Классификация сигналов

По виду физических процессов (или величин), используемых в качестве носителей, сигналы могут быть:

–  механические,

–  электрические,

–  электромагнитные,

–  световые,

–  акустические,

–  на базе ионизирующих излучений и т.п.

Очевидно, что этот перечень можно легко продолжить или детализировать. Однако мы этого делать не будем, а ограничимся некоторыми замечаниями общего плана.

При строгом рассмотрении видов сигналов может быть столько, сколько существует физических процессов и их характеристик с учетом различных аспектов их рассмотрения. Тем не менее, разобраться в этом неисчислимом множестве не так уж трудно, как это может показаться на первый взгляд, если обратить внимание на то, что существует такая наука, как физика, основная цель которой состоит в объяснении всех физических явлений через минимальное число фундаментальных сущностей и законов, которым они подчиняются. Если следовать логике существующих достижений в области физики, то классификация сигналов (как и физических процессов) должна повторять классификацию физических взаимодействий (поля – электромагнитное, гравитационное, сильное, слабое) и объектов, начиная с микрочастиц и заканчивая макротелами, с той лишь разницей, что для технических приложений реальный интерес представляют уже хорошо освоенные в технологическом плане объекты и виды взаимодействий.

В настоящее время подавляющее большинство информационных (искусственных) систем используют сигналы на основе электромагнитного взаимодействия (процессы в электрических цепях – это его частные проявления), что объясняется развитием электронной техники, обеспечивающей широкие возможности генерирования и обработки таких сигналов. Однако технология не стоит на месте, и уже сейчас с успехом осваивается оптический диапазон электромагнитных волн и ведутся небезрезультатные исследования по использованию некоторых «экзотических» видов взаимодействия, например гравитационных волн, потоков частиц нейтрино и т.п.

По характеру протекания во времени сигналы разделяются на два вида:

–  постоянные во времени;

–  переменные во времени.

С точки зрения классической теории информации (шенноновской), постоянные во временисигналы не представляют никакого интереса, поскольку количество информации, которое с их помощью можно перенести, равно нулю. Это нетрудно понять, если заметить, что сигнал с постоянным (неизменным) значением обладает только одним единственным возможным состоянием и, значит, с его помощью можно закодировать только одно сообщение. Но, поскольку при этом нет выбора, то это сообщение заранее известно и ничего нового получателю сигнала не дает.

Однако не все случаи практического использования сигналов укладываются в схему снятия неопределенности выбора, принятую в теории информации К. Шеннона. Один из таких случаев – это передача (в пространстве и во времени) единицы измеряемой величиныв средствах измерения с помощью меры, которая может рассматриваться как постоянный во времени сигнал. Причем, чем более постоянен этот сигнал, тем лучше он может выполнять функцию меры (с меньшей погрешностью воспроизведения единицы измеряемой величины).

Переменные во времени сигналы– это сигналы, значения которых изменяются во времени. Такие сигналы имеют широкое применение, и их классификацию можно рассмотреть более подробно, как это показано на Рис. 13.

Сигнал называется случайным,когда его значение в каждый момент времени есть случайная величина.

В отличие от неопределенных величин случайная величина обладает свойством статистической устойчивости, следствием которой является детерминированность (определенность) вероятностных характеристик, а именно — закона распределения плотности вероятности и всех его моментов. Детерминированность не налагает запрета на изменение вероятностных характеристик во времени по известным законам. Широкое применение случайных сигналов в качестве модели реальных физических сигналов объясняется, по крайней мере, двумя причинами. Во-первых, случайные сигналы хорошо вписываются в статистическую схему передачи информации по К. Шеннону и, во-вторых, существует хорошо развитый и удобный математический аппарат для описания и исследования свойств случайных процессов.

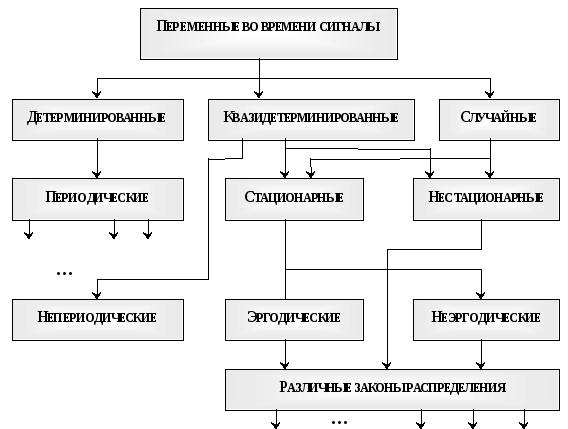
Рис. 13. Классификация переменных во времени сигналов

Случайные сигналы делятся на стационарныеинестационарные. У стационарных сигналов вероятностные характеристики не зависят от времени (постоянны), что позволяет значительно упростить их математическое описание.

В множестве стационарных сигналов выделяется подмножество эргодическихсигналов, не совсем строгое определение которых можно дать следующим образом. Вероятностные характеристики случайных сигналов могут быть получены либо усреднением по времени, т.е. путем рассмотрения всех значений одной реализации сигнала, либо усреднением по множеству (ансамблю) реализаций, т.е. путем рассмотрения значений всех реализаций случайного сигнала в один и тот же момент времени. Сигналы, для которых вероятностные характеристики не зависят от способа усреднения (по времени или по ансамблю), называются

эргодическими. Эргодические сигналы обладают целым рядом замечательных свойств, которые позволяют упростить решение многих задач, не разрешимых или трудно разрешимых для неэргодических сигналов.

Все случайные сигналы в конечном итоге классифицируются по виду закона распределения плотности вероятности; этот закон является полной и исчерпывающей характеристикой любого случайного сигнала.

Среди неслучайных сигналов наибольший интерес представляют детерминированные и квазидетерминированные сигналы.

Детерминированный сигнал

– это сигнал, закон изменения во времени и все параметры которого известны. В чистом виде детерминированный сигнал, так же как и постоянный во времени (и вследствие тех же соображений), не может переносить информацию.

Квазидетерминированный сигнал – это сигнал, закон изменения которого известен, но один или несколько параметров этого закона являются случайными величинами или процессами. Такой сигнал уже может рассматриваться как переносчик информации. В приложениях именно такие сигналы используются чаще всего.

Примером детерминированного сигнала является сигнал вида x(t)=A sin(ωt+φ), гдеA, ω, φ – заданные величины. Если же, хотя бы один из этих параметров является случайной величиной, то такой сигнал уже может рассматриваться, как квазидетерминированный и может быть носителем информации.

В зависимости от формы представления сигналы могут быть непрерывными,квантованными по уровню,дискретнымиицифровыми(Рис. 14). То, что существуют только четыре основные формы представления сигналов, легко понять, если заметить следующее. С математической точки зрения сигналx(t) есть функция, т.е. отображение множества значений времени {t} во множество значений сигнала {x}. Каждое из этих множеств может быть либо непрерывным, либо дискретным. Непрерывное множество (континуум) устроено так же, как и множество вещественных чисел. Основная особенность этого множества состоит в том, что любой конечный интервал (подмножество) содержит бесконечное число точек (элементов), причем мощность (количество элементов) любого подмножества совпадает с мощностью всего множества континуум, т.е. часть равна целому. Дискретное множество тоже содержит бесконечное число элементов, но их всегда можно упорядочить так, чтобы каждому элементу присвоить уникальный номер в виде целого числа. По этой причине дискретное множество называют также счетным множеством. Теперь, если допустить, что каждое из множеств {

x} и {t} может быть либо непрерывным, либо дискретным, то мы получим четыре возможные комбинации.

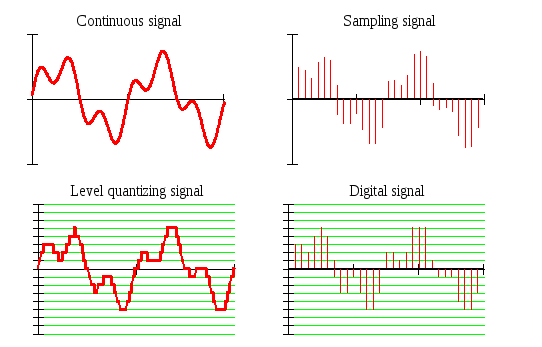
Рис. 14. Четыре формы представления сигналов

Как правило, непрерывная модель хорошо описывает входные сигналы, которые отражают поведение измеряемых физических величин. Для непосредственного же ввода в ЭВМ пригодны только цифровые сигналы. Поэтому в АСНИ (как и во всех других системах с компьютерной обработкой данных) всегда приходится осуществлять преобразование непрерывных сигналов в цифровую форму, что сопряжено с неизбежными потерями части информации. В связи с этим требуется решать задачу выбора такой процедуры преобразования сигнала из непрерывной формы в цифровую, чтобы погрешность от таких потерь не превышала заданной величины.

Квантованная по уровню и дискретная формы сигналов непосредственно применяются довольно редко, чаще они используются при теоретическом анализе промежуточных этапов преобразования сигналов из непрерывной в цифровую форму, а также при моделировании. В заключение отметим, что в математике существуют объекты, которые полностью соответствуют каждой из четырех рассмотренных форм представления сигналов, но имеют специальные названия. Непрерывному сигналу (continuoussignal) соответствуетнепрерывная функция,квантованному по уровню сигналу (levelquantizingsignal) –ступенчатая функция, дискретному сигналу (samplingsignal) –

решетчатая функцияилипоследовательность вещественных чисел, цифровому сигналу (digitalsignal) –последовательность целых чисел. Параллельные термины полезно знать, так как это может натолкнуть на мысль использовать в той или иной конкретной ситуации хорошо разработанный известный математический аппарат.

Обработка сигналов — Википедия

Материал из Википедии — свободной энциклопедии

Обработка сигналов — область радиотехники, в которой осуществляется восстановление, разделение информационных потоков, подавление шумов, сжатие данных, фильтрация, усиление сигналов.

Теория обработки сигналов — совокупность математических методов, описывающих преобразования аналоговых сигналов посредством технических устройств, представляемых в данной теории в идеализированном виде.

Например, приём сигнала на фоне шума описывается в виде процедуры фильтрации сигнала посредством фильтра, при этом ставится задача максимально ослабить шумы и помехи и минимально исказить принимаемый сигнал.

Сигналы могут быть как аналоговыми, так и цифровыми и иметь различные источники.

Существует множество направлений обработки сигналов, зависящие от их природы.

Для аналоговых сигналов обработка может включать усиление и фильтрацию, модуляцию и демодуляцию. Для цифровых сигналов также осуществляется сжатие, обнаружение и исправление ошибок и пр.

Анализ сигналов — извлечение информации из сигнала, например, выявление и обособление интересующих особенностей в экспериментально полученной функции. Существуют корреляционный анализ сигналов и спектральный анализ сигналов.

Спектральный анализ сигналов. Вероятно, наиболее распространённым видом анализа сигналов является преобразование Фурье временного сигнала в частотную область для получения спектра частот сигнала. Для анализа сигналов, в частности для получения временно-частотного представления также могут быть использованы другие преобразования, такие как оконное преобразование Фурье и непрерывное вейвлет-преобразование. Другие разновидности анализа сигналов включают подбор параметров, например поиск наилучшего приближения методом наименьших квадратов.

• Харкевич А. А. Спектры и анализ М: Физматгиз,1963,467 с.

Классификация сигналов: модели, функции, виды, схемы

Классификация сигналов

В теории электрической связи при описании сигналов и помех возникает задача поиска математических моделей, которые с необходимой степенью точности отображали бы реальные процессы в каналах передачи информации. Поскольку сигналы являются электрическими колебаниями, изменяющимися во времени, то их базовой математической моделью должна быть временнАя функция, т.е. функция, значения которой изменяются во времени.

Различают сигналы детерминированные и случайные.

«Детерминированным» называется сигнал, мгновенные значения которого в любой момент времени можно предсказать с вероятностью, равной единице.

Например, при ξ → 0 сигнал ν(t, ξ) переходит в единичную функцию включения (рис. 2.1):

Функция включения описывает процесс перехода некоторого физического объекта из нулевого состояния в единичное. Переход осуществляется по линейному закону за время t = 2ξ. При ξ → 0 в пределе переход производится мгновенно. Данная математическая модель получила название функции Хевисайда.

Рис. 2.1. Функция Хевисайда (функция включения)

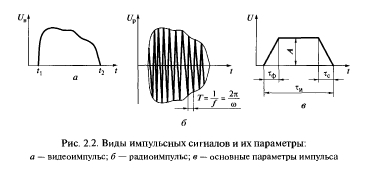
Рис. 2.2. Виды импульсных сигналов и их параметры:
а — видеоимпульс; б — радиоимпульс; в — основные параметры импульса

Важный класс сигналов представляют собой «импульсные» сигналы, под которыми понимают колебания, существующие только на конечном отрезке (в интервале) времени. При этом различают видеоимпульсы и радиоимпульсы (рис. 2.2).

Видеоимпульсу Uв(t) ≥ 0 соответствует радиоимпульс Uр(t) = Uв(t) cos(ωt + φ), где Uв(t) — огибающая радиоимпульса; cos(ωt + φ) — высокочастотное заполнение; ω, φ — соответственно частота и фаза сигнала, имеющие произвольные значения. В ТЭС видеоимпульсы принято задавать амплитудой (А), длительностью импульса (τи), длительностью фронта (τф) и длительностью спада (τс). Происхождение термина «видеоимпульс» объясняется тем, что данные колебания впервые стали применяться в технике телевидения.

Например, импульсный сигнал прямоугольной формы в пределе при ξ → 0 переходит в δ-функцию (рис. 2.3, 2.4):

Рис. 2.3. Прямоугольный видеоимпульс

Рис. 2.4. Определение δ-функции

Дельта-функция (функция Дирака) везде равна нулю за исключением точки t = 0, в которой

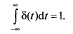Дельта-функция обладает важным свойством, называемым «фильтрующим»:

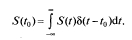
Физический смысл фильтрующего свойства заключается в том, что интеграл по времени от произведения непрерывной функции и дельта-функции равен значению этой непрерывной функции в точке, где сосредоточен δ-импульс.

Соответствующая схема измерения мгновенных значений аналогового сигнала в точке t0 показана на рис. 2.5. Точность измерения S (t0) зависит от ширины прямоугольного видеоимпульса, который приближенно представляет собой δ-функцию, широко применяемую в теории электрической связи.

Детерминированные сигналы можно подразделить на периодические и непериодические. Рассмотренные ранее сигналы являются непериодическими.

«Периодическим» называется повторяющийся во времени сигнал, для которого справедливо условие
S(t) = S(t ± kT), где k — любое целое число; Т — период, являющийся конечным отрезком.

Например, периодическим является гармонический сигнал S(t) =U cos(ωt + φ), −∞ < t < ∞. Здесь U, ω = 2π / Τ; φ — соответственно постоянные амплитуда, угловая частота и начальная фаза. Такой сигнал широко применяется в качестве переносчика информации при формировании модулированных сигналов.

«Случайными» называются сигналы, значения которых заранее неизвестны и могут быть предсказаны только с некоторой вероятностью, меньшей единицы. Например, электрические колебания, соответствующие речевому сигналу, музыке или последовательности знаков телеграфного кода при передаче неповторяющегося текста.

Рис. 2.5. Схема измерения мгновенных значений произвольного аналогового сигнала S(t)

Отметим, что любой сигнал, несущий в себе информацию, должен быть обязательно случайным. Приведенные ранее детерминированные сигналы, являющиеся полностью известными, информации не переносят.

Сигналы также подразделяются на одномерные и многомерные. «Одномерным» называется сигнал, который описывается одной функцией времени. Примером такого сигнала является напряжение на зажимах цепи или ток в ветви.

«Многомерным» («векторным») называется сигнал, образованный некоторым упорядоченным множеством одномерных сигналов (Формула), где Ν — размерность сигнала. Примером такого сигнала может служить последовательность посылок на выходе кодера, т.е. кодовая комбинация, или система напряжений на зажимах многополюсника.

Наконец, сигналы могут быть «дискретными» и «непрерывными», как во времени t, так и по уровню, о чем уже говорилось при рассмотрении сообщений.

Сигнал — Вікіпедія

Матеріал з Вікіпедії — вільної енциклопедії.

Сигна́л — зміна фізичної величини (наприклад, температури, тиску повітря, світлового потоку, сили струму тощо), що використовується для пересилання даних^[1]. Саме завдяки цій зміні сигнал може нести в собі якусь інформацію^[2]. Інше визначення: сигнал — фізичний процес, властивості якого визначаються взаємодією між матеріальним об’єктом та засобом його дослідження^[3].

Термін широко використовується у галузях науки й техніки, пов’язаних з обробкою й передаванням інформації, в кібернетиці, електроніці, радіотехніці, техніці зв’язку й ін.

Класифікація сигналів[ред. | ред. код]

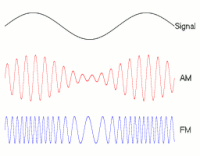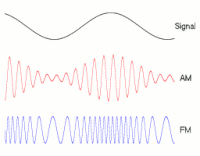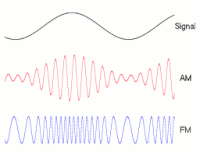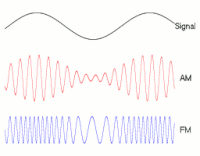Модулювання сигналу. Демонстрація накладення низьких частот на сигнал-носій (високочастотний). Амплітудна (AM) і частотна (FM) модуляції.

За фізичною природою носія інформації^[4]:

• механічний сигнал — сигнал у вигляді механічного діяння твердого тіла, у якого дієвою величиною є сила, момент сили або переміщення;
• електричний сигнал — сигнал у вигляді електричного діяння, дієвою величиною якого є сила струму або напруга;
• радіосигнал — сигнал у вигляді діяння електромагнітного випромінювання, дієвою величиною якого є напруженість електричного поля або магнітного поля;
• оптичний сигнал — сигнал у вигляді діяння оптичного випромінювання, дієвою величиною якого є потік випромінювання;
• акустичний сигнал — сигнал у вигляді діяння звуку, дієвою величиною якого є звуковий тиск;
• гідравлічний (пневматичний) сигнал — сигнал у вигляді механічного діяння рідини (газу), дієвою величиною якого є тиск.

За способом задання сигналу:

• регулярні (детерміновані), задані аналітичною функцією;
• нерегулярні (випадкові), які приймають довільні значення в будь-який момент часу. Для опису таких сигналів використовуються засоби теорії ймовірності;

Залежно від функції, що описує параметри сигналу, виділяють аналогові, дискретні, квантовані та цифрові сигнали.:

Аналоговий сигнал (АС)[ред. | ред. код]

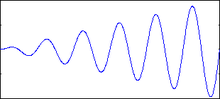Аналоговий сигнал

Більшість сигналів мають аналогову природу, тобто змінюються безперервно в часі і можуть набувати будь-яких значень на певному інтервалі. Аналогові сигнали описуються деякою математичною функцією часу.

Приклад АС — гармонічний сигнал s(t) = A·cos(ω·t + φ). Для передавання інформації змінюється в часі за законом модулюючого сигналу один або декілька параметрів сигналу s(t). При зміні амплітуди А, кругової частоти ω·t, фази φ, здійснюється відповідно амплітудна, частотна, фазова модуляція.

Дискретний сигнал[ред. | ред. код]

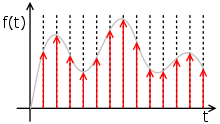Дискретний сигнал

Дискретизація аналогового сигналу полягає в тому, що сигнал подається у вигляді послідовності значень, взятих в дискретні моменти часу. Ці значення називаються відліками.. Δt називається інтервалом дискретизації.

Квантований сигнал[ред. | ред. код]

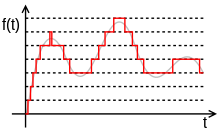Квантований сигнал

При квантуванні вся область значень сигналу розбивається на рівні. Відстань між цими рівнями називається кроком квантування Δ. Число цих рівнів рівне N (від 0 до N-1). Кожному рівню присвоюється деяке число. Відліки сигналу порівнюються з рівнями квантування і як сигнал вибирається число, що відповідає певному рівню квантування.

Цифровий сигнал[ред. | ред. код]

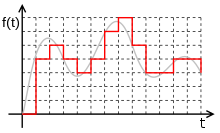Цифровий сигнал

Для того щоб представити аналоговий сигнал послідовністю чисел скінченної розрядності, його потрібно спочатку перетворити в дискретний сигнал, а потім квантувати. В результаті сигнал буде представлений таким чином, що на кожному заданому часовому проміжку відоме приблизне (квантоване) значення сигналу, яке можна записати цілим числом. Якщо записати ці цілі числа у двійковій системі, отримається послідовність нулів і одиниць, яка і буде цифровим сигналом.

Модуляція (лат. modulatio — розміреність, ритмічність) — процес зміни одного або декількох параметрів високочастотного носійного коливання за законом низькочастотного інформаційного сигналу (повідомлення).

Модуляція сигналу використовується для збільшення відстані передавання сигналу різними засобами передавання, підвищення завадозахищеності сигналу, нарощування пропускної спроможності каналів зв’язку тощо.

• Аналоговий сигнал — сигнал, інформаційний параметр якого змінюється безперервно.
• Анізохронний сигнал — сигнал, у якого інтервали часу між сусідніми значущими моментами не обов’язково рівні чи кратні одиничному інтервалу.
• Вхідний сигнал — сигнал, що надходить на вхід системи, пристрою чи елемента.
• Двійковий сигнал — сигнал, параметри якого можуть приймати тільки одне з двох можливих значень.
• Дискретний сигнал — сигнал, інформативний параметр якого може змінюватися тільки переривчасто та мати тільки скінченну кількість значень у заданому діапазоні протягом певного інтервалу часу.
• Ізохронний сигнал — сигнал, у якого інтервали часу між сусідніми значущими моментами рівні чи кратні одиничному інтервалу.
• Кодовий сигнал — дискретний сигнал, інформативний параметр якого визначений в умовних символах відповідно до певного коду.
• Модульований сигнал — сигнал, що є результатом взаємодії двох або більше сигналів, які модулюються та модулюють.
• Модулювальний сигнал — сигнал, що використовується для зміни якого-небудь параметра сигналу, що модулюється, в залежності від виду модуляції.
• Приведений сигнал — сигнал, перетворений в один із стандартизованих видів.
• Сигнал керування — сигнал, передбачений для впливу на об’єкт керування з метою виконання вказівки, яка є в команді.
• Сигнал лиха — сигнал або комбінація сигналів, які вказують, що передавач (судно, літак, особа, група осіб) терпить лихо і потребує допомоги.
• Сигнал синхронізації — періодичний сигнал для тимчасового узгодження всіх синхронних операцій.
• Сигнал стимуляції — сигнал, який подають на вхід об’єкта з метою отримання інформації про його технічний стан.
• Цифровий сигнал — дискретний сигнал з певним значенням інформативного параметра, яке визначається у цифровій формі.
• Сигнал розузгодження (Δ(y)) — векторна різниця між поточним значенням параметра і заданим. Цей сигнал звичайно надходить на вхід регулювального пристрою (у САР).

1. ↑ ДСТУ 2938-94. Системи оброблення інформації. Основні поняття. Терміни та визначення.
2. ↑ Лекція 1. Базові поняття цифрової електроніки Архівовано 28 квітень 2012 у Wayback Machine. // Intuit.ru (рос.)
3. ↑ ДСТУ 2681-94. Державна система забезпечення єдності вимірювань. Метрологія. Терміни та визначення.
4. ↑ ДСТУ 3956-2000. Технічні засоби вимірювання та керування у промислових процесах. Частина 1. Основні поняття. Терміни та визначення.