Схема соединения «Треугольник»
Дата публикации: .
Категория: Электротехника.
Соединение в треугольник трехфазного генератора или вторичной обмотки трансформатора.
Соединим конец x обмотки ax с началом b обмотки by, конец y обмотки by с началом c обмотки cz, конец z обмотки cz с началом a обмотки ax так, как показано на рисунке 1. Такое соединение по виду напоминает треугольник, откуда и происходит его название. Линейные провода присоединены в вершинах треугольника.

Рисунок 1. Соединение в треугольник генератора.
Основные соотношения:
1. При соединении в треугольник линейные и фазные напряжения равны потому, что каждые два линейных провода (как видно из рисунка 1) присоединены к началу и концу одной из фазных обмоток, а все фазные обмотки одинаковы.
2. Линейные токи Iл больше фазных Iф в √3 = 1,73 раза.
Как доказать, что Iл = 1,73 × Iф? Воспользуемся для этого векторной диаграммой рисунка 2.

Рисунок 2. Определение линейных токов при соединении в треугольник.
Фазные токи Iab, Ibc, Ica в трех электроприемниках ЭП (рисунок 2, а) изображаются векторной диаграммой (рисунок 2, б), которая получена путем перенесения параллельно самим себе векторов с рисунка 2, а. Вершины треугольника нагрузок a, b и c являются узловыми точками. Поэтому согласно первому закону Кирхгофа справедливы равенства
Ia + Ica = Iab, откуда Ia = Iab – Ica;
Ib + Iab = Ibc, откуда Ib = Ibc – Iab;
Ic + Ibc = Ica, откуда Ic = Ica – Ibc.
Понятно, что эти равенства геометрические, поэтому вычитание нужно выполнять по правилам вычитания векторов, что и сделано на рисунке 2, б. Непосредственное измерение длин векторов или вычисления по правилам геометрии показывают, что линейные токи Ia, Ib и Ic больше фазных токов Iab, Ibc и Ica в √3 = 1,73 раза.
На рисунке 2, б также видно, что векторная диаграмма симметричных линейных токов Ia, Ib и Ic сдвинута на 30° в сторону, обратную вращению векторов, относительно диаграммы фазных токов Iab, Ibc и Ica. Иными словами, ток Ia отстает на 30° от тока Iab. Ток Ib отстает на 30° от тока Ibc, ток Ic отстает на 30° от тока Ica.
Порядок индексов в обозначении фазных токов указывает на порядок вращения фаз. В нашем примере порядок следования (вращения) фаз: a, b, c.
На рисунке 2, в показано соединение в треугольник обмоток генератора или вторичных обмоток трансформатора. Векторы токов Iba, Iac, Icb, проходящих в обмотках генератора (вторичных обмотках трансформатора), и векторы токов в нагрузке (Iab, Ica, Ibc) соответственно параллельны, но повернуты на 180°. Причина такого расположения векторов станет ясна, если совместить рисунок 2, в с правой частью рисунка 2, а, что и выполнено на рисунке 2, г.
Обращается внимание на то, что все три обмотки внутри генератора (трансформатора) соединены последовательно и образуют замкнутую цепь. Подобное соединение в установках постоянного тока привело бы к короткому замыканию. В установках трехфазного тока в силу того, что электродвижущие силы (э. д. с.) сдвинуты по фазе на 120°, ток в этом замкнутом контуре отсутствует, так как в каждый момент сумма э. д. с. трех обмоток равна нулю 1.
Необходимо здесь же заметить, что для отсутствия тока в контуре обмоток генератора (трансформатора) необходимо, чтобы обмотки имели одинаковые числа витков, были сдвинуты на 120 электрических градусов и имели э. д. с. строго синусоидальные или во всяком случае не содержащие гармоник, кратных трем (смотрите статью «Понятие о магнитном равновесии трансформатора»).
Генераторы практически никогда не соединяют в треугольник. В трансформаторах такие соединения не только распространены, но иногда выполняются с целью получения внутри трансформатора токов третьих гармоник. Зачем? Понятно не затем, чтобы создавать в трансформаторе дополнительные потери. Причины здесь гораздо сложнее, смотрите статью «Понятие о магнитном равновесии трансформатора».
Соединение в треугольник обмоток трансформаторов в двух вариантах показано на рисунке 3. Подробно вопрос о соединениях обмоток трансформаторов рассмотрен в статье «Группы соединения трансформаторов».


Рисунок 3. Соединение в треугольник трансформаторов.
Соединение в треугольник электроприемников и конденсаторных батарей.
Соединение в треугольник обмоток электродвигателей показано на рисунках 4, а – в. При этом на рисунке 4, а обмотки и соединены и расположены треугольником; на рисунке 4, б обмотки соединены треугольником, но расположены произвольно; на рисунке 4, в обмотки расположены звездой, но соединены в треугольник. На рисунке 4, г обмотки расположены треугольником, но соединены в звезду.


Рисунок 4. Соединение в треугольник электроприемников.
Все эти рисунки подчеркивают, что дело отнюдь не в том, как расположены изображения электроприемников на чертежах (хотя их часто удобно располагать в соответствии с видом соединения), а в том, что с чем соединено: концы (начала) всех обмоток между собой или конец одной обмотки с началом другой. В первом случае получается соединение в звезду, во втором – в треугольник.
Соединение в треугольник конденсаторных батарей показано на рисунке 4, д.
На рисунке 4, е показано соединение в треугольник ламп. Хотя лампы территориально разбросаны по разным квартирам, но они объединены сначала в группы в пределах каждой квартиры, затем в группы по стоякам 2 и, наконец, эти группы соединены в треугольник на вводном щите 1. Заметьте: до вводного щита нагрузка трехфазная, после вводного щита (в стояках и квартирах) однофазная, хотя она и включена между двумя фазами.
На каком основании нагрузка, питающаяся от двух фаз названа однофазной? На том основании, что изменения тока в обоих проводах, к которым присоединена нагрузка, происходят одинаково, то есть в каждый момент ток проходит через одни и те же фазы.
Видео 1. Соединение треугольником
1 Отсутствие тока в замкнутом контуре еще не означает, что в фазных обмотках нет тока. Токи в фазных обмотках соответствуют их нагрузкам.
Источник: Каминский Е. А., «Звезда, треугольник, зигзаг» – 4-е издание, переработанное – Москва: Энергия, 1977 – 104с.
3.1.2 Соединение в треугольник. Схема, определения
Если конец каждой фазы обмотки генератора соединить с началом следующей фазы, образуется соединение в треугольник. К точкам соединений обмоток подключают три линейных провода, ведущие к нагрузке.
На рис. 5 изображена трехфазная цепь, соединенная треугольником. Как видно из рис. 5, в трехфазной цепи, соединенной треугольником, фазные и линейные напряжения одинаковы Uл = Uф
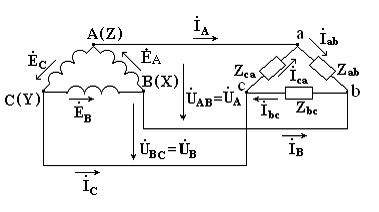
Рис. 5. Трехфазная цепь, соединенная треугольником
Линейные и фазные токи нагрузки связаны между собой первым законом Кирхгофа для узлов а, b, с:
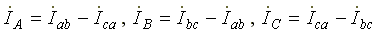
или
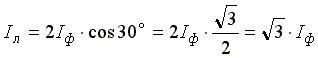
Следовательно, при симметричной нагрузке Iл = √3 Iф
Трехфазные цепи, соединенные звездой, получили большее распространение, чем трехфазные цепи, соединенные треугольником. Это объясняется тем, что, во-первых, в цепи, соединенной звездой, можно получить два напряжения: линейное и фазное. Во-вторых, если фазы обмотки электрической машины, соединенной треугольником, находятся в неодинаковых условиях, в обмотке появляются дополнительные токи, нагружающие ее. Такие токи отсутствуют в фазах электрической машины, соединенных по схеме «звезда».
3.2 Расчёт симметричных режимов работы трёхфазных цепей
Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в комплексной форме в полной мере распространяются на них.
Трёхфазный приемник и вообще трёхфазная цепь называются симметричными, если в них комплексные сопротивления соответствующих фаз одинаковы, т.е. ZA = ZB = ZC. В противном случае они являются несимметричными. Равенство модулей указанных сопротивлений не является достаточным условием симметрии

Рис. 6. Рис. 7.
Если к симметричной
трехфазной цепи приложена симметричная
трехфазная система напряжений генератора,
то в ней будет иметь место симметричная
система токов. Такой режим работы
трехфазной цепи называется симметричным. В этом режиме
токи и напряжения соответствующих фаз
равны по модулю и сдвинуты по фазе друг
по отношению к другу на угол 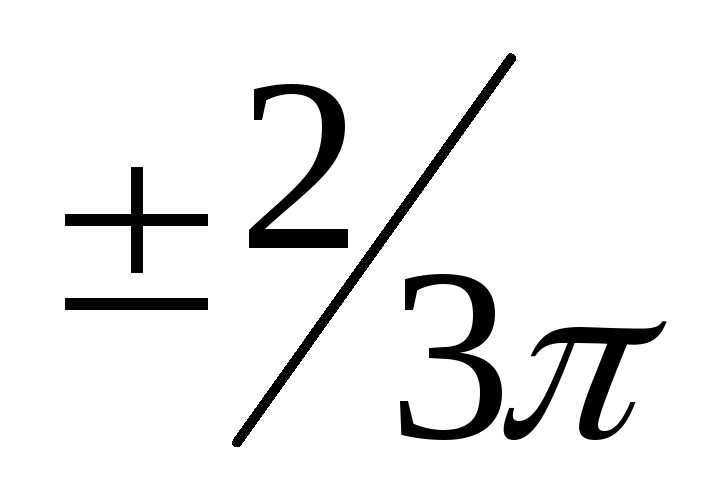
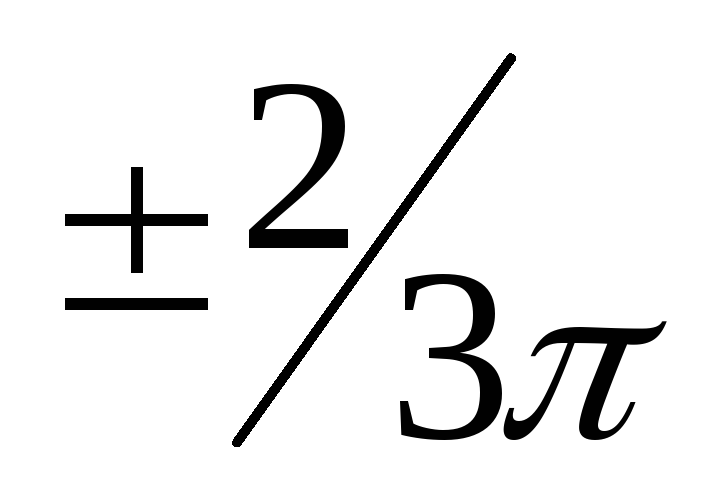 при сохранении неизменным ее модуля.
Так для симметричного режима работы
цепи на рис. 8
при сохранении неизменным ее модуля.
Так для симметричного режима работы
цепи на рис. 8 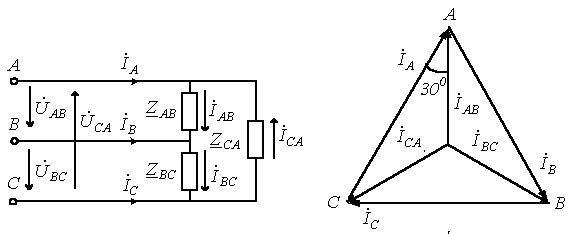
Рис. 8.
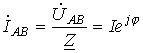
где угол фазового сдвига φ между напряжением и током определяется характером нагрузки Z.
Тогда на основании вышесказанного токи в других двух фазах равны:
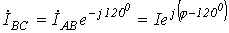
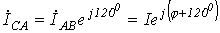
Комплексы линейных токов можно найти с использованием векторной диаграммы, из которой следует

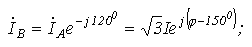

Пример расчёта симметричного режима работы трёхфазной цепи приведён в приложении 3.
4. Электрические цепи периодического несинусоидального тока
Периодические несинусоидальные токи и напряжения в электрических цепях возникают в случае действия в них несинусоидальных ЭДС или наличия в них нелинейных элементов. Реальные ЭДС, напряжения и токи в электрических цепях синусоидального переменного тока по разным причинам отличаются от синусоиды. В энергетике появление несинусоидальных токов или напряжений нежелательно, т.к. вызывает дополнительные потери энергии. Однако существуют большие области техники (радиотехника, автоматика, вычислительная техника, полупроводниковая преобразовательная техника), где несинусоидальные величины являются основной формой ЭДС, токов и напряжений.
Рассмотрим краткие теоретические сведения и методику расчёта линейных электрических цепей при воздействии на них источников периодических несинусоидальных ЭДС.
4.1.Разложение периодической функции в тригонометрический ряд
может быть разложена в тригонометрический ряд (ряд Фурье):

Первый член ряда называется постоянной составляющей, второй член – основной или первой гармоникой. Остальные члены ряда называются высшими гармониками.
Если в выражении раскрыть синусы суммы каждой из гармоник, то оно примет вид :

где
В случае аналитического задания функции f (ωt) коэффициенты ряда могут быть вычислены с помощью следующих выражений:

После чего производится расчёт амплитуд и начальных фаз гармонических составляющих ряда:

Коэффициенты ряда Фурье большей части периодических функций, встречающихся в технике, приводятся в справочных данных или в учебниках по электротехнике.
Соединение треугольником Википедия
Трёхфазная система электроснабжения — частный случай многофазных систем электрических цепей переменного тока, в которых действуют созданные общим источником синусоидальные ЭДС одинаковой частоты, сдвинутые друг относительно друга во времени на определённый фазовый угол. В трёхфазной системе этот угол равен 2π/3 (120°).
Многопроводная (шестипроводная) трёхфазная система переменного тока изобретена Николой Теслой. Значительный вклад в развитие трёхфазных систем внёс М. О. Доливо-Добровольский, который впервые предложил трёх- и четырёхпроводную системы передачи переменного тока, выявил ряд преимуществ малопроводных трёхфазных систем по отношению к другим системам и провёл ряд экспериментов с асинхронным электродвигателем.
Описание
Каждая из действующих ЭДС находится в своей фазе периодического процесса, поэтому часто называется просто «фазой». Также «фазами» называют проводники — носители этих ЭДС. В трёхфазных системах угол сдвига равен 120 градусам. Фазные проводники обозначаются в РФ латинскими буквами L с цифровым индексом 1…3, либо A, B и C[1].
Распространённые обозначения фазных проводов:
| Россия, EC (выше 1000 В) | Россия, ЕС (ниже 1000 В) | Германия | Дания |
|---|---|---|---|
| А | L1 | R | |
| B | L2 | L2 | S |
| C | L3 | L3 | T |
Преимущества
Возможная схема разводки трёхфазной сети в многоквартирных жилых домах- Экономичность.
- Экономичность передачи электроэнергии на значительные расстояния.
- Меньшая материалоёмкость 3-фазных трансформаторов.
- Меньшая материалоёмкость силовых кабелей, так как при одинаковой потребляемой мощности снижаются токи в фазах (по сравнению с однофазными цепями).
- Уравновешенность системы. Это свойство является одним из важнейших, так как в неуравновешенной системе возникает неравномерная механическая нагрузка на энергогенерирующую установку, что значительно снижает срок её службы.
- Возможность простого получения кругового вращающегося магнитного поля, необходимого для работы электрического двигателя и ряда других электротехнических устройств. Двигатели 3-фазного тока (асинхронные и синхронные) устроены проще, чем двигатели постоянного тока, одно- или 2-фазные, и имеют высокие показатели экономичности.
- Возможность получения в одной установке двух рабочих напряжений — фазного и линейного, и двух уровней мощности при соединении на «звезду» или «треугольник».
- Возможность резкого уменьшения мерцания и стробоскопического эффекта светильников на люминесцентных лампах путём размещения в одном светильнике трёх ламп (или групп ламп), питающихся от разных фаз.
Благодаря этим преимуществам, трёхфазные системы наиболее распространены в современной электроэнергетике.
Схемы соединений трёхфазных цепей
Звезда
Звездой называется такое соединение, когда концы фаз обмоток генератора (G) соединяют в одну общую точку, называемую нейтральной точкой или нейтралью. Концы фаз обмоток потребителя (M) также соединяют в общую точку.
Провода, соединяющие начала фаз генератора и потребителя, называются линейными. Провод, соединяющий две нейтрали, называется нейтральным.
Трёхфазная цепь, имеющая нейтральный провод, называется четырёхпроводной. Если нейтрального провода нет — трёхпроводной.
Если сопротивления Za, Zb, Zc потребителя равны между собой, то такую нагрузку называют симметричной.
Линейные и фазные величины
Напряжение между фазным проводом и нейтралью (Ua, Ub, Uc) называется фазным. Напряжение между двумя фазными проводами (UAB, UBC, UCA) называется линейным. Для соединения обмоток звездой, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями:
IL=IF;UL=3×UF{\displaystyle I_{L}=I_{F};\qquad U_{L}={\sqrt {3}}\times {U_{F}}}
Несложно показать, что линейное напряжение сдвинуто по фазе на π/6{\displaystyle \pi /6} относительно фазных:
uLab=uFa−uFb=UF[cos(ωt)−cos(ωt−2π/3)]=2UFsin(−π/3)sin(ωt−π/3)=3UFcos(ωt+π−π/3−π/2){\displaystyle u_{L}^{ab}=u_{F}^{a}-u_{F}^{b}=U_{F}[\cos(\omega t)-\cos(\omega t-2\pi /3)]=2U_{F}\sin(-\pi /3)\sin(\omega t-\pi /3)={\sqrt {3}}U_{F}\cos(\omega t+\pi -\pi /3-\pi /2)}
uL=3UFcos(ωt+π/6){\displaystyle u_{L}={\sqrt {3}}U_{F}\cos(\omega t+\pi /6)}
Мощность трёхфазного тока
Для соединения обмоток звездой, при симметричной нагрузке, мощность трёхфазной сети равна P=3UFIFcosφ=3UL3ILcosφ=3ULILcosφ{\displaystyle P=3U_{F}I_{F}cos\varphi =3{\frac {U_{L}}{\sqrt {3}}}I_{L}cos\varphi ={\sqrt {3}}U_{L}I_{L}cos\varphi }
Последствия отгорания (обрыва) нулевого провода в трёхфазных сетях
Существующие виды защиты от линейного напряжения, которые можно найти в продаже в электротехнических магазинах Шины для раздачи нулевых проводов (синяя) и проводов заземления (зелёная)При симметричной нагрузке в трёхфазной системе питание потребителя линейным напряжением возможно даже при отсутствии нейтрального провода. Несмотря на это, при питании нагрузки фазным напряжением, когда нагрузка на фазы не является строго симметричной, наличие нейтрального провода обязательно. При его обрыве или значительном увеличении сопротивления (плохом контакте) происходит так называемый перекос фаз, в результате которого подключенная нагрузка, рассчитанная на фазное напряжение, может оказаться под произвольным напряжением в диапазоне от нуля до линейного (конкретное значение зависит от распределения нагрузки по фазам в момент обрыва нулевого провода). Это зачастую является причиной выхода из строя бытовой электроники в квартирных домах, который может приводить к пожарам. Пониженное напряжение также может послужить причиной выхода из строя техники.
Проблема гармоник, кратных третьей
Современная техника всё чаще оснащается импульсными сетевыми источниками питания. Импульсный источник без корректора коэффициента мощности потребляет ток узкими импульсами вблизи пиков синусоиды питающего напряжения на интервалах зарядки конденсатора входного выпрямителя. Большое количество таких источников питания в сети создаёт повышенный ток третьей гармоники питающего напряжения. Токи гармоник, кратных третьей, вместо взаимной компенсации, математически суммируются в нейтральном проводнике (даже при симметричном распределении нагрузки) и могут привести к его перегрузке даже без превышения допустимой мощности потребления по фазам. Такая проблема существует, в частности, в офисных зданиях с большим количеством одновременно работающей оргтехники. Решением проблемы третьей гармоники является применение корректора коэффициента мощности (пассивного или активного) в составе схемы производимых импульсных источников питания. Требования стандарта IEC 1000-3-2 накладывают ограничения на гармонические составляющие тока нагрузки устройств мощностью от 50 Вт. В России количество гармонических составляющих тока нагрузки нормируется стандартами ГОСТ Р 54149-2010, ГОСТ 32144-2013 (с 1.07.2014), ОСТ 45.188-2001.
Треугольник
Треугольник — такое соединение, когда конец первой фазы соединяется с началом второй фазы, конец второй фазы с началом третьей, а конец третьей фазы соединяется с началом первой.
Соотношение между линейными и фазными токами и напряжениями
Для соединения обмоток треугольником, при симметричной нагрузке, справедливо соотношение между линейными и фазными токами и напряжениями:
IL=3×IF;UL=UF{\displaystyle I_{L}={\sqrt {3}}\times {I_{F}};\qquad U_{L}=U_{F}}
Мощность трёхфазного тока при соединении треугольником
Для соединения обмоток треугольником, при симметричной нагрузке, мощность трёхфазного тока равна:
P=3UFIFcosφ=3ULIL3cosφ=3ULILcosφ{\displaystyle P=3U_{F}I_{F}cos\varphi =3U_{L}{\frac {I_{L}}{\sqrt {3}}}cos\varphi ={\sqrt {3}}U_{L}I_{L}cos\varphi }
Распространённые стандарты напряжений
| Страна | Частота, Гц | Напряжение (фазное/линейное), Вольт |
|---|---|---|
| Россия [2] | 50 | 220/230 [3] (бытовые сети) 230/400, 380/660, 400/690, 380, 400, 220/380, 3000, 6000, 10000 (промышленные сети)[источник не указан 518 дней] |
| Страны ЕС | 50 | 230/400, 400/690 (промышленные сети) 660 450 |
| Япония | 50 (60) | 120/208 |
| США | 60 | 120/208, 277/480 240 (только треугольник) |
Маркировка
Проводники, принадлежащие разным фазам, маркируют разными цветами. Разными цветами маркируют также нейтральный и защитный проводники. Это делается для обеспечения надлежащей защиты от поражения электрическим током, а также для удобства обслуживания, монтажа и ремонта электрических установок и электрического оборудования — фазировка (чередование фаз, то есть очерёдность протекания токов по фазам) принципиальна, так как от неё зависит направление вращения трёхфазных двигателей, правильная работа управляемых трёхфазных выпрямителей и некоторых других устройств. В разных странах маркировка проводников имеет свои различия, однако многие страны придерживаются общих принципов цветовой маркировки проводников, изложенных в стандарте Международной Электротехнической Комиссии МЭК 60445:2010.
Трёхфазная двухцепная линия электропередачиЦвета фаз
Каждая фаза в трёхфазной системе имеет свой цвет. Он меняется в зависимости от страны. Используются цвета международного стандарта IEC 60446 (IEC 60445).
| Страна | L1 | L2 | L3 | Нейтраль / ноль | Земля / защитное заземление |
|---|---|---|---|---|---|
| Россия, Белоруссия, Украина, Казахстан (до 2009), Китай | Белый | Черный | Красный | Голубой | Жёлто/зелёный (в полоску) |
| Европейский союз и все страны которые используют европейский стандарт CENELEC с апреля 2004 (IEC 60446), Гонконг с июля 2007, Сингапур с марта 2009, Украина, Казахстан с 2009, Аргентина, Россия с 2009 | Коричневый | Чёрный | Серый | Голубой | Жёлто/зелёный (в полоску)[4] |
| Европейский союз до апреля 2004[5] | Красный | Жёлтый | Голубой | Чёрный | Жёлто/зелёный (в полоску) (зелёный в установках до 1970) |
| Индия, Пакистан, Великобритания до апреля 2006, Гонконг до апреля 2009, ЮАР, Малайзия, Сингапур до февраля 2011 | Красный | Жёлтый | Голубой | Чёрный | Жёлто/зелёный (в полоску) (зелёный в установках до 1970) |
| Австралия и Новая Зеландия | Красный (или коричневый)[6] | Белый (или чёрный) (ранее — жёлтый) | Тёмно синий (или серый) | Чёрный (или голубой) | Жёлто/зелёный (в полоску) (зелёный в очень старых установках) |
| Канада (обязательный)[7] | Красный | Чёрный | Голубой | Белый или серый | Зелёный или цвета меди |
| Канада (в изолированных трехфазных установках)[8] | Оранжевый | Коричневый | Жёлтый | Белый | Зелёный |
| США (альтернативная практика)[9] | Коричневый | Оранжевый (в системе треугольник), или фиолетовый (в системе звезда) | Жёлтый | Серый или белый | Зелёный |
| США (распространённая практика)[10] | Чёрный | Красный | Голубой | Белый или серый | Зелёный, жёлто/зелёный (в полоску),[11] или провод цвета меди |
| Норвегия | Чёрный | Белый/серый | Коричневый | Голубой | Жёлто/зелёный (в полоску), в более старых установках может встречаться только жёлтый или цвета меди |
См. также
Примечания
- ↑ Действующий в РФ ГОСТ 2.709-89 предписывает обозначение цепей фазных проводников трёхфазного переменного тока: L1, L2, L3, и при этом допускает обозначения A, B, C.
- ↑ Согласно ГОСТ 29322-2014
- ↑ Согласно ГОСТ 29322-2014
- ↑ Жёлто-зелёная маркировка была принята как международный стандарт для защиты от поражения эл.током дальтоников. От 7 % до 10 % людей не могут точно распознать красный и зелёные цвета.
- ↑ В Европе ещё осталось много установок со старой цветовой схемой начала 1970-х. В новых установках используются жёлто/зелёные шины заземления в соответствии с IEC 60446. (Фаза/ноль+земля; Германия: чёрный/серый + красный; Франция зелёный/красный + белый; Россия: красный/серый + чёрный; Швейцария: красныйd/серый + жёлтый или жёлтый и красный; Дания: белый/чёрный + красный
- ↑ В Австралии и Новой Зеландии фазы могут быть люього цвета, но только не жёлто-зелёного, зелёного, жёлтого, чёрного или голубого цвета.
- ↑ Canadian Electrical Code Part I, 23rd Edition, (2002) ISBN 1-55324-690-X, rule 4-036 (3)
- ↑ Canadian Electrical Code (англ.)русск. 23-е издание 2002 года, правила 24-208(c)
- ↑ Начиная с 1975 в США National Electric Code (англ.)русск. не имел специальных обозначений фаз. По сложившейся практике для соединения звезда 120/208 фазы маркировались чёрным, красным и голубым цветом, а при соединении звезда или треугольник 277/480 фазы обозначались коричневым, оранжевым и жёлтым. В системе 120/240 треугольник с наибольшим напряжением 208 вольт (обычно фаза B) всегда обозначалась оранжевым, общая фаза A была чёрного цвета, а фаза C — красной или голубой.
- ↑ See Paul Cook: Harmonised colours and alphanumeric marking Архивная копия от 4 марта 2016 на Wayback Machine. IEE Wiring Matters, Spring 2006.
- ↑ В США провод жёлто-зелёного цвета (в полоску) может обозначать изолированную землю[неизвестный термин]. Сегодня в большинстве стран, жёлто-зелёные (в полоску) провода используются для защитного заземления и не могут быть отсоеденины и использованы для других целей.
Ссылки
§61. Схема соединения «треугольником»
При соединении фазных обмоток источника трехфазного тока «треугольником» (рис. 211, а) конец первой фазы АВ соединяется с началом второй фазы ВС, конец второй фазы соединяется с началом третьей фазы СА и конец третьей фазы — с началом первой АВ. Три линейных провода 1, 2 и 3, идущих к приемникам электрической энергии, присоединяются к началам А, В и С этих фаз. Точно так же могут соединяться и отдельные группы приемников ZAB, ZBC, ZCA (фазы нагрузки). При этом каждая фаза нагрузки присоединяется к двум линейным проводам, идущим от источника, т. е. включается на линейное напряжение, которое одновременно будет и фазным напряжением. Таким образом, в схеме «треугольник» фазные напряжения Uф равны линейным Uл и не зависят от сопротивлений ZAB, ZBC, ZCA фаз нагрузки.
Как следует из формулы (77), при соединении «треугольником» трех фазных обмоток генератора или другого источника переменного тока сумма э. д. с, действующая в замкнутом контуре, образованном этими обмотками, равна нулю. Поэтому в этом контуре при отсутствии нагрузки не возникает тока. Но каждая из фазных э. д. с. может создавать ток в цепи своей фазы.
Линейные токи в схеме «треугольник» согласно первому закону Кирхгофа для узлов А, В и С соответственно:

iA = iAB – iCA; iB = iBC – iAB; iC = iCA – iBC
Переходя от мгновенных значений токов к их векторам, получим:
?A = ?AB – ?CA; ?B = ?BC – ?AB; ?C = ?CA – ?BC
Следовательно, линейный ток равен векторной разности соответствующих фазных токов.
По полученным векторным уравнениям можно для равномерной нагрузки фаз построить векторную диаграмму (рис. 211,б), которую можно преобразовать в диаграмму (рис. 211, в), из которой
Рис. 211. Схема «треугольник» (а) и векторные диаграммы токов для этой схемы при равномерной нагрузке (б и в)
видно, что при равномерной нагрузке фаз векторы линейных токов ?А, ?B, ?C образуют равносторонний треугольник ABC, внутри которого расположена трехлучевая звезда векторов фазных токов ?АВ, ?BC и ?СА. Отсюда по аналогии с диаграммой рис. 207,б следует, что
Iл = 2Iф cos 30° = 2Iф ?3 / 2 = ?3 Iф
т. е. при равномерной нагрузке фаз в схеме «треугольник» линейный ток больше фазного тока в ?3 раз.
Следовательно, при переключении приемников со «звезды» на «треугольник» фазные токи возрастают в ?3 раз, а линейные токи — в 3 раза. Возможность включения одних и тех же приемников по схеме «звезда» или «треугольник» расширяет область их применения. Например, если приемник рассчитан на фазное напряжение 220 В, то при соединении по схеме «треугольник» он может быть включен в сеть с линейным напряжением 220 В, а при соединении по схеме «звезда» — в сеть с линейным напряжением 220?3 = 380 В. Приемники, рассчитанные на фазное напряжение 127 В, могут работать в сетях с линейными напряжениями 127 и 127?3= 220 В.
Особенности подвода трехфазного тока к приемникам. В трех-проводной трехфазной сети (при схемах «звезда без нулевого провода» и «треугольник») алгебраическая сумма мгновенных значений линейных токов в любой момент времени равна нулю, поэтому такие токи совместно не создают магнитного поля. Это позволяет прокладывать три линейных провода в одной общей металлической трубе или в кабеле с металлической оболочкой без опасности образования вихревых токов. Не допускается прокладка линейных проводов по отдельности в металлических трубах, так как возникающие вихревые токи вызывали бы сильный нагрев металла. То же самое происходило бы при прокладке в кабеле с металлической оболочкой или в трубе трех линейных проводов при схеме «звезда с нулевым проводом», так как сумма токов в них не равна нулю.

Соединение потребителей электрической энергии в треугольник
При соединении фаз электроприемников в треугольник каждая фаза будет подключена к двум линейным проводам, как показано на рисунке ниже:

Поэтому при таком типе соединения, обратно звезде, независимо от характера и значения сопротивления приемника каждое фазное напряжение будет равно линейному, то есть UФ = UЛ. Если не брать во внимание сопротивления фазных проводов, то можно предположить, что напряжения источника и приемника электрической энергии равны.
На основании приведенной выше схемы и формулы можно сделать вывод, что соединение фаз приемников электрической энергии в треугольник следует применять тогда, когда каждая фаза трехфазного или двухфазного потребителя электрической энергии рассчитана на линейное напряжение сети.
В отличии от соединения звездой, где фазные и линейные токи равны, при соединении треугольником они равны не будут. Применив первый закон Кирхгофа к узловым точкам a, b, c получим соотношение между фазными и линейными токами:

Имея векторы фазных токов, используя данное соотношение, не трудно построить векторы линейных токов.
Симметричная нагрузка при соединении приемников треугольником
В отношении любой фазы можно применять формулы, которые справедливы для однофазных цепей:

Очевидно, что при симметричной нагрузке:

Векторная диаграмма фазных (линейных) напряжений и токов при активно-индуктивной симметричной нагрузке показана ниже:

В соответствии с формулой (1) были построены векторы линейных токов. Также стоит обратить внимание на то, что при построении векторных диаграмм для соединения треугольник вектор линейного напряжения Uab принято направлять вертикально вверх.
Векторы линейных токов часто изображают соединяющими векторы фазных токов, как это показано на рисунке b):

На основании данной векторной диаграммы можно записать:  . Такое же соотношение справедливо и для других фаз. Исходя из этого, можно вывести формулу зависимости между фазным и линейным током для соединения фаз потребителей треугольником при симметричной нагрузке
. Такое же соотношение справедливо и для других фаз. Исходя из этого, можно вывести формулу зависимости между фазным и линейным током для соединения фаз потребителей треугольником при симметричной нагрузке  .
.
Пример
Трехфазная сеть имеет линейное напряжение UЛ = 220 В. К ней необходимо подключить трехфазный электроприемник с фазным напряжением в 220 В и содержащим последовательно подключенные активное rф = 8,65 Ом и индуктивное xф = 5 Ом сопротивления.
Решение
Поскольку линейные и фазные напряжения в этом случае будут равны, то выбираем способ соединения обмоток потребителя в треугольник.
Линейные и фазные токи, а также полные сопротивления фаз будут равны:

Активная, реактивная и полная мощности электроприемника любой фазы будут равны:

Векторные диаграммы приведены выше.
Несимметричная нагрузка при соединении приемников треугольником
В случае несимметричного сопротивления фаз, как и при соединении в звезду, для подключения к сети электроприемники разбивают на три примерно одинаковые по мощности группы. Подключение каждой группы производится к двум фазным проводом, у которых есть отличия по фазе:

В пределах каждой группы подключение приемников производится параллельно.
После замены сопротивления нескольких приемников в одной фазе на одно эквивалентное получим такую схему:

Углы сдвига между напряжением и током, мощности и фазные токи можно найти из формулы (2). В случае несимметричной нагрузки (в нашем случае схема выше) фазные мощности, токи, а также углы сдвига (cos φ) не будут равны. Векторная диаграмма для случая, когда фаза ab имеет активную нагрузку, bc – активно-индуктивную, ca – активно-емкостную, показана ниже:

Для определения суммарной мощности всех фаз нужно применять выражение:

Пример
Дана несимметричная электрическая цепь, включенная по схеме выше, с параметрами: UЛ = 220 В, rab = 40 Ом, xLbc = 10 Ом, rbс = 17,3 Ом, xcа = 5 Ом, rCcа = 8,65 Ом. Нужно определить линейные и фазные токи, а также мощности.
Решение
Воспользовавшись выражением для определения комплексных значений получим:

Комплексные значения полных сопротивлений фаз: Zab = 40 Ом, Zbс = 17,3 + j10 Ом, Zbс = 8,65 – j5 Ом.
Комплексные и действующие значения линейных и фазных токов:

Дольше можно проводить расчеты, не прибегая к комплексному методу:

Общие активные и реактивные мощности:

Углы сдвига между токами и напряжениями:

Векторная диаграмма для несимметричного треугольника приводилась выше.
3.3 Соединение звездой. Трехпроводная система трехфазного тока.
В четырехпроводной системе трехфазного тока, включенной по схеме звезда, при симметричной нагрузке ток в нейтральном проводе равен нулю. Следовательно, в этом случае от нейтрального провода можно отказаться, и четырехпроводная система при этом превращается в трехпроводную систему трехфазного тока (рис. 3.7.)

Рис. 3.7 Трехпроводная трехфазная система «звезда».
Топографическая векторная диаграмма, токов и напряжений в трехпроводной системе «звезда» при симметричной нагрузке аналогична соответствующей диаграмме четырехпроводной системы (рис. 3.6.а).
При несимметричной нагрузке в трехфазной системе действующие значения токов IА, IВ, IC не будут равны между собой, однако, в соответствии с первым законом Кирхгофа, их геометрическая сумма должна быть равна нулю. Поэтому токи в этом случае не будут представлять собой симметричную трехфазную систему. Следовательно, изменятся и фазные напряжения на нагрузке, т.е. симметричные фазные напряжения станут несимметричными, их действующие значения не будут равны между собой, а сдвиги фаз между ними будут отличаться от 1200. Между нулевыми точками генератора N и нагрузки n появится напряжение UNn, называемое напряжением смещения.
Топографическая векторная диаграмма трехпроводной системы «звезда» при несимметричной активной нагрузке представлена ни рис. 3.8.
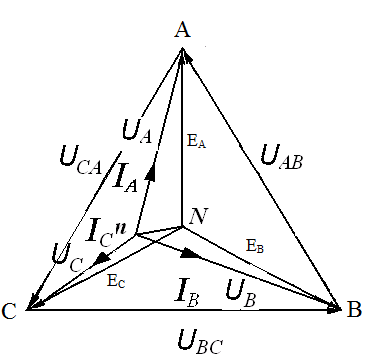
Рис.3.8. Топографическая векторная диаграмма трехпроводной трехфазной системы «звезда» при несимметричной активной нагрузке
Анализ векторной диаграммы позволяет сделать следующие выводы:
Напряжения между
линейными проводами остаются равными
по величине (UAB= UBC= UCA)
и взаимно сдвинутыми по фазе на 120о как при симметричной, так и при
несимметричной нагрузке фаз. Фазные же
напряжения в трехпроводной сети одинаковы
по величине только в случае симметричной
нагрузки фаз. При нарушении симметричности
нагрузки напряжения между линейными
проводами и нулевой точкой, т.е. фазные
напряжения потребителей UА,
UВ и UCбудут
неодинаковы. Поэтому соотношение UЛ= Uф в трехпроводной сети справедливо только
при симметричной нагрузке фаз.
Uф в трехпроводной сети справедливо только
при симметричной нагрузке фаз.
Электрические сети выполняются трехпроводными только для питания таких потребителей, которые обеспечивают симметричную нагрузку фаз (например, электрические двигатели).
3.4. Соединение по схеме «треугольник».
Если конец первой фазы трехфазного генератора соединить с началом второй, конец второй фазы с началом третьей, конец третьей фазы с началом первой, то получится соединение треугольником. По такому принципу могут быть соединены и сопротивления нагрузки. Одноименные вершины фаз генератора и фаз нагрузки соединяются между собой линейными проводами (рис. 3.9)
По сопротивлениям нагрузки проходят фазные токи IAB, IBC и IСА, а по линейным проводам линейные IA, IB и IC. Принятые положительные направления фазных и линейных токов обозначены стрелками. Напряжения, приложенные к сопротивлениям нагрузки ZAB, ZBC и ZСА называются фазными напряжениями.
Таким образом, при соединении потребителей трехфазного тока треугольником фазные напряжения равны линейным Uф= UЛ

Рис.3.9 Система трехфазного тока при соединении треугольником.
По первому закону Кирхгофа для узловых точек А, В, и С имеем
iA = iAB – iCA
iB = iBC – iAB (3.4)
iC= iCA – iBC
В действующих значениях токов система (3.4) справедлива в векторной форме:
A = 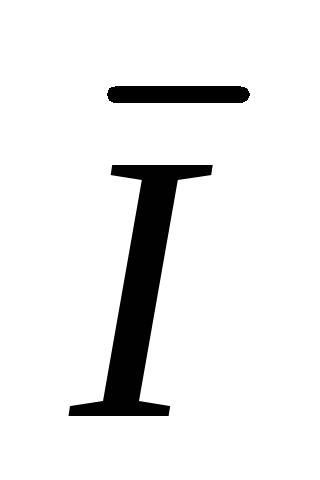 AB –
AB – 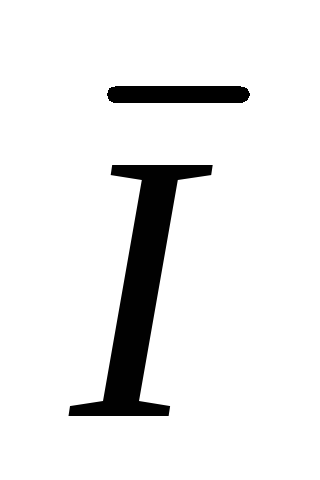 CA
CA
 B =
B = 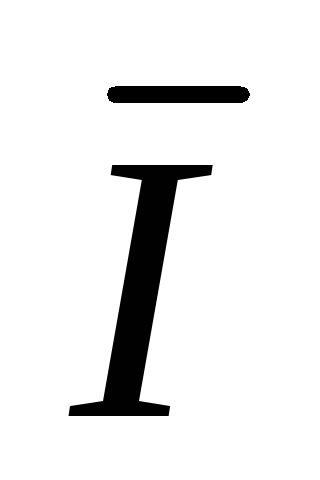 BC –
BC –  AB (3.5)
AB (3.5)
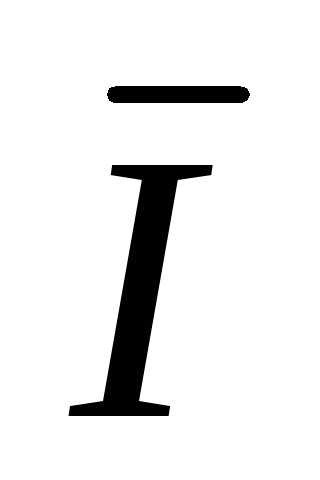 C=
C= 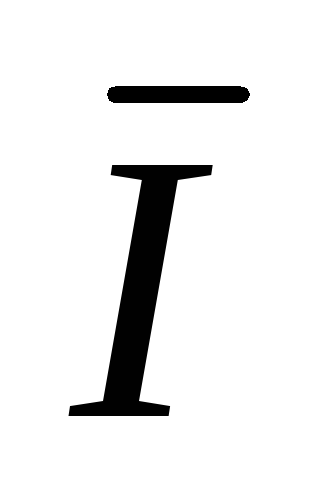 CA –
CA – 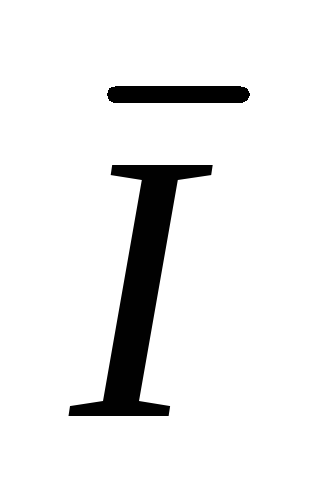 BC
BC
Из системы уравнений (3.5) следует:
1. Каждый линейный ток в трехфазной цепи при соединении треугольником равен геометрической разности двух прилегающих к узловой точке фазных токов;
2. При любых значениях фазных токов геометрическая сумма линейных токов равна нулю, как при симметричной, так и при несимметричной нагрузке.

На основании системы уравнений (3.5) построим векторную диаграмму фазных и линейных токов при соединении треугольником при симметричной нагрузке (рис. 3.10).

Рис. 3.10. Векторная диаграмма трехпроводной системы «треугольник» при симметричной нагрузке.
Из треугольника OEМ найдем связь между фазными и линейными токами, применив рассуждения, аналогичные рассмотренным для напряжений при соединении звездой (см. раздел 3.2), получаем
IЛ = 2 Iф cos300 =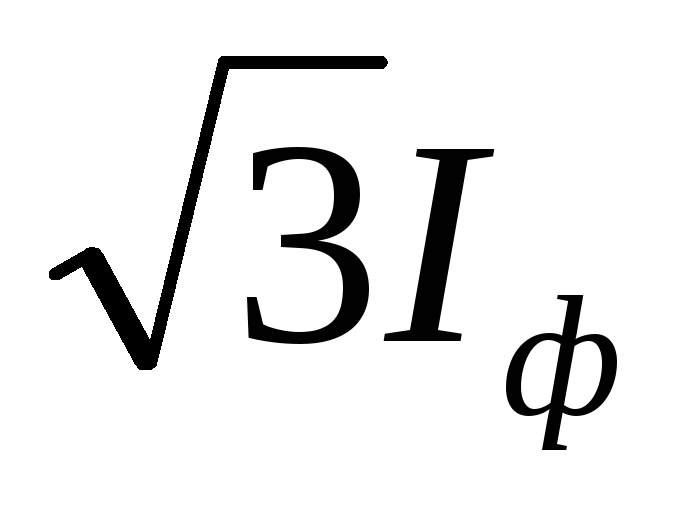 .
.
Таким образом, при
симметричной нагрузке системы, соединенной
в треугольник, линейные токи больше
фазных в  раз, а линейные напряжения равны фазным.
раз, а линейные напряжения равны фазным.
Соединение треугольником применяется только для питания потребителей, обеспечивающих симметричную нагрузку.
3.3. Соединение фаз треугольником
Несколько реже, чем соединение звездой, в трехфазных устройствах применяют соединение треугольником (условное обозначение ).
При соединении треугольником (рис. 3.9) обмотки фаз генератора соединяются так, чтобы начало одной обмотки фазы соединялось с концом предыдущей (АсZ;ВсXиСсY). Положительные направляя э.д.с. при таком соединении направлены внутри треугольника обмоток фаз одинаково; следовательно, внутри этого треугольника действует алгебраическая сумма мгновенных значений фазных э.д.с.еA + eB + еC = 0и поэтому уравнительного тока в мотках генератора не возникает6. Общие точки, созданные объединением двух зажимов обмоток, соединяются с линейными проводами, к которым подключаются фазы приемника. Ток в каждом из линейных проводов системы равен сумме двух токов, положительные направления которых противоположны (см. рис. 3.9). На основании сказанного ясно, что результирующие, токи линейных проводах равны векторной разности соответствующих фазных токов:
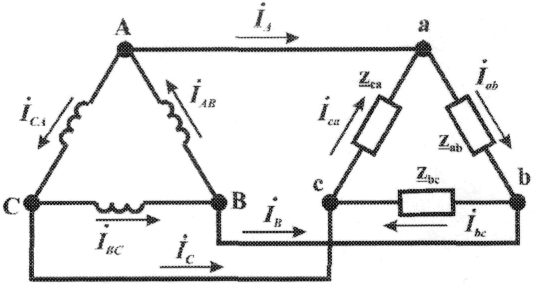
Рис. 3.9 Соединение фаз треугольником
İA = İAB — İCA ; İB = İBC — İAB ; İC = İCA – İBC; (3.5)
В этой системе три фазных напряжения будут вместе с тем линейными, поэтому как линейные, так и фазные токи, ими создаваемые, обозначают двумя индексами узлов («начал» обмоток генератора или фаз приемника).
Три линейных напряжения ŮAB.ŮBCиŮCAмогут быть исходными при построении векторной диаграммы системы (рис. 10а). Углы между ними равны120°. Векторы фазных токовİab,İbc,İcaсимметричной нагрузке сдвинуты по отношению создающим их напряжениям на некоторый угол φ значение которого зависит от отношения реактивного и активного сопротивлений приемника.
На основании соотношений (3.5), чтобы построить вектор линейного тока İA,нужно кİabприбавить (—İca), т. е. вектор, равный поİcaвеличине, но противоположный ему по направлению, На этом же основании определяются и два остальных линейных тока.
При симметричной нагрузке фазные токи по величине одинаковы: Iab=Ibc–Iфи должны быть равны между собой линейные токиIA=IB=IC=IЛ.
На диаграмме векторы фазных и линейных токов образуют три равнобедренных треугольника с острыми углами по 30°и тупым углом120°. В таком треугольнике, опустив из вершины угла перпендикуляр на противолежащую сторону (рис. 3.10б), найдем, что
Iф cos 30o = Iл / 2 или Iл = √3 Iф;(3.6)
Следовательно, в трехфазной симметричной системе, соединенной треугольником, фазные напряжения являются одновременно линейными: Uф=Uл, а линейные токи больше фазных в3 раз:
Iф = 3 Iф;
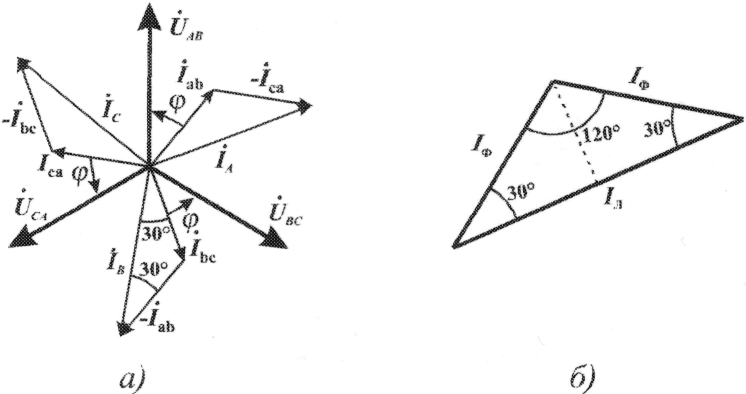
Рис. 3.10 Векторная диаграмма напряжений и токов трехфазной системы, соединенной треугольником (а), и векторные соединения между фазными и линейными токами (б)
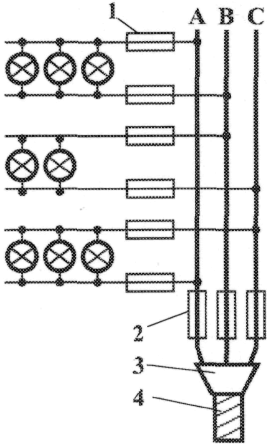
Рис. 3.11 Осветительная сеть, соединенная треугольником:
1 — квартирные предохранители, 2 — ломовые предохранители,
3 — муфт,. 4 — кабель.
Некоторым преимуществом соединения фаз треугольником является то, что при несимметричной нагрузке нет необходимости использовать четвертый провод. На рис. 3.11 показана схема осветительной сети жилого дома при соединении фаз приемников треугольником.
Приемники подключаются к трем проводам трехфазной сети, причем они могут быть соединены звездой или треугольником независимо от способа соединения фаз генератора, питающего сеть.
В ряде случаев целесообразно в зависимости от условий работы приемников изменять способ соединения фаз — переключать фазы приемника от звезды на треугольник и обратно. Такое переключение применяется для уменьшения пусковых токов трехфазных электродвигателей, для изменения температуры трехфазных электрических печей, для изменения вторичных напряжений трансформаторов.
При переключении со звезды, на треугольник фаз симметричных приемников, сопротивления которых не зависят от напряжения, линейные токи увеличиваются в три раза:
IЛ = 3IЛY
но фазные токи возрастают в 3 раз:
IФ = 3IФY;



