1.1 Расчет линейных электрических цепей постоянного тока

Задание

Для электрической цепи выполнить следующее:

1) составить на основании законов Кирхгофа систему уравнений для оп­ределения токов во всех ветвях схемы;

2) определить токи во всех ветвях схемы, используя метод контурных токов;

3) определить токи во всех ветвях схемы на основании метода нало­жения;

4) составить баланс мощностей для заданной схемы;

5) результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить;

6) определить ток во второй ветви методом эквивалентного генера­тора;

7) построить потенциальную диаграмму для любого замкнутого кон­тура, включающего обе ЭДС.

E1 B	E2 B	R1 Ом	R2 Ом	R3 Ом	R4 Ом	R5 Ом	R6 Ом	r01 Ом	r02 Ом
40	20	35	52	24	41	16	61	2	1

1.1.1 Составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы

Метод узловых и контурных уравнений основан на применении пер­вого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчета любой цепи.

При расчете данным методом произвольно задаем направление токов в ветвях

Составляем систему уравнений. В системе должно быть столько уравнений, сколько в цепи ветвей (неизвестных токов).

В заданной цепи 6 ветвей, значит, в системе должно быть 6 уравнений (т = 6). Сначала составляем уравнения для узлов по первому закону Кирхгофа. Для цепи с п узлами можно составить (n-1) независи­мых уравнений. В нашей цепи 4 узла (А, В, С,D), значит, число уравнений: n-1=4-1=3. Составляем 3 уравнения для любых 3-х узлов, например, для узлов А, В,C

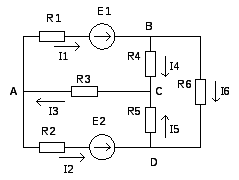
Всего в системе должно быть пять уравнений. Два уже есть. Три не­достающих составляем для линейно независимых контуров. Чтобы они были независимыми, в каждый следующий контур надо включить хотя бы одну ветвь, не входящую в предыдущие.

Задаемся обходом каждого контура и составляем уравнения по вто­рому закону Кирхгофа.

А: I₃=I₂+ I₁

B: I₁=I₄+ I₆

C: I₃=I₄+ I₅

Контур АВCА — обход по часовой стрелке

Контур ADCA — обход против часовой стрелки

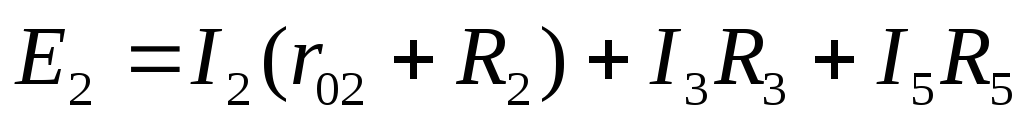
Контур DCBD — обход по часовой стрелке

Мы получили систему из 6 уравнений с 6 неизвестными:

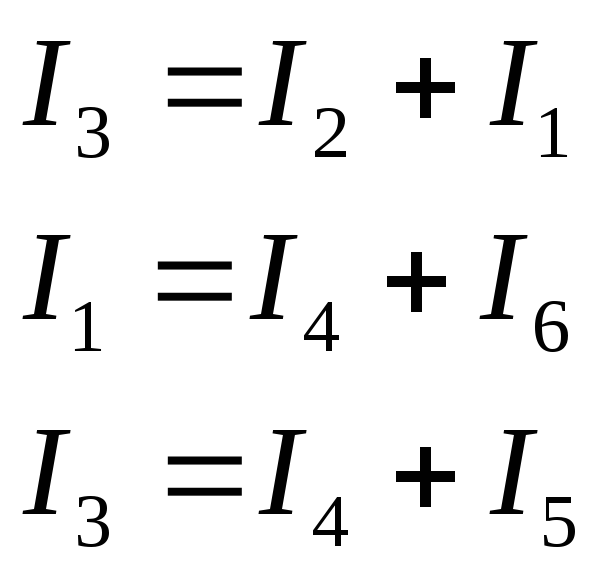
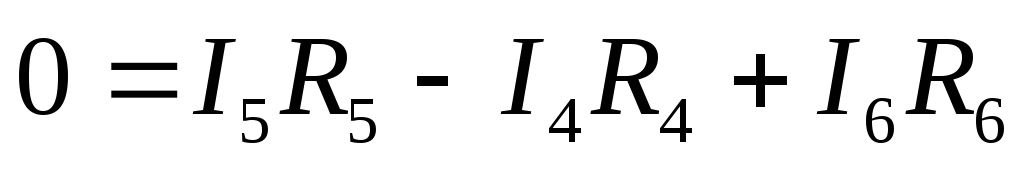
1.1.2 Определить токи во всех ветвях схемы, используя метод контурных токов

Метод контурных токов основан на использовании только второго за­кона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n-1_.

Достигается это разделением схемы на ячейки (независимые конту­ры) и введением для каждого контура-ячейки своего тока — контурного тока, являющегося расчетной величиной.

В заданной можно рассмотреть три контура-ячейки (ABCA, ADCА, DCBD) и ввести для них контурные токи I_k1, I_k2, I_k3.

Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.

При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются на­пряжения на сопротивлениях, входящих в этот контур, а также учитывает­ся падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура.

На основании вышеизложенного порядок расчета цепи методом кон­турных токов будет следующим:

стрелками указываем выбранные направления контурных токов I_k1, I_k2, I_k3в контурах-ячейках. Направление обхода контуров принимаем таким же;

составляем уравнения и решаем систему уравнений или методом

подстановки, или с помощью определителей.

Подставляем в уравнение численные значения ЭДС и сопротивлений.

Решим систему с помощью определителей. Вычислим определитель системы ∆ и частные определители ∆

1, ∆₂, ∆₃

Вычисляем контурные токи:

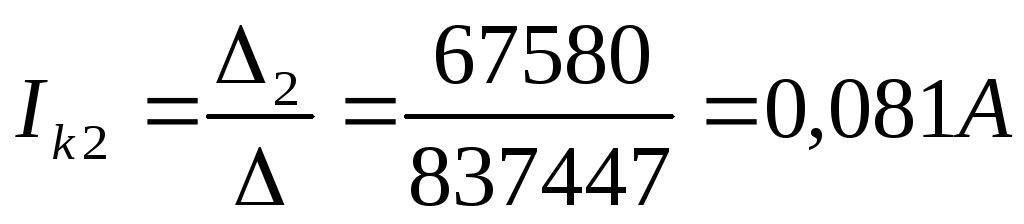
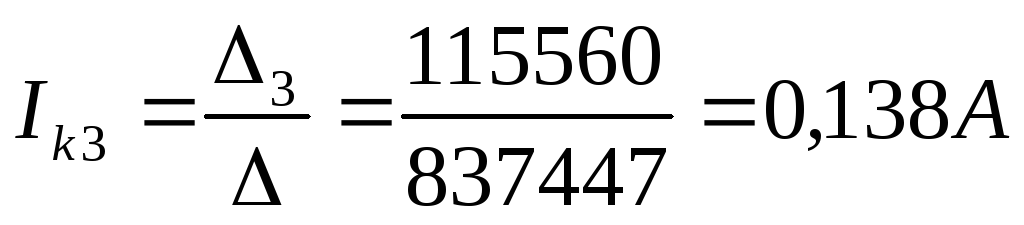
Действительные токи ветвей:

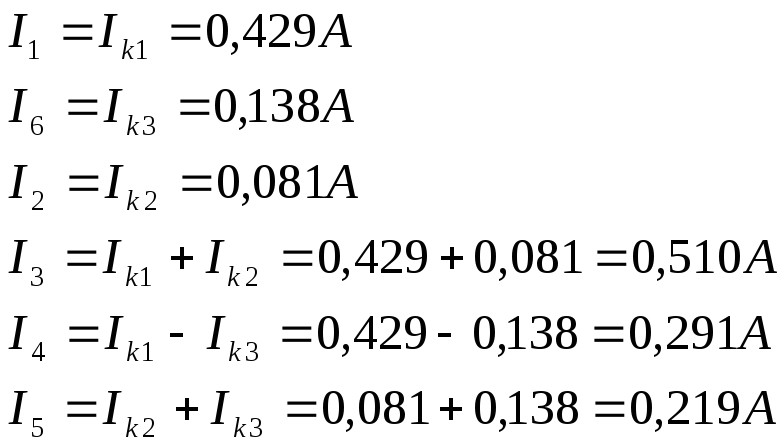
примеры решений задач / variant_77

Задания

1. Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.

2. Определить токи во всех ветвях схемы методом контурных токов.

3. Определить токи во всех ветвях схемы методом узловых потенциалов.

4. Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить между собой.

5. Составить баланс мощностей в исходной схеме, вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений).

6. Определить ток в заданной по условию схеме, используя теорему об активном двухполюснике и эквивалентном генераторе.

7. Начертить потенциальную диаграмму для любого замкнутого контура, включая обе э.д.с.

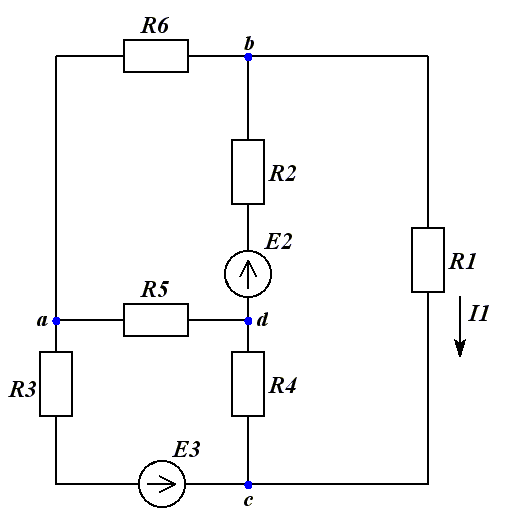
R₁=18Ом;

R₂=40Ом;

R₃=32Ом;

R₄=80Ом;

R₅=60Ом;

R₆=44Ом;

E₂=60В;

E₃=28В;

Линейные цепи постоянного тока.

1.Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.

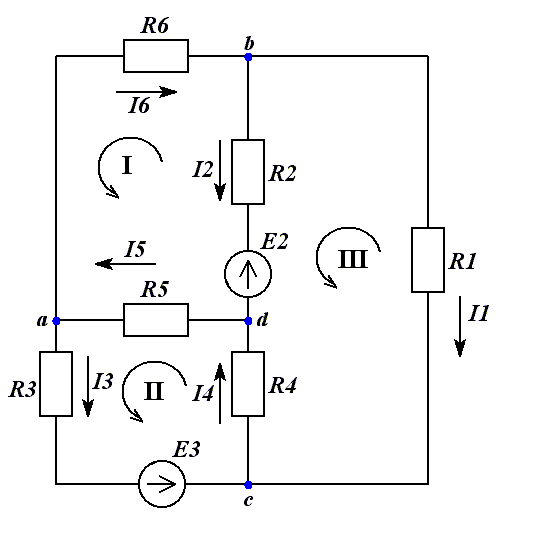
Направим произвольно токи в ветвях схемы. В схеме четыре узла значит по первому закону Кирхгофа составим три уравнения. Составим уравнения узлов а,b,с.

Для узла а -I₃

+I₅-I₆=0

Для узла b -I₁-I₂+I₆=0

Для узла c I₁+I₃-I₄=0

По второму закону Кирхгофа составим 3 уравнения. Так как общее число уравнений 6, то число неизвестных тоже 6. Примем направление обхода контуров против часовой стрелки.

Для контура I; —R₂I₂-R₅I₅— R₆I₆ =E₂

Для контура II; R₃I₃+R₄I₄+R₅I₅=E₃

Для контура III; -R₁I₁+R₂I₂-R₄I₄=-E₂

2. Определить токи во всех ветвях методом контурных токов.

Выберем направления обхода контуров против часовой стрелки.

Найдем сопротивления контуров

R₁₁=R₂+R₅+R₆=40+60+44=144Ом

R₂₂=R₃+R₄+R₅=32+80+60=172Ом

R₃₃=R₁+R₂+R₄=18+40+80=138Ом

Смежные сопротивления:

R₁₂=R₂₁=-R₅=-60Ом

R₁₃=R₃₁=-R₂=-40Ом

R₂₃=R₃₂=-R₄=-80Ом

E₁₁=E₂=60В E₂₂=E₃=28В E₃₃=-E₂=-60В

Записываем систему уравнений.

R₁₁I₁₁+R₁₂I₂₂+R₁₃I₃₃=E₁₁

R₂₁I₁₁+R₂₂I₂₂+R₂₃I₃₃=E₂₂

R₃₁I₁₁+R₃₂I₂₂+R₃₃I₃₃=E₃₃

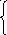144I₁₁—60I₂₂—40I₃₃=60

—60I₁₁+172I₂₂—80I₃₃=28

—40I₁₁—80I₂₂+138I₃₃=-60

Составляем определитель:

144 -60 -40

= -60 172 -80 =1340000

-40 -80  138

60 -60 -40

1= 28 172 -80 =660800

-60 -80  138

144 60 -40

2= -60 28 -80 =365200

-40 -28  138

144 -60 60

3= -60 172 28 =-179500

-40 -80  -60

I₁₁=1/= 0,493A; I₁=- I₃₃= 0,134A; I₄=I₂₂-I₃₃= 0,406A

I₂₂=2/= 0,272A; I₂=I₃₃-I₁₁= -0,627A; I₅=I₂₂-I₁₁= -0,221A

I₃₃=3/= -0,134A; I₃=I₂₂= 0,272 A; I₆=-I₁₁= -0,493A

Знаки « — » перед значениями токов указывают, что токи направлены в противоположную сторону от выбранных нами направлений.

3. Определить ток в схеме методом узловых потенциалов.

Заземлим точку c, приняв её потенциал равным 0.

Запишем общую систему уравнений.

φ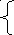₁₁G₁₁+φ₂₂G₁₂+φ₃₃G₁₃=I₁₁

φ₁₁G₂₁+φ₂₂G₂₂+φ₃₃G₃₂=I₂₂

φ₁₁G₃₁+φ₂₂G₃₂+φ₃₃G₃₁=I₃₃

Узловые проводимости:

G₁₁=1/R₃+1/R₅+1/R₆

G₂₂=1/R₂+1/R₄+1/R₅

G₃₃=1/R₁+1/R₂+1/R₆

Смежные проводимости:

G₁₂=G₂₁=-1/R₅

G₁₃=G₃₁=-1/R₆

G₂₃=G₃₂=-1/R₂

Узловые токи:

I₁₁=-E₃/R₃; I₂₂=-E₂/R₂; I₃₃=E₂/R₂

Подсчитываем проводимости и токи, и подставляя их в общую систему уравнений решаем её. Находим узловые потенциалы.

0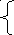,071φ₁₁-0,017φ₂₂-0,023φ₃₃=-0,857

-0,017φ₁₁+0,054φ₂₂—0,025φ₃₃=-1,5

-0,023φ₁₁-0,025φ₂₂+0,103φ₃₃=1,5

0,071 -0,017 -0,023

 = -0,017 0,054 -0,025 = 0,0002726

-0,023 -0,025 0,103

-0.857 -0,017 -0,023

1= -1,5 0,054 -0,025 = —0,00522

1,5 -0,025 0,103

0,071 —0,857 -0,023

2 = -0,017 -1,5 -0,025 = -0,00892

-0,023 1,5 0,103

0,071 -0,017 —0,857

3 = -0,017 0,054 -1,5 = 0,0006399

-0,023 -0,025 1,5

Получили значения потенциалов

φ₁₁= -19,144 В φ₂₂= -32,718 В φ₃₃= 2,347 В

Токи в ветвях схемы вычисляем по закону Ома. Причем не будем менять направления на противоположные для наглядности, что получили те же токи.

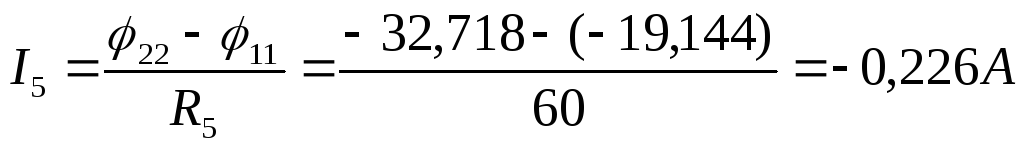
Т.к. не меняли направления токов то они как и во 2-ом пункте получились отрицательные.

4.Свести результаты расчета токов в таблицу и определить относительную и абсолютную погрешности.

Метод контурных токов	Метод узловых потенциалов	ε,%	∆I,А
I1=0,134А	I1= 0,13А	0,03	0,004
I2= -0,627А	I2= -0,623А	0,006	-0,004
I3= 0,272А	I3= 0,227А	0,018	-0,005
I4= 0,406А	I4= 0,409А	0,007	-0,003
I5= -0,221А	I5= -0,226А	0,023	0,005
I6= -0,493А	I6= -0,488А	0,01	-0,005

ε иI рассчитаны по формулам:

ε=|(I_К—I_φ)/I_К|*100%,где I_К-ток по МКТ.

I_φ-ток по МУП.

I=I_К-I_φ.

5.Составить баланс мощностей в исходной схеме, вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений).

Уравнение баланса: I²_кR_к=E_КI_К.

Как видим баланс мощностей сходится.

6. Определить ток I₁ в заданной по условию схеме, используя теорему об активном двухполюснике и эквивалентном генераторе.

Для нахождения тока I₁,преобразуем исходную схему, используя теорему об активном двухполюснике. И рассчитаем I₁ по формуле:

I₁=ε_экв / R_вх+R₁

Для нахождения ε_экв исключим из исходной схемы ветвь содержащую ток I₁.Произвольно направим токи в полученной схеме.

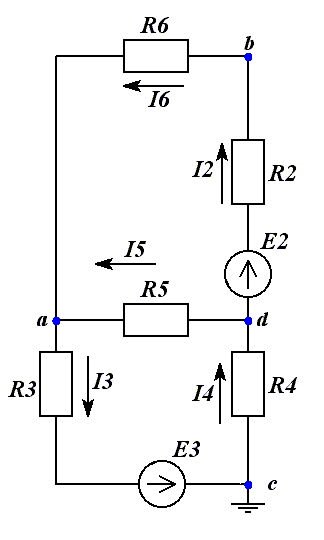
Потенциал узла c примем равным нулю.

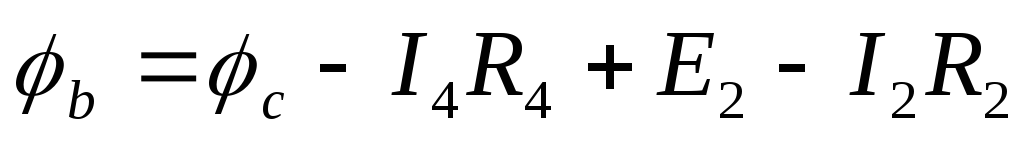
Для нахождения токов в преобразованной схеме воспользуемся методом двух узлов.

Полученные значения токов подставим в выражения для потенциалов. И получим ε_экв:

ε_экв =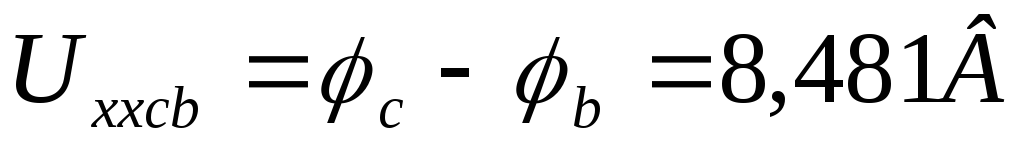

Найдем R_вх для чего исключим из схемы все источники ЭДС и найдем сопротивление схемы относительно зажимов (bc ).

Для нахождения входного сопротивления преобразуем треугольник R₄,R₅,R₆ в звезду R₄₅,R₅₃,R₃₄.

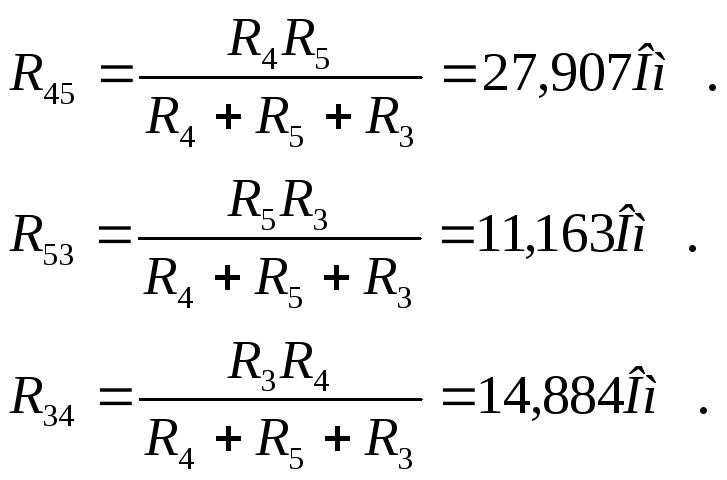
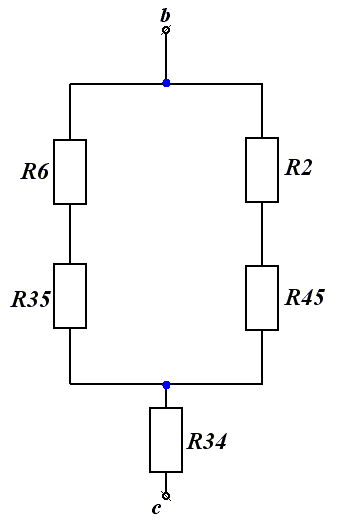
Теперь мы можем найти I₁.

7.Построить потенциальную диаграмму для любого замкнутого контура включающего обе ЭДС.

Выберем направление обхода контура fabkdcf. При этом не будем менять направления токов. А значения токов возьмем из второго задания с теми же знаками. Заземлим узел f.

φ_f = 0В

Рассчитаем потенциалы остальных точек контура.

φ_a = φ_f + R₃I₃= 8,7В

φ_b = φ_a –I₆R₆ = 30,4В

φ_k = φ_b – R₂I₂ = 55,5В

φ_d = φ_k — Е₂ = -4,5В

φ_c = φ_d + R₄I₄ =28В

φ_f = φ_k – E₃ = 0В

По полученным данным строим потенциальную диаграмму:

Определить Токи Электрической Схемы — tokzamer.ru

Подставив 1.


Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Реальная электрическая цепь может быть представлена в виде активного и пассивного двухполюсников рис.

Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Известны величины сопротивлений и ЭДС, необходимо определить токи.
Как научиться читать электрические схемы

Для исходной схемы своего варианта, см.

Последовательное включение источников питания источников ЭДС применяется тогда, когда требуется создать напряжение требуемой величины, а рабочий ток в цепи меньше или равен номинальному току одного источника ЭДС рис.

Выберем три независимых контура и укажем направления обхода контуров. В схеме имеются четыре узла, можно составить четыре уравнения по первому закону Кирхгофа.

Дальнейший расчет п.

На параллельную работу включают обычно источники с одинаковыми ЭДС, мощностями и внутренними сопротивлениями. Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода.

RL ЦЕПЬ │Теория и задача │Переменный ток

Рассчитайте схему цепи

Так как ток обоих участков цепи одинаков, а сумма напряжений на элементах равна приложенному рис. Приступаем к основному этапу — составлению системы уравнений контурных токов. Реальная электрическая цепь может быть представлена в виде активного и пассивного двухполюсников рис.

Выберем три независимых контура и укажем направления обхода контуров.

Линейные электрические цепи постоянного тока Для электрической схемы, соответствующей номеру варианта и изображенной на рис.

Задача 1. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений.

Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Последовательное соединение нелинейных элементов.

Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить между собой. Составляем систему уравнений по второму закону Кирхгофа для каждого замкнутого контура так, чтобы охватить каждый неизвестный ток в данной схеме имеем 3 таких контура.

Пользуясь характеристиками рис. При этом на нагрузке выделится активная мощность 1.
Как читать электрические схемы. Урок №6

Рекомендуем: Подключение 2 х клавишного выключателя

Основные понятия

Рассмотрим пример. В заданной схеме, см.

Токи в резисторах В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю. Выполняем все поэтапно.

В табл.

Ток в сопротивлении R3, являющийся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви с R3 встречно. Управляемые элементы работают под влиянием управляющего воздействия тиристоры, транзисторы и другие.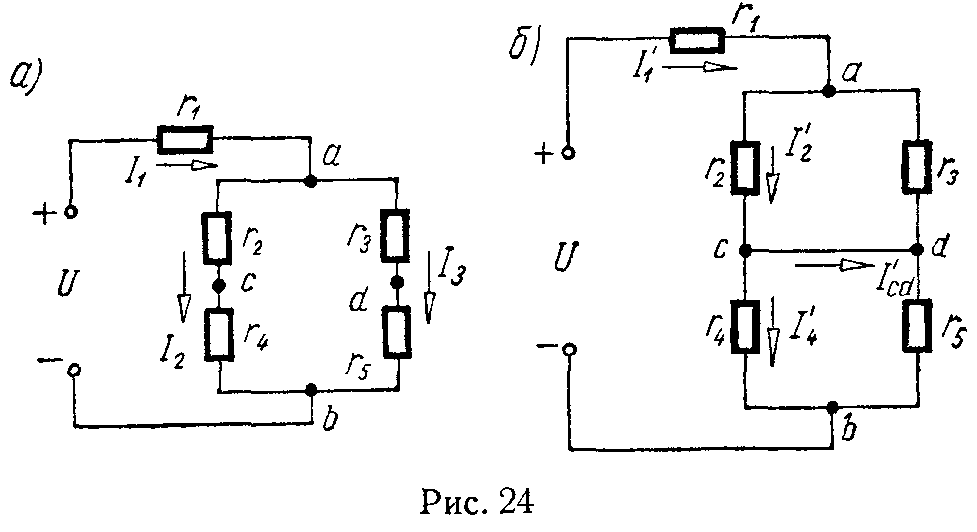

Пусть, например, задана величина приложенного к току напряжения U и требуется определить ток в цепи и распределение напряжений на ее участках. Последовательное соединение нелинейных элементов. Управляемые элементы работают под влиянием управляющего воздействия тиристоры, транзисторы и другие.

Примеры решения задач на законы Кирхгофа

В схеме рис. После проведенных преобразований рис.

Приступаем к основному этапу — составлению системы уравнений контурных токов. Про комплексные числа можно подробнее прочитать на нашем сайте. Определим параметры электрической цепи рис. Уравнения по второму закону составляют для независимых контуров. Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур.

Система уравнений 4. Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах. Запишем уравнения:: 4. В этом случае ток в нагрузке становится равным нулю, и как следует из соотношения 1.
КАК ТЕЧЁТ ТОК В СХЕМЕ — Читаем Электрические Схемы 1 часть

Переменный ток.

В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.

Последним этапом находим действительные токи, для этого нужно записать для них выражения. Работа активного двухполюсника под нагрузкой в номинальном режиме определяется уравнением 1.

Определим параметры электрической цепи рис. Неуправляемые нелинейные элементы имеют одну вольт-амперную характеристику; управляемые — семейство характеристик.

Определить ток I1 в заданной по условию схеме с источником тока, используя метод эквивалентного генератора. Чтобы решить такую систему можно воспользоваться программой MathCad. В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений.

Читайте дополнительно: Нормы прокладки кабеля под землей

АГЗ МЧС РГР №1 Расчёт линейных цепей постоянного тока

Уравнения по второму закону составляют для независимых контуров. Определим параметры электрической цепи рис. Контурный ток равен действительному току, который принадлежит только этому контуру. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений.

Направление обхода контура совпадает с направлением контурных токов. Режим работы электрической цепи рис. Переменный синусоидальный ток или напряжение задается уравнением: Здесь Im — амплитуда тока. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем. Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.

Определить токи во всех ветвях схемы на основании метода наложения.

Эта вольт-амперная характеристика строится по двум точкам 1 и 2 рис. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Следовательно, схема источника тока рис. Вычислим коэффициент подобия.

Составить баланс мощностей в исходной схеме схеме с источником тока , вычислив суммарную мощность источников и суммарную мощность нагрузок сопротивлений. Рекомендуется узлы схемы a, b, c, d заменить на 1, 2, 3, 4 соответственно. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. В нашем случае эти токи направлены по часовой стрелке.
Законы Кирхгофа — Теория и задача

Определить токи во всех ветвях схемы, используя метод контурных токов.

Метод контурных токов основан на использовании только второго за­кона Кирхгофа. Это позволяет уменьшить число уравнений в системе на .

Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока – контурного тока, являющегося расчетной величиной.

Итак, в заданной цепи можно рассмотреть три контура-ячейки (ACB, BDC, ADB) и ввести для них контурные токи .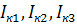

R₃R₅

I₃I_k1R₁I_k3I₅

E₁

I₄ E₁I₆

R₄I₁r₀₁R₆

I_k2I₂

E₂ r₀₂ R₂

Контуры-ячейки имеют ветвь, не входящую в другие контуры – это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей.

Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.

При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются на­пряжения на сопротивлениях, входящих в этот контур, а также учитывает­ся падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура.

На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим:

стрелками указываем выбранные направления контурных токов в контурах-ячейках. Направление обхода контуров принимаем таким же;

составляем уравнения и решаем систему уравнений с помощью определителей.

_E1=_Ik1(_R1+_r01+_R4+_R3)+_Ik2_R4+_Ik3(_R1+_r01)

E₂=I_k2(R₂+r₀₂+R₆+R₄)-I_k3R₆+I_k1R₄

E₁=I_k3(R₁+r₀₁+R₆+R₅)+I_k1(R₁-r₀₁)-I_k2R₆

Подставляем в уравнение численные значения ЭДС и сопротивлений:

30=I_k1(45+1+24+32)+24 I_k2+I_k3(45+1)

20= I_k1(53+1+15+24)-15 I_k3+24I_k1

30= I_k3(45+1+15+61)+ I_k1(45+1)-15 I_k2

Раскрываем скобки и приводим подобные:

30=102I_2k+46I_k3

20=24I_k1+93I_k2-15I_k3

30=46I_k1-15I_k2+122I_k3

Решим полученную систему уравнений с определителей. Вычислим определитель системы и частные определители .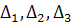

30 102 24 46 102 24 46

20 24 93 -15 ∆= 24 93 -15 =834162

30 46 -15 122 46 -15 122

30 24 46 102 30 46

∆₁= 20 93 -15 =122130 ∆₂= 24 20 -15 = 177040

30 -15 122 46 30 122

102 24 30

∆₃= 24 93 20 =180840

46 -15 30

Вычисляем контурные токи:

I_k1===0,146 А;

I_k2=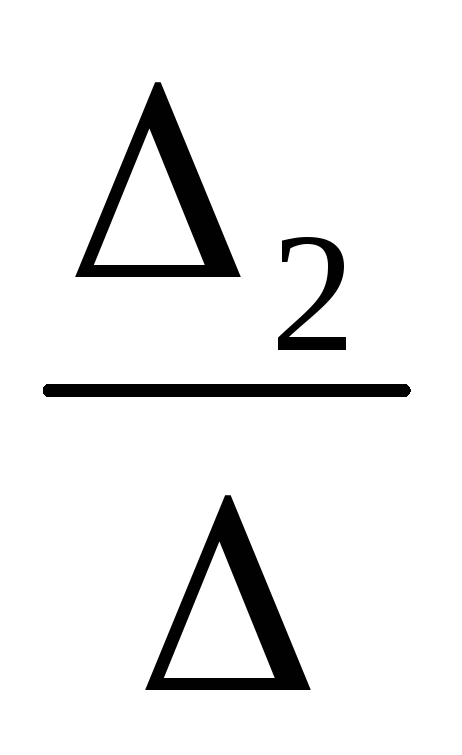==0,212 А;

I_k3=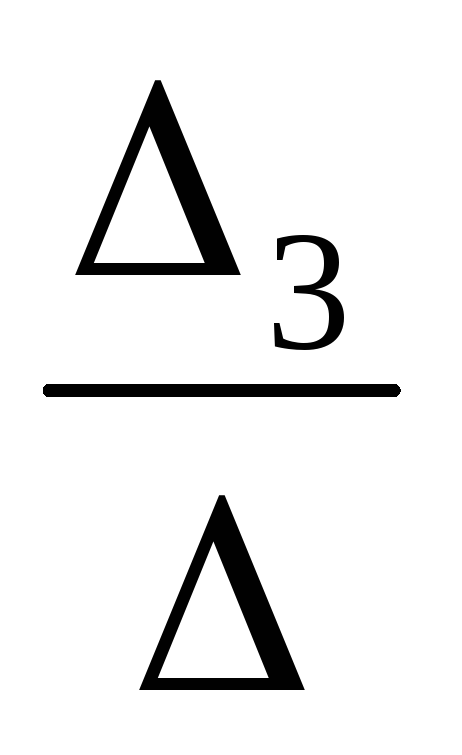==0,217 А.

Действительные токи ветвей:

I₁=I_k1+I_k3=0,146+0,217=0,363 A

I₂=I_k2=0,212 A

I₃=I_k1=0,146 A

I₄=I_k1+I_k2=0,146+0,212=0,358 A

I₅=I_k3=0,217 A

I₆=I_k3-I_k2=0,217-0,212=0,005 A

Определить токи во всех ветвях схемы, используя метод контурных токов.

Метод контурных токов основан на использовании только второго за­кона Кирхгофа. Это позволяет уменьшить число уравнений в системе на .

Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока – контурного тока, являющегося расчетной величиной.

Итак, в заданной цепи можно рассмотреть три контура-ячейки (ACB, BDC, ADB) и ввести для них контурные токи .

R₃R₅

I₃I_k1R₁I_k3I₅

E₁

I₄ E₁I₆

R₄I₁r₀₁R₆

I_k2I₂

E₂ r₀₂ R₂

Контуры-ячейки имеют ветвь, не входящую в другие контуры – это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей.

Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.

При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются на­пряжения на сопротивлениях, входящих в этот контур, а также учитывает­ся падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура.

На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим:

стрелками указываем выбранные направления контурных токов в контурах-ячейках. Направление обхода контуров принимаем таким же;

составляем уравнения и решаем систему уравнений с помощью определителей.

_E1=_Ik1(_R1+_r01+_R4+_R3)+_Ik2_R4+_Ik3(_R1+_r01)

E₂=I_k2(R₂+r₀₂+R₆+R₄)-I_k3R₆+I_k1R₄

E₁=I_k3(R₁+r₀₁+R₆+R₅)+I_k1(R₁+r₀₁)-I_k2R₆

Подставляем в уравнение численные значения ЭДС и сопротивлений:

50=I_k1(53+1+18+24)+18 I_k2+I_k3(53+1)

30= I_k1(34+1+442+18)-42 I_k3+18I_k1

50= I_k3(53+1+42+25)+ I_k1(53+1)-42 I_k2

Раскрываем скобки и приводим подобные:

50=96I­­_k1+­18I_k2+46I_k3

30=18I_k1+95I_k2-42I_k3

50=54I_k1-42I_k2+121I_k3

Решим полученную систему уравнений с определителей. Вычислим определитель системы 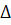и частные определители .

50 96 18 54 96 18 54

30 18 95 -42 ∆= 18 95 -42 =536304

50 54 -42 121 54 -42 121

50 18 54 96 50 54

∆₁= 30 95 -42 =58870 ∆₂= 18 30 -42 = 288900

50 -42 121 54 50 121

96 18 50

∆₃= 18 95 30 = 295620

54 -42 50

Вычисляем контурные токи:

I_k1===0,1098 А;

I_k2===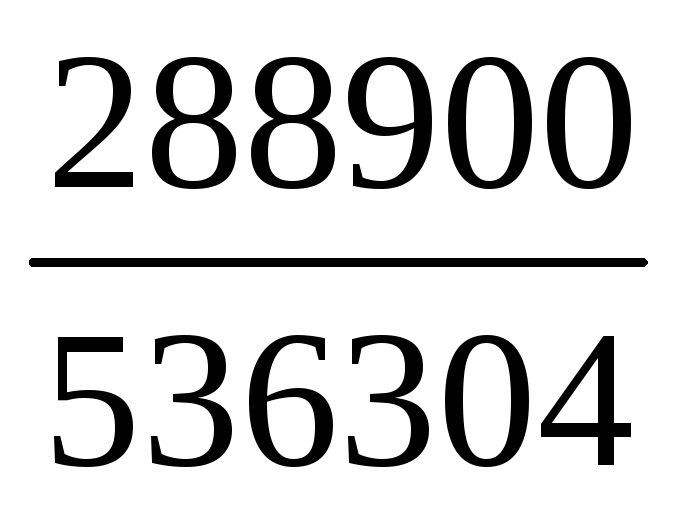0,5387 А;

I_k3===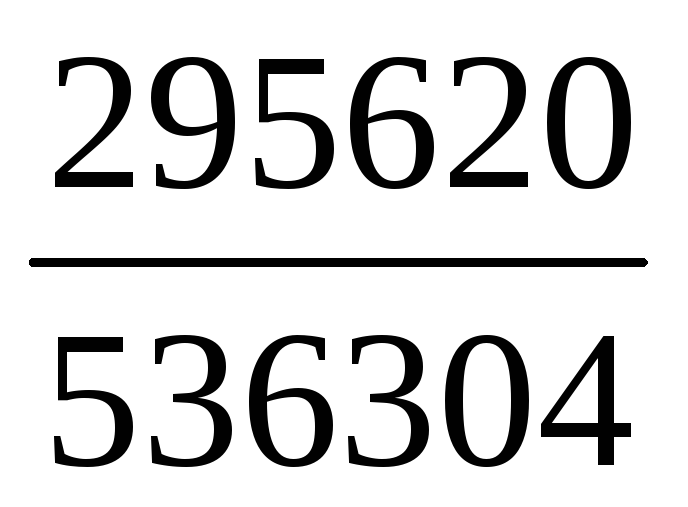0,5512 А.

Действительные токи ветвей:

I₁=I_k1+I_k3=0,1098+0,5512=0,661 A

I₂=I_k2=0,5387 A

I₃=I_k1=0,1098 A

I₄=I_k1+I_k2=0,1098+0,5387=0,6485 A

I₅=I_k3=0,5512 A

I₆=I_k3-I_k2=0,5512-0,5387=0,0125 A.

1.8. Расчет цепей методом контурных токов.

Этот метод рационально использовать при расчете цепей с большим количеством узлов, т.к. он позволяет почти вдвое сократить количество уравнений по сравнению с методом непосредственного применения законов Кирхгофа. В методе контурных токов независимыми переменными являются контурные токи, условно замыкающиеся по элементам независимых контуров.

Чтобы найти контурные токи каждого независимого контура, необходимо составить уравнения второго закона Кирхгофа и решить полученную систему уравнений.

П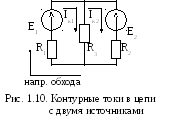ри расчете рекомендуется придерживаться следующей последовательности:

– выделить все независимые контуры

– указать направления обхода контуров (желательно одно и то же для всех контуров)

– указать направления контурных токов в каждом контуре (рекомендуется направления контурных токов выбирать совпадающими с направлением обхода)

– для всех независимых контуров составить уравнения второго закона Кирхгофа

– решить полученную систему уравнений любым известным методом

– по вычисленным значениям контурных токов определить величины токов в ветвях и их направления.

Рассмотрим цепь, представленную на рис. 1.10. Она имеет два независимых контура: E₁R₃R₁E₁и R₃E₂R₂R₃. Направления контурных токов и направления обхода указаны на рисунке. Нетрудно видеть, что в смежной ветви R₃, которая принадлежит двум контурам сразу, протекают два контурных тока I_K1и I_K2, но в противоположных направлениях.

E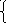₁ = I_K1 (R₁ + R₃) – I_K2R₃

– E₂= –I_K1R₃+I_K2(R₂+R₃)

Решение полученной системы уравнений проводится так же, как изложено выше для метода непосредственного применения законов Кирхгофа. Токи в ветвях, принадлежащих одному контуру, равны соответствующему контурному току. Если же контурный ток отрицателен, то ток в ветви, принадлежащей только этому контуру, будет равен контурному току по величине, но будет иметь противоположное направление.

Например, пусть контурные токи в ветвях цепи, представленной на рис. 1.10 равны: I_K1=7 A, I_K2= – 5 A. Тогда I₁= I_K1= 7 = 7 A и протекает в резисторе R₁так же, как контурный ток I_K1по схеме сверху вниз. Ток I₂= – I_K2= – 5 А и протекает в резисторе R₂по схеме снизу вверх. Токи в смежных ветвях, принадлежащие одновременно двум контурам и по которым протекают два контурных тока, находятся как алгебраическая сумма протекающих в этих ветвях контурных токов. Направление тока в смежной ветви определяется направлением большего контурного тока в этой ветви. Например, в ветви R₃ , цепи представленной на рис. 1.10, протекают контурный ток I_K1= 7 А по схеме сверху вниз и контурный ток I₂= – 5 А по схеме снизу вверх. I_K1> I_K2и I₃= I_K1– I_K2= 7 – (–5) = 12 А. Ток I₃имеет такое же направление, что и ток I_K1 , т.е. по схеме сверху вниз.

1.9. Расчет цепей методом эквивалентного преобразования.

Расчет цепей методом эквивалентного преобразования применяют для цепей с одним источником электроэнергии со смешанным соединением приемников. Смешанным соединением приемников называется сочетание их последовательных и параллельных соединений.

По методу эквивалентных преобразований отдельные участки цепи с последовательным или параллельным включением приемников заменяют одним эквивалентным приемником. Постепенным преобразованием участков цепь приводят к простейшей, состоящей из одного эквивалентного элемента.

Рис. 1.11. Цепь со смешанным соединением приемников (а) и эквивалентные ей схемы (б) и (в)

Например, в цепи представленной на рис. 1.11а приемники R₃и R₄соединены последовательно и их можно заменить одним эквивалентным с сопротивлением

R₃₄= R₃+ R₄.

После замены цепь принимает вид, представленный на рис. 1.11б, в которой приемник R₂ и эквивалентный приемник R₃₄включены параллельно. Параллельный участок R₂– R₃₄также можно заменить одним эквивалентным с сопротивлением

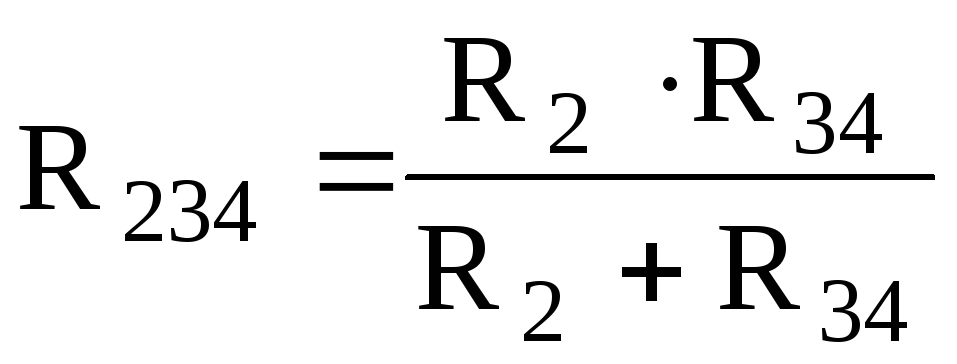
после чего цепь принимает вид, представленный на рис. 1.11.в, элементы которой соединены последовательно.

Входное сопротивление этой цепи R₁₂₃₄= R₁+ R₂₃₄

позволяет найти ток I₁исходной цепи рис. 1.11а, пользуясь законом Ома

.

Напряжение на участке R₂₃₄легко найти по закону Ома для пассивного участка цепи

U₂₃₄= I₁R₂₃₄.

Токи в ветвях R₂и R₃₄также находятся по закону Ома

.

Токи I₃= I₄, т.к. приемники R₃и R₄включены последовательно, они равны току I₃₄.

Определить токи во всех ветвях схемы, используя метод контурных токов.

Метод контурных токов основан на использовании только второго за­кона Кирхгофа. Это позволяет уменьшить число уравнений в системе на .

Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока – контурного тока, являющегося расчетной величиной.

Итак, в заданной цепи можно рассмотреть три контура-ячейки (ACB, BDC, ADB) и ввести для них контурные токи .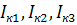

R₃R₅

I₃I_k1R₁I_k3I₅

E₁

I₄ E₁I₆

R₄I₁r₀₁R₆

I_k2I₂

E₂ r₀₂ R₂

Контуры-ячейки имеют ветвь, не входящую в другие контуры – это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей.

Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.

При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются на­пряжения на сопротивлениях, входящих в этот контур, а также учитывает­ся падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура.

На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим:

стрелками указываем выбранные направления контурных токов в контурах-ячейках. Направление обхода контуров принимаем таким же;

составляем уравнения и решаем систему уравнений с помощью определителей.

_E1=_Ik1(_R1+_r01+_R4+_R3)+_Ik2_R4+_Ik3(_R1+_r01)

E₂=I_k2(R₂+r₀₂+R₆+R₄)-I_k3R₆+I_k1R₄

E₁=I_k3(R₁+r₀₁+R₆+R₅)+I_k1(R₁-r₀₁)-I_k2R₆

Подставляем в уравнение численные значения ЭДС и сопротивлений:

30=I_k1(45+1+24+32)+24 I_k2+I_k3(45+1)

20= I_k1(53+1+15+24)-15 I_k3+24I_k1

30= I_k3(45+1+15+61)+ I_k1(45+1)-15 I_k2

Раскрываем скобки и приводим подобные:

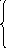30=102I_2k+46I_k3

20=24I_k1+93I_k2-15I_k3

30=46I_k1-15I_k2+122I_k3

Решим полученную систему уравнений с определителей. Вычислим определитель системы и частные определители .

30 102 24 46 102 24 46

20 24 93 -15 ∆= 24 93 -15 =834162

30 46 -15 122 46 -15 122

30 24 46 102 30 46

∆₁= 20 93 -15 =122130 ∆₂= 24 20 -15 = 177040

30 -15 122 46 30 122

102 24 30

∆₃= 24 93 20 =180840

46 -15 30

Вычисляем контурные токи:

I_k1===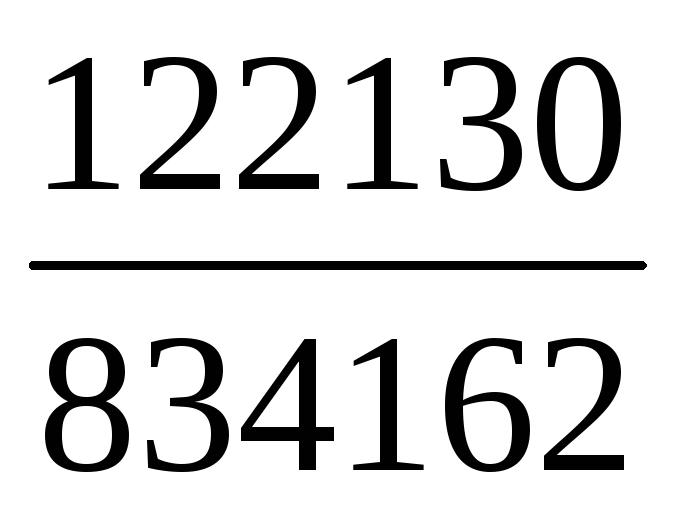0,146 А;

I_k2=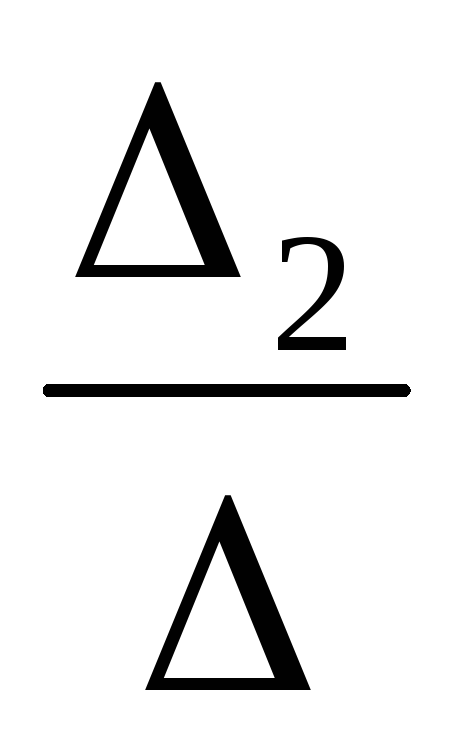==0,212 А;

I_k3===0,217 А.

Действительные токи ветвей:

I₁=I_k1+I_k3=0,146+0,217=0,363 A

I₂=I_k2=0,212 A

I₃=I_k1=0,146 A

I₄=I_k1+I_k2=0,146+0,212=0,358 A

I₅=I_k3=0,217 A

I₆=I_k3-I_k2=0,217-0,212=0,005 A