Задание №1 — Расчет сложной электрической цепи постоянного тока
Оглавление
Задание №1 — Расчет сложной электрической цепи постоянного тока 3
1.1 Расчёт токов в исследуемой электрической цепи путём непосредственного применения законов Кирхгофа. 4
1.3 Расчёт токов во всех ветвях схемы методом узловых потенциалов 8
Задание № 2 — Расчет электрической цепи переменного синусоидального тока 17
Активная мощность. Единица измерения — ватт (W, Вт). 26
Реактивная мощность. Единица измерения — вольт-ампер реактивный (var, вар) 26
Указания к выбору варианта задания
Электрические схемы, предлагаемые для расчета, пронумерованы. Соответствие варианта и расчетной схемы обозначено в таблице №1 и одинаково для обеих групп. Значения сопротивлений резисторов для студентов групп, номера которых заканчиваются цифрой 1 и 2 приведены в таблицах №3 и №4 соответственно. Значения ЭДС, действующих в ветвях, приведены в таблице №2 (первая строка для всех студентов группы, номер которой заканчивается цифрой 1, вторая строка – для группы, номер которой заканчивается цифрой 2). Внутренними сопротивлениями источников ЭДС следует пренебречь.
Содержание работы
1. Рассчитать токи во всех ветвях электрической цепи
а) методом непосредственного применения правил Кирхгофа;
б) методом контурных токов;
в) методом узловых потенциалов.
Результаты расчетов свести в таблицу.
2. Составить и решить уравнение баланса мощностей.
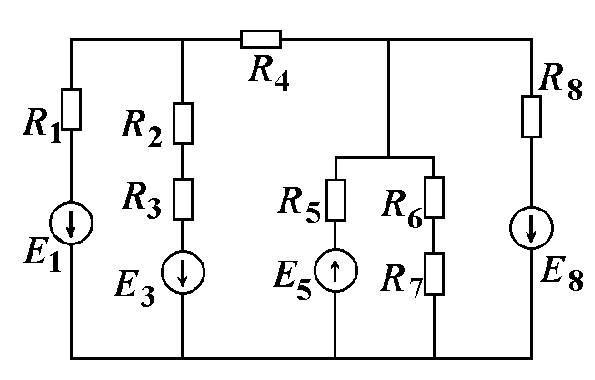
Рисунок 1.1
Таблица 1.1 – Значения параметров, вариант 10
R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | R7, Ом | R8, Ом | Е1, В | В | Е5, В | Е8, В |
15 | 29 | 8 | 22 | 39 | 19 | 25 | 30 | 10 | 36 | 27 | 26 |
1.1 Расчёт токов в исследуемой электрической цепи путём непосредственного применения законов Кирхгофа.
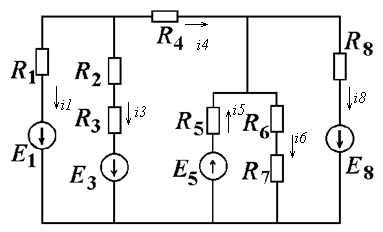
Рисунок 1.2 – Исследуемая схема цепи
Составим систему уравнений, согласно законам Кирхгофа для цепи (рисунок 1.2):
 (1)
(1)

Решим систему матричным методом:
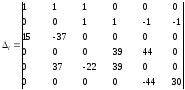

Находим токи в ветвях:
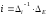 (2)
(2)

i1 = -0,257(A), i3 = 0,599(A), i4 = -0,342(A), i5 = 0,854(A), i6 = -0,144(A), i8 = 0,656(A),
1.2 Расчёт токов в ветвях методом контурных токов.
Для схемы (1.2 обход по часовой стрелке) составим систему уравнений:


Решая систему, получаем:


Находим токи в контурах:
 (4)
(4)

Рассчитаем токи в ветвях:
 (5)
(5)
 (6)
(6)
 (7)
(7)
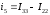 (8)
(8)
 (9)
(9)

i1 = -0,257(A), i3 = 0,599(A), i4 = -0,342(A), i5 = 0,854(A), i6 = -0,144(A), i8 = 0,656(A),
1.3 Расчёт токов во всех ветвях схемы методом узловых потенциалов
Найдём проводимости ветвей схемы.
g1 = 0,067(См), g23 = 0,027 (См), g4 = 0,045 (См),
g5 = 0,026(См), g67= 0,023 (См), g8 = 0,033 (См).

Запишем уравнения в матричной форме (φа=0):
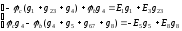 (11)
(11)
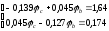
Решая систему, получаем:


Находим токи в контурах:
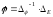

Рассчитаем токи в ветвях:
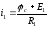 (13)
(13)
(14)
 (15)
(15)
 (16)
(16)

 (18)
(18)
i1 = -0,257(A), i3 = 0,599(A), i4 = -0,342(A), i5 = 0,854(A), i6 = -0,144(A),
i8 = 0,656(A),
Таблица 1.2 – Результаты расчётов
i1 | i3 | i4 | i5 | i6 | i8 | |
Законы Кирхгофа | -0,257 | 0,599 | -0,342 | 0,854 | -0,144 | 0,656 |
Метод контурных токов | -0,257 | 0,599 | -0,342 | 0,854 | -0,144 | 0,656 |
Метод двух узлов | -0,257 | 0,599 | -0,342 | 0,854 | -0,144 | 0,656 |
1.4 Баланс мощностей.
Уравнение баланса мощностей:
 (19)
(19)
Суммарная мощность источников:
 (20)
(20)

Суммарная мощность приёмников:
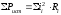 (21)
(21)


Контрольные вопросы по теме
«Расчет электрических цепей постоянного тока»
Дайте определение электрической цепи и ее схемы замещения.
Электрическая цепь — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитных процессов, в которых могут быть описаны с помощью понятий сила тока и напряжение.
Схема замещения — электрическая схема, в которой все реальные элементы заменены максимально близкими по функциональности цепями из идеальных элементов.
Какими моделями пользуются при описании свойств идеальных и реальных источников электродвижущей силы (Э.Д.С.)?
Источник напряжения — идеализированный элемент ЭЦ, напряжение на зажимах которого не зависит от протекающего через него тока.
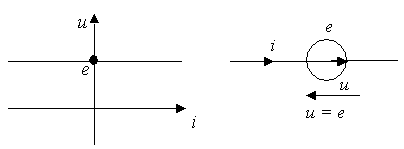
Какими моделями пользуются при описании свойств идеальных и реальных источников тока?
Источник тока – это идеализированный элемент ЭЦ, ток которого не зависит от напряжения на его зажимах.

Чем отличаются линейные и нелинейные элементы электрических цепей?
Элементы, ВАХ которых являются прямыми линиями, называются линейными. Электрические цепи, имеющие только линейные элементы, называются линейными электрическими цепями.
Элементы, ВАХ которых не являются прямыми линиями, называются нелинейными. Электрические цепи, имеющие хотя бы один нелинейный элемент, называются нелинейными.
Какие электрические цепи называются линейными электрическими цепями постоянного тока?
Элементы электрической цепи, ВАХ которых представляют собой прямые линии, называются линейными элементами, а цепи, состоящие из таких элементов, работающие от источника постоянного тока – линейными электрическими цепями постоянного тока.
Дайте определения ветви, узла и контура электрической цепи.
Ветвь – это участок электрической цепи от одного узла до другого узла. Ветвь обычно содержит один или несколько последовательно соединенных элементов цепи: сопротивления, источники ЭДС или источники тока.
Узел цепи в электронике — точка, в которой соединяются три (или более) проводника электрической цепи. Узел (наряду с контуром) является базовым понятием, необходимым при анализе электрических цепей.
Контур — это замкнутый участок электрической цепи. Любой замкнутый путь, проложенный через ветви цепи, и есть замкнутый контур.
Сформулируйте первое правило (закон) Кирхгофа. Какой принцип электромагнетизма утверждается в первом правиле Кирхгофа?
Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным.
Сформулируйте второе правило (закон) Кирхгофа. Какой принцип электромагнетизма утверждается во втором правиле Кирхгофа?
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю.
Докажите, что при последовательном соединении элементов в электрической цепи эквивалентное сопротивление равно сумме их сопротивлений.
Полное
напряжение в цепи при последовательном
соединении, или напряжение на полюсах
источника тока, равно сумме напряжений
на отдельных участках цепи: 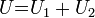 .
.
Так как ток в цепи один:

Докажите, что при параллельном соединении элементов в электрической цепи эквивалентная проводимость равна сумме их проводимостей.
При
параллельном соединении резисторов
складываются величины, обратно
пропорциональные сопротивлению (то
есть общая проводимость 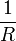 складывается
из проводимостей каждого резистора
складывается
из проводимостей каждого резистора ).
).
Для
двух параллельно соединённых резисторов
их общее сопротивление равно:  .
.
Если 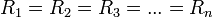 ,
то общее сопротивление равно:
,
то общее сопротивление равно: ,
то естьэквивалентная
проводимость равна сумме проводимостей.
,
то естьэквивалентная
проводимость равна сумме проводимостей.
Приведите пример расчета электрической цепи методом непосредственного применения правил Кирхгофа.
Пример приведён в работе.
Приведите пример расчета электрической цепи методом контурных токов.
Пример приведён в работе.
Приведите пример расчета электрической цепи методом узловых потенциалов.
Пример приведён в работе.
Приведите пример расчета электрической цепи методом эквивалентного генератора.
Метод эквивалентного генератора используется при расчёте сложных схем, в которых одна ветвь выделяется в качестве сопротивления нагрузки, и требуется исследовать и получить зависимость токов в цепи от величины сопротивления нагрузки. В соответствии с данным методом неизменная часть схемы преобразовывается к одной ветви, содержащей ЭДС и внутреннее сопротивление эквивалентного генератора.
ЭДС эквивалентного генератора определяется по формуле:


где:  —проводимость
участка цепи, равная
—проводимость
участка цепи, равная 
Для определения эквивалентного сопротивления генератора применяется расчет последовательно и параллельно соединённых сопротивлений, а также, в случае более сложных схем, применяют преобразование треугольник-звезда.
После определения параметров эквивалентного генератора можно определить ток в нагрузке при любом значении сопротивления нагрузки по формуле:

Параметры  и
и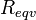 можно так же определить по исходной
схеме из опытовхолостого
хода
можно так же определить по исходной
схеме из опытовхолостого
хода 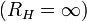 икороткого
замыкания
икороткого
замыкания 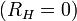 .
.
По
опыту холостого хода 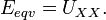 Для
определения
Для
определения в исходной схеме убирают сопротивление
нагрузки и полученную схему рассчитываютметодом
узловых потенциалов.
Через полученные значения потенциалов
определяют
в исходной схеме убирают сопротивление
нагрузки и полученную схему рассчитываютметодом
узловых потенциалов.
Через полученные значения потенциалов
определяют 
Значение  обычно определяется из опыта короткого
замыкания, для этого в исходной схеме
сопротивление нагрузки заменяют проводом
и пометоду
контурных токов
определяют ток
обычно определяется из опыта короткого
замыкания, для этого в исходной схеме
сопротивление нагрузки заменяют проводом
и пометоду
контурных токов
определяют ток 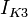 в
проводе. После этого эквивалентное
сопротивление генератора определяется
по формуле:
в
проводе. После этого эквивалентное
сопротивление генератора определяется
по формуле:

Приведите пример расчета электрической цепи методом эквивалентных преобразований.
Метод эквивалентных преобразований заключается в том, что электрическую цепь или ее часть заменяют более простой по структуре электрической цепью. При этом токи и напряжения в непреобразованной части цепи должны оставаться неизменными, т.е. такими, каким они были до преобразования. В результате преобразований расчет цепи упрощается и часто сводится к элементарным арифметическим операциям.
Одним из наиболее часто встречающихся случаев смешанного соединения сопротивлений.

Исходная
схема содержит параллельное соединение
ветвей, содержащих  и
и ,
т.е.
,
т.е. .
И этот участок с параллельным соединением
включен последовательно с
.
И этот участок с параллельным соединением
включен последовательно с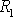 .
.
Поэтапным преобразованием эта цепь сводится к эквивалентному сопротивлению
 .
.
Как и для чего составляется уравнение баланса мощностей при расчете электрической цепи? Приведите пример его составления.
Для проверки правильности расчёта электрической цепи. Пример приведён в работе.
1. Произвольно задать направление токов в ветвях исследуемой цепи.
2. Исходную цепь, содержащую n источников, преобразовать в n подсхем, каждая из которых содержит только один из источников, прочие источники исключаются следующим образом: источники напряжения замыкаются накоротко, а ветви с источниками тока обрываются. При этом необходимо помнить, что внутренние сопротивления реальных источников играют роль потребителей, и поэтому они должны оставаться в подсхемах.
3. Определить токи каждой из подсхем, задавшись их направлением в соответствии с полярностью источника, любым из известных методов. В большинстве случаев расчет ведется по закону Ома с использованием метода эквивалентных преобразований пассивных цепей.
4. Полный ток в любой ветви исходной цепи определяется как алгебраическая сумма токов вспомогательных подсхем, причем при суммировании со знаком «+» берутся токи подсхем, направление которых совпадает с направлением тока в исходной цепи, со знаком «–» – остальные.
1.4. Пример расчета
1.4.1. Задание
Рассчитать цепь, изображенную графом а, с параметрами: Е1 = 20 В; Е6 = 40 В; J3 = 2А; R1 = R3 = R5 = R7 = 5,4 Ом; R2 = R4 = R6 = 6,8 Ом.
Подлежащая расчету цепь будет иметь вид (рис. 1.3).
1 .4.2.
Запись уравнений Кирхгофа
.4.2.
Запись уравнений Кирхгофа
Для произвольно выбранных и обозначенных на схеме (см. рис. 1.3) положительных направлений токов ветвей и совокупности независимых контуров запишем:
– уравнения по I закону Кирхгофа:
для узла А: I1 – I2 – J3 = 0,
для узла В: I7 – I6 – I4 – I1 = 0,
для узла С: I4 + I2 – I5 = 0,
– уравнения по II закону Кирхгофа:
для контура I: I1R1 + I2R2 – I4R4 = E1,
для контура II: I4R4 + I5R5 – I6R6 = –E6,
для контура III: I6R6 + I7R7 = E6,
для контура IV: J3R3 – I5R5 – I2R2 = UJ.
После
подстановки численных значений
коэффициентов получаем разрешимую
систему уравнений с семью неизвестными
величинами  :
:
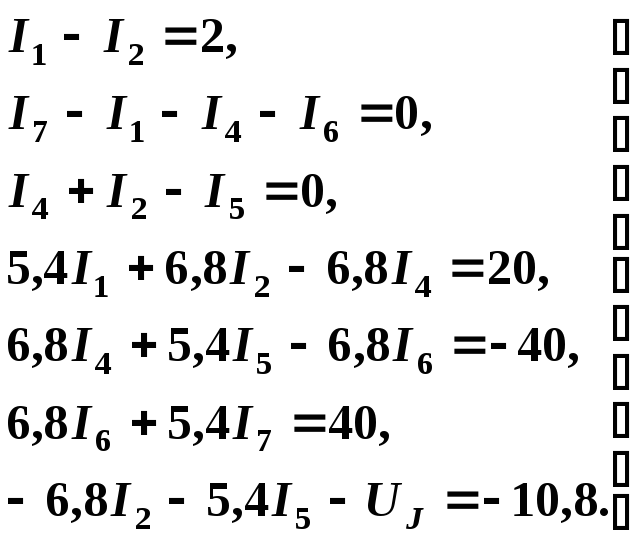
1.4.3. Метод контурных токов
Для рассматриваемой четырехконтурной цепи (см. рис. 1.3) система уравнений относительно контурных токов, совпадающих по направлению с обходом контуров, примет вид

Для выбранных контурных токов I44 = J3. Подсчитаем значения коэффициентов системы:
– собственные сопротивления контуров:

– общие сопротивления контуров:

– контурные ЭДС:
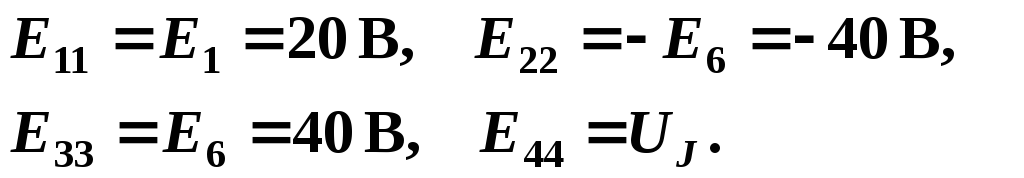
После подстановки численных значений коэффициентов и необходимых преобразований система уравнений примет вид
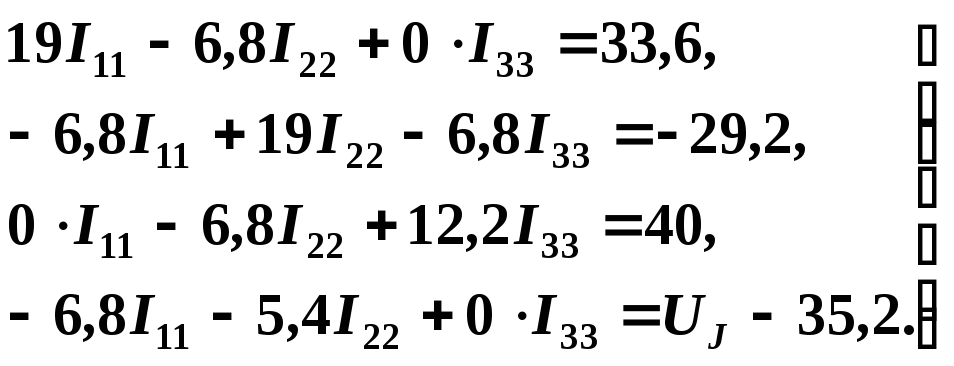
В случае решения данной системы при помощи определителей необходимо совместно решить систему из первых трех уравнений относительно неизвестных токов I11, I22, I33, а затем из четвертого уравнения системы определить UJ.
Результаты расчета системы уравнений следующие:
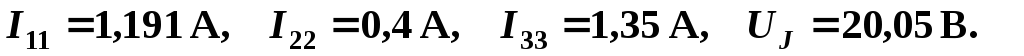
В соответствии с принятыми (см. рис. 1.3) положительными направлениями токов в ветвях вычисляем их значения:
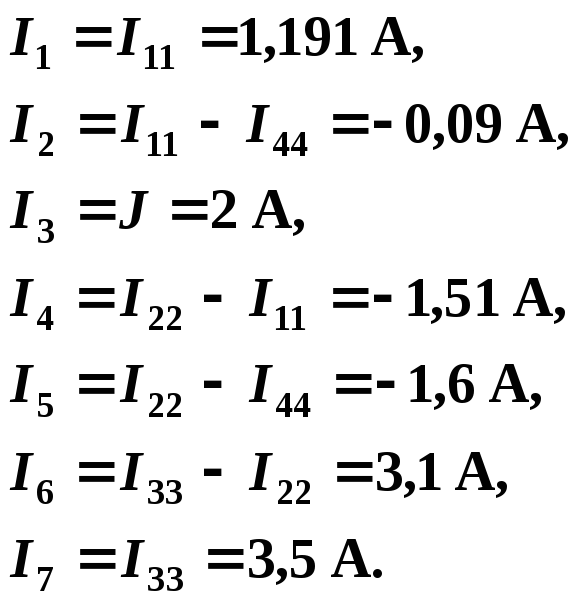
1.4.3. Баланс мощности
Мощность источников

Мощность потребителей
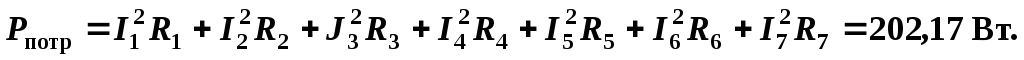
Оценим относительную погрешность расчета,

1.4.4. Метод узловых потенциалов
Принимаем потенциал узла А равным нулю (см. рис. 1.3). Составим систему уравнений по методу узловых потенциалов относительно В, С, D:

Выпишем и подсчитаем значения коэффициентов системы:
– собственная проводимость узлов
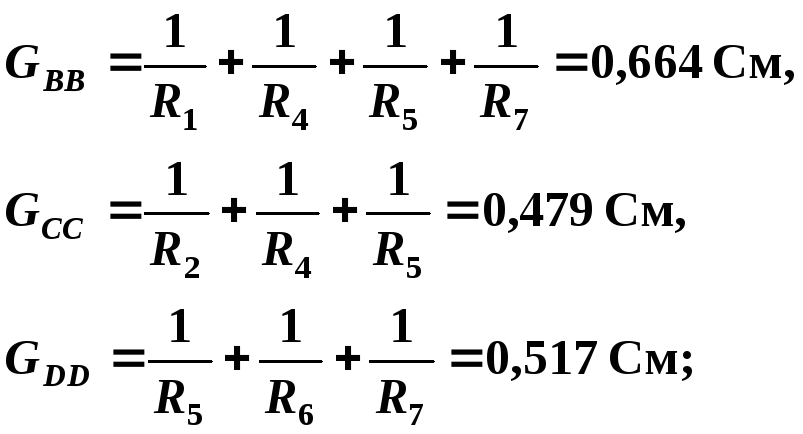
– общие проводимости узлов

– узловые токи

Система уравнений после подстановки численных значений коэффициентов примет вид

Результаты расчета системы уравнений:

Рассчитаем значения токов в ветвях по обобщенному закону Ома


вариант20
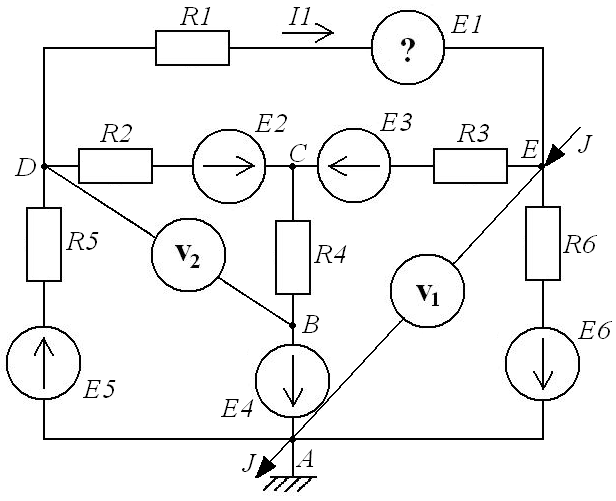
Дано: R1=5 Ом; R2=5 Ом; R3=6 Ом; R4=5 Ом; R5=2 Ом; R6=2 Ом; R7=2 Ом; R8=2 Ом; E2=50 В; E3=40 В; E4=30 В; E5=20 В; E6=10 В; J=4 A; I1=2 A;
 1.
Написать по законам Кирхгофа систему
уравнений для определения неизвестных
токов и ЭДС в ветвях схемы.
1.
Написать по законам Кирхгофа систему
уравнений для определения неизвестных
токов и ЭДС в ветвях схемы.
Рисуем расчетную схему цепи, на которой показываем выбранные и известные положительные направления всех токов и ЭДС, а также направления обходов контуров.

Пишем уравнения по первому закону Кирхгофа для узлов A, C, D:

По второму закону Кирхгофа можно
составить независимые контурные
уравнения 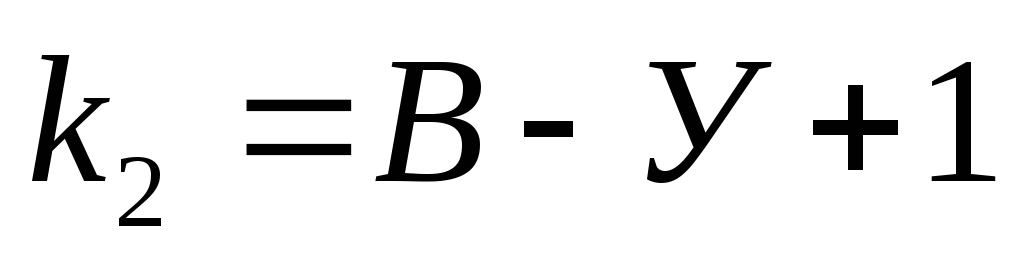 ,
где
,
где  -число
ветвей цепи,
-число
ветвей цепи,  -число
узлов. Для рассматриваемой цепи
-число
узлов. Для рассматриваемой цепи  .
.
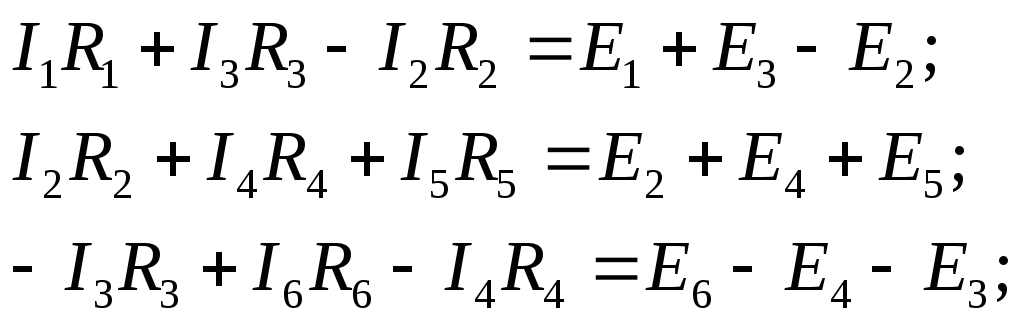
Решение системы из шести уравнений с шестью неизвестными достаточно сложно, поэтому для расчета рассматриваемой электрической цепи применяем другие методы.
2. Определить ЭДС в первой ветви и токи во всех ветвях методом контурных токов.
Составляем уравнения по методу контурных токов:

Решаем систему, находим корни:

Определяем токи во всех ветвях цепи:
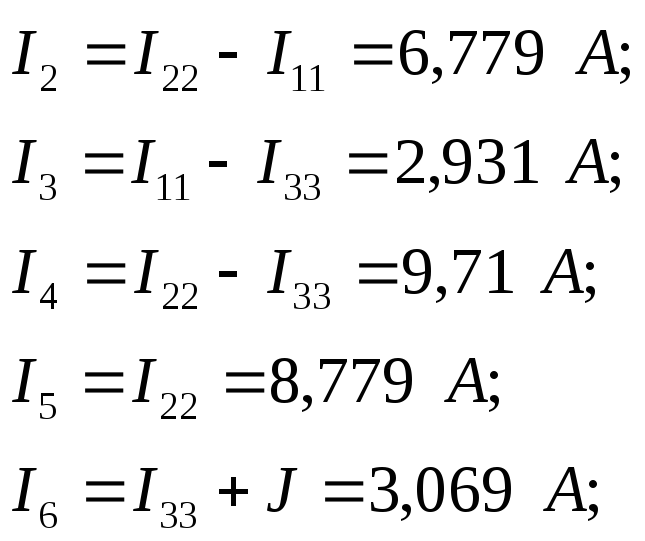
3. Проверка правильности определения искомых величин.
Так как расчет выполнен по методу контурных токов, первый закон Кирхгофа для всех узлов цепи выполняется автоматически. Чтобы убедиться в том, что токи определены верно, нужно проверить тождественность уравнений, составленных по второму закону Кирхгофа для отдельных контуров цепи.
Для первого контура

Подставив в это уравнение значения сопротивлений, токов и ЭДС, получаем:

Аналогично для второго контура

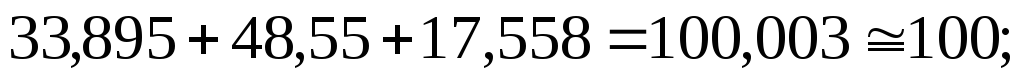
Для третьего контура


Итак, расчет выполнен верно.
4. Составить баланс мощностей.
Алгебраическая сумма мощностей
источников энергии должна быть равна
сумме мощностей в сопротивлениях цепи 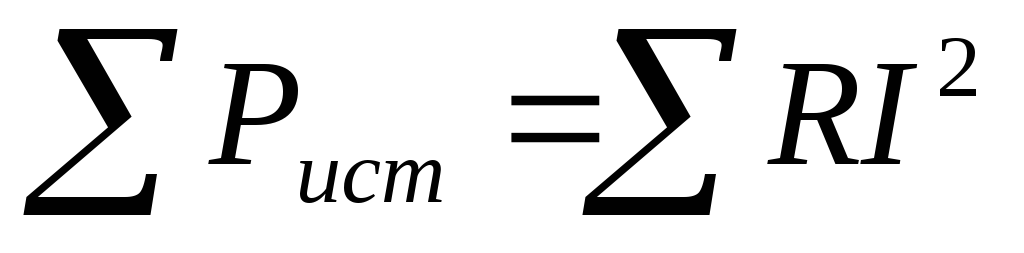 .
.
Мощность источников напряжения определяется как сумма произведений ЭДС ветвей на протекающие через них токи.

Мощность источника тока определяется
как произведение тока источника на
разность потенциалов узла 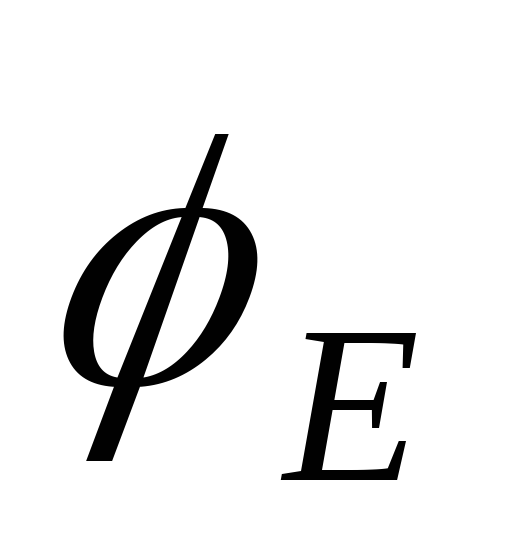 ,
к которому ток подтекает, и узла
,
к которому ток подтекает, и узла  ,
из которого ток вытекает.
,
из которого ток вытекает.

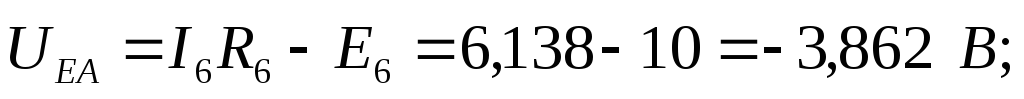

Суммарная мощность источников энергии

Мощность в сопротивлениях
5. Определить напряжения, измеряемые вольтметрами.
Вольтметр 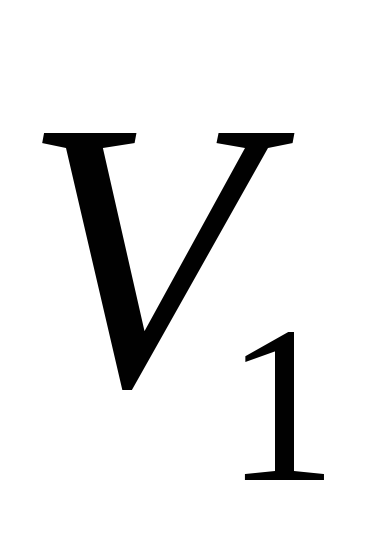 показывает разность потенциалов между
точками A и E цепи. По второму закону Кирхгофа
показывает разность потенциалов между
точками A и E цепи. По второму закону Кирхгофа

Показания вольтметра 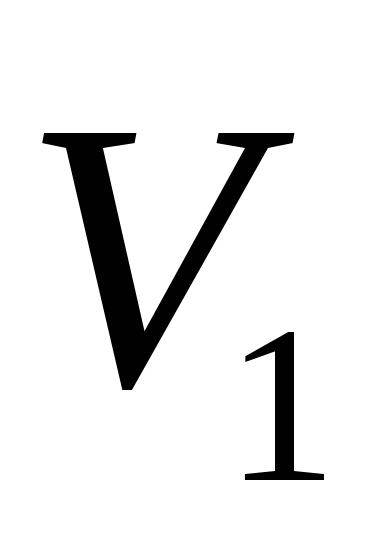 :
:

Вольтметр показывает разность потенциалов между точками B и D цепи.


6. Определение тока во второй ветви по методу эквивалентного генератора.
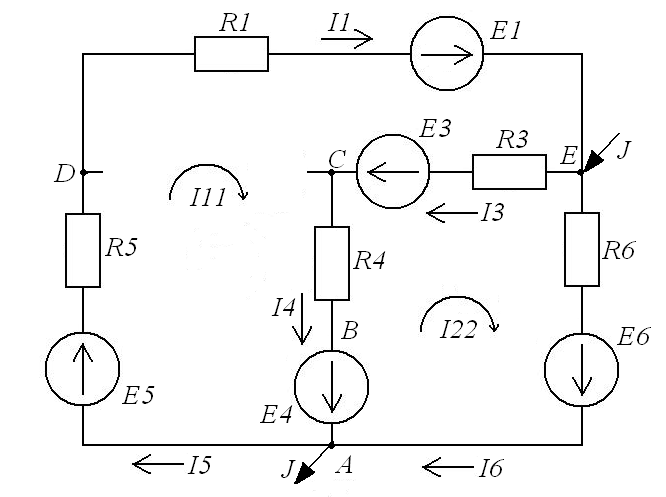


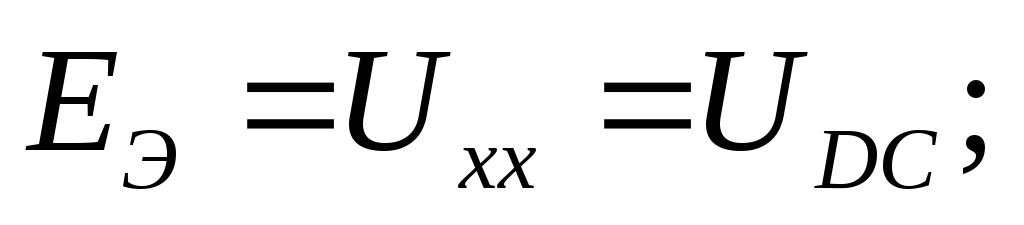

Решаем систему, находим корни:


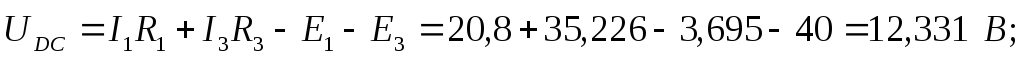

Составляем схему для определения входного сопротивления двухполюсника.

Треугольник сопротивлений  заменяем эквивалентной трехлучевой
звездой
заменяем эквивалентной трехлучевой
звездой 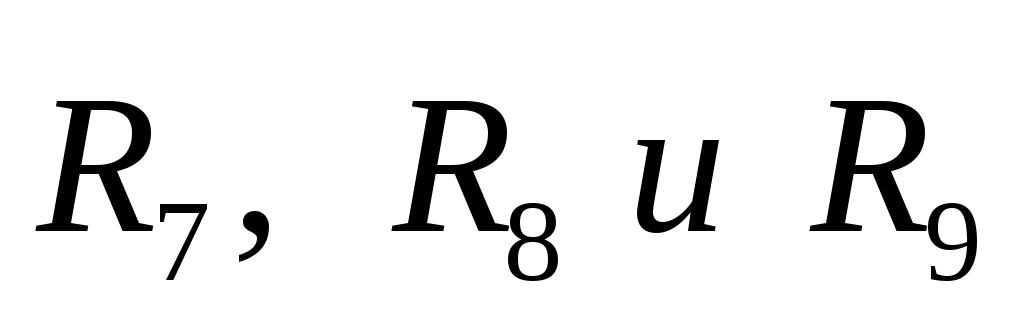 :
:


Определяем входное сопротивление, свертывая схему:
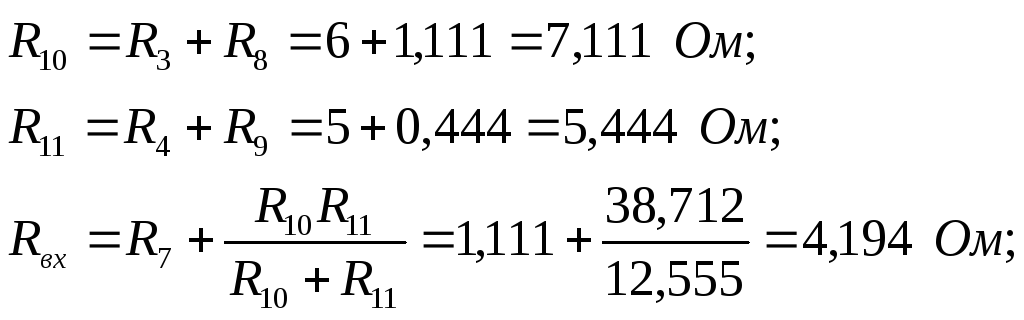

По записанной ранее формуле вычисляем ток во второй ветви:

Получено такое же значение тока  ,
как и при расчетах по методам контурных
токов и узловых потенциалов.
,
как и при расчетах по методам контурных
токов и узловых потенциалов.
7. Определение величины и направления ЭДС, которую нужно дополнительно включить, чтобы ток во второй ветви увеличился в два раза и изменил свое направление.
Тогда должно быть



8. Определение входной проводимости второй ветви.
Входное сопротивление второй ветви 
Входная проводимость 
9. Определение взаимной проводимости второй и третьей ветвей.
Пусть 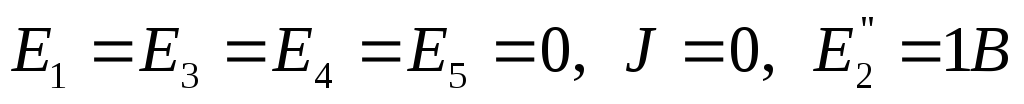 .
Тогда
.
Тогда  .
Этот ток будет распределяться по всем
ветвям схемы. Ток, протекающий через
сопротивление
.
Этот ток будет распределяться по всем
ветвям схемы. Ток, протекающий через
сопротивление 

Взаимная проводимость второй и третьей ветвей
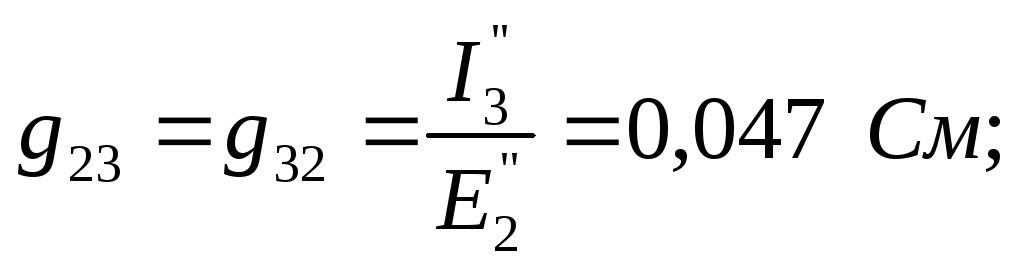
10. Другой способ определения взаимной проводимости.
Если изменится только ЭДС во второй ветви, то в соответствии с принципом линейности имеем

Вычтем второе уравнение из первого, получим
 откуда
откуда 
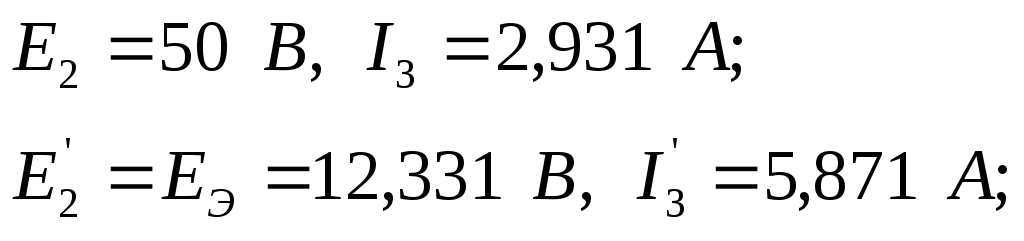

11. Определение зависимости тока в третьей ветви от сопротивления второй ветви при неизменных остальных параметрах цепи.

Нормальный режим работы цепи 
Режим холостого хода 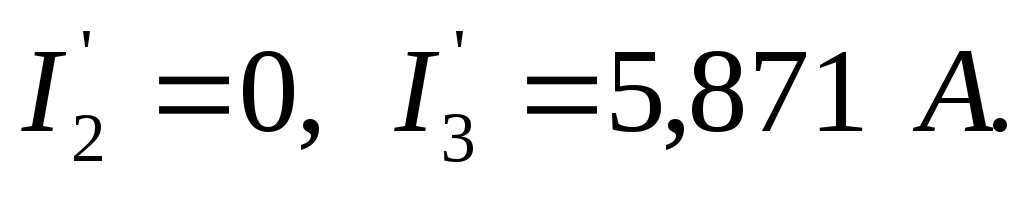
Составляем систему уравнений для
определения коэффициентов  и
и 


Таким образом получаем зависимость между токами во второй и в третьей ветви
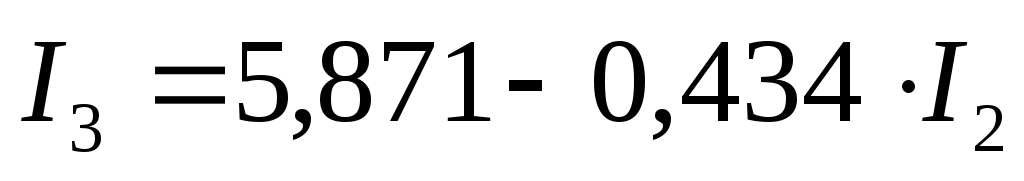

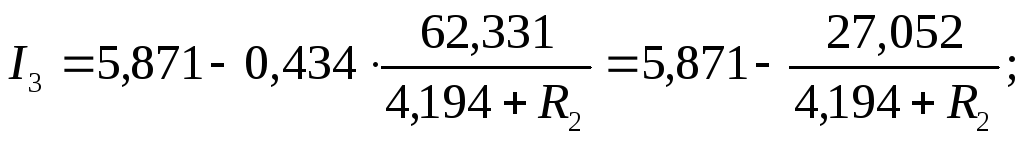

9
Метод двух узлов. Решение задач
Одним из распространенных методов расчета электрических цепей является метод двух узлов. Этот метод применяется в случае, когда в цепи всего два узла.
Алгоритм действий таков:
1 — Потенциал одного из узлов принимается равным нулю
2 — Составляется узловое уравнение для другого узла
3 — Определяется напряжение между узлами
4 — По закону Ома, находятся токи в ветвях
Рассмотрим пример

1 – Примем потенциал узла 2 равным нулю φ2=0. Тогда напряжение U12 будет направлено из точки с большим потенциалом, к точке с меньшим.
2 — Составим узловое уравнение для узла 1.

где g1,g2,g3 проводимости ветвей Знак ЭДС определяется её направлением, если к узлу, то положительное, если от узла – отрицательное.
Знак ЭДС определяется её направлением, если к узлу, то положительное, если от узла – отрицательное.
3 – Определим напряжение U12 между узлами

А так как φ2=0, то

Для общего случая формула напряжения выглядит следующим образом

4 – Найдем токи в ветвях. Причем если направление ЭДС совпадает с направление напряжения, то берем напряжение со знаком плюс. В противном случае со знаком минус.

Как всегда, лучше всего проверить задачу с помощью баланса мощностей. Напомним, что мощность источников ЭДС должна быть равна мощности приемников.

Таким образом, задача решена методом двух узлов. Спасибо за внимание!
Рекомендуем к прочтению — Метод узловых потенциалов



