Эквивалентное преобразование звезды в треугольник

Любые сложные электрические цепи можно упростить. Один из методов — эквивалентное преобразование звезды в треугольник. При этом в электрической схеме уменьшается количество узлов или количество ветвей. Преобразование треугольника в звезду возможно только для пассивных элементов, т.е. для потребителей электрической энергии.

Определение соединения сопротивлений звездой

Если соединение трех сопротивлений имеет общий узел и имеет внешний вид трехлучевой звезды, то такое соединение сопротивлений называется звездой. 

Способ соединения трех сопротивлений, находящихся в пассивных ветвях (ветвь не содержит источник ЭДС), при котором все 3 сопротивления имеют одну общую точку, называется звездой.

Ветви, составляющие звезду сопротивлений называются лучами.

В курсе теоретических основ электротехники обычно принято электрические элементы цепи изображать горизонтально и вертикально. Так что схема ниже так же является соединением звездой.

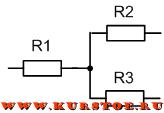
Определение соединения сопротивлений треугольником

Если три сопротивления соединены так, что образуют собою стороны треугольника, то такое соединение сопротивлений называют треугольником сопротивлений.

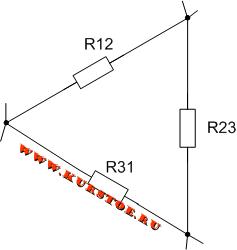
Причина использования преобразования звезды в треугольник

При выполении расчета сложной электрической цепи иногда необходимо выполнить упрощение (свертку, преобразование) схемы. Обычно для этого ищут сначала последовательное или параллельное соединений сопротивлений. Если таких соединений не находят то выполняют экивалентное преобразование звезды в треугольник, если в электрической цепи есть соединение сопротивлений звездой.

Если в электрической цепи нашли соединение сопротивлений звездой, то между концами лучей подставляем сопротивления в виде треугольника.

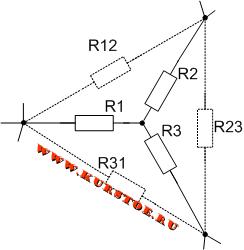
Удаляем соединение звездой. Получается эквивалентное преобразование звезды в треугольник.

Формулы для расчета эквивалентного преобразования звезды в треугольник

        

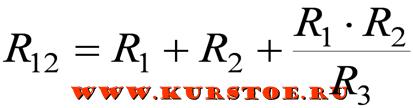
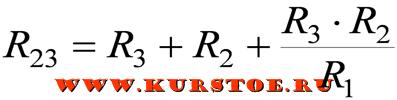
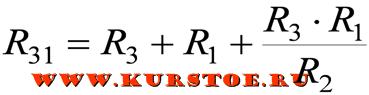
Пример преобразования

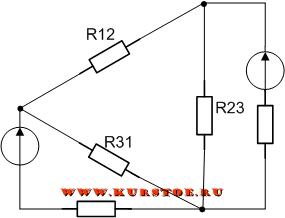
Для приведенной электрической цепи необходимо выполнить экивалентное преобразование звезды R1 -R2 -R3 в треугольник R12 — R23 — R31.

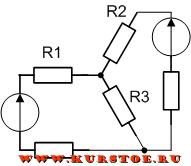
Дорисовываем три сопротивления R12, R23, R31 к концам лучей сопротивлений R1, R2 и R3.

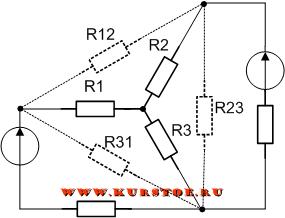
Удаляем сопротивления R1, R2 и R3. Параметры эквивалентных сопротивлений R12, R23, R31 рассчитываем по формулам.

Преобразование треугольник/звезда: что за сценой?

Добавлено 17 июня 2019 в 12:15

Сохранить или поделиться

Преобразования треугольник/звезда позволяют нам заменить часть схемы другой схемой, которая, хотя и эквивалентна в поведении, но может значительно упростить анализ общей схемы. Здесь мы узнаем, откуда берутся эти преобразования.

Зачем?

Когда мы начали изучать электронику, резисторы были соединены либо последовательно, либо параллельно, и мы научились заменять такие комбинации их эквивалентными сопротивлениями, часто с целью уменьшения всей сети сопротивлений до единственного эквивалентного сопротивления, видимого из источника питания. После этого появились схемы (рисунок 1), которые содержали резисторы, которые не были ни последовательными, ни параллельными, но их всё же можно было убрать, тщательно определяя и сокращая фрагменты схемы в правильном порядке. Обратите внимание, что R₁ не параллелен и не последователен ни с R₂, ни с R₃, но путем объединения R₂ последовательно с R₄, и объединяя R₃ последовательно с R₅, мы можем затем объединить эти два эквивалентных сопротивления параллельно и, наконец, объединив результат последовательно с R₁, получить полное сопротивление, видимое источнику питания, которое, используя закон Ома, поможет получить общий ток источника питания.

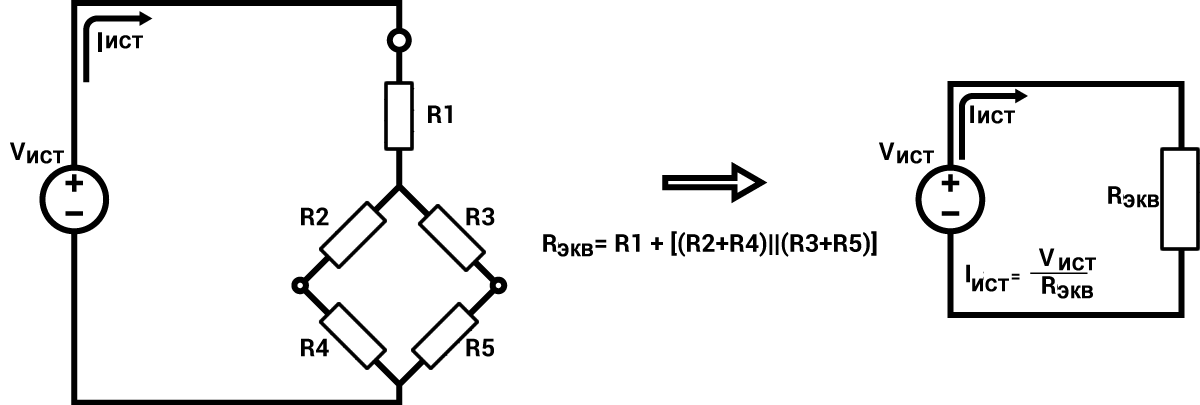Рисунок 1

Но теперь мы подошли к схемам (рисунок 2), где нет никаких пар резисторов, которые включены последовательно или параллельно, – похоже, мы зашли в тупик. Одним из способов анализа этой схемы является использование закона напряжений Кирхгофа (второй закон) и закона токов Кирхгофа (первый закон) для получения алгебраических уравнений, которые мы можем решить для напряжений и токов. Хотя этот подход будет работать всегда (для этой и большинства других типов схем), он может быть довольно громоздким. Мы могли бы смириться с этим как с ценой возможности анализа этих более сложных схем, но иногда мы можем избежать оплаты этого счета, изменяя или «преобразовывая» фрагменты схемы, чтобы превратить ее в нечто, что мы можем уменьшить, используя только правила последовательного/параллельного объединения.

Рисунок 2

Для простоты мы будем рассматривать только цепи постоянного тока с резисторами, но эти принципы применимы к любой линейной системе переменного или постоянного тока. Кроме того, чтобы сфокусировать обсуждение на преобразованиях, мы найдем только общий ток, поставляемый источником напряжения, что означает, что мы стремимся свести всю сеть резисторов в единое эквивалентное сопротивление.

Давайте рассмотрим эти две схемы немного подробнее (рисунок 3). Мы видим, что единственная разница между ними заключается в том, что находится внутри пунктирных окружностей. В каждом случае цепь в окружности имеет три контакта, которые пересекают окружность для взаимодействия с остальной частью схемы. В левой цепи (рисунок 3(a)) резисторы подключены к контактам в конфигурации «треугольник» (в англоязычной литературе, конфигурация «delta», «дельта», названная в честь заглавной греческой буквы Δ). А в правой цепи резисторы подключены в конфигурации «звезда» (в англоязычной литературе, конфигурация «wye», «уай», названная в честь заглавной английской буквы Y, хотя в схеме она перевернута).

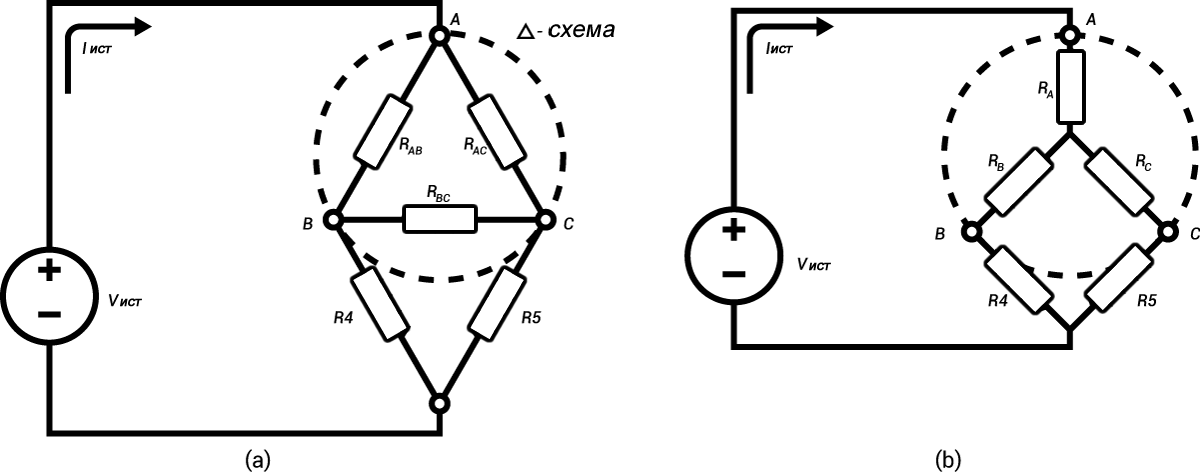Рисунок 3

Теперь представьте, что резисторы внутри пунктирной окружности в левой цепи помещены в черный ящик, этот ящик удален из схемы и заменен другим черным ящиком, который заставляет схему вести себя точно так же. Далее представьте, что, когда вы открываете, этот новый ящик он содержит три резистора, расположенных как в правой цепи. Кто бы ни придумал второй черный ящик, он очень тщательно выбрал значения резисторов так, чтобы эти два блока были неразличимы для остальной части схемы: мы знаем, как анализировать правую схему, и теперь мы знаем, что когда мы это делаем, результаты можно применить к левой схеме, потому что они эквивалентны. Вот зачем выполнять преобразования «треугольник→звезда» и «звезда→треугольник».

Основные соотношения

Чтобы определить уравнения, связывающие резисторы в цепи, соединенной треугольником, с резисторами в цепи, соединенной звездой, нам ничего не нужно, кроме наших надежных формул для последовательных/параллельных соединений (и немного алгебры). Идея заключается в выравнивании эквивалентных сопротивлений между соответствующими парами контактов при отключенном оставшемся контакте (рисунок 4)

Рисунок 4

Выполнив это для эквивалентного сопротивления между контактами B-C, мы получим:

\[R_B + R_C = \frac{R_{BC} \left( R_{AB} + R_{AC} \right) }{R_{AB} + R_{BC} + R_{AC}}\]

Если мы повторим этот процесс для каждой другой пары контактов по очереди, мы получим еще два аналогичных уравнения, и любое из них даст нам необходимую нам информацию (при условии, что мы распознаем задействованную симметрию).

Частный случай: симметричные схемы

Если сопротивления в каждом плече цепи, соединенной треугольником или звездой, равны, такая цепь считается «симметричной». Это означает, что

\[R_∆ = R_{AB} = R_{BC} = R_{AC}\]

\[R_Y = R_A = R_B = R_C\]

Комбинация этого условия с соотношением из предыдущего раздела сразу приводит к уравнению преобразования для случая симметрии.

\[2R_Y = \frac{R_∆(2R_∆)}{3R_∆}\]

\[R_Y = \frac{R_∆}{3}\]

\[R_∆ = 3R_Y\]

Это гораздо более значительный результат, чем может показаться на первый взгляд, и причина довольно проста – когда инженеры проектируют схемы с соединениями треугольник или звезда, они часто стараются сделать эти схемы симметричными. Хотя, конечно, это не всегда возможно, и поэтому мы должны иметь возможность разобраться с общим случаем, когда схема не симметрична.

Общий случай преобразования треугольник→звезда

Для преобразования треугольник/звезда нам дана известная схема, соединенная треугольником, и мы хотим найти значения для эквивалентной схемы, соединенной звездой, – поэтому мы пытаемся найти {R_A, R_B, R_C} для заданных {R_AB, R_BC, R_AC}.

Мы начнем с того, что запишем наши основные соотношения из первоначального вида в несколько более компактной форме, определив новую величину, R_ΔS, которая равна сумме сопротивлений всех резисторов в цепи, соединенной треугольником.

\[R_{ΔS}=R_{AB}+R_{BC}+R_{AC}\]

Затем мы делаем перестановку нашего соотношения для получения вида линейного алгебраического уравнения с неизвестными {R_A, R_B, R_C}.

\[(0)R_A+(R_{ΔS})R_B+(R_{ΔS})R_C=R_{AB}R_{BC}+R_{BC}R_{AC}\]

Поскольку у нас есть три неизвестных, нам нужно еще два уравнения. Они получаются из эквивалентных сопротивлений, видимых при рассмотрении двух других пар контактов. Выполнив это (или используя симметрию) мы получаем

\[(R_{ΔS})R_A+(0)R_B+(R_{ΔS})R_C=R_{AB}R_{AC}+R_{BC}R_{AC}\]

\[(R_{ΔS})R_A+(R_{ΔS})R_B+(0)R_C=R_{AB}R_{AC}+R_{AB}R_{BC}\]

Сложив эти два уравнения вместе и вычтя наше первое уравнение, мы получим

\[2(R_{ΔS})R_A=2R_{AB}R_{AC}\]

\[R_A= {R_{AB}R_{AC} \over R_{ΔS}}\]

Мы можем решить систему уравнению для двух других неизвестных сопротивлений (или использовать симметрию), чтобы получить

\[R_B= {R_{AB}R_{BC} \over R_{ΔS}}\]

\[R_C= {R_{AC}R_{BC} \over R_{ΔS}}\]

Эти отношения могут быть обобщены очень компактно. Сопротивление, подключенное к каждому узлу в эквивалентной цепи, соединенной звездой, равно произведению сопротивлений, подключенных к соответствующему узлу в цепи, соединенной треугольником, деленному на сумму сопротивлений всех резисторов в треугольнике. Обычно это выражается формулой, такой как

\[R_N= {R_{N1}R_{N2} \over R_{ΔS}}\]

где

• R_N – резистор, подключенный к контакту N в схеме «звезда»;
• R_N1 и R_N2 – резисторы, подключенные к контакту N в схеме «треугольник»

Общий случай преобразования звезда→треугольник

Для преобразования звезда→треугольник нам дана известная схема, соединенная звездой, и мы хотим найти значения для эквивалентной схемы, соединенной треугольником. Следовательно, мы пытаемся найти {R_AB, R_BC, R_AC} для заданных {R_A, R_B, R_C}.

Это не так просто, как в случае преобразования треугольник→звезда потому, что неизвестные сопротивления перемножаются вместе, делая результирующие уравнения нелинейными. К счастью, мы можем обойти это неудобство, рассмотрев отношения сопротивлений резисторов в каждой цепи. Например, взяв отношение R_A к R_B, мы получаем

\[{R_A \over R_B} = { R_{AB}R_{AC} \over R_{AB}R_{BC} } = {R_{AC} \over R_{BC} }\]

Другими словами, отношение сопротивлений резисторов, подключенных к любым двум контактам в схеме звезда, равно отношению сопротивлений резисторов, соединяющих те же самые два контакта с третьим контактом в схеме треугольник. Следовательно, два других соотношения будут следующими

\[{R_B \over R_C} = {R_{AB} \over R_{AC} }\]

\[{R_A \over R_C} = {R_{AB} \over R_{BC} }\]

Вооружившись этим, мы могли бы вернуться к нашим основным соотношениям и продолжить работу с ними, но в качестве отправной точки проще использовать одно из отношений из общего случая преобразования треугольник→звезда.

\[R_A= {R_{AB}R_{AC} \over R_{AB} + R_{BC}+R_{AC} }\]

\[R_{AB}R_{AC} = R_A (R_{AB} + R_{BC}+R_{AC})\]

\[R_{AB} = R_A \left( {R_{AB} + R_{BC}+R_{AC} \over R_{AC} } \right)\]

\[R_{AB} = R_A \left( {R_{AB} \over R_{AC}} + {R_{BC} \over R_{AC} } + 1 \right)\]

\[R_{AB} = R_A \left( {R_{B} \over R_{C}} + {R_{B} \over R_{A} } + 1 \right)\]

\[R_{AB} = R_A + R_B + {R_AR_B \over R_C } \]

Два других выражения получаются аналогично (или согласно симметрии):

\[R_{BC} = R_B + R_C + {R_B R_C \over R_A } \]

\[R_{AC} = R_A + R_C + {R_A R_C \over R_B } \]

Эти выражения могут быть обобщены очень компактно. Сопротивление, подключенное между каждой парой узлов в эквивалентной схеме, соединенной треугольником, равно сумме сопротивлений двух резисторов, подключенных к соответствующим узлам в схеме, соединенной звездой, плюс произведение сопротивлений этих двух резисторов, деленное на сопротивление третьего резистора.

Общий способ выразить это состоит в том, чтобы поместить правую часть под общим знаменателем, а затем отметить, что числитель в каждом выражении является суммой произведений каждой пары сопротивлений в цепи, соединенной звездой, а знаменатель – это сопротивление, подключенное к третьему контакту.

\[R_{AB}={R_P \over R_C}\]

\[R_P = R_A R_B + R_B R_C + R_A R_C\]

Пример

Рисунок 5

Давайте поработаем с задачей, показанной на рисунке 5. Прежде чем мы начнем, давайте определим ожидаемый ответ, чтобы у нас была хорошая проверка того, является ли наш окончательный ответ правильным. Для этого рассмотрим роль мостового резистора 150 Ом. Этот резистор служит для уменьшения общего сопротивления, обеспечивая путь между левой и правой сторонами цепи. Следовательно, самое высокое эффективное сопротивление будет иметь место, если этот резистор будет удален полностью, и в этом случае полное сопротивление будет равно параллельной комбинации левой и правой сторон, что приведет к

\[R_{экв.max}=(100 +220)||(470+330)=228,6 \; Ом\]

С другой стороны, наименьшее общее сопротивление было бы получено путем уменьшения мостового резистора до прямого короткого замыкания, и в этом случае общее сопротивление было бы равно параллельной комбинации двух верхних резисторов, включенной последовательно с параллельной комбинацией двух нижних резисторов, что приведет к

\[R_{экв.min}=(100||470)+(220||330)=214,5 \; Ом\]

Теперь мы ЗНАЕМ, что наш ответ ДОЛЖЕН быть между этими двумя предельными значениями. Во многих случаях простой анализ границ, такой как этот, приводит к ответу, который «достаточно хорошо» подходит для данной цели, но давайте предположим, что это не так. Используя приведенные выше уравнения преобразования треугольник→звезда, мы сначала определяем сумму сопротивлений резисторов треугольника.

\[R_{ΔS}=100+150+470=720 \; Ом\]

А затем находим значение R₁, перемножив сопротивления двух резисторов, которые подключены к верхнему контакту, и разделив это произведение на сумму всех трех сопротивлений.

\[R_1={100⋅470 \over 720}=65,28 \; Ом\]

Повторим это же для R₂.

\[R_2={100⋅150 \over 720}=20,83 \; Ом\]

Мы могли бы повторить это еще раз для R₃, но давайте, вместо этого, определим R₃, используя свойства отношений.

\[{R_3 \over R_1}={150 \over 100}⇒R_3=1,5R_1=97,92 \; Ом\]

Теперь, когда у нас есть все сопротивления для эквивалентной схемы звезда, мы можем очень легко определить общее сопротивление.

\[R_{экв.}=R_1+[(R_2+220)||(R_3+330)]=219,4 \; Ом\]

Поскольку это значение находится между нашими минимальной и максимальной границами, мы полностью уверены, что это правильный ответ, или, даже если мы допустили ошибку, наш ответ довольно близок к правильному. Поэтому суммарный ток равен

\[I={12\; В \over 219,4 \; Ом}=54,7 \; мА\]

Заключение

Теперь мы увидели, что преобразования треугольник/звезда полезны, и, что более важно, увидели, как их можно легко выполнить, используя не более чем концепцию эквивалентных сопротивлений с использованием последовательных/параллельных комбинаций резисторов. Это может хорошо вам помочь, поскольку дает вам возможность вывести эти формулы на лету, если когда-нибудь возникнет в них необходимость, и у вас не будет подходящего справочного материала. Но что еще более важно, это должно служить для более прочного закрепления фундаментальных понятий в наборе инструментов, который хранится у вас в голове, позволяя вам использовать в своей работе еще более эффективные навыки анализа цепей.

В конце мы должны принять к сведению распространенное заблуждение, заключающееся в том, что преобразования треугольник↔звезда являются ЕДИНСТВЕННЫМ способом анализа цепей, которые нельзя уменьшить другими способами. В действительности, хотя эти преобразования могут сделать нашу жизнь проще, они не обязательны, поскольку ЛЮБОЙ контур, который можно проанализировать с их помощью, также можно проанализировать с помощью правил Кирхгофа, либо напрямую, либо с помощью одного из более формализованных методов их применения, включая метод контурных токов или метод узловых напряжений, а также с методиками, такими как эквивалентная схема Тевенина.

Оригинал статьи:

Теги

Анализ цепейТреугольник-звезда

Сохранить или поделиться

Звезда треугольник разница в мощности — Moy-Instrument.Ru

Значения напряжения, тока и мощности при соединениях звездой и треугольником

Открытие великим Фарадеем закономерности: при пересечении проводником силовых линий магнитного поля, в проводнике наводится электродвижущая сила, вызывающая ток в цепи, в которую входит этот проводник, — послужило основой для создания электрогенераторов с вращающимся ротором — магнитом. ЭДС наводится при этом в обмотках статора (смотрите — Практическое применение закона электромагнитной индукции Фарадея).

Получаемые напряжения могут быть самые разные: все зависит от конструкции генератора, от числа обмоток в статоре и способах их соединения. Однако в практической электротехнике самое широкое распространении получила трехфазная система синусоидального тока, предложенная выдающимся русским инженером М.О. Доливо-Добровольским в 1888 году (через 57 лет после открытия Фарадея).

Из всех многофазных систем трехфазная обеспечивает наиболее экономичную передачу электрической энергии на дальние расстояния и позволяет создать надежные в работе и простые по устройству генераторы, электродвигатели и трансформаторы. Но и три обмотки могут быть соединены двумя способами: «треугольником» (рис. 1) и «звездой» (рис. 2).

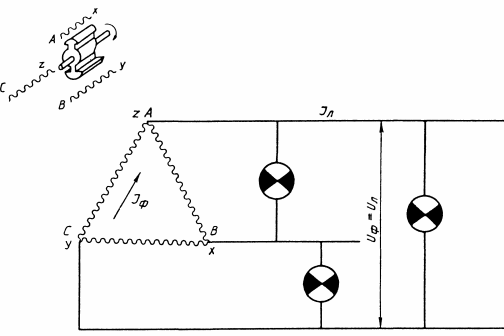
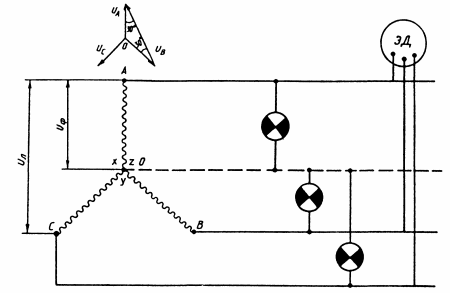
Фазным называют напряжение Uф создаваемое одной обмоткой, линейным Uл — напряжение между двумя линейными проводами. Другими словами, фазное напряжение — это напряжение между каждым из линейных проводов и нулевым проводом.

При соединении симметричного генератора в звезду линейное напряжение по значению в 1,73 раз больше фазного, т.е. Uk = 1,73•Uф. Это следует из того, что Uл — основание равнобедренного треугольника с острыми углами по 30°: Uл = U

АВ = Uф 2 cos 30° = 1,73•Uф.

При соединении и нагрузки в звезду соответствующий линейный ток равен фазному току нагрузки. Если трехфазная нагрузка симметричная, то ток в нулевом проводе будет равен 0. В этом случае надобность в нулевом проводе вообще отпадает и трехфазная цепь превращается в трехпроводную. Это соединение называют «звезда-звезда без нулевого провода». При симметричной нагрузке фаз линейные токи по величине в 1,73 больше фазных токов, Iл = 1,73•3Iф.

При соединении трехфазного генератора звездой используются два напряжения, что выгодно отличает это соединение от соединения треугольником. Но при соединении нагрузки треугольником все фазы находятся под одним и тем же по числовому значению линейным напряжением независимо от сопротивления фаз, что важно для осветительной нагрузки — ламп накаливания.

Трехфазная система с нулевым проводом применяется для питания приемников двух напряжений, различающихся в 1,73 раз, например, лапм, включаемых на фазное напряжение, и двигателей, включаемых на линейное напряжение.

Номинальное напряжение определяется конструкцией генераторов и способом соединения его обмоток.

На рисунке 3 показаны зависимости, определяющие значение мощности для цепи переменного тока при соединениях звездой и треугольником.

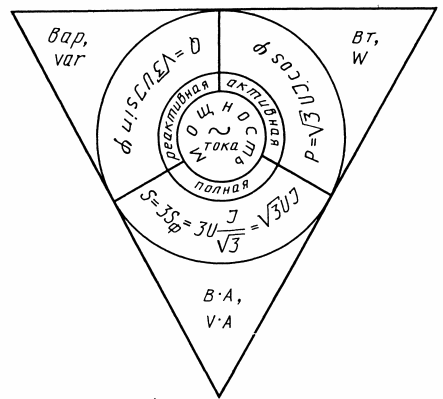
По виду формулы одинаковы, казалось бы нет ни выигрыша, ни проигрыша в мощности для этих двух разновидностей электроцепей. Но не спешите с выводами.

При пересоединении из треугольника в звезду на каждую фазную обмотку приходится в 1,73 раза более низкое напряжение, хотя напряжение в сети остается прежним. Уменьшение напряжения приводит к уменьшению и тока в обмотках в те же 1,73 раза. И еще — при соединении в треугольник линейный ток был в 1,73 раза больше фазного, а теперь эти токи равны. В итоге линейный ток при пересоединении в звезду уменьшился в 1,73 • 1,73 = 3 раза.

Новую мощность вычисляют действительно по той же формуле, но подставляя иные величины!

При пересоединении электродвигателя с треугольника на звезду и питании его от той же сети мощность, развиваемая этим двигателем, снижается в 3 раза. При переключении со звезды на треугольник обмоток генераторов или вторичных обмоток трансформаторов напряжение в сети понижается в 1,73 раза, например, с 380 до 220 В.

Мощность генератора или трансформатора остается прежней, потому что напряжение и ток в каждой фазной обмотке сохраняются, хотя ток в линейных проводах возрастает в 1,73 раза. При переключении обмоток генераторов или вторичных обмоток трансформаторов с треугольника на звезду происходят обратные явления: линейное напряжение сети повышается в 1,73 раза, токи в фазных обмотках остаются теми же, токи в линейных проводах уменьшаются в 1,73 раза.

Расчет мощности двигателя при схеме соединения звезда-треугольник

В этой статье я хотел бы рассказать как изменяется мощность двигателя при схеме соединения обмоток звезда – треугольник и наоборот.

В связи со спецификой своей работы я сталкиваюсь с ремонтов различных асинхронных двигателей и в большинстве случаев выход из строя двигателя происходит при неправильном переключении обмоток двигателя, так как люди не понимают, как изменяется мощность двигателя при переключении с треугольника на звезду и обратно, и как это может отразится на работоспособности самого двигателя.

Определение мощности при схеме соединения звезда

Известно [Л1. с. 34], что при соединении в звезду линейные токи Iл и фазные токи Iф равны между собой, при этом между фазным Uф и линейным напряжением Uл существует соотношение, где Uл = √3*Uф , в результате Uф = Uл/√3.

Исходя из этого, полная мощность определяется через линейные величины:

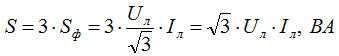
Определение мощности при схеме соединения треугольник

При схеме соединения в треугольник, фазные и линейные напряжения равны между собой Uл = Uф, при этом между токами существует соотношение: Iл = √3*Iф, в результате Iф = Iл/√3.

Исходя из этого, полная мощность определяется, как:

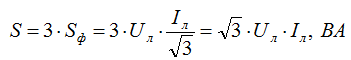
Для определения активной и реактивной мощности используются формулы:

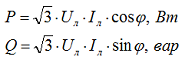
Из-за того что формулы для схемы соединения звезды и треугольника имеют одинаковый вид, у мало опытных инженеров происходят недоразумения, будто вид соединения безразличен и ни на что не влияет.

Рассмотрим на примере, на сколько ошибочные данные утверждения. В данном примере будем рассматривать электродвигатель типа АИР90L2, который имеет две схемы подключения ∆/Y, технические характеристики двигателя:

• коэффициент мощности cosφ = 0,84;
• коэффициент полезного действия, η = 78,5%;

Определяем ток двигателя при напряжении 380 В и схеме соединения треугольник, мощность при таком соединении составляет 3 кВт:

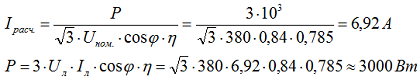
Теперь соединим обмотки двигателя в звезду. В результате на фазную обмотку пришлось на 1,73 раза более низкое напряжение Uф = Uл/√3, соответственно и ток уменьшился в 1,73 раза, но так как при соединении в треугольник Uл = Uф, а линейный ток был в 1,73 раза больше фазного Iл = √3*Iф, то получается, что при соединении в звезду, мощность уменьшится в √3*√3 = 3 раза, соответственно и ток уменьшиться в 3 раза.

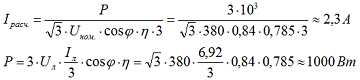
Из всего выше изложенного можно сделать, следующие выводы:

1. При переключении двигателя со звезды на треугольник, мощность двигателя увеличивается в 3 раза и наоборот. Использовать данные переключения, можно если схемы подключения двигателя позволяет выполнять переключения ∆/Y, в противном случае, двигатель может сгореть, когда Вы будете выполнять переключение со звезды на треугольник.

2. Как Вы уже поняли, используя схему переключения обмоток двигателя со звезды на треугольник, мы уменьшаем пусковые токи при пуске двигателя на пониженном напряжении, а затем его повышаем до номинального. Когда обмотки двигателя соединены в звезду, к каждой из них подводиться напряжение меньше номинального в 1,73 раза. В процессе пуска, двигатель увеличивает скорость вращения и ток снижается. В это время происходит переключение на треугольник.

Обращаю Ваше внимание, что двигатели, которые недогружены, работают с очень низким cosφ. Поэтому рекомендуется заменить недогруженный двигатель, на двигатель меньшей мощности. Если же у недогруженного двигателя, запас мощности велик, то cosφ можно поднять путем переключения обмоток с треугольника на звезду без риска перегреть двигатель.

Как мы видим ничего сложного нету в определении мощности при схеме звезда и треугольник.

1. Звезда и треугольник. Е.А. Каминский, 1961 г.

Звезда и треугольник принцип подключения. Особенности и работа

Для увеличения мощности передачи без увеличения напряжения сети, снижения пульсаций напряжения в блоках питания, для уменьшения числа проводов при подключении нагрузки к питанию, применяют различные схемы соединения обмоток источников питания и потребителей (звезда и треугольник).

Схемы

Обмотки генераторов и приемников при работе с 3-фазными сетями могут соединяться с помощью двух схем: звезды и треугольника. Такие схемы имеют между собой несколько отличий, различаются также нагрузкой по току. Поэтому, перед подключением электрических машин необходимо выяснить разницу в этих двух схемах — звезда и треугольник.

Схема звезды

Соединение различных обмоток по схеме звезды предполагает их подключение в одной точке, которая называется нулевой (нейтральной), и имеет обозначение на схемах «О», либо х, у, z. Нулевая точка может иметь соединение с нулевой точкой источника питания, но не во всех случаях такое соединение имеется. Если такое соединение есть, то такая система считается 4-проводной, а если нет такого соединения, то 3-проводной.

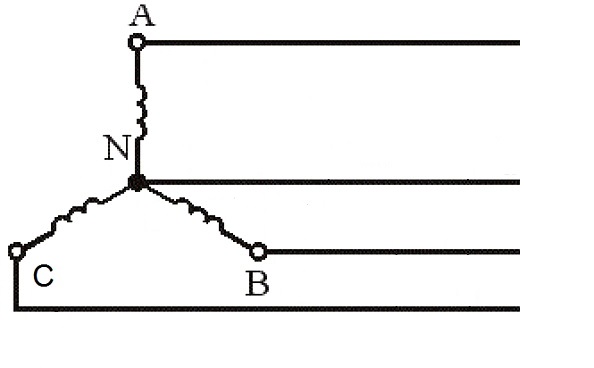
Схема треугольника

При такой схеме концы обмоток не объединяются в одну точку, а соединяются с другой обмоткой. То есть, получается схема, похожая по виду на треугольник, и соединение обмоток в ней идет последовательно друг с другом. Нужно отметить отличие от схемы звезды в том, что в схеме треугольника система бывает только 3-проводной, так как общая точка отсутствует.

В схеме треугольника при отключенной нагрузке и симметричной ЭДС равно 0.

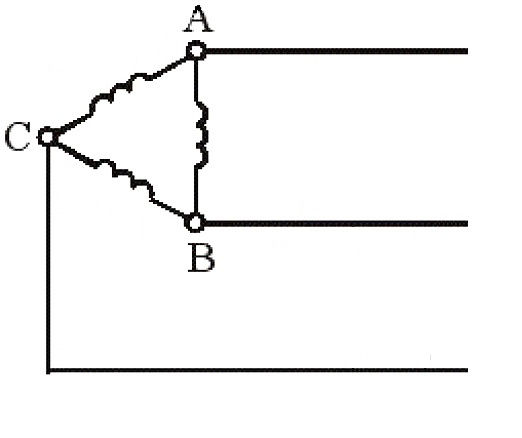
Фазные и линейные величины

В 3-фазных сетях питания имеется два вида тока и напряжения – это фазные и линейные. Фазное напряжение – это его величина между концом и началом фазы приемника. Фазный ток протекает в одной фазе приемника.

При применении схемы звезды фазными напряжениями являются U_a, U_b, U_c, а фазными токами являются I _a, I _b, I _c. При применении схемы треугольника для обмоток нагрузки или генератора фазные напряжения — U_aв, U_bс, U_cа, фазные токи – I _ac, I _bс, I _cа.

Линейные значения напряжения измеряются между началами фаз или между линейных проводников. Линейный ток протекает в проводниках между источником питания и нагрузкой.

В случае схемы звезды линейные токи равны фазным, а линейные напряжения равны U _ab, U_bc, U _ca. В схеме треугольника получается все наоборот – фазные и линейные напряжения равны, а линейные токи равны I _a, I _b, I _c.

Большое значение уделяется направлению ЭДС напряжений и токов при анализе и расчете 3-фазных цепей, так как его направление влияет на соотношение между векторами на диаграмме.

Особенности схем

Между этими схемами есть существенная разница. Давайте разберемся, для чего в различных электроустановках используют разные схемы, и в чем их особенности.

Во время пуска электрического мотора ток запуска имеет повышенную величину, которая больше его номинального значения в несколько раз. Если это механизм с низкой мощностью, то защита может и не сработать. При включении мощного электромотора защита обязательно сработает, отключит питание, что обусловит на некоторое время падение напряжения и перегорание предохранителей, или отключение электрических автоматов. Электродвигатель будет работать с малой скоростью, которая меньше номинальной.

Видно, что имеется немало проблем, возникающих из-за большого пускового тока. Необходимо каким-либо образом снижать его величину.

Для этого можно применить некоторые методы:

• Подключить на запуск электродвигателя реостат, дроссель, либо трансформатор.
• Изменить вид соединения обмоток ротора электродвигателя.

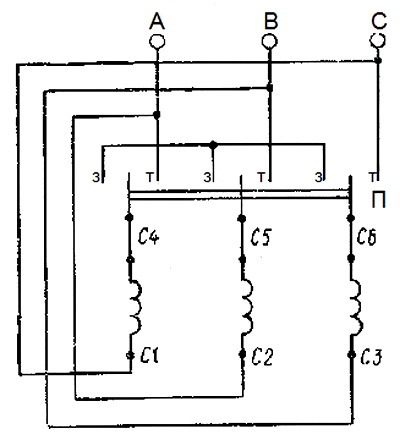
В промышленности в основном применяют второй способ, так как он наиболее простой и дает высокую эффективность. Здесь работает принцип переключения обмоток электромотора на такие схемы, как звезда и треугольник. То есть, при запуске мотора его обмотки имеют соединение «звезда», после набора эксплуатационных оборотов, схема соединения изменяется на «треугольник». Этот процесс переключения в промышленных условиях научились автоматизировать.

В электромоторах целесообразно применение сразу двух схем — звезда и треугольник. К нулевой точке необходимо подключить нейтраль источника питания, так как во время использования таких схем возникает повышенная вероятность перекоса фазных амплитуд. Нейтраль источника компенсирует эту асимметрию, которая возникает вследствие разных индуктивных сопротивлений обмоток статора.

Достоинства схем

Соединение по схеме звезды имеются важные преимущества:

• Плавный пуск электрического мотора.
• Позволяет функционировать электродвигателю с заявленной номинальной мощностью, соответствующей паспорту.
• Электродвигатель будет иметь нормальный рабочий режим при различных ситуациях: при высоких кратковременных перегрузках, при длительных незначительных перегрузках.
• При эксплуатации корпус электродвигателя не перегреется.

Основным достоинством схемы треугольника является получение от электродвигателя наибольшей возможной мощности работы. Целесообразно поддерживать режимы эксплуатации по паспорту двигателя. При исследовании электромоторов со схемой треугольника выяснилось, что его мощность повышается в 3 раза, по сравнению со схемой звезды.

При рассмотрении генераторов, схемы – звезда и треугольник по параметрам аналогичны при функционировании электродвигателей. Выходное напряжение генератора будет больше в схеме треугольника, чем в схеме звезды. Однако, при повышении напряжения снижается сила тока, так как по закону Ома эти параметры обратно пропорциональны друг другу.

Поэтому можно сделать вывод, что при разных соединениях концов обмоток генератора можно получить два разных номинала напряжения. В современных мощных электромоторах при запуске схемы – звезда и треугольник переключаются автоматически, так как это позволяет снизить нагрузку по току, возникающей при пуске мотора.

Процессы, происходящие при изменении схемы звезда и треугольник в разных случаях

Здесь, изменение схемы — имеется ввиду переключение на щитах и в клеммных коробках электрических устройств, при условии, что имеются выводы обмоток.

Обмотки генератора и трансформатора

При переходе со звезды в треугольник напряжение уменьшается с 380 до 220 вольт, мощность остается прежней, так как фазное напряжение не изменяется, хотя линейный ток увеличивается в 1,73 раза.

При обратном переключении возникают обратные явления: линейное напряжение увеличивается с 220 до 380 вольт, а фазные токи не изменяются, однако линейные токи снижаются в 1,73 раза. Поэтому можно сделать вывод, что если есть вывод всех концов обмоток, то вторичные обмотки трансформатора и генераторы можно применять на два типа напряжения, которые отличаются в 1,73 раза.

Лампы освещения

При переходе со звезды в треугольник лампы сгорят. Если переключение сделать обратное, при условии, что лампы при треугольнике горели нормально, то лампы будут гореть тусклым светом. Без нулевого провода лампы можно соединять звездой при условии, что их мощность одинакова, и распределяется равномерно между фазами. Такое подключение применяется в театральных люстрах.

Подключение звезда и треугольник – в чем разница?

Обмотки генераторов, трансформаторов, электродвигателей и других электрических приемников при их подключении к трехфазной сети соединяются двумя способами: звездой или треугольником. Эти схемы подключения сильно отличаются друг от друга и несут на себе разные токовые нагрузки. Поэтому есть необходимость разобраться в вопросе, как производится подключение звезда и треугольник – в чем разница?

Что собой представляют схемы

Подключение обмоток звездой – это их соединение в одной точке, которая носит название нулевая точка или нейтральная. Она обозначается буквой «О».

Схема подключения треугольником – это последовательное соединение концов рабочих обмоток, в которых начало одной обмотки соединяется с концом другой.

Разница очевидна. Но какую цель преследуют эти виды соединения, почему звезда треугольник применяются в разных электрических установках, в чем эффективность той и другой. Вопросов по данной теме возникает немало, с ними и надо разобраться.

Начнем с того, что при запуске того же электродвигателя ток, который называется пусковым, обладает высоким значением, который превышает номинальную его величину раз в шесть или восемь. Если это маломощный агрегат, то защита такую силу тока может выдержать, а если это электродвигатель большой мощности, то никакие защитные блоки не выдержат. И это вызовет обязательно «проседание» напряжения и выход из строя предохранителей или автоматических выключателей. Сам же двигатель начнет вращаться с небольшой скоростью, отличающуюся от паспортной. То есть, проблем с пусковым током немало.

Поэтому его надо просто снизить. Есть несколько для этого способов:

• установить в систему подключения электрического двигателя один из перечисленных приборов: трансформатор, дроссель, реостат;
• изменяется схема подключения обмоток ротора.

Именно второй вариант используется на производстве, как самый простой и эффективный. Просто производится преобразование схемы звезда в треугольник. То есть, во время пуска двигателя его обмотки соединяются по схеме звезда, затем как только мотор наберет обороты, переключается на треугольник. Процесс переключения звезды на треугольник производится автоматически.

Рекомендуется в электродвигателях, где используются одновременно два варианта соединения – звезда-треугольник, к соединению обмоток по схеме звезда, то есть, к их общей точке подключения, подсоединить нейтраль от сети питания. Для чего это необходимо делать? Все дело в том, что во время работы по данному варианту подсоединения появляется высокая вероятность асимметрии амплитуд разных фаз. Именно нейтраль будет компенсировать данную асимметрию, которая обычно появляется за счет того, что обмотки статора могут иметь разное индуктивное сопротивление.

Преимущества двух схем

У схемы звезда достаточно серьезные достоинства:

• плавный запуск электрического двигателя;
• номинальная его мощность будет соответствовать паспортным данным;
• двигатель будет работать нормально и при кратковременных высоких нагрузках, и при долгосрочных небольших перегрузов;
• в процессе работы корпус мотора не будет перегреваться.

Что касается схемы треугольник, то основное ее преимущество – это достижение электрическим двигателем в процессе его работы максимальной мощности. Но при этом рекомендуется строго придерживаться эксплуатационных режимов, которые расписаны в паспорте мотора. Тестирование электродвигателей, соединенных по схеме треугольник, показало, что его мощность в три раза больше, чем соединенных по схеме звезда.

Если говорить о генераторах, которые выдают ток в питающую сеть, то схемы соединения звезда и треугольник по своим техническим параметрам точно такие же. То есть, выдаваемое напряжение треугольником будет больше, правда, не в три раза, но не менее 1,73 раза. По сути, получается, что напряжение генератора при звезде, равное 220 вольт, преобразуется в 380 вольт, если провести переключение с одного варианта на другой. Но необходимо отметить, что мощность самого агрегата при этом остается неизменной, потому что все подчиняется закону Ома, в котором напряжение и сила тока находятся в обратной пропорциональности. То есть, увеличение напряжения в 1,73 раза, снижает ток точно на такую же величину.

Отсюда вывод: если в клеммной коробке генератора располагаются все шесть концов обмоток, то можно будет получить напряжение двух номиналов, отличающихся друг от друга коэффициентом 1,73.

Делаем выводы

Почему соединения треугольником и звездой сегодня присутствуют во всех современных мощных электродвигателях? Из всего вышесказанного становится понятным, что основное требование ситуации – это снизить токовую нагрузку, которая возникает в процессе пуска самого агрегата.

Если расписать формулы такого подключения, то они будут выглядеть вот так:

Uф=Uл/1,73=380/1,73=220, где Uф – напряжение на фазах, Uл – на питающей линии. Это соединение звездой.

После того, как электрический агрегат разгонится, то есть, скорость его вращения станет соответствовать паспортным данным, произойдет переход на треугольник со звезды. Отсюда фазное напряжение станет равным линейному.

Чем отличаются соединения звездой и треугольником

Питание асинхронного электродвигателя происходит от трехфазной сети с переменным напряжением. Такой двигатель, при простой схеме подключения, оснащен тремя обмотками, расположенными на статоре. Каждая обмотка имеет сдвиг друг относительно друга на угол 120 градусов. Сдвиг на такой угол предназначен для создания вращения магнитного поля.

Концы фазных обмоток электродвигателя выведены на специальную «колодку». Выполнено это с целью удобства соединения. В электротехнике используют основных 2 метода подключения асинхронных электродвигателей: методом соединения “треугольника” и метод “звезды”. При соединении концов применяют специально предназначенные для этого перемычки.

Различия между «звездой» и «треугольником»

Исходя из теории и практических знаний основ электротехники, способ подключения «звезда», позволяет электродвигателю работать плавнее и мягче. Но при этом данный способ не позволяет выйти двигателю на всю мощность, представленную в технических характеристиках.

Соединив фазные обмотки по схеме «треугольник», двигатель способен быстро выйти на максимальную рабочую мощность. Это позволяет использовать по полной КПД электродвигателя, согласно техпаспорта. Но у такой схемы соединения есть свой недостаток: большие пусковые токи. Для уменьшения значения токов применяют пусковой реостат, позволяя осуществить более плавный пуск двигателя.

Соединение «звездой» и его преимущества

Каждая из трех рабочих обмоток электродвигателя имеет два вывода – соответственно начало и конец. Концы всех трех обмоток соединяют в одну общую точку, так называемую нейтраль.

При наличии нейтрального провода в цепи схему называют 4-х проводной, в противном случае, она будет считаться 3-х проводной.

Начало выводов присоединяют к соответствующим фазам питающей сети. Приложенное напряжение на таких фазах составляет 380 В, реже 660 В.

Основные преимущества применения схемы «звезда»:

• Устойчивый и длительный режим безостановочной работы двигателя;
• Повышенная надежность и долговечность, за счет снижения мощности оборудования;
• Максимальная плавность пуска электрического привода;
• Возможность воздействия кратковременной перегрузки;
• В процессе эксплуатации корпус оборудования не перегревается.

Существует оборудование с внутренним соединением концов обмоток. На колодку такого оборудования будет выведено всего лишь три вывода, что не позволяет применить другие методы соединения. Выполненное в таком виде электрооборудование, для своего подключения не требует грамотных специалистов.

Подключение трехфазного двигателя к однофазной сети по схеме звезда

Соединение «треугольником» и его преимущества

Принцип соединения «треугольник» заключается в последовательном соединении конца обмотки фазы А с началом обмотки фазы В. И дальше по аналогии – конец одной обмотки с началом другой. В итоге конец обмотки фазы С замыкает электрическую цепь, создавая неразрывный контур. Данную схему можно назвать было кругом, если бы не структура монтирования. Форму треугольника предает эргономичное размещение соединения обмоток.

При соединении «треугольником» на каждой из обмоток, присутствует линейное напряжение равное 220В или 380В.

Основные преимущества применения схемы «треугольник»:

• Увеличение до максимального значения мощности электрооборудования;
• Использование пускового реостата;
• Повышенный вращающийся момент;
• Большие тяговые усилия.

Недостатки:

• Повышенный ток пуска;
• При длительной работе двигатель сильно греется.

Метод соединения обмоток двигателя «треугольником» широко используется при работе с мощными механизмами и наличия высоких пусковых нагрузок. Большой вращающий момент создается за счет увеличения показателей ЭДС самоиндукции, вызванных протекающими большими токами.

Подключение трехфазного двигателя к однофазной сети по схеме треугольник

Тип соединения «звезда-треугольник»

В сложных механизмах, зачастую используется комбинированная схема «звезда-треугольник». При таком переключении резко вырастает мощность, и если двигатель по техническим характеристикам не предназначен для работы по методу «треугольника», то он перегреется и сгорит.

В этом случае напряжение на соединении каждой обмотки будет в 1,73 раза меньше, следовательно, будет меньше и протекающий в этот период ток. Дальше происходит увеличение частоты и продолжение снижения показания тока. Тогда применяя релейно-контактную схему, произойдет переключение со «звезды» на «треугольник».

В итоге, используя данную комбинацию, получим максимальную надежность и эффективную продуктивность используемого электрического оборудования, не боясь вывести ее из строя.

Переключение «звезда-треугольник» допустимо для электродвигателей с облегченным режимом пуска. Этот метод неприменим, если необходимо понизить ток пуска и одновременно не снижать большой пусковой момент. В этом случае применяют двигатель с фазным ротором с пусковым реостатом.

Основные преимущества комбинации:

• Увеличение срока службы. Плавный пуск позволяет избежать неравномерности нагрузки на механическую часть установки;
• Возможность создания двух уровней мощности.

Свойства звезды и треугольника

Дата публикации: 17 июля 2013 .
Категория: Электротехника.

Типичные случаи соединений в звезду и треугольник генераторов, трансформаторов и электроприемников рассмотрены в статьях «Схема соединения «Звезда» и «Схема соединения «Треугольник». Остановимся теперь на важнейшем вопросе о мощности при соединениях в звезду и треугольник, так как для работы каждого механизма, приводимого в действие электродвигателем или получающего питание от генератора или трансформатора, в конечном итоге важна именно мощность.

При определении мощности генераторов в формулы входят э. д. с, при определении мощности электроприемииков – напряжения на их зажимах. При определении мощности электродвигателей учитывают также коэффициент полезного действия, так как на табличке электродвигателя указывается мощность на его валу.

Мощность при соединении в звезду

При соединении в звезду линейные токи I и фазные токи I_ф равны, а между фазными
и линейными напряжениями существует соотношение U = √3 × U_ф, откуда U_ф = U / √3.

Сопоставляя эти формулы, видим, что выраженные через линейные величины при соединении в звезду мощности равны:
полная S = 3 × S_ф = 3 × (U / √3) × I = √3 × U × I;
активная P = √3 × U × I × cos φ;
реактивная Q = √3 × U × I × sin φ.

Мощность при соединении в треугольник

При соединении в треугольник линейные U и фазные U_ф напряжения равны, а между фазными и линейными токами существует соотношение I = √3 × I_ф, откуда I_ф = I / √3.

Поэтому выраженные через линейные величины при соединении в треугольник мощности равны:
полная S = 3 × S_ф = 3 × U × (I / √3) = √3 × U × I;
активная P = √3 × U × I × cos φ;
реактивная Q = √3 × U × I × sin φ.

Важное замечание. Одинаковый вид формул мощности для соединений в звезду и треугольник иногда служит причиной недоразумений, так как наталкивает недостаточно опытных людей на неправильный вывод, будто вид соединений всегда безразличен. Покажем на одном примере, насколько ошибочен такой взгляд.

Электродвигатель был соединен в треугольник и работал от сети 380 В при токе 10 А с полной мощностью

S = 1,73 × 380 × 10 = 6574 В×А.

Затем электродвигатель пересоединили в звезду. При этом на каждую фазную обмотку пришлось в 1,73 раза более низкое напряжение, хотя напряжение в сети осталось тем же. Более низкое напряжение привело к тому, что ток в обмотках уменьшился в 1,73 раза. Но и этого мало. При соединении в треугольник линейный ток был в 1,73 раза больше фазного, а теперь фазный и линейный токи равны.

Таким образом, линейный ток при пересоединении в звезду уменьшился в 1,73 × 1,73 = 3 раза.

Иными словами, хотя новую мощность нужно вычислять по той же формуле, но подставлять в нее следует иные величины, а именно:

S₁ = 1,73 × 380 × (10 / 3) = 2191 В×А.

Из этого примера следует, что при пересоединении электродвигателя с треугольника в звезду и питании его от той же электросети мощность, развиваемая электродвигателем, снижается в 3 раза.

Что происходит при переключении со звезды в треугольник и обратно в наиболее распространенных случаях?

Оговариваем, что речь идет не о внутренних пересоединениях (которые выполняют в заводских условиях или в специализированных мастерских), а о пересоединениях на щитках аппаратов, если на них выведены начала и концы обмоток.
1. При переключении со звезды в треугольник обмоток генераторов или вторичных обмоток трансформаторов напряжение в сети понижается в 1,73 раза, например с 380 до 220 В. Мощность генератора и трансформатора остается такой же. Почему? Потому что напряжение каждой фазной обмотки остается таким же и ток в каждой фазной обмотке такой же, хотя ток в линейных проводах возрастает в 1,73 раза.

При переключении обмоток генераторов или вторичных обмоток трансформаторов с треугольника в звезду происходят обратные явления, то есть линейное напряжение в сети повышается в 1,73 раза, например с 220 до 380 В, токи в фазных обмотках остаются теми же, токи в линейных проводах уменьшаются в 1,73 раза.

Значит, и генераторы и вторичные обмотки трансформаторов, если у них выведены все шесть концов, пригодны для сетей на два напряжения, отличающихся в 1,73 раза.

2. При переключении ламп со звезды в треугольник (при условии их присоединения к той же сети, в которой лампы, включенные звездой, горят нормальным накалом) лампы перегорят.

При переключении ламп с треугольника в звезду (при условии, что лампы при соединении в треугольник горят нормальным накалом) лампы будут давать тусклый свет. Значит, лампы, например, на 127 В в сеть напряжением 127 В должны включаться треугольником. Если же их приходится питать от сети 220 В, необходимо соединение в звезду с нулевым проводом (подробнее смотрите статью «Схема соединения «Звезда»). Соединять в звезду без нулевого провода можно только лампы одинаковой мощности, равномерно распределенные между фазами, как, например, в театральных люстрах.

3. Все сказанное о лампах относится и к сопротивлениям, электрическим печам и тому подобным электроприемникам.

4. Конденсаторы, из которых собирают батареи для повышения cos φ, имеют номинальное напряжение, которое указывает напряжение сети, к которой конденсатор должен присоединяться. Если напряжение сети, например, 380 В, а номинальное напряжение конденсаторов 220 В, их следует соединять в звезду. Если напряжение сети и номинальное напряжение конденсаторов одинаковы, конденсаторы соединяют в треугольник.

5. Как объяснено выше, при переключении электродвигателя с треугольника в звезду мощность его снижается примерно втрое. И наоборот, если электродвигатель переключить со звезды в треугольник, мощность резко возрастает, но при этом электродвигатель, если он не предназначен для работы при данном напряжении и соединении в треугольник, сгорит.

Пуск короткозамкнутого электродвигателя с переключением со звезды в треугольник

применяют для снижения пускового тока, который в 5 – 7 раз превышает рабочий ток двигателя. У двигателей сравнительно большой мощности пусковой ток настолько велик, что может вызвать перегорание предохранителей, отключение автомата и привести к значительному снижению напряжения. Уменьшение напряжения снижает накал ламп, уменьшает вращающий момент электродвигателей 2 , может вызвать отключение контакторов и магнитных пускателей. Поэтому стремятся уменьшить пусковой ток, что достигается несколькими способами. Все они в итоге сводятся к понижению напряжения в цепи статора на период пуска. Для этого в цепь статора на период пуска вводят реостат, дроссель, автотрансформатор либо переключают обмотку со звезды в треугольник. Действительно, перед пуском и в первый период пуска обмотки соединены в звезду. Поэтому к каждой из них подводится напряжение, в 1,73 раза меньшее номинального, и, следовательно, ток будет значительно меньше, чем при включении обмоток на полное напряжение сети. В процессе пуска электродвигатель увеличивает частоту вращения и ток снижается. Тогда обмотки переключают в треугольник.

Предупреждения:
1. Переключение со звезды в треугольник допустимо лишь для двигателей с легким режимом пуска, так как при соединении в звезду пусковой момент примерно вдвое меньше момента, который был бы при прямом пуске. Значит, этот способ снижения пускового тока не всегда пригоден, и если нужно снизить пусковой ток и одновременно добиться большого пускового момента, то берут электродвигатель с фазным ротором, а в цепь ротора вводят пусковой реостат.
2. Переключать со звезды в треугольник можно только те электродвигатели, которые предназначены для работы при соединении в треугольник, то есть имеющие, обмотки, рассчитанные на линейное напряжение сети.

Переключение с треугольника в звезду

Известно, что недогруженные электродвигатели работают с очень низким коэффициентом мощности cos φ. Поэтому рекомендуется недогруженные электродвигатели заменять менее мощными. Если, однако, выполнить замену нельзя, а запас мощности велик, то не исключено повышение cos φ переключением с треугольника в звезду. Нужно при этом измерить ток в цепи статора и убедиться в том, что он при соединении в звезду не превышает при нагрузке номинального тока; в противном случае электродвигатель перегреется.

1 Активная мощность измеряется в ваттах (Вт), реактивная – в вольт-амперах реактивных (вар), полная – в вольт-амперах (В×А). Величины в 1000 раз большие соответственно называют киловатт (кВт), киловар (квар), киловольт-ампер (кВ×А).
2 Вращающий момент электродвигателя пропорционален квадрату напряжения. Следовательно, при снижении напряжения на 20% вращающий момент снижается не на 20, а на 36% (1² — 0,82² = 0,36).

Источник: Каминский Е.А., «Звезда, треугольник, зигзаг» — 4-е издание, переработанное — Москва: Энергия, 1977 — 104с.

Преобразование треугольника сопротивлений в эквивалентную звезду и обратно

Преобразование треугольника сопротивлений  в эквивалентную  звезду

Иногда для облегчения расчетов применяют преобразование треугольника сопротивлений  в эквивалентную  звезду. 

Треугольник сопротивлений представляет собой треугольник сторонами которого является сопротивления (рис. 1).

Преобразование треугольника в звезду значительно упрощает схему рис.2 а — до преобразования, б — после.

Итак начнём преобразование:

1. Для удобства обозначим узлы (углы) треугольника буквами A, B, C.
2. Найдём сопротивления лучей звезды по формулам. Сумма сопротивлений ветвей выходящих из узла (угла треугольника) делённая на сумму всех сопротивлений треугольника.
3. Начертим новую схему с преобразованным треугольником в звезду. (Рисунок 2,б)

Преобразование звезды сопротивлений в эквивалентный треугольник

В расчетах также возникает потребность обратной операции, то есть

преобразование звезды в треугольник. В задании нам известны сопротивление лучей звезды, и нам нужно рассчитать сопротивления сторон треугольника. По формуле — сопротивление стороны треугольника равно сумме сопротивлений лучей звезды прилегающих к данной стороне треугольника и произведения их, деленного на оставшийся луч звезды.

Некоторые ошибки при соединениях в звезду, треугольник, зигзаг

Дата публикации: 17 июля 2013.
Категория: Электротехника.

Ошибки при соединении в треугольник

При соединениях иногда допускают ошибки, в результате которых вместо треугольника (рисунок 1, а) получается другое соединение (рисунок 1, в). Его причина – другое направление намотки одной из обмоток или, проще, ошибочное определение ее конца и начала. Пока треугольник еще разомкнут, то есть точки y и z еще не соединены, между ними получается двойное фазное напряжение 2U. Если их соединить, произойдет короткое замыкание.

Рисунок 1. Ошибки при соединениях обмоток трансформаторов в треугольник.

Чтобы избежать этой ошибки, поступают следующим образом. Соединяют два каких-либо конца разных обмоток и измеряют напряжение между свободными концами, принимая необходимые меры предосторожности, например, проводя испытания при значительно пониженном напряжении. Если концы выбраны правильно, то вольтметр V покажет фазное напряжение U (рисунок 1, б). Если же напряжение будет в 1,73 раза больше фазного 1,73U (рисунок 1, г), то у одной из обмоток нужно переменить концы. Затем к одному из свободных концов присоединяют один конец третьей обмотки и снова измеряют напряжение между свободными концами (рисунок 1, д). Оно должно быть равно нулю. Но если третья обмотка «вывернута» (рисунок 1, в), то вольтметр покажет удвоенное фазное напряжение 2U. Тогда у третьей обмотки нужно переменить концы.

Следует здесь же заметить, что при наличии третьих гармоник (смотрите статью «Понятие о магнитном равновесии трансформатора») вольтметр может показать некоторое (меньше, чем двойное фазное) напряжение. В этом случае надо соединить концы через сопротивление R и амперметр А (рисунок 1, е). Если напряжение, показываемое вольтметром, происходит от третьих гармоник, то отклонение стрелки амперметра невелико. Это объясняется тем, что для токов тройной частоты обмотки представляют большое сопротивление. Если же перепутано направление обмотки, амперметр покажет значительный уравнительный ток.

Ошибки при соединении в звезду

Переворачивание одной из обмоток при соединении в звезду вместо звезды (рисунок 2, а) дает «веер» («елочку»), как показано на рисунке 2, б. Короткого замыкания при этом не будет, но напряжение, близкое к номинальному, сохранится только между фазами a и c. Между фазами a и b, b и c напряжение будет значительно понижено и равно примерно фазному напряжению. В сетях освещения «елочка» вместо звезды приведет к недокалу ламп.

Рисунок 2. Правильное (а) и неправильное (б) соединения вторичных обмоток трансформаторов в звезду.

В сетях, соединенных «елочкой» и питающих электродвигатели (а также при включении обмоток электродвигателя, соединенного «елочкой»), не только уменьшится мощность на валу (что может привести к остановке и сгоранию электродвигателя), но изменится направление его вращения. Почему? Потому что если при правильном соединении обмоток вращающееся магнитное поле имело направление a, b, c (смотрите стрелку на рисунке 2, а), то при соединении «елочкой» оно, а следовательно, и ротор электродвигателя меняют направление на обратное, а именно a, c, b, и, конечно, резко снижается вращающий момент из-за нарушения симметрии.

В трехфазных стержневых трансформаторах важно правильно соединить первичные обмотки, то есть соединить их так, чтобы в каждый данный момент поток в одном стержне был направлен вверх, а в двух других стержнях вниз (рисунок 3, а). Если же одну фазу «вывернуть» (неправильно определены ее конец и начало или намотка выполнена в другом направлении), то потоки Ф_A, Ф_B и Ф_C во всех стержнях будут иметь одинаковое направление (рисунок 3, б). Иными словами, поток одной фазы, направленный навстречу потокам других фаз, будет размагничивать их стержни, что приведет к увеличению намагничивающего тока.

Рисунок 3. Правильное (а) и неправильное (б) соединение в звезду первичных обмоток трехфазного стержневого трансформатора.

Ошибки при соединении в зигзаг

Все сказанное о соединениях в звезду еще в большей мере относится к соединению в зигзаг – звезду, так как приходится соединять значительно больше выводов. Результат неправильного определения конца и начала одной из обмоток (показано штриховой линией) иллюстрирует рисунок 4, б (сравните с векторной диаграммой на рисунке 4, а). Рисунок 4, в показывает, что в результате неправильного определения концов и начал трех обмоток получены √3 раз меньшие напряжения, чем нормальное. Кроме того, векторная диаграмма повернулась на 90°.

Рисунок 4. Соединение в зигзаг: правильное (а) и неправильные (б и в).

Источник: Каминский Е. А., «Звезда, треугольник, зигзаг» – 4-е издание, переработанное – Москва: Энергия, 1977 – 104с.