Преобразование треугольник/звезда: что за сценой?
Добавлено 17 июня 2019 в 12:15
Сохранить или поделиться
Преобразования треугольник/звезда позволяют нам заменить часть схемы другой схемой, которая, хотя и эквивалентна в поведении, но может значительно упростить анализ общей схемы. Здесь мы узнаем, откуда берутся эти преобразования.
Зачем?
Когда мы начали изучать электронику, резисторы были соединены либо последовательно, либо параллельно, и мы научились заменять такие комбинации их эквивалентными сопротивлениями, часто с целью уменьшения всей сети сопротивлений до единственного эквивалентного сопротивления, видимого из источника питания. После этого появились схемы (рисунок 1), которые содержали резисторы, которые не были ни последовательными, ни параллельными, но их всё же можно было убрать, тщательно определяя и сокращая фрагменты схемы в правильном порядке. Обратите внимание, что R1 не параллелен и не последователен ни с R2, ни с R3, но путем объединения R2 последовательно с R4, и объединяя R3 последовательно с R5, мы можем затем объединить эти два эквивалентных сопротивления параллельно и, наконец, объединив результат последовательно с R1, получить полное сопротивление, видимое источнику питания, которое, используя закон Ома, поможет получить общий ток источника питания.
Но теперь мы подошли к схемам (рисунок 2), где нет никаких пар резисторов, которые включены последовательно или параллельно, – похоже, мы зашли в тупик. Одним из способов анализа этой схемы является использование закона напряжений Кирхгофа (второй закон) и закона токов Кирхгофа (первый закон) для получения алгебраических уравнений, которые мы можем решить для напряжений и токов. Хотя этот подход будет работать всегда (для этой и большинства других типов схем), он может быть довольно громоздким. Мы могли бы смириться с этим как с ценой возможности анализа этих более сложных схем, но иногда мы можем избежать оплаты этого счета, изменяя или «преобразовывая» фрагменты схемы, чтобы превратить ее в нечто, что мы можем уменьшить, используя только правила последовательного/параллельного объединения.
Рисунок 2Для простоты мы будем рассматривать только цепи постоянного тока с резисторами, но эти принципы применимы к любой линейной системе переменного или постоянного тока. Кроме того, чтобы сфокусировать обсуждение на преобразованиях, мы найдем только общий ток, поставляемый источником напряжения, что означает, что мы стремимся свести всю сеть резисторов в единое эквивалентное сопротивление.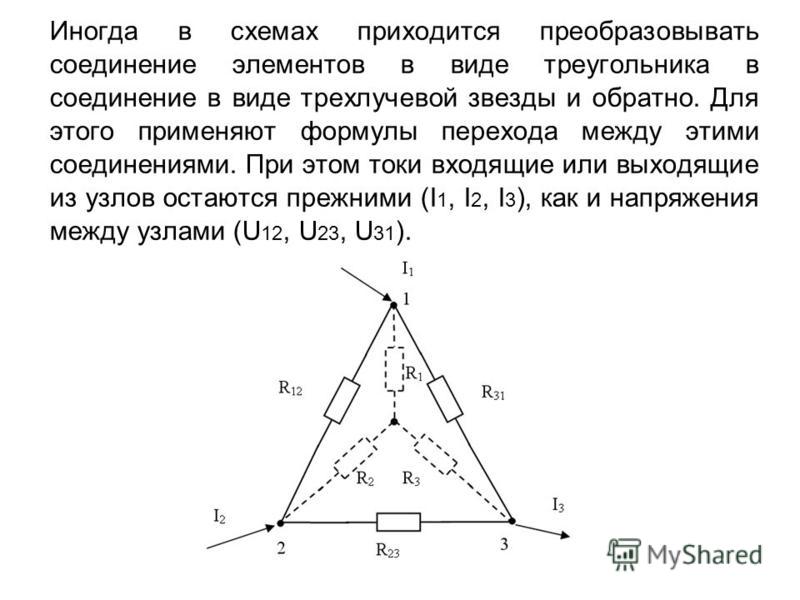
Давайте рассмотрим эти две схемы немного подробнее (рисунок 3). Мы видим, что единственная разница между ними заключается в том, что находится внутри пунктирных окружностей. В каждом случае цепь в окружности имеет три контакта, которые пересекают окружность для взаимодействия с остальной частью схемы. В левой цепи (рисунок 3(a)) резисторы подключены к контактам в конфигурации «треугольник» (в англоязычной литературе, конфигурация «delta», «дельта», названная в честь заглавной греческой буквы Δ). А в правой цепи резисторы подключены в конфигурации «звезда» (в англоязычной литературе, конфигурация «wye», «уай», названная в честь заглавной английской буквы Y, хотя в схеме она перевернута).
Рисунок 3Теперь представьте, что резисторы внутри пунктирной окружности в левой цепи помещены в черный ящик, этот ящик удален из схемы и заменен другим черным ящиком, который заставляет схему вести себя точно так же. Далее представьте, что, когда вы открываете, этот новый ящик он содержит три резистора, расположенных как в правой цепи.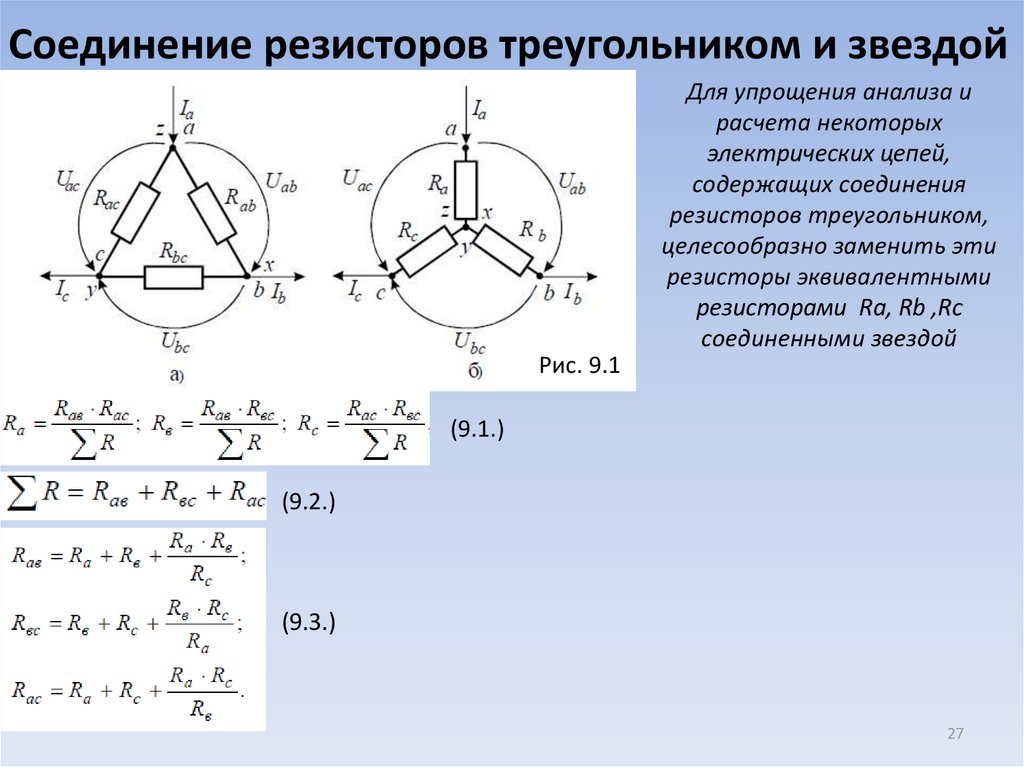
Кто бы ни придумал второй черный ящик, он очень тщательно выбрал значения резисторов так, чтобы эти два блока были неразличимы для остальной части схемы: мы знаем, как анализировать правую схему, и теперь мы знаем, что когда мы это делаем, результаты можно применить к левой схеме, потому что они эквивалентны. Вот зачем выполнять преобразования «треугольник→звезда» и «звезда→треугольник».
Основные соотношения
Чтобы определить уравнения, связывающие резисторы в цепи, соединенной треугольником, с резисторами в цепи, соединенной звездой, нам ничего не нужно, кроме наших надежных формул для последовательных/параллельных соединений (и немного алгебры). Идея заключается в выравнивании эквивалентных сопротивлений между соответствующими парами контактов при отключенном оставшемся контакте (рисунок 4)
Рисунок 4Выполнив это для эквивалентного сопротивления между контактами B-C, мы получим:
\[R_B + R_C = \frac{R_{BC} \left( R_{AB} + R_{AC} \right) }{R_{AB} + R_{BC} + R_{AC}}\]
Если мы повторим этот процесс для каждой другой пары контактов по очереди, мы получим еще два аналогичных уравнения, и любое из них даст нам необходимую нам информацию (при условии, что мы распознаем задействованную симметрию).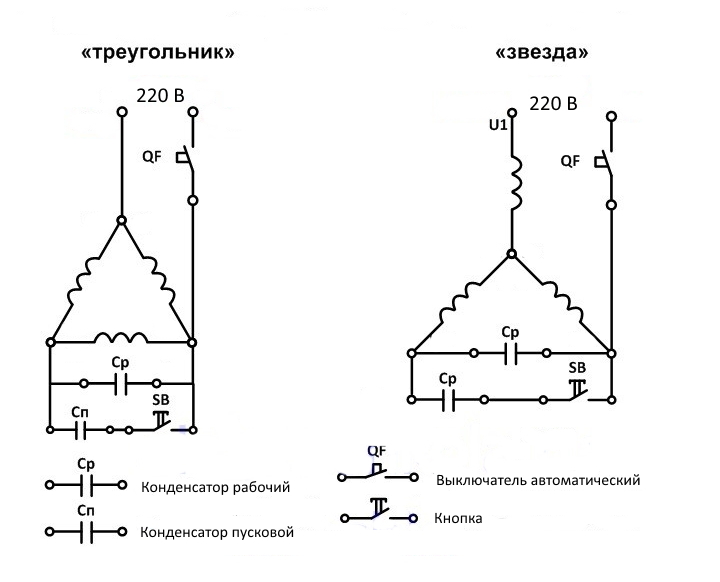
Частный случай: симметричные схемы
Если сопротивления в каждом плече цепи, соединенной треугольником или звездой, равны, такая цепь считается «симметричной». Это означает, что
\[R_∆ = R_{AB} = R_{BC} = R_{AC}\]
\[R_Y = R_A = R_B = R_C\]
Комбинация этого условия с соотношением из предыдущего раздела сразу приводит к уравнению преобразования для случая симметрии.
\[2R_Y = \frac{R_∆(2R_∆)}{3R_∆}\]
\[R_Y = \frac{R_∆}{3}\]
\[R_∆ = 3R_Y\]
Это гораздо более значительный результат, чем может показаться на первый взгляд, и причина довольно проста – когда инженеры проектируют схемы с соединениями треугольник или звезда, они часто стараются сделать эти схемы симметричными. Хотя, конечно, это не всегда возможно, и поэтому мы должны иметь возможность разобраться с общим случаем, когда схема не симметрична.
Общий случай преобразования треугольник→звезда
Для преобразования треугольник/звезда нам дана известная схема, соединенная треугольником, и мы хотим найти значения для эквивалентной схемы, соединенной звездой, – поэтому мы пытаемся найти {RA, RB, RC} для заданных {RAB, RBC, RAC}.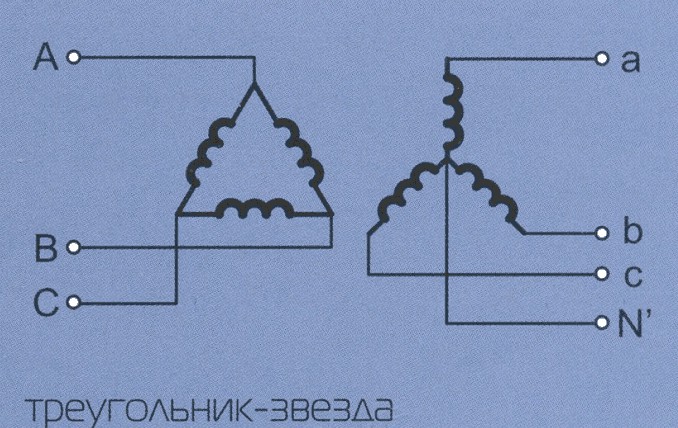
Мы начнем с того, что запишем наши основные соотношения из первоначального вида в несколько более компактной форме, определив новую величину, RΔS, которая равна сумме сопротивлений всех резисторов в цепи, соединенной треугольником.
\[R_{ΔS}=R_{AB}+R_{BC}+R_{AC}\]
Затем мы делаем перестановку нашего соотношения для получения вида линейного алгебраического уравнения с неизвестными {RA, RB, RC}.
\[(0)R_A+(R_{ΔS})R_B+(R_{ΔS})R_C=R_{AB}R_{BC}+R_{BC}R_{AC}\]
Поскольку у нас есть три неизвестных, нам нужно еще два уравнения. Они получаются из эквивалентных сопротивлений, видимых при рассмотрении двух других пар контактов. Выполнив это (или используя симметрию) мы получаем
\[(R_{ΔS})R_A+(0)R_B+(R_{ΔS})R_C=R_{AB}R_{AC}+R_{BC}R_{AC}\]
\[(R_{ΔS})R_A+(R_{ΔS})R_B+(0)R_C=R_{AB}R_{AC}+R_{AB}R_{BC}\]
Сложив эти два уравнения вместе и вычтя наше первое уравнение, мы получим
\[2(R_{ΔS})R_A=2R_{AB}R_{AC}\]
\[R_A= {R_{AB}R_{AC} \over R_{ΔS}}\]
Мы можем решить систему уравнению для двух других неизвестных сопротивлений (или использовать симметрию), чтобы получить
\[R_B= {R_{AB}R_{BC} \over R_{ΔS}}\]
\[R_C= {R_{AC}R_{BC} \over R_{ΔS}}\]
Эти отношения могут быть обобщены очень компактно.
Сопротивление, подключенное к каждому узлу в эквивалентной цепи, соединенной звездой, равно произведению сопротивлений, подключенных к соответствующему узлу в цепи, соединенной треугольником, деленному на сумму сопротивлений всех резисторов в треугольнике. Обычно это выражается формулой, такой как
\[R_N= {R_{N1}R_{N2} \over R_{ΔS}}\]
где
- RN – резистор, подключенный к контакту N в схеме «звезда»;
- RN1 и RN2 – резисторы, подключенные к контакту N в схеме «треугольник»
Общий случай преобразования звезда→треугольник
Для преобразования звезда→треугольник нам дана известная схема, соединенная звездой, и мы хотим найти значения для эквивалентной схемы, соединенной треугольником. Следовательно, мы пытаемся найти {RAB, RBC, RAC} для заданных {RA, RB, RC}.
Это не так просто, как в случае преобразования треугольник→звезда потому, что неизвестные сопротивления перемножаются вместе, делая результирующие уравнения нелинейными. К счастью, мы можем обойти это неудобство, рассмотрев отношения сопротивлений резисторов в каждой цепи. Например, взяв отношение RA к RB, мы получаем
\[{R_A \over R_B} = { R_{AB}R_{AC} \over R_{AB}R_{BC} } = {R_{AC} \over R_{BC} }\]
Другими словами, отношение сопротивлений резисторов, подключенных к любым двум контактам в схеме звезда, равно отношению сопротивлений резисторов, соединяющих те же самые два контакта с третьим контактом в схеме треугольник. Следовательно, два других соотношения будут следующими
\[{R_B \over R_C} = {R_{AB} \over R_{AC} }\]
\[{R_A \over R_C} = {R_{AB} \over R_{BC} }\]
Вооружившись этим, мы могли бы вернуться к нашим основным соотношениям и продолжить работу с ними, но в качестве отправной точки проще использовать одно из отношений из общего случая преобразования треугольник→звезда.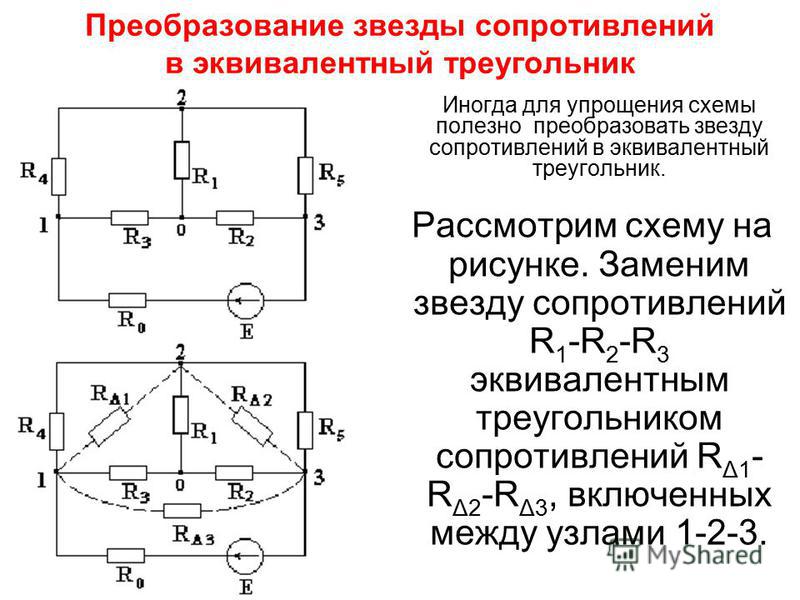
\[R_A= {R_{AB}R_{AC} \over R_{AB} + R_{BC}+R_{AC} }\]
\[R_{AB}R_{AC} = R_A (R_{AB} + R_{BC}+R_{AC})\]
\[R_{AB} = R_A \left( {R_{AB} + R_{BC}+R_{AC} \over R_{AC} } \right)\]
\[R_{AB} = R_A \left( {R_{AB} \over R_{AC}} + {R_{BC} \over R_{AC} } + 1 \right)\]
\[R_{AB} = R_A \left( {R_{B} \over R_{C}} + {R_{B} \over R_{A} } + 1 \right)\]
\[R_{AB} = R_A + R_B + {R_AR_B \over R_C } \]
Два других выражения получаются аналогично (или согласно симметрии):
\[R_{BC} = R_B + R_C + {R_B R_C \over R_A } \]
\[R_{AC} = R_A + R_C + {R_A R_C \over R_B } \]
Эти выражения могут быть обобщены очень компактно. Сопротивление, подключенное между каждой парой узлов в эквивалентной схеме, соединенной треугольником, равно сумме сопротивлений двух резисторов, подключенных к соответствующим узлам в схеме, соединенной звездой, плюс произведение сопротивлений этих двух резисторов, деленное на сопротивление третьего резистора.
Общий способ выразить это состоит в том, чтобы поместить правую часть под общим знаменателем, а затем отметить, что числитель в каждом выражении является суммой произведений каждой пары сопротивлений в цепи, соединенной звездой, а знаменатель – это сопротивление, подключенное к третьему контакту.
\[R_{AB}={R_P \over R_C}\]
\[R_P = R_A R_B + R_B R_C + R_A R_C\]
Пример
Рисунок 5Давайте поработаем с задачей, показанной на рисунке 5. Прежде чем мы начнем, давайте определим ожидаемый ответ, чтобы у нас была хорошая проверка того, является ли наш окончательный ответ правильным. Для этого рассмотрим роль мостового резистора 150 Ом. Этот резистор служит для уменьшения общего сопротивления, обеспечивая путь между левой и правой сторонами цепи. Следовательно, самое высокое эффективное сопротивление будет иметь место, если этот резистор будет удален полностью, и в этом случае полное сопротивление будет равно параллельной комбинации левой и правой сторон, что приведет к
\[R_{экв.max}=(100 +220)||(470+330)=228,6 \; Ом\]
С другой стороны, наименьшее общее сопротивление было бы получено путем уменьшения мостового резистора до прямого короткого замыкания, и в этом случае общее сопротивление было бы равно параллельной комбинации двух верхних резисторов, включенной последовательно с параллельной комбинацией двух нижних резисторов, что приведет к
\[R_{экв.
min}=(100||470)+(220||330)=214,5 \; Ом\]
Теперь мы ЗНАЕМ, что наш ответ ДОЛЖЕН быть между этими двумя предельными значениями. Во многих случаях простой анализ границ, такой как этот, приводит к ответу, который «достаточно хорошо» подходит для данной цели, но давайте предположим, что это не так. Используя приведенные выше уравнения преобразования треугольник→звезда, мы сначала определяем сумму сопротивлений резисторов треугольника.
\[R_{ΔS}=100+150+470=720 \; Ом\]
А затем находим значение R1, перемножив сопротивления двух резисторов, которые подключены к верхнему контакту, и разделив это произведение на сумму всех трех сопротивлений.
\[R_1={100⋅470 \over 720}=65,28 \; Ом\]
Повторим это же для R2.
\[R_2={100⋅150 \over 720}=20,83 \; Ом\]
Мы могли бы повторить это еще раз для R3, но давайте, вместо этого, определим R3, используя свойства отношений.
\[{R_3 \over R_1}={150 \over 100}⇒R_3=1,5R_1=97,92 \; Ом\]
Теперь, когда у нас есть все сопротивления для эквивалентной схемы звезда, мы можем очень легко определить общее сопротивление.
\[R_{экв.}=R_1+[(R_2+220)||(R_3+330)]=219,4 \; Ом\]
Поскольку это значение находится между нашими минимальной и максимальной границами, мы полностью уверены, что это правильный ответ, или, даже если мы допустили ошибку, наш ответ довольно близок к правильному. Поэтому суммарный ток равен
\[I={12\; В \over 219,4 \; Ом}=54,7 \; мА\]
Заключение
Теперь мы увидели, что преобразования треугольник/звезда полезны, и, что более важно, увидели, как их можно легко выполнить, используя не более чем концепцию эквивалентных сопротивлений с использованием последовательных/параллельных комбинаций резисторов. Это может хорошо вам помочь, поскольку дает вам возможность вывести эти формулы на лету, если когда-нибудь возникнет в них необходимость, и у вас не будет подходящего справочного материала. Но что еще более важно, это должно служить для более прочного закрепления фундаментальных понятий в наборе инструментов, который хранится у вас в голове, позволяя вам использовать в своей работе еще более эффективные навыки анализа цепей.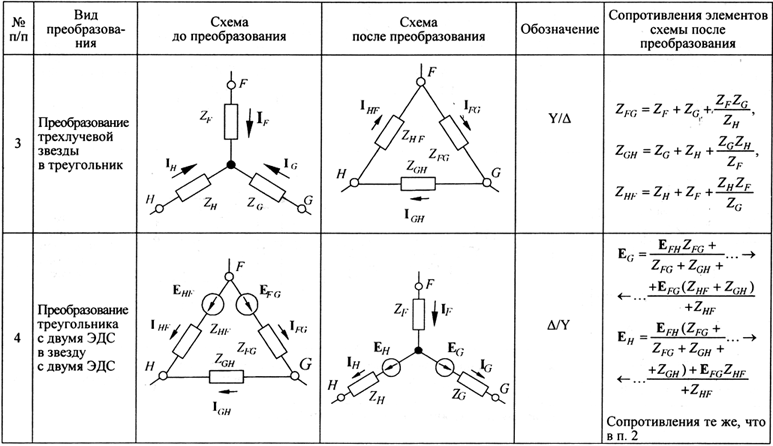
В конце мы должны принять к сведению распространенное заблуждение, заключающееся в том, что преобразования треугольник↔звезда являются ЕДИНСТВЕННЫМ способом анализа цепей, которые нельзя уменьшить другими способами. В действительности, хотя эти преобразования могут сделать нашу жизнь проще, они не обязательны, поскольку ЛЮБОЙ контур, который можно проанализировать с их помощью, также можно проанализировать с помощью правил Кирхгофа, либо напрямую, либо с помощью одного из более формализованных методов их применения, включая метод контурных токов или метод узловых напряжений, а также с методиками, такими как эквивалентная схема Тевенина.
Оригинал статьи:
Теги
Анализ цепейТреугольник-звездаСохранить или поделиться
Преобразование звезды в треугольник и преобразование треугольника в звезду
Содержание:
Преобразование звезды в треугольник и преобразование треугольника в звезду
Преобразуйте звезду в треугольник и преобразуйте треугольник в звезду.
Соединение называется «Звезда», соединение 3 резисторов в виде 3-проводной звезды (рис.25) и соединение 3 резисторов, образующих стороны треугольника (рис.26), называется соединением»треугольник». в узлах I, 2, 3(их потенциалы>. (Си + Си + г)= 0 Отсюда _ > 1(&»+£и> — » Prfft-1■■■ ’(1.27）
- Ток в цепи на рис. 25, 25 должен быть равен току / x. для 26 потенциальных значений ΦXX, φ2, φ» , а коэффициент φ8 на правой стороне (1.27) должен равняться коэффициенту φ3 на правой стороне. (1.26). Так… Точно так же . ..(1.28） ги + ГТ + гр I13 = гиг(1.29） ги + ГТ + ГТ ’ С%3-гиг*(1.30） ги + ГТ + ГТ ’
коэффициент φ2 на правой стороне (1.27) равен коэффициенту φ2 на правой стороне (1.26) Людмила Фирмаль
Формула (1.28)-(1.30)позволяет найти проводимость сторон треугольника через проводимость лучей звезды. Они имеют структуру, которую очень легко запомнить: индекс проводимости молекул справа соответствует индексу проводимости слева, а сумма проводимости лучей звезды находится в знаменателе.
- Утилита для преобразования треугольников в звезды может быть показана, например, на рисунке 3. 27.На рисунке 27 показана схема перед преобразованием, а преобразованный треугольник показан с пунктирной линией вокруг него. На рисунке 27b показана та же схема, но после преобразования.
Расчет тока в ней значительно проще, чем расчет тока в цепи на рисунке 2(например, по методу 2 узлов). 27 а. 28.In диаграмма диаграмма, диаграмма перед преобразованием показана.
полезность преобразования звезд в треугольники можно увидеть на примере схематической схемы.Людмила Фирмаль
Пунктирная линия окружает звезду, которая преобразуется в треугольник. Рисунок 28b показывает рисунок после преобразования. Схема была сведена к последовательному и параллельному подключению резистора. 。
Пример 14.Найти сопротивление в цепи Рисунок 27b сопротивление цепи f?18, Ф?32-27 а И Формула(1.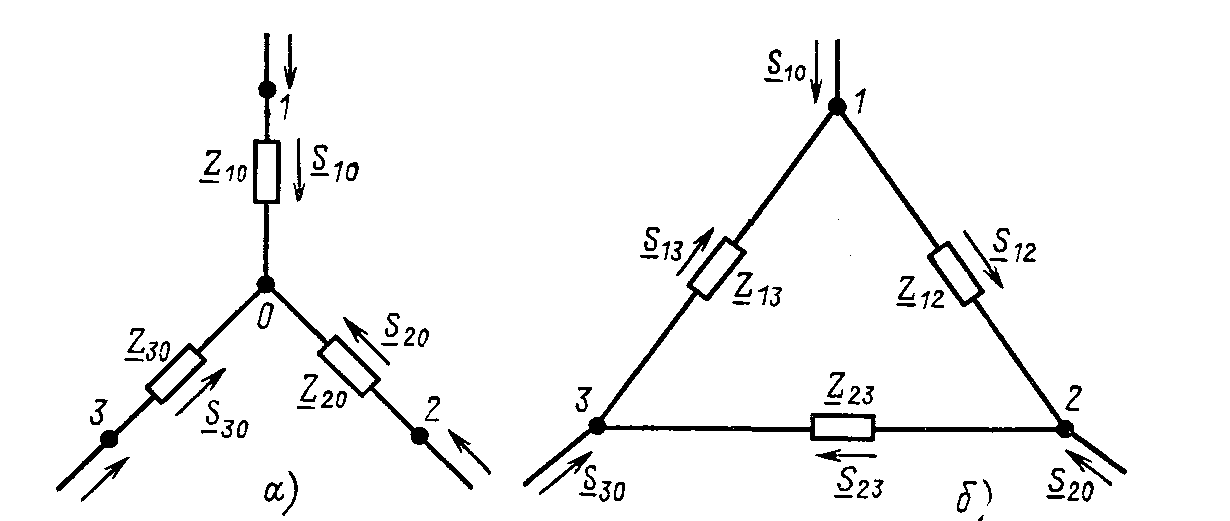
37） Каждый равен 2,3 5 ом. Двадцать восемь Решение. По формуле (1.35) Формула (1.36） s > 1 м 1 (Пр)） — ! 5 {ом}-
Смотрите также:
Предмет электротехника тоэ
| Шкаф управления электродвигателем по схеме «звезда-треугольник» ШУ-ЗТ 15кВт [32А], Uупр~220В, корпус навесной, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие EKF) | Регион-Автоматика / Elcada-32-СТ54-ШУЗТ-3574-Э | шт | 18297,05 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» ШУ-ЗТ 30кВт [63А], Uупр~220В, корпус навесной, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие EKF) | Регион-Автоматика / Elcada-63-СТ54-ШУЗТ-3874-Э | шт | 26145,93 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» ШУ-ЗТ 45кВт [100А], Uупр~220В, корпус навесной, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие EKF) | Регион-Автоматика / Elcada-100-СТ54-ШУЗТ-4074-Э | шт | 31181,45 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» ШУ-ЗТ 55кВт [115А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие EKF) | Регион-Автоматика / Elcada-115-СТ54-ШУЗТ-4174-Э | шт | 49154,88 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» ШУ-ЗТ 90кВт [160А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие EKF) | Регион-Автоматика / Elcada-160-СТ54-ШУЗТ-4374-Э | шт | 84641,75 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» ШУ-ЗТ 132кВт [265А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие EKF) | Регион-Автоматика / Elcada-265-СТ54-ШУЗТ-4574-Э | 110876,89 RUB | ||||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» ШУ-ЗТ 160кВт [330А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие EKF) | Регион-Автоматика / Elcada-330-СТ54-ШУЗТ-4574-Э | шт | 142453,09 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» реверсивный ШУ-ЗТ-Р 22кВт [50А], Uупр~220В, корпус навесной, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие EKF) | Регион-Автоматика / Elcada-50-СТ54-ШУЗТР-3774-Э | шт | 30478,22 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» реверсивный ШУ-ЗТ-Р 30кВт [63А], Uупр~220В, корпус навесной, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие EKF) | Регион-Автоматика / Elcada-63-СТ54-ШУЗТР-3874-Э | шт | 31349,44 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» реверсивный ШУ-ЗТ-Р 45кВт [100А], Uупр~220В, корпус навесной, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие EKF) | Регион-Автоматика / Elcada-100-СТ54-ШУЗТР-4074-Э | шт | 37468,14 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» реверсивный ШУ-ЗТ-Р 55кВт [115А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие EKF) | Регион-Автоматика / Elcada-115-СТ54-ШУЗТР-4174-Э | шт | 60103,39 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» реверсивный ШУ-ЗТ-Р 110кВт [225А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие EKF) | Регион-Автоматика / Elcada-225-СТ54-ШУЗТР-4474-Э | шт | 109362,67 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» реверсивный ШУ-ЗТ-Р 160кВт [330А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие EKF) | Регион-Автоматика / Elcada-330-СТ54-ШУЗТР-4574-Э | шт | 173319,75 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» ШУ-ЗТ 22кВт [50А], Uупр~220В, корпус навесной, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие Schneider-electric) | Регион-Автоматика / Elcada-50-СТ54-ШУЗТ-3774-Ш | шт | 31866,18 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» ШУ-ЗТ 30кВт [63А], Uупр~220В, корпус навесной, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие Schneider-electric) | Регион-Автоматика / Elcada-63-СТ54-ШУЗТ-3874-Ш | шт | 32890,37 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» ШУ-ЗТ 37кВт [80А], Uупр~220В, корпус навесной, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие Schneider-electric) | Регион-Автоматика / Elcada-80-СТ54-ШУЗТ-3974-Ш | шт | 36729,87 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» ШУ-ЗТ 45кВт [100А], Uупр~220В, корпус навесной, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие Schneider-electric) | Регион-Автоматика / Elcada-100-СТ54-ШУЗТ-4074-Ш | шт | 42654,88 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» ШУ-ЗТ 75кВт [150А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие Schneider-electric) | Регион-Автоматика / Elcada-150-СТ54-ШУЗТ-4274-Ш | шт | 66094,75 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» ШУ-ЗТ 132кВт [265А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие Schneider-electric) | Регион-Автоматика / Elcada-265-СТ54-ШУЗТ-4574-Ш | шт | 130779,82 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» реверсивный ШУ-ЗТ-Р 22кВт [50А], Uупр~220В, корпус навесной, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие Schneider-electric) | Регион-Автоматика / Elcada-50-СТ54-ШУЗТР-3774-Ш | шт | 43884,98 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» реверсивный ШУ-ЗТ-Р 55кВт [115А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие Schneider-electric) | Регион-Автоматика / Elcada-115-СТ54-ШУЗТР-4174-Ш | шт | 73079,37 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» реверсивный ШУ-ЗТ-Р 75кВт [150А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие Schneider-electric) | Регион-Автоматика / Elcada-150-СТ54-ШУЗТР-4274-Ш | шт | 86335,83 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» реверсивный ШУ-ЗТ-Р 90кВт [160А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие Schneider-electric) | Регион-Автоматика / Elcada-160-СТ54-ШУЗТР-4374-Ш | шт | 118612,20 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» реверсивный ШУ-ЗТ-Р 110кВт [225А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие Schneider-electric) | Регион-Автоматика / Elcada-225-СТ54-ШУЗТР-4474-Ш | шт | 133032,63 RUB | |||
| Шкаф управления электродвигателем по схеме «звезда-треугольник» реверсивный ШУ-ЗТ-Р 160кВт [330А], Uупр~220В, корпус напольный, ввод-снизу, вывод-снизу, IP54, УХЛ4 (комплектующие Schneider-electric) | Регион-Автоматика / Elcada-330-СТ54-ШУЗТР-4574-Ш | шт | 221736,23 RUB | |||
88″>
89″>Что такое «звезда» и «треугольник» в электродвигателе | ЭТМ для профессионалов
Понятия «звезда» и «треугольник» неразрывно связаны с системами трёхфазного переменного тока, и начинающие электрики или люди далёкие от электричества не понимают значения этих слов и практического различия этих параметров. В этой статье мы поговорим о том, что такое звезда и треугольник в электродвигателе.
Теория и схемы
Чтобы избежать путаницы давайте рассматривать этот вопрос на примере трёхфазного асинхронного электродвигателя с короткозамкнутым ротором как самого распространенного из электрических машин в быту и на производстве. Как правило, у такого двигателя 3 обмотки, также встречаются многоскоростные двигатели и там количество обмоток больше трёх, но кратное этому числу.
У каждой обмотки есть начало и конец, а на схеме начало обмотки обычно обозначается точкой.
Но питающих провода в трёхфазной сети у нас 3 или 4. Отсюда возникает вопрос: «Как правильно соединить шесть концов обмоток с тремя питающими проводами?». Вот здесь как раз и всплывают эти «геометрические фигуры» — звезда и треугольник.
Итак, звезда и треугольник – это названия схем соединения потребителей в трёхфазной электросети как обмоток электродвигателей, трансформаторов, так и любой другой нагрузки.
«Звезда»
При соединении обмоток звездой к началам обмоток присоединяют питающие провода (на схемах обозначены цветами), а концы обмоток соединяют между собой в одну точку, при этом подключение нулевого проводника в точку соединения концов обмоток необязательно так как это симметричная нагрузка. В свою очередь, точка соединения концов обмоток также называется нейтралью.
Есть два варианта представления этого соединения на электрических схемах, как в наглядном виде, действительно напоминающем трёхлучевую звезду (А), так и в более классическом для схем представлении (Б). Вас не должно смущать это отличие, когда вы читаете схему.
«Треугольник»
По схеме треугольника начало следующей и конец предыдущей обмотки соединяются между собой, то есть: конец первой обмотки соединяется с началом второй, конец второй обмотки соединяется с началом третьей, а конец третьей с началом первой обмотки, а питающие провода подключаются к точкам соединения обмоток.
Итого у нас получается три точки соединения начал и концов обмоток и, соответственно, возможно подключение только трёх питающих фазных проводов без нулевого.
На схеме такое соединение также может быть нарисовано по-разному — наглядным и похожим на треугольник, или в горизонтальном или вертикальном исполнении.
Если говорить о подключении другой нагрузки, не относящейся к трансформаторам и электроприводу, то понятия «начало» и «конец» там нет, поэтому провода подключаются произвольно, но с сохранением логики соединения этих схем.
Мощность, ток и напряжение
Всем известно, что в электросети есть два напряжения: фазное — 220В и линейное — 380В. Здесь линейное напряжение больше фазного в 1.73 раза (корень квадратный из 3). Дело в том, что вторичная обмотка питающего трансформатора соединяется звездой и между фазой и нейтралью получаются те самые 220В, а между двумя разноименными фазами — 380В.
Но это справедливо не только для питающей сети, но и при распределении напряжения между потребителями. Поэтому давайте рассмотрим подробнее схему соединения обмоток звездой — как в ней распределяются токи и напряжения.
Как мы уже отметили выше в «звезде» есть два напряжения — фазное (Uф) и линейное (Uл), и при этом они соотносятся следующим образом:
Uл=1,73*Uф
Токи также бывают фазными и линейными, и в схеме звезды они равны.
Iл=Iф
В «треугольнике» дела обстоят подобным образом, но здесь, наоборот — линейное (Uл) и фазное (Uф) напряжения равны, но при этом линейный ток превышает фазный в 1,73 раза.
Uл=Uф
Iл=1,73*Iф
Распределение токов и напряжений между элементами цепи в схемах звезды и треугольникаРаспределение токов и напряжений между элементами цепи в схемах звезды и треугольника
На рисунке выше важно выделить, что при соединении обмоток звездой на каждую обмотку приходится напряжение в 1.73 раза меньше линейного напряжения в питающей сети, то есть для 380В – 220, для 220В – 127, для 660 — 380 вольт. Запомните это, чуть позже мы вернемся к этому вопросу.
Формулы мощности для цепей соединенной по схеме звезды и по схеме треугольника не отличаются.
· полная S = 3*Sф = 3*(Uл/√3)*I = √3*Uл*I;
· активная P = √3*Uл*I*cos φ;
· реактивная Q = √3*Uл*I*sin φ.
Практика – для чего нужны эти схемы
Большинство электриков работают с электрическими сетями напряжением 220/380 вольт, поэтому давай рассмотрим, какую схему соединения обмоток выбрать для подключения электродвигателя к такой электросети.
Трёхфазные асинхронные двигатели по способу подключения к электросети условно можно разделить на 2 больших группы: с возможностью изменения схемы соединения обмоток и без неё.
В первом случае на клеммник в брно электродвигателя выведено 6 проводов, и вы можете, в зависимости от напряжения в электросети, к которой подключаете выбрать нужную схему соединения обмоток.
Внешний вид клеммника в брно электродвигателя с тремя (сверху) и с шестью выводами (внизу)Внешний вид клеммника в брно электродвигателя с тремя (сверху) и с шестью выводами (внизу)
При этом обмотки соединяются в ту или иную схему с помощью медных шинок (или перемычек из провода, если шины потеряли), клеммы расположены таким образом, что с помощью всего трёх перемычек может быть собрана нужная схема (см. рисунок ниже).
Соответствие начал и концов обмоток клеммам, и соответствие положения перемычек между клеммами схемам подключения (звезде и треугольнику)Соответствие начал и концов обмоток клеммам, и соответствие положения перемычек между клеммами схемам подключения (звезде и треугольнику)
Хоть и это должен помнить и знать каждый электрик, тем не менее производители зачастую отливают либо же клеят этикетку с указанием положения перемычек для каждой из схем на крышке брно.
Собранные схемы звезды (сверху) и треугольника (снизу), обратите внимания положение перемычек указано на крышке (в правой части фотографий).Собранные схемы звезды (сверху) и треугольника (снизу), обратите внимания положение перемычек указано на крышке (в правой части фотографий).
Если же в брно выведено всего 3 провода, то обмотки двигателя уже соединены по какой-то схеме внутри его корпуса, и для переключения звезды и треугольника нужно вскрывать корпус, искать концы обмоток, разъединять их и соединять так, как вам нужно. Но это скорее процедура из «народного хозяйства», нежели часто встречающаяся производственная необходимость.
Какую схему выбрать и какая лучше?
Итак, как соединить обмотки звездой и треугольником мы разобрались, но здесь как раз и начинается «все самые интересные вопросы», причем эти вопросы у людей возникают чаще всего либо при подключении трёхфазного двигателя к однофазной сети, либо при подключении двигателя к частотному преобразователю с однофазным входом и линейными 220В на выходе и в других ситуациях.
Возможность изменения схемы соединения обмоток нужна для того, чтобы один и тот же двигатель мог эксплуатироваться в электросетях с различным напряжением.
Какую схему лучше выбрать? Вопрос не корректный, нужно соединять обмотки в ту схему, номинальное напряжение которой соответствует напряжению в электросети. Эта информация указана на шильдике электродвигателя.
Номинальные напряжения для треугольника и звезды на шильдикеНоминальные напряжения для треугольника и звезды на шильдике
Если на шильдике вашего двигателя указано как на фото выше «Δ/Y 220/380» — это значит что если линейное напряжение в питающей сети 220В – нужно соединять обмотки треугольником, если 380В – звездой. Если вы будете его подключать к однофазной сети 220В с конденсаторами – обмотки также соединяются треугольником.
Если на шильдике указано только одно напряжение и значок схемы (см. рисунок ниже), то возможности изменить схему соединения нет, и в брно, скорее всего, выведено будет 3 провода.
Встречаются и двигатели, которые в сети 380В работают, соединенными по схеме треугольника, схема звезды в этом случае рассчитана на работу в сети 660В, что вы можете наблюдать на следующей фотографии.
Но зачастую такие двигатели используются для пуска с переключением со звезды на треугольник, это делают для понижения пусковых токов.
660В – это линейное напряжение в схеме звезды, а 380В – фазное, то есть каждая из обмоток такого двигателя рассчитана на 380В. Это наглядно показано на рисунке «Распределение токов и напряжений между элементами цепи схемах звезды и треугольника» приведенного в первой половине статьи.
В этом случае напряжение 380В подаётся сначала на обмотки соединенные по схеме звезды, так как номинальное напряжение для этой схемы 660В двигатель в момент пуска питается от пониженного напряжения и к каждой из обмоток прикладывается всего по 220В.
Когда обороты двигателя возрастают, происходит переключение на треугольник. И уже к каждой обмотке прикладываются их номинальные 380В.
Схема подключения электродвигателя с переходом со звезды на треугольник при пуске
Схема подключения электродвигателя с переходом со звезды на треугольник при пускеСхема подключения электродвигателя с переходом со звезды на треугольник при пуске
Что будет если перепутать звезду и треугольник?
Чтобы ответить на этот вопрос вспомним формулы мощности трёхфазной нагрузки:
· полная S = 3*Sф = 3*(Uл/√3)*I = √3*Uл*I;
· активная P = √3*Uл*I*cos φ;
· реактивная Q = √3*Uл*I*sin φ.
Для упрощения представим, что у нас есть сеть с каким-то определенным напряжением, пусть это будет 220/380 вольт, а также есть 3 лампы накаливания с номинальным напряжением 220В. И еще раз посмотрим на рисунок с распределением напряжений и токов в звезде и треугольнике.
Так как линейное напряжение у нас 380В, а в «звезде» фазное в 1.73 раза ниже линейного, то делаем вывод, что для работы в номинальном режиме нужно подключить эти лампочки звездой, тогда к каждой из них будет приложено 220В.
Теперь соединим их в треугольник, и что получится? Первое что бросается в глаза – к каждой лампе приложено уже 380В вместо 220В номинальных.
Несложно догадаться, что в этом случае наши лампочки просто сгорят, то же самое произойдет и с обмоткой двигателя.
Что при этом происходит с мощностью?
Если питающее напряжение и нагрузка неизменны, то при переключении со звезды на треугольник мощность, выделяемая на этой самой нагрузке, возрастёт в 3 раза. Это происходит потому, что напряжение на каждой лампе увеличилось в 1.73 раза, за ним настолько же вырос и ток.
Формулы для вычисления мощности в обоих случаях одинаковые, но цифры в них различаются, давайте проведем 1 расчет для примера.
Допустим, ток нагрузки в схеме звезды у нас был 1А, тогда полная мощность в звезде равна:
S = √3*Uл*Iл;
S=1.73*380В*1А=657,4 ВА
При этом мощность одной лампы в этом случае равна 220 ВА.
В треугольнике к каждой лампе приложено напряжение в 1.73 раза выше – 380В, соответственно и ток через лампу (фазный ток) возрастет на столько же. При этом не забывайте, что линейный ток в звезде и так будет в 1.73 раза больше, чем фазный. Найдем полную мощность по трём фазам:
S=√3*Uл*Iл=1.73*380В*(1.73А*1.73) = 1.73*380В*3А=1972 ВА
А на одной лампе выделится мощность равная:
W=380В*1.73А=657 ВА
Но это не значит, что при соединении по схеме треугольника двигатель будет выдавать в 3 раза большую мощность, при питании от номинального для этой схемы напряжения двигатель будет выдавать свою номинальную мощность.
Небольшое отступление от автора — я неоднократно сталкивался с фразами на форумах типа «на треугольнике двигатель работает мягче», «на звезде лучше тянет» или подобные. Однако эти фразы не несут за собой подкрепления какими-либо техническими или научными комментариями. И мне так и не удалось найти, откуда это пошло и почему, никто объяснить так и не смог (если вы можете аргументировано ответить о причинах таких высказываний – пишите об этом в комментариях, интересно почитать).
Алексей Бартош специально для ЭТМ
Электротехника: Расчёт с преобразованием звезда-треугольник
В статье «расчет сопротивления схемы с преобразованием треугольник-звезда» рассчитывалось сопротивление схемы на рисунке 1 относительно точек А и В.Рисунок 1 — Схема
Для упрощения расчёта было применено преобразование треугольника R1, R2, R3 в звезду. Для упрощения расчёта данной схемы можно также применить преобразование звезды образованной элементами R1, R3, R6 в треугольник. Преобразуем звезду R1, R3, R6 в треугольник R16, R31, R36:
Рисунок 2 — Схема с преобразованной звездой R1, R3, R6 в треугольник R16, R31, R36.
Исходные данные будут такими же как и в статье где выполнялось преобразование треугольник-звезда: R1=20, R2=20, R3=10, R4=20, R5=8, R6=4, R7=4.
Сопротивления резисторов R16, R31, R36 находятся по формулам:
Для нахождения сопротивления стороны треугольника нужно найти сумму сопротивлений прилегающих к данной стороне лучей звезды и произведения этих сопротивлений деленного на сопротивление оставшегося луча.
В схеме на рисунке 2 можно заменить параллельное соединение элементов R31 и R2 одним элементом R312 а параллельное соединение элементов R36 и R7 одним элементом R367:
Рисунок 3 — Схема с замененными параллельными соединениями элементов
Сопротивления резисторов R312 и R367 рассчитываются по формулам:Заменим последовательное соединение элементов R312 и R367 одним элементом R312367:
Рисунок 4 — Схема с преобразованным последовательным соединением R312 и R367
Сопротивление R312367 определяется по формуле:
Преобразуем параллельное соединение элементов R312367 и R16 одним элементом R16IIR312367:
Рисунок 5 — Схема с резистором R16IIR312367
Сопротивление R16IIR312367 находиться по формуле:
Схему на рисунке 5 можно преобразовать к одному элементу сопротивление которого будет равно сопротивлению схемы на рисунке 1 относительно точек А и В, для этого выражение для преобразования последовательного соединения элементов R5 и R16IIR312367 подставим в выражение для параллельного соединения R4 с последовательным соединением R5 и R16IIR312367.
Рисунок 6 — Эквивалентное сопротивление схемы 1
Rэ находиться по формуле:
Основы электротехники и электроники: Курс лекций, страница 7
Вернемся к схеме на Рис. 9.2. Здесь эквивалентное сопротивление двух параллельных ветвей:
.
Ток, втекающий в узел, – это, несомненно, . Согласно правилу параллельного разброса:
.
.
Теперь находим составляющие токов, создаваемых источником ЭДС. Для этого удаляем из схемы источник тока. Так как внутреннее сопротивление источника тока бесконечно велико, на его месте (между точками a и b) оставляем разрыв (Рис. 9.4).
Рис. 9.4
Цепь на Рис. 9.4 – это одноконтурная цепь. Здесь
,
.
С другой стороны, ток можно найти по закону Ома:
.
Наконец, находим реальные токи (см. Рис. 9.1):
.
Метод наложения не может использоваться для расчета мощности, поскольку мощность пропорциональна не току, а квадрату тока.
Заметим также, что метод наложения применим только к линейным цепям.
10. ПРЕОБРАЗОВАНИЕ ЗВЕЗДЫ В ТРЕУГОЛЬНИК И ТРЕУГОЛЬНИКА В ЗВЕЗДУ
Соединение трех сопротивлений, имеющее вид трехлучевой звезды (Рис. 10.1а), называют звездой, а соединение трех сопротивлений, при котором они образуют стороны треугольника (Рис. 10.1б), называют треугольником. В узлах 1, 2, 3 звезда и треугольник соединяются с остальной частью схемы (не показанной на рисунках).
а)
б)
Рис. 10.1
Токи, подтекающие к узлам 1, 2, 3, имеют обозначения . Потенциалы узлов 1, 2 и 3 – .
Часто при расчетах электрических цепей необходимо преобразовывать треугольник в звезду или звезду в треугольник. Если преобразование выполнить таким образом, что потенциалы узлов 1, 2, 3 и токи, подтекающие к этим узлам, останутся неизменными, то вся внешняя схема «не заметит» произведенной замены. Формулы преобразований получим из законов Ома и Кирхгофа.
Для звезды по первому закону Кирхгофа:
. (10.1)
Здесь и далее знак над током означает, что формула относится к звезде.
Но, с другой стороны, из закона Ома получаем соотношения:
. (10.2)
Подставим (10.2) в (10.1) и найдем :
. (10.3)
Так как в треугольнике нет узла 0, исключим потенциал этого узла из соотношений (10.2). Для этого подставляем (10.3) в (10.2) и, в частности, для тока получим выражение:
. (10.4)
Для треугольника по первому закону Кирхгофа:
. (10.5)
Здесь и далее знак над током означает, что формула относится к треугольнику.
Так как токи, подтекающие извне к звезде и треугольнику, равны, приравняем и из (10.4) и (10.5). Проделаем эту операцию и для других токов и после преобразований получим:
,
, (10.6)
, (10.7)
. (10.8)
Из выражений (10.6-10.8) получаются формулы сопротивлений при преобразовании звезды в треугольник:
, (10.9)
, (10.10)
. (10.11)
Из полученных формул выводятся обратные, для преобразования треугольника в звезду:
, (10.12)
, (10.13)
. (10.14)
Чтобы запомнить и правильно использовать формулы (10.9-10.14), можно порекомендовать следующий прием.
При преобразовании звезды в треугольник установить два пальца в те узлы, к которым будет подсоединяться ветвь треугольника. Искомое сопротивление ветви треугольника будет равно сумме сопротивлений лучей звезды, подходящих к пальцам, плюс произведение этих сопротивлений, деленное на сопротивление оставшегося луча.
При преобразовании треугольника в звезду установить один палец в тот узел, к которому будет подсоединяться луч звезды. Искомое сопротивление луча звезды – это произведение сопротивлений ветвей, подходящих к пальцу, деленное на сумму сопротивлений всех трех ветвей треугольника.
Если сопротивления всех ветвей звезды или треугольника равны, такие звезда и треугольник называются симметричными. Сопротивления ветвей эквивалентных симметричных звезды и треугольника связаны соотношением, которое можно вывести из (10.9-10.14):
.
Пример 10.1:
Решить задачу (Рис. 10.2).
Рис. 10.2
Преобразуем звезду R4, R5, R6 в эквивалентный треугольник Rab, Rbc, Rac (Рис. 10.3).
Рис. 10.3
Рассчитываем параметры треугольника:
.
Сворачиваем сопротивления параллельных ветвей:
.
Сворачиваем все сопротивления в одно эквивалентное:
.
Находим ток по закону Ома:
.
11. СВЕРТКА ПАРАЛЛЕЛЬНЫХ ВЕТВЕЙ В ОДНУ ЭКВИВАЛЕНТНУЮ
Пусть несколько параллельных ветвей (с источниками и без) располагаются между ветвями a и b (Рис. 11.1 а). При этом извне в узел a втекает ток I, а из узла b этот же ток вытекает. Заменим эти параллельные ветви одной эквивалентной, содержащей ЭДС Eэкв и сопротивление Rэкв (Рис. 11.1 б).
а)
б)
Рис. 11.1
Для этого запишем уравнения по первому закону Кирхгофа и закону Ома для параллельных ветвей:
, (11.1)
, (11.2)
, (11.3)
Познакомьтесь с Летним треугольником | Сегодня вечером
Яркие звезды Вега, Денеб и Альтаир образуют Летний треугольник, который легко обнаружить.Вега, Денеб и Альтаир
Летний треугольник — это астеризм, а не созвездие. Он состоит из трех ярких звезд в трех разных созвездиях. Эти звезды — Вега, Денеб и Альтаир. Мы в Северном полушарии можем видеть Летний треугольник часть ночи в любое время года. Но увидеть его летом — самое интересное! Это наиболее заметно в северном летнем сезоне.Итак, когда сумерки переходят в ночь теплой июньской или июльской ночью, посмотрите на восток в поисках этого огромного звездного узора.
Трудно передать огромные размеры Летнего треугольника. С наступлением темноты северным летом ищите самую яркую звезду на восточном небе. Это будет Вега, самая яркая звезда в созвездии Лира-Арфа.
Посмотрите на левую нижнюю часть Веги, чтобы увидеть еще одну яркую звезду. Это Денеб, ярчайшая звезда в созвездии Лебедя и Лебедя и третья по яркости звезда Летнего треугольника.Вытянутая рука на расстоянии вытянутой руки приблизительно равна расстоянию от Веги до Денеба.
Посмотрите в нижний правый угол от Веги, чтобы найти вторую по яркости звезду Летнего треугольника. Это Альтаир, самая яркая звезда в созвездии Орла Аквилы. Линейка на расстоянии вытянутой руки (12 дюймов или 30 см) заполняет промежуток между этими двумя звездами.
Летний треугольник, запечатленный и составленный нашей подругой Сьюзен Гис Дженсен в Одессе, Вашингтон.Летний треугольник как дорожная карта к Млечному Пути
Если вам посчастливится оказаться под темным небом в безлунную ночь, вы увидите огромную полосу звезд, известную как Млечный Путь, проходящую между звездами Летнего треугольника Вега и Альтаир.Звезда Денеб качается посреди этой звездной реки, которая проходит через Летний треугольник и изгибается по небу. Хотя каждая звезда, которую вы видите невооруженным глазом, на самом деле является членом нашей галактики Млечный Путь, часто термин Млечный Путь относится к поперечному сечению галактического диска, на котором бесчисленные далекие солнца собираются в облачный след. звезд.
Когда вы освоите Летний треугольник, вы всегда сможете найти Млечный Путь ясной темной ночью.Как насчет того, чтобы максимально использовать темную летнюю ночь, чтобы исследовать эту звездную полосу, этот залитый звездами бульвар, изобилующий небесными прелестями? Воспользуйтесь биноклем, чтобы рассмотреть тонкую красоту всего этого, призрачные туманности и звездные скопления из снов в летнюю ночь!
Некоторые видят в Летнем треугольнике большую букву «V» для отпуска , где Альтаир отмечает точку «V». Летом Летний треугольник появляется на востоке с наступлением темноты, высоко над головой после полуночи и на западе на рассвете.Всю ночь в летнюю ночь звезды Летнего треугольника — словно школьники на каникулах — вальсируют среди фонарей галактики Млечный Путь.
Посмотреть больше. | Великий Разлом Млечного Пути проходит через созвездие Кассиопеи и Летний треугольник.Летний треугольник как сезонный календарь природы
Летний треугольник служит звездным календарем, отмечающим времена года. Когда звезды Летнего треугольника освещают восточные сумеречные сумерки с середины до конца июня, это верный признак смены времен года, смены весны на лето.Однако, когда Летний треугольник виден высоко на юге в сумерках и ранним вечером, изменение положения Летнего треугольника указывает на то, что лето перешло в осень.
Итог: Как найти Летний треугольник — астеризм или заметный звездный узор — состоящий из трех ярких звезд Вега, Денеб и Альтаир.
Наборы для астрономииEarthSky идеально подходят для новичков. Закажите сегодня в магазине EarthSky
Нравится ли вам EarthSky? Подпишитесь на нашу бесплатную ежедневную рассылку новостей сегодня!
Пожертвовать: Ваша поддержка значит для нас весь мир
Брюс МакКлюр
Просмотр статейОб авторе:
Брюс МакКлюр работал ведущим автором популярных страниц «Сегодня вечером» на EarthSky с 2004 по 2021 год, когда он выбрал заслуженную пенсию.Он страстный поклонник солнечных часов, чья любовь к небу привела его к озеру Титикака в Боливии и плаванию в Северной Атлантике, где он получил свой сертификат астрономии в Школе океанского парусного спорта и навигации. Он также написал и организовал общественные астрономические программы и программы планетария в своем доме в северной части штата Нью-Йорк и вокруг него.
Летний треугольник | Фотографии, расположение, звезды и значение
Летний треугольник
Летний треугольник — это астеризм, который включает в себя три яркие звезды на ночном небе: Вегу, Денеб и Альтаир.Этот маяк более теплой погоды наблюдается в северном полушарии большую часть года, но самый высокий в небе наблюдается в июле-августе.
Каждая звезда Летнего треугольника является частью своего созвездия Лиры, Лебедя и Аквилы. Все они самые яркие звезды в созвездии, а Вега — вторая по яркости звезда в северном небесном полушарии. Единственная звезда в северном полушарии ярче Веги — это Сириус Большого Пса.
На этом изображении Млечного Пути с большой выдержкой видны 3 звезды Летнего треугольника.
Термин «Летний треугольник» популяризировал британский астроном Патрик Мур в 1950-х годах, хотя его образование было отмечено многими другими исследователями еще в 1800-х годах. Это имя можно найти в путеводителях по созвездиям еще в 1913 году.
Несмотря на то, что его называют «Летним» треугольником, те из нас, кто живет в северном полушарии, могут фактически наблюдать этот астеризм в течение части ночи в в любое время года.
Летний треугольник — один из нескольких астеризмов в ночном небе.Астеризмы — это, по сути, прозвище звездных образований, не являющихся созвездиями. Они могут охватывать несколько созвездий, как Летний треугольник, или вписываться в созвездие. Большая Медведица является прекрасным примером этого, поскольку этот астеризм является частью гораздо более крупного созвездия Большой Медведицы (Большая Медведица).
Созвездия и астеризмы интересно фотографировать с помощью цифровой зеркальной камеры и широкоугольного объектива. Часто они слишком велики, чтобы их можно было запечатлеть в телескоп, поскольку они лучше подходят для объектов глубокого космоса, обнаруженных внутри астеризма.
В статье Sky and Telescope я обнаружил, что самое раннее «официальное» письменное упоминание о Летнем треугольнике было только в 1839 году, когда австрийский астроном Иоганн Йозеф фон Литтроу в Атласе звездных небес заявил:
». . . Вы сразу можете распознать очень яркий, большой равнобедренный треугольник на небе, который образован тремя звездами первой величины, а именно Вегой, Денебом и Альтаиром ».
В моей фотографии Летнего треугольника использовался объектив Rokinon 14mm F / 2.8 (Amazon).
Как найти летний треугольник
Летний треугольник огромен и простирается через Великую трещину Млечного Пути. Он касается нескольких созвездий, но его легко идентифицировать, если вы понимаете масштаб этого звездного узора.
Вы, вероятно, сначала заметите самую яркую звезду в треугольнике, Вегу. Вега — вторая по яркости звезда в северном небесном полушарии, ярче только Арктур.
Из Веги отправляйтесь в созвездие Лебедя и найдите самую яркую звезду на Северном Кресте.Это Денеб, звезда номер 2 в нашем звездном образе.
Наконец, мы направляемся в летнее созвездие Орла Аквилы, чтобы завершить узор треугольника. Альтаир — вторая по яркости звезда в Летнем треугольнике, и по обе стороны от него расположены две более тусклые звезды.
Лучший способ насладиться Летним треугольником — это выехать из города и отправиться за город безлунной ночью. Этот астеризм обрамляет заполненный звездами яркий участок Млечного Пути.
Примечательной особенностью этой области является Звездное Облако Лебедя, которое интенсивно светится между Денебом и двойной звездой Альбирео.Те, кто пользуется биноклем, могут оценить этот богатый звездами район нашей Галактики, посмотрев в сторону основания Северного Креста.
Еще одна памятная достопримечательность — близлежащий Северный угольный мешок, который является частью Великой трещины в Млечном Пути. Туманность Воронкообразное Облако (как ее называют Небо и Телескоп) находится к востоку от Денеба, которая также является безымянной темной туманностью, расположенной здесь.
Звезды в Летнем треугольнике:
1. Вега- Созвездие: Лира
- Абсолютная звездная величина: 0.03
- Расстояние: 25 световых лет
- Созвездие: Лебедь
- Величина: 1.25
- Расстояние: 1500 световых лет
- Созвездие: Аквила
- Величина: 0.77
- Расстояние: 1500 световых лет
Когда можно увидеть Летний треугольник?
В северном полушарии в июне Летний треугольник с наступлением темноты начинает показывать свои 3 яркие звезды на восточном небе.Это один из лучших моментов, чтобы наблюдать и наслаждаться этим звездным узором, поскольку он всю ночь путешествует по ночному небу.
По мере смены сезонов меняются и позиции Веги, Денеба и Альтаира. Поздней осенью и зимой эти 3 звезды появляются высоко в небе на западе, а самая южная звезда (Альтаир) заходит примерно в 22:00.
Денеб
Для фотографии ниже использовался объектив Rokinon 14mm F / 2.8 для Canon EOS. Изображения были сделаны с сайта Bortle Scale Class 2 на вечеринке Cherry Springs Star Party в 2018 году.Я обозначил некоторые из самых популярных объектов глубокого космоса на Лебеде, хотя на этом широкоугольном изображении они довольно малы.
Объекты глубокого неба в Лебеде рядом с яркой звездой Денеб.
Вот более пристальный взгляд на туманность Северная Америка в Лебеде с помощью телеобъектива 300 мм. NGC 7000 находится чуть ниже Денеба, поэтому ее очень легко найти и сфотографировать. Эта туманность очень тусклая при визуальном наблюдении, но очень хорошо видна на изображении с длинной выдержкой.
Изображения Летнего треугольника, сделанные с использованием методов астрофотографии, которые улучшают отношение сигнал / шум, несомненно, будут содержать следы областей водородной эмиссионной туманности в Лебеде.
Туманность Северная Америка и стена Лебедя недалеко от Денеба.
Лебедь — не единственное созвездие, связанное с Летним треугольником с захватывающими объектами глубокого космоса внутри. В Лире есть несколько примечательных целей, в том числе известная планетарная туманность, известная как Мессье 57, или, чаще, Кольцевая туманность. .
Вега
Вега — голубовато-белая звезда главной последовательности с величиной 0,03. В северном полушарии он поразительно яркий и заметный на ночном небе. Вега в 40 раз ярче Солнца и является одной из самых ярких звезд в окрестностях нашей Солнечной системы.
С точки зрения астрофотографии Vega имеет ряд преимуществ. Это отличная звезда для фокусировки телескопа с маской Бахтинова, потому что она очень яркая.Сверхдлинные дифракционные звезды, созданные Vega, могут помочь вам добиться точной фокусировки вашего телескопа.
Еще одно преимущество Vega для астрофотографии — ее удобное расположение на ночном небе для выравнивания звезд. Для калибровки точности наведения опоры телескопа GoTo можно использовать процедуру юстировки по трем звездам. Поскольку Вега такая яркая и простирается высоко в небо, это одна из самых полезных звезд выравнивания, которые вы могли бы использовать.
Фактически, каждая из 3 звезд, образующих Летний треугольник, — удобный выбор, когда дело доходит до юстировки монтировки телескопа.В ограниченном пространстве, таком как внутренний дворик на заднем дворе, есть большая вероятность, что хотя бы одна из этих звезд будет видна большую часть времени года.
Мессье 57 (туманность Кольцо) находится в созвездии Лиры, недалеко от Веги.
Альтаир
Альтаир можно идентифицировать как яркую звезду в Аквиле с двумя более тусклыми звездами на каждой стороне. Я часто использую Альтаир во время процесса выравнивания звезд на моем экваториальном телескопе. Ядро Млечного Пути начинает впечатляюще проявляться чуть ниже Альтаира в северном полушарии.
Будучи самой южной звездой в этом астеризме, она также первая звезда, которая зайдет в конце ноября около 22:00. Восходящий астеризм Летнего треугольника в конце весны означает возвращение лета в северном полушарии, а исчезающий треугольник на западе означает, что здесь зима.
Астрофотография
Если вы хотите сфотографировать астеризм Летнего треугольника и красивые области туманностей и звезд, которые его окружают, темное небо окажет наибольшее влияние на ваш снимок.Раньше я пытался сфотографировать этот район из города (см. Фото ниже), но широкоугольные снимки невероятно сложны в районах с сильным световым загрязнением.
Лучше всего использовать цифровую зеркальную камеру в ручном режиме лампы, так как вам нужно экспонировать изображения в течение полных 30 секунд, чтобы позволить как можно большему количеству звездного света попасть на датчик. Мне нравится использовать баланс белого при дневном свете при съемке широкоугольных фотографий ночного неба, хотя обычно я все равно корректирую цветовой баланс при постобработке.
При съемке астрофотографических изображений с помощью цифровой зеркальной камеры важно всегда снимать в формате RAW, чтобы собрать максимальный объем данных. У вас будет гораздо больше контроля над изображением на этапах обработки с RAW над сжатым изображением .JPG. Объединение нескольких изображений в такое приложение, как DeepSkyStacker, действительно может помочь улучшить соотношение сигнал / шум (SNR) вашего окончательного изображения.
Широкоугольный объектив камеры, такой как Rokinon 14mm F / 2.8 или аналогичный — идеальный вариант, потому что такой объектив камеры может записывать большое количество сигнала за одну экспозицию. Хотя этот объектив очень светосильный, я не делал снимков с широко открытым объективом с F / 2.8. Для получения более резкого изображения я настроил кольцо управления ручной диафрагмой (соотношением f) объектива на F / 3,2. Следующее изображение было создано путем наложения 40 x 2-минутных экспозиций при ISO 1600 .
Млечный Путь к Лебедю, показывая Великий Разлом. Общая выдержка 1 час 20 минут.Щелкните, чтобы увеличить версию.
Использовалась камера Canon EOS Rebel T3i с модификацией полного спектра. Нет необходимости модифицировать камеру для астрофотографии (подробнее об этом здесь), но это поможет выявить гораздо больше красных водородно-альфа-туманностей в ночном небе. На фотографии выше это наиболее заметно в Лебеде, а именно в туманности Северная Америка, в регионе Садр и даже в туманности Слоновий хобот в Цефеусе.
Широкоугольная фотография Млечного Пути — одна из моих любимых дисциплин в хобби, и она возможна с использованием цифровой зеркальной камеры начального уровня и доступного широкоугольного объектива.
Связанное сообщение: Использование цифровой зеркальной камеры Canon EOS Rebel для астрофотографии
Звездный трекер не является необходимым для получения отличного изображения Летнего треугольника, но он, безусловно, поможет. Устройство слежения за камерой, такое как iOptron SkyTracker Pro, — это простой способ компенсировать вращение Земли и избежать появления следов звезды на ваших изображениях. При точном полярном выравнивании вы можете рассчитывать на получение изображений за 2-3 минуты (без управления) с помощью широкоугольного объектива камеры.
В конце концов, те же самые передовые методы, которые используются для получения изображений глубокого неба с помощью телескопа, применимы к широкоугольным фотографиям с помощью объектива камеры.Захватите как можно больше четких изображений и объедините их, чтобы усилить сигнал и уменьшить шум. Затем остается лишь немного растянуть данные в Photoshop, чтобы увеличить насыщенность и применить дополнительные настройки, такие как сведение к минимуму звезд.
Астрофотография города. Моя лучшая попытка создать этот астеризм под залитым светом небом.
Итог
Для меня Летний треугольник означает сердце летнего сезона астрофотографии, где ночи короткие и теплые.Это одно из лучших времен года, чтобы насладиться астрономией, потому что вы можете комфортно сидеть под звездами до поздней ночи.
После того, как вы познакомитесь с этим астеризмом, будет трудно игнорировать его всякий раз, когда вы увидите его в ночном небе. Поделитесь этой информацией со своими друзьями и семьей, чтобы они тоже могли глубже оценить наше невероятное ночное небо.
Чтобы узнать, как делать широкоугольные изображения ночного неба с помощью цифровой зеркальной камеры и объектива, ознакомьтесь с 7 моими лучшими советами по астрофотографии для начинающих.
Другие астеризмы в ночном небе
Астеризмы, подобные «Летнему треугольнику», — это альтернативные названия, данные образцу ярких звезд на ночном небе. Эти «связанные» звезды часто являются частью созвездия и будут различаться в зависимости от культуры и местоположения.
Наш разум творчески ищет узоры в пунктирных звездах на ночном небе, и некоторые люди видят, как нарисованы другие фигуры, чем другие. Например, Сью Френч ссылается на астеризм «Челюсти», о котором говорилось в книге: The Deep Sky: An Introduction в этой занимательной статье «Небо и телескоп».
Астеризм Челюсти в Деве — Сью Френч
Вот некоторые из самых известных астеризмов в ночном небе:
- Пояс Ориона
- Большая Медведица или Плуг
- Зимний шестигранник
- Каскад Кембла
- Великий алмаз
- Меч Ориона
- Алмазный крест
- Эйфелева башня
- Шляпа Наполеона
Полезные ресурсы:
Астеризм Зимнего Треугольника | Факты, информация, история и определения
Астеризм Зимнего Треугольника, также известный как Большой Южный Треугольник, представляет собой выдающийся астеризм, образованный Сириусом, Бетельгейзе и Проционом, главными звездами в трех зимних созвездиях Большого Пса, Ориона и Малого Пса.
Основные факты и резюме- Зимний треугольник — заметный астеризм в ночном небе в северном полушарии в зимние месяцы, с декабря по март.
- Астеризм Зимнего треугольника значительно меньше астеризма Летнего треугольника, который образован известными летними звездами Вега, Альтаир и Денеб и затмевается большим Зимним шестиугольником, также известным как Зимний круг, который доминирует в небе в зима.
- Зимний треугольник почти равносторонний и имеет две вершины — звезды Сириус и Процион, с Зимним шестиугольником.
- Бетельгейзе находится в центре Зимнего шестиугольника, примерно между Проционом и Альдебараном, но не является частью более крупного зимнего астеризма.
- Три звезды, образующие Зимний треугольник, являются одними из самых ярких звезд на ночном небе. Звезды Зимнего треугольника — это Сириус, самая яркая звезда на ночном небе, красный сверхгигант Бетельгейзе, которая является девятой по яркости звездой в небе, и Процион, восьмая по яркости звезда на ночном небе.
- Звезды Зимнего треугольника легко найти, поскольку они очень яркие и расположены в непосредственной близости от Пояса Ориона, одного из самых известных астеризмов в небе.
- Бетельгейзе, звезда на левом плече Ориона, находится чуть выше Альнитака, самой восточной звезды Пояса.
- Сириус можно найти, следуя линии, образованной звездами Пояса на юго-востоке, а Процион находится в верхнем левом углу Сириуса.
- Зимний треугольник полезен для поиска зимней части Млечного Пути в небе.
- Астеризм Зимнего треугольника также полезен при поиске множества известных объектов глубокого космоса, таких как скопление в форме сердца, туманность Конус, скопление рождественской елки, Мессье 41, Мессье 46, Мессье 47, Мессье 93 или Мессье 48.
В зимние месяцы астеризм Зимнего треугольника отчетливо виден в ночном небе из северного полушария. Это воображаемый равносторонний треугольник, нарисованный на небесной сфере с определяющими вершинами в Сириусе, Бетельгейзе и Проционе.
Эти три звезды являются главными звездами в своих созвездиях — Большого Пса, Ориона и Малого Пса соответственно. Этот астеризм часто используется для поиска других интересных объектов дальнего космоса.
ВидимостьАстеризм Зимнего треугольника виден большую часть ночи в северном полушарии, когда он находится высоко в небе в средних северных широтах, с декабря по март.
Однако Зимний треугольник также можно увидеть осенью ранним утром на востоке. Весной Зимний треугольник виден на западе ранним вечером еще до того, как его звезды зайдут за горизонт.
В южном полушарии Зимний треугольник в летние месяцы кажется перевернутым и ниже в небе. Зимний треугольник окружает большую часть слабого созвездия Единорога.
Две звезды в Зимнем треугольнике имеют вторую величину, а Сириус — самая яркая звезда на небе.Другие звезды зимнего неба лежат вокруг Зимнего треугольника, такие как Ригель — в Орионе, Альдебаран — в Тельце, Кастор и Поллукс в Близнецах и Капелла в Возничего.
Зимний треугольник Объекты дальнего космосаЯсной ночью полоса нашей галактики видна слева от Бетельгейзе и Сириуса и справа от Проциона. Он простирается до северо-запада неба через больший Зимний шестиугольник, между яркими звездами Альдебаран в Тельце и Капеллой в Возничего.
Зимний треугольник, таким образом, полезен для поиска многих интересных объектов глубокого космоса, поскольку они находятся в одной и той же области неба. К ним относятся скопление в форме сердца (Мессье 50), туманность Конус, скопление Рождественская елка в созвездии Единорога, Мессье 41, скопление Тау Canis Majoris, скопление Каролины в Большом Псове или рассеянные скопления Мессье 46, Мессье 47, Мессье. 93 в созвездии Пупписа и Мессье 48 в созвездии Гидры.
Звезды Зимнего треугольникаТри звезды, образующие астеризм Зимнего треугольника, — это Сириус, Бетельгейзе и Процион.Они входят в число самых известных и ярких звезд на ночном небе.
СириусСириус, обозначаемый как Alpha Canis Majoris, является самой яркой звездой в созвездии Большого Пса и самой яркой звездой на ночном небе.
Сириус — двойная звезда с видимой величиной -1,46, она вдвое ярче Канопуса, второй по яркости звезды Большого Пса. Сириус примерно в 25 раз ярче, чем наше Солнце, и он расположен примерно в 8 раз.В 6 световых годах от Земли.
Основная звезда звездной системы Сириуса, Сириус A, является звездой главной последовательности спектрального класса A0 или A1. Она на 200% массивнее нашего Солнца и имеет около 171% радиуса, что более чем в два раза горячее, чем наше Солнце.
Сириус сопровождает слабый белый карлик-компаньон, самый первый из обнаруженных белых карликов, обозначенный как Сириус B. Сириус B примерно на 100000 слабее, чем Сириус A. Древние знали Сириус, а некоторые записи датируются еще 4000 лет назад.
В 1868 году Сириус стал первой звездой, скорость которой была измерена. Он приближается к нашей Солнечной системе, и поэтому его яркость увеличивается. Примерно к 9000 году Сириус больше не будет виден из Северной и Центральной Европы.
Сириус — ближайшая к Земле звезда из звезд Зимнего треугольника и самая яркая, но только из-за ее близости к нам. Бетельгейзе затмила бы Сириус, будь он ближе к нам.
БетельгейзеБетельгейзе, обозначаемая как Альфа Ориона, является второй по яркости звездой Ориона, иногда превосходя по яркости Ригель, самую яркую звезду в созвездии.Бетельгейзе — красный сверхгигант полурегулярной переменной звезды с видимой величиной от +0,0 до +1,13. У нее самый широкий диапазон разной величины среди звезд первой величины, она является девятой по яркости звездой на ночном небе.
Бетельгейзе находится на расстоянии около 640 световых лет от Земли, а ее яркость составляет от 90 000 до 150 000 раз больше яркости нашего Солнца. Бетельгейзе — одна из крупнейших известных нам звезд, ее радиус составляет около 88,700% радиуса нашего Солнца и 1160% его массы.
Из-за своего размера Бетельгейзе холоднее нашего Солнца: средняя температура поверхности около 3500 К. Звезда окружена сложной оболочкой — туманностями, примерно в 250 раз превышающими ее размер.
Эта оболочка образовалась вокруг Бетелегейзе из-за ее утраченной массы, так как Бетельгейзе теряет около 1 солнечной массы каждые 10 000 лет. Бетельгейзе — самая далекая звезда из звезд Зимнего треугольника.
ПроционПроцион, обозначаемый как Альфа Малого Пса, является самой яркой звездой в созвездии Малого Пса и обычно восьмой по яркости звездой в ночном небе с визуальной величиной 0.34.
Процион — двойная звездная система, состоящая из Проциона А, который представляет собой белую звезду главной последовательности, и Проциона B, слабого белого карлика. Эта звездная система расположена на расстоянии около 11,45 световых лет от нас, Процион — вторая по близости к нам звезда из звезд Зимнего треугольника.
Основная звезда, Процион A, имеет около 150% массы нашего Солнца и примерно в семь раз ярче. В средневековый период Процион, наряду с Сириусом, был среди пятнадцати бехенских неподвижных звезд, используемых в магических ритуалах.
Помимо астеризма Треугольника Винера, Процион также отмечает одну из вершин большего Зимнего шестиугольника. Этот Шестиугольник или Зимний Круг — это Процион, Сириус, Поллукс, Капелла, Возничий, Альдебаран и Ригель.
Знаете ли вы?- Для полинезийцев, проживающих в основном в Южном полушарии, восхождение Сириуса ознаменовало приход зимы и было важным ориентиром для их навигации по Тихому океану.
- Восход Сириуса также ознаменовал разлив Нила в Древнем Египте.
- Процион достигает своей кульминации в полночь 14 -го января.
- В македонском фольклоре Сириус и Процион были известны как «волки» — Волчи — кружащие на плуге с волами, представленные созвездием Ориона, небесного охотника.
- Википедия
- Constellation-guide
- Earthsky
звёзд
Что такое звезда?
| …… | Если вы посмотрите энциклопедию, вы найдете несколько значений
слова звездочка : > «небесное тело» |
Вы можете определить: Звезда — это фигура, которая обычно состоит из
выпуклого многоугольника с треугольниками по бокам.
Треугольники называются точками.
Производство звезд наверху
Есть разные способы сделать звезду.
1-я возможность
Вы берете правильный многоугольник и
установите по бокам равносторонние треугольники.
2-й вариант:
Вы берете правильный многоугольник и отразите основные треугольники многоугольников по бокам. Эта процедура не приводит к звезде, если начать с треугольник или квадрат.
3-я возможность:
Вы берете правильный многоугольник с п углов и повернуть на 180 / п. Происхождение и образ вместе образуют звезду.
4-я возможность:
Создайте многоугольник и нарисуйте специальные диагонали. Они образуют звезды. Правильные многоугольники образуют звезды с богатой симметрией. Пентаграмма и гексаграмма — самые простые примеры.
5-й возможность:
Вы берете правильный многоугольник и установите по бокам равнобедренные треугольники, которые имеют большую высоту по сравнению с с основной стороны.Многоугольник, имеющий точки, может вырождаться в круг (крайний правый). ……………. Вырастают красивые звезды. Очевидно, вы ожидаете, что звезды должны имеют «заостренные точки».
6-я возможность:
Вы берете любой многоугольник и установите произвольные треугольники по бокам.
| …… | Звезда немецкого журнала «Stern» была натурщицей. эта звезда. |
Создание звезд наверху
Звезда — любимая тема для
многие люди занимаются рукоделием с бесчисленными вариациями.Я представляю
следующие две звезды.
| Звезда как силуэт | Звезда Фрёбеля |
Первая восьмерка остроконечная звезда — это силуэт.
| …… | Вы снова и снова складываете квадратный лист бумаги красная линия, пока не появится фиг.5. Затем вы отрезаете кусочки вдоль синие линии прочными кухонными ножницами. Рис.6 развивается.Пока разворачивается вы получите звезду. |
Вторая звезда — звезда Фробеля, который сделан из четырех полос. Это объясняется на другом сайте моего домашняя страница.
Оригами-цветы
| … | Ханна сделала эти красивые цветы с помощью бессербастельна.де
(URL-адрес ниже). Спасибо за подсказку. |
Пентаграмма сверху
Пентаграмма определенно является «звездой» среди звезд.
Его также называют Drudenfuß (нем.) Или звездой ведьмы.
| …… | Складывается, если нарисовать диагонали (черные) внутри обычная пентаграмма. |
| …… | Центральный угол (синий) в центральном треугольнике ABC
правильного пятиугольника составляет 360 ° / 5 = 72 °. Итак, два основных угла равны 54 °. Внутренний угол пятиугольника составляет 108 °. |
| …… | Предполагая, что маленький пятиугольник внутри пентаграммы
также является правильным, отмеченный оранжевый угол составляет 108 °. Дело в равнобедренном
72-36-72-треугольник. Есть второй желтый треугольник поменьше 72-36-72, лежащий внизу. |
| …… | Оба желтых треугольника похожи друг на друга, потому что
соответствующих таких же углов. Вы найдете формулы в следующей главе. |
| …… | Это PQ : QS = QS : QR или : x = x : (a-x) в желтых треугольниках. Это уравнение можно связать с линией PQ и точка R на прямой.Все расстояние до большей части, как этот больший раздел к меньшему. Вы также можете сказать: Большой раздел это (золотая) середина всего и меньшего сечения, x = sqr [a (a-x)] в формуле. |
Известный немецкий тележурналист Профессор Хайнц Хабер описал золотое сечение в 1960-х годах следующим образом.
| …… | Боковая доска и ваза с цветами в
экспериментальная комната. Испытуемые должны были поставить вазу на шкафчик в
таким образом, чтобы это выглядело красиво. Лишь немногие поместили его в центр. Это выглядит скучный. Большинство людей ставят вазу немного справа или слева, как показано на картинке.В результате ширина шкафа была делится в золотой пропорции. Возможно, это чувство прекрасного дало воспитание и принадлежит нашей западной культуре. |
Пентаграмма также называется Друденфус. или звезда ведьмы. Это ссылка на определенную тему, которую вы можете исследовать в интернете. Я рекомендую каталог изображений на google.com и поисковое слово «пентаграмма». Иногда думаешь, что попал в средневековье. (То же самое и с гексаграммой в следующей главе.)
Мой вклад может заключаться в следующем: Я увидел пентаграмму у двери. совмещенного конюшни с коровником на ферме в 1950-е гг. Он должен сохранить от болезней крупного рогатого скота.
| …… | Вы можете нарисовать пентаграмму или звезды с помощью 7, 9 … точек
свободной рукой после некоторой практики, не поднимая карандаш. Я уже многих впечатлил этим :-). |
Строка Игра
Гексаграмма вверху
Вторая звезда, которую стоит описать, — это гексаграмма.Его также называют звездой Давида или печатью Саломона.
| …… | Гексаграмма состоит из 12 равносторонних треугольников и следовательно, принадлежит к группе Polyiamonds . |
| …… | Вы также можете рассматривать гексаграмму как фигуру, которая образован двумя равносторонними треугольниками. На голове стоит один треугольник. |
| …… | Что-то ностальгическое: В прежние времена Салмиакпастиллен (леденцы с горьким вкусом) были в моде. Вы смочили (чистую?) Тыльную сторону ладони и сформировали на нем звезда из шести пастилок. Затем вы лизнули пастилки. |
Два из Karen Koeller’s Quilts топ
Трехмерный
Звезды наверх
Вы можете создавать трехмерные звезды из правильных тел.Вы положили
пирамиды с каждой стороны.
Вот пример октаэдра с восемью тетраэдрами.
Те, кто знаком с трехмерным изображением, могут увидеть звезду трехмерно.
Многогранники Кеплера-Пуансо
| …… | Если поставить правильные пятиугольные пирамиды
стороны додекаэдра и тетраэдра на икосаэдре, вы получите
«Малый звездчатый додекаэдр» и «Большой звездчатый додекаэдр» (Кеплер).Пуансо открыл два «многогранника Пуансо», «Большой додекаэдр».
и «Великий Икосаэдр». Большой додекаэдр известен как звезда Александра (слева) головоломка, принадлежащая семейству кубиков Рубика. Больше об этих интересных твердых телах можно найти в Интернете. страницы ниже. |
Есть трехмерные звезды, которые в декабре висят в холлах многих домов. У них есть лампочка в центр, чтобы они светились изнутри.Их называют Стернлампионами (= звезда Китайские фонарики) на немецком языке и звезды Моравии на английском языке. Среди них «Оригинальный Herrnhuter Weihnachtsstern» (звезда Herrnhut) известен во всем мире. мир.
Звезды — Рядом и
Far Away наверх
далеко
Многие страны имеют одну или несколько звезд в своей национальной
флаг. Вот небольшой выбор.
рядом
Здесь, в Липпе, в районе Северного Рейна-Вестфалии здесь много фахверковых домов с большим залом, так что лошадь и карета могла въезжать и раньше.Обычно есть надпись снаружи над залом со звездой (здесь семиконечной) «Бурга Штернберга» с одной стороны, а с другой — «липкая роза», похожая на звезду. ………. Дом «Gut Hovedissen» в Леопольдсхёэ, Крайс Липпе, В качестве примера.
Диковинка изображена на гербе города Барнтруп / Липпе. (справа). «Der halbe Stern erinnert an die Gründung der Stadt durch die Grafen zu Sternberg. Die halbe lippische Rose wurde von der Stadt nach dem Übergang der Grafschaft Sternberg an die Herrschaft Lippe in das städtische Siegel übernommen.»
Источник: http://www.lippe.de/new/allgemein/show.php3?s=3&n=wappen
Вы также найдете звезду и розу в исторической ратуше (1546 г.) моего родного города Бад-Зальцуфлен. ………
| …… | Липпийская роза также (хотя и небольшая) на флаге
земли Северный Рейн-Вестфалия. Это было следствием подключения государства Липпе в Северный Рейн-Вестфалия после Второй мировой войны. |
Звезды на других страницах моей домашней страницы
Кеплер-Пуансо-Керпер (Только на немецком языке)Звезды в Интернете наверху
Немецкий
HERRNHUTER STERNE GMBH
Bauanleitungen
für Herrnhuter Sterne
Иоахим Мор
умереть
stetige Teilung oder der goldene Schnitt und die Konstruktion des regelmäßigen
Fünfecks
Лена Полина Хёниш Хурадо (besserbasteln.де)
Videoanleitung:
Spitze Fleurogami Blüte falten
Мартин Мархейнеке
Das
Пентаграмма, Пифагор и Голден Шнитт
origamiseiten.de
Bildergalerie
nachgefalteter Modelle ( Sterne )
Википедия
Кормовой
(Геометрия)
Английский
БЕТСИ РОСС
Как
вырезать пятиконечную звезду одним ножом
Эрик У.Вайсштейн (Мир математики)
Звезда
Многоугольник,
Кеплер-Пуансо
Твердый
Харви Д. Хайнц
Магия
Звезды
Википедия
Звезда
многоугольник
Список литературы наверх
(1) Мартин Гарднер: Mathematischer Zirkus, Берлин 1988 г.
(ISBN 3550076924)
Отзыв: Адрес электронной почты на моей главной странице
Это страница также доступна на немецком языке.
URL из
моя домашняя страница:
http://www.mathemische-basteleien.de/
© 2003 Юрген Кёллер
topPHP Программа Star Triangle — javatpoint
Звездный треугольник в PHP создается с помощью цикла for и foreach. Есть много звездных узоров. Мы покажем некоторые из них здесь.
Образец 1
= 1; $ j -) {
эхо «*»;
}
эхо «
«;
}
?>
Выход:
Образец 2
«; } ?>
Выход:
Образец 3
= $ i; $ k -) {
эхо «»;
}
for ($ j = 1; $ j <= $ i; $ j ++) {
эхо "*";
}
эхо "
«;
}
for ($ i = 4; $ i> = 1; $ i -) {
for ($ k = 5; $ k> = $ i; $ k -) {
эхо «»;
}
for ($ j = 1; $ j <= $ i; $ j ++) {
эхо "*";
}
эхо "
«;
}
?>
Выход:
Образец 4
‘;
}
for ($ i = 5; $ i> = 1; $ i -) {
for ($ j = 1; $ j <= $ i; $ j ++) {
echo '*';
}
эхо '
‘;
}
?>
Выход:
Образец 5
«; } ?>
Выход:
Образец 6
= 1; $ i—)
{
если ($ i% 2! = 0)
{
для ($ j = 5; $ j> = $ i; $ j—)
{
эхо «*»;
}
эхо «
«;
}
}
для ($ i = 2; $ i <= 5; $ i ++)
{
если ($ i% 2! = 0)
{
для ($ j = 5; $ j> = $ i; $ j—)
{
эхо «*»;
}
эхо «
«;
}
}
?>
Выход:
Луна, Сатурн и звезда образуют небесный треугольник
Наблюдатели за небесами, которые находятся вне дома после колдовского часа полуночи сегодня вечером (январь.24) будет интересно полюбоваться небесным массивом: космический треугольник, созданный Луной, планетой Сатурн и яркой звездой.
Для звездочетов конфигурация неба сначала будет напоминать довольно большой равнобедренный треугольник, расположенный низко в небе с востока на юго-восток, если позволит погода.
Три точки треугольника начинаются с луны, которая не должна быть освещена на две трети в ее убывающей луны. [Как работают фазы Луны]
Далее идет Сатурн, проявляющийся в виде спокойного желтовато-белого свечения значительно выше и слева от Луны.Яркая голубоватая звезда Спика завершает треугольник в конечной точке ниже и слева от Луны в зодиакальном созвездии Девы.
Луна, конечно, кажется, проходит мимо Спики каждый месяц, когда она пересекает небо, но в этот конкретный момент Сатурн тоже оказывается поблизости, образуя своего рода «Треугольник Сатурна».
На этой карте звездного неба треугольника Сатурна показано, каким он будет наблюдателям с ясным темным небом в первые часы завтрашнего дня.
Равнобедренный треугольник (с двумя сторонами равной длины) делает то, что Сатурн будет расположен на одинаковом расстоянии от Луны и Спики: около 8 градусов неба.
Астрономы измеряют расстояния между объектами в ночном небе в градусах дуги. Например, ваш сжатый кулак на расстоянии вытянутой руки будет охватывать около 10 градусов.
Таким образом, стороны треугольника Сатурн-Луна и Сатурн-Спика будут немного меньше ширины кулака. Сторона треугольника от Луны до Спики составит всего 6 градусов.
Около 5:30 утра по восточному стандартному времени завтра (10:30 по Гринвичу), когда рассвет на востоке США вот-вот начнется.побережья, тройка переместится в точку почти на полпути в небе к югу. Но и треугольник будет выглядеть немного иначе.
Сатурн в настоящее время находится на расстоянии 859 миллионов миль (1,382 миллиарда километров) от Земли и не изменит своего положения относительно фоновых звезд в течение одной ночи. Но Луна находится всего в 228 700 милях (368 000 км) от нас, и в результате в течение ночи будет медленно перемещаться на восток.
На самом деле, менее чем через шесть часов после первого появления треугольника Луна будет двигаться примерно на 3 градуса ближе к Спике, в результате чего треугольник станет уже.
(Кажется, что Луна движется на восток на фоне звезд с примерно собственной видимой шириной — полградуса — в час.)
Астрономы измеряют яркость небесных объектов с помощью шкалы звездных величин. Чем меньше число, тем ярче объект. Например, полная луна имеет звездную величину около -12,7 по этой шкале.
Сатурн с величиной 0,6 примерно на половину ярче звезды Спика.
Если у вас есть телескоп, посмотрите на кольца Сатурна.Всего 16 месяцев назад кольца Сатурна были почти невидимы для нас, потому что они были повернуты ребром (или почти так), если смотреть с Земли. Однако теперь они наклонены к нам чуть более чем на 10 градусов и их легко увидеть, если вы используете увеличение не менее 30 крат.
Джо Рао работает инструктором и приглашенным лектором в планетарии Хайдена в Нью-Йорке. Он пишет об астрономии для The New York Times и других изданий, а также является метеорологом перед камерой для News 12 Westchester, N.Ю.
Джо Рао, SPACE.com Колумнист Skywatching
Скрытые угощения в Золотом треугольнике
▼ Регион 3Мы начинаем наш последний регион с нашей третьей золотой двойной звезды, Альмах. Жемчужина для телескопов всех размеров, главная звезда 2-й величины имеет сапфирового компаньона 5-й величины на расстоянии 10 дюймов. Прыгая на северо-запад к Фи (φ) Кассиопеи 5-й величины, мы достигаем очаровательного скопления Сов (NGC 457), одного из самые популярные экспонаты на любительских собраниях и объект, названный редактором астрономии Дэвидом Дж.Айхер. Скопление с величиной 6 имеет две выдающиеся звезды (Phi1 и Phi2) в качестве глаз, примерно Т-образное расположение более тусклых звезд и два изолированных солнца, обозначающих ноги совы.
Теперь давайте центрируем Эту Кассиопеи в наших телескопах. Названный «Двойник пасхального яйца», главная топазовая звезда с магнитудой 3,5 разделяет поле зрения с лиловым спутником магнитудой 7,5 в 13 дюймов на северо-запад. Короткий прыжок на 1½˚ на юго-восток приводит нас к еще одному сокровищу: туманности Пакмана неправильной формы (NGC 281). 30 ‘свечение в форме запятой содержит в своем ядре рассеянный кластер шириной 4’ (IC 1590).
Далее идет триада разрозненных кластеров. Начнем с веб-кластера Вдовы (NGC 7790) примерно в 2½˚ к северо-западу от Кафа. Хотя скопление тускло светит с блеском 8,5, его две дюжины или около того звезд сжаты в область неба шириной 5 футов и выглядят как высококонцентрированная сеть звездного света Y-образной формы с восточно-западным направлением на фоне богатого Млечного Пути. NGC 7788, скопление 9-й величины и шириной 9 футов, находится всего в 15 футах к северо-западу, в то время как рассеянное скопление 10-й величины Berkeley 58 находится примерно в 20 футах к юго-востоку и выглядит как призрачное скопление 5 футов шириной. минутные звезды.
Двигаясь на север к Gamma Cephei 3-й величины, мы смотрим примерно на 5½ ° к юго-востоку на 35-дюймовый диск туманности Галстук-бабочка (NGC 40). Центральная звезда планетарной звезды 12-й величины 11,5 величины подавляет окружающее свечение. Увеличения больше. более 150x требуется, чтобы увидеть темную полость между центральной звездой и ее оболочкой.
Давайте перейдем к Альфирку 3-й величины (Бета Цефеи), затем примерно в 3 ° к юго-западу к туманности Ирис 8-й величины (NGC 7023) — отражающей туманности с высокой поверхностной яркостью, окружающей звезду 7-й величины.Это одна из первых областей, где астрономы нашли прямые доказательства наличия пылинок в молекулярных облаках.
Еще один поворот на 3˚ к юго-западу приводит нас к небольшой (4 ‘) спиральной галактике с перемычкой 11-й величины NGC 6951, также находящейся в Цефеусе. Это незаметное внегалактическое чудо было обнаружено американским астрономом Льюисом Свифтом с помощью 4½-дюймового рефрактора. На изображениях это видно сквозь перистые облака галактики или облака межзвездной пыли.
Вернувшись к Драко, мы направляемся на остров Фи Драконис 4-й величины и смотрим примерно на 2¾˚ к северо-востоку на затерянную в космосе галактику 10-й величины (NGC 6503).Немецкий астроном Артур фон Ауверс обнаружил эту карликовую спираль длиной 6 футов с рефрактором 2,6 дюйма. Если смотреть с ребра всего в 16˚, он чем-то напоминает светящийся метеоритный поезд.
Мы заканчиваем наш тур всего в 4˚ к югу и немного восточнее от NGC 6503 у одной из самых красивых планетарных туманностей неба: туманности Кошачий глаз 8-й величины (NGC 6543). Эта огромная туманность шириной 23 дюйма, расположенная всего в 3 футах к востоку от звезды 8-й величины, светится бледно-зеленым цветом даже при малом увеличении. При высоком увеличении можно хорошо отделить ее резкую центральную звезду 11-й величины от ее светящегося внутреннего кольца.Тонкая внешняя оболочка из туманного вещества окружает эти детали, придавая планетарному аппарату слегка вытянутый вид.
Надеюсь, вам понравилось исследовать Золотой треугольник. Объекты, которые мы рассмотрели, являются лишь примерами чудес этого региона. Но, как и в любом путешествии, всегда лучше оставлять некоторые вещи незамеченными до следующего возвращения.