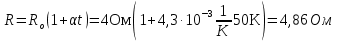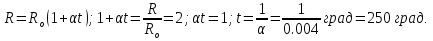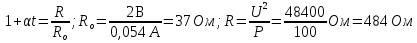Т. Зависимость сопротивления от температуры — PhysBook

Зависимость сопротивления проводника от температуры

Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что

1. возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
2. изменяется их концентрация при нагревании проводника.

Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:

\(~\rho_t = \rho_0 (1 + \alpha t) ,\) \(~R_t = R_0 (1 + \alpha t) ,\)

где ρ₀, ρ_t — удельные сопротивления вещества проводника соответственно при 0 °С и t °C; R₀, R_t — сопротивления проводника при 0 °С и t °С, α — температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К^-1). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.

Температурный коэффициент сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.

\(~\mathcal h \alpha \mathcal i = \frac{1 \cdot \Delta \rho}{\rho \Delta T} ,\)

где \(~\mathcal h \alpha \mathcal i\) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ.

Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. У чистых металлов α = 1/273 К^-1. У металлов концентрация свободных носителей зарядов (электронов)

n = const и увеличение ρ происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.

Для растворов электролитов α < 0, например, для 10%-ного раствора поваренной соли α = -0,02 К^-1. Сопротивление электролитов с ростом температуры уменьшается, так как увеличение числа свободных ионов из-за диссоциации молекул превышает рост рассеивания ионов при столкновениях с молекулами растворителя.

Формулы зависимости ρ и R от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором

α = const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.

Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.

Рис. 1

При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости. Металл переходит в сверхпроводящее состояние.

Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.

Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 256-257.

Расчёт сопротивления проводника. Удельное сопротивление. Примеры расчетов

Сопротивление в проводниках возникает из-за взаимодействия электронов с ионами кристаллической решетки. Если вдуматься, то можно заметить, что чем длиннее проводник, тем больше такое взаимодействие.

Также, логично предположить, что чем толще проводник, тем больший поток электронов может пройти через поперечное сечение.

И, конечно, мы знаем, что разные вещества по-разному проводят ток. Исходя из этих знаний, мы можем установить следующее:

Чем длиннее проводник, тем больше его сопротивление.

Чем толще проводник, тем меньше его сопротивление.

Сопротивления проводников одинаковой длины и толщины могут быть различны, в зависимости от вещества.

Ну а как именно зависит сопротивление проводника от его размеров, можно узнать только с помощью опытов. Мы уже немного знакомы с методикой проведения подобных экспериментов: нам нужно провести некоторые измерения, и, построив график, установить зависимость сопротивления от тех или иных величин. Данные опыты были проведены Георгом Омом.

Подключим проводник к источнику тока и, с помощью амперметра и вольтметра, измерим силу тока и напряжение. Мы используем, так называемый, мультиметр — современный прибор, который выполняет функции амперметра и вольтметра, в зависимости от настроек. Но, тем не менее, мы по-прежнему должны следовать правилам: когда мы хотим измерить силу тока, мультиметр подключается последовательно. На мультиметре есть переключатель между режимами измерения той или иной величины. Также, когда мы хотим измерить напряжение, мультиметр подключается параллельно. Используя закон Ома, мы можем вычислить сопротивление данного проводника.

Подобным способом, мы можем вычислить сопротивление проводников разной длины, но той же толщины, сделанных из того же материала. Проведя несколько измерений, выясним, что сопротивление проводника увеличивается ровно во столько раз, во сколько увеличивается его длина.

В таблице с данными можно увидеть незначительные несоответствия. Однако, мелкие погрешности в измерениях, при проведении любого опыта, неизбежны. Тем не менее, закономерность очевидна: сопротивление проводника прямо пропорционально длине проводника. Это подтверждается и графиком, который является прямой линией.

Проведем несколько иной опыт: сравним сопротивления проводников из того же материала, одинаковой длины, но разной толщины. Поскольку роль играет не сама толщина, а площадь поперечного сечения проводника, то мы попытаемся выяснять, как зависит сопротивление именно от этого параметра.

Полученные данные показывают, что на этот раз сопротивление проводника обратно пропорционально площади поперечного сечения проводника

. Наш график зависимости сопротивления от поперечного сечения имеет форму ветви гиперболы.

Как вы уже, наверное, догадались, удельное сопротивление проводников из того или иного материала тоже вычисляется экспериментальным путём. На этот раз, все проводники имеют одну и ту же длину и толщину, но состоят из разного вещества.

Удельное сопротивление проводника — это сопротивление проводника из данного вещества с площадью поперечного сечения 1 м² и длиной 1 м. В таблице даны значения удельного сопротивления для некоторых веществ.  

Однако, площадь поперечного сечения проводника удобнее измерять в квадратных миллиметрах, поскольку это больше соответствует размерам реальных проводников.

Итак, исходя из наших опытов, сопротивление проводника прямо пропорционально длине проводника, обратно пропорционально площади поперечного сечения и зависит от вещества:

Из формулы мы можем выразить удельное сопротивление и определить его единицы измерения:

Упражнения.

Задача 1. Железный провод длиной 250 м имеет площадь поперечного сечения 2 мм². Найдите сопротивление данного провода.

Задача 2. Какое напряжение должно быть на эбонитовом диске толщиной 1 мм, чтобы через него прошел ток в 1 мкА? Диаметр диска составляет 1 см.

Мы видим, что даже для того, чтобы через эбонит прошел очень маленький ток, нужно просто огромное напряжение. Такое напряжение создать практически невозможно. Даже в современных ускорителях частиц достигалось напряжение не больше нескольких ТВ. Поэтому, можно сказать, что мы не можем провести ток через эбонит. Этого следовало ожидать, поскольку удельное сопротивление эбонита огромно, и он является непроводником.

Задача 3. На рисунке показан график зависимости силы тока на участке цепи от неизвестной величины. Можете ли вы определить, что это за величина?

Итак, давайте вспомним, от чего вообще может зависеть сила тока. В первую очередь, сила тока — это количество заряда, прошедшего через поперечное сечение за единицу времени. Из формулы видно, что сила тока находится в линейной зависимости от количества заряда в единицу времени, а на рисунке мы видим график функции, который показывает нелинейную зависимость. Мы знаем, что график функции, описывающий любую линейную зависимость, будет являться прямой. Из формулы, описывающей закон Ома, мы видим, что сила тока прямо пропорциональна напряжению. Значит, неизвестная величина не является ни количеством заряда, ни напряжением. Сила тока обратно пропорциональна сопротивлению. Однако, мы уже знаем, что график функции зависимости силы тока от сопротивления представляет собой ветвь гиперболы, а на рисунке мы видим другой график.

Тогда следует заметить, что сила тока зависит от величин, которые, в свою очередь, зависят от других величин. Напряжение связано с работой по переносу заряда, но эта зависимость тоже линейная. Рассмотрим, от чего зависит сопротивление: от удельного сопротивления, от длины проводника и от площади поперечного сечения. Удельное сопротивление для каждого проводника — есть величина постоянная. Сопротивление находится в линейной зависимости от длины проводника, длина проводника — это независимая величина. Остается площадь поперечного сечения. Как раз-таки, она зависит не от радиуса, а от квадрата радиуса проводника, что приводит нас к нелинейной зависимости. Если мы преобразуем формулу, по которой вычисляется сила тока в проводнике, то увидим, что сила тока прямо пропорциональна квадрату радиуса проводника. Это единственная величина, которая могла привести к построению графика квадратичной функции. Действительно, если мы внимательно изучим график, то убедимся, что это парабола. Следует заметить, что это может быть график зависимости силы тока не от радиуса, а от диаметра. Однако, для того, чтобы это проверить, нам нужна дополнительная информация. Тем не менее, мы с уверенностью можем сказать, что это график зависимости силы тока либо от радиуса, либо от диаметра проводника (по форме эти два графика ничем не отличаются — существуют лишь числовые отличия).

Зависимость сопротивления проводника от температуры: почему увеличивается

 

Каждое вещество имеет свое удельное сопротивление. Причем сопротивление будет зависеть от температуры проводника. Убедимся в этом, проведя следующий опыт.

Пропустим ток через стальную спираль. В цепи со спиралью подключим последовательно амперметр. Он покажет некоторое значение. Теперь будем нагревать спираль в пламени газовой горелки. Значение силы тока, которое покажет амперметр, уменьшится. То есть, сила тока будет зависеть от температуры проводника.

Изменение сопротивления в зависимости от температуры

Пусть при температуре 0 градусов, сопротивление проводника равняется R0, а при температуре t  сопротивление равно R, тогда относительное изменение сопротивления будет прямо пропорционально изменению температуры t:

В данной формуле а – коэффициент пропорциональности, который называют еще температурным коэффициентом.  Он характеризует зависимость сопротивления, которым обладает вещество, от температуры. 

Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании его на 1 Кельвин.

Для всех металлов температурный коэффициент больше нуля. При изменениях температуры он будет незначительно меняться. Поэтому, если изменение температуры невелико, то температурный коэффициент можно считать постоянным, и равным среднему значению из этого интервала температур.

Растворы электролитов с ростом температуры сопротивление уменьшается. То есть для них температурный коэффициент будет меньше нуля.

Сопротивление проводника зависит от удельного сопротивления проводника и от размеров проводника. Так как размеры проводника при нагревании меняются незначительно, то основной составляющей изменения сопротивления проводника является удельное сопротивление.

Зависимость удельного сопротивления проводника от температуры

Попытаемся найти зависимость удельного сопротивления проводника от температуры.

Подставим в полученную выше формулу значения сопротивлений R=p*l/S R0=p0*l/S.

Получим следующую формулу:

Температурный коэффициент можно считать постоянным, следовательно, удельное сопротивление проводника будет прямо пропорционально температуре проводника.

Данная зависимость представлена на следующем рисунке.

Попробуем разобраться, почему увеличивается сопротивление

Когда мы повышаем температуру, то увеличивается амплитуда колебаний ионов в узлах кристаллической решетки. Следовательно, свободные электроны будут чаще с ними сталкиваться. При столкновении они будет терять направленность своего движения. Следовательно, сила тока будет уменьшаться.  

Зависимость сопротивления проводника от температуры, широко используется в технике и физике. Например, в изготовлении термометров сопротивления.

Нужна помощь в учебе?

Предыдущая тема: Опыт Милликена и Иоффе: суть эксперимента и как это было
Следующая тема:&nbsp&nbsp&nbspСверхпроводимость: определение, история открытия, свойства и перспективы

Все неприличные комментарии будут удаляться.

Тест по физике Удельное сопротивление проводников для 11 класса

Тест по физике Удельное сопротивление проводников. Зависимость удельного сопротивления проводников от температуры для 11 класса с ответами. Тест включает в себя 2 варианта. В каждом варианте по 5 заданий.

1 вариант

1. Металлический проводник имеет сопротивление 1 Ом. Каким сопротивлением будет обладать проводник, имею­щий в 2 раза большую длину и в 2 раза большую площадь сечения, сделанный из того же материала?

А. 0,25 Ом.
Б. 2 Ом.
В. 1 Ом.

2. Как изменится сопротивление проволоки, если ее сло­жить вдвое?

А. Уменьшится в 4 раза.
Б. Уменьшится в 2 раза.
В. Увеличится в 2 раза.

3. Какой график (рис. 5) соответствует зависимости удельного сопротивления металла от температуры?

4. Каким сопротивлением обладает нихромовый про­водник длиной 5 м и площадью поперечного сечения 0,75 мм²? Удельное сопротивление нихрома равно 1,1 Ом · мм²/м.

А. 10,5 Ом.
Б. 7,3 Ом.
В. 14,6 Ом.

5. Сопротивление угольного стержня уменьшилось от 5 до 4,5 Ом при повышении температуры от 50 до 545 °С. Каков температурный коэффициент сопротивле­ния угля?

А. 0,0002 К^-1
Б. 0,0004 К^-1
В. 0,0008 К^-1

2 вариант

1. Металлический проводник имеет сопротивление 2 Ом. Каким сопротивлением будет обладать проводник, имею­щий в 4 раза большую длину и в 2 раза меньшую пло­щадь сечения, сделанный из того же материала?

А. 32 Ом.
Б. 16 Ом.
В. 8 Ом.

2. Как изменится сопротивление проволоки, если ее сло­жить втрое?

А. Уменьшится в 3 раза.
Б. Уменьшится в 9 раз.
В. Увеличится в 3 раза.

3. Какой график (рис. 6) соответствует зависимости удельного сопротивления полупроводника от темпера­туры?

4. Чему равно сопротивление константановой проволоки длиной 8 м и площадью поперечного сечения 2 мм²? Удель­ное сопротивление константана равно 0,5 Ом · мм²/м.

А. 2 Ом.
Б. 20 Ом.
В. 30 Ом.

5. Сопротивление медного проводника при 0 °С равно 4 Ом. Каково его сопротивление при 100 °С, если тем­пературный коэффициент сопротивления меди равен 0,0043 К^-1?

А. 57,2 Ом.
Б. 6,43 Ом.
В. 5, 72 Ом.

Ответы на тест по физике Удельное сопротивление проводников. Зависимость удельного сопротивления проводников от температуры для 11 класса
1 вариант
1-В
2-А
3-А
4-Б
5-А
2 вариант
1-А
2-Б
3-В
4-А
5-В

Зависимость сопротивления проводника от температуры. Сверхпроводимость

Изучая закон Ома для участка цепи мы с вами ввели понятие электрического сопротивления, как физическую величину, характеризующую свойства проводника препятствовать прохождению электрического тока в нём.

При этом мы с вами показали, что сопротивление проводника прямо пропорционально его длине, обратно пропорционально площади поперечного сечения и зависит от вещества, из которого этот проводник изготовлен:

Напомним, что электрические свойства проводника характеризуются его удельным сопротивлением.

Как вы знаете, в таблицах удельных сопротивлений веществ очень часто указывается температура, при которой удельное сопротивление было измерено. Тогда логично предположить, что сопротивление проводника должно каким-то образом зависеть от температуры.

Проверим это предположение на опыте. Для этого соберём электрическую цепь, состоящую из источника тока, проволочной спирали и амперметра. Включим источник тока, и отметим показание амперметра.

А теперь давайте нагреем исследуемую спиральку, например, с помощью спиртовки. Не трудно увидеть, что показания амперметра начинают уменьшаться. Вывод очевиден: при увеличении температуры сопротивление металлов увеличивается.

Объясняется этот факт достаточно просто. Вы знаете, что удельное сопротивление вещества металлического проводника зависит от концентрации свободных носителей заряда и числа их столкновений с ионами кристаллической решётки, совершающими колебательные движения около положений устойчивого равновесия. В металлических проводниках концентрация свободных электронов практически постоянна для данного проводника и не зависит от температуры.

Однако число столкновений свободных электронов с ионами кристаллической решётки с ростом температуры возрастает. Это приводит к возрастанию удельного сопротивления металлического проводника при повышении температуры.

Если принять, что при 273 К (то есть при 0 ^оС) удельное сопротивление проводника равно ρ₀, а при температуре Т оно равно ρ, то, как показывает опыт, относительное изменение удельного сопротивления пропорционально изменению абсолютной температуры (которое, напомним, совпадает с изменением температуры по шкале Цельсия):

В записанном уравнении α — это температурный коэффициент. Он численно равен относительному изменению удельного сопротивления вещества проводника при изменении его температуры на 1 К:

Таким образом, удельное сопротивление вещества металлического проводника возрастает с увеличением температуры.

Поскольку сопротивление проводника прямо пропорционально удельному сопротивлению вещества, из которого изготовлен проводник, то, не учитывая незначительную температурную зависимость отношения l/S, можно записать такие соотношения:

Здесь R₀ и R — это сопротивления проводника соответственно при нуле градусов Цельсия и при данной температуре.

Отметим, что для металлических проводников эти формулы применимы при температурах более T >140 К.

У всех металлов при повышении температуры сопротивление возрастает. То для них температурный коэффициент сопротивления — это величина положительная. У растворов же электролитов наоборот с ростом температуры сопротивление уменьшается. Значит их температурный коэффициент сопротивления меньше нуля.

Для большинства металлов (но не сплавов) при температурах от 0 для 100 ^оС температурный коэффициент можно считать постоянным и равным его среднему значению на этом интервале температур:

Давайте, для примера определим сопротивление алюминиевого проводника при температуре 90 ^оС, если при температуре 20 ^оС его сопротивление равно 4 Ом. Температурный коэффициент сопротивления алюминия α = 4,2 · 10^–3 К^–1.

Зависимость сопротивления металлов от температуры используют в специальных приборах — термометрах сопротивления. Широкое распространение получили термометры сопротивления из чистых металлов, особенно платины и меди, которые конструктивно представляют собой металлическую проволоку, намотанную на жёсткий каркас (из кварца, фарфора или слюды), заключённый в защитную оболочку (из металла, кварца, фарфора, стекла). Платиновые термометры сопротивления применяют для измерения температуры в пределах от –263 до 1064 ^oС, а медные — от –50 до 180 ^oС.

Если при изготовлении электроизмерительных приборов требуются проводники, сопротивление которых должно как можно меньше зависеть от температуры окружающей среды, то используют специальные сплавы — константан и манганин.

В 1911 году голландский физик Хейке Камерлинг-Оннес исследуя зависимость сопротивления ртути от температуры обнаружил одно замечательное явление. Вначале эксперимента всё шло по плану: сопротивление металла при охлаждении постепенно уменьшалось. Однако при температуре меньше либо равной 4,12 К (по современным измерениям при 4,15 К) электрическое сопротивление ртути резко исчезало.

Явление падения до нуля сопротивления проводника при определённой температуре называется сверхпроводимостью, а проводник в этом состоянии — сверхпроводником.

Температуру, при которой электрическое сопротивление проводника обращается в ноль, называют критической температурой.

Открытие Камерлинг-Оннеса, за которое в 1913 году ему была присуждена Нобелевская премия, повлекло за собой исследования свойств веществ при низких температурах. Позже многочисленными опытами было установлено, что это явление характерно для многих проводников. Каждый сверхпроводящий металл характеризуется своей критической температурой.

У веществ в сверхпроводящем состоянии были отмечены резкие аномалии магнитных, тепловых и ряда других свойств. Так, например, если в кольцевом проводнике, находящемся в сверхпроводящем состоянии, создать ток, а затем удалить источник тока, то сила этого тока в таком проводнике не меняется сколь угодно долго. В обычном же (несверхпроводящем) проводнике электрический ток в этом случае прекращается. Это указывает на перспективу использования явления сверхпроводимости при передаче электрической энергии.

Сверхпроводящие соединения нашли применение в качестве материала обмоток электромагнитов для создания сильных магнитных полей в установках управляемого термоядерного синтеза, а также в мощных электрических двигателях и генераторах.

Объяснение сверхпроводимости возможно только на основе квантовой теории. Оно было дано лишь в 1957 году американскими учёными Джоном Бардиным, Леоном Купером и Джоном Шриффером, а также советским учёным и академиком Николаем Николаевичем Боголюбовым.

Очень упрощённо механизм сверхпроводимости можно объяснить так: при критической температуре электроны объединяются в правильную шеренгу и движутся, не сталкиваясь с кристаллической решёткой, состоящей из ионов. Это движение существенно отличается от обычного теплового движения, при котором свободный электрон движется хаотично.

В 1986 году была открыта высокотемпературная сверхпроводимость. Получены сложные оксидные соединения лантана, бария и других элементов с температурой перехода в сверхпроводящее состояние около 100 К. Это выше температуры кипения жидкого азота при атмосферном давлении (77 К).

Высокотемпературная сверхпроводимость в недалёком будущем приведёт наверняка к новой технической революции во всей электротехнике, радиотехнике и конструировании компьютеров.

План урока на тему «Зависимость сопротивления проводников от температуры» (10 класс)

Зависимость сопротивления проводников от температуры.

Сверхпроводимость.

Цель урока: объяснить физическую природу зависимости сопротивления проводников от температуры; ввести понятие температурного коэффициента сопротивления и сверхпроводимости.

Задачи урока:

Образовательные:

• на основе демонстрации опытов объяснить увеличения сопротивления металлов от температуры и уменьшения у электролитов, получить формулу связи R от t ;

• ознакомить с явлением сверхпроводимости

Развивающие:

• развитие речи, умения выражать и защищать свою точку зрения;

• развитие познавательных умений

Воспитательные:

• вовлечь всех учащихся в творческую работу;

• воспитание мотивов учения, положительного отношения к знаниям

Тип урока: комбинированный.

Формы организации урока: фронтальная, индивидуальная.

Методы: рассказ, демонстрация опытов, исследование, записи на доске, беседа.

Тип урока: комбинированный.

Формы организации урока: фронтальная, индивидуальная.

Методы: рассказ, демонстрация опытов, исследование, записи на доске, беседа.

Оборудование к уроку:

1) прибор для показа зависимости сопротивления металлов от температуры;

2) спиртовка, спичка;

3) раствор медного купороса;

4) амперметр постоянного тока;

5)гальванометр

6)U-образная трубка

7) источник постоянного тока.

8) ПК, мультимедиа-проектор, компьютерная презентация.

Ход урока

I. Оргмомент.

II. Фронтальный опрос (Слайд 1)

Электрический ток в металлах

а) Что называют электрическим током?

б) Сформулируйте закон Ома для полной цепи.

в) Перечислите хорошие проводники электрического тока.

г) Какой проводимостью обладают металлы? Чем это объясняется?

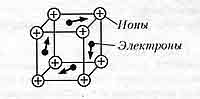
Носители свободных зарядов в металлах

— свободные электроны, которые упорядоченно перемещаются вдоль проводника под действием электрического поля с постоянной средней скоростью (из-за тормозного действия положительно заряженных ионов кристаллической решетки) (Слайд 4,5)

Металлы обладают электронной проводимостью.

III.Зависимость сопротивления проводника R от температуры:

а) Как можно рассчитать сопротивление проводника?

б) Что такое ρ?

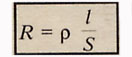
Различные вещества имеют разные удельные сопротивления (см. § 104).

Проблемный вопрос. Зависит ли сопротивление от состояния проводника? от его температуры? Выслушать мнение учащихся. Ответ должен дать опыт.

Если пропустить ток от аккумулятора через стальную спираль, а затем начать нагревать ее в пламени горелки, то амперметр покажет уменьшение силы тока. Это означает, что с изменением температуры сопротивление проводника меняется. (Опыт№1, рис 1.) Учащиеся наблюдают уменьшение накала спирали и уменьшение силы тока в цепи.

Вопросы учащимся: Как обьяснить данный опыт?

Как меняется сопротивление спирали в зависимости от температуры?

Выслушать рассуждения учащихся.

Увеличение сопротивления можно объяснить тем, при повышении температуры увеличивается скорость и амплитуда хаотического движения ионов кристаллической решетки металла и свободных электронов. Это приводит к более частым их соударениям, что затрудняет направленное движение электронов, то есть увеличивает электрическое сопротивление. (Слайд 7)

Если при температуре, равной 0°С, сопротивление проводника равно R_о, а при температуре t оно равно R, то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры t:

При нагревании размеры проводника меняются мало, а в основном меняется удельное сопротивление.

Удельное сопротивление проводника зависит от температуры:

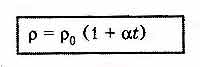
где ρ₀ — удельное сопротивление при 0 градусов,

t — температура,

α — температурный коэффициент сопротивления

( т.е. относительное изменение удельного сопротивления проводника при нагревании его на один градус)

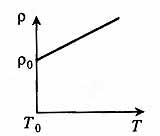
Для металлов и сплавов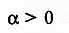

Обычно для чистых металлов принимается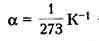

Таким образом, для металлических проводников с ростом температуры

Рис 1

увеличивается удельное сопротивление, увеличивается сопротивление проводника и уменьшается электрический ток в цепи.

Сопротивление проводника при изменении температуры можно рассчитать по формуле:

R = Ro (1 + αt)

где Ro — сопротивление проводника при 0 градусов Цельсия

t — температура проводника

α — температурный коэффициент сопротивления

(Слайды 8,9)

Хотя коэффициент α довольно мал, учет зависимости сопротивления от температуры при расчете нагревательных приборов совершенно необходим. Так, сопротивление вольфрамовой нити лампы накаливания увеличивается при прохождении по ней тока более чем в 10 раз.

У некоторых сплавов, например, у сплава меди с никелем (константан), температурный коэффициент сопротивления очень мал: α ≈ 10^-5 K^-1. Удельное сопротивление константана велико: ρ ≈ 10^-6 Ом∙м. Такие сплавы используют для изготовления эталонных сопротивлений и добавочных сопротивлений к измерительным приборам, т. е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.

Вывод. Удельное сопротивление (соответственно и сопротивление) металлов растет линейно с увеличением температуры.

(Дополнительно.) У растворов электролитов оно уменьшается при увеличении температуры. (рис.2)

(Опыт №2.) Учащиеся наблюдают увеличение силы тока, проходящего через раствор медного купороса при нагревании раствора.

Вопрос учащимся: Как обьяснить данный опыт?

Выслушать мнение учащихся по наблюдаемому опыту.

Уменьшение сопротивления объясняется увеличением степени диссоциации и образованием свободных носителей зарядов

(Слайд 10)

Рис. 2

IV. Явление сверхпроводимости

Сверхпроводимость – физическое явление, заключающееся в скачкообразном падении до нуля сопротивления вещества.

Сверхпроводник – вещество, которое может переходить в сверхпроводящее состояние.

Открытие низкотемпературной сверхпроводимости:

1911г. — голландский ученый Камерлинг — Онес

наблюдается при сверхнизких температурах (ниже 25 К) во многих металлах и сплавах;

при таких температурах удельное сопротивление этих веществ становится исчезающе малым.

(Слайды 11,12)

В 1957 г. дано теоретическое объяснение явления сверхпроводимости:

Купер (США), Боголюбов (СССР)

1957г. опыт Коллинза: ток в замкнутой цепи без источника тока не прекращался в течение 2,5 лет.

В 1986 г. открыта (для металлокерамики) высокотемпературная сверхпроводимость (при 100 К).

Трудность достижения сверхпроводимости:

— необходимость сильного охлаждения вещества

Применение явления сверхпроводимости (Слайд 13)

1)Экранирование

Сверхпроводник не пропускает магнитный поток, следовательно, он экранирует электромагнитное излучение. Используется в микроволновых устройствах, а также при создании установок для защиты от излучения при ядерном взрыве

2)Магниты

— научно-исследовательское оборудование

— магнитная левитация

— получение сильных магнитных полей;

— мощные электромагниты со сверхпроводящей обмоткой в ускорителях и генераторах.

НТСП магниты используются в ускорителях частиц и установках термоядерного синтеза

Интенсивно проводятся работы по созданию поездов на магнитной подушке. Прототип в Японии использует НТСП.

3)Передача энергии

4)Аккумулирование

Возможность аккумулировать электроэнергию в виде циркулирующего тока

5)Вычислительные устройства

Комбинация полупроводниковых и сверхпроводящих приборов открывает новые возможности в конструировании аппаратуры.

В настоящий момент в энергетике существует большая проблема

— большие потери электроэнергии при передаче ее по проводам.

Возможное решение проблемы:

при сверхпроводимости сопротивление проводников приблизительно равно 0 и потери энергии резко уменьшаются

Вещество с самой высокой температурой сверхпроводимости. В марте 1988 г. в Исследовательском центре компании ИБМ в Сан-Хосе, штат Калифорния, США, при температуре –148°С было получено явление сверхпроводимости. Проводником служила смесь оксидов таллия, кальция, бария и меди – Тl2Са2Ва2Сu3Оx.

???

1. Когда электрическая лампочка потребляет большую мощность: сразу после включения ее в сеть или спустя несколько минут?

2. Если бы сопротивление спирали электроплитки не менялось с температурой, то ее длина при номинальной мощности должна быть большей или меньшей?

V. Закрепление изученного материала методом решения задач. (Слайды 14-17)

1.Сопротивление медного провода при 0⁰С равно 4 Ом. Найдите его сопротивление при 50⁰С. Если температурный коэффициент сопротивления меди α = 4,3∙10^-3 К^-1.

2.(№864-Р). При какой температуре сопротивление серебряного проводника станет 2 раза больше, чем при 0⁰С?

3.(868 №) На сколько процентов изменится мощность, потребляемая электромагнитом, обмотка которого выполнена из медной проволоки. При изменении температуры от 0 до 30⁰С?

4. (№869-Р) На баллоне электрической лампы написано 220 В, 100 Вт. Для измерения сопротивления нити накала в холодном состоянии на лампу подали напряжение 2 В, при этом сила тока была 54 мА. Найти приблизительно температуру накала вольфрамовой нити

Решения задач:

1. 

2. (№864)

3. (868)

Ответ: уменьшится на 11%

4. (869)

1+=;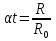

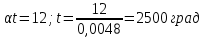
На дом:§113,114.

№865,870

5. Сопротивление вольфрамовой нити лампы при 20˚С равно 20 Ом, а при 3000˚С равно 250 Ом. Найти α вольфрамовой нити (0,0042 град^-1)

Дополнительный материал к уроку

Металлический термометр сопротивления

Представляет собой резистор, выполненный из металлической проволоки или плёнки и имеющий известную зависимость электрического сопротивления от температуры. Наиболее распространённый тип термометров сопротивления — платиновые термометры. Это объясняется тем, что платина имеет высокий температурный коэффициент сопротивления и высокую стойкость к окислению. Эталонные термометры изготавливаются из платины высокой чистоты с температурным коэффициентом не менее 0,003925. В качестве рабочих средств измерений применяются также медные и никелевые термометры. Действующий стандарт на технические требования к рабочим термометрам сопротивления: ГОСТ Р 8.625-2006 (Термометры сопротивления из платины, меди и никеля. Общие технические требования и методы испытаний). В стандарте приведены диапазоны, классы допуска, таблицы НСХ и стандартные зависимости сопротивление-температура. Стандарт соответствует международному стандарту МЭК 60751 (2008). В стандарте впервые отказались от нормирования конкретных номинальных сопротивлений. Сопротивление изготовленного термометра может быть любым. Промышленные платиновые термометры сопротивления в большинстве случаев используются со стандартной зависимостью сопротивление-температура (НСХ), что обуславливает погрешность не лучше 0,1 °C (класс АА при 0 °C). Термометры сопротивления на основе напыленной на подложку плёнки отличаются повышенной вибропрочностью, но меньшим диапазоном температур. Максимальный диапазон, в котором установлены классы допуска платиновых термометров для проволочных чувствительных элементов составляет 660 °C (класс С), для плёночных 600 °C (класс С).

Краткая теория сверхпроводимости.

Современная теория сверхпроводимости состоит в том, что при температурах, близких к нулю Кельвина, происходит особое взаимодействие между электронами (с порождением и поглощением фотонов), которое характеризуется притяжением между электронами. При таком взаимодействии фотонное притяжение электронов сильнее кулоновского отталкивания. А поэтому все электроны проводимости образуют связанный коллектив, который не может отдавать энергию малыми порциями. Энергия коллективизированных электронов не расходуется на тепловые колебания ионов. А поэтому сопротивление проводника практически равно нулю. Критическая температура (при которой удельное сопротивление резко падает) для сверхпроводников находится по таблице. Сверхпроводники применяются для получения мощных электромагнитов в ускорительных приборах.

Литература

1.Г.Я.Мякишев. Б.Б. Буховцев, Н.Н. Сотский. Физика 10

2. А.П. Рымкевич. Сборник задач по физике

http://class-fizika.narod.ru/10_9.htm

http://www.electrolibrary.info/history/sverkhprovodimost.htm

http://www.nado5.ru/e-book/zavisimost-soprotivleniya-provodnika-ot-temperatury

http://do.gendocs.ru/docs/index-380436.html?page=3

http://elementy.ru/lib/430825/430831

как сопротивление проводника зависит от температуры? кто-нибудь знает?

Удельное сопротивление проводников и непроводников зависит от температуры. Сопротивление металлических проводников увеличивается с повышением температуры. У полупроводников сопротивление сильно уменьшается при повышении температуры У некоторых металлов при температуре, близкой к абсолютному нулю, сопротивление скачком уменьшается до нуля (явление сверхпроводимости).

От повышения температуры сопротивление уменьшается.

Чем выше температура проводника, тем выше его сопротивление

повышается с повышением температуры.

Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры; изменяется их концентрация при нагревании проводника.