Зависимость электрического сопротивления от сечения, длины и материала проводника
Сопротивление различных проводников зависит от материала, из которого они изготовлены.
Можно проверить это практически на следующем опыте.
Рисунок 1. Опыт, показывающий зависимость электрического сопротивления от материала проводника
Подберем два или три проводника из различных материалов, возможно меньшего, но одинакового поперечного сечения, например, один медный, другой стальной, третий никелиновый. Укрепим на планке два зажима а и б на расстоянии 1 —1,5 м один от другого (рис. 1) и подключим к ним аккумулятор через амперметр. Теперь поочередно между зажимами а и б будем на 1—2 сек включать сначала медный, потом стальной и, наконец, никелиновый проводник, наблюдая в каждом случае за отклонением стрелки амперметра. Нетрудно будет заметить, что наибольший по величине ток пройдет по медному проводнику, а наименьший — по никелиновому.
Из этого следует, что сопротивление медного проводника меньше, чем стального, а сопротивление стального проводника меньше, чем никелинового.
Таким образом, электрическое сопротивление проводника зависит от материала, из которою он изготовлен.
Для характеристики электрического сопротивления различных материалов введено понятие о так называемом удельном сопротивлении.
Определение: Удельным сопротивлением называется сопротивление проводника длиной в 1 м и сечением в 1 мм2 при температуре +20 С°.
Удельное сопротивление обозначается буквой ρ («ро») греческого алфавита.
Каждый материал, из которого изготовляется проводник, обладает определенным удельным сопротивлением. Например, удельное сопротивление меди равно 0,0175 Ом*мм
Ниже приводится таблица удельных сопротивлений материалов, наиболее часто применяемых в электротехнике.
Удельные сопротивления материалов, наиболее часто применяемых в электротехнике
| Материал | Удельное сопротивление, Ом*мм2/м |
| Серебро | 0,016 |
| Медь | |
| Алюминий | 0,0295 |
| Железо | 0,09-0,11 |
| Сталь | 0,125-0,146 |
| Свинец | 0,218-0,222 |
| Константан | 0,4-0,51 |
| Манганин | 0,4-0,52 |
| Никелин | 0,43 |
| Вольфрам | 0,503 |
| Нихром | 1,02-1,12 |
| Фехраль | 1,2 |
| Уголь | 10-60 |
Любопытно отметить, что например, нихромовый провод длиною 1 м обладает примерно таким же сопротивлением, как медный провод длиною около 63 м (при одинаковом сечении).
Разберем теперь, как влияют размеры проводника, т. е. длина и поперечное сечение, на величину его сопротивления.
Воспользуемся для этого схемой, изображенной на рис. 1. Включим между зажимами а и б для большей наглядности опыта проволоку из никелина. Заметив показание амперметра, отключим от зажима б проводник, которой соединяет прибор с минусом аккумулятора, и освободившимся концом проводника прикоснемся к никелиновой проволоке на некотором удалении от зажима а (рис. 2). Уменьшив таким образом длину проводника, включенного в цепь, нетрудно заметить по показанию амперметра, что ток в цепи увеличился.
Рисунок 2. Опыт, показывающий зависимость электрического сопротивления от длины проводника
Это говорит о том, что с уменьшением длины проводника сопротивление его уменьшается. Если же перемещать конец проводника по никелиновой проволоке вправо, т. е. к зажиму б, то, наблюдая за показаниями амперметра, можно сделать вывод, что с увеличением длины проводника сопротивление его увеличивается.
Таким образом, сопротивление проводника прямо пропорционально его длине, т. е. чем длиннее проводник, тем больше его электрическое сопротивление..
Выясним теперь, как зависит сопротивление проводника от его поперечного сечения, т. е. от толщины.
Подберем для этого два или три проводника из одного и того же материала (медь, железо или никелин), но различного поперечного сечения и включим их поочередно между зажимами а и б, как указано на рис. 1.
Наблюдая каждый раз за показаниями амперметра, можно убедиться, что чем тоньше проводник, тем меньше ток в цепи, а следовательно, тем больше сопротивление проводника. И, наоборот, чем толще проводник, тем больше ток в цепи, а следовательно, тем меньше сопротивление проводника.
Чтобы лучше уяснить эту зависимость, представьте себе две пары сообщающихся сосудов (рис. 3), причем у одной пары сосудов соединяющая трубка тонкая, а у другой — толстая.
Рисунок 3. Вода по толстой трубке перейдет быстрее, чем по тонкой
Ясно, что при заполнении водой одного из сосудов (каждой пары) переход ее в другой сосуд по толстой трубке произойдет гораздо быстрее, чем по тонкой. Это значит, что толстая трубка окажет меньшее сопротивление течению воды. Точно так же и электрическому току легче пройти по толстому проводнику, чем по тонкому, т. е. первый оказывает ему меньшее сопротивление, чем второй.
Обобщая результаты произведенных нами опытов, можно сделать следующий общий вывод:
электрическое сопротивление проводника равно удельному сопротивлению материала, из которого этот проводник сделан, умноженному на длину проводника и деленному на площадь его поперечного сечения..
Математически эта зависимость выражается следующей формулой:
где R—сопротивление проводника в Ом;
ρ — удельное сопротивление материала в Ом*мм
l — длина проводника в м;
S—площадь поперечного сечения проводника в мм2.
Примечание. Площадь поперечного сечения круглого проводника вычисляется по формуле
где π—постоянная величина, равная 3,14;
d—диаметр проводника.
Указанная выше зависимость дает возможность определить длину проводника или его сечение, если известны одна из этих величин и сопротивление проводника.
Так, например, длина проводника определяется по формуле:
Если же необходимо определить площадь поперечного сечения проводника, то формула принимает следующий вид:
Решив это равенство относительно ρ, получим выражение для определения удельного сопротивления проводника:
Последней формулой приходится пользоваться в тех случаях, когда известны сопротивление и размеры проводника, а его материал неизвестен и к тому же трудно определим по внешнему виду. Определив по формуле удельное сопротивление проводника, можно найти материал, обладающий таким удельным сопротивлением.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Зависимость сопротивления проводника от температуры.
Если пропустить ток от аккумулятора через стальную спираль, то амперметр покажет уменьшение силы тока. Это означает, что с сопротивлением температуры сопротивление проводника меняется.
Если при температуре, равной 0С, сопротивление проводника равно R0, а при температуре t оно равно R, то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры t:
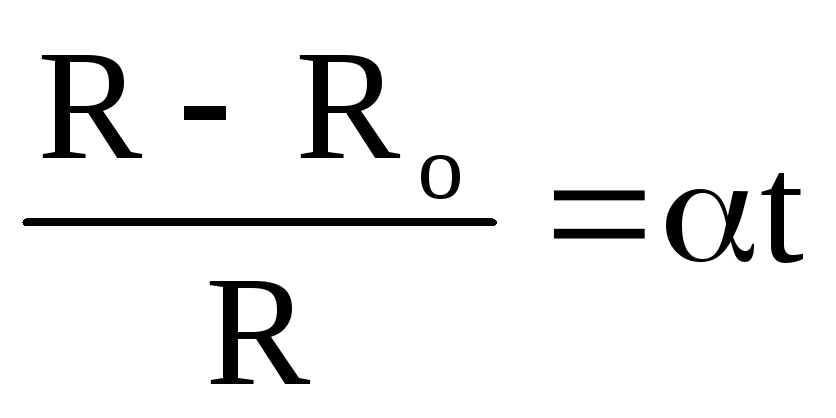 (1)
(1)
Коэффициент  называетсятемпературным
коэффициентом сопротивления.
Он характеризует зависимость сопротивления
вещества от температуры.
называетсятемпературным
коэффициентом сопротивления.
Он характеризует зависимость сопротивления
вещества от температуры.
Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при повышении температура на 1 К.
Для
всех металлов  >0
и незначительно меняется с изменением
температуры. У растворов электролитов
сопротивление с ростом температуры не
уменьшается, а увеличивается. Для них
>0
и незначительно меняется с изменением
температуры. У растворов электролитов
сопротивление с ростом температуры не
уменьшается, а увеличивается. Для них <0.
<0.
При нагревании проводника его геометрические размеры меняются незначительно. Сопротивление проводника меняется в основном за счет изменения его удельного сопротивления. Можно найти зависимость этого удельного сопротивления от температуры, если в формулу (1) подставить значения
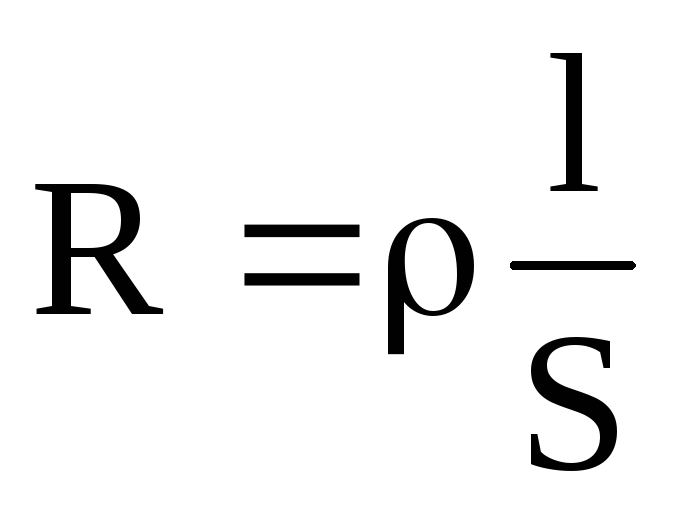 и
и 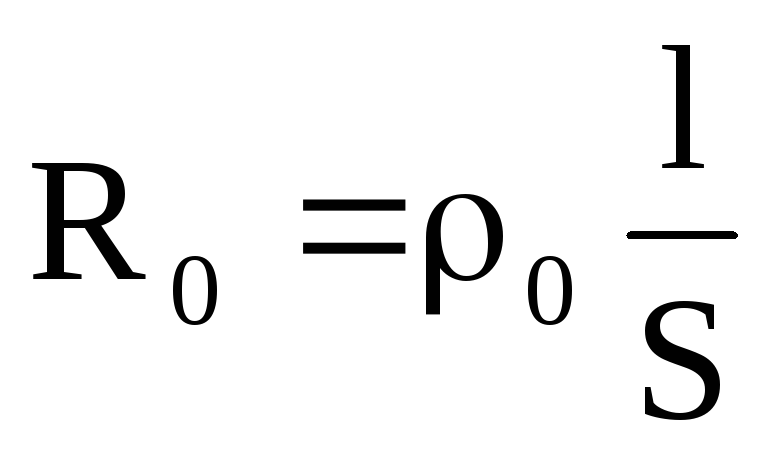 :
:
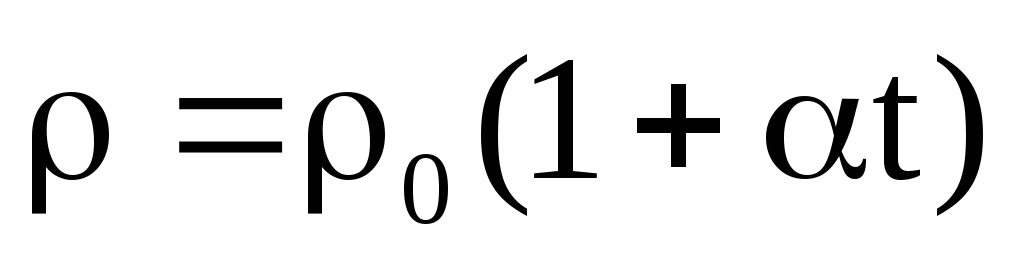
Так
как  мало меняется при изменении температуры,
то можно считать, что удельное
сопротивление проводника линейно
зависит от температуры.
мало меняется при изменении температуры,
то можно считать, что удельное
сопротивление проводника линейно
зависит от температуры.
С приближением температуры к абсолютному нулю удельное сопротивление монокристаллов становится очень малым. Этот факт свидетельствует о том, что в идеальной кристаллической решетке металла электроны перемещаются под действием электрического поля, не взаимодействуя с ионами решетки. Электроны взаимодействуют лишь с ионами, не находящимися в узлах кристаллической решетки.
При повышении температуры возрастает число дефектов кристаллической решетки из-за тепловых колебаний ионов, – и это приводит к возрастанию удельного сопротивления кристалла.
Сверхпроводимость
В 1911 г. нидерландский ученый Камерлинг-Оннес обнаружил, что при понижении температуры ртути до 4,1 К ее удельное сопротивление скачком уменьшается до нуля. Явление уменьшения удельного сопротивления до нуля при температуре, отличной от абсолютного нуля, называется сверхпроводимостью. Материалы, обнаруживающие способность переходить при некоторых температурах, отличных от абсолютного нуля, в сверхпроводящее состояние, называются сверхпроводниками.
Прохождение тока в сверхпроводнике происходит без потерь энергии, поэтому однажды возбужденный в сверхпроводящем кольце электрический ток может существовать неограниченно долго без изменения.
Сверхпроводящие вещества уже используются в электромагнитах. Однако получить сколь угодно сильное магнитное поле с помощью сверхпроводящего магнита нельзя, т. к. очень сильное магнитное поле разрушает сверхпроводящее состояние. Поэтому для каждого проводника в сверхпроводящем состоянии существует критическое значение силы тока, превзойти которое, не нарушая сверхпроводящего состояния, нельзя.
Объяснение сверхпроводимости возможно только на основе квантовой теории. Оно было дано лишь в 1957 г.
В 1986 г. была открыта высокотемпературная сверхпроводимость керамик – соединений лантана, бария, меди и кислорода. Сверхпроводимость таких керамик сохраняется до температур около 100 К.
II. Электрическое сопротивление проводника
Электрическое сопротивление проводника: 1) величина, характеризующая противодействие проводника или электрической цепи электрическому току;
2) структурный элемент электрической цепи, включаемый в цепь для ограничения или регулирования силы тока.
Электрическое сопротивление металлов зависит от материала проводника, его длины и поперечного сечения, температуры и состояния проводника (давления, механических сил растяжения и сжатия, т.е. внешних факторов, влияющих на кристаллическое строение металлических проводников).
Зависимость сопротивления от материала, длины и площади поперечного сечения проводника:
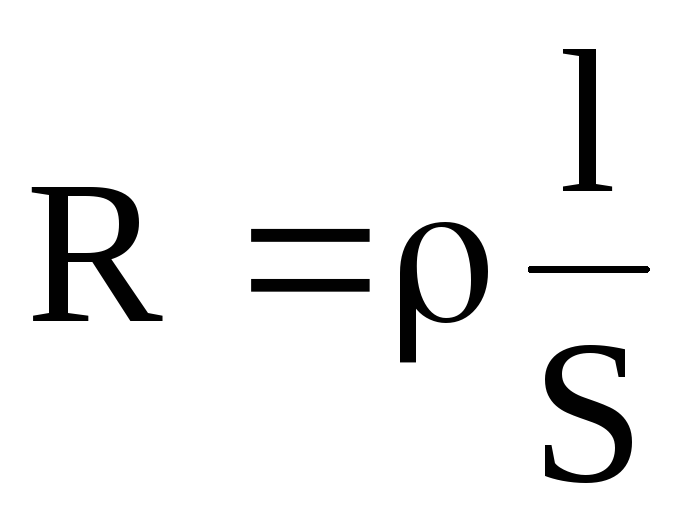 ,
,
где — удельное сопротивление проводника;
l – длина проводника;
S – площадь поперечного сечения проводника.
Зависимость сопротивления проводника от температуры:
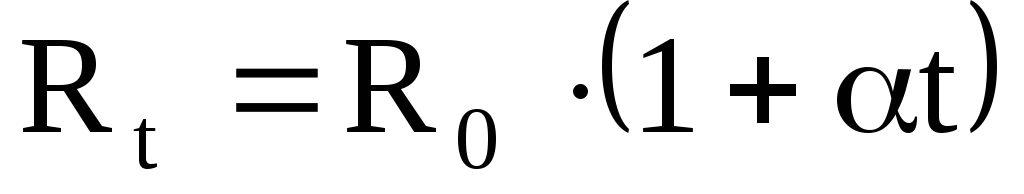 или
или 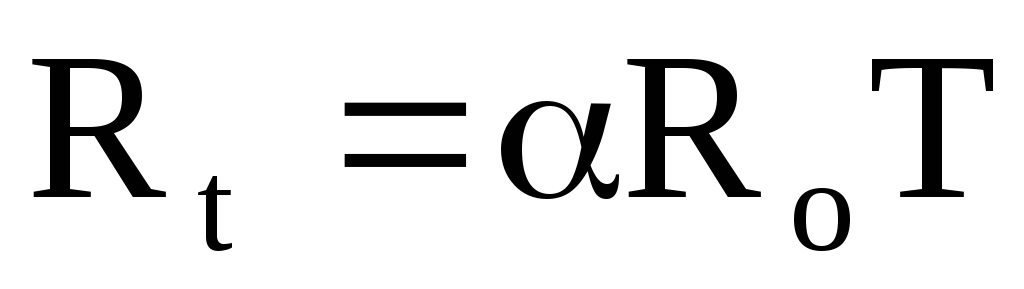 ,
,
где Rt – сопротивление при температуре t 0C;
R0 – сопротивление при 0 0C;
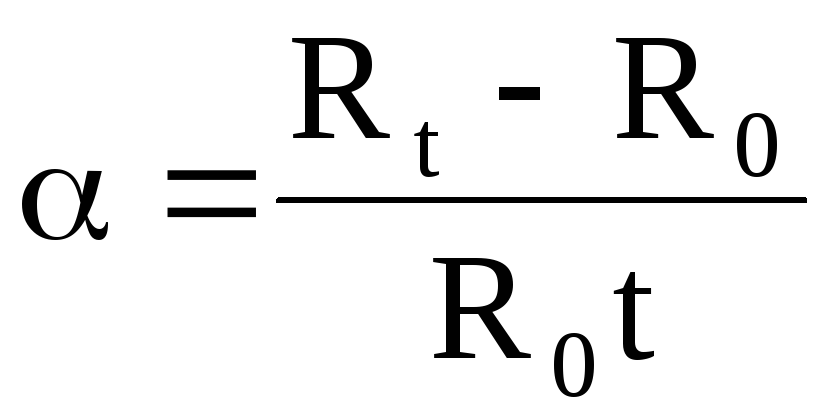 —
температурный коэффициент сопротивления,
который показывает, как изменяется
сопротивление проводника по отношению
к его сопротивлению при 0 0C,
если температура изменяется на один
градус;
—
температурный коэффициент сопротивления,
который показывает, как изменяется
сопротивление проводника по отношению
к его сопротивлению при 0 0C,
если температура изменяется на один
градус;
T – термодинамическая температура.
Соединения сопротивлений: последовательное, параллельное, смешанное.
а) Последовательное соединение сопротивлений представляет собой систему проводников (сопротивлений), которые включены один за другим, так что через каждое из сопротивлений протекает один и тот же ток:
I = I1 = I2 == In.
Напряжение при последовательном соединении сопротивлений равно сумме напряжений на каждом из сопротивлений:
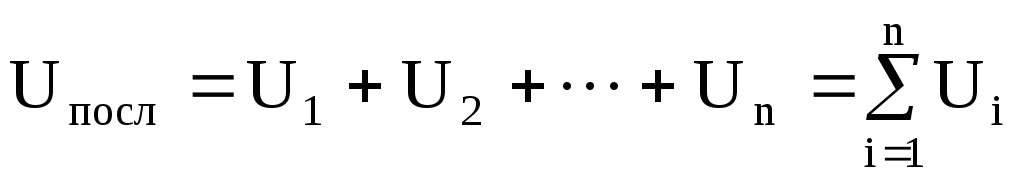 .
.
Напряжение на каждом из последовательно соединенных сопротивлений пропорционально значению данного сопротивления:
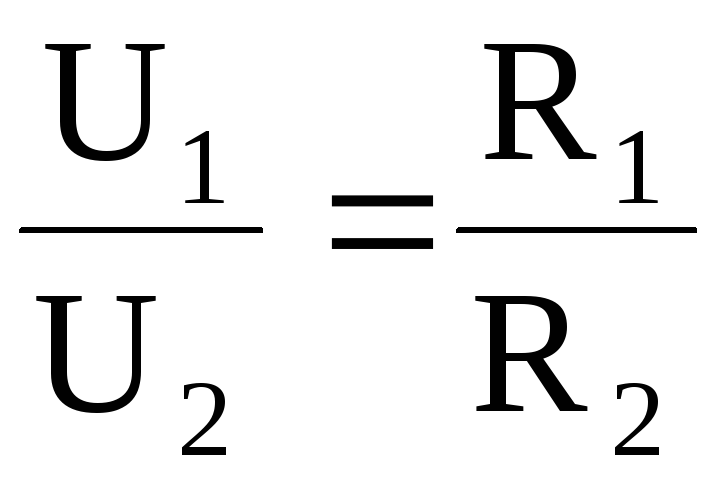 .
.
Распределение напряжения по последовательно соединенным элементам цепи (делитель напряжения):
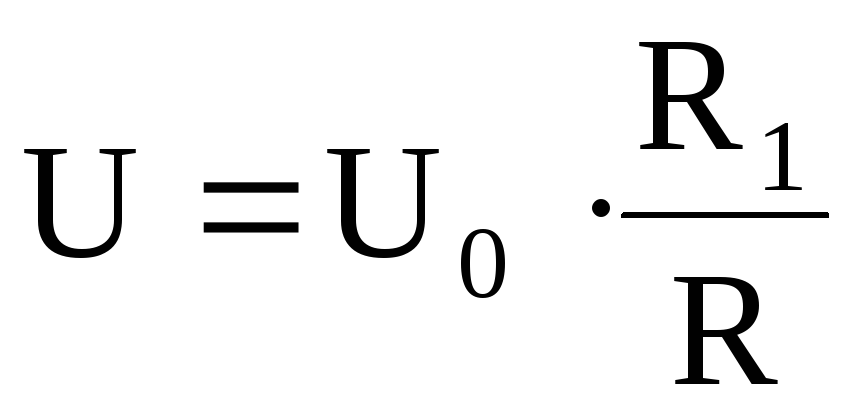 ,
,
где U0 – напряжение на всем соединении;
U – напряжение на участке цепи с сопротивлением R1;
R – полное сопротивление соединения;
R1 – сопротивление участка цепи с выбранным сопротивлением.
Общее сопротивление цепи при последовательном соединении равно сумме отдельно взятых сопротивлений и оно больше наибольшего из включенных:
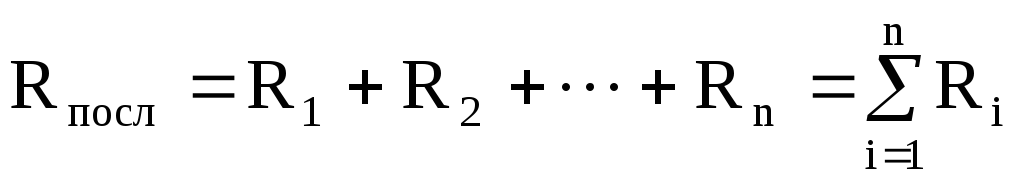 .
.
Общее сопротивление цепи при последовательном соединении n одинаковых сопротивлений:
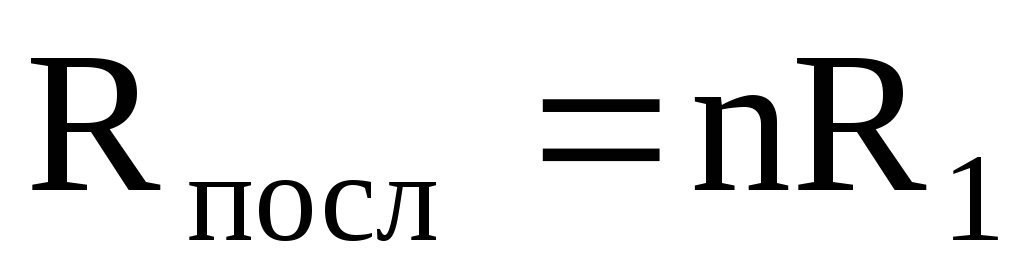 ,
,
где n – число сопротивлений, включенных последовательно;
R1 = значение отдельно взятого сопротивления.
б) Параллельное соединение сопротивлений: признаком такого соединения является разветвление тока I на отдельные токи через соответствующие сопротивления. При этом ток I равен сумме токов через отдельно взятое сопротивление:
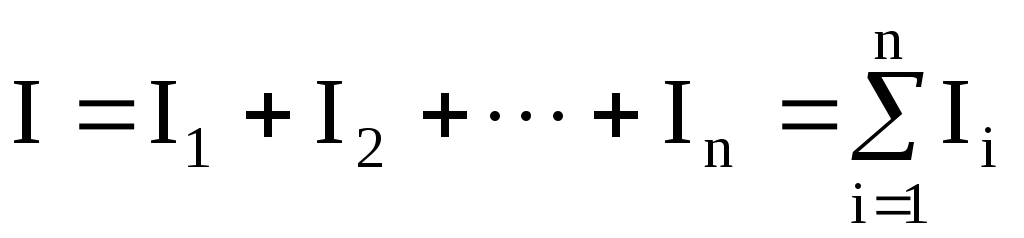 .
.
Общее напряжение при параллельном соединении равно напряжению на отдельно взятом сопротивлении:
U = U1 = U2 = = Ui.
Связь между током и сопротивлением при параллельном соединении: при параллельном соединении сопротивлений токи в отдельных проводниках обратно пропорциональны их сопротивлениям:
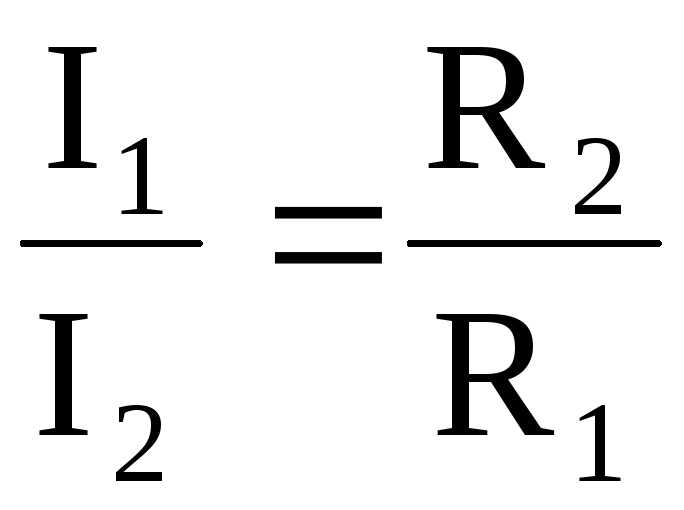 .
.
Величина, обратная полному сопротивлению цепи (общая проводимость) при параллельном соединении, равна сумме проводимостей отдельно взятых проводников. При этом общее сопротивление цепи меньше наименьшего сопротивления из включенных:
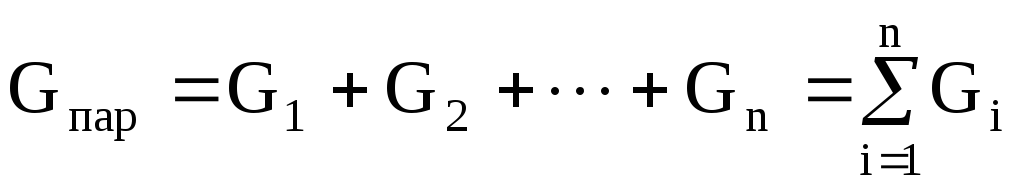 ;
; 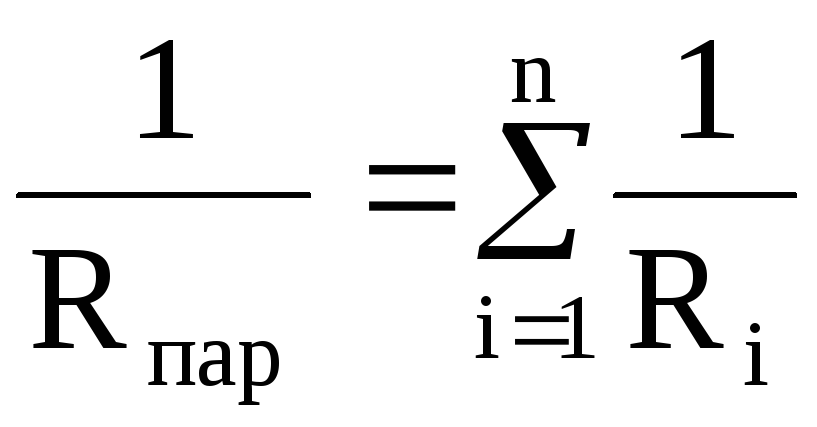 .
.
Общая проводимость цепи при параллельном соединении n проводников:
Gпар = nG1,
где Gпар – проводимость цепи;
G1 – проводимость отдельного взятого проводника.
Шунтирование электроизмерительных приборов – расширение предела измерения тока с помощью электроизмерительного прибора, к которому присоединяют параллельно проводник с малым сопротивлением (шунт). В этом случае
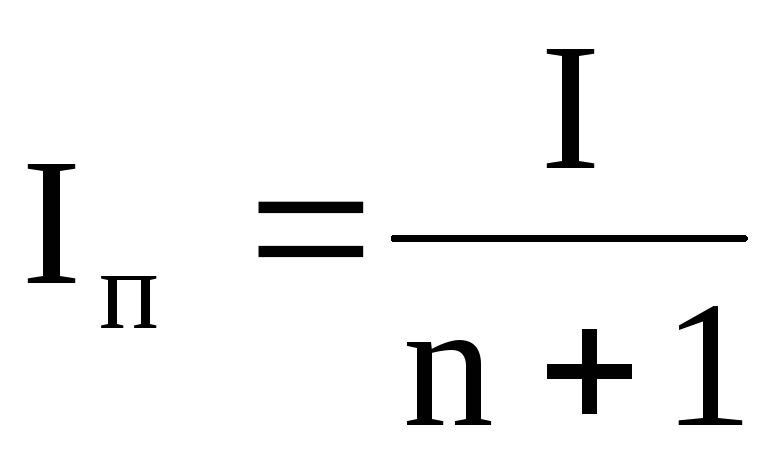 ,
,
где Iп – ток, протекающий через прибор;
I – ток в цепи;
n = Rп/Rш – отношение сопротивления прибора Rп к сопротивлению шунта Rш.
Добавочное сопротивление – сопротивление, которое присоединяют последовательно к электроизмерительному прибору для расширения предела измерения напряжения. При этом
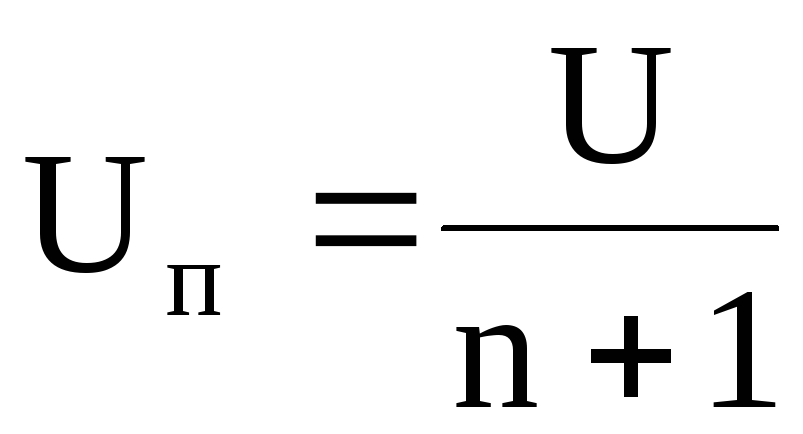 ,
,
где Uп – напряжение на приборе;
U – напряжение в цепи;
N = Rд/Rп – отношение величины добавочного сопротивления к сопротивлению прибора.
Электрическая проводимость – физическая величина, обратная сопротивлению проводника:
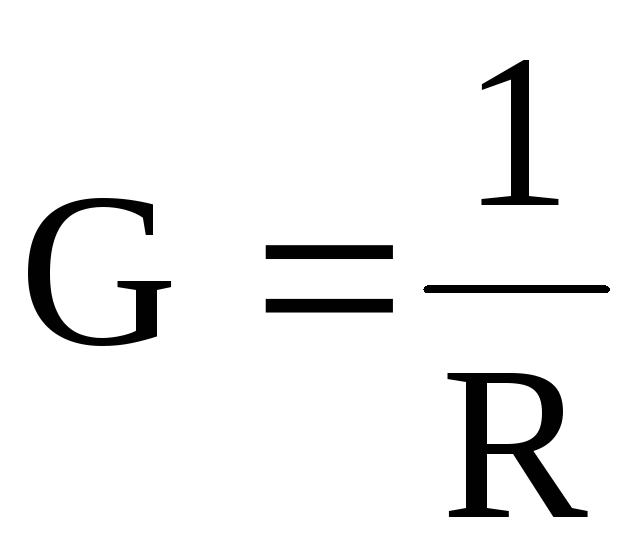 .
.
Сверхпроводимость – свойство многих проводников, состоящее в том, что их электрическое сопротивление скачком падает до нуля при охлаждении ниже определенной критической температуры Tk, характерной для данного материала.
Связь удельной проводимости с удельным сопротивлением (удельным электрическим сопротивлением) :
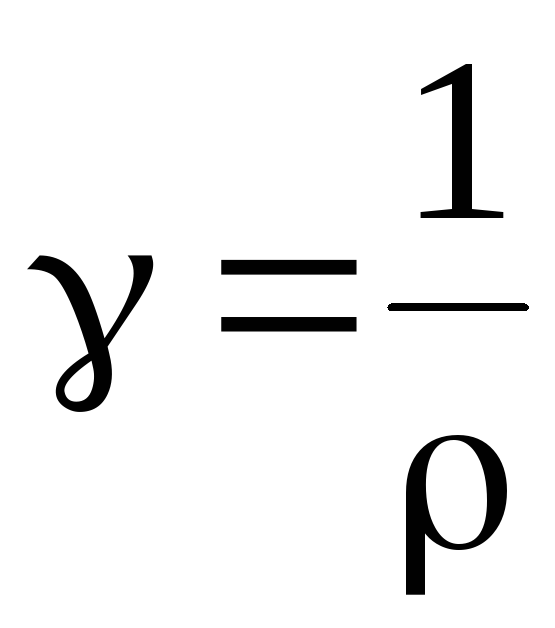 ;
; 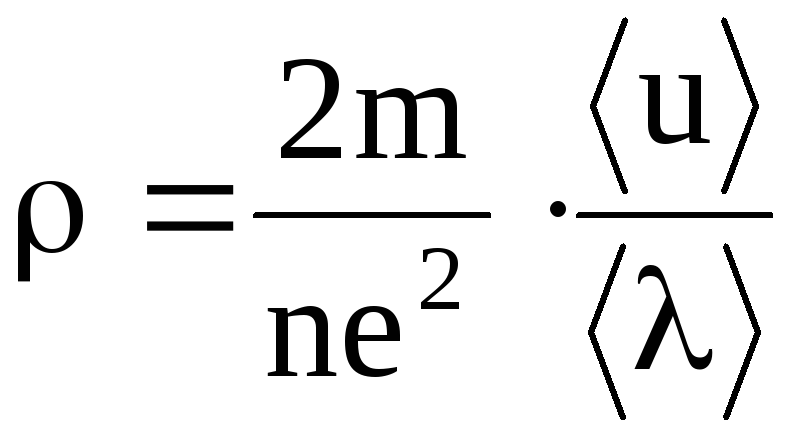 .
.
Зависимость удельного сопротивления проводника от температуры:
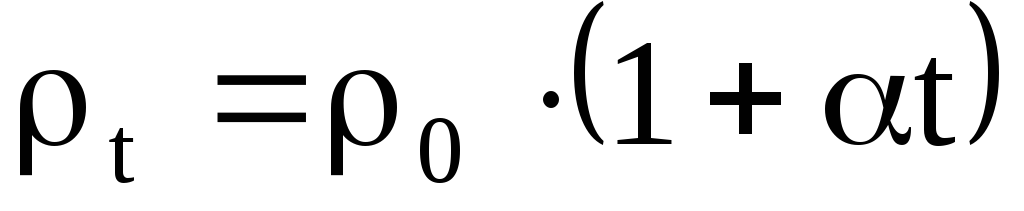 ,
,
где t – удельное сопротивление при температуре t 0C;
0 – удельное сопротивление при 0 0C;
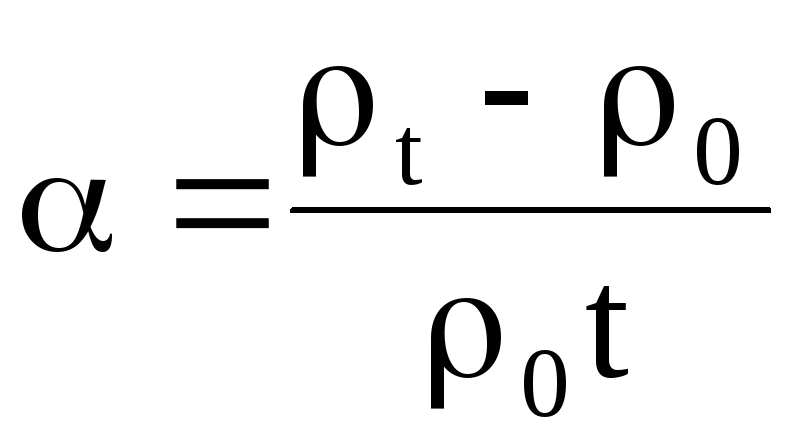 —
температурный коэффициент сопротивления,
который показывает, как изменяется
удельное сопротивление проводника по
отношению к его удельному сопротивлению
при 0 0C,
если температура изменяется на один
градус.
—
температурный коэффициент сопротивления,
который показывает, как изменяется
удельное сопротивление проводника по
отношению к его удельному сопротивлению
при 0 0C,
если температура изменяется на один
градус.
Задания: 1. Ознакомиться с применяемыми в работе электроизмерительными приборами. Результаты занести в табл. 1.
Таблица 1.
Наименование прибора | Заводской номер | Инвентарный номер | Система | Класс точности | Предел измерений | Число делений шкалы | Цена деления | Абсолютная погрешность | Внутреннее сопротивление | Чувствительность |
2. Измерить удельное электрическое сопротивление.
1. Измерить микрометром в нескольких местах рабочей части проводника его диаметр. Рассчитать среднее значение диаметра.
2. Установить подвижный контакт на 0,5 0,7 от длины рабочей части проводника. Занести значение длины в таблицу 2.
3. Включить установку в сеть переменного тока с напряжением 220 В. При этом должна загореться индикаторная лампочка.
4. Провести измерения тока и напряжения. Результаты занести в таблицу 2.
Таблица 2.
№ п/п | <d> 10-3, м | <d> 10-3, м | ℓ, м | <ℓ> 10-3, м | U, В | I 10-3, А | 10—6 Омм | <> 10—6, Омм | , % | <> 10—6, Омм |
5. Отключить установку. Установить подвижный контакт на другое значение рабочей части исследуемого проводника. Вновь включить установку и определить новые значения тока и напряжения.
Примечание. Изменение длины рабочей части проводника, определение тока и напряжения проводятся 3-5 раз.
6. Так как
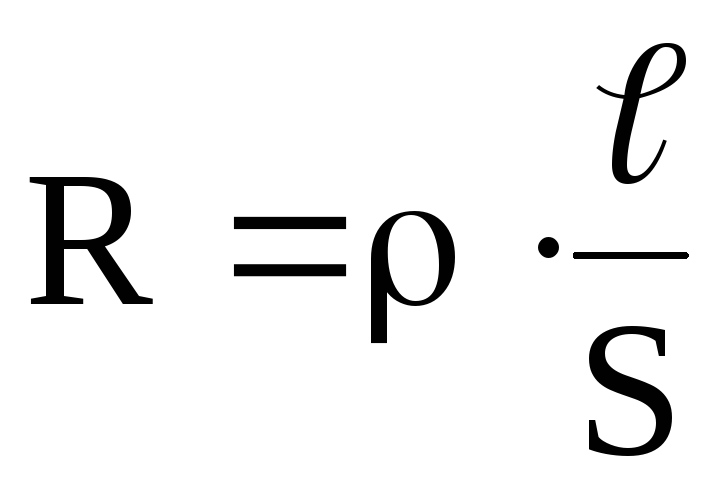 ,
,
то
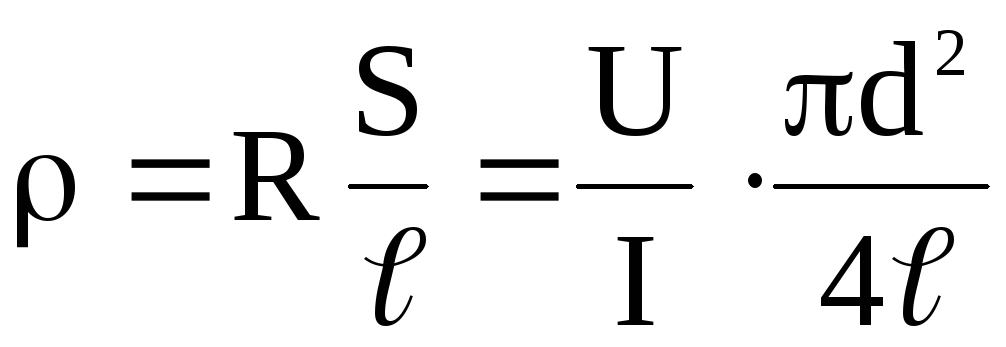 ,
(1)
,
(1)
где — удельное электросопротивление проводника;
ℓ — длина проводника;
S — площадь поперечного сечения.
По формуле (1) рассчитать удельное электрическое сопротивление исследуемого проводника и среднее его значение.
7. Рассчитать относительные погрешности проведенных измерений по формуле
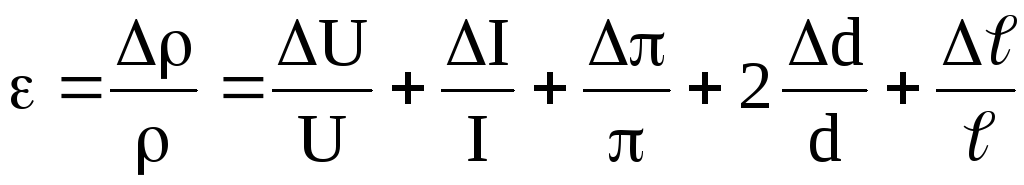 ,
(2)
,
(2)
где 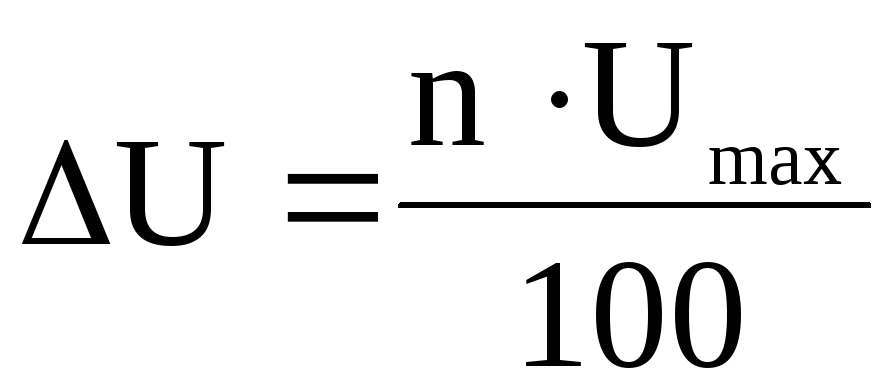 — погрешность вольтметра;
— погрешность вольтметра;
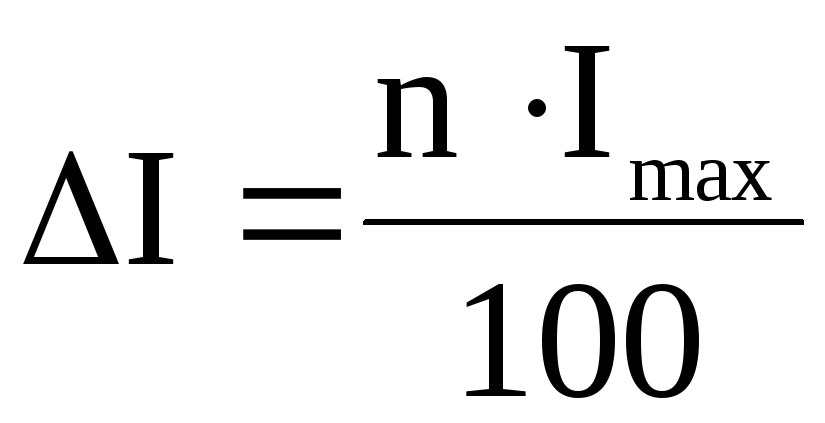 —
приборная погрешность миллиамперметра;
—
приборная погрешность миллиамперметра;
— задается преподавателем;
d, ℓ — определяются известными методами.
9. Зная среднее значение <> рассчитать среднее значение абсолютной погрешности <>.
10. Записать полученный результат в виде доверительного интервала
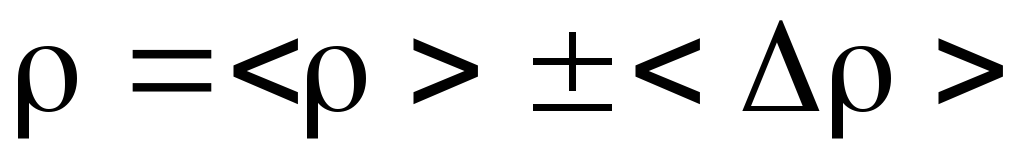 .
.
Зависимость сопротивления проводника от температуры. Сверхпроводимость
Зависимость сопротивления проводника от температуры. Сверхпроводимость
«Физика — 10 класс»
Какую физическую величину называют сопротивлением
От чего и как зависит сопротивление металлического проводника?
Различные вещества имеют разные удельные сопротивления. Зависит ли сопротивление от состояния проводника? от его температуры? Ответ должен дать опыт.
Если пропустить ток от аккумулятора через стальную спираль, а затем начать нагревать её в пламени горелки, то амперметр покажет уменьшение силы тока. Это означает, что с изменением температуры сопротивление проводника меняется.
Если при температуре, равной 0 °С, сопротивление проводника равно R0, а при температуре t оно равно R, то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры t:
Коэффициент пропорциональности α называют температурным коэффициентом сопротивления.
Температурный коэффициент сопротивления — величина, равная отношению относительного изменения сопротивления проводника к изменению его температуры.
Он характеризует зависимость сопротивления вещества от температуры.
Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании на 1 К (на 1 °С).
Для всех металлических проводников коэффициент α > 0 и незначительно меняется с изменением температуры. Если интервал изменения температуры невелик, то температурный коэффициент можно считать постоянным и равным его среднему значению на этом интервале температур. У чистых металлов
У растворов электролитов сопротивление с ростом температуры не увеличивается, а уменьшается. Для них α < 0. Например, для 10%-ного раствора поваренной соли α = -0,02 К-1.
При нагревании проводника его геометрические размеры меняются незначительно. Сопротивление проводника меняется в основном за счёт изменения его удельного сопротивления. Можно найти зависимость этого удельного сопротивления от температуры, если в формулу (16.1) подставить значения Вычисления приводят к следующему результату:
ρ = ρ0(1 + αt), или ρ = ρ0(1 + αΔТ), (16.2)
где ΔТ — изменение абсолютной температуры.
Так как а мало меняется при изменении температуры проводника, то можно считать, что удельное сопротивление проводника линейно зависит от температуры (рис. 16.2).
Увеличение сопротивления можно объяснить тем, что при повышении температуры увеличивается амплитуда колебаний ионов в узлах кристаллической решётки, поэтому свободные электроны сталкиваются с ними чаще, теряя при этом направленность движения. Хотя коэффициент а довольно мал, учёт зависимости сопротивления от температуры при расчёте параметров нагревательных приборов совершенно необходим. Так, сопротивление вольфрамовой нити лампы накаливания увеличивается при прохождении по ней тока за счёт нагревания более чем в 10 раз.
У некоторых сплавов, например у сплава меди с никелем (Константин), температурный коэффициент сопротивления очень мал: α ≈ 10-5 К-1; удельное сопротивление Константина велико: ρ ≈ 10-6 Ом • м. Такие сплавы используют для изготовления эталонных резисторов и добавочных резисторов к измерительным приборам, т. е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.
Существуют и такие металлы, например никель, олово, платина и др., температурный коэффициент которых существенно больше: α ≈ 10-3 К-1. Зависимость их сопротивления от температуры можно использовать для измерения самой температуры, что и осуществляется в термометрах сопротивления.
На зависимости сопротивления от температуры основаны и приборы, изготовленные из полупроводниковых материалов, — термисторы. Для них характерны большой температурный коэффициент сопротивления (в десятки раз превышающий этот коэффициент у металлов), стабильность характеристик во времени. Номинальное сопротивление термисторов значительно выше, чем у металлических термометров сопротивления, оно обычно составляет 1, 2, 5, 10, 15 и 30 кОм.
Обычно в качестве основного рабочего элемента термометра сопротивления берут платиновую проволоку, зависимость сопротивления которой от температуры хорошо известна. Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить.Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Сверхпроводимость.
Сопротивление металлов уменьшается с уменьшением температуры. Что произойдёт при стремлении температуры к абсолютному нулю?
В 1911 г. голландский физик X. Камерлинг-Оннес открыл замечательное явление — сверхпроводимость. Он обнаружил, что при охлаждении ртути в жидком гелии её сопротивление сначала меняется постепенно, а затем при температуре 4,1 К очень резко падает до нуля (рис. 16.3).
Явление падения до нуля сопротивления проводника при критической температуре называется сверхпроводимостью.
Открытие Камерлинг-Оннеса, за которое в 1913 г. ему была присуждена Нобелевская премия, повлекло за собой исследования свойств веществ при низких температурах. Позже было открыто много других сверхпроводников.
Сверхпроводимость многих металлов и сплавов наблюдается при очень низких температурах — начиная примерно с 25 К. В справочных таблицах приводятся температуры перехода в сверхпроводящее состояние некоторых веществ.
Температура, при которой вещество переходит в сверхпроводящее состояние, называется критической температурой.
Критическая температура зависит не только от химического состава вещества, но и от структуры самого кристалла. Например, серое олово имеет структуру алмаза с кубической кристаллической решёткой и является полупроводником, а белое олово обладает тетрагональной элементарной ячейкой и является серебристо-белым, мягким, пластичным металлом, способным при температуре, равной 3,72 К, переходить в сверхпроводящее состояние.
У веществ в сверхпроводящем состоянии были отмечены резкие аномалии магнитных, тепловых и ряда других свойств, так что правильнее говорить не о сверхпроводящем состоянии, а об особом, наблюдаемом при низких температурах состоянии вещества.
Если в кольцевом проводнике, находящемся в сверхпроводящем состоянии, создать ток, а затем удалить источник тока, то сила этого тока не меняется сколь угодно долго. В обычном же (несверхпроводящем) проводнике электрический ток в этом случае прекращается.
Сверхпроводники находят широкое применение. Так, сооружают мощные электромагниты со сверхпроводящей обмоткой, которые создают магнитное поле на протяжении длительных интервалов времени без затрат энергии. Ведь выделения тепла в сверхпроводящей обмотке не происходит.
Однако получить сколь угодно сильное магнитное поле с помощью сверхпроводящего магнита нельзя. Очень сильное магнитное поле разрушает сверхпроводящее состояние. Такое поле может быть создано и током в самом сверхпроводнике. Поэтому для каждого проводника в сверхпроводящем состоянии существует критическое значение силы тока, превысить которое, не нарушая сверхпроводящего состояния, нельзя.
Сверхпроводящие магниты используются в ускорителях элементарных частиц, магнитогидродинамических генераторах, преобразующих механическую энергию струи раскалённого ионизованного газа, движущегося в магнитном поле, в электрическую энергию.
Объяснение сверхпроводимости возможно только на основе квантовой теории. Оно было дано лишь в 1957 г. американскими учёными Дж. Бардиным, Л. Купером, Дж. Шриффером и советским учёным, академиком Н. Н. Боголюбовым.
В 1986 г. была открыта высокотемпературная сверхпроводимость. Получены сложные оксидные соединения лантана, бария и других элементов (керамики) с температурой перехода в сверхпроводящее состояние около 100 К. Это выше температуры кипения жидкого азота при атмосферном давлении (77 К).
Высокотемпературная сверхпроводимость в недалёком будущем приведёт наверняка к новой технической революции во всей электротехнике, радиотехнике, конструировании ЭВМ. Сейчас прогресс в этой области тормозится необходимостью охлаждения проводников до температур кипения дорогого газа — гелия.
Физический механизм сверхпроводимости довольно сложен. Очень упрощённо его можно объяснить так: электроны объединяются в правильную шеренгу и движутся, не сталкиваясь с кристаллической решёткой, состоящей из ионов. Это движение существенно отличается от обычного теплового движения, при котором свободный электрон движется хаотично.
Надо надеяться, что удастся создать сверхпроводники и при комнатной температуре. Генераторы и электродвигатели станут исключительно компактными (уменьшатся в несколько раз) и экономичными. Электроэнергию можно будет передавать на любые расстояния без потерь и аккумулировать в простых устройствах.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Электрический ток в различных средах — Физика, учебник для 10 класса — Класс!ная физика
Электрическая проводимость различных веществ. Электронная проводимость металлов — Зависимость сопротивления проводника от температуры. Сверхпроводимость — Электрический ток в полупроводниках. Собственная и примесная проводимости — Электрический ток через контакт полупроводников с разным типом проводимости. Транзисторы — Электрический ток в вакууме. Электронно-лучевая трубка — Электрический ток в жидкостях. Закон электролиза — Электрический ток в газах. Несамостоятельный и самостоятельный разряды — Плазма — Примеры решения задач по теме «Электрический ток в различных средах»
Зависимость сопротивления проводника от температуры
Практически в электротехнике выло выявлено, что с увеличением температуры сопротивление проводников из металла возрастает, а с понижением уменьшается. Для всех проводников из металла это изменение сопротивления почти одинаково и в среднем равно 0,4% на 1°С.
Если быть точным, то на самом деле при изменении температуры проводника изменяется его удельное сопротивление, которое имеет следующую зависимость:
где ρ и ρ0, R и R0 — соответственно удельные сопротивления и сопротивления проводника при температурах t и 0°С (шкала Цельсия), α — температурный коэффициент сопротивления, [α] = град-1.
Изменение удельного сопротивления проводника приводит к изменения самого сопротивления, что видно из следующего выражения:
Зная электронную теорию строения вещества можно дать следующее объяснение увеличению сопротивления металлических проводников с повышением температуры. При увеличении температуры проводник получает тепловую энергию, которая несомненно передается всем атомам вещества, в результате чего .возрастает их тепловое движение. Увеличившееся тепловое движение атомов создает большее сопротивление направленному движению свободных электронов (увеличивается вероятность столкновения свободных электронов с атомами), от этого и возрастает сопротивление проводника.
С понижением температуры направленное движение электронов облегчается (уменьшается возможность столкновения свободных электронов с атомами), и сопротивление проводника уменьшается. Этим объясняется интересное явление — сверхпроводимость металлов. Сверхпроводимость, т. е. уменьшение сопротивления металлов до нуля, наступает при огромной отрицательной температуре —273° С, называемой абсолютным нулем. При температуре абсолютного нуля атомы металла как бы застывают на месте, совершенно не препятствуя движению электронов.
График звисимости сопротивления металлического проводника от температуры представлен на рисунке 1.
Рисунок 1. График зависимости удельного сопротивления металлического проводника от температуры
Необходимо сказать, что сопротивление электролитов и полупроводников (уголь, селен и другие) с увеличением температуры уменьшается.
Температурная зависимость сопротивления электролита объясняется также в основном изменением удельного сопротивления,однако всегда температурный коэффициент сопротивления — α <0.
Поэтому кривая зависимости сопротивленя электролита от температуры имеет вид, представленый на рисунке 2.
Рисунок 1. График зависимости удельного сопротивления электролита от температуры
Ддя полупроводников характер изменения удельного сопротивления от температуры будет схож с таковым для элетролитов.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Электрическое сопротивление проводника
Электрическое сопротивление — физическая величина, которая показывает, какое препятствие создается току при его прохождении по проводнику. Единицами измерения служат Омы, в честь Георга Ома. В своем законе он вывел формулу для нахождения сопротивления, которая приведена ниже.

Рассмотрим сопротивление проводников на примере металлов. Металлы имеют внутреннее строение в виде кристаллической решетки. Эта решетка имеет строгую упорядоченность, а её узлами являются положительно заряженные ионы. Носителями заряда в металле выступают “свободные” электроны, которые не принадлежат определенному атому, а хаотично перемещаются между узлами решетки. Из квантовой физики известно, что движение электронов в металле это распространение электромагнитной волны в твердом теле. То есть электрон в проводнике движется со скоростью света (практически), и доказано, что он проявляет свойства не только как частица, но еще и как волна. А сопротивление металла возникает в результате рассеяния электромагнитных волн (то есть электронов) на тепловых колебаниях решетки и её дефектах. При столкновении электронов с узлами кристаллической решетки часть энергии передается узлам, вследствие чего выделяется энергия. Эту энергию можно вычислить при постоянном токе, благодаря закону Джоуля-Ленца – Q=I2Rt. Как видите чем больше сопротивление, тем больше энергии выделяется.
Удельное сопротивление
Существует такое важное понятие как удельное сопротивление, это тоже самое сопротивление, только в единице длины. У каждого металла оно свое, например у меди оно равно 0,0175 Ом*мм2/м, у алюминия 0,0271 Ом*мм2/м . Это значит, брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2 будет иметь сопротивление 0,0175 Ом, а такой же брусок, но из алюминия будет иметь сопротивление 0,0271 Ом. Выходит что электропроводность меди выше чем у алюминия. У каждого металла удельное сопротивление свое, а рассчитать сопротивление всего проводника можно по формуле

где p – удельное сопротивление металла, l – длина проводника, s – площадь поперечного сечения.
Значения удельных сопротивлений приведены в таблице удельных сопротивлений металлов (20°C)
|
Вещество |
p, Ом*мм2/2 |
α,10-3 1/K |
|
Алюминий |
0.0271 |
3.8 |
|
Вольфрам |
0.055 |
4.2 |
|
Железо |
0.098 |
6 |
|
Золото |
0.023 |
4 |
|
Латунь |
0.025-0.06 |
1 |
|
Манганин |
0.42-0.48 |
0,002-0,05 |
|
Медь |
0.0175 |
4.1 |
|
Никель |
0.1 |
2.7 |
|
Константан |
0.44-0.52 |
0.02 |
|
Нихром |
1.1 |
0.15 |
|
Серебро |
0.016 |
4 |
|
Цинк |
0.059 |
2.7 |
Кроме удельного сопротивления в таблице есть значения ТКС, об этом коэффициенте чуть позже.
Зависимость удельного сопротивления от деформаций
При холодной обработке металлов давлением, металл испытывает пластическую деформацию. При пластической деформации кристаллическая решетка искажается, количество дефектов становится больше. С увеличением дефектов кристаллической решетки, сопротивление течению электронов по проводнику растет, следовательно, удельное сопротивление металла увеличивается. К примеру, проволоку изготавливают методом протяжки, это значит, что металл испытывает пластическую деформацию, в результате чего, удельное сопротивление растет. На практике для уменьшения сопротивления применяют рекристаллизационный отжиг, это сложный технологический процесс, после которого кристаллическая решетка как бы, “расправляется” и количество дефектов уменьшается, следовательно, и сопротивление металла тоже.
При растяжении или сжатии, металл испытывает упругую деформацию. При упругой деформации вызванной растяжением, амплитуды тепловых колебаний узлов кристаллической решетки увеличиваются, следовательно, электроны испытывают большие затруднения, и в связи с этим, увеличивается удельное сопротивление. При упругой деформации вызванной сжатием, амплитуды тепловых колебаний узлов уменьшаются, следовательно, электронам проще двигаться, и удельное сопротивление уменьшается.
Влияние температуры на удельное сопротивление
Как мы уже выяснили выше, причиной сопротивления в металле являются узлы кристаллической решетки и их колебания. Так вот, при увеличении температуры, тепловые колебания узлов увеличиваются, а значит, удельное сопротивление также увеличивается. Существует такая величина как температурный коэффициент сопротивления (ТКС), который показывает насколько увеличивается, или уменьшается удельное сопротивление металла при нагреве или охлаждении. Например, температурный коэффициент меди при 20 градусах по цельсию равен 4.1 · 10 − 3 1/градус. Это означает что при нагреве, к примеру, медной проволоки на 1 градус цельсия, её удельное сопротивление увеличится на 4.1 · 10 − 3 Ом. Удельное сопротивление при изменении температуры можно вычислить по формуле


где r это удельное сопротивление после нагрева, r0 – удельное сопротивление до нагрева, a – температурный коэффициент сопротивления, t2 – температура до нагрева, t1 — температура после нагрева.
Подставив наши значения, мы получим: r=0,0175*(1+0.0041*(154-20))=0,0271 Ом*мм2/м. Как видите наш брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2, после нагрева до 154 градусов, имел бы сопротивление, как у такого же бруска, только из алюминия и при температуре равной 20 градусов цельсия.
Свойство изменения сопротивления при изменении температуры, используется в термометрах сопротивления. Эти приборы могут измерять температуру основываясь на показаниях сопротивления. У термометров сопротивления высокая точность измерений, но малые диапазоны температур.
На практике, свойства проводников препятствовать прохождению тока используются очень широко. Примером может служить лампа накаливания, где нить из вольфрама, нагревается за счет высокого сопротивления металла, большой длины и узкого сечения. Или любой нагревательный прибор, где спираль разогревается благодаря высокому сопротивлению. В электротехнике, элемент главным свойством которого является сопротивление, называется – резистор. Резистор применяется практически в любой электрической схеме.
Удельное сопротивление проводника: формула, сопротивление разных материалов
Многие люди, изучающие электрику, в первую очередь сталкиваются с таким понятием как удельное сопротивление. Что оно собой представляет, в каких единицах измеряется удельное сопротивление проводника, от чего зависит и как его найти по формуле далее.
Что это такое
Удельным сопротивлением проводника называется физический вид величины, который показывает, что материал может препятствовать электротоку. По-другому, это такое сопротивление металлов, которое оказывает материал с единичным сечением сопротивление протекающему току. Отличается удельное сопротивление постоянному току тем, что оно вызывается током на проводник. Что касается переменного тока, то он появляется в проводнике под действием вихревого поля.

Удельное электросопротивление
Важно также уточнить, что собой представляет удельная электрическая проводимость. Электропроводимость — это величина, которая обратна сопротивлению и называется электропроводностью. Это показатель, показывающий меру проводимости силы электротока.
Обратите внимание! Чем больше он, тем лучше способен проводник проводить электричество.

Общее определение из учебного пособия
В чем измеряется
Согласно международной системе единиц, измеряется величина в омах, умноженных на метр. В некоторых случаях применяется единица ом, умноженная на миллиметр в квадрате, поделенная на метр. Это обозначение для проводника, имеющего метровую длину и миллиметровую площадь сечения в квадрате.

Единица измерения
Формула как найти
Согласно положению из любого учебного пособия по электродинамики, удельное сопротивление материала проводника формула равна пропорции общего сопротивления проводника на площадь поперечного сечения, поделенного на проводниковую длину. Важно понимать, что на конечный показатель будет влиять температура и степень материальной чистоты. К примеру, если в медь добавить немного марганца, то общий показатель будет увеличен в несколько раз.

Главная формула расчета
Интересно, что существует формула для неоднородного изотропного материала. Для этого нужно знать напряженность электрополя с плотностью электротока. Для нахождения нужно поделить первую величину на другую. В данном случае получится не константа, а скалярная величина.

Закон ома в дифференциальной форме
Есть другая, более сложная для понимания формула для неоднородного анизотропного материала. Зависит от тензорного координата.
Важно отметить, что связь сопротивления с проводимостью также выражается формулами. Существуют правила для нахождения изотропных и анизотропных материалов через тензорные компоненты. Они показаны ниже в схеме.

Связь с проводимостью, выраженная в физических соотношениях
От чего зависит
Сопротивляемость зависит от температуры. Она увеличивается, когда повышается столбик термометра. Это поясняется физиками так, что при росте температуры атомные колебания в кристаллической проводниковой решетке повышаются. Это препятствует тому, чтобы свободные электроны двигались.
Обратите внимание! Что касается полупроводников и диэлектриков, то там величина понижается из-за того, что увеличивается структура концентрации зарядных носителей.

Зависимость от температуры как основное свойство проводниковой сопротивляемости
Удельное сопротивление разных материалов
Важно отметить, что сопротивление у металлических монокристаллов с металлами и сплавами разные. Значения различаются из-за химической металлической чистоты, способов создания составов и их непостоянства. Также стоит иметь в виду, что значения меняются при изменении температуры. Иногда сопротивляемость падает до нуля. В таком случае явление называется сверхпроводимостью.
Интересно, что под термической обработкой, например, отжигом меди, значение вырастает в 3 раза, несмотря на то, что доля примесей в проном, антикоррозийном и легком составе, как правило, равна не больше 0,1%.
Обратите внимание! Что касается отжига алюминия, свинца или железа, значение в таких же условиях вырастает в 2 раза, несмотря на наличие примесей в количестве 0,5% и необходимости большей энергии на плавление.

Таблица значений составов при температуре 20 градусов Цельсия
В целом, удельное электросопротивление представляет собой физическую величину, которая характеризует способность вещества препятствовать тому, чтобы проходил электроток. По СИ измеряется в омах, перемноженных на метры. Зависит от увеличения температуры вещества. Отыскать значение можно по формуле соотношения общего сопротивления и площади поперечного сечения, поделенного на длину проводника. Что касается удельного сопротивления сплавов, согласно изучениям разных ученых состав их непостоянный, может быть изменен под термообработкой.



