13. Зависимость сопротивления проводников от его размеров, материала и температуры.

В классической физике свободные электроны в металлах называют электронным газом и в первом приближении считают, что к нему применимы законы, установленные для идеального газа.

Сопротивление проводника прямо про­порционально его длине и обратно пропорционально площади его поперечного сечения. Величину р, характеризующую зависимость со­противления проводника от материала, из которого он сделан, и от внешних условий, называют удельным сопротивлением вещества.

Величину,^ обратную удельному сопротивлению, называют удельной проводимостью вещества и обозначают ơ:

Ơ =1/р.

Величину а, характеризующую зависимость изменения удельного сопротивления при нагревании от рода вещества, называют темпе­ратурным коэффициентом сопротивления. Температурный коэф­фициент сопротивления измеряют числом, показывающим, на ка­кую часть своей величины, взятой при О °С, изменяется удельное сопротивление при нагревании на 1 °С.

Зависимость сопротивления металлов от температуры исполь­зуется в термометрах сопротивления.

14. Последовательное соединение проводников.

1. При последовательном соединении сила тока во всех участках цепи одина­кова:

I=I₁=I₂=I₃

2. При последовательном соединении напряжение на внешней цепи равно сумме напряжений на отдельных участках цепи:

U_посл=U₁+U₂+U₃

3. Напряжения на отдельных участках цепи при последователь­ном соединении прямо пропорциональны сопротивлениям участков:

U₁ : U₂ : U₃=R₁ : R₂ : R₃.

4. При последовательном соединении эквивалентное сопротивле­ние всей цепи равно сумме сопротивлений отдельных участков цепи:

R_посл = R₁ + R₂ + R₃.

При размыкании цепи у одного из последовательно соединенных потребителей ток исчезает во всей цепи.

15. Параллельное соединение проводников.

Все вместе параллельно соединенные проводники составляют разветвление, а каж­дый из них называется ветвью.

1.При параллельном соединении напряжения на отдельных ветвях и на всем разветвлении одинаковы:

U₁=U₂=U₃=U.

2.Ток до и после разветвления равен сумме токов в отдельных ветвях:

I_пар=I₁+I₂+I₃.

3. Токи в отделных ветвях разветвления обратно пропорциональны сопротивлениям этих ветвей:

I₁:I₂:I₃=1/R₁: 1/R_2: 1/R₃

4.Проводимость всего разветвления равно сумме проводимостей отдельных ветвей:

1/R_пар=1/R₁+1/R₂+1/R₃.

Если напряжение между узлами остается постоянным, то токи в ветвях не зависят друг от друга.

16.Электродвижущая сила источника тока. Закон ома для полной цепи.

Источник электрической энергии всегда имеет некоторое сопротивление, тепло. Это сопротивление г назы­вают внутренним сопро­тивлением источника.

Закон Ома для всей цепи: сила тока в электрической цепи с одним источником э. д. с. прямо пропорциональна электродвижущей силе и обратно пропор­циональна сумме сопротивлений внешней и внутренней цепей.

В свою очеpедь, интегpал

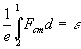
называется электpодвижущей силой (ЭДС) источника.

17. Работа и мощность электрического тока.

Полную работу тока на участке цепи, которой является потребителем, можно найти по формуле:

A_п=Uq.

Для вычисления работы тока на участке цепи без э. д. с.:

A = U²t/R.

При вычислении работы тока на участке цепи без э. д. с. можно пользоваться любой из формул.

Работа тока, определяющая электрическую энергию, которая затрачивается на тепловое действие в данном участке цепи, выражается формулой:

A_T=I²Rt.

Работа сторонних сил в генераторе, которой оце­нивают полученное в нем количество электрической энергии за счет других видов энергии, находится из соотноше­ния. Так как q=It, получаем:

A=EIt.

Мощность тока на участке цепи измеряют работой тока за единицу времени.

Мощность тока во всей внеш­ней цепи при любом соединении равна сумме мощностей на отдель­ных участках цепи. Мощность тока в подводящих про­водах часто называют потерей мощности.

Сопротивление проводника и его зависимость от размеров, материалов и температуры.

Любое тело, по которому протекает электрический ток, оказывает ему определенное сопротивление. Свойство материала проводника препятствовать прохождению через него электрического тока называется электрическим сопротивлением.

Сопротивление обозначается латинскими буквами R или r.

За единицу электрического сопротивления принят Ом.

Сопротивление различных проводников зависит от материала, из которого они изготовлены. Для характеристики электрического сопротивления различных материалов введено понятие так называемого удельного сопротивления.

Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм2. Удельное сопротивление обозначается буквой греческого алфавита ρ. Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.

Сопротивление проводника прямо пропорционально его длине, т. е. чем длиннее проводник, тем больше его электрическое сопротивление.

Сопротивление проводника обратно пропорционально площади его поперечного сечения, т. е. чем толще проводник, тем его сопротивление меньше, и, наоборот, чем тоньше проводник, тем его сопротивление больше.

Электрическое сопротивление проводника равно удельному сопротивлению материала, из которого этот проводник сделан, умноженному на длину проводника и деленному на площадь площадь поперечного сечения проводника

:

R = р l / S,

где — R — сопротивление проводника, ом, l — длина в проводника в м, S — площадь поперечного сечения проводника, мм².

Еще одной причиной, влияющей на сопротивление проводников, являетсятемпература.

Установлено, что с повышением температуры сопротивление металлических проводников возрастает, а с понижением уменьшается. С понижением же температуры создаются лучшие условия для направленного движения электронов, и сопротивление проводника уменьшается. Этим объясняется интересное явление — сверхпроводимость металлов.

 

ЭДС источника тока. Закон Ома для полной цепи с ЭДС.

При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.

Физическая величина, равная отношению работы A_ст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника(ЭДС):

Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).

 

Эта формула выражет закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.

Сопротивление r неоднородного участка можно рассматривать как внутреннее сопротивление источника тока.

63. Соединение проводников.

Проводники в электрических цепях могут соединяться последовательно и параллельно.

При последовательном соединении проводников сила тока во всех проводниках одинакова:

 

По закону Ома, напряжения U₁ и U₂ на проводниках равны

Общее напряжение U на обоих проводниках равно сумме напряжений U₁ и U₂:

U = U1 + U2 = I(R1 + R2) = IR,

где R – электрическое сопротивление всей цепи. Отсюда следует:

Зависимость сопротивления от материала, длины и площади поперечного сечения проводника

⇐ ПредыдущаяСтр 2 из 54Следующая ⇒

В металле подвижными носителями зарядов являются свободные электроны. Можно считать, что при своем хаотическом движении они ведут себя подобно молекулам газа. Поэтому в классической физике свободные электроны в металлах называют электронным газом и в первом приближении считают, что к нему применимы законы, установленные для идеального газа.

Плотность электронного газа и строение кристаллической решетки зависят от рода металла. Поэтому сопротивление проводника должно зависеть от рода его вещества. Кроме того, оно должно еще зависеть от длины проводника, площади его поперечного сечения и от температуры.

Влияние сечения проводника на его сопротивление объясняется тем, что при уменьшении сечения поток электронов в проводнике при одной и той же силе тока становится более плотным, поэтому и взаимодействие электронов с частицами вещества в проводнике становится сильнее.

Из формулы

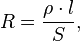
видно, что сопротивление проводника прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения. Величину ρ, характеризующую зависимость сопротивления проводника от материала, из которого он сделан, и от внешних условий, называют удельным сопротивлением вещества. Удельное сопротивление различных веществ при расчетах берут из таблиц.

Величину, обратную удельному сопротивлению, называют удельной проводимостью вещества и обозначают σ.

Сопротивление тела человека

· Для расчёта опасной величины силы тока, протекающего через человека при попадании его под электрическое напряжение частотой 50 Гц, сопротивление тела человека условно принимается равным 1 кОм

[5]. Эта величина имеет малое отношение к реальному сопротивлению человеческого тела. В реальности сопротивление человека не является омическим, так как эта величина, во-первых, нелинейна по отношению к приложенному напряжению, во-вторых меняется во времени, в третьих, гораздо меньше у человека, который волнуется и, следовательно, потеет и т. д.

· Серьёзные поражения тканей человека наблюдаются обычно при прохождении тока силой около 100 мА. Совершенно безопасным считается ток силой до 1 мА. Удельное сопротивление тела человека зависит от состояния кожных покровов. Сухая кожа обладает удельным сопротивлением порядка 10000 Ом·м, поэтому опасные токи могут быть достигнуты только при значительном напряжении. Однако при наличии сырости сопротивление тела человека резко снижается и безопасным может считаться напряжение только ниже 12 В. Удельное сопротивление крови 1 Ом·м при 50 Гц.

 

Электрическое сопротивление проводников

 

Рекомендуемые страницы:

ФиЗиКа. Как зависит сопротивление проводника от его длинны и от площади поперечного сечения?

R=p*l/S p-удельная плотность вещ-ва Cопротивление прямо пропорционально длине проводника, и обратно пропорционально площади его поперечного сечения, это видно из данной формулы

Направленному движению электрических зарядов в любом проводнике препятствуют его молекулы и атомы. Поэтому как внешняя цепь, так и сам источник энергии оказывают препятствие прохождению тока. Величина, характеризующая противодействие электрической цепи прохождению электрического тока, называется электрическим сопротивлением (или, короче, сопротивлением) . Источник электрической энергии, включенный в замкнутую электрическую цепь, расходует энергию на преодоление сопротив­ления внешней и внутренней цепей. В различных веществах содержится различное количество электронов, а атомы, между которыми эти электро­ны движутся, имеют различное расположение. Поэтому сопротив­ление проводников электрическому току зависит от материала, из которого они изготовлены, от длины и площади поперечного сече­ния проводника. Если сравнить два проводника, изготовленных из одного и того же материала, то более длинный проводник имеет большее сопротивление при равных площадях поперечных сечений, а проводник с большим поперечным сечением имеет меньшее сопро-тивление при равных длинах.

Цель: Исследовать зависимость сопротивления проводника от его длины и площади поперечного сечения

R=p*l/S p-удельная плотность вещ-ва

Метод расчета активного сопротивления цилиндрического провода с учетом поверхностного эффекта



В данной статье рассматривается вопрос влияния высших гармоник тока на активное сопротивление цилиндрического провода в диапазоне частот от 50 до 2000 Гц. Выведена расчетная формула для активного сопротивления цилиндрического провода на произвольной частоте. Проанализированы закономерности изменения активного сопротивления медных и алюминиевых проводов в зависимости от частоты и площади поперечного сечения.

Ключевые слова: поверхностный эффект, несинусоидальность, активное сопротивления медного провода, активное сопротивление алюминиевого провода

This article has shown the problem of high-harmonics influence on cylindrical wire resistance according to the frequency range from 50 to 2000 Hz. Cylindrical wire resistance estimation for any frequency has been deduced.We have also analyzed cylindrical wire resistance dependence of copper and aluminum wires due to the frequency and cross section area.

Keywords: skin effect, high-harmonics, copper wire resistance, aluminum wire resistance

В Российской Федерации системы электроснабжения общего назначения работают на фиксированной частоте 50 Гц. Кроме основной гармоники, в сетях присутствуют также высшие гармоники токов и напряжений [1]. Исследования указывают на то, что при наличии в сети нелинейных нагрузок, наибольшим искажениям подвергается форма кривой тока, в то время как кривая напряжения практически не изменяется [5, 6]. Это объясняется тем, что реальные генераторы по своим свойствам близки к идеальным источникам ЭДС. Высшие гармоники тока приводят к дополнительному нагреву проводников линии электропередачи, в результате чего, с одной стороны возникают дополнительные потери мощности, с другой происходит ускоренный износ изоляции, изоляторов, растяжение проводов и другие негативные последствия [2]. По мере увеличения частоты, начинает проявляться поверхностный эффект, приводящий к перераспределению плотности тока в сечении проводника, от центра к поверхности, в результате изменяется его сопротивление, что в свою очередь влияет на потери мощности и энергии в линиях электропередачи электрической распределительной сети.

Задача данного исследования: определить степень изменения плотности тока в сечении провода и его сопротивления в зависимости от частоты гармоники тока протекающего по проводнику. Это позволит более точно рассчитать дополнительные потери мощности на нагрев проводов, обусловленные несинусоидальностью питающего напряжения электрической распределительной сети.

Провод можно приближенно представить в виде цилиндрического проводника, длина которого многократно превышает радиус. Для нахождения плотности тока используют уравнения Максвелла, решение которых производится в цилиндрической системе координат [3]. В результате выражения для плотности тока и напряженности магнитного поля в любой точке сечения цилиндрического проводника:

(1)

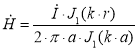(2)

где — комплексная плотность тока, А/м²; — напряженность магнитного поля, А/м; 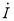— комплексный ток, А; J₀ — функция Бесселя 1-го рода 0-го порядка; J₁ — функция Бесселя 1-го рода 1-го порядка; r — радиус текущей поверхности тока в проводе, м; a — радиус провода, м; — комплексное волновое число, м^-1; 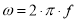— круговая частота, рад/с; f — циклическая частота, Гц; — абсолютная магнитная проницаемость, Гн/м; µ — относительная магнитная проницаемость; µ ₀= 4·π·10–⁷ Гн/м — магнитная постоянная.

Формулы (1), (2) не учитывают «эффект близости», т. к. для этого необходимо точно знать пространственное расположение проводников. При расстоянии между проводами многократно превышающем радиус и невысоких значениях тока «эффектом близости» можно пренебречь.

Мощность рассеиваемую цилиндрическим проводом определяют по закону Джоуля-Ленца в комплексной форме:

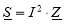(3)

С другой стороны рассеиваемую мощность находим, используя теорему Умова-Пойнтинга [3]:

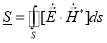(4)

Приравнивая выражения (3) и (4) получаем:

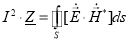(5)

В результате комплексное сопротивление выражаем формулой:

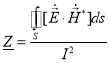(6)

Вектор напряженности электрического поля 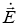вычисляем по формуле:

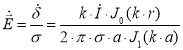(7)

где σ — удельная проводимость, См/м.

Учитывая, что площадь боковой поверхности цилиндрического проводника равна S=2·π·a·lи радиус поверхности равен радиусу провода r=a получаем:

где l — длина проводника, м.

Таким образом, окончательное выражение для комплексного сопротивления цилиндрического провода приняло вид:

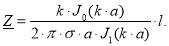
Активное сопротивление при этом определяем, как действительную часть полного комплексного сопротивления:

(8)

Рассчитаем сопротивления медных проводов и алюминиевых проводов марок А, АКП, АН, АНКП, АЖ, АЖКП. Сечения выберем самые распространенные: 16, 25, 35, 50, 70, 95, 120, 150, 185 мм² [4], хотя каких-либо ограничений по сечению проводов нет. Единственное условие данного метода: длина должна быть много больше радиуса l>>a. Удельная проводимость меди σ_Cu=56·10⁶ См/м, а удельная проводимость алюминия σ_Al=37·10⁶ См/м. Относительная магнитная проницаемость обоих материалов приблизительно равна µ=1 (медь является диамагнетиком, а алюминий парамагнетиком). Радиус провода выражаем из формулы площади круга:

,

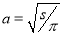где s — площадь сечения провода, мм².

Расчета активного сопротивления медных проводов различных сечений, выполнен в диапазоне частот 0–2 кГц (рисунок 1.). Аналогичный расчет проведен для алюминиевых проводов (рисунок 2.). Выбор диапазона обосновывается тем, что согласно ГОСТ Р54149–2010, гармоники нормируются до 40-й включительно, что соответствует наибольшему значению частоты 2кГц [1].

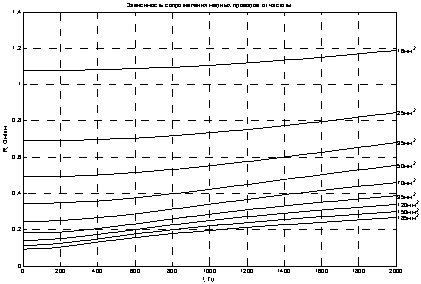
Рис. 1. Зависимость активного сопротивления медных проводов различных сечений от частоты

Семейства графиков (рисунки 1, 2) показывает зависимость погонного сопротивления проводов как от их сечения, так и от частоты. В полосе частот от 0 до 2000 Гц (рисунок 1.) величина возрастания сопротивления от 10,4 % до 183,9 %, в зависимости от сечения провода. Причем наибольший, в процентном отношении, прирост сопротивления наблюдается на больших сечениях. Например, при сечении 16 мм² погонное сопротивление увеличивается с 1,08 до 1,19 Ом/км, что составляет 10,4 %, а при наибольшем сечении 185 мм² погонное сопротивление увеличивается с 0,09 до 0,27 Ом/км, что в пересчете на проценты составляет 183,9 %. Это объясняется большей неравномерностью плотности тока при большем радиусе сечений проводов.

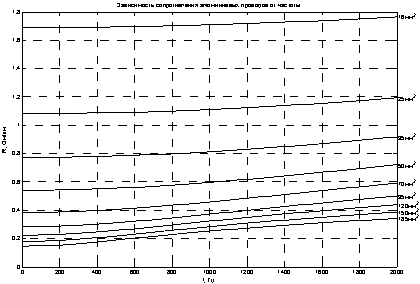
Рис. 2. Зависимость активного сопротивления алюминиевых проводов различных сечений от частоты

Результаты, полученные для алюминиевых проводов (рисунок 2.), аналогичны результатам для медных проводов. Сопротивление возрастает на величину от 4,4 % до 133,8 %, в зависимости от сечения провода, наименьший прирост погонного сопротивления наблюдается при сечении 16 мм², в этом случае погонное сопротивление увеличивается с 1,69 до 1,76 Ом/км, что составляет 4,4 %, а при наибольшем приведенном на графике сечении 185 мм² погонное сопротивление увеличивается с 0,15 до 0, 34 Ом/км, что в пересчете на проценты составляет 133,8 %.

Таким образом для проводников большего сечения поверхностный эффект оказывает более выраженное влияние на сопротивление (для меди сопротивление возросло на 183,9 %, а для алюминия на 133,8 %, в полосе частот от 0 до 2000 Гц), уменьшение же сечения приводит к существенному возрастанию активного сопротивления (рисунки 1,2.). Проводники с большей удельной проводимостью более подвержены влиянию поверхностного эффекта. При равном сечении, по мере увеличения частоты, активное сопротивление медного провода возрастает быстрее, чем активное сопротивление алюминиевого провода.

Литература:

1. ГОСТ 32144–2013 Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. [Текст] — М.: Стандартинформ — 2014г. — 38 с.
2. Григорьев О. Высшие гармоники в сетях электроснабжения 0,4 кВ/ О. Григорьев, В. Петухов, В. Соколов, И. Красилов [Текст] //«Новости электротехники», № 6(18) 2002–1(19) 2003.
3. Бессонов Л. А. Теоретические основы электротехники [Текст] — М.: Высшая школа — 1964г. — 750 с.
4. Будзко И. А. Элетроснабжение сельского хозяйства/ И. А. Будзко, Т. Б. Лещинская, В. И. Сукманов [Текст] — М: Колос — 2000 г. — 536 с.
5. Бессонов Л. А. Линейные электрические цепи / Л. А. Бессонов. — М: Высшая школа, 1983. — 336 с.
6. Лосев А. К. Теория Линейных электрических цепей / А. К. Лосев. — М: Высшая школа, 1987. — 512 с.

Основные термины (генерируются автоматически): активное сопротивление, погонное сопротивление, поверхностный эффект, цилиндрический провод, провод, сечение, цилиндрический проводник, радиус провода, сечение провода, алюминиевый провод.