Лабораторная работа №1 исследование зависимомти активного,индуктивного и емкостного сопротивления от частоты переменного тока.Проверка закона ома для пени переменного тока.
Цель работы: выяснить зависимость сопротивлений от частоты.
Приборы и принадлежности: генератор звуковой частоты, амперметр, вольтметр, активное сопротивление, катушка индуктивности, конденсатор, провода.
Краткая теория
Переменный электрический ток в электрических цепях является результатом возбуждения в них вынужденных электромагнитных колебаний. Эти вынужденные колебания создаются генераторами переменного тока, работающими на электростанциях.
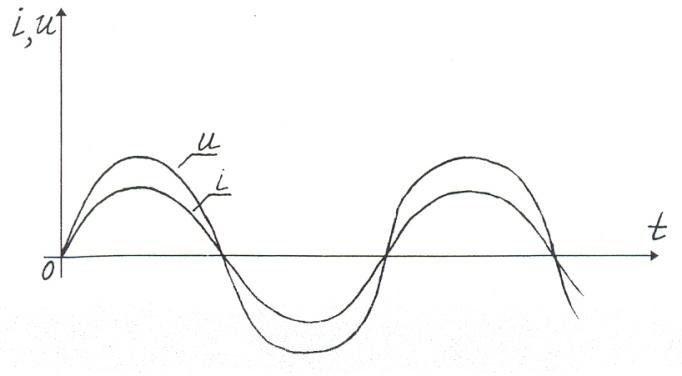
Электрический генератор создает синусоидальное напряжение. Соответственно синусоидальным оказывается и ток.
Зависимость напряжения от времени можно записать в виде:
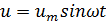
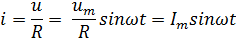
где i, u — мгновенные значения напряжения и силы тока.
Потенциал
периодически изменяется между 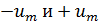
Величина 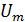 называется амплитудным значением
напряжения (или пиковым напряжением).
называется амплитудным значением
напряжения (или пиковым напряжением).

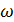 —
циклическая
частота.
—
циклическая
частота.
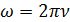 ,
где
,
где
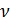 —
частота тока.
—
частота тока.
Частота переменного тока в России равна 50 Гц.
Рассмотрим процессы, происходящие в проводнике, включенном вцепь переменного тока.
I. Цепь, в которой разность потенциалов на реактивных сопротивлениях много меньше разности потенциалов на резисторе, будет являться цепью с активным сопротивлением.

Активным сопротивлением R называется физическая величина, определяемая отношением мощности Р переменного тока на участке электрической цепи к квадрату действующего значения силы тока на этом участке
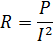
Действующим значением силы переменного тока называют силу такого постоянного тока, при прохождении которого по той же цепи и за то же время выделяется такое же количество теплоты, как и при прохождении переменного тока.
Выразим
действующее значение силы тока I через
амплитуду силы тока .
Согласно определению, бесконечно малое
количество теплоты, выделяемое постоянным
током, равно такому же количеству
теплоты, выделяемому переменным током.
.
Согласно определению, бесконечно малое
количество теплоты, выделяемое постоянным
током, равно такому же количеству
теплоты, выделяемому переменным током.
На основании закона Джоуля — Ленца имеем:

Приравнивая
значения 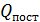 и
и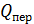 ,
получим:
,
получим:

Пусть теплота Q выделяется током в течение одного периода колебаний. Тогда, интегрируя данное выражение в пределах от 0 до Т получим:
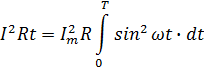
Найдем значение интеграла:
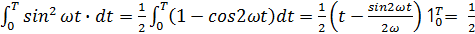
Тогда  ,откуда
,откуда
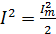
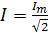
Аналогично для действующих значений напряжений получим:
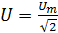 ,
,
где
действующее значение переменного
напряжения U в 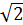
Колебания силы тока в цепи с активным сопротивлением происходят по закону:
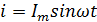 ,
,
где
амплитуда силы тока 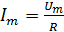
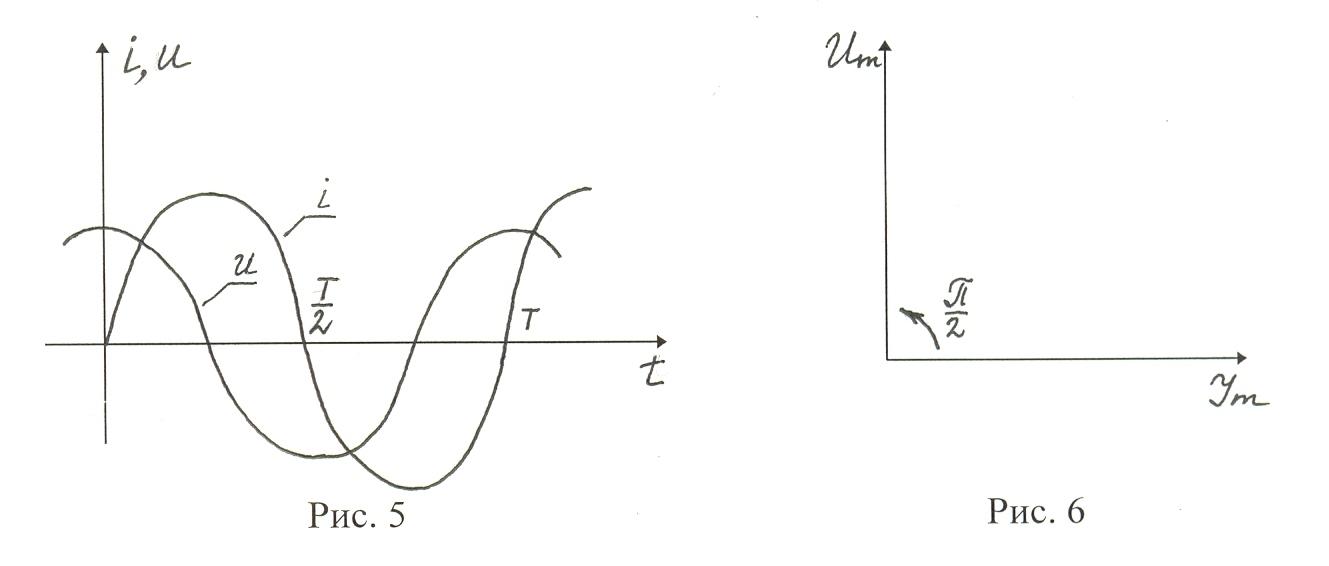
Частота и фаза переменного тока будут совпадать с частотой и фазой колебания напряжения (рис. 2,3).
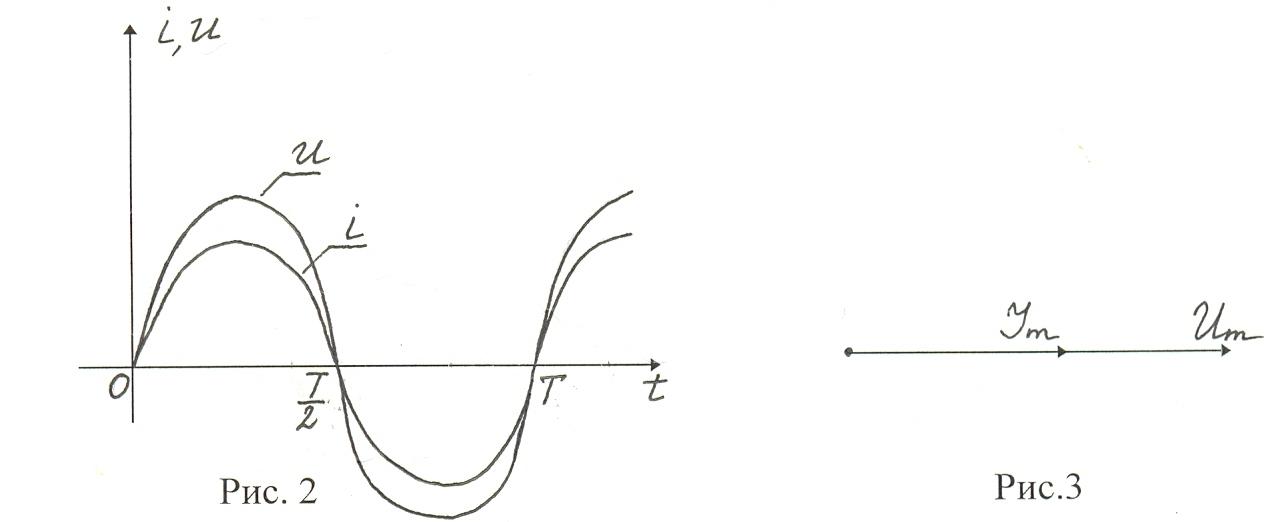
II. Рассмотрим цепь переменного тока с индуктивным сопротивлением, т.е. цепь, содержащую катушку.
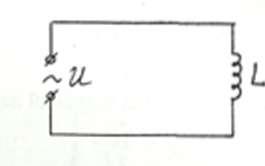
Рис. 4
Произведение
циклической частоты 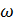 на
индуктивность L называется индуктивным
сопротивлением.
на
индуктивность L называется индуктивным
сопротивлением.
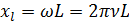
Через
катушку идёт ток, изменяющийся по закону: 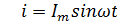 ,
,
При этом в катушке возникает ток самоиндукции, а ЭДС самоиндукции будет
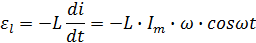
Приложенное
к катушке напряжение должно в любой
момент времени уравновешивать Э.Д.С.
самоиндукции в катушке, если 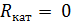 ,
то
,
то
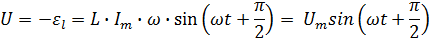
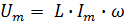
Связь
между амплитудой 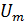 колебаний напряжения на концах проводника
индуктивностью L с амплитудой
колебаний напряжения на концах проводника
индуктивностью L с амплитудой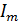 колебаний силы тока в нем совпадает по
форме с выражением закона Ома для участка
цепи постоянного тока.
колебаний силы тока в нем совпадает по
форме с выражением закона Ома для участка
цепи постоянного тока.
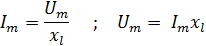
Хотя
данное выражение совпадает по форме с
выражением закона Ома для участка цепи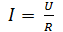
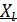 не является постоянной величиной, его
значение прямо пропорционально частоте
переменного тока.
не является постоянной величиной, его
значение прямо пропорционально частоте
переменного тока. Поэтому
амплитуда  колебаний силы тока в проводнике
индуктивностью L при постоянном значении
амплитуды
колебаний силы тока в проводнике
индуктивностью L при постоянном значении
амплитуды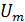
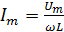
Индуктивное сопротивление энергию не потребляет. Из уравнений
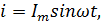

видно,
что сдвиг фаз между напряжением и током
равен  , колебания силы тока отстают от колебаний
напряжения на четверть периода.
, колебания силы тока отстают от колебаний
напряжения на четверть периода.
Индуктивное сопротивление выражают в омах, оно играет роль сопротивления в цепи переменного тока с катушкой индуктивности.
III. Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором.
При включении конденсатора в цепь переменного тока через диэлектрик, разделяющий обкладки конденсатора, электрические заряды проходить не будут. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора в проводах, соединенных с его выводами появится переменный ток.
Лампа накаливания, включенная последовательно с конденсатором в цепь переменного тока, кажется горящей непрерывно, т.к. человеческий глаз не замечает периодического ослабления свечения нити лампы.
Ток в цепи с емкостным сопротивлением меняется по гармоническому закону
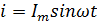
Напряжение
на обкладках конденсатора  ,
,
где 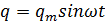
Ток
в цепи 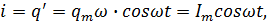
где 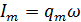
По
закону Ома 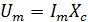 ,
,
где 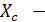 сопротивление конденсатора переменного
тока, называемое емкостным
сопротивлением.
сопротивление конденсатора переменного
тока, называемое емкостным
сопротивлением.
 ;
;
При 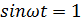 ,
напряжение
будет максимальным
,
напряжение
будет максимальным
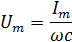
Отсюда следует, что
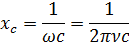
Как
и индуктивное сопротивление 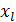 катушки,
емкостное сопротивление
катушки,
емкостное сопротивление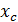 конденсатора не является постоянной
величиной. Значение
емкостного сопротивления обратно
пропорционально частоте переменного
тока.
конденсатора не является постоянной
величиной. Значение
емкостного сопротивления обратно
пропорционально частоте переменного
тока.
Поэтому
амплитуда 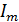 колебаний силы тока в цепи конденсатора
при постоянной амплитуде колебаний
напряжения на конденсаторе возрастает
прямо пропорционально частоте
колебаний силы тока в цепи конденсатора
при постоянной амплитуде колебаний
напряжения на конденсаторе возрастает
прямо пропорционально частоте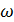 .
.
Емкостное сопротивление энергию не потребляет, поэтому как и индуктивное является реактивным.
Сдвиг фаз между током и напряжением на конденсаторе, как видно из
формул 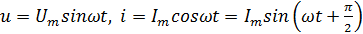
равен
четверти периода, колебания силы тока
опережают колебания внешнего напряжения
по фазе на 
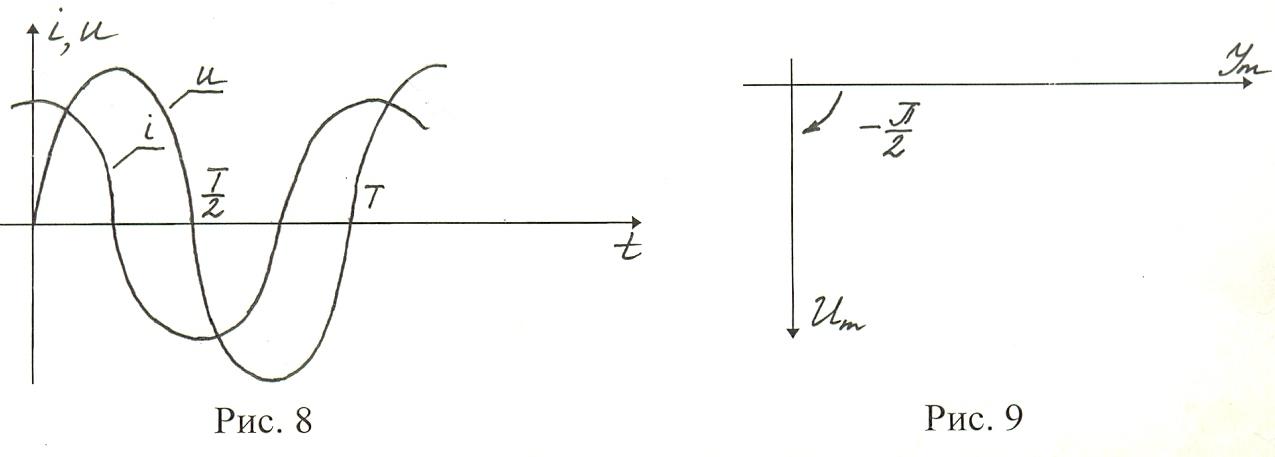
IV. Рассмотрим полную цепь переменного тока, содержащую активное, индуктивное, емкостное сопротивления.
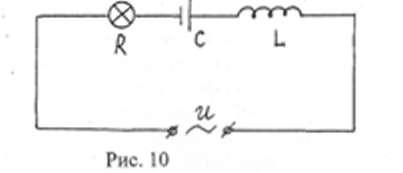
Ток на всех трёх участках один и тот же:
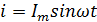
Разности потенциалов на всех трёх сопротивлениях имеют вид:
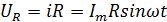
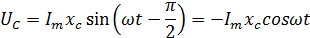
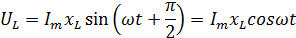
Частота колебаний результирующей разности потенциалов на клеммах генератора (совпадающей с его Э.Д.С.), равна частоте складываемых колебаний разности потенциалов.
Фаза
результирующей разности потенциалов
должна быть сдвинута по отношению к
колебаниям силы тока в общем случае на
угол 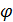
Для нахождения результирующей амплитуды напряжений (Э.Д.С.) в цепи, построим векторную диаграмму цепи:
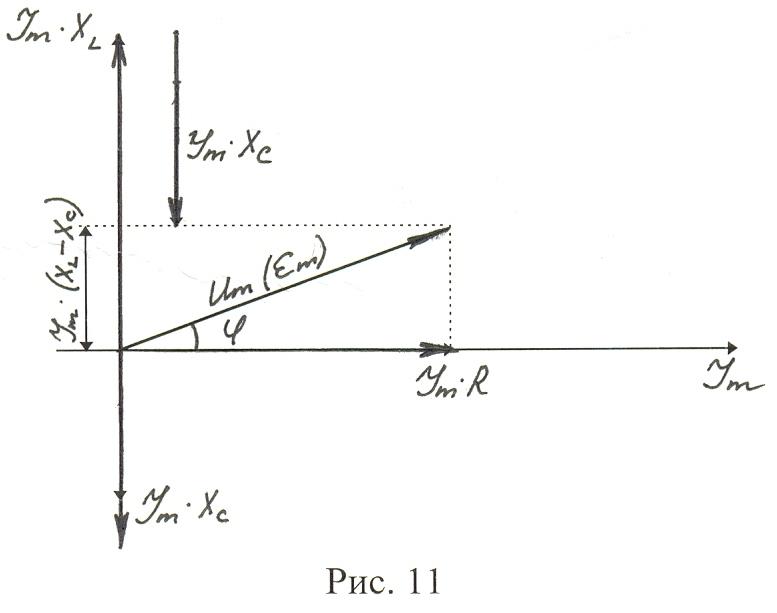
Так как сила тока в этом случае на всех участках цепи одинакова, то здесь в качестве базисного вектора выбирают вектор, изображающий амплитудное значение силы тока.
Векторы, изображающие амплитудные значения напряжений на отдельных участках строят под определенными углами к вектору силы тока. Эти углы равны сдвигам фаз на каждом из участков цепи. Результирующую амплитуду напряжений определяют как модуль результирующего вектора, который находят по правилу суммирования векторов, а фазу результирующего колебания просто измеряют соответствующим углом, отсчитанным в направлении против часовой стрелки от базисного вектора.
Из диаграммы видно:
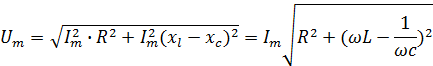
Как видно, амплитуды колебаний силы тока и напряжения связаны соотношением
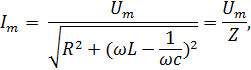
где
величину Z , равную выражению 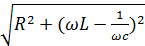 называют полным
сопротивлением цепи
переменного тока.
называют полным
сопротивлением цепи
переменного тока.
Выражение 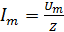 называется
законом Ома для цепи переменного
называется
законом Ома для цепи переменного
тока.
Разделив
левую и правую часть на 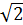 получим, что закон справедлив и для
действующих значений силы тока и
напряжения.
получим, что закон справедлив и для
действующих значений силы тока и
напряжения.
Из
формулы 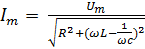 видно, что ток в цепи можно увеличить
не меняя напряжение, а изменяя частоту.
видно, что ток в цепи можно увеличить
не меняя напряжение, а изменяя частоту.
При изменении частоты может наступить такой момент, когда и при одинаковой силе тока одинаковыми оказываются и амплитуды колебаний напряжения на конденсаторе и катушке.
Колебания
напряжения на катушке и конденсаторе
противоположны по фазе, поэтому сумма
напряжений на них при 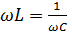 в любой момент
в любой момент
времени = 0.
В
результате напряжение на активном
сопротивлении при резонансе оказывается
равным полному напряжению 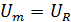 ,
а сила тока
,
а сила тока
в цепи достигает максимального значения, т.е. наступает резонанс.
Индуктивное реактивное сопротивление: формулы, схемы
В данной статье мы подробно поговорим про индуктивное сопротивление, реактивное сопротивление и треугольники напряжения, сопротивления и силы.
Введение
Итак, мы рассмотрели поведение индукторов, подключенных к источникам постоянного тока, и, надеюсь, теперь мы знаем, что когда на индуктор подается постоянное напряжение, рост тока через него происходит не мгновенно, а определяется индуктором, индуцированным самим индуктором или обратным значением ЭДС.
Также мы видели, что ток индукторов продолжает расти, пока не достигнет своего максимального установившегося состояния после пяти постоянных времени. Максимальный ток, текущий через индукционную катушку ограничиваются только резистивной частью катушек обмотки в омах, и как мы знаем из закона Ома, это определяется отношением напряжения к току V / R .
Когда переменное напряжение подается на катушку индуктивности, поток тока через него ведет себя совершенно иначе, чем при приложении постоянного напряжения. Эффект синусоидального питания приводит к разности фаз между напряжением и формами тока. Теперь в цепи переменного тока противодействие току, протекающему через обмотки катушек, зависит не только от индуктивности катушки, но и от частоты сигнала переменного тока.
Сопротивление току, протекающему через катушку в цепи переменного тока, определяется сопротивлением переменного тока, более известным как полное сопротивление (Z) цепи. Но сопротивление всегда связано с цепями постоянного тока, поэтому, чтобы отличить сопротивление постоянного тока от сопротивления переменного тока, обычно используется термин «реактивное сопротивление» .
Как и сопротивление, значение реактивного сопротивления также измеряется в омах, но ему присваивается символ X (заглавная буква «X»), чтобы отличить его от чисто резистивного значения.
Поскольку интересующий нас компонент является индуктором, реактивное сопротивление индуктора поэтому называется «Индуктивное реактивное сопротивление». Другими словами, электрическое сопротивление индуктивности при использовании в цепи переменного тока называется индуктивным сопротивлением .
Индуктивное сопротивление, которому дается символ X L , является свойством в цепи переменного тока, которое противодействует изменению тока. В наших уроках о конденсаторах в цепях переменного тока мы видели, что в чисто емкостной цепи ток I C «опережает» напряжение на 90 o . В чисто индуктивной цепи переменного тока верно обратное: ток I L отстает от напряжения на 90 o или (π / 2 рад).
Схема индуктивности переменного тока

В приведенной выше чисто индуктивной цепи индуктор подключен непосредственно через напряжение питания переменного тока. Когда напряжение питания увеличивается и уменьшается с частотой, самоиндуцированная обратная ЭДС также увеличивается и уменьшается в катушке по отношению к этому изменению.
Мы знаем, что эта самоиндуцированная ЭДС прямо пропорциональна скорости изменения тока через катушку и имеет наибольшее значение при переходе напряжения питания от положительного полупериода к отрицательному полупериоду или наоборот в точках 0о и 180о вдоль синусоиды.
Следовательно, минимальная скорость изменения напряжения возникает, когда синусоида переменного тока пересекается при своем максимальном или минимальном пиковом уровне напряжения. В этих положениях в цикле максимальный или минимальный токи протекают через цепь индуктора, и это показано ниже.
Векторная диаграмма индуктора переменного тока

Эти формы напряжения и тока показывают, что для чисто индуктивной цепи ток отстает от напряжения на 90 o . Также можно сказать, что напряжение опережает ток на 90 o . В любом случае общее выражение заключается в том, что ток отстает, как показано на векторной диаграмме. Здесь вектор тока и вектор напряжения показаны смещенными на 90 o . Ток отстает от напряжения .
Мы можем также написать это заявление как, V L = 0 ö и I L = -90 о по отношению к напряжению, V L . Если форма волны напряжения классифицируется как синусоида, то ток I L можно классифицировать как отрицательный косинус, и мы можем определить значение тока в любой момент времени как:

Где:
ω в радианах в секунду, а
t в секундах.
Поскольку ток всегда отстает от напряжения на 90 o в чисто индуктивной цепи, мы можем найти фазу тока, зная фазу напряжения или наоборот. Так что если мы знаем значение V L , то I L должно отставать на 90 o . Аналогичным образом, если мы знаем значение I L, то V L, следовательно, должно опережать на 90 o . Затем это отношение напряжения к току в индуктивном контуре будет производить уравнение, определяющее индуктивное сопротивление Х L катушки.

Мы можем переписать уравнение для индуктивного сопротивления в более привычную форму, которая использует обычную частоту питания вместо угловой частоты в радианах ω и это будет выглядеть так:

Где:
ƒ — частота,
L — индуктивность катушки и
2πƒ = ω .
Из приведенного выше уравнения для индуктивного реактивного сопротивления можно видеть, что, если увеличить частоту, либо индуктивность, общее значение индуктивного реактивного сопротивления также увеличится. Когда частота приближается к бесконечности, реактивное сопротивление индукторов также увеличивается до бесконечности, действуя как разомкнутая цепь.
Однако, когда частота приближается к нулю или постоянному току, реактивное сопротивление индукторов будет уменьшаться до нуля, действуя как короткое замыкание. Это означает, что индуктивное сопротивление «пропорционально» частоте.
Другими словами, индуктивное реактивное сопротивление увеличивается с частотой, в результате чего X L будет небольшим на низких частотах, а X L будет высоким на высоких частотах, что продемонстрировано на графике ниже.
Индуктивное сопротивление от частоты

Затем мы видим, что при постоянном токе индуктор имеет нулевое реактивное сопротивление (короткое замыкание), на высоких частотах индуктор имеет бесконечное реактивное сопротивление (разомкнутая цепь).
Питание от сети переменного тока серии LR
До сих пор мы рассматривали чисто индуктивную катушку, но невозможно иметь чистую индуктивность, поскольку все катушки, реле или соленоиды будут иметь определенное сопротивление, независимо от того, насколько мало связано с витками используемого провода. Тогда мы можем рассматривать нашу простую катушку как последовательное сопротивление с индуктивностью (LR).
В цепи переменного тока, которая содержит как индуктивность L и сопротивление R, напряжение V будет векторная сумма двух компонентов напряжения, V R и V L . Это означает, что ток, протекающий через катушку еще будет отставать от напряжения, но на величину меньше чем 90 ö в зависимости от значений V R и V L .
Новый фазовый угол между напряжением и током известен как фазовый угол цепи и обозначается греческим символом фи, Φ .
Чтобы получить векторную диаграмму зависимости между напряжением и током, необходимо найти эталонный или общий компонент. В последовательно соединенной цепи RL ток является общим, так как один и тот же ток течет через каждый компонент. Вектор этой эталонной величины обычно рисуется горизонтально слева направо.
Из наших руководств о резисторах и конденсаторах, мы знаем, что ток и напряжение в цепи переменного резистивного тока, оба «в фазе» и, следовательно, вектор V R рисуется с наложением на текущую или контрольную линию.
Из вышесказанного также известно, что ток «отстает» от напряжения в чисто индуктивной цепи и, следовательно, вектор V L отображается на 90 o перед опорным током и в том же масштабе, что и V R, это показано ниже.
Цепь переменного тока серии LR

На приведенной выше векторной диаграмме видно, что луч OB представляет текущую опорную линию, луч OA — это напряжение резистивного компонента, которое в фазе с током, луч OC показывает индуктивное напряжение, которое составляет 90 o перед током, поэтому видно, что ток отстает от напряжения на 90 o , луч OD дает нам результирующее или питающее напряжение в цепи. Треугольник напряжения выводится из теоремы Пифагора и имеет вид:

Треугольник сопротивления

В цепи постоянного тока отношение напряжения к току называется сопротивлением. Однако в цепи переменного тока это отношение известно как полное сопротивление Z с единицами измерения в омах. Полное сопротивление — это полное сопротивление току в «цепи переменного тока», содержащее как сопротивление, так и индуктивное сопротивление.
Если мы разделим стороны треугольника напряжения выше на ток, получим еще один треугольник, стороны которого представляют сопротивление, реактивное сопротивление и полное сопротивление катушки. Этот новый треугольник называется «Треугольник сопротивления».
Силовой треугольник индуктора переменного тока
Существует еще один тип конфигурации треугольника, который мы можем использовать для индуктивной цепи, и это «силовой треугольник». Мощность в индуктивной цепи называется реактивной мощностью или вольт-амперной реактивной, символ Var, который измеряется в вольт-амперах. В цепи переменного тока серии RL ток отстает от напряжения питания на угол Φ o .
В чисто индуктивной цепи переменного тока ток будет сдвинут по фазе на 90 o к напряжению питания. Таким образом, общая реактивная мощность, потребляемая катушкой, будет равна нулю, так как любая потребляемая мощность компенсируется генерируемой самоиндуцированной ЭДС-мощностью. Другими словами, полезная мощность в ваттах, потребляемая чистым индуктором в конце одного полного цикла, равна нулю, так как энергия берется из источника и возвращается к нему.
Реактивная мощность ( Q ) катушки может быть задана как: I 2 x X L (аналогично I 2 R в цепи постоянного тока). Затем три стороны силового треугольника в цепи переменного тока представлены кажущейся мощностью ( S ), реальной мощностью ( P ) и реактивной мощностью ( Q ), как показано.

Обратите внимание, что данный индуктор или катушка будет потреблять мощность в ваттах из — за сопротивления обмоток, создающих сопротивление Z.
3.1.Сопротивление параллельного контура при резонансе
Сопротивление параллельного контура при резонансе чисто активное; напряжение на контуре и ток в неразветвленной части цепи совпадают по фазе. Реальный контур отбирает от питающего генератора некоторое количество энергии, которое превращается в тепло на активном сопротивлении R (сопротивлении потерь) контура. На основании закона сохранения энергии мощность, отдаваемая генератором, и мощность, расходуемая на тепло в активном сопротивлении контура, равны.
Мощность, отдаваемая генератором, определяется выражением
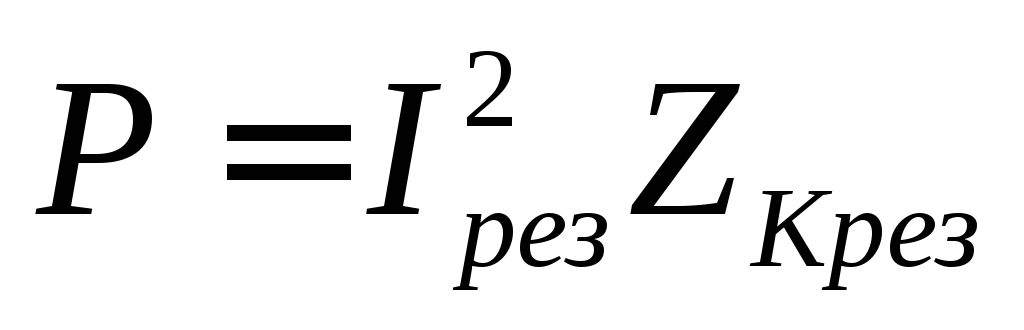
где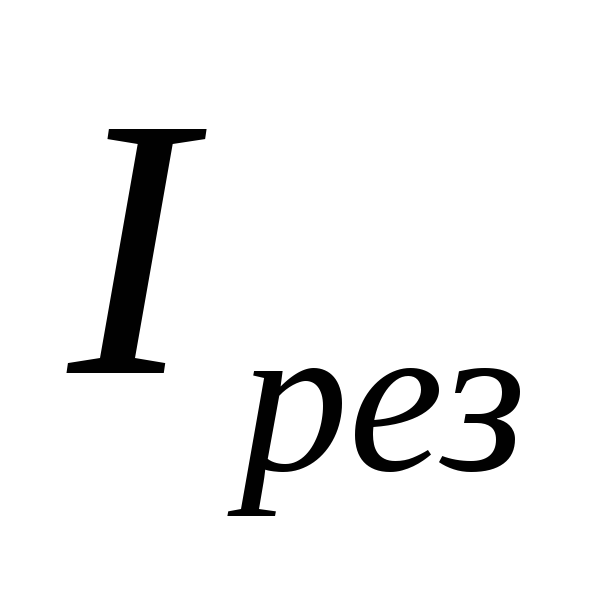 –ток в неразветвленной
части цепи при резонансе;
–ток в неразветвленной
части цепи при резонансе;
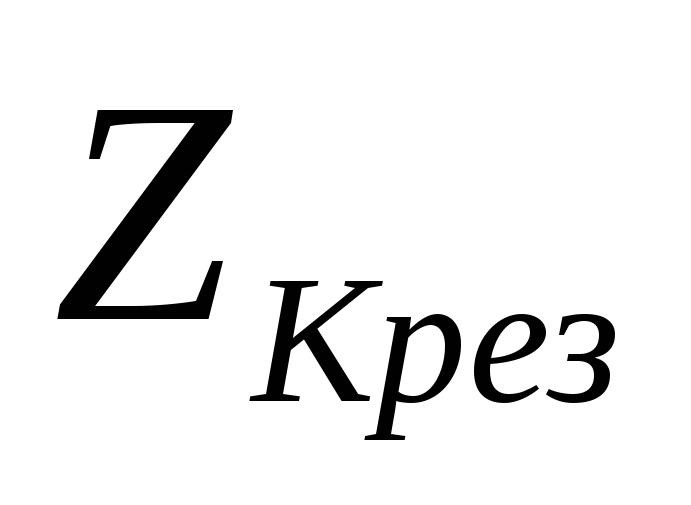 –сопротивление
контура при резонансе.
–сопротивление
контура при резонансе.
Мощность, расходуемая в активном сопротивлении R, равна
 ,
,
где 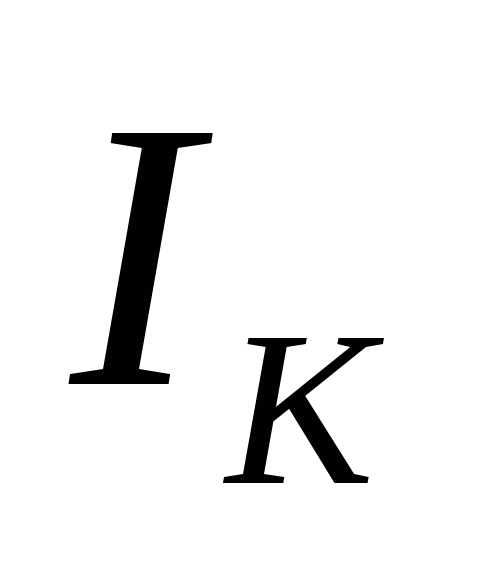 –ток внутри контура
при резонансе (
–ток внутри контура
при резонансе (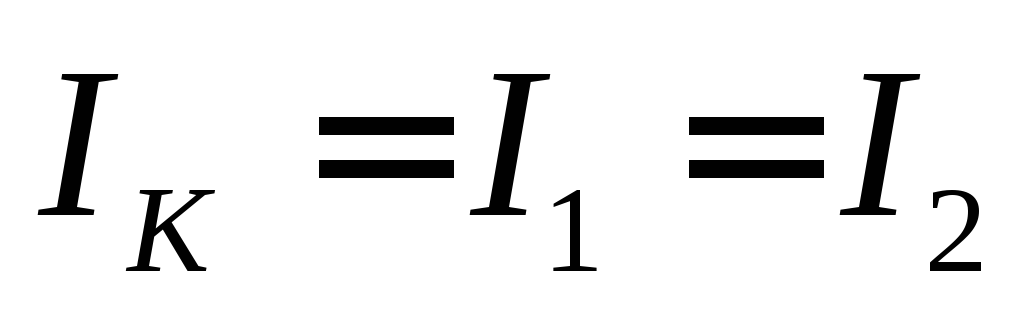 ).
).
R –активное сопротивление, учитывающее потери энергии вкатушке.
Если
напряжение на зажимах генератора 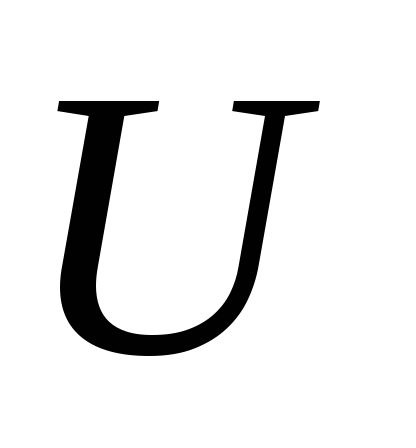 ,
то
,
то
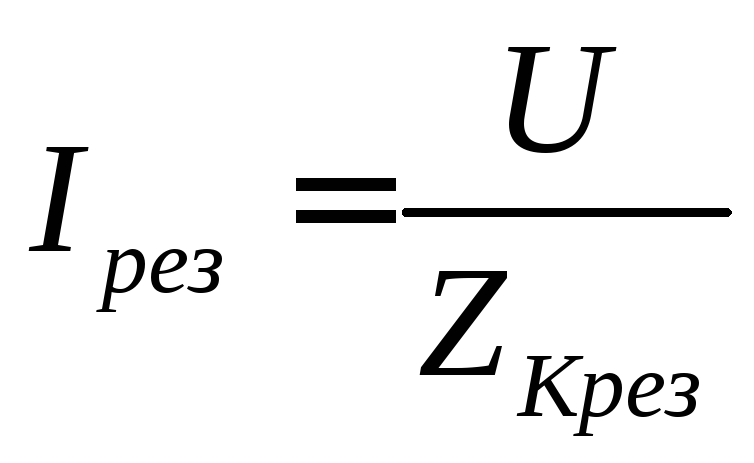
и
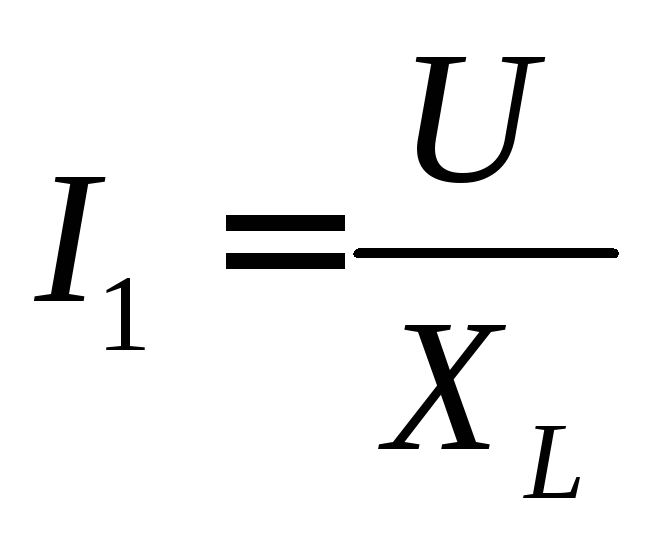 .
.
Имея
в виду последние два выражения, приравняем
мощности 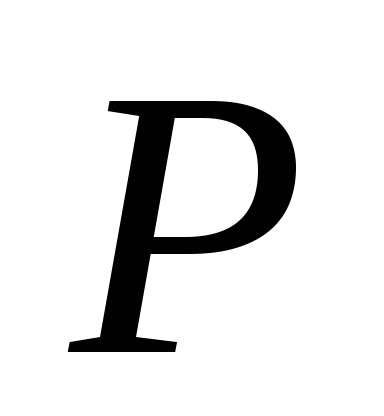 и
и :
:
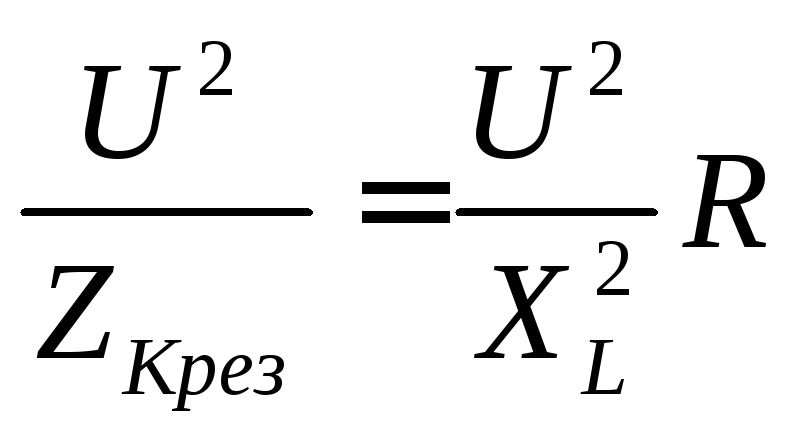 .
.
Отсюда
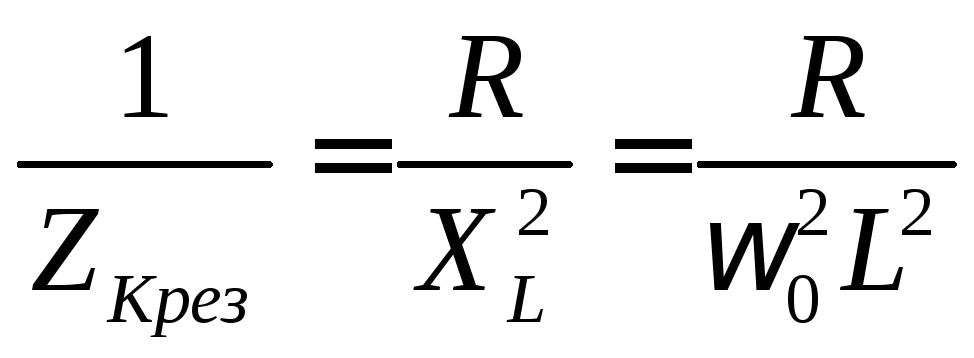 ,
,
или
.
Так
как 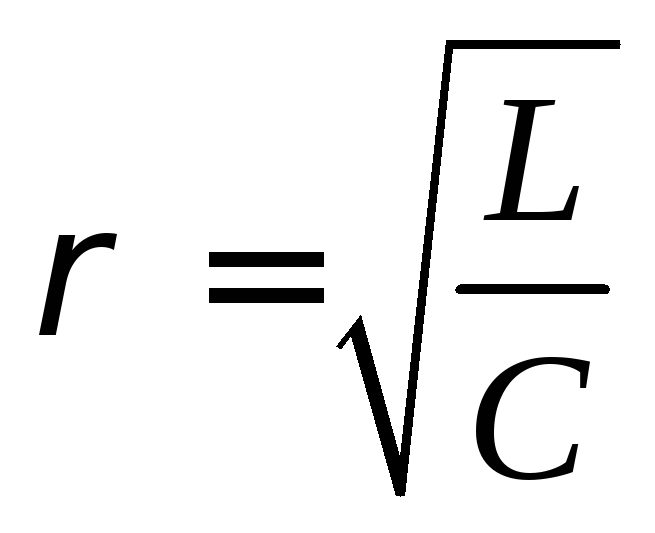 ,
то
,
то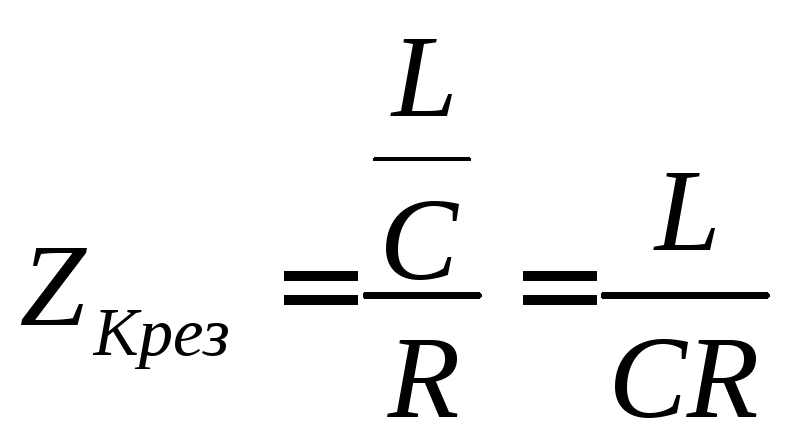 ,
,
где 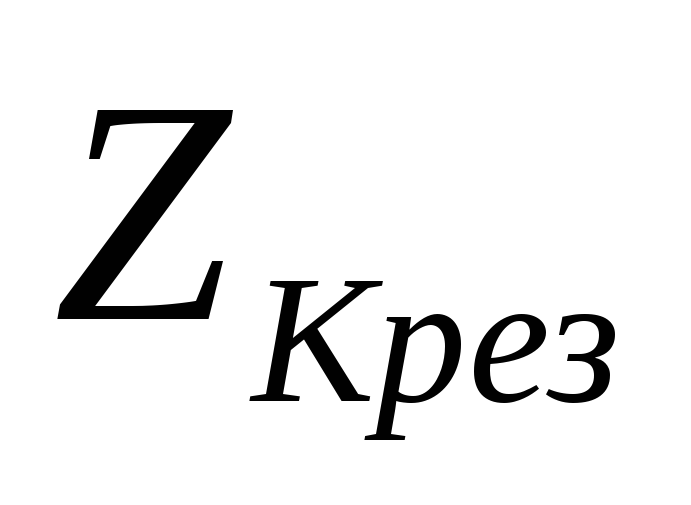 – резонансное сопротивление
контура в омах;
– резонансное сопротивление
контура в омах;
L –индуктивность контура в генри;
С –емкость контура в фарадах;
R – активное сопротивление в омах.
Резонансное
сопротивление параллельного контура
зависит от величины активного сопротивления
потерь R и от соотношения
величин L и С,
т. е. от волнового сопротивления контура.
Чем больше R,
тем больше энергии расходуется в нем
на тепло и тем больше энергии (большая
мощность) поступает от генератора в
контур. Следовательно, чем больше
сопротивление потерь R,
тем больше ток 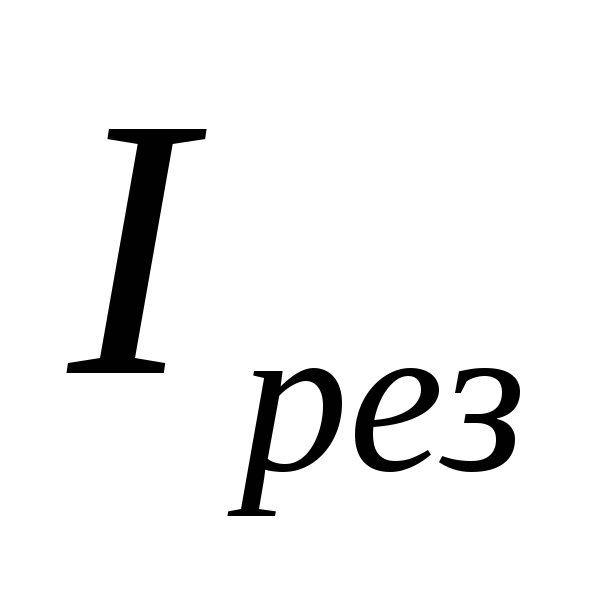 в общей части цепи. Но по величине тока
можно судить о величине сопротивления
контура: чем больше ток, тем меньше
сопротивление. Поэтому чем больше
сопротивление потерь, тем меньше
сопротивление параллельного контура
при резонансе. В отсутствиеR
в общей части цепи. Но по величине тока
можно судить о величине сопротивления
контура: чем больше ток, тем меньше
сопротивление. Поэтому чем больше
сопротивление потерь, тем меньше
сопротивление параллельного контура
при резонансе. В отсутствиеR 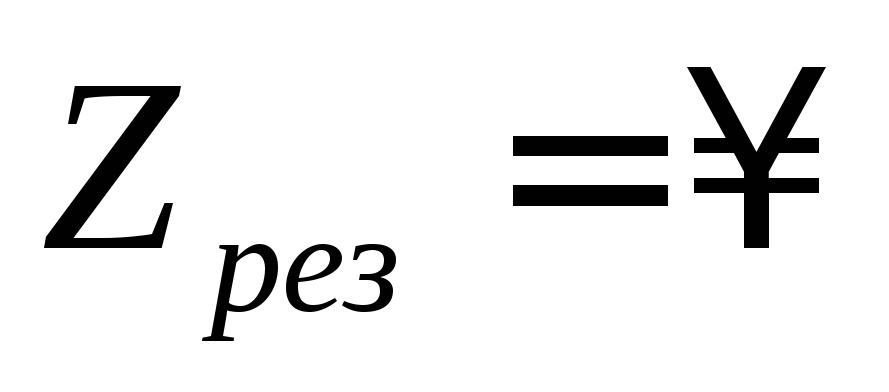 .
.
3.2. Зависимость сопротивления параллельного контура от частоты
Пусть частота генератора, питающего параллельный контур, изменяется в широких пределах. При повышении частоты генератора емкостное сопротивление конденсатора уменьшается:
 ,
,
а индуктивное сопротивление увеличивается:
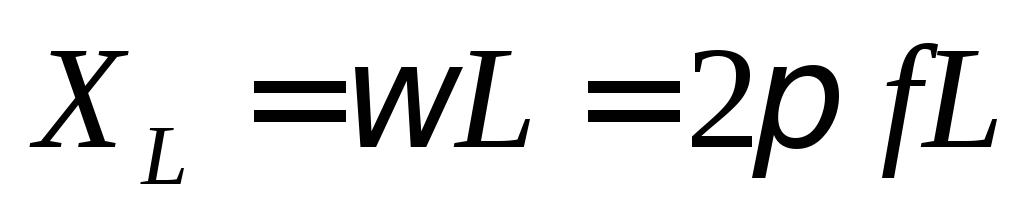 .
.
При этом ток в емкостной ветви увеличивается, а в индуктивной уменьшается. При частоте ниже резонансной в общей цепи преобладает индуктивный ток и контур ведет себя как индуктивное сопротивление. При частоте генератора, равной собственной частоте контура , емкостной и индуктивный токи равны по величине и реактивный ток в общей части цепи равен нулю (состояние резонанса). Сопротивление контура имеет чисто активный характер и значительную величину, определяемую формулой
 .
.
При частоте выше резонансной в общей цепи преобладает емкостной ток и контур ведет себя как емкостное сопротивление.
Чем
больше частота генератора отличается
от собственной (резонансной) частоты
контура, тем больше различаются токи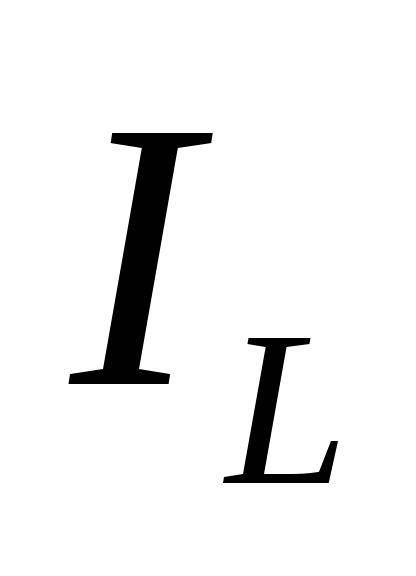 и
и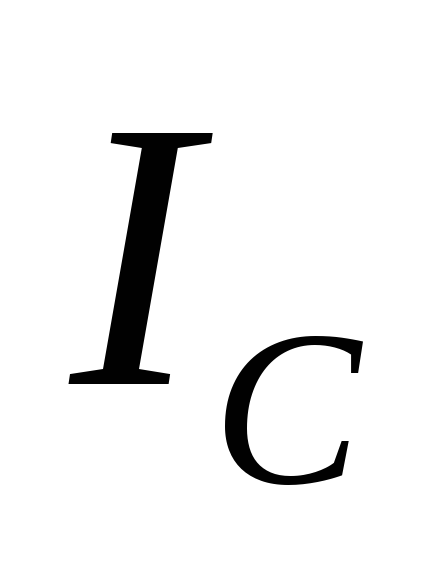 ,
тем больше реактивный ток в общей части
цепи и меньше реактивное сопротивление
контура. Исходя из этих рассуждений,
можно показать зависимость сопротивления
параллельного контура от частоты
питающего генератора (рис.14).
,
тем больше реактивный ток в общей части
цепи и меньше реактивное сопротивление
контура. Исходя из этих рассуждений,
можно показать зависимость сопротивления
параллельного контура от частоты
питающего генератора (рис.14).
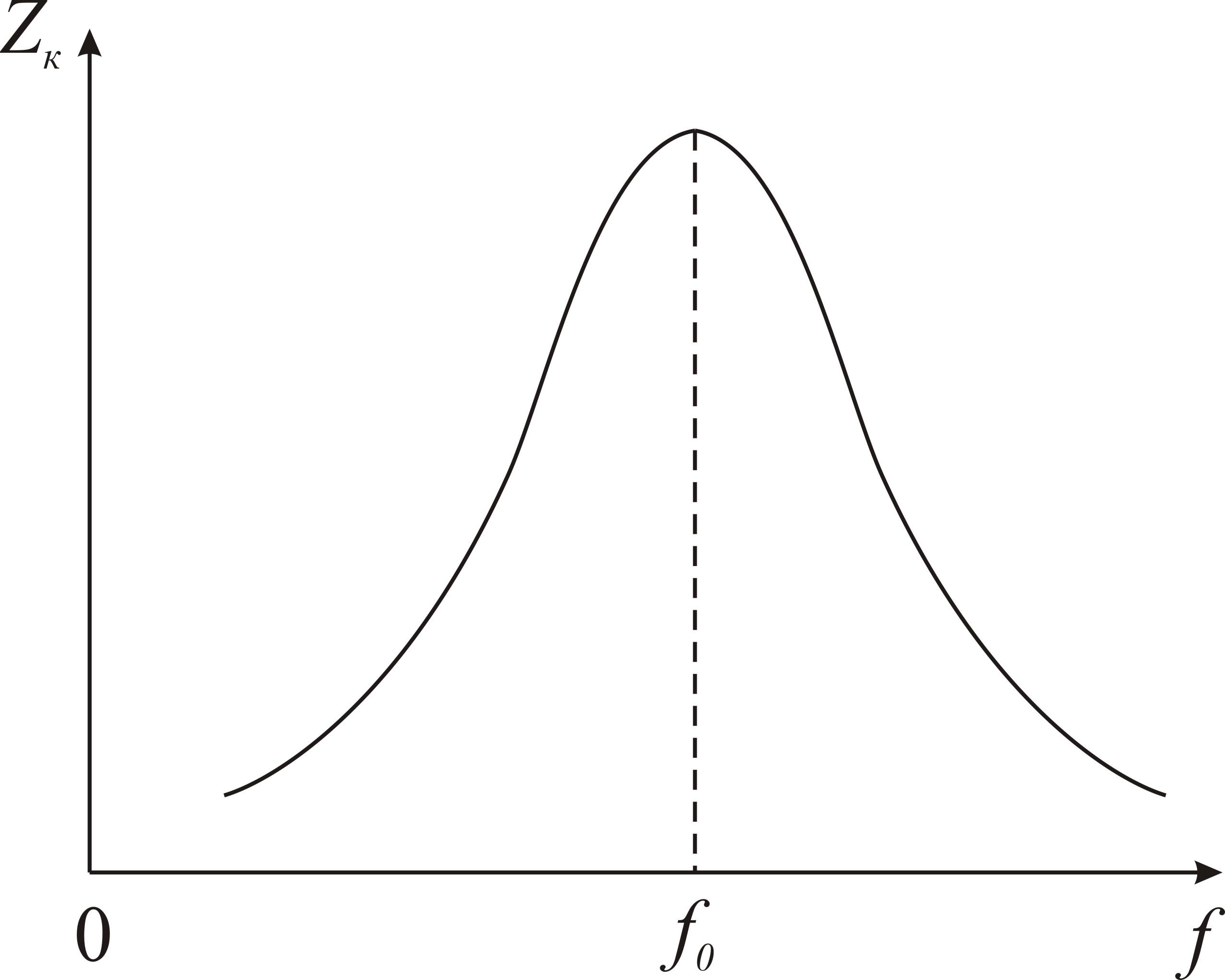
Рис.14. Зависимость сопротивления параллельного контура от частоты генератора
При
изменении частоты генератора изменяется
фазовый сдвиг между напряжением
генератора и током  ,
идущим через контур. Если частота
генератора значительно ниже собственной
(резонансной) частоты контура, то
сопротивление контура можно считать
чисто индуктивным, т.к. реактивный ток
в общей цепи во много раз больше активного.
Угол фазового сдвига между напряжением
генератора и током
,
идущим через контур. Если частота
генератора значительно ниже собственной
(резонансной) частоты контура, то
сопротивление контура можно считать
чисто индуктивным, т.к. реактивный ток
в общей цепи во много раз больше активного.
Угол фазового сдвига между напряжением
генератора и током 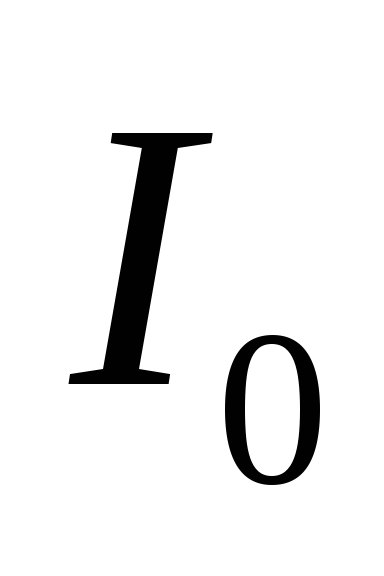 при этом близок к
при этом близок к .
По мере повышения частоты генератора
реактивная составляющая тока в общей
цепи и фазовый угол уменьшаются. При
резонансе сопротивление контура является
чисто активным и фазовый сдвиг между
напряжением генератора и током
.
По мере повышения частоты генератора
реактивная составляющая тока в общей
цепи и фазовый угол уменьшаются. При
резонансе сопротивление контура является
чисто активным и фазовый сдвиг между
напряжением генератора и током  равен нулю. Если частота генератора
превышает резонансную частоту контура,
то сопротивление контура состоит из
активной и емкостной составляющих. По
мере повышения частоты генератора
соотношение между активной и реактивной
составляющими изменяется и угол фазового
сдвига между напряжением генератора и
током
равен нулю. Если частота генератора
превышает резонансную частоту контура,
то сопротивление контура состоит из
активной и емкостной составляющих. По
мере повышения частоты генератора
соотношение между активной и реактивной
составляющими изменяется и угол фазового
сдвига между напряжением генератора и
током 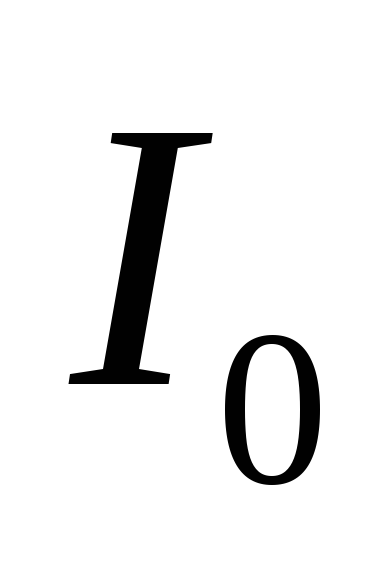 приближается к
приближается к .
.
Кривая, показывающая зависимость угла фазового сдвига между напряжением генератора и током через контур, называется фазо-частотной характеристикой параллельногоконтура(рис.15).
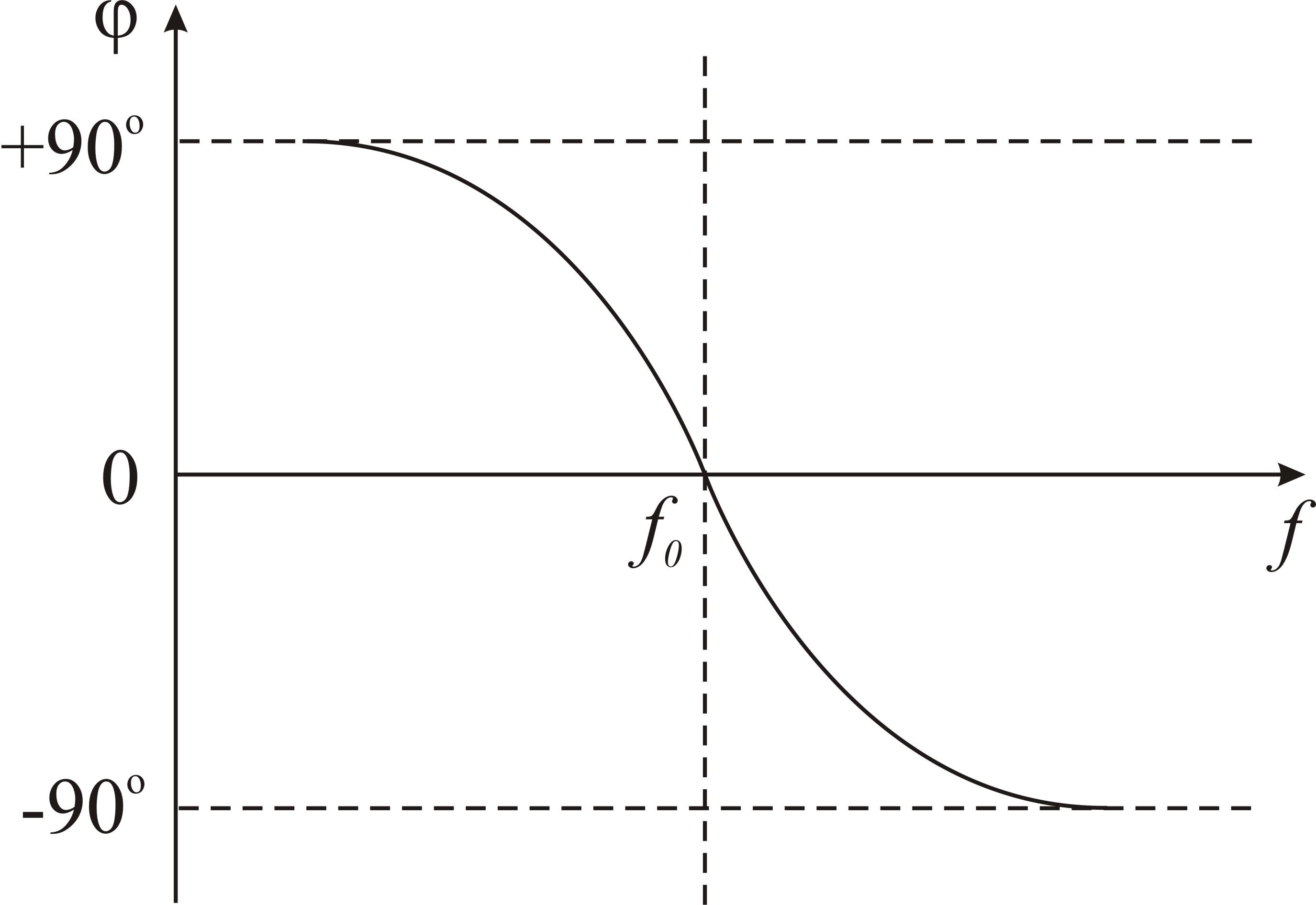
Рис.15. Фазо-частотная характеристика параллельного контура
Индуктивное сопротивление катушки — Основы электроники
Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением.
Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.
Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.
При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь. Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).
Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.
Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.
Индуктивное сопротивление обозначается буквой XL и измеряется в омах.
Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле
XL=2π• f •L
где XL — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн
Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так:
XL=ω•L
Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.
Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
5.5.1.2. Зависимость добротности контура q от сопротивления источника сигнала (Ri) и сопротивления нагрузки (Rн)
С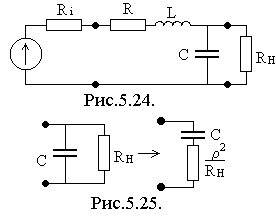 хема
замещения последовательного колебательного
контура с учетом добавочных элементовRi,
RH имеет вид (рис.5.24).
хема
замещения последовательного колебательного
контура с учетом добавочных элементовRi,
RH имеет вид (рис.5.24).
На
рис. 5.25 показано эквивалентное
преобразование паралельной RC цепи в
последовательную, где .
Добротность контура с учетом добавочных
элементовRi,
RH называется эквивалентной и определяется
из следующего выражения
.
Добротность контура с учетом добавочных
элементовRi,
RH называется эквивалентной и определяется
из следующего выражения
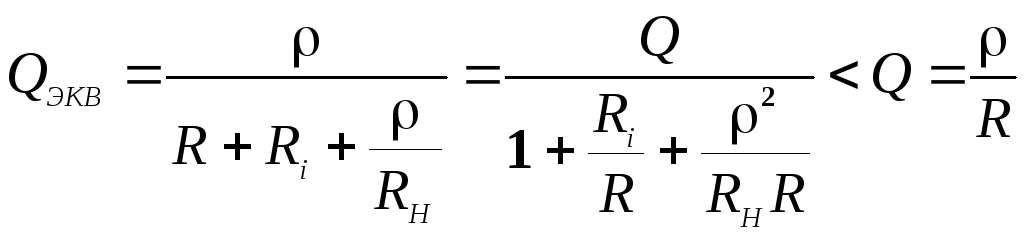 .
.
Она
меньше собственной добротности контура
Q.
Для того, чтобы  необходимо:
необходимо:
1)  .
Это означает, что последовательный
колебательный контур необходимо питать
от источника ЭДС, т.е. источника с нулевым
сопротивлением.
.
Это означает, что последовательный
колебательный контур необходимо питать
от источника ЭДС, т.е. источника с нулевым
сопротивлением.
2)  .
В этом случае нагрузка не будет влиять
на добротность контура.
.
В этом случае нагрузка не будет влиять
на добротность контура.
5.5.1.3. Последовательный колебательный контур как четырехполюсник
Н а
практике используются две схемы
включения рис.5.26. Для четырехполюсника
основной частотной характеристикой
является передаточная по напряжению.
а
практике используются две схемы
включения рис.5.26. Для четырехполюсника
основной частотной характеристикой
является передаточная по напряжению.
1) 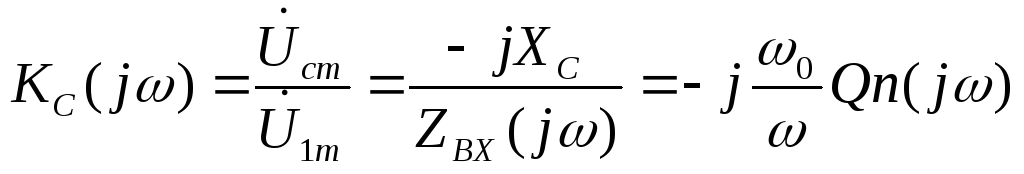
2 )
)
Построим графики амплитудно-частотные характеристик этих зависимостей рис.5.27. Подробный анализ показывает, что при высоких добротностях резонансные частоты обеих схем совпадают и равны ω0.
5.5.2. Параллельный колебательный контур
Он состоит из параллельно соединенных двух реактивных элементов L и C. Его принципиальная схема имеет вид, приведенный на рис.5.28а.
Схема замещения контура с учетом резистивных потерь реактивных элементов приведена на рис.5.28б.
Определим комплексное входное сопротивление параллельного колебательного контура
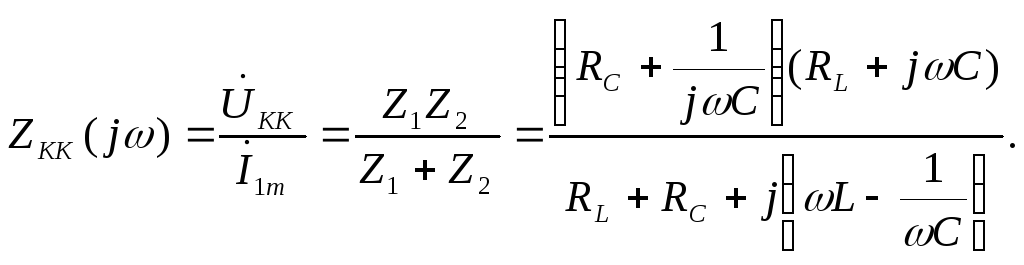
Обозначим 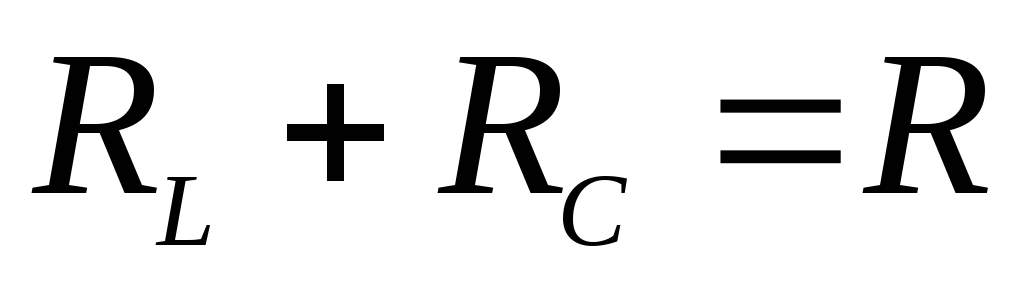 —
общие резистивные потери параллельного
контура. При условии, что вблизи от
резонанса
—
общие резистивные потери параллельного
контура. При условии, что вблизи от
резонанса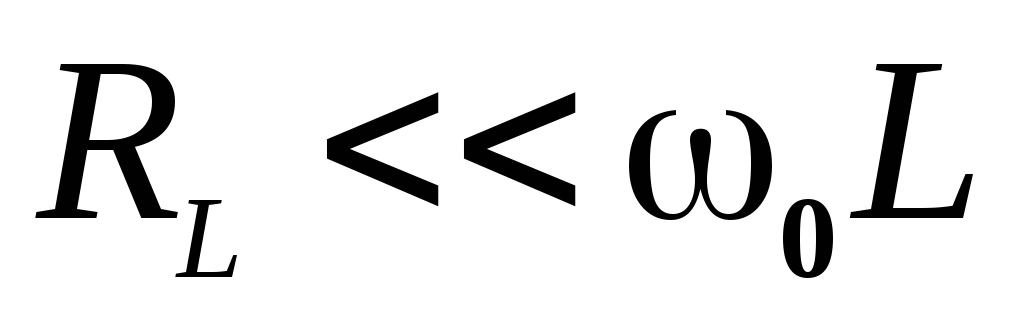 ,
, 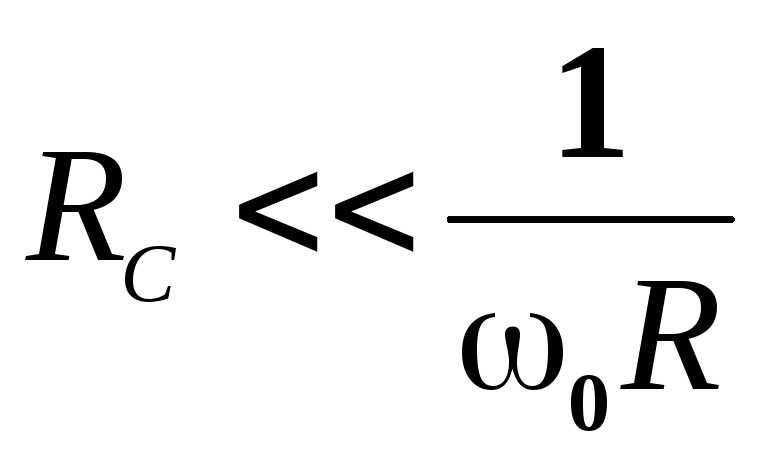 .
Получим окончательное выражение для
сопротивления параллельного колебательного
контура.
.
Получим окончательное выражение для
сопротивления параллельного колебательного
контура.
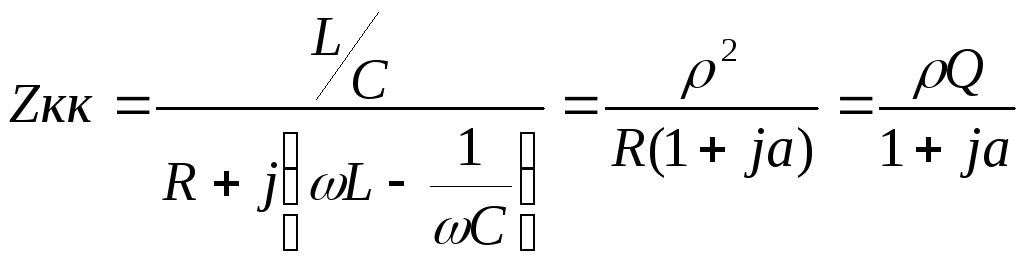 .
.
Характер сопротивления параллельного колебательного контура зависит от частоты.
1)
На НЧ  —
характер индуктивный. Схема замещения
состоит из элементовR,
L
и приведена на рис. 5.29а. Сопротивление
контура Zkk(ω
= 0) =RL.
—
характер индуктивный. Схема замещения
состоит из элементовR,
L
и приведена на рис. 5.29а. Сопротивление
контура Zkk(ω
= 0) =RL.
2)
На ВЧ  — сопротивление носит емкостной характер,
рис. 5.29б. Сопротивление контураZkk(ω
)
=RC.
— сопротивление носит емкостной характер,
рис. 5.29б. Сопротивление контураZkk(ω
)
=RC.
3)
На 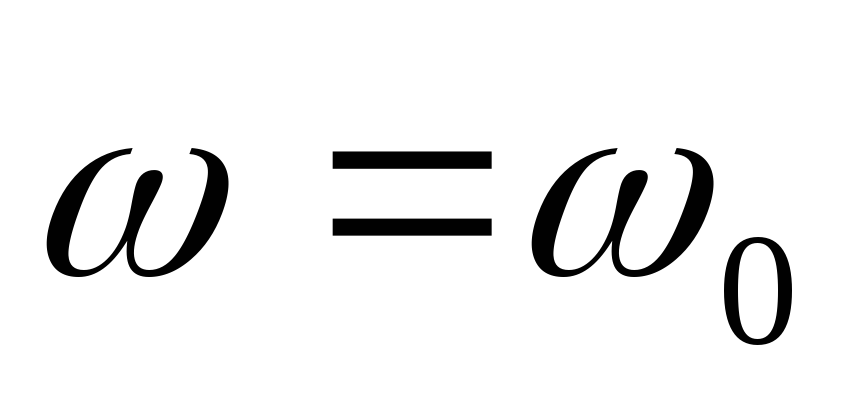 ,
когда
,
когда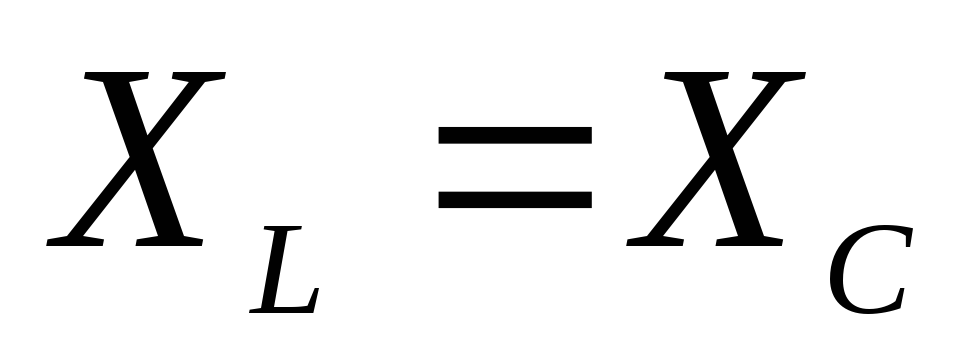 сопротивление контура имеет резистивный
характерZkk(ω0)
=ρQ,
рис. 5.29в, где ω0=(LC)1/2 – резонансная частота.
сопротивление контура имеет резистивный
характерZkk(ω0)
=ρQ,
рис. 5.29в, где ω0=(LC)1/2 – резонансная частота.

Отметим свойства параллельного контура на резонансной частоте.
Сопротивление контура имеет резистивный характер и его модуль имеет максимальное значение по сравнению с сопротивлением на других частотах.
Ток и напряжение совпадают по фазе.
 сопротивление
реактивных элементов одинаково и равно
сопротивление
реактивных элементов одинаково и равно  .
.Амплитуда тока через реактивные элементы в Q раз превышает ток во внешней цепи:
 ,
поэтому резонанс в параллельном контуре
называется резонансом токов. Это
вытекает из следующего
,
поэтому резонанс в параллельном контуре
называется резонансом токов. Это
вытекает из следующего
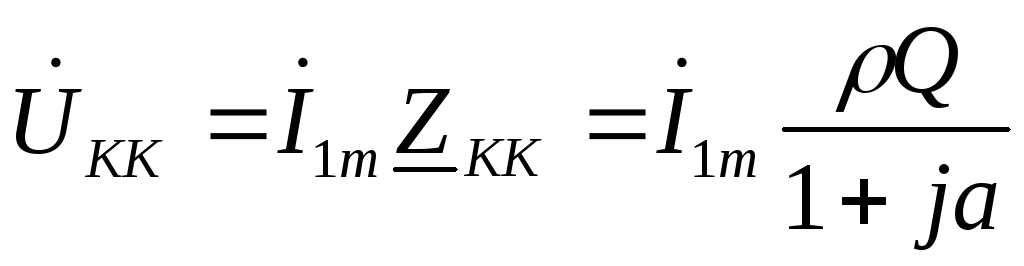 ;
; 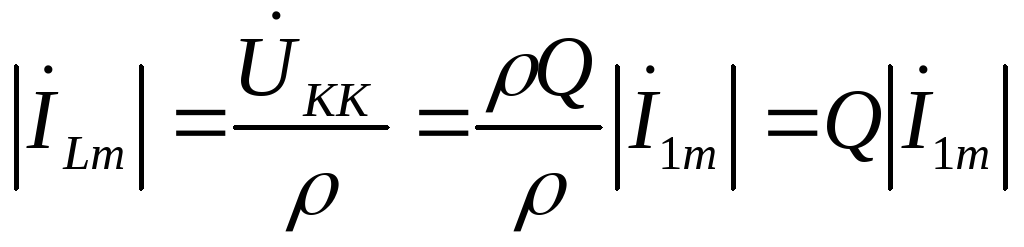 .
.
Токи через реактивные элементы сдвинуты по фазе на 1800.

Построим графики АЧХ и ФЧХ входного сопротивления параллельного контура, которые определяются выражениями
АЧХ: 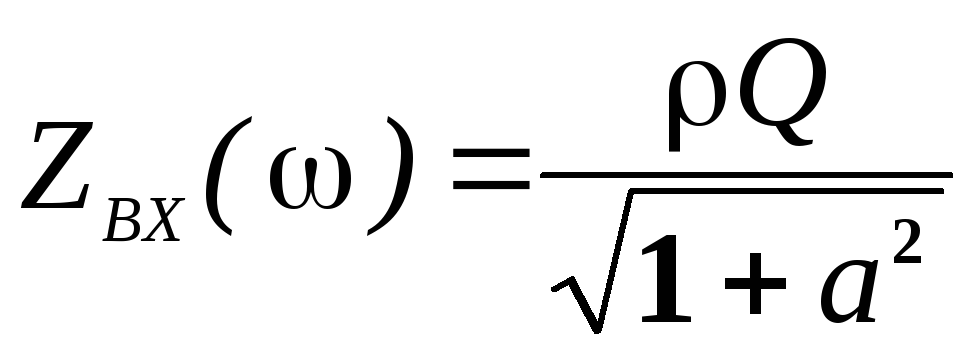 ;
ФЧХ:
;
ФЧХ: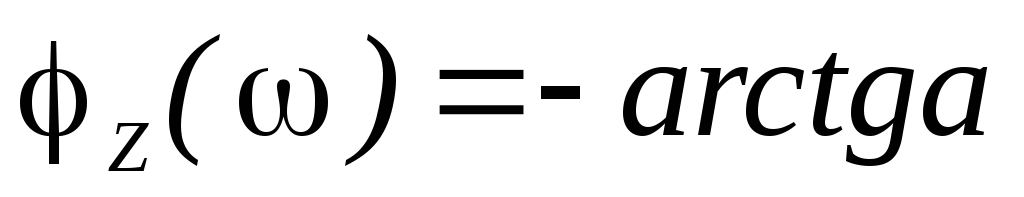 .
.
Построенные графики приведены на рис.5.30.
5.5.2.1. Резонансная характеристика параллельного колебательного контура
Она представляет собой зависимость от частоты отношения комплексной амплитуды напряжения на контуре к амплитуде напряжения на резонансной частоте.
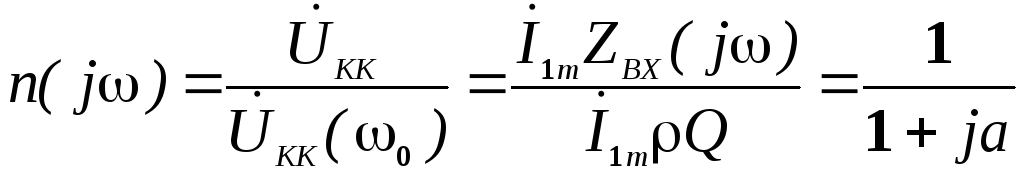
Вид резонансной характеристики для последовательного и параллельного контуров одинаковы, это их и объединяет. По характеру зависимости сопротивления от частоты они обладают противоположными свойствами (см. рис.5.30).
Резонанс напряжений в последовательном колебательном контуре
В радиотехнике широкое применение имеют электрические цепи, составленные из катушки индуктивности и конденсатора. Такие цепи в радиотехнике называются колебательными контурами. Источник переменного тока к колебательному контуру может быть присоединен двумя способами: последовательно (рисунок 1а) и параллельно (рисунок 1б).
Рисунок 1. Схемотическое обозначение колебательного контура. а) последовательный колебательный контур; б) параллельный колебательный контур.
Рассмотрим поведение колебательного контура в цепи переменного тока при последовательном соединении контура и источника тока (рис 1а).
Мы знаем, что такая цепь оказывает переменному току реактивное сопротивление, равное:
где RL— активное сопротивление катушки индуктивности в ом;
ωL,-индуктивное сопротивление катушки индуктивности в ом;
1/ωC-емкостное сопротивление конденсатора в ом.
Активное сопротивление катушки RL практически очень мало изменяется при изменении частоты (если пренебречь поверхностным эффектом). Индуктивное и емкостное сопротивления в очень сильной степени зависят от частоты, а именно: индуктивное сопротивление ωL увеличивается прямо пропорционально частоте тока, а емкостное сопротивление 1/ωC уменьшается при повышении частоты тока, т. е. оно связано с частотой тока обратно пропорциональной зависимостью.
Отсюда непосредственно следует, что реактивное сопротивление последовательного колебательного контура также зависит от частоты, и колебательный контур будет оказывать токам разных частот неодинаковое сопротивление.
Если мы будем измерять реактивное сопротивление колебательного контура при различных частотах, то обнаружим, что в области низких частот сопротивление последовательного контура очень велико; при увеличении частоты оно уменьшается до некоторого предела, а затем начинает снова возрастать.
Объясняется это тем, что в области низких частот ток испытывает большое сопротивление со стороны конденсатора, при увеличении же частоты начинает действовать индуктивное сопротивление, компенсирующее действие емкостного сопротивления.
При некоторой частоте индуктивное сопротивление становится равным емкостному, т. е.
Они будут взаимно компенсировать друг друга и общее реактивное сопротивление контура станет равным нулю:
При этом реактивное сопротивление последовательного колебательного контура будет равно только его активному сопротивлению, так как
При дальнейшем повышении частоты ток будет испытывать все большее и большее сопротивление со стороны индуктивности катушки, при одновременном уменьшении компенсирующего действия емкостного сопротивления. Поэтому реактивное сопротивление контура начнет снова возрастать.
На рисунке 2а приведена кривая, показывающая изменение реактивного сопротивления последовательного колебательного контура при изменении частоты тока.
Рисунок 2. Резонанс напряжений. а) зависимость изменения полного сопротивления от частоты; б) зависимость реактивного сопротивления от активного сопротивления контура; в) кривые резонанаса.
Частота тока, при которой сопротивление колебательного контура делается наименьшим, называется частотой резонанса или резонансной частотой колебательного контура.
При резонансной частоте имеет место равенство:
пользуясь которым, нетрудно определить частоту резонанса:
(1)
Единицами в этих формулах служат герцы, генри и фарады.
Из формулы (1) видно, что чем меньше величины емкости и самоиндукции колебательного контура, тем больше будет его резонансная частота.
Величина активного сопротивления RL не влияет на резонансную частоту, однако от нее зависит характер изменения Z. На рисунке 2б приведен ряд графиков изменения реактивного сопротивления колебательного контура при одних и тех же величинах L и С, но при разных RL. Из этого рисунка видно, что чем больше активное сопротивление последовательного колебательного контура, тем тупее становится кривая изменения реактивного сопротивления.
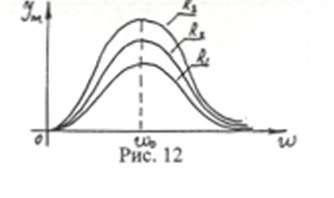
Теперь рассмотрим, как будет изменяться сила тока в колебательном контуре, если мы будем изменять частоту тока. При этом мы будем считать, что напряжение, развиваемое источником переменного тока, остается все время одним и тем же.
Так как источник тока включен последовательно с L и С контура, то сила тока, протекающего через катушку и конденсатор, будет тем больше, чем меньше реактивное сопротивление колебательного контура в целом, так как
Отсюда непосредственно следует, что при резонансе сила тока в колебательном контуре будет наибольшей. Величина тока при резонансе будет зависеть от напряжения источника переменного тока и от активного сопротивления контура:
На рисунке 2г изображен ряд графиков изменения силы тока в последовательном колебательном контуре при изменении частоты тока так называемых кривых резонанса. Из этого рисунка видно, что чем больше активное сопротивление контура, тем тупее кривая резонанса.
При резонансе сила тока может достигать огромных значений при сравнительно малой внешней ЭДС. Поэтому падения напряжения на индуктивном и емкостном сопротивлениях контура, т. е. на катушке и на конденсаторе, могут достигать очень больших величии и далеко превосходить величину внешнего напряжения.
Последнее утверждение на первый взгляд может показаться несколько странным, однако нужно помнить, что фазы напряжений на емкостном и индуктивном сопротивлениях сдвинуты друг относительно друга на 180°, т. е. мгновенные значения напряжений на катушке и конденсаторе направлены всегда в противоположные стороны. Вследствие этого большие напряжения, существующие при резонансе внутри контура на его катушке и конденсаторе, ничем не обнаруживают себя вне контура, взаимно компенсируя друг друга.
Разобранный нами случай последовательного резонанса называется резонансом напряжений, так как в этом случае в момент резонанса имеет место резкое увеличение напряжения на L и С колебательного контура.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Активное и реактивное сопротивление в цепи переменного тока
В электрической цепи переменного тока существует два вида сопротивлений: активное и реактивное. Это является существенным отличием от цепей постоянного тока.
Активное сопротивление
При прохождении тока через элементы, имеющие активное сопротивление, потери выделяющейся мощности необратимы. Примером может служить резистор, выделяющееся на нем тепло, обратно в электрическую энергию не превращается. Кроме резистора активным сопротивлением может обладать линии электропередач, соединительные провода, обмотки трансформатора или электродвигателя.
Отличительной чертой элементов имеющих чисто активное сопротивление – это совпадение по фазе тока и напряжения, поэтому вычислить его можно по формуле

Активное сопротивление зависит от физических параметров проводника, таких как материал, площадь сечения, длина, температура.
Реактивное сопротивление
При прохождении переменного тока через реактивные элементы возникает реактивное сопротивление. Оно обусловлено в первую очередь ёмкостями и индуктивностями.
Индуктивностью в цепи переменного тока обладает катушка индуктивности, причём в идеальном случае, активным сопротивлением её обмотки пренебрегают. Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.
Реактивное сопротивление катушки зависит от частоты тока и индуктивности катушки

Конденсатор обладает реактивным сопротивлением благодаря своей ёмкости. Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока.
Сопротивление конденсатора можно рассчитать по формуле
 Треугольник сопротивлений
Треугольник сопротивлений
Цепи переменного тока обладают полным сопротивлением. Полное сопротивление цепи определяется как сумма квадратов активного и реактивного сопротивлений

Графическим изображением этого выражения служит треугольник сопротивлений, который можно получить в результате расчёта последовательной RLC-цепи. Выглядит он следующим образом:
 На треугольнике видно, что катетами являются активное и реактивное сопротивление, а полной сопротивление гипотенуза.
На треугольнике видно, что катетами являются активное и реактивное сопротивление, а полной сопротивление гипотенуза.




 сопротивление
реактивных элементов одинаково и равно
сопротивление
реактивных элементов одинаково и равно 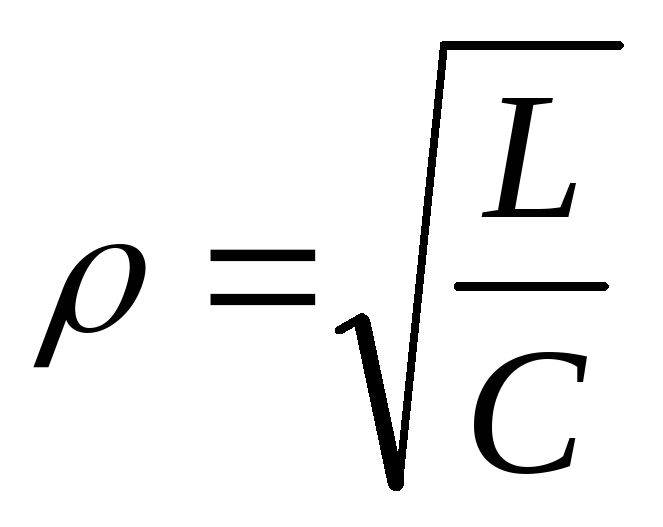 .
. ,
поэтому резонанс в параллельном контуре
называется резонансом токов. Это
вытекает из следующего
,
поэтому резонанс в параллельном контуре
называется резонансом токов. Это
вытекает из следующего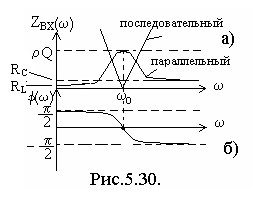
 Треугольник сопротивлений
Треугольник сопротивлений