Лабораторная работа «Исследование колебаний математического маятника» (Ерюткин Е. С.)

Цель: выяснить, как зависит период и частота свободных колебаний математического маятника от его длины.

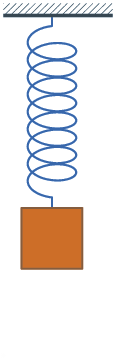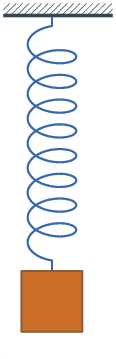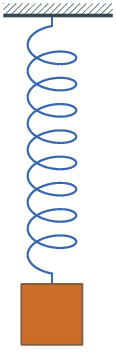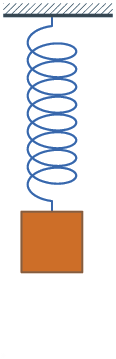
Оборудование: штатив с муфтой и лапкой, шарик с нитью, секундомер (рис. 1).

Рис. 1. Оборудование

Для выполнения работы нам потребуется таблица. Таблица будет состоять из следующих частей:

Величина/№	1	2	3	4	5
Длина (см)	5	20	45	80	125
Число колебаний	30	30	30	30	30
Время (с)
Период (с)
Частота (Гц)

Во-первых, нужно определить количество экспериментов. В данном случае их 5. По вертикали записаны те самые величины, которые мы будем измерять. В первую очередь, длина самого маятника в сантиметрах. Следующая величина – количество колебаний. Далее – полное время колебаний. Следующие две графы – это период колебаний, который измеряется в секундах, и частота в Гц. Обратите внимание, что мы заранее записали те величины, которые будем использовать. В первую очередь, это длина нитяного маятника. Начальная длина: 5 см – это очень короткий маятник. Дальше 20, 45, 80 и 125. 

Число колебаний мы будем использовать постоянное. Это 30 колебаний. В каждом эксперименте мы будем использовать по 30 колебаний.

Соберем экспериментальную установку. Установка состоит из шарика на нити. Нить продернута через ластик. Это сделано для того, чтобы можно было регулировать его длину. Обратите внимание, что сам ластик укреплен в лапке штатива.

Рис. 2. Грузик на нити, закрепленный в штативе

Для измерения длины будем использовать линейку и секундомер. Итак, мы отсчитали 30 колебаний, и время, которое мы зарегистрировали, оказалось равным 13,2 с (рис. 3).

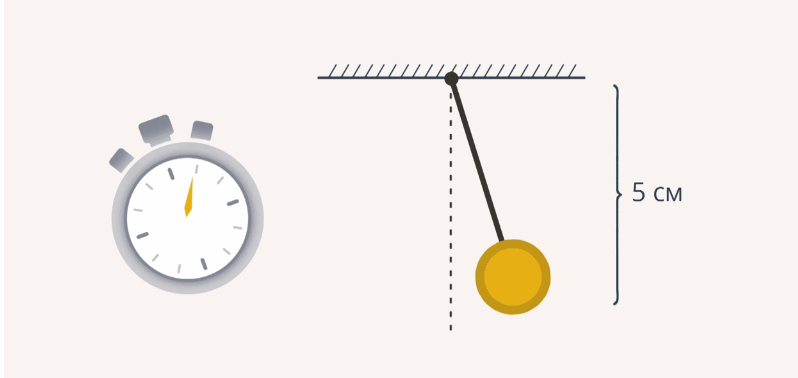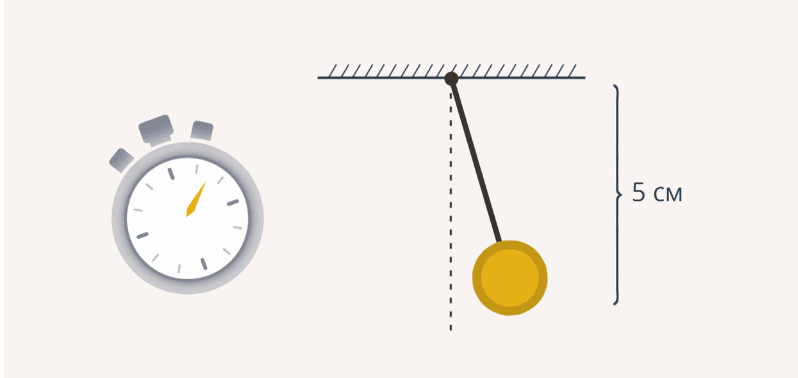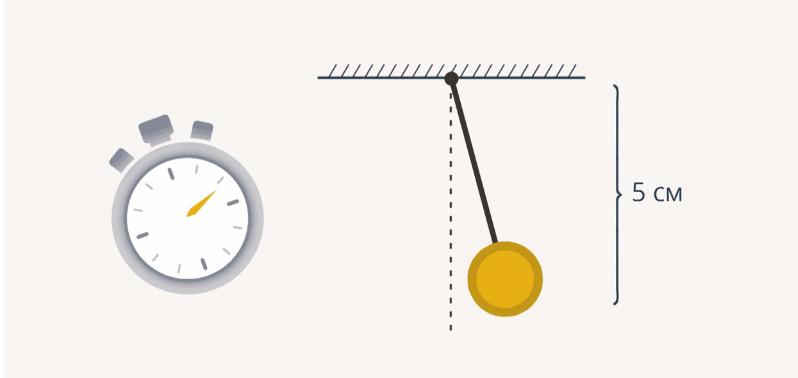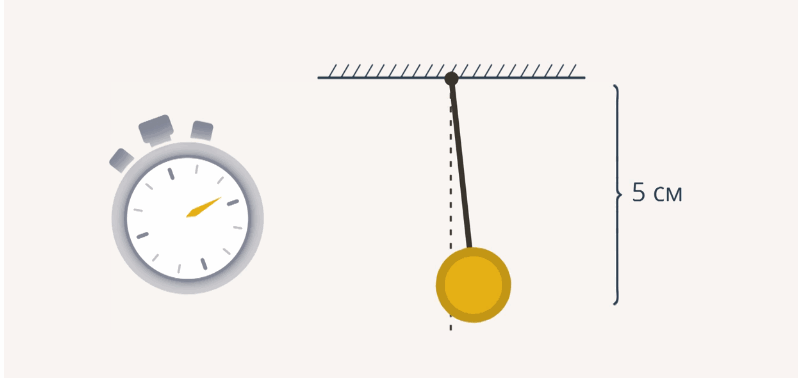
Рис. 3. Первый эксперимент с длиной нити 5 см

Заносим эти данные в таблицу и можем приступать к расчетам периода и частоты колебаний. Следующий шаг: увеличиваем длину маятника до 20 см. И весь эксперимент повторяем сначала. Вновь результаты заносим в таблицу. Итак, проведя наши эксперименты, мы получили конечные результаты и занесли их в таблицу.

Период колебаний: 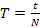 (с). Частота колебаний:  (Гц), где 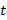 – это время, а  – количество колебаний, совершенных за время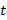

.

Обратите внимание: когда длина маятника составляла 5 см, 30 колебаний прошли за время 13,2 с. Период колебаний составил , а частота .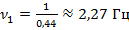

Следующий результат: те же 30 колебаний, но длина маятника была уже 20 см. В этом случае увеличилось время колебаний – 26,59 с, а период колебаний составил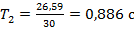

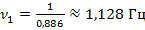. Частота уменьшилась почти в 2 раза, обратите внимание: .

Если мы посмотрим на третий результат, то увидим, что длина маятника еще больше, период стал больше, а частота уменьшилась еще на некоторое значение. Следующий, четвертый и пятый, постарайтесь посчитать сами. Обратите внимание на то, как при этом будет меняться период и частота колебаний нашего нитяного маятника.

Для 4 и 5 экспериментов посчитайте частоту и период самостоятельно.

Величина/№	1	2	3	4	5
Длина (см)	5	20	45	80	125
Число колебаний	30	30	30	30	30
Время (с)	13,2	26,59	40,32	52,81	66,21
Период (с)	0,44	0,886	1,344
Частота (Гц)	2,27	1,128	0,744

Табл. 1. Значения частоты и периода для первых трех экспериментов

Можно сделать вывод: с увеличением длины маятника увеличивается период колебаний и уменьшается частота (рис. 4). Хотелось бы, чтобы четвертый и пятый опыты вы проделали сами и убедились, что все действительно так, как мы получили в наших опытах.

Формула для вычисления периода колебания математического маятника: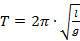

, где  – длина маятника, а – ускорение свободного падения.

Формула для вычисления частоты колебаний: .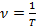

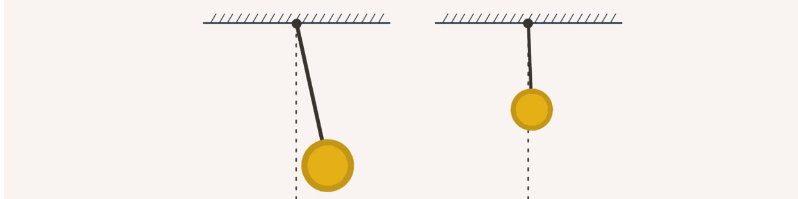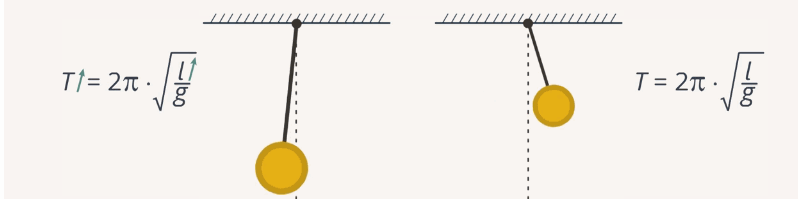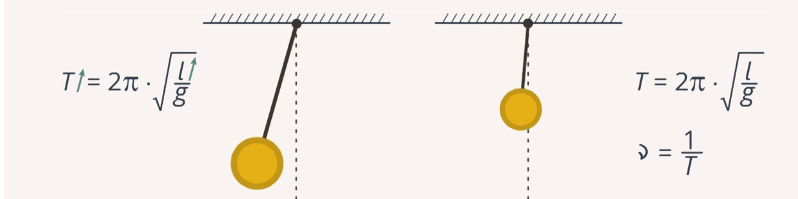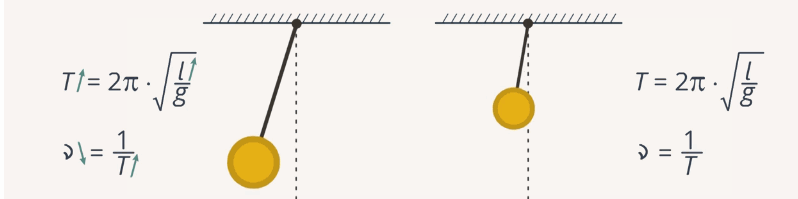
Рис. 4. Зависимость частоты и периода маятника от его длины

На этом лабораторная работа заканчивается, но есть дополнительная часть к лабораторной работе – дальнейшее исследование колебаний.

 

Ветка. Математическая зависимость между длиной маятника и периодом колебаний

Дополнительная часть лабораторной работы заключается в том, чтобы лучше определить взаимосвязь периода колебаний и длины нитяного маятника. Эта зависимость должна определяться математически. Цель дополнительного задания в том, чтобы выявить математическую зависимость между периодом и длиной маятника. Как это можно сделать? Нужно рассмотреть отношение периодов колебаний маятника и отношение длин маятника. Посмотрим на таблицу, которую используем, и обсудим те величины, которые будем туда заносить.

В первой части мы рассмотрим отношение периода из второго опыта, когда длина маятника составляла 20 см. Отношение мы будем искать к периоду, который получили, когда длина маятника составляла 5 см. Отношение самих длин мы рассмотрим в нижней строке. Итак, в верхней строке отношение периодов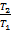 

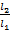, в нижней строке отношение длин маятника . Все необходимые данные мы возьмем из предыдущей таблицы. Обратим внимание, что эти вычисления в некоторых случаях получатся приближенными, но это зависит уже от чистоты эксперимента. Если мы обратимся к первой строке, то увидим, что во всех экспериментах отношение периодов будет составлять:

Далее рассмотрим отношение длин маятников. Обратите внимание: в первом случае это отношение равно 4, т. е. 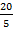. Во втором случае – 9. В третьем случае – 16. Видно сразу, как будут связаны эти величины. Посмотрите: в первом случае у нас 2 и 4. В другом случае – 3 и 9 и т. д.

Делаем вывод о том, что период будет пропорционален корню квадратному из длины маятника. Эту зависимость мы можем использовать в дальнейшем для анализа подобных колебаний: 

Из этого следует, что период мы можем записать как  .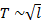

Другими словами, если мы увеличиваем длину маятника в 4 раза, то период увеличится в 2 раза. Если увеличим длину маятника в 3 раза, то увеличится период в  раз. И т. д. В этом и заключается результат лабораторной работы.

 

Список литературы

1. Аксенович Л.А. Физика в средней школе: Теория. Задания. Тесты: учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования/Л.А. Аксенович, Н.Н. Ракина, К.С. Фарино. Под ред. К.С. Фарино. – Минск.: Адукацыя i выхаванне, 2004.
2. Физика: механика. 10 кл.: учеб. для углубленного изучения физики/М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др. Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – 496 с.
3. Элементарный учебник физики. Под ред. Г.С. Ландсберга. Т. 3. – М., 1974.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «eduspb.com» (Источник)
2. Интернет-портал «physics.ru» (Источник)
3. Интернет-портал «fizmat.by» (Источник)

 

Домашнее задание

1. Что такое математический маятник? Запишите формулу для периода такого маятника.
2. Один математический маятник имеет период 10 с, а другой – период 6 с. Определите период колебаний третьего математического маятника, длина которого равна разности длин указанных маятников.
3. Длина математического маятника 25 см. Определите период и частоту его колебаний на Земле.

Гармонические колебания — Класс!ная физика

Гармонические колебания

«Физика — 11 класс»

Ускорение — вторая производная координаты по времени.

Мгновенная скорость точки — это производная координаты точки по времени.
Ускорение точки — это производная ее скорости по времени, или вторая производная координаты по времени.
Поэтому уравнение движения маятника можно записать так:

где х» — вторая производная координаты по времени.

При свободных колебаниях координата х изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.

Гармонические колебания

Из математики: вторые производные синуса и косинуса по их аргументу пропорциональны самим функциям, взятым с противоположным знаком, и никакие другие функции таким свойством не обладают.
Поэтому:
Координата тела, совершающего свободные колебания, меняется с течением времени по закону синуса или косинуса.

Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются гармоническими колебаниями.

Амплитуда колебаний

Амплитудой гармонических колебаний называется модуль наибольшего смещения тела от положения равновесия.

Амплитуда определяется начальными условиями, а точнее энергией, сообщаемой телу.

График зависимости координаты тела от времени представляет собой косинусоиду.

х = x_m cos ω₀t

где

Тогда уравнение движения, описывающее свободные колебания маятника:

Период и частота гармонических колебаний.

При колебаниях движения тела периодически повторяются.
Промежуток времени Т, за который система совершает один полный цикл колебаний, называется периодом колебаний.

Частота колебаний — это число колебаний в единицу времени.
Если одно колебание совершается за время Т, то число колебаний за секунду

В Международной системе единиц (СИ) единица частоты называется герцем (Гц) в честь немецкого физика Г. Герца.

Число колебаний за 2π с равно:

Величина ω₀ — это циклическая (или круговая) частота колебаний.
Через промежуток времени, равный одному периоду, колебания повторяются.

Частоту свободных колебаний называют собственной частотой колебательной системы.
Часто для краткости циклическую частоту называют просто частотой.

Зависимость частоты и периода свободных колебаний от свойств системы.

1. для пружинного маятника

Собственная частота колебаний пружинного маятника равна:

Она тем больше, чем больше жесткость пружины k, и тем меньше, чем больше масса тела m.
Жесткая пружина сообщает телу большее ускорение, быстрее меняет скорость тела, а чем тело массивнее, тем медленнее оно изменяет скорость под влиянием силы.

Период колебаний равен:

Период колебаний пружинного маятника не зависит от амплитуды колебаний.

2. для нитяного маятника

Собственная частота колебаний математического маятника при малых углах отклонения нити от вертикали зависит от длины маятника и ускорения свободного падения:

Период же этих колебаний равен:

Период колебаний нитяного маятника при малых углах отклонения не зависит от амплитуды колебаний.

Период колебаний возрастает с увеличением длины маятника. От массы маятника он не зависит.

Чем меньше g, тем больше период колебаний маятника и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут за сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета (высота 200 м). И это только за счет уменьшения ускорения свободного падения с высотой.

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Механические колебания. Физика, учебник для 11 класса — Класс!ная физика

Свободные, затухающие и вынужденные колебания — Условия возникновения свободных колебаний. Математический маятник — Динамика колебательного движения. Уравнение движения маятника — Гармонические колебания — Фаза колебаний — Превращение энергии при гармонических колебаниях — Вынужденные колебания. Резонанс — Примеры решения задач — Краткие итоги главы

Гармонический осциллятор — Википедия

У этого термина существуют и другие значения, см. Осциллятор.

Гармони́ческий осцилля́тор (в классической механике) — система, которая при выведении её из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x:

F=−kx{\displaystyle F=-kx},

где k — постоянный коэффициент.

Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Свободные колебания системы груз—пружина без затухания.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди немеханических аналогов гармонического осциллятора можно выделить электрический гармонический осциллятор (см. LC-цепь).

Свободные колебания консервативного гармонического осциллятора[править | править код]

Уравнение и его решения[править | править код]

Пусть x — смещение материальной точки относительно её положения равновесия, а F — действующая на точку возвращающая сила любой природы вида

F=−kx{\displaystyle F=-kx},

где k = const. Тогда, используя второй закон Ньютона, можно записать ускорение как

a=−kmx{\displaystyle a=-{\frac {k}{m}}x}.

Обозначая ω02=k/m{\displaystyle {\omega _{0}}^{2}=k/m} и заменяя a на вторую производную от координаты по времени x¨{\displaystyle {\ddot {x}}}, имеем

x¨+ω02x=0{\displaystyle {\ddot {x}}+\omega _{0}^{2}x=0}.

Это дифференциальное уравнение описывает поведение консервативного гармонического осциллятора. Величину ω0{\displaystyle \omega _{0}} называют циклической частотой. (Имеется в виду круговая частота, измеряющаяся в радианах за секунду. Чтобы перевести её в частоту, выражающуюся в герцах, надо разделить на 2π{\displaystyle 2\pi }.)

Будем искать решение этого уравнения в виде^[1]

x(t)=Asin⁡(ωt+φ){\displaystyle x(t)=A\sin \left(\omega t+\varphi \right)}.

Здесь A — амплитуда, ω — частота колебаний, φ — начальная фаза.

Подставляем в дифференциальное уравнение и получаем:

x¨(t)=−Aω2sin⁡(ωt+φ){\displaystyle {\ddot {x}}(t)=-A\omega ^{2}\sin(\omega t+\varphi )},

−Aω2sin⁡(ωt+φ)+ω02Asin⁡(ωt+φ)=0{\displaystyle -A\omega ^{2}\sin(\omega t+\varphi )+\omega _{0}^{2}A\sin(\omega t+\varphi )=0}.

Амплитуда сокращается. Значит, она может иметь любое значение (в том числе и нулевое — это означает, что материальная точка покоится в положении равновесия). На синус также можно сократить, так как равенство должно выполняться в любой момент времени t. Таким образом, остаётся условие для частоты колебаний:

−ω2+ω02=0,{\displaystyle -\omega ^{2}+\omega _{0}^{2}=0,}

ω=±ω0.{\displaystyle \omega =\pm \omega _{0}.}

Отрицательную частоту можно отбросить, так как произвол в выборе здесь знака покрывается произволом выбора начальной фазы.

Общее решение уравнения записывается в виде:

x(t)=Asin⁡(ω0t+φ),{\displaystyle x(t)=A\sin \left(\omega _{0}t+\varphi \right),}

где A и φ — произвольные постоянные. Эта запись исчерпывает все решения дифференциального уравнения, так как позволяет удовлетворить любым начальным условиям.

Итого, консервативный гармонический осциллятор может совершать чисто гармонические колебания с частотой, равной его собственной частоте, с амплитудой любой величины и с произвольной начальной фазой.

Простое гармоническое движение[править | править код]

Простое гармоническое движение. На этой анимированной картинке по вертикальной оси отложена координата частицы (x в формуле), а по горизонтальной оси отложено время (t).

Движение, совершаемое консервативным гармоническим осциллятором, носит название простого гармонического движения. Это движение не является ни вынужденным, ни затухающим.

Оно периодическое: тело колеблется с частотой ω₀ около положения равновесия по синусоидальному закону. Каждое последующее колебание такое же, как и предыдущее; период, частота и амплитуда колебаний остаются постоянными.

Учитывая, что ω₀ = 2πf, получим

f=12πkm,{\displaystyle f={\frac {1}{2\pi }}{\sqrt {\frac {k}{m}}},}

и, поскольку T = 1/f, где T — период колебаний,

T=2πmk.{\displaystyle T=2\pi {\sqrt {\frac {m}{k}}}.}

Эти формулы показывают, что период и частота не зависят от амплитуды и начальной фазы движения.

Частота движения определяется характерными свойствами системы (например, массой движущегося тела), в то время как амплитуда и начальная фаза определяются начальными условиями — координатой и скоростью тела в момент начала колебаний. Кинетическая и потенциальная энергии системы также зависят от этих свойств и условий.

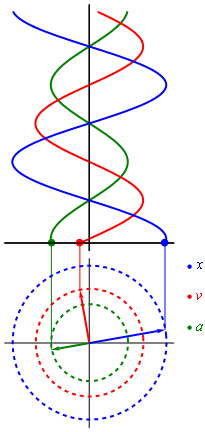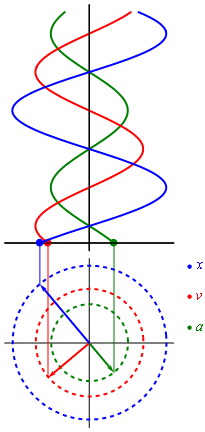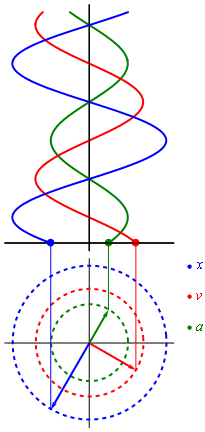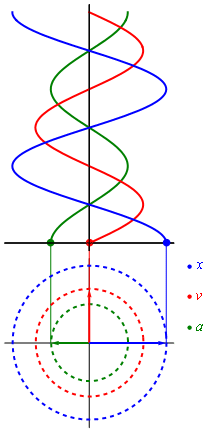Положение, скорость и ускорение простого гармонического движения на фазовой плоскости

Используя приёмы дифференциального исчисления, можно получить скорость и ускорение материальной точки как функции времени:

v(t)=dxdt=Aω0cos⁡(ω0t+φ){\displaystyle v(t)={\frac {\mathrm {d} x}{\mathrm {d} t}}=A\omega _{0}\cos(\omega _{0}t+\varphi )},

a(t)=d2xdt2=−Aω02sin⁡(ω0t+φ){\displaystyle a(t)={\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-A\omega _{0}^{2}\sin(\omega _{0}t+\varphi )}.

Кинетическая энергия записывается в виде

T=12mv2(t)=12kA2cos2⁡(ω0t+φ){\displaystyle T={\frac {1}{2}}mv^{2}(t)={\frac {1}{2}}kA^{2}\cos ^{2}(\omega _{0}t+\varphi )},

а потенциальная энергия составляет

U=12kx2(t)=12kA2sin2⁡(ω0t+φ){\displaystyle U={\frac {1}{2}}kx^{2}(t)={\frac {1}{2}}kA^{2}\sin ^{2}(\omega _{0}t+\varphi )}.

Тогда получается, что полная энергия

E=12kA2{\displaystyle E={\frac {1}{2}}kA^{2}}

имеет постоянное значение. Это отражает «консервативность» осциллятора, то есть отсутствие энергетических потерь.

Простое гармоническое движение можно рассматривать как математическую модель различных видов движения, таких, например, как колебание пружины. Другими случаями, которые могут приближённо рассматриваться как простое гармоническое движение, являются движение маятника и вибрации молекул.

Простое гармоническое движение является основой некоторых способов анализа более сложных видов движения. Одним из таких способов является способ, основанный на преобразовании Фурье, суть которого сводится к разложению более сложного вида движения в ряд простых гармонических движений.

Примеры осцилляторов[править | править код]

Любая система, в которой происходит простое гармоническое движение, обладает двумя ключевыми свойствами:

• когда система выведена из состояния равновесия, должна существовать возвращающая сила, стремящаяся вернуть систему в равновесие;
• возвращающая сила должна в точности или приближённо быть пропорциональна перемещению.

Ниже представлено несколько примеров.

Горизонтальная система груз—пружина

Положение, скорость и ускорение гармонического осциллятора

Типичным примером системы, в которой происходит простое гармоническое движение, является идеализированная система груз—пружина, в которой груз присоединён к пружине и находится на горизонтальной поверхности. Если пружина не сжата и не растянута, то на груз не действует никаких переменных сил и он находится в состоянии механического равновесия. Однако, если груз вывести из положения равновесия, пружина деформируется и с её стороны будет действовать сила, стремящаяся вернуть груз в положение равновесия. В случае системы груз—пружина такой силой является сила упругости пружины, которая подчиняется закону Гука:

F=−kx{\displaystyle F=-kx},

где k имеет вполне конкретный смысл — это коэффициент жёсткости пружины.

Однажды смещённый груз подвергается действию возвращающей силы, ускоряющей его и стремящейся вернуть в начальную точку, то есть в положение равновесия. По мере того, как груз приближается к положению равновесия, возвращающая сила уменьшается и стремится к нулю. Однако в положении x = 0 груз обладает некоторым количеством движения (импульсом), приобретённым благодаря действию возвращающей силы. Поэтому груз проскакивает положение равновесия, начиная снова деформировать пружину (но уже в противоположном направлении). Возвращающая сила будет стремиться замедлить его, пока скорость не станет равной нулю; и сила вновь будет стремиться вернуть груз в положение равновесия.

Если нет потерь энергии, груз будет колебаться как описано выше; такое движение является периодическим.

Вертикальная система груз—пружина

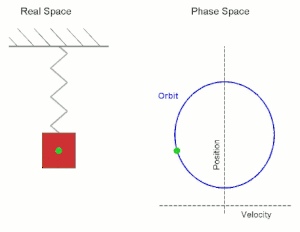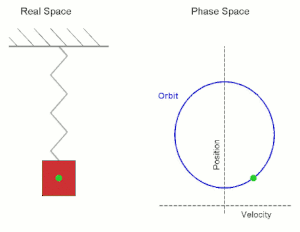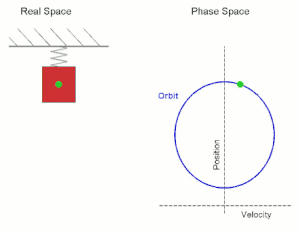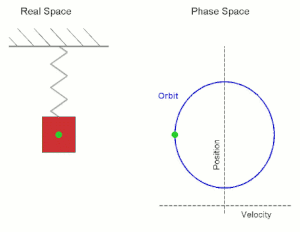Простое гармоническое движение, показанное одновременно в реальном пространстве и в фазовом пространстве. Real Space — реальное пространство; Phase Space — фазовое пространство; velocity — скорость; position — положение (позиция).

В случае вертикально подвешенного на пружине груза, наряду с силой упругости, действует сила тяжести, то есть суммарно сила составит

F=−kx−mg{\displaystyle F=-kx-mg}.

Если сделать замену переменной, чтобы оперировать не величиной x{\displaystyle x}, а величиной X=x+mg/k{\displaystyle X=x+mg/k}, то уравнение движения примет вид, идентичный случаю горизонтальной геометрии, только для переменной X{\displaystyle X}.

Колебания будут происходить с той же частотой ω0=k/m{\displaystyle \omega _{0}={\sqrt {k/m}}}. Однако, если в горизонтальном случае равновесию отвечало состояние недеформированной пружины, то в вертикальном варианте пружина в равновесии будет растянута. Зависимости частоты от величины ускорения свободного падения g{\displaystyle g} при этом нет; g{\displaystyle g} влияет лишь на сдвиг положения равновесия mg/k{\displaystyle mg/k}.

Измерения частоты (или периода) колебаний груза на пружине используются в устройствах для определения массы тела — так называемых массметрах, применяемых на космических станциях, когда весы не могут функционировать из-за невесомости.

Универсальное движение по окружности

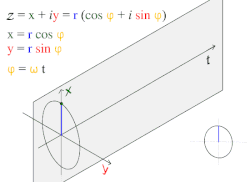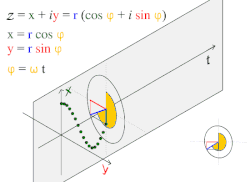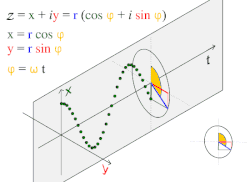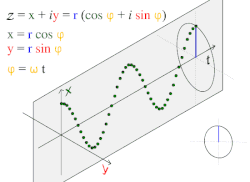Движение по кругу и гармоническое движение

Простое гармоническое движение в некоторых случаях можно рассматривать как одномерную проекцию универсального движения по окружности.

Если объект движется с постоянной угловой скоростью ω по окружности радиуса r, центром которой является начало координат плоскости x − y, то такое движение вдоль каждой из координатных осей является простым гармоническим с амплитудой r и круговой частотой ω.

Груз как простой маятник

Простое гармоническое движение маятника без затухания.

В приближении малых углов движение простого маятника является близким к простому гармоническому. Период колебаний такого маятника, прикреплённого к стержню длиной ℓ, даётся формулой

T=2πℓg.{\displaystyle T=2\pi {\sqrt {\frac {\ell }{g}}}.}

где g — ускорение свободного падения. Это показывает, что период колебаний не зависит от амплитуды и массы маятника, но зависит от g, поэтому, при той же самой длине маятника, на Луне он будет качаться медленнее, так как там слабее гравитация и меньше значение ускорения свободного падения.

Указанное приближение является корректным только при небольших углах отклонения, поскольку выражение для углового ускорения пропорционально синусу координаты:

ℓmgsin⁡θ=Iα,{\displaystyle \ell mg\sin \theta =I\alpha ,}

где I — момент инерции; в данном случае I = m ℓ ². Небольшие углы реализуются в условиях, когда амплитуда колебаний значительно меньше длины стержня.

Когда угол θ мал, можно считать, что sin θ ≈ θ, и выражение принимает вид:

ℓmgθ=Iα,{\displaystyle \ell mg\theta =I\alpha ,}

что делает угловое ускорение прямо пропорциональным углу θ, а это удовлетворяет определению простого гармонического движения.

Свободные колебания гармонического осциллятора с затуханием[править | править код]

Уравнение и его решения[править | править код]

При рассмотрении осциллятора с затуханием за основу берётся модель консервативного осциллятора, в которую добавляется сила вязкого трения. Сила вязкого трения направлена против скорости движения груза относительно среды и прямо пропорциональна этой скорости. Тогда полная сила, действующая на груз, записывается так:

F=−kx−αv.{\displaystyle F=-kx-\alpha v.}

Используя второй закон Ньютона, получаем дифференциальное уравнение, описывающее затухающий осциллятор:

x¨+2γx˙+ω02x=0.{\displaystyle {\ddot {x}}+2\gamma {\dot {x}}+\omega _{0}^{2}x=0.}

Здесь введены обозначения:

• 2γ=α/m{\displaystyle 2\gamma =\alpha /m}. Коэффициент γ{\displaystyle \gamma } носит название постоянной затухания. Он имеет размерность частоты.
• ω0=km{\displaystyle \omega _{0}={\sqrt {k \over m}}}. Величину ω0{\displaystyle \omega _{0}} называют собственной частотой системы. Она тоже имеет размерность частоты.

Решение распадается на три случая.

• При малом трении (γ<ω0{\displaystyle \gamma <\omega _{0}}) общее решение записывается в виде:

x(t)=Ae−γtsin(ωft+φ),{\displaystyle x(t)=Ae^{-\gamma t}sin(\omega _{f}t+\varphi ),}

где ωf=ω02−γ2{\displaystyle \omega _{f}={\sqrt {\omega _{0}^{2}-\gamma ^{2}}}} — частота свободных колебаний.

• Затухание γ=ω0{\displaystyle \gamma =\omega _{0}} называют критическим. Начиная с такого значения показателя затухания, осциллятор будет совершать так называемое неколебательное движение. В граничном случае движение происходит по закону:

 x(t)=(A+Bt)e−γt.{\displaystyle \ x(t)=(A+Bt)e^{-\gamma t}.}

• При сильном же трении γ>ω0{\displaystyle \gamma >\omega _{0}} решение выглядит следующим образом:

x(t)=Ae−β1t+Be−β2t,{\displaystyle x(t)=Ae^{-\beta _{1}t}+Be^{-\beta _{2}t},}

где β1,2=γ±γ2−ω02.{\displaystyle \beta _{1,2}=\gamma \pm {\sqrt {\gamma ^{2}-\omega _{0}^{2}}}.}

Движение при наличии затухания[править | править код]

Характер движения затухающего осциллятора зависит от постоянной затухания γ{\displaystyle \gamma }. Помимо указанной постоянной, затухание осциллятора также часто характеризуют безразмерным параметром, называемым добротностью. Добротность обычно обозначают буквой Q{\displaystyle Q}. По определению, добротность равна:

Q=ω02γ.{\displaystyle Q={\frac {\omega _{0}}{2\gamma }}.}

Чем больше добротность, тем медленнее затухают колебания осциллятора.

Критическое затухание γ=ω0{\displaystyle \gamma =\omega _{0}} примечательно тем, что именно при таком затухании осциллятор быстрее всего оказывается в положении равновесия. Если трение меньше критического, он дойдёт до положения равновесия быстрее, однако «проскочит» его по инерции и будет совершать колебания. Если трение больше критического, то осциллятор будет экспоненциально стремиться к положению равновесия, но тем медленнее, чем больше трение.

Поэтому в стрелочных индикаторах (например, в амперметрах) обычно стараются ввести именно критическое затухание, чтобы стрелка успокаивалась максимально быстро для считывания его показаний.

У осциллятора с критическим затуханием добротность равна 0,5. Соответственно, добротность указывает характер поведения осциллятора. Если добротность больше 0,5, то свободное движение осциллятора представляет собой колебания; теоретически, со временем он пересечёт положение равновесия неограниченное количество раз. Добротность, меньшая или равная 0,5, соответствует неколебательному движению осциллятора; в свободном движении он пересечёт положение равновесия не более одного раза.

Добротность иногда называют коэффициентом усиления осциллятора, так как при некоторых способах возбуждения при совпадении частоты возбуждения с резонансной частотой колебаний их амплитуда устанавливается примерно в Q{\displaystyle Q} раз больше, чем при возбуждении с той же интенсивностью на низкой частоте.

Также добротность примерно равна количеству колебательных циклов, за которое амплитуда колебаний уменьшается в e{\displaystyle e} раз, умноженному на π{\displaystyle \pi }.

В случае колебательного движения затухание ещё характеризуют такими параметрами, как:

• Время жизни колебаний (оно же время затухания, оно же время релаксации) τ — время, за которое амплитуда колебаний уменьшится в e раз.

τ=1/γ.{\displaystyle \tau =1/\gamma .}

Это время рассматривается как время, необходимое для затухания (прекращения) колебаний (хотя, формально, свободные колебания продолжаются бесконечно долго).

• Логарифмический декремент затухания. Определяется как логарифм отношения двух последовательных максимальных отклонений в одну сторону: d=ln⁡(xmaxn/xmaxn+1).{\displaystyle d=\operatorname {ln} (x_{{\text{max}}\;n}/x_{{\text{max}}\;n+1}).} Величина, обратная d, есть количество колебаний, которое пройдёт за время затухания τ.

Замечание о вынужденных колебаниях гармонического осциллятора[править | править код]

Колебания осциллятора называют вынужденными, когда на него производится некоторое дополнительное воздействие извне. Это воздействие может производиться различными средствами и по различным законам. Например, силовым возбуждением называется воздействие на груз силой, зависящей только от времени по определённому закону. Кинематическим возбуждением называют воздействие на осциллятор движением точки закрепления пружины по заданному закону. Возможно также воздействие трением, когда, например, среда, с которой груз испытывает трение, совершает движение по заданному закону.

Бутиков Е. И. Собственные колебания линейного осциллятора. Учебное пособие

1. ↑ Решение приведённого дифференциального уравнения можно записать как с помощью функции синуса:

   x(t)=Asin⁡(ωt+φ){\displaystyle x(t)=A\sin(\omega t+\varphi )},

   так и через косинус:

   x(t)=Acos⁡(ωt+φ){\displaystyle x(t)=A\cos(\omega t+\varphi )}.

   Оба варианта верны, поскольку известно общее равенство cos θ = sin(π/2 — θ). Используя тригонометрические соотношения, можно записать

   Acos⁡(ωt+φ)=Acos⁡(φ)cos⁡(ωt)−Asin⁡(φ)sin⁡(ωt),{\displaystyle A\cos(\omega t+\varphi )=A\cos(\varphi )\cos(\omega t)-A\sin(\varphi )\sin(\omega t),}

   и таким образом

   acos⁡(ωt)+bsin⁡(ωt){\displaystyle a\cos(\omega t)+b\sin(\omega t)}

   также является верным решением при соответствующим образом выбранных постоянных a и b.

3. Длина волны. Связь длины волны со скоростью её распространения и периодом (частотой)

Каждая волна распространяется с какой-то скоростью.

Под скоростью волны понимают скорость распространения возмущения.

Пример:

удар по торцу стального стержня вызывает в нём местное сжатие, которое затем распространяется вдоль стержня со скоростью около \(5\) км/с.

 

Обрати внимание!

Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую её скорость изменяется.

Помимо скорости, важной характеристикой волны является длина волны.

Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.

Рассмотрим процесс передачи колебаний от точки к точке при распространении поперечной волны.

Для этого используем: частицы среды, в которой будет распространяться волна, примем за цепочку пронумерованных шариков (рис. \(1\)).

Будем считать, что между шариками, как и между частицами среды, существуют силы взаимодействия, в частности при небольшом удалении шариков друг от друга возникает сила притяжения.

 

Рис. \(1\)

 

Если привести первый шарик в колебательное движение, то есть заставить его двигаться вверх и вниз от положения равновесия, то благодаря силам взаимодействия каждый шарик в цепочке будет повторять движение первого, но с некоторым запаздыванием (сдвигом фаз). Это запаздывание будет тем больше, чем дальше от первого шарика находится данный шарик.

 

Четвёртый шарик отстаёт от первого на \(1/4\) колебания (рис. \(2\)). Когда первый шарик прошёл \(1/4\) часть пути полного колебания, максимально отклонившись вверх, четвёртый шарик только начал движение из положения равновесия.

 

Рис. \(2\)

 

Движение седьмого шарика отстаёт от движения первого на \(1/2\) колебания (рис. \(3\)), десятого — на \(3/4\) колебания (рис. \(4\)).

 

Рис. \(3\)

 

Рис. \(4\)

 

Тринадцатый шарик отстаёт от первого на одно полное колебание (рис. \(5\)), то есть находится с ним в одинаковых фазах.

 

Рис. \(5\)

 

Движения этих двух шариков совершенно одинаковы (рис. \(6\)).

 

Рис. \(6\)

 

Расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, называется длиной волны.

Обрати внимание!

Длина волны обозначается греческой буквой \(λ\) («ламбда»).

Расстояние между первым и тринадцатым шариками (см. рис. \(6\)), вторым и четырнадцатым, третьим и пятнадцатым и так далее, то есть между всеми ближайшими друг к другу шариками, колеблющимися в одинаковых фазах, будет равно длине волны \(λ\).

 

Из рисунков выше видно, что колебательный процесс распространился от первого шарика до тринадцатого, то есть на расстояние, равное длине волны \(λ\), за то же время, за которое первый шарик совершил одно полное колебание, то есть за период колебаний \(T\).

 

Значит,

 

λ=VT,

 

где \(V\) — скорость волны.

 

Поскольку период колебаний связан с их частотой ν зависимостью

 

T=1ν,

 

то длина волны может быть выражена через скорость волны и частоту:

 

λ=Vν.

 

Обрати внимание!

Длина волны зависит от частоты ν (или периода \(T\)) колебаний источника, порождающего эту волну, и от скорости \(V\) распространения волны.

Из формул для определения длины волны можно выразить скорость волны:

 

V=λT

 

и

 

V=λν.

 

Обрати внимание!

Формулы для нахождения скорости волны справедливы как для поперечных, так и для продольных волн.

Длину волны при распространении продольных волн можно представить с помощью рисунка \(7\).

 

Рис. \(7\)

 

Обрати внимание!

Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна.

При переходе волны из одной среды в другую её частота не изменяется, меняются лишь скорость и длина волны.

Колебания — Википедия

Отличие колебания от волны

Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются все углы его отклонения относительно вертикали; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.

Колебания почти всегда связаны с превращением энергии из одной формы в другую и обратно.

Колебания различной физической природы имеют много общих закономерностей и тесно связаны c волнами. Поэтому исследованиями этих закономерностей занимается теория колебаний и волн. Принципиальное отличие волн в том, что их распространение сопровождается переносом энергии.

Выделение разных видов колебаний зависит от подчёркиваемых свойств систем с колебательными процессами (осцилляторов).

По используемому математическому аппарату[править | править код]

По периодичности[править | править код]

• Периодические
• Квазипериодические
• Апериодические
• Антипериодические^{[A: 1]}

Так, периодические колебания определены следующим образом:

По физической природе[править | править код]

По характеру взаимодействия с окружающей средой[править | править код]

• Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия.
• Свободные (или собственные) — это колебания в системе под действием внутренних сил после того, как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.
• Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы). Характерным отличием автоколебаний от вынужденных колебаний является то, что их амплитуда определяется свойствами самой системы, а не начальными условиями.
• Параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.

• Амплитуда — максимальное отклонение колеблющейся величины от положения равновесия, A{\displaystyle A\,\!} (м)
• Период — время полного колебания, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), T{\displaystyle T\,\!} (с)
• Частота — число колебаний в единицу времени, f{\displaystyle f\,\!} (Гц, с⁻¹).

Период колебаний T{\displaystyle T\,\!} и частота f{\displaystyle f\,\!} — обратные величины:

T=1f{\displaystyle T={\frac {1}{f}}\qquad } и f=1T{\displaystyle \qquad f={\frac {1}{T}}}

В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота ω{\displaystyle \omega \,\!} (рад/с, Гц, с⁻¹), показывающая число колебаний за 2π{\displaystyle 2\pi } единиц времени:

ω=2πT{\displaystyle \omega ={\frac {2\pi }{T}}\qquad } и T=2πω{\displaystyle \qquad T={\frac {2\pi }{\omega }}}

• Смещение — отклонение тела от положения равновесия, X{\displaystyle X\,\!} (м)
• Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.

Гармонические колебания были известны с XVII века.

Термин «релаксационные колебания» был предложен в 1926 г. ван дер Полем.^{[A: 2][A: 3]} Обосновывалось введение такого термина лишь тем обстоятельством, что указанному исследователю казались все подобные колебания связанными с наличием «времени релаксации» — то есть с концептом, который на тот исторический момент развития науки представлялся наиболее понятным и широко распространённым. Ключевым свойством колебаний нового типа, описанных рядом перечисленных выше исследователей, было то, что они существенно отличались от линейных, — что проявляло себя в первую очередь как отклонение от известной формулы Томсона. Тщательное историческое исследование показало^{[A: 4]}, что ван дер Поль в 1926 г. ещё не осознавал того обстоятельства, что открытое им физическое явление «релаксационные колебания» соответствует введённому Пуанкаре математическому понятию «предельный цикл», и понял он это лишь уже после вышедшей в 1929 г. публикации А. А. Андронова.

Иностранные исследователи признают^{[A: 4]} тот факт, что среди советских учёных мировую известность приобрели ученики Л. И. Мандельштама, выпустившие в 1937 г. первую книгу^{[B: 1]}, в которой были обобщены современные сведения о линейных и нелинейных колебаниях. Однако советские учёные «не приняли в употребление термин „релаксационные колебания“, предложенный ван дер Полем. Они предпочитали термин „разрывные движения“, используемый Блонделем, в частности потому, что предполагалось описывать этих колебаний в терминах медленных и быстрых режимов. Этот подход стал зрелым только в контексте теории сингулярных возмущений»^{[A: 4]}.

Краткая характеристика основных типов колебательных систем[править | править код]

Линейные колебания[править | править код]

Важным типом колебаний являются гармонические колебания — колебания, происходящие по закону синуса или косинуса. Как установил в 1822 году Фурье, любое периодическое колебание может быть представлено как сумма гармонических колебаний путём разложения соответствующей функции в ряд Фурье. Среди слагаемых этой суммы существует гармоническое колебание с наименьшей частотой, которая называется основной частотой, а само это колебание — первой гармоникой или основным тоном, частоты же всех остальных слагаемых, гармонических колебаний, кратны основной частоте, и эти колебания называются высшими гармониками или обертонами — первым, вторым и т. д.^{[B: 2]}

Нелинейные релаксационные колебания[править | править код]

Указывается^{[A: 4]}, что формулировка, представленная Ван дер Полем: «медленная эволюция, сопровождаемая внезапным прыжком» (в оригинале: «slow evolution followed by a sudden jump»), — недостаточна, чтобы избежать неоднозначной интерпретации, причём на это обстоятельство указывали ещё современники ван дер Поля.

Тем не менее, похожим образом релаксационные колебания определяются и в более поздних работах. Например, Е. Ф. Мищенко и соавт.^[2] определяют релаксационные колебания как такие «периодические движения» по замкнутой фазовой траектории, при которых «сравнительно медленные, плавные изменения фазового состояния чередуются с весьма быстрыми, скачкообразными». При этом далее указывается^[3], что «сингулярно возмущённую систему, допускающую такое периодическое решение, называют релаксационной».

Рассматривались отдельно в классической коллективной монографии А. А. Андронова и соав.^[4] под названием «разрывные колебания», более принятому в советской математической школе.

Позже сложилась в теорию сингулярных возмущений (см. напр.^{[B: 3]}).

1. ↑ Андронов А. А., Витт А. А., Хайкин С. Э. Теория колебаний. — 2-е изд., перераб. и испр.. — М.: Наука, 1981. — 918 с.
2. ↑ § 16. Резонансные явления при действии негармонической периодической силы. // Элементарный учебник физики / Под ред. Г.С. Ландсберга. — 13-е изд. — М.: ФИЗМАТЛИТ, 2003. — Т. 3. Колебания и волны. Оптика. Атомная и ядерная физика. — С. 41—44.
3. ↑ Мищенко Е. Ф., Колесов Ю. С., Колесов А. Ю., Розов Н. Х. Периодические движения и бифуркационные процессы в сингулярно возмущенных системах. — М.: Физматлит, 1995. — 336 с. — 1000 экз. — ISBN 5-02-015129-7.

• Физика. Большой энциклопедический словарь/Гл. ред. А. М. Прохоров. — 4-е изд. — М.: Большая Российская энциклопедия, 1999. — С. 293—295. ISBN 5-85270-306-0 (БРЭ)

Отрицательная частота — Википедия

Понятие отрицательной и положительной частоты может быть показано на примере вращающегося в ту или другую сторону вектора. Частота со знаком отражает как скорость, так и направление вращения. Скорость выражена в оборотах (циклах) в секунду (герцах) или рад/с (где 1 оборот соответствует 2π радианам).

Для заданного во времени сигнала такой вектор представляет его на комплексной плоскости. Зависимость значения сигнала от времени есть лишь зависимость проекции вектора на действительную ось от времени. Поэтому понятие отрицательной частоты не может быть представлено в виде некомплексных сигналов во временной области и распространяется только на частотную.

Чтобы сигнал был представим в некомплексном виде, формула Эйлера требует равенства коэффициентов при комплексных экспонентах частот разных знаков. Несимметричность спектра равноценна наличию в сигнале гармоник, заданных только для отрицательной частоты.

Рассмотрим сигнал с девиацией частоты ±Δω{\displaystyle \pm \Delta \omega } относительно несущей. При переносе несущей на ноль обычным гетеродином информация искажается. Поэтому для правильной обработки необходимо использовать квадратурный гетеродин, в котором вводится дополнительный канал, позволяющий сохранить информацию о несимметричности спектра (об отрицательной частоте относительно несущей) представляя огибающую двумя равноценными сигналами: исходный сигнал становится комплексным. Получить из такого сигнала вещественный можно лишь его переносом на несущую ωs>Δω{\displaystyle \omega _{s}>\Delta \omega }, иначе требуется два канала передачи.

Пример искажения сигнала при преобразовании несущей обычным гетеродином:

cos(ωst+Δωt)+2cos(ωst−Δωt)→ωs→03cos(Δωt)→ω0→ωs1.5cos(ωst+Δωt)+1.5cos(ωst−Δωt){\displaystyle cos\left(\omega _{s}t+\Delta \omega t\right)+2cos\left(\omega _{s}t-\Delta \omega t\right){\xrightarrow {\omega _{s}\to 0}}3cos\left(\Delta \omega t\right){\xrightarrow {\omega _{0}\to \omega _{s}}}1.5cos\left(\omega _{s}t+\Delta \omega t\right)+1.5cos\left(\omega _{s}t-\Delta \omega t\right)}

Преобразование квадратурным гетеродином:

cos(ωst+Δωt)+2cos(ωst−Δωt)→ωs→03cos(Δωt)−isin(Δωt)→ω0→ωscos(ωst+Δωt)+2cos(ωst−Δωt){\displaystyle cos\left(\omega _{s}t+\Delta \omega t\right)+2cos\left(\omega _{s}t-\Delta \omega t\right){\xrightarrow {\omega _{s}\to 0}}3cos\left(\Delta \omega t\right)-isin\left(\Delta \omega t\right){\xrightarrow {\omega _{0}\to \omega _{s}}}cos\left(\omega _{s}t+\Delta \omega t\right)+2cos\left(\omega _{s}t-\Delta \omega t\right)}

Для частотной области таким непредставимым понятием является временная асимметрия сигналов: лишь симметричные сигналы имеют некомплексный спектр.

Нечетная симметрия синусоиды во времени, в частотной области представлена сменой знака частоты: S(f)=−S(−f){\displaystyle S(f)=-S(-f)}, а значения косинуса не связаны со знаком частоты.

Таким образом, понятие отрицательной частоты столь же оправданно, как и понятие отрицательного времени. Наглядное представление вращающегося в разные стороны вектора можно получить на экране осциллографа, подавая синус на вертикальные, а косинус на горизонтальные пластины и меняя полуось времени (знак синуса).

Синус — это функция углового аргумента, циклично меняющая свою амплитуду с постоянным возрастанием и убыванием «угла» (фазы). Понятие отрицательной частоты используется для различения уменьшающегося или увеличивающегося аргумента. Но синус немонотонная функция: sin⁡(ωt+π2+θ){\displaystyle \sin(\omega t+{\frac {\pi }{2}}+\theta )} уже не сохраняет знак ω{\displaystyle \omega }, так же, как f(x)=x2{\displaystyle f(x)=x^{2}} не сохраняет знак x{\displaystyle x}. Хотя θ{\displaystyle \theta } обычно отражает неизвестное, случайное смещение фазы, в большинстве случаев использования отдельной взятой вещественной синусоиды достаточно «предположить», что ω{\displaystyle \omega } положительна.

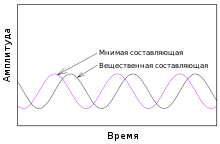Вещественная и комплексная части гармонического колебания.

Иногда два колебания одной частотой и известной фазой различны, к примеру:

R(t)=cos⁡(ωt+θ){\displaystyle R(t)=\cos(\omega t+\theta )}

и

I(t)=cos⁡(ωt+θ−π2)=sin⁡(ωt+θ){\displaystyle I(t)=\cos(\omega t+\theta -{\begin{matrix}{\frac {\pi }{2}}\end{matrix}})=\sin(\omega t+\theta )}

При ω>0{\displaystyle \omega >0}, R(t){\displaystyle R(t)} опережает I(t){\displaystyle I(t)} на 14{\displaystyle {\begin{matrix}{\frac {1}{4}}\end{matrix}}} периода (=π2{\displaystyle ={\begin{matrix}{\frac {\pi }{2}}\end{matrix}}} рад). Но когда ω<0{\displaystyle \omega <0}, их роли меняются. Так в этом случае возможно отличить отрицательные и положительные частоты: R(t){\displaystyle R(t)} рассматривается как реальная, а I(t){\displaystyle I(t)} как мнимая часть одного и того же колебания. И θ=0{\displaystyle \theta =0}. График показывает отрицательную частоту. Отрицательная частота (уменьшение фазы) может быть представлена вращением вектора комплексной амплитуды по часовой стрелке.

Параметрический график такой зависимости мнимой части от действительной выглядит как окружность. Добавление измерения времени представляет движение точки по такой окружности в виде спирали.

Комплексная синусоида.

Комплексная функция: cos⁡(ωt)+j⋅sin⁡(ωt){\displaystyle \cos(\omega t)+j\cdot \sin(\omega t)} облегчает многие виды операций с использованием cos⁡(ωt){\displaystyle \cos(\omega t)}, в значительной степени благодаря упрощению Эйлера:

ejωt=cos⁡(ωt)+j⋅sin⁡(ωt){\displaystyle e^{j\omega t}=\cos(\omega t)+j\cdot \sin(\omega t)}

Эта часто употребимая запись называются комплексной синусоидой, и она сохраняет различие между положительными и отрицательными ω{\displaystyle \omega }.

Преобразование Фурье от ejωt{\displaystyle e^{j\omega t}} — ненулевой отклик на единственной частоте ω{\displaystyle \omega }.

Алиасинг дискретизированных синусоид (косинусоид).

При дискретизации комплексной синусоиды с постоянным интервалом, её частота становится неотличима от некоторых других частот, в том числе от отрицательной (т. н. алиасинг). Частные случаи этого эффекта показаны на рисунке. Красная линия показывает 0 Hz (постоянная величина). Последовательно возрастающие частоты отмечены оранжевым, синим, пурпурным, фиолетовым, черным. Некоторые отсчёты отображают «R» и «I» одной частоты, а другие «I» разных частот, являющихся «алиасами» (ложными именами) друг друга.

Например, в четвертом кадре (пурпурные и зеленые) показано совпадение отсчетов мнимой компоненты дробной частоты +58{\displaystyle {\begin{matrix}{\frac {5}{8}}\end{matrix}}} и отрицательной частоты −38{\displaystyle -{\begin{matrix}{\frac {3}{8}}\end{matrix}}}. Другими словами: ej2π(+58)n=ej2π(−38)n{\displaystyle e^{j2\pi \left(+{\begin{matrix}{\frac {5}{8}}\end{matrix}}\right)n}=e^{j2\pi \left(-{\begin{matrix}{\frac {3}{8}}\end{matrix}}\right)n}} для целых n. Сигналы являются всего лишь мнимыми компонентами:  ej2π(+58)Fst{\displaystyle e^{j2\pi \left(+{\begin{matrix}{\frac {5}{8}}\end{matrix}}\right)F_{s}t}}  и  ej2π(−38)Fst{\displaystyle e^{j2\pi \left(-{\begin{matrix}{\frac {3}{8}}\end{matrix}}\right)F_{s}t}},  где Fs{\displaystyle F_{s}} — частота дискретизации (samples/sec).

Аналогично +78{\displaystyle {\begin{matrix}{\frac {7}{8}}\end{matrix}}} неотличимо от −18{\displaystyle -{\begin{matrix}{\frac {1}{8}}\end{matrix}}}. А 88{\displaystyle {\begin{matrix}{\frac {8}{8}}\end{matrix}}} (последний график) неотличимо от 08{\displaystyle {\begin{matrix}{\frac {0}{8}}\end{matrix}}} (первый график).

Отрицательные частоты как согласованный фильтр для положительных[править | править код]

Строки ДПФ матрицы начинаются с нулевой частоты, убывающей строка за строкой при смещении вниз. Каждая из функций этих строк как согласованный фильтр выявляет растущие положительные частоты в рассматриваемом сигнале. Например, верхняя строка ДПФ-матрицы 8 порядка выявляет постоянную составляющую сигнала, а следующая строка, являющаяся сигналом с дробной частотой −1/8, измеряет величину мощности при +1/8 дробной частоты в исследуемом сигнале.

Отрицательные частоты в радаре Доплера[править | править код]

В радаре Доплера регистрируемая разностная частота от объектов перемещающихся к и от радара отличается знаком.