формула, взаимное влияние, нормы, характеристики

Частота электрического тока выступает одним из параметров качества электроэнергии и основной характеристикой режима энергосистемы. Количественно частота в энергосети равна количеству периодов в секунду. Изменение частоты в сети влияет на функционирование и, соответственно, производительность работы потребителей. Также свое влияние оказывает отклонение частоты на работу всей энергосистемы.

Нормируемые требования к показателям

В РФ требования к качеству работы энергосистемы стандартизированы.

В соответствии с ГОСТ 13109-97 частота в энергосистеме должна непрерывно поддерживаться на уровне f = 50 ± 0,2 Гц, при этом допускается кратковременное отклонение частоты до значения ∆f = 0,4 Гц.

Анализируя зависимость силы тока от частоты, можно сделать вывод, что если подключаемая нагрузка имеет чисто активный характер (к примеру, резистор), то в широком диапазоне сила тока от частоты иметь зависимость не будет. В случае достаточно высоких частот, когда индуктивность и ёмкость подключаемой нагрузки будут характеризоваться сопротивлением, сравнимым с активным, то сила тока будет иметь определенную зависимость от частоты.

Другими словами, при варьировании частоты тока происходит изменение ёмкостного сопротивления, изменение которого, в свою очередь, приводит к изменению тока, протекающего по цепи.

То есть при повышении частоты, снижается ёмкостное сопротивление, и повышается ток, протекающий по цепи.

Математическое выражение зависимости будет иметь следующий вид: I = UCω;

Зависимость при учете активного сопротивления будет определяться следующим выражением: I (ω) = UCω √(R2 • C2 • ω2 + 1).

Влияние частоты тока на электроприборы

Далее рассмотрим влияние частоты электрического тока. Увеличение частоты до сравнительно невысоких величин (1 — 10 тыс. Гц), обычно является следствием исключительно повышения номинальной мощности электроаппаратуры, поскольку таким образом возрастает проводимость газовых промежутков. Для измерения частоты в системе используют частотомеры.

Паровая турбина разрабатываются и создаются таким образом, чтобы при номинальной скорости вращения (частоте) обеспечивалась максимальная выходная мощность на валу. При этом уменьшение номинальной частоты является следствием возникновения потерь на удар пара о лопатки с единовременным повышением момента вращения, а повышение частоты — к снижению момента вращения.

Таким образом, наиболее экономичный режим работы достигается при оптимальной частоте.

Помимо этого, работа на пониженных частотах приводит к ускоренному износу рабочих лопаток и прочих частей и механизмов. Снижение частоты оказывает влияние на расход на собственные нужды станций.

Зависимость частоты и напряжений от баланса мощности

Остановимся прежде всего на основном и общем для рассматриваемых задач вопросе: выясним, от чего зависят величины частоты и напряжений, устанавливающиеся в электроэнергетической системе.

Каждый из приемников энергии, присоединенных к электрической сети, потребляет активную и реактивную мощности, величины которых, как уже отмечалось ранее, определяются величиной напряжения на его зажимах и частотой. Мощность, идущая на питание приемников энергии и покрытие потерь в сети, соединяющей приемники с некоторой узловой точкой системы, в данном режиме нагрузки зависит только от частоты и величины напряжения в данной узловой точке.

Следовательно, нагрузка любой узловой точки однозначно (в области нормальных значений частоты и напряжения) определяется частотой и напряжением в этой точке. Статические характеристики нагрузки в некоторой узловой точке представляют собой, как известно, зависимости активной и реактивной мощностей этой нагрузки от напряжения при заданной частоте. Для различных значений частоты может быть построено семейство подобных характеристик (рис. 2).

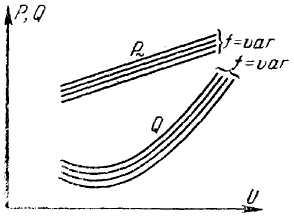
Рис. 2. Зависимости активной и реактивной мощности от напряжения

Обеспечить в данной узловой точке некоторые заданные значения частоты и напряжения можно, только передавая к ней из системы совершенно определенные величины активной и реактивной мощностей. Эти величины при заданных частоте и напряжении можно определить по соответствующим статическим характеристикам нагрузок. Если почему-либо из внешней сети в узловую точку будет поступать недостаточная активная или реактивная мощность, то заданные значения частоты и напряжения не могут установиться в этой узловой точке: параметры фактического режима будут иными. Рассмотрим несколько детальнее этот вопрос.

Пусть заданные семейства статических характеристик выражаются в неявной форме следующими зависимостями:

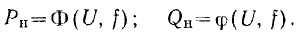
Величины активной и реактивной мощностей, притекающих к данной узловой точке системы, зависят как от величины

U и фазы  напряжения в этой узловой точке, так и от величин и фаз напряжений в смежных узловых точках и сопротивлений, соединяющих участки сети.

Допустим сначала для простоты, что напряжения у ближайших узловых точек неизменны по величине и фазе и имеют одинаковую частоту f. Тогда в данной узловой точке установится совершенно определенное напряжение, величина и фаза которого определяются из условия баланса активных и реактивных мощностей: суммарные потоки активной и реактивной мощностей в данную узловую точку (Р_г и Q_г) должны быть равны соответственно активной и реактивной мощностям нагрузки в данной узловой точке (

Р_н и Q_н). При заданной частоте последние будут только функциями напряжения. Тогда

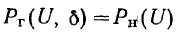
и

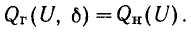
Эти два уравнения с двумя неизвестными и позволяют определить U и .

Покажем, как графически решается эта задача. Совместим на одной диаграмме (рис. 3) характеристику P_Н = Ф₁(U), соответствующую заданному значению

f, и семейство характеристик P_г=₁(U, ), соответствующих тому же значению f, но при разных значениях . Так как P_Г = P_Н, то из этой диаграммы по точкам пересечения может быть определена зависимость  = Ф(U), соответствующая балансу активных мощностей в узловой точке. Далее аналогичным образом совмещаем на одной диаграмме характеристику Q_H = Ф₂(U) и семейство характеристик Q_Г = ₂(U, ) для различных  (рис. 4) и заданного f. При помощи найденной зависимости  = Ф(U) на каждой из характеристик Q_Г  = ₂(U, ) получим точку, находящуюся на характеристике Q_Г = (U). Соединив эти точки, получим всю характеристику Q_Г = (U), соответствующую балансу активных мощностей. Тогда точка пересечения характеристик Q_H = Ф(U) и Q_Г = (U) определяет фактическое напряжение U_Н (рис. 4).

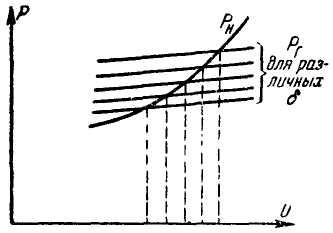
Рис. 3. Определение зависимости угла сдвига (фазы) от величины напряжения

Все наши предыдущие рассуждения относились к случаю неизменности по величине и фазе напряжений в смежных узловых точках и частоты в системе. В действительности такой неизменности нет и напряжения во всех узловых точках могут изменяться по величине и фазе; может также изменяться и частота системы.

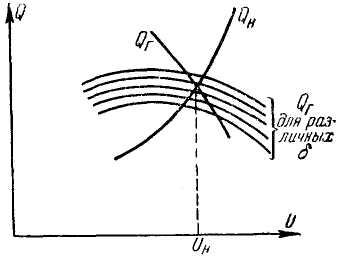
Рис. 4. Построение характеристики зависимости Q от U

Однако в системе можно найти такие узловые точки, в которых поддерживается неизменное по величине и фазе или только по величине напряжение или из которых в сеть передается определенная активная мощность.

При определенном впуске энергоносителя и нормальных значениях параметров режима первичный двигатель развивает мощность, зависящую только от частоты сети, и, следовательно, электромагнитная мощность генератора в этих условиях зависит только от частоты:

P_г=Ф(U).

При постоянстве тока возбуждения генератора неизменной является величина э.д.с. генератора E_d, а при наличии регуляторов возбуждения неизменной или почти неизменной будет величина напряжения на его выводах.

В системе должен быть баланс активных и реактивных мощностей: сумма активных и реактивных мощностей всех генераторов должна равняться сумме активных и реактивных мощностей нагрузок всех узловых точек и потерь активной и реактивной мощностей во всех элементах сетей. Следовательно, частота во всей системе, а также величина и фаза напряжения в каждой из узловых точек установятся как раз такими, которые требуются по условию баланса мощностей.

Пусть в системе установился некоторый режим. Изменим впуск энергоносителя в первичный двигатель одного из генераторов. Угол сдвига ротора этого генератора также изменится. Во всей системе произойдет изменение частоты, а также изменение величин и фаз напряжений во всех узловых точках. Эти изменения будут происходить во времени до тех пор, пока не установится новый режим баланса мощностей в системе. Процесс этот является далеко не таким простым, как можно было бы предполагать. В самом деле, например, уменьшение впуска энергоносителя вызовет уменьшение угла сдвига ротора данного генератора относительно других, активные нагрузки других генераторов возрастут. Появится небаланс на валах каждого из этих генераторов, и они начнут тормозиться. В связи с этим генератор, у первичного двигателя которого уменьшился впуск энергоносителя, также должен начать тормозиться, так как при уменьшении углов сдвига роторов остальных генераторов он должен принять добавочную нагрузку. Торможение всех генераторов будет приводить к снижению общей частоты в системе. По мере ее снижения будут уменьшаться активные мощности нагрузок узловых точек в соответствии с их частотными статическими характеристиками и увеличиваться мощности всех других генераторов в соответствии со статическими характеристиками регуляторов скорости первичных двигателей

.

Оба эти фактора приведут к тому, что при достаточно большом снижении частоты вновь наступит баланс на валу каждого из генераторов; мощности, развиваемые первичными двигателями, будут балансироваться с мощностями нагрузки

генераторов. Дальнейшее снижение частоты прекратится. Необходимо учесть, что снижение частоты вызывает изменение Э.Д.С. всех генераторов, реактивных сопротивлений всех ветвей системы, а, следовательно, и всех напряжений в сети, что в свою очередь приведет к изменению активных и реактивных нагрузок всех узловых точек в соответствии с их статическими характеристиками по напряжению и частоте. Таким образом, процесс оказывается достаточно сложным.

Рассмотрим другой случай. Пусть уставка регулятора возбуждения на одном из крупных генераторов системы будет снижена. Тогда уменьшится выпуск реактивной мощности от данного генератора, что приведет к снижению напряжения по крайней мере в близлежащем районе электрической сети. Снижение напряжения в свою очередь вызовет уменьшение активных и реактивных нагрузок всех узловых точек в соответствии с их статическими характеристиками по напряжению. Появится небаланс на валу каждого из генераторов; углы сдвига их роторов, а, следовательно, и скорости их вращения будут расти. Это приведет к повышению частоты, так как генераторы, особенно близлежащие, разгрузятся. Частота в системе будет расти, пока не наступит новый баланс, обусловленный ростом активных нагрузок системы. Рост частоты в свою очередь повлияет на увеличение напряжений.

Такова сложная взаимосвязь изменений частоты, напряжения и активных и реактивных мощностей в системе. Однако для решения практических вопросов можно упростить задачу путем некоторой идеализации.

Так, отвлекаясь от изменений напряжений и реактивных мощностей, можно считать, что изменение баланса активных мощностей в системе определенным образом сказывается только на изменении частоты.

Действительно, рост активной нагрузки потребителей или снижение активной мощности генераторов в первую очередь вызывает определенное для данного режима снижение частоты в системе. Практически именно это является наиболее существенным. Менее существенным является то, что это изменение частоты будет в некоторой степени различным в зависимости от того, в какой узловой точке выросла активная нагрузка или у какого именно генератора снизилась активная мощность. Это различие обусловлено влиянием других факторов (напряжений, реактивных мощностей) и не столь велико. Снижение частоты, обусловленное возникновением дефицита активной мощности, обязательно приведет к восстановлению баланса, так как при этом в связи со снижением частоты и напряжений активная нагрузка уменьшается. В то же время регуляторы скорости первичных двигателей и частоты увеличивают впуск энергоносителя, и активная мощность генераторов растет.

Количественное соотношение, т.е. зависимость относительного изменения частоты от относительного небаланса активной мощности, не является неизменным и в зависимости от режима работы системы может колебаться в довольно широких пределах.

Как зависит мощность от частоты тока. Зависимость частоты и напряжений от баланса мощности

В настоящее время все производство, практически все распределение и большая часть потребления электроэнергии в энергосистемах выполняются на переменном токе. Поэтому параметры переменного тока — частота, величина и форма кривой напряжения — приобрели значение унифицированных параметров, в соответствии с которыми конструируются все источники, средства передачи и приемники электрической энергии. В особенности это относится к частоте. Практически сохранилось лишь два стандартных значения частоты — 50 Гц в странах Европы, в том числе в России, и 60 Гц в США и Канаде.

В процессе работы энергосистемы все параметры переменного тока могут изменяться. Чем ближе они поддерживаются к номинальным, т.е. расчетным для оборудования, значениям, тем ближе режим к оптимальному. Таким образом, частота приобретает значение показателя, характеризующего качество продукции энергетической промышленности, качества электроэнергии. Согласно ГОСТ 13109—97 на качество электрической энергии частота в энергосистемах России в нормальном режиме должна поддерживаться с точностью ± 0,2 Гц (95 % времени суток). Допускается кратковременная (не более 72 мин в сутки) работа энергосистем с отклонением частоты в пределах ±0,4 Гц.

Столь жесткие требования объясняются тем, что частота переменного тока непосредственно связана с частотой вращения агрегатов, преобразующих механическую энергию в электрическую, т.е. генераторов, и агрегатов, преобразующих электрическую энергию в механическую, т.е. двигателей. Изменение же частоты вращения, даже небольшое, существенно влияет на режим работы вращающихся механизмов. Снижение частоты приводит к падению производительности насосов и других механизмов.

Примером механизма, предъявляющего весьма жесткие требования к точности поддержания частоты вращения, является паровая турбина. Турбостроительные заводы требуют, чтобы частота не оставалась длительно ниже 49,5 Гц и выше 50,5 Гц, иначе возможно повреждение лопаток турбин. Таким образом, наиболее серьезные требования к точности регулирования частоты предъявляются самими электростанциями.

Частота является не только показателем качества электроэнергии, но и важнейшим параметром режима энергосистемы. Непрерывность производства электроэнергии, отсутствие возможности запасать энергию и непрерывное изменение потребления требуют столь же непрерывного контроля за соответствием производства и потребления. Параметром, характеризующим это соответствие, и является частота.

Частота в энергосистеме определяется общим балансом генерируемой и потребляемой активной мощности. Если баланс соблюдается, то частота неизменна. При нарушении баланса мощности, т.е. при появлении небаланса мощности, возникает переходный процесс изменения частоты. По скорости и направлению изменения частоты можно судить о величине и знаке возникшего в энергосистеме небаланса активной мощности. Если частота в энергосистеме уменьшается, то для восстановления нормальной

Регулирование скорости асинхронного электродвигателя путем изменения частоты питающей сети

Наиболее экономичным способом регулирования скорости вращения асинхронных электрических машин с короткозамкнутым ротором является изменение частоты питающего напряжения последних. При изменении частоты также будут меняться и параметры асинхронной машины. Для обеспечения необходимых значений пускового и критического моментов, а также коэффициента мощности и коэффициента полезного действия КПД, необходимо с изменением частоты соответствующим образом изменять и напряжение, подводимое к зажимам электродвигателя.

Общие закономерности регулирования скорости асинхронных машин путем изменения частоты питающей сети были исследованы академиком М.П. Костенко еще в 1925 году.

Основное соотношение, связывающее изменение частоты и напряжения, в зависимости от характера статического момента механизма может быть выведено из общих соотношений, представляемых эквивалентной схемой замещения. При постоянной частоте питающей сети критический момент асинхронного электродвигателя будет равен:

Где: m₁ – количество фаз в обмотке статора; r₁ и x₁ – активное и индуктивное сопротивление статорной обмотки; х₂^/ — индуктивное сопротивление роторной обмотки, приведенной к первичной обмотке; f – частота питающей сети.

Если пренебречь активным сопротивлением статорной обмотки, выражение (1) примет вид:

Индуктивные сопротивления x₁  и х₂^/ зависят от частоты питающей сети. Поэтому при переменной частоте предыдущее выражение должно  быть записано как:

Для сохранения неизменной перегрузочной способности машины отношение критических моментов при любых скоростях должно быть равно отношению соответствующих статических моментов:

Где М_с1 и М_с2 – статические моменты, соответствующие скорости электрической машины при частотах f₁ и f₂; U₁ и U₂ – напряжения, подводимые к двигателю при тех же частотах.

Полученная формула (4) показывает, что оптимальный закон изменения напряжения при частотном регулировании определяется характером изменения статического момента в зависимости от частоты. В таблице ниже сопоставлены значения моментов, мощностей и напряжений при различных характерах зависимости статического момента от скорости.

Анализ, проведенный академиком М.П. Костенко на базе упрощенной круговой диаграммы, показал, что при соблюдении  условия (4) будет иметь место постоянство cosφ,  а КПД электрической машины будет функцией частоты и не зависит от нагрузки. Для всех видов зависимости момента от скорости: М_с ≡ 1/f, М_с = const, M_c ≡ f и M_c ≡ f². КПД двигателя при каждой заданной скорости будет примерно одинаков.

Для выявления поведения асинхронного электродвигателя при регулировании частоты питающего напряжения в случаях различной зависимости статического момента от скорости необходимо установить характер изменения пускового и критического моментов.

В основу рассмотрения легла эквивалентная схема асинхронной машины с намагничивающим контуром, вынесенным на зажимы машины. Влияние насыщения не учитывается. За исходные данные принимаем параметры машины при номинальном напряжении и частоте f_ном = 50 Гц. В качестве независимой переменной (определяющего параметра) удобно принять частоту, выраженную в относительных единицах:

Напряжение, приложенное к зажимам электрической машины, будет функцией частоты и одновременно, будет зависеть от характера изменения статического момента, и в общем случае будет иметь вид:

Показатель степени α зависит от желаемого характера М_дв и функции скорости. При построении механической характеристики асинхронной машины при любой f можно использовать общее выражение:

Индуктивное сопротивление обмоток можно выразить при f = 50 Гц, а именно:

Где х_1н и х_2н^/ — индуктивные сопротивления статора и ротора, приведенные к обмотке статора, при f = 50 Гц.

После введения относительных единиц выражение примет вид:

Где φ – частота в относительных единицах; α – коэффициент, определяемый характером зависимости момента от скорости электрической машины.

В (8) при переходе к относительным единицам U² превращается в U²_нφ^2α, однако за счет f, входящей в выражение синхронной скорости  ω₀ = 2πf_нφ, показатель степени у

φ становится 2α — 1.

Величина критического момента станет равна:

В случае пренебрежения активным сопротивлением статорной обмотки:

Выражение  (10) может быть представлено как:

Где М_кн – критический момент электрической машины при номинальном напряжении и f.

Критическое скольжение при переменной частоте:

В ряде случаев удобно воспользоваться выражением механической характеристики, содержащим значение критического момента:

Если пренебречь сопротивлением активным обмотки статора уравнение механической характеристики примет вид:

Подставляя в упрощенное выражение механической характеристики значения М_к и s_к без учета r₁ получим расчетную формулу:

На рисунке ниже приведены механические характеристики асинхронного электродвигателя для трех различных частот в относительных единицах для случая изменения f по закону (U/f) = const или α = 1.

Сравнение характеристик показывает, что критическое скольжение возрастает с понижением частоты. Это связано с изменением соотношения активного и индуктивного сопротивления. При уменьшении f критический момент в двигательном режиме уменьшается. Выражение для пускового момента равно:

Пусковой момент при небольших изменениях частоты несколько увеличивается, а затем, при дальнейшем уменьшении f, достигает максимума, а дальше падает. Понижение М, наблюдаемое при низких f, вызывается относительным увеличением активного сопротивления, а также уменьшением магнитного потока, влияние которого не учитывают приведенные выше формулы. Уменьшение потока обуславливается падением напряжения в обмотке статора и является функцией нагрузки электродвигателя. Уменьшение магнитного потока может быть устранено с помощью увеличения отношения U/f при малых значениях частоты. Увеличение отношения U/f в размере, необходимом для поддержания номинального значения магнитного потока при нагрузке, приведет к тому, что при малых нагрузках машина окажется перевозбужденной и, следовательно, возрастет намагничивающий ток.

Механическая характеристика асинхронного двигателя для случая α = 1/2 , то есть при изменении напряжения по закону  показаны ниже:

Регулирование скорости асинхронных короткозамкнутых машин в настоящее время применяется для самого широкого спектра рабочих механизмов. В высоко оборотистых электроприводах, где скорость вращения вала равна или превышает 3000 об/мин, применение коллекторных электромашин крайне нежелательно. Здесь больше подходит частотно-регулируемый асинхронный электропривод. Часто данный способ регулирования применяется при необходимости одновременного изменения скорости по одному закону нескольких рабочих органов машины, приводимых в движение отдельными электродвигателями. Примерами таких установок могут послужить электроприводы центрифуг вискозной промышленности, применяемые для получения вискозного волокна,  рогулечных прядильных машин текстильной промышленности, роликовых транспортеров прокатных цехов металлургических заводов, служащих для транспортировки как горячего, так и холодного металла в процессе прокатки. Во всех перечисленных случаях каждый отдельный элемент рабочей машины (отдельная центрифуга, рогулька прядильной машины, ролик транспортера и так далее) приводятся в движение отдельным асинхронным двигателем мощностью от нескольких десятков ватт, до киловатт, и целая группа подобных двигателей может питаться от одного преобразователя с регулируемой частотой.

В качестве источника регулируемых асинхронных электродвигателей могут быть использованы следующие типы преобразователей частоты:

1. Синхронный генератор, вращающийся с переменной частотой.
2. Асинхронный преобразователь частоты.
3. Преобразователь типа Леблана.
4. Коллекторные генераторы переменного тока с возбуждением со статора.
5. Полупроводниковые преобразователи частоты.

В таблице ниже представлены сопоставления технических показателей каждого типа перечисленных преобразователей:

Таблица выше показывает, что все системы машинных преобразователей, за исключением преобразователя Леблана, состоят из значительного количества электрических машин и обладают невысоким общим коэффициентом полезного действия и высокой первоначальной стоимостью. Преобразователь частоты Леблана свободен от указанных недостатков, однако, несовершенство коммутации ограничило возможности его широкого использования в недалеком прошлом. Современная электроника вывела на первое место полупроводниковые преобразователи частоты равных которым пока нет, и которые используются практически во всех частотно-регулируемых электроприводах.

Существует ли зависимость напряжения от частоты?

Казалось бы, раскрыть зависимость напряжения от частоты просто. Стоит только обратиться с соответствующим запросом ко всезнающим поисковым системам и… убедиться, что ответа на этот вопрос попросту нет. Что же предпринять? Давайте разбираться вместе в этом непростом вопросе.

Напряжение или разность потенциалов?

Надо заметить, что напряжение и разность потенциалов — это одно и то же. По сути, это сила, которая способна заставить электрические заряды двигаться потоком. Не имеет значения, куда будет направлено это движение.

Разность потенциалов — просто другое выражение для напряжения. Оно нагляднее и, может быть, понятнее, но сути дела не меняет. Поэтому главный вопрос состоит в том, откуда берется напряжение, и от чего оно зависит.

В том, что касается домашней сети 220 Вольт, ответ простой. На гидростанции поток воды вращает ротор генератора. Энергия вращения трансформируется в силу напряжения. Атомная электростанция вначале превращает воду в пар. Он и крутит турбину. В бензоэлектростанции ротор вращает сила сгорающего бензина. Есть и другие источники, но суть всегда одна и та же: энергия превращается в напряжение.

Самое время задаться вопросом о зависимости напряжения от частоты. Но мы еще не знаем, откуда берется частота.

Что является источником частоты

Тот же самый генератор. Частота его вращения превращается в одноименное свойство напряжения. Вращайте генератор быстрее — частота будет больше. И наоборот.

Хвост не может «вилять» собакой. По той же причине частота не может изменить напряжение. Следовательно, выражение «зависимость напряжения от частоты тока» не имеет смысла?

Чтобы найти ответ, надо правильно сформулировать вопрос. Есть такая присказка про глупца и 10 ученых мужей. Он задавал неправильные вопросы, а они не могли ответить.

Если назвать напряжение другим определением, все встанет на свои места. Оно применяется для цепей, состоящих из множества разных сопротивлений. «Падение напряжения». Оба выражения часто считаются синонимами, что почти всегда неправильно. Потому что падение напряжения действительно может зависеть от частоты.

С чего бы напряжению падать?

Да просто потому, что не может не падать. Итак. Если на одном полюсе источника потенциал равен 220 Вольт, а на другом — ноль, то это падение могло произойти только в цепи. Закон Ома говорит о том, что, если в сети имеется одно сопротивление, то все напряжение на нем и упадет. Если два и больше — каждое падение будет пропорционально его величине, а их сумма равна исходной разности потенциалов.

Ну и что? Где здесь указание на зависимость напряжения от частоты тока? Пока что все зависит от величины сопротивления. Вот, если бы найти такой резистор, который меняет свои параметры при изменении частоты! Тогда и падение напряжения на нем менялось бы автоматически.

Есть такие резисторы

Их еще называют реактивными, в отличие от активных собратьев. На что же они реагируют, изменяя свою величину? На частоту! Существует 2 вида реактивных сопротивлений:

• индуктивное;
• емкостное.

Каждый вид связан со своим полем. Индуктивное — с магнитным, емкостное — с электрическим. На практике они представлены в первую очередь, соленоидами.

Они представлены на фото выше. И конденсаторами (ниже).

Их можно считать антиподами, потому что реакция на изменение частоты прямопротивоположная. Индуктивное сопротивление растет с частотой. Емкостное, наоборот, падает.

Теперь, учитывая особенности реактивных сопротивлений, в соответствии с законом Ома, можно утверждать, что зависимость напряжения от частоты переменного тока существует. Она может быть рассчитана с учетом величин реактивных сопротивлений в цепи. Только для ясности надо помнить, что речь идет именно о падении напряжения на элементе цепи.

И все-таки она существует!

Вопросительный знак в заголовке статьи превратился в восклицательный. «Яндекс» реабилитирован. Осталось только привести формулы зависимости напряжения от частоты для разных видов реактивных сопротивлений.

Емкостное: XC = 1/(w · C). Здесь w — угловая частота, C — емкость конденсатора.

Индуктивное: XL = w · L, где w — то же, что и в предыдущей формуле, L — индуктивность.

Как видно, частота влияет на величину сопротивления, изменяя его, следовательно, изменяет и падение напряжения. Если в сети имеется активное сопротивление R, емкостное XC и индуктивное XL, то сумма падений напряжений на каждом элементе будет равна разности потенциалов источника: U = U_r + U_xc+ U_xl.

Поддержание нормальных значений частоты и напряжений в системе

Для поддержания нормальной частоты в системе в первую очередь должен быть обеспечен соответствующий этой частоте баланс активных мощностей, а следовательно, при росте активных нагрузок прежде всего должна соответственно увеличиваться активная мощность генераторов.

Возникающее при дефиците реактивных мощностей снижение напряжений также влияет на величину активных нагрузок в системе, но при обычном преобладании в составе нагрузки электродвигателей это обстоятельство является второстепенным и поддержание частоты при помощи регулирования напряжений, даже если бы оно было допустимо с точки зрения пределов изменений величины напряжений, возможно лишь в очень узком диапазоне.

Аналогично этому рост реактивной нагрузки потребителей или снижение реактивной мощности генераторов в первую очередь вызывает снижение напряжений во всех узловых точках системы. Однако здесь имеется существенное отличие от предыдущего: если частота изменяется во всей системе одинаково, то изменение напряжений существенно зависит от электрической удаленности данного места от источника изменения баланса по реактивной мощности. Снижение напряжений, вызванное изменением баланса по реактивной мощности, приведет к уменьшению реактивной нагрузки в близлежащих узловых точках системы и, кроме того, в большинстве случаев к росту реактивных мощностей генераторов. Особенно интенсивно растет генерация реактивной мощности в случае снижения напряжения в сети благодаря наличию у машин автоматических регуляторов возбуждения.

Таким образом, для поддержания нормальных напряжений в системе в первую очередь должен быть обеспечен соответствующий баланс реактивных мощностей. Возникающее при дефиците активных мощностей снижение частоты влияет на величину реактивных мощностей в системе, что в данном случае оказывается существенным, и обеспечить поддержание нормальных напряжений в системах при дефиците активной мощности и сниженной частоте не всегда удается.

Поскольку напряжения в различных точках системы различны, необходимо не только обеспечить баланс реактивных мощностей в системе, но и распределить в ней источники реактивной мощности так, чтобы напряжения во всех ее узловых точках не выходили из зоны допустимых значений. Произвольное распределение реактивных мощностей может привести к большим значениям потоков реактивной мощности на отдельных участках сети и, как следствие, к большим потерям напряжения и невозможности поддержания допустимых напряжений в отдельных пунктах системы. Следовательно, нужно стремиться устанавливать местные балансы реактивной мощности в отдельных районах сети, по возможности не допуская передачи значительной реактивной мощности, особенно через длинные линии.

Этим регулирование напряжения отличается от регулирования частоты. Произвольное распределение активных нагрузок не мешает регулированию частоты, если не учитывать изменения потерь активной мощности и если при этом не превышается пропускная способность электропередач. Однако распределение активных нагрузок в известной мере влияет на величину напряжений в отдельных узловых точках, особенно в сети с большими значениями отношений r/x.

Условия обеспечения надлежащих значений частоты и напряжений в сетях электроэнергетической системы сводятся к следующему:

1. Располагаемая активная мощность станций должна быть достаточной для того, чтобы покрыть всю активную нагрузку системы и потери активной мощности в сетях при нормальных напряжениях и частоте.

2. Располагаемая реактивная мощность генераторов и синхронных компенсаторов должна быть достаточной для того, чтобы покрыть всю реактивную нагрузку системы и потери реактивной мощности в сетях при нормальных напряжениях и частоте.

3. Распределение располагаемой реактивной мощности генераторов и синхронных компенсаторов в системе должно быть таким, чтобы в каждом районе, отделенном от других районов относительно длинными линиями, реактивная нагрузка всех потребителей вместе с потерями реактивной мощности в сетях в основном могла быть покрыта местными генераторами и компенсаторами и уравнительные потоки реактивной мощности между районами были небольшими и не приводили к значительной потере напряжений в сетях.

Невыполнение первого условия, т.е. появление дефицита (недостатка) активной мощности, приводит к невозможности поддержания нормальной частоты; невыполнение второго — к невозможности поддержания среднего уровня напряжений в сетях близ нормального значения. Наконец, невыполнение третьего условия, т.е. появление местных недостатков реактивной мощности в отдельных районах приводит к невозможности поддержания надлежащего уровня напряжений в этих районах.

Недостаток активной мощности в системе снижает не только частоту, но (при отсутствии надлежащего резерва реактивной мощности) также и напряжения, что частично уменьшает дефицит активной мощности.

Недостаток реактивной мощности не только приводит к снижению напряжений, но и увеличивает резерв активной мощности в системе за счет снижения активной мощности потребителей, что частично уменьшает недостаток реактивной мощности.

Располагая резервом активной мощности, можно несколько смягчить недостаток реактивной мощности и в очень узких пределах повысить слишком низкое напряжение, повышая для этой цели частоту в сети, что приводит к росту реактивной мощности генераторов и снижению реактивной мощности потребителей.

Имея повышенный уровень напряжений в системе, можно несколько снизить дефицит активной мощности в системе и в очень узких пределах повысить сниженную частоту, уменьшая уровень напряжений в сетях, что приводит к снижению активных нагрузок.

В заключение остановимся на характеристиках зависимости активной и реактивной мощностей потребителей от частоты и напряжения.

На рис. 5 и 6 представлены характеристики зависимости активной Р и реактивной Q мощностей потребителей от частоты f и напряжения U, построенные Теплоэлектропроектом.

Как видно из рис. 5, зависимость Р от f почти прямолинейна. Наклон этой характеристики зависит от состава нагрузок потребителей и главным образом от доли участия нагрузок в виде синхронных и асинхронных электродвигателей с постоянным моментом на валу и асинхронных электродвигателей с переменным (падающим) моментом на валу (приводы насосов и вентиляторов). Для первой группы потребителей активная мощность нагрузки почти пропорциональна первой степени частоты, т. е. при снижении частоты на 1% активная мощность снижается на 1 %. Для второй группы потребителей снижению частоты на 1 % соответствует снижение активной мощности примерно на 3%. Для других потребителей – освещения, бытовых приборов, дуговых печей – изменение частоты почти не приводит к изменению активной мощности, если при этом поддерживается неизменное напряжение.

Суммарные потери активной мощности в электрических сетях мало изменяются при изменениях частоты.

Для энергосистем в целом на 1 % снижения частоты суммарная активная нагрузка изменяется на величину 1,0 –2,0% в зависимости от состава потребителей.

Рис. 5. Характеристика зависимости активной и реактивной мощности от частоты

Из того же рис. 5 видно, что снижение частоты приводит к росту реактивной мощности потребителей. Этот рост обусловлен главным образом увеличением магнитной индукции в асинхронных двигателях и трансформаторах при снижении частоты и соответствующим значительным (вследствие насыщения) ростом токов их намагничивания. Указанное увеличение их реактивной мощности частично компенсируется снижением потерь реактивной мощности в реактивностях рассеяния линий, трансформаторов и асинхронных электродвигателей, а также ростом зарядной мощности линий электрических сетей. Для энергосистемы в целом на 1% снижения частоты (при неизменных напряжениях) реактивная мощность возрастает примерно на 1 – 1,5%.

Из рис. 6 видно, что зависимость активной мощности потребителей от напряжения почти прямолинейна.

От величины напряжения сильно зависит активная мощность, потребляемая бытовыми приборами, дуговыми печами, а также теряемая в электрических сетях. На 1 % снижения напряжения потребляемая этими нагрузками .активная мощность снижается на 1,6 – 2%. Мощность нагрузки асинхронных двигателей очень мало зависит от изменения напряжения (только за счет небольшого изменения скольжения). Мощность нагрузки синхронных двигателей совсем не зависит от напряжения. Потери в стали трансформатора снижаются при уменьшении напряжения. Для энергосистемы в целом на 1 % снижения напряжения активная мощность снижается на величину от 0,6 % (при малой доле бытовой нагрузки) до 2 % (при большой доле бытовой нагрузки).

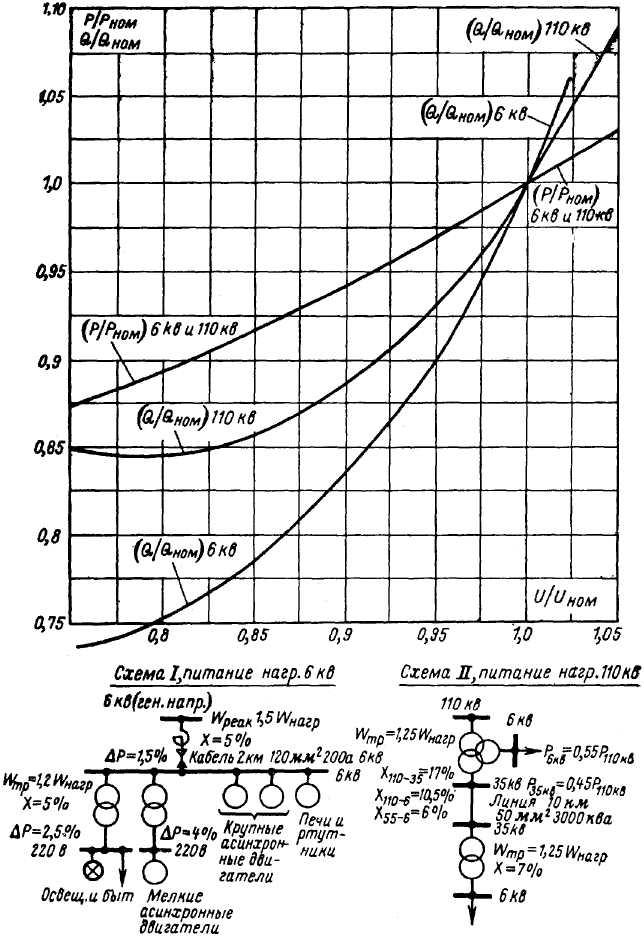
Рис. 6. Характеристика зависимости активной и реактивной мощности от напряжения

Зависимость реактивной нагрузки потребителей от напряжения имеет криволинейный характер по следующим причинам. Реактивная мощность намагничивания асинхронных двигателей и трансформаторов, составляющая значительную долю (60 – 70 %) всей реактивной нагрузки системы, резко уменьшается при снижении напряжения, что обусловливает крутой спад реактивной нагрузки при напряжениях, близких к нормальному значению (до 2 – 3 % на 1 % снижения напряжения). С другой стороны, снижение напряжения приводит к заметному росту реактивной мощности, теряемой в реактивных сопротивлениях рассеяния линий, трансформаторов и асинхронных двигателей (почти на 2 % при снижении напряжения на 1 %). Хотя при нормальном напряжении эта реактивная мощность составляет лишь 30 – 40 % всей нагрузки, но по мере снижения напряжения ее доля участия в суммарной реактивной нагрузке все время возрастает. Кроме того, зарядная мощность линий, частично покрывающая потребность энергосистемы в реактивной мощности, при снижениях напряжения падает по квадратичной зависимости, что также приводит к увеличению реактивной нагрузки энергосистемы. Поэтому при достаточно большом снижении напряжения реактивная нагрузка системы доходит до минимального значения и при дальнейшем снижении напряжения начинает возрастать. Этот минимум (Q _мин) в промышленных энергетических системах имеет место при снижении напряжения до 75 – 85% нормального. Определяющим для характеристики зависимости реактивной нагрузки от напряжения является состав потребителей и в особенности коэффициент загрузки асинхронных двигателей. Чем больше коэффициент загрузки асинхронных двигателей, тем больше доля реактивной нагрузки от полей рассеяния и тем меньше доля реактивной нагрузки от токов намагничивания и, следовательно, тем меньше спад реактивной нагрузки при напряжениях, близких к нормальным, и тем выше напряжение, соответствующее минимуму реактивной нагрузки. Кривые на рис. 6 построены при средней загрузке асинхронных двигателей порядка 75% и при следующем составе потребителей: освещение и быт – 22 %, асинхронная нагрузка – 50%, синхронная нагрузка – 9%, дуговые печи и ртутные выпрямители – 11 % и потери мощности в электрических сетях –8 %

Характерные зависимости Q_HАГ = f(U). Для нагрузок потребителей различных отраслей промышленности приведены в литературе.

Влияние повышения частоты питания на мощность двигателя — Электропривод

Ну, если подходить к вопросам частотного регулирования с точки зрения «как то крутится» то крутиться будет и в диапазоне зменения частоты +/-10% даже будет примерно сохранять свои параметры. Говорить о мощности вообше то бессмысленно, работает крутящий момент, а мощность как раз и есть производная величина, грубо — это момент умноженный на обороты.

Так что мощность может даже рости с увеличением оборотов, вот только нагрузку движок будет тянуть все хуже и хуже

Вот пара примеров:

1. настраиваем ДВС на динамометрическом стенде, естественно, стенд пишет графики момента и мощности. Так вот, малограмотные «дрфтеры-дристеры» видят и понимают только мощность и радуются, как дурачки — график мощности «добежал» аж до 600 л.с. Вот только «странность» на дороге машина нифига не едет. Потому, как эти 600 л.с. были где то в районе 11 т. оборотов, при моменте в пару кг/м.

2. На одном из Московских заводов СМС- стирально-моющих средств в составе технологической линии стояли насосы «Балестро» с частотным регулированием. Один из движков благополучно спалили по разгильдяйству, но разгильдяи ж всегда «умные»! Вот и притулили вместо фирменного движка, специально разработанного для систем с частотным регулированием, первый попавшийся на складе асинхронник аналогичной мощности. Вот только работал и качал пульпу нормально он примерно в диапазоне 45 — 55 гц (примерно в половину производительности линии). Дальше с увеличением частоты обороты почти не росли, мотор грелся как дурной, а в районе 100% производительности насос вообще останавливался. Вылечили просто — приобрели подходящий мотор отечественного производства, предназначенный для частотного регулирования.

Так что можете в меня хоть тапочками, хоть ботинками кидать, но восторгов от частотного регулирования обычного асинхронника я не разделяю.

А на специализированных движках в доке указывается рекомендуемый диапазон частот.

Изменено 26 июня, 2015 пользователем gktuning