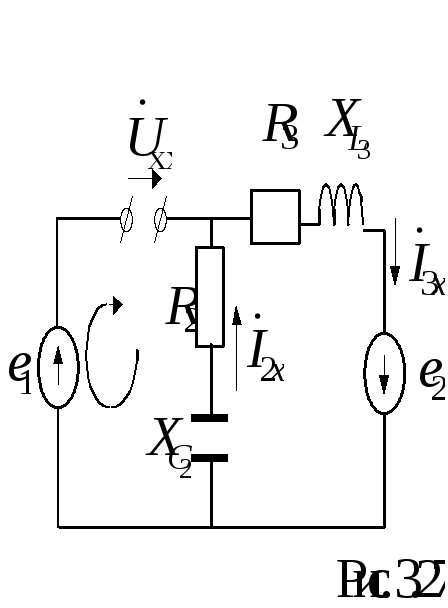
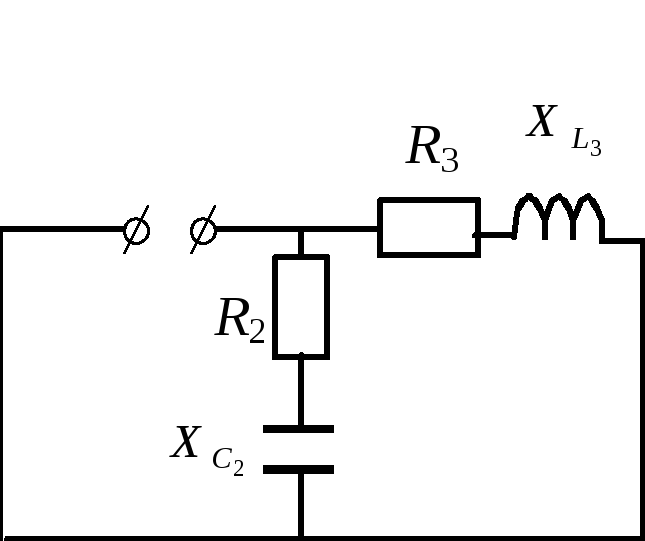
7.3. Законы Ома и Кирхгофа в операторной форме Благодаря линейности преобразования Лапласа, законы Ома и Кирхгофа можно написать для изображений токов и напряжений
Закон
Ома: 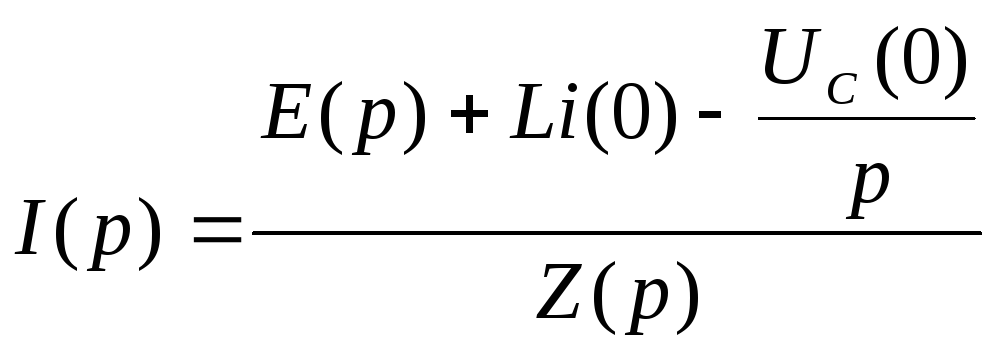 (7.7)
(7.7)
где
Z(p)=R+ZL(p)+ZC(p) — операторное сопротивление цепи;
ZL(p)=pL -операторное сопротивление индуктивности;
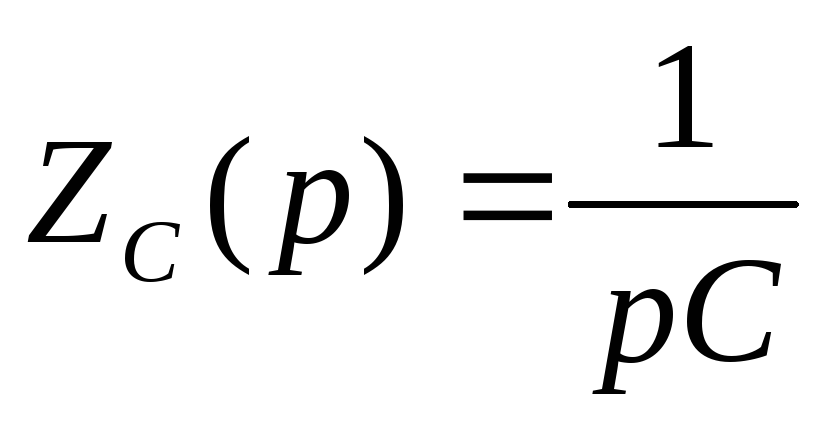 -операторное
сопротивление ёмкости;
-операторное
сопротивление ёмкости;
E(p) -изображение ЭДС;
Li(0) и 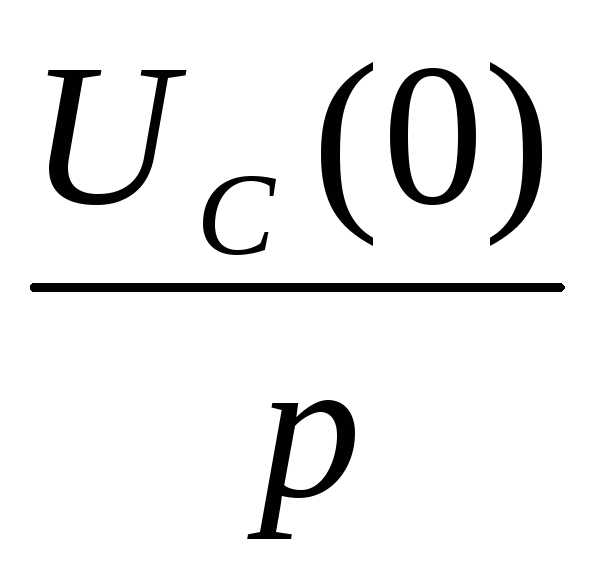 — расчётные напряжения,
характеризующие запасенную энергию в
индуктивности и ёмкости к моменту
коммутации.
— расчётные напряжения,
характеризующие запасенную энергию в
индуктивности и ёмкости к моменту
коммутации.
Первый
закон Кирхгофа: 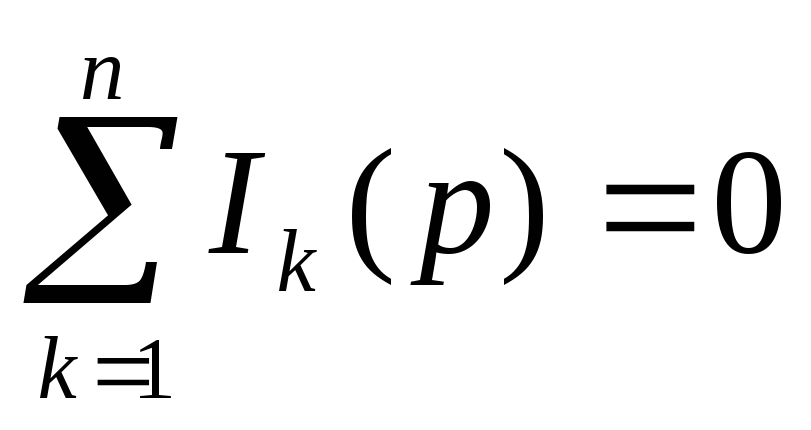 (7.8)
(7.8)
Второй
закон Кирхгофа: 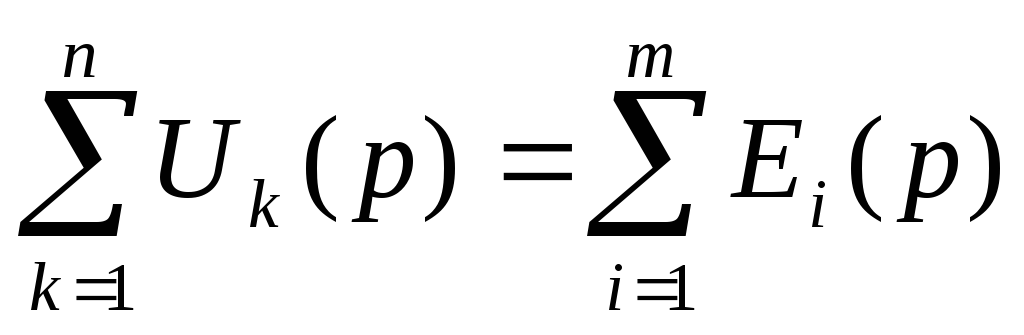 (7.9)
(7.9)
Т.к. для изображений справедливы законы Кирхгофа, то для нахождения изображений токов и напряжений и цепи можно использовать все методы расчёта ЭЦ. При этом удобно пользоваться эквивалентными операторными схемами (рис. 7.1), составленными на основании (7.3-7.6)

Рис. 7.1. Операторные схемы замещения элементов ЭЦ.
7.4. Определение оригинала функции по его изображению
Существуют три способа определения оригинала искомой функции по его изображению:
с помощью обратного преобразования Лапласа;
с помощью таблиц;
по теореме разложения.
Если изображение
F(p) получено
в виде рациональной дроби 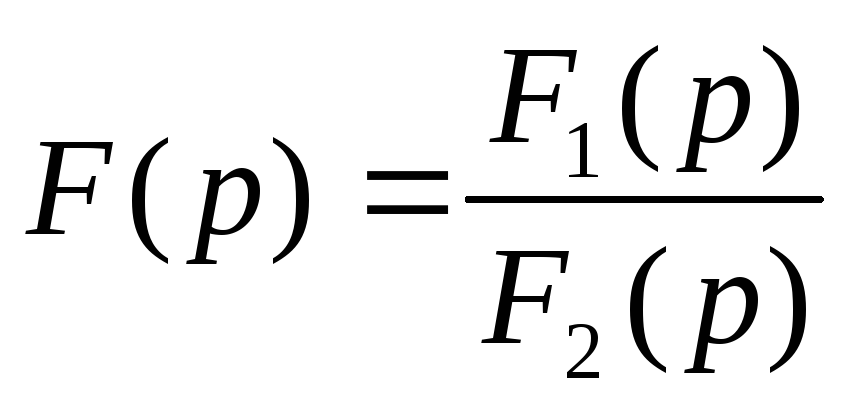 ,
то оригинал определяется по теореме
разложения. В зависимости от вида корней
уравнения F2(p)=0,
существуют следующие виды записи теоремы
разложения:
,
то оригинал определяется по теореме
разложения. В зависимости от вида корней
уравнения F2(p)=0,
существуют следующие виды записи теоремы
разложения:
корни вещественны и различны
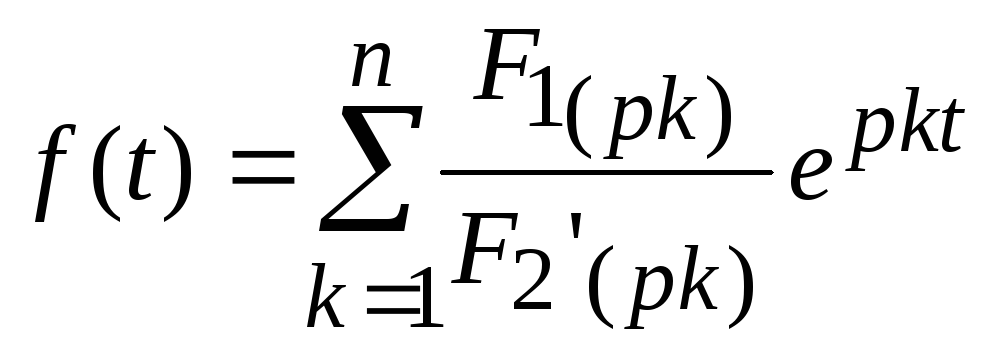 ,
где рк – корни функции
(7.10)
,
где рк – корни функции
(7.10)
F2(p)=0; n -число корней;
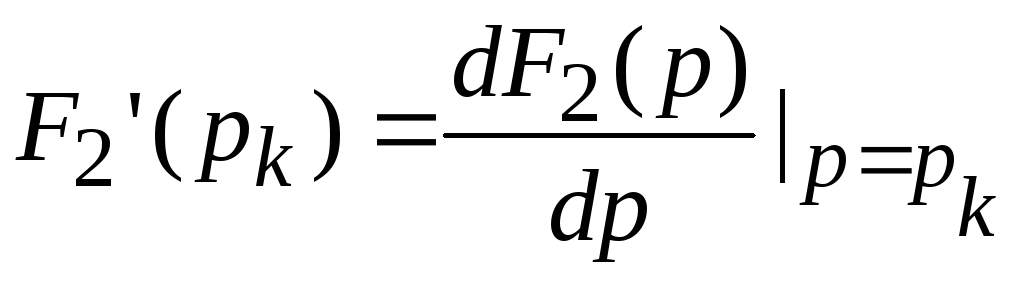 .
.
при наличии нулевого корня
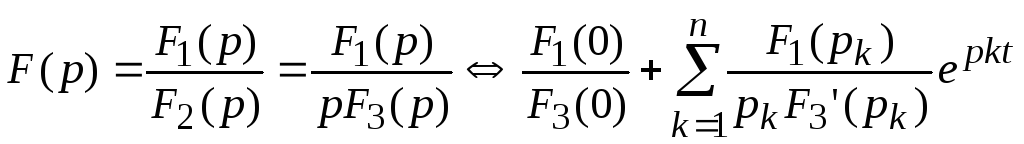 (7.11)
(7.11)
Пример: Определить оригинал функции 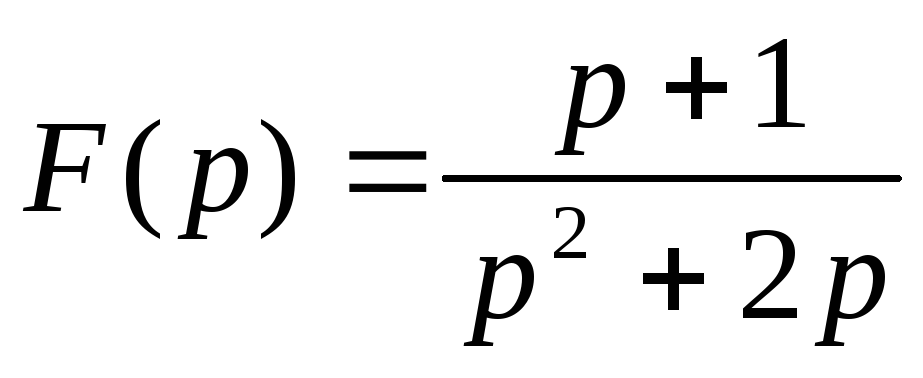
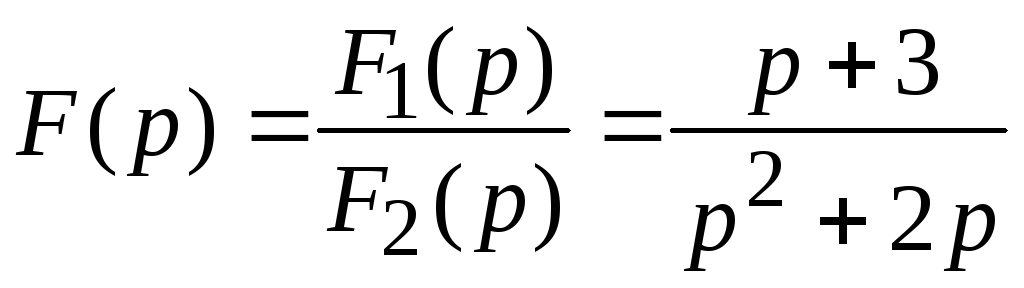 ;
; 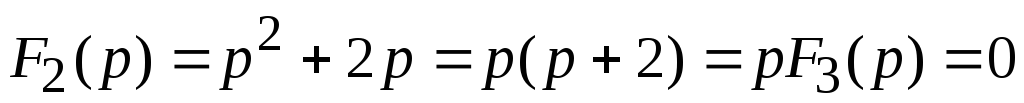
p1= -2; p2=0
F1(0)=3; F3(0)=2; F1(p1)=-2+3=1; F3’(p1)=2
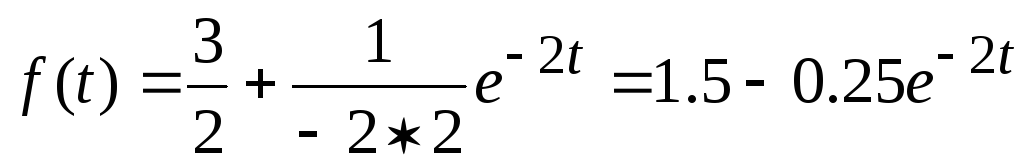 .
.
7.5. Порядок расчёта переходных процессов операторным методом
Расчёт производится в следующем порядке:
Определение независимых начальных условий
Составление эквивалентной операторной схемы цепи после коммутации
С помощью любого из методов расчёта определить изображение искомых величин
По полученному изображению определить оригинал искомой функции
Пример: Определить переходной ток в цепи рис. 7.2а операторным методом.
R1
L
i
R1
i(-0)
R1
I(p)













E
E
E/p







pL








R2
R2

Li(0)
б)
в)
a)
Рис. 7.2.
Независимые начальные условия определяются по схеме рис. 7.2б.
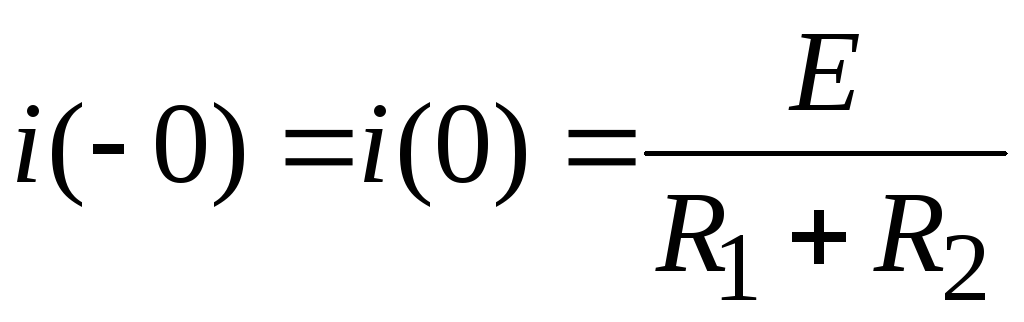 .
.
Эквивалентная операторная схема приведена на рис. 7.2в
По
закону Ома 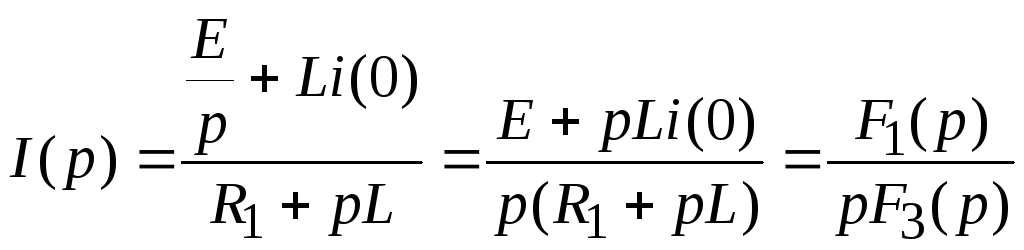
Определим оригинал тока:
1 способ — с помощью таблицы «оригинал-изображение»
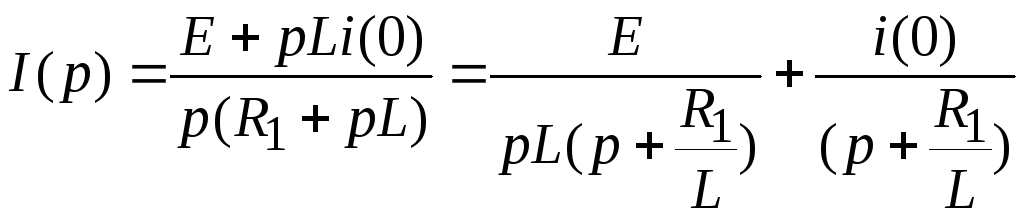
По
таблице 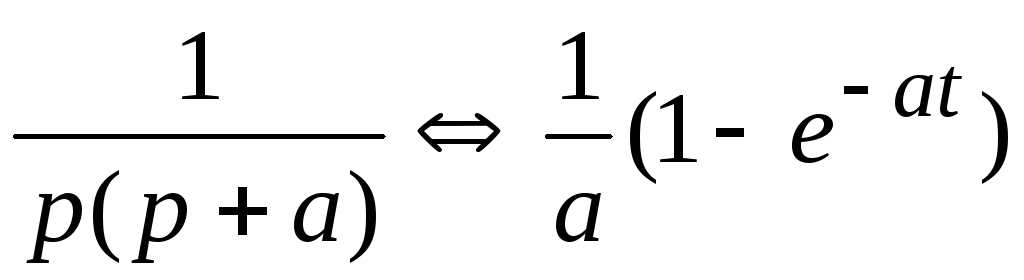

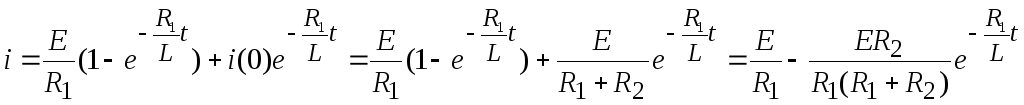
2 способ — по теореме разложения (7.11)
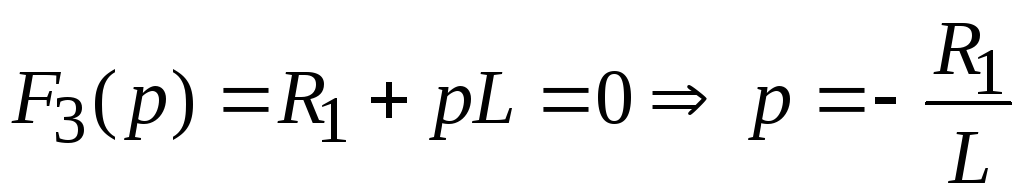 ;
;
F1(0)=E; F3(0)=R1; F3’(p)=L;
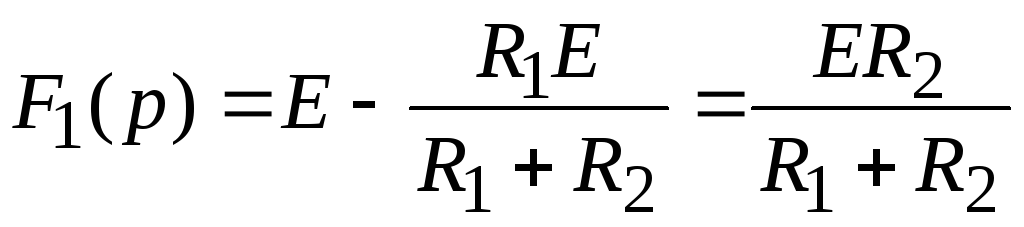 ,
,

7.6. Операторная передаточная функция
Важную роль в методах анализа и синтеза ЭЦ играет операторная передаточная функция H(p), равная отношению изображения реакции цепи и изображению воздействия при нулевых начальных условиях. Различают следующие виды передаточных функций:
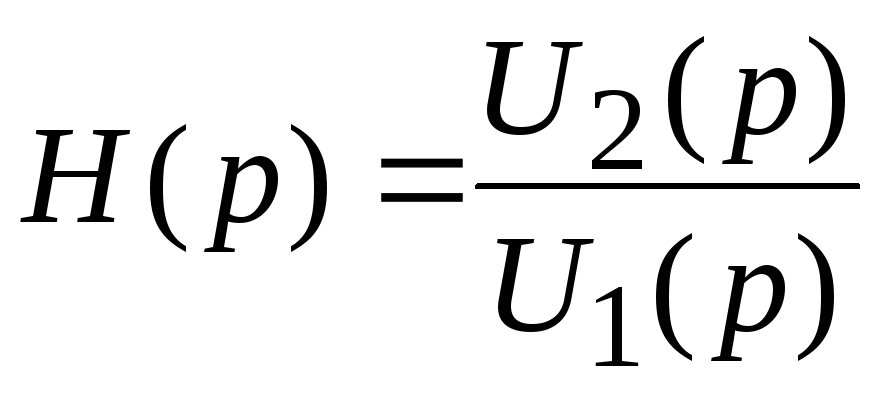 ;
; 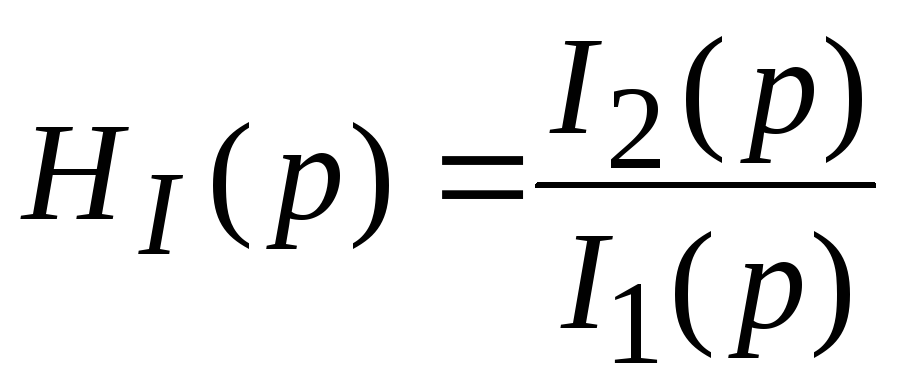 ;
; 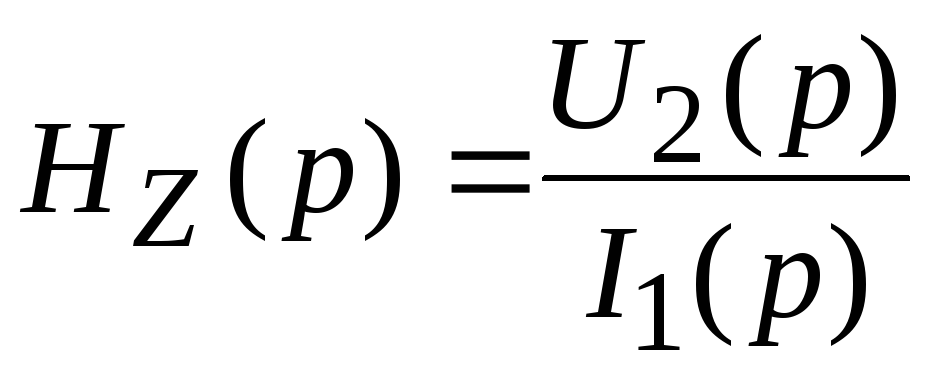 ;
; 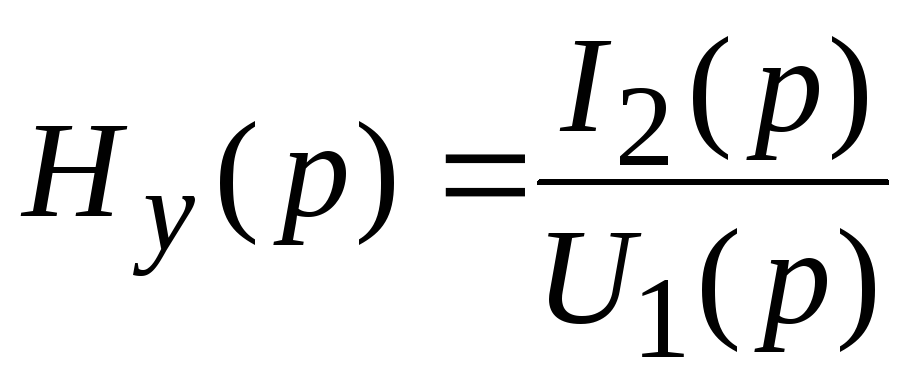 .
.
Операторная передаточная функция представляет собой дробно-рациональную функцию с вещественными коэффициентами
 .
(7.12)
.
(7.12)
Степени полиномов числителя и знаменателя зависят от числа реактивных элементов цепи и её схемы.
Устойчивыми называются ЭЦ, у которых при произвольных начальных условиях свободные колебания стремятся к нулю с неограниченным ростом времени, т.е. переходные процессы будут затухающими.
Цепь будет устойчивой, если все полюсы передаточной функции (корни уравнения N(p)=0) располагаются в левой полуплоскости комплексной переменной р. Они могут быть вещественными или комплексно- сопряженными. Для этого необходимо, чтобы полином N(p) содержал вещественные коэффициенты, т.е. являлся полиномом Гурвица.

Рис. 7.3. Расположение полюсов устойчивой цепи в случае
а) действительных корней; б) комплексно- сопряженных корней.
Зная операторную передаточную функцию, можно найти изображение реакции, а по нему и реакцию цепи на заданное воздействие.
Пример: Определить u2(t) цепи рис. 7.4а
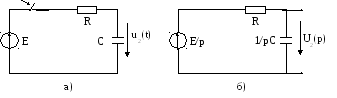
Рис. 7.4. Исходная схема а) и её операторная схема замещения б).
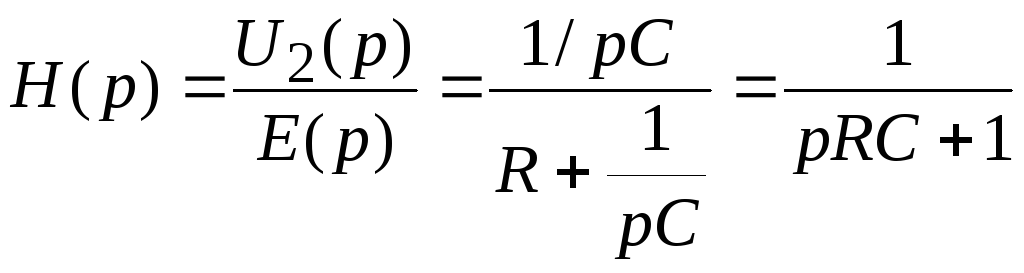 ;
;
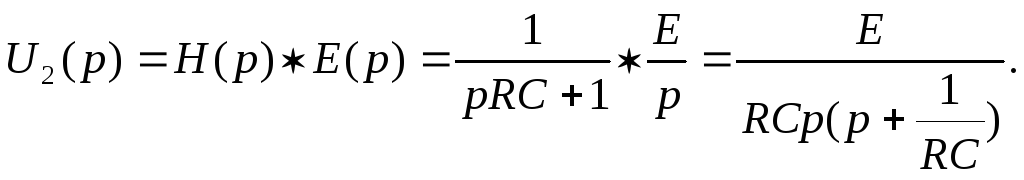
По таблице определим оригинал u2(t)

38) Закон Ома и Кирхгофа в символической форме
По
I
закону Кирхгофа алгебраическая сумма
мгновенных значений токов, сходящихся
в любом узле электрической цепи, равна
нулю, т.е.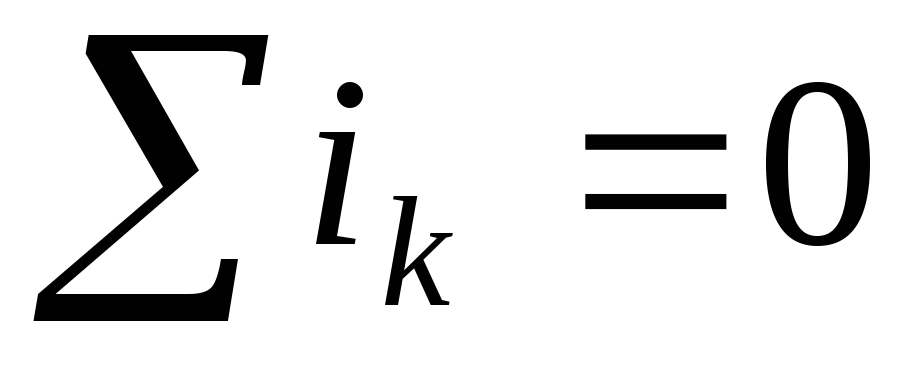 .
.
В
соответствии с теоремой о сумме I
закон Кирхгофа в символической или
комплексной форме записывается в виде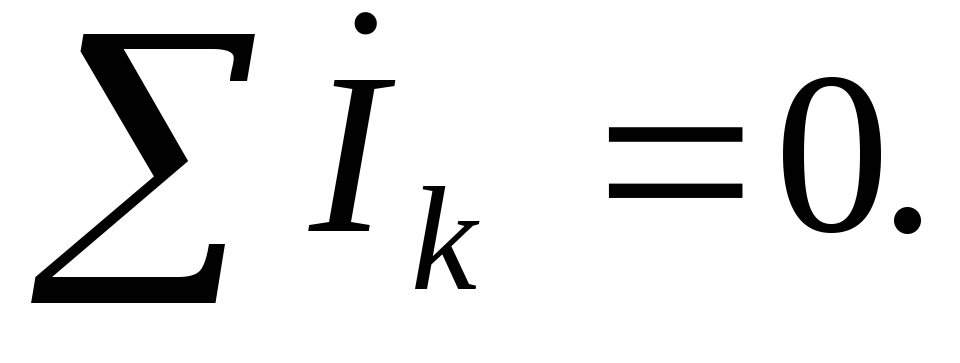
По II закону Кирхгофа алгебраическая сумма мгновенных значений падений напряжений в замкнутом контуре равна нулю, т.е.
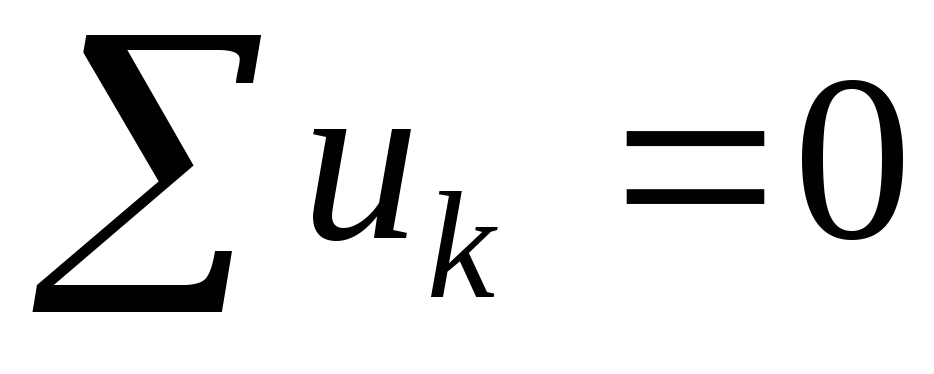 или
или 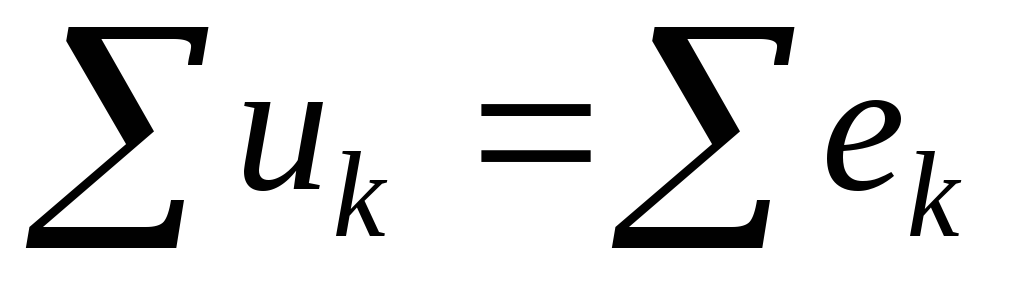 или
или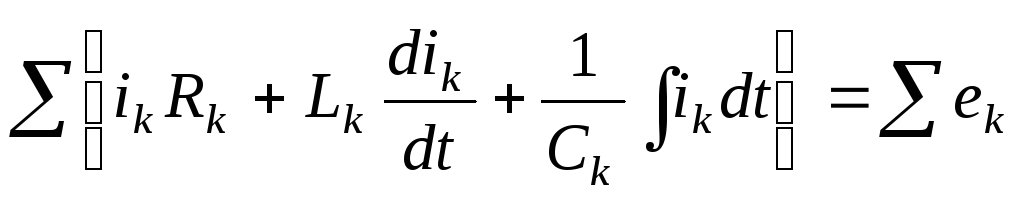 .
.
Но в соответствии с теоремами символического метода II закон Кирхгофа в символической или комплексной форме записи имеет следующий вид:
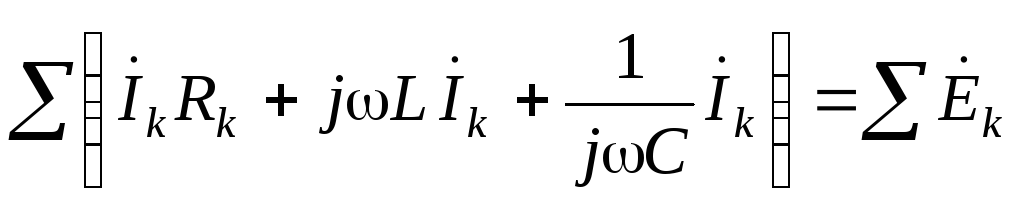 или
или 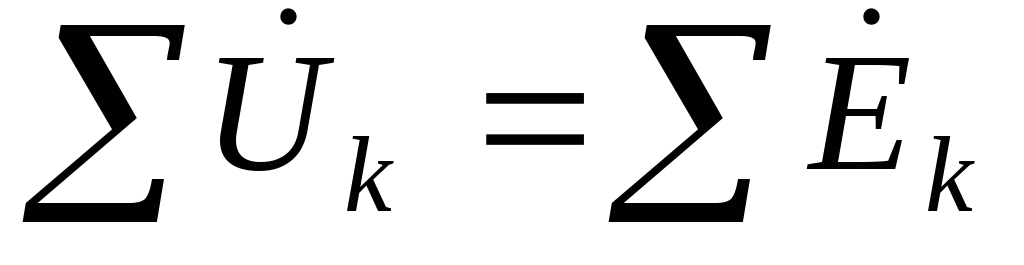 . (3.33)
. (3.33)
Рассмотрим закон Ома в символической форме записи для элементов цепи гармонического тока (рис. 3.15).
На рис. 3.16 приведены векторные диаграммы напряжений и токов соответственно для сопротивления, индуктивности и емкости.
39)Метод контурных токов (гармонический ток)
Алгоритм расчета цепей гармонического тока методом контурных токов аналогичен рассмотренному при изучении цепей постоянного тока (глава 2.3.2) с поправкой на символический метод.
При решении задачи данным методом составляется система уравнений вида
 ,
,
где 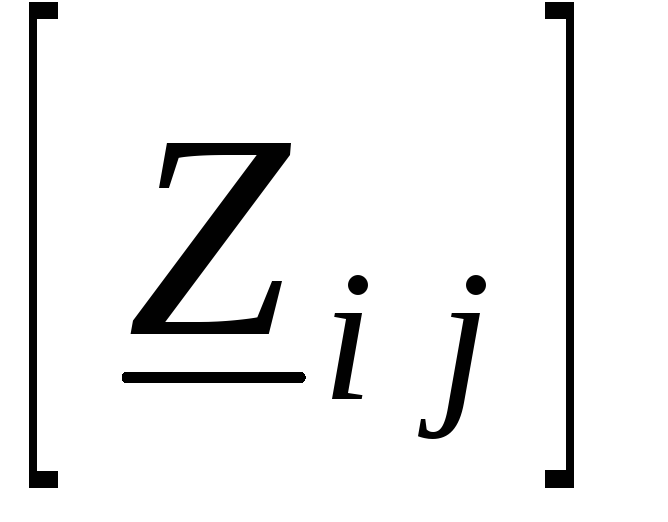 – квадратная матрица комплексных
сопротивлений, в которой
– квадратная матрица комплексных
сопротивлений, в которой – собственное
комплексное сопротивление,
– собственное
комплексное сопротивление,
 –общее
комплексное сопротивление i и j контуров;
–общее
комплексное сопротивление i и j контуров;
–матрица-столбец контурных токов;
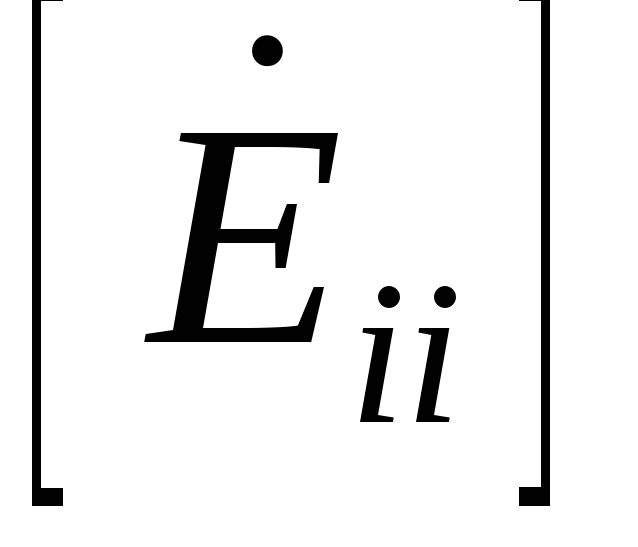 –матрица-столбец
контурных ЭДС.
–матрица-столбец
контурных ЭДС.
40)Метод узловых потенциалов (гармонический ток)
Алгоритм расчета цепей гармонического тока методом узловых потенциалов аналогичен рассмотренному при изучении цепей постоянного тока (глава 2.3.3) с поправкой на символический метод.
При решении задачи данным методом составляется система уравнений вида
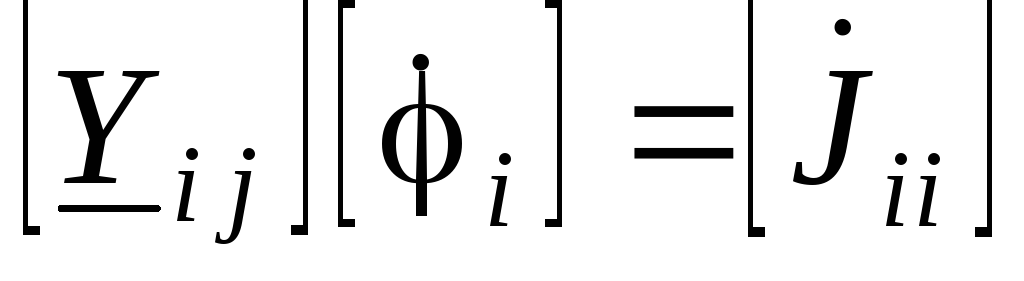 ,
,
где 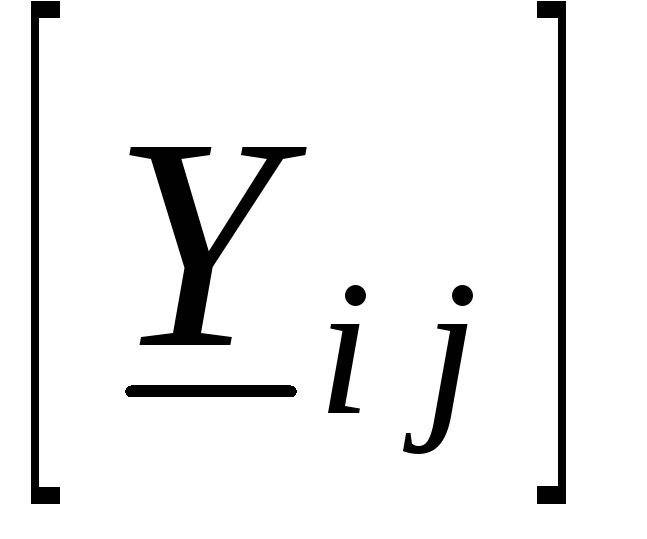 – квадратная матрица комплексных
проводимостей, в которой
– квадратная матрица комплексных
проводимостей, в которой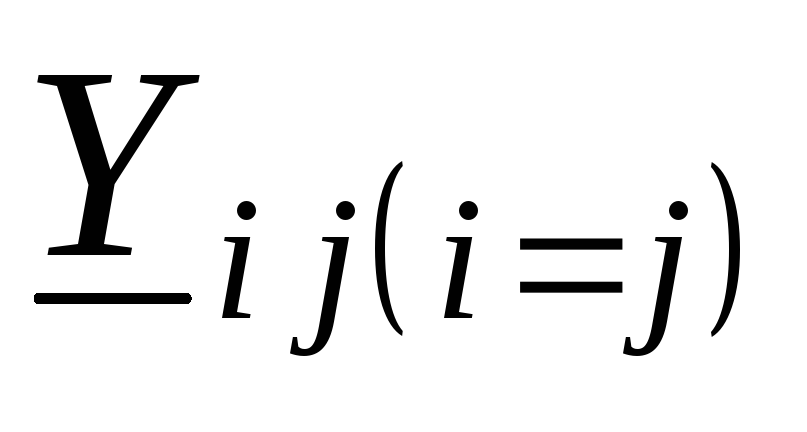 – собственная комплексная проводимость,
– собственная комплексная проводимость,
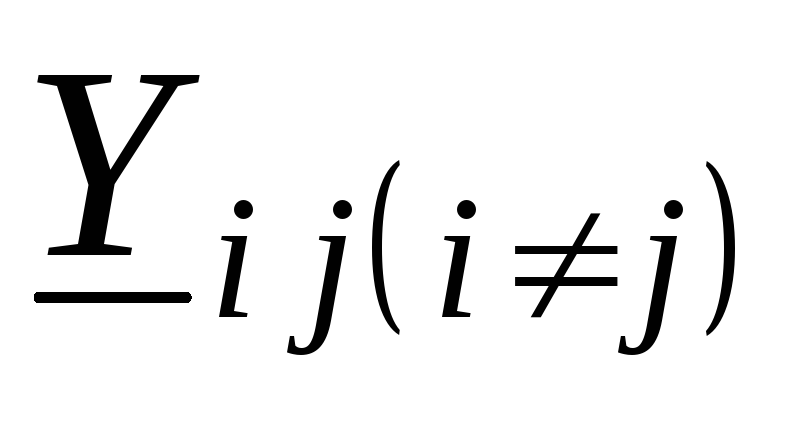 –общая
комплексная проводимость ветвей,
соединяющих i и j узлы;
–общая
комплексная проводимость ветвей,
соединяющих i и j узлы;
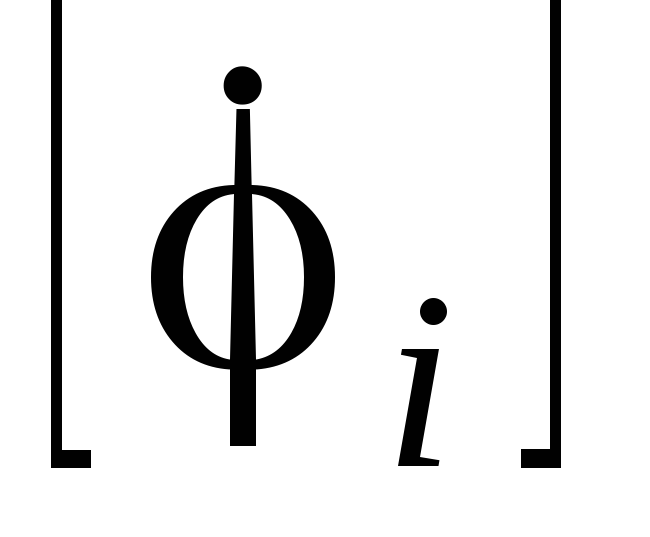 – матрица-столбец
потенциалов;
– матрица-столбец
потенциалов;
 –матрица-столбец
узловых токов.
–матрица-столбец
узловых токов.
Для представленной цепи на рис. 3.25 система уравнений вырождается в одно уравнение, поскольку в цепи два узла.
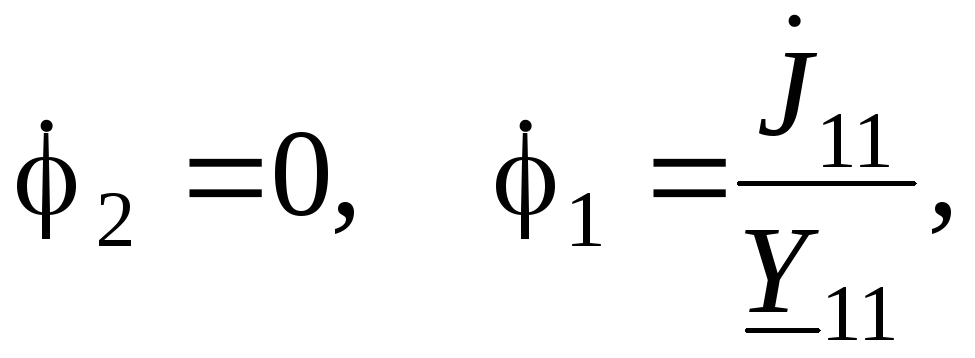
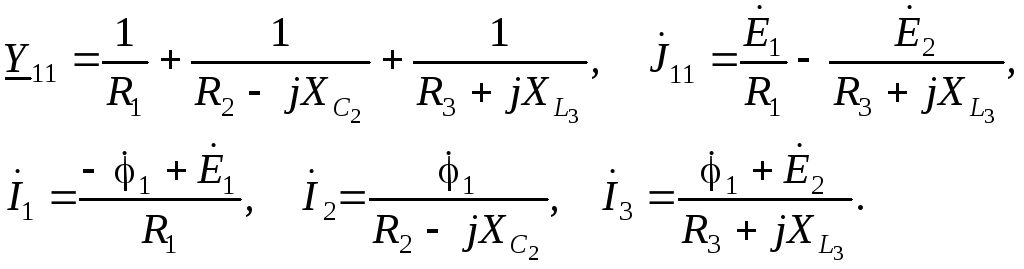
41) Метод эквивалентного генератора (гармонический ток)
Алгоритм
расчета аналогичен рассмотренному при
изучении цепей постоянного тока (глава
2.3.5). Рассмотрим применение этого метода
на примере определения тока 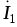 схемы на рис. 3.25. На рис. 3.27 представлены
схема цепи в режиме холостого хода
(обрыв потребителя в ветви, где ищется
ток) и пассивная схема, в которой удалены
источники (напоминаем, что источники
исключаются из схемы по следующему
правилу: источники ЭДС замыкаются
накоротко, а ветви с источниками тока
обрываются).
схемы на рис. 3.25. На рис. 3.27 представлены
схема цепи в режиме холостого хода
(обрыв потребителя в ветви, где ищется
ток) и пассивная схема, в которой удалены
источники (напоминаем, что источники
исключаются из схемы по следующему
правилу: источники ЭДС замыкаются
накоротко, а ветви с источниками тока
обрываются).
|
|
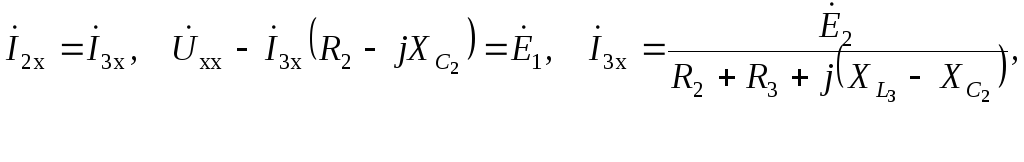
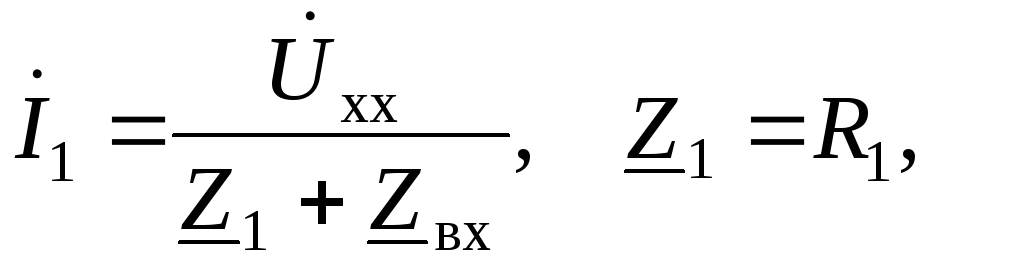
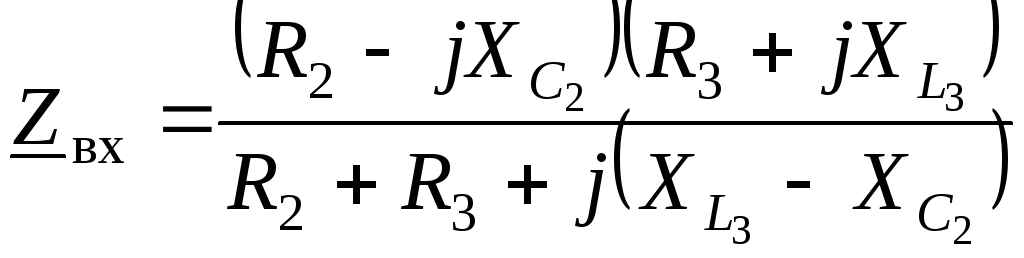 .
.
42) Метод наложения (гармонический ток)
Алгоритм расчета аналогичен рассмотренному при изучении цепей постоянного тока (глава 2.3.4). Рассмотрим применение этого метода на примере схемы на рис. 3.25, которую можно заменить на две составляющие подсхемы (рис. 3.26):
Законы Ома и Кирхгофа в комплексной форме
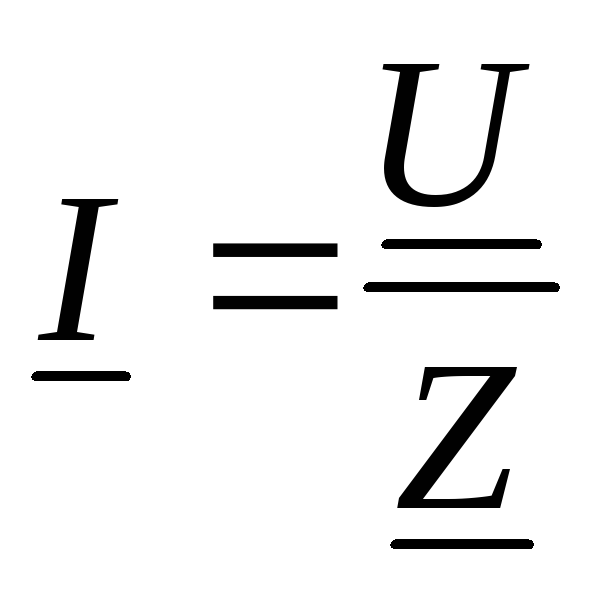 — закон Ома в комплексной форме, где
— закон Ома в комплексной форме, где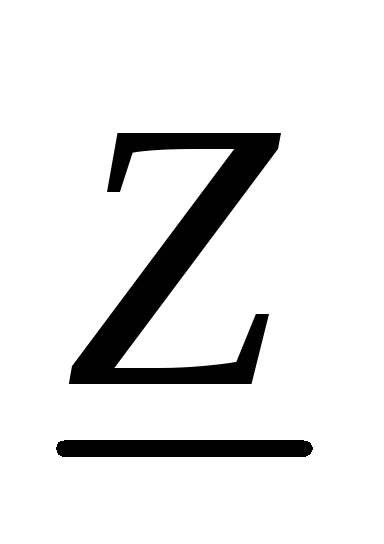 — комплексное сопротивление
— комплексное сопротивление
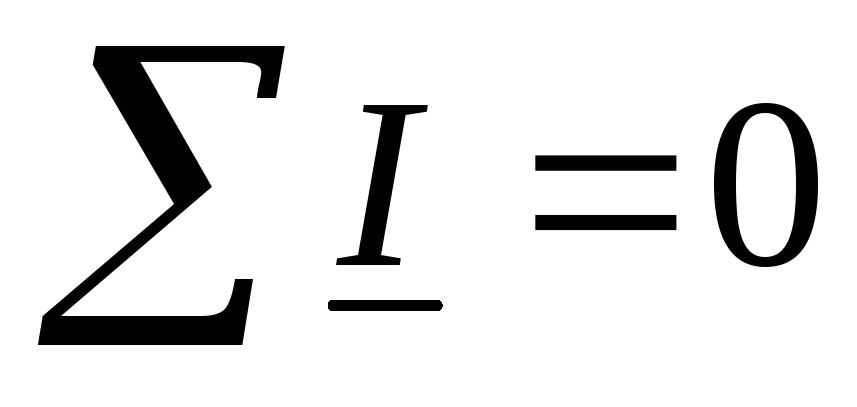 — первый закон Кирхгофа в комплексной
форме
— первый закон Кирхгофа в комплексной
форме
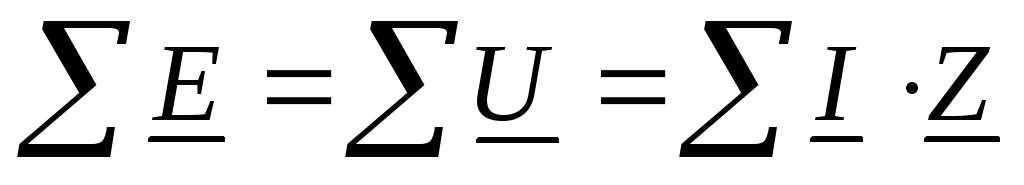 — второй закон Кирхгофа в комплексной
форме
— второй закон Кирхгофа в комплексной
форме
Комплексная мощность
Сопряжённымназывается комплекс, который по модулю равен комплексному выражению, но противоположен по знаку аргумента, например:


Комплексная мощность— произведение комплекса напряжения на сопряжённый комплекс тока.
Модуль комплексной мощности — полная мощность цепи S.
Действительная часть — активная мощность P.
Мнимая часть — реактивная мощность Q.
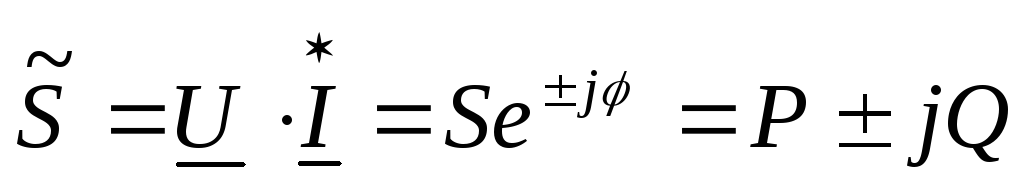
Пример: 
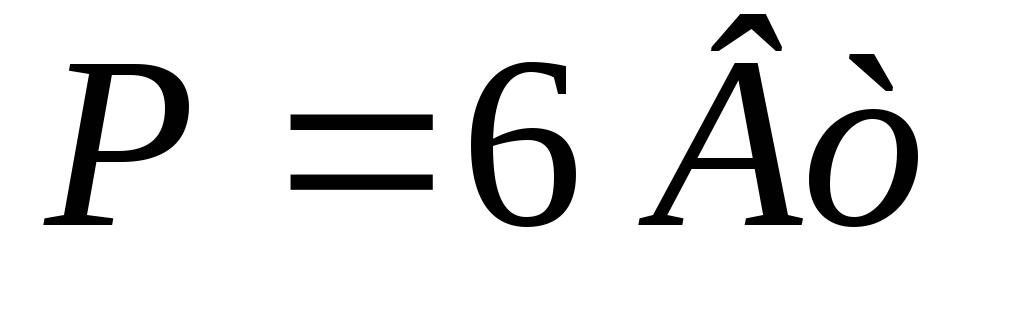
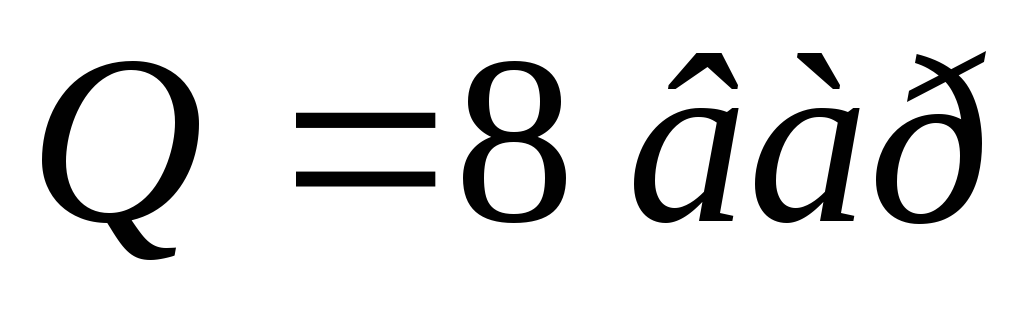
Неразветвлённая цепь с произвольным числом резистивных и реактивных элементов (L и C)
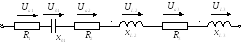
Воспользовавшись данными, найдём входное сопротивление этой цепи; построим векторную диаграмму напряжений:
Вопрос 38. Эквивалентные параметры сложной цепи, рассматриваемые в целом как двухполюсник. Схема замещения двухполюсника при заданной частоте (на примере).
Любой двухполюсник можно заменить
эквивалентным последовательным
двухполюсником с параметрами: 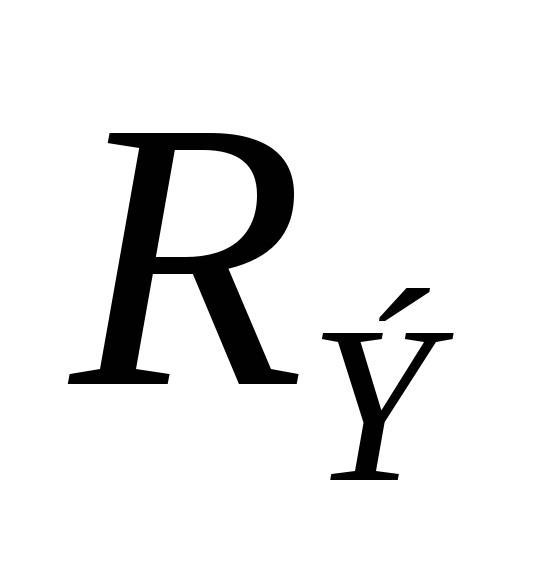 и
и .
.
Задача
Д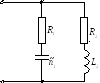 ано:
ано:
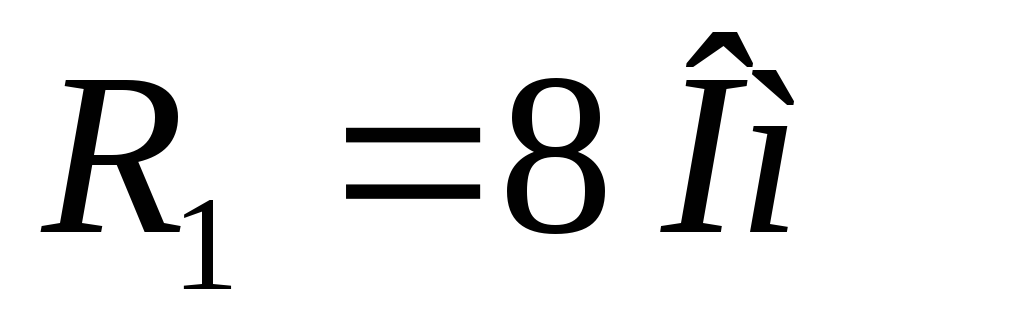
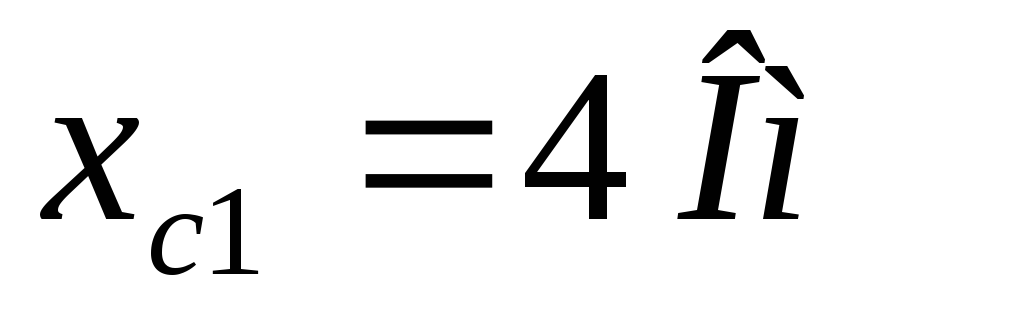
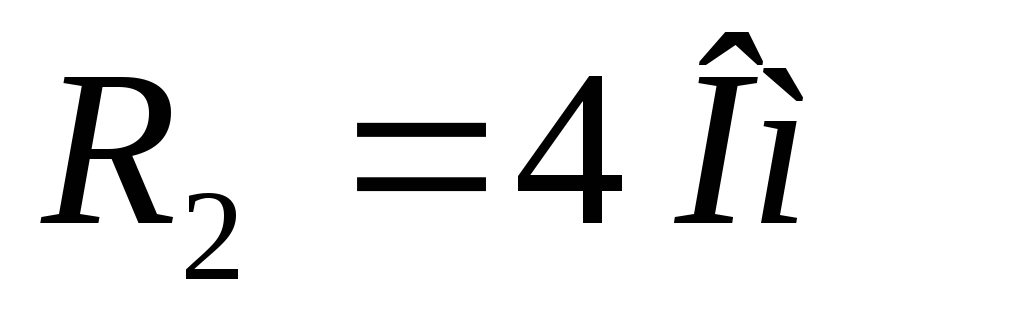
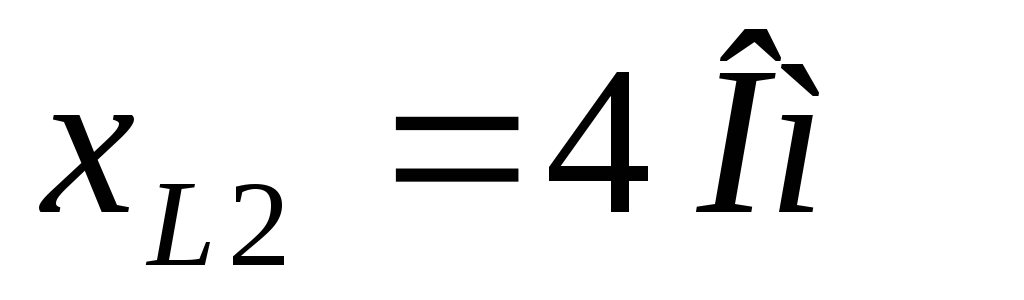
Найти: 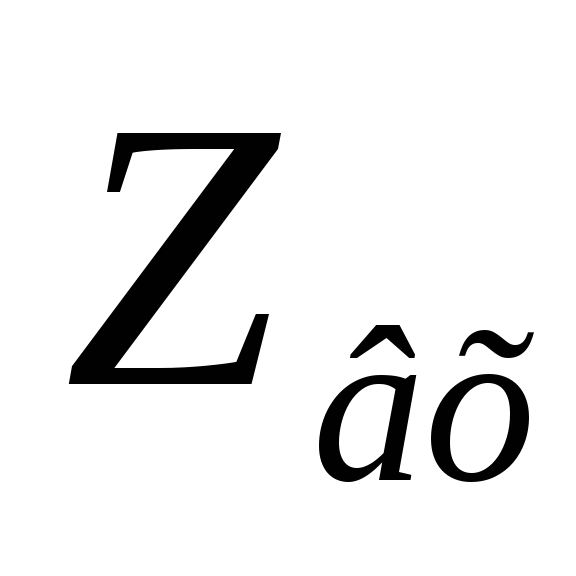 ,
,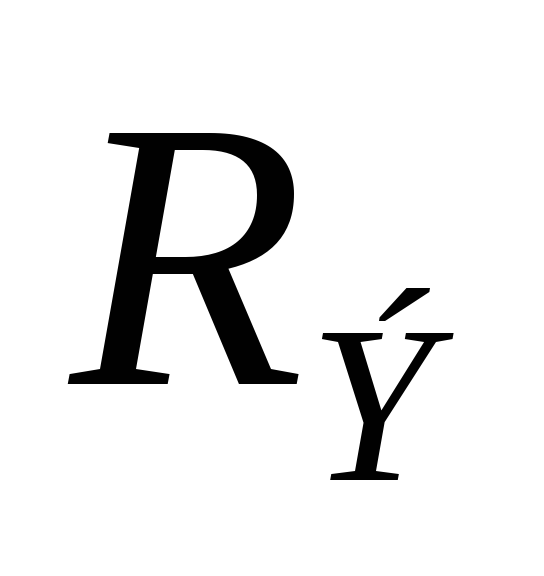 и
и ;
нарисовать схему замещения.
;
нарисовать схему замещения.
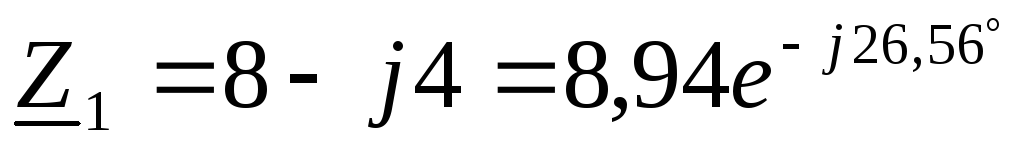
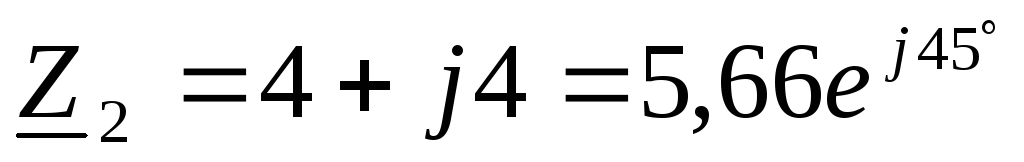
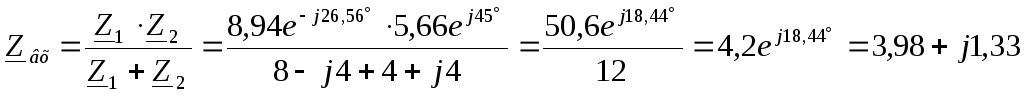
Следовательно:
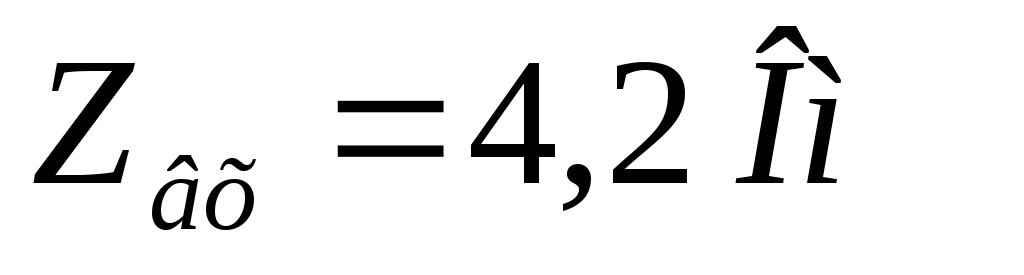
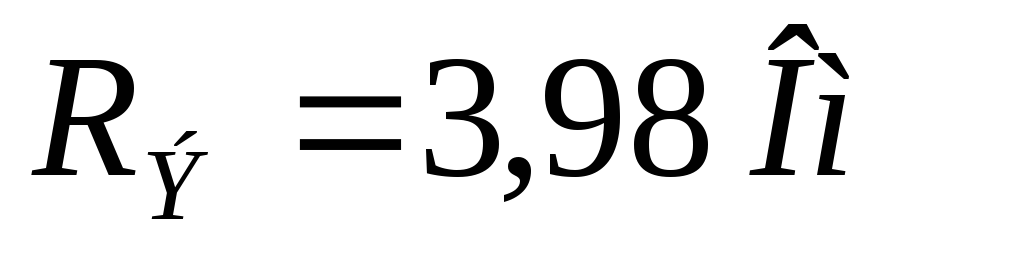

Нарисуем схему эквивалентного
четырёхполюсника (т. к. 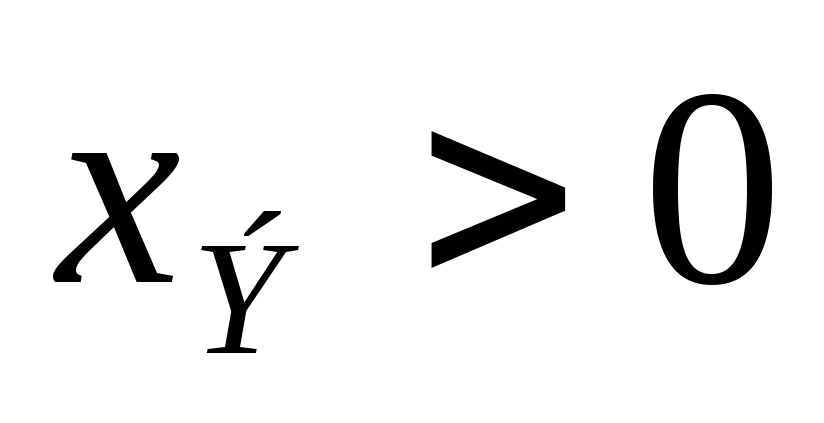 ,
то цепь носит индуктивный характер):
,
то цепь носит индуктивный характер):
Вопрос 39. Фазосдвигающие цепи. Пассивные и активные фазосдвигатели (схемы, анализ работы).


схема 1 схема 2
Фазосдвигающими
цепями называются четырехполюсники, у которых
фаза выходного напряжения 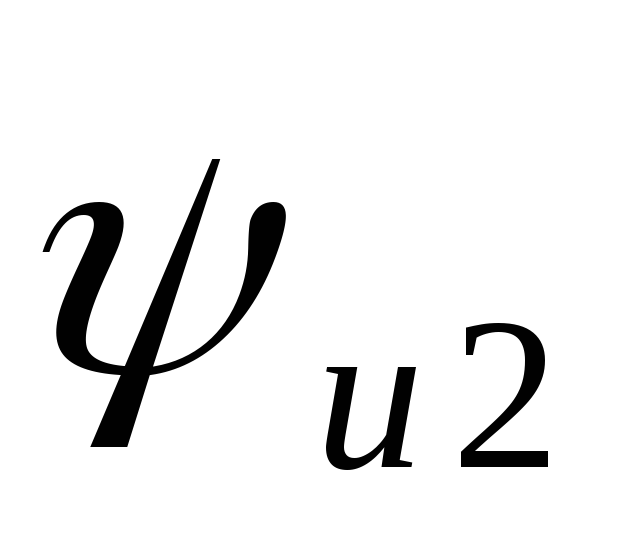 сдвинута относительно фазы входного
напряжения
сдвинута относительно фазы входного
напряжения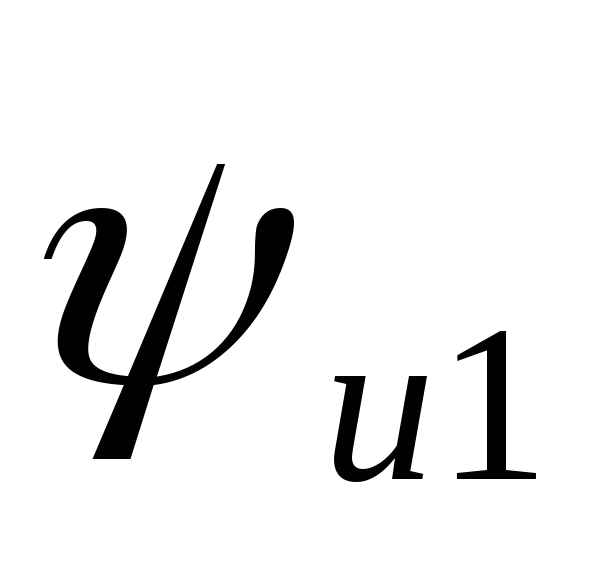 .
.
Четырехполюсники, у которых можно в широких пределах изменять разность начальных фаз, называются фазовращателями.
Пассивная фазосдвигающая цепь — это цепь RC
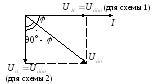
Обозначим
угол сдвига фаз между входным и выходным
напряжениями 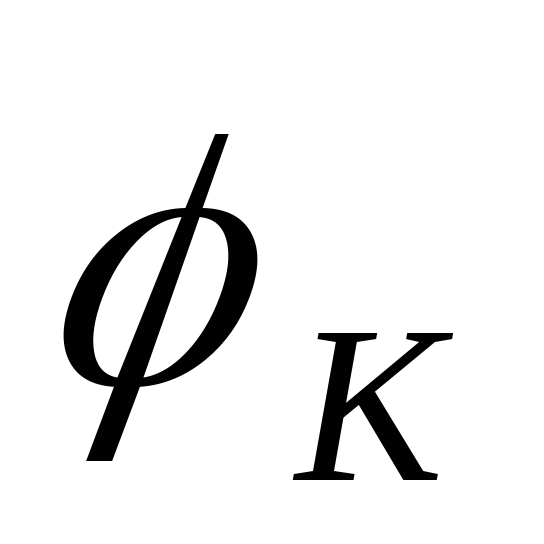 .
.
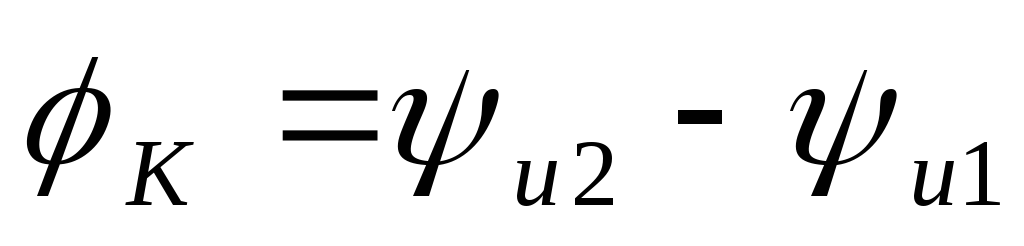
Из
векторной диаграммы видно, что  для первой схемы, и
для первой схемы, и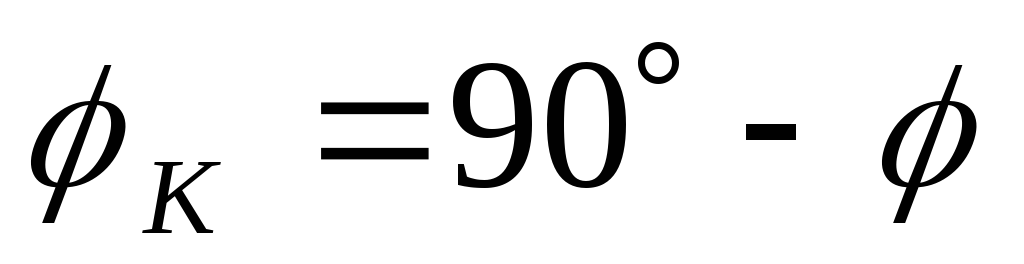 для второй схемы.
для второй схемы.
Используют фазосдвигающие цепи в RC-генераторах в цепях обратной связи. Там необходимо повернуть фазу выходного напряжения на 180° и затем подать это напряжение на вход усилителя (ПОС). Эта задача решается с помощью трёхзвенной фазосдвигающей цепи. Каждое звено осуществляет сдвиг фаз на 60°.
 (схема
1)
(схема
1)
 (схема
2)
(схема
2)
Обычно
выбирают  .
.
Такой сдвиг фаз обеспечивается на частотах:
(для первой схемы)
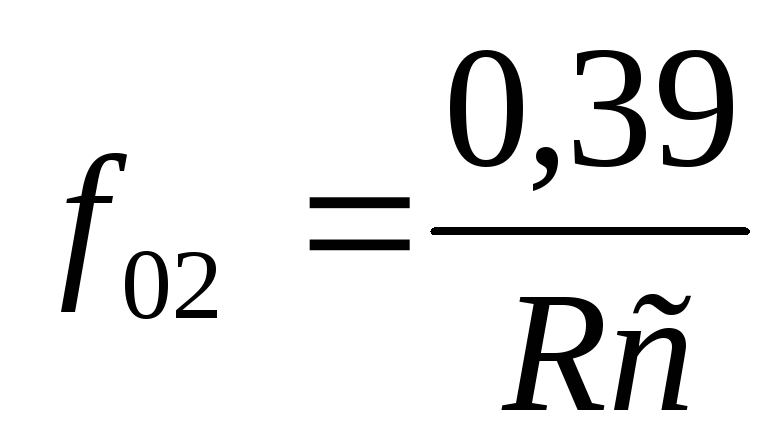 (для второй схемы)
(для второй схемы)
Эти частоты и будут определять частоту автоколебаний генератора.
Подбор Rисв произведении не имеет жестких ограничений. Надо только, чтобы входное сопротивление фазосдвигающей цепи было в 5 – 10 раз больше выходного сопротивления усилителя.
Активная фазосдвигающая цепь
Недостатком
пассивной фазосдвигающей цепи является
низкий коэффициент передачи (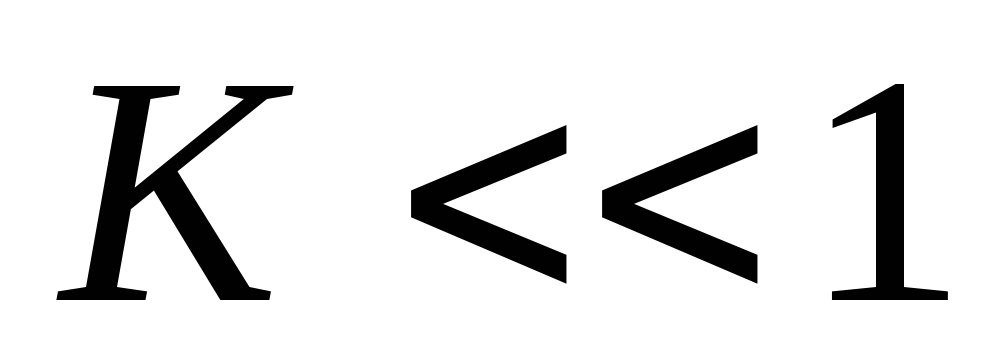 ).
Поэтому используют активную фазосдвигающую
цепь, построенную на основе ОУ, где
).
Поэтому используют активную фазосдвигающую
цепь, построенную на основе ОУ, где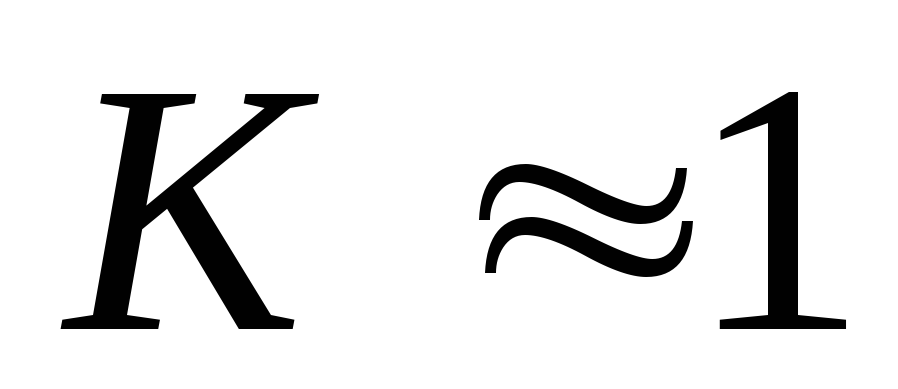 на любой частоте.
на любой частоте.
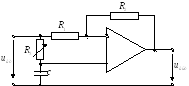
Рассчитано, что угол сдвига фаз между входным и выходным напряжениями
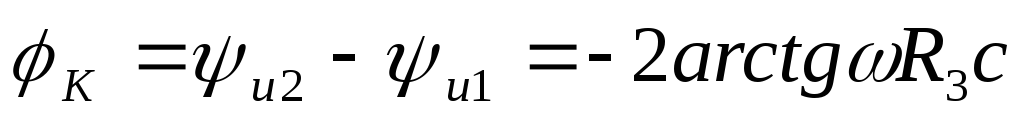 ,
,
поэтому регулировку фазы можно
осуществлять изменением резистора  .
Изменяя сопротивление
.
Изменяя сопротивление от 0 до
от 0 до ,
фаза изменяется от 0° до
,
фаза изменяется от 0° до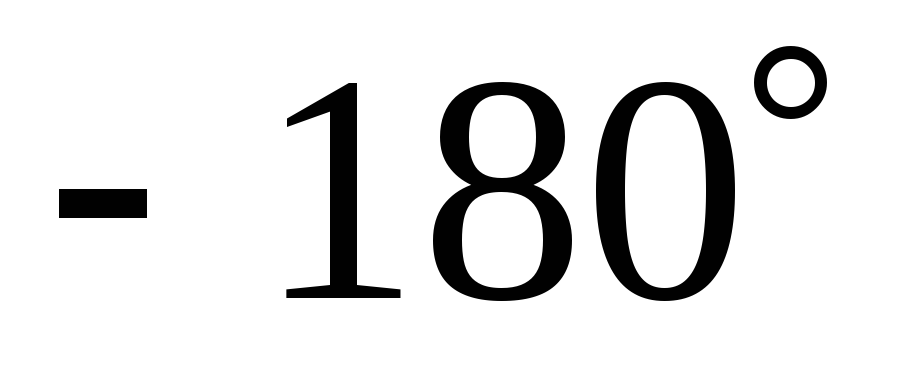 .
.
Вопрос 40. Входные АЧХ и ФЧХ RL неразветвлённых и разветвлённых цепей. Определение и понятие граничной частоты, построение входных характеристик.
Входные амплитудно-частотные (АЧХ) и фазо-частотные характеристики (ФЧХ)
Цепь первого порядка— цепь, в которой есть или одна катушка, или один конденсатор.
Отношение комплексного напряжения на входе к комплексному току на входе называется комплексным входным сопротивлением:
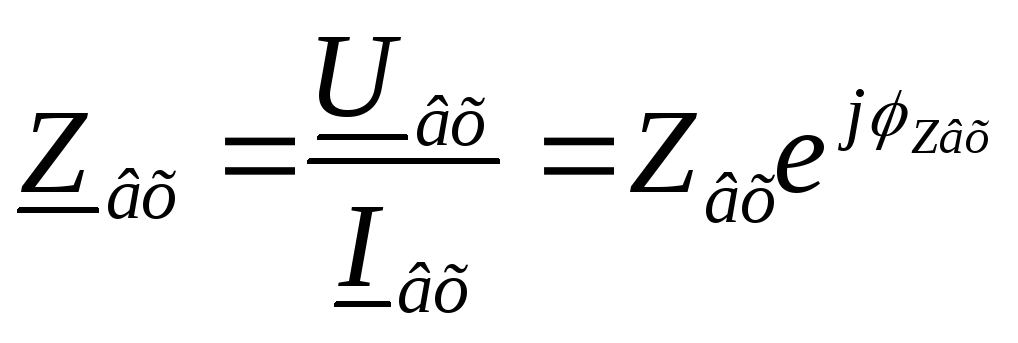
Зависимость модуля комплексного входного сопротивления от частоты, называется входной АЧХ.
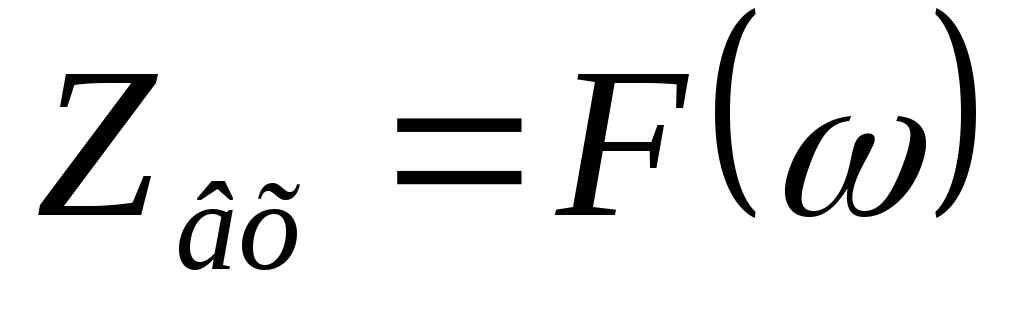 — входная АЧХ
— входная АЧХ
Зависимость аргумента комплексного входного сопротивления от частоты, называется входной ФЧХ.
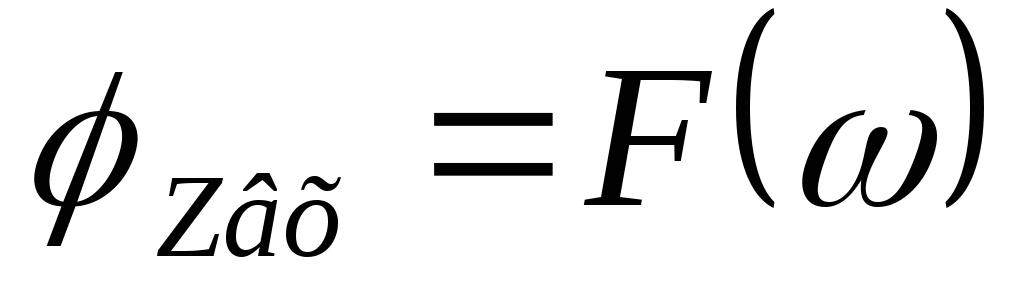 — входная ФЧХ
— входная ФЧХ
Частота, на которой действительная
и мнимая часть комплексного входного
сопротивления равны,называется
граничной(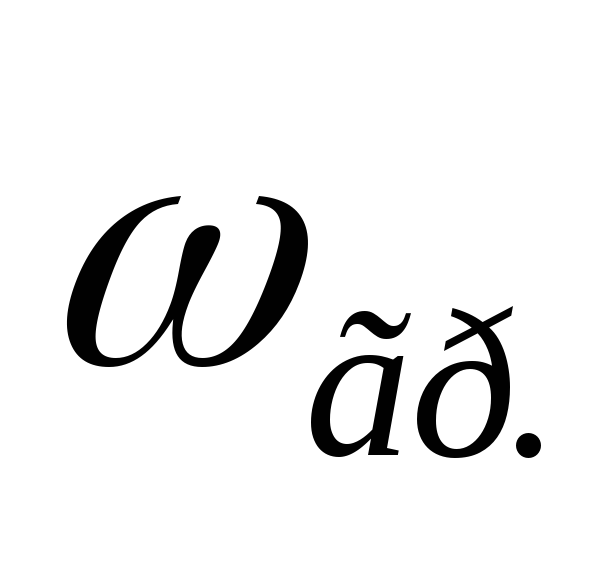 или
или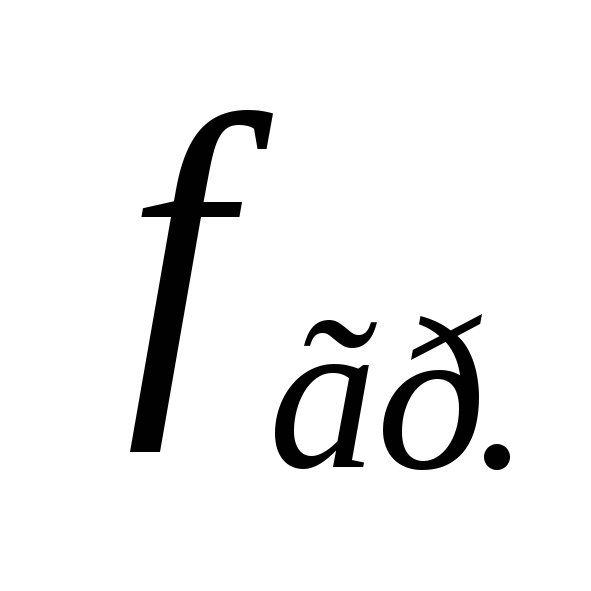 ).
).
Законы Кирхгофа, Ома, Джоуля — Ленца.
Законы Кирхгофа являются одной из форм закона сохранения энергии и потому относятся к фундаментальным законам природы.
Первый закон Кирхгофа является следствием принципа непрерывности электрического тока, в соответствии с которым суммарный поток зарядов через любую замкнутую поверхность равен нулю, т.е. количество зарядов выходящих через 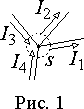 эту поверхность должно быть равно количеству входящих зарядов.
эту поверхность должно быть равно количеству входящих зарядов.
Можно считать токи направленные к узлу положительными, а от узла отрицательными. Тогда для узла рис. 1 уравнение Кирхгофа будет иметь вид I3+I4—I1—I2 = 0 или I3+I4=I1+I2 .
Обобщая сказанное на произвольное число ветвей сходящихся в узле, можно сформулировать первый закон Кирхгофа следующим образом:
- алгебраическая сумма токов в любом узле электрической цепи равна нулю
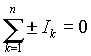 | (1) |
- в любом узле сумма токов направленных к узлу равна сумме токов направленных от узла
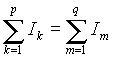 , где p+q=n. , где p+q=n.
| (2) |
в пределах описания одной электрической цепи нельзя для разных узлов использовать разные знаки для токов направленных к узлам или от узлов.
Второй закон Кирхгофа связан с понятием потенциала электрического поля, как работы, совершаемой при перемещении единичного точечного заряда в пространстве. Если такое перемещение совершается по замкнутому контуру, то суммарная работа при возвращении в исходную точку будет равна нулю. В противном случае путем обхода контура можно было бы получать положительную энергию, нарушая закон ее сохранения.
Сформулируем оба варианта второго закона Кирхгофа, т.к. они принципиально равноценны:
- алгебраическая сумма падений напряжения вдоль любого замкнутого контура электрической цепи равна нулю
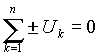 |
знак + выбирается перед падением напряжения на резисторе, если направление протекания тока через него и направление обхода контура совпадают; для падений напряжения на источниках ЭДС знак + выбирается, если направление обхода контура и направление действия ЭДС встречны независимо от направления протекания тока;
- алгебраическая сумма ЭДС вдоль любого замкнутого контура равна алгебраической сумме падений напряжения на резисторах в этом контуре
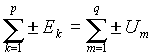 , где p+q=n , где p+q=n
| (4) |
знак + для ЭДС выбирается в том случае, если направление ее действия совпадает с направлением обхода контура, а для напряжений на резисторах знак + выбирается, если в них совпадают направление протекания тока и направление обхода.
Закон Ома — это закон, устанавливающий связь между падением напряжения U на любом неразветвленном (не содержащем узлов) участке электрической цепи и величиной тока I, протекающего по этому участку.
Если зависимость U(I) или I(U) какого-либо элемента электрической цепи линейна, то такой элемент называют линейным, а электрическую цепь, состоящую только из линейных элементов — линейной цепью.
Для линейного элемента справедливо
где r=1/g и g=1/r — некоторые постоянные коэффициенты имеющие размерность соответственно В/А=Ом (омы) и А/В=См (сименсы).Коэффициент r называется сопротивлением, а g — проводимостью. В резисторе ток и падение напряжения (напряжение) всегда имеют одинаковое направление (рис. 1).
Закон Джоуля-Ленца. Если по активному сопротивлению (проводнику) течет постоянный ток, то работа тока на этом участке идет на преобразование электрической энергии во внутреннюю. Увеличение внутренней энергии проводника приводит к повышению его температуры (проводник нагревается).
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля
Математически может быть выражен в следующей форме:
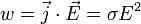
где w — мощность выделения тепла в единице объёма, 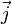 — плотность электрического тока,
— плотность электрического тока, 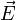 — напряжённость электрического поля, σ — проводимость среды.
— напряжённость электрического поля, σ — проводимость среды.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка
В математической форме этот закон имеет вид
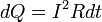
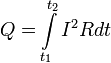
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. В случае постоянных силы тока и сопротивления:
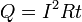
3.Анализ электрического состояния цепей постоянного тока В соответствии с методом свертывания, отдельные участки схемы упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному) сопротивлению, включенному к зажимам источника. Схема упрощается с помощью замены группы последовательно или параллельно соединенных сопротивлений одним, эквивалентным по сопротивлению. Определяют ток в упрощенной схеме, затем возвращаются к исходной схеме и определяют в ней токи.
Рассмотрим схему на рис. 3.1. Пусть известны величины сопротивлений R1, R2, R3, R4, R5, R6, ЭДС Е. Необходимо определить токи в ветвях схемы.
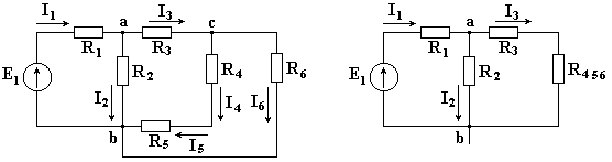
Рис. 3.1 Рис. 3.2 Сопротивления R4 и R5 соединены последовательно, а сопротивление R6 — параллельно с ними, поэтому их эквивалентное сопротивление
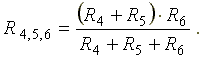
После проведенных преобразований схема принимает вид, показанный на рис. 3.2, а эквивалентное сопротивление всей цепи
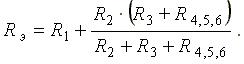
Ток I1 в неразветвленной части схемы определяется по формуле:

Найдем токи I2 и I3 в схеме на рис. 3.2 по формулам:
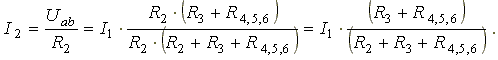
I3 = I1 — I2 — формула получается из уравнения, составленного по первому закону Кирхгофа:
I1 — I2 — I3 = 0.
Переходим к исходной схеме на рис. 3.1 и определим токи в ней по формулам:

I6 = I3 — I4 (в соответствии с первым законом Кирхгофа I3 — I4 — I6 =0).
4.Применение законов Кирхгофа и Ома для расчетов электрических цепей .Самое распространенное применение законов Кирхгофа мы наблюдаем в так называемых последовательных и параллельных цепях. В последовательной цепи (яркий пример такой цепи — елочная гирлянда, состоящая из последовательно соединенных между собой лампочек) электроны от источника питания по серии проводов последовательно проходят через все лампочки, и на сопротивлении каждой из них напряжение падает согласно закону Ома.
В параллельной цепи провода, напротив, соединены таким образом, что на каждый элемент цепи подается равное напряжение от источника питания, а это означает, что в каждом элементе цепи сила тока своя, в зависимости от его сопротивления. Пример параллельной цепи является — ламп «лесенкой»: напряжение подается на шины, а лампы смонтированы на поперечинах. Токи, проходящие через каждый узел такой цепи, определяются по второму закону Кирхгофа.
Все те, кто знаком с основами электротехники, представляют себе значение закона Ома в теории и практике электрических цепей. Не вдаваясь в подробности, перечислим некоторые примеры использования закона Ома при изучении электрических цепей.
В первую очередь, как уже упоминалось, закон Ома в виде 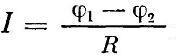
служит для определения сопротивления проводника. При наличии амперметра и вольтметра эта операция даже для неопытного экспериментатора не представит трудностей. Одним из наиболее точных и чувствительных способов определения сопротивления является метод мостовых схем, расчет которых производится также с использованием закона Ома.
Применяя закон Ома для полной цепи, можно, изменяя внешнее сопротивление, вычислить ЭДС и внутреннее сопротивление источника тока, решив для этого систему двух соответствующих выражений:

ПоказанияI1 и I2 при этом снимают с амперметра, включенного в цепь. Сопротивление R1 и R2 внешних участков цепи можно найти, измеряя вольтметром падение напряжения на этих участках и применяя формулу закона Ома для участка цепи.
Этот же закон позволяет рассчитать электрическую цепь, источником тока в которой является батарея, составленная из нескольких элементов.
В настоящее время в электротехнике широко применяются правила Кирхгофа, с помощью которых рассчитывают разветвленные цепи. Зная эти правила, можно, например, определить силу и направление тока в любой части разветвленной системы проводников, если заданы сопротивления и ЭДС всех его участков. Второе правило Кирхгофа получено в результате применения закона Ома к различным участкам замкнутой цепи. Первое правило также следует из теоретических рассуждений Ома, изложенных им в работе «Теоретические исследования электрических цепей».
Изучение нелинейных цепей обязано своим прогрессом также закону Ома. Важнейшие характеристики электронных ламп и полупроводниковых приборов — крутизна характеристики, внутреннее сопротивление — определяется в соответствии с законом Ома.
Закон Ома применяется ко всей цепи. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа
5.Метод эквивалентного преобразования схем . Эквивалентным называется преобразование, при котором напряжения и токи в частях схемы, не подвергшихся преобразованию, не меняются.
Последовательное соединение элементов
электрических цепей
На рис. 2.1 изображена электрическая цепь с последовательно соединенными сопротивлениями.
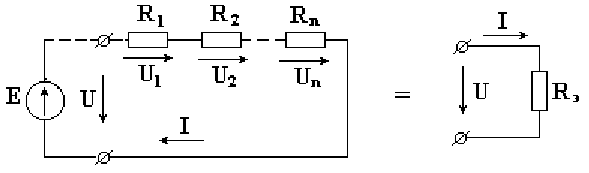
Рис. 2.1
Напряжение на зажимах источника ЭДС равно величине электродвижущей силы. Поэтому часто источник на схеме не изображают.
Падения напряжений на сопротивлениях определяются по формулам 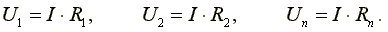 В соответствии со вторым законом Кирхгофа, напряжение на входе электрической цепи равно сумме падений напряжений на сопротивлениях цепи.
В соответствии со вторым законом Кирхгофа, напряжение на входе электрической цепи равно сумме падений напряжений на сопротивлениях цепи.  где
где  — эквивалентное сопротивление.
— эквивалентное сопротивление.
Эквивалентное сопротивление электрической цепи, состоящей из n последовательно включенных элементов, равно сумме сопротивлений этих элементов.
Параллельное соединение элементов
электрических цепей
На рис. 2.2 показана электрическая цепь с параллельным соединением сопротивлений.
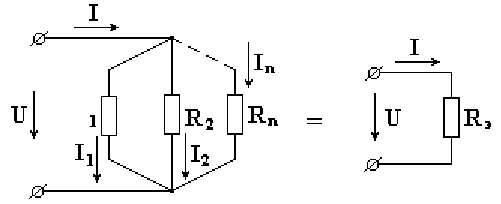
Рис. 2.2
Токи в параллельных ветвях определяются по формулам: 
где 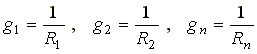 — проводимости 1-й, 2-й и n-й ветвей.
— проводимости 1-й, 2-й и n-й ветвей.
В соответствии с первым законом Кирхгофа, ток в неразветвленной части схемы равен сумме токов в параллельных ветвях.
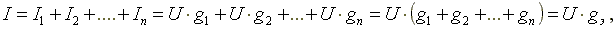 где
где 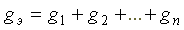
Эквивалентная проводимость электрической цепи, состоящей из n параллельно включенных элементов, равна сумме проводимостей параллельно включенных элементов.
Эквивалентным сопротивлением цепи называется величина, обратная эквивалентной проводимости 
Пусть электрическая схема содержит три параллельно включенных сопротивления.
Эквивалентная проводимость 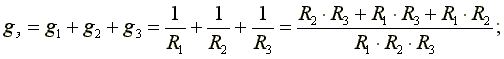
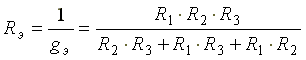 Эквивалентное сопротивление схемы, состоящей из n одинаковых элементов, в n раз меньше сопротивлений R одного элемента
Эквивалентное сопротивление схемы, состоящей из n одинаковых элементов, в n раз меньше сопротивлений R одного элемента 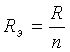
Возьмем схему, состоящую из двух параллельно включенных сопротивлений (рис. 2.3). Известны величины сопротивлений и ток в неразветвленной части схемы. Необходимо определить токи в параллельных ветвях.
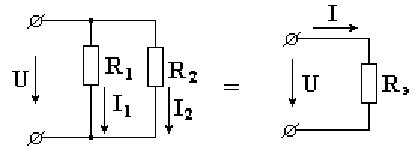
Рис. 2.3 Эквивалентная проводимость схемы
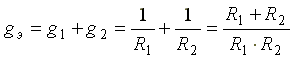 ,
,
а эквивалентное сопротивление 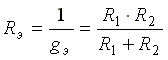 Напряжение на входе схемы
Напряжение на входе схемы 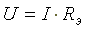 Токи в параллельных ветвях
Токи в параллельных ветвях 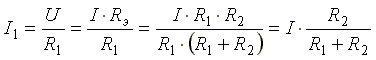
Аналогично 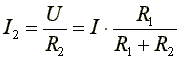
Ток в параллельной ветви равен току в неразветвленной части схемы, умноженному на сопротивление противолежащей, чужой параллельной ветви и деленному на сумму сопротивлений чужой и своей параллельно включенных ветвей.
Преобразование треугольника сопротивлений
в эквивалентную звезду
Встречаются схемы, в которых отсутствуют сопротивления, включенные последовательно или параллельно, например, мостовая схема, изображенная на рис. 2.4. Определить эквивалентное сопротивление этой схемы относительно ветви с источником ЭДС описанными выше методами нельзя. Если же заменить треугольник сопротивлений
R1-R2-R3, включенных между узлами 1-2-3, трехлучевой звездой сопротивлений, лучи которой расходятся из точки 0 в те же узлы 1-2-3, эквивалентное сопротивление полученной схемы легко определяется.
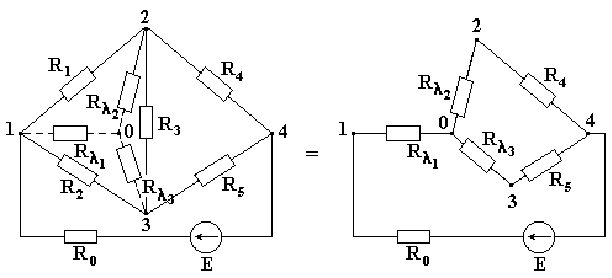
Рис. 2.4 Сопротивление луча эквивалентной звезды сопротивлений равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений всех сторон треугольника.
В соответствии с указанным правилом, сопротивления лучей звезды определяются по формулам:
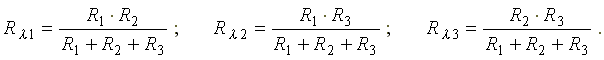 Эквивалентное соединение полученной схемы определяется по формуле
Эквивалентное соединение полученной схемы определяется по формуле
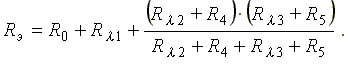 Сопротивления R0 и R?1 включены последовательно, а ветви с сопротивлениями R?1 + R4 и R?3 + R5 соединены параллельно.
Сопротивления R0 и R?1 включены последовательно, а ветви с сопротивлениями R?1 + R4 и R?3 + R5 соединены параллельно.
Преобразование звезды сопротивлений
в эквивалентный треугольник
Иногда для упрощения схемы полезно преобразовать звезду сопротивлений в эквивалентный треугольник.
Рассмотрим схему на рис. 2.5. Заменим звезду сопротивлений R1-R2-R3 эквивалентным треугольником сопротивлений R?1-R?2-R?3, включенных между узлами 1-2-3.

2.5. Преобразование звезды сопротивлений
в эквивалентный треугольник
Сопротивление стороны эквивалентного треугольника сопротивлений равно сумме сопротивлений двух прилегающих лучей звезды плюс произведение этих же сопротивлений, деленное на сопротивление оставшегося (противолежащего) луча. Сопротивления сторон треугольника определяются по формулам:
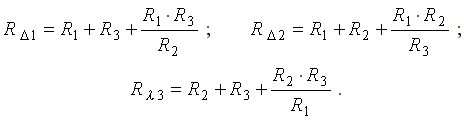
Эквивалентное сопротивление преобразованной схемы равно
При решении схемы методом непосредственного преобразования элементов используют серию эквивалентных преобразований схемы, направленных на упрощение схемы. Понятие эквивалентного преобразования подразумевает такое изменение состава и/или топологии фрагментасхемы, при котором не изменяются электрические показатели (токи и напряжения) в остальных частях схемы, не затронутых преобразованием. Такое обстоятельство означает, что величины, найденные для одной из эквивалентных схем (искомые или вспомогательные), действительны и для любой другой из эквивалентных схем.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Обобщенный закон Ома.
Закон
Ома выражаемый формулой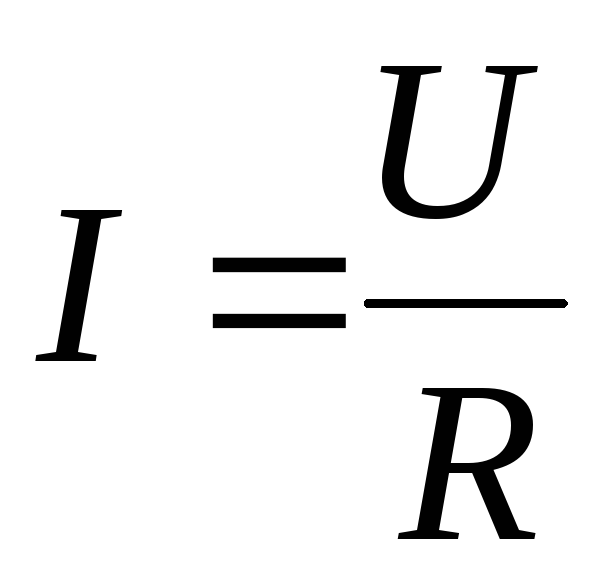 ,
определяет зависимость между током и
напряжением на пассивном участке
электрической цепи.
,
определяет зависимость между током и
напряжением на пассивном участке
электрической цепи.
Определим зависимость между током, напряжением и э.д.с. на активном участке (рис. 16).
Из формулы 15 следует:
a-b=I(R1+R2)- E1+E2 (16)
На положительное напряжение на участке a – b Uab=a-b
Следовательно, Uab= I(R1+R2)- E1+E2 (17)
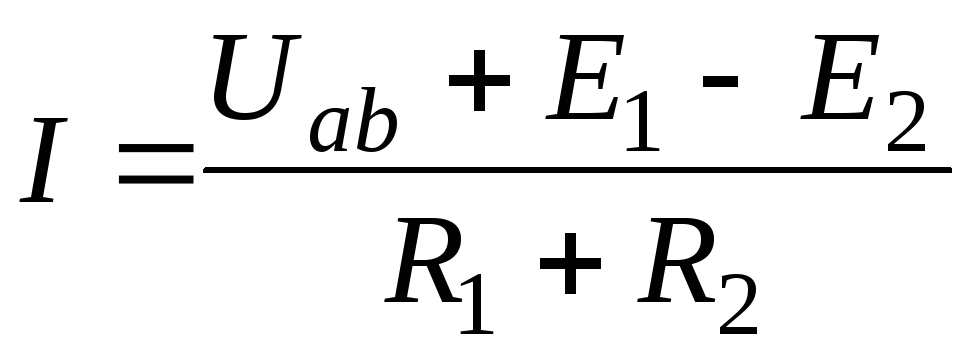 (18)
(18)
Формула (18) выражает обобщенный закон Ома, или закон Ома для участка, содержащего э.д.с.
Из формулы видно, что если ток, напряжение и э.д.с. совпадают по направлению, то в выражение закона Ома они входят с одинаковыми знаками. Если э.д.с. действует в сторону, противоположную положительному направлению тока, то в выражении ставится знак «-».
Закон Ома применяется для участка ветви и для одноконтурной замкнутой схемы.
Пример № 1 построения потенциальной диаграммы:
Построить потенциальную диаграмму для одноконтурной схемы:
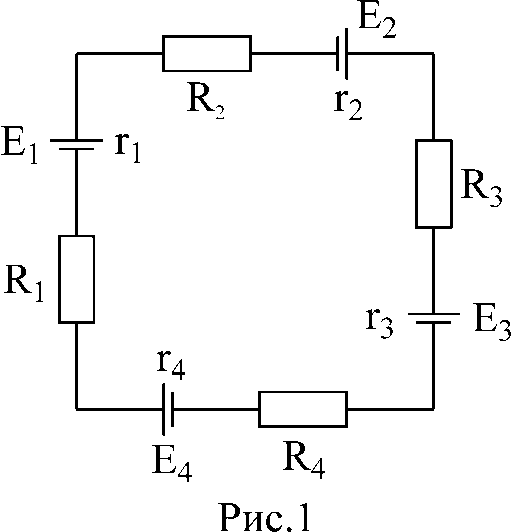
E1=25В; E2=5В; E3=20В; E4=35В,
R1=8 Ом; R2=24 Ом; R3=40 Ом; R4=4 Ом,
r1=2 Ом; r2=6 Ом; r3=2 Ом; r4=4 Ом.
Решение: 1. перерисуем заданный контур, вынося внутренние сопротивления э.д.с. (r1— r4) за их пределы; обозначим точки контура.
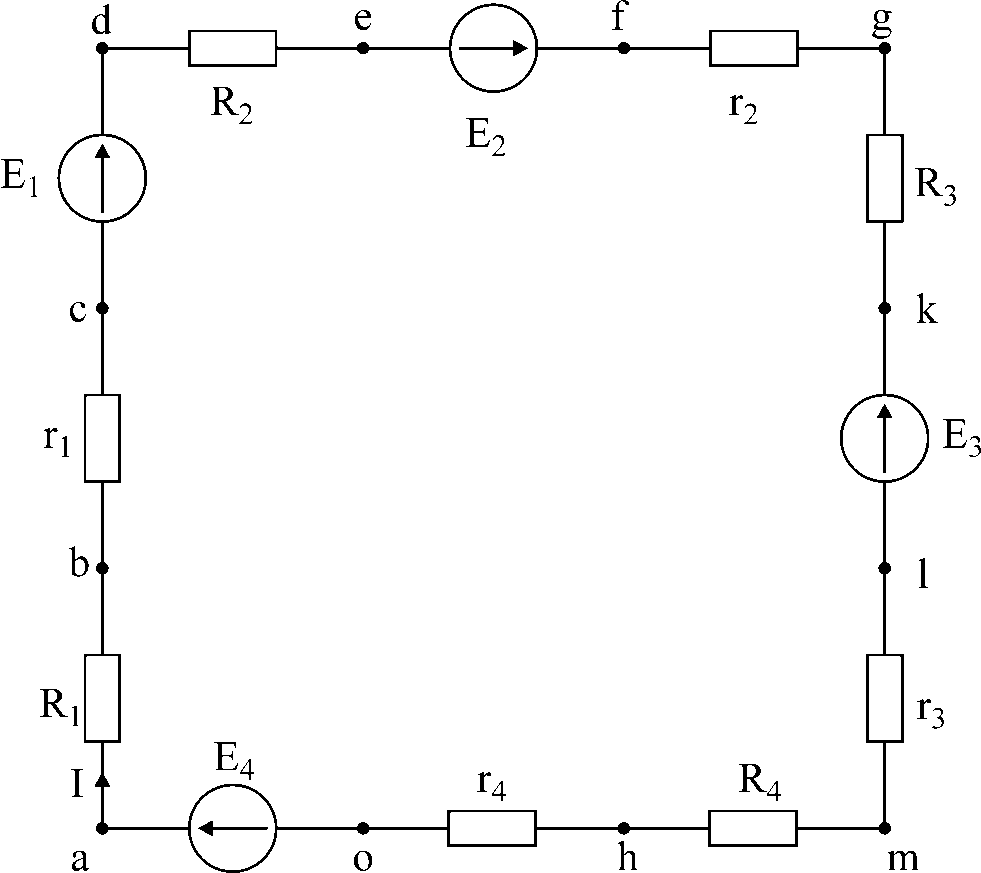
Рис.2
2. Выберем положительное направление тока I, определим его значение используя обобщенный закон Ома:

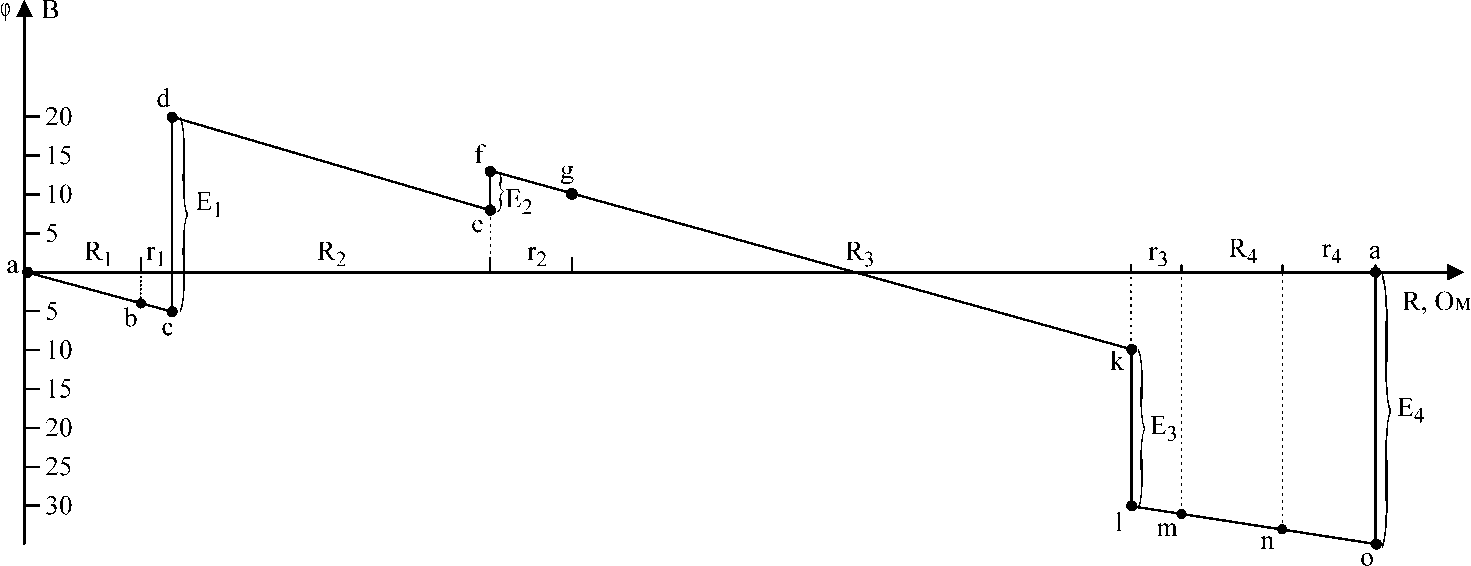
3. За базисную точку примем точку a. Найдем потенциалы остальных точек:
b= a– IR1 = — 4В e= d– IR2 = 8В
c= b– Ir1 = — 5В f= e+ E2 = 13В
d= c+ E1 = 20В q= f– Ir2 = 10В
k= q– IR3 = — 10В n= m– IR4 = — 33В
e = k – E3 = — 30В o = n – Ir4 = — 35В
m = e – Ir3 = — 31В a = o + E4 = 0
4. В системе координат строим потенциальную диаграмму:
Законы Кирхгофа.
Распределение токов по ветвям электрической цепи подчиняется первому закону Кирхгофа, а распределение напряжений по участкам цепи подчиняется второму закону Кирхгофа.
Законы Кирхгофа наряду с законом Ома являются основными в теории электрических цепей.
Первый закон Кирхгофа:
Алгебраическая сумма токов в узле равна нулю:
i = 0 (19)
Где i — число ветвей, сходящихся в данном узле.
Т.е., суммирование распространяется на токи в ветвях, которые сходятся в рассматриваемом узле.
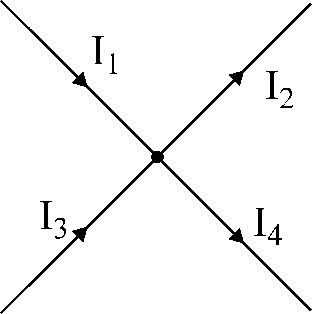
Рис.17. Иллюстрация к первому закону Кирхгофа.
Число уравнений, составляемых по первому закону Кирхгофа, определяется формулой:
Nуp = Nу – 1,
Где Nу – число узлов в рассматриваемой цепи.
Знаки токов в уравнении берутся с учетом выбранного положительного направления. Знаки у токов одинаковы, если токи одинаково ориентированы относительно данного узла.
Например, для узла, представленного на рис.17: припишем токам, подтекающим к узлу знаки «+», а к токам, оттекающим от узла – знаки «-».
Тогда уравнение по первому закону Кирхгофа запишется так:
I1 – I2 + I3 – I4 = 0.
Уравнения, составленные по первому закону Кирхгофа, называются узловыми.
Этот закон выражает тот факт, что в узле электрический заряд не накапливается и не расходуется. Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.
Второй закон Кирхгофа:
Алгебраическая сумма э.д.с. в любом замкнутом контуре цепи равна алгебраической сумме падений напряжения на элементах этого контура:
Ui = Ei
IiRi=Ei(20)
Где i – номер элемента(сопротивления или источника напряжения) в рассматриваемом контуре.
**Число уравнений, составляемых по второму закону Кирхгофа, определяется формулой:
Nуp = Nb – Nу + 1 – Nэ.д.с.
Где Nb – число ветвей электрической цепи;
Nу — число узлов;
Nэ.д.с. — число идеальных источников э.д.с.
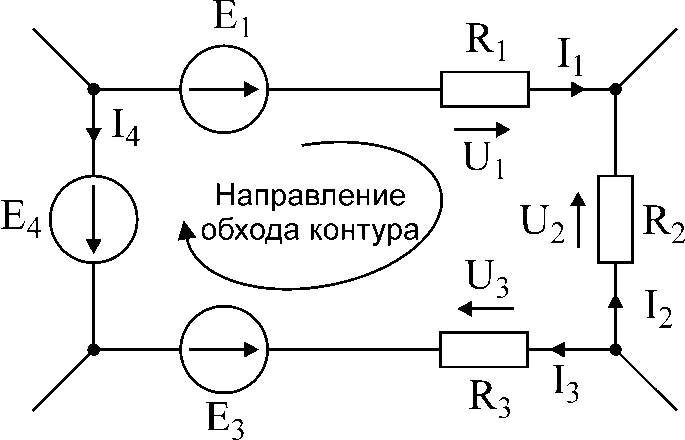
Рис.18. Иллюстрация ко второму закону Кирхгофа.
Для того, чтобы правильно записать второй закон Кирхгофа для заданного контура, следует выполнять следующие правила:
произвольно выбрать направление обхода контура, например, по часовой стрелке (рис.18).
э.д.с. и падения напряжения, которые совпадают по направлению с выбранным направлением обхода, записываются в выражении со знаком «+»; если э.д.с. и падения напряжения не совпадают с направлением обхода контура, то перед ними ставится знак «-».
Например, для контура рис.18, второй закон Кирхгофа запишется следующим образом:
U1 – U2 + U3 = E1 – E3 – E4 (21)
Уравнение (20) можно переписать в виде:
(Ui – Ei) = 0 (22)
Где (U – E) – напряжение на ветви.
Следовательно, второй закон Кирхгофа можно сформулировать следующим образом:
Алгебраическая сумма напряжений на ветвях в любом замкнутом контуре равна нулю.
Потенциальная диаграмма, рассмотренная ранее, служит графической интерпретацией второго закона Кирхгофа.
Задача №1.
В схеме рис.1 заданы токи I1 и I3, сопротивления и э.д.с. Определить токи I4, I5, I6 ; напряжение между точками a и b, если I1 = 10мA, I3 = -20 мA, R4 = 5kОм, E5 = 20B, R5 = 3kОм, E6 = 40B, R6 = 2kОм.
.
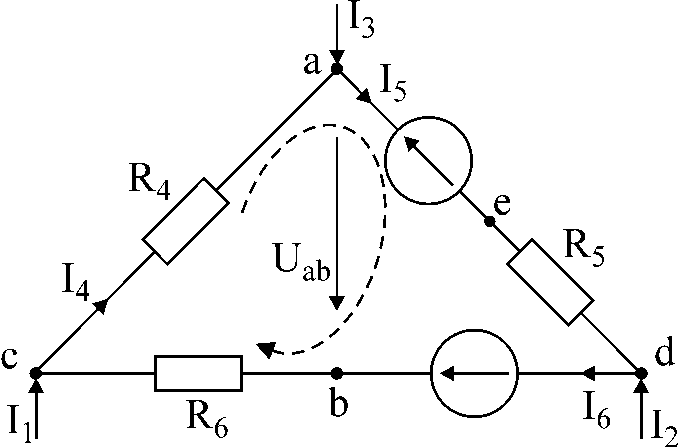
Рис.1
Решение:
Для заданного контура составим два уравнения по первому закону Кирхгофа и одно – по второму. Направление обхода контура указано стрелкой.
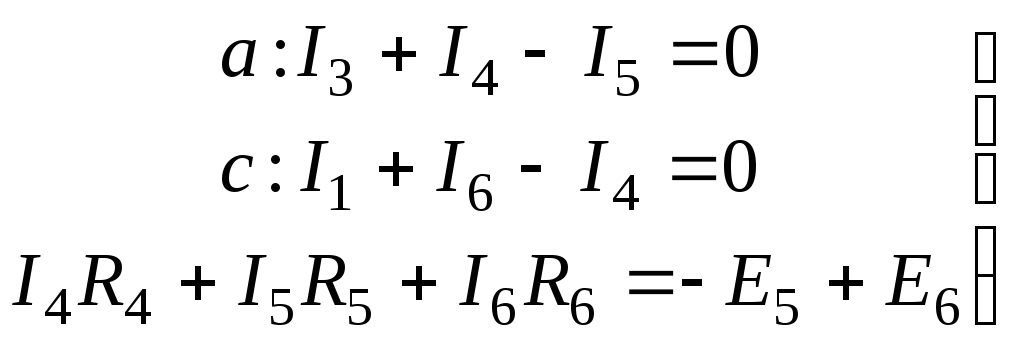
В результате решения получаем: I6 = 0; I4 = 10мA; I5 = -10мA
зададим направление напряжения между точками a и b от точки «a» к точке «b» — Uab. Это напряжение найдем из уравнения по второму закону Кирхгофа:
I4R4 + Uab + I6R6 = 0
Uab = — 50B.
Задача №2.
Для схемы рис.2 составить уравнения по законам Кирхгофа и определить неизвестные точки.
Дано: I1 = 20мA; I2 = 10мA
R1 = 5kОм, R3 = 4kОм, R4 = 6kОм, R5 = 2kОм, R6 = 4kОм.
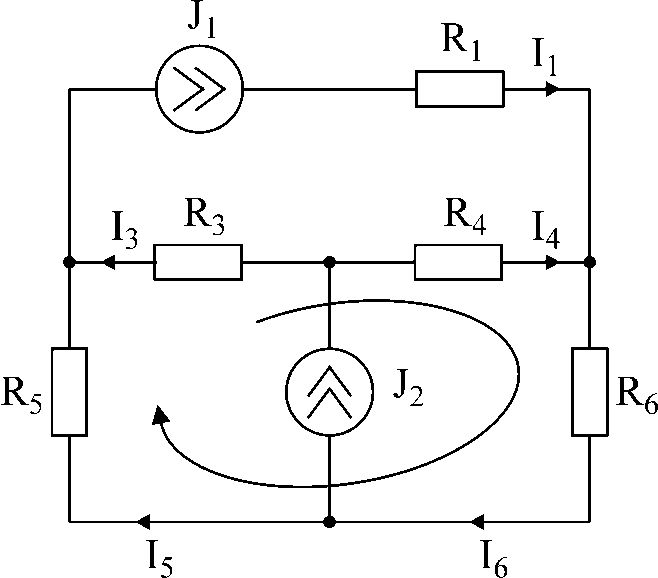
Рис.2
Решение:
Число узловых уравнений – 3, число контурных уравнений – 1.
Запомнить! При составлении уравнения по второму закону Кирхгофа выбираем контур, в который не входят источники тока. Направление контура указано на рисунке.
В данной цепи известны токи ветвей I1 и I2. Неизвестные токи I3, I4, I5, I6.
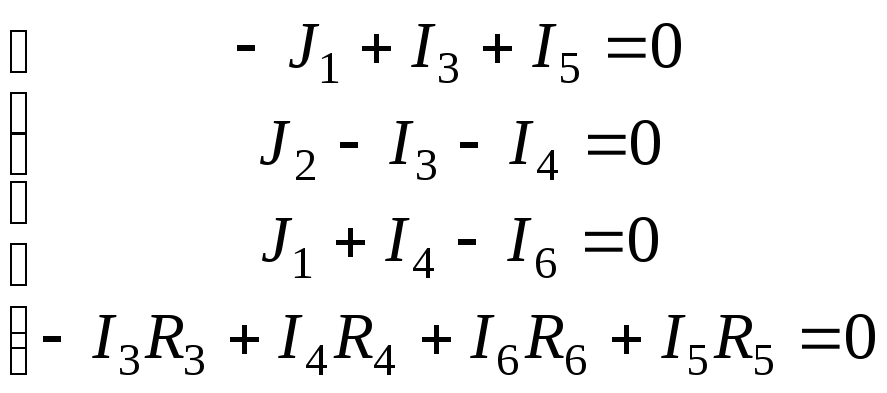
Решая систему, получаем: I3 = 13,75 мA; I4 = -3,75мA; I5 = 6,25мA; I6 = 16,25мA.