1.5. Задача анализа цепи. Законы Кирхгофа » СтудИзба

1.5. Задача анализа цепи. Законы Кирхгофа.

Задача анализа электрической цепи формулируется следующим образом: заданы схемы электрической цепи со значениями всех ее элементов, а также напряжения и токи источников, действующих в цепи, требуется найти токи в ветвях и напряжения на элементах цепи. Для определения искомых токов и напряжений необходимо составить уравнения цепи, которые определяются только геометрической конфигурацией и способами соединения элементов цепи. Эти уравнения составляются на основе двух законов Кирхгофа, которые связывают токи ветвей, сходящихся в узлах, и напряжения элементов, входящих в контуры.

Первый закон Кирхгофа, выражающий закон сохранения заряда, формулируется так: в любой момент алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю.

(1.12)

Знак тока ,при записи первого закона Кирхгофа, определяется выбором положительных направлений токов ветвей: например, токам, входящим в узел, приписывают условно знак плюс, а токам, выходящим из узла — знак минус. Так, для узла изображенного на рис. 1.10.

Второй закон Кирхгофа, выражающий закон сохранения энергии, формулируется следующим образом: в любой момент алгебраическая сумма напряжений в ветвях контура равна нулю.

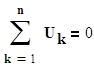(1.13)

          Рис  1.10                Суммирование напряжений производится с учетом их положительных направлений и выбранного направления обхода контура. Если положительное направление напряжения ветви совпадает с напряжением обхода контура, то оно входит в (1.13) со знаком плюс, в противном случае – со знаком минус.

Часто используется другая формулировка второго закона Кирхгофа: алгебраическая сумма э.д.с. источников, действующих в контуре, равна алгебраической сумме напряжений на элементах контура.

(1.14)

При этом напряжения на элементах контура и э.д.с. источников входят  в уравнение (1.14) со знаком плюс, если их положительные направления совпадают с направлением обхода контура, в обратном случае слагаемые в (1.14) берутся со знаком минус. Например, для схемы (рис 1.11) при обходе по часовой стрелке уравнение второго закона Кирхгофа запишется следующим образом:

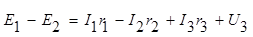
Для разветвленной цепи, содержащей q узлов и k ветвей, при определении неизвестных токов следует составить k уравнений по первому и второму законам Кирхгофа, т.к. число неизвестных токов

            Рис  1.11               равно числу ветвей цепи. Причем число уравнений, составленных по первому закону Кирхгофа, равно (q-1), а число уравнений, составленных по второму закону Кирхгофа, — (k-(q-1)).

Уравнение второго закона Кирхгофа может быть записано для участка цепи между точками «а» и «b» (см. рис. 1.12). При этом контур замыкается по стрелке, указывающей положительное направление напряжения между точками «a» и «b»

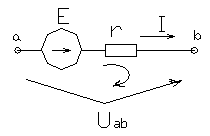 (1.15)   

Таким образом можно всегда определить напряжение между двумя любыми точками электрической цепи.

Пример 1.1. Записать уравнения по законам

        Рис  1.12                Кирхгофа для расчета токов цепи, представленной на                            рис. 1.13.

Решение.

Цепь содержит 3 ветви и два узла: «a» и «b», следовательно, по первому закону Кирхгофа составим одно уравнение, а остальные два – по  второму закону Кирхгофа. Выбрав положительные направления токов I₁, I₂, I₃ такими, как показано на рисунке 1.13, и обходя контур I и II по часовой стрелке, получим                                                                                        Рис  1.13                              

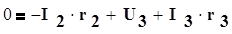
После решения и подстановки числовых значений полученные результаты могут быть либо положительными, либо отрицательными. В случае отрицательного значения действительное направление тока будет противоположным указанному на рисунке.

2.2. Законы Кирхгофа

Согласно первого закона Кирхгофа алгебраическая сумма токов в любом узле электрической цепи равна нулю

∑I = 0.

Поскольку речь идет об алгебраической сумме ∑I, необходимо учитывать знаки слагаемых токов. Входящие в узел токи принято считать положительными, выходящие – отрицательными. Для узла «а» (рис. 2.5) имеем

I₁ + I₂ — I₃ = 0.

Согласно второго закона Кирхгофа алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах контура

∑E = ∑R·I.

Для составления уравнения по второму закону Кирхгофа произвольно выбирают направление обхода контура. Принято ЭДС, токи и напряжения считать положительными, если они совпадают по направлению с направлением обхода контура, а если не совпадают – отрицательными. При обходе контура

E₁, E₂, R₂, R₁ электрической цепи (рис. 2.5) по часовой стрелке имеем

E₁ — E₂ = R₁·I₁ — R₂I₂.

2.3. Преобразования в электрических цепях

При расчётах сложных электрических цепей применяют формулы последовательного (смотреть пункт 2.1), параллельного, смешанного соединения элементов, а также преобразования «треугольника» в «звезду» и обратно. Рассмотрим эти соотношения.

2.3.1. Параллельное соединение (рис. 2.6)

Рис. 2.6. – Параллельное соединение элементов

При таком соединении элементов общее сопротивление определяется выражением

При двух сопротивлениях, соединенных параллельно

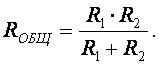
Если R₁ = R₂ = … R_n, то

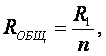
где п – число параллельно соединенных элементов.

2.3.2. Смешанное соединение (рис. 2.7)

Смешанным соединением называют сочетание последовательного и парал­лельного соединений резисторов.

При смешанном соединении элементов для эквивалентного преобразования пользуются

методом последовательных эквивалентных преобразований, т.е. последовательно преобразуются участки цепи, имеющие простое (только последовательное, или только параллельное) соединение элементов.

Поясним это на конкретном примере расчета электрической цепи (рис.1.3).

Рис.1.3. Смешанное соединение элементов.

Рис. 2.7. – Смешанное соединение элементов

2.3.3. Преобразование «треугольника» в «звезду» (рис. 2.8)

2.2.4. Преобразование «звезды» в «треугольник» (рис. 2.8)

Рис. 2.8. – Соединение сопротивлений в «треугольник» и «звезду»

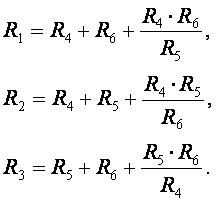
2.4. Расчет разветвленной электрической цепи с одним источником энергии

При расчете электрических цепей в большинстве случаев известны параметры источников ЭДС, сопротивления элементов электрической цепи. Задача расчета электрической цепи сводится к определению токов в ветвях. По найденным токам можно рассчитать напряжения на элементах цепи, мощность отдельных элементов и электрической цепи в целом, мощность источников, сечения проводников.

Для расчета электрических цепей с одним источником энергии применяется метод эквивалентных преобразований, заключающийся в постепенном преобразовании и замене последовательно и параллельно соединенных элементов эквивалентными. Всю группу элементов цепи заменяют одним эквивалентным. Преобразования начинают в ветвях, наиболее удалённых от источника. Затем в преобразованной (предельно простой) цепи по закону Ома определяют ток. Полученные в процессе преобразования расчетные схемы позволяют определить токи во всех остальных ветвях.

Пример 1: Рассчитать эквивалентное сопротивление цепи R_экв

и, токи в каждом резисторе.

Дано: R₁ = 3 Ом; R₂ = 2 Ом; R₃ = 5 Ом; R₄ = 10 Ом; E = 50 В.

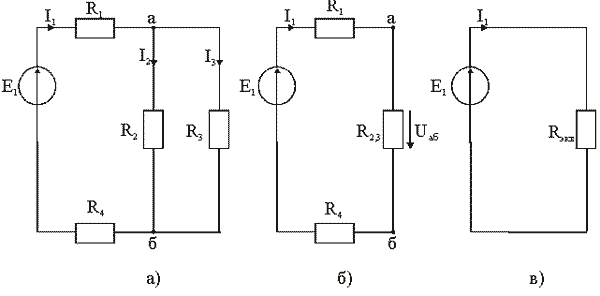Рис. 2.9 — Пример эквивалентных преобразований: а) схема электрической цепи до преобразования; б) расчетная схема после первого преобразования; в) — расчетная схема после второго (окончательного) преобразования

Определить токи в ветвях схемы, представленной на рис. 2.9, а.

Выбираем направления токов в ветвях. Преобразуем параллельно соединенные резисторы R₂ и R₃, заменяя их эквивалентным элементом R

_{2, 3}

Расчетная схема после первого преобразования показана на рис. 2.9, б.

Проводим второе преобразование. Для этого последовательно соединенные резисторы R₁, R_{2, 3}, R₄ заменяем одним эквивалентным R_ЭКВ.

R_ЭКВ = R₁ + R_{2, 3} + R₄ = 3 + 1,43 + 10 = 14,43 Ом.

Теперь исходная схема сведена к простейшей, показанной на рис. 2.9, в, в которой

Для определения токов I₂ и I₃, необходимо определить напряжение U_аб, рис. 2.9, а, которое рассчитываем по рис. 2.9, б

U_аб = R_{2, 3}·I₁ = 1,43·3,47 = 4,96 В.

Возвращаясь к схеме рис 2.9, а, получим

Для проверки правильности расчета токов составляем баланс мощности. Мощность, вырабатываемая всеми источниками энергии в цепи, должна быть равна мощности, потребляемой всеми приёмниками электрической энергии (нагрузкой). Относительная погрешность расчета не должна превышать одного процента.

Мощность, вырабатываемая источником ЭДС

Р

_И = Е·I₁ = 50·3,47 = 173,5 Вт.

Мощность, потребляемая нагрузкой

Погрешность баланса мощности

Если баланс сходится с допустимой погрешностью, то расчет токов выполнен верно.

Пример выполнения задачи 1.

Для электрической цепи постоянного тока, приведенной на рис. 4:

1. Рассчитать эквивалентное сопротивление цепи.

2. Рассчитать ток в каждом резисторе.

3. Проверить выполнение первого закона Кирхгофа во всех узлах схемы и второго Закона Киhхгофа для одного из контуров.

4. Определить мощности, рассеиваемые на резисторах схемы.

5. Проверить выполнение баланса мощностей

Рис. 4. Электрическая цепь постоянного тока

1. Расчет эквивалентного сопротивления цепи проводим методом последовательных эквивалентных преобразований..

а) б) в)

Рис. 5. «Этапы эквивалентного преодразования электрической цепи

Эквивалентное сопротивление ветвей R₃ и R₄ соединенных параллельно определяем по формуле:

,

.

Эквивалентное сопротивление элементов R₂, R₃₄ и R₅, соединенных последовательно находим по формуле:

,

.

Эквивалентное сопротивление всей цепи (R₂₃₄₅ и R₁ -соединены параллельно):

,

.

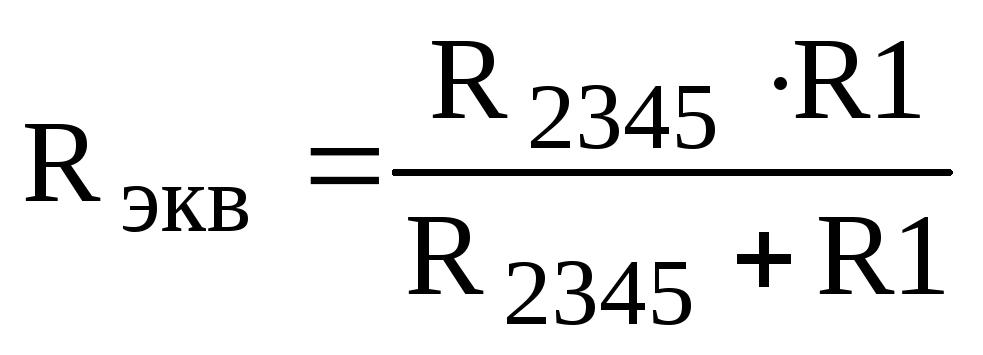
2. Рассчитаем токи во всех ветвях.

Ток, потребляемый цепью от источника питания:

,

_.

Ток в ветви R1:

Ток в ветви R₂₃₄₅:

,

.

Определяем потенциал узла «б»:

,

.

Определяем потенциал узла «в»:

.

Очевидно, что I₅ = I₂, откуда

.

Определяем разность потенциалов между узлами «б» и «в»:

,

.

Определяем токи в ветвях R3 и R4:

,

;

,

.

3. Проверяем выполнение первого закона Кирхгофа для токов в узлах.

Для узла «а»: ,

.

Для узла «б»: ,

.

Для узла «в»: ,

.

Проверяем выполнение второго закона Кирхгофа для контура R₅, R₃, R₂, R₁:

,

,

.

4. Определяем мощности, рассеиваемые на резисторах:

,

;

,

;

,

;

,

;

,

.

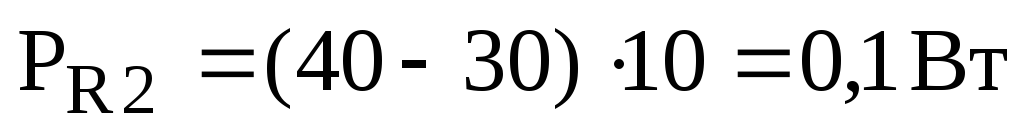5. Проверяем выполнение баланса мощностей.

Мощность, потребляемая цепью от источника питания:

,

.

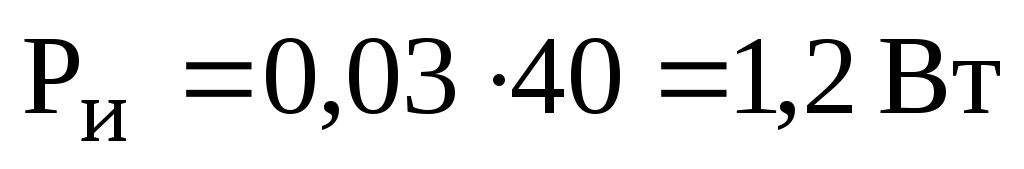Составляем уравнение для проверки баланса мощностей:

,

,

.

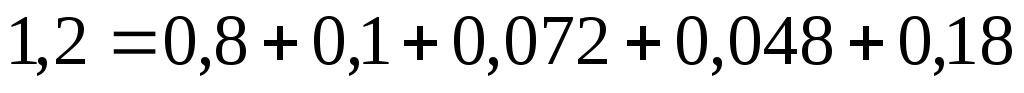Баланс мощностей выполняется.

Методические указания к выполнению задания 2.

Методы расчета цепей постоянного (переменного) тока

Под расчетом цепи, в общем случае, понимают нахождение токов во всех ветвях схемы.

Основные методы расчета:

1. Метод токов ветвей.

2.Метод контурных токов.

3. Метод узловых напряжений.

4. Метод наложения.

5. Метод эквивалентных преобразований

Метод токов ветвей

• В общем случае токи сложной электрической цепи могут быть определены в результате совместного решения уравнений, составленных по первому и второму законам Кирхгофа. Для однозначного нахождения всех токов необходимо составить в уравнений, где в— число ветвей схемы (без источников тока).

• Последовательность расчета следующая:

1. Проводят топологический анализ схемы.

1.1. обозначают токи во всех ветвях (I1, I2, …,Iв), произвольно выбирают их положительное направление и обозначают на схеме стрелками;

1.2. подсчитывают общее число узлов у и определяют число независимых узлов Nу=у-1 и показывают их на схеме;

1.3. подсчитывают число независимых контуров Nk = в-у+1, и показывают их на схеме дугой.

2. По первому закону Кирхгофа для независимых узлов и по второму закону Кирхгофа для независимых контуров относительно токов ветвей записывают уравнения. После приведения подобных членов они сводятся к системе линейных алгебраических уравнений (ЛАУ)

где x_i =Ii– искомые токи ветвей; a_ji – постоянные коэффициенты, зависящие от параметров пассивных элементов схемы; в_i – постоянные величины, зависящие от параметров активных элементов схемы.

3. Решая систему из в уравнений относительно токов, по методу Крамера находят токи во всех ветвях схемы:

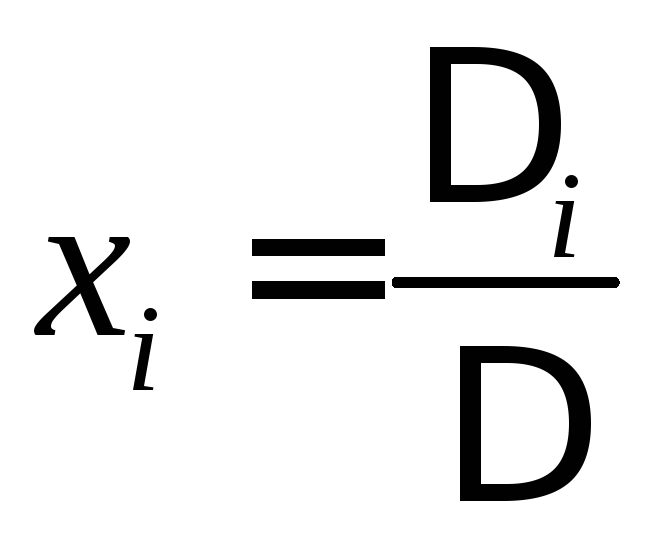
где D – главный определитель системы; Di – определитель, получается из главного D путем замены i-го столбца на столбец свободных членов в_i.

Если значения некоторых токов отрицательные, то действительные направления их будут противоположны первоначально выбранным направлениям. I1

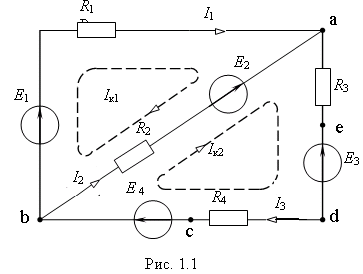
Пример 1. Для электрической цепи рис. 1.1 n = 2, m = 3, и расчет токов цепи осуществляется путем решения следующей системы уравнений

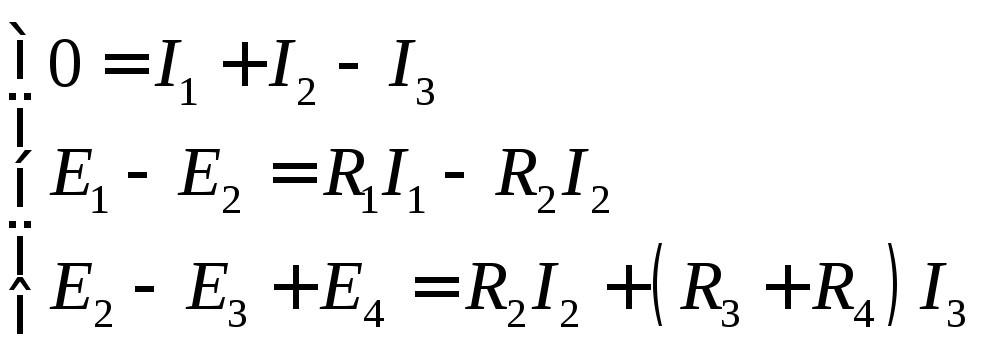
1.3. Расчет сложных цепей. Правила Кирхгофа

Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.

1. В разветвленных цепях можно выделитьузловые точки(узлы), в которых сходятся не менее трех проводников (рис. 1). Токи,втекающие в узел, принято считать положительными; токи, вытекающие из узла – отрицательными.

Рис. 1. Узел электрической цепи. I₁, I₂ > 0; I₃, I₄ < 0

2.Первое правило Кирхгофа:

Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:

I₁ + I₂ + I₃ + … + I_n = 0 или =0

При этом при расчетах уравнения по первому закону Кирхгофа записываются для (m-1) узлов, так как при записи уравнений для всехm узлов одно (любое) из них будет линейно зависимым от других, т.е. не дает дополнительной информации.

Первое правило Кирхгофа является следствием закона сохранения электрического заряда.

3. Контуры– это замкнутые пути в разветвленной цепи, состоящие из однородных и неоднородных участков. На разных участках выделенного контура могут протекать различные токи. Нарис. 2представлен пример разветвленной цепи. Цепь содержит узлыaиd, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d)

Рис. 2.Пример разветвленной электрической цепи. Цепь содержит один независимый узел (aилиd) и два независимых контура (например,abcd иadef).

В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например,abcd и adef), так как третий не содержит никаких новых участков.

4. Второе правило Кирхгофаявляется следствием обобщенного закона Ома.

Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 2, например, abcd. Для этого на каждом участке нужно задатьположительное направление токаиположительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдатьопределенные «правила знаков»,которые поясняются нарис. 3.

Для участков контура abcd обобщенный закон Ома записывается в виде:

Для участка bc: I₁R₁ = Δφ_bc – Е₁.

Для участка da: I₂R₂ = Δφ_da – Е₂.

Складывая левые и правые части этих равенств и принимая во внимание, что Δφ_bc = – Δφ_da, получимI₁R₁ + I₂R₂ = Δφ_bc + Δφ_da – Е₁ + Е₂ = –Е₁ – Е₂.:

Рис. 3. «Правила знаков».

Аналогично, для контура adef можно записать:

– I₂R₂ + I₃R₃ = Е₂ + Е₃.

Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.

Первое и второе правила Кирхгофа, записанные длявсехнезависимых узлов и контуров разветвленной цепи, дают в совокупностинеобходимое и достаточное число алгебраических уравненийдля расчета электрической цепи. Для цепи, изображенной нарис. 2,системаиз трех уравненийдля определениятрех неизвестных токов I₁, I₂ и I₃имеет вид:

I₁R₁ + I₂R₂ = – Е₁ – Е₂,

– I₂R₂ + I₃R₃ = Е₂ + Е₃,

– I₁ + I₂ + I₃ = 0.

Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению.

Применение правил Кирхгофа. При использовании правил Кирхгофа надо иметь в виду:

1. Число составляемых уравнений должно соответствовать числу неизвестных.

2. Составляя уравнение, надо следить, чтобы в каждое последующее входила хотя бы одна неизвестная величина, которая не входила в предыдущие уравнения.

3. Для каждого контура направление его обхода, определяющее знаки сил токов и ЭДС, выбирают произвольно. Если в результате решения получают отрицательное значение силы тока на каком–либо участке, то это означает, что ток на этом участке идет в направлении, противоположном выбранному обходу контура.

Урок на тему Законы Кирхгофа

П л а н у р о к а № 4 Дата____________

Законы Кирхгофа. (2 часа)

П 00. Профессиональный цикл

ОПД 13. Основы электротехники

Преподаватель: А.А. Гурьянов

— о первом законе Кирхгофа;

— о втором законе Кирхгофа;

— способах соединения проводников.

Воспитательная цель

Сформировать у учащихся усидчивость, внимательность, аккуратность, ответственность; организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

Развивающая цель

Сформировать у учащихся навыки:

— выбирать методы расчета в зависимости от типа цепей тока;

— составлять уравнения Кирхгофа для расчета электрических цепей;

— составлять исходные уравнения для расчетов сложной цепи постоянного тока.

Тип учебного

занятия

изучение нового материала.

Формируемые компетенции

ПК 1.2. Взаимодействовать с о специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности.

ПК 1.3. Производить модификацию отдельных модулей информационной системы в соответствии с рабочим заданием, документировать произведенные изменеия.

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.

Вид учебного

занятия

смешанный

Межпредметные связи

математика, физика

Оснащение,

оборудование

Учебник, компьютер, проектор, экран, интерактивная доска

Структура урока.

1. Организационный момент.

2. Актуализация знаний.

3. Формирование новых понятий и способов действий.

4. Формирование умений и навыков.

5. Итог урока.

6. Домашнее задание.

Ход урока.

1. Организационный момент.

Учет отсутствующих, проверка домашнего задания, сообщение темы и постановка целей урока.

2. Актуализация знаний.

1. Верно ли, что напряжение равно работе электрического тока?

2. От чего зависит сопротивление проводника?

3. Медный и стальной провода имеют одинаковые диаметр и длину. Какой из них сильнее нагревается при одной и той же силе тока?

4. Как определить длину мотка медной проволоки, не разматывая его?

5. Что представляют собой сверхпроводники?

6. Как зависит от длины кабеля электрическое сопротивление его жилы и сопротивление изоляции?

3. Формирование новых понятий и способов действий.

Электрическая цепь может иметь сложную форму, содержать несколько источников и большое количество потребителей электрической энергии, соединенных различными способами.

Характерными элементами такой цепи являются ветвь, узел и контур.

Ветвью электрической цепи называют участок, в котором ток в данный момент времени имеет одно и то же значение и изменяется одновременно и одинаково на всем про­тяжении участка. В частном случае ток может оставаться постоянным и одинаковым в пределах всего участка цепи, называемого ветвью.

Ветвь может содержать один или несколько последовательно соединенных источников ЭДС, может совсем не содержать источников ЭДС. Участки agf, af, ab и т.д. являются ветвями цепи, изображенной на рис. 1.7.

Точка электрической схемы, представляющая собой место соединения трёх или большего числа ветвей, называется узлом. В цепи, изображенной на рис. 1.7, четыре такие точки: a, b, d, /.

Замкнутая фигура, образованная ветвями электрической цепи, называется контуром. В рассматриваемой цепи можно выделить шесть контуров: afga, abdfa, bcdb, abdfga, abcdfa, abcdfga.

Первый закон Кирхгофа устанавливает, что алгебраическая сумма токов в узле равна нулю:

ΣI = 0.

Первый закон Кирхгофа непосредственно следует из того факта, что ни в одном узле схемы не (происходит накапливания электрических зарядов, т.е. количество зарядов, притекающих к узлу в единицу времени, равно количеству зарядов, утекающих от узла.

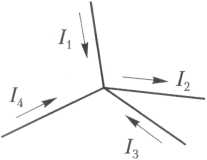На рис. изображен узел некоторой сложной цепи. Условимся токи, приходящие к узлу, считать положительными, а токи, уходя­щие от узла, — отрицательными. Тогда в соответствии с (1.15) мож­но написать уравнение

I₁ + (–I₂) + I₃+ I₄= 0.

Если токи, имеющие знак минус, перенести в правую часть уравнения, то получим

I₁ + I₃+ I₄=I₂

Последнее равенство позволяет дать первому закону Кирхгофа несколько иную формулировку: сумма токов, приходящих к узлу равна сумме токов, уходящих от узла.

Сложная электрическая цепь, основные определения.

Первый закон Кирхгофа (331)

Сколько в этой электрической цепи:

а) узлов;

б) ветвей?

а) 3;

б) 7

164

а) 4;

б) 6

54

а) 4;

б) 5

165

а) 4;

б) 4

53

Сколько контуров в цепи, изображенной выше?

7

166

3

52

5

167

6

51

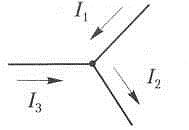
I₁ = – 5 А

I₂ = 2 A

Найдите I₃

7 А

168

3 А

50

–3 А

169

–7 А

49

I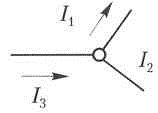₃ = 10 А

I₁ = 5 A

Определите действительное направление тока I, (направление движения положительных зарядов).

От узла

170

К узлу

48

Задача не определена

171

Приборы показывают, что к узлу притекают токи 3 А и 8 А, а утекают токи 5 А и 7 А. Сколько ветвей сходится в узле?

3

47

4

172

5

46

Не менее пяти

173

Второй закон Кирхгофа можно сформулировать следующим образом: в любом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения на сопротивлениях, входящих в контур:

ΣE = ΣIR

Отсюда следует также, что падение напряжения на каком-либо участке контура равно сумме падений напряжения на сопротивлениях, входящих в этот участок.

При записи уравнения ΣE = ΣIR необходимо произвольно выбрать направление обхода контура; токи и ЭДС, направление которых совпадает с выбранным направлением обхода, считать положительными, а токи и ЭДС, направление которых противоположно направлению обхода контура, считать отрицательными.

Например, обходя контур abdfa против часовой стрелки, запишем:

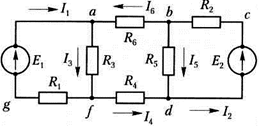
0 = I₃R₃ + I₄R₄ – I₅R₅ + I₆R₆,

обходя контур bcdb по часовой стрелке, запишем –Е = –I₂R₂ – I₅R₅

и т.д. для всех контуров.

Второй закон Кирхгофа выражает тот факт, что в потенциальном поле работа сил поля, совершаемая при обходе зарядом замкнутого контура, равна нулю.

Второй закон Кирхгофа(282)

Какие из величин I₁, I₂, I₃, E₁, E₂ войдут в уравнения второго закона Кирхгофа со знаком минус?

E₁, I₁

174

E₂, I₂

45

I₃

175

Это зависит от выбора направления обхода контуров электрической цепи

44

В какой строке уравнения второго закона Кирхгофа для изображенной выше цепи записаны правильно?

E₁ = I₁R₁; E₂ = –I₂R₂ + I₃R₃

176

–E₁ = I₁R₁ + I₃R₃; E₂ = I₃R₃ –I₂R₂

43

–E₁ = I₁R₁ + I₃R₃; E₂ = –I₂R₂

177

Е₁ = 110 В;

R₁ = 1 Ом;

I₁ = 10 А.

Найдите напряжение между точками ab изображенной выше цепи.

120 В

42

110 В

178

100 В

41

Задача не определена, т.к. неизвестны R₃, I₃

179

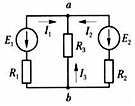
Е₂ = 24 В;

R₂ = 1 Ом;

I₂ = 6 А.

Определите U_ba

18 В

40

24 В

180

30 В

39

Для решения задачи недостаточно данных

181

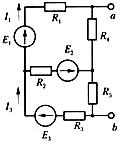
I₁ = 5 А.

I₃ = 10 А.

R₄ = 2 Ом;

R₅ = 3 Ом;

Определите U_ba

20 В

38

40 В

182

–40 В

37

Для решения задачи недостаточно данных

183

4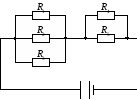. Формирование умений и навыков.

66. Сформулируйте законы Кирхгофа.

67. Сколько узлов, ветвей и контуров имеет электрическая цепь, изображенная на рис. 12?

Рис. 12

6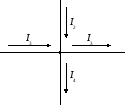8. Напишите уравнение согласно первому закону Кирхгофа для узла, изображенного на рис. 13.

Рис. 13

69. Нарисуйте электрический узел, для которого согласно первому закону Кирхгофа составлено следующее уравнение:

I₁ + I₂ – I₃ + I₄ – I₅ – I₆ = 0.

7

R₁

R₂

0. Напишите уравнения согласно второму закону Кирхгофа для контуров а-б-д-е и б-в-г-д, изображенных на рис. 14.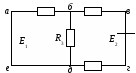

R₄

Рис. 14

7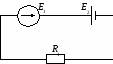1. Определите ток в цепи, изображенной на рис. 15, если ЭДС генератора Е₁ = 36 В, его внутреннее сопротивление r₁ = 0,5 Ом, ЭДС батареи Е₂ = 30 В, его внутреннее сопротивление r₂ = 0,2 Ом, сопротивление потребителя R₁ = 1,5 Ом.

Р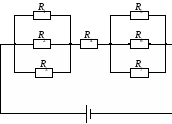ис. 15

72. В электрической цепи, схема которой приведена на рис. 16, резисторы имеют сопротивления R₁ = 2 Ом, R₂ = 6 Ом, R₃ = 18 Ом, R₄ = 10 Ом, R₅ = 3 Ом, R₆ = 9 Ом, R₇ = 27 Ом. Определите общий ток в цепи и напряжение на резисторе R₄, если к зажимам подведено напряжение 24 В.

Рис. 16

73. Напряжение сети составляет 12 В, общий ток, потребляемый четырьмя параллельно включёнными одинаковыми лампами, равен 6 А. Определите сопротивление каждой лампы.

7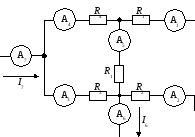4. Имеется разветвление, состоящее из четырёх параллельно включенных резисторов сопротивлениями 10, 5, 3 и 8 Ом. Ток, протекающий к точке разветвления, равен 20 А. Определите ток, протекающий по каждой ветви.

Рис. 17

75. Показания амперметров А₇, А₁ и А₆в сложной цепи (рис. 17) соответственно равны 10, 8 и 1 А, показание амперметра А₅ равно нулю. Определите значения и направления неизвестных токов.

76. Напряжение генератора 110 В. В сеть включены параллельно тридцать ламп сопротивлением по 200 Ом каждая. Определите ЭДС генератора, если его внутреннее сопротивление 0,5 Ом.

5. Итог урока.

Проверка выполнения задач, выставление оценок, сообщение домашнего задания.

6. Домашнее задание.

Выполнить упражнения, которые остались не выполненными.

РАСЧЕТ ЦЕПЕЙ ПО ЗАКОНАМ КИРХГОФА

⇐ ПредыдущаяСтр 5 из 9Следующая ⇒

Пример решения задачи

-первый закон Кирхгофа

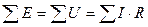— второй закон Кирхгофа

Составляем уравнения по законам Кирхгофа для данной схемы

Пример решения задачи:

Дано:

E₁ = 24 B

E₂ = 18 B

R_i1 = 0, Ом

R_i2 = 0, Ом

R₁ = 1,5Ом

R₂ = 1,8Ом

R₃ = 2 Ом

Найти: I_1-3 — ?

Подставляя исходные данные

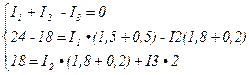
Сокращаем коэффициенты в уравнениях

Выражаем I₁ из первого уравнения и подставляем во второе

I₁=I₃-I₂

3=I₃-I₂-I₂=I₃-2I₂

Совместно записываем второе и третье уравнение и вычитаем почленно

3=I₃-2I₂

9=I₃+I₂

_{_————————}

-6=-3I₂

I₂=2A

Подставляем найденные I₂=2A в третье уравнение

9= I₂+I₃=2+I₃

I₃=9-2=7A

Подставляем I₂ и I₃ в первое уравнение

I₁= I₃-I₂ =7-2=5A

Ответы:

I₁=5A

I₂ =2A

I₃=7A

Оба источника работают в режиме генератора, так как ток и ЭДС совпадают по направлению

Тестовые задания:

Задание	Схема к заданию
1.Составьте в общем виде необходимое количество уравнений по законам Кирхгофа.

 

МЕТОД КОНТУРНЫХ ТОКОВ

Этот метод позволяет уменьшать количество уравнений в системе.

Порядок расчёта:

1. Выбираем производное направление контурного тока;

2. Составляем уравнение по второму закону Кирхгофа для контурных токов. При записи учитываем падение напряжения от собственного контурного тока и контурных токов соседних контуров;

3. Решаем полученную систему уравнений и определяем контурные токи;

4. Рассчитываем действительные токи ветвей по правилу:

если в ветви течёт один контурный ток, то действительный ток равен этому контурному; если течет несколько, то действительный равен алгебраической сумме.

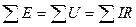— второй закон Кирхгофа

-E₁ — E₂ = I_1к∙(R₄ + R_i1 + R₁ + R_i2 + R₂) — I_2к∙(R₂ + R_i2)

E₂ — E₃ = I_2к∙(R₂ + R_i2 + R₃ + R_i3) — I_1к∙(R₂ + R_i2)

Пусть при решении получилось

I_1к=3A I_2к=2A

Тогда I₁ = I_1к=3A и направлен вверх

I₂ = I_1к — I_2к=3-2=1A и направлен вниз

I₃ = I_2к=2A и направлен вниз

Пример решения задачи

Дано:

E₁ = 24 B

E₂ = 18 B

R_i1 = 0,5 Ом

R_i2 = 0,2 Ом

R₁ = 1,5 Ом

R₂ = 1,8 Ом

R₃ = 2 Ом

Найти: I_1-3-?

30=6I_1к 6=4∙5-2I_2к

I_1к=5A I_2к=7A

_______________

I₃₌I_2к=7A

I₁= I_1к=5A

I₂= I_2к— I_1к=7-5=2A

 

Тестовые задания:

Задание	Схема к заданию
1.Составьте в общем виде необходимое количество уравнений по методу контурных токов.

 

МЕТОД ДВУХ УЗЛОВ

1.Обозначим узлы (А;В)

Под узлом А обозначим узел, к которому направлено больше ЭДС

2.Все токи направляем к узлу А

3. Рассчитываем проводимость каждой ветви по формуле единица разделить на сумму всех сопротивлений ветви.

G₁= 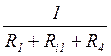См

G₂= См

G₃= См

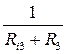G₄= См

4) Определяем напряжение между двумя узлами, в эту формулу Е входит со знаком «плюс» если она направлена к узлу А и со знаком «минус» , если от узла

∙

5) Записываем токи ветвей

I₁=(E₁-U_AB)∙G₁

I₂=(E₁-U_AB)∙G₂

I₃=(-E₃-U_AB)∙G₃

I₄=(-U_AB)∙G₄

6) Меняем направлен отрицательных токов (I₃, I₄)

 

 

Пример решения задачи

Дано:

E₁=120 В

E₈=128 В

R_i1=1 Ом

R₁=10 Ом

R₂=19 Ом

R₃=40 Ом

R₄=3 Ом

R₅=20 Ом

Найти: I_1-5=?

G₁

G₂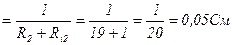

G₃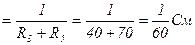

U_AB=

I₁=(E₁-U_АВ)∙G₁=(120-108)∙ = = =0,8A

I₂=( E₂-U_АВ )∙G₂=(128-108)∙ =1A

I₃=- U_АВ∙G₃ =(-108)∙

I₃^‘=1,8A

Ответ:I₁= I_i1=0,8A

I₂=1A

I₃=I₅=1,8A

Тестовые задания:

Задание	Схема к заданию
1.Составьте в общем виде решение задачи по методу двух узлов.

 

МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА

Этим методом удобно рассчитывать ток в одной ветви, особенно, если сопротивление этой ветви меняется.

Цель называется активной, если она содержит внутри себя источники или усилительные элементы и пассивной, если нет (R, L, C).

Согласно теории об эквивалентном генераторе любой активный двухполюсник можно заменить эквивалентным ЭДС с эквивалентным внутренним сопротивлением.

 

Схема с активным двухполюсником из нее следует

Чтобы найти Е_э надо разомкнуть ветвь АВ и найти напряжение на зажимах разомкнутой ветви.

Пример решения задачи методом эквивалентного генератора.

 

Дано

U_АВ = U_хх = Е_э

E₁ = 15 B

E₂ = 5 B

R₁ = 3 Ом

R₂ = 5 Ом

R₃ = 19,6 Ом

R_i = 1 Ом

I₃-?

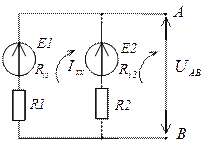
Обходим контур, который замыкается через U_AB по второму закону Кирхгофа.

E₂ = — I_xx∙(R₂ + R_i2) + U_AB

5 = — 6 + U_AB

U_AB = 11 B

U_AB=Eэ = 11 В

Чтобы найти R_э надо разомкнуть ветвь АВ, исключить все ЭДС, оставив их внутренне сопротивление и рассчитать входное сопротивление цепи по отношению к зажимам разомкнутой ветви.

R_i1,1=R_i1+R₁=1+3=4 ОМ

R_i2,2=R_i2+R₂=1+5=6 Ом

I₃= A

Дано:

E₁=150B

E₂=10 B

E₃= 80B

R_i1=R_i2= R_i3=1Ом

R₁=10 Ом

R₂=118 Ом

R₃=29 Ом

R₄=80 Ом

R₅=20 Ом

I₅-?

Пример решения задачи.

E₃ -E₂=-I_xx(R_i3+R₂+R_i2)+U_AB

80-10=-0,5∙120+U_AB

U_AB=130B

E_э=U_AB=130B

R_i1,1-3=R₁+R_i1+R₃=10+1+29=40Ом

R_i2,2-3=1+118+1=120Ом

I₅=

 

ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ

Активные элементы — это источники и усилительные элементы.

Пассивные — резисторы, катушки индуктивности и конденсаторы.

Операционный усилитель — активный резистивный элемент, который выполняет в технике связи основной усилительный эффект. Представляет собой то или иное число транзисторов (до 20) и резисторов. Выполняется в виде интегральных микросхем.

Схемное изображение операционного усилителя:

Операционный усилитель имеет 8 выводов: 2 входных, 1 выходной, 1 заземлённый и 2 для регулировки, 2 источника питания. Напряжение питания 12-15 В.

Достоинства:

1) очень высокий коэффициент усиления μ = 10⁴ — 10⁵;

2) очень высокое входное сопротивление R_вх = 10⁵ и выше;

3) маленькое выходное сопротивление R_вых = единицы Ом.

Неинвертируемый (положительный) вход операционного усилителя — это такой вход, при подаче на который напряжения одной полярности на выходе получается напряжение той же полярности.

Инвертируемый (отрицательный) вход операционного усилителя — это такой вход, при подаче на который напряжения одной полярности на выходе получается напряжение другой полярности.

Работа операционного усилителя сводится к тому, что напряжение источника питания преобразуется по закону входного напряжения, но напряжение на выходе не может быть больше, чем напряжение источника питания. Поэтому, если операционный усилитель работает без обратной связи, то на его выходе всегда будет сигнал прямоугольной формы, равный напряжению источника питания.

Схема включения операционного усилителя без обратной связи:

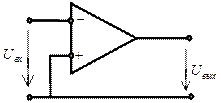
Понятие об обратной связи

Обратная связь — это цепи, через которые часть напряжения с выхода четырёхполюсника снова подаётся на вход того же четырехполюсника.

ООС — отрицательная обратная связь — это когда выходное напряжение подаётся на вход со знаком противоположным знаку входного.

ПОС — когда выходное напряжение подаётся на вход с тем же знаком, что и знак входного напряжения.

Операционный усилитель всегда работает с глубокой отрицательной обратной связью. Поэтому его коэффициент передачи уменьшается, но зато улучшаются его другие свойства (стабильность, полоса пропускания).

Схема операционного усилителя с обратной связью:

R_вх = R₁

R_обр.св. = R₂

 

 

Тестовые задания:

Задание	Варианты ответов
1.Является ли операционный усилитель активным элементом?	Да; Нет.
2.Можно ли на выходе операционного усилителя получить напряжение больше чем напряжение питания?	Да; Нет.
3.Является ли очень высокий коэффициент передачи операционного усилителя его достоинством?	Да; Нет.

 

МЕТОД НАЛОЖЕНИЯ

Основан на принципе, согласно которому, ток в которой ветви может быть найден, как алгебраическая сумма токов от действия каждой ЕДС в отдельности

Порядок расчета

1. Поочередно оставляем в схеме по одному источнику

2. Внутренние сопротивления исключаемых источников остаются

3. Получаем расчет схемы для нахождения частичных токов. Эти токи обозначаем со « ′ » и рассчитываем по закону Ома

4. Находим действительные токи ветви, как алгебраическую сумму частичных токов. Действительный ток направлен в сторону большего действительного

 

 

 

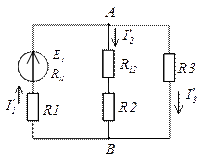
Пусть при решении получилось

, , . Тогда

Пример решения задачи:

 

 

Рекомендуемые страницы:

Методы анализа, основанные на законах Ома и Кирхгофа

Главная → Примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ – МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 1 Методы расчета электрических цепей при постоянных токах и напряжениях → 1.1 Методы анализа, основанные на законах Ома и Кирхгофа Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ – МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ → 1 Методы расчета электрических цепей при постоянных токах и напряжениях

1.1 Методы анализа, основанные на законах Ома и законах Кирхгофа

Закон Ома устанавливает зависимость между напряжением и током на пассивной ветви, а также позволяет определить ток по известным потенциалам на концах ветви с источником напряжения.

Законы Кирхгофа применяют для нахождения токов в ветвях линейных и нелинейных схем при любом законе изменения во времени токов и напряжений.

Метод эквивалентных преобразований. При эквивалентных преобразований отдельные участки электрической цепи заменяются более простыми. Эквивалентность преобразования состоит в том, что токи и напряжения в непреобразованной части схемы не изменяются.

Последовательное упрощение схемы продолжается до ее преобразования в одноконтурную схему, после чего для расчета используется закон Ома.

Метод эквивалентных преобразований используется для нахождения внутреннего сопротивления эквивалентного генератора.

При помощи метода эквивалентных преобразований облегчают расчет расчет нелинейной цепи, упростив линейную часть цепи эквивалентными преобразованиями.

---

Принято пользоваться приведенным ниже алгоритмом метода законов Кирхгофа.

1. Произвольно выбирают положительные направления токов в ветвях и обозначают их на схеме.

2. Составляют уравнения по первому закону Кирхгофа: на одно уравнение меньше числа узлов (для последнего узла уравнение будет зависимым от предыдущих уравнений).

3. Выбирают независимые (главные) контуры и направление их обхода. Удобно для всех контуров выбрать одинаковое направление обхода.

4. Записывают уравнения по второму закону Кирхгофа для выбранных контуров.

5. Решая полученную систему уравнений, определяют искомые токи.

---

Решение задач на закон Ома и законы Кирхгофа

---

Задача 1.1. Определить эквивалентное сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К методом эквивалентных преобразований (рис. 1.1, a).

Рис. 1.1

Решение. Сохраняя топологию схемы, трансформируем ее к виду, удобному для анализа (отправная точка – потенциалы узлов c и d равны между собой).

Из рис. 1.1, б следует:

1. При разомкнутом ключе К

Rab=R1⋅R3R1+R3+ (R47+R5+R6)⋅R2 (R47+R5+R6)+R2.

2. При замкнутом ключе К

R47=R1⋅R3R1+R3+R47⋅R2R47+R2,

где

R47=R4⋅R7R4+R7.

---

Задача 1.2. Определить методом эквивалентных преобразований сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К для схемы, изображенной на рис. 1.2.

Рис. 1.2

Решение. Совершим поворот части схемы относительно зажимов c и d. В результате получим (рис. 1.3):

Рис. 1.3

1. При разомкнутом ключе К

Rab= (R1+R3)⋅ (R2+R4) (R1+R3)+ (R2+R4).

2. При замкнутом ключе К

Rab=R1⋅R4R1+R4+R2⋅R3R2+R3.

Задача 1.3. Найти сопротивление между зажимами a и b для схемы, изображенной на рис. 1.4.

Рис. 1.4

Решение. К точке 2 подходят условные «начало» сопротивления R₂ и  «концы» сопротивлений R_l и R₃.

К точке 3 подходят «начала» сопротивлений R₁ и R₃ и  «конец» сопротивления R₂.

Но тогда, все «начала» сопротивлений и все их «концы» соединяются соответственно в одни точки. А значит, по определению, имеем параллельное соединение приемников (рис. 1.5).

Рис. 1.5

Таким образом, сопротивление между зажимами a и b:

Rab=1Yab=11R1+1R2+1R3.

---

Задача 1.4. Найти сопротивление R₁₃, R₁₄, R₁₇ между различными парами вершин куба, ребра которого имеют заданное сопротивление R (рис. 1.6).

Рис. 1.6

Решение. Задачу проще всего решить методом амперметра и вольтметра. Суть метода заключается в следующем. Если к фиксированным точкам схемы a и b подвести условно известное напряжение U_ab и определить ток I во внешней цепи, то искомое сопротивление R_ab = U_ab/I. При этом напряжение U_ab (показание вольтметра) в соответствии с законами Кирхгофа определяется как функция тока I (показание амперметра).

1. Расчетная схема для определения сопротивления R₁₃ имеет вид, представленный на рис. 1.7.

Рис. 1.7

В силу симметрии потенциалы точек 2 и 6 (4 и 8) равны между собой. Поэтому токи в ребрах. 2 – 6 и 4 – 8 отсутствуют.

Перераспределение токов I₁ и I₂ легко находится из первого закона Кирхгофа и соответствует рисунку 1.7.

Соотношение между токами найдем из второго закона Кирхгофа:

U14=U15+U58+U84;I1⋅R=I2⋅R+12I2⋅R+0=32I2⋅R.

Откуда:

I1=32I2;  I2=23I1.

А значит, общий ток

I=2I1+I2=2I1+23I1=83I1.

Но

U13=I⋅R13=83I1⋅R13=U12+U23=2I1⋅R.

Откуда, сокращая на I₁, имеем 8/3·R₁₃ = 2R. Или, что-то          же, искомое R₁₃ = 3/4·R.

2. Расчетная схема для определения сопротивления R₁₄ имеет вид, представленный на рис. 1.8.

Рис. 1.8

В силу симметрии токи в ребрах 1 – 2, 1 – 4, 2 – 3 и 4 – 3 равны между собой. А значит, в соответствии с первым законом Кирхгофа, токи в ребрах 2 – 6 и 4 – 8 отсутствуют.

Перераспределение неизвестных токов I₁, I₂, I₃, I₄ находится из первого закона Кирхгофа (и симметрии цепи) и соответствует рис. 1.8.

Поскольку падение напряжения

U23=U26+U67+U73;I4⋅R=I3⋅R+2I3⋅R+I3⋅R=4I3⋅R,

то, сокращая на R, имеем:

I4=4I3

или

I3=14I4.

Ток

I2=I3+I4=14I4+I4=54I4

или

I4=45I2.

Но

U14=U15+U58+U84;I1⋅R=I2⋅R+I4⋅R+I2⋅R=I2⋅R+54I2⋅R+I2⋅R=145I2⋅R.

Откуда, сокращая на R, имеем:

I1=145I2

или

I2=514I1.

Но

U14=I⋅R14= (I1+2I2)⋅R14= (I1+1014I1)⋅R14=2414I1⋅R14=I1⋅R.

Или, что то же, искомое R₁₄ = 14/24·R = 7/12·R.

3. Расчетная схема для определения сопротивления R₁₇ имеет вид, представленный на рис. 1.9.

Рис. 1.9

В силу диагональной симметрии схемы полный ток I = 3I₁.

Падение напряжения

U17=U14+U43+U37;I⋅R17=I1⋅R+12I1⋅R+I1⋅R=52I1⋅R.

Откуда искомое сопротивление R₁₇ = 5/6·R.

---

Задача 1.5. Определить методом эквивалентных преобразований токи в ветвях цепи (рис. 1 10, а) и показание вольтметра, включенного между точками c и d, считая, что его сопротивление во много раз превышает сопротивление каждого из элементов цепи.

Чему равно показание амперметра, включенного между точками c и d, сопротивление которого считать равным нулю?

Рис. 1.10

Сопротивления элементов цепи: R₁ =10 Ом, R₂ = R₃ = R₅ = 25 Ом и R₄ = 50 Ом, а приложенное к ней напряжение U = 120 В.

Решение. Расчет показания вольтметра. Из условия вытекает, что его включение не оказывает влияния на распределение токов в цепи. Для расчета токов сначала определяем эквивалентное сопротивление всей цепи (рис. 1.10, а):

R=R1+ (R2+R4)⋅ (R3+R5) (R2+R4)+ (R3+R5)=10+75⋅50125=40   Ом.

В неразветвленной части цепи протекает ток

I1=UR=12040=3  A.

Токи, протекающие через сопротивления (R₂ + R₄) и (R₃ + R₅) можно найти различными способами.

1. В параллельных ветвях токи распределяются обратно пропорционально их сопротивлениям (формула разброса токов):

I2=I1⋅R3+R5 (R2+R4)+ (R3+R5)=3⋅50125=1,2  A;I3=I1⋅R2+R4 (R2+R4)+ (R3+R5)=3⋅75125=1,8  A.

2. Найдем напряжение на зажимах параллельных ветвей:

Uab=I1⋅ (R2+R4)⋅ (R3+R5) (R2+R4)+ (R3+R5)=3⋅75⋅50125=90   B.

Токи в ветвях с сопротивлениями R₂ + R₄ и R₃ + R₅ равны:

I2=UabR2+R4=9075=1,2  A;  I3=UabR3+R5=9050=1,8  A.

Напряжение на зажимах параллельных ветвей может быть найдено как разность между приложенным напряжением и падением напряжения на сопротивлении R₁: U_ab = U – R₁·I₁.

Найдем показание вольтметра, равное напряжению между точками с и d:

UV=Ucd=−I2⋅R2+I3⋅R3=−1,2⋅25+1,8⋅25=15  B.

Наконец, вычислим ток, проходящий через амперметр; он равен току короткого замыкания I’_cd (рис. 1.10, б). Для его нахождения вычислим токи:

I′1=UR1+R2⋅R3R2+R3+R4⋅R5R4+R5=14447  A;I′2=I′1⋅R3R2+R3=7247  A;  I′4=I′1⋅R5R4+R5=4847  A.

Искомый ток, проходящий через амперметр,

IA=I′cd=I′2−I′4=2447=0,51  A.

---

Задача 1.6. В схеме рис. 1.11 заданы сопротивления приемников, величины ЭДС и источника тока отдельных ветвей. Рассчитать неизвестные токи, ЭДС E₂ и сопротивление R₅, пользуясь законами Кирхгофа.

Рис. 1.11

Правильность решения проверить по балансу мощностей. Для наружного контура построить потенциальную диаграмму и определить показание вольтметра.

Решение

1. Всего в схеме пять ветвей, неизвестных токов I₁, I₂, I₅ – три, неизвестных величин E₂ и R₅ – две, для нахождения которых составам три уравнения по первому закону Кирхгофа и два – по второму закону Кирхгофа:

для узла  b:   J=I4+I5;для узла  d:   −I5−I3+I1=0;для контура  I:   I5R5−I4R4=E3+E4;для контура  II:   I1R1+I2R2=E1+E2−E3.

Из первых трех уравнений находим токи:

I5=J−I4=4−2=2  A;I1=I5+I3=2+3=5  A;I2=−J+I1=−4+5=1  A.

из четвертого уравнения

R5=E3+E4+I4⋅R4I5=10+6+142=15  Ом.

Величину E₂ определяем из последнего уравнения:

E2=I1⋅R1+I2⋅R2−E1+E3=5⋅10+10⋅1−100+10=−30  B.

2. Для построения потенциальной диаграммы найдем потенциалы всех точек контура abcdea, приняв исходный потенциал точки a равным нулю:

φe=φa−I1⋅R1=0+5⋅10=50  B;φd=φe−E1=50−100=−50  B;φb=φd+I5⋅R5=−50+2⋅15=−20  B.

3. По найденным потенциалам строим потенциальную диаграмму, откладывая по оси ординат потенциалы точек, а по оси абсцисс – сопротивления участков (рис. 1.12).

Рис. 1.12

3. Из потенциальной диаграммы легко определить разность потенциалов между точками b и c U_bc = 70 В, что и будет показывать вольтметр.

4. Произведем проверку баланса мощностей:

Pисточников=E1⋅I1+E2⋅I2+E3⋅ (−I3)+E4⋅ (−I4)+Uba⋅J;Pпотребителей=I12⋅R1+I22⋅R2+I42⋅R4+I52⋅R5.

В этом уравнении нам неизвестно напряжение на зажимах источника тока U_ba, которое легко найти из потенциальной диаграммы: U_ba = –20 В. С учетом этого

Pисточников=100⋅5+ (−30)⋅1+10⋅ (−3)+6⋅ (−2)+ (−20)⋅4=348  Вт;Pпотребителей=52⋅10+12⋅10+32⋅0+22⋅7+22⋅15=348  Вт;Pисточников=Pпотребителей=348  Вт.

---

Закон Ома, законы Кирхгофа в статье ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. Основные положения и соотношения. Упражнения и задачи

второй закон Кирхгофа,  первый закон Кирхгофа,  Законы Кирхгофа,  закон Ома 

16.10.2011, 74175 просмотров.

Первый и второй законы Кирхгофа(метод непосредственного применения законов Кирхгофа)

Дано
R₁=16 Ом;
R₂=31 Ом;
R₃=24 Ом;
R₄=13 Ом;
R₅=33 Ом;
R₆=40 Ом;
R₇=22 Ом;
R₈=7 Ом;
E₁=30 В;
E₂=24 В;
E₇=16 В;
E₈=11 В.

Найти
Токи в цепи непосредственным применением законов Кирхгофа.

Решение

Составляем уравнения по законам Кирхгофа. Первый закон Кирхгофа говорит о том, что сумма втекающих и вытекающих токов в любом узле схемы равна нулю. Второй закон Кирхгофа гласит, что алгебраическая сумма падений напряжений по замкнутому контуру равна сумме ЭДС в этом контуре. В приведенной схеме m=7 ветвей и n=4 узла. Следовательно, по первому закону Кирхгофа должно быть составлено n-1=3 уравнения, а по второму закону Кирхгофа m-(n-1)=4 уравнения. Размечаем произвольно выбранные направления токов, контуры обходов, узлы схемы.

Ответ:
I₁=0,265 А; I₂=0,082 А; I₃=0,347 А; I₅=0,131 А; I₆=0,214 А; I₇=0,140 А; I₈=-0,273 А.

Найденные токи совпадают с токами, вычисленными с использованием метода контурных токов, что подтверждает правильность решения.