Второй закон Кирхгофа — FREEWRITERS
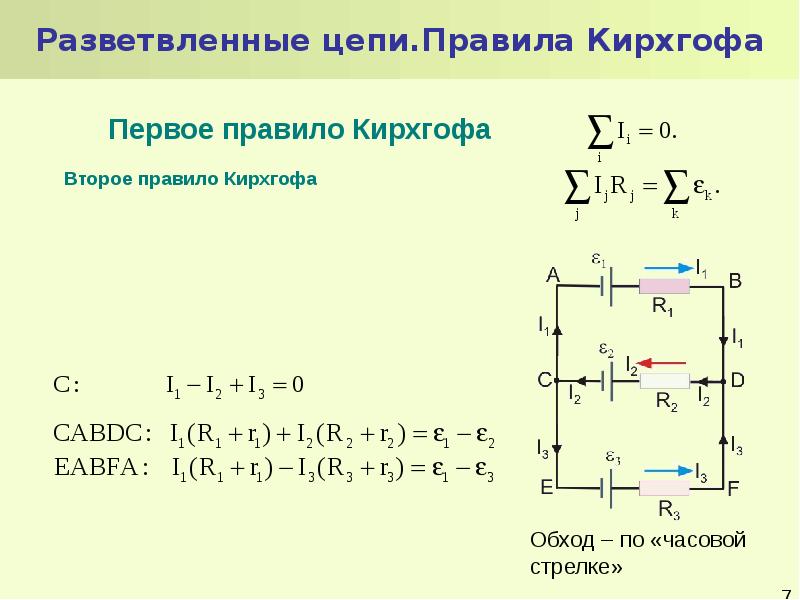
«Обойдем» любой контур в любой схеме, например контур ACDBA в схеме (рис. 1, б).
Рис. 1.
Смотрите еще:
Пример решения задачи по правилам Кирхгофа № 1
Пример решения задачи по правилам Кирхгофа № 2
Пример решения задачи по правилам Кирхгофа № 3
В той же самой схеме контур ADCBA:
В общем случае (рис. 2) для контура в разветвленной цепи определим разность потенциалов между отдельными точками цепи:
Рис. 2.
Добавив эти уравнения, получим, что:
или
В этом уравнении со знаком «плюс» берутся те ЭДС, где направление действия сторонних сил (внутренняя стрелочка) совпадает с направлением обхода контура, и со знаком «минус» — в противоположном случае; падение напряжения I·R имеет положительное значение, если направление тока и обхода совпадают, и со знаком «минус», когда ток направлен навстречу.
Если учесть, что ЭДС на идеальной части источника равняется соответствующему напряжению , то, согласно с указанным выше, имеем, что:
Т.
 е. алгебраическая сумма всех напряжений в контуре равняется нулю. Обобщив это, получим второй закон Кирхгофа:
е. алгебраическая сумма всех напряжений в контуре равняется нулю. Обобщив это, получим второй закон Кирхгофа:или
Таким образом, алгебраическая сумма ЭДС всех веток контура и падение напряжений на сопротивлениях ветвей одинаковы, или алгебраическая сумма напряжений в контуре равняется нулю.
Напомним, что под контуром понимают замкнутый путь обхода вдоль ветвей цепи (рис. 3)
Рис. 3.
Не следует путать с замкнутой цепью, как замкнутым путем прохождения тока (рис. 2). Уравнение справедливо как для цепи (рис. 3), где ветвь 5 – 8 разорвана кА для тока, так и для цепи (рис. 2), где все ветви замкнуты.
pravilo_Kirkhgofa — презентация онлайн
1.
 Расчет сложных цепей постоянного тока по I и II законам Кирхгофа
Расчет сложных цепей постоянного тока по I и II законам Кирхгофа2. Повторение изученного материала
3. Дайте определение сложной электрической цепи
• Сложными называются разветвленныеэлектрические цепи со многими источниками
энергии.
4. Дайте формулировку I закону Кирхгофа
• Алгебраическая сумма токов в каждомузле любой цепи равна нулю. При этом
направленный к узлу ток принято считать
положительным, а направленный от узла
— отрицательным.
n
I
i
0
5. Дайте формулировку II закону Кирхгофа
• Алгебраическая сумма паденийнапряжений на всех ветвях,
принадлежащих любому замкнутому
контуру цепи, равна алгебраической
сумме ЭДС ветвей этого контура.
n
n
U E
i 1
i
i 1
i
6. Решение задачи
7. Определить токи во всех ветвях данной электрической цепи
8. Найдем общее количество уравнений
• Для определения токов во всех ветвяхданной электрической цепи,
необходимо составить систему
уравнений по законам Кирхгофа.
• Общее число уравнений в системе должно
соответствовать числу неизвестных
токов, т. е. числу ветвей.
9. Посчитаем количество ветвей в нашей электрической цепи
R1Итого
5 ветвей, т.е.
R2
I2
I4
Е1
R4
Е2
R5
I5
I1
R3
I3
Е3
10. Найдем количество уравнений по I закону Кирхгофа
• По первому закону Кирхгофа составляетсячисло уравнений, на единицу меньшее
числа узлов цепи, т.к. уравнение для
последнего узла есть следствие всех
предыдущих уравнений и не дает
ничего нового для расчета.
11. Посчитаем количество узлов электрической цепи
2R1
Итого
3 узла, т.е.
2 уравнения
R2
I2
I4
Е1
R4
Е2
R5
I5
I1
R3
1
I3
Е3
3
12. Зададим направление токов во всех ветвях цепи
2R1
R2
I2
I4
Е1
R4
Е2
R5
I5
I1
R3
1
I3
Е3
3
13.
 Составим уравнения по I закону Кирхгофа • Токи, подходящие к узлу, будем считать
Составим уравнения по I закону Кирхгофа • Токи, подходящие к узлу, будем считатьа токи, отходящие от узла – (–).
2
R1
R2
I2
I4
Е1
R4
Е2
R5
I5
I1
R3
1
I3
Е3
Для узла № 1: –I1 – I3 – I4 = 0
Для узла № 2: I1 – I2 + I4 + I5 = 0
3
15. Найдем количество уравнений по II закону Кирхгофа
• По второму закону Кирхгофасоставляются все недостающие
уравнения для любых произвольно
выбранных контуров цепи.
• Посчитаем количество недостающих
уравнений: 5 – 2 = 3.
16. Зададим направление обхода выбранных контуров
2R1
R2
I2
I
Е1
III
I4
R4
Е2
R5
II
I5
I1
R3
1
I3
Е3
3
17. Составим уравнения по II закону Кирхгофа
• При составлении уравнений ЭДС итоки, совпадающие с выбранным
брать со знаком (+), а несовпадающие –
со знаком (–).

2
R1
R2
I2
I
Е1
III
I4
R4
Е2
R5
II
I5
Е3
I1
R3
1
I3
3
Для I контура: I1R1 – I4R4 = Е1
Для II контура: I4R4 – I5R5 – I3R3 = Е3
Для III контура: I2R2 + I5R5 = –Е2
19. Получилась система уравнений
–I1 – I3 – I4 = 0I1 – I2 + I4 + I5 = 0
I1R1 – I4R4 = E1
I4R4 – I5R5 – I3R3 = E3
I2R2 + I4R4 = –E2
Решив ее, получаем пять значений
токов.
Решение задач по методу Кирхгофа
§ 4. Решение задач по методу Кирхгофа
етоды изученные в предыдущих параграфах позволяют решить любую схему. Но чем сложнее схема, тем с большим количеством преобразований придется столкнуться. К примеру, сначала схему необходимо будет свернуть до одного контура, найти необходимые значения, затем постепенно её разворачивать производя все новые и новые вычисления.
Это
достаточно неудобно, и хотя закон Ома доказал свою универсальность, со временем
стали появляться и другие более удобные методы. Основой для каждого из методов
служит базисный закон – закон Георга Ома.
Основой для каждого из методов
служит базисный закон – закон Георга Ома.
Густав Роберт Кирхгоф (1824-1887), профессор физики Гейдельберского университета в Берлине, в 1846 году установил два правила, названные в его честь[18] – «Первое и Второе правило Кирхгофа для электрических цепей»[19].
§ 4.1. Первый закон Кирхгофа
Первый закон Кирхгофа. Алгебраическая сумма токов в любом узле равна нулю.
При выведении первого закона Кирхгоф опирался на закон сохранения электрического заряда[20]. Если в разветвление X, проводящей цепи входит ток силой I, а выходят токи I1 и I2, за время ∆t в область разветвления втекает электрический заряд , а вытекает заряд . Приравнивая эти величины, друг к другу находим:
Если же в узле сходится n проводников, то
где
под Ii понимают алгебраическую величину силы тока, которая берется
со знаком «плюс», если ток входит в узел, и со знаком «минус» если выходит. Это правило называется правилом знаков.
Это правило называется правилом знаков.
Таким образом, мы получаем, что в один узел не могут втекать все токи из прилегающих ветвей, и из одного узла не могут вытекать все токи. Так как это нарушит закон сохранения заряда.
§ 4.2. Второй закон Кирхгофа для участка цепи.
Как уже говорилось, законы Кирхгофа включают в себя закон Ома. И второй закон для участка цепи
а закон Ома приобретает вид:
Когда
на участке AB имеется
источник тока с ЭДС E, разность потенциалов
изменяется на величину , где знак выбирается в
зависимости от полярности включения источника (по току или против него). Тогда соотношение 4.4 принимает вид:
Тогда соотношение 4.4 принимает вид:
Если цепь сложная рис 4.3, то на пути от точки А к точке В может встретиться m источников тока ЭДС Ei и n сопротивлений Rk, по которым протекают токи Ik. Тогда второй закон Кирхгофа для участка цепи записывается так:
Из соотношения 4.6 выразим силу тока:
В такой записи это соотношение получило название обобщенный закон Ома. Для электрической схемы изображенной на рисунке 4.3 сила тока по обобщенному закону Ома будет выглядеть так:
§ 4.3. Второй закон Кирхгофа для замкнутого контура.
Второй закон Кирхгофа для замкнутого контура. В любом контуре электрической цепи алгебраическая сумма ЭДС, источников напряжения, равна алгебраической сумме падений напряжения вдоль этого контура.
Второй
закон Кирхгофа для замкнутого контура также основан на законе Ома и
законе сохранения энергии – в замкнутой системе, сколько энергии излучается,
столько же энергии и поглощается, таким образом, общее количество энергии
остается неизменным.
Возьмем, к примеру, электрическую схему изображенную на рисунке 4.4. Стрелкой в верхнем левом углу обозначен обход контура. Обычно, но не обязательно, его направление выбирается по часовой стрелке. Обход необходим для правильного составления уравнения, так как при записи уравнений по второму[22] закону Кирхгофа используется следующее
Если заданные или выбранные направления ЭДС, напряжений и токов в ветвях совпадают с обходом контура, то ЭДС в суммах слева, напряжения и токи в суммах справа записывают со знаком «плюс», если не совпадают с обходом контура – со знаком «минус».
Теперь составим уравнение для принципиальной электрической схемы, изображенной на рис 4.4. Направление токов выбрано совершенно случайно, только для этого примера.
§ 4.3. Метод решения задач на основе законов Кирхгофа.
Для того чтобы уметь
применять законы Кирхгофа решим трех контурную электрическую цепь изображенную
на рис. 4.5.
4.5.
Раздел долгосрочного плана 10.3В – Постоянный ток | Школа: ФИО учителя: | |||||||
Дата: |
| |||||||
Класс: 10 | Количество присутствующих: |
отсутствующих: — | ||||||
Тема урока | Законы Кирхгофа
| |||||||
Вид урока | Урок отработки навыков решения задач | |||||||
Цели обучения, которые достигаются на данном уроке | 10.4.2.6 — применять законы Кирхгофа к разветвленным электрическим цепям
| |||||||
Цели урока | — применять первый закон Кирхгофа при решении задач; — применять второй закон Кирхгофа при решении задач; — применять
универсальный метод для расчета сложных цепей. | |||||||
Критерии оценки | Знание : понятия – узел. Ветвь, контур Понимание: Понимать первый и второй законы Кирхгофа Применение: законы при решении задач Анализ: анализировать условие задачи и результат расчетов. Синтез: решение задач практического характера. Оценивание: самооценка своей деятельности | |||||||
Языковые цели | Учащиеся могут …читать сложные цепи, записывать уравнения по первому и второму законам Кирхгофа Словарь специфических терминов и терминология: узел, ветвь, контур направление обхода контура. Набор полезных фраз для общения/письма: для расчета цепи необходимо найти токи на всех участках цепи; Сила тока на участке цепи прямо пропорциональна… Общее сопротивление цепи при смешанном соединении…; падение напряжения на концах проводника; | |||||||
Привитие ценностей
| Развивать
мышление учащихся, интерес к изучению физики. Обучение на протяжении всей жизни | |||||||
Межпредметные связи | Умение решать систему линейных уравнений ученики научились на математике | |||||||
Первоначальные знания | Закон Ома для полной цепи; источники постоянного тока; закон Ома для участка цепи; элементы электрических схем и их обозначения; последовательное и параллельное соединение проводников; энергия и мощность электрического тока. Законы Кирхгофа. | |||||||
План | ||||||||
Этапы урока | Запланированная деятельность на уроке | Ресурсы | ||||||
Начало 1 мин.
2-3 мин
1 мин
|
2. « Проверка и актуализация опорных знаний » Цель: Проверить понимание темы предыдущего урока.Систематизировать знания учеников, настроить на отработку навыков решения задач на расчет сложных цепей Описание: Ученики открывают тетради с
выполненным домашним заданием. Учитель узнает – нет ли вопросов по решению
домашней задачи у учеников. Если вопросов нет, то учитель задает наводящие
вопросы по решению задачи. Отвечает ученик по выбору учителя.Если есть
вопросы, то учитель просит ответить на них учеников, справившихся с решением. Деятельность учителя: задает вопросы, контролирует ответы учеников и их обсуждение. Деятельность ученика: отвечает на вопрос. Слушают остальных учеников, дополняет и комментирует ответы. Оценивание: самооценка. Взаимооценка, проверка знаний по теме.
Деятельность учителя: Учитель сообщает тему урока “Применение законов Кирхгофа для расчета сложных цепей”. Сообщает цель обучения и цели урока. |
Слайд № 2-4
Слайд № 5-7
| ||||||
Середина 10 мин
15 мин
5-7 мин |
4. Цель: Познакомить учеников с практическим применением законов Кирхгофа.. Описание: Ученики просматривают видео, зарисовывают схемы в тетрадь, записывают результаты опыта, делают выводы. Ученики выполняют работу самостоятельно. (Используются индивидуальные компьютеры или видео транслируются на интерактивной доске)Деятельность учителя: Учитель контролирует выполнение задание всеми учениками, оказывает поддержку ученикам, не справляющимся с заданием. Учитель может останавливать трансляцию видео, задавать дополнитнльные вопросы. Деятельность ученика: Ученики самостоятельно выполняют задание. Делают выводы, правильно зарисовывают схемы и подключение измерительных приборов. Оценивание: Самооценка
5. «Решение задач» Цель: Отработать навыки решения задач по теме — законы Кирхгофа» Описание: Задачи №10.86 (задачник по физике авт. Волькенштейн В.Л.) и № 21.30 ( задачник по физике авт. Гольдфабр Н.И.). Если
нет задачника, условие можно взять из видео «Урок265». При необходимости
можно ученикам дать возможность просмотреть решение задачи или проверить
решение после самостоятельного решения. Волькенштейн В.Л.) и № 21.30 ( задачник по физике авт. Гольдфабр Н.И.). Если
нет задачника, условие можно взять из видео «Урок265». При необходимости
можно ученикам дать возможность просмотреть решение задачи или проверить
решение после самостоятельного решения.Деятельность учителя: Учитель объясняет алгоритм решения задач, контролирует выполнение всеми учениками, оказывает поддержку ученикам, не справляющимся с заданием. Ведет беседу с учениками и демонстрирует выводы на доске. Деятельность ученика: Ученики ведут записи в тетрадях, Ведут совместные рассуждения, выполняют самостоятельно расчеты, сравнивают результаты. По готовым ответам проверяют себя. Оценивание: Самооценка
6. «Проверка усвоения знаний и умений» Цель: Проверка усвоения материала . Описание: Тестовые задания, которые позволят быстро проверить первичные знания учеников. Ученики выполняют самостоятельно.Деятельность учителя: Учитель объясняет правила
выполнения теста, контролирует выполнение всеми учениками, оказывает
поддержку ученикам, не справляющимся с заданием. Деятельность ученика: Ученики самостоятельно выполняют задание. По готовым ответам проверяют себя. Оценивание: Самооценка (по слайду) |
Видео 1 и 2 закон Слайд № 8
Видео урок № 265 Слайды №10
Приложение 4
Слайд № 12
| ||||||
Конец 2 мин
1 мин |
1. «Рефлексия» Цель: проверить усвоение материала Описание: беседа – что узнали нового? – где используется изученное? – что вам дает умение вести расчеты сложных цепей? Оценивание: обратная связь
Задача № 10.91 , (задачник по физике авт. Волькенштейн В.Л.
|
Слайд № 13
Слайд № 14
| ||||||
Дополнительная информация | ||||||||
Дифференциация – как Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащихся? | Межпредметные связи | ||||||
При объяснении нового материала трудно дифференцировать подаче материала. Для учеников самостоятельно изучающих физику и опережающих программу следует подготовить дополнительные задания с критериями оценивания. | Самооценка
учеников по готовым ответам при выполнении теста. Во время изучения нового материала – обратная связь и поддержка со стороны учителя. | При решении системы линейных уравнений ученики используют знания, полученные на уроках математики. | ||||||
Общая оценка
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: Коллективная работа при осмыслении нового материала. 2:Использование слайдов при поэтапном разборе решения задачи. Какие две вещи могли бы улучшить урок (подумайте как о преподавании, так и об обучении)? 1: Просмотр видеоролика каждым учеником самостоятельно, позволит ускорить понимание продвинутым ученикам и при необходимости, повторить просмотр некоторым ученикам 2: Проверить выполнение законов Кирхгофа ри выполнении практической работы. Что я узнал(а) за время урока о классе или отдельных учениках такого, что поможет мне подготовиться к следующему уроку? Следующий урок
следует начать с проверки решения домашней задачи.
| ||||||||
Презентация по физике на тему «Закон Кирхгофа» 10 класс профиль
Урок-практикум в 10 классе
Расчет сложных электрических цепей. Законы Кирхгофа.
Цели урока:
формирование понятия о законах Кирхгофа
применение законов Кирхгофа для расчёта разветвлённых цепей
формирование чувства взаимопомощи, умения работать в группах
развитие самостоятельности мышления
развитие творческих способностей
1. Информационный модуль. Законы Кирхгофа.
Все э.д.с., токи и сопротивления любой цепи связаны между собой уравнениями, выражающими законы Кирхгофа. Эти уравнения могут быть записаны, если известны не только величины э.д.с. и токов, но и их направления.
I закон Кирхгофа: сумма токов, протекающих к точке разветвления (узловой точке), равна сумме токов, утекающих от этой точки (слайд 3)
II закон Кирхгофа: во всяком замкнутом контуре алгебраическая сумма э. д.с. равна алгебраической сумме падений напряжений на отдельных участках этого контура (Слайд 4)
д.с. равна алгебраической сумме падений напряжений на отдельных участках этого контура (Слайд 4)
Расчет сложной цепи при помощи уравнений Кирхгофа проводят в следующей последовательности (слайд 5):
по возможности упрощают расчетную схему (заменив, например, несколько параллельно соединенных сопротивлений одним эквивалентным сопротивлением
наносят на схеме известные направления э.д.с.
задаются произвольными положительными направлениями токов
составляют уравнения по первому закону Кирхгофа для всех узловых точек схемы, кроме одной, так как для получения требуемого числа независимых уравнений следует применить первый закон Кирхгофа ко всем узловым точкам, кроме одной, т. е. составить (n—1) уравнений, если число узлов равно п. Недостающие уравнения должны быть составлены по второму закону Кирхгофа так, чтобы каждое следующее уравнение не могло быть получено из предыдущих.
составляют недостающие уравнения по второму закону Кирхгофа, обходя замкнутые контуры по часовой стрелке или против часовой стрелки.
 При этом э.д.с. и токи, совпадающие с направлением обхода, принимаются положительными, а э.д.с. с. и токи, противоположные (т. е. встречные) этому направлению, — отрицательными;
При этом э.д.с. и токи, совпадающие с направлением обхода, принимаются положительными, а э.д.с. с. и токи, противоположные (т. е. встречные) этому направлению, — отрицательными;решают составленную систему уравнений и определяют неизвестные токи. Если некоторые значения токов получаются со знаком «минус», то это означает, что они имеют направления, обратные тем, которые были условно приняты для этих токов в начале расчета.
Если в результате расчета сложной цепи фактическое направление тока в энергопреобразующем устройстве (электрической машине или аккумуляторе) совпадает с направлением его э.д.с., то это свидетельствует о том, что рассматриваемое устройство работает в качестве источника электроэнергии, а не электроприемника. Если направление тока обратно направлению э.д.с., то это означает, что устройство является электроприемником.
Рис. 1.Схема разряда (а) и заряда (б) аккумулятора
На рисунке 1. а) аккумулятор работает как генератор, в схеме 1. б) он является потребителем электрической энергии.
б) он является потребителем электрической энергии.
2. Модуль практической деятельности. Применение законов Кирхгофа для расчета сложных цепей.
Демонстрационная задача (слайд 6):
В электрической цепи ЭДС первого источника , а второго В.
Сопротивления всех резисторов одинаковые Ом. Определить токи во всех участках цепи.
Произвольно выбираем направления токов I, I1, I2 и две узловые точки А и В (слайд 7)
Так как требуется найти три неизвестных, то составим систему из трёх уравнений. Одно уравнение запишем согласно I закону Кирхгофа и два по II закону Кирхгофа
Считаем > 0 — так как ток переходит от «-» к «+», < 0 — так как ток переходит от «+» к «-»
Один из способов решения полученной системы:
Выразим из уравнений (2) значение тока
(2/)
Подставим полученное выражение (2/) в уравнение (3)
После сокращений и преобразований находим значение тока
(3/)
Из формул (1), (2/) и (3/) рассчитываем значения сил токов и получаем:
I1 = 5 А, I2 = 2 А, I= 7 А
Отработка алгоритма решения задач с использованием законов Кирхгофа.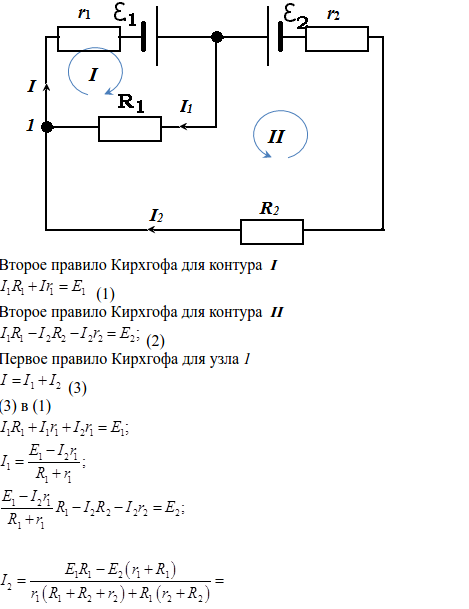 Задачи для самостоятельного решения (слайд 8):
Задачи для самостоятельного решения (слайд 8):
Работа в группах предполагает обсуждение и совместное решение.
Задача 1 – подобная демонстрационной задаче
Дана схема, и известны сопротивления резисторов и ЭДС источников. Требуется найти токи в ветвях, используя законы Кирхгофа.
Возможное решение:
Используя первый закон Кирхгофа, можно записать n-1 уравнений для цепи. В нашем случае количество узлов n=2, а значит нужно составить только одно уравнение.
Напомним, что по первому закону, сумма токов, сходящихся в узле равна нулю. При этом, условно принято считать входящие токи в узел положительными, а выходящими отрицательными. Значит для нашей задачи
Затем используя второй закон (сумма падений напряжения в независимом контуре равна сумме ЭДС в нем) составим уравнения для первого и второго контуров цепи. Направления обхода выбраны произвольными, при этом если направление тока через резистор совпадает с направлением обхода, берем со знаком плюс, и наоборот если не совпадает, то со знаком минус. Аналогично с источниками ЭДС.
Направления обхода выбраны произвольными, при этом если направление тока через резистор совпадает с направлением обхода, берем со знаком плюс, и наоборот если не совпадает, то со знаком минус. Аналогично с источниками ЭДС.
На примере первого контура – ток I1 и I3 совпадают с направлением обхода контура (против часовой стрелки), ЭДС E1 также совпадает, поэтому берем их со знаком плюс.
Уравнения для первого и второго контуров по второму закону будут:
Все эти три уравнения образуют систему
Подставив известные значения и решив данную линейную систему уравнений, найдем токи в ветвях (способ решения может быть любым).
Проверку правильности решения можно осуществить разными способами, но самым надежным является проверка балансом мощностей.
Задача 2
Зная сопротивления резисторов и ЭДС трех источников найти ЭДС четвертого и токи в ветвях.
Возможное решение:
Как и в предыдущей задаче начнем решение с составления уравнений на основании первого закона Кирхгофа. Количество уравнений n-1= 2
Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче.
На основании этих уравнений составляем систему с 5-ью неизвестными
Решив эту систему любым удобным способом, найдем неизвестные величины
Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей, полученных приемниками.
Баланс мощностей сошелся, а значит токи и ЭДС найдены верно.
3. Модуль контроля знаний и умений
Внимательно рассмотрите схему и выполните задания по ней (слайд 9):
Запишите 1 закон Кирхгофа для узла АЗапишите 1 закон Кирхгофа для узла С.

Запишите второй закон Кирхгофа для контура АСD
Запишите второй закон Кирхгофа для контура АСB
Домашнее задание: решить задачу, используя законы Кирхгофа
Какую силу тока покажет амперметр, включенный в схему, изображенную на рисунке, если R1 = 1,25 Ом, R2 = 1 Ом, R3 = 3 Ом, R4= 7 Ом и ЭДС источника 2,8 В? Сопротивлением амперметра и источника пренебречь.
Пример решения задачи по теме «Расчеты электрических цепей по правилам Кирхгофа» | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Тема: Примеры решения задач по электродинамике
| Рис. 5.28. К задаче на правило Кирхгофа |
Задача.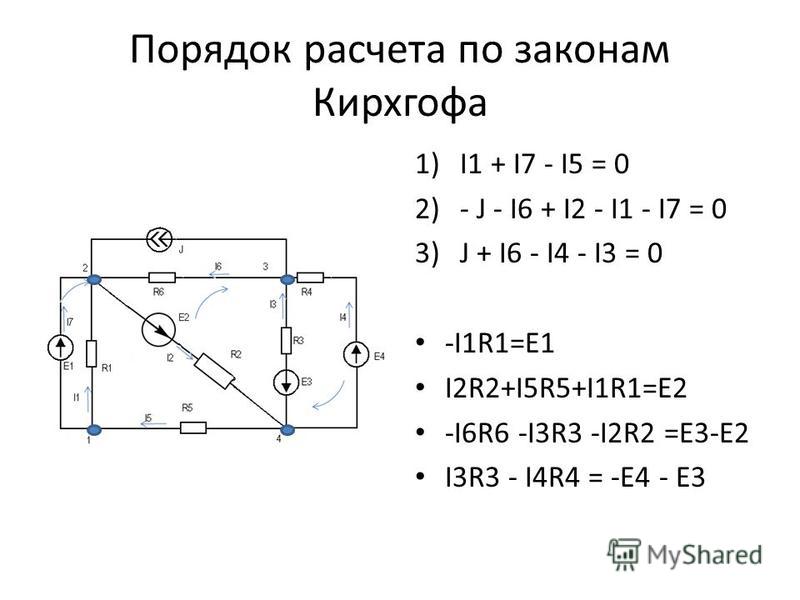 Три одинаковых источника тока с электродвижущими силами Ɛ = 2 В и внутренними сопротивлениями r = 1 Ом и два одинаковых резистора с сопротивлениями R = 1 Ом включены так, как показано на схеме (рис. 5.28, а). Определить силы тока в точках A, B, C электрической цепи.
Три одинаковых источника тока с электродвижущими силами Ɛ = 2 В и внутренними сопротивлениями r = 1 Ом и два одинаковых резистора с сопротивлениями R = 1 Ом включены так, как показано на схеме (рис. 5.28, а). Определить силы тока в точках A, B, C электрической цепи.
Решение:
Для решения задачи в электрической цепи необходимо определить узлы (D и К) и контуры, по которым осуществляются обходы. Выберем «внешний» (I) и «внутренний» (II) обходы, осуществляя их по направлению движения часовой стрелки (можно выбрать и другие контуры).
Поскольку неизвестны значения трех сил токов, то минимальным количеством уравнений для решения задачи есть три. Избираем направления токов, как показано на рис. 5.28, б, и для узла D записываем первое уравнение Кирхгофа:
I — I1 — I2 = 0.
Для контуров I и II записываем другие уравнения Кирхгофа:
Ir + I1r + I1R = Ɛ + Ɛ;
Ir + I2r + I2R = Ɛ — Ɛ;
Из 1-го уравнения имеем: I = I1 + I2. Это значение подставляем во второе и третье, и получаем:
Это значение подставляем во второе и третье, и получаем:
I12r + I2r + I1R = 2Ɛ;
I1r + I22r + I2R = 0;
Преобразовав эти уравнения, имеем:
I1 = -(I2(2r + R)) / r;
I2 = 2Ɛr / ((2r + R)2 — r2). Материал с сайта http://worldofschool.ru
Имея в виду, что Ɛ = 2 В, a r = R = 1 Ом, находим значение I2 = -0,5 А. Знак минус в полученном результате означает, что в процессе решения задачи мы избрали направление, противоположное действительному направлению тока в этой ветке.
Теперь легко находим значения I1 = 1,5 А и I = 1,0 А.
Ответ: I = 1,0 А; I1 = 1,5 А; I2 = 0,5 А.
На этой странице материал по темам:Задачи на правило кирхгофа с решениями когда 2 сопротивление
Задачи по теме правила кирхгофа
Примеры решения задач по правилу кирхгофа
Задачи на правила кирхгофа
Простые задачи на правило кирхгофа с эдс решение
1.5. Задача анализа цепи. Законы Кирхгофа
1.5. Задача анализа цепи. Законы Кирхгофа.
Задача анализа электрической цепи формулируется следующим образом: заданы схемы электрической цепи со значениями всех ее элементов, а также напряжения и токи источников, действующих в цепи, требуется найти токи в ветвях и напряжения на элементах цепи. Для определения искомых токов и напряжений необходимо составить уравнения цепи, которые определяются только геометрической конфигурацией и способами соединения элементов цепи.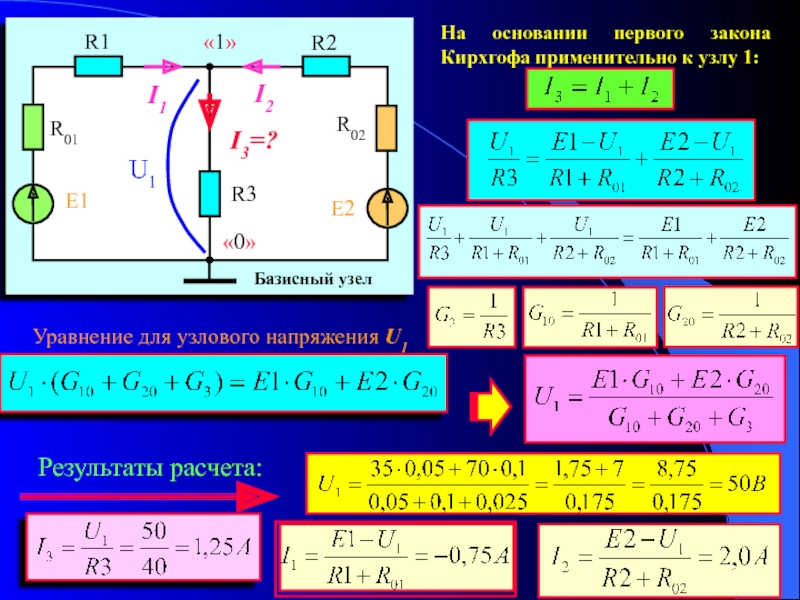 Эти уравнения составляются на основе двух законов Кирхгофа, которые связывают токи ветвей, сходящихся в узлах, и напряжения элементов, входящих в контуры.
Эти уравнения составляются на основе двух законов Кирхгофа, которые связывают токи ветвей, сходящихся в узлах, и напряжения элементов, входящих в контуры.
Первый закон Кирхгофа, выражающий закон сохранения заряда, формулируется так: в любой момент алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю.
(1.12)
Знак тока ,при записи первого закона Кирхгофа, определяется выбором положительных направлений токов ветвей: например, токам, входящим в узел, приписывают условно знак плюс, а токам, выходящим из узла — знак минус. Так, для узла изображенного на рис. 1.10.
Второй закон Кирхгофа, выражающий закон сохранения энергии, формулируется следующим образом: в любой момент алгебраическая сумма напряжений в ветвях контура равна нулю.
(1.13)
Рис 1.10 Суммирование напряжений производится с учетом их положительных направлений и выбранного направления обхода контура. Если положительное направление напряжения ветви совпадает с напряжением обхода контура, то оно входит в (1.13) со знаком плюс, в противном случае – со знаком минус.
Если положительное направление напряжения ветви совпадает с напряжением обхода контура, то оно входит в (1.13) со знаком плюс, в противном случае – со знаком минус.
Часто используется другая формулировка второго закона Кирхгофа: алгебраическая сумма э.д.с. источников, действующих в контуре, равна алгебраической сумме напряжений на элементах контура.
Рекомендуемые файлы
(1.14)
При этом напряжения на элементах контура и э.д.с. источников входят в уравнение (1.14) со знаком плюс, если их положительные направления совпадают с направлением обхода контура, в обратном случае слагаемые в (1.14) берутся со знаком минус. Например, для схемы (рис 1.11) при обходе по часовой стрелке уравнение второго закона Кирхгофа запишется следующим образом:
Для разветвленной цепи, содержащей q узлов и k ветвей, при определении неизвестных токов следует составить k уравнений по первому и второму законам Кирхгофа, т.к. число неизвестных токов
Рис 1. 11 равно числу ветвей цепи. Причем число уравнений, составленных по первому закону Кирхгофа, равно (q-1), а число уравнений, составленных по второму закону Кирхгофа, — (k-(q-1)).
11 равно числу ветвей цепи. Причем число уравнений, составленных по первому закону Кирхгофа, равно (q-1), а число уравнений, составленных по второму закону Кирхгофа, — (k-(q-1)).
Уравнение второго закона Кирхгофа может быть записано для участка цепи между точками «а» и «b» (см. рис. 1.12). При этом контур замыкается по стрелке, указывающей положительное направление напряжения между точками «a» и «b»
(1.15)
Таким образом можно всегда определить напряжение между двумя любыми точками электрической цепи.
Пример 1.1. Записать уравнения по законам
Рис 1.12 Кирхгофа для расчета токов цепи, представленной на рис. 1.13.
Информация в лекции «13. Организация взаимодействия и полномочия» поможет Вам.
Решение.
Цепь содержит 3 ветви и два узла: «a» и «b», следовательно, по первому закону Кирхгофа составим одно уравнение, а остальные два – по второму закону Кирхгофа. Выбрав положительные направления токов I1, I2, I3 такими, как показано на рисунке 1.13, и обходя контур I и II по часовой стрелке, получим Рис 1.13
После решения и подстановки числовых значений полученные результаты могут быть либо положительными, либо отрицательными. В случае отрицательного значения действительное направление тока будет противоположным указанному на рисунке.
Закон Кирхгофа — проблемы и решения
1. Если R 1 = 2 Ом, R 2 = 4 Ом, R 3 = 6 Ом, определите электрический ток, протекающий в схеме ниже.
Известный:
Резистор 1 (R 1 ) = 2 Ом
Резистор 2 (R 2 ) = 4 Ом
Резистор 3 (R 3 ) = 6 Ом
Источник ЭДС 1 (E 1 ) = 9 В
Источник ЭДС 2 (E 2 ) = 3 В
Требуется: Электрический ток (I)
Решение:
Этот вопрос относится к закону Кирхгофа.Как решить эту проблему:
Сначала , выберите направление тока. Вы можете выбрать противоположный ток или направление по часовой стрелке.
Второй , при прохождении тока через резистор (R) происходит уменьшение потенциала, так что V = IR со знаком отрицательного значения. Третий , если ток переходит от низкого напряжения к высокому (- к +), то источник ЭДС (E) имеет положительный знак из-за зарядки энергии в источнике ЭДС. Если ток переходит от высокого к низкому напряжению (+ к -), то источник ЭДС (E) имеет отрицательный знак из-за потери энергии в источнике ЭДС.
В этом решении направление тока такое же, как и направление вращения по часовой стрелке.
— I R 1 + E 1 — I R 2 — I R 3 — E 2 = 0
— 2 I + 9 — 4 I — 6 I — 3 = 0
— 12 I + 6 = 0
— 12 I = — 6
I = -6 / -12
I = 0,5
Электрический ток, протекающий в цепи, равен 0,5 A. Знак электрического тока положительный означает, что направление электрического тока совпадает с направлением вращения по часовой стрелке.Если электрический ток отрицательный, то электрический ток направлен против часовой стрелки.
2. Определите электрический ток, протекающий в цепи, как показано на рисунке ниже.
Решение:
В этом решении направление тока такое же, как и направление вращения по часовой стрелке.
-20 — 5I -5I — 12 — 10I = 0
-32 — 20I = 0
-32 = 20I
I = -32 / 20
I = -1,6 А
Поскольку электрический ток отрицательный, направление электрического тока фактически противоположно направлению по часовой стрелке.Направление электрического тока не совпадает с оценкой.
3. Определите электрический ток, протекающий в цепи, как показано на рисунке ниже.
Решение:
В этом решении направление тока такое же, как и направление вращения по часовой стрелке.
— I — 6I + 12 — 2I + 12 = 0
-9I + 24 = 0
-9I = -24
I = 24/9
I = 8/3 А
4. Электрическая цепь состоит из четырех резисторов, R 1 = 12 Ом, R 2 = 12 Ом, R 3 = 3 Ом и R 4 = 6 Ом, подключенных к источнику ЭДС E 1 = 6 Вольт, E 2 = 12 Вольт.Определите электрический ток, протекающий в цепи, как показано на рисунке ниже.
Известный:
Резистор 1 (R 1 ) = 12 Ом
Резистор 2 (R 2 ) = 12 Ом
Резистор 3 (R 3 ) = 3 Ом
Резистор 4 (R 4 ) = 6 Ом
Источник ЭДС 1 (E 1 ) = 6 Вольт
Источник ЭДС 2 (E 2 ) = 12 Вольт
Разыскивается: Электрический ток течет в цепи (I)
Решение:
Резистор 1 (R 1 ) и резистор 2 (R 2 ) подключены параллельно.Эквивалентный резистор:
1/ 12 = 1/ 1 + 1/ 2 = 1/12 + 1/12 = 2/12
R 12 = 12/2 = 6 Ом
В этом решении направление тока такое же, как и направление вращения по часовой стрелке.
— I R 12 — E 1 — I R 3 — I R 4 + E 2 = 0
— 6 I — 6 — 3I — 6I + 12 = 0
— 6I — 3I — 6I = 6-12
— 15I = — 6
I = -6 / -15
I = 2/5 А
5.Определите электрический ток, протекающий в цепи, как показано на рисунке ниже.
Известный:
Резистор 1 (R 1 ) = 10 Ом
Резистор 2 (R 2 ) = 6 Ом
Резистор 3 (R 3 ) = 5 Ом
Резистор 4 (R 4 ) = 20 Ом
Источник ЭДС 1 (E 1 ) = 8 Вольт
Источник ЭДС 2 (E 2 ) = 12 Вольт
Разыскивается: Электрический ток, протекающий в цепи
Решение:
Резистор 3 (R 3 ) и резистор 4 (R 4 ) подключены параллельно.Эквивалентный резистор:
1/ 34 = 1/ 3 + 1/ 4 = 1/5 + 1/20 = 4/20 + 1/20 = 5/20
R 34 = 20/5 = 4 Ом
В этом решении направление тока такое же, как и направление вращения по часовой стрелке.
— I R 1 — I R 2 — E 1 — I R 34 + E 2 = 0
— 10I — 6I — 8 — 4I + 12 = 0
— 10I — 6I — 4I = 8 — 12
— 20I = — 4
I = -4 / -20
I = 1/5 А
I = 0.2 А
6. Определите электрический ток, протекающий в цепи, как показано на рисунке ниже.
Известный:
Резистор 1 (R 1 ) = 1 Ом
Резистор 2 (R 2 ) = 6 Ом
Резистор 3 (R 3 ) = 6 Ом
Резистор 4 (R 4 ) = 4 Ом
Источник ЭДС 1 (E 1 ) = 12 Вольт
Источник ЭДС 2 (E 2 ) = 6 Вольт
Разыскивается: Электрический ток, протекающий в цепи
Решение:
Резистор 1 (R 1 ) и резистор 2 (R 2 ) подключены параллельно.Эквивалентный резистор:
1/ 12 = 1/ 1 + 1/ 2 = 1/1 + 1/6 = 6/6 + 1/6 = 7/6
R 12 = 6/7 Ом
Направление тока такое же, как и при вращении по часовой стрелке.
E 1 — I R 12 — E 2 — I R 4 — I R 3 = 0
12 — (6/7) I — 6 — 4I — 6I = 0
12-6 — (6/7) I — 4I — 6I = 0
6 — (6/7) I — 10I = 0
6 = (6/7) I + 10I
6 = (6/7) I + (70/7) I
6 = (76/7) I
(6) (7) = 76I
42 = 76I
I = 42/76
I = 0.5 А
Урок 13 — Решение цепей по законам Кирхгофа
«Покупка DVD с репетитором по алгебре, математике и физике была лучшим вложением в образование».
«В прошлом семестре я перешел с« C »на
и« пятёрку »!»
Les J.
Matawan, NJ
«DVD-диски Math Tutor просто фантастические!
Джейсон представляет материал в ясной и хорошо организованной форме.«
С. Дидс-Рубин
Лос-Анджелес, Калифорния
«Ваши методы настолько ясны, что мой семилетний сын, которому
год, усваивал уроки тригонометрии. Я тоже подбираю
новый материал».
Гэри Г.
«Смотреть справочные видео по математике — это замечательно, потому что, работая над задачами, вы показываете и объясняете каждый шаг».
М. Далримпл
Ланкастер, Калифорния
«Все инструкции
и примеры на DVD с репетитором математики очень четко объяснены, и стиль преподавания Джейсона определенно делает зрителя очень комфортным с представленным материалом.«
Д. Форбс
Мидлтаун, штат Нью-Джерси
«Я нашел лекции
очень четкими, прямо по делу, и темп был как раз для меня, который не видел никаких расчетов или триггеров за последние 10 лет и должен быстро набрать скорость».
София
«Просто хотел сообщить вам, что благодаря
основанию, которое я получил от вашего DVD с справкой по математике (особенно DVD с предварительным расчетом), я смог сдать свой курс по предварительному расчету в этом семестре на пятерку!»
Дж.Ректон
«У вас серьезный педагогический дар.
Доказательство того, что я смотрю ваши DVD, когда я обычно бываю
вне дома. Никогда не думал, что смогу выучить математику. Я сразу перехожу к исчислению, а затем к физике. Я действительно наслаждайтесь этим, и я подумываю о смене карьеры. Отличная работа! »
Д. Смит
Правила Кирхгофа: примеры решенных задач
Пример решения решенных задач: первое правило Кирхгофа (правило тока или правило соединения), второе правило Кирхгофа (правило напряжения или правило петли), мост Уитстона, измерительный мост
Первое правило Кирхгофа (текущее правило или правило соединения): решенные примеры проблем
ПРИМЕР 2.20
Из данной схемы найдите значение I.
Решение
Применив правило Кирхгофа к точке P в схеме,
Стрелки, указывающие на P, положительны, а от P — отрицательны.
Следовательно, 0,2A — 0,4A + 0,6A — 0,5A + 0,7A — I = 0
1,5A — 0,9A — I = 0
0,6A — I = 0
I = 0,6 A
Второе правило Кирхгофа (правило напряжения или правило петли): решенные примеры проблемПРИМЕР 2.21
На следующем рисунке показана сложная сеть проводников, которую можно разделить на два замкнутых контура, такие как ACE и ABC. Примените правило Кирхгофа по напряжению.
Решение
Таким образом, применение второго закона Кирхгофа к замкнутому контуру EACE
I 1 R 1 + I 2 R 2 + I 3 R 3 = ξ
и для замкнутого контура ABCA
I 4 R 4 + I 5 R 5- I 2 R 2 = 0
ПРИМЕР 2.22
Рассчитайте ток, протекающий через резистор 1 Ом в следующей схеме.
Решение
Мы можем обозначить ток, который течет от батареи 9 В, как I1, и он разделяется на I2 и I1 — I2 в переходе в соответствии с правилом тока Кирхгофа (KCR). Это показано ниже.
Теперь рассмотрим петлю EFCBE и применим KVR, получаем
1I2 + 3I1 + 2I1 = 9
5I1 + I2 = 9 (1)
Применяя KVR к петле EADFE, получаем
3 (I1 — I2 ) — 1I2 = 6
3I1 — 4I2 = 6 (2)
Решая уравнения (1) и (2), получаем
I1 = 1.83 A и I2 = -0,13 A
Это означает, что ток в резисторе 1 Ом течет от F к E.
Мост Уитстона: решенные примеры проблем
ПРИМЕР 2.23
В мосте Уитстона P = 100 Ом, Q = 1000 Ом и R = 40 Ом. Если гальванометр показывает нулевое отклонение, определите значение S.
Решение
ПРИМЕР 2.24
Какое значение имеет значение x , когда сеть Уитстона сбалансирована?
P = 500 Ом, Q = 800 Ом, R = x + 400, S = 1000 Ом
Решение
P / Q = R / S
x + 400 = 0.625 × 1000
x + 400 = 625
x = 625-400
x = 225 Ом
Измерительный мост: решенные примеры проблем
ПРИМЕР 2.25
В измерительном мосту со стандартным сопротивлением 15 Ом в правый зазор, соотношение балансировочной длины 3: 2. Найдите значение другого сопротивления.
Раствор
ПРИМЕР 2.25
В метровом мосту значение сопротивления в ячейке сопротивления составляет 10 Ом.Балансировочная длина л 1 = 55 см. Найдите значение неизвестного сопротивления.
Решение
Q = 10 Ом
Учебные материалы, Примечания к лекциям, Задания, Ссылка, Описание Wiki, краткие детали
12-я Физика: Электричество тока: Правила Кирхгофа: Решенные примеры задач |
Закон Кирхгофа по току и напряжению (KCL и KVL)
Первый и второй законы Кирхгофа с решенным примеромНемецкий физик Роберт Кирхгоф ввел в 1847 году два важных электрических закона, с помощью которых мы можем легко найти эквивалентное сопротивление сложная сеть и протекающие токи в разных проводниках.Цепи переменного и постоянного тока могут быть решены и упрощены с помощью этих простых законов, которые известны как закон Кирхгофа по току (KCL) и закон Кирхгофа по напряжению (KVL).
Также обратите внимание, что KCL выводится из уравнения непрерывности заряда в электромагнетизме, в то время как KVL выводится из уравнения Максвелла-Фарадея для статического магнитного поля (производная B по времени равна 0)
Закон Кирхгофа по току (KCL):Согласно KCL, в любой момент алгебраическая сумма текущих токов через точку (или соединение) в сети равна нулю (0) или в любой электрической сети, алгебраическая сумма токов, встречающихся в точке (или соединение) равно нулю (0).Этот закон также известен как Точечный закон или Текущий закон.
В любой электрической сети алгебраическая сумма входных токов в точку и выходных токов из этой точки равна нулю. Или токи на входе в точку равны токам на выходе из этой точки.
Другими словами, сумма токов, текущих к точке, равна сумме токов, текущих от нее. Или алгебраическая сумма токов, входящих в узел, равна алгебраической сумме выходящих из него токов.
Объяснение KCL:Предположим, что некоторые проводники встречаются в точке «A», как показано на рис. 1.a. в некоторых проводниках токи поступают в точку «А», в то время как в других проводниках токи уходят или исходят из точки «А».
Считайте входящие или входящие токи «положительными (+) в направлении точки« A », в то время как уходящие или исходящие токи из точки« A »считаются« отрицательными (-) ».
, затем:
I 1 + (-I 2 ) + (-I 3 ) + (-I 4 ) + I 5 = 0
OR
I 1 + I 5 -I 2 -I 3 -I 4 = 0
OR
I 1 + I 5 = I 2 + I 3 + I 4 = 0
и.е.
Входящие или входящие токи = выходящие или исходящие токи
или
ΣI Вход = ΣI Выход
Например, 8A приближается к точке, а 5A плюс 3A выходят из этой точки на рис. 1.b, следовательно,
8A = 5A + 3А
8А = 8А.
Второй закон Кирхгофа гласил:
В любом замкнутом пути (или цепи) в сети алгебраическая сумма IR-продукта равна ЭДС в этом пути.
Другими словами, в любом замкнутом контуре (который также известен как Mesh) алгебраическая сумма приложенной ЭДС равна алгебраической сумме падений напряжения в элементах. Второй закон Кирхгофа также известен как закон напряжения или закон сетки.
ΣIR = ΣE
Замкнутый контур показан на рис., Который содержит два соединения батарей E 1 и E 2 . Общая сумма E.M.F батарей обозначается E 1 -E 2 .Воображаемое направление тока также показано на рис.
E 1 управляют током в таком направлении, которое должно быть положительным, в то время как E 2 мешает в направлении тока (то есть в направлении, противоположном предполагаемому направлению тока), следовательно, это принято как отрицательный. Падение напряжения в этой замкнутой цепи зависит от произведения напряжения и тока.
Падение напряжения в предполагаемом направлении тока известно как положительное падение напряжения, а другое — отрицательное падение напряжения.
На приведенном выше рисунке I 1 R 1 и I 2 R 2 — положительное падение напряжения, а I 3 R 3 и I 4 R 4 — отрицательное напряжение V.D.
Если мы обойдем замкнутую цепь (или каждую сетку) и умножим сопротивление проводника на протекающий в нем ток, то сумма IR будет равна сумме приложенных источников ЭДС, подключенных к цепи.
Общее уравнение для вышеуказанной схемы:
E 1 -E 2 = i 1 R 1 + i 2R 2 — i 3 3 R 3 — i 4 R 4
Если мы пойдем в предполагаемом направлении тока, как показано на рис., То произведение IR принимается как положительное, в противном случае — отрицательное.
Полезно знать:
Направление тока:
Очень важно определять направление тока при решении схем по законам Кирхгофа.
Направление тока можно предполагать по часовой стрелке или против часовой стрелки. После того, как вы выберете собственное направление тока, вам нужно будет применить и поддерживать одно и то же направление для всей цепи до окончательного решения схемы.
Если мы получили окончательное значение как положительное, это означает, что предполагаемое направление тока было правильным.В случае отрицательных значений, тогда ток направления меняется на противоположный по сравнению с предполагаемым.
Анализ схемы по законам Кирхгофа Решенный пример для KCL и KVL (законы Кирхгофа)Пример:
Резисторы R 1 = 10 Ом, R 4 Ом и 4 Ом = 8 Ом подключаются до двух батарей (с незначительным сопротивлением), как показано. Найдите ток через каждый резистор.
Решение:
Предположим, что токи текут в направлениях, указанных стрелками.
Примените KCL к соединениям C и A.
Следовательно, ток в сетке ABC = i 1
Ток в сетке CA = i 2
Затем ток в сетке CDA = i 1 — i 2
Теперь примените KVL к сетке ABC, 20 В действуют по часовой стрелке. Приравнивая сумму IR произведений, получаем:
10 i 1 + 4 i 2 = 20 ……………. (1)
В сети ACD 12 вольт действуют по часовой стрелке, затем:
8 ( i 1 — i 2 ) — 4 i 2 = 12
8 i 1 — 8 i 2 — 4 i 2 = 12
8 i 1 — 12 i 2 = 12 …………….(2)
Умножение уравнения (1) на 3;
30 i 1 + 12 i 2 = 60
Решение для i 1
30 i 1 + 12 i 2 = 60823 908 1 — 12 i 2 = 12
______________
38 i 1 = 72
i 1 = 72/38 = 1,895 Ампер = Ток в резисторе 10 Ом
Подставляя это значение в (1), получаем:
10 (1,895) + 4 i 2 = 20
4 i 2 = 20 — 18,95
i 2 = 0,263 Ампер = Ток в резисторах 4 Ом.
Сейчас,
i 1 — i 2 = 1.895 — 0,263 = 1,632 Ампер
- Законы Кирхгофа можно использовать для определения значений неизвестных значений, таких как ток, напряжение, ток, а также направление потока. значения в цепи.
- Эти законы могут быть применены к любой цепи * (см. Ограничение законов Кирхгофа в конце статьи), но полезны для поиска неизвестных значений в сложных схемах и сетях.
- Также используется в узловом и сеточном анализе для определения значений тока и напряжения.
- Ток через каждую независимую петлю передается за счет применения KVL (каждая петля) и тока в любом элементе схемы путем подсчета всего тока (применимо в методе тока петли).
- Ток через каждую ветвь передается за счет применения KCL (каждый переход) KVL в каждом контуре цепи (применимо в методе тока контура).
- Законы Кирхгофа полезны для понимания передачи энергии через электрическую цепь.
Полезно знать:
При упрощении и анализе электрических цепей по законам Кирхгофа необходимо учитывать эти полезные правила:
- Падение напряжения в контуре из-за тока по часовой стрелке считается положительным (+) Падение напряжения.
- Падение напряжения в контуре из-за тока, направленного против часовой стрелки, считается отрицательным (-) падением напряжения.
- Ток, потребляемый батареей по часовой стрелке, считается положительным (+).
- Ток, потребляемый батареей против часовой стрелки, считается положительным (-).
- KCL применяется при условии, что ток течет только по проводам и проводам. В то время как в высокочастотных цепях, где паразитная емкость больше не может игнорироваться. В таких случаях ток может течь в разомкнутой цепи, потому что в этих случаях проводники или провода действуют как линии передачи.
- KVL применимо при условии отсутствия флуктуирующего магнитного поля, связывающего замкнутый контур.В то время как в присутствии изменяющегося магнитного поля в высокочастотных, но коротковолновых цепях переменного тока электрическое поле не является консервативным векторным полем. Таким образом, электрическое поле не может быть градиентом какого-либо потенциала, а линейный интеграл электрического поля вокруг контура не равен нулю, что прямо противоречит KVL. Поэтому КВЛ в таком состоянии неприменим.
- Во время передачи энергии от магнитного поля к электрическому полю, когда в KVL необходимо ввести помаду, чтобы заставить P.d (разности потенциалов) вокруг схемы равны 0.
Вы также можете проверить больше схем, анализируя теоремы:
Проблемы закона Кирхгофа с решением
Листинг результатов Проблемы с решением закона Кирхгофа
Закон Кирхгофа — проблемы и решения Решенные проблемы
9 часов назад Решение : Этот вопрос относится к закону Кирхгофа . Как решить эту проблему : Сначала выберите направление тока.Вы можете выбрать противоположный ток или направление по часовой стрелке. Во-вторых, когда ток через резистор (R)…
Расчетное время чтения: 3 минуты
Предварительный просмотр / Показать еще
Добавлено в : Kirchhoff current law example Show details
Законы Кирхгофа CPP
6 часов назад Закон Кирхгофа Напряжение Закон (KVL): Алгебраическая сумма всех напряжений вокруг замкнутого контура всегда должна быть равна нулю.где vn — n-е напряжение. N — количество элементов в цикле. Распространенное назначение: если сначала встречается положительная (+) сторона напряжения, назначьте…
Предварительный просмотр / Показать еще
Добавлено в : Закон Кирхгофа пример проблемы решены Показать подробности
Практические задачи: правила Кирхгофа Решения физика
5 часов назад Практика Задачи : Правила Кирхгофа Решения .1. (умеренно) Студент утверждает, что правило петли, примененное к простой электрической цепи, подтверждает принцип сохранения заряда. Прав ли ученик? Объясните свой ответ. Студент не прав. Правило цикла основано на сохранении энергии.
Расчетное время чтения: 1 мин.
Предварительный просмотр / Показать еще
Опубликовано в : Закон Кирхгофа практика проблема Показать подробности
Текущий закон Кирхгофа Примеры с решением В этой статье мы решили 10 различных
Кирхгофа Текущий закон Пример с рисунками и контрольными подсказками.Итак, приступим к решению. Итак, приступим к решению. Пример 1 найдите величину и направление неизвестных токов на рисунке 1.Расчетное время чтения: 5 минут
Предварительный просмотр / Показать еще
Размещено в : законы Кирхгофа пример Показать подробности
Правила Кирхгофа: примеры решенных задач
5 часов назад Второе правило Кирхгофа (правило напряжения или правило петли): решенный пример Проблемы .ПРИМЕР 2.21. На следующем рисунке показана сложная сеть проводников, которую можно разделить на два замкнутых контура, такие как ACE и ABC. Примените правило Кирхгофа по напряжению. Решение . Таким образом, применяя второй закон Кирхгофа к замкнутому контуру EACE. I 1 R 1 + I 2 R 2 + I 3
Предварительный просмотр / Показать еще
Размещено в : Проблемы закона Кирхгофа рабочий лист Показать подробности
Закон Кирхгофа с примерами задач и расчетов
3 часа назад Используя закон Кирхгофа для напряжения , KVL, уравнения представлены как; Петля 1 задается как: 10 = R1 x I1 + R3 x I3 = 10I1 + 40I3.Контур 2 задается как: 20 = R2 x I2 + R3 x I3 = 20I2 + 40I3. Контур 3 задается как: 10-20 = 10I1 — 20I2. Поскольку I3 является суммой I1 + I2, мы можем переписать уравнения как; Уравнение
Предварительный просмотр / Показать еще
Опубликовано в : Закон Кирхгофа действующий закон практика проблемПоказать подробности
Законы Ома и Кирхгофа
1 час назад Предоставлено Академическим центром совершенства 5 Ом и Законы Кирхгофа 19.01.17.Теперь примените закон Ома к каждому резистору. Обратите внимание, что, поскольку через резистор 20 Ом протекает ток (I 2), на этом резисторе имеется напряжение (V a — 0) = I 2 * 20 Ом или I 2 = V a / 20 Ом. Начиная с
Preview «PDF / Adobe Acrobat»
Preview / Показать еще
Размещено в : правила петли Кирчоффа решены проблемПоказать детали
Kirchhoff’s Circuit Laws 9069 ч. назад • Пример
Проблемы . Законы Кирхгофа • Что такое Законы Кирхгофа ? Законы Кирхгофа регулируют сохранение заряда и энергии в электрических цепях. • Законы Кирхгофа 1. Правило соединения 2. Правило замкнутого цикла « Бесплатные Материалы онлайн-курса. Физика. MIT OpenCourseWare». Интернет. 28 февраля 2012 г.«PDF / Adobe Acrobat»
Предварительный просмотр / Показать еще
Размещено в : Закон об энергетике Показать подробности
Раздел текста 28.3 Правила цепи Кирхгофа
2 часа назад Правила цепи Кирхгофа Практика: Глава 28, проблемы 17, 19, 25, 26, 43 Правило перехода: общий ток на входе = общий ток на выходе на каждом переходе (из-за сохранения заряда) . Правило цикла: сумма ЭДС и разностей потенциалов вокруг любого замкнутого контура равна нулю (из-за сохранения энергии).
«PDF / Adobe Acrobat»
Предварительный просмотр / Показать еще
Опубликовано в : Закон об энергии Показать подробности
Примеры закона напряжения Кирхгофа с решением
4 часа назад В этой статье мы решили десять разные Кирхгофа Напряжение Закон Примеры с раствором и рисунком.Итак, приступим к решению. Решая этот вопрос, мы предполагаем, что у вас есть базовые знания о Закон Кирхгофа Current и Закон Кирхгофа о напряжении Закон . Проверьте Закон Кирхгофа Current Закон Примеры с решением
17 Показать Предварительный просмотр подробнее
Размещено в : Law Commons Показать подробности
Закон Кирхгофа по току и напряжению (KCL и KVL) Решенный пример
8 часов назад Первый и второй законы Кирхгофа с решенным примером Немецкий физик “ Роберт Кирхгоф »ввел два важных электрических закона в 1847 году, с помощью которых мы можем легко найти эквивалентное сопротивление сложной сети и текущих токов в различных проводниках.Цепи переменного и постоянного тока могут быть решены и упрощены с помощью этих простых законов , который известен как Закон Кирхгофа Текущий Закон (KCL) и
Предварительный просмотр / Показать больше
Опубликовано в : Law CommonsПоказать подробности
Руководство для начинающих по законам Кирхгофа KCL & KVL
7 часов назад Рассмотрим текущее направление, показанное на рисунке. Применим закон Кирхгофа , действующий закон на обоих перекрестках, и мы получим.На стыке 1 I = I1 + I2. В соединении 2 I1 + I2 = I. Подайте закон напряжения Кирхгофа на оба контура, и мы получим. В первом контуре 1,5 В — 100 I1 = 0. I1 = 1,5 / 100. = 0,015 Ампер.
Предварительный просмотр / Показать еще
Размещено в : Law Commons Показать подробности
Проблемы с законом Кирхгофа
7 часов назад Законы Кирхгофа Пример faqlaw.com. 4 часа назад Закон Кирхгофа Решатель цепей.Just Now Faq- law .com Подробнее. Кирхгоф Законы CPP. 6 часов назад Cpp.edu Показать подробности. Закон Кирхгофа Напряжение Закон (KVL): Алгебраическая сумма всех напряжений вокруг замкнутого контура всегда должна быть равна нулю. где vn — n-е напряжение. N — количество элементов в цикле. Распространенное назначение: если положительная (+) сторона
Предварительный просмотр / Показать еще
Размещено в : Law Commons Показать подробности
Практика правил Кирхгофа — гипертекст по физике
5 часов назад практика задача 1.военно-морской персонал.pdf. Ниже представлена довольно сложная трехпроводная схема. Напряжение источника составляет 120 В между центральным (нейтралью) и внешним (горячим) проводами. Токи нагрузки в верхней половине схемы равны 10, 4 и 8 А для нагрузочных резисторов j, k и l соответственно. Токи нагрузки в нижней половине
Предварительный просмотр / Показать еще
Опубликовано в : Pdf Law, Air Law Показать подробности
Закон Кирхгофа Проблемы и решения IIT JEE и NEET
Just Now Solution .Чтобы решить эту проблему , мы можем использовать базовую концепцию Кирхгофа первый закон . Он говорит вам, что токи, идущие к точке, — это токи, выходящие из соединения. Далее мы можем записать ток на любом элементе как отношение разности потенциалов на нем и его сопротивления. Это базовое понимание, что напряжение на переходе
Предварительный просмотр / Показать еще
Опубликовано в : Law CommonsПоказать подробности
Практические проблемы: правила Кирхгофа Physicsprep.com
1 час назад Практика Проблемы : Правила Kirchhoff Щелкните здесь, чтобы просмотреть решения . 1. (умеренно) Студент утверждает, что правило петли, примененное к простой электрической цепи, подтверждает принцип сохранения заряда. Прав ли ученик? Объясните свой ответ. 2. (умеренно) Студент анализирует простую электрическую цепь, так что следующий цикл
Предварительный просмотр / Показать еще
Опубликовано в : Law Commons Показать подробности
ЗАКОН НАПРЯЖЕНИЯ КИРХОФА: ПРИМЕР 1
1 часов назад РЕШЕНИЕ : (a) Сначала мы идентифицируем петли в цепи.Как показано ниже, мы можем выбрать любые две из трех петель. Напряжение Кирхгофа Закон : Сумма падений напряжения вокруг любого замкнутого контура равна нулю. Применение KVL к петле 1: Применение закона Ома к R1 дает результаты. . .
«PDF / Adobe Acrobat»
Preview / Показать еще
Размещено в : Law Commons Показать подробности
KIRCHHOFF’S LAWS TINA Design Suite
7 часов назад Решение Kirch 9038 9038 с использованием решения 9038 закон : -VS + V 1 + V 2 = 0 или VS = V 1 + V 2.отсюда: V 2 = V S — V 1 = 100-40 = 60 В. Обратите внимание, что обычно мы не знаем напряжения резисторов (если мы их не измеряем), и нам нужно использовать оба закона Кирхгофа для решения .
Предварительный просмотр / Показать еще
Опубликовано в : Law Commons Показать подробности
Текущий закон Кирхгофа: Практические проблемы WiscOnline OER
3 часа назад Кирхгоф Текущие проблемы Закон о практике :Терри Бартельт. Учащиеся рассматривают Кирхгофа Текущий закон и работают шесть практикующих задач . Дается обратная связь. Скачать Object. Скачать Object. Международная лицензия Creative Commons Attribution-NonCommercial 4.0. Узнать больше о лицензии ». 75.
Предварительный просмотр / Показать еще
Опубликовано в : Международное право, Коммерческое право Показать подробности
Закон Кирхгофа Проблемы Уровень Физика YouTube
3 часа назад Я пытался придумать Кирхгофа закон физика задач для студентов для решения на практике.Мои решения даются после каждой задачи .
Предварительный просмотр / Показать еще
Размещено в : Law Commons Показать подробности
Законы Кирхгофа и решенные примеры — QuantumStudy
9 часов назад Для показанной диаграммы нам дает KCL. I 1 — (I 2) + (−I 3) = 0. или, I 1 = I 2 + I 3. KCL является прямым следствием принципа сохранения электрического заряда. KVL ( закон напряжения Кирхгофа закон ): закон напряжения Кирхгофа утверждает, что алгебраическая сумма разностей потенциалов в любом контуре, включая те, которые связаны с ЭДС, должна быть равна нулю.
Предварительный просмотр / Показать больше
Размещено в : Study Law Показать подробности
Kirchho s Laws Mercer University
4 часа назад Kirchho’s Laws 5 Процедура и анализ данных Проверка ‘s Текущий закон Kirchho cation Закон В этом эксперименте будет проверяться экспериментально закон о токе Кирхгофа / узел , который гласит, что сумма токов °, протекающих в узел, должна быть равна нулю.1. С помощью мультиметра измерьте значение сопротивления каждого из трех
«PDF / Adobe Acrobat»
Предварительный просмотр / Показать еще
Опубликовано в : Университетское право Показать подробности
Законы Кирхгофа Кирхгофа Текущий закон, Закон Кирхгофа
1 час назад Согласно Закон Кирхгофа Напряжение Закон , напряжение вокруг контура равно сумме всех падений напряжения в том же контуре для любой замкнутой сети, а также равно нулю.Иными словами, алгебраическая сумма каждого напряжения в контуре должна быть равна нулю, и это свойство закона Кирхгофа называется сохранением энергии.
Предварительный просмотр / Показать еще
Размещено в : Закон о собственности, Закон об энергии Показать подробности
Эпизод 117: Законы Кирхгофа IOPSpark
9 часов назад Эпизод 117-3: Проверка Кирхгофф Законы (Word, 64 КБ) Рабочие примеры: Акцент на втором законе .Студентам вряд ли потребуется решать сложные задачи , включающие схемы с двумя или более петлями. Однако они должны иметь возможность применять законы Кирхгофа к простым схемам. Первый закон не сложен; второй закон сложнее.
Предварительный просмотр / Показать еще
Размещено в : Law CommonsПоказать подробности
Пример действующего закона Кирхгофа Проблемы и решения KCL
3 часа назад Закон KCL Ома Действующий закон Кирхгофа Как решить Kirchhoff ‘s Rules Problem — Простой примерПример: Kirchhoff ‘s Current Law
Preview / Показать больше
Опубликовано в разделе : Law Commons Показать подробности 9114 Законы Кирхгофа и их применение
8 часов назад Решение : следовательно, ток, протекающий через R 3 = 0 A (уравновешенная мостовая схема).Пример 2.2. Найдите значение тока в R 1, как показано на рисунке 2.3. Остальные параметры такие же, как в примере 2.1. Ответ I = 2,5 A Хотя на данный момент это может быть неочевидным, суть проблемы заключается в существовании множества неизвестных величин.
Предварительный просмотр / Показать еще
Размещено в : Law CommonsПоказать подробности
Пример законов Кирхгофа faqlaw.com
4 часа назад Закон Кирхгофа Решатель цепей.Just Now Faq- law .com Подробнее. Кирхгоф Законы CPP. 6 часов назад Cpp.edu Показать подробности. Закон Кирхгофа Напряжение Закон (KVL): Алгебраическая сумма всех напряжений вокруг замкнутого контура всегда должна быть равна нулю. где vn — n-е напряжение. N — количество элементов в цикле. Распространенное назначение: если сначала встречается положительная (+) сторона напряжения, назначьте
Предварительный просмотр / Показать больше
Опубликовано в : Law Commons Показать подробности
Закон Кирхгофа Примеры вашего электрического руководства
3 часа назад Этот закон гласит, что «алгебраическая сумма всех токов, встречающихся в точке или соединении в электрической цепи, равна нулю».Рассмотрим пять проводов, по которым проходит ток I 1, I 2, I 3, I 4, I 5, пересекающиеся в точке O .; Чтобы получить алгебраическую сумму, нужно учитывать силу тока. Если принять поток тока к точке O как положительный, то поток тока от точки O будет
Предварительный просмотр / Показать еще
Опубликовано в : Law Commons Показать подробности
РЕШЕННЫЕ ПРОБЛЕМЫ Закон Кирхгофа (KCL)
2 часа назад Сначала мы должны применить KCL 1 к сети.См. Рисунок 8.5. Основы переменного тока (решенный пример 2) 1) Найдите среднеквадратичное значение, V (t) = Sin 2πt + Sin 6πt Ответ Прежде всего, мы должны найти t РЕШЕННЫЕ ПРОБЛЕМЫ Q1) Определите эквивалентную схему Тевенина между клеммами A и B. схема, показанная на рисунке 11.1.
Предварительный просмотр / Показать еще
Опубликовано в : Law Commons Показать подробности
Законы Кирхгофа для тока и напряжения
3 часа назад В 1845 году немецкий физик Густав Кирхгоф 90 впервые описал два закона , которые впоследствии стали центральное место в электротехнике. Закон Кирхгофа по току , также известный как Закон Кирхгофа и Первый закон Кирхгофа , определяют способ распределения электрического тока, когда он проходит через соединение — a точка, где встречаются три или более проводника. Другими словами, Закон Кирхгофа Закон гласит, что…
Предварительный просмотр / Показать еще
Размещено в : Law Commons Показать подробности
Закон Кирхгофа Проблема Основана на Законе Кирхгофа
Бытие 9 часов назад Первый закон также известен как — Закон Кирхгофа Текущий закон (KCL).Этот закон основан на законе сохранения заряда . Когда ток в цепи постоянный, заряд не может накапливаться или возникать в любой точке цепи. Таким образом, независимо от того, какой заряд течет к соединению в любом временном интервале, равный заряд должен течь от этого соединения в
Preview / Показать больше
Опубликовано в : Law Commons Показать подробности
Ток и напряжение Кирхгофа Законы Северо-западный
3 часа назад
1 .Закон Кирхгофа (KCL) гласит, что ток, идущий в соединение или узел, равен току, выходящему из узла. Другими словами, сумма токов, входящих в узел, должна быть равна нулю (если мы рассматриваем токи, выходящие из узла, как отрицательный ток, входящий в узел). Рассмотрим следующую диаграмму: Для узла A в центре i1 и i2 входят в узел, а i3 и i4 покидают узел. Мы бы написали: что также может быть записано как Обратите внимание, что i7 равно i2; мы можем доказать это, проанализировав узел B.Мы также можем рассматривать все между узлами C и D как один большой узел и заключить, что i5 равно i6, без необходимости знать значение любого из токов внутри. Решая для токов в реальной задаче, мы можем произвольно выбирать, в каком направлении указывают стрелки. Если ток течет в направлении, противоположном направлению стрелки, значение, которое мы получаем после вычисления тока, будет отрицательным. Если вы нарисуете i4 как выходящий узел A, как на диаграмме выше, то …Предварительный просмотр / Показать еще
Размещено в : Law Commons Показать подробности
Второе право Кирхгофа, решенные примеры
7 часов назад Второй закон Кирхгофа . Закон Кирхгофа или схема Законы состоит из двух математических уравнений равенства, которые имеют дело с сопротивлением, током и напряжением в сосредоточенной элементарной модели электрических цепей. Законы являются фундаментальными в теории цепей. Они количественно определяют, как токи и напряжения изменяются в контуре в цепи.
Предварительный просмотр / Показать больше
Размещено в : Law Commons Показать подробности
8. Законодательство Кирхгофа Окончание Королевской инженерной академии
7 часов назад Справочная информация — Кирхгофа первый закон анализ цепи может быть осуществляется по законам Кирхгофа . Первый закон Кирхгофа применяется к токам на стыке в цепи. В нем говорится, что в соединении в электрической цепи сумма токов, протекающих в соединении, равна…
Предварительный просмотр / Показать еще
Опубликовано в : Law Commons Показать подробности
Kirchhoff’s Laws TechnologyUK
4 часа назад
1 . Законы Кирхгофа раскрывают уникальную алгебраическую взаимосвязь между током, напряжением и сопротивлением в электрических цепях, которая жизненно важна для нашего понимания анализа электрических цепей.Многие схемы очень сложные, с несколькими источниками питания и ответвлениями и не могут быть решены с помощью одного закона Ома. В ходе экспериментов в 1857 году немецкий физик Густав Кирхгоф разработал методы решения сложных схем, известные сегодня как законы напряжения и тока Кирхгофа. Закон Кирхгофа по току: в любом соединении в электрической цепи полный ток, текущий к этому соединению, равен полному току, текущему от соединения. Закон Кирхгофа о напряжении: в любом замкнутом контуре в сети алгебраическая сумма падений напряжения (т.е. произведения тока и сопротивления), взятые вокруг контура, равна результирующей электродвижущей силе, действующей в этом контуре. Эти законы могут показаться очевидными на основе того, что мы уже знаем о теории цепей, но они являются мощными инструментами для анализа …Предварительный просмотр / Показать еще
Опубликовано в : Law Commons Показать подробности
Проблема закона Кирхгофа ! (Действительно сложно!) Форумы по физике
9 часов назад Смысл в том, чтобы найти токи i1,2,3,4 и 5 на картинке.R1 = 14 Ом R2 = 6 Ом Пока это моя работа. 5 токов, 5 петель, 5 уравнений, это правило (или я так думаю). Как я смотрю на это, есть 6 петель, поэтому, если кто-то может уменьшить их до 5, это немного поможет
Предварительный просмотр / Показать еще
Размещено в : Law Commons Показать подробности
Лекция 13: Текущий закон Кирхгофа Видео-лекции
6 часов назад Итак, закон , Закон Кирхгофа в этой точке собирается сказать мне, что поток w_2 плюс w_3 минус w_5 будет равен нулю, если нет текущего источника, или если я подаю туда ток, какой-то текущий f_3, тогда он будет соответствовать f_3.Так что, может быть, только что сказав эти слова, позвольте мне просто сказать, w_2, я скажу это еще раз, w_2 плюс w_3 минус w_5, и я
Preview / Показать еще
Добавлено в : Law CommonsShow подробности
Закон Кирхгофа обзор ScienceDirect Темы
2 часа назад Законы Кирхгофа , один для напряжения и один для тока, определяют, что означает связь между элементами схемы. Эти законы могут помочь нам проанализировать это схема.Места присоединения элементов схемы друг к другу называются узлами. • Закон Кирхгофа В каждом узле сумма всех токов, входящих в узел, должна равняться нулю.
Предварительный просмотр / Показать еще
Размещено в : Law Commons Показать подробности
Закон Кирхгофа о напряжении и сохранение энергии
5 часов назад Густав Закон Кирхгофа является вторым из его фундаментальных законов. законы мы можем использовать для анализа схем.Его закон напряжения гласит, что для последовательного тракта с замкнутым контуром алгебраическая сумма всех напряжений вокруг любого замкнутого контура в цепи равна нулю. Это потому, что контур цепи равен…
Preview / Show more
Опубликовано в : Закон об энергетике Показать подробности
Текущий закон Кирхгофа (KCL) и Правило перекрестка
5 часов назад Таким образом, мы можем подтвердить анализом, что Закон Кирхгофа , действующий закон (KCL), который утверждает, что алгебраическая сумма токов в точке соединения в цепи цепи всегда равен нулю, это верно и верно в этом примере. Закон Кирхгофа Текущий Закон Пример №2. Найдите токи, протекающие по следующей цепи, используя только Закон Кирхгофа Тока .
Предварительный просмотр / Показать еще
Опубликовано в : Law Commons Показать подробности
Рабочий лист законов Кирхгофа Электрические цепи постоянного тока
Just Now Красный провод на A, черный провод на H = 24 вольт. Красный провод на C, черный провод на G = 12 вольт. Красный провод на F, черный провод на B = -12 вольт.Красный провод на F, черный провод на A = -18 вольт. Примечания: Закон Кирхгофа Voltage Закон (KVL) очень легко изучить в реальной жизни с помощью набора батарей и соединений «перемычки».
Предварительный просмотр / Показать еще
Размещено в : Law CommonsПоказать подробности
Законы Кирхгофа по электротехнике Справка по назначению
5 часов назад
Предварительный просмотр / Показать еще
89 Закон CommonsShow details
Законы Кирхгофа, Закон Кирхгофа о напряжении и Закон Кирхгофа
4 часа назад Введение: Законы Кирхгофа : эти законы используются для определения силы тока в различных ветвях электрической сети, которая может быть легко решена с помощью омов закон , Законы Кирхгофа — это два числа Закон Кирхгофа первый закон или Закон Кирхгофа текущий закон «KCL» Петля Кирхгофа закон или Закон Кирхгофа Закон Кирхгофа Закон Кирхгофа Закон «КВЛ».
Предварительный просмотр / Показать еще
Размещено в : Law Commons Показать подробности
1 часов назад 34. Кирхгоф Первый Закон о говорит, что текущее течение теряет силу Схема: Напряжение теряет силу при протекании по цепи. Проводам нужна изоляция, чтобы электроны не вытекли из провода. Полный ток, протекающий в точку, такой же, как ток, текущий из этой точки.35. KCL используется при решении схем с….
Предварительный просмотр / Показать еще
Размещено в : Law Commons Показать подробности
Первый закон Кирхгофа, второй закон Кирхгофа и как это сделать плата. Электрический ток через металлический проводник представляет собой поток отрицательных
свободных электронов (электрических зарядов), текущий из одной точки в другую. Эти заряды не накапливаются в какой-либо точке цепи, но они движутся по цепи непрерывно, и проводник не накапливается. не заряжается во время протекания электрического тока.Предварительный просмотр / Показать еще
Размещено в : Law Commons Показать подробности
Закон Кирхгофа Викторина по схемам Викторина
Just Now SURVEY. 900 секунд. В. «Полный ток в параллельной цепи равен сумме токов отдельных ветвей». варианты ответа. Закон Ома Закон . Kirchhoff ‘s Voltage Law . Действующий закон Кирхгофа .
Предварительный просмотр / Показать еще
Размещено в : Law Commons Показать подробности
Проблемы юридической практики Кирхгофа pdf merge — Telegraph
6 часов назад как решить проблемы закона Кирхгофа объяснить законы kcl и kv с примером закон Кирхгофа решено проблем Текущий закон Кирхгофа пример проблем с решениями Правила схемы Кирхгофа .Практика: Глава 28, задач 17, 19, 25, 26, 43. Правило соединения: общий ток на входе = общий ток на выходе на каждом переходе (из консервации. Kirchhoff ‘s
Preview / Show more
Опубликовано в : Pdf Law Показать подробности
Тип фильтра: За все время Последние 24 часа Прошлая неделя Прошлый месяц
Пожалуйста, оставьте свои комментарии здесь:
Как вы решаете проблемы закона Кирхгофа? Приведите пример.
Вопрос:
Как вы решаете проблемы закона Кирхгофа? Приведите пример.
Закон Кирхгофа
Законы Кирхгофа являются основой для решения любой электрической схемы.
1-й закон Кирхгофа. Закон о сетке
Сумма всех падений напряжения на ячейке (участок замкнутого контура, состоящий только из одного провода) всегда равна нулю. 3I_i = 0 \\ I_t-I_1-I_2 = 0 \\ I_t = I_1 + I_2 \\ {/ eq}
Чтобы применить 1-й закон Кирхгофа, предположим, что падение напряжения отрицательное, а повышение напряжения положительное.2V_i = 0 \\ V-RI_2 = 0 \\ {/ eq}
Теперь мы получили систему уравнений, с помощью которой можно найти требуемые параметры в соответствии с поставленной задачей.
{eq} \ left \ {\ begin {matrix} V = RI_1 \\ V = RI_2 \\ I_t = I_1 + I_2 \ end {matrix} \ right. {/ eq}
Лекция (L2-2) Законы Кирхгофа (KCL, KVL)
| Вопрос дня: |
| Что такое законы Кирхгофа и как их применять? (Напишите себе поваренную книгу с подробностями для решения неизвестных I и V в схемах с использованием KCL и KVL). |
| Самооценка: ECE1250_Assess2_2.pdf |
Введение: Законы Кирхгофа — это первый из нескольких методов, которые мы будем использовать для решения схемных задач. Мы также будем использовать этот метод, чтобы ПОЛУЧИТЬ несколько других методов. Две основные концепции законов Кирхгофа являются ключевыми в электротехнике: (1) сумма напряжений в замкнутом контуре равна нулю и (2) сумма токов, приходящих в узел, = сумма выходящих токов.
Справочный материал:
Учебник: Глава 2-2
Поваренная книга: законы Кирхгофа KCL KVL на одной странице.pdf
поваренная книга KVL KCl с матрицами.pdf
Поваренная книга (подробнее): KVL KCL Eq’ns и Cookbook: KVL KCL Complete Guide
Карты ECE Toolbox для планирования процедуры решения KVL languages.pdf
Делители напряжения и тока: поваренная книга VI.pdf
Видео-лекция:
L (2-2) Законы Кирхгофа KVL, KCL
Power Point для заметок: L (2-2) — законы Кирхгофа KCL KVL [режим совместимости].pdf
Указатель для L (2-2): pdf | docx
ДОПОЛНИТЕЛЬНЫЕ ПРИМЕРЫ:
Ниже я привел несколько дополнительных примеров. Вам НЕ нужно смотреть их перед уроком. Они здесь для вашего будущего обзора по мере необходимости.
1. Дополнительный (Furse) видео пример законов Кирхгофа:
kvl.pdf (для заметок)
квл Пример закона Кирхгофа (с настроенной матрицей)
2. И еще пример
1 Уравнения KVL / KCL для получения I2 из I и V найти мощность 3 Найдите напряжения в узлах 4 Набор инструментов ECE4. Дополнительные практические примеры (спасибо Арну Столпу):
Дополнительные примеры законов Кирхгофа.pdf
5. Другой пример, аналогичный задаче 2.27
Пример Кирхгофа
6. Дополнительные примеры
R последовательно и параллельно (2) и KVCL с Matlab и схемами проверки.pdf
7. KVL KCL.pdf
8. Наши домашние задания в виде матричных уравнений:
Домашнее задание КВЛ с использованием матричных уравнений.







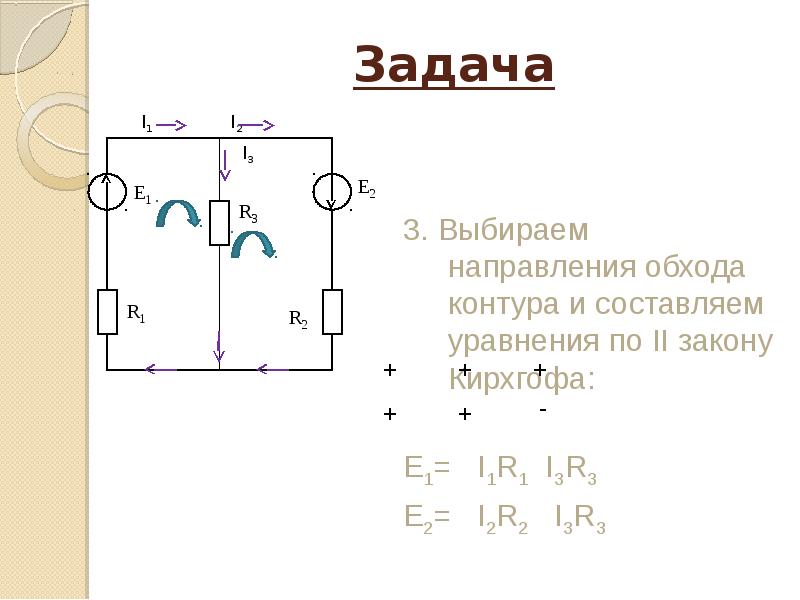
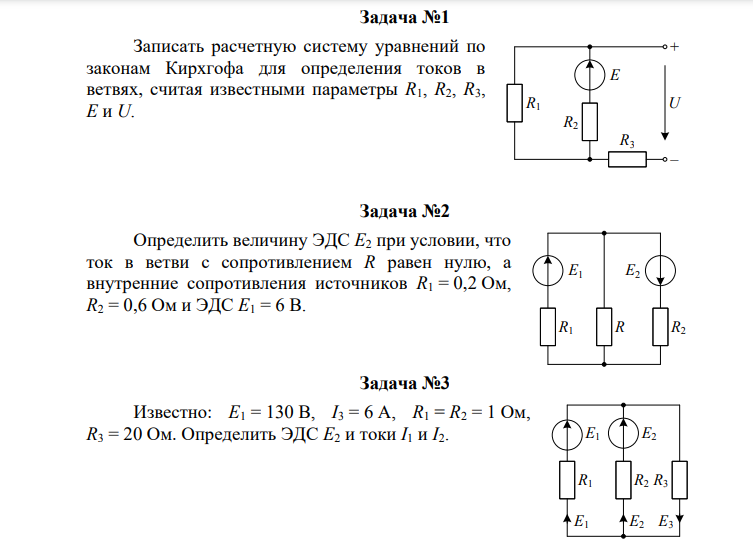 «Практическое
применение законов Кирхгофа»
«Практическое
применение законов Кирхгофа»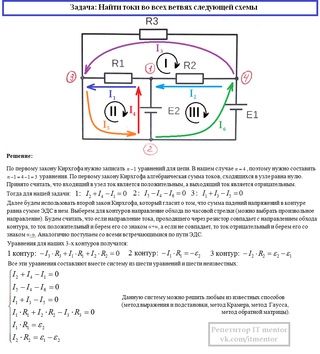
 ,- Алматы
«Мектеп» ,2010
,- Алматы
«Мектеп» ,2010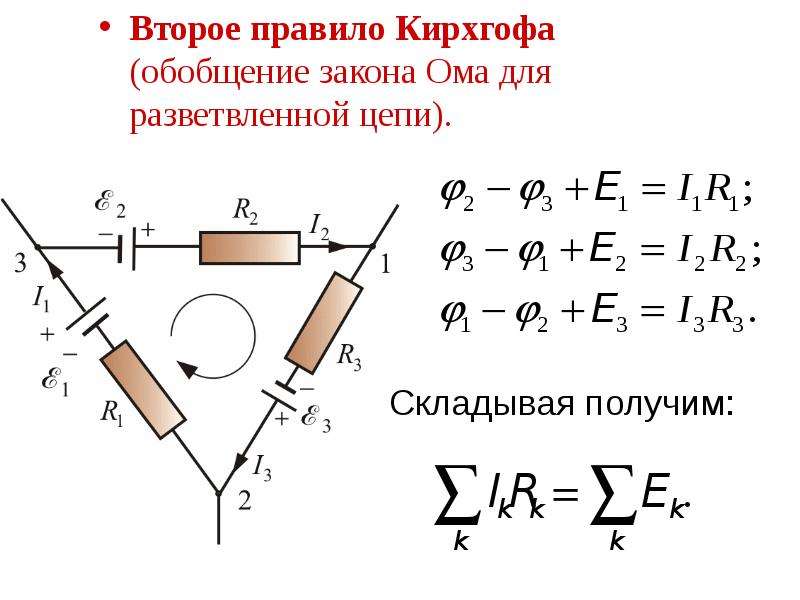
 Обязательно про решать
несколько задач на расчет сложных цепей.
Обязательно про решать
несколько задач на расчет сложных цепей. При этом э.д.с. и токи, совпадающие с направлением обхода, принимаются положительными, а э.д.с. с. и токи, противоположные (т. е. встречные) этому направлению, — отрицательными;
При этом э.д.с. и токи, совпадающие с направлением обхода, принимаются положительными, а э.д.с. с. и токи, противоположные (т. е. встречные) этому направлению, — отрицательными;