Законы Ома для участка цепи и для полной цепи
В 1826 году немецкий ученый Георг Ом совершил открытие и описал
эмпирический закон о соотношении между собой таких показателей как сила тока, напряжение и особенности проводника в цепи. Впоследствии, по имени ученого он стал называться закон Ома.
В дальнейшем выяснилось, что эти особенности не что иное, как сопротивление проводника, возникающее в процессе его контакта с электричеством. Это внешнее сопротивление (R). Есть также внутреннее сопротивление (r), характерное для источника тока.
Закон Ома для участка цепи
Согласно обобщенному закону Ома для некоторого участка цепи, сила тока на участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению.
I = U/ R
Где U – напряжение концов участка,I– сила тока, R– сопротивление проводника.
Беря во внимание вышеприведенную формулу, есть возможность найти неизвестные значенияUиR, сделав несложные математические операции.
U = I*R
R = U / I
Данные выше формулы справедливы лишь когда сеть испытывает на себе одно сопротивление.
Закон Ома для замкнутой цепи
Сила тока полной цепи равна ЭДС, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Замкнутая сеть имеет одновременно сопротивления внутреннего и внешнего характера. Поэтому формулы отношения будут уже другими.
I = E/ Rвн+r
Где E – электродвижущая сила (ЭДС), R- внешнее сопротивление источника, r-внутреннее сопротивление источника.
Закон Ома для неоднородного участка цепи
Замкнутая электрическая сеть содержит участки линейного и нелинейного характера. Участки, не имеющие источника тока и не зависящие от стороннего воздействия являются линейными, а участки, содержащие источник – нелинейными.
Закон Ома для участка сети однородного характера был изложен выше. Закон на нелинейном участке будет иметь следующий вид:
I = U/ R = f1 – f2 + E/ R
Где f1 – f2 – разница потенциалов на конечных точках рассматриваемого участка сети
R – общее сопротивление нелинейного участка цепи
ЭДС нелинейного участка цепи бывает боль
Решение задач на закон Ома для участка и полной цепи
Решение задач на закон Ома сводится к нахождению одной из трех неизвестных составляющих: тока, сопротивления или напряжения. Сам же закон описывает, как они соотносятся между собой.
Напомним, что согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
Формула закона Ома для участка цепи:

Формула закона Ома для полной цепи:
 Задача 1
Задача 1
Утюг включенный в сеть напряжением 220 В, потребляет ток 1,2 А. Определите сопротивление утюга.
|
Дано U = 220 В I = 1,2 А |
Решение Согласно закону Ома для участка цепи:
|
|
R — ? |
|
|
Ответ: R = 183,3 Ом. |
|
Задача 2
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.

|
Дано E = 12 В I = 0,5 А Rл = Rр/2 Rр = 10 Ом |
Решение Найдем экв. сопротивление двух параллельно соединённых резисторов:
Сопротивление лампочки:
Согласно закону Ома для полной цепи:
|
|
Найти r — ? |
|
|
Ответ: r = 14 Ом. |
|
Задача 3
К участку цепи с напряжением 12 В через резистор сопротивлением 2 Ом подключены десять одинаковых лампочек сопротивлением 10 Ом. Найти напряжение на каждой лампочке.

|
Дано Uобщ = 10 В Rр = 2 Ом Rл = 10 Ом |
Решение Так как лампочки подключены параллельно, напряжение на них будет одинаковым, согласно закону Ома для участка цепи:
При последовательном соединении ток в цепи общий:
Выразим Uл через Uобщ:
Найдем Rэкв:
Окончательно получим:
|
|
Найти Uл — ? |
|
|
Ответ: Uл = 4 В. |
|
Задача 4
Как определить длину мотка медной проволоки, не разматывая его?
Решение:
Для решения данной задачи необходимо воспользоваться формулой:


отсюда длина проволоки


В этой формуле, l – длина проволоки, R – сопротивление, S – площадь поперечного сечения, ρ – удельное сопротивление металлов, в данном случае ρ для меди равно 0.0175 Ом/м.
Сопротивление R проволоки можно измерить с помощью омметра, а площадь S с помощью штангенциркуля, измерив диаметр проволоки и по формуле Πr2 вычислив ее значение. Значение удельного сопротивления ρ не только для меди, но и других металлов можно найти в справочнике, или тут. Подставив все известные величины в формулу, приведенную выше, получим длину проволоки.
Задача 5
Начертите схему электрической цепи, состоящей из источника тока, выключателя и двух ламп, включенных параллельно. Что произойдет в цепи при перегорании одной лампы?
Решение:


При перегорании одной из лампочек, вторая будет гореть, так как, при параллельном включении проводников токи I1 и I2 проходящие через них не зависят друг от друга и при разрыве параллельной цепочки ток продолжает протекать.
Закон Ома для участка цепи
Скажу сразу, что закон Ома – основной закон электротехники и применяется для расчета таких величин, как: ток, напряжение и сопротивление в цепи.
Рассмотрим электрическую цепь, приведенную на рисунке 1.
Рисунок 1. Простейшая цепь, поясняющея закон Ома.
Мы знаем, что электрический ток, то есть поток электронов, возникает в цепи между двумя точками (на рисунке А и Б) с разными потенциалами. Тогда следует считать, что чем больше разность потенциалов, тем большее количество электронов переместятся из точки с низким потенциалом (Б) в точку с высоким потенциалом (А). Количественно ток выражается суммой зарядов прошедших через заданную точку и увеличение разности потенциалов, то есть приложенного напряжения к резистору R, приведет к увеличению тока через резистор.
С другой стороны сопротивление резистора противодействует электрическому току. Тогда следует сказать, что чем больше сопротивление резистора, тем меньше будет средняя скорость электронов в цепи, а это ведет к уменьшению тока через резистор.
Совокупность двух этих зависимостей (тока от напряжения и сопротивления) известна как закон Ома для участка цепи и записывается в следующем виде:
I=U/R
Это выражение читается следующим образом: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
Следует знать что:
I – величина тока, протекающего через участок цепи;
U – величина приложенного напряжения к участку цепи;
R – величина сопротивления рассматриваемого участка цепи.
При помощи закона Ома для участка цепи можно вычислить приложенное напряжение к участку цепи (рисунок 1), либо напряжение на входных зажимах цепи (рисунок 2).
Рисунок 2. Последовательная цепь, поясняющая расчет напряжения на зажимах цепи.
В этом случае формула (1) примет следующий вид:
U = I *R
Но при этом необходимо знать ток и сопротивление участка цепи.
Третий вариант закона Ома для участка цепи, позволяющий рассчитать сопротивление участка цепи по известным значениям тока и напряжения имеет следующий вид:
R =U/I
Как запомнить закон Ома: маленькая хитрость!
Для того, что бы быстро переводить соотношение, которое называется закон Ома, не путаться, когда необходимо делить, а когда умножать входящие в формулу закона Ома величины, поступайте следующим образом. Напишите на листе бумаги величины, которые входят в закон Ома, так как показано на рисунке 3.
Рисунок 3. Как запомнить закон Ома.
Теперь закройте пальцем, ту величину, которую необходимо найти. Тогда относительное расположение оставшихся незакрытыми величин подскажет, какое действие необходимо совершить для вычисления неизвестной величины.
Подробнее можно узнать в мультимедийном учебнике по основам электротехники и электроники.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Закон Ома для полной цепи: определение для замкнутого участка
 Одним из принципов электротехники является закон Ома для полной цепи. Используя установленную учёным закономерность, можно вычислить сопротивление электрической цепи или источника тока, рассчитать электродвижущую силу (ЭДС). Практическое же применение полученным при расчёте данным велико. Это подбор шунтирующих и предохранительных элементов, вычисление необходимой мощности используемых деталей, согласование электронных узлов.
Одним из принципов электротехники является закон Ома для полной цепи. Используя установленную учёным закономерность, можно вычислить сопротивление электрической цепи или источника тока, рассчитать электродвижущую силу (ЭДС). Практическое же применение полученным при расчёте данным велико. Это подбор шунтирующих и предохранительных элементов, вычисление необходимой мощности используемых деталей, согласование электронных узлов.
История открытия
Зависимость между током, напряжением и сопротивлением в электрической цепи была установлена опытным путём в 1827 году. Занимаясь исследованиями электричества, Георг Симон Ом проводил ряд экспериментов над проводниками, изучая их проводимость, и в частности, подключая последовательно к источнику энергии тонкие проводники, выполненные из различных материалов. Изменяя их длину, он получал определённую силу тока. Им было установлено, что на результаты экспериментов влияет источник электрической энергии, сопротивление которого оказывалось выше, чем у используемых в опытах проводников.
 По совету своего наставника Поггендорфа Ом собрал термоэлектрическую батарею, отказавшись от использования химических элементов, применив вместо них открытую Зеебеком термопару медь-висмут. Для измерения параметров цепи им использовались крутильные весы, с магнитной стрелкой сконструированные Кулоном.
По совету своего наставника Поггендорфа Ом собрал термоэлектрическую батарею, отказавшись от использования химических элементов, применив вместо них открытую Зеебеком термопару медь-висмут. Для измерения параметров цепи им использовались крутильные весы, с магнитной стрелкой сконструированные Кулоном.
На основании своих исследований физик-экспериментатор пришёл к выводу, что отклонение стрелки зависит от определённой силы, названной силой тока. Когда стрелка отклонялась, Ом закручивал весы таким образом, чтобы она возвращалась в своё начальное положение. Угол, на который закручивалась нить, он считал пропорциональной силе тока. Изменяя условия, Ом вывел математическую зависимость, составив уравнение. Выглядело оно следующим образом: Х = а/b + x, где за Х принималась сила, отклоняющая магнитную стрелку, за а — длина исследуемого образца, а b+x обозначали интенсивность и считались постоянной величиной.
В 1862 году в журнале «Физика и химия» публикуется статья Ома под названием «Определение закона, по которому металлы проводят контактное электричество». Результаты его исследований не производят впечатления на других ученых, и его выводы остаются незамеченными. Ом продолжает эксперименты, выясняя, что электричество можно рассмотреть наподобие теплового потока. Подобно разнице температур, благодаря которой совершается тепловое движение, некой величиной можно описать движение электрического заряда. Так он вводит понятие ЭДС.
Открытие Ома было принято учёным миром уже после его смерти. Существенный вклад в это внесли русские учёные Ленц и Якоби. В 1842 году Лондонское Королевское общество наградило физика золотой медалью, а закон, открытый им, был назван его именем.
Понятие тока и напряжения
Закономерность учёного устанавливает зависимость между собой трёх электрических величин: тока, напряжения и сопротивления. Поэтому для того чтобы разобраться в сути закона Ома для полной электрической цепи, необходимо понимать, что же из себя они представляют.
 В любом теле существуют свободные элементарные частички, обладающие определённым количеством энергии — зарядом. Если тело находится в спокойном состоянии, то есть на него не оказывается никакого воздействия, то происходит их хаотичное перемещение. Если же к телу приложено электрическое поле, то их перемещение становится упорядоченным, и они начинают передвигаться в одну сторону.
В любом теле существуют свободные элементарные частички, обладающие определённым количеством энергии — зарядом. Если тело находится в спокойном состоянии, то есть на него не оказывается никакого воздействия, то происходит их хаотичное перемещение. Если же к телу приложено электрическое поле, то их перемещение становится упорядоченным, и они начинают передвигаться в одну сторону.
Такое направленное движение называют электрическим током. Мерой его служит сила тока, скалярная величина, определяемая отношением количества зарядов прошедших через поперечное сечение проводника за единицу времени: I = dq/dt. За единицу измерения силы тока принят ампер.
Если направление перемещения зарядов остаётся неизменным, то движение тока считается постоянным, а если изменяется — переменным. Возникновение тока возможно только в замкнутой цепи. Для того чтобы заряд переместился, приложенное поле должно выполнить работу. То есть затратить какую-то энергию для перемещения заряда с одной точки в другую. Если принять, что в начальном положении частичка обладает нулевым зарядом, то тогда переместившись, она уже будет иметь другое его значение. Разность между этими величинами называется разностью потенциалов или напряжением.
Для поддержания силы тока в полной цепи необходим источник, постоянно воздействующий на свободные заряды и поддерживающий разности потенциалов на различных участках цепи. Величина силы, которая действует на цепь, называется ЭДС. Физически она представляет собой отношение работы, затрачиваемой на передвижение заряда от одного своего полюса к другому, к значению заряда: E = A/q. Измеряется ЭДС, так же как и напряжение, в вольтах.
При перемещении заряд из-за особенностей строения кристаллической решётки вещества, он сталкивается с различными дефектами и примесями. В результате этого происходит частичное рассеивание его потенциала, а скорость движения замедляется. Потеря энергии характеризуется электрической величиной-сопротивлением. Другими словами, сопротивление — это величина, препятствующая прохождению тока.
Импеданс цепи
Немецкий физик, проводя эксперименты, смог обнаружить зависимость между током и напряжением. Их связь определялась через постоянную величину, которая после была названа сопротивлением. Так, формула закона Ома для полной цепи может быть записана в виде выражения:
I = E/Z, где:
- I — сила тока цепи;
- E — электродвижущая сила, приложенная к цепи;
- Z — постоянная величина (полное сопротивление).
Полное сопротивление (импеданс) электрической цепи важный параметр, определяющий силу тока и полезную мощность. Состоит она из нескольких составляющих: внутреннего сопротивления источника тока и сопротивления элементов, из которых состоит схема.

Поэтому в отличие от участка цепи, где берётся во внимание только сопротивление проводников, закон для всей цепи учитывает и электрическое сопротивление источника тока. В то же время характер происхождения сопротивления может носить как активную составляющую, так и реактивную, учитывающуюся для переменного тока.
Активная составляющая
Такое сопротивление называется активным, так как оно забирает на себя часть мощности, поступающей от источника питания. Эта забираемая энергия, проходя через проводник, превращается в тепло. При этом можно обнаружить, что если проводник подключить к переменному источнику сигнала, то его сопротивление будет немного больше. Связано это с тем, что индуцируемая ЭДС в материале в любой его точке неодинаковая. Ближе к центру она будет больше, чем у поверхности. То есть при переменном сигнале как бы происходит уменьшение полезного сечения проводника.

Сопротивление зависит от физических параметров материала. Математически это может быть описано выражением: R = p*L/S, где L — длина проводника, S — поперечное сечение, p — удельное сопротивление (табличное значение). Активное сопротивление слабо зависит от частоты сигнала, но при его увеличении возрастает.
Отличительной чертой элемента, обладающего активным сопротивлением, будет совпадение по фазе, протекающего через него тока и напряжения. Поэтому вычисляться оно по формуле: R = U/I.
Реактивное сопротивление
Индуктивное сопротивление связано с ЭДС самоиндукции. При протекании через элемент, обладающий индуктивностью, переменного тока, возникает магнитное поле, создающее ЭДС. Эта сила противодействует внешнему полю и препятствует его распространению. Затрачиваемая энергия увеличивает мощность магнитного поля. Как только ток уменьшается, значение магнитного поля начинает тоже снижаться, индуцируя ток самоиндукции. Его направление совпадает с убывающим током. В результате энергия, отобранная магнитным полем, начинает отдаваться обратно в цепь. То есть фактически, в отличие от активного сопротивления, потерь энергии не возникает.
Величина индуктивного сопротивления находится по формуле X L = 2 p * f * L, где: f — частота сигнала, L — значение индуктивности. Напряжение, приложенное к индуктивности и ток, поступающий от источника энергии, сдвинуты относительно друг друга по фазе на 900, при этом ток отстаёт от напряжения.

Ёмкостное же сопротивление обусловлено возникновением электродвижущей силы. При прохождении через ёмкость энергия, поступающая от источника питания должна преодолеть ёмкостное сопротивление, затрачивая часть мощности для её заряда. Но как только подаваемый сигнал изменит знак, весь накопленный заряд ёмкостью начнёт возвращаться в цепь, увеличивая энергию электрического поля.
Другими словами, ёмкость становится источником ЭДС. Ёмкостное сопротивление описывается выражением: X c = 1/ (2 p * f * C), где: C — величина ёмкости. При таком роде сопротивления ток будет опережать напряжение по фазе на 900.
Таким образом, реактивное сопротивление зависит от частоты сигнала. Общий же импеданс определяется не как сумма всех сопротивлений, а по формуле Z = (R2+ X l2+ X c2)½.
Суть закона
Общепринятая формулировка закона Ома гласит, что сила тока в полной цепи прямо пропорциональна электродвижущей силе источника, делённой на общее сопротивление всех элементов замкнутой цепи. Классическая формула закона Ома для цепи постоянного тока выглядит следующим образом:
I = E /(r+R), где:
- R — сопротивление внешней части цепи, Ом;
- r — внутренний импеданс источника энергии.
В замкнутой схеме ток течёт от источника энергии, протекает через различные элементы, последовательно или параллельно подключённые к нему, и возвращается обратно. Изучая открытие Ома можно сформулировать основной физический принцип, на котором строится электротехника. Заключается он в том, что чем больше ЭДС, тем большей энергией будут обладать носители заряда, а значит и их скорость перемещения будет больше. При увеличении сопротивления в цепи скорость движения, а значит, и энергия носителей заряда уменьшается, соответственно снижается и ток.

Величина ЭДС зависит от характеристик источника энергии, а сопротивление от физических параметров материала и температуры. Значение активного сопротивления не может быть изменено увеличением направленного движения частиц или напряжения, но при этом реактивная составляющая зависит от частоты сигнала.
Поэтому закон Ома для полного участка цепи переменного тока и учитывает индуктивную и ёмкостную составляющую, причём как источника питания, так и самой цепи. Описывается математически он формулой: I = Um /Z, где:
- Um — ЭДС источника питания;
- Z — импеданс всей замкнутой цепи: Z = (R2+(wL — 1/wC)2)½.
То есть для переменного тока закон будет описываться выражением вида:
I = Um/ (R2+(wL -1/wC)2)½.
Однако следует понимать, что в формуле используются амплитудные значения величин, а не мгновенные.
Дифференциальное уравнение
Так как сопротивление зависит не только от физических свойств материала, но и от его геометрических параметров, часто последнее при использовании закона Ома исключается из формулы. Открытие учёного, учитывающее только электропроводящие свойства, записывают в так называемой дифференциальной форме.
Такая формула имеет вид: J = σ*E, где:
- J — плотность, характеризующая силу электричества протекающего через единицу площади;
- σ — удельная проводимость, величина обратная удельному сопротивлению;
- E — напряжённость поля, определяется в определённой точке как отношение силы действующей на неподвижный заряд к его величине.
Составляющие уравнения представляются в виде функции координат и времени. Удельная проводимость выражается в виде единичной матрицы. Поэтому закон можно представить формулой:

Таким образом, закон Ома для замкнутой цепи практически ничем не отличается от его формулировки для неполной схемы, лишь только дополнительно учитывает внутреннее сопротивление источника ЭДС. При этом его формулировка не изменяется.
Закон Ома для полной цепи
Зако́н Ома — это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома. Суть закона проста: сила тока в проводнике прямо пропорциональна напряжению между концами проводника, если при прохождении тока свойства проводника не изменяются. Следует также иметь в виду, что закон Ома является фундаментальным и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа, однако, такое приложение этого закона используется крайне редко в рамках узко специализированных расчётов.
Закон Ома формулируется так: Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна характеристике участка, которую называют электрическим сопротивлением этого участка.
| Ток, А | Напряжение, В | Сопротивление, Ом | Мощность, Вт |
|---|---|---|---|
| I | U | R | P |
История закона Ома
Георг Ом, проводя эксперименты с проводником, установил, что сила тока I в проводнике пропорциональна напряжению U, приложенному к его концам:
 ,
,
или
 .
.
Коэффициент пропорциональности 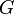 назвали электропроводностью, а величину
назвали электропроводностью, а величину 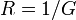 принято именовать электрическим сопротивлением проводника.
принято именовать электрическим сопротивлением проводника.
Закон Ома был открыт в 1827 году.
Закон Ома в интегральной форме
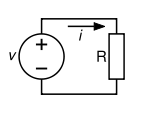
Схема, иллюстрирующая три составляющие закона Ома
Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления
Закон Ома для участка электрической цепи имеет вид:
- U = RI
где:
- U — напряжение или разность потенциалов,
- I — сила тока,
- R — сопротивление.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:
 ,
,
где:
Закон Ома в дифференциальной форме
Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
где:
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).
Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.
Закон Ома для переменного тока
Если цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), а ток является синусоидальным с циклической частотой ω, то закон Ома обобщается; величины, входящие в него, становятся комплексными:
где:
- U = U0eiωt — напряжение или разность потенциалов,
- I — сила тока,
- Z = Re—iδ — комплексное сопротивление (импеданс),
- R = (Ra2+Rr2)1/2 — полное сопротивление,
- Rr = ωL — 1/ωC — реактивное сопротивление (разность индуктивного и емкостного),
- Rа — активное (омическое) сопротивление, не зависящее от частоты,
- δ = —arctg Rr/Ra — сдвиг фаз между напряжением и силой тока.
При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведен взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, U = U0sin(ωt + φ) подбором такой 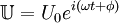 , что
, что 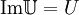 . Тогда все значения токов и напряжений в схеме надо считать как
. Тогда все значения токов и напряжений в схеме надо считать как 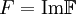
Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.
Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
Объяснение закона Ома
Закон Ома можно просто объяснить при помощи теории Друде
См. также
Wikimedia Foundation. 2010.
Закон Ома для однородного участка цепи
Обязательным условием существования электрического тока является наличие электрического поля, для существования которого, в свою очередь, необходима разность потенциалов (напряжение). Ток будет направлен в сторону уменьшения потенциалов (на рисунке – влево), а свободные электроны будут двигаться в обратную сторону.

На концах участка проводника заданы потенциалы φ_1 и φ_2, причем φ_1>φ_2. Напряжение в таком случае можно найти по формуле:

В 1826 году Георг Ом, обобщив итоги опытов, показавших, что, чем больше напряжение на участке, тем больше сила тока, проходящего через него, получил зависимость, названную законом Ома. В ходе экспериментов Ом выявил, что различные проводники при одинаково заданном напряжении будут проводить ток по-разному, т.е., каждый проводник обладает различной мерой проводимости. Эту величину назвали электрическим сопротивлением.
Определеение Закона Ома для однородного участка цепи гласит: сила тока для однородного проводника на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению проводника.
Формула закона Ома для однородного участка цепи

- I [А] – сила тока,
- U [В] – напряжение,
- R [Ом] – электрическое сопротивление.
Сопротивление – главная характеристика проводника. В зависимости от строения проводника, в них существует различное количество узлов кристаллической решетки и атомов примесей, взаимодействуя с которыми электроны замедляются.
Сопротивление будет зависеть от рода и размеров проводника:
 где:
где:- P
 — удельное сопротивление проводника (табличная величина, характеризующая способность материала к сопротивлению).
— удельное сопротивление проводника (табличная величина, характеризующая способность материала к сопротивлению). - l [м] – длина проводника,
- S [мм2] – площадь поперечного сечения проводника.
Решение задачи по теме Закон Ома для однородного участка цепи
Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 1 мм2, если к концам провода приложено напряжение 8,5 В.




 Задача 1
Задача 1








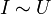 ,
,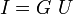 .
.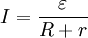 ,
,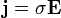
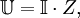
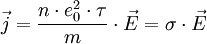
 — удельное сопротивление проводника (табличная величина, характеризующая способность материала к сопротивлению).
— удельное сопротивление проводника (табличная величина, характеризующая способность материала к сопротивлению).