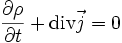Закон сохранения электрических зарядов
Многие физические явления, наблюдаемые в природе и окружающей нас жизни, не могут быть объяснены только на основе законов механики, молекулярно-кинетической теории и термодинамики. В этих явлениях проявляются силы, действующие между телами на расстоянии, причем эти силы не зависят от масс взаимодействующих тел и, следовательно, не являются гравитационными. Эти силы называют электромагнитными силами.
Закон сохранения электрических зарядов
В обычных условиях микроскопические тела являются электрически нейтральными, потому что положительно и отрицательно заряженные частицы, которые образуют атомы, связаны друг с другом электрическими силами и образуют нейтральные системы. Если электрическая нейтральность тела нарушена, то такое тело называется наэлектризованное тело. Для электризации тела необходимо, чтобы на нём был создан избыток или недостаток электронов или ионов одного знака.
Способы электризации тел, которые представляют собой взаимодействие заряженных тел, могут быть следующими:
- Электризация тел при соприкосновении. В этом случае при тесном контакте небольшая часть электронов переходит с одного вещества, у которого связь с электроном относительно слаба, на другое вещество.
- Электризация тел при трении. При этом увеличивается площадь соприкосновения тел, что приводит к усилению электризации.
- Влияние. В основе влияния лежит явление электростатической индукции, то есть наведение электрического заряда в веществе, помещённом в постоянное электрическое поле.
- Электризация тел под действием света. В основе этого лежит фотоэлектрический эффект
Многочисленные опыты показывают, что когда имеет место электризация тела, то на телах возникают электрические заряды, равные по модулю и противоположные по знаку.
Отрицательный заряд тела обусловлен избытком электронов на теле по сравнению с протонами, а положительный заряд обусловлен недостатком электронов.
Когда происходит электризация тела, то есть когда отрицательный заряд частично отделяется от связанного с ним положительного заряда, выполняется
Закон сохранения электрического заряда формулируется следующим образом:
В замкнутой системе алгебраическая сумма зарядов всех частиц остаётся неизменной:
q1 + q2 + q3 + … + qn = const
где
q1, q2 и т.д. – заряды частиц.
Закон сохранения электрических зарядов
Элементарные частицы могут иметь эл. заряд, тогда они называются заряженными;
Электрический заряд — физическая величина, определяет интенсивность электромагнитных взаимодействий.
Существует 2 знака эл.зарядов:
- положительный
- отрицательный
Частицы с одноименными зарядами отталкиваются, с разноименными — притягиваются. Протон имеет положительный заряд, электрон — отрицательный, нейтрон — электрически нейтрален.
Элементарный заряд
Чем объяснить наличие электромагнитных сил в природе? — в состав всех тел входят заряженные частицы.
В обычном состоянии тела электрически нейтральны (т.к. атом нейтрален), и электромагнитные силы не проявляются.
Тело заряжено, если имеет избыток зарядов какого-либо знака:
- отрицательно заряжено — если избыток электронов;
- положительно заряжено — если недостаток электронов.
Электризация тел — это один из способов получения заряженных тел, например, соприкосновением).
При этом оба тела заряжаются , причем заряды противоположны по знаку, но равны по модулю.
Закон сохранения электрических зарядов
Взаимодействие тел, имеющих заряды одинакового или разного знака, можно продемонстрировать на следующих опытах. Наэлектризуем эбонитовую палочку трением о мех и прикоснёмся ею к металлической гильзе, подвешенной на шёлковой нити.
На гильзе и эбонитовой палочке распределяются заряды одного знака (отрицательные заряды). Приближая заряженную отрицательно эбонитовую палочку к заряженной гильзе, можно увидеть, что гильза будет отталкиваться от палочки (рис. 1.1).
Если теперь поднести к заряженной гильзе стеклянную палочку, потёртую о шёлк (положительно заряженную), то гильза будет к ней притягиваться (рис. 1.2).
Закон сохранения электрических зарядов
Возьмём два одинаковых электрометра и один из них зарядим (рис. 2.1). Его заряд соответствует 6 делениям шкалы.
Если соединить эти электрометры стеклянной палочкой, то никаких изменений не произойдёт. Это подтверждает тот факт, что стекло является диэлектриком. Если же для соединения электрометров использовать металлический стержень А (рис. 2.2), держа его за не проводящую электричество ручку В, то можно заметить, что первоначальный заряд разделится на две равные части: половина заряда перейдёт с первого шара на второй. Теперь заряд каждого электрометра соответствует 3 делениям шкалы. Таким образом, первоначальный заряд не изменился, он только разделился на две части.
Если заряд передать от заряженного тела к незаряженному телу такого же размера, то заряд разделится пополам между двумя этими телами. Но если второе, незаряженное тело, будет больше, чем первое, то на второе перейдёт больше половины заряда. Чем больше тело, которому передают заряд, тем большая часть заряда на него перейдёт.
Но общая сумма заряда при этом не изменится. Таким образом, можно утверждать, что заряд сохраняется. Т.е. выполняется закон сохранения электрического заряда.
Электрические заряды не существуют сами по себе, а являются внутренними свойствами элементарных частиц – электронов, протонов и др.
Опытным путем в 1914 г. американский физик Р. Милликен показал
В реакции образования электронно-позитронной пары действует закон сохранения заряда.
qэлектрона + qпозитрона = 0.
Позитрон — элементарная частица, имеющая массу, приблизительно равную массе электрона; заряд позитрона положительный и равен заряду электрона.
На основании закона сохранения электрического заряда
Как известно, все тела состоят из атомов, в состав которых входят электроны и протоны. Количество электронов и протонов в составе незаряженного тела одинаковое. Поэтому такое тело не проявляет электрического действия на другие тела. Если же два тела находятся в тесном контакте (при натирании, сжатии, ударе и т.п.), то электроны, связанные с атомами значительно слабее, чем протоны, переходят с одного тела на другое.
Тело, на которое перешли электроны, будет иметь их избыток. Согласно закону сохранения электрический заряд этого тела будет равняться алгебраической сумме положительных зарядов всех протонов и зарядов всех электронов. Этот его заряд будет отрицательным и по значению равным сумме зарядов избыточных электронов.
У тела с излишком электронов отрицательный заряд.
Тело, утратившее электроны, будет иметь положительный заряд, модуль которого будет равен сумме зарядов электронов, потерянных телом.
У тела, имеющего положительный заряд, электронов меньше, чем протонов.
Электрический заряд не изменяется при переходе тела в другую систему отсчета.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Конспект «Закон сохранения электрического заряда»
«Закон сохранения электрического заряда»
Закон сохранения электрического заряда — один из фундаментальных законов природы. Закон сохранения заряда был открыт в 1747 г. Б. Франклином.
Электрон — частица, входящая в состав атома. В истории физики существовало несколько моделей строения атома. Одна из них, позволяющая объяснить ряд экспериментальных фактов, в том числе явление электризации, была предложена Э. Резерфордом. На основании проделанных опытов он сделал вывод о том, что в центре атома находится положительно заряженное ядро, вокруг которого по орбитам движутся отрицательно заряженные электроны. У нейтрального атома положительный заряд ядра равен суммарному отрицательному заряду электронов. Ядро атома состоит из положительно заряженных протонов и нейтральных частиц нейтронов. Заряд протона по модулю равен заряду электрона. Если из нейтрального атома удалены один или несколько электронов, то он становится положительно заряженным ионом; если к атому присоединяются электроны, то он становится отрицательно заряженным ионом.
Знания о строении атома позволяют объяснить явление электризации трением. Электроны, слабо связанные с ядром, могут отделиться от одного атома и присоединиться к другому. Это объясняет, почему на одном теле может образоваться недостаток электронов, а на другом — их избыток. В этом случае первое тело становится заряженным положительно, а второе — отрицательно.

При электризации происходит перераспределение заряда, электризуются оба тела, приобретая равные по модулю заряды противоположных знаков. При этом алгебраическая сумма электрических зарядов до и после электризации остаётся постоянной:
q1 + q2 + … + qn = const.
Алгебраическая сумма зарядов пластин до и после электризации равна нулю. Записанное равенство выражает фундаментальный закон природы — закон сохранения электрического заряда.

Как и любой физический закон, он имеет определённые границы применимости: он справедлив для замкнутой системы тел, т.е. для совокупности тел, изолированных от других объектов.

Конспект урока «Закон сохранения электрического заряда».
Следующая тема: «Электрическое поле. Проводники и диэлектрики».
Закон сохранения электрического заряда — урок. Физика, 8 класс.
Возьмём два одинаковых электрометра и один из них зарядим (рис. 1). Его заряд соответствует \(6\) делениям шкалы.


Если соединить эти электрометры стеклянной палочкой, то никаких изменений не произойдёт. Это подтверждает тот факт, что стекло является диэлектриком. Если же для соединения электрометров использовать металлический стержень А (рис. 2), держа его за не проводящую электричество ручку В, то можно заметить, что первоначальный заряд разделится на две равные части: половина заряда перейдёт с первого шара на второй. Теперь заряд каждого электрометра соответствует \(3\) делениям шкалы. Таким образом, первоначальный заряд не изменился, он только разделился на две части.
Если заряд передать от заряженного тела к незаряженному телу такого же размера, то заряд разделится пополам между двумя этими телами. Но если второе, незаряженное тело, будет больше, чем первое, то на второе перейдёт больше половины заряда. Чем больше тело, которому передают заряд, тем большая часть заряда на него перейдёт.
Но общая сумма заряда при этом не изменится. Таким образом, можно утверждать, что заряд сохраняется. Т.е. выполняется закон сохранения электрического заряда.
В замкнутой системе алгебраическая сумма зарядов всех частиц остаётся неизменной:
q1+q2+q3+…+qn \(=\) const,
где q1, q2 и т.д. — заряды частиц.
Замкнутой считают систему, в которую не входят заряды извне, а также не выходят из неё наружу.
Экспериментально установлено, что при электризации тел тоже выполняется закон сохранения электрического заряда. Нам уже известно, что электризация — это процесс получения электрически заряженных тел из электронейтральных. При этом заряжаются оба тела. Например, при натирании стеклянной палочки шёлковой тканью стекло приобретает положительный заряд, а шёлк становится отрицательно заряженным. В начале эксперимента ни одно из тел заряжено не было. В конце эксперимента оба тела заряжены. Экспериментально установлено, что эти заряды противоположны по знаку, но одинаковы по численному значению, т.е. их сумма равна нулю. Если тело заряжено отрицательно и при электризации оно ещё приобретает отрицательный заряд, то заряд тела возрастает. Но суммарный заряд этих двух тел не меняется.
Пример:
До электризации первое тело имеет заряд \(-2\) у.е (у.е. — условная единица заряда). В ходе электризации оно приобретает еще \(4\) отрицательных заряда. Тогда после электризации его заряд становится равен \(-2 + (-4) = -6\) у.е. Второе тело в результате электризации отдаёт \(4\) отрицательных заряда, и его заряд будет равным \(+4\) у.е. Суммируя заряд первого и второго тела в конце эксперимента, получим \(-6 + 4 = -2\) у.е. А такой заряд был у них до эксперимента.
Источники:
Пёрышкин А.В. Физика, 8 класс// ДРОФА, 2013.
http://fizika.in/elektrodinamika/elekrostatika/70-elektroskop-delimost-elektricheskogo-zaryada.html
Закон сохранения электрического заряда — это… Что такое Закон сохранения электрического заряда?
- Закон сохранения электрического заряда
Закон сохранения электрического заряда гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.

Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу. В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако, такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. То есть был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме.
Закон сохранения заряда в интегральной форме
Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность можно записать в математической форме:

Здесь Ω — некоторая произвольная область в трёхмерном пространстве,
 — граница этой области, ρ — плотность заряда,
— граница этой области, ρ — плотность заряда,  — плотность тока (плотность потока электрического заряда) через границу.
— плотность тока (плотность потока электрического заряда) через границу.Закон сохранения заряда в дифференциальной форме
Переходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса можно переписать закон сохранения заряда в локальной дифференциальной форме (уравнение непрерывности)

Закон сохранения заряда в электронике
Правила Кирхгофа для токов напрямую следуют из закона сохранения заряда. Объединение проводников и радиоэлектронных компонентов представляется в виде незамкнутой системы. Суммарный приток зарядов в данную систему равен суммарному выходу зарядов из системы. В правилах Кирхгофа предполагается что электронная система не может значительно изменять свой суммарный заряд.
Wikimedia Foundation. 2010.
- Закон соответственных состояний
- Закон стила (фильм)
Смотреть что такое «Закон сохранения электрического заряда» в других словарях:
ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА — один из основных законов природы, состоящий в том, что алгебраическая сумма электрических зарядов любой замкнутой (электрически изолированной) системы остаётся неизменной, какие бы процессы ни происходили внутри этой системы … Большая политехническая энциклопедия
закон сохранения электрического заряда — krūvio tvermės dėsnis statusas T sritis fizika atitikmenys: angl. charge conservation law; law of conservation of electric charge vok. Erhaltungssatz der elektrischen Ladung, m; Ladungserhaltungssatz, m rus. закон сохранения заряда, m; закон… … Fizikos terminų žodynas
Закон сохранения заряда — закон сохранения электрического заряда закон, согласно которому алгебраическая сумма электрических зарядов всех частиц изолированной системы не меняется при происходящих в ней процессах. Электрический заряд любой частицы или системы частиц… … Концепции современного естествознания. Словарь основных терминов
Закон сохранения — Законы сохранения фундаментальные физические законы, согласно которым при определённых условиях некоторые измеримые физические величины, характеризующие замкнутую физическую систему, не изменяются с течением времени. Некоторые из законов… … Википедия
закон сохранения заряда — krūvio tvermės dėsnis statusas T sritis fizika atitikmenys: angl. charge conservation law; law of conservation of electric charge vok. Erhaltungssatz der elektrischen Ladung, m; Ladungserhaltungssatz, m rus. закон сохранения заряда, m; закон… … Fizikos terminų žodynas
Закон сохранения заряда — Закон сохранения электрического заряда гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется. Закон сохранения заряда выполняется абсолютно точно. На данный момент его происхождение объясняют следствием принципа… … Википедия
Закон сохранения лептонного числа — Аромат в физике элементарных частиц Ароматы и квантовые числа: Лептонное число: L Барионное число: B Странность: S Очарование: C Прелесть: B Истинность: T Изоспин: I или Iz Слабый изоспин: Tz … Википедия
Закон сохранения энергии — Закон сохранения энергии фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и… … Википедия
ЗАРЯДА СОХРАНЕНИЯ ЗАКОН — один из фундаментальных строгих законов природы, состоящий в том, что алгебр. сумма электрич. зарядов любой замкнутой (электрически изолированной) системы остаётся неизменной, какие бы процессы ни происходили внутри этой системы. Установлен в 18… … Физическая энциклопедия
Сохранения законы — физические закономерности, согласно которым численные значения некоторых физических величин не изменяются со временем в любых процессах или в определённом классе процессов. Полное описание физической системы возможно лишь в рамках… … Большая советская энциклопедия
Книги
- 10класс. Физика, Сборник. Аудиокурс поможет учащимся в освоении необходимого материала по курсу физики в 10 классе общеобразовательной школы. Важной темой аудиокурса является раздел «Механика», включающая динамику… Подробнее Купить за 124 руб аудиокнига
- Курсы «Подготовка к ЕГЭ по физике», Коллектив авторов. Данный курс посвящен подготовке к итоговой аттестации по школьному курсу по физике, подготовке к сдаче единого государственного экзамена и дальнейшему поступлению школьника в ВУЗ. Главные… Подробнее Купить за 124 руб аудиокнига
Закон сохранения заряда — это… Что такое Закон сохранения заряда?
Зако́н сохране́ния электри́ческого заря́да гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.
Закон сохранения заряда выполняется абсолютно точно. На данный момент его происхождение объясняют следствием принципа калибровочной инвариантности[1][2]. Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу. В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. То есть был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме.
Физическая теория утверждает, что каждый закон сохранения основан на соответствующем фундаментальном принципе симметрии. Со свойствами симметрий пространства-времени связаны законы сохранения энергии, импульса и момента импульса. Законы сохранения электрического, барионного и лептонного зарядов связаны не со свойствами пространства-времени, а с симметрией физических законов относительно фазовых преобразований в абстрактном пространстве квантовомеханических операторов и векторов состояний. Заряженные поля в квантовой теории поля описываются комплексной волновой функцией, где x — пространственно-временная координата. Частицам с противоположными зарядами соответствуют функции поля, различающиеся знаком фазы , которую можно считать угловой координатой в некотором фиктивном двумерном «зарядовом пространстве». Закон сохранения заряда является следствием инвариантности лагранжиана относительно глобального калибровочного преобразования типа , где Q — заряд частицы, описываемой полем , а — произвольное вещественное число, являющееся параметром и не зависящее от пространственно-временных координат частицы. Такие преобразования не меняют модуля функции, поэтому они называются унитарными U(1).[3][4]
Закон сохранения заряда в интегральной форме
Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность, можно записать в математической форме:
Здесь — некоторая произвольная область в трёхмерном пространстве, — граница этой области, — плотность заряда, — плотность тока (плотность потока электрического заряда) через границу.
Закон сохранения заряда в дифференциальной форме
Переходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса можно переписать закон сохранения заряда в локальной дифференциальной форме (уравнение непрерывности)
Закон сохранения заряда в электронике
Правила Кирхгофа для токов напрямую следуют из закона сохранения заряда. Объединение проводников и радиоэлектронных компонентов представляется в виде незамкнутой системы. Суммарный приток зарядов в данную систему равен суммарному выходу зарядов из системы. В правилах Кирхгофа предполагается, что электронная система не может значительно изменять свой суммарный заряд.
Экспериментальная проверка
Наилучшей экспериментальной проверкой закона сохранения электрического заряда является поиск таких распадов элементарных частиц, которые были бы разрешены в случае нестрогого сохранения заряда. Такие распады никогда не наблюдались.[5] Лучшее экспериментальное ограничение на вероятность нарушения закона сохранения электрического заряда получено из поиска фотона с энергией mec2/2 ≈ 255 кэВ, возникающего в гипотетическом распаде электрона на нейтрино и фотон:
однако существуют теоретические аргументы в пользу того, что такой однофотонный распад не может происходить даже в случае, если заряд не сохраняется.[7] Другой необычный несохраняющий заряд процесс — спонтанное превращение электрона в позитрон[8] и исчезновение заряда (переход в дополнительные измерения, туннелирование с браны и т. п.). Наилучшие экспериментальные ограничения на исчезновение электрона вместе с электрическим зарядом и на бета-распад нейтрона без эмиссии электрона:
Примечания
- ↑ Яворский Б. М. «Справочник по физике для инженеров и студентов вузов» / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев, 8-ое изд., М., ООО «Издательство Оникс», ООО «Издательство Мир и образование», 2006, ISBN 5-488-00330-4 (ООО «Издательство Оникс»), ISBN 5-94666-260-0 (ООО «Издательство Мир и образование»), ISBN 985-13-5975-0 (ООО «Харвест»), УДК 530(035) ББК 22.3, Разд. VII «Основы ядерной физики и физики элементарных частиц», Гл. 4 «Элементарные частицы», п. 3 «Гравитация. Квантовая электродинамика.», с. 952;
- ↑ Ландау Л. Д., Лифшиц Е. М. «Теоретическая физика», учебн. пособ. для вузов, в 10 т. / т. 4, «Квантовая электродинамика», 4-е изд., исправл., М., «Физматлит», 2001, 720 с., тир. 2000 экз., ISBN 5-9221-0058-0 (т. 4), гл. 5 «Излучение», п. 43 «Оператор электромагнитного взаимодействия», с. 187—190.
- ↑ Окунь Л. Б. Лептоны и кварки, изд 3-е, стереотипное, М.: Едиториал УРСС, 2005, 352 с., ISBN 5-354-01084-5, гл. 19 Калибровочная инвариантность. Глобальная абелева симметрия U(1)., с. 179
- ↑ Яворский Б. М. Справочник по физике для инженеров и студентов вузов. / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев, 8-е изд. перераб. и испр., М., ООО «Издательство Оникс», ООО «Издательство Мир и Образование», 2006, 1056 стр., ил., ISBN 5-488-00330-4 (ООО «Издательсто Оникс»), ISBN 5-94666-260-0 (Издательство «Мир и Образование»), ISBN 985-13-5975-0 (ООО «Харвест»), Раздел VII. Основы ядерной физики и физики элементарных частиц. Глава 4. «Элементарные частицы» п. 1 «Принципы теории» cтр. 912—925.
- ↑ J. Beringer et al. (2012). «Tests of Conservation Laws». Phys. Rev. D 86: 010001.
- ↑ H.O. Back et al. (2002). «Search for electron decay mode e → γ + ν with prototype of Borexino detector». Physics Letters B 525 (1-2): 29–40. DOI:10.1016/S0370-2693(01)01440-X. Bibcode: 2002PhLB..525…29B.
- ↑ L.B. Okun (1989). «Comments on Testing Charge Conservation and Pauli Exclusion Principle». Comments on Nuclear and Particle Physics 19 (3): 99–116.
- ↑ R.N. Mohapatra (1987). «Possible Nonconservation of Electric Charge». Physical Review Letters 59 (14): 1510–1512. DOI:10.1103/PhysRevLett.59.1510. Bibcode: 1987PhRvL..59.1510M.
- ↑ DOI:10.1016/S0370-2693(99)01091-6. Bibcode: 1999PhLB..465..315B..
- ↑ Norman E.B., Bahcall J.N., Goldhaber M. (1996). «Improved limit on charge conservation derived from 71Ga solar neutrino experiments». Physical Review D53 (7): 4086–4088. DOI:10.1103/PhysRevD.53.4086. Bibcode: 1996PhRvD..53.4086N.
Закон сохранения электрического заряда — Википедия
Материал из Википедии — свободной энциклопедии
Зако́н сохране́ния электри́ческого заря́да — закон физики, утверждающий, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется:
- q1+q2+q3+……+qn=const.{\displaystyle q_{1}+q_{2}+q_{3}+……+q_{n}=const.}
Закон сохранения заряда выполняется абсолютно точно. На данный момент его происхождение объясняют следствием принципа калибровочной инвариантности[1][2]. Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу. В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. То есть был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме.
Физическая теория утверждает, что каждый закон сохранения основан на соответствующем фундаментальном принципе симметрии. Со свойствами симметрий пространства-времени связаны законы сохранения энергии, импульса и момента импульса. Законы сохранения электрического, барионного и лептонного зарядов связаны не со свойствами пространства-времени, а с симметрией физических законов относительно фазовых преобразований в абстрактном пространстве квантовомеханических операторов и векторов состояний. Заряженные поля в квантовой теории поля описываются комплексной волновой функциейϕ(x)=|ϕ(x)|eiψ(x){\displaystyle \phi (x)=|\phi (x)|e^{i\psi (x)}}, где x — пространственно-временная координата. Частицам с противоположными зарядами соответствуют функции поля, различающиеся знаком фазы ψ{\displaystyle \psi }, которую можно считать угловой координатой в некотором фиктивном двумерном «зарядовом пространстве». Закон сохранения заряда является следствием инвариантности лагранжиана относительно глобального калибровочного преобразования типа ϕ′=eiαQϕ{\displaystyle \phi ‘=e^{i\alpha Q}\phi }, где Q — заряд частицы, описываемой полем ϕ{\displaystyle \phi }, а α{\displaystyle \alpha } — произвольное вещественное число, являющееся параметром и не зависящее от пространственно-временных координат частицы[3]. Такие преобразования не меняют модуля функции, поэтому они называются унитарными U(1).[4][5]
Другие соображения
Предположим, что нам известен процесс, нарушающий закон сохранения заряда, в ходе которого, затратив энергию E{\displaystyle E}, можно создать заряд e{\displaystyle e}. Пользуясь этим процессом, создадим заряд e{\displaystyle e}, затратив энергию E{\displaystyle E} в клетке Фарадея с потенциалом φ{\displaystyle \varphi }. Извлечём затем созданный заряд и переместим его подальше от клетки. Получим энергию в виде работы электростатических сил eφ{\displaystyle e\varphi }. Обратим теперь процесс создания заряда и получим ранее затраченную энергию E{\displaystyle E}. Повторяя такой процеcc, можно создать вечный двигатель I рода. Следовательно, допущение о возможности нарушения закона сохранения электрического заряда является ложным. Данное рассуждение показывает связь между законом сохранения электрического заряда и предположением о ненаблюдаемости абсолютной величины электрического потенциала.[6]
Закон сохранения заряда в интегральной форме
Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность, можно записать в математической форме:
- ∂∂t∫ΩρdV=−∮∂Ωj→⋅dS →.{\displaystyle {\frac {\partial }{\partial t}}\int \limits _{\Omega }\rho dV=-\oint \limits _{\partial \Omega }{\vec {j}}\cdot d{\vec {S\ }}.}
Здесь Ω{\displaystyle \Omega } — некоторая произвольная область в трёхмерном пространстве, ∂Ω{\displaystyle \partial \Omega } — граница этой области, ρ{\displaystyle \rho } — плотность заряда, j→{\displaystyle {\vec {j}}} — плотность тока (плотность потока электрического заряда) через границу.
Закон сохранения заряда в дифференциальной форме
Переходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса, можно переписать закон сохранения заряда в локальной дифференциальной форме (уравнение непрерывности):
- ∂ρ∂t+divj→=0.{\displaystyle {\frac {\partial \rho }{\partial t}}+{\mbox{div}}{\vec {j}}=0.}
Закон сохранения заряда в электронике
Правила Кирхгофа для токов напрямую следуют из закона сохранения заряда. Объединение проводников и радиоэлектронных компонентов представляется в виде незамкнутой системы. Суммарный приток зарядов в данную систему равен суммарному выходу зарядов из системы. В правилах Кирхгофа предполагается, что электронная система не может значительно изменять свой суммарный заряд.
Экспериментальная проверка
Наилучшей экспериментальной проверкой закона сохранения электрического заряда является поиск таких распадов элементарных частиц, которые были бы разрешены в случае нестрогого сохранения заряда. Такие распады никогда не наблюдались[7]. Лучшее экспериментальное ограничение на вероятность нарушения закона сохранения электрического заряда получено из поиска фотона с энергией mec2/2 ≈ 255 кэВ, возникающего в гипотетическом распаде электрона на нейтрино и фотон:
однако существуют теоретические аргументы в пользу того, что такой однофотонный распад не может происходить даже в случае, если заряд не сохраняется[10]. Другой необычный несохраняющий заряд процесс — спонтанное превращение электрона в позитрон[11] и исчезновение заряда (переход в дополнительные измерения, туннелирование с браны и т. п.). Наилучшие экспериментальные ограничения на исчезновение электрона вместе с электрическим зарядом и на бета-распад нейтрона без эмиссии электрона:
| e → любые частицы | время жизни больше 6,4·1024 лет (68 % CL)[12] | |
| n → pνν | относительная вероятность несохраняющего заряд распада менее 8·10−27 (68 % CL) при бета-распаде нейтрона в ядре галлия-71, превращающегося при этом в германий-71[13] |
Примечания
- ↑ Яворский Б. М. «Справочник по физике для инженеров и студентов вузов» / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев, 8-ое изд., М., ООО «Издательство Оникс», ООО «Издательство Мир и образование», 2006, ISBN 5-488-00330-4 (ООО «Издательство Оникс»), ISBN 5-94666-260-0 (ООО «Издательство Мир и образование»), ISBN 985-13-5975-0 (ООО «Харвест»), УДК 530(035) ББК 22.3, Разд. VII «Основы ядерной физики и физики элементарных частиц», Гл. 4 «Элементарные частицы», п. 3 «Гравитация. Квантовая электродинамика.», с. 952;
- ↑ Ландау Л. Д., Лифшиц Е. М. «Теоретическая физика», учебн. пособ. для вузов, в 10 т. / т. 4, «Квантовая электродинамика», 4-е изд., исправл., М., «Физматлит», 2001, 720 с., тир. 2000 экз., ISBN 5-9221-0058-0 (т. 4), гл. 5 «Излучение», п. 43 «Оператор электромагнитного взаимодействия», с. 187—190.
- ↑ Наумов А. И. Физика атомного ядра и элементарных частиц. — М., Просвещение, 1984. — С. 281-282
- ↑ Окунь Л. Б.Лептоны и кварки, изд 3-е, стереотипное, М.: Едиториал УРСС, 2005, 352 с., ISBN 5-354-01084-5, гл. 19 Калибровочная инвариантность. Глобальная абелева симметрия U(1)., с. 179
- ↑ Яворский Б. М. Справочник по физике для инженеров и студентов вузов. / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев, 8-е изд. перераб. и испр., М., ООО «Издательство Оникс», ООО «Издательство Мир и Образование», 2006, 1056 стр., ил., ISBN 5-488-00330-4 (ООО «Издательство Оникс»), ISBN 5-94666-260-0 (Издательство «Мир и Образование»), ISBN 985-13-5975-0 (ООО «Харвест»), Раздел VII. Основы ядерной физики и физики элементарных частиц. Глава 4. «Элементарные частицы» п. 1 «Принципы теории» стр. 912—925.
- ↑ Вигнер Э.И. Инвариантность и законы сохранения. Этюды о симметрии. — М.: Едиториал УРСС, 2002. — С. 17-18. — ISBN 5-354-00191-9.
- ↑ J. Beringer et al. (2012). «Tests of Conservation Laws». Phys. Rev. D 86: 010001.
- ↑ Agostini, M.; et al. (Borexino Coll.) (2015). «Test of Electric Charge Conservation with Borexino». Physical Review Letters 115 (23): 231802. arXiv:1509.01223. DOI:10.1103/PhysRevLett.115.231802.
- ↑ Back, H. O.; et al. (Borexino Coll.) (2002). «Search for electron decay mode e → γ + ν with prototype of Borexino detector». Physics Letters B 525 (1—2): 29—40. DOI:10.1016/S0370-2693(01)01440-X. Bibcode: 2002PhLB..525…29B.
- ↑ Okun L. B. (1989). «Comments on Testing Charge Conservation and Pauli Exclusion Principle». Comments on Nuclear and Particle Physics 19 (3): 99—116. (недоступная ссылка)
- ↑ Mohapatra R. N. (1987). «Possible Nonconservation of Electric Charge». Physical Review Letters 59 (14): 1510—1512. DOI:10.1103/PhysRevLett.59.1510. Bibcode: 1987PhRvL..59.1510M. (недоступная ссылка)
- ↑ Belli P. et al. (1999). «Charge non-conservation restrictions from the nuclear levels excitation of 129Xe induced by the electron’s decay on the atomic shell». Physics Letters B 465 (1—4): 315—322. DOI:10.1016/S0370-2693(99)01091-6. Bibcode: 1999PhLB..465..315B..
- ↑ Norman E.B., Bahcall J.N., Goldhaber M. (1996). «Improved limit on charge conservation derived from 71Ga solar neutrino experiments». Physical Review D53 (7): 4086—4088. DOI:10.1103/PhysRevD.53.4086. Bibcode: 1996PhRvD..53.4086N. (недоступная ссылка)
Закон сохранения электрического заряда.
Рассмотрим поток вектора плотности тока через замкнутую поверхность, ориентированную наружу:
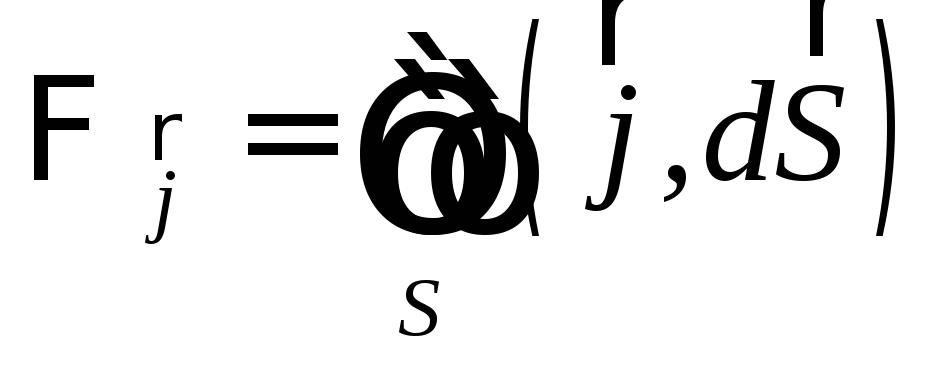 .
.
Если 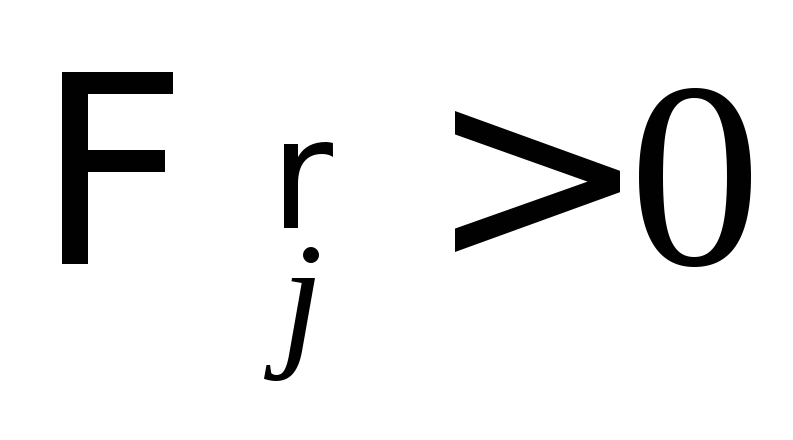 ,
то это означает, что положительные
частицы выходят из объёма, охваченного
этой поверхностью (или отрицательные
входят в объём). Поэтому алгебраическая
величина заряда (с учётом знака)
уменьшается внутри объёма, охваченного
поверхностьюS:
,
то это означает, что положительные
частицы выходят из объёма, охваченного
этой поверхностью (или отрицательные
входят в объём). Поэтому алгебраическая
величина заряда (с учётом знака)
уменьшается внутри объёма, охваченного
поверхностьюS: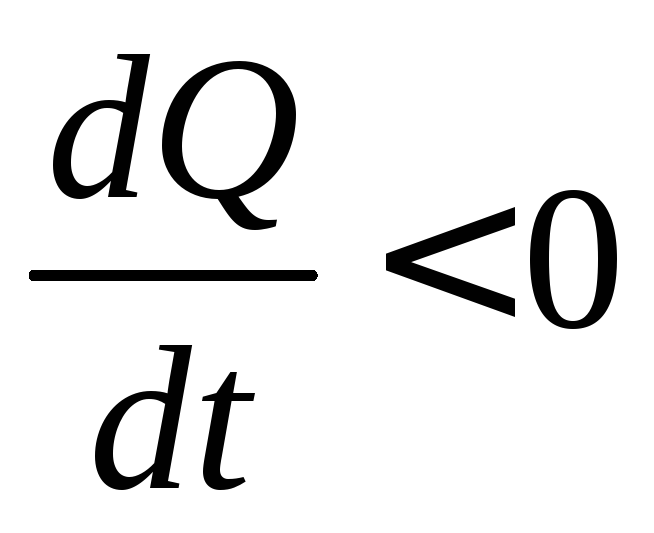 .
Следовательно, должно быть справедливо
равенство
.
Следовательно, должно быть справедливо
равенство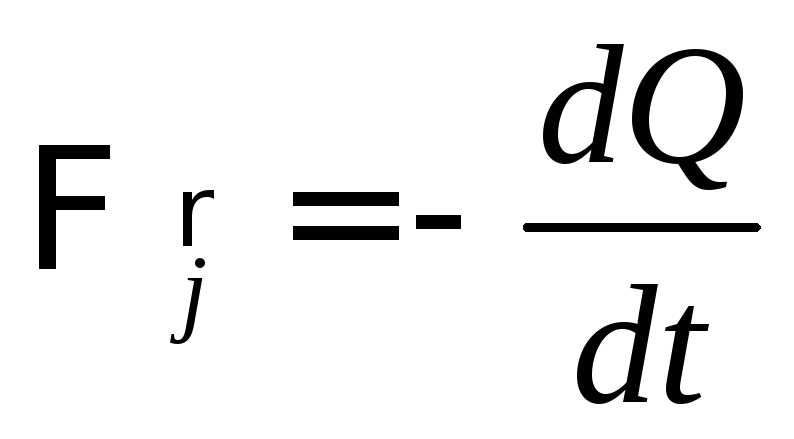 .
Т.е.
.
Т.е.
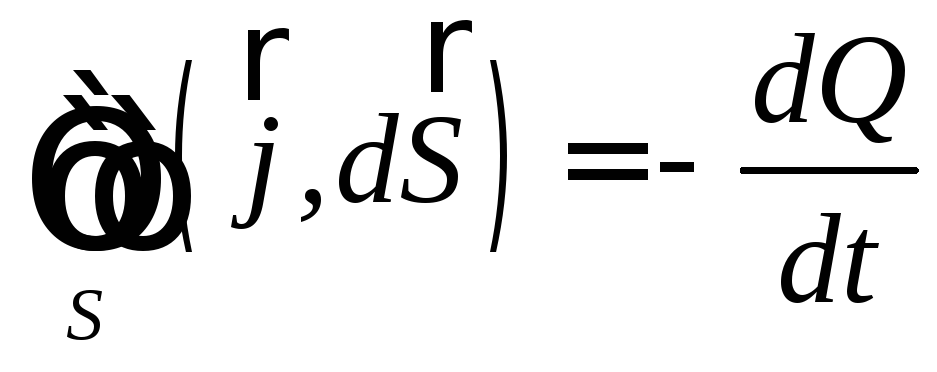
Это
соотношение называется законом
сохранения электрического зарядав
интегральной форме. Если ввести функцию
объёмной плотности заряда,
то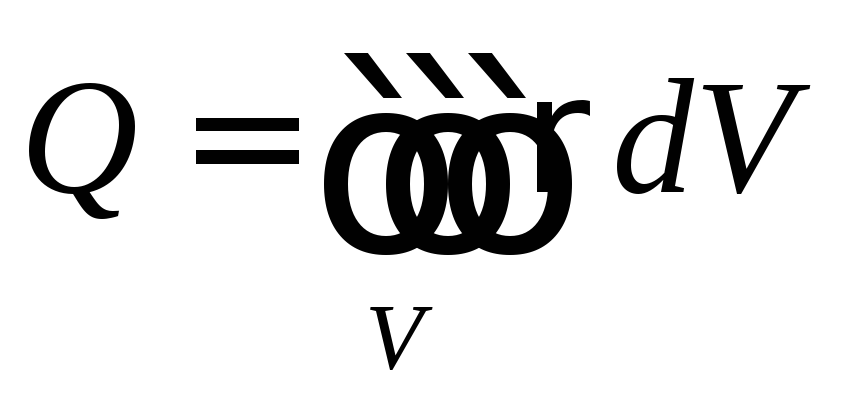 .
.
Получаем
равенство  .
.
Воспользуемся
теоремой Остроградского-Гаусса 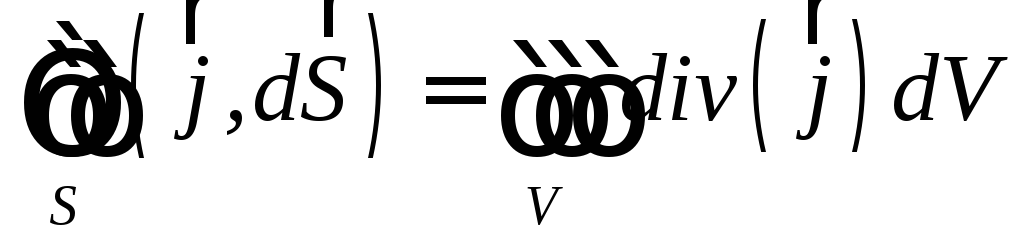 .
.
Если
поверхность Sнеподвижная,
то можно написать равенство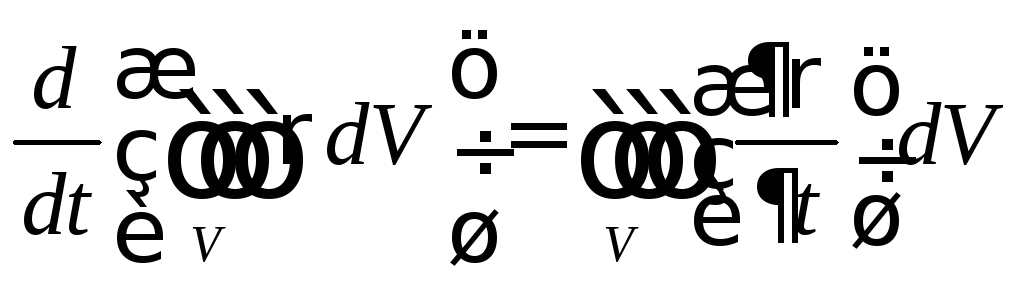 .
.
Тогда
из равенства 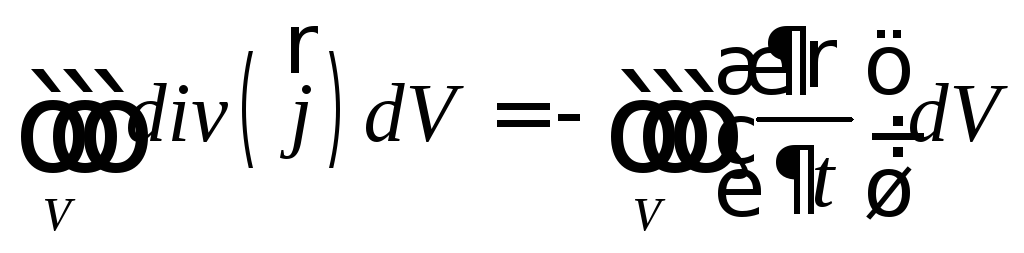 следуетзакон сохранения заряда в
дифференциальной форме
следуетзакон сохранения заряда в
дифференциальной форме
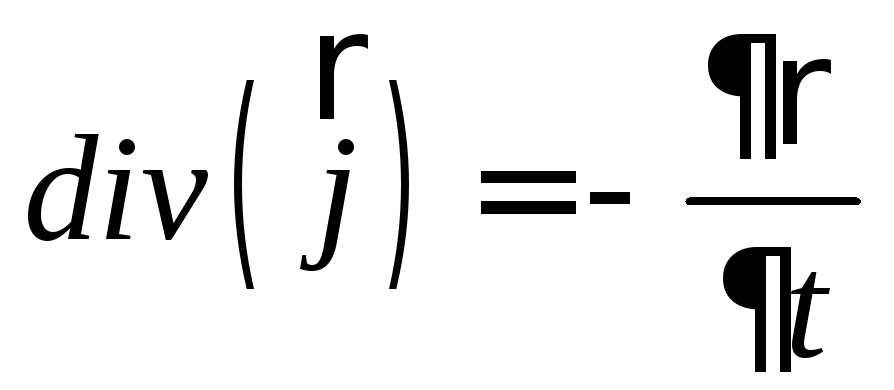 или
или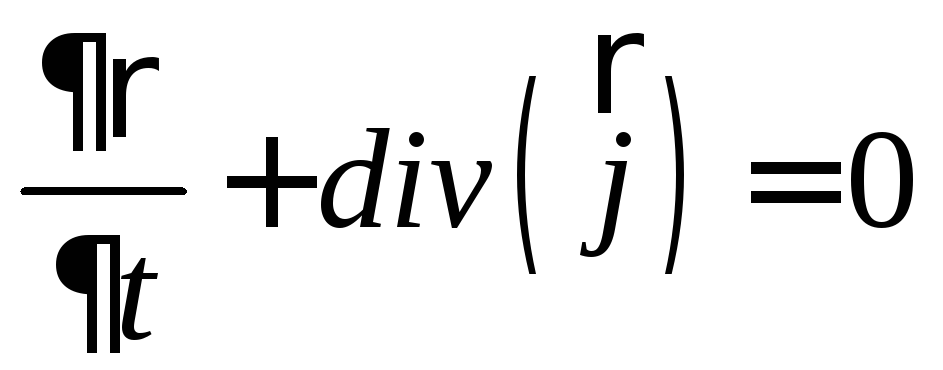 .
.
Следствие.
Если внутри замкнутой поверхности
величина заряда не изменяется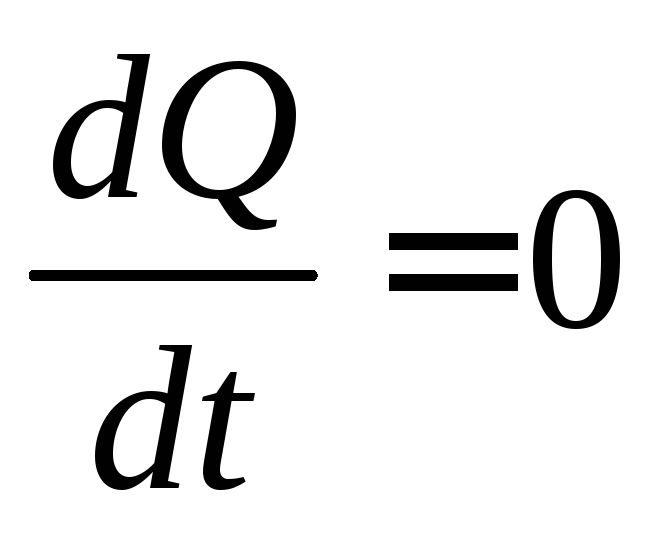 ,
то это означает, что суммарный поток
плотности тока через эту поверхность
равен нулю
,
то это означает, что суммарный поток
плотности тока через эту поверхность
равен нулю
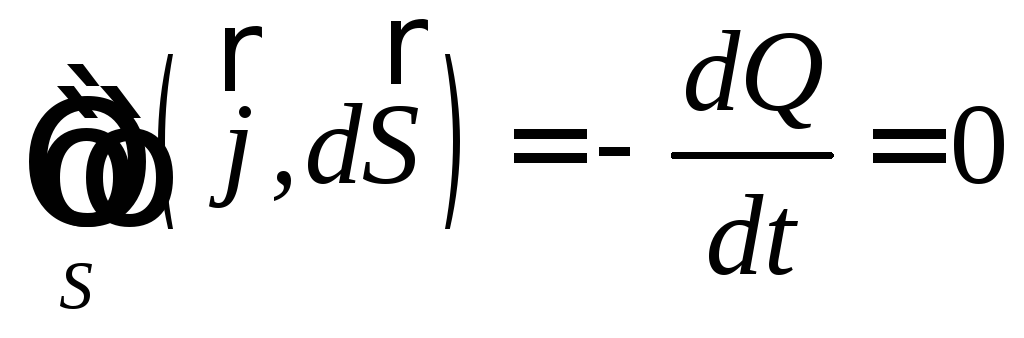 .
.
Так как замкнутая поверхность ориентирована наружу, то поток векторного поля, направленного наружу — положительный, а направленного внутрь – отрицательный. Поэтому можно сказать, что сила втекающего тока имеет отрицательный знак, а втекающего — положительный: Тогда

Т.е. в случае постоянного заряда сила втекающего тока равна силе вытекающего тока.
Сторонние силы.
Кроме кулоновской силы (со стороны электростатического поля) на заряженную частицу могут действовать и другие силы. Например, сила тяжести. В химических источниках тока заряженные частицы движутся под действием сил межмолекулярного взаимодействия т .д..
Силы, действующие на заряженную частицу
и отличные от кулоновских, называются сторонними. При перемещении заряда
эти силы тоже совершают работу АСТОР.
Отношение работы сторонних сил по
перемещению электрического заряда
между двумя точками поля к величине
перенесенного заряда называетсяэлектродвижущей силой (ЭДС):  .
.
Как видно из определения, ЭДС измеряется в Вольтах.
Пример. Электрон под действием силы тяжести опустился вниз на 10 м. Найти величину ЭДС силы тяжести между начальной и конечной точками.
Решение.
Работа силы тяжести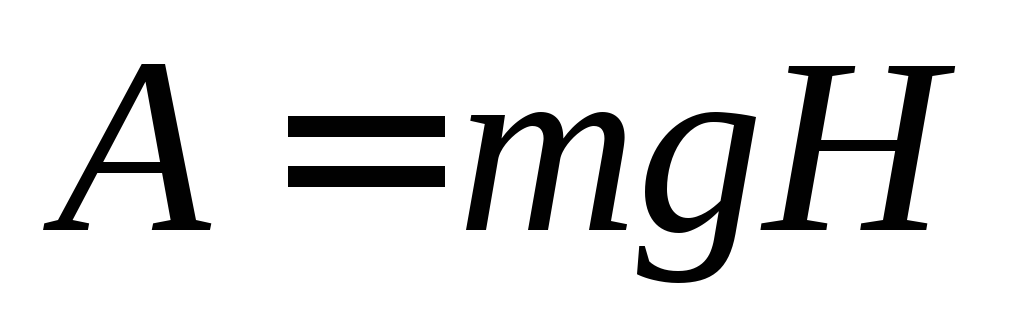 ,
масса электрона
,
масса электрона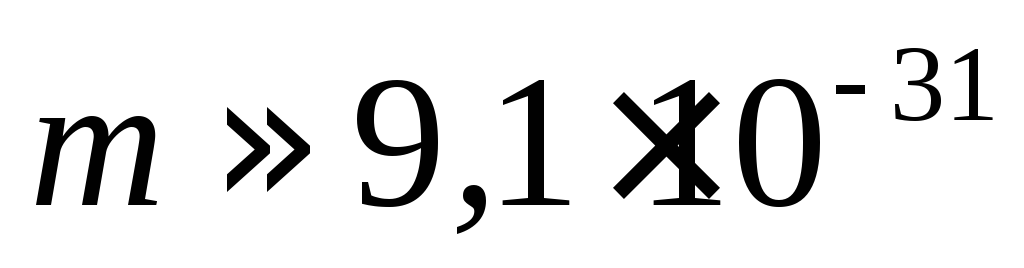 кг, заряд электрона
кг, заряд электрона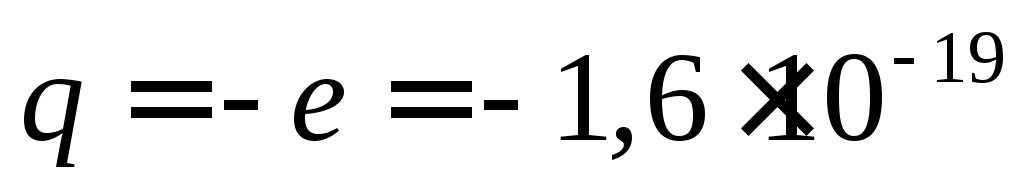 Кл. Поэтому ЭДС силы тяжести между
начальной и конечной точками
Кл. Поэтому ЭДС силы тяжести между
начальной и конечной точками
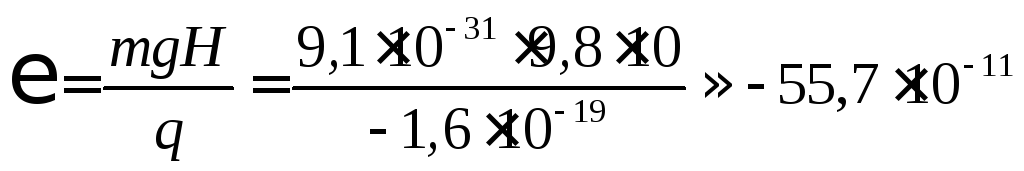 В.
В.
Напряженностью
поля сторонней силыназывается
векторная величина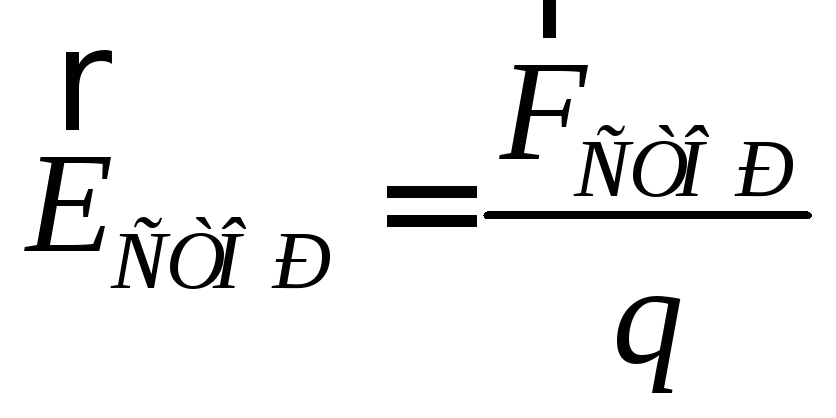 .
.
Пример.
Напряженность поля силы тяжести как
сторонней силы равна по величине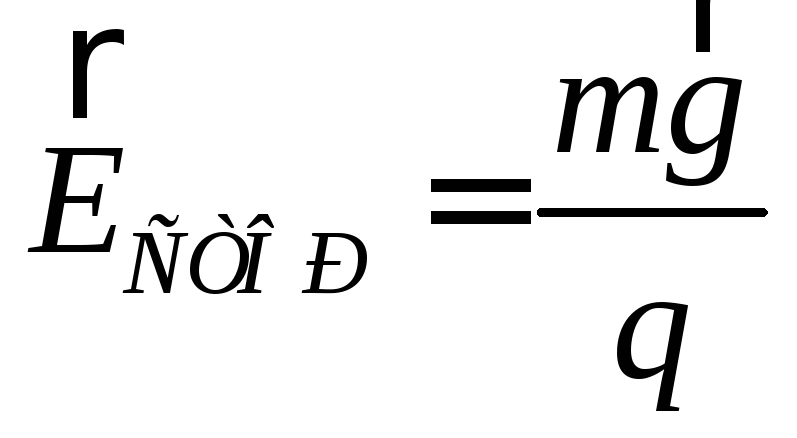
Для ЭДС
между двумя точками поля можно записать 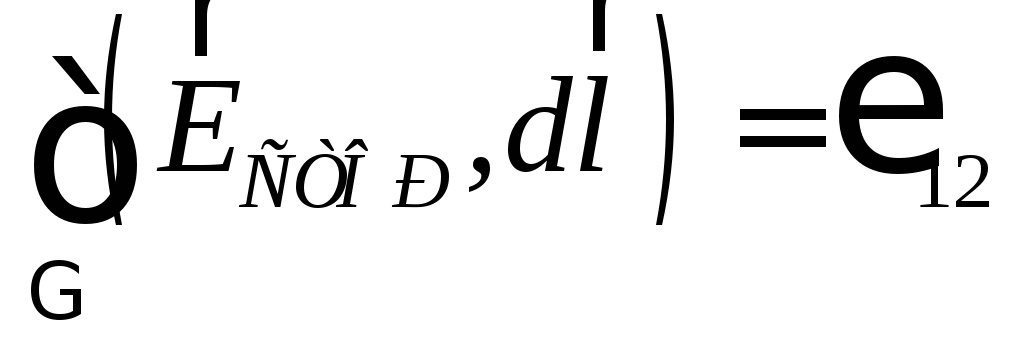 .
.
Полным напряжениеммежду двумя точками поля называется величина отношения работы всех сил по переносу заряда между этими точками к величине этого заряда:
 .
.
Т.к. 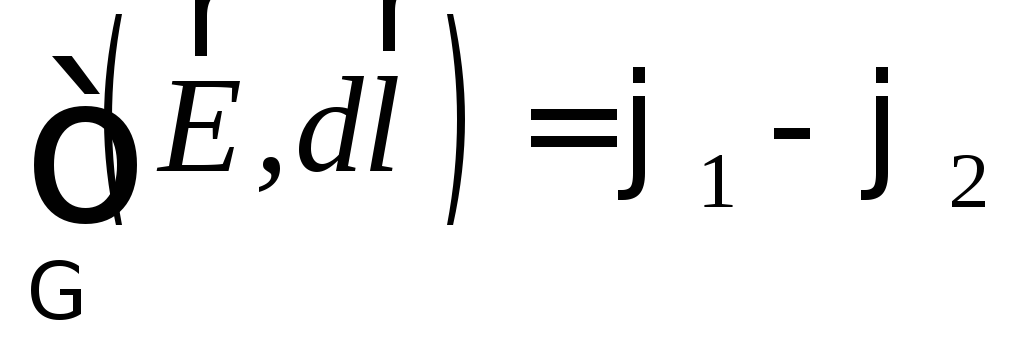 ,
то
,
то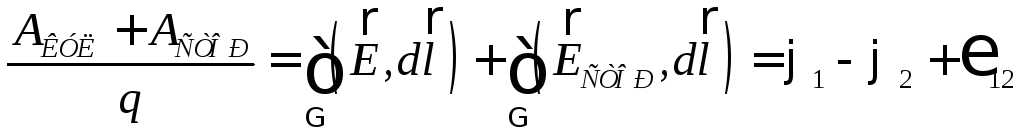 ,
поэтому
,
поэтому
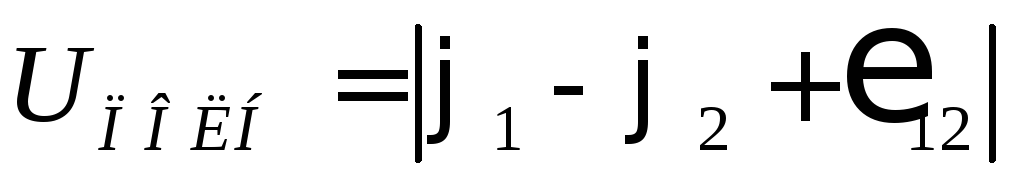 .
.
Величина  называетсянапряжением между точками
поля.
называетсянапряжением между точками
поля.
Источники эдс.
Р ассмотрим
две точки в пространстве: А и В. Пусть
нам необходимо перенести между этими
точками некоторый положительный
электрический зарядQ.
Так как этот заряд кратен элементарному
ассмотрим
две точки в пространстве: А и В. Пусть
нам необходимо перенести между этими
точками некоторый положительный
электрический зарядQ.
Так как этот заряд кратен элементарному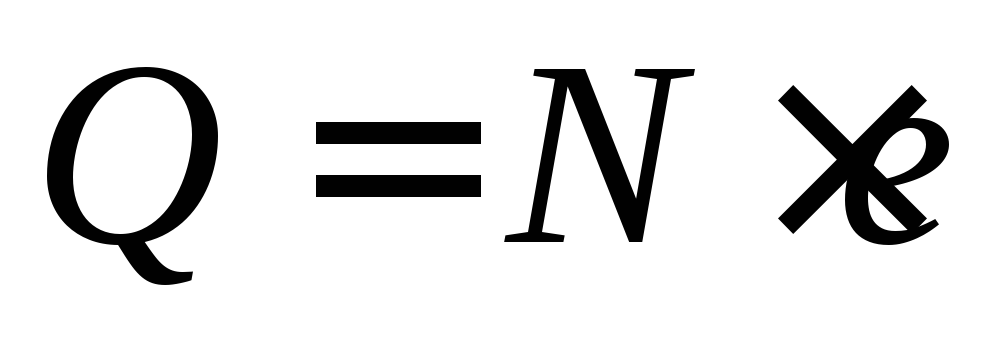 ,
то фактически требуется перенестиNэлементарных положительных зарядов.
Перенос зарядов осуществляют кулоновские
силы, работа которых
,
то фактически требуется перенестиNэлементарных положительных зарядов.
Перенос зарядов осуществляют кулоновские
силы, работа которых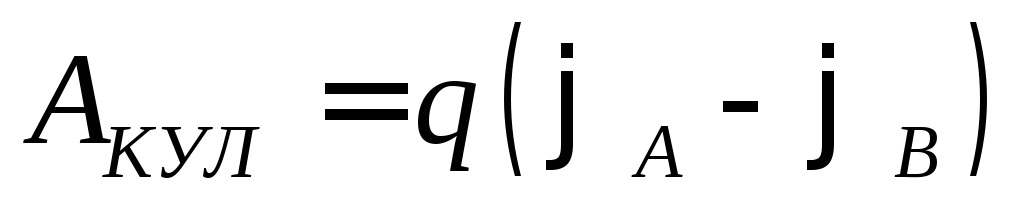 .
Работа кулоновской силы будетбольше
нуля
.
Работа кулоновской силы будетбольше
нуля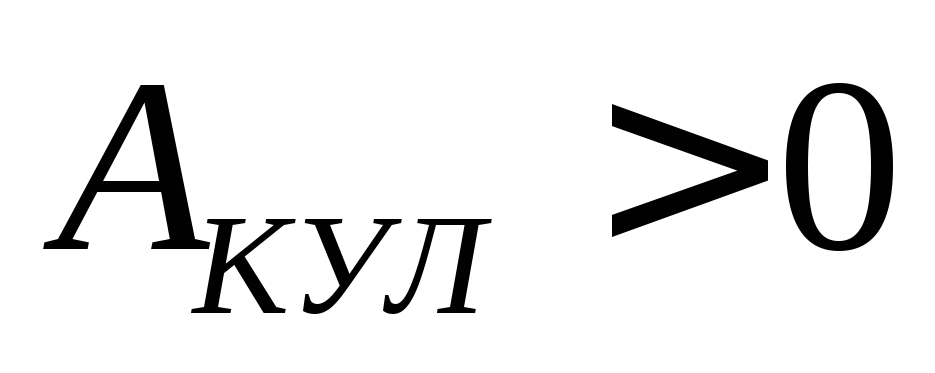 при переносе положительного заряда
при переносе положительного заряда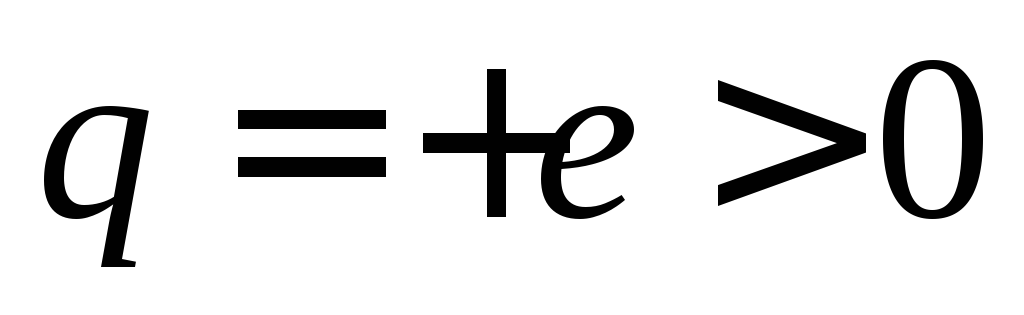 если
если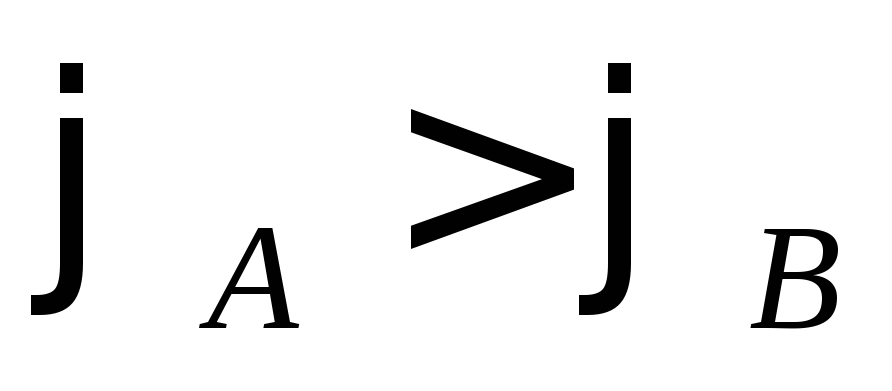 .
Т.е. кулоновские силы смогут переносить
заряд между этими точками, пока
.
Т.е. кулоновские силы смогут переносить
заряд между этими точками, пока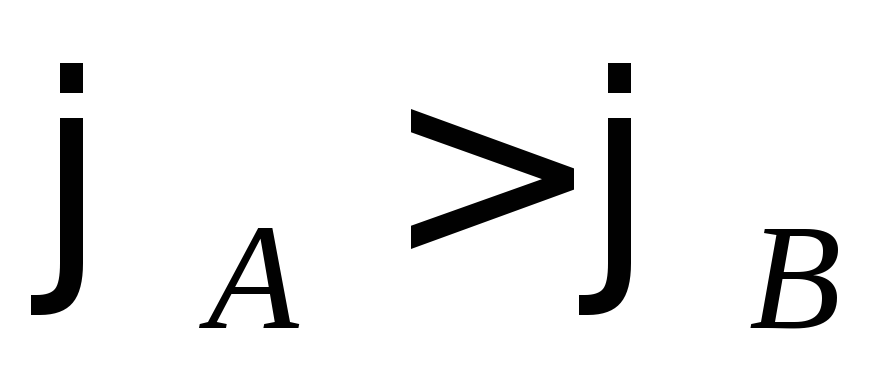 .
Но т.к. положительные заряды будут
уходить из точки А, то её потенциал будет
уменьшаться. И т.к. заряды будут приходить
в точку В, то её потенциал будет
увеличиваться. И в какой-то момент
времени неравенство
.
Но т.к. положительные заряды будут
уходить из точки А, то её потенциал будет
уменьшаться. И т.к. заряды будут приходить
в точку В, то её потенциал будет
увеличиваться. И в какой-то момент
времени неравенство перестанет выполняться. Т.е. кулоновские
силы больше не смогут переносить заряд
между этими точками.
перестанет выполняться. Т.е. кулоновские
силы больше не смогут переносить заряд
между этими точками.
Однако, если каким-то образом убирать
заряды из точки В и переносить их обратно
в А, то неравенство  будет выполняться. Кулоновские силы не
могут сделать такой перенос (т.к. они
при этом совершили бы отрицательную
работу), поэтому нужны силы, отличные
от кулоновских, т.е.сторонние. Таким
образом,сторонние силы должны
переносить положительный заряд из
области с низким потенциалом в область
высокого потенциала.
будет выполняться. Кулоновские силы не
могут сделать такой перенос (т.к. они
при этом совершили бы отрицательную
работу), поэтому нужны силы, отличные
от кулоновских, т.е.сторонние. Таким
образом,сторонние силы должны
переносить положительный заряд из
области с низким потенциалом в область
высокого потенциала.
Элементы цепи, в которых действуют
сторонние силы, называются элементами
ЭДС и обозначаются  . Область высокого потенциала обозначается
«длинной тонкой палочкой», а низкого –
«толстой и короткой». Область высоко
потенциала обозначают знаком «+», а
область низкого «».
. Область высокого потенциала обозначается
«длинной тонкой палочкой», а низкого –
«толстой и короткой». Область высоко
потенциала обозначают знаком «+», а
область низкого «».
Таким образом, элемент ЭДС работает как
«насос», перекачивая положительные
заряды из области с низким потенциалом
в область с более высоким потенциалом.
При этом сторонние силы совершают работу  .
Внутри источника ЭДС кулоновские силы
совершают отрицательную работу
.
Внутри источника ЭДС кулоновские силы
совершают отрицательную работу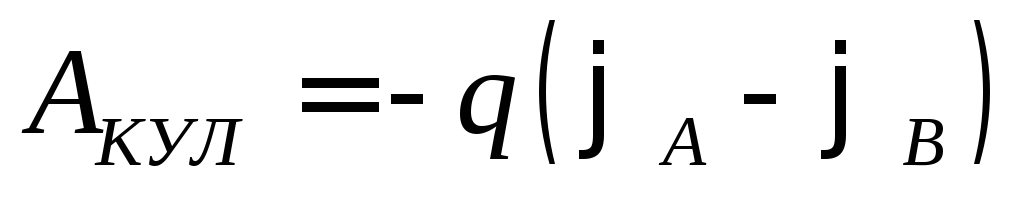 ,
так как они препятствуют перемещению
положительного заряда от низкого
потенциала к высокому.
,
так как они препятствуют перемещению
положительного заряда от низкого
потенциала к высокому.
Суммарная работа всех сил на замкнутой траектории движения зарядов будет равна сумме работ вне элемента ЭДС и внутри ЭДС АСУМ=АВНЕШ+АВНУТР.
Но  ,
,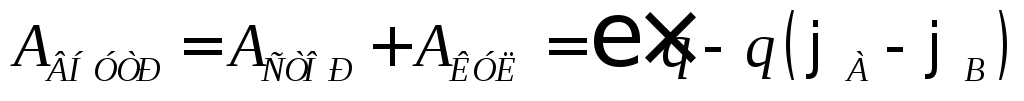
Поэтому
на замкнутой линии тока  ,
т.е. суммарная работа равна работе
сторонних сил.
,
т.е. суммарная работа равна работе
сторонних сил.
ЗАКОН ОМА
Опыт показывает, что в большинстве проводников на движущиеся заряженные частицы кроме внешних сил, вызывающих движение, действуют силы сопротивления движению. Поэтому скорость частиц ограничена по величине. При этом величина средней скорости упорядоченного движения заряженной частицы пропорциональна величине внешней силы.
Пример. Опишем прямолинейное движение
частицы массыmпод
действием постоянной внешней силыFи силы сопротивления .
Второй закон Ньютона вдоль прямой
.
Второй закон Ньютона вдоль прямой .
Установившееся значение скорости
определяется условиемa=0:
.
Установившееся значение скорости
определяется условиемa=0: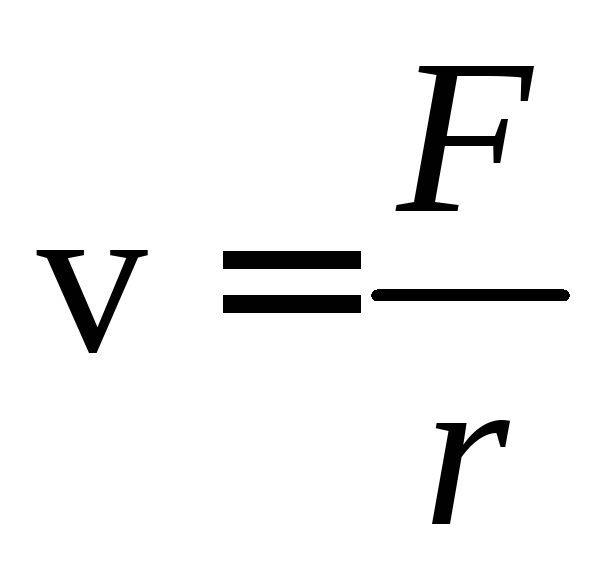 .
Если внешняя сила, например, — электрическая,
т.е.
.
Если внешняя сила, например, — электрическая,
т.е.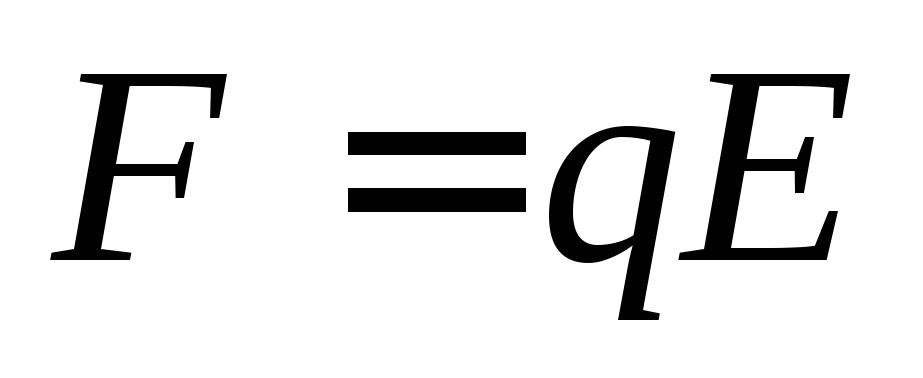 ,
то величина установившейся скорости
пропорциональна напряжённости
электрического поля
,
то величина установившейся скорости
пропорциональна напряжённости
электрического поля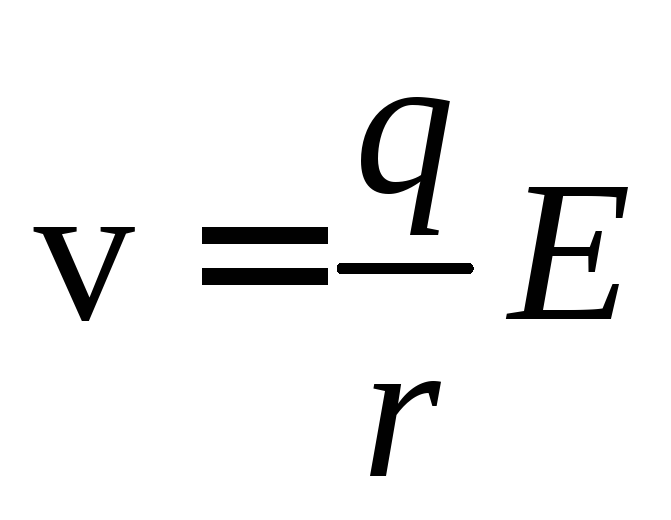 .
.
Силы
сопротивления могут быть вызваны
различными причинами (неоднородностями,
нарушениями кристаллической структуры,
тепловыми колебаниями и т.д.). Но для
данного вещества существует прямая
зависимость между величиной средней
скорости упорядоченного движения
носителей и величиной напряжённости
электрического поля или поля сторонних
сил 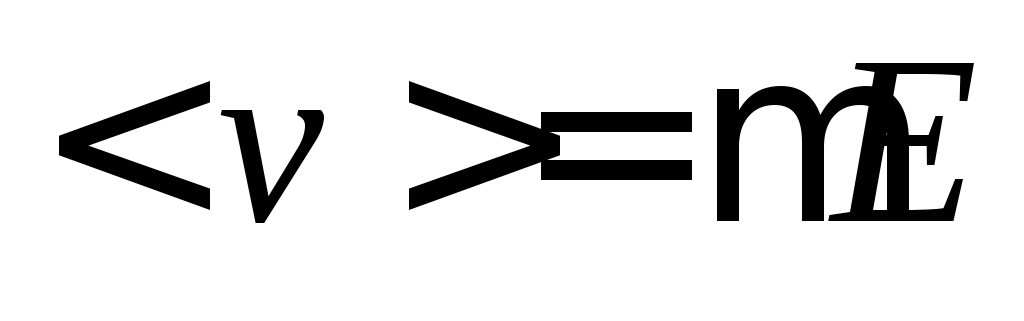 .
Коэффициент
.
Коэффициент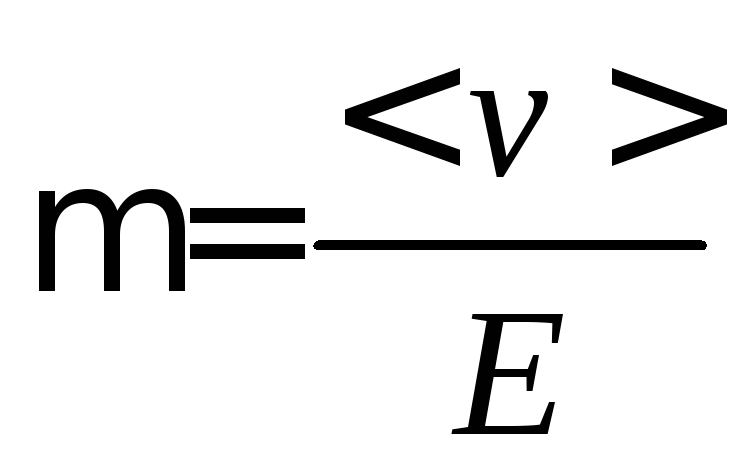 называетсякоэффициентом подвижности
носителей, единицы измерения
называетсякоэффициентом подвижности
носителей, единицы измерения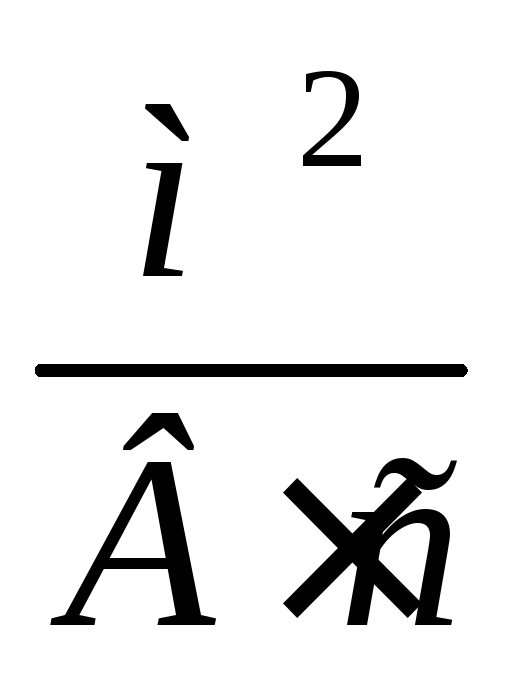 .
.
Замечание. Если в проводнике несколько видов носителей, то у каждого вида свой коэффициент подвижности.
Тогда
для вектора плотности тока можно написать 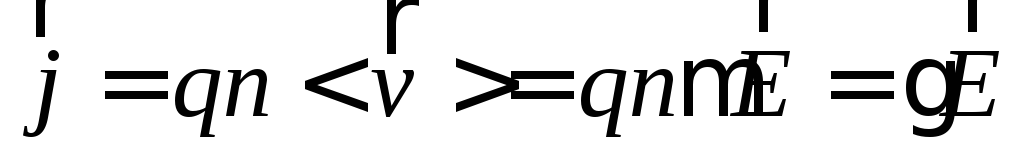 .
.
Коэффициент 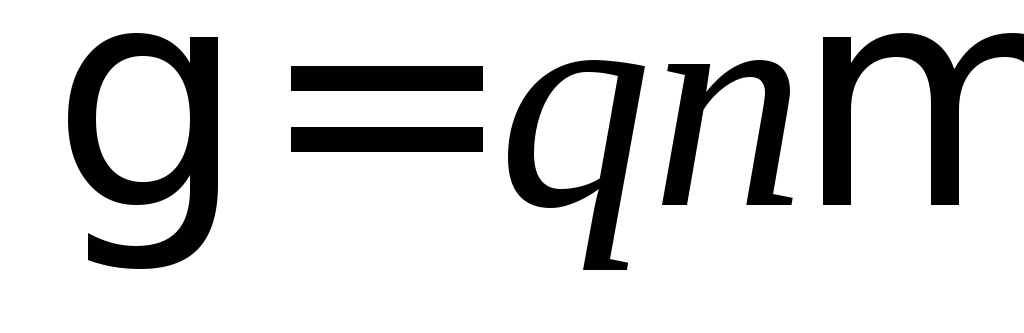 называетсякоэффициентом удельной
электропроводности(удельной
проводимости) вещества. Единица
измерения удельной проводимости См/м
(Сименс/метр). Обратная величина
называетсякоэффициентом удельной
электропроводности(удельной
проводимости) вещества. Единица
измерения удельной проводимости См/м
(Сименс/метр). Обратная величина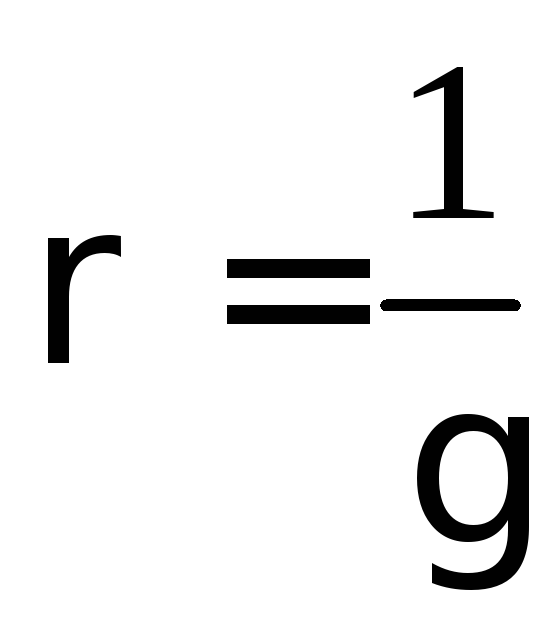 называетсяудельным сопротивлениемвещества. Единица измерения удельного
сопротивления Омм.
называетсяудельным сопротивлениемвещества. Единица измерения удельного
сопротивления Омм.
Выражение
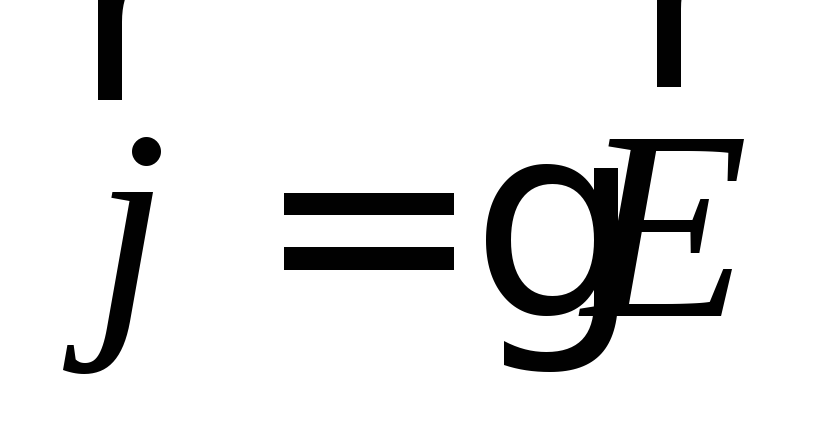
является выражением закона Омав дифференциальной форме. Из этого закона следует, в частности, что линии тока и силовые линии электрического поля (поля сторонних сил) в проводнике совпадают.
Участок проводника, на котором действуютсторонние силы, называетсянеоднородным.
Участок проводника, на котором не действуютсторонние силы, называетсяоднородным.
Будем
считать, что неоднородный участок
проводника имеет вид цилиндра (постоянного
сечения), в котором задано однородное
векторное поле плотности тока.
Проинтегрируем закон Ома 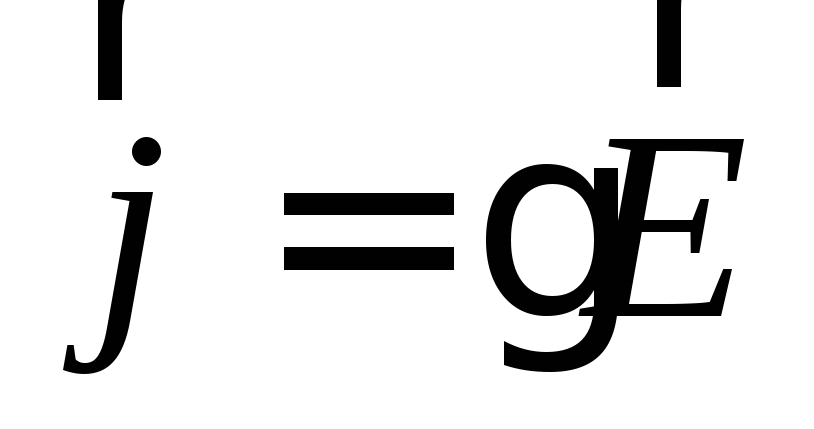 вдоль кривой Г, являющейся линией тока:
вдоль кривой Г, являющейся линией тока:
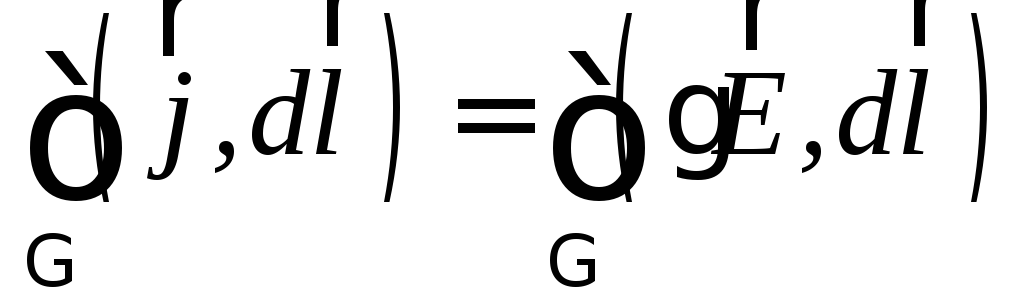 .
.
Вдоль
линии тока  и
и ,
поэтому
,
поэтому и
и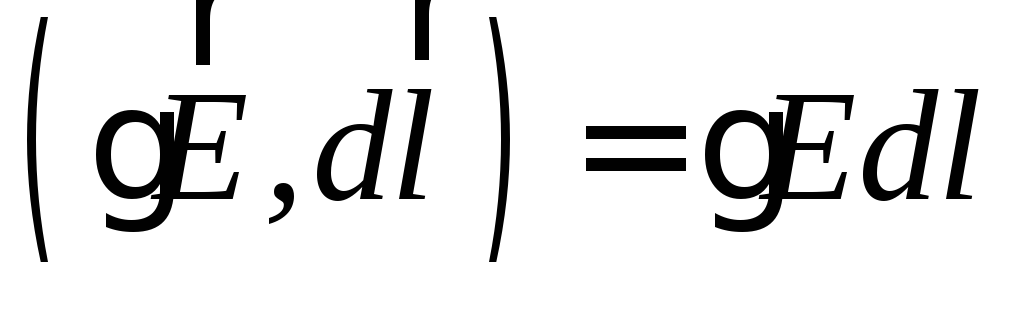 .
.
Т.к.
поперечное сечение и вектор плотности
тока взаимно перпендикулярны в каждой
точке сечения и вдоль сечения 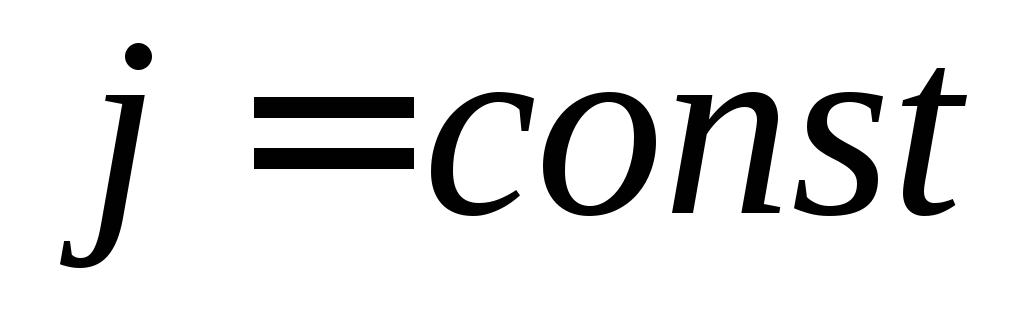 ,
то сила тока через сечение
,
то сила тока через сечение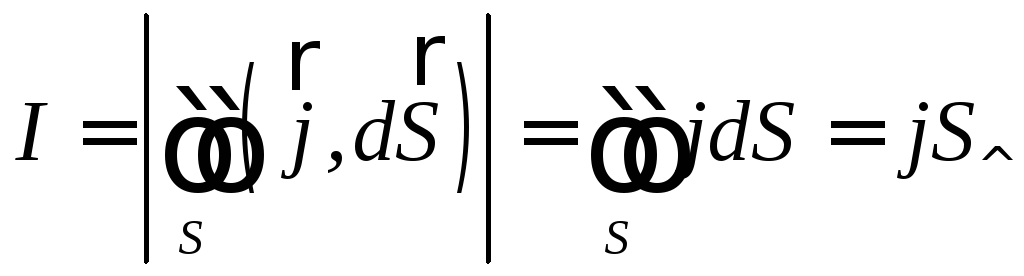 ,
гдеS— площадь поперечного сечения. Откуда
,
гдеS— площадь поперечного сечения. Откуда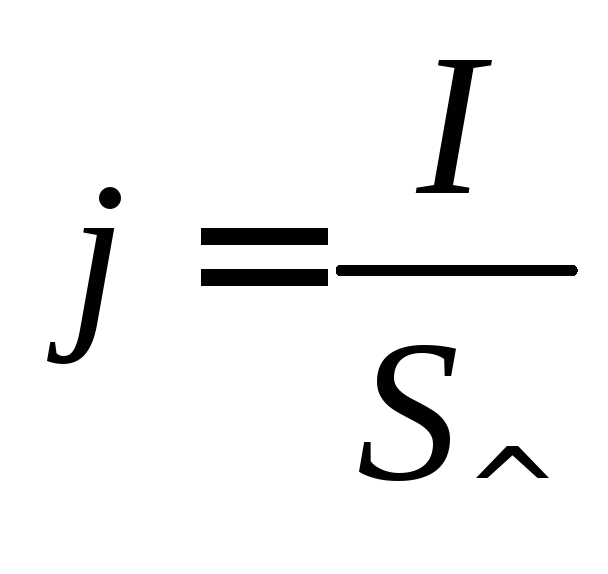 .
Тогда
.
Тогда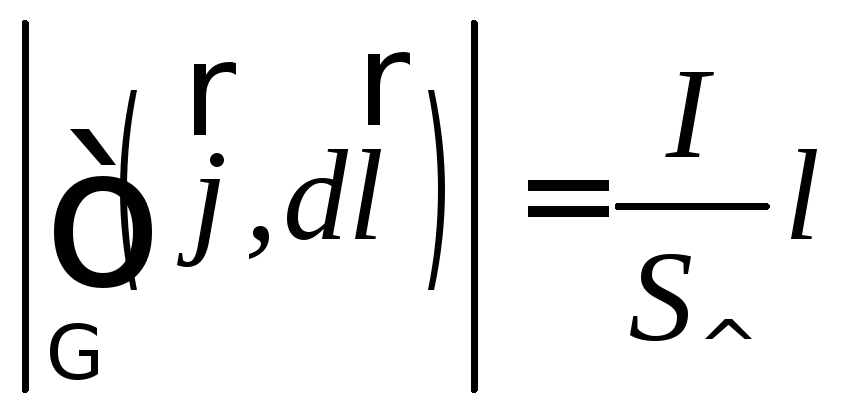 .
.
Т.к. 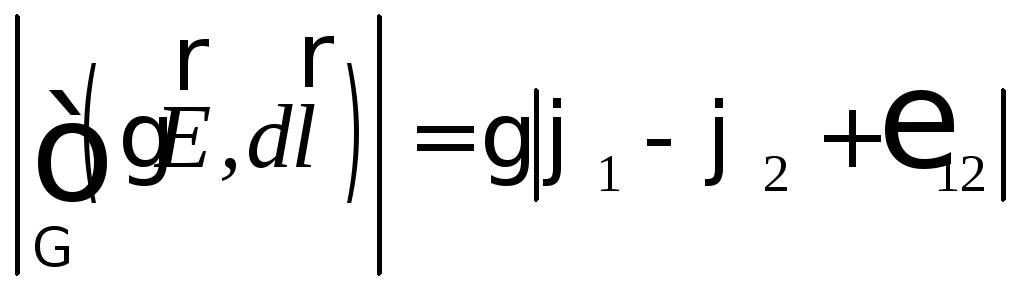 ,
то получаем соотношение
,
то получаем соотношение
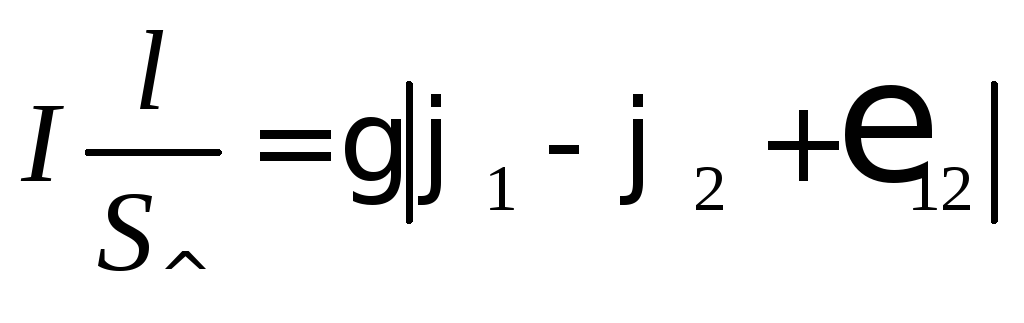 .
.
Величина  называется (электрическим)сопротивлениемпроводника. Единицы измерения сопротивления
– Ом. Тогда получаем соотношение
называется (электрическим)сопротивлениемпроводника. Единицы измерения сопротивления
– Ом. Тогда получаем соотношение
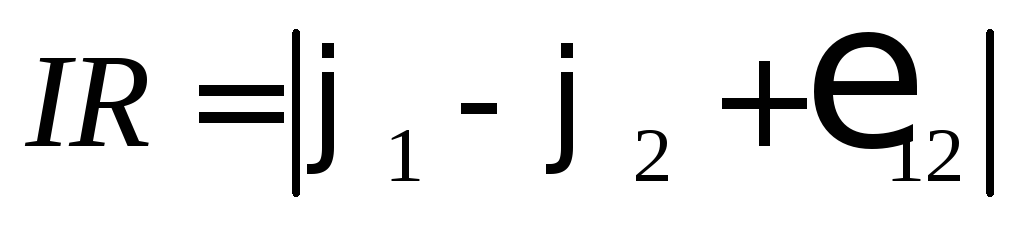 .
.
Это выражение называется законом Ома в интегральной форме.
Величина силы тока в проводнике прямо пропорциональна полному напряжению на этом проводнике и обратно пропорциональна сопротивлению этого проводника
 .
.
Замечание.
Если силу тока считать алгебраической
величиной, то это выражение можно
записать в виде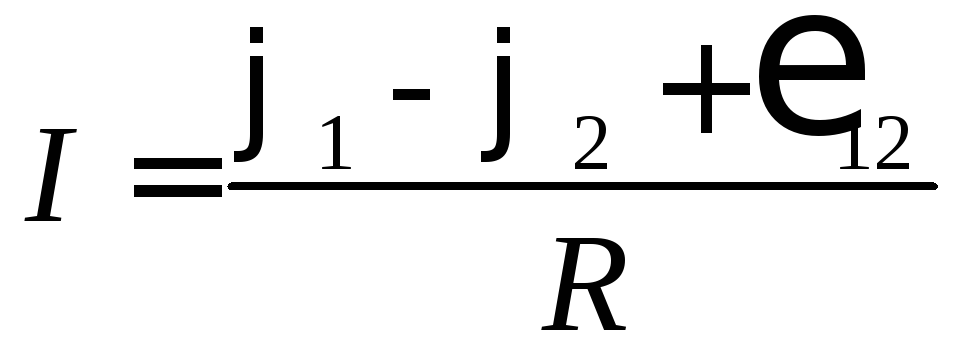 .
.
На однородном участкепроводника не
действуют сторонние силы, т.е.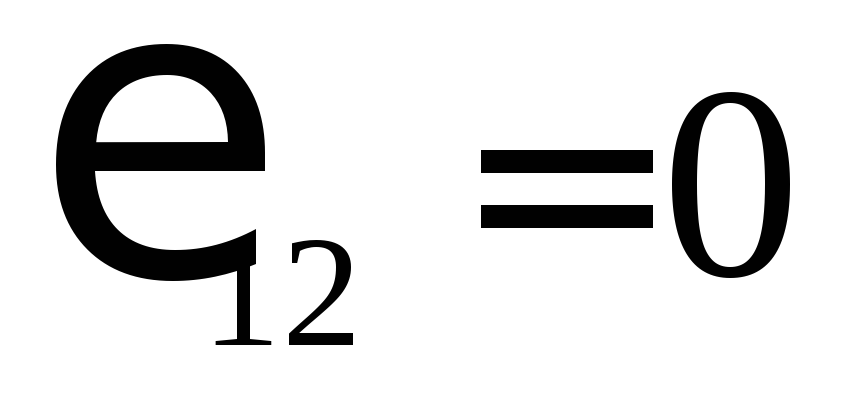 .
Тогда закон Ома для однородного участка
.
Тогда закон Ома для однородного участка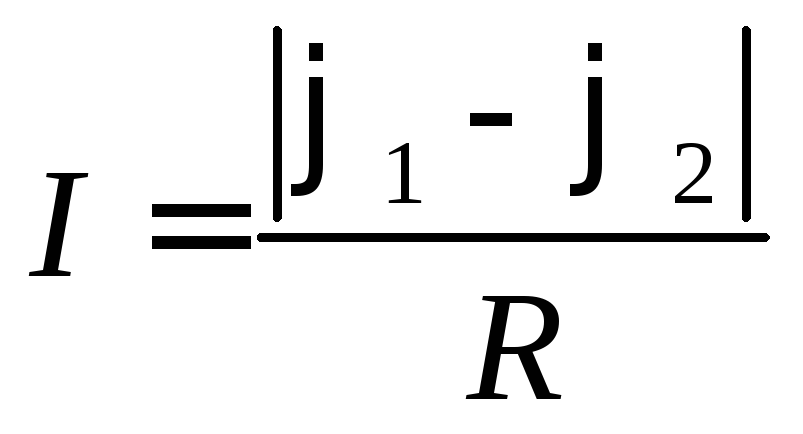 (или с учётом знака
(или с учётом знака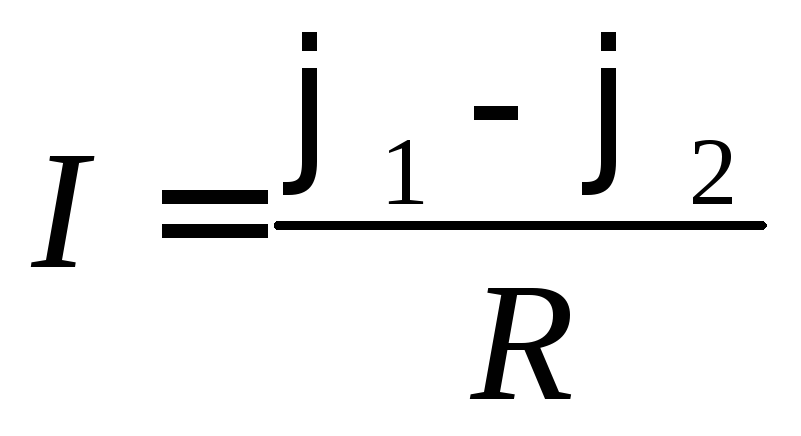 ).
).
Величина
силы тока на однородном участке прямо
пропорциональна напряжению на участке
и обратно пропорциональна сопротивлению
участка: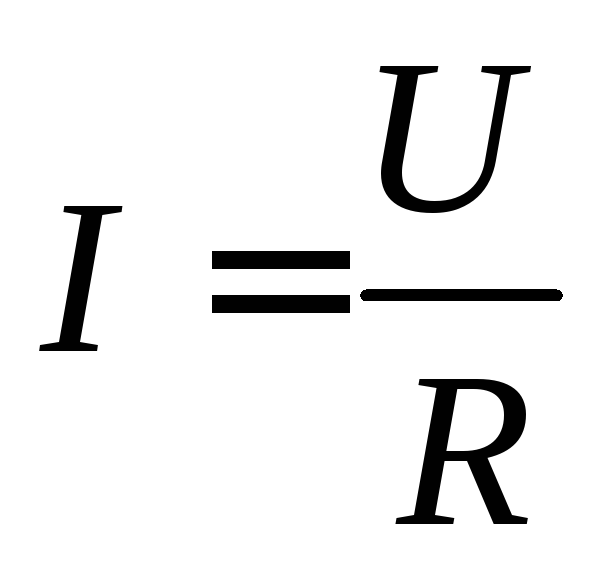 .
.
Замечание.
Из соотношения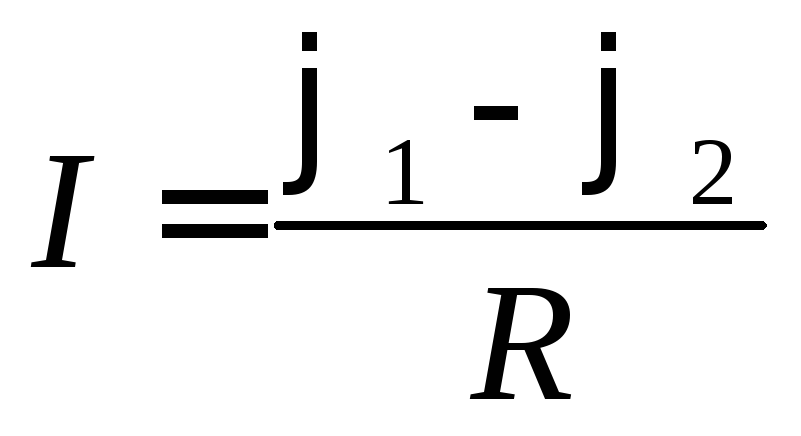 видно, что на однородном проводнике
положительным направлением для тока
является направление от точки с высоким
потенциалом к точке с низким потенциалом
видно, что на однородном проводнике
положительным направлением для тока
является направление от точки с высоким
потенциалом к точке с низким потенциалом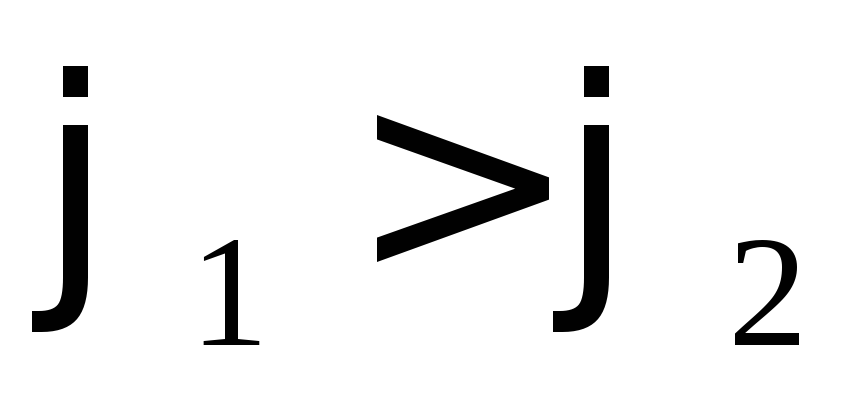 .
Поэтому можно записать вдоль положительного
направления тока:
.
Поэтому можно записать вдоль положительного
направления тока: или
или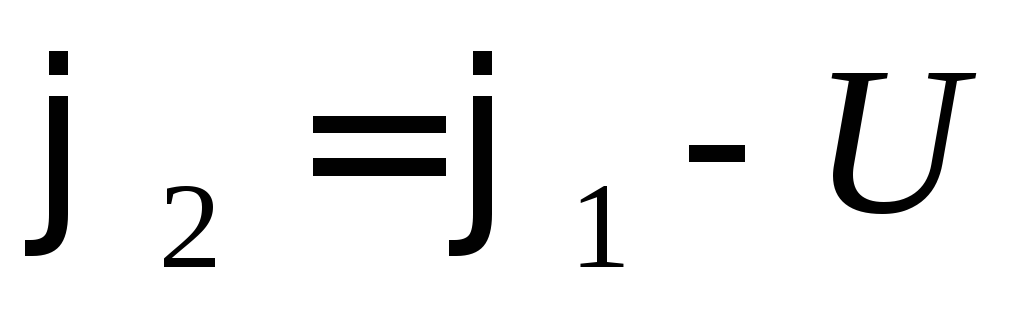 .
Т.е.потенциал на однородном участке
уменьшается в направлении тока на
величину напряжения на этом участке.
Поэтому часто напряжение называютпадением напряжения.
.
Т.е.потенциал на однородном участке
уменьшается в направлении тока на
величину напряжения на этом участке.
Поэтому часто напряжение называютпадением напряжения.
Соединение проводников, по которым может протекать электрический ток, называется электрической цепью.
Узломэлектрической цепи называется место соединения более двух проводников.
Так как заряд каждого узла остается постоянным, то сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла(Это утверждение называется1-е правило Кирхгофа).
Элемент
электрической цепи, сопротивление
которого значительно отличается от
сопротивления проводников цепи,
называется резистором(сопротивлением).
Резистор условно обозначается
прямоугольником  .
.
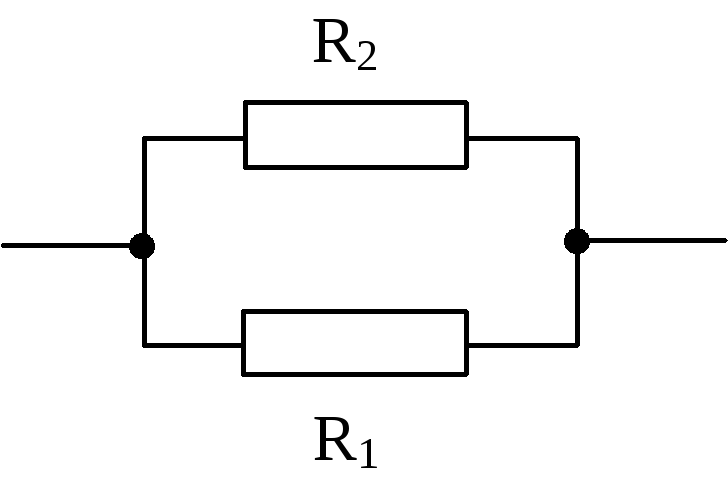
Расчет сопротивлений при параллельном соединении
Пусть сопротивления R1иR2соединены параллельно. Найдем общее сопротивление этого участка. Пусть напряжение на этом участке равноU. Тогда на каждом из сопротивленийU1=U2=U. Сила тока в цепи равна сумме сил токов через каждое из сопротивлений:I=I1+I2или
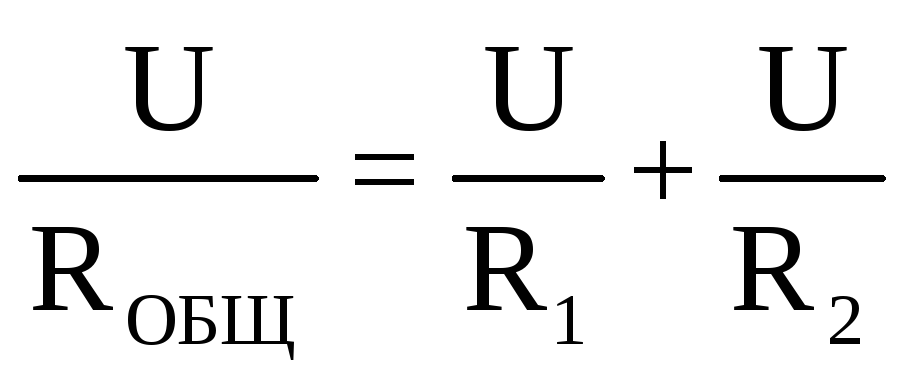
 откуда
откуда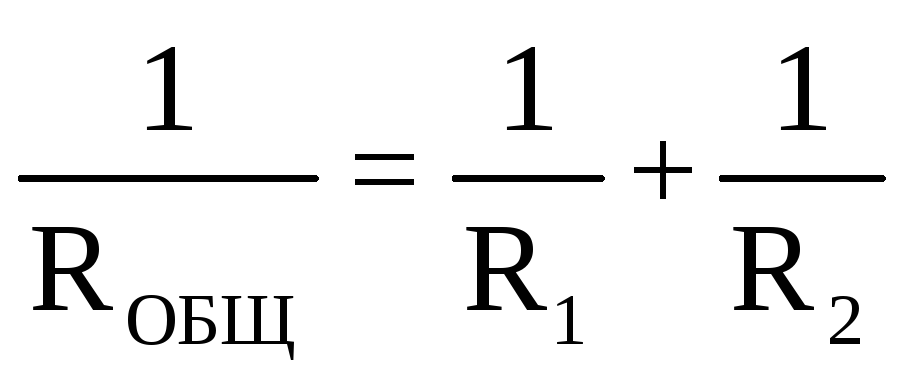 .
.
Таким образом, при параллельном соединении сопротивления складываются по закону обратных чисел.
Расчет сопротивлений при последовательном соединении:
Т ак
как сопротивления соединены последовательно,
то сила тока одинаковая, а напряжение
равно сумме напряжений на каждом из
участковU=U1+U2илиIRОБЩ=IR1+IR2.
ак
как сопротивления соединены последовательно,
то сила тока одинаковая, а напряжение
равно сумме напряжений на каждом из
участковU=U1+U2илиIRОБЩ=IR1+IR2.
Поэтому RОБЩ=R1+R2.При последовательном соединении сопротивления суммируются.




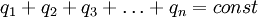
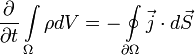
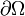 — граница этой области, ρ — плотность заряда,
— граница этой области, ρ — плотность заряда, 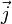 — плотность тока (плотность потока электрического заряда) через границу.
— плотность тока (плотность потока электрического заряда) через границу.