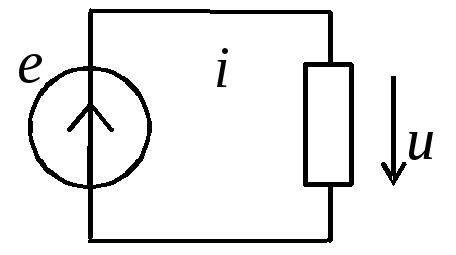
Магнитные и нелинейные цепи
4.1. Магнитное поле и его параметры
Направление магнитных линий и направление создающего их тока связаны между собой известным правилом правоходового винта (буравчика) (рис. 4.1).
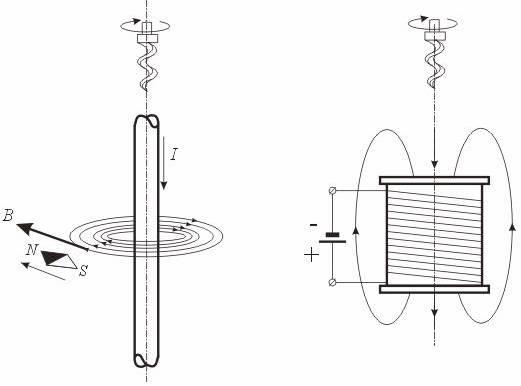
Рис. 4.1. Магнитное поле прямолинейного проводника и катушки. Правило Буравчика
Основной
величиной, характеризующей интенсивность
и направление магнитного поля является
– вектор магнитной индукции 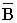 ,
которая измеряется в Теслах [Тл].
,
которая измеряется в Теслах [Тл].
Вектор 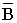 направлен
по касательной к магнитной линии,
направление вектора совпадает с осью
магнитной стрелки, помещенной в
рассматриваемую точку магнитного поля.
направлен
по касательной к магнитной линии,
направление вектора совпадает с осью
магнитной стрелки, помещенной в
рассматриваемую точку магнитного поля.
Величина 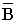 определяется
по механической силе, действующей на
элемент проводника с током, помещенный
в магнитное поле.
определяется
по механической силе, действующей на
элемент проводника с током, помещенный
в магнитное поле.
Если 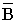 во
всех точках поля имеет одинаковую
величину и направление, то такое поле
называется равномерным.
во
всех точках поля имеет одинаковую
величину и направление, то такое поле
называется равномерным.
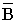 зависит
не только от величины I, но и от магнитных
свойств окружающей среды.
зависит
не только от величины I, но и от магнитных
свойств окружающей среды.
Второй
важной величиной, характеризующей
магнитное поле является – магнитный
поток 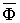
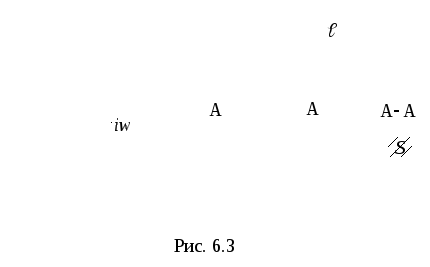
Элементарным магнитным потоком Ф сквозь бесконечно малую площадку называется величина (рис. 4.2)
dФ = B cos dS,
где
– угол между направлением
и
нормалью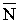 к
площадке dS.
к
площадке dS.
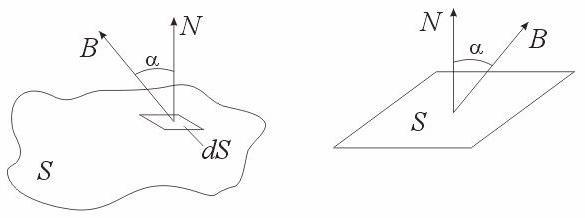
а) б)
Рис. 4.2. Определение магнитного потока, пронизывающего: а) произвольную поверхность; б) плоскую поверхность в равномерном магнитном поле
Сквозь поверхность S [м2]
Ф = s∫ dФ = s∫ B cos α dS,
Если магнитное поле равномерное, а поверхность S представляет собой плоскость
Ф = B S.
При
исследовании магнитных полей и расчете
магнитных устройств пользуются расчетной
величиной  –
напряженность магнитного поля [А/м]
–
напряженность магнитного поля [А/м]
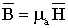
где а – абсолютная магнитная проницаемость среды.
Для неферромагнитных материалов и сред (дерево, бумага, медь, алюминий, воздух) а не отличается от магнитной проницаемости вакуума и равна
o = 4 · 10-7, Гн/м (Генри/метр).
У ферромагнетиков а переменная и зависит от В.
4.2. Магнитные цепи
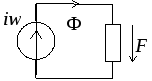
Всякий электромагнит состоит из стального сердечника – магнитопровода и намотанной на него катушки с витками изолированной проволоки, по которой проходит электрический ток.
Совокупность нескольких участков: ферромагнитных (сталь) и неферромагнитных (воздух), по которым замыкаются линии магнитного потока, составляют магнитную цепь.
4.3. Закон полного тока
В основе расчета магнитных цепей лежит закон полного тока (рис. 4.3)
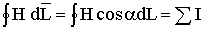 ,
,
где: Н –
напряженность магнитного поля в данной
точке пространства;
dL – элемент длины
замкнутого контура L;
– угол между направлениями векторов  и
и ;
I – алгебраическая сумма токов,
пронизывающих контур L.
;
I – алгебраическая сумма токов,
пронизывающих контур L.
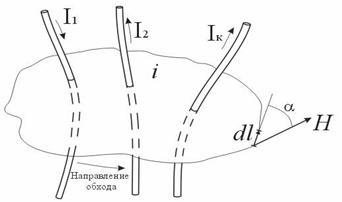
Рис. 4.3. Закон полного тока
Ток Iк, пронизывающий контур L считается положительным, если принятое направление обхода контура и направление этого тока связаны правилом правоходового винта (буравчика).
Применение закона полного тока для расчета магнитных цепей
Рассмотрим простейшую магнитную цепь, выполненную в виде кольца тороида из однородного материала (рис. 4.4).

Рис. 4.4. Кольцевая магнитная цепь
Обмотка
имеет W витков и обтекается током I.
Магнитные линии внутри кольца представляют
собой концентрические окружности с
центров точке О. Применим к контуру C
 и
и  совпадают,
следовательно = 0;
совпадают,
следовательно = 0;величина Нх во всех точках контура одинакова;
сумма токов, пронизывающих контур, равна IW.
Тогда
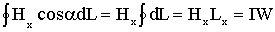
Отсюда
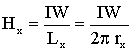 [А/м],
[А/м],
где Lx – длина контура, вдоль которого велось интегрирование; rx – радиус окружности.
Вектор  внутри
кольца зависит от расстояния rх.
Если
– ширина кольца << d, то эта
разница между значениями Н в пределах
сердечника не велика. При этом в расчет
допустимо принять для всего поперечного
сечения магнитопровода одно значение
напряженности магнитного поля:
внутри
кольца зависит от расстояния rх.
Если
– ширина кольца << d, то эта
разница между значениями Н в пределах
сердечника не велика. При этом в расчет
допустимо принять для всего поперечного
сечения магнитопровода одно значение
напряженности магнитного поля:
Hср = IW / L ,
где L – длина средней магнитной линии.
Магнитные цепи
Магнитной цепью называют устройство, в котором замыкается магнитный поток. Бывают разветвленные и неразветвленные.
|
|
Неразветвленная цепь | Разветвленная цепь |
Кроме того, магнитные цепи бывают однородные и неоднородные. Однородные цепи изготавливают из одного материала, они имеют одинаковую площадь сечения.
Закон Ома и закон Кирхгофа для магнитных цепей
Закон
Ома: магнитное
напряжение на любом участке 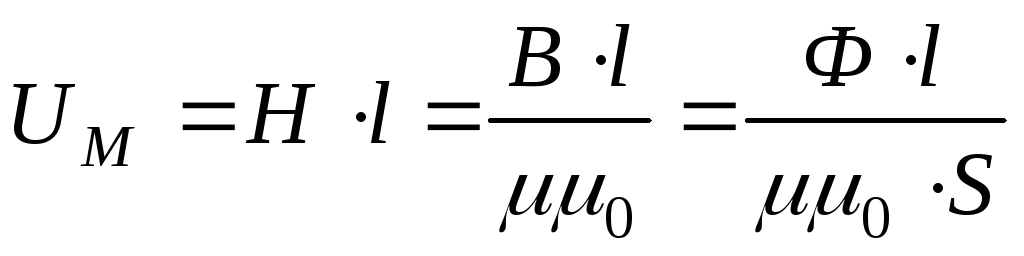 т.к.
т.к.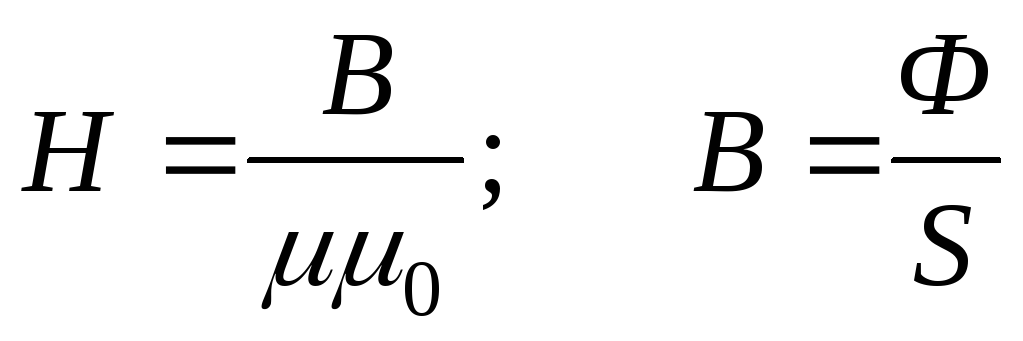 .
.
Если 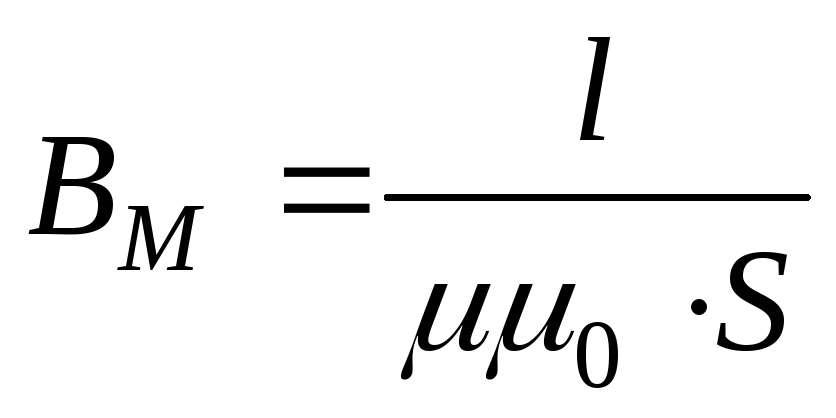
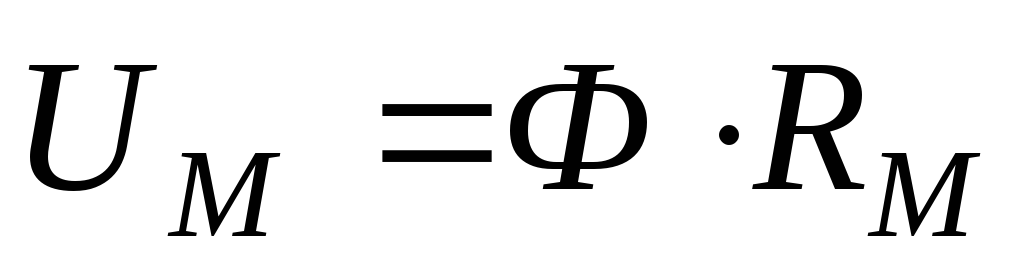 ,
где
,
где — магнитное сопротивление.
— магнитное сопротивление.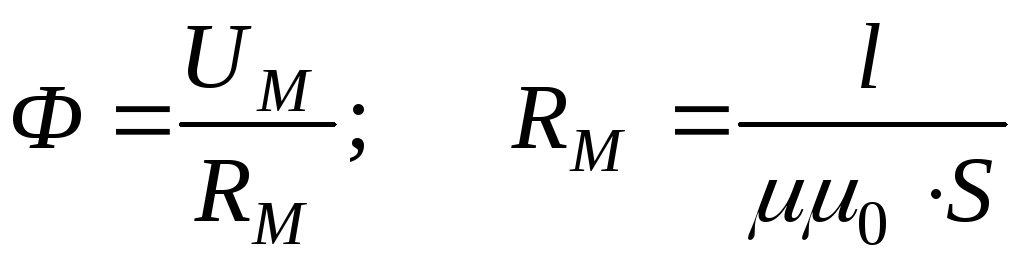

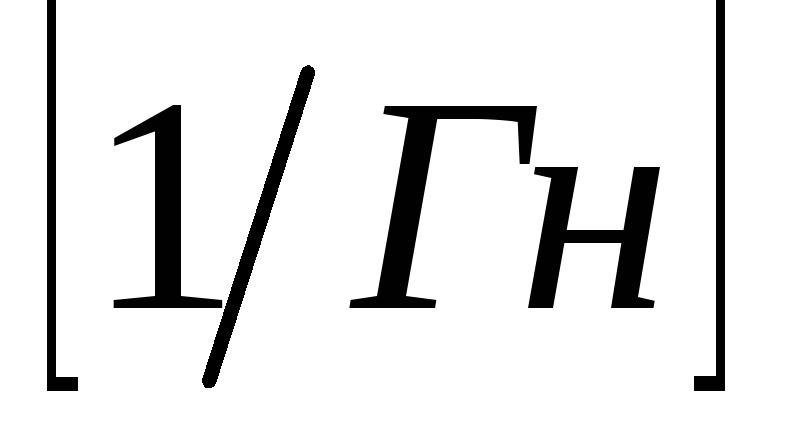 .
.Магнитный поток прямо пропорционален магнитному напряжению и обратно пропорционален магнитному сопротивлению.
Закон
Кирхгофа
1 правило: алгебраическая сумма магнитных токов в точке разветвления равна 0.
2
правило: основано на законе полного тока 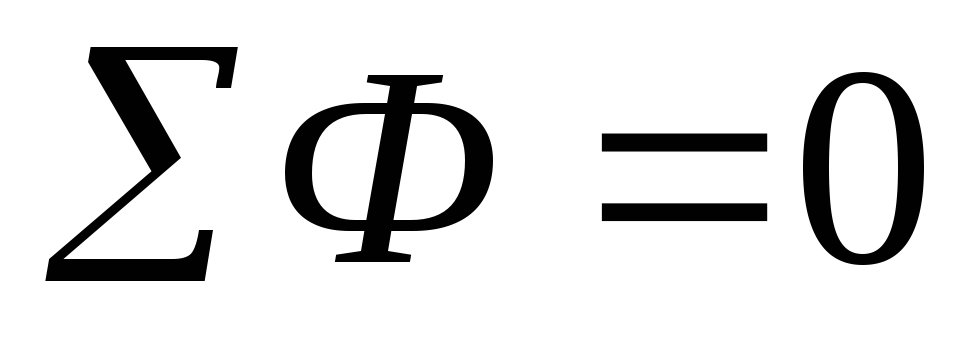 .
.
Алгебраическая сумма МДС равна алгебраической сумме магнитных напряжений на отдельных участках цепи.
 .
.
Закон Ома и закон Кирхгофа для расчета магнитных цепей не используют, т.к. магнитное сопротивление, в отличие от электрического, зависит от величины магнитного напряжения.
Для расчета магнитных цепей используют закон полного тока.
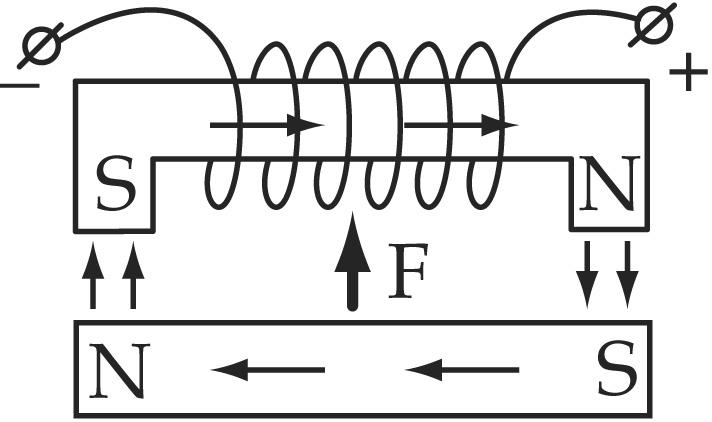
Электромагниты и реле
1. Подъемная сила электромагнита
| Состоит из стального сердечника С, на котором размещена катушка. Магнитный поток, созданный током катушки, замыкается по сердечнику. Якорь притягивается к сердечнику с отрывной силой: |
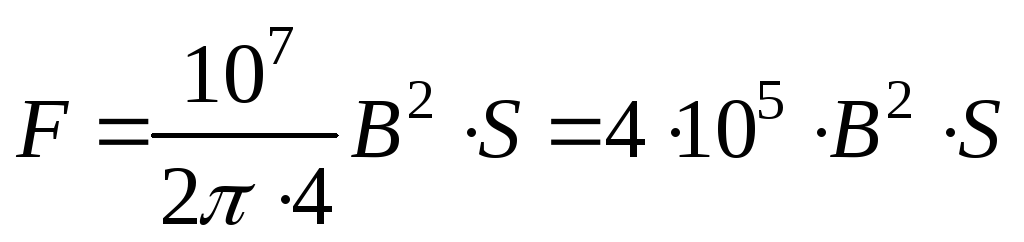 .
.
Если 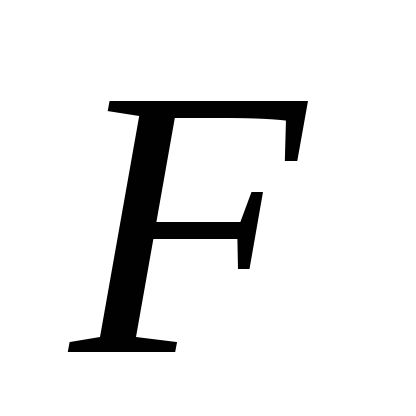 выражена вкг,ВвТл,S– всм2, то
выражена вкг,ВвТл,S– всм2, то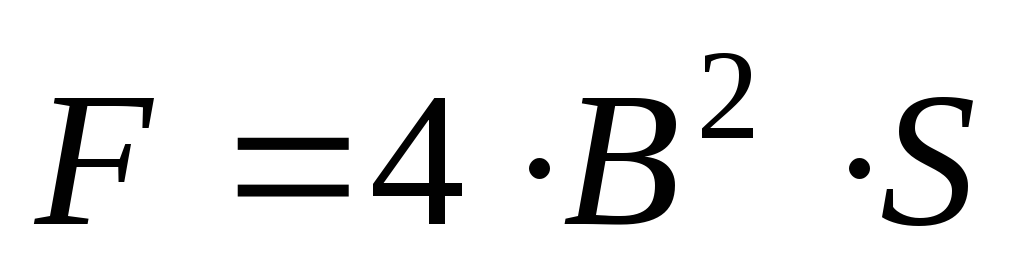 .
Сердечник и якорь изготовлены из мягкой
стали, поэтому при размыкании цепи они
размагнитятся и
.
Сердечник и якорь изготовлены из мягкой
стали, поэтому при размыкании цепи они
размагнитятся и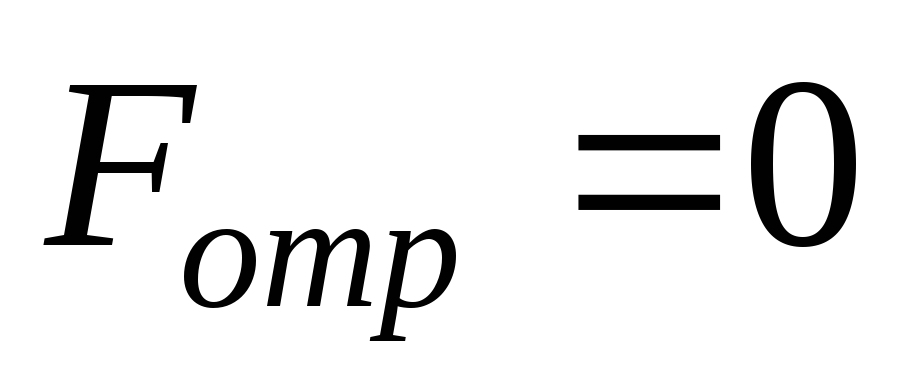 .
.
Применяются в устройствах автоматики, связи, измерительной технике.
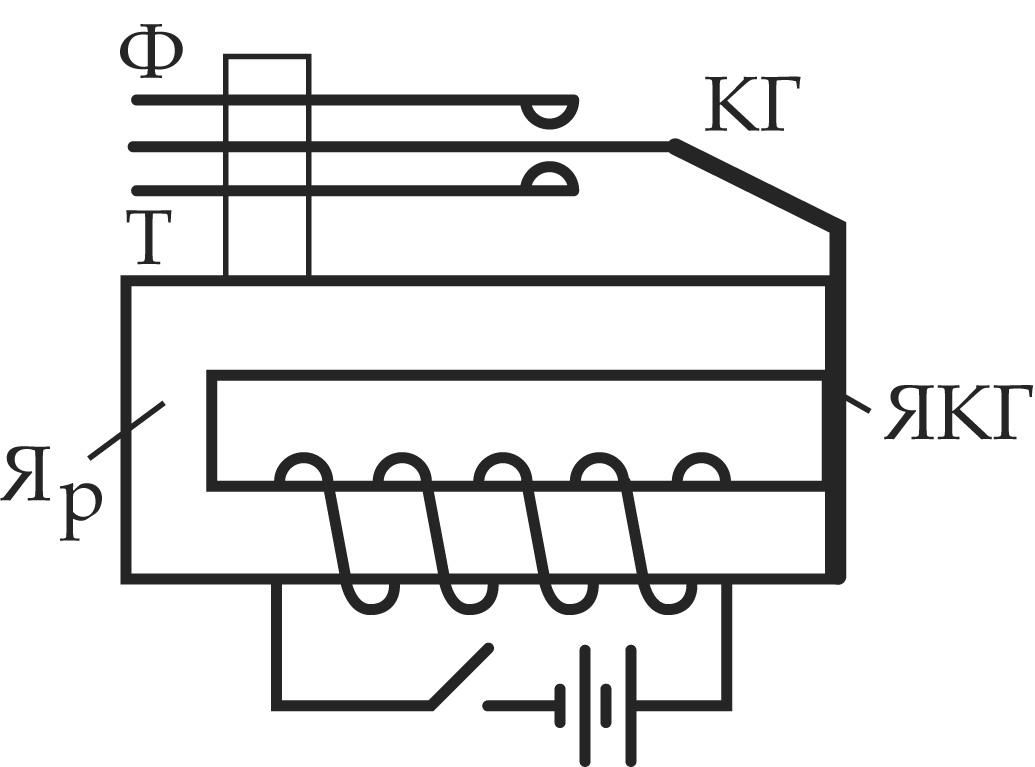
2. Устройство и применение магнитных реле
| Реле автоблокировки состоит из сердечника С, якоря, ярма с обмоткой, контактной группы, имеющей осевую О, фронтовой Ф и тыловой Т контакты. При отсутствии тока в цепи якорь под действием противовеса отпадает, осевой контакт контактной группы касается тылового контакта. |
При наличии тока – якорь притянут к сердечнику, осевой контакт касается фронтового.
Путевое реле называется нейтральным, т.к. его якорь притягивается к сердечнику независимо от направления тока.
3. Поляризованное реле
Поляризованное реле – якорь отклоняется от нейтрального положения в одну или другую сторону в зависимости от направления тока обмотки.
Порядок расчета магнитных цепей
Расчет заключается:
1. определении намагничивающей силы по заданному магнитному потоку, размерам магнитной цепи и ее материалу.
2. определении магнитного потока по заданной намагничивающей силе и размерам магнитной цепи:
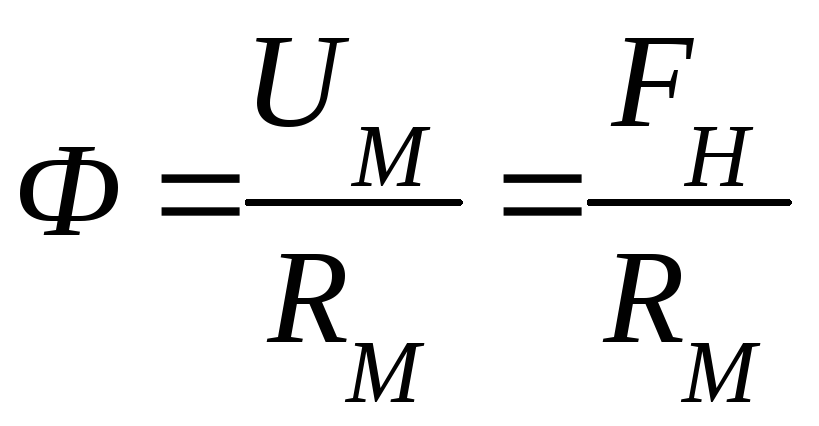
Для этого разбивают магнитную цепь на ряд однородных участков, имеющих одинаковое поперечное сечение и выполненных из одного материала.
Длины участков определяют по средней магнитной силовой линии. Для каждого участка определяют значение магнитной индукции.
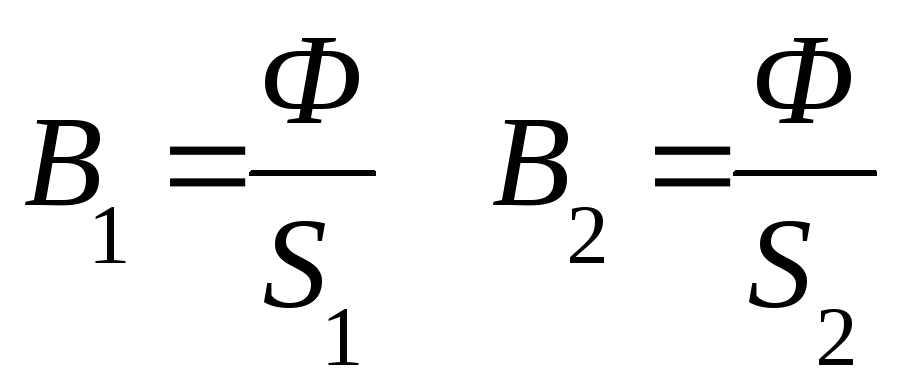 и т.д.
и т.д.
Для каждого участка по кривым намагничивания определяют напряженность магнитного поля (по графику или в таблице): Н1,Н2и т.д.
Для воздушного зазора напряженность определяется по формуле:
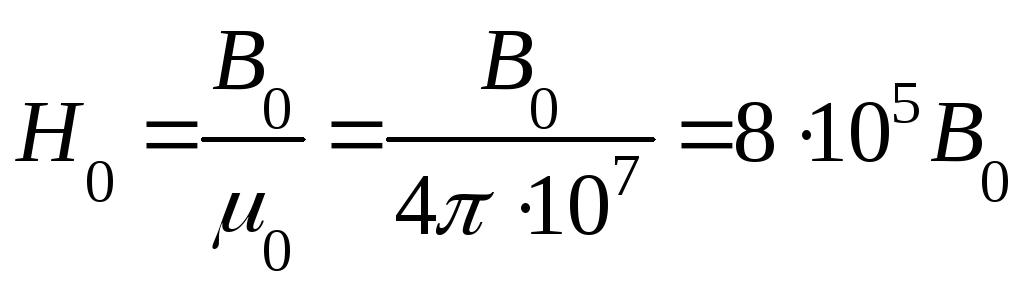
Для каждого участка определяют магнитное напряжение
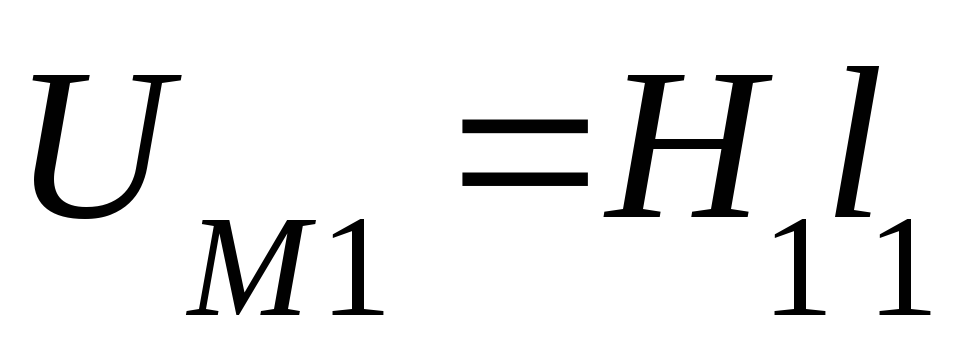
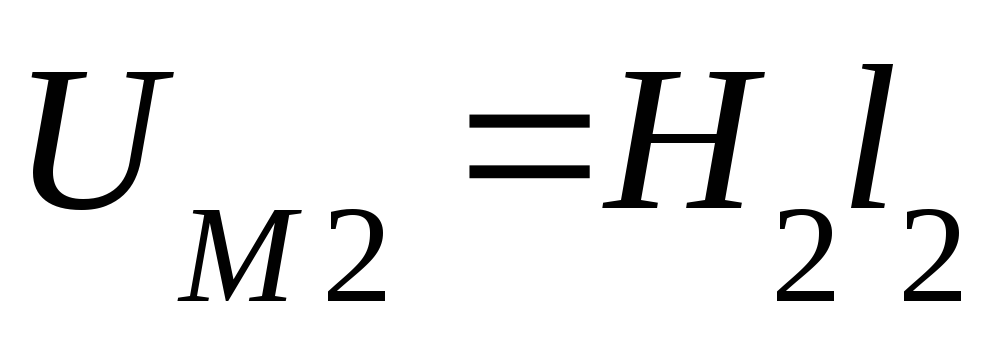
По закону полного тока определяют намагничивающую силу. Она равна:
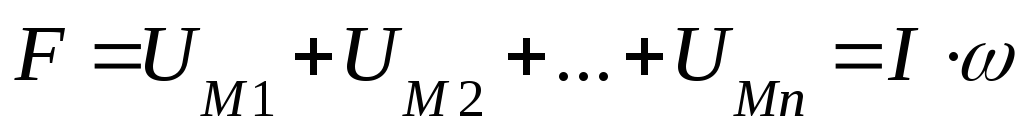
По заданному току находим число витков в катушке ей необходимое для создания требуемого магнитного потока.
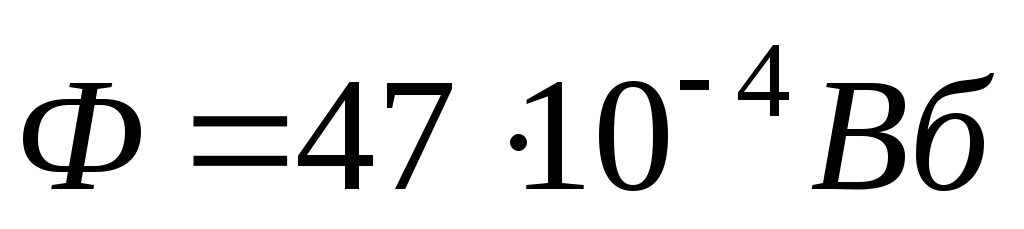
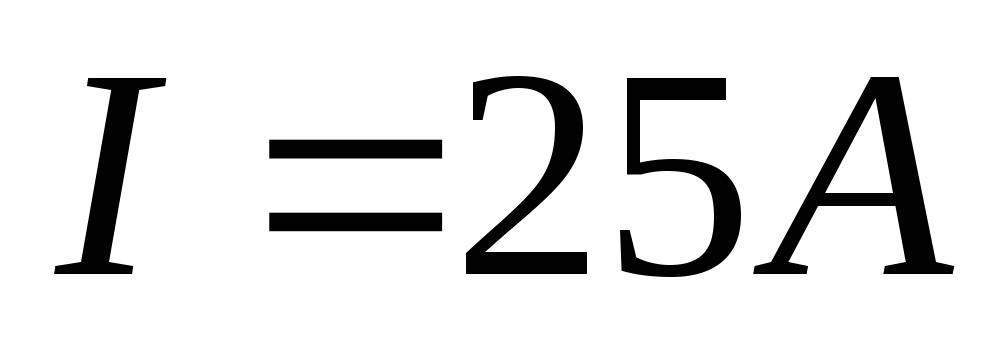
Законы и параметры магнитных цепей
Определим магнитный
поток 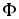 для сердечника с постоянным поперечным
сечением
для сердечника с постоянным поперечным
сечением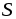 (рис. 6.3), считая м.д.с.
(рис. 6.3), считая м.д.с. катушки известной.
катушки известной.
Учитывая допущение
о равномерном распределении потока по
сечению, из определения магнитного
потока 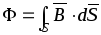 получим для рассматриваемой магнитной
цепи
получим для рассматриваемой магнитной
цепи
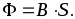
Применяя закон
полного тока в интегральной форме к
контуру 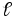 ,
являющемуся средней линией сердечника,
можем записать
,
являющемуся средней линией сердечника,
можем записать
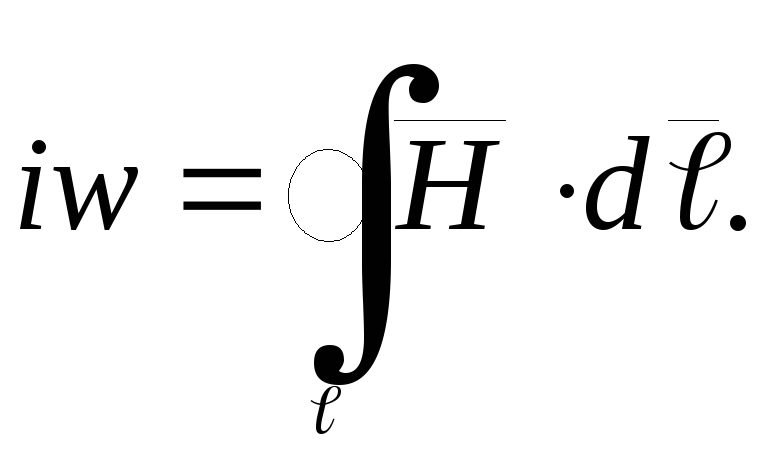
Используя допущение
о неизменности потока вдоль контура 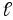 при постоянном сечении
при постоянном сечении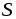 ,
получим
,
получим
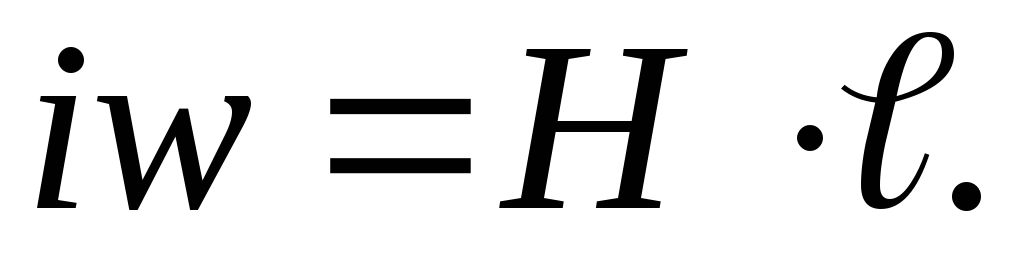
Соотношение 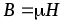 ,
с учетом полученных ранее выражений,
приводит к равенству
,
с учетом полученных ранее выражений,
приводит к равенству
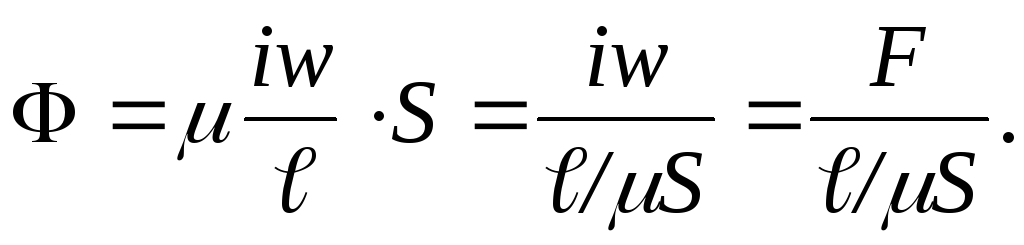
Отношение
магнитодвижущей силы (м.д.с.) 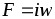 вдоль всей магнитной
цепи к магнитному потоку
вдоль всей магнитной
цепи к магнитному потоку 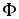 называютмагнитным
сопротивлением такой цепи
называютмагнитным
сопротивлением такой цепи
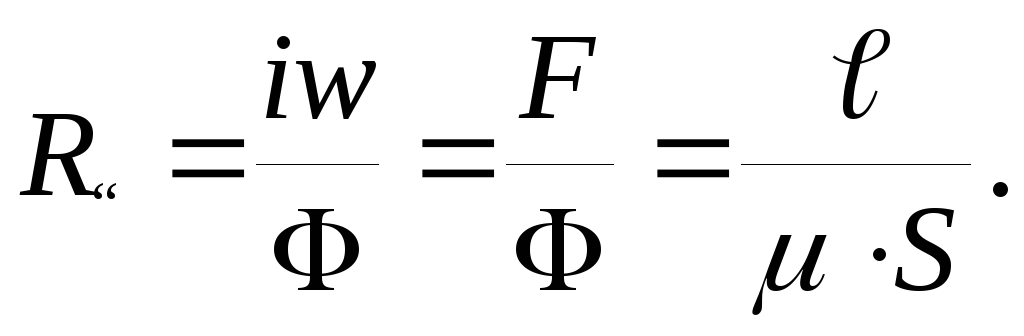
Размерность
магнитного сопротивления [ ]
= 1/Гн.
]
= 1/Гн.
Понятие
магнитного сопротивления можно ввести
и для участка магнитной цепи. В этом
случае 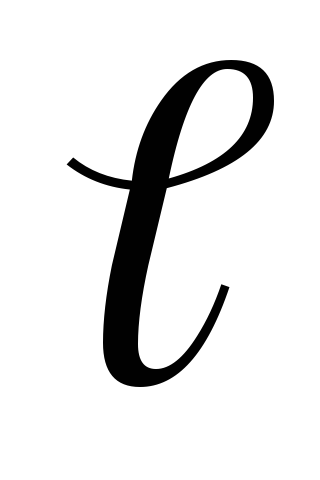 представляет собой длину участка
магнитопровода с сечением
представляет собой длину участка
магнитопровода с сечением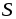 .
Магнитное сопротивление является
основным параметром магнитной цепи.
.
Магнитное сопротивление является
основным параметром магнитной цепи.
Соотношение
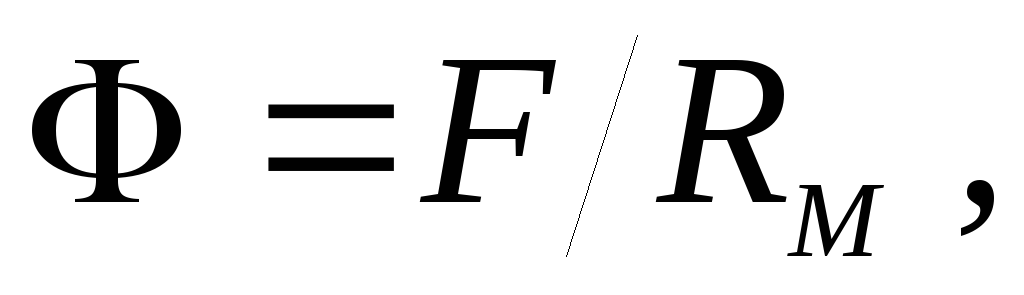
связывающее магнитный поток, м.д.с. и магнитное сопротивление сердечника, называют законом Ома для магнитной цепи.
Полученное выражение аналогично закону Ома для электрической цепи
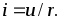
Сравнивая интегральные характеристики магнитных и электрических цепей, можно установить аналогию между ними.
Таблица 6.1
Магнитная цепь | Электрическая цепь |
Магнитный
поток М.д.с. М.д.с. на
участке АВ Магнитное
сопротивление Закон Ома для участка магнитной
цепи Схема магнитной цепи | Электрический
ток Э.д.с. Напряжение на
участке АВ Электрическое
сопротивление Закон Ома для участка электрической
цепи Схема электрической цепи
|
Расчет магнитной цепи
Рассмотрим
магнитную цепь (рис. 6.4), состоящую из
последовательных участков с различными
сечениями 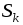 ,
различными магнитными проницаемостями
,
различными магнитными проницаемостями 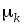 и воздушным промежутком
и воздушным промежутком 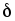 .
Величина воздушного зазора
.
Величина воздушного зазора 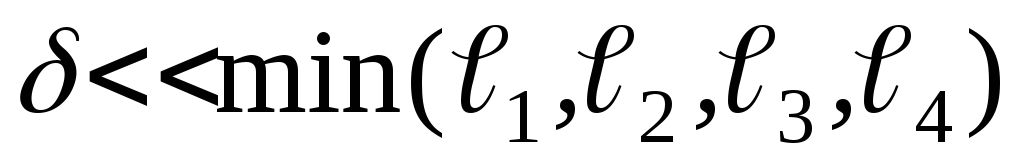 .
.
П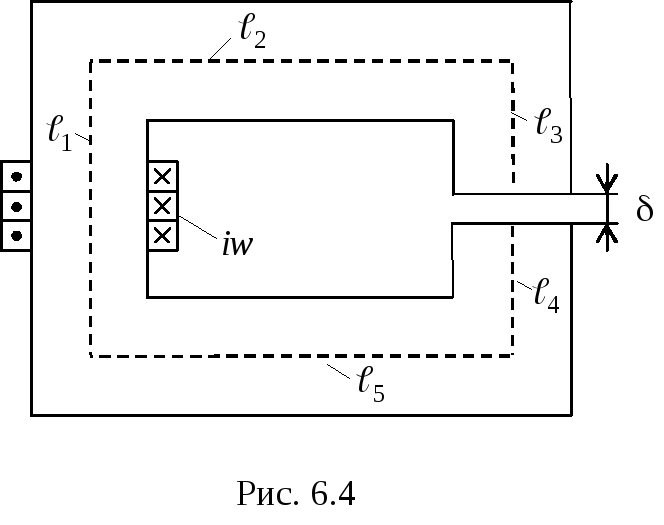 ри
расчете магнитной цепи выделяют участки
магнитной цепи с постоянным сечением,
постоянной магнитной проницаемостью
и одинаковым магнитным потоком вдоль
участка. Каждый участок характеризуется
магнитным сопротивлением
ри
расчете магнитной цепи выделяют участки
магнитной цепи с постоянным сечением,
постоянной магнитной проницаемостью
и одинаковым магнитным потоком вдоль
участка. Каждый участок характеризуется
магнитным сопротивлением 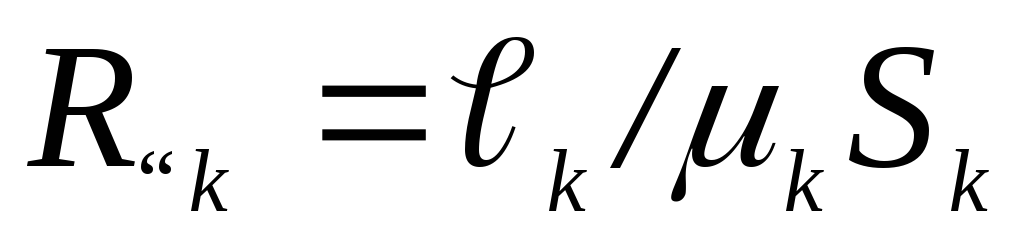 ,
где длину участка
,
где длину участка 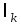 можно вычислять вдоль линии, проходящей
через середину сечений стержней
магнитопровода
можно вычислять вдоль линии, проходящей
через середину сечений стержней
магнитопровода
При малой длине зазора конфигурация поля в нем существенно не отличается от конфигурации поля в прилегающем участке магнитопровода. Поэтому сечение, сквозь которое проходит магнитный поток в зазоре, можно взять таким же, как и сечение прилегающего к зазору ферромагнитного участка цепи.
Для замкнутого контура рассматриваемой магнитной цепи имеем
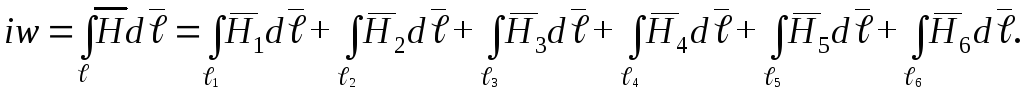
Обозначим 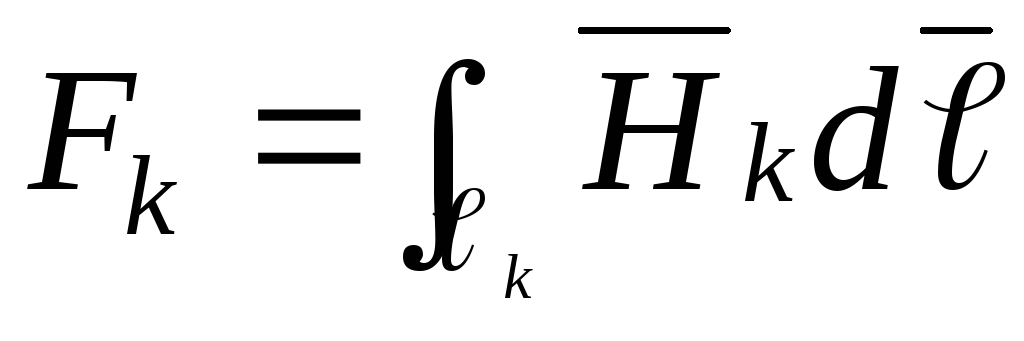 — м.д.с. на
— м.д.с. на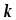 -м участке магнитной цепи, тогда
-м участке магнитной цепи, тогда
или с учетом закона Ома для участка магнитной цепи, получим
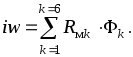
Это соотношение, полученное из закона полного тока, остается справедливым для любого контура разветвленной магнитной цепи, т.е. м.д.с. вдоль замкнутого контура магнитной цепи равна сумме произведений магнитного сопротивления на магнитный поток во всех участках (ветвях) цепи, входящих в этот контур.
Последнее уравнение аналогично уравнению второго закона Кирхгофа, составленному для контура электрической цепи при постоянном токе,
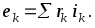
В
рассматриваемом примере одноконтурной
магнитной цепи (рис. 6.4) магнитный поток 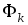 одинаков на различных участках.
Следовательно, имеем
одинаков на различных участках.
Следовательно, имеем
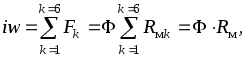 причем
причем 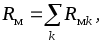
то есть, как и для электрических цепей, магнитное сопротивление последовательно соединенных участков магнитной цепи равно сумме магнитных сопротивлений каждого из участков.
Для напряженности магнитного поля в зазоре можно написать
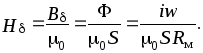
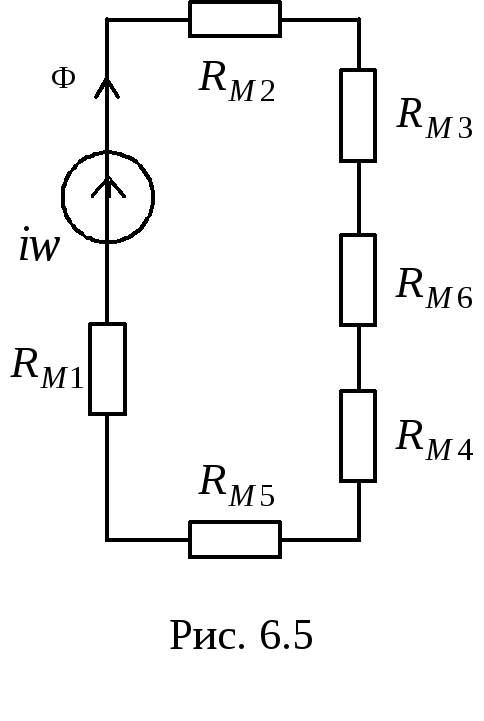
Эквивалентная схема рассматриваемой магнитной цепи представлена на рис.6.5,
где 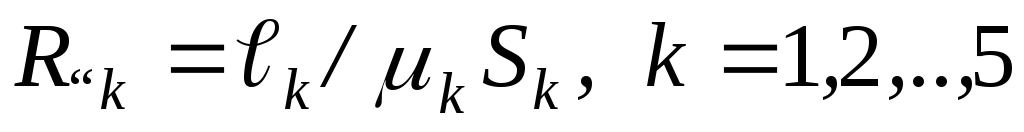 ;
;
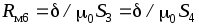
Зная магнитную проницаемость вещества сердечника и его размеры, нетрудно рассчитать эквивалентное магнитное сопротивление сердечника и затем при заданной м.д.с. определить магнитный поток
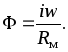
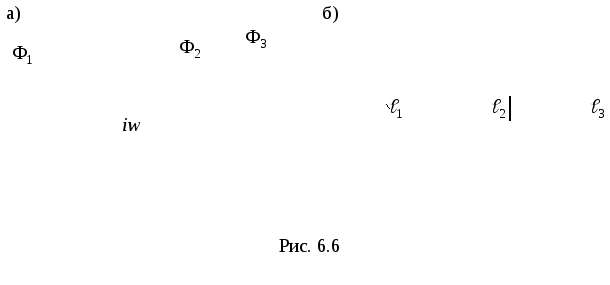
Для разветвленной
магнитной цепи (например, рис. 6.6) из
условия непрерывности магнитного потока 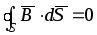 с учетом пренебрежения потоками рассеяния
следует, что сумма магнитных потоков в
участках цепи, отходящих от узла магнитной
цепи, равна нулю
с учетом пренебрежения потоками рассеяния
следует, что сумма магнитных потоков в
участках цепи, отходящих от узла магнитной
цепи, равна нулю
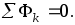
Это соотношение аналогично уравнению для узла электрической цепи, записанному согласно первому закону Кирхгофа
Уравнений
подобного типа должно быть составлено  ,
если
,
если
число узлов магнитной цепи. Уравнений,
составленных по аналогии с уравнениями
второго закона Кирхгофа, должно быть
число узлов магнитной цепи. Уравнений,
составленных по аналогии с уравнениями
второго закона Кирхгофа, должно быть 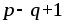 ,
где
,
где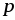
число ветвей магнитной цепи.
число ветвей магнитной цепи.
Таким образом, расчет магнитных цепей, если можно пренебречь потоками рассеяния и считать магнитную проницаемость материала участков магнитопровода постоянной, аналогичен расчету линейных электрических цепей постоянного тока.
Рассмотрим
разветвленную магнитную цепь (рис.
6.6а). Участки магнитной цепи 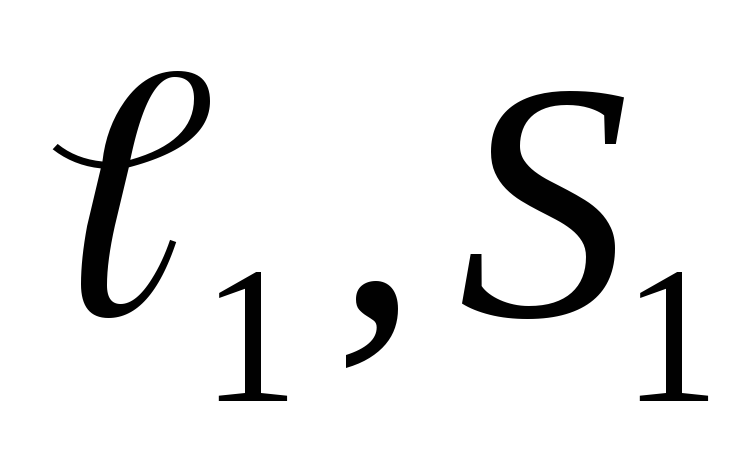 ,
,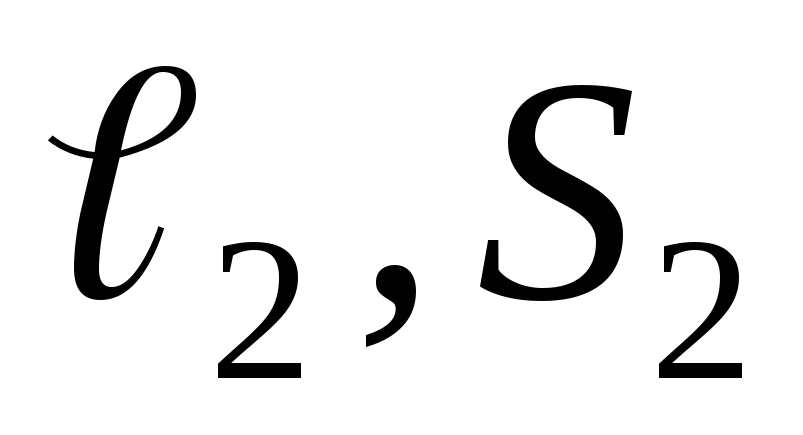 ,
,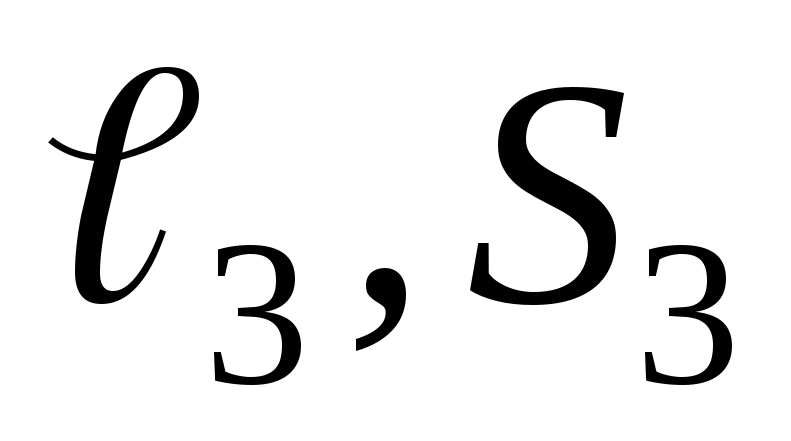 (рис. 6.6б) выбраны так, чтобы потоки
(рис. 6.6б) выбраны так, чтобы потоки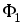 ,
,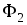 ,
,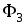 вдоль этих участков были постоянными.
вдоль этих участков были постоянными.
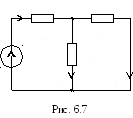
Схема
замещения рассматриваемой магнитной
цепи изображена на рис.6.7. Для этой схемы
имеем 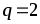 ,
, ,
тогда аналог уравнений Кирхгофа для
магнитной цепи можно записать следующим
образом
,
тогда аналог уравнений Кирхгофа для
магнитной цепи можно записать следующим
образом
где 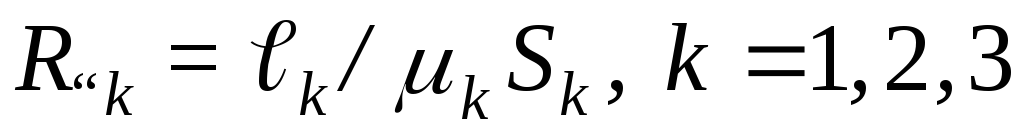 .
.
В результате решения системы уравнений определим магнитные потоки в каждом участке, а через них найдем значения магнитной индукции и напряженности магнитного поля на этих участках.
Аналогия магнитных цепей с электрическими цепями постоянного тока позволяет использовать для расчета магнитной цепи все рассмотренные ранее методы расчета цепей постоянного тока.
Рассмотрим магнитную цепь, в которой имеются катушки с токами в различных ветвях магнитной цепи (рис.6.8а)
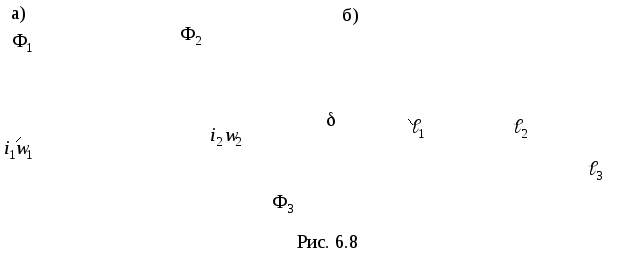
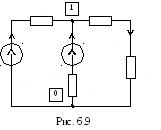 Схема
замещения магнитной цепи (рис. 6.8а)
изображена на рисунке 6.9. Значения
магнитных сопротивлений участков цепи
определяются из соотношений
Схема
замещения магнитной цепи (рис. 6.8а)
изображена на рисунке 6.9. Значения
магнитных сопротивлений участков цепи
определяются из соотношений
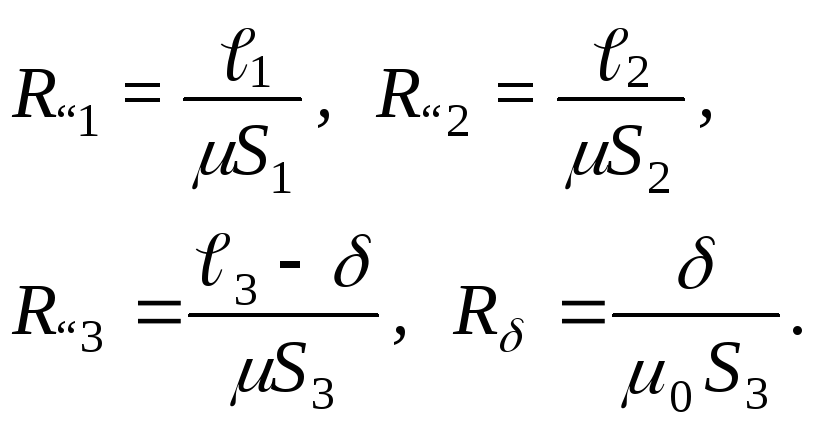
Применяя
для расчета этой цепи метод узловых
напряжений и используя соотношение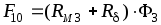 можем записать
можем записать
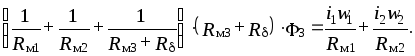
Определив из
последнего соотношения значение
магнитного потока 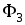 ,
значения остальных потоков получим на
основании равенств
,
значения остальных потоков получим на
основании равенств
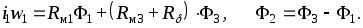
Схему
замещения магнитной цепи можно также
использовать для определения собственных
индуктивностей обмоток 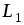 и
и 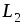 и взаимной индуктивности
и взаимной индуктивности 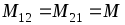 .
.
 В
соответствии с определением собственной
индуктивности для первой обмотки имеем
В
соответствии с определением собственной
индуктивности для первой обмотки имеем
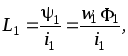
где
поток 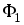 создается только
током
создается только
током 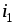 в
первой обмотке.
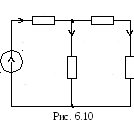
Рассчитаем схему, изображенную на
рис.6.10.
в
первой обмотке.
Рассчитаем схему, изображенную на
рис.6.10.
Выражение для
потока 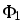 имеет вид
имеет вид
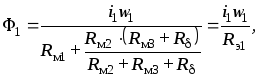 откуда
откуда 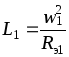 .
.
Взаимную
индуктивность 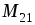 ,
в соответствии с определением, рассчитаем
из соотношения
,
в соответствии с определением, рассчитаем
из соотношения
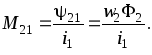
Значение
магнитного потока 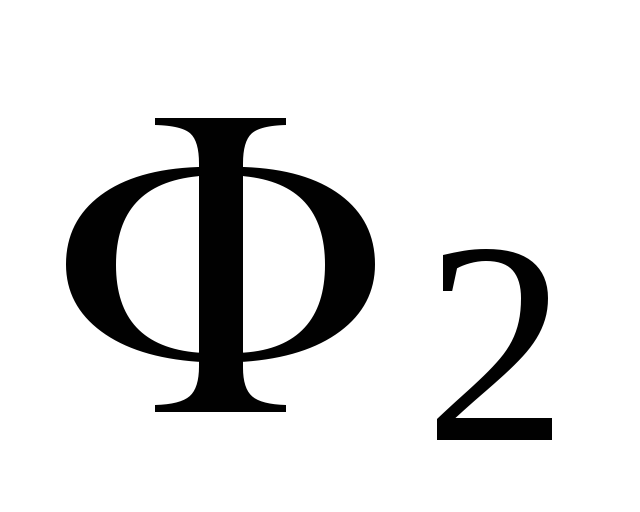 также определяется из расчета схемы
(рис.
6.10), поскольку
также определяется из расчета схемы
(рис.
6.10), поскольку 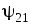 представляет собой потокосцепление со
второй обмоткой, создаваемое током в
первой.
представляет собой потокосцепление со
второй обмоткой, создаваемое током в
первой.
Можно записать
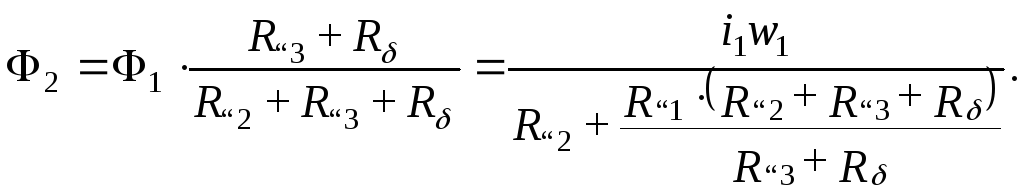
Окончательно получим
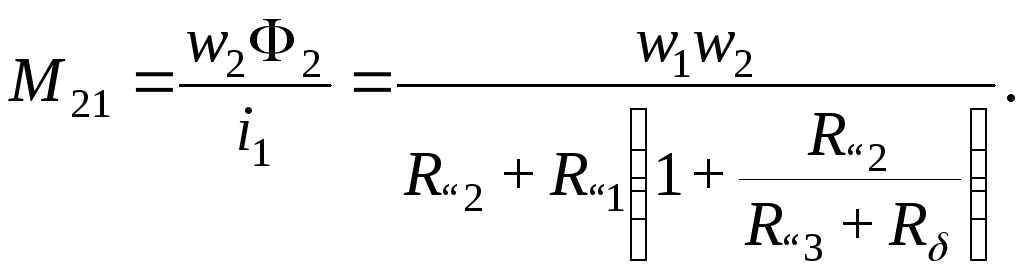
 Аналогично
проведем расчет собственной индуктивности
Аналогично
проведем расчет собственной индуктивности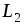 второй обмотки и взаимной индуктивности
второй обмотки и взаимной индуктивности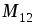 ,
для чего используем схему замещения
магнитной цепи, изображенную на рис.6.11.
,
для чего используем схему замещения
магнитной цепи, изображенную на рис.6.11.
Для
собственной индуктивности 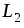 второй обмотки имеем
второй обмотки имеем
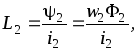
причем 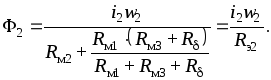
В результате
получим 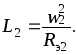
Взаимную
индуктивность 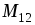 определим из соотношения
определим из соотношения
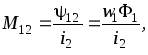 где
где 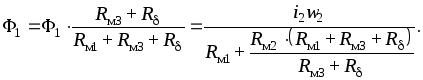
Окончательно
имеем 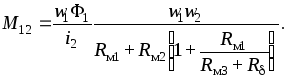
Отметим, что в обоих случаях получены одинаковые выражения для взаимной индуктивности двух катушек
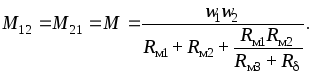
Поскольку собственные
и взаимные индуктивности не зависят от
величин токов в обмотках, то в схемах
для их расчета (рис. 6.10 и 6.11), значения
токов 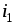 и
и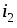 выбираются произвольно. В частности,
можно принять
выбираются произвольно. В частности,
можно принять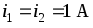 .
.
Для иллюстрации приведенных ранее теоретических положений рассмотрим решение нескольких задач.
Задача
1. Определить
минимальную силу тока 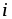 электромагнита (рис. 6.12), удерживающего
стальной лист массой
электромагнита (рис. 6.12), удерживающего
стальной лист массой 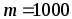 кг, если средний зазор
кг, если средний зазор 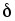 между магнитом и листом, обусловленный
неровностями соприкасающихся поверхностей,
равен одному миллиметру. Число витков
обмотки электромагнита
между магнитом и листом, обусловленный
неровностями соприкасающихся поверхностей,
равен одному миллиметру. Число витков
обмотки электромагнита 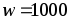 ,
площадь поперечного сечения сердечника
,
площадь поперечного сечения сердечника 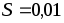 м2.
При решении считать магнитную проницаемость
м2.
При решении считать магнитную проницаемость 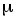 вещества сердечника магнита и стального
листа бесконечно большой.
вещества сердечника магнита и стального
листа бесконечно большой.
Решение.Сопротивление
магнитной цепи магнитному потоку ,
создаваемому током
,
создаваемому током электромагнита, определяется только
магнитным сопротивлением зазоров,
поскольку магнитные сопротивления
участков ферромагнитного сердечника
равны нулю (в силу допущения
электромагнита, определяется только
магнитным сопротивлением зазоров,
поскольку магнитные сопротивления
участков ферромагнитного сердечника
равны нулю (в силу допущения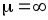 ).
).
Величина магнитного потока определяется выражением
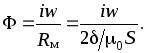
Электромагнитную силу, действующую на стальной лист в магнитном поле, определим из соотношения
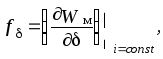
где 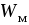 энергия магнитного
поля системы.
энергия магнитного
поля системы.
Напряженность
магнитного поля в ферромагнетике равна
нулю (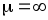 ),
поэтому вся энергия магнитного поля
),
поэтому вся энергия магнитного поля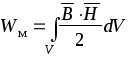 сосредоточена в
области воздушного зазора под полюсами
электромагнита.
сосредоточена в
области воздушного зазора под полюсами
электромагнита.
Считая магнитное поле в зазоре однородным, можно записать
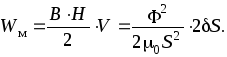
Итак, выражение для электромагнитной силы примет вид
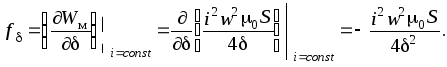
Знак «−» в
последнем выражении указывает на то,
что сила стремится уменьшить параметр 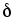 ,
то есть притянуть стальной лист к
электромагниту.
,
то есть притянуть стальной лист к
электромагниту.
Условием удержания
стального листа является неравенство 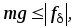
отсюда минимальное значение тока, необходимое для этого, равно
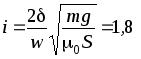 А.
А.
Задача 2.Построить линейную эквивалентную схему
замещения постоянного магнита (рис.6.13)
для рабочего участка характеристики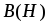 .
.
Определить энергию магнитного поля постоянного магнита.

Решение.Для
построения линейной эквивалентной
схемы замещения постоянного магнита
аппроксимируем реальную характеристику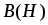 на рабочем участке отрезком прямой
(рис. 6.13б). В соответствии с законом
полного тока имеем
на рабочем участке отрезком прямой
(рис. 6.13б). В соответствии с законом
полного тока имеем
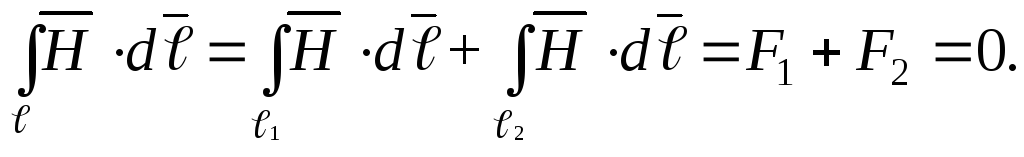
В этом соотношении
контур  .
образован участками
.
образован участками и
и ,
совпадающими с линиями напряженности
,
совпадающими с линиями напряженности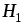 и
и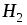 внутри магнита и в зазоре, а
внутри магнита и в зазоре, а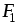 и
и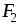 представляют собой магнитодвижущие
силы на этих же участках.
представляют собой магнитодвижущие
силы на этих же участках.
Считая поле в магните однородным, можем записать
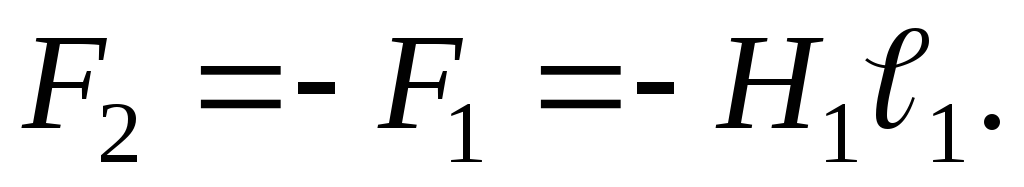
С учетом линейной
аппроксимации зависимости 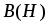 ,
связь напряженности
,
связь напряженности в теле магнита с индукцией
в теле магнита с индукцией имеет вид
имеет вид
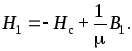
Домножая
обе части последнего равенства на длину 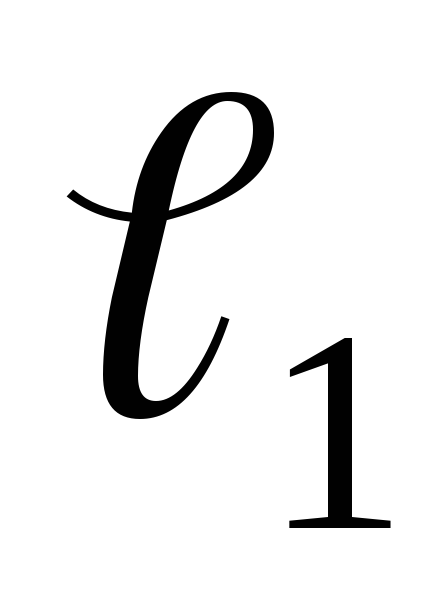 участка вдоль среднейлинии
внутри магнита с площадью поперечного
сечения
участка вдоль среднейлинии
внутри магнита с площадью поперечного
сечения 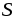 ,
получим
,
получим
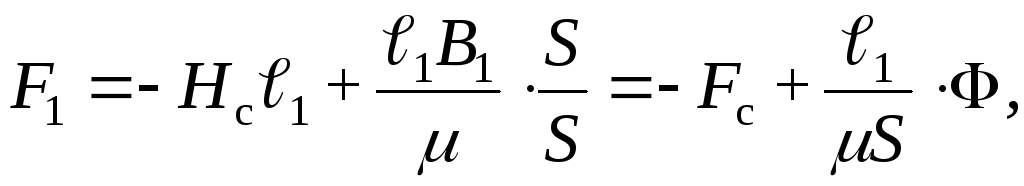
откуда с учетом 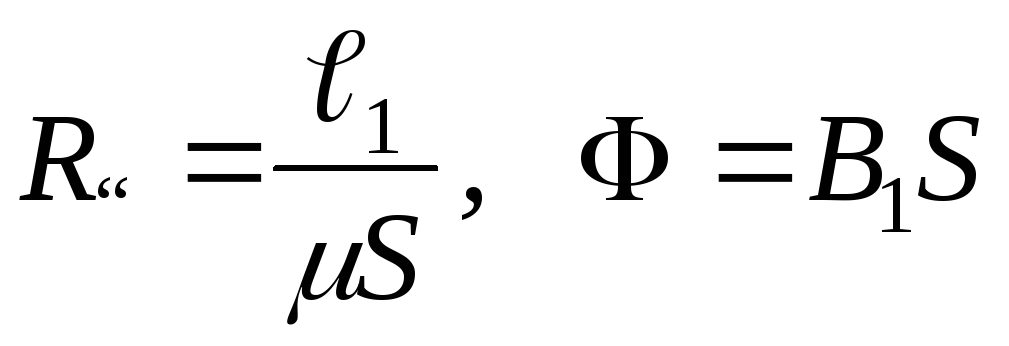 имеем
имеем
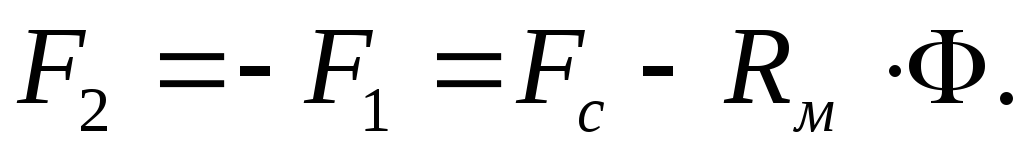
 На
основе последнего соотношения можно
построить схему замещения постоянного
магнита (рис.6.14). Заметим, что магнитный
поток
На
основе последнего соотношения можно
построить схему замещения постоянного
магнита (рис.6.14). Заметим, что магнитный
поток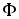 ,
создаваемый постоянным магнитом, зависит
от параметров внешней магнитной цепи.
,
создаваемый постоянным магнитом, зависит
от параметров внешней магнитной цепи.
Определим энергию  однородного магнитного поля в объеме
однородного магнитного поля в объеме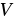 длиной
длиной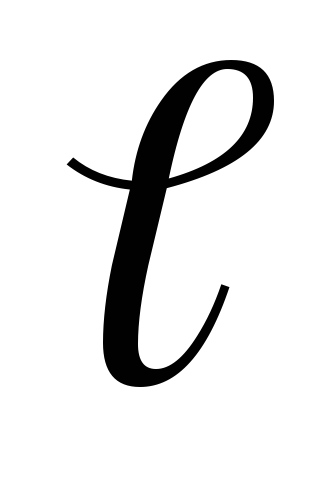 и площадью поперечного сечения
и площадью поперечного сечения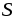 .
.
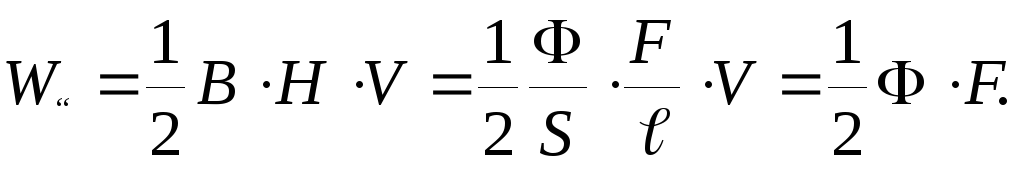
В случае, когда источником однородного магнитного поля является постоянный магнит, энергия магнитного поля определяется выражением
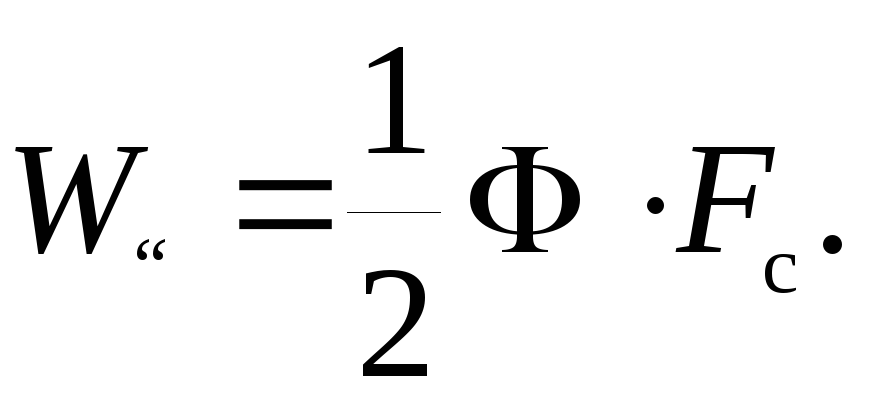
В рассматриваемой задаче энергия магнитного поля магнита может быть определена из соотношения
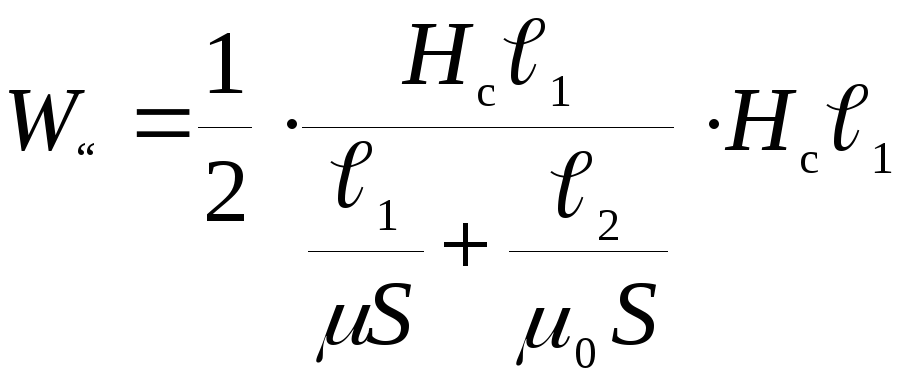 .
.
З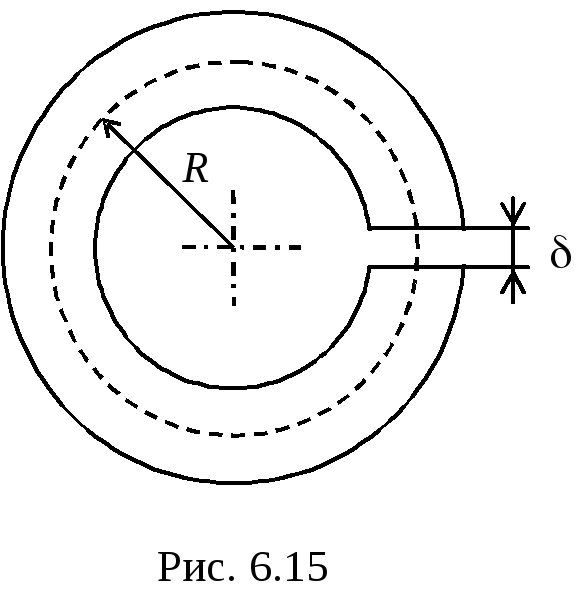 адача
3.Определить напряженность магнитного
поля в зазоре тороидального магнита
(рис.6.15). Характеристика материала
магнита имеет вид, изображенный на рис.
6.13,б, с параметрами
адача
3.Определить напряженность магнитного
поля в зазоре тороидального магнита
(рис.6.15). Характеристика материала
магнита имеет вид, изображенный на рис.
6.13,б, с параметрами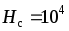 А/м,
А/м,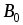 = 1 Тл,
= 1 Тл,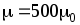 .
Средний радиус тора
.
Средний радиус тора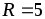 см, поперечное сечение
см, поперечное сечение см2.
см2.
Решение.Полагая
магнитное поле в зазоре однородным,
рассчитаем магнитное сопротивление
соответственно зазора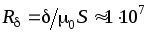 1/ Гн, и магнита
1/ Гн, и магнита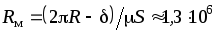 1/ Гн.
1/ Гн.
Используя схему замещения постоянного магнита, построенную в предыдущей задаче, изобразим схему замещения постоянного магнита с зазором (рис.6.16).
 Для
определения напряженности
Для
определения напряженности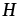 магнитного поля в зазоре рассчитаем
магнитный поток
магнитного поля в зазоре рассчитаем
магнитный поток
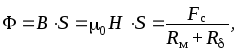
причем
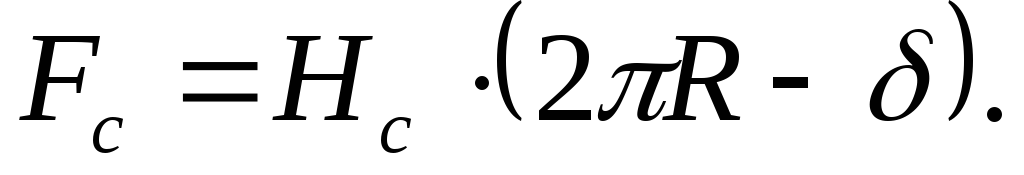
Для магнитной индукции в зазоре имеем
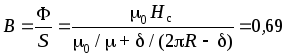 Тл,
Тл,
при этом напряженность магнитного поля в зазоре равна
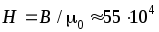 А/м.
А/м.
З адача
4.Система из двух постоянных Гобразных
магнитов (рис. 6.17), разделенных выполненным
из ферромагнитного материала штифтом,
притягивает стальной лист. Определить,
во сколько раз отличается сила притяженияпри наличии
ферромагнитного штифта и без него.
адача
4.Система из двух постоянных Гобразных
магнитов (рис. 6.17), разделенных выполненным
из ферромагнитного материала штифтом,
притягивает стальной лист. Определить,
во сколько раз отличается сила притяженияпри наличии
ферромагнитного штифта и без него.
Средний зазор
между магнитами и стальным листом 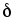 = 0,5 мм, а между магнитами и штифтом
= 0,5 мм, а между магнитами и штифтом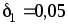 мм. При расчете считать магнитную
проницаемость листа и штифта бесконечно
большой. Поперечное сечение магнита
мм. При расчете считать магнитную
проницаемость листа и штифта бесконечно
большой. Поперечное сечение магнита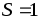 см2, средняя длина вдоль оси
магнитов
см2, средняя длина вдоль оси
магнитов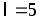 см, длина штифта
см, длина штифта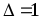 см. Параметры характеристики
см. Параметры характеристики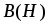 материала магнита
материала магнита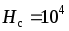 А/м,
А/м,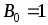 Тл,
Тл,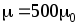 .
.
Решение.Схема замещения рассматриваемой магнитной системы изображена на рис.6.18.
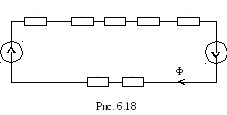
При построении схемы замещения учитывалось, что магнитное сопротивление стального листа равно нулю вследствие бесконечно большого значения магнитной проницаемости материала листа. Нетрудно заметить, что
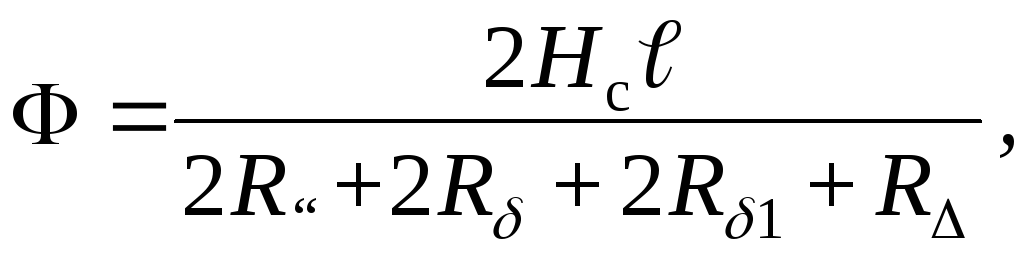
где 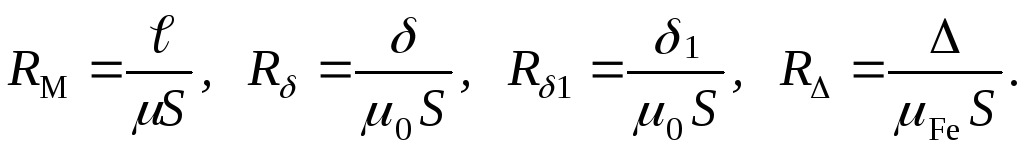
Электромагнитную
силу, действующую на стальной лист,
определим из закона сохранения энергии 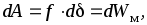 так как работа
так как работа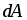 ,
совершенная при перемещении листа на
расстояние
,
совершенная при перемещении листа на
расстояние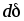 ,
равна изменению энергии магнитного
поля системы. Следовательно, выражение
для силы примет вид
,
равна изменению энергии магнитного
поля системы. Следовательно, выражение
для силы примет вид
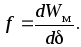
Энергию магнитного поля системы можно рассчитать, суммируя энергии, запасенные в постоянных магнитах
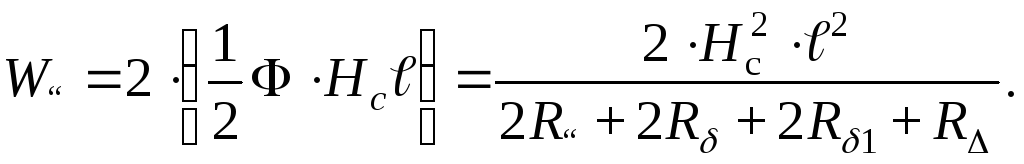
Тогда для
электромагнитной силы 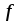 имеем
имеем
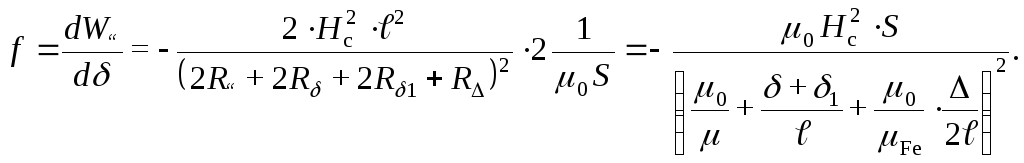
Поскольку
магнитная проницаемость 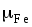 материала штифта принята бесконечно
большой, имеем
материала штифта принята бесконечно
большой, имеем 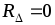 .
Тогда из последнего соотношения получим
выражение для силы
.
Тогда из последнего соотношения получим
выражение для силы 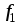 притяжения листа к постоянным магнитам
при наличии штифта
притяжения листа к постоянным магнитам
при наличии штифта
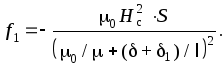
При отсутствии
штифта в выражении для силы 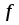 следует положить
следует положить .
В этом случае значение силы
.
В этом случае значение силы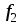 притяжения листа к постоянным магнитам
определится из соотношения
притяжения листа к постоянным магнитам
определится из соотношения
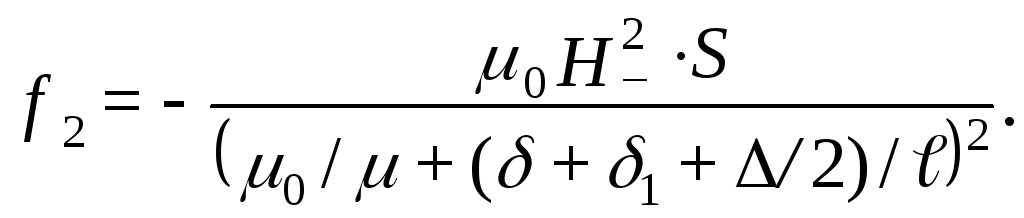
Отношение сил притяжения при наличии штифта и без него получается равным
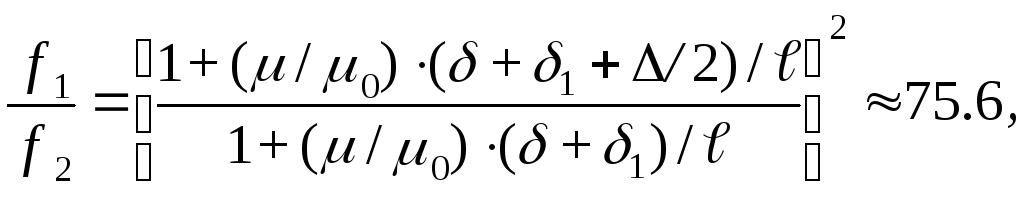
то есть сила притяжения стального листа к магнитам при наличии штифта увеличивается в 75,6 раза.
Значение силы
притяжения листа к магнитам со штифтом
приблизительно равно 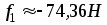 .
Знак «минус» в последнем соотношении
указывает, что
.
Знак «минус» в последнем соотношении
указывает, что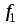 является силой притяжения.
является силой притяжения.
11. Методы расчёта трёхфазных электрических цепей.
Приемники, включаемые в трехфазную цепь, могут быть либо однофазными, либо трехфазными. К однофазным приемникам относятся электрические лампы накаливания и другие осветительные приборы, различные бытовые приборы, однофазные двигатели и т.д. К трехфазным приемникам относятся трехфазные асинхронные двигатели и индукционные печи. Обычно комплексные сопротивления фаз трехфазных приемников равны между собой:
Za = Zb = Zc = Zejφ. (3.9)
Такие приемники называют симметричными. Если это условие не выполняется, то приемники называют несимметричными. При этом, если Za = Zb = Zc, то трехфазный приемник называют равномерным, если φa = φb = φc, то однородным.
Д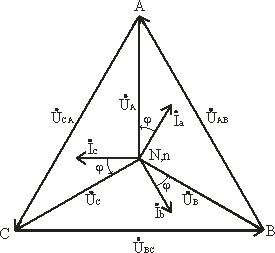 ля
расчета трехфазной цепи применимы все
методы, используемые для расчета линейных
цепей. Обычно сопротивления проводов
и внутреннее сопротивление генератора
меньше сопротивлений приемников, поэтому
для упрощения расчетов таких цепей
(если не требуется большая точность)
сопротивления проводов можно не учитывать
(ZЛ = 0, ZN = 0). Тогда фазные напряжения
приемника Ua, Ub и Uc будут равны соответственно
фазным напряжениям источника электрической
энергии(генератора или вторичной обмотки
трансформатора), т.е. Ua = UA; Ub = UB; Uc = UC. Если
полные комплексные сопротивления фаз
приемника равны Za = Zb = Zc, то токи в каждой
фазе можно определить по формулам
ля
расчета трехфазной цепи применимы все
методы, используемые для расчета линейных
цепей. Обычно сопротивления проводов
и внутреннее сопротивление генератора
меньше сопротивлений приемников, поэтому
для упрощения расчетов таких цепей
(если не требуется большая точность)
сопротивления проводов можно не учитывать
(ZЛ = 0, ZN = 0). Тогда фазные напряжения
приемника Ua, Ub и Uc будут равны соответственно
фазным напряжениям источника электрической
энергии(генератора или вторичной обмотки
трансформатора), т.е. Ua = UA; Ub = UB; Uc = UC. Если
полные комплексные сопротивления фаз
приемника равны Za = Zb = Zc, то токи в каждой
фазе можно определить по формулам
İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc. (3.10)
В соответствии с первым законом Кирхгофа ток в нейтральном проводе
İN = İa + İb + İc = İA + İB + İC. (3.11)
Симметричная нагрузка приемника
При симметричной системе напряжений и симметричной нагрузке, когда Za = Zb = Zc, т.е. когда
Ra = Rb = Rc = Rф и Xa = Xb = Xc = Xф,
фазные токи равны по значению и углы сдвига фаз одинаковы
I a
= Ib = Ic = Iф = Uф
/ Zф, (3.12)
a
= Ib = Ic = Iф = Uф
/ Zф, (3.12)
φa = φb = φc = φ = arctg (Xф/Rф). (3.13)
Построив векторную диаграмму токов для симметричного приемника (рис. 3.8), легко установить, что геометрическая сумма трех векторов тока равна нулю: İa + İb + İc = 0. Следовательно, в случае симметричной нагрузки ток в нейтральном проводе IN = 0, поэтому необходимость в нейтральном проводе отпадает.
Рис. 3.8
Несимметричная нагрузка приемника
При симметричной системе напряжений и несимметричной нагрузке, когда Za ≠ Zb ≠ Zc и φa ≠ φb ≠ φc токи в фазах потребителя различны и определяются по закону Ома
İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc.
Ток в нейтральном проводе İN равен геометрической сумме фазных токов
İN = İa + İb + İc.
Напряжения будут Ua = UA; Ub = UB; Uc = UC, UФ = UЛ / , благодаря нейтральному проводу при ZN = 0.
Следовательно, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке.
Поэтому в четырехпроводную сеть включают однофазные несимметричные нагрузки, например, электрические лампы накаливания. Режим работы каждой фазы нагрузки, находящейся под неизменным фазным напряжением генератора, не будет зависеть от режима работы других фаз.
12. Магнитные цепи. Элементы магнитной цепи. Закон полного тока.
В конструкцию многих электротехнических устройств (электрических машин, трансформаторов, электрических аппаратов, измерительных приборов и т.д.) входят магнитные цепи.
Магнитной цепью называется часть электротехнического устройства, содержащая ферромагнитные тела, в которой при наличии намагничивающей силы возникает магнитный поток и, вдоль которой замыкаются линии магнитной индукции. Источниками намагничивающей силы могут быть катушки с токами, постоянные магниты.
В конструктивном отношении магнитные цепи выполняют разветвлёнными и неразветвлёнными, причём применение того или иного вида цепи определяется в основном назначением электромагнитного устройства.
Ферромагнитные материалы и их магнитные свойства
По магнитным свойствам все материалы разделяют на две группы: ферромагнитные (железо, кобальт, никель и их сплавы и др.) и неферромагнитные материалы (все материалы, за исключением ферромагнитных).
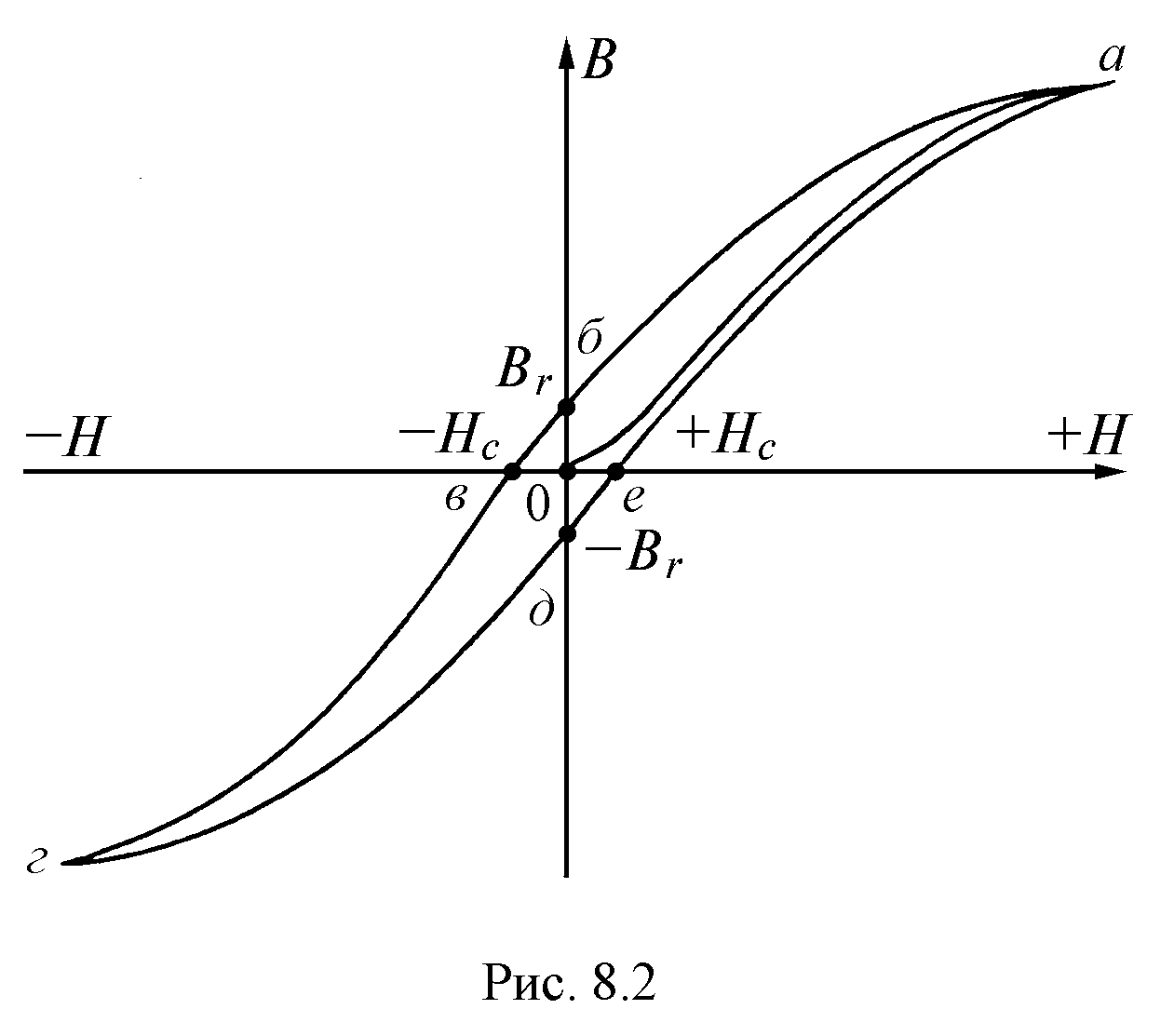
Особенностью неферромагнитных материалов является то, что зависимость между магнитной индукцией В и напряженностью магнитного поля Н в них является линейной. Их абсолютная магнитная проницаемость есть величина постоянная и практически равна магнитной постоянной
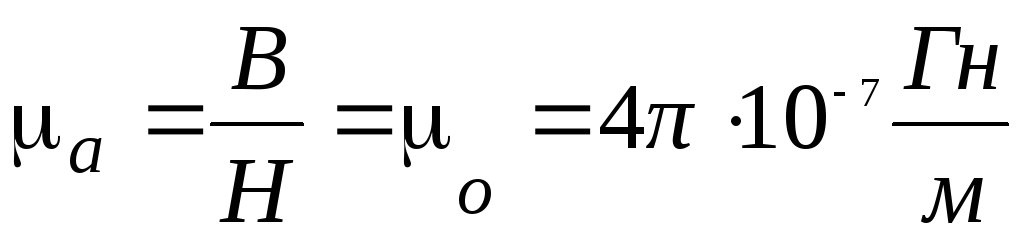 .
.  (7.1)
(7.1)
 Материалы,
магнитная проницаемость которых
достигает больших значений и зависит
от внешнего магнитного поля и
предшествующего состояния, называютферромагнитными.
Свойства ферромагнитных материалов
принято характеризовать зависимостью
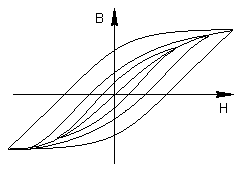
магнитной индукции В от напряженности магнитного поля Н.
Если перемагничивать образец в
периодическом магнитном поле, то кривая
Материалы,
магнитная проницаемость которых
достигает больших значений и зависит
от внешнего магнитного поля и
предшествующего состояния, называютферромагнитными.
Свойства ферромагнитных материалов
принято характеризовать зависимостью
магнитной индукции В от напряженности магнитного поля Н.
Если перемагничивать образец в
периодическом магнитном поле, то кривая 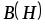 имеет вид петли, называемойпетлей
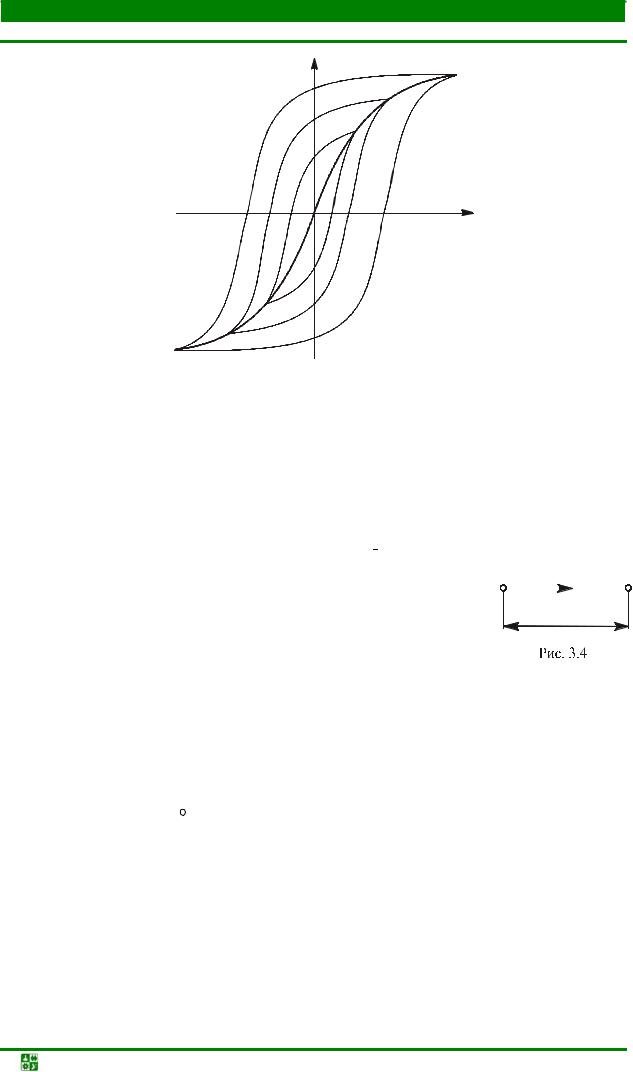
гистерезиса (рис. 7.1).
Участок 0а является кривой намагничивания, поскольку
поле возникает при нулевом значении
индукции. Точки б и д соответствуют остаточной индукции
имеет вид петли, называемойпетлей
гистерезиса (рис. 7.1).
Участок 0а является кривой намагничивания, поскольку
поле возникает при нулевом значении
индукции. Точки б и д соответствуют остаточной индукции 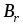 ,
а напряженность в точкахв и е называют задерживающей, или коэрцитивной,
силой
,
а напряженность в точкахв и е называют задерживающей, или коэрцитивной,
силой 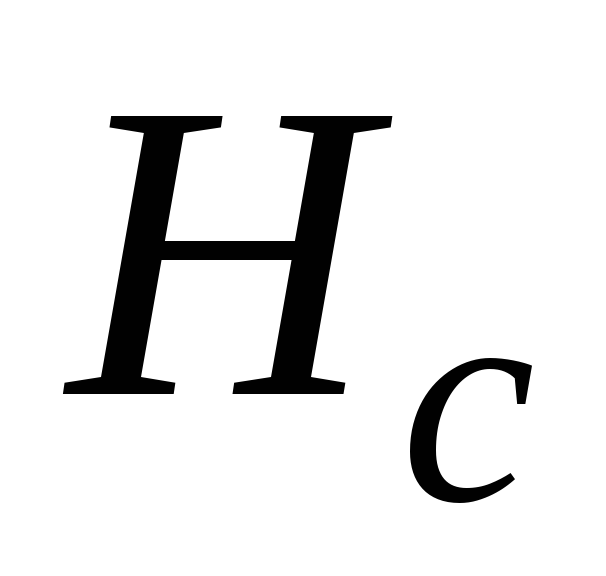 .
.
В зависимости от магнитной проницаемости ферромагнитные материалы разделяют на две группы:
1)
магнитомягкие с большой магнитной
проницаемостью и с малой коэрцитивной
силой  .
К ним относят электротехнические стали,
пермаллой и ферриты;
.
К ним относят электротехнические стали,
пермаллой и ферриты;
2)
магнитотвердые с малой магнитной
проницаемостью, большой коэрцитивной
силой 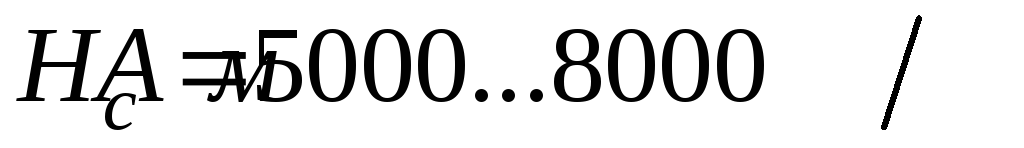 и большой остаточной индукцией
и большой остаточной индукцией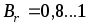 Тл.
Тл.
Магнитотвердые материалы применяют для изготовления постоянных магнитов. К ним относятся углеродистые, вольфрамовые, хромистые и кобальтовые сплавы.
Ферромагнитные материалы играют важную роль в электротехнике, так как дают возможность при относительно небольших напряженностях получать сильные магнитные поля и конструировать электромагнитные устройства, обладающие заданными характеристиками.
Ферромагнитные магнитопроводы используют во всех электрических машинах, трансформаторах, электромагнитах, реле и др.
Закон полного тока и его применение для расчета магнитного поля
Магнитной цепью называется совокупность магнитодвижущих сил (МДС), ферромагнитных тел или каких-либо иных сред, по которым замыкается магнитный поток.
Произведение числа витков катушки на протекающий в ней ток называют магнитодвижущей силой (МДС)
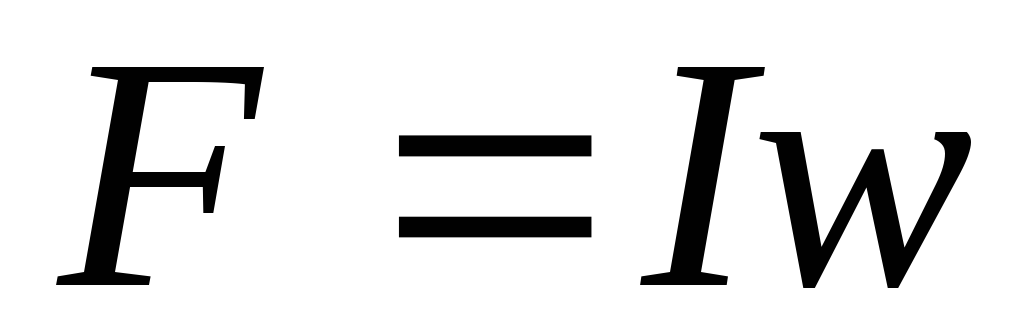 ,
[А].
(7.2)
,
[А].
(7.2)
МДС вызывает в магнитной цепи магнитный поток подобно тому, как ЭДС вызывает ток в электрической цепи. На схемах МДС указывают стрелкой, положительное направление которой совпадает с направлением движения правоходного винта, если его вращать по направлению тока в обмотке (рис. 7.2 а).
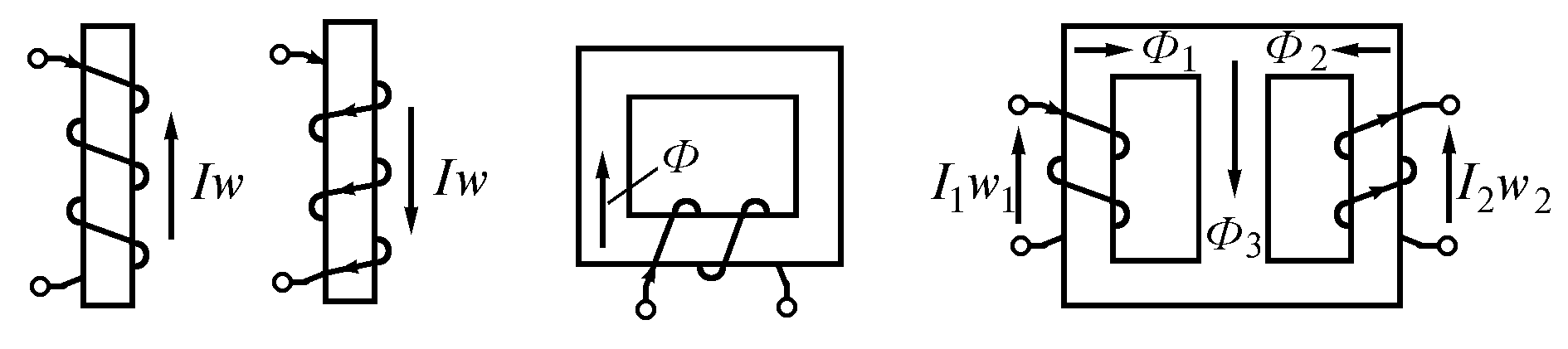 Магнитная
цепь, во всех сечениях которой магнитный
поток одинаков, называется неразветвленной
(рис. 7.2 б).
Магнитная
цепь, во всех сечениях которой магнитный
поток одинаков, называется неразветвленной
(рис. 7.2 б).
а) б) в) г)
Рис. 7.2
В
разветвленной магнитной цепи потоки
на различных участках неодинаковы
(рис. 7.2 в).Одним из основных законов,
используемых при расчете магнитной
цепи, является закон полного тока: циркуляция
вектора напряженности магнитного
поля Н по замкнутому контуру равна алгебраической
сумме токов, которые охвачены этим
контуром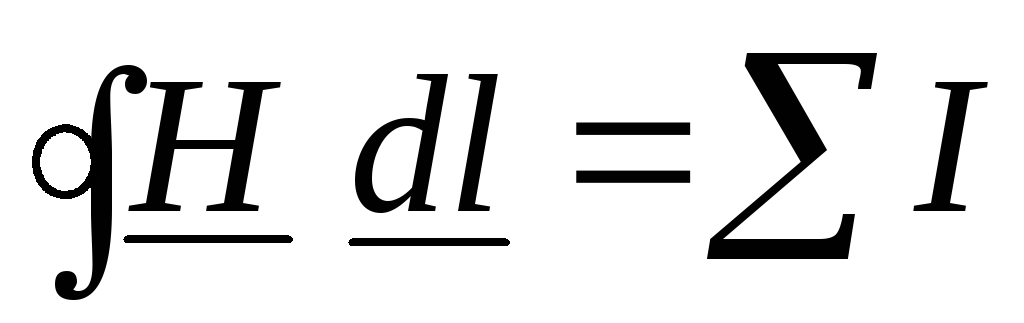 .
(7.3)
.
(7.3)
Если
контур интегрирования охватывает 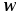 витков катушки, которым протекает токI, то закон полного тока принимает вид:
витков катушки, которым протекает токI, то закон полного тока принимает вид: .
(7.4)
.
(7.4)
Закон полного тока для магнитного поля: формулы и определение
Знакомый многим предмет под названием «Электротехника» содержит в своей программе ряд основополагающих законов, определяющих принципы физического взаимодействия для магнитного поля. Они распространяют свое действие на различные элементы электротехнических устройств, а также на входящие в их состав структуры и среды. Физика происходящих в них процессов касается таких базовых понятий, как потоки электричества и поля. Закон полного тока устанавливает зависимость между перемещением электрических зарядов и создаваемым им магнитным полем (точнее – его напряженностью). Современная наука утверждает, что его применение распространяется практически на все среды.
Суть закона
Рассматриваемый закон, применимый в магнитных цепях, определяет следующую количественную связь между входящими в него составляющими. Циркуляция вектора магнитного поля по замкнутому контуру пропорциональна сумме токов, пронизывающих его. Чтобы понять физический смысл закона полного тока – потребуется ознакомиться с графическим представлением описываемых им процессов.

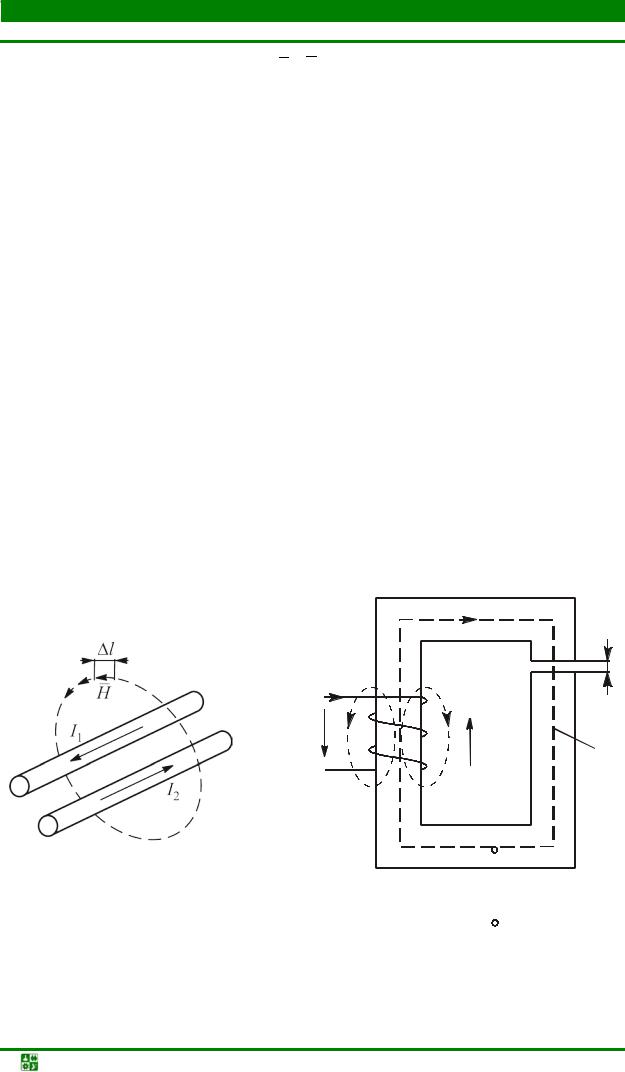
Из рисунка видно, что около двух проводников с протекающими по ним токами I1 и I2 образуется поле, ограниченное контуром L. Оно вводится как мысленно представляемая замкнутая фигура, плоскость которой пронизывают проводники с движущимися зарядами. Простыми словами этот закон можно выразить так. При наличии нескольких потоков электричества через мысленное представляемую поверхность, охватываемую контуром L, в ее пределах формируется магнитное поле с заданным распределением напряженности.
За положительное направление движения вектора в соответствии с законом для контура магнитной цепи выбирается ход часовой стрелки. Оно также является мысленно представляемым.
Такое определение создаваемого токами вихревого поля предполагает, что направление каждого из токов может быть произвольным.
Для справки! Вводимую полевую структуру и описывающий ее аппарат следует отличать от циркуляции электростатического вектора «Е», который при обходе контура всегда равен нулю. Вследствие этого такое поле относится к потенциальным структурам. Циркуляция же вектора «В» магнитного поля никогда не бывает нулевой. Именно поэтому оно называется «вихревым».
Основные понятия
В соответствии с рассматриваемым законом для расчета магнитных полей применяется следующий упрощенный подход. Полный ток представляется в виде суммы нескольких составляющих, протекающих через поверхность, охватываемую замкнутым контуром L. Теоретические выкладки могут быть представлены следующим образом:
- Полный электрический поток, пронизывающих конур Σ I – это векторная сумма I1 и I2.
- В рассматриваемом примере для его определения используется формула:
ΣI = I1- I2 (минус перед вторым слагаемым означает, что направления токов противоположны). - Они, в свою очередь, определяются по известному в электротехнике закону (правилу) буравчика.
Напряженность магнитного поля вдоль контура вычисляется на основании полученных выкладок по специальным методикам. Для ее нахождения придется проинтегрировать этот параметр по L, используя уравнение Максвелла, представленное в одной из форм.Оно может быть применено и в дифференциальной форме, но это несколько усложнит выкладки.
Упрощенный подход в интегральном виде
Если воспользоваться дифференциальным представлением – выразить закон полного тока в упрощенном виде будет очень сложно (в этом случае в него приходится вводить дополнительные компоненты). Добавим к этому, что магнитное вихревое поле, создаваемое движущимся в пределах контура токами, определяется в этом случае с учетом тока смещения, зависящего от скорости изменения электрической индукции.
Поэтому на практике в ТОЭ большей популярностью пользуется представление формул для полных токов в виде суммирования микроскопически малых отрезков контура с создаваемыми в них вихревыми полями. Этот подход предполагает применение уравнения Максвелла в интегральной форме. При его реализации контур разбивается на мелкие отрезки, в первом приближении считающиеся прямолинейными (согласно закону предполагается, что магнитное поле однородно). Эта величина, обозначаемая как Um для одного дискретного участка длиной ΔL магнитного поля, действующего в вакууме, определяется так:
Um= HL*ΔL
Суммарная напряженность вдоль полного контура L, представленная кратко в интегральном виде, находится по следующей формуле:
UL= Σ HL*ΔL.
Закон полного тока для вакуума
В окончательном виде, оформленном по всем правилам интегрирования, закон полного тока выглядит так. Циркуляция вектора «В» по замкнутому контуру может быть представлена как произведение магнитной постоянной m на сумму токов:
Интеграл от B по dL = интегралу от Bl по dL= m Σ In
где n – это обще число проводников с разнонаправленными токами, охватываемыми мысленно представляемым контуром L произвольной формы.
Каждый ток учитывается в этой формуле столько раз, сколько он полностью охватывается данным контуром.
На окончательный вид полученных выкладок для закона полного тока большое влияние оказывает среда, в которой действует наведенная электромагнитная сила (поле).
Влияние среды
Рассмотренные отношения для закона токов и полей, действующих не в вакууме, а в магнитной среде, приобретают несколько иной вид. В этом случае помимо основных токовых составляющих вводится понятие микроскопических токов, возникающих в магнетике, например, или в любом подобном ему материале.
Нужное соотношение в полном виде выводится из теоремы о векторной циркуляции магнитной индукции B. Простым языком она выражается в следующем виде. Суммарное значение вектора B при интегрировании по выбранному контуру равно сумме охватываемых им макро токов, умноженной на коэффициент магнитной постоянной.
В итоге формула для «В» в веществе определяется выражением:
Интеграл от B по dL = интегралу от Bl по dL= m(I+I1)
где: dL – дискретный элемент контура, направленный вдоль его обхода, Вl– составляющая в направлении касательной в произвольной точке,бI и I1 – ток проводимости и микроскопический (молекулярный) ток.
Если поле действует в среде, состоящей из произвольных материалов – должны учитываться микроскопические токи, характерные именно для этих структур.
Эти выкладки также верны для поля, создаваемого в соленоиде или в любой другой среде, обладающей конечной магнитной проницаемостью.
Для справки
В самой полной и объемлющей системе измерений СГС напряженность магнитного поля представляется в эрстедах (Э). В другой действующей системе (СИ) она выражается в амперах на один метр (А/метр). Сегодня эрстед постепенно вытесняется более удобной в работе единицей – ампером на метр. При переводе результатов измерений или расчетов из СИ в СГС используется следующее соотношение:
1 Э = 1000/(4π) А/м ≈ 79,5775 Ампер/метр.
В заключительной части обзора отметим, что независимо от того, какая используется формулировка закона полных токов – суть его остается неизменной. Своими словами это можно представить так: он выражает отношения между токами, пронизывающими данный контур и создаваемыми в веществе магнитными полями.
Напоследок рекомендуем просмотреть полезное видео по теме статьи:
Материалы по теме:
ГЛАВА 8 МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА

8.1. Основныевеличины, характеризующие магнитныецепи
Магнитная цепь – это совокупность тел для замыкания магнитного потока.
Все вещества по магнитным свойствам делят на три группы:
1. Диамагнитные, у которых относительная магнитная проницаемость
µ <1.
2.Парамагнитные, у которых µ >1.
3.Ферромагнитные, у которых µ >>1.
Относительная магнитная проницаемость показывает, во сколько раз абсолютная магнитная проницаемость вещества µà больше магнитной про-
ницаемости | вакуума μ0 , т. е. µ = | µà . Величина µ0 не изменяется |
|
| µ0 |
(µ0 = 4π 10 −7 | Ãí /ì ), ее называют магнитной постоянной. Магнитную прони- | |
цаемость воздуха принимают равной магнитной постоянной, поэтому воздушные магнитные цепи являются линейными.
Для создания магнитных цепей используют преимущественно ферромагнитные материалы. Основными ферромагнитными материалами являются, прежде всего, электротехнические стали Э11, Э21, Э32, Э44 и т. д. Первая цифра обозначает процентное содержание кремния, вторая – гарантированный уровень потерь. Относительная магнитная проницаемость электротехнических сталей порядка 1800–1900.
Более качественными являются сплавы пермалой и перминвар, содержащие до 78,5 % никеля. У них относительная магнитная проницаемость µ =
=200000 – 800000.
Врадиотехнике широко применяют ферриты.
Магнитные цепи из ферромагнитных материалов являются нелинейными, так как у них относительная магнитная проницаемость– величина переменная.
Вокруг каждого проводника с током возникает магнитное поле. Интенсивность магнитного поля в каждой его точке определяют вектором маг-
нитной индукции В. Единицей измерения магнитной индукции является тесла (Тл).
Магнитная индукция магнитного поля Земли составляет 10–4 Тл. В электрических реле В = (0,2–0,3) Тл, в трансформаторах В = 1,4 Тл, пр е- дельное значение магнитной индукции в машинах постоянного тока составляет 1,71 Тл. В ускорителях В = (2–3) Тл, в МГД-генераторах В = 5 Тл достигают за счет явления сверхпроводимости.
Магнитное поле характеризуют также вектором напряженности маг-
Теоретические основы электротехники. Учеб. пособие | -229- |
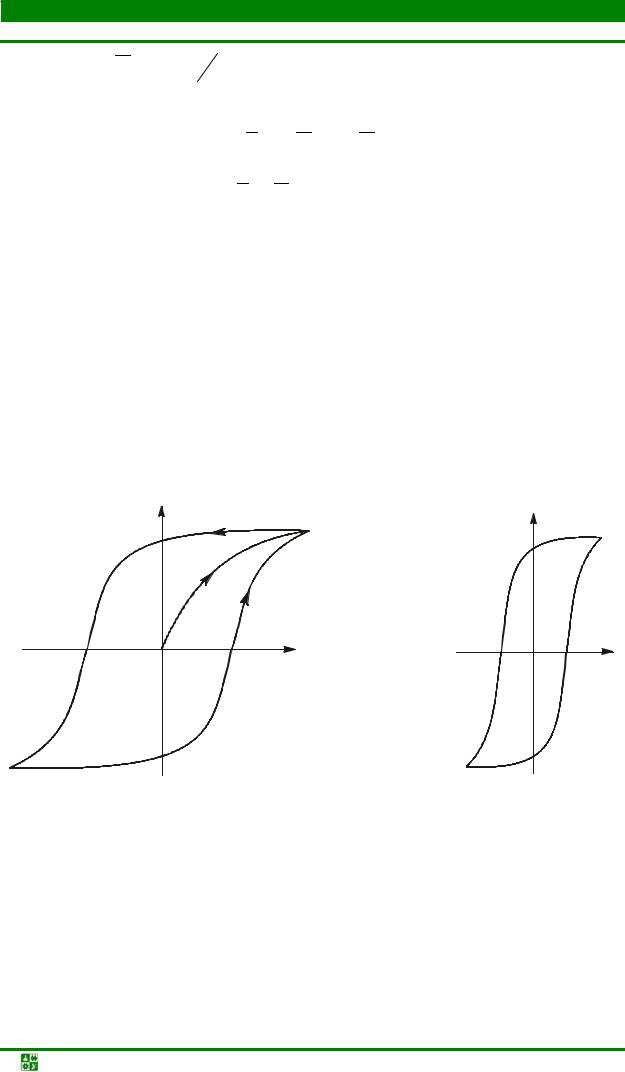
ГЛАВА 8. МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
8.1. Основные величины, характеризующие магнитные цепи
нитного поля Н . [Í ]= À ì .
Величины В и Н связаны зависимостью
 = µà Í = µ0µÍ .
Направления векторов В и Н совпадают, поэтому можно записать:
 = µ0µÍ .
Характер зависимости В(Н) был впервые установлен в 1871 г. русским физиком А. Г. Столетовым.
В общем случае эта зависимость сложна. Ее устанавливают экспериментально и представляют графически в виде кривой намагничивания, называемой циклом (петлей) магнитного гистерезиса (рис. 8.1). Для каждого значения Hmax получается свой цикл гистерезиса.
Явление гистерезиса – это отставание изменения магнитной индукции В от изменения напряженности магнитного поля Н. Как видно из рис. 8.1, когда Н = 0, В имеет остаточное значение.
B | B |
H | H |
РисРис. 8.1. 3.1 | Рис. 3.2 |
Рис. 8.2 |
Материалы с широким циклом магнитного гистерезиса (рис. 8.1) называют магнитотвердыми, с узким (рис. 8.2) – магнитомягкими.
При расчетах, если позволяет требуемая точность, пользуются основной кривой намагничивания.
Основная кривая намагничивания – это геометрическое место вершин симметричных циклов магнитного гистерезиса (рис. 8.3). Она практически совпадает с кривой первоначального намагничивания.
Теоретические основы электротехники. Учеб. пособие | -230- |
ГЛАВА 8. МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
8.1. Основные величины, характеризующие магнитные цепи
B |
H |
Рис. 8.3 |
Рис. 3.3 |
Магнитный поток – поток магнитной индукции через площадь S:
Ф = В S .
Магнитный поток измеряют в веберах (Вб).
Магнитное напряжение между двумя точками магнитного поля
Uм = | Н | l (рис. 8.4). При расчетах выбирают l по направле- |
|
|
|
|
| ||
H | |||||||||
нию | H | . Тогда можно записать: Uì = H l . [Uì ]= A . |
|
|
|
|
| ||
|
|
|
|
| |||||
|
| Магнитодвижущая сила F =WI , |
| l | |||||
где W – число витков катушки; I – ток в ней. |
|
|
|
|
| ||||
|
| Очевидно, что единицей измерения магнитодвижущей |
| Рис. 8.4 |
| ||||
силы является ампер (А). |
|
|
|
|
| ||||
|
|
|
|
| |||||
8.2.Основныезаконымагнитныхцепей
1.Принцип непрерывности магнитного потока. Линии магнитной индукции непрерывны и замкнуты. Поэтому магнитный поток через замкну-
тую поверхность Ф = ∫В dS = 0. Отсюда следует, что в неразветвленных це-
пях магнитный поток на всех участках одинаков, а в разветвленных цепях алгебраическая сумма магнитных потоков в точке разветвления равна нулю:
ΣÔ = 0.
2. Закон полного тока. Линейный интеграл напряженности магнитного поля вдоль замкнутого контура равен алгебраической сумме токов, пронизывающих этот контур:
Теоретические основы электротехники. Учеб. пособие | -231- |
ГЛАВА 8. МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
8.2. Основные законы магнитных цепей
∫ Í d l = ∑I .
Правило знаков: со знаком плюс записывают токи, связанные с выбранным направлением обхода контура интегрирования правилом правоходового винта (правой руки).
Контур интегрирования выбирают совпадающим с магнитной силовой линией, тогда обозначения векторов можно убрать. Закон полного тока для рис. 8.5 имеет следующий вид:
∫ Í d l = I1 − I2 .
Если внутри контура интегрирования находятся не линейные проводники, а индуктивные катушки, то в правой части уравнения по закону полного тока нужно записать алгебраическую сумму магнитодвижущих сил:
∫ Í d l = ΣF = ΣWI .
Напряженность магнитного поля принимают для средней силовой линии. Воспользуемся законом полного тока для анализа неразветвленной неоднородной магнитной цепи. Эта цепь представляет собой индуктивную катушку с сердечником из ферромагнитного материала, который усиливает
магнитный поток и придает ему требуемую форму (рис. 8.6).
| Ф |
|
I | Фs | lв |
| ||
U | F | l |
| ||
|
|
Рис. 8.5
РисРис..83..66
Сердечник изготавливают разборным, чтобы на стержень можно было надеть катушку. В местах стыков возникают зазоры, которые на рис. 8.6 учтены одним с суммарной длиной lâ . Даже небольшой воздушный зазор до-
вольно резко уменьшает магнитный поток. Иногда воздушные зазоры делают
Теоретические основы электротехники. Учеб. пособие | -232- |

ГЛАВА 8. МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
8.2. Основные законы магнитных цепей
специально, чтобы сердечник не намагничивался до состояния насыщения. Основная часть магнитного потока Ф замыкается по сердечнику. Маг-
нитный поток рассеяния Ôs замыкается по воздуху (см. рис. 8.6). Строгий
расчет магнитной цепи может быть выполнен только с привлечением методов теории электромагнитного поля.
Для приближенного решения делают следующие допущения: 1) пренебрегают магнитным потоком рассеяния (Ôs = 0) ;
2) площадь Sâ , которую пронизывает поток Ф в зазоре, считают равной
площади поперечного сечения S сердечника магнитопровода, т. е. пренебрегают выпучиванием магнитных линий в зазоре;
3) при расчете пользуются основной кривой намагничивания.
Если сечение магнитопровода одинаково, то представленную на рис. 8.6 магнитную цепь делим на два участка: сердечник и воздушный зазор. По закону полного тока
|
|
|
|
| Hl + Hâlâ = F . |
|
|
|
|
|
|
|
| |
Так как H = | B | и H |
| = | Bâ | , а B = B = | Ô | , то H = | Ô | и H |
| = | Ô | . |
| µ µ0 |
| â |
| µ0 | â | S |
| µ µ0S |
| â |
| µ0S | |
Подставив эти формулы в закон полного тока, получим:
| l |
| lâ |
| = F . | |
Ô | + |
| ||||
µ µ0S |
| |||||
|
| µ0S |
| |||
По аналогии с электрическим сопротивлением R = γlS , где γ – удель-
ная проводимость, вводят понятие магнитного сопротивления сердечника
R = | l | и зазора R | = | lâ | . |
ì | µ µ0S | ì â |
| µ0S | |
Тогда уравнение по закону полного тока примет вид
Φ(Rì + Rì â ) = F .
Отсюда
| F | |
Φ = |
| . |
R + R | ||
| ì ì â |
|
Эта формула похожа по структуре на формулу, выражающую закон Ома для полной электрической цепи. Уравнение по закону полного тока похоже на уравнение по второму закону Кирхгофа для электрической цепи,
Теоретические основы электротехники. Учеб. пособие | -233- |
ГЛАВА 8. МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
8.2. Основные законы магнитных цепей
уравнение ΣÔ = 0 – на уравнение по первому закону Кирхгофа.
На основании этого говорят о формальной аналогии между магнитными и электрическими цепями. По своему физическому содержанию процессы, происходящие в этих цепях, существенно отличаются.
По аналогии с электрической цепью в магнитной цепи можно выделить узлы и ветви, составить ее схему замещения.
Схема замещения магнитной цепи рис. 8.6 и ее аналоговая электрическая схема приведены на рис. 8.7, а и б.
Рис. 8.7
Схема замещения содержит два последовательно соединенных элемента: линейный, сопротивление Rì â которого равно магнитному сопротивле-
нию воздушного зазора, и нелинейный, сопротивление Rì которого равно
магнитному сопротивлению сердечника.
Расчет магнитных цепей аналогичен расчету нелинейных электрических цепей с сосредоточенными параметрами, причем МДС F соответствует ЭДС Е, поток Ф – току I, магнитное сопротивление Rì – электрическому сопротивле-
нию R , магнитное напряжение Uì – электрическому напряжению U.
По аналогии с электрическими цепями основные законы магнитных цепей нередко называют законами Кирхгофа для магнитных цепей и формулируют следующим образом:
1) алгебраическая сумма магнитных потоков в узле равна нулю:
ΣÔ = 0 ;
2) алгебраическая сумма магнитных напряжений в контуре равна алгебраической сумме действующих в этом контуре МДС:
∑Uì = ∑F ; ∑H l = ∑W I или ∑Rì Φ = ∑F .
Магнитное напряжение направлено по потоку. Для определения направления МДС можно использовать правило правой руки: если сердечник мысленно охватить правой рукой, расположив четыре пальца по направлению тока в катушке, то отогнутый большой палец укажет направление МДС.
Теоретические основы электротехники. Учеб. пособие | -234- |
Магнитные цепи
Расчёт магнитных цепей при постоянных магнитодвижущих силах.
Магнитной цепью называется совокупность устройств, содержащих ферромагнитные тела, служащих для сосредоточения магнитного потока в определённой части пространства.
В силу непостоянства магнитной проницаемости µ магнитные цепи нелинейны.
Если магнитная цепь выполнена из одного ферромагнитного материала, то её называют однородной, если из различных материалов – неоднородной. Магнитная цепь, во всех сечениях которой магнитный поток одинаков, называется неразветвлённой магнитной цепью.
Основные законы магнитных цепей.
Закон полного
тока: циркуляция вектора  по замкнутому контуру равна алгебраической
сумме токов, охватываемых этим контуром,
то есть
по замкнутому контуру равна алгебраической
сумме токов, охватываемых этим контуром,
то есть
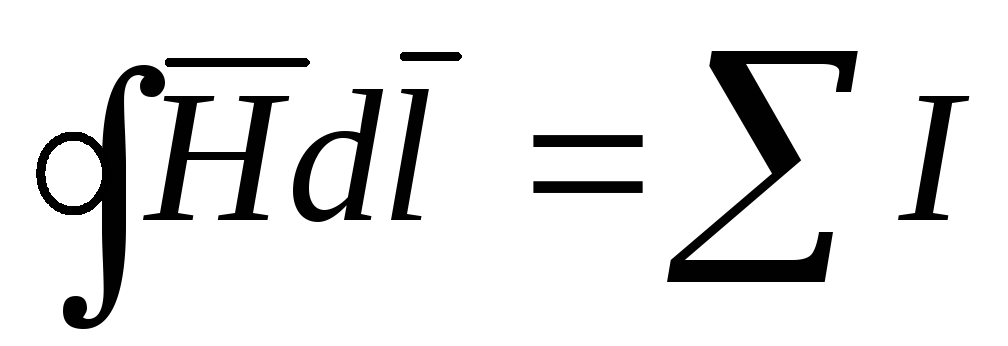 ;
;
знак тока выбирается
по правилу правого винта, 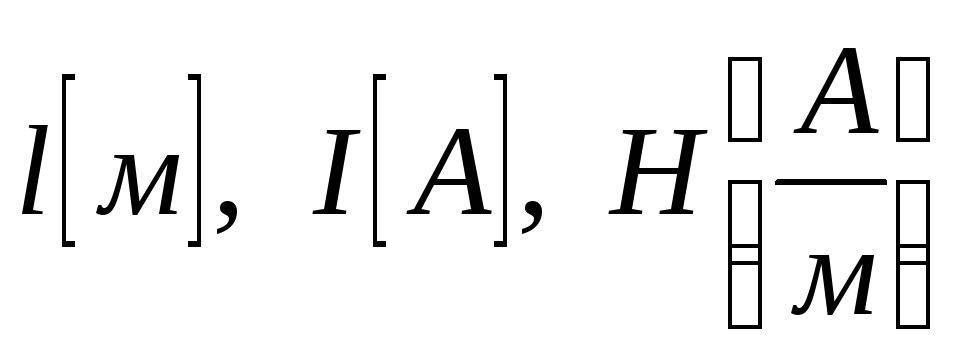 .
.
В случае когда
контур интегрирования охватывает W
витков катушки 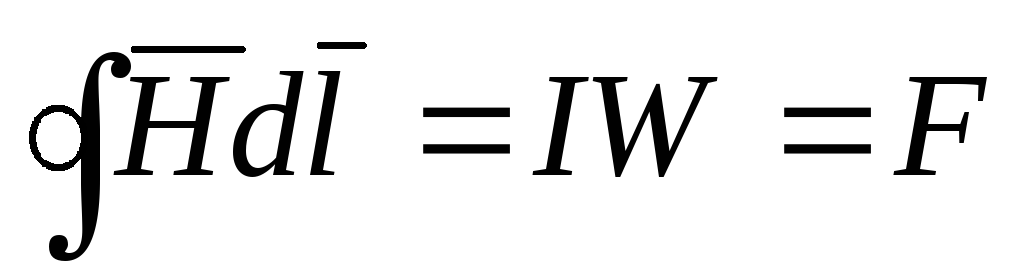 ,
где
,
где 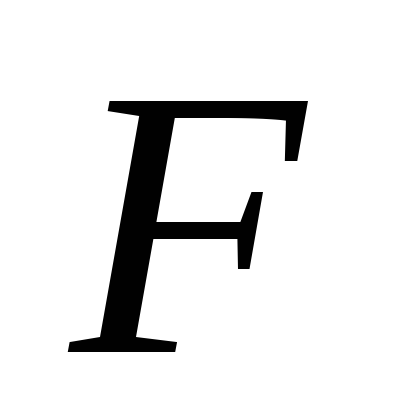 —
намагничивающая сила (НС) или магнитодвижущая
сила (МДС),
—
намагничивающая сила (НС) или магнитодвижущая
сила (МДС), 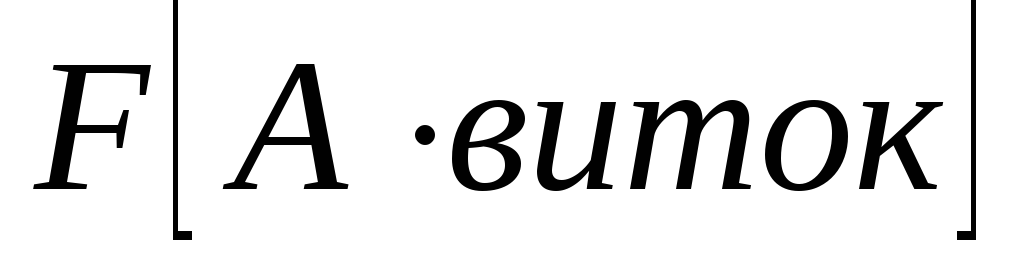 .
.
С вектором  связан вектор магнитной индукции
связан вектор магнитной индукции 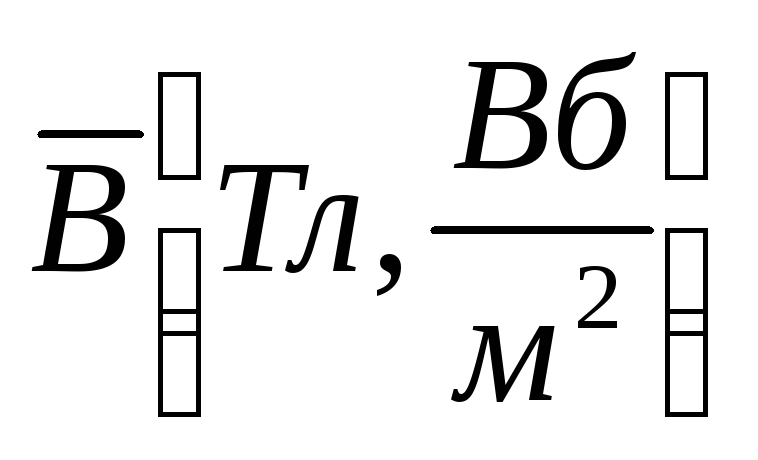 .
.
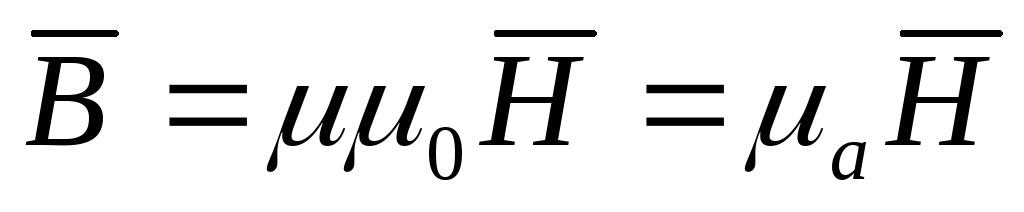 ,
,
где µ — относительная магнитная проницаемость, µ=4·10-7 Гн/м — магнитная постоянная, µа – абсолютная магнитная проницаемость.
Контур интегрирования обычно выбирают таким образом, чтобы он совпадал с линией вектора напряжённости, что позволяет заменить подынтегральное выражение в законе полного тока произведением скалярных величин.
Для практических
расчётов интеграл заменяют суммой
произведений  ,
где k
– участок с неизменной µ.
В результате имеем закон для магнитных
цепей:
,
где k
– участок с неизменной µ.
В результате имеем закон для магнитных
цепей:
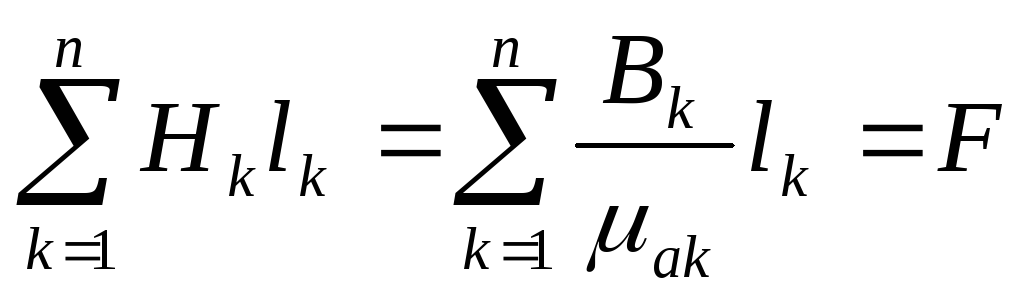 ,
,
где n
– число участков, 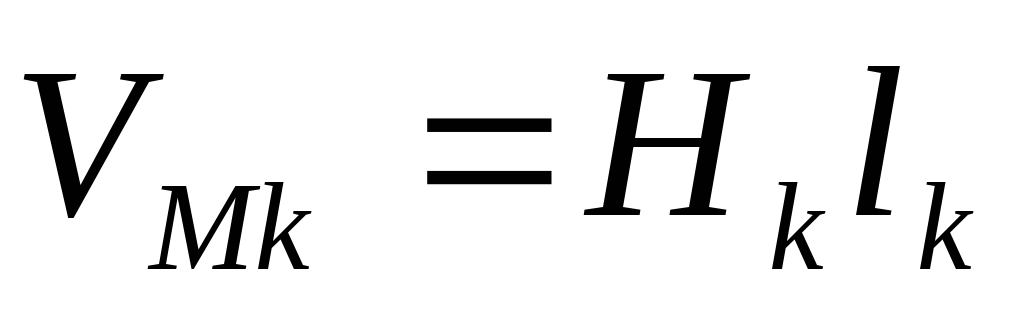 —
разность скалярных магнитных потенциалов.
—
разность скалярных магнитных потенциалов.
Алгебраическая сумма МДС в любом контуре равна произведению алгебраической суммы потока и соответствующего магнитного сопротивления:
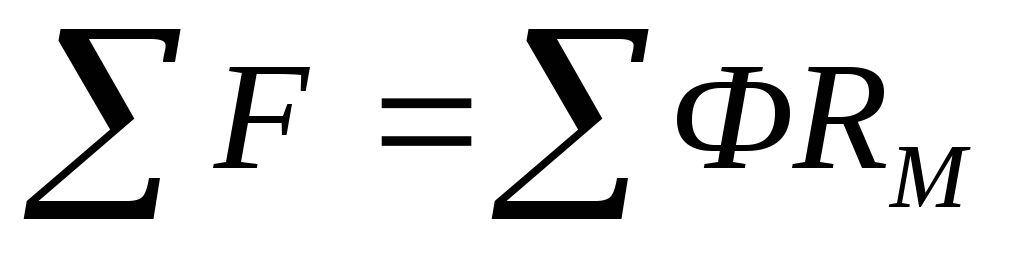 .
.
Для воздушных
зазоров µ=µ0 ,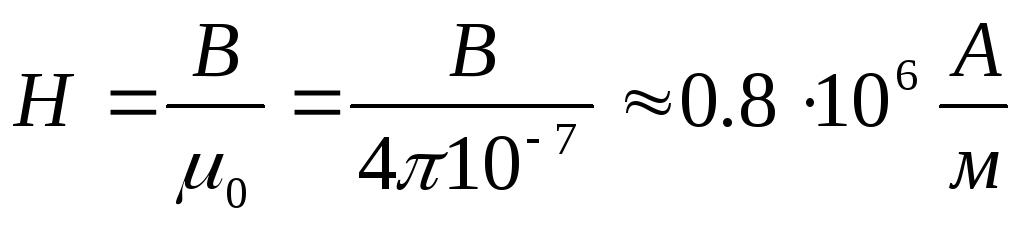 .
.
Свойство: в неразветвлённой магнитной цепи поток на всех участках одинаков, а в разветвлённой цепи поток на участке подходящем к месту разветвления равен сумме потоков.
В разветвлённой магнитной цепи поток подчиняется первому закону Кирхгофа для магнитной цепи: алгебраическая сумма магнитных потоков в узле равна нулю, то есть
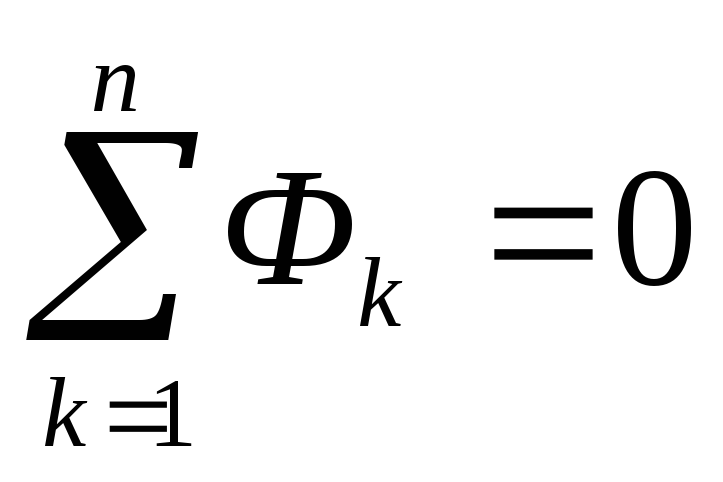 .
.
Если считать, что
вектор 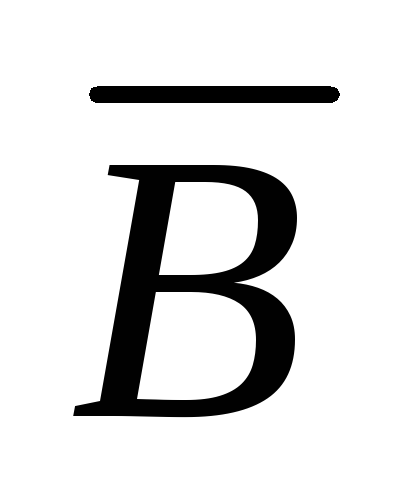 одинаков во всех точках поперечного
сечения S
магнитной цепи и направлен перпендикулярно
этому сечению, то
одинаков во всех точках поперечного
сечения S
магнитной цепи и направлен перпендикулярно
этому сечению, то 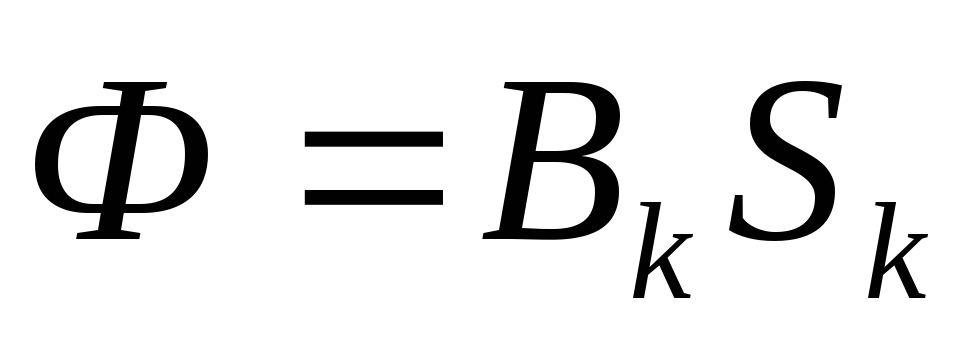 ,
где k
– участок магнитной цепи с неизменным
потоком
,
где k
– участок магнитной цепи с неизменным
потоком  .
.
Закон Ома для магнитной цепи:
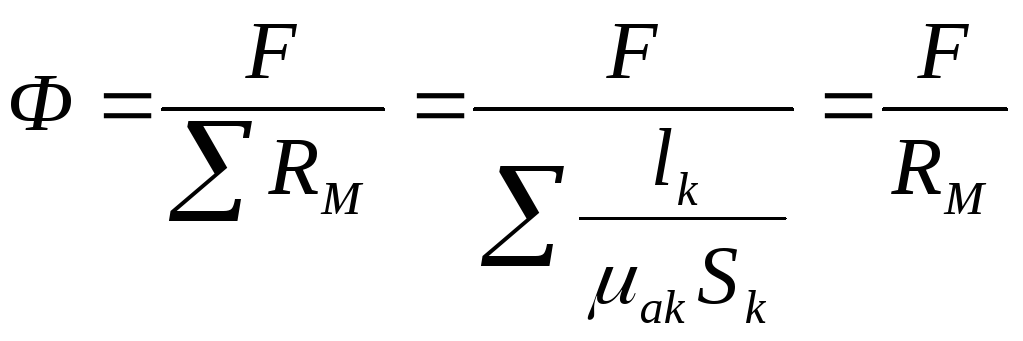 ,
,
где 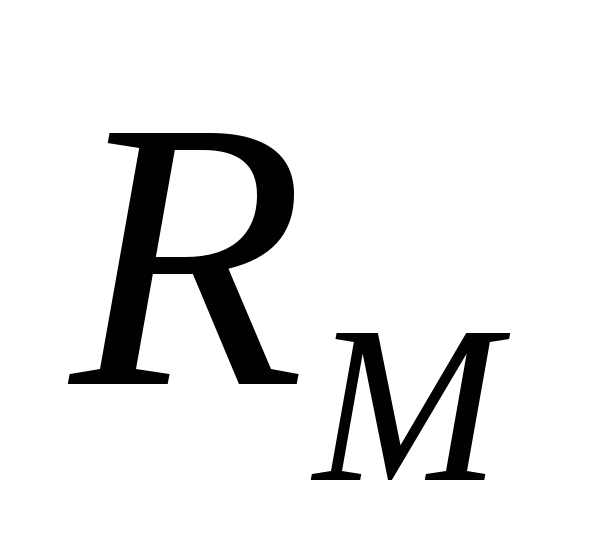 —
магнитное сопротивление [1/Гн],
—
магнитное сопротивление [1/Гн], 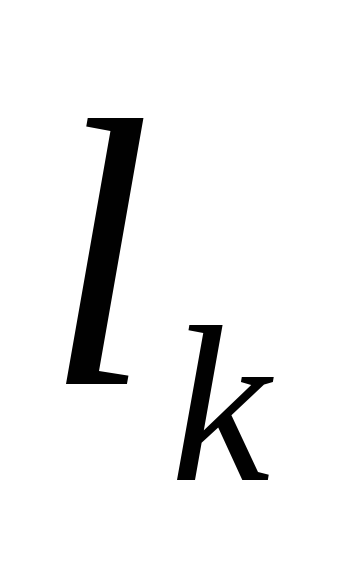 —
длина средней линии.
—
длина средней линии.
Закон Ома для
магнитных цепей применим только для
тех случаев, когда связь между индукцией 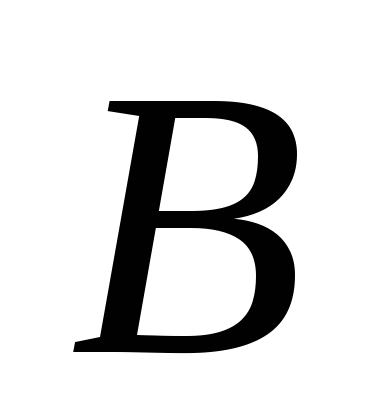 и напряжённостью магнитного поля
и напряжённостью магнитного поля  принята линейной.
принята линейной.
Формальная аналогия между электрическими и магнитными цепями.
Электрическая цепь | Магнитная цепь |
E I R I=0 IR=E I=E/R R=l/S | F Ф RM µ Ф=0 Hl=F Ф=F/RM RM=l/µS |
Допущения принимаемые при анализе магнитных цепей.
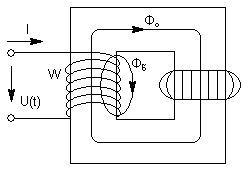
Поток рассеивания
 пренебрежимо мал. Расчёт осуществляется
по основному потоку
пренебрежимо мал. Расчёт осуществляется
по основному потоку  .
.Э
 ффектом
выпучивания магнитных силовых линий
в воздушном зазоре пренебрегаем, то
есть площадь поперечного сечения стали
и воздушного промежутка одинакова.
ффектом
выпучивания магнитных силовых линий
в воздушном зазоре пренебрегаем, то
есть площадь поперечного сечения стали
и воздушного промежутка одинакова.Расчёт магнитной цепи осуществляем по основной кривой намагничивания, которая получается в результате соединения вершин частных петель гистерезиса.
Расчёт неразветвлённой магнитной цепи.
Различают прямую и обратную задачу расчёта магнитных цепей.
П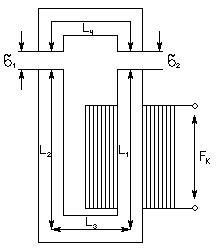 рямая
задача.
рямая
задача.
При заданном  или
или  ,
,  определяем как сумму падений магнитного
напряжений на отдельных участках
ферромагнитных тел и воздушных зазоров,
то есть используем второй закон Кирхгофа
для магнитной цепи:
определяем как сумму падений магнитного
напряжений на отдельных участках
ферромагнитных тел и воздушных зазоров,
то есть используем второй закон Кирхгофа
для магнитной цепи:
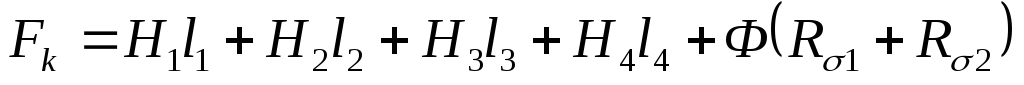 ,
,
где 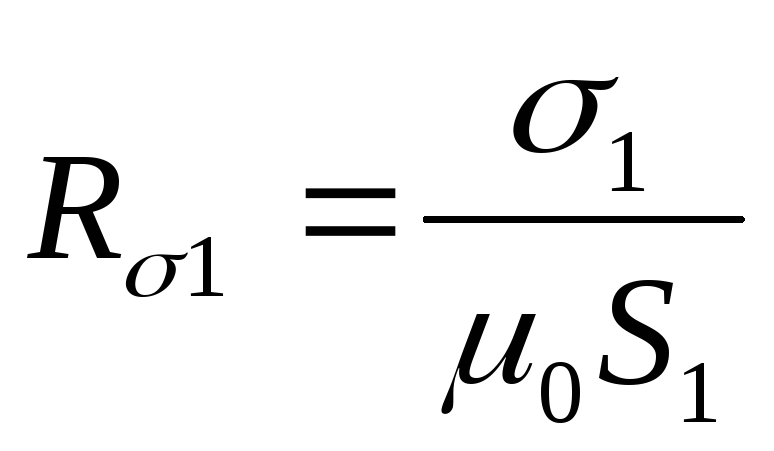 и
и 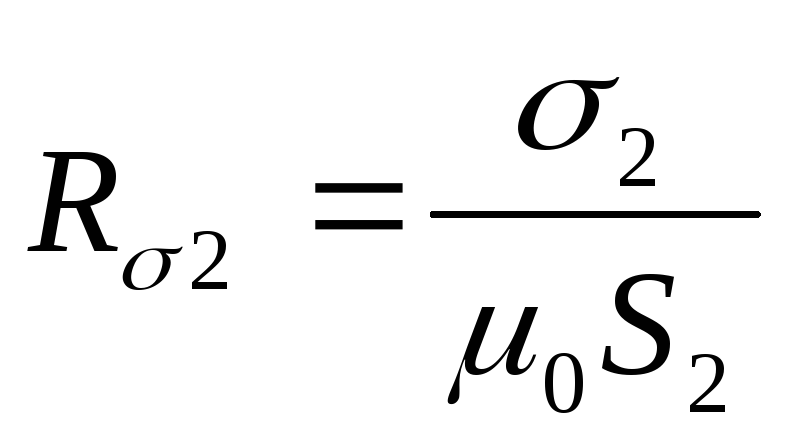 .
.
Н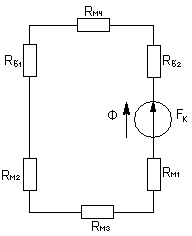 аходим
аходим 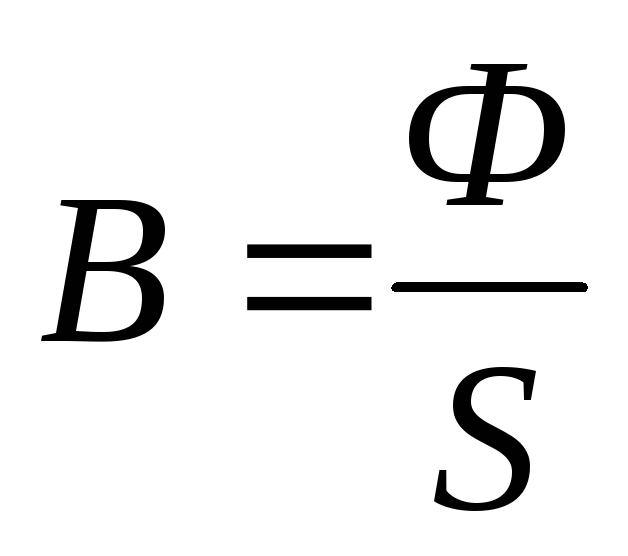 ,
далее определяем из графика
,
далее определяем из графика 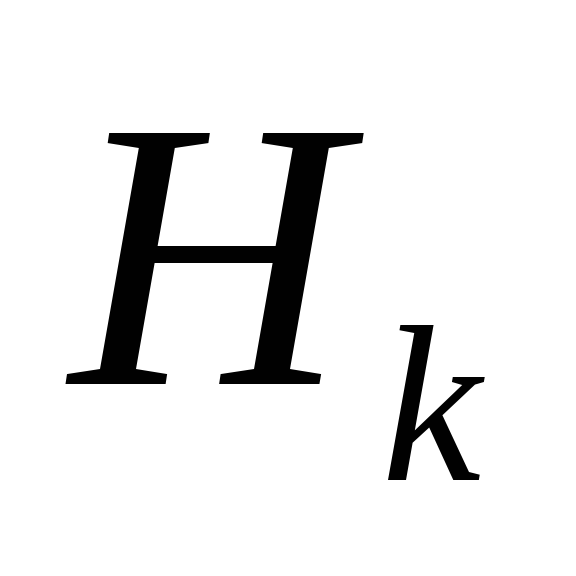 и подставляем его значение во второй
закон Кирхгофа для магнитной цепи.
и подставляем его значение во второй
закон Кирхгофа для магнитной цепи.
Расчёт неразветвлённой магнитной цепи методом последовательных приближений.
Обратная задача.
Определяем какую необходимо создать намагничивающую силу, для того чтобы сформировать заданный магнитный поток.
Определяем значение
 без учёта магнитного сопротивления
стали:
без учёта магнитного сопротивления
стали:
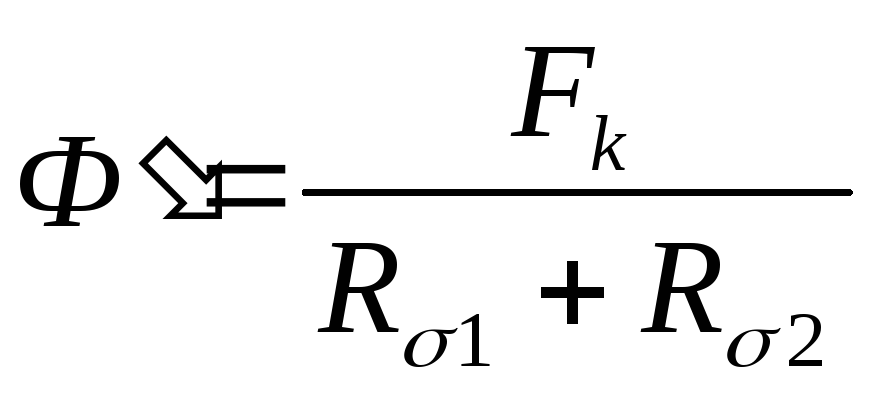
По известной
 определяем
определяем  на отдельных участках. Пользуясь кривой
намагничивания находим
на отдельных участках. Пользуясь кривой
намагничивания находим  ,
,  ,
,  и
и  .
.Определяем
 на основе второго закона Кирхгофа для
магнитной цепи.
на основе второго закона Кирхгофа для
магнитной цепи.
Далее аналогично
определяем значения  ,
при условии, что
,
при условии, что  ,
так как учитываем магнитное сопротивление
стали,
,
так как учитываем магнитное сопротивление
стали,  ,
,  ,
,  ,
,  и
и  .
.
С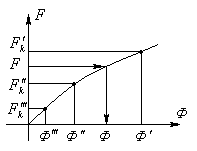 троим
по полученной вспомогательной
характеристике
троим
по полученной вспомогательной
характеристике 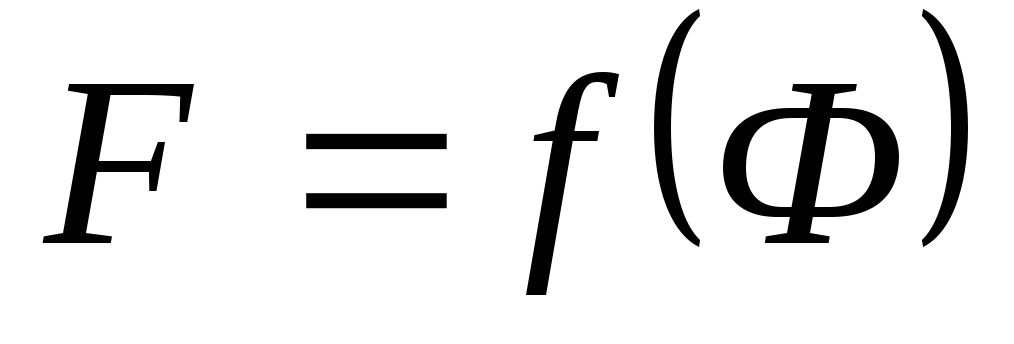 и при заданном значении
и при заданном значении 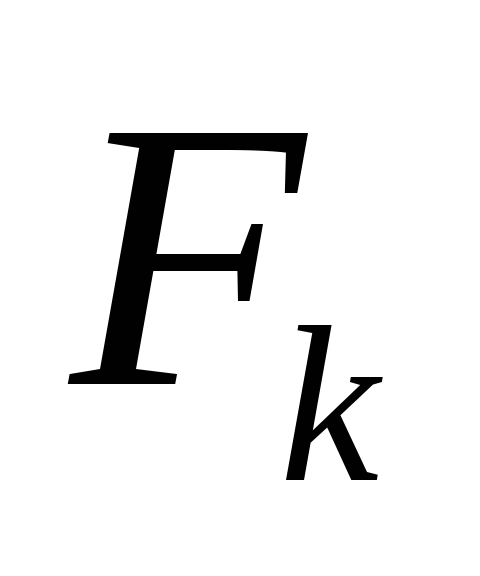 находим
находим  .
.
Графоаналитический метод расчёта.
Предположим, что сечения сердечников одинаковы, тогда:
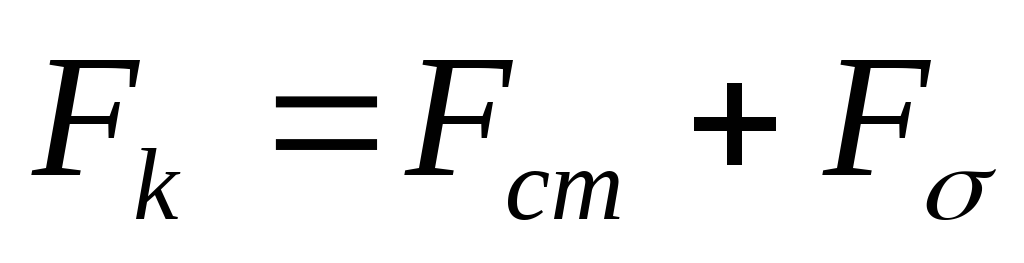 ,
,
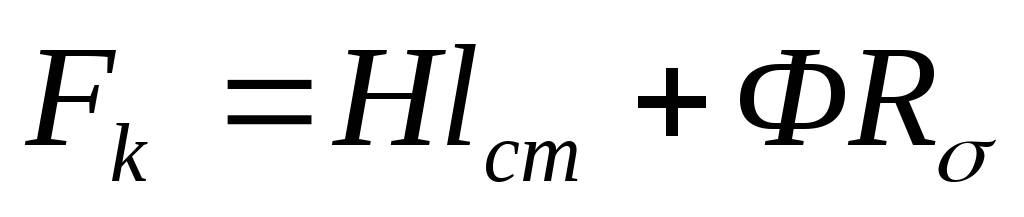 ,
,
где 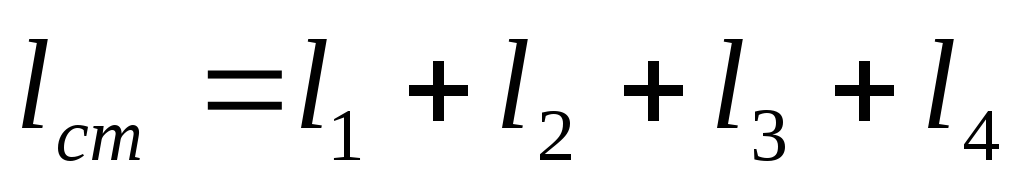 и
и 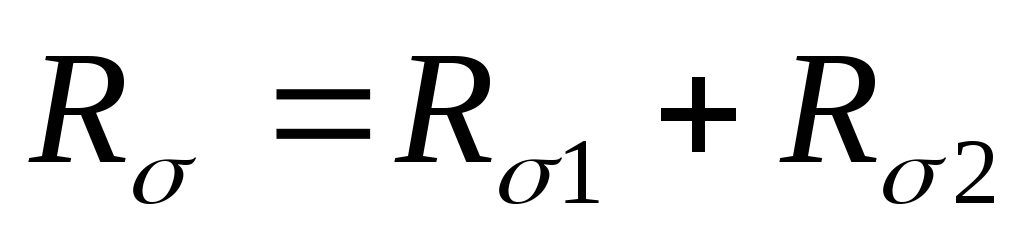 .
.
Представим МДС катушки на единицу длины магнитопровода:
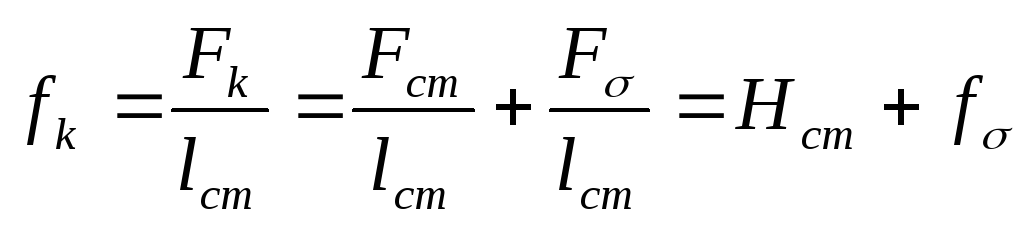 (1).
(1).
Значения 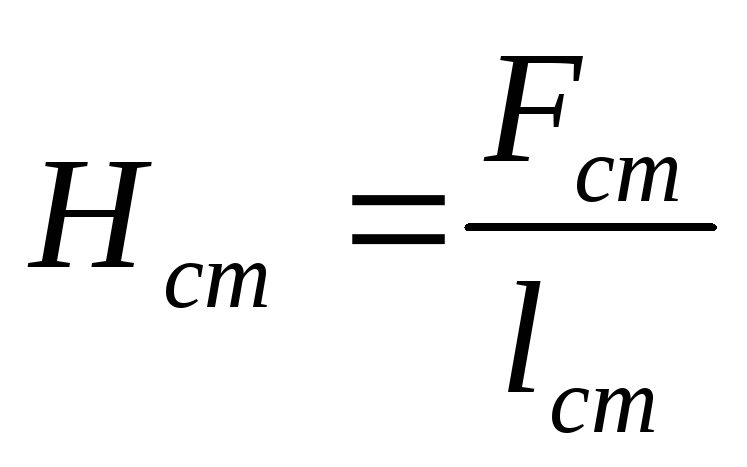 и
и 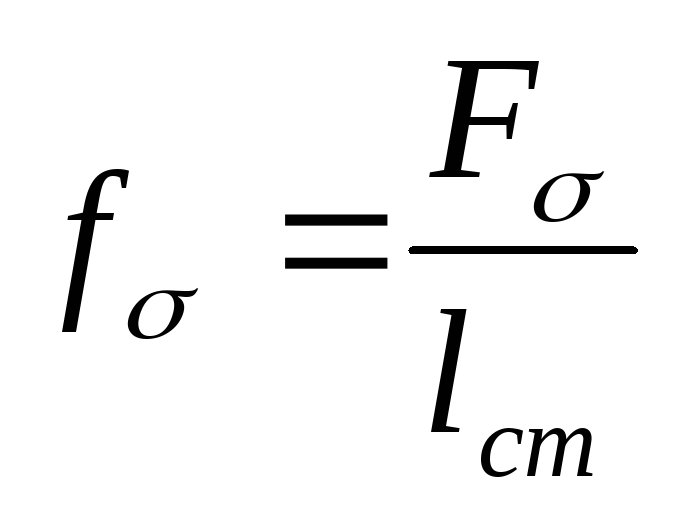 отображены на рисунке:
отображены на рисунке:
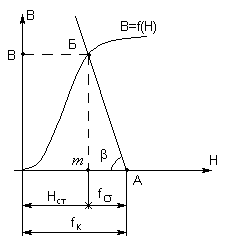 Для
решения поставленной задачи возьмём
Для
решения поставленной задачи возьмём 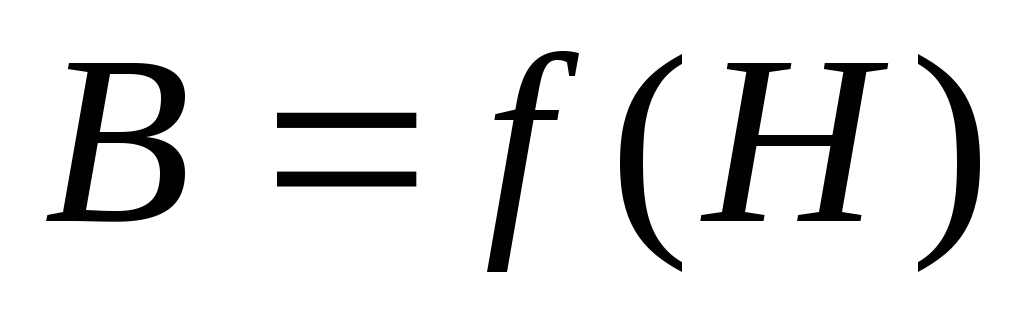 —
(2) и уравнение прямой АБ:
—
(2) и уравнение прямой АБ: 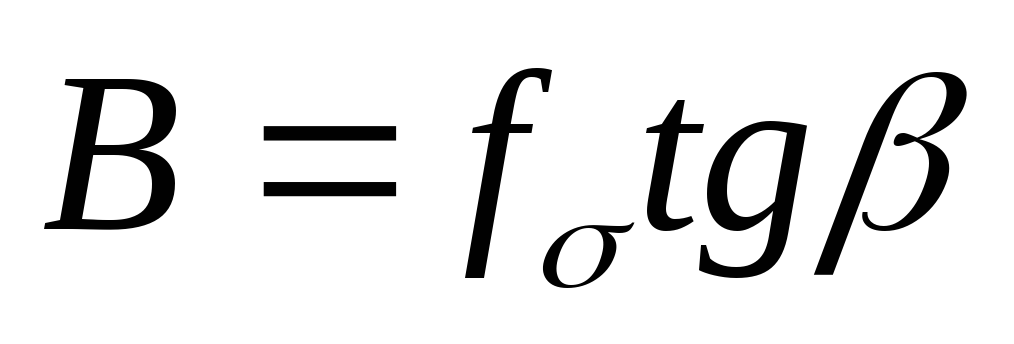 —
(3).
—
(3).
Имеем (1), (2) и (3) с
неизвестными 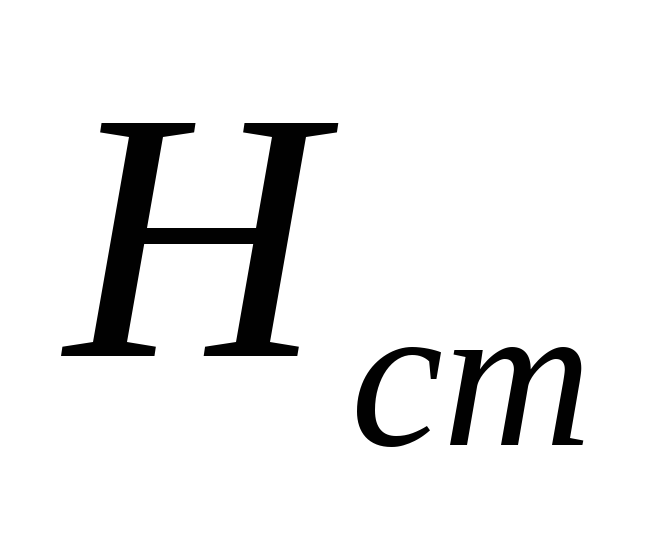 ,
, 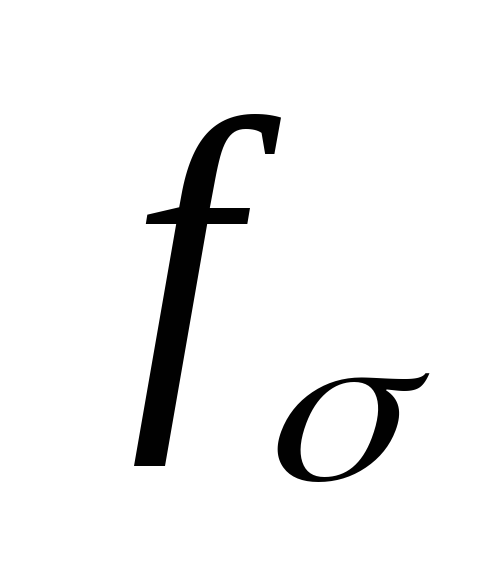 и
и  .
.
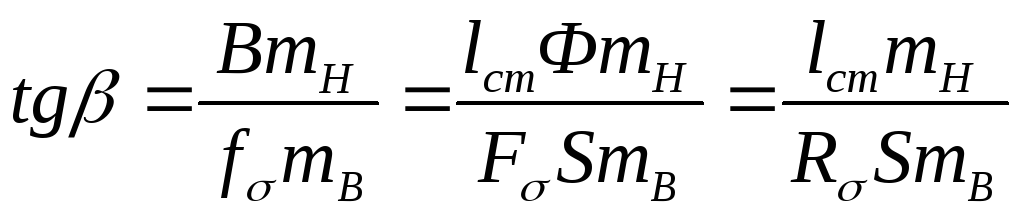 .
.
Порядок расчёта.
По заданной
 и (1) находим
и (1) находим  .
.Из точки О проводим прямую под углом до пересечения с кривой намагничивания в точке .
Опускаем перпендикуляр ОМ и МА и определяем величины МДС, идущие на сталь
 и воздушные зазоры
и воздушные зазоры  .
.По величинам М определяем
 .
.
По заданному потоку
 требуется определить
требуется определить  .
. ,
определяем .
,
определяем .По точке Б определяем
 .
.Под углом из точки Б проводим АБ до пересечения с осью абсцисс, что даёт величину
 и
и  .
.
Разветвлённая магнитная цепь.
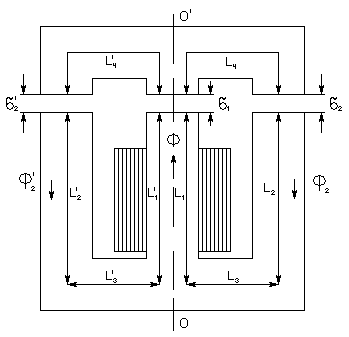
Е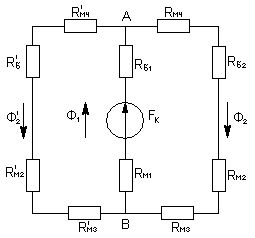 сли
сли 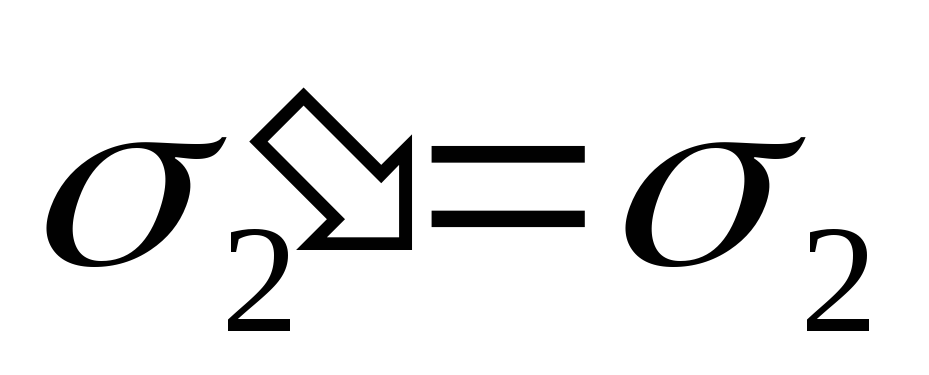 магнитная цепь относительно ООстановится
симметрич-ной, то есть если правую
половину положить на левую, то получим
П-образный магнитопровод с удвоенным
сечением при той же МДС катушки. Таким
образом, такая разветвлённая цепь легко
приводится к неразветвлённой, расчёт
которой был изложен ранее.
магнитная цепь относительно ООстановится
симметрич-ной, то есть если правую
половину положить на левую, то получим
П-образный магнитопровод с удвоенным
сечением при той же МДС катушки. Таким
образом, такая разветвлённая цепь легко
приводится к неразветвлённой, расчёт
которой был изложен ранее.
В случае 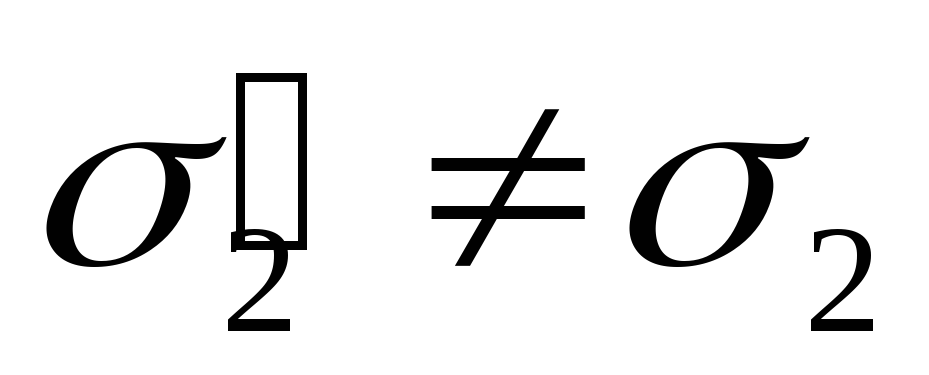 расчёт магнитной цепи значительно
усложняется.
расчёт магнитной цепи значительно
усложняется.
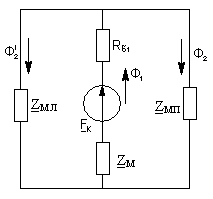
Пусть имеем магнитную цепь, схема замещения которой представлена на рисунке.
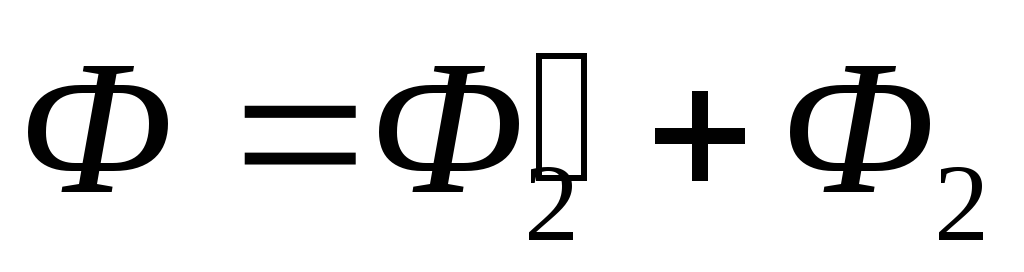 (4),
(4),
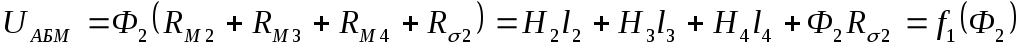 (5),
(5),
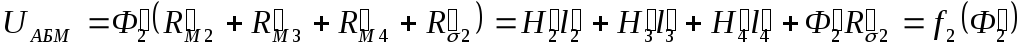 (6),
(6),
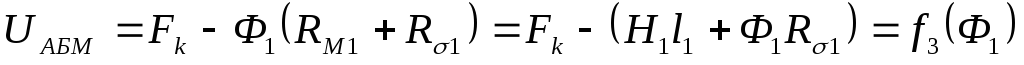 (7).
(7).
Прямая задача.
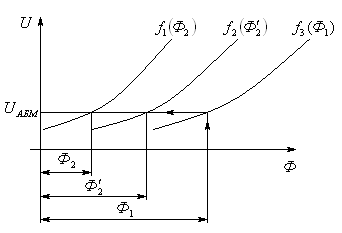
При известном
 задаёмся рядом
задаёмся рядом  и
и  .
.Определяем
 и
и  по заданным сечениям.
по заданным сечениям.По кривой намагничивания определяем
 и
и  .
.По (5) и (6) строим
 и
и  .
.Результирующая
 по (4).
по (4).По заданному
 и
и  находим
находим  .
. и
и  находим по точке пересе-чения.
находим по точке пересе-чения.
Обратная задача.
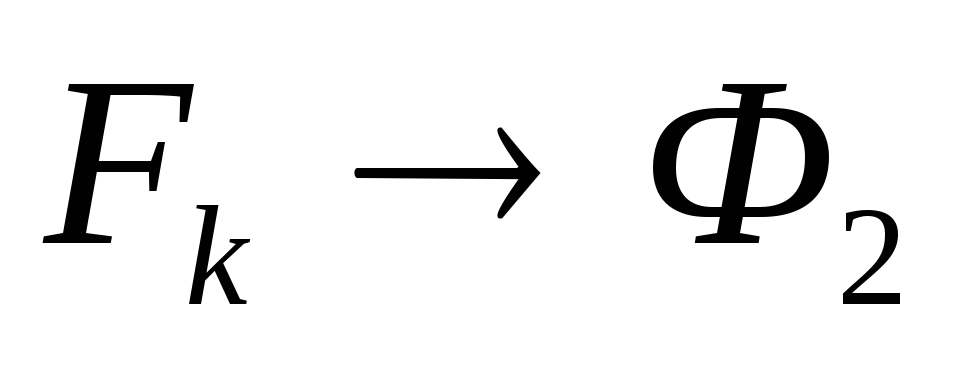 ,
,  ,
, 
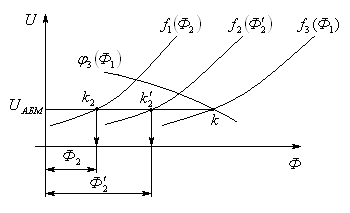
Строим
 и
и  .
.Находим
 .
.Задаваясь различными значениями
 по (7) рассчитываем и строим
по (7) рассчитываем и строим  .
.Точка пересечения
 и
и  даёт истинный
даёт истинный  и
и  в точке
в точке  .
.По пересечениям в точках
 и
и  определяем
определяем  и
и  .
.
Расчёт разветвлённой магнитной цепи с помощью электрической схемы замещения.
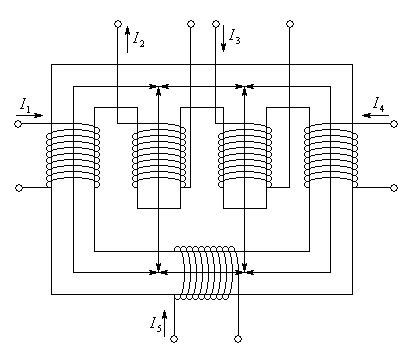
С формируем
для реальной магнитной цепи электрическую
схему замещения.
формируем
для реальной магнитной цепи электрическую
схему замещения.
Основные методы расчёта магнитных цепей.
Первый и второй законы Кирхгофа для магнитной цепи (аналитический метод).
Графическая реализация первого и второго законов Кирхгофа, МЭГ, М2У и т.д.
Использование формальной аналогии между магнитной и электрической цепью.
Однократный расчёт без применения магнитных характеристик.




 и
и 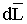 совпадают,
следовательно = 0;
совпадают,
следовательно = 0;
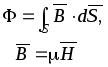
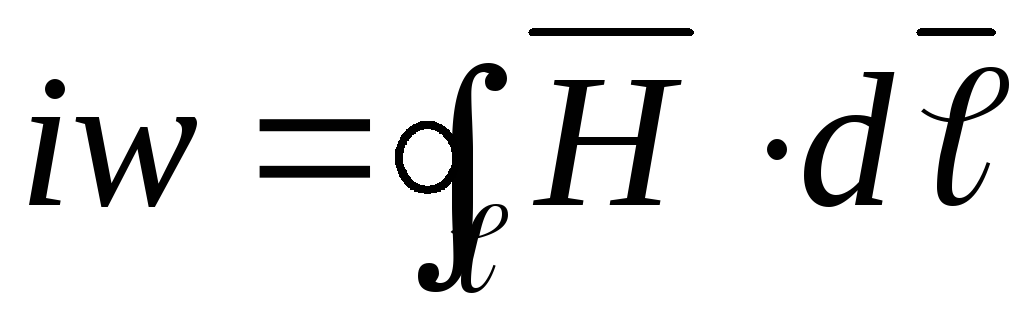
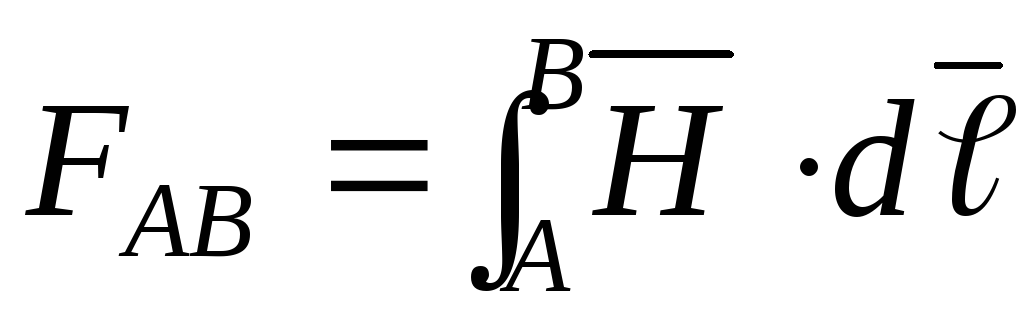
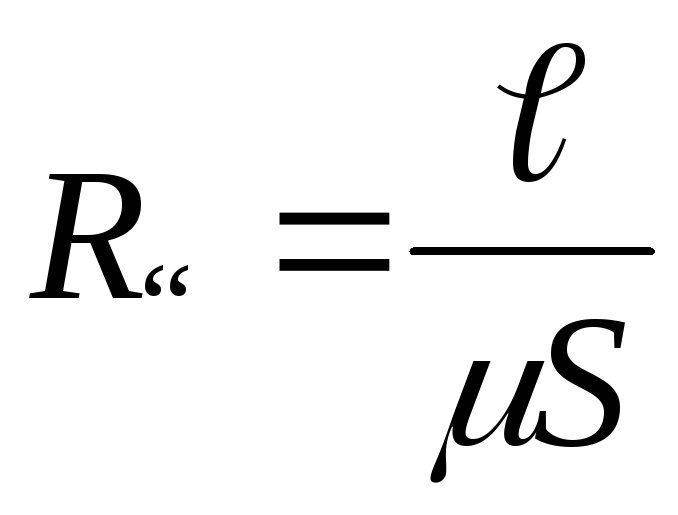
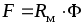
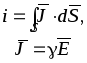
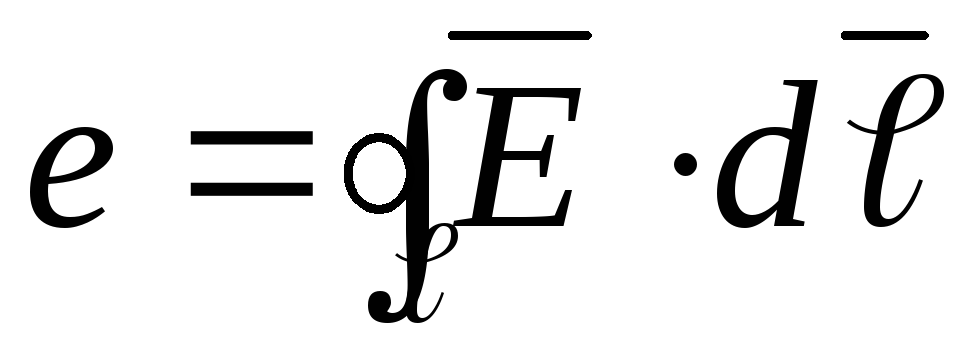
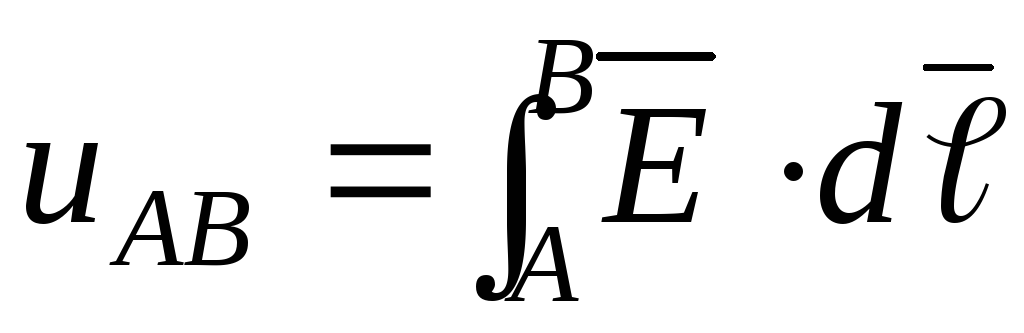
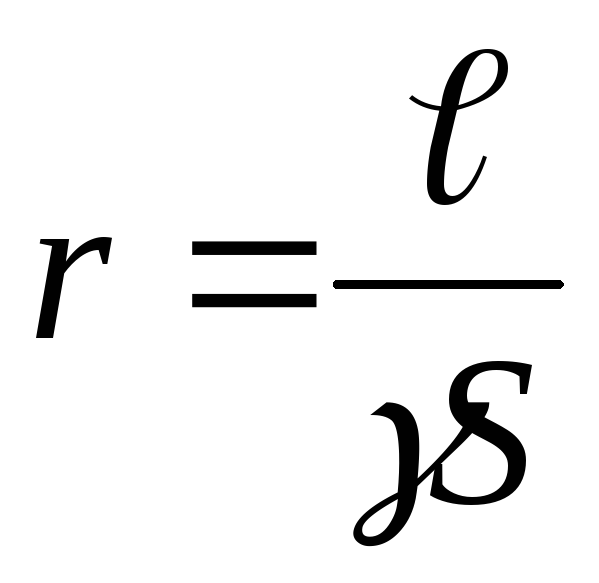
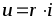
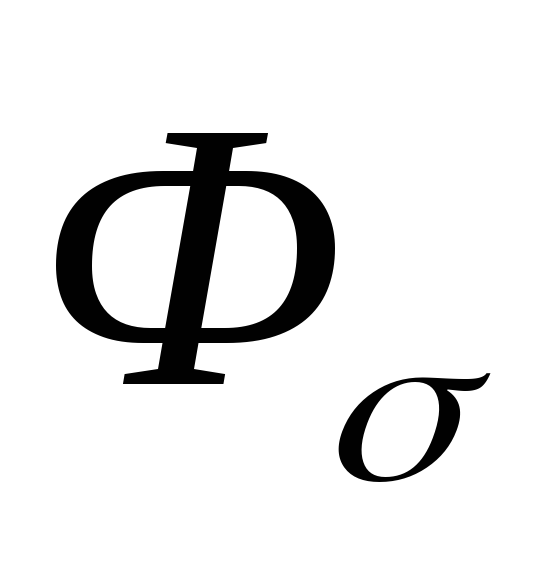 пренебрежимо мал. Расчёт осуществляется
по основному потоку
пренебрежимо мал. Расчёт осуществляется
по основному потоку 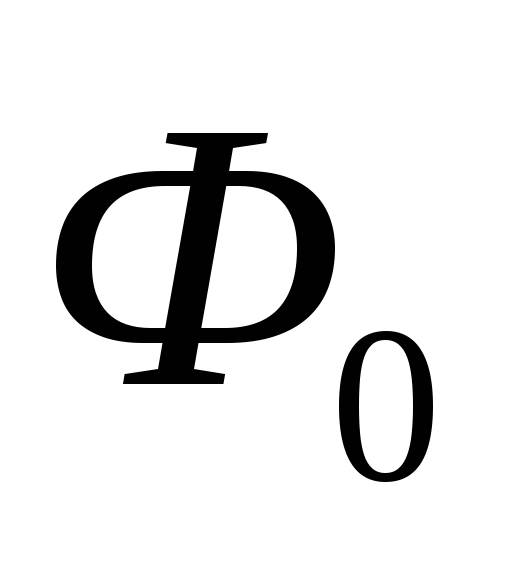 .
. ффектом
выпучивания магнитных силовых линий
в воздушном зазоре пренебрегаем, то
есть площадь поперечного сечения стали
и воздушного промежутка одинакова.
ффектом
выпучивания магнитных силовых линий
в воздушном зазоре пренебрегаем, то
есть площадь поперечного сечения стали
и воздушного промежутка одинакова. без учёта магнитного сопротивления
стали:
без учёта магнитного сопротивления
стали: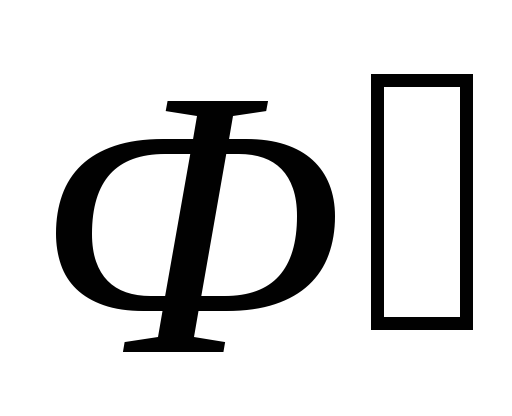 определяем
определяем  на отдельных участках. Пользуясь кривой
намагничивания находим
на отдельных участках. Пользуясь кривой
намагничивания находим  ,
,  ,
, 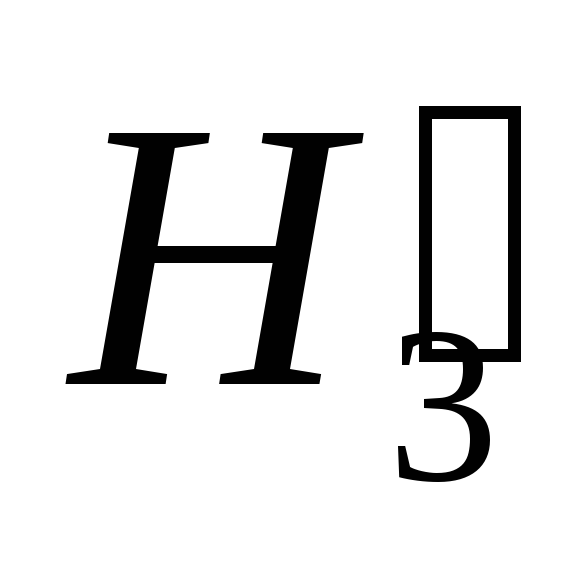 и
и 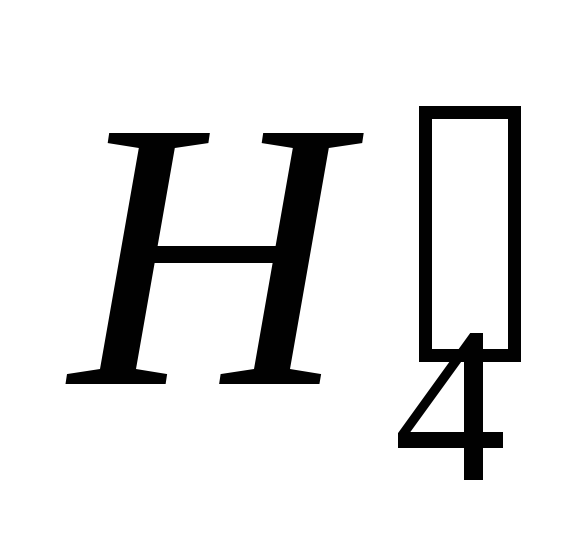 .
.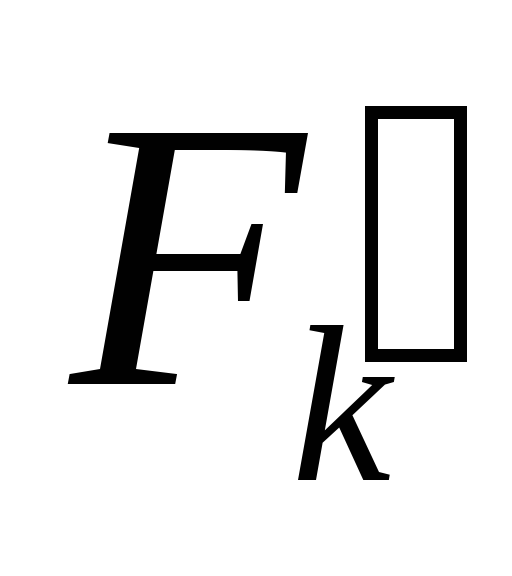 на основе второго закона Кирхгофа для
магнитной цепи.
на основе второго закона Кирхгофа для
магнитной цепи.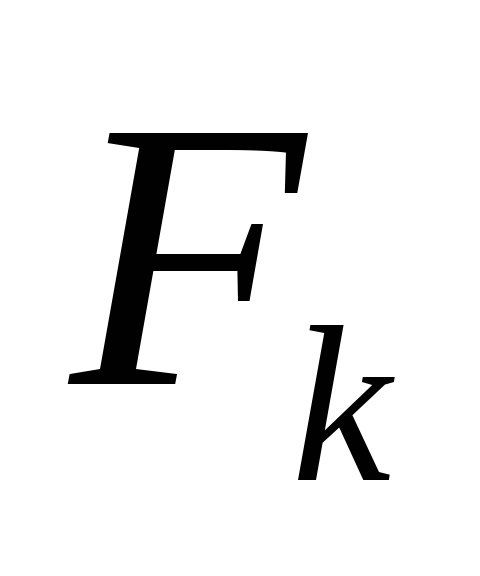 и (1) находим
и (1) находим 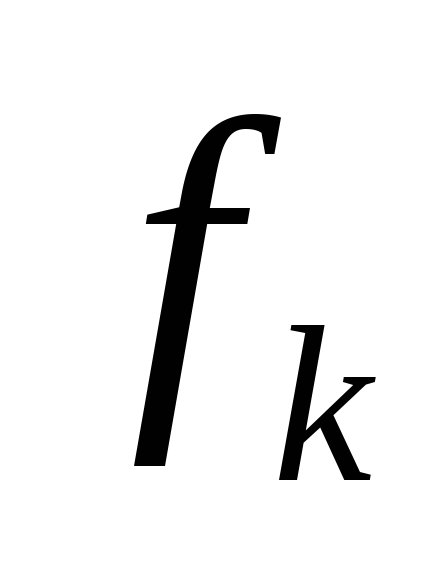 .
.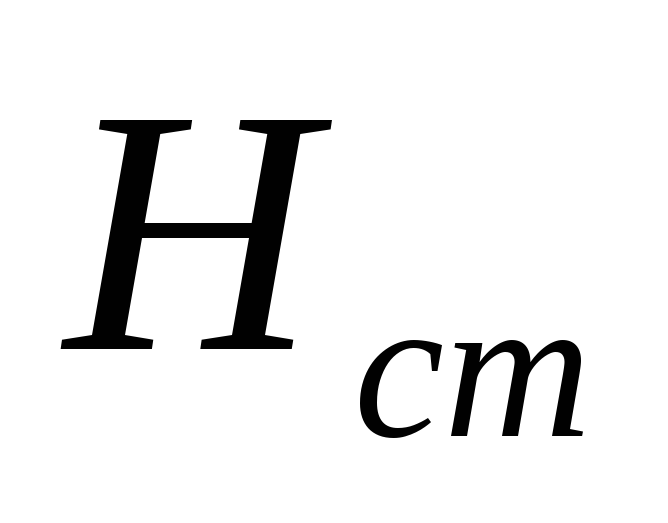 и воздушные зазоры
и воздушные зазоры 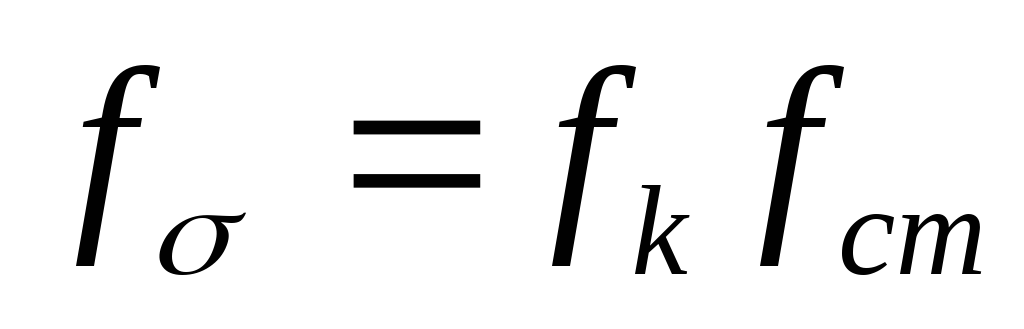 .
. .
. требуется определить
требуется определить 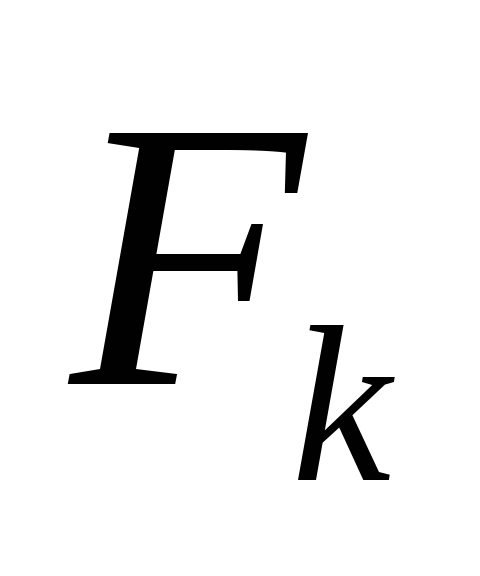 .
.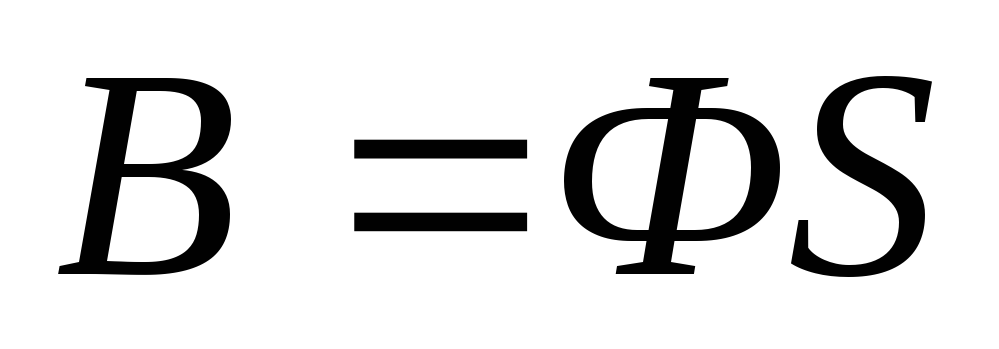 ,
определяем .
,
определяем . .
. и
и 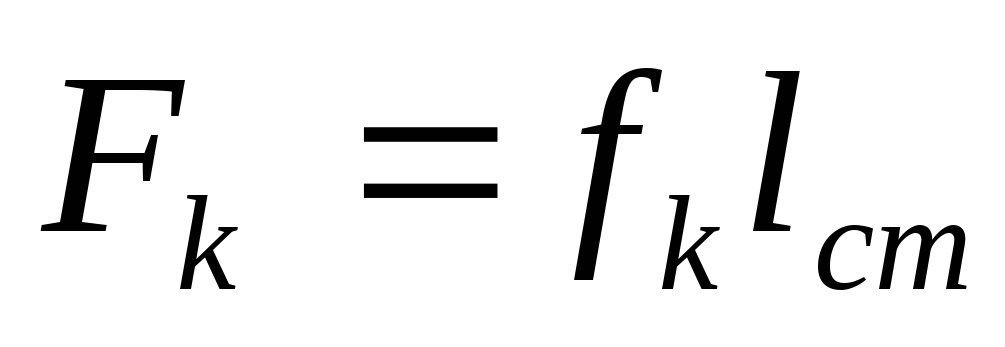 .
. задаёмся рядом
задаёмся рядом 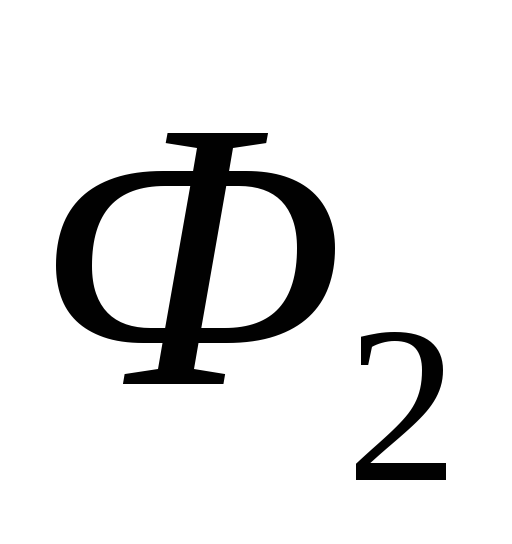 и
и  .
.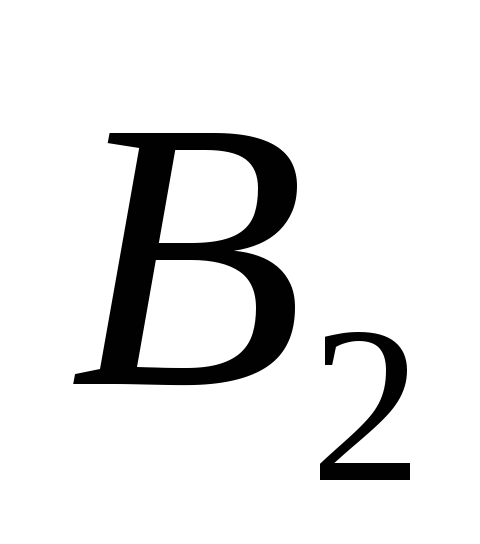 и
и  по заданным сечениям.
по заданным сечениям.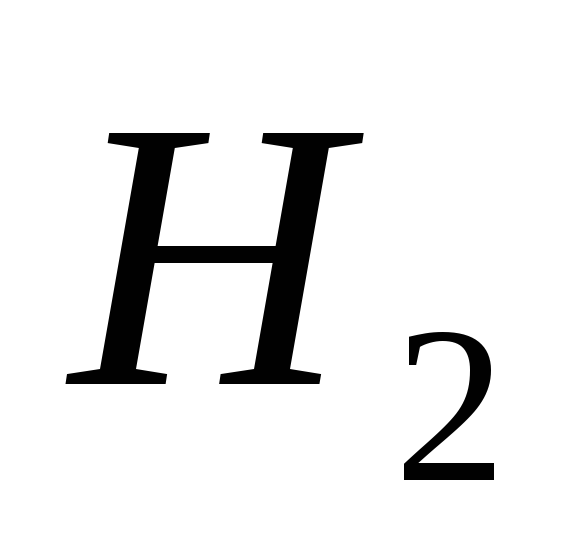 и
и 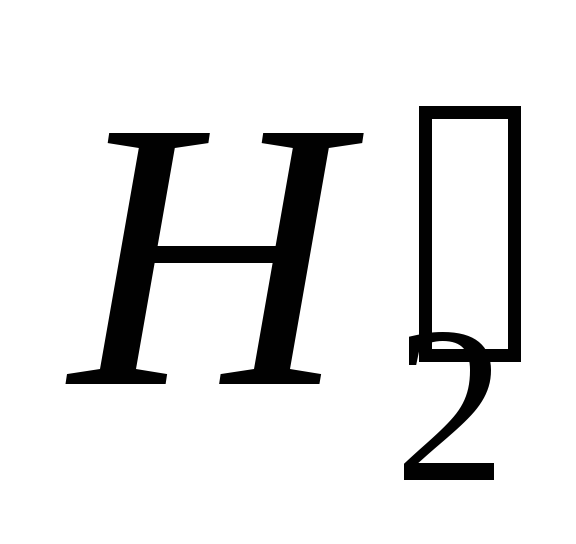 .
.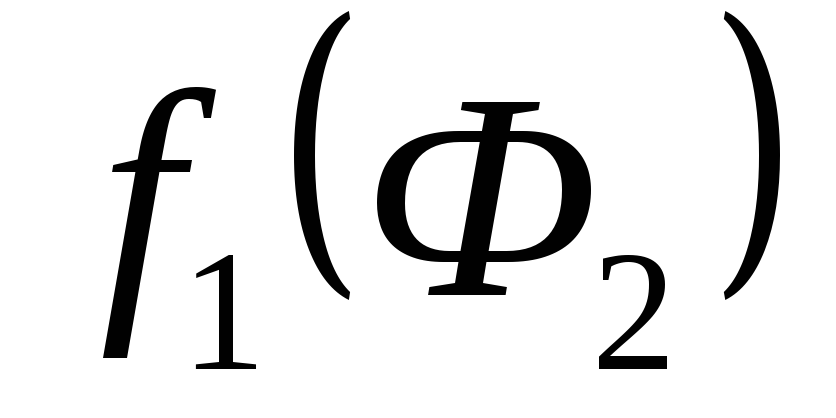 и
и 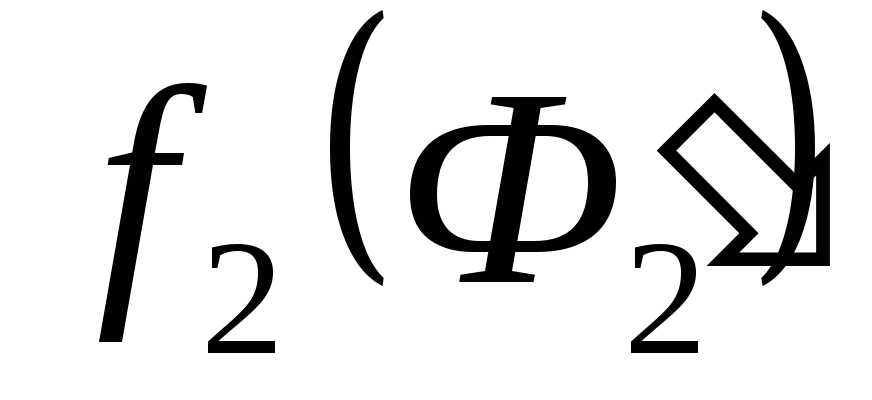 .
.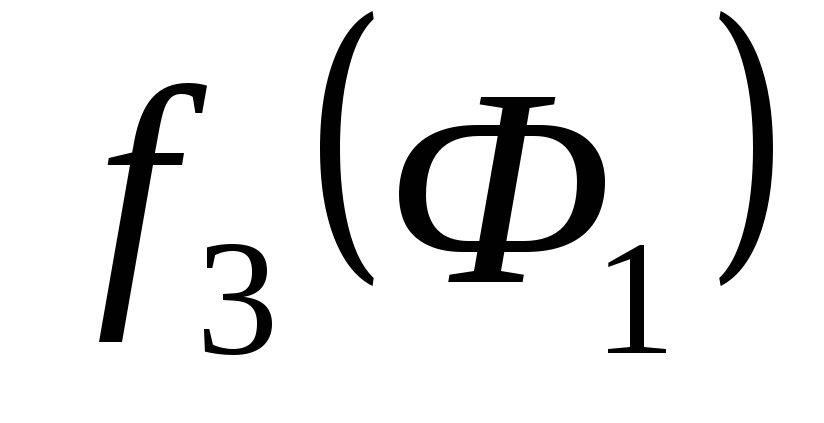 по (4).
по (4). и
и 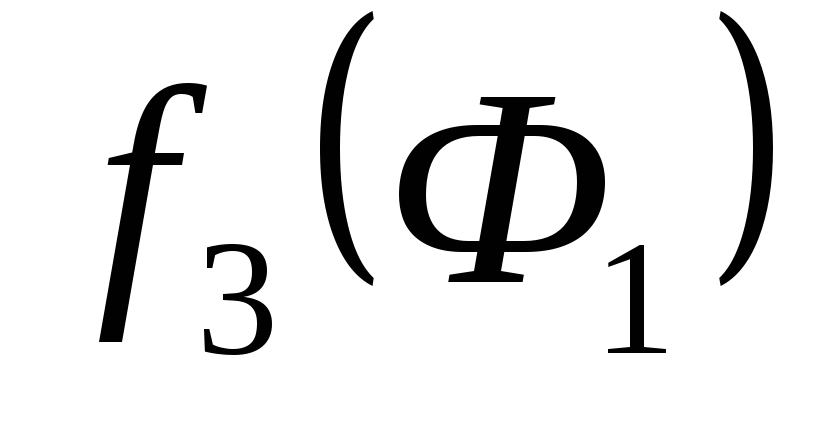 находим
находим 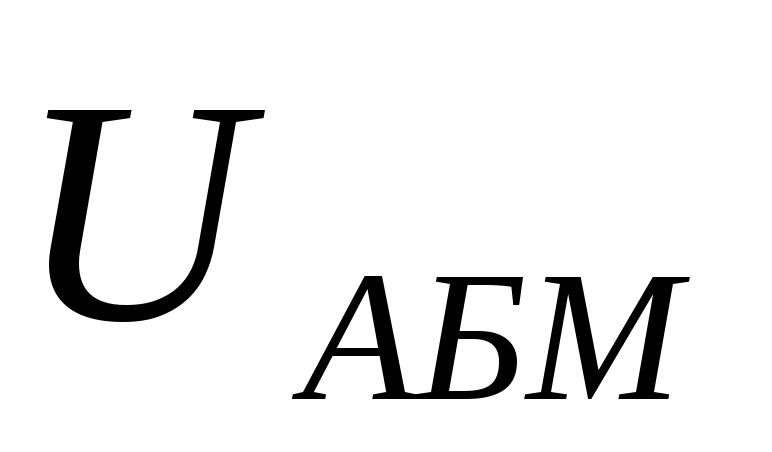 .
.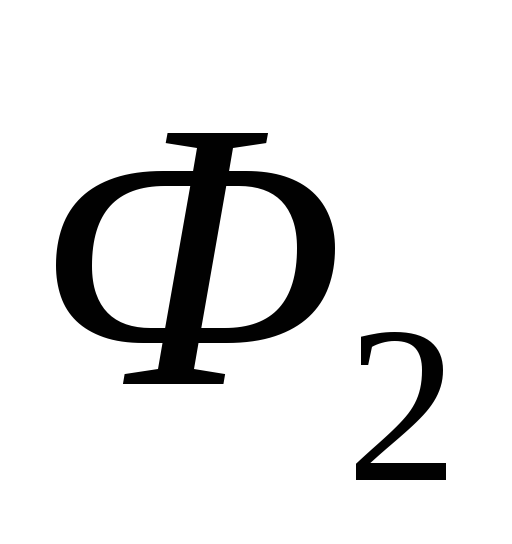 и
и  находим по точке пересе-чения.
находим по точке пересе-чения.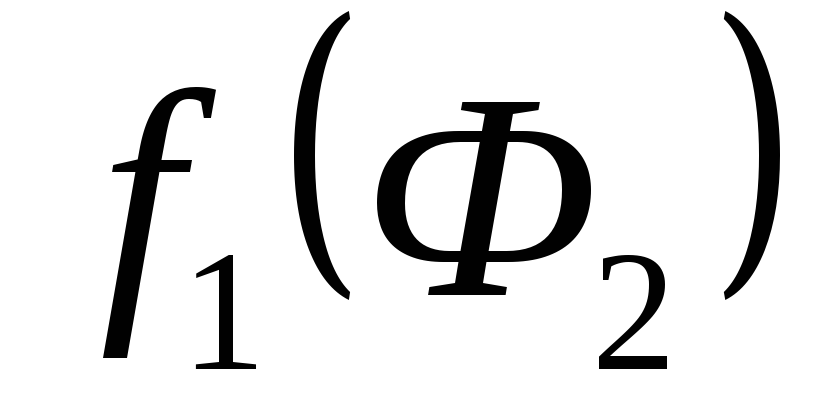 и
и 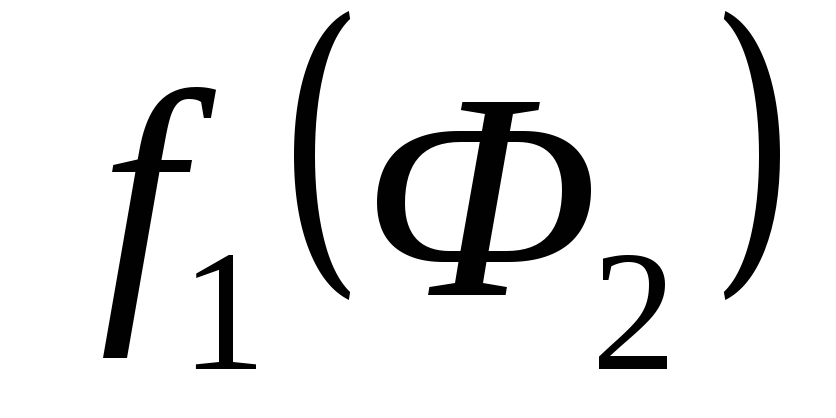 .
.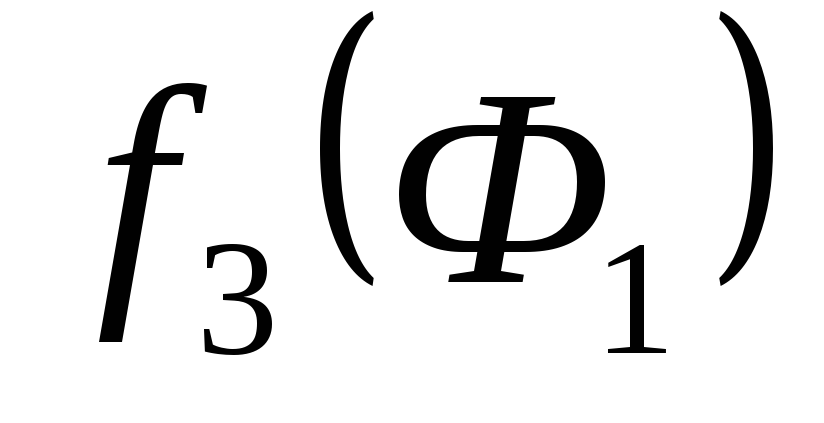 .
. по (7) рассчитываем и строим
по (7) рассчитываем и строим 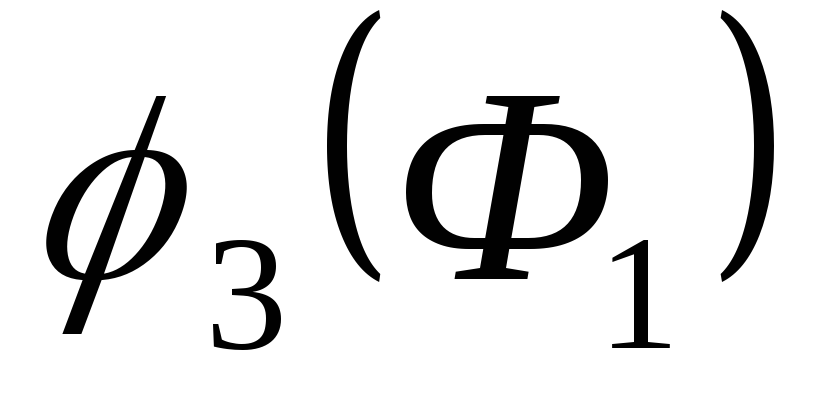 .
.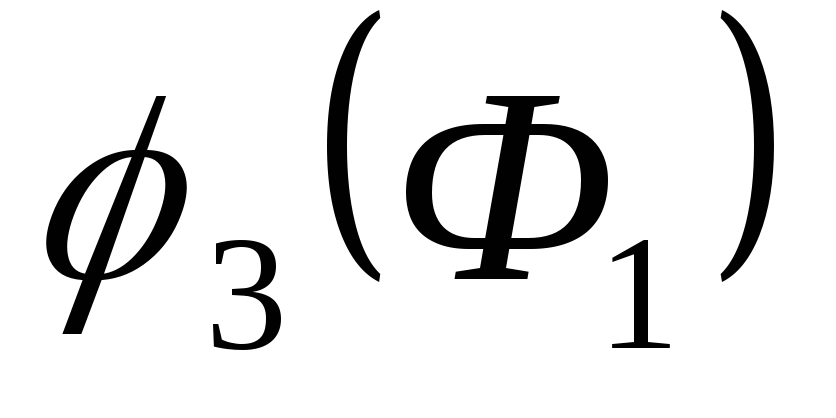 и
и 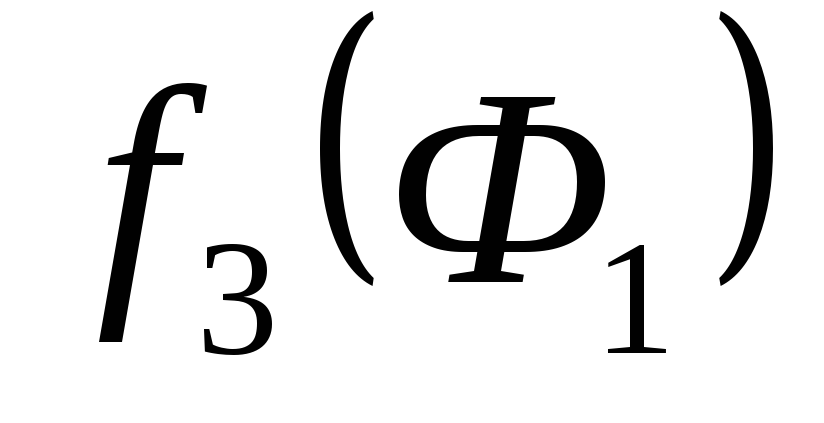 даёт истинный
даёт истинный  и
и 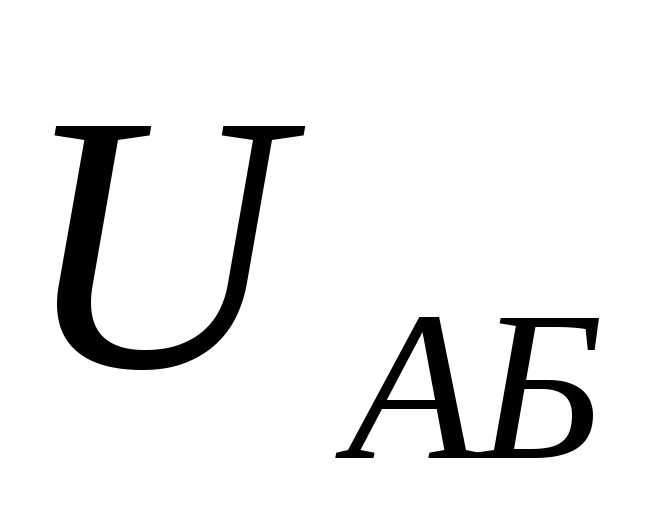 в точке
в точке  .
.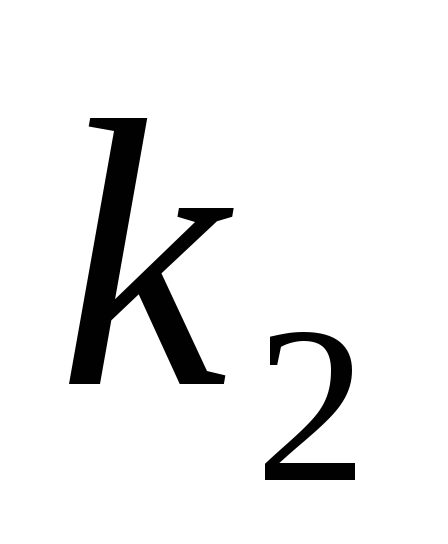 и
и  определяем
определяем 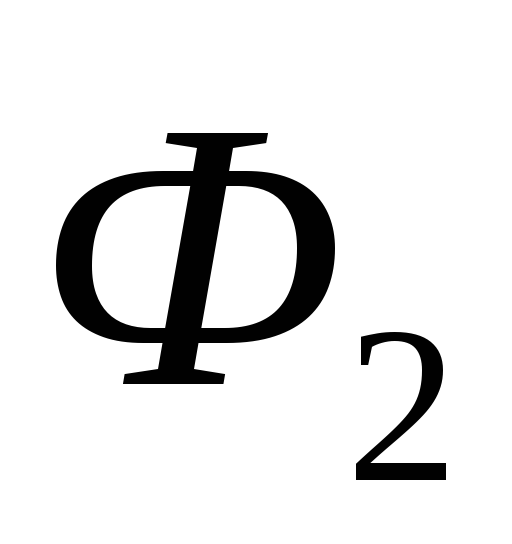 и
и  .
.