Закон полного тока для магнитного поля: физический смысл, формулы

В электрических цепях всегда присутствует магнитное поле, которое оказывает электромагнитное взаимодействие с токами этих цепей. Данный фактор учитывается при расчетах цепей, а закон полного тока для магнитного поля является инструментом для подобных вычислений.

Если поднести магнитную стрелку к проводнику, по которому течёт ток, её положение изменится. Это говорит о наличии вокруг проводника кроме электрического ещё и магнитного поля. В результате многочисленных исследований электромагнитных явлений установлено, что существует взаимное влияние полей, имеющих электрическую и магнитную природу.

Физический смысл закона

Рассмотрим упрощённый вариант влияния магнитной индукции на электрическое поле. Для этого представим себе два параллельных проводника, по которым циркулируют постоянные токи, например, I₁ и I₂. Вблизи этих проводников образуется поле, которое мысленно можно ограничить неким контуром L – воображаемой замкнутой фигурой, плоскость которой пересекает потоки движущихся зарядов.

В пределах плоскости, охватываемой контуром L, формируется магнитное поле, напряжённость которого распределена в соответствии с направлениями токов. При этом циркуляция вектора магнитного поля в плоскости замкнутого контура прямо пропорциональна сумме токов, пронзающих данный контур. Полный электрический ток равен векторной сумме его составляющих:

Направления векторов I₁ и I₂ определяется по правилу буравчика.

Приведённые выше рассуждения можно рассматривать в качестве примера изображающего упрощённую модель частного случая рассматриваемого закона. В действительности же, процессы взаимного влияния магнитных и электрических полей намного сложнее, и они описываются интегральными и дифференциальными уравнениями Максвелла.

Упрощенный подход

Выразить закон в дифференциальном представлении довольно сложно. Потребуется вводить дополнительные компоненты. Необходимо учитывать влияние молекулярных токов. Наличие вихревых токов является причиной образования магнитного вихревого поля в пределах контура.

Вектор электрического смещения сравним с вектором напряжённости присутствующего магнитного поля H. При этом Ориентация вектора смещения зависит от быстроты изменения магнитной индукции.

Для упрощения вычислений на практике часто пользуются формулами закона для магнитного поля полных токов, представленных в виде суммирования предельно малых участков контура, с учётом влияния вихревых полей. При реализации этого метода контур мысленно разбивают на бесконечно малые отрезки. На этих отрезках проводники считаются прямолинейными, а магнитное поле на таких участках контура считают однородным.

На одном дискретном участке вектор напряженности U_m определяется по формуле: U_m= H_L×ΔL, где H_L– циркуляция вектора напряжённости на участке ΔL контура L. Тогда суммарная напряжённость U_L вдоль всего контура вычисляется по формуле:

U_L= Σ H_L× ΔL.

Закон в интегральном представлении

Рассмотрим бесконечно прямой проводник, по которому циркулирует электрический ток, образующий поле, ограниченное контуром в виде окружности. Плоскость, пронизывающая проводник, – это круг, очерчённый линией данной окружности (см. рис. 1).

Рис. 1. Поле бесконечно прямого тока

Воспользуемся методом разбиения контура на мизерные участки dl (элементарные векторы длины контура).  Пусть φ – угол между векторами dl и B. В нашем случае, при суммировании отрезков, вектор индукции B поворачивается так, что он очерчивает круг, то есть угол φ

→ 2π.

Из теоремы Остроградского-Гаусса вытекает формула:

Учитывая, что cos φ = 1,

следовательно:

Данная формула – постулат, подтверждённый экспериментально. Согласно этому постулату, циркуляция вектора B по окружности, то есть по замкнутому контуру, равна μ

0I, где μ₀ = 1/c² ε₀ – магнитная постоянная.

Ориентация вектора dB определяется путём применения правила буравчика. Это направление всегда перпендикулярно вектору плотности. Если проводников будет несколько (например, N), тогда

Каждый ток, с учётом знака, необходимо учитывать такое количество раз, которое соответствует числу его охватов контуром.

Ток берётся со знаком «+», если он по направлению обхода образует правовинтовую систему. При этом, отрицательным считается ток противоположного направления.

Заметим, что формула справедлива только для вакуума. В обычных условиях необходимо учитывать проницаемость среды.

Если ток распределён в пространстве (произвольный ток), тогда

где S – натянутая на контур поверхность, j – объёмная плотность тока. С учётом последнего выражения, формулу полного тока в вакууме можно записать:

Рис. 2. Иллюстрация закона для вакуума

Отсюда вытекает:

1. Закон справедлив не только для бесконечно прямолинейного проводника, но и для контуров, произвольной конфигурации.
2. Циркуляция вектора магнитной индукции B сориентированного вдоль магнитных линий, всегда отлична от нуля.
3. Ненулевая циркуляция свидетельствует о том, что магнитное поле прямолинейного, бесконечно длинного проводника не потенциально. Такое поле называют вихревым, либо соленоидным.

Влияние среды

На результат взаимодействия магнитных потоков и постоянных токов влияет среда. Вещества обладают магнитной проницаемостью в потоке вектора индукции, что вносит коррективы на взаимодействие магнитной среды с токами проводимости. В однородной изотопной среде, где значение вектора электромагнитной индукции одинаково во всех точках, векторы B и H связаны между собой следующим соотношением:

где H — напряжённость магнитного поля, символом μ обозначена магнитная проницаемость.

Носители электрических зарядов создают собственные микротоки. Циркуляция вектора, характеризующего электростатическое поле, всегда нулевая. Поэтому электростатические поля, в отличие от магнитных, являются потенциальными.

Вектор B отображает результирующее значение полей макро- и микротоков. Линии электростатической индукции всегда остаются замкнутыми, в том числе и на положительных зарядах.

Рис. 3. Закон полного тока в веществе

Для полей, которые действуют в среде, состоящей из разных веществ, необходимо учитывать микротоки, характерные именно для конкретных структур, образующих данную среду.

Утверждение, изложенное выше, верно для полей соленоидов или любой другой структуры, обладающей свойствами конечной магнитной проницаемости.

Торойд

В электротехнике часто приходится иметь дело с катушками разных видов и размеров. Катушка, образованная витками намотанными на сердечник тороидальной формы (в виде бублика), называется тороидом. Важными характеристиками сердечника тора являются его радиусы — внутренний (R

1) и внешний (R₂).

Поле внутри соленоида на расстоянии r от центра равно:

Выводы

На основании изложенного, приходим к заключению:

1. Закон полного тока устанавливает зависимость между напряжённостью магнитного поля и перемещением в этом поле электрических зарядов.
2. Действие закона распространяется на все среды, при допустимых плотностях тока.
3. Закон также выполняется в полях постоянных магнитов.

При вычислениях не имеет значения, какую формулу мы используем – суть закона остаётся неизменной: он выражает взаимодействия, которые происходят между токами и создаваемыми ими магнитными полями, пронизывающими замкнутый контур.

Выводы закона учитываются при конструировании электромагнитных устройств. Наличие завихрений в электромагнитных полях приводит к снижению КПД. Кроме того, вихревые поля негативно влияют на работоспособность электронных элементов, расположенных в зоне их действий.

Конструкторы электротехнических приборов стремятся свести к минимуму таких влияний. Например, вместо обычных соленоидов применяют тороидальные катушки, за пределами которых отсутствуют электромагнитные поля.

III. Закон полного тока для магнитного поля в веществе

Циркуляция вектора напряженности магнитного поля по любому замкнутому контуру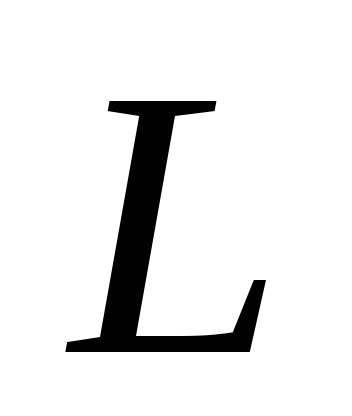равна алгебраической сумме макротоков, охватываемых этим контуром:

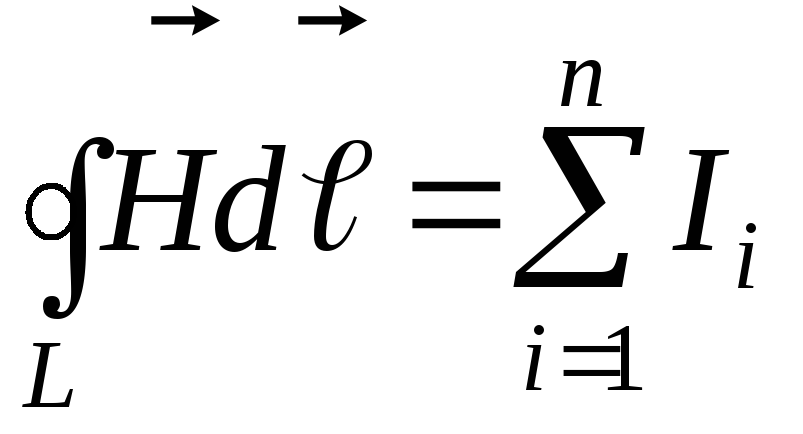. (19)

Это важнейший закон электромагнетизма. Макротоками называются токи, текущие по проводам, в отличие от микротоков, циркулирующих в атомах и молекулах вещества (движение электронов в атомах).

На рисунке 14 показан произвольный замкнутый контур и направление его обхода указанно стрелкой. Внутри контура находятся т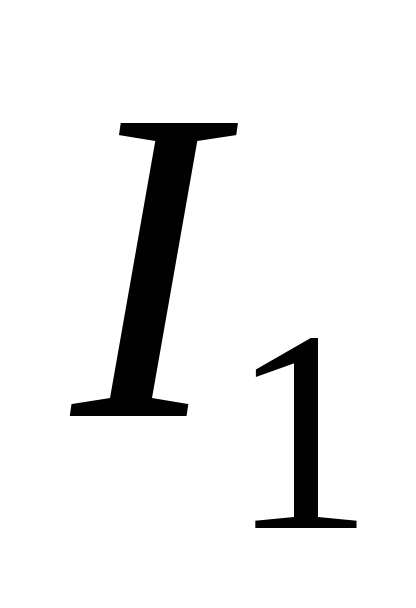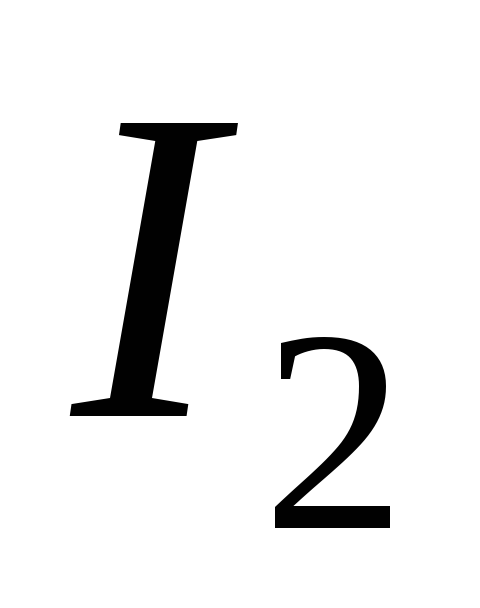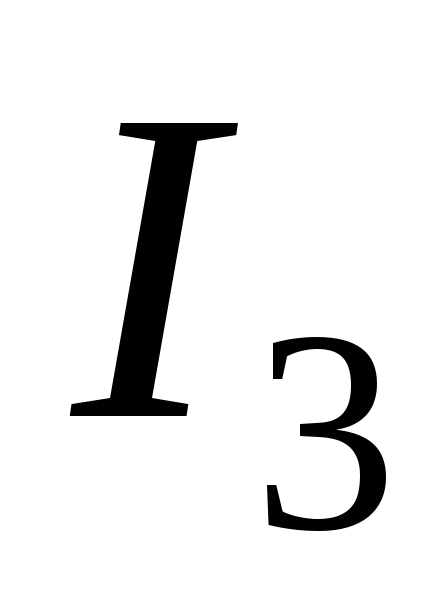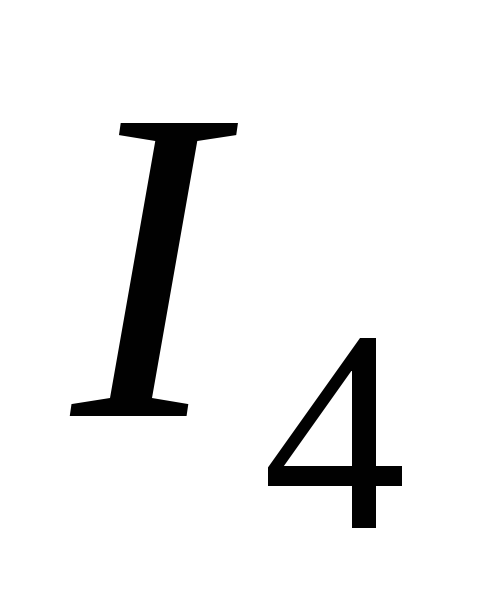оки,,,, токи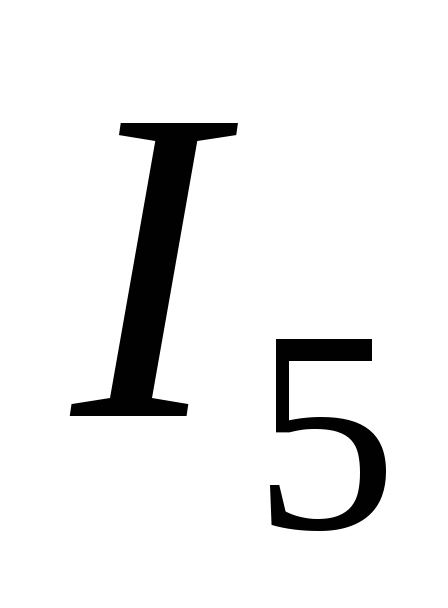,— вне контура. Для случая, изображённого на рис. 14 закон полного тока запишется так:

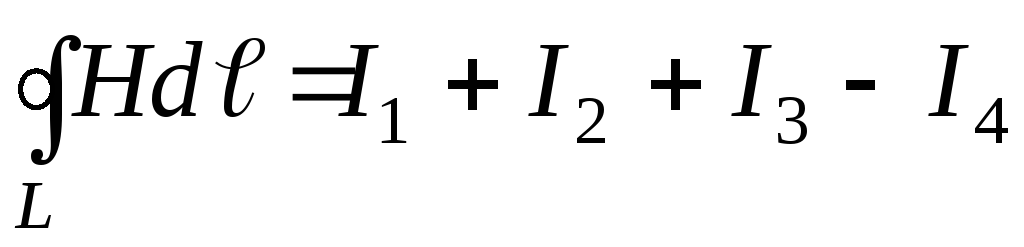. (20)

Те токи, которые связаны правилом правого винта по направлению обхода контура, считаются положительными, а противоположного направления – отрицательными. Суммируются только те токи, которые заключены внутри контура, а те, что вне контура 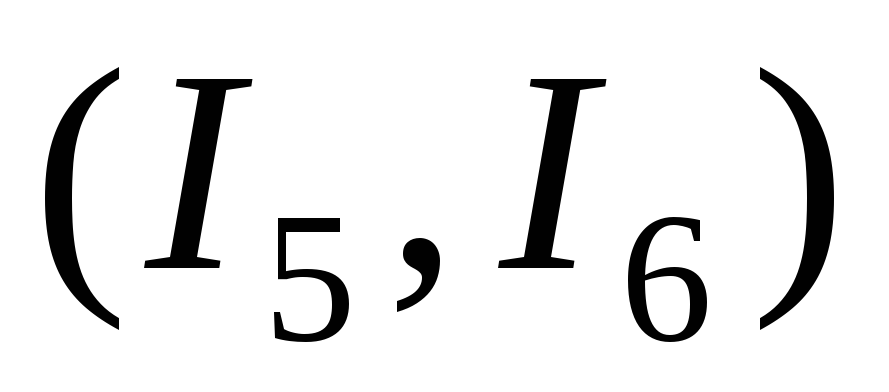, не учитываются, поэтому в правой части выражения (20) их нет.

Закон полного тока (19) неравенство нулю циркуляции вектора напряжённости по замкнутому контуру служит доказательством вихревого характера магнитного поля.

В данной лабораторной работе косвенным методом проверяется справедливость закона полного тока для магнитного поля в веществе.

Идея проверки закона заключается в следующем. Сначала по заданному значению индукции магнитного поля в зазоре электромагнита рассчитываются токи в обмотке электромагнита с помощью закона полного тока. Затем производится соответствующие измерения и определяется значение индукции экспериментально. Если совпадают результаты лабораторной работы, полученные экспериментальным путём с заданными (теоретическими), то можно говорить о справедливости закона полного тока для магнитного поля в веществе.

IV. Описание установки и методика измерения индукции магнитного поля электромагнита

Э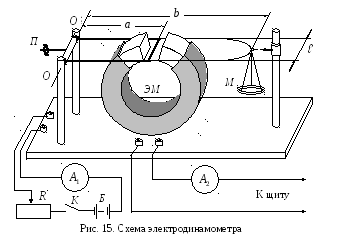кспериментальная установка представлена на рис. 15. Она состоит из электромагнита ЭМ, выполненного в виде тороида с малым зазором. Обмотка электромагнита содержит = 3100 витков толстой медной проволоки. Сердечник стальной. В зазор электромагнита помещен проводник длиной , укрепленный так, что он может вращаться вокруг оси 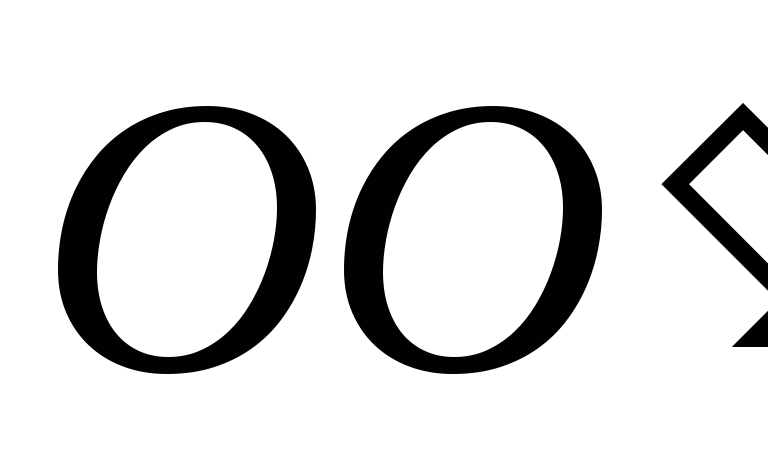. Ту же ось вращения имеет и чашка 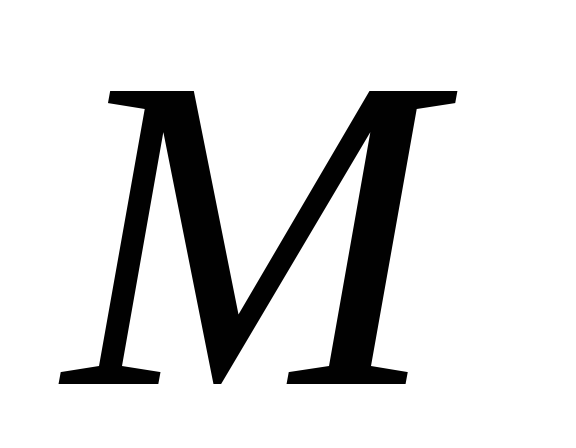, предназначенная для грузов. На противоположном конце рычага расположен противовес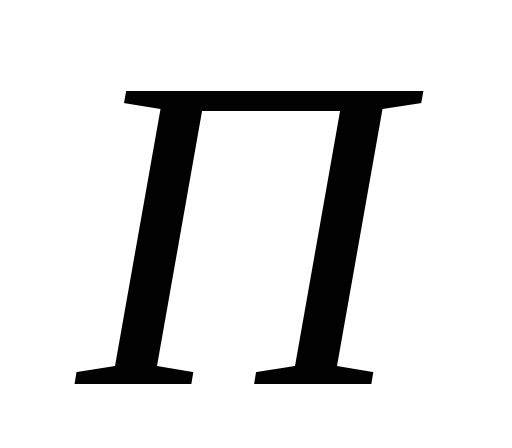для приведения системы в равновесие перед выполнением эксперимента.

Найдем силу тока 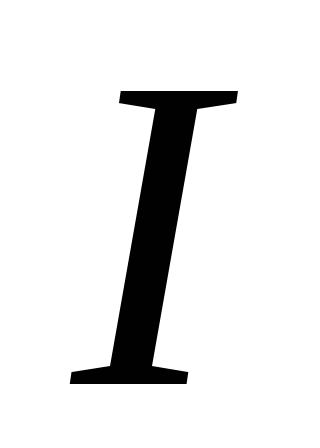, который нужно пропустить через обмоткуЭМ для того, чтобы получить в зазоре магнитное поле с индукцией .

При протекании тока в обмотке сердечника в нём возникает магнитное поле, картина которого показана на рис. 16. Так как силовые линии этого поля непрерывны, то значения магнитного потока внутри сердечника и в зазореодинаковы. Вследствие малости зазора по отношению к диаметру сердечника ЭМ линии идут в зазоре практически параллельно, т.е. плотность линий остается такой же, как и в сердечнике, поэтому величина в сердечнике и зазоре одинакова .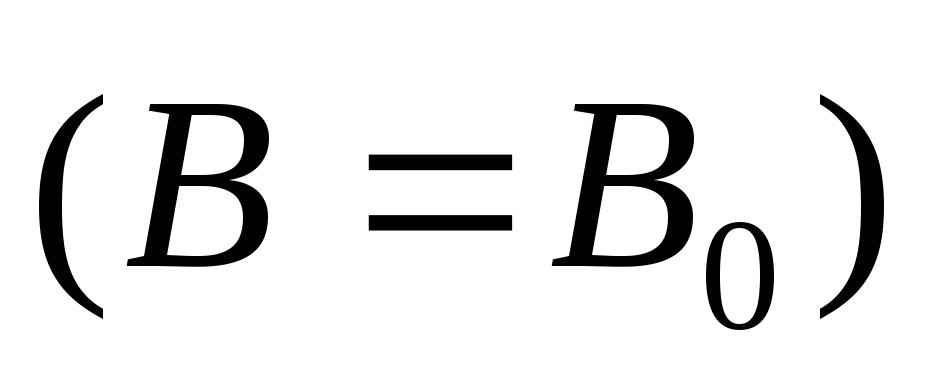

В качестве контура 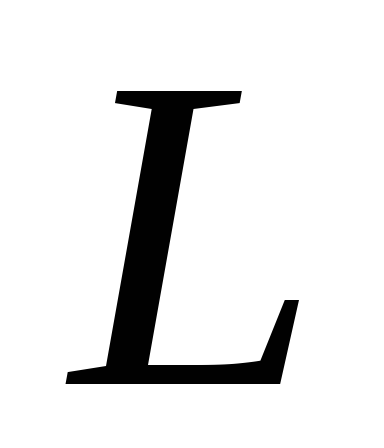возьмем осевую линию тороида и применим к нему закон полного тока. Тогда

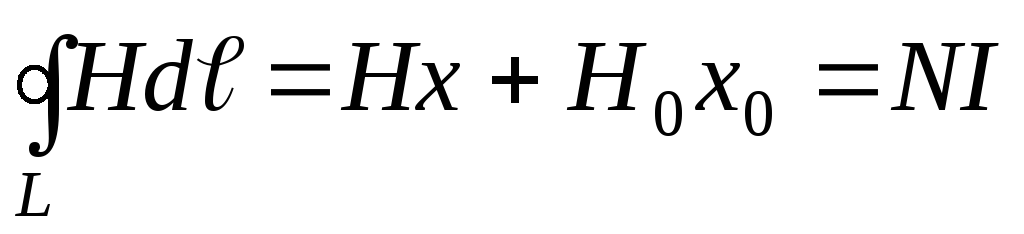, (21)

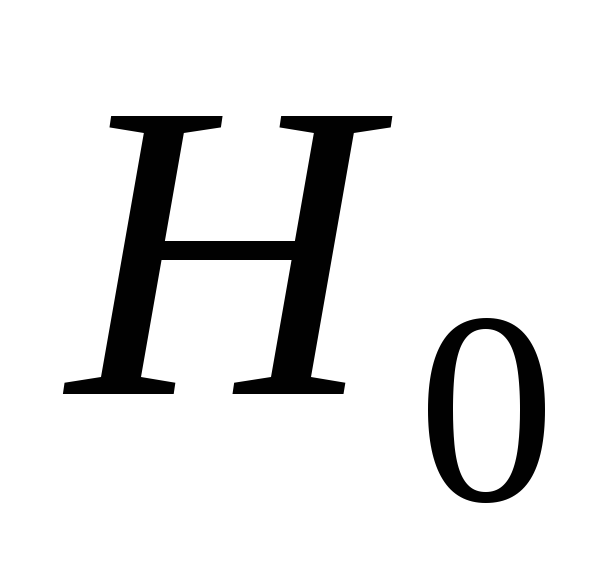здесь — напряжённость поля внутри сердечника,— напряжённость поля в зазоре,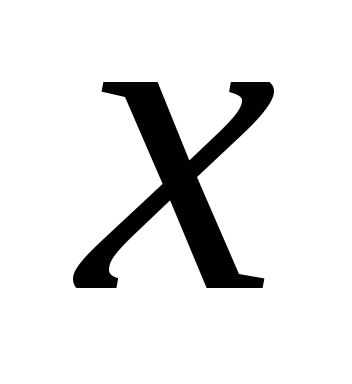— длина осевой линии сердечника,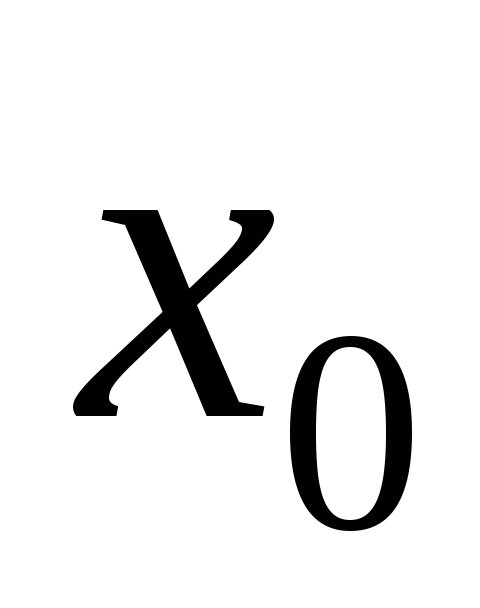— ширина зазора.

Значение 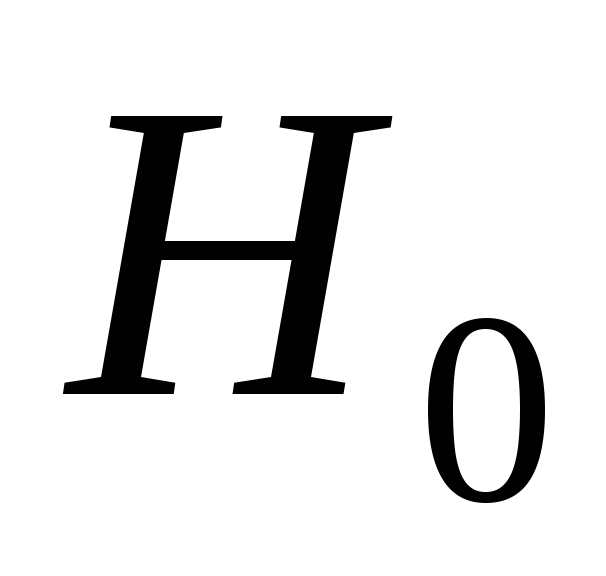можно определить, воспользовавшись соотношением (16) в котором для воздуха. Тогда

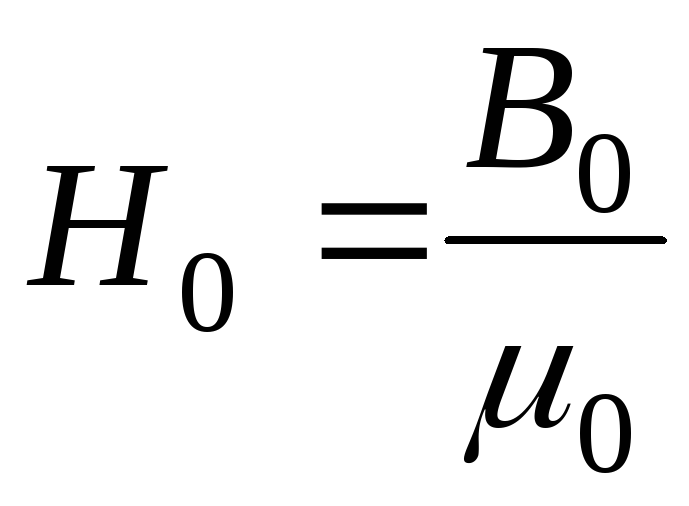. (22)

Из формулы (21) следует

.

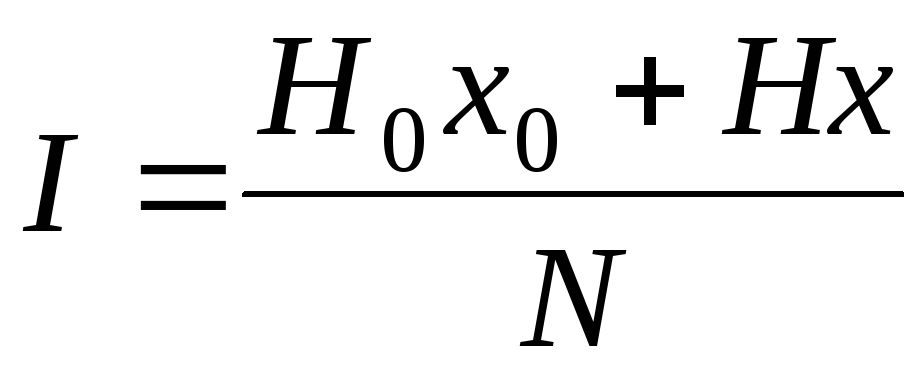Или с учетом выражения (22):

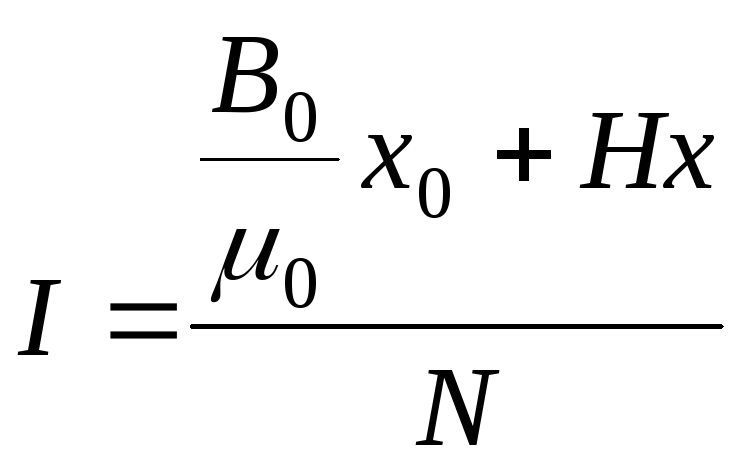. (23)

Для ферромагнетиков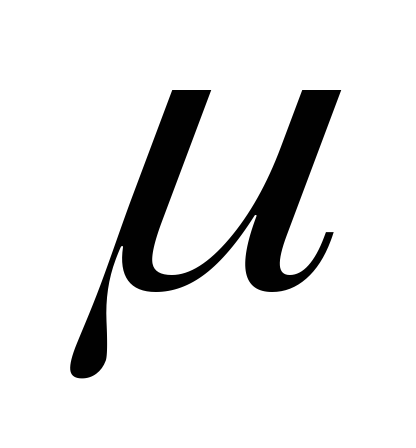является сложной функцией напряжённости внешнего поля. Поэтому зависимость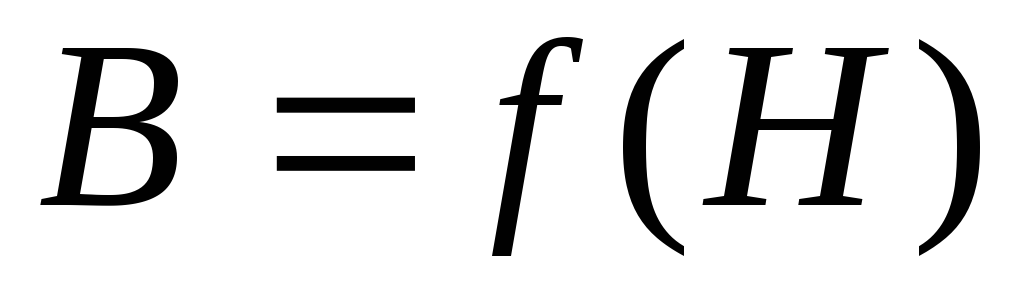 тоже сложна и обычно определяется экспериментально для каждого типа магнитного материала. Для того вещества, из которого изготовлен сердечник нашего ЭМ, кривая зависимости 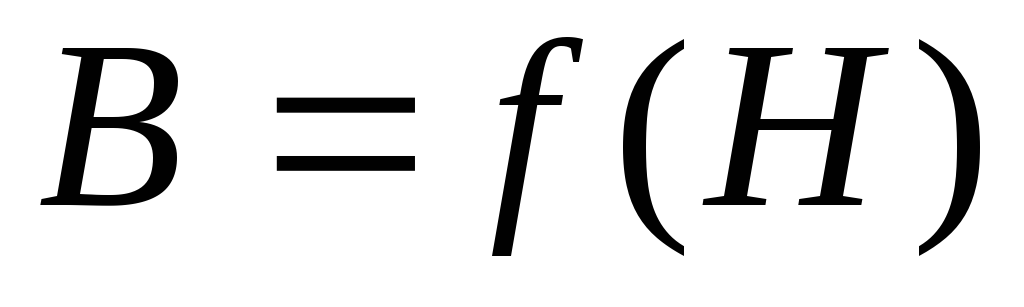приведена на рис. 17.

Пользуясь этой кривой по известному значению можно найти соответствующее ему значение напряжённости , и по формуле (23) рассчитать силу тока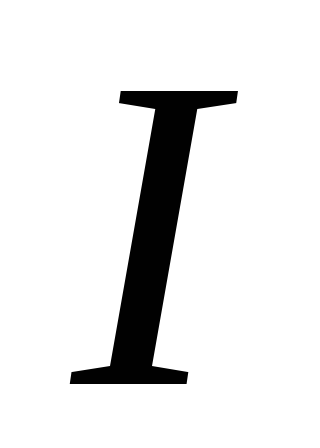в обмотке электромагнита, который обеспечивает в зазоре индукцию.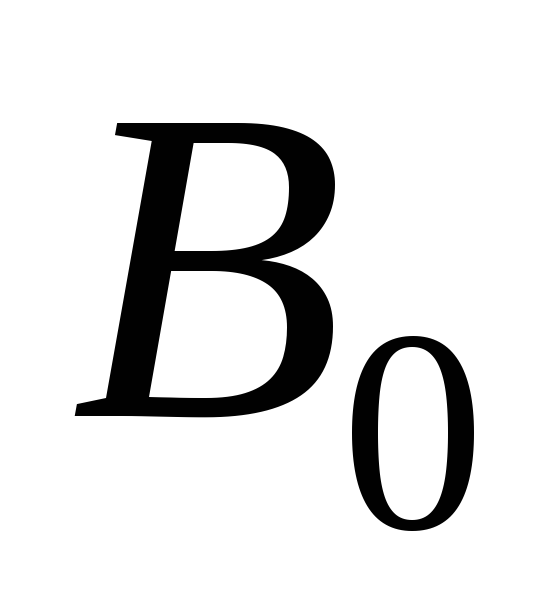

По закону Ампера (10) на проводник с током в магнитном поле действует сила, равная

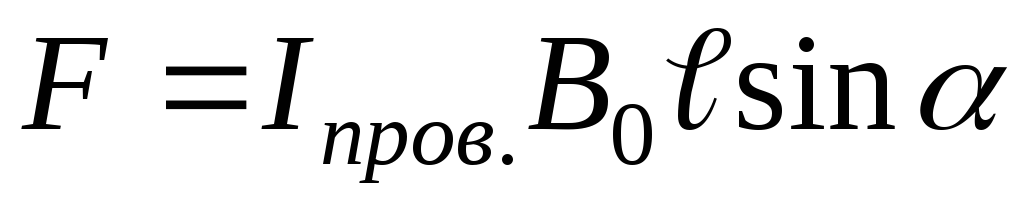, (24)

здесь — сила тока в проводнике, 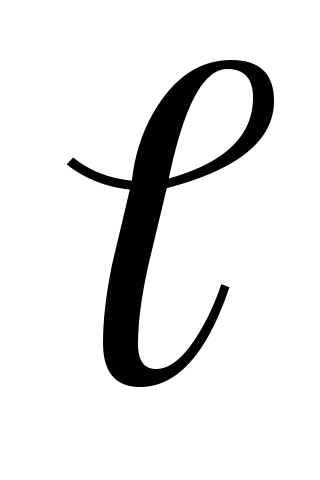— длина проводника,— угол между направлением тока и вектором.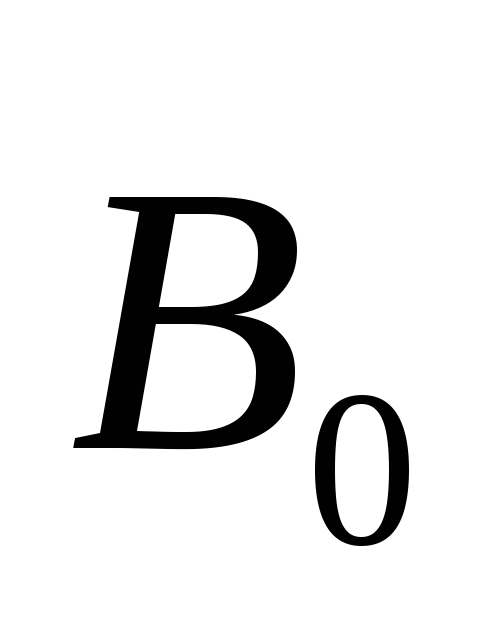

Направление тока в проводнике подбирается так, чтобы поле выталкивало проводник вверх. Сила тока 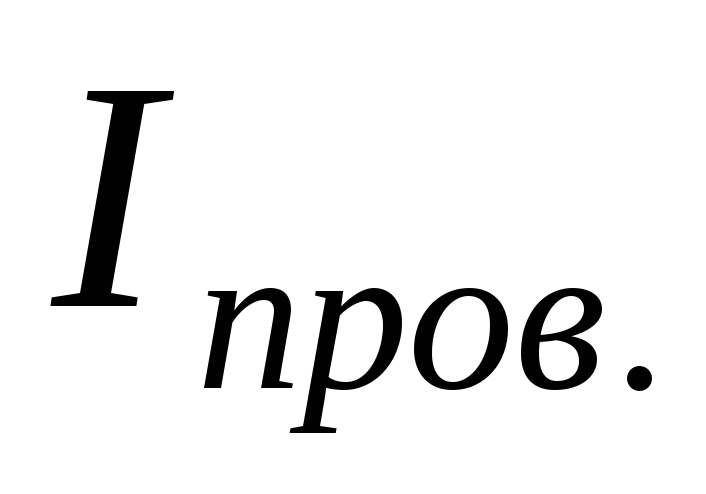в проводнике берётся равной 1A. Используя равенство моментов сил относительно оси 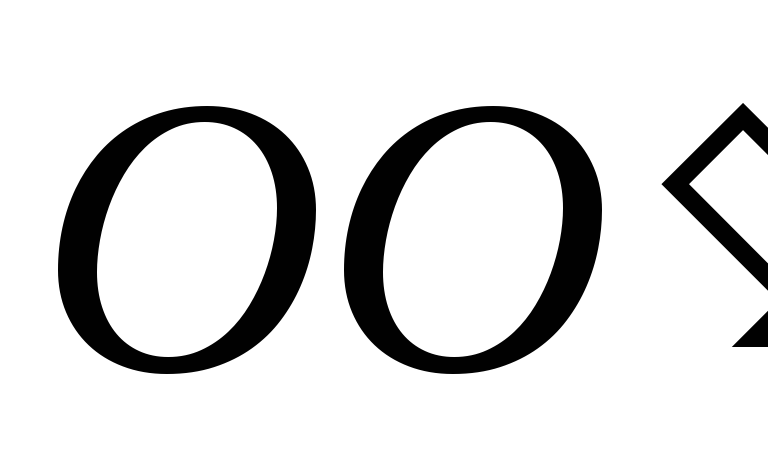индукции магнитного поля в зазоре ЭМ:

или , (25)

где 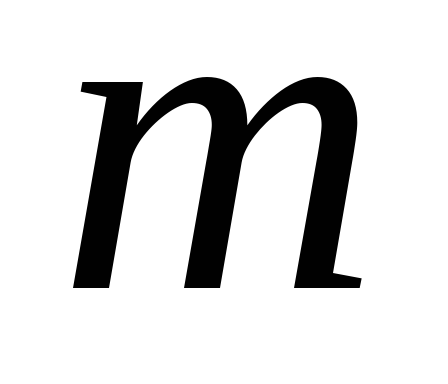— масса гирь,и— расстояние от точек приложения сил 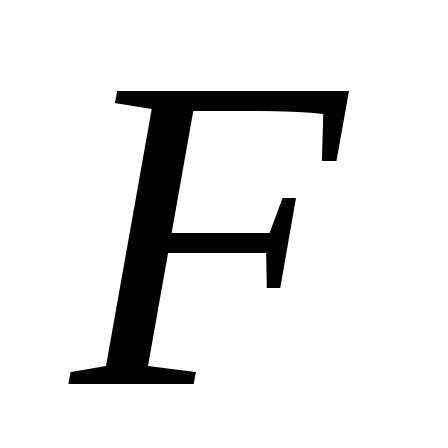и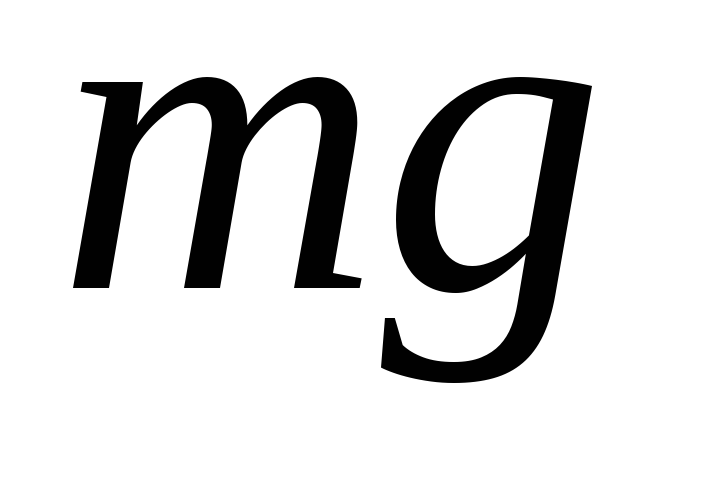до оси вращения.

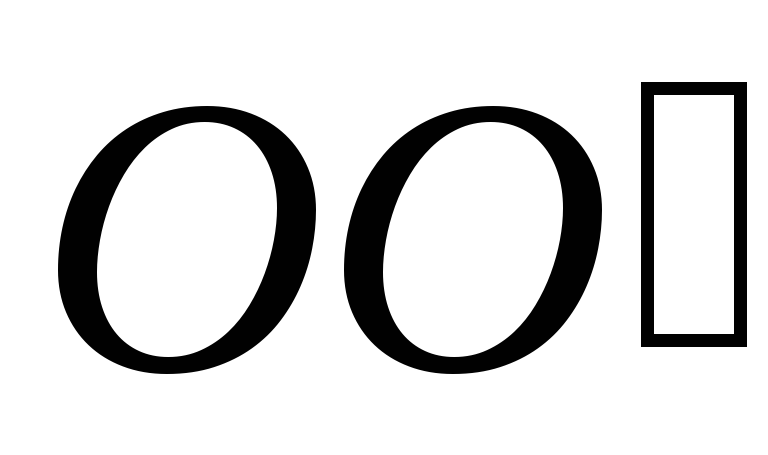Так как в нашем случае , то из формулы (24) получаем

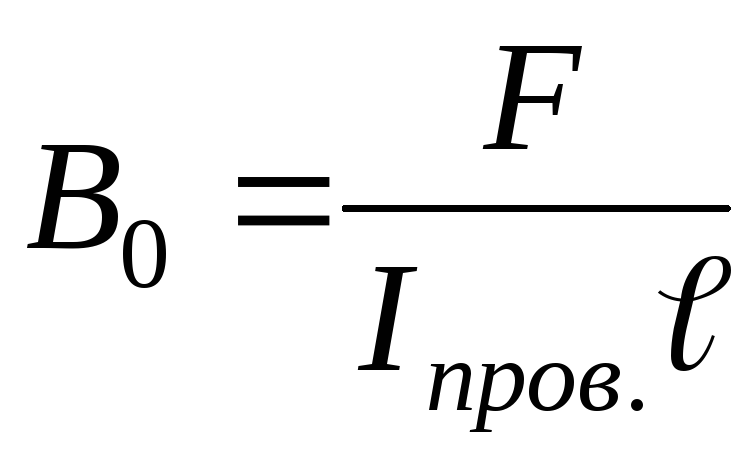. (26)

Решая (25) и (26) совместно, получаем

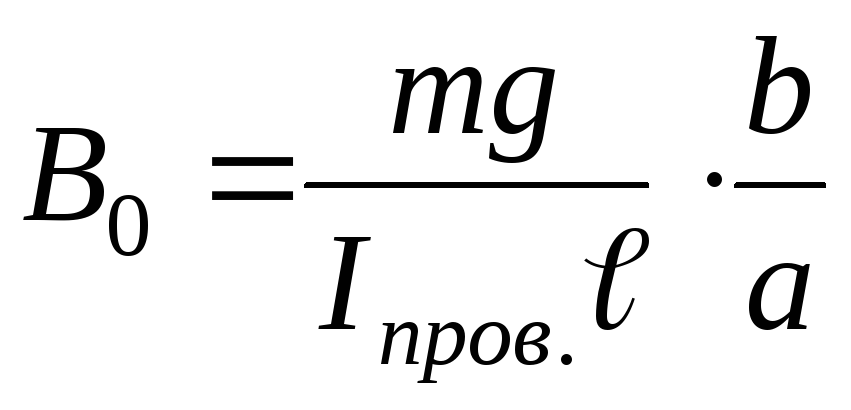, (27)

здесь 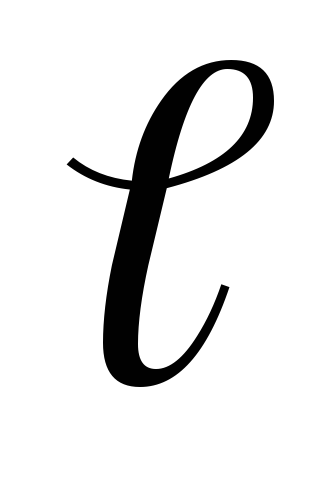,,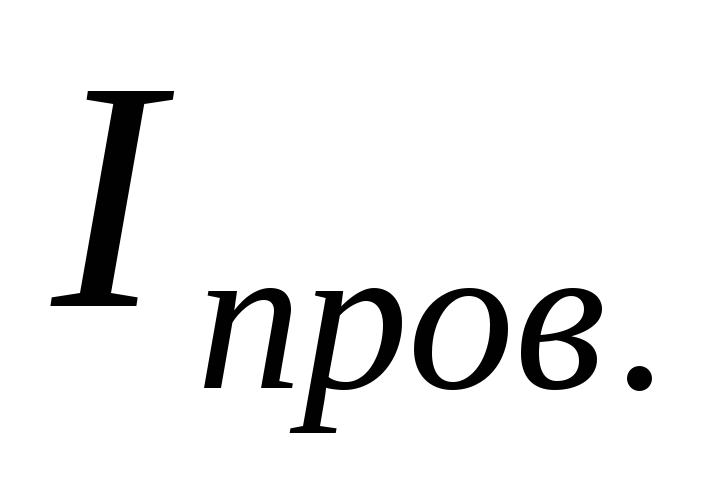,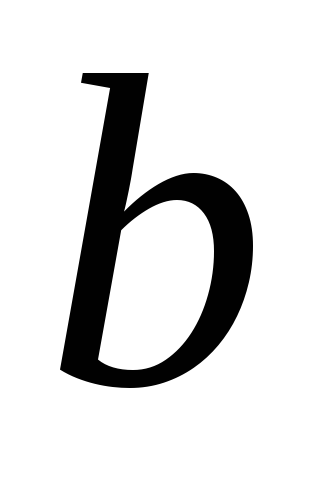— постоянные величины, поэтому можно ввести :

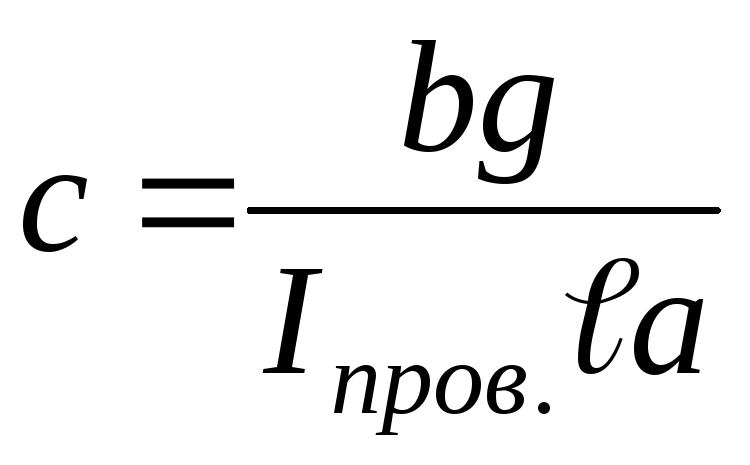— постоянная прибора. (28)

Тогда формула (27) примет вид:

. (29)

Напряженность магнитного поля. Закон полного тока

Понятие напряженности магнитного поля построено на формальной аналогии полей неподвижных зарядов и неподвижных намагниченных тел. Такая аналогия часто оказывается весьма полезной, т.к. позволяет перенести в теорию магнитного поля методы, разработанные для электростатических полей.

Напряженность магнитного поля первоначально была введена в форме закона Кулона через понятие магнитной массы, аналогичной электрическому заряду, как механическая сила взаимодействия двух точечных магнитных масс в однородной среде, которая пропорциональна произведению этих масс и обратно пропорциональна квадрату расстояния между ними

,

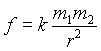где m₁ и m₂ — взаимодействующие магнитные массы; r — расстояние между точками, в которых магнитные массы считаются сосредоточенными; k — коэффициент, зависящий от свойств среды и системы единиц измерения.

Сила f направлена по прямой, соединяющей центры магнитных масс.

Магнитные массы одного знака отталкиваются, а противоположного — притягиваются.

Для количественной характеристики магнитного поля можно воспользоваться механической силой, действующей на положительный полюс пробного магнита, в той точке, где он расположен в пространстве. Напряженностью магнитного поля называется отношение механической силы, действующей на положительный полюс пробного магнита, к величине его магнитной массы или механическая сила, действующая на положительный полюс пробного магнита единичной массы в данной точке поля.

Напряженность изображается вектором H, имеющим направление вектора механической силы f.

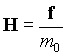
Если определить напряженность во всех точках магнитного поля, то можно построить линии, направление касательных к которым в каждой точке поля будет совпадать с направлением напряженности. Такие линии называются линиями напряженности или силовыми линиями.

Можно также ввести понятие о силовой трубке магнитного поля аналогично тому, как это было сделано для магнитного потока.Силовые линии, в отличие от линий индукции магнитного поля, начинаются на положительных магнитных массах и заканчиваются на отрицательных, т.е. прерываются.

Д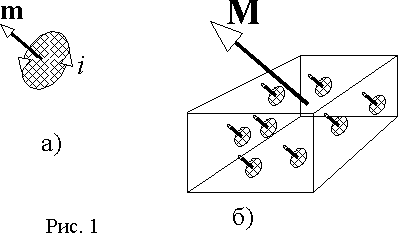ля изотропной среды существует связь между индукцией и напряженностью магнитного поля

Последнее соотношение можно использовать для определения магнитной проницаемости  как отношения индукции к напряженности магнитного поля.

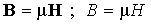или .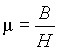

При помещении в магнитное поле вещества в нем происходят процессы ориентации различных структур, обладающих дипольным магнитным моментом.  Так электроны, перемещаясь по орбитам, образуют элементарные токи и соответствующие магнитные поля или магнитные диполи (рис. 1 а)). Кроме этого, электроны создают магнитный момент за счет вращения вокруг собственной оси, называемый спиновым магнитным моментом.

Магнитный диполь можно характеризовать вектором магнитного момента, численно равным произведению величины элементарного тока на площадь контура, ограниченного этим током в пространстве

m = is,

и направленным по нормали к площади контура.

Геометрическая сумма всех магнитных моментов образует магнитный момент тела

M =  m,

который обычно соотносят с объемом вещества V и называют намагниченностью или интенсивностью намагничивания

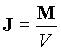
Единицу измерения намагниченности можно определить из выражения (1) [J] = [M/V] = Ам²/м³ = А/м.

Вектор намагниченности совпадает с направлением вектора напряженности и связан с ним линейной зависимостью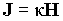

Безразмерный коэффициент  называется магнитной восприимчивостью вещества.

Для магнитного поля, существующего в некоторой среде, можно представить магнитную индукцию в виде суммы двух составляющих, индукции B₀ , соответствующей вакууму, и дополнительной индукции B_н, создаваемой намагниченностью вещества

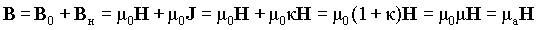
г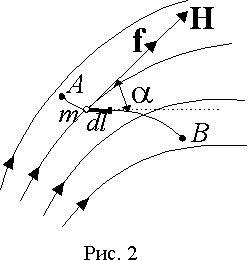де  ₀ — магнитная проницаемость вакуума;  _а и  =1+ — соответственно абсолютная и относительная магнитные проницаемости вещества.

В зависимости от значения  все вещества разделяются на диамагнитные парамагнитные и ферромагнитные. К диамагнетикам относятся вещества, у которых <0 и  <1, т.е. их магнитная проницаемость меньше чем у вакуума. Наиболее сильно диамагнитные свойства выражены у висмута, у которого  =0,99983. У парамагнетиков  >0 и  >1. Например, у платины относительная магнитная проницаемость составляет 1,00036.

Особую группу веществ, представляющих большой интерес с практической точки зрения, составляют ферромагнетики, у которых  >>1 и составляет величину порядка 10^4 10⁶.

Определение напряженности магнитного поля через магнитные силы и массы не вполне адекватно физической картине явлений в магнитном поле, т.к., в отличие от электрического заряда, не существует массы или заряда магнитного. На практике удобнее пользоваться явлениями, связывающими между собой электрический ток и магнитное поле.

Пусть некая точечная магнитная масса m перемещается по произвольному пути из точки A в точку B магнитного поля (рис. 2). Действующая на магнитную массу механическая сила f в любой точке поля направлена по касательной к силовой линии и равна f=mH , где H — напряженность поля.

Работа по перемещению массы m по пути AB равна

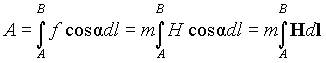
где  — угол между направлением вектора H и касательной к направлению перемещения. В этом выражении линейный интеграл вектора напряженности магнитного поля, взятый вдоль некоторого пути AB, называетсямагнитодвижущей силой (МДС) F, действующей вдоль этого пути

т.е. магнитодвижущая сила численно равна работе по перемещению единичной магнитной массы по заданному пути.

Рассмотрим теперь перемещение магнитной массы m по замкнутому пути в магнитном поле витка с постоянным значением тока i.

Сначала допустим, что существует только воздействие со стороны поля витка на массу m (рис. 3 а)).

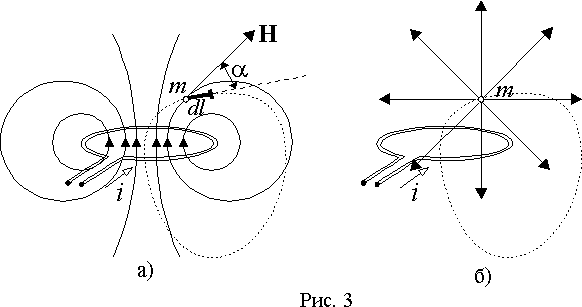
В соответствии с выражением (4), работа перемещения по замкнутому пути будет равна

Теперь предположим, что мы перемещаемся по тому же замкнутому контуру, но воздействие существует только со стороны магнитной массы m на виток с током (рис. 3 б)). При анализе электромагнитной силы было установлено, что элементарная работа по перемещению отрезка проводника с током i в магнитном поле равна dA = idФ = idN, где — число линий индукции магнитного поля, пересекаемых при перемещении.

Если магнитная масса m переместится по изображенному на рисунке контуру, то виток пересечет все исходящие из нее линии индукции и работа по перемещению, с учетом того, что полный магнитный поток перемещаемой массы численно равен ее значению, будет равна

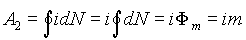
Но на основании закона сохранения энергии A₁ = A₂ , отсюда

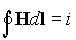
Очевидно, что задачу можно дополнить другими контурами (витками) с токами. Однако, в этом случае ее можно рассмотреть по отдельности, для каждого витка. Тогда в правой части выражения (8) окажется алгебраическая сумма всех токов, охваченных контуром интегрирования

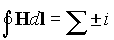
Полученное выражение называется законом полного тока. Линейный интеграл вектора напряженности магнитного поля, взятый по замкнутому контуру, равен полному (суммарному) электрическому току, проходящему через поверхность, ограниченную этим контуром или МДС вдоль замкнутого контура равна полному току, охватываемому этим током.

Закон полного тока является одним из важнейших законов, устанавливающим неразрывную связь между электрическим током и магнитным полем. Из него следует, что любая магнитная линия обязательно охватывает электрический ток и, наоборот, электрический ток всегда окружен магнитным полем. Причем, не являются исключением из этого закона и постоянные магниты, т.к. в них магнитные линии создаются элементарными микроскопическими токами, также входящими в правую часть выражения (9).

Переход магнитного потока из одной среды в другую сопровождается некоторыми явлениями на границе раздела этих сред.

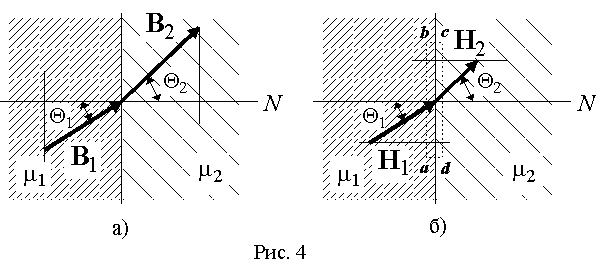
Пусть магнитный поток переходит из среды с магнитной проницаемостью  ₁ в среду с магнитной проницаемостью  ₂ (рис. 4). Из условия непрерывности магнитного потока следует, что при переходе из одной среды в другую через границу раздела площадью S он должен сохраняться, т.е. Ф₁ = Ф₂ . Но магнитный поток для изотропной среды можно представить через индукцию в виде

,

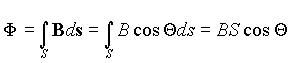где  — угол между направлением вектора индукции и нормалью к поверхности границы раздела сред, а произведение Bcos — проекция вектора индукции на нормаль или нормальная проекция.

Отсюда — Ф₁= B₁Scos ₁= Ф₂= B₂Scos ₂ или

B₁cos ₁ = B₂cos_

т.е. при переходе из одной среды в другую магнитная индукция изменяет свое значение, но сохраняет нормальную проекцию.

В изотропной среде векторы индукции и напряженности магнитного поля совпадают по направлению, поэтому и углы с нормалью векторов H₁ и H₂ будут такими же как у векторов B₁ и B₂ (рис. 4 б)). Выделим вблизи поверхности раздела замкнутый прямоугольный контур abcd так, чтобы его противоположные стороны длиной l располагались в разных средах на бесконечно малом расстоянии от границы (рис. 4 б)).Найдем линейный интеграл от вектора напряженности поля вдоль этого контура и по закону полного тока приравняем его нулю, т.к. внутри контура отсутствует электрический ток:

.

Отсюда — H₁sin ₁ = H₂sin₂.

Это означает, что при переходе из одной среды в другую вектор напряженности магнитного поля сохраняет тангенциальную составляющую, т.е. проекцию на границу раздела сред.

Если разделить выражение (10) на выражение (11), то мы получим соотношение, связывающее углы векторов с нормалью и магнитные проницаемости.

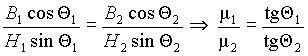
Из выражения (12) следует, что при большом отличии магнитных проницаемостей ( ₁/ ₂=1000), например, при выходе магнитного потока из ферромагнетика в воздушную среду почти параллельно границе раздела ( ₁=87 ), угол с нормалью вектора индукции составит около 1 , т.е. можно считать, что магнитные линии в воздухе нормальны к поверхностям тел из ферромагнетиков.

2.2. Применение закона полного тока для расчета магнитных полей

2.2.1. Напряженность поля бесконечно длинного соленоида

Соленоидом называют катушку цилиндрической формы из провода, витки которой намотаны в одном направлении и прилегают плотно друг к другу.

Магнитное поле соленоида представляет собой результат сложения полей, создаваемых несколькими круговыми токами, расположенными рядом и имеющими общую ось (рис. 2.6).

Внутри соленоида силовые линии каждого отдельного витка имеют одинаковое направление. Поэтому принято считать поле бесконечно длинного соленоида (такого, у которого диаметр гораздо меньше длины – d<<L) однородным, существующим только внутри его.

Р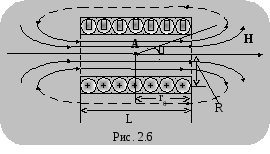ассчитаем напряженность магнитного поля внутри соленоида, длина которогоL, радиус витка R, число витков N, сила тока I. Будем считать, что в любой точке соленоида вектор H направлен параллельно оси.

Для расчета напряженности воспользуемся законом полного тока в виде

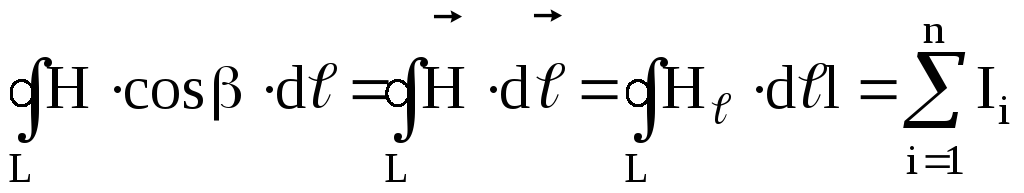. (2.7)

В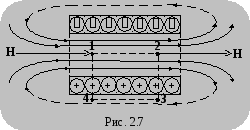ыберем замкнутый контур прямоугольной формы (рис. 2.7), участок 1-2 которого расположен внутри соленоида вдоль его оси.

Левую часть выражения (2.7) можно представить в виде

,

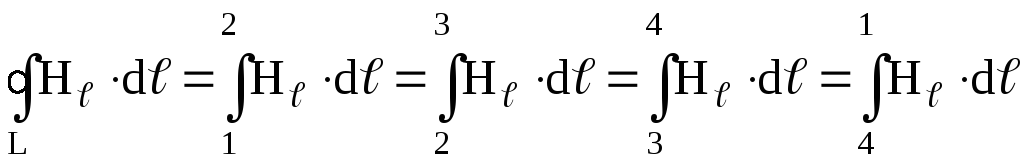где 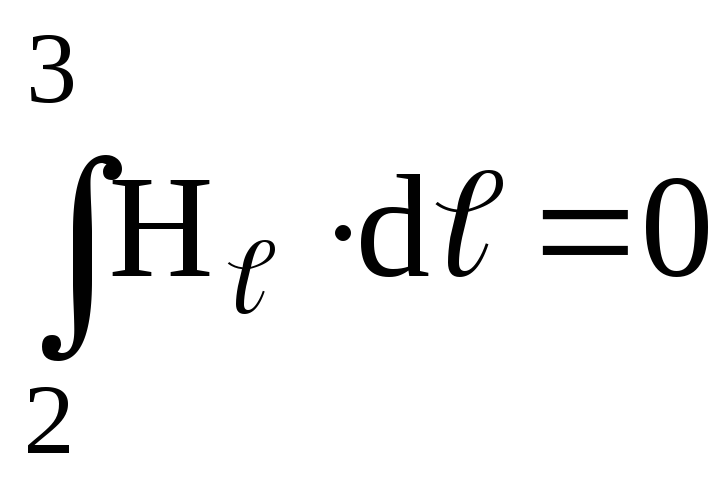, так как H перпендикулярен участку 2-3;

, так как H перпендикулярен участку 4-1;

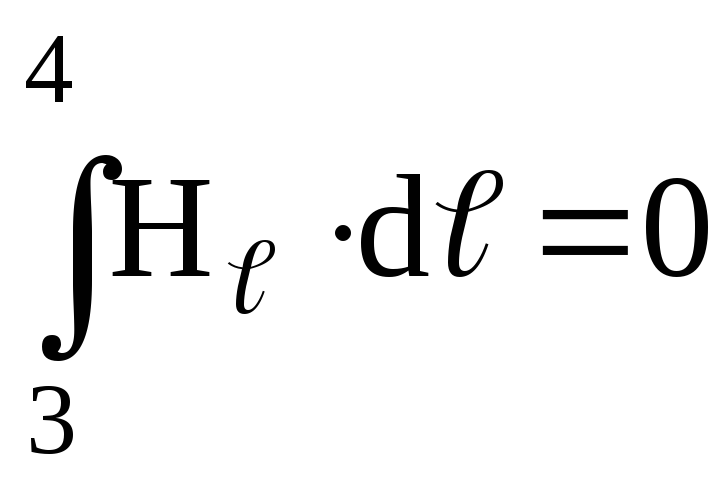, так как участок 3-4 находится вне соленоида.

Следовательно,

.

Правая часть выражения (2.16) может быть представлена так:

,

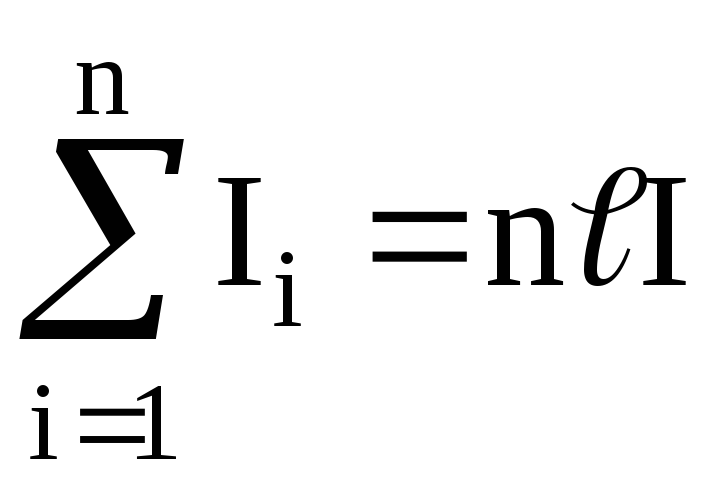где n — число витков на единице длины соленоида;

— длина участка;

I — величина тока в соленоиде.

Таким образом, имеем

.

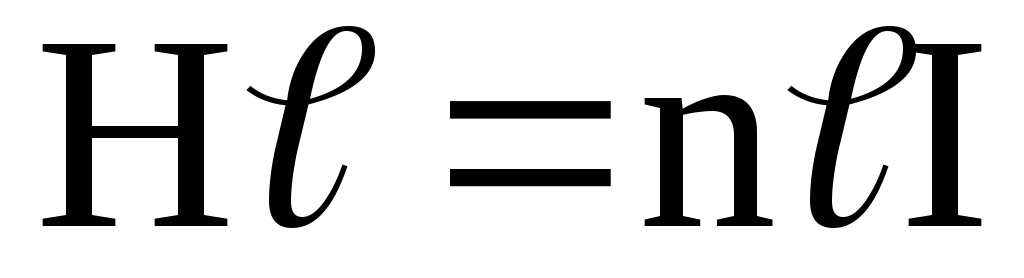Откуда

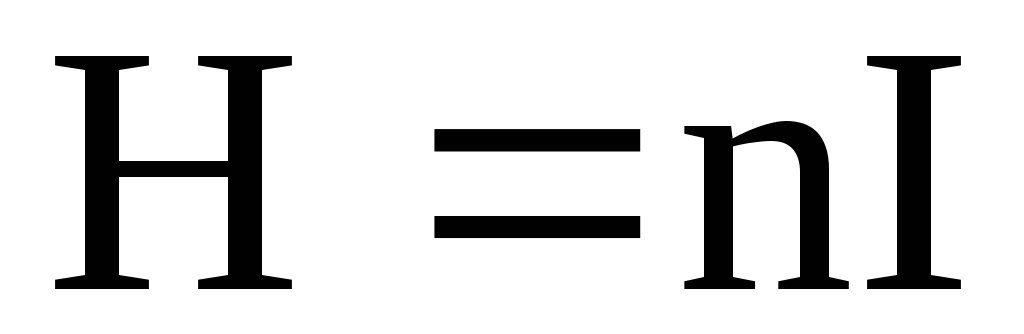. (2.8)

Формула (2.8) согласуется с формулой, полученной с применением закона Био-Савара-Лапласа.

Из полученного результата действительно видно, что напряженность магнитного поля внутри бесконечно длинного соленоида имеет одно и тоже значение, а следовательно, оно действительно однородно.

Таким образом, действительно внутри бесконечно длинного соленоида напряженность магнитного поля практически везде одинакова. Она направлена вдоль оси соленоида в соответствии с правилом правого винта.

2.2.2. Напряженность магнитного поля тороида

Магнитное поле тороида (тороид – это соленоид, свитый в кольцо) однородное, сосредоточено внутри самого тороида. Вне тороида поле отсутствует. Линии вектора H представляют собой концентрические окружности, центры которых совпадают с центром тороида. Краевой эффект у тороида (такого соленоида) отсутствует (рис. 2.8).

В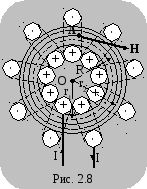ыбирая одну из линий вектора H за контур обхода, радиус которого r (r₁, r₂), и применяя закон полного тока, будем иметь

;

,

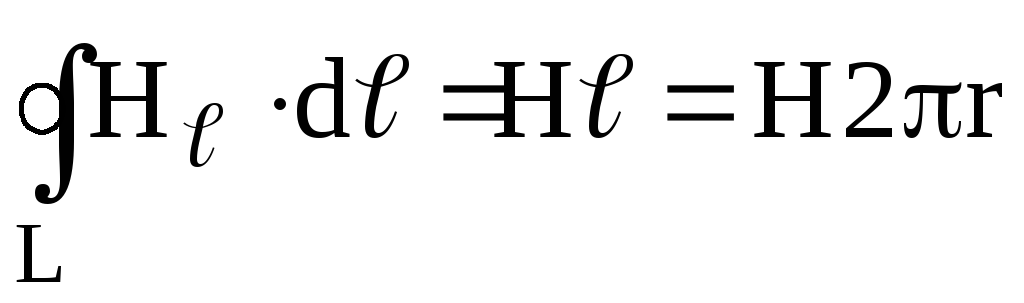где R — радиус тороида (радиус линии вектора H, расположенной в средней части тороида).

Имеем

.

Откуда

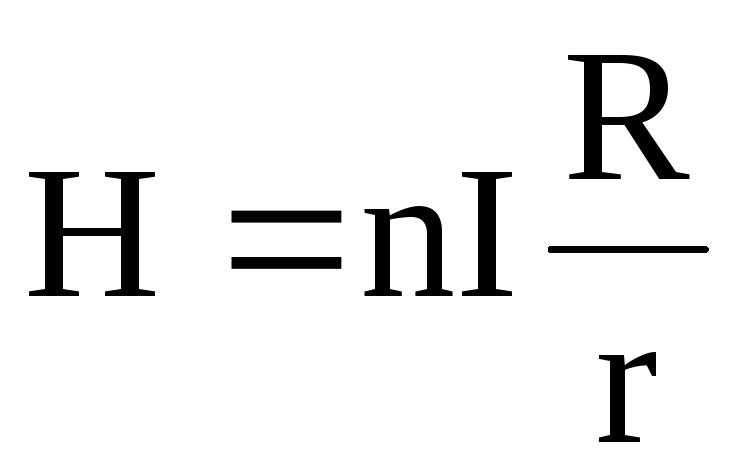
. (2.9)

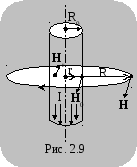
Так как в нашем случае R = r, то

. (2.10)

Внутри тороида напряженность магнитного поля имеет различные направления, поэтому говорить о его однородности можно только условно, т.е.

.

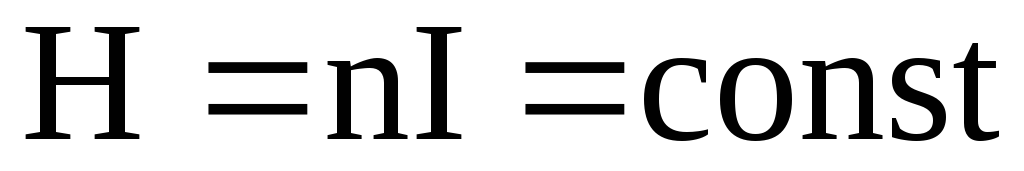2.2.3. Напряженность магнитного поля внутри толстых проводников с током

Пусть ток с постоянной плотностью протекает по проводнику радиуса (рис. 2.9). Вне проводника, согласно теореме о циркуляции вектора напряженности магнитного поля,

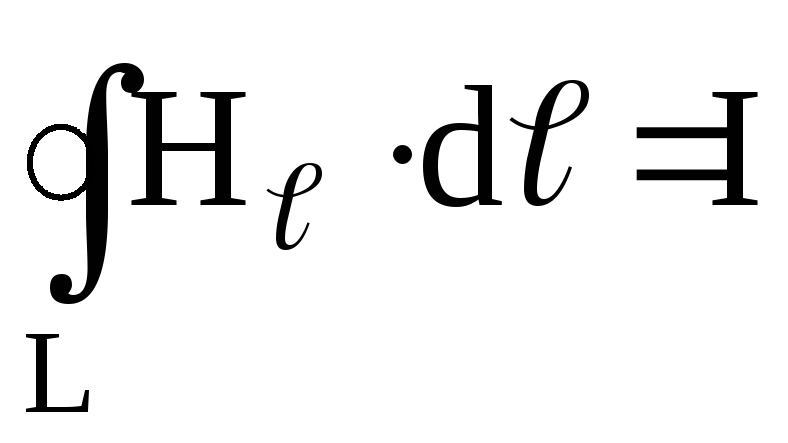, (2.11)

где 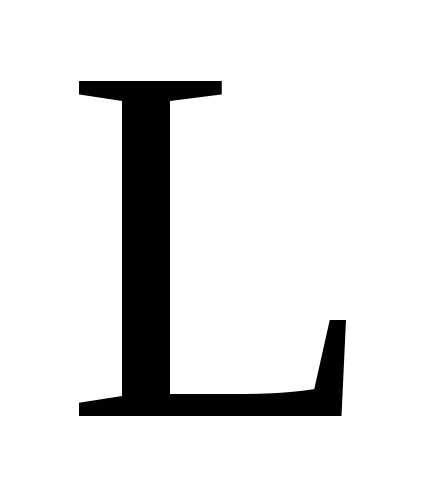— контур, представляющий собой окружность радиуса, центр которой лежит на оси цилиндрического проводника.

Имеем

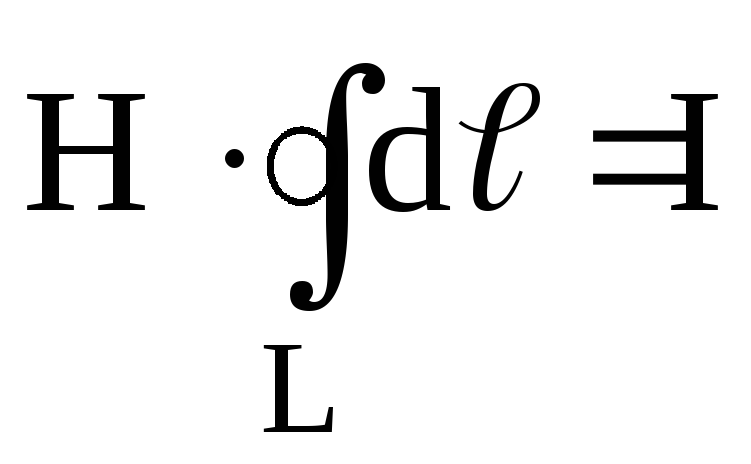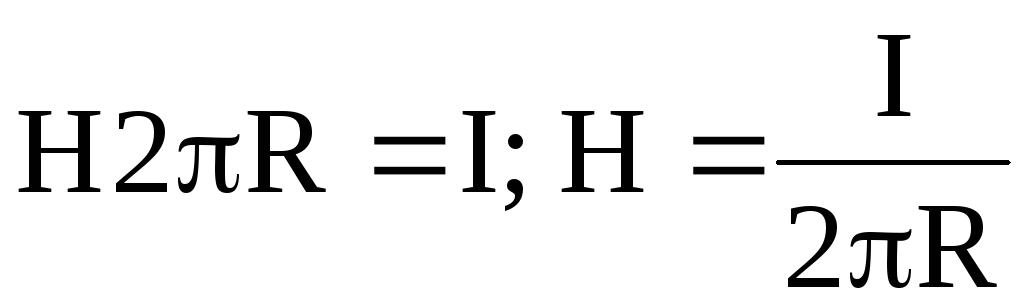или . (2.12)

Величина тока

,

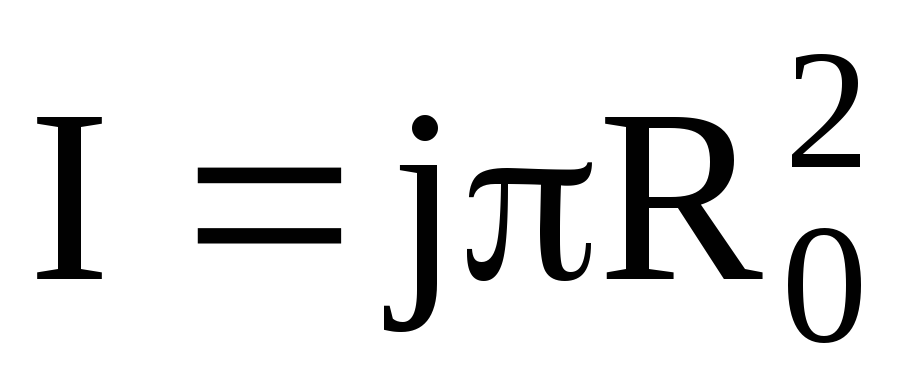где 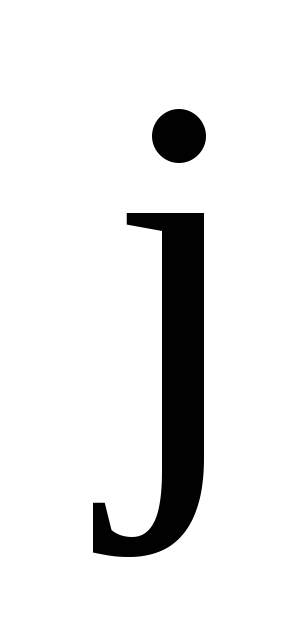— плотность тока.

Тогда

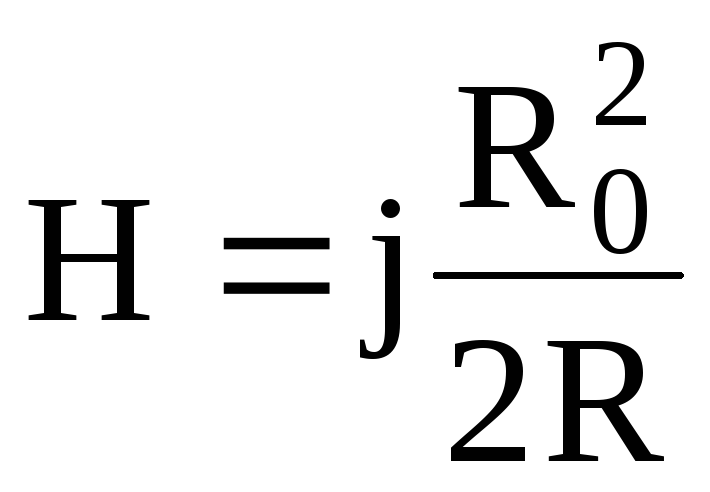, (2.13)

Анализ полученного соотношения показывает:

1. Если расстояние от оси проводника меньше его радиуса (r<R₀), то

.

Напряженность магнитного поля линейно возрастает.

2. Если расстояние от оси проводника равно его радиусу, то

.

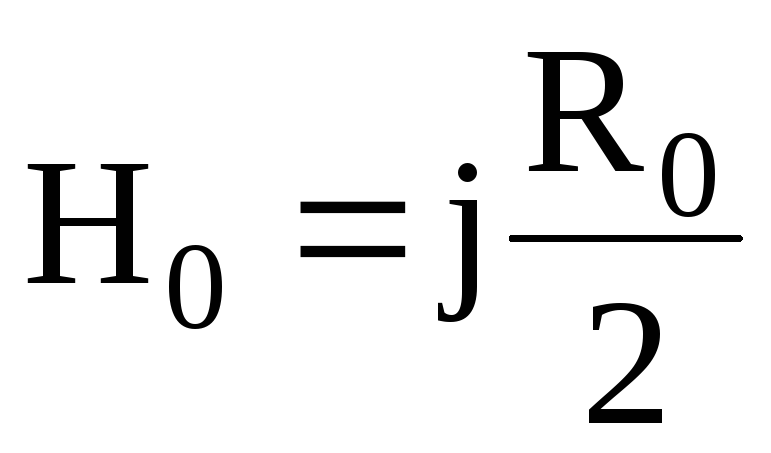Н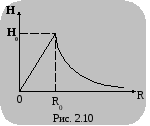апряженность магнитного поля достигает максимального значения.

3. Если расстояние от оси проводника больше его радиуса (r<>R₀), то

.

Напряженность магнитного поля убывает и при R равна нулю.

Графически изменение напряженности магнитного поля проводника от расстояния до его оси можно представить так, как показано на рис. 2.10.

1.6. Закон полного тока для магнитного поля в вакууме(теорема о циркуляции вектора в).@

В разделе “Электростатика” было доказано, что циркуляция вектора напряженности электростатического поля вдоль замкнутого контура равна нулю, откуда следует потенциальный характер электростатического поля. Одним из основных отличий магнитного поля от электростатического поля является его непотенциальность. Для доказательства этого рассмотрим линейный интеграл от В по замкнутому пути в магнитном поле, создаваемом током, т.е.

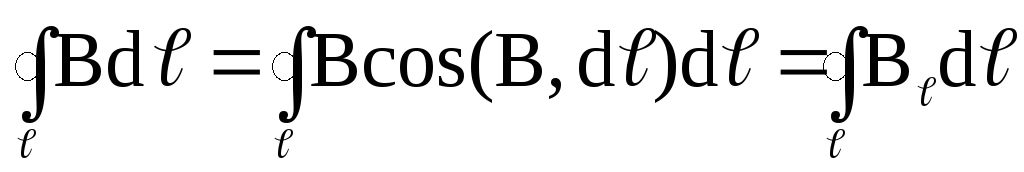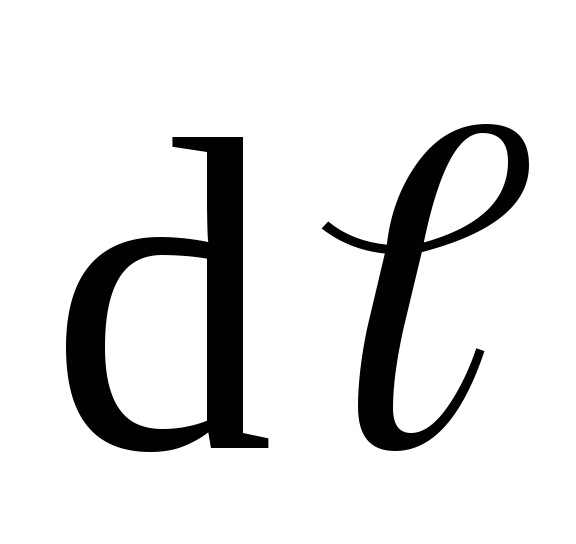где– вектор элемента длины контура, направленный вдоль обхода контура; В_ℓ– проекция вектора на направление касательной к контуру. Данный интеграл называется циркуляцией векторапо заданному замкнутому контуруℓ.

Рассмотрим частный случай: круговой путь ℓ является силовой линией радиуса R магнитного поля прямолинейного бесконечного проводника с током (рис.1.9). Магнитная индукция для этого случая была подсчитана ранее, и во всех точках окружности вектор составляет:

У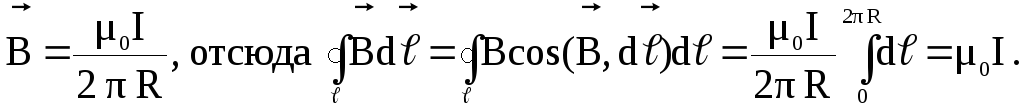гол между векторамии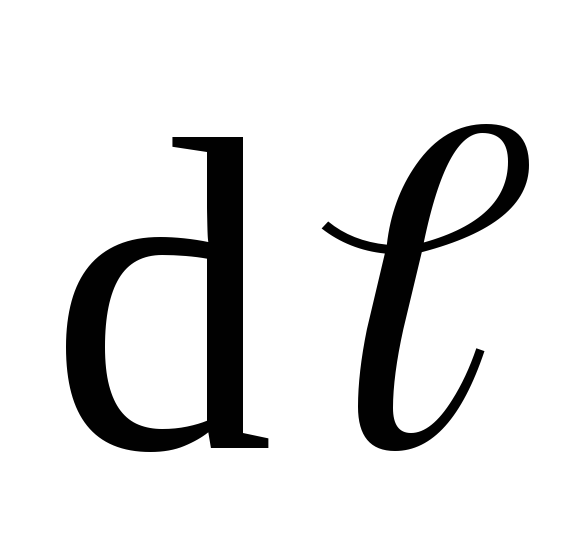равен нулю, поэтомуcos(,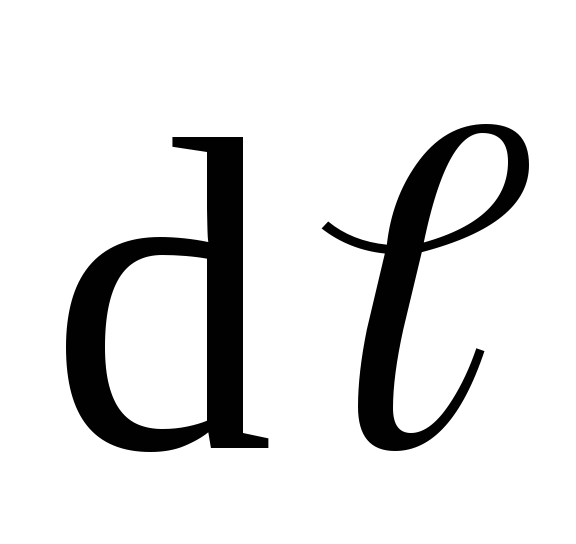)=1. Из полученного результата следует, что циркуляция вектора магнитной индукции вдоль силовой линии прямолинейного проводника с током не равна нулю, т.е. поле такого проводниканепотенциально. Оно называется вихревым. Полученная формула справедлива для любой формы замкнутого контура, охватывающего проводник с током.

Пусть теперь наш контур ℓ произвольной формы охватывает n проводников с токами I₁, …I_n. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. При этом положительным считается ток, если он с направлением обхода контура образует правовинтовую систему. Ток противоположного направления считается отрицательным.

Р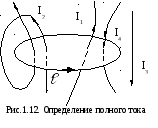азберем пример, изображенный на рис.1.12. Найдем сумму токов, т.е. полный ток, охватываемый контуромℓ:

Т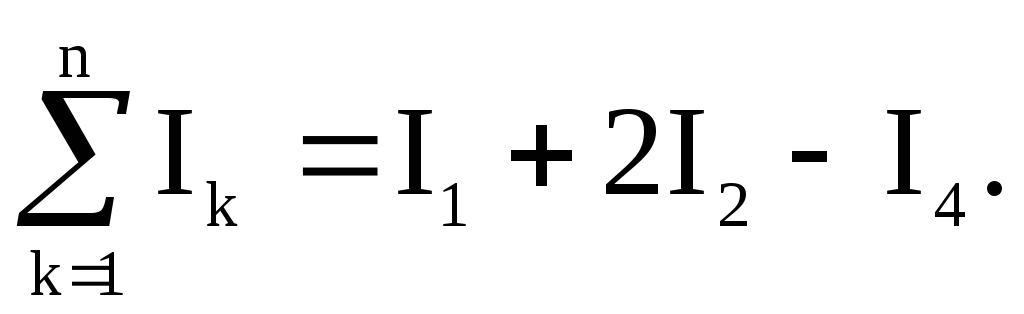окI₃ не учитывается, т.к. он не охватывается контуром. В результате имеем

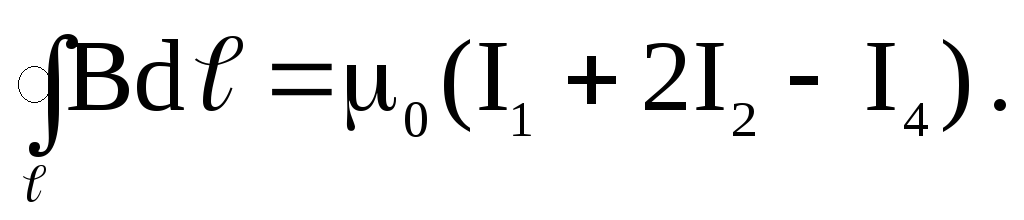
Таким образом, циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром:

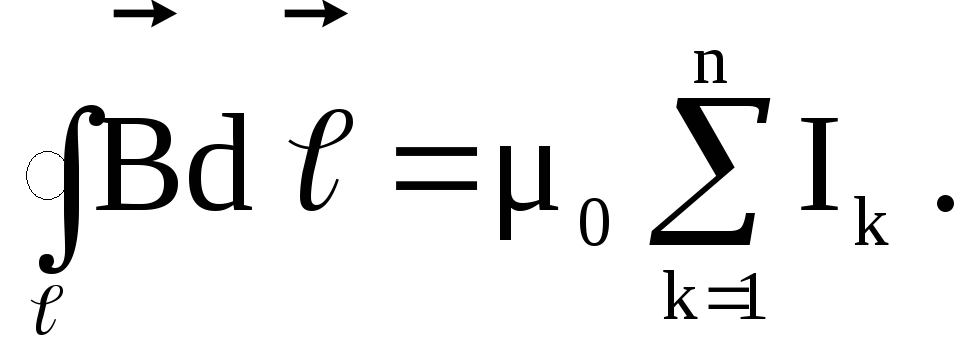
Данное выражение представляет собой закон полного тока для магнитного поля в вакууме, или теорему о циркуляции вектора В.

Все вышерассмотренное относится к вакууму. Можно доказать, что циркуляция вектора вдоль замкнутого контура, не охватывающего проводник с током, равна нулю.

Рассмотренная нами теорема имеет в магнитостатике такое же значение, как теорема Гаусса в электростатике. Она позволяет находить магнитную индукцию различных полей без применения закона Био-Савара-Лапласа.

1.7. Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля.@

Аналогично определению электрического потока, или числа силовых линий Е, пересекающих поверхностьS, определим магнитный поток, поток вектора магнитной индукции, или число силовых линий , пересекающих поверхностьS. Потоком вектора магнитной индукции через элементарную площадку dS называется физическая величина dФ_m, равная произведению величины этой площадки и проекции вектора В на направление нормали к площадке dS (рис. 1.13):

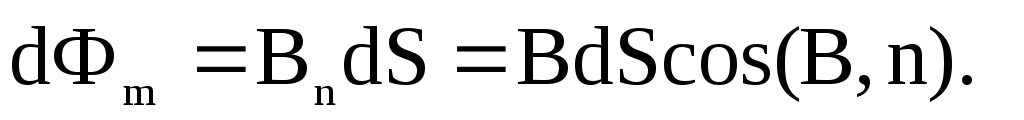
Интегрируя это выражение по S, получим магнитный поток Ф_mсквозь произвольную замкнутую поверхностьS: .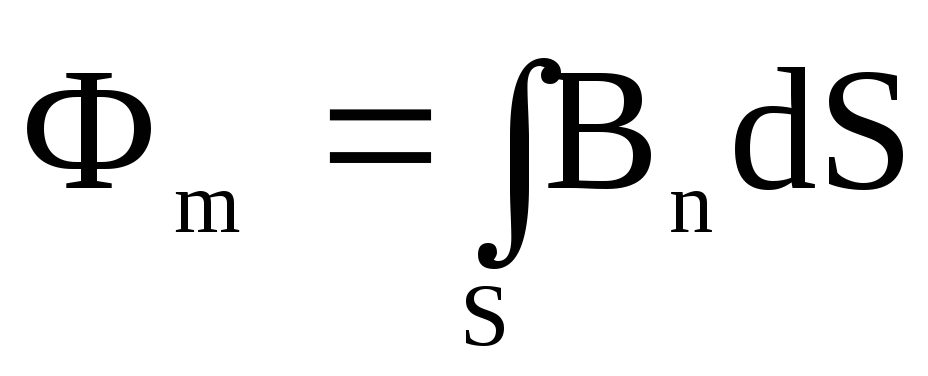

Для однородного поля и плоской поверхности, расположенной перпендикулярно В, поток рассчитывают по формуле Ф = ВS, из которой можно определить единицу магнитного потока, которая называется вебер (Вб). 1 Вб – это такой магнитный поток, который проходит через плоскую поверхность площадью 1 м², расположенную перпендикулярно магнитному полю, индукция которого равна 1Тл: 1Вб=1Тл∙1 м².

Мы уже знаем, что силовые линии магнитного поля замкнуты. Поэтому, интеграл ∫ Вds по любой замкнутой поверхности должен быть равен нулю, так как внутрь поверхности входит тот же поток, что и выходит из нее. Если имеется k токов, то создаваемый ими магнитный поток: 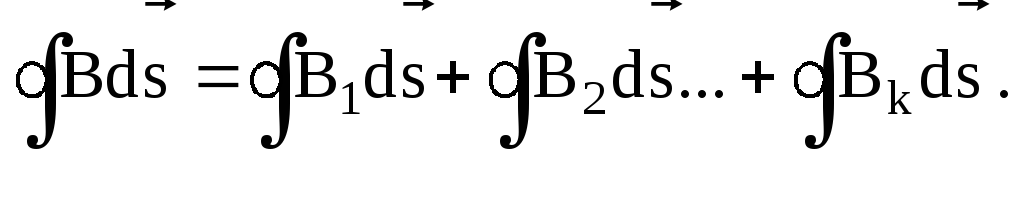Здесь В_n — проекция В на нормаль к ds. Поскольку каждый интеграл по отдельности равен нулю, то и

в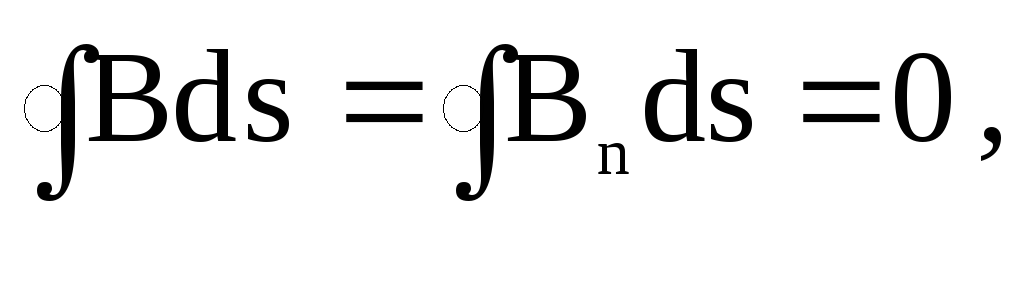ышеизложенное составляет суть теоремы Гаусса для потока магнитного поля Ф_m. Поток магнитного поля через любую замкнутую поверхность равен нулю. Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

2.2. Применение закона полного тока для расчета магнитных полей

2.2.1. Напряженность поля бесконечно длинного соленоида

Соленоидом называют катушку цилиндрической формы из провода, витки которой намотаны в одном направлении и прилегают плотно друг к другу.

Магнитное поле соленоида представляет собой результат сложения полей, создаваемых несколькими круговыми токами, расположенными рядом и имеющими общую ось (рис. 2.6).

Внутри соленоида силовые линии каждого отдельного витка имеют одинаковое направление. Поэтому принято считать поле бесконечно длинного соленоида (такого, у которого диаметр гораздо меньше длины – d<<L) однородным, существующим только внутри его.

Р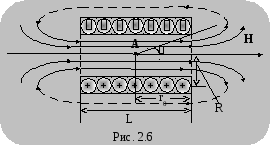ассчитаем напряженность магнитного поля внутри соленоида, длина которогоL, радиус витка R, число витков N, сила тока I. Будем считать, что в любой точке соленоида вектор H направлен параллельно оси.

Для расчета напряженности воспользуемся законом полного тока в виде

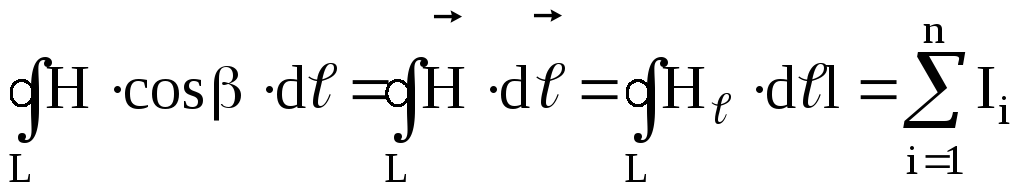. (2.7)

В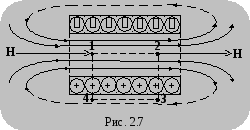ыберем замкнутый контур прямоугольной формы (рис. 2.7), участок 1-2 которого расположен внутри соленоида вдоль его оси.

Левую часть выражения (2.7) можно представить в виде

,

где 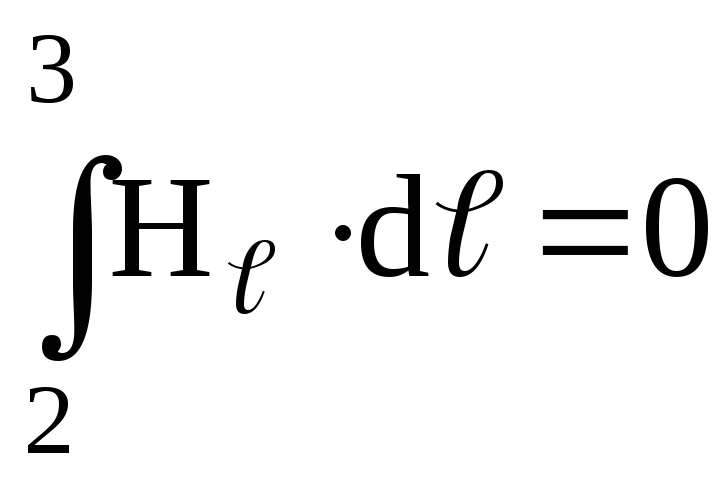, так как H перпендикулярен участку 2-3;

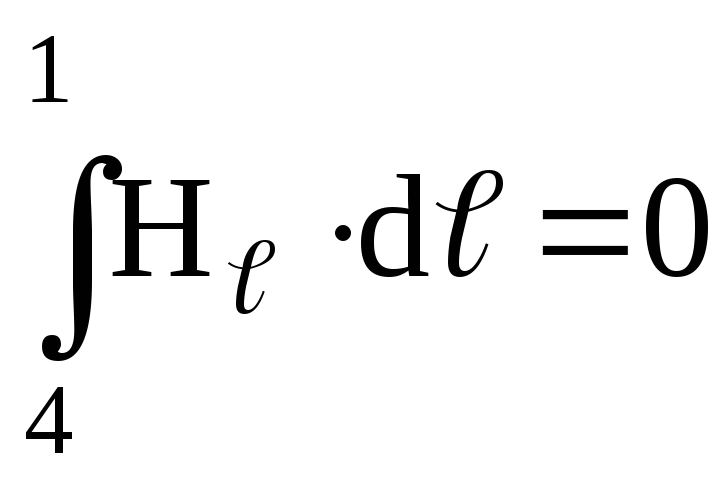, так как H перпендикулярен участку 4-1;

, так как участок 3-4 находится вне соленоида.

Следовательно,

.

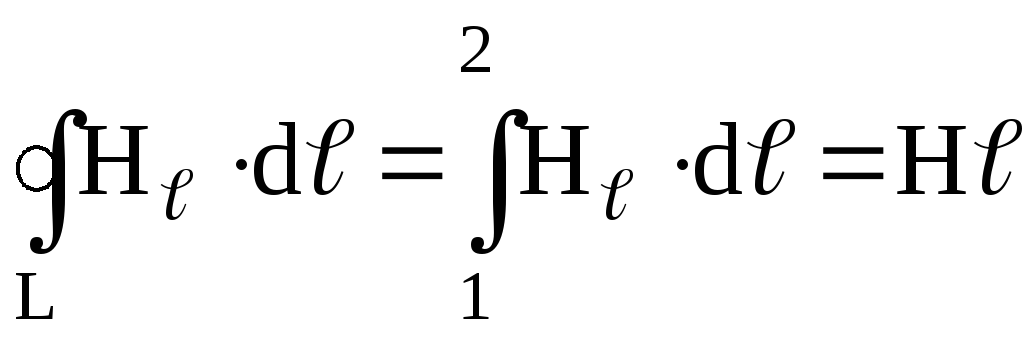Правая часть выражения (2.16) может быть представлена так:

,

где n — число витков на единице длины соленоида;

— длина участка;

I — величина тока в соленоиде.

Таким образом, имеем

.

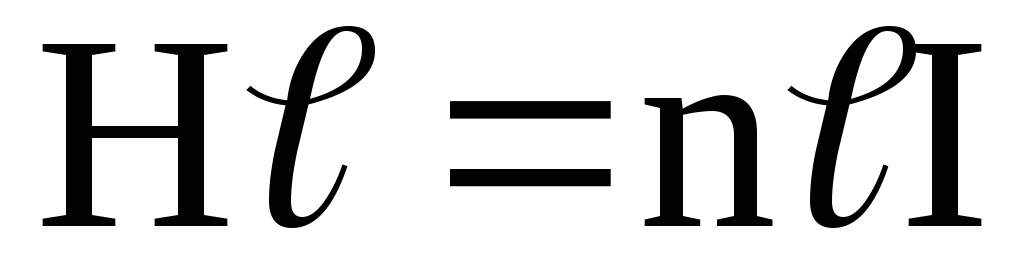Откуда

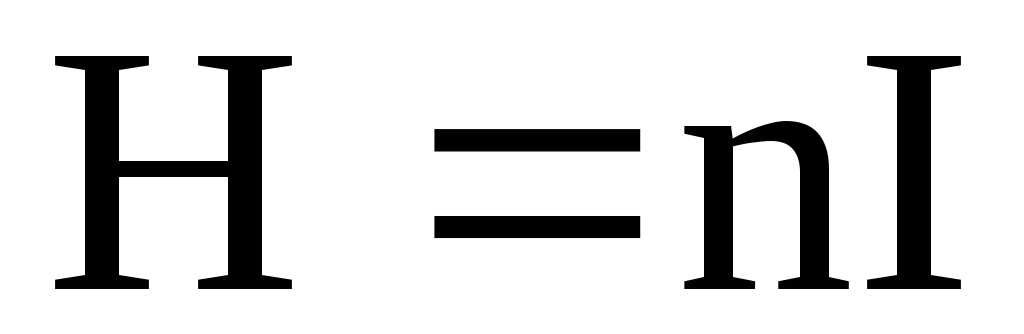. (2.8)

Формула (2.8) согласуется с формулой, полученной с применением закона Био-Савара-Лапласа.

Из полученного результата действительно видно, что напряженность магнитного поля внутри бесконечно длинного соленоида имеет одно и тоже значение, а следовательно, оно действительно однородно.

Таким образом, действительно внутри бесконечно длинного соленоида напряженность магнитного поля практически везде одинакова. Она направлена вдоль оси соленоида в соответствии с правилом правого винта.

2.2.2. Напряженность магнитного поля тороида

Магнитное поле тороида (тороид – это соленоид, свитый в кольцо) однородное, сосредоточено внутри самого тороида. Вне тороида поле отсутствует. Линии вектора H представляют собой концентрические окружности, центры которых совпадают с центром тороида. Краевой эффект у тороида (такого соленоида) отсутствует (рис. 2.8).

В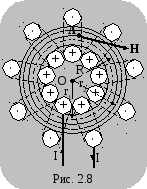ыбирая одну из линий вектора H за контур обхода, радиус которого r (r₁, r₂), и применяя закон полного тока, будем иметь

;

,

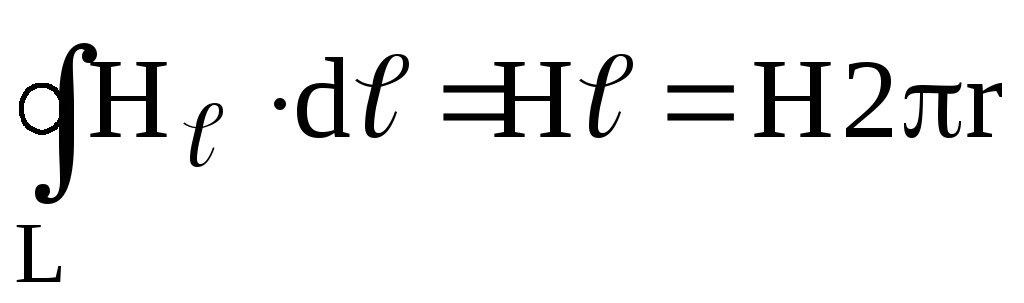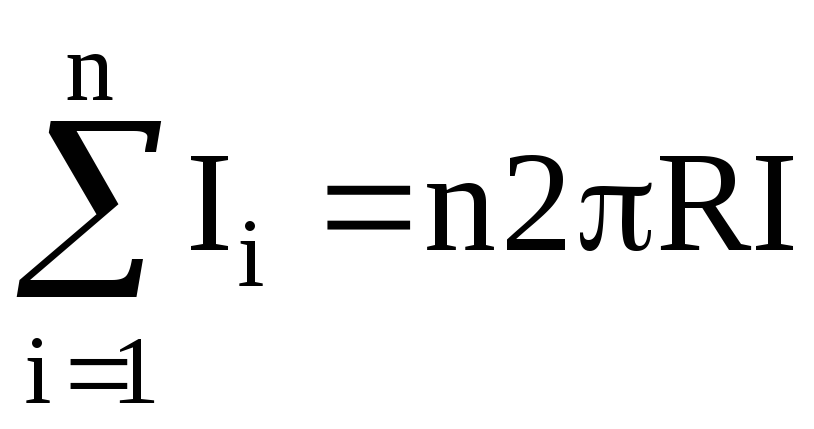где R — радиус тороида (радиус линии вектора H, расположенной в средней части тороида).

Имеем

.

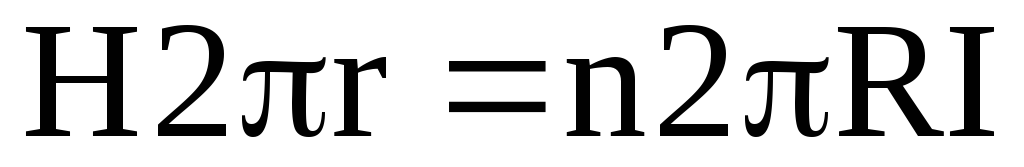Откуда

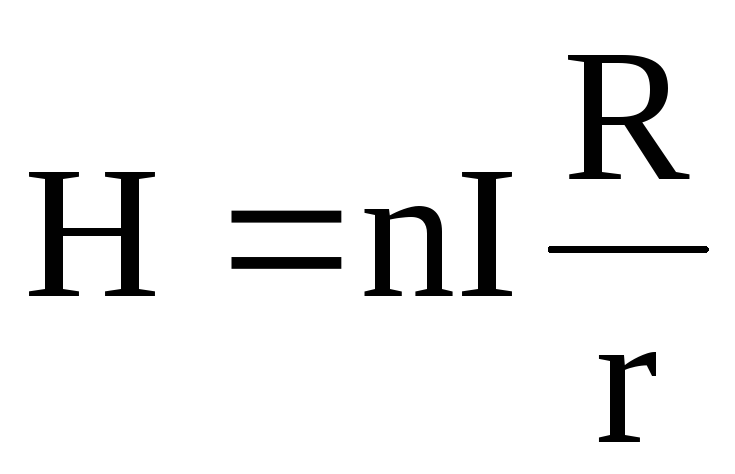
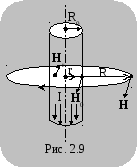. (2.9)

Так как в нашем случае R = r, то

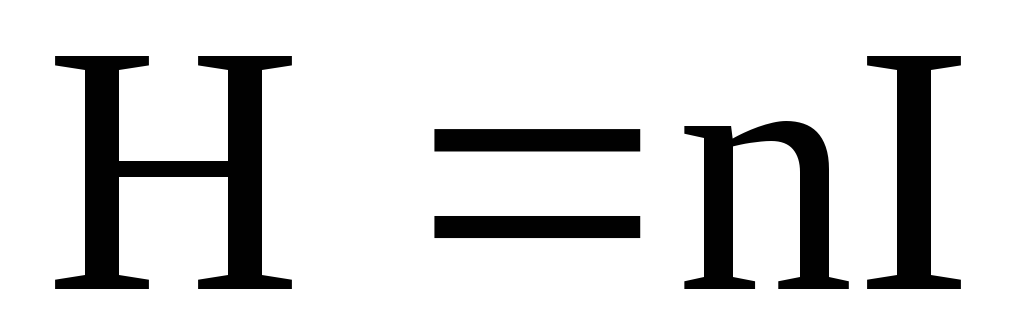. (2.10)

Внутри тороида напряженность магнитного поля имеет различные направления, поэтому говорить о его однородности можно только условно, т.е.

.

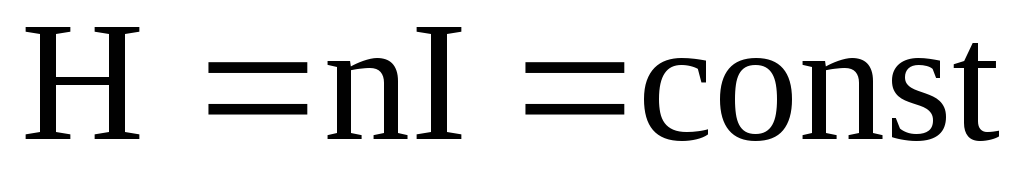2.2.3. Напряженность магнитного поля внутри толстых проводников с током

Пусть ток с постоянной плотностью протекает по проводнику радиуса (рис. 2.9). Вне проводника, согласно теореме о циркуляции вектора напряженности магнитного поля,

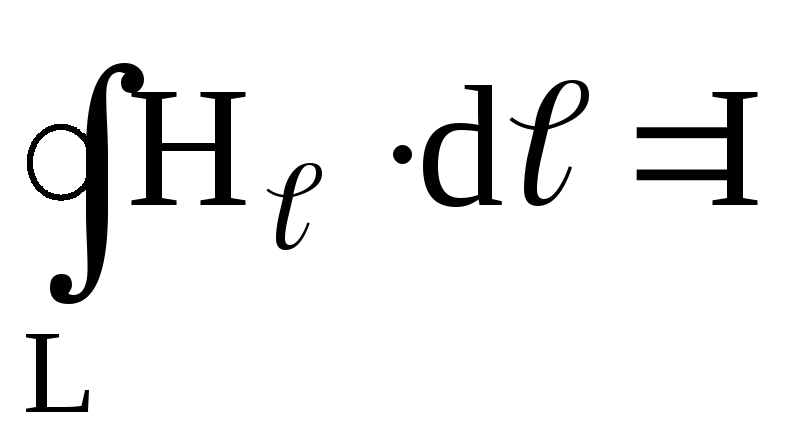, (2.11)

где 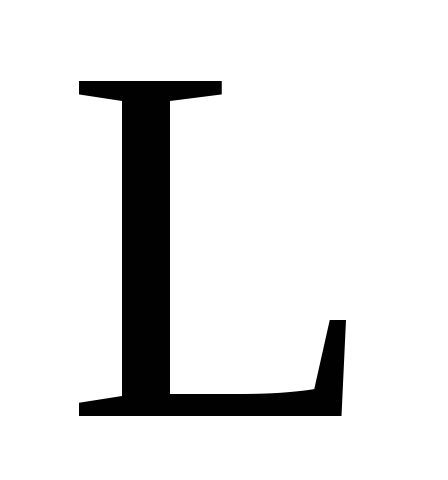— контур, представляющий собой окружность радиуса, центр которой лежит на оси цилиндрического проводника.

Имеем

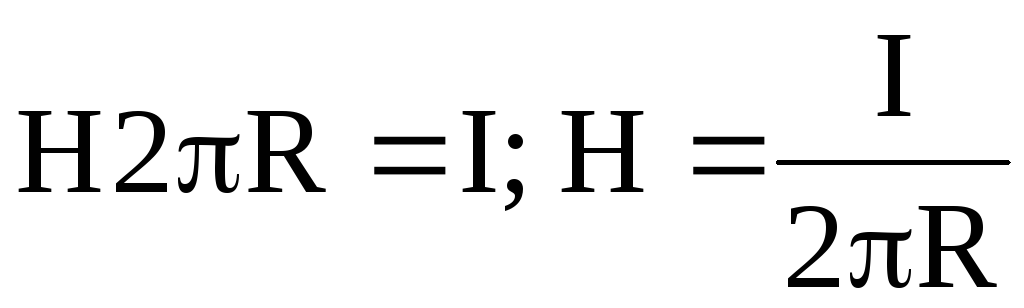или . (2.12)

Величина тока

,

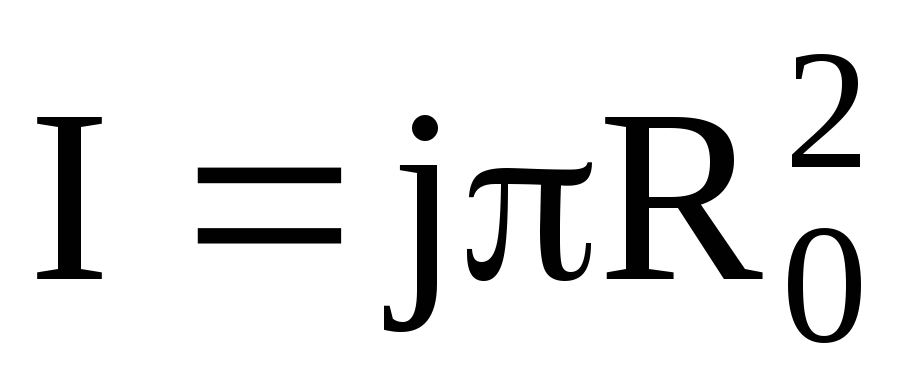где 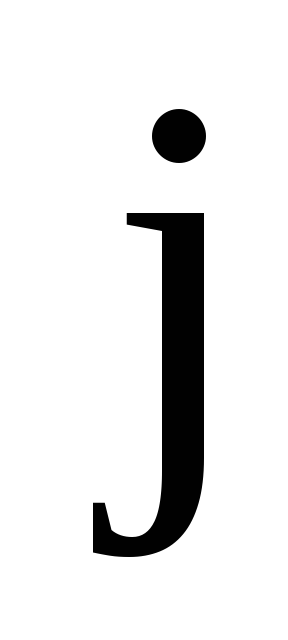— плотность тока.

Тогда

, (2.13)

Анализ полученного соотношения показывает:

1. Если расстояние от оси проводника меньше его радиуса (r<R₀), то

.

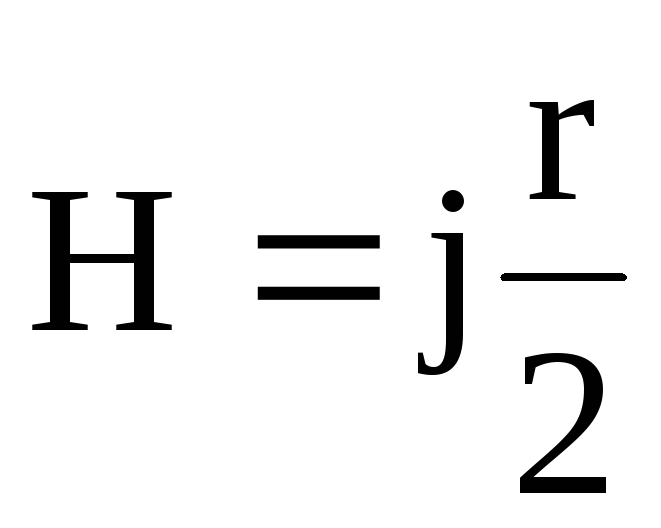Напряженность магнитного поля линейно возрастает.

2. Если расстояние от оси проводника равно его радиусу, то

.

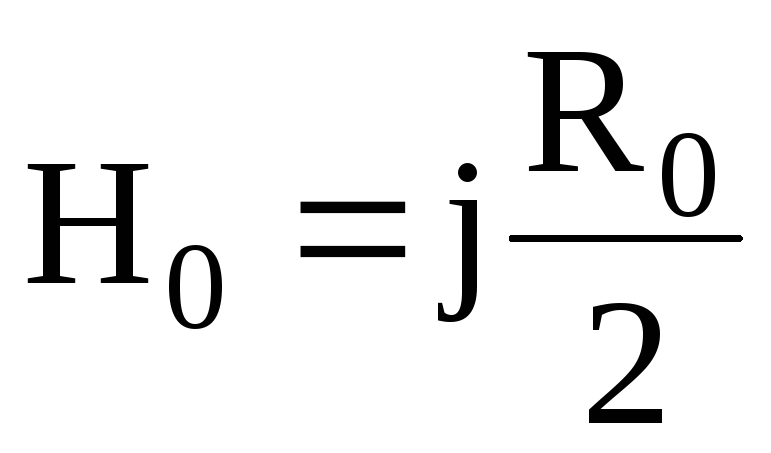Н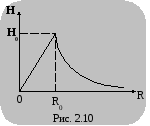апряженность магнитного поля достигает максимального значения.

3. Если расстояние от оси проводника больше его радиуса (r>R₀), то

.

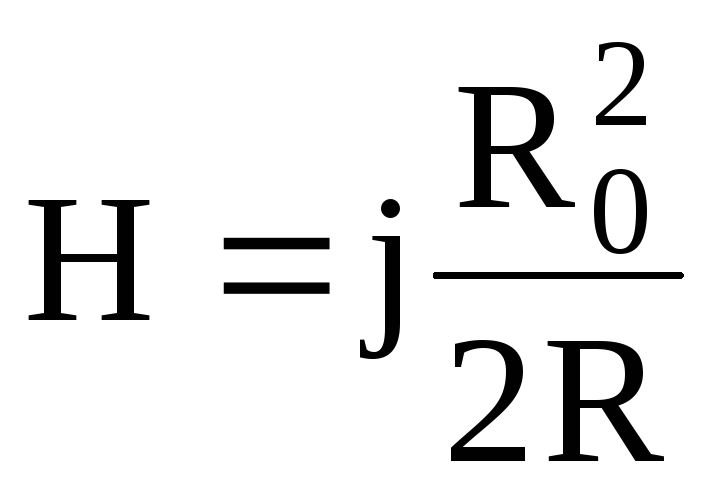Напряженность магнитного поля убывает и при R равна нулю.

Графически изменение напряженности магнитного поля проводника от расстояния до его оси можно представить так, как показано на рис. 2.10.

6 Закон полного тока для магнитного поля в вакууме. Вихревой характер магнитного поля.

Аналогично циркуляции вектора напряженности электростатического поля введем циркуляцию вектора магнитной индукции. Циркуляцией вектора В по заданному замкнутому контуру называется интеграл

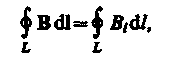
где dl — вектор элементарной длины контура, направленной вдоль обхода контура, B₁ = Bcos — составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода),  — угол между векторами В и dl.

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной m₀ на алгебраическую сумму токов, охватываемых этим контуром:

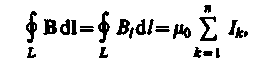(118.1)

где n — число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого .образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Например, для системы токов, изображенных на рис. 173,

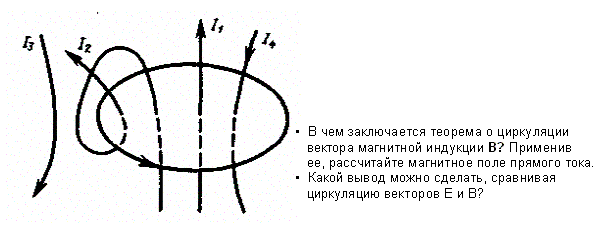
Рис. 173

Выражение (118.1) справедливо только для поля в вакууме, поскольку, как будет показано ниже, для поля в веществе необходимо учитывать молекулярные токи.

Продемонстрируем справедливость теоремы о циркуляции вектора В на примере магнитного поля прямого тока /, перпендикулярного плоскости чертежа и направленного к нам (рис. 174). Представим себе замкнутый контур в виде окружности радиуса к. В каждой точке этого контура вектор В одинаков по модулю и направлен по касательной к окружности (она является и линией магнитной индукции). Следовательно, циркуляция вектора В равна

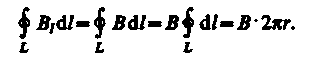
Согласно выражению (118.1), получим В2r =m₀I (в вакууме), откуда

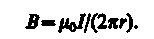
Рис. 174

Таким образом, исходя из теоремы о циркуляции вектора В получили выражение для магнитной индукции поля прямого тока, выведенное выше (см. (110.5)).

Сравнивая выражения 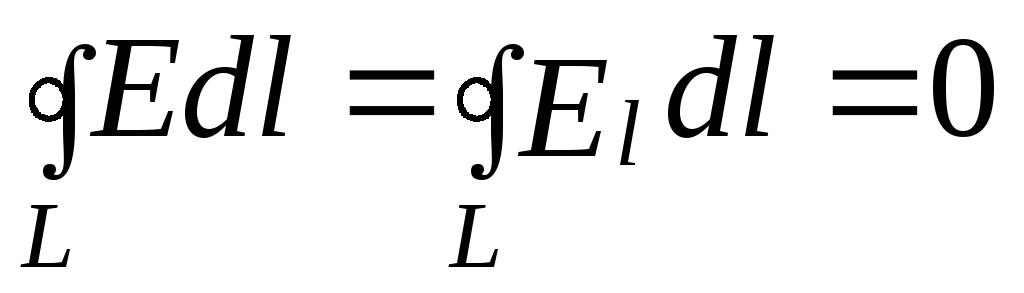и для циркуляции векторов Е и В, видим, что между ними существует принципиальное различие. Циркуляция вектора В электростатического поля всегда равна нулю, т. е. электростатическое поле является потенциальным. Циркуляция вектора В магнитного поля не равна нулю. Такое поле называется вихревым,

Теорема о циркуляции вектора В имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био — Савара — Лапласа.

7.Магнитное поле земли. Магнитные полюсы Земли. Элементы земного магнетизма.

Магнитное поле Земли (геомагнитное поле) — магнитное поле, генерируемое внутриземными источниками. В 1600 году английский ученый Уильям Гильберт в своей книге «О магните, магнитных телах

и большом магните — Земле». представил Землю, как гигантский постоянный магнит, ось которого

не совпадает с осью вращения Земли (угол между этими осями называют магнитным склонением). Гильберт подтвердил свое предположение на опыте:он выточил из естественного магнита большой шар и, приближая к поверхности шара магнитную стрелку, показал, что она всегда устанавливается так же, как стрелка компаса на 3емле.

Графически магнитное поле Земли похоже на магнитное поле постоянного магнита. Основная причина наличия магнитного поля Земли в том, что ядро Земли состоит из раскаленного железа (хорошего проводника электрических токов, возникающих внутри Земли).Магнитное поле Земли образует магнитосферу, простирающуюся на 70-80 тыс. км

в направление Солнца. Она экранирует поверхность Земли, защищает от вредного влияния заряженных частиц, высоких энергий и космических лучей, определяет характер погоды.

Северный магнитный полюс — условная точка на земной поверхности, в которой магнитное поле Земли направлено строго вниз (под углом 90° к поверхности). Следует отметить, что с физической точки зрения этот полюс является «южным», поскольку притягивает северный полюс стрелки компаса. Расположение северного магнитного полюса не совпадает с географическим северным полюсом. Противоположностью северного магнитного полюса является южный магнитный полюс, который расположен в Антарктике. Если провести условную линию от одного полюса до другого, то она не пройдёт точно через центр Земли. Это связано с тем, что магнитное поле Земли не совсем симметрично.

Магнитное склонение, наклонение, горизонтальная и вертикальная составляющие вектора напряженности магнитного поля Земли являются элементами земного магнетизма. Величины этих элементов изменяются во времени, что вызывает необходимость периодического проведения магнитометрических измерений. По данным этих измерений составляются магнитные карты, на которые наносятся элементы земного магнетизма в виде изолиний, то есть линий, соединяющих точки с одинаковым значением какого-либо элемента. Магнитные карты составляются к определенному моменту времени, который принято называть эпохой магнитной карты. Обычно этим моментом является 00 ч 00 мин по гринвичскому времени на 1 июля.

Изолинии магнитных склонений называются изогонами, магнитного наклонения — изоклинами, вертикальной и горизонтальной составляющих — изодинами (иногда изодинамами). Изогоны магнитного склонения наносятся на все аэронавигационные карты.

Кроме изогон на полетных и бортовых картах указываются магнитные аномалии (районы со значительным изменением магнитного склонения).