Закон полного тока

Дата публикации: 20 февраля 2015.
Категория: Электротехника.

Пусть произвольная замкнутая линия l пронизывает проводник с током (рисунок 1), то есть они сцепляются друг с другом как два звена цепи. Вокруг проводника возникает магнитное поле.

Рисунок 1. Закон полного тока

Построим вектор напряженности H, создаваемой током в точке А, расположенной на линии l. Если линия охватывает несколько проводников с током, то для каждого тока строятся векторы напряженности в данной точке линии. Складывая геометрически отдельные векторы напряженности, находим вектор результирующей напряженности магнитного поля.

Вектор результирующей напряженности H в общем случае образует с элементом длины Δl угол α. Поэтому продольная или тангенциальная составляющая H_l результирующей напряженности H будет:

H_l = H

× cos α.

Если разбить замкнутую линию на n элементов длины и сложить произведения длин всех элементов на тангенциальные составляющие результирующей напряженности в этих элементах, получим следующую сумму:

Эту сумму можно представить так:

где знак  означает сумму от k = 1 до k = n.

В теоретической электротехнике доказывается, что указанная сумма равна алгебраической сумме токов, сцепляющихся с контуром суммирования подобно тому, как сцепляются между собой два смежных звена цепи.

Следовательно, можно записать так:

Эта формулировка называется законом полного тока. Для случая, когда контур многократно пронизывает один и тот же виток, как, например,  при наличии обмотки с числом витков w, полный ток будет:

Если замкнутый контур суммирования совпадает с магнитной линией, то вектор напряженности в любой точке контура будет направлен по касательной к элементу длины Δ

l.

В этом случае

и закон полного тока принимает вид:

Если значение напряженности для всех точек контура при этом одинаково, а сумма Δl по контуру равна l, то формула закона полного тока запишется так:

Закон полного тока является основным законом при расчете магнитных цепей и дает возможность в некоторых случаях легко определять напряженность поля.

Например, применяя закон полного тока для определения напряженности на расстоянии a от прямолинейного проводника с током, имеем:

l = 2 × π × a .

Поэтому

H × 2 × π × a = I ,

откуда

Рисунок 2. К определению напряженности поля катушки, намотанной на кольцо

Чтобы определить напряженность поля внутри катушки, намотанной на кольцо (рисунок 2), воспользуемся опять законом полного тока. Контуром здесь является окружность радиуса r. Контур пронизывает w витков с токами одного направления:

H × 2 × π × r = I × w .

Обозначая длину средней линии кольца через l = 2 × π × r , получаем:

H × l = I × w ,

откуда

Таким образом, напряженность поля катушки пропорциональна произведению числа ампер на число витков или числу ампер-витков.

I × w называется намагничивающей силой и обозначается буквой F. Так как w – число отвлеченное, то намагничивающая сила измеряется в амперах.

Магнитная индукция внутри катушки будет:

Если площадь поперечного сечения кольца по всей длине одинакова и равна S, то, зная магнитную индукцию B, можно определить магнитный поток Ф:

Эту же формулу можно представить в ином виде:

По своему строению эта формула напоминает формулу Ома. Выше было указано, что произведение I × w называется намагничивающей силой. Выражение

 стоящее в знаменателе, называется магнитным сопротивлением и обозначается буквой R_м:

Из этой формулы видно, что магнитное сопротивление пропорционально длине пути и обратно пропорционально сечению материала, по которому проходит магнитный поток.

Таким образом, магнитный поток Ф пропорционален намагничивающей силе F и обратно пропорционален магнитному сопротивлению R_м:

Рисунок 3. Закон полного тока для вакуума

Источник: Кузнецов М.И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.

Закон полного тока

Еще в 19-м веке экспериментальным путем было установлено, что электрический ток, протекающий по проводникам, вызывает появление магнитного поля в окружающем пространстве. На основании этого научного факта был сформулирован закон полного тока. Это положение нашло широкое применение в электротехнике, особенно в тех областях, где имеет место непосредственное использование электромагнетизма.

Основные понятия закона полного тока

Для того чтобы наглядно представить себе, как работает этот закон, необходимо ограничить в пространстве условную поверхность S таким же условным контуром L. Направление обхода на нем устанавливается таким образом, чтобы движение от конца вектора происходило против часовой стрелки, вдоль контура элементарной площадки dS.

Затем необходимо представить себе поверхность S, которую пронизывает отдельно взятая система токов. В случае дискретного характера такой системы в нее могут входить отдельные проводники, или она может непрерывно распределяться, как это происходит с электронным потоком. Если не рассматривать конкретно физическую природу этих токов, следует теоретически предположить их непрерывное распределение в пространстве с какой-то плотностью .

В этом случае значение полного тока, пронизывающего контур, будет выглядеть в виде следующей формулы:

Таким образом, в соответствии с законом полного тока, вектор напряженности магнитного поля, циркулирующий вдоль контура L, инициированный протекающим током , становится равным полному току, согласно формуле:

Данное соотношение закон полного тока легко переводит в интегральную форму, то есть плотность тока оказывается непосредственно связанной с напряженностью магнитного поля:

Если принять за факт, что , то в этом случае  получается формула, отражающая закон полного тока в дифференциальной форме:

Как рассчитать полный ток

Расчеты полного тока можно выполнить довольно простым способом. Контур в магнитном поле обходится в определенном направлении, которое условно принимается за положительное. Токи, пронизывающие данный контур, также могут считаться положительными, если их направление полностью совпадает с тем же направлением, в каком поступательно двигается буравчик. Рукоятка этого буравчика должна вращаться в том же направлении, в каком осуществляется обход контура – в положительном. Пронизывающие токи могут иметь положительное и отрицательное значение. Поэтому сумма полного тока будет выглядеть следующим образом: ∑I = I₁ – I₂, где I₁ является положительным током, а I₂ – отрицательным.

Значения магнитной индукции и напряженности поля в отдельно взятых точках могут быть одинаковыми или разными. Если предположить, что в некоторой точке а образуется угол между вектором напряженности поля и элементом длины контура dl. 

Таким образом, появляется формула: H_L = Hcosa, представляющую собой касательную с контуром и вектором напряженности магнитного поля. Величина магнитного напряжения HLdl, затрагивающего элементарный участок контура dl будет положительной при условии совпадения вектора H_L с направлением, выбранным в обход контура. В противном случае оно будет иметь отрицательное значение.

В соответствии законом полного тока, магнитодвижущая сила (F), проходящая вдоль контура, равна значению полного тока, проходящего через поверхность, ограниченную данным контуром. Это будет выглядеть следующим образом:

или

В некоторых случаях значения индукции и напряженности поля во всех точках будут одинаковыми. В этом случае закон полного тока в самом простом варианте представляет собой такую формулу: H_L =∑I, где вектор напряженности магнитного поля циркулирует по окружности замкнутого контура.

3.6.Закон полного тока

Закон полного тока, или теорема о циркуляции вектора , которая будет рассмотрена ниже, позволяет находить напряженность магнитного поля при наличии симметрии токов без применения закона Био – Савара — Лапласа. Это дает возможность существенно упростить вычисления в ряде случаев.

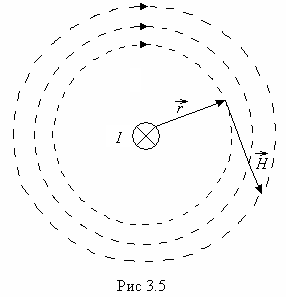
Основное отличие магнитного поля от электростатического состоит в том, что магнитное поле непотенциально . Докажем это. Рассмотрим магнитное поле бесконечного прямолинейного проводника с током. Силовые линии (линии напряженности) этого поля представляют собой окружности, плоскости которых перпендикулярны к проводнику, а центры лежат на оси проводника ( рис.3.5). Циркуляция вектора напряженности магнитного поля вдоль произвольной силовой линии L равна

.

При этом L — окружность радиуса r, модуль напряженности по закону Био –Савара-Лапласа равен

.

Вектор направлен по касательной к окружности, поэтому. Тогда(3.1)

— циркуляция вектора вдоль силовой линии не равна нулю, следовательно,

магнитное поле прямолинейного тока непотенциально.

Из выражения (1) следует, что циркуляция вектора магнитного поля прямолинейного тока одинакова вдоль любой силовой линии и равна силе тока.

Формула (3.1) справедлива для замкнутого контура L произвольной формы, охватывающего бесконечно длинный прямолинейный проводник с током I.

Действительно, рассмотрим контур (силовую линию) произвольной формы (рис.3.6). ТочкаА этого контура находится на расстоянии r от оси проводника с током. Из оси проводника проведем окружность радиуса r через точку А. Тогда вектор направлен по касательной к этой окружности, следовательно, он перпендикулярен к радиус – вектору. Элемент силовой линиив точкеА направлен по касательной к контуру L. Тогда ,

где – длина проекции векторана направление вектора. Но малый отрезоккасательной к окружности радиусаr можно заменить дугой этой окружности: , где 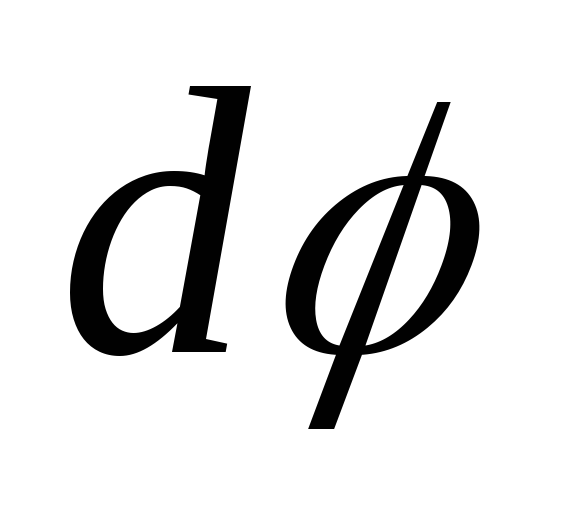– центральный угол, под которым виден элементконтураL из центра окружности. Тогда:

,

ациркуляция вектораравна:

(3.2)

— результат тот же, что и для случая, когда L — окружность.

Таким образом, циркуляция вектора напряженности магнитного поля прямолинейного проводника с током I вдоль замкнутого контура произвольной формы, охватывающего проводник, не зависит от формы контура и численно равна силе тока I.

Рассмотрим случай, когда контур не охватывает проводник с током (рис.3.7). В этом случае циркуляция векторапо контуруL равна сумме циркуляций вектора по участку контура 1a2 и участку контура 2b1, т.е.

(3.3)

— циркуляция вектора напряженности магнитного поля прямолинейного проводника с током вдоль замкнутого контура, не охватывающего этот проводник, равна нулю.

Можно показать, что формулы (3.2) и (3.3) являются универсальными, т.е. справедливы для проводника любой формы и размеров.

На практике магнитное поле создается, как правило, несколькими проводниками, по которым текут токи ,, … ,. Каждый проводник с током создает магнитное поле напряженностью ( ). Согласно принципу суперпозиции, напряженность результирующего поля равна:

.

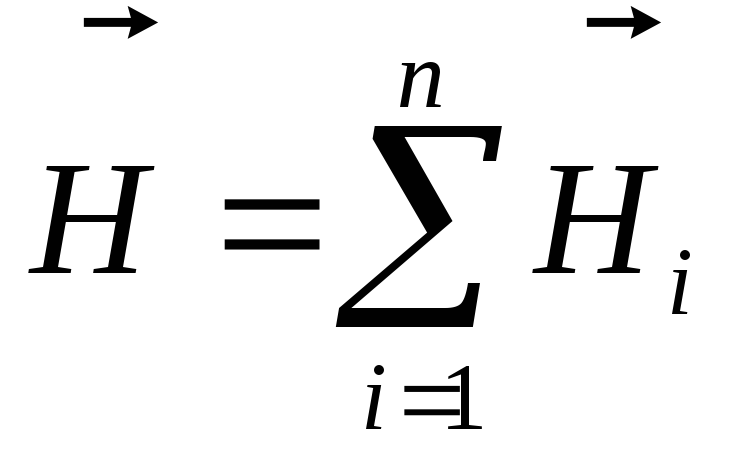Циркуляция вектора напряженности вдоль произвольного замкнутого контураL равна:

.

Но, согласно формулам (2) и (3),

,если контур L охватывает ток ;

0 , если контур L не охватывает тока .

Таким образом, . (3.4)

В выражении (3.4) индекс i заменен индексом к для того, чтобы подчеркнуть, что в эту сумму входят только токи, охватываемые контуром L. Формула (3.4) выражает закон полного тока для токов проводимости: циркуляция вектора напряженности магнитного поля постоянного электрического тока вдоль замкнутого контура равна алгебраической сумме токов, охватываемых эти контуром.

Если контур несколько раз охватывает ток, то величина тока учитывается столько раз, сколько раз контур обвивается вокруг тока с учетом направления обхода и знака тока.

Если токи текут непрерывно по поверхности S, то сумму токов можно заменить интегралом:

,

где — вектор плотности тока. Тогда закон полного тока (3.4) принимает вид:

,

или

. ( 3.5)

Здесь ( мы рассматриваем поле в вакууме),L – контур, на который опирается поверхность S. Согласно теореме Стокса , тогда из (3.5) получаем:

, (3.6)

— ротор вектора магнитной индукции отличен от нуля – магнитное поле непотенциально.

Поле, ротор которого отличен от нуля, называется вихревым или соленоидальным.

Выражение (3.6) представляет собой дифференциальную форму записи закона полного тока.

С помощью закона полного тока (3.6) найдем напряженность магнитного поля внутри соленоида. Пусть длина соленоида много больше его радиуса, . Такой соленоид можно

считать соленоид бесконечным. Если витки соленоида расположены вплотную или очень близко друг к другу, то соленоид можно приближенно рассматривать как систему большого числа последовательно соединенных круговых токов одинакового радиуса, центры которых лежат на оси соленоида, а плоскости ортогональны ей. Легко видеть, что линии магнитной индукции соленоида параллельны его оси (рис.3. 8). Все поле сосредоточено внутри соленоида, вне соленоида поля нет и .

Для нахождения H выделим участок соленоида длины , на котором расположеновитков, (n— число витков на участке соленоида единичной длины), и проведем контур 1234 . Согласно (рис. 3.8) закону полного тока (3.4) имеем:

.

На участках 1,2 и 3,4 контур перпендикулярен к вектору , поэтому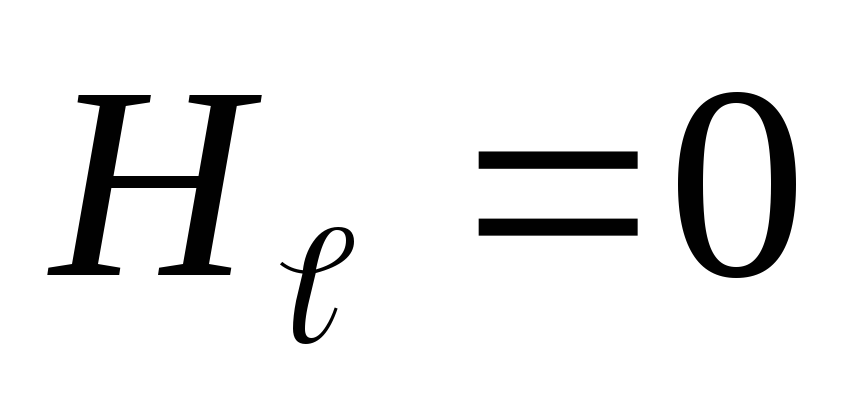и

.

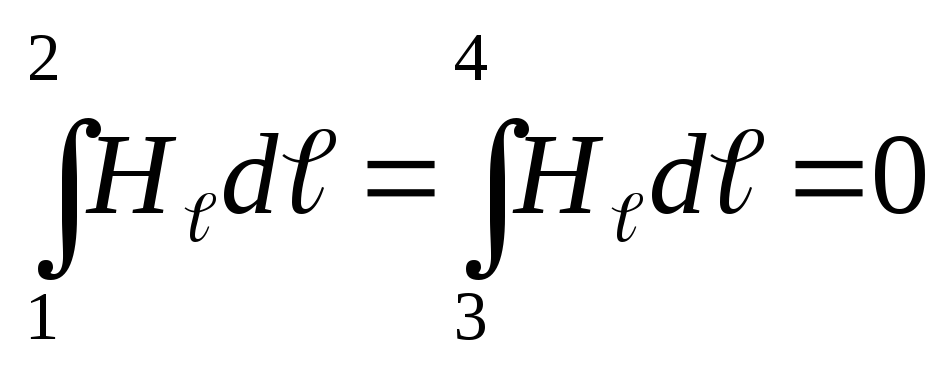Участок 4,1 находится вне соленоида, следовательно, и , следовательно,.

Тогда , и . Сократив на , окончательно получаем:

.

Из этого выражения видно, что не зависит ни от расстояния до оси соленоида, ни от размеров самого соленоида. При фиксированном значении силы тока, поле соленоида однородно.

ЛЕКЦИЯ13

7.2. Закон полного тока

Напряженность магнитного поля может быть найдена расчетным путем из закона полного тока, согласно которому линейный интеграл напряженности магнитного поля вдоль замкнутого контура равен полно­му току, охватываемому этим контуром:

(7.3)

где dl — вектор, равный по модулю элементу длины dl и направлен­ный по касательной к контуру в сторону обхода контура; ∑I — полный ток, т. е. алгебраическая сумма токов, пронизывающих по­верхность, ограниченную контуром интегрирования. Выбрав произвольно положительное направление обхода контура, считают положительными те токи, направление которых совпадает с поступательным движением правоходового винта, вращающегося по направлению обхода контура, т. е. направление магнитного поля которых совпадает с направлением об­хода контура. Например, для контура рис. 7.3 токи I₁ и I₂ положительны, а ток I₃ отрицателен.

Векторы Н и В в изотропной среде направлены в одну сторону, в анизотропной среде их направления могут не совпадать. Так, в цепях с постоянными магнитами векторы В и Н могут быть сдвинуты отно­сительно друг друга на 180°. Однако на практике в большинстве случаев расчеты производят в предположении, что векторы В и Н совпадают по направлению. Если интегрирование производится по контуру, состоящему из W витков, через которые проходит ток I, то закон полного тока имеет вид

(7.4)

Интеграл напряженности магнитного поля вдоль рассматриваемого замкнутого контура называют магнитодвижущей силой (м. д. с.) этого контура. Магнитодвижущую силу обычно принято обозначать F. Едини­цей м. д. с. является ампер или ампер-виток. Магнитодвижущая сила -скалярная величина, которая характеризует намагничивающее действие электрического тока. Введя понятие м. д. с., закон полного тока можно сформулировать следующим образом: м. д. с. вдоль замкнутого контура равна полному току, охватываемому этим контуром.

При расчете напряженности магнит­ного поля согласно закону полного тока целесообразно замкнутый контур выби­рать совпадающим с замкнутой линией магнитной индукции, а направление об­хода контура — совпадающим с направ­лением этой линии. В этом случае угол между векторами Н и dl равен нулю, Hdl = Hdl и закон полного тока имеет вид

(7.5)

Понятие м. д. с. можно применить к любому участку аb линии напряжен­ности магнитного поля.

При этом м. д. с.

Следовательно, напряжен­ность магнитного поля т. е. численно равна м. д. с., приходящейся на единицу длины в направлении линии напря­женности поля. Если магнитное поле существует в изотроп­ной среде, то напряженность магнитного поля можно рассматри­вать как м. д. с., приходящуюся на единицу длины линии магнитной индукции. Когда физические условия вдоль всей рассматриваемой линии магнитной индукции одинаковы, тогда напряженность поля Н вдоль этой линии равна частному от деления м. д. с. на длину линии магнитной индукции.

В большинстве электротехнических устройств напряженность магнит­ного поля вдоль линии магнитной индукции изменяется в зависимости от физических условий участков, через которые она проходит. Путь, в котором имеются ферромагнитные тела или какие-либо другие тела или среды, образующие замкнутую систему, в которой при наличии м. д. с. образуется и замыкается магнитный поток и физические условия на участках различны, делится на ряд участков, в пределах каждого из которых напряженность поля практически можно считать постоянной. Это позволяет в формуле закона полного тока заменить интегрирование суммированием. Далее будет показано, что закон полного тока, устанавливающий связь между магнитным полем и создающим его электрическим током, лежит в основе расчета магнитных цепей.

3.2. Закон полного тока

Напряженность магнитного поля Н является векторной величиной. Если определить напряженность во всех точках магнитного поля, то можно провести линии, во всех точках которых направление касательных к ним совпадает с направление вектора Н. Эти линии называют линиями напряженности магнитного поля. Единицей напряженности магнитного поля в СИ является А/м.

Напряженность магнитного поля может быть найдена из закона полного тока, согласно которому линейный интеграл напряженности магнитного поля вдоль замкнутого контура равен полному току, охватываемому этим контуром

,

где dl – вектор, равный по модулю элементу длины dl и направленный по касательной к контуру в сторону обхода контура; − полный ток, т. е. алгебраическая сумма токов, пронизывающих поверхность, ограниченную контуром интегрирования. Выбрав произвольно положительное направление обхода контура, считают положительными токи, направление магнитного поля которых совпадает с направлением обхода контура. Если интегрирование производится по контуру, состоящему изW витков, через которые проходит ток I, то закон полного тока имеет вид .

Интеграл напряженности магнитного поля вдоль рассматриваемого замкнутого контура называют магнитодвижущей силой (МДС) этого контура F. Единицей МДС является ампер или ампер-виток. Магнитодвижущая сила F характеризует намагничивающее действие электрического тока. Введя понятие МДС, закон полного тока можно сформулировать следующим образом: МДС вдоль замкнутого контура равна полному току, охватываемому этим контуром.

Понятие МДС можно применить к любому участку ab линии напряженности магнитного поля. ,

следовательно, напряженность магнитного поля H = dF/dl, т.е. численно равна МДС, приходящейся на единицу длины в направлении линии напряженности поля.

Закон полного тока, устанавливающий связь между магнитным полем и создающим его электрическим током, лежит в основе расчета магнитных цепей.

3.3. Основные характеристики ферромагнитных материалов

Магнитная индукция зависит не только от тока, возбуждающего магнитное поле, но и от среды, в которой она существует. Влияние среды на магнитное поле характеризуется абсолютной магнитной проницаемостью среды ,

где − относительная магнитная проницаемость среды; Гн/м. Здесь Гн (генри) – единица индуктивности.

Вещества, у которых > 1, называются парамагнетиками, а< 1 –диамагнетиками. Для диамагнетиков и парамагнетиков,= 1. Эти вещества – неферромагнитные.

Особо важное значение в практической электротехнике имеют ферромагнитные материалы, обладающие исключительно большой магнитной проницаемостью, , эта разница (железо, никель, и их сплавы) может быть в сотни раз. Ферромагнетики, способны намагничиваться в магнитном поле до насыщения, при отсутствии внешнего поля суммарный момент ферромагнетика равен нулю. Под действием внешнего поля намагниченные области ориентируются в направлении поля, во много раз усиливая его. Поэтому в ферромагнитных материалах при одной и той же напряженности магнитного поля магнитная индукция во много раз больше, чем в неферромагнитных материалах. Большая магнитная проницаемость ферромагнетиков используется для усиления магнитных полей в электрических машинах.

Если вектор магнитной индукции поля, созданного током катушки в неферромагнитной среде, , то в намагниченном ферромагнетике имеется добавочное поле, с магнитной индукцией, которая усиливает поле, создаваемое током катушки. Вектор магнитной индукции результирующего поля намагниченного ферромагнетикаВ в этом случае равен геометрической сумме вектором и..

Если поместить ферромагнетик, магнитный момент которого первоначально был равен нулю, в магнитное поле, то линия 0 — 1 на рис. 3.3. будет соответствовать кривой первоначального намагничивания В(Н). Если намагнитить ферромагнетик до насыщения (1 на рис. 3.3.), а затем начать размагничивать его, т.е. уменьшать напряженность поля от до 0, получим кривую, которая не совпадает с кривой первоначального намагничивания. В отсутствие внешнего поля (Н = 0) намагничивание ферромагнетика не исчезает и характеризуется некоторым значением остаточной индукции . Для полного размагничивания необходимо к ферромагнетику приложить поле с напряженностью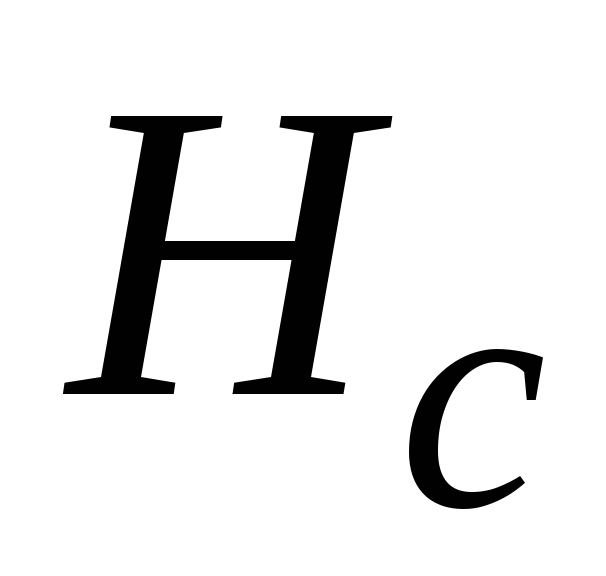, имеющее направление, противоположное намагничивающему полю –коэрцитивную силу.Способность ферромагнетиков обладать остаточной индукцией дает возможность изготовлять постоянные магниты.

Рис. 3.3.

Если периодически намагничивать ферромагнетик в прямом и обратном направлении, то зависимость В(Н) имеет вид петли гистерезиса (рис. 3.4., сплошная кривая 1-2-3-4-5-1). Явление отставания измерений магнитной индукции В от изменения напряженности поля Н называется магнитным гистерезисом. Частых циклов может быть сколько угодно много, все они будут находится внутри петли гистерезиса.

Для увеличения магнитного потока магнитопроводы изготовляют из ферромагнитных материалов. Магнитопроводы бывают разнообразной формы. Часть электротехнического устройства, которая необходима для создания в нем магнитного поля необходимой интенсивности, называется магнитной цепью. Магнитная цепь состоит из магнитопровода и элементов, возбуждающих магнитное поле, например обмоток с током, надеваемых на магнитопровод. Простейшей магнитной цепью является кольцевой магнитопровод из ферромагнитного материала с равномерно нанесенной на нем намагничивающей катушкой.

Закон полного тока (Ампера)

В начале XIXвека датский физик Эрстед установил важнейший для теории электромагнетизма экспериментальный факт, который заключается в том, что протекание электрического тока по проводникам приводит к возникновению в окружающем пространстве магнитного поля. Это открытие позволило французскому ученому Амперу сформулировать закон, носящий в настоящее время название закона полного тока.

Рассмотрим в пространстве воображаемый контур , ограничивающий поверхность. Зададим на этом контуре направление обхода так, чтобы движение вдоль контура с конца вектора элементарной площадки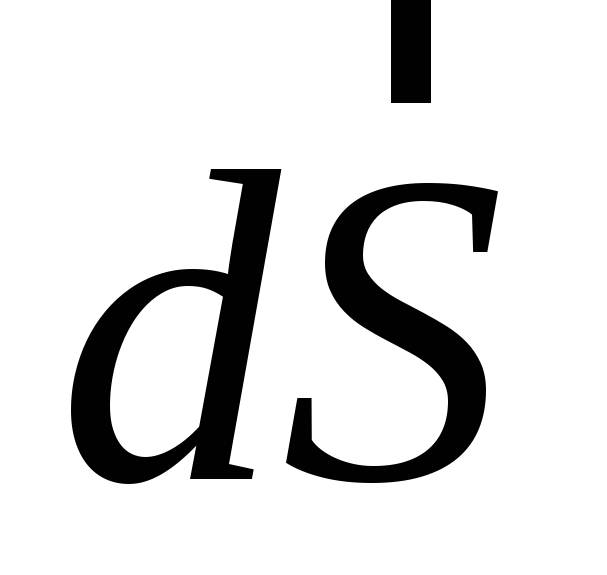наблюдалось в направлении против часовой стрелки (рисунок Рисунок 27 ). Предположим далее, что поверхностьпронизывается векторным полем токов, распределенных в пространстве с некоторой плотностью. Это может быть как система дискретных проводников, так и непрерывно распределенный электронный поток. Тогда полный ток, пронизывающий контур, определится как поток вектора плотности токачерез поверхностьв виде

,

где − вектор плотности тока проводимости,− поверхность, ограниченная контуром.

27. −К закону полного тока

Закон полного тока гласит, что циркуляция по контуру вектора напряженности магнитного поля, вызванного протеканием тока, равна полному току:

,

.

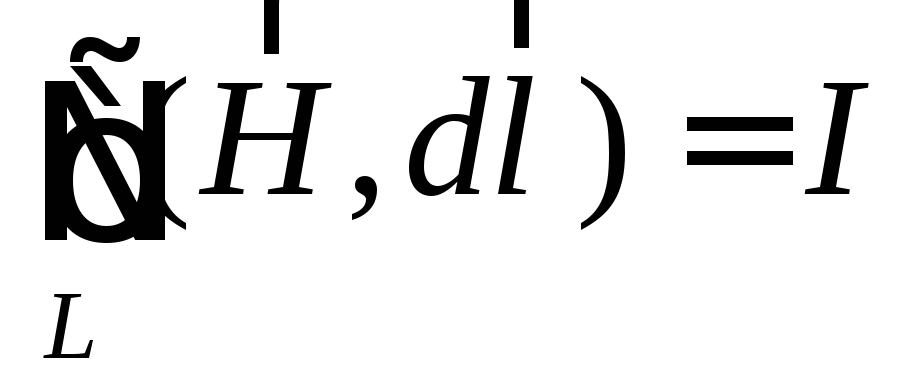Физический смысл этой формулы заключается в том, что при перемещении электрических зарядов, выражающемся в появлении электрического тока, появляется магнитное поле.

4. Параметры сред, классификация сред

Векторы исвязаны с векторамиичерез макроскопические, т.е., усредненные параметры среды:− электрическая проницаемость,− магнитная проницаемость,−удельная проводимость.

Параметры ,,полностью характеризуют реакцию среды на электромагнитное поле, определяют макроскопические электромагнитные свойства среды. Диэлектрическая проницаемостьхарактеризует способность среды поляризоваться при воздействии электрического поля. Магнитная проницаемостьхарактеризует способность среды намагничиваться при воздействии магнитного поля. Удельная проводимость средыхарактеризует степень электропроводности.

Связь между соответствующей парой векторов поля в веществе выражается через параметры ,,следующими уравнениями состояния:

,,.

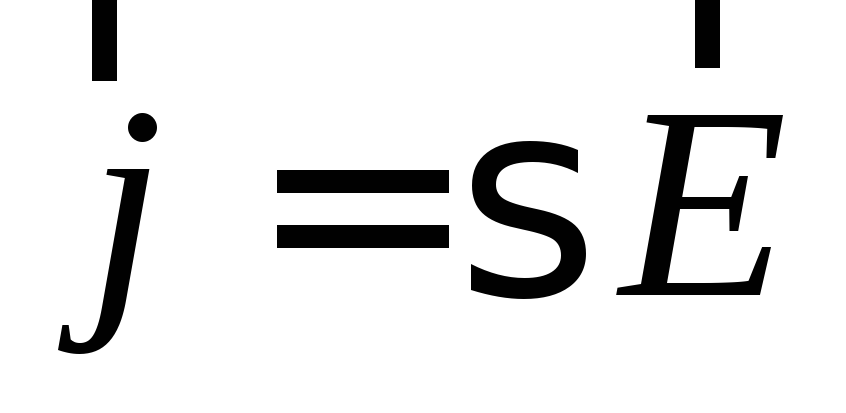Макроскопические электромагнитные параметры среды определяются экспериментально.

В вакууме векторы и,исвязаны соотношениями

,,

где − диэлектрическая проницаемость свободного пространства (вакуума),− магнитная проницаемость свободного пространства (вакуума).

Часто, особенно в курсе антенн и устройств СВЧ, пользуются не абсолютными величинами диэлектрической и магнитной проницаемостей, а относительными, взятыми по отношению к и:− относительная диэлектрическая проницаемость,− относительная магнитная проницаемость.

На рисунке Рисунок 28 приведена фотография прибора AgilentE4991A, используемого для измерения параметров сред. Этот прибор есть у нас в институте.

28. −Прибор AgilentE4991Aдля определения параметров сред

В зависимости от свойств параметров ,исреды подразделяются на линейные и нелинейные.

Линейные среды – среды, в которых параметры ,ине зависят от величин и направлений электрического и магнитного полей; в этом случае зависимости,являются линейными ()

29. − Нелинейные и линейные среды

Нелинейные среды – среды, в которых параметры ,,, или хотя бы один из них, зависят от величины электрического или магнитного полей. В этом случае соотношения,оказываются нелинейными функциями.

Строго говоря, все реальные среды являются нелинейными. Однако при не очень сильных полях в большинстве случаев, представляющих практический интерес, можно пренебречь зависимостью параметров ,,от величины электрического и магнитного полей и считать рассматриваемые среды линейными. В нашем курсе в дальнейшем мы будем рассматривать только линейные среды. Примерами нелинейных сред при слабых полях являются ферромагнетики (магнитная нелинейность) и сегнетоэлектрики (электрическая нелинейность).

Линейные среды, в свою очередь, делятся на неоднородные и однородные, изотропные и неизотропные.

Однородными называют среды, параметры которых ,,не зависят от координат, т.е., одинаковы во всех точках рассматриваемой среды.

Неоднородными называют среды, у которых хотя бы один из параметров ,,является функцией пространственных координат:,,.

Изотропными называют среды, электромагнитные свойства которых одинаковы по всем направлениям, т.е. не зависят от направления векторов внешнего поля. Для изотропных сред параметры ,,являются скалярами, а векторыи,ипараллельны друг другу и связаны соотношениями

,.

Подавляющее большинство сред относится к изотропным. Однако существует ряд сред, свойства которых существенно зависят от направления векторов внешнего электромагнитного поля. Такие среды называют анизотропными. В них пары векторов и,имогут быть непараллельными и, по крайней мере, один из параметров,,является тензором.

Например, вектор направлен по оси, т.е., имеет одну составляющую, а векторне совпадает по направлению с вектороми имеет все три составляющие:,,(рисунок Рисунок 30 ). Каждая из составляющих векторапропорциональна векторус разными коэффициентами пропорциональности:

,,.

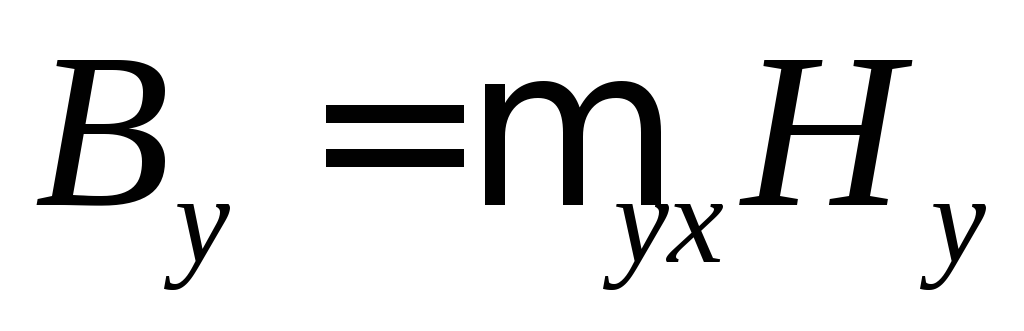30. −Анизотропная система

В общем случае каждая проекция вектора на оси координат зависит от всех трех составляющих вектора, связь между ними определяется системой уравнений:

Таким образом, параметр анизотропной ферромагнитной среды характеризуется девятью коэффициентами, записываемыми в виде матрицы − тензора:

.

В этом случае векторы исвязаны соотношением

.

Аналогично для анизотропного диэлектрика

,

где − тензор диэлектрической проницаемости.

Примерами анизотропных сред являются кристаллы, намагниченные ферриты и др.

Следует отметить, что для большинства сред можно считать , и тогда.

5.2. Закон полного тока для магнитного поля в веществе

Закон полного тока для магнитного поля в вакууме состоит в том, что циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром. Запишем его:

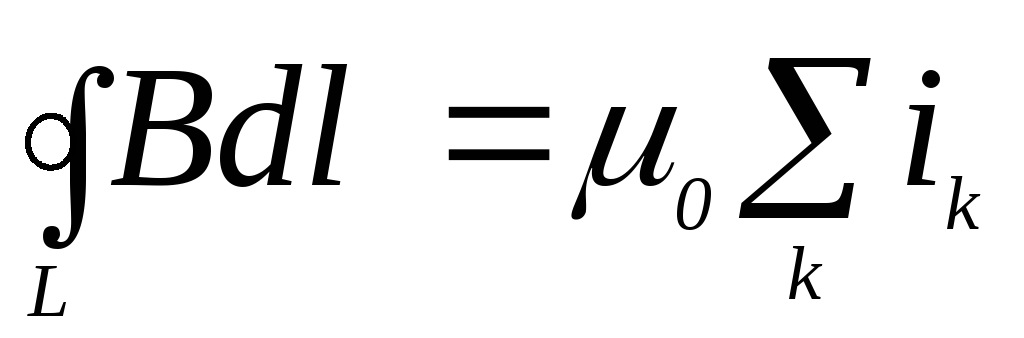. (5.4)

Обобщим закон полного тока на случай магнитного поля в веществе. Для этого нужно учесть все токи, охватываемые контуром: как макротоки (токи проводимости), так и микротоки (молекулярные токи).

Тогда для магнитного поля в веществе имеем:

. (5.5)

Здесь — алгебраическая сумма молекулярных токов, охватываемых замкнутым контуромL. Выразим ее через вектор намагниченности.

Рассмотрим произвольный замкнутый контурL. Контур охватывает множество молекулярных токов (рис.5.2). Но вклад в сумму будут вносить только те токи, плоскость которых пересекается контуром (1, 2, 3, 4).

Пусть некоторый элемент контура образует с вектором намагниченностиугол(рис.5.3). Тогда элементпересекает только те молекулярные токи, центры которых попали внутрь косого цилиндра, основания которого равныS^/ (площади, охватываемой отдельным молекулярным током). Объём этого цилиндра равен

. (5.6)

Число молекулярных токов, охватываемых элементом , равно:

. (5.7)

Здесь n – концентрация молекул.

Сумма молекулярных токов, охватываемых всем замкнутым контуром, равна:

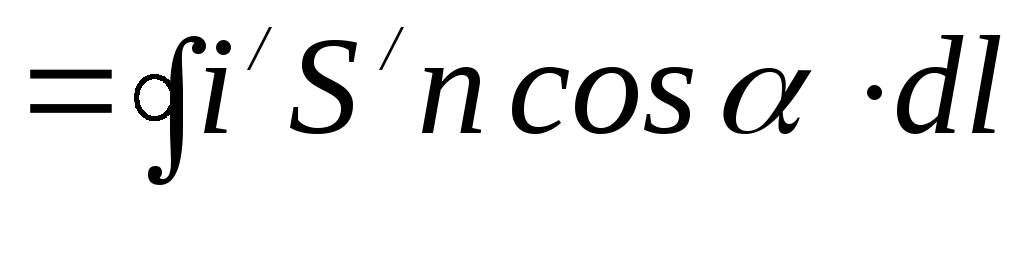. (5.8)

В этом выражении произведение равно магнитному моменту отдельной молекулы, а— магнитному моменту единицы объема вещества или вектору намагниченности . Тогда

или . (5.9)

Подставим выражение (5.9) в формулу (5.5), получим:

. (5.10)

Перенесем интеграл из правой части формулы (5.10 в левую, и разделим все выражение на :

. (5.11)

Обозначим

. (5.12)

Вектор называетсянапряжённостью магнитного поля.Учитывая обозначение (5.12), формулу (5.11) можно записать в виде:

. (5.13)

Выражение (5.13) называется законом полного тока для магнитного поля в веществе. Циркуляция вектора напряженности по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов проводимости, охватываемых этим контуром.

Примечание. Из формул (5.12) и (5.13) следует:

• напряженность магнитного поля и намагниченность имеют одинаковую размерность;

• напряженность характеризует магнитное поле, создаваемое токами проводимости.

5.3. Магнитные моменты электронов и атомов

Магнитные свойства вещества, в конечном счете, обусловлены магнитными свойствами составляющих его частиц. Исследования показали, что магнитные моменты протонов и нейтронов малы по сравнению с магнитными моментами электронов. Следовательно, магнитные свойства атома целиком определяются электронами.

Всякий атом можно рассматривать как динамическую систему, состоящую из ядра и движущихся вокруг его электронов.

Будем считать, что электроны в атомах движутся по круговым орбитам. Движение электрона по замкнутой орбите представляет собой ток. Направление тока противоположно движению электрона (рис.5.4).

Пусть – угловая скорость вращения электрона. Вектор угловой скорости образует с направлением движения электрона правовинтовую систему.

Величина орбитального тока равна

. (5.14)

Ему соответствует орбитальный магнитный момент электрона

. (5.15)

Магнитный момент образует с создающим его током правовинтовую систему и направлен противоположно вектору угловой скорости:

, . (5.16)