 Рис.3.16 Рис.3.16 | Пусть по проводнику длиной l и сечением S течет ток I. В проводнике создается электрическое поле напряженности E, а j1 и j2 – потенциалы на концах проводника (рис.3.16). В случае однородного проводника величину j1 — j2 = U можно назвать падением напряжения на участке проводника. |
Закон Ома: сила тока, текущего по однородному участку проводника, прямо пропорциональна падению напряжения на проводнике:
 (3.47)
(3.47)
где R – электрическое сопротивление проводника.
(3.47) – закон Ома в интегральной форме.
Размерность сопротивления в СИ: [R] = В/А = Ом.
Ом – сопротивление такого проводника, в котором при напряжении в 1 В течет ток 1А.
Сопротивление зависит от геометрических размеров и формы проводников, материала и температуры проводников. Для цилиндрического проводника
 (3.48)
(3.48)
где r — удельное сопротивление проводника.
Удельное сопротивление численно равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м2. Размерность удельного сопротивления в СИ: [r] = Ом×м.
Величина, обратная сопротивлению, называется проводимостью.
Величина, обратная удельному сопротивлению, называется удельной проводимостью:
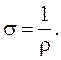
Единица, обратная Ом, называется Сименсом [См].
Учитывая (3.46) — (3.49), а также  , получим:
, получим:
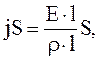

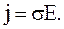 (3.50)
(3.50)
(3.50) – закон Ома в дифференциальной форме.
 Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике:
Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике:
 (Интегральная форма закона) (20.10)
(Интегральная форма закона) (20.10)
Однородным называется проводник, в котором не действуют сторонние силы, т.е. отсутствуют источники ЭДС. В этом случае, как мы видели, напряжение U совпадает с разностью потенциалов j1 — j
Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника
 (20.11)
(20.11)
где l — длина проводника, S — площадь его поперечного сечения, r — зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества. В СИ 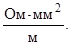
Закон Ома можно записать в дифференциальной форме.
Это уравнение устанавливает связь между дифференциальными характеристиками поля и тока, т.е. между j и Ев одной и той же точке проводника.
Преобразуем выражение (20.10) применительно к цилиндрическому проводнику, являющемуся однородным участком электрической цепи

Если поле однородно, то U = E×l,  и тогда
и тогда

Обозначим 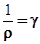 и назовем удельной проводимостью, а
и назовем удельной проводимостью, а  — плотность тока.
— плотность тока.

 (20.12)
(20.12)
В анизотропных телах направления векторов j и Е могут не совпадать.
Закон Ома в интегральной форме
Закон Ома для участка электрической цепи имеет вид:
U = RI
где:
U — напряжение или разность потенциалов,
I — сила тока,
R — сопротивление.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:
I=E/(R+r),
где:
e — ЭДС цепи,
R — сопротивление всех элементов цепи,
r — внутреннее сопротивление источника питания.
Закон Ома в дифференциальной форме
Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
j=σ*E
где
j- вектор плотности тока,
σ — удельная проводимость,
E — вектор напряжённости электрического поля.
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).
Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.
Исто́чник то́ка
Исто́чник то́ка (также генератор тока) — двухполюсник, который создаёт ток , не зависящий от сопротивления нагрузки, к которой он присоединён. В быту «источником тока» часто неточно называют любой источник электрического напряжения (батарею, генератор, розетку), но в строго физическом смысле это не так, более того, обычно используемые в быту источники напряжения по своим характеристикам гораздо ближе к источнику ЭДС, чем к источнику тока.
Идеальный источник тока[править]
Напряжение на клеммах идеального источника тока зависит только от сопротивления внешней цепи:
Мощность, отдаваемая источником тока в сеть, равна:
Так как для источника тока , напряжение и мощность, выделяемая им, неограниченно растут при росте сопротивления.
Реальный источник тока[править]
Реальный источник тока, так же как и источник ЭДС, в линейном приближении может быть описан таким параметром, как внутреннее сопротивление . Отличие состоит в том, что чем больше внутреннее сопротивление, тем ближе источник тока к идеальному (источник ЭДС, наоборот, чем ближе к идеальному, тем меньше его внутреннее сопротивление). Реальный источник тока с внутренним сопротивлением эквивалентен реальному источнику ЭДС, имеющему внутреннее сопротивление и ЭДС .
Напряжение на клеммах реального источника тока равно:
Сила тока в цепи равна:
Мощность, отдаваемая реальным источником тока в сеть, равна:
ЭДС.
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил висточниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.
ЭДС можно выразить через напряжённость электрического поля сторонних сил ( ). В замкнутом контуре ( ) тогда ЭДС будет равна:
, где — элемент длины контура.
ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.
Закон Ома для участка цепи утверждает: сила тока I прямо пропорциональна напряжению U на участке цепи и обратно пропорциональна сопротивлению R
.
Закон Ома можно представить в дифференциальной форме. Через поперечное сечение проводника течет ток силой dI равной dI = jdS. Напряжение, приложенное на концах проводника, будет равно Е·dl (т.к. и dφ = -Edl). Для проводника постоянного сечения длиной l будем иметь
.
Отсюда , где — удельная проводимость проводника. Таким образом, выражение закона Ома в дифференциальной форме в векторном виде будет
j = γ E.
Плотность тока в проводнике прямо пропорциональна напряженности электрического поля в нем.
Рассмотрим замкнутую электрическую цепь, содержащую ЭДС. Источник тока в такой цепи обладает внутренним сопротивлением r. Сопротивление внешней части цепи R называют внешним или сопротивлением нагрузки. Падение напряжения на внутреннем участке цепи равно U1 = Ir, а на внешнем — U =IR. При замкнутой внешней цепи ЭДС источника тока ε равна сумме падений напряжения на внутреннем сопротивлении источника тока и во внешней цепи, ε = Ir + IR, откуда
I = ε / (r + R).
Это есть выражение закона Ома в интегральной форме.
Опытом установлено, что если в проводнике течет ток, то работа сторонних сил расходуется на его нагревание. Предположим, что на концах участка проводника имеется разность потенциалов U = φ1 – φ2.
Тогда работа по переносу заряда Q на этом участке равна
A = Q (φ1 – φ2) = QU.
Если ток постоянный, то
и
A = I · U · t.
Эта работа равна количеству теплоты Q, и формула Q = I · U · t выражает закон Джоуля-Ленца в интегральной форме.
Используя выражение закона Ома получим
.
Преобразуем закон Джоуля–Ленца. Введем плотность тепловой мощности w – величину, равную энергии, выделяемой за время t прохождения тока в единице объема проводника:
,
где S — сечение, l — длина проводника. Подставляя Q = I2 R t и , получим .
Здесь — плотность тока, , и учитывая, что j = γE, получим
.
Это есть выражение закона Джоуля-Ленца в дифференциальной форме. Плотность тепловой мощности в проводнике, по которому течет ток, прямо пропорциональна квадрату напряженности поля в проводнике. Коэффициентом пропорциональности является удельная проводимость проводника.
Магнитное поле.
Магнитное поле – это особая форма материи, которая создается магнитами, проводниками с током (движущимися заряженными частицами) и которую можно обнаружить по взаимодействию магнитов, проводников с током (движущихся заряженных частиц).
Вектор магнитной индукции(В)— это основная силовая характеристика магнитного поля (обозначается В). Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил М.
Бесконечно длинный ток величины I создает на расстоянии r от себя магнитное поле:
где Мо — магнитная постоянная, R — расстояние, I — сила тока в проводнике.
Магнитная индукция — это векторная физическая величина, являющаяся силовой характеристикой в данной точке магнитного поля.
Единица магнитной индукции — тесла (Тл).
Мы бы никогда не знали о магнитном поле, если бы оно себя не проявляло. Определить наличие поля можно стрелкой компаса. Стрелка компаса будет только сигнализатором наличия поля. Для получения количественных величин стрелка непригодна. В качестве измерителя поля можно использовать вращающуюся рамку.
Амплитуда напряжения на токосъемных кольцах равна
Где:
N – число витков в рамке;
Ф – магнитный поток Вб;
ω – угловая частота вращения равная 2π f
По замеренному напряжению можно рассчитать магнитный поток, измеряемый в веберах (Вб). Магнитный поток и есть величина, характеризующая поле. Зная магнитный поток, можно рассчитать напряжение, которое мы можем получить в генераторе. На практике чаще пользуются понятием плотности магнитного потока, т.е. потоком, проходящим сквозь площадку площадью 1 квадратный метр. Плотность магнитного потока называется магнитной индукцией.
B = Ф/ S
Магнитная индукция измеряется в теслах (Тл).
Причиной возникновения магнитного потока является электрический ток. Магнитная индукция на расстоянии r от прямолинейного проводника равна:
По центру витка с током радиуса r магнитная индукция будет равна
Этой характеристикой магнитного потока – индукцией и можно было бы ограничиться при изучении магнетизма. Но традиционно преподается, что электрический ток порождает напряженность магнитного поля, а уж та в свою очередь порождает индукцию.
Это напоминает индийский уклад офиса. В Индии начальник, чтобы включить вентилятор вызывает секретаршу. Та говорит: «Хорошо», — кланяется и уходит; через полчаса приходит электрик и, наконец, вентилятор начинает вращаться..
Напряженность магнитного поля измеряется в А/м.
Для прямолинейного провода с током
Для витка с током напряженность в центре витка равна
Это те же самые формулы, которые приведены выше для индукции. Различаются они лишь магнитной постоянной μ0.
Индукция в вакууме или воздухе равна
Где:
μ0 — магнитная постоянная, равная 4π·10-7
То есть, индукция и напряженность различаются только масштабом единиц. И одно из этих понятий для наших сугубо практических целей излишне. И можно было бы все формулы и графики пересчитать на B , но читателям этой статьи придется пользоваться специальной литературой, где H наличествует, поэтому я оставлю по большинству традиционный стиль формул.
Немецкий физик Георг Ом в XIX веке экспериментально вывел основную закономерность, по которой функционируют и проектируются электрические цепи. Она заключается в том, что сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Данная формулировка описывает закон Ома в интегральной форме.
Дифференциальный вид закона Ома
Действие электродвижущих сил
Работая с электричеством, следует помнить, что сопротивление проводника зависит от его размера, формы и материала, из которого он изготовлен. Поэтому данный показатель при решении теоретических и прикладных задач рассчитывается как отношение длины к площади, умноженное на величину удельного сопротивления материала.
Дополнительная информация. Величина сопротивления также зависит и от температуры, где находится проводник. Как правило, такая зависимость носит линейный характер: чем выше температура, тем больше сопротивление проводящего вещества.
Чтобы в цепи появилось электричество, необходимо наличие в ней свободных заряженных частиц (обычно электронов). Кроме того, они должны обладать способностью перемещаться в определенном направлении (от источника тока к его потребителю, от отрицательно заряженного предмета к месту с положительным зарядом). Такое движение создает электрическое поле. Следовательно, чтобы движение частиц не прекращалось, необходимо энергию этого поля каким-либо образом восполнять.
Если соединить проводом два тела, у одного из которых положительный, а у другого отрицательный заряд, из-за кулоновских сил начнется движение электронов. Однако достаточно быстро такое перемещение прекратится, поскольку разница потенциалов из-за действия законов природы восстановится. Таким образом, наличие в электрической цепи только электростатических сил явно недостаточно, чтобы обеспечить постоянное движение электронов в сети.
Важно! Чтобы поддерживать постоянное наличие тока в сети, необходимо обеспечивать разность потенциалов на ее концах. Естественным образом такую ситуацию создать невозможно. Следовательно, необходимы сторонние силы, которые называются электродвижущими.
Электродвижущие силы
Благодаря внешнему воздействию, электроны движутся в направлении, противоположном действию электрического поля, за счет чего поддерживается постоянная разница потенциалов. Создает электродвижущие силы источник тока за счет механического действия, химической реакции и так далее. Следовательно, интегрального вида записи закона Ома для описания функционирования электрической цепи недостаточно, поскольку, помимо разницы потенциалов и сопротивления проводника, на движение электронов действует еще ряд факторов. Решить эту задачу позволяет закон Ома в дифференциальной форме.
Движение тока по неоднородным проводникам
Дифференциальная форма записи выявленной Омом закономерности особенно актуальна, когда проводящий элемент по своему составу неоднороден – на всем протяжении движения электронов у него меняется площадь сечения и уровень сопротивления. Это создает определенные сложности при расчете мощности источника тока, параметров изоляции и так далее, чтобы обеспечить стабильность работы сети, а главное – ее безопасность.
Чтобы сформулировать закон Ома в дифференциальной форме, следует представить проводник не как однородное тело, а как набор бесконечного числа бесконечно малых частей. Это позволит считать каждый элемент однородным, а значит, у него постоянная толщина и постоянный уровень сопротивления, и на таком бесконечно малом участке действуют стандартные принципы закона Ома.
Обратите внимание! При записи закономерности Ома в дифференциальном виде необходимо ввести такие понятия, как плотность тока и удельная проводимость, поскольку именно они являются ключевыми для расчета параметров электрической цепи с неоднородным проводником.
Под плотностью понимается векторная величина, которая демонстрирует уровень силы тока, протекающий через единицу площади. Учет плотности приводит к тому, что при неоднородном проводящем элементе в схеме потребуется установка различных дополнительных устройств для выравнивания напряжения и обеспечения стабильности и безопасности работы.
Плотность и проводимость проводника
Удельная проводимость – это величина, обратная удельному сопротивлению, которая позволяет оценить способность единицы какого-либо вещества обеспечивать прохождение через себя электронов. Знание такой характеристики также позволяет корректно спроектировать схему из различных проводников.
Итак, закон Ома является базовым для понимания устройства электрической цепи. Возможность записать его в разных видах позволяет учесть при проектировании схем устройств и приборов толщину, проводимость и другие характеристики материалов. Необходимо отметить, что такая деятельность требует знаний в области высшей математики (владение основами дифференциальных и интегральных вычислений).
Видео
Оцените статью:Немецкий физик Г. Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника: I = U/R, где R — электрическое сопротивление проводника. Это уравнение выражает закон Ома для участка цепи (не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. Формула позволяет установить единицу сопротивления — ом (Ом): 1 Ом — сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А. Величина
G = 1/R называется электрической проводимостью проводника. Единица проводимости — сименс (См): 1 См — проводимость участка электрической цепи сопротивлением 1 Ом.
Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S:
R = ρl/S, где r — коэффициент пропорциональности, характеризующий материал проводника и называемыйудельным электрическим сопротивлением. Единица удельного электрического сопротивления — ом×метр (Ом×м). Наименьшим удельным сопротивлением обладают серебро (1,6×10–8 Ом×м) и медь (1,7×10–8 Ом×м). На практике наряду с медными применяются алюминиевые провода.
Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления в закон Ома, получим
I/S = U/ρl, где величина, обратная удельному сопротивлению, γ = 1/ρ называетсяудельной электрической проводимостью вещества проводника. Ее единица — сименс на метр (См/м). Учитывая, что U/l = Е — напряженность электрического поля в проводнике, I/S = j — плотность тока, формулу можно записать в виде
j= γE. Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора Е, то направления j и Е совпадают.
Последняя формула — закон Ома в дифференциальном форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.
Опыт показывает, что в первом приближении изменение удельного сопротивления, а значит и сопротивления, с температурой описывается линейным законом:
ρ = ρ0(1+αt), R = R0(1+αt), где r и r0, R и R0 — соответственно удельные сопротивления и сопротивления проводника при t и 0°С, a —температурный коэффициент сопротивления, для чистых металлов (при не очень низких температурах) близкий к 1/273 К–1. Следовательно, температурная зависимость сопротивления может быть представлена в виде R = R0αT
где Т — термодинамическая температура.
Впоследствии было обнаружено, что сопротивление многих металлов (например, Al, Pb, Zn и др.) и их сплавов при очень низких температурах TK (0,14—20 К), называемыхкритическими, характерных для каждого вещества, скачкообразно уменьшается до нуля, т. е. металл становится абсолютным проводником. Явление сверхпроводимости объясняется на основе квантовой теории. Практическое использование сверхпроводящих материалов (в обмотках сверхпроводящих магнитов, в системах памяти ЭВМ и др.) затруднено из-за их низких критических температур. В настоящее время обнаружены и активно исследуются керамические материалы, обладающие сверхпроводимостью при температуре выше 100 К.
Сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении участка и обратно пропорциональна сопротивлению участка при постоянном напряжении.
В диф: 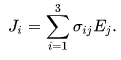
В интегральной 
Электросопротивление, его температурная зависимость. Сверхпроводимость. Свойства сверхпроводников. Высокотемпературные сверхпроводники
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему
Удельное сопротивление меняется с изменением температуры ΔT:
Сверхпроводи́мость — свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении ими температуры ниже определённого значения
Свойства сверхпроводников:
· Нулевое сопротивление
· Фазовый переход в сверхпроводящее состояние
· Эффект Мейсснера
· Изотопический эффект
· Момент Лондона
Высокотемпературные сверхпроводники- сверхпроводящие соединения, имеющие рекордно высокие критические температуры тс перехода в сверхпроводящее состояние
Закон Ома для неоднородного участка цепи. , правила Кирхгофа
Произведение силы тока I на сопротивление участка цепи R равно сумме разности потенциалов на этом участке и ЭДС всех источников тока, включенных на данном участке цепи 
Разветвленная цепь состоит из совокупности однородных и неоднородных участков цепи, электрическое соединение которых происходит в узлах. Узлом в разветвленной цепи называется точка, в которой имеется более двух возможных направлений тока . В узле сходится более двух проводников.
Правила Кирхгофа:
1. Алгебраическая сумма токов в узле равна 0
2. Алгебраическая сумма падений напряжений на элементах замкнутого контура равна сумме ЭДС
3. Выбирают направление обхода контура и берут токи с (+) , которые совпадают с направлением обхода и т.е ЭДС которых гонят ток в том же направлении
Страница не найдена | MIT
Перейти к содержанию ↓- образование
- Исследовательская работа
- новаторство
- Прием + помощь
- Студенческая жизнь
- Новости
- Alumni
- О MIT
- Больше ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Alumni
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Посмотреть больше результатов
Предложения или отзывы?
,Закон об амперах в дифференциальной форме
Что такое закон Ампера?
В соответствии с законом Ампера «Интеграл от линии магнитного поля B вдоль замкнутого пути, вызванного током, равен произведению проницаемости свободного пространства и тока, приложенного замкнутым путем».
Математически это выражается как:

Где
μ 0 = проницаемость свободного пространства
i = ток, протекающий через проводник.
Доказательство: 
Рассмотрим прямой проводник, по которому течет ток i. Ток создает магнитное поле B вокруг проводника. Линии магнитного поля имеют форму концентрических окружностей.
Ампер показал, что плотность потока B в любой точке вблизи проводника прямо пропорциональна току i и обратно пропорциональна расстоянию ‘r’ от проводника, поэтому: 

Где длина пути, называемая окружность круга?
Разделите круг, представляющий линию магнитного поля, на большое количество мелких элементов, каждый из которых имеет длину dl.Величина B.dl рассчитывается для каждого элемента следующим образом:
B.dl = Bdlcos = Bdlcos0 = Bdl
Для полного круга:

Интегральная форма кругового закона ампера

Дифференциальная форма закона ампера
Поскольку интегральная форма закона Ампера равна:

Вышеупомянутое соотношение известно как дифференциальная форма кругового закона Ампера.
Применение кругового закона Ампера
Рассмотрим соленоид, имеющий n витков на единицу длины.Когда ток проходит через соленоид, магнитное поле создается внутри соленоида, который направлен вдоль оси соленоида. Магнитное поле в пространстве снаружи настолько слабо, что считается нулевым.

Чтобы рассчитать значение магнитного поля B внутри соленоида по закону Ампера, мы рассматриваем abcda с замкнутым контуром в форме прямоугольника. Этот замкнутый путь известен как путь Amperian, как видно на рисунке.
Пусть этот путь будет разделен на четыре элемента длины:
ab = L1
bc = L2
cd = L3
da = L4
Таким образом, что сумма точек Произведение магнитного поля и длина элемента составляет:
∑ B.ΔL = BL1 Cos θ1 + BL2 Cos θ2 + BL3 Cos θ3 + BL4 Cos θ4 ………. (1)
Поскольку L1 параллельна линиям магнитного поля внутри соленоида, следовательно, θ = 0 °
BL1 Cos θ1 = BL1
L2 и L4 перпендикулярны магнитному полю, т. Е. Θ2 = 90 ° и θ4 = 90 °
BL2 Cos θ2 = 0
BL4 Cos θ4 = 0
и линии L3 вне соленоида, где поле слабее, т.е. B = 0
oR BL3 Cos θ3 = 0
Поместите все эти значения в уравнение (1), получим:
∑ B.ΔL = BL1 + 0 + 0 + 0
∑ B.ΔL = BL1 ………… .. (2)
Согласно закону Ампера
∑ B.ΔL = μ0I ……… (3)
Если N — число витков катушки, то
Ток = NI
А если «n» — это число витков на единицу длины, то
n = N / L1
N = nL1
Ток = n L1I
∑ B.ΔL = μ0n L1I ………… (4)
Сравнивая уравнения (2) и (4), получаем
μ0n L1I = BL1
B = μ0nI
Похожие темы на нашем сайте находятся:
5.7: закон Гаусса — дифференциальная форма
Интегральная форма закона Гаусса — это расчет вложенного заряда \ (Q_ {encl} \) с использованием плотности окружающего электрического потока:
\ [\ oint _ {\ mathcal S} {\ bf D} \ cdot d {\ bf s} = Q_ {encl} \ label {m0045_eGLIF} \]
где \ ({\ bf D} \) — плотность электрического потока, а \ ({\ mathcal S} \) — окружающая поверхность. Иногда также необходимо выполнить обратный расчет (то есть определить электрическое поле, связанное с распределением заряда).Иногда это возможно, используя уравнение \ ref {m0045_eGLIF}, если позволяет симметрия задачи; см. примеры в разделах 5.5 и 5.6. Если проблема не проявляет необходимой симметрии, то, по-видимому, следует обратиться к семейству методов, представленных в разделе 5.4, требующих прямой интеграции по заряду, что вытекает из закона Кулона.
Тем не менее, даже подход кулоновского закона / прямой интеграции имеет ограничение, которое очень важно признать: оно не учитывает наличие структур, которые могут влиять на электрическое поле.Например, электрическое поле из-за заряда в свободном пространстве отличается от электрического поля из-за того же заряда, расположенного вблизи идеально проводящей поверхности. Фактически, эти подходы не учитывают возможность пространственных изменений в составе материала , что исключает их использование во многих инженерных приложениях.
Для решения этого более широкого круга проблем нам требуется альтернативная форма закона Гаусса, которая применяется в отдельных точках пространства. То есть нам требуется закон Гаусса, выраженный в форме дифференциального уравнения, а не интегрального уравнения.Это облегчает использование закона Гаусса даже в задачах, которые не проявляют достаточной симметрии и которые включают в себя границы материала и пространственные изменения материальных составляющих параметров. Учитывая это дифференциальное уравнение и граничные условия, налагаемые структурой и материалами, мы можем затем решить для электрического поля в этих более сложных сценариях. В этом разделе мы выводим искомую дифференциальную форму закона Гаусса. В другом месте (в частности, в разделе 5.15) мы используем это уравнение в качестве инструмента для поиска электрических полей в задачах, касающихся границ материала.3 \)) в точке, в которой мы сходимся после того, как объем упадет до нуля. По определению левая часть — это дивергенция из \ ({\ bf D} \), обозначенная в математической записи как «\ (\ nabla \ cdot {\ bf D} \)» (раздел 4.6). Таким образом, мы имеем закон Гаусса в дифференциальной форме :
\ [\ boxed {\ nabla \ cdot {\ bf D} = \ rho_v} \ label {m0045_eGLDF} \]
Чтобы интерпретировать это уравнение, напомним, что дивергенция — это просто поток (в данном случае электрический поток ) на единицу объема.
Закон Гаусса в дифференциальной форме (уравнение \ ref {m0045_eGLDF}) гласит, что электрический поток на единицу объема, исходящий из точки в пространстве, равен плотности объемного заряда в этой точке.
Вывод по теореме дивергенции
Уравнение \ ref {m0045_eGLDF} также может быть получено из уравнения \ ref {m0045_eGLIF} с использованием теоремы расхождения, которая в данном случае может быть записана:
\ [\ int _ {\ mathcal V} \ left (\ nabla \ cdot {\ bf D} \ right) dv = \ oint _ {\ mathcal S} {\ bf D} \ cdot d {\ bf s} \]
Из уравнения \ ref {m0045_eGLIF} мы видим, что правая часть уравнения может быть заменена вложенным зарядом:
\ [\ int _ {\ mathcal V} \ left (\ nabla \ cdot {\ bf D} \ right) dv = Q_ {encl} \]
Кроме того, вложенный заряд может быть выражен как интеграция плотности объемного заряда \ (\ rho_v \) по \ ({\ mathcal V} \): \ [\ int _ {\ mathcal V} \ left (\ nabla \ cdot {\ bf D} \ right) dv = \ int _ {\ mathcal V} \ rho_v dv \] Приведенные выше отношения должны выполняться независимо от конкретного расположения или формы \ ({\ mathcal V} \).4 \). Какова плотность заряда при \ ({\ bf r} = \ hat {\ bf x} 2 — \ hat {\ bf y} 2 \) m?
Решение
Сначала мы используем \ ({\ bf D} = \ epsilon {\ bf E} \), чтобы получить \ ({\ bf D} \). Поскольку проблема в свободном пространстве, \ (\ epsilon = \ epsilon_0 \). Таким образом, мы имеем, что объемная плотность заряда составляет
\ [\ begin {align} \ rho _ {v} & = \ nabla \ cdot \ mathbf {D} \\ & = \ nabla \ cdot \ left (\ epsilon _ {0} \ mathbf {E} \ right) = \ epsilon _ {0} \ nabla \ cdot \ mathbf {E} \\ & = \ epsilon _ {0} \ left [\ frac {\ частичный} {\ частичный x} \ left (A x ^ {2} \ правый) + \ frac {\ частичный} {\ частичный y} (B z) + \ frac {\ частичный} {\ частичный z} \ left (C x ^ {2} z \ right) \ right] \\ & = \ epsilon _ {0} \ left [2 A x + 0 + C x ^ {2} \ right] \ end {align} \]
Теперь вычисляем плотность заряда в указанном месте \ ({\ bf r} \):
\ [\ begin {array} {l} {\ epsilon _ {0} \ left [2 \ left (3 \: \ mathrm {V} / \ mathrm {m} ^ {3} \ right) (2 \: \ mathrm {m}) + 0 + \ left (1 \: \ mathrm {V} / \ mathrm {m} ^ {4} \ right) (2 \: \ mathrm {m}) ^ {2} \ right] } \\ {= \ epsilon _ {0} (16 \: \ mathrm {V} / \ mathrm {m})} \\ {= 142 \: \ mathrm {pC} / \ mathrm {m} ^ {3} } \ end {array} \]
Чтобы получить электрическое поле из распределения заряда при наличии граничных условий, налагаемых материалами и структурой, мы должны применить соответствующие граничные условия.Эти граничные условия представлены в разделах 5.17 и 5.18. Часто возможен более простой подход, требующий только граничных условий на электрический потенциал (\ (V (\ bf {r}) \)); это представлено в разделе 5.15.
Кроме того, читатель должен отметить следующее. Закон Гаусса не всегда обязательно ограничивает возможные решения для электрического поля. Для этого нам также может понадобиться закон напряжения Кирхгофа; см. раздел 5.11.
Прежде чем двигаться дальше, стоит отметить, что уравнение \ ref {m0045_eGLDF} может быть решено в особом случае, когда нет граничных условий для удовлетворения; я.3} ~ \ rho_v ({\ bf r} ‘) ~ dv} \]
, который мы признаем одним из результатов, полученных в Разделах 5.4 (после деления обеих сторон на \ (\ epsilon \), чтобы получить \ ({\ bf E} \)). Разумно сделать вывод, что закон Гаусса (в интегральной или дифференциальной форме) является фундаментальным, тогда как закон Кулона является лишь следствием закона Гаусса.
участников и атрибутов
,ЗаконОм | Статья о законе Ома в «Свободном словаре»
, который гласит, что постоянная плотность тока I в проводнике прямо пропорциональна разности потенциалов (напряжению) U между двумя фиксированными точками или сечениями проводника:
(1) RI = U
Константа пропорциональности R , которая зависит от геометрических и электрических свойств проводника и от температуры, называется омическим сопротивлением или просто сопротивлением данного участка проводник.Закон Ома был открыт в 1826 году немецким физиком Г. С. Омом.
В общем случае соотношение между I и U является нелинейным; однако на практике всегда можно предположить, что он является линейным для определенного диапазона напряжений, и применять закон Ома для этого диапазона. Для металлов и их сплавов ассортимент практически неограничен.
ЗаконОма в форме (1) действителен для тех участков цепи, которые не содержат источников электродвижущей силы (ЭДС).Если такие источники (аккумуляторы, термопары или динамо) присутствуют, закон Ома принимает форму
(2) RI = U + E
, где E — ЭДС всех источников, подключенных в секции схемы, которая рассматривается. Для замкнутого контура закон Ома принимает следующую форму:
(3) R t I = E
, где R t = R + R i является полное сопротивление всей цепи, которое равно сумме внешнего сопротивления R цепи и внутреннего сопротивления R i источника ЭДС.Законы Кирхгофа обобщают закон Ома для случая разветвленных цепей.
Закон Ома также может быть записан в дифференциальной форме, которая связывает плотность тока j и общую напряженность электрического поля для каждой точки проводника. Потенциальное электрическое поле напряженности E, создаваемое в проводниках микроскопическими зарядами — электронами и ионами — самих проводников, не может поддерживать устойчивое движение свободных зарядов (тока), поскольку работа, выполняемая полем в замкнутом контуре, равна нулю ,Ток поддерживается неэлектростатическими силами различного происхождения (индукционными, химическими, термическими и т. Д.), Которые активны в источниках ЭДС и могут быть представлены в виде некоторого эквивалентного, непотенциального поля напряженности E и , называемого внешним полем. В общем случае общая напряженность поля, действующего на заряды в проводнике, составляет E + E и . Соответственно, дифференциальный закон Ома принимает форму
(4) ρj = E + E ext или j = σ (E + E ext )
где ρ — удельное электрическое сопротивление материала проводника, а σ = 1 / ρ — удельная электропроводность.
Закон Ома в сложной форме также действителен для синусоидальных квазистационарных токов:
(5) ZI = E
, где Z — полное комплексное сопротивление, равное R + iX и R и iX — это сопротивление и реактивное сопротивление цепи, соответственно. Если индуктивность L и емкость C присутствуют в цепи, несущей квазистационарный ток частоты ω, то X = ω L — 1 / ω В.
ЛИТЕРАТУРА
Курсфизики , вып. 2. Под редакцией Н. Д. Папалекси. Москва-Ленинград, 1948.Калашников С.Г. Электричество. , Москва, 1964. ( Общий курс физики , вып. 2.)
Физические основы электротехники. Генеральный редактор К. М. Поливанов. Москва-Ленинград, 1950..



