Законы электротехники | elesant.ru

class=»eliadunit»>

 

Законы электротехники

• Закон Ома
• Законы Кирхгофа
• Закон Джоуля-Ленца

Основной закон электротехники закон Ома

Основным законом электротехники, несомненно, является Закон Ома. Названый, как и большинство, законы в физики, в честь его открывателя немецкого физика Ома, он гласит:

Сила тока участка электрической сети прямо пропорциональна напряжению, приложенному к этому участку и обратно пропорциональна его сопротивлению.

В символическом выражении Закон Ома выглядит так:

I=U÷R, где I-Сила тока в цепи (Ампер), U-Напряжение сети (Вольт), R-Сопротивление сети (Ом).

В таком виде закон Ома не имеет практического применения в электрике жилых и промышленных зданий. Напомню, что для электропитания зданий применяется переменное напряжение и здесь работают немного другие законы электротехники. Но закон Ома является одной из баз лежащей в основе всех формул и всех электротехнический расчетов.

Практическое применения имеет закон взаимосвязи (соответствия) напряжения, силы тока и мощности в электрической цепи. Он математически выводится из закона Ома и основан на двух алгебраических формулах, выражающих физические законы:

P=U×I, где P-мощность электрической сети (Ватт), U-напряжение, I-сила тока.

I=U÷R, где I-сила тока, U-напряжение, R-сопротивление.

Если немного посидеть, вспомнить простую алгебру и поманипулировать с эти двумя формулами, можно получить диаграмму-подсказку, в которой все четыре величины:U; I; R; P математически связаны друг с другом.

Практическое применение этих математических формул законов электрики можно применить в расчете простой электросети напряжением 220 Вольт без электродвигателей.

Например: Освещение одной комнаты из 20 лампочек накаливания. Напряжение сети величина постоянная и равна 220 вольт. Мощность каждой лампочки 25 Ватт.

Простым умножением получаем следующие результаты:

Общая потребляемая мощность сети:25 Ватт×20 лампочек=500ватт.

Сила тока в сети:500ватт÷220 вольт=2,3 ампера.

Если таких комнат в квартире три, то суммарный рабочий ток в сети составит 3×2,3 ватта=6,9 Ампер.

class=»eliadunit»>

В соответствии с этим расчетом можно выбрать номинал автомата защиты освещения всей квартиры. Округляем 6,9 ампер в большую сторону, до значения номиналов автоматов имеющихся в продаже. Это 10 ампер.

Вывод: Простой расчет по основному закону электропроводки позволил рассчитать номинал нужного автомата защиты.

Законы Кирхгофа

Электрика любого помещения выполняется в виде замкнутых, рабочих электрических цепей. Два главных закона, которые определяют процессы в электрических сетях, являются законы Кирхгофа. Их два. Оба из них применяются и для постоянных и для переменных токов.

Первый закон Кирхгофа утверждает:

Суммарная величина токов направленная к узлу электрической сети равна суммарной величине токов направленных от узла.

В практике на основе первого закона Кирхгофа основана работа Устройств защитного отключения (УЗО). Работа УЗО заключается в отключении электропитания сети при возникновении токов утечки. При нормальном режиме работы суммарное значение тока, втекающая в электрическую сеть равна значению тока утекающему из нее. Если равенство токов нарушается, значит, в сети есть утечка. УЗО сконструировано и подключено таким образом, что при утечке тока УЗО его обнаруживает и размыкает питание электросети.

Второй закон Кирхгофа гласит:

Любой замкнутый контур переменной электрической сети имеет равные значения комплексных напряжений и ЭДС (электродвижущих сил) на всех пассивных элементах сети.

Примечание: Комплексное напряжение это значение напряжение в сети переменного тока.

Практическое применение можно пояснить на любой квартирной группе электропитания. Для пояснения рассмотрим квартиру.

Сколько бы групп электропитания в квартире не было, на любой розетке или светильнике напряжение в сети (при рабочем режиме) будет 220 вольт.

Еще один основной закон электрики нужно вспомнить.

Закон Джоуля-Ленца

Закон Джоуля-Ленца устанавливает связь между током «бегающему» по проводнику, его сопротивлению и теплом которое при этом выделяется.

В математическом символизме закон Джоуля-Ленца выглядит так:

Q=I²×R×t,где Q это количество выделяемого тепла в проводнике, в Джоулях;I-сила тока;R-сопротивление проводника;t-время прохождения тока в секундах.

В качестве информации: Ленц это русский физик Эмилий Христианович Ленц. Русский физик, электротехник, физический географ.1804-1865 года жизни.

Говоря о практическом применении закона Джоуля-Ленца, трудно назвать в какой части электрики он не проявляется. Электрические обогреватели, электрические водонагреватели, тепловые завесы, выбор автоматов защиты, тепловые реле в автоматике и многое другое.

Конечно это не все основные законы электрики. На по своему значению эти законы имеют фундаментальное значение.

Другие статьи сайта

 

 

class=»eliadunit»>

Электротехника. Основы. Закон Ома — Всё об энергетике

Электротехника. Основы. Закон Ома

В электротехнике, как и в любой другой науке, существуют базовые понятия, без понимания которых не удастся овладеть этой областью знаний. Здесь такими понятиями являются электрическое напряжение, электрический ток и электрическое сопротивление.

Закон Ома

Закон Ома был открыт в результате экспериментов Георга Ома с гальванометром и простой электрической цепью из источника ЭДС и сопротивления. Со временем формула полученная Омом претерпела несколько изменений.

Закон Ома для участка цепи без ЭДС

Может быть сформулирован через сопротивление [1, стр.33][2, стр.15]:

\begin{equation} I = {U_{ab}\over R}; \end{equation}

Где:

• I — ток через участок ab электрической цепи;
• U_ab — напряжение на участке ab электрической цепи;
• R — сопротивление участка ab электрической цепи.

Или через проводимость:

\begin{equation} I = U_{ab} × G; \end{equation}

Где:

• G — проводимость участка ab электрической цепи.

Формула (1, 2) справедлива для электрической цепи представленной ниже на рисунке 1.

Рисунок 1 — Участок цепи без ЭДС

Закон Ома для участка цепи содержащего ЭДС

Или обобщённый закон Ома. Формулируется следующим образом [1, стр.34][2, стр.17]:

\begin{equation} I = {U_{ab} + E\over R}; \end{equation}

Где:

• I — ток через участок ac электрической цепи;
• U_ab — напряжение на участке ab электрической цепи;
• E — ЭДС на участке bс электрической цепи;
• R — сопротивление участка ab электрической цепи.

Или через проводимость:

\begin{equation} I = {(U_{ab} + E) × G}; \end{equation}

Где:

• G — проводимость участка ab электрической цепи.

Формула (3, 4) справедлива для электрической цепи представленной ниже на рисунке 2.

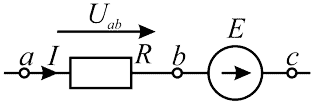
Рисунок 2 — Участок цепи содержащий ЭДС

Закон Ома для полной цепи

Закон формулируется следующим образом [1, стр.34][2, стр.17]:

\begin{equation} I = {E\over {R + r}}; \end{equation}

Где:

• I — ток в электрической цепи;
• E — ЭДС электрической цепи;
• R — сопротивление электрической цепи;
• r — внутреннее сопротивление источника ЭДС.

Формулировка выражения (5) через проводимость неудобна и здесь приведена не будет. Ниже на рисунке 3 изображена схема электрической цепи для которой справедливо выражение (5).

Рисунок 3 — Полная цепь

На схеме видно, что

R и r соединены последовательно, а в формуле это отражено как сумма R (сопротивления цепи) и r (внутреннего сопротивления источника ЭДС). Заменим выражение R + r на R_п

\begin{equation} I = {E\over R_п}; \end{equation}

Где:

• R_п — полное сопротивление электрической цепи (включая сопротивление источника ЭДС).

Закон Ома в дифференциальной форме

Закон Ома в дифференциальной форме, представленный в выражении (7), справедлив для неоднородного, но изотропного вещества [3].

\begin{equation} \vec E = {ρ × \vec\jmath}; \end{equation}

Где:

• \(\vec\jmath\) — плотность тока;
• ρ — удельное сопротивление;
• \(\vec E\) — напряжённость электрического поля.

Примеры применения

Ниже приведены несколько примеров для демонстрации применения разных формулировок закона Ома.

Пример 1

Схема задания приведена на рисунке 4. На схеме R = 5,2 Ом, U = 26 В. Определить I.

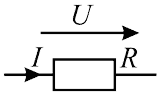
Рисунок 4 — Схема к 1 и 2-му примеру

Для решения задания воспользуемся выражением (1):

\begin{equation} I = {U\over R} = {26\over 5,2} = {5 \ А;} \end{equation}

Пример 2

Схема задания приведена на рисунке 4. К данному участку цепи приложено напряжение 24 В и по нему протекает ток 1,5 А. Определить проводимость участка цепи.

Для решения задания преобразуем выражение (2) относительно G:

\begin{equation} I = {U × G} \ \Rightarrow \ G = {I\over U} = {1,5\over 24} = {0,0625 \ См;} \end{equation}

Пример 3

Схема задания приведена на рисунке 5. На схеме U = 220 В, I = 0,5 А, R = 140 Ом. Определить E.

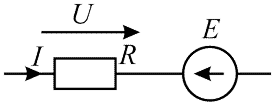
Рисунок 5 — Схема к 3-му примеру

Для решения задания преобразуем выражение (3) относительно E:

\begin{equation} I = {U — E\over R} \ \Rightarrow \ {I × R} = {U — E} \ \Rightarrow \ E = {U — I × R}; \end{equation}

Подставим в выражение (10) известные величины:

\begin{equation} E = {U — I × R} = {220 — 0,5 × 140} = {150 \ В;} \end{equation}

Пример 4

Сопротивление электрической цепи, приведенной на рисунке 3 составляет 12 Ом, напряжение источника ЭДС включенного в цепь — 9 В. Измерения показали, что по цепи протекает ток 0,72 А. Необходимо определить внутреннее сопротивление источника ЭДС.

Преобразуем выражение (5) относительно r:

\begin{equation} I = {E\over {R + r}} \ \Rightarrow \ {I × (R + r)} = E \ \Rightarrow \ {I × r} = {E — I × R} \ \Rightarrow \ r = {E — I × R\over I}; \end{equation}

Определим внутренней сопротивление источника ЭДС, подставив в выражение (10) известные величины:

\begin{equation} r = {E — I × R\over I} = {9 — 0,72 × 12\over 0,72} = {0,36\over 0,72} = {0,5 \ Ом;} \end{equation}

Использованные термины

Электрический потенциал точки:

Физическая величина, равная потенциальной энергии, которой обладает элементарный положительный заряд, помещенный в электрическое поле.

Потенциал обозначается буквой φ греческого алфавита и измеряется в вольтах (В). Он не имеет направления и записывается как скаляр.

Электрическое напряжение:

Физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из точки А в точку Б электромагнитного поля, определяемая как разность потенциалов этих точек: U_ab = φ_a — φ_b.

Напряжение обозначается буквой U (u) латинского алфавита и измеряется в вольтах (В). Напряжение — скалярная величина, но на электрических схемах указывают его положительное направление.

Электродвижущая сила (ЭДС):

Также как и напряжение это физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из одной точки электромагнитного поля в другую.

ЭДС обозначается буквой E (e) латинского алфавита и измеряется в вольтах (В). ЭДС — скалярная величина, но на электрических схемах указывают её положительное направление. Она численно равна напряжению на зажимах не подключенного источника.

Электрическое ток:

Физическая величина, равная количеству заряженных частиц прошедших через поперечное сечение проводника за единицу времени. Как явление — направленное движение заряженных частиц.

Напряжение обозначается буквой I (i) латинского алфавита и измеряется в амперах (А). Ток, так же как и напряжение, величина скалярная, и на электрических схемах тоже указывают его положительное направление [2, стр.11].

Плотность тока:

Физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади.

Плотность тока обозначается буквой \(\vec\jmath\) латинского алфавита и измеряется в амперах на метр квадратный (А/м²). Плотность тока — векторная величина [4].

Электрическое сопротивление:

Физическая величина, характеризующая способность проводника препятствовать прохождению по нему тока.

Сопротивление обозначается буквами R (r), X (x) или Z (z) латинского алфавита (последние два обозначения применяются для реактивного и комплексного сопротивления соответственно) и измеряется в омах (Ом). Как и предыдущие, сопротивление — скалярная величина.

Электрическая проводимость:

Физическая величина, характеризующая насколько хорошо проводник проводит электрический ток, является обратной сопротивлению: G = 1/R.

Проводимость обозначается буквами G (g) латинского алфавита и измеряется в сименсах (См). Так же как и сопротивление проводимость — скалярная величина.

Удельное сопротивление:

Физическая величина, численно равная сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².

Удельная проводимость обозначается буквами ρ греческого алфавита и измеряется в омах на метр (Ом×м). Является скалярной величиной. [3].

В дальнейшем при использовании вышеперечисленных терминов слово «электрический» будет упускаться.

Список использованных источников

1. Бессонов, Л.А. Теоретические основы электротехники: учебник / Л.А. Бессонов — Москва: Высшая школа, 1996. — 623 с.
2. Иванова, С.Г. Теоретические основы электротехники: Версия 1.0 [Электронный ресурс] : учеб. пособие / С. Г. Иванова, В. В. Новиков – Красноярск: ИПК СФУ, 2008. — 318 с.
3. Википедия — Удельное электрическое сопротивление [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Удельное_электрическое_сопротивление
4. Википедия — Плотность тока [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Плотность_тока

Электротехника. Основы. Закон Ома — Всё об энергетике

Электротехника. Основы. Закон Ома

В электротехнике, как и в любой другой науке, существуют базовые понятия, без понимания которых не удастся овладеть этой областью знаний. Здесь такими понятиями являются электрическое напряжение, электрический ток и электрическое сопротивление.

Закон Ома

Закон Ома был открыт в результате экспериментов Георга Ома с гальванометром и простой электрической цепью из источника ЭДС и сопротивления. Со временем формула полученная Омом претерпела несколько изменений.

Закон Ома для участка цепи без ЭДС

Может быть сформулирован через сопротивление [1, стр.33][2, стр.15]:

\begin{equation} I = {U_{ab}\over R}; \end{equation}

Где:

• I — ток через участок ab электрической цепи;
• U_ab — напряжение на участке ab электрической цепи;
• R — сопротивление участка ab электрической цепи.

Или через проводимость:

\begin{equation} I = U_{ab} × G; \end{equation}

Где:

• G — проводимость участка ab электрической цепи.

Формула (1, 2) справедлива для электрической цепи представленной ниже на рисунке 1.

Рисунок 1 — Участок цепи без ЭДС

Закон Ома для участка цепи содержащего ЭДС

Или обобщённый закон Ома. Формулируется следующим образом [1, стр.34][2, стр.17]:

\begin{equation} I = {U_{ab} + E\over R}; \end{equation}

Где:

• I — ток через участок ac электрической цепи;
• U_ab — напряжение на участке ab электрической цепи;
• E — ЭДС на участке bс электрической цепи;
• R — сопротивление участка ab электрической цепи.

Или через проводимость:

\begin{equation} I = {(U_{ab} + E) × G}; \end{equation}

Где:

• G — проводимость участка ab электрической цепи.

Формула (3, 4) справедлива для электрической цепи представленной ниже на рисунке 2.

Рисунок 2 — Участок цепи содержащий ЭДС

Закон Ома для полной цепи

Закон формулируется следующим образом [1, стр.34][2, стр.17]:

\begin{equation} I = {E\over {R + r}}; \end{equation}

Где:

• I — ток в электрической цепи;
• E — ЭДС электрической цепи;
• R — сопротивление электрической цепи;
• r — внутреннее сопротивление источника ЭДС.

Формулировка выражения (5) через проводимость неудобна и здесь приведена не будет. Ниже на рисунке 3 изображена схема электрической цепи для которой справедливо выражение (5).

Рисунок 3 — Полная цепь

На схеме видно, что R и r соединены последовательно, а в формуле это отражено как сумма R (сопротивления цепи) и r (внутреннего сопротивления источника ЭДС). Заменим выражение R + r на R_п

\begin{equation} I = {E\over R_п}; \end{equation}

Где:

• R_п — полное сопротивление электрической цепи (включая сопротивление источника ЭДС).

Закон Ома в дифференциальной форме

Закон Ома в дифференциальной форме, представленный в выражении (7), справедлив для неоднородного, но изотропного вещества [3].

\begin{equation} \vec E = {ρ × \vec\jmath}; \end{equation}

Где:

• \(\vec\jmath\) — плотность тока;
• ρ — удельное сопротивление;
• \(\vec E\) — напряжённость электрического поля.

Примеры применения

Ниже приведены несколько примеров для демонстрации применения разных формулировок закона Ома.

Пример 1

Схема задания приведена на рисунке 4. На схеме R = 5,2 Ом, U = 26 В. Определить I.

Рисунок 4 — Схема к 1 и 2-му примеру

Для решения задания воспользуемся выражением (1):

\begin{equation} I = {U\over R} = {26\over 5,2} = {5 \ А;} \end{equation}

Пример 2

Схема задания приведена на рисунке 4. К данному участку цепи приложено напряжение 24 В и по нему протекает ток 1,5 А. Определить проводимость участка цепи.

Для решения задания преобразуем выражение (2) относительно G:

\begin{equation} I = {U × G} \ \Rightarrow \ G = {I\over U} = {1,5\over 24} = {0,0625 \ См;} \end{equation}

Пример 3

Схема задания приведена на рисунке 5. На схеме U = 220 В, I = 0,5 А, R = 140 Ом. Определить E.

Рисунок 5 — Схема к 3-му примеру

Для решения задания преобразуем выражение (3) относительно E:

\begin{equation} I = {U — E\over R} \ \Rightarrow \ {I × R} = {U — E} \ \Rightarrow \ E = {U — I × R}; \end{equation}

Подставим в выражение (10) известные величины:

\begin{equation} E = {U — I × R} = {220 — 0,5 × 140} = {150 \ В;} \end{equation}

Пример 4

Сопротивление электрической цепи, приведенной на рисунке 3 составляет 12 Ом, напряжение источника ЭДС включенного в цепь — 9 В. Измерения показали, что по цепи протекает ток 0,72 А. Необходимо определить внутреннее сопротивление источника ЭДС.

Преобразуем выражение (5) относительно r:

\begin{equation} I = {E\over {R + r}} \ \Rightarrow \ {I × (R + r)} = E \ \Rightarrow \ {I × r} = {E — I × R} \ \Rightarrow \ r = {E — I × R\over I}; \end{equation}

Определим внутренней сопротивление источника ЭДС, подставив в выражение (10) известные величины:

\begin{equation} r = {E — I × R\over I} = {9 — 0,72 × 12\over 0,72} = {0,36\over 0,72} = {0,5 \ Ом;} \end{equation}

Использованные термины

Электрический потенциал точки:

Физическая величина, равная потенциальной энергии, которой обладает элементарный положительный заряд, помещенный в электрическое поле.

Потенциал обозначается буквой φ греческого алфавита и измеряется в вольтах (В). Он не имеет направления и записывается как скаляр.

Электрическое напряжение:

Физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из точки А в точку Б электромагнитного поля, определяемая как разность потенциалов этих точек: U_ab = φ_a — φ_b.

Напряжение обозначается буквой U (u) латинского алфавита и измеряется в вольтах (В). Напряжение — скалярная величина, но на электрических схемах указывают его положительное направление.

Электродвижущая сила (ЭДС):

Также как и напряжение это физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из одной точки электромагнитного поля в другую.

ЭДС обозначается буквой E (e) латинского алфавита и измеряется в вольтах (В). ЭДС — скалярная величина, но на электрических схемах указывают её положительное направление. Она численно равна напряжению на зажимах не подключенного источника.

Электрическое ток:

Физическая величина, равная количеству заряженных частиц прошедших через поперечное сечение проводника за единицу времени. Как явление — направленное движение заряженных частиц.

Напряжение обозначается буквой I (i) латинского алфавита и измеряется в амперах (А). Ток, так же как и напряжение, величина скалярная, и на электрических схемах тоже указывают его положительное направление [2, стр.11].

Плотность тока:

Физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади.

Плотность тока обозначается буквой \(\vec\jmath\) латинского алфавита и измеряется в амперах на метр квадратный (А/м²). Плотность тока — векторная величина [4].

Электрическое сопротивление:

Физическая величина, характеризующая способность проводника препятствовать прохождению по нему тока.

Сопротивление обозначается буквами R (r), X (x) или Z (z) латинского алфавита (последние два обозначения применяются для реактивного и комплексного сопротивления соответственно) и измеряется в омах (Ом). Как и предыдущие, сопротивление — скалярная величина.

Электрическая проводимость:

Физическая величина, характеризующая насколько хорошо проводник проводит электрический ток, является обратной сопротивлению: G = 1/R.

Проводимость обозначается буквами G (g) латинского алфавита и измеряется в сименсах (См). Так же как и сопротивление проводимость — скалярная величина.

Удельное сопротивление:

Физическая величина, численно равная сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².

Удельная проводимость обозначается буквами ρ греческого алфавита и измеряется в омах на метр (Ом×м). Является скалярной величиной. [3].

В дальнейшем при использовании вышеперечисленных терминов слово «электрический» будет упускаться.

Список использованных источников

1. Бессонов, Л.А. Теоретические основы электротехники: учебник / Л.А. Бессонов — Москва: Высшая школа, 1996. — 623 с.
2. Иванова, С.Г. Теоретические основы электротехники: Версия 1.0 [Электронный ресурс] : учеб. пособие / С. Г. Иванова, В. В. Новиков – Красноярск: ИПК СФУ, 2008. — 318 с.
3. Википедия — Удельное электрическое сопротивление [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Удельное_электрическое_сопротивление
4. Википедия — Плотность тока [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Плотность_тока

1. Основные законы электротехники

Расчет и анализ электрических цепей основан на использовании законов Ома, Кирхгофа и Джоуля-Ленца. При рассмотрении принципа действия различных электротехнических устройств, а также расчета и анализа их параметров и характеристик необходимо дополнительное знание закона Ампера, закона электромагнитной индукции, закона полного тока и ряда других законов.

В настоящей работе основные законы электротехники формулируются применительно к электрическим цепям постоянного тока.

В цепях переменного тока такая формулировка законов оказывается справедливой только для мгновенных значений напряжений и токов, в связи с чем их использование имеет ряд особенностей, рассматриваемых в соответствующих разделах курса «Электротехника и электроника»: «Электрические цепи синусоидального тока», «Переходные процессы в линейных электрических цепях» и др.

1.1. Закон Ома

Закон Ома показывает причинно-следственную связь между напряжением Uи величиной токаI. Различают закон Ома для участка цепи и замкнутой цепи, а также закон Ома для участка цепи, содержащего источник электродвижущей силы (э.д.с.).

Закон Ома для участка цепи

На рисунке 1 показан участок электрической цепи, представляющей собой резистор R, на концах которого действует напряжение U (разность электрических потенциалов) и по которому протекает электрический ток I.

Резисторомназывается элемент электрической цепи,который предназначен для ограничения величины тока, и параметром которого является электрическое сопротивление R. В резисторе происходит необратимый процесс преобразования энергии электрической в энергию тепловую.

Закон Ома для участка цепиформулируется следующим образом:токIпрямо пропорционален напряжениюUи записывается в виде:

(1)

где I – сила тока (ток, величина тока). Единица измерения тока – ампер [A]^. Ампер – такая величина тока, при которой через поперечное сечение проводника в одну секунду протекает электрический заряд q в один кулон [Кл]. 1 А = Кл/с. Таким образом, сила тока I – это количество электричества q, протекающее через сечение проводника в единицу времени t. Математически ток i представляет собой в общем случае производную от заряда q по времени t:;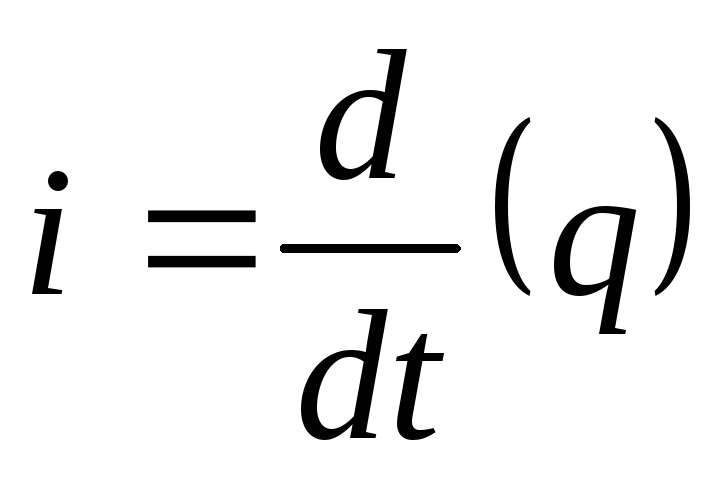

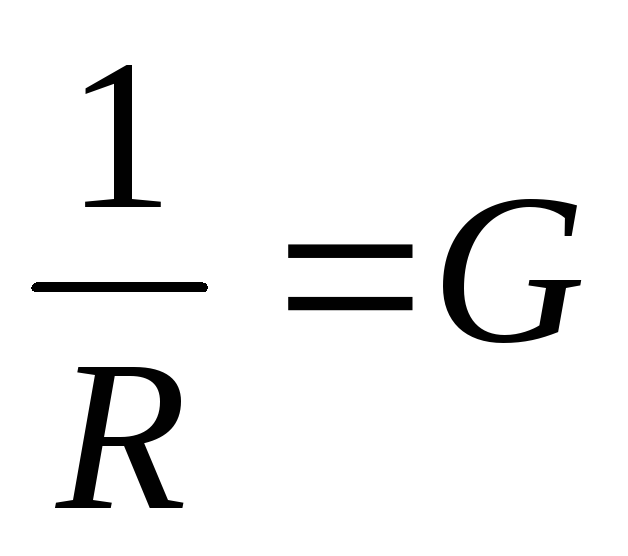–коэффициент пропорциональности между током и напряжением. R – электрическое сопротивление, измеряемое в омах [Ом]. Проводник обладает сопротивлением в один Ом, если по нему протекает ток один ампер при напряжении в один вольт [Ом] = [В] / [A];

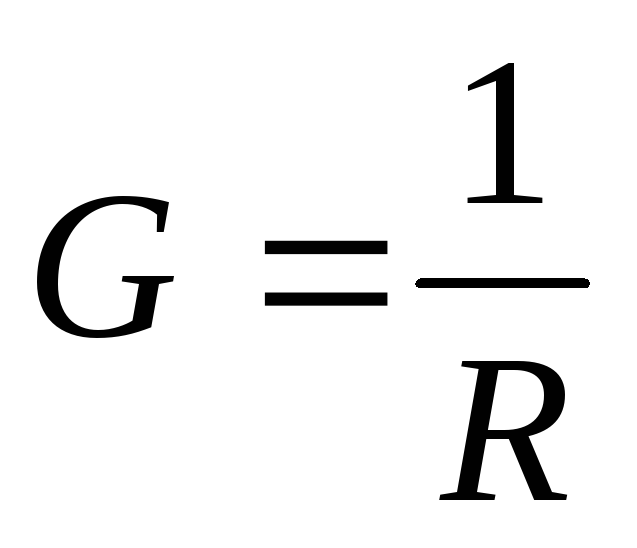–электрическая проводимость, то есть величина, обратная сопротивлению; единица ее измерения – сименс [См], [См] = [Ом^-1].

Электрическое сопротивление твердого проводника зависит от его геометрических размеров и материала, из которого он изготовлен. Оно рассчитывается по формуле:

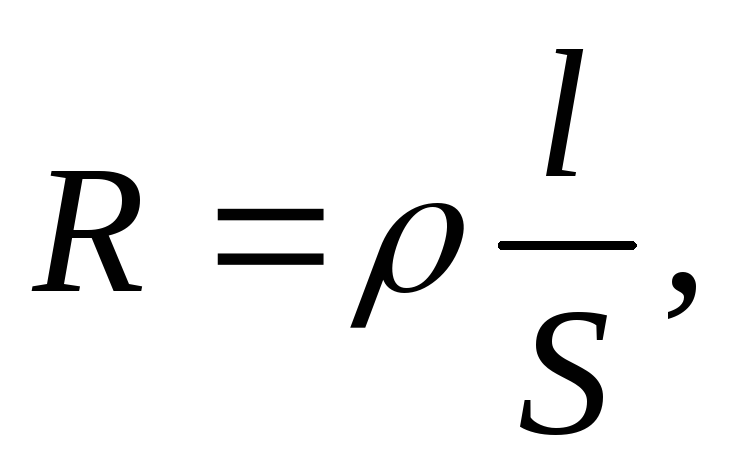
(2)

где l– длина проводника в метрах [м];

S– сечение проводника [м²];

ρ – удельное сопротивление материала [Ом∙м].

В формулу (2) можно подставить величину удельной проводимости материала :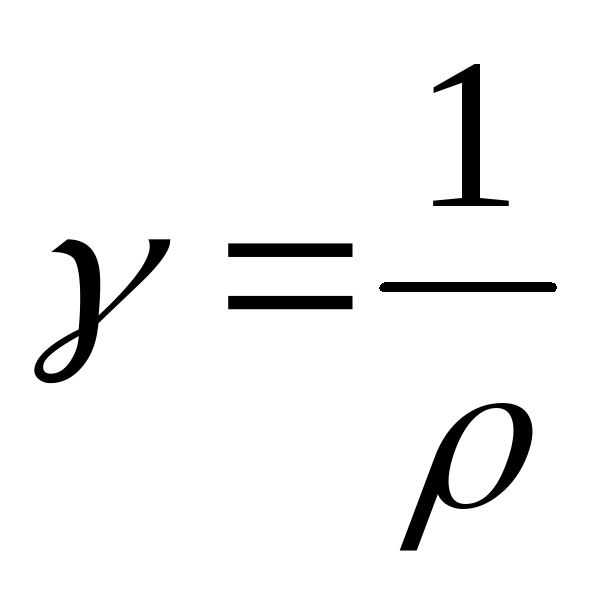

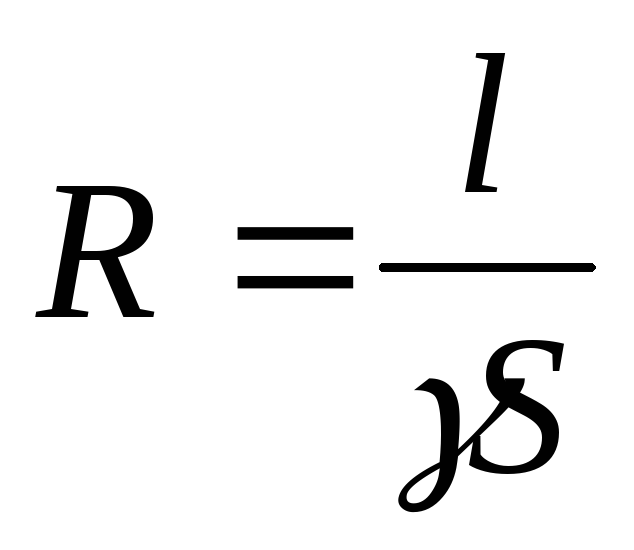
(2а)

Э

(3)

лектрическое сопротивление проводников зависит от температуры. Эта зависимость может быть рассчитана по формуле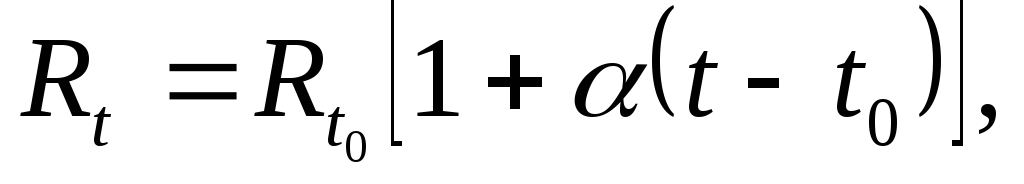

где R_t– сопротивление при температуреt;

R_t0– сопротивление при температуреt₀;

t₀– начальная температура проводника, которая принимается равной 20°С;

α[град^-1] –температурный коэффициент сопротивления–ТКR, который для металлов и большинства их сплавов – положительная величина (α> 0).

В частности для меди и алюминия ТКRα0,004 град^-1. Например, приt₀= 20°С и повышении температуры до величиныt= 120°С (рабочая температура большинства электротехнических установок) согласно выражению (3)

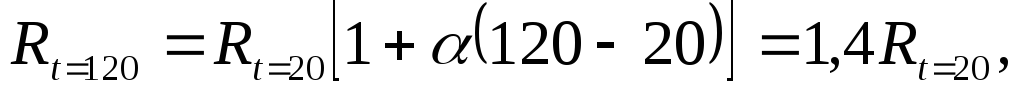
то есть сопротивление медных и алюминиевых проводов увеличивается на 40%, что необходимо учитывать при тепловых и вентиляционных расчетах на стадии проектирования электрических машин, трансформаторов и другого электрооборудования.

Увеличение электрического сопротивления металлов (ТКR > 0) объясняется тем, что при повышении температуры увеличиваются частота и амплитуда колебаний узлов кристаллической решетки, и повышается число их столкновений с движущимися направленно электронами.

Закон Ома для переменного тока

Приветствую всех на нашем сайте! В этот раз речь пойдёт про закон Ома для переменного тока.

Когда-то люди жили без электричества. Потом научились делать батарейки, и так появился постоянный электрический ток. Есть у электриков шутка: «Что такое переменный ток? Это нет-нет, да шарахнет…» А вот тут возникает логичный вопрос: «Почему не остановились на постоянном токе, раз он безопаснее»? Исключительно с экономической точки зрения. Переменный ток гораздо удобнее и дешевле преобразовывать, то есть повышать или понижать. Точнее не сам ток, а напряжение. Когда протекает ток, он совершает работу, работа сопровождается выделением тепла. Мощность, это произведение тока и напряжения, а значит, повышая напряжение и понижая ток мы передадим ту же мощность, но с меньшим тепловыделением, а значит и с меньшими потерями. А ещё, чем выше напряжение, тем меньше сопротивление проводов, по которым протекает ток, это оказывает влияние на потери напряжения. Как-нибудь поговорим более подробно об этом. А пока обратимся к школьному курсу физики – ток протекает только по замкнутому контуру и возможен только при условии, что к этому контуру будет приложено напряжение и контур будет иметь какое-то сопротивление. Подробно об этом вы можете прочитать в статье Закон Ома для замкнутой цепи. А мы двинемся дальше.

Сейчас вы поймете, почему так важен и что даёт закон Ома для цепи переменного тока. В современной жизни без этого закона никак не обойтись. Поскольку ток, это работа, а работа есть выделение тепла, то существенная задача электротехники в том, чтобы соблюдался термический режим, проще говоря, чтобы не произошло перегрева электроцепей. Итак, закон Ома гласит, что:

Измерить напряжение довольно просто, для этого понадобится вольтметр, в нашем случае для переменного напряжения. В цепях постоянного тока измерить сопротивление тоже не составляет сложности, для этого потребуется омметр. Почему же возникают сложности с переменным током? А проблема, именно, в его переменности, а точнее понятиях емкости и индукции, которые ведут себя при переменном токе несколько иначе, нежели при постоянном.

Формула Закона Ома для переменного тока:

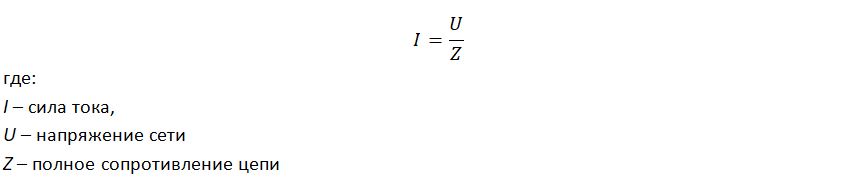
Кому-то эта формула может показаться неожиданной, потому что все привыкли видеть другую формулу:

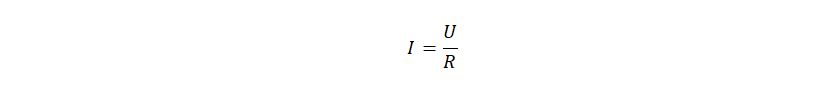
Теперь давайте разберёмся, что такое полное сопротивление цепи и всё сразу встанет на свои места. В цепях постоянного тока конденсаторы могут только накапливать заряд, а катушки индуктивности становятся обычным проводом, но в цепях переменного тока они становятся сопротивлениями. Поэтому в переменном токе существует две составляющие: активный ток и реактивный. Как это происходит, сейчас увидите.

Ёмкостное сопротивление. При подаче напряжения на конденсатор сначала возникает сильный ток и потом поднимается напряжение, то есть в идеальных условиях ток опережает напряжение на угол 90. Другими словами, ток совершает работу из-за наличия сопротивления в цепи, которое можно посчитать по формуле: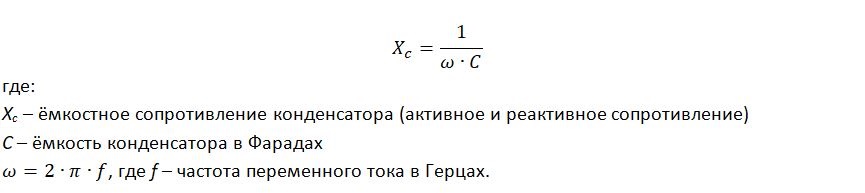

Таким образом, чем выше частота переменного тока и чем выше емкость конденсатора, тем меньше ёмкостное сопротивление.

Индуктивное сопротивление. Здесь все происходит наоборот, сначала возникает напряжение, затем запускается индукционный процесс который препятствует возрастанию тока. Подробнее об этом читайте в статьях про индукцию.

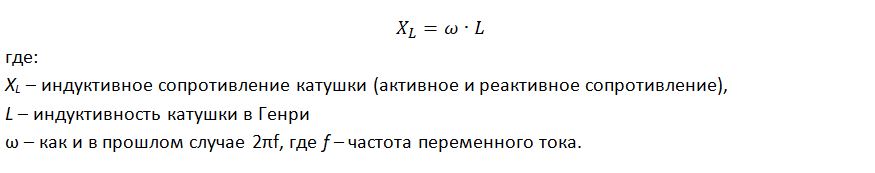
Поэтому здесь мы видим уже обратную картину – чем выше частота и чем больше индуктивность катушки, тем больше индуктивное сопротивление переменному току.

Почему эти понятия не встречаются в цепях постоянного тока? Ответ можно узнать, посмотрев на формулы. Если ток постоянный, то f=0. То есть, емкостное сопротивление станет бесконечно большим, а это значит, что конденсатор в цепи постоянного тока становится похож на выключатель, который размыкает цепь и ток по ней не идёт, но при этом, конденсатор будет пропускать переменный ток. А индуктивное сопротивление станет равно нулю, значит, у нас останется просто провод, который имеет свое собственное сопротивление, которое еще называется активным, и его можно измерить обычным омметром. В отличие от конденсатора, у которого нет активного сопротивления, сопротивление катушки, если оно довольно большое, должно приниматься в расчёт. Как правило, активное сопротивление катушки очень маленькое по сравнению с индуктивным, поэтому его в расчёт не берут, но всё же правильно формула сопротивления катушки выглядит так:

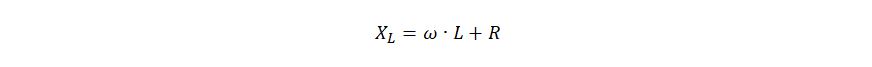
По такому принципу в электронике изготавливают фильтры, которые должны отсечь переменный ток от постоянного, то есть пропускать только переменный ток или наоборот заглушить переменный ток, оставив только постоянный, или даже заглушить токи какой-то одной или нескольких частот.

А сейчас совсем вас запутаю… И катушка может иметь ёмкостные свойства и конденсатор – индуктивные, но как правило они слишком малы и носят паразитический характер.

Ну а сейчас мы рассмотрим закон Ома для электрической цепи переменного тока наглядно.

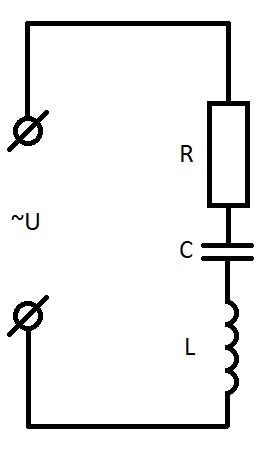
Допустим, у нас есть цепь из последовательно включенных резистора (активное сопротивление), конденсатора (реактивное ёмкостное сопротивление) и катушка (активно-реактивное индуктивное сопротивление). Теперь, чтобы узнать силу тока в цепи нам нужно правильно посчитать полное сопротивление цепи.

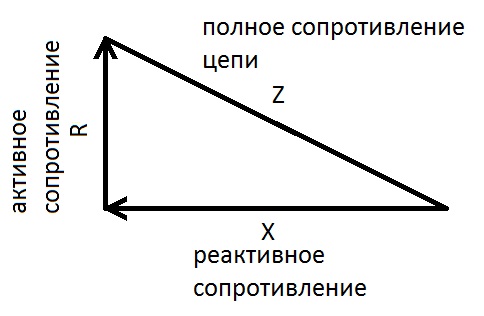
Осталось применить всё изложенное выше.

Реактивное сопротивление Х это разница между индуктивным сопротивлением X_L и ёмкостным сопротивлением X_C. Ну а дальше векторным сложением можем узнать полное реактивное сопротивление

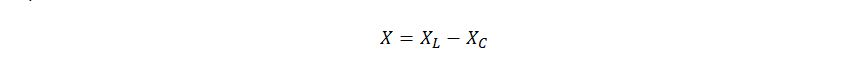
следовательно:

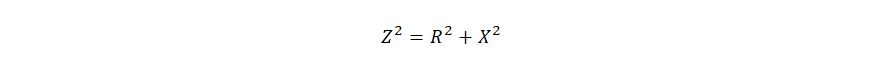
дальнейший расчет:

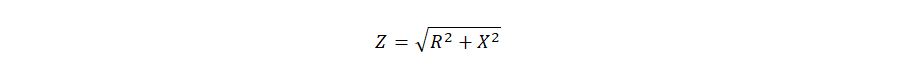
или:

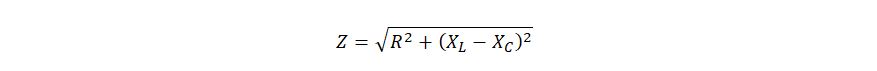
Что можно сказать в заключении. Как вы можете видеть, закон Ома для переменного тока точно такой же, как и для постоянного. Разница лишь в том, как считать сопротивление. Если в постоянном токе мы имеем только активное сопротивление, то в переменном токе добавляется еще и реактивное, а именно индуктивное и емкостное. И, кстати говоря, реактивный ток – явление, с которым в электротехнике стараются бороться различными методами, поскольку эти токи паразитные и не несут полезной нагрузки. Об этом мы поговорим в других статьях. Пока сообщу лишь, что идеальный вариант, к которому пока никто не смог приблизиться, чтобы нагрузка была исключительно активной.

Поделиться ссылкой:

Похожее

Закон Ома для переменного тока: формула

Содержание:

1. Закон ома для участка цепи
2. Закон ома для полной цепи
3. Закон ома для цепи переменного тока
4. Видео

Закон Ома был открыт немецким физиком Георгом Омом в 1826 году и с тех пор начал широко применяться в электротехнической области в теории и на практике. Он выражается известной формулой, с посредством которой можно выполнить расчеты практически любой электрической цепи. Тем не менее, закон Ома для переменного тока имеет свои особенности и отличия от подключений с постоянным током, определяемые наличием реактивных элементов. Чтобы понять суть его работы, нужно пройти по всей цепочке, от простого к сложному, начиная с отдельного участка электрической цепи.

Закон ома для участка цепи

Закон Ома считается рабочим для различных вариантов электрических цепей. Более всего он известен по формуле I = U/R, применяемой в отношении отдельного отрезка цепи постоянного или переменного тока.

В ней присутствуют такие определения, как сила тока (I), измеряемая в амперах, напряжение (U), измеряемое в вольтах и сопротивление (R), измеряемое в Омах.

Широко распространенное определение этой формулы выражается известным понятием: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению на конкретном отрезке цепи. Если увеличивается напряжение, то возрастает и сила тока, а рост сопротивления, наоборот, снижает ток. Сопротивление на этом отрезке может состоять не только из одного, но и из нескольких элементов, соединенных между собой последовательно или параллельно.

Формулу закона Ома для постоянного тока можно легко запомнить с помощью специального треугольника, изображенного на общем рисунке. Он разделяется на три секции, в каждой из которых помещен отдельно взятый параметр. Такая подсказка дает возможность легко и быстро найти нужное значение. Искомый показатель закрывается пальцем, а действия с оставшимися выполняются в зависимости от их положения относительно друг друга.

Если они расположены на одном уровне, то их нужно перемножить, а если на разных – верхний параметр делится на нижний. Данный способ поможет избежать путаницы в расчетах начинающим электротехникам.

Закон ома для полной цепи

Между отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами.

Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока.

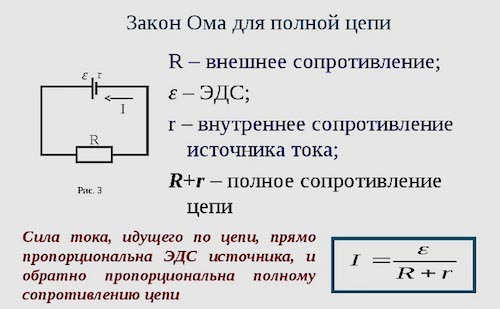
Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта. Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания. Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R.

Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока. По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами. Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет разность потенциалов.

Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела. Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r). На размеры силы тока влияет такое понятие, как электродвижущая сила – ЭДС, прилагаемая к электродам, обозначенная символом Е.

Значение ЭДС возможно измерить на выводах батареи с использованием вольтметра при отключенном внешнем контуре. После подключения нагрузки на вольтметре появится наличие напряжения U. Таким образом, при отключенной нагрузке U = E, в при подключении внешнего контура U < E.

ЭДС дает толчок движению зарядов в полной цепи и определяет силу тока I = E/(R+r). Данная формула отражает закон Ома для полной электрической цепи постоянного тока. В ней хорошо просматриваются признаки внутреннего и наружного контуров. В случае отключения нагрузки внутри батареи все равно будут двигаться заряженные частицы. Это явление называется током саморазряда, приводящее к ненужному расходу металлических частиц катода.

Под действием внутренней энергии источника питания сопротивление вызывает нагрев и его дальнейшее рассеивание снаружи элемента. Постепенно заряд батареи полностью исчезает без остатка.

Закон ома для цепи переменного тока

Для цепей переменного тока закон Ома будет выглядеть иначе. Если взять за основу формулу I = U/R, то кроме активного сопротивления R, в нее добавляются индуктивное XL и емкостное ХС сопротивления, относящиеся к реактивным. Подобные электрические схемы применяются значительно чаще, чем подключения с одним лишь активным сопротивлением и позволяют рассчитать любые варианты.

Сюда же включается параметр ω, представляющий собой циклическую частоту сети. Ее значение определяется формулой ω = 2πf, в которой f является частотой этой сети (Гц). При постоянном токе эта частота будет равной нулю, а емкость примет бесконечное значение. В данном случае электрическая цепь постоянного тока окажется разорванной, то есть реактивного сопротивления нет.

Цепь переменного тока ничем не отличается от постоянного, за исключением источника напряжения. Общая формула остается такой же, но при добавлении реактивных элементов ее содержание полностью изменится. Параметр f уже не будет нулевым, что указывает на присутствие реактивного сопротивления. Оно тоже оказывает влияние на ток, протекающий в контуре и вызывает резонанс. Для обозначения полного сопротивления контура используется символ Z.

Отмеченная величина не будет равной активному сопротивлению, то есть Z ≠ R. Закон Ома для переменного тока теперь будет выглядеть в виде формулы I = U/Z. Знание этих особенностей и правильное использование формул, помогут избежать неправильного решения электротехнических задач и предотвратить выход из строя отдельных элементов контура.

Закон Ома.

Закон Ома.

Программа КИП и А

В программу «КИП и А», в разделе «Электрика» включен блок расчета закона Ома для постоянного и переменного тока. Сначала немного теории..

Для постоянного тока

Закон Ома определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи. Наиболее популярна формулировка:

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, т.е.

I = U / R	где	I — сила тока, измеряемая в Амперах, (A)
		U — напряжение, измеряемое в Вольтах, (V)
		R — сопротивление, измеряется в Омах, (Ω)

Закон Ома, является основополагающим в электротехнике и электронике. Без его понимания также не представляется работа подготовленного специалиста в области КИП и А. Когда-то была даже распространена такая поговорка, — «Не знаешь закон Ома, — сиди дома..».

Помимо закона Ома, важнейшим является понятие электрической мощности, P:

Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U), т.е.

P = I × U	где	P — эл. мощность, измеряемая в Ваттах, (W)
		I — сила тока, измеряемая в Амперах, (A)
		U — напряжение, измеряемое в Вольтах, (V)

Комбинируя эти две формулы, выведем зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:

Сила тока,	I=	U/R	P/U	√(P/R)
Напряжение,	U=	I×R	P/I	√(P×R)
Сопротивление,	R=	U/I	P/I²	U²/P
Мощность,	P=	I×U	I²×R	U²/R

Практический пример использования таблицы: Покупая в магазине утюг, мощностью 1 кВт (1 кВт = 1000 Вт), высчитываем на какой минимальный ток должна быть рассчитана розетка в которую предполагается включать данную покупку:
Несмотря на то, что утюг включается в сеть переменного тока, пренебрегаем его реактивным сопротивлением (см. ниже), и используем упрощенную формулу для постоянного тока. Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В (напряжение сети) = 4,5 Ампера. Это и есть минимальный ток, который должна выдерживать розетка, при подключении к ней нагрузки мощностью 1 кВт.

Наиболее распространенные множительные приставки:

• Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А. 1 миллиампер (1 mA) = 0,001 A. 1 микроампер (1 µA) = 0,000001 A.
• Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V. 1 милливольт (1 mV) = 0,001 V. 1 микровольт (1 µV) = 0,000001 V.
• Сопротивление, Омы (Om): 1 мегаом (1 MOm) = 1000000 Om. 1 килоом (1 kOm) = 1000 Om.
• Мощность, Ватты (W): 1 мегаватт (1 MW) = 1000000 W. 1 киловатт (1 kW) = 1000 W. 1 милливатт (1 mW) = 0,001 W.

Для переменного тока

В цепи переменного тока закон Ома может иметь некоторые особенности, описанные ниже.

Импеданс, Z

В цепи переменного тока, сопротивление кроме активной (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.

Последовательное включение R, L, C
Параллельное включение R, L, C

Также, полное сопротивление, Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.

Импеданс, Полное сопротивление, Z
При последовательном включении R, L, C	При параллельном включении R, L, C
Z=√(R2+(ωL-1/ωC)2)	Z=1/ √(1/R2+(1/ωL-ωC)2)
где,
ω = 2πγ — циклическая, угловая частота; γ — частота переменного тока.

Коэффициент мощности, Cos(φ)

Коэффициент мощности, в самом простом понимании, это отношение активной мощности (P) потребителя электрической энергии к полной (S) потребляемой мощности, т. е.

Cos(φ) = P / S

Он также показывает насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице.
Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи.

Исходя из вышеперечисленных понятий импеданса Z и коэффициента мощности Cos(φ), характерных для переменного тока, выведем формулу закона Ома, коэффициента мощности и их производные для цепей переменного тока:

I = U / Z	где	I — сила переменного тока, измеряемая в Амперах, (A)
		U — напряжение переменного тока, измеряемое в Вольтах, (V)
		Z — полное сопротивление (импеданс), измеряется в Омах, (Ω)

Производные формулы:

Сила тока,	I=	U/Z	P/(U×Cos(φ))	√(P/Z)
Напряжение,	U=	I×Z	P/(I×Cos(φ))	√(P×Z)
Полное сопротивление, импеданс	Z=	U/I	P/I²	U²/P
Мощность,	P=	I²×Z	I×U×Cos(φ)	U²/Z

Программа «КИП и А» имеет в своем составе блок расчета закона Ома как для постоянного и переменного тока, так и для расчета импеданса и коэффициента мощности Cos(φ). Скриншоты представлены на рисунках внизу:

Закон Ома для постоянного тока
Закон Ома для переменного тока
Расчет полного сопротивления
Расчет коэффициента мощности Cos(φ)