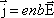Закон Ома в интегральной и дифференциальной форме. — КиберПедия
Закон Ома в интегральной форме:
— для участка цепи: «Сила тока 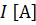 на однородном участке электрической цепи прямо пропорциональна напряжению на данном участке
на однородном участке электрической цепи прямо пропорциональна напряжению на данном участке 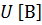 и обратно пропорциональна сопротивлению этого участка
и обратно пропорциональна сопротивлению этого участка 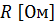 »:
»:
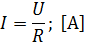
— для всей цепи:
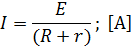
где 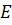 – электродвижущая сила, В;
– электродвижущая сила, В;
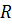 – сопротивление всех элементов цепи, Ом;
– сопротивление всех элементов цепи, Ом;
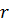 – внутреннее сопротивление источника питания, Ом;
– внутреннее сопротивление источника питания, Ом;
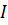 – сила тока, А.
– сила тока, А.
Закон Ома в дифференциальной форме:
— для участка цепи: «Плотность тока в каждой точке однородного участка цепи пропорциональна напряженности электрического поля в этой же точке»:
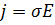
Где 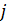 – вектор плотности тока, А/м²;
– вектор плотности тока, А/м²;
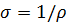 – удельная проводимость, См=
– удельная проводимость, См= 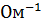 ;
;
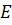 – вектор напряженности электрического поля, В/м.
– вектор напряженности электрического поля, В/м.
Работа и мощность электрического тока. Закон Джоуля-Ленца в интегральной и дифференциальной форме.
За время t по участку электрической цепи будет перенесён заряд и при этом будет совершена работа:
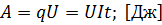
где 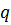 – электрический заряд, Кл;
– электрический заряд, Кл;
 – напряжение, В;
– напряжение, В;
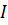 – сила тока, А;
– сила тока, А;
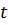 – время, с.
– время, с.
Работа, совершаемая в единицу времени – мощность электрического тока:
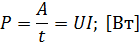
Закон Джоуля-Ленца в дифференциальной форме: «Мощность тепла 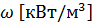 , выделяемого в единице объёма среды при протекании постоянного электрического тока, равна произведению плотности электрического тока
, выделяемого в единице объёма среды при протекании постоянного электрического тока, равна произведению плотности электрического тока 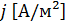 на величину напряженности электрического поля
на величину напряженности электрического поля 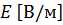 »:
»:
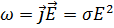
где 
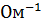 .
.Закон Джоуля-Ленца в интегральной форме:
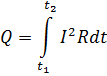
где 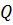 – полное количество теплоты, выделенное за промежуток времени от
– полное количество теплоты, выделенное за промежуток времени от 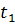 до
до 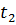
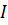 – сила тока, А;
– сила тока, А;
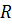 – сопротивление. Ом.
– сопротивление. Ом.
Закон Ома для участка цепи и для замкнутой цепи, содержащей э.д.с.
Закон Ома для участка цепи:
«Сила тока 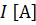 на однородном участке электрической цепи прямо пропорциональна напряжению на данном участке
на однородном участке электрической цепи прямо пропорциональна напряжению на данном участке 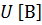 и обратно пропорциональна сопротивлению этого участка
и обратно пропорциональна сопротивлению этого участка 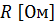
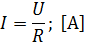
Закон Ома для неоднородного участка цепи (содержащего ЭДС):
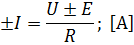
где 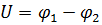 – разность потенциалов (напряжение), В;
– разность потенциалов (напряжение), В;
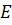 – электродвижущая сила, В;
– электродвижущая сила, В;
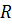
Если направление тока совпадает с направлением обхода, его принято считать положительным; если источник тока повышает потенциал в направлении обхода (источник посылает ток в направлении обхода), то ЭДС такого источника считается положительной.
Закон Ома для замкнутой цепи, содержащей ЭДС:
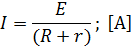
где 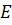 – электродвижущая сила, В;
– электродвижущая сила, В;
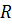
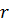 – внутреннее сопротивление источника питания, Ом;
– внутреннее сопротивление источника питания, Ом;
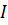 – сила тока, А.
– сила тока, А.
Законы Кирхгофа.
Первое правило Кирхгофа: «Алгебраическая сумма токов, сходящихся в узле, равна нулю:
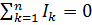 ».
».
Второе правило Кирхгофа:
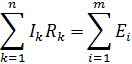
где 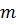 – число источников ЭДС;
– число источников ЭДС;
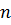 – число ветвей в замкнутом контуре;
– число ветвей в замкнутом контуре;
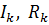 – ток и сопротивление -той ветви, А, Ом».
– ток и сопротивление -той ветви, А, Ом».
Правило знаков:
1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;
2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.
Закон Ома (интегральная форма)
Основной закон электрических цепей (закон Ома) установил экспериментально в 1826 году немецкий физик Георг Ом.
В общем случае закон Ома (обобщённый) формулируется так: сила тока на участке цепи прямо пропорциональна напряжению на этом участке:
I = GU, (8)
Коэффициент пропорциональности G называется проводимостью участка цепи.
Величина, обратная проводимости, называется электросопротивлением (или просто — сопротивлением) участка цепи:
R = 1/G. (9)
Обобщённый закон Ома обычно выражается так:
I = 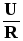 .
(10)
.
(10)
Сопротивление проводников зависит от его размеров, формы и материала, из которого проводник изготовлен. Для однородного проводника с одинаковой по всей длине площадью поперечного сечения s сопротивление равно:
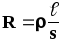 ,
(11)
,
(11)
где — удельное сопротивление материала проводника.
В области температур, близких или выше комнатных, сопротивление линейно зависит от температуры:
R = R0(1 + T), (12)
где R0 — сопротивление проводника при некоторой температуре Т0 (обычно Т0=00С), R — сопротивление этого проводника при температуре Т=Т0+T, — термический коэффициент сопротивления.
В конкретных электротехнических задачах закон Ома удобно представлять в виде —
— для однородного участка цепи (не содержащего ЭДС):
I = 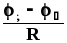 ,
(13)
,
(13)
— для неоднородного участка цепи (содержащего ЭДС):
I = 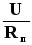 =
=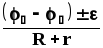 ,
(14)
,
(14)
— для замкнутой цепи:
I = 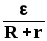 .
(15)
.
(15)
Здесь (1 — 2) — разность потенциалов на концах участка, — алгебраическая сумма ЭДС неоднородного участка цепи или всего контура (в случае замкнутой цепи), R — полное сопротивление всех однородных участков цепи, r — общее внутреннее сопротивление всех источников ЭДС, Rп=R+r — полное сопротивление неоднородного участка цепи. Перед ставятся знаки «+» или «-» в зависимости от полярности источника ЭДС по отношению к полярности внешнего напряжения (1 — 2), приложенного к участку цепи.
Закон Ома (дифференциальная форма).
Закон Ома можно представить в дифференциальной форме, если в уравнении (10) использовать вместо интегральных характеристик — силы тока I, напряжения U и сопротивления R, дифференциальные, характеризующие электрическое состояние среды в одной точке, — плотность тока J, напряжённость поля E и удельное сопротивление проводника соответственно.
Для проводника,
имеющего форму цилиндра, сопротивление
определяется формулой (11). Подстановка
её в формулу (10) даёт: 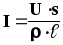 или
или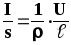 .
Поскольку
.
Поскольку =J,
=J, 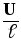 =Е,
=Е, 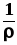 = (удельная проводимостью материала
проводника), то
= (удельная проводимостью материала
проводника), то
закон Ома принимает вид:
J = E. (16)
Плотность тока 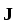 и напряжённость поля
и напряжённость поля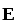 являются коллинеарными векторами. Таким
образом,закон
Ома в дифференциальной форме можно представить так:
являются коллинеарными векторами. Таким
образом,закон
Ома в дифференциальной форме можно представить так:
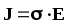 .
(17)
.
(17)
24. «Закон Ома в дифференциальной и интегральной формах» Закон Ома в дифференциальной форме


Найдем
связь между 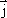 и
и  в
бесконечно малом объеме проводника
– закон
Ома в дифференциальной форме.
в
бесконечно малом объеме проводника
– закон
Ома в дифференциальной форме.
В
изотропном проводнике (в данном случае
с постоянным сопротивлением) носители
зарядов движутся в направлении действия
силы, т.е. вектор плотности тока 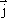 и
вектор напряженности поля
и
вектор напряженности поля  коллинеарны
(рис. 7.6).
коллинеарны
(рис. 7.6).
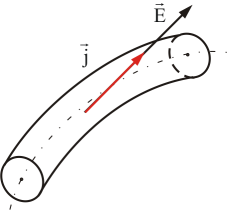
Рис. 7.6
Исходя из закона Ома (7.6.1), имеем:
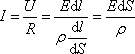
А
мы знаем, что 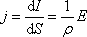 или
или 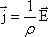 .
Отсюда можно записать
.
Отсюда можно записать
|
| (7.6.3) |
|
это запись закона Ома в дифференциальной форме.
Здесь 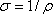 – удельная
электропроводность.
– удельная
электропроводность.
Размерность
σ – [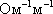 ].
].
Плотность
тока можно выразить через заряд
электрона е,
количество зарядов n и
дрейфовую скорость 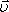 :
:
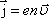 .
.
Обозначим 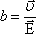 ,
тогда
,
тогда  ;
;
|
| (7.6.4) |
|
Теперь,
если удельную электропроводность σ
выразить через е, n и b: 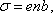 то
вновь получим выражение закона
Ома в дифференциальной форме:
то
вновь получим выражение закона
Ома в дифференциальной форме:
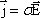 .
.

Закон Ома в интегральной форме
Для однородного участка цепи, т.е. для
участка, на котором не действуют сторонние
силы, закон Ома записывается в форме
(2.8). Рассмотрим теперь неоднородный участок
цепи 1-2 (рис. 2.8), где действует ЭДС
источника 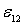 и
на концах которого приложена разность
потенциалов
и
на концах которого приложена разность
потенциалов  .
.

На
рассматриваемом участке работа 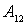 всех
приложенных сил (сторонних и
электростатических), совершаемая над
носителями тока, согласно (2.6) равна:
всех
приложенных сил (сторонних и
электростатических), совершаемая над
носителями тока, согласно (2.6) равна:
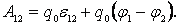
В
этой формуле ЭДС  берется
либо с положительным, либо с отрицательным
знаком. Если ЭДС способствует движению
положительных зарядов в направлении
обхода (в направлении 1-2), т.е. внутри
источника обход совпадает с перемещением
зарядов от катода к аноду, то
берется
либо с положительным, либо с отрицательным
знаком. Если ЭДС способствует движению
положительных зарядов в направлении
обхода (в направлении 1-2), т.е. внутри
источника обход совпадает с перемещением
зарядов от катода к аноду, то 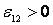 (рис.
2.8, а).
Если ЭДС препятствует движению
положительных зарядов в направлении
обхода, то
(рис.
2.8, а).
Если ЭДС препятствует движению
положительных зарядов в направлении
обхода, то 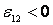 (рис.
2.8, б).
По закону сохранения и превращения
энергии работа
(рис.
2.8, б).
По закону сохранения и превращения
энергии работа 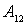 равна
теплоте, выделяющейся на участке 1-2 за
время t (эта
теплота определяется согласно
закону Джоуля-Ленца):
равна
теплоте, выделяющейся на участке 1-2 за
время t (эта
теплота определяется согласно
закону Джоуля-Ленца):
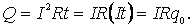 (2.20)
(2.20)
Приравнивая (2.6) и (2.20), получим:
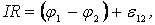 (2.21)
(2.21)
или
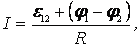 (2.22)
(2.22)
где R – суммарное сопротивление, включающее в себя внутреннее сопротивление r источника тока и сопротивление внешней цепи. Выражение (2.21) или (2.22) есть закон Ома в интегральной (обобщенной) форме для цепи постоянного тока.
25
Исто́чник то́ка (в теории электрических цепей) — двухполюсник, создающий в нагрузке электрический ток, причем сила тока не зависит от сопротивления нагрузки. Используются также термины генератор тока и идеальный источник тока. Источник тока — модель реального источника электроэнергии или часть такой модели.
Смещение под действием электрического поля зарядов в проводнике всегда происходит таким образом, что электрическое поле в проводнике исчезает и ток прекращается. Для протекания тока в течение продолжительного времени на заряды в электрической цепи должны действовать силы, отличные по природе от сил электростатического поля, такие силы получили название сторонних сил.
Эти силы могут быть обусловлены химическими процессами, диффузией носителей тока в неоднородной среде, электрическими (но не электростатическими) полями, порождаемыми переменными во времени магнитными полями, и т. д. Всякое устройство, в котором возникают сторонние силы, называется источником электрического тока.
Сторонние силы характеризуют работой, которую они совершают над перемещаемыми по электрической цепи носителями заряда. Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой (ЭДС) , действующей в электрической цепи или на ее участке.
26
Преодолевая сопротивление проводника, электрический ток выполняет работу, в процессе которой в проводнике выделяется тепло. Свободные электроны при своем движении сталкиваются с атомами и молекулами и при этих столкновениях механическая энергия движущихся электронов переходит в тепловую.
Зависимость тепловой энергии от силы тока в проводнике определяется по закону Джоуля-Ленца. При прохождении электрического тока по проводнику количество тепла, выделяемого током в проводнике, прямо пропорционально силе тока, взятой во второй степени, величине сопротивления проводника и времени действия тока.
Если количество тепла обозначать буквой Q, силу тока в а — I, сопротивление в ом — R и время в сек.— t, то математически закон Джоуля-Ленца можно представить так:
Q = aI2Rt
При а=1 количество тепла Q получится в джоулях. При а=0,24 количество тепла Q получится в малых калориях. Коэффициент 0,24 в формуле фигурирует потому, что ток в 1 а в проводнике с сопротивлением в 1 ом за 1 сек. выделяет 0,24 малых калорий тепла. Малая калория служит единицей для измерения количества тепла. Малая калория равна количеству тепла, которое необходимо для нагревания 1 г воды на 1° С.
Этот закон независимо друг от друга открыли в 1840-м году английский физик Джеймс Джоуль и русский физик Эмилий Христианович Ленц. Этот физический закон определяет количество теплоты Q, выделяемой в проводнике при прохождении через него электрического тока.
Итак, тепло всегда выделяется в проводнике, когда в нем проходит ток. Однако, чрезмерный нагрев проводников и электротехнических устройств допускать нельзя, так как это приведет к их повреждению. Особенно опасен перегрев при коротком замыкании проводов, то есть при электрическом соединении проводников, подводящих электрическую энергию к потребителю.
При коротком замыкании обычно сопротивление остающихся под током проводников ничтожно, ток из-за этого достигает большой силы, и тепло выделяется в таком количестве, которое вызывает аварию. Для предохранения от коротких замыканий и чрезмерных перегревов в цепь включаются плавкие предохранители. Они представляют собой небольшие куски тонкой проволоки или пластинки, которые перегорают как только ток достигает определенной величины. Выбор плавких предохранителей производится в зависимости от площади сечения проводов.
27
Первое правило Кирхгофа утверждает, что алгебраическая сумма токов, сходящихся в любом узле цепи равна нулю:
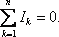
В случае установившегося постоянного тока в цепи ни в одной точке проводника, ни на одном из его участков не должны накапливаться электрические заряды (узел – любой участок цепи, где сходятся более двух проводников (рис. 7.8)).
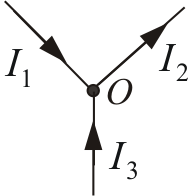
Рис. 7.8
Токи, сходящиеся к узлу, считаются положительными:
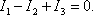
Второе правило Кирхгофа является обобщением закона Ома для разветвленной цепи.
Для произвольного замкнутого контура с произвольным числом разветвлений (рис. 7.9) можно записать для каждого элемента контура:
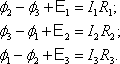
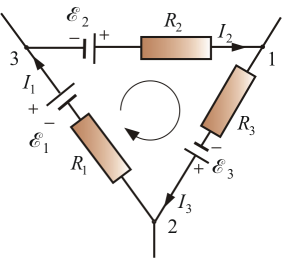
Рис. 7.9
Складывая эти уравнения получим второе правило Кирхгофа:
В любом замкнутом контуре электрической цепи алгебраическая сумма произведения тока на сопротивление равна алгебраической сумме ЭДС, действующих в этом же контуре.
Обход контуров осуществляется по часовой стрелке, если направление обхода совпадает с направлением тока, то ток берется со знаком «плюс».
Обобщенный закон Ома в интегральной и дифференциальной формах.
Обобщенный закон Ома в интегральной и дифференциальной формах.Немецкий физик Г. Ом (1787-1854) экспериментально установил, что сила тока в однородном проводнике пропорциональна разности потенциалов на его концах и обратно пропорциональна сопротивлению проводника (закон Ома для участка цепи):
где R – электрическое сопротивление проводника, определяющее упорядоченность перемещения свободных носителей тока.
Электрическое сопротивление металлического проводника обусловлено тем, что свободные электроны при своем движении взаимодействуют (соударяются) с положительными ионами кристаллической решетки. Поэтому сопротивление проводников зависит прежде всего от материала проводника, т.е. строения его кристаллической решетки. Для однородного цилиндрического проводника длиной l и площадью поперечного сечения S сопротивление определяется по формуле
Удельное электрическое сопротивление проводника зависит не только от рода вещества, но и от температуры (по Цельсию):
У чистых металлов α = 1/273 1/KДля полной цепи, содержащей ЭДС, справедлив обобщенный закон Ома в интегральной форме
Для участка с источником тока и для участка с внешним сопротивлением будем иметьСложив, получим закон Ома для полной цепи
I(r+R)=ε
Разности потенциалов сократились, потому что работа электростатических сил по замкнутому контуру равна нулю. В случае многих источников направление тока заранее неизвестно; выбираем его произвольно и проходим контур в этом направлении. Записав соответствующие уравнения, получим
I∑Ri=∑±εi
Если сила тока окажется отрицательной, то направление тока надо изменить на противоположное.
Закон Ома в интегральной форме
Ляпин Али Ибрагимович, доцент БРУ
1. | Однородный и неоднородный участки цепи. | 2 |
| ρ dl | 2 |
| r | r | 2 r | r | |
| Вывод закона Ома в интегральной форме | для | I ∫ |
|
| =∫Eк dl | +∫Eстор dl | ||||
|
| S | |||||||||
| неоднородного участка цепи |
| 1 |
| 1 |
|
|
| 1 |
| |
|
|
|
|
|
|
|
|
|
|
| |
2. | Разность потенциалов, электродвижущая |
|
|
| 2 r | r |
|
|
| 2 r | r |
| сила, напряжение | ϕ1 | −ϕ2 = ∫Eк dl | ; | ε1−2 | = ∫Eстор dl | |||||
|
|
|
| 1 |
|
|
|
| 1 |
| |
3. | Правила Кирхгофа для электрических цепей |
|
|
| N |
|
| N |
|
| N |
|
|
|
| ∑Ik = 0 ; | ∑Ik Rk = ∑εk | ||||||
|
|
|
| k =1 |
|
| k =1 |
| k =1 | ||

2Ляпин Али Ибрагимович, доцент БРУ
1.Однородный и неоднородный участки цепи. Вывод закона Ома в интегральной форме для неоднородного участка цепи.
Однородный и неоднородный участки цепи.
Если в проводнике действует только электростатическое поле, то в нем может возникнуть только кратковременный электрический ток. Действительно, если обкладки конденсатора, заряженного до некоторой разности потенциалов Δφ, соединить проводником, то в проводнике возникнет электрический ток. По мере протекания тока конденсатор будет разряжаться, и разность потенциалов будет уменьшаться. С течением времени потенциал во всех точках системы уравняется и ток прекратится.
Например, если обкладки заряженного конденсатора емкостью 1Ф замкнуть проводником, имеющим сопротивление 1Ом, то электрический ток в цепи будет протекать примерно в течение 1с.
В электростатическом поле заряды перемещаются из точек с большим потенциалом в точки с меньшим потенциалом, что приводит к выравниванию потенциалов. Для поддержания электрического тока достаточно длительное время, необходим источник, в котором за счет сил не электростатического происхождения осуществлялся бы перенос носителей тока в исходную точку с большим потенциалом. Указанные силы называются сторонними.
Таким образом, для поддержания электрического тока в цепи необходимо наличие сторонних сил, действующих либо во всей цепи, либо на отдельных ее участках.
Сторонние силы могут быть химической, электромагнитной природы и др. Например, в большинстве аккумуляторов роль сторонних сил играют силы химического взаимодействия, приводящие к разделению молекул электролитов на разноименные заряды. В этом случае разность потенциалов на электродах аккумулятора поддерживается за счет энергии химической реакции.
Участок цепи, на котором не действуют сторонние силы, называется однородным. Участок цепи, на котором действуют сторонние силы, называется неоднородным.
Вывод закона Ома в интегральной форме для неоднородного участка цепи.
В общем случае на неоднородном участке цепи действуют и кулоновские и сторонние силы. Обозначим напряженность поля электростатических (кулоновских) сил через Ек, а напряженность поля сторонних сил через Естор. Тогда в любой точке внутри проводника результирующая напряженность равна
E = Eк + Eстор
и закон Ома в дифференциальной форме будет иметь вид
|
|
|
|
|
|
| r | 1 |
|
| r |
| r |
|
| |
|
|
|
|
|
|
| j = |
|
| (E | к | + E | ) | . (1) | ||
|
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
| ρ |
|
|
|
| стор |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Обе части уравнения (1) умножим |
| скалярно на вектор dl , | ||||||||||||||
численно равный элементу dl длины проводника и совпадающий | ||||||||||||||||
по направлению с вектором j плотности тока |
|
|
|
| ||||||||||||
r | r |
| 1 | r | r | r |
|
|
|
| r |
|
|
|
| |
j | dl | = |
| (E | dl | + E |
|
| dl ) . (2) |
| ||||||
ρ |
|
|
| |||||||||||||
|
|
| к |
|
| стор |
|
|
|
|
|
|
| |||
Так как плотность тока j постоянного |
| равна | j = I / S и скалярное произведение | |||||||||||||
сонаправленных векторов | rj и | dl равно произведению их модулей, то формулу (2) можно | ||||||||||||||
записать в следующей форме |
| ρ dl |
|
| r |
|
|
| r | r | r | |||||
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
| I |
|
| = | E | к | dl + E | dl . (3) | ||||
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
| S |
|
|
|
|
|
| стор |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
3 | Ляпин Али Ибрагимович, доцент БРУ |
Формула (3) представляет собой закон Ома для бесконечно малого элемента dl неоднородного участка цепи от сечения 1 с потенциалом φ1 до сечения 2 с потенциалом φ2. Проинтегрировав выражение (3) по всей длине участка цепи от сечения 1 с потенциалом φ1
до сечения 2 с потенциалом φ2 получим формулу обобщенного закона Ома в интегральной форме для неоднородного участка цепи
2 | ρ dl | 2 | r | r | 2 | r | r |
| |
I ∫ |
| =∫Eк dl | +∫Eстор dl | . (4) | |||||
S | |||||||||
1 | 1 |
|
| 1 |
|
|
| ||
Так как сила постоянного тока во всех сечениях проводника постоянна, то сила тока вынесена за знак интеграла.
2. Разность потенциалов, электродвижущая сила, напряжение
Проанализируем интегралы, входящие в формулу (4). Нетрудно видеть, что подынтегральное выражение в интеграле левой части формулы (4) определяет электрическое сопротивление элемента dl проводника, а сам интеграл выражает электрическое сопротивление цепи на рассматриваемом участке
R | = | 2 | ρ dl | . (5) |
∫1 |
| |||
1−2 |
| S | ||
|
| |||
При этом, сопротивление R1-2 включает в себя как сопротивление R проводника, так и сопротивление r промежутка цепи между электродами источника тока (сопротивление электролита или внутреннее сопротивление источника)
R1-2=R+r. (6)
Первый интеграл правой части формулы (4) выражает работу сил электростатического поля по перемещению единичного положительного заряда из точки с потенциалом φ1 в точку
с потенциалом φ2. Эта работа в электростатике была названа разностью потенциалов, поэтому
ϕ1 −ϕ2 = ∫2 Erк dlr. (7)
1
Второй интеграл правой части формулы (4) выражает работу сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи. Указанная работа сторонних сил называется электродвижущей силой (ЭДС) и часто
обозначается символом ε
ε1−2 = ∫2 Erстор dlr. (8)
1
Из формулы (8) следует физический смысл ЭДС:
ЭДС на участке цепи называется физическая величина, численно равная работе сторонних сил по перемещению единичного положительного заряда на этом участке.
ЭДС, так же как и разность потенциалов, измеряется в вольтах.
С учетом введенных обозначений для интегралов, формулу (4) можно записать в следующем виде
I R1−2 = (ϕ1 −ϕ2 ) +ε1−2 . (9)
Формула (9) также является математическим выражением закона Ома для неоднородного участка цепи в интегральной форме.
ЭДС, так же как и сила тока, является величиной алгебраической. Поэтому следует учитывать ее знак.
Если ЭДС способствует перемещению положительных зарядов в данном направлении, то она считается положительной. Если ЭДС препятствует перемещению положительных зарядов в данном направлении, то она считается отрицательной.
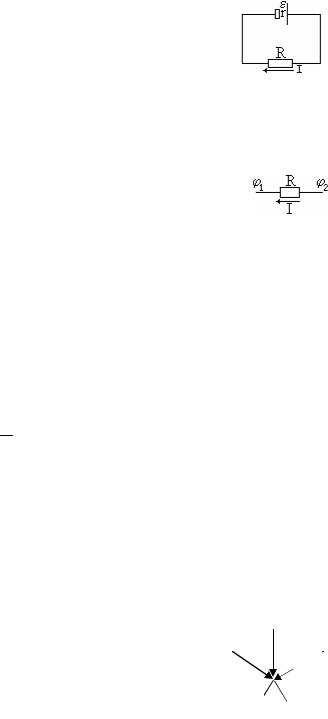
4 Ляпин Али Ибрагимович, доцент БРУ
Произведение величины сопротивления участка цепи и силы тока в нем называется падением напряжения. Из формулы (9) следует физический смысл напряжения:
напряжением на участке цепи называется физическая величина, численно равная сумме работ электростатических и сторонних сил по перемещению единичного положительного заряда вдоль этого участка.
Формула (9) называется также формулой обобщенного закона Ома, так как она справедлива для различных цепей.
Если на приведенном выше рисунке участок цепи замкнуть проводником, то получим замкнутую цепь. В этом случае φ1=φ2 и из формулы (9), с учетом формулы (6), получим закон Ома в следующем виде
I (R + r)= ε или I = | ε | . (10) | |
R + r | |||
|
|
В случае замкнутой неразветвленной цепи ЭДС равна работе по перемещению единичного положительного заряда по всей цепи.
Из формулы (10) следует, что ЭДС равна сумме падений напряжений на внутреннем и внешнем участках цепи.
В случае однородного (в отсутствие ЭДС) участка цепи с током I, ε=0,
r=0 и формула (9) принимает следующий вид |
|
|
| |||
I = | ϕ1 | −ϕ2 | или | I = | U | , (11) |
| R | R | ||||
|
|
|
|
| ||
где φ1-φ2=U называется падением напряжения на сопротивлении R.
Если неоднородная цепь не замкнута, то I=0 и формула (9) принимает следующий вид
(ϕ1 −ϕ2 ) = ε , (12)
то есть в этом случае ЭДС равна разности потенциалов на клеммах источника тока.
Для каждого проводника в неизменном состоянии существует однозначная зависимость между разностью потенциалов, приложенной к его концам, и силой тока в нем I=f(U). Эта зависимость называется вольтамперной характеристикой (ВАХ). Для многих проводников, особенно металлических, эта зависимость выражается законом Ома
I = R1 U . (13)
То есть значение силы тока изменяется прямо пропорционально с изменением значения U. Обобщенный закон Ома в интегральной форме позволяет рассчитывать различные электрические цепи.
3. Правила Кирхгофа для разветвленных электрических цепей
Расчеты сложных (разветвленных) электрических цепей значительно упрощаются с помощью правил Кирхгофа (Г. Кирхгоф, нем. ученый, 1847г.). Любую разветвленную цепь можно представить как совокупность точек разветвления и замкнутых контуров.
Узлом называется точка разветвления цепи, в которой сходится больше
двух проводников с током. | I | I2 | I3 |
Первое правило Кирхгофа выражает условие постоянства тока в цепи. В |
|
|
|
случае постоянного тока электрические заряды не должны накапливаться на | I5 |
| I4 |
каком либо участке цепи. |
| ||
Первое правило Кирхгофа гласит: алгебраическая сумма токов, |
|
|
|
сходящихся в узле, равна нулю: |
|
|
|
N
∑Ik = 0 , (14)
k =1
где N– число проводников, сходящихся в узле; Ik– сила тока в k-м проводнике, причем токи, подходящие к узлу считаются положительными, а токи, отходящие от него– отрицательными
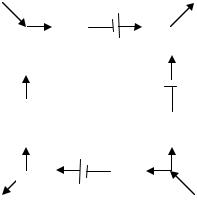
5 | Ляпин Али Ибрагимович, доцент БРУ |
Второе правило Кирхгофа является обобщением закона Ома (9) на разветвленные цепи.
Второе правило гласит: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма напряжений на всех участках этого контура равна алгебраической сумме Э.Д.С. всех источников электрической энергии, включенных в контур
N | N |
∑Ik Rk = ∑εk , (15) | |
k =1 | k =1 |
где N– число участков, на которые контур разбивается узлами; Ik, Rk и εk– сила тока, сопротивление и Э.Д.С. соответствующие k-му участку.
При составлении уравнения (15) необходимо |
|
|
|
|
|
|
| ε1 |
|
|
|
|
|
|
|
|
| |||||
выбрать направление обхода контура. Все токи в |
|
| A R1 |
|
| I1 |
| B |
|
|
| |||||||||||
участках, | совпадающие | по | направлению с |
|
|
|
|
|
|
| – | + |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
направлением | обхода контура, | следует | считать |
|
|
|
|
|
|
|
|
|
|
|
| I2 | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
положительными, а не совпадающие с направлением |
|
|
|
|
|
|
|
|
|
|
|
| + |
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ε2 | |||||||
обхода – отрицательными. | Э.Д.С. | источников тока |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
| – |
|
| ||||||||
считать положительными, если они создают ток, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
R4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
совпадающий | с направлением | обхода | контура. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| R2 | |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
Например, в случае обхода приведенного контура |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
I4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
ABCD по часовой стрелке уравнение имеет вид |
|
| + |
| – |
|
|
|
|
|
|
| C | |||||||||
I1 R1 − I2 R2 + I3 R3 + I4 R4 =ε1 −ε2 +ε3 . |
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
| D | ε3 |
|
|
|
| I3 | ||||||||||||||
|
|
| R3 |
|
|
|
| |||||||||||||||
Вопросы для самопроверки:
1.Что понимают под сторонними силами и какова их роль в электрической цепи? Укажите природу сторонних сил.
2.Какой участок цепи называется однородным, и какой неоднородным? Вывести закон Ома в интегральной форме для неоднородного участка цепи. Как выбирается знак Э.Д.С. при записи закона Ома?
3.Пояснить физический смысл разности потенциалов, электродвижущей силы и напряжения на участке электрической цепи. Указать на отличие между этими величинами.
4.Сформулировать правила Кирхгофа. Как выбираются знаки Э.Д.С. и токов при записи правил Кирхгофа?
Закон Ома в дифференциальной форме.
Рассмотрим небольшой участок однородного
проводника постоянного сечения,
находящегося под напряжением  .
Поделив напряжение на сопротивление
участка и, учитывая, что
.
Поделив напряжение на сопротивление
участка и, учитывая, что
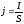 ,
,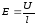 ,
,
находим
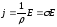 ,
,
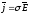 .
.
Плотность тока в каждой точке проводника пропорциональна напряжённости электрического поля. Полученное соотношение выражает локальный закон Ома и называется законом Ома в дифференциальной форме.
Отметим, что в случае постоянноготока избыточный заряд внутриоднородногопроводника равен нулю. Действительно, при постоянном токе, заряд, входящий в выделенный объём, равен заряду, выходящему из объема, т.е.
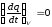 ,
,
откуда следует
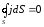 .
.
Учитывая, что
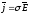 ,
,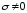 ,
,
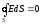 ,
,
т.е. 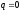 .
.
Избыточный заряд может появиться только на поверхности однородного проводника, где проводник имеет неоднородность.
В проводнике при постоянном токе распределение зарядов не изменяется с течением времени, хотя и происходит движение зарядов, так как в каждой точке на место уходящих зарядов непрерывно поступают новые. Эти движущиеся заряды создают электрическое поле аналогичноеполю неподвижных зарядов той же конфигурации, т.е. является потенциальным.
Закон Ома для участка, содержащего сторонние силы.
Сторонниминазывают силы не
электростатического происхождения.
Они могут быть обусловлены химической
и физической неоднородностью проводника,
например, таковы силы, возникающие при
соприкосновении разнородных проводников
(гальванические элементы, аккумуляторы)
или проводников различной температуры
(термоэлементы) и др.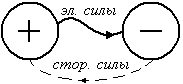
Постоянный ток возможен только при наличии сторонних сил, так как одни электростатические силы могут вызвать только кратковременный ток.
Сторонние силы должны переносить положительные носители на участках своего действия в сторону возрастания потенциала, компенсируя действие электростатических сил.
Для количественной характеристики сторонних сил вводят понятие поля сторонних сил и его напряженность аналогично полю электрических сил:
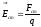 .
.
Очевидно, плотность тока в местах, где существуют электрические и сторонние силы определяется соотношением:
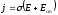 ,
,
которое называется обобщенным законом Ома в дифференциальной форме.
Закон Ома в интегральной форме для участка, содержащего источник тока.
Для простоты рассмотрим участок
проводника в форме цилиндра (см. рисунок),
к торцам которого приложена разность
потенциалов 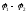 и в пределах которого действуют сторонние
силы.
и в пределах которого действуют сторонние
силы.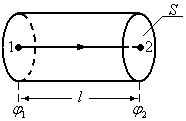
Умножим выражение локального закона Ома:
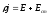
скалярно
на вектор перемещения 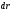 вдоль линии тока и проинтегрируем от
точки 1 до точки 2:
вдоль линии тока и проинтегрируем от
точки 1 до точки 2:
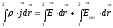 .
.
После интегрирования получаем:
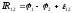 ,
,
где 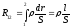 — сопротивление участка цепи между
сечениями 1 и 2,
— сопротивление участка цепи между
сечениями 1 и 2,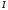 – сила тока на участке,
– сила тока на участке,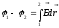 — разность потенциалов,
— разность потенциалов,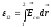 —
электродвижущая сила (э.д.с.), действующая
на данном участке цепи, равная работе
сторонних сил по перемещению единичного
положительного заряда. Произведение
—
электродвижущая сила (э.д.с.), действующая
на данном участке цепи, равная работе
сторонних сил по перемещению единичного
положительного заряда. Произведение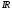 называютпадениемнапряжения на
участке.
называютпадениемнапряжения на
участке.
Э.д.с., как и сила тока 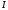 и соответственно падение напряжения,
является величиной алгебраической:
если э.д.с. способствует движению
положительных носителей в выбранном
направлении, то
и соответственно падение напряжения,
является величиной алгебраической:
если э.д.с. способствует движению
положительных носителей в выбранном
направлении, то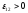 ,
если же препятствует, то
,
если же препятствует, то .
.
Полученное соотношение выражает интегральную форму закона Ома для участка, содержащего сторонние силы.
Обычно сторонние силы действуют на
ограниченном участке, которые называют
источником постоянного тока. Условно
источник обозначают двумя вертикальными
черточками, короткой и длинной. Короткая
относится к отрицательному полюсу,
длинная – к положительному. Э.д.с.
направлена от минуса к плюсу, так как
сторонние силы в источнике всегда
действуют против электрических сил.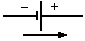
Пример.
Рассмотрим участок, содержащий источник и сопротивление (см. рисунок).
Выразим
разность потенциалов: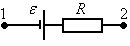
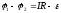 .
.
В
нашем примере 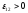 .
.
Пусть ток на участке течёт от 1 и 2 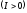 .
Алгебраическая сумма в правой части
может оказаться отрицательной.
Следовательно
.
Алгебраическая сумма в правой части
может оказаться отрицательной.
Следовательно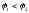 ,
т.е. ток течёт в сторону повышения
потенциала. Это возможно потому, что на
участке действует э.д.с. в положительном
направлении (от 1 и 2). Если
,
т.е. ток течёт в сторону повышения
потенциала. Это возможно потому, что на
участке действует э.д.с. в положительном
направлении (от 1 и 2). Если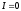 ,
то
,
то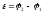 ,
т.е. э.д.с. источника равна разности
потенциалов между полюсами источника.
,
т.е. э.д.с. источника равна разности
потенциалов между полюсами источника.
Закон Ома в дифференциальной форме.
Рассмотрим небольшой участок однородного
проводника постоянного сечения,
находящегося под напряжением 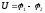 .
Поделив напряжение на сопротивление
участка и, учитывая, что
.
Поделив напряжение на сопротивление
участка и, учитывая, что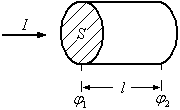
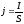 ,
,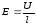 ,
,
находим
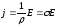 ,
,
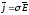 .
.
Плотность тока в каждой точке проводника пропорциональна напряжённости электрического поля. Полученное соотношение выражает локальный закон Ома и называется законом Ома в дифференциальной форме.
Отметим, что в случае постоянноготока избыточный заряд внутриоднородногопроводника равен нулю. Действительно, при постоянном токе, заряд, входящий в выделенный объём, равен заряду, выходящему из объема, т.е.
 ,
,
откуда следует
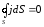 .
.
Учитывая, что
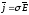 ,
,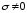 ,
,
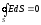 ,
,
т.е. 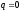 .
.
Избыточный заряд может появиться только на поверхности однородного проводника, где проводник имеет неоднородность.
В проводнике при постоянном токе распределение зарядов не изменяется с течением времени, хотя и происходит движение зарядов, так как в каждой точке на место уходящих зарядов непрерывно поступают новые. Эти движущиеся заряды создают электрическое поле аналогичноеполю неподвижных зарядов той же конфигурации, т.е. является потенциальным.
Закон Ома для участка, содержащего сторонние силы.
Сторонниминазывают силы не
электростатического происхождения.
Они могут быть обусловлены химической
и физической неоднородностью проводника,
например, таковы силы, возникающие при
соприкосновении разнородных проводников
(гальванические элементы, аккумуляторы)
или проводников различной температуры
(термоэлементы) и др.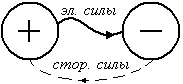
Постоянный ток возможен только при наличии сторонних сил, так как одни электростатические силы могут вызвать только кратковременный ток.
Сторонние силы должны переносить положительные носители на участках своего действия в сторону возрастания потенциала, компенсируя действие электростатических сил.
Для количественной характеристики сторонних сил вводят понятие поля сторонних сил и его напряженность аналогично полю электрических сил:
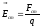 .
.
Очевидно, плотность тока в местах, где существуют электрические и сторонние силы определяется соотношением:
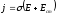 ,
,
которое называется обобщенным законом Ома в дифференциальной форме.
Закон Ома в интегральной форме для участка, содержащего источник тока.
Для простоты рассмотрим участок
проводника в форме цилиндра (см. рисунок),
к торцам которого приложена разность
потенциалов  и в пределах которого действуют сторонние
силы.
и в пределах которого действуют сторонние
силы.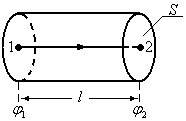
Умножим выражение локального закона Ома:
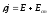
скалярно
на вектор перемещения 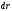 вдоль линии тока и проинтегрируем от
точки 1 до точки 2:
вдоль линии тока и проинтегрируем от
точки 1 до точки 2:
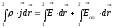 .
.
После интегрирования получаем:
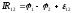 ,
,
где 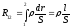 — сопротивление участка цепи между
сечениями 1 и 2,
— сопротивление участка цепи между
сечениями 1 и 2,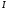 – сила тока на участке,
– сила тока на участке,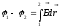 — разность потенциалов,
— разность потенциалов,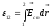 —
электродвижущая сила (э.д.с.), действующая
на данном участке цепи, равная работе
сторонних сил по перемещению единичного
положительного заряда. Произведение
—
электродвижущая сила (э.д.с.), действующая
на данном участке цепи, равная работе
сторонних сил по перемещению единичного
положительного заряда. Произведение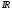 называютпадениемнапряжения на
участке.
называютпадениемнапряжения на
участке.
Э.д.с., как и сила тока 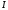 и соответственно падение напряжения,
является величиной алгебраической:
если э.д.с. способствует движению
положительных носителей в выбранном
направлении, то
и соответственно падение напряжения,
является величиной алгебраической:
если э.д.с. способствует движению
положительных носителей в выбранном
направлении, то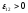 ,
если же препятствует, то
,
если же препятствует, то .
.
Полученное соотношение выражает интегральную форму закона Ома для участка, содержащего сторонние силы.
Обычно сторонние силы действуют на
ограниченном участке, которые называют
источником постоянного тока. Условно
источник обозначают двумя вертикальными
черточками, короткой и длинной. Короткая
относится к отрицательному полюсу,
длинная – к положительному. Э.д.с.
направлена от минуса к плюсу, так как
сторонние силы в источнике всегда
действуют против электрических сил.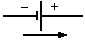
Пример.
Рассмотрим участок, содержащий источник и сопротивление (см. рисунок).
Выразим
разность потенциалов: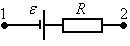
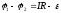 .
.
В
нашем примере 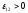 .
.
Пусть ток на участке течёт от 1 и 2 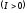 .
Алгебраическая сумма в правой части
может оказаться отрицательной.
Следовательно
.
Алгебраическая сумма в правой части
может оказаться отрицательной.
Следовательно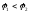 ,
т.е. ток течёт в сторону повышения
потенциала. Это возможно потому, что на
участке действует э.д.с. в положительном
направлении (от 1 и 2). Если
,
т.е. ток течёт в сторону повышения
потенциала. Это возможно потому, что на
участке действует э.д.с. в положительном
направлении (от 1 и 2). Если ,
то,
т.е. э.д.с. источника равна разности
потенциалов между полюсами источника.
,
то,
т.е. э.д.с. источника равна разности
потенциалов между полюсами источника.




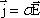 ,
,