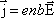Закон Ома в дифференциальной и интегральной формах
Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике:
I=
Однородным называется проводник, в котором не действуют сторонние силы. В этом случае, как мы видели, напряжение U совпадает с разностью потенциалов —
— , поддерживаемой на концах проводника. Величина R называется электрическим сопротивлением проводника. Единицей сопротивления служит ом, равный сопротивлению такого проводника, в котором при напряжении в 1 в течет ток силой в 1 а.
, поддерживаемой на концах проводника. Величина R называется электрическим сопротивлением проводника. Единицей сопротивления служит ом, равный сопротивлению такого проводника, в котором при напряжении в 1 в течет ток силой в 1 а.
Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника
R=
где l— длина проводника, S — площадь его поперечного сечения,  — зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества. Если l=1 и S= 1, то R численно равно
— зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества. Если l=1 и S= 1, то R численно равно  . В СИ
. В СИ 
 в (ом×мм2)/м.
в (ом×мм2)/м.Закон Ома можно записать в дифференциальной форме. Выделим мысленно в окрестности некоторой точки внутри проводника элементарный цилиндрический объем с образующими, параллельными вектору плотности тока j в данной точке. Через поперечное сечение цилиндра течет ток силой
jdS. Напряжение, приложенное к цилиндру, равно Edl где Е — напряженность поля в данном месте. Наконец, сопротивление цилиндра, согласно формуле равно 
jdS= ×Edt
×Edt
Носители заряда в каждой точке движутся в направлении вектора Е. Поэтому направления j и Е совпадают. Таким образом, можно написать
j=
где 
 — величина, называемая коэффициентом электропроводности или просто проводимостью материала. Формула выражает закон Ома в дифференциальной форме.
— величина, называемая коэффициентом электропроводности или просто проводимостью материала. Формула выражает закон Ома в дифференциальной форме.
Для любой точки внутри проводника напряженность  результирующего поля равна сумме напряженности поля кулоновских сил и поля сторонних сил
результирующего поля равна сумме напряженности поля кулоновских сил и поля сторонних сил 

Умножим скалярно обе части на вектор  , численно равный элементу
, численно равный элементу 


Так как скалярное произведение совпадающих по направлению векторов 
 , равно произведению их модулей, то это равенство можно переписать в виде
, равно произведению их модулей, то это равенство можно переписать в виде
С учетом 

Интегрируя по длине проводника  от сечения 1 до некоторого сечения 2 и учитывая, что сила тока во всех сечениях проводника одинакова, получаем
от сечения 1 до некоторого сечения 2 и учитывая, что сила тока во всех сечениях проводника одинакова, получаем
|
|
Интеграл  численно равен работе, совершаемой кулоновскими силами при перенесении единичного положительного заряда с точки 1 в точку 2. В электростатике было показано, что
численно равен работе, совершаемой кулоновскими силами при перенесении единичного положительного заряда с точки 1 в точку 2. В электростатике было показано, что

Таким образом,

где
 и
и  — значение потенциала в т.1 и т.2.
— значение потенциала в т.1 и т.2.Интеграл, содержащий вектор 
 , действующей на участке 1-2
, действующей на участке 1-2|
|
Интеграл
|
|
равен сопротивлению участка цепи 1-2.
Подставляя окончательно получим
|
|
Последнее уравнение выражает собой закон Ома в интегральной форме для участка цепи, содержащего эдс и формулируется следующим образом: падение напряжения на участке цепи равно сумме падений электрического потенциала на этом участке и эдс всех источников электрической энергии, включённых на участке.
Законы Ома для участка цепи
Закон Ома в интегральной форме
Немецкий физик Георг Ом в 1826 году экспериментально установил, что сила тока, протекающего по металлическому проводнику прямо пропорциональна разности потенциалов (напряжению) на концах проводника:
I=(1–2) =U. (6.8)
Коэффициент пропорциональности,
связывающий силу тока в проводник и
напряжение — ,
называется электрической проводимостью.
Величина, обратная проводимости —
электрическое сопротивление проводника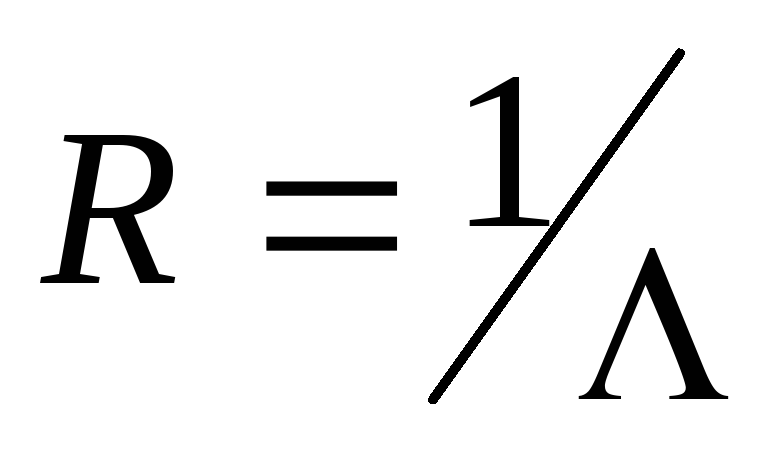 .
Сопротивление зависит от материала
проводника, его формы, размеров и
состояния. Например, сопротивление
цилиндрического проводника (проволоки):
.
Сопротивление зависит от материала
проводника, его формы, размеров и
состояния. Например, сопротивление
цилиндрического проводника (проволоки):
 . (6.9)
. (6.9)
Здесь: — удельное сопротивление вещества, из которого сделан проводник;
lиS— длина и площадь поперечного сечения проводника.
Сопротивление измеряется в омах. 1 Ом — это сопротивление такого проводника, в котором течёт ток I= 1 А при напряженииU= 1 В:
 .
.
Удельное сопротивление в системе СИ измеряется в Омм:
 .
.
Удельное сопротивление вещества зависит от температуры. В не слишком широком диапазоне температур удельное сопротивление многих проводников является линейной функцией температуры:
=0(1 +t). (6.10)
Здесь: 0— удельное электрическое сопротивление вещества при 0С;
— температурный коэффициент сопротивления.
Для всех чистых металлов = 0.037, то есть
температурный коэффициент их удельного
сопротивления близок к температурному
коэффициенту расширения идеальных
газов. Температурный коэффициент
сопротивления проводниковIрода (металлов)I> 0, аIIрода (электролитов)II< 0. Это означает, что с понижением
температуры удельное сопротивление
металлов уменьшается, а электролитов
— растёт.
0.037, то есть
температурный коэффициент их удельного
сопротивления близок к температурному
коэффициенту расширения идеальных
газов. Температурный коэффициент
сопротивления проводниковIрода (металлов)I> 0, аIIрода (электролитов)II< 0. Это означает, что с понижением
температуры удельное сопротивление
металлов уменьшается, а электролитов
— растёт.
При температурах близких к абсолютному нулю (0.2 20 К) сопротивление многих металлов и их сплавов скачком уменьшается до нуля. Это состояние вещества называется сверхпроводящим. Впервые явление сверхпроводимости было обнаружено для ртути в 1911 году голландским физиком Камерлинг-Оннесом.
Не так давно обнаружено сверхпроводящее состояние ряда керамических материалов, которое наступает при достаточно высоких температурах ~100 К («высокотемпературная сверхпроводимость»).
Рассмотренный закон пропорциональности тока в проводнике и напряжения:
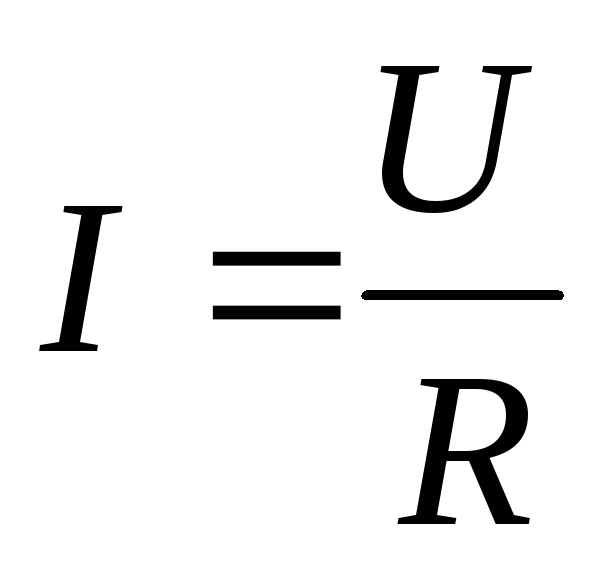 (6.11)
(6.11)
называется законом Ома в интегральной форме. Он позволяет вычислить ток, текущий в цилиндрических проводниках. Но как быть, если электрический ток течёт, например, в электропроводящей среде, заполняющей пространство между обкладками сферического или цилиндрического конденсатора? В подобных случаях на помощь приходит другой закон Ома, к изучению которого мы и приступаем.
Закон Ома в дифференциальной форме
Представим себе электрический ток не в привычном для нас проводнике, а однородной изотропной проводящей среде. В своём направленном движении носители заряда перемещаются по траекториям, которые называются «линии тока». Выделим в среде небольшую поверхность S. Линии тока, коснувшиеся границы этой поверхности, в дальнейшем вырезают в пространстве «трубку тока» (рис. 6.4.). Особенность этой трубки состоит в том, что заряженные частицы, движущиеся внутри трубки тока, не пересекают её боковую поверхность, то есть они никогда не покидают свою трубку тока.
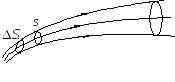
Рис. 6.4.
Выделим в трубке тока два эквипотенциальных сечения S1иS2, отстоящие друг от друга на расстоянииl(рис. 6.5.). Потенциалы этих сечений1и2=1+. Для выделенного элемента трубки тока запишем закон Ома (6.11):
 .
.

Рис. 6.5.
Сократив Sи введя удельную электропроводимость=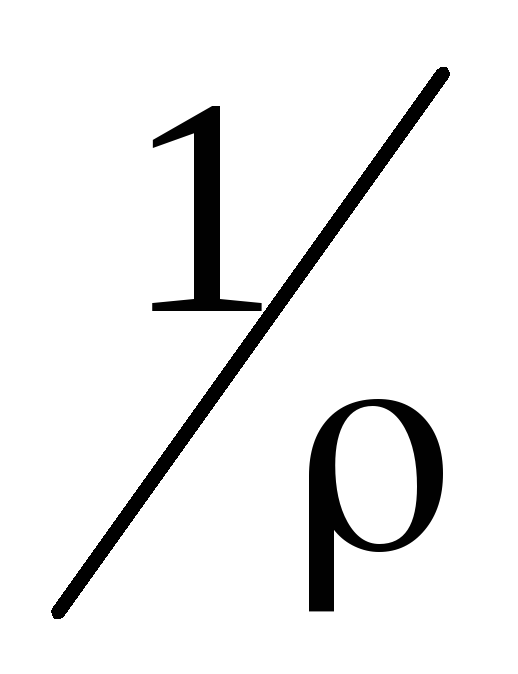 ,
получим:
,
получим:
 .
.
Этот результат становится совсем точным, если перейти к пределу, устремив lк нулю. ТогдаS=S1=S2, так как трубка становится цилиндрической. Кроме того:
 . (6.12)
. (6.12)
Учитывая этот результат, плотность тока запишем так:
i=E,
или в векторном виде:
 . (6.13)
. (6.13)
Уравнение (6.13) — математическая записьзакона Ома в дифференциальной форме.
В этом законе связываются две «локальные»
характеристики тока: плотность тока в любойточкепространства и
напряжённость электрического поля
в любойточкепространства и
напряжённость электрического поля в той же точке. В соответствии с этим
законом, плотность электрического
тока прямо пропорциональна напряжённости
поля в рассматриваемой точке пространства.
в той же точке. В соответствии с этим
законом, плотность электрического
тока прямо пропорциональна напряжённости
поля в рассматриваемой точке пространства.
В приведённых рассуждениях есть момент, который не может не настораживать: в законе (6.13) Е— напряжённость электрического поля в проводящей среде с током. А для вычисления этой характеристики мы воспользовались связью напряжённости и потенциала электростатического поля в вакууме (6.12). Однако можно показать, что напряжённость электрического поля внутри однородной проводящей среды совпадает с электростатическим полем, которое существует в вакууме, если обеспечивается то же пространственное распределение потенциала, что и в проводящей среде при наличии тока (см., например, [2]).
Теперь на примере расчёта тока утечки в сферическом конденсаторе покажем, как используется закон Ома в дифференциальной форме для решения вполне реальных задач.
Электрический ток. Сила и плотность тока. Основные законы постоянного тока. Законы Ома и Джоуля-Ленца в интегральной и дифференциальной формах. Плотность тока и скорость носителей тока.
I. Любое упорядоченное (направленное) движение электрических зарядов называется ЭЛЕКТРИЧЕСКИМ ТОКОМ. При приложении внешнего электрического поля Е в проводнике начинается движение зарядов, т.е. возникает электрический ток. При этом положительные заряды движутся по полю, а отрицательные — против поля. За направление тока принимают направление движения положительных зарядов. Для возникновения и существования электрического тока необходимо выполнение двух условий :
1. наличие свободных носителей зарядов (т.е. вещество должно быть проводником или полупроводником при высоких температурах),
2.Наличие внешнего электрического поля.
Для количественного описания электрического тока вводится — СИЛА ТОКА – скалярная физическая велична, равная количеству электрического заряда, переносимосму за единицу времени через поперечное сечение проводника S.
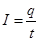 — для постоянного тока, и
— для постоянного тока, и
 — для переменного тока.
— для переменного тока.
Ток, сила и направление которого не изменяются со временем, называетсяпостоянным.
ПЛОТНОСТЬ ТОКА  — векторная физическая величина, численно равная силе тока, проходящего через единицу площади, перпендикулярной к току:
— векторная физическая величина, численно равная силе тока, проходящего через единицу площади, перпендикулярной к току:

1. Закон Ома для однородного участка цепи.
Однороднымназывается участок не содержащий ЭДС.
Сила тока на однородном участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению цепи



1 Ом – сопротивление такого проводника, в котором при напряжении 1 В течёт ток 1 А.

G — электрическая проводимость.  (Сименс).
(Сименс).
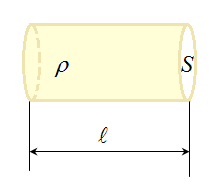 Сопротивление R проводника зависит от его размеров и формы, а также от материала проводника.
Сопротивление R проводника зависит от его размеров и формы, а также от материала проводника.
 ,
,
где ρ — удельное сопротивление проводника — сопротивление единицы длины проводника. 
ℓ — длина проводника; S — площадь поперечного сечения проводника.
2.Закон Ома для неоднородного участка цепи
НЕОДНОРОДНЫМназывается участок цепи, содержащий ЭДС.
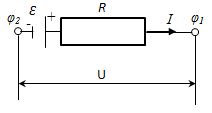

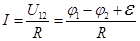
— Закон Ома для неоднородного участка цепи в интегральной форме.
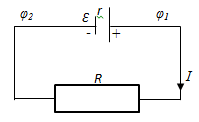 3. Закон Ома для замкнутой цепи (для полной цепи).
3. Закон Ома для замкнутой цепи (для полной цепи).

где  где R — сопротивление внешней цепи,
где R — сопротивление внешней цепи,
г — сопротивление источника ЭДС, тогда
 — Закон Ома для полной цепи
— Закон Ома для полной цепи
4. Закон Ома в дифференциальной форме.
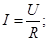

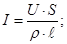

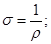

σ — удельная электропроводность; 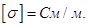
 — Закон Ома в дифференциальной форме.
— Закон Ома в дифференциальной форме.
Плотность тока  прямо пропорциональна напряженности электрического поля Е, Коэффициент пропорциональности σ — удельная электропроводность.
прямо пропорциональна напряженности электрического поля Е, Коэффициент пропорциональности σ — удельная электропроводность.
Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов  , тогда работу по переносу заряда q на этом участке равна
, тогда работу по переносу заряда q на этом участке равна 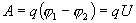
По определению I= q/t. откуда q= I t. Следовательно 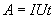
Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил
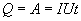 | (17.13) |
Соотношение (17.13) выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности  , равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника
, равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника

где S — поперечное сечение проводника,  — его длина. Используя (1.13) и соотношение
— его длина. Используя (1.13) и соотношение  , получим
, получим  . Но
. Но 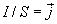 — плотность тока, а
— плотность тока, а  , тогда
, тогда 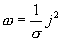 с учетом закона Ома в дифференциальной форме
с учетом закона Ома в дифференциальной форме 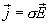 , окончательно получаем
, окончательно получаем
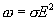 | (17.14) |
Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.
Подвижность (скорость) носителей тока в твёрдом теле, отношение скорости направленного движения электронов проводимости и дырок (дрейфовой скорости υдр), вызванного электрическим полем, к напряжённости Е этого поля:
μ = υдр/Е.
У разных типов носителей в одном и том же веществе μ различны, а в анизотропных кристаллахразличны μ каждого типа носителей для разных направлений поля Е. Величина μ определяется процессамирассеяния электронов в кристалле. Рассеяние происходит на заряженных и нейтральных примесныхчастицах и дефектах кристаллической решётки, а также на тепловых колебаниях кристаллической решётки (фононах). Испуская или поглощая фонон, носитель изменяетсвой Квазиимпульс и, следовательно, скорость. Поэтому μ сильно изменяется при изменении температуры.При T ≥ 300 К преобладает рассеяние на фононах, с понижением температуры вероятность этого процессападает и доминирующим становится рассеяние на заряженных примесях или дефектах, вероятностькоторого растет с уменьшением энергии носителей.
Законы Кирхгофа.
Первый закон Кирхгофа.
1) Первый закон (правило) Кирхгофа — алгебраическая сумма токов сходящихся в узле равна нулю.
Ветви — это проводящие участки цепи между узлами.
Узел — это область соединения двух (или трёх) и более ветвей.
Алгебраическая сумма — это значит в неё входят слагаемые со знаком плюс и со знаком минус.
На рисунке ниже показан узел в котором соединяются четыре ветви с токами: I1, I2, I3, I4.

Рисунок 1 — Узел с ветвями
Направления токов показаны стрелочками. От узла направлены токи I1 и I2, к узлу направлены токи I3 и I4. Примем направления к узлу — положительными, а от узла — отрицательными. Запишем, с учётом выбранных положительных и отрицательных направлений токов, уравнение по первому закону Кирхгофа для узла на рисунке 1:

Ток I1 вошел в уравнение (1) со знаком минус так как этот ток направлен от узла (см. рисунок 1).
Ток I2 входит в уравнение (1) со знаком минус по той же причине. Токи I3 и I4 входят в уравнение (1) со знаком плюс так как они направлены к узлу (см. рисунок 1). Вся эта алгебраическая сумма равна нулю.
Токи I1 и I2 можно перенести в правую часть уравнения с противоположным знаком:

Также можно поступить и с любым уравнением записанным по первому закону Кирхгофа.
Учитывая это можно дать другое определение первого закона (правила) Кирхгофа:
2) сумма токов входящих в узел равна сумме токов выходящих из него.
Уравнение (2) можно привести к виду:

перенеся в правую часть уравнения токи I3 и I4 с противоположным знаком.
Уравнение (3) можно привести к виду:

Тоже самое можно проделать с любым уравнением записанным по первому закону Кирхгофа. Это значит что не имеет значения то какое направление (от узла или к узлу) принято за положительное а какое за отрицательное, главное чтобы все одинаковые направления имели один знак а все противоположные другой.
Иногда бывает так что один узел принимается за два и более при невнимательном осмотре схемы что приводит к ошибкам в расчётах. Рассмотрим схему на рисунке 2:
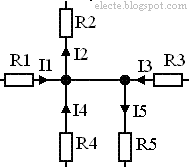
Рисунок 2 — Схема с одним узлом
В этой схеме один узел, для этого узла можно составить уравнение по первому закону Кирхгофа:
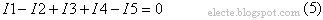 Токи в узлах не протекают т.к. узел имеет один потенциал на всем его протяжении и на всей его площади.
Токи в узлах не протекают т.к. узел имеет один потенциал на всем его протяжении и на всей его площади.
10) Классическая теория электропроводности металлов. Закон Ома для проводника в дифференциальной и интегральной форме.
Изучив основные законы постоянного тока, познакомимся с тем, как их объясняет классическая теория в случае металлических проводников.
Прежде всего, согласимся с тем, что свободными носителями заряда в металлах являются не ионы, а электроны.
По теории Друде-Лоренца, свободные электроны в металле движутся также как атомы идеального газа. Эта аналогия позволила вычислить среднюю скорость теплового движения электронов. Для температуры Т = 300 К она составила гигантскую величину: 105 м/с

105 м/с.
105 м/с.Теперь обратимся к рассмотрению направленного движения электронов в электрическом поле. Электрон движется равноускоренно под действием постоянной силы F = eE. Ускорение движения (II закон Ньютона):
 За
время свободного пробега
За
время свободного пробега  электрон достигнет максимальной
скорости в своём направленном движении:
электрон достигнет максимальной
скорости в своём направленном движении:  .
.
после каждого столкновения скорость направленного движения вновь начинает нарастать от 0 до Vmax. Тогда средняя скорость направленного движения оказывается равной половине максимальной:
 .
Воспользовавшись этим результатом в
уравнении (6.2), получим:
.
Воспользовавшись этим результатом в
уравнении (6.2), получим: 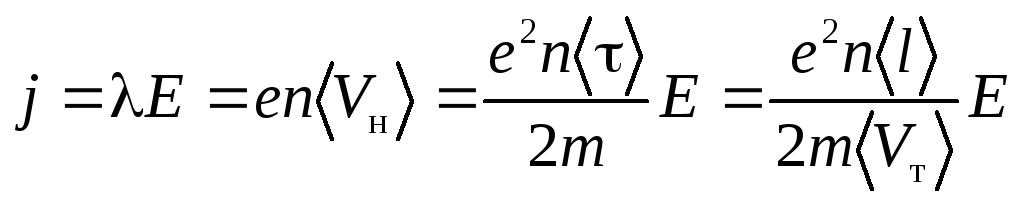 .
.
Коэффициент пропорциональности, связывающий плотность тока с напряженностью электростатического поля — удельная электропроводность металла:

К концу своего свободного пробега электрон достигает скорости:
 и энергии:
и энергии:  .
.
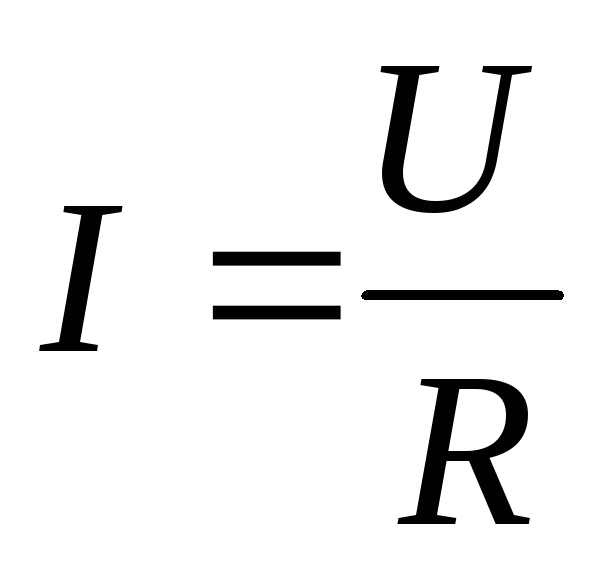 называется
законом Ома в интегральной форме.
называется
законом Ома в интегральной форме.
Уравнение  . — математическая запись закона Ома в
дифференциальной форме.
. — математическая запись закона Ома в
дифференциальной форме.
11) Закон Ома для замкнутой цепи. Сторонние силы. Электродвижущая сила элемента.
Нельзя организовать циркуляцию заряда по замкнутому контуру под действием только электростатической силы. Для переноса заряда в область высокого потенциала (2-b-1) придётся использовать силы неэлектростатической природы. Такие силы получили название сторонних сил. В качестве сторонних сил могут выступать любые силы кроме электростатических. Приборы, в которых на электрические заряды действуют сторонние силы, называются источниками тока. В аккумуляторах, например, сторонние силы возникают в результате химической реакции взаимодействия электродов с электролитом, в генераторах сторонними являются силы, действующие на заряды, движущиеся в магнитном поле и т.д. Именно в источниках тока благодаря работе сторонних сил создаётся генерируемая энергия, которая затем расходуется в электрической цепи.
Работа, которую
совершают сторонние силы  при перемещении единичного положительного
заряда — одна из основных характеристик
источника, его электродвижущая сила :
при перемещении единичного положительного
заряда — одна из основных характеристик
источника, его электродвижущая сила :
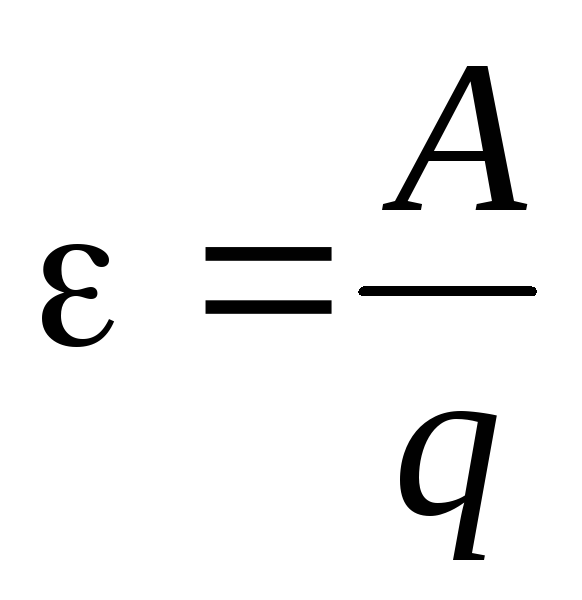
Поле сторонних
сил, также как и электростатическое
поле, характеризуется вектором
напряжённости  :
:
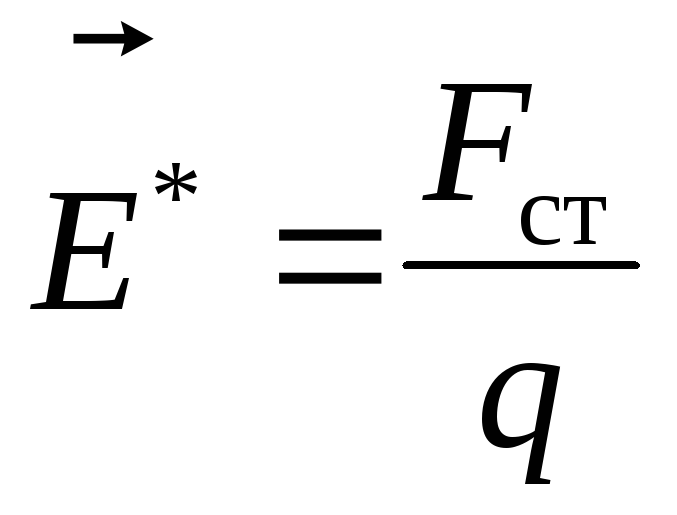
Электродвижущая сила источника равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда по замкнутому контуру.
На участке цепи
1-а-2 движение носителей заряда происходит
под действием только электростатической
силы  = q
= q .
Такие участки называются однородными.
.
Такие участки называются однородными.
Участок замкнутого контура, где наряду с электростатической силой действуют и сторонние силы, называют неоднородным.
Можно показать,
что на однородном участке цепи средняя
скорость направленного движения
носителей заряда пропорциональна
действующей на них силе. Для этого
достаточно сравнить формулы, полученные
на прошлой лекции: 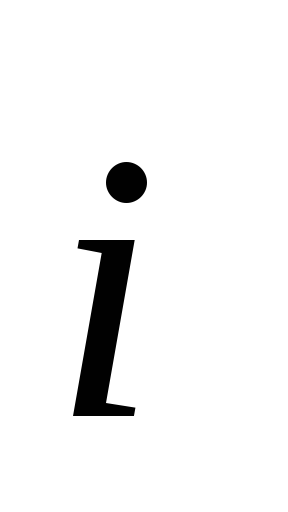 =
=  (6.3) и
(6.3) и  =
= 
Пропорциональность
скорости силе, а плотности тока —
напряжённости сохранится и в случае
неоднородного участка цепи. Но теперь
напряжённость поля равна сумме
напряжённостей электростатического
поля  и поля сторонних сил
и поля сторонних сил  :
:  .
.
Это уравнение закона Ома в локальной дифференциальной форме для неоднородного участка цепи.
Теперь перейдём к закону Ома для неоднородного участка цепи в интегральной форме.
Для замкнутого
контура уравнение закона Ома несколько
видоизменяется, так как разность
потенциалов в этом случае равна нулю:  .
.
В законе Ома для замкнутой цепи (7.8) R — полное сопротивление контура, складывающееся из внешнего сопротивления цепи R0 и внутреннего сопротивления источника r: R = R0 + r.
12) Закон Джоуля-Ленца в дифференциальной форме и интегральной форме.
Пусть на участке электрической цепи протекает постоянный ток I . Напряжение U на концах этого участка численно равно работе, совершаемой электрическими силами при перемещении единичного положительного заряда по этому участку. Это следует из определения напряжения.
Отсюда работа A = q U. За время t по участку будет перенесён заряд q = I t и при этом будет совершена работа: A = q U = U I t.
Это выражение работы электрического тока справедливо для любых проводников.
Работа, совершаемая
в единицу времени — мощность электрического
тока:  .
.
Работа электрического тока (6.14) может затрачиваться на нагревание проводника, совершение механической работы (электродвигатель) и на химическое действие тока при его течении через электролит (электролиз).
Если химическое действие и механическая работа при течении тока не производятся, то вся работа электрического тока расходуется только на нагревание проводника: Q = A = U I t = I2 R t. (6.15)
Закон о тепловом эффекте электрического тока (6.15) был экспериментально установлен независимо английским учёным Д. Джоулем и русским академиком Э.Х. Ленцем. Формула (6.15) — математическая запись закона Джоуля-Ленца в интегральной форме, позволяющая вычислить количество теплоты, выделяющейся в проводнике.
 .
.
Перед нами закон
Джоуля-Ленца в дифференциальной форме.
Учитывая, что i = E = 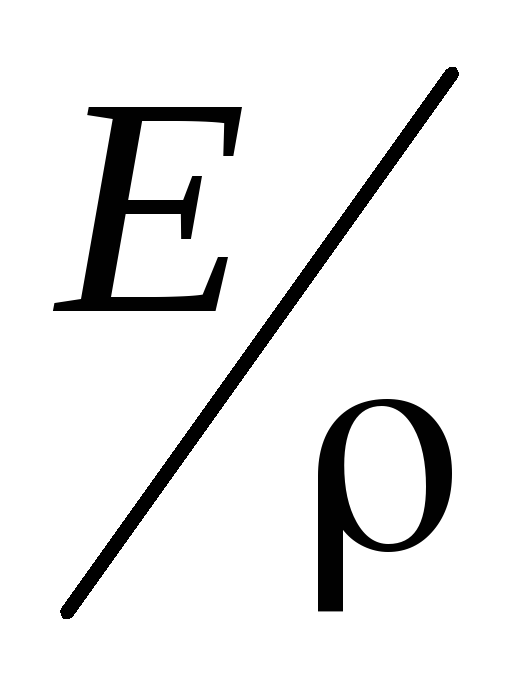 ,
это выражение можно записать ещё и так:
,
это выражение можно записать ещё и так:

Закон Джоуля-Ленца в интегральной и дифференциальной формах
Теперь подробнее обсудим величину DU (которая представляет в расчетах изменение внутренней энергии) применительно к проводнику, по которому начинает течь ток.
Постепенно, выбранный проводник будет нагреваться, а это значит, что будет увеличиваться его внутренняя энергия. По мере нагрева разность между температурой проводника и окружающей его среды будет увеличиваться. Согласно закономерности Ньютона, вместе с этим возрастать будет и мощность теплоотдачи проводника. Таким образом, через какое-то время температура проводника, достигнув определенного значения, перестанет увеличиваться. В этот момент величина DU будет равной нулю, и перестанет изменяться внутренняя энергия проводника.
Тогда для этого состояния первый закон термодинамики будет выглядеть так: A = – Q. То есть когда не меняется внутренняя энергия проводника, работа тока целиком превращается в теплоту. Используя этот вывод, можем записать все три рассмотренные формулы для расчета работы тока в несколько ином виде, в конечном итоге получаем закон Джоуля-Ленца в интегральной форме:
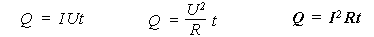 На
первый взгляд все формулы могут считаться
равноправными, однако только последняя
справедлива всегда, поэтому она и
считается законом. А вот остальные две
справедливы только при определенных
условиях, поэтому законом считаться не
могут.
На
первый взгляд все формулы могут считаться
равноправными, однако только последняя
справедлива всегда, поэтому она и
считается законом. А вот остальные две
справедливы только при определенных
условиях, поэтому законом считаться не
могут.
Закон Джоуля-Ленца в дифференциальной форме выглядит совершенно по-иному, мы рассмотрим только общий вариант, без дополнительных выведений и вычислений, который выглядит так:
 Где:
Где:
 —
является мощностью тепла, выделяемого
в единице объёма;
—
является мощностью тепла, выделяемого
в единице объёма; —
плотность электрического тока;
—
плотность электрического тока; —
это напряжённость электрического поля;
—
это напряжённость электрического поля; —
проводимость выбранной среды.
—
проводимость выбранной среды.
Так в общих чертах выглядит закон Джоуля-Ленца и его интегральная и дифференциальная формы. Хотя, если проводить дальнейшие вычисления, то закон может принимать и другие формы.
21. Закон Ома для неоднородного участка цепи (обобщенный закон Ома). Закон Ома для замкнутой цепи.
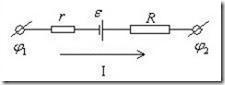
Участок цепи, содержащий источник ЭДС, называется неоднородным(рис.5.11). Всякий источник ЭДС характеризуется величиной ЭДС ε ивнутренним сопротивлением r.
 —
напряжение на концах участка цепи.
—
напряжение на концах участка цепи.
Рис.5.11. Неоднородный участок цепи.
Закон Ома для неоднородного участка цепи имеет вид:
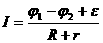
При
соединении концов неоднородного участка
цепи идеальнымпроводником
образуется замкнутая цепь, в
которой потенциалы φ1 иφ2 выравниваются
и мы приходим к закону
Ома для замкнутой (или полной) цепи:
потенциалы φ1 иφ2 выравниваются
и мы приходим к закону
Ома для замкнутой (или полной) цепи:

Если
сопротивление внешней цепи  ,
то имеем случай короткого
замыкания.
В этом случае в цепи течетмаксимальный ток:
,
то имеем случай короткого
замыкания.
В этом случае в цепи течетмаксимальный ток:
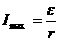
При  имеем разомкнутую цепь.
В этом случае ток в цепи равен
нулю:
имеем разомкнутую цепь.
В этом случае ток в цепи равен
нулю:
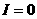
22. Правила Кирхгофа для разветвленных цепей постоянного тока
Правило 1: в любом узле сумма входящих токов и выходящих равна нулю. Оно учитывает закон сохранения электрического заряда.

При этом токи, идущие к узлу, и токи, исходящие из узла, следует считать величинами разных знаков.
Правило 2: алгебраическая сумма произведений сил токов на сопротивления при обходе контура равна сумме ЭДС в контуре. Учитывается закон сохранения энергии.
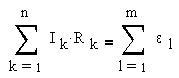
Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.
В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.
|
Рисунок 1.10.1. Узел электрической цепи. I1, I2 > 0; I3,I4 < 0 |
В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа:
Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:
|
Первое правило Кирхгофа является следствием закона сохранения электрического заряда.
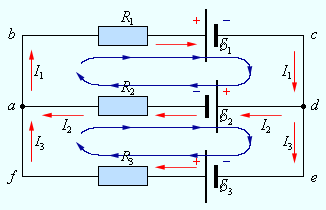
В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 1.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).
|
Рисунок 1.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef) |
В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.
Второе правило Кирхгофа является следствием обобщенного закона Ома.
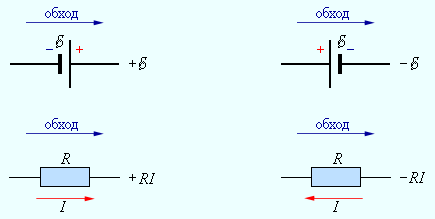
Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.
|
Рисунок 1.10.3. «Правила знаков» |
Для участков контура abcd обобщенный закон Ома записывается в виде:
Для
участка bc: I1R1 = Δφbc –  1.
1.
Для
участка da: I2R2 = Δφda –  2.
2.
Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:
I1R1 + I2R2 = Δφbc + Δφda – |
Аналогично, для контура adef можно записать:
– I2R2 + I3R3 = |
Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.
Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:
I1R1 + I2R2 = – |
– I2R2 + I3R3 = |
– I1 + I2 + I3 = 0 |
23. Работа и мощность постоянного электрического тока. КПД источника тока.
Работа А электрического тока на участке цепи с электрическим сопротивлением R за время D t равна:
A = I · U · ? t = I2 · R · ? t
Мощность P электрического тока равна отношению работы А тока ко времени D t, за которое эта работа совершена:
P = A / ? t = I · U = I2 R = U2 / R.
Работа А электрического тока равна количеству теплоты Q, выделяемому проводником (если не совершается механическая работа и не происходят химические реакции):
Q = I2 · R · ? t
Этот закон был экспериментально установлен английским ученым Джеймсом Джоулем (1818-1889) и русским ученым Эмилием Ленцем (1804-1865) и поэтому носит название закона Джоуля — Ленца.
Рассмотрим элементарную электрическую цепь, содержащую источник ЭДС с внутренним сопротивлением r, и внешним сопротивлением R (рис. 7.5).
КПД всегда определяем как отношение полезной работы к затраченной:
| | (7.8.1) |
|
Полезная
работа –
мощность, выделяемая на внешнем
сопротивлении Rв
единицу времени. По закону Ома
имеем:  а
а 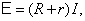 тогда
тогда
 .
.
24. Вывод закона Ома из классической теории электропроводимости металлов.
Друде считал, что сразу после очередного соударения электрона с ионом кристаллической решетки скорость упорядоченного движения электрона равна нулю. Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение равное

и к концу пробега скорость упорядоченного движения достигнет значения
| (18.2) |
где
t — среднее время между двумя последовательными
соударениями электрона с ионами решетки.
Друде не учитывал распределение
электронов по скоростям и приписывал
всем электронам одинаковое значение
средней скорости  .
В этом приближении
.
В этом приближении 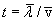 ,
где
,
где 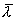 —
среднее значение длины свободного
пробега,
—
среднее значение длины свободного
пробега,  —
скорость теплового движения электронов.
Подставим это значение t в формулу (18.2)
—
скорость теплового движения электронов.
Подставим это значение t в формулу (18.2)
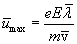
Скорость изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального

Подставив это выражение в
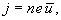
получим

Плотность
тока оказалась пропорциональной
напряженности поля. Следовательно, мы
получили закон Ома. Согласно 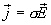 коэффициент
пропорциональности между j и Е представляет
собой проводимость
коэффициент
пропорциональности между j и Е представляет
собой проводимость
| (18.3) |
Если бы электроны не сталкивались с ионами решетки, длина свободного пробега, а, следовательно, и проводимость были бы бесконечно велики. Таким образом, электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами.
Вывод закона Джоуля-Ленца из классической теории электропроводности металлов. Затруднения этой теории.
К
концу свободного пробега электрон
приобретает скорость 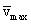 ,
и, следовательно, дополнительную
кинетическую энергию, средняя величина
которой
,
и, следовательно, дополнительную
кинетическую энергию, средняя величина
которой
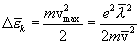
Столкнувшись
с ионом, электрон по предположению
полностью теряет приобретенную им за
время пробега скорость, и передает
энергию кристаллической решетке. Эта
энергия идет на увеличение внутренней
энергии металла, проявляющееся в его
нагревании. Каждый электрон претерпевает
за секунду в среднем 1/t соударений,
сообщая всякий раз решетке энергию  .
Следовательно, в единице объема за
единицу времени должно выделяться тепло
.
Следовательно, в единице объема за
единицу времени должно выделяться тепло

где
n — число электронов проводимости в
единице объема. Величина 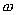 есть
не что иное, как удельная мощность тока.
Множитель при
есть
не что иное, как удельная мощность тока.
Множитель при  совпадает
со значением
совпадает
со значением  (18.3)
для закона Ома. Таким образом. Мы пришли
к выражению закона Джоуля-Ленца в
дифференциальной форме.
(18.3)
для закона Ома. Таким образом. Мы пришли
к выражению закона Джоуля-Ленца в
дифференциальной форме.
Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость диэлектриков, у которых нет свободных электронов. Согласно закону Дюлонга и Пти (см. §73), теплоемкость одноатомного кристалла равна 3R. Учтем, что теплоемкость одноатомного электронного газа равна 3/2R. Тогда атомная теплоемкость металлов должна быть близка к 4,5R. Однако опыт доказывает, что она равна 3R, т. е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классической электронной теорией.
Указанные расхождения теории с опытом можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла — Больцмана, а квантовой статистикой. Поэтому объяснить затруднения элементарной классической теории электропроводности металлов можно лишь квантовой теорией, которая будет рассмотрена в дальнейшем. Надо, однако, отметить, что классическая электронная теория не утратила своего значения и до настоящего времени, так как во многих случаях (например, при малой концентрации электронов проводимости и высокой температуре) она дает правильные качественные результаты и является по сравнению с квантовой теорией простой и наглядной.
Несамостоятельный и самостоятельный газовые разряды.
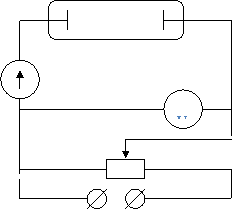
Несамостоятельный газовый разряд. Процесс прохождения электрического тока через газ называется газовым разрядом. Если электропроводность газа создается внешними ионизаторами, то электрический ток, возникающий в нем, называется несамостоятельным газовым разрядом. С прекращением действия внешних ионизаторов несамостоятельный разряд прекращается. Несамостоятельный газовый разряд не сопровождается свечением газа. Ниже изображен график зависимости силы тока от напряжения при несамостоятельном разряде в газе. Для построения графика использовалась стеклянная трубка с двумя впаянными в стекло металлическими электродами. Цепь собрана как показано на рисунке ниже.
|
+ —
Самостоятельный
газовый разряд.
Электрический разряд в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным газовым разрядом. Для его осуществления необходимо, чтобы в результате самого разряда в газе непрерывно образовывались свободные заряды. Основным источником их возникновения является ударная ионизация молекул газа.
Если после достижения насыщения продолжать увеличивать разность потенциалов между электродами, то сила тока при достаточно большом напряжении станет резко возрастать (график 2).
Это означает, что в газе появляются дополнительные ионы, которые образуются за счет действия ионизатора. Сила тока может возрасти в сотни и тысячи раз, а число заряженных частиц, возникающих в процессе разряда, может стать таким большим, что внешний ионизатор будет уже не нужен для поддержания разряда. Поэтому ионизатор теперь можно убрать.

I
|
27. Магнитное поле, Магнитная индукция. Принцип суперпозиции магнитных полей. Закон Ампера.
Зако́н
Ампе́ра —
закон взаимодействия электрических
токов.
Впервые был установлен Андре
Мари Ампером в 1820 для
постоянного тока. Из закона Ампера
следует, что параллельные проводники с
электрическими токами, текущими в одном
направлении, притягиваются, а в
противоположных — отталкиваются.
Законом Ампера называется также закон,
определяющий силу, с которой магнитное
поле действует
на малый отрезок проводника с током.
Сила 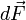 ,
с которой магнитное поле действует на
элемент объёма
,
с которой магнитное поле действует на
элемент объёма 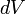 проводника
с током плотности
проводника
с током плотности  ,
находящегося в магнитном поле с
индукцией
,
находящегося в магнитном поле с
индукцией  :
:
 .
.
Модуль силы Ампера можно найти по формуле:
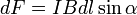 ,
,
где 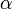 —
угол между векторами магнитной индукции
и тока.
—
угол между векторами магнитной индукции
и тока.
Сила  максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции ():
максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции ():
 .
.
Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1], магнитная составляющая электромагнитного поля[2]
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).
Магни́тная
инду́кция 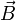 — векторная величина,
являющаяся силовой характеристикой магнитного
поля (его
действия на заряженные частицы) в данной
точке пространства. Определяет, с
какой силой
— векторная величина,
являющаяся силовой характеристикой магнитного
поля (его
действия на заряженные частицы) в данной
точке пространства. Определяет, с
какой силой 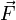 магнитное
поле действует на заряд
магнитное
поле действует на заряд  ,
движущийся со скоростью
,
движущийся со скоростью  .
.
Более
конкретно, 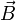 —
это такой вектор, что сила
Лоренца
—
это такой вектор, что сила
Лоренца 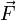 ,
действующая со стороны магнитного
поля[1] на
заряд
,
действующая со стороны магнитного
поля[1] на
заряд  ,
движущийся со скоростью
,
движущийся со скоростью  ,
равна
,
равна
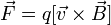
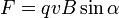
где
косым крестом обозначено векторное
произведение,
α — угол между векторами скорости и
магнитной индукции (направление
вектора  перпендикулярно
им обоим и направлено по правилу
буравчика).
перпендикулярно
им обоим и направлено по правилу
буравчика).
6.5. Закон Джоуля-Ленца в дифференциальной и интегральной формах
Двигаясь под действием силы F = eE, электрон проводимости приобретает некоторую энергию
 .
(6.53)
.
(6.53)
Провзаимодействовав с ионом кристаллической решетки, он отдает ему эту энергию, которая выделяется в проводнике в виде тепла.
Если взаимодействие электрона проводимости с ионом кристаллической решетки происходило в течение времени t, то за это время в проводнике выделится в виде тепла энергия
 ,
(6.54)
,
(6.54)
где 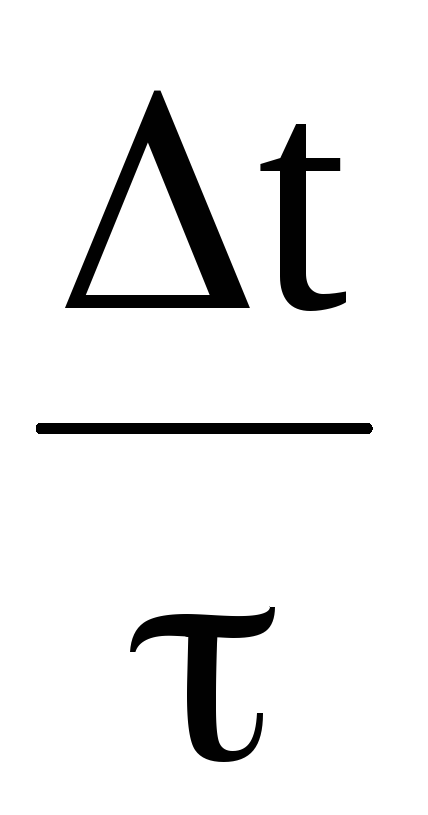 – число взаимодействий электрона
проводимости с ионом кристаллической
решетки.
– число взаимодействий электрона
проводимости с ионом кристаллической
решетки.
Так как

то
 ,
(6.55)
,
(6.55)
где  – время свободного пробега электрона
проводимости.
– время свободного пробега электрона
проводимости.
Если в объеме проводника содержится n электронов проводимости, то энергия, переданная единице объема проводника в единицу времени всеми электронами,
 .
(6.56)
.
(6.56)
Выражение (6.56) является математической формой записи закона Джоуля-Ленца в дифференциальной форме.
Из формулы (6.56) можно получить формулу закона Джоуля Ленца в интегральной форме. Имеем
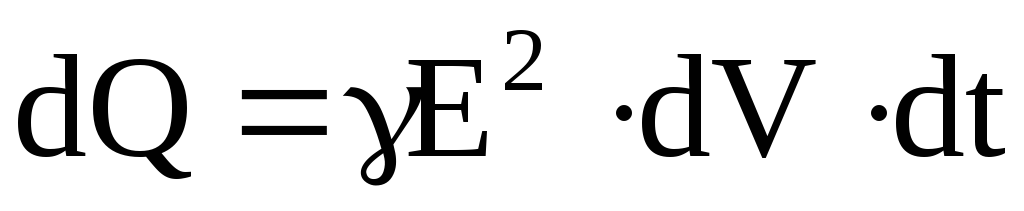 ,
,
где = 1/; E = U/dl, dV = S dl.
Следовательно,

или
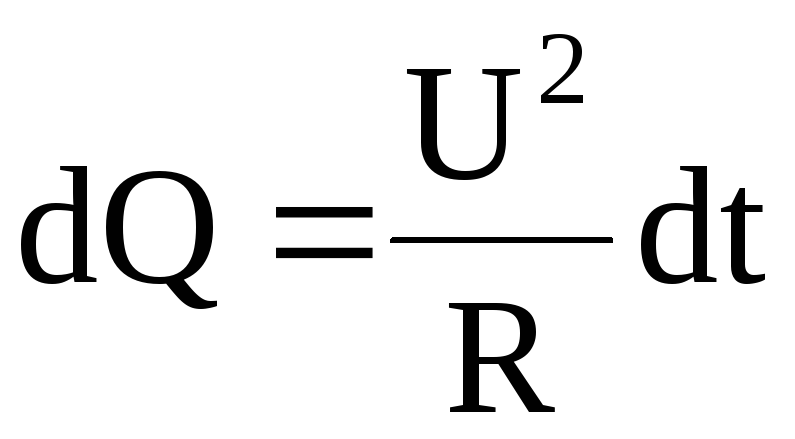 ,
(6.57)
,
(6.57)
где  — сопротивление проводника;
— сопротивление проводника;
U = IR – напряжение.
Количество тепла, выделившееся в проводнике за время t,
 .
(6.58)
.
(6.58)
Выражение (6.58) является математической формой записи закона Джоуля-Ленца в интегральной форме.
В случае постоянного тока
 .
(6.59)
.
(6.59)
Классическая электронная теория проводимости металлов смогла объяснить не только электропроводность металлов и сплавов, но и их теплопроводность, некоторые оптические свойства вещества, что является её крупным достижением. Однако с её помощью невозможно объяснить такие экспериментальные факты, как независимость теплоемкости металлов от наличия электронов проводимости и сверхпроводимости. Это связано с тем, что в ней электроны проводимости подчиняются законам идеального газа, законам статистики Максвелла-Больцмана. В действительности же для электронов проводимости справедлива квантовая статистика, и они подчиняются закону статистики Ферми-Дирака.
6.6. Энергия, выделяющаяся в цепи постоянного тока. Коэффициент полезного действия (кпд) источника постоянного тока
На участке цепи, не содержащей ЭДС, силы электрического поля совершают работу по перемещению электрического заряда, которая выделяется в проводнике в виде тепла:
 .
(6.60)
.
(6.60)
Если в цепи имеется ЭДС, то работа по перемещению электрического заряда совершается сторонними и электрическими силами, численно равная энергии, выделяющейся в этой цепи:
 .
(6.61)
.
(6.61)
В замкнутой цепи энергия, выделяющаяся в проводнике численно равна работе:
 .
(6.62)
.
(6.62)
Таким образом, в замкнутой цепи внутри источника сторонние силы совершают работу по разделению зарядов, создают электрическое поле и запасают энергию, которая расходуется во внешней цепи на поддержание электрического поля, или выделяется в виде тепла. В замкнутой цепи совершают работу только сторонние силы.
Известно, что работа, совершаемая в единицу времени, называется мощностью:
 . (6.63)
. (6.63)
Это оказывается справедливым и для постоянного электрического тока. Поэтому для участка цепи, в котором отсутствует ЭДС, мощность
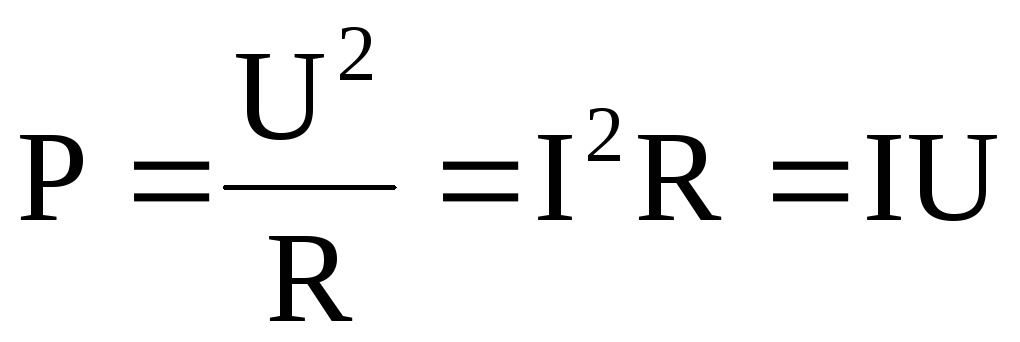 . (6.64)
. (6.64)
При наличии ЭДС
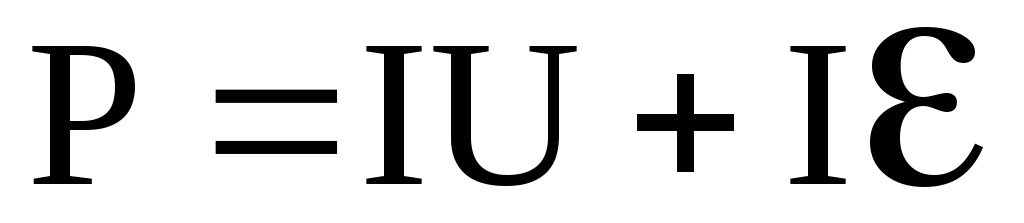 .
(6.65)
.
(6.65)
В замкнутой цепи
 .
(6.66)
.
(6.66)
Мощность во внешней цепи является полезной мощностью
 .
(6.67)
.
(6.67)
Отношение полезной мощности (мощности во внешней цепи) к мощности, развиваемой источником тока (полной мощности), называют коэффициентом полезного действия (КПД):
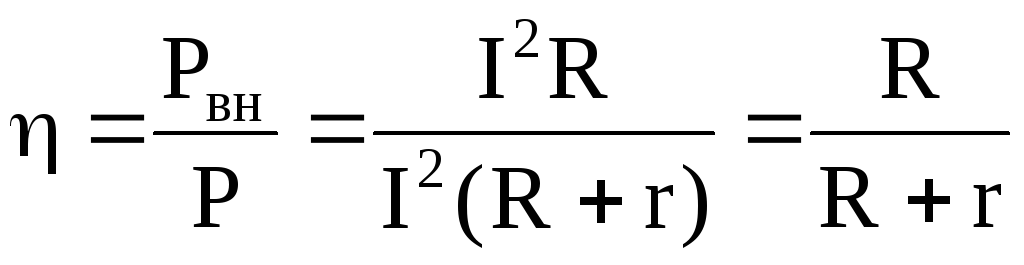 .
(6.68)
.
(6.68)
Из выражения (6.67) видно, что при r0, 1.
Найдем соотношение между R и r, при котором полезная мощность максимальна. Для этого проведем исследование функции Pвн = f(R). Определяем первую производную и приравниваем её к нулю:
 .
(6.69)
.
(6.69)
Определяем вторую производную и исследуем её знак:
 . (6.70)
. (6.70)
Из формул (6.64) и (6.65) видно, что в том случае, когда сопротивление внешнего участка цепи равно внутреннему сопротивлению источника тока (R = r), мощность во внешней цепи максимальна:
 . (6.71)
. (6.71)
При этом коэффициент полезного действия (при максимальном значении мощности во внешней цепи)
 . (6.72)
. (6.72)
Можно установить зависимость КПД источника тока от тока во внешней цепи ( = f (I)):
 .
(6.73)
.
(6.73)
Г рафики
зависимости мощности во внешней цепи,
полной мощности и коэффициента полезного
действия источника тока от тока в цепи
представлены на рис. 6. 12. Зависимость
КПД от сопротивления внешнего участка
цепи
= f(R)
рафики
зависимости мощности во внешней цепи,
полной мощности и коэффициента полезного
действия источника тока от тока в цепи
представлены на рис. 6. 12. Зависимость
КПД от сопротивления внешнего участка
цепи
= f(R)
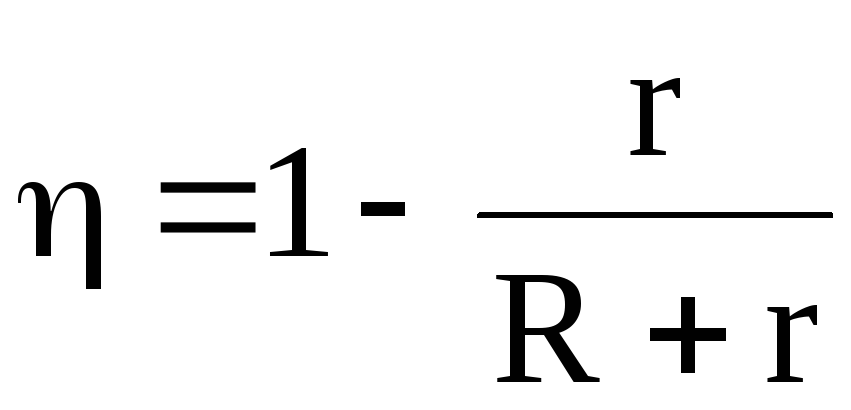 . (6.74)
. (6.74)
Из вышеизложенного видно, что получение Pmax и max невозможно, т.к. при Pвн = Pmax, = 0,5, а при 1, Pвн0.
Вопрос 5. Законы Ома в интегральной и дифференциальной форме
Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)
|
| (7.6.1) |
|
Для однородного линейного проводника выразим R через ρ:
|
| (7.6.2) |
|
ρ – удельное объемное сопротивление; [ρ] = [Ом·м].
Найдем
связь между 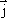 и
и  в
бесконечно малом объеме проводника
– закон
Ома в дифференциальной форме.
в
бесконечно малом объеме проводника
– закон
Ома в дифференциальной форме.
В
изотропном проводнике (в данном случае
с постоянным сопротивлением) носители
зарядов движутся в направлении действия
силы, т.е. вектор плотности тока  и
вектор напряженности поля коллинеарны
(рис. 7.6).
и
вектор напряженности поля коллинеарны
(рис. 7.6).
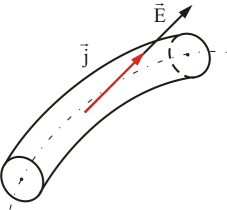
Рис. 7.6
Исходя из закона Ома (7.6.1), имеем:

А
мы знаем, что  или
или 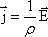 .
Отсюда можно записать
.
Отсюда можно записать
|
| (7.6.3) |
|
это запись закона Ома в дифференциальной форме.
Здесь  – удельная
электропроводность.
– удельная
электропроводность.
Размерность
σ – [ ].
].
Плотность
тока можно выразить через заряд
электрона е,
количество зарядов n и
дрейфовую скорость 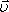 :
:
 .
.
Обозначим  ,
тогда
,
тогда  ;
;
|
| (7.6.4) |
|
Теперь,
если удельную электропроводность σ
выразить через е, n и b:  то
вновь получим выражение закона
Ома в дифференциальной форме:
то
вновь получим выражение закона
Ома в дифференциальной форме:
 .
.









105 м/с.
105 м/с. За
время свободного пробега
За
время свободного пробега  электрон достигнет максимальной
скорости в своём направленном движении:
электрон достигнет максимальной
скорости в своём направленном движении:  .
. и энергии:
и энергии:  .
. —
является мощностью тепла, выделяемого
в единице объёма;
—
является мощностью тепла, выделяемого
в единице объёма; —
плотность электрического тока;
—
плотность электрического тока;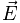 —
это напряжённость электрического поля;
—
это напряжённость электрического поля;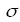 —
проводимость выбранной среды.
—
проводимость выбранной среды.
 1 +
1 + 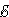 2 = –
2 = –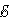 1 –
1 –  2.
2.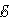 2 +
2 + 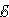 3.
3.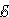 1 –
1 – 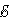 2,
2,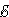 2 +
2 +  3,
3,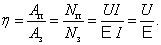
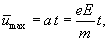
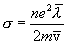

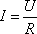
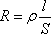 ,
, ,
,