Закон Ома в дифференциальной форме. Второй закон Кирхгофа в дифференциальной форме
Содержание:
Закон Ома в дифференциальной форме. Второй закон Кирхгофа в дифференциальной форме
Закон Ома в дифференциальной форме. Второй закон Кирхгофа в дифференциальной форме. Для проводящих носителей выберите параллелепипед с небольшим объемом dR.
- Длина ребра параллелепипеда D /, как площадь поперечного сечения. Разместите этот объем так, чтобы
напряженность электрического поля в нем была параллельна ребру (рис. 431, а). Людмила Фирмаль
Поскольку объем мал, можно предположить, что электрическое поле E одинаково во всем основном объеме: D / = D / 1 °, As = Asn ‘, где nQ — единичный вектор в направлении D /, As и E. Ток I = j 6 ds = d As. Напряжение на элементе объема U = E M = /? /. Формула /?
Подставляя эквиваленты R и / для / = ED /, получить — ~ 6Asn == £ D / l °. yZ g * = yE отсюда. (14.1) Соотношение (14.1) называется законом Ома в дифференциальной форме. Он устанавливает связь между плотностью тока в конкретной точке проводящей среды и напряженностью электрического поля в той же точке.
(14.1) Соотношение (14.1) называется законом Ома в дифференциальной форме. Он устанавливает связь между плотностью тока в конкретной точке проводящей среды и напряженностью электрического поля в той же точке.
- Уравнение (14.1) справедливо для области за пределами источника e. Помимо области d.s., «кулоновского» (электростатического) поля, занимаемого источником d.s e, существует также так называемое внешнее электрическое поле, которое гарантирует непрерывное движение заряда в электрической цепи.
Внешнее электрическое поле означает электрическое поле неэлектростатического характера
например, в результате химических, электрохимических, термических, термоэлектрических, механических или электромагнитных процессов.Людмила Фирмаль
Напряженность внешнего поля обозначается Est (, p. В области, занятой источником ЭДС, общая напряженность поля равна геометрической сумме «кулона» и внешнего поля E — \ — Estor. Состоит из источника питания цепи постоянного тока и нагрузки, источник ЭДС стороннего производителя создает напряженность внешнего поля Eestor в источнике питания.
Состоит из источника питания цепи постоянного тока и нагрузки, источник ЭДС стороннего производителя создает напряженность внешнего поля Eestor в источнике питания.
Линейный интеграл напряженности поля стороннего производителя в источнике называется источником ЭДС (EJ). : S Эстор при воздействии внешнего поля m в источнике, заряд непрерывно отделяется, положительный заряд перемещается к положительному источнику, отрицательный заряд перемещается в отрицательный, постоянный ток в цепь из положительного в отрицательный заряд
Поскольку ток течет, некоторые заряды непрерывно заменяются другими, как и раньше, поэтому изображение поля в макроскопическом смысле повторяется в смежные моменты времени. Статичен по своей природе
Эта ситуация служит основой для поля, созданного в проводящей среде разделенным зарядом, называемым кулоновским полем, а его напряженность E называется интенсивностью кулоновского поля.
Направлено на боковое поле, общая напряженность поля в источнике E Estor, а вне источника кулоновское поле направлено от положительного к отрицательному, под воздействием этого поля упорядоченный заряд
Движение происходит в области вне источника, когда ток протекает по цепи | £ g / ent |> 1 £ I-разомкнутая цепь | £ rmop | = | £ | Закон Ома дифференциальной формы занимающей области, ds записывается как d = T (E + Efmo;,) (14. указывает на сопротивление секции 123, а R указывает на сопротивление секции 341.
указывает на сопротивление секции 123, а R указывает на сопротивление секции 341.
D1 в той же точке, где можно предположить, что площадь поперечного сечения всех участков замкнутого контура достаточно мала и что направление напряженности электрического поля в определенной точке совпадает с направлением элемента пути.
Умножьте на обе стороны (14.Г) и циркулируйте вдоль замкнутого Y контура. 431, c: интеграл от суммы равен сумме интегралов. Следовательно, Φ (e + EPtor) d? = EdF + $ Eo0Pdl.
Из-за потенциальной природы поля «кулона» 1 £ dl = 0. -123 341 ke 341 ЭДС третьей стороны для расчета величины (p, умножить интегрирование на сечение S и заменить на плотность тока 6-1 dl ток / сопротивление сечения (1R. ~ 5dl S Idl v S ~ yS ~ R ‘123 341 Следовательно, / ++ +?) = £. (A) Следовательно, уравнение (a) ) Сформирован.
Смотрите также:
Если вам потребуется заказать решение по электротехнике (ТОЭ) вы всегда можете написать мне в whatsapp.
4.3. Закон Ома
Немецкий
физик Г. Ом экспериментально установил закон, согласно которому сила
тока, текущего по однородному (отсутствуют сторонние силы) металлическому
проводнику, пропорциональна падению напряжения на проводнике:
.
Сопротивление проводника. Величина R называется электрическим сопротивлением проводника. Единица сопротивления — 1 Ом. Для однородного цилиндрического проводника,
где l — длина проводника; S — площадь его поперечного сечения; — зависящий от свойств материала коэффициент, называемыйДифференциальная форма закона Ома. Найдем связь между плотностью
тока j и напряженностью поля Е в одной и той же точке проводника. В изотропном проводнике упорядоченное движение носителей тока происходит
в направлении вектора Е. Поэтому направления векторов j и Е совпадают.
В изотропном проводнике упорядоченное движение носителей тока происходит
в направлении вектора Е. Поэтому направления векторов j и Е совпадают.
Рассмотрим в однородной изотропной среде элементарный объем с образующими,
параллельными вектору
Обозначим их потенциалы и , а среднюю площадь сечения через . Используя закон Ома, получим для тока , или для плотности тока , следовательно
.
Перейдем к пределу при , тогда рассматриваемый объем можно считать цилиндрическим, а поле внутри него однородным, так что,
где Е — напряженность электрического поля внутри проводника. Учитывая, что j и Е совпадают по направлению, получаем Это соотношение является дифференциальной формой закона Ома для однородного
участка цепи. Величина
называется удельной проводимостью.
Это соотношение является дифференциальной формой закона Ома для однородного
участка цепи. Величина
называется удельной проводимостью.На неоднородном участке цепи на носители тока действуют, кроме электростатических
сил ,
еще и сторонние силы ,
следовательно, плотность тока в этих участках оказывается пропорциональной
сумме напряженностей. Учет этого приводит к дифференциальной форме
закон Ома для неоднородного участка цепи.
Вследствие закона сохранения заряда сила постоянного тока в каждом сечении
должна быть одинаковой.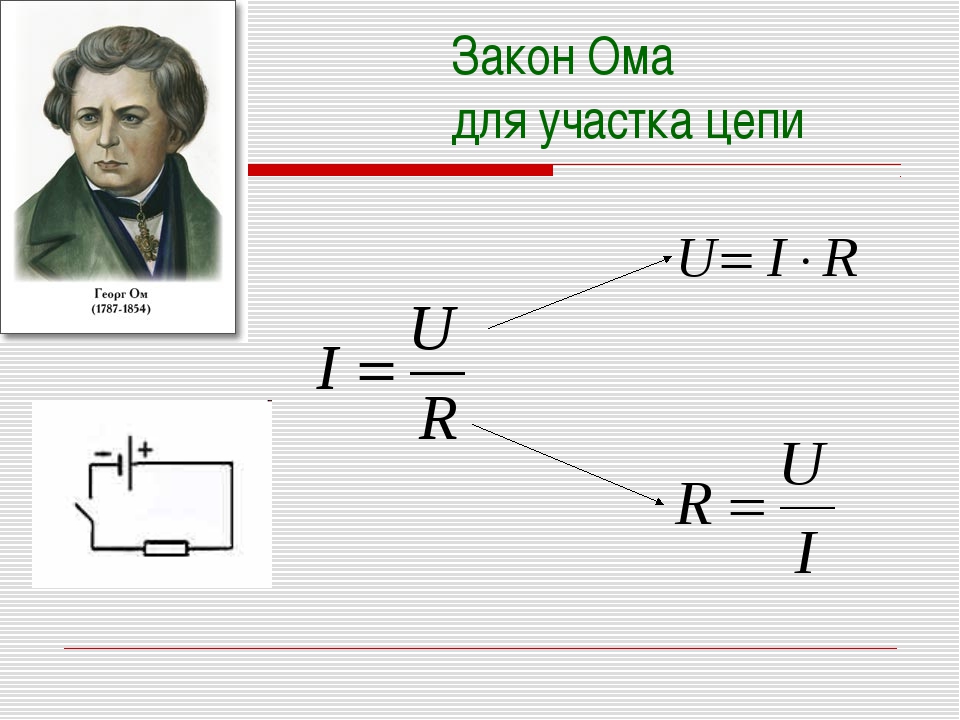 Поэтому величина
постоянна вдоль контура. Тогда, заменяя j отношением ,
получаем
Поэтому величина
постоянна вдоль контура. Тогда, заменяя j отношением ,
получаем
Умножим это соотношение на dl и проинтегрируем вдоль контура:
,
где представляет собой суммарное сопротивление участка цепи, первый интеграл в правой части — разность потенциалов на концах участка, а второй интеграл определяет ЭДС , действующую на участке цепи. Таким образом .ЭДС ,
как и сила тока I, величина алгебраическая. В случае, когда ЭДС
способствует движению положительных носителей тока в выбранном направлении
(в направлении 1-2), .
Если ЭДС препятствует движению положительных носителей в данном направлении,
то :
.
Последняя формула выражает,
где R — сопротивление нагрузки, r — внутреннее сопротивление источника тока.
Вопросы
1) Какова связь между проводимостью и сопротивлением, удельной проводимостью и удельным сопротивлением2) Какой вид имеет вольт-амперная характеристика металлического элемента: линейный или экспоненциальный
3) Каковы правила знаков для силы тока и ЭДС при записи закона Ома для неоднородного участка цепи
Закон Ома — Лаборатория радиолюбителя — Каталог статей
Электроны в цепи постоянного тока падают, как парашютисты, не нарушая второго закона Ньютона. Как должно двигаться тело, на которое действует Постоянная сила?
Ответ: тело под действием постоянной силы движется равно-ускоренно. Этого требует один из основных законов механики — второй закон Ньютона. Как же должны двигаться свободные электроны в металле, если на них действует с постоянной силой электрическое поле? Не спешите с ответом. Электроны движутся с постоянной средней скоростью, причем легко убедиться, что эта скорость пропорциональна напряженности электрического поля, т. е. действующей силе. Именно этот факт выражается законом Ома, который в школьном учебнике для IX класса формулируется так: для однородной цепи сила тока прямо пропорциональна приложенному напряжению.
Электроны движутся с постоянной средней скоростью, причем легко убедиться, что эта скорость пропорциональна напряженности электрического поля, т. е. действующей силе. Именно этот факт выражается законом Ома, который в школьном учебнике для IX класса формулируется так: для однородной цепи сила тока прямо пропорциональна приложенному напряжению.
Вспомним, что сила тока в проводнике определяется зарядом, прошедшим через поперечное сечение проводника за единицу времени. Так, если сила тока равна 1 А, то через сечение проводника за 1 с проходит 6,2-1018 электронов. Ясно, что сила тока прямо пропорциональна средней скорости движения электронов. Приложенное напряжение, в свою очередь, пропорционально напряженности электрического поля, т.е. силе, действующей на электроны.
В чем же кажущееся противоречие между законом Ома и вторым законом Ньютона? Оно вызвано тем, что мы забыли о непрерывных столкновениях электронов с ионами кристаллической решетки. Разогнавшийся в электрическом поле электрон при столкновении с ионом теряет приобретенную кинетическую энергию и вновь разгоняется. -8 см.
-8 см.
Не кажется ли вам странным полученный результат? Электрон «проявляет удивительную ловкость», пробегая мимо девяти притягивающих его ионов, и сталкивается в среднем только с каждым десятым (рис. 8)
Вы вправе удивляться. В самом деле, объяснить такое движение, основываясь лишь на законах классической физики, нельзя. Мы здесь впервые сталкиваемся с тем обстоятельством, что такие фундаментальные законы, как законы Ньютона, закон Кулона, закон Ома, еще недостаточны для полного описания наблюдаемых явлений. Мы должны сделать вывод о том, что эти законы классической физики характеризуют поведение электрона в металле лишь приближенно. Более точный, расчет, движения электронов в металле стал возможен лишь с развитием, на заре XX в. квантовой физики.
Однако не спешите отбрасывать как «устаревшие» законы классической физики. Многие и очень многие опытные факты они описывают с такой высокой точностью, что применять в этих случаях квантовые законы было бы совершенно неразумно. 22 электронов на 1 см3) свободных электронов. Электроны являются носителями электрического заряда в металле. Движению свободных электронов в металле мешают попы кристаллической решетки и тем больше, чем выше температура металла. Поэтому электропроводимость металлов с повышением температуры уменьшается.
22 электронов на 1 см3) свободных электронов. Электроны являются носителями электрического заряда в металле. Движению свободных электронов в металле мешают попы кристаллической решетки и тем больше, чем выше температура металла. Поэтому электропроводимость металлов с повышением температуры уменьшается.
Такова простейшая модель, поясняющая протекание тока через металл.
Поделись с друзьями в социальных сетях
Реклама
Похожие материалы:
К сожалению, похожего ничего не нашлось!
| | Адрес этой страницы (вложенность) в справочнике dpva. ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Постоянный электрический ток. Закон Ома для участка цепи. Работа и мощность постоянного тока. Закон Джоуля-Ленца. Закон Ома для полной цепи. Закон электролиза Фарадея. Электрические цепи — последовательное и параллельное соединение. Правила Кирхгофа. ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Постоянный электрический ток. Закон Ома для участка цепи. Работа и мощность постоянного тока. Закон Джоуля-Ленца. Закон Ома для полной цепи. Закон электролиза Фарадея. Электрические цепи — последовательное и параллельное соединение. Правила Кирхгофа.Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||
Чему равно напряжение замкнутой цепи.
 Закон ома простым языком
Закон ома простым языкомГеорг Симон Ом, выдающийся немецкий физик. Именно ему принадлежит одно из важнейших открытий, без которого сложно себе представить работу всех тех людей, которые работают с электричеством. Конечно, в жизни мы пользуемся и другими законами, не менее важны, например первый и второй законы Кирхгофа, но именно благодаря Георгу Ому и его закону мы сейчас можем довольно легко посчитать, какой ток будет протекать в проводе при заданной мощности или посчитать мощность, которую можно присоединить на провод.
Конечно, на этом использование его закона не заканчивается и имеет более широкое применение, но в целом, для бытовых нужд мы используем один из его законов: закон Ома для участка цепи, который гласит –сила тока в цепи прямопропорциональна приложенному напряжению и обратнопропорциональна сопротивлению цепи
. В виде формулы это выглядит так: I=U/R. Как известно, мощность – это произведение тока и напряжения (P=U I), отсюда легко узнать напряжение или ток, если известна мощность, но неизвестна одна из требуемых величин: ток или напряжение. Чтобы не писать здесь все эти формулы, настоятельно рекомендую сохранить себе вот такую диаграмму
Чтобы не писать здесь все эти формулы, настоятельно рекомендую сохранить себе вот такую диаграмму
И тогда вам не придется все запоминать или выводить. Очень простая диаграмма. Внутри круга искомая величина, снаружи формула, по которой ее можно найти, используя известные величины.
Но Ом вывел и другие более сложные законы. Например: закон Ома для полной цепи. В этом случае учитывается не только сопротивление самой цепи, но и сопротивление источника питания. И звучит он так: Сила тока в замкнутой цепи, состоящей из источника тока (или напряжения) с внутренним сопротивлением и нагрузки, которая также, естественно имеет сопротивление, равна отношению величины ЭДС (электродвижущей силы) источника к сумме внутреннего сопротивления источника и сопротивления нагрузки.
где ɛ — это ЭДС источника, r – внутреннее сопротивление источника, R – внешнее сопротивление цепи.
В таком виде этот закон справедлив для напряжения, которое носит характер постоянного, то есть не меняет своего значения с течением времени. Если проще выразиться, у которого есть плюс и минус. Типичным примером источника постоянного напряжения является батарейка.
Если проще выразиться, у которого есть плюс и минус. Типичным примером источника постоянного напряжения является батарейка.
В переменном токе закон Ома так же справедлив, но вносится небольшая корректировка. Дело в том, что в сетях переменного напряжения присутствуют такие элементы, как индуктивность и емкость. Об этом мы немного говорили в статье «Общее сопротивление электрической цепи». Поэтому для переменного напряжения будет справедлива формула I=U/Z, где Z – это полное сопротивление цепи. Для индуктивности она будет равна а для емкости Таким образом, реактивное сопротивление будет выглядеть так ну а полное сопротивление цепи В итоге, мы получаем формулу закона Ома для полной цепи, которая выглядит так.
Вряд ли в жизни вам пригодится эта формула, ибо мне, как электрику, который делает ремонты в домах, квартирах и других сооружениях, она еще ни разу не пригодилась. В основном я пользуюсь формулой, которую ошибочно называют «Законом Ома» для участка цепи, о которой я писал выше, и которая более востребована для расчетов.
На практике закон Ома для полной цепи может потребоваться лишь только для того, чтобы вычислить внутреннее сопротивление источника ЭДС. Так же величина тока важна при . В большинстве случаев мы сталкиваемся с этим законом только в школе на уроках физики и благополучно об этом забываем.
Вернёмся ещё раз к рис. 7.1. Здесь изображена замкнутая проводящая цепь. На участке цепи 1-а -2 движение носителей заряда происходит под действием только электростатической силы=q . Такие участки называютсяоднородными .
Совсем по-другому обстоят дела на участке контура 2-b -1. Здесь на заряды действует не только электростатическая, но и сторонняя сила. Полную силунайдем, сложив эти две:
.
Участок замкнутого контура, где наряду с электростатической силой действуют и сторонние силы, называют неоднородным .
Можно показать, что на однородном участке
цепи средняя скорость направленного
движения носителей заряда пропорциональна
действующей на них силе.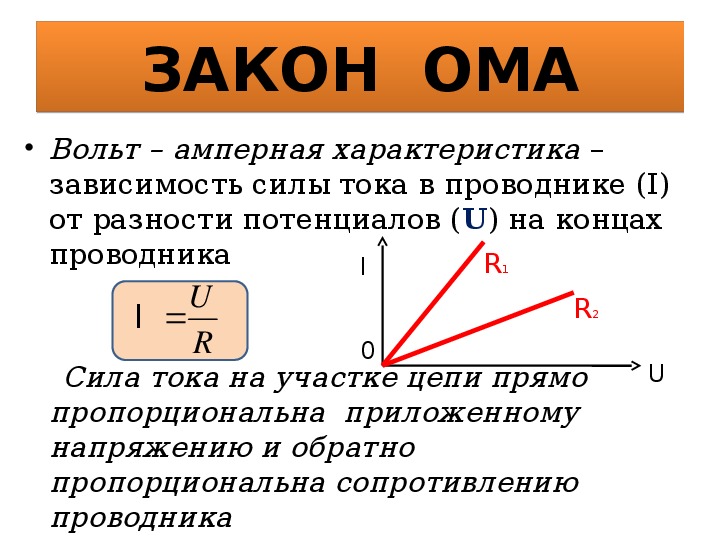 Для этого
достаточно сравнить формулы, полученные
на прошлой лекции:
=
Для этого
достаточно сравнить формулы, полученные
на прошлой лекции:
=
(6.3) и=(6.13).
Пропорциональность скорости силе, а
плотности тока — напряжённости сохранится
и в случае неоднородного участка цепи.
Но теперь напряжённость поля равна
сумме напряжённостей электростатического
поля
и поля сторонних сил
:
. (7.5)
Это уравнение закона Ома в локальной дифференциальной форме для неоднородного участка цепи.
Теперь перейдём к закону Ома для неоднородного участка цепи в интегральной форме.
Выделим двумя близкими сечениями S участокdl трубки тока (рис. 7.3.). Сопротивление этого участка:
,
а плотность тока можно связать с силой тока:
.
Рис. 7.3.
Эти два выражения используем в уравнении (7.5), спроецировав его предварительно на линию тока:
Проинтегрировав последнее уравнение по неоднородному участку 1-2, получим:
.
Произведение IR 1-2 =U — напряжение на участке 1-2;
первый интеграл справа == 1 – 2 — разность потенциалов на концах участка;
второй интеграл
== 1-2 — э. д.с.
источника тока.
д.с.
источника тока.
Учтя всё это, конечный результат запишем в виде:
. (7.6)
Это закон Ома для неоднородного участка цепи в интегральной форме . Обратите внимание, что напряжение на неоднородном участке цепиU не совпадает с разностью потенциалов на его концах ( 1 – 2):
IR 1-2 =U 1-2 = ( 1 – 2) + 1-2 . (7.7)
Эти две величины равны только в случае однородного участка, где источники тока отсутствуют и 1-2 = 0. Тогда:
U 1-2 = 1 – 2 .
Для замкнутого контура уравнение закона Ома (7.6) несколько видоизменяется, так как разность потенциалов в этом случае равна нулю:
. (7.8)
В законе Ома для замкнутой цепи (7.8) R — полное сопротивление контура, складывающееся из внешнего сопротивления цепи R 0 и внутреннего сопротивления источника r :
R =R 0 +r .
Правила Кирхгофа
Рассмотренные нами законы постоянного
тока позволяют рассчитать токи в сложных
разветвлённых электрических цепях. Эти
расчёты упрощаются, если пользоваться
правилами Кирхгофа.
Эти
расчёты упрощаются, если пользоваться
правилами Кирхгофа.
Правил Кирхгофа два: правило токов иправило напряжений .
Правило токов относится к узлам цепи, то есть, к таким точкам схемы, где сходятся не менее трёх проводников (рис. 7.4.). Правило токов гласит: алгебраическая сумма токов в узле равняется нулю:
. (7.9)
Рис. 7.4.
При составлении соответствующего уравнения, токи, втекающие в узел, берутся со знаком плюс, а покидающие его — со знаком минус. Так, для узла А (рис. 7.3.) можно записать:
I 1 –I 2 –I 3 +I 4 –I 5 = 0.
Это первое правило Кирхгофа является следствием уравнения непрерывности (см. (6.7)) или закона сохранения электрического заряда.
Правило напряжений относится к любому замкнутому контуру разветвлённой цепи.
Выделим, например, в разветвлённой
сложной цепи замкнутый элемент 1-2-3-1
(рис. 7.5.). Произвольно обозначим в ветвях
контура направления токов I 1 ,I 2 ,I 3 . Для каждой ветви запишем уравнение
закона Ома для неоднородного участка
цепи:
Для каждой ветви запишем уравнение
закона Ома для неоднородного участка
цепи:
Участок
.
Здесь R 1 ,R 2 ,R 3 —полное сопротивление соответствующих ветвей. Сложив эти уравнения, получим формулу второго правила Кирхгофа:
I 1 R 1 –I 2 R 2 –I 3 R 3 = 1 + 2 – 3 – 4 + 5 .
Правило напряжений формулируется так: в любом замкнутом контуре алгебраическая сумма падений напряжения равна алгебраической сумме э.д.с., встречающихся в этом контуре:
. (7.10)
Рис. 7.5.
При составлении уравнения (7.10) второго правила Кирхгофа задаются направлением обхода: в нашем примере — по часовой стрелке. Токи, совпадающие с направлением обхода, берутся со знаком плюс (I 1), токи противоположного направления — со знаком минус (–I 2 , –I 3).
Э.д.с. источника берётся со знаком плюс,
если он создаёт ток, совпадающий с
направлением обхода (+ 1 ,
+ 2 , + 5). В противном случае э.д.с. отрицательна
(– 3 , – 4).
В противном случае э.д.с. отрицательна
(– 3 , – 4).
В качестве примера составим уравнения правил Кирхгофа для конкретной электрической схемы — измерительного моста Уитстона (рис. 7.6.). Мост образуют четыре резистора R 1 ,R 2 ,R 3 ,R 4 . В точкахA иB к мосту подключен источник питания (,r ), а в диагоналиBD — измерительный гальванометр с сопротивлениемR g .
Рис. 7.6.
Во всех ветвях схемы произвольно обозначим направления токовI 1 ,I 2 , I 3 , I 4 , I g , I .
В схеме четыре узла: точки A ,B ,C ,D . Для трёх из них составим уравнения первого правила Кирхгофа — правила токов:
точка А : I – I 1 – I 4 = 0; (1)
точка B : I 1 – I 2 – I g = 0; (2)
точка D : I 4
+ I g
– I 3
= 0. (3)
(3)
Для трёх контуров цепи ABDA ,BCDB иADC A составим уравнения второго правила Кирхгофа. Во всех контурах направление обхода по часовой стрелке.
ABDA : I 1 R 1 + I g R g – I 4 R 4 = 0; (4)
BCDB : I 2 R 2 – I 3 R 3 – I g R g = 0; (5)
ADC A : I 4 R 4 + I 3 R 3 + I r = . (6)
Таким образом, мы получили систему шести уравнений, решая которую можно найти все шесть неизвестных токов.
Но чаще мост Уитстона используется для измерения неизвестного сопротивления R x R 1 . В этом случае резисторыR 2 ,R 3 иR 4 — переменные. Меняя их сопротивления, добиваются того, чтобы ток в измерительной диагонали моста оказался равным нулюI g = 0. Это означает, что:
I 1 =I 2 см. (1),
(1),
I 3 =I 4 см.(3),
I 1 R 1 = I 4 R 4 см. (4),
I 2 R 2 = I 3 R 3 см. (5).
Учитывая эти упрощающие обстоятельства, приходим к выводу, что:
,
.
Замечательно, что для определения неизвестного сопротивления нужно знать лишь сопротивления резисторов моста R 2 ,R 3 иR 4 . Э.д.с. источника, его внутреннее сопротивление, как и сопротивление гальванометра при таком измерении не играют никакой роли.
Закон Ома — физический закон, определяющий зависимость между электрическими величинами — напряжением, сопротивлением и током для проводников.
Впервые открыл и описал его в 1826 году немецкий физик Георг Ом, показавший (с помощью гальванометра) количественную связь между электродвижущей силой, электрическим током и свойствами проводника, как пропорциональную зависимость.
Впоследствии свойства проводника, способные противостоять электрическому току на основе этой зависимости,
стали называть электрическим сопротивлением (Resistance), обозначать в расчётах и на схемах буквой R и измерять в Омах в честь первооткрывателя.
Сам источник электрической энергии также обладает внутренним сопротивлением, которое принято обозначать буквой r .
Закон Ома для участка цепи
Со школьного курса физики всем хорошо известна классическая трактовка Закона Ома:
Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.
Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер.
Отсюда следуют ещё два полезных соотношения:
Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения).
Если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.
Вышеописанные формулы в таком виде могут быть применимы для переменного тока лишь в том случае, если цепь состоит только из активного сопротивления R .
Кроме того, следует помнить, что Закон Ома справедлив только для линейных элементов цепи.
Предлагается простой Онлайн-калькулятор для практических расчётов.
Закон Ома. Расчёт напряжения, сопротивления, тока, мощности.
После сброса ввести два любых известных параметра.
Закон Ома для замкнутой цепи
Если к источнику питания подключить внешнюю цепь сопротивлением R , в цепи пойдёт ток с учётом внутреннего сопротивления источника:
I — Сила тока в цепи.
— Электродвижущая сила (ЭДС) — величина напряжения источника питания не зависящая от внешней цепи (без нагрузки).
Характеризуется потенциальной энергией источника.
r — Внутреннее сопротивление источника питания.
Для электродвижущей силы внешнеее сопротивление R и внутреннее r соединены последовательно, значит величина тока в цепи определится значением ЭДС и суммой сопротивлений: I = /(R+r) .
Напряжение на выводах внешней цепи определится исходя из силы тока и сопротивления R соотношением, которое уже рассматривалось выше: U = IR .
Напряжение U , при подключении нагрузки R , всегда будет меньше чем ЭДС на величину произведения I*r , которую называют падением напряжения на внутреннем сопротивлении источника питания.
С этим явлением мы сталкиваемся достаточно часто, когда видим в работе частично разряженные батарейки или аккумуляторы.
По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника,
значит уменьшается внешнее напряжение U = — I*r .
Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах U .
Если ток в цепи равен нулю, следовательно, = U . Цепь разомкнута, ЭДС источника равна напряжению на его выводах.
В случаях, когда внутренним сопротивлением источника можно пренебречь (r ≈ 0), напряжение на выводах источника будет равно ЭДС ( ≈ U )
независимо от сопротивления внешней цепи R .
Такой источник питания называют источником напряжения .
Закон Ома для переменного тока
При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление.
В таком случае запись Закона Ома будет иметь вид:
Здесь Z — полное (комплексное) сопротивление цепи — импеданс . В него входит активная R и реактивная X составляющие.
Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи.
Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс .
С учётом сдвига фаз φ , созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме :
Комплексная амплитуда тока. = I amp e jφ
— комплексная амплитуда напряжения. = U amp e jφ
— комплексное сопротивление. Импеданс.
φ — угол сдвига фаз между током и напряжением.
e — константа, основание натурального логарифма.
j — мнимая единица.
I amp , U amp — амплитудные значения синусоидального тока и напряжения.
Нелинейные элементы и цепи
Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников.
Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы.
Такие элементы и цепи, в которых они используются, называют нелинейными.
В
1826 г. немецкий ученый Георг Ом
экспериментально установил прямую
пропорциональную зависимость между
силой тока I
в проводнике и напряжением U
на его концах:
,
гдеG
— электрическая
проводимость проводника .
Величина, обратная проводимости
называется электрическим
сопротивлением проводника R . Таким образом, закон
Ома для участка цепи, не содержащего
источника э.д.с. ,
имеет вид
. Учитывая,
что в общем случае участок цепи может
содержать и э.д.с.,закон
Ома следует
представить в виде
.
Таким образом, закон
Ома для участка цепи, не содержащего
источника э.д.с. ,
имеет вид
. Учитывая,
что в общем случае участок цепи может
содержать и э.д.с.,закон
Ома следует
представить в виде
.
Сопротивление проводника зависит от его размеров, формы и материала, из которого он изготовлен. Для однородного линейного проводника , гдеl — длина, S — площадь поперечного сечения проводника, — удельное электрическое сопротивление, зависящее от материала, из которого изготовлен проводник. Единица сопротивления 1 Ом — это сопротивление такого проводника, в котором при напряжении 1В течет ток в 1А.
Если цепь замкнута, то ,, гдеR — общее сопротивление всей цепи, включая сопротивление источника э.д.с. Тогда закон Ома для замкнутой цепи следует записать , где — алгебраическая сумма всех э.д.с., имеющихся в этой цепи.
Принято
называть сопротивление источника тока
r
— внутренним ,
а сопротивление всей остальной цепи
R
— внешним .
Окончательный вид формулы закона Ома
для замкнутой цепи
. В системе единиц СИ напряжение и э.д.с.
измеряются в Вольтах (В), сопротивление
— в Омах (Ом), удельное электрическое
сопротивление — в Ом-метрах (Омм),
электрическая проводимость в Сименсах (См).
В системе единиц СИ напряжение и э.д.с.
измеряются в Вольтах (В), сопротивление
— в Омах (Ом), удельное электрическое
сопротивление — в Ом-метрах (Омм),
электрическая проводимость в Сименсах (См).
Рис.2.1. Отрезок проводника.
Закон Ома можно записать и для плотности тока. Рассмотрим участок электрической длиной dl и поперечным сечением dS (рис.2.1). Сила тока на этом участке , сопротивление, падение напряжения, где Е — напряженность электрического поля в проводнике. Подставив эти параметры в закон Ома для участка цепи, получим. Отсюдаили, где-удельная электрическая проводимость проводника или удельная электропроводность . В векторном виде имеем (единицей измерения в системе СИ является сименс на метр (См/м)). Полученное выражение есть закон Ома в дифференциальной форме: плотность тока в любой точке внутри проводника прямо пропорциональна напряженности поля в этой точке .1.14
Сопротивление проводника. Явление
сверхпроводимости.
Способность вещества проводить ток характеризуется его удельной проводимостью , либо удельным сопротивлением . Их величина определяется химической природой проводника и условиями, в частности температурой, при которой он находится. Для большинства металлов растет с температурой приблизительно по линейному закону: ,- удельное сопротивление при 0С, t — температура по шкале Цельсия, — температурный коэффициент сопротивления близкий к 1/273 К -1 при не очень низких температурах. Так как R, то , где- сопротивление при 0С. Преобразовав две последние формулы, можно записать и, где Т – температура по Кельвину. На основе температурной зависимости сопротивления металлов созданытермометры сопротивления — термисторы , позволяющие определять температуру с точностью до 0.003 К.
При
низких температурах нарушается линейность
зависимости сопротивления металлов от
температуры и при температуре 0 К
наблюдается остаточное сопротивление
R ост.
Величина R ост
зависит от чистоты материала и наличия
в нем механических напряжений. Лишь у
идеально чистого металла с идеально
правильной кристаллической решеткой
R ост
0
при Т0
(пунктирная часть кривой).
Лишь у
идеально чистого металла с идеально
правильной кристаллической решеткой
R ост
0
при Т0
(пунктирная часть кривой).
Кроме
этого, в 1911 г. Г.Каммерлинг-Оннес
обнаружил, что при Т к = 4.1К
сопротивление ртути скачкообразно
уменьшается практически до нуля. Эта
температура была названа критической ,
а наблюдаемое явление — сверхпроводимостью .
Впоследствии этот эффект был обнаружен
у целого ряда других металлов (Ti,
Al ,
Pb,
Zn,
V
и др.) и их сплавов в интервале
температур 0.14-20 К. Вещества в сверхпроводящем
состоянии обладают необычными свойствами.
Однажды возбужденный в них ток может
длительно существовать без источника
тока. Переход в сверхпроводящее состояние
сопровождается скачкообразным изменением
теплоемкости, теплопроводности,
магнитных свойств вещества. Выяснилось,
что внешнее магнитное поле не проникает
в толщину сверхпроводника, т.е.
магнитная индукция внутри него всегда
равна нулю. Явление сверхпроводимости
объясняется на основе квантовой теории.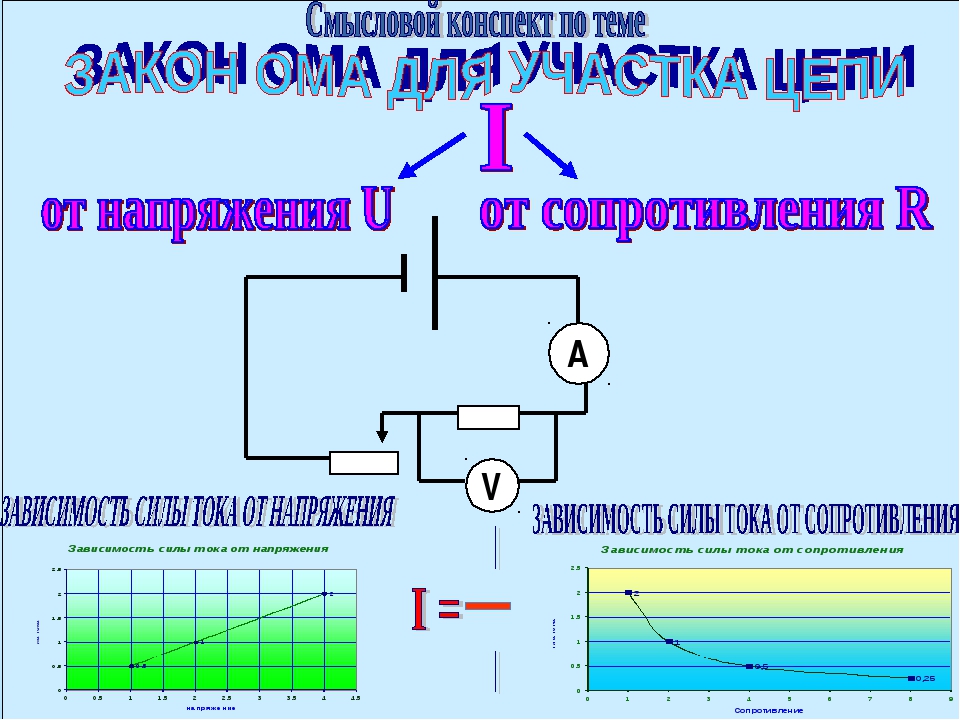 К настоящему времени это явление
обнаружено также у ряда композиционных
веществ (например, соединений металлов
и диэлектриков), при этом критическая
температура доходит до температуры
сжижения азота, что позволяет достаточно
экономично использовать явление
высокотемпературной сверхпроводимости
в инженерной практике. Данное явление
позволяет создавать: системы передачи
без потерь электрического тока по
проводам из таких веществ, системы для
накопления электроэнергии, мощные
электромагниты, магнитные подвески для
различных целей.
К настоящему времени это явление
обнаружено также у ряда композиционных
веществ (например, соединений металлов
и диэлектриков), при этом критическая
температура доходит до температуры
сжижения азота, что позволяет достаточно
экономично использовать явление
высокотемпературной сверхпроводимости
в инженерной практике. Данное явление
позволяет создавать: системы передачи
без потерь электрического тока по
проводам из таких веществ, системы для
накопления электроэнергии, мощные
электромагниты, магнитные подвески для
различных целей.
1.15 Работа и мощность тока, закон Джоуля-Ленца.
Определим работу, совершаемую постоянным током в проводнике, имеющем сопротивление R и находящемся под напряжением . Так как ток представляет собой перемещение зарядаq под действием поля, то работу тока можно определить по формуле . Учитывая формулуи закон Ома, получим, или, или, гдеt — время протекания тока. Поделив обе части равенства на t, получим выражения для мощности постоянного тока N
Работа тока в системе единиц СИ измеряется
в доулях (Дж), а мощность — в ваттах (Вт). На практике применяются также внесистемные
единицы работы тока: ватт-час (Втч)
и киловатт-час (кВтч).
1Втч
— работа тока мощностью 1Вт в течение
одного часа. 1Втч=3.610 3
Дж.
На практике применяются также внесистемные
единицы работы тока: ватт-час (Втч)
и киловатт-час (кВтч).
1Втч
— работа тока мощностью 1Вт в течение
одного часа. 1Втч=3.610 3
Дж.
Опыт показывает, что ток всегда вызывает некоторое нагревание проводника. Нагревание обусловлено тем, что кинетическая энергия движущихся по проводнику электронов (т.е. энергия тока) при каждом их столкновении с ионами металлической решетки переходит в теплоту Q. Если ток идет по неподвижному металлическому проводнику, то вся работа тока расходуется на его нагревание и, следуя закону сохранения энергии, можно записать . Данные соотношения выражаютзакон Джоуля-Ленца . Впервые этот закон был установлен опытным путем Д.Джоулем в 1843 г. и независимо от него Э.Ленцем в 1844 г. Применение теплового действия тока в технике началось с открытия в 1873 г. русским инженером А.Ладыгиным лампы накаливания .
На
тепловом действии тока основан целый
ряд электрических приборов и установок:
тепловые электроизмерительные приборы,
электропечи, электросварочная аппаратура,
бытовые электронагревательные приборы
— чайники, кипятильники, утюги. В пищевой
промышленности широко применяется
метод электроконтактного нагрева,
заключающийся в том, что электрический
ток, проходя через продукт, обладающий
определенным сопротивлением, вызывает
его равномерное нагревание. Например,
для производства колбасных изделий
через дозатор фарш поступает в формы,
торцевые стенки которых служат
электродами. При такой обработке
обеспечивается равномерность
нагрева по всему объему продукта,
возможность поддержания определенного
температурного режима, наивысшая
биологическая ценность изделия,
наименьшие длительность процесса и
расход энергии.
В пищевой
промышленности широко применяется
метод электроконтактного нагрева,
заключающийся в том, что электрический
ток, проходя через продукт, обладающий
определенным сопротивлением, вызывает
его равномерное нагревание. Например,
для производства колбасных изделий
через дозатор фарш поступает в формы,
торцевые стенки которых служат
электродами. При такой обработке
обеспечивается равномерность
нагрева по всему объему продукта,
возможность поддержания определенного
температурного режима, наивысшая
биологическая ценность изделия,
наименьшие длительность процесса и
расход энергии.
Определим удельную
тепловую мощность тока ,
т.е. количество теплоты, выделяющееся
в единице объема за единицу времени.
Выделим в проводнике элементарный
цилиндрический объем dV
с поперечным сечением dS
и длиной dl параллельной направлению тока, и
сопротивлением
,.
По закону Джоуля-Ленца, за времяdt
в этом объеме выделится теплота
.
Тогдаи,
используя закон Ома для плотности токаи соотношение,
получим. Эти соотношения выражаютзакон
Джоуля-Ленца в дифференциальной форме .
Эти соотношения выражаютзакон
Джоуля-Ленца в дифференциальной форме .
1.16. Правило Кирхгофа для разветвленных электрических цепей.
До сих пор нами рассматривались простейшие электрические цепи, состоящие из одного замкнутого неразветвленного контура. На всех его участках силы тока одинаковы. Расчет I, R, в такой цепи выполняется с помощью законов Ома.
Рис.2.2.Разветвленная электрическая цепь.
Более сложной является разветвленная электрическая цепь , состоящая из нескольких замкнутых контуров, имеющих общие участки. В каждом контуре может быть несколько источников тока. Силы тока на отдельных участках замкнутого контура могут быть различными по величине и направлению (рис.2.2). В 1847 г. Г.Кирхгоф сформулировал два правила, значительно упрощающих расчет разветвленных цепей.Первое
правило Кирхгофа : алгебраическая
сумма сил токов в узле равна нулю: .Узел — точка цепи, в которой сходятся не менее
трех проводников. В электрической
цепи на рис.2.2 имеются два узла А и В.
Ток, входящий в узел, считается
положительным, выходящий — отрицательным.
Например, для узла А первое правило
Кирхгофа следует записать
.
В электрической
цепи на рис.2.2 имеются два узла А и В.
Ток, входящий в узел, считается
положительным, выходящий — отрицательным.
Например, для узла А первое правило
Кирхгофа следует записать
.
Первое правило выражает закон сохранения электрического заряда, так как ни в одной точке цепи они не могут возникать или исчезать.
Второе
правило Кирхгофа относится к любому замкнутому контуру,
выделенному в разветвленной цепи: алгебраическая
сумма произведений токов на сопротивления,
включая и внутренние, на всех участках
замкнутого контура равна алгебраической
сумме электродвижущих сил, встречающихся
в этом контуре .
Контур ‑ это замкнутый участок
схемы, по которому можно пройти и
вернуться в исходную точку. Второе
правило Кирхгофа получается из закона
Ома, записанного для всех участков от
узла до узла (ветвей) разветвленной
схемы. В электрической цепи на рис.2.2
имеются три контура:AMNBA,
CABDC,
CMNDC.
При этом, токи I i
в ветвях контура, совпадающие с произвольно
выбранным направлением обхода
контура, считаются положительными, а
направленные навстречу обхода —
отрицательными. Э.д.с., проходимые от
«+» к «-» считаются положительными и
наоборот. В рассматриваемой электрической
цепи (рис.2.2) выберем обход контуров по
часовой стрелке и запишем для них
уравнения по II
правилу Кирхгофа: для AMNBА
;
дляCABDС
;
дляCMNDС
.
В данном примере внутренними сопротивлениями
источников тока пренебрегаем. Первое
и второе правила Кирхгофа позволяют
составить систему линейных алгебраических
уравнений, которые связывают параметры
(I,
R,
)
и позволяют, зная одни, найти другие.
Э.д.с., проходимые от
«+» к «-» считаются положительными и
наоборот. В рассматриваемой электрической
цепи (рис.2.2) выберем обход контуров по
часовой стрелке и запишем для них
уравнения по II
правилу Кирхгофа: для AMNBА
;
дляCABDС
;
дляCMNDС
.
В данном примере внутренними сопротивлениями
источников тока пренебрегаем. Первое
и второе правила Кирхгофа позволяют
составить систему линейных алгебраических
уравнений, которые связывают параметры
(I,
R,
)
и позволяют, зная одни, найти другие.
Рис.2.3. а) Последовательное соединение сопротивлений; б) Параллельное соединение сопротивлений.
Простые электрические цепи имеют очень большое практическое применение. В повседневной жизни полезно знать, как подключить динамики или проигрыватель к стереосистеме, как подсоединить сигнализацию для охраны или автомобильный кассетный проигрыватель, как зарядить аккумуляторы или осветить новогоднюю елку.Большинство
электрических цепей содержит комбинацию
последовательно или параллельно
подключенных резисторов (резистор — это
элемент цепи, обладающий только
сопротивлением).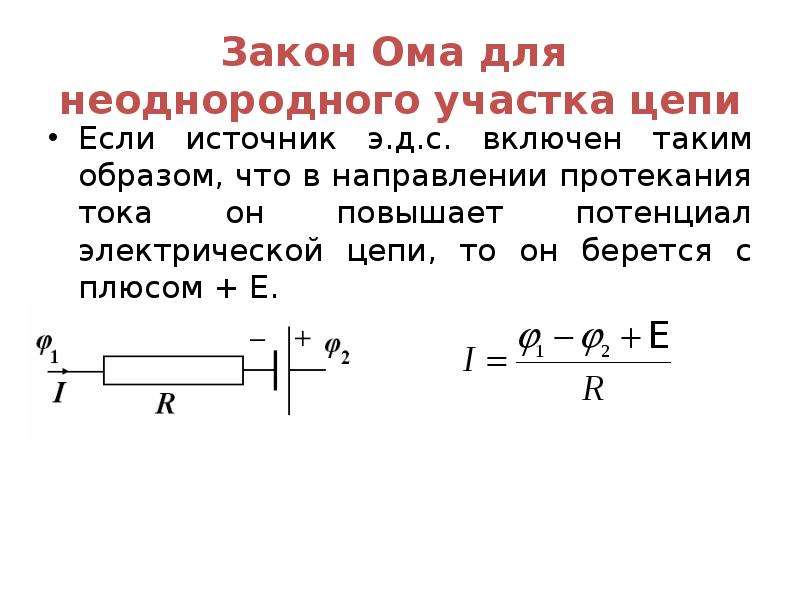 Полное сопротивление
участка цепи определяется отношением
падения напряжения на нем к величине
силы тока
.
При последовательном соединении
(рис.2.3 а) через все резисторы течет
один и тот же ток. При параллельном
соединении (рис.2.3 б) полный ток равен
сумме токов, текущих в отдельных
резисторах.
Полное сопротивление
участка цепи определяется отношением
падения напряжения на нем к величине
силы тока
.
При последовательном соединении
(рис.2.3 а) через все резисторы течет
один и тот же ток. При параллельном
соединении (рис.2.3 б) полный ток равен
сумме токов, текущих в отдельных
резисторах.
При последовательном соединении падение напряжения на участке АВ равно , т.е. сумме падений напряжения на трех резисторах. Разделим обе части равенства наI и получим , т.е.. Таким образом, полное сопротивление участка цепи, состоящего из последовательно соединенных резисторов, равно их алгебраической сумме.
При параллельном соединении (рис..2.3 б) мы имеем . Разделим обе части равенства наU, где U — падение напряжения на участке цепи АВ, причем , и получим. Из этого равенства следует. Величина обратная полному сопротивлению параллельно соединенных резисторов равна алгебраической сумме величин их обратных сопротивлений.
В
электрическую цепь может быть включено
регулируемое (изменяющееся с помощью
специального движка), сопротивление,
которое называется реостатом . По назначению реостаты делятся на
пусковые, служащие для ограничения силы
тока во время пуска двигателей, и
регулирующие — для регулировки силы
тока в цепи (постепенное снижение
освещенности в театральных залах),
регулировки скорости вращения
электродвигателей и т.д. Реостат может
быть использован в качестве так
называемого датчика
перемещения .
В автоматических регуляторах уровня
жидкости в резервуарах применяется
поплавково-реостатный датчик. Специальный
поплавок крепится к движку реостата.
Изменение уровня жидкости сдвигает
поплавок, изменяет сопротивление
реостата, и следовательно, силы тока в
цепи, величина которого дает информацию
об уровне.
По назначению реостаты делятся на
пусковые, служащие для ограничения силы
тока во время пуска двигателей, и
регулирующие — для регулировки силы
тока в цепи (постепенное снижение
освещенности в театральных залах),
регулировки скорости вращения
электродвигателей и т.д. Реостат может
быть использован в качестве так
называемого датчика
перемещения .
В автоматических регуляторах уровня
жидкости в резервуарах применяется
поплавково-реостатный датчик. Специальный
поплавок крепится к движку реостата.
Изменение уровня жидкости сдвигает
поплавок, изменяет сопротивление
реостата, и следовательно, силы тока в
цепи, величина которого дает информацию
об уровне.
Каждый специалист, ремонтирующий и обслуживающий электроустановки, должен хорошо знать и применять на практике закон Ома для замкнутой цепи. Это действительно так, поскольку закономерности, открытые немецким физиком Георгом Омом, лежат в основе всей электротехники. Данный закон стал весомым вкладом в дальнейшее развитие научных знаний в области электричества.
Физические свойства закона Ома
Прямая взаимосвязь между силой тока, напряжением, подведенным к сети, и была обнаружена Омом в 1826 году. В дальнейшем, понятие напряжения было заменено на более точный термин — электродвижущую силу (ЭДС). После теоретического обоснования этой зависимости был выведен закон для замкнутой цепи. Его важной особенностью считается обязательное отсутствие какого-либо внешнего возмущения. Поэтому стандартные формулировки потеряют свою актуальность, если, например, поместить проводник в переменное магнитное поле.
Для экспериментов по выводу закона использовалась простейшая схема, состоящая из источника питания, обладающего ЭДС и подключенных к нему двух выводов, соединенных с резистором. В проводнике начинают в определенном направлении перемещаться элементарные частицы, несущие заряд. Таким образом, представляется в виде отношения ЭДС к общему сопротивлению всей цепи: I = E/R.
В представленной формуле Е — является электродвижущей силой, измеряемой в вольтах, I — сила тока в амперах, а R выступает в роли электрического сопротивления резистора, измеряемого в омах. При этом, учитываются все составляющие сопротивления и при расчетах используется их суммарное значение. Они включают сопротивление самого резистора, проводника (r) и источника питания (r0). Окончательно формула будет выглядеть так: I = E/(R+r+r0). Если значение внутреннего сопротивления источника тока r0 превышает сумму R+r, то в этом случае отсутствует зависимость силы тока от характеристик подключенной нагрузки, а источник ЭДС исполняет роль источника тока. Когда r0 ниже суммы R+r, получается обратная пропорция тока с суммарным внешним сопротивлением, а напряжение поступает за счет источника питания.
При этом, учитываются все составляющие сопротивления и при расчетах используется их суммарное значение. Они включают сопротивление самого резистора, проводника (r) и источника питания (r0). Окончательно формула будет выглядеть так: I = E/(R+r+r0). Если значение внутреннего сопротивления источника тока r0 превышает сумму R+r, то в этом случае отсутствует зависимость силы тока от характеристик подключенной нагрузки, а источник ЭДС исполняет роль источника тока. Когда r0 ниже суммы R+r, получается обратная пропорция тока с суммарным внешним сопротивлением, а напряжение поступает за счет источника питания.
Закон Ома для выполнения расчетов
Точные расчеты требуют учета всех потерь напряжения, в том числе и в местах соединений. Для определения электродвижущей силы на выводах источника тока замеряется разность потенциалов при разомкнутой цепи, когда нагрузка полностью отключена. В этом случае применяется не только закон Ома для замкнутой цепи, но и закон, действующий . Данный участок считается однородным, поскольку здесь принимается в расчет только разность потенциалов, без учета ЭДС.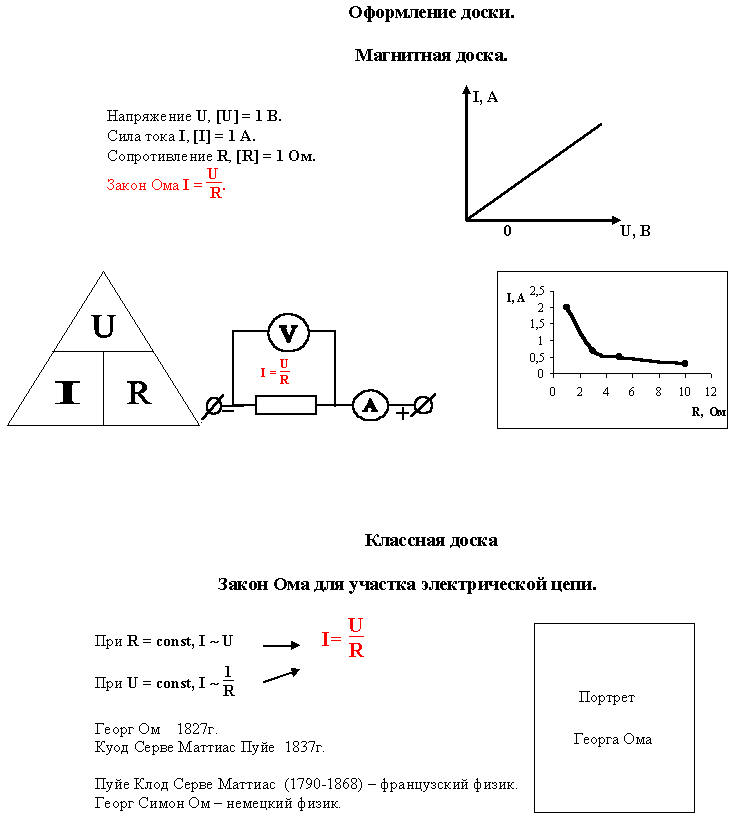 Это дает возможность рассчитать каждый элемент электрической цепи по формуле I=U/R, в которой U является разностью потенциалов или напряжением, измеряемым в вольтах.
Это дает возможность рассчитать каждый элемент электрической цепи по формуле I=U/R, в которой U является разностью потенциалов или напряжением, измеряемым в вольтах.
Замеры выполняются с помощью вольтметра при подключении щупов к выводам нагрузки или сопротивления. Полученное значение напряжения будет всегда ниже электродвижущей силы. Это наиболее распространенная формула, позволяющая найти любую составляющую при наличии двух известных.
Закон Ома для замкнутой цепи имеет много общего с законом, выведенным для магнитной цепи. В этой системе проводник выполнен в виде замкнутого магнитопровода. В качестве источника выступает обмотка катушки по виткам которой протекает электрический ток. Появляющийся магнитный поток (Ф) замыкается на магнитопровод и начинает циркулировать по контуру. Он находится в непосредственной зависимости от магнитодвижущей силы и сопротивления материала, через который проходит. Данное явление выражено формулой Ф=F/Rm, в которой F представляет собой магнитодвижущую силу, а Rm служит сопротивлением, вызывающим затухание.
Как рассчитать цепи
Закон первого Ома — MR WATT Shop
Мы можем сказать, что в электрической цепи, если разность потенциалов, приложенная между двумя ее точками, равна 1 вольт, а частичное сопротивление участка между этими двумя точками составляет 1 Ом на этом участке. циркулирует ток в 1 ампер.
Закон Ома очень просто устанавливает взаимосвязь между тремя следующими электрическими величинами: напряжением (В), током (I) и сопротивлением (R)
Этот закон был провозглашен известным немецким физиком Джорджем Симоном Омом и, безусловно, является наиболее подходящим. важны из тех, что связаны с электричеством.
Заявление звучит именно так:
«Сила тока в цепи прямо пропорциональна приложенному к ней напряжению и обратно пропорциональна сопротивлению самой цепи».
Его математическое выражение:
I = V / R
, которое позволяет рассчитать ток, зная напряжение и сопротивление. Получено по этой формуле:
Получено по этой формуле:
V = I * R
R = V / I
, что позволяет определить напряжение или сопротивление, когда две другие величины известны.Если схема применяется к одному ф.э.м. (Электродвижущая сила) значения E, мы видим, что формула закона Ома принимает следующий вид:
I = E / (R + r)
где «r» — внутреннее сопротивление генератора. . Если мы рассмотрим схему с одним резистором и предположим, что разность потенциалов между клеммами A и B имеет значение V, ток, протекающий через сопротивление R, будет:
I = V / R
Тогда как с другой стороны, схема с двумя резисторами, питаемыми от ЭДС генератора E и внутренним сопротивлением r, если R1 и R2 являются внешними резисторами или нагрузкой, соединенными последовательно, мы будем иметь:
I = E / (R1 + R2 + r)
, что дает
E = I (R1 + R2 + r) = I R1 + I R2 + I r.
Продукты I R1, I R2 и I r (резисторы тока) соответственно выражают разность потенциалов, существующую между точками (AC) и (CB), а также внутреннее падение напряжения генератора.
Мы видим, что ф.э.м. И приложенная к цепи сумма разностей парциальных потенциалов равна сумме, которые также называют «падениями напряжения».
Падения напряжения IR1 и IR2 возникают во внешней цепи и могут иметь полезный эффект. Падение напряжения Ir возникает внутри генератора и не имеет значения.
Предположим, что теперь переключатель разомкнут: в цепи нет тока и, поскольку I = 0, внутреннее падение напряжения будет нулевым, а ddp между двумя выводами A и B генератора будет равно ЭДС самого генератора. : VAB = E.
Если вместо этого цепь замкнута и циркулирует ток I, между A и B будет разность потенциалов (ddp)
VAB = E — I * r
Другой случай, при котором возникает условие VAB = E — когда внутреннее сопротивление генератора равно нулю (r = 0).
Несмотря на то, что большинство из нас знает и правильно использует «Закон Ома», мы не должны забывать, что есть люди, начинающие, которые, зная о существовании этого закона, не знают, как использовать его на практике, чтобы получить как можно больше преимуществ. .
Мы обращаемся к симулятору за любыми примерами и приложениями.
Сопротивление и простые схемы — College Physics
Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, розетки и т. Д., Которые необходимы для поддержания тока.Все такие устройства создают разность потенциалов и условно называются источниками напряжения. Когда источник напряжения подключен к проводнику, он создает разность потенциалов, которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Закон Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к ним напряжению. Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
.
Это важное соотношение известно как закон Ома.Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием. Это эмпирический закон, подобный закону трения — явление, наблюдаемое экспериментально. Такая линейная зависимость возникает не всегда.
Сопротивление и простые схемы
Если напряжение управляет током, что ему мешает? Электрическое свойство, препятствующее току (примерно такое же, как трение и сопротивление воздуха), называется сопротивлением. Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток.Сопротивление обратно пропорционально току, или
.Таким образом, например, ток уменьшается вдвое, если сопротивление увеличивается вдвое. Комбинируя отношения тока к напряжению и тока к сопротивлению, получаем
Это соотношение также называется законом Ома. Закон Ома в такой форме действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален. Многие вещества, для которых действует закон Ома, называются омическими. К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах.Омические материалы обладают сопротивлением, не зависящим от напряжения и тока. Объект с простым сопротивлением называется резистором , даже если его сопротивление невелико. Единицей измерения сопротивления является ом, который обозначается символом (заглавная греческая омега). Перестановка дает, и поэтому единицы сопротивления 1 Ом = 1 вольт на ампер:
(рисунок) показывает схему простой схемы. Простая схема имеет один источник напряжения и один резистор.Можно предположить, что провода, соединяющие источник напряжения с резистором, имеют незначительное сопротивление, или их сопротивление можно включить.
Простая электрическая цепь, в которой замкнутый путь для прохождения тока обеспечивается проводниками (обычно металлическими), соединяющими нагрузку с выводами батареи, представленной красными параллельными линиями. Зигзагообразный символ представляет собой единственный резистор и включает любое сопротивление в соединениях с источником напряжения.
Расчет сопротивления: автомобильная фара
Какое сопротивление проходит у автомобильной фары? 2.50 А при подаче на него 12,0 В?
Стратегия
Мы можем изменить закон Ома, как указано в, и использовать его, чтобы найти сопротивление.
Решение
Перестановка и замена известных значений дает
Обсуждение
Это относительно небольшое сопротивление, но оно больше, чем хладостойкость фары. Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампа имеет меньшее сопротивление при первом включении и потребляет значительно больший ток во время короткого периода прогрева.
Сопротивление может быть разным. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление или более. Сухой человек может иметь сопротивление руки к ноге, тогда как сопротивление человеческого сердца составляет около. Кусок медного провода большого диаметра длиной в метр может иметь сопротивление, а сверхпроводники вообще не имеют сопротивления (они неомичны). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделах «Сопротивление и удельное сопротивление».
Дополнительную информацию можно получить, решив дать
Это выражение для можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока . Для этого напряжения часто используется фраза падение . Например, у фары на (Рисунок) падение составляет 12,0 В. Если напряжение измеряется в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости.Источник напряжения подобен насосу, создающему перепад давления, вызывая ток — поток заряда. Резистор похож на трубу, которая снижает давление и ограничивает поток из-за своего сопротивления. Здесь сохранение энергии имеет важные последствия. Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию). В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, так как и то же самое течет через каждый.Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. (Рисунок).)
Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Установление соединений: сохранение энергии
В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. Здесь о сохранении энергии свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму только с помощью резистора.Мы обнаружим, что сохранение энергии имеет и другие важные применения в схемах и является мощным инструментом анализа схем.
Открытия Георга ОмаВ своей первой статье, опубликованной в 1825 году, Ом исследует уменьшение электромагнитной силы, создаваемой проводом, по мере увеличения длины провода.В статье были выведены математические соотношения, основанные исключительно на экспериментальных данных, которые Ом вывел в таблицу. В двух важных статьях 1826 года Ом дал математическое описание проводимости в схемах, смоделированных на основе исследования теплопроводности Фурье. Эти статьи продолжают вывод Ома результатов из экспериментальных данных, и, особенно во втором случае, он смог предложить законы, которые во многом помогли объяснить результаты других, работающих над гальваническим электричеством. Вторая статья, безусловно, является первым шагом в всеобъемлющей теории, которую Ом смог изложить в своей знаменитой книге, опубликованной в следующем году. То, что сейчас известно как закон Ома, появилось в этой знаменитой книге Die galvanische Kette, Mathematisch Bearbeitet (1827), в которой он дал свою полную теорию электричества. Книга начинается с математической подготовки, необходимой для понимания остальной работы. Здесь следует отметить, что такая математическая подготовка была необходима даже ведущим немецким физикам для понимания работы, поскольку в то время упор делался на нематематический подход к физике.Следует также отметить, что, несмотря на попытки Ома в этом введении, ему не удалось убедить немецких физиков старшего возраста в правильности математического подхода. Как указано выше, эта работа включала теорию «Закона Ома»: отношение тока, проходящего через большинство материалов, прямо пропорционально разности потенциалов, приложенной к материалу. Хотя работа Ома сильно повлияла на теорию, поначалу она была воспринята без особого энтузиазма.Тем не менее, его работа была в конечном итоге признана Королевским обществом, награжденным медалью Копли в 1841 году. Он стал иностранным членом Королевского общества в 1842 году, а в 1845 году он стал полноправным членом Баварской академии. Закон ОмаЗакон Ома, названный в честь его первооткрывателя, гласит, что разность потенциалов V между концами проводника или резистора R и ток I , протекающий через R , пропорциональны при данной температуре:
Закон строго верен только для резисторов, сопротивление которых не зависит от приложенного напряжения, которые называются омическими или идеальными резисторами или омическими устройствами. Закон Ома никогда не бывает полностью точным, если R предполагается постоянным, для «реальных» устройств, потому что ни одно реальное устройство не является омическим устройством для каждого напряжения и тока — на каком-то уровне устройство откроется или закроется, например, путем возгорания или образования дуги. Более того, температура является важным фактором, определяющим точность закона Ома.Когда температура металла увеличивается, количество столкновений между электронами и атомами увеличивается, поэтому, когда вещество нагревается из-за протекающего через него электричества (или в результате любого другого процесса нагрева), сопротивление увеличивается. Отношение V / I = R справедливо даже для неомических устройств, но тогда сопротивление R зависит от V и больше не является постоянным. Чтобы проверить, является ли данное устройство омическим или нет, строят график V и I и сравнивают график с прямой линией, проходящей через начало координат. Важно отметить, что закон Ома — это не фактический математически выведенный закон, а наблюдение, подтвержденное значительными эмпирическими данными. В 1845 году немецкий физик Густав Кирхгоф (1824–1887) объявил об открытии законов Кирхгофа, которые позволяют рассчитывать токи, напряжения и сопротивления электрических сетей. Расширяя теорию Георга Ома, он обобщил уравнения, описывающие течение тока, на случай электрических проводников в трех измерениях.В дальнейших исследованиях он продемонстрировал, что ток течет по проводнику со скоростью света. Эксперименты по закону ОмаЭксперименты по закону ОмаЭксперимент с законом Ома — Кафедра астрономии и физики МГУ Характеристики тока / напряжения и закон Ома — Davidson Physics Круговая диаграмма и калькуляторы с законом Ома — 12volt.com Закон Ома — Р. Виктор Джонс Закон Ома, электрическая мощность, ЭДС и внутренние сопротивление — PMB Отношения закона Ома — Уолтер Банцаф, Э.К. Смит, Уинфилд Янг Закон Ома — Рэндалл Дж. Скалайс Закон Ома — Омические резисторы JL Stanbrough Закон Ома против лампочек — UBC Эксперименты по законам Кирхгофа Законы Кирхгофа — Университет Гвельфа, факультет физики Закон Ома и правила Кирхгофа — Крис Одом, Университет Клемсона Фон закона Ома Закон Ома — Национальная лаборатория сильных магнитных полей. Закон Ома — Гиперфизика. Закон Ома — Университет Гвельфа, факультет физики.com Демонстрация закона Ома — Science Joy Wagon Биографии Георга Ома Георг Симон Ом — MacTutor Книги& nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp & nbsp |
Определение закона Ома в физике.
Примеры закона Ома в следующих темах:
Закон Ома
- Эта важная взаимосвязь известна как закон Ома .
- Это соотношение также называется законом Ома закон .
- Закон Ома (как и закон Гука ) не является универсальным.
- Многие вещества, для которых действует закон Ома , называются омическими.
- Два других устройства не подчиняются закону Ома .
Измерения тока и напряжения в цепях
- Согласно закону Ома , электрический ток I или движение заряда, протекающего через большинство веществ, прямо пропорционально приложенному к нему напряжению V.
- Закон Ома , следовательно, можно записать следующим образом:
- Точнее, закон Ом гласит, что R в этом отношении является постоянным, не зависящим от тока.
- Чтобы решить эту проблему, мы просто подставим указанные значения в закон Ом : I = 1,5 В / 5 Ом; I = 0,3 ампера.
- Если нам известны ток и сопротивление, мы можем переставить уравнение Ом закон и решить для напряжения V:
Резисторы в цепях переменного тока
- В цепи с резистором и источником питания переменного тока все еще применяется закон Ом (V = IR).
- Закон Ома применяется как к цепям переменного тока, так и к цепям постоянного тока.
- Применить закон Ом для определения силы тока и напряжения в цепи переменного тока
Конденсаторы в цепях переменного тока: емкостное сопротивление и фазорные диаграммы
- Здесь мы использовали закон Ом (V = IR), чтобы получить соотношение между напряжением и током в цепях переменного тока.
- В этом и последующих атомах мы обобщим закон Ом Ом, чтобы мы могли использовать его, даже когда в цепи есть конденсаторы и катушки индуктивности.
- Поскольку это по-прежнему напряжение, деленное на ток (например, сопротивление), его единицей является Ом .
- Считается, что это эффективное сопротивление конденсатора переменному току, поэтому среднеквадратичный ток Irms в цепи, содержащей только конденсатор C, определяется другой версией закона Ом как $ I_ {rms} = \ frac {V_ {rms}} {X_C} $, где Vrms — действующее значение напряжения.
- Обратите внимание, что XC заменяет R в версии закона Ом закона для постоянного тока.
Резисторы серии
- Использование закона Ом для расчета изменений напряжения в резисторах серии
- Согласно закону Ом падение напряжения V на резисторе при протекании через него тока рассчитывается по формуле V = IR, где I — ток в амперах (A), а R — сопротивление в Ом (Ом).
- Краткое введение в анализ последовательных цепей и последовательных цепей, включая Закон Кирхгофа (KCL) и Закон Кирхгофа по напряжению (KVL).
Параллельные резисторы
- Согласно закону Ома , токи, протекающие через отдельные резисторы, равны $ I_1 = \ frac {V} {R_1} $, $ I_2 = \ frac {V} {R_2} $ и $ I_3 = \ frac {V} {R_3} $.
- Цепь серии
RLC: на больших и малых частотах; Фазорная диаграмма
- Путем комбинирования закона Ом (Irms = Vrms / Z; Irms и Vrms — среднеквадратичные ток и напряжение) и выражение для импеданса Z из:
- Этот отклик имеет смысл, потому что на высоких частотах закон Ленца предполагает, что полное сопротивление индуктора будет большим.
Различные типы токов
- Ряд законов об электротехнике применяется ко всем электрическим сетям.
- К ним относятся закон Ом , который обсуждался в модуле «Сопротивление и резисторы», законы тока и напряжения Кирхгофа , которые рассматриваются в модуле «Правила Кирхгофа».
- Два закона Кирхгофа вместе с вольт-амперной характеристикой (ВАХ) каждого электрического элемента полностью описывают цепь.
- Ток i, протекающий по цепи, определяется законом Ом .
Дроссели в цепях переменного тока: индуктивно-реактивные и фазовые диаграммы
- В цепи переменного тока с катушкой индуктивности напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца .
- Среднеквадратичный ток Irms через катушку индуктивности L определяется версией закона Ом : $ I_ {rms} = \ frac {V_ {rms}} {X_L} $, где Vrms — среднеквадратичное напряжение на катушке индуктивности, а $ X_L = 2 \ pi \ nu L $, где $ \ nu $ — частота источника переменного напряжения в герцах.
- Поскольку катушка индуктивности препятствует прохождению тока, XL имеет единицы измерения Ом (1 H = 1 Ωs, так что частота, умноженная на индуктивность, имеет единицы (циклов / s) (Ωs) = Ω), что соответствует его роли в качестве эффективное сопротивление.
- Напряжение на катушке индуктивности «ведет» ток в соответствии с законом Ленца .
Введение и важность
- Схема Кирхгофа законы — это два уравнения, впервые опубликованные Густавом Кирхгофом в 1845 году.
- Кирхгоф, скорее, использовал работу Георга Ома в качестве основы для действующего закона Кирхгофа (KCL) и закона Кирхгофа по напряжению (KVL).
- Закон Кирхгофа чрезвычайно важен для анализа замкнутых цепей.
- В заключение, законы Кирхгофа зависят от определенных условий.
- Закон напряжения является упрощением закона индукции Фарадея и основан на предположении, что в замкнутом контуре нет флуктуирующего магнитного поля.
Ома — калькулятор, формула, определение, уравнение, объяснение колеса
Содержание
Закон ОмаЗакон Ома гласит, что ток, протекающий по проводнику между двумя точками, прямо пропорционален напряжению в двух точках при определенной температуре. Здесь сопротивление вводится как коэффициент пропорциональности. Сопротивление — это противодействие току в цепи. Закон Ома выражает союз между напряжением, током и сопротивлением.
Ом формулирует этот закон в очень простой форме уравнения. Этот закон упрощает понимание электрических цепей. Согласно закону Ома соотношение между током в цепи и напряжением в этой цепи определяется следующим образом.
I ∝ V
V
I = -
р
Где I — ток, протекающий по цепи, V — напряжение в цепи, а R — сопротивление проводника току. Ток — это поток электронов или электричества в электрической цепи, тогда как напряжение — это разность потенциалов в заряде между двумя точками проводника или цепи.Ом помогает нам вывести формулы для напряжения, тока и сопротивления из его закона. Ток в цепи можно измерить по следующей формуле
В
I = -
R Напряжение в цепи можно измерить по следующей формуле
В = IR
Сопротивление в цепи можно измерить по следующей формуле
В
R = -
I Закон Ома Единица
Закон Ома Единица Согласно закону Ома единицы измерения тока, напряжения и сопротивления следующие:
- Единица измерения электрического тока, протекающего по цепи, равна Ампер .Поток тока в один ампер создается на сопротивлении 1 Ом напряжением одного напряжения. Ампер обозначается как ‘A.’
- Единица измерения напряжения в цепи — Вольт . Один вольт — это разность потенциалов, по которой через сопротивление в один Ом проходит ток в один ампер. Вольт обозначается как ‘V.’
- Единица сопротивления, противодействующего току, составляет Ом . Один Ом — это сопротивление, возникающее при прохождении тока в один ампер через разность потенциалов в один вольт.Обозначается цифрой ‘’. Это греческая заглавная буква Омега. Кроме того, когда говорится о сопротивлении, это называется Ом.
1 Вольт
1 Ом = ―――
1 ампер
Таблица формул для закона Ома
| Закон Ома | Напряжение (В) | Ток (I) | Сопротивление (R) | Мощность (P) | Ток 9 | V = IR | — | — | P = I 2 R | |||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ток и мощность | P V = — I | — | P R = — I | — | ||||||||||||||||||||||||||||||||||||||||||
| Напряжение и ток | — | — | В R = — I | P = VI | ||||||||||||||||||||||||||||||||||||||||||
| Напряжение и сопротивление | — R = — R = — | В 2 p = — R | — | |||||||||||||||||||||||||||||||||||||||||||
| Напряжение и мощность | — | P I = — V | V 2 R = — | P —
| Мощность и сопротивление tance | V = √PR | I = √ (P / R) | — | — |
Также прочтите: Закон Ом Мультфильм-Вольт, Ампер, Объяснение Ом
Закон Ома для Комбинация резисторов в схемах
Есть два способа подключения резисторов.Резисторы могут быть соединены последовательно, параллельно или последовательно и параллельно.
НАКОПЛЕНИЕ РЕЗИСТОРОВ СЕРИИ
В последовательной схеме резисторы соединены рядом друг с другом, т.е. они соединены в линию. Никакой другой элемент схемы не подключен между любыми двумя цепями. Только один конец резистора подключен к концу дополнительного резистора. Можно подключить «N» резисторов. При последовательном соединении ток, протекающий через все резисторы, одинаков, а напряжение на каждом резисторе разное.Последовательная комбинация резисторов показана ниже.
Предположим, что «I» — это ток, протекающий через эти резисторы. Сопротивление первого резистора равно «, второго резистора» и так далее. Пусть напряжение на первом резисторе будет «, а на втором резисторе».
Тогда по закону Ома напряжение на каждом резисторе определяется как:
В 1 = I × R 1 V 1 = I × R 2
V 3 = I × R 3 и т. Д.Общее эквивалентное напряжение в цепи равно V эквивалент = V 1 1+ V 2 + V 3 +…. + V n ИК эквивалент = ИК 1 + ИК 2 + ИК 3 + ……. + ИК № Таким образом, общая сумма сопротивления, приложенного цепью, определяется выражением R Эквивалент = R 1 + R 2 + R 3 + ……. + R № .
ПАРАЛЛЕЛЬНОЕ НАКОПЛЕНИЕ РЕЗИСТОРОВ
В параллельной цепи сопротивления могут быть соединены параллельно друг другу i.е. они прикреплены друг к другу. Оба конца резистора подключены к обоим концам другого резистора. В схеме соединение «N» резисторов может быть выполнено параллельно друг другу.
При параллельном подключении напряжение на одном резисторе совпадает с напряжением на разных резисторах, подключенных в этой цепи, в то время как ток, протекающий через каждый резистор, изменяется в зависимости от каждого резистора. Параллельная комбинация резисторов показана ниже
. Предположим, что напряжение на этих резисторах равно «V».Сопротивление первого резистора R 1 , второго резистора R 2 и так далее. Пусть ток, протекающий через первый резистор, будет «I 1 », а через второй резистор — «I 2 ».
Тогда по закону Ома ток через каждый резистор определяется как:
В
Я 1 = -
руб. 1
V
Я 2 = -
R 2
V
Я 3 = -
R 3
Полный эквивалентный ток в цепи равен I эквиваленту = I 1 + I 2 + I 3 +….+ I n Таким образом, при подстановке мы получаем V / R_equivalent = V / R 1 + V / R 2 2+ V / R 3 +… .. + V / R n .
Таким образом, общая сумма сопротивления, приложенного цепью, определяется как
1 / R эквивалент = 1 / R 1 + 1 / R 2 + 1 / R 3 + …… +1 / R n
Уравнение закона Ома
Как гласит закон Ома, ток прямо пропорционален напряжению, а сопротивление является константой пропорциональности.Получаем
Напряжение = Ток x Сопротивление V = I × R
Ток противодействует протеканию тока, который называется сопротивлением. Ток — это разряд электронов. Но при прохождении через провод цепи он должен преодолевать сопротивление, создаваемое проводом, и течь по цепи. Уравнение закона Ома. Сопротивление равно
В.
R = -
я
Пример 1
Если сопротивление цепи равно 50, через который ток равен 3.2 А, затем найдите напряжение в этой цепи.
Решение:
Мы должны найти напряжение, когда нам заданы сопротивление и ток в цепи. Итак, воспользуемся формулой напряжения.
По закону Ома
В = ИК V = 3,2 х 50 V = 160 Вольт.
Итак, напряжение, полученное в предоставленной цепи, измеряется как 160 вольт.
Пример 2
Если сопротивление цепи составляет 25, через которую протекает ток 6 А, то найдите напряжение на этой цепи.
Решение:
Мы должны найти напряжение, когда нам заданы сопротивление и ток в цепи. Итак, воспользуемся формулой напряжения.
По закону Ома
В = ИК Подставляя заданные значения сопротивления и тока в формулу, получаем V = 6 х 25 V = 150 Вольт.
Итак, напряжение, полученное в предоставленной цепи, измеряется как 150 вольт.
Пример 3
Напряжение в цепи составляет 6,56 В, а сопротивление той же цепи равно 1.6 Ом. К какому току прилагается сопротивление или противодействие?
Решение:
Мы должны найти ток в цепи, когда нам даны напряжение и сопротивление цепи. Так что воспользуемся током и решим эту проблему.
По закону Ома
В
I = -
р
Подставляя заданные значения напряжения и сопротивления в формулу, получаем
6,56
I = -
1.6
I = 4,1 А
Ток, протекающий по данной цепи, равен 4.1 А. Пример 4
Найдите ток в цепи, к которой приложено сопротивление 9,75 Ом. Напряжение в цепи составляет 8 В.
Решение:
Мы должны найти ток в цепи, когда нам даны напряжение и сопротивление цепи. Так что воспользуемся током и решим эту проблему.
По закону Ома
В
I = -
р
Подставляя заданные значения напряжения и сопротивления в формулу, получаем
8
I = -
9.75
I = 0,82 А
Ток, протекающий по данной цепи, составляет 0,82 А. Пример 5
Ток, протекающий по цепи, составляет 5 А, а напряжение в цепи составляет 200 В. Какое сопротивление, прикладываемое цепью к протеканию тока?
Решение:
Мы должны найти сопротивление цепи, когда нам даны напряжение и ток в цепи. Итак, воспользуемся формулой сопротивления для решения этой задачи.
По закону Ома
В
R = -
я
Подставляя заданные значения напряжения и тока в формулу, получаем
200
R = -
5
R = 40 Ом
Итак, сопротивление току в данной цепи составляет 40 Ом.Пример 6
Ток, протекающий по цепи, составляет 4,2 А, а напряжение в цепи составляет 210 В. Какое сопротивление прикладывает цепь к протеканию тока?
Решение:
Мы должны найти сопротивление цепи, когда нам даны напряжение и ток в цепи. Итак, воспользуемся формулой сопротивления для решения этой задачи.
По закону Ома
В
R = -
я
Подставляя заданные значения напряжения и тока в формулу, получаем
210
R = -
4.2
R = 50 Ом
Итак, сопротивление току в данной цепи составляет 50 Ом.
Треугольник уравнения Ома
Треугольник уравнения Ома состоит из всех членов закона Ома. Он включает в себя напряжение, ток и сопротивление. Этот треугольник помогает быстро решать проблемы. Если треугольник показывает слова, расположенные горизонтальной линией, то они умножаются. Когда он показывает термины вертикальной линией, значит, они находятся в разделе. Формулы можно угадать, просто взглянув на них.
Треугольник уравнения ОмаШаги по использованию треугольника закона Ома
Шаг 1
Обратите внимание на термин, который вы пытаетесь найти: ток (I), напряжение (В), сопротивление (R) или мощность (P).
Step 2
Теперь обратите внимание на два члена, значение которых вам дано: ток (I), напряжение (В), сопротивление (R) или мощность (P).
Step 3
Допустим, вам даны значения тока и сопротивления, и вам нужно найти напряжение в цепи. Это означает, что даны I и R.
Шаг 4
Если треугольник показывает, что члены размещены на горизонтальной линии, то они умножаются.
Шаг 5
Если треугольник показывает, что термины расположены вертикально, то они попадают в разделение.
Шаг 6
Теперь держите руку на значении, которое вы должны найти, то есть на напряжении.
Шаг 7
Так как ток и сопротивление оба видны на горизонтальной линии, можно сказать, что они оба находятся в умножении
Шаг 8
Отсюда вы получаете формулу напряжения, которая означает, что напряжение равно сопротивлению в ток
Определение закона Ома
Постоянный ток или ток, протекающий через резистор, прямо пропорционален напряжению на этом сопротивлении и наоборот.Это означает, что когда напряжение увеличивается без изменения сопротивления цепи, тогда ток также будет в порядке возрастания.
I ∝ V V ∝ I
Объяснение: Для измерения тока используйте формулу: I = V / R Здесь сопротивление остается постоянным, а напряжение увеличивается каждый раз на небольшую величину. С каждым увеличением напряжения происходит постепенное увеличение тока.
| Напряжение | Сопротивление | Ток |
| 200 вольт | 50 Ом | 4 ампера | 9016 5016 9016 9016 9016 300 В | 50 Ом | ампер |
Ток, проходящий через резистор, обратно симметричен противодействию току в этом резисторе.Это означает, что при увеличении сопротивления цепи ток будет уменьшаться. Условием для этого является постоянное напряжение.
1
Я ∝ -
р
Пояснение: Для измерения силы тока используйте формулу: I = V / R. Здесь напряжение поддерживается постоянным, а сопротивление каждый раз увеличивается на небольшую величину. По мере увеличения сопротивления наблюдается уменьшение тока.
| Сопротивление | Напряжение | Ток |
| 20 Ом | 200 вольт | 10 ампер |
| 40158 9015 9016 9015 50 Ом | 200 В | 4 ампера |
Напряжение на резисторе проводника прямо пропорционально сопротивлению этого резистора.Это означает, что при повышении напряжения без изменения протекающего тока наблюдается увеличение сопротивления цепи.
В ∝ R
Пояснение: Для измерения тока используйте формулу: R = V / I. Здесь ток поддерживается постоянным, а напряжение увеличивается каждый раз на небольшую величину. Наблюдается увеличение сопротивления по мере постепенного увеличения напряжения.
| Напряжение | Ток | Сопротивление |
| 200 вольт | 4 ампер | 50 Ом | 240168 9016 9016 9015 9016 9016 | 9015 280 В4 ампера | 70 Ом |
Колесо в форме пирога для закона Ома
Колесо в форме пирога для закона Ома используется для упрощения решения проблем.Это представление закона Ома с использованием формулы пирога. Это колесо представляет собой разновидность диаграммы формул.
Колесо разделено на четыре части. Каждая часть представляет собой отдельный термин. В каждой части есть по три формулы. Разделение колеса производится на следующие части.
- Ток обозначен I
- Напряжение обозначено V
- Сопротивление обозначено R
- Мощность обозначено P
Как использовать круговое колесо закона Ома
- Шаг 1: Обратите внимание на термин пытается найти: ток (I), напряжение (В), сопротивление (R) или мощность (P).
- Шаг 2: Теперь обратите внимание на два термина, значения которых у вас есть: ток (I), напряжение (В), сопротивление (R) или мощность (P).
- Шаг 3: Затем найдите часть колеса, которая соответствует всем трем членам (термин, который вам нужен, и два других, которые у вас уже есть.)
- Шаг 4: Когда вы найдете соответствующую формулу, вы можете решить проблема легко.
ПРИМЕЧАНИЕ. Важно помнить, что единицы используемых и подлежащих поиску терминов должны быть совместимы. I.е. вам нужно преобразовать миллиамперы в амперы, киловольты в вольты, киловольты в омы и т.д. Но на самом деле основных формул всего две.
Легко понять закон Ома
Электричество — очень трудная глава для всех, так что нервничайте, если вам трудно его изучить или понять.давайте попробуем упростить концепции, используя простые слова.
Напряжение- Напряжение простыми словами можно определить как стабильность заряда между двумя точками.
- Единица измерения Вольт используется для измерения напряжения.
- E или V — это символ напряжения.
- Ток простыми словами можно определить как количество электронов, проходящих через точку. Другой способ выразить силу тока — это сила тока.
- Ампер используется для измерения силы тока.
- «I» — это символ, используемый для обозначения силы тока.
- Сопротивление можно просто определить как противодействие потоку электронов в проводе.
- Ом используется для измерения сопротивления.
- R — символ, используемый для обозначения сопротивления.
- Мощность можно просто определить как передачу электрической энергии в другую форму.
- Вт используется для масштабирования мощности.
- P — символ, используемый для обозначения мощности.
Давайте рассмотрим электричество как воду в резервуаре, которая течет по шлангу. Когда вода проходит по шлангу, к ней прилагается сила или давление. Допустим, это давление Напряжение . Из-за этого давления поток воды через шланг можно считать Current . У каждого шланга есть свои вариации. Эти вариации противодействуют потоку воды, иначе через него может пройти меньше воды.Можно сказать, что это вариации сопротивления и сопротивления . А теперь представьте, как вода разбрызгивается. Эта водяная струя заставляет воду вращаться. Можно сказать, что это Power .
Закон Ома связывает термины «напряжение», «ток» и «сопротивление» математически, выраженное как «напряжение есть ток», с сопротивлением.
Используя указанные выше обозначения, вы можете записать это как V = I x R .
Также можно записать I = V / R и R = V / I.
Пример 1
Давайте рассмотрим пример, чтобы легко это понять. У вас есть схема с батареей на 10 В и резистором с сопротивлением 2 Ом. Теперь вам нужно найти значение тока в вашей цепи.
Если вы поместите данные вам значения в приведенное выше уравнение, то мы получим простое уравнение, которое выглядит так: 10 В = I x 2 Ом.
Теперь разделите 10 В на 2 Ом.
Получаем I = 5А.
Пример 2
Теперь предположим, что вы используете ту же батарею на 10 В, но на этот раз вы знаете, что ток, протекающий по цепи, составляет 1 ампер.Теперь вам нужно найти сопротивление. Давайте выполним описанные выше шаги и введем заданные значения в уравнение.
На этот раз наше уравнение выглядит так: 10 В = 1 A x R
Теперь разделите 10 вольт на 1 ампер.
Это дает значение R как 10 Ом.
Пример 3
Для последнего примера возьмем батарею, напряжение которой неизвестно. На этот раз вы знаете, что сила тока составляет 2 ампера, а сопротивление — 5 Ом. Мы будем использовать то же уравнение, чтобы найти напряжение батареи.
Когда мы помещаем данные значения в приведенное выше уравнение, это выглядит как V = 2 A x 5 Ом.
Это дает значение заряда батареи 10 В.
Для простого решения этих проблем используйте треугольник закона Ома, который объясняется выше.
График закона Ома
Проводник при постоянной температуре:
Согласно закону Ома, если металлический проводник имеет постоянную температуру, то ток, протекающий через этот проводник, прямо пропорционален напряжению на нем с сопротивлением, как его постоянная пропорциональность.Давайте построим график, учитывая приведенное выше утверждение. Для этого графика давайте рассмотрим напряжение на проводнике по оси x и ток, протекающий через проводник по оси y. Построив этот график, мы получим прямую линию. Сопротивление проводника — это наклон этого прямолинейного графика.
Наклон этого графика определяется соотношением I / V = 1 / R.
Изменение наклона по постоянному сопротивлению приведено ниже
R = V / I.
Шаги по построению графика закона Ома при постоянной температуре
- Шаг 1. Возьмите миллиметровку и начертите на ней оси x и y.
- Шаг 2: Отметьте ось X как напряжение, а ось Y как ток.
- Шаг 3: Теперь нанесите значения напряжения и тока на оси x и y соответственно.
- Шаг 4: Теперь соедините точки, нанесенные на график.
- Шаг 5: Вы увидите, что когда точки соединены, мы получаем прямую линию на графике. Полученная прямая линия представляет собой температуру проводника.
Проводник при разных температурах
По закону Ома температура проводника постоянна.График температуры проводника выглядит иначе, чем график с проводником при постоянной температуре. На этом графике мы получаем две прямые.
Шаги по построению графика закона Ома для проводника при разных температурах:
Для этого графика две разные температуры. Предположим, что температуры равны T1 и T2 соответственно. Пусть температура T1 больше T2.
- Шаг 1. Возьмите миллиметровку и нарисуйте на ней оси x и y.
- Шаг 2: Отметьте ось X как напряжение, а ось Y как ток.
- Шаг 3: Теперь нанесите значения напряжения и тока для температуры T1 на оси x и y соответственно.
- Шаг 4: Теперь соедините точки температуры T1 на графике.
- Шаг 5: Аналогичным образом постройте значения напряжения и тока для температуры T2 по оси x и оси y соответственно.
- Шаг 6: Теперь соедините точки, нанесенные на график для температуры T2.
- Шаг 7: Вы увидите две прямые линии на графике. Эти две прямые представляют сопротивление проводника при температурах t1 и t2 соответственно.
Лабораторный эксперимент по закону Ома Цель
Лабораторный эксперимент Ома проводится для определения взаимосвязи между током, протекающим через резистор, и разностью потенциалов на том же резисторе проводника или цепи.
АппаратДля этого эксперимента не так много требований. Аппаратура, необходимая для этого эксперимента, — электрические элементы, резисторы, амперметр, вольтметр и некоторые соединительные провода.
ПроцедураЭтот эксперимент разделен на две части. Для первой части мы будем колебать напряжение на резисторе. Будет отмечен полученный ток в цепи. Аналогично для второй части мы будем колебать ток, протекающий по цепи. Будет отмечено полученное напряжение в цепи. С помощью этих собранных данных о токе и напряжении в цепи можно изучить взаимосвязь между ними.
Шаги для сбора различных измерений напряжения в цепи следующие:
- Шаг 1: В соответствии с принципиальной схемой вы должны настроить цепь. Сначала добавьте всего одну ячейку.
- Шаг 2. Обязательно проверьте цепь перед включением питания.
- Шаг 3. С помощью вольтметра измерьте напряжение на резисторе.
- Шаг 4: Теперь с помощью амперметра измерьте ток, протекающий в цепи.
- Шаг 5: Затем добавьте еще одну ячейку в схему и измерьте ток и напряжение в цепи.
- Шаг 6. Повторите процедуру, добавляя каждый раз по одной ячейке. Продолжайте так, пока у вас не будет 4 ячеек.
Шаги для сбора различных измерений напряжения в цепи следующие:
- Шаг 1: В соответствии с принципиальной схемой вы должны настроить цепь. Сначала добавьте только один резистор.
- Шаг 2. Обязательно проверьте цепь перед включением питания.
- Шаг 3. С помощью вольтметра измерьте напряжение на резисторе.
- Шаг 4: Теперь с помощью амперметра измерьте ток, протекающий в цепи.
- Шаг 5: Затем добавьте в схему еще один резистор и измерьте ток и напряжение в цепи.
- Шаг 6: Повторите процедуру, добавляя каждый раз по одному резистору. Продолжайте так, пока ваша схема не будет иметь 4 резистора.
- Шаг 7: Запишите все показания в следующую таблицу:
Наблюдение и результаты
Для первой части:
| Напряжение | Ток |
| 2.5 V | 0,1 A |
| 5 V | 0,2 A |
| 10 V | 0,4 A |
| 15 V | 0,6 A |
Для этого анализа мы рисуем график, который показывает взаимосвязь между током и напряжением.Здесь во время эксперимента берется изменение напряжения. Итак, напряжение — независимая переменная. Поскольку ток зависит от напряжения, он становится зависимой переменной. Независимые переменные нанесены на ось x, а зависимая переменная — на ось y. Итак, мы наносим напряжение на ось x, а ток — на ось y.
Анализ переменного токаДля этого анализа мы рисуем график, который показывает взаимосвязь между напряжением и током.Здесь, управляя экспериментом, берется изменение тока. Таким образом, ток — это независимая переменная. Изменение напряжения зависит от тока и становится зависимой переменной. Независимые переменные нанесены на ось x, а зависимая переменная — на ось y. Итак, мы наносим ток на ось x, а напряжение на ось y.
ЗаключениеВ первой части эксперимента, когда добавляется аккумулятор или элемент, показание амперметра увеличивается с увеличением показания вольтметра.Здесь мы узнаем, что когда напряжение на резисторе увеличивается, ток также постепенно увеличивается.
Аналогично во второй части эксперимента, когда добавляется резистор, показание вольтметра увеличивается с увеличением показания амперметра. Здесь мы узнаем, что когда ток, протекающий через резистор, увеличивается, напряжение также постепенно увеличивается.
Из этих наблюдений мы можем заключить, что для напряжения и тока, если одна величина увеличивается, другая также увеличивается, тогда как если одна величина уменьшается, другая увеличивается одновременно.Это показывает, что напряжение на проводнике прямо пропорционально току, протекающему по тому же проводнику. Это то, что мы называем законом Ома. Таким образом, этот эксперимент подтверждает закон Ома.
Лаборатория закона Ома Экспериментальное использование
Основные области применения закона Ома приведены ниже:
- Определение напряжения в цепи, тока, протекающего по ней, и приложенного сопротивления выполняется с помощью Закон Ома.Некоторые другие факторы, такие как удельное сопротивление, скорость дрейфа и т. Д., Определяются с использованием этих терминов.
- Потребляемая мощность также может быть рассчитана по этому закону.
- Падение напряжения на электронных компонентах может поддерживаться по вашему желанию с помощью этого закона.
- Отвод тока в амперметре постоянного тока и других шунтах также осуществляется по закону Ома.
Использование закона Ома в повседневной жизни
Помимо экспериментального использования закона Ома, он также имеет множество эмпирических приложений в различных электрических компонентах или приборах.Закон Ома важен. Таким образом, мы сталкиваемся с множеством его приложений в нашей повседневной жизни. Некоторые из этих применений объясняются ниже:
- Закон Ома для управления скоростью вентиляторов: Электрический компонент с переменным сопротивлением называется потенциометром. Большинство из нас знает, что такое потенциометр. Этот компонент используется для регулирования скорости стандартного вентилятора. Результат можно достичь с помощью регулятора или круглой ручки. Когда ручка вращается, значение выходной составляющей сопротивления изменяется, поскольку ручка установлена на потенциометре.Значение сопротивления и протекающего тока можно рассчитать для конкретного значения входного сопротивления. Мощность можно рассчитать по закону Ома.
- Требуемая мощность электрических компонентов: Большое количество резисторов используется для работы любого электрического прибора, такого как электрический чайник, утюг и т. Д. Резисторы помогают в правильном функционировании прибора. При правильной мощности этих резисторов можно добиться бесперебойной работы. Для этого мощность можно рассчитать, используя P = V x I.
- Потребление и подача энергии электронным устройством: для определения мощности электрического нагревателя используются катушка в нагревателе и приложенное к ней напряжение. После расчета мощности время, в течение которого использовался нагреватель, умножается. Таким образом, количество дней использования умножается на него. это может помочь нам получить сумму, которую мы должны заплатить в качестве счета за электроэнергию.
- Выбор предохранителей: Предохранитель используется для защиты цепи. Мы можем использовать закон Ома, чтобы решить, какой предохранитель использовать.Это позволяет нам определить значение тока, протекающего через предохранители, подключенные последовательно с прибором. Вы можете выбрать известное или неизвестное сопротивление предохранителя. Чтобы защитить ваше устройство или прибор от взрыва, сила тока не должна быть слишком большой.
Ограничения по закону Ома:
- Поскольку односторонние электрические компоненты, такие как диоды, транзисторы и т. Д., Позволяют току течь только в одном направлении, закон Ома не может применяться к этой сетевой схеме.
- Трудно использовать закон Ома в нелинейных электрических компонентах, которые состоят из емкости, сопротивления и т. Д. Это происходит из-за того, что напряжение и ток в этих электрических компонентах не будут постоянными.
Закон Ома Электрическая мощность:
Скорость, с которой электрическая энергия движущихся зарядов преобразуется в другую форму энергии, называется электрической мощностью. Электрическая энергия может быть преобразована в механическую энергию, тепло, магнитные поля и т. Д.
Электрическая мощность может быть измерена по следующей формуле:
P = V x I.
Единица измерения электрической мощности цепи выражается в ваттах.
1 Вт — это мощность, вырабатываемая при протекании через цепь тока силой 1 ампер через разность потенциалов 1 вольт. «W» используется для обозначения ватт.
Закон Ома можно использовать для расчета электрической мощности в терминах напряжения, тока и сопротивления.
Если указаны напряжение и ток, мы используем
p = vI
Если указаны напряжение и сопротивление, мы используем
V 2
P = -
R Если даны ток и сопротивление, мы используем
p = I 2 R
Треугольник силы закона Ома
Треугольник электрической мощности состоит из напряжения тока и электрической мощности.Этот треугольник помогает легко решить проблемы, связанные с электроэнергией. Использование этого треугольника аналогично треугольнику уравнения закона Ома.
Треугольник силы закона Ома:Закон Ома — AP Physics 2
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Что такое закон Ома? Калькулятор теории, формул и закона Ома
Итак, вы задаетесь вопросом, почему так важно изучать закон Ома?
Что такое закон Ома на самом деле?
Как им пользоваться?
Сначала мы запутаемся его название, почему это должен быть закон Ома? Я знаю это.Само название происходит от того, кто открыл его впервые.
Этот закон существует для измерения « электрического сопротивления ».
Закон Ома — самый фундаментальный и самый основной закон для электрических и электронных схем. Вы можете найти все основные элементы в электрической цепи: напряжение, ток и сопротивление.
Для цепи переменного тока вы замените сопротивление импедансом. Если у нас есть значения двух из трех элементов, мы можем легко найти третий элемент значения.
Почему нам так важно усвоить закон Ома? Потому что его элементы в уравнении являются основными переменными. Вы найдете напряжение, ток и сопротивление (или импеданс) в каждой электрической цепи, которую вы найдете или используете.
Мало того, закон Ома используется для сложных законов, теорем и вычислений. Закон Ома используется во всех аспектах электрических и электронных цепей, где протекает электрический ток.
В этом посте мы узнаем все о законе Ома.Я расскажу об анализе схемы, его применении и более простом методе использования. Какова формула закона Ома? — наш главный приоритет.
Здесь вы найдете не только его уравнение, здесь вы найдете более простую иллюстрацию, чтобы хорошо его запомнить.
Прежде чем изучать закон Ома, будет разумно сначала прочитать, что такое электрическая цепь.
Первое открытие закона ОмаФормула закона Ома не была открыта на пустом месте. Этот закон Ома устанавливает связь между напряжением, током и сопротивлением в электрической цепи.Позже мы прочитаем про определение закона Ома .
Если мы хотим отдать должное закону Ома, то он должен относиться к Георгу Ому. Он немецкий ученый, который провел множество экспериментов, чтобы найти взаимосвязь между напряжением, током и сопротивлением в одном уравнении. Этот закон является «отцом» всех электрических законов и теорем.
Что такое закон ОмаЕсли вы поищете формулу закона Ома, вы получите следующие определения:
Википедия:
закон, согласно которому электрический ток пропорционален напряжению и обратно пропорционален сопротивлению.
Словарь Коллинза:
принцип, согласно которому электрический ток, проходящий через проводник, прямо пропорционален разности потенциалов на нем, при условии, что температура остается постоянной. Константа пропорциональности — это сопротивление проводника.
Формула закона Ома или уравнение закона Ома показывает, как ток течет через любой материал при приложении напряжения. Следует помнить о разнице между низким и высоким сопротивлением.Электрический провод или любой проводник имеет низкое сопротивление, значит, ток будет течь легко. В противном случае, если сопротивление велико, току будет трудно протекать.
Определение закона Ома , приведенное выше, не очень помогает, если мы не знаем, что есть что. Нам нужно знать, какие переменные мы используем, что такое уравнение и как его использовать.
Из того, что мы нашли в словаре американского английского, говорится, что закон Ома — это пропорциональное отношение тока цепи постоянного тока к приложенному к ней напряжению и обратно пропорциональное сопротивлению.Не только для постоянного тока, закон Ома применим к цепи переменного тока.
Немецкий физик Георг Ом изобрел этот закон в 1827 году.
Чтобы упростить задачу, поскольку величина тока, протекающего в цепи, определяется делением напряжения на сопротивление, большее сопротивление означает меньший ток и наоборот.
Обычно любой проводник имеет очень маленькое сопротивление, поэтому мы можем не учитывать его при расчетах. С другой стороны, любой материал, который не может проводить электрический ток, является изолятором.
Сопротивление, измеряемое в омах, определяется материалом. Разные материалы разных размеров обеспечивают разное сопротивление друг от друга.
Закон Ома представлен графиком линейной зависимости между напряжением (V) и током (I) в электрической цепи. Мы можем представить закон Ома, используя иллюстрацию водопроводной трубы:
- Водопроводная труба — это сопротивление (R) в цепи, измеряемое в омах (Ом).
- Вода — это электрический ток (I), протекающий в цепи, измеряемый в амперах (A).
- Разница высот воды — это напряжение (В) в цепи, измеренное в вольтах (В).
Рисунок выглядит следующим образом:
- Если водопроводная труба тонкая (высокое сопротивление), она ограничивает протекание воды (электрического тока) в цепи.
- Если водопроводная труба широкая (сопротивление низкое), это увеличивает воду (электрический ток), протекающую в цепи.
Каждый материал обладает уникальными характеристиками, препятствующими прохождению электрического заряда.Их физическая способность противостоять току известна как сопротивление с символом R.
Рисунок 1. СопротивлениеИз рисунка (1a) мы заключаем, что сопротивление материала с однородным поперечным сечением A зависит от площади поперечного сечения A и длина l.
Следовательно, математическое уравнение сопротивления можно увидеть ниже:
(1)
Где:
ρ = удельное сопротивление материала, измеренное в ом-метрах.
Чем ниже удельное сопротивление, тем выше проводимость материала как проводника.
Пример хороших проводников — алюминий и медь. В противном случае примером хороших изоляторов является слюда и бумага, обладающие высоким удельным сопротивлением.
Если вы хотите узнать другие примеры хороших проводников и хороших изоляторов, вы можете бесплатно найти их в Интернете. Просто дерзайте и хорошо их запомните.
За исключением этих двух, мы узнаем о полупроводниковых материалах, но пока что пропустим.
Если мы говорим о сопротивлении, то в основном будем говорить о резисторах.Но что это такое? Резистор — это простейший пассивный элемент, сделанный из металлических сплавов и соединений углерода, чтобы выдерживать электрический ток.
Его обозначение цепи показано на рисунке (1b), где R обозначает значение сопротивления.
Закон Ома представляет соотношение между током и напряжением на резисторе. Этот закон был приписан Георгу Симону Ому (1787-1854) и записан как:
Закон Ома гласит, что напряжение v на резисторе прямо пропорционально току i , протекающему через резистор.
Следовательно,
(2)
Для краткости,
Закон Ома утверждает , что напряжение на резисторе пропорционально току, протекающему через него.
Напряжение, ток и сопротивлениеЭлектрическая цепь сделана из проводящей проволоки, позволяющей электрическому заряду проходить через нее. Движение этого электрического заряда называется током.
Электрическая сила, называемая напряжением, дает энергию электрическому заряду, протекающему в цепи.Для научного объяснения напряжение — это разность потенциалов между двумя выводами (точками).
Если мы измеряем напряжение, это означает, что мы измеряем разность потенциалов для перемещения электрического заряда из одной точки в другую.
Если нет двух точек, нет напряжения.
Ток движется по проводнику с некоторым противодействием или трением. Это трение или противодействие известно как сопротивление.
Даже жилой провод имеет небольшое сопротивление току.Величина тока зависит от того, сколько напряжения и сопротивления.
Чем меньше сопротивление, тем выше ток.
Единицы измерения: вольт, ампер и омЗнание значений напряжения, тока и сопротивления не имеет для нас большого значения. Нам нужно понимать величины для электрической цепи.
Ниже приведены стандартные единицы измерения электрического напряжения, тока и сопротивления:
Сокращение для каждого измерения близко к первому слову.Сокращенное обозначение напряжения — «V», а «R» — «сопротивление». Хотя «я» немного странно, потому что далеко от нынешнего.
Буква «I» обозначает французскую фразу «tensité du courant» (сила тока). Мы найдем еще один символ «E», который означает «Электродвижущая сила».
И «V», и «E» одинаковы, но вместо этого мы будем использовать «V». Обычно «E» обозначает напряжение на источнике.
Эти сокращения написаны заглавными буквами, потому что здесь мы будем использовать термины DC.Заглавные буквы означают, что значение остается постоянным в течение определенного периода времени.
Но мы будем использовать строчные буквы, если они имеют периодическое значение в течение периодического времени.
Уравнение закона ОмаИз приведенного выше определения мы знаем, что:
Закон Ома гласит, что разность потенциалов (напряжение) между двумя точками пропорциональна току, протекающему через резистор, а также сопротивлению резистора. схема. Таким образом, формула закона Ома просто V = IxR.
Нам нужен простейший пример схемы, чтобы понять этот основной закон. Мы будем использовать простую схему ниже, чтобы объяснить уравнение закона Ома , состоящее из источника напряжения и резистора.
Ток обозначается буквой I и измеряется в амперах (A), равном напряжению (V), деленному на сопротивление резистора (R), измеренное в омах (Ω).
Следовательно, уравнение. (2) становится
(3)
, которое является математическим уравнением закона Ома .Таким образом, R в уравнении (3) измеряется в Ом или Ом.
В — это напряжение в цепи, измеряемое в вольтах (В), но некоторые люди вместо этого используют E. Где E — электродвижущая сила или напряжение.
I — ток, протекающий в цепи через каждый элемент (резистор в примере схемы), измеренный в амперах (A).
R — сопротивление резистора, измеренное в Ом (Ом).
Делаем вывод, что:
- Если напряжение увеличится, то увеличится и ток.
- При увеличении сопротивления ток уменьшится.
Итак,
Сопротивление R элемента обозначает его способность сопротивляться прохождению электрического тока, измеряемую в омах (Ом).
Мы можем вывести уравнение к
(4)
, так что
1 Ом = 1 В / А
Чтобы успешно реализовать формулу закона Ома, используемую для определения сопротивления , нам нужно заплатить Обратите внимание на полярность напряжения или направление тока.
Мы можем найти значения напряжения, тока и сопротивления по закону Ома, если у нас есть две из трех переменных. Например:
Расчет напряжения Формула закона Ома
Если у нас есть значение сопротивления и тока, мы сможем найти значение напряжения с помощью:
[V = I x R] —– Напряжение (Вольт) = Ток (Ампер) x Сопротивление (Ом)
Расчет тока Формула закона Ома
[I = V / R] —– Ток (Ампер) = Напряжение (В) / Сопротивление (Ом)
Расчет сопротивления Формула закона Ома
Если у нас есть значение напряжения и тока, мы сможем найти значение сопротивления с помощью:
[R = V / I] —– Сопротивление (Ом) = Напряжение (В) / ток (Ампер)
Значение R изменяется от нуля до бесконечности.Следовательно, важно принять во внимание два крайних возможных значения R.
Нулевое сопротивление и короткое замыканиеЭлемент со значением R = 0 на рисунке (2a) является коротким замыканием.
Рисунок 2. Короткое замыкание и обрыв цепиИтак,
(5)
, указывающее, что напряжение равно нулю, но ток может быть любым. Другими словами, короткое замыкание обычно предполагает соединительный провод, который является идеальным проводником. Следовательно.
Короткое замыкание — это элемент цепи с сопротивлением, близким к нулю.
Бесконечное сопротивление и разрыв цепиНапротив, элемент с R = ∞ является разомкнутой цепью, как показано на рисунке (2b). Для разомкнутой цепи
(6)
, указывающее, что ток равен нулю через напряжение, может иметь любые значения. Следовательно,
Разрыв цепи — это элемент схемы с сопротивлением, приближающимся к бесконечности.
Как работает закон Ома?Закон Ома — это метод анализа для анализа токов в цепи с определенным сопротивлением, подаваемой источником напряжения.Для аналогии мы можем представить себе использование водопровода.
Напор воды является источником напряжения, сопротивление — диаметром трубы, а сила тока — объемом воды.
Чем выше напряжение, тем выше ток, и наоборот. Но чем выше сопротивление, тем меньше ток.
Это доказывает пропорциональное соотношение между напряжением и током, но обратно пропорциональное соотношение между током и сопротивлением.
Закон Ома Простые задачиОзнакомьтесь с этими простыми задачами, чтобы лучше понять закон Ома.
- Если у нас есть электрическая цепь с источником постоянного напряжения и увеличивается сопротивление, что будет с током?
Ответ: прокрутите вверх и прочтите уравнение закона Ома, если вы его забыли. С текущей точки зрения мы будем использовать [I = V / R]. Если напряжение остается постоянным, но сопротивление увеличивается, ток будет уменьшаться.
- Если напряжение источника удвоить, сколько тока мы получим?
Ответ: используя то же уравнение [I = V / R], если V становится 2V, то ток равен 2V / R.Таким образом, ток удваивается.
Анализ цепи по закону ОмаДавайте попробуем проанализировать электрическую цепь, используя закон Ома. Не волнуйтесь, мы просто воспользуемся батареей, резистором и проводом.
Ток движется по часовой стрелке, поскольку полярность напряжения находится в верхнем левом углу. Эти три соединены последовательно, чтобы упростить задачу.
Представьте, что у нас есть батарея на 10 В и резистор 5 Ом, сколько будет тока?
Уравнение верно, потому что если вы используете [I = V / R], вы получите [I = 10/5 = 2 A].
Что произойдет, если мы заменим резистор на резистор 10 Ом?
И снова закон Ома применим для получения результата 1A.
Мы можем поменять местами переменное уравнение, если оно удовлетворяет треугольнику закона Ома, о котором вы прочитаете позже в этом посте. Мы будем использовать этот закон для схемы с несколькими резисторами, соединенными следующим образом:
- Последовательное соединение
- Параллельное соединение
Зная две из трех переменных из закона Ома, мы легко найдем сомнительная переменная.
Следовательно, если мы хотим знать значение тока, мы должны знать значения напряжения и сопротивления.
Ниже представлен хорошо известный треугольник закона Ома.
Как указано выше:
Для расчета напряжения (В)
[В = I x R] —– Напряжение (Вольт) = Ток (Ампер) x Сопротивление (Ом)
Для расчета тока (I)
[I = V / R] —– Ток (Ампер) = Напряжение (В) / Сопротивление (Ом)
Для расчета сопротивления (Ом)
[R = V / I] —– Сопротивление (Ом) = Напряжение (В) / Ток (Ампер)
Закон Ома показывает взаимосвязь между напряжением (V или E), током (I) и сопротивлением (R).
Таким образом, мы добавляем закон Джоуля, чтобы усовершенствовать колесо закона Ома. Закон Джоуля гласит, что мощность — это произведение напряжения и тока.
В результате комбинация этих двух даст нам 12 формул с 2 известными переменными.
Таким образом, мы получаем колесо закона Ома вместе с их единицами измерения.
Закон Ома ПрименениеИз приведенного выше объяснения мы можем сделать вывод, что закон Ома полезен для определения значений напряжения, тока и сопротивления.
Но как это помогает нам в реальной жизни? Ниже приведены примеры применения закона Ома в реальной жизни:
- Определение напряжения, тока и сопротивления в цепи.
- Поддерживайте падение напряжения на элементе схемы на желаемом уровне.
- Этот закон применяется для амперметров постоянного тока.
Даже это самый простой анализ схемы, он все еще имеет некоторые ограничения, такие как:
- Не может использоваться для односторонней электрической сети (диодный транзистор и т. Д.), Которая не работает. t имеют линейную зависимость напряжения от тока.
- Невозможно реализовать для нелинейной схемы.
Резистор может быть постоянным или переменным. Но он имеет фиксированное значение, что означает, что значение остается постоянным. На рисунке (3) показаны два распространенных типа постоянных резисторов (с проволочной обмоткой и составные). Один резистор образует ответвление в цепи.
Рисунок (3a) проволочного типа имеет меньшее сопротивление с большим порогом мощности, в то время как Рисунок (3b) является составным типом, имеет более высокое сопротивление с меньшим порогом мощности.
Рисунок 3. Постоянный резисторПеременные резисторы имеют регулируемое сопротивление, его символ можно увидеть на рисунке. (4a).
Обычный переменный резистор также известен как потенциометр или для краткости потенциометр, его символ показан на рисунке. (4b).
Рисунок 4. Переменный резисторПоток представляет собой трехконтактный элемент со скользящим контактом или грязесъемником. Использование скользящего контакта изменит сопротивление. Точно так же переменный резистор также имеет проволочную обмотку и состав, как показано на рисунке.(5a) для композиции и рис. (5b) для ползунка.
Рисунок 5. ПотенциометрНе все резисторы подчиняются закону Ома. Но резистор, подчиняющийся закону Ома, называется линейным резистором. Имеет постоянное сопротивление.
Следовательно, его вольт-амперная характеристика показана на рисунке (6a): график i-v представляет собой прямую линию, проходящую через начало координат.
Нелинейный резистор не подчиняется закону Ома, его сопротивление изменяется в зависимости от тока, а его i-v характеристика показана на рисунке (6b).
Примером нелинейного сопротивления являются лампочка и диоды.
Рис. 6. Характеристика iv резистора ПроводимостьДругая полезная величина в анализе электрических цепей — величина, обратная сопротивлению R, известному как проводимость, и обозначается символом G:
(7)
Проводимость измеряет, насколько хорошо элемент будет проводить электрический ток и его единица измерения — mho (ом, записанный в обратном порядке) или обратный ом с символом ℧, перевернутой омегой.
В этом блоге мы будем использовать сименс (S) вместо mho в качестве единицы проводимости в системе СИ:
(8)
Следовательно,
Проводимость — это способность элемента проводить электрический ток; измеряется в mhos () или сименсах (S)
То же сопротивление может быть выражено в омах или сименсах, например, 10 Ом равно 0.1 S. Рассматривая уравнение. (7), мы можем написать:
(9)
Мощность, рассеиваемая резистором, может быть выражена с помощью R с уравнением. (3),
(10)
Мощность, рассеиваемая резистором. резистор может быть выражен с помощью G,
(11)
Линейный график закона ОмаМы можем нарисовать график закона Ома с двухмерной осью, напряжением и током, как показано ниже. Напряжение и ток образуют линейный график для каждого типа резистора, который мы используем, будь то постоянный резистор, переменный резистор или просто простой провод различной длины.
Можно сделать вывод, что удвоение напряжения удвоит ток, протекающий через элемент схемы.
Примеры закона Ома
1.) Электрический утюг потребляет 2 А при 120 В. Вычислите его сопротивление.
Решение:
Используя закон Ома:
2.) В соответствии со схемой ниже вычислите ток i , проводимость G и мощность p .
Решение:
Ток:
Проводимость:
Мощность:
Часто задаваемые вопросыТеперь давайте ответим на наиболее часто задаваемые вопросы ниже:
ЧТО ТАКОЕ в законе Ома?
Закон Ома гласит, что разность потенциалов (напряжение) между двумя точками пропорциональна току, протекающему через резистор, а также пропорциональна сопротивлению цепи.Таким образом, формула закона Ома просто V = IxR.
Как рассчитать закон Ома?
Ток (I) в цепи равен напряжению (V) на резисторе, деленному на сопротивление (R) резистора.
Почему важен закон Ома?
Закон Ома очень важен для анализа электрической цепи, связанной с напряжением, током и сопротивлением в цепи, и определения их взаимосвязи.




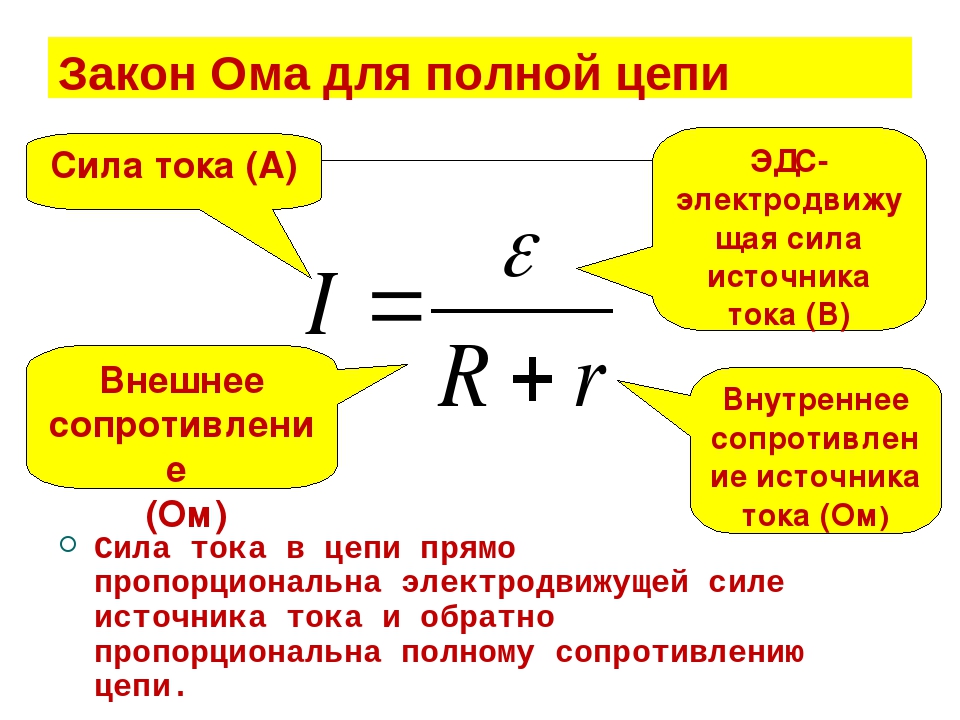 Введите свой запрос:
Введите свой запрос: