Закон Ома для полной (замкнутой) цепи
Закон Ома для полной цепи определяет значение тока в реальной цепи, который зависит не только от сопротивления нагрузки, но и от сопротивления самого источника тока. Другое название этого закона — закон Ома для замкнутой цепи. Рассмотрим смысл закона Ома для полной цепи более подробно.
Потребители электрического тока (например, электрические лампы) вместе с источником тока образуют замкнутую электрическую цепь. На рисунке 1 показана замкнутая электрическая цепь, состоящая из автомобильного аккумулятора и лампочки.
Рисунок 1. Замкнутая цепь, поясняющея закон Ома для полной цепи.
Ток, проходящий через лампочку, проходит также и через источник тока. Следовательно, проходя по цепи, ток кроме сопротивления проводника встретит еще и то сопротивление, которое ему будет оказывать сам источник тока (сопротивление электролита между пластинами и сопротивление пограничных слоев электролита и пластин).
Сопротивление нагрузки, присоединенной к источнику тока, принято называть внешним сопротивлением, а сопротивление самого источника тока — внутренним сопротивлением. Внутреннее сопротивление обозначается буквой r.
Если по цепи, изображенной на рисунке 1, протекает ток I, то для поддержания этого тока во внешней цепи согласно закону Ома между ее концами должна существовать разность потенциалов, равная I*R. Но этот же ток I протекает и по внутренней цепи. Следовательно, для поддержания тока во внутренней цепи, также необходимо существование разности потенциалов между концами сопротивления r. Эта разность потенциалов па закону Ома должна быть равна I*r.
Поэтому для поддержания тока в цепи электродвижущая сила (ЭДС) аккумулятора должна иметь величину:
E=I*r+I*R
Эта формула показывает, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения. Вынося I за скобки, получим:
Вынося I за скобки, получим:
E=I(r+R)
или
I=E/(r+R)
Две последние формулы выражают закона Ома для полной цепи.
Закон Ома для полной замкнутой цепи формулируется так: сила тока в замкнутой цепи прямо пропорциональна ЭДС в цепи и обратно пропорциональна общему сопротивлению цепи.
Под общим сопротивлением подразумевается сумма внешнего и внутреннего сопротивлений.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Закон Ома для замкнутой цепи
Закон Ома для замкнутой цепи показывает — значение тока в реальной цепи зависит не только от сопротивления нагрузки, но и от сопротивления источника.
Формулировка закона Ома для замкнутой цепи звучит следующим образом: величина тока в замкнутой цепи, состоящей из источника тока, обладающего внутренним и внешним нагрузочным сопротивлениями, равна отношению электродвижущей силы источника к сумме внутреннего и внешнего сопротивлений.
Впервые зависимость тока от сопротивлений была экспериментально установлена и описана Георгом Омом в 1826 году.
Формула закона Ома для замкнутой цепи записывается в следующем виде:
где:
- I [А] – сила тока в цепи,
- ε [В] – ЭДС источника напряжения,
- R [Ом] – сопротивление всех внешних элементов цепи,
- r [Ом] – внутреннее сопротивление источника напряжения
Физический смысл закона
Потребители электрического тока вместе с источником тока образуют замкнутую электрическую цепь. Ток, проходящий через потребитель, проходит и через источник тока, а значит, току кроме сопротивления проводника оказывается сопротивление самого источника. Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника.
Физический смысл зависимости тока от ЭДС источника и сопротивления цепи заключается в том, что чем больше ЭДС, тем больше энергия носителей зарядов, а значит больше скорость их упорядоченного движения. При увеличении сопротивления цепи энергия и скорость движения носителей зарядов, следовательно, и величина тока уменьшаются.
При увеличении сопротивления цепи энергия и скорость движения носителей зарядов, следовательно, и величина тока уменьшаются.
Зависимость можно показать на опыте. Рассмотрим цепь, состоящую из источника, реостата и амперметра. После включения в цепи идет ток, наблюдаемый по амперметру, двигая ползунок реостата, увидим, что при изменении внешнего сопротивления ток будет меняться.
Примеры задач на применение закона Ома для замкнутой цепи
К источнику ЭДС 10 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 4 Ом. Найти силу тока в цепи и напряжение на зажимах источника.
| Дано: | Решение: |
|---|---|
|
|
При подключении к батарее гальванических элементов резистора сопротивлением 20 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 10 Ом сила тока стала 1,5 А. Найти ЭДС и внутреннее сопротивление батареи.
| Дано: | Решение: |
|---|---|
|
|
формулы и определения / Блог / Справочник :: Бингоскул
Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.
Закон Ома для участка цепи:
Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.
- I — сила тока
- Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
- Формула: I=\frac{U}{R}
- U — напряжение (в системе СИ измеряется — Вольт)
- Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
- Формула: U=IR
- R — электрическое сопротивление (в системе СИ измеряется — Ом).
- Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
- Формула R=\frac{U}{I}
Определение единицы сопротивления — Ом
1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).
Закон Ома для полной цепи
Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника
Формула I=\frac{\varepsilon}{R+r}
- \varepsilon — ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Как запомнить формулы закона Ома
Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.
.
- U — электрическое напряжение;
- I — сила тока;
- P — электрическая мощность;
- R — электрическое сопротивление
Смотри также:
Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.
Закон Ома для замкнутой цепи
Каждый специалист, ремонтирующий и обслуживающий электроустановки, должен хорошо знать и применять на практике закон Ома для замкнутой цепи. Это действительно так, поскольку закономерности, открытые немецким физиком Георгом Омом, лежат в основе всей электротехники. Данный закон стал весомым вкладом в дальнейшее развитие научных знаний в области электричества.
Физические свойства закона Ома
Прямая взаимосвязь между силой тока, напряжением, подведенным к сети, и сопротивлением проводника была обнаружена Омом в 1826 году. В дальнейшем, понятие напряжения было заменено на более точный термин – электродвижущую силу (ЭДС). После теоретического обоснования этой зависимости был выведен закон для замкнутой цепи. Его важной особенностью считается обязательное отсутствие какого-либо внешнего возмущения. Поэтому стандартные формулировки потеряют свою актуальность, если, например, поместить проводник в переменное магнитное поле.
Для экспериментов по выводу закона использовалась простейшая схема, состоящая из источника питания, обладающего ЭДС и подключенных к нему двух выводов, соединенных с резистором. В проводнике начинают в определенном направлении перемещаться элементарные частицы, несущие заряд. Таким образом, сила тока представляется в виде отношения ЭДС к общему сопротивлению всей цепи: I = E/R.
В проводнике начинают в определенном направлении перемещаться элементарные частицы, несущие заряд. Таким образом, сила тока представляется в виде отношения ЭДС к общему сопротивлению всей цепи: I = E/R.
В представленной формуле Е – является электродвижущей силой, измеряемой в вольтах, I – сила тока в амперах, а R выступает в роли электрического сопротивления резистора, измеряемого в омах. При этом, учитываются все составляющие сопротивления и при расчетах используется их суммарное значение. Они включают сопротивление самого резистора, проводника (r) и источника питания (r0). Окончательно формула будет выглядеть так: I = E/(R+r+r0).
Если значение внутреннего сопротивления источника тока r0 превышает сумму R+r, то в этом случае отсутствует зависимость силы тока от характеристик подключенной нагрузки, а источник ЭДС исполняет роль источника тока. Когда r0 ниже суммы R+r, получается обратная пропорция тока с суммарным внешним сопротивлением, а напряжение поступает за счет источника питания.
Закон Ома для выполнения расчетов
Точные расчеты требуют учета всех потерь напряжения, в том числе и в местах соединений. Для определения электродвижущей силы на выводах источника тока замеряется разность потенциалов при разомкнутой цепи, когда нагрузка полностью отключена. В этом случае применяется не только закон Ома для замкнутой цепи, но и закон, действующий для участка цепи. Данный участок считается однородным, поскольку здесь принимается в расчет только разность потенциалов, без учета ЭДС. Это дает возможность рассчитать каждый элемент электрической цепи по формуле I=U/R, в которой U является разностью потенциалов или напряжением, измеряемым в вольтах.
Замеры выполняются с помощью вольтметра при подключении щупов к выводам нагрузки или сопротивления. Полученное значение напряжения будет всегда ниже электродвижущей силы. Это наиболее распространенная формула, позволяющая найти любую составляющую при наличии двух известных.
Закон Ома для замкнутой цепи имеет много общего с законом, выведенным для магнитной цепи. В этой системе проводник выполнен в виде замкнутого магнитопровода. В качестве источника выступает обмотка катушки по виткам которой протекает электрический ток. Появляющийся магнитный поток (Ф) замыкается на магнитопровод и начинает циркулировать по контуру. Он находится в непосредственной зависимости от магнитодвижущей силы и сопротивления материала, через который проходит. Данное явление выражено формулой Ф=F/Rm, в которой F представляет собой магнитодвижущую силу, а Rm служит сопротивлением, вызывающим затухание.
В этой системе проводник выполнен в виде замкнутого магнитопровода. В качестве источника выступает обмотка катушки по виткам которой протекает электрический ток. Появляющийся магнитный поток (Ф) замыкается на магнитопровод и начинает циркулировать по контуру. Он находится в непосредственной зависимости от магнитодвижущей силы и сопротивления материала, через который проходит. Данное явление выражено формулой Ф=F/Rm, в которой F представляет собой магнитодвижущую силу, а Rm служит сопротивлением, вызывающим затухание.
Как рассчитать цепи
Закон Ома для участка цепи, формула, определение
электрика, сигнализация, видеонаблюдение, контроль доступа (СКУД) и другие инженерно технические системы (ИТС)
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит.
Возьмем замкнутую электрическую цепь (рисунок 1) и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I — ток, протекающий по участку цепи.
- R — сопротивление этого участка.
- φ1-φ2 — разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R
Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+.
 ..+Rn
..+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
ПРАВИЛО ЗНАКОВ ДЛЯ ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной (рис.3.1). В противном случае — ЭДС считается отрицательной (рис.3.2).
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис. 3.3) E=E1+E2-E3.
3.3) E=E1+E2-E3.
При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ
Закон Ома для полной цепи — его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r).
Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС.
Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r — сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной.
Такая ситуация вполне может быть реальной.
Закон Ома рассмотрен здесь достоточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
© 2012-2021 г. Все права защищены.
Представленные на сайте материалы имеют информационный характер и не могут быть использованы в качестве руководящих и нормативных документов
Закон Ома для замкнутой цепи
Закон Ома для замкнутой цепи часто находит применение в работе с электричеством. Благодаря закономерности, найденной немецким физиком Георгом Омом, сегодня мы можем рассчитать величину тока, протекающего в проводе или необходимую толщину провода для подключения к сети.
История открытия
Будущий ученый с малых лет интересовался природой электрического тока. Он провел множество испытаний, связанных с измерением напряжения и силы тока. Ввиду несовершенства измерительных приборов того времени, первые результаты исследований были ошибочны и препятствовали дальнейшему развитию вопроса. Георг опубликовал первую научную работу, в которой описывал возможную связь между напряжением и силой тока. Последующие его работы подтвердили предположения, и Ом сформулировал свой знаменитый закон. Все труды были внесены в доклад 1826 года, но научное сообщество не заметило труды молодого физика.
Ввиду несовершенства измерительных приборов того времени, первые результаты исследований были ошибочны и препятствовали дальнейшему развитию вопроса. Георг опубликовал первую научную работу, в которой описывал возможную связь между напряжением и силой тока. Последующие его работы подтвердили предположения, и Ом сформулировал свой знаменитый закон. Все труды были внесены в доклад 1826 года, но научное сообщество не заметило труды молодого физика.
Через пять лет, когда известный французский учёный Пулье пришел к такому же выводу, Георга Ома наградили медалью Копли, за внесение большого вклада в развитии физика как науки.
Сегодня закон Ома используется по всему миру, признанный истинным законом природы. .
Детальное описаниеЗакон Георга показывает значение электричества в определенной сети, имеющее зависимость от сопротивления к нагрузке и внутренним элементам источника питания. Рассмотрим это детально.
Условное устройство, использующее электроэнергию (например, звуковой динамик) при подключении к источнику питания образует замкнутую цепь (рисунок 1). Подсоединим динамик к аккумулятору. Следующий через динамик ток тоже следует через источник питания. Поток заряженных частиц встретит сопротивление провода и внутренней электроники устройства, а также сопротивление аккумулятора (электролит внутри банки оказывает определенное воздействие на электрический ток). Исходя из этого, значение сопротивления закрытой сети складывается из сопротивления:
Подсоединим динамик к аккумулятору. Следующий через динамик ток тоже следует через источник питания. Поток заряженных частиц встретит сопротивление провода и внутренней электроники устройства, а также сопротивление аккумулятора (электролит внутри банки оказывает определенное воздействие на электрический ток). Исходя из этого, значение сопротивления закрытой сети складывается из сопротивления:
- Источника питания;
- Электрического устройства.
Подключение условного электрического прибора (динамика) к источнику питания (автомобильному аккумулятору)
Первый параметр называют внутренним, второй – внешним сопротивлением. Противодействие источника электричества маркируется символом r.
Представим, что по сети источник питания/электрическое устройство проходит определённый ток T. Для сохранения стабильного значения электричества внешней сети, в соответствии с законом, на её окончаниях должна наблюдаться потенциальная разность, которая равна R*T. Ток такой же величины проходит и внутри цепи. Вследствие этого – сохранение постоянного значения электричества внутри сети требует потенциальной разности на окончаниях сопротивления r. Она, согласно закону, должна равняться T*r. При сохранении стабильного тока в сети, значение электродвижущей силы равно:
Вследствие этого – сохранение постоянного значения электричества внутри сети требует потенциальной разности на окончаниях сопротивления r. Она, согласно закону, должна равняться T*r. При сохранении стабильного тока в сети, значение электродвижущей силы равно:
E=T*r+T*R
Из формулы следует, что ЭДС равна сумме падения напряжений во внутренней и внешней сети. Если вынести значение T за скобки, получим:
Е=T(r+R)
или
T=E/(r+R)
Примеры задач на применение закона для соединенной сети1) К источнику ЭДС 15 В и сопротивлением 2 Ом подсоединен реостат с сопротивлением 5 Ом. Задача – вычислить силу тока и напряжение на зажимах.
Вычисление
- Представим закон Ома для соединенной сети: T=E/(r+R).
- Снижение напряжения вычислим по формуле: U= E-Tr=ER/(R+r).
- Подставим имеющиеся значения в формулу: T= (15 В)/((5+2) Ом) = 2.
 1 А, U=(15 В* 5 Ом)/(5+1) Ом = 12.5 В
1 А, U=(15 В* 5 Ом)/(5+1) Ом = 12.5 В
Ответ: 2.1 А, 12.5 В.
2) При подсоединении к гальваническим элементам резистора с сопротивлением 30 Ом, сила тока в сети приняла значение в 1.5 А, а при подсоединении такого же элемента с сопротивлением 15 Ом сила тока стала 2.5 А. Задача – узнать значение ЭДС и внутреннее сопротивление цепи из гальванических элементов.
Вычисление
- Запишем закон Георга Ома для соединённой сети: T=E/(r+R).
- Из него выведем формулы для внутреннего и внешнего сопротивления: E=T_1 R_1+T_1 r, E= T_2 R_2 + T 2r.
- Приравняем части формулы и вычислим внутреннее сопротивление: r=(T_1 R_1-T_2 R_2)/(T_2-T_1 ).
- Полученные значения подставим в закон: E=(T_1 T_2 (R_2-R_1))/(T_2-T_1 ).
- Проведем вычисления: r=(1.5 А∙30 Ом-2.5А∙15 Ом)/(2,5-1,5)А=7.5 Ом, E=(1.5 А∙2.5А(30-15)Ом)/((2.5-1.5)А)=56 В.
Ответ: 7.5 Ом, 56 В.
Сфера применения закона Ома для замкнутой цепи
Закон Ома – универсальный инструмент электрика. Он позволяет правильно рассчитать силу тока и напряжение в сети. В основе принципа работы некоторых устройств лежит закон Ома. В частности, предохранителей короткого замыкания.
Он позволяет правильно рассчитать силу тока и напряжение в сети. В основе принципа работы некоторых устройств лежит закон Ома. В частности, предохранителей короткого замыкания.
Короткое замыкание – случайное замыкание двух участков сети, не предусмотренное конструкцией оборудования и приводящее к неисправностям. Для предотвращения таких явлений используют специальные устройства, отключающие питание сети.
Если произойдет случайное замыкание цепи с большой перегрузкой, устройство автоматически прекратит подачу тока.
Закон Ома в данном случае находит место на участке цепи постоянного тока. В полной схеме процессов может быть гораздо больше. Многие действия при построении электрической сети или ее ремонте следует проводить с учетом закона Георга Ома.
Для полного изучения соотношения параметров тока в проводниках представлены формулы:
Более сложное выражение закона для практического применения:
Сопротивление представлено отношением напряжения к силе тока в цепи. Если напряжение увеличить в n раз, значение тока также увеличится в n раз.
Если напряжение увеличить в n раз, значение тока также увеличится в n раз.
Не менее известны в электротехнике труды Густава Киргофа. Его правила находят применения в расчетах разветвленных сетей. В основе этих правил лежит закон Ома для электрической цепи.
Труды ученого нашли применение при изобретении многих повседневных вещей, таких как лампы накаливания и электрические плиты. Современные достижения в электронике многим обязаны открытиям 1825 года.
Поделиться ссылкой:
ПохожееЗаконы Ома для участка цепи и для полной цепи
Автор Alexey На чтение 4 мин. Просмотров 6.4k. Опубликовано Обновлено
В 1826 году немецкий ученый Георг Ом совершил открытие и описал
эмпирический закон о соотношении между собой таких показателей как сила тока, напряжение и особенности проводника в цепи. Впоследствии, по имени ученого он стал называться закон Ома.
В дальнейшем выяснилось, что эти особенности не что иное, как сопротивление проводника, возникающее в процессе его контакта с электричеством. Это внешнее сопротивление (R). Есть также внутреннее сопротивление (r), характерное для источника тока.
Закон Ома для участка цепи
Согласно обобщенному закону Ома для некоторого участка цепи, сила тока на участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению.
I = U/ R
Где U – напряжение концов участка,I– сила тока, R– сопротивление проводника.
Беря во внимание вышеприведенную формулу, есть возможность найти неизвестные значенияUиR, сделав несложные математические операции.
U = I*R
R = U / I
Данные выше формулы справедливы лишь когда сеть испытывает на себе одно сопротивление.
Закон Ома для замкнутой цепи
Сила тока полной цепи равна ЭДС, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Замкнутая сеть имеет одновременно сопротивления внутреннего и внешнего характера. Поэтому формулы отношения будут уже другими.
I = E/ Rвн+r
Где E – электродвижущая сила (ЭДС), R- внешнее сопротивление источника, r-внутреннее сопротивление источника.
Закон Ома для неоднородного участка цепи
Замкнутая электрическая сеть содержит участки линейного и нелинейного характера. Участки, не имеющие источника тока и не зависящие от стороннего воздействия являются линейными, а участки, содержащие источник – нелинейными.
Участки, не имеющие источника тока и не зависящие от стороннего воздействия являются линейными, а участки, содержащие источник – нелинейными.
Закон Ома для участка сети однородного характера был изложен выше. Закон на нелинейном участке будет иметь следующий вид:
I = U/ R = f1 – f2 + E/ R
Где f1 – f2 – разница потенциалов на конечных точках рассматриваемого участка сети
R – общее сопротивление нелинейного участка цепи
ЭДС нелинейного участка цепи бывает больше нуля или меньше. Если направление движения тока, идущего из источника с движением тока в электрической сети, совпадают, будет преобладать движение зарядов положительного характера и ЭДС будет положительная. В случае же совпадения направлений, в сети будет увеличено движение отрицательных зарядов, создаваемых ЭДС.
Закон Ома для переменного тока
При имеющейся в сети емкости или инертности, необходимо учитывать при проводимых вычислениях, что они выдают свое сопротивление, от действия которого ток приобретает переменный характер.
Закон Ома для переменного тока выглядит так:
I = U/ Z
где Z – сопротивление по всей длине электрической сети. Его еще называют импеданс. Импеданс составляют сопротивления активного и реактивного характера.
Закон Ома не является основным научным законом, а лишь эмпирическим отношением, причем в некоторых условиях оно может не соблюдаться:
- Когда сеть обладает высокой частотой, электромагнитное поле меняется с большой скоростью, и при расчетах необходимо учитывать инертность носителей заряда;
- В условиях низкой температуры с веществами, которые обладают сверхпроводимостью;
- Когда проводник сильно нагревается проходящим напряжением, отношение тока к напряжению становится переменным и может не соответствовать общему закону;
- При нахождении под высоким напряжением проводника или диэлектрика;
- В светодиодных лампах;
- В полупроводниках и полупроводниковых приборах.

В свою очередь элементы и проводники, соблюдающие закон Ома, называются омическими.
Закон Ома может дать объяснение некоторым явлениям природы. Например, когда мы видим птиц, сидящих на высоковольтных проводах, у нас возникает вопрос – почему на них не действует электрический ток? Объясняется это довольно просто. Птицы, сидя на проводах, представляют собой своеобразные проводники. Большая часть напряжения приходится на промежутки между птицами, а та доля, что приходится на сами «проводники» не представляет для них опасности.
Но это правило работает лишь при единичном соприкосновении. Если птица заденет клювом или крылом провод или телеграфный столб, она неминуемо погибнет от огромного количества напряжения, которое несут в себе эти участки. Такие случаи происходят повсеместно. Поэтому в целях безопасности в некоторых населенных пунктах установлены специальные приспособления, защищающие птиц от опасного напряжения. На таких насестах птицы находятся в полной безопасности.
Закон Ома также широко применятся на практике. Электричество смертельно опасно для человека при одном лишь касании к оголенному проводу. Но в некоторых случаях сопротивление человеческого тела может быть разным.
Так, например, сухая и неповрежденная кожа обладает большим сопротивлением к воздействию электричества нежели рана или кожа, покрытая потом. В следствие переутомления, нервного напряжения и опьянения, даже при небольшом напряжении тока человек может получить сильный удар током.
В среднем, сопротивление тела человека – 700 Ом, значит, для человека является безопасным напряжение в 35 В. Работая с большим напряжением, специалисты используют специальные средства защиты.
ЗаконОма для замкнутой цепи, соотношение между ЭДС (VB) электрического элемента и напряжением на его полюсах
Закон Ома ЭДС электрического элемента (батареи — источника) — это общая работа, выполняемая внутри и снаружи элемента по передаче электрических зарядов в электрической цепи. Если мы обозначим ЭДС батареи через (V B ), общая сила тока в цепи (I), внешнее сопротивление (R) и внутреннее сопротивление ячейки (r).
Если мы обозначим ЭДС батареи через (V B ), общая сила тока в цепи (I), внешнее сопротивление (R) и внутреннее сопротивление ячейки (r).
Тогда: V B = I R + I r
В В = I (R + r)
I = V B / (R + r)
Это известно как закон Ома для замкнутой цепи, где:
Сила электрического тока = Общая электродвижущая сила / Общее сопротивление цепи
Закон Ома
Отношение между ЭДС (В B ) электрического элемента и напряжением на его полюсах (В)По закону Ома для замкнутой цепи:
В В = I R + I r, V = I R
∴ V B = V + I r, ∴ V = V B — I r
Из предыдущего соотношения мы видим, что при с внешнее сопротивление (R) увеличивается, электрический ток (I), проходящий в цепи, постепенно уменьшается, а разность потенциалов (V) между полюсами ячейки увеличивается.
Разность потенциалов (V) между полюсами ячейки становится равной ЭДС источника (V B ). Когда значение тока становится очень маленьким, (I r) можно не учитывать.
ЭДС электрического элемента больше, чем разность потенциалов между выводами его внешней цепи, когда цепь включена, потому что внутреннее сопротивление электрического элемента потребляет работу, чтобы пропустить ток внутри электрического элемента на основе соотношения (V B = V + I r) и, следовательно, (V
Следовательно, мы можем определить ЭДС ячейки как:
ЭДС ячейки (V B ) — это разность потенциалов на полюсах ячейки в случае отсутствия тока в цепи (выключатель разомкнут), или это общая работа, проделанная внутри и снаружи ячейки для передачи электрический заряд 1 Кл (единица электрических зарядов) в электрической цепи, ЭДС источника измеряется в вольтах.
Когда ЭДС электрического элемента = 3 В, общая работа, проделанная внутри и снаружи элемента для передачи электрического заряда 1 Кл в электрической цепи = 3 Дж.
Закон Ома
В случае включения в цепь одного электрического элемента:Где V B — показания вольтметра на батарее, имеющей внутреннее сопротивление r, батарея подключена последовательно с сопротивлением, которое имеет разность потенциалов 2 , и она подключена последовательно с амперметр.
Если переключатель K замкнут:
I = V B / (R + r)
I = V B — V 1 / r
I = V 2 / R
V 2 = I R, V 1 = V B — I r
Если выключатель К разомкнут:
I = 0
В 2 = 0, В 1 = В В
При последовательном включении в цепь двух электрических ячеек Где, В 1 — это показание вольтметра на первой батарее с внутренним сопротивлением r 1 , В 2 — это показание вольтметра на второй батарее с внутренним сопротивлением r 2 , разность потенциалов на двух батареях составляет V 3 .
I = [(V B ) 1 + (V B ) 2 ] / (R + r 1 + r 2 )
V 1 = (V B ) 1 — I r 1
V 2 = (V B ) 2 — I r 2
В 3 = В 1 + В 2
Когда две батареи подключены в противоположных направлениях, Где (V B ) 2 <(V B ) 1 :I = [(V B ) 1 — (V B ) 2 ] / (R + r 1 + r 2 )
V 1 = (V B ) 1 — I r 1 (нагнетательный корпус)
В 2 = (В B ) 2 + I r 2 (зарядный кейс)
В 3 = В 1 — В 2
Электрический ток, разность потенциалов, электрическое сопротивление и закон Ома
Подключение сопротивлений (последовательно и параллельно), Электроэнергия и Электроэнергия
Первый закон Кирхгофа, второй закон Кирхгофа и способы решения проблем, связанных с законами Кирхгофа
ЗаконОма: сопротивление и простые схемы
Цели обучения
К концу этого раздела вы сможете:
- Объясните происхождение закона Ома.

- Рассчитайте напряжения, токи или сопротивления по закону Ома.
- Объясните, что такое омический материал.
- Опишите простую схему.
Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, розетки и т. Д., Которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и условно называются источниками напряжения. Когда источник напряжения подключен к проводнику, он прикладывает разность потенциалов В , которая создает электрическое поле.Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В . Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
[латекс] I \ propto {V} \\ [/ латекс].
Это важное соотношение известно как закон Ома . Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием. Это эмпирический закон, подобный закону трения — явление, наблюдаемое экспериментально. Такая линейная зависимость возникает не всегда.
Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием. Это эмпирический закон, подобный закону трения — явление, наблюдаемое экспериментально. Такая линейная зависимость возникает не всегда.
Сопротивление и простые схемы
Если напряжение управляет током, что ему мешает? Электрическое свойство, препятствующее току (примерно такое же, как трение и сопротивление воздуха), называется сопротивлением R .Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток. Сопротивление обратно пропорционально току, или
[латекс] I \ propto \ frac {1} {R} \\ [/ latex].
Таким образом, например, ток уменьшается вдвое, если сопротивление увеличивается вдвое. Комбинируя отношения тока к напряжению и тока к сопротивлению, получаем
[латекс] I = \ frac {V} {R} \\ [/ латекс].
Это соотношение также называется законом Ома. Закон Ома в такой форме действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален. Многие вещества, для которых действует закон Ома, называются омическими . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление R , которое не зависит от напряжения В и тока I . Объект с простым сопротивлением называется резистором , даже если его сопротивление невелико.Единица измерения сопротивления — Ом, и обозначается символом Ω (греческая омега в верхнем регистре). Перестановка I = V / R дает R = V / I , и поэтому единицы сопротивления равны 1 Ом = 1 вольт на ампер:
Закон Ома в такой форме действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален. Многие вещества, для которых действует закон Ома, называются омическими . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление R , которое не зависит от напряжения В и тока I . Объект с простым сопротивлением называется резистором , даже если его сопротивление невелико.Единица измерения сопротивления — Ом, и обозначается символом Ω (греческая омега в верхнем регистре). Перестановка I = V / R дает R = V / I , и поэтому единицы сопротивления равны 1 Ом = 1 вольт на ампер:
[латекс] 1 \ Omega = 1 \ frac {V} {A} \\ [/ latex].
На рисунке 1 показана схема простой схемы. Простая схема имеет один источник напряжения и один резистор. Можно предположить, что провода, соединяющие источник напряжения с резистором, имеют незначительное сопротивление, или их сопротивление можно включить в R .
Можно предположить, что провода, соединяющие источник напряжения с резистором, имеют незначительное сопротивление, или их сопротивление можно включить в R .
Рис. 1. Простая электрическая цепь, в которой замкнутый путь для прохождения тока обеспечивается проводниками (обычно металлическими), соединяющими нагрузку с выводами батареи, представленной красными параллельными линиями. Зигзагообразный символ представляет собой единственный резистор и включает любое сопротивление в соединениях с источником напряжения.
Пример 1. Расчет сопротивления: автомобильная фара
Какое сопротивление проходит у автомобильной фары 2.50 А течет при подаче на него 12,0 В?
СтратегияМы можем изменить закон Ома, как указано в формуле I = V / R , и использовать его для определения сопротивления.
РешениеПерестановка I = V / R и замена известных значений дает
[латекс] R = \ frac {V} {I} = \ frac {\ text {12} \ text {. } \ Text {0 V}} {2 \ text {.} \ Text {50 A}} = \ text {4} \ text {.} \ text {80 \ Omega} \\ [/ latex].
} \ Text {0 V}} {2 \ text {.} \ Text {50 A}} = \ text {4} \ text {.} \ text {80 \ Omega} \\ [/ latex].
Это относительно небольшое сопротивление, но оно больше, чем хладостойкость фары.Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампа имеет меньшее сопротивление при первом включении и потребляет значительно больший ток во время короткого периода прогрева.
Сопротивление может быть разным. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 12 Ом или более. Сопротивление сухого человека может составлять 10 5 Ом, тогда как сопротивление человеческого сердца составляет примерно 10 3 Ом.Кусок медного провода большого диаметра длиной в метр может иметь сопротивление 10 −5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомичны). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделах «Сопротивление и удельное сопротивление». Дополнительное понимание можно получить, решив I = V / R для V , что дает
Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделах «Сопротивление и удельное сопротивление». Дополнительное понимание можно получить, решив I = V / R для V , что дает
В = ИК
Это выражение для В можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока I .Фраза IR drop часто используется для этого напряжения. Например, фара в Примере 1 выше имеет падение IR на 12,0 В. Если напряжение измеряется в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор похож на трубу, которая снижает давление и ограничивает поток из-за своего сопротивления.Здесь сохранение энергии имеет важные последствия. Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию). В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, так как PE = q Δ V , и то же самое q протекает через каждую. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны.(См. Рисунок 2.)
Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию). В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, так как PE = q Δ V , и то же самое q протекает через каждую. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны.(См. Рисунок 2.)
Рис. 2. Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Установление соединений: сохранение энергии В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. Здесь о сохранении энергии свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним резистором. Мы обнаружим, что сохранение энергии имеет и другие важные применения в схемах и является мощным инструментом анализа схем.
Посмотрите, как уравнение закона Ома соотносится с простой схемой. Отрегулируйте напряжение и сопротивление и посмотрите, как изменяется ток по закону Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Щелкните, чтобы запустить моделирование.
Сводка раздела
- Простая схема — это схема , в которой есть один источник напряжения и одно сопротивление.
- Одно из утверждений закона Ома дает соотношение между током I , напряжением В и сопротивлением R в простой схеме как [латекс] I = \ frac {V} {R} \\ [/ latex] .
- Сопротивление выражается в единицах Ом (Ом), относящихся к вольтам и амперам на 1 Ом = 1 В / А.
- На резисторе возникает падение напряжения или IR , вызванное протекающим через него током, равным V = IR .
Концептуальные вопросы
- Падение напряжения IR на резисторе означает изменение потенциала или напряжения на резисторе.
 Изменится ли ток при прохождении через резистор? Объяснять.
Изменится ли ток при прохождении через резистор? Объяснять. - Как падение IR в резисторе похоже на падение давления в жидкости, протекающей по трубе?
Задачи и упражнения
1. Какой ток протекает через лампочку фонаря на 3,00 В, когда ее горячее сопротивление составляет 3,60 Ом?
2. Вычислите эффективное сопротивление карманного калькулятора с батареей на 1,35 В, через которую протекает ток 0,200 мА.
3.Каково эффективное сопротивление стартера автомобиля, когда через него проходит 150 А, когда автомобильный аккумулятор подает на двигатель 11,0 В?
4. Сколько вольт подается для работы светового индикатора DVD-плеера с сопротивлением 140 Ом, если через него проходит 25,0 мА?
5. (a) Найдите падение напряжения в удлинителе с сопротивлением 0,0600 Ом, через который проходит ток 5,00 А. (b) Более дешевый шнур использует более тонкую проволоку и имеет сопротивление 0.300 Ом. Какое в нем падение напряжения при протекании 5.00 А? (c) Почему напряжение на любом используемом приборе снижается на эту величину? Как это повлияет на прибор?
6. ЛЭП подвешена к металлическим опорам со стеклянными изоляторами, имеющими сопротивление 1,00 × 10 9 Ом. Какой ток протекает через изолятор при напряжении 200 кВ? (Некоторые линии высокого напряжения — постоянного тока.)
Глоссарий
- Закон Ома:
- эмпирическое соотношение, указывающее, что ток I пропорционален разности потенциалов V , V ; его часто записывают как I = V / R , где R — это сопротивление
- сопротивление:
- электрическое свойство, препятствующее току; для омических материалов это отношение напряжения к току, R = V / I
- Ом:
- единица сопротивления, равная 1Ω = 1 В / A
- омическое:
- тип материала, для которого действует закон Ома
- простая схема:
- схема с одним источником напряжения и одним резистором
Избранные решения проблем и упражнения
1.0,833 А
3. 7,33 × 10 −2 Ом
5. (а) 0,300 В
(б) 1,50 В
(c) Напряжение, подаваемое на любой используемый прибор, снижается, поскольку общее падение напряжения от стены до конечного выхода прибора является фиксированным. Таким образом, если падение напряжения на удлинителе велико, падение напряжения на приборе значительно уменьшается, поэтому выходная мощность прибора может быть значительно уменьшена, что снижает способность прибора работать должным образом.
закон Ома | физика | Britannica
Закон Ома , описание взаимосвязи между током, напряжением и сопротивлением. Величина постоянного тока через большое количество материалов прямо пропорциональна разности потенциалов или напряжению на материалах. Таким образом, если напряжение В, (в единицах вольт) между двумя концами провода, сделанного из одного из этих материалов, утроится, ток I (амперы) также утроится; и отношение V / I остается постоянным.Отношение V, / I для данного куска материала называется его сопротивлением, R, измеряется в единицах, называемых омами. Сопротивление материалов, для которых действует закон Ома, не изменяется в огромных диапазонах напряжения и тока. Математически закон Ома может быть выражен как V / I = R . То, что сопротивление или отношение напряжения к току для всей или части электрической цепи при фиксированной температуре, как правило, является постоянным, было установлено к 1827 году в результате исследований немецкого физика Георга Симона Ома.
Альтернативные утверждения закона Ома заключаются в том, что ток I в проводнике равен разности потенциалов В на проводнике, деленной на сопротивление проводника, или просто I = В / R , и что разность потенциалов в проводнике равна произведению тока в проводнике и его сопротивления, В = IR . В цепи, в которой разность потенциалов или напряжение постоянна, ток можно уменьшить, добавив большее сопротивление, или увеличить, удалив некоторое сопротивление.Закон Ома также может быть выражен в терминах электродвижущей силы или напряжения E источника электроэнергии, такого как батарея. Например, I = E / R .
С изменениями закон Ома применяется также к цепям переменного тока, в которых соотношение между напряжением и током более сложное, чем для постоянного тока. Именно из-за того, что ток меняется, помимо сопротивления возникают другие формы противодействия току, называемые реактивным сопротивлением.Комбинация сопротивления и реактивного сопротивления называется импедансом, Z. Когда полное сопротивление, эквивалентное отношению напряжения к току, в цепи переменного тока является постоянным, обычно применяется закон Ома. Например, V / I = Z .
С дальнейшими изменениями закон Ома был расширен до постоянного отношения магнитодвижущей силы к магнитному потоку в магнитной цепи.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.Подпишитесь сейчас19,1 Закон Ома — Физика
Постоянный и переменный ток
Так же, как вода течет с большой высоты на низкую, электроны, которые могут свободно перемещаться, будут перемещаться из места с низким потенциалом в место с высоким потенциалом. Батарея имеет две клеммы с разным потенциалом. Если клеммы соединены проводом, электрический ток (заряды) будет течь, как показано на рисунке 19.2. Затем электроны будут перемещаться от низкопотенциальной клеммы батареи (отрицательный конец ) через провод и попадут в высокопотенциальную клемму батареи (положительный конец ).
Рис. 19.2 У батареи есть провод, соединяющий положительную и отрицательную клеммы, который позволяет электронам перемещаться от отрицательной клеммы к положительной.
Teacher Support
Teacher Support
Подчеркните, что электроны движутся от отрицательного вывода к положительному, потому что они несут отрицательный заряд, поэтому они отталкиваются кулоновской силой от отрицательного вывода.
Электрический ток — это скорость, с которой движется электрический заряд.Большой ток, такой как тот, который используется для запуска двигателя грузовика, перемещает большое количество очень быстро, тогда как небольшой ток, такой как тот, который используется для работы портативного калькулятора, перемещает небольшое количество заряда медленнее. В форме уравнения электрический ток I определяется как
, где ΔQΔQ — это количество заряда, которое проходит через заданную область, а ΔtΔt — время, за которое заряд проходит мимо этой области. Единицей измерения электрического тока в системе СИ является ампер (А), названный в честь французского физика Андре-Мари Ампера (1775–1836).Один ампер — это один кулон в секунду, или
Электрический ток, движущийся по проволоке, во многом похож на ток воды, движущийся по трубе. Чтобы определить поток воды через трубу, мы можем подсчитать количество молекул воды, которые проходят мимо данного участка трубы. Как показано на рисунке 19.3, электрический ток очень похож. Мы подсчитываем количество электрических зарядов, протекающих по участку проводника; в данном случае провод.
Рис. 19.3 Электрический ток, движущийся по этому проводу, — это заряд, который проходит через поперечное сечение A, деленный на время, необходимое этому заряду, чтобы пройти через участок A .
Поддержка учителя
Поддержка учителя
Обратите внимание на то, что носители заряда на этом рисунке положительны, поэтому они движутся в том же направлении, что и электрический ток.
Предположим, что каждая частица q на рисунке 19.3 несет заряд q = 1nCq = 1nC, и в этом случае общий заряд будет равен ΔQ = 5q = 5nCΔQ = 5q = 5nC. Если эти заряды пройдут мимо области A за время Δt = 1 нсΔt = 1 нс, то ток будет
I = ΔQΔt = 5nC1ns = 5A.I = ΔQΔt = 5nC1ns = 5A.19,1
Обратите внимание, что мы присвоили зарядам на рис. 19.3 положительный заряд. Обычно отрицательные заряды — электроны — являются подвижным зарядом в проводах, как показано на рисунке 19.2. Положительные заряды обычно застревают в твердых телах и не могут свободно перемещаться. Однако, поскольку положительный ток, движущийся вправо, совпадает с отрицательным током такой же величины, движущимся влево, как показано на рисунке 19.4, мы определяем обычный ток, который течет в том направлении, в котором протекал бы положительный заряд, если бы он мог двигаться. .Таким образом, если не указано иное, предполагается, что электрический ток состоит из положительных зарядов.
Также обратите внимание, что один кулон — это значительная величина электрического заряда, поэтому 5 А — это очень большой ток. Чаще всего вы увидите ток порядка миллиампер (мА).
Рис. 19.4 (a) Электрическое поле направлено вправо, ток движется вправо, а положительные заряды движутся вправо. (б) Эквивалентная ситуация, но с отрицательными зарядами, движущимися влево.Электрическое поле и ток по-прежнему справа.
Поддержка учителя
Поддержка учителя
Укажите, что электрическое поле одинаково в обоих случаях, и что ток направлен в направлении электрического поля.
Предупреждение о заблуждении
Убедитесь, что учащиеся понимают, что ток — это , определяемый как как направление, в котором будет течь положительный заряд, даже если электроны чаще всего являются мобильными носителями заряда. Математически результат один и тот же, независимо от того, предполагаем ли мы положительный заряд в одну сторону или отрицательный заряд в противоположном направлении.Однако физически ситуация совершенно иная (хотя разница уменьшается после определения отверстий).
Snap Lab
Vegetable Current
Эта лабораторная работа помогает студентам понять, как работает ток. Учитывая, что частицы, заключенные в трубе, не могут занимать одно и то же пространство, толкание большего количества частиц в один конец трубы приведет к вытеснению того же количества частиц из противоположного конца. Это создает поток частиц.
Найдите соломинку и сушеный горох, которые могут свободно перемещаться в соломе.Положите соломинку на стол и засыпьте ее горошком. Когда вы вдавливаете одну горошину с одного конца, другая горошина должна выходить из другого конца. Эта демонстрация представляет собой модель электрического тока. Определите часть модели, которая представляет электроны, и часть модели, которая представляет собой подачу электроэнергии. В течение 30 секунд подсчитайте, сколько горошин вы можете протолкнуть через соломинку. Когда закончите, вычислите горошин, текущий , разделив количество горошин на время в секундах.
Обратите внимание, что поток гороха основан на том, что горох физически сталкивается друг с другом; электроны толкают друг друга за счет взаимно отталкивающих электростатических сил.
Проверка захвата
Предположим, у вас есть резервуар с горохом, каждый заправлен до 1 нКл. Если вы пропустите горошек через соломинку со скоростью четыре горошины в секунду, как бы вы рассчитали электрический ток, проводимый заряженным горошком?
- Измерьте длину соломинки, затем разделите на расход гороха и умножьте на расход на горошину.
- Умножьте расход гороха на расход гороха.
- Измерьте длину соломинки, затем умножьте на скорость потока гороха и разделите на количество заряда на горошину.
- Разделите скорость потока гороха на расход гороха.
Направление обычного тока — это направление, в котором течет положительный заряд . В зависимости от ситуации могут перемещаться положительные заряды, отрицательные заряды или и то, и другое.В металлических проводах, как мы видели, ток переносится электронами, поэтому отрицательные заряды движутся. В ионных растворах, таких как соленая вода, движутся как положительно заряженные, так и отрицательно заряженные ионы. То же самое и с нервными клетками. Чистые положительные токи относительно редки, но встречаются. История отмечает, что американский политик и ученый Бенджамин Франклин описал ток как направление, в котором положительные заряды проходят через провод. Он назвал тип заряда, связанный с электронами, отрицательным задолго до того, как стало известно, что они переносят ток во многих ситуациях.
Когда электроны движутся по металлической проволоке, они сталкиваются с препятствиями, такими как другие электроны, атомы, примеси и т. Д. Электроны рассеиваются от этих препятствий, как показано на рисунке 19.5. Обычно электроны теряют энергию при каждом взаимодействии. Таким образом, чтобы электроны двигались, требуется сила, создаваемая электрическим полем. Электрическое поле в проводе направлено от конца провода с более высоким потенциалом к концу провода с более низким потенциалом. Электроны, несущие отрицательный заряд, движутся в среднем (или дрейф ) в направлении, противоположном электрическому полю, как показано на рисунке 19.5.
Рис. 19.5. Свободные электроны, движущиеся в проводнике, совершают множество столкновений с другими электронами и атомами. Показан путь одного электрона. Средняя скорость свободных электронов находится в направлении, противоположном электрическому полю. Столкновения обычно передают энергию проводнику, поэтому для поддержания постоянного тока требуется постоянный запас энергии.
До сих пор мы обсуждали ток, который постоянно движется в одном направлении. Это называется постоянным током, потому что электрический заряд течет только в одном направлении.Постоянный ток часто называют током DC .
Многие источники электроэнергии, такие как плотина гидроэлектростанции, показанная в начале этой главы, вырабатывают переменный ток, направление которого меняется взад и вперед. Переменный ток часто называют . Переменный ток . Переменный ток перемещается вперед и назад через равные промежутки времени, как показано на рисунке 19.6. Переменный ток, который исходит из обычной розетки, не меняет направление внезапно.Скорее, он плавно увеличивается до максимального тока, а затем плавно уменьшается до нуля. Затем он снова растет, но в противоположном направлении, пока не достигнет того же максимального значения. После этого он плавно уменьшается до нуля, и цикл начинается снова.
Рисунок 19.6 При переменном токе направление тока меняется на противоположное через равные промежутки времени. График вверху показывает зависимость тока от времени. Отрицательные максимумы соответствуют движению тока влево.Положительные максимумы соответствуют току, движущемуся вправо. Ток регулярно и плавно чередуется между этими двумя максимумами.
Teacher Support
Teacher Support
Помогите ученикам интерпретировать график, подчеркнув, что ток не меняет направление мгновенно, а плавно переходит от одного максимума к противоположному максимуму и обратно. Объясните, что четыре изображения внизу показывают ток в соответствующих максимумах. Обратите внимание, что для упрощения интерпретации операторы мобильной связи на изображении считаются положительными.
Устройства, использующие переменный ток, включают пылесосы, вентиляторы, электроинструменты, фены и многие другие. Эти устройства получают необходимую мощность, когда вы подключаете их к розетке. Настенная розетка подключена к электросети, которая обеспечивает переменный потенциал (потенциал переменного тока). Когда ваше устройство подключено к сети, потенциал переменного тока толкает заряды вперед и назад в цепи устройства, создавая переменный ток.
Однако во многих устройствах используется постоянный ток, например в компьютерах, сотовых телефонах, фонариках и автомобилях.Одним из источников постоянного тока является аккумулятор, который обеспечивает постоянный потенциал (потенциал постоянного тока) между своими выводами. Когда ваше устройство подключено к батарее, потенциал постоянного тока толкает заряд в одном направлении через цепь вашего устройства, создавая постоянный ток. Другой способ получения постоянного тока — использование трансформатора, который преобразует переменный потенциал в постоянный. Маленькие трансформаторы, которые вы можете подключить к розетке, используются для зарядки вашего ноутбука, мобильного телефона или другого электронного устройства. Люди обычно называют это зарядным устройством или батареей , но это трансформатор, который преобразует напряжение переменного тока в напряжение постоянного тока.В следующий раз, когда кто-то попросит одолжить зарядное устройство для ноутбука, скажите им, что у вас нет зарядного устройства для ноутбука, но они могут одолжить ваш преобразователь.
Рабочий пример
Ток при ударе молнии
Удар молнии может передать до 10201020 электронов из облака на землю. Если удар длится 2 мс, каков средний электрический ток в молнии?
Стратегия
Используйте определение тока, I = ΔQΔtI = ΔQΔt. Заряд ΔQΔQ из 10201020 электронов ΔQ = neΔQ = ne, где n = 1020n = 1020 — количество электронов, а e = −1.60 · 10−19Ce = −1.60 · 10−19C — заряд электрона. Это дает
ΔQ = 1020 × (-1,60 × 10-19 ° C) = -16,0 ° C. ΔQ = 1020 × (-1,60 × 10-19 ° C) = -16,0 ° C.19,2
Время Δt = 2 × 10–3 с Δt = 2 × 10–3 с — это продолжительность удара молнии.
Решение
Ток в ударе молнии
I = ΔQΔt = −16,0C2 × 10−3s = −8kA.I = ΔQΔt = −16,0C2 × 10−3s = −8kA.19,3
Обсуждение
Отрицательный знак отражает тот факт, что электроны несут отрицательный заряд.Таким образом, хотя электроны текут от облака к земле, положительный ток должен течь от земли к облаку.
Рабочий пример
Средний ток для заряда конденсатора
В цепи, содержащей конденсатор и резистор, заряд конденсатора емкостью 16 мкФ с использованием батареи 9 В. занимает 1 мин. Какой средний ток в это время?
Стратегия
Мы можем определить заряд конденсатора, используя определение емкости: C = QVC = QV.Когда конденсатор заряжается батареей 9 В, напряжение на конденсаторе будет V = 9VV = 9V. Это дает заряд
Подставляя это выражение для заряда в уравнение для тока, I = ΔQΔtI = ΔQΔt, мы можем найти средний ток.
Решение
Средний ток
I = ΔQΔt = CVΔt = (16 × 10−6F) (9V) 60s = 2,4 × 10−6A = 2,4 мкА I = ΔQΔt = CVΔt = (16 × 10−6F) (9V) 60s = 2,4 × 10−6A = 2,4 мкА.19,5
Обсуждение
Этот небольшой ток типичен для тока, встречающегося в таких цепях.
Сопротивление и закон Ома
Как упоминалось ранее, электрический ток в проводе во многом похож на воду, текущую по трубе. На поток воды, который может течь по трубе, влияют препятствия в трубе, такие как засорения и узкие участки в трубе. Эти препятствия замедляют ток через трубу. Точно так же электрический ток в проводе может быть замедлен многими факторами, включая примеси в металле провода или столкновения между зарядами в материале.Эти факторы создают сопротивление электрическому току. Сопротивление — это описание того, насколько провод или другой электрический компонент препятствует прохождению через него заряда. В XIX веке немецкий физик Георг Симон Ом (1787–1854) экспериментально обнаружил, что ток через проводник пропорционален падению напряжения на проводнике с током.
Константа пропорциональности — это сопротивление материала R , что приводит к
Это соотношение называется законом Ома.Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием. Закон Ома — это эмпирический закон, подобный закону трения, что означает, что это экспериментально наблюдаемое явление. Единицы сопротивления — вольт на ампер или В / А. Мы называем V / A Ом , что обозначается заглавной греческой буквой омега (ΩΩ). Таким образом,
1 Ом = 1 В / А (1,4). 1 Ом = 1 В / А (1,4). ЗаконОма справедлив для большинства материалов и при обычных температурах. При очень низких температурах сопротивление может упасть до нуля (сверхпроводимость).При очень высоких температурах тепловое движение атомов в материале препятствует потоку электронов, увеличивая сопротивление. Многие вещества, для которых действует закон Ома, называются омическими. Омические материалы включают в себя хорошие проводники, такие как медь, алюминий и серебро, а также некоторые плохие проводники при определенных обстоятельствах. Сопротивление омических материалов остается практически неизменным в широком диапазоне напряжения и тока.
Watch Physics
Введение в электричество, схемы, ток и сопротивление
В этом видео представлен закон Ома и простая электрическая схема.Говорящий использует аналогию давления, чтобы описать, как электрический потенциал заставляет заряд двигаться. Он обращается к электрическому потенциалу как , электрическому давлению . Другой способ размышления об электрическом потенциале — это представить, что множество частиц одного знака скопилось в небольшом замкнутом пространстве. Поскольку эти заряды имеют одинаковый знак (все они положительные или все отрицательные), каждый заряд отталкивает другие вокруг себя. Это означает, что множество зарядов постоянно выталкивается за пределы пространства.Полная электрическая цепь подобна открытию двери в небольшом пространстве: какие бы частицы ни толкали к двери, теперь у них есть способ убежать. Чем выше электрический потенциал, тем сильнее каждая частица толкает друг друга.
Проверка захвата
Если вместо одного резистора R на принципиальной схеме, показанной в видео, нарисовать два резистора с сопротивлением R каждый, что вы можете сказать о токе, протекающем в цепи?
- Сила тока в цепи должна уменьшиться вдвое.
- Величина тока в цепи должна увеличиться вдвое.
- Ток в цепи должен оставаться неизменным.
- Количество тока в цепи увеличится вдвое.
Виртуальная физика
Закон Ома
Это моделирование имитирует простую схему с батареями, обеспечивающими источник напряжения, и резистором, подключенным к батареям.Посмотрите, как на ток влияет изменение сопротивления и / или напряжения. Обратите внимание, что сопротивление моделируется как элемент, содержащий малых центров рассеяния . Они представляют собой загрязнения или другие препятствия, препятствующие прохождению тока.
Проверка захвата
В цепи, если сопротивление оставить постоянным, а напряжение удвоить (например, с 3 \, \ text {V} до 6 \, \ text {V}), как изменится ток? Соответствует ли это закону Ома?
- Сила тока удвоится.Это соответствует закону Ома, поскольку ток пропорционален напряжению.
- Сила тока удвоится. Это не соответствует закону Ома, поскольку сила тока пропорциональна напряжению.
- Ток увеличится вдвое. Это соответствует закону Ома, поскольку ток пропорционален напряжению.
- Ток уменьшится вдвое. Это не соответствует закону Ома, поскольку сила тока пропорциональна напряжению.
Рабочий пример
Сопротивление фары
Каково сопротивление автомобильной фары, через которую проходит 2,50 А при подаче на нее 12,0 В?
Стратегия
ЗаконОма говорит нам, что Vheadlight = IRheadlightVheadlight = IRheadlight. Падение напряжения при прохождении через фару — это просто повышение напряжения, обеспечиваемое аккумулятором, Vheadlight = VbatteryVheadlight = Vbattery. Мы можем использовать это уравнение и изменить закон Ома, чтобы найти сопротивление RheadlightRheadlight фары.
Решение
Решение закона Ома для сопротивления фары дает
Vheadlight = IRheadlight Vbattery = IRheadlight Rheadlight = Vbattery I = 12V2.5A = 4.8Ω. Vheadlight = IRheadlight Vbattery = IRheadlightRheadlight = VbatteryI = 12V2.5A = 4.8Ω.19,6
Обсуждение
Это относительно небольшое сопротивление. Как мы увидим ниже, сопротивление в цепях обычно измеряется в кВт или МВт.
Рабочий пример
Определите сопротивление по графику «ток-напряжение»
Предположим, вы подаете на цепь несколько различных напряжений и измеряете ток, протекающий по цепи.График результатов показан на рисунке 19.7. Какое сопротивление цепи?
Рисунок 19.7 Линия показывает зависимость тока от напряжения. Обратите внимание, что ток указан в миллиамперах. Например, при 3 В ток составляет 0,003 А или 3 мА.
Стратегия
График показывает, что ток пропорционален напряжению, что соответствует закону Ома. По закону Ома (V = IRV = IR) константа пропорциональности — это сопротивление R . Поскольку на графике показан ток как функция напряжения, мы должны изменить закон Ома в следующей форме: I = VR = 1R × VI = VR = 1R × V.Это показывает, что наклон линии I по сравнению с V составляет 1R1R. Таким образом, если мы найдем наклон линии на рисунке 19.7, мы сможем вычислить сопротивление R .
Решение
Наклон линии равен подъему , разделенному на отрезок . Глядя на нижний левый квадрат сетки, мы видим, что линия поднимается на 1 мА (0,001 А) и проходит через напряжение 1 В. Таким образом, наклон линии равен
наклон = 0.001A1V. Наклон = 0,001A1V.19,7
Приравнивая наклон к 1R1R и решая для R , получаем
1R = 0,001A1R = 1V0,001A = 1000 Ом 1R = 0,001A1R = 1V0,001A = 1000 Ом19,8
или 1 кОм.
Обсуждение
Это сопротивление больше, чем мы обнаружили в предыдущем примере. Подобные сопротивления часто встречаются в электрических цепях, как мы узнаем в следующем разделе. Обратите внимание, что если бы линия на рисунке 19.7 не была прямой, то материал не был бы омическим, и мы не смогли бы использовать закон Ома.Материалы, которые не подчиняются закону Ома, называются безомными.
20.2: Закон Ома — сопротивление и простые схемы
Что управляет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, розетки и т. Д., Которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и условно называются источниками напряжения. Когда источник напряжения подключен к проводнику, он создает разность потенциалов \ (V \), которая создает электрическое поле.Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Закон Ома
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению \ (В \). Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
\ [I \ propto V. \ label {20.3.1} \]
Это важное соотношение известно как закон Ома .Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток — следствием. Это эмпирический закон, подобный закону трения — явление, наблюдаемое экспериментально. Такая линейная зависимость возникает не всегда.
Сопротивление и простые схемы
Если напряжение управляет током, что ему мешает? Электрическое свойство, препятствующее току (примерно такое же, как трение и сопротивление воздуха), называется сопротивлением \ (R \). Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток.Сопротивление обратно пропорционально току, или
\ [I \ propto \ frac {1} {R}. \ label {20.3.2} \]
Таким образом, например, ток уменьшается вдвое, если сопротивление увеличивается вдвое. Комбинируя отношения тока к напряжению и тока к сопротивлению, получаем
\ [I = \ frac {V} {R}. \ label {20.3.3} \]
Это соотношение также называется законом Ома. Закон Ома в такой форме действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален.Многие вещества, для которых действует закон Ома, называются омическими . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление \ (R \), которое не зависит от напряжения \ (V \) и тока \ (I \). Объект с простым сопротивлением называется резистором , даже если его сопротивление невелико. Единица измерения сопротивления — Ом и обозначается символом \ (\ Omega \) (греческая омега в верхнем регистре). Перестановка \ (I = V / R \) дает \ (R = V / I \), и поэтому единицы сопротивления равны 1 Ом = 1 вольт на ампер:
\ [1 \ Omega = 1 \ frac {V} {A}.\ label {20.3.4} \]
На рисунке \ (\ PageIndex {1} \) показана схема простой схемы. Простая схема имеет один источник напряжения и один резистор. Можно предположить, что провода, соединяющие источник напряжения с резистором, имеют незначительное сопротивление, или их сопротивление можно включить в \ (R \).
Рисунок \ (\ PageIndex {1} \): Простая электрическая цепь, в которой замкнутый путь для прохождения тока обеспечивается проводниками (обычно металлическими), соединяющими нагрузку с выводами батареи, представленной красными параллельными линиями.Зигзагообразный символ представляет собой единственный резистор и включает любое сопротивление в соединениях с источником напряжения.Пример \ (\ PageIndex {1} \): Расчет сопротивления: автомобильная фара:
Каково сопротивление автомобильной фары, через которую проходит 2,50 А при подаче на нее 12,0 В?
Стратегия
Мы можем изменить закон Ома, как указано в \ (I = V / R \), и использовать его для определения сопротивления.
Решение:
Преобразование уравнения \ ref {20.3.3} и замена известных значений дает
\ [\ begin {align *} R & = \ frac {V} {I} \\ [5pt] & = \ frac {12,0 V} {2,50 A} \\ [5pt] & = 4,80 \ Omega. \ end {align *} \]
Обсуждение:
Это относительно небольшое сопротивление, но оно больше, чем хладостойкость фары. Как мы увидим, сопротивление металлов обычно увеличивается, , а увеличивает температуру , поэтому колба имеет меньшее сопротивление при первом включении и потребляет значительно больший ток во время короткого периода прогрева.{-5} \ Omega \), а сверхпроводники вообще не имеют сопротивления (они неомичны). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделах «Сопротивление и удельное сопротивление».
Дополнительное понимание можно получить, решив \ (I = V / R \) для \ (V \), что дает
\ [V = ИК. \ label {20.3.5} \]
Выражение для \ (V \) можно интерпретировать как падение напряжения на резисторе, вызванное минимальным током \ (I \). Для обозначения этого напряжения часто используется фраза \ (IR \) drop .Например, у фары в примере падение \ (IR \) составляет 12,0 В. Если напряжение измеряется в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор похож на трубу, которая снижает давление и ограничивает поток из-за своего сопротивления. Здесь сохранение энергии имеет важные последствия. Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию).В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку \ (PE = q \ Delta V \), и то же самое \ (q \) проходит через каждую . Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразованная резистором, равны (Рисунок \ (\ PageIndex {2} \)).
Рисунок \ (\ PageIndex {2} \): Падение напряжения на резисторе в простой схеме равно выходному напряжению батареи.ПОДКЛЮЧЕНИЕ: СОХРАНЕНИЕ ЭНЕРГИИ
В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму.Здесь о сохранении энергии свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним резистором. Мы обнаружим, что сохранение энергии имеет и другие важные применения в схемах и является мощным инструментом анализа схем.
ЗаконОма | Электрические цепи
11,2 Закон Ома (ESBQ6)
Три основные величины для электрических цепей: ток, напряжение (разность потенциалов) и сопротивление .Напомним:
Электрический ток, \ (I \), определяется как скорость прохождения заряда через цепь.
Разность потенциалов или напряжение \ (В \) — это количество энергии на единицу заряда, необходимое для перемещения этого заряда между двумя точками в цепи.
Сопротивление, \ (R \), является мерой того, насколько «трудно» протолкнуть ток через элемент схемы.
Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.
Важная взаимосвязь между током, напряжением и сопротивлением в цепи была обнаружена Георгом Симоном Омом и называется законом Ома .
- Закон Ома
Величина электрического тока через металлический проводник при постоянной температуре в цепи пропорциональна напряжению на проводнике и может быть описана как
\ (I = \ frac {V} {R} \)где \ (I \) — ток через проводник, \ (V \) — напряжение на проводнике, а \ (R \) — сопротивление проводника.Другими словами, при постоянной температуре сопротивление проводника постоянно, независимо от приложенного к нему напряжения или проходящего через него тока.
Закон Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий через проводник, прямо пропорционален напряжению на нем. Это означает, что если мы нанесем напряжение на ось x графика, а ток — на ось y графика, мы получим прямую линию.
Наклон прямолинейного графика связан с сопротивлением проводника как \ [\ frac {I} {V} = \ frac {1} {R}.\] Это можно изменить с точки зрения постоянного сопротивления как: \ [R = \ frac {V} {I}. \]
Закон Ома
Цель
Для определения взаимосвязи между током, протекающим через резистор, и разностью потенциалов (напряжением) на том же резисторе.
Аппарат
4 ячейки, 4 резистора, амперметр, вольтметр, соединительные провода
Метод
Этот эксперимент состоит из двух частей. В первой части мы будем изменять приложенное к резистору напряжение и измерять результирующий ток в цепи.Во второй части мы будем изменять ток в цепи и измерять результирующее напряжение на резисторе. После получения обоих наборов измерений мы исследуем взаимосвязь между током и напряжением на резисторе.
Изменение напряжения:
Установите схему в соответствии со схемой 1), начиная с одной ячейки.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Количество ячеек
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)
Попросите учителя проверить электрическую цепь перед включением питания.
Измерьте напряжение на резисторе с помощью вольтметра и ток в цепи с помощью амперметра.
Добавьте в схему еще одну ячейку \ (\ text {1,5} \) \ (\ text {V} \) и повторите измерения.
Повторяйте, пока не получите четыре ячейки и не заполните таблицу.
Изменение тока:
Установите схему в соответствии со схемой 2), начиная с одного резистора в цепи.
Нарисуйте следующую таблицу в своем лабораторном журнале.
Напряжение, В (\ (\ text {V} \))
Ток, I (\ (\ text {A} \))
Попросите учителя проверить вашу схему перед включением питания.
Измерьте ток и напряжение на единственном резисторе.
Теперь добавьте еще один резистор последовательно в схему и снова измерьте ток и напряжение только на исходном резисторе. Продолжайте добавлять резисторы, пока у вас не будет четырех последовательно, но не забывайте каждый раз измерять напряжение только на исходном резисторе. Введите измеренные вами значения в таблицу.
Анализ и результаты
Используя данные, записанные в первой таблице, постройте график зависимости тока от напряжения.Поскольку напряжение — это переменная, которую мы изменяем напрямую, это независимая переменная, которая будет отложена по оси \ (x \). Ток является зависимой переменной и должен быть нанесен на ось \ (y \).
Используя данные, записанные во второй таблице, постройте график зависимости напряжения от тока. В этом случае независимой переменной является ток, который должен быть нанесен на ось \ (x \), а напряжение является зависимой переменной и должно быть нанесено на ось \ (y \).
Выводы
Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? т.е. увеличивается или уменьшается?
Изучите график, который вы построили на основе второй таблицы. Что происходит с напряжением на резисторе, когда ток через резистор увеличивается? т.е. увеличивается или уменьшается?
Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.
Вопросы и обсуждение
- Для каждого из ваших графиков вычислите градиент и по нему определите сопротивление исходного резистора. Получаете ли вы одно и то же значение, когда рассчитываете его для каждого из ваших графиков?
Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_0 \)?
Зарегистрируйтесь, чтобы получить стипендию и возможности карьерного роста.Используйте практику Сиявулы, чтобы получить наилучшие возможные оценки.
Зарегистрируйтесь, чтобы открыть свое будущееЗакон Ома
Упражнение 11.1Постройте график напряжения (по оси X) и тока (по оси Y).
Какой тип графика вы получите (прямой, парабола, другая кривая)
прямая линия
Рассчитайте градиент графика.
Градиент графика (\ (m \)) — это изменение тока, деленное на изменение напряжения:
\ begin {align *} m & = \ frac {\ Delta I} {\ Delta V} \\ & = \ frac {(\ text {1,6}) — (\ text {0,4})} {(\ text {12}) — (\ text {3})} \\ & = \ текст {0,13} \ end {выровнять *}Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.
Да. График с прямой линией получается, когда мы строим график зависимости напряжения от тока.
Как вы можете найти сопротивление неизвестного резистора, используя только источник питания, вольтметр и известный резистор \ (R_ {0} \)?
Вы начинаете с подключения известного резистора в цепь с источником питания. Теперь вы читаете напряжение источника питания и записываете его.
Затем вы последовательно подключаете два резистора.Теперь вы можете измерить напряжение на каждом из резисторов.
Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:
\ [V = IR \]Итак, используя это, а также тот факт, что для резисторов, включенных последовательно, ток одинаков во всей цепи, мы можем найти неизвестное сопротивление.
\ begin {align *} V_ {0} & = IR_ {0} \\ I & = \ frac {V_ {0}} {R_ {0}} \\ V_ {U} & = IR_ {U} \\ I & = \ frac {V_ {U}} {R_ {U}} \\ \ frac {V_ {U}} {R_ {U}} & = \ frac {V_ {0}} {R_ {0}} \\ \ поэтому R_ {U} & = \ frac {V_ {U} R_ {0}} {V_ {0}} \ end {выровнять *}Омические и неомические проводники (ESBQ7)
Проводники, подчиняющиеся закону Ома, имеют постоянное сопротивление, когда на них изменяется напряжение или увеличивается ток, проходящий через них.Эти проводники называются омическими проводниками. График зависимости тока от напряжения на этих проводниках будет прямолинейным. Некоторыми примерами омических проводников являются резисторы цепи и нихромовая проволока.
Как вы видели, когда мы говорим о законе Ома, есть упоминание о постоянной температуре . Это связано с тем, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводников называются неомическими проводниками , потому что они не подчиняются закону Ома.Лампочка — типичный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.
В лампочке сопротивление нити накала резко возрастает по мере того, как она нагревается от комнатной до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы, то увеличение тока приведет к увеличению температуры нити накала, что приведет к увеличению ее сопротивления. Это эффективно ограничивает увеличение тока.В этом случае напряжение и ток не подчиняются закону Ома.
Явление изменения сопротивления при изменении температуры присуще почти всем металлам, из которых сделано большинство проводов. Для большинства приложений эти изменения сопротивления достаточно малы, чтобы их можно было игнорировать. При применении металлических нитей накала ламп, температура которых сильно повышается (примерно до \ (\ text {1 000} \) \ (\ text {℃} \) и начиная с комнатной температуры), изменение довольно велико.
В общем, для неомических проводников график зависимости напряжения от тока не будет прямолинейным, что указывает на то, что сопротивление не является постоянным для всех значений напряжения и тока.
Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат данные о токе и напряжении для резистора и лампочки и определят, какой из них подчиняется закону Ома. Вам потребуются лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр. Учащиеся должны обнаружить, что резистор подчиняется закону Ома, а лампочка — нет.
Омические и неомические проводники
Aim
Чтобы определить, подчиняются ли два элемента схемы (резистор и лампочка) закону Ома
Аппарат
4 ячейки, резистор, лампочка, соединительные провода, вольтметр, амперметр
Метод
Две схемы, показанные на схемах выше, одинаковы, за исключением того, что в первой есть резистор, а во второй — лампочка.Настройте обе схемы, указанные выше, начиная с 1 ячейки. Для каждой цепи:
Измерьте напряжение на элементе схемы (резисторе или лампочке) с помощью вольтметра.
Измерить ток в цепи с помощью амперметра.
Добавьте еще одну ячейку и повторяйте измерения, пока в вашей цепи не будет 4 ячейки.
Результаты
Нарисуйте в своей книге две таблицы, которые выглядят следующим образом.У вас должна быть одна таблица для измерений первой цепи с резистором и другая таблица для измерений второй цепи с лампочкой.
Количество ячеек | Напряжение, В (\ (\ text {V} \)) | Ток, I (\ (\ text {A} \)) |
\ (\ text {1} \) | ||
\ (\ text {2} \) | ||
\ (\ text {3} \) | ||
\ (\ text {4} \) |
Анализ
Используя данные в ваших таблицах, нарисуйте два графика \ (I \) (\ (y \) — ось) vs.\ (V \) (\ (x \) — ось), один для резистора и один для лампочки.
Вопросы и обсуждение
Внимательно изучите свои графики и ответьте на следующие вопросы:
Как должен выглядеть график зависимости \ (I \) от \ (V \) для проводника, подчиняющегося закону Ома?
Один или оба ваших графика выглядят так?
Какой можно сделать вывод о том, подчиняются ли резистор и / или лампочка закону Ома?
Имеет ли лампочка омический или неомический провод?
Использование закона Ома (ESBQ8)
Теперь мы готовы увидеть, как закон Ома используется для анализа схем.
Рассмотрим схему с ячейкой и омическим резистором R. Если сопротивление резистора равно \ (\ text {5} \) \ (\ text {Ω} \), а напряжение на резисторе равно \ (\ text { 5} \) \ (\ text {V} \), то мы можем использовать закон Ома для расчета тока, протекающего через резистор. Наша первая задача — нарисовать принципиальную схему. При решении любой проблемы с электрическими схемами очень важно составить схему схемы перед тем, как производить какие-либо расчеты. Принципиальная схема для этой проблемы выглядит следующим образом:
Уравнение закона Ома: \ [R = \ frac {V} {I} \]
, который можно преобразовать в: \ [I = \ frac {V} {R} \]
Ток, протекающий через резистор:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {5} \ text {V}} {\ text {5} \ Omega} \\ & = \ текст {1} \ текст {А} \ end {align *}
Рабочий пример 1: Закон Ома
Изучите электрическую схему ниже:
Сопротивление резистора равно \ (\ text {10} \) \ (\ text {Ω} \), а ток, проходящий через резистор, равен \ (\ text {4} \) \ (\ text {A} \ ).Какова разность потенциалов (напряжение) на резисторе?
Определите, как подойти к проблеме
Нам задают сопротивление резистора и ток, проходящий через него, и просят вычислить напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя: \ [R = \ frac {V} {I}. \]
Решить проблему
Измените приведенное выше уравнение и замените известные значения на \ (R \) и \ (I \), чтобы найти \ (V \). \ begin {align *} R & = \ frac {V} {I} \\ R \ times I & = \ frac {V} {I} \ times I \\ V & = I \ раз R \\ & = \ текст {10} \ times \ text {4} \\ & = \ текст {40} \ текст {V} \ end {align *}
Напишите окончательный ответ
Напряжение на резисторе равно \ (\ text {40} \) \ (\ text {V} \).
Зарегистрируйтесь, чтобы получить стипендию и возможности карьерного роста. Используйте практику Сиявулы, чтобы получить наилучшие возможные оценки.
Зарегистрируйтесь, чтобы открыть свое будущееЗакон Ома
Упражнение 11.2Рассчитайте сопротивление резистора, разность потенциалов которого равна \ (\ text {8} \) \ (\ text {V} \), когда ток равен \ (\ text {2} \) \ (\ text {A} \) протекает через него. Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {8} {2} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}Какой ток будет проходить через резистор \ (\ text {6} \) \ (\ text {Ω} \) при разности потенциалов \ (\ text {18} \) \ (\ text {V} \) на концах? Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {18} {6} \\ & = \ текст {3} \ текст {А} \ end {выровнять *}Какое напряжение на резисторе \ (\ text {10} \) \ (\ text {Ω} \) при токе \ (\ text {1,5} \) \ (\ text {A} \) течет хоть это? Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора составляет:
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {1,5}) (10) \\ & = \ текст {15} \ текст {V} \ end {выровнять *}Переплет резисторов последовательно и параллельно (ESBQ9)
В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы подключены последовательно и параллельно.В последовательной цепи есть один путь, по которому течет ток. В параллельной цепи есть несколько путей, по которым течет ток.
Когда в цепи более одного резистора, мы обычно можем вычислить общее суммарное сопротивление всех резисторов. Это известно как сопротивление , эквивалентное .
Эквивалентное последовательное сопротивление
В цепи, в которой резисторы включены последовательно, эквивалентное сопротивление — это просто сумма сопротивлений всех резисторов.
- Эквивалентное сопротивление в последовательной цепи,
Для последовательно подключенных резисторов n эквивалентное сопротивление:
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + \ ldots + R_ {n} \]
Применим это к следующей схеме.
Резисторы включены последовательно, следовательно:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {3} \ text {Ω} + \ text {10} \ text {Ω} + \ text {5} \ text {Ω} \\ & = \ текст {18} \ текст {Ω} \ end {align *}Эквивалентное параллельное сопротивление
В схеме, в которой резисторы включены параллельно, эквивалентное сопротивление определяется следующим определением.
- Эквивалентное сопротивление в параллельной цепи
Для резисторов, включенных параллельно \ (n \), эквивалентное сопротивление составляет:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ ldots + \ frac {1} {R_ {n}} \]
Применим эту формулу к следующей схеме.
Какое полное (эквивалентное) сопротивление в цепи?
\ begin {align *} \ frac {1} {R_ {p}} & = \ left (\ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}) } \верно) \\ & = \ left (\ frac {1} {\ text {10} \ text {Ω}} + \ frac {1} {\ text {2} \ text {Ω}} + \ frac {1} {\ text { 1} \ text {Ω}} \ right) \\ & = \ left (\ frac {\ text {1} \ text {Ω} + \ text {5} \ text {Ω} + \ text {10} \ text {Ω}} {\ text {10} \ text { Ω}} \ right) \\ & = \ left (\ frac {\ text {16} \ text {Ω}} {\ text {10} \ text {Ω}} \ right) \\ R_ {p} & = \ text {0,625} \ text {Ω} \ end {align *}Последовательное и параллельное сопротивление
Упражнение 11.3Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) соединены последовательно. Рассчитайте эквивалентное сопротивление.
Поскольку резисторы включены последовательно, мы можем использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {10} \ text {kΩ} + \ text {10} \ text {kΩ} \\ & = \ текст {20} \ текст {кОм} \ end {выровнять *}Два резистора соединены последовательно.Эквивалентное сопротивление равно \ (\ text {100} \) \ (\ text {Ω} \). Если один резистор равен \ (\ text {10} \) \ (\ text {Ω} \), вычислите номинал второго резистора.
Поскольку резисторы включены последовательно, мы можем использовать:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ R_ {2} & = R_ {s} — R_ {1} \\ & = \ text {100} \ text {Ω} — \ text {10} \ text {Ω} \\ & = \ текст {90} \ текст {Ω} \ end {выровнять *}Два резистора \ (\ text {10} \) \ (\ text {kΩ} \) подключены параллельно.Рассчитайте эквивалентное сопротивление.
Поскольку резисторы включены параллельно, можно использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {100}} + \ frac {1} {\ text {10}} \\ & = \ frac {1 + 10} {\ text {100}} \\ & = \ frac {11} {\ text {100}} \\ R_ {p} & = \ text {9,09} \ text {kΩ} \ end {выровнять *}Два резистора подключены параллельно.Эквивалентное сопротивление равно \ (\ text {3,75} \) \ (\ text {Ω} \). Если сопротивление одного резистора равно \ (\ text {10} \) \ (\ text {Ω} \), каково сопротивление второго резистора?
Поскольку резисторы включены параллельно, можно использовать:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {R_ {2}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} \\ & = \ frac {1} {\ text {3,75}} — \ frac {1} {\ text {10}} \\ & = \ frac {\ text {10} — \ text {3,75}} {\ text {37,5}} \\ & = \ frac {\ text {6,25}} {\ text {37,5}} \\ R_ {2} & = \ текст {6} \ текст {Ω} \ end {выровнять *}Рассчитайте эквивалентное сопротивление в каждой из следующих цепей:
a) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {3}} + \ frac {1} {\ text {2}} \\ & = \ frac {\ text {2} + \ text {3}} {\ text {6}} \\ & = \ frac {\ text {5}} {\ text {6}} \\ R & = \ текст {1,2} \ текст {Ω} \ end {выровнять *}b) Резисторы включены параллельно, поэтому мы используем:
\ [\ frac {1} {R_ {p}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ frac {1} {R_ {4}} \]Эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\ & = \ frac {1} {\ text {2}} + \ frac {1} {\ text {3}} + \ frac {1} {\ text {4}} + \ frac {1} {\ text { 1}} \\ & = \ frac {\ text {6} + \ text {4} + \ text {3} + \ text {12}} {\ text {12}} \\ & = \ frac {\ text {25}} {\ text {12}} \\ R & = \ text {0,48} \ text {Ω} \ end {выровнять *}c) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}d) Резисторы включены последовательно, поэтому мы используем:
\ [R_ {s} = R_ {1} + R_ {2} + R_ {3} + R_ {4} \]Эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ & = \ text {2} \ text {Ω} + \ text {3} \ text {Ω} + \ text {4} \ text {Ω} + \ text {1} \ text {Ω} \\ & = \ текст {10} \ текст {Ω} \ end {выровнять *}Использование закона Ома в последовательных и параллельных цепях (ESBQB)
Используя определения эквивалентного сопротивления для резисторов, включенных последовательно или параллельно, мы можем проанализировать некоторые схемы с этими установками.
Цепи серии
Рассмотрим схему, состоящую из трех резисторов и одиночная ячейка соединена последовательно.
Первый принцип, который нужно понять в отношении последовательных цепей, заключается в том, что величина тока одинакова через любой компонент в цепи. Это потому, что существует только один путь для движения электронов в последовательной цепи. По способу подключения батареи мы можем сказать, в каком направлении будет течь ток. Мы знаем, что ток по условию течет от положительного к отрицательному.Обычный ток в этой цепи будет течь по часовой стрелке от точки A к B, от C к D и обратно к A.
Мы знаем, что в последовательной цепи ток должен быть одинаковым во всех компонентах. Итак, мы можем написать:
\ [I = I_ {1} = I_ {2} = I_ {3}. \]Мы также знаем, что полное напряжение цепи должно быть равно сумме напряжений на всех трех резисторах. Итак, мы можем написать:
\ [V = V_ {1} + V_ {2} + V_ {3} \]Используя эту информацию и то, что мы знаем о вычислении эквивалентного сопротивления резисторов, включенных последовательно, мы можем решить некоторые проблемы схемы.
Рабочий пример 2: Закон Ома, последовательная цепь
Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как подойти к проблеме
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако в цепи два резистора, и нам нужно найти полное сопротивление.
Найдите полное сопротивление в цепи
Поскольку резисторы включены последовательно, общее (эквивалентное) сопротивление R составляет:
\ [R = R_ {1} + R_ {2} \]Следовательно,
\ begin {align *} R & = \ текст {2} + \ текст {4} \\ & = \ текст {6} \ текст {Ω} \ end {align *}Применить закон Ома
\ begin {align *} R & = \ frac {V} {I} \\ R \ times \ frac {I} {R} & = \ frac {V} {I} \ times \ frac {I} {R} \\ I & = \ frac {V} {R} \\ & = \ frac {12} {6} \\ & = \ текст {2} \ текст {А} \ end {align *}
Напишите окончательный ответ
В цепи протекает ток \ (\ text {2} \) \ (\ text {A} \).
Рабочий пример 3: Закон Ома, последовательная цепь
Два омических резистора (\ (R_ {1} \) и \ (R_ {2} \)) соединены последовательно с ячейкой. Найдите сопротивление \ (R_ {2} \), учитывая, что ток, протекающий через \ (R_ {1} \) и \ (R_ {2} \), равен \ (\ text {0,25} \) \ ( \ text {A} \) и что напряжение на ячейке равно \ (\ text {1,5} \) \ (\ text {V} \). \ (R_ {1} \) = \ (\ text {1} \) \ (\ text {Ω} \).
Нарисуйте схему и введите все известные значения.
Определите, как подойти к проблеме.
Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление, используя:
\ [R = R_ {1} + R_ {2} \], потому что он находится в последовательной цепи.
Найдите общее сопротивление
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {\ text {1,5}} {\ text {0,25}} \\ & = \ текст {6} \ текст {Ω} \ end {align *}Найдите неизвестное сопротивление
Мы знаем, что:
\ [R = \ text {6} \ text {Ω} \]и что
\ [R_ {1} = \ text {1} \ text {Ω} \]С
\ [R = R_ {1} + R_ {2} \] \ [R_ {2} = R — R_ {1} \]Следовательно,
\ [R_ {1} = \ text {5} \ text {Ω} \]Рабочий пример 4: Закон Ома, последовательная цепь
Для следующей схемы рассчитайте:
падение напряжения \ (V_1 \), \ (V_2 \) и \ (V_3 \) на резисторах \ (R_1 \), \ (R_2 \) и \ (R_3 \)
сопротивление \ (R_3 \).
Определите, как подойти к проблеме
Нам даны напряжение на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для расчета падения напряжения на известных резисторах. Поскольку резисторы включены в последовательную цепь, напряжение равно \ (V = V_1 + V_2 + V_3 \), и мы можем вычислить \ (V_3 \). Теперь мы можем использовать эту информацию, чтобы найти напряжение на неизвестном резисторе \ (R_3 \).
Рассчитать падение напряжения на \ (R_1 \)
Используя закон Ома: \ begin {align *} R_1 & = \ frac {V_1} {I} \\ I \ cdot R_1 & = I \ cdot \ frac {V_1} {I} \\ V_1 & = {I} \ cdot {R_1} \\ & = 2 \ cdot 1 \\ V_1 & = \ текст {2} \ текст {V} \ end {align *}
Рассчитать падение напряжения на \ (R_2 \)
Снова используя закон Ома: \ begin {align *} R_2 & = \ frac {V_2} {I} \\ I \ cdot R_2 & = I \ cdot \ frac {V_2} {I} \\ V_2 & = {I} \ cdot {R_2} \\ & = 2 \ cdot 3 \\ V_2 & = \ текст {6} \ текст {V} \ end {align *}
Рассчитать падение напряжения на \ (R_3 \)
Поскольку падение напряжения на всех резисторах вместе должно быть таким же, как падение напряжения на ячейке в последовательной цепи, мы можем найти \ (V_3 \), используя: \ begin {align *} V & = V_1 + V_2 + V_3 \\ V_3 & = V — V_1 — V_2 \\ & = 18-2-6 \\ V_3 & = \ текст {10} \ текст {V} \ end {align *}
Найдите сопротивление \ (R_3 \)
Нам известны напряжение на \ (R_3 \) и ток через него, поэтому мы можем использовать закон Ома для вычисления значения сопротивления: \ begin {align *} R_3 & = \ frac {V_3} {I} \\ & = \ frac {10} {2} \\ R_3 & = \ text {5} \ Omega \ end {align *}
Напишите окончательный ответ
\ (V_1 = \ text {2} \ text {V} \)
\ (V_2 = \ text {6} \ text {V} \)
\ (V_3 = \ text {10} \ text {V} \)
\ (R_1 = \ text {5} \ Omega \)
Параллельные цепи
Рассмотрим схему, состоящую из одной ячейки и трех резисторов, соединенных параллельно.
Первый принцип, который нужно понять в отношении параллельных цепей, заключается в том, что напряжение одинаково на всех компонентах в цепи. Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени. Итак, для показанной схемы верно следующее:
\ [V = V_ {1} = V_ {2} = V_ {3}. \]Второй принцип параллельной схемы состоит в том, что все токи, проходящие через каждый резистор, должны составлять общий ток в цепи:
\ [I = I_ {1} + I_ {2} + I_ {3}.\]Используя эти принципы и наши знания о том, как рассчитать эквивалентное сопротивление параллельных резисторов, мы можем теперь подойти к некоторым проблемам схемы, связанным с параллельными резисторами.
Рабочий пример 5: Закон Ома, параллельная цепь
Вычислите ток (I) в этой цепи, если оба резистора имеют омическую природу.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как подойти к проблеме
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома.Однако в цепи два резистора, и нам нужно найти полное сопротивление.
Найдите эквивалентное сопротивление в цепи
.Поскольку резисторы включены параллельно, общее (эквивалентное) сопротивление R составляет:
\ [\ frac {1} {R} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}}. \] \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {2 + 1} {4} \\ & = \ frac {3} {4} \\ \ text {Следовательно,} R & = \ text {1,33} \ Omega \ end {align *}Применить закон Ома
\ begin {align *} R & = \ frac {V} {I} \\ R \ cdot \ frac {I} {R} & = \ frac {V} {I} \ cdot \ frac {I} {R} \\ I & = \ frac {V} {R} \\ I & = V \ cdot \ frac {1} {R} \\ & = (12) \ left (\ frac {3} {4} \ right) \\ & = \ текст {9} \ текст {А} \ end {align *}Напишите окончательный ответ
В цепи протекает ток \ (\ text {9} \) \ (\ text {A} \).
Рабочий пример 6: Закон Ома, параллельная цепь
Два омических резистора (\ (R_1 \) и \ (R_2 \)) подключены параллельно ячейке. Найдите сопротивление \ (R_2 \), учитывая, что ток, протекающий через ячейку, равен \ (\ text {4,8} \) \ (\ text {A} \) и что напряжение на ячейке равно \ (\ текст {9} \) \ (\ text {V} \).
Определите, что требуется
Нам нужно рассчитать сопротивление \ (R_2 \).
Определите, как подойти к проблеме
Поскольку резисторы омические и нам даны напряжение на ячейке и ток в ячейке, мы можем использовать закон Ома, чтобы найти эквивалентное сопротивление в цепи.\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {\ text {4,8}} \\ & = \ text {1,875} \ \ Omega \ end {align *}
Рассчитайте значение для \ (R_2 \)
Поскольку мы знаем эквивалентное сопротивление и сопротивление \ (R_1 \), мы можем использовать формулу для параллельных резисторов, чтобы найти сопротивление \ (R_2 \). \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \ end {выровнять *} Переставляем решение для \ (R_2 \): \ begin {align *} \ frac {1} {R_2} & = \ frac {1} {R} — \ frac {1} {R_1} \\ & = \ frac {1} {\ text {1,875}} — \ frac {1} {3} \\ & = \ текст {0,2} \\ R_2 & = \ frac {1} {\ text {0,2}} \\ & = \ текст {5} \ \ Omega \ end {align *}
Напишите окончательный ответ
Сопротивление \ (R_2 \) равно \ (\ text {5} \) \ (\ Omega \)
Рабочий пример 7: Закон Ома, параллельная цепь
Ячейка на 18 В подключена к двум параллельным резисторам \ (\ text {4} \) \ (\ Omega \) и \ (\ text {12} \) \ (\ Omega \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов.
Сначала нарисуйте схему, прежде чем производить какие-либо вычисления
Определите, как подойти к проблеме
Нам нужно определить ток через ячейку и каждый из параллельных резисторов. Нам дана разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для расчета тока.
Рассчитать ток через ячейку
Чтобы рассчитать ток через элемент, нам сначала нужно определить эквивалентное сопротивление остальной части цепи.Резисторы включены параллельно и поэтому: \ begin {align *} \ frac {1} {R} & = \ frac {1} {R_1} + \ frac {1} {R_2} \\ & = \ frac {1} {4} + \ frac {1} {12} \\ & = \ frac {3 + 1} {12} \\ & = \ frac {4} {12} \\ R & = \ frac {12} {4} = \ text {3} \ \ Omega \ end {выровнять *} Теперь, используя закон Ома, чтобы найти ток через ячейку: \ begin {align *} R & = \ frac {V} {I} \\ I & = \ frac {V} {R} \\ & = \ frac {18} {3} \\ I & = \ text {6} \ text {A} \ end {align *}
Теперь определим ток через один из параллельных резисторов
.Мы знаем, что для чисто параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из параллельных резисторов.Для этой схемы: \ begin {align *} V & = V_1 = V_2 = \ text {18} \ text {V} \ end {выровнять *} Начнем с расчета тока через \ (R_1 \) по закону Ома: \ begin {align *} R_1 & = \ frac {V_1} {I_1} \\ I_1 & = \ frac {V_1} {R_1} \\ & = \ frac {18} {4} \\ I_1 & = \ text {4,5} \ text {A} \ end {align *}
Рассчитайте ток через другой параллельный резистор
Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_2 \): \ begin {align *} R_2 & = \ frac {V_2} {I_2} \\ I_2 & = \ frac {V_2} {R_2} \\ & = \ frac {18} {12} \\ I_2 & = \ text {1,5} \ text {A} \ end {выровнять *} Альтернативный метод вычисления \ (I_2 \) заключался бы в использовании того факта, что токи через каждый из параллельных резисторов должны складываться в общий ток через ячейку: \ begin {align *} I & = I_1 + I_2 \\ I_2 & = I — I_1 \\ & = 6 — 4.5 \\ I_2 & = \ text {1,5} \ text {A} \ end {align *}
Напишите окончательный ответ
Ток через ячейку равен \ (\ text {6} \) \ (\ text {A} \).
Ток через резистор \ (\ text {4} \) \ (\ Omega \) равен \ (\ text {4,5} \) \ (\ text {A} \).
Ток через резистор \ (\ text {12} \) \ (\ Omega \) равен \ (\ text {1,5} \) \ (\ text {A} \).
Закон Ома в последовательной и параллельной цепях
Упражнение 11.4Рассчитать номинал неизвестного резистора в цепи:
Сначала мы используем закон Ома для вычисления полного последовательного сопротивления:
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {9} {1} \\ & = \ текст {9} \ текст {Ω} \ end {выровнять *}Теперь мы можем найти неизвестное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} + R_ {4} \\ R_ {4} & = R_ {s} — R_ {1} — R_ {2} — R_ {3} \\ & = 9 — 3 — 3 — 1 \\ & = \ текст {2} \ текст {Ω} \ end {выровнять *}Рассчитайте значение тока в следующей цепи:
Сначала находим общее сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ text {1} + \ text {2,5} + \ text {1,5} \\ & = \ текст {5} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать ток:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {5} \\ & = \ текст {1,8} \ текст {А} \ end {выровнять *}Три резистора с сопротивлением \ (\ text {1} \) \ (\ text {Ω} \), \ (\ text {5} \) \ (\ text {Ω} \) и \ (\ text {10} \) \ (\ text {Ω} \) соответственно соединены последовательно с батареей \ (\ text {12} \) \ (\ text {V} \).Рассчитайте значение тока в цепи.
Рисуем принципиальную схему:
Теперь мы находим полное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {2} + R_ {3} \\ & = \ текст {1} + \ текст {5} + \ текст {10} \\ & = \ текст {16} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать ток:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {12} {16} \\ & = \ текст {0,75} \ текст {A} \ end {выровнять *}Рассчитайте ток через ячейку, если оба резистора имеют омическую природу.
Сначала находим общее сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {3}} \\ & = \ frac {3 + 1} {\ text {3}} \\ & = \ frac {4} {\ text {3}} \\ & = \ текст {0,75} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать ток:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {9} {\ text {0,75}} \\ & = \ текст {12} \ текст {А} \ end {выровнять *}Рассчитайте номинал неизвестного резистора \ (R_ {4} \) в цепи:
Сначала находим общее сопротивление:
\ begin {align *} R & = \ frac {V} {I} \\ & = \ frac {24} {\ text {2}} \\ & = \ текст {12} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать неизвестное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + \ гидроразрыв {1} {R_ {4}} \\ \ frac {1} {R_ {4}} & = \ frac {1} {R_ {p}} — \ frac {1} {R_ {1}} — \ frac {1} {R_ {2}} — \ гидроразрыв {1} {R_ {3}} \\ & = \ frac {1} {\ text {12}} — \ frac {1} {\ text {120}} — \ frac {1} {\ text {40}} — \ frac {1} {\ text { 60}} \\ & = \ frac {10 — 1 — 3 — 2} {\ text {120}} \\ & = \ frac {4} {\ text {120}} \\ & = \ текст {30} \ текст {Ω} \ end {выровнять *}значение тока через АКБ
Рисуем принципиальную схему:
Чтобы рассчитать значение тока через аккумулятор, нам сначала нужно рассчитать эквивалентное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {\ text {1}} + \ frac {1} {\ text {5}} + \ frac {1} {\ text {10}} \\ & = \ frac {10 + 2 + 1} {\ text {10}} \\ & = \ frac {13} {\ text {10}} \\ & = \ текст {0,77} \ текст {Ω} \ end {выровнять *}Теперь можем посчитать ток через батарею:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {0,77}} \\ & = \ текст {26} \ текст {А} \ end {выровнять *}значение тока в каждом из трех резисторов.
Для параллельной схемы напряжение на ячейке такое же, как напряжение на каждом из резисторов. Для этой схемы:
\ [V = V_ {1} = V_ {2} = V_ {3} = \ text {20} \ text {V} \]Теперь мы можем рассчитать ток через каждый резистор. Начнем с \ (R_ {1} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {1}} \\ & = \ текст {20} \ текст {А} \ end {выровнять *}Затем мы вычисляем ток через \ (R_ {2} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {5}} \\ & = \ текст {4} \ текст {А} \ end {выровнять *}И наконец вычисляем ток через \ (R_ {3} \):
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {20} {\ text {10}} \\ & = \ текст {2} \ текст {А} \ end {выровнять *}Вы можете проверить, что они в сумме составляют общий ток.
Последовательные и параллельные сети резисторов (ESBQC)
Теперь, когда вы знаете, как работать с простыми последовательными и параллельными цепями, вы готовы заняться цепями, которые объединяют эти две схемы, например, следующей цепью:
Рисунок 11.1: Пример последовательно-параллельной сети. Пунктирными прямоугольниками обозначены параллельные участки цепи.Проработать такие схемы относительно легко, потому что вы используете все, что вы уже узнали о последовательных и параллельных схемах.Единственная разница в том, что вы делаете это поэтапно. На рисунке 11.1 схема состоит из 2 параллельных частей, которые затем включены последовательно с ячейкой. Чтобы вычислить эквивалентное сопротивление для схемы, вы начинаете с вычисления общего сопротивления каждой из параллельных частей, а затем последовательно складываете эти сопротивления. Если бы все резисторы на рисунке 11.1 имели сопротивление \ (\ text {10} \) \ (\ text {Ω} \), мы можем вычислить эквивалентное сопротивление всей цепи.
Начнем с расчета общего сопротивления параллельной цепи 1 .{-1} \\ & = \ текст {5} \, \ Omega \ end {align *}
Теперь вы можете рассматривать схему как простую последовательную схему следующим образом:
Следовательно, эквивалентное сопротивление: \ begin {align *} R & = R_ {p1} + R_ {p2} \\ & = 5 + 5 \\ & = 10 \, \ Omega \ end {align *}
Эквивалентное сопротивление цепи на рисунке 11.1 равно \ (\ text {10} \) \ (\ text {Ω} \).
Последовательные и параллельные сети
Упражнение 11.5Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {4} + \ frac {1} {2} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {3} + R_ {p} \\ & = \ текст {2} + \ текст {1,33} \\ & = \ текст {3,33} \ текст {Ω} \ end {выровнять *}Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ & = \ frac {1} {1} + \ frac {1} {2} \\ & = \ frac {3} {2} \\ R_ {p} & = \ text {0,67} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с тремя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {3} + R_ {4} + R_ {p} \\ & = \ текст {4} + \ текст {6} + \ текст {0,67} \\ & = \ текст {10,67} \ текст {Ω} \ end {выровнять *}Начнем с определения эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}ток \ (I \) через ячейку.
Чтобы найти ток \ (I \), нам сначала нужно найти эквивалентное сопротивление. Начнем с расчета эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {3} + \ frac {1} {5} + \ frac {1} {1} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,652} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ & = \ текст {2} + \ текст {0,652} \\ & = \ текст {2,652} \ текст {Ω} \ end {выровнять *}Значит, ток через ячейку:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {12}} {\ text {2,652}} \\ & = \ текст {4,52} \ текст {А} \ end {выровнять *}ток через резистор \ (\ text {5} \) \ (\ text {Ω} \).
Ток через параллельную комбинацию резисторов равен \ (\ text {4,52} \) \ (\ text {A} \). (Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через параллельную комбинацию резисторов (не забудьте использовать эквивалентное параллельное сопротивление, а не эквивалентное сопротивление цепи):
\ begin {align *} V & = I \ cdot R \\ & = (\ text {4,52}) (\ text {0,652}) \\ & = \ текст {2,95} \ текст {V} \ end {выровнять *}Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторе \ (\ text {5} \) \ (\ text {Ω} \).
Итак, теперь мы можем рассчитать ток через резистор:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {2,95}} {\ text {5}} \\ & = \ текст {0,59} \ текст {А} \ end {выровнять *}Если ток, протекающий через ячейку, равен \ (\ text {2} \) \ (\ text {A} \), и все резисторы омические, рассчитайте напряжение на ячейке и на каждом из резисторов, \ (R_1 \ ), \ (R_2 \) и \ (R_3 \) соответственно.
Чтобы найти напряжение, нам сначала нужно найти эквивалентное сопротивление.Начнем с расчета эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {2} + \ frac {1} {4} \\ & = \ frac {3} {4} \\ R_ {p} & = \ text {1,33} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {p} \\ & = \ text {4,66} + \ text {1,33} \\ & = \ текст {5,99} \ текст {Ω} \ end {выровнять *}Итак, напряжение на ячейке:
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {5,99}) \\ & = \ текст {12} \ текст {V} \ end {выровнять *}Ток через параллельную комбинацию резисторов равен \ (\ text {2} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение на каждом из резисторов. Начнем с нахождения напряжения на \ (R_ {1} \):
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {4,66}) \\ & = \ текст {9,32} \ текст {V} \ end {выровнять *}Теперь находим напряжение на параллельной комбинации:
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2}) (\ текст {1,33}) \\ & = \ текст {2,66} \ текст {V} \ end {выровнять *}Поскольку напряжение на каждом резисторе в параллельной комбинации одинаково, это также напряжение на резисторах \ (R_ {2} \) и \ (R_ {3} \).
ток через ячейку
Чтобы найти ток, сначала нужно найти эквивалентное сопротивление. Начнем с расчета эквивалентного сопротивления параллельной комбинации:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {1} + \ frac {1} {1} \\ & = 2 \\ R_ {p} & = \ text {0,5} \ text {Ω} \ end {выровнять *}Теперь у нас есть цепь с двумя последовательно включенными резисторами, поэтому мы можем вычислить эквивалентное сопротивление:
\ begin {align *} R_ {s} & = R_ {1} + R_ {4} + R_ {p} \\ & = \ text {2} + \ text {1,5} + \ text {0,5} \\ & = \ текст {4} \ текст {Ω} \ end {выровнять *}Значит, ток через ячейку:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {10}} {\ text {4}} \\ & = \ текст {2,5} \ текст {А} \ end {выровнять *}падение напряжения на \ (R_4 \)
Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через \ (R_ {4} \):
\ begin {align *} V & = I \ cdot R \\ & = (\ текст {2,5}) (\ текст {1,5}) \\ & = \ текст {3,75} \ текст {V} \ end {выровнять *}ток через \ (R_2 \)
Ток через все резисторы равен \ (\ text {2,5} \) \ (\ text {A} \).(Ток одинаков при последовательном соединении резисторов, и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти ток через \ (R_ {2} \).
Сначала нам нужно найти напряжение на параллельной комбинации:
\ begin {align *} V & = I \ cdot R \\ & = (\ text {2,5}) (\ text {0,5}) \\ & = \ текст {1,25} \ текст {V} \ end {выровнять *}Теперь мы можем найти ток через \ (R_ {2} \), используя тот факт, что напряжение одинаково на всех резисторах в параллельной комбинации:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {1,25}} {\ text {1}} \\ & = \ текст {1,25} \ текст {А} \ end {выровнять *} ЗаконОм — обзор
8.2.2 Паразитная емкость
Закон Ома, как указано в формуле. (8.1) не выполняется, когда модель устройства включает реактивные (емкостные или индуктивные) компоненты и учитываются изменяющиеся во времени напряжения / токи. В таких случаях обобщенная форма закона Ома, показанная в формуле. (8.4) описывает взаимосвязь между напряжением и током через понятие электрического импеданса Z .
(8.4) V = ZIwithZ = R + jX
Электрический импеданс Z представлен комплексным числом, действительной частью которого является сопротивление R , как определено ранее, а мнимая часть X , называемое реактивным сопротивлением, учитывает реактивные эффекты.
Некоторые датчики несут информацию, относящуюся к измеряемой величине, как в резистивных, так и реактивных компонентах импеданса, поэтому интерфейсные схемы должны иметь возможность выполнять одновременную оценку R и X . С другой стороны, если полезная информация содержится только в резистивном компоненте, как это обычно бывает с резистивными датчиками, реактивный компонент считается паразитным элементом, влияние которого следует минимизировать.
При работе с резистивными датчиками обычно основной паразитный вклад имеет емкостный характер.В отличие от неидеальности большинства компонентов схемы, эти емкостные эффекты не могут быть компенсированы правильной калибровкой схемы, поскольку они зависят от конкретного датчика и условий эксплуатации. Если не принять во внимание надлежащим образом, такие эффекты могут вызвать ошибки в оценке сопротивления, как будет разъяснено в следующих разделах.
Одна из наиболее распространенных причин возникновения паразитных емкостных эффектов связана с производством датчиков. Если эффект обнаружения достигается определенными явлениями, происходящими на поверхности датчика (например,g., с фотодетекторами и датчиками газа), обычный способ улучшить чувствительность датчика — это максимизировать поверхностные эффекты путем реализации метода, основанного на встречно-штыревых электродах, показанном на рис. 8.3. К сожалению, эта структура приводит к увеличению паразитной емкости C ee между электродами, как показано на рис. 8.3, которая становится еще более заметной по мере повторения встречно-штыревой структуры (Polese et al., 2017).
Рисунок 8.3. Паразитно-емкостный эффект в датчиках с встречно-штыревыми электродами.
Другая ситуация, в которой появляются паразитные емкостные эффекты, характерна для газовых датчиков. Некоторым устройствам для обнаружения газа необходимо работать при гораздо более высокой температуре, чем температура окружающей среды, и по этой причине они обычно снабжены встроенной нитью накала R h , которая действует как нагреватель (Samà et al. , 2017). Нить накала нагревателя представляет собой проводник, реализованный на той же подложке чувствительного компонента R s и разделенный диэлектрическим материалом, который электрически изолирует два компонента датчика.Однако небольшой размер реализованных устройств заставляет эти два компонента взаимодействовать друг с другом из-за емкостных эффектов, как показано на рис. 8.4.
Рисунок 8.4. Паразитно-емкостный эффект в газовых сенсорах со встроенной нитью нагревателя.
В дополнение к этим возможным внутренним источникам емкостные эффекты могут возникать из-за внешних причин, таких как соединение между датчиком и измерительной системой, как показано на рис. 8.5. Фактически, разъемы и провода, используемые для соединения датчика с электронной схемой, демонстрируют распределенную емкостную характеристику C c , которая, с точки зрения приборов, наблюдается параллельно датчику.
Рисунок 8.5. Паразитно-емкостный эффект из-за связи датчика с измерительной системой.
Расчет общего емкостного паразитного эффекта далеко не прост и часто требует полного понимания характеристик датчика, в том числе на микроскопическом уровне. По этой причине, когда необходимо учитывать паразитную емкость, обычно рассматривается упрощенная модель датчика, в которой паразитный конденсатор C с представлен параллельно с сопротивлением датчика R с , с учетом всех возможных емкостных паразитных эффектов.





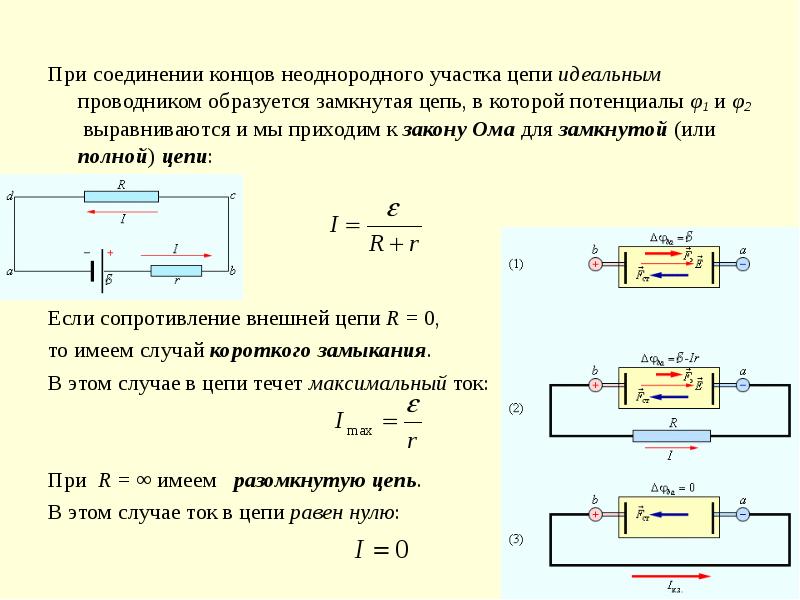 ..+Rn
..+Rn 1 А, U=(15 В* 5 Ом)/(5+1) Ом = 12.5 В
1 А, U=(15 В* 5 Ом)/(5+1) Ом = 12.5 В

 Изменится ли ток при прохождении через резистор? Объяснять.
Изменится ли ток при прохождении через резистор? Объяснять.