Закон Ома для замкнутой цепи
Закон Ома для замкнутой цепи показывает — значение тока в реальной цепи зависит не только от сопротивления нагрузки, но и от сопротивления источника.
Формулировка закона Ома для замкнутой цепи звучит следующим образом: величина тока в замкнутой цепи, состоящей из источника тока, обладающего внутренним и внешним нагрузочным сопротивлениями, равна отношению электродвижущей силы источника к сумме внутреннего и внешнего сопротивлений.
Впервые зависимость тока от сопротивлений была экспериментально установлена и описана Георгом Омом в 1826 году.
Формула закона Ома для замкнутой цепи записывается в следующем виде:

где:
- I [А] – сила тока в цепи,
- ε [В] – ЭДС источника напряжения,
- R [Ом] – сопротивление всех внешних элементов цепи,
- r [Ом] – внутреннее сопротивление источника напряжения
Физический смысл закона
Потребители электрического тока вместе с источником тока образуют замкнутую электрическую цепь. Ток, проходящий через потребитель, проходит и через источник тока, а значит, току кроме сопротивления проводника оказывается сопротивление самого источника. Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника.
Физический смысл зависимости тока от ЭДС источника и сопротивления цепи заключается в том, что чем больше ЭДС, тем больше энергия носителей зарядов, а значит больше скорость их упорядоченного движения. При увеличении сопротивления цепи энергия и скорость движения носителей зарядов, следовательно, и величина тока уменьшаются.

Зависимость можно показать на опыте. Рассмотрим цепь, состоящую из источника, реостата и амперметра. После включения в цепи идет ток, наблюдаемый по амперметру, двигая ползунок реостата, увидим, что при изменении внешнего сопротивления ток будет меняться.
Примеры задач на применение закона Ома для замкнутой цепи
К источнику ЭДС 10 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 4 Ом. Найти силу тока в цепи и напряжение на зажимах источника.
| Дано: | Решение: |
|---|---|
|
|
При подключении к батарее гальванических элементов резистора сопротивлением 20 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 10 Ом сила тока стала 1,5 А. Найти ЭДС и внутреннее сопротивление батареи.
| Дано: | Решение: |
|---|---|
|
|
Закон Ома для участка и полной замкнутой цепи
В
1826 г. немецкий ученый Георг Ом
экспериментально установил прямую
пропорциональную зависимость между
силой тока I
в проводнике и напряжением U
на его концах: 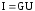 ,
гдеG
— электрическая
проводимость проводника.
Величина, обратная проводимости
называется электрическим
сопротивлением проводника R.
Таким образом, закон
Ома для участка цепи, не содержащего
источника э.д.с.
,
гдеG
— электрическая
проводимость проводника.
Величина, обратная проводимости
называется электрическим
сопротивлением проводника R.
Таким образом, закон
Ома для участка цепи, не содержащего
источника э.д.с.
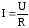 . Учитывая,
что в общем случае участок цепи может
содержать и э.д.с.,закон
Ома следует
представить в виде
. Учитывая,
что в общем случае участок цепи может
содержать и э.д.с.,закон
Ома следует
представить в виде 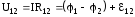 .
. Сопротивление
проводника зависит от его размеров,
формы и материала, из которого он
изготовлен. Для однородного линейного
проводника 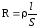 ,
гдеl — длина, S
— площадь поперечного сечения проводника,
— удельное электрическое
сопротивление, зависящее от материала,
из которого изготовлен проводник.
Единица сопротивления 1 Ом — это
сопротивление такого проводника, в
котором при напряжении 1В течет ток в
1А.
,
гдеl — длина, S
— площадь поперечного сечения проводника,
— удельное электрическое
сопротивление, зависящее от материала,
из которого изготовлен проводник.
Единица сопротивления 1 Ом — это
сопротивление такого проводника, в
котором при напряжении 1В течет ток в
1А.
Если
цепь замкнута, то  ,
, ,
гдеR
— общее сопротивление всей цепи, включая
сопротивление источника э.д.с. Тогда закон Ома
для замкнутой цепи следует записать
,
гдеR
— общее сопротивление всей цепи, включая
сопротивление источника э.д.с. Тогда закон Ома
для замкнутой цепи следует записать  ,
где
— алгебраическая сумма всех э.д.с.,
имеющихся в этой цепи.
,
где
— алгебраическая сумма всех э.д.с.,
имеющихся в этой цепи.
Принято называть сопротивление источника тока r —
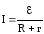 .
В системе единиц СИ напряжение и э.д.с.
измеряются в Вольтах (В), сопротивление
— в Омах (Ом), удельное электрическое
сопротивление — в Ом-метрах (Омм),
электрическая проводимость в Сименсах (См).
.
В системе единиц СИ напряжение и э.д.с.
измеряются в Вольтах (В), сопротивление
— в Омах (Ом), удельное электрическое
сопротивление — в Ом-метрах (Омм),
электрическая проводимость в Сименсах (См). 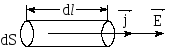
Рис.2.1. Отрезок проводника.
Закон Ома можно записать и для плотности тока. Рассмотрим участок электрической длиной d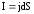 ,
сопротивление
,
сопротивление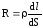 ,
падение напряжения
,
падение напряжения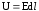 ,
где Е — напряженность электрического
поля в проводнике. Подставив эти
параметры в закон Ома для участка цепи,
получим
,
где Е — напряженность электрического
поля в проводнике. Подставив эти
параметры в закон Ома для участка цепи,
получим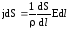 .
Отсюда
.
Отсюда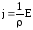 или
или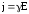
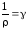 —удельная электрическая
проводимость проводника или удельная электропроводность.
В векторном виде имеем
—удельная электрическая
проводимость проводника или удельная электропроводность.
В векторном виде имеем 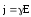 (единицей измерения
в системе СИ является сименс на метр
(См/м)). Полученное выражение есть закон
Ома в дифференциальной форме : плотность
тока в любой точке внутри проводника
прямо пропорциональна напряженности
поля в этой точке.
(единицей измерения
в системе СИ является сименс на метр
(См/м)). Полученное выражение есть закон
Ома в дифференциальной форме : плотность
тока в любой точке внутри проводника
прямо пропорциональна напряженности
поля в этой точке.1.14 Сопротивление проводника. Явление сверхпроводимости.
Способность
вещества проводить ток характеризуется
его удельной
проводимостью ,
либо удельным
сопротивлением .
Их величина определяется химической
природой проводника и условиями, в
частности температурой, при которой он
находится. Для большинства металлов
растет с температурой приблизительно
по линейному закону: 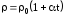 ,
,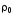 — удельное сопротивление при 0С,
t
— температура по шкале Цельсия,
— температурный коэффициент
сопротивления близкий к 1/273 К-1
— удельное сопротивление при 0С,
t
— температура по шкале Цельсия,
— температурный коэффициент
сопротивления близкий к 1/273 К-1
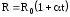 ,
где
,
где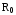 — сопротивление при 0С.
Преобразовав две последние формулы,
можно записать
— сопротивление при 0С.
Преобразовав две последние формулы,
можно записать 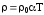 и
и ,
где Т – температура по Кельвину. На
основе температурной зависимости
сопротивления металлов созданытермометры
сопротивления — термисторы,
позволяющие определять температуру с
точностью до 0.003 К.
,
где Т – температура по Кельвину. На
основе температурной зависимости
сопротивления металлов созданытермометры
сопротивления — термисторы,
позволяющие определять температуру с
точностью до 0.003 К. При
низких температурах нарушается линейность
зависимости сопротивления металлов от
температуры и при температуре 0 К
наблюдается остаточное сопротивление
R
Кроме этого, в 1911 г. Г.Каммерлинг-Оннес обнаружил, что при Тк = 4.1К сопротивление ртути скачкообразно уменьшается практически до нуля. Эта температура была названа критической, а наблюдаемое явление — сверхпроводимостью. Впоследствии этот эффект был обнаружен у целого ряда других металлов (Ti, A
1.15 Работа и мощность тока, закон Джоуля-Ленца.
Определим
работу, совершаемую постоянным током
в проводнике, имеющем сопротивление R
и находящемся под напряжением 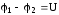 .
Так как ток представляет собой
перемещение зарядаq
под действием поля, то работу тока можно
определить по формуле
.
Так как ток представляет собой
перемещение зарядаq
под действием поля, то работу тока можно
определить по формуле 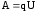 .
Учитывая формулу
.
Учитывая формулу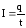 и закон Ома, получим
и закон Ома, получим ,
или
,
или ,
или
,
или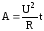 ,
гдеt
— время протекания тока. Поделив обе
части равенства на t,
получим выражения для мощности постоянного тока N
,
гдеt
— время протекания тока. Поделив обе
части равенства на t,
получим выражения для мощности постоянного тока N
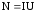 ,
,  ,
,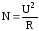 .
Работа тока в системе единиц СИ измеряется
в доулях (Дж), а мощность — в ваттах (Вт).
На практике применяются также внесистемные
единицы работы тока: ватт-час (Втч)
и киловатт-час (кВтч).
1Втч
— работа тока мощностью 1Вт в течение
одного часа. 1Втч=3.6103 Дж.
.
Работа тока в системе единиц СИ измеряется
в доулях (Дж), а мощность — в ваттах (Вт).
На практике применяются также внесистемные
единицы работы тока: ватт-час (Втч)
и киловатт-час (кВтч).
1Втч
— работа тока мощностью 1Вт в течение
одного часа. 1Втч=3.6103 Дж.
Опыт
показывает, что ток всегда вызывает
некоторое нагревание проводника.
Нагревание обусловлено тем, что
кинетическая энергия движущихся по
проводнику электронов (т.е. энергия
тока) при каждом их столкновении с ионами
металлической решетки переходит в
теплоту Q.
Если ток идет по неподвижному
металлическому проводнику, то вся
работа тока расходуется на его нагревание
и, следуя закону сохранения энергии,
можно записать  .
Данные соотношения выражаютзакон
Джоуля-Ленца.
Впервые этот закон был установлен
опытным путем Д.Джоулем в 1843 г. и независимо
от него Э.Ленцем в 1844 г. Применение
теплового действия тока в технике
началось с открытия в 1873 г. русским
инженером А.Ладыгиным лампы
накаливания.
.
Данные соотношения выражаютзакон
Джоуля-Ленца.
Впервые этот закон был установлен
опытным путем Д.Джоулем в 1843 г. и независимо
от него Э.Ленцем в 1844 г. Применение
теплового действия тока в технике
началось с открытия в 1873 г. русским
инженером А.Ладыгиным лампы
накаливания.
На тепловом действии тока основан целый ряд электрических приборов и установок: тепловые электроизмерительные приборы, электропечи, электросварочная аппаратура, бытовые электронагревательные приборы — чайники, кипятильники, утюги. В пищевой промышленности широко применяется метод электроконтактного нагрева, заключающийся в том, что электрический ток, проходя через продукт, обладающий определенным сопротивлением, вызывает его равномерное нагревание. Например, для производства колбасных изделий через дозатор фарш поступает в формы, торцевые стенки которых служат электродами. При такой обработке обеспечивается равномерность нагрева по всему объему продукта, возможность поддержания определенного температурного режима, наивысшая биологическая ценность изделия, наименьшие длительность процесса и расход энергии.
Определим удельную
тепловую мощность тока ,
т.е. количество теплоты, выделяющееся
в единице объема за единицу времени.
Выделим в проводнике элементарный
цилиндрический объем dV
с поперечным сечением dS
и длиной dl параллельной направлению тока, и
сопротивлением 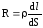 ,
,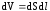 .
По закону Джоуля-Ленца, за времяdt
в этом объеме выделится теплота
.
По закону Джоуля-Ленца, за времяdt
в этом объеме выделится теплота 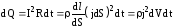 .
Тогда
.
Тогда и,
используя закон Ома для плотности тока
и,
используя закон Ома для плотности тока и соотношение
и соотношение ,
получим
,
получим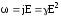 .
Эти соотношения выражаютзакон
Джоуля-Ленца в дифференциальной форме.
.
Эти соотношения выражаютзакон
Джоуля-Ленца в дифференциальной форме.
1.16. Правило Кирхгофа для разветвленных электрических цепей.
До сих пор нами рассматривались простейшие электрические цепи, состоящие из одного замкнутого неразветвленного контура. На всех его участках силы тока одинаковы. Расчет I, R, в такой цепи выполняется с помощью законов Ома.

Рис.2.2.Разветвленная электрическая цепь.
Более сложной является разветвленная электрическая цепь, состоящая из нескольких замкнутых контуров, имеющих общие участки. В каждом контуре может быть несколько источников тока. Силы тока на отдельных участках замкнутого контура могут быть различными по величине и направлению (рис.2.2). В 1847 г. Г.Кирхгоф сформулировал два правила, значительно упрощающих расчет разветвленных цепей. Первое
правило Кирхгофа: алгебраическая
сумма сил токов в узле равна нулю: 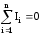 .Узел — точка цепи, в которой сходятся не менее
трех проводников. В электрической
цепи на рис.2.2 имеются два узла А и В.
Ток, входящий в узел, считается
положительным, выходящий — отрицательным.
Например, для узла А первое правило
Кирхгофа следует записать
.Узел — точка цепи, в которой сходятся не менее
трех проводников. В электрической
цепи на рис.2.2 имеются два узла А и В.
Ток, входящий в узел, считается
положительным, выходящий — отрицательным.
Например, для узла А первое правило
Кирхгофа следует записать 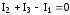 .
.
Первое правило выражает закон сохранения электрического заряда, так как ни в одной точке цепи они не могут возникать или исчезать.
Второе
правило Кирхгофа относится к любому замкнутому контуру,
выделенному в разветвленной цепи: алгебраическая
сумма произведений токов на сопротивления,
включая и внутренние, на всех участках
замкнутого контура равна алгебраической
сумме электродвижущих сил, встречающихся
в этом контуре 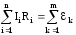 .
Контур ‑ это замкнутый участок
схемы, по которому можно пройти и
вернуться в исходную точку. Второе
правило Кирхгофа получается из закона
Ома, записанного для всех участков от
узла до узла (ветвей) разветвленной
схемы. В электрической цепи на рис.2.2
имеются три контура:AMNBA,
CABDC,
CMNDC.
При этом, токи Ii в ветвях контура, совпадающие с произвольно
выбранным направлением обхода
контура, считаются положительными, а
направленные навстречу обхода —
отрицательными. Э.д.с., проходимые от
«+» к «-» считаются положительными и
наоборот. В рассматриваемой электрической
цепи (рис.2.2) выберем обход контуров по
часовой стрелке и запишем для них
уравнения по II
правилу Кирхгофа: для AMNBА
.
Контур ‑ это замкнутый участок
схемы, по которому можно пройти и
вернуться в исходную точку. Второе
правило Кирхгофа получается из закона
Ома, записанного для всех участков от
узла до узла (ветвей) разветвленной
схемы. В электрической цепи на рис.2.2
имеются три контура:AMNBA,
CABDC,
CMNDC.
При этом, токи Ii в ветвях контура, совпадающие с произвольно
выбранным направлением обхода
контура, считаются положительными, а
направленные навстречу обхода —
отрицательными. Э.д.с., проходимые от
«+» к «-» считаются положительными и
наоборот. В рассматриваемой электрической
цепи (рис.2.2) выберем обход контуров по
часовой стрелке и запишем для них
уравнения по II
правилу Кирхгофа: для AMNBА  ;
дляCABDС
;
дляCABDС 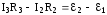 ;
дляCMNDС
;
дляCMNDС 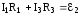 .
В данном примере внутренними сопротивлениями
источников тока пренебрегаем. Первое
и второе правила Кирхгофа позволяют
составить систему линейных алгебраических
уравнений, которые связывают параметры
(I,
R,
.
В данном примере внутренними сопротивлениями
источников тока пренебрегаем. Первое
и второе правила Кирхгофа позволяют
составить систему линейных алгебраических
уравнений, которые связывают параметры
(I,
R, 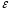 )
и позволяют, зная одни, найти другие.
)
и позволяют, зная одни, найти другие.
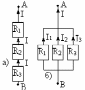
Рис.2.3. а) Последовательное соединение сопротивлений; б) Параллельное соединение сопротивлений.
Простые электрические цепи имеют очень большое практическое применение. В повседневной жизни полезно знать, как подключить динамики или проигрыватель к стереосистеме, как подсоединить сигнализацию для охраны или автомобильный кассетный проигрыватель, как зарядить аккумуляторы или осветить новогоднюю елку. Большинство
электрических цепей содержит комбинацию
последовательно или параллельно
подключенных резисторов (резистор — это
элемент цепи, обладающий только
сопротивлением). Полное сопротивление
участка цепи определяется отношением
падения напряжения на нем к величине
силы тока 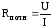 .
При последовательном соединении
(рис.2.3 а) через все резисторы течет
один и тот же ток. При параллельном
соединении (рис.2.3 б) полный ток равен
сумме токов, текущих в отдельных
резисторах.
.
При последовательном соединении
(рис.2.3 а) через все резисторы течет
один и тот же ток. При параллельном
соединении (рис.2.3 б) полный ток равен
сумме токов, текущих в отдельных
резисторах.
При
последовательном соединении падение
напряжения на участке АВ равно 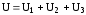 ,
т.е. сумме падений напряжения на трех
резисторах. Разделим обе части равенства
наI
и получим
,
т.е. сумме падений напряжения на трех
резисторах. Разделим обе части равенства
наI
и получим 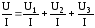 ,
т.е.
,
т.е.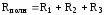 .
Таким образом, полное сопротивление
участка цепи, состоящего из последовательно
соединенных резисторов, равно их
алгебраической сумме
.
Таким образом, полное сопротивление
участка цепи, состоящего из последовательно
соединенных резисторов, равно их
алгебраической сумме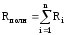 .
.
При
параллельном соединении (рис..2.3 б)
мы имеем 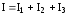 .
Разделим обе части равенства наU,
где U
— падение напряжения на участке цепи
АВ, причем
.
Разделим обе части равенства наU,
где U
— падение напряжения на участке цепи
АВ, причем 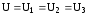 ,
и получим
,
и получим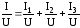 .
Из этого равенства следует
.
Из этого равенства следует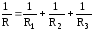 .
Величина обратная полному сопротивлению
параллельно соединенных резисторов
равна алгебраической сумме величин их
обратных сопротивлений
.
Величина обратная полному сопротивлению
параллельно соединенных резисторов
равна алгебраической сумме величин их
обратных сопротивлений .
.
В электрическую цепь может быть включено регулируемое (изменяющееся с помощью специального движка), сопротивление, которое называется реостатом. По назначению реостаты делятся на пусковые, служащие для ограничения силы тока во время пуска двигателей, и регулирующие — для регулировки силы тока в цепи (постепенное снижение освещенности в театральных залах), регулировки скорости вращения электродвигателей и т.д. Реостат может быть использован в качестве так называемого датчика перемещения. В автоматических регуляторах уровня жидкости в резервуарах применяется поплавково-реостатный датчик. Специальный поплавок крепится к движку реостата. Изменение уровня жидкости сдвигает поплавок, изменяет сопротивление реостата, и следовательно, силы тока в цепи, величина которого дает информацию об уровне.
Закон Ома для замкнутой цепи
 Закон Ома для замкнутой цепи часто находит применение в работе с электричеством. Благодаря закономерности, найденной немецким физиком Георгом Омом, сегодня мы можем рассчитать величину тока, протекающего в проводе или необходимую толщину провода для подключения к сети.
Закон Ома для замкнутой цепи часто находит применение в работе с электричеством. Благодаря закономерности, найденной немецким физиком Георгом Омом, сегодня мы можем рассчитать величину тока, протекающего в проводе или необходимую толщину провода для подключения к сети.
История открытия
Будущий ученый с малых лет интересовался природой электрического тока. Он провел множество испытаний, связанных с измерением напряжения и силы тока. Ввиду несовершенства измерительных приборов того времени, первые результаты исследований были ошибочны и препятствовали дальнейшему развитию вопроса. Георг опубликовал первую научную работу, в которой описывал возможную связь между напряжением и силой тока. Последующие его работы подтвердили предположения, и Ом сформулировал свой знаменитый закон. Все труды были внесены в доклад 1826 года, но научное сообщество не заметило труды молодого физика.
Через пять лет, когда известный французский учёный Пулье пришел к такому же выводу, Георга Ома наградили медалью Копли, за внесение большого вклада в развитии физика как науки.
Сегодня закон Ома используется по всему миру, признанный истинным законом природы. .
Детальное описание
Закон Георга показывает значение электричества в определенной сети, имеющее зависимость от сопротивления к нагрузке и внутренним элементам источника питания. Рассмотрим это детально.
Условное устройство, использующее электроэнергию (например, звуковой динамик) при подключении к источнику питания образует замкнутую цепь (рисунок 1). Подсоединим динамик к аккумулятору. Следующий через динамик ток тоже следует через источник питания. Поток заряженных частиц встретит сопротивление провода и внутренней электроники устройства, а также сопротивление аккумулятора (электролит внутри банки оказывает определенное воздействие на электрический ток). Исходя из этого, значение сопротивления закрытой сети складывается из сопротивления:
- Источника питания;
- Электрического устройства.

Подключение условного электрического прибора (динамика) к источнику питания (автомобильному аккумулятору)
Первый параметр называют внутренним, второй – внешним сопротивлением. Противодействие источника электричества маркируется символом r.
Представим, что по сети источник питания/электрическое устройство проходит определённый ток T. Для сохранения стабильного значения электричества внешней сети, в соответствии с законом, на её окончаниях должна наблюдаться потенциальная разность, которая равна R*T. Ток такой же величины проходит и внутри цепи. Вследствие этого – сохранение постоянного значения электричества внутри сети требует потенциальной разности на окончаниях сопротивления r. Она, согласно закону, должна равняться T*r. При сохранении стабильного тока в сети, значение электродвижущей силы равно:
E=T*r+T*R
Из формулы следует, что ЭДС равна сумме падения напряжений во внутренней и внешней сети. Если вынести значение T за скобки, получим:
Е=T(r+R)
или
T=E/(r+R)
Примеры задач на применение закона для соединенной сети
1) К источнику ЭДС 15 В и сопротивлением 2 Ом подсоединен реостат с сопротивлением 5 Ом. Задача – вычислить силу тока и напряжение на зажимах.
Вычисление
- Представим закон Ома для соединенной сети: T=E/(r+R).
- Снижение напряжения вычислим по формуле: U= E-Tr=ER/(R+r).
- Подставим имеющиеся значения в формулу: T= (15 В)/((5+2) Ом) = 2.1 А, U=(15 В* 5 Ом)/(5+1) Ом = 12.5 В
Ответ: 2.1 А, 12.5 В.
2) При подсоединении к гальваническим элементам резистора с сопротивлением 30 Ом, сила тока в сети приняла значение в 1.5 А, а при подсоединении такого же элемента с сопротивлением 15 Ом сила тока стала 2.5 А. Задача – узнать значение ЭДС и внутреннее сопротивление цепи из гальванических элементов.
Вычисление
- Запишем закон Георга Ома для соединённой сети: T=E/(r+R).
- Из него выведем формулы для внутреннего и внешнего сопротивления: E=T_1 R_1+T_1 r, E= T_2 R_2 + T 2r.
- Приравняем части формулы и вычислим внутреннее сопротивление: r=(T_1 R_1-T_2 R_2)/(T_2-T_1 ).
- Полученные значения подставим в закон: E=(T_1 T_2 (R_2-R_1))/(T_2-T_1 ).
- Проведем вычисления: r=(1.5 А∙30 Ом-2.5А∙15 Ом)/(2,5-1,5)А=7.5 Ом, E=(1.5 А∙2.5А(30-15)Ом)/((2.5-1.5)А)=56 В.
Ответ: 7.5 Ом, 56 В.
Сфера применения закона Ома для замкнутой цепи
Закон Ома – универсальный инструмент электрика. Он позволяет правильно рассчитать силу тока и напряжение в сети. В основе принципа работы некоторых устройств лежит закон Ома. В частности, предохранителей короткого замыкания.
Короткое замыкание – случайное замыкание двух участков сети, не предусмотренное конструкцией оборудования и приводящее к неисправностям. Для предотвращения таких явлений используют специальные устройства, отключающие питание сети.
Если произойдет случайное замыкание цепи с большой перегрузкой, устройство автоматически прекратит подачу тока.
Закон Ома в данном случае находит место на участке цепи постоянного тока. В полной схеме процессов может быть гораздо больше. Многие действия при построении электрической сети или ее ремонте следует проводить с учетом закона Георга Ома.
Для полного изучения соотношения параметров тока в проводниках представлены формулы: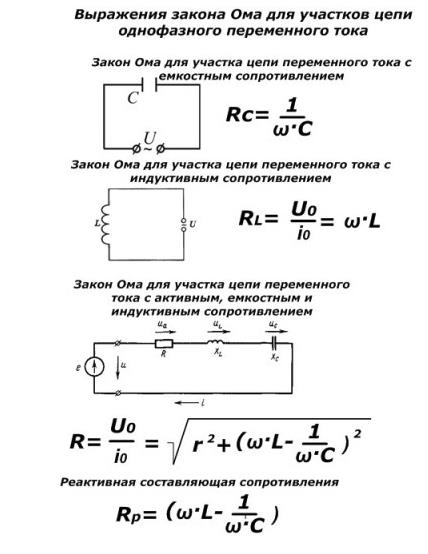
Более сложное выражение закона для практического применения: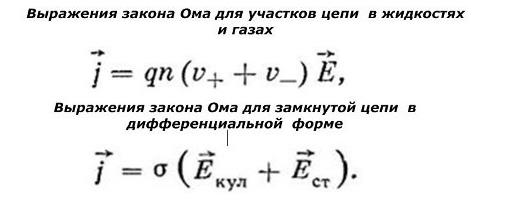
Сопротивление представлено отношением напряжения к силе тока в цепи. Если напряжение увеличить в n раз, значение тока также увеличится в n раз.
Не менее известны в электротехнике труды Густава Киргофа. Его правила находят применения в расчетах разветвленных сетей. В основе этих правил лежит закон Ома для электрической цепи.
Труды ученого нашли применение при изобретении многих повседневных вещей, таких как лампы накаливания и электрические плиты. Современные достижения в электронике многим обязаны открытиям 1825 года.
Поделиться ссылкой:
Похожее
согласованный, рабочий, холостого хода, короткого замыкания.
Закон Ома справедлив для всех значений.
Закон Ома для участка цепи:
 — для мгновенных значений
— для мгновенных значений
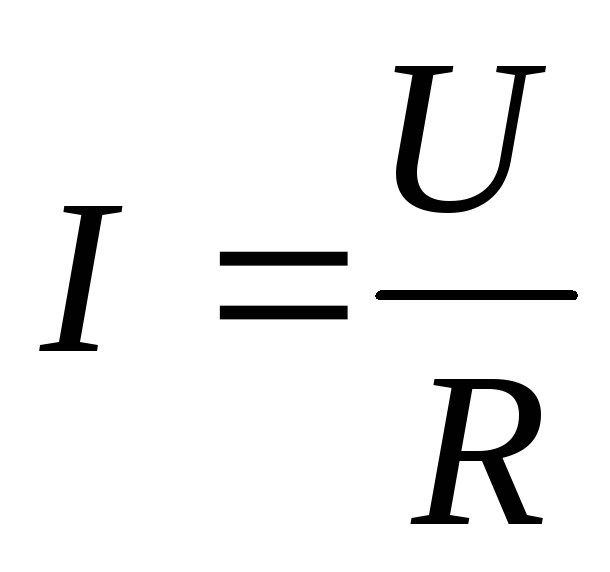 — для действующих значений
— для действующих значений
 — для максимальных значений
— для максимальных значений
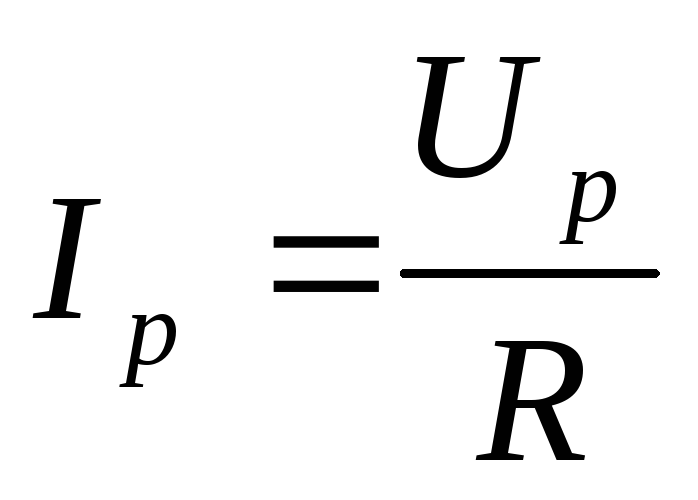 — для размаха
— для размаха
Закон Ома для замкнутой цепи:
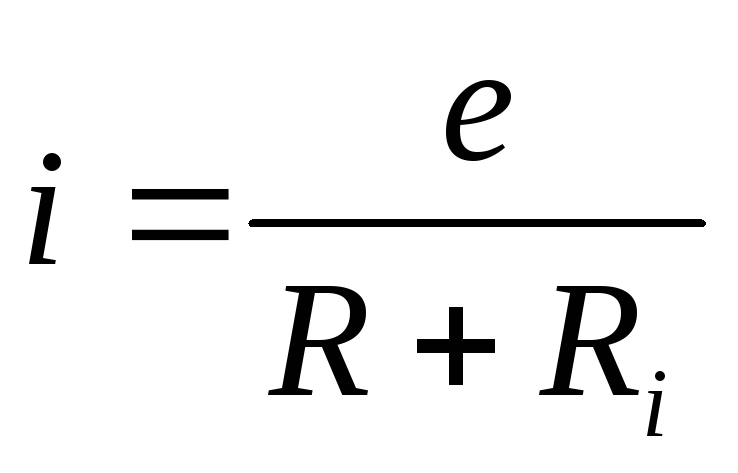
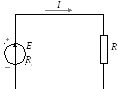 — для мгновенных значений
— для мгновенных значений
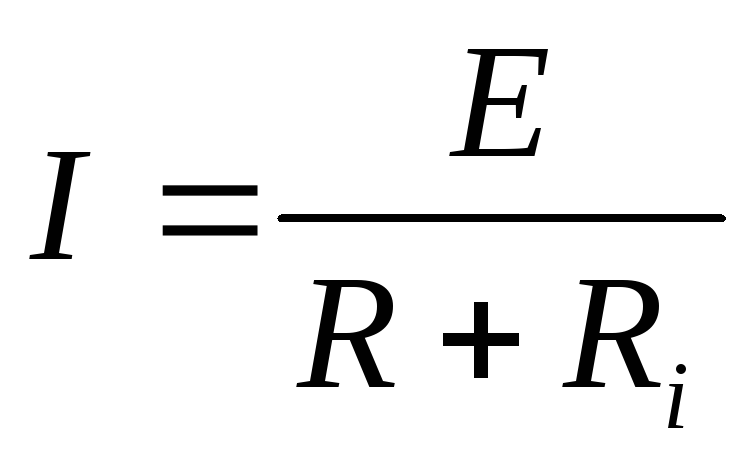 — для действующих значений
— для действующих значений
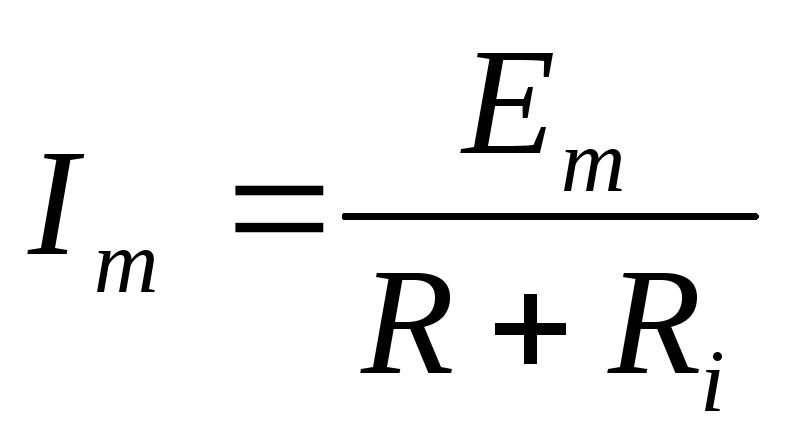 — для максимальных значений
— для максимальных значений
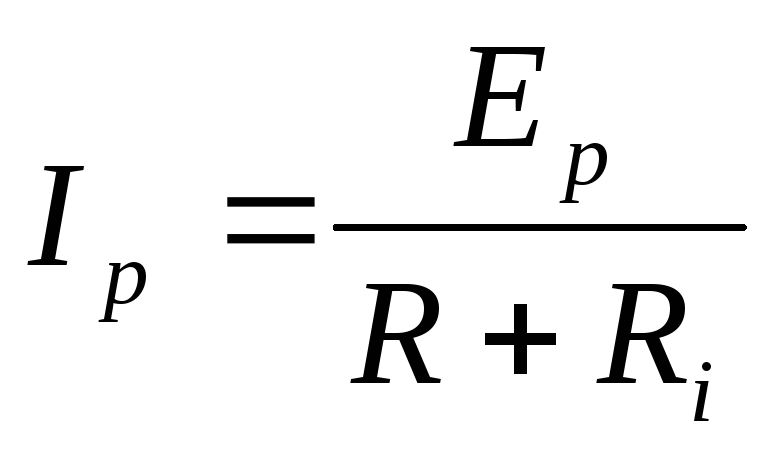 — для размаха
— для размаха
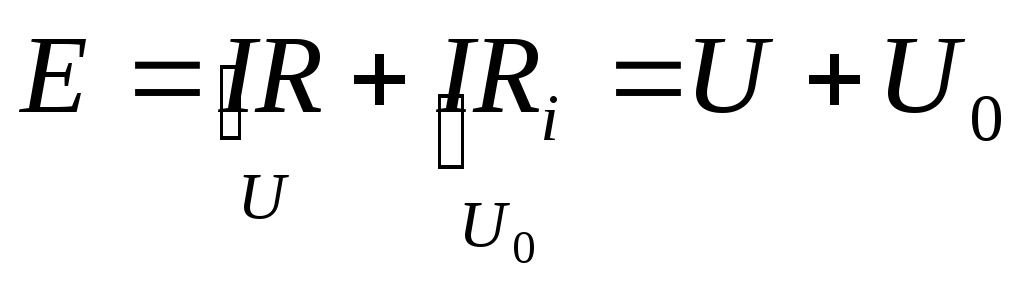 ,
,
где  — напряжение на зажимах источника,
— напряжение на зажимах источника,
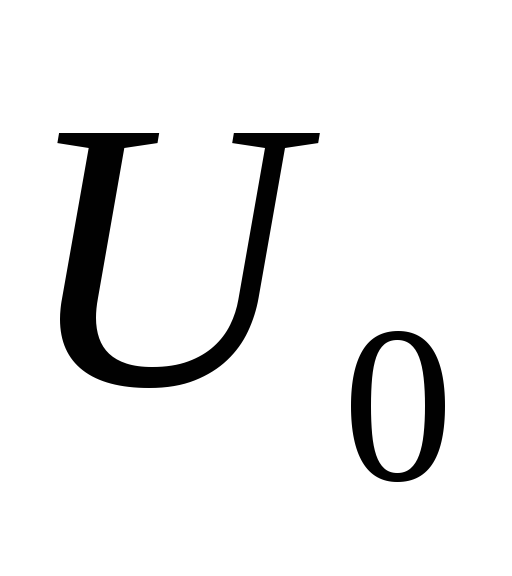 — внутренне падение напряжение
источника.
— внутренне падение напряжение
источника.
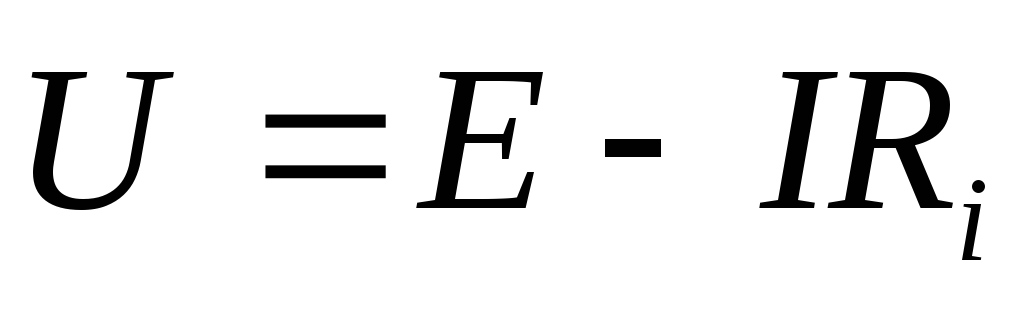
Напряжение на зажимах источника меньше ЭДС на величину внутреннего падения напряжения.
Чтобы измерить ЭДС источника, надо на его зажимы включить вольтметр, а внешнюю цепь разомкнуть:

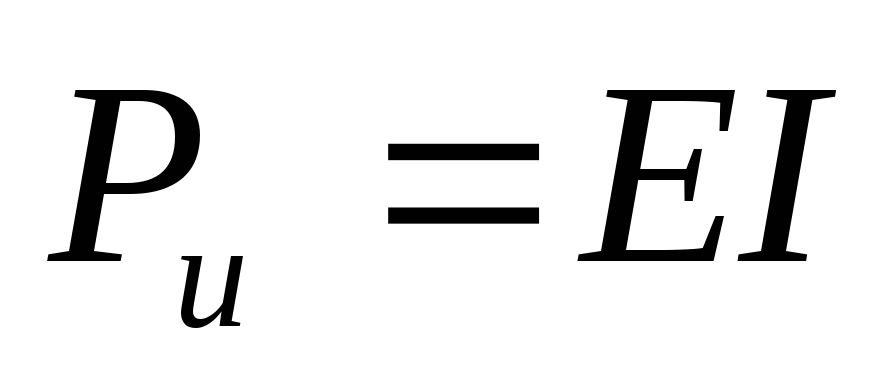 — мощность источника
— мощность источника
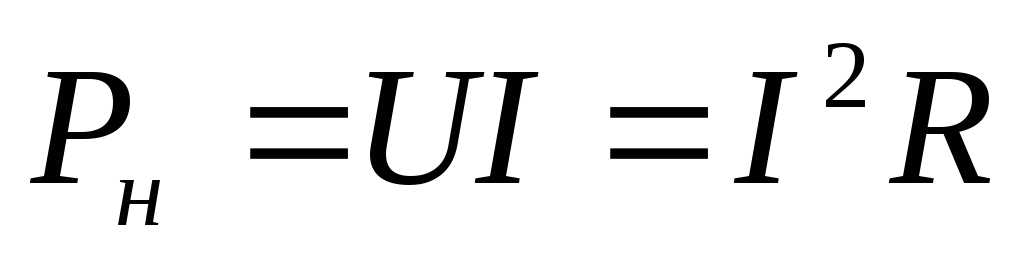 — мощность нагрузки
— мощность нагрузки
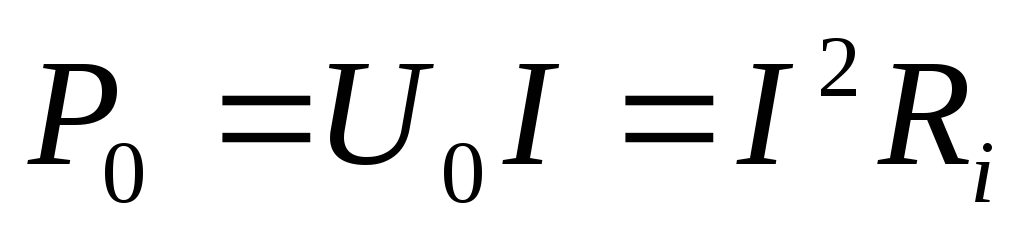 — мощность потерь внутри источника
— мощность потерь внутри источника
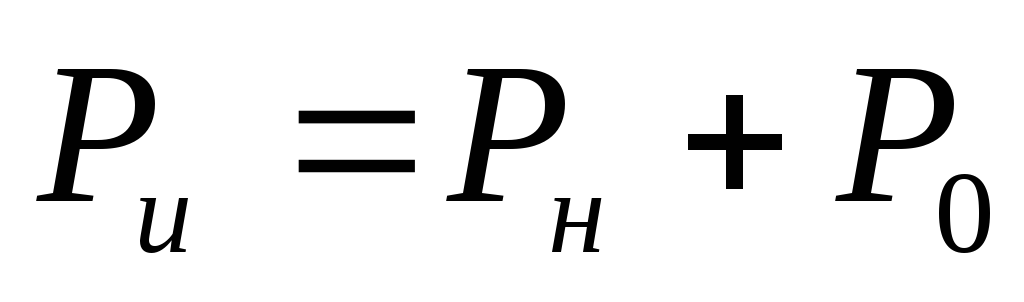 —уравнение баланса мощностей
—уравнение баланса мощностей
КПД источника:

Режимы работы источника:
Режим холостого хода(ХХ):

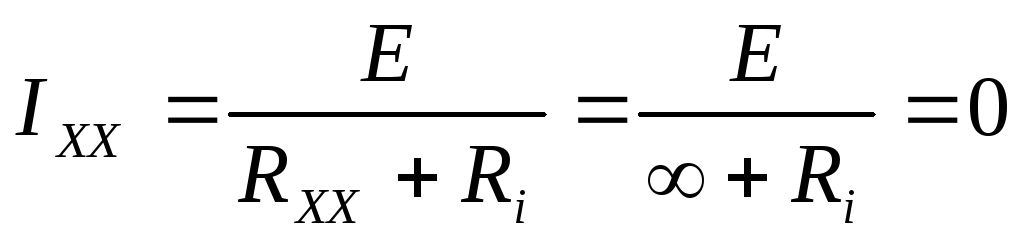
Чтобы получить режим холостого хода, надо цепь разомкнуть.
Короткое замыкание(КЗ):
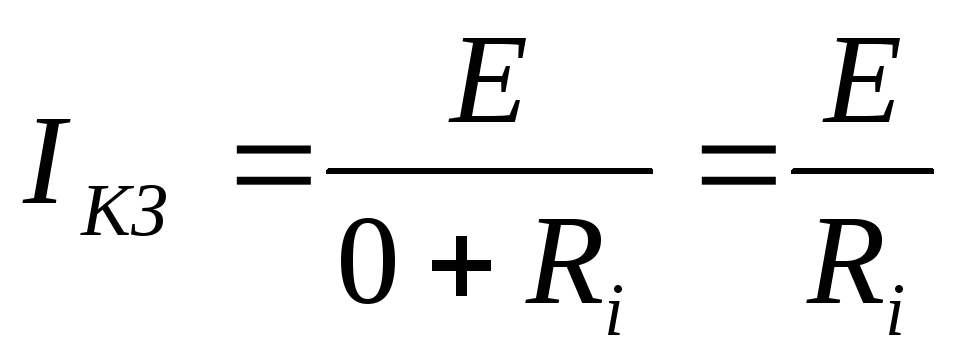 — максимум тока
— максимум тока
Чтобы получить режим КЗ, нужно цепь перемкнуть проводом:

Согласованный режим— сопротивление нагрузки равно внутреннему сопротивлению источника:


Рабочий (реальный) режим
Вопрос 13. Последовательное и параллельное соединения резисторов. Входное сопротивление и свойства цепей данных соединений. Последовательное соединение источников ЭДС.
Последовательное соединение резисторов
Последовательным называется такое соединение, когда элементы соединяются один вслед за другим, без разветвлений:
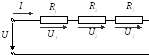
Свойства последовательного соединения:
Ток на всех участках цепи одинаковый
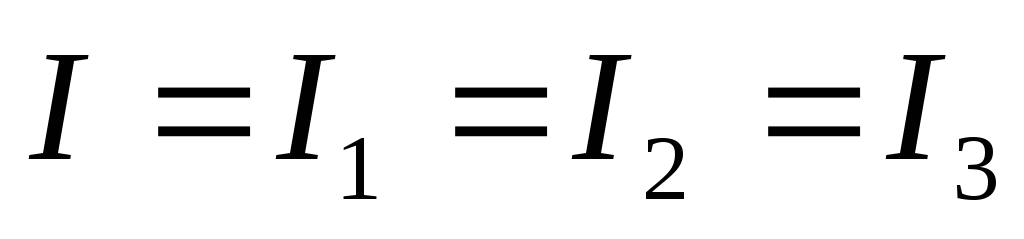
Общее напряжение равно сумме напряжений на отдельных участках
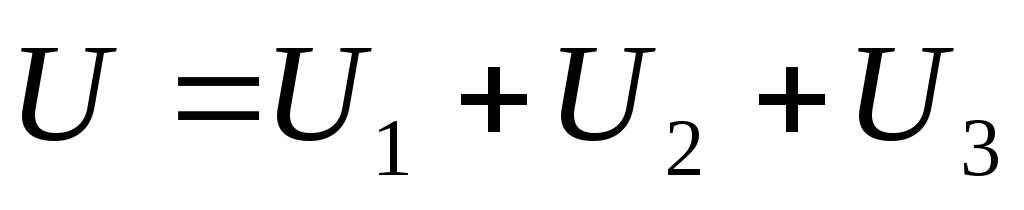
Сопротивление по отношению к входным зажимам называется входным.
Входное сопротивление равно сумме сопротивлений участков
Напряжение участков прямо пропорционально сопротивлению

Если последовательно соединяются несколько источников напряжения, то общая ЭДС равна сумме ЭДС отдельных источников, а общее внутреннее сопротивление — сумме внутренних сопротивлений источников:

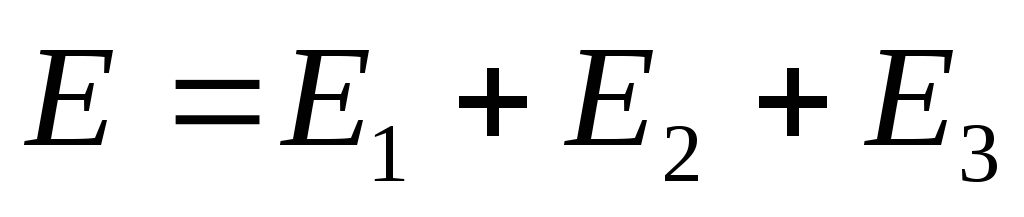
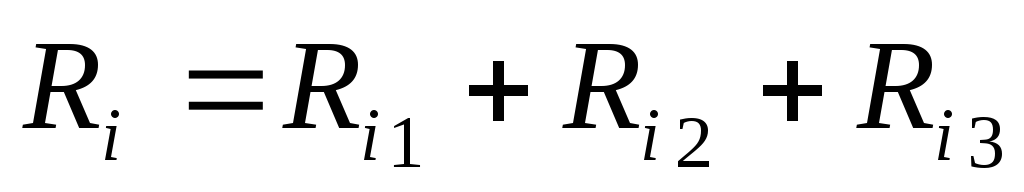
Параллельное соединение
Параллельным называется такое соединение, когда все начала элементов соединяются в одну общую точку, а все концы во вторую общую точку, и к этим точкам подводится напряжение:
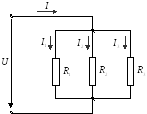
Свойства параллельного соединения:
Общее напряжение равно напряжению всех участков
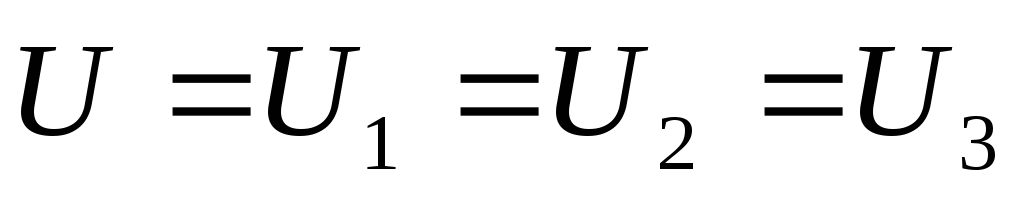
Ток до и после разветвления (общий ток) равен сумме токов в каждой ветви
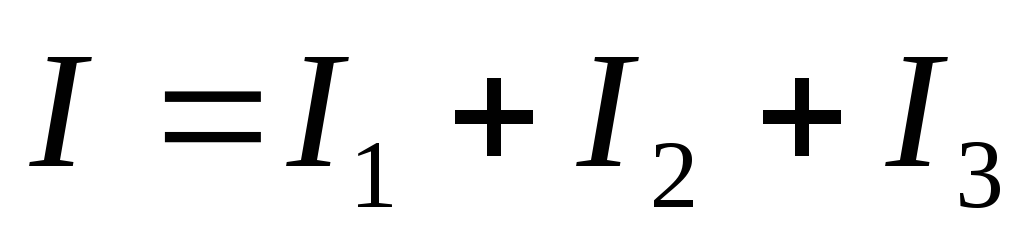
Величина, обратная входному сопротивлению, равна сумме величин, обратных сопротивлениям каждой ветви в отдельности
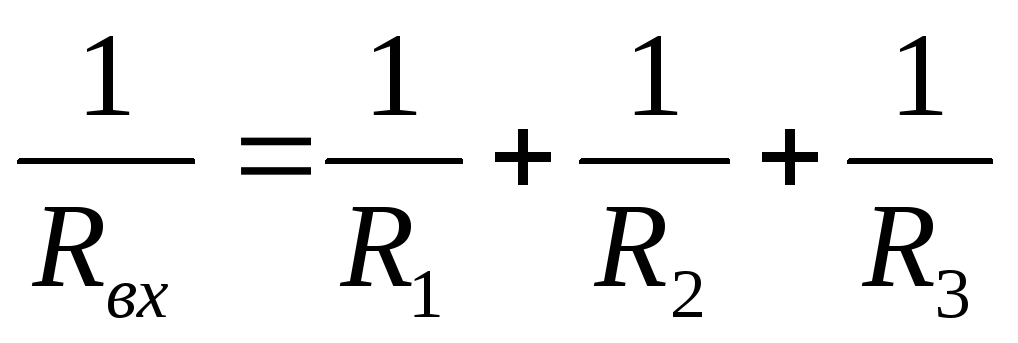
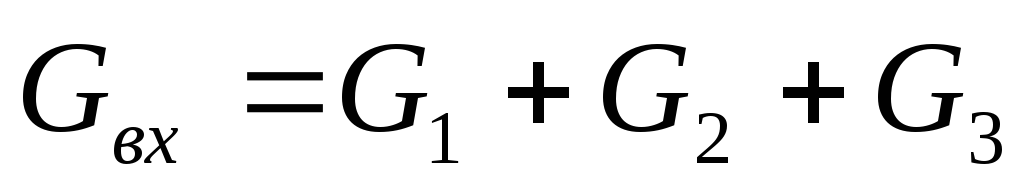
При параллельном соединении резисторов общее сопротивление меньше меньшего.
Токи ветвей обратно пропорциональны их сопротивлениям
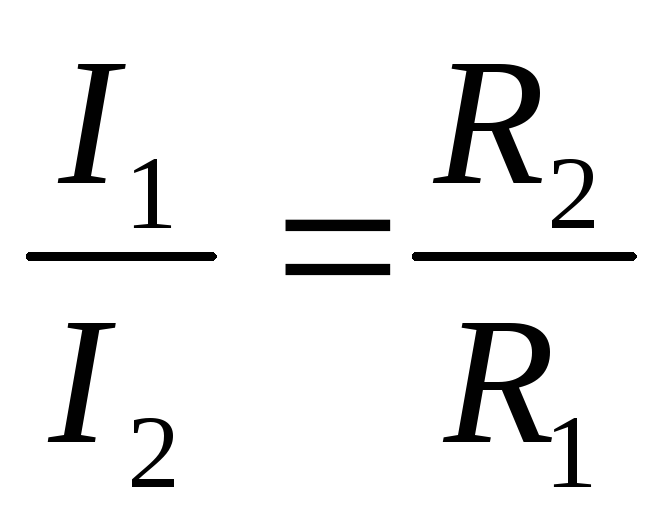
Если параллельно соединяются два резистора, то:
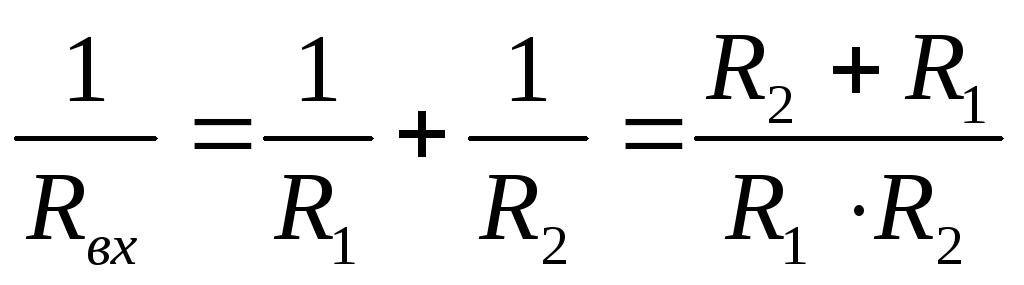
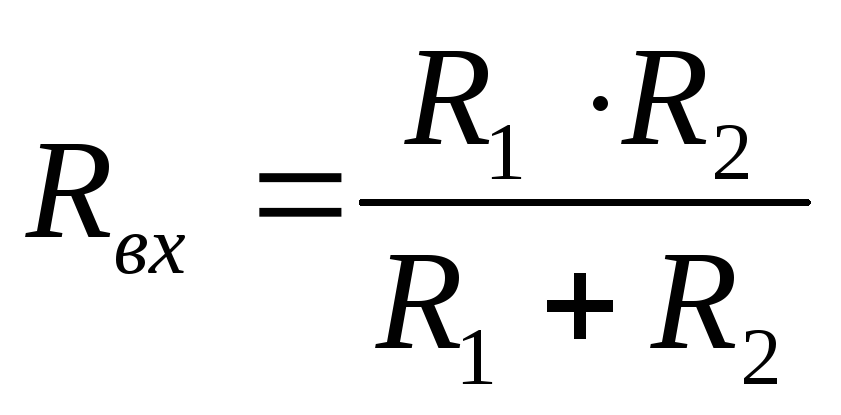
Если известен общий ток, то при параллельном соединении двух резисторов токи ветвей можно найти по формулам:
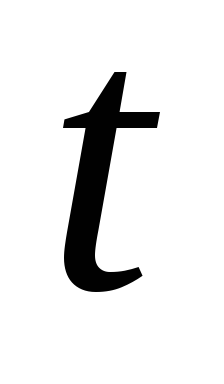
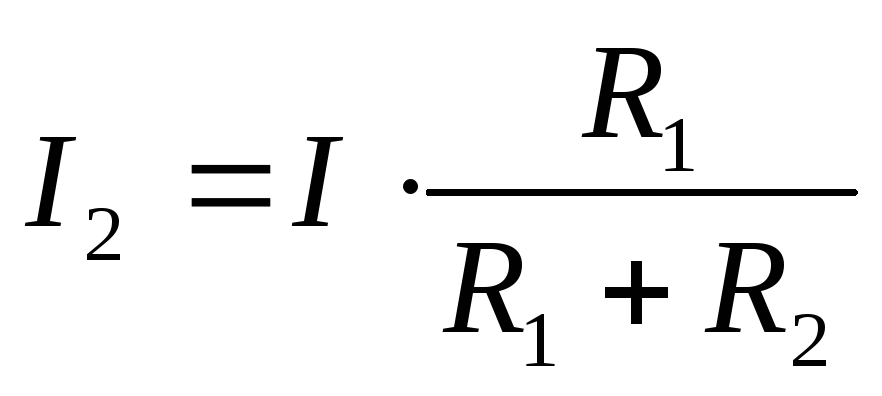
Вопрос 14. Смешанное соединение резисторов. Расчёт входного сопротивления, токов, напряжений и мощностей.
Задача
Д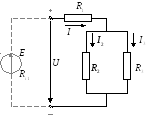 ано:
ано:
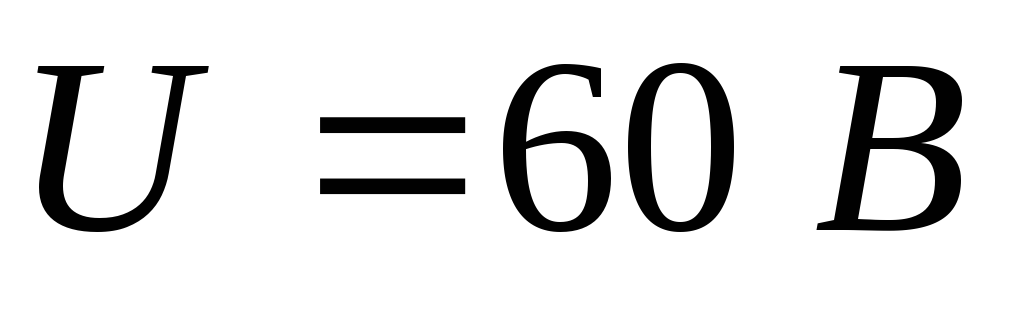
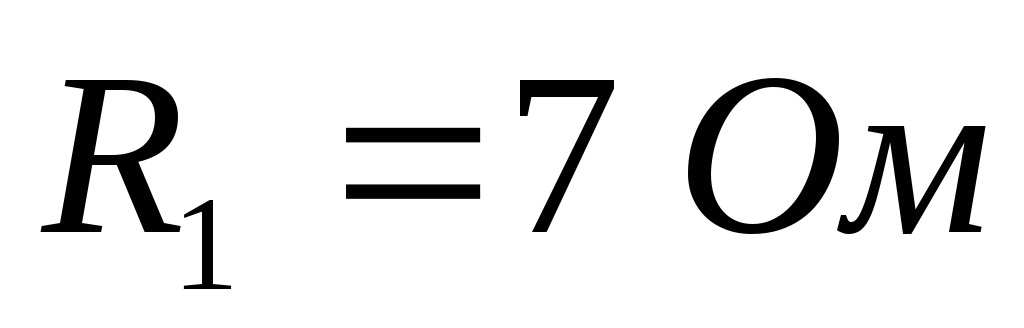
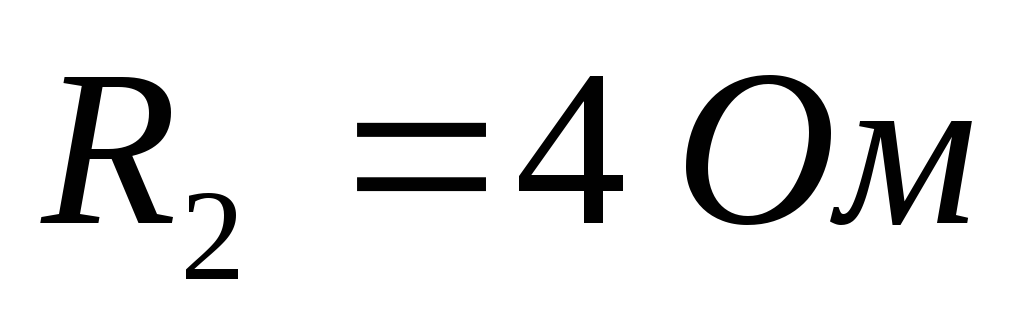
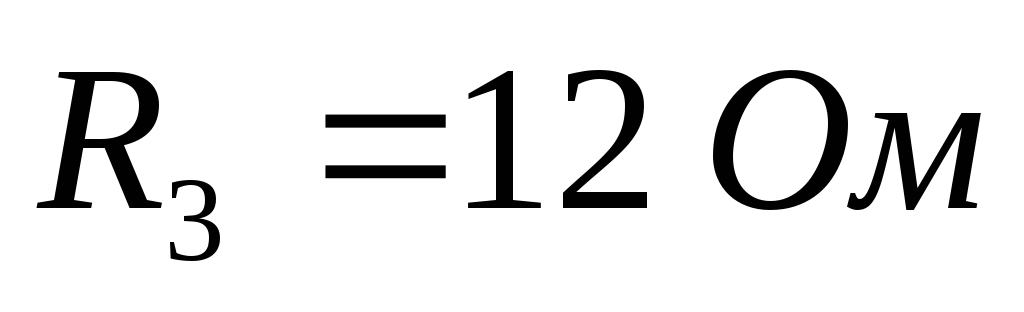
Рассчитайте все токи и направьте их
В задачах такого типа используются свойства последовательного и параллельного соединения, законы Ома, формулы нахождения мощностей:
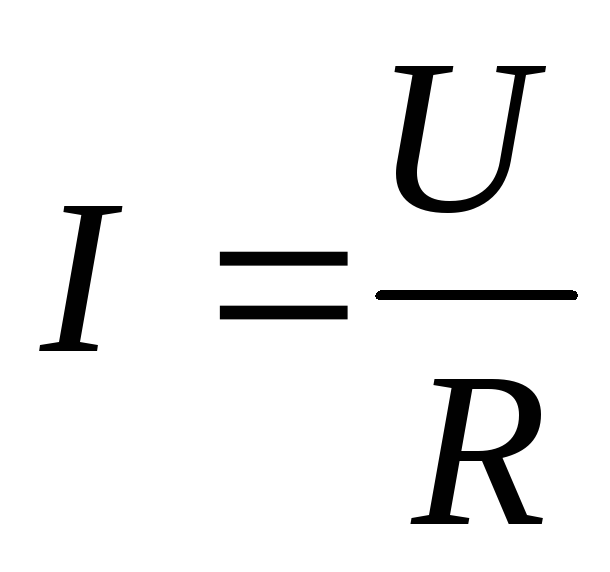 — закон Ома для участка цепи
— закон Ома для участка цепи
 — закон Ома для замкнутой цепи
— закон Ома для замкнутой цепи
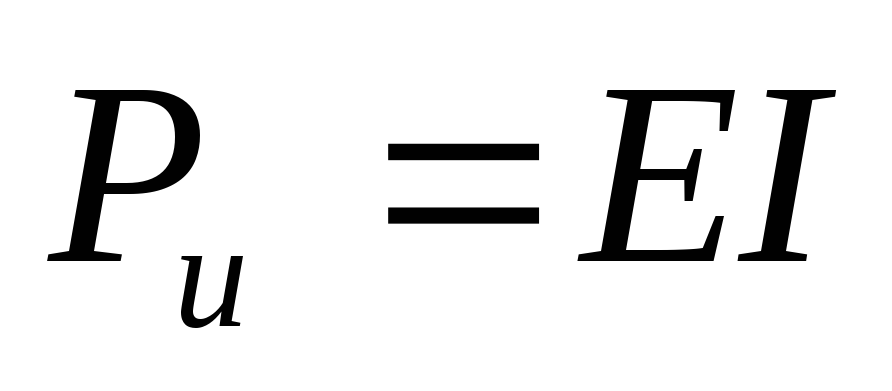 — мощность источника
— мощность источника
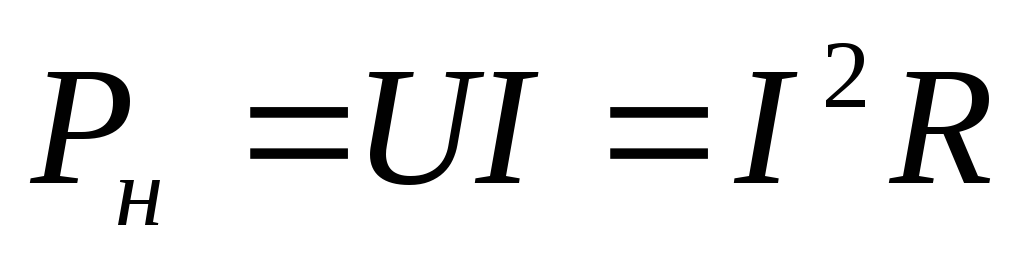 — мощность нагрузки
— мощность нагрузки
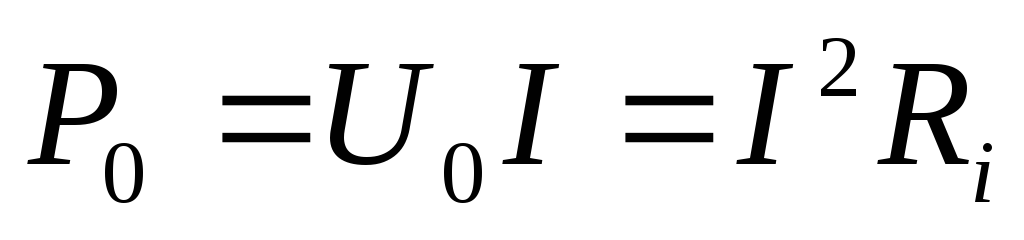 — мощность потерь внутри источника
— мощность потерь внутри источника
Находим входное сопротивление:
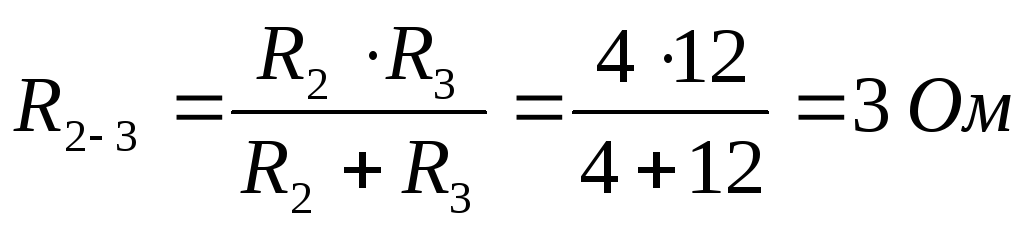
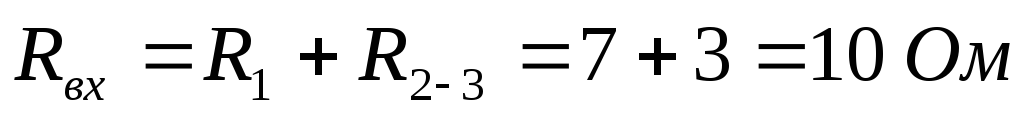
Находим общий ток (который идёт через источник):
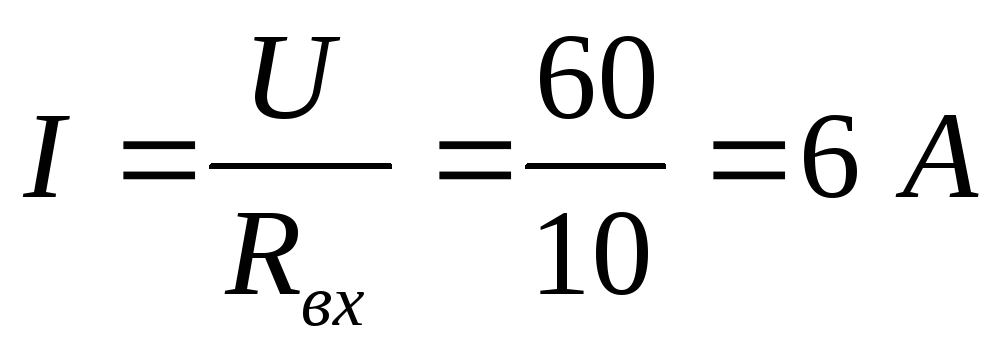
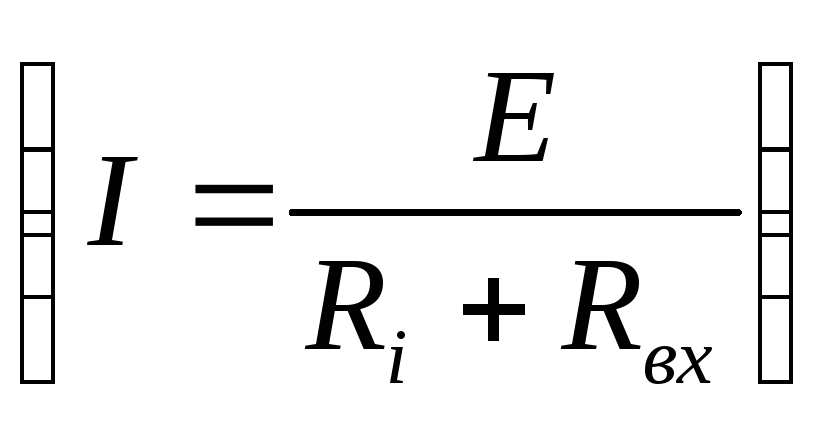

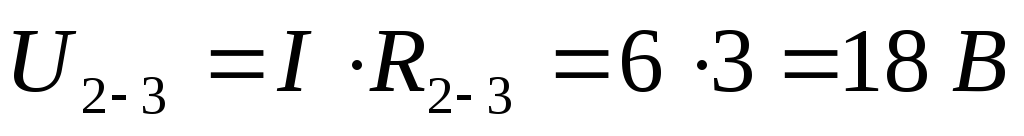
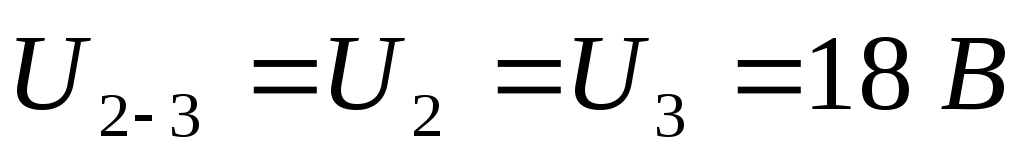
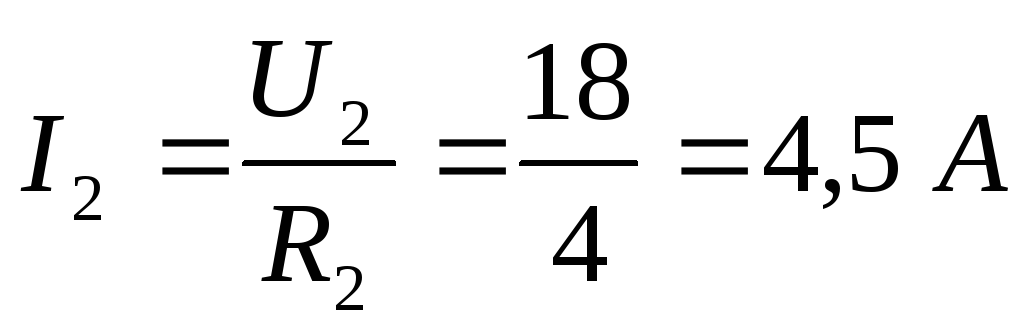
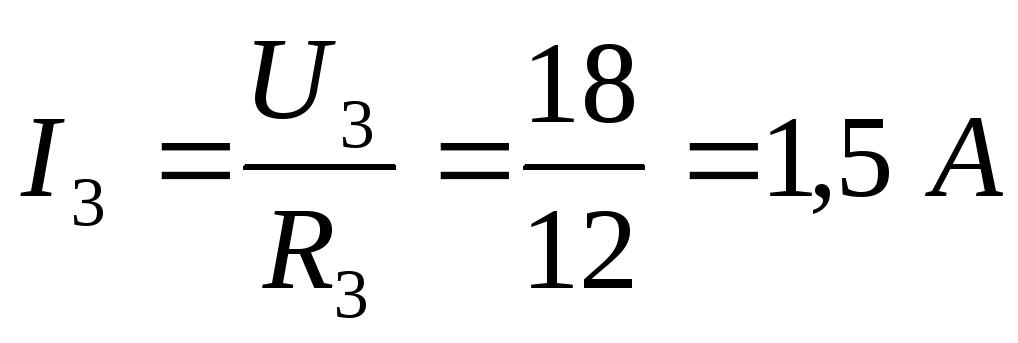
Закон Ома для замкнутой цепи
Н а
рисунке 2 показана простейшая замкнутая
цепь, состоящая из реального источника
э.д.с. Е, имеющего внутреннее сопротивлениеRвти нагрузочного
резистора с сопротивлениемR(сопротивление соединительных проводов
включено в сопротивлениеRрезистора).
а
рисунке 2 показана простейшая замкнутая
цепь, состоящая из реального источника
э.д.с. Е, имеющего внутреннее сопротивлениеRвти нагрузочного
резистора с сопротивлениемR(сопротивление соединительных проводов
включено в сопротивлениеRрезистора).
Закон Ома для замкнутой цепиформулируется следующим образом:сила тока (ток, величина тока) прямо пропорциональна электродвижущей силе (э.д.с.) источника и записывается в виде:
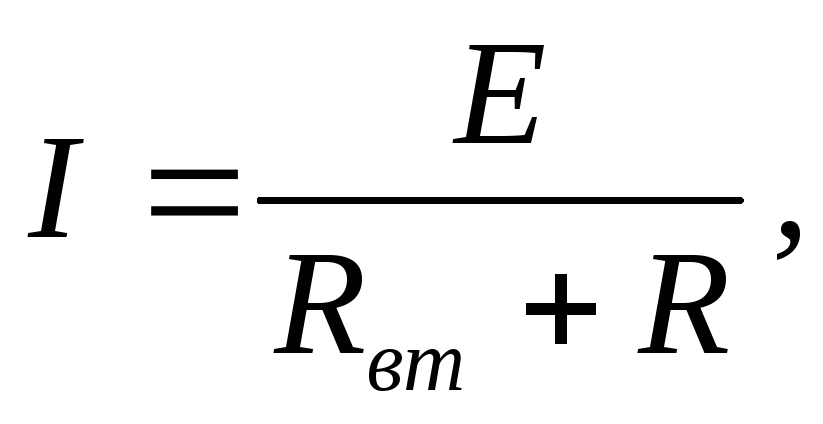
(4)
где 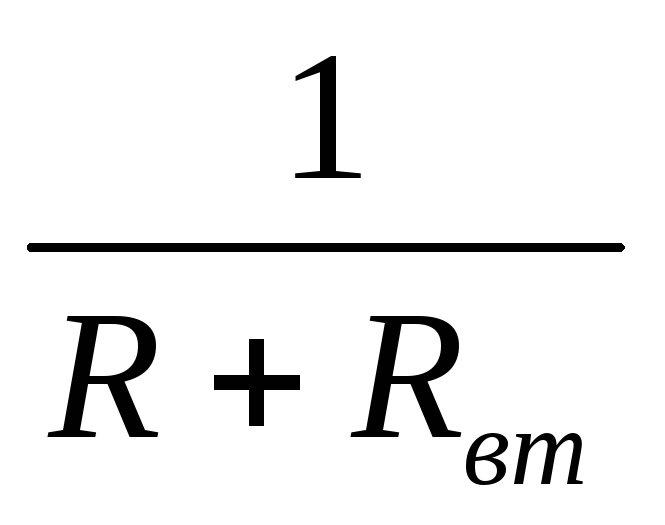 – коэффициент пропорциональности.
– коэффициент пропорциональности.
П
(4а)
ерепишем равенство (4) в виде 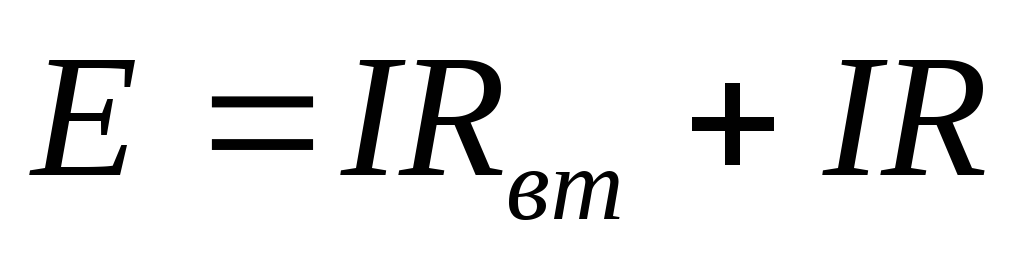
и введем обозначение U=IR– напряжение на выходных зажимах источника э.д.с. (генератора), которое одновременно является падением напряжения, создаваемым токомIна внешнем сопротивленииRнагрузочного резистора.
П
(5)
одставив это обозначение в правую часть равенства (4а), можно получить следующую зависимость:  ,
,
к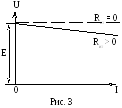 оторая
представляет собой аналитическое
выражение внешней характеристики
источника э.д.с. Эту зависимость можно
сокращенно записать в видеU = F(I) при E = const, Rвт = const. Внешней
характеристикой принято называть графическую
зависимость U = F(I),
показанную на рисунке 3.
оторая
представляет собой аналитическое
выражение внешней характеристики
источника э.д.с. Эту зависимость можно
сокращенно записать в видеU = F(I) при E = const, Rвт = const. Внешней
характеристикой принято называть графическую
зависимость U = F(I),
показанную на рисунке 3.
Сплошной линией показана внешняя характеристика реального источника э.д.с., в котором с ростом тока I увеличивается падение напряжения на внутреннем сопротивлении IRвт, в результате чего с ростом тока выходное напряжение источника U уменьшается. Пунктирной линией на рисунке 3 показана внешняя характеристика идеального источника э.д.с., у которого отсутствует внутреннее сопротивление (Rвт = 0), а, следовательно, и внутреннее падение напряжения (IRвт = 0). В результате равенство (5) принимает вид
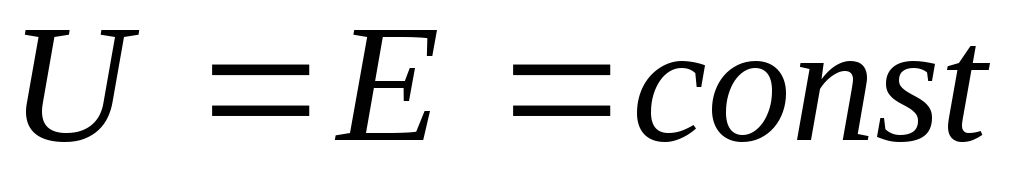
(5а)
,и характеристика представляет собой горизонтальную линию. Такой идеальный источник называют источником (генератором) бесконечной мощности, поскольку он гарантирует постоянство напряжения при сколь угодно больших токах нагрузки.
Закон Ома для участка цепи, содержащего источник э.Д.С. (обобщенный закон Ома)
На рисунках 4а и 4б показаны одинаковые участки, содержащие последовательно включенные резистор R и источник э.д.с. Е, по которым протекает ток I одного и того же направления. Что касается источников, то э.д.с. в схеме на рисунке 4а совпадает с направлением тока, а на рисунке 4б – действует встречно с током.
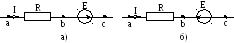
Рис. 4
К
(6)
ак известно,под напряжением Uна участке цепипонимают разность электрических потенциаловφмежду крайними точками этого участка (аисна рисунке 4). Ток всегда течет от более высокого потенциала к более низкому потенциалу. Поскольку ток в обоих случаях (рис. 4а и 4б) направлен от точкиак точкес, то напряжение 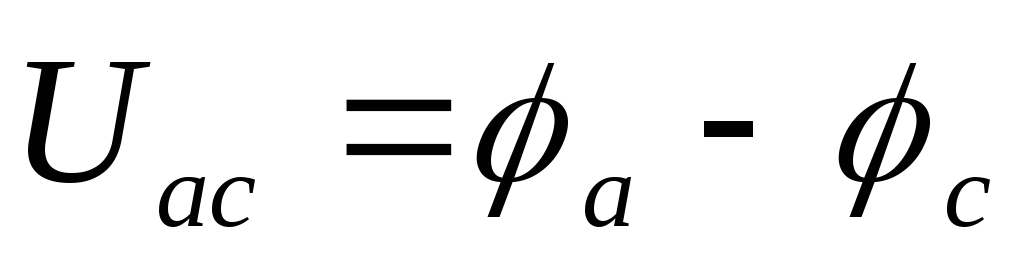
Выразим более высокий потенциал точки ачерез потенциал точкис. При
перемещении (рис. 4а) от точкиск
точкеb(встречно к
направлению э.д.с. Е) потенциал точкиbоказывается ниже потенциала точкисна величину э.д.с. Е, то есть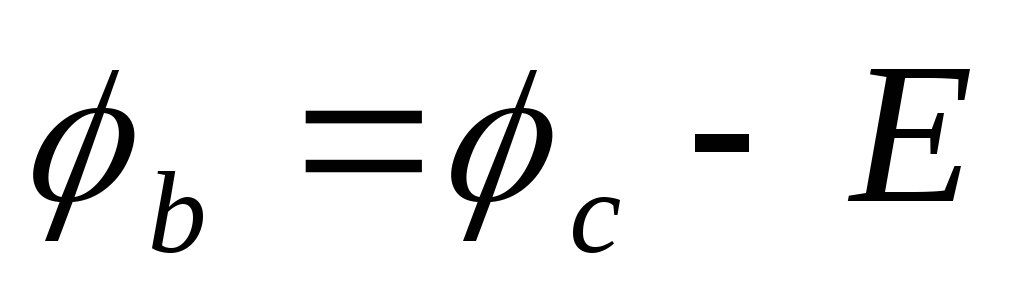 .
Применительно к схеме на рисунке 4б
потенциал точкиbбудет выше на величину э.д.с. Е, то есть
.
Применительно к схеме на рисунке 4б
потенциал точкиbбудет выше на величину э.д.с. Е, то есть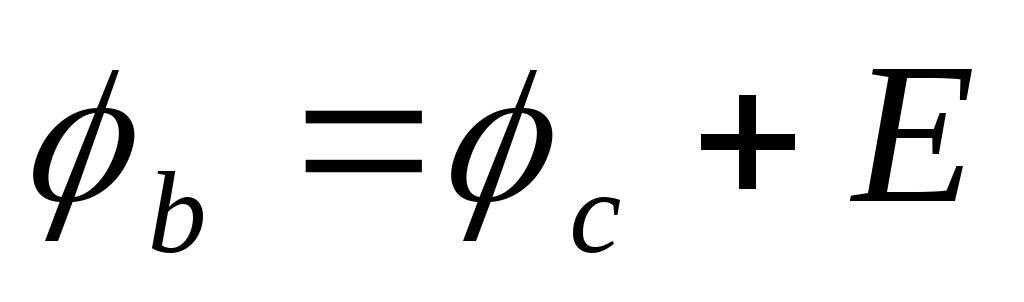 .
Поскольку потенциал точкиавыше
потенциала точкиbна
величину падения напряженияIRна резисторе с сопротивлениемR,
то
.
Поскольку потенциал точкиавыше
потенциала точкиbна
величину падения напряженияIRна резисторе с сопротивлениемR,
то .
.
Таким образом, для рисунка 4а: 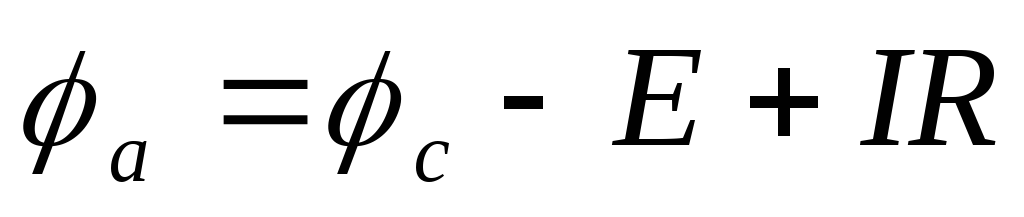 ,
а для рисунка 4б:
,
а для рисунка 4б: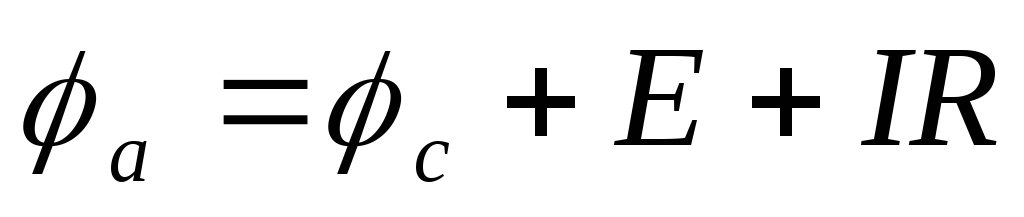 .
.
Соответственно напряжение между границами аисучастка:
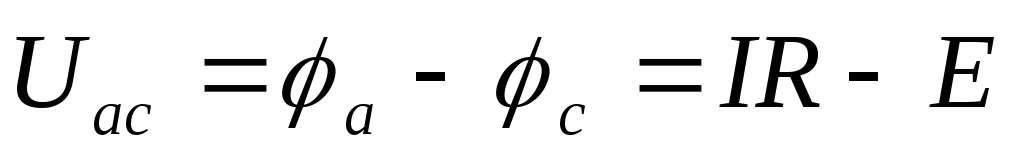 ;
;
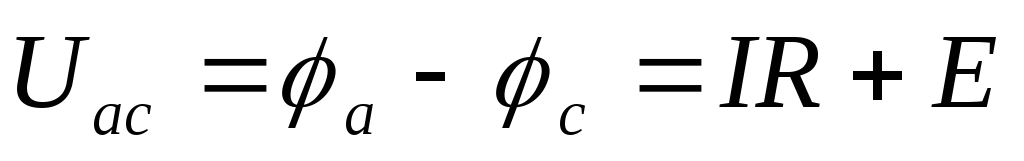 .
.
Решив равенства (6а) и (6б) относительно тока, получим обобщенный закон Ома (закон Ома для участка цепи, содержащего источник э.д.с.):
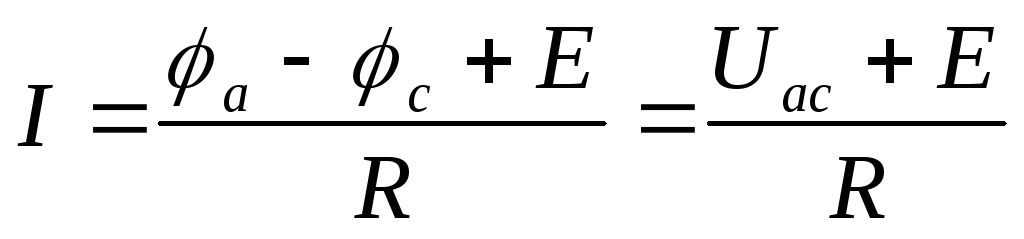 ;
;
 .
.
В общем случае
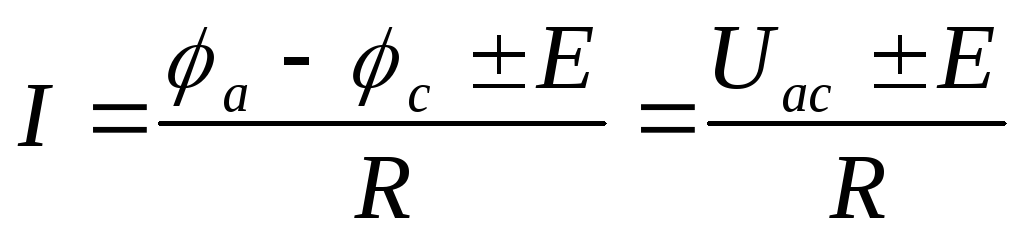
(7)
В частном случае, когда э.д.с. отсутствует (Е = 0) уравнение (7) превращается в закон Ома для участка цепи, не содержащего э.д.с. (1).
формулы и определения / Блог :: Бингоскул
Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.
Закон Ома для участка цепи:
Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.
- I — сила тока (в системе СИ измеряется — Ампер)
- Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
- Формула: I=\frac{U}{R}
- U — напряжение (в системе СИ измеряется — Вольт)
- R — электрическое сопротивление (в системе СИ измеряется — Ом).
- Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
- Формула R=\frac{U}{I}
Определение единицы сопротивления — Ом
1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1(Вольт) протекает ток 1 (Ампер).
Закон Ома для полной цепи
Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника
Формула I=\frac{\varepsilon}{R+r}
- \varepsilon — ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Как запомнить формулы закона Ома
Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.
.
- U — электрическое напряжение;
- I — сила тока;
- P — электрическая мощность;
- R — электрическое сопротивление
Смотри также:
Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.
Закон Ома для неоднородного участка цепи
На практике видно, что для поддержания стабильного тока в замкнутой цепи необходимы силы принципиально иной природы, нежели кулоновские, тогда наблюдается случай, когда на участке цепи на свободные электрические заряды одновременно действуют как силы электрического поля, так и сторонние силы (любые неконсервативные силы, действующие на заряд, за исключением сил электрического сопротивления (кулоновских сил)). Такой участок называется неоднородным участком цепи. На рисунке ниже приведен пример такого участка.

Напряженность поля в любой точке цепи равна векторной сумме поля кулоновских сил и поля сторонних сил:

Сформулируем закон Ома для неоднородного участка цепи — Сила тока прямо пропорциональна напряжению на этом участке и обратно пропорциональна его полному сопротивлению:
 – формула закона Ома для неоднородного участка цепи.
– формула закона Ома для неоднородного участка цепи.Где
- I – сила тока,
- U12 – напряжение на участке,
- R – полное сопротивление цепи.
Работа на неоднородном участке цепи
Разность потенциалов характеризует работу силы электрического поля по переносу единичного положительного заряда (q) из точки 1 в точку 2:
 — где φ1 и φ 2 – потенциалы на концах участка.
— где φ1 и φ 2 – потенциалы на концах участка.ЭДС характеризует работу сторонних сил по переносу единичного положительного заряда точки 1 в точку 2:  — где ε12 – ЭДС, действующая на данном участке, численно равна работе по перемещению единичного положительного заряда вдоль контура.
— где ε12 – ЭДС, действующая на данном участке, численно равна работе по перемещению единичного положительного заряда вдоль контура.
Напряжение на участке цепи представляет собой суммарную работу сил ЭП и сторонних сил:

Тогда закон Ома примет вид: 
ЭДС может быть как положительной, так и отрицательной. Это зависит от полярности включения ЭДС в участок. Если внутри источника тока обход совершается от отрицательного полюса к положительному, то ЭДС положительная (см. рисунок). Сторонние силы при этом совершают положительную работу. Если же обход совершается от положительного полюса к отрицательному, то ЭДС отрицательная. Проще говоря, если ЭДС способствует движению положительных зарядов, то ε>0, иначе ε

Решение задач по закону ому для неоднородного участка цепи
Определить ток, идущий по изображенному на рисунке участку АВ. ЭДС источника 20 В, внутреннее сопротивление 1 Ом, потенциалы точек А и В соответственно 15 В и 5 В, сопротивление проводов 3 Ом.

| Дано: | Решение: |
|---|---|
|
|
Два элемента соединены «навстречу» друг другу, как показано на рисунке. Определить разность потенциалов между точками А и В, если ε1 = 1,4 В, r1 = 0,4 Ом, ε2 = 1,8 В, r2 = 0,6 Ом.

| Дано: | Решение: |
|---|---|
|
|




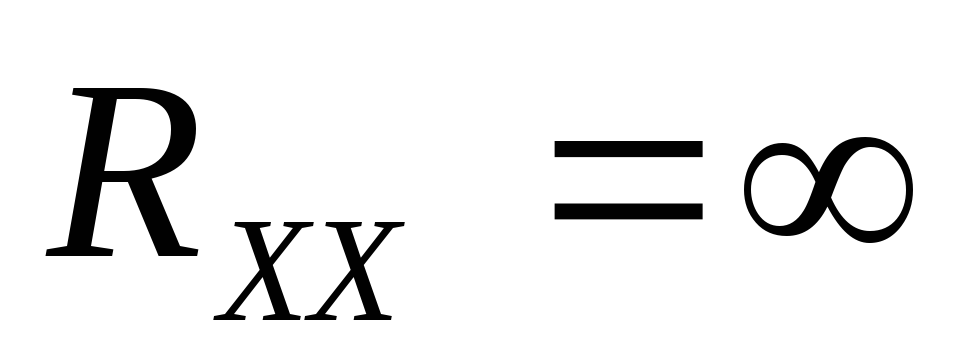
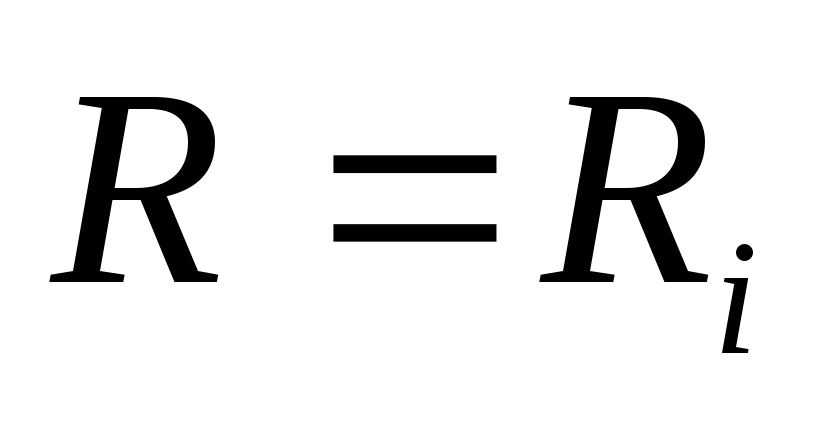

 — для первого участка цепи,
— для первого участка цепи,  — для второго участка.
— для второго участка.