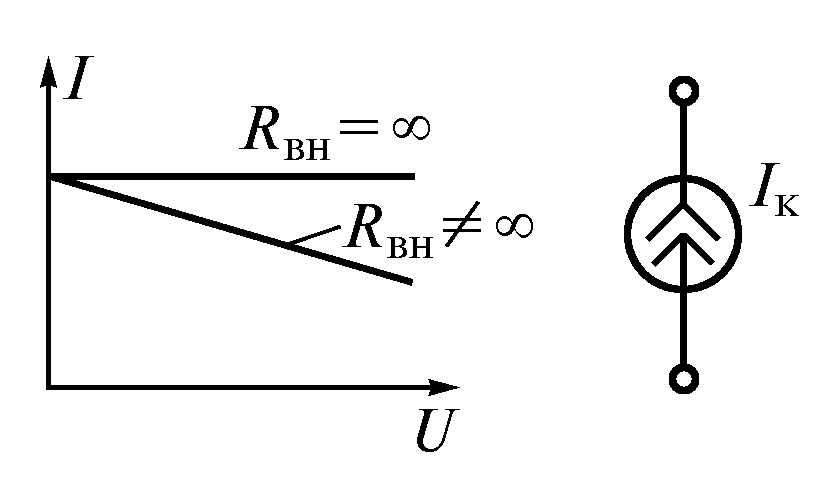Закон Ома для участка цепи, не содержащего источника ЭДС. — Студопедия.Нет
Закон (правило) Ома для участка цепи, не содержащего источник ЭДС, устанавливает связь между током и напряжением на этом участке. Применительно к рис. 2.5
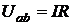
или
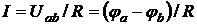 (2.4)
(2.4)
Закон Ома для участка цепи, содержащего источник ЭДС. Обобщенный закон Ома.
Закон (правило) Ома для участка цепи, содержащего источник ЭДС, позволяет найти ток этого участка по известной разности потенциалов (φа — φс) на концах участка цепи и имеющейся на этом участке ЭДС Е. Так, по уравнению (2.2) для схемы рис. 2.6а
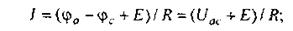
по уравнению (2.3) для схемы рис. 2.6
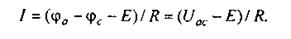
В общем случае
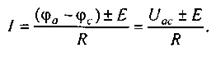 (2.5)
(2.5)
Уравнение (2.5) математически выражает закон Ома для участка цепи, содержащего источник ЭДС:
— знак плюс перед Е соответствует рис. 2.5а ;
— знак минус — рис. 2.5б.
В частном случае при E = 0 уравнение (2.5) переходит в уравнение (2.4).
Неразветвленные и разветвленные электрические цепи.
Электрические цепи подразделяют на неразветвленные и разветвленные. На рис. 2.6
Ветвь — участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами.
Узел — это точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рис. 2.6в), то в этом месте есть электрическое соединение двух линий, в противном случае (рис. 2.6
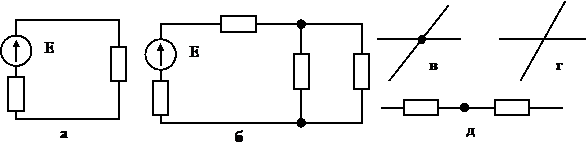
Рис.2.6
Кроме термина «узел» иногда используют термин «устранимый узел». Под устранимым узлом понимают точку, в которой соединены два последовательных сопротивления (рис. 2.6д). Этим понятием пользуются при введении данных в ЭВМ о значении и характере сопротивлений.
Последовательное соединение элементов —это соединение элементов, в которых протекает один и тот же ток (рис.2.6а).
Это соединение элементов можно заменить одним эквивалентным сопротивлением, вычисленным по формуле:
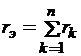
Эквивалентная проводимость определяется по формуле:
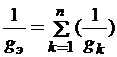 .
.
Параллельное соединение элементов – это соединение элементов, когда напряжение на каждом из элементов имеет одно и тоже значение.
Это соединение элементов можно заменить одним эквивалентным сопротивлением, вычисленным по формуле:
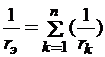
Эквивалентная проводимость определяется по формуле:
 .
.
Смешанное соединение резистивных элементов
При наличии в цепи только одного источника ЭДС внешнюю по отношению к источнику часть электрической цепи можно в большинстве случаев рассматривать как смешанное (последовательно-параллельное) соединение элементов.
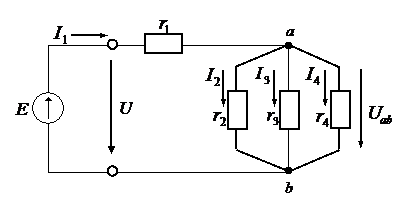
Рис.2.7.
В приведенной схеме (рис.2.7) несколько резистивных элементов, которые соединены параллельно.
Расчет смешанного соединения нужно начинать с определения эквивалентной проводимости
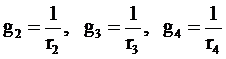 ;
;
эквивалентная проводимость равна:
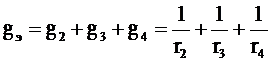 .
.
После замены параллельного соединения резистивных элементов эквивалентным резистивным элементом с сопротивлением 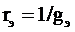 (рис.2.12) получается эквивалентная схема с последовательным соединением двух резистивных элементов r
(рис.2.12) получается эквивалентная схема с последовательным соединением двух резистивных элементов r
BILET_dlya_1_kursa_6_8_7
Закон Ома для участка цепи без ЭДС. Сопротивление проводника. Падение напряжения. Потеря напряжения.
Закон Ома был установлен экспериментально.
Для участка, который не содержит источника тока, и, следовательно, сторонние силы отсутствуют, и перемещение носителей происходит только под действием кулоновских сил, закон формулируется следующим образом.
Сила тока на однородном участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
С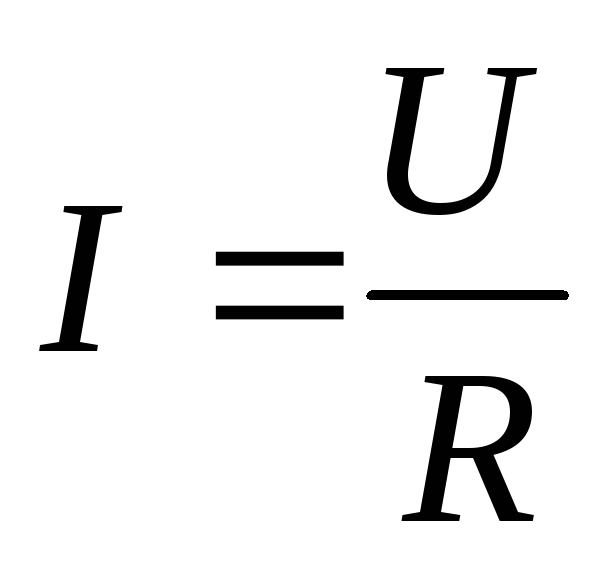 ила
тока – скалярная физическая величина, равная
отношению заряда q,
прошедшего через поперечное сечение
проводника за промежуток времени t,
к этому промежутку.
ила
тока – скалярная физическая величина, равная
отношению заряда q,
прошедшего через поперечное сечение
проводника за промежуток времени t,
к этому промежутку.
Е диница
измерения силы тока – 1 А. Это
сила такого неизменяющегося тока,
который, проходя по двум бесконечно
длинным прямолинейным параллельным
проводникам очень малого сечения,
расположенным на расстоянии 1 м друг от
друга в вакууме, вызывает силу
взаимодействия между ними 2 10
диница
измерения силы тока – 1 А. Это
сила такого неизменяющегося тока,
который, проходя по двум бесконечно
длинным прямолинейным параллельным
проводникам очень малого сечения,
расположенным на расстоянии 1 м друг от
друга в вакууме, вызывает силу
взаимодействия между ними 2 10
Н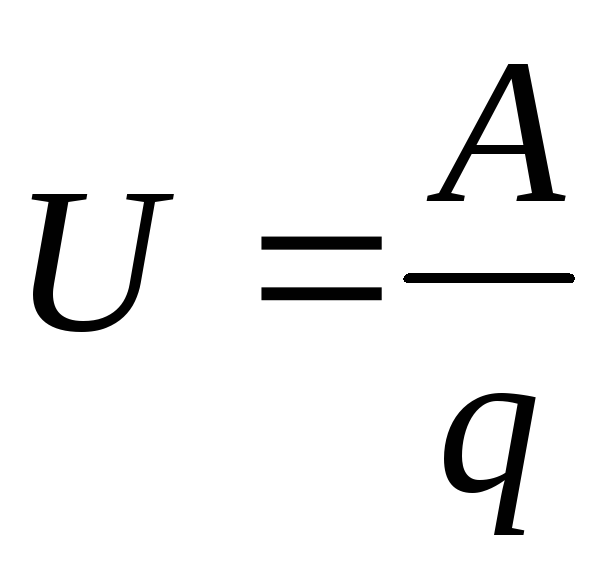 апряжением на участке
цепи называется скалярная физическая
величина, численно равная полной работе
А, которая совершается кулоновскими и
сторонними силами по перемещению вдоль
участка цепи единичного положительного
заряда.
апряжением на участке
цепи называется скалярная физическая
величина, численно равная полной работе
А, которая совершается кулоновскими и
сторонними силами по перемещению вдоль
участка цепи единичного положительного
заряда.
Е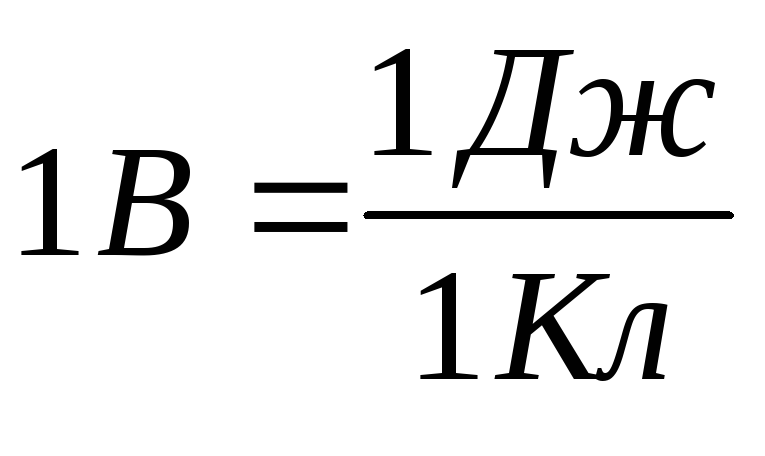 диница
измерения напряжения – 1 В.
диница
измерения напряжения – 1 В.
Электрическое сопротивление – физическая величина, характеризующая свойство проводника уменьшать скорость упорядоченного движения свободных носителей заряда в проводнике.
Сопротивление металла связано с рассеянием электронов проводимости на ионах кристаллической решётки и структурных неоднородностях (дефектах и примесях решётки).
Единица измерения сопротивления – 1 Ом. Проводник имеет сопротивление 1 Ом, если при напряжении 1 В сила тока в нём 1 А.
С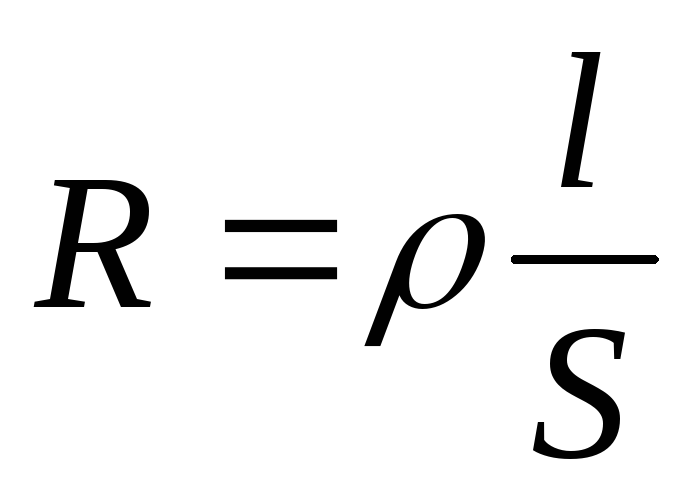 опротивление
зависит от рода вещества проводника,
его геометрических размеров и формы.
опротивление
зависит от рода вещества проводника,
его геометрических размеров и формы.
Где — удельное сопротивление проводника, l – длина проводника, S – сечение проводника.
Удельное сопротивление проводника зависит от вещества и температуры
г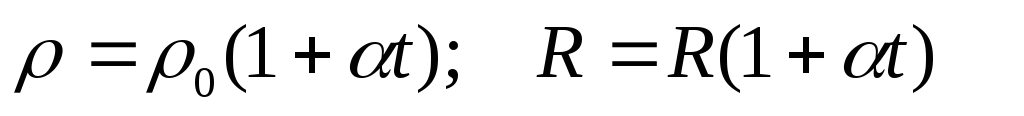 де
0 – удельное сопротивление проводника
при 00С,
— удельное сопротивление проводника
при t0C,
-температурный коэффициент сопротивления,
для чистых металлов он равен 1/273.
де
0 – удельное сопротивление проводника
при 00С,
— удельное сопротивление проводника
при t0C,
-температурный коэффициент сопротивления,
для чистых металлов он равен 1/273.
Сопротивление проводника определяет вид зависимости тока от напряжения.
Зависимость силы тока от напряжения называется вольт-амперной характеристикой. Для металлов это линейная зависимость.
Падением напряжения
U=IR
Для однородного участка цепи падение напряжения равно напряжению.
Потерями напряжения называется падение напряжения на подводящих проводах.
БИЛЕТ 8
Работа и мощность электрического тока. Тепловое действие электрического тока. Закон Джоуля-Ленца.
Электрическое поле, перемещающее заряды по проводнику, совершает работу. Эту работу называют работой тока. При напряжении U между точками цепи работа электрического поля определяется выражением
A=qU
где q – переносимый заряд.
При постоянном токе q=It, где I – сила тока в проводнике, t — время прохождения тока. Тогда А=IUt
Работа тока на участке цепи равна произведению силы тока на напряжение на этом участке и на время прохождения тока.
Единица измерения работы тока – 1 Дж=1 В 1А 1 с
Е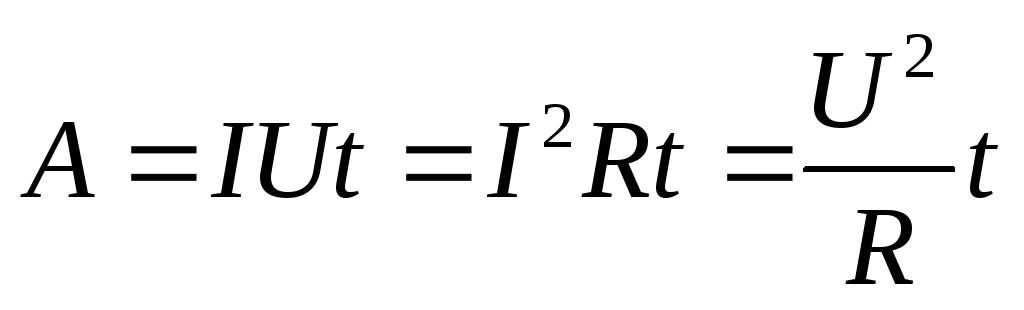 сли
ток протекает по однородному участку
цепи сопротивлением R,
то на основании закона Ома для однородного
участка цепи, можно получить следующие
формулы для расчёта работы тока
сли
ток протекает по однородному участку
цепи сопротивлением R,
то на основании закона Ома для однородного
участка цепи, можно получить следующие
формулы для расчёта работы тока
М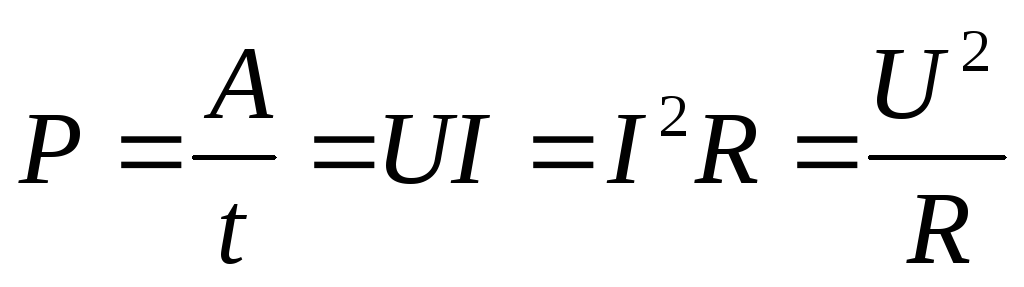 ощность
электрического тока равна работе, которая совершается током
за единицу времени
ощность
электрического тока равна работе, которая совершается током
за единицу времени
Единица измерения мощности – 1 Вт=1 Дж/1 с.
Внесистемная единица измерения работы тока – 1 киловатт-час. 1кВт ч=1000 Дж3600 с=3,6 106 Дж.
Под действием электрического поля электроны приобретают дополнительную кинетическую энергию. При соударении электрона с ионом решётки эта энергия полностью передаётся решётке и идёт на увеличение внутренней энергии проводника, т.е. проводник нагревается.
Количество теплоты, которое выделяется в проводнике при прохождении электрического тока, определяется законом Джоуля-Ленца.
Количество теплоты, выделяющееся в проводнике при прохождении электрического тока, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени протекания тока.
Q=I2Rt
Если на участке цепи не совершается механическая работа и ток не производит химического действия, то вся работа тока затрачивается на нагревание проводника Q=А.
Е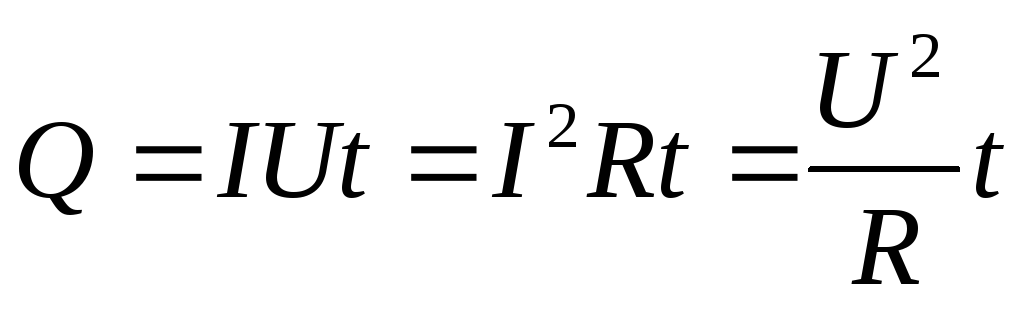 сли
участок цепи однородный, то на основании
закона Ома для однородного участка цепи
можно записать
сли
участок цепи однородный, то на основании
закона Ома для однородного участка цепи
можно записать
Если два проводника сопротивлениями R1 и R2 соединены последовательно, то
К оличество
теплоты, выделяемое током на последовательно
соединённых проводниках, пропорционально
сопротивлениям этих проводников.
оличество
теплоты, выделяемое током на последовательно
соединённых проводниках, пропорционально
сопротивлениям этих проводников.
Если два проводника сопротивлениями R1 и R2 соединены параллельно, то
К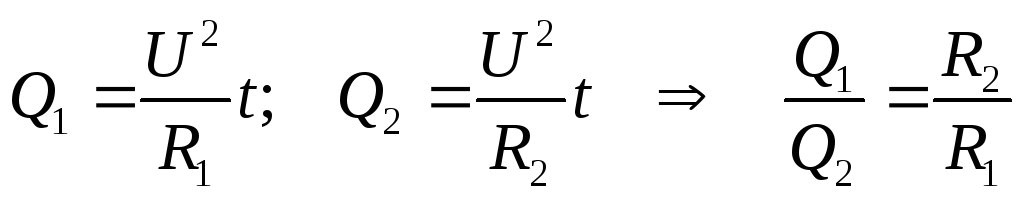 оличество
теплоты, выделяемое током на параллельно
соединённых проводниках, обратно
пропорционально сопротивлениям этих
проводников.
оличество
теплоты, выделяемое током на параллельно
соединённых проводниках, обратно
пропорционально сопротивлениям этих
проводников.
На законе Джоуля-Ленца основано действие многих электронагревательных приборов.
БИЛЕТ 7
Внешний и внутренний участки цепи. Закон Ома для замкнутой цепи с одной ЭДС.
Для существования постоянного тока в цепи необходимо поддерживать неизменную разность потенциалов на её концах. Эту функцию выполняет устройство, которое называется источником тока. Внутри источника тока за счёт сил неэлектростатической природы, так называемых сторонних сил, происходит перенос положительного заряда от меньшего потенциала к большему, т.е. происходит разделение зарядов, в результате которого на одном из полюсов источника накапливается положительный заряд, а на другом – отрицательный, т.е. поддерживается разность потенциалов между полюсами источника тока.
Характеристикой действия сторонних сил является электродвижущая сила – ЭДС.
ЭДС численно равна работе сторонних сил по перемещению единичного положительного заряда по замкнутой цепи.
Е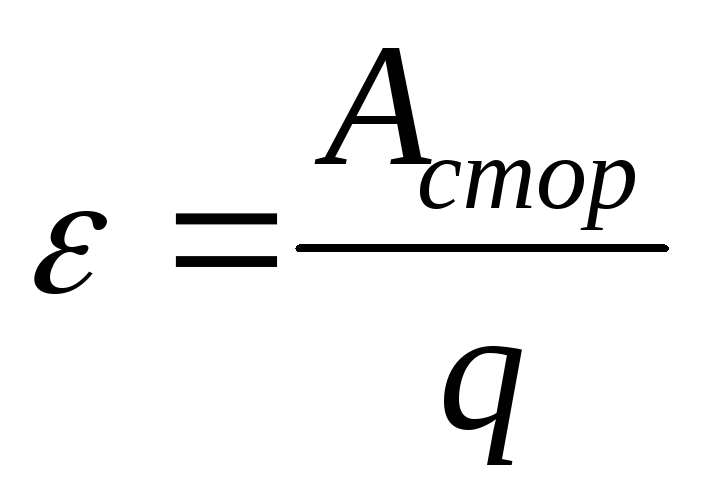 диница
измерения ЭДС – 1 В.
диница
измерения ЭДС – 1 В.
Замкнутая цепь состоит из внутренней и внешней частей. Внутренняя часть цепи представляет собой источник тока, обладающий внутренним сопротивлением r; внешняя – различные потребители, соединительные провода, приборы и т.д. с общим сопротивлением R.
Работа сторонних сил по перемещению по замкнутой цепи заряда q равна
Аст=q
Если в цепи не совершается механическая работа и ток не производит химического действия, то вся работа затрачивается на нагревание проводника.
По закону Джоуля-Ленца
Q=I2Rt+I2rt=I2(R+r)t
Т ак
как Аст= Q, то q=
It=
I2(R+r)t
и =
I(R+r). Отсюда получаем закон Ома для
замкнутой цепи
ак
как Аст= Q, то q=
It=
I2(R+r)t
и =
I(R+r). Отсюда получаем закон Ома для
замкнутой цепи
Сила тока в замкнутой цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна полному сопротивлению цепи.
Если сопротивление внешней цепи стремится к нулю, то в цепи возникает максимально возможный ток, который называется током короткого замыкания.
З акон
Ома можно записать в следующем виде
акон
Ома можно записать в следующем виде
= IR+ I r=U+Ir
Это значит, что ЭДС источника равна сумме падений напряжений на внешнем и внутреннем участках замкнутой цепи.
Полная мощность источника
Р= I= I2(R+r)
Мощность, выделяемая на внешнем участке цепи, называется полезной мощностью
М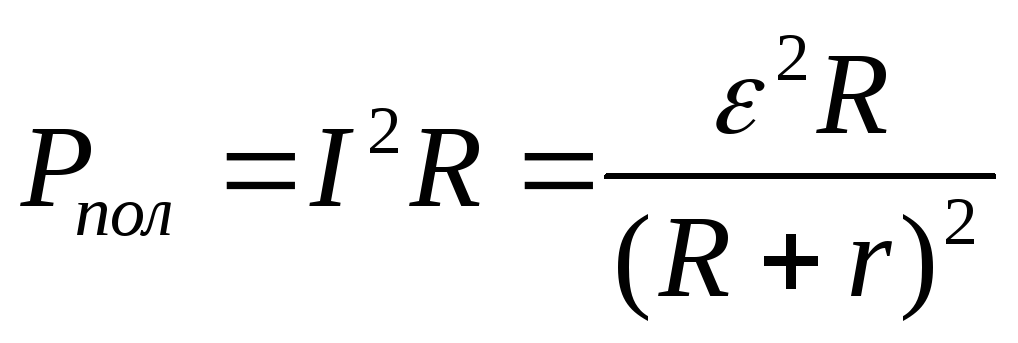 ощность,
выделяемая на внутреннем сопротивлении
в источнике тока, называется теряемой
мощностью
ощность,
выделяемая на внутреннем сопротивлении
в источнике тока, называется теряемой
мощностью
К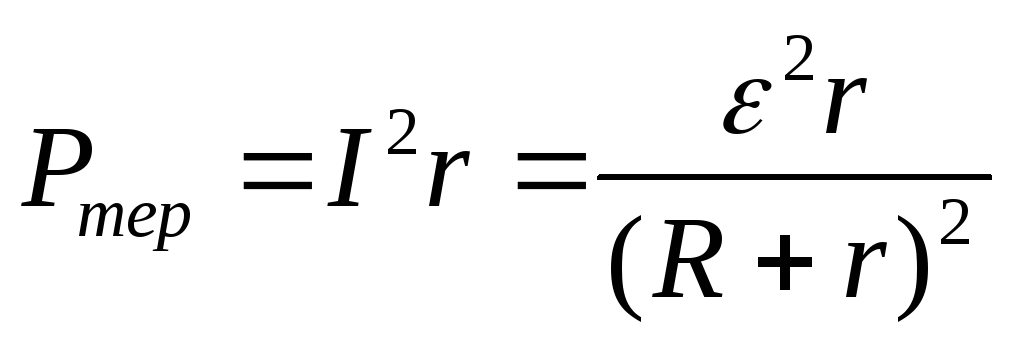
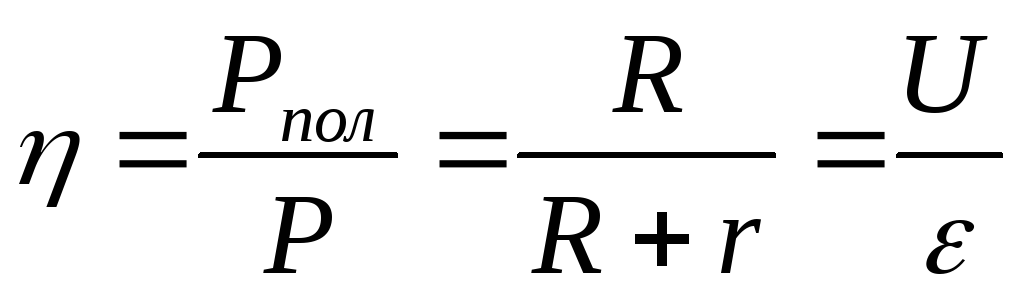 оэффициент
полезного действия источника тока
равен отношению полезной мощности Рпол к полной мощности Р
оэффициент
полезного действия источника тока
равен отношению полезной мощности Рпол к полной мощности Р
ЭДС. Закон Ома для полной цепи
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против движения заряда (т.е. против направления тока).
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :
(1)
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь
Наша задача — найти силу тока в цепи и напряжение на резисторе .
За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу:
(2)
Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:
(3)
Итак, , и мы приравниваем правые части формул (2) и (3):
После сокращения на получаем:
Вот мы и нашли ток в цепи:
(4)
Формула (4) называется законом Ома для полной цепи.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:
(5)
Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.
Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .
1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .
2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина неотличима от , и формула (5) снова даёт нам .
Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи — это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
Закон Ома для неоднородного участка
Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.
Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.
На рис. 3показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (усли внутреннее сопротивление источника равно , можно просто заменить резистор на резистор ).

Рис. 3. ЭДС «помогает» току:
Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.
Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.
Напряжение на нашем участке равно: . За время через участок проходит заряд , при этом стационарное электрическое поле совершает работу:
Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):
Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным элетрическим полем и сторонними силами источника, целиком превращается в тепло: .
Подставляем сюда выражения для , и закон Джоуля–Ленца:
Сокращая на , получаем закон Ома для неоднородного участка цепи:
(6)
или, что то же самое:
(7)
Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .
Отметим два следствия выведенных формул (6) и (7).
1. Если участок однородный, то . Тогда из формулы (6) получаем — закон Ома для однородного участка цепи.
2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на :
Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:
Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.
Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:
Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!
Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:
Тогда закон Ома для неоднородного участка примет вид:
(8)
или:
где по-прежнему — напряжение на участке.
Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:
Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».
Закон Ома для участка цепи
Закон для участка электрической цепи без источника тока
Если в проводнике течет ток, то потенциал в разных его точках различается. Падение напряжения означает, что отлична от нуля составляющая напряженности поля, которая направлена вдоль проводника ($E_{\tau }$).
Напряжённостью поля называется векторная физическая величина, являющаяся отношением силы, действующей на заряд, к величине этого заряда.
Следовательно, напряженность поля у поверхности проводника с током не перпендикулярна к проводящей поверхности.
Для того чтобы в проводнике существовал постоянный ток, необходимо чтобы действовала внешняя сила, которая равна $E_{\tau }\cdot q_e$, где $q_e$ — заряд электрона, то значит, на движущиеся электроны действует сила трения. Или иначе говорят, что проводники имеют сопротивление ($R$). Сопротивление — это тот коэффициент, который связывает силу тока и напряжение.
Свой закон Ом получил эмпирически. Если построить вольтамперную характеристику электрического проводника, то легко заметить, что $I\sim U$. В соответствии с законом сила тока, которая течет по металлическому проводнику, может быть найдена:
где $R$ — сопротивление проводника или просто сопротивление.
Данная формула — это общая формулировка закона Ома.
В том случае, если источников ЭДС в электрической цепи нет (иногда в таком случае говорят, что проводник однороден в смысле сторонних сил), то напряжение $U$ — совпадает с разностью потенциалов.
Для неоднородного участка цепи
Для участков электрических цепей с источником ЭДС закон Ома запишем в виде:
$I=\frac{\left({\varphi }_1-{\varphi }_2\right)+\mathcal{E}}{R}\ \left(2\right)$, где:
- $\mathcal{E}$ — ЭДС источника тока,
- $R$ —сопротивление рассматриваемого участка цепи.
$\mathcal{E}$, как и сила тока является алгебраической величиной. В том случае, если выбор положительного $\mathcal{E}$ совпадает с направлением положительных зарядов, то $\mathcal{E}$ считается положительной. Если $\mathcal{E}$ препятствует перемещению зарядов, то $\mathcal{E}$ получают, используя то, что в такой цепи ${\varphi }_1={\varphi }_2$, следовательно:
$I=\frac{\mathcal E}{R}\left(3\right)$
где $R$ — сумма вех сопротивлений.
Применение закона Ома
Закон Ома используется, например, при измерении напряжения с помощью вольтметра. Вольтметр — это гальванометр, последовательно с которым соединено небольшое сопротивление. При подключении вольтметра к точкам участка цепи, напряжение между которыми мы планируем измерить, в вольтметр ответвляется часть тока. Сила данного тока $(I)$ по закону Ома в виде (1) пропорциональна напряжению между заданными точками. Следовательно, зная чувствительность вольтметра по току и его сопротивление, можно найти напряжение, используя подходящую формулировку закона Ома. Это напряжение наносят на шкалу прибора.
Ток через вольтметр должен быть очень небольшим, для того чтобы подключение вольтметра сильно не изменяло силу тока и распределение напряжения в цепи. С этой целью сопротивление самого вольтметра делают очень большим в сравнении с сопротивлением внешнего (по отношению к вольтметру) участка цепи.
Закон Ома — один из самых важных законов электричества. Но он имеет смысл только в случае, когда сопротивление проводника не зависит от приложенного к нему напряжению и силы тока. К такому типу проводников относят: металлы, уголь, электролиты. Для ионизированных газов закон Ома не всегда справедлив.
Задание № 1: Используя закон Ома, получите формулу для расчёта суммарного сопротивления трех последовательно соединенных проводников имеющих сопротивления $R_1,R_2,R_3$. Обобщите полученную формулу для $n$ проводников.
Рисунок 1. Схема соединения. Автор24 — интернет-биржа студенческих работ
Решение:
При последовательном соединении проводников (рис.1), $I=const$, а суммарное напряжение в цепи находится как сумма напряжений на концах каждого проводника:
$I=const,\ U=U_1+U_2+U_3\left(1.1\right)$
В качестве основы для решения задачи можно использовать закон Ома для однородного участка цепи. Для всей цепи запишем:
$U=IR\ (1.2)$
в формуле (1.2) $R$ — искомое напряжение, обратно пропорциональное сопротивлению.
Для одного сопротивления:
где $R_1$ — сопротивление первого проводника, $U_1$ — напряжение на нем.
Подставим в закон Ома (1.2) выражение для напряженности (1.1) и выражения для токов, которые текут через отдельные проводники (1.3) получим:
Сократим в (1.4) токи, получим формулу для расчета суммарного сопротивления для цепи из трех последовательных сопротивлений:
Ответ: Для трех сопротивлений $R=R_1+R_2+R_3.$ Для n — сопротивлений: $R=R_1+R_2+\dots +R_n.$
Задание № 2: Чему равно ЭДС ($\mathcal E$) и сопротивление источника $\mathcal E$, если он эквивалентен двум источникам тока, которые характеризуются ЭДС: $ \mathcal E_1 и\ \mathcal E_2$ и внутренними сопротивлениями: $r_1и\ r_2$, соединенными параллельно (рис.2).
Рисунок 2. Схема соединения. Автор24 — интернет-биржа студенческих работ
Решение:
За основу решения задачи примем закон Ома. Запишем его дважды для неоднородного участка цепи 1-2, учитываем, что соединение источников тока параллельное:
Выразим токи из (2.1), получим:
Суммарный ток, который дают источники можно найти как сумму токов:
По условиям задачи эквивалентный источник должен давать ток равный $I$ (2.3), и разность потенциалов в точках 1 и 2 равна $U_{21}\ $(2.4), для него запишем:
Сравним формулу (2.5) и (2.4).
Ответ: $\mathcal E=\frac{r_2\mathcal E_1+r_1\mathcal E_2}{r_1+r_2}$,
$r=\frac{r_1r_2}{r_1+r_2}$.
1.3. Закон Ома
В 1827 г. немецкий физик Г. Ом, проведя серию точных экспериментов, установил один из основных законов электрического тока. Он гласит: постоянный электрический ток в участке электрической цепи прямо пропорционален напряжению на этом участке.
Закон Ома имеет различные формы записи.
В дифференциальной форме для участка цепи без ЭДС он имеет вид
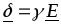 ,
(1.2)
,
(1.2)
где 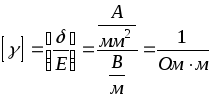 – удельная проводимость.
– удельная проводимость.
Рассмотрим
прямолинейный проводник постоянного
сечения s (рис. 1.6): 
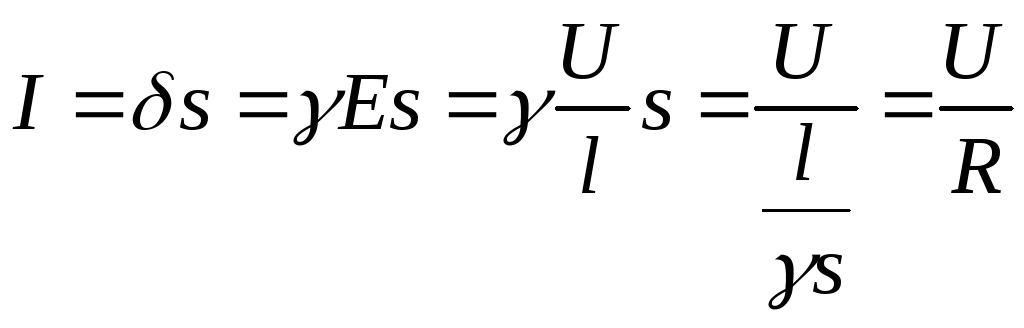 .
(1.3)
.
(1.3)
Рис. 1.6
Это вторая форма записи закона Ома для участка цепи без ЭДС, которая называется интегральной. Он формулируется следующим образом: ток в проводнике равен отношению падения напряжения на участке проводника к электрическому сопротивлению участка.
Электрическое сопротивление прямо
пропорционально длине
прямо
пропорционально длине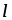 и обратно пропорционально площади
поперечного сечения проводника:
и обратно пропорционально площади
поперечного сечения проводника:
 .
(1.4)
.
(1.4)
Размерность сопротивления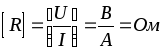 .
.
Таким образом, сопротивление– это скалярная величина, характеризующая проводящие свойства цепи. Оно равно отношению постоянного напряжения на участке цепи к току в нем при отсутствии на участке ЭДС:
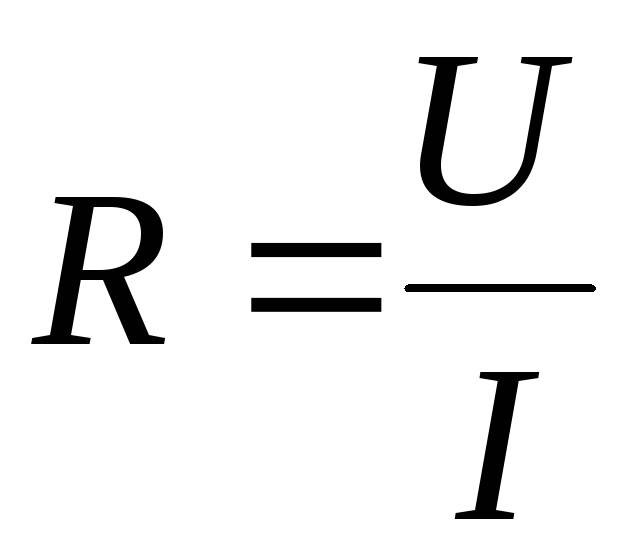 .
(1.5)
.
(1.5)
Сопротивление – это величина, показывающая, что в данном участке цепи происходит преобразование энергии.
Величина, обратная сопротивлению, называется проводимостью:
 .
(1.6)
.
(1.6)
Размерность проводимости – сименс (См). 1 См = 1/Ом.
Удельное сопротивление:
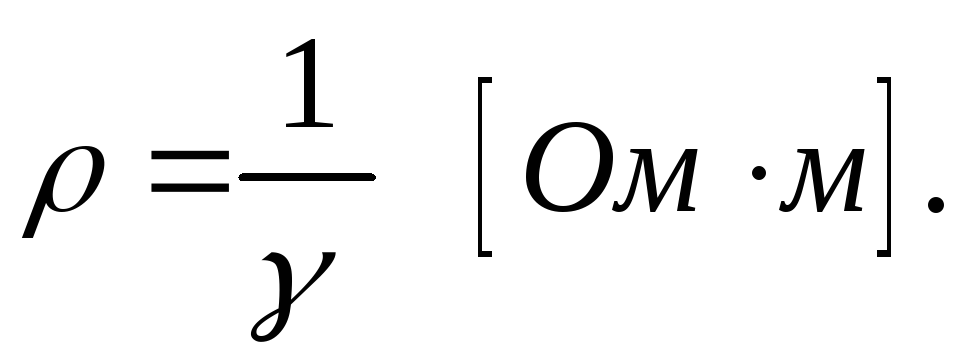 (1.7)
(1.7)
Тогда
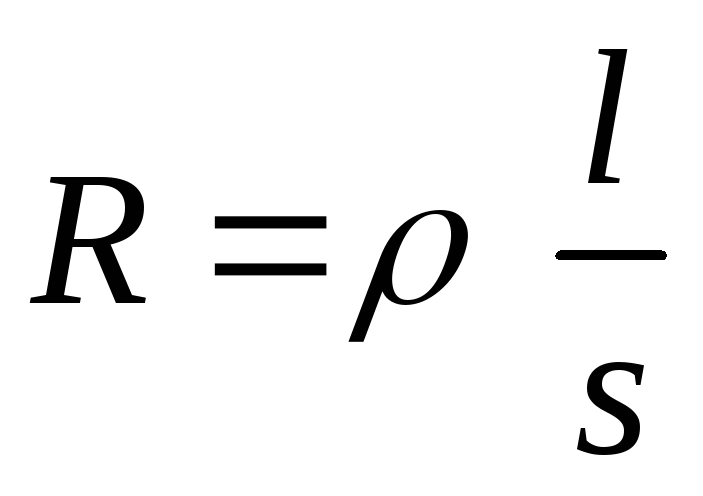 .
(1.8)
.
(1.8)
Удельное сопротивление получено экспериментально для всех материалов и приведено в справочниках.
Обмотки реостатов и нагревательных приборов изготавливают из сплавов с большим удельным сопротивлением (нихром, фехраль и т.п.).
Устройства, которые включают в электрическую цепь для ограничения или регулирования тока, называются резисторами или реостатами.
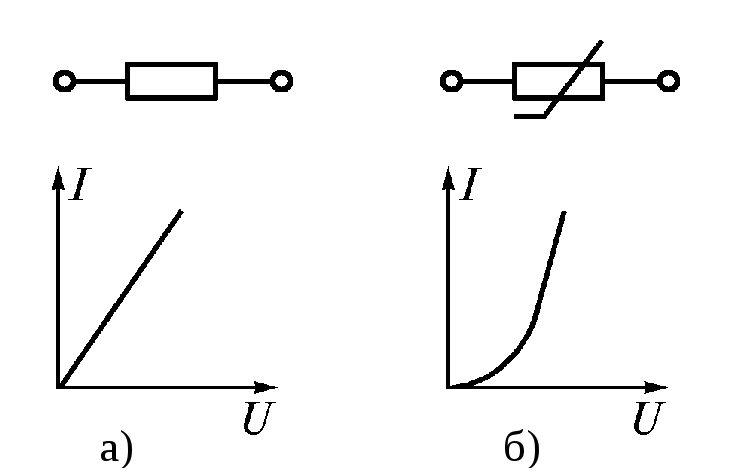
Рис. 1.7
Зависимость тока резистораIот подводимого напряженияUназывается еговольтамперной характеристикой(ВАХ). Если сопротивление резистора не зависит от тока, то его ВАХ представляет собой прямую линию (рис. 1.7 а), проходящую через начало координат. Такой резистор называетсялинейным. Резистор, ВАХ которого не является прямой линией (рис. 1.7 б), называетсянелинейным. Электрические цепи, содержащие только линейные элементы, называют линейными. Если в цепи имеется хотя бы один нелинейный элемент, вся цепь называетсянелинейной.1.4. Источник эдс и источник тока
При преобразовании
любого вида энергии в электрическую
энергию в источниках происходит за
счет электродвижущей силы (ЭДС). Электродвижущая
сила 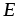 характеризует действие сторонних
(неэлектрических) сил в источниках
постоянного или переменного тока. В
замкнутом проводящем контуре она
равна работе этих сил по перемещению
единичного положительного заряда
вдоль этого контура. Сторонние силы
приводят в движение заряженные частицы
внутри источника электрической
энергии: генераторов, гальванических
элементов и т.д. ЭДС определяется как
отношение работы
характеризует действие сторонних
(неэлектрических) сил в источниках
постоянного или переменного тока. В
замкнутом проводящем контуре она
равна работе этих сил по перемещению
единичного положительного заряда
вдоль этого контура. Сторонние силы
приводят в движение заряженные частицы
внутри источника электрической
энергии: генераторов, гальванических
элементов и т.д. ЭДС определяется как
отношение работы 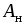 ,
совершаемой сторонними силами при
переносе заряженной частицы внутри
источника, к ее заряду:
,
совершаемой сторонними силами при
переносе заряженной частицы внутри
источника, к ее заряду:
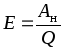 .
.
Если 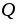 =
1Кл, то
=
1Кл, то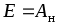 .
.
Следовательно, ЭДС равна работе, совершаемой сторонними силами при переносе единицы заряда внутри источника от зажима с меньшим потенциалом к зажиму с большим потенциалом. Ее можно представить разностью потенциалов или напряжением между положительным и отрицательным зажимами источника энергии при отсутствии в нем тока.
В замкнутой электрической цепи под действием ЭДС источника возникает ток. Цепь, в которой ток не изменяется во времени, называют цепью постоянного тока. При расчете и анализе электрических цепей источник электрической энергии представляют либо источником ЭДС, либо источником тока.
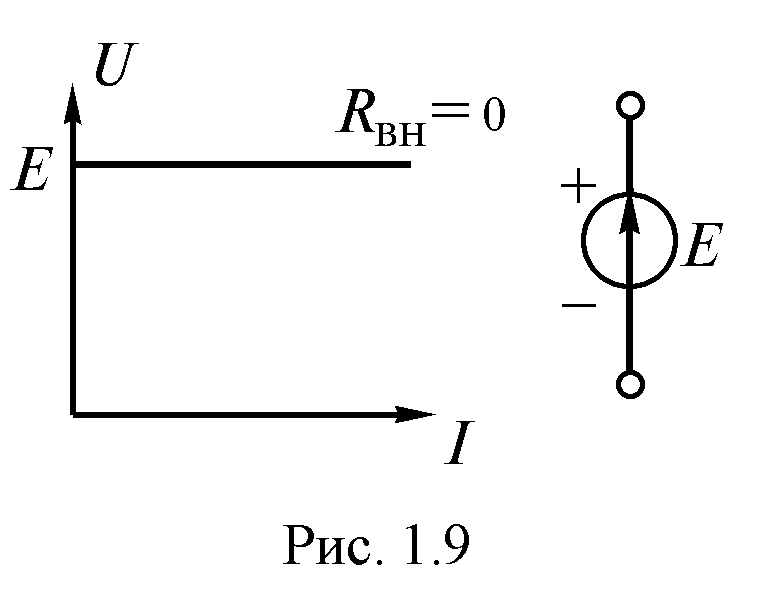
Идеальным источником ЭДС (рис. 1.8) называют такой источник энергии, ЭДС которого не зависит от протекающего через него тока и равна ЭДС реального источника, а его внутреннее сопротивление равно нулю. На рис. 1.8 показаны условные обозначения и вольтамперная характеристика идеального источника ЭДС.
За положительное направление ЭДС
источника принимается направление
возрастания потенциала внутри этого
источника. Внутреннее сопротивление  показывает, что часть энергии,
вырабатываемой источником, используется
внутри источника. Схема замещения
реального источника (
показывает, что часть энергии,
вырабатываемой источником, используется
внутри источника. Схема замещения
реального источника (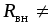 0)
может быть представлена в виде
последовательного соединения идеального
источника ЭДС и внутреннего сопротивления
(рис. 1.9). Реальный источник называют
источником напряжения.
0)
может быть представлена в виде
последовательного соединения идеального
источника ЭДС и внутреннего сопротивления
(рис. 1.9). Реальный источник называют
источником напряжения.
|
|
Рис. 1.8 | Рис. 1.9 |
Ток в цепи (рис. 1.9) определяется по закону Ома:
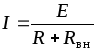 .
(1.9)
.
(1.9)
Из последней формулы видно, что внутреннее сопротивление оказывает влияние на ток в электрической цепи.
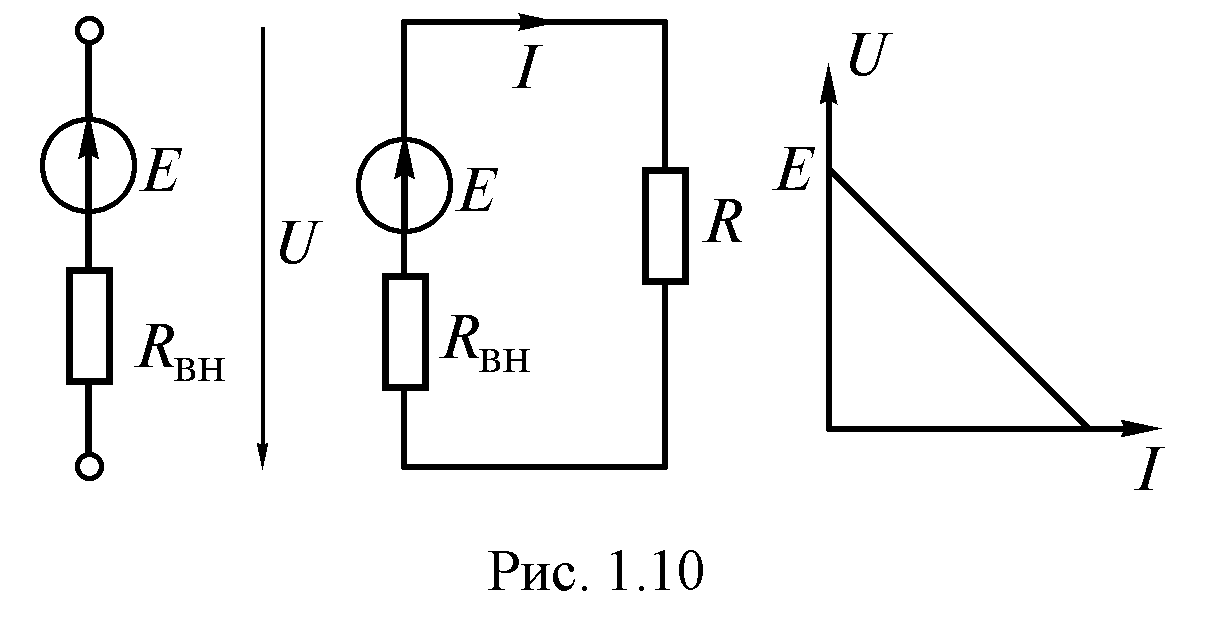
Напряжение на зажимах источника или на нагрузке (рис. 1.9) определяется по формуле
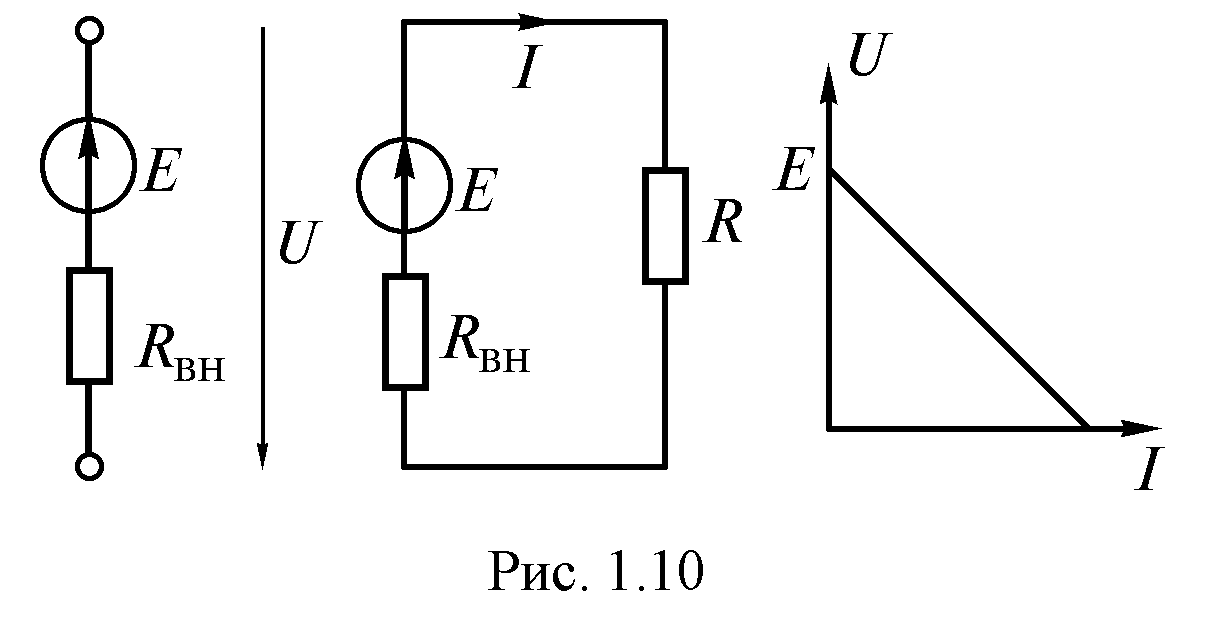
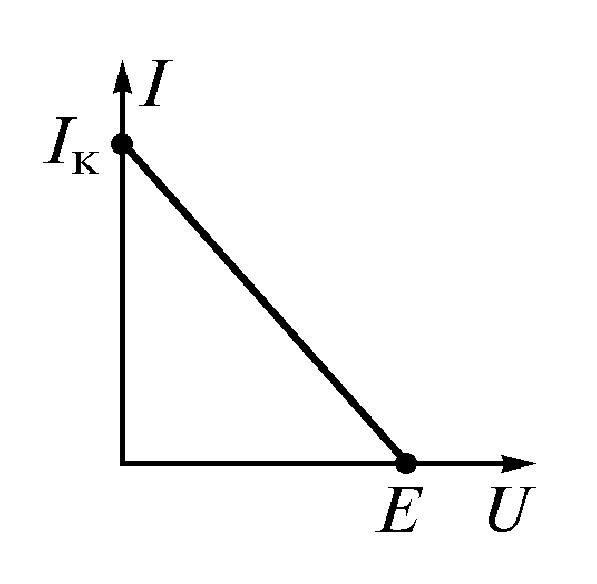
Рис. 1.10
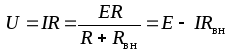 .
(1.10)
.
(1.10)ВАХ источников электрической энергии часто называют внешними характеристиками. Внешняя характеристика реального источника описывается уравнением (1.10). Ее можно построить по данным двух опытов (рис. 1.10):
холостого хода 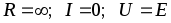 ;
;
короткого замыкания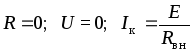 .
.
Источником токаназывают такой
идеализированный источник электрической
энергии, который вырабатывает ток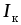 ,
не зависящий от нагрузки
,
не зависящий от нагрузки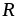 цепи и равный частному от деления ЭДС
реального источника на его внутреннее
сопротивление:
цепи и равный частному от деления ЭДС
реального источника на его внутреннее
сопротивление:
 .
(1.11)
.
(1.11)
Чтобы обеспечить постоянство тока 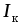 независимо от нагрузки
независимо от нагрузки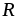 ,
необходимо выполнить условия: а)
,
необходимо выполнить условия: а)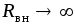 ;
б)
;
б)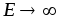 .
.
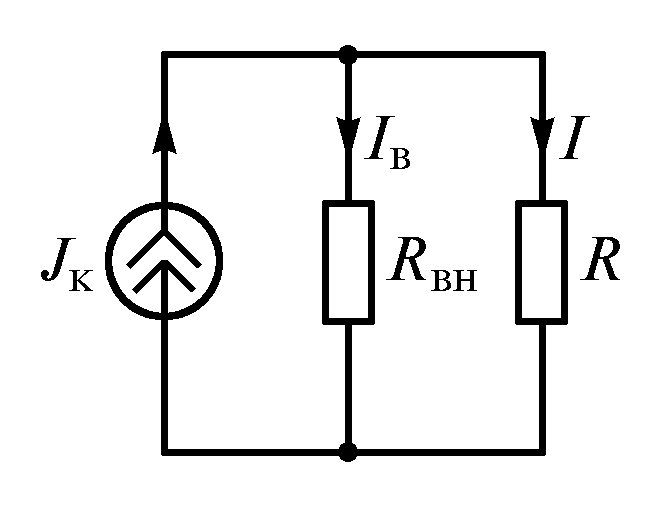
Идеальный источник тока можно считать
реальным, если внутреннее сопротивление 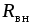 подключить параллельно сопротивлению
нагрузки. ВАХ и условное обозначение
источника тока показаны на рис. 1.11. Схема
замещения реального источника представлена
на рис. 1.12.
подключить параллельно сопротивлению
нагрузки. ВАХ и условное обозначение
источника тока показаны на рис. 1.11. Схема
замещения реального источника представлена
на рис. 1.12.
Ток в нагрузке
 .
(1.12)
.
(1.12)
| |
Рис. 1.11 | Рис. 1.12 |
Следовательно, при расчете цепей источники тока могут быть заменены источниками ЭДС и наоборот.
Каждый из двух расчетных эквивалентов является равноценным. В дальнейшем будем использовать в основном источник ЭДС.
Эквивалентность источников обеспечивается при равенстве напряжений при холостом ходе и равенстве токов при коротком замыкании.
Сформулируйте закон Ома для полной цепи?
закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
I = E/(R+r) сила тока полной цепи равна ЭДС деленной на сумму сопротивлений однородного и неоднородного участков цепи
Закон Ома для полной цепи Для замкнутой цепи работа сторонних сил источника тока равна количеству теплоты, выделившейся на внешнем и внутреннем участках цепи
Сила тока прямопропорциональна напряжению и обратнопропорциональна сопротивлению.




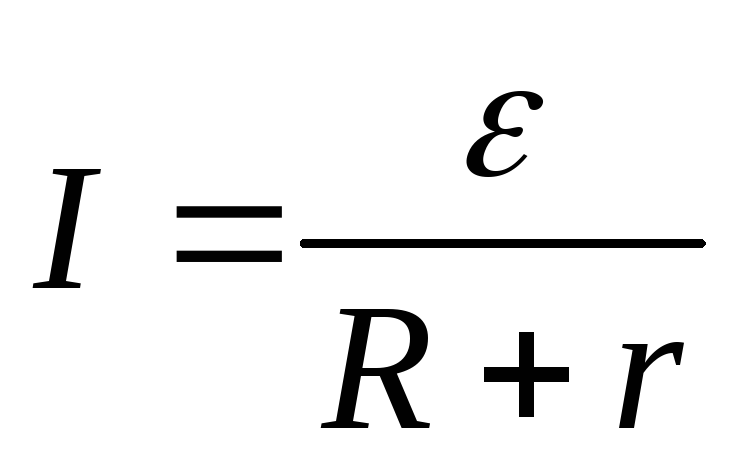 ак
как Аст= Q, то q=
It=
I2(R+r)t
и =
I(R+r). Отсюда получаем закон Ома для
замкнутой цепи
ак
как Аст= Q, то q=
It=
I2(R+r)t
и =
I(R+r). Отсюда получаем закон Ома для
замкнутой цепи акон
Ома можно записать в следующем виде
акон
Ома можно записать в следующем виде