Переменный электрический ток. Закон Ома

Переменный электрический ток. Закон Ома.

Переме́нный ток, AC (англ. alternating current — переменный ток) — электрический ток, который периодически изменяется по модулю и направлению.

Под переменным током также подразумевают ток в обычных одно- и трёхфазных сетях. В этом случае мгновенные значения тока и напряжения изменяются по гармоническому закону.

В устройствах-потребителях постоянного тока переменный ток часто преобразуется выпрямителями для получения постоянного тока.

 Закон ома для переменного тока в общем случае имеет такой же вид, как и для постоянного. То есть при увеличении напряжения в цепи ток также в ней будет увеличиваться. Отличием же является то, что в цепи переменного тока сопротивление ему оказывают такие элементы как катушка индуктивности и емкость. Учитывая этот факт, запишем закон ома для переменного тока.

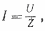
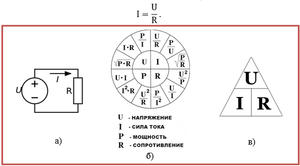
Формула 1 — закон ома для переменного тока

 где z это полное сопротивление цепи.

Формула 2 — полное сопротивление цепи

 

 В общем случае полное сопротивление цепи переменного тока будет состоять из активного емкостного и индуктивного сопротивления. Проще говоря, ток в цепи переменного тока, зависит не только от активного омического сопротивление, но и от величины емкости и индуктивности.

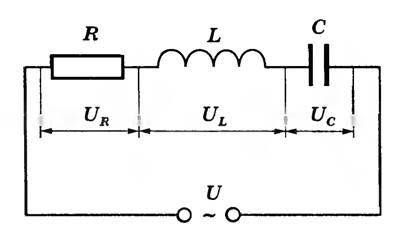
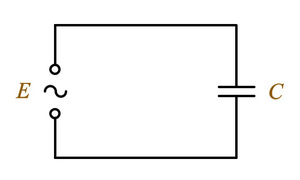
Рисунок 1 — цепь, содержащая омическое индуктивное и емкостное сопротивление

 

 Если, например, в цепь постоянного тока включить конденсатор то тока в цепи не будет, так как конденсатор на постоянном токе является разрывом цепи. Если же в цепи постоянного тока появится индуктивность, то ток не изменится. Строго говоря, изменится, так как катушка будет обладать омическим сопротивлением. Но изменение будет ничтожным.  Если же конденсатор и катушку включить в цепи переменного тока, то они будут оказывать сопротивление току пропорционально величине ёмкости и индуктивности соответственно. Кроме этого в цепи буде наблюдаться сдвиг фаз между напряжением и током. В общем случае ток в конденсаторе опережает напряжение на 90 градусов. В индуктивности же отстает на 90 градусов.  Емкостное сопротивление зависит от величины емкости и частоты переменного тока. Эта зависимость обратно пропорциональна, то есть с увеличением частоты и ёмкости сопротивление будет уменьшаться.

Формула 3 — емкостное сопротивление

 

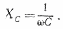
 Индуктивное сопротивление прямо пропорционально частоте и индуктивности. Чем больше индуктивность и частота, тем больше сопротивление переменному току будет оказывать данная катушка.

формула взаимосвязи между электрическими величинами, порядок расчета

Фундаментальным положением, описывающим зависимость тока, сопротивления и напряжения друг от друга является закон Ома для цепи переменного тока. Основное его отличие от одноимённого положения для участка цепи заключается в учёте полного сопротивления. Эта величина зависит от активной и реактивной составляющей линии, то есть учитывает ёмкость и индуктивность. Поэтому и расчёт параметров для полной цепи по сравнению с участком выполнить будет сложнее.

Основные понятия

Вся наука электротехника построена на оперировании такими понятиями, как заряд и потенциал. Кроме этого, важными явлениями в цепи являются электрические и магнитные поля. Для того чтобы разобраться в сущности закона Ома, необходимо понимать, что представляют собой эти величины, и от чего зависят те или иные электромагнитные процессы.

Электричеством называется явление, обусловленное взаимодействием зарядов между собой и их движением. Это слово было введено в обиход Уильямом Гилбертом в 1600 году после открытия им способности некоторых тел наэлектризовываться. Так как свои эксперименты он проводил с кусочками янтаря, то и свойство притягивать или отталкивать ими другие вещества им было названо «янтарностью», что в переводе с греческого звучит как электричество.

В дальнейшем различными ученными, такими как Эрстед, Ампер, Джоуль, Фарадей, Вольт, Ленц и Ом был открыт ряд явлений. Благодаря их исследованиям в обиходе появились понятия: электромагнитная индукция и поле, гальванический элемент, ток и потенциал. Ими была открыта связь между электричеством и магнетизмом, что привело к появлению науки, изучающей теорию электромагнитных явлений.

В 1880 году русский инженер Лачинов теоретически указал, какие условия необходимы для передачи электричества на расстояния. А через 8 лет Генрих Рудольф Герц во время экспериментов зарегистрировал электромагнитные волны.

Таким образом было установлено, что электрические заряды способны создавать вокруг себя электрическое излучение. Условно их разделили на частицы с положительным и отрицательным знаком заряда. Было установленно, что одноимённого знака заряды притягиваются, а разноимённого — отталкиваются. Для возникновения их движения к физическому телу необходимо приложить какую-либо энергию. При их перемещении возникает магнитное поле.

Свойство материалов обеспечивать движение зарядов получило название проводимость, а величина, обратная ей, — сопротивление. Способность пропускать через себя заряды зависит от структуры кристаллической решётки вещества, её связей, дефектов и содержания примесей.

Определение напряжения

Учёными было установлено, что существует два вида перемещения зарядов — хаотичное и направленное. Первый тип не приводит ни к каким процессам, так как энергия находится в сбалансированном состоянии. Но если к телу приложить силу, заставляющую заряды следовать в одну сторону, то возникнет электрический ток.

Существует два вида:

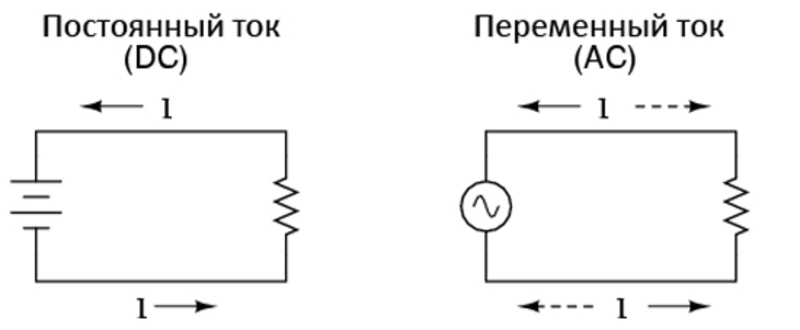
1. Постоянный — сила и направление которого остаются постоянными во времени.
2. Переменный — имеющий разную величину в определённой точке времени и изменяющий своё движение, при этом повторяющий через равные интервалы времени своё изменение (цикл). Эта переменчивость описывается по гармоническому закону синуса или косинуса.

Заряд характеризуется таким понятием, как потенциал, то есть количеством энергии, которой он обладает. Необходимая сила для перемещения заряда из одной точки тела в другую называется напряжением.

Определяется она относительно изменения потенциала заряда. Сила тока определяется отношением количества заряда, прошедшего через тело за единицу времени, к величине этого периода. Математически она описывается выражением: Im = ΔQ/ Δt, измеряется в амперах (A).

Относительно переменного сигнала вводится дополнительная величина — частота f, которая определяет цикличность прохождения сигнала f = 1/T, где T — период. За её единицу измерения принят герц (Гц). Исходя из этого синусоидальный ток выражается формулой:

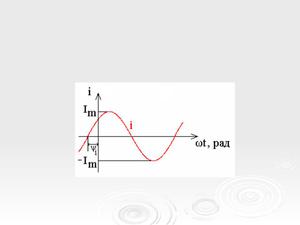I = Im * sin (w*t+ Ψ), где:

• Im — это сила тока в определённый момент времени;
• Ψ — фаза, определяемая смещением волны тока по отношению к напряжению;
• w — круговая частота, эта величина зависит от периода и равна w = 2*p*f.

Напряжение же характеризуется работой, которую совершает электрическое поле для переноса заряда из одной точки в другую. Определяется она как разность потенциалов: Um = φ1 — φ2. Затрачиваемая работа же складывается из двух сил: электрических и сторонних, называется электродвижущей (ЭДС). Зависит она от магнитной индукции. Потенциал же равен отношению энергии взаимодействия заряда окружающего поля к значению его величины.

Поэтому для гармонического изменения сигнала значение напряжения выражается как:

U = Um * sin (w*t + Ψ).

Где Um — амплитудное значение напряжения. Измеряется переменное напряжение в вольтах (В).

Импеданс цепи

Каждое физическое тело имеет своё сопротивление. Обусловлено оно внутренним строением вещества. Характеризуется эта величина свойством проводника препятствовать прохождению тока и зависит от удельного электрического параметра. Определяется по формуле: R = ρ*L/S, где ρ — удельное сопротивление, являющееся скалярной величиной, Ом*м; L — длина проводника; м; S — площадь сечения, м

2. Таким выражением определяется постоянное сопротивление, присущее пассивным элементам.

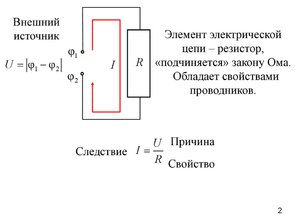В то же время импеданс, полное сопротивление, находится как сумма пассивной и реактивной составляющей. Первая определяется только активным сопротивлением, состоящим из резистивной нагрузки источника питания и резисторов: R = R0 + r. Вторая находится как разность между ёмкостным и индуктивным сопротивлением: X = XL-Xc.

Если в электрическую цепь поместить идеальный конденсатор (без потерь), то после того, как на него поступит переменный сигнал, он зарядится. Ток начнёт поступать далее, в соответствии с периодами его заряда и разряда. Количество электричества, протекающее в цепи, равно: q = C * U, где С — ёмкость элемента, Ф; U — напряжение источника питания или на обкладках конденсатора, В.

Так как скорости изменения тока и напряжения прямо пропорциональны частоте w, то будет справедливым следующее выражение: I = 2* p * f * C * U. Отсюда получается, что ёмкостной импеданс вычисляется по формуле:

Xc = 1/ 2* p * f * C = 1/ w * C, Ом.

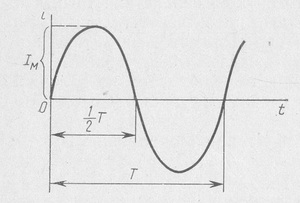Индуктивное же сопротивление возникает вследствие появления в проводнике собственного поля, называемого ЭДС самоиндукции EL. Зависит она от индуктивности и скорости изменения тока. В свою очередь индуктивность зависит от форм и размеров проводника, магнитной проницаемости среды: L =Ф / I, измеряется в теслах (Тл). Поскольку напряжение, приложенное к индуктивности, по своей величине равно ЭДС самоиндукции, то справедливо EL = 2* p * f * L * I. При этом скорость изменения тока пропорциональна частоте w. Исходя из этого индуктивное сопротивление равно:

Xl = w * L, Ом.

Таким образом, импеданс цепи рассчитывается как: Z = (R ² +(X c-X l) ²) ^½, Ом.

То есть он зависит от частоты переменного сигнала, индуктивности и ёмкости цепи, а также активного сопротивления источника и электрической линии. При этом в качестве реактивной составляющей чаще всего выступают паразитные величины.

Закон для переменного тока

Классический закон был открыт физиком из Германии Симоном Омом в 1862 году. Проводя эксперименты, он обнаружил связь между током и напряжением. В результате ученый сформулировал утверждение, что сила тока пропорциональна разности потенциалов и обратно пропорциональна сопротивлению. Если в электрической цепи ток уменьшится в несколько раз, то и напряжение в ней станет меньше на столько же.

Математически закон Ома был описан как:

I = U / R, А.

Это выражение справедливо как для синусоидального, так и для постоянного тока. Но такая зависимость величин соответствует идеальной ситуации, в которой не учитываются паразитные составляющие и сопротивление источника тока. В случае же гармоничного сигнала на его прохождение влияет частота, из-за присутствия ёмкостной и индуктивной составляющей в электрической линии.

Поэтому закон Ома для переменного тока описывается формулой:

I = U / Z, где:

• I — сила переменного тока, А;
• U — разность потенциалов, В;
• Z — полное сопротивление цепи, Ом.

Полное сопротивление зависит от частоты гармоничного сигнала и вычисляется по следующей формуле:

Z = ((R+r)² + (w*L — 1/w*C)²)^½ = ((R+r)²+X²)^½.

При прохождении тока переменной величины электромагнитное поле совершает работу, при этом из-за сопротивления, оказываемого в цепи, выделяется тепло. То есть электрическая энергия переходит в тепловую. Мощность же пропорциональна току и напряжению. Формула, описывающая мгновенное значение, выглядит как: P = I*U.

В то же время для переменного сигнала необходимо учитывать амплитудную и частотную составляющую. Поэтому:

P = I *U*cosw*t*cos (w*t+ Ψ), где I, U — амплитудные значения, а Ψ — фазовый сдвиг.

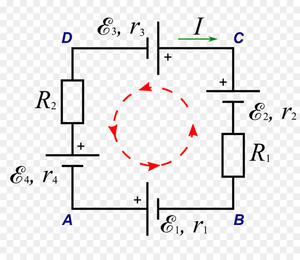Для анализа процессов в электрических цепях переменного тока вводится понятие комплексного числа. Связанно это со смещением фаз, появляющихся между током, и разностью потенциалов. Обозначается это число латинской буквой j и состоит из мнимой Im и вещественной Re частей.

Так как на активном сопротивлении происходит трансформирование мощности в тепло, а на реактивном она преобразуется в энергию электромагнитного поля, возможны её переходы из любой формы в любую. Можно записать: Z = U / I = z * e^j*Ψ.

Отсюда полное сопротивление цепи: Z = r + j * X, где r и x — соответственно активное и реактивное сопротивление. Если же сдвиг фаз принимается равный 90⁰, то комплексное число можно не учитывать.

Использование формулы

Использование закона Ома позволяет построить временные характеристики различных элементов. С помощью него несложно рассчитать нагрузки для электрических схем, выбрать нужное сечение проводов, правильно подобрать защитные автоматы и предохранители. Понимание закона даёт возможность применить правильный источник питания.

Использование Закона Ома можно применить на практике для решения задачи. Например, пускай есть электрическая линия, состоящая из последовательно соединённых элементов, таких как: ёмкость, индуктивность и резистор. При этом ёмкость C = 2*Ф, индуктивность L=10 мГн, а сопротивление R = 10 кОм. Требуется вычислить импеданс полной цепи и рассчитать силу тока. При этом блок питания работает на частоте равной f = 200 Гц и выдаёт сигнал с амплитудой U = 12 0 В. Внутреннее сопротивление источника питании составляет r = 1 кОм .

Вначале необходимо рассчитать реактивное сопротивление в цепи переменного тока. Так, ёмкостное сопротивление находится из выражения: Xc = 1/ (2 *p *F*C) и на частоте 200 Гц оно равно: Xc = 588 Ом.

Индуктивное сопротивление находится из выражения: XL = 2*p*F* L. На f = 200 Гц и оно оставляет: X*L = 1,25 Ом. Полное сопротивление RLC цепи будет: Z = ((10 *10 ³ +1*10 ³ ) ² + (588−1,25) ² ) ^½ = 11 кОм.

Разность потенциалов, изменяющаяся по гармоническому закону синуса, будет определяться: U (t) = U * sin (2* p *f*t) = 120*sin (3,14*t). Ток будет равен: I (t) = 10* 10 ⁻³ + sin (3,14*t+p/2).

По рассчитанным данным можно построить график тока, соответствующий частоте 100 Гц. Для этого в декартовой системе координат отображается зависимость тока от времени.

Следует отметить, закон Ома для переменного сигнала отличается от использующегося для классического расчёта лишь учётом полного сопротивления и частоты сигнала. А учитывать их важно, так как любой радиокомпонент обладает как активным, так и реактивным сопротивлением, что в итоге сказывается на работе всей схемы, особенно на высоких частотах. Поэтому при проектировании электронных конструкций, в частности импульсных устройств, для расчётов используется именно полный закон Ома.

Закон Ома для переменного тока в цепи, содержащей только емкость

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПРОВЕРКА ПОЛНОГО ЗАКОНА ОМА ДЛЯ ПЕРЕМЕННОГО ТОКА

Методические указания к выполнению лабораторной работы №16 по электричеству для студентов физического факультета

УФА

РИЦ БашГУ

2010

Печатается по решению кафедры общей физики

от 17 сентября 2010г., протокол №2

Составители:

д. ф.-м. н. Альмухаметов Р.Ф.,

к. ф.-м. н. Гафуров И.Г., Горбенко А.П.

ПРОВЕРКА ПОЛНОГО ЗАКОНА ОМА ДЛЯ ПЕРЕМЕННОГО ТОКА

Цель работы: проверка выполнения полного закона Ома для цепи переменного тока, исследование индуктивности и коэффициента мощности дросселя в цепи переменного тока.

Приборы и принадлежности: катушка индуктивности (с ферромагнитным сердечником), магазин емкостей, амперметр, вольтметр, ваттметр, лабораторный автотрансформатор.

Краткая теория

При рассмотрении электрических колебаний приходится иметь дело с токами, изменяющимися во времени. Закон Ома и правила Кирхгофа были установлены для постоянного тока. Однако они остаются справедливыми и для мгновенных значений изменяющихся тока и напряжения, если только эти изменения происходят не слишком быстро (нужно помнить, что электромагнитные возмущения передаются по цепи со скоростью света).

Пусть длина цепи равна 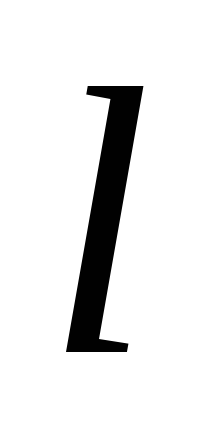. Если за время , необходимое для передачи возмущения в самую удаленную точку цепи, сила тока изменится незначительно, то мгновенные значения силы тока во всех сечениях цепи будут практически одинаковыми. Токи, удовлетворяющие таким условиям, называются КВАЗИСТАЦИОНАРНЫМИ. Для переменного тока условие квазистационарности имеет вид

,

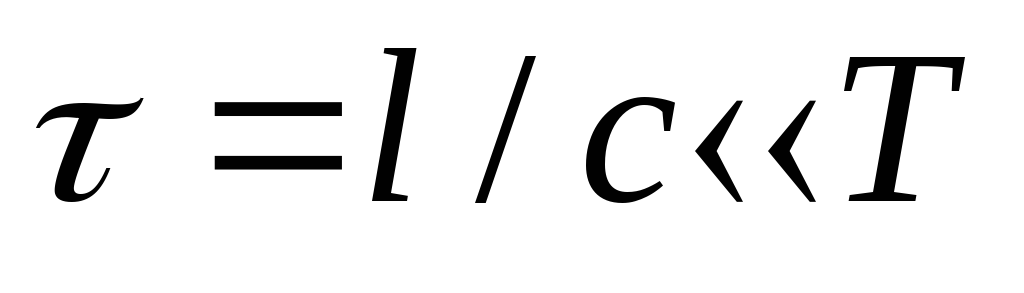где – период изменений.

Для цепи длиной 3м время запаздывания τ=10^-8 с. Таким образом, вплоть до Т~10^-6 с (что соответствует частоте 10⁶ Гц) ток в цепи можно считать квазистационарным. Ток промышленной частоты 50Гц квазистационарен для цепей длиной до 100км.

Мгновенные значения квазистационарного тока подчиняются закону Ома, следовательно, для них справедливы и правила Кирхгофа.

Для характеристики переменного тока используют сопоставление средней мощности тока с мощностью постоянного тока соответствующей силы. Полученное таким образом значение силы переменного тока I называется ДЕЙСТВУЮЩИМ (или эффективным) значением, математически представляющим собой среднеквадратичное за период значение силы тока. Аналогично определяется и действующее значение напряжения U переменного тока.

В простейшем и наиболее важном случае мгновенное значение силы I переменного тока меняется во времени t по синусоидальному закону:

(1)

где 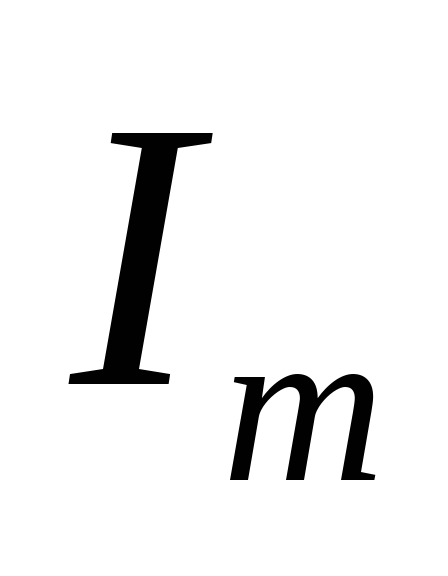— амплитуда тока, — его круговая частота, — начальная фаза.

Синусоидальный (гармонический) ток создается синусоидальным напряжением U той же частоты:

(2)

где — амплитуда напряжения, — начальная фаза (рис.1).

+

с.1. Графики напряжения и тока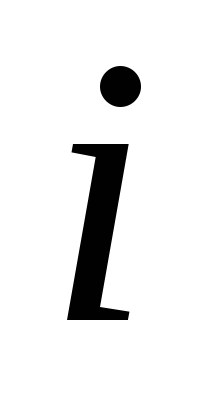

в цепи переменного тока.

Действующие значения такого переменного тока равны:

(3)

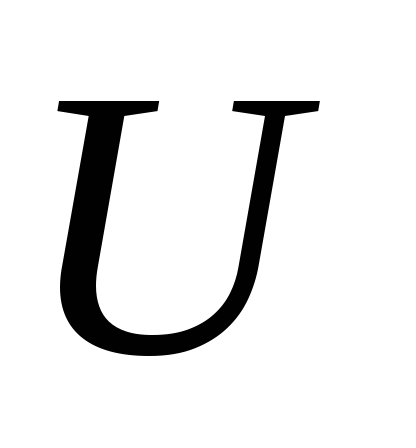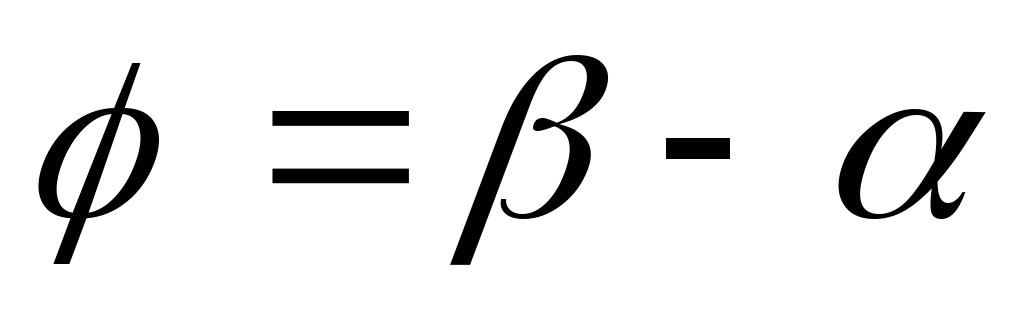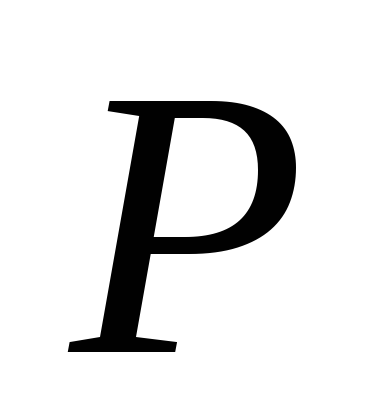Как уже говорилось выше, для квазистационарных токов справедлив закон Ома. Из–за наличия в цепи переменного тока индуктивности L или емкости C между силой тока I и напряжением в общем случае возникает сдвиг фаз , зависящий от параметров цепи (R, L, C, где R – активное сопротивление, L – индуктивность, С — емкость) и частоты ω. Вследствие сдвига фаз средняя мощность переменного тока, измеряемая, например, ваттметром, меньше произведения действующих значений тока и напряжения:

(4)

Закон Ома для переменного тока в цепи, содержащей только активное сопротивление

В цепи, не содержащей ни индуктивности, ни емкости, ток совпадает по фазе с напряжением (рис. 2) .

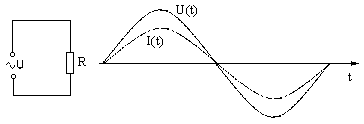
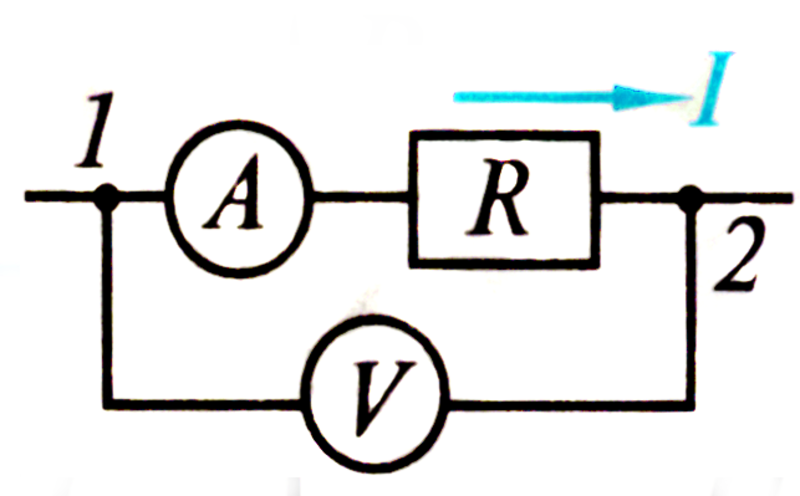
рис. 2 Схема цепи и графики напряжения U(t) и силы тока I(t) в цепи, содержащей только активное сопротивление R

Закон Ома для действующих значений этой цепи имеет такую же форму, как и для цепи постоянного тока:

(5)

АКТИВНОЕ СОПРОТИВЛЕНИЕ цепи 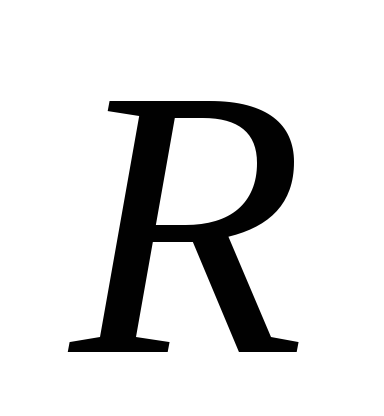определятся по активной мощности , затрачиваемой в цепи:

Закон Ома для переменного тока в цепи, содержащей только индуктивность

При наличии в цепи индуктивности L переменный ток индуцирует в ней ЭДС самоиндукции:

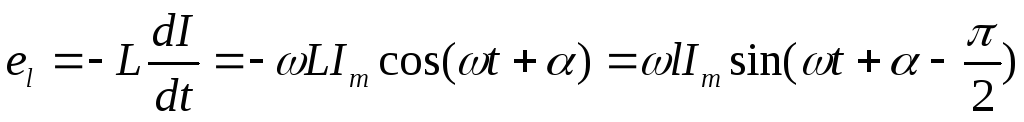(6)

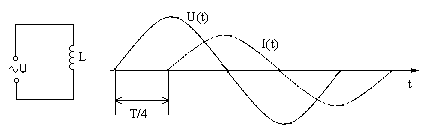
рис. 3 Схема цепи и графики напряжения U(t) и

силы тока I(t) в цепи, содержащей только индуктивность L.

ЭДС самоиндукции противодействует изменению тока, и в цепи, содержащей только индуктивность, ток отстает по фазе от напряжения на четверть периода, т.е. (рис. 3).

Действующее значение равно:

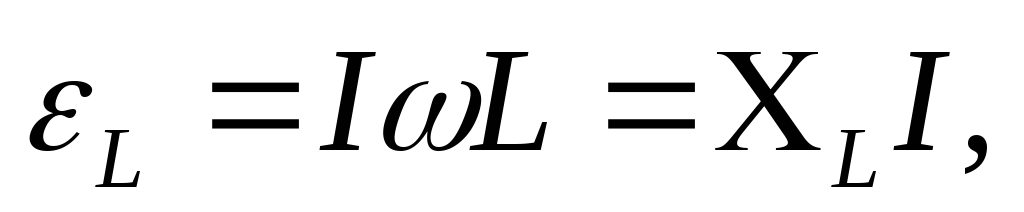(7)

где 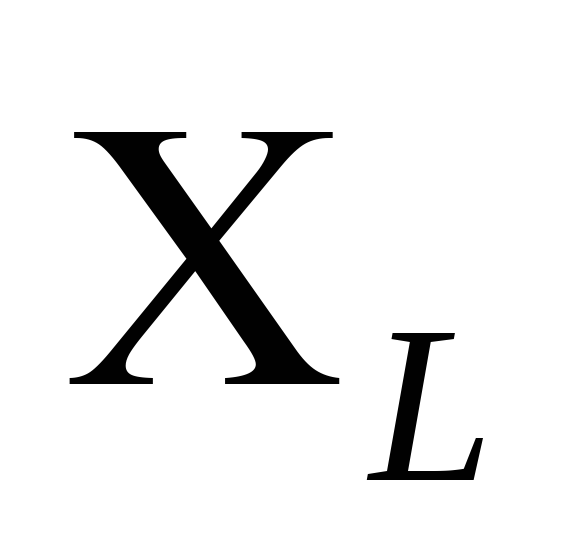— индуктивное сопротивление цепи.

Закон Ома для такой цепи имеет вид:

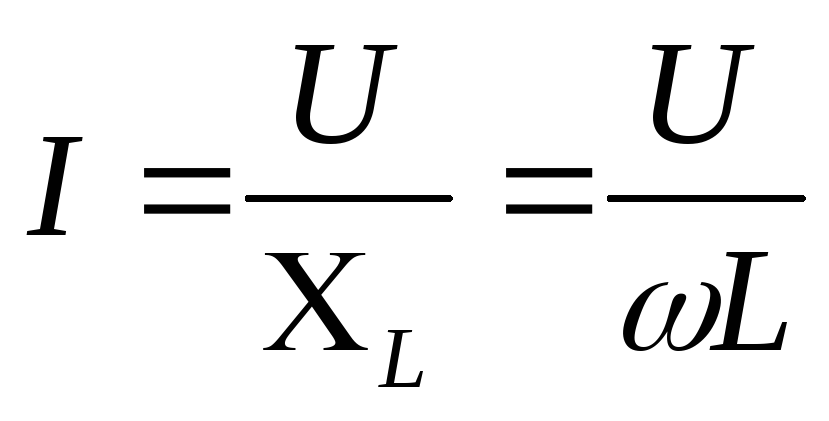(8)

А значение

(9)

называется индуктивным сопротивлением.

При напряжении 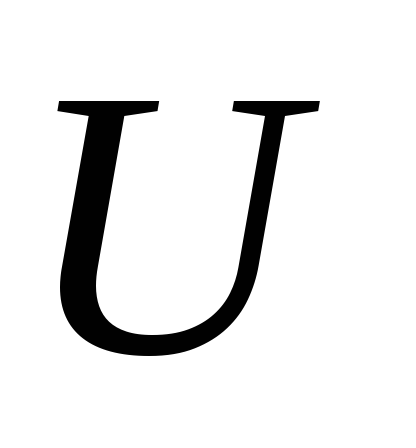на конденсаторе с емкостью заряд на его обкладках будет равен 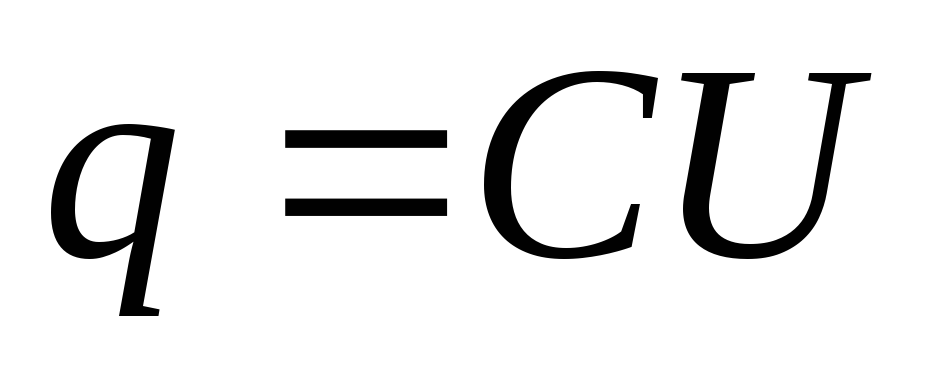. Периодические изменения вызывают периодическое изменение , и возникает ток, протекающий через конденсатор:

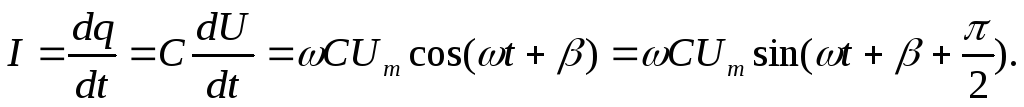(10)

Таким образом, синусоидальный переменный ток, проходящий через емкость, опережает по фазе напряжение на её зажимах на четверть периода, т.е. (рис. 4).

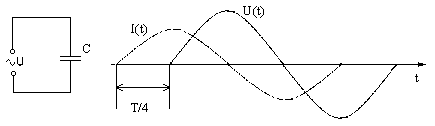
рис. 4 Схема цепи и графики напряжения U(t) и

силы тока I(t) в цепи, содержащей только емкость С.

Эффективные значения силы тока и напряжения в такой цепи связаны соотношением (закон Ома для цепи, содержащей только емкость):

(11)

где

(12)

емкостное сопротивление цепи.

Закон Ома для переменного тока в цепи, содержащей активное сопротивление, индуктивность и емкость

Если в цепь переменного тока последовательно включены активное сопротивление R, индуктивность L и емкость C, то её ПОЛНОЕ СОПРОТИВЛЕНИЕ равно:

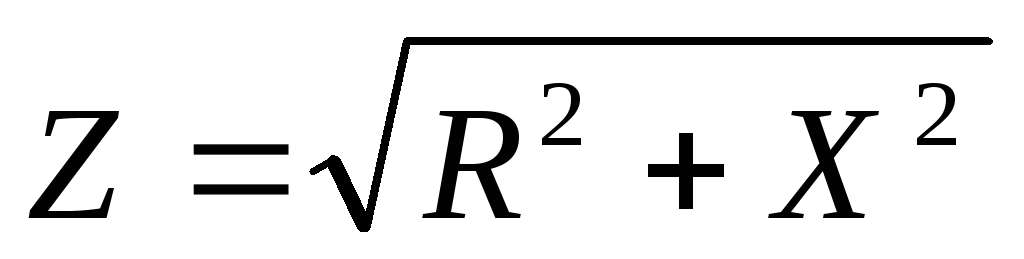(13)

где 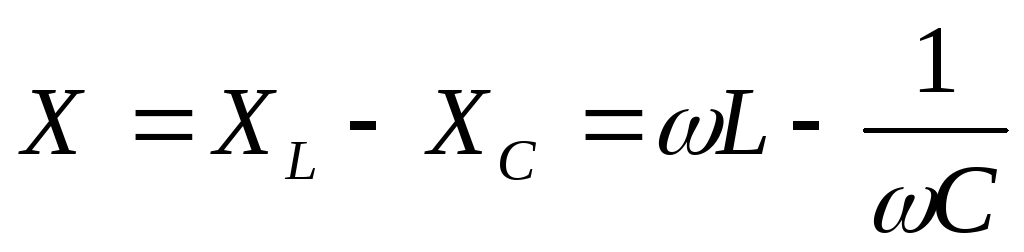— реактивное сопротивление цепи.

Соответственно закон Ома переменного тока имеет вид:

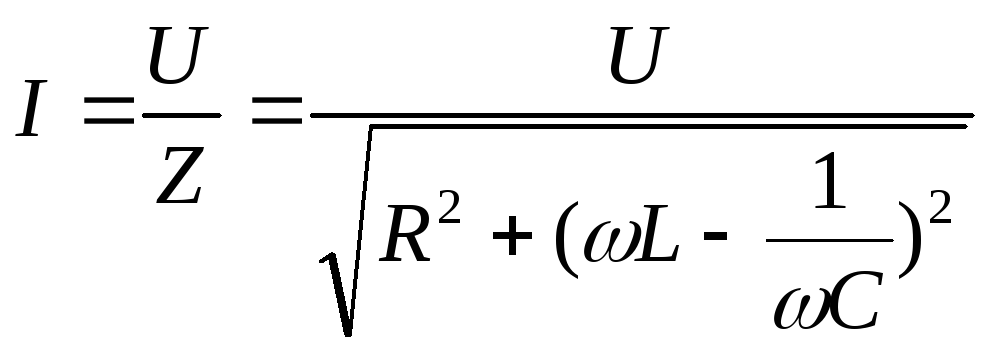( 14)

Сдвиг фаз между током и напряжением определяется отношением реактивного сопротивления к активному: .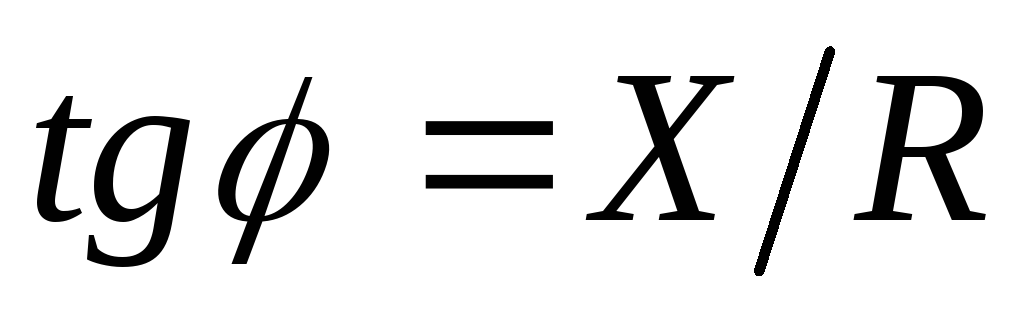

Закон Ома для цепи переменного тока можно получить, используя метод векторной диаграммы (рис.5) на комплексной плоскости:

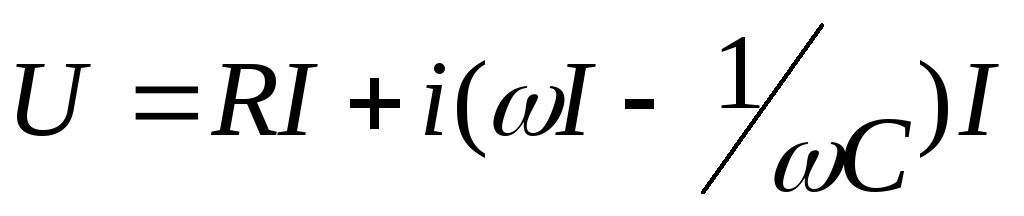
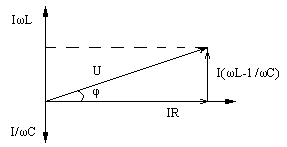
рис. 5

В такой цепи при совпадении частоты вынужденных колебаний, создаваемых источником переменного тока с резонансной частотой 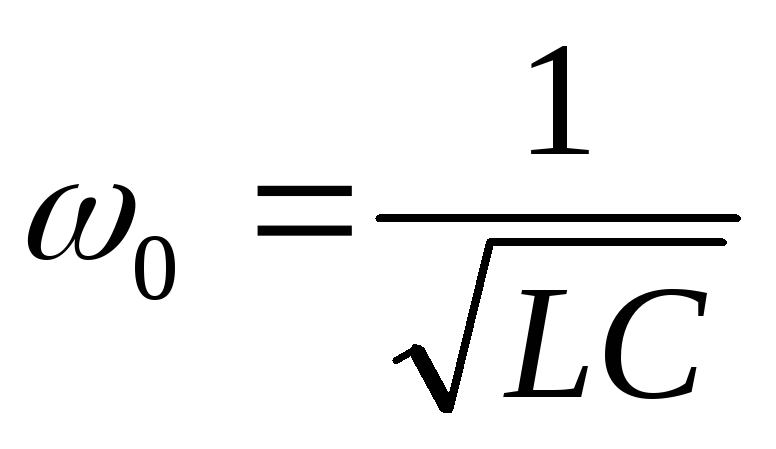, индуктивное и емкостное сопротивление равны и полностью компенсируют друг друга, сила тока максимальна и наблюдается явление РЕЗОНАНСА. В условиях резонанса напряжения на индуктивности и емкости могут значительно (часто во много раз) превышать напряжение на зажимах цепи.

Упражнение 1. Исследование индуктивности и коэффициента мощности дросселя в цепи переменного тока.

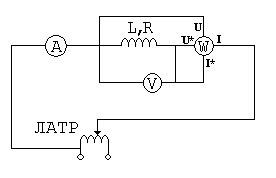
рис. 6. Экспериментальная установка.

На рис.6 представлена схема экспериментальной установки для проведения соответствующих измерений. Дроссель с индуктивностью и активным сопротивлением 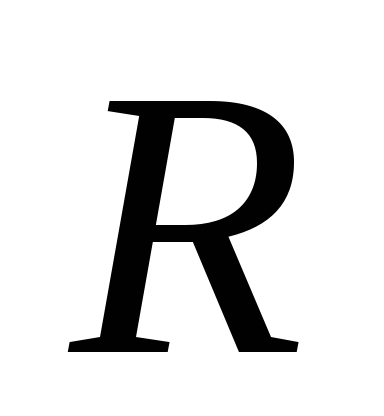питается от автотрансформатора ЛАТР. Измерительными приборами являются амперметр, вольтметр и ваттметр.

Полное сопротивление цепи определи по уравнению:

(15)

Показания измерительных приборов позволяют найти коэффициент мощности:

(16)

Активное сопротивление определяется по формуле:

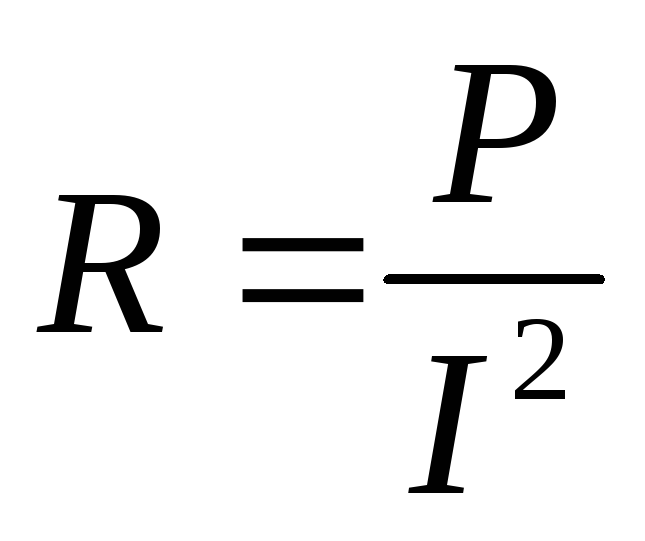(17)

Легко видеть, что индуктивность дросселя:

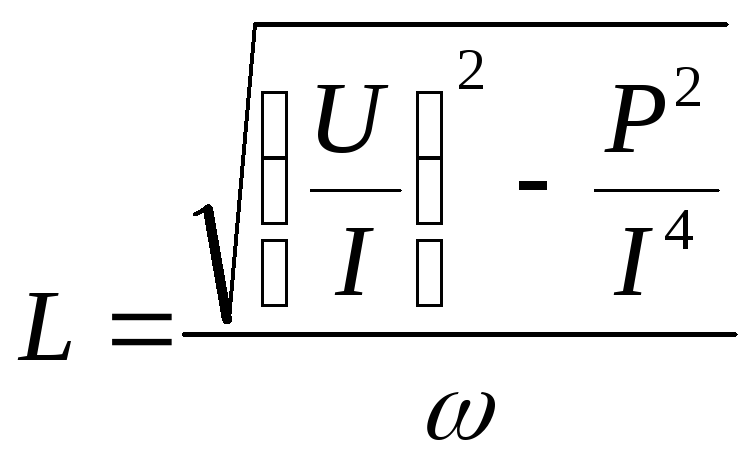. (18)

Если сопротивление соединительных проводов и обмоток дросселя обозначить , то потери энергии в сердечнике будет характеризоваться выражением:

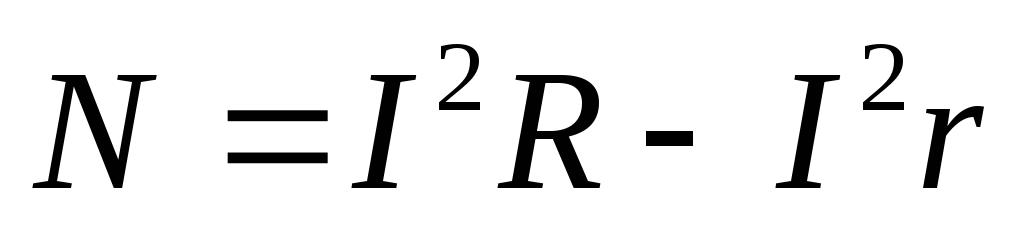, (19)

где — мощность, выделяемая в проводах.

Таким образом, для исследования цепи, содержащей индуктивность и активное сопротивление, следует найти индуктивность дросселя, коэффициент мощности и потери энергии в железном сердечнике дросселя.

Рекомендуется следующий порядок выполнения измерений:

1. Ознакомиться с устройством и принципом действия ваттметра (в нашем случае электродинамического типа) по техническому описанию; собрать схему по рис. 6, проверить правильность ее исполнения у лаборанта;

2. Записать в тетрадь значение активного сопротивления дросселя;

3. Пользуясь схемой рис. 6, определить индуктивность катушки без ферромагнитного сердечника, пользуясь соотношением:

(20)

4. Вставить сердечник и при 3 – 5 значениях тока определить активное сопротивление (по формуле 17), коэффициент мощности (формула 16), индуктивность дросселя (18) и потери мощности в сердечнике (19). Полученные результаты внести в таблицу, в которую занести показания приборов, результаты измерений и погрешности определения измеряемых величин;

I, A

U, B

P, Вт

R, Ом

cosφ

L, Гн

N, Вт

5. Согласно данным эксперимента постройте векторную диаграмму напряжений (рис.5) на индуктивности и активном сопротивлении.

Есть ли отличия закона Ома для цепей переменного и постоянного напряжения?

Закон Ома является одним из основных законов электротехники. Он довольно прост и применяется при расчете практически любых электрических цепей. Но данный закон имеет некоторые особенности работы в цепях переменного и постоянного тока при наличии в цепи реактивных элементов. Эти особенности нужно помнить всегда.

Закон Ома для цепи постоянного тока

Классическая схема закона Ома выглядит так:

А звучит и того проще – ток, протекающей на участке цепи, будет равен отношению напряжения цепи к ее сопротивлению, что выражается формулой:

Но ведь мы знаем, что помимо активного сопротивления R, существует и реактивные сопротивления индуктивности Х_L и емкости X_C. А ведь согласитесь, что электрические схемы с чисто активным сопротивлением встречаются крайне редко. Давайте рассмотрим схему, в которой последовательно включена катушка индуктивности L, конденсатор С и резистор R:

Помимо чисто активного сопротивления R, индуктивность L и емкость С имеют и реактивные сопротивления  Х_L и X_C, которые выражены формулами:

Где ω это циклическая частота сети, равная ω = 2πf. f – частота сети в Гц.

Для постоянного тока частота равна нулю (f = 0), соответственно реактивное сопротивление индуктивности станет равным нулю (формула (1)), а емкости – бесконечности (2), что приведет к разрыву электрической цепи. Отсюда можно сделать вывод, что реактивное сопротивление элементов в цепях постоянного напряжения отсутствует.

Закон Ома для цепи переменного тока

Если рассматривать классическую электрическую цепь и на переменном токе, то она практически ничем не будет отличаться от постоянного тока, только источником напряжения (вместо постоянного — переменное):

Соответственно и формула для такого контура останется прежней:

Но если мы усложним схему и добавим к ней реактивных элементов:

Ситуация изменится кардинально. Теперь f у нас не равна нулю, что сигнализирует о том, что помимо активного, в цепь вводится и реактивное сопротивление, которое также может влиять на величину тока, протекаемого в контуре и приводить к резонансу. Теперь полное сопротивление контура (обозначается как Z) и оно не равно активному Z ≠ R. Формула примет следующий вид:

Соответственно немного изменится и формула для закона Ома:

Почему это важно?

Знание этих нюансов позволит избежать серьезных проблем, которые могут возникнуть при неправильном подходе к решению некоторых электротехнических задач. Например, в контур переменного напряжения подключена катушка индуктивности со следующими параметрами: f_ном = 50 Гц, U_ном = 220 В, R = 0,01 Ома, L = 0,03 Гн. Ток, протекающий через данную катушку будет равен:

Где:

В случае, если подать на эту же катушку постоянное напряжение с таким же значением, получим:

Мы видим, что ток катушки возрастает в разы, что приводит к выходу из строя элементов контура.

Активное, емкостное и индуктивное сопротивление. Закон Ома для цепей переменного тока

Активное сопротивление

Определение 1

Пусть источник переменного тока включен в цепь, в которой индуктивностью и емкостью можно пренебречь. Переменный ток изменяется в соответствии с законом:

\[I\left(t\right)=I_m{sin \left(\omega t\right)\ \left(1\right).\ }\]

Рисунок 1.

Тогда, если применить к участку цепи ($а R в$) (рис.1) закон Ома получим:

\[U=IR=I_m{Rsin \left(\omega t\right)\ \left(2\right),\ }\]

где $U$ — напряжение на концах участка. Разность фаз между током и напряжением равна нулю. Амплитудное значение напряжения ($U_m$) равно:

\[U_m=RI_m\left(3\right),\]

где коэффициент $R$ — называется активным сопротивлением. Наличие активного сопротивления в цепи всегда приводит к выделению тепла.

Ёмкостное сопротивление

Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$.

Рисунок 2.

Мы можем использовать следующие соотношения:

Если $I(t)$ определена уравнением (1), то заряд выражен как:

где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно:

Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $\frac{\pi }{2}.$ Амплитуда напряжения на емкости равна:

Величину $X_C=\frac{1}{\omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=\infty $. Это значит, что постоянный ток не течет через конденсатор. Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.

Индуктивное сопротивление

Пусть участок цепи имеет только индуктивность (рис.3). Будем считать $I>0$, если ток направлен от $а$ к $в$.

Рисунок 3.

Если в катушке течет ток, то в индуктивности появляется ЭДС самоиндукции, следовательно, закон Ома примет вид:

По условию $R=0. \mathcal E$ самоиндукции можно выразить как:

Из выражений (8), (9) следует, что:

Амплитуда напряжения в данном случае равна:

где $X_L-\ $индуктивное сопротивление (кажущееся сопротивление индуктивности).

Закон Ома для цепей переменного тока

Определение 2

Выражение вида:

\[I_m=\frac{U_m}{\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}}\left(12\right).\]

где

\[Z=\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}(13)\]

называют полным электросопротивлением, или импедансом, иногда называют законом Ома для переменного тока. Однако необходимо помнить, что формула (12) относится к амплитудам тока и напряжения, а не мгновенным их значениям.

Пример 1

Задание: Чему равно действующее значение силы тока в цепи. Цепь переменного тока состоит из последовательно соединенных: конденсатора емкостью $C$, катушки индуктивности $L$, активного сопротивления $R$. На зажимы цепи подается напряжение действующее напряжение $U$ частота которого $\nu$.

Решение:

Так как все элементы цепи соединены последовательно, то сила тока во всех элементах одинакова.

Амплитудное значение силы тока выражается «законом Ома для переменного тока»:

\[I_m=\frac{U_m}{\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}}\left(1.1\right)\]

оно связано с действующим значением силы тока как:

\[I=\frac{I_m}{\sqrt{2}}\left(1.2\right).\]

В условиях задачи мы имеем действующее значение напряжения $U$, нам в формуле (1.1) требуется амплитуда напряжения, используя формулу:

\[U=\frac{U_m}{\sqrt{2}}\to U_m=\sqrt{2}U\left(1.3\right).\]

Подставим в формулу (1.2) формулы (1.1) и (1.3), получим:

\[I=\frac{1}{\sqrt{2}}\frac{\sqrt{2}U}{\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}}=\frac{U}{\sqrt{R^2+{\left(\omega L-\frac{1}{\omega C}\right)}^2}}=\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}},\]

где $\omega =2\pi \nu .$

Ответ: $I=\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}}.$

Пример 2

Задание: Используя условия задачи в первом примере, найдите действующие значения напряжений на катушке индуктивности ($U_L$), сопротивлении ($U_R$), конденсаторе ($U_C$).

Решение:

Используем результат примера 1. Напряжение на катушке индуктивности выражается формулой:

\[U_L=I\omega L=2 \pi \nu L\frac{U}{\sqrt{R^2+{\left(2 \pi \nu L-\frac{1}{2 \pi \nu C}\right)}^2}}.\]

Напряжение на активном сопротивлении ($U_R$) равно:

\[U_R=IR=\frac{UR}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}}.\]

Напряжение на конденсаторе ($U_C$) определяется как:

\[U_C=\frac{I}{C2 \pi \nu}=\frac{1}{C2 \pi \nu}\frac{U}{\sqrt{R^2+{\left(2 \pi \nu L-\frac{1}{2 \pi \nu C}\right)}^2}}.\]

Ответ: $U_L=2\pi \nu L\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}},\ U_R=\frac{UR}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}},U_C=\frac{1}{C2\pi \nu }\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}}.$

Закон Ома для цепи переменного тока. Мощность

В 2.3 были выведены соотношения, связывающие амплитуды переменных токов и напряжений на резисторе, конденсаторе и катушке индуктивности:

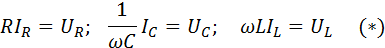
Эти соотношения во виду напоминают закон Ома для участка цепи постоянного тока, но только теперь в них входят не значения постоянных токов и напряжений на участке цепи, а амплитудные значения переменных токов и напряжений.

Соотношения (*) выражают закон Ома для участка цепи переменного тока, содержащего один из элементов R, L и C.

Физические величины R, 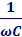 и ωL называются активным сопротивлением резистора, емкостным сопротивлением конденсатора и индуктивным сопротивлением катушки.

При протекании переменного тока по участку цепи электромагнитное поле совершает работу, и в цепи выделяется джоулево тепло. Мгновенная мощность в цепи переменного тока равна произведению мгновенных значений тока и напряжения: p = J · u. Практический интерес представляет среднее за период переменного тока значение мощности

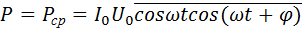
Здесь I₀ и U₀ – амплитудные значения тока и напряжения на данном участке цепи, φ – фазовый сдвиг между током и напряжением. Черта означает знак усреднения. Если участок цепи содержит только резистор с сопротивлением R, то фазовый сдвиг φ = 0:

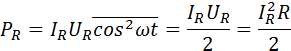
Для того, чтобы это выражение по виду совпадало с формулой для мощности постоянного тока, вводятся понятия действующих или эффективных значений силы тока и напряжения:

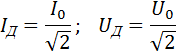
Средняя мощность переменного тока на участке цепи, содержащем резистор, равна

Если участок цепи содержит только конденсатор емкости C, то фазовый сдвиг между током и напряжением 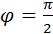 . Поэтому

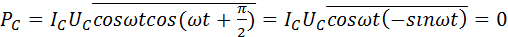
Аналогично можно показать, что PL = 0.

Таким образом, мощность в цепи переменного тока выделяется только на активном сопротивлении. Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю.

Рассмотрим теперь электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки. Цепь подключена к источнику переменного тока частоты ω. На всех последовательно соединенных участках цепи протекает один и тот же ток. Между напряжением внешнего источника e (t) и током J (t) возникает фазовый сдвиг на некоторый угол φ. Поэтому можно записать

J (t) = I0 cos ωt;   e (t) = 0 cos (ωt + φ).

Такая запись мгновенных значений тока и напряжения соответствует построениям на векторной диаграмме (рис. 2.3.2). Средняя мощность, развиваемая источником переменного тока, равна

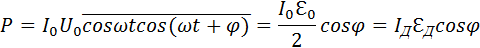
Как видно из векторной диаграммы, UR = 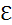₀ · cos φ, поэтому

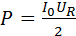 . Следовательно, вся мощность, развиваемая источником, выделяется в виде джоулева тепла на резисторе, что подтверждает сделанный ранее вывод.

В 2.3 было выведено соотношение между амплитудами тока I₀ и напряжения 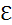₀ для последовательной RLC-цепи:

 

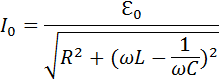
Величину

называют полным сопротивлением цепи переменного тока. Формулу, выражающую связь между амплитудными значениями тока и напряжения в цепи, можно записать в виде

ZI0 = 0.

(**)

Это соотношение называют законом Ома для цепи переменного тока. Формулы (*), приведенные в начале этого параграфа, выражают частные случаи закона Ома (**).

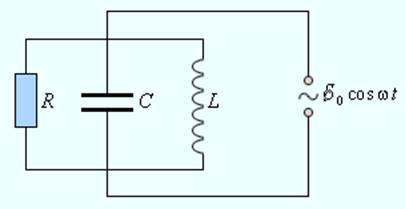
Понятие полного сопротивления играет важную роль при расчетах цепей переменного тока. Для определения полного сопротивления цепи во многих случаях удобно использовать наглядный метод векторных диаграмм. Рассмотрим в качестве примера параллельный RLC-контур, подключенный к внешнему источнику переменного тока (рис. 2.4.1).

Рисунок 2.4.1. Параллельный RLC-контур

При построении векторной диаграммы следует учесть, что при параллельном соединении напряжение на всех элементах R, C и L одно и то же и равно напряжению внешнего источника. Токи, текущие в разных ветвях цепи, отличаются не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Поэтому полное сопротивление цепи нельзя вычислить по законам параллельного соединения цепей постоянного тока. Векторная диаграмма для параллельного RLC-контура изображена на рис. 2.4.2.

Рисунок 2.4.2. Векторная диаграмма для параллельного RLC-контура

Из диаграммы следует:

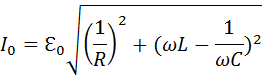
Поэтому полное сопротивление параллельного RLC-контура выражается соотношением

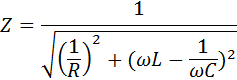
При параллельном резонансе (ω² = 1 / LC) полное сопротивление цепи принимает максимальное значение, равное активному сопротивлению резистора:

Фазовый сдвиг φ между током и напряжением при параллельном резонансе равен нулю.