12.3. Закон Ома для однородного участка цепи. Сопротивление проводников.
Г. Ом в 1826 г. экспериментально установил закон, который называется законом Ома для однородного участка цепи: Ток, текущий по однородному металлическому проводнику, пропорционален падению напряжения на проводнике.
I=(), (12-14)
где R — сопротивление проводника, измеряется в СИ в омах [Ом]; из (12-14) следует, что 1Ом =1 В/1 А.
Сопротивление проводника
R =ρl / S , (12-15)
где — удельное сопротивление, измеряется в СИ в Ом м. Оно зависит от температуры: =T, где — удельное сопротивление при температуре
Найдем связь между векторами и. Для этого мысленно выделим в окрестности некоторой точки проводника элементарный цилиндрический объем с образующими, параллельными векторам и, (рис.12.4).
Между концами проводника длиной dl
Сопротивление цилиндрического проводника, в нашем случае, равно
R = .
Используя закон Ома для участка цепи I = , находим:
jdS = ,
откуда и получаем закон Ома в дифференциальной форме
= =, (12-16)
где =удельная электропроводность; [] = 1 / (Ом м).
12.4. Закон Ома для неоднородного участка цепи
. (12-17)
Рассмотрим цилиндрический проводник длиной l с площадью поперечного сечения S. Умножим обе части равенства (12-17) на перемещение dl вдоль оси проводника и проинтегрируем получившееся соотношение по длине проводника от 0 до l:
что дает
j l = (+). (12-18)
Заменив j на I/S, а на , из (12-18) получим I =+ , откуда следует закон Ома для неоднородного участка цепи
I = (+) / R (12-19)
где R=l / S — сопротивление участка цепи 12. Для замкнутой цепи формула (12-19) запишется в виде
I = / R (12-20)
где R — суммарное сопротивление всей цепи; — ЭДС источника.
Пусть замкнутая цепь состоит из источника электрической энергии с ЭДС и внутренним сопротивлением r, а также внешней цепи потребителя, имеющей сопротивление R. Согласно (12-20)
I = / (R + r). (12-21)
азность потенциалов на электродах источника, рис.12.5, равна напряжению на внешнем участке цепи:
U == IR =- Ir. (12-22)
Если цепь разомкнуть, то ток в ней прекратится и напряжение U на зажимах источника станет равным его ЭДС, т.е. U = .
Таким образом, напряжение на внешнем участке цепи, будет равно
U = IR = R / (R + r).(12-23)
В пределе, когда R 0 (источник тока замкнут накоротко), то в этом случае, в соответствии с (12-21), ток максимален
I= I= / R, (12-24)
а напряжение во внешней цепи равно нулю.
В противоположном предельном случае, R, цепь разомкнута и ток отсутствует:
U = R / (R + r)= , т. к. lim R / (R + r) = 1. (12-25)
Закон Ома для однородного и неоднородного участка цепи
Дифференциальная форма закона Ома. Найдем связь между плотностью тока j и напряженностью поля Е в одной и той же точке проводника. В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора Е
 ,
ограниченной двумя эквипотенциальными
сечениями 1 и 2 (рис. 4.3).
,
ограниченной двумя эквипотенциальными
сечениями 1 и 2 (рис. 4.3). 
Обозначим
их потенциалы  и
и  ,
а среднюю площадь сечения через
,
а среднюю площадь сечения через 
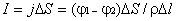 ,
или для плотности тока
,
или для плотности тока  ,
следовательно
,
следовательно  .
.
Перейдем
к пределу при  ,
тогда рассматриваемый объем можно
считать цилиндрическим, а поле внутри
него однородным, так что
,
тогда рассматриваемый объем можно
считать цилиндрическим, а поле внутри
него однородным, так что
 ,
,
где Е — напряженность электрического поля внутри проводника. Учитывая, что j и Есовпадают по направлению, получаем
 .
.
Это
соотношение является дифференциальной
формой закона Ома для однородного
участка цепи.
Величина 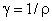 называется
удельной проводимостью. На
неоднородном участке цепи на носители
тока действуют, кроме электростатических
сил
называется
удельной проводимостью. На
неоднородном участке цепи на носители
тока действуют, кроме электростатических
сил 
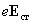 ,
следовательно, плотность тока в этих
участках оказывается пропорциональной
сумме напряженностей. Учет этого приводит
к дифференциальной
форме закон Ома для неоднородного
участка цепи.
,
следовательно, плотность тока в этих
участках оказывается пропорциональной
сумме напряженностей. Учет этого приводит
к дифференциальной
форме закон Ома для неоднородного
участка цепи. 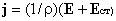 .
.
При прохождении электрического тока в замкнутой цепи на свободные заряды действуют силы со стороны стационарного электрического поля и сторонние силы. При этом на отдельных участках этой цепи ток создается только стационарным электрическим полем. Такие участки цепи называются
Для того чтобы выяснить, от чего зависит сила тока на этих участках, необходимо уточнить понятие напряжения.

Рис. 1
Рассмотрим вначале однородный участок цепи (рис. 1, а). В этом случае работу по перемещению заряда совершают только силы стационарного электрического поля, и этот участок характеризуют разностью потенциалов Δ
U=AKq+Astorq=φ1−φ2+ε.
Из этой формулы видно, что в общем случае напряжение на данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС на этом участке. Если же на участке действуют только электрические силы (ε = 0), то U=φ1−φ2. Таким образом, только для однородного участка цепи понятия напряжения и разности потенциалов совпадают.
Закон Ома для неоднородного участка цепи имеет вид:
I=UR=φ1−φ2+εR,
где R — общее сопротивление неоднородного участка.
ЭДС ε может быть как положительной, так и отрицательной. Это связано с полярностью включения ЭДС в участок: если направление, создаваемое источником тока, совпадает с направлением тока, проходящего в участке (направление тока на участке совпадает внутри источника с направлением от отрицательного полюса к положительному), т.е. ЭДС способствует движению положительных зарядов в данном направлении, то ε > 0, в противном случае, если ЭДС препятствует движению положительных зарядов в данном направлении, то ε < 0.
Закон Ома для однородного участка цепи. Сопротивление проводников.
Между
падением потенциала — напряжением U и силой тока в проводнике I существует функциональная зависимость  ,
называемаявольтамперной характеристикой данного проводника (ВАХ). Вид этой
зависимости для разных проводников и
устройств может быть самым разнообразным.
,
называемаявольтамперной характеристикой данного проводника (ВАХ). Вид этой
зависимости для разных проводников и
устройств может быть самым разнообразным.
К ак
показывает опыт, для многих проводящих
материалов выполняется зависимость:
ак
показывает опыт, для многих проводящих
материалов выполняется зависимость:  ,
получившая название закона
Ома (Ohm
G.,
1787-1854) для однородного
участка цепи. (ВАХ приведена на рис. 3.1.).
,
получившая название закона
Ома (Ohm
G.,
1787-1854) для однородного
участка цепи. (ВАХ приведена на рис. 3.1.).
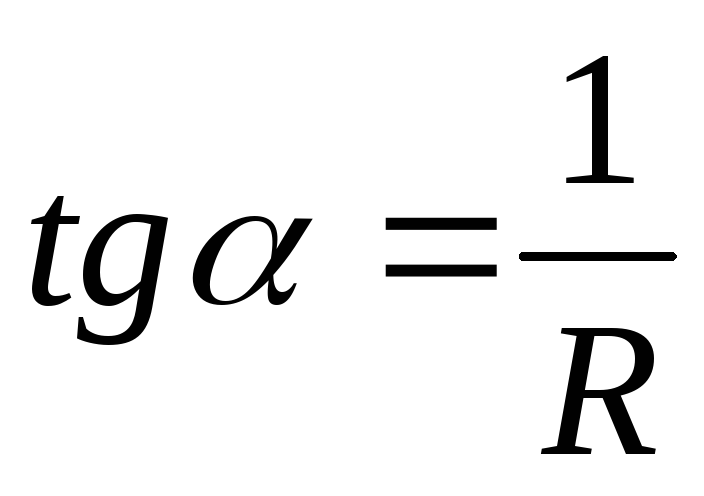
Коэффициент пропорциональности R называется сопротивлением проводника. Сопротивление однородного проводника зависит от материала, из которого он изготовлен, его формы, размеров, а также от температуры.
Рисунок 3.1 Вольтамперная
характеристика.
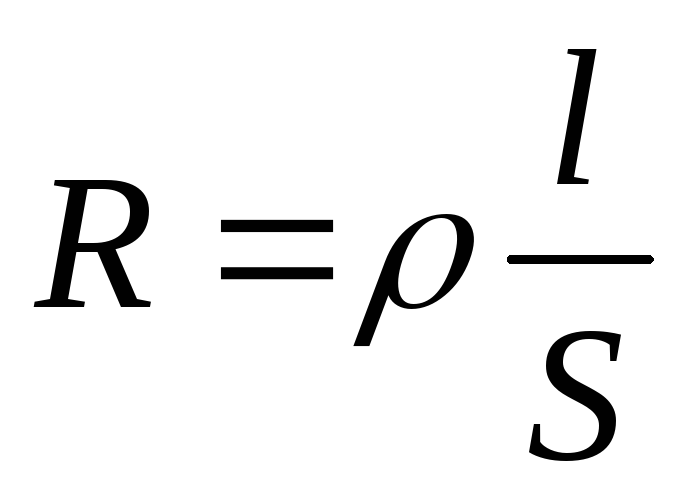
Размерность
сопротивления: [R]
= 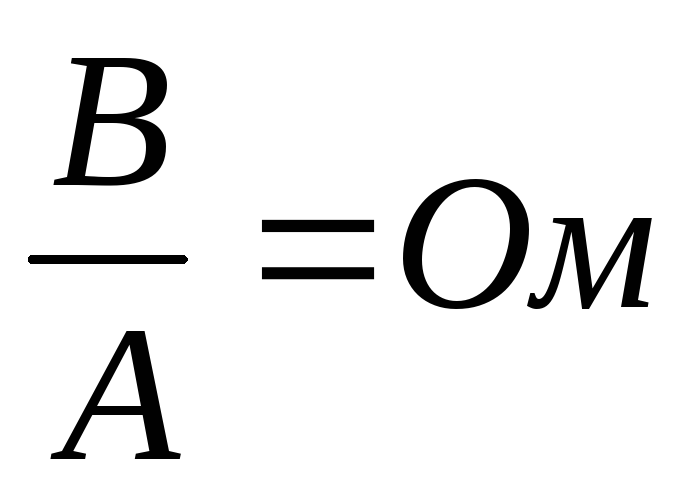 .
.
Кратные единицы измерения: 1кОм = 103Ом ; 1Мом = 106Ом.
ρ – удельное сопротивление. Размерность ρ в СИ: [ρ] = Ом∙м.
Для многих веществ зависимость сопротивления от температуры в широком интервале температур вблизи Т≈300К определяется эмпирической зависимостью от температуры их удельного сопротивления:
 ,
,
где α – температурный коэффициент сопротивления;  —
значение
—
значение при
при  .
.
Для металлов  ,
поэтому сопротивление металлов в
указанной области температур
пропорционально температуре (рис. 3.2.).
,
поэтому сопротивление металлов в
указанной области температур
пропорционально температуре (рис. 3.2.).

Рисунок 3.2. Зависимость сопротивления от температуры (для металлов).
Для электролитов α<0, зависимость их сопротивления от температуры имеет вид, изображенный на рис.. Для разных электролитов α различно.

Рис. 3. Зависимость сопротивления от температуры (для электролитов).
Дифференциальная форма закона Ома.
Если
проводник неоднороден по своему составу
и/или имеет неодинаковое сечение, то
для характеристики тока в различных
частях проводника используют закон
Ома в
дифференциальной форме.
Для его вывода выделим внутри проводника
элементарный цилиндрический объем с
образующими, параллельными вектору
плотности тока  .
Если выделенный объем достаточно мал,
его можно считатьоднородным и
применить к нему закон Ома:
.
Если выделенный объем достаточно мал,
его можно считатьоднородным и
применить к нему закон Ома:
 ,
где
,
где

 ,
откуда
,
откуда
Или в векторном виде:
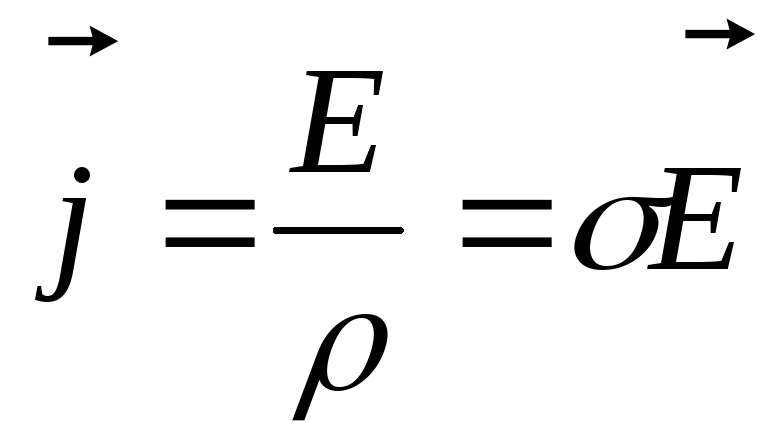
Величина 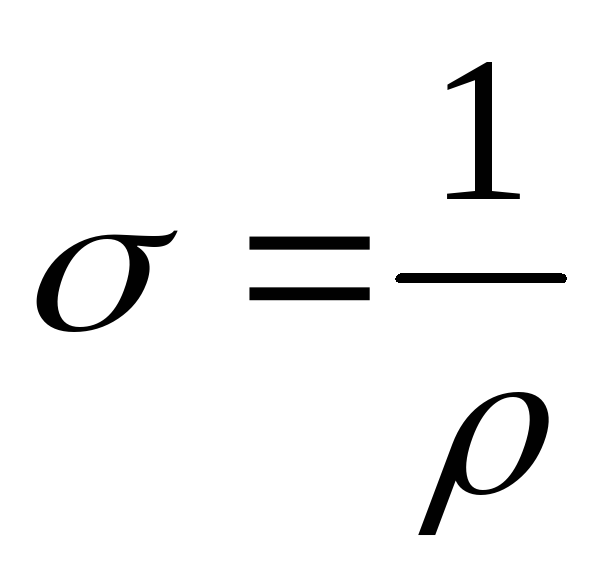 называетсякоэффициентом
электропроводности или проводимостью материала. Единицей
измерения σ в
СИ является (Ом∙м)-1=См
(сименс).
называетсякоэффициентом
электропроводности или проводимостью материала. Единицей
измерения σ в
СИ является (Ом∙м)-1=См
(сименс).
Работа и мощность постоянного тока. Закон Джоуля – Ленца.
При протекании по проводнику электрического тока проводник нагревается. Нагревание происходит за счет работы, совершаемой силами поля над носителями заряда:
 ,
,


Джоуль (Joule J., 1818-1889) и независимо от него Э.Х.Ленц (1804-1865) установили экспериментально, что количество теплоты, выделяющейся в проводнике, пропорционально квадрату силы тока, сопротивлению проводника и времени протекания тока:
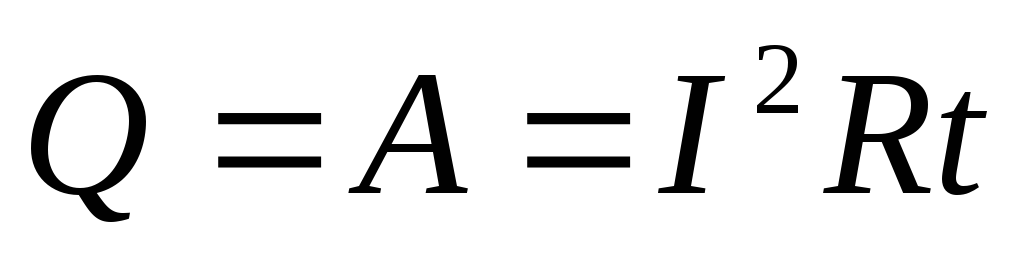
Если
сила тока изменяется со временем, то за
промежуток времени Δt = t2 – t1 выделится теплота: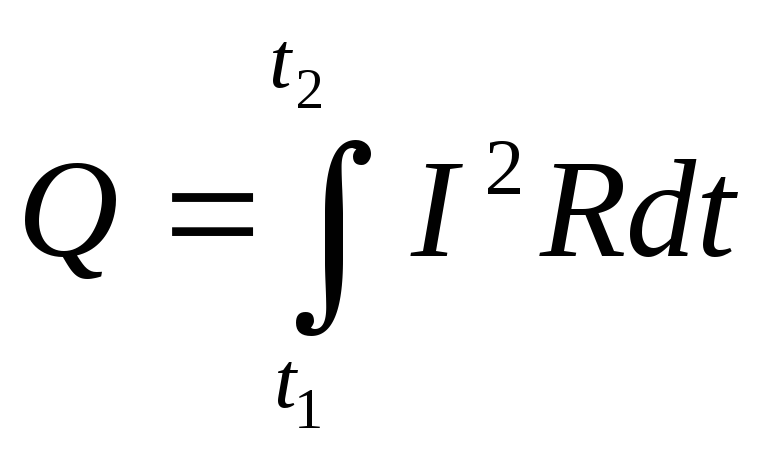
Написанные соотношения выражают собой закон Джоуля – Ленца.
Если
теплоту измерять в калориях,
то:  .
.
Количество теплоты, выделяющееся в единице объема проводника за единицу времени, называется удельной мощностью:
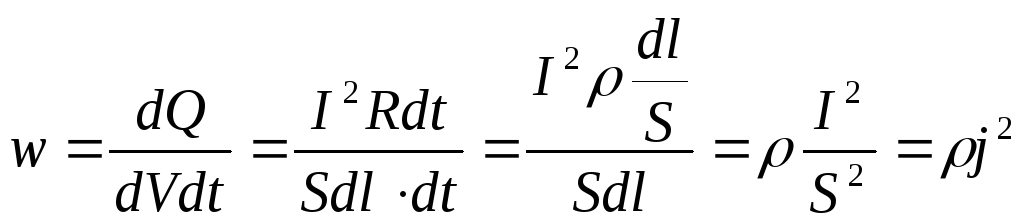 ,
где
,
где  —
плотность тока.
—
плотность тока.
Это
соотношение представляет собой закон
Джоуля-Ленца в дифференциальной форме: 
Работа, производимая током за единицу времени, называется мощностью:
 .
.
Размерность
мощности в СИ:  (ватт).
(ватт).
Закон Ома для однородного участка цепи. Сопротивление проводников.
Однородным называется проводник, в котором не действуют сторонние силы, т.е. нет источника тока.
В 1826 году Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику пропорциональна падению напряжения U на проводнике.
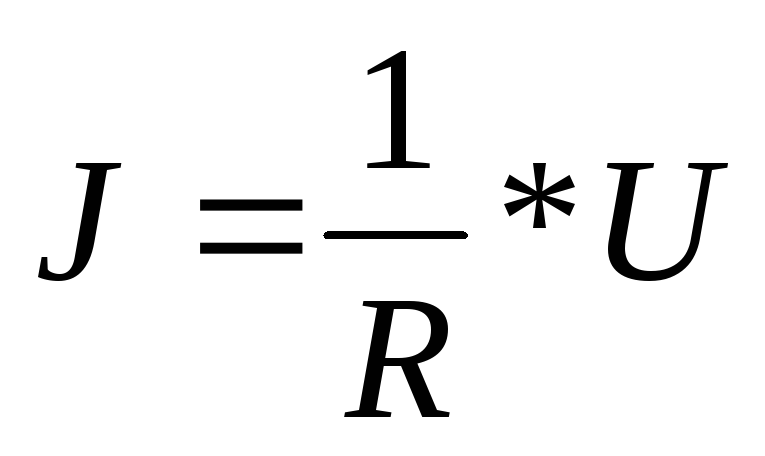 (1)
(1)
U-напряжение,
или падение напряжения, оно равно
разности потенциалов  ,поддерживаемой
на концах проводника.
,поддерживаемой
на концах проводника.
Величина R называется электрическим сопротивлением проводника. Единицей сопротивления в системе СИ является Ом.
 ;
СИ: 1Ом=
;
СИ: 1Ом= ;
;
Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого сделан проводник. Для однородного цилиндрического проводника
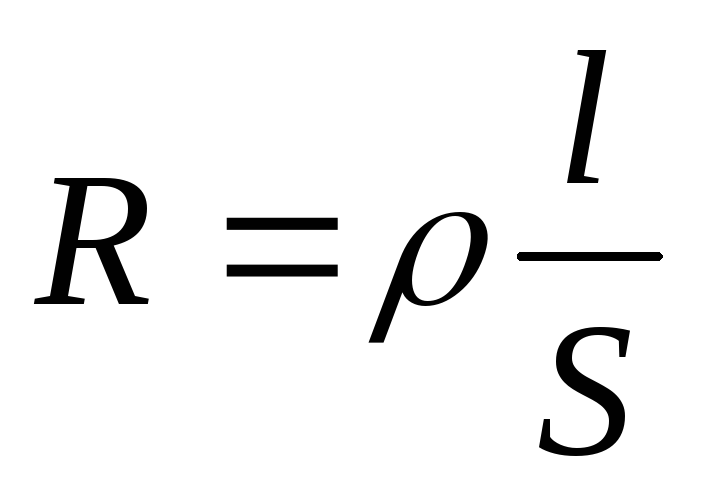
ρ- зависящий от свойств материала коэффициент, называемый удельным сопротивлением вещества.
В
СИ сопротивление измеряется в Ом*м,
часто измеряют в  ;
Сопротивление зависит от температуры.
Для большинства металлов
растет с температурой по линейному
закону
;
Сопротивление зависит от температуры.
Для большинства металлов
растет с температурой по линейному
закону
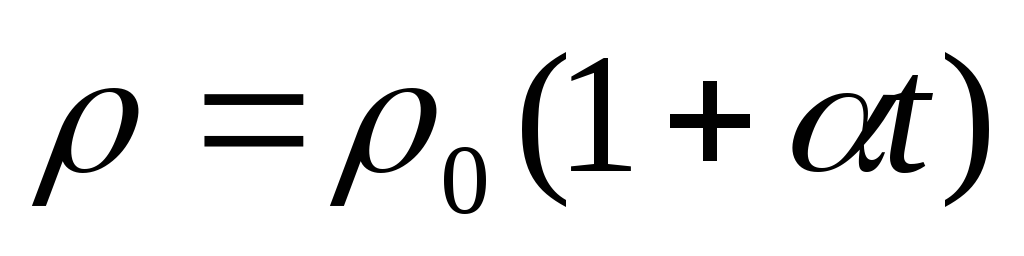
Уравнение (1) определяет соотношение между током и напряжением для конечного участка цепи и поэтому иногда называется законом Ома в интегральной форме.
Закон Ома можно записать также в дифференциальной форме.
В ыделим
мысленно в окрестности некоторой точки
внутри проводника элементарный
цилиндрический объем с образующими,
параллельными вектору плотности тока
ыделим
мысленно в окрестности некоторой точки
внутри проводника элементарный
цилиндрический объем с образующими,
параллельными вектору плотности тока  в данной точке.
в данной точке.
Тогда закон Ома в применении к такому элементарному участку проводника можно записать так:
dI
=  (2)
(2)
dI = jdS ; dU = Edl ; dR = (dl/dS)
Подставляя все эти выражения в (2) , получим:
jdS
=  ;
; 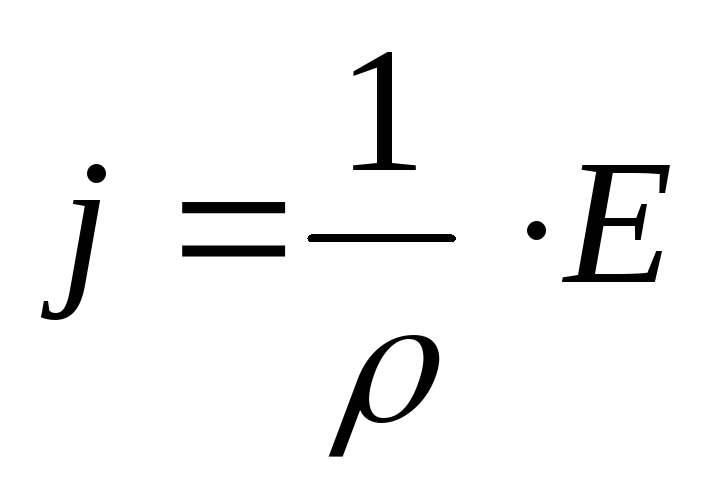 (3)
(3)
Носители
заряда в каждой точке движутся в
направлении  .
Поэтому направления
.
Поэтому направления 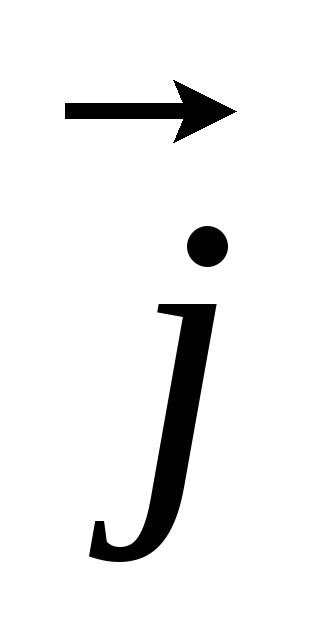 и
и  совпадают, и следовательно можно
записать в векторном виде
совпадают, и следовательно можно
записать в векторном виде
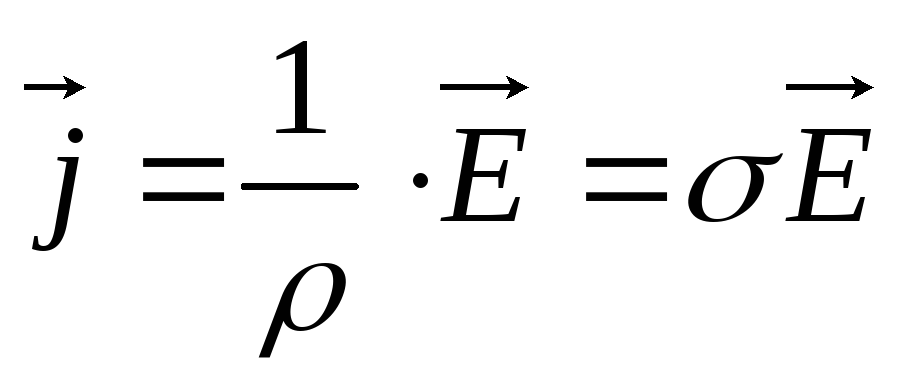 (4)
(4)
 коэффициент
электропроводности или просто
проводимость материала.
коэффициент
электропроводности или просто
проводимость материала.
Формула (4) выражает закон Ома для однородного участка цепи в дифференциальной форме.
Закон Ома для неоднородного участка цепи.
Участок цепи, в котором действуют сторонние силы, то есть, например, включен гальванический элемент, называется неоднородным. Обозначим через
Е*
=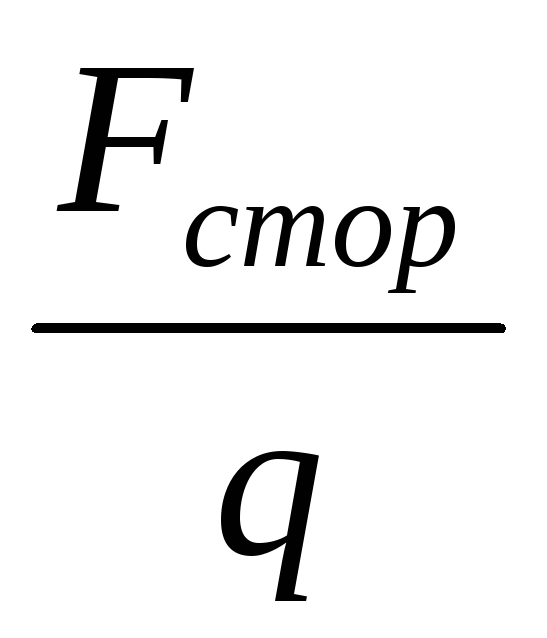
напряженность поля сторонних сил. При наличии сторонних сил закон Ома в дифференциальной форме примет более общий вид
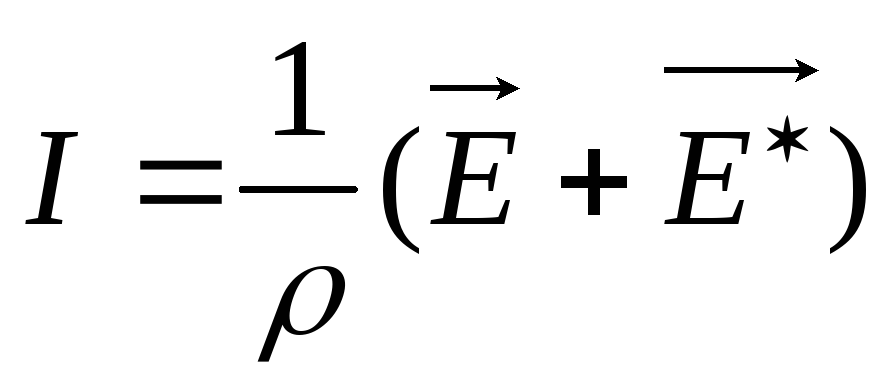 (1)
(1)
(1)- закон Ома для неоднородного участка цепи в дифференциальной форме.
Перейдем
к интегральной форме. Умножим скалярно
обе части равенства (1) на вектор  ,
численно равный элементу dl длины
проводника и направленный в направлении
,
численно равный элементу dl длины
проводника и направленный в направлении 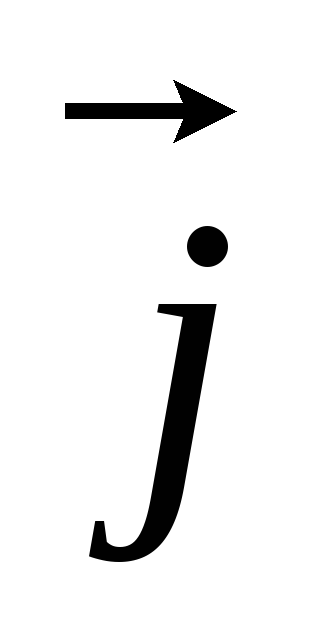 .
.

 (2)
(2)


Е -проекция
-проекция  на направление
на направление 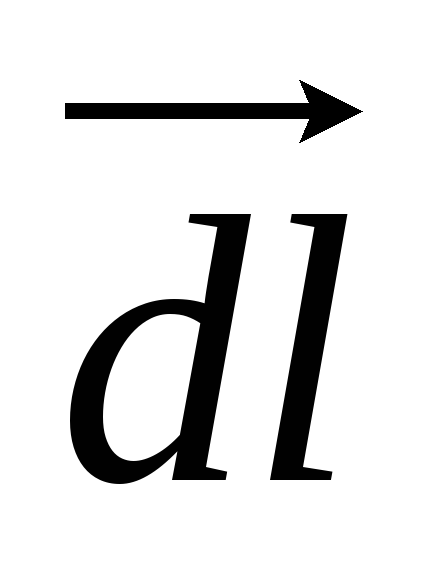

С
учетом этих соотношений и заменяя 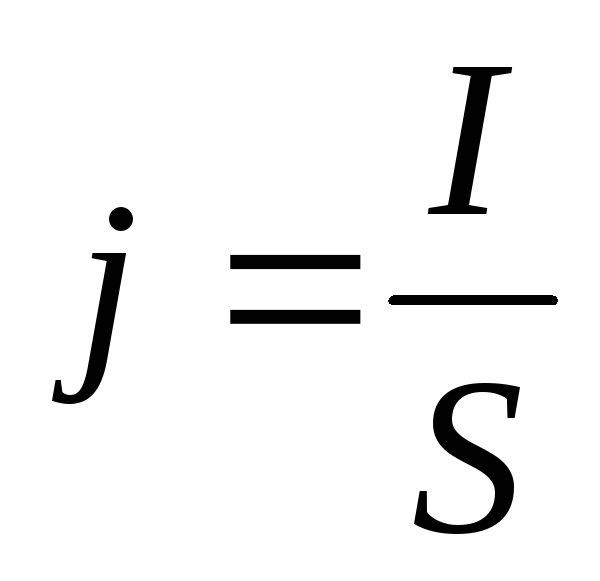 (2) можно
переписать в виде:
(2) можно
переписать в виде:

Интегрируя
по длине l проводника от сечения 1 до
сечения 2, получаем: 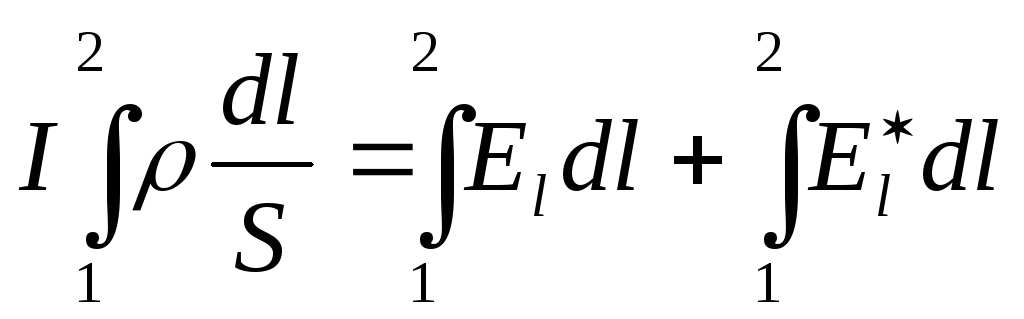 (3)
(3)
Рассмотрим физический смысл всех членов входящих в уравнение (3)
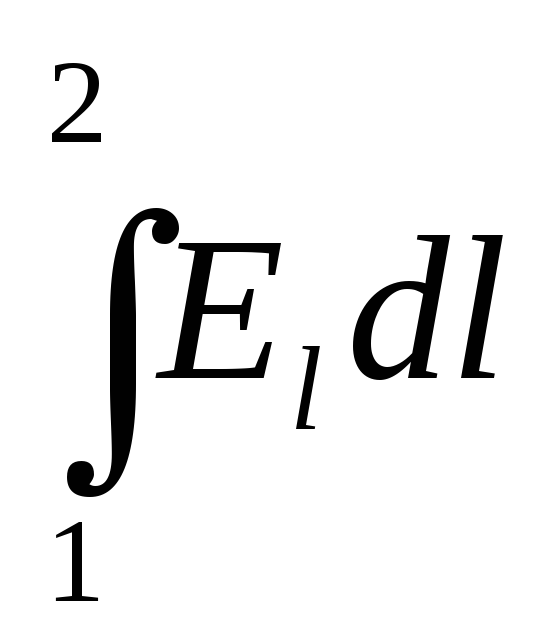 —
численно равен работе, совершаемой
кулоновскими (т.е. электрическими)
силами при перенесении единичного
положительного заряда из точки 1 в точку
2.
—
численно равен работе, совершаемой
кулоновскими (т.е. электрическими)
силами при перенесении единичного
положительного заряда из точки 1 в точку
2.
В электростатике мы нашли связь между напряженностью поля и потенциалом
 ;
;
 (4)
(4)
где  и
и 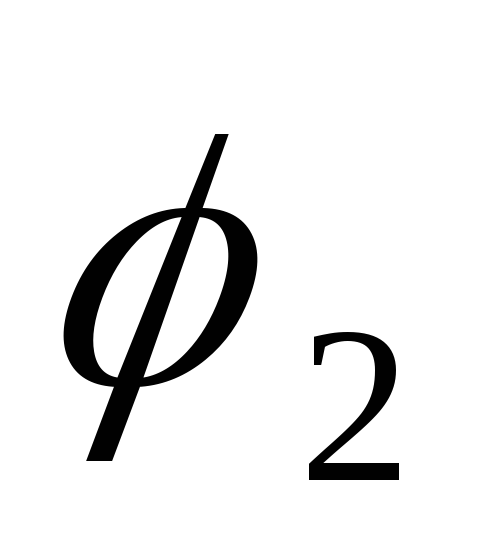 — значения потенциала в точках 1 и 2.
— значения потенциала в точках 1 и 2.
Аналогичный
интеграл содержащий вектор  напряженности поля сторонних сил
называется электродвижущей силой (ЭДС)
напряженности поля сторонних сил
называется электродвижущей силой (ЭДС)  действующей на участке цепи 1-2.
действующей на участке цепи 1-2.
 (5)
(5)
ЭДС численно равна работе, совершаемой сторонними силами при перемещении по проводнику единичного положительного заряда из точки 1 в точку 2. Эта работа производится за счет энергии, затрачиваемой в источнике тока.
Падением напряжения U21 или просто напряжением, на участке цепи 1-2 называется физическая величена, численно равная работе, совершаемой суммарным полем кулоновских и сторонних сил при перемещении вдоль цепи единичного положительного заряда из точки 1 в точку 2.
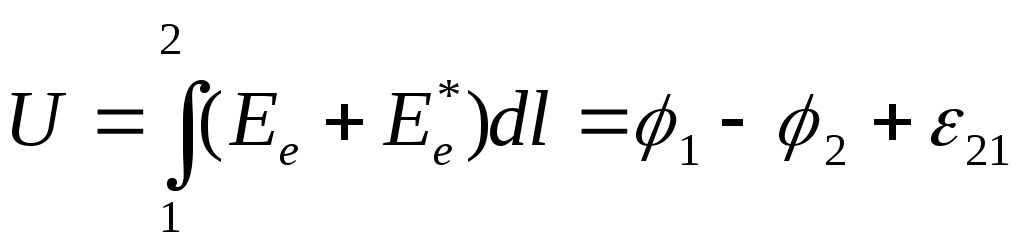 (6)
(6)
Если на участке не приложена ЭДС, т.е. участок однородный, то напряжение равно разности потенциалов на концах этого участка.
Интеграл
 (7)
(7)
представляет
собой сопротивление участка цепи между
сечениями 1 и2. Для однородного линейного
проводника  =const
, S =const и
=const
, S =const и
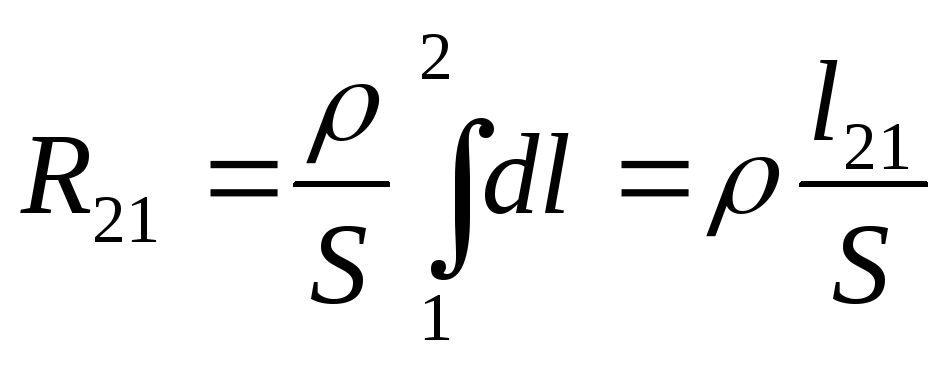 ,
,
где l21 – длина проводника между сечениями 1 и 2
Из ф. (3) – (7) следует, что
I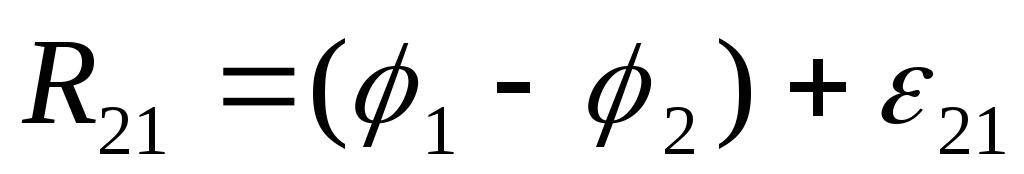 (8)
(8)
Или

Формула (8) выражает собой закон Ома в интегральной форме для неоднородного участка цепи.
Рассмотрим частные случаи формулы (8) :
 ,это
означает, что точки 1 и 2 совпадают, т.е.
цепь замкнута.
,это
означает, что точки 1 и 2 совпадают, т.е.
цепь замкнута.
При
этом 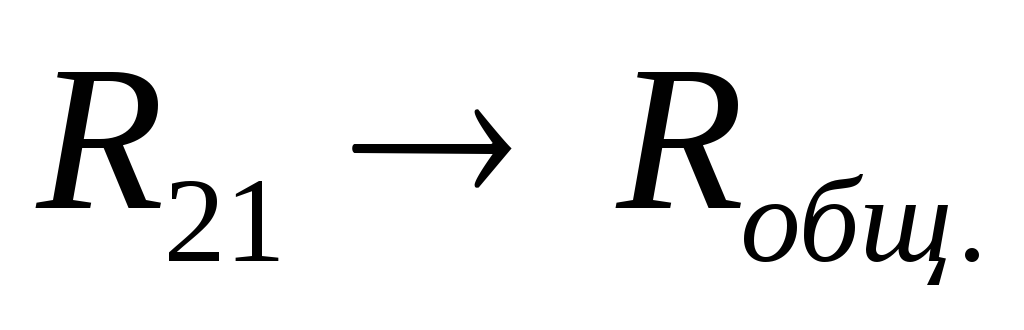 сопротивление всей цепи
сопротивление всей цепи

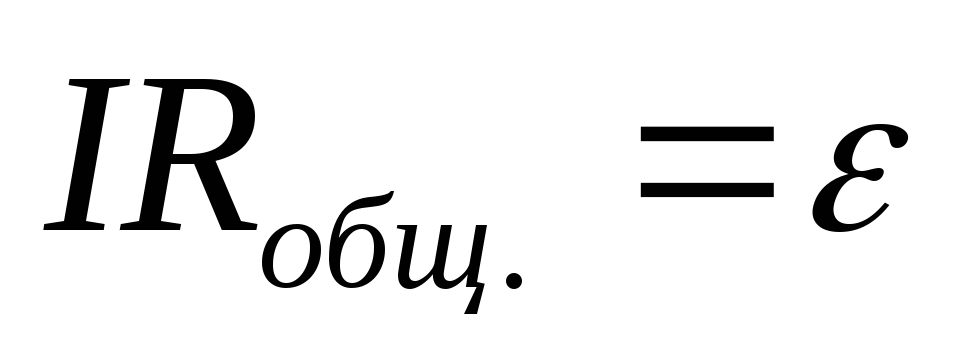 (9)
(9)
 Часто
Rобщ. представляют в виде суммы внешнего
сопротивления R
и внутреннего сопротивления источника
тока r
Часто
Rобщ. представляют в виде суммы внешнего
сопротивления R
и внутреннего сопротивления источника
тока r
 закон
Ома для замкнутой цепи.
закон
Ома для замкнутой цепи.
2.
Если  ,
то из (8) получается закон Ома для
однородного участка цепи.
,
то из (8) получается закон Ома для
однородного участка цепи.
 или
или
3.Если цепь разомкнута, и след.I=0, то из (8) следует, что
 это
значит, что ЭДС равна разности потенциалов
на концах разомкнутой цепи. Поэтому
при точных измерениях ЭДС применяются
схемы, при которых ток через измеряемую
ЭДС делается равным нулю. Разность
потенциалов на её концах дает при этом
точное значение ЭДС.
это
значит, что ЭДС равна разности потенциалов
на концах разомкнутой цепи. Поэтому
при точных измерениях ЭДС применяются
схемы, при которых ток через измеряемую
ЭДС делается равным нулю. Разность
потенциалов на её концах дает при этом
точное значение ЭДС.
Приближенно ЭДС измеряют с помощью вольтметра. По закону Ома для замкнутой цепи:

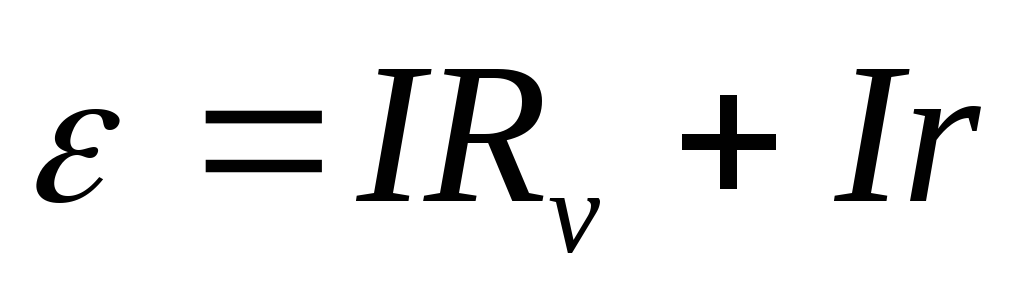
Вольтметр в данном случае показывает напряжение во внешней цепи, т.е. на самом себе

Поскольку Rv>>r, то Uvε
7.5. Закон Ома для неоднородного участка цепи.

Рис. 3 Перемещение заряда на этих участках возможно лишь с помощью сил
неэлектрического происхождения (сторонних сил): химические процессы, диффузия носителей заряда, вихревые электрические поля. Аналогия: насос, качающий воду в водонапорную башню, действует за счет негравитационных сил (электромотор).
Сторонние силы можно характеризовать работой, которую они совершают над перемещающимися зарядами.
Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой. Э.Д.С. действующей в цепи.
ε = | A |
| Дж | =[В]; |
| |
| ; |
|
| (7.4.1) | ||
q |
| |||||
|
| Кл |
|
| ||
Ясно, что размерность Э.Д.С. совпадает с размерностью потенциала, т.е. измеряется в вольтах.
Стороннюю силу, действующую на заряд, можно представить в виде:
r | Fст. = Eст.q , | (7.4.2) |
Eст. | – напряженность поля сторонних сил. |
|
| Работа сторонних сил на участке 1 – 2 |
|
| 2 r | r | 2 | r | r |
| ||
A12 | = ∫Fст.dl | = q∫Eст.dl , | (7.4.3) | |||||
| 1 |
| 1 |
|
|
| ||
|
|
|
| A12 |
| 2 r | r |
|
тогда | ε12 | = |
|
| = ∫Eст.dl . | (7.4.4) | ||
| q | |||||||
|
|
|
| 1 |
|
| ||
Для замкнутой цепи: ε = ∑εi | = ∫Eст.dl . | (7.4.5) | ||||||
Циркуляция вектора напряженности сторонних сил равна Э.Д.С., действующей в замкнутой цепи (алгебраической сумме Э.Д.С.).
При этом необходимо помнить, что поле сторонних сил не является потенциальным, и к нему нельзя применять термин – разность потенциалов или напряжение.
Рассмотрим неоднородный участок цепи, участок, содержащий источник Э.Д.С.
(т.е. участок, – где действуют неэлектрические силы). Напряженность E поля в любой точке цепи равна векторной сумме поля кулоновских сил и поля сторонних сил, т.е.
E = Eq +Eст. .
67

Величина, численно равная работе по переносу единичного положительного заряда суммарным полем кулоновских и сторонних сил на участке цепи (1 – 2), называется напряжением на этом участке U12 (Рис. 4)
| Рис. 4 |
|
| ||
| 2 r r | 2 | r | r |
|
| U12 = ∫Eq dl + | ∫Eст.dl ; | (7.5.1) | ||
| 1 | 1 |
|
|
|
| 2 | r | r |
|
|
т. к. | Eq dl = −dφ и ∫Eq dl | = φ1 −φ2 ; | (7.5.2) | ||
| 1 |
|
|
|
|
тогда | U12 = (φ1 – φ2) + ε12 | (7.5.3) | |||
Напряжение на концах участка цепи совпадает с разностью потенциалов только в | |||||
случае, если на этом участке нет Э.Д.С., т.е. на однородном участке цепи. |
| ||||
| I·R12 = (φ1 – φ2) + ε12 | (7.5.4) | |||
Это обобщенный закон Ома. Обобщенный закон Ома выражает закон сохранения энергии применительно к участку цепи постоянного тока. Он в равной мере справедлив как для пассивных участков (не содержащих Э.Д.С.), так и для активных.
В электротехнике часто используют термин падения напряжения – изменение напряжения вследствие переноса заряда через сопротивление
U = I R |
| (7.5.5) | |||
В замкнутой цепи: φ1 = φ2 ; |
|
| ε |
| |
I RΣ= ε | или | I = | |||
R∑ | |||||
|
|
| |||
Где R Σ =R + r; r – внутреннее сопротивление активного участка цепи (Рис. 5).
Тогда закон Ома для замкнутого участка цепи, содержащего Э.Д.С. запишется в
виде:
I = | ε | ; | (7.5.6) | |
R + r | ||||
|
|
|
Рис. 5
7.6. Закон Ома в дифференциальной форме.
Закон Ома в интегральной форме для однородного участка цепи (не содержащего Э.Д.С.)
I = U | ; |
| (7.6.1) | ||
R |
|
|
| ||
Для однородного линейного проводника выразим R через ρ |
| ||||
R = ρ | l |
| ; | (7.6.2) | |
S | |||||
|
|
| |||
ρ – удельное объемное сопротивление; [ρ] = [Ом м].
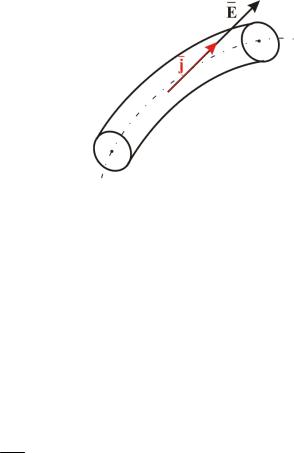
Найдем связь между j и E в бесконечно малом объеме проводника – закон Ома в
дифференциальной форме.
В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов (Рис.6) движутся в направлении действия силы, т.е. плотность тока
j ↑↑ E , следовательно, векторы коллинеарны.
|
|
|
|
|
|
| Рис. 6 |
|
| |||||||
|
|
|
| I = | U |
| = |
| Edl |
| = | EdS | ; | |||
|
|
|
| R |
| ρ |
| dl |
| ρ | ||||||
|
|
|
|
| r | dS |
| |||||||||
|
|
|
|
|
|
|
|
|
| |||||||
| dI |
| 1 |
|
|
|
|
| 1 r |
|
| |||||
А мы знаем что: j = |
| = |
| E , т.е. | j = |
|
|
| E j или |
| ||||||
dS | ρ |
| ρ |
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
| j = σE |
|
|
|
|
|
|
| (7.6.3) | ||||
это запись закона Ома в дифференциальной форме.
Здесь σ – удельная электропроводность. Размерность j – [ Oм−1 м−1 ]; Плотность тока можно выразить через заряд, n и vrдр. .
j = envrдр.
r
обозначим: b = vEдр. , то vrдр. = bE ;
j = enbE ,
а если σ = enb,
где n – число пар ионов, b – расстояние. j = jE
– закон Ома в дифференциальной форме.

7.7. Работа и мощность тока. Закон Джоуля — Ленца.
Рассмотрим произвольный участок цепи, к концам которого приложено напряжение U. За время dt через каждое сечение проводника проходит заряд
dq = I dt | (7.7.1) |
При этом силы электрического поля, действующего на данном участке совершают | |
работу: |
|
dA = U dq = U I dt | (7.7.2) |
Разделив работу на время, получим выражение для мощности: |
|
N = dA =UI | (7.7.3) |
dt |
|
Полезно вспомнить и другие формулы для мощности и работы:
| N = RI2 | (7.7.4) |
| A = RI2t | (7.7.5) |
| В 1841г. Английский физик Джеймс Джоуль и русский физик | |
| Эмилий Ленц установили закон теплового действия электрического | |
| тока. |
|
| ДЖОУЛЬ Джеймс Пресскотт (Рис. 6) |
|
| (24.12.1818 – 11. 10.1889) – английский физик, один |
|
| из первооткрывателей закона сохранения энергии. |
|
| Первые уроки по физике ему давал Дж. Дальтон, под |
|
| влиянием которого Джоуль начал свои эксперименты. |
|
| Работы посвящены электромагнетизму, кинетической |
|
Рис. 6 | теории газов. |
|
ЛЕНЦ Эмилий Христианович (Рис. 7) (24.2.1804 |
| |
|
| |
– 10.2.1865) – русский физик. Основные работы в области |
| |
электромагнетизма. В 1833 установил правило определения | Рис. 7 | |
электродвижущей силы индукции (закон Ленца), а в 1842 (независимо | ||
от Дж. Джоуля) – закон теплового действия электрического тока (закон Джоуля — Ленца). Открыл обратимость электрических машин. Изучал зависимость сопротивление металлов от температуры. Работы относятся также к геофизике.
Независимо друг от друга Джоуль и Ленц показали, что при протекании тока в проводнике выделится количество теплоты:
Q = RI2t | (7.7.6) | |
Если ток изменяется со временем, то |
| |
Q = ∫2 | RI 2dt ; | (7.7.7) |
1
(7.7.7) это закон Джоуля – Ленца в интегральной форме.
Следовательно, нагревание происходит за счет работы, совершаемой силами поля над зарядом (мощность выделения тепла N = RI2).
Получим закон Джоуля – Ленца в дифференциальной форме.
dQ = RI 2dt = ρ dSdl (jdS )2 dt = ρj2dldSdt = ρj2dldSdt = ρj2 dVdt,
где dV = dl dS – элементарный объем. |
|
Количество тепла выделяющегося в единицу объема в единицу времени |
|
Q уд = ρj2 | (7.7.8) |
22) Закон Ома для однородного и неоднородного участка цепи.
Законы Ома.
Закон Ома для однородного участка цепи.
Сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении участка и обратно пропорциональна сопротивлению участка при постоянном напряжении.

где U — напряжение на участке, R — сопротивление участка.

Закон Ома для произвольного участка цепи, содержащего источник постоянного тока.

где φ1 — φ2 + ε = U напряжение на заданном участке цепи, R — электрическое сопротивление заданного участка цепи.

Закон Ома для полной цепи.
Сила тока в полной цепи равна отношению электродвижущей силы источника к сумме сопротивлений внешнего и внутреннего участка цепи.

где R — электрическое сопротивление внешнего участка цепи, r — электрическое сопротивление внутреннего участка цепи.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
Закон Ома для однородного участка цепи
Рассмотрим произвольный источник положительной ЭДС. Являясь неоднородным участком, он обладает двумя неотъемлемыми характеристиками: сопротивлением, которое называется внутренним и обозначается буквой r, и ЭДС e. Закон Ома для неоднородного участка позволяет дать практическое определение положительной e. Сначала дадим определение: разомкнутым источником ЭДС называется источник, по которому не протекает электрический ток. Схему разомкнутого источника легко изобразить:
Рис.17.4
Закон Ома для этого участка выглядит так:
Þ
ЭДС источника равна модулю разности потенциалов на разомкнутом источнике.
§17.5. Закон Ома для однородного участка цепи (I-я форма интегрального закона Ома)
Однородным называется участок, на котором отсутствуют источники ЭДС. Электрическая схема участка выглядит так:
Рис.17.5
На однородном участке на носитель действуют только сила сопротивления и электростатическая сила в качестве движущей. Единственной неотъемлемой характеристикой однородного участка является сопротивление R. Закон Ома для такого участка легко получается из выражения для неоднородного участка с помощью обнуления ЭДС:
или
Словесная формулировка будет звучать так:
на однородном участке цепи постоянного тока напряжение равно падению напряжения.
17.5.1. Последовательное соединение сопротивлений
Рис.17.6
Очевидно, что через все сопротивления течёт один и тот же ток. Проинтегрируем закон Ома для элементарного участка по всему (от клеммы 1 до клеммы 2) однородному участку:
.
Падение напряжения всего однородного участка раскладывается на сумму падений напряжения на каждом отдельном сопротивлении:
Þ .
Напряжение на всем участке:
Итак, при последовательном соединении ток через все сопротивления течёт один и тот же, напряжение на всём участке равно сумме напряжений на отдельных сопротивлениях, общее сопротивление участка равно сумме отдельных сопротивлений.
17.5.2. Параллельное соединение сопротивлений
Рис.17.7
Очевидно, что общий ток равен сумме токов через каждое сопротивление:
,
а напряжение на всех сопротивлениях одинаковы и равны . Тогда
Þ
Итак, при параллельном соединении напряжение на всех сопротивлениях одно и то же, ток на всём участке равен сумме токов на отдельных сопротивлениях, общее обратное сопротивление участка равно сумме отдельных обратных сопротивлений
17.5.3. Мостиковое соединение
Аналогично соединениям (батареям) конденсаторов резисторы (сопротивления) можно соединять не только в последовательно-параллельные схемы, но и в мостиковые, которые в общем случае невозможно свести ни последовательным, ни к параллельным соединениям.
Рис.17.8
В общем случае расчёт токов, текущих по участкам отдельных сопротивлений рассчитывается по законам Кирхгофа (далее), но при выполнении условия уравновешенности мостика
через резистор R0 ток не течёт, и его с одинаковым успехом можно заменить на короткое замыкание, сводя мостик к глобально последовательной схеме, или игнорировать, сводя схему к глобально параллельной.
§17.6. Закон Ома для простого контура (III-я форма интегрального закона Ома)
Простым контуром называется контур, состоящий из неоднородного участка (источник), замкнутого однородным участком (нагрузка):
Рис.17.9
Проинтегрируем закон Ома для элементарного участка по всему контуру в направлении ЭДС:
Интеграл сопротивления распадается на два интеграла: по участку источника (внутренний участок контура) и по участку нагрузки (внешний участок контура).
.
Интеграл напряжения по замкнутому контуру равен 0:
.
Интеграл ЭДС по контуру равен ЭДС источника. В результате получаем:
.
Отсюда видно, что ток в простом контуре течёт всегда по направлению ЭДС.
§17.7. Законы Кирхгофа
Законы Кирхгофа позволяют рассчитать силы токов, текущих в сложных контурах. Разветвлённым или сложным контуром называется цепь постоянного тока, состоящая из нескольких смежных простых контуров.
Рис.17.10
На рисунке 17.10 изображён сложный контур, состоящий из двух смежных контуров. Необходимым элементом схем сложных контуров являются узлы: точки, в которые втекают и вытекают более двух токов (на рисунке отмечены кружками). Для узлов справедлив I-й закон Кирхгофа:
алгебраическая сумма токов одного узла равна 0:
.
В этой алгебраической сумме токи, втекающие в данный узел, и токи, вытекающие из данного узла, должны иметь разные знаки. Суммирование ведётся по всем токам, связанным с данным узлом. Очевидно, что I-й закон Кирхгофа является следствием уравнения неразрывности для постоянного тока.
При использовании I-го закона Кирхгофа необходимо следить за тем, чтобы обозначения токов разных узлов было единым для всей схемы, так чтобы выполнялось правило: на участке между двумя соседними узлами ток не меняет ни силы, ни направления.
Если проинтегрировать по одному простому контуру закон Ома для элементарного участка:
,
то получим II-й закон Кирхгофа, справедливый для каждого простого контура:
алгебраическая сумма падений напряжения контура равна алгебраической сумме его ЭДС:
.
Знаки падений напряжения и ЭДС определяются по отношению к направлению обхода контура (по часовой или против часовой стрелки), которое для данного контура выбирается произвольно и независимо от выбора, сделанного для других простых контуров. Если ток течёт против направления обхода, он считается отрицательным. Если ЭДС включена против направления обхода, она считается отрицательной.
Уравнения I-го и II-го законов Кирхгофа для всего сложного контура должны составить замкнутую систему линейных уравнений, которая позволяет однозначно определить силы тока контура по ЭДС и сопротивлениям, включённым в контур. Запишем уравнения I-го и II-го законов Кирхгофа для рассматриваемого контура:
· верхний узел: (1)
· нижний узел: (1’)
· левый простой контур: (2)
· правый простой контур: (3)




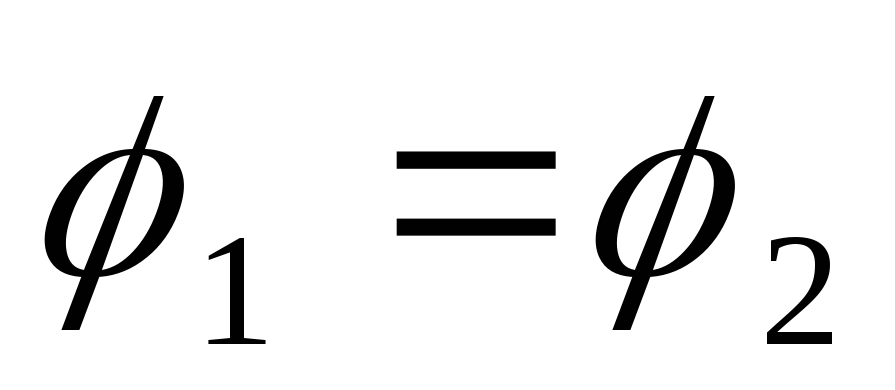 ,это
означает, что точки 1 и 2 совпадают, т.е.
цепь замкнута.
,это
означает, что точки 1 и 2 совпадают, т.е.
цепь замкнута.