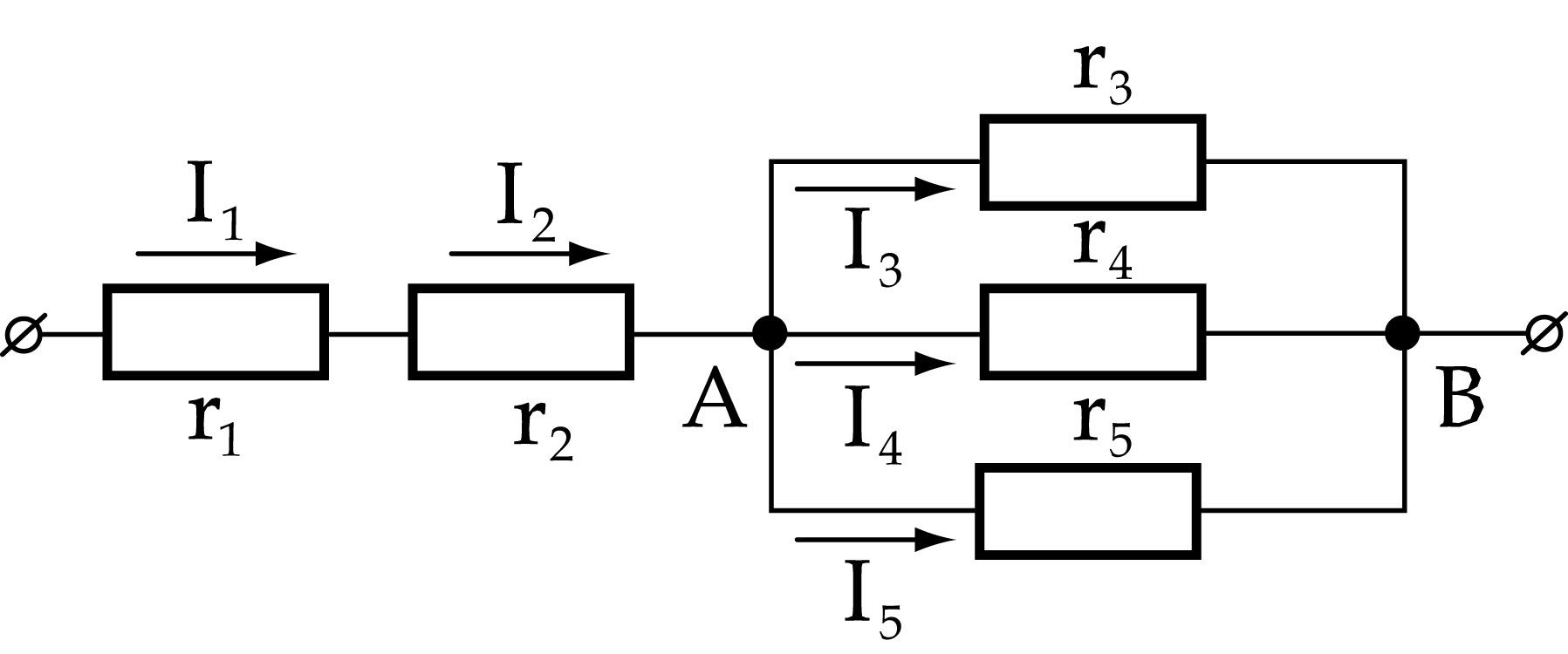
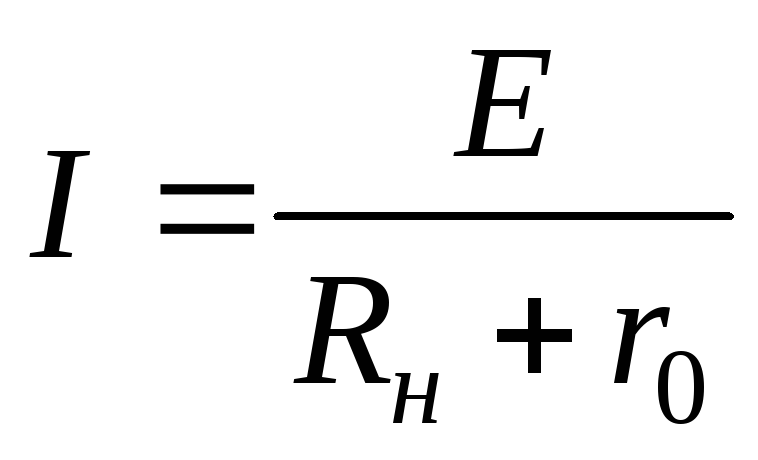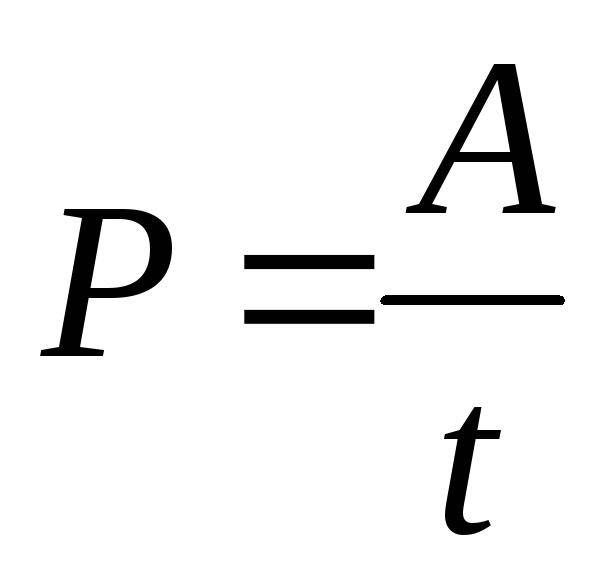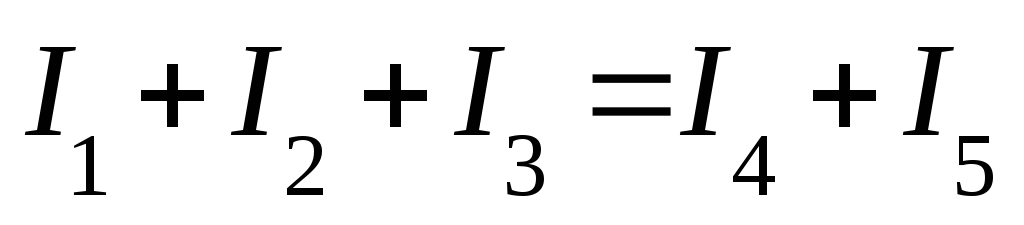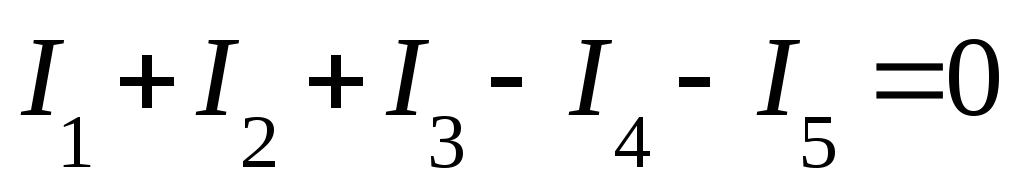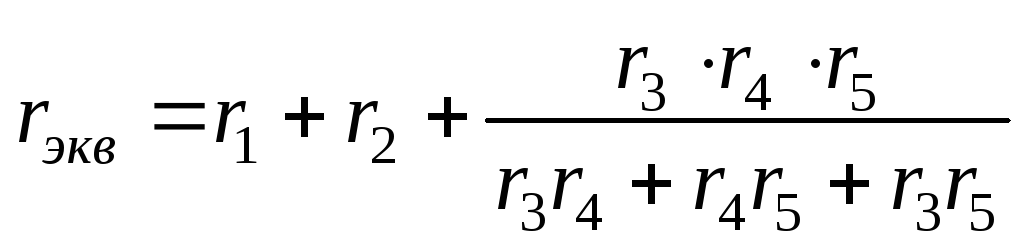Закон Ома для электрической цепи

Электрический ток, как и любое другое физическое явление подчиняется определенным законам. Так, в 1826 году, Георг Ом вывел эмпирический закон, который способен объяснить зависимость силы тока, напряжения, а также особенностей проводника в электроцепи. В дальнейшем вносились определенные изменения, сам закон Ома для электрической цепи модифицировался, и на данный момент ученые его интерпретируют в четырех вариантах, которые мы и рассмотрим.

В ходе практических исследований, на их базе, ученый смог определить зависимость силы тока и напряжения от специфики проводника, по которому протекает ток. Если быть точнее, то каждый материал имеет определенное сопротивление и на определенном участке цепи, сила тока вычисляется отношением напряжения и сопротивления.

I = U/ R,

где I – сила тока, U – напряжение, R – сопротивление проводника.

Фактически, этот закон аналогичен прохождению воды по трубам: чем больше диаметр трубы и напор, тем больше ее выльется в конечной точке.

Закон Ома для замкнутой цепи

Подобная интерпретация подразумевает наличие источника питания, а также проводника, по которому протекает ток. В этом случае, помимо сопротивления на отдельно взятом участке следует учитывать и то, которое возникает в ИП. Учитывая эти факторы, можно сказать, что сила тока будет равна отношению электродвижущей силы к сумме сопротивлений.

I = E/ Rвн+r,

где Е – ЭДС, Rвн – внешнее сопротивление, а r соответственно внутреннее.

Закон Ома для замкнутой цепи можно объяснить доступным языком. Электродвижущая сила по определению должна полноценно обеспечивать постоянную разницу потенциалов, и эта сила может иметь неприродное происхождение: химическое, если в качестве источника используется батарейка или механическая, в случае подключения к электрической цепи генератора. При подключении медной проволоки с идентичным сечением к батарейке и аккумулятору. Эффект должен быть таким, что по этому проводнику, в котором сопротивление практически отсутствует, должен пойти ток с величиной, стремящейся к бесконечности. Однако этого не происходит и разница в показателях будет существенной, а во втором случае, проволока и вовсе может перегореть. Именно поэтому в расчет берется внутреннее сопротивление источника питания, чтобы описать подобное явление.

Закон ома для неоднородного участка цепи

Перед тем, как записать формулу для подобной интерпретации закона, следует разобраться в таких понятиях, как линейные и нелинейные участки цепи.

Если сопротивление никаким образом не зависит от тока и подаваемого напряжения, то с ростом второго параметра, первый будет прямо пропорционально возрастать и наоборот, то есть зависимость можно описать прямой линией. Подобная зависимость относится к линейным участкам цепи и сопротивление имеет аналогичное название.

Однако вышеизложенный вариант считается идеальным и его можно смоделировать лишь в идеальных условиях, что фактически невозможно, ведь, как минимум, окружающая среда вносит свои коррективы. В этом случае, рост напряжения не будет прямо пропорциональным силе тока и на графике зависимость будет изображаться в виде кривой.

На рисунке изображено два графика, первый из которых описывает линейную зависимость, а второй нелинейную.

Чтобы отчетливо понимать разницу между этими понятиями, рассмотрим принцип работы обычной электрической лампы накаливания. При прохождении тока по нити, температура в значительной степени повышается, что приводит к заметному росту сопротивления. Соответственно, при возрастании напряжения, сила тока будет увеличиваться медленнее, то есть не линейно.

Примечание: в некоторых ситуациях, некоторыми внешними факторами пренебрегают по причине того, что они очень незначительны и в числовом эквиваленте никоим образом не могут повлиять на общую картину. Это значит, что нелинейная зависимость на графике фактически совпадает с линейной.

Учитывая вышесказанное, можно установить следующую зависимость:

I = U/ R = (f1 – f2) + E/ R,

Где f1 и f2 – потенциалы (соответственно f1 – f2 называется разницей потенциалов), E – ЭДС неоднородного участка цепи, а R – суммарное сопротивление на этом же участке.

Нужно упомянуть и о том, что электродвижущая сила не всегда в этом случае будет иметь положительное значение. Если направление тока источника будет аналогичным с направлением в электрической сети, протонов будет больше, чем электронов (положительных и отрицательных частиц), то в этом случае величина E будет иметь значение со знаком «+», в иной ситуации, этот параметр будет со знаком «-».

Закон Ома для переменного тока

Если в электроцепи имеется емкость или инертность, то этот факт следует однозначно учитывать при расчётах силы тока. Они имеют собственные показатели сопротивления, что приводит к ситуации, которая будет иметь переменный характер. В случае Закона Ома для переменного тока формула записывается следующим образом:

I = U/ Z, где

I – сила тока, U – напряжение, а Z – суммарное значение сопротивления на всех участках электрической цепи (этот параметр именуется еще, как импеданс).

Как говорилось изначально, закон Ома считается эмпирическим. Это обозначает то, что он может не всегда работать и выполнять вычисления на его основе не представляется возможным. Подобная ситуация может сложиться в нескольких случаях:

• в ситуации, когда электросеть имеет высокую частоту и электромагнитное поле может сильно изменяться за короткие промежутки времени;
• при наличии проводников, которые обладают свойствами сверхпроводимости, расположенных в условиях низких температурных показателей;
• при перегреве проводника под воздействием проходящего по нему тока, отношение напряжения и сопротивления может носить переменный, неоднородный характер;
• если проводник (диэлектрик) находится под высоким напряжением;
• светодиодных лампах;
• в полупроводниках и аналогичных устройствах.

На основе этого закона, можно произвести вывод некоторых формул математическим путем. С их помощью можно производить разнообразные расчеты.

Поделиться ссылкой:

Похожее

Закон Ома для полной цепи и для участка цепи: формулы, описание и объяснение

Профессиональному электрику, специалисту электронщику никак не обойти в собственной деятельности закон Ома, решая любые задачи, связанные с наладкой, настройкой, ремонтом электронных и электрических схем.

Собственно, понимание этого закона необходимо каждому. Потому что каждому в быту приходится иметь дело с электричеством.

И хотя учебным курсом средней школы закон немецкого физика Ома и предусмотрен, но на практике не всегда своевременно изучается. Поэтому рассмотрим в нашем материале такую актуальную для жизни тему и разберемся с вариантами записи формулы.

Содержание статьи:

Отдельный участок и полная электрическая цепь

Рассматривая электрическую цепь с точки зрения применения к схеме закона Ома, следует отметить два возможных варианта расчета: для отдельно взятого участка и для полноценной схемы.

Расчет тока участка электрической схемы

Участком электрической цепи, как правило, рассматривается часть схемы, исключающая источник ЭДС, как обладающий дополнительным внутренним сопротивлением.

Поэтому расчетная формула, в данном случае, выглядит просто:

I = U/ R,

Где, соответственно:

• I – сила тока;
• U – приложенное напряжение;
• R – сопротивление.

Трактовка формулы простая – ток, протекающий по некоему участок цепи, пропорционален приложенному к нему напряжению, а сопротивлению – обратно пропорционален.

Так называемая графическая «ромашка», посредством которой представлен весь набор вариаций формулировок, основанных на законе Ома. Удобный инструмент для карманного хранения: сектор “P” – формулы мощности; сектор “U” – формулы напряжения; сектор “I” – формулы тока; сектор “R” – формулы сопротивления

Таким образом, формулой чётко описывается зависимость протекания тока по отдельному участку электрической цепи относительно определенных значений напряжения и сопротивления.

Формулой удобно пользоваться, например, рассчитывая параметры сопротивления, которое требуется впаять в схему, если заданы напряжение с током.

Закон Ома и два следствия, которыми необходимо владеть каждому профессиональному электромеханику, инженеру-электрику, электронщику и всем, кто связан с работой электрических цепей. Слева направо: 1 – определение тока; 2 – определение сопротивления; 3 – определение напряжения, где I – сила тока, U – напряжение, R – сопротивление

Вышеприведенный рисунок поможет определить, например ток, протекающий через 10-омное сопротивление, к которому приложено напряжение 12 вольт. Подставив значения, найдем – I = 12 / 10 = 1.2 ампера.

Аналогично решаются задачи поиска сопротивления (когда известны ток с напряжением) или напряжения (когда известны напряжение с током).

Тем самым всегда можно подобрать требуемое рабочее напряжение, нужную силу тока и оптимальный резистивный элемент.

Формула, которой предложено пользоваться, не требует учитывать параметры источника напряжения. Однако, схема, содержащая, например, аккумулятор, будет рассчитываться по другой формуле. На схеме: А – включение амперметра; V – включение вольтметра.

Кстати, соединительные провода любой схемы – это сопротивления. Величина нагрузки, которую им предстоит нести, определяется напряжением.

Соответственно, опять же пользуясь законом Ома, становится допустимым точный подбор необходимого сечения проводника, в зависимости от материала жилы.

У нас на сайте есть подробная инструкция по по мощности и току.

Вариант расчета для полной цепи

Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС.

Поэтому логичным является некоторое изменение выше рассмотренной формулы:

I = U / (R + r)

Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС.

Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.

Для расчетов в условиях полноценной электрической цепи всегда берется к учету резистивное значение источника ЭДС. Это значение суммируется с резистивным сопротивлением непосредственно электрической цепи. На схеме: I – прохождение тока; R – резистивный элемент внешний; r – резистивный фактор ЭДС (источника энергии)

Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины.

Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.

Рассмотрение действия закона к переменной величине

Понятие «сопротивление» к условиям прохождения переменного тока следует рассматривать уже больше как понятие «импеданса».  Здесь имеется в виду сочетание активной резистивной нагрузки (Ra) и нагрузки, образованной реактивным резистором (Rr).

Обусловлены подобные явления параметрами индуктивных элементов и законами коммутации применительно к переменной величине напряжения – синусоидальной величине тока.

Такой видится эквивалентная схема электрической цепи переменного тока под расчет с применением формулировок, исходящих из принципов закона Ома: R – резистивная составляющая; С – емкостная составляющая; L – индуктивная составляющая; ЭДС -источник энергии; I -прохождение тока

Другими словами, имеет место эффект опережения (отставания) токовых значений от значений напряжения, что сопровождается появлением активной (резистивной) и реактивной (индуктивной или емкостной) мощностей.

Расчёт подобных явлений ведётся при помощи формулы:

Z = U / I или Z = R + J * (X_L – X_C)

где: Z – импеданс; R – активная нагрузка; X_L , X_C – индуктивная и емкостная нагрузка; J – коэффициент.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.

Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

• I = I₁ = I₂ ;
• U = U₁ + U₂ ;
• R = R₁ + R₂

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.

Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U, U1, U2 – приложенное напряжение

Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.

Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

• I = I₁ + I₂ … ;
• U = U₁ = U₂ … ;
• 1 / R = 1 / R₁ + 1 / R₂ + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.

Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U – подведённое напряжение; А, В – точки входа/выхода

Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.

Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E

Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ   

Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Выводы и полезное видео по теме

Подробный разбор закона Ома в видеоролике, представленном ниже, поможет окончательно закрепить знания в этом направлении.

Своеобразный видеоурок качественно подкрепляет теоретическое письменное изложение:

Работа электрика или деятельность электронщика неотъемлемо связана с моментами, когда реально приходится наблюдать закон Георга Ома в действии. Это своего рода прописные истины, которые следует знать каждому профессионалу.

Объёмных знаний по данному вопросу не требуется – достаточно выучить три основных вариации формулировки, чтобы успешно применять на практике.

Хотите дополнить изложенный выше материал ценными замечаниями или выразить свое мнение? Пишите, пожалуйста, комментарии в блоке под статьей. Если у вас остались вопросы, не стесняйтесь задавать их нашим экспертам.

Закон Ома для электрической цепи

Сила тока в цепи прямо пропорциональна ЭДС источника и обратно пропорциональна сумме сопротивлений внешнего и внутреннего участков цепи.

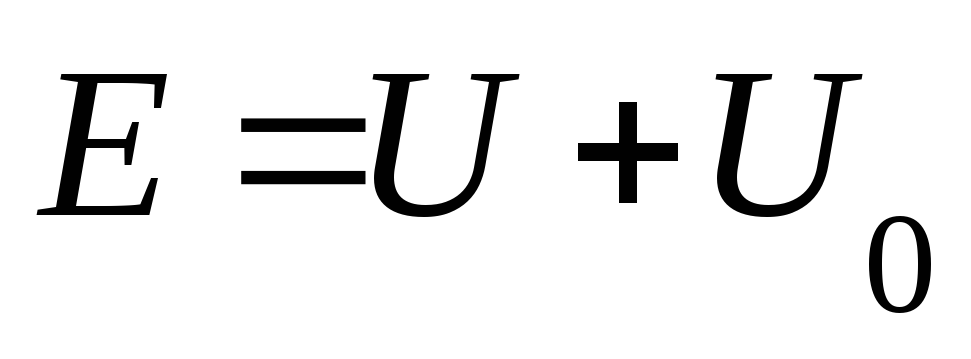
Т.е. ЭДС уравновешивается суммой падений напряжений на внешних и внутренних участках цепи.

Закон Ома для участка цепи

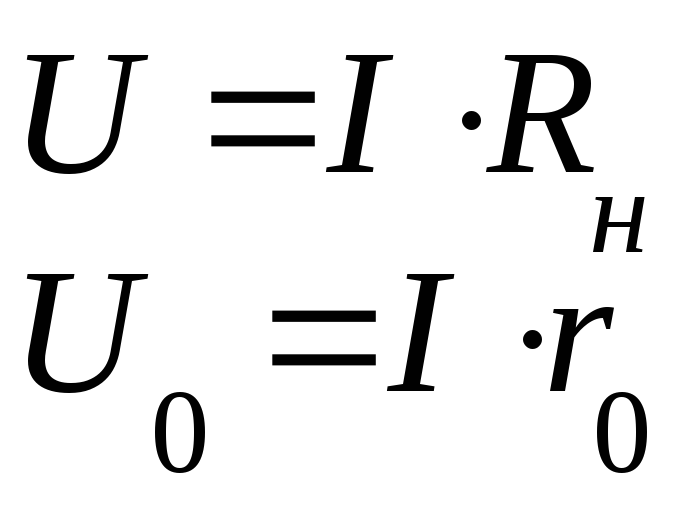
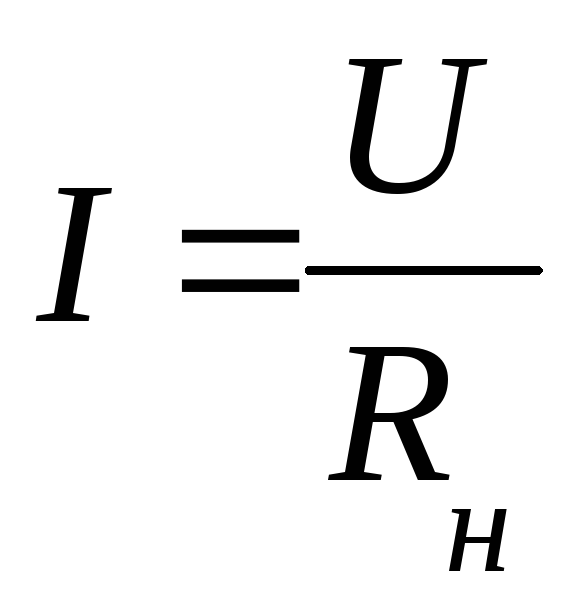
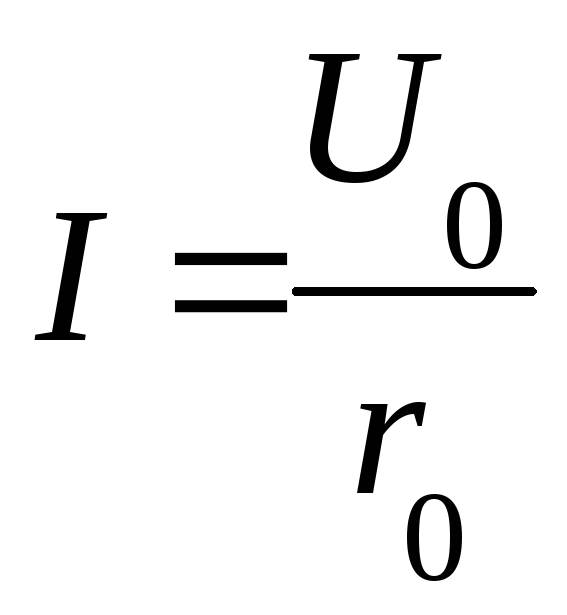
Сила тока на участке цепи прямо пропорциональна направлению на этом участке и обратно пропорциональна сопротивлению участка.

1. При разомкнутой цепи ЭДС равна напряжению:

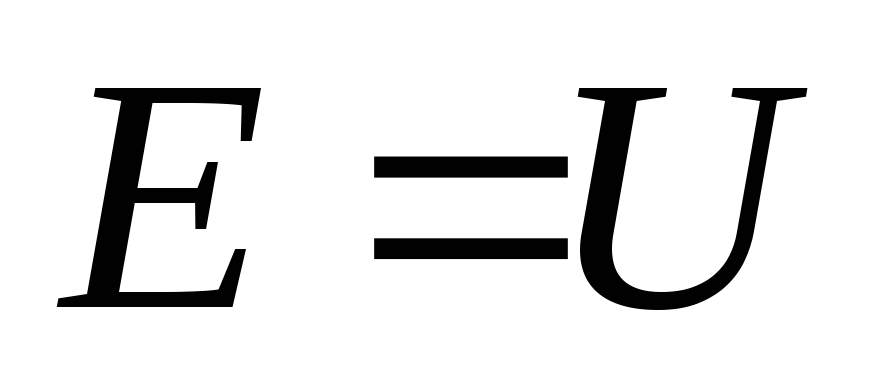
2. При коротком замыкании 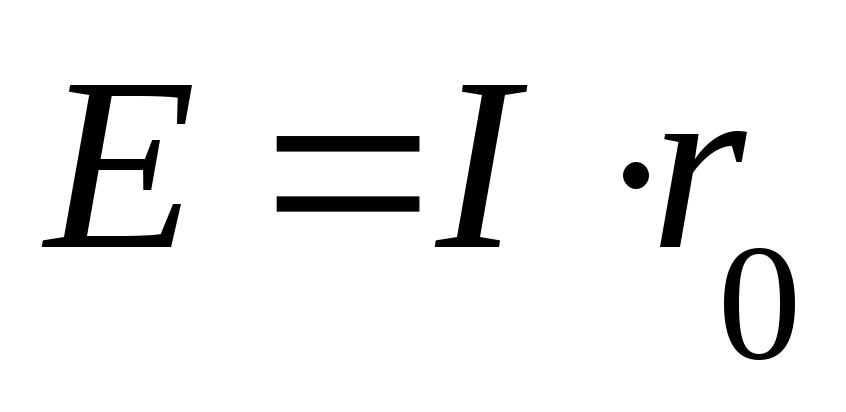, т.к.r₀ очень мало, то ток достигает большой величины.

Работа и мощность электрического тока

В электрических генераторах под действием электромагнитной индукции происходит разделение зарядов, при этом генератором совершается работа

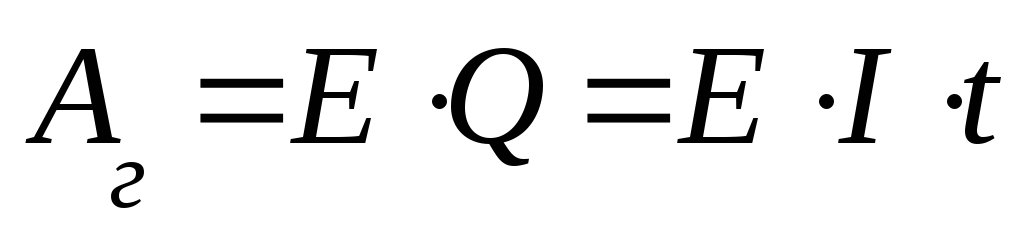
По закону сохранения энергии электрическая энергия, выработанная генератором за то же время, преобразуется в другие виды энергии. Часть этой энергии затрачивается на внешнем участке цепи, , а часть этой энергии теряется внутри источника

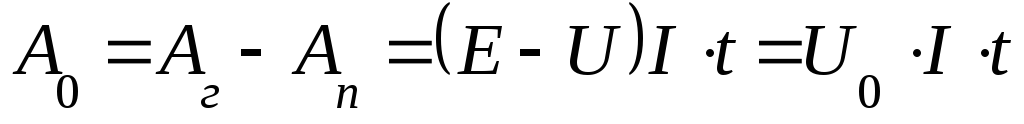
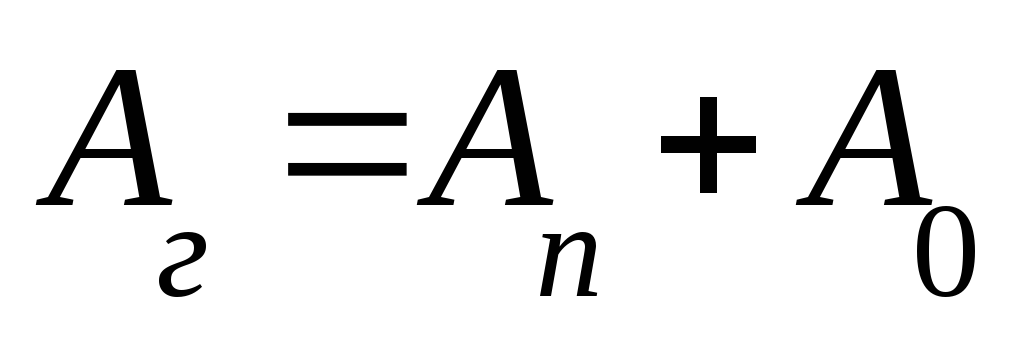
Отношение работы к промежутку времени, в течении которого она совершалась, называется мощностью.

Мощность характеризует скорость, с которой выполняется работа.

Скорость, с которой происходят преобразования механической или какой-либо другой энергии в электрическую, называется мощностью генератора

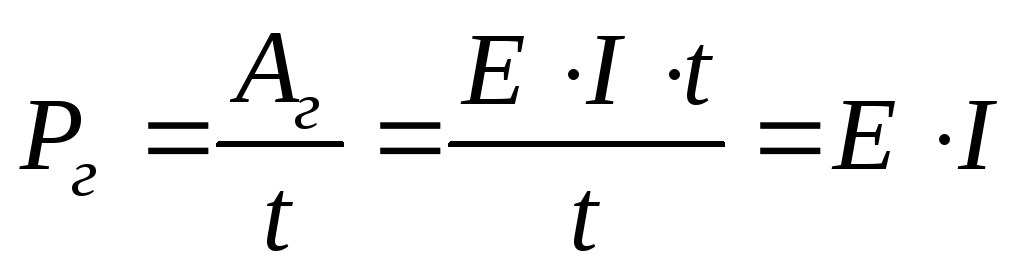
Скорость, с которой происходят преобразования электрической энергии в другие виды энергии во внешнем участке цепи, называется мощностью потребителя

Мощность, определяющая непроизводительные потери энергии в источнике (тепловые потери), называется мощностью потерь

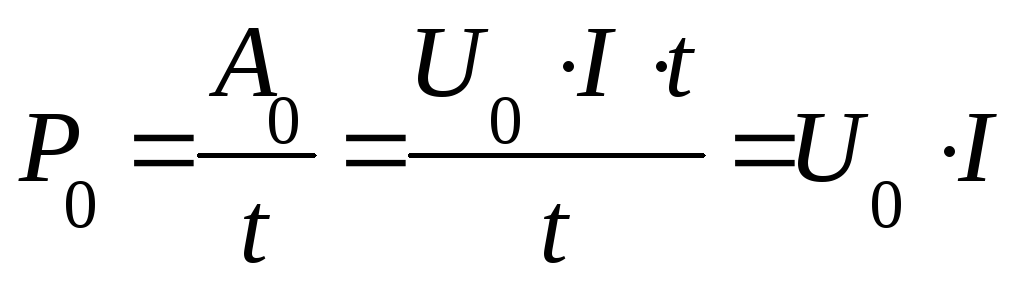
Таким образом, мощность, вырабатываемая генератором, равна сумме мощностей потребителя и потерь.

уравнение баланса мощностей

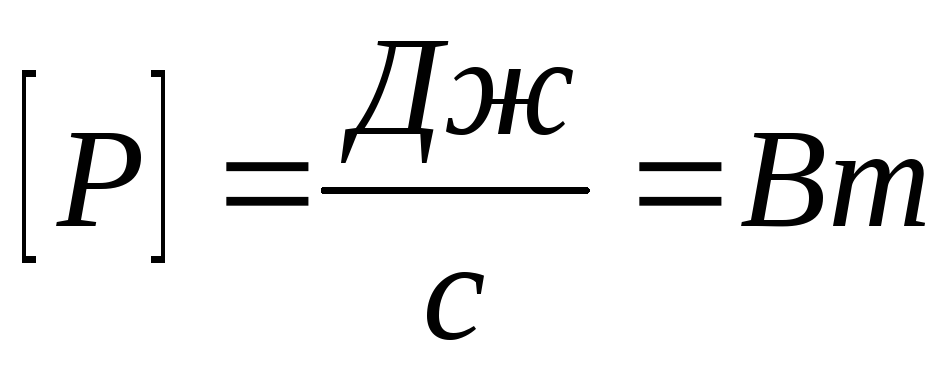
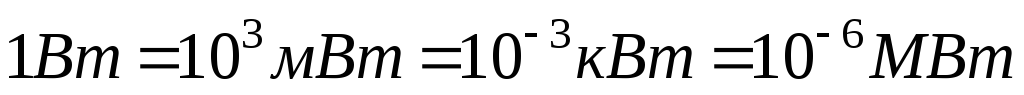
Законы кирхгофа

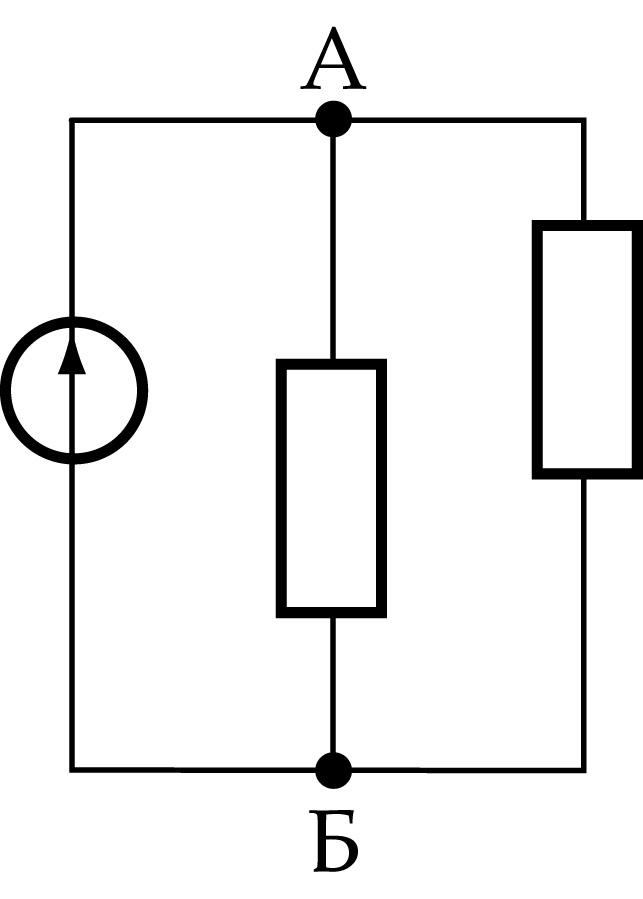
Точка электрической цепи называется узлом, если в ней сходится три или более провода. Ветвью эл. цепи называется ее участок, состо-ящий из одного или нескольких последовательно соединенных элементов, расположенных между двумя узлами.

Контуром эл. цепи называется замкнутый путь, проходящий по нескольким ветвям.

I закон Кирхгофа Сумма токов, направленных к узлу, равна сумме токов, выходящих из узла.

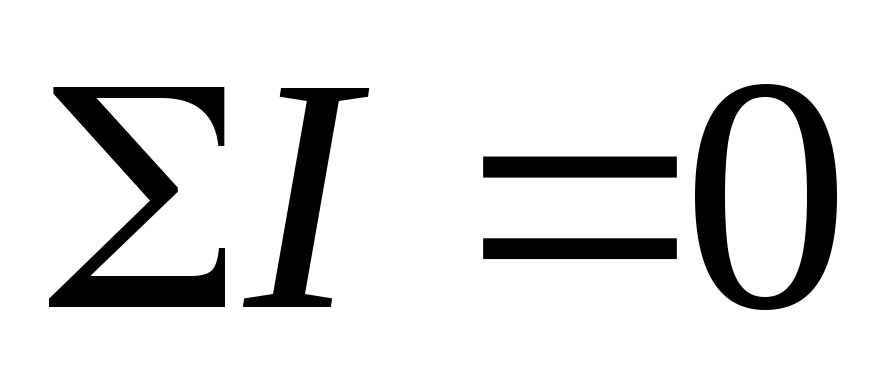
Алгебраическая сумма токов в узле равна нулю.

II закон Кирхгофа

Во всяком замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех сопротивлениях контура.

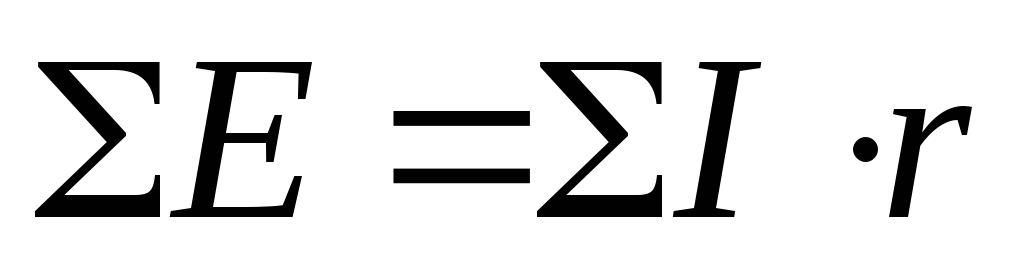
При составлении уравнений по второму правилу Кирхгофа ЭДС записывается со знаком «+», если ее направление совпадает с произвольно выбранным направлением обхода контура.

Падение напряжения берется со знаком «+», если направление тока в резисторе совпадает с направлением обхода.

Соединение сопротивлений (резисторов)

1. Последовательное соединение резисторов

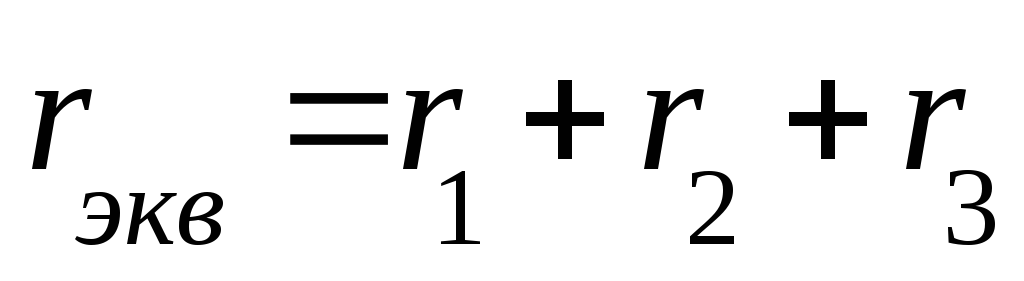
Падение напряжения на резисторах при их последовательном соединении распределяются прямо пропорционально сопротивлению этих резисторов.

2. Параллельное соединение резисторов

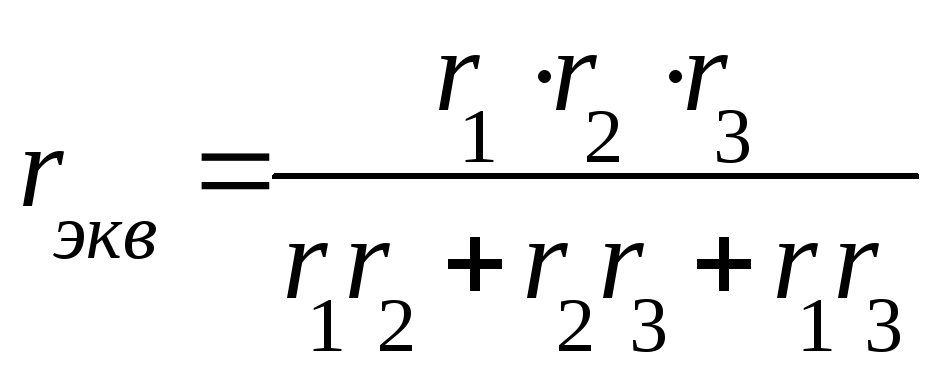
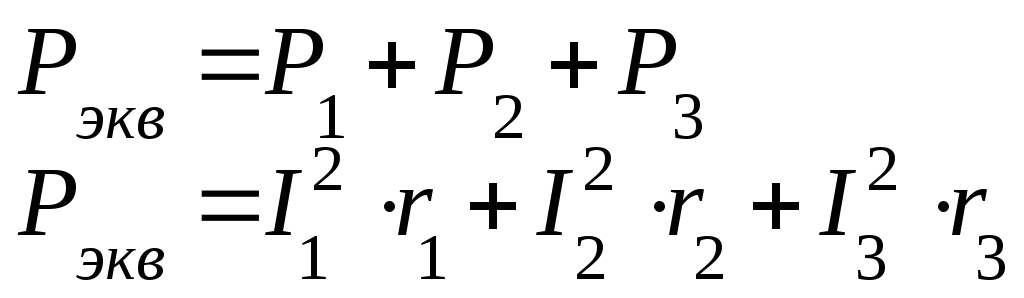
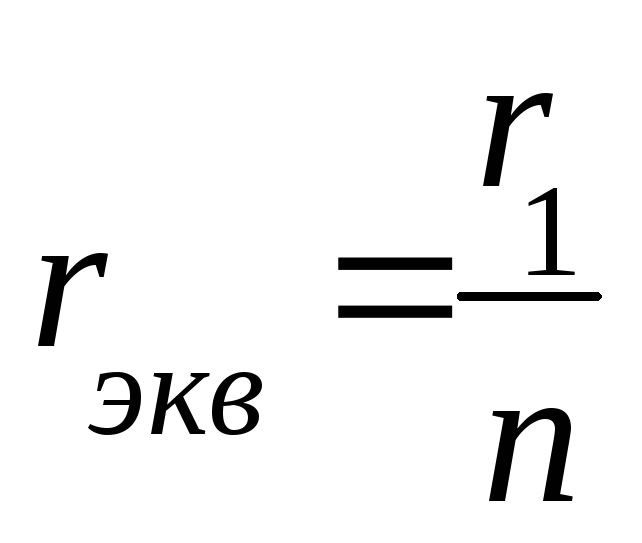
3. Смешанное соединение резисторов

Способы соединения химических

источников энергии в батарее

1. Виды источников энергии и их основные электрические характеристики

Химические источники энергии делятся на первичные элементы и аккумуляторы. В первичных элементах происходит необратимый процесс преобразования химической энергии в электрическую. В технике применяются элементы марганцево-цинковой и воздушно-марганцево-цинковой систем, ртутно-цинковые элементы.

В отличие от первичный элементов активные вещества аккумуляторов можно восстановить, пропуская через тих ток, по своему направлению обратный току разряда. Этот процесс называется зарядом аккумуляторов.

В технике применяются свинцовые (кислотные), никель-железные и никель-кадмиевые (щелочные), серебряно-цинковые аккумуляторы.

Количество электричества, которое можно получить от элемента во время его разряда, называется емкостью элемента.

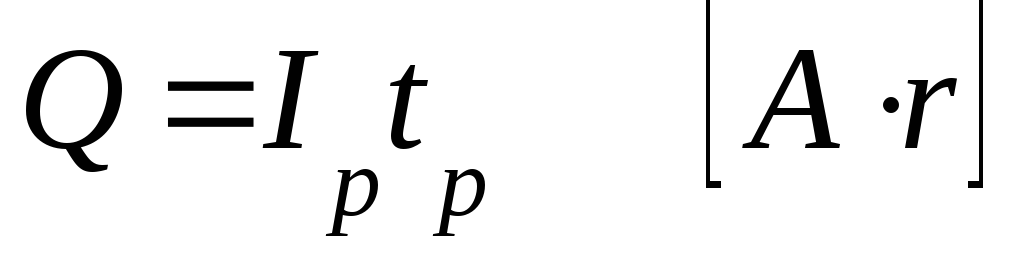
где 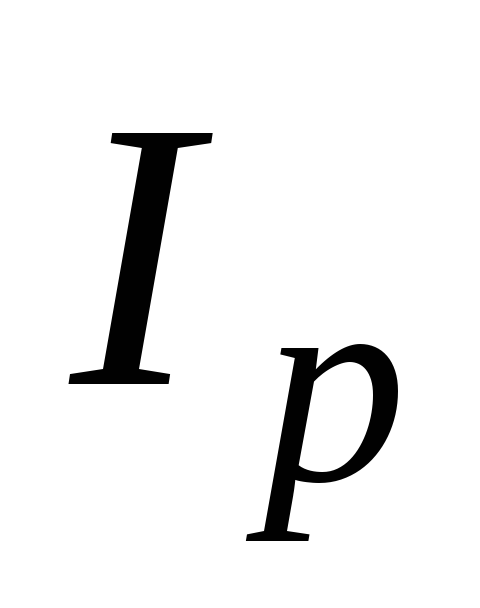— разрядный ток,— время разряды.

Первичные элементы и аккумуляторы имеют сравнительно низкую ЭДС.

Первичные элементы с большим внутренним сопротивлением могут разряжаться небольшими токами.

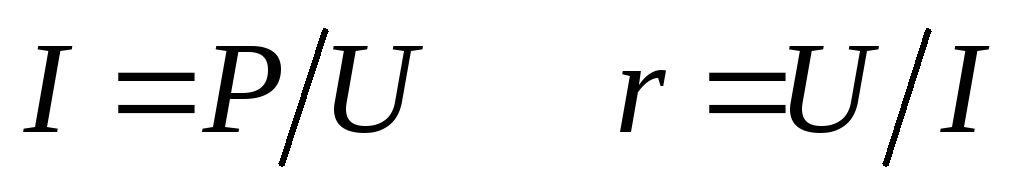
1. Электрическое сопротивление. Закон Ома для участка электрической цепи

Соберём электрическую цепь, состоящую из источника тока (который позволяет плавно менять напряжение), амперметра, спирали из никелиновой проволоки (проводника), ключа и параллельно присоединённого к спирали вольтметра (схема этой цепи показана рядом, прямоугольником условно обозначен проводник).

 

 

Замкнём цепь и отметим показания приборов. Затем при помощи источника тока плавно изменим напряжение (лучше всего увеличить его вдвое). Напряжение на спирали при этом тоже увеличится вдвое, и амперметр покажет вдвое большую силу тока. Увеличивая напряжение в \(3\) раза, напряжение на спирали увеличивается втрое, во столько же раз увеличивается сила тока.
Таким образом, опыт показывает, что во сколько раз увеличивается напряжение, приложенное к одному и тому же проводнику, во столько же раз увеличивается сила тока в нём. Другими словами:

 

Обрати внимание!

Сила тока в проводнике прямо пропорциональна напряжению на концах проводника.

Эту зависимость можно изобразить графически. Её называют зависимостью силы тока в проводнике от напряжения между концами этого проводника.

 

 

Включая в электрическую цепь источника тока различные проводники и амперметр, можно заметить, что при разных проводниках показания амперметра различны, т.е. сила тока в данной цепи различна.

 

 

Графики тоже будут отличаться.

 

 

Вольтметр, поочерёдно подключаемый к концам этих проводников, показывает одинаковое напряжение. Значит, сила тока в цепи зависит не только от напряжения, но и от свойств проводников, включённых в цепь. Зависимость силы тока от свойств проводника объясняется тем, что разные проводники обладают различным электрическим сопротивлением.

 

Обрати внимание!

Электрическое сопротивление — физическая величина. Обозначается оно буквой R.

За единицу сопротивления принимают \(1\) ом — сопротивление такого проводника, в котором при напряжении на концах \(1\)вольт сила тока равна \(1\) амперу.

Кратко это записывают так: 1 Ом =1 В1 А.Применяют и другие единицы сопротивления: миллиом (мОм), килоом (кОм), мегаом (МОм).

 

\(1\) мОм = \(0,001\) Ом;

\(1\) кОм = \(1000\) Ом;

\(1\) МОм = \(1 000 000\) Ом.

 

Причина сопротивления заключается в следующем: электроны взаимодействуют с ионами кристаллической решётки металла. При этом замедляется упорядоченное движение электронов, и сквозь поперечное сечение проводника проходит за \(1\) с меньшее их число. Соответственно, уменьшается и переносимый электронами за \(1\) с заряд, т.е. уменьшается сила тока. Таким образом, каждый проводник как бы противодействует электрическому току, оказывает ему сопротивление. Итак:

 

Обрати внимание!

Причиной сопротивления является взаимодействие движущихся электронов с ионами кристаллической решётки.

Чтобы ответить на вопрос, как зависит сила тока в цепи от сопротивления, обратимся к опыту.

 

 

На рисунке изображена электрическая цепь, источником тока в которой является аккумулятор. В эту цепь по очереди включают проводники, обладающие различным сопротивлением. Напряжение на концах проводника во время опыта поддерживается постоянным. За этим следят по показаниям вольтметра. Силу тока в цепи измеряют амперметром. Ниже приведены результаты опытов с тремя различными проводниками.

 

Напряжение на концах проводника, В	Сопротивление проводника, Ом	Сила тока в цепи, А
\(2\)	\(1\)	\(2\)
\(2\)	\(2\)	\(1\)
\(2\)	\(4\)	\(0,5\)

Обобщая результаты опытов, приходим к выводу, что:

 

Обрати внимание!

Сила тока в проводнике обратно пропорциональна сопротивлению проводника.

Зависимость силы тока от напряжения на концах участка цепи и сопротивления этого участка называется законом Ома — по имени немецкого учёного Георга Ома, открывшего этот закон в \(1827\) году.
Закон Ома читается так:

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.

И записывается так:

 

I=UR,

 

где \(I\) — сила тока в участке цепи, \(U\) — напряжение на этом участке, \(R\) — сопротивление участка.

Зависимость силы тока от сопротивления проводника при одном и том же напряжении на его концах может быть показана графически:

 

 

 

Найти сопротивление экспериментально можно несколькими способами:

 

 

Где  — обозначение омметра в цепи (или мультиметра в режиме измерения сопротивления).

Источники:

Пёрышкин А.В. Физика, 8 класс// ДРОФА, 2013.

http://xn--h2adlho.xn--g1ababalj7azb.xn--p1ai/375/
http://radiolove.ucoz.com/index/ne_znaesh_zakona_oma_sidi_doma/0-8

7. Закон Ома для электрической цепи.

С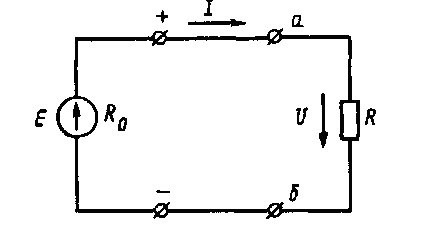огласно этому законуcила тока I прямо пропорциональна напряжению U и обратно пропорциональна электрическому сопротивлению R цепи. Полное сопротивление замкнутой электрической цепи (рис. 9) можно представить в виде суммы сопротивления внешней цепи R (например, какого-либо приемника электрической энергии) и внутреннего сопротивления R_o источника.

Поэтому сила тока : I = E/(R + R_o )

Чем больше э. д. с. Е источника и чем меньше сопротивление электрической цепи, тем больший ток проходит по этой цепи.

При применении Закона Ома к участку цепи, например между точками а и б (см. рис. 9) э. д. с. Е источника в формуле должна быть заменена разностью потенциалов между началом и концом рассматриваемого участка, т. е. напряжением U, а вместо сопротивления всей цепи в формулу должно быть подставлено сопротивление R данного участка. В этом случае закон Ома выражается формулой:

I = U/R

Из формулы следует, что напряжение U, действующее на некотором участке цепи, равно произведению силы тока I на сопротивление R этого участка:

U = IR

Так как потенциал электрического поля в начале участка электрической цепи больше, чем в конце, разность потенциалов, или напряжение U, приложенное к участку электрической цепи, часто называют падением напряжения на данном участке.

Исходя из закона Ома, если известны напряжение, приложенное к данному участку и сила тока на этом участке, можно найти сопротивление R этого участка

R = U/I

8. Использование резисторов для регулирования тока в электрической цепи.

З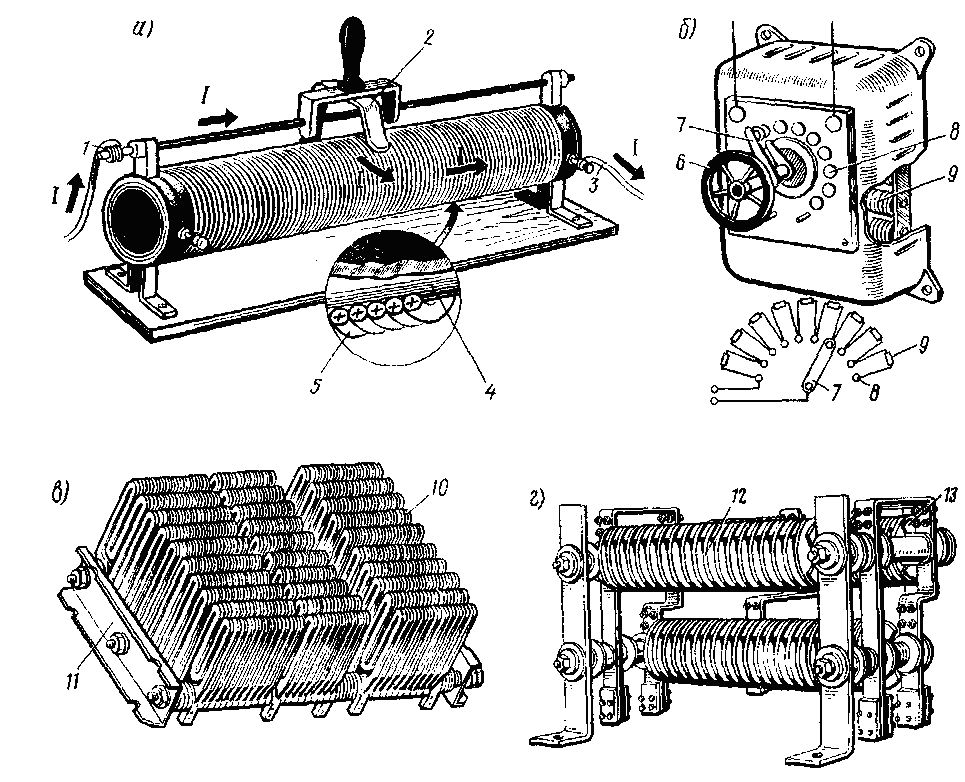акон Ома показывает, что силу тока в электрической цепи можно изменять, включая в нее различные сопротивления. Электрический аппарат, предназначенный для включения в электрическую цепь с целью регулирования или ограничения проходящего по ней тока, называютрезистором. Резисторы бывают с постоянным или регулируемым сопротивлением (реостатами).

Р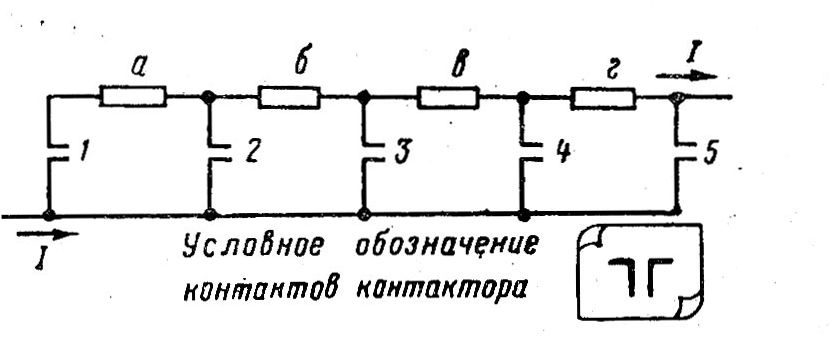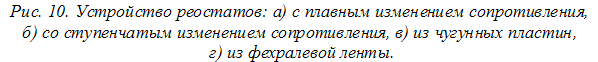езисторы обычно изготовляют из проволоки или ленты, материалом для которых служат сплавы металлов, обладающие высоким удельным сопротивлением (константан, никелин, манганин, фехраль). Это дает возможность для изготовления резисторов применять проволоку наименьшей длины. Реостаты могут выполняться с плавным или ступенчатым изменением сопротивления.

Д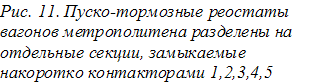ля регулирования тока при пуске тяговых двигателей постоянного тока применяют реостаты со ступенчатым изменением сопротивления (пусковые реостаты). Отдельные секции реостата в процессе пуска замыкаются накоротко контакторами (рис.11).

Пусковые реостаты электропоездов выполняют из фехралевой ленты 12, намотанной на фарфоровые изоляторы 13 (рис. 10,г).

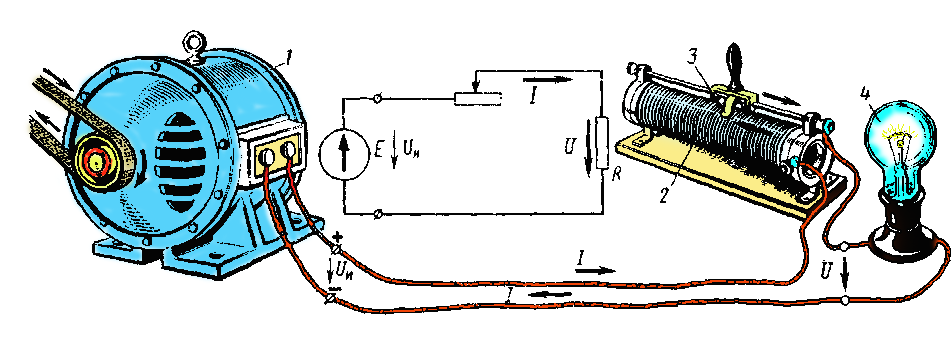
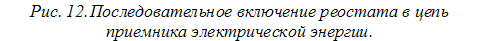
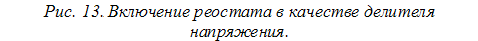
Схемы включения реостатов. Реостат 2 (рис. 12) может быть включен последовательно в цепь между источником 1 и приемником 4 электрической энергии. В этом случае при изменении сопротивления реостата, т. е. при перемещении подвижного контакта 3, изменяется сила тока в приемнике. Этот ток проходит только по части сопротивления реостата. Однако реостат можно включать в цепь таким образом, чтобы ток проходил по всему его сопротивлению, а к приемнику ответвлялась только часть тока источника. В этом случае два крайних зажима 2 и 4 реостата (рис. 13) подключают к источнику 5, а один из этих зажимов, например 4, и подвижной контакт 3 реостата — к приемнику 1. Очевидно, что при таком включении к приемнику будет подаваться напряжение U, равное падению напряжения между зажимом 4 и подвижным контактом 3 реостата. Следовательно, передвигая подвижной контакт реостата, можно изменять напряжение U, подводимое к приемнику, и силу тока в нем. Напряжение U представляет собой только часть напряжения U_и на зажимах источника.

Реостат, включенный по схеме рис. 13, называется делителем напряжения, или потенциометром.

Закон Ома для участка цепи. Сопротивление

Закон Ома для участка цепи. Сопротивление

«Физика — 10 класс»

Что заставляет заряды двигаться вдоль проводника?
Как электрическое поле действует на заряды?

Вольт-амперная характеристика.

В предыдущем параграфе говорилось, что для существования тока в проводнике необходимо создать разность потенциалов на его концах. Сила тока в проводнике определяется этой разностью потенциалов. Чем больше разность потенциалов, тем больше напряжённость электрического поля в проводнике и, следовательно, тем большую скорость направленного движения приобретают заряженные частицы. Это означает увеличение силы тока.

Для каждого проводника — твёрдого, жидкого и газообразного — существует определённая зависимость силы тока от приложенной разности потенциалов на концах проводника.

Зависимость силы тока в проводнике от напряжения, подаваемого на него, называют вольт-амперной характеристикой проводника.

Её находят, измеряя силу тока в проводнике при различных значениях напряжения. Знание вольт-амперной характеристики играет большую роль при изучении электрического тока.

Закон Ома.

Наиболее простой вид имеет вольт- амперная характеристика металлических проводников и растворов электролитов. Впервые (для металлов) её установил немецкий учёный Георг Ом, поэтому зависимость силы тока от напряжения носит название закона Ома.

На участке цепи, изображённой на рисунке 15.3, ток направлен от точки 1 к точке 2. Разность потенциалов (напряжение) на концах проводника равна U = φ₁ — φ₂. Так как ток направлен слева направо, то напряжённость электрического поля направлена в ту же сторону и φ₁ > φ₂.

Измеряя силу тока амперметром, а напряжение вольтметром, можно убедиться в том, что сила тока прямо пропорциональна напряжению.

Закон Ома для участка цепи:

Сила тока на участке цепи прямо пропорциональна приложенному к нему напряжению U и обратно пропорциональна сопротивлению этого участка R.

Применение обычных приборов для измерения напряжения — вольтметров — основано на законе Ома. Принцип устройства вольтметра такой же, как и у амперметра. Угол поворота стрелки прибора пропорционален силе тока.

Сила тока, проходящего по вольтметру, определяется напряжением между точками цепи, к которой он подключён. Поэтому, зная сопротивление вольтметра, можно по силе тока определить напряжение. На практике прибор градуируют так, чтобы он сразу показывал напряжение в вольтах.

Сопротивление.

Основная электрическая характеристика проводника — сопротивление. От этой величины зависит сила тока в проводнике при заданном напряжении.

Свойство проводника ограничивать силу тока в цепи, т. е. противодействовать электрическому току, называют электрическим сопротивлением проводника.

С помощью закона Ома (15.3) можно определить сопротивление проводника:

Для этого нужно измерить напряжение на концах проводника и силу тока в нём.

На рисунке 15.4 приведены графики вольт-амперных характеристик двух проводников. Очевидно, что сопротивление проводника, которому соответствует график 2, больше, чем сопротивление проводника, которому соответствует график 1.

Сопротивление проводника не зависит от напряжения и силы тока.

Сопротивление зависит от материала проводника и его геометрических размеров.

Сопротивление проводника длиной l с постоянной площадью поперечного сечения S равно:

где ρ — величина, зависящая от рода вещества и его состояния (от температуры в первую очередь).

Величину ρ называют удельным сопротивлением проводника.

Удельное сопротивление материала численно равно сопротивлению проводника из этого материала длиной 1 м и площадью поперечного сечения 1 м².

Единицу сопротивления проводника устанавливают на основе закона Ома и называют её омом.

Проводник имеет сопротивление 1 Ом, если при разности потенциалов 1 В сила тока в нём 1 А.

Единицей удельного сопротивления является 1 Ом • м. Удельное сопротивление металлов мало. А вот диэлектрики обладают очень большим удельным сопротивлением. Например, удельное сопротивление серебра 1,59 • 10^-8 Ом • м, а стекла порядка 10¹⁰ Ом • м. В справочных таблицах приводятся значения удельного сопротивления некоторых веществ.

Значение закона Ома.

Из закона Ома следует, что при заданном напряжении сила тока на участке цепи тем больше, чем меньше сопротивление этого участка. Если по какой-то причине (нарушение изоляции близко расположенных проводов, неосторожные действия при работе с электропроводкой и пр.) сопротивление между двумя точками, находящимися под напряжением, оказывается очень малым, то сила тока резко возрастает (возникает короткое замыкание), что может привести к выходу из строя электроприборов и даже возникновению пожара.

Именно из-за закона Ома нельзя говорить, что чем выше напряжение, тем оно опаснее для человека. Сопротивление человеческого тела может сильно изменяться в зависимости от условий (влажности, температуры окружающей среды, внутреннего состояния человека), поэтому даже напряжение 10—20 В может оказаться опасным для здоровья и жизни человека. Следовательно, всегда необходимо учитывать не только напряжение, но и силу электрического тока. При работе в физической лаборатории нужно строго соблюдать правила техники безопасности!

Закон Ома — основа расчётов электрических цепей в электротехнике.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Законы постоянного тока — Физика, учебник для 10 класса — Класс!ная физика

Электрический ток. Сила тока — Закон Ома для участка цепи. Сопротивление — Электрические цепи. Последовательное и параллельное соединения проводников — Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» — Работа и мощность постоянного тока — Электродвижущая сила — Закон Ома для полной цепи — Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»

Закон Ома

В 1826 величайший немецкий физик Георг Симон Ом публикует свою работу «Определение закона, по которому металлы проводят контактное электричество», где дает формулировку знаменитому закону. Ученые того времени встретили враждебно публикации великого физика. И лишь после того, как другой ученый – Клод Пулье, пришел к тем же выводам опытным путем, закон Ома признали во всем мире.

Закон Ома – физическая закономерность, которая определяет взаимосвязь между током, напряжением и сопротивлением проводника. Он имеет две основные формы.

Закон Ома для участка цепи

Формулировка закона Ома для участка цепи – сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению.

Это простое выражение помогает на практике решать широчайший круг вопросов. Для лучшего запоминания решим задачу.

  Задача 1.1

Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм², если к концам провода приложено напряжение 12 B.

Задача простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.

Закон Ома для полной цепи

Формулировка закона Ома для полной цепи — сила тока прямо пропорциональна сумме ЭДС цепи, и обратно пропорциональна сумме сопротивлений источника и цепи , где E – ЭДС, R- сопротивление цепи, r – внутреннее сопротивление источника.

Здесь могут возникнуть вопросы. Например, что такое ЭДС? Электродвижущая сила — это физическая величина, которая характеризует работу внешних сил в источнике ЭДС. К примеру, в обычной пальчиковой батарейке, ЭДС является химическая реакция, которая заставляет перемещаться заряды от одного полюса к другому. Само слово электродвижущая говорит о том, что эта сила двигает электричество, то есть заряд.

В каждом источнике присутствует внутреннее сопротивление r, оно зависит от параметров самого источника. В цепи также существует сопротивление R, оно зависит от параметров самой цепи.

Формулу закона Ома для полной цепи можно представить в другом виде. А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.

Для закрепления материала, решим две задачи на формулу закона Ома для полной цепи.

  Задача 2.1

Найти силу тока в цепи, если известно что сопротивление цепи 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.

 

Теперь решим задачу посложнее.

  Задача 2.2

Источник ЭДС подключен к резистору сопротивлением 10 Ом с помощью медного провода длиной 1 м и площадью поперечного сечения 1 мм². Найти силу тока, зная что ЭДС источника равно 12 В, а внутреннее сопротивление 1,9825 Ом.

Приступим.

Мнемоническая диаграмма

Для лучшего запоминания закона Ома существует мнемоническая диаграмма, благодаря которой можно всегда напомнить себе формулу. Пользоваться этой диаграммой очень просто. Достаточно закрыть искомую величину и две другие укажут, как её найти. Потренируйтесь, это может вам пригодится.

Успехов в изучении электричества! Рекомендуем прочесть статью — законы Кирхгофа.

Просмотров: 11436