Закон индукции Фарадея | энергетик
 Закон индукции Фарадея — Изменение потока магнитной индукции, проходящего через незамкнутую поверхность S, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре, l который является границей поверхности S.
Закон индукции Фарадея — Изменение потока магнитной индукции, проходящего через незамкнутую поверхность S, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре, l который является границей поверхности S.

Таким образом:
Закон Фарадея для электромагнитной индукции — для любого замкнутого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур.

Обозначение в формуле:
B — поток магнитной индукции;
E — электрическое поле;
dL — бесконечно малый элемент контура;
dS — бесконечно малый элемент вектора поверхности.
Анализируя результаты, полученные опытным путем, Фарадей пришел к количественному закону электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Значение индукционного тока, а, следовательно, и э.д.с. электромагнитной индукции определяется только скоростью изменения магнитного потока, т.е.

Теперь необходимо выяснить знак e. Вообще, знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали определяется правилом правого винта. Следовательно, выбирая положительное направление нормали, мы определяем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре.

Пользуясь этими представлениями и выводами, можно соответственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э.д.с (обоз. знаком E, ε или e).
Знак минус показывает, что увеличение потока (dФ/dt>0) вызывает э.д.с e < 0, т.е. поле индукционного тока направленно навстречу потоку; уменьшение потока (dФ/dt<0) вызывает e > 0, т.е. направление потока и поля индукционного тока совпадают. Знак минус в формуле правилом Ленца — общим правилом для нахождения направления индукционного тока, выведенного в 1833 г.
 Закон Фарадея можно сформулировать еще таким образом: э.д.с. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.
Закон Фарадея можно сформулировать еще таким образом: э.д.с. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.
Этот закон является универсальным: э.д.с. не зависит от способа изменения магнитного потока. Э.Д.С. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим:
 .
.
Законы электромагнитной индукции Фарадея • Джеймс Трефил, энциклопедия «Двести законов мироздания»
После того как в начале XIX века было установлено, что электрические токи порождают магнитные поля (см. Открытие Эрстеда, Закон Био—Савара), ученые заподозрили, что должна наблюдаться и обратная закономерность: магнитные поля должны каким-то образом производить электрические эффекты. В 1822 году в своей записной книжке Майкл Фарадей записал, что должен найти способ «превратить магнетизм в электричество». На решение этой задачи у него ушло почти десять лет.
Не раз за эти годы он возвращался к этой проблеме, пока не придумал серию экспериментов, кажущихся крайне незамысловатым по современным меркам. На железную катушку в форме бублика, например, он с одной стороны намотал плотные витки длинного, заизолированного от железного сердечника проводника, подключаемые к сильной электрической батарее, а с другой — плотные витки электрического проводника, подключенного к гальванометру — прибору для обнаружения электрического тока. Железный сердечник был нужен для «поимки» силовых линий образующегося магнитного поля и передачи их внутрь контура второй обмотки.
Первые результаты пришли не сразу. Сначала, сколько Фарадей ни наблюдал за своей установкой, при протекании электрического тока по первичной обмотке тока во вторичной обмотке не возбуждалось. Могло показаться, что предположения Фарадея относительно «преобразования» электричества в магнетизм и обратно ошибочны. И тут на помощь пришел случай: обнаружилось, к полному удивлению Фарадея, что стрелка гальванометра в цепи вторичной обмотки скачкообразно отклоняется от нулевого положения лишь при подключении или отключении батареи. И тогда Фарадея посетило великое прозрение: электрическое поле возбуждается лишь при
Повторяя свои опыты и анализируя результаты, Фарадей вскоре пришел к выводу, что протекающий по контуру электрический заряд пропорционален изменению т. н. магнитного потока, проходящего через него. Представьте себе, что замкнутый электропроводящий контур положен на лист бумаги, через который проходят силовые линии магнитного поля. Магнитным потоком называется произведение площади контура на напряженность (условно говоря, число силовых линий) магнитного поля, проходящего через эту площадь перпендикулярно ей. В первоначальной формулировке закон электромагнитной индукции Фарадея гласил, что при изменении магнитного потока, проходящего через контур, по проводящему контуру протекает электрический заряд, пропорциональный изменению магнитного потока, который возбуждается без всякого внешнего источника питания типа электрической батареи. Не будучи до конца удовлетворенным формулировкой, в которой фигурировала столь трудноизмеримая величина, как электрический заряд, Фарадей вскоре объединил свой закон с законом Ома и получил формулу (иногда ее принято называть
Изменить магнитный поток через контур можно тремя способами:
- изменить площадь контура;
- изменить интенсивность магнитного поля;
- изменить взаимную ориентацию магнитного поля и плоскости, в которой лежит контур.
Последний метод работает, поскольку при таком движении изменяется проекция магнитного поля на перпендикуляр к площади контура, хотя ни напряженность магнитного поля, ни площадь контура не меняются. Это очень важно с практической точки зрения, поскольку именно это явление лежит в основе действия любого электрогенератора. В самом простом варианте генератора проволочный контур вращается между полюсами сильного магнита. Поскольку в процессе вращения магнитный поток, проходящий через контур, постоянно меняется, по нему всё время протекает электрический ток. Согласно правилу Ленца, на протяжении одного полуоборота контура ток будет течь в одну сторону, а на протяжении следующего полуоборота — в другую. Собственно, по этому принципу и вырабатывается так хорошо нам знакомый
Электрогенераторы играли, играют и будут играть важнейшую роль в развитии нашей технологической цивилизации, поскольку позволяют получать энергию в одном месте, а использовать ее в другом. Паровая машина, например, может преобразовывать энергию сгорания угля в полезную работу, но использовать эту энергию можно только там, где установлены угольная топка и паровой котел. Электростанция же может размещаться весьма далеко от потребителей электроэнергии — и, тем не менее, снабжать ею заводы, дома и т. п.
Рассказывают (скорее всего, это всего лишь красивая сказка), будто Фарадей, демонстрировал прототип электрогенератора Джону Пилу (John Peel), Канцлеру казначейства Великобритании, и тот спросил ученого: «Хорошо, мистер Фарадей, всё это очень интересно, а какой от всего этого толк?»
«Какой толк? — якобы удивился Фарадей. — Да вы знаете, сэр, сколько налогов в казну эта штука со временем будет приносить?!»
См. также:
Обсуждение:Закон электромагнитной индукции Фарадея — Википедия
Материал из Википедии — свободной энциклопедии
что за бардак в статье? вы её читать пробывали?
читием заголовок: Пример 2: петля, движущаяся в постоянном магнитном поле
текст: На рис. 4 показан шпиндель, образованный двумя дисками с проводящими ободами, и проводящая петля, расположенная вертикально между этими ободами.
подпись к рисунку 4:
Рис. 4. Замкнутый прямоугольный провод вращается с угловой скоростью ω в радиальном, направленном наружу магнитном поле B фиксированной величины. Ток снимается щётками, касающимися верхнего и нижнего дисков с проводящими ободами.
ну что тут можно сказать «петля» практически тоже самое что и «Замкнутый прямоугольный провод», а нарисована ваще пластина ибо ток в одном направлении с каждой стороны. попробуйте в петле направить ток как на рисунке. так получится если это не петля, а два отдельных проводика замкнутые на обод.
к слову говоря и «ток снимается» это что? типа закон сохранения энергии не указ? и крутится и снимается — само по сибе. и проще всего обяснить не силой Лоренца, а силой Ампера там сразу блина проводна а не единичный заряд.
кстати говоря не надо мучатся что петля что пластина а что замкнутый прямоугольный провод — один провод будет отлично вращаться есали к дискам подвести ток.
интересны коментарии.
объяснениее же здесь — наукообразный бред. фишка это конструкции в том чтто тут не работает закон электромагнитной индукции Фарадея — вообще напрочь. вот такой вот парадокс Фарадея.
вот ваш эффект — так сказать наглядная демонстрация.
а вот здесь ничего написано и картинка правильная Рельсотрон
а вобще статью написал какойто вредитель.там ниже идет обяснение что если весь путь отследить, то будет изменение площади контура, одна загвоздка — он не замкунут. цитаты извесных людей притянуты за уши. тут надо все переписывать от начала и до конца.
есть графоман с физическим образованием? —109.238.81.229 08:54, 13 сентября 2016 (UTC)
и еще пять копек к правке.
можно говорить об ЭДС, но нужен источник потока магнитной индукци. Меня что-то мучают некоторые сомнения(с чего бы это? опять закон сохранения энергии? — вот шайтан ведь), что ситема выйдет на самоподдержку. такой генератор называют униполярным — описан в начале статьи. вообще случай «рамки» в равномерном поле это просто часный случай униполярного двигателя или генератора. кстати исторически это называется «парадокс Фарадея». т.е. Фарадей сам не смог прикрутить туда свой закон. готов написать математику (упрощенный вывод через закон Фарадея или силу Лоренца, а можно то и то) мне нужны картинки. последовательное описание еффекта дается в ОТО — это мне не по-зубам.
—109.238.81.229 11:00, 19 сентября 2016 (UTC)
Закон электромагнитной индукции (закон Фарадея) — Мегаобучалка
В результате многочисленных опытов Фарадей установил основной количественный закон электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток. Возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Фарадей установил, что значение ЭДС электромагнитной индукции E
Ei = -К , (27.1)
где К – коэффициент пропорциональности, зависящий только от выбора единиц измерения.
В системе единиц СИ коэффициент К = 1, т.е.
Ei = — . (27.2)
Эта формула и представляет собой закон электромагнитной индукции Фарадея. Знак минус в этой формуле соответствует правилу (закону) Ленца.
Закон Фарадея можно сформулировать еще таким образом: ЭДС электромагнитной индукции Ei в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: ЭДС E
Знак минус в (27.2) показывает, что увеличение потока ( > 0) вызывает ЭДС Ei < 0, т.е. магнитный поток индукционного тока направлен навстречу потоку, вызвавшему его; уменьшение потока ( < 0) вызывает Ei > 0 т. е. направления магнитного потока индукционного тока и потока, вызвавшего его, совпадают. Знак минус в формуле (27.2) является математическим выражением правила Ленца — общего правила для нахождения направления индукционного тока (а значит и знака и ЭДС индукции), выведенного в 1833 г. Правило Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Иначе говоря, индукционный ток создает магнитный поток, препятствующий изменению магнитного потока, вызывающего ЭДС индукции.
ЭДС индукции выражается в вольтах (В). Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим:
.
Если замкнутый контур, в котором индуцируется ЭДС индукции, состоит из N витков, то Ei будет равна сумме ЭДС, индуцируемых в каждом из витков. И если магнитный поток, охватываемый каждым витком, одинаков и равен Ф, то суммарный поток сквозь поверхность N витков, равен (NФ) – полный магнитный поток (потокосцепление). В этом случае ЭДС индукции равна:
Ei = -N× , (27.3)
Формула (27.2) выражает закон электромагнитной индукции в общей форме. Она применима как к неподвижным контурам, так и к движущимся проводникам в магнитном поле. Входящая в нее производная от магнитного потока по времени в общем случае состоит из двух частей, одна из которых обусловлена изменением магнитной индукции во времени, а другая – движением контура относительно магнитного поля (или его деформацией). Рассмотрим некоторые примеры применения этого закона.
Пример 1. Прямолинейный проводник длиной l движется параллельно самому себе в однородном магнитном поле (рисунок 38). Этот проводник может входить в состав замкнутой цепи, остальные части которой неподвижны. Найдем ЭДС, возникающую в проводнике.
Если мгновенное значение скорости проводника есть v, то за время dt он опишет площадь dS = l×v×dt и за это время пересечет все линии магнитной индукции, проходящие через dS. Поэтому изменение магнитного потока через контур, в состав которого входит движущийся проводник, будет dФ = Bn×l×v×dt. Здесь Bn — составляющая магнитной индукции, перпендикулярная к dS. Подставляя это в формулу (27.2) получаем величину ЭДС:
Ei = Bn×l×v. (27.4)
Направление индукционного тока и знак ЭДС определяются правилом Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток. В некоторых случаях возможно определение направления индукционного тока (полярности ЭДС индукции) согласно другой формулировке правила Ленца: индукционный ток в движущемся проводнике направлен таким образом, что возникающая при этом сила Ампера противоположна вектору скорости (тормозит движение).
Разберем численный пример. Вертикальный проводник (автомобильная антенна) длиной l = 2 м движется с востока на запад в магнитном поле Земли со скоростью v = 72 км/час = 20 м/с. Вычислим напряжение между концами проводника. Так как проводник разомкнут, то тока в нем не будет и напряжение на концах будет равно ЭДС индукции. Учитывая, что горизонтальная составляющая магнитной индукции поля Земли (т.е. составляющая, перпендикулярная к направлению движения) для средних широт равна 2×10-5 Тл, по формуле (27.4) находим
U = Bn×l×v = 2×10-5×2×20 = 0,8×10-3 В,
т.е. около 1 мВ. Магнитное поле Земли направлено с юга на север. Поэтому мы находим, что ЭДС направлена сверху вниз. Это значит, что нижний конец провода будет иметь более высокий потенциал (зарядится положительно), а верхний – более низкий (зарядится отрицательно).
Пример 2. В магнитном поле находится замкнутый проволочный контур, пронизываемый магнитным потоком Ф. Предположим, что этот поток уменьшается до нуля, и вычислим полную величину заряда, прошедшего по цепи. Мгновенное значение ЭДС в процессе исчезновения магнитного потока выражается формулой (27.2). Следовательно, согласно закону Ома мгновенное значение силы тока есть
I = — , (27.5)
где R – полное сопротивление цепи.
Величина прошедшего заряда равна
q = = — = . (27.6)
Полученное соотношение выражает закон электромагнитной индукции в форме, найденной Фарадеем, который из своих опытов заключил, что величина заряда, прошедшего по цепи, пропорциональна полному числу линий магнитной индукции, пересеченных проводником (т.е. изменению магнитного потока Ф1-Ф2), и обратно пропорциональна сопротивлению цепи R. Соотношение (27.6) позволяет дать определение единицы магнитного потока в системе СИ: вебер – магнитный поток, при убывании которого до нуля в сцепленном с ним контуре сопротивлением 1 Ом проходит заряд 1 Кл.
Согласно закону Фарадея, возникновение ЭДС электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае она не может быть причиной возникновения ЭДС индукции. Максвелл для объяснения ЭДС индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция вектора напряженности этого поля по любому неподвижному контуру L проводника представляет собой ЭДС электромагнитной индукции:
Ei = = — . (27.7)
Линии напряженности вихревого электрического поля представляют собой замкнутые кривые, поэтому при перемещении заряда в вихревом электрическом поле по замкнутому контуру совершается отличная от нуля работа. В этом заключается отличие вихревого электрического поля от электростатического, линии напряженности которого начинаются и заканчиваются на зарядах.
Закон электромагнитной индукции (закон Фарадея).
Федун В.И. Конспект лекций по физике Электромагнетизи
Лекция 26.
Электромагнитная индукция. Открытие Фарадея.
В 1831 г. М. Фарадеем было сделано одно из важнейших фундаментальных открытий в электродинамике – обнаружено явлениеэлектромагнитной индукции.
В замкнутом проводящем
контуре при изменении магнитного потока
(потока вектора 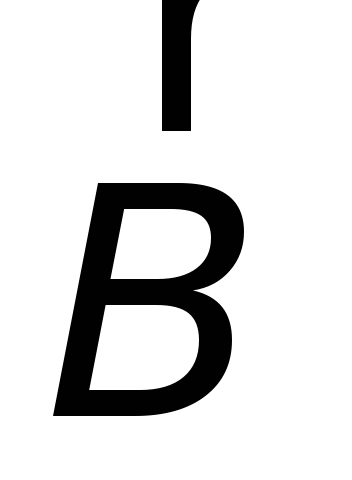 ),
охватываемого этим контуром, возникает
электрический ток.
),
охватываемого этим контуром, возникает
электрический ток.
Этот ток получил название индукционного.
Появление индукционного тока означает, что при изменении магнитного
Фарадей обнаружил, что индукционный ток можно вызвать двумя различными способами, которые удобно объяснить с помощью рисунка.
1-й способ: перемещение рамки 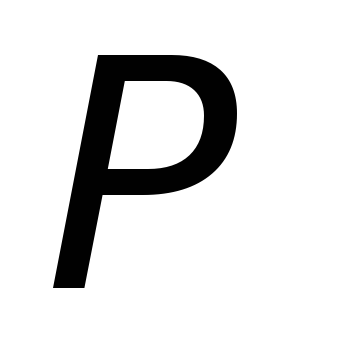 в магнитном поле неподвижной катушки
в магнитном поле неподвижной катушки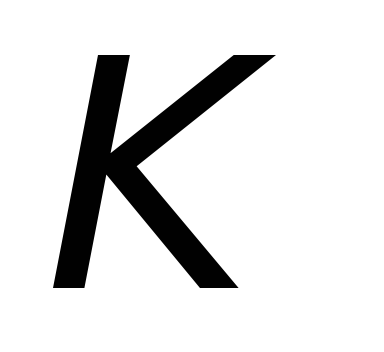 (см.
рис.26.1).
(см.
рис.26.1).
2-й способ: изменение магнитного поля 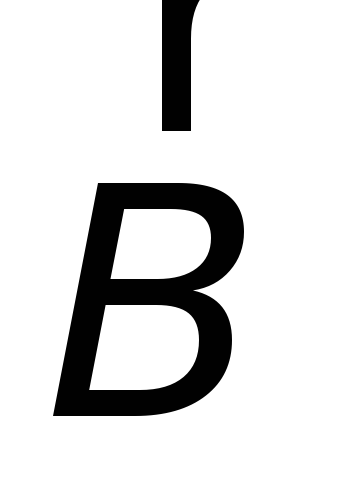 ,
создаваемого катушкой
,
создаваемого катушкой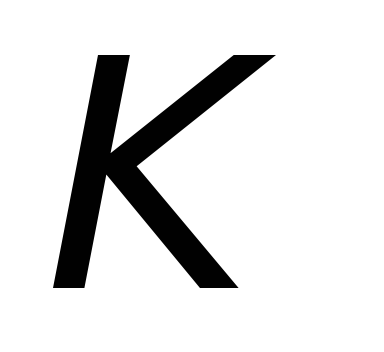 ,
за счет ее движения или вследствие
изменения силы тока
,
за счет ее движения или вследствие
изменения силы тока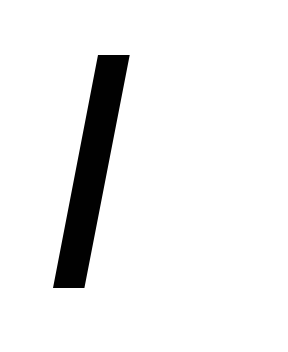 в ней (или того и другого вместе). Рамка
в ней (или того и другого вместе). Рамка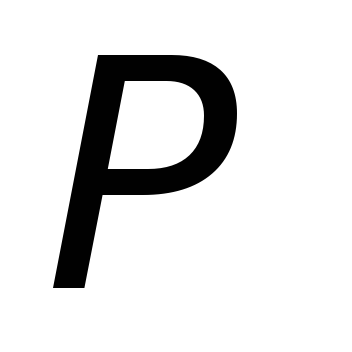 при этом неподвижна.
при этом неподвижна.
В обоих этих случаях гальванометр 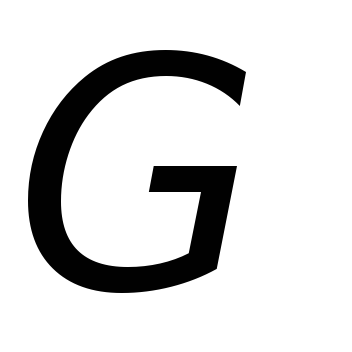 будет показывать наличие индукционного
тока в рамке
будет показывать наличие индукционного
тока в рамке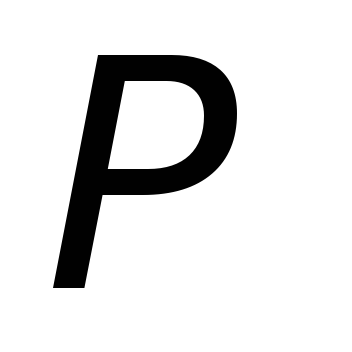 .
.
Направление индукционного тока и,
соответственно, знак э.д.с. индукции  определяются правилом Ленца.
определяются правилом Ленца.
Правило Ленца.
Индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей.
Правило Ленца выражает важное физическое свойство – стремление системы противодействовать изменению ее состояния. Это свойство называют электромагнитной инерцией.
Какова бы ни была причина изменения магнитного потока, охватываемого замкнутым проводящим контуром, возникающая в контуре э.д.с. индукции определяется формулой
| (26.1) |
Природа электромагнитной индукции.
С целью выяснения физических причин, которые приводят к возникновению э.д.с. индукции, последовательно рассмотрим два случая.
1. Контур движется в постоянном магнитном поле.
| Пусть контур
с подвижной перемычкой длиной |
Рисунок 26.2 |
действовать сила
|
вызывающая перемещение электронов по перемычке вниз, т.е. потечет ток, направленный вверх.
Перераспределившиеся заряды создадут электрическое поле, которое возбудит ток и в остальных участках контура.
Это и есть индукционный ток.
Магнитная сила 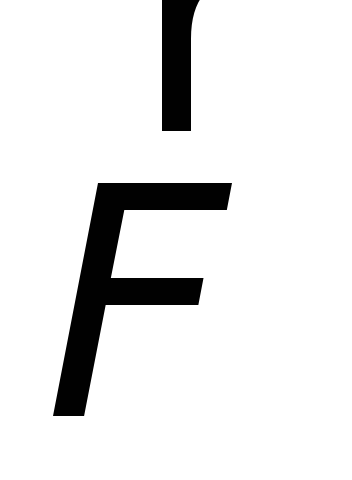 играет роль сторонней силы. Ей можно
сопоставить эквивалентное поле сторонних
сил
играет роль сторонней силы. Ей можно
сопоставить эквивалентное поле сторонних
сил
| (26.2) |
Электродвижущая сила,
создаваемая этим полем, называется электродвижущей
силой индукции  .
В нашем случае
.
В нашем случае
| (26.3) |
Здесь знак «минус» поставлен
потому, что стороннее поле
направлено против положительного обхода
контура, определяемого правилом правого
винта. Произведение есть скорость приращения площади контура
(приращение площади в единицу времени),
поэтому
есть скорость приращения площади контура
(приращение площади в единицу времени),
поэтому
|
где  — приращение магнитного потока сквозь
контур.
— приращение магнитного потока сквозь
контур.
Тогда,
| (26.4) |
Полученный результат можно обобщить
на случай произвольной ориентации
вектора индукции магнитного поля 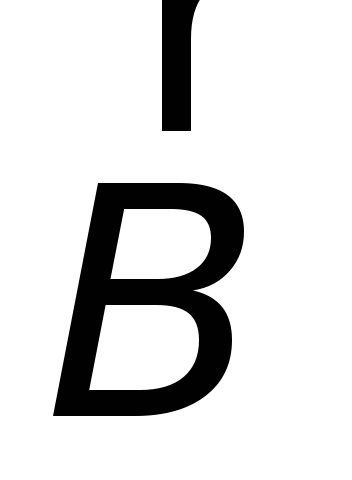 относительно плоскости контура и на
любой контур, движущийся (и/или
деформируемый) произвольным образом в
постоянном неоднородном внешнем
магнитном поле.
относительно плоскости контура и на
любой контур, движущийся (и/или
деформируемый) произвольным образом в
постоянном неоднородном внешнем
магнитном поле.
Итак, возбуждение э.д.с. индукции при
движении контура в постоянном магнитном
поле объясняется действием магнитной
составляющей силы Лоренца, пропорциональной 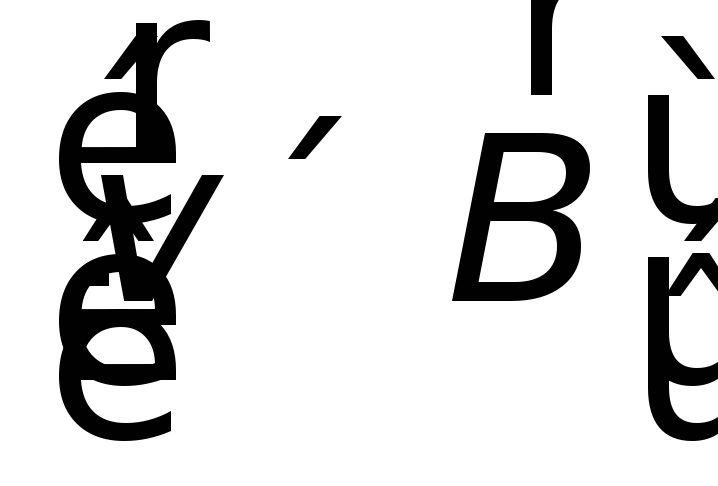 ,
которая возникает при перемещении
проводника.
,
которая возникает при перемещении
проводника.
2. Контур покоится в переменном магнитном поле.
Наблюдаемое на опыте возникновение индукционного тока свидетельствует о том, что и в этом случае в контуре появляются сторонние силы, которые теперь связаны с изменяющимся во времени магнитным полем. Какова же их природа? Ответ на этот принципиальный вопрос был дан Максвеллом.
Поскольку проводник покоится, то скорость
упорядоченного движения электрических
зарядов 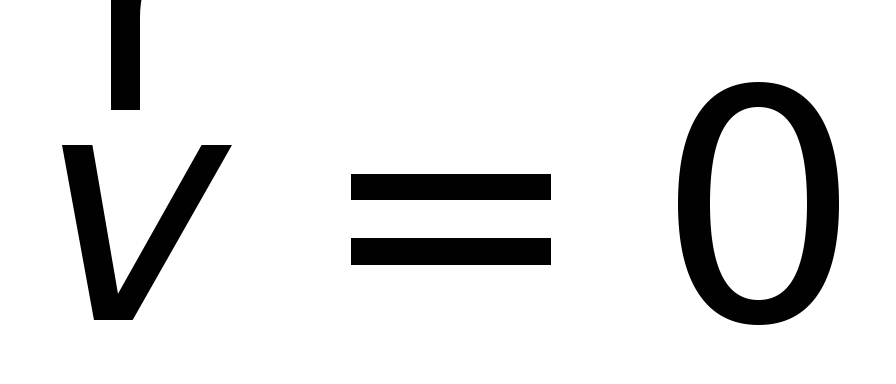 и, следовательно, магнитная сила,
пропорциональная
и, следовательно, магнитная сила,
пропорциональная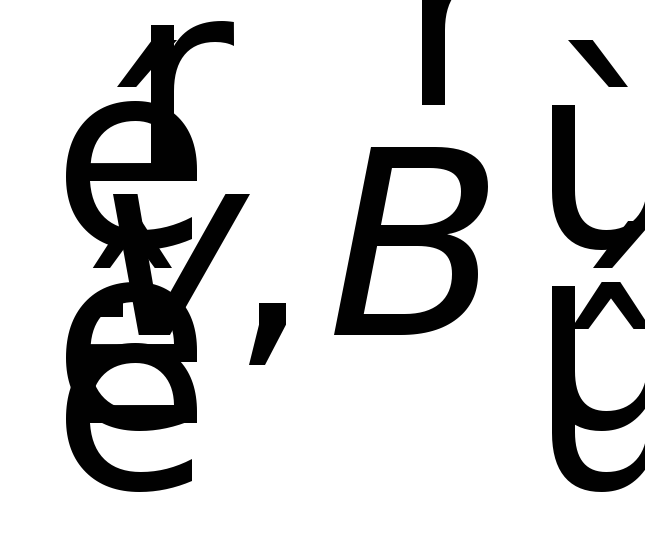 ,
также равна нулю и уже не может привести
заряды в движение. Однако кроме магнитной
силы на электрический заряд может
действовать только сила со стороны
электрического поля, равная
,
также равна нулю и уже не может привести
заряды в движение. Однако кроме магнитной
силы на электрический заряд может
действовать только сила со стороны
электрического поля, равная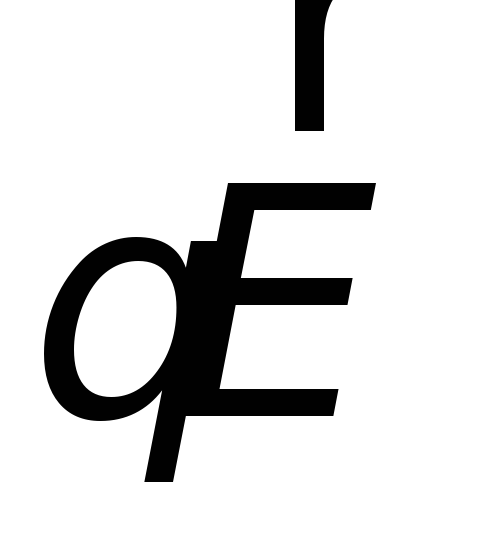 .
Поэтому остается заключить, чтоиндукционный ток обусловлен
электрическим полем
.
Поэтому остается заключить, чтоиндукционный ток обусловлен
электрическим полем 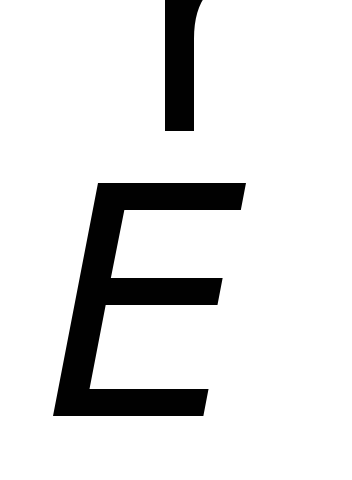 ,
возникающим при изменении во времени
внешнего магнитного поля. Именно
это электрическое поле и ответственно
за появление э.д.с. индукции в неподвижном
контуре. Согласно Максвеллу,изменяющееся
во времени магнитное поле порождает в
окружающем пространстве электрическое
поле. Возникновение электрического
поля не связано с наличием проводящего
контура, который лишь позволяет обнаружить
по возникновению в нем индукционного
тока существование этого поля.
,
возникающим при изменении во времени
внешнего магнитного поля. Именно
это электрическое поле и ответственно
за появление э.д.с. индукции в неподвижном
контуре. Согласно Максвеллу,изменяющееся
во времени магнитное поле порождает в
окружающем пространстве электрическое
поле. Возникновение электрического
поля не связано с наличием проводящего
контура, который лишь позволяет обнаружить
по возникновению в нем индукционного
тока существование этого поля.
Формулировка закона электромагнитной индукции, данная Максвеллом, принадлежит к числу наиболее важных обобщений электродинамики.
Всякое изменение магнитного поля во времени возбуждает в окружающем пространстве электрическое поле.
Математическая формулировка закона электромагнитной индукции в понимании Максвелла имеет вид:
Циркуляция вектора
напряженности 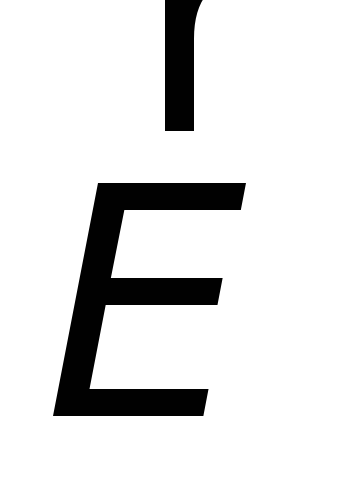 этого поля по любому неподвижному
замкнутому контуру
этого поля по любому неподвижному
замкнутому контуру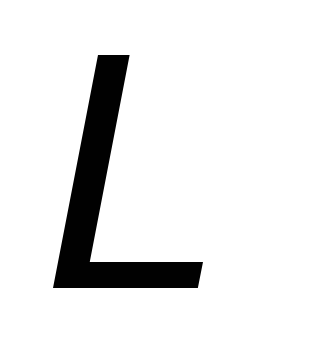 определяется выражением
определяется выражением
| (26.5) |
где 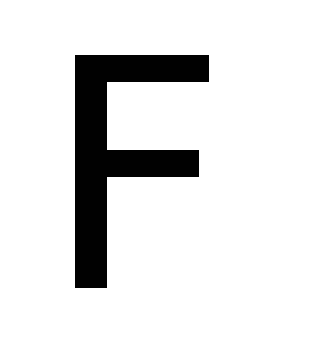 — магнитный поток, пронизывающий контур
— магнитный поток, пронизывающий контур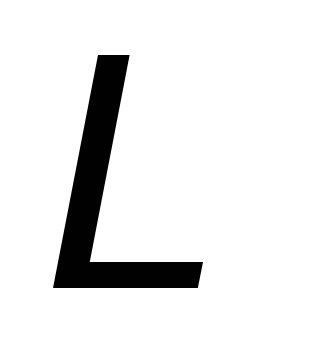 .
.
Используемый для обозначения скорости изменения магнитного потока знак частной производной указывает на то, что контур является неподвижным.
Поток вектора 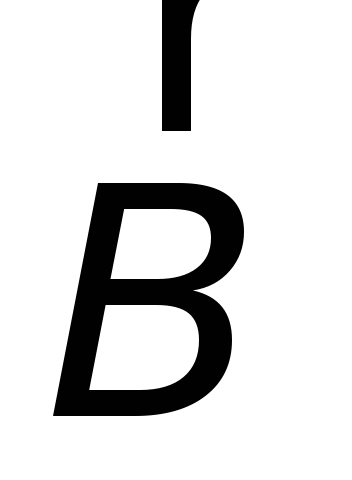 через поверхность, ограниченную контуром
через поверхность, ограниченную контуром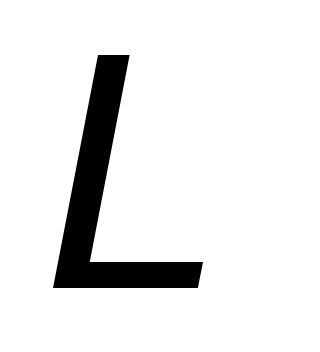 ,
равен
,
равен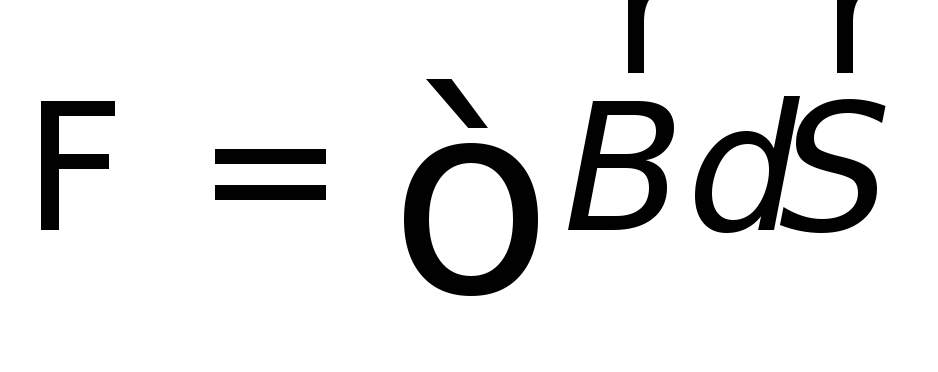 ,
поэтому выражение закона электромагнитной
индукции можно переписать следующим
образом:
,
поэтому выражение закона электромагнитной
индукции можно переписать следующим
образом:
| (26.6) |
Воспользовавшись теоремой Стокса можно получить закон электромагнитной индукции в дифференциальной форме:
| (26.7) |
Это одно из уравнений системы уравнений Максвелла.
Тот факт, что циркуляция электрического поля, возбуждаемого переменным во времени магнитным полем, отлична от нуля, означает, что рассматриваемое электрическое поле не потенциальное.Оно, как и магнитное поле, являетсявихревым.
В общем случае электрическое поле 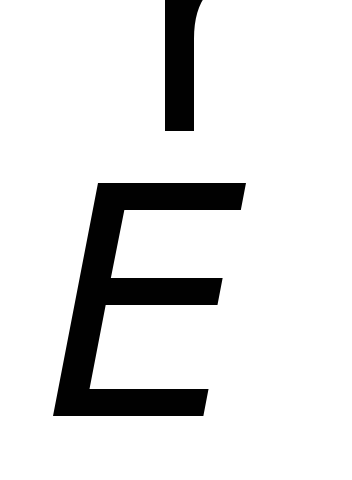 может быть представлено векторной
суммой потенциального (поля статических
электрических зарядов, циркуляция
которого равна нулю) и вихревого
(обусловленного изменяющимся во времени
магнитным полем) электрических полей.
может быть представлено векторной
суммой потенциального (поля статических
электрических зарядов, циркуляция
которого равна нулю) и вихревого
(обусловленного изменяющимся во времени
магнитным полем) электрических полей.
В основе рассмотренных нами явлений,
объясняющих закон электромагнитной
индукции, не просматривается общего
принципа, позволяющего установить
общность их физической природы. Поэтому
эти явления следует рассматривать как
независимые, а закон электромагнитной
индукции — как результат их совместного
действия. Тем более удивительным
оказывается тот факт, что э.д.с. индукции
в контуре всегда равна скорости изменения
магнитного потока сквозь контур. В тех
случаях, когда меняется и поле 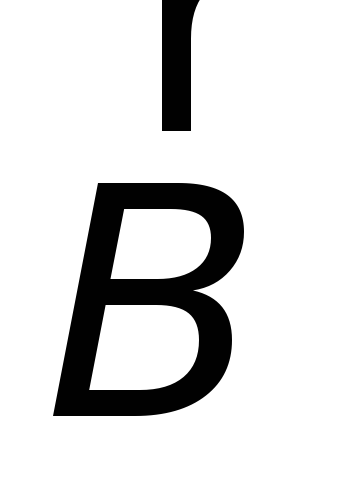 и расположение или конфигурация контура
в магнитном поле, э.д.с. индукции следует
рассчитывать по формуле
и расположение или конфигурация контура
в магнитном поле, э.д.с. индукции следует
рассчитывать по формуле
| (26.8) |
а закон электромагнитной индукции можно представить в виде
| (26.9) |
Выражение, стоящее в правой части этого равенства, представляет собой полную производную магнитного потока по времени: первое слагаемое связано с изменением магнитного поля во времени, второе – с движением контура.
Можно сказать, что во всех случаях индукционный ток вызывается полной силой Лоренца
|
Какая часть индукционного тока вызывается электрической, а какая магнитной составляющей силы Лоренца — зависит от выбора системы отсчета.
О работе сил Лоренца и Ампера.
Из самого определения работы следует, что сила, действующая в магнитном поле на электрический заряд и перпендикулярная его скорости, не может совершать работы. Однако при движении проводника с током, увлекающего за собой заряды, сила Ампера все же работу совершает. Наглядным подтверждением этого служат электромоторы.
Это противоречие исчезает, если принять
во внимание, что движение проводника в
магнитном поле неизбежно сопровождается
явлением электромагнитной индукции.
Поэтому наряду с силой Ампера работу
над электрическими зарядами совершает
и возникающая в проводнике электродвижущая
сила индукции. Т.о., полная работа сил
магнитного поля складывается из
механической работы, обусловленной
силой Ампера, и работы э.д.с., индуцируемой
при движении проводника. Обе работы
равны по модулю и противоположны по
знаку, поэтому их сумма равна нулю.
Действительно, работа амперовой силы
при элементарном перемещении проводника
с током в магнитном поле равна 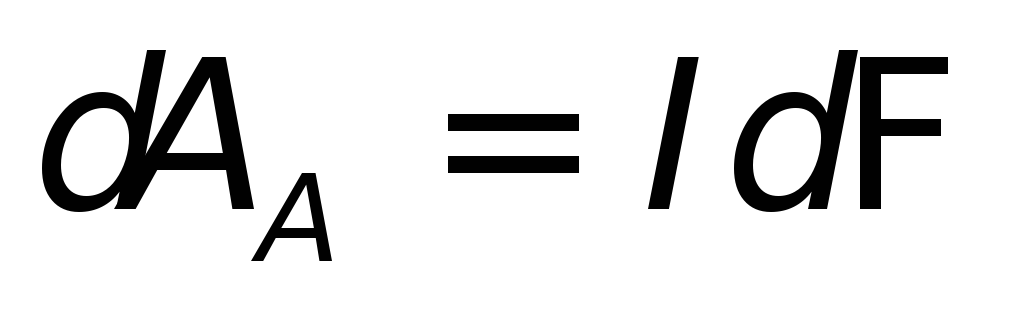 ,
за это же время э.д.с. индукции совершает
работу
,
за это же время э.д.с. индукции совершает
работу
| (26.10) |
тогда полная работа  .
.
Силы Ампера совершают работу не за счет энергии внешнего магнитного поля, которое может оставаться постоянным, а за счет источника э.д.с., поддерживающего ток в контуре.
Закон электромагнитной индукции Фарадея Википедия
Электромагнитная индукция была обнаружена независимо друг от друга Майклом Фарадеем и Джозефом Генри в 1831 году, однако Фарадей первым опубликовал результаты своих экспериментов[3][4].
В первой экспериментальной демонстрации электромагнитной индукции (август 1831) Фарадей обмотал двумя проводами противоположные стороны железного тора (конструкция похожа на современный трансформатор). Основываясь на своей оценке недавно обнаруженного свойства электромагнита, он ожидал, что при включении тока в одном проводе особого рода волна пройдёт сквозь тор и вызовет некоторое электрическое влияние на его противоположной стороне. Он подключил один провод к гальванометру и смотрел на него, когда другой провод подключал к батарее. В самом деле, он увидел кратковременный всплеск тока (который он назвал «волной электричества»), когда подключал провод к батарее, и другой такой же всплеск, когда отключал его.[5] В течение двух месяцев Фарадей нашёл несколько других проявлений электромагнитной индукции. Например, он увидел всплески тока, когда быстро вставлял магнит в катушку и вытаскивал его обратно, он генерировал постоянный ток во вращающемся вблизи магнита медном диске со скользящим электрическим проводом («диск Фарадея»)[6].

Фарадей объяснил электромагнитную индукцию с использованием концепции так называемых силовых линий. Однако, большинство учёных того времени отклонили его теоретические идеи, в основном потому, что они не были сформулированы математически.[7] Исключение составил Максвелл, который использовал идеи Фарадея в качестве основы для своей количественной электромагнитной теории.[7][8][9] В работах Максвелла аспект изменения во времени электромагнитной индукции выражен в виде дифференциальных уравнений. Оливер Хевисайд назвал это законом Фарадея, хотя он несколько отличается по форме от первоначального варианта закона Фарадея и не учитывает индуцирование ЭДС при движении. Версия Хевисайда является формой признанной сегодня группы уравнений, известных как уравнения Максвелла.
Эмилий Христианович Ленц сформулировал в 1834 году закон (правило Ленца), который описывает «поток через цепь» и даёт направление индуцированной ЭДС




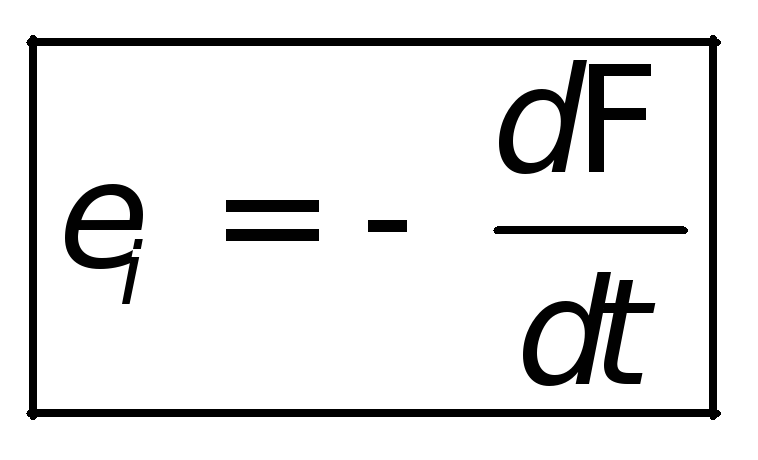
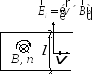
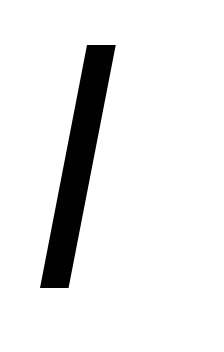 находится в магнитном поле,
перпендикулярном плоскости контура
(см.Рисунок
26.2). Если двигать перемычку со
скоростью
находится в магнитном поле,
перпендикулярном плоскости контура
(см.Рисунок
26.2). Если двигать перемычку со
скоростью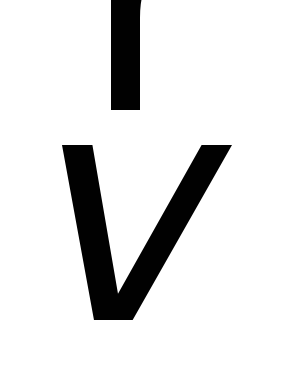 вправо, то с такой же скоростью начнут
двигаться и носители тока в перемычке
– электроны. В результате на каждый
электрон начинает
вправо, то с такой же скоростью начнут
двигаться и носители тока в перемычке
– электроны. В результате на каждый
электрон начинает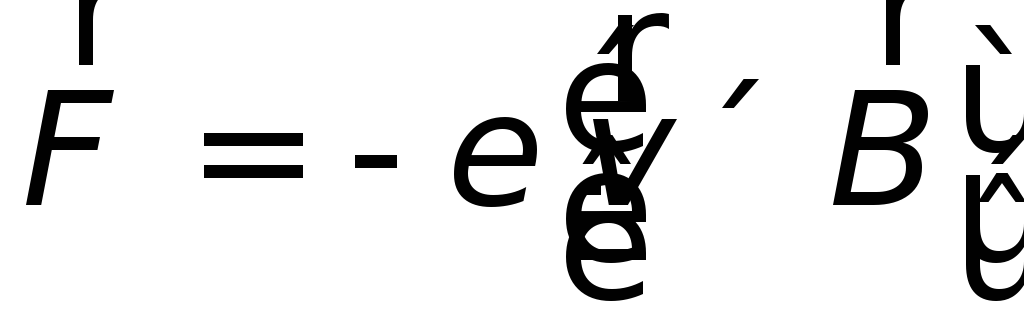 ,
,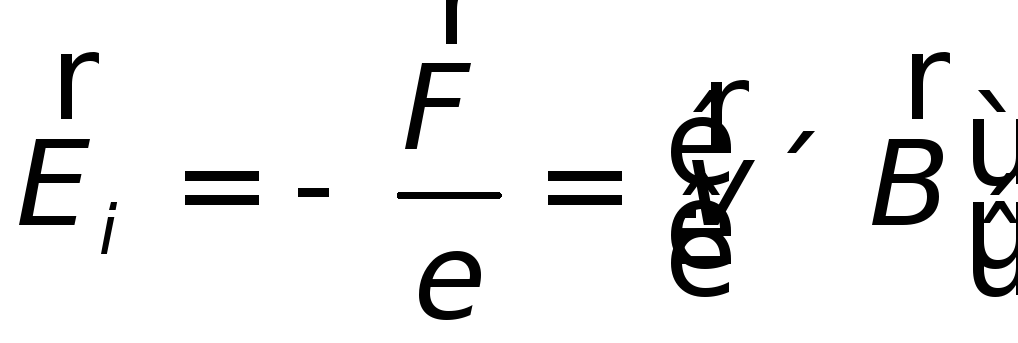 .
.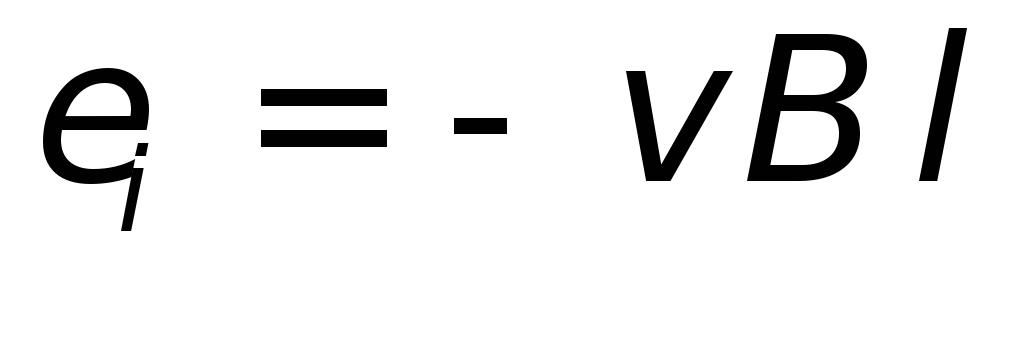 .
.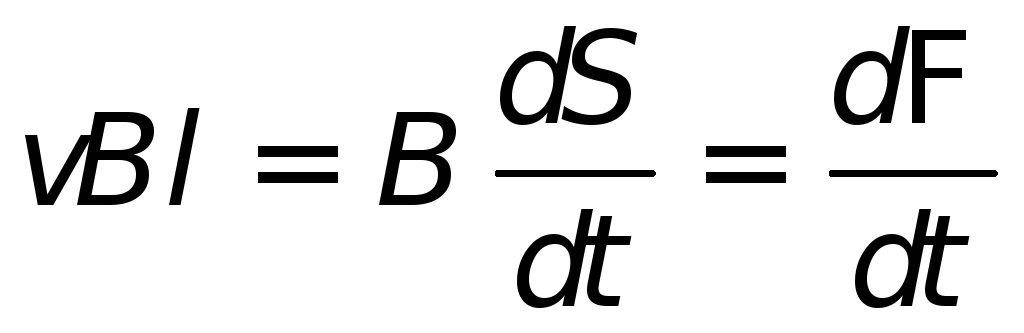 ,
,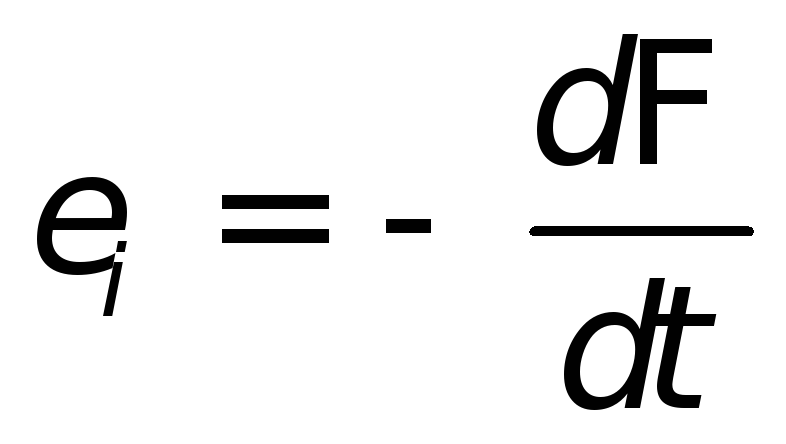 .
.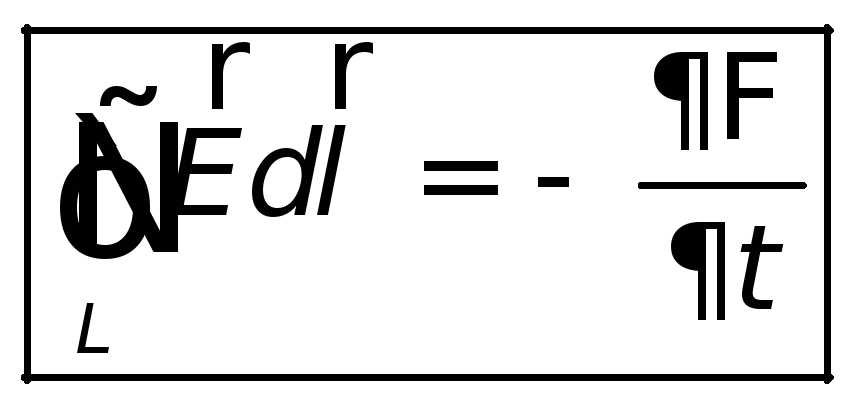 ,
,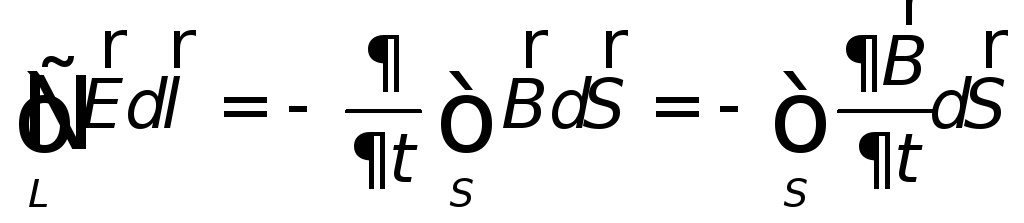 .
.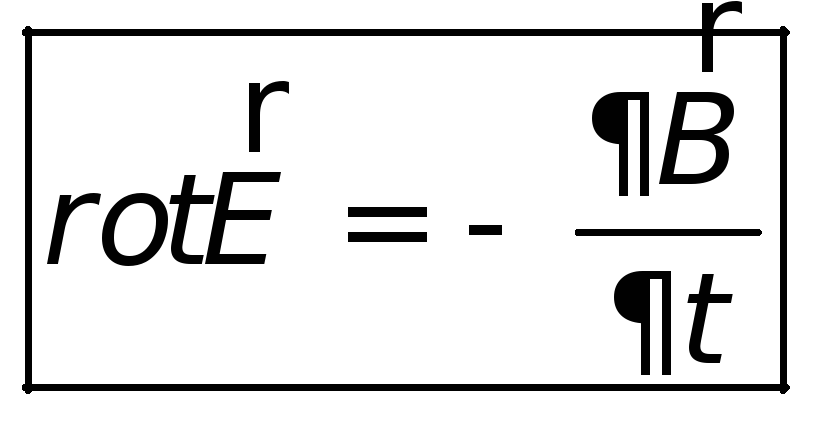 .
.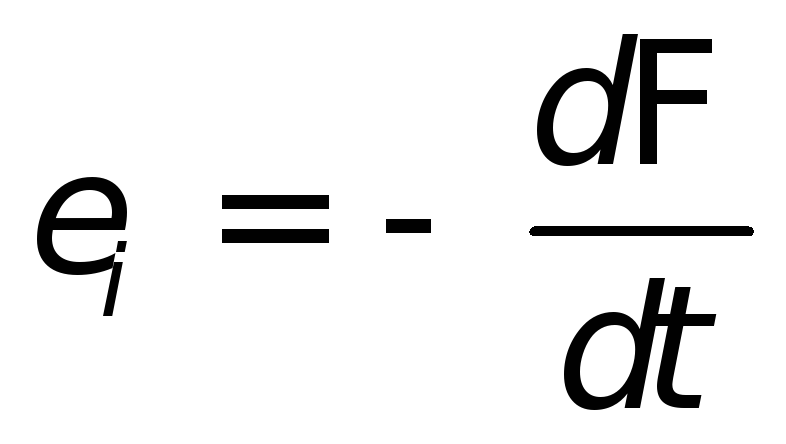 ,
,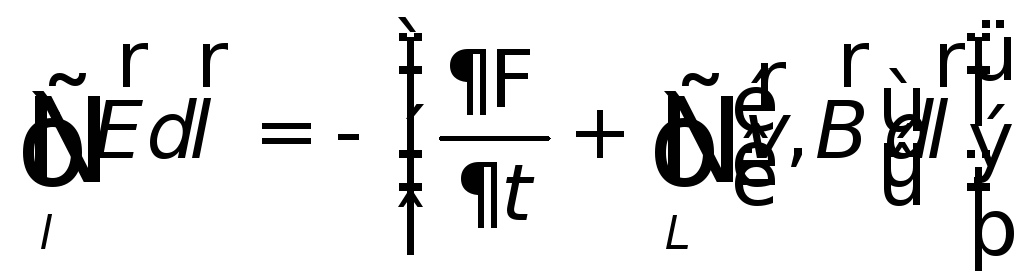 .
.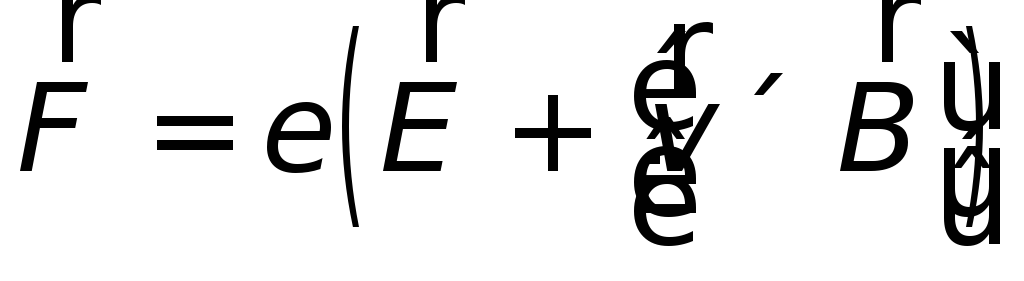 .
.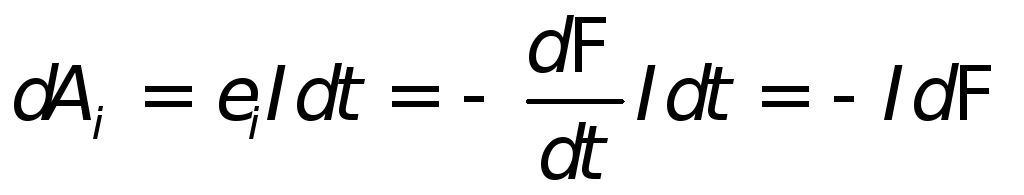 ,
,