Примеры решения задач на законы Кирхгофа
Рассмотрим на примерах как можно использовать законы Кирхгофа при решении задач.
Задача 1
Дана схема, и известны сопротивления резисторов и ЭДС источников. Требуется найти токи в ветвях, используя законы Кирхгофа.

Используя первый закон Кирхгофа, можно записать n-1 уравнений для цепи. В нашем случае количество узлов n=2, а значит нужно составить только одно уравнение.
Напомним, что по первому закону, сумма токов сходящихся в узле равна нулю. При этом, условно принято считать входящие токи в узел положительными, а выходящими отрицательными. Значит для нашей задачи

Затем используя второй закон (сумма падений напряжения в независимом контуре равна сумме ЭДС в нем) составим уравнения для первого и второго контуров цепи. Направления обхода выбраны произвольными, при этом если направление тока через резистор совпадает с направлением обхода, берем со знаком плюс, и наоборот если не совпадает, то со знаком минус. Аналогично с источниками ЭДС.
На примере первого контура – ток I1 и I3 совпадают с направлением обхода контура (против часовой стрелки), ЭДС E1 также совпадает, поэтому берем их со знаком плюс.
Уравнения для первого и второго контуров по второму закону будут:

Все эти три уравнения образуют систему

Подставив известные значения и решив данную линейную систему уравнений, найдем токи в ветвях (способ решения может быть любым).

Проверку правильности решения можно осуществить разными способами, но самым надежным является проверка балансом мощностей.
Задача 2
Зная сопротивления резисторов и ЭДС трех источников найти ЭДС четвертого и токи в ветвях.

Как и в предыдущей задаче начнем решение с составления уравнений на основании первого закона Кирхгофа. Количество уравнений n-1= 2
 Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче.
Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче.

На основании этих уравнений составляем систему с 5-ью неизвестными

Решив эту систему любым удобным способом, найдем неизвестные величины
 Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей полученных приемниками.
Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей полученных приемниками.
 Баланс мощностей сошелся, а значит токи и ЭДС найдены верно.
Баланс мощностей сошелся, а значит токи и ЭДС найдены верно.
Читайте также — расчет простых цепей постоянного тока
Законы Кирхгофа: решение задач
Прочитав статейки про первый и второй законы Кирхгофа, уважаемый читатель может сказать: «Хорошо, MyElectronix, ты рассказал мне, конечно, интересные штуки, но что мне дальше с ними делать? Пока по твоим словам я заключил, что если я соберу ручками схему, то я смогу в каждом ее узле и в каждом контуре намерить вот такие вот зависимости. Это здорово, но я хотел бы рассчитывать схемы, а не просто наблюдать зависимости!»
Господа, все эти замечания абсолютно верные и в ответ на них можно лишь рассказать о расчете электрических схем с помощью законов Кирхгофа. Без лишних слов перейдем сразу к делу!
Начнем с самого простейшего случая. Он изображен на рисунке 1. Допустим, ЭДС источника питания равна Е1=5 В, а сопротивления R1=100 Ом, R2=510 Ом, R3=10 кОм. Требуется рассчитать напряжения на резисторах и ток через каждый резистор.
Господа, замечу сразу, эту задачу можно решить гораздо более простым способом, чем с применением законов Кирхгофа. Однако сейчас наша задача не искать оптимальные способы решения, а на наглядном примере рассмотреть методику применения законов Кирхгофа при расчете схем.
Рисунок 1 – Простая схема
В этой схеме мы можем видеть три контура. Если возник вопрос – а почему три, то рекомендую посмотреть статью про второй закон Кирхгофа. В той статье имеется практически такая же схема с наглядным пояснением методики расчета числа контуров.
Господа, хочу отметить один тонкий момент. Хоть контура и три, независимых из них только два. Третий контур включает в себя все остальные и не может считаться независимым. И вообще всегда при всех расчетах мы должны использовать только независимые
Итак, будем использовать два независимых контура. Для этого зададимся в каждом контуре направлением обхода контура. Как мы уже говорили, это некоторое направление в контуре, которое мы принимаем за положительное. Можно в какой-то степени назвать это аналогом осей координат в математике. Направление обхода каждого контура нарисуем синей стрелкой.
Далее зададимся направлением токов в ветвях: просто проставим его наугад. Не важно, угадаем мы сейчас направление или нет. Если угадали, то в конце расчета мы получим ток со знаком плюс, а если ошиблись – со знаком минус. Итак, обозначим токи в ветвях черными стрелочками с подписями I
Мы видим, что в контуре №1 направление токов I1 и I3, а также направление источника питания совпадают с направлением обхода, поэтому будем считать их со знаком плюс. В контуре №2 ток I2 совпадет с направлением обхода, поэтому будет со знаком плюс, а ток I3 направлен в другую сторону, поэтому будет со знаком минус. Запишем второй закон Кирхгофа для контура №1:
А теперь запишем этот же закон для контура №2:
Видим, что в контуре №2 нет источников питания, поэтому в левой части (где у нас согласно второму закону Кирхгофа стоит сумма ЭДС) у нас нолик. Итак, у нас есть два уравнения, а неизвестных-то у нас три (I
Господа, теперь полный порядок, у нас есть три уравнения и три неизвестных и нам остается только решить вот такую вот систему уравнений
Подставим конкретные числа. Все расчеты будем вести в кошерной системе СИ. Рекомендую всегда считать только в ней. Не поддавайтесь искушению подставлять куда-то миллиметры, мили, килоамперы и прочее. Возможно возникновение путаницы.
Решение таких систем рассматривается чуть ли не в начальной школе и, полагаю, не должно вызывать трудностей . Если что, есть куча математических пакетов, которые сделают это за вас, если вам лень самим ручками считай. Поэтому мы опустим процесс решения, а сразу приведем результат
Видим, что все токи получились у нас со знаком плюс. Это значит, что мы верно угадали их направление. Да, то есть токи в схеме текут именно в том направлении, как мы нарисовали стрелочки на рисунке 1. Однако из условия задачи необходимо найти не только токи через резисторы, но и падение напряжения на них. Как это сделать? Например, с помощью уже изученного нами закона Ома. Как мы помним, закон Ома связывает между собой ток, напряжение и сопротивление. Если нам известны любые две из этих величин, мы легко можем найти третью. В данном случае мы знаем сопротивление и ток, который течет через это сопротивление. Поэтому, используя вот эту формулу
находим напряжение на каждом резисторе
Заметим, господа, что напряжения на резисторах R2 и R3 равны между собой. Это и логично, поскольку они соединены между собой параллельно. Однако пока не будем на этом акцентировать большое внимание, рассмотрим это лучше в другой раз.
Итак, господа, мы решили эту простую задачку с помощью двух законов Кирхгофа и закона Ома. Но это был совсем простой пример. Давайте попробуем решить более сложную задачу. Взгляните на рисунок 2.
Рисунок 2 – Схема посложнее
Схема выглядит внушительно, не правда ли? Возможно, вам даже не верится, что эту схему можно легко рассчитать. Однако, господа, уверяю вас, вы обладаете всеми необходимыми знаниями для расчета этой схемы, если уже изучили мои предыдущие статьи. Сейчас вы в этом убедитесь.
Для начала зададимся конкретными цифрами значений сопротивлений резисторов и напряжений источников.
Пусть Е1=15 В, Е2=24 В, R1= 10 Ом, R2 = 51 Ом, R3=100 Ом, R4=1 кОм, R5=10 Ом, R6=18 Ом, R7=10 кОм.
Найти, как и в прошлой задаче, требуется все токи в схеме и напряжения на всех резисторах.
В этой схеме мы можем видеть три независимых контура. Обозначим их римскими цифрами I, II, III. В каждом контуре зададимся направлением обхода. Они показаны синими стрелками.
Дальше как и в прошлый раз наугад расставим направления токов во всех ветвях и подпишем где какой ток. Видно, что всего у нас 6 ветвей и, соответственно, 6 разных токов (I1…I6).
Теперь запишем второй закон Кирхгофа для всех трех независимых контуров.
Второй закон Кирхгофа для контура I:
Второй закон Кирхгофа для контура II:
Второй закон Кирхгофа для контура III:
У нас есть три уравнения, однако неизвестных токов аж 6. Как и в прошлой задаче для получения недостающих уравнений запишем первые законы Кирхгофа для узлов.
Первый закон Кирхгофа для узла А:
Первый закон Кирхгофа для узла В:
Первый закон Кирхгофа для узла С:
Собственно, у нас теперь есть система из 6 уравнений с 6 неизвестными. Остается только решить эту систему
Подставляя числа, заданные в условии, получаем
Опуская решения за пределами статьи, приведем итоговый результат
Господа, мы видим, что почти все токи, кроме I4 получились у нас со знаками «минус». Это значит, что мы не угадали их направление, когда рисовали стрелочки на рисунке 2 . То есть все токи, кроме тока I4 на самом деле текут в противоположные стороны. А ток I4 течет так, как мы нарисовали. Хотя бы с ним мы угадали верно.
Теперь все по тому же закону Ома ровно как в прошлом примере рассчитаем напряжения на резисторах:
Вот и все, господа: схема рассчитана, а задачка решена. Таким образом, вы теперь обладаете весьма мощным инструментом по расчету электрических схем. С помощью двух законов Кирхгофа и закона Ома вы сможете рассчитать весьма непростые схемы, найти величины токов и их направления, а также напряжения на всех нагрузках цепи. Более того, зная токи и напряжения вы легко сможете рассчитать и мощности, которые на этих резисторах выделяются, если воспользуетесь рекомендациями из моей предыдущей статьи.
На этом на сегодня все господа. Огромной вам всем удачи и успешных расчетов!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Алгоритм решения задач на законы Кирхгофа
Задачи на применение закона Кирхгофа решаются в школе не часто, и не во всех классах. Работая в школе, я давала законы Кирхгофа только тем ребятам, кто готовился к олимпиадам по физике, и учащимся, которые готовились в ВУЗы.
Задачи на использование законов Кирхгофа есть даже не всех сборниках задач, рекомендованных для использования в средней школе.
Ниже приведён алгоритм решения задач по данной теме. Алгоритм не сложен. Использование данного алгоритма поможет Вам в решении задач по этой теме.
Итак, начнем. Сначала необходимо выполнить некоторые подготовительные операции.
- перерисовать схему
- указать направление ЭДС источников тока
- указать предполагаемое направление токов, текущих в каждом резисторе (если итоговый ответ будет отрицательным, то направление тока было изначально выбрано не верно)
- выбрать направление обхода для всех линейно независимых контуров
После проведения предварительных операций, приступаем собственно к решению самой задачи.
- Записываем первый закон Кирхгофа: сумма токов, втекающих и вытекающих в данный узел, равна нулю.
Важно! Если ток втекает в узел, то он берётся со знаком «плюс», если вытекает, то со знаком «минус». Число уравнений второго закона Кирхгофа равно n-1, где n — число узлов в данной схеме. (Узел — точка, в которой соединяются три проводника и более).
- Записываем второй закон Кирхгофа для всех линейно независимых контуров: Сумма ЭДС в контуре равно сумме падений напряжений в каждом из этих контуров.
Важно! Если направление ЭДС совпадает с направлением обхода контура, то значение ЭДС берётся со знаком «плюс». Если направление ЭДС не совпадает с направлением обхода контура, то значение ЭДС берётся со знаком «минус». Если направление тока совпадает с направлением обхода контура, то падение напряжения на данном участке берётся со знаком «плюс». Если направление тока через какой-либо резистор не совпадает с направлением обхода в данном контуре, то падение напряжения берётся со знаком «минус».
Решаем систему получившихся уравнений, относительно неизвестных величин.
Чаще всего в задачах этого типа, основную сложность представляет именно решение системы получившихся уравнений.
Ниже показан пример решения задачи с использованием законов Кирхгофа. Обратите внимание ещё раз на основные этапы решения. Они полностью соответствуют алгоритму, описанному выше.
Вот условие этой задачи.
Электрическая цепь состоит из двух гальванических элементов, трех резисторов и амперметра. В этой цепи R1 = 100 Ом, R2 = 50 Ом, R3 = 20 Ом, ЭДС элемента ?1 = 2 В. Амперметр регистрирует ток I3 = 50 мА, идущий в направлении, указанном стрелкой. Определить ЭДС ?2 второго элемента. Сопротивлением амперметра и внутренним сопротивлением источников пренебречь.
Удачи в освоении этой довольно сложной темы!
Возникающие вопросы можете оставлять в комментариях.
Вы можете оставить комментарий, или поставить трэкбек со своего сайта.Написать комментарий
7.2. Порядок решения задач на законы Кирхгофа
1. Нарисовать схему цепи. На рисунке выбрать и показать направления токов на всех участках цепи, при этом надо учесть, что в узел токи не могут только входить или только выходить из узла. Это следует из первого закона Кирхгофа.
2. Выбрать замкнутые контуры обхода для применения второго закона Кирхгофа. Показать на рисунке направление обхода по контуру. Контуров может быть несколько. Число независимых уравнений, которые можно составить по второму закону Кирхгофа, меньше чем число контуров. Чтобы составить необходимое число независимых уравнений надо придерживаться следующего правила: Выбирать контуры так, чтобы в каждый новый контур входил хотя бы один участок цепи, которого бы не было нив одном ранее рассмотренных контуров.
3. Используя первый закон Кирхгофа можно написать ( n – 1) уравнений, где n— число узлов в рассматриваемой цепи.
4. Воспользоваться вторым законом Кирхгофа и записать такое число уравнений, чтобы число уравнений, составленных по первому и второму законам Кирхгофа, равнялось числу неизвестных величин в задаче. При этом надо учитывать следующее правило знаков: падение напряжения на каждом участке записывается со знаком «+», если направление обхода по этому участку совпадает с направлением тока на нем. И наоборот, если обход совершался по этому сопротивлению обратно направлению тока, то ставится знак « – ».
ЭДС записывается со знаком «+» в том случае, когда направление обхода совпадает с направлением поля сторонних сил в источнике тока и наоборот.
Поле сторонних сил внутри источника всегда направлено от отрицательного полюса к положительному.
5. Решить полученную систему уравнений и найти искомые величины.
В результате решения полученной системы уравнений определяемые величины могут получаться отрицательными. Отрицательное значение тока указывает на то, что фактическое направление тока на данном участке цепи обратно тому, которое мы выбрали.
7.3. Примеры решения задач на законы Кирхгофа
П р и м е р 1.
Два элемента с одинаковыми ЭДС e1 = e2 = 2В и внутренними сопротивлениями r1 = 1 Ом, r2 = 2 Ом замкнуты на внешнее сопротивление R. Через первый элемент течет ток I1 = 1 А. Найдите сопротивление R, ток I2, текущий через второй элемент, и ток I, текущий через сопротивление R. Схема соединения показана на рисунке.
Д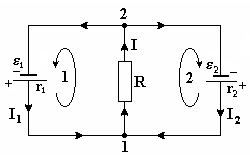 ано:
ано:
e 1 = e2 = 2 D;
1 = e2 = 2 D;
r1 = 1 Ом;
r2 = 2 Ом;
I1 = 1 A
________
Найти:
I2 =? R=? I=?
Решение:
1.Выберем направления токов на всех участках цепи так, как показано на рисунке. Видим, что в узлах 1 и 2 есть входящие и есть выходящие токи, значит, направления токов выбраны разумно.
2. Выберем контуры обхода и покажем направления обхода по ним. Контуров выбрали два и нарисовали направления обхода по ним.
3. Составим уравнение, используя первый закон Кирхгофа. Узлов два, поэтому можно составить только одно уравнение, например для первого узла:
I1 + I2 — I = 0.
Токи, входящие в узел, пишем со знаком «+», а выходящие с знаком»–». Уравнение для второго узла будет тождественно первому.
4. Применим второй закон Кирхгофа для первого контура обхода. Падение напряжения на всех участках этого контура пишем со знаком «+», т.к. направление обхода на всех участках совпадает с направлением тока на этих участках
Uå = IR +I1 r.
В этот контур входит только один источник тока e1, и направление обхода по контуру совпадает с направлением поля сторонних сил, т.к. силы этого поля направлены от отрицательного полюса к положительному, т.е. вниз.
Запишем уравнение
IR + I1r1 = e1.
Для второго контура, рассуждая аналогично, получим U2 = +I2r2 + IR. ЭДС будет входить в уравнение также со знаком «+».
Второе уравнение имеет вид: I2R2 + IR = e2.
5. Получили систему из трех уравнений с тремя неизвестными.
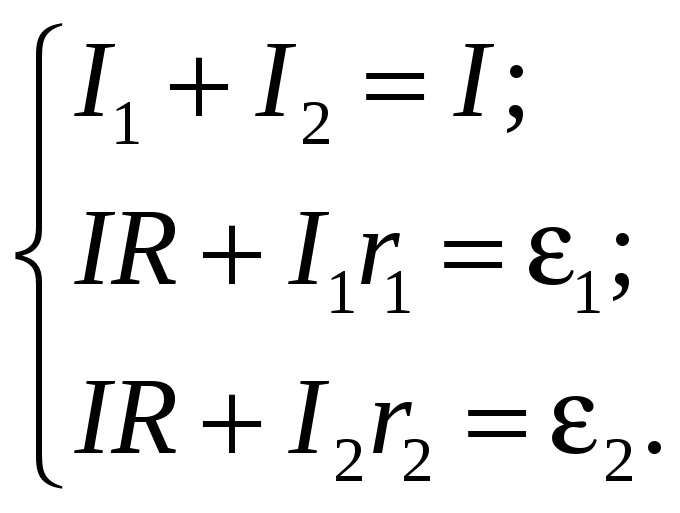
Решая систему, находим величину тока I2
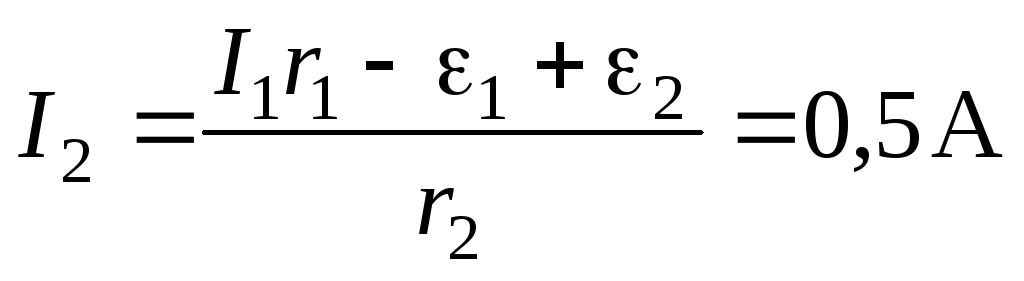 .
.
Полный ток через сопротивление R равен сумме токов
I = I1 + I2 = 1,5 A.
Сопротивление R находим из одного из уравнений системы:
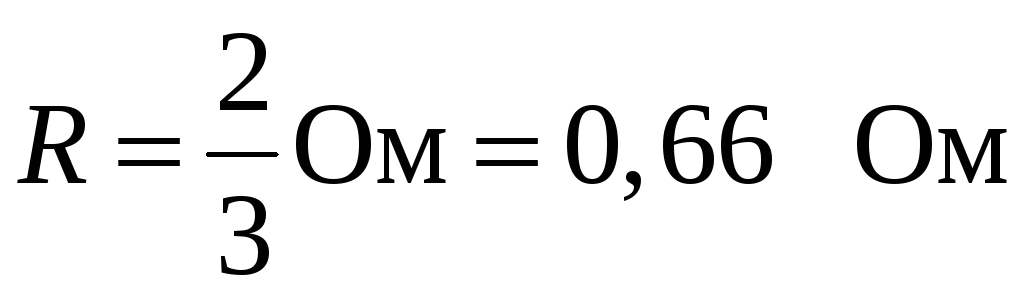 .
.
Ответ: ток через второй источник равен I2 = 0,5 А, суммарный ток
I = I1 + I2 = 1,5 А. Внешнее сопротивление R = 0,66 Ом.
П р и м е р 2.
Два одинаковых элемента имеют ЭДС e1 = e2 = 2 В и внутренние сопротивления r1 = r 2 = 0,5 Ом. Найдите токи I1 и I2, текущие через сопротивления R1 = 0,5 Ом и R2 = 1,5 Ом, а также ток I через первый элемент. Схема заданной цепи изображена на рисунке.
Д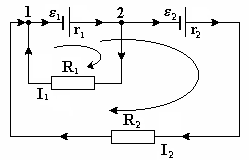 ано:
ано:
e 1 = e2 = 2 В;
1 = e2 = 2 В;
r1=r2=0,5 Ом;
R1 = 0,5 Ом;
R 2 = 1,5 Ом
2 = 1,5 Ом
I1 – ? I2 – ? I – ?
Решение:
1. Выберем направления токов на всех участках так, как показано на рисунке. Видим, что в узлах 1 и 2 есть входящие и есть выходящие токи, значит, направления токов выбраны верно.
2. Выберем два контура обхода: большой и малый. Укажем направления обходов по контурам. Контуров обхода в заданной цепи можно выбрать три, но для нахождения трех неизвестных величин достаточно трех уравнений. Узлов всего два, поэтому можно составить только одно уравнение, применяя первый закон Кирхгофа. Недостающих два уравнения составим используя второй закон Кирхгофа.
3. Для первого узла запишем:
I2 + I1 – I = 0.
4. Учитывая правила определения знаков всех слагаемых при применении второй закон Кирхгофа для большого контура, получаем уравнение:
I r1 + I2r2 + I2R2 = e1 + e2.
Для малого контура:
I r1 + I1R1 = e1.
5.Получили систему из трех уравнений с тремя неизвестными величинами I1; I2 и I.
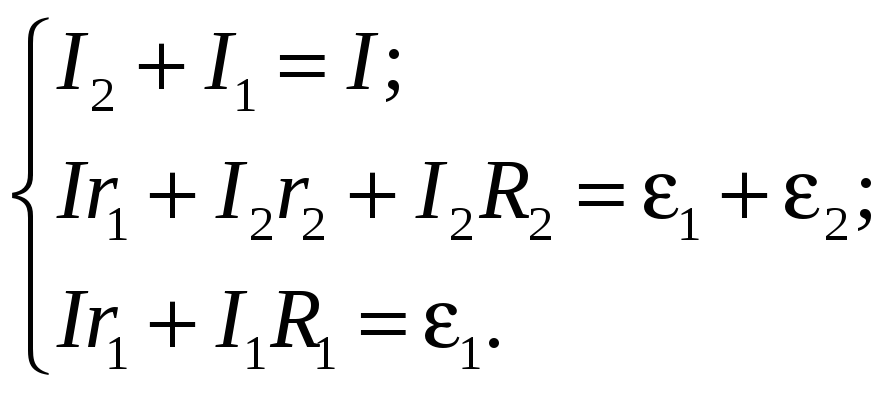
Решать
систему линейных уравнений можно разными
способами. В случае, когда система
состоит из большого числа уравнений
удобно пользоваться методом Крамера
(методом определителей). Проиллюстрируем
применение этого метода решения на
нашей системе уравнений. Для этого
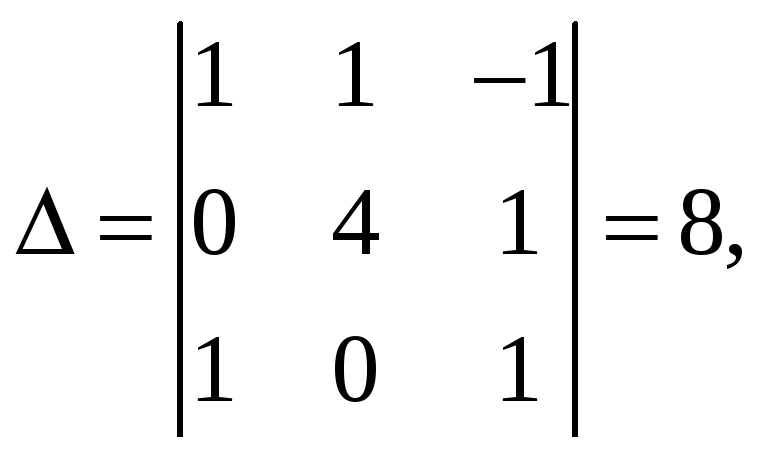
перепишем систему ещё раз: 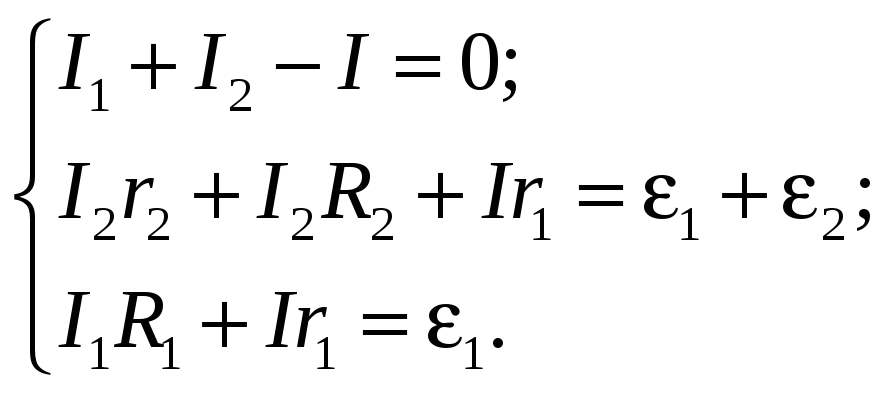
или
в численном виде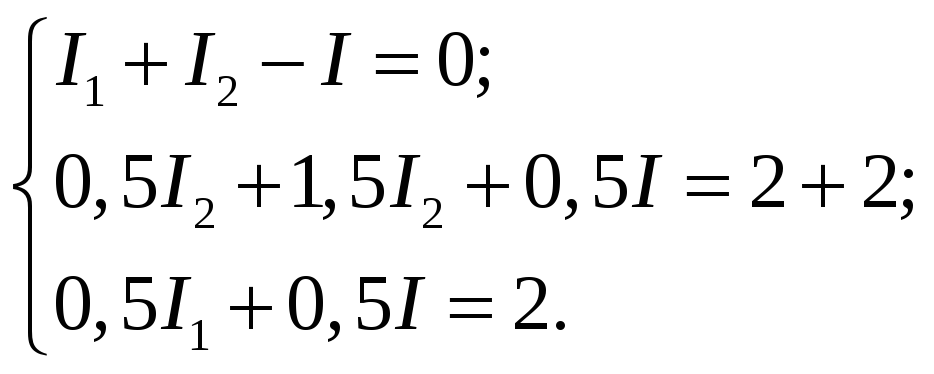 ;
если поделить правую и левую части
второго и третьего уравнении на « 0,5»
получим
;
если поделить правую и левую части
второго и третьего уравнении на « 0,5»
получим 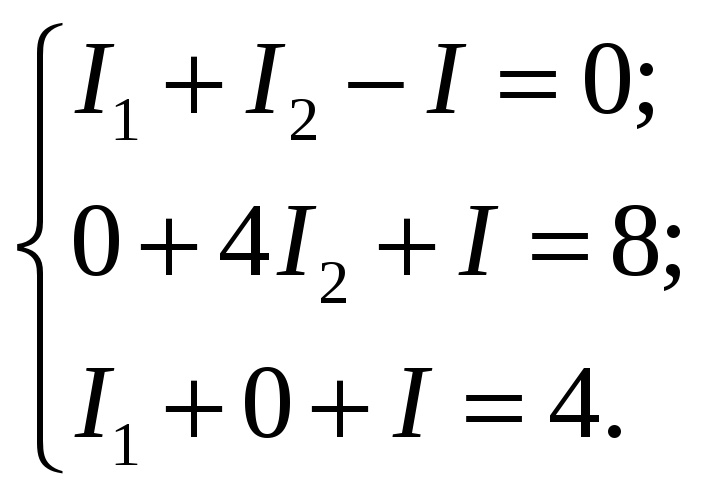
Искомые
величины токов по методу определителей
находятся следующим образом: 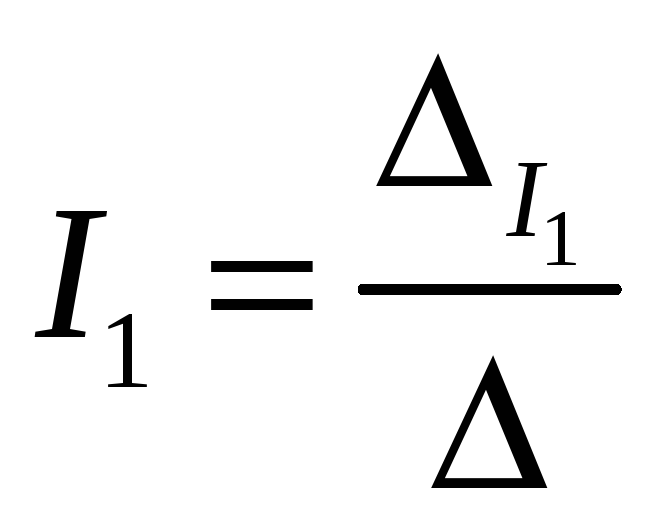 и
и 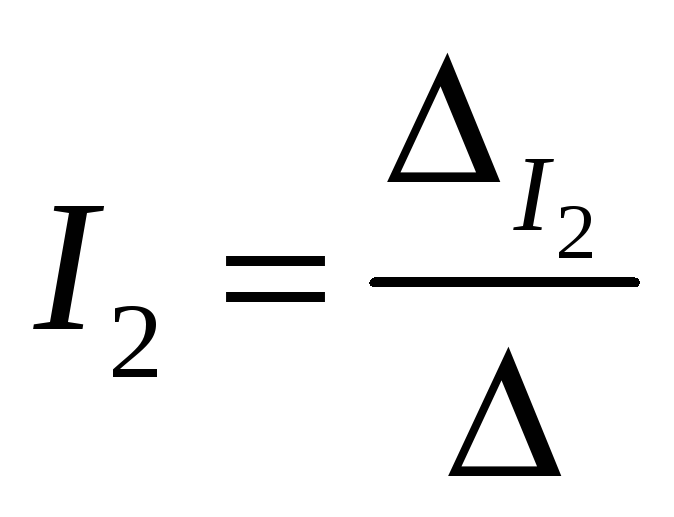 ,
,
где
определители  —
определитель системы уравнений,
—
определитель системы уравнений, 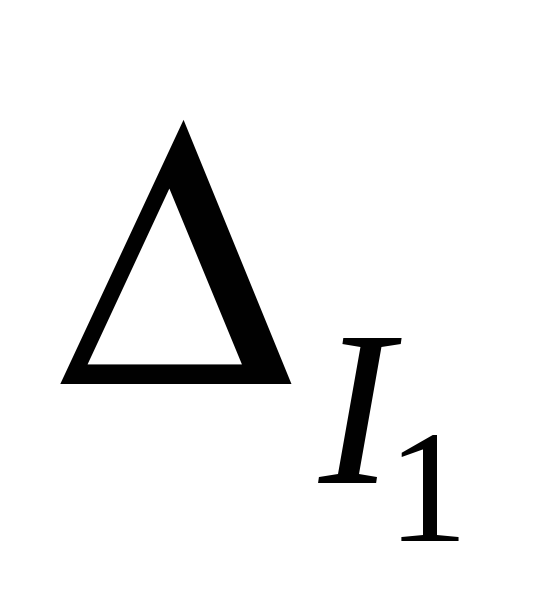 и
и 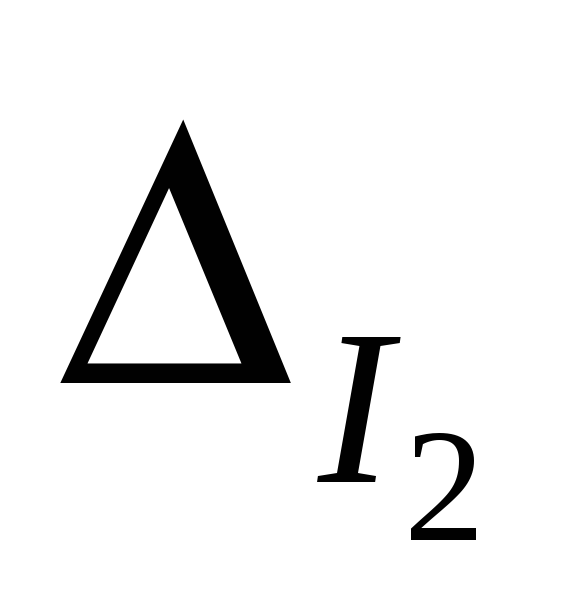 -определители,
которые получаются заменой соответствующих
столбцов определителя
-определители,
которые получаются заменой соответствующих
столбцов определителя  столбцами,
полученными из свободных членов уравнений
образующих систему (с учетом заданных
числовых значений). Запишем эти
определители:
столбцами,
полученными из свободных членов уравнений
образующих систему (с учетом заданных
числовых значений). Запишем эти
определители:
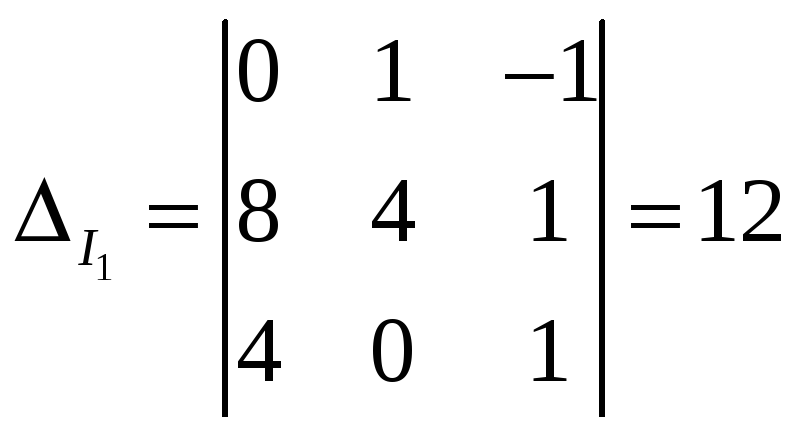
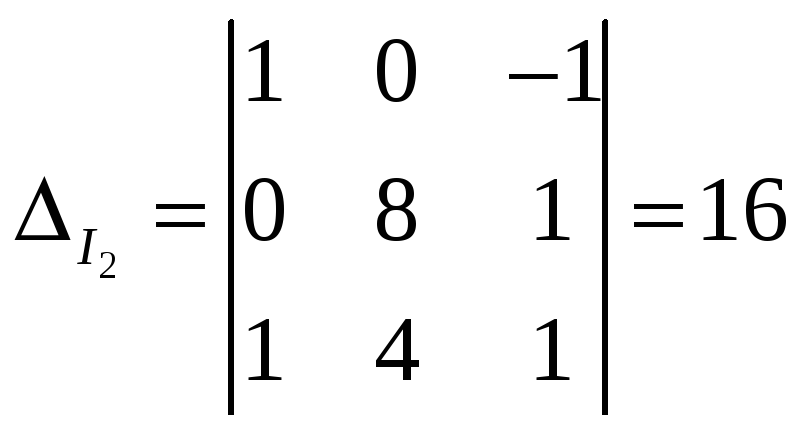
По приведенным выше формулам, получаем
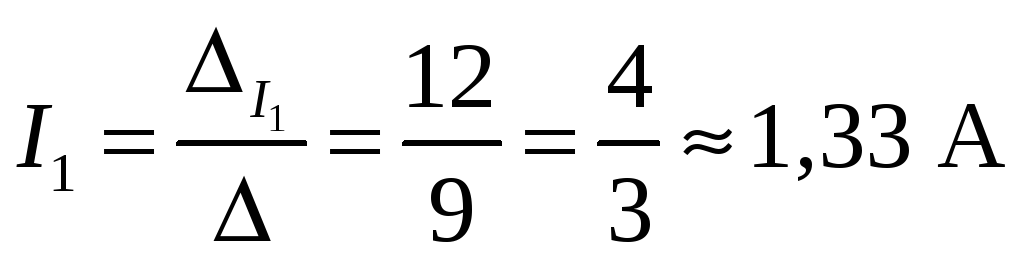 и
и 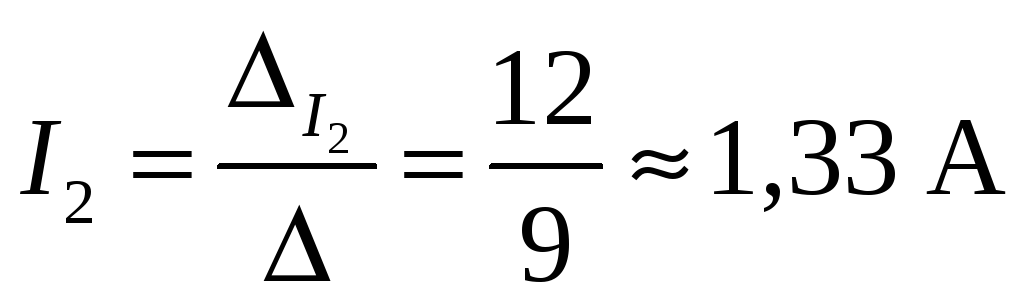 .
.
Значение третьего тока можно найти аналогичным способом, но проще его значение получить из первого уравнения нашей системы:
I2 + I1 – I = 0 или I = I2 + I1 = 1,33 + 1,33 = 2,66 А
Знаки у всех полученных значений силы тока положительные, это свидетельствует о том, что при произвольном выборе направлений токов, указанных на рисунке, все направления токов были выбраны правильно.
Ответ: I1 = 1,33 А ; I2 = 1.33 А;I = I1 + I2 = 2.66 А.
П р и м е р 3.
Два элемента с одинаковыми ЭДС 1 = 2 = 2В и внутренними сопротивлениями r1 = 1 Ом, r2 = 2 Ом замкнуты на внешнее сопротивление R. Через элемент с ЭДС 1 — течет ток I1 = 1 А. Найти сопротивление R и ток I2, текущий через элемент с ЭДС 2. Какой ток течет через сопротивление R. Схема соединения показана на рисунке.
Д
 ано:
ано:
1 = 2 = 2 D;
r1 = 1 Ом;
r2 = 2 Ом;
I1 = 1 A
__________
+I2 — ?
R — ? I — ?
Выберем направления токов на всех участках цепи. Видим, что в узлах 1 и 2 есть входящие и есть выходящие токи, значит, направления токов выбраны разумно.
Выберем контуры обхода и покажем направления обхода по ним.
Составим уравнение, используя первый закон Кирхгофа для первого узла:
I1 + I2 — I = 0.
Токи, входящие в узел, пишем со знаком «+», а входящие с «–». Всего можно написать одно уравнение, т.к. второе будет тождественно первому.
Воспользуемся вторым законом Кирхгофа. Запишем уравнение для первого контура обхода. Падение напряжения на всех участках 1-го контура напишем со знаком «+», т.к. направление обхода на этих участках совпадает с направлением тока
U = IR +I1 r.
В этот контур входит только ЭДС 1, и направление обхода по контуру совпадает с направлением поля сторонних сил, т.к. силы этого поля направлены от отрицательного полюса к положительному.
Запишем уравнение
IR + I1r1 = 1.
Для второго контура U2 = +I2r2 + IR. И ЭДС будет входить в уравнение также со знаком «+».
Запишем уравнение I2R2 + IR = 2.
Получим систему из трех уравнений с тремя неизвестными.
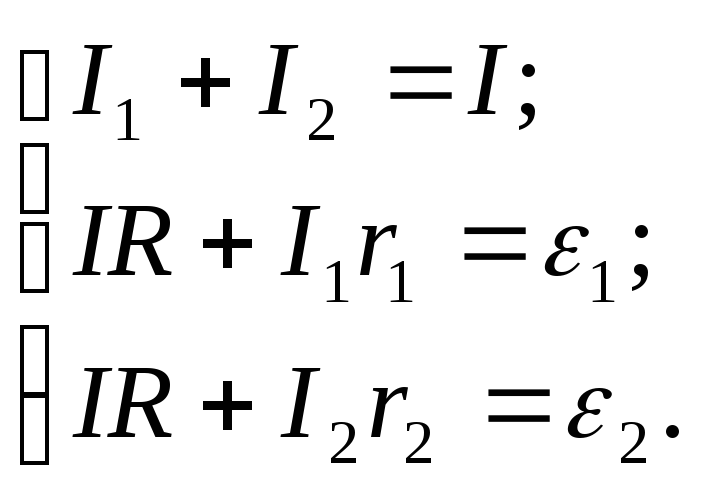
Решая систему, получаем
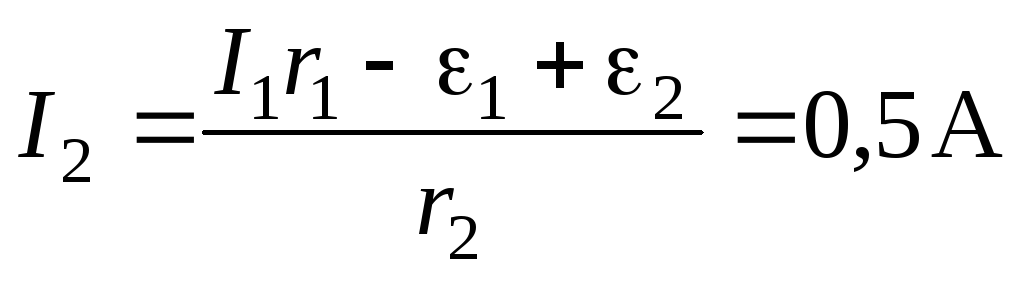 .
.
Полный ток через сопротивление R равен сумме токов
I = I1 + I2 = 1,5 A.
Сопротивление R находим из одного из уравнений
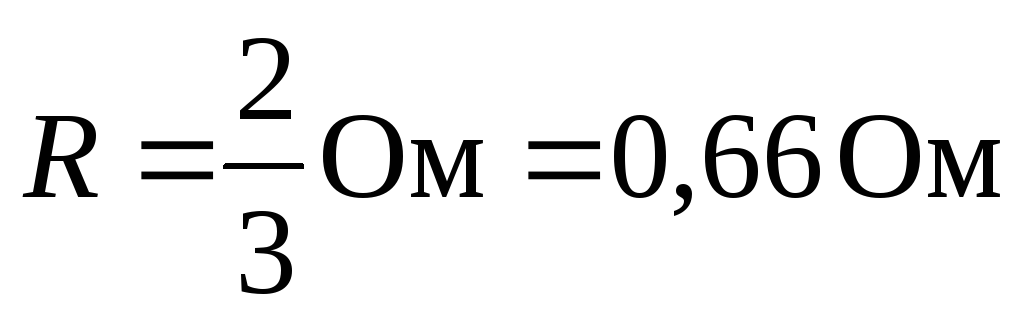 .
.
Ответ. Ток через второй источник равен I2 = 0,5 А, суммарный ток
I = I1 + I2 = 1,5 А. Внешнее сопротивление R = 2/3 Ом.
П р и м е р 4.
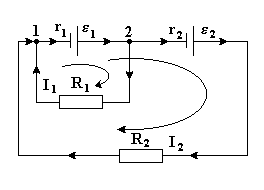
Два одинаковых элемента имеют ЭДС 1 = 2 = 2 В и внутренние сопротивления r1 = l2 =0,5 Ом. Найти токи I1 и I2, текущие через сопротивления R1 = 0,5 Ом и R2 = 1,5 Ом, а также ток I через элемент с ЭДС. Схема изображена на рисунке.
Д
 ано:
ано:
1 = 2 = 2 В;
r1 = r2 = 0,5 Ом;
R1 = 0,5 Ом;
R2 = 1,5 Ом
_____________
I1 — ?
I2 — ?
I — ?
Решение:
Выберем направления токов на всех участках. Запишем первый закон Кирхгофа для 1-го узла
I2 + I1 = I .
Выберем большой и малый контуры обхода. Для большого контура уравнение будет иметь вид:
Ir1 + I2r2 + I2R2 = 1 + 2.
Для малого контура
Ir1 + I1R1 = 1.
Получили три уравнения
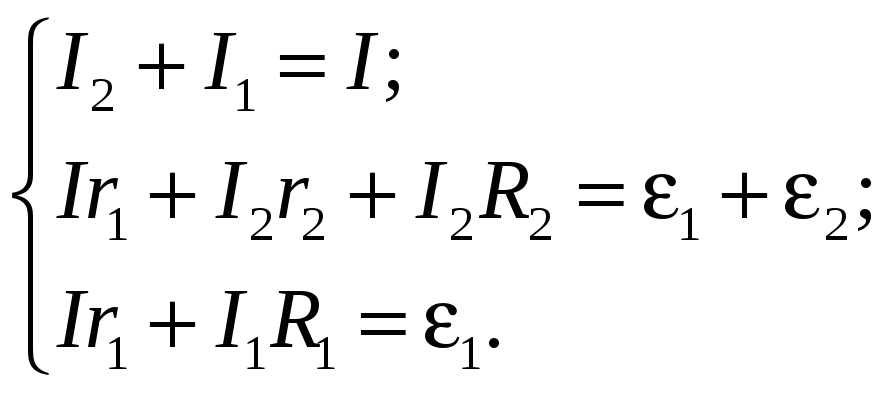
В эти уравнения входят три неизвестных величины I1; I2 и I. Решаем систему уравнений и находим
I1 = 2,28 А ; I2 = 0,56 А;I = I1 + I2 = 1,72 А.
Правила Кирхгофа, теория и примеры задач
Очень часто электрическая цепь включает несколько источников тока и сопротивлений, которые соединены разными способами. Такую цепь называют сложной разветвленной электрической цепью. Значимыми для составления систем уравнений, позволяющих провести расчеты в сети постоянного тока, являются ее узлы и замкнутые контуры. Расчеты любой сети можно проводить, используя закон Ома и закон сохранения заряда. Но использование специальных правил, которые называют правилами Кирхгофа (иногда законами Кирхгофа) позволяют упростить процедуру составления уравнений для вычислений. Всего выделяют два правила Кирхгофа.
Первое правило Кирхгофа
Довольно часто в электрической цепи в одной точке сходятся более двух проводников, по которым текут токи. Такие точки в цепи называют узлами или разветвлениями. В любом узле, если ток в цепи постоянен, полное изменение заряда за некоторый промежуток времени равно:
где суммирование проводят с учетом знаков силы тока. Если мы имеем дело с постоянным током в цепи, то потенциалы всех ее точек остаются неизменными. Значит, в узлах не может накапливаться заряд. Поэтому рассматривая силу тока, как алгебраическую величину запишем:
где N – число токов, которые сходятся в узле. Выражение (2) носит название первого правила Кирхгофа (правило узлов): сумма токов, текущих через сопротивления в цепи постоянного тока, с учетом их знака, сходящихся в узле, равна нулю.
Знак у тока (плюс или минус) выбирают произвольно, но при этом следует считать, что все входящие в узел токи имеют одинаковые знаки, а все исходящие из узла токи имеют противоположные входящим, знаки. Допустим, все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными.
Первое правило Кирхгофа дает возможность составить независимое уравнение, если в цепи k узлов.
Второе правило Кирхгофа
Во втором правиле Кирхгофа рассматривают замкнутые контуры, поэтому оно называется правилом контуров. Формулируется это правило Кирхгофа следующим образом: Суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних ЭДС (), которые входят в рассматриваемый контур. В математическом виде второй закон Кирхгофа записывают как:
Величины называют падениями напряжения. Прежде, чем применять второй закон Кирхгофа определяются с направлением положительного обхода контура. Выбирается направление произвольно, либо по часовой стрелке, либо против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго закона для данного контура входит с положительным знаком. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника. Более правильно было бы сказать, сто ЭДС считают положительной, если работа сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи в заданном направлении обхода контура является положительной величиной.
Второе правило Кирхгофа является следствием закона Ома.
Примеры решения задач
Постоянный ток: законы Кирхгофа
При решении задач на законы Кирхгофа лучше придерживаться определенного алгоритма: 1. определить число неизвестных токов – столько уравнений должно быть в системе ; 2. определить количество узлов – уравнений по первому закону тогда нужно составить на одно меньше; 3. проложить контуры и записать для них уравнения по второму закону. Кто хочет разобраться досконально – есть видео.
Задача 1. Два элемента с  В и
В и  В соединены по схеме, показанной на рисунке . Сопротивление
В соединены по схеме, показанной на рисунке . Сопротивление  Ом. Внутреннее сопротивление элементов одинаково
Ом. Внутреннее сопротивление элементов одинаково  Ом. Определить силу тока, идущего через сопротивление
Ом. Определить силу тока, идущего через сопротивление  .
.

К задаче 1
Обозначим токи в ветвях произвольно. По первому закону Кирхгофа сумма токов, сходящихся в узле, равна 0:
![Rendered by QuickLaTeX.com \[I_1+I_2-I_R=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-91663c0cb35c91e14e80fc039cf263e5_l3.png)
Будем обходить верхний контур против часовой стрелки. По второму закону Кирхгофа сумма падений напряжений в контуре равна сумме ЭДС:
![Rendered by QuickLaTeX.com \[U_R+U_{r1}=E_1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a5a1e364afe0b443b325f52f486cdb2e_l3.png)
![Rendered by QuickLaTeX.com \[I_RR+I_1r_1=E_1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-30659f5b5f5a38c81bdb90a1abc94f1b_l3.png)
Будем обходить второй контур по часовой стрелке:
![Rendered by QuickLaTeX.com \[U_R+U_{r2}=E_2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-14060a2858fafeb82c3147f6bfdb9a34_l3.png)
![Rendered by QuickLaTeX.com \[I_RR+I_2r_2=E_2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ed2b284902a6633a4948a0f1b766c692_l3.png)
Неизвестных токов – три, мы составили три уравнения. Этого достаточно, чтобы найти токи:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{ I_1+I_2-I_R=0}\\{ I_RR+I_1r_1=E_1}\\{ I_RR+I_2r_2=E_2}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bf74ee4b0d88bc4e91c1b202d61626db_l3.png)
Выразим  из второго уравнения, а
из второго уравнения, а  – из третьего:
– из третьего:
![Rendered by QuickLaTeX.com \[I_1=\frac{ E_1- I_RR }{ r_1}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-dc961817a8374faee6c400fd0fca3273_l3.png)
![Rendered by QuickLaTeX.com \[I_2=\frac{ E_2- I_RR }{ r_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d7f46bd2003bd5bdd79e452e2eb9c4c7_l3.png)
Подставим эти выражения в первое уравнение:
![Rendered by QuickLaTeX.com \[\frac{ E_1- I_RR }{ r_1}+\frac{ E_2- I_RR }{ r_2}-I_R=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-07789dd4acb3a91c4c792ee479570831_l3.png)
![Rendered by QuickLaTeX.com \[\frac{ E_1}{r_1}-\frac{ I_RR }{ r_1}+\frac{ E_2}{r_2}-\frac{ I_RR }{ r_2}-I_R=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-feeeb1f911dea5854244f08328526119_l3.png)
![Rendered by QuickLaTeX.com \[\frac{ E_1}{r_1}+\frac{ E_2}{r_2} = \frac{ I_RR }{ r_1}+\frac{ I_RR }{ r_2}+I_R\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-33594f4b2ad4077dd79d20b027d69c69_l3.png)
![Rendered by QuickLaTeX.com \[I_R=\frac{\frac{ E_1}{r_1}+\frac{ E_2}{r_2}}{\frac{ R }{ r_1}+\frac{ R }{ r_2}+1 }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-320e6d7f81cf618f766db437189f8f1f_l3.png)
![Rendered by QuickLaTeX.com \[I_R=\frac{\frac{ 2}{1}+\frac{ 1}{1}}{\frac{ 0,5 }{ 1}+\frac{ 0,5 }{ 1}+1 }=1,5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b5c61c6b8ee5de57950c08702f450f79_l3.png)
Тогда токи  и
и 
![Rendered by QuickLaTeX.com \[I_1=\frac{ E_1- I_RR }{ r_1}=\frac{ 2- 1,5\cdot0,5 }{1}=1,25\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a331cc32989cad53b129c24ca7e3e276_l3.png)
![Rendered by QuickLaTeX.com \[I_2=\frac{ E_2- I_RR }{ r_2}=\frac{ 1- 1,5\cdot0,5 }{ 1}=0,25\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6ea30286dd45b1330863796498268bb6_l3.png)
Ответ:  A,
A,  A,
A,  A.
A.
Задача 2. Найти силу тока на всех участках цепи‚ если  В,
В,  В‚
В‚  В,
В,  Ом‚
Ом‚  Ом‚
Ом‚  Ом‚
Ом‚  Ом‚
Ом‚  Ом,
Ом,  Ом.
Ом.

К задаче 2
Обозначаем токи в ветвях произвольно, выбираем направления обходов контуров и сами контуры. Составляем систему уравнений. Сначала составим уравнение по первому закону Кирхгофа – у нас два узла, поэтому уравнение будет одно. Затем, обходя контуры, составим два уравнения по второму закону: их нужно составить два, так как неизвестных токов в цепи три.
![Rendered by QuickLaTeX.com \[\begin{Bmatrix I_1+I_2+I_3=0}\\{ I_1(R_1+r_1)-I_2(R_2+r_2)=E_1-E_2}\\{ I_2(R_2+r_2)-I_3(R_3+r_3)=E_2-E_3}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4e5842a75727e3b87a316265a503aa22_l3.png)
Решаем систему и находим ответ (я решала с помощью он-лайн калькулятора):  ,
,  ,
,  .
.
Ответ:  ,
,  ,
,  .
.
Задача 3. В схеме, показанной на рисунке, найти силу тока через гальванометр, если  В,
В,  кОм;
кОм;  В,
В,  кОм. Сопротивлением гальванометра пренебречь.
кОм. Сопротивлением гальванометра пренебречь.

К задаче 3
Нам неизвестно сопротивление гальванометра, запишем для напряжения на нем два уравнения:
![Rendered by QuickLaTeX.com \[U=E_1-I_1R_1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8dcec034d1aacdd00f4d22c7991d620a_l3.png)
![Rendered by QuickLaTeX.com \[U=E_2-I_2R_2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3fdbbcbc61fe4dda4dfa23ce57a95298_l3.png)
Приравнивая, получим
![Rendered by QuickLaTeX.com \[E_1-I_1R_1= E_2-I_2R_2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f03790fe700a54e48434a31b242d74fd_l3.png)
Заметим, что, если  , то равенство будет выполнено. Таким образом, ток через гальванометр не течет.
, то равенство будет выполнено. Таким образом, ток через гальванометр не течет.
Ответ:  .
.
Задача 4. В цепи  В‚
В‚  В,
В,  Ом,
Ом,  Ом. Найти распределение токов в цепи. Внутреннее сопротивление источников тока не учитывать.
Ом. Найти распределение токов в цепи. Внутреннее сопротивление источников тока не учитывать.

К задаче 4
Обозначаем токи в ветвях произвольно, выбираем направления обходов контуров и сами контуры. Составляем систему уравнений. Сначала составим уравнение по первому закону Кирхгофа – у нас три узла, поэтому уравнений будет два. Затем, обходя контуры, составим три уравнения по второму закону: их нужно составить именно три, так как неизвестных токов в цепи шесть.
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{ I_1+I_6+I_5=0}\\{ -I_3-I_1+I_2=0}\\{- I_2-I_4-I_5=0}\\{ I_1R_1-I_3R_3=-E_1}\\{ I_2R_2+I_3R_3-I_4R_4=0}\\{ I_4R_4-I_5R_5=E_1-E_2}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-35bf061026341dedd0456866eb0fe0e7_l3.png)
Решаем систему и находим ответ (я решала с помощью он-лайн калькулятора):  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Ответ:  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Задача 5. Какую силу тока покажет амперметр в схеме, изображенной на рисунке? Сопротивлением амперметра пренебречь.

К задаче 5
Обозначим токи в цепи произвольно. Обозначим направления обхода контуров. Запишем систему уравнений: составим три уравнения по первому закону (на одно меньше, чем количество узлов) и три уравнения по второму закону, так как неизвестных токов шесть и система должна состоять из шести уравнений.
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{ -I_4+I_5+I_6=0}\\{ I_2-I_3-I_5=0}\\{ I_1-I_2-I_6=0}\\{ I_2\cdot6r+I_5\cdot6r =0}\\{ I_4\cdot6r +I_5\cdot6r -I_3\cdot6r =0}\\{ I_2\cdot6r +I_3\cdot6r +I_1\cdot2r =-E}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5c703937678e6bc9829cca3caadbc6de_l3.png)
Чтобы воспользоваться калькулятором, я задала  Ом и
Ом и  В. В итоге получилось:
В. В итоге получилось:  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Минусы свидетельствуют о противоположном направлении тока в этой ветви тому, что мы нарисовали.
2.5.1. Метод непосредственного применения законов Кирхгофа
Пример . Методом непосредственного применения законов Кирхгофа рассчитать токи в схеме на рис.
Число ветвей обозначим m, а число узлов n. Произвольно выбираем положительные направления токов в ветвях и направления обхода контуров. Поскольку в каждой ветви протекает свой ток, то число токов, которое следует определить, а следовательно, и число уравнений, которое нужно составить, равно m. По первому закону Кирхгофа составляем n-1 уравнений. Недостающие m-(n-1) уравнений следует составить по второму закону Кирхгофа для взаимно независимых контуров.
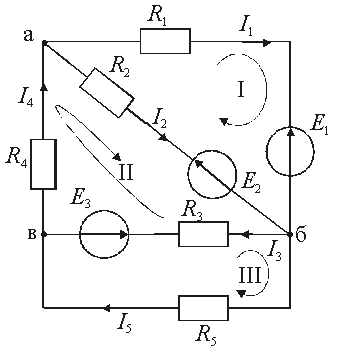 Рис.
2.20. Схема замещения сложной электрической
цепи
с несколькими источниками энергии:
I,
II, III – номера контуров
Рис.
2.20. Схема замещения сложной электрической
цепи
с несколькими источниками энергии:
I,
II, III – номера контуров
1. Проводим топологический анализ.
Она содержит пять ветвей и три узла, m = 5, n = 3. Составляем два уравнения по первому закону Кирхгофу, т. к. n – 1 = 2 (например, для узлов а и б).
2. Составляем уравнения по певому и второму законам Кирхгофа
Для узла «а» — I1 — I2 + I4 = 0.
Для узла «б» — I1 + I2 — I3 — I5 = 0.
Остальные m — (n — 1) = 3 уравнения составляем по второму закону Кирхгофа.
Для контура I — R1·I1 — R2·I2 = — E1 + E2.
Для контура II — R2·I2 + R3·I3 + R4·I4 = — E2 — E3.
Для контура III — — R3·I3 + R5·I5 = E3.
Решив систему, состоящую из пяти уравнений, находим пять неизвестных токов. Если какие-либо значения токов оказались отрицательными, то это означает, что действительные направления этих токов противоположны первоначально выбранным.
При расчётах сложных цепей с использованием ЭВМ удобна матричная форма записи. Уравнения, составленные по законам Кирхгофа, запишем в виде
— I1 — I2 + 0 + I4 + 0 = 0
I1 + I2 — I3 + 0 — I5 = 0
R1·I1 — R2·I2 + 0 + 0 + 0 = — E1 + E2
0 + R2·I2 + R3·I3 + R4·I4 + 0 = — E2 — E3
0 + 0 + — R3·I3 + 0 + R5·I5 = E3.
В матричной форме
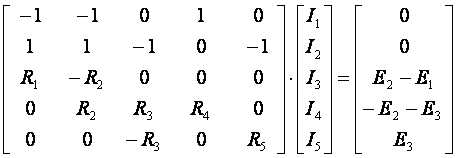
или [R]·[I] = [Е],
где [R] – квадратная (5 х 5) матрица, элементами которой являются коэффициенты при неизвестных токах в исходных уравнениях;
[I] – матрица — столбец неизвестных токов;
[E] – матрица — столбец, элементами которой могут быть алгебраическая сумма ЭДС.
Решение матричного уравнения ищут в виде
[I] = [R]-1·[E],
где [R]-1 – матрица, обратная матрице [R].
Рассмотренный метод расчета неудобен, если в цепи имеется большое количество узлов и контуров, поскольку потребуется решать громоздкую систему уравнений. В таких случаях рекомендуется применять метод контурных токов, позволяющий значительно сократить число расчетных уравнений 2.
Метод контурных токов
Метод основан на 2-м законе Кирхгофа. При его использовании в составе анализируемой схемы выбирают независимые контуры и предполагают, что в каждом из контуров течет свой контурный ток. Для каждого из независимых контуров составляют уравнение по 2-му закону Кирхгофа и их решают. Токи в ветвях находят как алгебраическую сумму контурных токов, протекающих по данной ветви.
Все источники сигналов, представленные источниками тока, заменяют источниками ЭДС (рис. 4.29).
Э та
схема эквивалентна, если
та
схема эквивалентна, если
а
 )E = IZiI;
)E = IZiI;
б) ZiII = ZiI.
1) Топологический анализ схемы.
а) Как и в предыдущем методе, определяют число ветвей b.
б) Определяют число узлов у.
в) Подсчитывают число независимых контуров Nk = b – y + 1.
Все независимые контуры обозначены дугами со стрелками на них, которые показывают положительное направление обхода.
Все контуры нумеруют и каждому контуру присваивают свой контурный ток: Ik1; Ik2;IkNk.
За положительное направление контурного тока принимают положительное направление обхода контура.
2) По второму закону Кирхгофа относительно контурных токов записывают уравнения, которые после приведения подобных членов образуют систему линейных уравнений Nk = Nkпорядка:
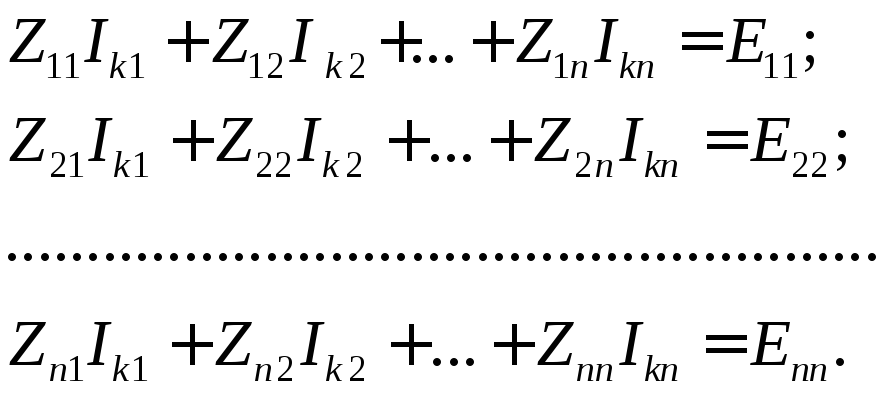
где Iki– контурный токi-го контура;
Zii– собственное сопротивлениеi-го контура и равно алгебраической сумме сопротивлений, входящих вi-й контур;
Zji– сопротивление смежных ветвей междуi-м иj-м контурами. Оно представляет собой алгебраическую сумму, причем ее члены берутся со знаком «+», если контурные токи направлены одинаково, и со знаком «–», если они направлены встречно;
Eki– контурная ЭДСi-ого контура. Она равна алгебраической сумме ЭДС, входящих вi-й контур. Контурная ЭДСEkiберется со знаком «+», когда направление источника ЭДС и направление тока совпадают, и со знаком «–», если они направлены встречно.
3 )
По правилу Крамера находят контурные
токиIki=
)
По правилу Крамера находят контурные
токиIki=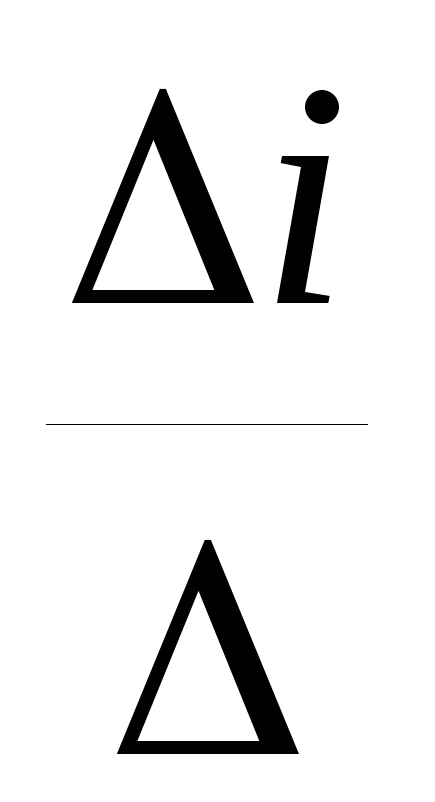 .
.
4) Токи в ветвях находят как алгебраическую сумму контурных токов, протекающих через данную ветвь. В алгебраической сумме контурные токи берутся со знаком «+» , если ток ветви и совпадает с контурным током и «–» если не совпадает.
Если токи ветви оказались положительными, то выбранное направление тока совпадает с истинным и наоборот.
Пример.Дана комплексная схема замещения электрической цепи (рис. 4.30). Определить токи во всех ветвях.
1. Проводим топологический анализ
а) b= 6; б)y= 4;в)Nk= 6 – 4 + 1=3.
2) Составим систему уравнений по методу МКТ
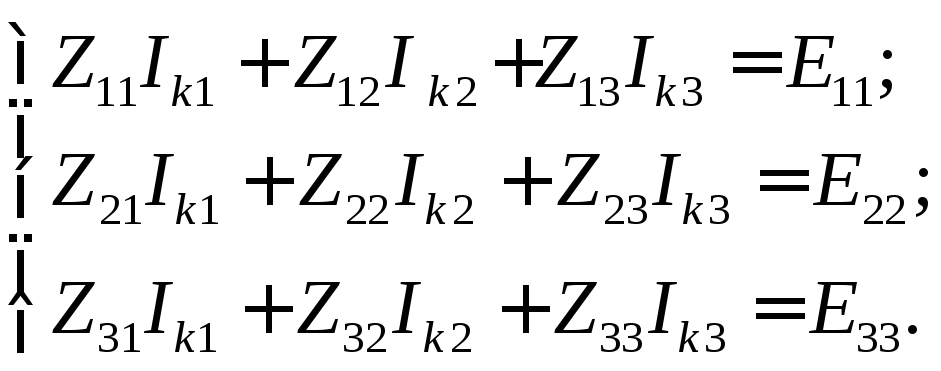
г де:
де: 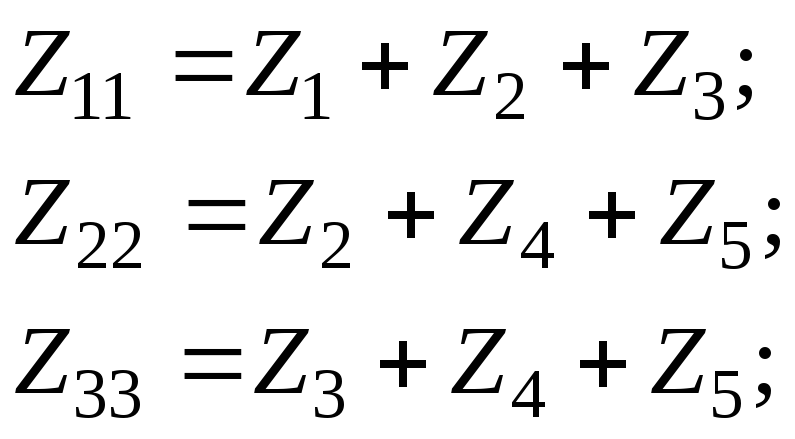
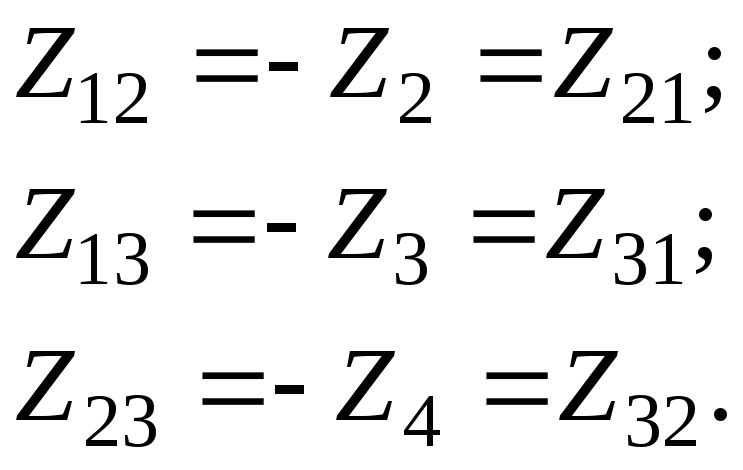
E


 11= E1; E22 = 0;E33 = 0.
11= E1; E22 = 0;E33 = 0.
3) По методу Крамера находим контурные
токи Iki =  .
.
4













 )
Находим токи
в ветвях: I1 = Ik1; I2 = = Ik1 – Ik2; I3 = Ik1 – Ik3; I4 =
–Ik2 + Ik3; I5 = Ik2; I6 = Ik3.
)
Находим токи
в ветвях: I1 = Ik1; I2 = = Ik1 – Ik2; I3 = Ik1 – Ik3; I4 =
–Ik2 + Ik3; I5 = Ik2; I6 = Ik3.
Пример 2. Рассмотрим электрической цепи постоянного тока, рис. 2.21.
1. Проводим топологический анализ
а) b= 5; б)y= 3;в)Nk= 5 – 3 + 1=3.
2) Для каждого контура записывают уравнение второго закона Кирхгофа,
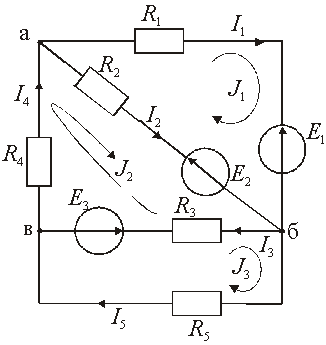 Рис.
2.21. – Расчетная схема для метода контурных
токов
Рис.
2.21. – Расчетная схема для метода контурных
токов
В каждом из трех контуров протекает свой контурный ток J1, J2, J3. Произвольно выбираем направление этих токов, например, по часовой стрелке. Составляем уравнения по второму закону Кирхгофа для каждого контура с учетом соседних контурных токов, протекающих по смежным ветвям
(R1 + R2)·J1 — R2·J2 = E2 — E1
— R2·J1 + (R2 + R3 + R4)·J2 — R3·J3 = — E2 — E3
— R3·J2 + (R3 + R5)·J3 = E3.
Решив систему уравнений, находят контурные токи J1, J2, J3. Затем определяют реальные токи в ветвях, причем токи во внешних ветвях равны контурным, а в смежных – алгебраической сумме 2-х контурных токов, протекающих в данной ветви
I1 = J1; I2 = J2 — J1; I3 = J2 — J3; I4 = J2; I5 = J3.
Исходная система уравнений в матричной форме
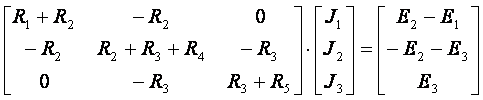
или
[R]·[J] = [E],
где [R] – квадратная матрица коэффициентов контурных токов;
[J] – матрица – столбец контурных токов; [E] – матрица – столбец ЭДС.
Решением матричного уравнения является матрица
[J] = [R]-1 ·[E],
где [R]-1 – матрица, обратная матрице [R]
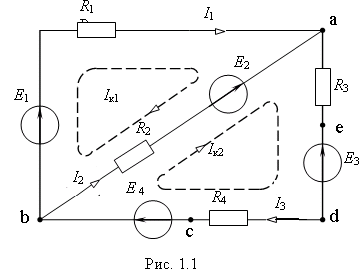
Пример 3. Для электрической цепи, схема которой приведена на рис. 1.1, получим следующие уравнения:
получим следующие уравнения:
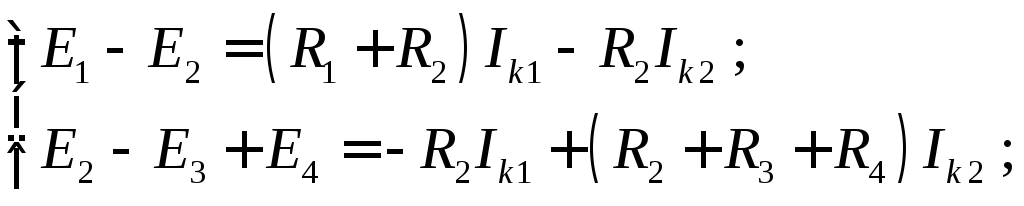
П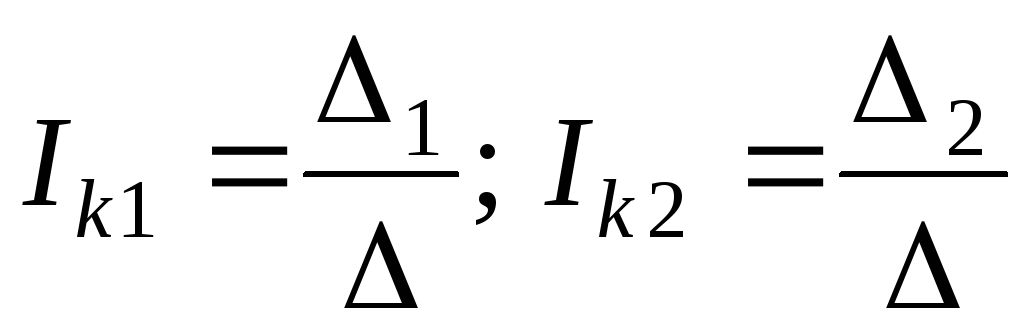 о
методу Крамера найдем контурные токи:
о
методу Крамера найдем контурные токи:
Действительные токи в ветвях: I1 = Ik1; I2 = Ik2 – Ik1; I3 = Ik2.
Пример 4. Расчет цепи методом контурных токов на рис. 2.22.
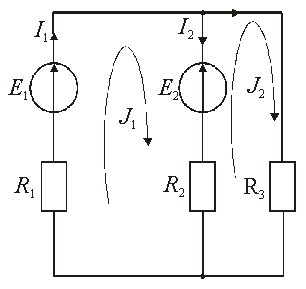 Рис.
2.22. – Расчет цепи методом контурных
токов
Рис.
2.22. – Расчет цепи методом контурных
токов
Для схемы замещения электрической цепи, показанной на рис. 2.22, задано: E1 = 30 B; E2 = 10 В; R1 = 8 Ом; R2 = 15 Ом; R3 = 36 Ом. Требуется определить токи в ветвях методом контурных токов. Составить баланс мощности.
Схема содержит три ветви (m = 3), два узла (n = 2). Выбираем положительные направления токов в ветвях произвольно. Число уравнений, составленных по методу контурных токов, равно m — (n — 1) = 2. Задаем направление контурных токов (например, по часовой стрелке) и составляем систему уравнений
(R1 + R2)·J1 — R2·J2 = E1 — E2
— R2·J1 + (R2 + R3)·J2 = E2.
Подставляя численные значения сопротивлений резисторов и ЭДС в приведённые уравнения, находим контурные токи J1, J2 (Например, методом определителей)
20 = 23·J1 – 15·J2
10 = — 15·J1 + 51·J2
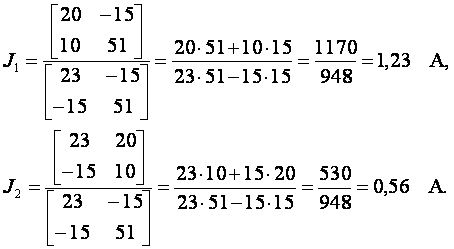
Токи в ветвях
I1 = J1 = 1,23 А; I2 = — J2 + J1 = 1,23 — 0,56 = 0,67 А; I3 = J2 = 0,56 А.
Составляем баланс мощностей.
Мощность генераторов (источников)
РИ = Е1·I1 — Е2·I2 = 30·1,23 – 10·0,67 = 30,2 Вт,
где произведение Е2·I2 имеет знак минус (ток через источник не совпадает с ЭДС, значит источник ЭДС работает в режиме потребителя электрической энергии).
Мощность, потребляемая нагрузкой, составляет
РН = R1·I12 + R2·I22 + R3·I32 = 8·1,232 + 15·0,562 + 36·0,562 = 30,13 Вт.
Погрешность
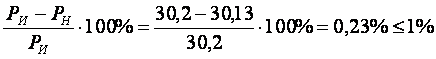
составляет менее 1%, т. е. токи найдены верно.
Метод узловых потенциалов (МУП)
Метод основан на применении первого закона Кирхгофа. В нем за неизвестные величины принимают потенциалы узлов. По закону Ома определяют токи во всех ветвях схемы.
Все источники ЭДС, имеющиеся в схеме, заменяют источниками тока (рис. 4.31).
а) I = E/ZiI;
б) ZiII = ZiI.
1) Топологический анализ.
а) Подсчитывают число ветвей bи число узловy.Определяется количество независимых узловNy =y – 1.
б) Нумеруют все узлы. Один из узлов, к
которому сходится наибольшее число
ветвей, считают нулевым, где  – потенциал нулевого узла.
– потенциал нулевого узла.
2) По 1-му закону Кирхгофа составляют уравнения для Nузлов схемы и решают их относительно потенциалов узлов:
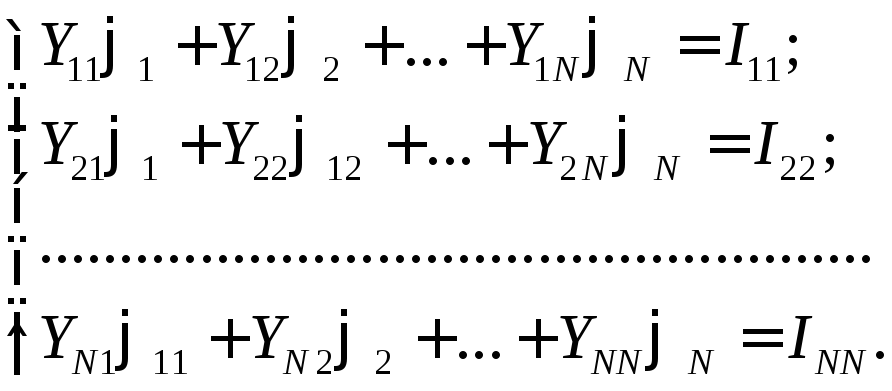


 ,
,
где Yii– собственная узловая проводимость. Она равна сумме проводимостей всех ветвей, сходящихся вi-м узле, все они берутся со знаком «+»;
Yij– межузловая проводимость междуi-м иj-м узлами. Проводимости всех узлов берутся со знаком «–»;
Iii– алгебраическая сумма токов источников тока, сходящихся вi-м узле. Втекающие токи записываются в эту сумму со знаком «+», а вытекающие – со знаком «–».
3) Потенциалы узлов находят по формуле Крамера
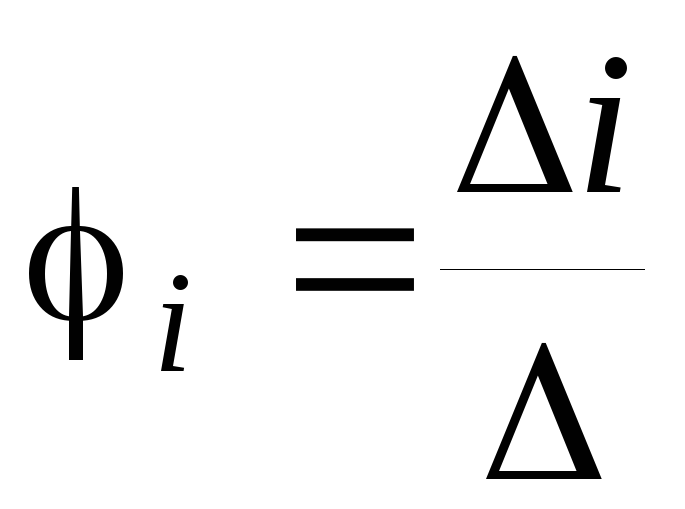 .
.
4) Токи в ветвях находят по закону Ома
I= (1 –2)/Z.
Пример.Дана электрическая цепь (рис. 4.32). Рассчитать токи во всех ветвях.
П
I2
Z2
редварительно преобразуем все источники напряжения (рис. 4.32) в источники тока (рис. 4.33). 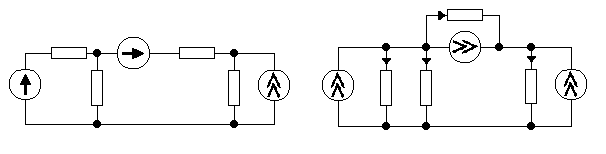
Z1
Z2
Z3
Z4
E1
E2
I
I1
I2
I4
I
I3
I1
Z1
Z3
Z4
Рис. 4.32 Рис. 4.33Проведем топологический анализ.
а) число ветвей b= 4;
б) число независимых узлов Nу= 2, их потенциалы: φ1и φ2(рис. 4.33).
Составим систему уравнений по методу узловых потенциалов:
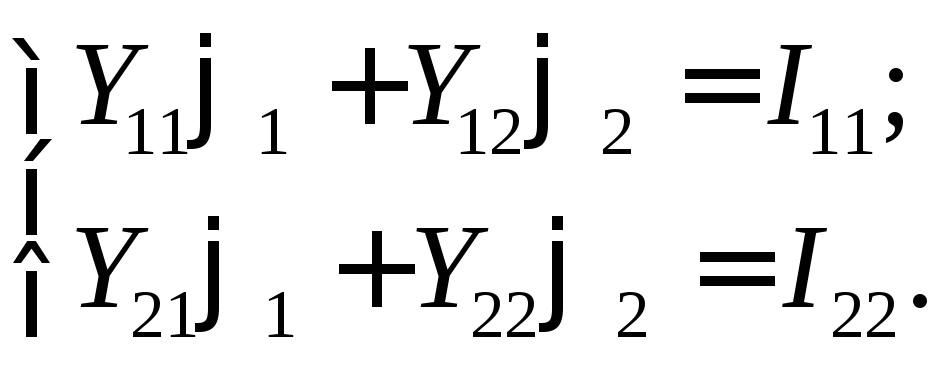


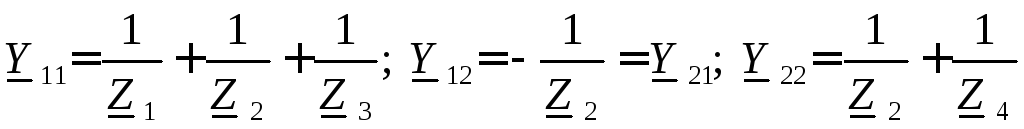





 ;
;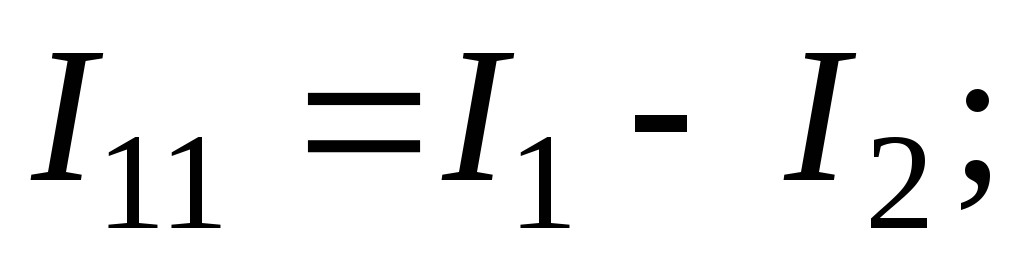
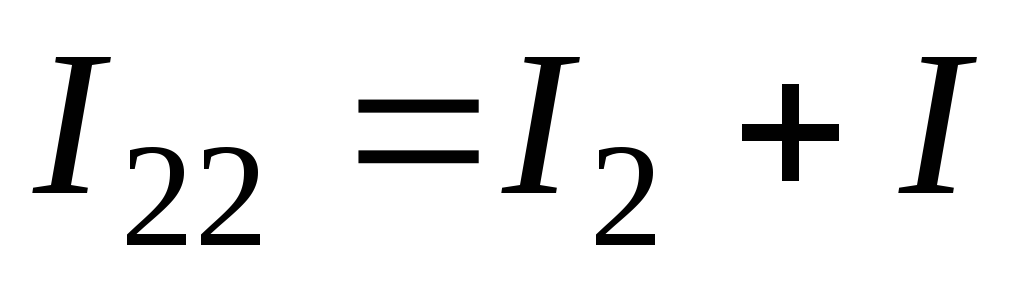 .
.
По методу Крамера найдем потенциалы
узлов 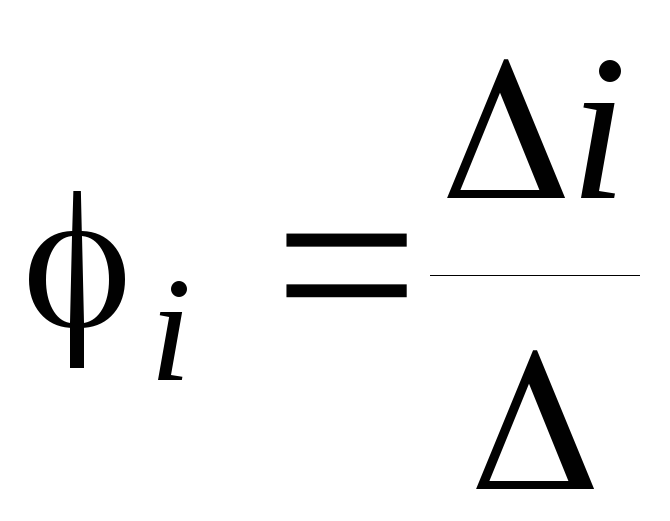 .
.
По закону Ома найдем токи во всех ветвях схемы:
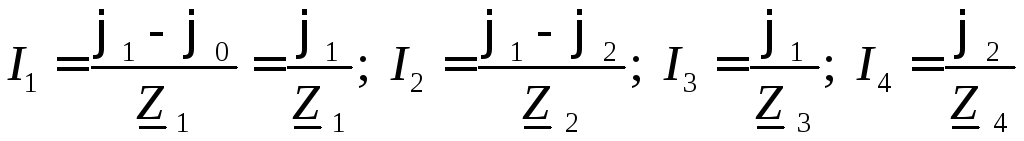



 .
.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЙ по теме цепи переменного тока



