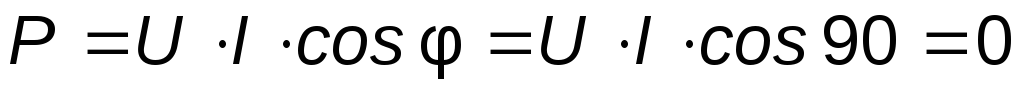1.4. Законы Ома и Кирхгофа
1.4. Законы Ома и Кирхгофа
Закон Ома для всей цепи выражает соотношение между электродвижущей силой (ЭДС), сопротивлением и током. Согласно этому закону ток в замкнутой цепи равен ЭДС источника деленной на сопротивление всей цепи:
 , (1.19)
, (1.19)
где I – ток, протекающий по цепи;
E – ЭДС, генератора, подключенного к электрической цепи;
Rг – сопротивление генератора;
Rц – сопротивление цепи.
Закон Ома для участка цепи. Ток на участке цепи прямо пропорционален напряжению между началом и концом участка и обратно пропорционален сопротивлению участка. Аналитически закон выражается в следующем виде:
 , (1.20)
, (1.20)
где I – ток, протекающий на участке цепи;
R – сопротивление участка цепи;
U – напряжение на участке цепи.
Обобщенный закон Ома. Сила тока в контуре цепи прямо пропорциональна алгебраической сумме ЭДС всех источников цепи и обратно пропорциональна арифметической сумме всех активных сопротивлений цепи.
 , (1.21)
, (1.21)
где m и n – количество источников и резисторов в контуре цепи.
При алгебраическом суммировании со знаком “плюс” берутся те ЭДС, направление которых совпадает с направлением тока, а со знаком “минус”– те ЭДС, направление которых не совпадает с направлением тока.
Первый закон Кирхгофа. Электрические цепи подразделяют на неразветвленные и разветвленные. На рис. 1.10 представлена простейшая разветвленная цепь.

Рис. 1.10 Схема разветвленной цепи.
Разветвленной называется такая электрическая цепь, в которой ток от какого-либо источника может идти по различным путям и, в которой, следовательно, имеются точки, где сходятся два и более проводников. Эти точки называютузлами. Токи, текущие к узлу считаются имеющими один знак, а от узла – другой.
Учитывая это правило для схемы, изображенной на рис. 1.11,а можно записать

 .
.
Для цепи, имеющей n ветвей, сходящихся в одном узле, имеем:
 , (1.22)
, (1.22)
т.е. алгебраическая сумма токов ветвей, сходящихся в любом узле, равна
нулю.

Рис. 1.11 Схема поясняющая законы Кирхгофа.
Физически первый закон Кирхгофа означает, что движение зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются.
Второй закон Кирхгофа устанавливает связь между ЭДС, токами и сопротивлениями в любом замкнутом контуре, который можно выделить в рассматриваемой цепи.
В соответствии со вторым законом Кирхгофа алгебраическая сумма ЭДС, действующих в любом контуре разветвленной электрической цепи, равна алгебраической сумме падений напряжений на всех сопротивлениях контура
 , (1.23)
, (1.23)
Рассмотрим электрическую цепь, изображенную на рис. 1.11,б. Обозначим стрелкой направление обхода контура. При составлении уравнений будем брать со знаком “плюс” те ЭДС и падения напряжений, направления которых совпадают с направлением обхода контура и со знаком “минус” те, которые направлены против обхода. Для цепи, изображенной на рис. 1.11,б второй закон Кирхгофа запишется в следующем виде:
 .
.
ЗАКОНЫ ОМА И КИРХГОФА
Всякая электрическая цепь состоит из источника электрической энергии (генератора), замкнутого проводящего контура (соединительных проводов) и потребителя (нагрузки).
Источники электрической энергии делятся на источники заданной ЭДС (напряжения) и источники заданного тока [1]. У идеального источника заданной ЭДС (рис.1.1,а) полагаем, что напряжение на его клеммах не зависит от нагрузки (внутреннее сопротивление равно нулю), а у идеального источника заданного тока (рис.1.1,б) полагаем, что его ток не зависит от нагрузки (внутреннее сопротивление стремится к ∞).
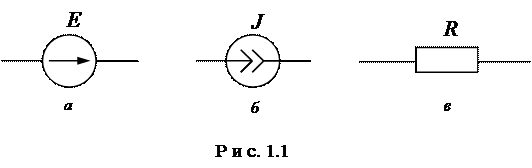 |
Омическое сопротивление R участка цепи (нагрузка) (рис.1.1,в) может быть определено по формуле
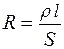 ,
,
где ρ – удельное сопротивление проводника; l – длина проводника; S – площадь поперечного сечения проводника.
Для расчета процессов в электрической цепи ее изображают в виде схемы.
Схемой электрической цепи называется её графическое изображение, показывающее последовательность соединения участков и отображающее свойства рассматриваемой цепи.
В электрической цепи (схеме) различают узлы, ветви и контуры.
Узел – точка цепи (схемы), где сходятся не менее 3 ветвей. Ветвь – участок цепи (схемы), соединяющий два узла. Контур – замкнутый путь, проходящий по нескольким ветвям цепи (схемы).
Любая часть электрической цепи, имеющая два зажима (полюса), называется двухполюсником.
Расчёт электрических цепей базируется на законе Ома и двух законах (правилах) Кирхгофа.
Закон Ома для участка цепи – ток Ik k-того участка прямо пропорционален напряжению Uk на этом участке и обратно пропорционален сопротивлению Rk этого участка:
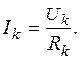
Типичная ошибка при применении закона Ома заключается в том, что при определении тока берется напряжение на одном участке и делится на сопротивление другого участка, что не соответствует этому закону.
Первый закон Кирхгофа применяется к узлам электрической цепи и вытекает из принципа непрерывности электрического тока:
«Алгебраическая сумма» означает, что втекающие в узел и вытекающие из него токи берутся с противоположными знаками.
Перед составлением уравнений по первому закону Кирхгофа необходимо произвольно задаться условными положительными направлениями токов в ветвях. Пример приведён на рис.1.2.
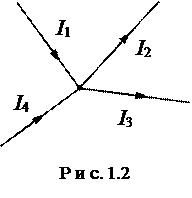 |
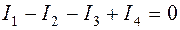
или
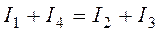
Если в результате расчета для какого-либо тока будет получено отрицательное значение, то это означает, что действительное направление данного тока противоположно выбранному.
Второй закон Кирхгофа применяется к контурам электрической цепи: алгебраическая сумма падений напряжения в замкнутом контуре равна алгебраической сумме ЭДС, действующих в этом контуре.
Электрический ток, протекая по сопротивлению, создаёт на нём падение напряжения, совпадающее по направлению с током, поэтому, выбрав направление тока в ветви, мы задаём и направление падения напряжения.
Рассмотрим пример (рис.1.3).
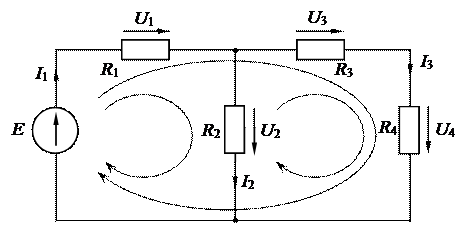
Для трёх указанных контуров схемы уравнения по второму закону Кирхгофа будут следующие:
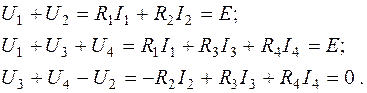
Необходимо отметить, что ток в ветви можно определить двумя путями:
— по закону Ома для участка цепи – когда известны напряжение и сопротивление данного участка;
— по первому закону Кирхгофа – когда в узле известны все токи, кроме искомого.
— В свою очередь напряжение между двумя точками цепи можно определить следующим образом:
— по закону Ома для участка цепи 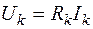 ;
;
— по второму закону Кирхгофа, причём контур может быть замкнут искомым напряжением;
— как разность потенциалов на концах рассматриваемого участка цепи.
1.2. Последовательное соединение сопротивлений
Пусть даны два сопротивления
Один зажим сопротивления R1 подключаем к клемме (+) источника, а другой – к клемме сопротивления R2; свободную клемму R2 подключаем к клемме (–) источника. Получим замкнутый проводящий контур, состоящий из одной ветви, включающей в себя источник с напряжением U и два сопротивления R1 и R2 (рис.1.4).
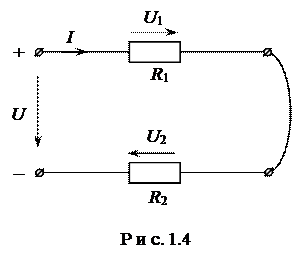 |
Аналогично можно включить и большее число сопротивлений. Через любое сечение проводника проходит одинаковое число электрических зарядов. Это следует из закона сохранения заряда. Следовательно, по всем сопротивлениям протекает один и тот же ток. Такое соединение называется последовательным.
Итак, признаком последовательного соединения является то, что по элементам протекает один и тот же ток, т.е. элементы включены в одну общую ветвь.
Для цепи (рис.1.4) запишем уравнение по второму закону Кирхгофа
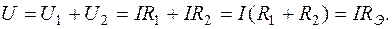 (1.1)
(1.1)
Таким образом, напряжение на входе цепи U можно выразить через ток I в цепи и эквивалентное сопротивление цепи RЭ.
Эквивалентным (входным) сопротивлением цепи называется такое одно сопротивление, при подключении которого (вместо всех сопротивлений цепи) к зажимам источника режим его работы не изменится, т.е. не изменятся ток I и напряжение U источника.
Эквивалентное сопротивление находится путём последовательного преобразования цепи от конца, противоположного источнику, к зажимам источника.
Конечная схема этих преобразований всегда одна (рис.1.5).
 |
Итак, для цепи (см. рис.1.4) получаем
 (1.2)
(1.2)
Из (1.2) следует:
— при последовательном соединении сопротивления складываются;*
— последовательные соединения удобнее рассчитывать через сопротивления.
Обратите внимание, что последовательное подключение сопротивления увеличивает эквивалентное сопротивление цепи, т.е. уменьшает потребляемый ток и мощность, отдаваемую источником.
1.3. Параллельное соединение сопротивлений
Те же два сопротивления R1 и R2 можно подключить к источнику и по-другому: R1 подключим к зажимам «+» и «–» и аналогично подключим R2. Получим схему, содержащую три ветви и два узла (рис.1.6).
 |
Такое соединение называется параллельным. Из полученной схемы соединений видно, что признаком параллельного соединения является то, что сопротивления находятся под одним и тем же напряжением, т.е. подключены к двум общих узлам (а и b).
Для цепи (см. рис.1.6) по первому закону Кирхгофа имеем
 (1.3)
(1.3)
По закону Ома токи в ветвях схемы
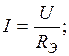


Подставляя в (1.3), получаем
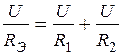 . (1.4)
. (1.4)
Поделив левую и правую части уравнения (1.4) на общую величину U, получим
 .
.
Обозначим 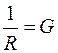 . Величина G, обратная сопротивлению, называется проводимостью. Размерность [G] = Ом-1 = См.
. Величина G, обратная сопротивлению, называется проводимостью. Размерность [G] = Ом-1 = См.
Получаем выражение для эквивалентной проводимости
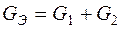 . (1.5)
. (1.5)
Из (1.5) следует:
— при параллельном соединении элементов проводимости складываются;*
— параллельные соединения удобнее рассчитывать через проводимости.
Для частного случая, когда параллельно соединены два сопротивления R1 и R2, эквивалентное сопротивление будет
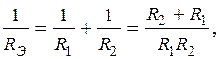

Обратите внимание, что параллельное подключение сопротивления уменьшает эквивалентное сопротивление цепи, т.е. увеличивает потребляемый ток и мощность, отдаваемую источником.
1.4. Смешанное соединение сопротивлений
Если электрическая цепь содержит три и более сопротивлений, то наряду с последовательным и параллельным соединениями возможно смешанное соединение.
Смешанным соединением называют сочетание последовательного и параллельного соединений (рис.1.7).
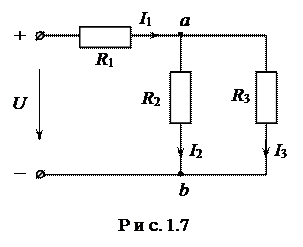 |
Схему смешанного соединения можно «свернуть», т.е. найти эквивалентное сопротивление RЭ.
На схеме (см. рис.1.7) сопротивления R2 и R3 включены параллельно. Заменим их одним сопротивлением R4 :
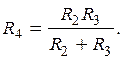
Получим новую схему (рис.1.8), эквивалентную заданной:
 |
В полученной схеме сопротивления R1 и R4 включены последовательно, так как по ним протекает один ток I1.
Следовательно, эквивалентное сопротивление цепи (рис. 1.9)

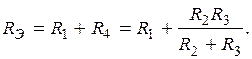
Более сложные электрические цепи могут не сводиться к последовательному и параллельному соединению элементов. Если при нахождении RЭ вы убедились, что в схеме нет последовательно или параллельно соединённых сопротивлений, необходимо воспользоваться преобразованием «звезды» в «треугольник» или наоборот [1,2,3].
1.5. Расчет простых электрических цепей
Электрические цепи можно условно разделить на простые и сложные.
Простой электрической цепью будем считать цепь, содержащую один источник электрической энергии. Если в одной ветви имеется несколько источников, то их всегда можно привести к одному эквивалентному.
Сложной электрической цепью будем называть цепь, содержащую два и более источников в различных ветвях. Расчёт сложных электрических цепей будет рассмотрен позже.
Различают прямую и обратную задачи расчёта простых цепей.
Прямой задачей называется расчет такой цепи, когда в схеме заданы ЭДС (напряжение) источника и сопротивления всех нагрузок. Требуется определить токи (напряжения, мощности) во всех ветвях.
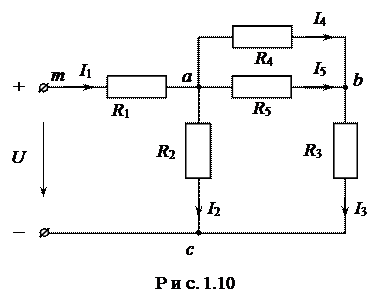 Пример.Дана электрическая цепь, схема которой приведена на рис.1.10.
Пример.Дана электрическая цепь, схема которой приведена на рис.1.10.
Известны параметры цепи и источника:
U = 20 В; R1 = 3 Ом; R2 = 4 Ом; R3 = 1.6 Ом; R4 = 6 Ом; R5 = 4 Ом.
Требуется определить токи во всех ветвях I1, I2, I3, I4, I5.
Расчёт прямой задачи ведётся в два этапа.
Первый этап. Цепь надо «свернуть», т.е. найти ее эквивалентное (входное) сопротивление RЭ.
Выберем положительные направления токов в ветвях и укажем их стрелками.
Поэтапно преобразуем цепь. Сопротивления R4 и R5 включены параллельно, следовательно,
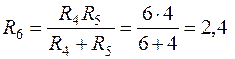 Ом.
Ом.
 Получаем схему, эквивалентную заданной (рис.1.11).
Получаем схему, эквивалентную заданной (рис.1.11).
В полученной схеме сопротивления R6 и R3 соединены последовательно, следовательно,
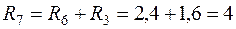 Ом.
Ом.
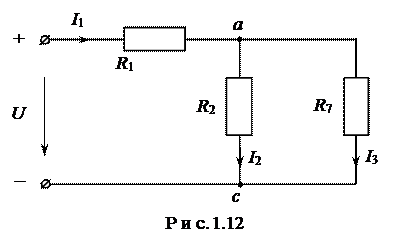 Получим схему, эквивалентную предыдущей (рис.1.12).
Получим схему, эквивалентную предыдущей (рис.1.12).
Здесь R2 и R7 включены параллельно. Заменим их сопротивлением R8 :
 Ом.
Ом.
Новая эквивалентная схема показана на рис.1.13.
Сопротивления R1 и R8 включены последовательно, т.е. эквивалентное сопротивление цепи (рис.1.14)

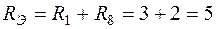 Ом.
Ом.
Второй этап. Теперь «развернём» схему, т.е. идем по эквивалентным схемам в обратном порядке и находим токи в ветвях.
В схеме (см. рис.1.14) известны U = 20 В, RЭ = 5 Ом.
Следовательно, ток
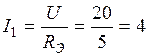 А.
А.
Переходим к схеме (см. рис.1.13). Здесь найдены все величины.
Переходим к схеме на рис.1.12. В схеме неизвестны токи I2 и I3. Их можно найти по закону Ома:

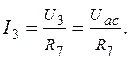
Найдём напряжение Uaс. Здесь возможны два пути.
1. Запишем уравнение по второму закону Кирхгофа для контура, куда входит напряжение Uaс:
 .
.
Отсюда получаем искомое напряжение на участке ac:
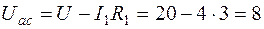 В.
В.
2. Напряжение Uaс можно определить по закону Ома для участка ac схемы (см. рис.1.13)
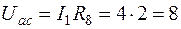 В.
В.
Зная напряжение Uaс, находим токи I2 и I3 по закону Ома:
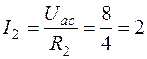 A;
A; 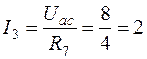 A.
A.
Аналогично найдём напряжение Uab:
 В.
В.
Тогда токи  A;
A;  A.
A.
Таким образом, прямая задача решена.
Проверить расчёт можно по законам Кирхгофа.
1. По первому закону Кирхгофа:
для узла «а» 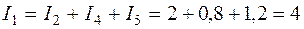 A;
A;
для узла «b» 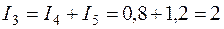 A;
A;
для узла «c» 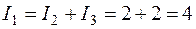 A.
A.
2. По второму закону Кирхгофа
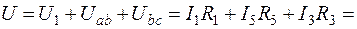
 В.
В.
Одним из точных способов проверки правильности расчёта токов является проверка по балансу мощностей. В основе баланса мощностей лежит закон сохранения энергии, в соответствии с которым суммарная мощность, отдаваемая источниками в цепь (Рист), должна равняться суммарной мощности всех потребителей (Рпотр).
В рассматриваемом примере мощность источника
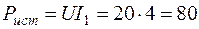 Вт.
Вт.
Суммарная мощность потребителей

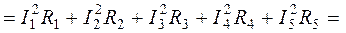
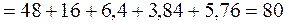 Вт.
Вт.
Таким образом,
 .
.
Баланс мощностей соблюдается, следовательно, токи в ветвях схемы найдены правильно.
Для рассматриваемого примера построим потенциальную диаграмму для внешнего контура.
Потенциальная диаграмма показывает, как изменяется потенциал j при движении вдоль замкнутого контура цепи. По оси абсцисс откладываются сопротивления R участков цепи вдоль контура, по оси ординат – потенциалы точек рассматриваемого контура.
Электрический потенциал j – величина относительная, и его значение зависит от того, какая из точек цепи принимается за базисную и мысленно заземляется, т.е. её потенциал условно считается равным нулю.
Необходимо помнить, что во внешней цепи ток протекает от точки с бóльшим потенциалом к точке с меньшим потенциалом (катится с горки), поэтому при определении потенциала надо учитывать, что если направление тока совпадает с направлением перехода от одной точки к другой, то потенциал понижается на величину падения напряжения IR на этом участке. В противном случае потенциал повышается.
Возьмем замкнутый контур abcma. Пусть потенциал точки а цепи (см. рис.1.10) равен нулю: ja = 0. Так как ток протекает из точки с бóльшим потенциалом в точку с меньшим потенциалом, то потенциал точки b будет меньше потенциала точки а на величину падения напряжения на сопротивлении R4 или на сопротивлении R5:
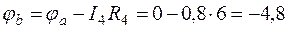 В.
В.
Потенциал точки с ниже потенциала точки b по той же причине, т.е.
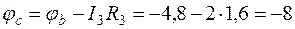 В.
В.
Потенциал точки m выше потенциала точки с из-за наличия на участке cm источника с напряжением U, в котором за счёт работы сторонних сил происходит повышение потенциала, т.е.
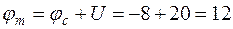 В.
В.
Потенциал точки а
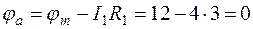 В.
В.
Контур abcma замкнулся.
Потенциальная диаграмма приведена на рис.1.15.
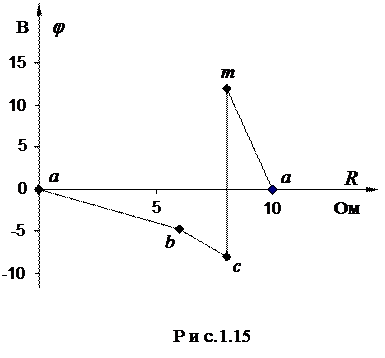
Тангенс угла наклона α любого участка потенциальной диаграммы пропорционален току цепи на этом участке.
Например, для участка ab
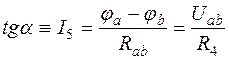 .
.
По заданной потенциальной диаграмме контура можно определить потенциалы точек, сопротивления участков, напряжения на участках, токи на участках этого контура.
Рассмотрим обратную задачу.
Обратная задача: по известным току (напряжению или мощности) на одном из участков и сопротивлениям цепи определить остальные токи и напряжение (мощность) источника.
Рассмотрим эту задачу на том же примере (см. рис.1.10), считая, что заданы ток в пятой ветви (I5 = 1,2 A) и те же сопротивления нагрузок.
Решение. Определим напряжение Uab по закону Ома:
 В.
В.
Так как R4 и R5 соединены параллельно, ток в четвертой ветви
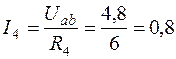 А.
А.
Теперь по первому закону Кирхгофа найдем ток в третьей ветви:
 A.
A.
Напряжение Uac определим по второму закону Кирхгофа. Для этого возьмем контур с сопротивлениями R5, R3, R2:
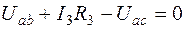 .
.
Отсюда находим
 В.
В.
Ток в ветви сопротивлением R2
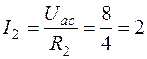 A.
A.
Ток в ветви с источником находим по первому закону Кирхгофа:
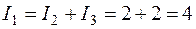 A.
A.
Напряжение на зажимах источника
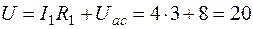 В.
В.
Этот приём можно использовать и для расчёта прямой задачи.
Для этого в наиболее удаленной от источника ветви произвольно задаемся некоторым значением тока (например, 1 А). Далее, продвигаясь к входным зажимам, рассчитываем токи в ветвях и напряжения на участках схемы. В результате расчета получим значение напряжения источника U’, если бы в исходной ветви протекал ток в 1 А.
Так как полученное значение напряжения U’ в общем случае будет отличаться от действительного значения напряжения U источника, то находим коэффициент K, равный отношению
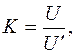
на который следует умножить все найденные токи и напряжения, чтобы получить их действительные значения. Этот метод расчёта линейных электрических цепей называют методом пропорциональных величин.
1.6. Расчет сложных электрических цепей
Сложной электрической цепью называется цепь, содержащая два и более источников электрической энергии, находящихся в различных ветвях.
Для анализа сложной электрической цепи её необходимо описать системой независимых уравнений, решив которые можно определить токи во всех ветвях, а следовательно, найти напряжения и мощности на всех участках.
В зависимости от поставленной задачи расчёта цепи можно применять любой из пяти ниже рассмотренных методов.
Дата добавления: 2017-09-01; просмотров: 5557;
Похожие статьи:
Законы Ома и Кирхгофа в комплексной форме.
Урав-ие представляет собой закон Ома для цепи синусоидального тока в комплексной форме
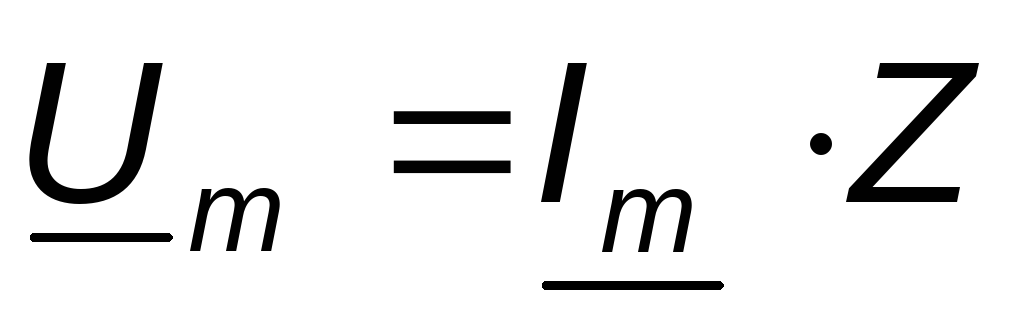 (3,9)
(3,9)
где Z – комплексное сопротивление, Ом.
В общем случае Z имеет некоторую действительную часть R и некоторую мнимую часть jX,
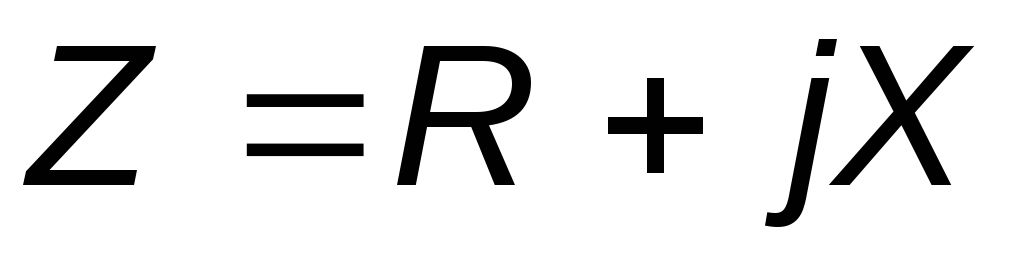
Уравнение 3.9 можно
записать иначе. Разделим обе его части
на 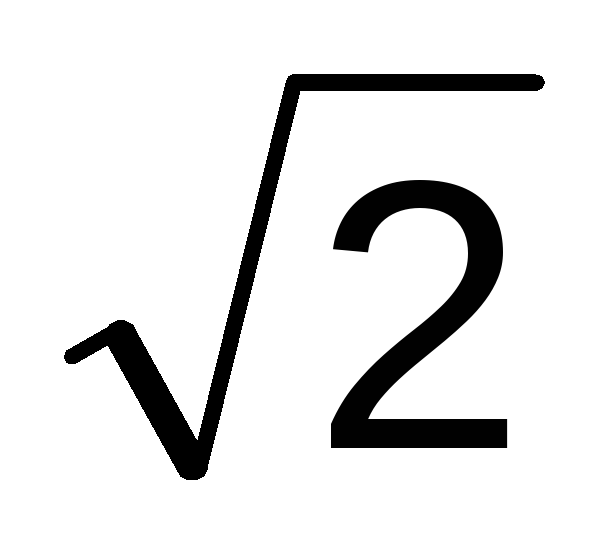 и перейдём от комплексных амплитуд
и перейдём от комплексных амплитуд и
и к комплексам действующих значений
к комплексам действующих значений и
и
По первому закону Кирхгофа, алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы равна нулю:

Подставив вместо 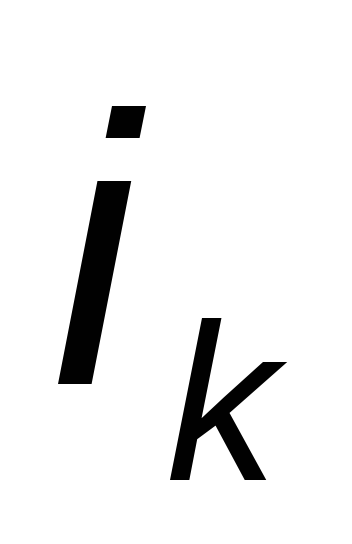 выражение
выражение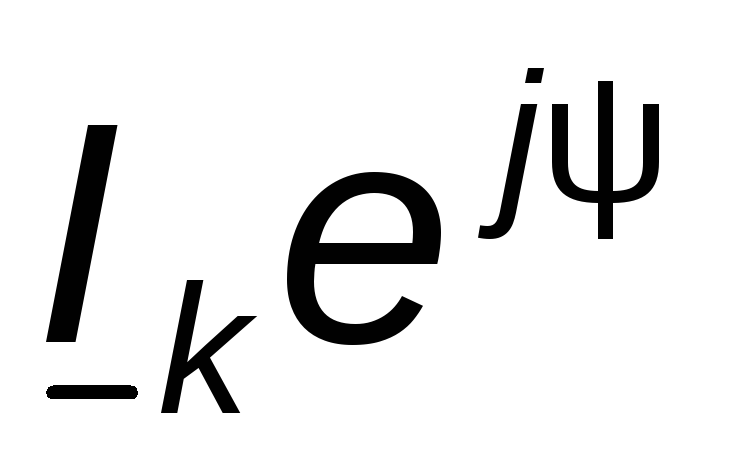 и вынеся
и вынеся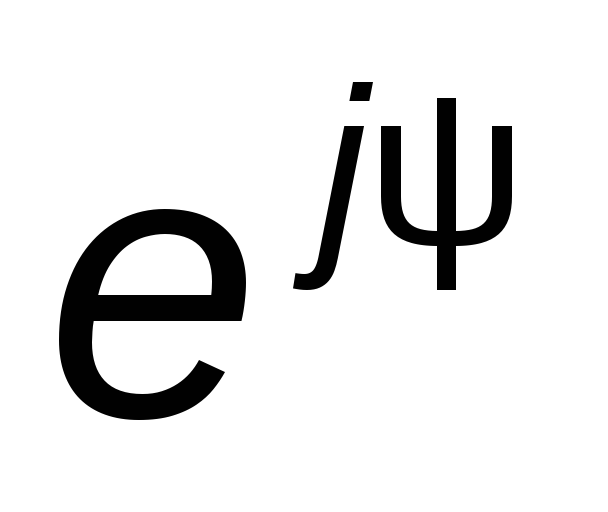 за скобку, получим
за скобку, получим .
Таким образом,
.
Таким образом,
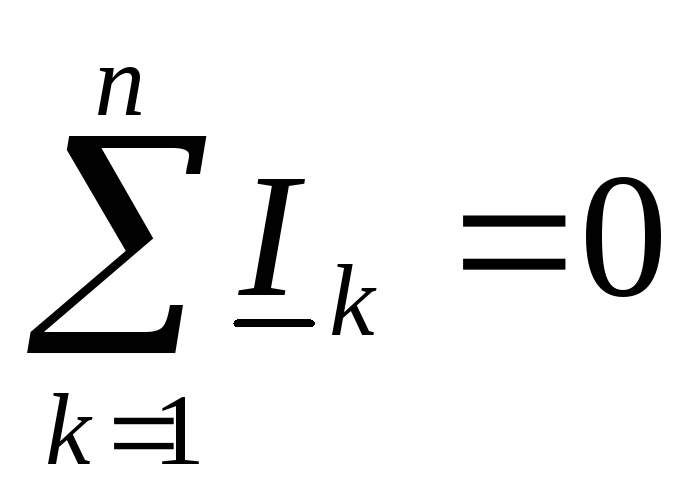 — первый
закон Кирхгофа в комплексной форме.
— первый
закон Кирхгофа в комплексной форме.
Для замкнутого контура сколь угодно сложной электрической цепи синусоидального тока можно составить уравнение по второму закону Кирхгофа и представить в комплексной форме:
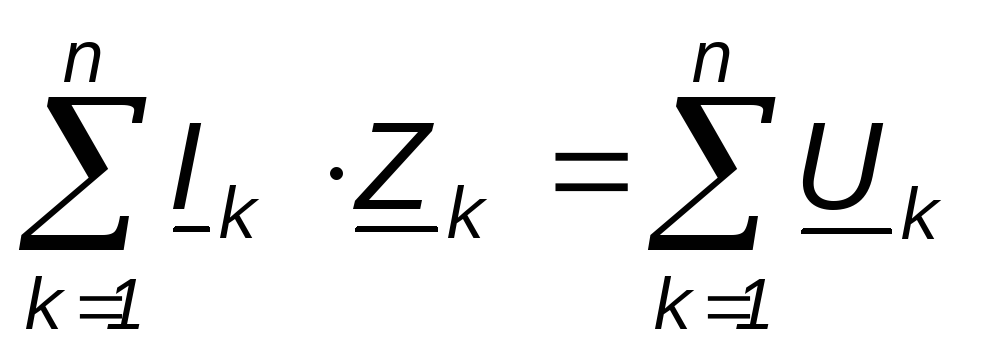
Пассивные элементы r, l, c в цепи синусоидального тока
1) Резистивный элемент
В электрической
цепи с резистивным элементом R ток
изменяется по синусоидальному закону
с начальной фазой  ,то
есть
,то
есть
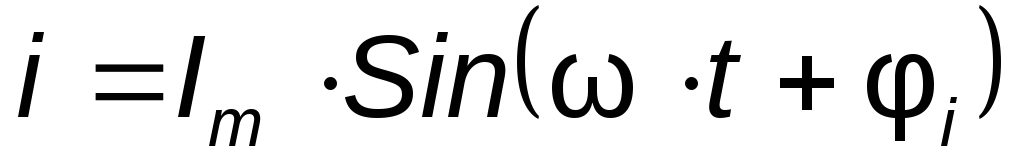
Напряжение на зажимах резистора
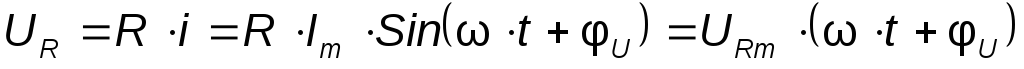 где
где 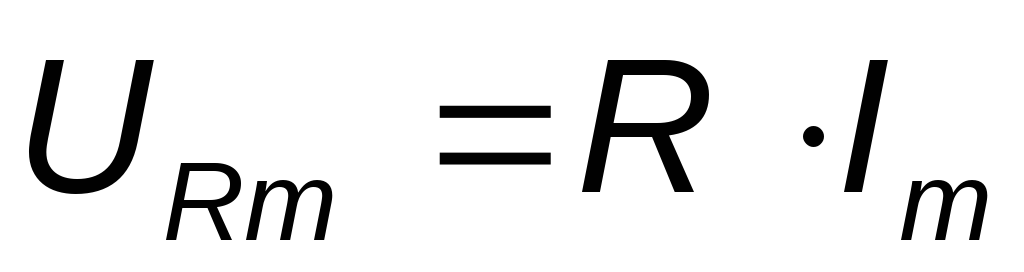 — амплитудное значение напряжения на
зажимах резистора,
— амплитудное значение напряжения на
зажимах резистора,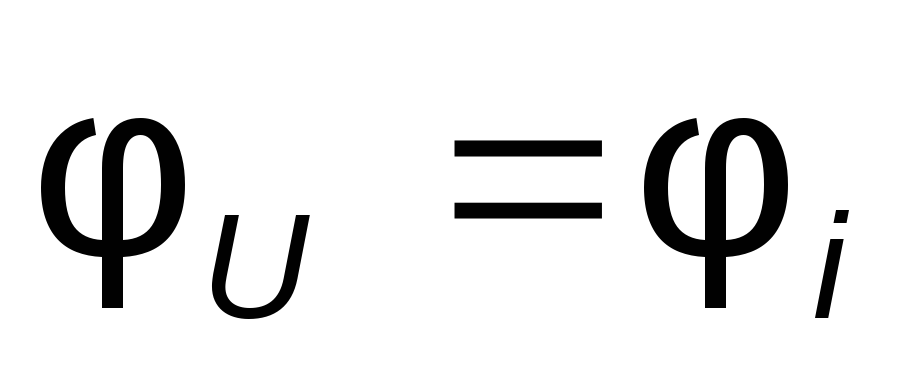 — начальные фазы напряжения и тока.
Кривые изменения напряжения
— начальные фазы напряжения и тока.
Кривые изменения напряжения и токаi (рис. 3.6б) в один и тот же момент времени
t достигают максимального значения
и одновременно проходят нулевые
значения. Иначе говоря, обе кривые
совпадают по фазе (рис. 3.6в).
и токаi (рис. 3.6б) в один и тот же момент времени
t достигают максимального значения
и одновременно проходят нулевые
значения. Иначе говоря, обе кривые
совпадают по фазе (рис. 3.6в).
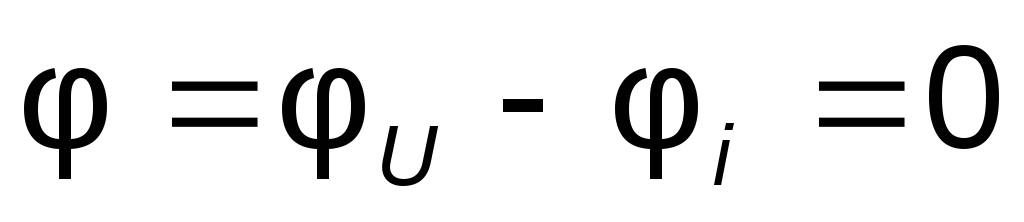
Векторы  и
и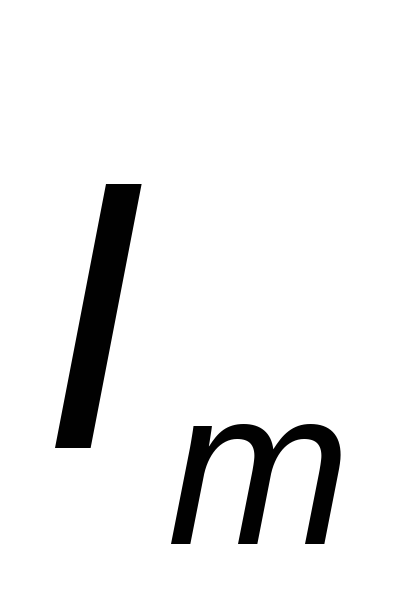 совпадают по направлению (уголφ=0).
Переходя к действующим значениям
можно записать
совпадают по направлению (уголφ=0).
Переходя к действующим значениям
можно записать
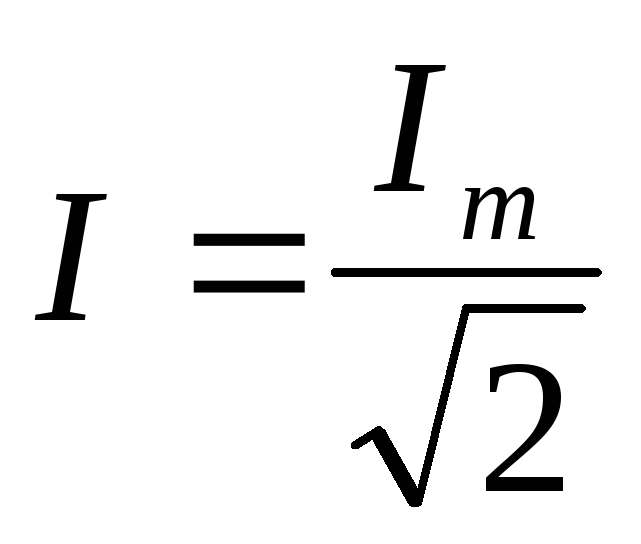
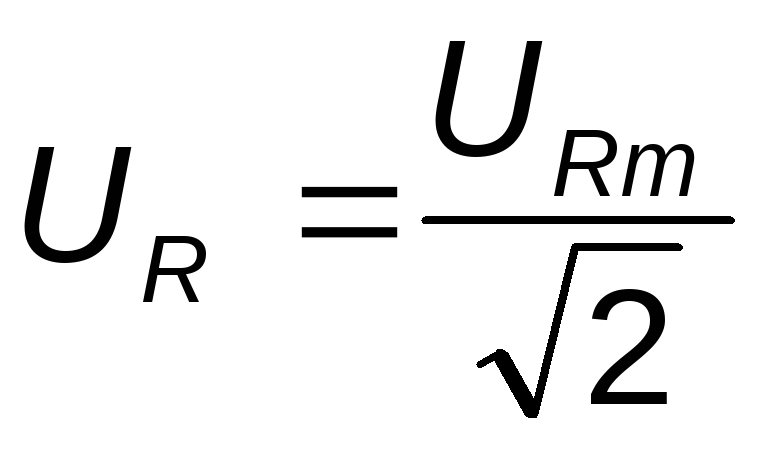
Сопротивление переменному току будет больше, чем постоянному за счет неравномерного распределения тока в проводе и потерь энергии в окружающую среду. Поэтому в отличие от сопротивления постоянному току сопротивление R в цепи переменного тока называется активным.
2) Индуктивный элемент
Изменение тока в
цепи с индуктивностью L (рис. 3.7а)
вызывает возникновение Э.Д.С. самоиндукции 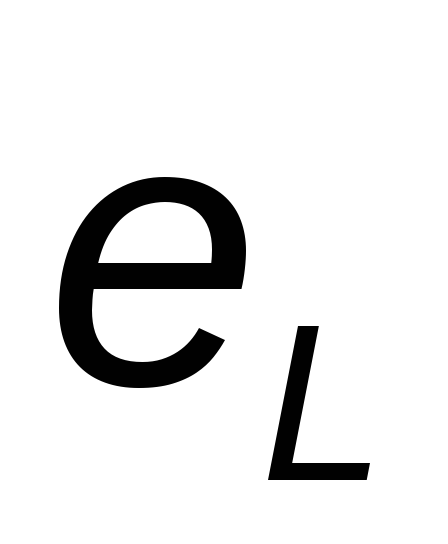 ,
которая по закону Ленца противодействует
изменению тока. При увеличении тока
Э.Д.С.
,
которая по закону Ленца противодействует
изменению тока. При увеличении тока
Э.Д.С.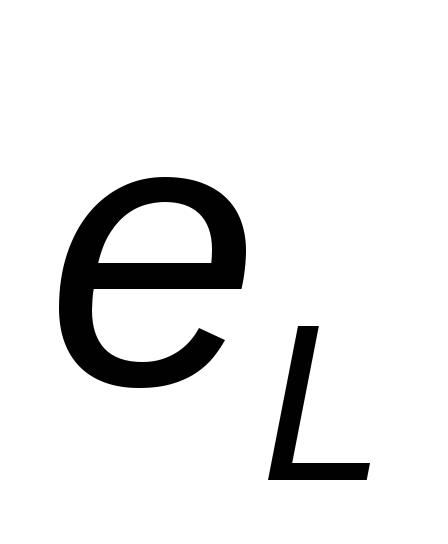 действует навстречу току, а при
уменьшении — в направлении тока,
противодействуя его изменению.
Показанные на рис. 3.7а положительные
направления
действует навстречу току, а при
уменьшении — в направлении тока,
противодействуя его изменению.
Показанные на рис. 3.7а положительные
направления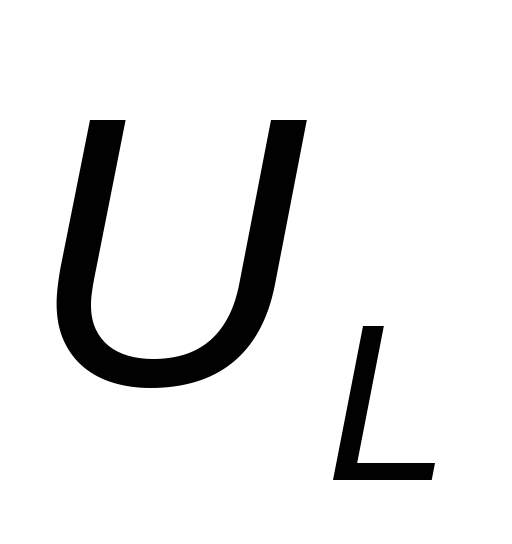 и
и имеют место только в течение некоторого
узкого
промежутка времени. Для тока, изменяющегося
по гармоническому закону
имеют место только в течение некоторого
узкого
промежутка времени. Для тока, изменяющегося
по гармоническому закону 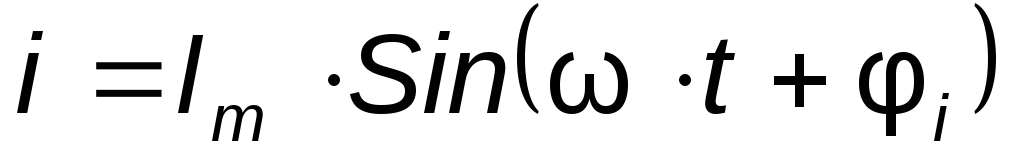 и приL= const Э.Д.С.
самоиндукции
и приL= const Э.Д.С.
самоиндукции

Чтобы в цепи протекал ток, требуется иметь на зажимах напряжение, уравновешивающее Э.Д.С. самоиндукции, равное ей по значению и противоположное по знаку.
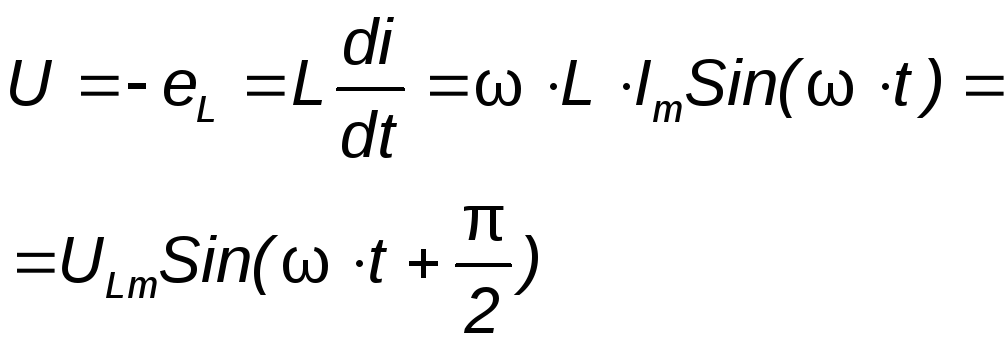
где 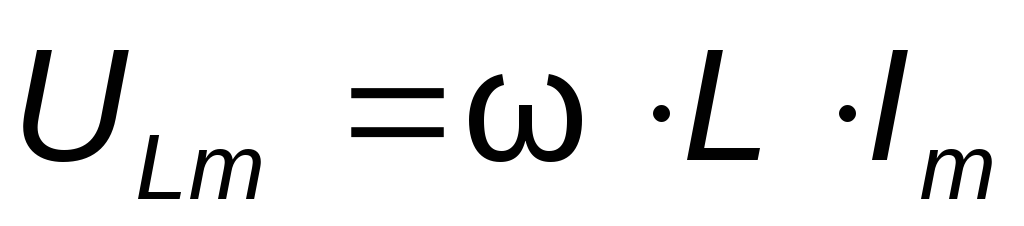 — амплитуда напряжения.
— амплитуда напряжения.
Произведение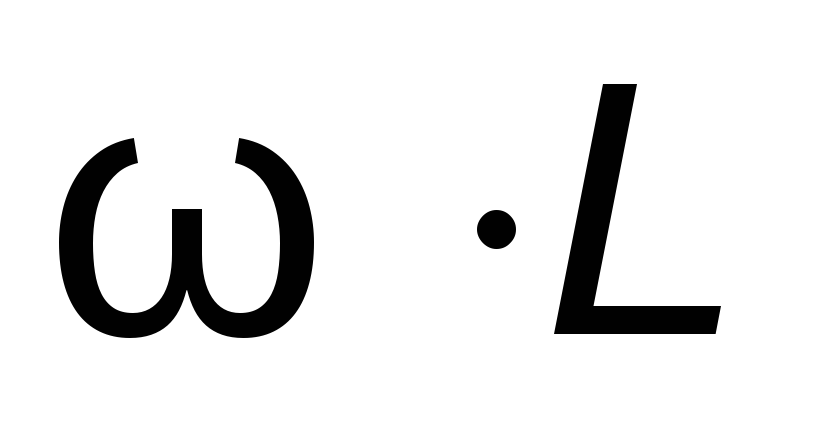 обозначается
обозначается ,называетсяиндуктивным
сопротивлением и измеряется в Омах:
,называетсяиндуктивным
сопротивлением и измеряется в Омах:
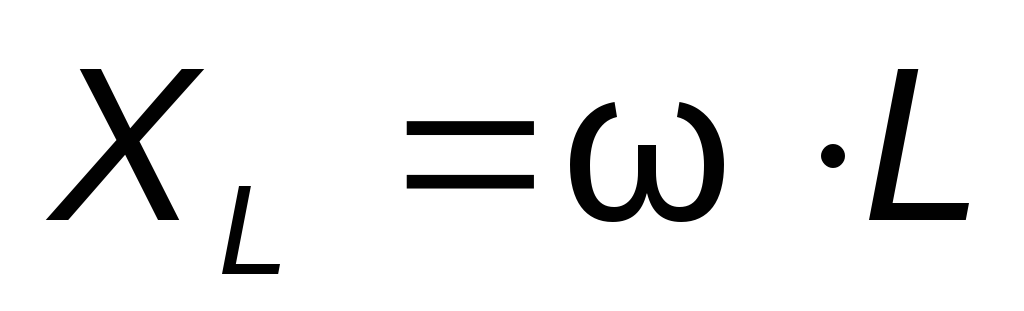
Из выражения 3.18
следует, что на участке цепи с
индуктивностью L
напряжение опережает ток на четверть
периода. На рис. 3.7в вектор напряжения  опережает вектор токаi на 900,
а комплекс (вектор) Э.Д.С. самоиндукции
находится в противофазе с комплексом
напряжения
опережает вектор токаi на 900,
а комплекс (вектор) Э.Д.С. самоиндукции
находится в противофазе с комплексом
напряжения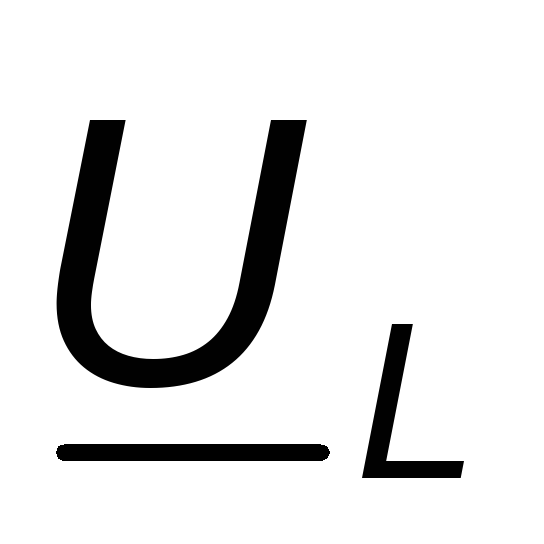
индуктивное
сопротивление пропорционально 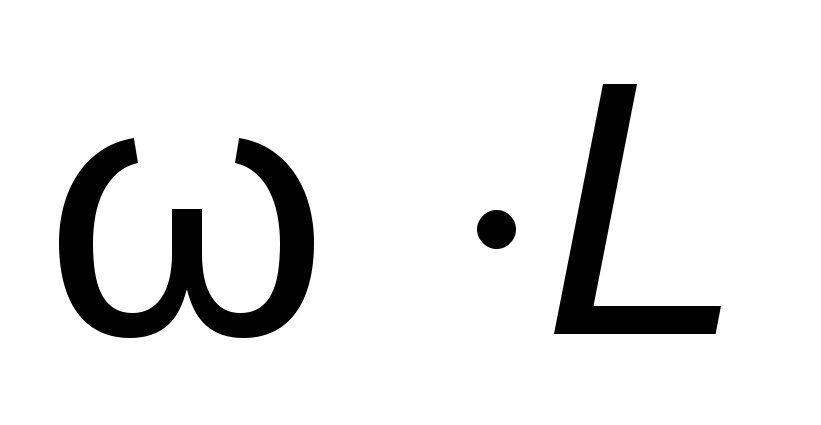 Если R =0, то средняя активная мощность
равна 0
Если R =0, то средняя активная мощность
равна 0
Законы Кирхгофа и Ома

|
|
|
|
|
| 29 | ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.17. Схема замещения катушки индуктивности а –– на постоянном токе; б –– на низких частотах; в –– на высоких частотах
Rк –– активное сопротивление катушки; Cп –– паразитная межвитковая ёмкость
пользовать один резистивный элемент). С ростом частоты возрастёт влияние межвитковой ёмкости (витки выполнены из изолированного провода, таким образом два соседних можно рассматривать как конденсатор) (рис. 1.17).
На сверхвысоких частотах резко возрастает роль индуктивности и ёмкости выводов катушки индуктивности.
1.3. Законы Кирхгофа и Ома
Закон Ома и два закона (иногда их называют правилами) Кирхгофа являются основополагающими законами электротехники. Они полностью определяют электрическое состояние электрических цепей и лежат в основе всех электротехнических расчетов.
1.3.1. Закон Ома
Закон Ома, связывающий напряжение и ток в электрической цепи, был экспериментально открыт немецким физиком Георгом Симоном Омом (1787 –– 1854 гг.) в 1827 г.
Для пассивного участка цепи (рис. 1.18) закон Ома имеет вид:
i = Ru
где R –– сопротивление цепи.
2.4.2. Законы ома и кирхгофа в комплексном виде
Закон Ома в комплексном виде:
Ỉ=Ủ/Zили Ỉ=Y∙Ủ, (2.26)
где Ỉ – ток, протекающий в электрической цепи,
Ủ – напряжение. приложенное к электрической цепи,
Y– комплексная проводимость электрической цепи,
Z– комплексное сопротивление электрической цепи.
Первый закон Кирхгофа. Сумма токов в проводах, сходящихся в узле электрической цепи равна нулю:
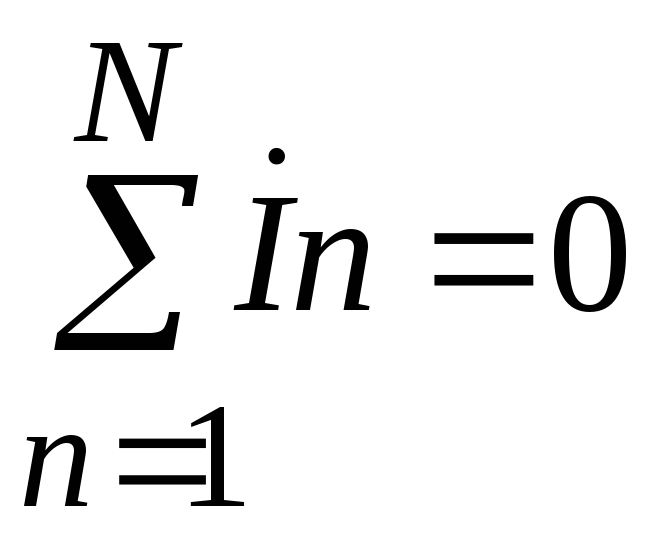 .
(2.27)
.
(2.27)
Второй закон Кирхгофа. Сумма комплексных э.д.с. или напряжений, действующих в замкнутом контуре, равна сумме падений напряжений на элементах этого контура.
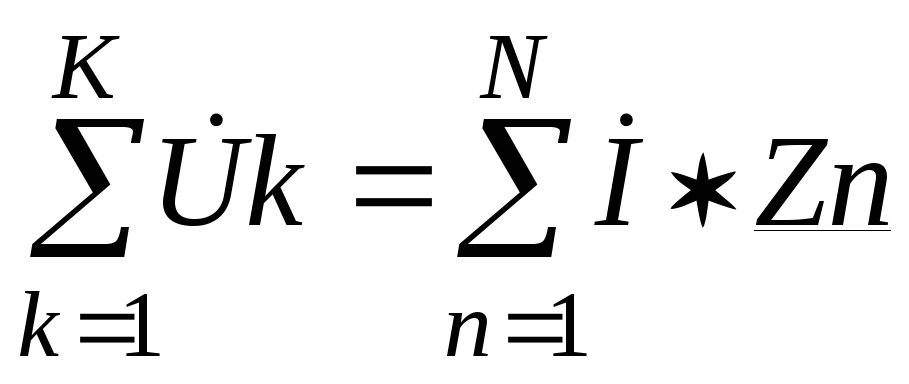 (2.28)
(2.28)
Законы Ома и Кирхгофа справедливы как для мгновенных, так и для действующих значений э.д.с. напряжений и токов.
Действующие(эффективное или среднеквадратическое напряжение) определяется выражением:
 ,
(2.29)
,
(2.29)
где T – период колебаний напряжения, равный 1/f,
f – частота колебаний напряжения.
При
строго синусоидальной форме колебаний
действующее напряжение, равно:
U=Um/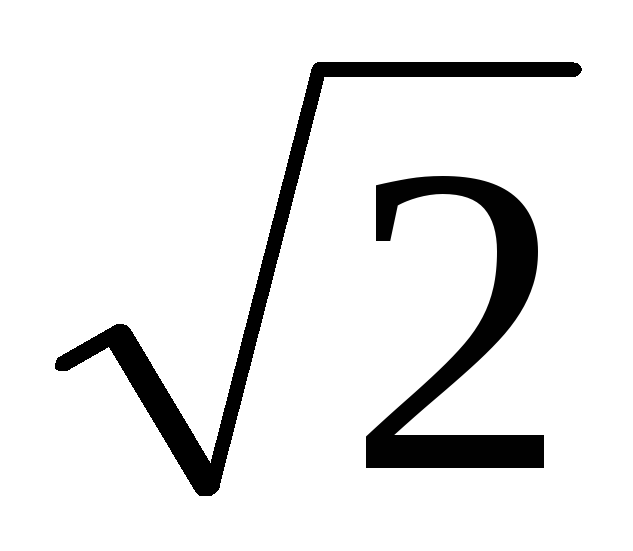 ,
(2.30)
,
(2.30)
где Um-максимальное значение напряженияu(t).
Аналогично определяются действующие значения э.д.с. и токов.
2.4.3. Построение векторных диаграмм на вращающейся комплексной плоскости
Для облегчения построения векторных диаграмм на вращающейся плоскости необходимо запомнить следующие основные положения:
а) В цепи с активным сопротивлением ток и напряжение совпадают по фазе.
б) В идеализированной цепи только с индуктивным сопротивлением без потерь напряжение по фазе опережает ток на угол, равный 90 градусов
в) В цепи с чисто емкостным сопротивлением без потерь ток опережает по фазе напряжение на угол +90 градусов.
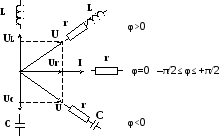
Рис.2.1.Мнемоническая схема, поясняющая возможные повороты
радиусов-векторов при различном включении r-L-Cэлементов.
При построении векторных диаграмм надо начинать построение с вектора напряжения или тока общего для всей анализируемой цепи. В частности при последовательном включение элементов цепи надо начинать с построения вектора тока, протекающего через все элементы цепи. При параллельном включении элементов цепи построение векторной диаграммы надо начинать с вектора общего приложенного напряжения, а затем строить вектора токов, протекающих через каждую из ветвей электрической цепи. Возможные сдвиги фаз векторов напряжения в электрических цепях, состоящих из различных комбинаций r-L-C элементов, приведены на мнемонической схеме (см. рис.2.1.).
Радиус-вектора на схеме и ниже выделяются жирным шрифтом или точками (черточками) над ними.
2.4.4. Резонанс напряжений в цепи, состоящей из последовательно включеных катушки индуктивности и конденсатора
Рассмотрим примеры такого анализа в предположении, что величины сопротивления, емкости и индуктивности не изменяются во времени и не зависят от приложенного напряжения и токов (см. рис.2.2).
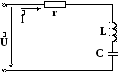
Рис.2.2.Электрическая схема последовательно включенных r-L-C- элементов.
Процессы, происходящие в исследуемой цепи (в соответствии со вторым законом Кирхгофа) описываются (при постоянстве величин элементов во времени и независимости их от величины протекающего тока) линейным интегрально-дифференциальным уравнением:
u(t)=ri(t)+Ldi(t)/dt+1/C ∫i(t)dt, (2.31)
где u(t) – переменное напряжение, подаваемое от источника на колебательный контур,
i(t) – переменный ток, протекающий в цепи,
L – индуктивность,
r – активное сопротивление катушки индуктивности,
С – емкость конденсатора.
Сопротивление (r), индуктивность (L) и емкость (C) образуют колебательный контур, в котором возможен резонанс напряжений. Термин «резонанс напряжения» подразумевает, что при равенстве Хl=Хc, переменные напряжения на элементах контура L и C увеличивается в Q раз по сравнению с напряжением подаваемым от источника на контур. Под величиной Q понимается добротность контура, равная Q=Хс/r.
При принятых предположениях уравнение (2.31) может быть представлено в следующем виде:
u(t)=i(t)*{r+j[Xl+Xc]}. (2.32)
Откуда следует выражение для комплексного сопротивления контура
Z=r+j{Xl–Xc}.
При резонансе напряжений, когда Хl=Хс, Z=r, то есть сопротивление контура оказывается активным, а ток, протекающий через контур, достигает максимальной величины, равной i(t)макс=u(t)/r.
В данном случае построение векторной диаграммы надо начинать с общего для цепи вектора тока (Ỉ), затем строятся векторы напряжений. При последовательном соединении катушки индуктивности и емкости общее реактивное сопротивление цепи X равно алгебраической разности индуктивного и емкостного сопротивлений Xl и Хc. Приложенное к такой цепи напряжение можно представить в виде векторной суммы вектора падения напряжения на активном сопротивлении (U r), совпадающего по фазе с вектором тока; вектора падения напряжения на индуктивности (Ul), опережающего ток по фазе на угол 90° и вектора падения напряжения на емкости (Uc), отстающего по фазе от вектора тока на угол 90°.При этом возможны следующие случаи:
а) Индуктивное сопротивление больше емкостного (Хl>ХС). В этом случае входное напряжение будет опережать ток по фазе на угол φ (см. рис. 2.3.).
б) Емкостное сопротивление больше индуктивного (Хl<Хс). При этом ток опережает напряжение на угол φ. Векторная диаграмма тока и напряжений показана на рис. 2.4.
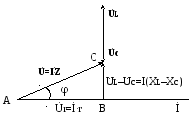

Uс–UL
Рис. 2.3 Рис. 2.4
в). Индуктивное сопротивление равно емкостному (Хl=Xс). Соответственно полное реактивное сопротивление цепи (Х) равно нулю, а полное сопротивление цепиZ=r, т.е. достигает своего минимального значения. При этом ток будет по фазе совпадать с напряжением, т.е. уголφ=0.Векторная диаграмма токов и напряжений для этого случая приведена на рис. 2.5.

Явление резонанса напряжений происходит также в кварцевых резонаторах, которые широко используются в автогенераторах колебаний.
Законы Ома и Кирхгофа в комплексной форме.
Урав-ие представляет собой закон Ома для цепи синусоидального тока в комплексной форме
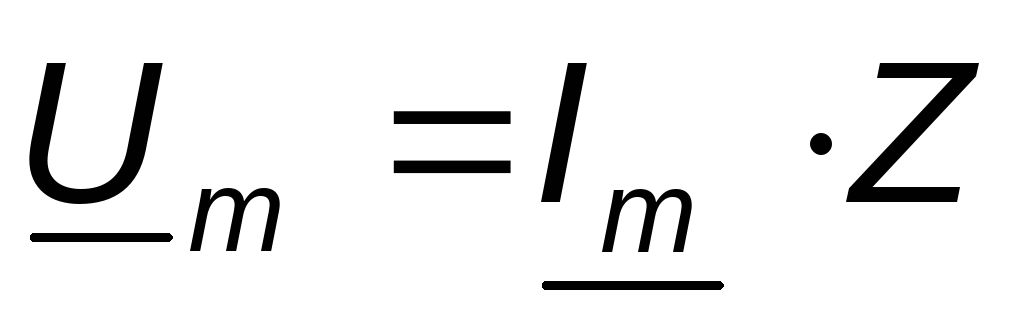 (3,9)
(3,9)
где Z – комплексное сопротивление, Ом.
В общем случае Z имеет некоторую действительную часть R и некоторую мнимую часть jX,
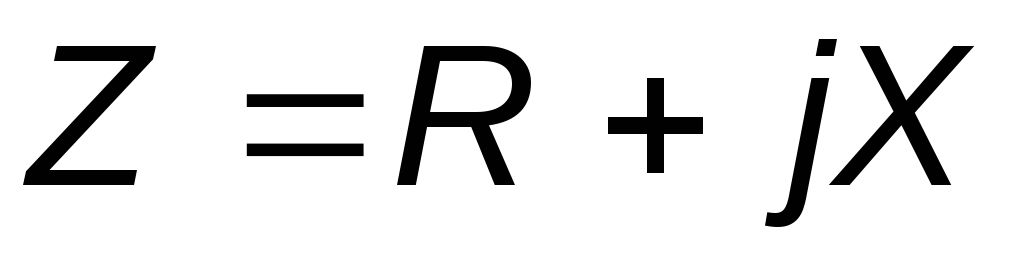
Уравнение 3.9 можно
записать иначе. Разделим обе его части
на  и перейдём от комплексных амплитуд
и перейдём от комплексных амплитуд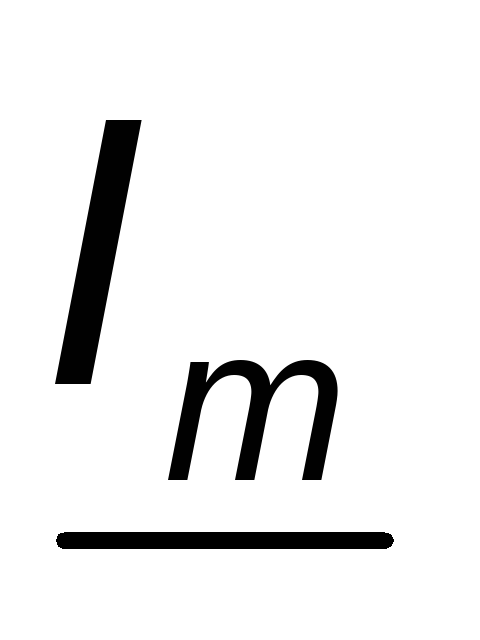 и
и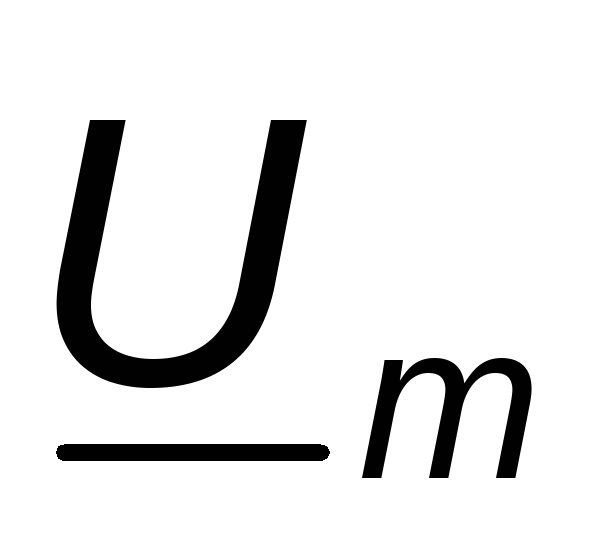 к комплексам действующих значений
к комплексам действующих значений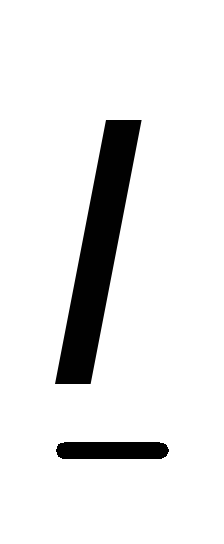 и
и
По первому закону Кирхгофа, алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы равна нулю:
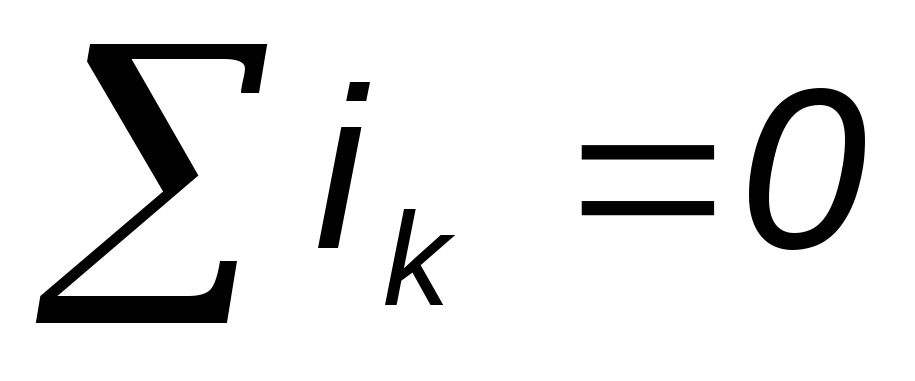
Подставив вместо 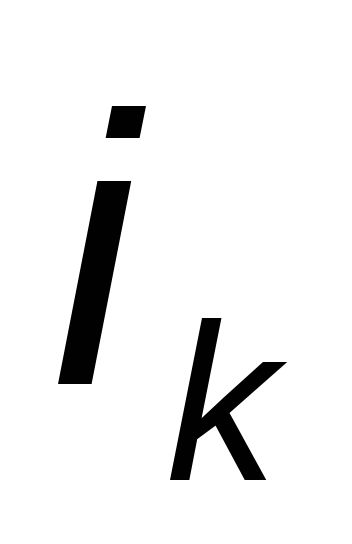 выражение
выражение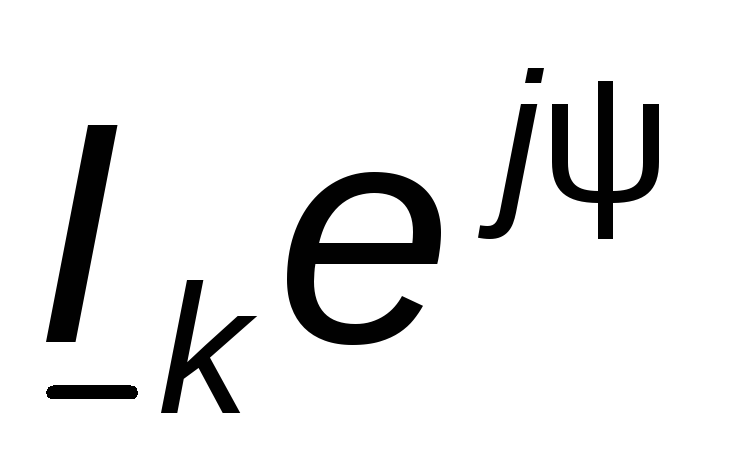 и вынеся
и вынеся за скобку, получим
за скобку, получим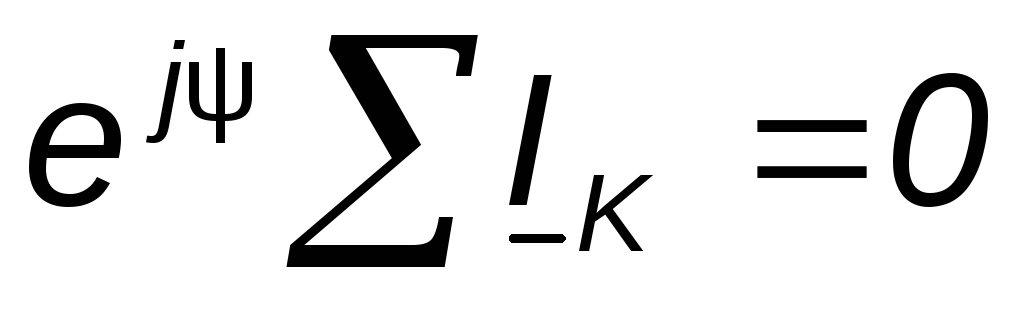 .
Таким образом,
.
Таким образом,
 — первый
закон Кирхгофа в комплексной форме.
— первый
закон Кирхгофа в комплексной форме.
Для замкнутого контура сколь угодно сложной электрической цепи синусоидального тока можно составить уравнение по второму закону Кирхгофа и представить в комплексной форме:
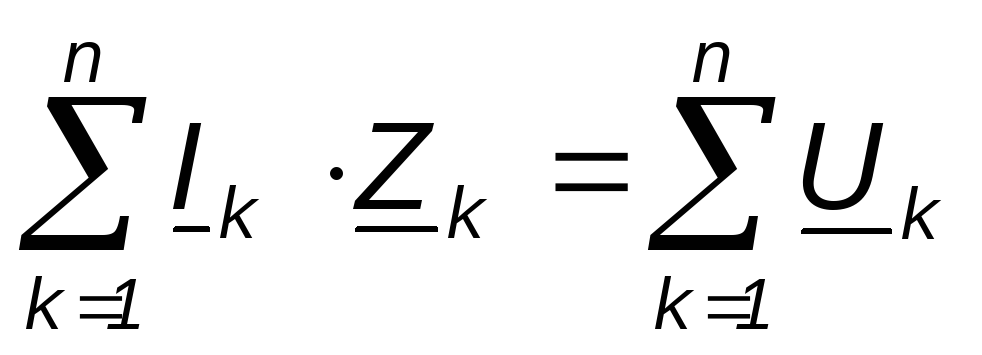
Пассивные элементы r, l, c в цепи синусоидального тока
1) Резистивный элемент
В электрической
цепи с резистивным элементом R ток
изменяется по синусоидальному закону
с начальной фазой  ,то
есть
,то
есть
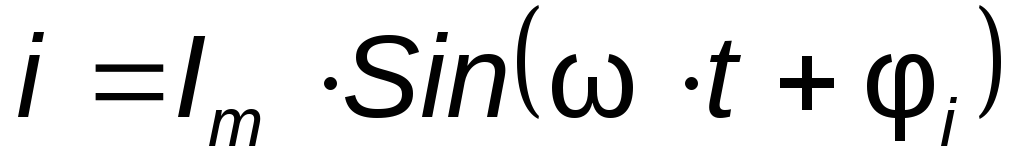
Напряжение на зажимах резистора
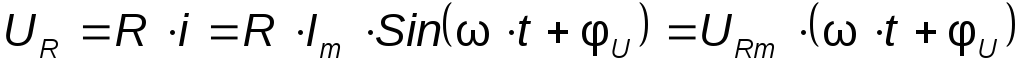 где
где 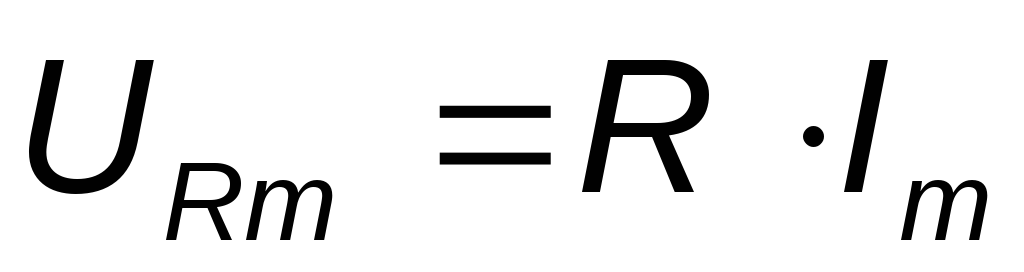 — амплитудное значение напряжения на
зажимах резистора,
— амплитудное значение напряжения на
зажимах резистора,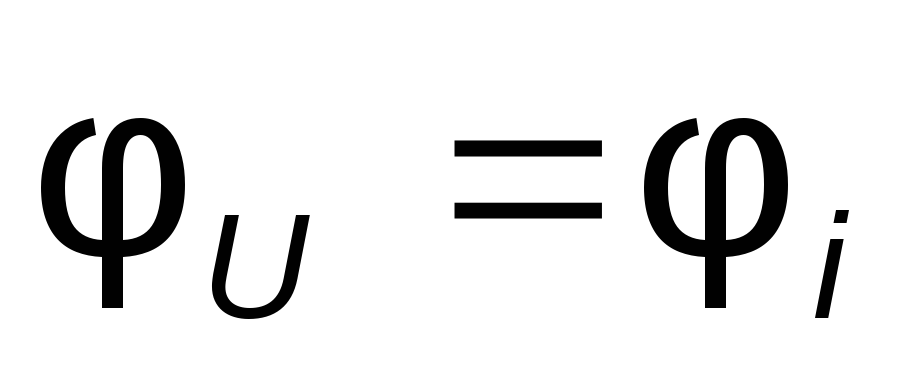 — начальные фазы напряжения и тока.
Кривые изменения напряжения
— начальные фазы напряжения и тока.
Кривые изменения напряжения и токаi (рис. 3.6б) в один и тот же момент времени
t достигают максимального значения
и одновременно проходят нулевые
значения. Иначе говоря, обе кривые
совпадают по фазе (рис. 3.6в).
и токаi (рис. 3.6б) в один и тот же момент времени
t достигают максимального значения
и одновременно проходят нулевые
значения. Иначе говоря, обе кривые
совпадают по фазе (рис. 3.6в).

Векторы  и
и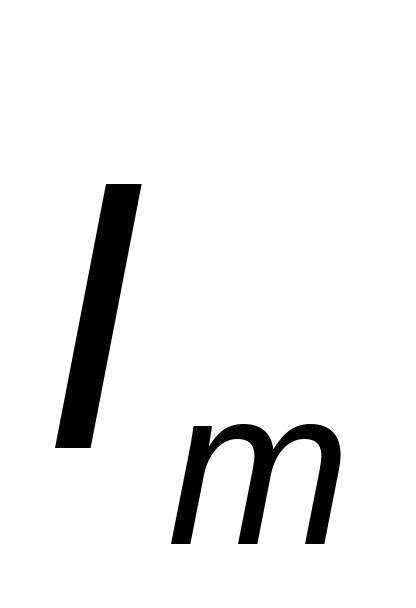 совпадают по направлению (уголφ=0).
Переходя к действующим значениям
можно записать
совпадают по направлению (уголφ=0).
Переходя к действующим значениям
можно записать
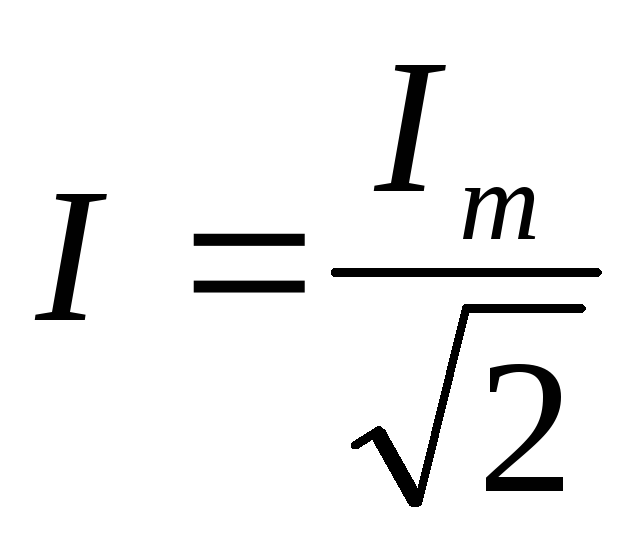
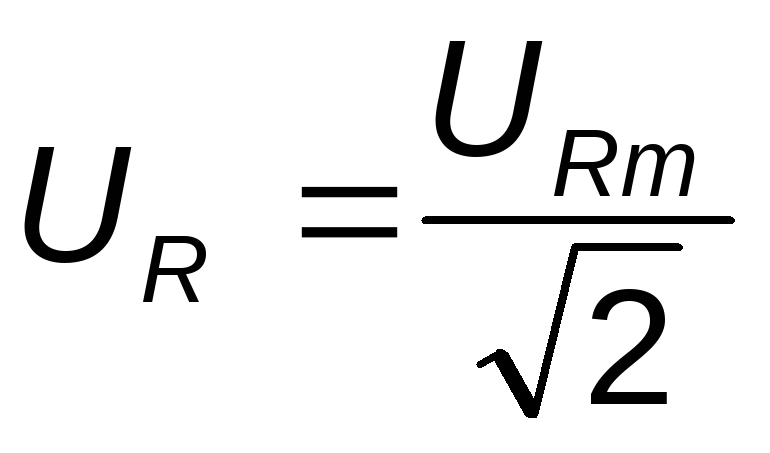
Сопротивление переменному току будет больше, чем постоянному за счет неравномерного распределения тока в проводе и потерь энергии в окружающую среду. Поэтому в отличие от сопротивления постоянному току сопротивление R в цепи переменного тока называется активным.
2) Индуктивный элемент
Изменение тока в
цепи с индуктивностью L (рис. 3.7а)
вызывает возникновение Э.Д.С. самоиндукции 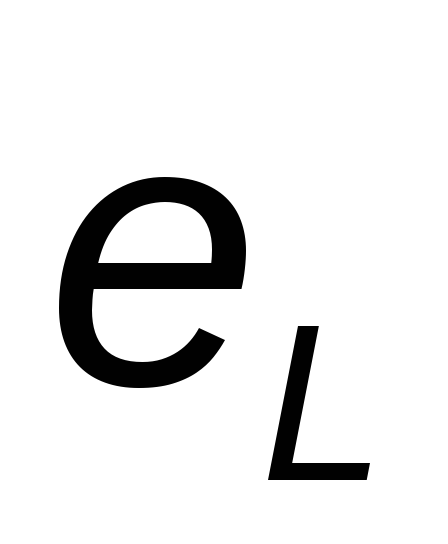 ,
которая по закону Ленца противодействует
изменению тока. При увеличении тока
Э.Д.С.
,
которая по закону Ленца противодействует
изменению тока. При увеличении тока
Э.Д.С. действует навстречу току, а при
уменьшении — в направлении тока,
противодействуя его изменению.
Показанные на рис. 3.7а положительные
направления
действует навстречу току, а при
уменьшении — в направлении тока,
противодействуя его изменению.
Показанные на рис. 3.7а положительные
направления и
и имеют место только в течение некоторого
узкого
промежутка времени. Для тока, изменяющегося
по гармоническому закону
имеют место только в течение некоторого
узкого
промежутка времени. Для тока, изменяющегося
по гармоническому закону 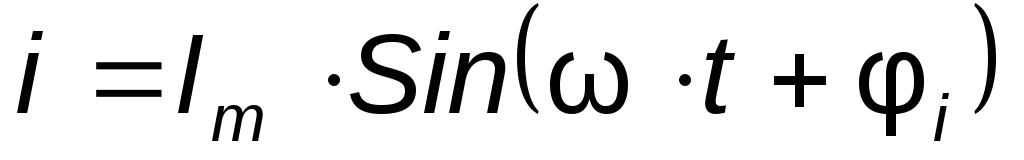 и приL= const Э.Д.С.
самоиндукции
и приL= const Э.Д.С.
самоиндукции
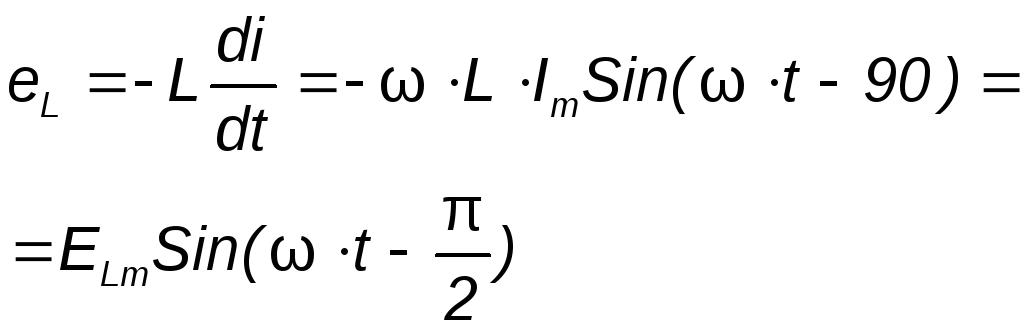
Чтобы в цепи протекал ток, требуется иметь на зажимах напряжение, уравновешивающее Э.Д.С. самоиндукции, равное ей по значению и противоположное по знаку.
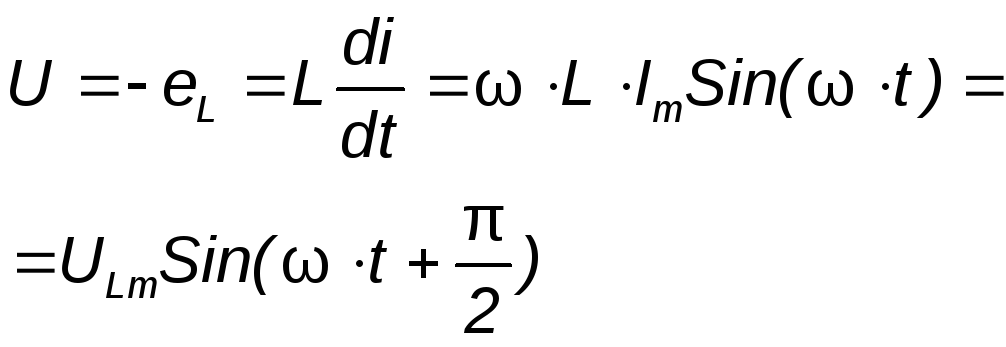
где 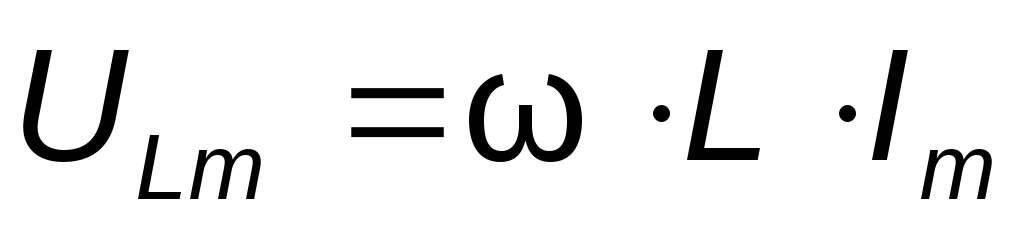 — амплитуда напряжения.
— амплитуда напряжения.
Произведение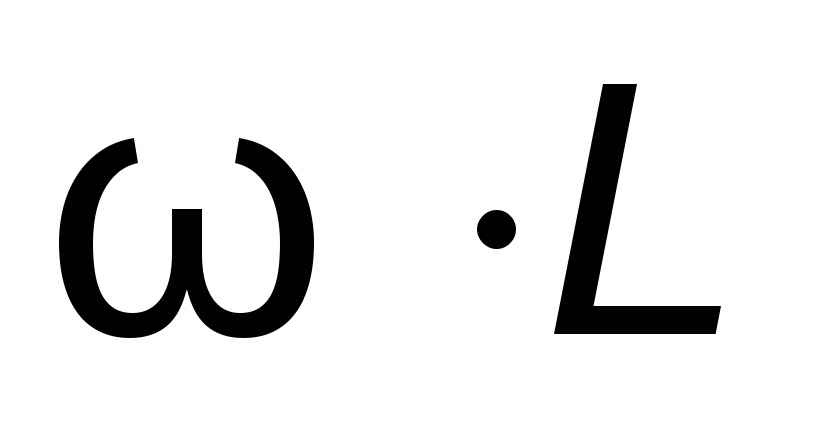 обозначается
обозначается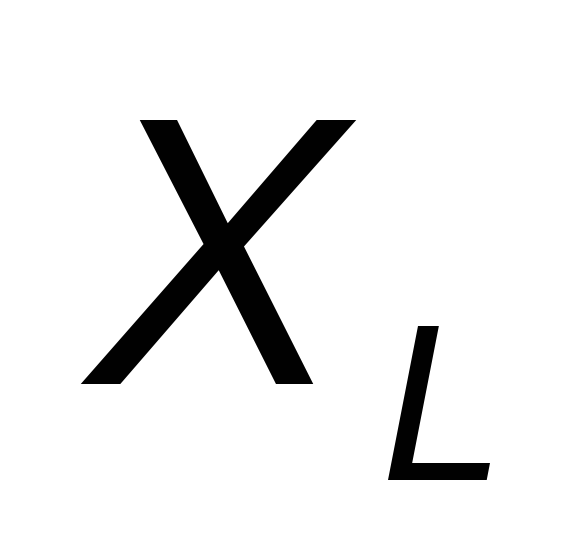 ,называетсяиндуктивным
сопротивлением и измеряется в Омах:
,называетсяиндуктивным
сопротивлением и измеряется в Омах:
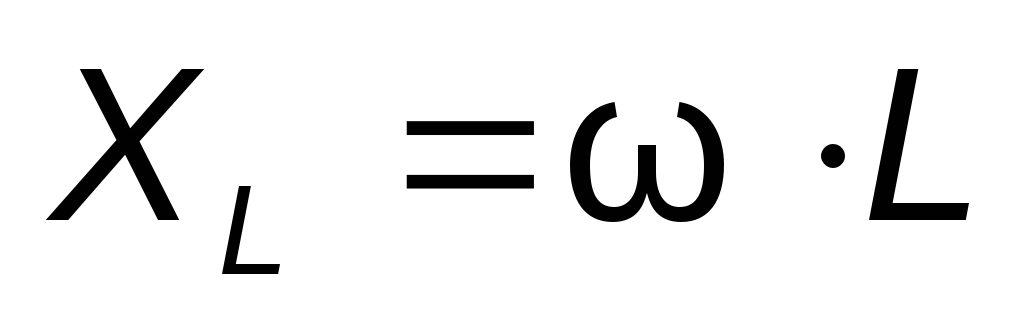
Из выражения 3.18
следует, что на участке цепи с
индуктивностью L
напряжение опережает ток на четверть
периода. На рис. 3.7в вектор напряжения 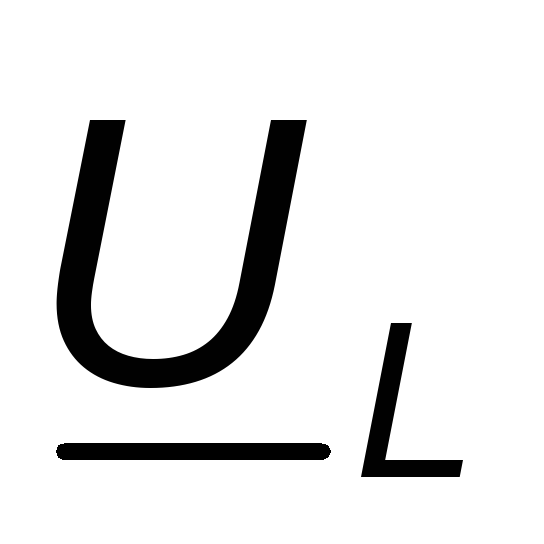 опережает вектор токаi на 900,
а комплекс (вектор) Э.Д.С. самоиндукции
опережает вектор токаi на 900,
а комплекс (вектор) Э.Д.С. самоиндукции  находится в противофазе с комплексом
напряжения
находится в противофазе с комплексом
напряжения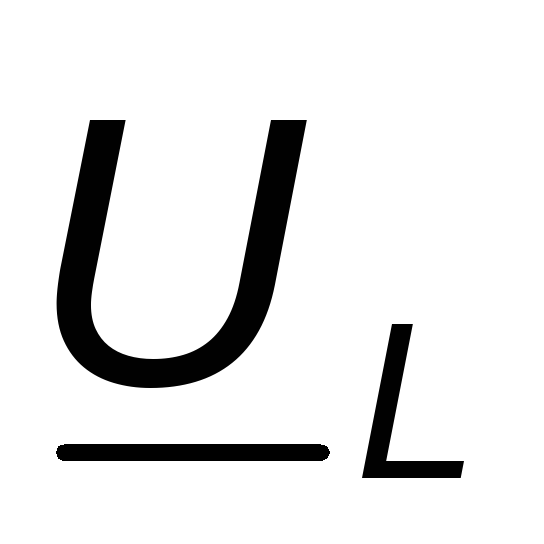
индуктивное
сопротивление пропорционально 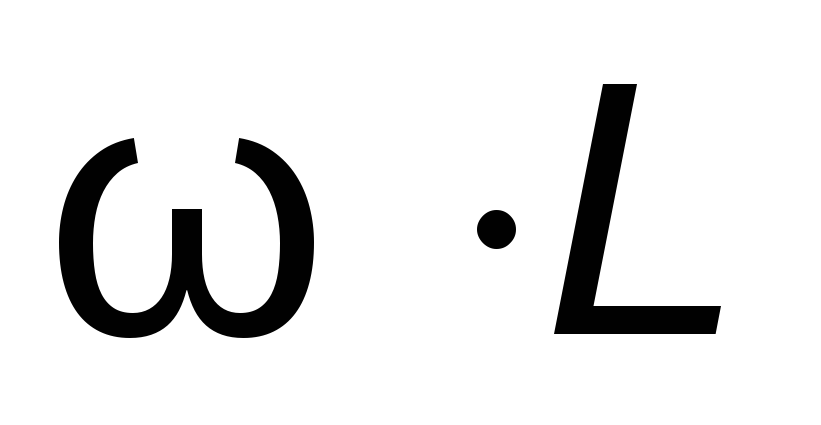 Если R =0, то средняя активная мощность
равна 0
Если R =0, то средняя активная мощность
равна 0