Расчет электрических цепей с применением законов Кирхгофа и Ома
Законы Кирхгофа наиболее общие. Они являются отдельным случаем универсальных уравнений электрического поля относительно произвольных электрических цепей с сосредоточенными параметрами. Закон Ома используется для расчета только линейных цепей.
Алгоритм расчета:
1. Начертить по принципиальной схеме схему замещения; упростить схему, преобразовав последовательно и параллельно соединенные резисторы в эквивалентные, пронумеровать ЭДС соответствующих ветвей, узлы; произвольно выбрать и обозначить положительные направления токов в ветвях.
2. Записать n – 1 уравнений по первому и m – (n – 1) уравнений по второму закону Кирхгофа, где n – количество узлов, m – количество ветвей в цепи. Если бы мы записывали n уравнений по первому закону Кирхгофа, то одно из них – это линейная комбинация оставшихся, что привело бы к линейной зависимости уравнений.
Источник тока J входит только в уравнение первого закона Кирхгофа (баланс тока в узлах) и переносится как известное в правую часть уравнения.
Смотрите еще:
Пример решения задачи по правилам Кирхгофа № 1
Пример решения задачи по правилам Кирхгофа № 2
Пример решения задачи по правилам Кирхгофа № 3
Рис. 1.
Ветвь с идеальным источником тока не учитывается, поскольку ее сопротивление бесконечно велико.
Уравнение по первому закону Кирхгофа при n – 1 = 2 для узла 1: – I1 – I3 + I4 + J = 0; для узла 2: I1 + I2 – I4 = 0.
Уравнение по второму закону Кирхгофа при m – (n – 1) = 4 – 2 = 2 для контура 1 (направление обхода указано пунктиром):
I1R1 + I2R2 = E1; для контура 2 (направление обхода то же самое, но можно было взять и противоположное): I2R2 – I3R3 – I4R4 = – E2.
Если среди компонент вектора I есть отрицательные, то это означает, что их направление противоположно положительному направлению, приведенному в схеме (рис. 1).
4. По закону Ома определить напряжения на элементах.
Сложность использования этого метода связана с чрезмерно большой размерностью систем уравнений.
Расчет сложных цепей постоянного тока по I и II законам Кирхгофа
Технология урока: интерактивная.
Тип урока: урок усвоения новых знаний.
Цели урока:
образовательные:
- помочь учащимся получить представление об основах расчета сложных цепей постоянного тока по I и II законам Кирхгофа;
- разобраться в выборе направлений протекания токов и обходов контуров;
воспитательные:
- воспитание информационной культуры учащихся, внимательности, аккуратности, дисциплинированности, организованности;
развивающие:
- развитие познавательных интересов;
- самоконтроля;
- умения конспектировать;
- памяти.
Оборудование: доска, компьютер, мультимедиа проектор, программа презентаций Microsoft Office PowerPoint 2003.
Методическое обеспечение урока: компьютерная презентация, электронные тесты, карточки самоконтроля учащихся, карточка контроля учащихся
План проведения урока.
Организационный момент – 2 мин.
Проверка и актуализация опорных знаний – 5 мин.
Объяснение нового материала – 20 мин.
Проверка усвоения новых знаний и умений – 12 мин.
Подведение итогов – 4 мин.
Домашнее задание – 2 мин.
План урока
| Этапы урока | Время | Организация работы |
| 1. Организационный момент | 1 мин. |
|
| 2. Формулировка темы урока. Постановка цели урока | 2 мин. |
|
| 3. Проверка опорных знаний | 4 мин. |
|
| 4. Объяснение нового материала | 20 мин. |
|
| 5. Проверка усвоения новых знаний и умений | 12 мин. |
|
| 6. Подведение итогов | 4 мин. |
|
| 7. Домашнее задание | 2 мин. |
|
Ход урока
Организационный момент
Учащиеся заходят в класс, приветствуют преподавателя, рассаживаются, достают тетради и ручки
Формулировка темы урока. Постановка цели урока
Учитель сообщает тему урока “Расчет сложных цепей постоянного тока по I и II законам Кирхгофа” и его план.
Сегодня мы проверим, как вы усвоили материал прошлого урока и научимся рассчитывать сложные цепи постоянного тока по законам Кирхгофа. Затем мы проверим, как вы усвоили новый материал.
У вас на столах лежат карточки самоконтроля. В них вы будете заносить полученные баллы за ответы на уроке, а также за тест. За каждый правильный устный ответ вы будете ставить себе один балл. За каждый правильный ответ на вопрос из теста оценивается также в один балл. На доске находится таблица соответствия набранных баллов оценке. При подведении итогов урока вы выставите эти оценки в карточки самоконтроля и сдадите их. Эти оценки будут выставлены в журнал.
В конце урока вы получите домашнее задание.
Проверка опорных знаний
Дайте определение сложной электрической цепи.
Сложными называются разветвленные электрические цепи со многими источниками энергии.
Дайте формулировку I закону Кирхгофа.
Алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным. Алгебраическая сумма токов, направленных к узлу равна сумме токов, направленных от узла.
где Ii – ток в узле,
n – число проводников, сходящихся в узле
Иными словами, сколько тока втекает в узел, столько из него и вытекает.
Дайте формулировку II закону Кирхгофа
Алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС, то суммарное падение напряжений равно нулю.
Объяснение нового материала
На рисунке представлена схема электрической цепи.
Для ее расчета, т.е. для определения токов во всех ее ветвях, необходимо составить систему уравнений по законам Кирхгофа. Общее число уравнений в системе должно соответствовать числу неизвестных токов, т.е. числу ветвей.
Давайте посчитаем количество ветвей в нашей электрической цепи.
Получилось пять ветвей, а значит и пять
неизвестных токов I1, I
По первому закону Кирхгофа составляется число уравнений, на единицу меньшее числа узлов цепи, поскольку уравнение для последнего узла есть следствие всех предыдущих уравнений и не дает ничего нового для расчета.
Посчитаем количество узлов электрической цепи.
В цепи три узла, значит по 1-му закону Кирхгофа надо составить (3 – 1 = 2) два уравнения.
По второму закону Кирхгофа составляются все недостающие уравнения для любых произвольно выбранных контуров цепи.
Посчитаем количество недостающих уравнений: 5 – 2 = 3.
В нашем примере по II закону Кирхгофа надо составить три уравнения.
Предварительно следует задаться (произвольно) направлением токов во всех ветвях цепи и направлением обхода выбранных контуров.
Заметим, что произвольность выбора направлений токов в ветвях цепи и направлений обхода контуров не влияет на конечный результат расчета. Если в результате расчетов некоторые из найденных токов будут иметь знак (–), то это будет означать, что их истинное направление противоположно предварительно принятому.
Зададим направление токов во всех ветвях цепи.
При составлении уравнений по первому закону Кирхгофа токи, подходящие к узлу, будем считать положительными и брать со знаком (+), а токи, отходящие от узла – отрицательными и брать со знаком (–).
По I закону Кирхгофа надо составить два уравнения. Для этого выберем любые два узла цепи. Например, первый и второй.
Узел 1: –I1 – I3 – I4 = 0
Узел 2: I1 – I2 + I4 + I5 = 0
Зададим направление обхода выбранных контуров.
При составлении уравнений по II закону Кирхгофа ЭДС и токи, совпадающие с выбранным направлением обхода контура будем брать со знаком (+), а несовпадающие – со знаком (–).
Контур I: I1R1 – I4R4 = E1
Контур II: I4R4 – I5R5 – I3R3 = E3
Контур III: I2R2 + I4R4 = –E2
Запишем систему уравнений.
–I1 – I3 – I4 = 0
I1 – I2 + I4 + I5 = 0
I1R1 – I4R4 = E1
I4R4 – I5R5 – I3R3 = E3
I2R2 + I4R4 = –E2
Решим полученную систему уравнений и определим токи во всех пяти ветвях этой цепи.
Выводы.
Количество уравнений по законам Кирхгофа = количество неизвестных токов цепи, т.е. количеству ветвей цепи.
- Количество уравнений по I закону Кирхгофа = количество узлов цепи – 1.
- Количество уравнений по II закону Кирхгофа = общее количество уравнений – количество уравнений по I закону Кирхгофа.
- Для уравнений по I закону Кирхгофа: токи входящие в узел записываются со знаком (+), а выходящие – со знаком (–).
- Для уравнений по II закону Кирхгофа: ЭДС и токи, совпадающие с выбранным направлением обхода контура записываются со знаком (+), а несовпадающие – со знаком (–).
Проверка усвоения новых знаний и умений.
Учащиеся выполняют тест (приложение 1). Проверяют его сами (приложение 2). Заполняют карточки самоконтроля (приложение 3). Выставляют себе отметки. Таблица соответствия отметок и баллов определяется учителем и выводится на доске.
Рефлексия.
Домашнее задание.
Учащиеся получают домашнее задание.
Презентация
Статья по физике (11 класс) по теме: Решение задач на применение законов Кирхгофа
Решение задач на применение законов Кирхгофа
Некрасов Александр Григорьевич, учитель физики
Статья относится к разделу : преподавание физики
Цели:
- Образовательная. Формировать понятие электрической цепи и ее элементов. Научится применять законы Кирхгофа для расчета сложных электрических цепей. Развивающая. Совершенствовать умения, активизировать познавательную деятельность учащихся через решение задач на расчет сложных электрических цепей.
- Воспитательная. Прививать культуру умственного труда, аккуратность, умение анализировать, видеть практическую ценность получаемых знаний, продолжить формирование коммуникативных умений.
Вид урока: практикум по решению задач.
Законы Кирхгофа применяются для расчета сложных электрических цепей.
Первый закон Кирхгофа: k=1nIk=0.
Второй закон Кирхгофа: k=1nuk=kEk.
Напомним правила знаков. Направления токов в узле выбирается произвольно. Притекающие в узел токи будем брать со знаком плюс, а вытекающие из узла – со знаком минус. Выбираем положительное направление обхода контура (обозначено овалом со стрелкой). Выбираем направление напряжения по направлению тока. Если «направление» напряжения совпадает с направлением обхода контура, то напряжение берется со знаком плюс. В противном случае – со знаком минус. Обозначим стрелкой над ЭДС направление возрастания потенциала (от катода к аноду). Если эта стрелка совпадает с направлением обхода контура, то E берется со знаком плюс, если нет, то с минусом.
Рассмотрим стандартную задачу на расчет сложной электрической цепи постоянного тока.
Задача1. Даны две батареи аккумуляторов с ЭДС E1=10 B с внутренним сопротивлением r1=1 Ом, E2=8 В и r2=2 Ом. Реостат имеет сопротивление R=6 Ом. Элементы цепи соединены по схеме, показанной на рисунке. Найти силу тока в батареях и реостате.
Дано:
E1=10 B
E2=8 B
r1=1 Ом
r2=2 Ом
R=6 Ом
Найти: I1, I2, I3=?
Решение:
Запишем уравнения законов Кирхгофа в соответствии с обозначениями на рисунке.
I1+I2-I3=0 u1-u2+0=E1-E20+u2+u3=E2
Так как u1=I1r1, u2=I2r2, u3=I3R, то
I1 +I2-I3=0 I1r1-I2r2+0=E1-E20+I2r2+I3R=E2.
Подставим в полученную систему данные, получим:
I1+I2-I3=0
1I1-2I2-I3=2
0+2I2+6I3=8 .
Решим эту систему по правилу Крамера. Найдем определитель системы:
∆=11-11-20026=1∙-2026-1∙1006-1∙1-206=-20.
Дополнительные определители для неизвестных:
∆I1=01-12-20826=0∙-2026-1∙2026-1∙2-282=-12-4+16=-32.
∆I2=10-1120086=1∙2086-0∙1006-1∙1-208=12-8=4.
∆I3=1101-22028=1∙-2286-1∙1208+0∙1-202=-20-8=-28.
Искомые значения токов определим по формуле Ik=∆Ik∆:
I1=3220=1,6 A, I2=-420=- 0,2 A, I3=2820=1,4 A.
Как видно, пришлось находить определители третьего порядка. Напомним один из способов их определения. Схема расчета определителя третьего порядка:
∆=a11a12a13a21a22a23a31a32a33=a11∙a22a23a32a33-a12∙a21a23a31a33+a13∙a21a22a31a32=
=a11a22a33-a32a23-a12a21a33-a31a23+a13(a21a32-a31a22).
Рассмотрим другие примеры.
Задача2. Резисторы с сопротивлениями R1=R2=1 Ом и R3=2 Ом и конденсаторы емкостью C1=2 нФ, C2=3 нФ включены в цепь с ЭДС E=10 B (смотри рисунок), Внутренним сопротивлением которого можно пренебречь. Определите заряды, установившиеся на конденсаторах [1].
Дано:
R1=R2=1 Ом
R3=2 Ом
E=10 B
C1=2 нФ
С2=3 нФ
q1=?; q2=?.
Решение:
Через конденсаторы постоянный ток не протекает. Тогда ток, который протекает по цепи, равен
I0=ER1+R2+R3=10 B4 Ом=2,5 А. Этот ток протекает через все резисторы. Чтобы определить заряды на конденсаторах, необходимо знать напряжения на них. Для этого воспользуемся вторым законом Кирхгофа. Поскольку всего два неизвестных, то и уравнений составим два.
u2+uC2=Eu2+u3+uC1=0.
Напряжение u2=I0R2=2,5∙1=2,5 B. Из первого уравнения находим uC2=E-u2=7,5 B. Найдем напряжение на R3: u3=I0R3=2,5∙2 = 5 B. Из второго уравнения uC1=-u2-u3=
=-7,5 B. Заряды определим по формуле q=Cu:
q1=C1uC1=2∙7,5=15 нКл
q2=C2uC2=3∙7,5=22,5 нКл. Это и есть ответы.
Приведем еще одну задачу в качестве примера применения законов Кирхгофа.
Задача 3. В схеме, изображенной на рисунке, ЭДС батареи E, сопротивление резистора R, индуктивности сверхпроводящих катушек — L1 и L2, причем L1>L2. Сначала замыкают ключ К1, а через некоторое ключ К2. Известно, что установившиеся токи через катушки L1 и L2 оказались одинаковыми. Определите силу тока, протекающего через резистор R в момент замыкания ключа К2. Внутренним сопротивлением батареи пренебречь [2].
Решение этой задачи, как и предыдущей, в указанных ссылках не приведено. Для решения также воспользуемся законами Кирхгофа.
Составим второе уравнение Кирхгофа при замкнутом ключе К1. Так как катушки индуктивности сверхпроводящие, то их омическое сопротивление равно нулю. Пусть в установившемся режиме сила тока равна I0. Имеем
uR+uL1=E. (1)
В некоторый момент времени сила тока равна i1. Перепишем (1) в виде:
i1R+L1∆i1∆t=E.
При замыкании ключа К2 соответствующие уравнения примут вид
uR+uL2=E и i2R+L2∆i2∆t=E.
Здесь необходимо отметить, что после установившегося режима ∆i∆t=0. Только в момент включения ключей эти производные отличны от нуля. Пусть ток i и есть тот ток, который изменяется в момент включения ключа К2. По правилу Ленца, этот ток будет направлен навстречу внешнему току I0=ER. А это значит, что в момент включения ключа К2 ток через резистор R уменьшится. Составим еще одно уравнение: uL2-uL1=0, или uL1=uL2. Так как uL=L∆I∆t, то L1∆I1∆t=
=L2∆I2∆t. В установившемся режиме сила тока I0. По условию задачи силы тока в катушках одинаковые, т. е. по I02 после установления при замыкании ключа К 2. Изменения ∆I1=i-I02, ∆I2=I02. Имеем L1i-L1I02=L2I22, откуда i=I02L1L1+L2. Ток, который протечет через резистор в момент включения ключа К 2 равен IR=I0-I02L1L1+L2=
=I0L1-L22L1. Так как I0=ER, тогда окончательно получим IR=EL1-L22RL1. По-видимому, это и будет ответом. Такого рода задачи хорошо проверяются на опыте. По крайне мере, можно зафиксировать скачок тока в резисторе и в какую сторону.
Задача4. Какой должна быть ЭДС E источника тока, чтобы напряженность электрического поля в плоском конденсаторе была равна E=2 кВ/м, если внутреннее сопротивление источника тока r=2 Ом, сопротивление резистора R=10 Ом, расстояние между пластинами конденсатора d=2 мм[3].
Для решения задачи воспользуемся вторым законом Кирхгофа для двух контуров, в которых указаны положительные направления обхода контуров.
uR+ur=E
uC-uR=0 .
Так как uR=I0R, ur=I0r, то I0=ER+r. Из второго уравнения uC=uR=ERR+r. Для плоского конденсатора uC=Ed. Тогда
E=uC(R+r)R = Ed(R+r)R. Это ответ.
Список использованной литературы.
- Москалев А. Н., Никулова Г. А..Физика. Готовимся к единому государственному экзамену. – М.: Дрофа, 2008. – 224.
- Физика. Большой справочник для школьников и поступающих в вузы / Ю. И. Дик, В. А. Ильин, Д. А. Исаев и др. – М.: Дрофа, 2008, — 735 с.
- Отличник ЕГЭ. Физика. Решение сложных задач. Под ред. В. А. Макарова, М. В. Семенова, А. А. Якуты. ФИПИ. – М.: — Интеллект-Центр, 2010.-368 с.
Законы Кирхгофа для электрической цепи
Правильнее было бы говорить правила Кирхгофа для расчетов сложных электрических цепей постоянного тока. Электрическая цепь на практике может состоять из нескольких резисторов и источников тока. Такие цепи называют разветвленными. Уравнения позволяющие провести расчеты, например, сил токов, текущих в сопротивлениях, в любых сетях можно составить, воспользовавшись законом Ома и законом сохранения заряда. Правила Кирхгофа являются следствиями вышеназванных законов и принципиально нового ни чего не привносят, однако, с их помощью можно упростить процедуру написания необходимых уравнений. Существует два правила Кирхгофа для электрических цепей постоянного тока. Одно правило называют правилом узлов, так как оно связывает в одно уравнение токи, сходящиеся в узле. Второе правило касается замкнутых контуров, которые можно выделить в сложной цепи.
Первый закон (правило) Кирхгофа
В электрической цепи в одной точке могут сходиться более двух проводников с токами, тогда такую точку цепи называют узлом (разветвлением). Учитывая, что сила тока алгебраическая величина для любого узла:
где N – число токов, которые сходятся в узле. Выражение (1) называют первым правилом Кирхгофа (правило узлов): сумма токов, текущих через сопротивления в цепи постоянного тока, с учетом их знака, сходящихся в узле, равна нулю.
Знак у тока (плюс или минус) выбирают произвольно, но при этом следует считать, что все входящие в узел токи имеют одинаковые знаки, а все исходящие из узла токи имеют противоположные входящим, знаки. Допустим, все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными.
Первое правило Кирхгофа дает возможность составить независимое уравнение, если в цепи k узлов.
Первое правило Кирхгофа является следствием закона сохранения заряда.
Второй закон (правило) Кирхгофа
Во втором правиле Кирхгофа рассматриваются замкнутые контуры, поэтому оно носит название правила контуров: Суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних электродвижущих сил (ЭДС) (), которые входят в рассматриваемый контур. В математическом виде второй закон Кирхгофа записывают как:
Величины называют падениями напряжения. До применения второго закона Кирхгофа выбирают положительное направление обхода контура. Это направление берется произвольно, либо по часовой стрелке, либо против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго правила для данного контура входит со знаком плюс. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника. Более правильно было бы сказать, что ЭДС считают положительной, если работа сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи в заданном направлении обхода контура является положительной величиной.
Второе правило Кирхгофа является следствием закона Ома.
Примеры решения задач
1.7. Законы Кирхгофа
Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа.
Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, чтоалгебраическая сумма токов, сходящихся в любом узле, равна нулю

Рис. 1.15
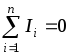 ,
(1.29)
,
(1.29) где 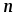 – число токов, сходящихся в данном узле.
– число токов, сходящихся в данном узле.
Например, для узла электрической цепи (рис. 1.15) уравнение по первому закону Кирхгофа можно записать в виде
 .
.
В этом уравнении токи, направленные к узлу, приняты положительными.
Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре
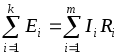 ,
(1.30)
,
(1.30)
где k– число источников
ЭДС;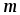 – число ветвей в замкнутом контуре;
– число ветвей в замкнутом контуре;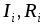 –
ток и сопротивление
–
ток и сопротивление -й
ветви.
-й
ветви.

Рис. 1.16
Так, для замкнутого контура схемы (рис. 1.16) 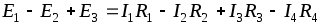 .
.
Замечание о знаках полученного уравнения:
1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;
2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.
1.8. Преобразование линейных электрических схем
Расчет и исследование сложных электрических схем во многих случаях можно значительно облегчить за счет преобразования. Суть преобразования заключается в замене участков цепи эквивалентными, но более простыми, т.е. не вызывающими изменения напряжения и токов в остальной части цепи.
1.8.1. Последовательное соединение резисторов
Если несколько резисторов соединены
один за другим без разветвлений и по
ним протекает один и тот же ток, такое
соединение называется последовательным(рис. 1.17 а). Обозначим сопротивления
отдельных резисторов через ,
а напряжения на них соответственно
,
а напряжения на них соответственно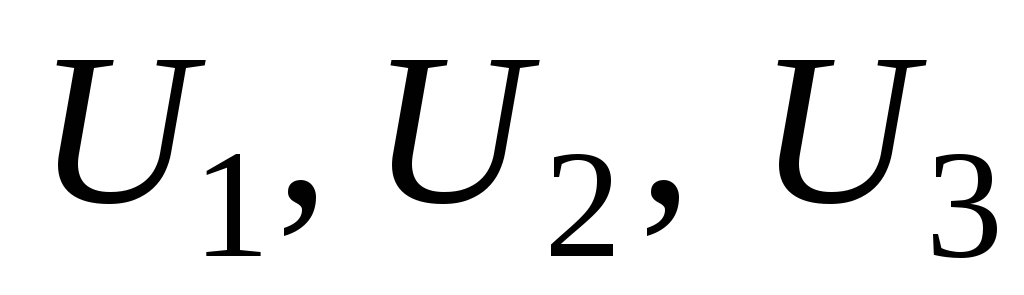 .
.
По второму закону Кирхгофа имеем
 .
(1.31)
.
(1.31)
Разделим обе части формулы (1.31) на ток 


или
 .
(1.32)
.
(1.32)
Таким образом, при последовательном соединении эквивалентное или общее сопротивление равно сумме сопротивлений отдельных участков цепи (рис. 1.17 б). В общем случае
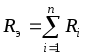 ,
(1.33)
,
(1.33)
где 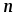 – число последовательно соединенных
резисторов.
– число последовательно соединенных
резисторов.
Ток в этой цепи
 .
.
Напряжения на отдельных участках определяются по формулам
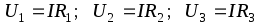 .
.
Последовательное соединение приемников энергии нашло широко применяется в различных областях техники. Оно используется обычно в тех случаях, когда расчетное напряжение приемника меньше напряжения источника электрической энергии.
1.8.2. Параллельное соединение резисторов
Параллельнымсоединением приемников называется такое соединение, при котором к одним и тем же двум узлам электрической цепи присоединяется несколько ветвей (рис. 1.18).

Рис. 1.18
В соответствии с законом Ома и первым законом Кирхгофа  ;
;
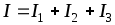
или
 .
(1.34)
.
(1.34)
Сократив обе части равенства на 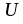 ,
получим
,
получим
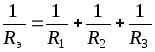
или
 .
(1.35)
.
(1.35)
Таким образом, общая (эквивалентная) проводимость при параллельном соединении приемников равна сумме проводимостей параллельных ветвей.
Из формулы (1.34) определяем общее сопротивление трех ветвей
 .
(1.36)
.
(1.36)
Если параллельно включены  одинаковых резисторовRi,
то эквивалентное сопротивление цепи
одинаковых резисторовRi,
то эквивалентное сопротивление цепи в
в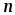 раз меньше сопротивления одной ветви
раз меньше сопротивления одной ветви
 .
(1.37)
.
(1.37)
Во всех случаях параллельного соединения эквивалентное сопротивление меньше самого малого из параллельно включенных.
Практический интерес представляет цепь с двумя параллельными резисторами (рис. 1.19). Эквивалентное сопротивление ее рассчитывают по формуле

Рис. 1.19
 . (1.38)
. (1.38)Токи в ветвях можно выразить через общий ток
 ;
;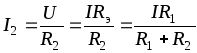 .
.
Параллельное соединение имеет свои особенности: все приемники находятся под одним напряжением; при неизменном напряжении отключение одного или нескольких приемников энергии не нарушает режима работы оставшихся включенными приемников.



