Законы Кирхгофа: решение задач

Прочитав статейки про первый и второй законы Кирхгофа, уважаемый  читатель может сказать: «Хорошо, MyElectronix, ты рассказал мне, конечно, интересные штуки, но что мне дальше с ними делать? Пока по твоим словам я заключил, что если я соберу ручками схему, то я смогу в каждом ее узле и в каждом контуре намерить вот такие вот зависимости. Это здорово, но я хотел бы рассчитывать схемы, а не просто наблюдать зависимости!»

Господа, все эти замечания абсолютно верные и в ответ на них можно лишь рассказать о расчете электрических схем с помощью законов Кирхгофа. Без лишних слов перейдем сразу к делу!

Начнем с самого простейшего случая. Он изображен на рисунке 1. Допустим, ЭДС источника питания равна Е1=5 В, а сопротивления R1=100 Ом, R2=510 Ом, R3=10 кОм. Требуется рассчитать напряжения на резисторах и ток через каждый резистор.

Господа, замечу сразу, эту задачу можно решить гораздо более простым способом, чем с применением законов Кирхгофа.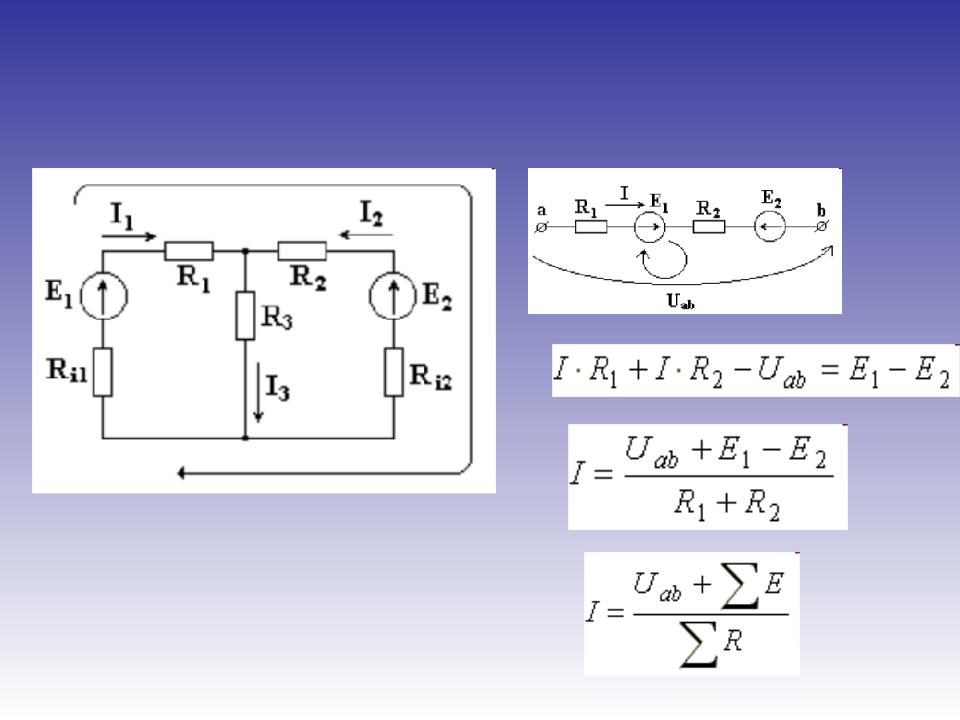

Однако сейчас наша задача не искать оптимальные способы решения, а на наглядном примере рассмотреть методику применения законов Кирхгофа при расчете схем.

Рисунок 1 – Простая схема

В этой схеме мы можем видеть три контура. Если возник вопрос – а почему три, то рекомендую посмотреть статью про второй закон Кирхгофа. В той статье имеется практически такая же схема с наглядным пояснением методики расчета числа контуров.

Господа, хочу отметить один тонкий момент. Хоть контура и три, независимых из них только два. Третий контур включает в себя все остальные и не может считаться независимым. И вообще всегда при всех расчетах мы должны использовать только

независимые контура. Не поддавайтесь искушению записать еще одно уравнение за счет этого общего контура, ничего хорошего не выйдет .

Итак, будем использовать два независимых контура. Для этого зададимся в каждом контуре направлением обхода контура. Как мы уже говорили, это некоторое направление в контуре, которое мы принимаем за положительное. Можно в какой-то степени назвать это аналогом осей координат в математике. Направление обхода каждого контура нарисуем синей стрелкой.

Далее зададимся направлением токов в ветвях: просто проставим его наугад. Не важно, угадаем мы сейчас направление или нет. Если угадали, то в конце расчета мы получим ток со знаком плюс, а если ошиблись – со знаком минус. Итак, обозначим токи в ветвях черными стрелочками с подписями I₁, I₂, I₃.

Мы видим, что в контуре №1 направление токов I₁ и I₃, а также направление источника питания совпадают с направлением обхода, поэтому будем считать их со знаком плюс. В контуре №2 ток I₂ совпадет с направлением обхода, поэтому будет со знаком плюс, а ток I₃ направлен в другую сторону, поэтому будет со знаком минус. Запишем второй закон Кирхгофа для контура №1:

А теперь запишем этот же закон для контура №2:

Видим, что в контуре №2 нет источников питания, поэтому в левой части (где у нас согласно второму закону Кирхгофа стоит сумма ЭДС) у нас нолик. Итак, у нас есть два уравнения, а неизвестных-то у нас три (I₁, I₂, I₃). А нам известно, что для нахождения трех неизвестных нужна система с тремя независимыми уравнениями. Где же взять третье недостающее уравнение? А, например, из первого закона Кирхгофа! Согласно этому закону мы можем записать

Господа, теперь полный порядок, у нас есть три уравнения и три неизвестных и нам остается только решить вот такую вот систему уравнений

Подставим конкретные числа. Все расчеты будем вести в кошерной системе СИ. Рекомендую всегда считать только в ней. Не поддавайтесь искушению подставлять куда-то миллиметры, мили, килоамперы и прочее. Возможно возникновение путаницы.

Решение таких систем рассматривается чуть ли не в начальной школе и, полагаю, не должно вызывать трудностей . Если что, есть куча математических пакетов, которые сделают это за вас, если вам лень самим ручками считай.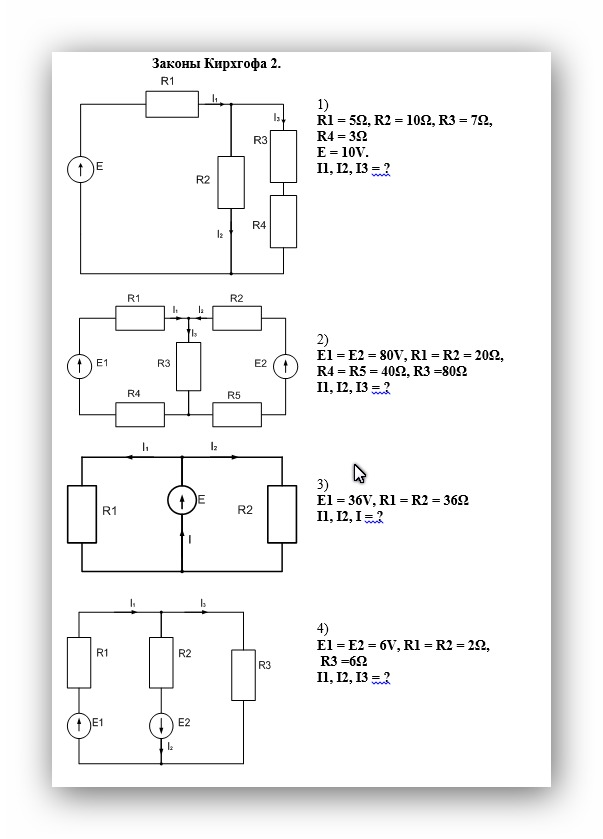

Поэтому мы опустим процесс решения, а сразу приведем результат

Видим, что все токи получились у нас со знаком плюс. Это значит, что мы верно угадали их направление. Да, то есть токи в схеме текут именно в том направлении, как мы нарисовали стрелочки на рисунке 1. Однако из условия задачи необходимо найти не только токи через резисторы, но и падение напряжения на них. Как это сделать? Например, с помощью уже изученного нами закона Ома. Как мы помним, закон Ома связывает между собой ток, напряжение и сопротивление. Если нам известны любые две из этих величин, мы легко можем найти третью. В данном случае мы знаем сопротивление и ток, который течет через это сопротивление. Поэтому, используя вот эту формулу

находим напряжение на каждом резисторе

Заметим, господа, что напряжения на резисторах R2 и R3 равны между собой. Это и логично, поскольку они соединены между собой параллельно. Однако пока не будем на этом акцентировать большое внимание, рассмотрим это лучше в другой раз.

Итак, господа, мы решили эту простую задачку с помощью двух законов Кирхгофа и закона Ома. Но это был совсем простой пример. Давайте попробуем решить более сложную задачу. Взгляните на рисунок 2.

Рисунок 2 – Схема посложнее

Схема выглядит внушительно, не правда ли? Возможно, вам даже не верится, что эту схему можно легко рассчитать. Однако, господа, уверяю вас, вы обладаете всеми необходимыми знаниями для расчета этой схемы, если уже изучили мои предыдущие статьи. Сейчас вы в этом убедитесь.

Для начала зададимся конкретными цифрами значений сопротивлений резисторов и напряжений источников.

Пусть Е1=15 В, Е2=24 В, R1= 10 Ом, R2 = 51 Ом, R3=100 Ом, R4=1 кОм, R5=10 Ом, R6=18 Ом, R7=10 кОм.

Найти, как и в прошлой задаче, требуется все токи в схеме и напряжения на всех резисторах.

В этой схеме мы можем видеть три независимых контура. Обозначим их римскими цифрами I, II, III. В каждом контуре зададимся направлением обхода.

Они показаны синими стрелками.

Дальше как и в прошлый раз наугад расставим направления токов во всех ветвях и подпишем где какой ток. Видно, что всего у нас 6 ветвей и, соответственно, 6 разных токов (I1…I6).

Теперь запишем второй закон Кирхгофа для всех трех независимых контуров.

Второй закон Кирхгофа для контура I:

Второй закон Кирхгофа для контура II:

Второй закон Кирхгофа для контура III:

У нас есть три уравнения, однако неизвестных токов аж 6. Как и в прошлой задаче для получения недостающих уравнений запишем первые законы Кирхгофа для узлов.

Первый закон Кирхгофа для узла А:

Первый закон Кирхгофа для узла В:

Первый закон Кирхгофа для узла С:

Собственно, у нас теперь есть система из 6 уравнений с 6 неизвестными. Остается только решить эту систему

 

Подставляя числа, заданные в условии, получаем

 

Опуская решения за пределами статьи, приведем итоговый результат

 

Господа, мы видим, что почти все токи, кроме I₄ получились у нас со знаками «минус».

Это значит, что мы не угадали их направление, когда рисовали стрелочки на рисунке 2 . То есть все токи, кроме тока I₄ на самом деле текут в противоположные стороны. А ток I₄ течет так, как мы нарисовали. Хотя бы с ним мы угадали верно.

Теперь все по тому же закону Ома ровно как в прошлом примере рассчитаем напряжения на резисторах:

Вот и все, господа: схема рассчитана, а задачка решена. Таким образом, вы теперь обладаете весьма мощным инструментом по расчету электрических схем. С помощью двух законов Кирхгофа и закона Ома вы сможете рассчитать весьма непростые схемы, найти величины токов и их направления, а также напряжения на всех нагрузках цепи. Более того, зная токи и напряжения вы легко сможете рассчитать  и мощности, которые на этих резисторах выделяются, если воспользуетесь рекомендациями из моей предыдущей статьи. 

На этом на сегодня все господа. Огромной вам всем удачи и успешных расчетов!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Законы кирхгофа 1 и 2 примеры. Первый закон кирхгофа

Большое количество электрических цепей на практике являются сложными. Однако в цепь любого уровня сложности имеет элементы двух простейших видов. Это узлы и замкнутые контуры. Узел — это любая точка разветвления цепи, в которой сошлось три или более проводников, по которым текут токи.

Второе правило (закон) Кирхгофа является следствием обобщенного закона Ома. Так, если в изолированной замкнутой цепи есть один источник ЭДС, то сила тока в цепи будет такой, что сумма падения напряжения на внешнем сопротивлении и внутреннем сопротивлении источника будет равна сторонней ЭДС источника. Если источников ЭДС несколько, то берут их алгебраическую сумму. Знак ЭДС выбирается положительным, если при движении по контуру в положительном направлении первым встречается отрицательный полюс источника. (За положительное направление обхода контура принимают направление обхода цепи либо по часовой стрелке, либо против нее).

Формулировка второго закона Кирхгофа

Произведение алгебраической величины силы тока (I) на сумму вешних и внутренних сопротивлений всех участков замкнутого контура равно сумме алгебраических значений сторонних ЭДС () рассматриваемого контура:

Каждое произведение определяет разность потенциалов, которая существовала бы между концами соответствующего участка, если бы ЭДС в нем была равно нулю. Величину называют падением напряжения, которое вызывается током.

Второй закон Кирхгофа иногда формулируют следующим образом:

Для замкнутого контура сумма падений напряжения есть сума ЭДС в рассматриваемом контуре.

Правила Кирхгофа служат для того, чтобы составить систему уравнений, позволяющих найти силу тока для сложной цепи. Направление положительного обхода выбирают для всех контуров одинаковым. При составлении уравнений, используя правила Кирхгофа необходимо внимательно следить за расстановкой знаков токов и ЭДС.

Система уравнений, которая получается при использовании первого и второго закона Кирхгофа является полной и дает возможность отыскать все токи. При составлении уравнений, используя правила Кирхгофа, надо следить за тем, чтобы новое уравнение имело хотя бы одну величину, которая еще не вошла в предыдущие уравнения. Кроме того, необходимо, чтобы система уравнений имела число уравнений равное количеству неизвестных.

Второй закон Кирхгофа следует из того, что электрическое напряжение по замкнутому контуру равно нулю, то есть это правило является следствием основного свойства электростатического поля, которое заключается в том, что работа поля при движении заряда по замкнутой траектории равна нулю.

Примеры решения задач

ПРИМЕР 1

Задание	Примените второе правило Кирхгофа для рис.1 и запишите уравнения рассмотрев контуры: ABDCA; ABFEA
Решение	Направление обхода контура зададим при помощи последовательности букв в его обозначении. Так для контура имеем направление обхода по часовой стрелке. Рассматривая эту цепь в дальнейшем направления обхода контуров изменять нельзя. Положительными будем считать токи, которые совпадают с направлением обхода контура. Для контура со знаком плюс будут во второе правило Кирхгофа входить ток: , со знаком минус ток . В соответствии с правилом выбора знака ЭДС, сформулированном в теоретической части, в рассматриваемый контур и будут положительными. Уравнение, соответствующее второму правилу Кирхгофа для контура запишем как: где и — внутренние сопротивления источников ЭДС; и — внешние сопротивления. Рассмотрим контур . Ток согласно избранным нами направлениям будет положительным во втором законе Кирхгофа, то — отрицательным. ЭДС войдет в уравнение со знаком минус. Получим:
Ответ	Для контура . Для контура получили:

ПРИМЕР 2

Задание

Пусть n одинаковых источников ЭДС соединены последовательно и замкнуты на внешнюю цепь (рис.2). Чему равна ЭДС данной цепи, если ЭДС каждого источника равна , внутренне сопротивление каждого источника ? Сопротивление внешней цепи R.

В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, ЭДС и сопротивлением всей цепи или, между напряжением и сопротивлением на каком-либо участке цепи определяется законом Ома .

На практике в цепях, токи, от какой-либо точки, идут по разным путям.
Точки, где сходятся несколько проводников, называются узлами, а участки цепи, соединяющие два соседних узла, ветвями.

В замкнутой электрической цепи ни в одной ее точке не могут скапливаться электрические заряды так, как это вызвало бы изменение потенциалов точек цепи. Поэтому электрические заряды притекающие к какому-либо узлу в единицу времени, равны зарядам, утекающим от этого узла за ту же единицу.
Разветвлённая цепь.
В узлеА цепь разветвляется на четыре ветви, которые сходятся в узел В .

Обозначим токи в неразветвленной части цепи —I , а в ветвях соответственно

I1 , I2 , I3 , I4 .

У этих токов в такой цепи будет соотношение:

I = I1+I2+I3+I4;

Cумма токов, подходящих к узловой точке электрической цепи,
равна сумме токов, уходящих от этого узла.

При параллельном соединении резисторов ток проходит по четырем направлениям, что уменьшает общее сопротивление или увеличивает общую проводимость цепи, которая равна сумме проводимостей ветвей.

Обозначим силу тока в неразветвленной ветви буквойI .
Силу тока в отдельных ветвях соответственно I1 , I2 , I3 и I4 .
Напряжение между точками A и B — U .
Общее сопротивление между этими точками — R .

По закону Ома напишем:

I = U/R ; I1 = U/R1 ; I2 = U/R2 ; I3 = U/R3 ; I4 = U/R4 ;

Согласно первому закону Кирхгофа:

I = I1+I2+I3+I4 ; или U/R = U/R1+U/R2+U/R3+U/R4 .

Сократив обе части полученного выражения на U получим:

1/R = 1/R1+1/R2+1/R3+1/R4 , что и требовалось доказать.

Cоотношение для любого числа параллельно соединенных резисторов.
В случае, если в цепи содержится два параллельно соединенных резистора
R1 и R2 , то можно написать равенство:

1/R =1/R1+1/R2 ;

Из этого равенства найдем сопротивление R , которым можно заменить два параллельно соединенных резистора:

Полученное выражение имеет большое практическое применение.
Благодаря этому закону производятся расчёты электрических цепей.

Второй закон Кирхгофа

В замкнутом контуре электрической цепи сумма всех эдс равна
сумме падения напряжения в сопротивлениях того же контура.

E1 + E2 + E3 +…+ En = I1R1 + I2R2 + I3R3 +…+ InRn . При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.

Если в электрической цепи включены два источника энергии, эдс которых совпадают по направлению, т. е. согласно изо1, то эдс всей цепи равна сумме эдс этих источников,
т. е.
E = E1+E2 .

Если же в цепь включено два источника, эдс которых имеют противоположные направления, т. е. включены встречно изо2, то общая эдс цепи равна разности эдс этих источников
Е = Е1-Е2 .

Благодаря этим законам производятся расчёты электрических цепей.
Существует несколько методов расчёта, один из них «Метод узловых напряжений»

Два приема, которые применяют для упрощения процесса составления уравнений, необходимых при расчетах сложных разветвленных цепей постоянного тока называют законами (вернее было бы сказать правилами) Кирхгофа. Прежде чем перейти к самим правила Кирхгофа введем два необходимых определения.

Разветвлёнными цепями названы цепи, которые имеют несколько замкнутых контуров, несколько источников электродвижущей силы (ЭДС).

Узлом разветвлённой цепи называют точку, в которой сходятся три или более проводников с токами.

Первый закон (правило) Кирхгофа, простыми словами

Первое правило Кирхгофа называют правилом узлов, так как оно касается сил токов в узах цепи. Словесно первый закон Кирхгофа формулируют следующим образом: Алгебраическая сумма сил токов в узле равна нулю. В виде формулы это правило запишем как:

С каким знаком сила тока будет входить в сумму (1), зависит от произвольного выбора. Но при этом следует считать, что все входящие в узел токи имеют одинаковые знаки, а все исходящие из узла токи имеют противоположные входящим, знаки. Пусть все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными. Если направления токов изначально не заданы, то их задают произвольно. Если при расчетах получено, что сила тока отрицательна, значит, что верное направление тока является противоположным тому, которое предполагали.

Первый закон Кирхгофа является следствием закона сохранения заряда. Если в цепи текут только постоянные токи, то нет в этой цепи точек, которые накапливали бы заряд. Иначе токи не были бы постоянными.

Первый закон Кирхгофа дает возможность составить независимое уравнение, при наличии в цепи k узлов.

Второй закон (правило) Кирхгофа, простыми словами

Второй закон Кирхгофа относят к замкнутым контурам, поэтому его называют правилом контуров. Согласно этому правилу суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних ЭДС (), входящих в рассматриваемый контур. В виде формулы второй закон Кирхгофа запишем как:

где величину часто называют падением напряжения; N — число рассматриваемых участков избранного контура. При использовании второго правила Кирхгофа важно помнить о направлении обхода контура. Как это делается? Произвольно выберем направление обхода рассматриваемого в задаче контура (по часовой стрелке или против нее). В случае совпадения направления обхода контура с направлением силы тока в рассматриваемом элементе, величина входит в (2) со знаком плюс. ЭДС войдет в сумму правой части выражения (2) со знаком плюс, если при движении вдоль контура, в соответствии с избранным направлением обхода первым мы встречаем отрицательный полюс источника ЭДС.

Используя второе правило Кирхгофа можно получить независимые уравнения для тех контуров цепи, которые не получены наложением уже описанных контуров. Количестов независимых контуров (n) равно:

где p — количество ветвей в цепи; k — число узлов.

Количество независимых уравнений, которые дадут оба правила Кирхгофа равно (s):

Делаем вывод о том, что число независимых уравнений будет равно числу разных токов в исследуемой цепи.

Второе правило Кирхгофа — следствие закона Ома. В принципе любую цепь можно рассчитать, применяя только закон Ома и закон сохранения заряда. Правила Кирхгофа являются всего лишь упрощающими приемами для решения задач, рассматривающих цепи постоянного тока.

Используя правила Кирхгофа для составления уравнений необходимо внимательно следить за расстановкой знаков токов и ЭДС.

Первое и второе правила Кирхгофа дают метод расчета цепи, то есть используя их можно найти все токи в цепи, если известны все ЭДС и сопротивления, в том числе и внутренние сопротивления источников.

Примеры решения задач

ПРИМЕР 1

Задание	Как следует записать уравнение для токов, используя первое правило Кирхгофа для узла А, изображенного на рис.1
Решение	Прежде чем применять первое правило Кирхгофа определим для себя, что положительными будут токи, которые входят в узел А, тогда выходящие из этого узла токи мы должны будем записать в первом правиле Кирхгофа со знаком минус. Из рис. 1 в узел А входят токи: Из узла А выходят токи: Тогда согласно правилу узлов имеем:
Ответ

ПРИМЕР 2

Задание	Составьте систему независимых уравнений, используя правила Кирхгофа, которая позволит найти все токи в цепи, представленной на рис. 2, если известны все ЭДС и все сопротивления (они указаны на рисунке)?
Решение	Направления токов выберем произвольно, обозначим их на рис.1. Пусть через сопротивление течет ток . На рис.2 видно, что в нашей цепи два узла. Это точки A и С. Запишем первое правило Кирхгофа для узла А:

При расчете электрических цепей нам часто приходится встречаться с цепями, которые образуют замкнутые контуры. В состав таких контуров, помимо сопротивлений, могут входить еще электродвижущие силы, то есть источники напряжений. На рисунке 1 представлен участок сложной электрической цепи. Задана полярность всех (э. д. с.). Произвольно выбираем положительные направления токов. Обходим контур от точки А в произвольном направлении, например по часовой стрелке. Рассмотрим участок АБ . На этом участке происходит падение потенциала (ток идет от точки с высшим потенциалом к точке с низшим потенциалом).

На участке АБ :

φ А + E 1 – I 1 × r 1 = φ Б .

На участке БВ :

φ Б – E 2 – I 2 × r 2 = φ В .

На участке ВГ :

φ В – I 3 × r 3 + E 3 = φ Г .

На участке ГА :

φ Г – I 4 × r 4 = φ А .

Складывая почленно четыре приведенных уравнения, получим:

φ А + E 1 – I 1 × r 1 + φ Б – E 2 – I 2 × r 2 + φ В – I 3 × r 3 + E 3 + φ Г – I 4 × r 4 = φ Б + φ В + φ Г + φ А

E 1 – I 1 × r 1 – E 2 – I 2 × r 2 – I 3 × r 3 + E 3 – I 4 × r 4 = 0.

Перенеся произведения I × r в правую часть, получим:

E 1 – E 2 + E 3 = I 1 × r 1 + I 2 × r 2 + I 3 × r 3 + I 4 × r 4 .

В общем виде

Это выражение представляет собой . Формула второго закона Кирхгофа показывает, что во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжений. Бывают случаи, когда в замкнутом контуре отсутствуют источники э. д. с., тогда применимо другое определение второго закона Кирхгофа – алгебраическая сумма падений равна нулю.

Видео 1. Второй закон Кирхгофа

Рассмотрим простой замкнутый контур (рисунок 2).

Рисунок 2. Простой замкнутый контур

По второму закону Кирхгофа

E = I × r 0 + I × r = I × (r 0 + r ),

Имеем три уравнения с тремя неизвестными. Решая их, находим величину и направление токов. Подставляя значение тока I 3 из уравнения (3) в уравнение (1), получим:

6 = 2 × I 1 + 5 × I 1 + 5 × I 2 ;

Сложим уравнения для двух контуров почленно:

(6 = 7 × I 1 + 5 × I 2) + (2 = I 1 – 2 × I 2)

(12 = 14 × I 1 + 10 × I 2) + (10 = 5 × I 1 – 10 × I 2).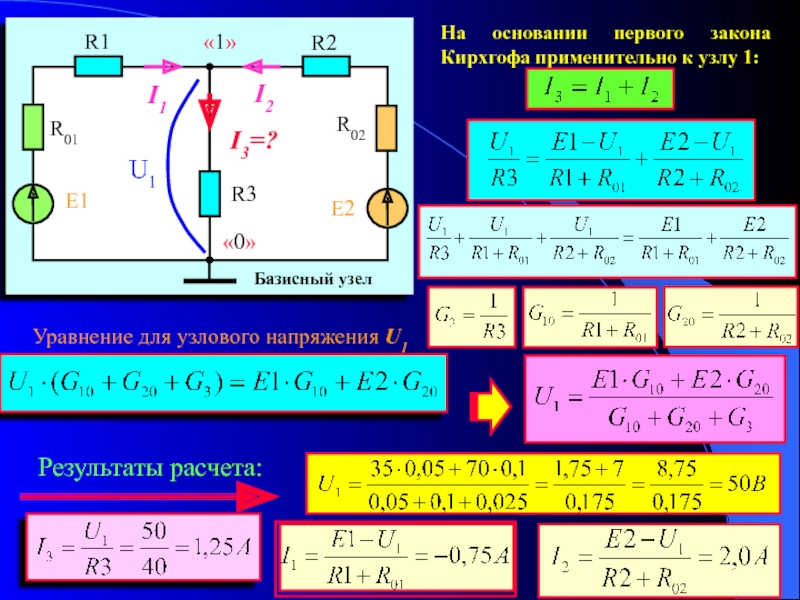

Сложив два последних уравнения, имеем:

22 = 19 × I 1 , откуда I 1 = 1,156 А,

подставляем значение I 1 в уравнение (1):

6 = 2 × 1,156 + 5 × I 3 ,

Подставляем значение I 1 в уравнение (2):

2 = 1,156 – 2 × I 2 ,

Знак минус показывает, что действительное направление тока I 2 обратно принятому нами направлению.

Законы Кирхгофа (Реферат) — TopRef.ru

Академия ФСО России

Кафедра Физики

Тема:

«Законы Кирхгофа и их применение для расчета электрических цепей»

Орел-2009

Содержание

Первый закон Кирхгофа

Второй закон Кирхгофа

Расчет сложных цепей с помощью уравнений Кирхгофа

Первый закон Кирхгофа

Алгебраическая сумма токов в ветвях, сходящихся к любому узлу электрической цепи, тождественно равна нулю. Согласно этому закону, если к некоторому узлу цепи подсоединено n ветвей с токами i₁, i₂, …, i_n, то в любой момент времени

,

где , если направление тока положительно и ориентировано от узла (ток выходит из узла), или , если ток входит в узел. Таким образом, любому узлу цепи соответствует уравнение, связывающее токи в ветвях цепи, соединенных с данным узлом.

В качестве примера приведем схему на рисунке 1.

Рис.1.

В соответствии с первым законом Кирхгофа:

.

Общее число уравнений, которое можно составить по первому закону Кирхгофа для цепи, равно числу узлов цепи .

Так, для четырех узлов графа (рисунок 2) можно составить следующие четыре уравнения:

Р
ис.2.

узел 1: ,

узел 2: ,

узел 3: ,

узел 4: .

Первый закон Кирхгофа часто называют законом Кирхгофа для токов и сокращенно в тексте обозначают ЗКТ.

Число независимых уравнений равно трем, так как любое из этих уравнений отличается от суммы трех остальных только знаком. Итак, если цепь содержит узлов, то для неё можно составить по первому закону Кирхгофа независимых уравнений. Совокупность из N узлов цепи, уравнения для которых образуют систему линейно независимых уравнений, называют совокупностью независимых узлов цепи.

Примеры на применение первого закона Кирхгофа. Параллельное соединение элементов

В качестве примера на применение первого закона Кирхгофа рассмотрим параллельное соединение нескольких элементов активных сопротивлений, конденсаторов, катушек индуктивности.

Особенностью параллельного соединения нескольких элементов является равенство напряжений, приложенных к зажимам любого из элементов, входящих в соединение. Цепь при таком соединении характеризуется только одним независимым узлом.

Пусть параллельно соединены n элементов активного сопротивления. Если выбрать направления отчетов токов в элементах такими как это показано на рисунке 3, то согласно первому закону Кирхгоффа при параллельном соединении элементов запишем:

Р

u

ис.3.

;

учитывая, что , имеем ,

где .

Зависимость не отличается от зависимости между напряжением на зажимах и током в элементе активного сопротивления с проводимостью G. Следовательно, цепь, составленная из нескольких сопротивлении, включенных параллельно, может быть заменена одним активным сопротивлением, при этом проводимость эквивалентного элемента равна сумме проводимостей элементов, входящих в соединение.

При параллельном соединении конденсаторов (рисунок 4) ток ветви можно определить по формуле: .

Рис.4.

Для вычисления общего тока необходимо просуммировать токи ветвей:

,

где _..

Таким образом, при параллельном соединении нескольких конденсаторов эквивалентная ёмкость равна сумме емкостей, входящих в соединение.

В случае параллельного соединения катушек индуктивностей (рисунок 5)
ток каждой из ветвей равен: .

Рис.5.

Уравнение для вычисления общего тока имеет вид:

.

Следовательно , то есть .

Это означает, что значение эквивалентной индуктивности будит меньше наименьшего из значений соединённых параллельно индуктивностей.

Второй закон Кирхгофа

Второй закон Кирхгофа формулируется следующим образом: алгебраическая сумма напряжений ветвей в любом контуре цепи тождественно равна нулю. Для замкнутого контура, изображённого на рисунке 6, можно записать соотношение:

.

Рис.6.

В соответствии со вторым законом Кирхгофа при обходе контура по часовой стрелке справедливо соотношение:

.

Изменение направления обхода эквивалентно изменению знаков напряжений на противоположные (умножению на минус единицу).

Примеры на применение второго закона Кирхгофа

Последовательное соединение элементов

П
усть n элементов активного сопротивления соединены последовательно (рисунок 7).

Рис.7.

В соответствии с выбранным направлением обхода по второму закону Кирхгофа получим уравнение:

.

характерной особенностью последовательного соединения является равенство токов в каждом из элементов, входящих в соединение.

При запишем:

, то есть .

Таким образом, при последовательном соединении нескольких резисторов эквивалентное сопротивление равно сумме сопротивлений, входящих в соединение.

При последовательном соединении катушек индуктивности (рисунок 8) можно записать:

.

Рис.8.

Если , то ,

следовательно .

Это означает, что эквивалентная индуктивность равна сумме индуктивностей, входящих в последовательное соединение.

В случае последовательного соединения конденсаторов (рисунок 9) по второму закону Кирхгофа можно записать:

.

Рис.9.

Заменяя получим: .

Обратная ёмкость всех конденсаторов, соединенных последовательно, равна сумме обратных ёмкостей конденсаторов, входящих в соединение:

.

При этом эквивалентная ёмкость соединения будет меньше наименьшей ёмкости конденсатора, входящего в последовательное соединение.

Расчет сложных цепей с помощью уравнений Кирхгофа

Пример 1

Далеко не во всех случаях цепь представляет собой совокупность лишь последовательно и параллельно соединенных ветвей. В качестве примера рассмотрим вариант расчета с помощью уравнений Кирхгофа электрической цепи (рисунок 10). Цепь содержит = 4 узлов и = 6 ветвей, включая источники напряжения.

Рис.10.

Для определения всех токов и напряжений в схеме достаточно найти значения токов во всех ветвях цепи. Зная ток, проходящий через любую из ветвей цепи, можно найти как напряжение этой ветви, так и напряжение между любой парой узлов цепи.

Если мы зададимся произвольно положительными направлениями токов в ветвях цепи и пронумеруем произвольно эти токи, то по первому закону Кирхгофа можно составить уравнений относительно токов в ветвях цепи.

По второму закону Кирхгофа будет линейно-независимых уравнений для напряжений ветвей схемы.

Совокупность из уравнений по первому закону Кирхгофа, и уравнений, составленных по второму закону Кирхгофа, образует систему линейно – независимых уравнений. Эта система будет неоднородной системой уравнений, так как ее свободными членами являются заданные напряжения источников.

Подобная система уравнений имеет единственное решение, позволяющее найти токи в ветвях цепи, а по ним и значения напряжений между любой парой узлов цепи.

Для примера составим систему уравнений по первому закону Кирхгофа (рисунок 10).

Число уравнений: .

Узел 1: ,

узел 2: ,

узел 3: .

В тоже время по второму закону Кирхгофа для контуров I, II, III можно составить систему из уравнений.

.

Контур I: ,

контур II: ,

контур III: .

Таким образом, решая систему из 6 уравнений с шестью неизвестными токами, например по методу Крамера, определим неизвестные. Если в цепи будет источник тока, то в системе уравнений неизвестным будет напряжение на зажимах этого источника, а ток через источник будет равен току задающего источника. Общее число неизвестных сохранится прежним.

Пример 2

Для цепи (рисунок 11) определить токи и , если E = 20 В, I₀ = 2 A, R₁ = 15 Ом, R₂ = 85 Ом.

Р
ис.11.

Решение

Выберем направления токов , и обхода в контуре, составим уравнения по законам Кирхгофа. Число уравнений, составляемых по первому закону Кирхгофа:

.

Число уравнений по второму закону Кирхгофа:

.

Уравнение токов для узла 1:

. (a)

Уравнение по второму закону Кирхгофа:

. (б)

Подставим в уравнения (а) и (б) числовые значения получим:

,

.

Решив эту систему, определим токи и :

; .

Литература

1. Белецкий А.Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986.

2. Бакалов В.П. и др. Теория электрических цепей. – М.: Радио и связь, 1998.

3. Качанов Н. С. и др. Линейные радиотехнические устройства. М.: Воен. издат., 1974.

4. В.П. Попов Основы теории цепей – М.: Высшая школа, 2000

Решение задач ТОЭ – методы, алгоритмы и примеры решения

Главная → Примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ – МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ

Решение задач занимают важное место в курсе ТОЭ, так как в процессе их решения проверяется степень усвоения теоретического материала, и приобретаются навыки, необходимые для приложения теории к практике.

На примерах решения задач по ТОЭ представлены основные разделы современной теории электрических цепей, составляющие предмет теоретических основ электротехники (ТОЭ).

Объем теоретического материала курса ТОЭ, представленный в виде кратких физических схем и подробно изложенных алгоритмов, позволяет непосредственно перейти к решению как типовых, так и задач, выходящих за рамки курса ТОЭ.

Реализуется естественный принцип выборочного прочтения и быстрого нахождения нужной информации.

Решение задач по ТОЭ делится на разделы, каждый из которых содержит краткое описание методов и алгоритмов решения задач ТОЭ.

---

Общие рекомендации при решении задач ТОЭ:

• заданные условия задачи должны быть тщательно проанализированы. Для этого их необходимо прочесть, как минимум, дважды: сначала бегло, схватывая смысл задания в целом, а затем медленно, стараясь подметить мелкие и, на первый взгляд, незначительные детали;

• не стоит решать задачу по схеме, изображенной в расчетной работе, билете. Схему следует перерисовать в привычном для себя виде;

• краткие условия задачи желательно приводить справа от расчетной схемы. На схеме должны быть обозначены все необходимые токи и напряжения, причем, желательно, все величины, относящиеся к одной ветви, обозначать одинаковым индексом: E₁, U₁, I₁, R₁. В расчетах не должно быть величин, которые не были бы обозначены на схеме;

• полученный результат (результаты) расчета должен быть проверен, будь это баланс мощностей, векторная диаграмма, отдельное уравнение по одному из законов Кирхгофа или просто логическое рассуждение.

---

Решение экзаменационных задач ТОЭ онлайн ВКонтаке Василий Новицкий

---

Содержание

1 Методы расчета электрических цепей при постоянных токах и напряжениях

1.1 Методы решения, основанные на законах Ома и Кирхгофа

1.2 Метод наложения

1.3 Метод контурных токов

1.4 Метод узловых потенциалов. Метод узлового напряжения (двух узлов)

1.5 Метод эквивалентного генератора (источника ЭДС)

1.6 Методы расчета нелинейных электрических цепей постоянного тока

2 Магнитное поле и магнитные цепи при постоянных токах

2.1 Методы расчета магнитных цепей постоянного тока

2.2 Катушки и трансформаторы со стальными сердечниками

2.3 Магнитное поле, индуктивность

3 Методы расчета линейных цепей синусоидального тока

3.1 Расчет цепей переменного тока методом векторных диаграмм

3.2 Символический метод расчета цепей синусоидального тока

3.3 Резонанс в электрической цепи

3.4 Цепи со взаимными индуктивностями

4 Анализ схем при несинусоидальных (негармонических) периодических воздействиях

4.1 Алгоритм расчета схем при несинусоидальных периодических воздействиях

4.2 Примеры расчета схем при несинусоидальных периодических воздействиях

5 Трехфазные цепи

5.1 Основные определения и отношения

5.2 Расчет симметричных режимов работы трехфазных цепей

5.3 Расчет несимметричных режимов работы трехфазных цепей (метод симметричных составляющих)

6 Анализ общих свойств пассивных четырехполюсников

7 Методы анализа переходных процессов в линейных цепях с сосредоточенными параметрами

7.1 Физические основы переходных процессов

7.2 Математический аппарат и алгоритмы расчетов

7.2.1 Классический метод анализа переходного процесса

7.2.2 Операторный метод расчета (метод преобразования Лапласа)

7.2.3 Расчет методом интеграла Дюамеля

8 Нелинейные цепи переменного тока

8.1 Графические и графоаналитические методы расчета

8.2 Аналитические методы расчета

Методы и примеры решения задач ТОЭ → РЕШЕНИЕ ЗАДАЧ ТОЭ – МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ

RSS

ЗАКОНЫ Кирхгофа

Нажмите или коснитесь приведенных ниже примеров схем, чтобы вызвать TINACloud, и выберите интерактивный режим DC, чтобы проанализировать их в Интернете.
Получите недорогой доступ к TINACloud для редактирования примеров или создания собственных схемУЗЕЛ ПОТЕНЦИАЛЬНЫЙ МЕТОД

Многие схемы слишком сложны, чтобы их можно было решить, используя правила для последовательных или параллельных схем или методы преобразования в более простые схемы, описанные в предыдущих главах. Для этих схем нам нужны более общие методы решения. Наиболее общий метод дается законами Кирхгофа, которые позволяют вычислять все напряжения и токи цепей по решению системы линейных уравнений.

Есть два Законы Кирхгофа, закон напряжения И текущий закон. Эти два закона могут быть использованы для определения всех напряжений и токов в цепях.

Закон напряжения Кирхгофа (KVL) гласит, что алгебраическая сумма повышений напряжения и падений напряжения вокруг контура должна быть равна нулю.

Цикл в вышеприведенном определении означает замкнутый путь в цепи; то есть путь, который покидает узел в одном направлении и возвращается к тому же узлу из другого направления.

В наших примерах мы будем использовать направление по часовой стрелке для циклов; однако те же результаты будут получены при использовании направления против часовой стрелки.

Для применения KVL без ошибок, мы должны определить так называемое опорное направление. Опорное направление неизвестного напряжения от точки к + — знак предполагаемых напряжений. Представьте себе использование вольтметра. Вы положили бы положительный пробник вольтметра (обычно красный) на клемму + опоры компонента. Если реальное напряжение положительное, оно в том же направлении, что и мы, и наше решение, и вольтметр покажут положительное значение.

При выводе алгебраической суммы напряжений, мы должны присвоить знак плюс к тем напряжениям, где опорное направление совпадает с направлением петли, и отрицательными знаками в противоположном случае.

Другой способ сформулировать закон напряжения Кирхгофа состоит в том, что приложенное напряжение последовательной цепи равно сумме падений напряжения на последовательных элементах.

Следующий короткий пример показывает использование закона напряжения Кирхгофа.

Найти напряжение на резисторе R_2, учитывая, что напряжение источника, В_S = 100 В и это напряжение на резисторе R₁ это V₁ = 40 V.

Рисунок ниже может быть создан с помощью TINA Pro версии 6 и выше, в которой инструменты рисования доступны в редакторе схем.

Решение с использованием закона напряжения Кирхгофа: -V_S + V₁ + V₂ = 0 или V_S V =₁ + V₂

следовательно: V₂ V =_S — V₁ = 100-40 = 60V

Обратите внимание, что обычно мы не знаем напряжения резисторов (если мы не измеряем их), и нам нужно использовать оба закона Кирхгофа для решения.

Текущий закон Кирхгофа (KCL) гласит, что алгебраическая сумма всех токов, входящих и выходящих из любого узла в цепи, равна нулю.

Далее мы даем знак + токам, выходящим из узла, и знак — токам, входящим в узел.

Вот основной пример, демонстрирующий действующий закон Кирхгофа.

Найти тока я₂ если источник тока I_S = 12 A, и я₁ = 8 A.

Используя текущий закон Кирхгофа в обведенном узле: -I_S + Я₁ + Я₂ = 0, следовательно: I₂= Я_S — Я₁ = 12 — 8 = 4 A, как вы можете проверить с помощью TINA (следующий рисунок).

В следующем примере мы будем использовать как законы Кирхгофа, так и закон Ома, чтобы рассчитать ток и напряжение на резисторах.

На рисунке ниже вы заметите Напряжение Стрелка выше резисторы. Это новый компонент, доступный в Версия 6 TINA и работает как вольтметр. Если подключить его через компонент, стрелка определяет опорное направление (сравнить с вольтметром, представьте размещения красного щупа в хвосте стрелки, а черный зонд на конце). При запуске анализа постоянного тока фактическое напряжение на компоненте будет отображаться на стрелке.

Нажмите / коснитесь схемы выше для анализа в режиме онлайн или нажмите эту ссылку, чтобы Сохранить в Windows

Чтобы начать использовать текущий закон Кирхгофа, мы видим, что токи через все компоненты одинаковы, поэтому давайте обозначим этот ток через I.

Согласно закону напряжения Кирхгофа: V_S V =₁+V₂+V₃

Теперь используя закон Ома: V_S= I * R₁+ I * R₂+ I * R₃

И отсюда ток цепи:

I = V_S /(Р₁+R₂+R₃) = 120 / (10 + 20 + 30) = 2 A

Наконец напряжения на резисторах:

V₁= I * R₁ = 2 * 10 = 20 V; V₂ = I * R₂ = 2 * 20 = 40 V; V₃ = I * R₃ = 2 * 30 = 60 V

Те же результаты можно увидеть на стрелках напряжения, просто запустив интерактивный анализ постоянного тока TINA.

В этой следующей, более сложной схеме мы также используем как законы Кирхгофа, так и закон Ома, но мы обнаруживаем, что мы наиболее решаем линейную систему уравнений.

Общее количество независимых применений законов Кирхгофа в цепи — это число ветвей цепи, а общее количество неизвестных (ток и напряжение каждой ветви) вдвое больше. Тем не менее, также используя закон Ома на каждом резисторе и Из простых уравнений, определяющих приложенные напряжения и токи, мы получаем систему уравнений, где число неизвестных совпадает с числом уравнений.

Найти токи ветвления I1, I2, I3 в схеме ниже.

Нажмите / коснитесь схемы выше для анализа в режиме онлайн или нажмите эту ссылку, чтобы Сохранить в Windows

Система уравнений выглядит следующим образом:

Узловое уравнение для обведенного узла:

– I₁ – I₂ — Я₃ = 0

или умножение на -1

I₁ + I₂ + Я₃ = 0

Уравнения цикла (с использованием направления по часовой стрелке) для цикла L1, содержащего V₁, R₁ и R₃

-V₁+I₁*R₁-I₃*R₃ = 0

и для цикла L2, содержащего V₂, R₂ и R₃

I₃*R₃ — Я₂*R₂ +V₂ = 0

Подставляя значения компонентов:

I₁+ Я₂+ Я₃ = 0 -8 + 40 * I₁ — 40 * I₃ = 0 40 * I₃ -20 * I₂ + 16 = 0

Экспресс я₁ используя узловое уравнение: I₁ = -Я₂ — Я₃

затем подставьте его во второе уравнение:

-V₁ — (Я₂ + Я₃)*Р₁ -Я₃*R₃ = 0 or –8- (я₂ + Я₃) * 40 — я₃* 40 = 0

Экспресс я₂ и подставим его в третье уравнение, из которого вы уже можете рассчитать I₃:

I₂ = — (V₁ + Я₃*(Р₁+R₃))/Р₁ or I₂ = — (8 + I₃* 80) / 40

I₃*R₃ + R₂* (V₁ + Я₃*(Р₁+R₃))/Р₁ +V₂ = 0 or I₃* 40 + 20 * (8 + I₃* 80) / 40 + 16 = 0

А также: I₃ = — (V₂ + V₁*R₂/R₁)/(Р₃+ (R₁+R₃)*Р₂/R₁) or I₃ = -(16+8*20/40)/(40 + 80*20/40)

Поэтому I₃ = — 0.25 А; I₂ = — (8-0.25 * 80) / 40 = 0.3 A и I₁ = — (0.3-0.25) = — 0.05 А

Или: I₁ = -50 мА; I₂ = 300 мА; I₃ = -250 мА.

Теперь давайте решим те же уравнения с интерпретатором TINA:

{Решение переводчика TINA} Sys I1, I2, I3 I1 + I2 + I3 = 0 -V1+I1*R1-I3*R3=0 I3*R3-I2*R2+V2=0 конец; I1 = [- 50m] I2 = [300m] I3 = [- 250m]

Наконец, давайте проверим Результаты с использованием TINA:

Далее, давайте проанализируем следующую, еще более сложную схему и определим ее ответвления токами и напряжениями.

Нажмите / коснитесь схемы выше для анализа в режиме онлайн или нажмите эту ссылку, чтобы Сохранить в Windows

Обозначим неизвестные напряжения и токи, добавив стрелки напряжения и тока к компонентам, а также покажем петли (L1, L2, L3) и узлы (N1, N2), где мы будем использовать уравнения Кирхгофа.

Вот набор Уравнения Кирхгофа для петель (с использованием направления по часовой стрелке) и узлов.

-I_L + Я_R1 — Я_s = 0 (для N1)

— Я_R1 + Я_R2 + Я_s3 = 0 (для N2)

-V_s1 — V_R3 + V_Is + V_L = 0 (для L1)

-V_Is + V_s2 +V_R2 +V_R1 = 0 (для L2)

-V_R2 — V_s2 + V_s3 = 0 (для L3)

Применяя закон Ома:

V_L = Я_L*R_L

V_R1 =I_R1*R₁

V_R2 = Я_R2*R₂

V_R3 = — Я_L*R₃

Это 9 неизвестных и 9 уравнений. Самый простой способ решить эту проблему — использовать TINA.

переводчик. Однако, если мы вынуждены использовать ручные вычисления, отметим, что этот набор уравнений может быть легко сведен к системе из 5 неизвестных путем подстановки последних 4 уравнений в уравнения цикла L1, L2, L3. Кроме того, добавив уравнения (L1) и (L2), мы можем устранить V_Is , сводя задачу к системе уравнений 4 для неизвестных 4 (I_L, I_R1 I_R2, I_s3). Когда мы нашли эти токи, мы можем легко определить V_L, V_R1, V_R2, и V_R3 используя последние четыре уравнения (закон Ома).

Подставляя V_L ,V_R1,V_R2 ,V_R3 :

-I_L + Я_R1 — Я_s = 0 (для N1)

— Я_R1 + Я_R2 + Я_s3 = 0 (для N2)

-V_s1 + Я_L*R₃ + V_Is + Я_L*R_L = 0 (для L1)

-V_Is + V_s2 + Я_R2*R₂ + Я_R1*R₁ = 0 (для L2)

— Я_R2*R₂ — V_s2 + V_s3 = 0 (для L3)

Добавляя (L1) и (L2) мы получаем

-I_L + Я_R1 — Я_s = 0 (для N1)

— Я_R1 + Я_R2 + Я_s3 = 0 (для N2)

-V_s1 + Я_L*R₃ + Я_L*R_L + V_s2 + Я_R2*R₂ + Я_R1*R₁ = 0 (L1) + (L2)

— Я_R2*R₂ — V_s2 + V_s3 = 0 (для L3)

После подстановки значений компонентов решение этих уравнений приходит легко.

-I_L+I_R1 — 2 = 0 (для N1)

-I_R1 + Я_R2 + Я_S3 = 0 (для N2)

-120 — + Я_L* 90 + I_L* 20 + 60 + I_R2* 40 + I_R1* 30 = 0 (л₁) + (L₂)

-I_R2* 40 — 60 + 270 = 0 (для L₃)

от L₃ I_R2 = 210 / 40 = 5.25 A (I)

из N₂ I_S3 — Я_R1 = — 5.25 (II),

от L₁+L₂ 110 I_L + 30 I_R1 = -150 (III),

и для N₁ I_R1 — Я_L = 2 (IV)

Умножьте (IV) на –30 и добавьте к (III) 140 I_L = -210 следовательно I_L = — 1.5 А

Заменить я_L в (IV) I_R1 = 2 + (-1.5) = 0.5 A

и я_R1 в (II), I_S3 = -5.25 + I_R1 = -4,75 A

И напряжения: V_R1 = Я_R1*R₁ = 15 V; V_R2 = Я_R2*R₂ = 210 V;

V_R3 = — Я_L*R₃= 135 V; V_L = Я_L*R_L = — 30 В; V_Is V =_S1+V_R3-V_L = 285 V

{Решение исходных уравнений интерпретатором TINA} Sys IL,IR1,IR2,Is3,VIs,VL,VR1,VR3,VR2 -IL-Is + IR1 = 0 -IR1 + IR2 + Is3 = 0 -Vs1 + VR3 + Вис-VL = 0 -Vis + VR1 + VR2 + Vs2 = 0 -Vs3 + VR2 + Vs2 = 0 VR1 = IR1 * R1 VR2 = IR2 * R2 VR3 = -IL * R3 VL = IL * RL конец; IL = [- 1.5] IR1 = [500m] IR2 = [5.25] Is3 = [- 4.75] = ВП [285] VL = [- 30] VR1 = [15] VR2 = [210] VR3 = [135]

Решение приведенной системы уравнений с использованием интерпретатора:

{Решение сокращенной системы уравнений интерпретатором TINA} Sys Il, Ir1, Ir2, Is3 -Il + Ir1-2 = 0 -Ir1 + Ir2 + Is3 = 0 -120+110*Il+60+40*Ir2+30*Ir1=0 -40 * Ir2 + 210 = 0 конец; Ил = [- 1.5] Ir1 = [500m] Ir2 = [5.25] Is3 = [- 4.75]

Мы также можем ввести выражения для напряжений и заставить интерпретатора TINA рассчитать их:

Il: = — 1.5; Ir1: = 0.5; Ir2: = 5.25; Is3: = — 4.75; Вл: = Il * RL; Vr1: = Ir1 * R1 Vr2: = Ir2 * R2; Vr3: = — Il * R3; ВП: = Vs1-Vl + Vr3; Vl = [- 30] Vr1 = [15] Vr2 = [210] Vr3 = [135] = ВП [285]

Мы можем проверить результат с TINA, просто включив интерактивный режим постоянного тока TINA или используя Анализ / Анализ постоянного тока / Узловое напряжение

---

УЗЕЛ ПОТЕНЦИАЛЬНЫЙ МЕТОД

Второй закон Кирхгофа — Заявление, ограничения, применения и примеры

Густав Кирхгоф, физик из Германии, исследовал и нашел два закона, касающихся электрических цепей, включающих сосредоточенные электрические элементы. В 1845 году он исследовал концепции закона Ома и закона Максвелла и определил первый закон Кирхгофа (KCL) и второй закон Кирхгофа (KVL).

Текущий закон Кирхгофа или KCL основан на законе сохранения заряда. В соответствии с этим входной ток узла должен быть равен выходному току узла.Далее второй закон подробно обсуждается ниже.

Государственный Второй закон Кирхгофа

Второй закон Кирхгофа также известен как закон напряжения Кирхгофа (KVL). Согласно KVL, сумма разности потенциалов в замкнутой цепи должна быть равна нулю. Или электродвижущая сила, действующая на узлы в замкнутом контуре, должна быть равна сумме разности потенциалов, найденной на этом замкнутом контуре.

2-й закон Кирхгофа также следует закону сохранения энергии, и это можно вывести из следующих утверждений.

• В замкнутом контуре полученный заряд равен количеству энергии, которую он теряет. Эта потеря энергии происходит из-за резисторов, включенных в эту замкнутую цепь.

• Кроме того, сумма падений напряжения в замкнутой цепи должна быть равна нулю. Математически это можно представить как ∑V = 0.

Ограничение и применение закона Кирхгофа

Согласно Кирхгофа, закон выполняется только при отсутствии флуктуирующих магнитных полей в этой цепи.Таким образом, его нельзя применять при наличии флуктуирующего магнитного поля. Взгляните на приложения KVL.

Обратитесь к этому изображению выше, чтобы найти признаки напряжения, когда направление тока в этой петле такое, как показано.

Давайте разберемся с законом напряжения Кирхгофа на примере.

1. Возьмите замкнутую схему или нарисуйте ее, как показано на рисунке.

2. Нарисуйте направление тока в цепи, которое может не совпадать с фактическим направлением тока.

3. В точках A и B I3 становится суммой I1 и I2. Итак, мы можем написать I3 = I1 + I2.

4. Согласно второму закону Кирхгофа, сумма падения потенциала в замкнутой цепи будет равна напряжению. Из этого оператора имеем

В цикле 1: I1 * R1 + I3 * R3 = 10.

В цикле 2: I2 * R2 + I3 * R3 = 20.

В цикле 3: 10 * I1 — 20 * I2 = 10-20.

Если подставить значения R1, R2 и R3 в приведенные выше уравнения, мы получим

в цикле 1: 10 I1 + 40 I3 = 10 или I1 + 4I3 = 1.

В цикле 2:20 I2 + 40 I3 = 20 или I2 + 2 I3 = 1.

В цикле 3: 2 I2 — I1 = 1.

5. Согласно 1-му закону Кирхгофа I3 = I1 + I2. Подставляя это во все 3 уравнения, мы получаем

В цикле 1: I1 + 4 (I1 + I2) = 1 или 5 I1 + I2 = 1. ………………… (1)

В цикле 2: I2 + 2 (I1 + I2) = 1, или 2I1 + 3I2 = 1. ………………. (2)

Приравнивая уравнения 1 и 2, мы получаем

5 I1 + I2 = 2I1 + 3I2, или 3 I1 = 2 I2

Следовательно, I1 = -1/3 I2

Подставляя значение I1 в уравнение цикла 3, мы получаем

I1 = -0.143 A.

I2 = 0,429 A.

I3 = 0,286 A.

Приведенные выше предположения и расчеты доказывают, что закон Кирхгофа по напряжению справедлив для этих сосредоточенных электрических цепей.

Впоследствии вы сможете лучше понять KVL, приобретя учебные материалы из нашего приложения Vedantu. Вы можете скачать приложение, чтобы начать обучение, не выходя из дома.

% PDF-1.7 % 387 0 объект > эндобдж xref 387 126 0000000016 00000 н. 0000003964 00000 н. 0000004109 00000 п. 0000004145 00000 н. 0000005507 00000 н. 0000006007 00000 н. 0000006589 00000 н. 0000007257 00000 н. 0000007882 00000 н. 0000007983 00000 п. 0000008020 00000 н. 0000008513 00000 н. 0000008625 00000 н. 0000008739 00000 н. 0000009135 00000 н. 0000010243 00000 п. 0000010879 00000 п. 0000011259 00000 п. 0000011620 00000 п. 0000012199 00000 п. 0000012468 00000 п. 0000012746 00000 п. 0000012976 00000 п. 0000013327 00000 п. 0000014325 00000 п. 0000015441 00000 п. 0000016293 00000 п. 0000017125 00000 п. 0000018093 00000 п. 0000045987 00000 п. 0000046981 00000 п. 0000063752 00000 п. 0000067230 00000 п. 0000072243 00000 п. 0000074892 00000 п. 0000075017 00000 п. 0000075096 00000 п. 0000075193 00000 п. 0000075342 00000 п. 0000075455 00000 п. 0000078613 00000 п. 0000097513 00000 п. 0000097544 00000 п. 0000097619 00000 п. 0000141645 00000 н. 0000141973 00000 н. 0000142039 00000 н. 0000142155 00000 н. 0000142230 00000 н. 0000142546 00000 н. 0000142601 00000 н. 0000142717 00000 н. 0000142748 00000 н. 0000142823 00000 н. 0000144331 00000 п. 0000144658 00000 н. 0000144724 00000 н. 0000144840 00000 н. 0000144871 00000 н. 0000144946 00000 н. 0000145275 00000 п. 0000145341 00000 п. 0000145457 00000 н. 0000145488 00000 н. 0000145563 00000 н. 0000145892 00000 н. 0000145958 00000 н. 0000146074 00000 н. 0000146105 00000 н. 0000146180 00000 п. 0000146509 00000 н. 0000146575 00000 н. 0000146691 00000 н. 0000146722 00000 н. 0000146797 00000 н. 0000147126 00000 н. 0000147192 00000 н. 0000147308 00000 н. 0000147339 00000 н. 0000147414 00000 н. 0000147741 00000 п. 0000147807 00000 н. 0000147923 00000 п. 0000148649 00000 н. 0000148930 00000 н. 0000149252 00000 н. 0000165053 00000 н. 0000165092 00000 н. 0000165479 00000 н. 0000165576 00000 н. 0000165722 00000 н. 0000166124 00000 н. 0000166221 00000 н. 0000166367 00000 н. 0000166442 00000 н. 0000166567 00000 н. 0000166869 00000 н. 0000166944 00000 н. 0000167070 00000 н. 0000167145 00000 н. 0000167892 00000 н. 0000167940 00000 н. 0000169975 00000 н. 0001195510 00000 п. 0001195897 00000 п. 0001196487 00000 п. 0001196562 00000 п. 0001196852 00000 п. 0001196927 00000 н. 0001197221 00000 п. 0001197296 00000 п. 0001197590 00000 п. 0001197665 00000 п. 0001197959 00000 п. 0001198034 00000 п. 0001198328 00000 п. 0001198403 00000 п. 0001198697 00000 п. 0001208025 00000 п. 0001213050 00000 п. 0001673491 00000 п. 0001677530 00000 п. 0001681569 00000 н. 0001701973 00000 п. 0001771455 00000 п. 0000002816 00000 н. трейлер ] / Назад 4188790 >> startxref 0 %% EOF 512 0 объект > поток h ތ T [lTU]>) v

j-M «4B2ь1BÏ2

+» W0UBV && «~? B ܧ Cc sg {(@ QT ه m% V

Примеры и формулы закона Кирхгофа | Закон Кирхгофа по току и напряжению — Видео и стенограмма урока

Закон Кирхгофа по току и напряжению

Итак, что такое закон Кирхгофа? На самом деле существует два варианта этих законов.Они известны как закон тока Кирхгофа

• : ток, входящий в соединение, должен быть равен току, выходящему из соединения.
• Закон Кирхгофа по напряжению: изменение потенциала вокруг замкнутого контура должно быть нулевым.

Эти законы были разработаны путем применения сохранения электрического заряда и сохранения энергии в замкнутых цепях. Они позволяют анализировать сложные цепи, чтобы определить ток в каждой ветви цепи.

Текущий закон Кирхгофа

Текущий закон Кирхгофа , или правило соединения, гласит, что в любой точке соединения или узле сумма всего тока, входящего в соединение, должна равняться сумме всех токов, покидающих соединение или узел.Формула закона Кирхгофа для тока:

{eq} \ sum I_ {in} = \ sum I_ {out} {/ eq}

Это следствие сохранения электрического заряда. Общий электрический заряд в замкнутой системе никогда не меняется. Итак, ток, который идет в узел, должен быть равен выходному току. На рис. 2 мы видим пример узла, который представляет собой соединение четырех токоведущих маршрутов с тремя токами, входящими в узел, и одним выходящим.

Рис. 2: Иллюстрация узла с тремя входящими токами и одним выходящим.

Согласно действующему закону Кирхгофа, следующее относительно рис. 2 должно выполняться.

{eq} I_1 + I_2 + I_4 = I_3 {/ eq}

Закон напряжения Кирхгофа

Закон напряжения Кирхгофа , или правило петли, основан на сохранении энергии. В нем говорится, что сумма изменений потенциала вокруг любого контура цепи должна быть равна нулю. Математически это можно записать как

{eq} \ sum_ {n} V_n = 0 {/ eq}

Для схемы с {eq} n {/ eq} элементами.

На рис. 3 показан пример схемы с источником напряжения, {eq} V_S {/ eq} и тремя элементами, вызывающими падение напряжения, {eq} V_1 {/ eq}, {eq} V_2 {/ eq} и {eq} V_3 {/ eq}. Важно отметить направление напряжения вокруг контура. Напряжения от отрицательного к положительному складываются, а напряжения от положительного к отрицательному вычитаются.

Рис. 3: Схема с источником напряжения и тремя падениями напряжения.

Следовательно, общее напряжение в системе следующее, согласно закону напряжения Кирхгофа

{eq} \ sum V_n = 0 {/ eq}

В цепи четыре напряжения, три из них — напряжение падает, поэтому они отрицательны по сравнению с напряжением источника.Следовательно, сумма напряжений равна

{eq} V_S — V_1 — V_2 — V_3 = 0 {/ eq}

, что дает

{eq} V_S = V_1 + V_2 + V_3 {/ eq}

Закон Кирхгофа. Примеры

При решении проблем с использованием законов Кирхгофа может быть полезно разбить проблему на следующие этапы:

1. Обозначьте ток в каждой ветви цепи и обозначьте направление.
2. Определите количество неизвестных, это укажет количество необходимых уравнений.
3. Применить текущий закон Кирхгофа на одном или нескольких перекрестках.
4. Примените закон напряжения Кирхгофа для одного или нескольких контуров.
5. Решите уравнения.

Рис. 4: Пример схемы с источниками напряжения и резисторами.

Рассмотрим пример схемы, показанной на рис. 4. Эта схема содержит два источника напряжения, 2 В и 6,5 В, и два резистора, 150 {eq} \ Omega {/ eq} и 400 {eq} \ Omega {/ eq}.Законы Кирхгофа можно использовать для определения тока через резисторы и полного тока в цепи. Первый шаг — это маркировка силы тока и направления в цепи. На диаграмме есть три неизвестных: полный ток, {eq} I_T {/ eq}, ток через резистор 150 {eq} \ Omega {/ eq}, {eq} I_1 {/ eq} и ток через резистор 400 {eq} \ Omega {/ eq}, {eq} I_2 {/ eq}. Поскольку существует три неизвестных, для решения этой задачи требуются три уравнения. Следующим шагом будет применение действующего закона Кирхгофа.

Рис. 5: Пример схемы, показывающей направление тока.

Применение закона Кирхгофа на первом переходе дает

{eq} I_T = I_1 + I_2 {/ eq}

Поскольку ток, идущий в переход, {eq} I_T {/ eq}, должен равняться току выходит, {eq} I_1 {/ eq} и {eq} I_2 {/ eq}. Следующим шагом является применение закона Кирхгофа по напряжению к двум петлям по часовой стрелке, как показано на рис.6.

Рис. 6: Пример схемы, показывающей две петли для закона напряжения.

Для левого контура это дает

{eq} \ sum V_n = 0 \\ \\ 2V — V_R = 0 {/ eq}

Где {eq} V_R {/ eq} — напряжение через Резистор 150 {eq} \ Omega {/ eq}. Используя закон Ома, уравнение принимает вид

{eq} 2V — 150 \ Omega \ times I_1 = 0 {/ eq}

Теперь мы можем решить эту проблему для тока.

{eq} — 150 \ Omega \ times I_1 = -2V \\ I_1 = 0,013A {/ eq}

Следовательно, ток через резистор 150 {eq} \ Omega {/ eq} равен {eq} I_1 = 0,013 А {/ экв}. В правом контуре напряжение через два резистора снова можно определить по закону Ома. Уравнение для правого контура:

{eq} \ sum V_n = 0 \\ \\ 150 \ Omega \ times (I_1 — I_2) — 6.5 V — 400 \ Omega \ times I_2 = 0 \\ 150 \ Omega \ times I_1 — 150 \ Omega \ times I_2 — 6.5V — 400 \ Omega \ times I_2 = 0 {/ eq}

Обратите внимание, что значение для {eq} I_2 {/ eq} вычитается из {eq} I_1 {/ eq} потому что они текут в противоположных направлениях через резистор 150 {eq} \ Omega {/ eq}.Затем мы подставляем значение, вычисленное для {eq} I_1 {/ eq} в приведенное выше уравнение.

{eq} 150 \ Omega \ times 0,013A — 150 \ Omega \ times I_2 — 6.5V — 400 \ Omega \ times I_2 = 0 \\ \\ 1.95V — 150 \ Omega \ times I_2 — 6.5V — 400 \ Omega \ times I_2 = 0 \\ -550 \ Omega \ times I_2 = 4.55V \\ I_2 = -0.008A {/ eq}

Таким образом, мы обнаружили, что ток через 400 {eq} \ Omega { / eq} резистор равен {eq} I_2 = -0,008 A {/ eq}. Эти значения затем можно подставить в уравнение, полученное из текущего закона Кирхгофа, которое дает

{eq} I_T = 0.013 A — 0,008 A {/ eq}

Следовательно, общий ток в цепи составляет {eq} I_T = 0,005 A {/ eq}.

Ограничения законов Кирхгофа для цепей

Законы Кирхгофа — мощный инструмент для анализа цепей в цепях постоянного тока и цепях переменного тока ниже определенного предела низких частот. Однако в цепях переменного тока на более высоких частотах они теряют силу. Это связано с тем, что оба закона зависят от предположений, которые не выполняются с увеличением частоты.

Текущий закон предполагает, что чистый заряд в цепи постоянный.Закон напряжения основан на предположении, что магнитные поля не изменяются в замкнутой цепи или что любое изменение магнитного поля ограничивается отдельными компонентами. Однако в высокочастотных цепях переменного тока это не всегда так. Когда присутствует флуктуирующее магнитное поле, которое не ограничено отдельными компонентами, электрические поля могут индуцироваться в других компонентах, что нарушает законы Кирхгофа. В результате они обеспечивают лишь грубое приближение для высокочастотных цепей переменного тока.

Резюме урока

Законы Кирхгофа можно использовать для анализа сложных схем.Есть два варианта этих законов, которые возникают в результате сохранения электрического заряда и сохранения энергии в замкнутых цепях. Закон Кирхгофа гласит, что ток, входящий в переход, должен быть равен току, выходящему из перехода, поскольку электрический заряд сохраняется. Закон напряжения Кирхгофа гласит, что изменение потенциала вокруг замкнутого контура должно быть нулевым из-за сохранения энергии.

приложений, ограничения и решенные примеры!

Законы Кирхгофа для цепей считаются основой любого анализа электрических цепей.Существует два типа законов Кирхгофа для цепей: закон Кирхгофа по току и закон Кирхгофа по напряжению. С помощью этих законов и уравнения для отдельных компонентов (резистора, конденсатора и катушки индуктивности) мы анализируем цепи. В 19 веке ученый по имени Густав Роберт Кирхгоф внес большой вклад в эту теорию и дал лучшее понимание электрических цепей. Он также обнаружил, что ток течет по проводнику со скоростью света.

Чтобы получить подробную информацию о кинетической теории газов, кандидаты могут посетить связанную статью.

Терминология цепи

1. Контур: Это замкнутый путь, по которому течет ток.
2. Путь: Путь рассматривается как одна линия, состоящая из элементов схемы и источников.
3. Узел: Узел определяется как терминал или соединение, в котором два или более элемента будут соединены вместе и, таким образом, будут иметь общую точку для более чем одной ветви.
4. Ветвь : Ветвь состоит из таких элементов, как резисторы и источники, подключенные между двумя узлами.
5. Цикл: Цикл — это замкнутый путь, в котором элементы подсчитываются только один раз.
6. Сетка: Сетка — это открытый контур без каких-либо элементов.

Если элементы соединены последовательно, ток, протекающий через каждый из них, будет одинаковым. Если элементы соединены параллельно, напряжение на каждом компоненте остается неизменным.

Подробнее о расстоянии и смещении см. В связанной статье.

Густав Роберт Кирхгоф

Густав Роберт Кирхгоф, немецкий физик, родился 12 марта 1824 года.Он внес вклад в фундаментальное понимание электрических цепей, спектроскопии и излучения черного тела нагретыми объектами. В XIX веке Густав Роберт Кирхгоф внес большой вклад в эту теорию и обеспечил лучшее понимание электрических цепей. Он также обнаружил, что ток течет по проводнику со скоростью света.

Первый закон — Закон Кирхгофа (KCL)

Первый закон Кирхгофа касается тока в цепи.Согласно этому закону алгебраическая сумма токов в любом узле цепи равна нулю. Полный ток, поступающий в переход, в точности равен полному току, выходящему из перехода. Этот закон основан на сохранении сборов.

Из изображения ниже мы можем сказать, что:

\ ((i_2 + i_3 + i_5 + i_6 + i_7) = (i_1 + i_4 + i_8) \)

∑ incoming = ∑ outgoing

Вы также можете подробности о Векторе.

В. Найдите ток в данной цепи.

Ответ. В узле возможно только одно значение тока

Итак, здесь нарушение KCL

Итак, ток в цепи невозможен.

См. Статью о равномерном круговом движении здесь.

Наконечник памяти

• KCL применяется к любой сосредоточенной сети независимо от ее характера; односторонние или двусторонние, активные или пассивные, линейные или нелинейные.
• KCL не распространяется на распределенные сети.
• Ток всегда проходит менее устойчивым путем.
• KCL всегда обеспечивает сохранение заряда.
• Максимальный ток протекает при коротком замыкании из-за нулевого сопротивления.
• Нет протекания тока в разомкнутой цепи из-за бесконечного сопротивления.

Получите подробную информацию о вихревых токах и токах смещения.

Второй закон — Закон напряжения Кирхгофа (KVL)

Закон напряжения Кирхгофа или второй закон касается падения напряжения в цепи.Когда в цепи протекает ток, величина тока изменяется в зависимости от произведения тока на сопротивление или ЭДС, с помощью которой он подключен в цепи. Согласно этому закону алгебраическая сумма напряжения (или падений напряжения) на любом замкнутом пути сети в определенном направлении равна нулю.

Знак при движении в цикле полностью зависит от пользователя,

Если мы рассмотрим переход от положительного (+) к отрицательному (-) (это зависит от пользователя), он действует как капля или прирост.

Этот знак не влияет на ответ.

Предположим, мы рассматриваем это как падение (-) при переходе от положительного (+) к отрицательному (-).

• Начнем с сопротивления R1. Ток идет от одной точки к другой (от положительной к отрицательной), а падение напряжения считается отрицательным (-).
• При переходе от ЭДС ток E2 меняется с положительного на отрицательный, и падение принимается как –E2
• Аналогично для R2 и R3
• Наконец, при переходе от E1 ток меняется с отрицательного на положительный, и здесь берется усиление.

-iR1 — E2 — iR2 + E1 = 0

E1 — E2 = iR1 + iR2

Q. Найдите ток I в данной цепи.

Ответ. Применим KVL в данном контуре, тогда мы получим,

120-30 I — 2VA + VA = 0

120 = 30 I + VA …………… (1)

Также из закона Ома на выходе мы можно получить

ВА = — 15 I ……………… .. (2)

Решая уравнения (1) и (2), получаем

I = 8 ампер.

Итак, в цепи протекает ток 8А.

Проверьте питание в цепи переменного тока для получения подробной информации здесь.

Наконечник памяти

• KVL применяется к любой сосредоточенной сети независимо от характера сети; односторонние или двусторонние, активные или пассивные, линейные или нелинейные.
• KVL не распространяется на распределенные сети.
• Падение напряжения при коротком замыкании равно нулю из-за нулевого сопротивления.
• КВЛ всегда экономит энергию.
• Максимальное напряжение возникает в разомкнутой цепи из-за бесконечного сопротивления.
• Напряжение постоянно в параллельном тракте и делится в последовательном тракте.

Применение закона Кирхгофа

С помощью закона Кирхгофа можно найти:

1. Значения тока, напряжения и внутреннего сопротивления в цепях постоянного тока.
2. Применяя этот закон, мы также можем найти неизвестное сопротивление в цепи.
3. Мост Уитстона — важное приложение закона Кирхгофа. Он используется при анализе сетки и узлов.

Ограничения закона Кирхгофа

1. Законы KCL и KVL не подходят для цепей переменного тока высокой частоты.Текущий закон применяется только тогда, когда электрический заряд в цепи постоянный.
2. Где KVL применяется в предположении, что магнитные поля не изменяются в замкнутой цепи. Таким образом, мы не можем применять KVL, когда магнитное поле изменяется внутри цепи.

Прочтите об атомах и ядрах здесь.

Законы Кирхгофа для цепей: краткое изложение

1. Густав Кирхгоф дает лучшее понимание решения и применения электрических цепей.
2. Первый закон Кирхгофа гласит, что полный ток, который входит в узел или переход, равен полному току или заряду, выходящему из узла.В его основе лежит принцип сохранения заряда. Это также известно как правило соединения.
3. Второй закон Кирхгофа гласит, что сумма падений напряжения равна сумме повышений напряжения. Этот закон основан на сохранении энергии. Это также известно как правило цикла.

Мы надеемся, что приведенные выше примечания к законам Кирхгофа помогли вам лучше понять предстоящие экзамены JEE и другие конкурсные экзамены. Попрактикуйтесь прямо сейчас в приложении Testbook с помощью бесплатных пробных тестов.

Также подробно ознакомьтесь с типами термодинамических процессов, чтобы улучшить вашу подготовку.

Часто задаваемые вопросы о законах Кирхгофа об округах

Q.1 Что такое первый закон Кирхгофа?

Ans.1 Согласно этому закону алгебраическая сумма токов в любом узле цепи равна нулю. Полный ток, поступающий в переход, в точности равен полному току, выходящему из перехода. Этот закон основан на сохранении сборов.

Q.2 Что такое второй закон Кирхгофа?

Ans.2 Согласно этому закону алгебраическая сумма напряжения (или падений напряжения) на любом замкнутом пути сети в определенном направлении равна нулю.

Q.3 Что такое цепь?

Ans.3 Цепь — это замкнутая цепь, по которой протекает ток.

Q.4 Что такое петля?

Ans.4 Цикл — это замкнутый путь, в котором элементы подсчитываются только один раз.

Q.5 Что такое узел?

Ans.5 Узел определяется как терминал или соединение, в котором два или более элемента будут соединены вместе и, таким образом, имеют общую точку для более чем одной ветви.

Создайте бесплатную учетную запись, чтобы продолжить чтение

• Получайте мгновенные оповещения о вакансиях бесплатно!

• Получите ежедневный GK и текущие новости Капсула и PDF-файлы

• Получите более 100 бесплатных пробных тестов и викторин

Подпишитесь бесплатно Уже есть аккаунт? Войти

Следующая запись

Законы Кирхгофа

Законы Кирхгофа

Далее: Проблемы Up: цепей предыдущий: резисторы, включенные параллельно

Хотя полезно иметь возможность уменьшить количество последовательных и параллельных резисторов в схемы, когда они возникают, схемы в целом не состоят исключительно таких комбинаций.Для таких случаев есть мощный набор соотношения, называемые законами Кирхгофа , которые позволяют анализировать произвольные схемы. Таких законов два:

• 1 ^st law or the junction rule : for a given junction или узла в цепи, сумма входящих токов равна сумме выходящих токов. Этот закон является утверждением сохранения заряда. Например, на рис. 17.6,
  

  Рисунок 17.6: Иллюстрация правила пересечения Кирхгофа

  
  правило соединения говорит нам I ₁ = I ₂ + I ₃ .
• 2 ^{nd закон} или правило петли : вокруг любого замкнутого петля в цепи, сумма разностей потенциалов по всем элементам равно нулю. Этот закон является заявлением о сохранении энергии, в этом любое обвинение, что начинается и заканчивается в той же точке, что и та же скорость должна была набрать столько же энергии, сколько и потерянный. Например, на рис. 17.7,
  

  Рисунок 17.7: Иллюстрация правила петли Кирхгофа

  
  , где прямоугольниками обозначен элемент схемы, правило цикла говорит нам 0 = ( V _b — V _a ) + ( V _c — V _b ) + ( V _d — V _c ) ( V _d — V _a ).

Второй закон влечет за собой определенные условные обозначения для потенциальных различий. по элементам схемы. Для батарей и резисторов эти условные обозначения следующие: резюмировано на рис. 17.8. Обратите внимание, что в этих соглашениях ток всегда течет от высокого к низкому потенциалу.

Рисунок 17.8: Условные обозначения для правила петли Кирхгофа

При анализе схем с использованием законов Кирхгофа полезно иметь в виду следующие рекомендации.

1.

Нарисуйте схему и присвойте метки известным и неизвестным количества, включая токи в каждой ветви. Вы должны назначить направления течениям; не волнуйся, если ты неправильно угадать направление определенного неизвестного тока, поскольку ответ в результате анализа в этом случае просто выйдет отрицательным, но с нужной величиной.

2.

Примените правило соединения к как можно большему числу соединений в цепи. для получения максимального количества независимых отношений.

3.

Примените правило цикла к необходимому количеству петель в схеме. чтобы решить неизвестное. Обратите внимание, что если у одного n неизвестных в схеме потребуется n независимых уравнений. В общем есть будет больше петель в цепи, чем нужно решить для всех неизвестные; отношения, полученные в результате этих « лишних » циклов, могут быть использованы в качестве проверки последовательности ваших окончательных ответов.

4.

Решите полученную систему одновременных уравнений для неизвестные количества.

Умение анализировать схемы по законам Кирхгофа, особенно с с учетом условных обозначений и решения одновременных уравнений, приходит с практикой.

---

Далее: Проблемы Up: цепей предыдущий: резисторы, включенные параллельно

[email protected]
09.10.1997

Первый и Второй законы Кирхгофа

Кирхгоф получил огромное имя в физике, просто применив два принципа физики к электрическим цепям.Это первый:

В любом соединении в цепи сумма токов, поступающих в соединение, = сумме токов, покидающих соединение.

Другими словами — заряд сохраняется . Если этого не произойдет, вы либо получите массивное скопление электронов на стыке в цепи, либо создадите заряд из ниоткуда! Это не произойдет.

Входной ток = Выходной ток

I ₁ = I ₂ + I ₃ + I ₄

Вот второй принцип:

В любом контуре (пути) вокруг цепи сумма ЭДС = сумме pds.

Другими словами — энергии сохраняется. Общее количество вложенной энергии (сумма ЭДС) совпадает с общим количеством отведенной энергии (сумма pds).

Примечание: pd = V = IR, поэтому

Энергия на входе = Энергия на выходе

ЭДС = pd ₁ + pd ₂ + pd ₃ + pd ₄

Причина, по которой Законы Кирхгофа вселяют страх в студентов A-level, заключается в том, что вы должны осторожно применять их.Как только вы освоите их, они не так уж и сложны. Придерживайтесь этих правил, и все будет в порядке.

Примеры вопросов с использованием законов Кирхгофа:

1. Используйте законы Кирхгофа, чтобы найти внутреннее сопротивление ячейки.

   Есть несколько способов ответить на этот вопрос, но вот один пример, использующий 2-й закон …

   Энергия на входе = Энергия на выходе и V = IR, поэтому

   10 В = (0.3 x 4) + (0,3 x 3) + (0,3 x r)

   10 = 1,2 + 0,9 + 0,3r

   7,9 = 0,3r, поэтому r = 26,3 Ом

2. Используйте законы Кирхгофа, чтобы найти ЭДС клетки.

   Опять же, к этому можно подойти разными способами, но на этот раз мы начнем с Правила 1 …

   Входной ток = Выходной ток

   Это говорит о том, что ток через каждый резистор 5 Ом составляет 1,5 А.

   Закон 2 говорит нам, что:

   ЭДС = (3×4) + (1.5×5) + (3×2,5)

   ЭДС = 12 + 7,5 + 7,5 = 27 В

   Теперь ваша очередь!

   Вопрос, который стоит попробовать:

   Используйте законы Кирхгофа, чтобы найти Э.М. показания ячейки на вольтметре и значения неизвестного резистора.

10.3 Правила Кирхгофа — Университетская физика, Том 2

Цели обучения

К концу этого раздела вы сможете:

• Государственное правило пересечения Кирхгофа
• Государственное правило петли Кирхгофа
• Анализировать сложные схемы по правилам Кирхгофа

Мы только что видели, что некоторые схемы можно проанализировать, сведя схему к одному источнику напряжения и эквивалентному сопротивлению.Многие сложные схемы не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в предыдущих разделах. В этом разделе мы подробно рассмотрим использование правил Кирхгофа для анализа более сложных схем. Например, схема на рис. 10.19 известна как многоконтурная схема, состоящая из переходов. Соединение, также известное как узел, представляет собой соединение трех или более проводов. В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы имеют четкую последовательную или параллельную конфигурацию, которую можно уменьшить.Попробуйте. Резисторы R1R1 и R2R2 включены последовательно и могут быть уменьшены до эквивалентного сопротивления. То же самое и с резисторами R4R4 и R5R5. Но что же тогда делать?

Несмотря на то, что эта схема не может быть проанализирована с помощью уже изученных методов, два правила анализа схемы могут использоваться для анализа любой схемы, простой или сложной. Эти правила известны как правила Кирхгофа в честь их изобретателя Густава Кирхгофа (1824–1887).

Фигура 10,19 Эта схема не может быть сведена к комбинации последовательного и параллельного подключения.Однако мы можем использовать правила Кирхгофа для его анализа.

Правила Кирхгофа

• Первое правило Кирхгофа — правило соединения. Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения: ∑Iin = ∑Iout.∑Iin = ∑Iout.

  10,4

• Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любого пути (контура) замкнутой цепи должна быть равна нулю:

Теперь мы даем объяснения этих двух правил, за которыми следуют советы по их применению и рабочий пример, в котором они используются.

Первое правило Кирхгофа

Первое правило Кирхгофа (правило соединения) применяется к заряду, входящему в соединение и выходящему из него (рис. 10.20). Как указывалось ранее, соединение или узел — это соединение трех или более проводов. Ток — это поток заряда, и заряд сохраняется; таким образом, любой заряд, попадающий в переход, должен вытекать.

Фигура 10.20 Заряд должен быть сохранен, поэтому сумма токов в переходе должна быть равна сумме токов вне перехода.

Хотя это чрезмерное упрощение, можно провести аналогию с водопроводными трубами, соединенными в водопроводной разводке. Если провода на рис. 10.20 были заменены водопроводными трубами и вода считалась несжимаемой, объем воды, протекающей в разветвление, должен был равняться объему воды, вытекающей из разветвления.

Второе правило Кирхгофа

Второе правило Кирхгофа (правило петли) применяется к разности потенциалов. Правило петли сформулировано в терминах потенциала V , а не потенциальной энергии, но они связаны между собой, поскольку U = qV.U = qV. В замкнутом контуре, какая бы энергия ни поступала от источника напряжения, энергия должна передаваться в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в цепь или из нее. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей потенциалов, включая напряжение, подаваемое источниками напряжения и резистивными элементами, в любой петле должна быть равна нулю. Например, рассмотрим простой контур без стыков, как на рисунке 10.21.

Фигура 10.21 Простая петля без стыков. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей напряжений равна нулю.

Схема состоит из источника напряжения и трех внешних нагрузочных резисторов. Ярлыки a , b , c и d служат в качестве ссылок и не имеют другого значения. Скоро станет очевидна полезность этих этикеток. Петля обозначается как Loop abcda , и метки помогают отслеживать разницу напряжений при перемещении по цепи.Начните с точки a и двигайтесь к точке b . Напряжение источника напряжения добавляется к уравнению и вычитается падение потенциала резистора R1R1. От точки b до c падение потенциала на R2R2 вычитается. От c до d падение потенциала на R3R3 вычитается. От точек d до a ничего не делается, потому что нет компонентов.

На рис. 10.22 показан график напряжения при перемещении по контуру.Напряжение увеличивается при прохождении через батарею, тогда как напряжение уменьшается при прохождении через резистор. Падение потенциала или изменение электрического потенциала равно току через резистор, умноженному на сопротивление резистора. Поскольку провода имеют незначительное сопротивление, напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.

Фигура 10,22 График напряжения при движении по цепи. Напряжение увеличивается, когда мы пересекаем батарею, и уменьшается, когда мы пересекаем каждый резистор.Поскольку сопротивление провода довольно мало, мы предполагаем, что напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.

Тогда правило петли Кирхгофа утверждает

V-IR1-IR2-IR3 = 0. V-IR1-IR2-IR3 = 0.

Уравнение петли можно использовать, чтобы найти ток через петлю:

I = VR1 + R2 + R2 = 12,00 В, 1,00 Ом + 2,00 Ом + 3,00 Ом = 2,00 А. I = VR1 + R2 + R2 = 12,00 В, 1,00 Ом + 2,00 Ом + 3,00 Ом = 2,00 А.

Этот цикл можно было бы проанализировать с помощью предыдущих методов, но мы продемонстрируем мощь метода Кирхгофа в следующем разделе.

Применение правил Кирхгофа

Применяя правила Кирхгофа, мы генерируем набор линейных уравнений, которые позволяют нам находить неизвестные значения в схемах. Это могут быть токи, напряжения или сопротивления. Каждый раз, когда применяется правило, оно создает уравнение. Если независимых уравнений столько же, сколько неизвестных, то проблема может быть решена.

Использование метода анализа Кирхгофа требует нескольких шагов, перечисленных в следующей процедуре.

Стратегия решения проблем

Правила Кирхгофа

1. Обозначьте точки на принципиальной схеме строчными буквами a , b , c ,….Эти ярлыки просто помогают сориентироваться.
2. Найдите соединения в цепи. Соединения — это точки, в которых соединяются три или более проводов. Обозначьте каждое соединение токами и направлениями в него и из него. Убедитесь, что хотя бы один ток направлен на соединение и хотя бы один ток выходит из соединения.
3. Выбрать петли в схеме. Каждый компонент должен содержаться по крайней мере в одном цикле, но компонент может содержаться более чем в одном цикле.
4. Примените правило соединения.Опять же, некоторые стыки не следует включать в анализ. Вам нужно использовать достаточно узлов только для включения каждого тока.
5. Примените правило петли. Используйте карту на рисунке 10.23.

Фигура 10,23 Каждый из этих резисторов и источников напряжения проходит от до до b . (a) При перемещении через резистор в том же направлении, что и ток, вычтите падение потенциала. (b) При перемещении через резистор в направлении, противоположном току, добавьте падение потенциала.(c) При перемещении источника напряжения от отрицательного вывода к положительному, добавьте падение потенциала. (d) При перемещении через источник напряжения от положительной клеммы к отрицательной вычтите падение потенциала.

Давайте более подробно рассмотрим некоторые этапы этой процедуры. При размещении переходов в цепи не обращайте внимания на направление токов. Если направление потока тока неочевидно, выбора любого направления достаточно, если хотя бы один ток направлен в соединение и хотя бы один ток выходит из соединения.Если стрелка находится в направлении, противоположном обычному течению тока, результат для рассматриваемого тока будет отрицательным, но ответ все равно будет правильным.

Количество узлов зависит от схемы. Каждый ток должен быть включен в узел и, таким образом, включен по крайней мере в одно уравнение соединения. Не включайте узлы, которые не являются линейно независимыми, то есть узлы, содержащие одинаковую информацию.

Рассмотрим рисунок 10.24. В этой цепи два перехода: переход b и переход e .Точки a , c , d и f не являются соединениями, потому что соединение должно иметь три или более соединений. Уравнение для перехода b : I1 = I2 + I3I1 = I2 + I3, а уравнение для перехода e — I2 + I3 = I1I2 + I3 = I1. Это эквивалентные уравнения, поэтому необходимо оставить только одно из них.

Фигура 10,24 На первый взгляд, эта схема содержит два соединения, соединение b и соединение e , но следует рассматривать только один, поскольку их уравнения соединения эквивалентны.

При выборе петель в схеме вам необходимо достаточное количество петель, чтобы каждый компонент был покрыт один раз, без повторения петель. На рис. 10.25 показаны четыре варианта петель для решения типовой схемы; варианты (a), (b) и (c) содержат достаточное количество циклов для полного решения схемы. Вариант (d) отражает больше петель, чем необходимо для решения схемы.

Фигура 10,25 Панели (a) — (c) достаточно для анализа схемы. В каждом случае два показанных контура содержат все элементы схемы, необходимые для полного решения схемы.Панель (d) показывает три использованных контура, что больше, чем необходимо. Любые две петли в системе будут содержать всю информацию, необходимую для решения схемы. Добавление третьего цикла дает избыточную информацию.

Рассмотрим схему на рис. 10.26 (а). Давайте проанализируем эту схему, чтобы найти ток через каждый резистор. Сначала промаркируйте схему, как показано в части (b).

Фигура 10,26 (а) Многоконтурная схема. (b) Пометьте цепь, чтобы облегчить ее ориентацию.

Далее определяем стыки. В этой схеме точки b и e имеют по три соединенных провода, что делает их соединениями. Начните применять правило соединения Кирхгофа (∑Iin = ∑Iout) (∑Iin = ∑Iout), нарисовав стрелки, представляющие токи, и пометив каждую стрелку, как показано на рисунке 10.27 (b). Соединение b показывает, что I1 = I2 + I3I1 = I2 + I3, а соединение e показывает, что I2 + I3 = I1I2 + I3 = I1. Поскольку соединение e дает ту же информацию, что и соединение b , ее можно не принимать во внимание.Эта схема имеет три неизвестных, поэтому для ее анализа нам понадобятся три линейно независимых уравнения.

Фигура 10,27 (a) Эта схема имеет два соединения, обозначенных b и e , но в анализе используется только узел b . (b) Обозначенные стрелки представляют токи в переходах и на выходе из них.

Далее нам нужно выбрать петли. На рисунке 10.28 контур abefa включает в себя источник напряжения V1V1 и резисторы R1R1 и R2R2.Цикл начинается в точке a , затем проходит через точки b , e и f , а затем возвращается к точке a . Второй контур, контур ebcde , начинается в точке e и включает в себя резисторы R2R2 и R3R3 и источник напряжения V2V2.

Фигура 10,28 Выбираем петли в схеме.

Теперь мы можем применить правило цикла Кирхгофа, используя карту на рисунке 10.23. Начиная с точки a и двигаясь к точке b , резистор R1R1 пересекается в том же направлении, что и ток I1I1, поэтому падение потенциала I1R1I1R1 вычитается.Двигаясь от точки b к точке e , резистор R2R2 пересекается в том же направлении, что и ток I2I2, поэтому падение потенциала I2R2I2R2 вычитается. Двигаясь от точки e к точке f , источник напряжения V1V1 пересекается от отрицательной клеммы к положительной клемме, поэтому добавляется V1V1. Между точками f и a нет компонентов. Сумма разностей напряжений должна равняться нулю:

Петля: −I1R1 − I2R2 + V1 = 0 или V1 = I1R1 + I2R2.Петля: −I1R1 − I2R2 + V1 = 0 или V1 = I1R1 + I2R2.

Наконец, мы проверяем цикл ebcde . Мы начинаем с точки e и переходим к точке b , пересекая R2R2 в направлении, противоположном течению тока I2I2. Добавляется падение потенциала I2R2I2R2. Затем мы пересекаем R3R3 и R4R4 в том же направлении, что и ток I3I3, и вычитаем падения потенциала I3R3I3R3 и I3R4.I3R4. Обратите внимание, что ток через резисторы R3R3 и R4R4 одинаковый, потому что они соединены последовательно.Наконец, источник напряжения пересекается с положительной клеммы на отрицательную, а источник напряжения V2V2 вычитается. Сумма этих разностей напряжений равна нулю и дает уравнение контура

Цикл: I2R2-I3 (R3 + R4) -V2 = 0. Цикл: I2R2-I3 (R3 + R4) -V2 = 0.

Теперь у нас есть три уравнения, которые мы можем решить относительно трех неизвестных.

(1) Узел b: I1 − I2 − I3 = 0. (2) Петля: I1R1 + I2R2 = V1. (3) Петля: I2R2 − I3 (R3 + R4) = V2. (1) Узел b: I1 − I2 − I3 = 0. (2) Цикл: I1R1 + I2R2 = V1. (3) Цикл: I2R2-I3 (R3 + R4) = V2.

Чтобы решить три уравнения для трех неизвестных токов, начните с исключения тока I2I2. Сначала добавьте уравнение. (1) умножить на R2R2 по формуле. (2). Результат обозначен как уравнение. (4):

(R1 + R2) I1 − R2I3 = V1. (4) 6ΩI1−3ΩI3 = 24В. (R1 + R2) I1 − R2I3 = V1. (4) 6ΩI1−3ΩI3 = 24V.

Затем вычтите уравнение. (3) из уравнения. (2). Результат обозначен как уравнение. (5):

I1R1 + I3 (R3 + R4) = V1 − V2. (5) 3ΩI1 + 7ΩI3 = −5V. I1R1 + I3 (R3 + R4) = V1 − V2. (5) 3ΩI1 + 7ΩI3 = −5V.

Мы можем решить уравнения. (4) и (5) для тока I1I1. Сложив в семь раз уравнение. (4) и троекратное уравнение.(5) дает 51 Ом I1 = 153 В, 51 Ом I1 = 153 В или I1 = 3,00 А. I1 = 3,00 А. Используя уравнение. (4) дает I3 = −2.00A.I3 = −2.00A. Наконец, уравнение. (1) дает I2 = I1 − I3 = 5,00 A. I2 = I1 − I3 = 5,00 A. Один из способов проверить соответствие решений — проверить мощность, подаваемую источниками напряжения, и мощность, рассеиваемую резисторами:

Вывод = I1V1 + I3V2 = 130 Вт, Pout = I12R1 + I22R2 + I32R3 + I32R4 = 130 Вт. Вывод = I1V1 + I3V2 = 130 Вт, Pout = I12R1 + I22R2 + I32R3 + I32R4 = 130 Вт.

Обратите внимание, что решение для тока I3I3 отрицательное. Это правильный ответ, но он предполагает, что стрелка, первоначально нарисованная при анализе соединений, имеет направление, противоположное направлению обычного тока.Мощность, отдаваемая вторым источником напряжения, составляет 58 Вт, а не −58 Вт.

Пример 10,6

Расчет тока по правилам Кирхгофа

Найдите токи, протекающие в цепи на рисунке 10.29. Фигура 10.29 Эта схема представляет собой комбинацию последовательной и параллельной конфигураций резисторов и источников напряжения. Эта схема не может быть проанализирована с использованием методов, обсуждаемых в «Электродвижущей силе», но может быть проанализирована с использованием правил Кирхгофа.

Стратегия

Эта схема достаточно сложна, чтобы токи нельзя было найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. На рисунке токи обозначены I1, I1, I2, I2 и I3I3, и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от до до h . В решении мы применяем правила соединения и петли, ища три независимых уравнения, которые позволят нам найти три неизвестных тока.

Решение

Применение правил соединения и петли дает следующие три уравнения. У нас есть три неизвестных, поэтому требуется три уравнения. Соединениеc: I1 + I2 = I3.Loopabcdefa: I1 (R1 + R4) −I2 (R2 + R5 + R6) = V1-V3.Loopcdefc: I2 (R2 + R5 + R6) + I3R3 = V2 + V3. Соединениеc: I1 + I2 = I3.Loopabcdefa: I1 (R1 + R4) −I2 (R2 + R5 + R6) = V1 − V3.Loopcdefc: I2 (R2 + R5 + R6) + I3R3 = V2 + V3.

Упростите уравнения, поместив неизвестные в одну сторону уравнений.

Соединениеc: I1 + I2-I3 = 06 В + 2,30 В. Соединениеc: I1 + I2-I3 = 0, замкнутый контур: I1 (3 Ом) -I2 (8 Ом) = 0,5 В-2,30 В. Замкнутый контур: I2 (8 Ом) + I3 (1 Ом) = 0,6 В + 2,30 В .

Упростите уравнения. Уравнение первого цикла можно упростить, разделив обе части на 3,00. Уравнение второго цикла можно упростить, разделив обе части на 6,00.

Переход c: I1 + I2 − I3 = 0 .Loopabcdefa: I1 (3 Ом) −I2 (8 Ом) = — 1,8 В. Loopcdefc: I2 (8 Ом) + I3 (1 Ом) = 2,9 В.

Результатов:

I1 = 0,20 А, I2 = 0,30 А, I3 = 0.50 A. I1 = 0,20 A, I2 = 0,30 A, I3 = 0,50 A.

Значение

Метод проверки расчетов заключается в вычислении мощности, рассеиваемой резисторами, и мощности, подаваемой источниками напряжения: PR1 = I12R1 = 0,04W.PR2 = I22R2 = 0,45W.PR3 = I32R3 = 0,25W.PR4 = I12R4 = 0,08W.PR5 = I22R5 = 0,09W.PR6 = I22R6 = 0,18W.Pdissipated = 1,09W.Psource = I1V1 + I2V3 + I3V2 = 0,10 Вт + 0,69 Вт + 0,30 Вт = 1,09 Вт. PR1 = I12R1 = 0,04 Вт. PR2 = I22R2 = 0,45 Вт. PR3 = I32R3 = 0,25 Вт. PR4 = I12R4 = 0,08 Вт. PR5 = I22R5 = 0,09 W.PR6 = I22R6 = 0,18 Вт. Рассеиваемая мощность = 1,09 Вт. Источник питания = I1V1 + I2V3 + I3V2 = 0,10 Вт + 0,69 Вт + 0.30 Вт = 1,09 Вт.

Подаваемая мощность равна мощности, рассеиваемой резисторами.

Проверьте свое понимание 10,6

Проверьте свое понимание При рассмотрении следующей схемы и мощности, подаваемой и потребляемой цепью, всегда ли источник напряжения обеспечивает питание цепи или источник напряжения может потреблять энергию?

Пример 10,7

Расчет тока по правилам Кирхгофа

Найдите ток, протекающий в цепи на рисунке 10.30.

Фигура 10.30 Эта схема состоит из трех резисторов и двух последовательно соединенных батарей. Обратите внимание, что батареи подключены с противоположной полярностью.

Стратегия

Эту схему можно проанализировать с помощью правил Кирхгофа. Есть только один цикл и нет узлов. Выберите направление тока. В этом примере мы будем использовать направление по часовой стрелке от точки a до точки b . Рассмотрим цикл abcda и воспользуемся рисунком 10.23, чтобы написать уравнение цикла. Обратите внимание, что согласно рисунку 10.23, батарея V1V1 будет добавлена, а батарея V2V2 вычтена.

Решение

Применение правила соединения дает следующие три уравнения. У нас есть одно неизвестное, поэтому требуется одно уравнение: Loopabcda: -IR1-V1-IR2 + V2-IR3 = 0. Loopabcda: -IR1-V1-IR2 + V2-IR3 = 0.

Упростите уравнения, поместив неизвестные в одну сторону уравнений. Используйте значения, указанные на рисунке.

I (R1 + R2 + R3) = V2 − V1. I = V2 − V1R1 + R2 + R3 = 24 В − 12 В 10.0 Ом + 30,0 Ом + 10,0 Ом = 0,20 А. I (R1 + R2 + R3) = V2-V1.I = V2-V1R1 + R2 + R3 = 24 В-12 В 10,0 Ом + 30,0 Ом + 10,0 Ом = 0,20 А.

Значение

Мощность, рассеиваемая или потребляемая схемой, равна мощности, подаваемой в схему, но обратите внимание, что ток в батарее V1V1 протекает через батарею от положительной клеммы к отрицательной клемме и потребляет мощность. PR1 = I2R1 = 0,40WPR2 = I2R2 = 1,20WPR3 = I2R3 = 0,80WPV1 = IV1 = 2,40WPdissipated = 4,80WPsource = IV2 = 4,80WPR1 = I2R1 = 0,40WPR2 = I2R2 = 1,20WPR3 = I2R3 = 0,801WPWP40 = 2,801 4.80WPsource = IV2 = 4,80 Вт

Подаваемая мощность равна мощности, рассеиваемой резисторами и потребляемой батареей V1.V1.

Проверьте свое понимание 10,7

Проверьте свое понимание При использовании законов Кирхгофа вам необходимо решить, какие петли использовать, и направление тока, протекающего через каждую петлю. При анализе схемы в Примере 10.7 направление тока было выбрано по часовой стрелке от точки a до точки b .Как бы изменились результаты, если бы направление тока было выбрано против часовой стрелки, от точки b до точки a ?

Несколько источников напряжения

Для многих устройств требуется более одной батареи. Несколько источников напряжения, например батареи, могут быть подключены в последовательной конфигурации, параллельной конфигурации или их комбинации.

Последовательно положительная клемма одной батареи соединена с отрицательной клеммой другой батареи.Любое количество источников напряжения, в том числе аккумуляторы, можно подключать последовательно. Две последовательно соединенные батареи показаны на рисунке 10.31. Использование правила петли Кирхгофа для схемы в части (b) дает результат

ε1 − Ir1 + ε2 − Ir2 − IR = 0, [(ε1 + ε2) −I (r1 + r2)] — IR = 0. ε1 − Ir1 + ε2 − Ir2 − IR = 0, [(ε1 + ε2) — I (r1 + r2)] — IR = 0.

Фигура 10.31 (а) Две батареи, соединенные последовательно с нагрузочным резистором. (b) Принципиальная схема двух батарей и нагрузочного резистора, каждая из которых моделируется как идеализированный источник ЭДС и внутреннего сопротивления.

Когда источники напряжения включены последовательно, их внутренние сопротивления можно складывать вместе, а их ЭДС можно складывать вместе, чтобы получить общие значения. Последовательное соединение источников напряжения является обычным явлением, например, в фонариках, игрушках и других приборах. Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС. На рисунке 10.31 напряжение на клеммах равно

. Vterminal = (ε1 − Ir1) + (ε2 − Ir2) = [(ε1 + ε2) −I (r1 + r2)] = (ε1 + ε2) + Ireq.Vterminal = (ε1 − Ir1) + (ε2 − Ir2) = [(ε1 + ε2) −I (r1 + r2)] = (ε1 + ε2) + Ireq.

Обратите внимание, что одинаковый ток I присутствует в каждой батарее, потому что они соединены последовательно. Недостаток последовательного соединения ячеек в том, что их внутренние сопротивления складываются.

Батареи соединены последовательно для увеличения напряжения, подаваемого в цепь. Например, светодиодный фонарик может иметь две батареи типа AAA, каждая с напряжением на клеммах 1,5 В, чтобы обеспечить 3,0 В для фонарика.

Любое количество аккумуляторов может быть подключено последовательно.Для аккумуляторов N последовательно напряжение на зажимах равно

Vterminal = (ε1 + ε2 + ⋯ + εN − 1 + εN) −I (r1 + r2 + ⋯ + rN − 1 + rN) = ∑i = 1Nεi − IreqVterminal = (ε1 + ε2 + ⋯ + εN − 1 + εN) −I (r1 + r2 + ⋯ + rN − 1 + rN) = ∑i = 1Nεi − Ireq

10,6

, где эквивалентное сопротивление req = ∑i = 1Nrireq = ∑i = 1Nri.

Когда нагрузка подключается к источникам напряжения последовательно, как показано на рисунке 10.32, мы можем найти ток:

(ε1 − Ir1) + (ε2 − Ir2) = IR, Ir1 + Ir2 + IR = ε1 + ε2, I = ε1 + ε2r1 + r2 + R. (ε1 − Ir1) + (ε2 − Ir2) = IR, Ir1 + Ir2 + IR = ε1 + ε2, I = ε1 + ε2r1 + r2 + R.

Как и ожидалось, внутреннее сопротивление увеличивает эквивалентное сопротивление.

Фигура 10,32 Две батареи подключаются последовательно к светодиодной лампочке, как в фонарике.

Источники напряжения, такие как батареи, также можно подключать параллельно. На рисунке 10.33 показаны две батареи с одинаковыми ЭДС, подключенные параллельно и подключенные к сопротивлению нагрузки. Когда батареи подключаются параллельно, положительные клеммы соединяются вместе, а отрицательные клеммы соединяются вместе, а сопротивление нагрузки подключается к положительной и отрицательной клеммам.Обычно источники напряжения, включенные параллельно, имеют идентичные ЭДС. В этом простом случае, поскольку источники напряжения подключены параллельно, общая ЭДС равна индивидуальной ЭДС каждой батареи.

Фигура 10,33 (a) Две батареи подключаются параллельно к нагрузочному резистору. (b) На принципиальной схеме показана батарея как источник ЭДС и внутренний резистор. Два источника ЭДС имеют идентичные ЭДС (каждый из которых обозначен как εε), соединенные параллельно, которые создают одинаковую ЭДС.

Рассмотрим анализ Кирхгофа схемы на рисунке 10.33 (б). Есть две петли и узел в точке b и ε = ε1 = ε2ε = ε1 = ε2.

Узел b : I1 + I2-I = 0I1 + I2-I = 0.

Цикл abcfa : ε − I1r1 + I2r2 − ε = 0, I1r1 = I2r2.ε − I1r1 + I2r2 − ε = 0, I1r1 = I2r2.

Цикл fcdef : ε2-I2r2-IR = 0, ε-I2r2-IR = 0. ε2-I2r2-IR = 0, ε-I2r2-IR = 0.

Решение для тока через резистор нагрузки приводит к I = εreq + RI = εreq + R, где req = (1r1 + 1r2) −1req = (1r1 + 1r2) −1. Напряжение на клеммах равно падению потенциала на нагрузочном резисторе IR = (εreq + R) IR = (εreq + R).Параллельное соединение снижает внутреннее сопротивление и, таким образом, может производить больший ток.

Любое количество аккумуляторов может быть подключено параллельно. Для аккумуляторов N , включенных параллельно, напряжение на зажимах равно

Vterminal = ε − I (1r1 + 1r2 + ⋯ + 1rN − 1 + 1rN) −1 = ε − IreqVterminal = ε − I (1r1 + 1r2 + ⋯ + 1rN − 1 + 1rN) −1 = ε − Ireq

10,7

, где эквивалентное сопротивление req = (∑i = 1N1ri) −1req = (∑i = 1N1ri) −1.

Например, в некоторых грузовиках с дизельным двигателем параллельно используются две батареи на 12 В; они производят полную ЭДС 12 В, но могут обеспечивать больший ток, необходимый для запуска дизельного двигателя.

Таким образом, напряжение на клеммах последовательно соединенных батарей равно сумме индивидуальных ЭДС минус сумма внутренних сопротивлений, умноженная на ток. Когда батареи соединены параллельно, они обычно имеют равные ЭДС, а напряжение на клеммах равно ЭДС минус эквивалентное внутреннее сопротивление, умноженное на ток, где эквивалентное внутреннее сопротивление меньше, чем отдельные внутренние сопротивления. Аккумуляторы подключаются последовательно для увеличения напряжения на клеммах нагрузки.Аккумуляторы подключаются параллельно для увеличения тока нагрузки.

Массив солнечных батарей

Другой пример, имеющий дело с несколькими источниками напряжения, — это комбинация солнечных элементов, соединенных как последовательно, так и параллельно, чтобы обеспечить желаемое напряжение и ток. Фотогальваническая генерация, которая представляет собой преобразование солнечного света непосредственно в электричество, основана на фотоэлектрическом эффекте. Фотоэлектрический эффект выходит за рамки этой главы и рассматривается в книге «Фотоны и волны материи», но в целом фотоны, ударяясь о поверхность солнечного элемента, создают в нем электрический ток.

Большинство солнечных элементов изготовлено из чистого кремния. Большинство отдельных элементов имеют выходное напряжение около 0,5 В, в то время как выходной ток зависит от количества солнечного света, падающего на элемент (падающее солнечное излучение, известное как инсоляция). При ярком полуденном солнечном свете типичные монокристаллические элементы вырабатывают ток на единицу площади около 100 мА / см 2100 мА / см 2 площади поверхности ячейки.

Индивидуальные солнечные элементы электрически соединены в модулях для удовлетворения потребностей в электроэнергии.Их можно соединить последовательно или параллельно — как батареи, о которых говорилось ранее. Группа или модуль солнечных элементов обычно состоит из 36-72 элементов с выходной мощностью от 50 до 140 Вт.

Солнечные элементы, как и батареи, вырабатывают напряжение постоянного тока. Ток от источника постоянного напряжения однонаправлен. Для большинства бытовых приборов требуется напряжение переменного тока.

.