2. Закон изменения тока в цепи при подключении
и отключении источника.
Применение закона для определения индуктивности
Найдем
изменение тока в цепи, состоящей из
последовательно соединенных соленоида,
индуктивность которой равна 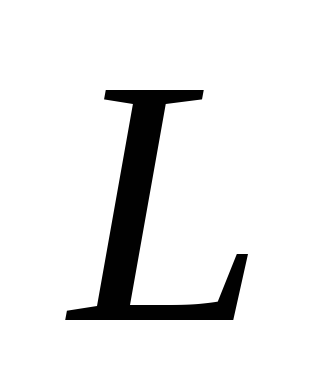 ,
и резистора, активное сопротивление
которого
,
и резистора, активное сопротивление
которого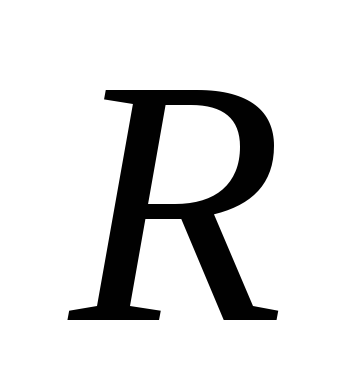 .
.
Если внешнее магнитное поле отсутствует или постоянно, а контур неподвижен, то индукционные явления обусловлены только самоиндукцией.
Из
закона Ома для замкнутой цепи, в которой
действует источник ЭДС 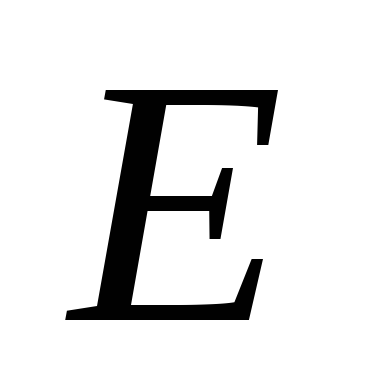 ,
а общее активное сопротивление
,
а общее активное сопротивление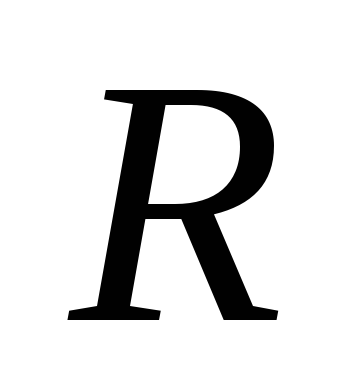
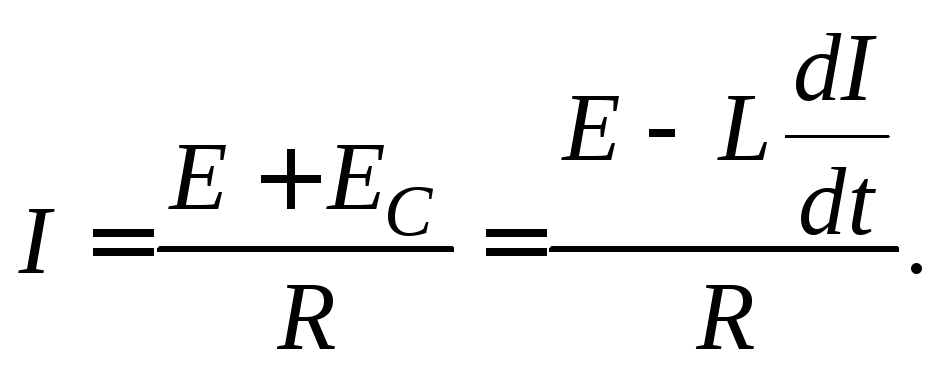
Для нахождения зависимости силы тока от времени разделим переменные
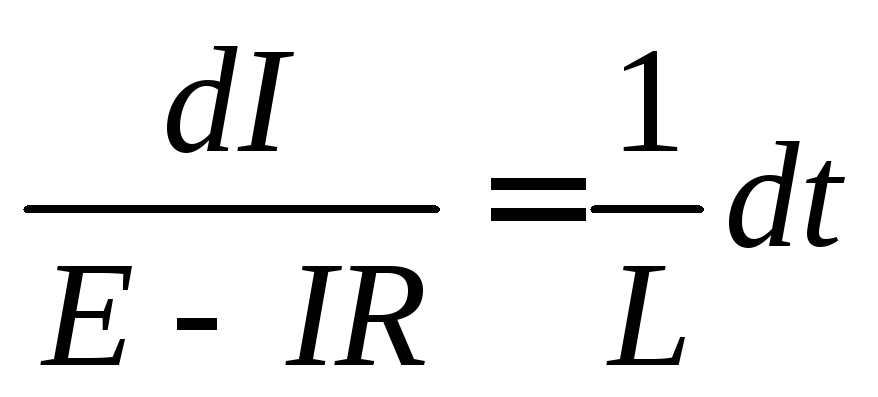 .
.
Полагая  постоянными и интегрируя, получаем
постоянными и интегрируя, получаем
где  –
постоянная интегрирования, значение
которой определяется начальными
условиями решаемой задачи.
–
постоянная интегрирования, значение
которой определяется начальными
условиями решаемой задачи.
Пусть
в момент времени  сила тока
сила тока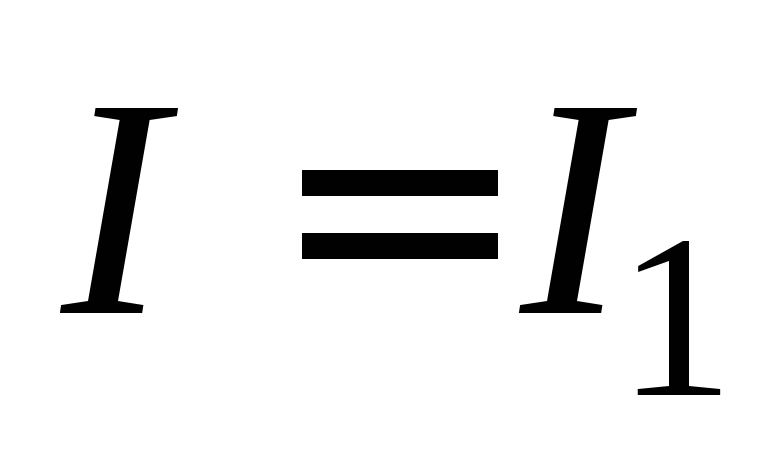 .
Тогда
.
Тогда
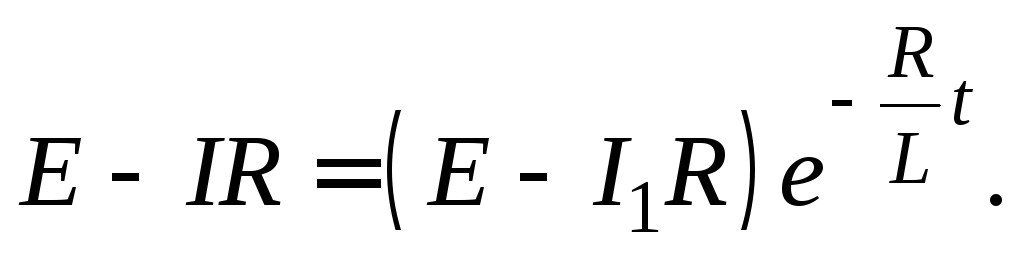
Выразив силу тока, получим
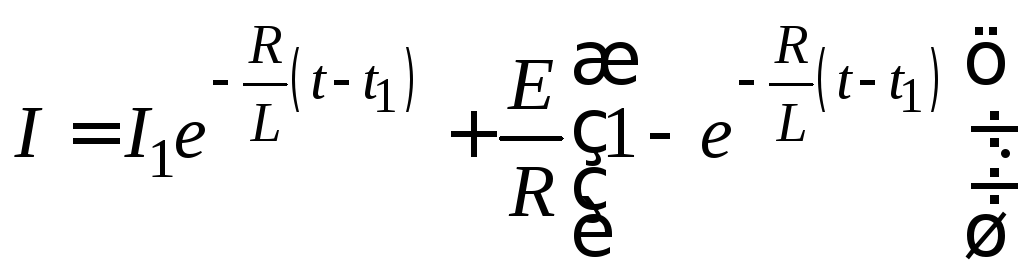 (15.5)
(15.5)
Из
этой общей формулы можно получить
зависимость силы тока от времени при
замыкании цепи. В этом случае начальный
ток равен нулю 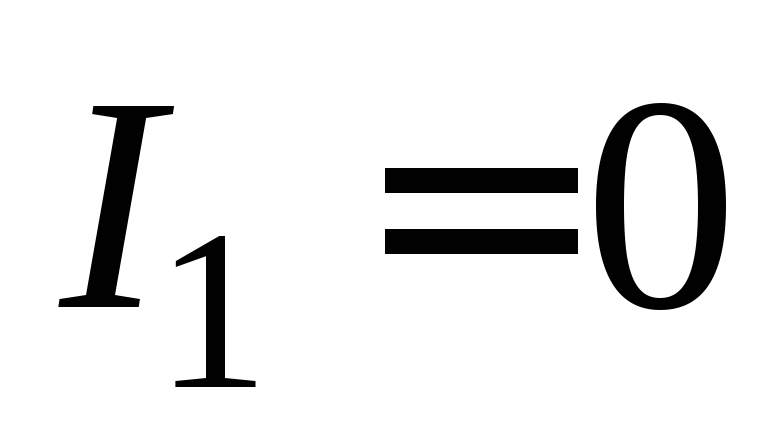
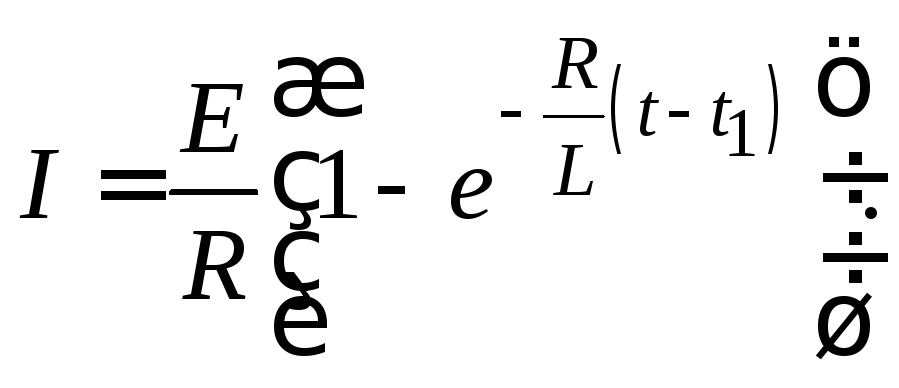 (15.6)
(15.6)
Из
этой формулы видно, что сила тока при
замыкании цепи постепенно увеличивается,
стремясь к 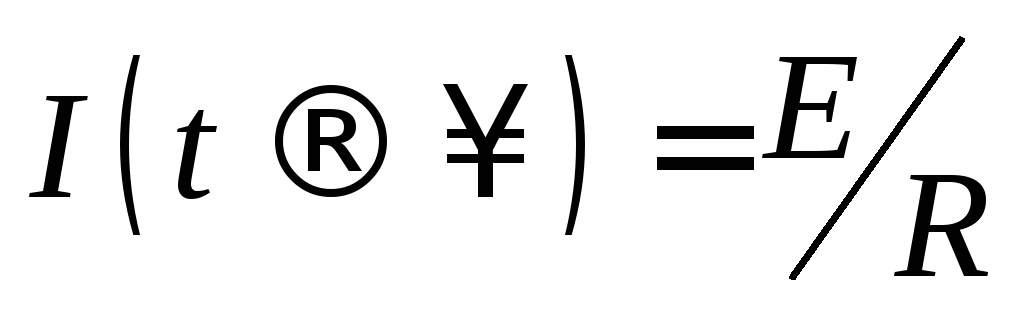 ,
соответствующей величине постоянного
тока (рис. 15.1). Нарастание тока происходит
тем медленнее, чем меньше отношение
,
соответствующей величине постоянного
тока (рис. 15.1). Нарастание тока происходит
тем медленнее, чем меньше отношение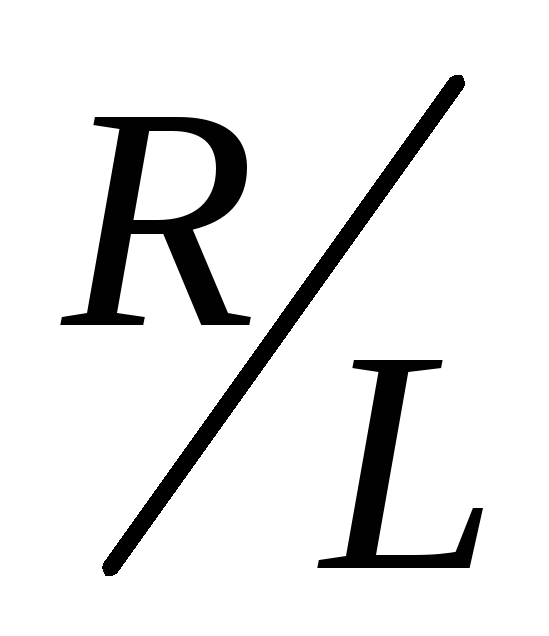
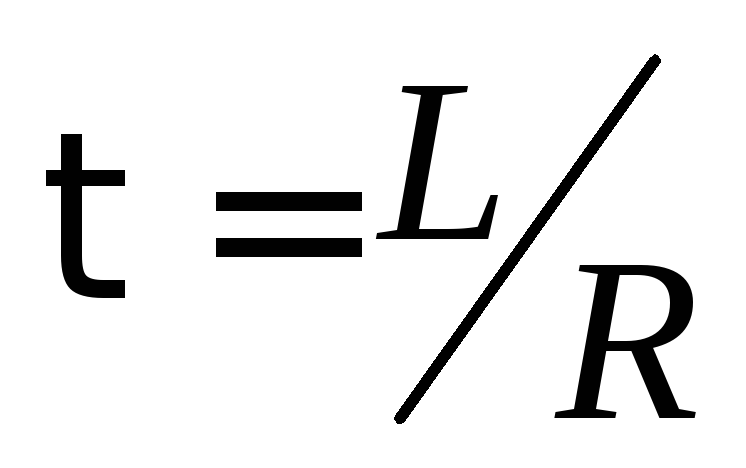 ,
физический смысл которого обсуждается
ниже.
,
физический смысл которого обсуждается
ниже. Если
же в момент времени 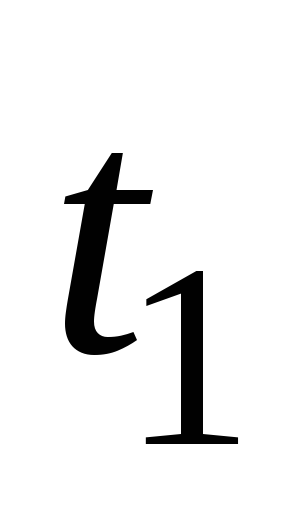 при силе тока
при силе тока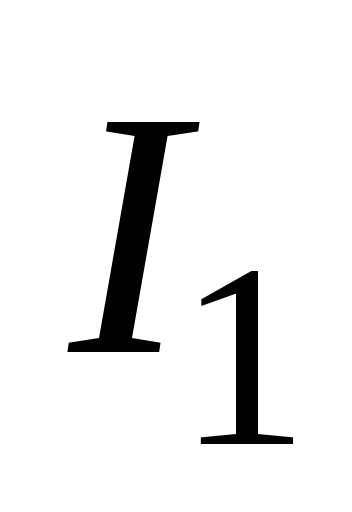 источник ЭДС отключить (
источник ЭДС отключить ( ),
сохранив замкнутость цепи, то из формулы
(15.5), получим следующую зависимость силы
тока от времени:
),
сохранив замкнутость цепи, то из формулы
(15.5), получим следующую зависимость силы
тока от времени:
 (15.7)
(15.7)
В
этом случае сила тока в цепи постепенно
уменьшается от начального значения 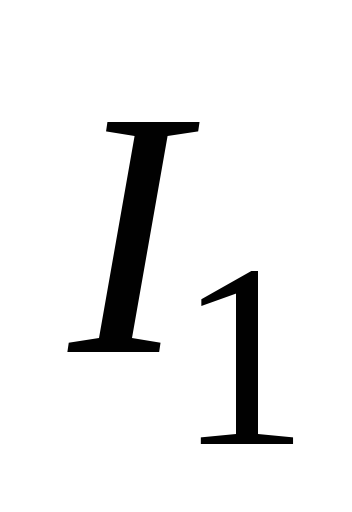 ,
стремясь к нулю. При этом за время
,
стремясь к нулю. При этом за время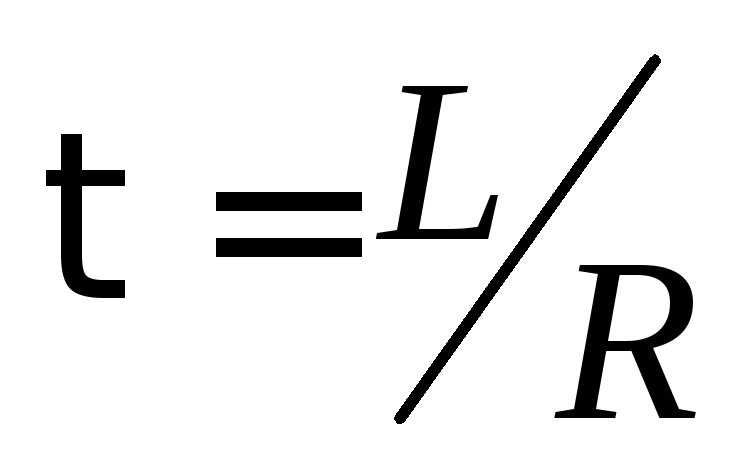 (время
релаксации)
сила тока изменяется в
(время
релаксации)
сила тока изменяется в 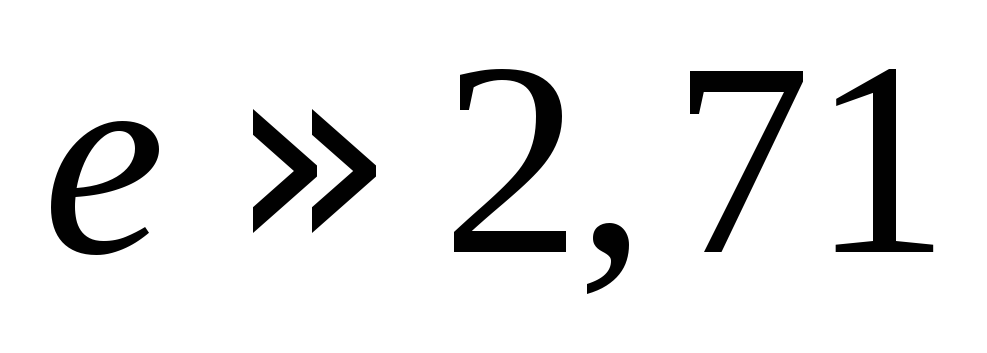 раза.
раза.

Рис. 15.1
Следует
заметить, что в опыте удобнее снимать
вместо зависимости силы тока в цепи от
времени  зависимость напряжения на некотором
известном активном сопротивлении
зависимость напряжения на некотором
известном активном сопротивлении ,
последовательно включенном в цепь, от
времени
,
последовательно включенном в цепь, от
времени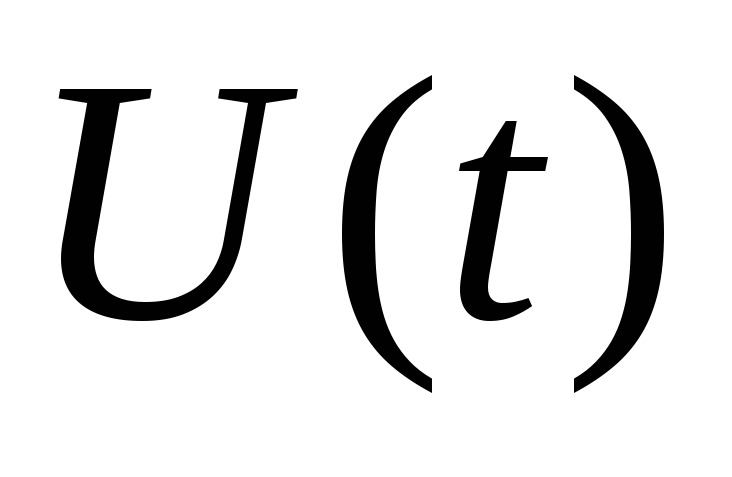 .
Напряжение в этом случае будет
пропорционально силе тока.
.
Напряжение в этом случае будет
пропорционально силе тока.
Из
сказанного ясно, что, измерив силу токов
(или напряжения) в некоторые моменты
времени 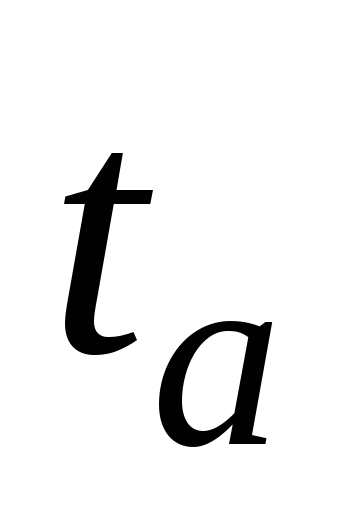
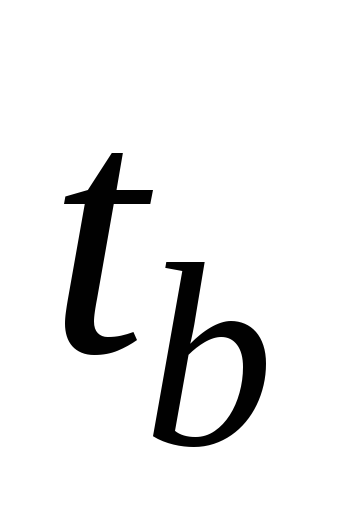 и зная, кроме того, величину общего
активного сопротивления контура
и зная, кроме того, величину общего
активного сопротивления контура ,
можно с помощью зависимостей (15.6) или
(15.7) определить индуктивность контура
,
можно с помощью зависимостей (15.6) или
(15.7) определить индуктивность контура .
. Особенно
просто, зная активное сопротивление
цепи 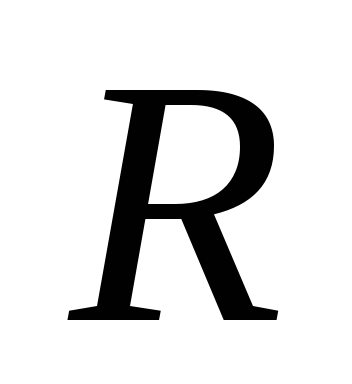 ,
определить её индуктивность, измерив
время релаксации,
,
определить её индуктивность, измерив
время релаксации,
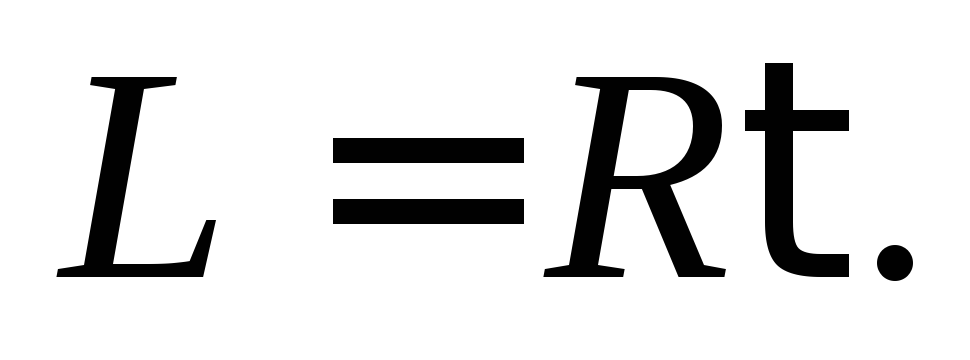 (15.8)
(15.8)3. Вынужденные электромагнитные колебания в контуре,
их применение для измерения индуктивности
Рассмотрим
контур, состоящий из последовательно
соединенных конденсатора емкостью  ,
активного сопротивления
,
активного сопротивления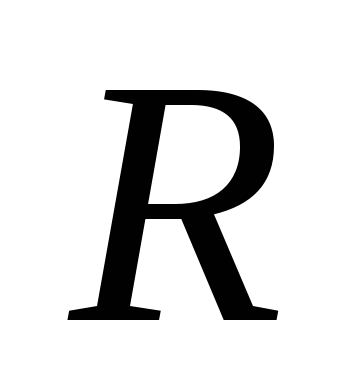 и соленоида индуктивностью
и соленоида индуктивностью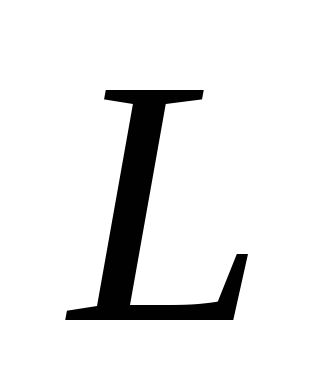 .
.
Для получения незатухающих электромагнитных колебаний необходимо включить в контур источник тока с периодически изменяющейся ЭДС (рис. 15.2).
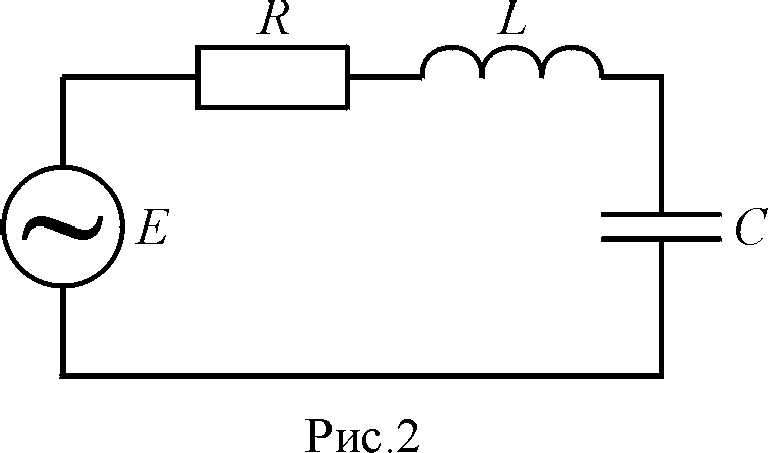
Рис. 15.2
В этом случае колебания в контуре являются вынужденными.
Пусть внешняя ЭДС изменяется по гармоническому закону
 .
.
Тогда, используя закон Ома, можно получить следующее дифференциальное уравнение вынужденных электромагнитных колебаний
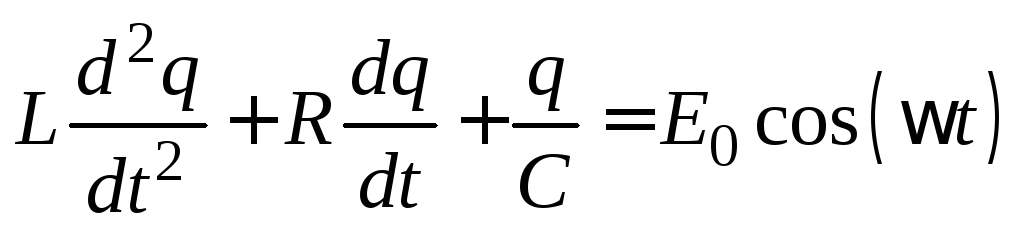
и, решив это уравнение, найти для установившихся вынужденных колебаний связь амплитудных значений силы тока и внешней ЭДС
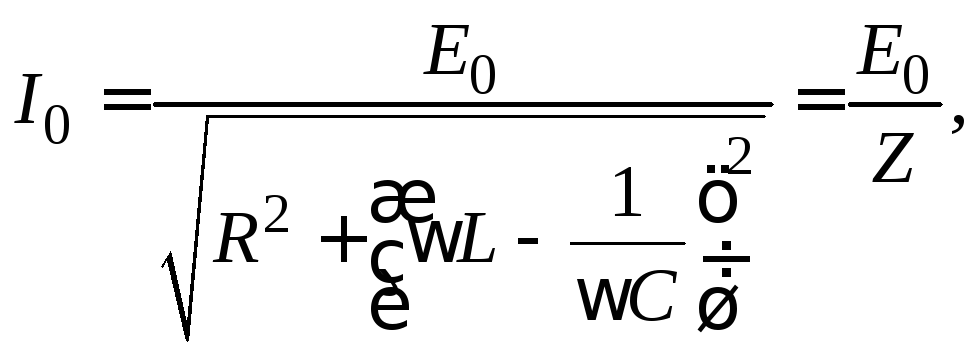 (15.9)
(15.9)
где
величина  называется полным сопротивлением
электрической цепи переменного тока.
называется полным сопротивлением
электрической цепи переменного тока.
В
нее входят активное
сопротивление 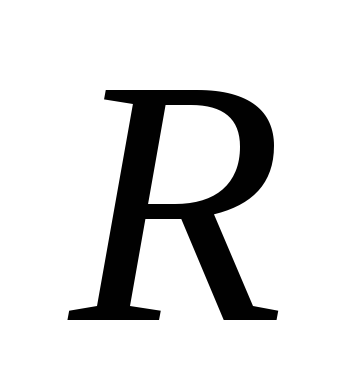 контура, емкостное
сопротивление
контура, емкостное
сопротивление 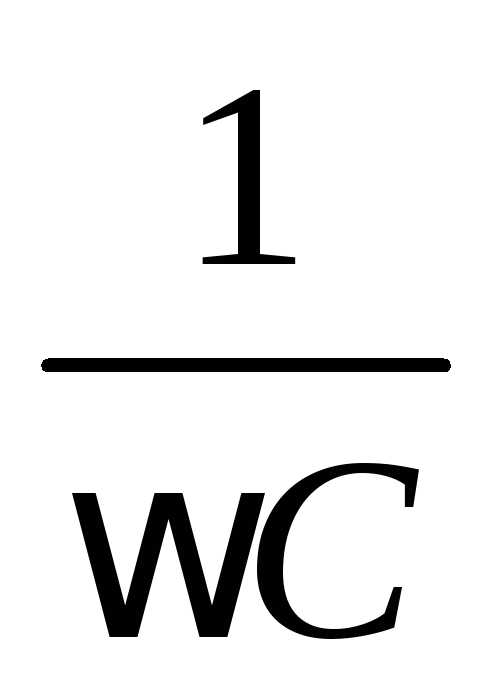
 .
. Если
электрическая емкость контура стремится
к бесконечности  ,
то есть емкостное сопротивление к нулю,
то формула (15.9) упрощается
,
то есть емкостное сопротивление к нулю,
то формула (15.9) упрощается
 (15.10)
(15.10)
Используя это выражение, получаем рабочую формулу для экспериментального определения индуктивности соленоида. При этом учтем, что амплитуда падения напряжения на активном сопротивлении
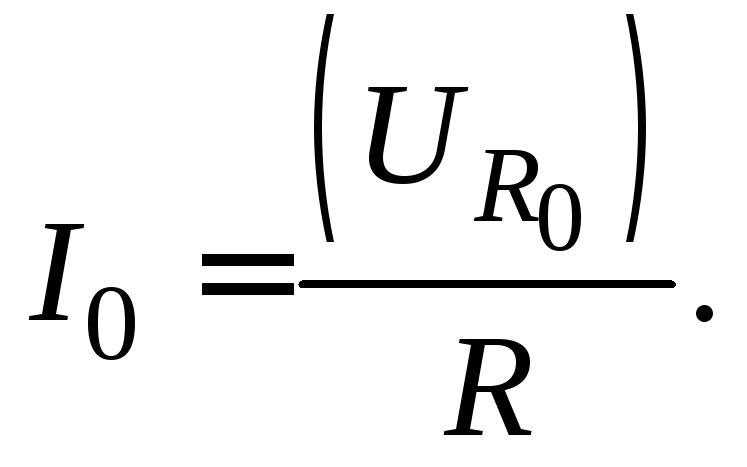 (15.11)
(15.11)
Из выражений (15.10) и (15.11) получим
 (15.12)
(15.12)
2. Закон изменения тока в цепи при подключении
Применение закона для определения индуктивности
Найдем
изменение тока в цепи, состоящей из
последовательно соединенных соленоида,
индуктивность которой равна  ,
и резистора, активное сопротивление
которого
,
и резистора, активное сопротивление
которого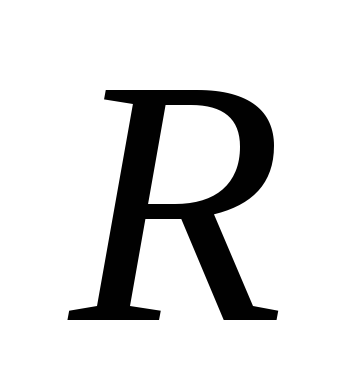 .
.
Если внешнее магнитное поле отсутствует или постоянно, а контур неподвижен, то индукционные явления обусловлены только самоиндукцией.
Из
закона Ома для замкнутой цепи, в которой
действует источник ЭДС 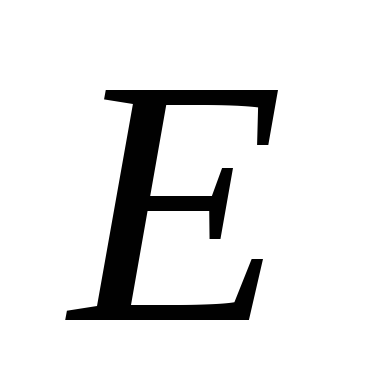 ,
а общее активное сопротивление
,
а общее активное сопротивление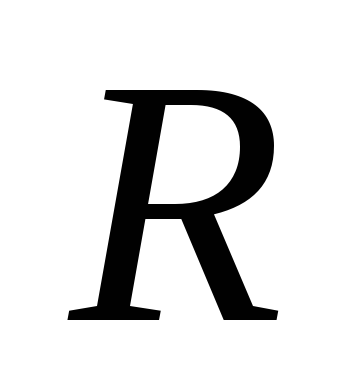 ,
сила тока равна
,
сила тока равна

Для нахождения зависимости силы тока от времени разделим переменные
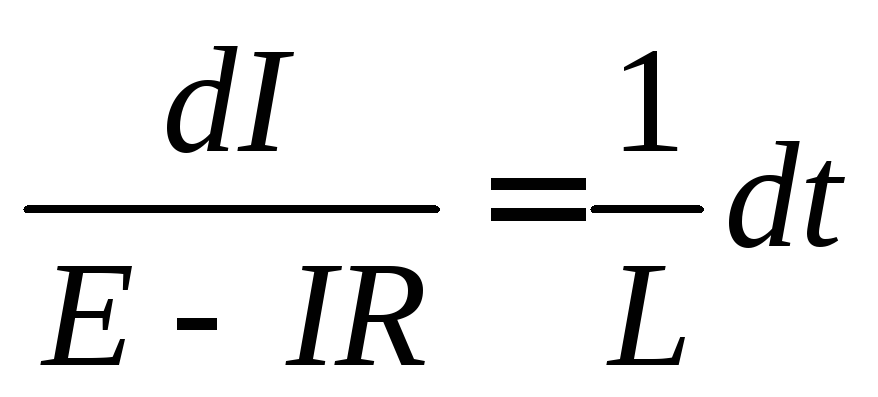 .
.
Полагая  постоянными и интегрируя, получаем
постоянными и интегрируя, получаем

где  –
постоянная интегрирования, значение
которой определяется начальными
условиями решаемой задачи.
–
постоянная интегрирования, значение
которой определяется начальными
условиями решаемой задачи.
Пусть
в момент времени 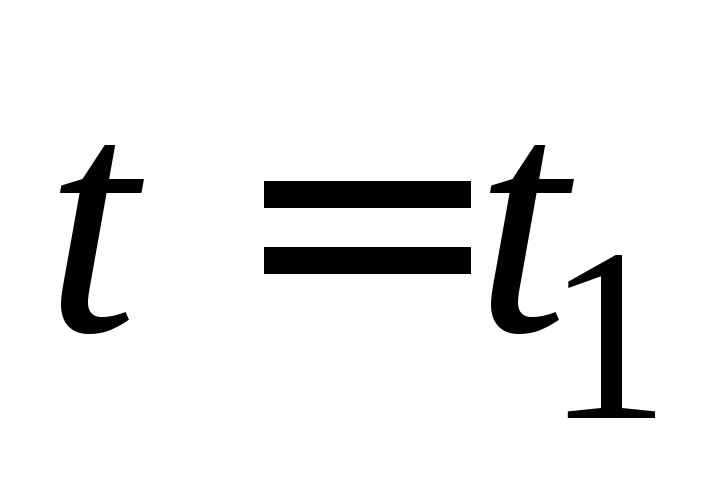 сила тока
сила тока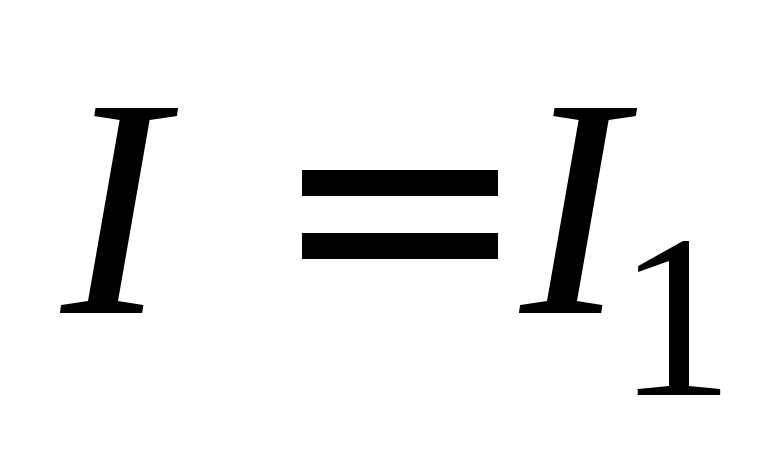 .
Тогда
.
Тогда

Выразив силу тока, получим
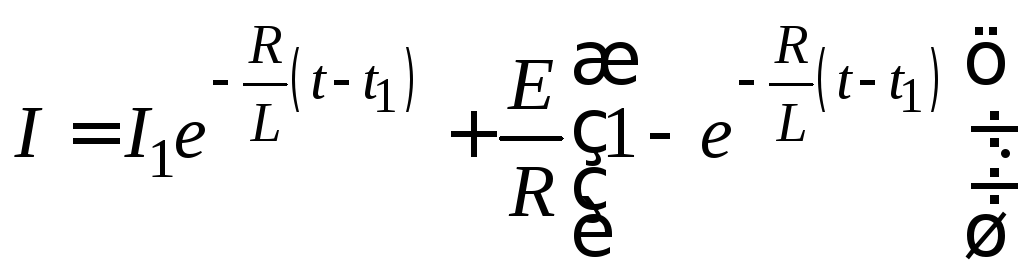 (15.5)
(15.5)
Из
этой общей формулы можно получить
зависимость силы тока от времени при
замыкании цепи. В этом случае начальный
ток равен нулю  и выражение (15.5) приобретает вид
и выражение (15.5) приобретает вид
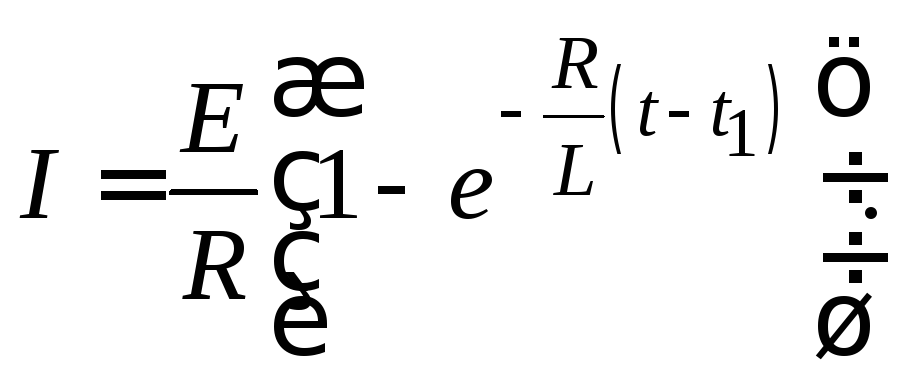 (15.6)
(15.6)
Из
этой формулы видно, что сила тока при
замыкании цепи постепенно увеличивается,
стремясь к 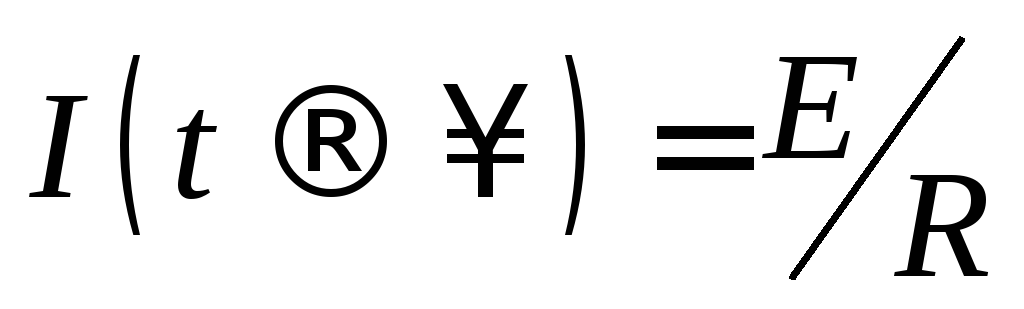 ,
соответствующей величине постоянного
тока (рис. 15.1). Нарастание тока происходит
тем медленнее, чем меньше отношение
,
соответствующей величине постоянного
тока (рис. 15.1). Нарастание тока происходит
тем медленнее, чем меньше отношение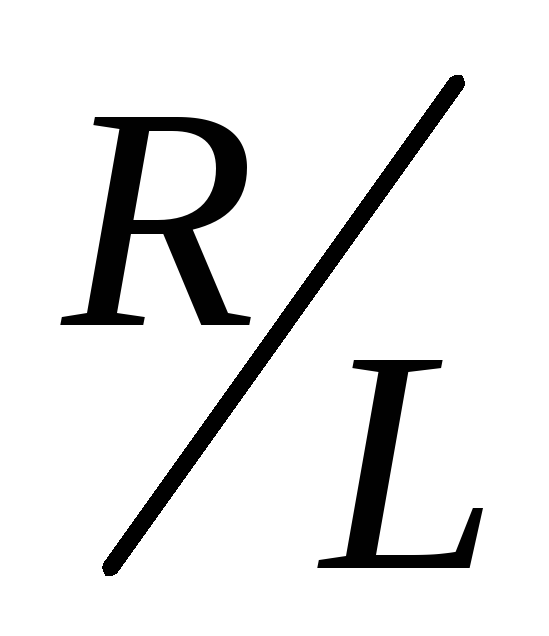 в показателе степени экспоненты или
больше обратное отношение
в показателе степени экспоненты или
больше обратное отношение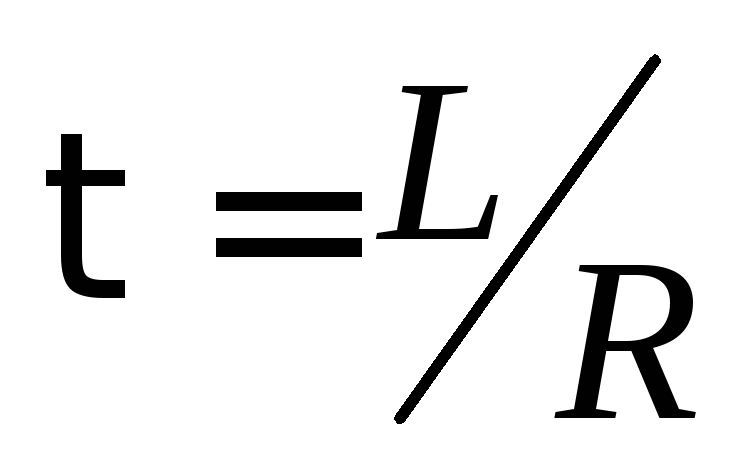 ,
физический смысл которого обсуждается
ниже.
,
физический смысл которого обсуждается
ниже.
Если
же в момент времени 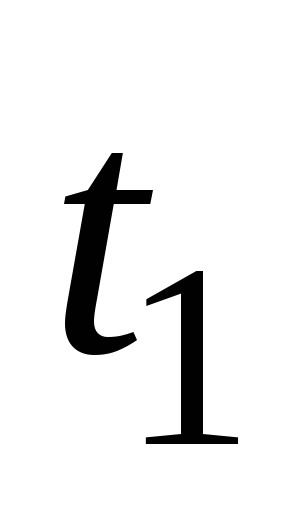 при силе тока
при силе тока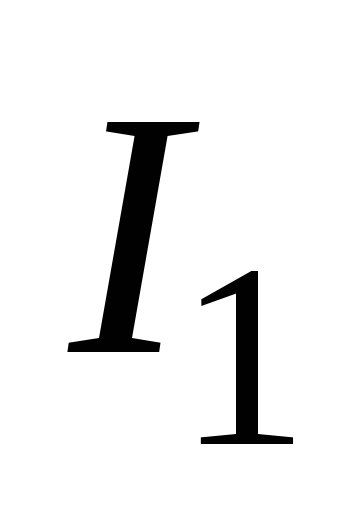 источник ЭДС отключить (
источник ЭДС отключить (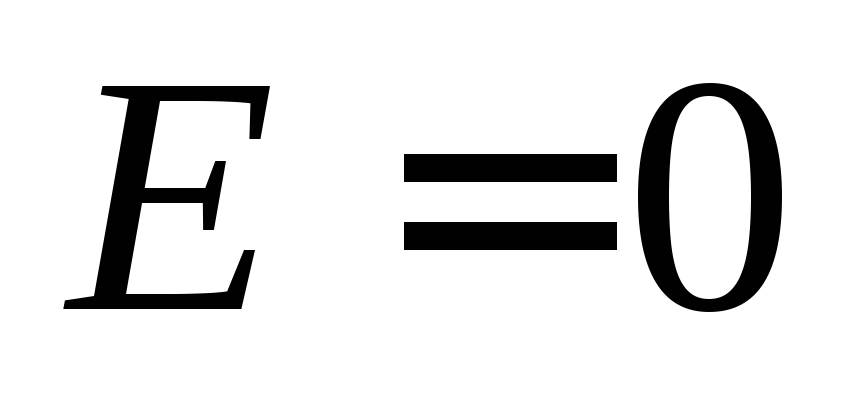 ),
сохранив замкнутость цепи, то из формулы
(15.5), получим следующую зависимость силы
тока от времени:
),
сохранив замкнутость цепи, то из формулы
(15.5), получим следующую зависимость силы
тока от времени:
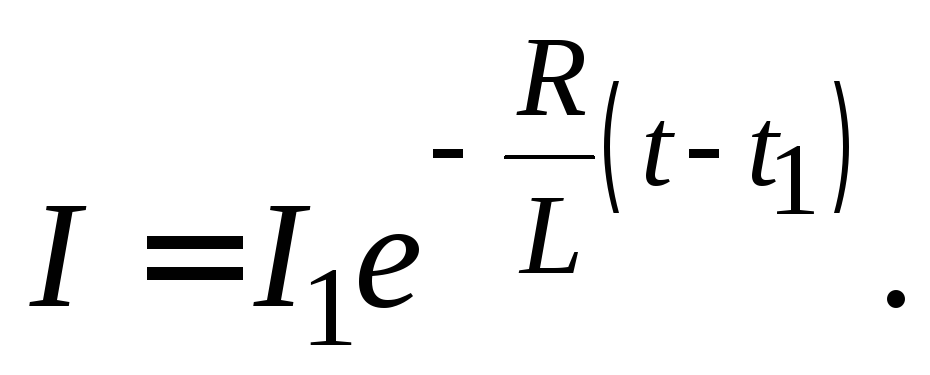 (15.7)
(15.7)
В
этом случае сила тока в цепи постепенно
уменьшается от начального значения 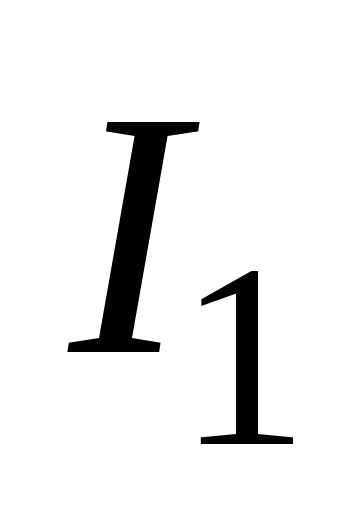 ,
стремясь к нулю. При этом за время
,
стремясь к нулю. При этом за время (время
релаксации)
сила тока изменяется в
(время
релаксации)
сила тока изменяется в 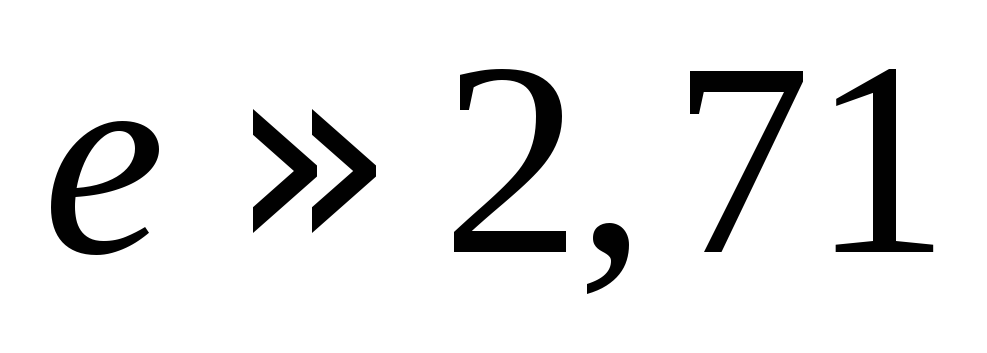 раза.
раза.

Рис. 15.1
Следует
заметить, что в опыте удобнее снимать
вместо зависимости силы тока в цепи от
времени  зависимость напряжения на некотором
известном активном сопротивлении
зависимость напряжения на некотором
известном активном сопротивлении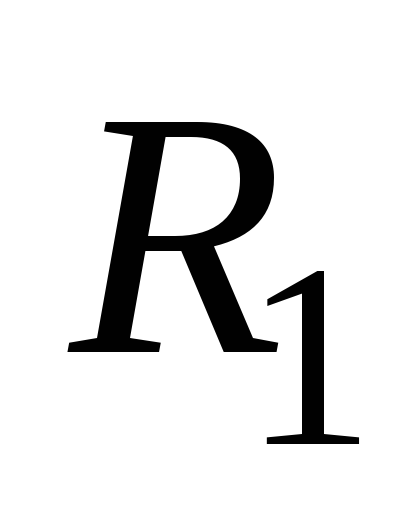 ,
последовательно включенном в цепь, от
времени
,
последовательно включенном в цепь, от
времени .
Напряжение в этом случае будет
пропорционально силе тока.
.
Напряжение в этом случае будет
пропорционально силе тока.
Из
сказанного ясно, что, измерив силу токов
(или напряжения) в некоторые моменты
времени 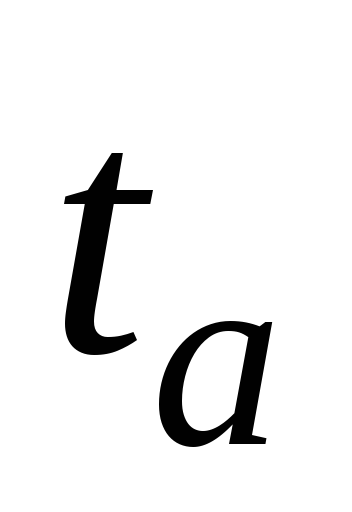 ,
,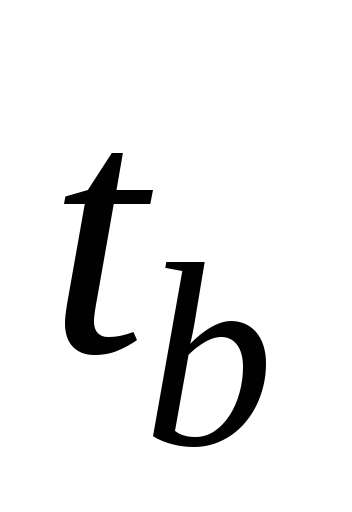 и зная, кроме того, величину общего
активного сопротивления контура
и зная, кроме того, величину общего
активного сопротивления контура ,
можно с помощью зависимостей (15.6) или
(15.7) определить индуктивность контура
,
можно с помощью зависимостей (15.6) или
(15.7) определить индуктивность контура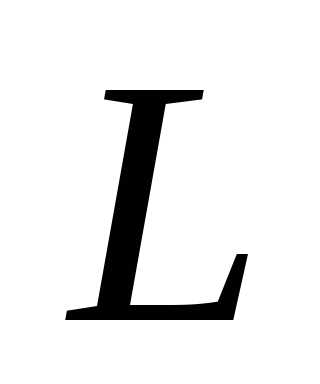 .
.
Особенно
просто, зная активное сопротивление
цепи 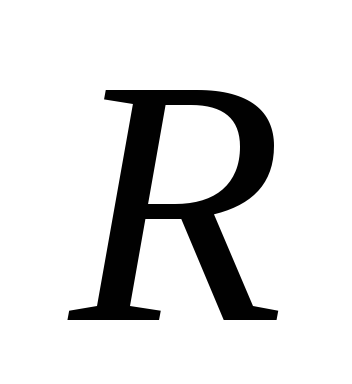 ,
определить её индуктивность, измерив
время релаксации,
,
определить её индуктивность, измерив
время релаксации,
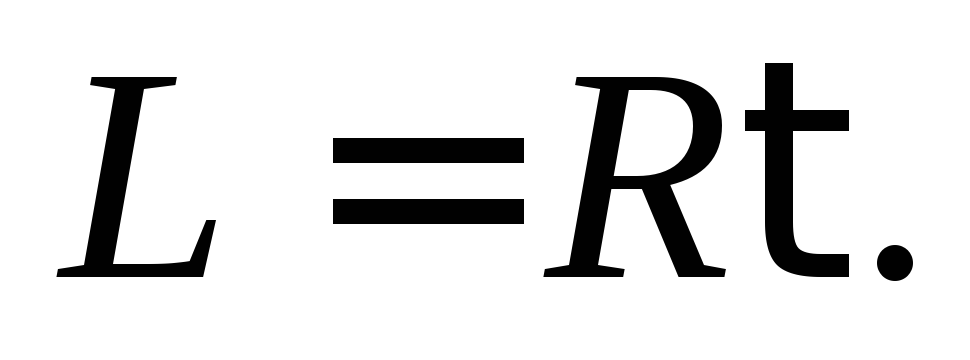 (15.8)
(15.8)
3. Вынужденные электромагнитные колебания в контуре,
их применение для измерения индуктивности
Рассмотрим
контур, состоящий из последовательно
соединенных конденсатора емкостью  ,
активного сопротивления
,
активного сопротивления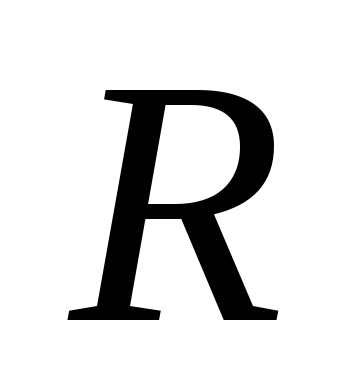 и соленоида индуктивностью
и соленоида индуктивностью .
.
Для получения незатухающих электромагнитных колебаний необходимо включить в контур источник тока с периодически изменяющейся ЭДС (рис. 15.2).
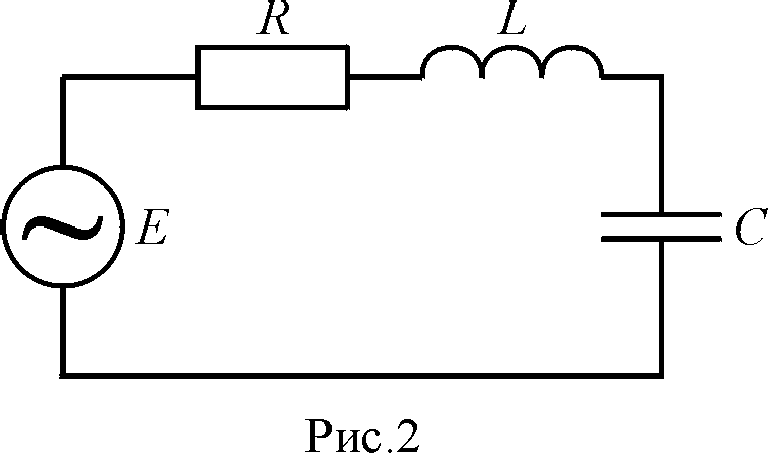
Рис. 15.2
В этом случае колебания в контуре являются вынужденными.
Пусть внешняя ЭДС изменяется по гармоническому закону
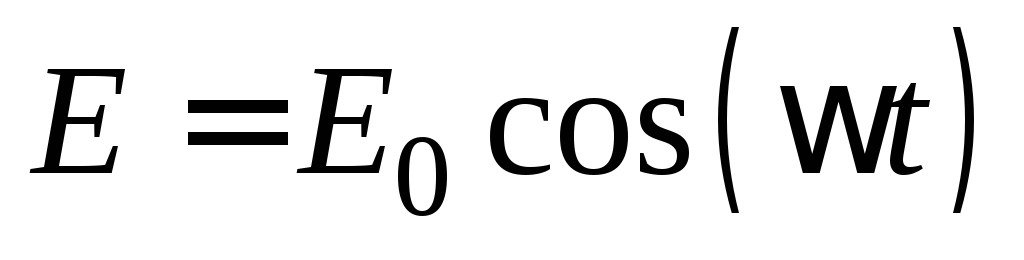 .
.
Тогда, используя закон Ома, можно получить следующее дифференциальное уравнение вынужденных электромагнитных колебаний

и, решив это уравнение, найти для установившихся вынужденных колебаний связь амплитудных значений силы тока и внешней ЭДС
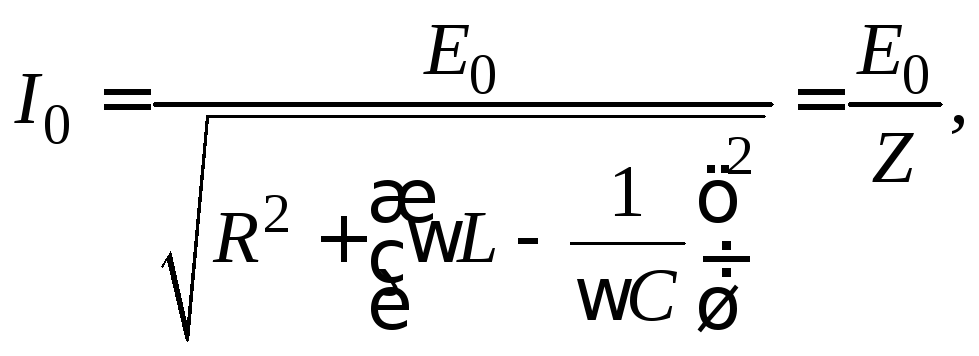 (15.9)
(15.9)
где
величина  называется полным сопротивлением
электрической цепи переменного тока.
называется полным сопротивлением
электрической цепи переменного тока.
В
нее входят активное
сопротивление 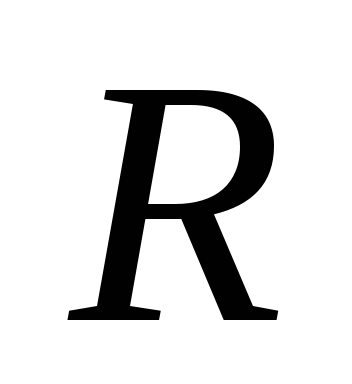 контура, емкостное
сопротивление
контура, емкостное
сопротивление 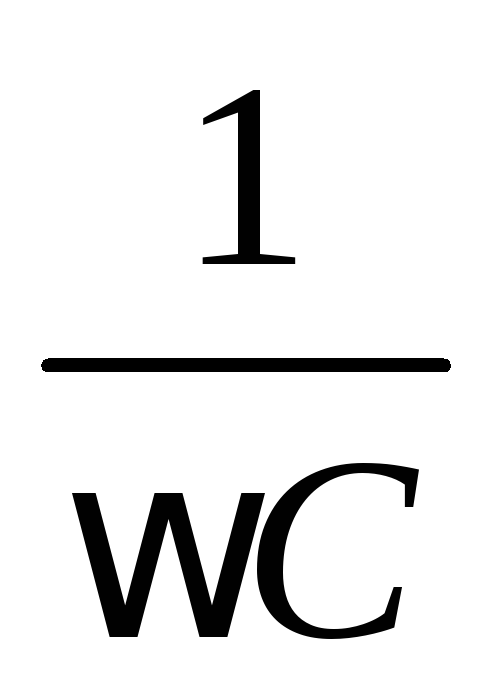 и индуктивное
сопротивление
и индуктивное
сопротивление 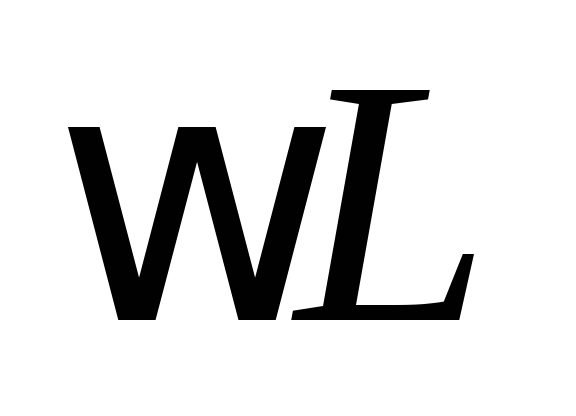 .
.
Если
электрическая емкость контура стремится
к бесконечности  ,
то есть емкостное сопротивление к нулю,
то формула (15.9) упрощается
,
то есть емкостное сопротивление к нулю,
то формула (15.9) упрощается
 (15.10)
(15.10)
Используя это выражение, получаем рабочую формулу для экспериментального определения индуктивности соленоида. При этом учтем, что амплитуда падения напряжения на активном сопротивлении R связана с амплитудой силы тока в цепи формулой
 (15.11)
(15.11)
Из выражений (15.10) и (15.11) получим
 (15.12)
(15.12)
Законы изменения тока и напряжения для участков цепи содержащих элементы: резистор, катушка индуктивности, конденсатор.
Кафедра Физики и математики, информационных технологий
 |
Отчет по лабораторной работе №2.2
Цепи переменного тока. Реактивные сопротивления
Выполнила ст. группы СБ-13-15
Пустовая Елена
Проверил:
ст. преподаватель Соболева В.В.
| Дата | Подпись | |
| Допуск | ||
| Результат | ||
| Отчет |
Цель работы: Ознакомиться с основными элементами электрических цепей синусоидального тока. Освоить методы электрических измерений в цепях синусоидального тока. Получить экспериментальное подтверждение закона Ома для цепей переменного тока.
Требуемое оборудование:
Модульный учебный комплекс: МУК-ЭМ1(2).
Приборы:
1. Генератор звуковых частот ЗГ1 1 шт.
2. Амперметр-вольтметр АВ1 1 шт.
3. Стенд с объектами исследования С3-ЭМ01 1 шт.
4. Комплект проводников 1 шт.
Ответы на контрольные вопросы:
Переменный ток. Мгновенное значение тока. Периодические токи. Период, частота.
Переменным током называют ток, изменяющийся во времени. Значение тока i(t) в любой момент времени называют мгновенным. Токи, мгновенные значения которых повторяются через равные промежутки времени в той же самой последовательности, называют периодическими, а наименьший промежуток времени T, через который эти повторения наблюдаются, — периодом. Величина, обратная периоду, называется частотой ν=1/T. Частота измеряется в герцах [Гц]. Постоянный ток можно рассматривать как частный случай периодического тока, период изменения которого бесконечно велик, т. е. частота равна нулю.
Уравнения мгновенного значения силы тока и напряжения, определение величин, входящих в данные уравнения.
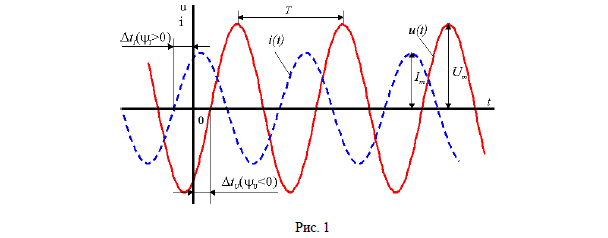
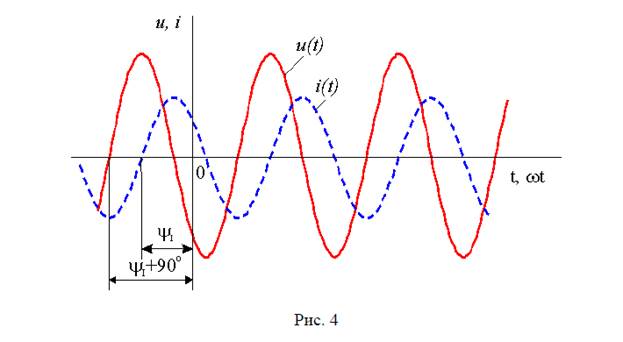
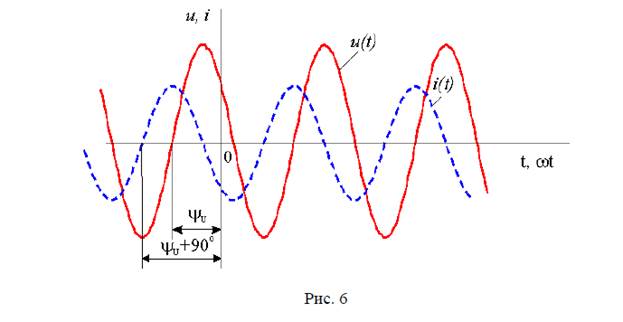
Пусть на некотором участке цепи мгновенные значения тока и напряжения меняются гармонически, т. е по синусоидальному закону (рис. 1)
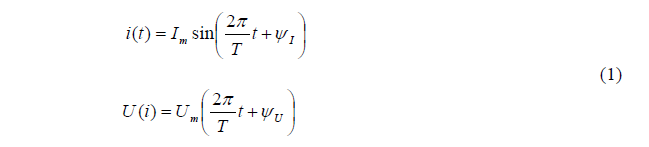
где Im – максимальное или амплитудное значение тока;
ψI – начальная фаза колебаний тока
ψU – начальная фаза колебаний напряжения.
Начальная фаза отсчитывается всегда от момента, соответствующего началу синусоиды (нулевое значение синусоидальной величины при переходе ее от отрицательных к положительным значениям), до момента начала отсчета времени t=0 (начало координат). Если начало синусоиды сдвинуто влево, то начальная фаза имеет положительное значение, а если вправо – отрицательное.
Найти численное значение начальной фазы, например тока (рис. 1), можно путем определения величины ΔtI :

Поскольку начало синусоиды смещено влево, то начальная фаза ψI имеет положительное значение.
Сдвиг фаз.
Если у нескольких синусоидальных функций, изменяющихся с одной частотой, начальные фазы не совпадают, то говорят, что они имеют сдвиг фаз (или разность фаз). Сдвиг фаз определяется как разность начальных фаз. Так, например, под разностью фаз ϕ напряжения и тока понимают разность начальных фаз напряжения ψU и тока ψI
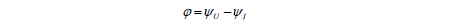
Физические процессы, протекающие в цепях переменного тока, отличаются от процессов, протекающих в цепях постоянного тока. При переменном токе электрические и магнитные поля изменяются во времени. Изменяющееся магнитное поле наводит ЭДС, изменение электрического поля сопровождается изменением зарядов на проводниках.
Законы изменения тока и напряжения для участков цепи содержащих элементы: резистор, катушка индуктивности, конденсатор.
Основными элементами схем цепей переменного тока являются резисторы, конденсаторы и индуктивности. Рассмотрим законы изменения тока и напряжения для участков цепи содержащих эти элементы.
Резистор
В резистивном элементе с сопротивлением R электромагнитная энергия преобразуется в тепло. Мгновенная мощность, с которой происходит преобразование энергии, определяется соотношением: 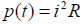 . Резистивные (или их ещё называют активные) сопротивления вводятся в схемы замещения также для учета необратимого преобразования электромагнитной энергии в другие виды (например, механическую, энергию излучения и т. п.).
. Резистивные (или их ещё называют активные) сопротивления вводятся в схемы замещения также для учета необратимого преобразования электромагнитной энергии в другие виды (например, механическую, энергию излучения и т. п.).
В резистивном элементе (рис. 2,а) напряжение связано с током законом Ома: 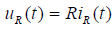 . Если ток в резисторе
. Если ток в резисторе  , то и напряжение
, то и напряжение
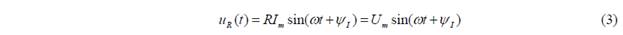
имеет синусоидальную форму и такую же фазу, что и ток в резисторе (т. е. ψI=ψU). Говорят, что ток и напряжение совпадают по фазе или синфазны, т. е. ϕ=0 (рис. 2,б).

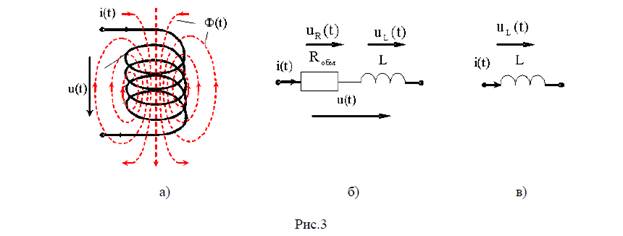
Если через катушку индуктивности (рис. 3,а) пропустить переменный синусоидальный ток 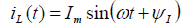 , то он создаст переменный магнитный поток, пронизывающий витки катушки. По закону электромагнитной индукции на зажимах катушки этот переменный поток наведёт синусоидальное напряжение:
, то он создаст переменный магнитный поток, пронизывающий витки катушки. По закону электромагнитной индукции на зажимах катушки этот переменный поток наведёт синусоидальное напряжение:

где n – число витков катушки;
Ψ=wФ – потокосцепление;
L= потокосцепление;
L=dΨ/di — индуктивность;
xL=Lω= — реактивное индуктивное сопротивление.
В системе единиц СИ индуктивность L имеет размерность Генри (Гн), а индуктивное сопротивление – (Ом).
Индуктивность L учитывает энергию магнитного поля катушки 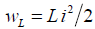
Из соотношения (4) видно, что ток через индуктивность i(t) отстаёт от напряжения 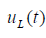 на угол
на угол 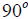 (рис. 4).
(рис. 4).
Переменный ток, протекая по виткам катушки, создаёт в проводниках тепловые потери мощности 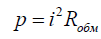 , где
, где 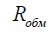 — активное сопротивление обмотки. На рис. 3,б показана низкочастотная схема замещения катушки индуктивности, состоящая из индуктивности L и активного сопротивления обмотки . Если сопротивлением обмотки можно пренебречь, то такую катушку считают идеальной индуктивностью (рис. 3,в). Для высоких частот в схеме замещения необходимо учитывать межвитковую ёмкость катушки.
— активное сопротивление обмотки. На рис. 3,б показана низкочастотная схема замещения катушки индуктивности, состоящая из индуктивности L и активного сопротивления обмотки . Если сопротивлением обмотки можно пренебречь, то такую катушку считают идеальной индуктивностью (рис. 3,в). Для высоких частот в схеме замещения необходимо учитывать межвитковую ёмкость катушки.
Из (4) следует, что при заданном напряжении  можно найти по соотношению
можно найти по соотношению

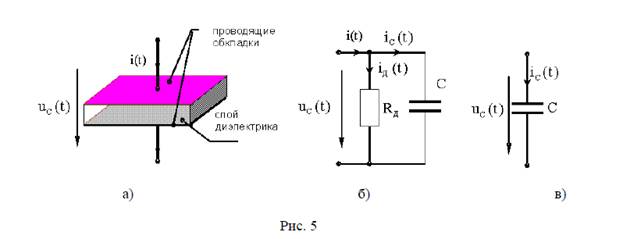
Конденсатор
Конденсатор является элементом электрической цепи, имеющим две проводящие обкладки, между которыми находится слой диэлектрика (рис. 5,а). Если к зажимам конденсатора (рис. 5,а) подключить источник синусоидального напряжения 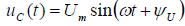 то на его обкладках возникнет изменяющийся во времени электрический заряд q(t), т. е. через конденсатор будет протекать электрический ток
то на его обкладках возникнет изменяющийся во времени электрический заряд q(t), т. е. через конденсатор будет протекать электрический ток

В (2) 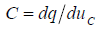 ёмкость конденсатора, которая определяет зависимость изменения величины заряда на обкладках конденсатора от изменения напряжения, приложенного к его обкладкам
ёмкость конденсатора, которая определяет зависимость изменения величины заряда на обкладках конденсатора от изменения напряжения, приложенного к его обкладкам 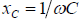 — реактивное ёмкостное сопротивление.
— реактивное ёмкостное сопротивление.
В системе единиц СИ ёмкость C имеет размерность Фарада (Ф), а ёмкостное сопротивление – (Ом).
Из соотношения (4) видно, что ток через конденсатор i(t) опережает напряжение 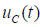 на угол 90 (рис. 6).
на угол 90 (рис. 6).
Основной особенностью конденсатора является его способность запасать энергию электрического поля 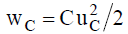 . Кроме того, в конденсаторе имеют место тепловые потери энергии в диэлектрике и обкладках, а также происходит запас энергии в магнитном поле. На рис. 5,б показана низкочастотная схема замещения конденсатора, состоящая из параллельного соединения ёмкости C и активного сопротивления с проводимостью – RД, учитывающей потери в диэлектрике и обкладках. Если потерями можно пренебречь, то конденсатор будет представлять собой идеальную ёмкость (рис. 5,в).
. Кроме того, в конденсаторе имеют место тепловые потери энергии в диэлектрике и обкладках, а также происходит запас энергии в магнитном поле. На рис. 5,б показана низкочастотная схема замещения конденсатора, состоящая из параллельного соединения ёмкости C и активного сопротивления с проводимостью – RД, учитывающей потери в диэлектрике и обкладках. Если потерями можно пренебречь, то конденсатор будет представлять собой идеальную ёмкость (рис. 5,в).
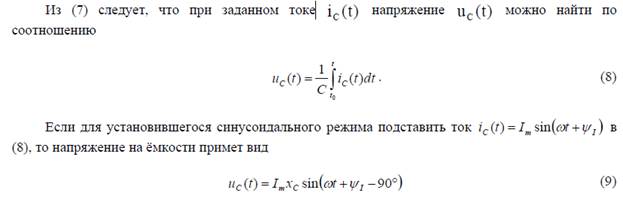
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
2. Закон изменения тока в цепи при подключении
и отключении источника.
Применение закона для определения индуктивности
Найдем
изменение тока в цепи, состоящей из
последовательно соединенных соленоида,
индуктивность которой равна 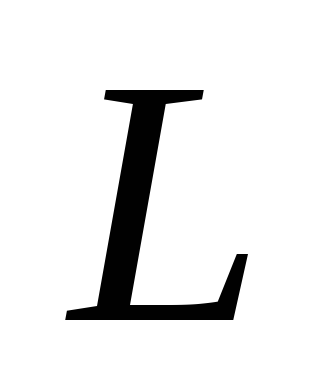 ,
и резистора, активное сопротивление
которого
,
и резистора, активное сопротивление
которого .
.
Если внешнее магнитное поле отсутствует или постоянно, а контур неподвижен, то индукционные явления обусловлены только самоиндукцией.
Из
закона Ома для замкнутой цепи, в которой
действует источник ЭДС 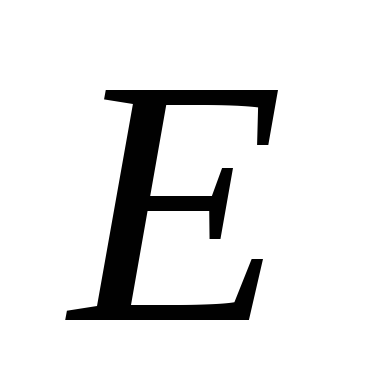 ,
а общее активное сопротивление
,
а общее активное сопротивление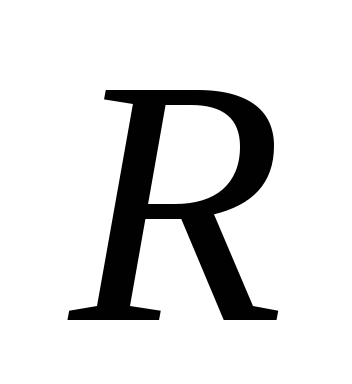 ,
сила тока равна
,
сила тока равна
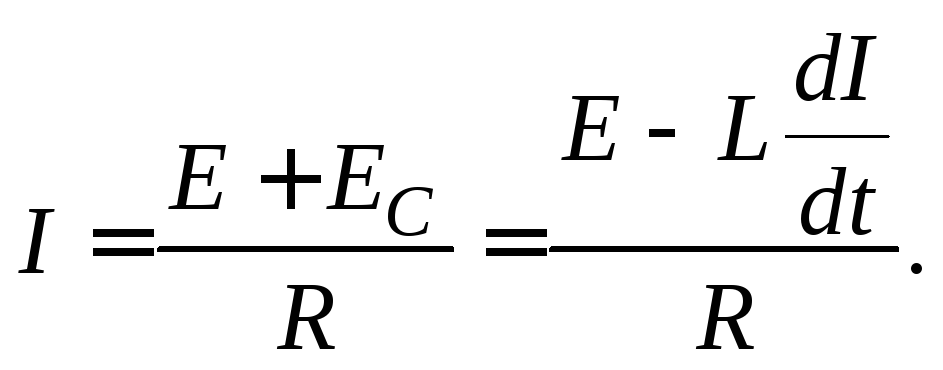
Для нахождения зависимости силы тока от времени разделим переменные
 .
.
Полагая 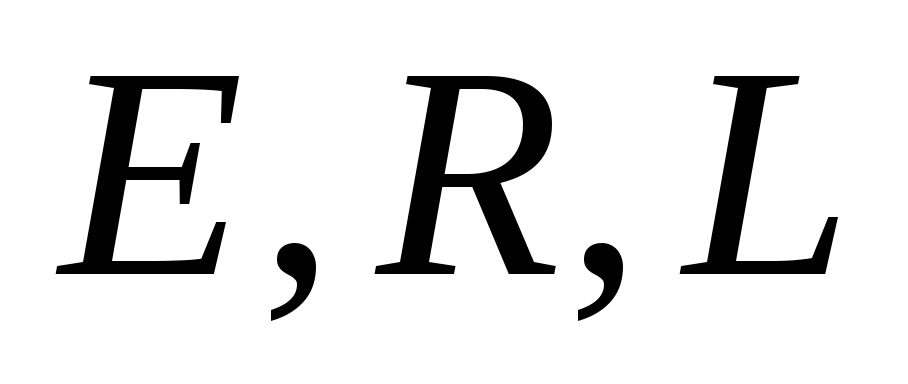 постоянными и интегрируя, получаем
постоянными и интегрируя, получаем
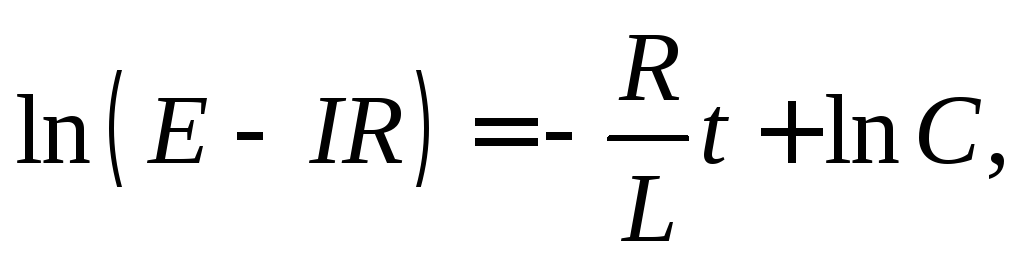
где  –
постоянная интегрирования, значение
которой определяется начальными
условиями решаемой задачи.
–
постоянная интегрирования, значение
которой определяется начальными
условиями решаемой задачи.
Пусть
в момент времени 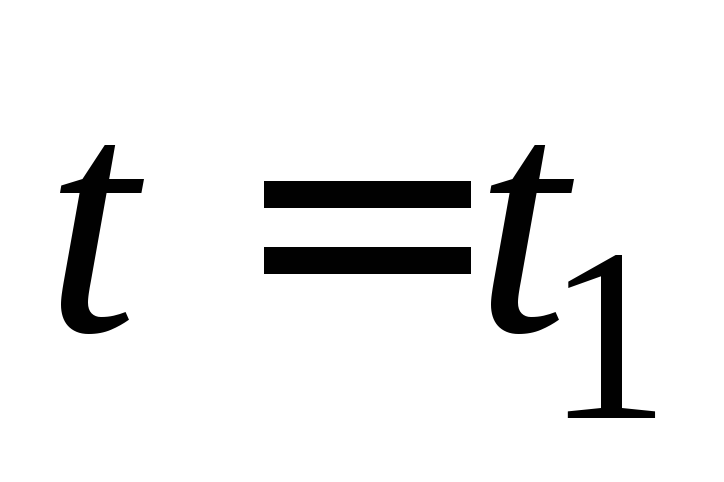 сила тока
сила тока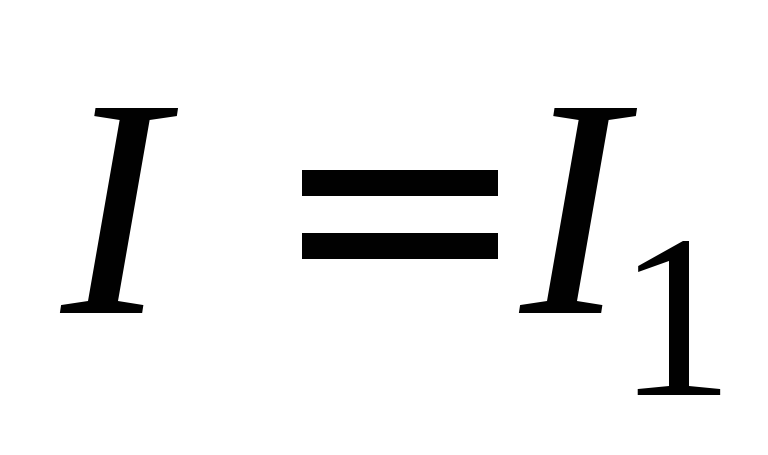 .
Тогда
.
Тогда
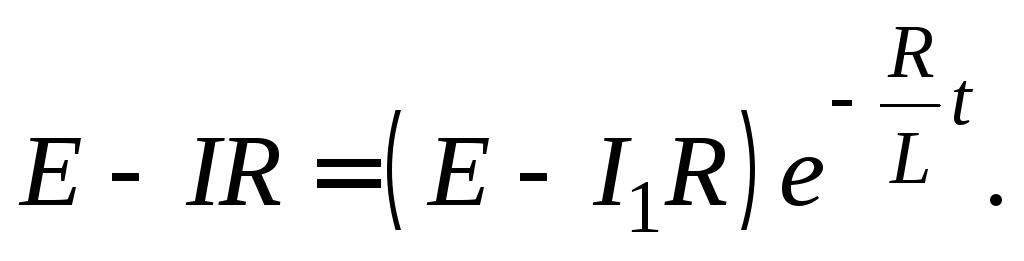
Выразив силу тока, получим
 (15.5)
(15.5)
Из
этой общей формулы можно получить
зависимость силы тока от времени при
замыкании цепи. В этом случае начальный
ток равен нулю  и выражение (15.5) приобретает вид
и выражение (15.5) приобретает вид
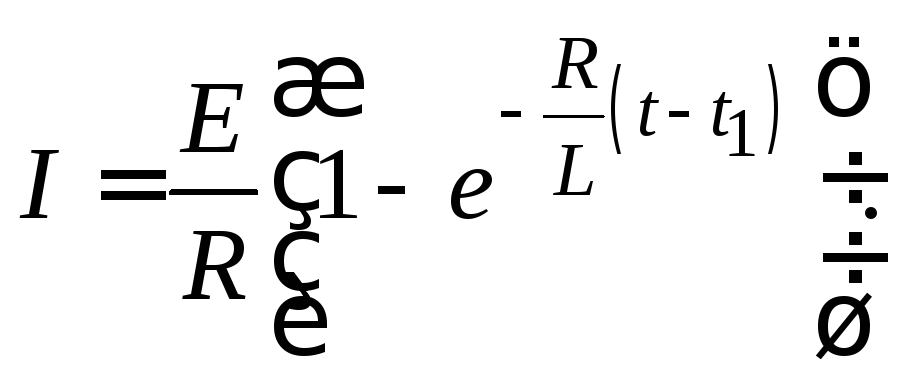 (15.6)
(15.6)
Из
этой формулы видно, что сила тока при
замыкании цепи постепенно увеличивается,
стремясь к 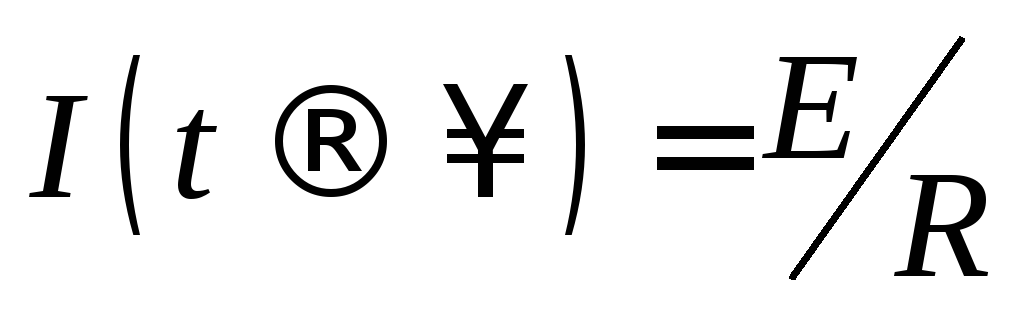 ,
соответствующей величине постоянного
тока (рис. 15.1). Нарастание тока происходит
тем медленнее, чем меньше отношение
,
соответствующей величине постоянного
тока (рис. 15.1). Нарастание тока происходит
тем медленнее, чем меньше отношение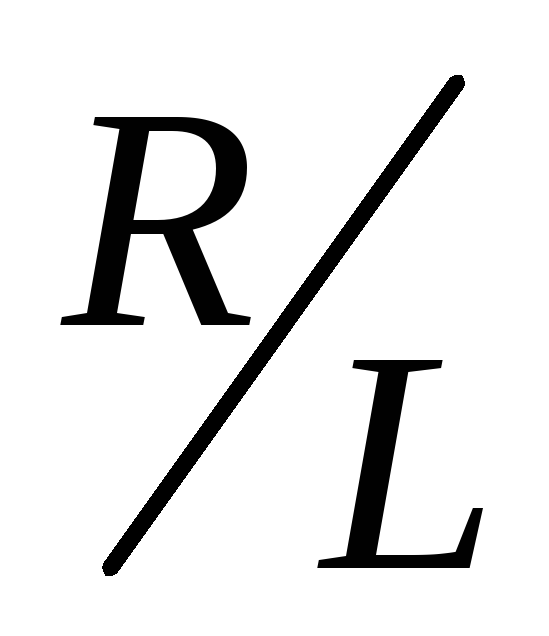 в показателе степени экспоненты или
больше обратное отношение
в показателе степени экспоненты или
больше обратное отношение ,
физический смысл которого обсуждается
ниже.
,
физический смысл которого обсуждается
ниже.
Если
же в момент времени  при силе тока
при силе тока источник ЭДС отключить (
источник ЭДС отключить (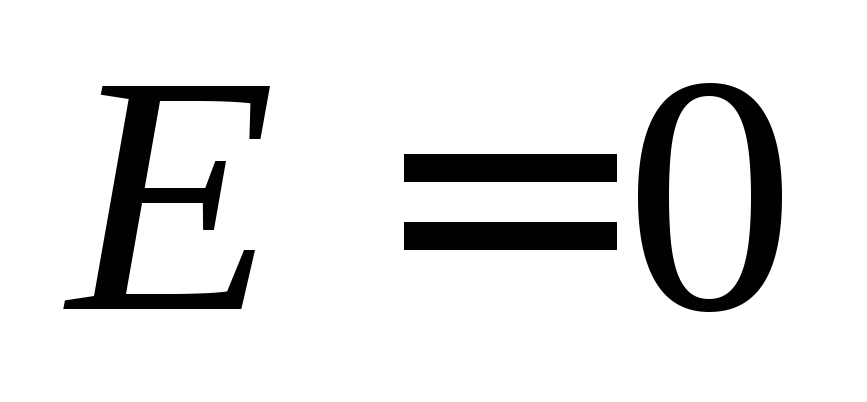 ),
сохранив замкнутость цепи, то из формулы
(15.5), получим следующую зависимость силы
тока от времени:
),
сохранив замкнутость цепи, то из формулы
(15.5), получим следующую зависимость силы
тока от времени:
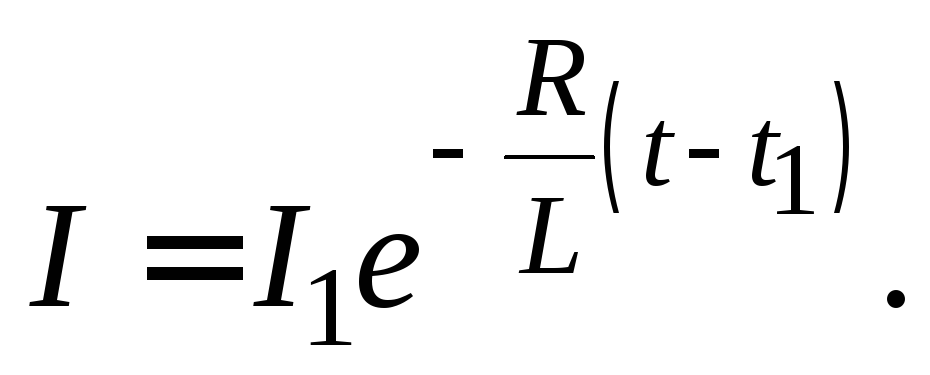 (15.7)
(15.7)
В
этом случае сила тока в цепи постепенно
уменьшается от начального значения 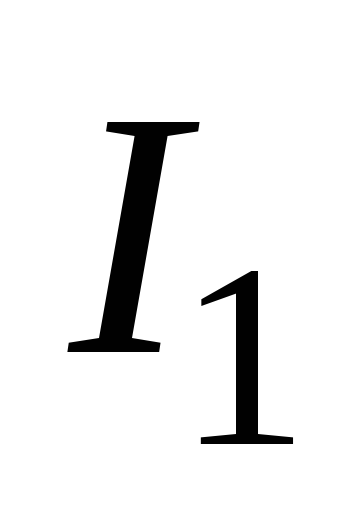 ,
стремясь к нулю. При этом за время
,
стремясь к нулю. При этом за время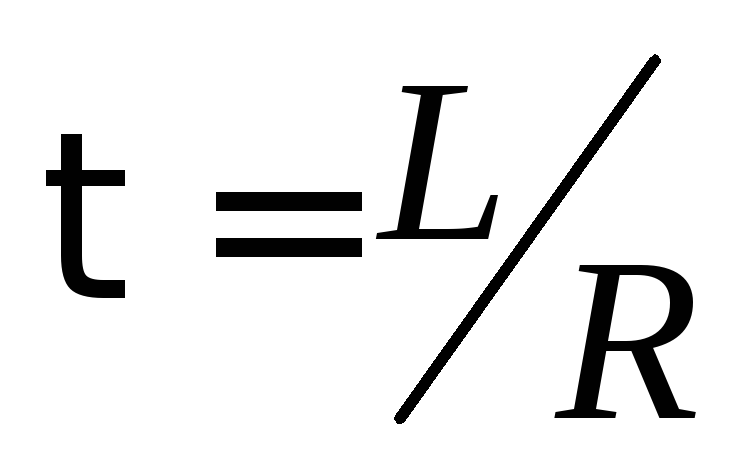 (время
релаксации)
сила тока изменяется в
(время
релаксации)
сила тока изменяется в 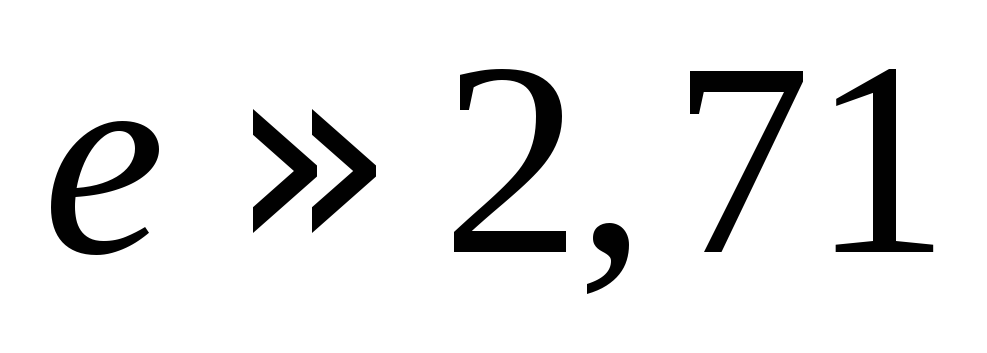 раза.
раза.
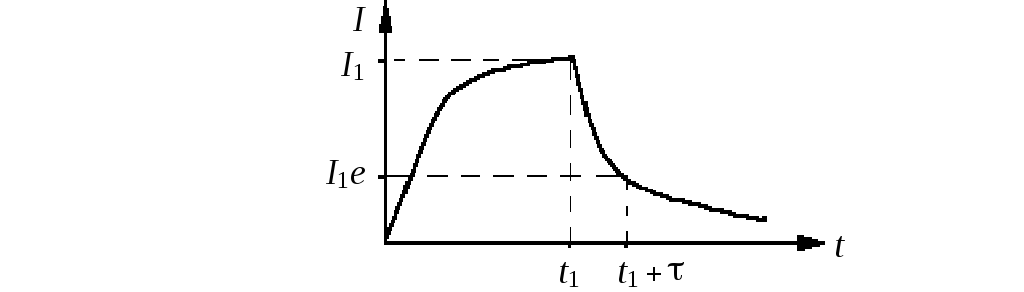
Рис. 15.1
Следует
заметить, что в опыте удобнее снимать
вместо зависимости силы тока в цепи от
времени  зависимость напряжения на некотором
известном активном сопротивлении
зависимость напряжения на некотором
известном активном сопротивлении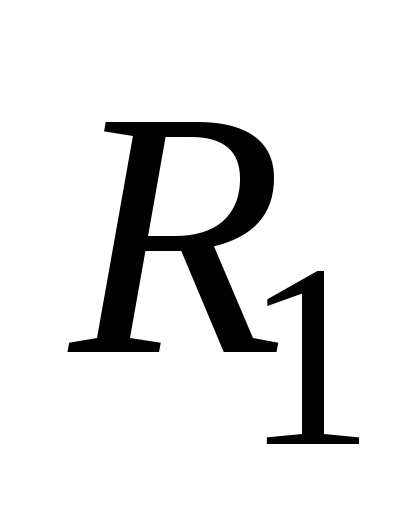 ,
последовательно включенном в цепь, от
времени
,
последовательно включенном в цепь, от
времени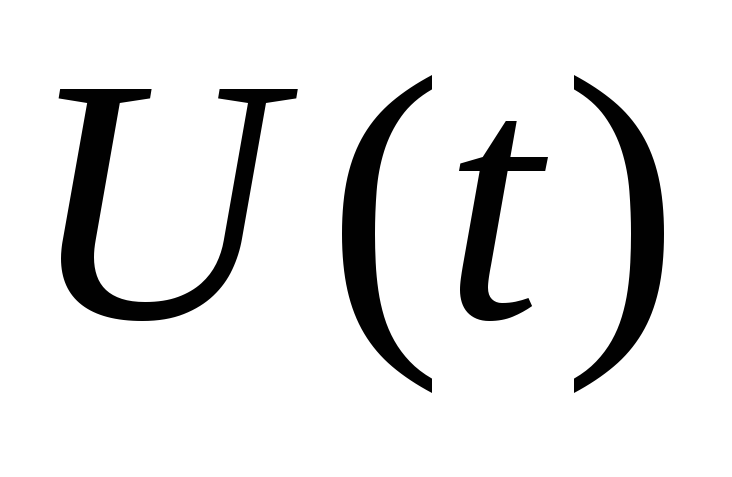 .
Напряжение в этом случае будет
пропорционально силе тока.
.
Напряжение в этом случае будет
пропорционально силе тока.
Из
сказанного ясно, что, измерив силу токов
(или напряжения) в некоторые моменты
времени 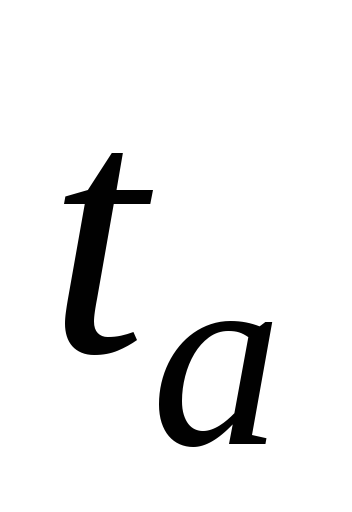 ,
,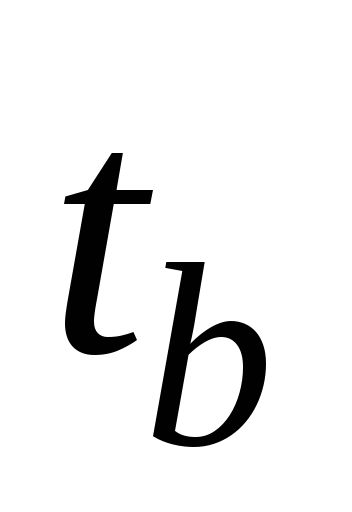 и зная, кроме того, величину общего
активного сопротивления контура
и зная, кроме того, величину общего
активного сопротивления контура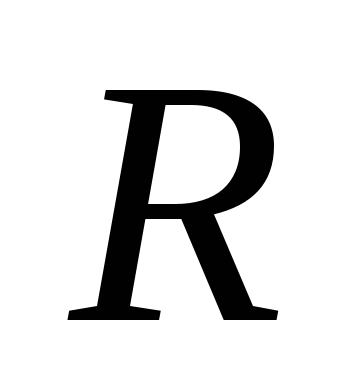 ,
можно с помощью зависимостей (15.6) или
(15.7) определить индуктивность контура
,
можно с помощью зависимостей (15.6) или
(15.7) определить индуктивность контура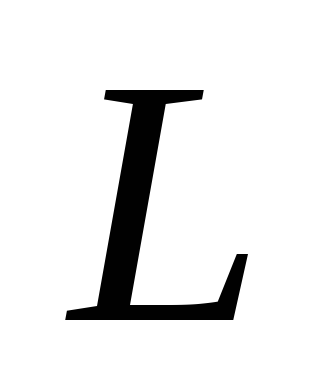 .
.
Особенно
просто, зная активное сопротивление
цепи 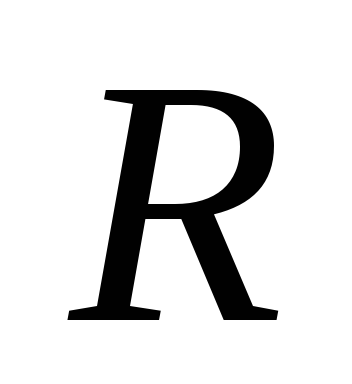 ,
определить её индуктивность, измерив
время релаксации,
,
определить её индуктивность, измерив
время релаксации,
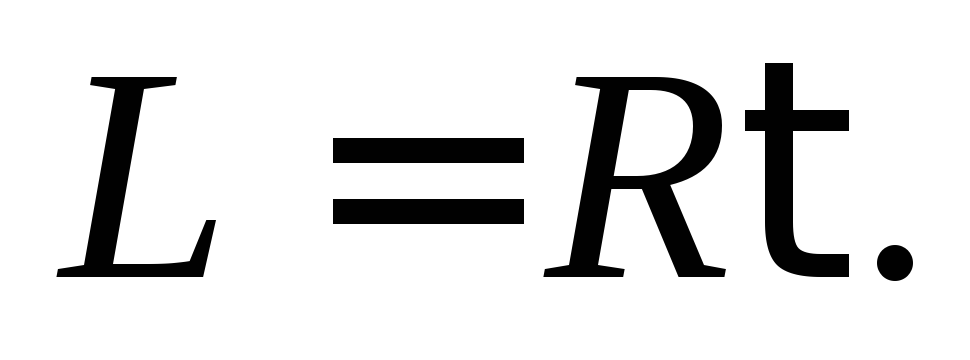 (15.8)
(15.8)
3. Вынужденные электромагнитные колебания в контуре,
их применение для измерения индуктивности
Рассмотрим
контур, состоящий из последовательно
соединенных конденсатора емкостью  ,
активного сопротивления
,
активного сопротивления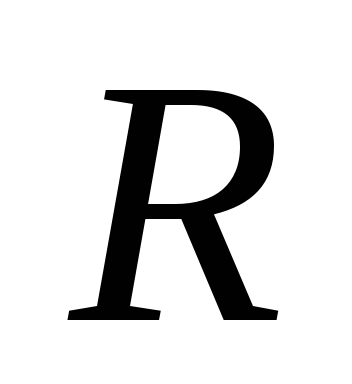 и соленоида индуктивностью
и соленоида индуктивностью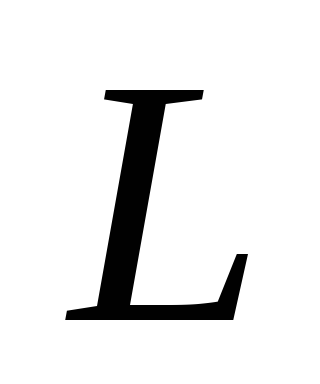 .
.
Для получения незатухающих электромагнитных колебаний необходимо включить в контур источник тока с периодически изменяющейся ЭДС (рис. 15.2).
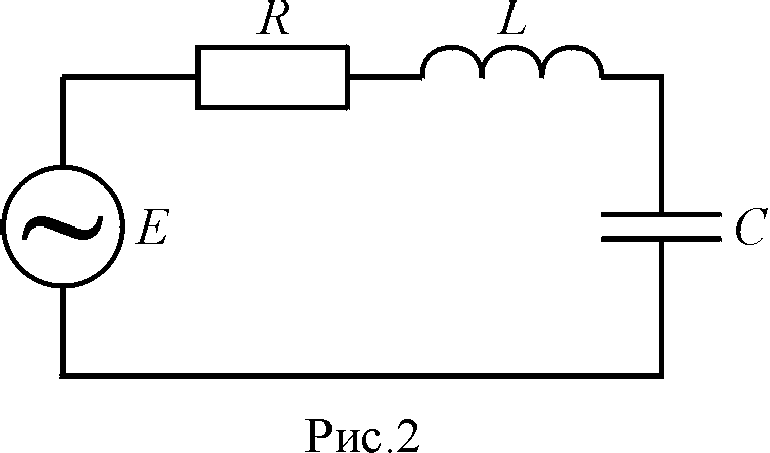
Рис. 15.2
В этом случае колебания в контуре являются вынужденными.
Пусть внешняя ЭДС изменяется по гармоническому закону
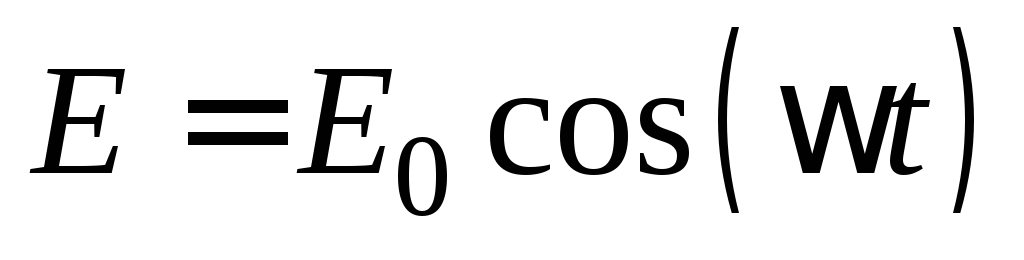 .
.
Тогда, используя закон Ома, можно получить следующее дифференциальное уравнение вынужденных электромагнитных колебаний

и, решив это уравнение, найти для установившихся вынужденных колебаний связь амплитудных значений силы тока и внешней ЭДС
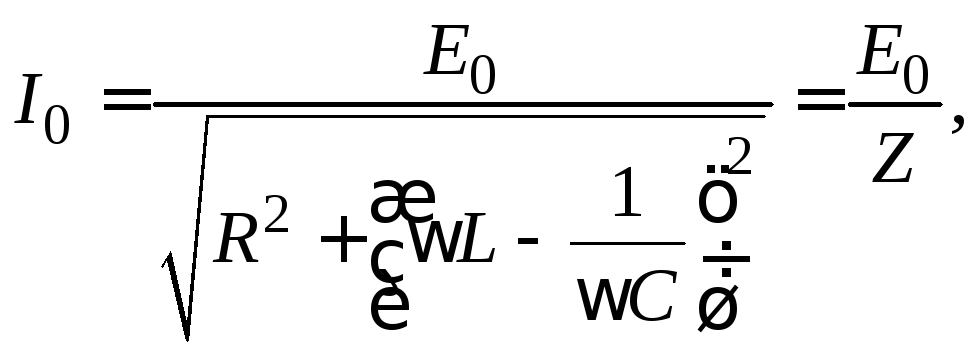 (15.9)
(15.9)
где
величина  называется полным сопротивлением
электрической цепи переменного тока.
называется полным сопротивлением
электрической цепи переменного тока.
В
нее входят активное
сопротивление 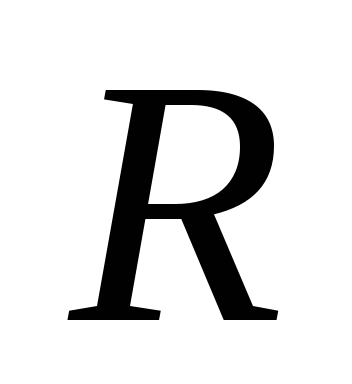 контура, емкостное
сопротивление
контура, емкостное
сопротивление  и индуктивное
сопротивление
и индуктивное
сопротивление 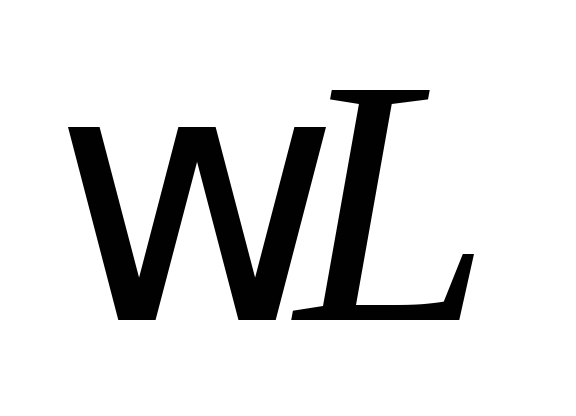 .
.
Если
электрическая емкость контура стремится
к бесконечности  ,
то есть емкостное сопротивление к нулю,
то формула (15.9) упрощается
,
то есть емкостное сопротивление к нулю,
то формула (15.9) упрощается
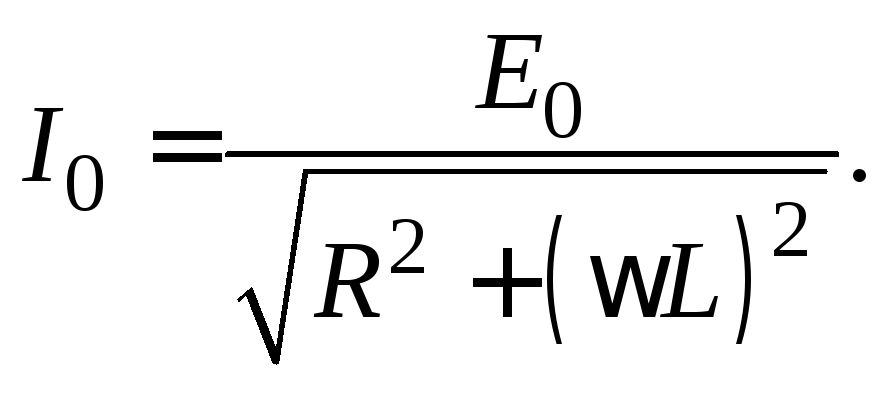 (15.10)
(15.10)
Используя это выражение, получаем рабочую формулу для экспериментального определения индуктивности соленоида. При этом учтем, что амплитуда падения напряжения на активном сопротивлении R связана с амплитудой силы тока в цепи формулой
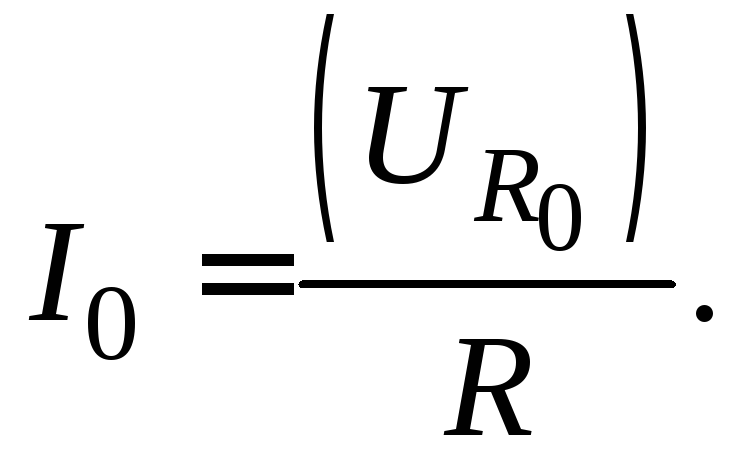 (15.11)
(15.11)
Из выражений (15.10) и (15.11) получим
 (15.12)
(15.12)
2. Закон изменения тока в цепи при подключении и отключении источника, его применение для определения индуктивности.
Найдем изменение тока в цепи, индуктивность
которой равна  ,
а активное сопротивление
—
,
а активное сопротивление
—  .
.
Если внешнее магнитное поле отсутствует или постоянно, а контур неподвижен, то индукционные явления обусловлены только самоиндукцией.
Из закона Ома для замкнутой цепи, в
которой действует источник
ЭДС  ,
а общее активное сопротивление
,
а общее активное сопротивление  ,
сила тока равна
,
сила тока равна
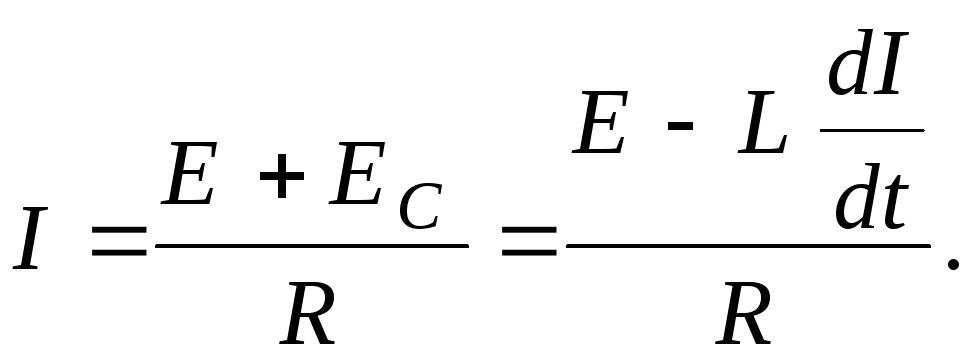
Для нахождения зависимости силы тока от времени разделим переменные:
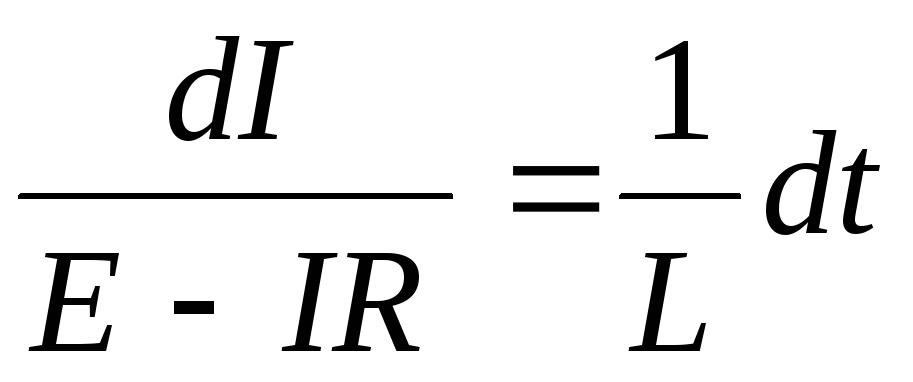 .
.
Полагая 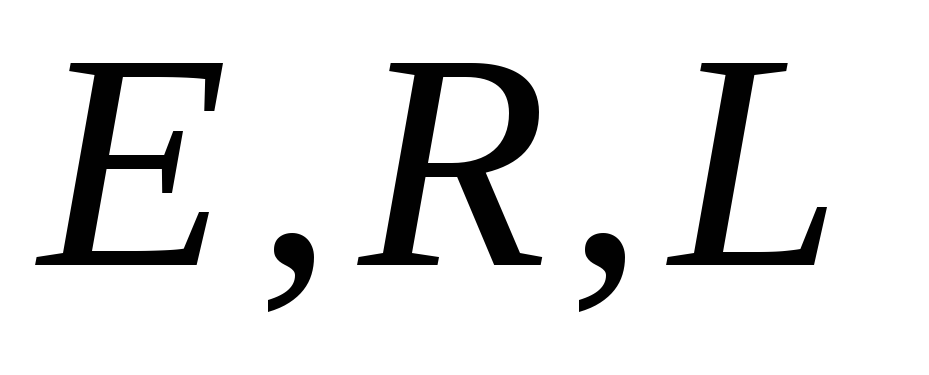 постоянными интегрируя, получаем:
постоянными интегрируя, получаем:
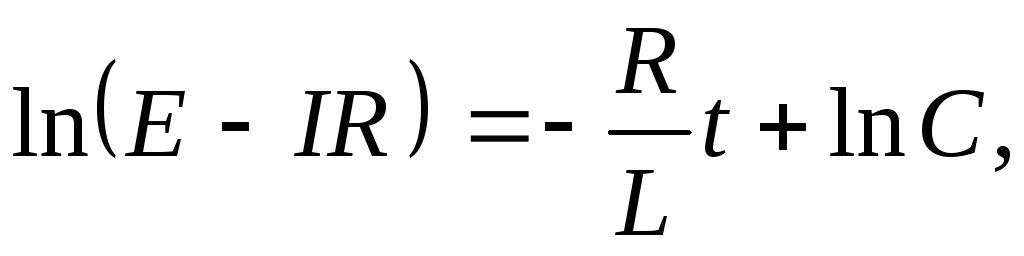
где  — постоянная интегрирования, значение
которой определяется начальными
условиями решаемой задачи.
— постоянная интегрирования, значение
которой определяется начальными
условиями решаемой задачи.
Пусть в момент времени 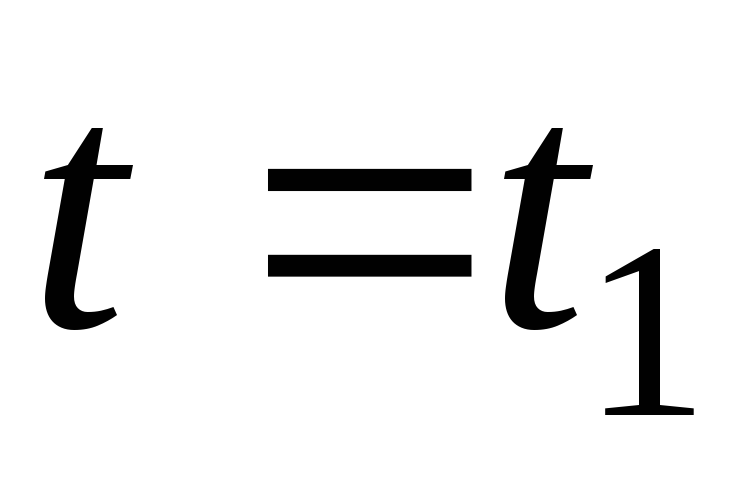 сила тока
сила тока 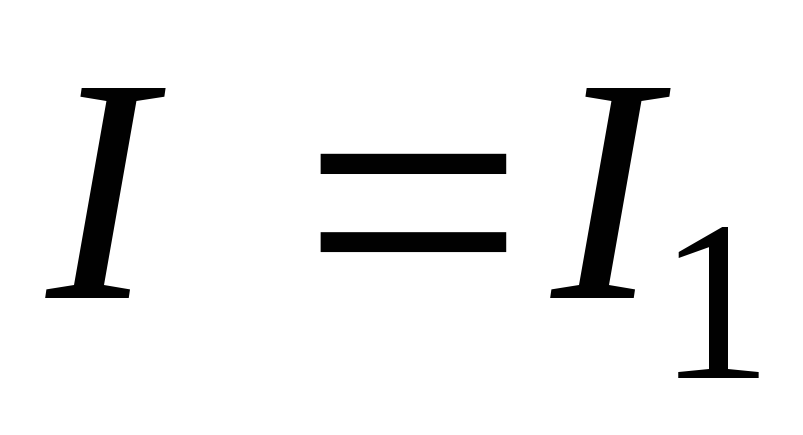 .
Тогда
.
Тогда

Выразив силу тока, получим
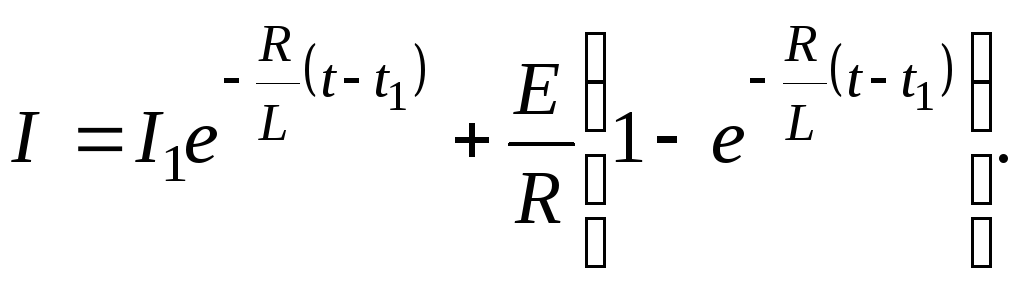 (5)
(5)
Из этой общей формулы можно получить
зависимость силы тока от времени при
замыкании цепи. В этом случае начальный
ток равен нулю  и выражение (5) приобретает вид:
и выражение (5) приобретает вид:
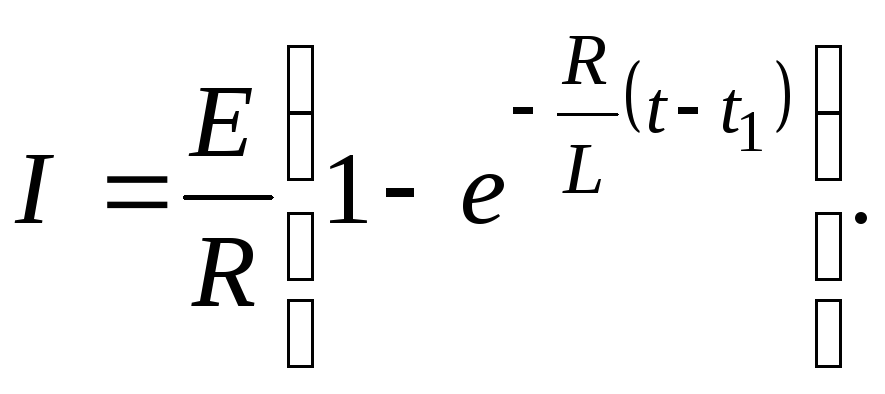 (6)
(6)
Из этой формулы видно, что сила тока при
замыкании цепи постепенно увеличивается,
стремясь к  ,
соответствующей величине постоянного
тока (Рис. 1). Нарастание тока происходит
тем медленнее, чем меньше отношение
,
соответствующей величине постоянного
тока (Рис. 1). Нарастание тока происходит
тем медленнее, чем меньше отношение  в показателе степени экспоненты или
больше обратное отношение
в показателе степени экспоненты или
больше обратное отношение 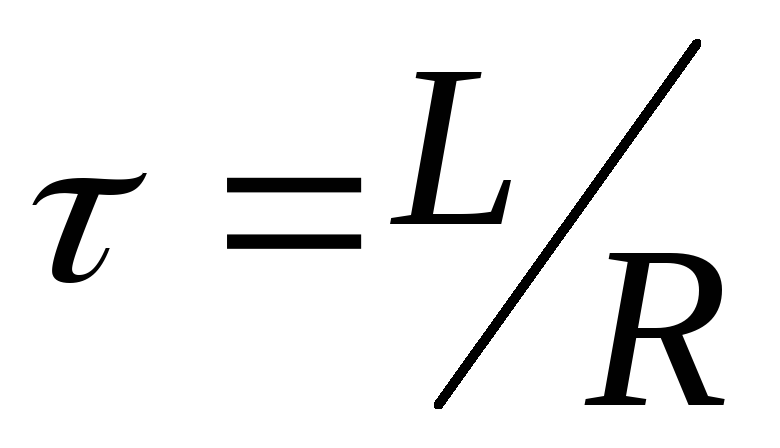 ,
физический смысл которого обсуждается
ниже.
,
физический смысл которого обсуждается
ниже.
Если же в момент времени 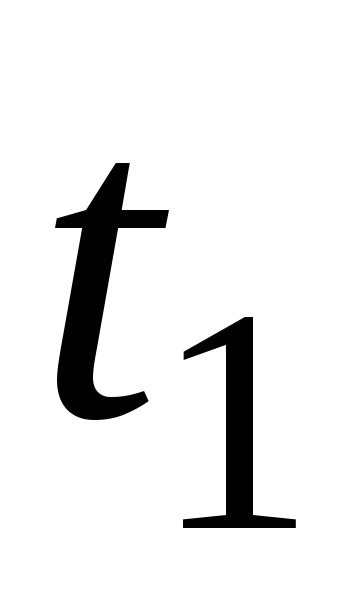 при силе тока
при силе тока 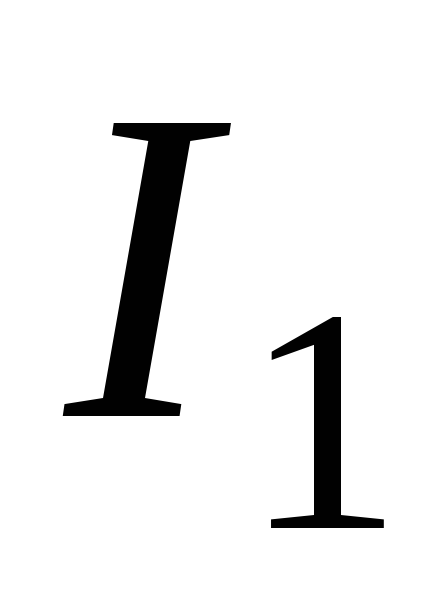 источник ЭДС отключить (
источник ЭДС отключить (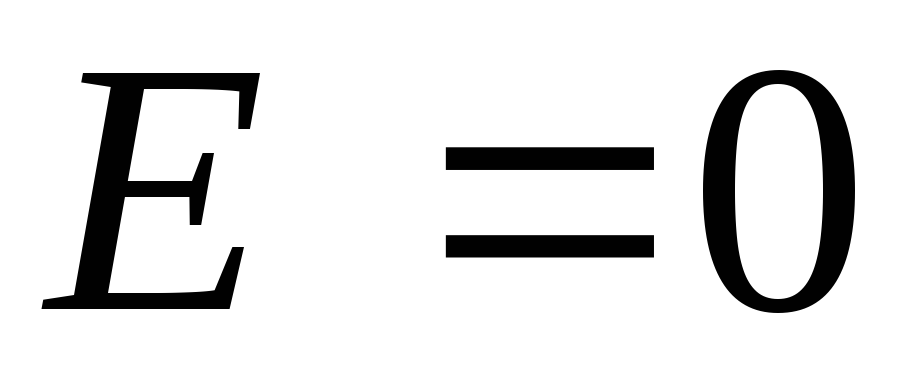 )
сохранив замкнутость цепи, то из формулы
(5) получим следующую зависимость силы
тока от времени:
)
сохранив замкнутость цепи, то из формулы
(5) получим следующую зависимость силы
тока от времени:
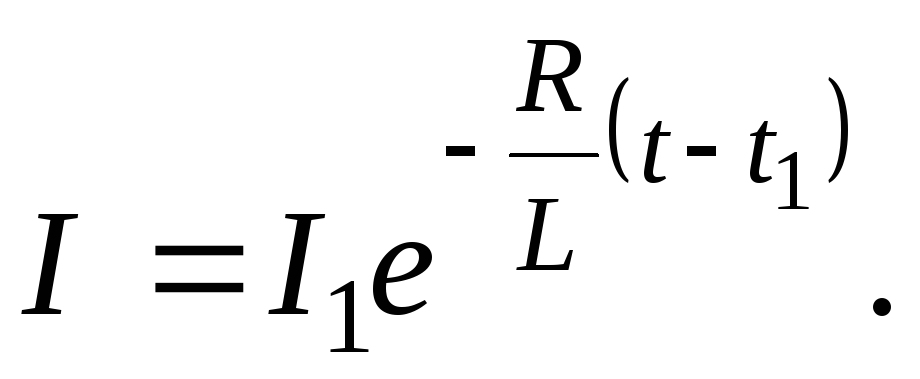 (7)
(7)
В этом случае сила тока в цепи постепенно
уменьшается от начального значения  ,
стремясь к нулю. При этом за время
,
стремясь к нулю. При этом за время  (время релаксации) сила тока
изменяется в
(время релаксации) сила тока
изменяется в 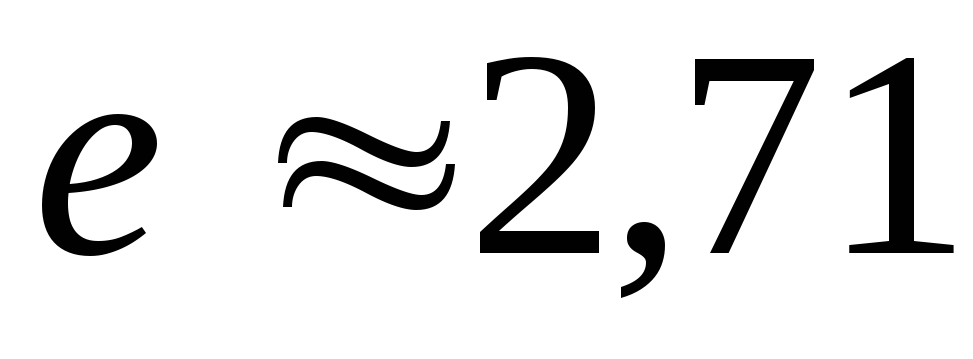 раз.
раз.

Рис. 1
Из сказанного ясно, что, измерив силу
токов в некоторые моменты
времени 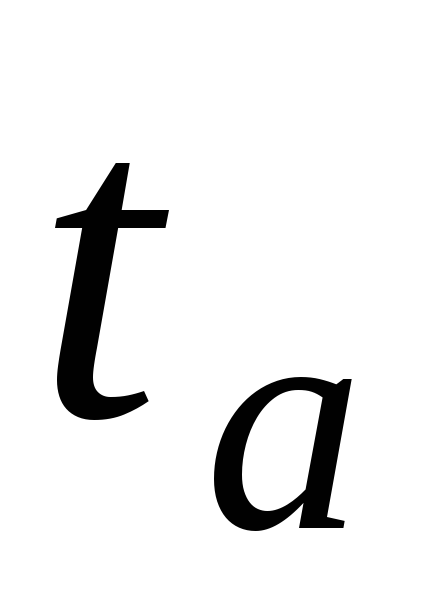 ,
, 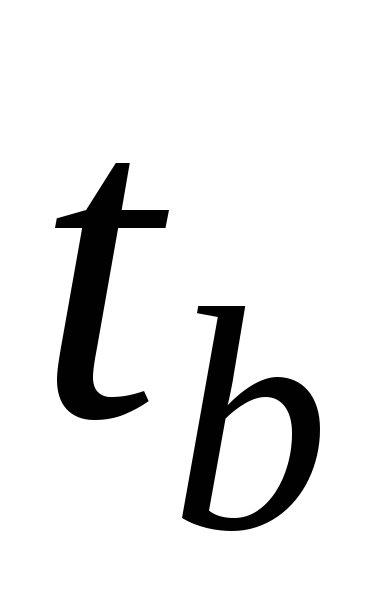 и зная, кроме того, величину активного
сопротивления
и зная, кроме того, величину активного
сопротивления
 ,
можно с помощью зависимостей (6) или
(7) определить индуктивность контура
,
можно с помощью зависимостей (6) или
(7) определить индуктивность контура 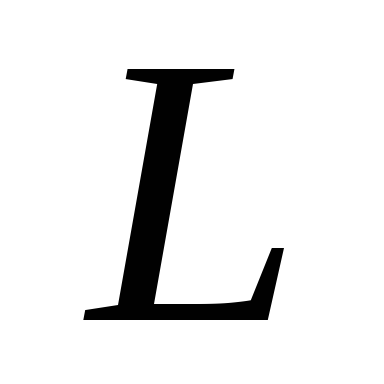
Особенно просто определить индуктивность, измерив время релаксации:
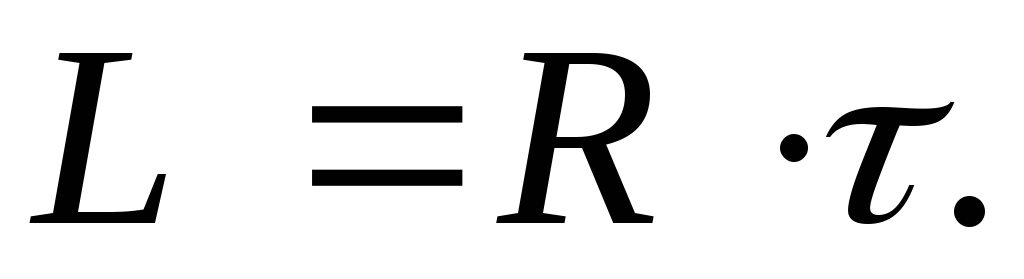 (8)
(8)
3. Вынужденные электромагнитные колебания в контуре, их применение для измерения индуктивности.
Рассмотрим контур, состоящий из
последовательно соединенных
конденсатора емкостью  ,
активного сопротивления
,
активного сопротивления  и соленоида индуктивностью
и соленоида индуктивностью 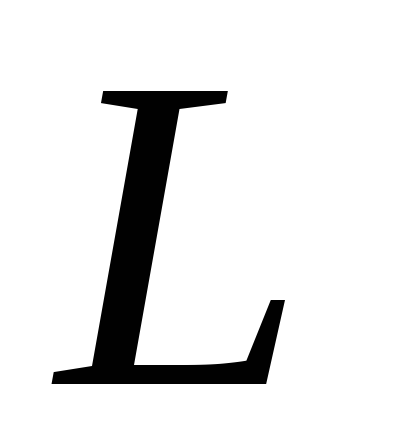 .
.
Для получения незатухающих электромагнитных колебаний необходимо включить в контур источник тока с периодически изменяющейся ЭДС (Рис.2).
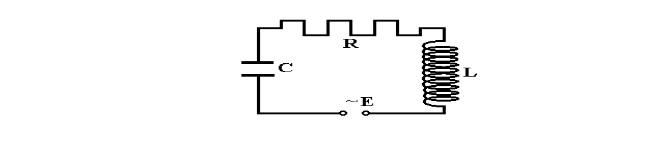
Рис.2
В этом случае колебания в контуре являются вынужденными.
Пусть, внешняя ЭДС изменяется по гармоническому закону
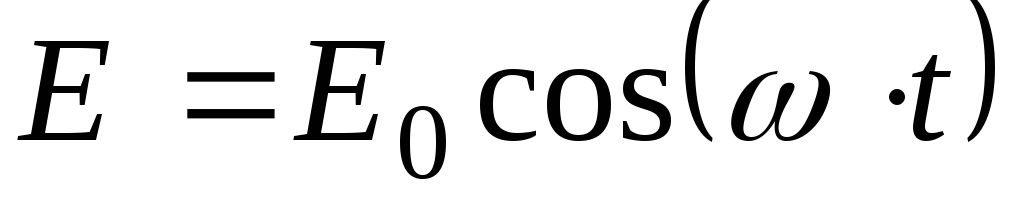 .
.
Тогда, используя закон Ома, можно получить следующее дифференциальное уравнение вынужденных электромагнитных колебаний

и, решив это уравнение, получить для установившихся вынужденных колебаний следующую связь амплитудных значений силы тока и внешней ЭДС:
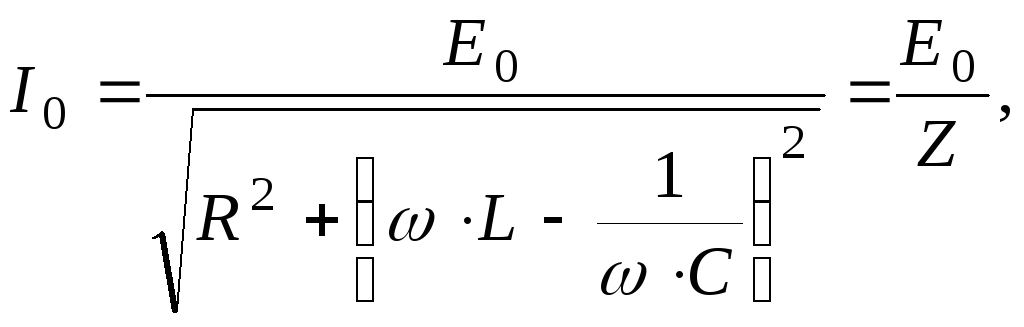 (9)
(9)
где величина 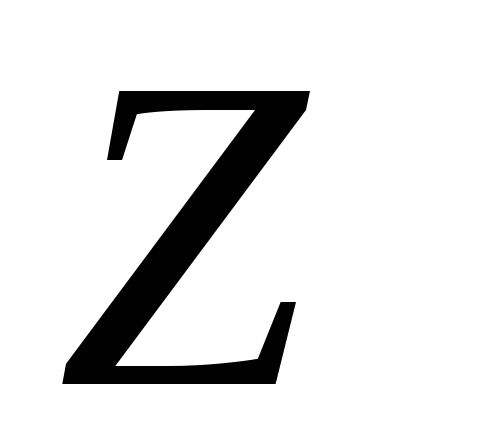 называется полным сопротивлением
электрической цепи переменного тока.
называется полным сопротивлением
электрической цепи переменного тока.
В нее входят активное сопротивление  , емкостное сопротивление
, емкостное сопротивление 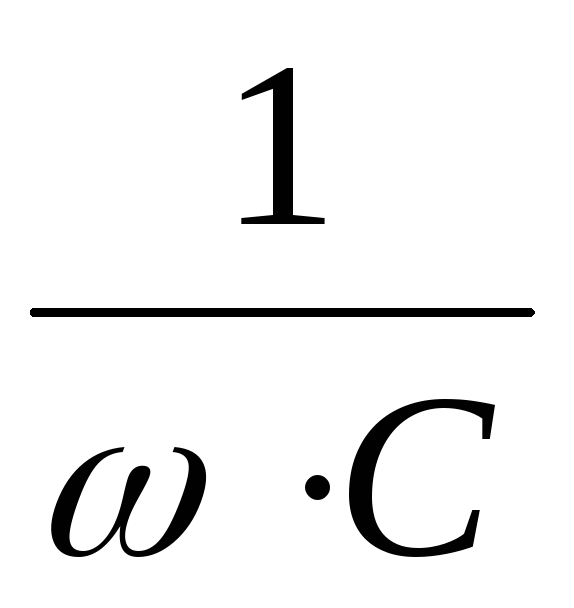 и индуктивное сопротивление
и индуктивное сопротивление 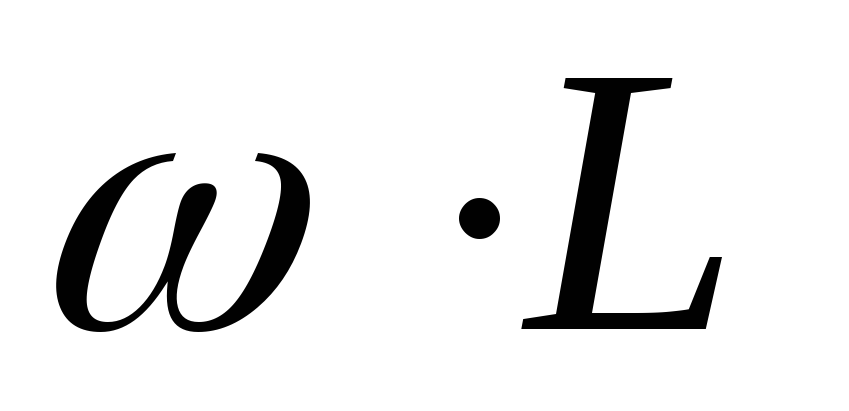 .
.
Если электрическая емкость контура
стремится к бесконечности  ,
то есть емкостное сопротивление к нулю,
то формула (9) упрощается:
,
то есть емкостное сопротивление к нулю,
то формула (9) упрощается:
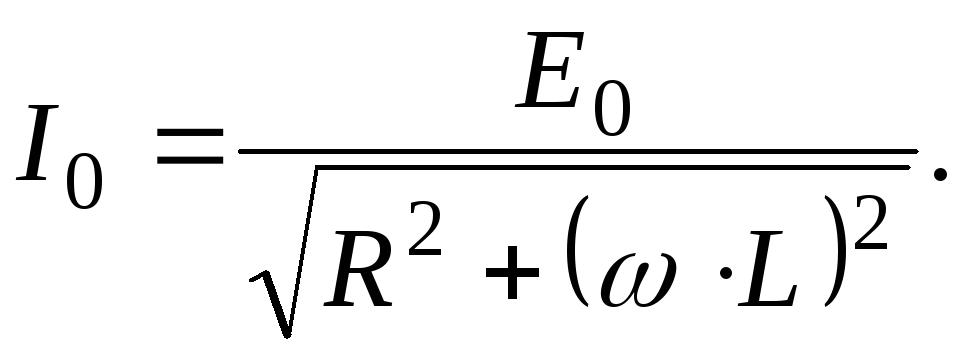 (10)
(10)
Используя это выражение, получим рабочую формулу для экспериментального определения индуктивности соленоида. При этом учтем, что амплитуда падения напряжения на активном сопротивлении R связана с амплитудой силы тока в цепи формулой
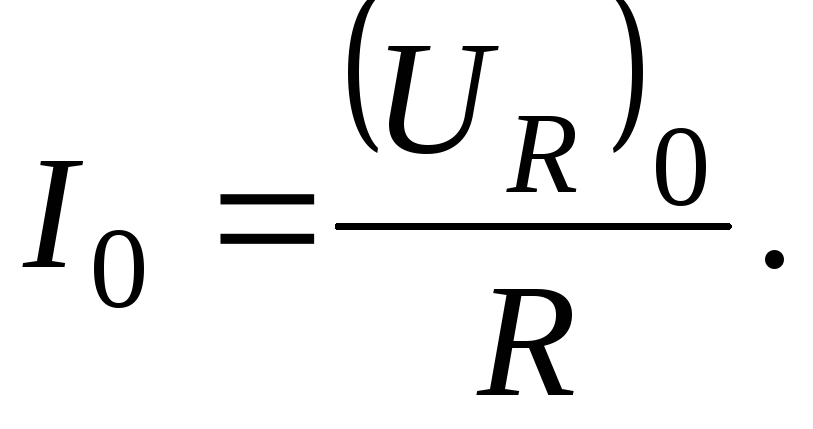 (11)
(11)
Из выражений (10) и (11) получим
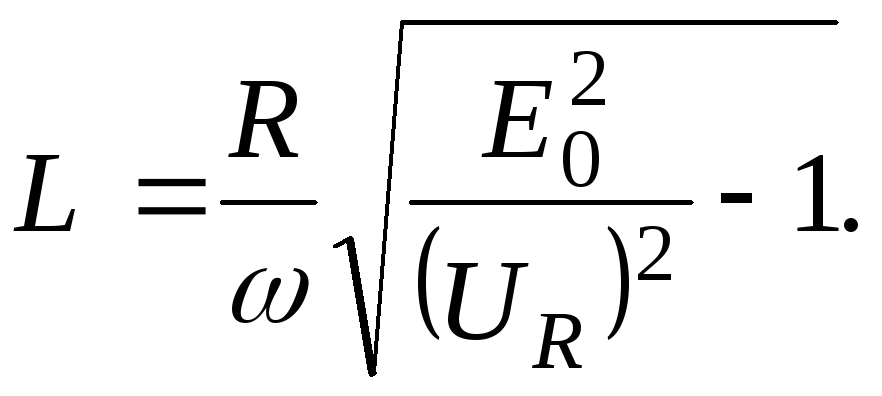 (12)
(12)
Законы изменения токов и напряжения
1 СОДЕРЖАНИЕ ЗАДАНИЯ
1.1 Дана схема однофазной цепи переменного тока (рисунок 1). Величина напряжения: U=100 В, величина частоты тока f=400 Гц, величины сопротивлений: R1=150 Ом, R2=25 Ом, величины индуктивностей L1=0,15 Гн, L2=0,4 Гн, величина емкости конденсатора C1=100 мкФ.

Рисунок 1 — Схема однофазной цепи переменного тока
1.2 Требуется:
-определить токи в ветвях и общий ток, записать законы их изменения;
-определить напряжения на всех элементах цепи, записать законы их изменения;
-составить баланс мощностей и определить погрешности расчета;
-построить векторную диаграмму.
2 ВЫПОЛНЕНИЕ
2.1 Обозначим направления тока в ветвях (рисунок 2). Найдем сопротивление каждого элемента цепи.
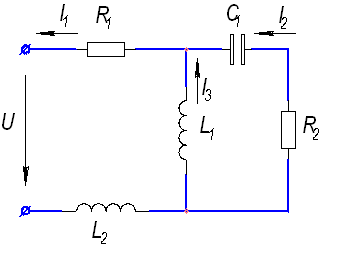
Рисунок 2 — Схема цепи с указанием направления тока в ветвях
Сопротивления индуктивностей:
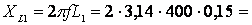 376,99 Ом;
376,99 Ом;
 1005,31 Ом.
1005,31 Ом.
Сопротивление конденсатора:
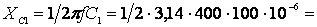 3,979 Ом.
3,979 Ом.
2.2 Найдем комплексные сопротивления участков цепи:
 Ом;
Ом;
 Ом;
Ом;
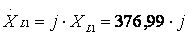 Ом;
Ом;
 Ом;
Ом;
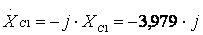 Ом.
Ом.
2.3 Представим схему с полными сопротивлениями для каждой ветви (рисунок 3). Укажем направления контурных токов.
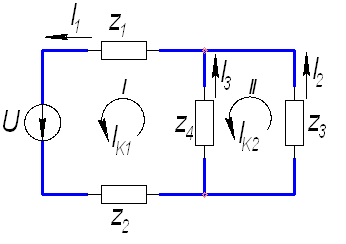
Рисунок 3 — Схема цепи с полными сопротивлениями
Полные комплексные сопротивления:
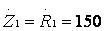 Ом;
Ом;
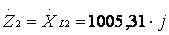 Ом;
Ом;
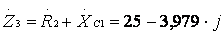 Ом;
Ом;
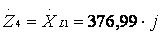 Ом.
Ом.
2.4 Используем метод контурных токов. По II закону Кирхгофа получаем:
для I контура: 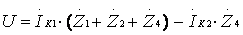 ;
;
для II контура: 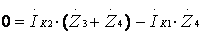 .
.
Подставляем значения напряжения и полных комплексных сопротивлений.
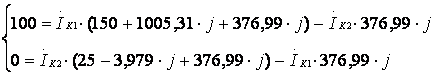 ;
;
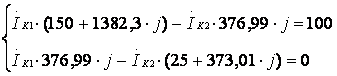 ;
;
Решаем полученную систему с помощью правила Крамера.
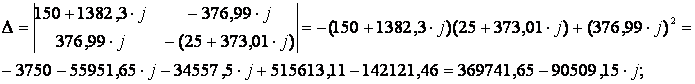
 ;
;
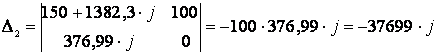 ;
;

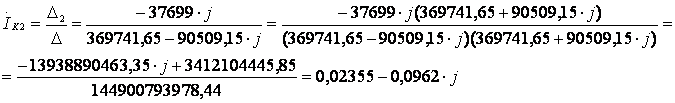
Получили контурные токи:
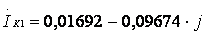 А;
А;
 А.
А.
2.5 Найдем токи в каждой ветви цепи:
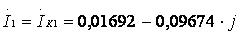 А;
А;
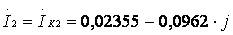 А;
А;
 А.
А.
3. Закон изменения искомого тока после первой и второй коммутаций.
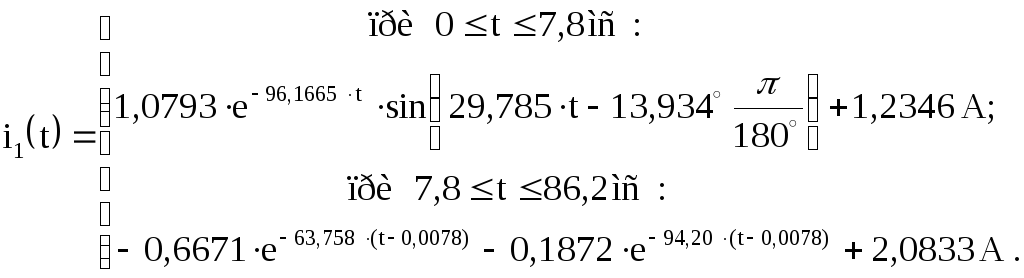 (17)
(17)
4. График изменения искомого тока во времени.
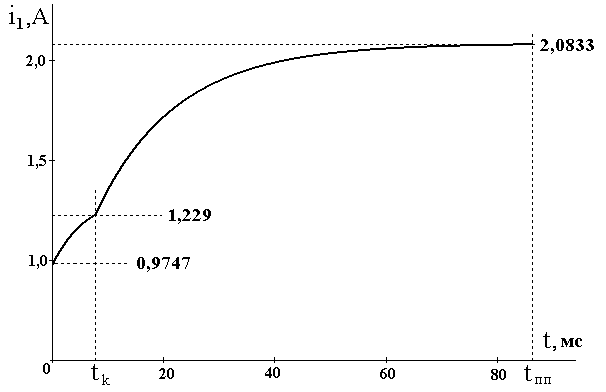
Рисунок 9 – Закон изменения тока
Методические указания к задаче 2
Рассчитать операторным методом переходный процесс в цепи индивидуального варианта № 30 (базовые параметры элементов электрической цепи – вариант №7).
Исходные данные варианта:
№ схемы | КR | КL | КC | Элементы электрической цепи в схеме рисунка 2 | Источник энергии в схеме рисунка 2 | Определить ток |
30 | 1,50 | 1,20 | 1,00 | R11, R12, R21, R32, C1, L2 | j(t) | i3(t) |
№ варианта | Jm, A | fj, град. | R10, Ом | R20, Ом | R30, Ом | RК, Ом | C10, мкФ | L20, мГн |
7 | 6 | 150 | 12 | 11 | 25 | 6 | 60 | 400 |
Замыкается ключ К12 = К.
Схема электрической цепи, в которой происходит коммутация, показана на рисунке 10.
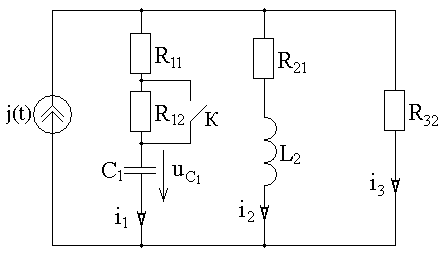
Рисунок 10 – Схема электрической цепи
Параметры элементов схемы электрической цепи (рисунок 10):
C1 = kC× C10 = 1,0 60 = 60 мкФ = 60 106 Ф;
L2 = kL× L20 = 1,2 400 = 480 мГн = 0,48 Гн;
R1 = kR × R10 = 1,5 12 = 18,0 Ом;
R2 = kR× R20 = 1,5 11 = 16,5 Ом;
R3 = kR× R30 = 1,5 25 = 37,5 Ом; R11 = R1 = 18,0 Ом ; R12 = 2,0 R1 = 36,0 Ом;
R21 = R2 = 22,5 Ом ; R32 = 3,0 R3 = 112,5 Ом;
RК = 6,0 Ом .
Решение
Указываем на схеме электрической цепи положительные направления токов ветвей.
1. Рассматриваем установившийся режим электрической цепи до коммутации и находим независимые начальные условия – внутренние источники энергии в эквивалентной операторной схеме.
В установившемся режиме электрической цепи до коммутации токи и напряжения изменяются по синусоидальному закону. Расчёт режима цепи до коммутации выполняем комплексным методом. Расчётная схема в комплексной форме для установившегося режима электрической цепи до коммутации (ключ К разомкнут) приведена на рисунке 11.

Рисунок 11 – Расчётная схема установившегося режима
электрической цепи до коммутации
Угловая частота синусоидального источника энергии:
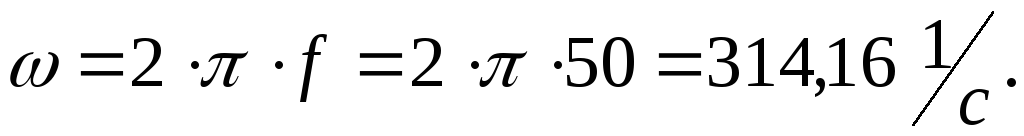
Реактивные сопротивления индуктивности и ёмкости токам частоты источника энергии:
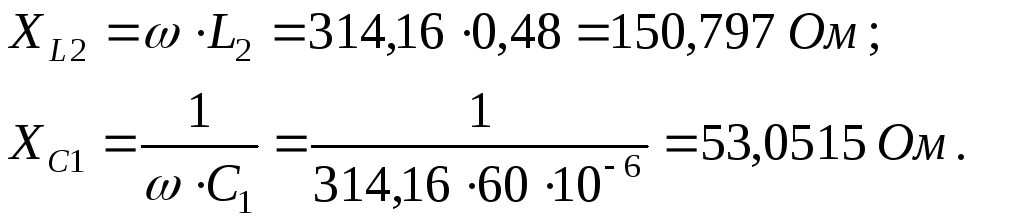
Комплексное действующее значение тока источника тока:
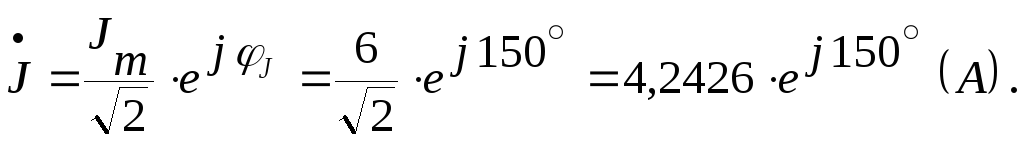
Комплексные
сопротивления ветвей электрической
цепи: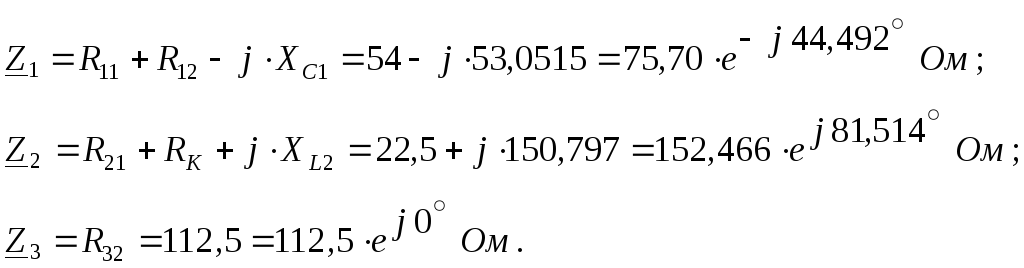
По методу двух узлов комплексное действующее значение напряжения между узлами схемы определится:

По закону Ома в комплексной форме имеем:
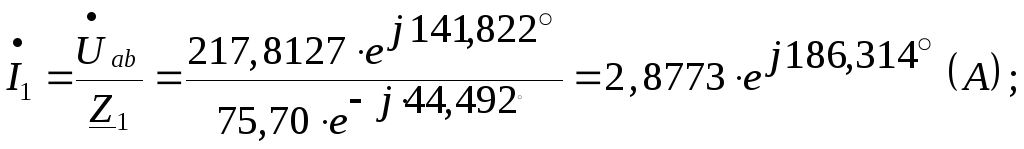
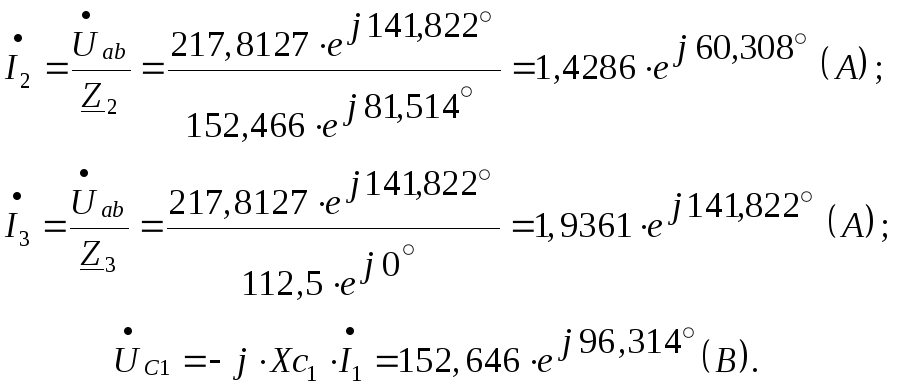
Законы изменения тока в индуктивности и напряжения на ёмкости в установившемся режиме до коммутации запишутся:
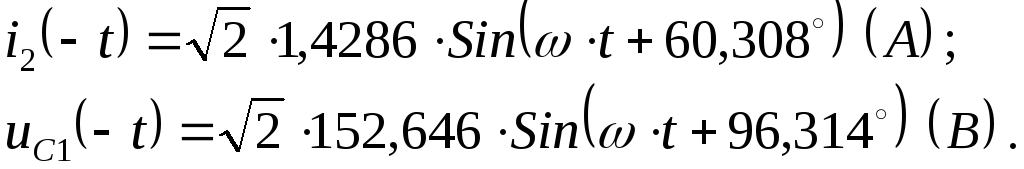
Независимые начальные условия для расчёта переходного процесса (законы коммутации) для электрической цепи (рисунок 10) запишутся:
 (18)
(18)
2. Эквивалентная операторная схема замещения электрической цепи после коммутации (ключ К замкнулся).
На операторной схеме замещения электрической цепи после коммутации указываем изображения токов ветвей, тока источника тока, операторные сопротивления элементов электрической цепи, внутренние источники энергии:
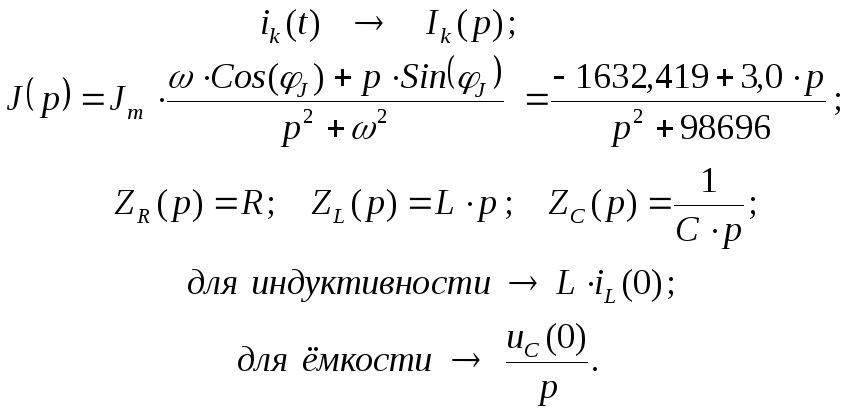

Рисунок 12 – Эквивалентная операторная схема замещения
3. По операторной схеме замещения (рисунок 12) находим изображение искомого тока I3(p).
Для упрощения дальнейших преобразований на операторной схеме замещения цепи (рисунок 12) обозначим (рисунок 13):


Рисунок 13 – Операторная схема замещения цепи
Изображение искомого тока по операторной схеме замещения можно найти методом контурных токов (в случае наличия в схеме источника ЭДС) или методом узловых потенциалов (в случае наличия в схеме источника тока).
При составлении уравнений для изображений по методу контурных токов целесообразно выбирать контуры таким образом, чтобы искомое изображение тока входило только в один контур.
Для полученной схемы замещения найдём выражение для изображения тока с помощью метода двух узлов в операторной форме:
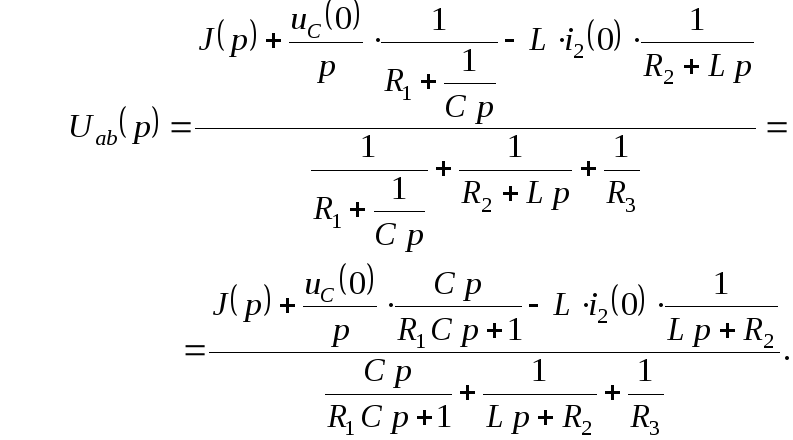
Изображение искомого тока определится на основании закона Ома в операторной форме:
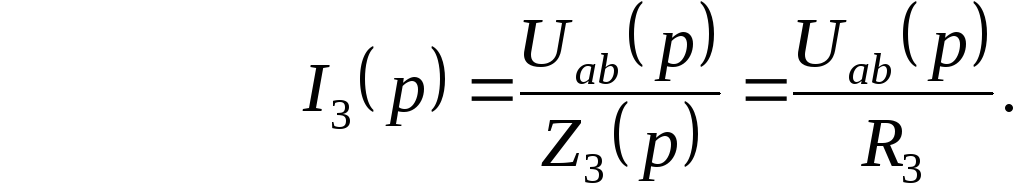
После подстановки изображения тока источника тока, преобразования полученного выражения, получим изображение искомого тока в виде правильной несократимой дроби:
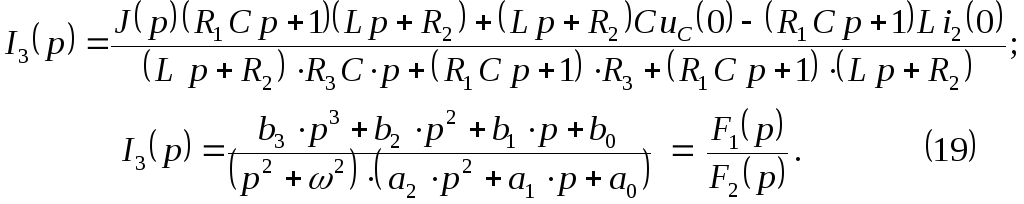
После преобразований и подстановки числовых значений параметров элементов электрической цепи, имеем:
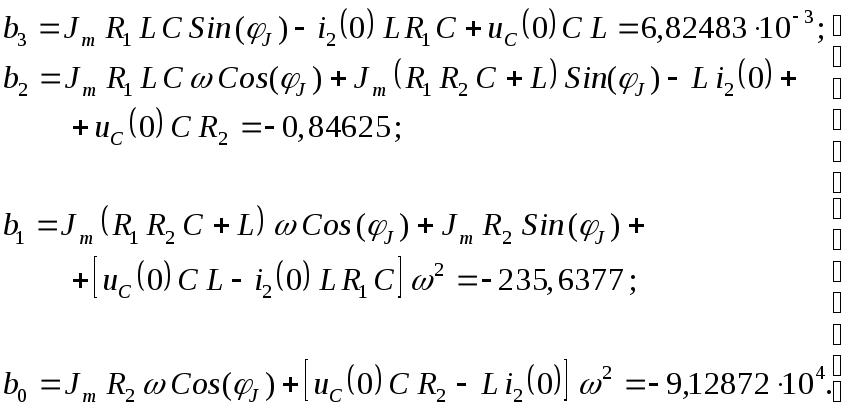 (20)
(20)
 (21)
(21)
4. По найденному изображению тока с помощью формулы разложения находим оригинал – закон изменения тока во времени:
 (22)
(22)
Корни полинома
знаменателя изображения 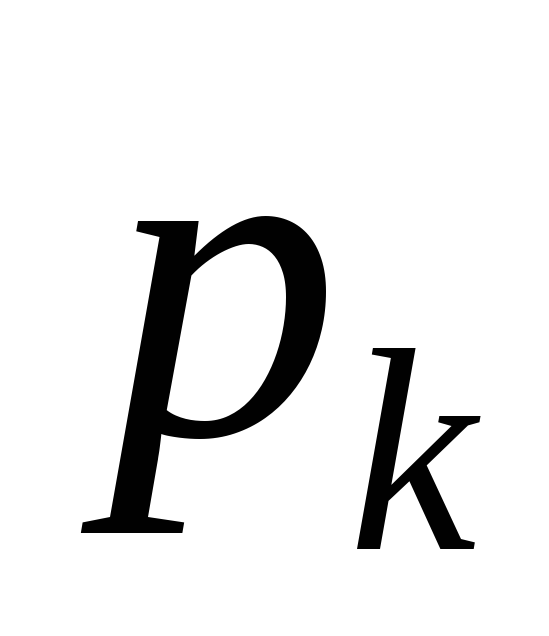 определятся:
определятся:


Таким образом, для изображения тока имеем одну пару сопряжённых мнимых корней (определяющих установившуюся составляющую тока), и другую пару сопряжённых комплексных корней (определяющих свободную составляющую тока):
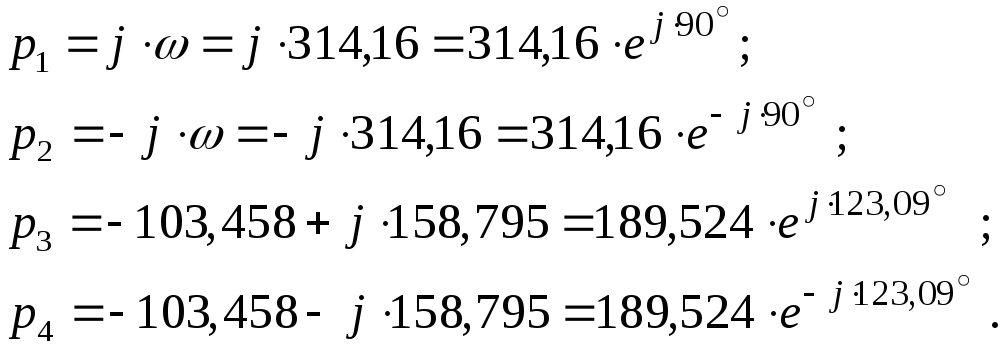 (23)
(23)
Для случая сопряжённых мнимых и комплексных корней формула разложения (22) упрощается (мнимые части выражений оригинала уничтожаются, а действительные – суммируются):
 (24)
(24)
Определяем значения выражения числителя в формуле разложения для изображения тока (20, 21) для найденных корней (23):

Значения выражения производной знаменателя (20, 22) в формуле разложения (24) для найденных корней (23) определятся:

После подстановки найденных значений в формулу разложения тока (24), получаем закон изменения тока ветви во времени:
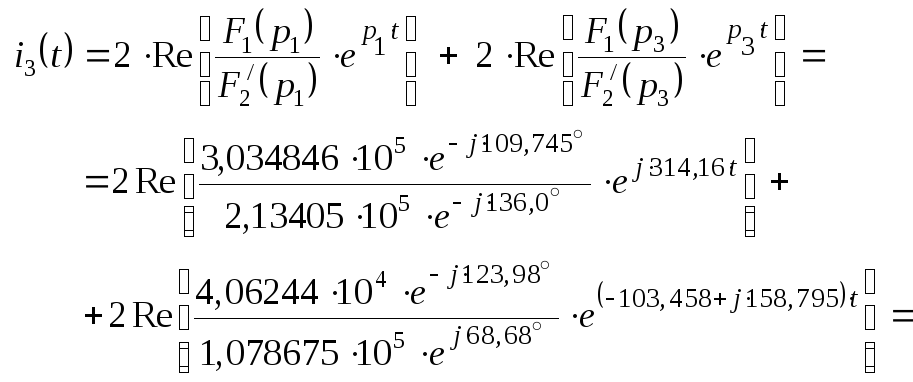
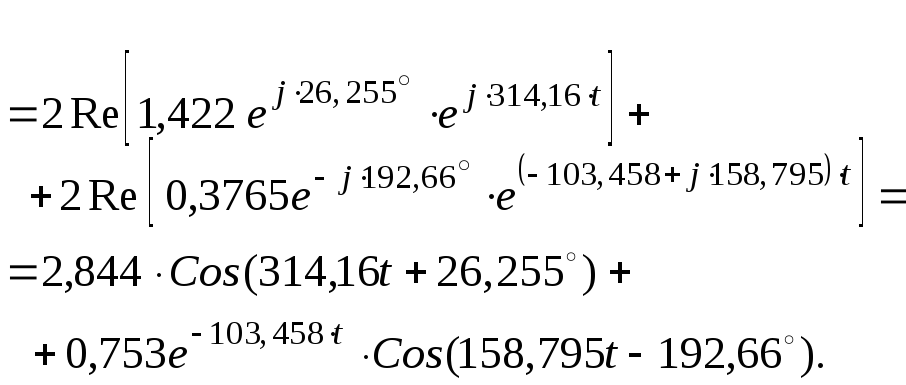
5. Закон изменения тока ветви во времени запишется:
 (25)
(25)
6. Проверку найденного операторным методом закона изменения тока ветви выполним с помощью классического метода расчёта переходных процессов в электрической цепи.
Исходя из полученного закона изменения тока ветви (25), принуждённая и свободная составляющие тока ветви запишутся:
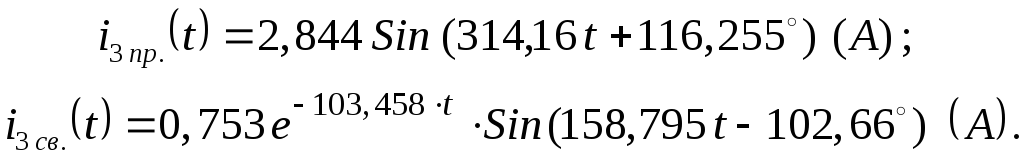
Классическим методом принуждённая составляющая тока ветви определится из рассмотрения установившегося режима электрической цепи после коммутации. Расчёт этого режима выполняется комплексным методом аналогично расчёту установившегося режима электрической цепи до коммутации:
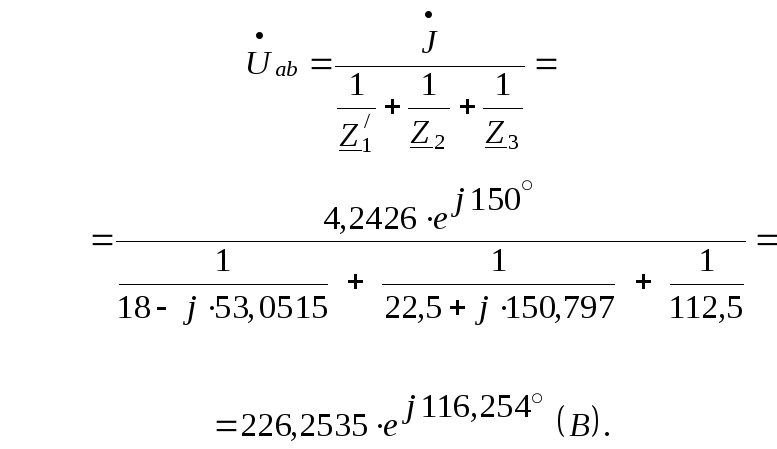
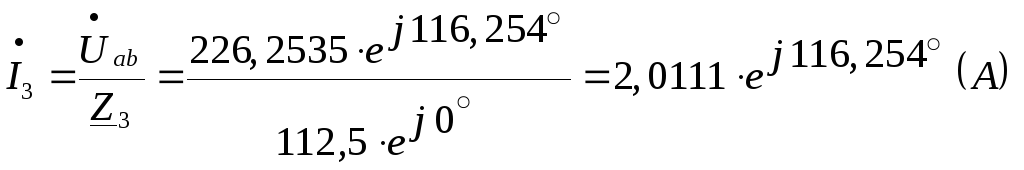
Закон изменения тока в ветви в установившемся режиме после коммутации (принуждённое значение тока) запишется:
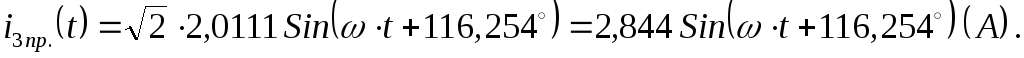
Корни характеристического уравнения электрической цепи после коммутации определятся приравниванием к нулю входного операторного сопротивления цепи:
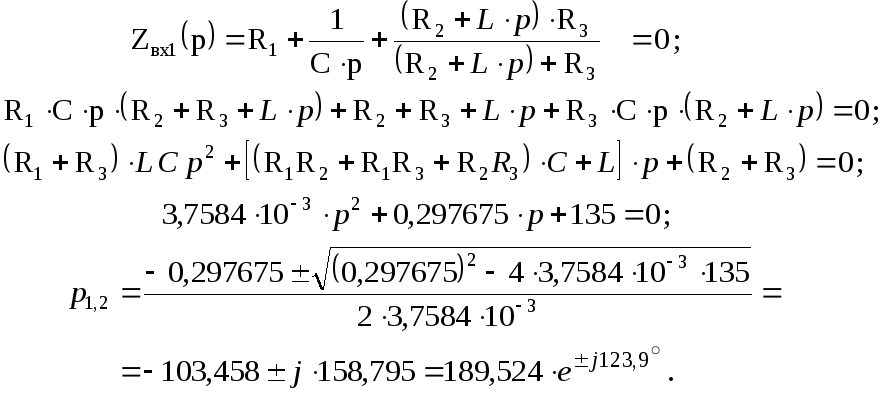
Корни характеристического
уравнения комплексные сопряжённые,
т.е. переходный процесс после коммутации
будет периодическим (колебательным).
Коэффициент затухания процесса 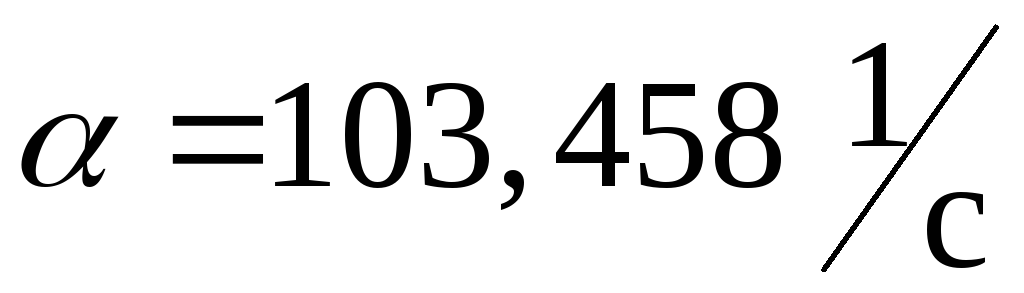 ,частота затухающих
колебаний
,частота затухающих
колебаний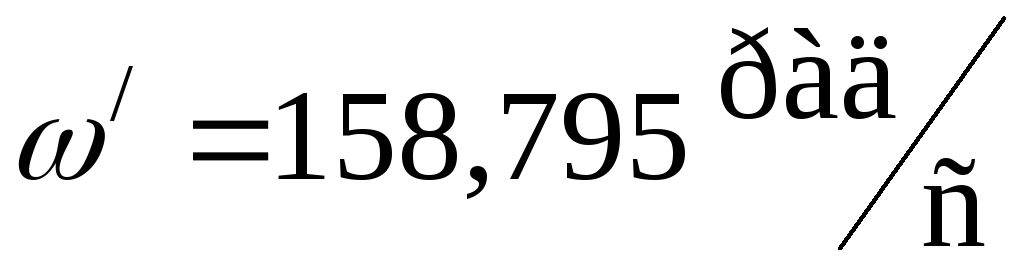 .
.
Свободная составляющая искомого тока запишется:
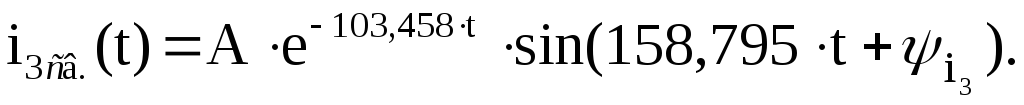
Постоянные интегрирования определятся решением системы уравнений:
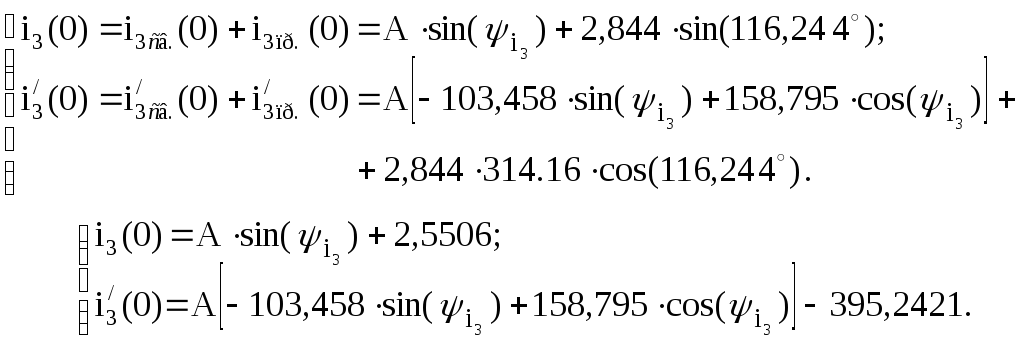
Зависимые начальные
условия определятся из системы уравнений
для цепи после коммутации (рисунок 10),
записанных по законам Кирхгофа для
момента времени  :
:

С учётом известных
независимых начальных условий (18) имеем
систему трёх уравнения с тремя
неизвестными. Решив полученную систему
уравнений, находим для момента коммутации
зависимые начальные условия  :
:
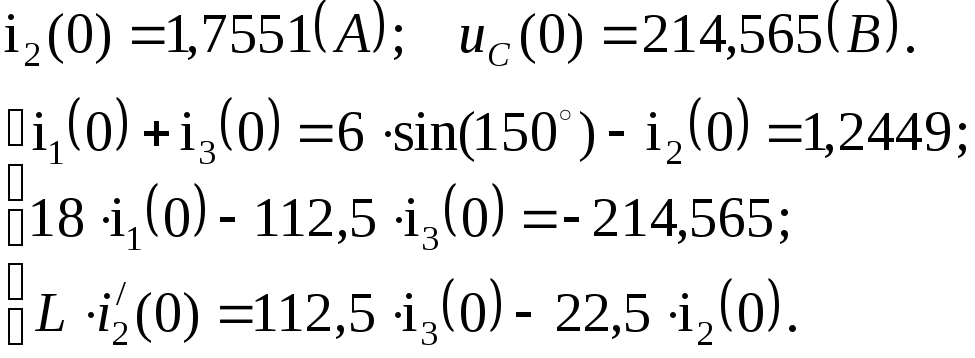

Для нахождения начальных значений первых производных токов имеем систему уравнений:
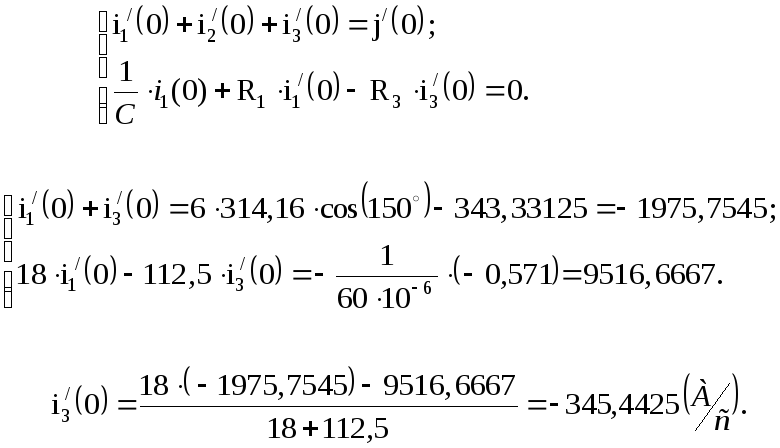
Для определения постоянных интегрирования для искомого тока ветви имеем систему уравнений:
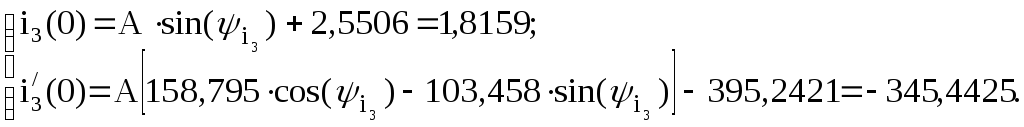
Решение полученной
системы уравнений:

Закон изменения искомого тока, найденный классическим методом расчёта:
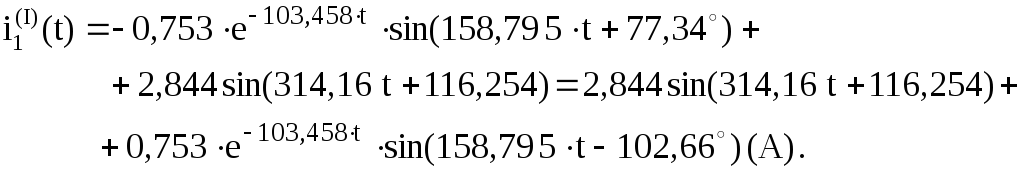
Полученный закон изменения тока совпал с операторным методом – расчёты, выполненные двумя методами, верны.
7. Закон изменения тока ветви во времени после коммутации приведён на рисунке 13. Время переходного процесса определится практическим временем затухания свободной составляющей тока:
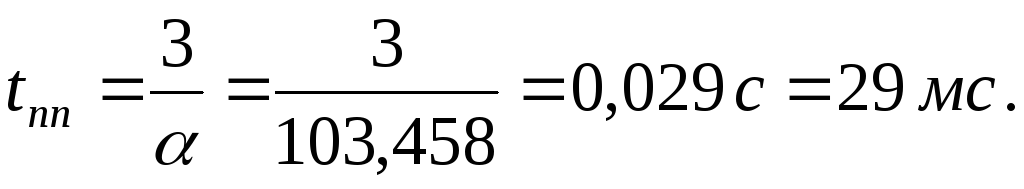
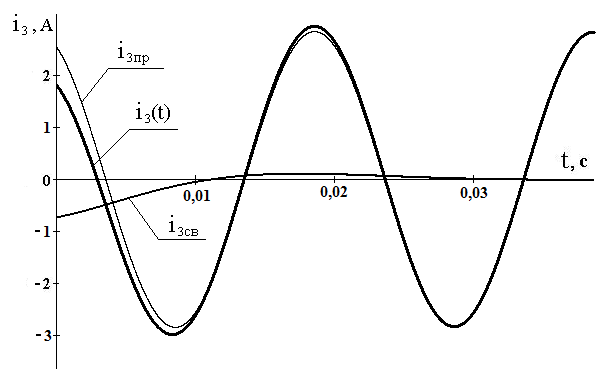
Рисунок 13 – Закон изменения тока



