Формула закона электромагнитной индукции
Это основной закон, который используют при вычислениях, которые связаны с электромагнитной индукцией.
Формула данного закона выглядит следующим образом:
где – электродвижущая сила (ЭДС) индукции, которая возникает в проводнике, если он находится в переменном магнитном поле. Если проводящим телом является, например, замкнутый контур, то в нем течет электрический ток, который называют током индукции. – магнитный поток, через поверхность, ограниченную этим контуром. Формула (1) означает то, что ЭДС индукции равна по модулю и противоположна по знаку скорости изменения магнитного потока через некоторую поверхность.
Магнитный поток, который пронизывает контур, может изменяться из-за разных причин, например, перемещения контура, его деформации, изменения самого магнитного поля. Полная производная в формуле закона электромагнитной индукции охватывает весь спектр действия этих причин.
Следует учесть, что из конца вектора нормали к контуру обход контура должен проходить против часовой стрелки.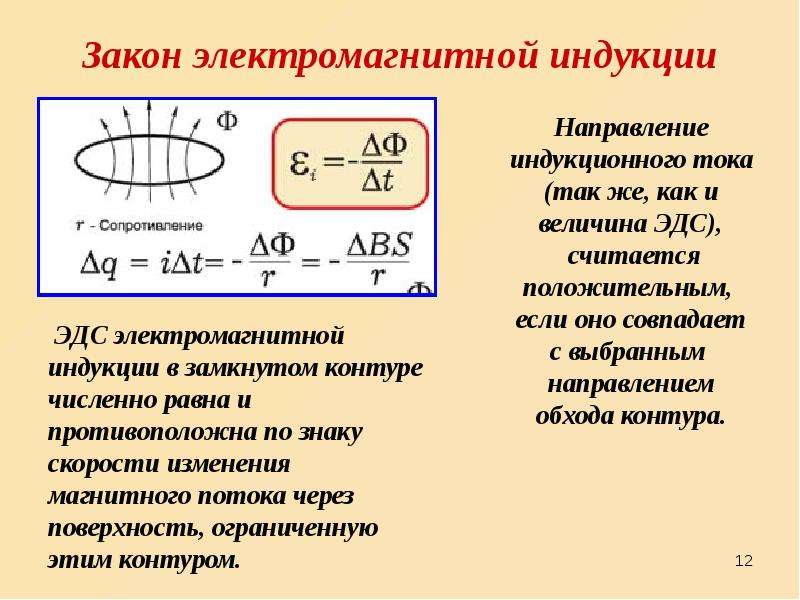
Знак минус в законе индукции отражает правило Ленца.
В виде (1), закон электромагнитной индукции записывается в международной системе единиц (СИ).
Если изменение магнитного потока происходит равномерно, то формулу закона электромагнитной индукции можно записать как:
Формулу закона для электромагнитной индукции, если контур состоит из N витков, соединенных последовательно, записывают в виде:
где – потокосцепление.
Результаты применения основного закона электромагнитной индукции
Формулы ЭДС индукции для частных случаев
ЭДС индукции в прямом проводнике, имеющем длину l, движущемся в магнитном поле и пересекающем линии магнитной индукции, если скорость его движения () перпендикулярна вектору магнитной индукции (), равна:
Разность потенциалов (U), возникающая на концах проводника длиной l, движущегося в однородном магнитном поле со скоростью v равна:
где – угол между направлением вектора скорости и направлением вектора магнитной индукции.
Если в однородном магнитном поле вращается плоский контур со скоростью , при этом ось вращения находится в плоскости витка и составляет угол в 900 с направлением вектора внешнего магнитного поля, то в контуре появляется ЭДС индукции равная:
где S – площадь, которую ограничивает виток; – мгновенное значение угла между и вектором нормали к плоскости рамки; – поток самоиндукции витка.
Если в рамке, вращающейся со скоростью в однородном магнитном поле, имеется N витков, то
в формуле (6) самоиндукцией витков пренебрегли.
Пусть проводник находится в покое, при этом изменяется во времени само магнитное поле, тогда ЭДС индукции можно найти как:
Примеры решения задач по теме «Закон электромагнитной индукции»
Какая формула выражает основной закон электромагнитной индукции — MOREREMONTA
История развития и опыты Фарадея
До середины XIX века считалось, что электрическое и магнитное поле не имеют никакой связи, и природа их существования различна.
Фарадей проделал следующий опыт: он замыкал цепь в катушке I и вокруг нее возрастало магнитное поле. Далее линии индукции данного магнитного поля пересекали катушку II, в которой возникал индукционный ток.
Рис. 1. Схема опыта Фарадея
Сколько бы экспериментов не проводил Фарадей, неизменным оставалось одно условие: для образования индукционного тока важным является изменение магнитного потока, пронизывающего замкнутый проводящий контур (катушку).
Закон Фарадея
Явление электромагнитной индукции определяется возникновением электрического тока в замкнутом электропроводящем контуре при изменении магнитного потока через площадь этого контура.
Основной закон Фарадея заключается в том, что электродвижущая сила (ЭДС) прямо пропорциональна скорости изменения магнитного потока.
Формула закона электромагнитной индукции Фарадея выглядит следующим образом:
Рис. 2. Формула закона электромагнитной индукции
И если сама формула, исходя из вышесказанных объяснений не порождает вопросов, то знак «-» может вызвать сомнения. Оказывается существует правило Ленца – русского ученого, который проводил свои исследования, основываясь на постулатах Фарадея. По Ленцу знак «-» указывает на направление возникающей ЭДС, т.е. индукционный ток направлен так, что магнитный поток, который он создает, через площадь, ограниченную контуром, стремится препятствовать тому изменению потока, которое вызывает данный ток.
Закон Фарадея-Максвелла
В 1873 Дж.К.Максвелл по-новому изложил теорию электромагнитного поля. Уравнения, которые он вывел, легли в основу современной радиотехники и электротехники. Они выражаются следующим образом:
- Edl = -dФ/dt – уравнение электродвижущей силы
- Hdl = -dN/dt – уравнение магнитодвижущей силы.

Где E – напряженность электрического поля на участке dl; H – напряженность магнитного поля на участке dl; N – поток электрической индукции, t – время.
Симметричный характер данных уравнений устанавливает связь электрических и магнитных явлений, а также магнитных с электрическими. физический смысл, которым определяются эти уравнения, можно выразить следующими положениями:
- если магнитное поле изменяется, то это изменение всегда сопровождается электрическим полем.
Рис. 3. Возникновение вихревого магнитного поля
Что мы узнали?
Ученикам 11 класса необходимо знать, что электромагнитную индукцию впервые как явление обнаружил Майкл Фарадей. Он доказал, что электрическое и магнитное поле имеют общую природу. Самостоятельные исследования на основе опытов Фарадея также проводили такие великие деятели как Ленц и Максвелл, которые расширили наши познания в области электромагнитного поля.
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ) , площади поверхности ( S ) , пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ) , единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным ( ( alpha ) ( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ) :
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec ) ЭДС электромагнитной индукции равна:
где ( alpha ) – угол между векторами ( vec ) и ( vec ) .
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле.
 Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле; - вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
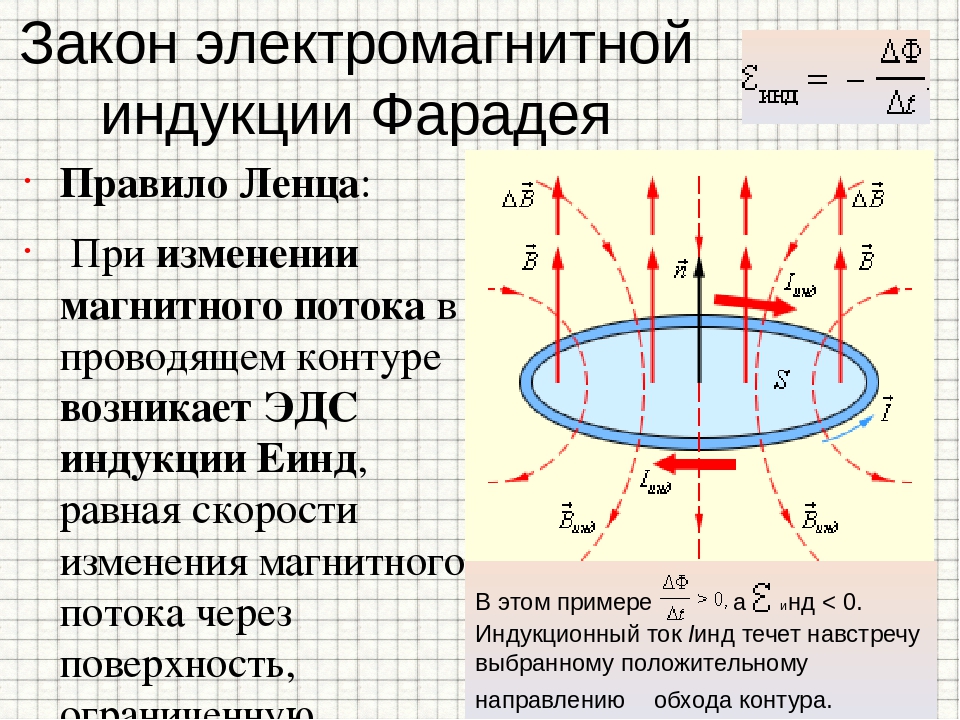
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током.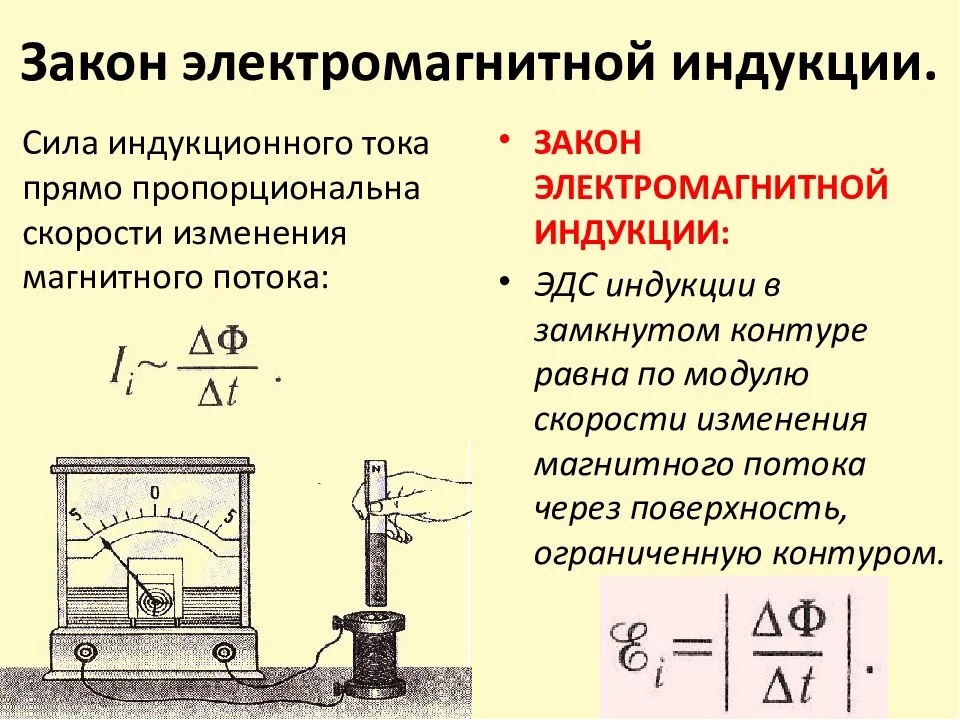 Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_ ) , возникающая в катушке с индуктивностью ( L ) , по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ) , создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
М. Фарадеем было установлено, что сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:
Возникновение тока в замкнутом контуре означает наличие сторонних сил, работа которых по перемещению единичного заряда в контуре называется электродвижущей силой (ЭДС). Это означает, что при изменении потока через поверхность, ограниченную замкнутым контуром, в контуре возникает ЭДС ɛi которую называют ЭДС индукции. Согласно закону Ома для замкнутой цепи, . Следовательно, ЭДС индукции пропорциональна ΔФ/Δt, поскольку сопротивление R не зависит от изменения магнитного потока.
Закон электромагнитной индукции формулируется так:
ЭДС индукции ɛi в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:
.
Применение правила Ленца к замкнутому контуру с положительной нормалью приводит к выражению:
.
Формула ( ) выражает основной закон электромагнитной индукции .
На рисунке внешнее магнитное поле индукции В возрастает со временем и направлено вдоль положительной нормали к контуру с током. Индуцированный ток противоположен выбранному направлению обхода в соответствии с индуцированным магнитным полем В’.
Описанные выше опыты свидетельствуют о том, что электромагнитная индукция — это возникновение электрического поля и электрического тока при изменении во времени магнитного поля или при движении проводника в магнитном поле. Эти два типа эффектов электромагнитной индукции отличаются физической природой процессов, отвечающих за их возникновение. Первый тип обусловлен наведением вихревого электрического поля переменным магнитным полем, второй — действием сил Лоренца на движущиеся заряды в стационарном магнитном поле. В обоих случаях выполняется основной закон индукции, выраженный формулой ().
Содержание:
Если взять замкнутую проводящую систему и создать в ней условия для того чтобы магнитный поток изменился в магнитном поле, то в результате этих движений появится электрический ток. Данное обстоятельство описывает закон электромагнитной индукции Фарадея – английского ученого, который при проведении опытов добился превращения магнитной энергии в электричество. Оно получило название индукционного, поскольку до того времени его можно было создать лишь гальваническим путем. История открытияЯвление электромагнитной индукции было открыто сразу двумя учеными. Это были Майкл Фарадей и Джозеф Генри, сделавшие свое открытие в 1831 году. Публикация Фарадеем результатов проведенных экспериментов была сделана раньше его коллеги, поэтому индукцию связывают именно с этим ученым. В дальнейшем это понятие было включено в систему СГС. Для демонстрации явления использовался железный тор, напоминающий конфигурацию современного трансформатора. Противоположные стороны его были обмотаны двумя проводниками с целью использования электромагнитных свойств. К одному из проводов подключался ток, вызывающий своеобразную электрическую волну при прохождении сквозь тор, и некоторый электрический всплеск с противоположной стороны. Наличие тока было зафиксировано гальванометром. Точно такой же всплеск электричества наблюдался и в момент отключения провода. Постепенно были обнаружены и другие формы проявления электромагнитной индукции. Кратковременное возникновение тока наблюдалось во время генерации его на медном диске, вращающемся возле магнита. На самом диске был установлен скользящий электропровод. Наибольшие представление о том, что такое индуктивность, дал эксперимент с двумя катушками. Одна из них, с меньшими размерами, подключена к жидкостной батарее, расположенной на рисунке с правой стороны. Таким образом, через эту катушку начинает протекать электрический ток, под действием которого возникает магнитное поле. Когда обе катушки находятся в неподвижном положении относительно друг друга, никаких явлений не происходит. Когда небольшая катушка начинает двигаться, то есть выходить из большой катушки или входить в нее, наступает изменение магнитного потока. В результате, в большой катушке наблюдается появление электродвижущей силы. Открытие Фарадея доработал другой ученый – Максвелл, который обосновал его математически, отображая данное физическое явление дифференциальными уравнениями. Еще одному ученому-физику – Ленцу удалось определить направление электротока и ЭДС, полученных под действием электромагнитной индукции. Законы электромагнитной индукцииСущность электромагнитной индукции определяется замкнутым контуром с электропроводностью, площадь которого пропускает через себя изменяющийся магнитный поток. В этот момент под влиянием магнитного потока появляется электродвижущая сила Еi и в контуре начинает течь электрический ток. Закон Фарадея для электромагнитной индукции заключается в прямой зависимости ЭДС и скорости, составляющих пропорцию. Данная скорость представляет собой время, в течение которого магнитный поток подвергается изменениям. Данный закон выражается формулой Еi = — ∆Ф/∆t, в которой Еi – значение электродвижущей силы, возникающей в контуре, а ∆Ф/∆t является скоростью изменения магнитного потока. В этой формуле не совсем понятным остается знак «минус», но ему тоже имеется свое объяснение. Совет В соответствии с правилом русского ученого Ленца, изучавшего открытия Фарадея, этот знак отображает направление ЭДС, возникающей в контуре. То есть, направление индукционного тока происходит таким образом, что создаваемый им магнитный поток на площади, ограниченной контуром, препятствует изменениям, вызванным этим током. Открытия Фарадея были доработаны Максвеллом, у которого теория электромагнитного поля получила новые направления. В результате, появился закон Фарадея и Максвелла, выраженный в следующих формулах:
В этих формулах Е соответствует напряженности электрического поля на определенном участке dl, Н является напряженностью магнитного поля на этом же участке, N – поток электрической индукции, t – период времени. Оба уравнения отличаются симметричностью, позволяющей сделать вывод, что магнитные и электрические явления связаны между собой. С физической точки зрения эти формулы определяют следующее:
Изменяющийся магнитный поток, проходящий сквозь замкнутую конфигурацию проводящего контура, приводит к возникновению в этом контуре электрического тока. Это основная формулировка закона Фарадея. Если изготовить проволочную рамку и поместить ее внутри вращающегося магнита, то в самой рамке появится электричество. Это и будет индукционный ток, в полном соответствии с теорией и законом Майкла Фарадея. Изменения магнитного потока, проходящего через контур, могут быть произвольными. Следовательно, формула ∆Ф/∆t бывает не только линейной, а в определенных условиях принимает любую конфигурацию. Если изменения происходят линейно, то ЭДС электромагнитной индукции, возникающей в контуре, будет постоянной.
Если же изменения магнитного потока принимают более сложную форму, то ЭДС индукции уже не будет постоянной, а будет зависеть от данного промежутка времени. В этом случае временной интервал рассматривается в качестве бесконечно малой величины и тогда соотношение ∆Ф/∆t с точки зрения математики станет производной от изменяющегося магнитного потока. Существует еще один вариант, трактующий закон электромагнитной индукции Фарадея. Его краткая формулировка объясняет, что действие переменного магнитного поля вызывает появление вихревого электрического поля. Этот же закон можно трактовать как одну из характеристик электромагнитного поля: вектор напряженности поля может циркулировать по любому из контуров со скоростью, равной скорости изменения магнитного потока, проходящего через тот или иной контур. |
| Понравился сайт? Расскажи друзьям! |
Источник: http://ru.solverbook.com/spravochnik/formuly-po-fizike/formula-zakona-elektromagnitnoj-indukcii/
§23. Закон электромагнитной индукции Фарадея
В 1831 г. Фарадей экспериментально открыл явление электромагнитной индукции. Суть явления состояла в том, что если через замкнутый контур происходило изменение магнитного потока, то в контуре возникала электродвижущая сила, приводящая к возникновению замкнутого тока.
Этот ток был назван индукционным током. Правило, устанавливающее направление индукционного тока было сформулировано в 1833г. Э. Х. Ленцем (1804 — 1865) и называется правилом Ленца.
Оно гласит: индукционный ток направлен так, что создаваемый им магнитный поток стремится компенсировать изменение магнитного потока, вызывающего данный ток.
Опыты Фарадея состояли в следующем: катушка индуктивности подключалась к чувствительному гальванометру и в катушку вдвигался и выдвигался постоянный магнит.
Из опытов следовало, что. Но сила тока зависит еще и от сопротивления контура. Поэтому закон электромагнитной индукции формулируется не для индукционного тока, а для причины, вызывающий этот ток, т. е. для. В 1845г. Ф. Э. Нейман (1799 — 1895) дал математическое определение закона электромагнитной индукции в современной форме:
(23.1)
Хотя внешне формулы (22.6) и (23.1) одинаковы, между ними существует принципиальное различие. Возникновениев (22.6) связано с движением проводников в магнитном поле и с действием на заряды силы Лоренца. Тогда как в (23.
1) на заряды в контуре действует электрическое поле, причем сам контур лишь только инструмент или прибор, который может обнаружить это изменяющееся электрическое поле, которое возникает в пространстве. Следовательно закон Фарадея отражает новое физическое явление, а именно: изменяющееся магнитное поле порождает изменяющееся электрическое поле.
Совет
А это означает, что электрическое поле порождается не только зарядами, но и изменяющимся магнитным полем. Закон электромагнитной индукции является фундаментальным законом природы.
Дифференциальная формулировка закона
, а тогда магнитный поток, а.
.
К левой части применим формулу Стокса. Тогда. После того как перенесем все слагаемые в одну сторону получим:
В силу произвольностиможно заключить, что подынтегральная функция равна нулю, а значит
(23.2)
Уравнение (23.2) является дифференциальной формой закона электромагнитной индукции. В переменных магнитных полях, а значити следовательно, в отличие от электростатического поля, порождаемого неподвижными зарядами, переменное электрическое поле не является потенциальным и работапри перемещении зарядапо замкнутому контуру не равна нулю:
.
Так как закон электромагнитной индукции не затрагивает закона порождения магнитного поля, то уравнение (18.6)остается в силе, а значит в силе остается и выражение (19.2):.
Если подставить (19.2) в (23.2), то, а значит
. (23.3)
Отсюда следует, что в переменных полях потенциальным является вектор, а значит он равен градиенту скалярной функции, т. е., а значит
. (23.4)
Второе слагаемое в (23.4) означает, что электрическое поле может порождаться неподвижными зарядами, а первое означает, что электрическое поле может порождаться переменным магнитным полем.
Источник: https://www.webpoliteh.ru/23-zakon-elektromagnitnoj-indukcii-faradeya/
Явление электромагнитной индукции. Закон Фарадея
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Обратите внимание
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года.
Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром.
Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
Явление электромагнитной индукции можно обнаружить в таких ситуациях:
1. при относительном движении катушки и магнита;
2. при изменении индукции магнитного поля в контуре, который расположен перпендикулярно линиям магнитного поля.
3. при изменении положения контура, расположенного в постоянном магнитном поле.
Закон Фарадея.
Согласно закону электромагнитной индукции Фарадея (в СИ):
где
— электродвижущая сила, действующая вдоль произвольно выбранного контура,
— магнитный поток через поверхность, ограниченную этим контуром.
Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
где
— электродвижущая сила,
— число витков,
— магнитный поток через один виток,
— потокосцепление катушки.
Векторная формула:
В дифференциальной форме закон Фарадея можно записать в следующем виде:
(в системе СИ)
или
(в системе СГС).
В интегральной форме (эквивалентной):
(СИ)
или
(СГС)
Важно
Здесь— напряжённость электрического поля,— магнитная индукция,— произвольная поверхность,— её граница. Контур интегрированияподразумевается фиксированным (неподвижным).
Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).
· В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)[2].
Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенствопродолжает соблюдаться, но ЭДС в левой части теперь не сводится к(которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула верна так же, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).
· Некоторые авторы, например, М. Лившиц в журнале «Квант» за 1998 год[3] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции и т. п.
к формулев случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока)[4].
В таком понимании закон Фарадея — это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.
· Однако возможность (пусть с некоторыми оговорками, уточняющими область применимости) совпадающей формулировки «правила потока» с законом электромагнитной индукции нельзя назвать чисто случайной.
Дело в том, что, по крайней мере для определенных ситуаций, это совпадение оказывается очевидным проявлением принципа относительности.
А именно, например, для случая относительного движения катушки с присоединенным к ней вольтметром, измеряющим ЭДС, и источника магнитного поля (постоянного магнита или другой катушки с током), в системе отсчета, связанной с первой катушкой, ЭДС оказывается равной именно циркуляции электрического поля, тогда как в системе отсчета, связанной с источником магнитного поля (магнитом), происхождение ЭДС связано с действием силы Лоренца на движущиеся с первой катушкой носители заряда. Однако та и другая ЭДС обязаны совпадать, поскольку вольтметр показывает одну и ту же величину, независимо от того, для какой системы отсчета мы её рассчитали.
· Потенциальная форма
При выражении магнитного поля через векторный потенциал закон Фарадея принимает вид:
(в случае отсутствия без вихревого поля, то есть тогда, когда электрическое поле порождается полностью только изменением магнитного, то есть электромагнитной индукцией).
В общем случае, при учёте и без вихревого (например, электростатического) поля имеем:
.
Источник: https://megapredmet.ru/1-64669.html
Математическая запись закона электромагнитной индукции
В статье расскажем что такое электромагнитная индукция, подробно опишем закон Фарадея и правило Ленца, а так же немного затронем тему уравнений Максвелла.
Электромагнитная индукция
Суть электромагнитной индукции заключается в том, что изменение магнитного поля, покрывающего электрическую цепь, вызывает возникновение электродвижущей силы в этой цепи, которая в случае замкнутой цепи вызывает протекание электрического тока. Если цепь, в которой мы должны генерировать электродвижущую силу, состоит из катушки и прикрепленного к ней амперметра, то источник изменяющегося магнитного поля, который включает в себя катушку, может быть адекватно перемещен постоянным магнитом или движущимся электромагнитом, в котором мы меняем ток питания. В каждом из этих случаев магнитное поле, которое пронизывает катушку, изменяется со временем.
В общем, изменение магнитного потока в цепи амперметра вызывает электрический ток в этой цепи.
Источником индуктивных явлений снова является сила Лоренца F, которая возникает, когда заряд q движется со скоростью v в магнитном поле B
F = q * v * B
Когда направляющая перемещается в поле B, подвижные носители нагрузки будут смещаться под действием силы Лоренца до тех пор, пока в проводнике не появится электрическое поле E, а сила, действующая на носители, F = q * E, уравнивает силу Лоренца. Когда линейный проводник длины l движется с постоянной скоростью v в однородном магнитном поле B, направленном перпендикулярно оси проводника и вектору скорости v , как на чертеже:
тогда мы сохраним условие баланса между силой Лоренца и силой отталкивания между зарядами в виде уравнения:
v*B = E = V / l ,
где V — разность потенциалов на концах проводника длиной l. Следовательно, значение этой разности потенциалов:
Если вектор v не перпендикулярен полю B , но образует с ним угол N , то разность потенциалов на концах направляющей будет:
V = v * B * l * sin θ
Это означает, что перемещение проводника вдоль направления поля B не будет генерировать в нем электродвижущую силу. Нетрудно доказать, что в случае направляющей любой формы разность потенциалов между точками а и b направляющей равна:
Когда прямоугольная рамка со сторонами a и b вращается в однородном магнитном поле B с постоянной угловой скоростью T
это электродвижущая сила V, генерируемая с обеих сторон рамы:
Магнитные силы, действующие в двух других сторонах петли, перпендикулярны этим сторонам и не влияют на электродвижущую силу. Посредством соответствующего способа получения генерируемого напряжения можно реализовать простейшие модели генераторов переменного тока (а) и постоянного тока (b), как показано на рисунке:
В природе и технике существует огромное количество явлений, вызванных электромагнитной индукцией, то есть генерацией электродвижущей силы в пространстве, где существует изменяющееся магнитное поле. Все эти явления описываются одним замечательным, компактным уравнением, являющимся содержанием закона Фарадея.
Формулы и объяснение закона Фарадея
Большое открытие Майкла Фарадея (1791 — 1867) состояло в том, что он нашел правило, управляющие электромагнитной индукцией. В результате многолетних экспериментов Фарадей заявил, что электродвижущая сила E появляется в проводнике при изменении магнитного поля, окружающего этот проводник, величина генерируемой электродвижущей силы пропорциональна скорости магнитного поля, и что направление индуцированной электродвижущей силы зависит от направления, в котором изменяется магнитное поле. Все эти факты содержатся только в одном уравнении:
где dΦ B — элементарный поток магнитного поля
В общем случае, даже когда проводников нет, электродвижущая сила равна циркуляции электрического поля E вдоль замкнутого контура:
Таким образом , закон Фарадея может быть записан в обобщенной форме:
Обратите внимание, сколько факторов может изменить значение потока:
1. Изменение значения вектора B ;
2. Изменение значения площади поверхности d A ;
3. Путем изменения угла между B и d А ;
4. Одновременное изменение B и d А ;
5. Одновременное изменение В и угла ;
6. Одновременное изменение d A и угла.
Нельзя не заметить появившийся здесь знак минус! Этот знак минус в законе Фарадея был назван правилом Ленца, который можно понимать как правило неповиновения в электродинамике.
Правило Ленца
Правило Ленца (знак минуса в законе Фарадея) определяет, что индукционный электрический ток в проводнике, возникающий при изменении магнитного потока, направлен таким образом, что его магнитное поле противодействует изменению магнитного потока.
Закон индукции Фарадея вместе с правилом Ленца представляет собой анимацию, в которой движение постоянного магнита вызывает создание электродвижущей силы в катушке, покрытой полем магнита.
Индукционный ток может создаваться не только в обмотках, но и в сплошных металлических блоках, помещенных в изменяющиеся магнитные поля.
Пример: так называемый вихревой ток, схематически показанный на рисунке:
Когда постоянное магнитное поле приложено к вращающейся алюминиевой мишени, то в мишени создаются два семейства противоположно направленных токов. Магнитное поле вихревых токов направлено так, что часть диска, которая выходит из поля, будет втянута обратно в поле, а часть диска, которая входит в область поля, будет вытеснена из этого поля.
Вихревые токи часто нежелательны, например, в сердечниках трансформатора, где они вызывают потери тепла. Для ограничения вихревых токов сердечники трансформатора выполнены в виде стопок из листового металла.
Уравнения Максвелла в интегральной форме
Закон Фарадея содержит: обобщенный закон Ампера, закон Гаусса для электрического поля и закон Гаусса для магнитного поля в системе из четырех уравнений Максвелла. Эти уравнения были представлены применительно к макроскопическим контурам и замкнутым поверхностям. По этой причине мы говорим, что это уравнения Максвелла в интегральной форме. Давайте посмотрим на эти уравнения еще раз.
Закон Фарадея
Обобщенный закон Ампера
Закон Гаусса для электрического поля
Закон Гаусса для магнитного поля
Интегральные уравнения Максвелла описывают электрические и магнитные явления в макроскопическом масштабе. Ведь для их формулировки нужны контуры, замкнутые поверхности, токи и потоки полей. Однако чрезвычайно важно знать, что происходит с электрическими и магнитными полями в отдельных точках, то есть в микроскопическом масштабе. Тогда можно будет описать такие явления как электромагнитные волны.
Для микроскопического описания электрических и магнитных явлений используются уравнения Максвелла в дифференциальной форме. Чтобы получить их, мы применим две математические теоремы к уравнениям в интегральной форме: теорема Гаусса-Остроградского и теорема Стокса.
Следует отметить, что преобразование уравнений Максвелла между целочисленной и дифференциальной формами получается в результате только математических операций. Это означает физическую эквивалентность этих двух форм уравнений Максвелла.
Теорема Гаусса-Остроградского и теорема Стокса, несмотря на их кажущуюся сложность, концептуально совершенно просты и легко интуитивно принимаются. Обе эти тему будут представлены в следующей статье.
Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
История развития и опыты Фарадея
До середины XIX века считалось, что электрическое и магнитное поле не имеют никакой связи, и природа их существования различна. Но М. Фарадей был уверен в единой природе этих полей и их свойств. Явление электромагнитной индукции, обнаруженное им, впоследствии стало фундаментом для устройства генераторов всех электростанций. Благодаря этому открытию знания человечества о электромагнетизме шагнули далеко вперед.
Фарадей проделал следующий опыт: он замыкал цепь в катушке I и вокруг нее возрастало магнитное поле. Далее линии индукции данного магнитного поля пересекали катушку II, в которой возникал индукционный ток.
Рис. 1. Схема опыта Фарадея
Сколько бы экспериментов не проводил Фарадей, неизменным оставалось одно условие: для образования индукционного тока важным является изменение магнитного потока, пронизывающего замкнутый проводящий контур (катушку).
Закон Фарадея
Явление электромагнитной индукции определяется возникновением электрического тока в замкнутом электропроводящем контуре при изменении магнитного потока через площадь этого контура.
Основной закон Фарадея заключается в том, что электродвижущая сила (ЭДС) прямо пропорциональна скорости изменения магнитного потока.
Формула закона электромагнитной индукции Фарадея выглядит следующим образом:
Рис. 2. Формула закона электромагнитной индукции
И если сама формула, исходя из вышесказанных объяснений не порождает вопросов, то знак «-» может вызвать сомнения. Оказывается существует правило Ленца – русского ученого, который проводил свои исследования, основываясь на постулатах Фарадея. По Ленцу знак «-» указывает на направление возникающей ЭДС, т.е. индукционный ток направлен так, что магнитный поток, который он создает, через площадь, ограниченную контуром, стремится препятствовать тому изменению потока, которое вызывает данный ток.
Закон Фарадея-Максвелла
В 1873 Дж.К.Максвелл по-новому изложил теорию электромагнитного поля. Уравнения, которые он вывел, легли в основу современной радиотехники и электротехники. Они выражаются следующим образом:
- Edl = -dФ/dt – уравнение электродвижущей силы
- Hdl = -dN/dt – уравнение магнитодвижущей силы.
Где E – напряженность электрического поля на участке dl; H – напряженность магнитного поля на участке dl; N – поток электрической индукции, t – время.
Симметричный характер данных уравнений устанавливает связь электрических и магнитных явлений, а также магнитных с электрическими. физический смысл, которым определяются эти уравнения, можно выразить следующими положениями:
- если электрическое поле изменяется, то это изменение всегда сопровождается магнитным полем.
- если магнитное поле изменяется, то это изменение всегда сопровождается электрическим полем.
Рис. 3. Возникновение вихревого магнитного поля
Что мы узнали?
Ученикам 11 класса необходимо знать, что электромагнитную индукцию впервые как явление обнаружил Майкл Фарадей. Он доказал, что электрическое и магнитное поле имеют общую природу. Самостоятельные исследования на основе опытов Фарадея также проводили такие великие деятели как Ленц и Максвелл, которые расширили наши познания в области электромагнитного поля.
М. Фарадеем было установлено, что сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:
Возникновение тока в замкнутом контуре означает наличие сторонних сил, работа которых по перемещению единичного заряда в контуре называется электродвижущей силой (ЭДС). Это означает, что при изменении потока через поверхность, ограниченную замкнутым контуром, в контуре возникает ЭДС ɛi которую называют ЭДС индукции. Согласно закону Ома для замкнутой цепи,
. Следовательно, ЭДС индукции пропорциональна ΔФ/Δt, поскольку сопротивление R не зависит от изменения магнитного потока.Закон электромагнитной индукции формулируется так:
ЭДС индукции ɛi в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:
.Применение правила Ленца к замкнутому контуру с положительной нормалью приводит к выражению:
.Формула ( ) выражает основной закон электромагнитной индукции .
На рисунке внешнее магнитное поле индукции В возрастает со временем и направлено вдоль положительной нормали к контуру с током. Индуцированный ток противоположен выбранному направлению обхода в соответствии с индуцированным магнитным полем В’.
Описанные выше опыты свидетельствуют о том, что электромагнитная индукция — это возникновение электрического поля и электрического тока при изменении во времени магнитного поля или при движении проводника в магнитном поле. Эти два типа эффектов электромагнитной индукции отличаются физической природой процессов, отвечающих за их возникновение. Первый тип обусловлен наведением вихревого электрического поля переменным магнитным полем, второй — действием сил Лоренца на движущиеся заряды в стационарном магнитном поле. В обоих случаях выполняется основной закон индукции, выраженный формулой (
).По какой формуле рассчитывается закон электромагнитной индукции. Закон электромагнитной индукции формула
В 1831 году мир впервые узнал о понятии электромагнитной индукции. Именно тогда Майкл Фарадей обнаружил это явление, ставшее в итоге важнейшим открытием в электродинамике.
История развития и опыты Фарадея
До середины XIX века считалось, что электрическое и магнитное поле не имеют никакой связи, и природа их существования различна. Но М. Фарадей был уверен в единой природе этих полей и их свойств. Явление электромагнитной индукции, обнаруженное им, впоследствии стало фундаментом для устройства генераторов всех электростанций. Благодаря этому открытию знания человечества о электромагнетизме шагнули далеко вперед.
Фарадей проделал следующий опыт: он замыкал цепь в катушке I и вокруг нее возрастало магнитное поле. Далее линии индукции данного магнитного поля пересекали катушку II, в которой возникал индукционный ток.
Рис. 1. Схема опыта Фарадея
На самом деле, одновременно с Фарадеем, но независимо от него, другой ученый Джозеф Генри обнаружил это явление. Однако Фарадей опубликовал свои исследования раньше. Таким образом, автором закона электромагнитной индукции стал Майкл Фарадей.
Сколько бы экспериментов не проводил Фарадей, неизменным оставалось одно условие: для образования индукционного тока важным является изменение магнитного потока, пронизывающего замкнутый проводящий контур (катушку).
Закон Фарадея
Явление электромагнитной индукции определяется возникновением электрического тока в замкнутом электропроводящем контуре при изменении магнитного потока через площадь этого контура.
Основной закон Фарадея заключается в том, что электродвижущая сила (ЭДС) прямо пропорциональна скорости изменения магнитного потока.
Формула закона электромагнитной индукции Фарадея выглядит следующим образом:
Рис. 2. Формула закона электромагнитной индукции
И если сама формула, исходя из вышесказанных объяснений не порождает вопросов, то знак «-» может вызвать сомнения. Оказывается существует правило Ленца – русского ученого, который проводил свои исследования, основываясь на постулатах Фарадея. По Ленцу знак «-» указывает на направление возникающей ЭДС, т.е. индукционный ток направлен так, что магнитный поток, который он создает, через площадь, ограниченную контуром, стремится препятствовать тому изменению потока, которое вызывает данный ток.
Закон Фарадея-Максвелла
В 1873 Дж.К.Максвелл по-новому изложил теорию электромагнитного поля. Уравнения, которые он вывел, легли в основу современной радиотехники и электротехники. Они выражаются следующим образом:
- Edl = -dФ/dt – уравнение электродвижущей силы
- Hdl = -dN/dt – уравнение магнитодвижущей силы.
Где E – напряженность электрического поля на участке dl; H – напряженность магнитного поля на участке dl; N – поток электрической индукции, t – время.
Симметричный характер данных уравнений устанавливает связь электрических и магнитных явлений, а также магнитных с электрическими. физический смысл, которым определяются эти уравнения, можно выразить следующими положениями:
- если электрическое поле изменяется, то это изменение всегда сопровождается магнитным полем.
- если магнитное поле изменяется, то это изменение всегда сопровождается электрическим полем.
Рис. 3. Возникновение вихревого магнитного поля
Также Максвелл установил, что распространение электромагнитного поля равна скорости распространения света.
Всего получено оценок: 134.
В 1831 году английский ученый физик в своих опытах М.Фарадей открыл явление электромагнитной индукции . Затем изучением этого явления занимались русские ученый Э.Х. Ленц и Б.С.Якоби.
В настоящее время, в основе многих устройств лежит явление электромагнитной индукции, например в двигателе или генераторе электрического тока тока, в трансформаторах, радиоприемниках, и многих других устройствах.
Электромагнитная индукция — это явление возникновения тока в замкнутом проводнике, при прохождении через него магнитного потока. То есть, благодаря этому явлению мы можем преобразовывать механическую энергию в электрическую — и это замечательно. Ведь до открытия этого явления люди не знали о методах получения электрического тока , кроме гальваники.
Когда проводник оказывается под действием магнитного поля, в нем возникает ЭДС, которую количественно можно выразить через закон электромагнитной индукции.
Закон электромагнитной индукции
Электродвижущая сила, индуцируемая в проводящем контуре, равна скорости изменения магнитного потока, сцепляющегося с этим контуром.
В катушке, которая имеет несколько витков, общая ЭДС зависит от количества витков n:
Но в общем случае, применяют формулу ЭДС с общим потокосцеплением:
ЭДС возбуждаемая в контуре, создает ток. Наиболее простым примером появления тока в проводнике является катушка, через которую проходит постоянный магнит . Направление индуцируемого тока можно определить с помощью правила Ленца .
Правило Ленца
Ток, индуцируемый при изменении магнитного поля проходящего через контур, своим магнитным полем препятствует этому изменению.
В том случае, когда мы вводим магнит в катушку, магнитный поток в контуре увеличивается, а значит магнитное поле, создаваемое индуцируемым током, по правилу Ленца, направлено против увеличения поля магнита. Чтобы определить направление тока, нужно посмотреть на магнит со стороны северного полюса. С этой позиции мы будем вкручивать буравчик по направлению магнитного поля тока, то есть навстречу северному полюсу. Ток будет двигаться по направлению вращения буравчика, то есть по часовой стрелке.
В том случае, когда мы выводим магнит из катушки, магнитный поток в контуре уменьшается, а значит магнитное поле, создаваемое индуцируемым током, направлено против уменьшения поля магнита. Чтобы определить направление тока, нужно выкручивать буравчик, направление вращения буравчика укажет направление тока в проводнике – против часовой стрелки.
>>Физика и астрономия >>Физика 11 класс >> Закон электромагнитной индукции
Закон Фарадея. Индукция
Электромагнитной индукцией называют такое явление, как возникновение электрического тока в замкнутом контуре, при условии изменения магнитного потока, который проходит через этот контур.
Закон электромагнитной индукции Фарадея записывается такой формулой:
И гласит, что:
Каким же образом ученым удалось вывести такую формулу и сформулировать этот закон? Мы с вами уже знаем, что вокруг проводника с током всегда существует магнитное поле, а электричество обладает магнитной силой. Поэтому в начале 19го века и возникла задача о необходимости подтверждения влияния магнитных явлений на электрические, которую пытались решить многие ученые, и английский ученый Майкл Фарадей был в их числе. Почти 10 лет, начиная с 1822 года, он потратил на различные опыты, но безуспешно. И только 29 августа 1831 года наступил триумф.
После напряженных поисков, исследований и опытов, Фарадей пришел к выводу, что только меняющееся со временем магнитное поле может создать электрический ток.
Опыты Фарадей
Опыты Фарадей состояли в следующем:
Во-первых, если взять постоянный магнит и двигать его внутри катушки, к которой присоединен гальванометр, то в цепи возникал электрический ток.
Во-вторых, если этот магнит выдвигать из катушки, то мы наблюдаем, что гальванометр так же показывает ток, но этот ток имеет противоположное направление.
А теперь давайте попробуем этот опыт немного изменить. Для этого мы попробуем на неподвижный магнит одевать и снимать катушку. И что мы в итоге видим? А мы с вами наблюдаем то, что во время движения катушки относительно магнита в цепи снова появляется ток. А если в катушке прекратилось, то и ток сразу же исчезает.
Теперь давайте проделаем еще один опыт. Для этого мы с вами возьмем и поместим в магнитное поле плоский контур без проводника, а его концы попробуем соединить с гальванометром. И что мы наблюдаем? Как только контур гальванометр поворачивается, то мы наблюдаем появление в нем индукционного тока. А если попробовать вращать магнит внутри него и рядом с контуром, то в этом случае также появится ток.
Думаю, вы уже заметили, ток появляется в катушке тогда, когда изменяется магнитный поток, который пронизывает эту катушку.
И тут возникает вопрос, при всяких ли движениях магнита и катушки, может возникнуть электрический ток? Оказывается не всегда. Ток не возникнет в том случае, когда магнит вращается вокруг вертикальной оси.
А из этого следует, что при любом изменении магнитного потока, мы наблюдаем то, что в этом проводнике возникает электрический ток, который существовал в течении всего процесса, пока происходили изменения магнитного потока. Именно в этом и заключается явление электромагнитной индукции. А индукционным током является тот ток, который был получен данным методом.
Если мы с вами проанализируем данный опыт, то увидим, что значение индукционного тока совершенно не зависит от причины изменения магнитного потока. В данном случае, первостепенное значение имеет лишь скорость, которая влияет на изменения магнитного потока. Из опытов Фарадея следует, что чем быстрее двигается магнит в катушке, тем больше отклоняется стрелка гальванометра.
Теперь мы можем подвести итог данного урока и сделать вывод, что закон электромагнитной индукции является одним из основных законом электродинамики. Благодаря изучению явлений электромагнитной индукции, учеными разных стран были созданы различные электродвигатели и мощные генераторы. Огромный вклад в развитие электротехники внесли и такие известные ученые, как Ленц, Якоби, и другие.
Что может быть лучше, чем вечером понедельника почитать про основы электродинамики . Правильно, можно найти множество вещей, которые будут лучше. Тем не менее, мы все равно предлагаем Вам прочесть эту статью. Времени занимает не много, а полезная информация останется в подсознании. Например, на экзамене, в условиях стресса, можно будет успешно извлечь из недр памяти закон Фарадея. Так как законов Фарадея несколько, уточним, что здесь мы говорим о законе индукции Фарадея.
Электродинамика – раздел физики, изучающий электромагнитное поле во всех его проявлениях.
Это и взаимодействие электрического и магнитного полей, электрический ток, электро-магнитное излучение, влияние поля на заряженные тела.
Здесь мы не ставим целью рассмотреть всю электродинамику. Упаси Боже! Рассмотрим лучше один из основных ее законов, который называется законом электромагнитной индукции Фарадея .
История и определение
Фарадей, параллельно с Генри, открыл явление электромагнитной индукции в 1831 году. Правда, успел опубликовать результаты раньше. Закон Фарадея повсеместно используется в технике, в электродвигателях, трансформаторах, генераторах и дросселях. В чем суть закона Фарадея для электромагнитной индукции, если говорить просто? А вот в чем!
При изменении магнитного потока через замкнутый проводящий контур, в контуре возникает электрический ток. То есть, если мы скрутим из проволоки рамку и поместим ее в изменяющееся магнитное поле (возьмем магнит, и будем крутить его вокруг рамки), по рамке потечет ток!
Этот ток Фарадей назвал индукционным, а само явление окрестил электромагнитной индукцией.
Электромагнитная индукция – возникновение в замкнутом контуре электрического тока при изменении магнитного потока, проходящего через контур.
Формулировка основного закона электродинамики – закона электромагнитной индукции Фарадея, выглядит и звучит следующим образом:
ЭДС , возникающая в контуре, пропорциональна скорости изменения магнитного потока Ф через контур.
А откуда в формуле минус, спросите Вы. Для объяснения знака минус в этой формуле есть специальное правило Ленца . Оно гласит, что знак минус, в данном случае, указывает на то, как направлена возникающая ЭДС. Дело в том, что создаваемое индукционным током магнитное поле направлено так, что препятствует изменению магнитного потока, который вызвал индукционный ток.
Примеры решения задач
Вот вроде бы и все. Значение закона Фарадея фундаментально, ведь на использовании данного закона построена основа почти всей электрической промышленности. Чтобы понимание пришло быстрее, рассмотрим пример решения задачи на закон Фарадея.
И помните, друзья! Если задача засела, как кость в горле, и нет больше сил ее терпеть — обратитесь к нашим авторам! Теперь вы знаете . Мы быстро предоставим подробное решение и разъясним все вопросы!
В результате многочисленных опытов Фарадей установил основной количественный закон электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток. Возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Фарадей установил, что значение ЭДС электромагнитной индукции E i пропорционально скорости изменения магнитного потока:
E i = -К , (27.1)
где К – коэффициент пропорциональности, зависящий только от выбора единиц измерения.
В системе единиц СИ коэффициент К = 1, т.е.
E i = — . (27.2)
Эта формула и представляет собой закон электромагнитной индукции Фарадея. Знак минус в этой формуле соответствует правилу (закону) Ленца.
Закон Фарадея можно сформулировать еще таким образом: ЭДС электромагнитной индукции E i в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: ЭДС E i не зависит от способа изменения магнитного потока.
Знак минус в (27.2) показывает, что увеличение потока ( > 0) вызывает ЭДС E i 0 т. е. направления магнитного потока индукционного тока и потока, вызвавшего его, совпадают. Знак минус в формуле (27.2) является математическим выражением правила Ленца — общего правила для нахождения направления индукционного тока (а значит и знака и ЭДС индукции), выведенного в 1833 г. Правило Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Иначе говоря, индукционный ток создает магнитный поток, препятствующий изменению магнитного потока, вызывающего ЭДС индукции.
ЭДС индукции выражается в вольтах (В). Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим:
Если замкнутый контур, в котором индуцируется ЭДС индукции, состоит из N витков, то E i будет равна сумме ЭДС, индуцируемых в каждом из витков. И если магнитный поток, охватываемый каждым витком, одинаков и равен Ф, то суммарный поток сквозь поверхность N витков, равен (NФ) – полный магнитный поток (потокосцепление). В этом случае ЭДС индукции равна:
E i = -N× , (27.3)
Формула (27.2) выражает закон электромагнитной индукции в общей форме. Она применима как к неподвижным контурам, так и к движущимся проводникам в магнитном поле. Входящая в нее производная от магнитного потока по времени в общем случае состоит из двух частей, одна из которых обусловлена изменением магнитной индукции во времени, а другая – движением контура относительно магнитного поля (или его деформацией). Рассмотрим некоторые примеры применения этого закона.
Пример 1. Прямолинейный проводник длиной l движется параллельно самому себе в однородном магнитном поле (рисунок 38). Этот проводник может входить в состав замкнутой цепи, остальные части которой неподвижны. Найдем ЭДС, возникающую в проводнике.
Если мгновенное значение скорости проводника есть v , то за время dt он опишет площадь dS = l×v ×dt и за это время пересечет все линии магнитной индукции, проходящие через dS. Поэтому изменение магнитного потока через контур, в состав которого входит движущийся проводник, будет dФ = B n ×l×v ×dt. Здесь B n — составляющая магнитной индукции, перпендикулярная к dS. Подставляя это в формулу (27.2) получаем величину ЭДС:
E i = B n ×l×v . (27.4)
Направление индукционного тока и знак ЭДС определяются правилом Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток. В некоторых случаях возможно определение направления индукционного тока (полярности ЭДС индукции) согласно другой формулировке правила Ленца: индукционный ток в движущемся проводнике направлен таким образом, что возникающая при этом сила Ампера противоположна вектору скорости (тормозит движение).
Разберем численный пример. Вертикальный проводник (автомобильная антенна) длиной l = 2 м движется с востока на запад в магнитном поле Земли со скоростью v = 72 км/час = 20 м/с. Вычислим напряжение между концами проводника. Так как проводник разомкнут, то тока в нем не будет и напряжение на концах будет равно ЭДС индукции. Учитывая, что горизонтальная составляющая магнитной индукции поля Земли (т.е. составляющая, перпендикулярная к направлению движения) для средних широт равна 2×10 -5 Тл, по формуле (27.4) находим
U = B n ×l×v = 2×10 -5 ×2×20 = 0,8×10 -3 В,
т.е. около 1 мВ. Магнитное поле Земли направлено с юга на север. Поэтому мы находим, что ЭДС направлена сверху вниз. Это значит, что нижний конец провода будет иметь более высокий потенциал (зарядится положительно), а верхний – более низкий (зарядится отрицательно).
Пример 2. В магнитном поле находится замкнутый проволочный контур, пронизываемый магнитным потоком Ф. Предположим, что этот поток уменьшается до нуля, и вычислим полную величину заряда, прошедшего по цепи. Мгновенное значение ЭДС в процессе исчезновения магнитного потока выражается формулой (27.2). Следовательно, согласно закону Ома мгновенное значение силы тока есть
где R – полное сопротивление цепи.
Величина прошедшего заряда равна
q = = — = . (27.6)
Полученное соотношение выражает закон электромагнитной индукции в форме, найденной Фарадеем, который из своих опытов заключил, что величина заряда, прошедшего по цепи, пропорциональна полному числу линий магнитной индукции, пересеченных проводником (т.е. изменению магнитного потока Ф 1 -Ф 2), и обратно пропорциональна сопротивлению цепи R. Соотношение (27.6) позволяет дать определение единицы магнитного потока в системе СИ: вебер – магнитный поток, при убывании которого до нуля в сцепленном с ним контуре сопротивлением 1 Ом проходит заряд 1 Кл.
Согласно закону Фарадея, возникновение ЭДС электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае она не может быть причиной возникновения ЭДС индукции. Максвелл для объяснения ЭДС индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция вектора напряженности этого поля по любому неподвижному контуру L проводника представляет собой ЭДС электромагнитной индукции:
E i = = — . (27.7)
Линии напряженности вихревого электрического поля представляют собой замкнутые кривые, поэтому при перемещении заряда в вихревом электрическом поле по замкнутому контуру совершается отличная от нуля работа. В этом заключается отличие вихревого электрического поля от электростатического, линии напряженности которого начинаются и заканчиваются на зарядах.
§23. Закон электромагнитной индукции Фарадея
В 1831 г. Фарадей экспериментально открыл явление электромагнитной индукции. Суть явления состояла в том, что если через замкнутый контур происходило изменение магнитного потока, то в контуре возникала электродвижущая сила, приводящая к возникновению замкнутого тока. Этот ток был назван индукционным током. Правило, устанавливающее направление индукционного тока было сформулировано в 1833г. Э. Х. Ленцем (1804 — 1865) и называется правилом Ленца. Оно гласит: индукционный ток направлен так, что создаваемый им магнитный поток стремится компенсировать изменение магнитного потока, вызывающего данный ток.
Опыты Фарадея состояли в следующем: катушка индуктивности подключалась к чувствительному гальванометру и в катушку вдвигался и выдвигался постоянный магнит.
Из опытов следовало, что
. Но сила тока зависит еще и от сопротивления контура. Поэтому закон электромагнитной индукции формулируется не для индукционного тока, а для причины, вызывающий этот ток, т. е. для . В 1845г. Ф. Э. Нейман (1799 — 1895) дал математическое определение закона электромагнитной индукции в современной форме: (23.1)Хотя внешне формулы (22.6) и (23.1) одинаковы, между ними существует принципиальное различие. Возникновение
в (22.6) связано с движением проводников в магнитном поле и с действием на заряды силы Лоренца. Тогда как в (23.1) на заряды в контуре действует электрическое поле, причем сам контур лишь только инструмент или прибор, который может обнаружить это изменяющееся электрическое поле, которое возникает в пространстве. Следовательно закон Фарадея отражает новое физическое явление, а именно: изменяющееся магнитное поле порождает изменяющееся электрическое поле. А это означает, что электрическое поле порождается не только зарядами, но и изменяющимся магнитным полем. Закон электромагнитной индукции является фундаментальным законом природы.Дифференциальная формулировка закона
, а тогда магнитный поток , а ..К левой части применим формулу Стокса. Тогда
. После того как перенесем все слагаемые в одну сторону получим:В силу произвольности
можно заключить, что подынтегральная функция равна нулю, а значит (23.2)Уравнение (23.2) является дифференциальной формой закона электромагнитной индукции. В переменных магнитных полях
, а значит и следовательно, в отличие от электростатического поля, порождаемого неподвижными зарядами, переменное электрическое поле не является потенциальным и работа при перемещении заряда по замкнутому контуру не равна нулю:.Так как закон электромагнитной индукции не затрагивает закона порождения магнитного поля, то уравнение (18.6)
остается в силе, а значит в силе остается и выражение (19.2): .Если подставить (19.2) в (23.2), то
, а значит. (23.3)Отсюда следует, что в переменных полях потенциальным является вектор
, а значит он равен градиенту скалярной функции, т. е., а значит. (23.4)Второе слагаемое в (23.4) означает, что электрическое поле может порождаться неподвижными зарядами, а первое означает, что электрическое поле может порождаться переменным магнитным полем.
в чем заключается, определение, как выглядит формула Фарадея
Закон электромагнитной индукции — история открытия, в чем суть
ОпределениеЭлектродвижущая сила, ЭДС — физическая величина, выражающая работу сил, которые действуют в электрических цепях, за исключением электростатических и диссипативных сил. Обозначение — греческая буква \(\varepsilon\), для электродвижущей силы индукции — \(\varepsilon_i\).
ОпределениеЗакон электромагнитной индукции является основным законом электродинамики, касающимся принципов работы трансформаторов, дросселей, многих видов электродвигателей и генераторов. Закон гласит: для любого замкнутого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур.
На проводник с током, находящийся в магнитном поле, воздействует сила Ампера, которую можно выразить в виде векторного произведения:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(d\overrightarrow F\;=\;Id\overrightarrow l\;\times\;\overrightarrow B\)
Величина В здесь — магнитная индукция, силовая характеристика магнитного поля. Она определяет силу, с которой магнитное поле воздействует на заряд.
Основной вклад Фарадея в физику электромагнитных явлений заключается в отказе от ньютонова принципа дальнодействия и во введении понятия поля — пространства, сплошь заполненного силовыми линиями.
Фарадей опытным путем выяснил, что при каждом пересечении проводника с магнитными силовыми линиями по проводнику проходит заряд \(\triangle Q\). С числом \triangle Ф пересеченных линий магнитного поля его связывает следующая зависимость:
\(\triangle Q\;=\;\alpha\frac{\triangle Ф}R\)
\(\alpha\) здесь — коэффициент пропорциональности, Ф — магнитный поток. Единица измерения магнитного потока — вебер.
Это соотношение считается количественным выражением закона индукции.
Максвелл решил придать закону Фарадея математическую форму. Представив замкнутый контур С, в котором действует электродвижущая сила индукции \(\varepsilon_i\), Максвелл, чтобы высчитать количество линий магнитного поля \(\triangle Ф\), соприкасающихся с контуром за время \(\triangle t\), отождествлял контур с поверхностью S, поделенной на элементарные площадки \(\triangle S\), и приравнял Ф к магнитному потоку сквозь всю поверхность. В итоге Максвелл получил следующее выражение:
\(Ф\;=\;\sum_{\triangle S}\;\;B\triangle S\)
Объединив это соотношение с законом Фарадея, Максвелл вывел собственную формулировку закона электромагнитной индукции:
\(\varepsilon_i\;=\;-\;\frac1с\;\times\;\frac{dФ}{dt}\)
Ленц добавил к закону Фарадея важное пояснение: индукционный ток в любом случае направлен так, чтобы противодействовать причине, которая его вызвала.{2}Rdt + IdФ\)
\(I = \frac{\epsilon — \frac{dФ}{dt}}{R}\)
Как выглядит формула закона электромагнитной индукции
\(\varepsilon_i\;=\;-\;\alpha\frac{\triangle Ф}{\triangle t}\)
Если проводник неподвижен, то индукционный ток вызывает само электрическое поле, это явление называется самоиндукцией. В соответствии с основной теоремой электростатики работа электростатического поля при переносе единичного заряда по замкнутой траектории равняется нулю. Значит, в проводнике возникает вихревое электрическое поле, работа которого равна электродвижущей силе индукции:
\(\varepsilon_i\;=\;\underset С{\oint\;}\;(\overrightarrow{Е\;}\times\;d\overrightarrow l)\\\)
ОпределениеВихревое электрическое поле — поле, порождаемое переменным магнитным током и имеющее замкнутые линии напряженности.
Тогда закон записывается в интегральной форме так:
\(\;\underset С{\oint\;}\;(\overrightarrow{Е\;}\times\;d\overrightarrow l) = — \frac{1}{c}\frac{d}{dt}\int \underset S{\int\;}\;(\overrightarrow{B} \times d\overrightarrow{S})\)
Левая часть выражения описывает циркуляцию \(\overrightarrow{Е\;}\) по замкнутому контуру С. Правая часть — скорость изменения магнитного потока Ф, который вычисляется как интеграл по поверхности S, «натянутой» на контур С.
Применение закона электромагнитной индукции на практике
В быту распространено использование этого явления для изменения величины напряжения тока в катушках индуктивности, или дросселях. Дроссели используют для подавления помех, ограничения переменного тока, накопления энергии и т. д.
В некоторых случаях, например, при очень маленьком размере электронной схемы, вместо катушек индуктивности используют специальные устройства — гираторы, которые заставляют электрические цепи проявлять индуктивные свойства.
Существуют также магнитные газовые генераторы, для создания тока в которых создается магнитное поле, в свою очередь создающее электродвижущую силу.
В учебных задачах часто требуется применение закона Фарадея, чтобы найти ЭДС, силу тока в проводнике или изменение магнитного потока. Рассмотрим на примере.
Задача 1
Магнитный поток, проходящий через контур, равномерно изменился за 5 секунд на 0,013 Вб. Сопротивление проводника равно 0,04 Ом. Найти силу тока.
Решение
Подставим известные значения в формулу закона Ома, учитывая закон Фарадея:
\(I_{i} = \frac{\epsilon_{i}}{R} = — \frac{\triangleФ} {\triangle t} \times \frac{1}{R}\)
\(I_{i} = \frac{0,013}{5\times0,04} = \frac{0,013}{0,2} = 0,065\)
Ответ: 0,065 А.
Задача 2
Ток силой 6 Ампер течет по катушке, индуктивность которой L равна 8 мкГн. За время \({\triangle t},\) равное 5 мс, сила тока падает почти до нуля. Найти среднее значение электродвижущей силы самоиндукции.
Решение
\(Ф = L \times I\)
\(\epsilon_{i} = \frac{\triangleФ}{\triangle t} = — L \times \frac{\triangle I}{\triangle t}\)
Так как магнитный поток меняется только за счет падения силы тока, то
\(\epsilon_{i} = — L \times \frac{I}{\triangle t}\)
Подставим известные значения:
\(\epsilon_{i} = — 8\times 10^{-6} \times \frac{6}{5\times 10^{-3}} = — 9,6 \times 10^{-3}\)
Ответ: — 9,6 мВ.
Определение, принцип, законы, эксперименты и приложения
Закон электромагнитной индукции Фарадея был собственным открытием двух ученых Майкла Фарадея в 1831 году и Джозефа Генри в 1832 году. Первые результаты его экспериментов были опубликованы Фарадеем. В своем первоначальном эксперименте он обнаружил принцип электромагнитной индукции. При этом он намотал на железное кольцо две полосы из металлической проволоки. Так он узнал принцип работы электромагнитов.Он считал, что когда на одном конце провода протекает ток, это стимулирует генерацию волн по всему кольцу и вырабатывает электрическую энергию на другом конце провода. Этот принцип послужил основой для разработки множества экспериментов по электромагнитной индукции. И это история открытия закона Фарадея. В этой статье четко объясняются концепции того, как действует закон Фарадея, усиление ЭДС в катушке, его законы и приложения.
Что такое закон Фарадея?
Закон электромагнитной индукции Фарадея в основном называется законом Фарадея.Это фундаментальный принцип электромагнетизма, который предусматривает концепцию того, как ЭДС (электродвижущая сила) будет генерироваться при взаимодействии электрического тока с магнитным полем. Этот сценарий называется электромагнитной индукцией.
Основной принцип закона Фарадея
При открытии этого закона один его сценарий, который представлял собой трансформаторную ЭДС, был позже сформулирован как уравнение Максвелла-Фарадея. Это означает, что закон Фарадея может быть получен с помощью уравнения Максвелла-Фарадея, которое описывает ЭДС трансформатора, и через Лоренца, где это констатируется относительно ЭДС движения.Рассматривая интегральную форму Максвелла-Фарадея, можно проиллюстрировать только трансформаторную ЭДС, тогда как рассмотрение неотъемлемой части закона Фарадея иллюстрирует как движущую, так и трансформаторную ЭДС.
Закон Фарадея — это одно уравнение, в котором говорится о двух различных явлениях: ЭДС движения (которая создается за счет магнитной силы в случае движущегося провода) и ЭДС трансформатора (которая создается электрической силой, возникающей из-за изменение магнитного поля). Это считается двумя явлениями закона Фарадея.
Формула
Основной принцип закона Фарадея гласит, что ЭДС, которая проходит через замкнутую поверхность, равна отрицательному изменению магнитного потока на замкнутом пути относительно скорости времени. Здесь замкнутый путь считается проводящим. Учтите, что проволочная петля, помещенная в магнитное поле, имеет магнитный поток Ф B , поверхность имеет любую поверхность, а Σ является границей предоставленной петли. Поскольку в проволочной петле будет движение, необходимо учитывать Σ (t) для предоставленной поверхности.Теперь магнитный поток представлен как:
B = ʃʃ Σ t) B (t). dA
Здесь «dA» рассматривается как элемент площади на движущейся поверхности Σ (t), а «B» рассматривается как магнитное поле, «B.dA» представляет элемент потока вокруг dA. Проще говоря, это можно определить как магнитный поток через проволочную петлю прямо пропорционально силовым линиям магнитного поля, которые проходят от петли.
Когда происходит изменение магнитного потока, B изменяется или, иначе, при изменении проволочной петли или и того, и другого, тогда, согласно принципу Фарадея, проволочная петля получает ЭДС, которая выражается как энергия, полученная от единицы заряда, который ушел полностью. поперек петли.Уравнение было выбрано для совместимости с условиями специальной теории относительности. Точно так же это напряжение, которое рассчитывается путем разрезания проволоки на куски для образования разомкнутой цепи и последующего подключения вольтметра по краям провода.
Закон Фарадея определяет, что электродвижущая сила представлена как изменение магнитного потока, которое показано как
Є = — (dФ B / dt)
Здесь Ф B обозначается как магнитный поток и є — электродвижущая сила.Путь ЭМП определяется принципом Ленца. Принцип Фарадея объясняет связь между путями переменных и их величинами. Несмотря на то, что отношения не были четко изображены, они были известны через математическую формулу.
Благодаря закону Фарадея можно узнать путь ЭМП, не обращаясь к закону Ленца. Для этого будет полезно правило левой руки, и направление может быть известно следующим образом:
Правило большого пальца левой руки Закон Фарадея
- Совместите изогнутые пальцы левой руки с петлей.
- Вытяните большой палец, и направление большого пальца обозначает путь «n», который является общим для области, окруженной петлей.
- Знайте знак ΔФ B , который представляет собой изменение потока. Найдите начальное и последнее значения потока, соответствующие ‘n’, как сигнализирует расширенный большой палец
- Когда изменение потока ΔФ B, представляет положительное значение, тогда изогнутые пальцы представляют путь ЭДС
- Тогда как, когда изменение в поток ΔФ B, представляет собой отрицательное значение, тогда путь ЭДС будет в направлении, противоположном изогнутым пальцам.
- В случае плотно окруженной проволочной катушки, состоящей из ‘N’ одинаковых витков с одинаковым Ф B, , тогда закон Фарадея противоречит тому, что
Є = -N (dФ B / dt)
Где «N» соответствует общему количеству витков в проводе, а Ф B соответствует магнитному потоку в одном контуре.
И это подробное объяснение формулы закона Фарадея .
Закон электромагнитной индукции Фарадея
В законе электромагнитной индукции Фарадея в основном есть два закона.Первый определяет индукцию ЭДС в движущемся проводнике, а второй определяет генерируемую ЭДС в проводнике. Давайте подробно рассмотрим оба закона.
Первый закон Фарадея
Электромагнитная индукция — это изобретение расширенной серии экспериментов, проведенных учеными Генри и Фарадеем. С результатами, полученными в результате этих экспериментов, Фарадей пришел к конечному результату, заключающемуся в том, что в катушке возникает индукция электродвижущей силы, когда магнитный поток, проходящий через катушку, изменяется во времени.На основе этой базовой концепции был изобретен первый закон Фарадея. Это можно представить на картинке, как показано ниже.
Изменение напряженности магнитного поля в закрытой петле Закон Фарадея
Итак, когда проводник находится в изменяющемся магнитном поле, возникает индукция ЭДС. Когда цепь, в которой размещается проводник, замкнута, генерируемый ток называется индуцированным током.
Ниже приведены способы изменения напряженности магнитного поля в замкнутом контуре:
- Путем вращения катушки, соответствующей магниту
- Путем изменения катушки либо внутренней, либо внешней по отношению к магнитному полю
- Путем изменения расположение области, в которой размещено магнитное поле.
- Сделав катушку и магнит как в сторону, так и в сторону закрытия.
Второй закон Фарадея
Электродвижущая сила, индуцируемая в катушке, равна скорости изменения магнитной связи. Магнитный поток считается произведением магнитного потока, связанного с катушкой, и общего количества витков, присутствующих в катушке. Формула имеет вид
Є = -N (dФ / dt)
Где «N» соответствует общему количеству витков в проводе, Ф соответствует магнитному потоку в одной петле, а «Є» соответствует магнитному поток.
Отрицательный знак означает, что путь индуцированной электродвижущей силы и изменение пути магнитных полей имеют противоположные направления.Вдобавок к этому, благодаря принципу Ленца, можно узнать об электромагнитной индукции.
Эксперимент
Главный эксперимент, который побудил Фарадея ввести принцип Фарадея, был не так уж и сложен. Этот закон был открыт с помощью небольшого количества бытовой техники. Здесь мы используем картонную трубку, экранированную проволокой, чтобы сформировать катушку. Для этого устройства через катушку подключается вольтметр, и генерируемая электродвижущая сила считывается как магнит, проходящий через катушку.Схема показана ниже.
В ходе этого эксперимента были сделаны следующие наблюдения:
- Когда магнит находится в постоянном положении или расположен близко к катушке, не будет напряжения.
- Когда магнит начинает движение в направлении катушки, будет некоторое напряжение, и оно увеличивается до пикового значения, когда дело доходит до средней точки катушки
- Когда магнит начинает удаляться от средней точки, будет изменение знака рассчитанного напряжения
- Когда магнит выходит наружу и находится далеко от катушки, то рассчитанное напряжение в обратном направлении по сравнению с предыдущим сценарием движения магнита близко к катушкам.
Что касается положения магнита и расчетной ЭДС, графическое представление показано как
Это стабильные наблюдения закона Фарадея. Несмотря на то, что постоянный магнит может генерировать огромное магнитное поле, будет возникать нулевая ЭДС, индуцированная по той причине, что поток через катушку не изменится. Когда магнит приближается к катушке, поток быстро увеличивается, пока положение магнита не окажется внутри катушки. Когда он начинает проходить по катушке, магнитный поток в катушке имеет тенденцию к уменьшению.В результате наведенная ЭДС изменится на противоположную.
Начальные эксперименты
Поскольку Фарадей провел множество экспериментов, начальными тремя были:
- В эксперименте 1 st было продемонстрировано, что сила магнитного поля изменяется при наведении тока. При подключении амперметра к этой установке он отклоняется, когда магнит приближается в направлении провода.
- В примере 2 и он показал, что прохождение тока по железному стержню может формировать его как электромагнитное.Он узнал, что когда существует относительное движение между катушкой и магнитом, возникает индукция ЭДС. Когда магнит вращался вокруг оси, ЭДС не возникало. Тогда как в случае, когда магнит вращается поперек своей оси, то возникает наведенная ЭДС. Из-за этого амперметр не прогибается, когда магнит остается постоянным.
- И в эксперименте 3 rd Фарадей заметил, что гальванометр не показывает отклонения и в катушке нет индуцированной ЭДС, когда катушка помещена в постоянное магнитное поле.Амперметр отклоняется в обратном направлении, когда магнит перемещается далеко от петли.
Приведенные выше экспериментальные наблюдения были сведены в таблицу:
| Положение магнита | Отклонение гальванометра |
| Магнит не движется | Гальванометр не показывает отклонения |
| катушка | Гальванометр отклоняется в одну сторону |
| Магнит постоянен рядом с катушкой | Гальванометр не показывает отклонения |
| Магнит движется далеко от катушки | Гальванометр отклоняется в обратном направлении |
| Магнит постоянен вдали от катушки | Гальванометр не показывает отклонения |
Примеры закона Фарадея
Постоянный магнит диаметром 10 мм генерирует значение поля 100 мТл.Поле быстро спадает по мере увеличения расстояния и является очень минимальным, что на 1 мм больше от границы. Когда магнит движется со скоростью 1 метр / секунду через катушку со 100 витками, имеющую длину 1 мм и диаметр несколько больше, чем у магнита. Тогда какова величина наведенной ЭДС?
Решение
1). Чтобы найти наведенную ЭДС, можно использовать закон Фарадея. Для этого нужно знать об изменении потока в катушке и о том, как быстро это изменение происходит.
Это может быть инициировано путем независимого наблюдения за ситуациями, когда магнит находится внутри и вне катушки. Поскольку мы знаем, что поле быстро уменьшается, можно подумать, что поток становится равным нулю, когда магниты находятся вне катушки. Поскольку катушка плотно соединена с магнитом, считалось, что положение поля ортогонально положению катушки, а магнитный поток равен
Ф = BA
Поскольку магнитное движение составляет 1000 мм / сек, это считалось внутренним по отношению к катушке длиной 1 мм в течение 1/1000 сек.Используя закон Фарадея,
Є = -N (dФ / dt)
= — (100) [(100,10 -3T ) ∏ (5,10 -3 ) 2 ] / ( 1 * 10 -3 )
= 0,78 В
2). Учтите, что поле направлено в прямом направлении, имеющее постоянную напряженность B = 5T, прядь квадратной формы с одной проволочной петлей и длиной сторон 0,1 м.
Решение
Площадь контура A = 0.1 × 0,1 = 0,01 м2
По мере того, как квадратная петля движется к полю в направлении «x» со скоростью 0,02 м / сек. Это означает, что в течение определенного периода времени Δt = 5 секунд петля переместится из полностью вне поля в полностью внутреннюю по отношению к нему, и нормаль к полю будет связана с магнитным полем в каждом временном интервале. Это означает, что ϴ = 0.
ΔФ = B ΔA cos (ϴ)
= 5T × 0,01 × cos (ϴ)
= 0.05 Wb
Повышение наведенной ЭДС в катушке
Ниже приведены процедуры, объясняющие, как увеличить ЭДС, наведенную в катушке
- Путем увеличения значения «N», что означает увеличение числа витков катушки в соответствии с формулой Фарадея. Было ясно, что при увеличении витков катушки индуцированная электродвижущая сила также увеличивается.
- С увеличением напряженности магнитного поля «B», окружающего катушку. Согласно статистическим расчетам, когда поток увеличивается, наведенная ЭДС также будет увеличиваться.И теоретически, когда катушка проходит через сильное магнитное поле, будут увеличиваться силовые линии для разделения, и поэтому ЭДС возрастает.
- Когда относительная скорость движения между магнитом и катушкой увеличивается по сравнению с ее предыдущим значением, катушка будет быстрее разделять силовые линии, и это создает большую наведенную ЭДС.
Приложения
Закон Фарадея является наиболее важным и фундаментальным законом в концепции электромагнетизма.Этот принцип находит применение во многих отраслях и сферах. Некоторые из приложений закона Фарадея :
Работа силовых трансформаторов зависит от закона Фарадея
- Основные функции электрического генератора основаны на принципе взаимной индукции закона Фарадея
- Мы все знаем, что индукционные плиты — это устройства, которые в наши дни можно найти в каждом доме. Это устройство также работает на основе концепции взаимной индукции.Когда ток проходит через медную катушку, которая находится на дне посуды для приготовления пищи, она создает переменное магнитное поле. Это изменяющееся или изменяющееся магнитное поле индуцирует электродвижущую силу, поэтому в сосуде генерируется ток, и вместе с этим в устройстве происходит выделение тепла.
- Электромагнитный расходомер — это устройство, которое используется для расчета скорости некоторых жидкостей. Когда есть приложение магнитного поля в электрически изолированной трубе, где присутствуют проводящие жидкости, тогда в соответствии с принципом закона Фарадея будет индукция ЭДС.Эта ЭДС прямо пропорциональна скорости потока жидкости.
- Уравнения Максвелла — прекрасное применение закона Фарадея. Согласно этому закону, изменение магнитного поля вызывает изменение электрического поля, и обратный принцип применим и к уравнениям Максвелла.
- Наиболее увлекательное применение закона Фарадея — светофоры. Здесь в светильниках используются проводные петли, чтобы узнать влияние наведенного магнитного поля. Под дорогой, проволочные петли, включая переменный ток, создают переменное магнитное поле, и когда любое транспортное средство движется по ним, оно создает индуцированные вихревые токи в транспортном средстве.Согласно принципу Ленца, эти токи образуют обратное магнитное поле, которое показывает влияние на ток, присутствующий в исходном проводном контуре. Этот эффект подразумевает присутствие транспортного средства, которое заставляет светофор соответственно менять цвет.
- Применяется в музыкальных устройствах, таких как электрические скрипки и гитары, и во многих других.
Наконец, это подробная информация о законе Фарадея. Эта статья предоставила четкую и точную информацию о принципе действия закона Фарадея, экспериментах, законах индукции, приложениях и примерах.Также более важно знать, как все связано с законом Фарадея?
(PDF) Общий закон для электромагнитной индукции
(Einduced ЭДС; ~
Bмагнитное поле; поверхность Sany, которая имеет замкнутый контур
электрической цепи в качестве контура). Однако иногда признается
, что правило потока создает некоторые проблемы, когда часть электрической цепи
движется. Некоторые авторы говорят об исключениях из правила потока [2]; другие сохраняют правило потока
путем специального выбора пути интегрирования, по которому вычисляется индуцированная ЭДС
[3].Справедливость правила потока
отстаивалась также в недавних статьях [4] [5]: в обоих случаях предполагается, что правило потока действует
, и авторам удается показать, как оно работает в нескольких критических ситуациях.
Наконец, следует подчеркнуть, что в литературе полностью игнорируется возможный вклад в индуцированную
ЭДС скорости дрейфа зарядов. Как показано в этой статье
, это верно только в том случае, если электрическая цепь представляет собой огнестойкую цепь
(или эквивалентную противопожарной цепи; см. Ниже случай перемещения стержня в магнитном поле
): когда часть цепи является сделанный из протяженного проводника, скорость дрейфа
вносит свой вклад (см. ниже трактовку Corbino
и диска Фарадея).
Подход, принятый в настоящей статье, радикально отличается и основан на определении наведенной ЭДС, приведенном в уравнении (3): он непосредственно приводит к «общему закону» для явлений электромагнитной индукции, равному
.применялся, например, к трем важным случаям (подвижный стержень, диск Фарадея и
диск Корбино). Затем показано, что правило потока не является ни полевым законом, ни причинным законом: его следует рассматривать как сокращение для расчетов, когда электрическая цепь
является пожарной (или эквивалентной).Наконец, следует напомнить, что Максвелл
записал «общие уравнения электродвижущей силы», которые, проинтегрированные
по замкнутому контуру, дают «общий закон» для электромагнитной индукции de-
, приведенный в этой статье, если скорость появляется в уравнениях Максвелла правильно интерпретируется
.
Этот вопрос имеет базовое концептуальное значение, не ограничиваясь преподаванием физики —
; он также имеет исторические и эпистемологические аспекты, которые заслуживают рассмотрения 2.
2 Изложенная в этой статье трактовка индукционных явлений была впервые представлена в сообщении на XXXIX Конгрессе AIF (Associazione per
l’Insegnamento della Fisica — Ассоциация преподавателей физики) [6]; затем в лекции
во время повышения квалификации учителей средней школы [7]; он также встречается в итальянском учебнике
[8] и, схематично, в [9]. Все эти отчеты на итальянском языке. Возможно, стоит представить эту обработку в международном журнале
.
2
Закон электромагнитной индукции Фарадея
Майкл Фарадей открыл явление электромагнитной индукции в 1831 году, что стало большим прорывом и привело к изобретению электродвигателя и генератора. Закон электромагнитной индукции Фарадея описывает два явления: взаимодействие между проводником и магнитным полем и ЭДС, создаваемую магнитным полем, которая широко известна как Первый закон Фарадея и Второй закон Фарадея соответственно.
законы Фарадея:
После открытия Эрстеда, который показал, что проводник с током создает магнитное поле, Фарадей предположил, что магнитное поле должно также производить электрический ток. Он провел несколько экспериментов в своей лаборатории в Лондоне более 10 лет. Эти эксперименты, наконец, привели к открытию Электромагнитная индукция .
Первый закон индукции Фарадея
Первый закон индукции Фарадея гласит, что «электродвижущая сила индуцируется в проводе, помещенном в переменное магнитное поле».Это явление известно как электромагнитная индукция .
Статическое магнитное поле не вызывает индукции. Между магнитным полем и проводом должно быть относительное движение. Например, перемещается либо магнит, либо проволока, либо само магнитное поле должно изменяться или изменяться. Если есть изменяющееся магнитное поле, оно заставит заряженные частицы в проводе двигаться. Эта сила известна как электродвижущая сила.
Второй закон индукции Фарадея
Второй закон индукции Фарадея гласит, что «величина наведенной ЭДС пропорциональна скорости изменения магнитного поля, в которое помещен провод».
Уравнение закона Фарадея
ЭДС, индуцированная в катушке из-за изменения магнитного поля, определяется вторым законом электромагнитной индукции, который формирует связь между магнитным полем и наведенной ЭДС. Величину наведенной ЭДС можно сформулировать следующим образом:
Где e — величина наведенной ЭДС, ϕ — величина магнитного потока, связывающего катушку, а N — количество витков катушки.Отрицательный знак указывает на то, что индуцированный ток будет течь в направлении, противодействующем изменению магнитного поля.
Подробнее о направлении индуцированного тока в законе Ленца.
Уравнение закона Фарадея показывает, что ЭДС, индуцированная в катушке, может быть увеличена следующим образом:
- Увеличение числа витков катушки.
- Увеличение скорости относительного движения между катушкой и магнитным полем.Чем быстрее изменение магнитного поля, тем выше будет наведенная ЭДС.
- Повышение напряженности магнитного поля. Чем выше поток, связывающий катушку, тем выше будет наведенная ЭДС.
Применение закона Фарадея
Электромагнитная индукция является основой электрических трансформаторов, двигателей и генераторов.
- В трансформаторе электрическая энергия передается от первичной обмотки ко вторичной за счет электромагнитной индукции.
- В электродвигателях и генераторах мощность передается от ротора к статору и наоборот за счет электромагнитной индукции.
- Индукционные плиты используют принцип электромагнитной индукции.
Майкл Фарадей (22 сентября 1791 — 25 августа 1867)
Майкл Фарадей был английским физиком и химиком. Он открыл явление электромагнитной индукции в 1831 году. Кроме того, он придумал слова анод, катод и электролиз.Помимо этого, он также изобрел бензол.
Оксфордский университет присвоил ему почетную степень доктора гражданского права, от которой он отказался по некоторым причинам. В его честь названа единица емкости фарад.
Эксперименты Фарадея
Фарадей провел несколько экспериментов, чтобы подтвердить свою гипотезу. Первым из них была демонстрация электромагнитной индукции. Он намотал две катушки в железное кольцо. К одной из катушек были подключены батарея и переключатель, а к другой — гальванометр.Он обнаружил, что гальванометр отклоняется, когда он замыкает переключатель, и отклоняется в другом направлении, когда он размыкает переключатель.
Несколькими неделями позже он провел еще один эксперимент, в котором он переместил постоянный магнит к катушке, соединенной с гальванометром. Он обнаружил, что гальванометр отклоняется в одном направлении, когда магнит перемещается к катушке, и отклоняется в другом направлении, когда магнит перемещается. Эти два эксперимента привели к открытию закона Фарадея электромагнитной индукции.
Артикул:
Электромагнитная индукция: законы Фарадея и приложения
Ученый Майкл Фарадей открыл и опубликовал книгу «Электромагнитная индукция» в 1831 году. В 1832 году американский ученый Джозеф Генри был независимо открыт. Основное понятие электромагнитной индукции взято из идеи силовых линий. Хотя на момент открытия ученые просто отбросили его идеи, потому что они не были созданы математически.Джеймс Клерк Максвелл использовал идеи Фарадея как основу своей количественной электромагнитной теории. В 1834 году Генрих Ленц изобрел закон, объясняющий поток во всем контуре. Направление индуцированной ЭДС может быть получено из закона Ленца, а ток является результатом электромагнитной индукции.
Что такое электромагнитная индукция?
Определение электромагнитной индукции — это создание напряжения или электродвижущей силы на проводнике в изменяющемся магнитном поле.Как правило, Майкл Фарадей получил признание за нововведение индукции в 1831 году. Джеймс Клерк Максвелл описал это с научной точки зрения с помощью закона индукции Фарадея. Направление индуцированного поля может быть обнаружено с помощью закона Ленца. Позже закон Фарадея был обобщен уравнением Максвелла-Фарадея. Применение электромагнитной индукции включает электрические компоненты, такие как трансформаторы, индукторы, а также такие устройства, как генераторы и двигатели.
Закон индукции Фарадея и закон Ленца
Закон индукции Фарадея использует ΦB-магнитный поток во всей области пространства, окруженной проволочной петлей.Здесь поток можно описать поверхностным интегралом.
магнитный поток Где «dA» — элемент поверхности.
«Σ» заключен в проволочную петлю.
«B» — магнитное поле.
‘B • dA’ — это скалярное произведение, которое связано с величиной магнитного потока.
Магнитный поток по проволочной петле может быть пропорционален ном. линий магнитного потока, превышающих по всей петле.
Каждый раз, когда поток на поверхности изменяется, закон Фарадея гласит, что проволочная петля приобретает ЭДС (электродвижущую силу).Наиболее распространенный закон гласит, что наведенная ЭДС в любой замкнутой цепи может быть эквивалентна скорости изменения магнитного потока, включенного в цепь.
Где «ε» — ЭДС, а «ΦB» — магнитный поток. Направление электродвижущей силы может быть задано законом Ленца, и этот закон гласит, что индуцированный ток, который будет течь внутри, будет сопротивляться преобразованию, которое его породило. Это из-за отрицательного сигнала в предыдущем уравнении.
Чтобы увеличить генерируемую электромагнитную силу, обычный подход заключается в создании магнитной связи путем создания туго намотанной петли из проволоки, собранной с N равными витками, каждый с одинаковым магнитным потоком, проходящим через них. Тогда результирующая ЭДС будет в N раз больше, чем у одиночного провода.
ε = -N δΦB / ∂t
ЭДС может возникать за счет отклонения магнитного потока по всей поверхности проволочной петли. Это можно получить разными способами.
- Магнитное поле (B) изменяется
- Петля провода может быть искажена, а также поверхность (Σ) будет изменена.
- Направление поверхности (dA) изменяется и любая вышеуказанная комбинация
Закон Ленца Электромагнитная индукция
Закон Ленца об электромагнитной индукции гласит, что всякий раз, когда создается электромагнитная сила путем регулирования магнитного потока на основе закона Фарадея, тогда наведенная полярность ЭДС генерирует ток, а магнитное поле сопротивляется изменению, которое его порождает.
ε = -N δΦB / ∂t
В приведенном выше уравнении электромагнитной индукции отрицательный сигнал указывает на то, что наведенная ЭДС, а также изменения в магнитном потоке (δΦB) имеют обратные сигналы.
Где,
Ε — это вынужденная ЭДС
δΦB изменяется в магнитном потоке
N — нет. витков в катушке
Уравнение Максвелла-Фарадея
Как правило, связь между электромагнитной силой, которая известна как ε внутри проволочной петли вокруг поверхности, подобной Σ, и электрическим полем (E) внутри провода может быть задана формулой
электрическое поле в максвелле В приведенном выше уравнении «dℓ» — это элемент кривой поверхности, который известен как «Σ», объединяющий его с определением магнитного потока.
Интегральную форму уравнения Максвелла-Фарадея можно записать как
Приведенное выше уравнение является одним из уравнений Максвелла из четырех уравнений и, следовательно, играет важную роль в классической теории электромагнетизма.
интегральная форма уравнения Максвелла – ФарадеяЗакон Фарадея и теория относительности
Закон Фарадея утверждает два разных факта. Один из них заключается в том, что электромагнитная сила может создаваться посредством магнитной силы над движущимся проводом, а также ЭДС трансформатора ЭДС может генерироваться с помощью электрической силы из-за изменения магнитного поля.
В 1861 году Джеймс Клерк Максвелл обратил внимание на отдельный физически наблюдаемый факт. Это можно рассматривать как исключительный пример в физических концепциях, где такой основной закон приводится, чтобы прояснить два таких несходных факта.
Альберт Эйнштейн заметил, что оба условия связаны с относительным движением магнита и проводника, и результат не изменился из-за того, какой из них перемещался. Это был один из главных путей, которые привели его к расширению частной теории относительности.
Эксперимент с электромагнитной индукцией
Мы знаем, что электричество может переноситься потоком электронов в противном случае током. Одна из основных и очень полезных характеристик тока заключается в том, что он создает собственное магнитное поле, которое применимо в некоторых типах двигателей, а также в приборах. Здесь мы собираемся дать представление об этой концепции, объясняя эксперимент с электромагнитной индукцией.
эксперимент с электромагнитной индукциейНеобходимые материалы для этого эксперимента в основном включают тонкий медный провод, аккумуляторную батарею 12 В, длинный металлический гвоздь, батарею 9 В, тумблер, кусачки, изоленту и скрепки.
- Подключения и все работает
- Возьмите длинный провод и подключите его к плюсу тумблера.
- Оберните провод как минимум 50 раз вокруг металлического гвоздя, чтобы получился соленоид.
- После скручивания провода подключите провод к отрицательной клемме аккумулятора.
- Возьмите кусок провода и подключите его к положительной клемме аккумулятора и отрицательной клемме тумблера.
- Включите переключатель.
- Поместите скрепки рядом с металлическим гвоздем.
Поток тока в цепи сделает металлический гвоздь намагниченным, а также намагнитит скрепки. Здесь батарея 12 В будет генерировать более сильный магнит по сравнению с батареей 9 В.
Приложения
Принципы электромагнитной индукции могут применяться во многих устройствах, а также в системах. Некоторые из примеров электромагнитной индукции включают следующее.
- Трансформаторы
- Двигатели асинхронные
- Электрогенераторы
- Электромагнитное формование
- Измерители на эффекте Холла
- Токовые клещи
- Индукционная готовка
- Магнитные расходомеры
- Графический планшет
- Индукционная сварка
- Индуктивная зарядка
- Катушки индуктивности
- Фонарик с механическим приводом
- Кольцо Роуленда
- Пикапы
- Транскраниальная магнитная стимуляция
- Беспроводная передача энергии
- Индукционное уплотнение
Итак, это все об электромагнитной индукции.Это метод, при котором проводник находится в изменяющемся магнитном поле, что приведет к появлению напряжения на проводнике. Это вызовет электрический ток. Принцип электромагнитной индукции может применяться в различных приложениях, таких как трансформаторы, индукторы и т. Д. Это основа всех видов электродвигателей и генераторов, которые могут использоваться для выработки электричества из движения электричества. Вот вам вопрос, кто открыл электромагнитную индукцию?
Электромагнитная индукция — GeeksforGeeks
Электромагнитная индукция, часто известная как индукция, — это процесс, при котором проводник помещается в определенное положение, а магнитное поле изменяется или остается неподвижным при движении проводника.В результате этого в электрическом проводнике создается напряжение или ЭДС (электродвижущая сила). В 1830 году Майкл Фарадей открыл закон индукции. Давайте подробнее рассмотрим электромагнитную индукцию.
Электромагнитная индукция
Допустим, вы ходите за покупками без наличных, а ваши родители используют кредитные карты. Карту всегда сканирует или проводит владелец магазина. Владелец магазина не фотографирует и не трогает карту. Однако он смахивает / сканирует его. Как это считывание карты удаляет деньги? Это происходит из-за явления, известного как «электромагнитная индукция».’
Могут ли движущиеся предметы генерировать электрический ток? Как узнать, существует ли связь между электричеством и магнетизмом? Подумайте, какой была бы жизнь, если бы не было компьютеров, телефонов и электричества. Эксперименты Фарадея привели к созданию генераторов и трансформаторов.
Индукция электродвижущей силы при прохождении проводника через магнитное поле или при изменении магнитного потока в магнитном поле называется электромагнитной индукцией.
Это происходит, когда проводник помещается в движущееся магнитное поле или когда он движется в фиксированном магнитном поле.
Майкл Фарадей открыл это правило электромагнитной индукции. Он протянул подводящий провод, аналогичный показанному на схеме выше, который он подключил к устройству, измеряющему напряжение в цепи. Напряжение в цепи измеряется, когда стержневой магнит проходит через устройство. Смысл этого в том, что это метод создания электрической энергии в цепи с использованием магнитных полей, а не батарей.Принцип электромагнитной индукции используется такими устройствами, как генераторы, трансформаторы и двигатели.
Закон электромагнитной индукции Фарадея
Фарадей дал два закона электромагнитной индукции:
Первый закон: Когда проводник помещается в изменяющееся магнитное поле, возникает наведенная ЭДС, а если проводник замкнут, индуцированная через него течет ток.
Второй закон: Величина наведенной ЭДС равна скорости изменения магнитного потока.
Фарадей в своем эксперименте обнаружил, что различные элементы влияют на генерацию напряжения. Они следующие:
- Количество витков: Индуцированное напряжение пропорционально количеству витков / витков провода. Чем больше витков, тем большее напряжение создается.
- Изменение магнитного поля: На индуцированное напряжение влияют изменения магнитного поля. Этого можно достичь, вращая магнитное поле вокруг проводника или вращая проводник внутри магнитного поля.
Следовательно, закон электромагнитной индукции Фарадея гласит, что величина напряжения, генерируемого в катушке, пропорциональна изменяющемуся магнитному полю и количеству витков катушки.
В результате индуцированное напряжение теперь равно:
E = N (dϕ ⁄ dt)
где,
- N = количество витков в катушке
- dϕ = изменение магнитного поток
- dt = временной интервал
- E = индуцированное напряжение
Закон электромагнитной индукции Ленца
Закон Ленца гласит, что когда ЭДС индуцирует согласно закону Фарадея, полярность (направление) этой индуцированной ЭДС противодействует причине его создание.
Согласно закону Ленца,
E = — N (dϕ ⁄ dt)
Отрицательный знак указывает на то, что индуцированная ЭДС противодействует причине ее возникновения.
Применение электромагнитной индукции
- Электромагнитная индукция в генераторе переменного тока
- Электрические трансформаторы
- Магнитный расходомер
Электрические трансформаторы
Электрический трансформатор — еще одно важное применение электромагнитной индукции.Трансформатор — это устройство, которое использует магнитное поле для преобразования электроэнергии переменного тока с одного уровня напряжения на другой. Напряжение в первичной обмотке понижающего трансформатора выше, чем во вторичной обмотке. Повышающий трансформатор — это трансформатор, в котором вторичное напряжение имеет дополнительные витки. Чтобы повысить напряжение до 100 кВ, поставщики электроэнергии используют ступенчатый трансформатор, который снижает ток и снижает потери мощности в линиях электропередачи. А в бытовых цепях используются понижающие трансформаторы для понижения напряжения до 120 или 240 В.
Электромагнитная индукция в генераторе переменного тока
Производство переменного тока является одним из наиболее важных приложений электромагнитной индукции.
Более совершенным оборудованием является генератор переменного тока с выходной мощностью 100 МВ. Эффективная площадь контура, когда катушка вращается в магнитном поле B, равна A cos θ , где θ — угол между A и B. Принцип работы основного генератора переменного тока заключается в следующем способе создания магнитного потока. изменение.Ось вращающейся катушки перпендикулярна направлению магнитного поля. Магнитный поток через катушку изменяется по мере вращения катушки, вызывая индукцию ЭДС в катушке.
Примеры проблем
Проблема 1: Когда стержневой магнит помещается рядом с круглой катушкой, имеющей 50 витков, плотность магнитного поля изменяется со скоростью 0,10 Тл / с. Найти наведенную в катушке ЭДС.
Решение:
Дано:
Число витков, N = 50 витков
Скорость изменения магнитного потока, dϕ ⁄ dt = 0.10 Тл / с
E = — N (dϕ / dt)
= — 50 × 0,10 В
= — 5 В
Следовательно, наведенная в катушке ЭДС составляет 5 В .
Проблема 2: Что такое электромагнитная индукция?
Решение:
Электромагнитная индукция — это индукция электродвижущей силы за счет движения проводника через магнитное поле или за счет изменения магнитного потока в магнитном поле.
Задача 3. Что такое закон электромагнитной индукции Фарадея?
Решение:
Закон электромагнитной индукции Фарадея гласит, что величина напряжения, генерируемого в катушке, пропорциональна количеству витков и изменяющемуся магнитному полю катушки.
Задача 4: Что такое закон Ленца?
Решение:
Согласно закону Ленца, наведенная ЭДС противодействует причине ее возникновения, то есть E = — N (dϕ ⁄ dt). Отрицательный знак указывает на то, что наведенная ЭДС противодействует причине ее возникновения.
Задача 5: Упомяните о применении электромагнитной индукции.
Решение:
Применение электромагнитной индукции:
- Электромагнитная индукция в генераторе переменного тока
- Электрические трансформаторы
- Магнитный расходомер
Внимание, читатель! Не прекращайте учиться сейчас.Присоединяйтесь к курсу First-Step-to-DSA для учащихся 9–12 классов , , специально разработанного для ознакомления со структурами данных и алгоритмами учащихся 9–12 классов
комментарий к Максвеллу (1865) ‘A динамическая теория электромагнитного поля »
Philos Trans A Math Phys Eng Sci. 2015 Apr 13; 373 (2039): 20140473.
Кавендишская лаборатория, Дж. Дж. Томсон-авеню, Кембридж CB3 0HE, Великобритания
© Авторы 2015. Опубликовано Королевским обществом в соответствии с условиями лицензии Creative Commons Attribution License http: // creativecommons.org / licenses / by / 4.0 /, что разрешает неограниченное использование при условии указания автора и источника.Abstract
В большой статье Максвелла 1865 года была установлена его динамическая теория электромагнитного поля. Истоки статьи лежат в его более ранних работах 1856 г., в которых он начал математическую разработку исследований Фарадея по электромагнетизму, и 1861–1862 гг., В которых был введен ток смещения. Эти более ранние работы были основаны на механических аналогиях.В статье 1865 г. акцент смещается на роль самих полей как описания электромагнитных явлений. Отчасти искусственные механические модели, с помощью которых он пришел к своим уравнениям поля несколькими годами ранее, были отброшены. Введение Максвеллом концепции полей для объяснения физических явлений обеспечило существенную связь между механическим миром ньютоновской физики и теорией полей, разработанной Эйнштейном и другими, которая лежит в основе физики двадцатого и двадцать первого веков.Этот комментарий был написан в ознаменование 350-летия журнала Philosophical Transactions of the Royal Society .
Ключевые слова: Максвелл, электромагнетизм, уравнения электромагнитного поля, открытие уравнений Максвелла
1. Прелюдия
16 июня 1865 года статья Джеймса Клерка Максвелла «Динамическая теория электромагнитного поля» была отправлена в типографии. Тейлора и Фрэнсиса для публикации в Philosophical Transactions of the Royal Society [1]. 1 Шесть дней назад, 10 июня того же года, состоялась мировая премьера произведения Рихарда Вагнера « Тристан и Изольда » в Мюнхенском театре «Корт». Слово революционный — единственное прилагательное, которое начинает отдавать должное исключительному влиянию этих двух событий 1865 года, одного в области физических наук, другого в музыке, опере и драме. Ошеломляющие нововведения Вагнера в музыкальной гармонии, структуре и драматургии произвели революцию в подходах композиторов и глубоко повлияли на музыку конца девятнадцатого и двадцатого веков — музыка уже никогда не будет прежней.Точно так же монументальная статья Максвелла заложила основы нововведений физики двадцатого века, поместив поля в основу теории электромагнетизма и всех последующих полей, которые описывают, как материя и излучение ведут себя на фундаментальном уровне.
Эйнштейн [2, с. 71] подытожил достижения Максвелла в 1931 году по случаю столетия со дня рождения Максвелла:
Мы можем сказать, что до Максвелла физическая реальность, поскольку она должна была представлять процесс природы, рассматривалась как состоящая из материальных частиц, вариации которых заключаются только в движениях, управляемых уравнениями в частных производных.Со времен Максвелла физическая реальность рассматривалась как представленная непрерывными полями, управляемая уравнениями в частных производных и не поддающаяся какой-либо механической интерпретации. Это изменение в представлении о Реальности является наиболее глубоким и наиболее плодотворным, которое физика пережила со времен Ньютона.
Достижения Максвелла обеспечили существенный мост между физикой Ньютона и Эйнштейна. Глубокая природа этого изменения восприятия прекрасно сформулирована Фрименом Дайсоном [3, с.4]:
Теория Максвелла становится простой и понятной только тогда, когда вы отказываетесь от мышления в терминах механических моделей. Вместо того чтобы думать о механических объектах как о первичных, а электромагнитные напряжения как о вторичных последствиях, вы должны думать об электромагнитном поле как о первичных, а механические силы как о вторичных. Идея о том, что первичными составляющими Вселенной являются поля, нелегко пришла в голову физикам поколения Максвелла. Поля — понятие абстрактное, далекое от привычного мира вещей и сил.Полевые уравнения Максвелла являются уравнениями в частных производных. Их нельзя выразить простыми словами, такими как закон движения Ньютона, сила равна массе, умноженной на ускорение. Теории Максвелла пришлось ждать, пока следующее поколение физиков, Герц, Лоренц и Эйнштейн, раскроет ее силу и прояснит ее концепции. Следующее поколение выросло с уравнениями Максвелла и было как дома во вселенной, построенной из полей. Примат полей был для Эйнштейна столь же естественным, как примат механических структур для Максвелла.
В этом эссе я помещаю статью Максвелла 1865 года в контекст эволюции его взглядов на природу физических явлений.
2. Акт 1. Предварительные сведения
К концу восемнадцатого века были установлены многие из основных экспериментальных свойств электростатики и магнитостатики. В 1770-х и 1780-х годах Шарль-Огюстен Кулон провел очень чувствительные эксперименты, которые прямо установили законы обратных квадратов электростатики и магнитостатики, которые в то время казались совершенно отдельными физическими явлениями.Это изменилось с развитием науки текущего электричества . В 1791 году итальянский анатом Луиджи Гальвани показал, что электрические эффекты могут стимулировать сокращение лягушачьих лапок. В 1791 году он показал, что при использовании двух разнородных металлов для соединения нервов и мышц в ногах лягушек наблюдалась такая же форма мышечного сокращения. Об этом было объявлено об открытии животных электричества . Алессандро Вольта подозревал, что электрический ток был связан с присутствием различных металлов в контакте с влажным телом.В 1800 году он продемонстрировал это, построив гальваническую батарею , которая состояла из чередующихся слоев меди и цинка, разделенных слоями картона, пропитанного проводящей жидкостью. Самым важным аспектом экспериментов Вольта было то, что он открыл управляемый источник электрического тока. Гальванический элемент имел короткий срок службы, так как картон высох, и поэтому он изобрел свою корону из чашек , в которой электроды были помещены в электролитическую жидкость в серии стеклянных сосудов, как в современных батареях.
Ключевой экспериментальный прогресс был сделан в 1820 году, когда Ганс Кристиан Эрстед продемонстрировал, что всегда существует магнитное поле, связанное с электрическим током — это положило начало науке об электромагнетизме . Сразу же физики Жан-Батист Био и Феликс Савар приступили к обнаружению зависимости напряженности магнитного поля на расстоянии r от элемента тока длиной d l , в котором ток I течет.В системе СИ их ответ, закон Био – Савара , может быть записан
2,1
d l — длина текущего элемента в направлении тока I и r измеряется от текущего элемента d l до точки на векторном расстоянии r .
Затем Андре-Мари Ампер расширил закон Био-Савара, чтобы связать ток, протекающий через замкнутый контур, с интегралом составляющей плотности магнитного потока вокруг контура.В современной векторной записи можно записать круговой закон Ампера в свободном пространстве
2,2
где I, , , — полный электрический ток, протекающий через область, ограниченную петлей C . В 1827 году Ампер опубликовал свой знаменитый трактат [4], в котором было показано, что магнитное поле токовой петли может быть представлено эквивалентной магнитной оболочкой. Он также сформулировал уравнение для силы между двумя токовыми элементами d l 1 и d l 2 несущие токи I 1 и I 2 :
2.3
d F 2 — сила, действующая на элемент тока d l 2 , r измеряется от d l 1 . Ампер продемонстрировал связь этого закона с законом Био – Савара.
В 1827 году Георг Саймон Ом сформулировал соотношение между разностью потенциалов В и током I , которое сейчас известно как закон Ома , В = RI , где R — сопротивление материал, по которому течет ток.Это было спорным результатом до 1876 года, когда Максвелл и его ученик Джордж Кристал установили закон экспериментально с высокой точностью в недавно основанной Кавендишской лаборатории, первым главой которой и Кавендишским профессором экспериментальной физики в 1871 году был назначен Максвелл. результаты были установлены к 1830 году и включают в себя все статического электричества, , силы между стационарными зарядами, зарядами, магнитами и токами. Суть уравнений Максвелла состоит в том, что они также имеют дело с изменяющимися во времени явлениями.За последующие 20 лет были установлены все основные экспериментальные особенности изменяющихся во времени электрических и магнитных полей.
В 1820-е годы в научные журналы было отправлено множество статей, описывающих электромагнитные эффекты и пытающихся их объяснить. Редактор журнала Philosophical Magazine пригласил Майкла Фарадея для обзора этой массы экспериментов и предположений, и так начал свое систематическое исследование электромагнитных явлений. Эти эксперименты привели Фарадея к введению ключевой концепции магнитных силовых линий , чтобы представить направление, в котором сила, действующая на магнитный полюс, действует при помещении в магнитное поле.Чем больше количество силовых линий на единицу площади в плоскости, перпендикулярной силовым линиям, тем больше сила, действующая на магнитный полюс.
Твердо веря в симметрию природы, Фарадей предположил, что, поскольку электрический ток может создавать магнитное поле, также должна быть возможность генерировать электрический ток из магнитного поля. В 1831 году он узнал об экспериментах Джозефа Генри, в которых использовались очень мощные электромагниты. Фарадею сразу пришла в голову идея наблюдать деформацию в материале сильного электромагнита, вызванную силовыми линиями.Он построил сильный электромагнит, намотав изолирующий провод, через который можно было пропускать ток, на толстое железное кольцо, создав таким образом магнитное поле внутри кольца. Эффекты деформации должны были регистрироваться другой обмоткой на кольце, которая была присоединена к гальванометру для измерения количества производимого электрического тока.
Эффект оказался совсем не таким, как ожидал Фарадей. Когда первичная цепь была замкнута, произошло смещение стрелки гальванометра во вторичной обмотке — электрический ток был индуцирован во вторичном проводе через среду железного кольца.Отклонения гальванометра были , только наблюдались при включении и выключении тока в электромагните. Это было открытие электромагнитной индукции . Еще в 1831 году Фарадей установил качественную форму своего закона индукции в терминах концепции силовых линий , электродвижущая сила, индуцированная в токовой петле, напрямую связана со скоростью, с которой пересекаются линии магнитного поля , добавление этого
Под магнитными кривыми я имею в виду силовые линии магнитного поля, которые были бы изображены железными опилками.
В 1834 году Ленц провозгласил закон, который прояснил вопрос о направлении наведенной электродвижущей силы в цепи — электродвижущая сила действует в таком направлении, чтобы противодействовать изменению магнитного потока .
Фарадей не мог математически сформулировать свои теоретические идеи, но он был убежден, что концепция силовых линий дает ключ к пониманию электромагнитных явлений. В 1846 году он предположил в своем выступлении перед Королевским институтом, что свет может быть некой формой возмущения, распространяющегося вдоль силовых линий, но эта идея была воспринята со значительным скептицизмом.
Фарадей инстинктивно верил в единство сил природы, особенно между светом, электричеством и магнетизмом. В 1846 году он пропустил свет через свинцово-боратное стекло в присутствии сильного магнитного поля. Он продемонстрировал явление, теперь известное как вращение Фарадея , при котором плоскость поляризации линейно поляризованного света поворачивается, когда световые лучи проходят вдоль направления магнитного поля в присутствии прозрачного диэлектрика. Уильям Томсон, позже лорд Кельвин, интерпретировал это явление как доказательство того, что магнетизм по своей природе вращается, и это должно было сильно повлиять на размышления Максвелла о физической природе магнитных полей.
3. Акт 2. Максвелл о «Силовых линиях Фарадея» (1856 г.)
Максвелл проявил свои таланты как физика-экспериментатора и физика-теоретика с раннего возраста. Его первая степень по естественной философии в Эдинбургском университете, за которой последовали математические исследования в Тринити-колледже в Кембридже, а также его всеядный аппетит к наиболее требовательным текстам великих европейских математиков и натурфилософов обеспечили идеальную подготовку к его исследованиям в области электромагнетизма. 2 По замечанию Сведриса [13, с. 428],
[Максвелл] был одним из очень немногих британских физиков, которые объединили экспериментальные и философские шотландские традиции с математической подготовкой, полученной в Кембридже.
Отличительной чертой мышления Максвелла была его способность работать по аналогии . В 1856 году он описал свой подход в эссе под названием Аналогий в природе , написанном для Клуба апостолов в Кембридже.Его суть можно уловить из следующего отрывка.
Каждый раз, когда [мужчины] видят связь между двумя хорошо известными им вещами и думают, что они видят аналогичную связь между менее известными вещами, они рассуждают от одного к другому. Это предполагает, что, хотя пары вещей могут сильно отличаться друг от друга, отношение в одной паре может быть таким же, как и в другой. Теперь, поскольку с научной точки зрения отношение является наиболее важной вещью, которую нужно знать, знание одной вещи ведет нас долгий путь к познанию другой.[14, стр. 381–382]
В отношении электромагнетизма он нашел формальные аналогии между математикой механических и гидродинамических систем и явлениями электродинамики. На протяжении всей этой работы он признавал свой долг Уильяму Томсону, впоследствии лорду Кельвину, который сделал существенные шаги в математизации электрических и магнитных явлений.
В том же 1856 году Максвелл опубликовал первую из своей серии статей по электромагнетизму «О силовых линиях Фарадея» [15].В предисловии к его Трактату об электричестве и магнетизме 1873 г. [16, с. viii], он вспоминал:
до того, как я начал изучать электричество, я решил не читать математику по этому предмету, пока я сначала не прочитаю «Экспериментальные исследования электричества » Фарадея .
Первая часть статьи расширяет технику аналогии и обращает особое внимание на ее применение к потоку несжимаемой жидкости и магнитным силовым линиям.Для ясности мы переработаем анализ Максвелла в единицах СИ, используя выражения векторных операторов div, grad и curl. Использование векторных методов было введено Максвеллом только в его статье 1870 г., озаглавленной «О математической классификации физических величин» [5,17] — он изобрел термины «наклон» (теперь «градиент»), «curl» . 3 и «конвергенция» (противоположность «расхождению»), чтобы интуитивно понять смысл этих векторных операторов. В 1856 году частные производные были явно выписаны в декартовой форме.Математика вращательного потока жидкости и эквиваленты div, grad и curl были знакомы физикам-математикам в то время. Томсон и Максвелл, например, нуждались в этих инструментах для описания потока жидкости в моделях атомов вихревых колец.
Максвелл начал с аналогии между потоком несжимаемой жидкости и магнитными силовыми линиями. Скорость u аналогична плотности магнитного потока B . Если силовые трубки или паропроводы расходятся, напряженность поля уменьшается, как и скорость жидкости.Это позволило Максвеллу немедленно записать математическое выражение поведения магнитных полей в свободном пространстве:
3,1
Те же рассуждения применимы к электрическим полям в свободном пространстве, но они могут возникать на зарядах, поэтому в правой части есть источник.
3,2
где E — напряженность электрического поля, а ρ e — плотность электрического заряда.
Закон электромагнитной индукции Фарадея был впервые преобразован в математическую форму Нейманом в 1845 году.Индуцированная электродвижущая сила пропорциональна скорости изменения магнитного потока в цепи.
3,3
где Φ — полный магнитный поток, пронизывающий цепь. Математически это в точности эквивалентно более мощному векторному уравнению, описывающему то, что происходит в точке пространства. Используя теорему Стокса,
3,4
Для токов и создаваемых ими магнитных полей существует аналогичное соотношение, выведенное из закона Ампера:
3.5
где H — напряженность магнитного поля, а J — плотность тока.
Последним достижением этой статьи было формальное введение того, что сейчас называется векторным потенциалом А . Такой вектор уже был введен Нейманом, Вебером и Кирхгофом для расчета индуцированных токов,
3,6
Это определение явно согласуется с (3.1), поскольку div curl A = 0.Максвелл пошел дальше и показал, как индуцированное электрическое поле E может быть связано с A . Включая определение (3.6) в (3.4), получаем
3,7
Меняя местами порядок временной и пространственной производных в правой части, получаем
3.8
Эти анализы обеспечивают формальную согласованность явлений электромагнетизма. Максвелл получил примитивную, но неполную систему уравнений для электромагнитных полей, представленных соотношениями (3.1), (3.2), (3.4) и (3.5). Однако ему все еще не хватало физической модели — механического аналога Максвелла — поведения электромагнитных явлений.
4. Акт 3. Максвелл «О физических силовых линиях» (1861–1862)
Максвелл разработал свое решение в 1861–1862 гг. В серии статей, озаглавленных «О физических силовых линиях» [18–21]. Начиная с его более ранней работы по аналогии между u и B , он становился все более и более убежденным в том, что магнетизм, по сути, имеет вращательную природу.Его целью было разработать модель среды, заполняющей все пространство, которая могла бы объяснить напряжения, которые Фарадей связал с магнитными силовыми линиями, — другими словами, механическую модель для эфира , который, как предполагалось, был средой через какой свет распространялся. В своей интригующей книге Innovation in Maxwell’s Electrodynamics [22] Дэвид Сигел провел подробный анализ этих работ, ярко продемонстрировав богатство идей Максвелла в проведении физических аналогий между механическими и электромагнитными явлениями.
Модель основана на аналогии между вращающейся вихревой трубкой и трубкой магнитного потока. Аналогия заключается в следующем. Если оставить их сами по себе, силовые линии магнитного поля расширяются, точно так же, как это происходит в случае жидкостной вихревой трубки, если вращательные центробежные силы не уравновешены. Кроме того, кинетическая энергия вращения вихрей может быть записана
4,1
где ρ — плотность жидкости, а u — ее скорость вращения.Это выражение формально идентично выражению для энергии, содержащейся в распределении магнитного поля,. И снова u аналогично B — чем больше скорость вращения трубки, тем сильнее магнитное поле. Максвелл постулировал, что локальная плотность магнитного потока везде пропорциональна угловой скорости вихревой трубки, так что вектор углового момента L параллелен оси вихря и, следовательно, параллелен вектору плотности магнитного потока В .
Максвелл начал с модели, в которой все пространство заполнено вихревыми трубками. Однако возникает непосредственная механическая проблема. Трение между соседними вихрями привело бы к их разрушению. Максвелл принял практическое инженерное решение, вставив «холостые колеса» или «шарикоподшипники» между вихрями, чтобы все они могли вращаться в одном направлении без трения. Опубликованное Максвеллом изображение вихрей, представленных массивом вращающихся шестиугольников, показано на рисунке.Затем он отождествил холостые колеса с электрическими частицами, которые, если бы они могли свободно двигаться, переносили бы электрический ток, как в проводнике. В изоляторах , включая свободное пространство , они не могут свободно перемещаться через распределение вихревых трубок и, следовательно, не могут проводить электрический ток. Я не сомневаюсь, что этот довольно крайний пример техники работы по аналогии был одной из причин «чувства дискомфорта и часто даже недоверия…», на которое ссылался Пуанкаре, когда французские физики-математики впервые столкнулись с работами Максвелла [ 23].
Акварель Джемаймы Веддерберн, изображающая детей, играющих на замерзшем озере на острове Сент-Мэри, недалеко от семейного дома в Гленлере, 23 декабря 1853 года. На заднем плане взрослые играли в керлинг. (С любезного разрешения The Maxwell at Glenlair Trust и James Clerk Maxwell Foundation.)
Диаграмма Максвелла из Philosophical Magazine за 1861 г., показывающая вращающиеся вихри, представленные шестиугольниками, и холостые колеса между ними [18, пластина V, рис. 2].
Примечательно, что эта механическая модель эфира могла объяснить все известные явления электромагнетизма. 4 В качестве примера индукции рассмотрим эффект включения второго провода в магнитное поле провода, по которому проходит ток I . Если ток постоянный, то во втором проводе нет никаких изменений. Однако, если ток изменяется, вращательный импульс передается через промежуточные холостые колеса и вихри, а во втором проводе индуцируется обратный ток.
Часть III статьи содержит вспышку гения, которая привела к открытию полного набора уравнений Максвелла.Теперь он подумал, как изоляторы хранят электрическую энергию. Он сделал предположение, что в изоляторах холостые колеса или электрические частицы могут быть на смещены на из своих «фиксированных» положений равновесия под действием электрического поля. Затем он приписал электростатическую энергию в среде упругой потенциальной энергии , связанной со смещением электрических частиц. В своей последующей статье 1865 года он называет это ключевое нововведение электрической упругостью .
Этот постулат имел два непосредственных следствия. Во-первых, когда электрическое поле, приложенное к среде, изменяется, есть небольшие изменения в положениях электрических частиц в изолирующей среде или вакууме, и поэтому возникают небольшие токи, связанные с этим движением частиц. Другими словами, существует ток J D , связанный со смещением на электрических частиц из их положений равновесия. Уравнения стали:
4.2
Во-вторых, из-за того, что электрические частицы упруго связаны, любое возмущение приводит к распространению волн через среду. Затем Максвелл мог бы выполнить простой расчет, чтобы определить физическую природу и скорость c , с которой возмущения могут распространяться через изолятор или вакуум. Для этого ему пришлось решить модифицированную версию полевых уравнений электромагнетизма (4.2) в вакууме. Простая версия аргументации приведена в приложении A.Ответ был c = ( εε 0 μμ 0 ) −1/2 , где ε и μ — диэлектрическая проницаемость и проницаемость среды.
Обратите внимание, что даже в вакууме, для которого μ = 1, ϵ = 1, скорость распространения волн конечна, c = ( ϵ 0 μ 0 ) −1/2 . Максвелл использовал экспериментальные значения Вебера и Кольрауша для произведения ϵ 0 μ 0 и, к своему изумлению, обнаружил, что c почти точно соответствует скорости света.В письмах Максвелла от 1861 года Майклу Фарадею и Уильяму Томсону он показал, что значения совпадают в пределах примерно 1%. По словам самого Максвелла, с его собственным акцентом, в третьей части его серии статей в Philosophical Magazine :
Скорость поперечных модуляций в нашей гипотетической среде, рассчитанная из электромагнитных экспериментов ММ. Кольрауш и Вебер точно согласны со скоростью света, вычисленной из оптических экспериментов М.Физо, что мы едва ли можем избежать вывода о том, что свет состоит из поперечных модуляций одной и той же среды, которая является причиной электрических и магнитных явлений . [20, с. 22]
Этот замечательный расчет представляет объединение света с электричеством и магнетизмом.
Максвелл прекрасно осознавал замечательную механическую основу своей модели вакуума, которая послужила источником вдохновения для его открытия. Как он писал [19, с. 346],
Представление о частице, движение которой связано с движением вихря за счет идеального контакта качения, может показаться несколько неудобным.Я не выдвигаю его как способ связи, существующий в Природе … Однако это способ связи, который механически мыслим, и он служит для выявления действительных механических связей между известными электромагнитными явлениями.
Никто не мог отрицать виртуозность Максвелла в определении скорости света по его механической модели электромагнитных сил.
5. Акт 4. Максвелл о «Динамической теории электромагнитного поля» (1865)
Максвелл хорошо осознавал тот факт, что теория, изложенная в его статье «О физических силовых линиях», была «неудобной» и считал это лишь «предварительной и временной гипотезой».Механическую основу его идей можно было неправильно понять или даже высмеять, но они поставили Максвелла на верный путь к окончательной теории электромагнитного поля. Поэтому он приступил к пересмотру теории на гораздо более абстрактной основе без каких-либо специальных предположений о природе среды, через которую распространяются электромагнитные явления. В 1865 году он опубликовал свою большую статью под названием «Динамическая теория электромагнитного поля» [1]. Цитируя Уиттекера [25, т.1, стр. 255]:
Здесь была показана архитектура его системы, лишенная строительных лесов, с помощью которых она была впервые возведена.
Интересно, что есть только одна, несколько извиняющаяся, ссылка в сноске к его статьям «О физических силовых линиях» 1861–1862 гг. В этой статье.
Как указал Сигель [6,26, с. 187–188], с самого начала своих исследований в области электромагнетизма он преследовал три цели:
«во-первых, разработать теорию, которая охватила бы все известные факты электричества и магнетизма;
второй, чтобы выполнить это объединение, используя подход Майкла Фарадея к электричеству и магнетизму — приближение силовых линий или поля ;
и, в-третьих, чтобы новая теория вышла за рамки того, что было известно из экспериментов… » эксперимент.
Собственное мнение Максвелла о значении этой статьи раскрывается в том, что C.W.F. В письме к своему кузену Чарльзу Кею Эверитт называет «редким моментом явного изобилия»:
У меня также есть газета, содержащая электромагнитную теорию света, которую я считаю великой пушкой, пока я не убежден в обратном. [7, с. 203]
Статья 1865 года объемная и разделена на семь частей. Все они содержат идеи и нововведения, которые иллюстрируют, как развивалось его мышление со времени его публикаций 1861–1862 годов.В этом эссе я перевел обозначения Максвелла в более знакомые символы для ясности аргументации для современного читателя — эти переводы показаны на. Обратите внимание, что система уравнений записана в смеси Максвелла электростатических и электромагнитных единиц, то есть в нерационализированных единицах. 5
Таблица 1.
Таблица перевода из нотации Максвелла в нерационализированные единицы.
количество масса корпуса C 168 168 силы, действующие в точках A и B A B → F A F B 9015 v w → v A v B v C с уменьшенными массами M N → L A M 9 0017 AB L B сопротивления R S → R A R A R сила, действующая на контур
ξ η → ε A ε B в контуре x y → I A I B количество электроэнергии → X X Q A Q B ч есть генерируется сопротивлением H → H собственная энергия токов E работа, выполненная при изменении индуктивности Вт → Вт угловая частота 16 9 9016 908 9 напряжения A C D → V A V 9016 9016 C V C 908 электромагнитный момент F G H 9137 6 →A x A y A z напряженность магнитного поля 904 γ → H x H y H z → E x E y E z 908 908 9 истинный ток проводимости 908 q r → J x 9 0168 J y J z электрическое смещение f g 904 x D y D z общий ток p ′ 4 q84 q8 →J ′ x J ′ y J ′ z ee количество свободной электроэнергии → ρ e электрический p потенциал Ψ → ϕ магнитный потенциал удельное сопротивление ρ → ϱ удельная индуктивность 9 ϵ (a) Часть I — введение в газете.Фактически, это введение само по себе могло бы найти подходящее место в любом вводном курсе бакалавриата по электромагнетизму. Вначале он подчеркивает разницу в подходах своей теории по сравнению с подходами Вебера и Неймана. Их подходы включали использование «действия на расстоянии» без учета того, как силы передаются от их источника к другим телам. Максвелл заявляет, что он
… предпочел искать объяснение этого факта в другом направлении, предполагая, что они вызываются действиями, которые происходят в окружающей среде, а также в возбужденных телах…
(3) Предлагаемая мной теория поэтому ее можно назвать теорией электромагнитного поля , потому что она имеет отношение к пространству в окрестности электрических и магнитных тел, и ее можно назвать динамической теорией , потому что она предполагает, что в этом пространстве есть это движущаяся материя, из-за которой возникают наблюдаемые электромагнитные явления.
Центральным элементом его теории была упругость среды, через которую должны распространяться электромагнитные явления, что привело к концепции тока смещения как необходимой части теоретического аппарата. Не менее важна формализация процессов электромагнитной индукции, которые могут создавать токи — они могут привести к диссипативным потерям энергии в сопротивлениях и химической диссоциации в электролитах.
Максвеллу пришлось предположить, что существует эфирная среда
пронизывающий все тела и изменяемый только по степени их присутствия; что части среды могут приводиться в движение электрическим током и магнитами; что это движение передается от одной части среды к другой силами, исходящими от соединений этих частей.
Максвеллу нужно было предположить, что эфир был физическим компонентом Вселенной, и его логика была изложена с поразительной ясностью в его вкладе в девятое издание Британской энциклопедии , в 1878 году [27].
Затем он противопоставляет свой подход подходам других исследователей, таких как Гельмгольц и Томсон, которые вывели феномен индукции из своих механических воздействий. Максвелл предлагает следовать противоположной программе — вывести механические воздействия из законов индукции.Для этого ему нужны общих уравнений электромагнитного поля , которые состоят из 20 уравнений с 20 переменными. В статье изложены истоки этих уравнений, и среди многих приложений есть ключевой результат, заключающийся в том, что электромагнитное излучение распространяется со скоростью света — объединение света и электромагнитного излучения. Максвелл признает вдохновение работы Фарадея «Мысли о лучевых вибрациях» [28]: 6
Электромагнитная теория света, предложенная (Фарадеем), по сути совпадает с той, которую я начал развивать в в этой статье, за исключением того, что в 1846 г. не было данных для расчета скорости распространения.…
(б) Часть II — об электромагнитной индукции
Затем Максвелл приступает к пространному обсуждению электромагнитной индукции. Механическое происхождение его мысли определяет его подход к определению форм уравнений самоиндукции и взаимной индуктивности между двумя индукторами. Здесь он применяет свою технику работы по аналогии с поразительным эффектом. Как он пишет:
Итак, если магнитное состояние поля зависит от движений среды, должна быть приложена определенная сила, чтобы увеличить или уменьшить эти движения, и когда движения возбуждаются, они продолжаются, так что эффект связи между током и окружающим его электромагнитным полем должно придавать току своего рода импульс, точно так же, как связь между точкой движения машины и маховиком наделяет точку движения дополнительным импульсом, который можно назвать импульс маховика уменьшился до точки движения.Неуравновешенная сила, действующая на движущую точку, увеличивает этот импульс и измеряется скоростью его увеличения.
Источником вдохновения для этого подхода послужила модель Méchanique Analytique Лагранжа. Максвелл изучал « Traité de Méchanique » Пуассона в Эдинбургском университете и был знаком с французской школой аналитической динамики, особенно хвалявшей идеи Лагранжа. Он представляет то, что он называет уменьшенным импульсом , связанным с действием сил F A и F B , действующих на тело в точках движения A и B.Сложив силы трения, для которых коэффициенты сопротивления равны R A и R B , общие силы, действующие на A и B, F A ‘и F B ‘, находятся
5,1
Обратите внимание, что Максвелл использует идентичные символы, которые будут повторяться в теории самоиндукции, взаимной индуктивности и сопротивления для этих механических эффектов. F A ‘и F B ‘ — силы, относящиеся к точкам A и B, соответственно.Затем, по словам Максвелла,
Если скорость A увеличивается со скоростью d v A / d t , то, чтобы предотвратить перемещение силы B, F ′ B = (d / d t ) ( M AB v A ).
Этот эффект на B из-за увеличения скорости A соответствует электродвижущей силе в одной цепи, возникающей из-за увеличения силы соседней цепи.
Особое значение для Максвелла имеет демонстрация уменьшенного импульса , количества ( L A v A + M AB v B ) и ( M AB v A + L B v B ) в механике. Соответствующие величины в электромагнитной индукции — это электромагнитный импульс или то, что Фарадей назвал электротоническим состоянием .
С помощью этой эквивалентности Максвелл немедленно преобразует уравнения в уравнения индукции между двумя проводниками с током. Тогда уравнение для тока I A в A имеет вид
5,2
и I B в B
5,3
где и — электродвижущие силы, I A и I B — токи, а R A и R B — сопротивления в A и B, соответственно.
С этими отождествлениями Максвелл приступает к формальному изложению процессов индукции для одного и двух токов. Из них он вывел выражения для работы и энергии, тепла, производимого токами, внутренней энергии токов и механического воздействия между проводниками, а также решил конкретные примеры для одного, двух и шести проводников. Этот последний пример имел практическое значение, поскольку шесть проводников могли формировать баланс электрического тока для практического измерения индуктивности.Здесь, как и везде в этой статье, Максвелл предлагает теорию точного измерения электрических величин, что было для него главной задачей, например, чтобы определить, насколько точно его теоретическое значение скорости света соответствует отношению электростатических и электромагнитных величин. единиц заряда.
Эта часть завершается обсуждением исследования «Исследование электромагнитного поля », линий магнитной силы и магнитных эквипотенциальных поверхностей , последние две темы возникли в результате его внимательного прочтения «Экспериментальные исследования электричества » Фарадея .В первой он описывает эксперименты, которые показывают, как можно продемонстрировать и измерить индуцированные электромагнитные эффекты.
(c) Часть III — общие уравнения электромагнитного поля
В этой части, в основе статьи, полный набор уравнений Максвелла для электромагнитного поля сформулирован с необычайной ясностью и убедительной логикой. Представленные здесь уравнения описываются алфавитной нумерацией, использованной в его статье. Таким образом, это:
Три уравнения магнитной силы ( H x , H y , H z )
Три уравнения электрических токов ( J x , J y , J z )
Три уравнения электродвижущей силы ( E x , E y , E z )
Три уравнения электрической упругости ( D x , D y , D z )
Три уравнения электрического сопротивления ( ϱ )
Три уравнения полных токов ( J ′ x , J ′ y , J ′ z )
Одно уравнение свободного электричества ( ρ e )
Одно уравнение неразрывности (d ρ e / d t )
В результате получается 20 уравнений для 20 переменных:
Написанные в современном понимании, уравнения имеют знакомый вид.Если мы идентифицируем μ H с B , уравнения (A) — (H) могут быть записаны с использованием обозначений векторных операторов следующим образом:
Таким образом, первое уравнение Максвелла
находится путем взятия ротора (D) и исключения члена v × B .
Второе уравнение Максвелла (C).
Третье уравнение Максвелла — (G).
Четвертое уравнение Максвелла находится из дивергенции (B).
(A) поглощается (C).
(D) содержит выражение для силы ( v × B ), действующей на частицу, обычно называемой силой Лоренца.
(E) — конститутивное выражение, связывающее E и D .
(F) — закон Ома, который Максвелл признал только эмпирическим соотношением.
(H) — уравнение неразрывности электрического заряда.
Хотя Хевисайду и Герцу обычно приписывают преобразование уравнений Максвелла в их обычную форму, очевидно, что по сравнению с исходной версией Максвелла потребовались только простейшие модификации.Это будет включать последовательное использование гауссовых единиц, которые будут заменены системой СИ в 1960 году.
Есть некоторые интересные особенности способа, которым Максвелл представляет эти уравнения.
— В то время как электрическое смещение ( D x , D y , D z ) появилось в его документах 1861–1862 гг. глубоко укоренившиеся в структуре электромагнетизма во втором разделе этой части статьи как
противоположная электризация сторон молекулы или частицы тела, которая может сопровождаться или не сопровождаться передачей через тело.
Холостые колеса были ненужным артефактом — явление электрического смещения обязательно должно происходить, и его изменение во времени вносит вклад в общий ток.
— Электромагнитный импульс A x , A y , A z отождествляется с тем, что мы теперь называем векторным потенциалом. Происхождение этой идентификации очевидно из уравнения (3.8) выше, но это также предвещает четырехвекторную нотацию специальной теории относительности, в которой четырехвектор для четырехпотенциала записан [ ϕ / c , A x , A y , A z ]. Максвелл широко использует векторный потенциал при разработке уравнений, в отличие от современной практики работы с полями E , D , B , H и Дж .
— Интересно, что Максвелл включает закон Ома в свое описание структуры уравнений, чего избегают в современной системе уравнений. Максвелл хорошо знал эмпирическую основу закона Ома в отличие от уравнений электромагнитной индукции. Как уже упоминалось, одним из первых его успешных проектов в качестве профессора Кавендиша было установление закона Ома с гораздо большей точностью.
Заключительный раздел этой части статьи — определение различных форм энергии, связанных с полями.Он снова начинает с электромагнитного импульса или векторного потенциала, A x , A y , A z и находит полную энергию из выражения
5,4
суммируя все пространство, занимаемое токами. Полная энергия может быть связана с полной энергией, существующей в самих полях:
5,5
Максвелл затем описывает ключевое значение этого выражения.
(74) Однако, говоря об Энергии поля, я хочу, чтобы меня понимали буквально.Всякая энергия тождественна механической энергии, независимо от того, существует ли она в форме движения, в форме упругости или в любой другой форме. Энергия в электромагнитных явлениях — это механическая энергия. Вопрос только в том, где он находится? Согласно старым теориям, он находится в наэлектризованных телах, проводящих цепях и магнитах в форме неизвестного качества, называемого потенциальной энергией, или способностью производить определенные эффекты на расстоянии. Согласно нашей теории, он находится в электромагнитном поле, в пространстве, окружающем наэлектризованные и магнитные тела, а также в самих этих телах и находится в двух различных формах, которые можно без гипотезы описать как магнитную поляризацию и электрическую поляризацию, или согласно очень вероятной гипотезе, как движение и деформация одной и той же среды.
(d) Часть IV — механические воздействия в поле
Следующая задача Максвелла — показать, как эти выражения для различных полей приводят к известным законам сил между различными электромагнитными объектами. Обратите внимание, что эти законы силы не были явно включены в формулировку уравнений электромагнетизма. В этой части он выводит из уравнений поля известные законы силы проводника, движущегося через магнитное поле, механическую силу, действующую на магнит, и силу, действующую на электрифицированное тело. 7
Максвелл также указывает, что коэффициент «электрической упругости» k , который появляется в уравнении (E) его уравнений, напрямую связан с соотношением электростатических и электромагнитных единиц измерения v через выражение k = 4 πv 2 . Вебер и Кольраух уже определили это отношение экспериментально и нашли, что оно составляет v = 310 740 000 м с -1 .
Последний раздел этой части включает попытку применить те же методы, чтобы понять законы гравитации.Здесь Максвелл затрагивает проблему универсальной силы притяжения гравитации, которая приводит к отрицательным значениям энергии гравитирующей системы. Он признается: «Поскольку я не могу понять, каким образом среда может обладать такими свойствами, я не могу идти дальше в этом направлении в поисках причины гравитации».
(e) Часть V — теория конденсаторов
Этот раздел касается определения емкости и поглощения конденсаторов различной конструкции.Это был вопрос большой важности для прокладки подводных телеграфных кабелей большой длины, о чем свидетельствует провал проекта по прокладке первого трансатлантического телеграфного кабеля в 1858 году. 8 Максвелл уже принимал активное участие в вопросах, касающихся определение фундаментальных констант и абсолютных стандартов сопротивления. На заседании Британской ассоциации в 1861 году был назначен комитет для наблюдения за определением фундаментальных стандартов, и Максвелл присоединился к нему в 1862 году, вскоре после публикации его статей по электромагнетизму 1861–1862 годов.
Он принимал активное участие в проверке своей теории точным экспериментом, в частности, в определении отношения электростатических и электромагнитных единиц электрического заряда. Деятельность Комитета стала более математической и теоретической, что напрямую связано с сильными сторонами Максвелла. Вместе со своими коллегами Бальфуром Стюартом и Флимингом Дженкином из Королевского колледжа Лондона он приступил к контролю за проектированием и изготовлением аппарата, чтобы сделать очень точное определение сопротивления [31].Успех этих экспериментов убедил Комитет в том, что абсолютное значение сопротивления, определенное этим и подобными методами, является явно предпочтительным стандартом.
В последующие годы работа над стандартами была фрагментирована, но Максвелл сохранил свой большой интерес и ведущую роль в этой теме и сделал ее одной из центральных тем исследовательской программы новой Кавендишской лаборатории в 1874 году. Определение абсолютного стандарта устойчивости было передано из обсерватории Кью в Кавендиш.Эта работа должна была оставаться одной из центральных ролей Кавендиша до тех пор, пока она не была передана Национальной физической лаборатории при ее основании в 1900 году.
(f) Часть VI — электромагнитная теория света
Часть VI — еще один памятный эпизод в Эта бумага. Максвелл теперь пытается определить, согласуются ли волны, которые могут распространяться через любую материальную среду, с постулатом о том, что свет можно отождествить с электромагнитными волнами. Анализ выглядит почти идентично тому, который появляется во всех современных стандартных текстах по электромагнетизму.Установив условия проводимости равными нулю, он выводит уравнения распространения электромагнитных волн в направлениях x , y , z за страницу или около того:
5,6
Он продолжает
(95) Если предположить, что H x , H y , H z являются функциями lx + my nz — В t = w , первое уравнение принимает вид
5.7
или
5,8
Другие уравнения дают такое же значение V , так что волна распространяется в любом направлении со скоростью V .
Эта волна полностью состоит из магнитных возмущений, причем направление намагниченности находится в плоскости волны. Никакое магнитное возмущение, направление намагничивания которого не находится в плоскости волны, вообще не может распространяться как плоская волна.
Следовательно, магнитные возмущения, распространяемые через электромагнитное поле, согласуются со светом в том, что возмущение в любой точке поперечно направлению распространения, и такие волны могут обладать всеми свойствами поляризованного света.
Для случая воздуха, для которого μ = 1, скорость распространения света, измеренная Фуко, составила 298 000 000 м с -1 по сравнению со значением, полученным Вебером и Кольраушем, которые нашли v = 310 740 000 м с −1 от их измеренного значения k . Эти цифры также совпадали в пределах экспериментальной ошибки со значением скорости света, определенным по астрономической аберрации световых лучей.
Далее Максвелл показывает, что показатель преломления непроводящего материала n дается квадратным корнем из удельной индуктивной способности среды.Он пишет
и, следовательно
5,9
или удельная индуктивная емкость равна квадрату показателя преломления, деленному на коэффициент магнитной индукции.
Максвелл затем проводит предварительное исследование случая анизотропных кристаллических материалов. Он был хорошо осведомлен о том, что кристаллы могут иметь разные показатели преломления вдоль разных осей, и поэтому изучает случай, когда μ принимает разные значения вдоль направлений x , y , z .
Следующее приложение — соотношение между электрическим сопротивлением и прозрачностью материалов. Его цель заключалась в том, чтобы учесть тот факт, что, как он выразился, «большинство прозрачных твердых тел являются хорошими изоляторами, тогда как все хорошие проводники очень непрозрачны». Он исследует распространение света по оси x поперечного возмущения. A y . С учетом удельного сопротивления среды ϱ уравнение распространения принимает вид
5.10
Если A y принимает вид
5,11
где α — коэффициент поглощения,
5,12
где V — скорость света в воздухе, а n — показатель преломления. Доля интенсивности падающего света, прошедшего через толщину x , равна
5,13
Если R — сопротивление образца материала толщиной x , шириной b и длиной l , то
5.14
установление количественной связи между α , n и R .
(ж) Часть VII — расчет коэффициентов электромагнитной индукции
Заключительная часть статьи касается точной оценки коэффициентов электромагнитной индукции. Это может показаться спуском с высот частей III, IV и VI статьи, но эти расчеты имели решающее значение для абсолютного определения сопротивления, что было одной из забот Максвелла на всю оставшуюся жизнь.Достаточно сказать, что Максвелл довольно подробно описывает различные способы измерения собственной и взаимной индуктивности в контексте экспериментов, которые он и его коллеги проводили в Королевском колледже Лондона и которые содержались в Отчете для Комитета. Британской ассоциации. Соображения должны были найти свое применение в кропотливых экспериментах Рэлея и его коллег [32,33] по определению абсолютного значения ома после смерти Максвелла.
6. Финал — последствия
Отождествление света с электромагнитным излучением было триумфом, обеспечив физическую основу волновой теории света, которая могла успешно объяснить явления отражения, преломления, поляризации и так далее. Однако поразительно, сколько времени потребовалось, чтобы глубокие идеи Максвелла стали общепринятыми в сообществе физиков. Он разработал теорию в своем великом Трактате об электричестве и магнетизме , как только он поселился в своем доме в Гленлере в регионе Дамфрис и Галлоуэй на юге Шотландии в 1865 году.
Примечательно, что, когда он писал Трактат , он также был экзаменатором Кембриджского математического трипоса и осознал острую потребность в подходящих учебниках. Двухтомный Трактат , однако, в отличие от многих других великих трактатов, таких как «Принципы » Ньютона, состоит в том, что это не систематическое изложение предмета, а незавершенная работа, отражающая собственный подход Максвелла к этим исследованиям. В более позднем разговоре Максвелл заметил, что цель Трактата заключалась не в том, чтобы окончательно изложить свою теорию миру, а в том, чтобы обучить себя, представив взгляд на стадию, которой он достиг.К сожалению, Максвелл посоветовал читать четыре части Трактата параллельно, а не последовательно.
Преимущество этого подхода состояло в том, что Максвелл ясно изложил свое собственное восприятие физического содержания теории, а также то, как с ней можно сопоставить точный эксперимент. На эти темы сильно повлияла его работа для комитета Британской ассоциации по фундаментальным стандартам. Он посвящает большую часть «Трактата » основным измерениям и электрическому оборудованию, при этом предлагая множество экспериментальных задач, которыми будут заниматься студенты-исследователи в Кавендишской лаборатории.Например, он анализирует пять методов абсолютного определения стандарта сопротивления, занимая всю гл. XVIII.
Затем, достигнув раздела 585, в середине второго тома, Максвелл заявляет, что он «должен снова начать с нового основания без каких-либо предположений, кроме предположений динамической теории» [16, т. 2, стр. 229]. Как резюмировал Питер Харман, Максвелл подчеркивает выражение физических величин, свободное от прямого представления механической моделью. Это потребовало новых математических подходов к электромагнетизму, включая кватернионы, интегральные теоремы, такие как теорема Стокса, топологические концепции и лагранжиано-гамильтоновы методы аналитической динамики.
Один из наиболее важных результатов появляется в разделе 792 Тома 2, в котором Максвелл вычисляет давление, которое излучение оказывает на проводник на основе электромагнитной теории. Этот глубокий результат обеспечивает связь между давлением p и плотностью энергии ε излучения, полученной исключительно из свойств электромагнитных полей, p = ε /3 c 2 . Этот результат должен был быть использован Больцманом в своей статье 1884 года, в которой он вывел закон Стефана – Больцмана из классической термодинамики.Опубликованный в 1873 году Трактат оказал немедленное влияние и вместе с Трактатом по естественной философии Томсона и Тейта предоставил студентам исчерпывающий обзор как экспериментальной, так и теоретической физики.
Максвелл был на удивление скромным в отношении своего вклада. Как заметил Фриман Дайсон, когда Максвелл был президентом секции математических и физических наук Британской ассоциации развития науки в 1870 году, его президентская лекция была прекрасной возможностью для описания своих новых идей, и тем не менее он почти не упомянул о своей недавней работе. о электромагнетизме, просто непринужденно говоря: «Другая теория электричества, которую я предпочитаю», даже не упомянув, что это была его собственная теория.По словам Дайсона [3, с. 3 примечания]: «Мораль этой истории состоит в том, что скромность не всегда является добродетелью».
Но проблемы были гораздо глубже. Не только теория Максвелла была сложной, но и открытие уравнений электромагнитного поля также потребовало серьезного сдвига в перспективе для физиков конца девятнадцатого века. Стоит процитировать Дайсона немного дальше.
Были и другие причины, помимо скромности Максвелла, по которым его теорию было трудно понять. Он заменил ньютоновскую вселенную материальных объектов, взаимодействующих друг с другом на расстоянии, вселенной полей, простирающихся через пространство и взаимодействующих только локально с осязаемыми объектами.Понятие поля было трудно понять, потому что поля нематериальны. Ученые того времени, включая самого Максвелла, пытались представить поля как механические структуры, состоящие из множества маленьких колес и вихрей, распространяющихся по всему пространству. Эти структуры должны были нести механические нагрузки, которые электрические и магнитные поля передают между электрическими зарядами и токами. Чтобы поля удовлетворяли уравнениям Максвелла, система колес и вихрей должна была быть чрезвычайно сложной.Если вы попытаетесь визуализировать теорию Максвелла с помощью таких механических моделей, это будет похоже на возврат к птолемеевской астрономии с планетами, движущимися на циклах, и эпициклами в небе. Это не похоже на изящную астрономию Ньютона. [3, с. 3]
Максвелл умер в 1879 году до того, как были получены прямые экспериментальные доказательства существования электромагнитных волн. Дело было окончательно решено через десять лет после смерти Максвелла в классической серии экспериментов Генриха Герца, почти через 30 лет после того, как Максвелл отождествил свет с электромагнитным излучением.Великая монография Герца Об электрических волнах [34] прекрасно излагает его замечательную серию экспериментов.
Герц обнаружил, что он может обнаруживать эффекты электромагнитной индукции на значительных расстояниях от своего устройства. Примеры типов излучателей и детекторов, которые он использовал, показаны на. Электромагнитное излучение испускалось, когда между большими сферами возникали искры при приложении высокого напряжения от индукционной катушки. Метод обнаружения поля излучения заключался в наблюдении искр в зазоре между парой малых сфер детектора.
Аппарат Герца для генерации и обнаружения электромагнитного излучения. Излучатель и создавал электромагнитное излучение в разрядах между сферическими проводниками. Детектор b состоял из аналогичного устройства с зажимами детектора, расположенными как можно ближе друг к другу для достижения максимальной чувствительности. Излучатель помещался в фокус цилиндрического параболоидного отражателя для получения направленного пучка излучения. (Из [34].)
После большого количества проб и ошибок Герц обнаружил, что для определенных устройств существует сильный резонанс, соответствующий резонансным частотам излучателя и детектора.Частоту резонансных волн можно было определить по резонансной частоте излучателя и детектора, которую он принял равной ω = ( LC ) −1/2 , где L и C — индуктивность и емкость диполя. Он измерил длину волны излучения, поместив отражающую пластину на некотором расстоянии от излучателя искрового промежутка, чтобы стоячие волны возникали вдоль линии между излучателем и пластиной. Скорость волн может быть найдена из соотношения c = ν λ.
Скорость оказалась почти равной скорости света в свободном пространстве. Затем он начал серию экспериментов, которые убедительно продемонстрировали, что эти волны во всех отношениях ведут себя точно так же, как свет — прямолинейное распространение, поляризация, отражение, преломление. Некоторые эксперименты были весьма примечательными по своему исполнению. Чтобы продемонстрировать преломление, он сконструировал призму весом 12 центнеров из так называемого «твердого материала, такого как асфальт».
Эксперименты убедительно показали, что существуют электромагнитные волны с частотой приблизительно 1 ГГц и длиной волны 30 см, которые во всех отношениях ведут себя как свет.Эти великие эксперименты были убедительным доказательством справедливости уравнений Максвелла.
Приложение A
В линейно-упругой среде смещение электрических частиц пропорционально напряженности электрического поля.
А 1
Когда напряженность поля меняется, заряды перемещаются, вызывая то, что Максвелл назвал током смещения . Если N q — это плотность числа электрических частиц, а q — заряд каждой из них, то плотность тока смещения равна
А 2
Максвелл утверждал, что эта плотность тока смещения должна быть включена в уравнение curl H = J , которое теперь должно читаться
А 3
На этом этапе , α, и , β, являются неизвестными константами, которые необходимо определить из известных электрических и магнитных свойств среды.
Прежде всего, вычислим скорость распространения возмущения в среде. Если предположить, что токи отсутствуют, Дж = 0, первые два уравнения Максвелла сводятся к
А 4
Дисперсионное соотношение для этих волн, то есть соотношение между волновым вектором k и угловой частотой ω , можно найти с помощью стандартной процедуры. Мы ищем волновые решения вида e i ( k ⋅ r — ωt ) , и поэтому заменяем векторные операторы скалярными и векторными произведениями согласно рецепту:
Тогда уравнения (A 4) сводятся к
А 5
Исключая E из уравнений (A 5),
А 6
где мы использовали линейное определяющее соотношение B = мкм 0 H , мкм — проницаемость среды.Используя векторную связь A × ( B × C ) = B ( A ⋅ C ) — C ( A ⋅ B ), находим, что
А 7
Не существует решения для k параллельно H , то есть продольных волн , так как тогда левая часть (A 6) равна нулю.Однако существуют решения для поперечных волн , для которых k ⋅ H = 0. Они представляют собой плоские поперечные волны с векторами E и H , перпендикулярными друг другу и направлению распространения волны. Соотношение дисперсии для волн, таким образом, составляет k 2 = ω 2 βμμ 0 . Поскольку скорость распространения волны равна c = ω / k , находим, что
А 8
Обратите внимание, что из-за линейной пропорциональности k и ω фазовая скорость c p и групповая скорость волнового пакета c g = dω / d k , оба имеют одинаковое значение, c , заданное формулой (A 8).
Теперь Максвелл знал, как вычислить константу β . Плотность энергии, запасенная в диэлектрике, — это просто работа, совершаемая на единицу объема при перемещении электрических частиц на расстояние r , то есть
А 9
Но
А 10
и, следовательно
А 11
Поэтому проделанная работа
А 12
Но это равно плотности электростатической энергии в диэлектрике, где ϵ — диэлектрическая проницаемость среды.Следовательно, β = ϵϵ 0 . Подставляя это значение в (A 8) для скорости волн, находим
A 13
Сноски
1 Обратите внимание, что дата на отсканированной версии статьи на веб-сайте Королевского общества неверна (1 января 1865 г.). Эта ошибка является артефактом того, как статья была оцифрована.
2 Дополнительную информацию о жизни и науке Максвелла см. В [3,5–12].
3 По словам доктора Дэвида Ричи из Фонда Джеймса Клерка Максвелла, «[Максвелл] использовал термин« завиток »для описания двумерных электрических и магнитных волн.Он сказал, что это не «вращение», которое подразумевает трехмерность ». Есть восхитительная акварель Джемаймы Веддерберн, на которой изображены дети, играющие на замерзшем озере на острове Сент-Мэри 23 декабря 1853 года (). На заднем плане можно увидеть взрослых керлингов, среди которых предположительно Максвелл, которые дома на рождественские каникулы из Кембриджа. Вращение камней для завивки двухмерное.
4 Я привожу несколько таких примеров в своей книге Теоретические концепции в физике [24, гл.5].
5 Более подробную информацию о различных системах единиц, используемых в электромагнетизме, можно найти в эссе Системы единиц в электромагнетизме по адресу http://info.ee.surrey.ac.uk/Workshop/advice/coils/unit_systems /.
6 Эта статья была впервые опубликована в Philosophical Magazine [29] после его лекции в Королевском институте в апреле 1846 года.
7 Многие части этого анализа аналогичны тем, которые я описал в своей книге [24, гл.6]. Там я начал с уравнений Максвелла как набора дифференциальных уравнений в частных производных, а затем придал им физическое значение, выполнив различные векторные манипуляции, чтобы показать, что все известные явления электромагнетизма могут быть выведены из постулируемого набора уравнений. Пока я не написал настоящее эссе, я не осознавал, что этот подход, который мы преподавали на уроках теоретической физики в Кембридже, был почти в точности тем, что Максвелл опубликовал в 1865 году. Кабель и его важность для продвижения использования методов теоретической физики в электротехнических проектах прекрасно рассказывается К.Смит и Н. М. Уайз в своей биографии Уильяма Томсона [30].
Профиль автора
Малькольм Лонгэр — джексонский профессор естественной философии Кембриджского университета и директор по развитию Кавендишской лаборатории в Кембридже. С 1980 по 1990 год он был королевским астрономом Шотландии и директором Королевской обсерватории в Эдинбурге. С 1997 по 2005 год он был главой Кавендишской лаборатории. Его исследовательские интересы лежат в области астрофизики высоких энергий и астрофизической космологии.Недавняя деятельность включала научную историю физики, астрономии, астрофизики и космологии. В 2013 году он опубликовал историю квантовой механики и в настоящее время пишет научную историю лаборатории Кавендиша.
Ссылки
1. Максвелл Дж. 1865 г. Динамическая теория электромагнитного поля. Фил. Пер. R. Soc. 155, 459–512. (10.1098 / rstl.1865.0008) [CrossRef] [Google Scholar] 2. Эйнштейн А. 1931 г. Влияние Максвелла на развитие представлений о физической реальности.В Джеймсе Клерке Максвелле — памятном томе 1831–1931 гг. (Ред. Томсон Дж. Дж. И др.), Стр. 66–73. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar] 3. Дайсон Ф. 1999 г. Памятный буклет Джеймса Клерка Максвелла. Эдинбург, Великобритания: Фонд Джеймса Клерка Максвелла. [Google Scholar] 4. Ампер А-М. 1827 г. Mémoir sur la Theorie Mathématiques des Phénomènes électrodynamiques, уникальность déduite de l’expérience. В Mémoires de l’Académie Royale des Sciences, 1823, vol. VI, стр. 175–388. [Google Scholar] 5. Максвелл Дж.1890 г. О математической классификации физических величин. В научных статьях Дж. Клерка Максвелла (ред. Нивен У. Д.), т. 2. С. 257–266. Кембридж, Великобритания: Издательство Кембриджского университета; (Перепечатано в 1965 году. Нью-Йорк: Dover Publications Inc.) [Google Scholar] 6. Флад Р., Маккартни М., Уитакер А. (ред.). 2014 г. Джеймс Клерк Максвелл: перспективы его жизни и работы. Оксфорд, Великобритания: Издательство Оксфордского университета. [Google Scholar] 7. Harman PM. (ред.). 1995 г. Научные письма и статьи Джеймса Клерка Максвелла, т.2 Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar] 8. Buchwald JZ. 1985 г. От Максвелла до микрофизики: аспекты теории электромагнетизма в последней четверти девятнадцатого века. Чикаго, Иллинойс: Издательство Чикагского университета. [Google Scholar] 9. Кэмпбелл Л., Гарнетт В. 1882 г. Жизнь Джеймса Кларка Максвелла. Лондон, Великобритания: MacMillan & Co. [Google Scholar] 10. Харман П. 1990 г. Научные письма и статьи Джеймса Клерка Максвелла. Том I, 1846–1862 гг. Кембридж, Великобритания: Издательство Кембриджского университета.[Google Scholar] 11. Харман П. 2002 г. Научные письма и статьи Джеймса Клерка Максвелла. Том III, 1874–1879 гг. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar] 12. Харман П. 1998 г. Натурфилософия Джеймса Клерка Максвелла. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar] 13. Сведрис Р. 1976 г. Расцвет физических лабораторий в Великобритании. Hist. Stud. Phys. Sci. 7, 405–436. (10.2307 / 27757360) [CrossRef] [Google Scholar] 14. Максвелл Дж. 1856 г. Аналогии в природе. В научных письмах и статьях Джеймса Клерка Максвелла (изд.Харман П.М.), т. 1. С. 376–383. Кембридж, Великобритания: Издательство Кембриджского университета (1990). [Google Scholar] 15. Максвелл Дж. 1856 г. О силовых линиях Фарадея. Пер. Camb. Фил. Soc. 10, 155–188. [Google Scholar] 16. Максвелл Дж. 1873 г. Трактат об электричестве и магнетизме, 2 тт. Оксфорд, Великобритания: Clarendon Press; (Перепечатка 3-го изд., 1998. Серия Oxford Classics.) [Google Scholar] 17. Максвелл Дж. 1871 г. О математической классификации физических величин. Proc. Лондон. Математика. Soc. 3, 224–233. [Google Scholar] 18.Максвелл Дж. 1861 г. О физических силовых линиях. I. Теория молекулярных вихрей применительно к магнитным явлениям. Фил. Mag. 21, 161–175. [Google Scholar] 19. Максвелл Дж. 1861 г. О физических силовых линиях. II. Теория молекулярных вихрей применительно к электрическим токам. Фил. Mag. 21, 338–348. [Google Scholar] 20. Максвелл Дж. 1862 г. О физических силовых линиях. III. Теория молекулярных вихрей применительно к статическому электричеству. Фил. Mag. 23, 12–24. [Google Scholar] 21. Максвелл Дж. 1862 г. О физических силовых линиях.IV. Теория молекулярных вихрей применима к действию магнетизма на поляризованный свет. Фил. Mag. 23, 85–95. [Google Scholar] 22. Siegel DM. 1991 г. Нововведение в электромагнитной теории Максвелла. Молекулярные вихри, ток смещения и свет. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar] 23. Хейлброн Дж. 1977 г. Лекции по истории атомной физики 1900–1922 гг. В истории физики двадцатого века: 57-я Международная школа физики Варенны, Энрико Ферми (редактор Вайнер К.), стр. 40–108. Нью-Йорк, штат Нью-Йорк: Academic Press. [Google Scholar] 24. Лонгэр М. 2003 г. Теоретические понятия в физике. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar] 25. Уиттакер Э. 1951 г. История теорий эфира и электричества, 2 тт. Лондон, Великобритания: Thomas Nelson & Sons Ltd. [Google Scholar] 26. Siegel DM. 2014 г. Вклад Максвелла в электричество и магнетизм. Джеймс Клерк Максвелл: взгляд на его жизнь и работу (ред. Флуд Р., Маккартни М., Уитакер А.), стр. 187–203.Оксфорд, Великобритания: Издательство Оксфордского университета. [Google Scholar] 27. Максвелл Дж. 1878 г. Эфир. В Британской энциклопедии, 9-е изд., Т. 8. С. 568–572. Эдинбург, Великобритания: А. и К. Блэк. [Google Scholar] 28. Фарадей М. 1846 г. Мысли о лучевых вибрациях. В исследованиях Фарадея по электричеству, т. 3. С. 447–452. Лондон, Великобритания: Ричард Тейлор и Уильям Фрэнсис. [Google Scholar] 29. Фарадей М. 1846 г. Мысли о лучевых вибрациях. Фил. Mag. Сер. 3 28, 345–350. [Google Scholar] 30. Томсон В. 1989 г. Энергия и империя: биографическое исследование лорда Кельвина.Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar]31. Максвелл Дж. К., Стюарт Б., Дженкин Ф. 1863 г. Описание экспериментального измерения электрического сопротивления, проведенного в Королевском колледже, стр. 140–158. Отчеты Британской ассоциации.
32. Рэлей Дж. У., Шустер А. 1881 г. Об определении Ом в абсолютной мере. Proc. R. Soc. 32, 104–141. (10.1098 / rspl.1881.0015) [CrossRef] [Google Scholar] 33. Рэйли Дж. У., Сиджвик Э. М.. 1883 г. Эксперименты по методу Лоренца для дальнейшего определения абсолютного значения единицы сопротивления Британской ассоциации с приложением по определению высоты звука в качестве стандартного камертона.Фил. Пер. R. Soc. 174, 295–322. (10.1098 / rstl.1883.0007) [CrossRef] [Google Scholar] 34. Герц Х. 1893 г. Электрические волны. С. 183–184. Лондон, Великобритания: Macmillan and Company; (Пер. Untersuchungen über die Ausbreitung der elektrischen Kraft, , Иоганн Амброзиус Барт, Лейпциг, 1892 г.) [Google Scholar]Укажите законы электромагнитной индукции Фарадея.
Законы электромагнитной индукции, данные Фарадеем:
- Всякий раз, когда происходит изменение магнитного потока, связанного с замкнутым контуром, индуцируется ЭДС, то есть индуцируется электромагнитное поле.
- Величина наведенной ЭДС прямо пропорциональна скорости изменения магнитного потока в этой цепи.
- Индуцированная ЭДС длится до тех пор, пока в контуре продолжается изменение магнитного потока.
Закон индукции Фарадея (кратко, закон Фарадея ) — это основной закон электромагнетизма, предсказывающий, как магнитное поле будет взаимодействовать с электрической цепью, создавая электродвижущую силу (ЭДС) — явление, известное как электромагнитная индукция.Это основной принцип работы трансформаторов, индукторов и многих типов электродвигателей, генераторов и соленоидов.
Уравнение Максвелла – Фарадея (указанное как одно из уравнений Максвелла) описывает тот факт, что пространственно изменяющееся (а также, возможно, изменяющееся во времени, в зависимости от того, как магнитное поле изменяется во времени) электрическое поле всегда сопровождает изменяющееся во времени магнитное поле. поле, в то время как закон Фарадея гласит, что существует ЭДС (электродвижущая сила, определяемая как электромагнитная работа, совершаемая над единичным зарядом, когда он прошел один виток проводящей петли) в проводящей петле, когда магнитный поток через поверхность, заключенную в петлю, изменяется во время.
Был открыт закон Фарадея, и один из его аспектов (трансформаторная ЭДС) был позже сформулирован как уравнение Максвелла – Фарадея. Уравнение закона Фарадея может быть получено с помощью уравнения Максвелла – Фарадея (описывающего ЭДС трансформатора) и силы Лоренца (описывающей ЭДС движения). Интегральная форма уравнения Максвелла – Фарадея описывает только ЭДС трансформатора, в то время как уравнение закона Фарадея описывает как ЭДС трансформатора, так и ЭДС движения.
Электромагнитная или магнитная индукция — это создание электродвижущей силы через электрический проводник в изменяющемся магнитном поле.
Майклу Фарадею обычно приписывают открытие индукции в 1831 году, а Джеймс Клерк Максвелл математически описал это как закон индукции Фарадея. Закон Ленца описывает направление индуцированного поля. Позднее закон Фарадея был обобщен и стал уравнением Максвелла – Фарадея, одним из четырех уравнений Максвелла в его теории электромагнетизма.
Электромагнитная индукция нашла множество применений, включая электрические компоненты, такие как индукторы и трансформаторы, а также такие устройства, как электродвигатели и генераторы.
Читать все
.




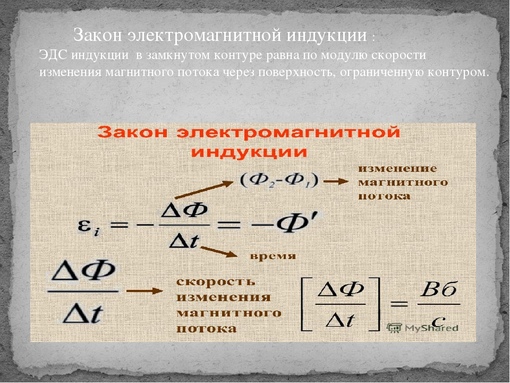
 Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле; Правильно, можно найти множество вещей, которые будут лучше. Тем не менее, мы все равно предлагаем Вам прочесть эту статью.
Правильно, можно найти множество вещей, которые будут лучше. Тем не менее, мы все равно предлагаем Вам прочесть эту статью.