Закон электромагнитной индукции и его вывод из закона сохранения энергии, также на основе электронной теории.

Обобщая результаты своих многочисленных опытов, Фарадей пришел к количественному закону электромагнитной индукции:

Знак минусопределяется правилом Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызва­вшему этот индукционный ток.

Закон Фарадея может быть непосредственно получен из закона со­хранения энергии, как это впервые сделал Г. Гельмгольц. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное плоско­сти контура, и может свободно перемещаться. Под действием силы Ампера F, направление которой показано на рисунке, проводник перемещается на отрезок dx. Таким образом, сила Ампера производит работу dA=IdФ, где dФ — пересеченный проводником магнитный поток.

Согласно закону сохранения энергии, работа источника тока за время dt () будет складываться из работы на джоулеву теплоту  и работы по перемещению проводника в магнитном поле (IdФ):

где R — полное сопротивление контура. Тогда
где -dФ/dt=ξ_i  есть не что иное, как закон Фарадея Закон Фарадея можно сформулировать еще таким образом: э.д.с. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: э. д. с. не зависит от способа изменения магнитного потока. Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим

Какова природа э.д.с. электромагнитной индукции? Если проводник движется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводником, будет направлена противоположно току, т. е. она будет создавать в проводнике индукционный ток противоположного направления (за направление электрического тока принимается движение положительных зарядов). Таким образом, возбуждение э.д.с. индукции при движения контура в постоянном магнитном поле объясняется действием силы Лоренца, возникающей при движении проводника.

Согласно закону Фарадея, возникновение э.д.с. электромагнитной индукции воз­можно и в случае неподвижного контура, находящегося в переменноммагнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае ею нельзя объяснить возникновение э.д.с. индукции. Максвелл для объяснения э.д.с. индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция вектора ЕB этого поля по любому неподвижному контуру L проводника представляет собой э. д. с. электромагнитной индукции:

          

Объяснение возникновения ЭДС индукции из электронной теории.

Пусть в магнитном поле с индукцией В перпендикулярно полю перемещается проводник длиной l со скоростью v, вектор v перпендикулярен вектору  В (рис. 118). На свободные электроны в проводнике при перемещении его будет действовать сила Лоренца F_Л=evB, где е – заряд электрона. Под действием этой силы F_Л произойдет перемещение зарядов и в проводнике возникнет разность потенциалов φ₁– φ₂, т.е. в самом проводнике возникает электрическое поле, которое будет препятствовать перемещению электронов под действием силы Лоренца. Сила, препятствующая перемещению, будет F_Э= еЕ, где Е =- напряженность поля в проводнике. В некоторый момент сила F_Э уравновешивается силой Лоренца F_Л

F_Э= -F_Л;      еЕ = -еvB;    E= -vB

 или        φ₁– φ₂= -vBl.

Если концы проводника замкнуть, то по нему потечет ток.

Движущийся в магнитном поле проводник можно рассматривать как своеобразный источник тока, обладающий ЭДС, называемой ЭДС индукции ε_i. Следовательно, на концах проводника_{длинойl, движущегося со скоростьюvв магнитном поле с индукцией В, индуцируется ЭДС индукции}

ε_i = -vBl_sinα.

Если за время dtпроводник переместился на расстояниеdx, то его скорость будет

ε_i= .

ldx=dS – это площадь, пересекаемая проводником за времяdt.

 Положив   , получим ε_i= ;     ε_i

выражение закона Фарадея-Максвелла, для ЭДС индукции, исходя из электронных представлений

ε_i= 

4.2. Вывод основного закона электромагнитной индукции из закона сохранения и превращения энергии

Основной закон электромагнитной индукции (закон Фарадея) можно вывести из закона сохранения и превращения энергии, что и было сделано Гельмгольцем (1847 г.).

Пусть имеется замкнутая цепь (контур с током), содержащая источник ЭДС, величина которой , и пусть полное сопротивление этой цепи равно R. Обозначим силу тока в цепи через I. Количество энергии, затрачиваемое источником ЭДС за время dt, как известно, равно

.

Если внешнее магнитное поле отсутствует или контур неподвижен, то вся эта энергия превращается в тепло, количество которого определяется законом Джоуля-Ленца:

.

Имеем

.

Откуда после сокращения на dt получим закон Ома для замкнутой (полной) цепи в интегральной форме:

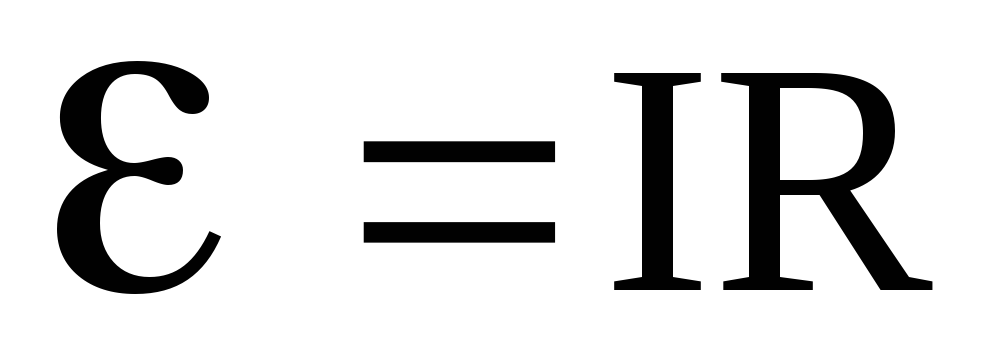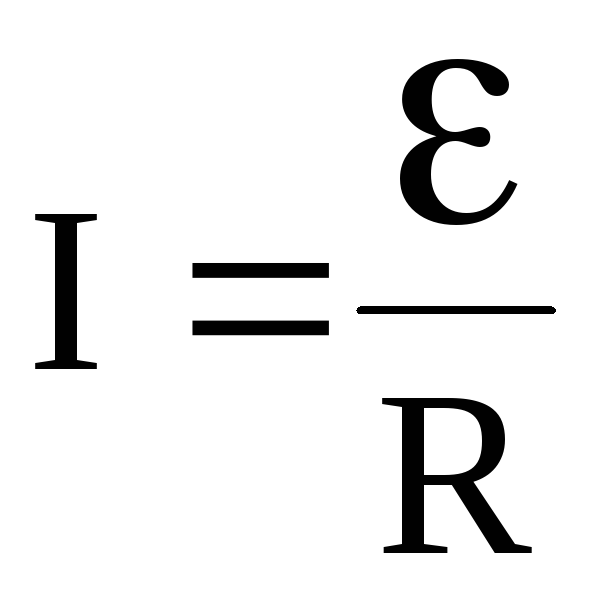и . (4.11)

При перемещении такого контура с источником ЭДС (с током) в магнитном поле часть энергии источника тока будет расходоваться против перемещения контура в магнитном поле, а часть выделяться в контуре в виде тепла. Расходование энергии источника тока против перемещения контура с током в магнитном поле связано с тем, что для получения индукционных токов методом перемещения проводника в магнитном поле необходимо совершить работу, так как сила, действующая на индукционный ток, препятствует перемещению проводника.

Известно, что работа по перемещению проводника с током в магнитном поле dA = IdФ, где dФ – величина изменения магнитного потока, сцепленного с данным контуром.

Так как при таком перемещении магнитное поле остается неизменным, то эта работа может совершаться лишь за счет энергии источника тока.

На основании закона сохранения и превращения энергии будем иметь

или

.

Откуда

. (4.12)

Решая уравнение (4.12) относительно силы тока, найдем

. (4.13)

Принимая равенство (4.13) за математическое выражение закона Ома и сравнивая его с полученным ранее для этого же контура в отсутствие магнитного поля, можно установить, что благодаря изменению потока магнитной индукции к имевшейся в цепи ЭДС источника прибавилась ЭДС:

. (4.14)

Как видно, величина ЭДС электромагнитной индукции не зависит от величины  источника тока и, значит, сохранит свое значение и при  = 0, т.е. будет возникать вне зависимости от всяких других ЭДС, действующих в той же цепи.

Знак «минус» служит математическим выражением правила (закона) Ленца.

Таким образом, формула (4.14) является математическим выражением основного закона электромагнитной индукции (в формулировке Максвелла).

Аналогично можно получить вывод этого закона и для отрезка проводника (в формулировке Фарадея).

4.3. Явление самоиндукции. Магнитное поле бесконечно длинного соленоида. Коэффициенты индуктивности и взаимной индуктивности

И

звестно, что вокруг любого проводника с током возникает магнитное поле. Следовательно, с любым контуром тока всегда связан поток магнитной индукции. Этот поток будет изменяться при изменении силы тока в контуре, а также формы контура или магнитной проницаемости окружающей среды. Изменение же магнитного потока, согласно закону электромагнитной индукции, возбудит в контуре ЭДС. ЭДС электромагнитной индукции, которая возникает в каком-либо контуре вследствие изменения магнитного потока, создаваемого электрическим током этого контура, называют ЭДС самоиндукции (рис. 4.4).

Величина ЭДС самоиндукции может быть определена по общей формуле, выражающей основной закон электромагнитной индукции:

.

Рассчитаем ЭДС самоиндукции, возникающую в бесконечно длинном соленоиде, магнитное поле которого однородно находится внутри объема соленоида, заполненного средой с магнитной проницаемостью .

Магнитный поток Ф₁, пронизывающий каждый виток соленоида сечением S,

. (4.15)

При изменении тока в соленоиде в каждом витке возникает ЭДС самоиндукции:

. (4.16)

В N последовательно соединенных витках соленоида возникает ЭДС самоиндукции:

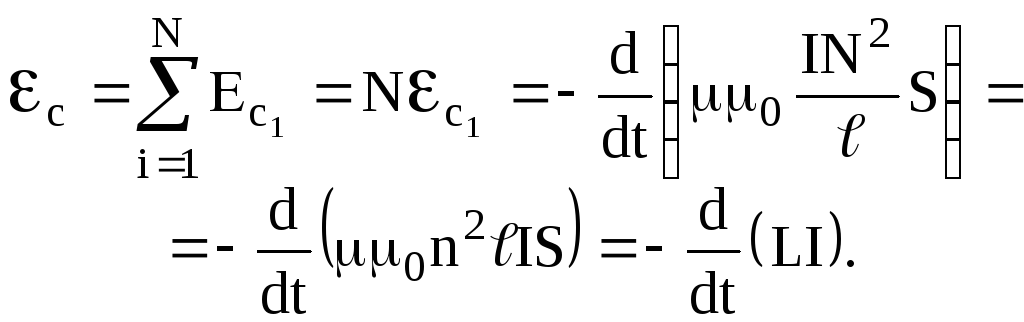(4.17)

где — коэффициент самоиндукции или индуктивность.

Индуктивность L зависит от формы, размеров проводника и магнитной проницаемости среды, окружающей проводник.

При 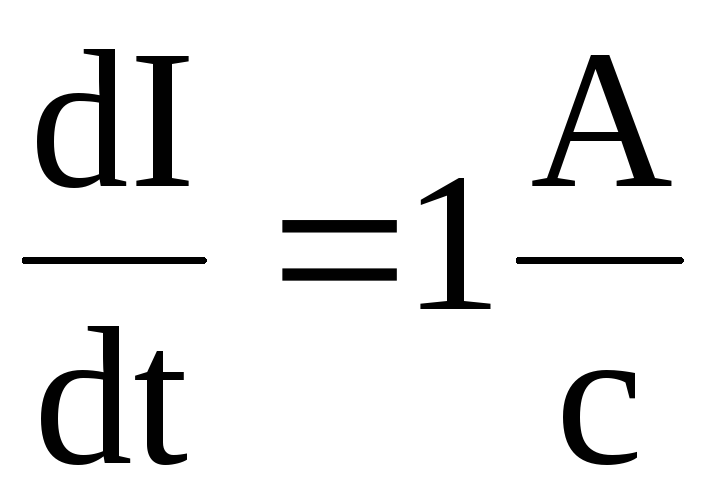_с = L, т.е. индуктивность (коэффициент самоиндукции) – это физическая величина, численно равная ЭДС самоиндукции, возникающей в проводнике при скорости изменения тока в нем, равной 1 А/с. В системе СИ индуктивность проводников измеряется в «генри» (Гн).

Один Гн (генри) – это индуктивность такого проводника, в котором при скорости изменения тока в 1 А/с индуцируется ЭДС самоиндукции, равная 1 В.

Если L = const,

. (4.18)

Следовательно, ЭДС самоиндукции прямо пропорциональна скорости изменения тока в проводнике. Оказывается, что данное утверждение справедливо для любых проводников.

Если L  const, что возможно при  = f(H),

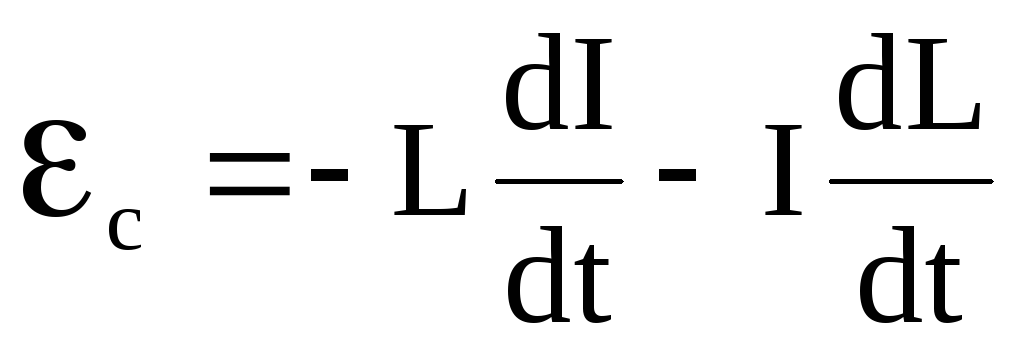. (4.19)

То есть при наличии ферромагнетиков и в переменных магнитных полях коэффициент пропорциональности в выражении для ЭДС самоиндукции не равен L.

Таким образом, в проводниках с переменным током существуют одновременно две ЭДС — источника тока и самоиндукции.

При возрастании тока ,_с<0, а это означает, что ЭДС самоиндукции «тормозит» движение зарядов в проводнике, совершая отрицательную работу, т.е. уменьшает ток в проводнике.

Если ток в проводнике убывает ,_с>0 — ЭДС самоиндукции препятствует уменьшению тока в проводнике.

Следовательно, _с противодействует причине, которая порождает ее (препятствует изменению тока в проводнике).

Сравнивая выражения идля магнитного потока, имеем

Ф = LI. (4.20)

4.3.1. Взаимная индукция. Коэффициент взаимной индукции

Взаимная индукция, явление, в котором обнаруживается магнитная связь двух или более электрических цепей. Благодаря этой связи возникает ЭДС индукции в одном из контуров при изменении тока в другом. Количественной характеристикой магнитной связи электрических цепей является взаимная индуктивность.

Если два контура (два замкнутых проводника) находятся в магнитных полях друг друга, то при всяком изменении тока в одном из них происходит изменение магнитного потока, пронизывающего (сцепленного) другой контур, что вызывает в нем появление ЭДС индукции (рис. 4.5).

Магнитный поток через первый контур с током I₁ частично пронизывает площадь, ограниченную вторым контуром. Причем магнитный поток Ф₁₂ через контур два прямо пропорционален току I₁:

, (4.21)

где М₁₂ — коэффициент пропорциональности, зависящий от размеров, формы контуров, расстояния между ними, от их взаимного расположения, а также от магнитной проницаемости окружающей среды. Он называется взаимной индуктивностью или коэффициентом взаимной индукции контуров. В системе СИ измеряется в генри (Гн).

Если ток I₂ течет в контуре «два», то магнитный поток Ф₂₁ через контур «один» также пропорционален току I₂:

. (4.22)

Согласно закону электромагнитной индукции,

; (4.23)

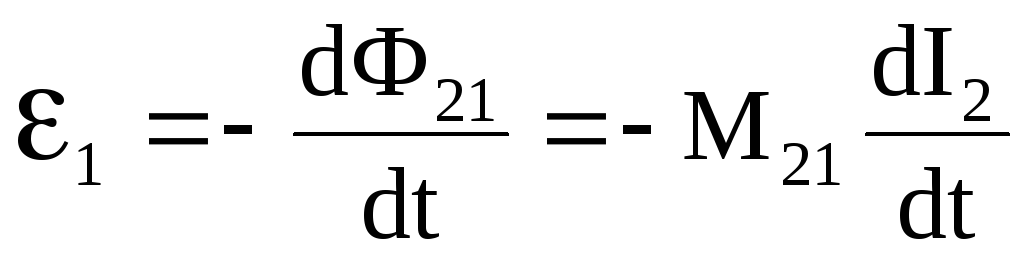, (4.24)

где ₂ и ₁ — возникающие во втором и в первом контурах ЭДС индукции;

и — скорости изменения магнитных потоков через соответствующие контуры.

Взаимная индукция лежит в основе действия трансформаторов.

ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ. ЗАКОН ФАРАДЕЯ И ЕГО ВЫВОД ИЗ ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ.

⇐ ПредыдущаяСтр 15 из 22Следующая ⇒

Рис. 71.

Электромагнитная индукция — это возникновение электрического тока в замкнутом проводящем контуре при изменении потока вектора магнитной индукции, охватываемого этим контуром. Величина индукционного тока не зависит от способа изменения магнитного потока и определяется только скоростью его изменения.

Возникновение индукционного тока указывает на наличие в цепи электродвижущей силы (Э.Д.С. индукции).

E_i = — dФ/dt. (13.1)

Знак минус показывает, что увеличение потока (dФ/dt > 0) вызывает Э.Д.С. Е_i < 0, (13.2)

т.е. поле индукционного тока направлено навстречу потоку. Уменьшение потока (dФ/dt < 0) вызывает

E_i > 0, (13.3)

т.е. направление потока и поля индукционного тока совпадают.

Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.

Если полное сопротивление контура равноR, то, согласно закону сохранения энергии, работа источника тока за времяdt

(E_i.I.dt) (13.4)

будет складываться из работы на джоулеву теплоту

(I².R.dt) (13.5)

и работы по перемещению проводника в магнитном поле (I.dФ):

E_i.I.dt = I².R.dt + I.dФ, (13.6)

откуда

I = [E_i — dФ/dt]/R, (13.7)

где–

dФ/dt = E_i. (13.8)

Рис. 72. Иллюстрация правила Ленца. В этом примере ∆Ф/∆t > 0. а инд < 0. Индукционный ток Iинд течет навстречу выбранному положительному направлению l обхода контура.

Закон Фарадея является универсальным: Э.Д.С. не зависит от способа изменения магнитного потока. Если проводник движется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводником, будет направлена противоположно току, т.е. она будет создавать в проводнике индукционный ток противоположного направления. Возникновение Э.Д.С. индукции при движении контура в постоянном магнитном поле объясняется действием силы Лоренца при движении проводника.

По закону Фарадея, возникновениеЭ.Д.С. электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Cила Лоренца на неподвижные заряды не действует и в этом случае ею нельзя объяснить возникновение Э.Д.С. индукции. Максвелл для объяснения Э.Д.С. индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока. Циркуляция вектораЕ_В этого поля по любому неподвижному контуруL проводника представляет собой Э.Д.С. индукции:

E_i = òE_B.dl = — dФ/dt. (13.9)

Рис. 73. Возникновение ЭДС индукции в движущемся проводнике. Указана составляющая силы Лоренца, действующей на свободный электрон.

Какова природа э.д.с. электромагнитной индукции? Если проводник (подвижная перемычка контура на рис. ) движется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводни­ком, будет направлена противоположно току, т. е. она будет создавать в проводнике индукционный ток противоположного направления (за направление электрического тока принимается движение положительных зарядов). Таким образом, возбуждение э.д.с. индукции при движения контура в постоянном магнитном поле объясняется действием силы Лоренца, возникающей при движении проводника.

 

ВРАЩЕНИЕ РАМКИ В МАГНИТНОМ ПОЛЕ.

Явление электромагнитной индукции применяется для преобразования механической энергии в энергию электрического тока. Для этого используют генераторы, принцип действия которых можно рассмотреть на примере плоской рамки, вращающейся в однородном магнитном поле. Рамка вращается с постоянной угловой скоростью w = const. Магнитный поток, сцепленный с рамкой площадьюS, в момент времениt, равен:

Ф = B_n.S = B.S.cosa = B.S.coswt, (13.10.)

где a = wt — угол поворота рамки в момент времени t. При вращении рамки в ней возникает переменная Э.Д.С. индукции

Е_i = — dФ/dt = B.S.w.sinwt. (13.11.)

При

sinwt = 1, (13.12.)

E_max = B.S.w. (13.13.)

Рис. 74.Модель. Генератор переменного тока.

ВИХРЕВЫЕ ТОКИ (ТОКИ ФУКО).

Индукционный ток возникает в массивных сплошных проводниках, помещенных в переменное магнитное поле. Эти токи оказываются замкнутыми в толще проводника и поэтому называются вихревыми (токами Фуко). Токи Фуко, как и индукционные токи в линейных проводниках подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать изменению магнитного потока, индуцирующего вихревые токи. В электрических машинах, где имеются массивные проводники, токи Фуко вызывают их нагревание, что приводит к потерям энергии. Поэтому массивные цепи электрических машин, якоря динамомашин, сердечники трансформаторов делаются не сплошными, а собираются из отдельных тонких листов, изолированных друг от друга специальным лаком или окалиной и располагаются параллельно линиям магнитной индукции. Токи Фуко образуются в плоскостях, перпендикулярных к линиям магнитной индукции, т.е. перпендикулярных к пластинам трансформатора, что сильно увеличивает их электрическое сопротивление. Для увеличения электрического сопротивления магнитных цепей и сердечников электрических установок используются в качестве материалов магнитодиэлектрики. Токи Фуко находят практическое применение для плавки металлов в индукционных печах. Тормозящим действием токов Фуко пользуются также для устройства магнитных успокоителей (демпферов).

Индукционная печь представляет собой тигель, помещаемый внутрь катушки, в кото­рой пропускается ток высокой частоты. В металле возникают интенсивные вихревые токи, способные разогреть его до плавления. Такой способ позволяет плавить металлы в вакууме, в результате чего получаются сверхчистые материалы.

Направление вихревых токов при возрастании первичного тока в проводнике и при его убывании. В обоих случаях направление вихревых токов таково, что они противодействуют изменению первичного тока внутри проводника и способ­ствуют его изменению вблизи поверхности. Таким образом, вследствие возникновения вихревых токов быстропеременный ток оказывается распределенным по сечению про­вода неравномерно — он как бы вытесняется на поверхность проводника. Это явление получило название скин-эффекта (от англ. skin — кожа) или поверхностного эффекта. Так как токи высокой частоты практически текут в тонком поверхностном слое, то провода для них делаются полыми. Если сплошные проводники нагревать токами высокой частоты, то в результате скин-эффекта происходит нагревание только их поверхностного слоя. На этом основан метод поверхностной закалки металлов. Меняя частоту поля, он позволяет произ­водить закалку на любой требуемой глубине.

ЛЕКЦИЯ № 14.

Рекомендуемые страницы:

§ 123. Закон Фарадея и его вывод из закона сохранения энергии

Обобщая результаты своих многочислен­ных опытов, Фарадей пришел к количе­ственному закону электромагнитной ин­дукции. Он показал, что всякий раз, когда происходит изменение сцепленного с кон­туром потока магнитной индукции, в кон-

194

туре возникает индукционный ток; возник­новение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой элек­тромагнитной индукции. Значение индук­ционного тока, а следовательно, и э. д. с, электромагнитной индукции ξ_i определя­ются только скоростью изменения магнит­ного потока, т. е.

Теперь необходимо выяснить знак ξ_i. В § 120 было показано, что знак магнитно­го потока зависит от выбора положитель­ной нормали к контуру. В свою очередь, положительное направление нормали свя­зано с током правилом правого винта (см. § 109). Следовательно, выбирая опре­деленное положительное направление нор­мали, мы определяем как знак потока маг­нитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими пред­ставлениями и выводами, можно соответ­ственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватыва­емого замкнутым проводящим контуром, возникающая в контуре э.д.с.

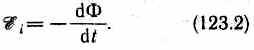
Знак минус показывает, что увеличе­ние потока (dФ/dt>0) вызывает э.д.с.

ξξ_i<0, т. е. поле индукционного тока на­правлено навстречу потоку; уменьшение

потока (dФ/dt<0 ) вызывает ξ_i>0,

т. е. направления потока и поля индукци­онного тока совпадают. Знак минус в фор­муле (123.2) является математическим выражением правила Ленца — общего правила для нахождения направления ин­дукционного тока, выведенного в 1833 г.

Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного по­тока, вызвавшего этот индукционный ток.

Закон Фарадея (см. (123.2)) может быть непосредственно получен из закона сохранения энергии, как это впервые сде­лал Г. Гельмгольц. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное плоско­сти контура, и может свободно переме­щаться (см. рис. 177). Под действием си­лы Ампера F, направление которой пока­зано на рисунке, проводник перемещается на отрезок dx. Таким образом, сила Ампе­ра производит работу (см.(121.1)) dA=IdФ, где dФ — пересеченный проводни­ком магнитный поток.

Если полное сопротивление контура равно R, то, согласно закону сохранения энергии, работа источника тока за вре­мя dt (ξIdt) будет складываться из рабо­ты на джоулеву теплоту (I²Rdt) и работы по перемещению проводника в магнитном поле (IdФ):

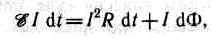
откуда

где-dФ/dt=ξ_i есть не что иное, как закон Фарадея (см. (123.2)).

Закон Фарадея можно сформулиро­вать еще таким образом: э.д.с. ξ_i элек­тромагнитной индукции в контуре числен­но равна и противоположна по знаку ско­рости изменения магнитного потока сквозь поверхность, ограниченную этим конту­ром. Этот закон является универсальным: э.д.с. ξ_i не зависит от способа изменения магнитного потока.

Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим

Какова природа э.д.с. электромагнит­ной индукции? Если проводник (подвиж­ная перемычка контура на рис. 177) дви-

195

жется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводником, будет направлена противо­положно току, т. е. она будет создавать в проводнике индукционный ток противо­положного направления (за направление электрического тока принимается движе­ние положительных зарядов). Таким обра­зом, возбуждение э.д.с. индукции при движении контура в постоянном магнит­ном поле объясняется действием силы Ло­ренца, возникающей при движении про­водника.

Согласно закону Фарадея, возникнове­ние э.д.с. электромагнитной индукции возможно и в случае неподвижного кон­тура, находящегося в переменном магнит­ном поле. Однако сила Лоренца на непод­вижные заряды не действует, поэтому в данном случае ею нельзя объяснить воз­никновение э.д.с. индукции. Максвелл для объяснения э.д.с. индукции в непод­вижных проводниках предположил, что всякое переменное магнитное поле воз­буждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция векто­ра Е_В этого поля по любому неподвижному контуру L проводника представляет собой э.д.с. электромагнитной индукции:

Закон Фарадея и его вывод из закона сохранения энергии — Мегаобучалка

Обобщая результаты своих многочислен­ных опытов, Фарадей пришел к количе­ственному закону электромагнитной ин­дукции. Он показал, что всякий раз, когда происходит изменение сцепленного с кон­туром потока магнитной индукции, в контуре возникает индукционный ток; возник­новение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой элек­тромагнитной индукции.Значение индук­ционного тока, а следовательно, и э. д. с, электромагнитной индукции ξ_iопределя­ются только скоростью изменения магнит­ного потока, т. е.

Теперь необходимо выяснить знак ξ_i. В § 120 было показано, что знак магнитно­го потока зависит от выбора положитель­ной нормали к контуру. В свою очередь, положительное направление нормали свя­зано с током правилом правого винта (см. § 109). Следовательно, выбирая опре­деленное положительное направление нор­мали, мы определяем как знак потока маг­нитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими пред­ставлениями и выводами, можно соответ­ственно прийти к формулировке закона электромагнитной индукции Фарадея:какова бы ни была причина изменения потока магнитной индукции, охватыва­емого замкнутым проводящим контуром, возникающая в контуре э.д.с.

Знак минус показывает, что увеличе­ние потока (dФ/dt>0) вызывает э.д.с.

ξξ_i<0, т. е. поле индукционного тока на­правлено навстречу потоку; уменьшение

потока (dФ/dt<0 ) вызывает ξ_i>0,

т. е. направления потока и поля индукци­онного тока совпадают. Знак минус в фор­муле (123.2) является математическим выражением правила Ленца — общего правила для нахождения направления ин­дукционного тока, выведенного в 1833 г.

Правило Ленца:индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного по­тока, вызвавшего этот индукционный ток.

Закон Фарадея (см. (123.2)) может быть непосредственно получен из закона сохранения энергии, как это впервые сде­лал Г. Гельмгольц. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное плоско­сти контура, и может свободно переме­щаться (см. рис. 177). Под действием си­лы Ампера F, направление которой пока­зано на рисунке, проводник перемещается на отрезок dx. Таким образом, сила Ампе­ра производит работу (см.(121.1)) dA=IdФ, где dФ — пересеченный проводни­ком магнитный поток.

Если полное сопротивление контура равно R, то, согласно закону сохранения энергии, работа источника тока за вре­мя dt (ξIdt) будет складываться из рабо­ты на джоулеву теплоту (I²Rdt) и работы по перемещению проводника в магнитном поле (IdФ):

откуда

где-dФ/dt=ξ_iесть не что иное, как закон Фарадея (см. (123.2)).

Закон Фарадеяможно сформулиро­вать еще таким образом: э.д.с. ξ_i элек­тромагнитной индукции в контуре числен­но равна и противоположна по знаку ско­рости изменения магнитного потока сквозь поверхность, ограниченную этим конту­ром. Этот закон является универсальным: э.д.с. ξ_iне зависит от способа изменения магнитного потока.

Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер(Вб), получим

Какова природа э.д.с. электромагнит­ной индукции? Если проводник (подвиж­ная перемычка контура на рис. 177) движется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводником, будет направлена противо­положно току, т. е. она будет создавать в проводнике индукционный ток противо­положного направления (за направление электрического тока принимается движе­ние положительных зарядов). Таким обра­зом, возбуждение э.д.с. индукции при движении контура в постоянном магнит­ном поле объясняется действием силы Ло­ренца, возникающей при движении про­водника.

Согласно закону Фарадея, возникнове­ние э.д.с. электромагнитной индукции возможно и в случае неподвижного кон­тура, находящегося в переменном магнит­ном поле. Однако сила Лоренца на непод­вижные заряды не действует, поэтому в данном случае ею нельзя объяснить воз­никновение э.д.с. индукции. Максвелл для объяснения э.д.с. индукции в непод­вижных проводниках предположил, что всякое переменное магнитное поле воз­буждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция векто­ра Е_Вэтого поля по любому неподвижному контуру L проводника представляет собой э.д.с. электромагнитной индукции:

Закон Фарадея и его вывод из закона сохранения энергии — КиберПедия

Обобщая результаты своих многочислен­ных опытов, Фарадей пришел к количе­ственному закону электромагнитной ин­дукции. Он показал, что всякий раз, когда происходит изменение сцепленного с кон­туром потока магнитной индукции, в контуре возникает индукционный ток; возник­новение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой элек­тромагнитной индукции.Значение индук­ционного тока, а следовательно, и э. д. с, электромагнитной индукции ξ_iопределя­ются только скоростью изменения магнит­ного потока, т. е.

Теперь необходимо выяснить знак ξ_i. В § 120 было показано, что знак магнитно­го потока зависит от выбора положитель­ной нормали к контуру. В свою очередь, положительное направление нормали свя­зано с током правилом правого винта (см. § 109). Следовательно, выбирая опре­деленное положительное направление нор­мали, мы определяем как знак потока маг­нитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими пред­ставлениями и выводами, можно соответ­ственно прийти к формулировке закона электромагнитной индукции Фарадея:какова бы ни была причина изменения потока магнитной индукции, охватыва­емого замкнутым проводящим контуром, возникающая в контуре э.д.с.

Знак минус показывает, что увеличе­ние потока (dФ/dt>0) вызывает э.д.с.

ξξ_i<0, т. е. поле индукционного тока на­правлено навстречу потоку; уменьшение

потока (dФ/dt<0 ) вызывает ξ_i>0,

т. е. направления потока и поля индукци­онного тока совпадают. Знак минус в фор­муле (123.2) является математическим выражением правила Ленца — общего правила для нахождения направления ин­дукционного тока, выведенного в 1833 г.

Правило Ленца:индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного по­тока, вызвавшего этот индукционный ток.

Закон Фарадея (см. (123.2)) может быть непосредственно получен из закона сохранения энергии, как это впервые сде­лал Г. Гельмгольц. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное плоско­сти контура, и может свободно переме­щаться (см. рис. 177). Под действием си­лы Ампера F, направление которой пока­зано на рисунке, проводник перемещается на отрезок dx. Таким образом, сила Ампе­ра производит работу (см.(121.1)) dA=IdФ, где dФ — пересеченный проводни­ком магнитный поток.

Если полное сопротивление контура равно R, то, согласно закону сохранения энергии, работа источника тока за вре­мя dt (ξIdt) будет складываться из рабо­ты на джоулеву теплоту (I²Rdt) и работы по перемещению проводника в магнитном поле (IdФ):

откуда

где-dФ/dt=ξ_iесть не что иное, как закон Фарадея (см. (123.2)).

Закон Фарадеяможно сформулиро­вать еще таким образом: э.д.с. ξ_i элек­тромагнитной индукции в контуре числен­но равна и противоположна по знаку ско­рости изменения магнитного потока сквозь поверхность, ограниченную этим конту­ром. Этот закон является универсальным: э.д.с. ξ_iне зависит от способа изменения магнитного потока.

Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер(Вб), получим

Какова природа э.д.с. электромагнит­ной индукции? Если проводник (подвиж­ная перемычка контура на рис. 177) движется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводником, будет направлена противо­положно току, т. е. она будет создавать в проводнике индукционный ток противо­положного направления (за направление электрического тока принимается движе­ние положительных зарядов). Таким обра­зом, возбуждение э.д.с. индукции при движении контура в постоянном магнит­ном поле объясняется действием силы Ло­ренца, возникающей при движении про­водника.

Согласно закону Фарадея, возникнове­ние э.д.с. электромагнитной индукции возможно и в случае неподвижного кон­тура, находящегося в переменном магнит­ном поле. Однако сила Лоренца на непод­вижные заряды не действует, поэтому в данном случае ею нельзя объяснить воз­никновение э.д.с. индукции. Максвелл для объяснения э.д.с. индукции в непод­вижных проводниках предположил, что всякое переменное магнитное поле воз­буждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция векто­ра Е_Вэтого поля по любому неподвижному контуру L проводника представляет собой э.д.с. электромагнитной индукции:

Закон Фарадея и его вывод из закона сохранения энергии

Явление электромагнитной индукции.

 

В гл. 3 было показано, что электрические токи создают вокруг себя магнитное поле. Связь магнитного поля с током привела к многочисленным попыткам возбудить ток в контуре с помощью магнитного поля. Эта фундаментальная задача была блестяще решена в 1831 г. английским физиком М. Фарадеем, открывшим явление электромагнитной индукции, заключающееся в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.

Опытным – путем было также установлено, что значение индукционного тока совершенно не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения.

Открытие явления электромагнитной индукции имело большое значение, так как была доказана возможность получения электрического тока с помощью магнитного поля. Этим была установлена взаимосвязь между электрическими и магнитными явлениями, что послужило в дальнейшем толчком для разработки теории электромагнитного поля.

Обобщая результаты своих многочисленных опытов, Фарадей пришел к количественному закону электромагнитной индукции.

Закон электромагнитной индукции Фарадея:

(4.1)

Знак минус показывает, что увеличение потока вызывает э. д. с. , т. е. магнитное поле индукционного тока направлено навстречу потоку; уменьшение потока вызывает т. е. направления потока и поля индукционного тока совпадают. Знак минус в формуле (4.1) является математическим выражением правила Ленца общего правила для нахождения направления индукционного тока, выведенного в 1833 г.

Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток. Закон Фарадея может быть непосредственно получен из закона сохранения энергии, как это впервые сделал Г. Гельмгольц. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное плоскости контура, и может свободно перемещаться (рис. 4.1). Под действием силы Ампера , направление которой показано на рисунке, проводник перемещается на отрезок dx. Таким образом, сила Ампера производит работу , где – пересеченный проводником магнитный поток.

Если полное сопротивление контура равно R, то, согласно закону сохранения энергии, работа источника тока за время будет складываться из работы на джоулеву теплоту и работы по перемещению проводника в магнитном поле :

откуда

где есть не что иное, как закон Фарадея.

Закон Фарадеяможно сформулировать еще таким образом: э. д. с. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: э. д. с. не зависит от способа изменения магнитного потока.

Э. д. с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим

Какова природа э. д. с. электромагнитной индукции? Если проводник (подвижная перемычка контура на рис. 4.1) движется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводником, будет направлена противоположно току, т. е. она будет создавать в проводнике индукционный ток противоположного направления (за направление электрического тока принимается движение положительных зарядов). Таким образом, возбуждение э. д. с. индукции при движении контура в постоянном магнитном поле объясняется действием силы Лоренца, возникающей при движении проводника.

Согласно закону Фарадея, возникновение э. д. с. электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае ею нельзя объяснить возникновение э. д. с. индукции. Максвелл для объяснения э. д. с. индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция вектора Е_В этого поля по любому неподвижному контуру L проводника представляет собой э. д. с. электромагнитной индукции:

(4.2)

Читайте также:

Рекомендуемые страницы:

Поиск по сайту