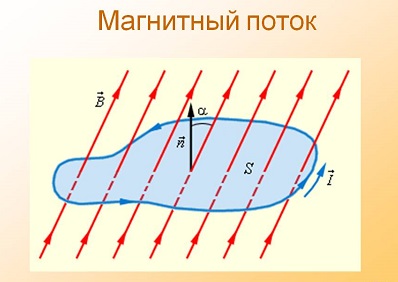
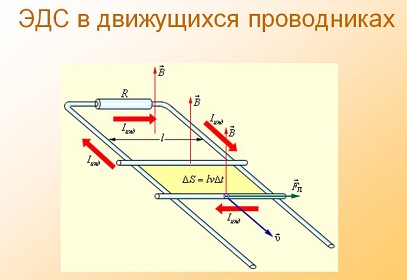
Формула закона электромагнитной индукции

Это основной закон, который используют при вычислениях, которые связаны с электромагнитной индукцией.

Формула данного закона выглядит следующим образом:

   

где – электродвижущая сила (ЭДС) индукции, которая возникает в проводнике, если он находится в переменном магнитном поле. Если проводящим телом является, например, замкнутый контур, то в нем течет электрический ток, который называют током индукции. – магнитный поток, через поверхность, ограниченную этим контуром. Формула (1) означает то, что ЭДС индукции равна по модулю и противоположна по знаку скорости изменения магнитного потока через некоторую поверхность.

Магнитный поток, который пронизывает контур, может изменяться из-за разных причин, например, перемещения контура, его деформации, изменения самого магнитного поля. Полная производная в формуле закона электромагнитной индукции охватывает весь спектр действия этих причин.

Следует учесть, что из конца вектора нормали к контуру обход контура должен проходить против часовой стрелки.

Знак минус в законе индукции отражает правило Ленца.

В виде (1), закон электромагнитной индукции записывается в международной системе единиц (СИ).

Если изменение магнитного потока происходит равномерно, то формулу закона электромагнитной индукции можно записать как:

   

Формулу закона для электромагнитной индукции, если контур состоит из N витков, соединенных последовательно, записывают в виде:

   

где – потокосцепление.

Результаты применения основного закона электромагнитной индукции

Формулы ЭДС индукции для частных случаев

ЭДС индукции в прямом проводнике, имеющем длину l, движущемся в магнитном поле и пересекающем линии магнитной индукции, если скорость его движения () перпендикулярна вектору магнитной индукции (), равна:

   

Разность потенциалов (U), возникающая на концах проводника длиной l, движущегося в однородном магнитном поле со скоростью v равна:

   

где – угол между направлением вектора скорости и направлением вектора магнитной индукции.

Если в однородном магнитном поле вращается плоский контур со скоростью , при этом ось вращения находится в плоскости витка и составляет угол в 900 с направлением вектора внешнего магнитного поля, то в контуре появляется ЭДС индукции равная:

   

где S – площадь, которую ограничивает виток; – мгновенное значение угла между и вектором нормали к плоскости рамки; – поток самоиндукции витка.

Если в рамке, вращающейся со скоростью в однородном магнитном поле, имеется N витков, то

   

в формуле (6) самоиндукцией витков пренебрегли.

Пусть проводник находится в покое, при этом изменяется во времени само магнитное поле, тогда ЭДС индукции можно найти как:

   

Примеры решения задач по теме «Закон электромагнитной индукции»

Закон электромагнитной индукции — Класс!ная физика

Закон электромагнитной индукции

«Физика — 11 класс»

Опыты Фарадея показали, что сила индукционного тока I_i в проводящем контуре пропорциональна скорости изменения числа линий магнитной индукции , пронизывающих поверхность, ограниченную этим контуром, т.е. скорости изменения магнитного потока.

ЭДС индукции

В цепи появляется электрический ток, когда на свободные заряды проводника действуют сторонние силы.
Величину, численно равную работе этих сил при перемещении единичного положительного заряда вдоль замкнутого контура, называют электродвижущей силой (ЭДС).

При изменении магнитного потока через поверхность, ограниченную контуром, в контуре появляются сторонние силы, действие которых характеризует ЭДС индукции.
Обозначение ЭДС индукции — .

Согласно закону Ома для замкнутой цепи индукционный ток в контуре

Закон электромагнитной индукции.

ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.

Как в законе электромагнитной индукции учесть направление индукционного тока (или знак ЭДС индукции) в соответствии с правилом Ленца?

Пусть положительное направление обхода контура — против часовой стрелки.
Нормаль к контуру образует правый винт с направлением обхода.

Если магнитная индукция В внешнего магнитного поля направлена вдоль нормали к контуру и возрастает со временем.
Тогда магнитный поток Ф > 0 и скорость измененеия магнитного потока тоже > 0.
По правилу Ленца индукционный ток создает магнитный поток Ф’ меньше 0.

Индукционный ток I_i по правилу буравчика направлен по часовой стрелке (против направления положительного обхода).
ЭДС индукции отрицательна.
Поэтому в формуле для закона электромагнитной индукции должен стоять знак «-»,
указывающий на то, что ЭДС индукции и скорость изменения магнитного потока имеют разные знаки:

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитная индукция. Физика, учебник для 11 класса — Класс!ная физика

Электромагнитная индукция. Магнитный поток — Направление индукционного тока. Правило Ленца — Закон электромагнитной индукции — ЭДС индукции в движущихся проводниках. Электродинамический микрофон — Вихревое электрическое поле — Самоиндукция. Индуктивность. Энергия магнитного поля тока — Электромагнитное поле — Примеры решения задач — Краткие итоги главы

Закон электромагнитной индукции. Правило Ленца

В 1831 году английский ученый физик в своих опытах М.Фарадей открыл явление электромагнитной индукции. Затем изучением этого явления занимались русские ученый Э.Х. Ленц и Б.С.Якоби.

В настоящее время, в основе многих устройств лежит явление электромагнитной индукции, например в двигателе или генераторе электрического тока тока, в трансформаторах, радиоприемниках, и многих других устройствах.

Электромагнитная индукция — это явление возникновения тока в замкнутом проводнике, при прохождении через него магнитного потока. То есть, благодаря этому явлению мы можем преобразовывать механическую энергию в электрическую — и это замечательно. Ведь до открытия этого явления люди не знали о методах получения электрического тока, кроме гальваники.

Когда проводник оказывается под действием магнитного поля, в нем возникает ЭДС, которую количественно можно выразить через закон электромагнитной индукции.

Закон электромагнитной индукции

Электродвижущая сила, индуцируемая в проводящем контуре, равна скорости изменения магнитного потока, сцепляющегося с этим контуром. 

В катушке, которая имеет несколько витков, общая ЭДС зависит от количества витков n: 

Но в общем случае, применяют формулу ЭДС с общим потокосцеплением: 

ЭДС возбуждаемая в контуре, создает ток. Наиболее простым примером появления тока в  проводнике является катушка, через которую проходит постоянный магнит. Направление индуцируемого тока можно определить с помощью

правила Ленца.

 

Правило Ленца

Ток, индуцируемый при изменении магнитного поля проходящего через контур, своим магнитным полем препятствует этому изменению.

 

В том случае, когда мы вводим магнит в катушку, магнитный поток в контуре увеличивается, а значит магнитное поле, создаваемое индуцируемым током, по правилу Ленца, направлено против увеличения поля магнита. Чтобы определить направление тока, нужно посмотреть на магнит со стороны северного полюса. С этой позиции мы будем вкручивать буравчик по направлению магнитного поля тока, то есть навстречу северному полюсу. Ток будет двигаться по направлению вращения буравчика, то есть по часовой стрелке.

В том случае, когда мы выводим магнит из катушки, магнитный поток в контуре уменьшается, а значит магнитное поле, создаваемое индуцируемым током, направлено против уменьшения поля магнита. Чтобы определить направление тока, нужно выкручивать буравчик, направление вращения буравчика укажет направление тока в проводнике – против часовой стрелки.

Рекомендуем к прочтению — закон Ампера 

Просмотров: 13724

Закон электромагнитной индукции. Курсы по физике

Тестирование онлайн

• Электромагнитная индукция. Основные понятия

• Закон электромагнитной индукции

ЭДС индукции в движущемся проводнике

Взаимосвязь электрических и магнитных явлений всегда интересовала физиков. Английский физик Майкл Фарадей был совершенно уверен в единстве электрических и магнитных явлений. Он рассуждал, что электрический ток способен намагнитить кусок железа. Не может ли магнит в свою очередь вызвать появление электрического тока? Эта задача была решена.

Если в постоянном магнитном поле перемещается проводник, то свободные электрические заряды внутри него тоже перемещаются (на них действует сила Лоренца). Положительные заряды концентрируются в одном конце проводника (провода), отрицательные — в другом. Возникает разность потенциалов —

ЭДС электромагнитной индукции. Явление возникновения ЭДС индукции в проводнике, движущемся в постоянном магнитном поле, называется явлением электромагнитной индукции.

Правило определения направления индукционного тока (правило правой руки):

В проводнике, движущемся в магнитном поле, возникает ЭДС индукции, энергия тока в этом случае определяется по закону Джоуля-Ленца:

Работа внешней силы по перемещению проводника с током в магнитном поле

ЭДС индукции в контуре

Рассмотрим изменение магнитного потока через проводящий контур (катушку). Явление электромагнитной индукции было открыто опытным путем:

Закон электромагнитной индукции (закон Фарадея): ЭДС электромагнитной индукции, возникающая в контуре, прямо пропорциональна скорости изменения магнитного потока через него.

Знак «минус» является математическим выражением следующего правила. Направление индукционного тока, возникающего в контуре, определяется по правилу Ленца: возникающий в контуре индукционный ток имеет такое направление, что созданный им магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.

4. Явление электромагнитной индукции. Основной законэлектромагнитной индукции. Правило (закон) Ленца. Самоиндукция. Энергия магнитного поля. Объемная плотность энергии магнитного поля.

Электромагнитная индукция – возникновение электродвижущей силы (эдс индукции) в проводящем контуре, находящемся в переменном магнитном поле или движущимся в постоянном магнитном поле.

ЭДС возникающую в проводниках при изменении магнитного потока называют электродвижущей силой (ЭДС) электромагнитной индукции E_i, а ток в замкнутом проводнике – индукционным. ЭДС электромагнитной индукции является распределенной в отличие от ЭДС источника тока, которую называют сосредоточенной.

Основной закон электромагнитной индукции (закон Фарадея):

«При пересечении потока магнитной индукции отрезком проводника в последнем возникает ЭДС электромагнитной индукции, прямо пропорциональная скорости изменения величины магнитного потока.»

E_i,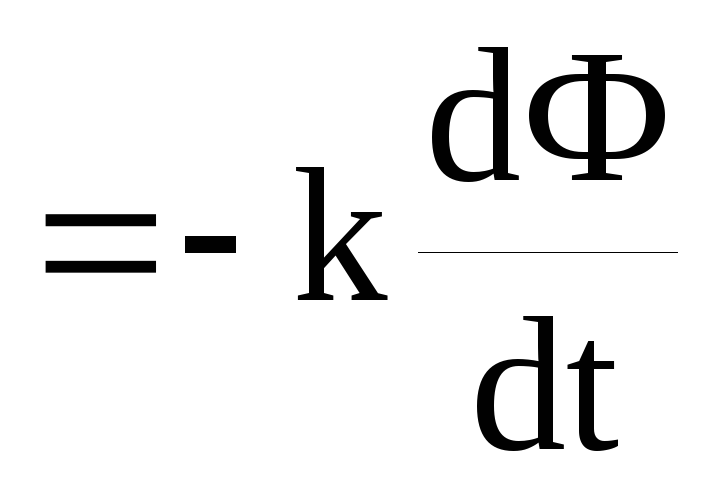

где k – коэффициент пропорциональности, зависящий от выбора системы единиц измерения физических величин;

dФ/dt – скорость изменения магнитного потока.

В системе СИ k=1значитE_i =-

Правило Ленца: «Индукционный ток всегда направлен так, чтобы своим действием препятствовать причине его порождающей или индукционный ток направлен так, что создаваемое им поле препятствует изменению магнитного потока».

Дифференциальная форма закона электромагнитной индукции

rotE=-dB/dt.

Самоиндукция – явление возникновения ЭДС электромагнитной индукции в каком-либо контуре вследствие изменения магнитного потока, создаваемого электрическим током этого контура.

Величина ЭДС самоиндукции определяется по общей формуле, выражающей основной закон электромагнитной индукции

E_с=-dФ/dt.

ЭДС самоиндукции, возникающая в бесконечно длинном соленоиде



где L= ₀n²S=₀n²V=(₀N²S)/– коэффициент самоиндукции или индуктивность соленоида.

Индуктивность L зависит от формы, размеров проводника и магнитной проницаемости среды, окружающей проводник.

При di/dt=1 А/с: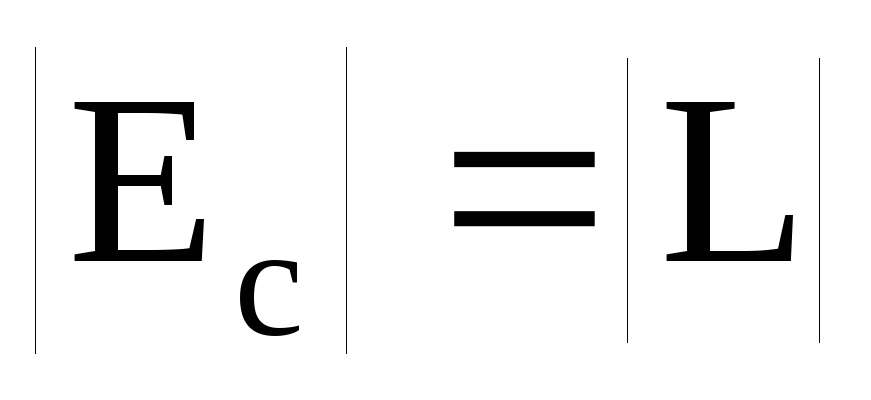

Индуктивность (коэффициент индуктивности) – физическая величина, численно равная ЭДС самоиндукции, возникающей в проводнике при скорости изменения тока в нем равной 1 А/с.

При L=const E_с=-Ldi/dt.

Если L const, что возможно при=f(H)



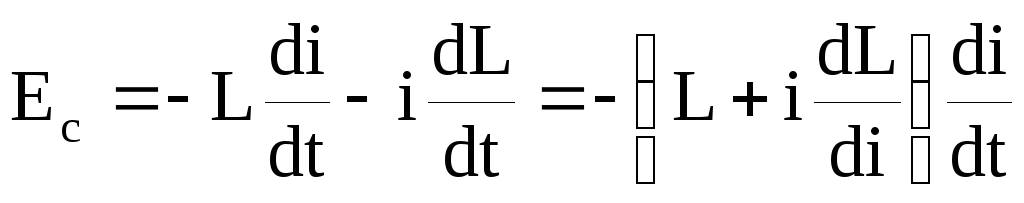
Связь потока магнитной индукции с током в проводнике

Ф=Li.

Взаимная индукция, явление, в котором обнаруживается магнитная связь двух или более электрических цепей. Благодаря этой связи возникает ЭДС индукции в одном из контуров при изменении тока в другом. Количественной характеристикой магнитной связи электрических цепей является взаимная индуктивность.

При включении источника с ЭДС Eв цепь, состоящую из сопротивления R и соленоида с индуктивностью L, которые соединены последовательно, сила тока в цепи возрастает согласно закону

i=E/R-E/Rexp(-Rt/L)=E/R[1-exp(-Rt/L)],

т.е. ток постепенно возрастает от i=0 до i=E/R при t.

При выключении постоянного источника сторонних ЭДС, сила тока уменьшается согласно уравнению:

i(t)=E/R[exp(-Rt/L)].

За время нарастания, убывания силы тока в цепи принять такое значение t, при котором показатель экспоненты обращается в минус единицу, т.е. t=L/R.

Закон Ома, при наличии в цепи конденсатора и сопротивления, записывается в виде уравнения IR=U₀-q/C,

где q – заряд на обкладке конденсатора;

q/C – разность потенциалов между обкладками конденсатора.

При выключении постоянной ЭДС из цепи, с емкостью и сопротивлением, изменение тока в цепи подчиняется уравнению

,

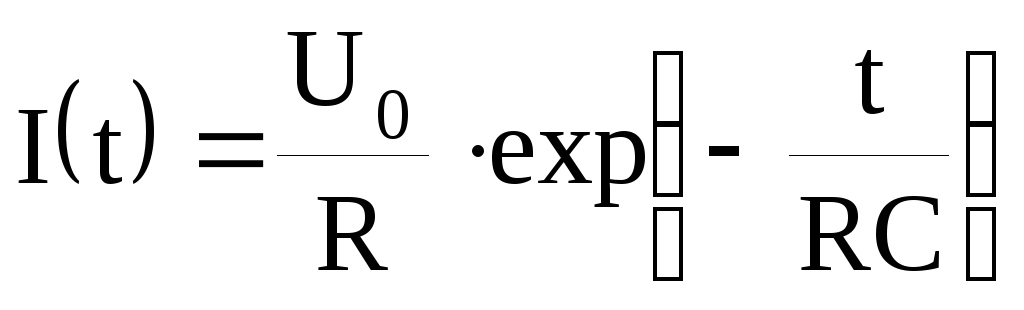при включении

.

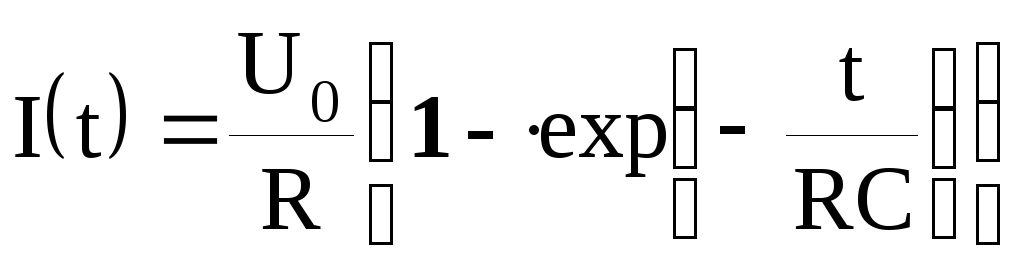Время убывания, возрастания тока в цепи определяется соотношением

t=RC.

В общем случае, когда цепь состоит из емкости C, индуктивности L, сопротивления R и источника тока с ЭДС E, уравнение для тока в цепи имеет вид



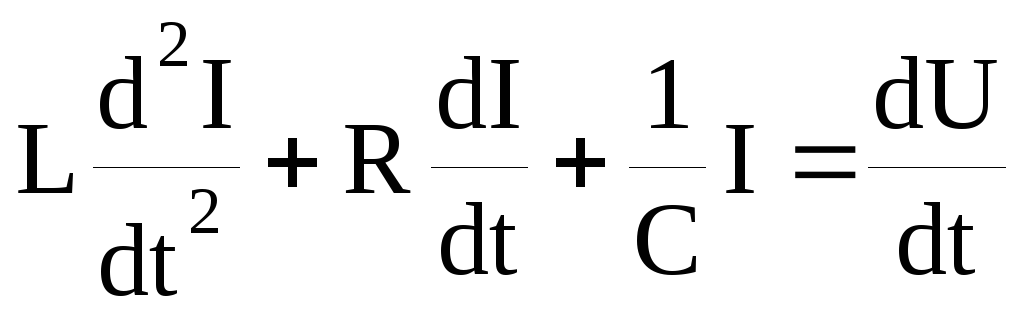
Энергия магнитного поля: W=.

Энергия магнитного поля двух контуров с током



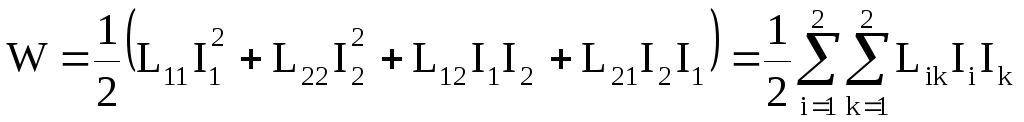
В случае N контуров:



где L_ik– при i=k называется индуктивностью i-го контура, а при ik – взаимной индуктивностью i-го и k-го контуров.

Величину Lik можно определить по формуле



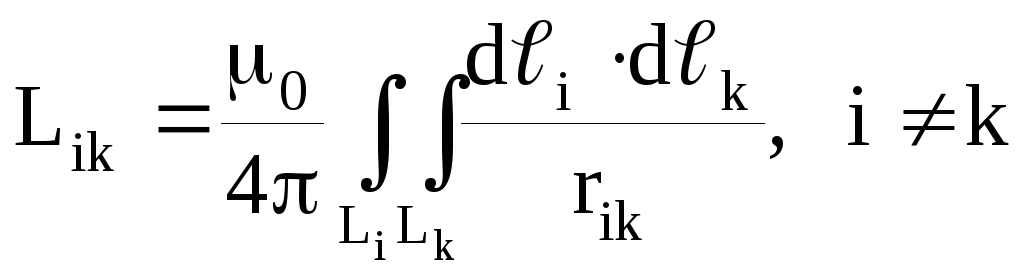
где d_i, d_k– элементы i-го и k-го контуров;

r_ik– расстояние между ними.

Энергия магнитного поля соленоида



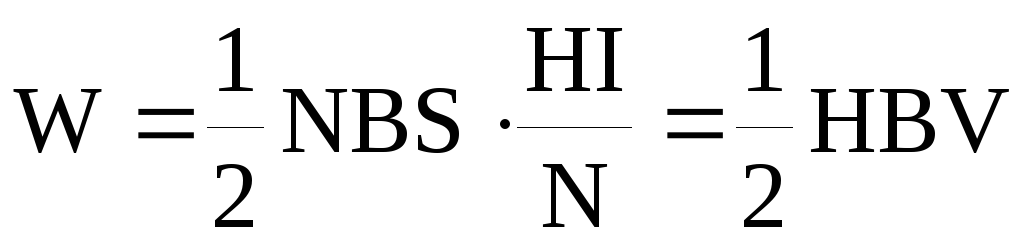
где V=S– объем соленоида, заполненный однородным магнитным полем.

Объемная плотность энергии магнитного поля – энергия поля отнесенная к его объему, т.е. объёмная плотность энергии магнитного поля – физическая величина, которая показывает, какой энергией обладает магнитное поле, занимающее единицу объема пространства:

w_o=W/V.

Объемная плотность магнитного поля длинного соленоида



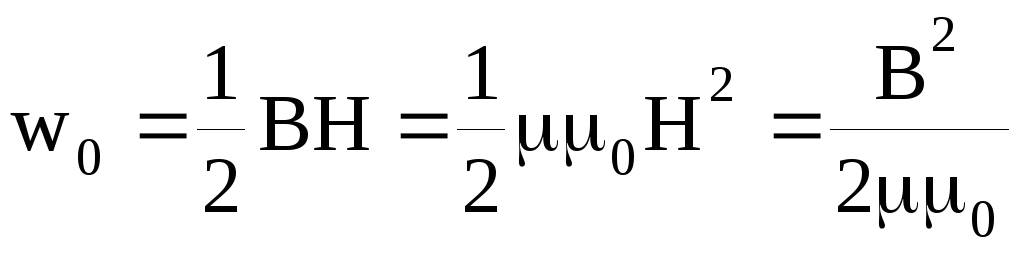
В неоднородном магнитном поле, энергия dW магнитного поля элемента объема dV, равна:

dW=w_odV.

Энергию неоднородного магнитного поля, занимающего какой-либо объем пространства, можно определить по формуле:



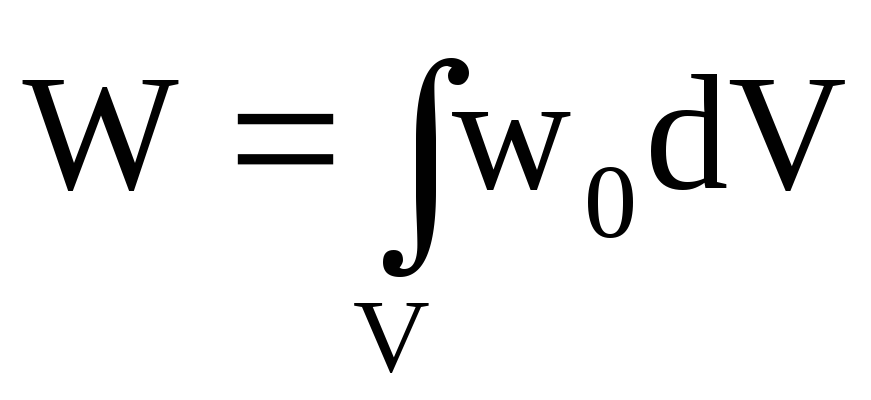
4.1. Примеры решения задач.

4.1.1. В однородном магнитном поле с индукцией 10,010^-2Тл расположена прямоугольная рамка (контур) abcd, подвижная сторона которой ad длиной==0,10 м перемещается со скоростью v=25 м/с перпендикулярно линиям индукции поля. Определить ЭДС индукции, возникающую в контуре.

Решение. При движении проводника ad площадь рамки увеличивается, магнитный поток Ф сквозь рамку возрастает, а значит, согласно закону Фарадея, в рамке должна при этом возникать ЭДС индукции. Чтобы ее определить, сначала выразим магнитный поток Ф через индукцию поля B и стороны рамки, x (x – расстояние от bc до ad. Согласно формуле



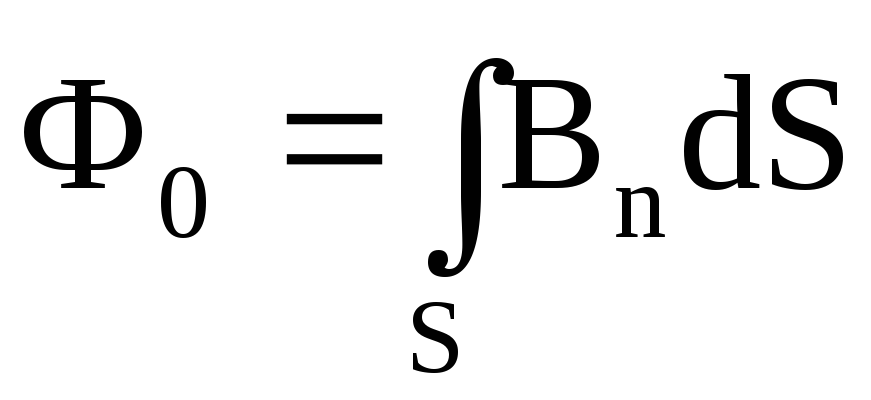
имеем Ф=BS=Bx.

Подставив это значение Ф в формулу E=– dФ/dt и учитывая, что B,– величины постоянные, запишем

E=– dФ/dt=-Bl(dx/dt),

где v=dx/dt – скорость перемещения проводника ad. Поэтому

E=-Blv. (1)

Размерность полученного результата очевидна.

Сделав подстановку числовых значений величин B, , v (все даны в единицах системы СИ), получим ответ

E=– 10,010^-20,1025=-2,510^-2В.

Ответ: E=-2,510^-2В.

Знак «минус» в формуле (1) показывает, что ЭДС индукции действует в контуре в таком направлении, при котором связанная с ним правилом правого винта нормаль к контуру противоположна вектору B. Отсюда заключаем, что и индукционный ток направлен в данном контуре против часовой стрелки. К такому же результату придем, применив правило правой руки для проводника ad.

Заметим, что если бы проводник ad двигался влево, то положительному приращению времени соответствовало бы отрицательное приращение (убыль) величины x. В этом случае индукционный ток направлен по часовой стрелке.

Замечание. При решении задачи допущена неточность: не принималось в расчет магнитное поле, созданное индукционным током. Это поле образует некоторый поток Ф’ сквозь рамку. При движении проводника ad поток Ф’ изменяется, что приводит к появлению дополнительной ЭДС Очевидно, что этот эффект тем слабее, чем меньше сила тока. Поскольку она обратно пропорциональна сопротивлению цепи, можно утверждать, что решение задачи верно при условии достаточно большого сопротивления цепи.

4.1.2.Короткая катушка, содержащая N=10³витков, равномерно вращается с частотой n=10 с^-1относительно оси АВ, лежащей в плоскости катушки и перпендикулярной линиям однородного магнитного поля (B=0,04 Тл). Определить мгновенное значение ЭДС индукции для тех моментов времени, когда плоскость катушки составляет угол=60⁰c линиями поля. Площадь катушки S=100 см².

Решение. Мгновенное значение ЭДС индукцииE_iопределяется основным уравнением электромагнитной индукции Фарадея-Максвелла

E_i=-d/dt, (1)

где =NФ – потокосцепление;

N – число витков катушки;

Ф – магнитный поток, пронизывающий каждый виток катушки.

Подставив выражение в формулу (1), получим

E_i=-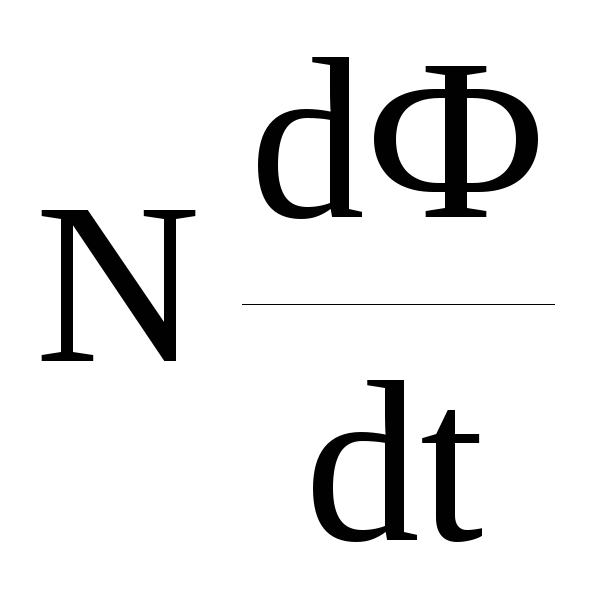. (2)

При вращении катушки магнитный поток Ф, пронизывающий катушку в момент времени t, изменяется по закону

Ф=BScost

где B – индукция магнитного поля

S-площадь сечения катушки

 – угловая скорость вращения

Подставив в формулу (2) выражение магнитного потока Ф и продифференцировав по временинайдём мгновенное значение ЭДС индукции

E_i=NBSsint

Заметив, что угловая скорость связана с частотой вращения n катушки соотношением=2n и что уголt=/2 –, получим (учтено, что sin(/2 –)==cos)

E_i=2nNBS.cos. (3)

Выразив величины, входящие в полученное соотношение, в единицах системы СИ, подставив их в формулу (3), и выполнив вычисление, получим

E_i=23,141010³0,0410^-20,5=25 В.

Ответ: E_i=25 В.

4.1.3. Квадратная проволочная рамка со стороной а=5 см и сопротивлением R=10 мОм находится в однородном магнитном поле (B=40 мТл). Нормаль к плоскости рамки составляет угол=30⁰с линиями магнитной индукции. Определить заряд, который пройдет по рамке, если выключить магнитное поле.

Решение. При выключении магнитного поля произойдет изменение магнитного потока. Вследствие этого в рамке возникнет ЭДС индукции, определяемая основным законом электромагнитной индукции

E_i=-dФ/dt.

Возникшая ЭДС индукции вызовет в рамке индукционный ток, мгновенное значение которого можно определить воспользовавшись законом Ома для полной цепи I_i=E_i/R,

где R – сопротивление рамки.

Тогда 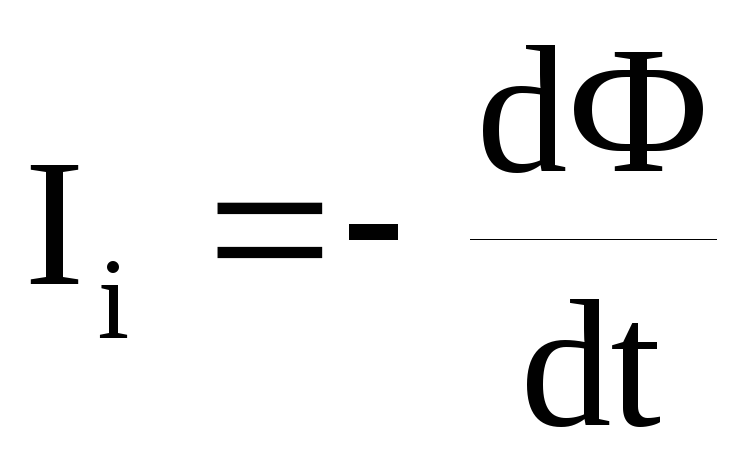(1)

Так как мгновенное значение силы индукционного тока I_i=dQ/dt, то выражение (1) можно переписать в виде

,

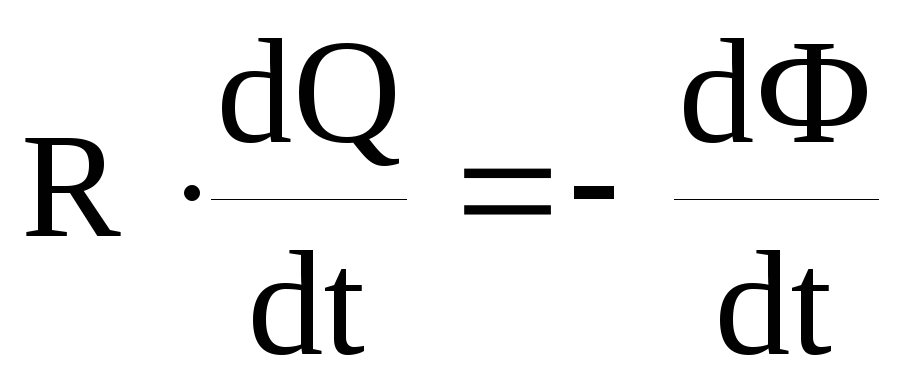откуда dQ=– dФ/R. (2)

Проинтегрировав (2), найдем

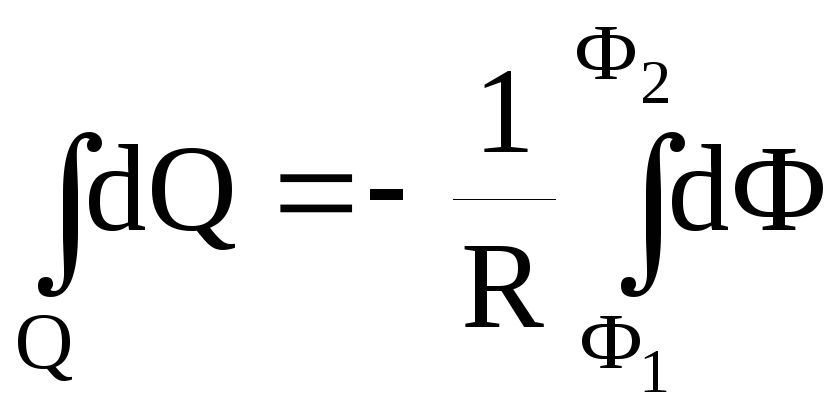
 тогда Q=(Ф₁-Ф₂)/R

Заметив, что при выключенном поле (конечное состояние) Ф₂=0, последнее равенство перепишем в виде

Q=Ф₁/R. (3)

Найдем магнитный поток Ф₁. По определению магнитного потока имеем

Ф₁=BScos,

где S – площадь рамки.

В нашем случае (рамка квадратная) S=а².

Тогда

Ф₁=Bа²cos. (4)

Подставив (4) в (3), получим

Q=(Bа²cos)/R.

Выразив величины, входящие в полученное соотношение, в единицах системы СИ, подставив их, и выполнив вычисление, получим



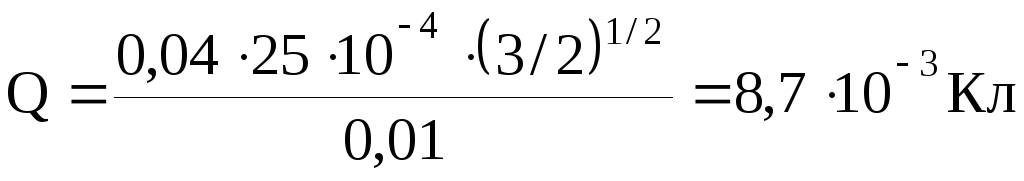
Ответ: Q=8,710^-3Кл.

4.1.4. В однородном магнитном поле с индукцией B вращается в плоскости, перпендикулярной линиям индукции, медный диск радиуса r, совершая n оборотов в секунду. При помощи скользящих контактов диск подключен к цепи, сопротивление которой R. Определить ЭДС индукции, возникающую при вращении диска, количество электричества q, протекающего по цепи, а также количество теплоты Q, выделенное в цепи за время, в течение которого диск совершил N оборотов.

Решение. При вращении диска в магнитном поле в контуре abcd, состоящем из цепи с сопротивлением R возникает индукционный ток, а значит, возникает ЭДС электромагнитной индукции. Так как магнитный поток сквозь этот контур не меняется, то, следовательно, закон Фарадея для электромагнитной индукции не может дать правильного результата. При движении проводников в магнитном поле закон Фарадея применяется лишь для контура, проходящего через одни и те же точки движущегося проводника. Здесь же участок контура проходит все время через различные радиусы вращающегося диска.

В контуре должна возникать ЭДС, так как один из его участков, например ad, представляет собой движущийся проводник, и поэтому на его свободные электроны, движущиеся вместе с диском, действуют силы Лоренца. Эти силы будут перемещать электроны относительно диска от точки a к точке d. Поэтому, чтобы найти ЭДС индукции, воспользуемся формулой определяющей любую ЭДС

E=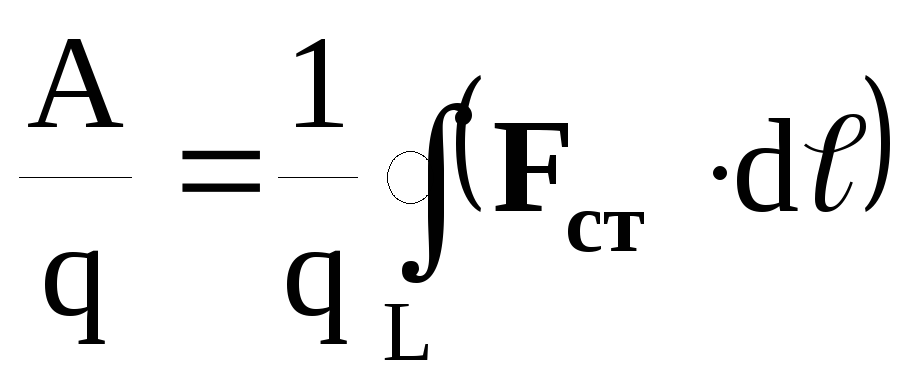

В данном случае в качестве сторонней силы, действующей только на участке ad, выступает сила Лоренца, численное значение которой равно:

F_л=еvBsina=еvB,

где е – заряд электрона.

E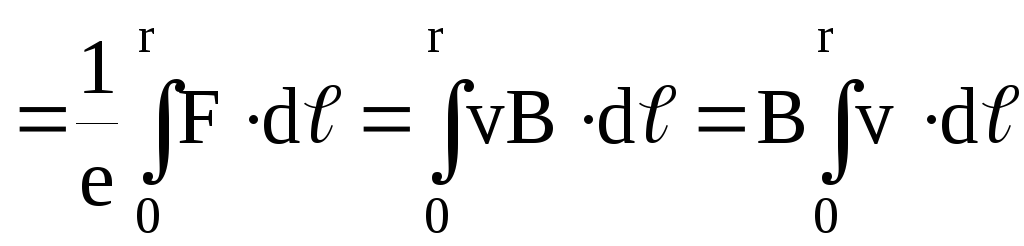(1)

Интегрирование проводится не по замкнутому контур L, а только по длине участка ad, которая меняется от нуля до r.

Находясь в различных точках участка ad, электроны имеют разную линейную скорость v, но одинаковую угловую скорость . Для электрона, находящегося на расстоянииот центра диска, v==2n.

Подставив это значение v в формулу (1), получим

E. (2)

Таким образом, при равномерном вращении диска, в цепи действует постоянная ЭДС, создавая в ней постоянный ток.

Количество электричества q, перемещенное индукционным током, определяется формулой q=-Ф/R.

Однако последняя формула имеет смысл только в тех же случаях, что и закон Фарадея. Поэтому величину q можно определить, воспользовавшись известным соотношением для цепи постоянного тока:

q=It=Et/R.

Подставив вместо Eее значение по формуле (2) и учитывая, что t=N/n, найдем

q=r²NB/R. (3)

Количество теплоты Q, выделенное в цепи постоянного тока, с учетом формул (2), (3) выразим так

Q=EIt=Eq=²r⁴nNB²/R.

Из полученных результатов видно, что при заданном числе оборотов величина q не зависит от скорости вращения диска, тогда как величина Q, будучи пропорциональной n, зависит.

Замечание.При решении задачи в качестве сторонних сил, действующих на свободные электроны во вращающемся диске, рассматривалась лишь сила Лоренца. Строго говоря, надо учесть еще центробежные силы инерции (если рассматривать явление в системе отсчета, связанной с вращающимся диском). Эти силы действуют на электроны независимо от магнитного поля, отбрасывая их к краям диска и создают добавочную ЭДС Таким образом, в рассматриваемом случае имеется, по существу, два генератора ЭДС: один электромагнитный, второй «инерционный», работающий по принципу центробежного насоса. В данном случае обе ЭДСEиE’ создают индукционный ток одного направления. При изменении направления вращения диска, ток изменит свое направление.

ЭДС «инерционного» генератора можно определить из следующих соображений. На электрон массы m, находящийся на расстоянии от центра диска, действует центробежная сила инерции

F_ин=-ma=-m²=-4²n²m,

где а – центростремительное ускорение электрона, обусловленное его вращением вместе с диском.

Подставив это значение F_ин(опуская знак «-«) в формулу (1), получим

E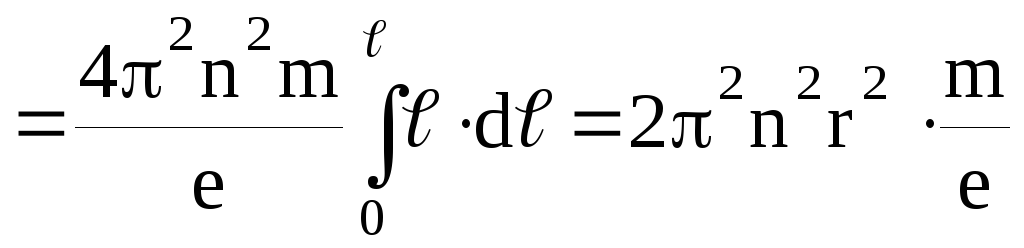. (4)

Сравнив величины E,E’ по формулам (4) и (2), имеем

E^’/E=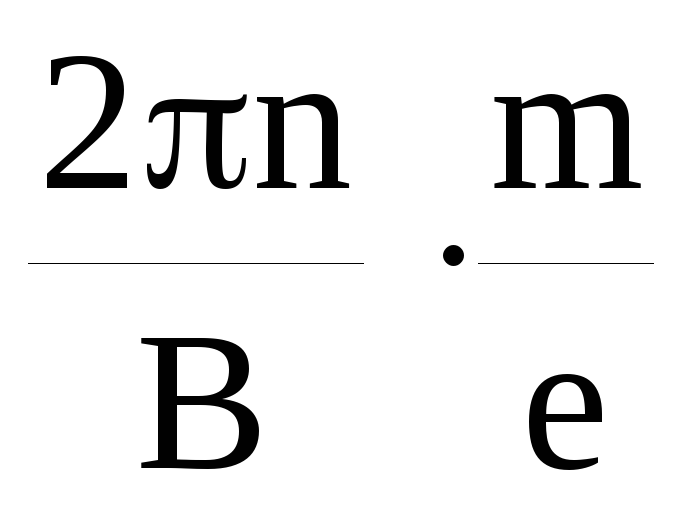

Так как для электрона m/e=5,710^-12кг/Кл, то данное отношение весьма мало, а это означает, что величиной E’ можно пренебречь. Однако в случае слабых магнитных полей и больших скоростей вращения диска действие «инерционного» генератора необходимо учитывать.

4.1.5. В цепи, состоящей из параллельно включенных: катушки индуктивности, активное сопротивление которой R₁=5,0 Ом, а L=0,34 Гн; сопротивления R₂=95 Ом; источника с ЭДСE=38 В, имеется ключ К, с помощью которого можно либо включать источник тока, либо его выключать. Внутреннее сопротивление батареи пренебрежимо мало. Определить силу тока в резисторе R₂в трех случаях: 1) до размыкания цепи; 2) в первый момент после размыкания; 3) через 0,01 с после размыкания.

Решение. 1. Силу тока I₂до размыкания цепи найдём по второму правилу Кирхгофа, применив его для контура, состоящего из R₂и батареи сE

I₂R₂+Ir=E,

где I – сила тока в батарее;

r – внутреннее сопротивление источника.

Поскольку внутренним сопротивлением батареи можно пренебречь, получим

I₂R₂=E, I₂=E/R₂=0,40 А.

2. Найдем силу тока I₂‘ в резисторе R₂сразу же после размыкания ключа К. Если в первом случае резистор R₂и катушка L были соединены между собой параллельно, то после отключения батареи они, образуя один неразветвленный контур, оказываются соединенными последовательно. Следовательно, по ним должен течь одинаковый ток. Так как из двух участков только один обладает индуктивностью, то именно ток I₁, проходивший до размыкания цепи по этому участку, должен сохраниться. Такой результат приобретает простой физический смысл: поскольку индуктивность является мерой инертности тока в проводнике, то ток I₂в резисторе R₂, практически лишенный инертности, сразу исчезнет после отключения батареи и по всему контуру потечет ток I₁. Таким образом, получаем ответ

I₂‘=I₁=E/R₁=7,6 А.

3. Так как в данном случае цепь отключена от батареи, ток начнет убывать. Его величину I₂» в заданный момент времени t=0,01 с можно определить по формуле для изменения тока при замыкании и размыкании

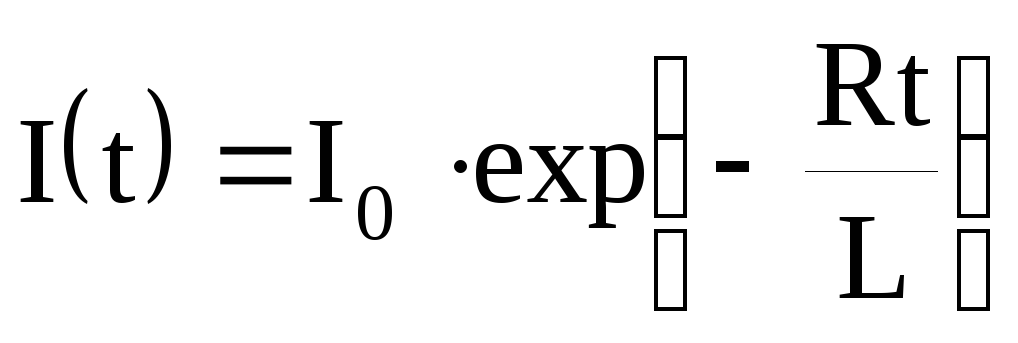E/R,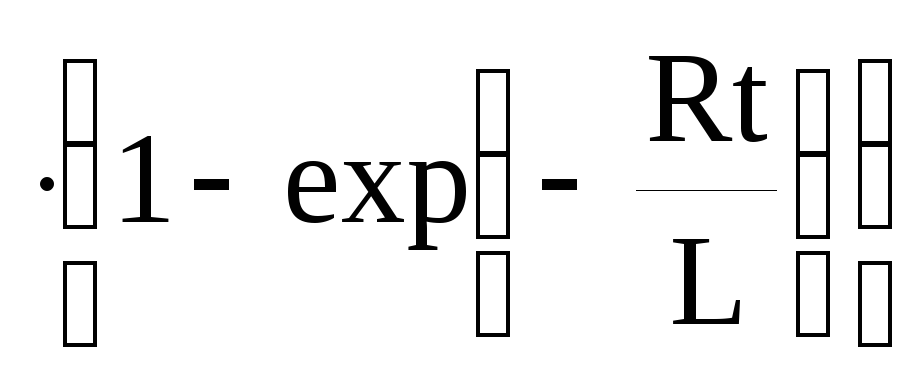

где I₀=0 – начальная сила тока при замыкании цепи;

E=0 – при размыкании цепи.

В рассматриваемом случае E=0 (случай размыкания), I₀=I₁.

Следовательно, имеем

I₂»=I₁exp(-Rt/L), (1)

где R=(R₁+R₂) – общее сопротивление цепи.

Подставив числовые значения величин I₁, R₁, R₂, L, t, в формулу (1) и произведя вычисления, найдем:

I₂»=0,4 А.

Ответ: I₂=0,4 А; I₂‘=7,6 А; I₂»=0,4 А.

4.1.6. Резистор сопротивлением R присоединен к верхним концам двух вертикальных медных стержней, отстоящих на расстояниидруг от друга. Стержни замкнуты медной перемычкой массы m, которая без трения может скользить по ним. В окружающем пространстве создано однородное магнитное поле с индукцией B, перпендикулярное плоскости, в которой расположены стержни. Перемычку отпустили, после чего она начала падать без нарушения электрического контакта. Пренебрегая сопротивлением стержней и перемычки, найти установившуюся скорость v последней. Принять индуктивность единицы длины системы стержней равной k.

Решение. При падении перемычки площадь контура, образованного резистором, стержнями и перемычкой, растет, и магнитный поток сквозь него увеличивается. Согласно закону Фарадея, в контуре появляется ЭДС электромагнитной индукции, вызывающая индукционный ток. Следовательно, на перемычку кроме силы тяжести mgдействует со стороны магнитного поля сила Ампера F_А, определяемая формулой:

dF_А=I[B].

Так как для всех элементов длины перемычки, по которой идет ток силой I, sina=1 и B=const, то

F_А=IB.

Согласно правилу Ленца, сила F_Анаправлена против силы mg. С ростом скорости падения перемычки увеличивается ЭДС индукции, сила тока I и, следовательно, сила Ампера F_А. Скорость перестанет возрастать, когда наступит равновесие сил mg иFА, т.е.

mg=IB. (1)

Из условия (1) можно найти силу тока I, а последнюю связать с искомой скоростью, применив закон Ома и закон электромагнитной индукции. По закону Ома для замкнутой цепи

I=E/R, (2)

где E=(E_i+E_s) – ЭДС, действующая в контуре;

E_i– ЭДС индукции, возникающая при изменении сквозь контур магнитного потока Ф₁вектора B;

E_s– ЭДС самоиндукции, которая появляется при изменении магнитного потока Фs сквозь контур, созданного индукционным током. Этот поток изменяется вследствие роста площади контура.

Величину E_iможно определить из следующих соображений:

E=(3)

где q – величина заряда.

При движении в магнитном поле проводника ad вместе с ним движутся со скоростью v его свободные заряды (электроны). Поэтому на каждый из них действует сила Лоренца, выполняющая роль сторонней силы F_ст, входящей в формулу (3). Поскольку векторv перпендикулярен векторуB, то силу Лоренца можно определить по формуле

F_л=qvBsin=qvB.

Так как она действует только вдоль участка ad длиной , интеграл, стоящий в (3), равен



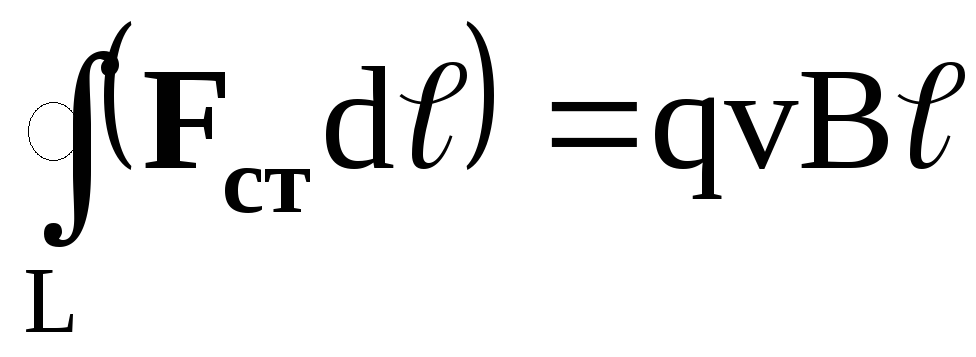
Подставив это значение интеграла в формулу (3), получим

E=vB. (4)

Чтобы определить величину E_s, учтем, что в данном случае индуктивность контура величина переменная. Действительно, индуктивность L=kx, где x – длина вертикальных стержней, измеренная на участке, по которому идет ток. При падении перемычки величины x и L возрастают. На основании законов электромагнитной индукции и самоиндукции, для ЭДС самоиндукции запишем

E_s=. (5)

Так как при установившейся скорости падения перемычки I=const, то первое слагаемое в (5) равно нулю и тогда

E_s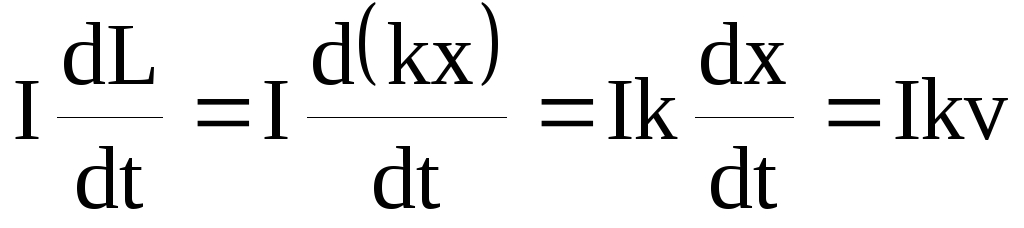=. (6)

Величины E_iиE_sимеют в данном случае противоположные знаки, поскольку магнитные потоки Ф_iи Ф_sнаправлены, согласно правилу Ленца, противоположно; при этом оба потока растут по абсолютному значению.

Учитывая это, из уравнений (2) – (4) и (6) найдем:

I=(Bv – Ikv)/R. (7)

Исключив из формул (1) и (7) силу тока I, определим установившуюся скорость перемычки:

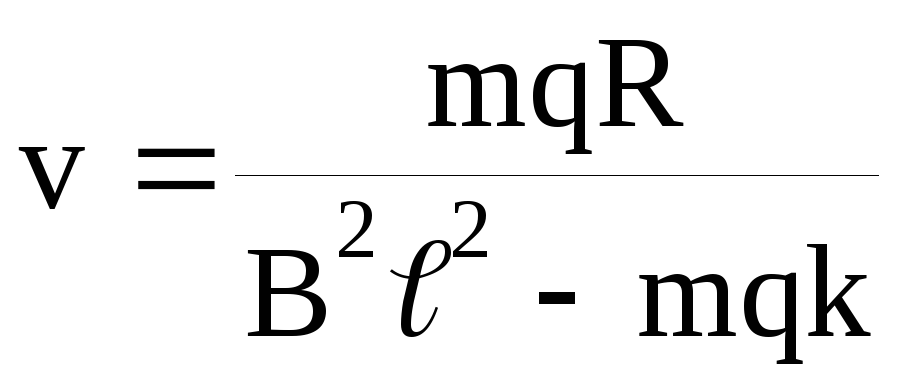. (8)

Проанализируем полученный результат.

1. Если k=0, то v=mgR/B²²и направлена вниз. Так как при наличии индуктивности скорость, будучи величиной конечной, направлена также вниз, то приходим к выводу, что формула (8) верна лишь при значениях заданных величин, удовлетворяющих неравенству

B²²>mgk. (9)

Выясним физический смысл этого соотношения. Из (1) следует, что значение I, необходимое для равновесия приложенных к перемычке сил, равно:

I=mg/B. (10)

Однако индуктивность цепи ограничивает рост силы тока в контуре, происходящий при увеличении скорости перемычки. Действительно, из (7) находим

I=B/(R/v+k).

Отсюда, предположив v, получим предельную силу тока:

I_пред=B/k. (11)

Сопоставляя формулы (9) – (11), видим, что неравенство (9) эквивалентно очевидному условию I_пред>I. Следовательно

1Если соотношение (9) не выполняется, то это означает, что сила тока в контуре, ограниченная в процессе самоиндукции величиной I_пред, не достигает значения, необходимого для равновесия сил mg иF_А, приложенных к перемычке, ни при каких конечных значениях ее скорости. Другими словами, скорость перемычки неограниченно возрастает и ее установившееся значение недостижимо.

2. Если R, то v. В этом случае ток по контуру не идет и перемычка падает под действие силы тяжести с ускорение g.

3. Если R=0 и выполняется условие (9), то v=0: перемычка будет неподвижно висеть в магнитном поле, несмотря на действие силы тяжести. Этот парадоксальный результат можно осуществить, если охладить проводника рассматриваемого контура, помещенного в достаточно сильное магнитное поле, до сверхпроводящего состояния.

формула явления, силы индукционного тока и скорости изменения магнитного потока

В нашем мире все виды существующих сил, за исключением сил тяготения, представлены электромагнитными взаимодействиями. Во Вселенной, несмотря на удивительное разнообразие воздействий тел друг на друга, в любых веществах, живых организмах всегда встречается проявление электромагнитных сил. Как произошло открытие электромагнитной индукции (ЭИ), расскажем ниже.

…

Вконтакте

Facebook

Twitter

Мой мир

Открытие ЭИ

Поворот магнитной стрелки вблизи проводника с током в опытах Эрстеда впервые указал на связь электрических и магнитных явлений. Очевидно: электроток «окружает» себя магнитным полем.

Так нельзя ли добиться его возникновения посредством магнитного поля — подобную задачу поставил Майкл Фарадей. В 1821 году он отметил это свойство в своем дневнике о превращении магнетизма в электричество.

Успех к ученому пришел не сразу. Лишь глубокая уверенность в единстве природных сил и упорный труд привели его через десять лет к новому великому открытию.

Решение задачи долго не давалось Фарадею и другим его коллегам, потому как они пытались получить электричество в неподвижной катушке, используя действие постоянного магнитного поля. Между тем, впоследствии выяснилось: изменяется количество силовых линий, пронизывающих провода, и возникает электроэнергия.

Явление ЭИ

Процесс появления в катушке электричества в результате изменения магнитного поля характерен для электромагнитной индукции и определяет это понятие. Вполне закономерно, что разновидность тока, возникающего в ходе данного процесса, называется индукционным. Эффект сохранится, если саму катушку оставить без движения, но перемещать при этом магнит. С использованием второй катушки можно и вовсе обойтись без магнита.

Если пропустить электричество через одну из катушек, то при их взаимном перемещении во второй возникнет индукционный ток. Можно надеть одну катушку на другую и менять величину напряжения одной из них, замыкая и размыкая ключ. При этом магнитное поле, пронизывающее катушку, на которую воздействуют ключом, меняется, и это становится причиной возникновения индукционного тока во второй.

Закон

Во время опытов легко обнаружить, что увеличивается число пронизывающих катушку силовых линий — стрелка используемого прибора (гальванометр) смещается в одну сторону, уменьшается – в иную. Более тщательное исследование показывает, что сила индукционного тока прямо пропорциональна скорости изменения числа силовых линий. В этом заключен основной закон электромагнитной индукции.

Данный закон выражает формула:

Она применяется, если за период времени t магнитный поток изменяется на одну и ту же величину, когда скорость изменения магнитного потока Ф/t постоянна.

Важно! Для индукционных токов справедлив закон Ома: I=/R, где — это ЭДС индукции, которую находят по закону ЭИ.

Замечательные опыты, проведенные когда-то знаменитым английским физиком и ставшие основой открытого им закона, сегодня без особого труда способен проделать любой школьник. Для этих целей используются:

• магнит,
• две проволочные катушки,
• источник электроэнергии,
• гальванометр.

Закрепим на подставке магнит и поднесем к нему катушку с присоединенными к гальванометру концами.

Поворачивая, наклоняя и перемещая ее вверх и вниз, мы меняем число силовых линий магнитного поля, пронизывающих ее витки.

Гальванометр регистрирует возникновение электричества с постоянно меняющимися в ходе опыта величиной и направлением.

Находящиеся же относительно друг друга в покое катушка и магнит не создадут условий и для возникновения электричества.

Это интересно! Что такое закон всемирного тяготения: формула великого открытия

Другие законы Фарадея

На основе проведенных исследований были сформированы еще два одноименных закона:

1. Суть первого состоит в такой закономерности: масса вещества m, выделяемая электрическим напряжением на электроде, пропорциональна количеству электричества Q, прошедшему через электролит.
2. Определение второго закона Фарадея, или зависимости электрохимического эквивалента от атомного веса элемента и его валентности формулируется так: электрохимический эквивалент вещества пропорционален его атомному весу, а также обратно пропорционален валентности.

Из всех существующих видов индукции огромное значение имеет обособленный вид данного явления – самоиндукция. Если мы возьмем катушку, которая имеет большое количество витков, то при замыкании цепи, лампочка загорается не сразу.

На этот процесс может уйти несколько секунд. Очень удивительный на первый взгляд факт. Чтобы понять, в чем здесь дело, необходимо разобраться, что же происходит в момент замыкания цепи. Замкнутая цепь словно «пробуждает» электроток, начинающий свое движение по виткам провода. Одновременно в пространстве вокруг нее мгновенно создается усиливающееся магнитное поле.

Катушечные витки оказываются пронизанными изменяющимся электромагнитным полем, концентрирующимся сердечником. Возбуждаемый же в витках катушки индукционный ток при нарастании магнитного поля (в момент замыкания цепи) противодействует основному. Мгновенное достижение им своего максимального значения в момент замыкания цепи невозможно, оно «растет» постепенно. Вот и объяснение, почему лампочка не вспыхивает сразу. Когда цепь размыкается, основной ток усиливается индукционным в результате явления самоиндукции, и лампочка ярко вспыхивает.

Важно! Суть явления, названного самоиндукцией, характеризуется зависимостью изменения, возбуждающего индукционный ток электромагнитного поля от изменения силы текущего по цепи электротока.

Направление тока самоиндукции определяет правило Ленца. Самоиндукция легко сравнима с инерцией в области механики, поскольку оба явления обладают схожими характеристиками. И действительно, в результате инерции под влиянием силы тело приобретает определенную скорость постепенно, а не сиюминутно. Не сразу – под действием самоиндукции — при включении батареи в цепь появляется и электричество. Продолжая сравнение со скоростью, заметим, он так же не способен мгновенно исчезнуть.

Вихревые токи

Наличие вихревых токов в массивных проводниках может послужить еще одним примером электромагнитной индукции.

Специалисты знают, что металлические трансформаторные сердечники, якоря генераторов и электродвигателей никогда не бывают сплошными. При их изготовлении на отдельные тонкие листы, из которых они состоят, накладывается слой лака, изолирующий один лист от другого.

Нетрудно понять, какая сила заставляет человека создавать именно такое устройство. Под действием электромагнитной индукции в переменном магнитном поле сердечник пронизывают силовые линии вихревого электрополя.

Представим, что сердечник изготовлен из сплошного металла. Поскольку его электрическое сопротивление невелико, возникновение индукционного напряжения большой величины было бы вполне объяснимым. Сердечник бы в итоге разогревался, и немалая часть электрической энергии терялась бесполезно. Кроме того, возникла бы необходимость принятия специальных мер для охлаждения. А изолирующие слои не позволяют достигать больших величин.

Индукционные токи, присущие массивным проводникам, называются вихревыми не случайно – их линии замкнуты подобно силовым линиям электрополя, где они и возникают. Чаще всего вихревые токи применяются в работе индукционных металлургических печей для выплавки металлов. Взаимодействуя с породившим их магнитным полем, они иногда становятся причиной занимательных явлений.

Возьмем мощный электромагнит и поместим между вертикально расположенными его полюсами, к примеру, пятикопеечную монету. Вопреки ожиданию, она не упадет, а будет медленно опускаться. Для прохождения нескольких сантиметров ей потребуются секунды.

Поместим, например, пятикопеечную монету между вертикально расположенными полюсами мощного электромагнита и отпустим ее.

Вопреки ожиданию, она не упадет, а будет медленно опускаться. Для прохождения нескольких сантиметров ей потребуются секунды. Передвижение монеты напоминает перемещение тела в вязкой среде. Почему такое происходит.

По правилу Ленца направления возникающих при передвижении монеты вихревых токов в неоднородном магнитном поле таковы, что поле магнита выталкивает монету вверх. Эту особенность используют для «успокоения» стрелки в измерительных приборах. Алюминиевая пластина, находящаяся между магнитными полюсами, прикрепляется к стрелке, и вихревые токи, возникающие в ней, способствуют быстрому затуханию колебаний.

Демонстрацию явления электромагнитной индукции поразительной красоты предложил профессор Московского университета В.К. Аркадьев. Возьмем свинцовую чашу, обладающую сверхпроводящей способностью, и попробуем уронить над ней магнит. Он не упадет, а будет словно «парить» над чашей. Объяснение здесь простое: равное нулю электрическое сопротивление сверхпроводника способствует возникновению в нем электричества большой величины, способных сохраняться продолжительное время и «удерживать» магнит над чашей. По правилу Ленца, направление магнитного поля их таково, что отталкивает магнит и не дает ему упасть.

Изучаем физику — закон электро-магнитной индукции

Правильна формулировка закона Фарадея

Вывод

Электромагнитные силы – это силы, которые позволяют людям видеть окружающий мир и чаще других встречаются в природе, например, свет — тоже пример электромагнитных явлений. Жизнь человечества невозможно представить без данного явления.

Это интересно! Специальная теория относительности Эйнштейна: кратко и простыми словами

Закон электромагнитной индукции формула

Явление электромагнитной индукции представляет собой возникновение электрического тока в условиях замкнутого проводящего контура, в то время как магнитный поток, пронизывающий этот контур, изменяется во времени. На этом явлении основан закон электромагнитной индукции, формула которого была выведена английским физиком Фарадеем. Понятия электромагнитной индукции Одной из основных величин, связанных с электромагнитной индукцией является магнитный поток. Чтобы понять его физический смысл, следует рассмотреть формулу, определяющую эту величину: Φ = B • S • cos α. Здесь В выступает в роли модуля вектора магнитной индукции, S – площадь проводящего контура, α – угол между нормалью к плоскости контура и вектором магнитной индукции. При неоднородном магнитном поле и неплоском контуре, значение магнитного потока можно обобщить. Для этого, в системе СИ существует обозначение единицы магнитного потока, называемое вебером. Для создания 1 Вб требуется магнитное поле в 1 Тл, которое пронизывает плоский контур, площадь которого составляет 1 м2. (1 Вб = 1 Тл • 1 м2) Фарадей открыл закон электромагнитной индукции, формула которого выражается в следующих показателях:  Эта формула наглядно демонстрирует, что изменение магнитного потока в контуре, приводит к возникновению ЭДС индукции. ЭДС, в свою очередь, равна скорости, с какой изменяется магнитный поток при прохождении через площадь, ограниченную контуром. Все значение ЭДС берется со знаком минус. Это и есть закон Фарадея. Причины изменения магнитного потока Магнитный поток, пронизывающий замкнутый контур, может изменяться в силу ряда причин. Прежде всего, эти изменения происходят, когда контур перемещается в магнитном поле, постоянном по времени. В этом случае, проводники вместе со свободными носителями зарядов передвигаются в магнитном поле. ЭДС индукции возникает под воздействием сторонних сил, которые влияют на свободные заряды, находящиеся в движущихся проводниках. Другая причина, изменяющая магнитный поток, заключается в изменении во времени магнитного поля, когда контур неподвижен. В неподвижном проводнике, электроны могут двигаться только под действием электрического поля. Это поле, в свою очередь, возникает воздействия магнитного поля, изменяющегося во времени. Работа магнитного поля, затрачиваемая на перемещение одного положительного заряда в замкнутом контуре, равна ЭДС индукции для неподвижного проводника. Такое поле, полученное с помощью изменяющегося магнитного поля, получило название вихревого электрического поля.