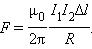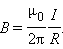3.4. Сила Лоренца и закон Ампера.
3.4.1.Сила Лоренца.
Обобщение опытных фактов приводит к выводу о том, что на движущийся заряд в магнитном поле действует сила, определяемая выражением:
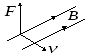
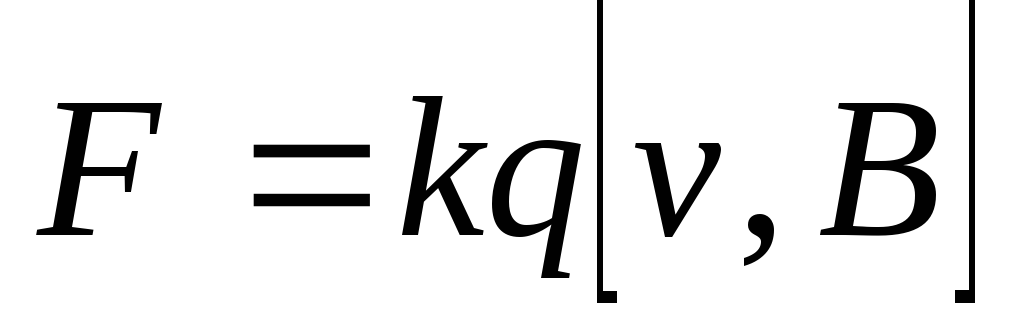 ,
(3.15)
,
(3.15)
где 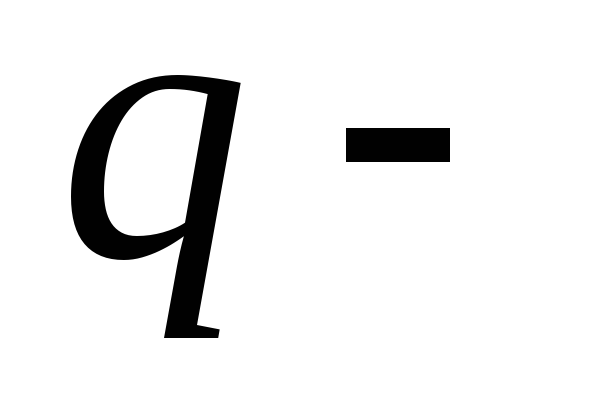 заряд,
заряд,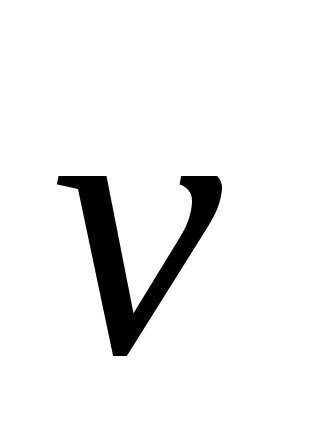 — скорость заряда,
— скорость заряда,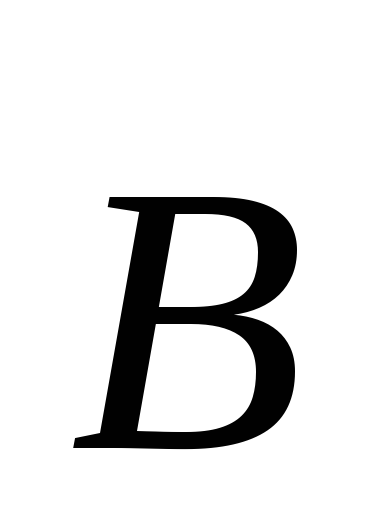 — индукция магнитного поля.
— индукция магнитного поля.
Здесь 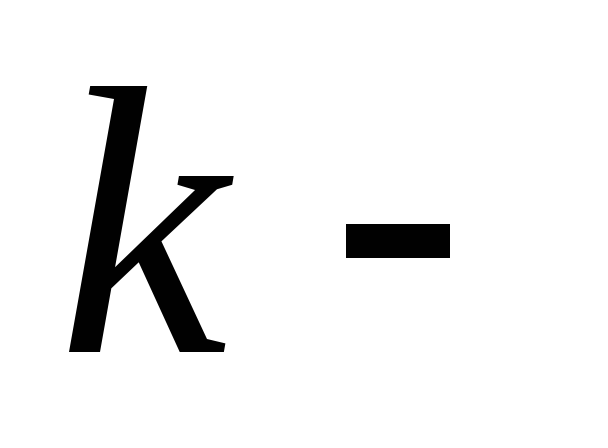 некоторая
константа, которая определяется выбранной
некоторая
константа, которая определяется выбранной
системой единиц.
В системе Гаусса 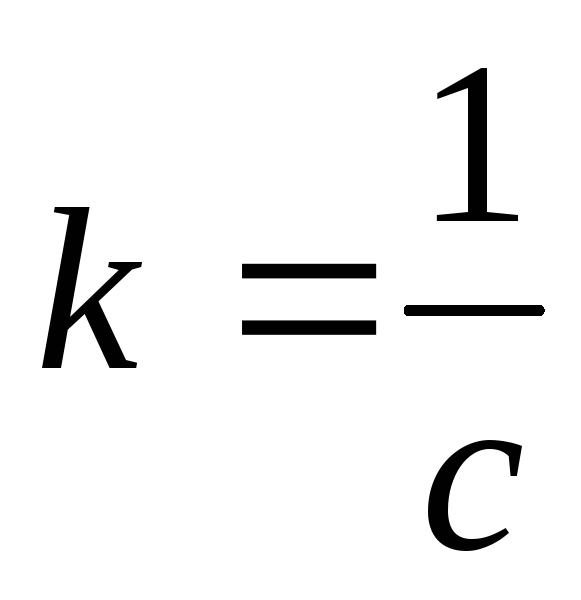 ,
где
,
где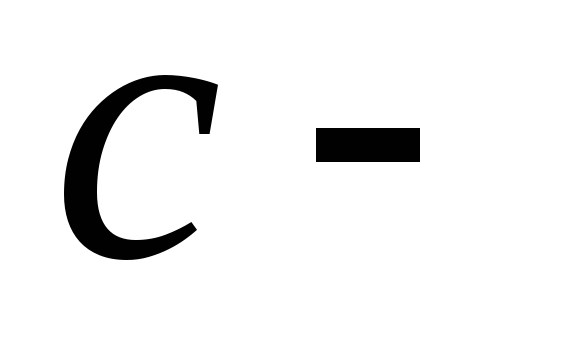 скорость
света.
скорость
света.
В СИ 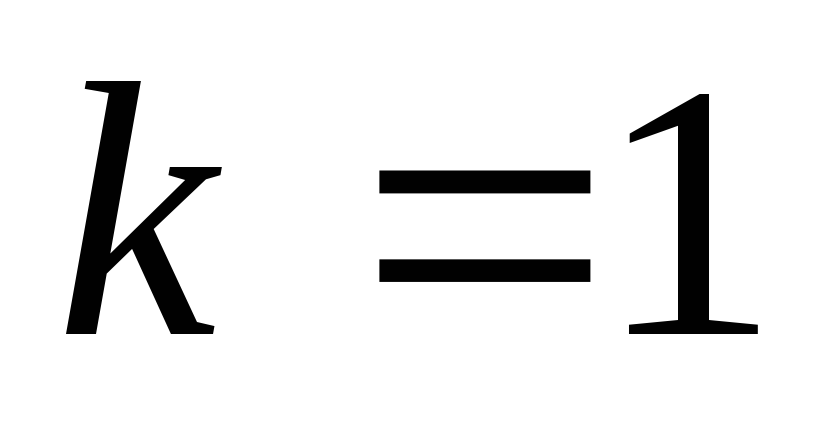
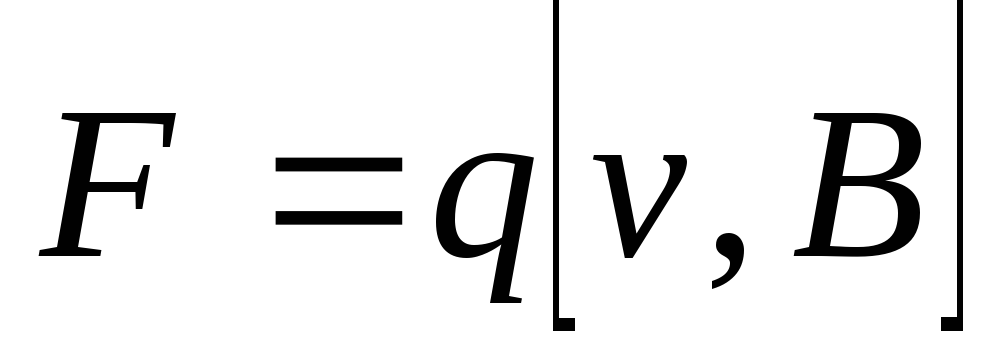 .
(3.16)
.
(3.16)
Таким образом, это соотношение может
служить определением единиц магнитной
индукции 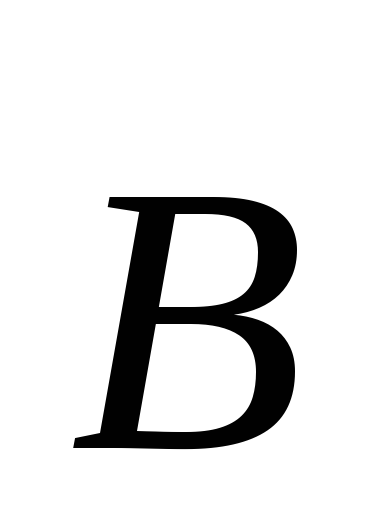 .
.
В системе СИ: 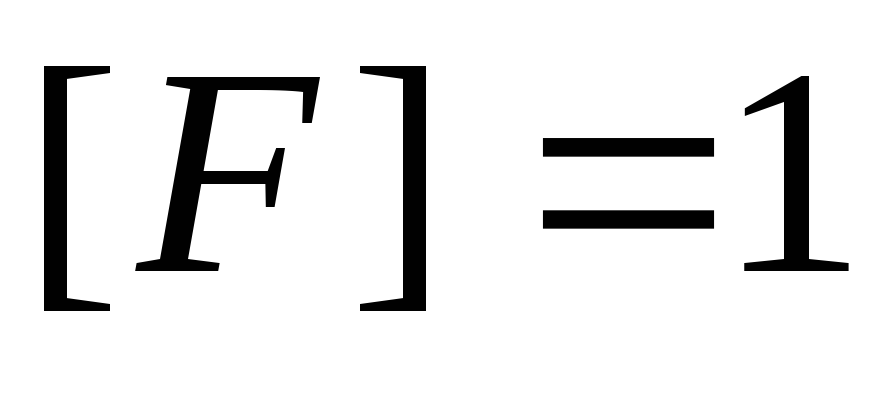 Н,
Н,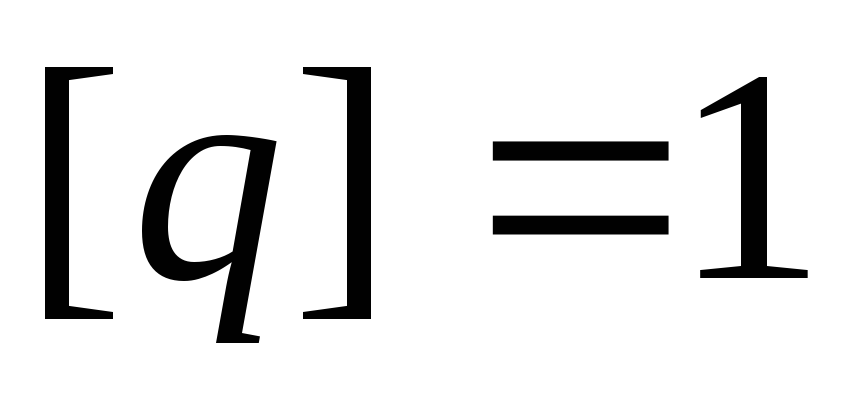
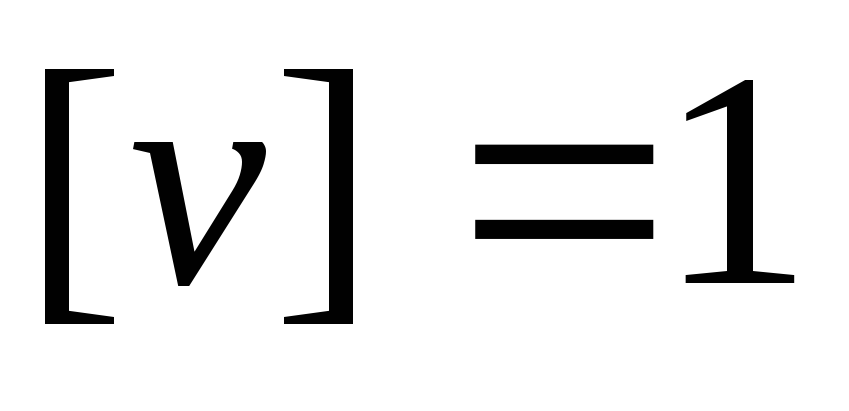 м/с,
тогда
м/с,
тогда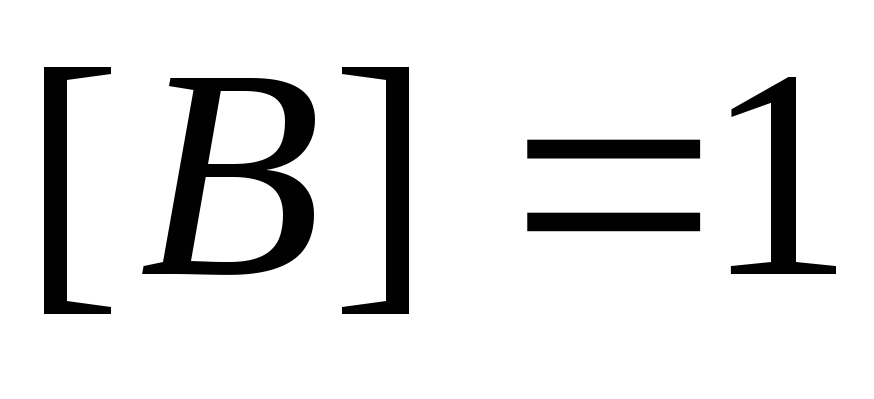 Тл
(тесла).
Тл
(тесла).Если движение заряда происходит в магнитном и электрическом полях, то сила Лоренца приобретает вид:
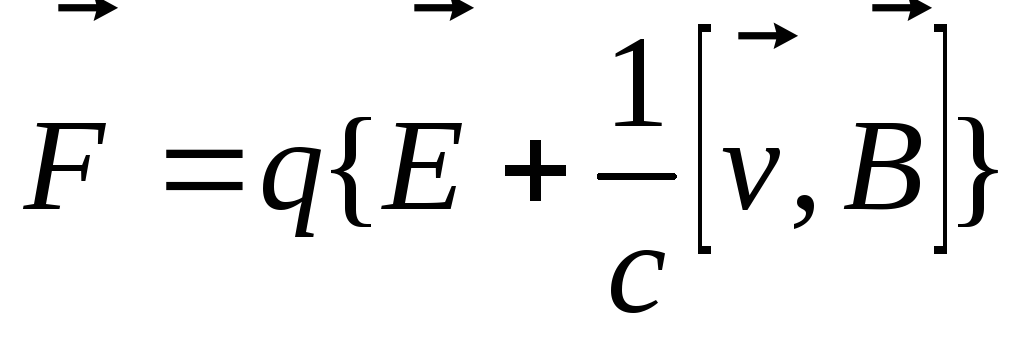 .
(3.17)
.
(3.17)
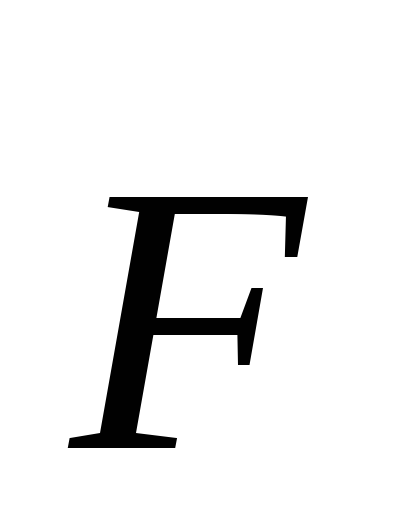 не должна изменяться при переходе из
одной ИСО в другую, поэтому разделение
силы Лоренца на электрическую и магнитную
части зависит от выбора системы отсчета.
Без указания системы отсчета такое
разделение теряет смысл.
не должна изменяться при переходе из
одной ИСО в другую, поэтому разделение
силы Лоренца на электрическую и магнитную
части зависит от выбора системы отсчета.
Без указания системы отсчета такое
разделение теряет смысл.Движение заряда в постоянном однородном магнитном поле.
 Если рассматривать движение частицы
с зарядом
Если рассматривать движение частицы
с зарядом
однородном магнитном поле 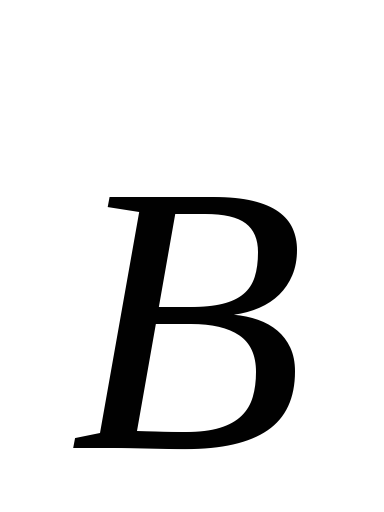 ,
то уравнение движения примет вид
,
то уравнение движения примет вид
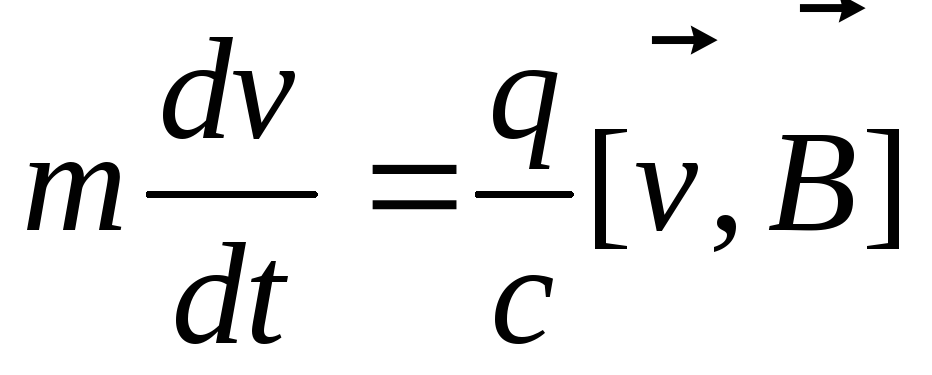 .
(3.18)
.
(3.18)
Чтобы определить траекторию частицы, рассмотрим её движение
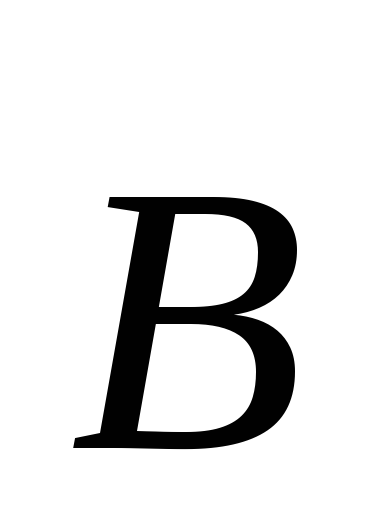 и в перпендикулярном ему направлении.
и в перпендикулярном ему направлении.Из свойств векторного произведения следует, что при движении
заряженной частицы в направлении, параллельном магнитному
полю, сила, действующая со стороны поля
на заряд 
т.е. параллельная полю компонента скорости заряда сохраняет свое
значение.
В то же время движение в направлении,
перпендикулярном полю, совершается с
ускорением  ,
определяемым уравнением
,
определяемым уравнением
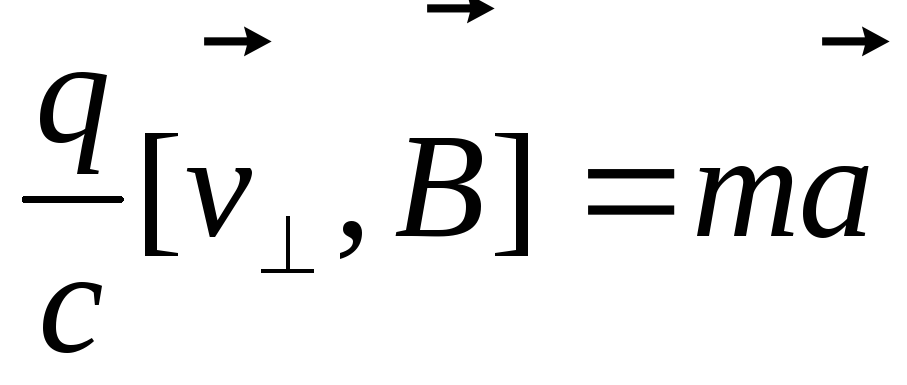
откуда следует, что ускорение
перпендикулярно векторам 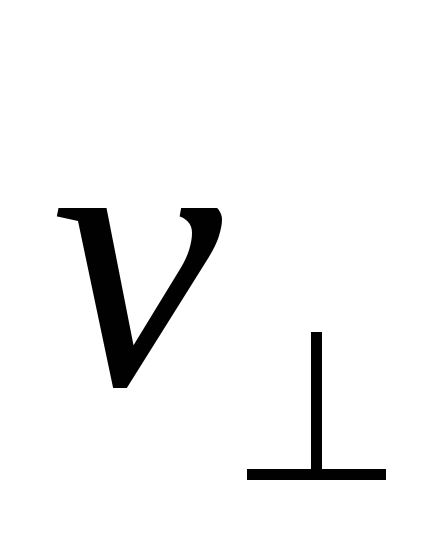 и
и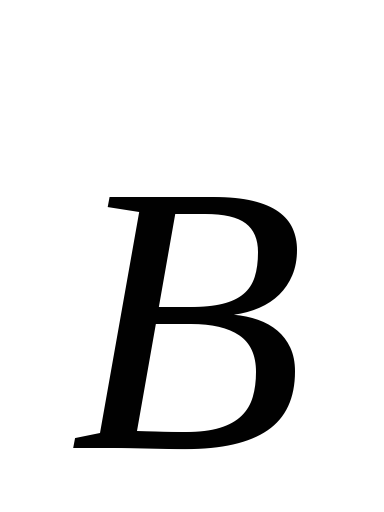 ,
т.е. частица движется с нормальным
ускорением
,
т.е. частица движется с нормальным
ускорением
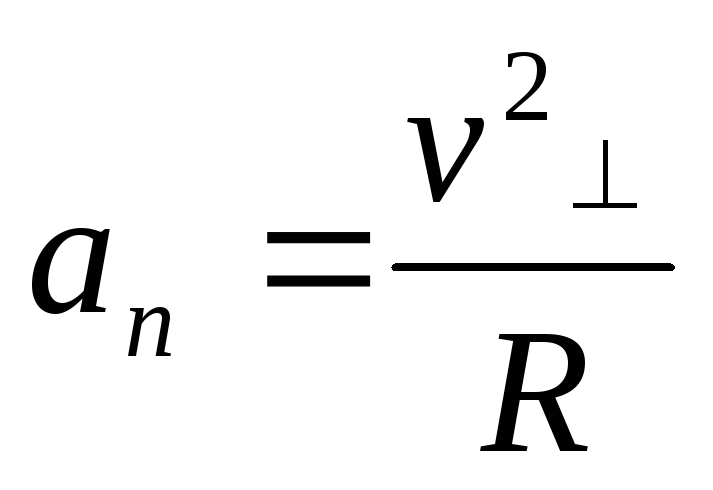 ,
,
по окружности радиусом:
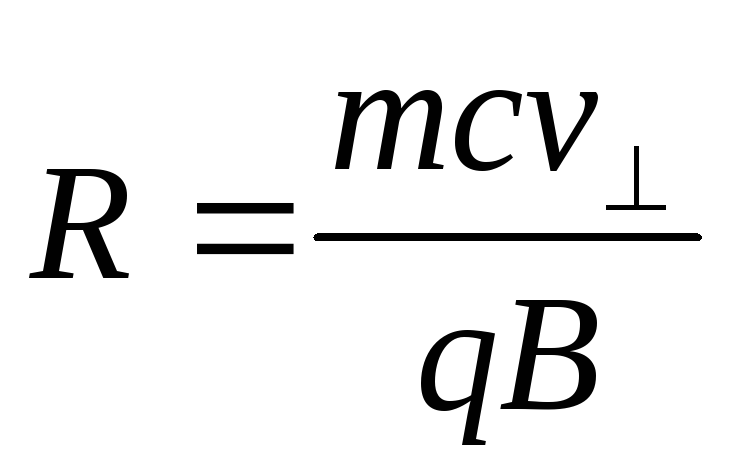
 Суммируя сказанное находим, что
траекторией движения частицы, влетевшей
в магнитное поле под произвольным углом
Суммируя сказанное находим, что
траекторией движения частицы, влетевшей
в магнитное поле под произвольным углом к вектору
к вектору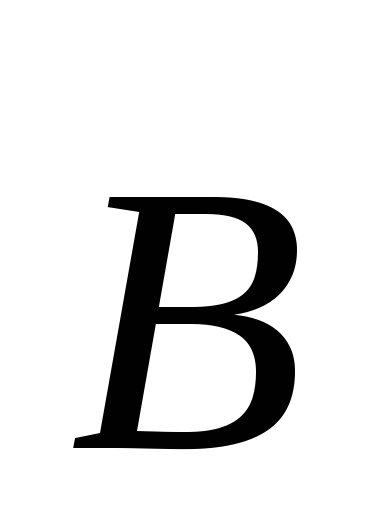 ,
являетсявинтовая линия, вырождающаяся
в прямую при
,
являетсявинтовая линия, вырождающаяся
в прямую при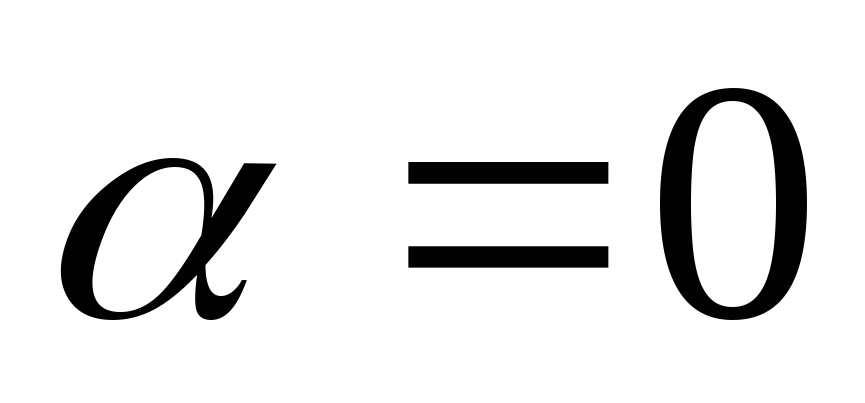 и окружность при
и окружность при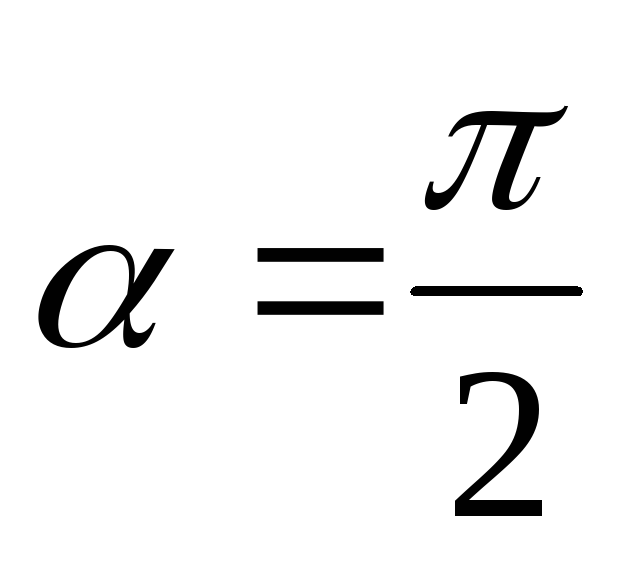
Шаг винтовой линии определяется как
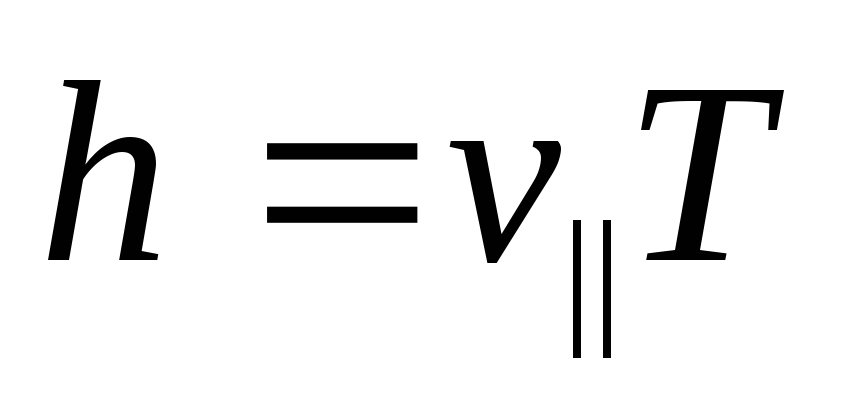 ,
,
где
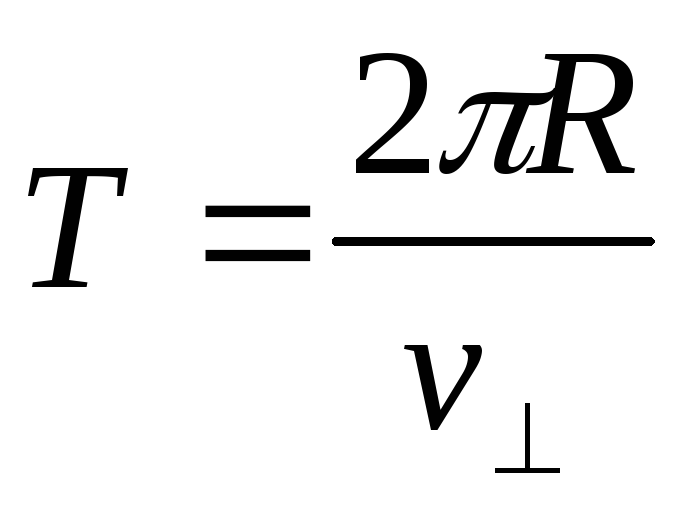 ;
;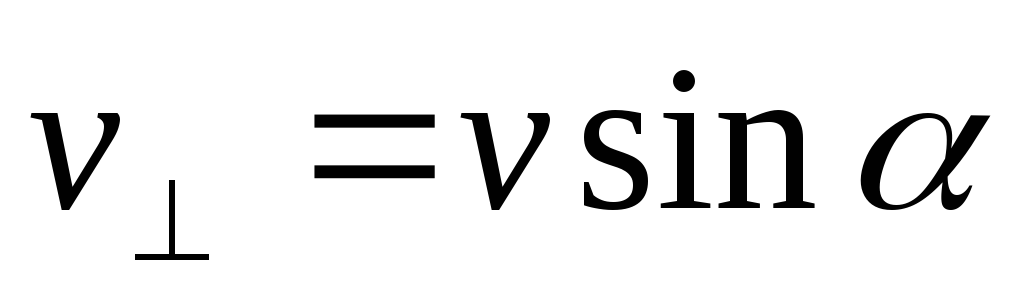 ;
;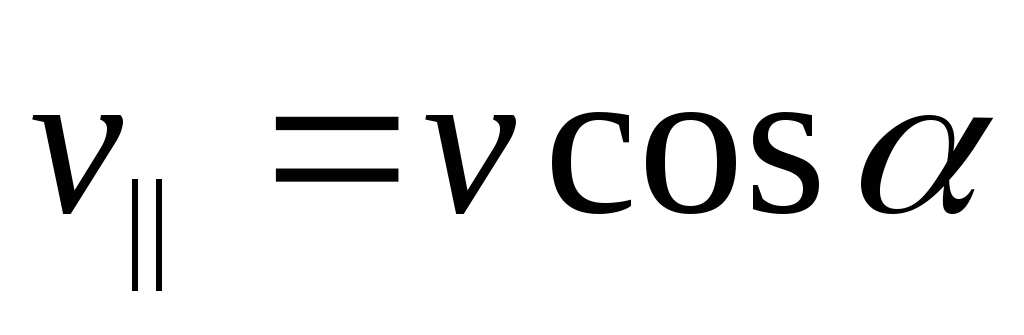 .
.
3.4.3. Закон Ампера
Каждый носитель тока в проводнике испытывает действие магнитной силы. В результате магнитное поле действует с определенной силой на сам проводник с током
Пусть имеем провод с током, помещенный в магнитное поле. На каждый заряд (носитель) действует сила Лоренца
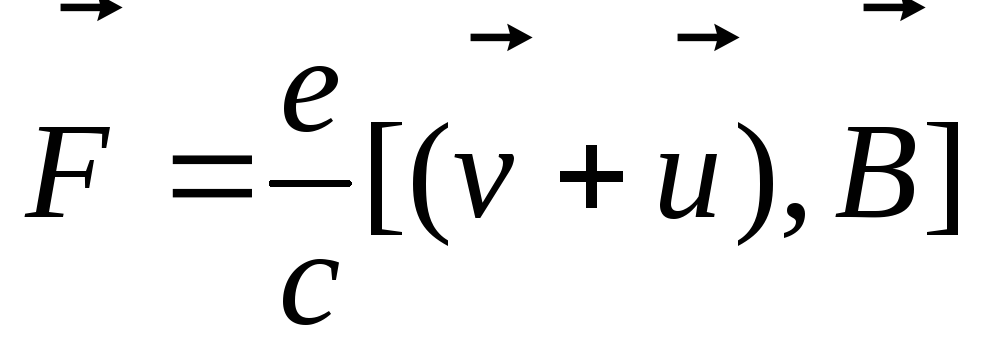 ,
(3.19)
,
(3.19)
где
— скорость хаотического движения,
 —
сечение проводника,
—
сечение проводника,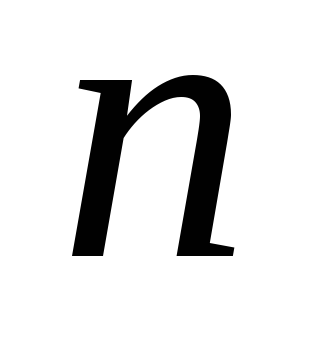 — концентрация носителей, то на элемент
тока длиной
— концентрация носителей, то на элемент
тока длиной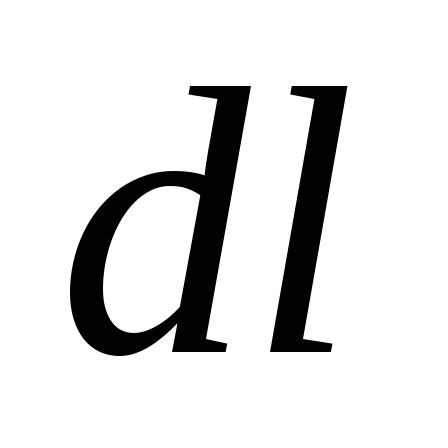 будет действовать сила
будет действовать сила 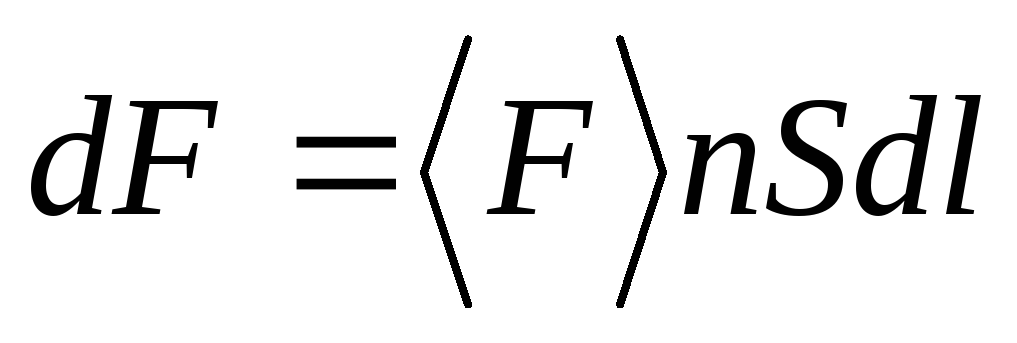 ,
(3.20)
,
(3.20)
где 
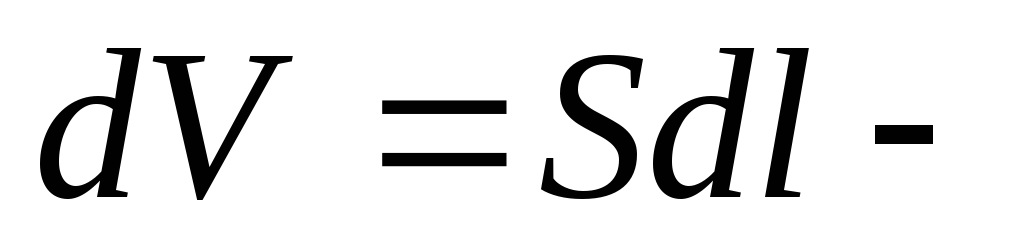 элементарный
объем проводника.
элементарный
объем проводника. 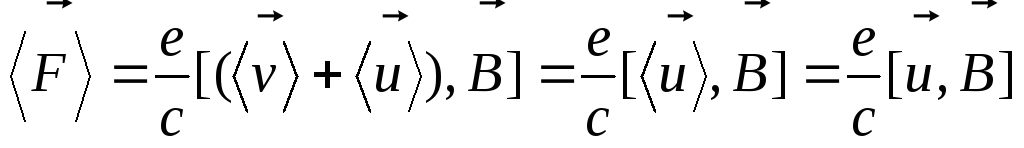 ,
,
т.к.
и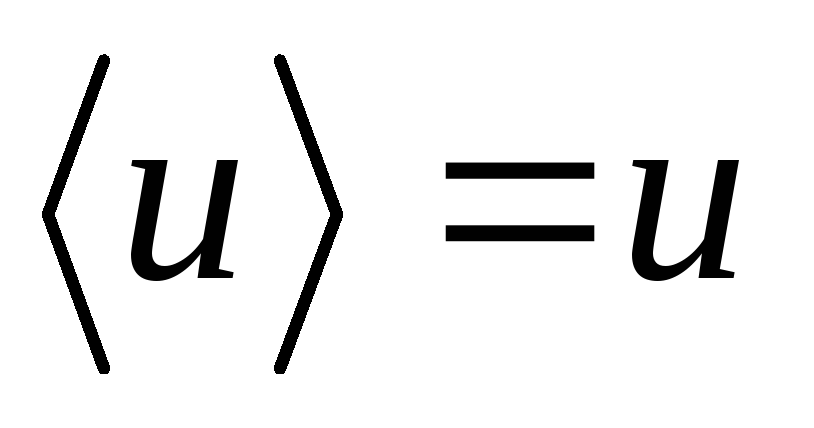 .
.
Тогда сила, действующая на элемент
проводника длиной 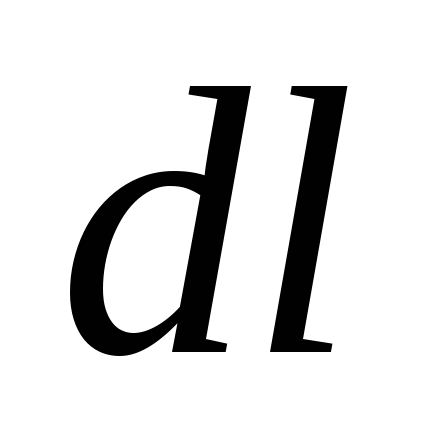
 ,
т.к.
,
т.к.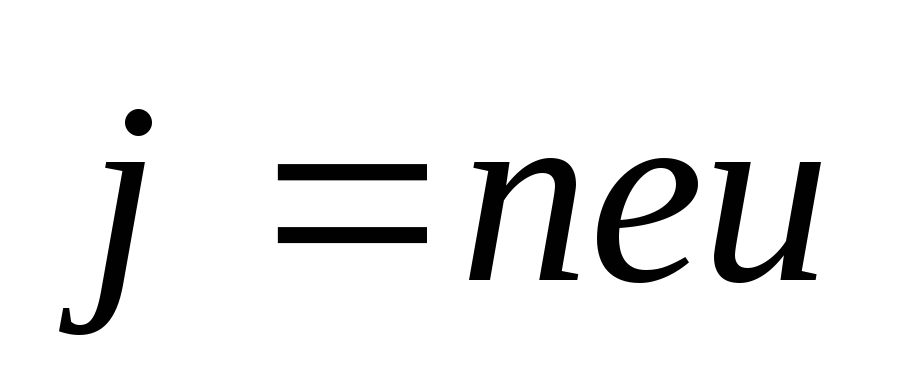 .
.
Итак,
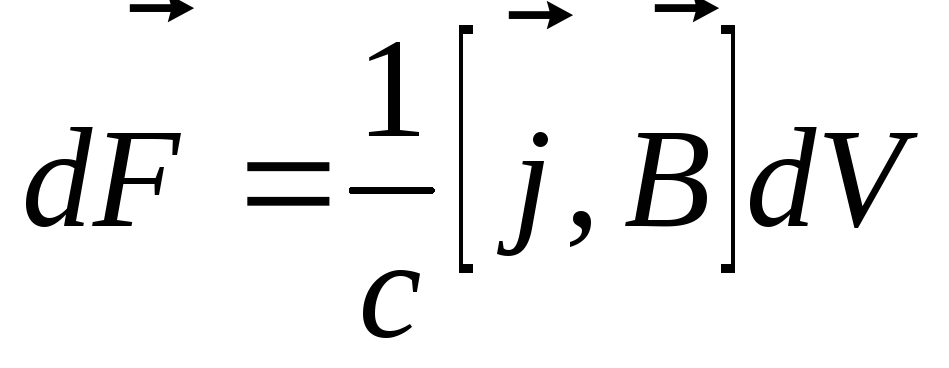 .
(3.21)
.
(3.21)
Если объемный элемент тока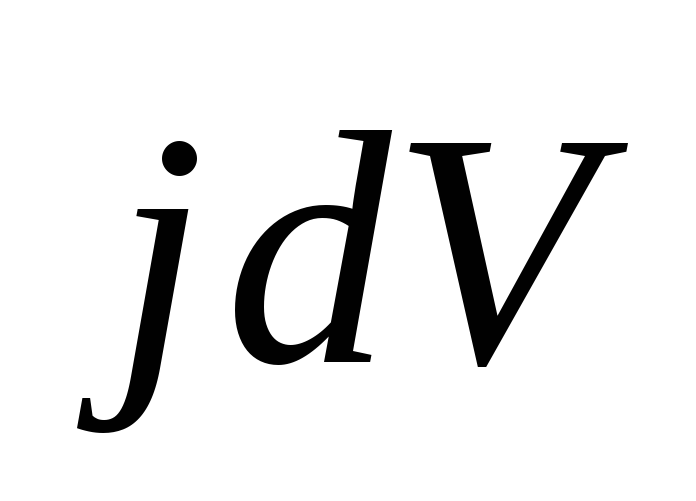 выразим черезлинейный элементтока
выразим черезлинейный элементтока 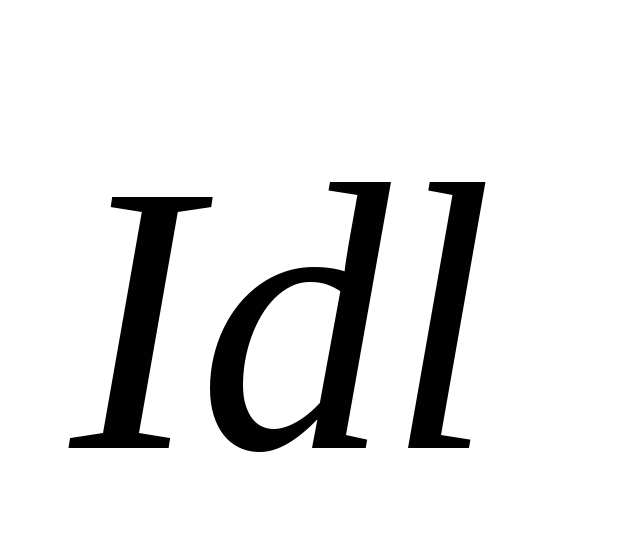 ,
то для тонкого провода с площадью
поперечного сечения
,
то для тонкого провода с площадью
поперечного сечения можно записать
можно записать
 .
(3.22)
.
(3.22)
Тогда сила, действующая на провод длиной 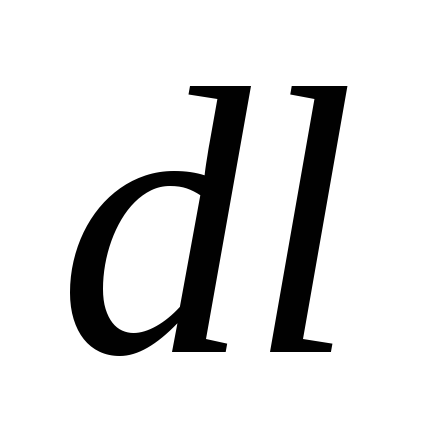 ,
определяется как
,
определяется как
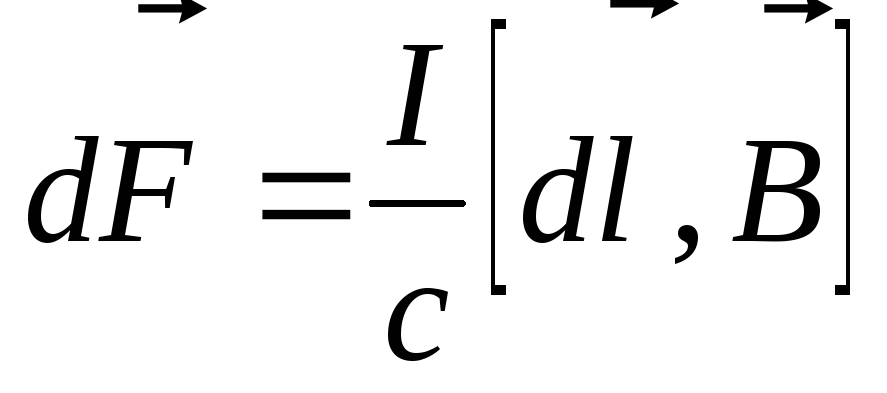 .
(3.23)
.
(3.23)
Сила, действующая на провод конечной длины:
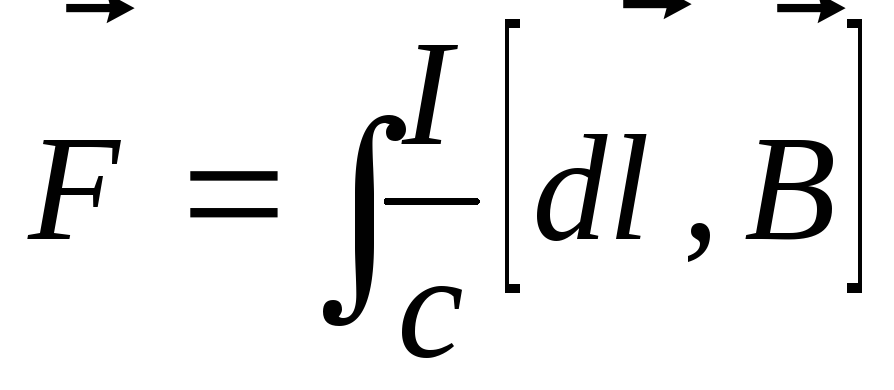 .
(3.24)
.
(3.24)
Эти соотношения и определяют закон Ампера (1820г.).
§ 35. ЗАКОН АМПЕРА. СИЛА ЛОРЕНЦА
Закон Био-Савара-Лапласа–Ампера экспериментально проверить нельзя, но следствия из него подтверждаются на практике.
Во всех точках пространства, окружающего произвольный ток, всегда существует обусловленное этим током поле сил, которое по сложившейся исторически терминологии называется магнитным полем.
По аналогии с электростатикой можно ввести силовую характеристику точки магнитного поля – вектор магнитной индукции: 
 — закон Био-Савара-Лапласа для расчета индукции магнитного поля, создаваемого элементом тока в некоторой точке (рис.69). Экспериментально проверить эту формулу нельзя, но можно рассчитать индукцию магнитного поля, созданного всем контуром с током, используя установленный на опыте принцип суперпозиции магнитных полей:
— закон Био-Савара-Лапласа для расчета индукции магнитного поля, создаваемого элементом тока в некоторой точке (рис.69). Экспериментально проверить эту формулу нельзя, но можно рассчитать индукцию магнитного поля, созданного всем контуром с током, используя установленный на опыте принцип суперпозиции магнитных полей:  .
.  -лишь формальная запись, на практике интегрирование возможно лишь для проекций вектора магнитной индукции.
-лишь формальная запись, на практике интегрирование возможно лишь для проекций вектора магнитной индукции.
 Тл (Тесла).
Тл (Тесла).
Если задана объемная плотность тока,
то:  . Тогда
. Тогда 
Магнитное поле порождается движущимися зарядами(токами). Если скорость направленного движения зарядов в проводнике  , то
, то  . Тогда:
. Тогда: 
Индукцию магнитного поля точечного заряда, движущегося с постоянной нерелятивистской скоростью (рис.70) можно определить по формуле: 
Вземли~5*10-5Тл, Вмозга~10-11Тл.
Вmax ~150 Тл — получена в виде импульса.
САМОСТОЯТ. XI: рассчитать индукцию магнитного поля: 1)бесконечного длинного прямого проводника с током I в точке на расстоянии b от него;
2)полубесконечного длинного прямого проводника с током I в точке на расстоянии b от него.
В законе Био-Савара-Лапласа-Ампера рассматривалось взаимодействие элементов токов двух контуров.
Выражение  определяет индукцию магнитного поля, созданного элементом тока
определяет индукцию магнитного поля, созданного элементом тока  в месте расположения элемента тока
в месте расположения элемента тока  .
.
Используя принцип суперпозиции магнитных полей, можно найти индукцию магнитного поля, создаваемого всем первым контуром с током в месте расположения второго элемента тока. В этом случае на второй элемент тока будет действовать сила  .
.
Сила, действующая на элемент тока в магнитном поле, называется силой Ампера, а формула, позволяющая рассчитать эту силу – закон Ампера:

Так как  , то закон Ампера может быть записан в виде:
, то закон Ампера может быть записан в виде: 
Интегрируя эти выражения по объемным или линейным элементам тока, можно найти силу, действующую на тот или иной объем проводника или его линейный участок.
Экспериментально показано, что магнитное поле также действует на движущиеся заряды. Сила, действующая на движущийся электрический заряд со стороны электромагнитного поля, называется силой Лоренца.
Получим формулу для магнитной составляющей силы Лоренца. Используем для этого формулу для силы Ампера, действующей на элемент тока в магнитном поле: 
Если ток прекращается, то исчезает сила Ампера, но сила тока
 , где q0 — величина свободного заряда, а N – число свободных зарядов, проходящих через поперечное сечение проводника за dt.
, где q0 — величина свободного заряда, а N – число свободных зарядов, проходящих через поперечное сечение проводника за dt.
Если средняя скорость направленного движения свободных зарядов  , то
, то 
 — сила, действующая со стороны магнитного поля на движущийся заряд.
— сила, действующая со стороны магнитного поля на движущийся заряд.
Если заряд двигается в пространстве, в котором существуют одновременно электрическое и магнитное поле, то на него действует сила Лоренца:

Сила Лоренца является причиной появления силы Ампера.
Закон Ампера. Сила Лоренца — Мегаобучалка
Причина возникновения сил магнитного взаимодействия токов (§ 5.21) заключается в появлении вокруг проводников с током магнитного поля (§ 5.22). Это магнитное поле в свою очередь действует на второй проводник с током. Сила взаимодействия двух контуров с током конечных размеров складывается из взаимодействия отдельных элементов тока. Она зависит от размеров контуров, их формы и взаимного расположения, и поэтому сформулировать общий закон взаимодействия контуров с током нельзя. Однако такой закон можно дать для элементов тока.
Оба контура с током мысленно разбиваем на элементы тока. Применяя закон Био-Савара-Лапласа совместно с принципом суперпозиции, довольно просто рассчитать конкретное поле, создаваемое одним из контуров в точке пространства, где располагается элемент тока другого контура. Затем, используя принцип суперпозиции для силы, можно рассчитать результирующую силу магнитного взаимодействия контуров с током. Согласно третьему закону Ньютона силы взаимодействия двух контуров равны по модулю и противоположны по направлению.
Результаты опытов Ампера и последующих многочисленных исследований можно сформулировать следующим образом. Сила , действующая на элемент тока I× , равна
= , (24.1)
где — вектор магнитной индукции.
Соотношение (24.1) было установлено экспериментально Ампером и носит название закона Ампера. Полную силу, действующую на проводник, можно найти суммированием элементарных сил на отдельных элементах проводника, т.е. = . Силы, действующие на токи в магнитном поле, называют амперовыми или силами Ампера.
Если имеется прямолинейный отрезок провода и магнитная индукция во всех его точках постоянна, то сила Ампера согласно (24.1):
= . (24.2)
Величина этой силы равна
F = I×l×B×sina, (24.3)
где a — угол между векторами и .
Направление силы перпендикулярно к и и подчиняется правилу правого винта: при движении головки винта от вектора к вектору поступательное движение винта происходит в направлении силы . Взаимное расположение векторов , и показано на рисунке 33.
Закон Ампера позволяет определить единицу измерения магнитной индукции. Предположим, что проводник длиной l с током I перпендикулярен вектору магнитной индукции. Тогда закон Ампера (24.3) запишется в виде F = I×l×B, и
B = ,
откуда определяем, что 1 Тл — магнитная индукция такого однородного магнитного поля, которое действует с силой в 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику протекает ток в 1 А, т.е. 1 Тл = 1 Н/(А×м).
Одним из методов измерения магнитной индукции В является использование зависимости электрического сопротивление висмута от величины индукции магнитного поля (примерно на 5 % на каждую десятую долю тесла). Помещая предварительно проградуированную висмутовую спираль в магнитное поле, и измеряя относительное изменение ее сопротивления, можно определить магнитную индукцию поля. Следует отметить, что у других металлов электрическое сопротивление также возрастает в магнитном поле, но в гораздо меньшей степени. У меди, например, увеличение сопротивления примерно в 104 раз меньше, чем у висмута.
Применим закон Ампера для вычисления силы взаимодействия двух находящихся в вакууме параллельных бесконечно длинных прямых токов. Если расстояние между токами R (рисунок 34), то каждый элемент тока I2 будет находиться в магнитном поле, индукция которого равна В1 = (m0/2p)×(I1/R) (см. формулу (22.4)). Угол a между элементами тока I2 и вектором прямой. Следовательно, согласно (24.3) на единицу длины (l2 = 1 м) тока I2 действует сила
F2 = I2l2B1 = I1I2. (24.4)
Нетрудно убедиться, что токи, одинаково направленные, притягиваются, а противоположно направленные – отталкиваются. Для силы F1, действующей на единицу длины тока I1, получается аналогичное (24.4) выражение.
В § 1.1 уже отмечалось, что единица силы тока (ампер) – определяется через магнитное взаимодействие токов. Если в (24.4) положить I1 = I2 = 1 А, а R = 1 м, то можно дать следующее определение: 1 А – сила постоянного тока, протекающего по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывающего между этими проводниками силу, равную 2×10-7 Н на каждый метр длины. Из этого определения следует, что магнитная постоянная должна иметь значение m0 = 4p×10-7 единицы системы СИ.
Так как всякий ток есть движение заряженных частиц (электронов или ионов), то очевидно, что на движущийся заряд в магнитном поле действует сила. Нетрудно определить величину этой силы. На проводник длиной l с током I в однородном магнитном поле с индукцией В действует сила Ампера
FA = I×l×B×sina,
где a — угол между векторами и .
С другой стороны
I×l = Nev,
где N – полное число движущихся заряженных частиц, е – заряд частицы (носителя тока), v — скорость движения частиц.
Учитывая, что направление совпадает с направлением скорости движения положительных частиц (с направлением тока), мы можем выражение для силы представить в следующем виде:
FА = Nev×B×sina,
где a — угол между векторами и .
Сила, действующая на проводник, пропорциональна полному числу движущихся частиц, а значит, сила, действующая на одну частицу, равна:
F = ev×B×sina. (24.5)
Заменяя в (24.5) заряд носителя тока на q, получаем
F = qv×B×sina. (24.6)
Полученный результат можно выразить в векторной форме:
= . (24.7)
Направление этой силы перпендикулярно к плоскости, в которой лежат векторы и , и подчиняется правилу правого винта. Скорость в этой формуле есть скорость заряда относительно магнитного поля. Если заряд q положителен, направление силы совпадает с направлением векторного произведения . В случае отрицательного заряда q направления и противоположны. Сила всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется. Причем на покоящуюся заряженную частицу ( =0) магнитное поле не действует ( =0).
Если одновременно имеются электрическое и магнитное поля, сила, действующая на заряженную частицу, равна:
= q + . (24.8)
Это выражение было получено Лоренцем путем обобщения экспериментальных данных, и носит название силы Лоренца.
Сила Лоренца складывается из двух слагаемых: = + , где = q и = , которые называют, соответственно, электрической и магнитной составляющими силы Лоренца. Разделение полной силы Лоренца на электрическую и магнитную составляющие зависит от выбора системы отсчета. Без указания системы отсчета такое разделение не имеет смысла.
БИЛЕТ. Магнитное взаимодействие постоянных токов. Вектор магнитной индукции. Закон Ампера. Сила Лоренца. Движение зарядов в электрических и магнитных полях.
⇐ ПредыдущаяСтр 3 из 9Следующая ⇒
Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот.
Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I1 и I2 в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:
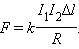 |
В Международной системе единиц СИ коэффициент пропорциональности k принято записывать в виде:
где μ0 – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно
| μ0 = 4π·10–7 H/A2 ≈ 1,26·10–6 H/A2. |
Формула, выражающая закон магнитного взаимодействия параллельных токов, принимает вид:
|
Отсюда нетрудно получить выражение для индукции магнитного поля каждого из прямолинейных проводников. Магнитное поле прямолинейного проводника с током должно обладать осевой симметрией и, следовательно, замкнутые линии магнитной индукции могут быть только концентрическими окружностями, располагающимися в плоскостях, перпендикулярных проводнику. Это означает, что векторы B1 и B2 магнитной индукции параллельных токов I1 и I2 лежат в плоскости, перпендикулярной обоим токам. Поэтому при вычислении сил Ампера, действующих на проводники с током, в законе Ампера нужно положить sin α = 1. Из закона магнитного взаимодействия параллельных токов следует, что модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением
|
Для того, чтобы при магнитном взаимодействии параллельные токи притягивались, а антипараллельные отталкивались, линии магнитной индукции поля прямолинейного проводника должны быть направлены по часовой стрелке, если смотреть вдоль проводника по направлению тока. Для определения направления вектора B магнитного поля прямолинейного проводника также можно пользоваться правилом буравчика: направление вращения рукоятки буравчика совпадает с направлением вектора B если при вращении буравчик перемещается в направлении тока Магнитное взаимодействие параллельных проводников с током используется в Международной системе единиц (СИ) для определения единицы силы тока – ампера:
Вектор магнитной индукции— это основная силовая характеристика магнитного поля (обозначается В).
Сила Лоренца — сила, действующая на одну заряженную частицу, равна
Под действием силы Лоренца электрические заряды в магнитном поле движутся по криволинейным траекториям. Рассмотрим наиболее характерные случаи движения заряженных частиц в однородном магнитном поле.
а) Если заряженная частица попадает в магнитное поле под углом α = 0°, т.е.летит вдоль линий индукций поля, то Fл= qvBsma = 0. Такая частица будет продолжать свое движение так, как если бы магнитного поля не было. Траектория частицы будет представлять собой прямую линию.
б)Частица с зарядом q попадает в магнитное поле так, что направление ее скорости v перпендикулярно индукции ^ В магнитного поля (рисунок — 3.34). В таком случае сила Лоренца обеспечивает центростремительное ускорение a = v2/R и частица движется по окружности радиусом R в плоскости, перпендикулярной линиям индукции магнитного поля.под действием силы Лоренца: Fn = qvB sinα, учитывая, что α = 90°, запишем уравнение движения такой частицы: т v2/R= qvB. Здесь m — масса частицы, R – радиус окружности по которой движется частица. Откуда можно найти отношение e/m — называют удельным зарядом,который показывает заряд единицы массы частицы.
с) Если заряженная частица влетает со скоростью v0 в магнитное поле под любым углом α , то данное движение можно представить ее как сложное и разложить ее на две составляющие по . Траектория движения представляет собой винтовую линию, ось которой совпадает с направлением В. Направление, в котором закручивается траектория, зависит от знака заряда частицы. Если заряд положителен, траектория закручивается против часовой стрелки. Траектория, по которой движется отрицательно заряженная частица, закручивается по часовой стрелке (предполагается, что мы смотрим на траекторию вдоль направления В; частица при этом летит от нас.
На частицу с зарядом q, помещенную в электрическое поле с напряженностью 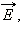 действует сила
действует сила 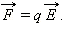 В однородном электрическом поле под действием этой силы частица движется по параболе, аналогично движению тела под действием силы тяжести вблизи поверхности Земли.
В однородном электрическом поле под действием этой силы частица движется по параболе, аналогично движению тела под действием силы тяжести вблизи поверхности Земли.
БИЛЕТ 10. Закон Био-Савара-Лапласа. Теорема о циркуляции (закон полного тока).
Закон Био-Савара-Лапласа гласит что магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока: 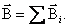
Элемент тока длины dl создает поле с магнитной индукцией: 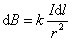 или в векторной форме:
или в векторной форме: 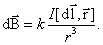
Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.
Рекомендуемые страницы:
Закон Ампера — это… Что такое Закон Ампера?
Зако́н Ампе́ра — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Выражение для силы , с которой магнитное поле действует на элемент объёма проводника с током плотности , находящегося в магнитном поле с индукцией , в Международной системе единиц (СИ) имеет вид:
- .
Если ток течёт по тонкому проводнику, то , где — «элемент длины» проводника — вектор, по модулю равный и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:
Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.
Модуль силы Ампера можно найти по формуле:
где — угол между векторами магнитной индукции и тока.
Сила максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ():
Два параллельных проводника
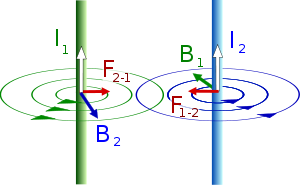 Два бесконечных параллельных проводника в вакууме
Два бесконечных параллельных проводника в вакуумеНаиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи и . Требуется найти силу, действующую на единицу длины проводника.
В соответствии с законом Био — Савара — Лапласа бесконечный проводник с током в точке на расстоянии создаёт магнитное поле с индукцией
где — магнитная постоянная.
Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:
По правилу буравчика, направлена в сторону первого проводника (аналогично и для , а значит, проводники притягиваются).
Модуль данной силы ( — расстояние между проводниками):
Интегрируем, учитывая только проводник единичной длины (пределы от 0 до 1):
Полученная формула используется в СИ для установления численного значения магнитной постоянной . Действительно, ампер, являющийся одной из основных единиц СИ, определяется в ней как «сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10−7ньютона»[1].
Таким образом, из полученной формулы и определения ампера следует, что магнитная постоянная равна Н/А² или, что то же самое, Гн/ м точно.
Проявления
- Электродинамическая деформация шин (токопроводов) трёхфазного переменного тока на подстанциях при воздействии токов короткого замыкания.
- Раздвигание токопроводов рельсотронов при выстреле.