30. Действие магнитного поля на проводник с током. Закон Ампера. Единицы измерения магнитной индукции.
Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента дли-
ной dl проводника на магнитную индукцию В:
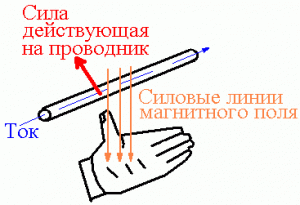
dF = I[dl, В]. (111.1)
Направление вектора dF может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
Модуль силы Ампера (см. (111.1)) вычисляется по формуле
dF = IBdlsin, (111.2)
где a — угол между векторами dl и В.
Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I1 и I2 (направления токов указаны на рис. 167), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока
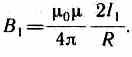

dF1=I2B1dl, или, подставляя значение для В1, получим
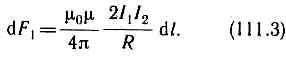
Рассуждая аналогично, можно показать, что сила d
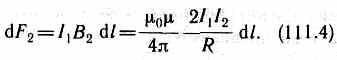
Сравнение выражений (111.3) и (111.4) показывает, что
dF1=dF2,
т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой

Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда закон Ампера (см. (111.2)) запишется в виде
dF=IBdl,
откуда
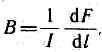
Единица магнитной индукции — тесла (Тл): 1 Тл—магнитная индукция такого однородного магнитного поля, которое действует с силой в 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток в 1 А:
1Тл=1Н/(А•м).
Так как 0= 4•10-7 Н/А2, а в случае вакуума (=1), согласно (1.09.3), В =0H, то для данного случая
H=В/0.
Единица напряженности магнитного поля — ампер на метр (А/м): 1 А/м — напряженность такого поля, магнитная индукция которого в вакууме равна 4•10-7 Тл.
3.7. Магнитное взаимодействие постоянных токов. Закон ампера
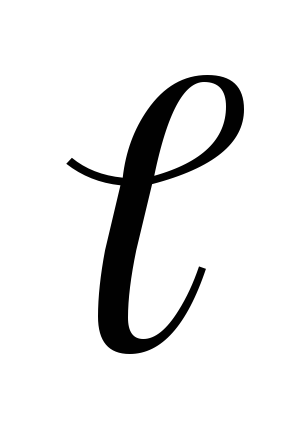 ,
магнитной индукции
,
магнитной индукции и синусу угла
и синусу угла между направлениями тока в проводнике
и вектором
между направлениями тока в проводнике
и вектором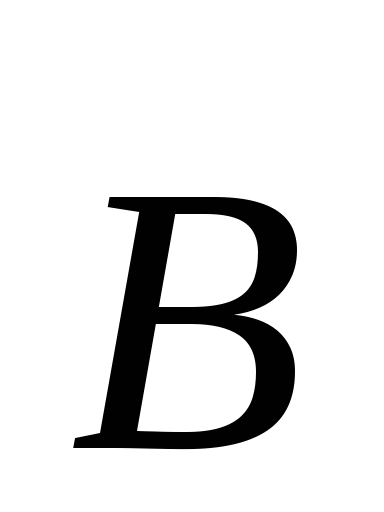
 .
.
В случае неоднородного магнитного поля и проводника произвольной формы перейдем к бесконечно малым приращениям, имеем:
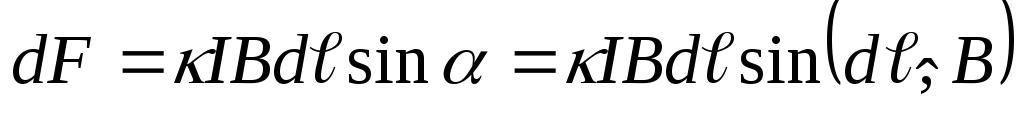 .
.
 -коэффициент
пропорциональности, зависящий от выбора
единицы измерения. В СИ
-коэффициент
пропорциональности, зависящий от выбора
единицы измерения. В СИ 
Будем
считать, что элемент проводника 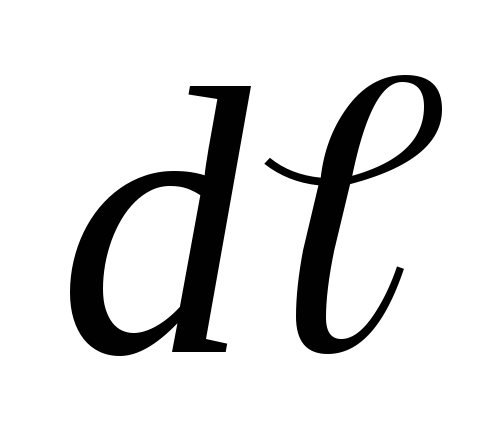 перпендикулярен вектору
перпендикулярен вектору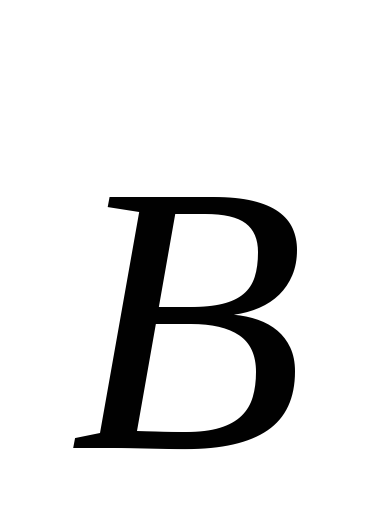 ,
тогда
,
тогда -магнитная индукция
-магнитная индукция численно равна силе, действующей со
стороны поля на единицу длины проводника,
по которому течет электрический ток
единичной силы и который расположен
перпендикулярно к направлению магнитного
поля. Т.е. магнитная индукция
численно равна силе, действующей со
стороны поля на единицу длины проводника,
по которому течет электрический ток
единичной силы и который расположен
перпендикулярно к направлению магнитного
поля. Т.е. магнитная индукция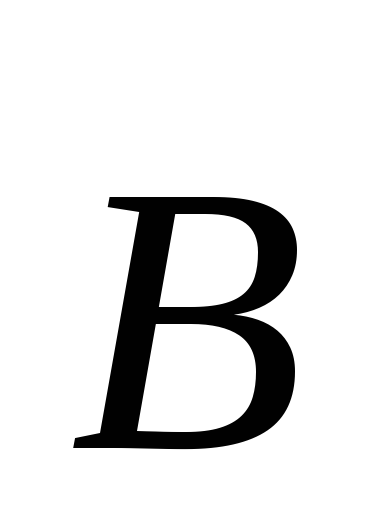
Направление
силы  определяется по правилу левой руки:
если ладонь левой руки расположить так,
чтобы в нее входили линии магнитной
индукции, а четыре вытянутых пальца
расположить по направлению электрического
тока в проводнике, то отставленный
большой палец укажет направление силы,
действующей на проводник со стороны
поля.
определяется по правилу левой руки:
если ладонь левой руки расположить так,
чтобы в нее входили линии магнитной
индукции, а четыре вытянутых пальца
расположить по направлению электрического
тока в проводнике, то отставленный
большой палец укажет направление силы,
действующей на проводник со стороны
поля.
Если 
 ,
то векторсовпадает по направлению с векторным
произведением
,
то векторсовпадает по направлению с векторным
произведением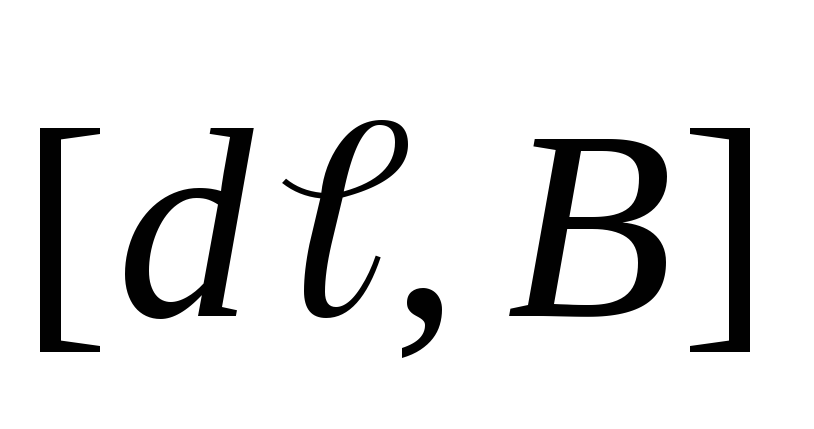 —
вектор
—
вектор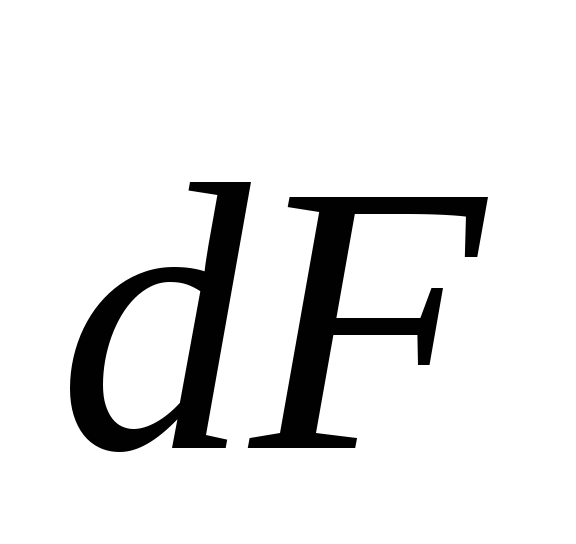 направлен перпендикулярно к плоскости,
образованной векторами
направлен перпендикулярно к плоскости,
образованной векторами и
и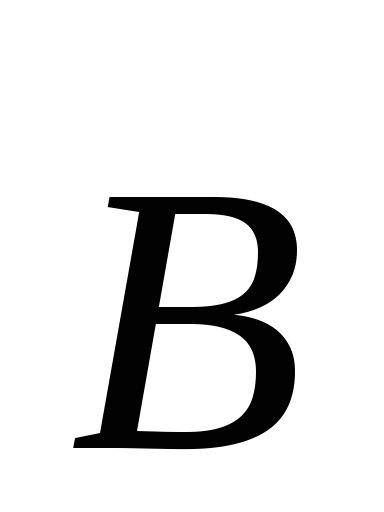 таким образом, чтобы из конца вектора
таким образом, чтобы из конца вектора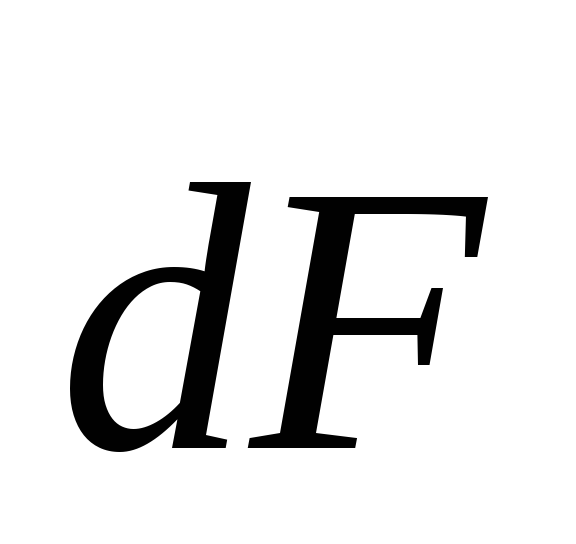
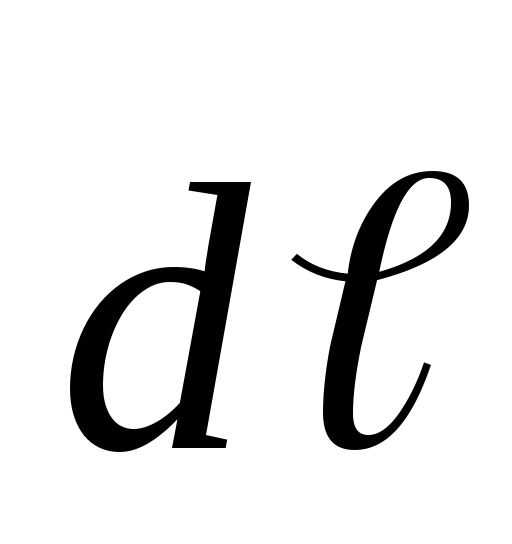 к вектору
к вектору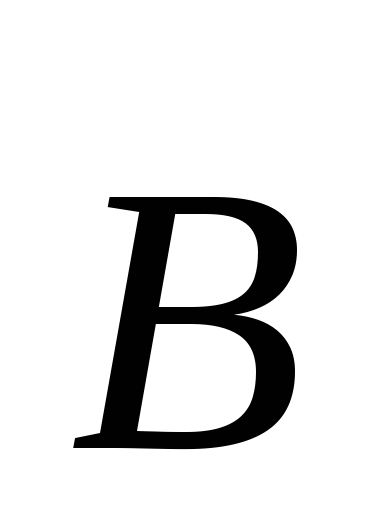 по кратчайшему пути происходило против
часовой стрелки.
по кратчайшему пути происходило против
часовой стрелки.Закон Ампера в векторной форме имеет вид:
 .
.
Силы электромагнитного взаимодействия не являются центральными и всегда перпендикулярны к линиям магнитной индукции.
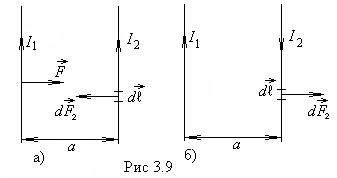 Рассмотрим
два длинных прямолинейных проводника,
которые расположены параллельно друг
к другу. Расстояние между проводниками а.
При пропускании тока по проводникам
между ними возникает сила взаимодействия.
Рассмотрим некоторые частные случаи.
Рассмотрим
два длинных прямолинейных проводника,
которые расположены параллельно друг
к другу. Расстояние между проводниками а.
При пропускании тока по проводникам
между ними возникает сила взаимодействия.
Рассмотрим некоторые частные случаи. 1.Пусть
токи 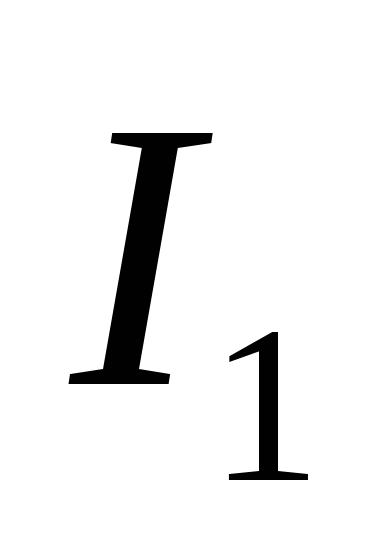 и
и в проводниках направлены в одну сторону
(рис.3.9а). В этом случае проводники
притягиваются друг к другу. Каждый из
проводников создает вокруг себя магнитное
поле, которое действует по закону Ампера
на другой проводник. При этом на элемент
в проводниках направлены в одну сторону
(рис.3.9а). В этом случае проводники
притягиваются друг к другу. Каждый из
проводников создает вокруг себя магнитное
поле, которое действует по закону Ампера
на другой проводник. При этом на элемент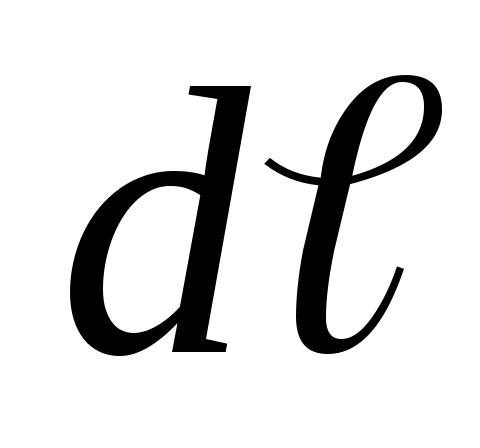 второго проводника с током
второго проводника с током действует сила
действует сила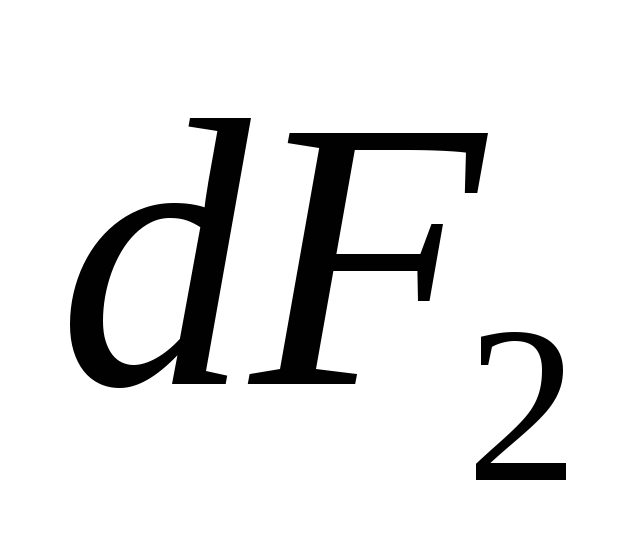 :
:
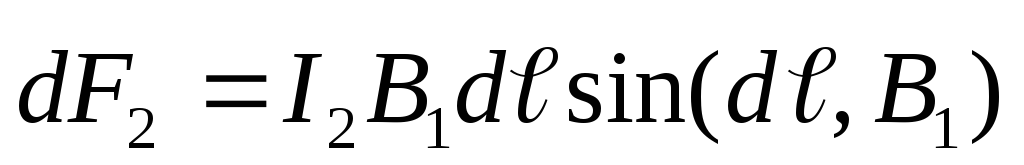 .
.
Если а << 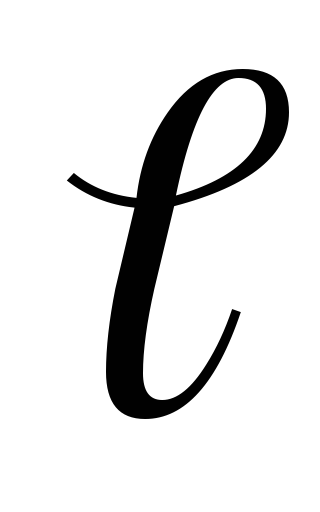 ,
то проводник можно считать бесконечно
длинным, тогда
,
то проводник можно считать бесконечно
длинным, тогда
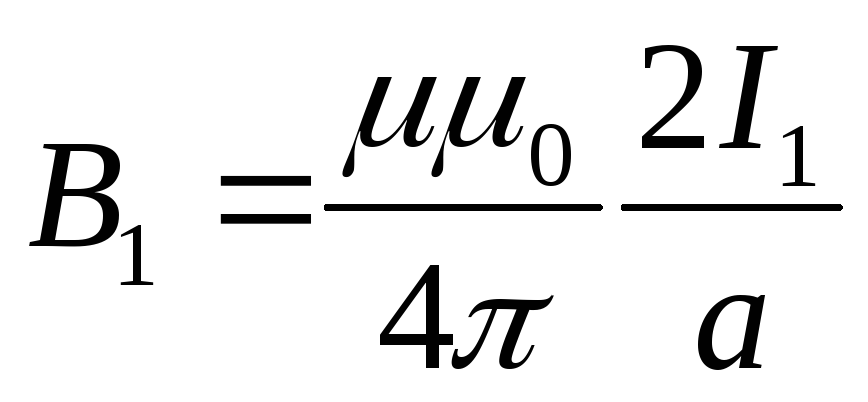 ,
при этом
,
при этом 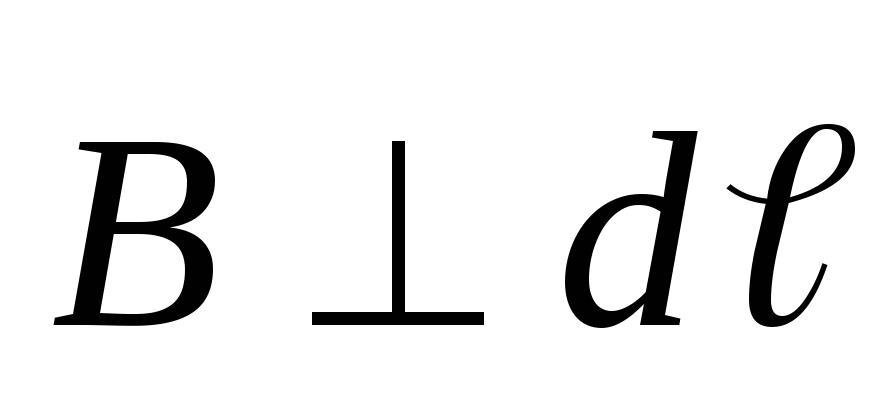 ,
,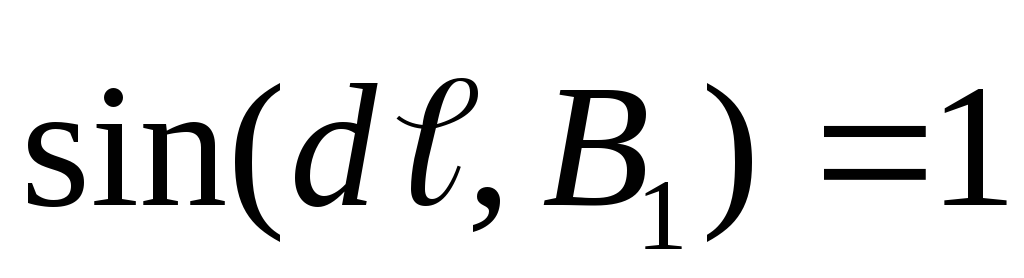 ,
имеем
,
имеем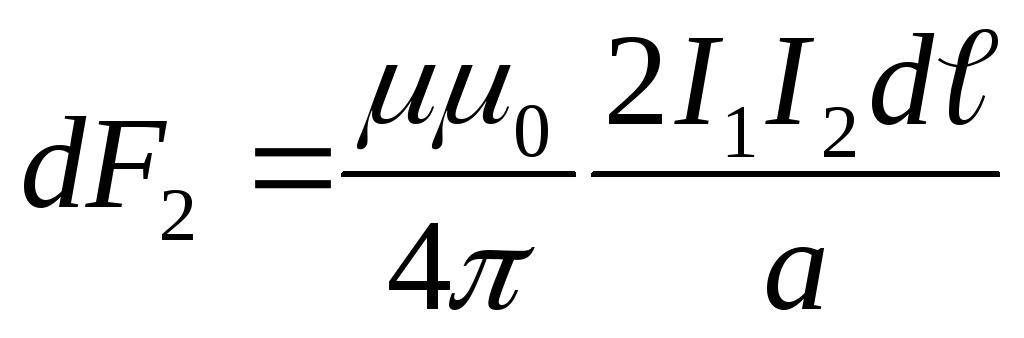 .
.
Для  выражение примет такой же вид. Оно
симметрично для обоих проводников,
поэтому
выражение примет такой же вид. Оно
симметрично для обоих проводников,
поэтому
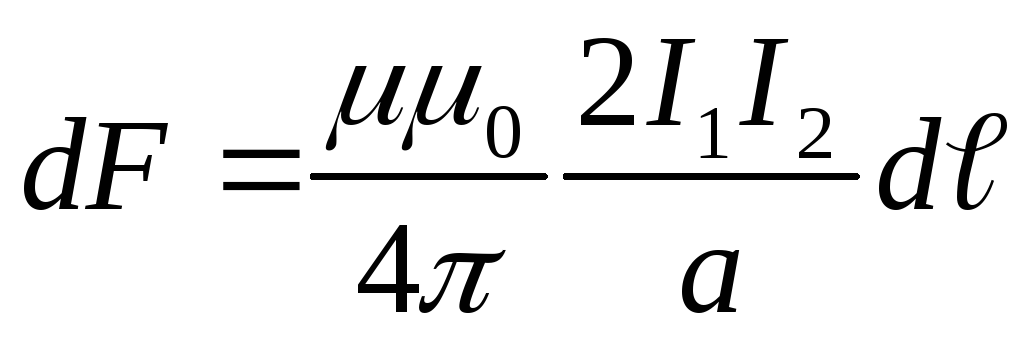 ,
тогда
,
тогда 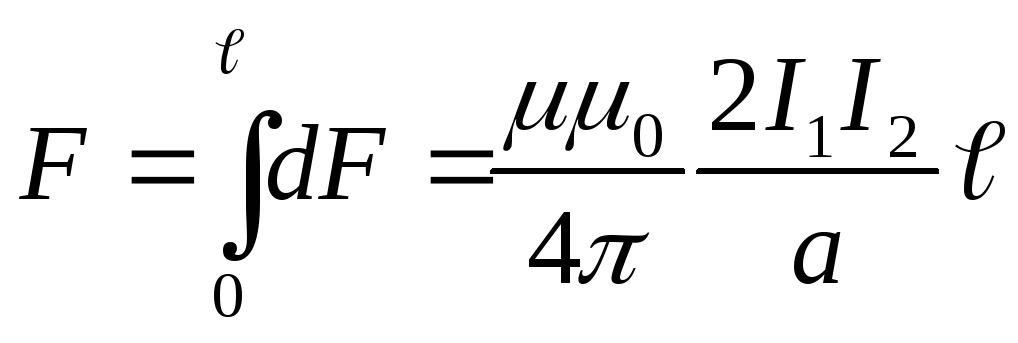 .
.
2. Если токи противоположны по направлению, то проводники отталкиваются (рис.9б).
Е диницы
измерения в системе СИ: магнитная
индукция —B=[Тл]
– тесла; напряженность магнитного поля H=[
диницы
измерения в системе СИ: магнитная
индукция —B=[Тл]
– тесла; напряженность магнитного поля H=[ ]
— ампер на метр.
]
— ампер на метр.
Рассмотрим
контур с током, находящийся в магнитном
поле. Сила Ампера, действующая на контур,
равна 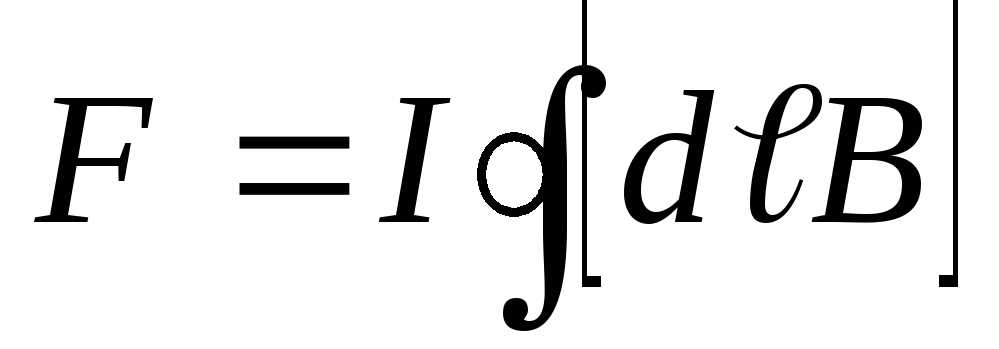 ,
интегрирование проводится по контуру
с током. Если поле однородно, вектор
,
интегрирование проводится по контуру
с током. Если поле однородно, вектор можно
вынести за знак интеграла. Интеграл
можно
вынести за знак интеграла. Интеграл представляет собой замкнутую цепочку
элементарных векторов
представляет собой замкнутую цепочку
элементарных векторов ,
поэтому он равен нулю. Поэтому
результирующая амперова сила равна
нулю в однородном магнитном поле. Если
же поле неоднородно, результирующая
сила отлична от нуля . Рассмотрим плоский
контур, размеры которого малы. Такой
контур называют элементарным. Его
магнитный момент
,
поэтому он равен нулю. Поэтому
результирующая амперова сила равна
нулю в однородном магнитном поле. Если
же поле неоднородно, результирующая
сила отлична от нуля . Рассмотрим плоский
контур, размеры которого малы. Такой
контур называют элементарным. Его
магнитный момент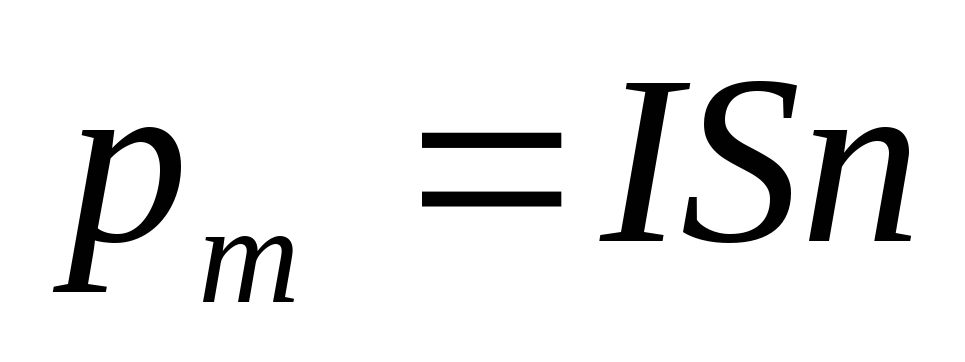 ,
где
,
где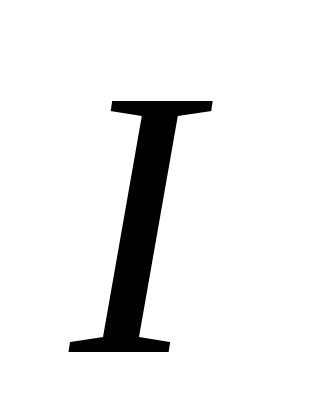 —
ток в контуре,
—
ток в контуре, —
его площадь,
—
его площадь, — единичный вектор нормали к поверхности
контура, связанный с направлением тока
правилом правого винта. Сила Ампера,
действующая на такой контур в неоднородном
магнитном поле, равна
— единичный вектор нормали к поверхности
контура, связанный с направлением тока
правилом правого винта. Сила Ампера,
действующая на такой контур в неоднородном
магнитном поле, равна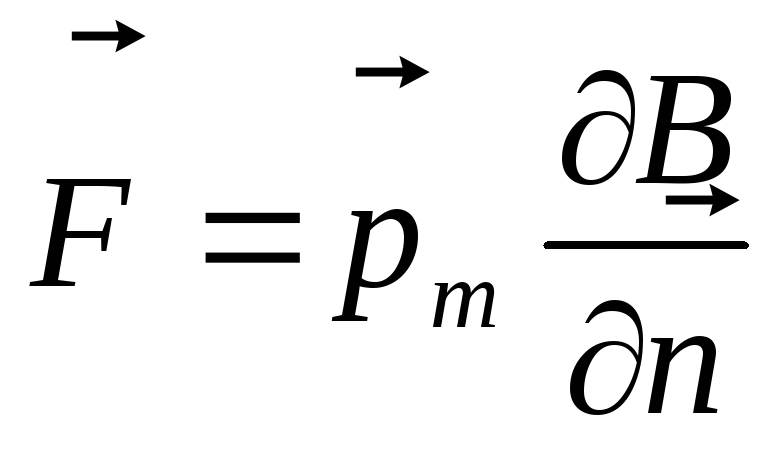 ,
где
,
где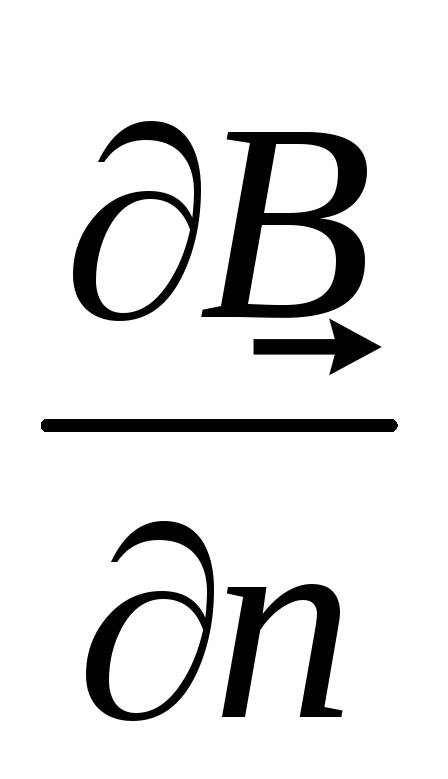 — производная магнитной индукции на
направление магнитного момента. Из этой
формулы следует:
— производная магнитной индукции на
направление магнитного момента. Из этой
формулы следует:
в
 однородном магнитном поле
однородном магнитном поле ,
т.к.
,
т.к. ;
;направление вектора
 в общем случае не совпадает ни с
вектором
в общем случае не совпадает ни с
вектором ,
ни с вектором
,
ни с вектором ;
вектор
;
вектор совпадает лишь с направлением
элементарного перемещения
совпадает лишь с направлением
элементарного перемещения ,
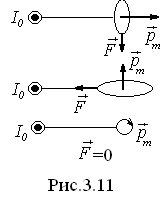
взятого в направлении вектора
,
взятого в направлении вектора в месте расположения контура. На рис.
3.11 представлены три расположения
контура в поле прямого тока. Проекция
силы на направлениеХ равна
в месте расположения контура. На рис.
3.11 представлены три расположения
контура в поле прямого тока. Проекция
силы на направлениеХ равна
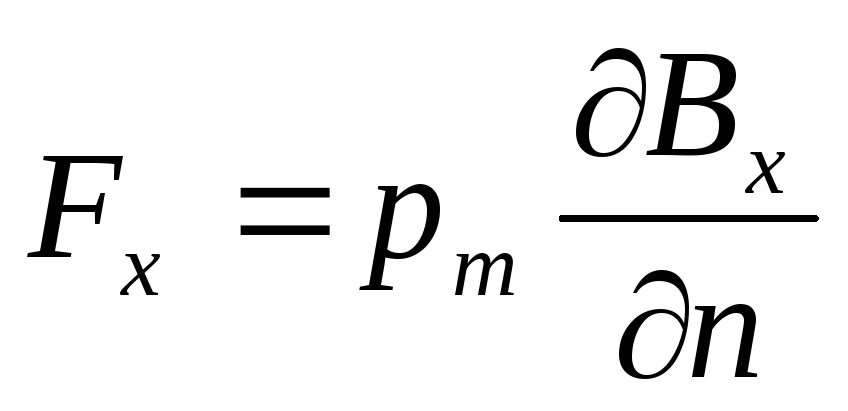 .
.
Найдем
момент сил Ампера, действующий на контур
с током в магнитном поле. В однородном
поле результирующая сил, действующих
на контур, равна нулю, следовательно,
суммарный момент этих сил не зависит
от точки О, относительно
которой определяют моменты этих сил. В
этом случае говорят просто о моменте
амперовых сил. Результирующий момент
этих сил  .
Таким образом, результирующий момент
амперовых сил , действующих на контур
с током в однородном магнитном поле,
перпендикулярен магнитному моменту
контура и вектору магнитной индукции.
.
Таким образом, результирующий момент
амперовых сил , действующих на контур
с током в однородном магнитном поле,
перпендикулярен магнитному моменту
контура и вектору магнитной индукции.
Закон Ампера. Взаимодействие параллельных токов.
7
Лекция 9. Действие магнитного поля на
проводники с током и движущиеся электрические заряды
[1] гл.14
План лекции
Закон Ампера. Взаимодействие параллельных токов.
Контур с током в магнитном поле. Работа перемещения проводника с током в магнитном поле.
Сила Лоренца. Движение заряженных частиц в магнитном поле.
З акон
Ампера: сила
акон
Ампера: сила  с которой магнитное поле действует на
элемент проводника
с которой магнитное поле действует на
элемент проводника  с током
с током 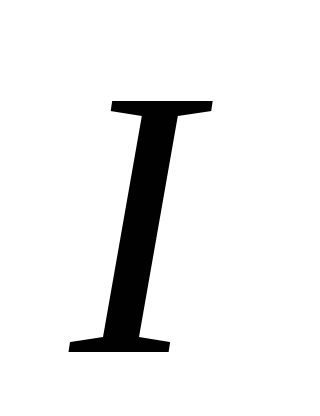 ,
находящегося в магнитном поле, прямо
пропорциональна силе тока
,
находящегося в магнитном поле, прямо
пропорциональна силе тока 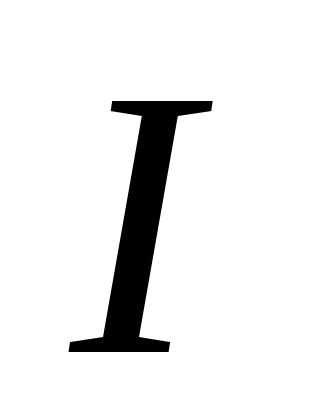 и векторному произведению элемента
длины
и векторному произведению элемента
длины 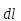 на
магнитную индукцию
на
магнитную индукцию  :
:
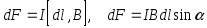
Если  ,
, 
Направление силы Ампера определяется правилом левой руки (рис. 1).
Закон Ампера применяется для определения
силы взаимодействия двух бесконечных
прямолинейных параллельных проводников
с токами  и
и 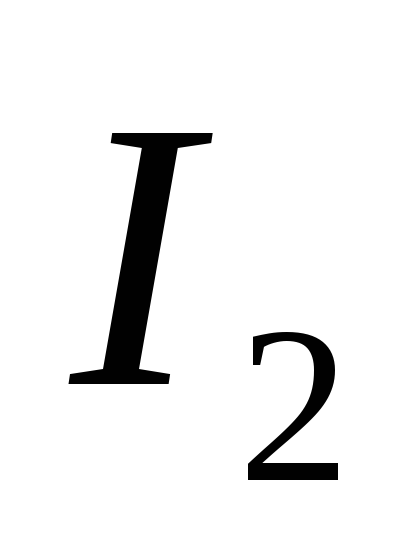 ,
расположенных в вакууме на расстоянии
,
расположенных в вакууме на расстоянии 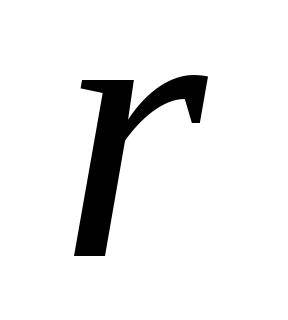 .
Каждый из проводников создает магнитное
поле, которое, по закону Ампера, действует
на другой проводник.
.
Каждый из проводников создает магнитное
поле, которое, по закону Ампера, действует
на другой проводник.
О пределим
силу, с которой магнитное поле тока
пределим
силу, с которой магнитное поле тока 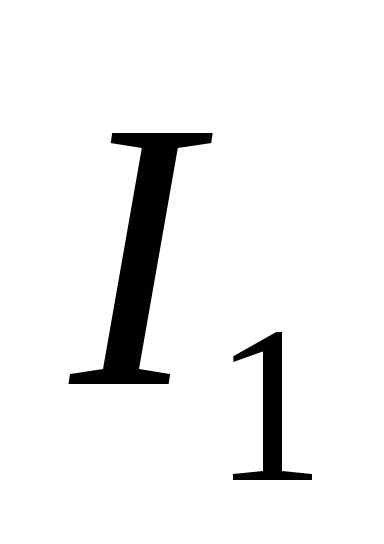 действует на элемент
действует на элемент 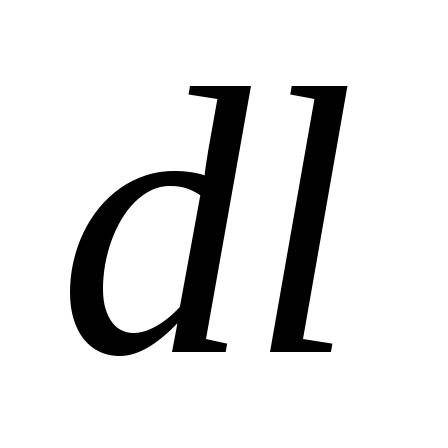 второго проводника с током
второго проводника с током 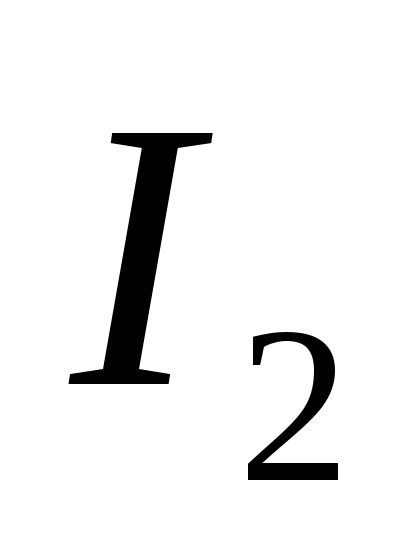 (рис. 2).
(рис. 2).
 ,
,
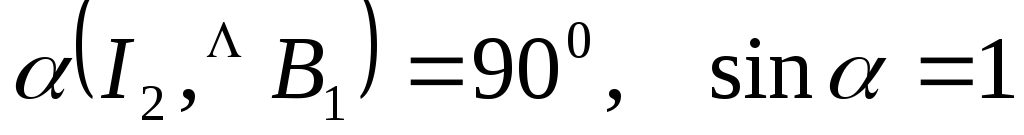 ,
,
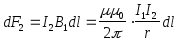 .
.
Рассуждая аналогично, можно показать, что
 .
.
По III закону Ньютона  т.е. два параллельных тока одинакового
направления притягиваются друг к другу
с силой
т.е. два параллельных тока одинакового
направления притягиваются друг к другу
с силой
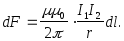
Аналогично можно доказать, что токи противоположного направления отталкиваются с такой же силой.
Если I1 = I2 = 1A, r=1м, l=1м, F1 = F2 = 210-7H , что соответствует определению величины 1 ампера.
Контур с током в магнитном поле. Работа перемещения проводника с током в магнитном поле.
Магнитный момент контура с током — это векторная физическая величина, численно равная произведению силы тока на площадь контура.
 .
.
1 Ам2 — это магнитный момент контура с током силой 1а, площадь которого равна 1м2.

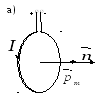 — единичный вектор внешней нормали к
поверхности S, ограниченной
контуром с током.
— единичный вектор внешней нормали к
поверхности S, ограниченной
контуром с током.

В нешней
(положительной) называется нормаль,
которая связана с направлением тока в
контуре правилом правого винта (рис.
3а). Таким образом, направление
нешней
(положительной) называется нормаль,
которая связана с направлением тока в
контуре правилом правого винта (рис.
3а). Таким образом, направление  определяется правилом правого винта:
если рукоятку винта вращать по току в
контуре, поступательное движение винта
совпадет с направлением
определяется правилом правого винта:
если рукоятку винта вращать по току в
контуре, поступательное движение винта
совпадет с направлением 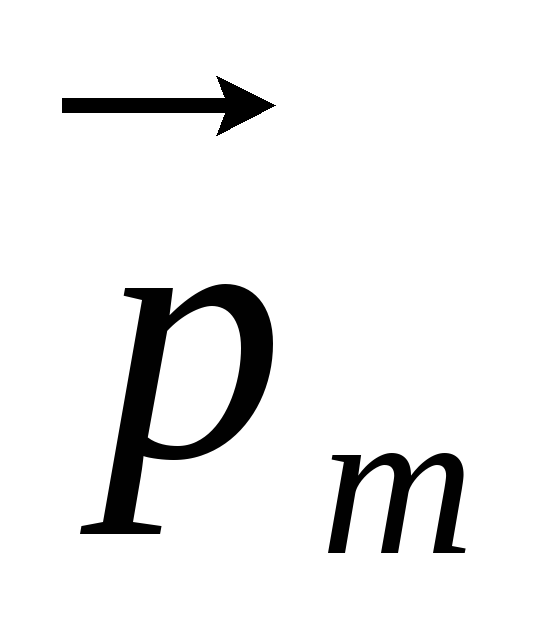 (рис. 3 а,б).
(рис. 3 а,б).
Поместим в однородное магнитное поле
с индукцией 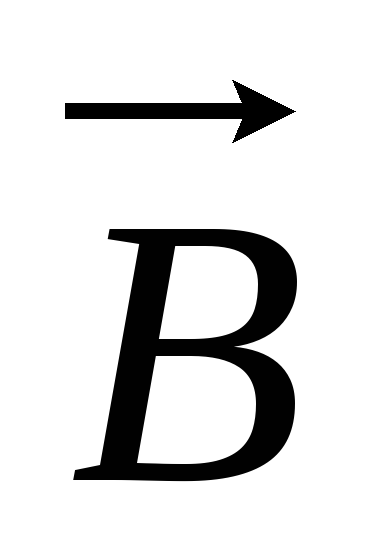 рамку с током
рамку с током 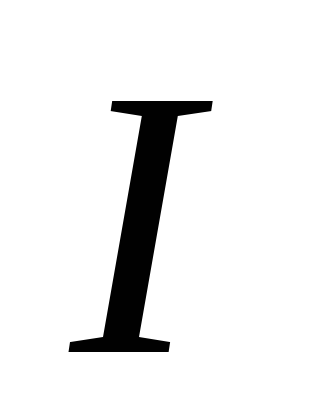 так, чтобы плоскость рамки была параллельна
магнитным силовым линиям (рис. 4). При
этом на стороны рамки, перпендикулярные
силовым линиям (
так, чтобы плоскость рамки была параллельна
магнитным силовым линиям (рис. 4). При
этом на стороны рамки, перпендикулярные
силовым линиям (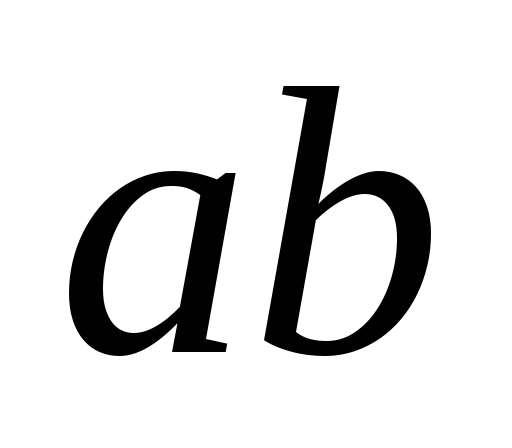 и
)
будут действовать силы
и
)
будут действовать силы  и
и 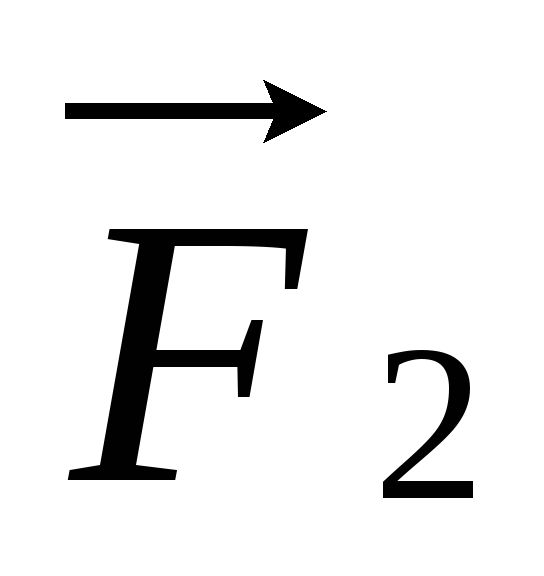 ,
создающие вращающий момент сил
относительно закрепленной оси вращения
00.
,
создающие вращающий момент сил
относительно закрепленной оси вращения
00.
 где
где 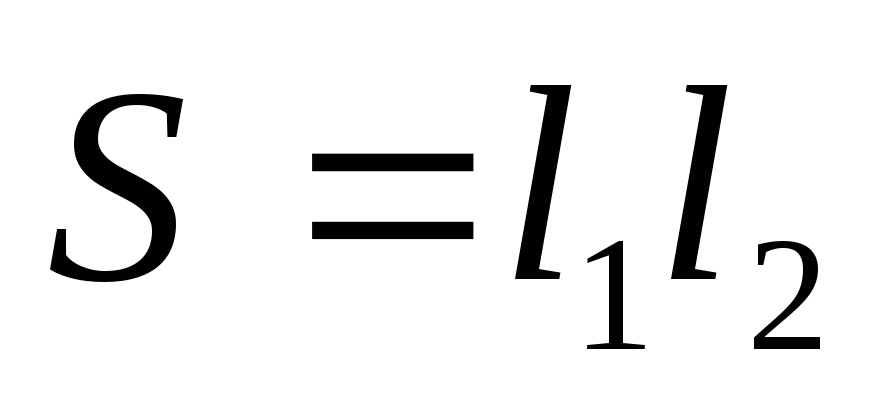 — площадь рамки, pm — магнитный момент рамки с током.
— площадь рамки, pm — магнитный момент рамки с током.
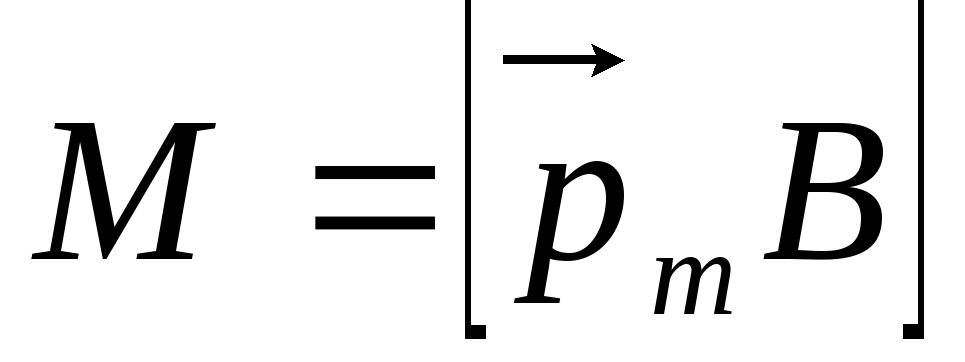 .
.
Вращающий момент стремится привести
контур в положение устойчивого равновесия,
при котором векторы  и
и 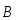 сонаправлены (рис.5), т.е. ориентированы
параллельно друг другу. При этом М=0,
силы
сонаправлены (рис.5), т.е. ориентированы
параллельно друг другу. При этом М=0,
силы  действуют в одной плоскости, они лишь
деформируют рамку (растягивают).
действуют в одной плоскости, они лишь
деформируют рамку (растягивают).
С ледовательно,
действие однородного магнитного поля
на рамку (контур) с током сводится к
повороту
ледовательно,
действие однородного магнитного поля
на рамку (контур) с током сводится к
повороту 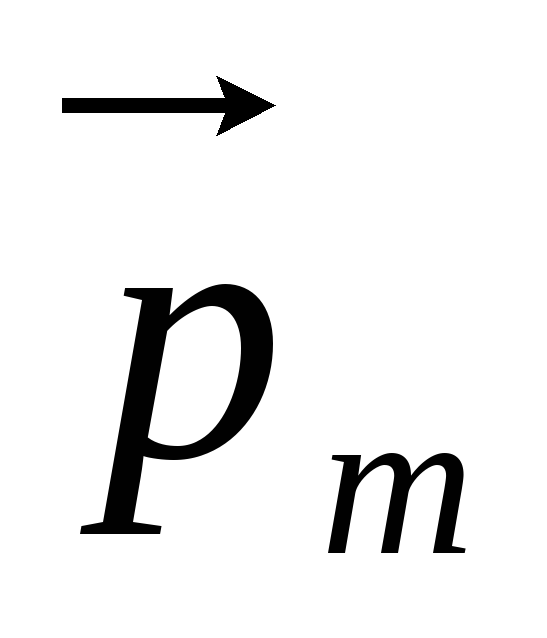 в направлении, параллельном
в направлении, параллельном 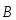 (
(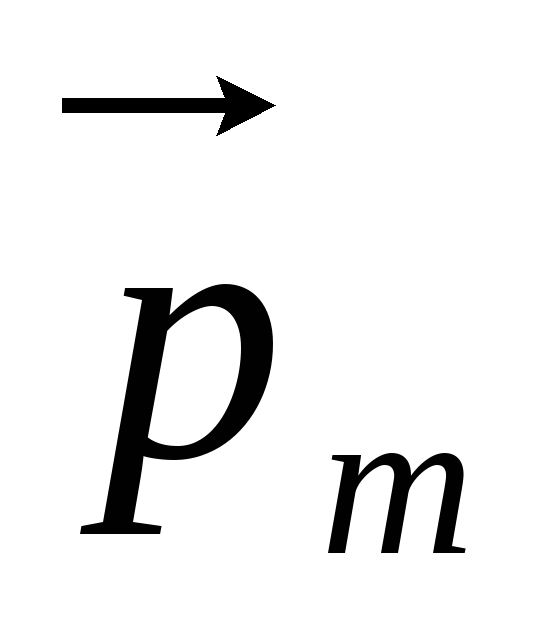 сонаправлено
сонаправлено 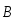 ).
).
Из предыдущей формулы может быть дано
определение 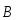 :
модуль вектора магнитной индукции в
данной точке магнитного поля равен
максимальному вращающему моменту сил,
действующих на рамку с током, обладающую
единичным магнитным моментом:
:
модуль вектора магнитной индукции в
данной точке магнитного поля равен
максимальному вращающему моменту сил,
действующих на рамку с током, обладающую
единичным магнитным моментом:
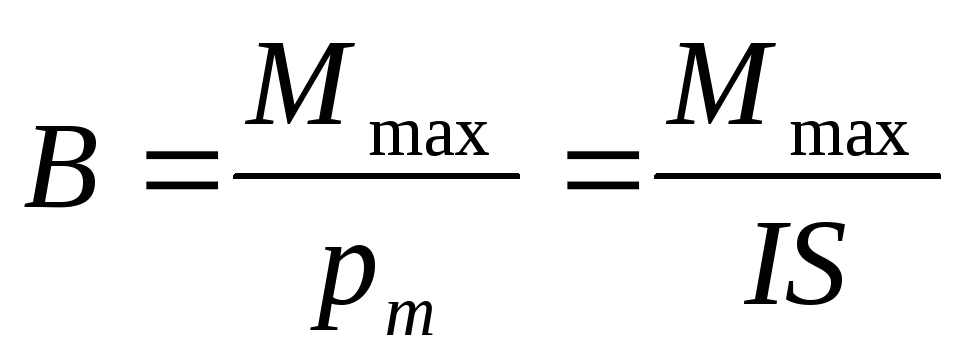 .
.
Если поле неоднородно, под действием силы незакрепленный контур с током втягивается в область более сильного магнитного поля.
Н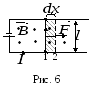 а
проводник с током в магнитном поле
действует сила Ампера. Если проводник
не закреплен (например, одна сторона
контура изготовлена в виде подвижной
перемычки), то под действием силы Ампера
он будет перемещаться в магнитном поле,
т.е. сила Ампера совершает работу. Для
ее определения рассмотрим проводник
длиной
а
проводник с током в магнитном поле
действует сила Ампера. Если проводник
не закреплен (например, одна сторона
контура изготовлена в виде подвижной
перемычки), то под действием силы Ампера
он будет перемещаться в магнитном поле,
т.е. сила Ампера совершает работу. Для
ее определения рассмотрим проводник
длиной  с током I, который может
свободно перемещаться в однородном
магнитном поле с индукцией
с током I, который может
свободно перемещаться в однородном
магнитном поле с индукцией 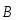 (рис. 6),
(рис. 6),  .
.
Под действием этой силы проводник
переместится параллельно самому себе
на 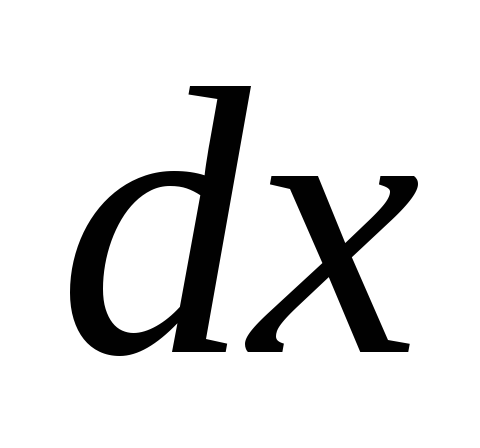 из положения 1 в положение 2 . Работа,
совершенная при этом:
из положения 1 в положение 2 . Работа,
совершенная при этом:
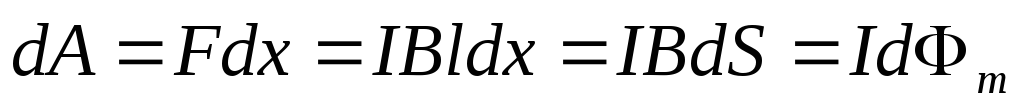 ,
,
где 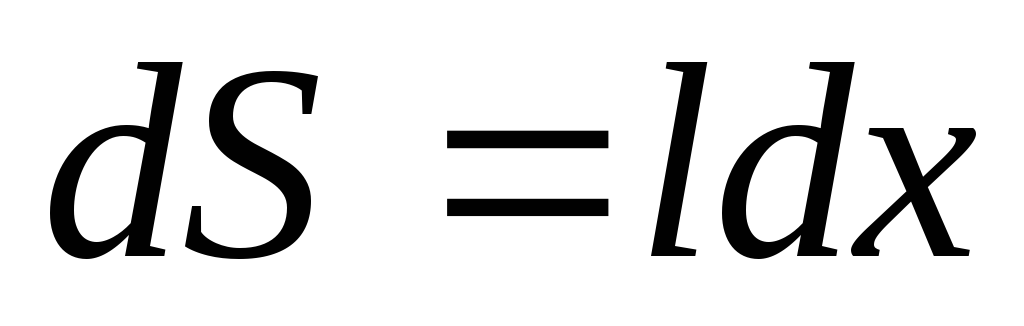 — площадь, пересекаемая проводником при
его движении;
— площадь, пересекаемая проводником при
его движении;
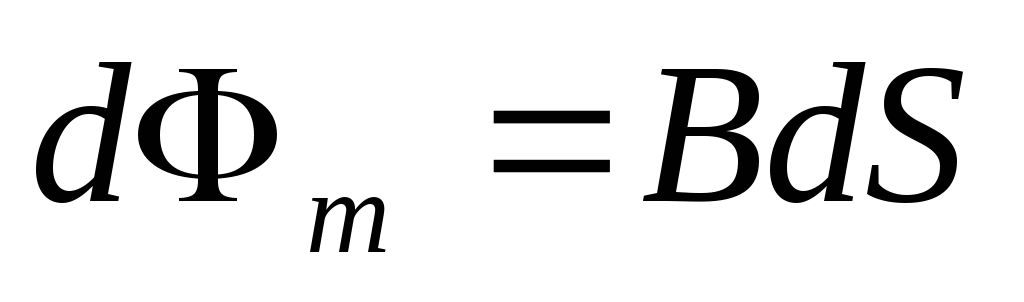 — магнитный поток, пронизывающий эту
площадь.
— магнитный поток, пронизывающий эту
площадь.
Полученная формула справедлива и для
произвольного направления вектора 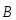 ,
т.к.
,
т.к. 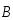 можно разложить на нормальную
можно разложить на нормальную 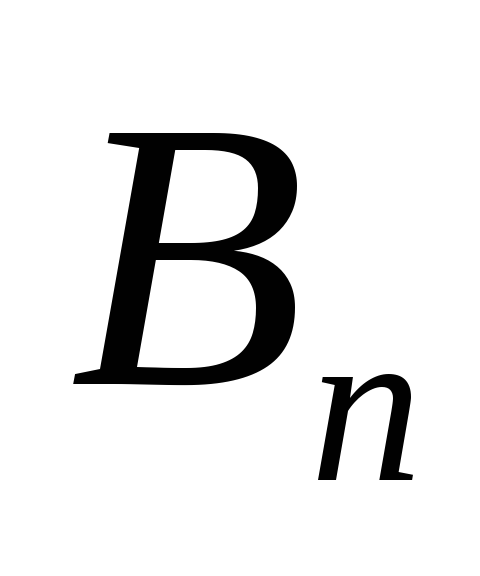 и тангенциальную
и тангенциальную 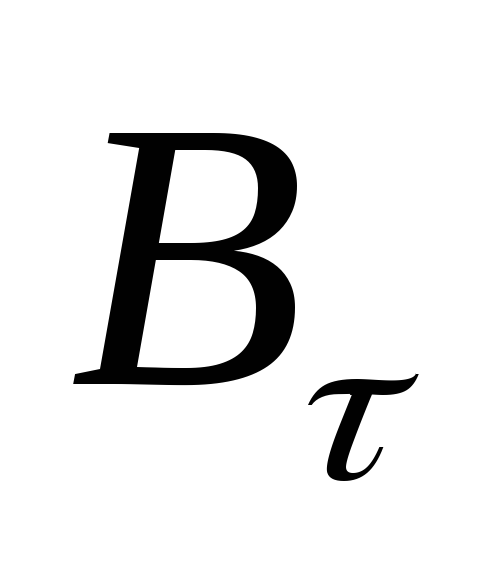 (по
отношению к плоскости контура)
составляющие.
(по
отношению к плоскости контура)
составляющие.
Поскольку 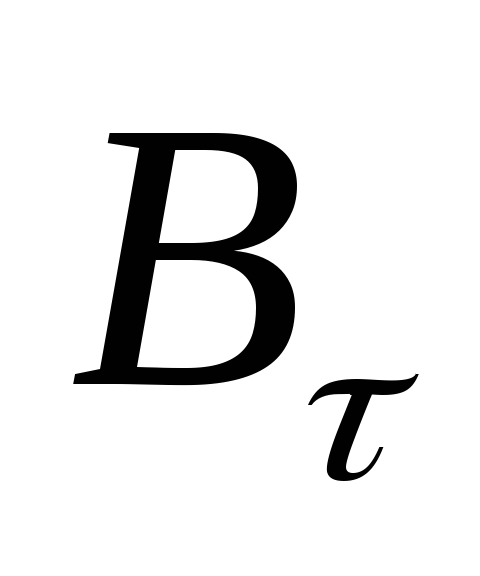 в создании силы ампера не участвует, то
в создании силы ампера не участвует, то
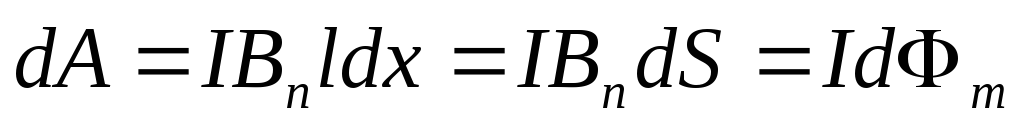 .
.
Если  ,
,
т.е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.
Работа совершается не за счет энергии внешнего магнитного поля, а за счет источника, поддерживающего неизменным ток в контуре, или в перемещаемом проводнике.
 Вычислим
работу по перемещению замкнутого контура
с током в магнитном поле. Для упрощения
вычислений рассмотрим контур прямоугольной
формы, плоскость которого перпендикулярна
Вычислим
работу по перемещению замкнутого контура
с током в магнитном поле. Для упрощения
вычислений рассмотрим контур прямоугольной
формы, плоскость которого перпендикулярна 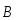 и с которым сцеплен магнитный поток
и с которым сцеплен магнитный поток 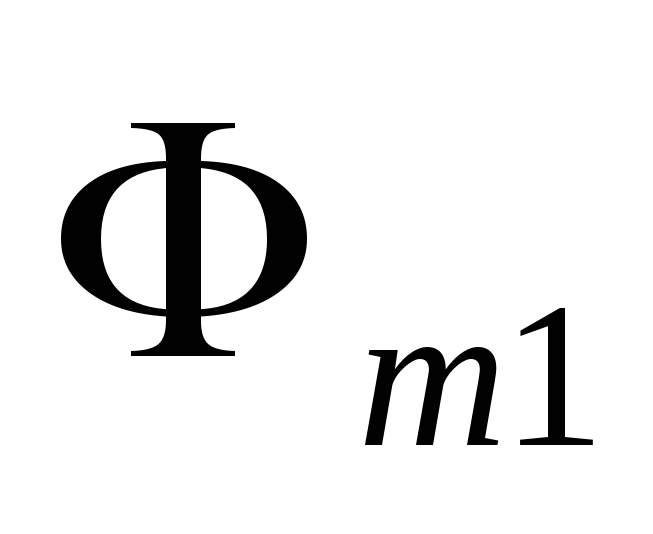 (рис. 7). Поскольку магнитное поле в общем
случае может быть неоднородным, при
перемещении контура 1234 в плоскости
чертежа в новое положение 1234
с ним будет сцеплен магнитный поток
(рис. 7). Поскольку магнитное поле в общем
случае может быть неоднородным, при
перемещении контура 1234 в плоскости
чертежа в новое положение 1234
с ним будет сцеплен магнитный поток 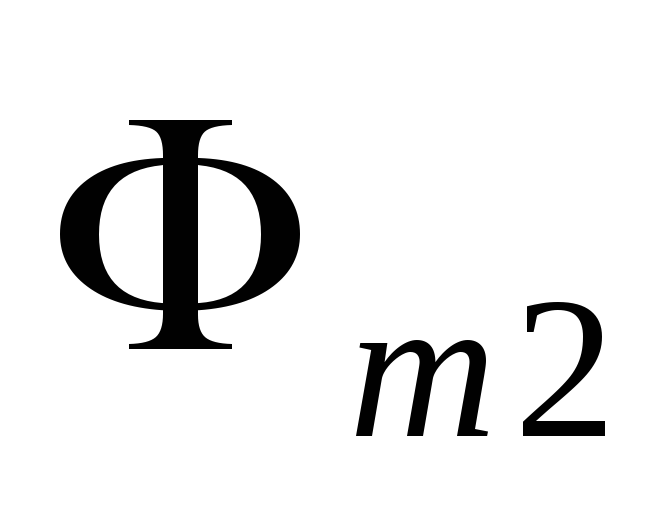 .
Магнитный поток сквозь площадку 4321
обозначим
.
Магнитный поток сквозь площадку 4321
обозначим 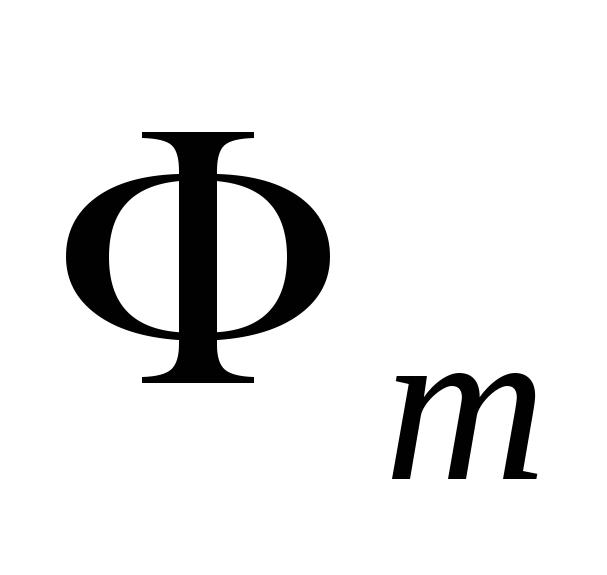 .
.
Полная работа, совершаемая при перемещении контура, равна алгебраической сумме работ, совершаемых при перемещении 4-х сторон:
 ,
,
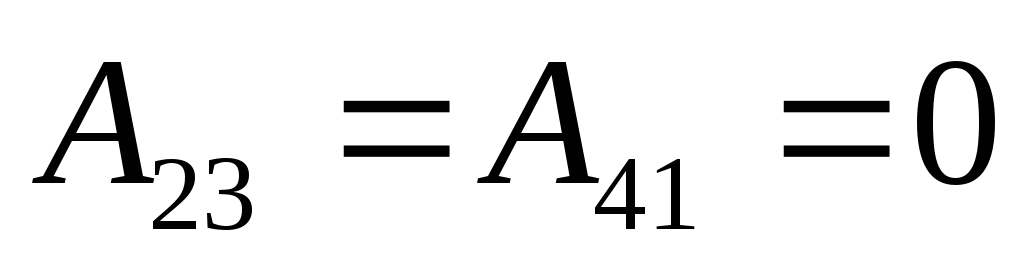 (т.к.
(т.к. 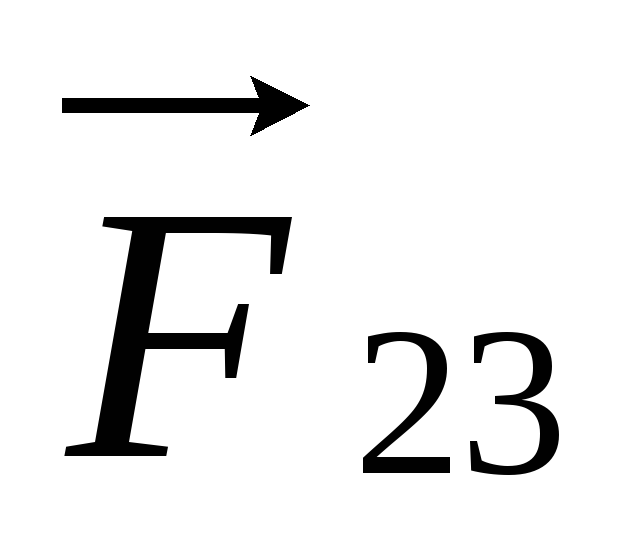 и
и 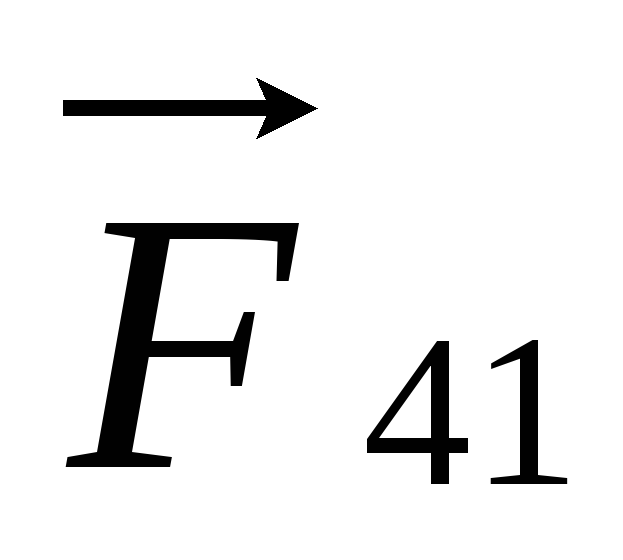 перпендикулярны перемещению).
перпендикулярны перемещению).
Т.к. сила  составляет с вектором перемещения 1800,
составляет с вектором перемещения 1800,  <0,
<0,
 .
.
Сила 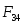 сонаправлена с вектором перемещения,
сонаправлена с вектором перемещения,  >0.
>0.
 ,
,
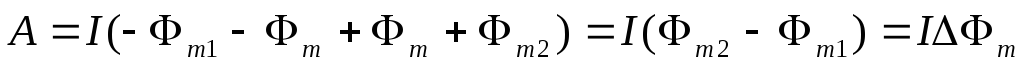 , (1)
, (1)
где  — изменение магнитного потока через
площадку, ограниченную замкнутым
контуром.
— изменение магнитного потока через
площадку, ограниченную замкнутым
контуром.
Работа, совершаемая силами Ампера при перемещении замкнутого контура с током в магнитном поле, равна произведению силы тока на изменение магнитного потока, сцепленного с контуром.
Соотношение (1), полученное для простейшего случая, справедливо для контура любой конфигурации в произвольном магнитном поле при любых его перемещениях (вращении, сминании и т.п.).
В частности, при повороте контура в
однородном магнитном поле (рис. 8) из
положения 1, при котором
частности, при повороте контура в
однородном магнитном поле (рис. 8) из
положения 1, при котором 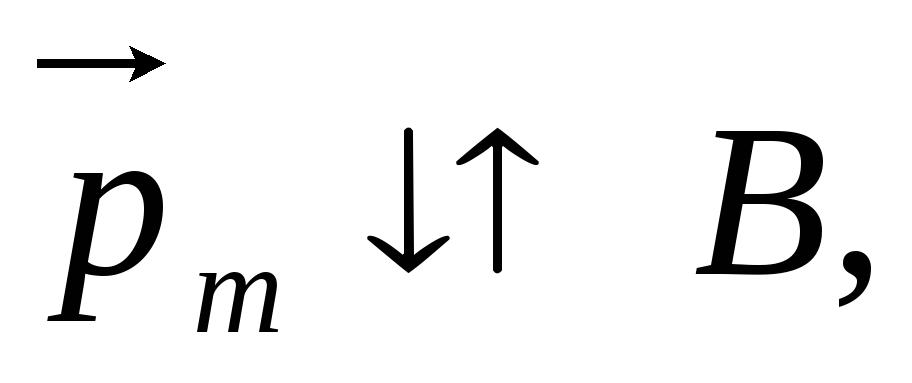 в положение 2, при котором
в положение 2, при котором  над контуром совершается работа:
над контуром совершается работа:
 .
.
Если контур неподвижен, а изменяется
значение или направление  ,
работа рассчитывается также по формуле
(1).
,
работа рассчитывается также по формуле
(1).
Тема 4. Действие магнитного поля на проводник с током (закон Ампера) и на движущийся заряд (сила Лоренца)
Закон Ампера. На элемент проводника  с током I , помещённый
в магнитное поле с индукцией
с током I , помещённый
в магнитное поле с индукцией  действует сила
действует сила  (
( –сила
Ампера):
–сила
Ампера):  .
.
М одуль
вектора
одуль
вектора :
: 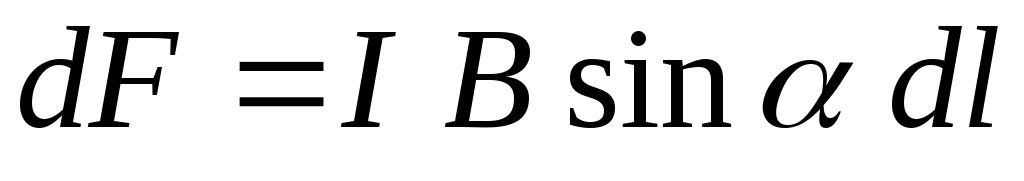 ,
,
где  –
угол между векторами
–
угол между векторами  и
и  .
.
Направление вектора  можно определить поправилу
левой руки:
если силовые линии входят в ладонь, а
четыре вытянутых пальца располагаются
по току, то отведённый большой палец
укажет направление силы
Ампера (рис.
13, сила
можно определить поправилу
левой руки:
если силовые линии входят в ладонь, а
четыре вытянутых пальца располагаются
по току, то отведённый большой палец
укажет направление силы
Ампера (рис.
13, сила  перпендикулярна плоскости рисунка).
перпендикулярна плоскости рисунка).
С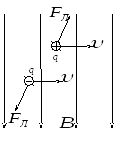 ила
Лоренца. На
заряд q , движущийся со скоростью в магнитном
поле с индукцией , действует сила
ила
Лоренца. На
заряд q , движущийся со скоростью в магнитном
поле с индукцией , действует сила (
–сила Лоренца ):
(
–сила Лоренца ):  .
.
Модуль вектора  :
: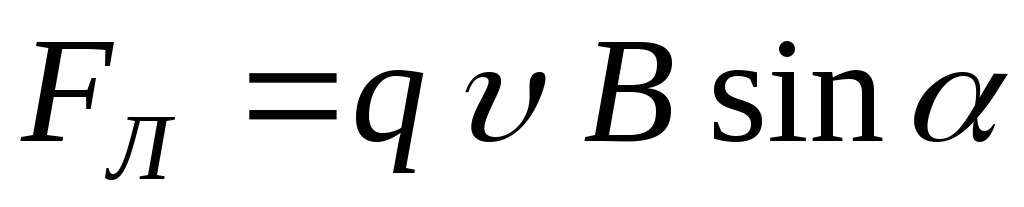 ,
,
где α – угол
между векторами  и
и  .
.
Н
Рис. 14
аправление вектора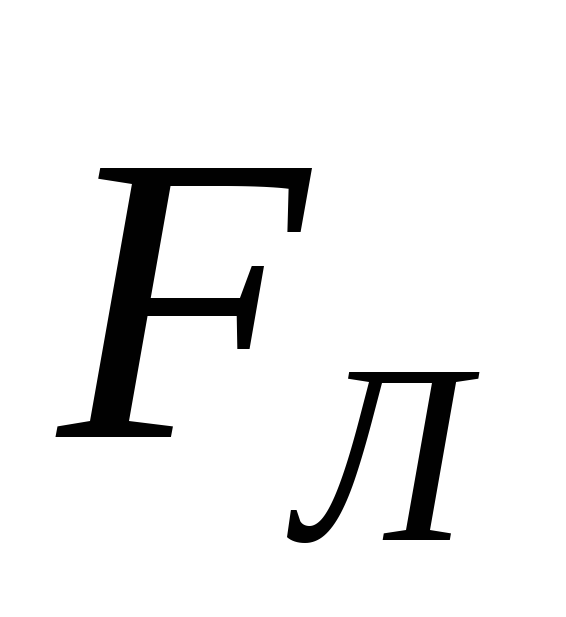 может быть определено поправилу
левой руки для движущихся
положительных зарядов и по правилу
правой руки для движущихся
отрицательных зарядов: если силовые
линии магнитного поля входят в ладонь,
а четыре вытянутых пальца располагаются
по скорости движения частицы, то
отведённый большой палец укажет
направление силы Лоренца (рис.14, сила
может быть определено поправилу
левой руки для движущихся
положительных зарядов и по правилу
правой руки для движущихся
отрицательных зарядов: если силовые
линии магнитного поля входят в ладонь,
а четыре вытянутых пальца располагаются
по скорости движения частицы, то
отведённый большой палец укажет
направление силы Лоренца (рис.14, сила 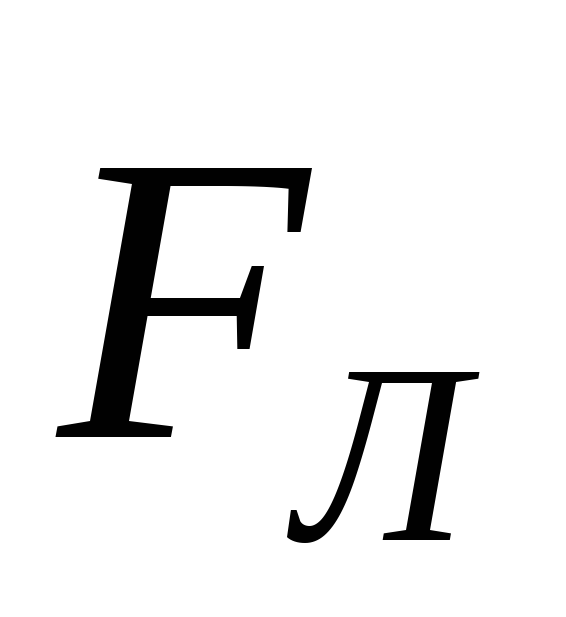 перпендикулярна плоскости рисунка).
перпендикулярна плоскости рисунка).Тема. 5. Магнитный поток. Теорема Гаусса для магнитного поля
Поток
вектора магнитной индукции  (или магнитный поток) через произвольную площадку S характеризуется числом силовых линий
магнитного поля, пронизывающих данную
площадку S. Если площадка S расположена перпендикулярно
силовым линиям магнитного поля (рис.
15), то поток ФB
(или магнитный поток) через произвольную площадку S характеризуется числом силовых линий
магнитного поля, пронизывающих данную
площадку S. Если площадка S расположена перпендикулярно
силовым линиям магнитного поля (рис.
15), то поток ФB
вектора
индукции  через данную площадкуS :
через данную площадкуS :  .
.
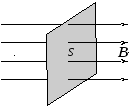
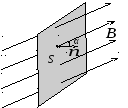
Рис. 15 Рис. 16
Если
площадка S расположена
неперпендикулярно силовым линиям
магнитного поля (рис. 16), то поток ФB вектора индукции  через данную площадкуS :
через данную площадкуS :
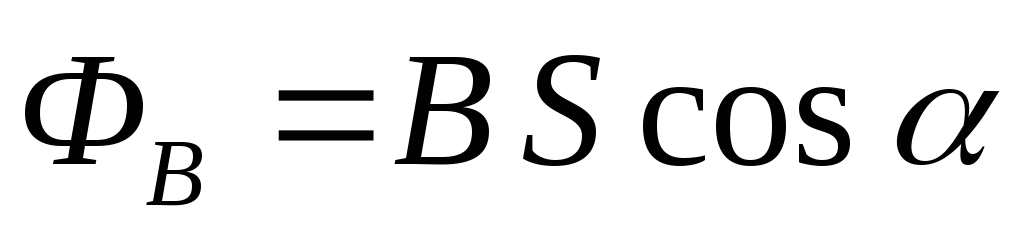 ,
,
где α – угол между векторами  и нормали
и нормали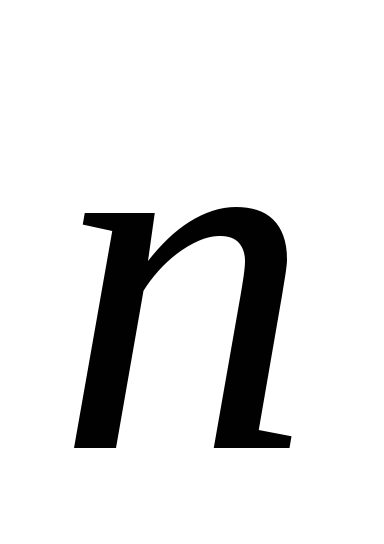 к площадкеS.
к площадкеS.
Д
Рис. 17
 ля
того, чтобы найти потокФB вектора магнитной индукции
ля
того, чтобы найти потокФB вектора магнитной индукции  через произвольную поверхностьS,
необходимо разбить
эту поверхность на элементарные площадки dS (рис.
17) и определить элементарный
поток
через произвольную поверхностьS,
необходимо разбить
эту поверхность на элементарные площадки dS (рис.
17) и определить элементарный
поток 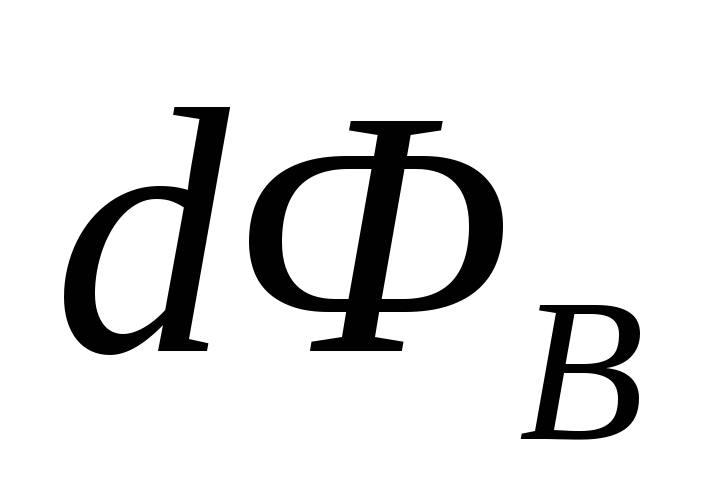 вектора
вектора через каждую площадкуdS по формуле:
через каждую площадкуdS по формуле: 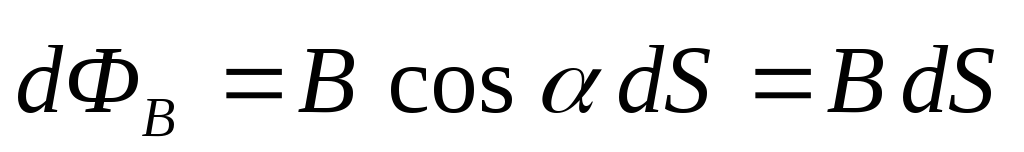 ,
, где α – угол между векторами  и нормали
и нормали к данной площадкеdS;
к данной площадкеdS;
 –вектор,
равный по величине площади площадки dS и направленный по вектору
нормали к данной площадке dS .
–вектор,
равный по величине площади площадки dS и направленный по вектору
нормали к данной площадке dS .
Тогда
поток вектора  через произвольную поверхностьS равен
алгебраической сумме элементарных
потоков
через произвольную поверхностьS равен
алгебраической сумме элементарных
потоков  через все элементарные площадки dS,
на которые разбита поверхность S,
что приводит к интегрированию:
через все элементарные площадки dS,
на которые разбита поверхность S,
что приводит к интегрированию:
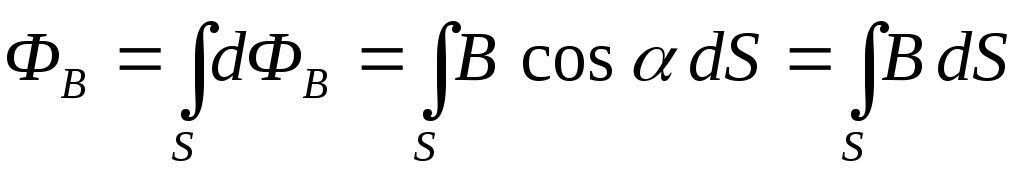 .
.
Теорема Гаусса для магнитного поля
Д ля
произвольной замкнутой поверхностиS (рис. 18) поток вектора индукции
ля
произвольной замкнутой поверхностиS (рис. 18) поток вектора индукции  магнитного поля через эту поверхностьS можно рассчитать по формуле:
магнитного поля через эту поверхностьS можно рассчитать по формуле:
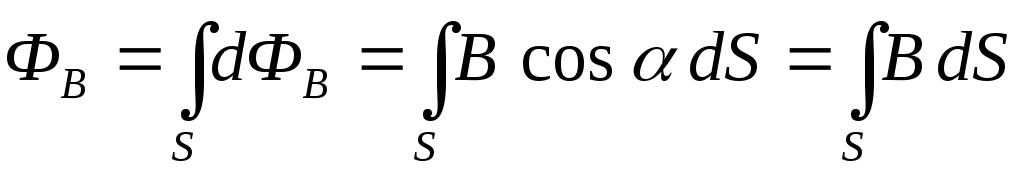 .
.
С
другой стороны, число линий магнитной
индукции, входящих внутрь объема,
ограниченного этой замкнутой поверхностью,
равно числу линий, выходящих из этого
объема (рис. 18). Поэтому, с учетом того,
что поток вектора индукции  магнитного поля считается положительным,
если силовые линии выходят из поверхности S,
и отрицательным для линий, входящих в
поверхность S, суммарный
поток ФB вектора индукции
магнитного поля считается положительным,
если силовые линии выходят из поверхности S,
и отрицательным для линий, входящих в
поверхность S, суммарный
поток ФB вектора индукции  через произвольную замкнутую поверхность S равен нулю,
то есть:
через произвольную замкнутую поверхность S равен нулю,
то есть:
 ,
,
что составляет формулировку теоремы Гаусса для магнитного поля.
Закон Ампера — Вікіпедія
Матеріал з Вікіпедії — вільної енциклопедії.
Взаємодія двох елементарних струмів: а — паралельних, б — антипаралельних (всі відрізки (вектори) лежать в одній площині)Закон Ампера — закон взаємодії постійних струмів. Установлений Андре-Марі Ампером в 1820 році. Із закону Ампера виходить, що паралельні провідники з постійними струмами, що течуть в одному напрямі, притягуються, а в протилежному — відштовхуються. Законом Ампера називається також закон, що визначає силу, з якою магнітне поле діє на малий відрізок провідника із струмом.
Сила Ампера — це сила, з якою магнітне поле діє на провідник зі струмом .
- F=BILsinα{\displaystyle F=BIL\sin \alpha \!}
Сила Ампера залежить від сили струму I{\displaystyle I}, елемента (частини) довжини провідника dl{\displaystyle dl}, кута між напрямом струму і напрямом ліній магнітного поля α{\displaystyle \alpha } та магнітної індукції B{\displaystyle B}, і задається формулою
- dF=BIdlsinα{\displaystyle dF=BIdl\sin \alpha \!}
У векторній формі сила Ампера записується
- dF=I[dl,B]{\displaystyle d\mathbf {F} =I[\mathbf {dl} ,\mathbf {B} ]}.
- dF=BIdlsinα{\displaystyle dF=BIdl\sin \alpha \!}
Взаимодействие параллельных токов. Закон Ампера.
Взаимодействие параллельных токов. Закон Ампера.
Закон Ампера — закон взаимодействия постоянных токов. Установлен Андре Мари Ампером в 1820.
Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположном — отталкиваются.
Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током.
Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию : . Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки:
— руку вдоль тока
— разворачиваем ладонь навстречу магнитным линям (перпендикулярно) (рука по-прежнему вытянута вдоль тока)
— отогнутый на 90 градусов большой палец покажет направление силы Ампера
(Направление магнитного поля провода с током по правилу буравчика или правой руки:
Модуль силы Ампера можно найти по формуле: ,где α — угол между векторами магнитной индукции и тока.
Сила dF максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции (): .Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии r друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи I1 и I2. Требуется найти силу, действующую на единицу длины проводника.
Бесконечный проводник с током I1 в точке на расстоянии r создаёт магнитное поле с индукцией:
Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:
По правилу буравчика поле тока I1 в месте нахождения второго проводника
По правилу буравчика, направлена в сторону первого проводника (аналогично и для , а значит, проводники притягиваются).Модуль данной силы (r — расстояние между проводниками):
Интегрируя, получаем для проводника единичной длины (пределы l от 0 до 1):
Явление электромагнитной индукции [править]
Основная статья: Электромагнитная индукция
Если поток вектора магнитной индукции через замкнутый контур меняется во времени, в этом контуре возникает ЭДСэлектромагнитной индукции, порождаемая (в случае неподвижного контура) вихревым электрическим полем, возникающим вследствие изменения магнитного поля со временем (в случае неизменного со временем магнитного поля и изменения потока из-за движения контура-проводника такая ЭДС возникает посредством действия силы Лоренца).
Закон Био-Савара-Лапласа Закон Био Савара Лапласа — Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.

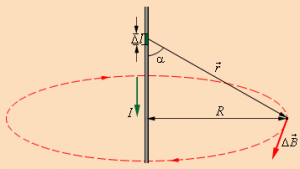
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
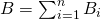
Закон Био-Савара-Лапласа для некоторых токов:
Магнитное
поле прямого тока : 
Магнитное
поле кругового тока : 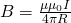
В формуле мы использовали :
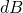 —
Магнитная
индукция
—
Магнитная
индукция
 —
Вектор,
по модулю равный длине dl элемента
проводника и совпадающий по направлению
с током
—
Вектор,
по модулю равный длине dl элемента
проводника и совпадающий по направлению
с током
 —
Магнитная
постоянная
—
Магнитная
постоянная
 —
Относительная
магнитная проницаемость (среды)
—
Относительная
магнитная проницаемость (среды)
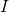 —
Сила
тока
—
Сила
тока
 —
Расстояние
от провода до точки, где мы вычисляем
магнитную индукцию
—
Расстояние
от провода до точки, где мы вычисляем
магнитную индукцию
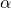 —
Угол
между вектором dl и r
—
Угол
между вектором dl и r
Закон Ампера — Если провод, по которому течет ток, находится в магнитном поле, то на каждый из носителей тока действует сила Ампера

Закон Ампера в векторной форме
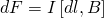
Закон Ампера устанавливает, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля
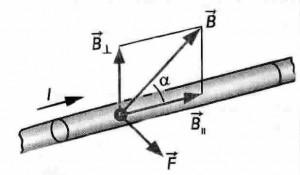
Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B. Для определения направления силы, действующей на проводник с током, помещенный в магнитное поле, применяется правило левой руки.
Чтоб найти силу Ампера для двух бесконечных параллельных проводников, токи которых текут в одном направлении и эти проводники находятся на расстоянии r, необходимо :

Бесконечный проводник с током I1 в точке на расстоянии r создаёт магнитное поле с индукцией:
По
закону Био-Савара-Лапласа для прямого
тока : 
Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:
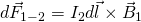
По
правилу буравчика, 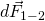 направлена
в сторону первого проводника (аналогично
и для
направлена
в сторону первого проводника (аналогично
и для  ,
а значит, проводники притягиваются).
,
а значит, проводники притягиваются).
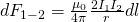
Интегрируем, учитывая только проводник единичной длины (пределы l от 0 до 1) и сила Ампера получается:
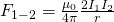
В формуле мы использовали :
 —
Сила
Ампера
—
Сила
Ампера
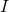 —
Значение
тока
—
Значение
тока
 —
Скорость
хаотического движения носителя
—
Скорость
хаотического движения носителя
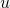 —
Скорость
упорядоченного движения
—
Скорость
упорядоченного движения
 —
Магнитная
постоянная
—
Магнитная
постоянная
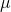 —
Относительная
магнитная проницаемость (среды)
—
Относительная
магнитная проницаемость (среды)
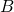 —
Магнитная
индукция
—
Магнитная
индукция
 —
Элементарная
длина провода
—
Элементарная
длина провода
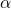 —
Угол
между векторами dl и B
—
Угол
между векторами dl и B
Вопрос | Чему равна работа по перемещению проводника с током в магнитном поле? |
Ответ |
|
Савельев И.В, т.2, стр.143 | Чтобы найти работу, совершаемую при конечном произвольном перемещении контура, просуммируем выражение (48.10) по всем элементарным перемещениям: Здесь Ф1 и Ф2 – значения магнитного потока через контур в начальном и конечном положениях. Таким образом, работа, совершаемая магнитными силами над контуром, равна произыведению силы тока на приращение магнитного потока через контур. |
Википедия | Поляризация не изменяет суммарного заряда в любом макроскопическом объеме внутри однородного диэлектрика. Однако она сопровождается появлением на его поверхности связанных электрических зарядов с некоторой поверхностной плотностью σ. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле с напряженностью Е1, направленное против внешнего поля с напряженностью Е0. Результирующая напряженность поля Е внутри диэлектрика Е=Е0-Е1 |




 однородном магнитном поле
однородном магнитном поле ,
т.к.
,
т.к. ;
; в общем случае не совпадает ни с
вектором
в общем случае не совпадает ни с
вектором ,
ни с вектором
,
ни с вектором ;
вектор
;
вектор совпадает лишь с направлением
элементарного перемещения
совпадает лишь с направлением
элементарного перемещения ,
взятого в направлении вектора
,
взятого в направлении вектора в месте расположения контура. На рис.
3.11 представлены три расположения
контура в поле прямого тока. Проекция
силы на направлениеХ равна
в месте расположения контура. На рис.
3.11 представлены три расположения
контура в поле прямого тока. Проекция
силы на направлениеХ равна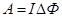
 (48.11)
(48.11)