Метод контурных токов.Решение задач

Один из методов анализа электрической цепи является метод контурных токов. Основой для него служит второй закон Кирхгофа. Главное его преимущество это уменьшение количества уравнений до m – n +1, напоминаем что m — количество ветвей, а n  — количество узлов в цепи. На практике такое уменьшение существенно упрощает расчет.

Основные понятия

Контурный ток — это величина, которая одинакова во всех ветвях данного контура.  Обычно в расчетах они обозначаются двойными индексами, например  I₁₁, I₂₂ и тд.

Действительный ток в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.

Контурная ЭДС — это сумма всех ЭДС входящих в этот контур.

Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.

Общим сопротивлением контура называется сопротивление ветви, смежное двум контурам.

Общий план составления уравнений

1 – Выбор направления действительных токов.

2 – Выбор независимых контуров и направления контурных токов в них.

3 – Определение собственных и общих сопротивлений контуров

4 – Составление уравнений и нахождение контурных токов

5 – Нахождение действительных токов

Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.

Выполняем все поэтапно.

1. Произвольно выбираем направления действительных токов I₁-I₆. 

2. Выделяем три контура, а затем указываем направление контурных токов I₁₁,I₂₂,I₃₃. Мы выберем направление по часовой стрелке.

3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.

R₁₁=R₁+R₄+R₅=10+25+30= 65 Ом

R₂₂=R₂+R₄+R₆=15+25+35 = 75 Ом

R₃₃=R₃+R₅+R₆=20+30+35= 85 Ом

Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R₄ принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.

R₁₂=R₂₁=R₄=25 Ом

R₂₃=R₃₂=R₆=35 Ом

R₃₁=R₁₃=R₅=30 Ом

4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС источников данного контура.

Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом: 

Ток первого контура I₁₁, умножаем на собственное сопротивление R₁₁ этого же контура, а затем вычитаем ток I₂₂, помноженный на общее сопротивление первого и второго контуров R₂₁ и ток I₃₃, помноженный на общее сопротивление первого и третьего контура R₃₁. Данное выражение будет равняться ЭДС E

1 этого контура.  Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.

Те же действия проделываем с двумя другими контурами и в итоге получаем систему: 

В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом.  

5.  Последним этапом находим действительные токи, для этого нужно записать для них выражения.

Контурный ток равен действительному току, который принадлежит только этому контуру

. То есть другими словами, если ток протекает только в одном контуре, то он равен контурному. 

Но, нужно учитывать направление обхода, например, в нашем случае ток I2 не совпадает с направлением, поэтому берем его со знаком минус. 

Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода. 

Например, через резистор R₄ протекает ток I₄, его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть

 

А для остальных 

Так решаются задачи методом контурных токов. Надеемся что вам пригодится данный материал, удачи!

Рекомендуем — Метод двух узлов

Просмотров: 133072

Пример решения задачи методом контурных токов

Скачайте приложение для онлайн решения разветвленной цепи. Вам потребуется только нарисовать схему в редакторе программы и задать численные значения элементов.
Программа сама выдаст подробное пошаговое решение как если бы вы сами делали это РГР.

Для электрической цепи рис. 1, выполнить следующее:

1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа. Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Построить потенциальную диаграмму для любого замкнутого контура, содержащего обе ЭДС.
4. Определить режимы работы активных элементов и составить баланс мощностей.

Значения ЭДС источников и сопротивлений приемников:
E1 = 130 В, Е2 = 110 В, R1 = 4 Ом, R2 = 8 Ом, R3 = 21 Ом, R4 = 16 Ом, R5 = 19 Ом, R6 = 16 Ом.

Смотрите также
 Пример решения схемы методом контурных токов № 1
 Пример решения схемы методом контурных токов № 2
 Пример решения схемы методом контурных токов № 3

 Пример решения схемы методом контурных токов № 4
 Пример решения схемы методом контурных токов № 5
 Посмотреть видео «Метод контурных токов 2»   (пример решения конкретной задачи)  
 

Рис.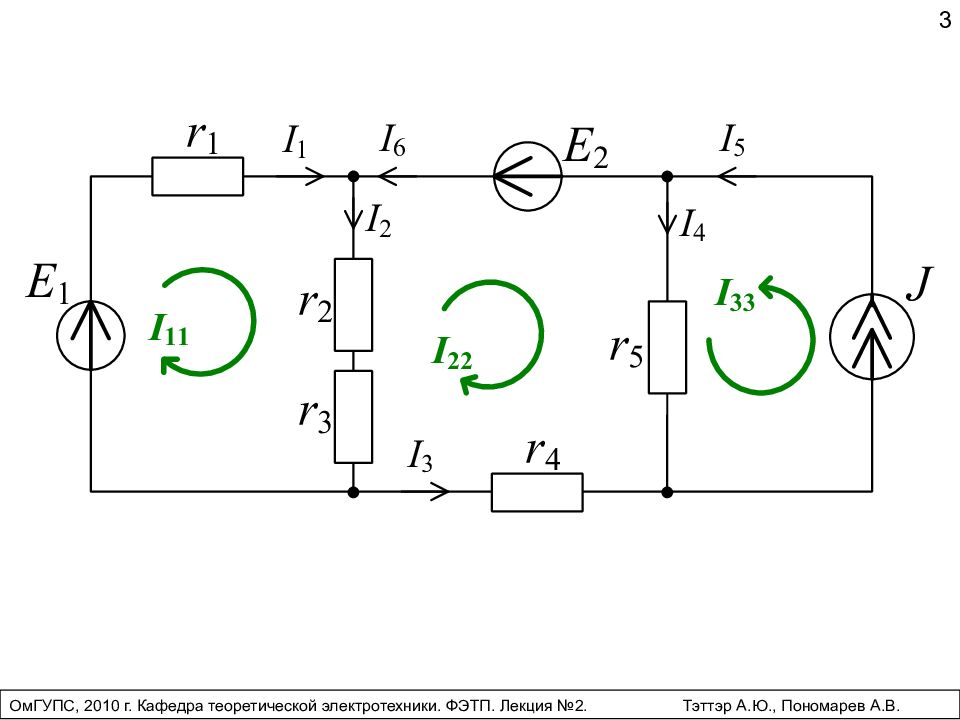 1. Схема

Решение. Заказать работу!    Решить онлайн! (New!!!)

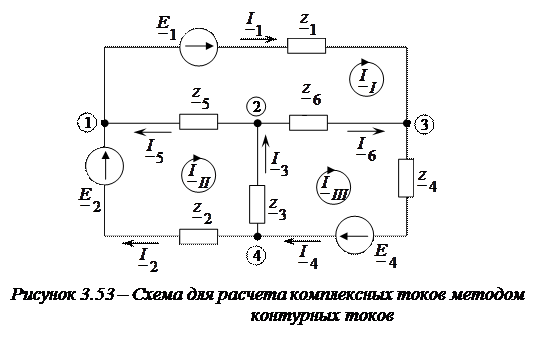
1. Произвольно расставим направления токов в ветвях цепи, примем направления обхода контуров (против часовой стрелки), обозначим узлы.

Рис. 2

2. Для получения системы уравнений по законам Кирхгофа для расчета токов в ветвях цепи составим по 1-му закону Кирхгофа 3 уравнения (на 1 меньше числа узлов в цепи) для узлов 1,2,3:

По второму закону Кирхгофа составим m – (р – 1) уравнений (где m – кол-во ветвей, р – кол-во узлов ), т.е. 6 – (4 – 1) = 3 для контуров I11, I22, I33:



Токи и напряжения совпадающие с принятым направлением обхода с «+», несовпадающие с «-».
Т.е. полная система уравнений для нашей цепи, составленная по законам Кирхгофа:







3. Определим токи в ветвях методом контурных токов. Зададимся направлениями течения контурных токов в каждом контуре схемы и обозначим их I11, I22, I33 (см. рис. 2)

4.

Определим собственные сопротивления трех контуров нашей цепи, а так же взаимное сопротивление контуров:

(Ом)
(Ом)
(Ом)
(Ом)
(Ом)
(Ом)

5. Составим систему уравнений для двух контуров нашей цепи:

Подставим числовые значения и решим.

(А)
(А)
(А)

Определим фактические токи в ветвях цепи:
(А) направление совпадает с выбранным
(А) направление совпадает с выбранным
(А) направление совпадает с выбранным
(А) направление тока потивоположно выбранному
(А) направление совпадает с выбранным
(А) направление совпадает с выбранным

6. Проверим баланс мощностей:

(ВА)
Небольшая разница в полученных результатах является результатом погрешности при округлении числовых значений токов и сопротивлений.

7. Построим потенциальную диаграмму контура изображенного на рис. 3. В качестве начальной точки примем узел 1.

Рис.3

Для построения потенциальной диаграммы определим падения напряжения на каждом сопротивлении, входящем в выбранный контур.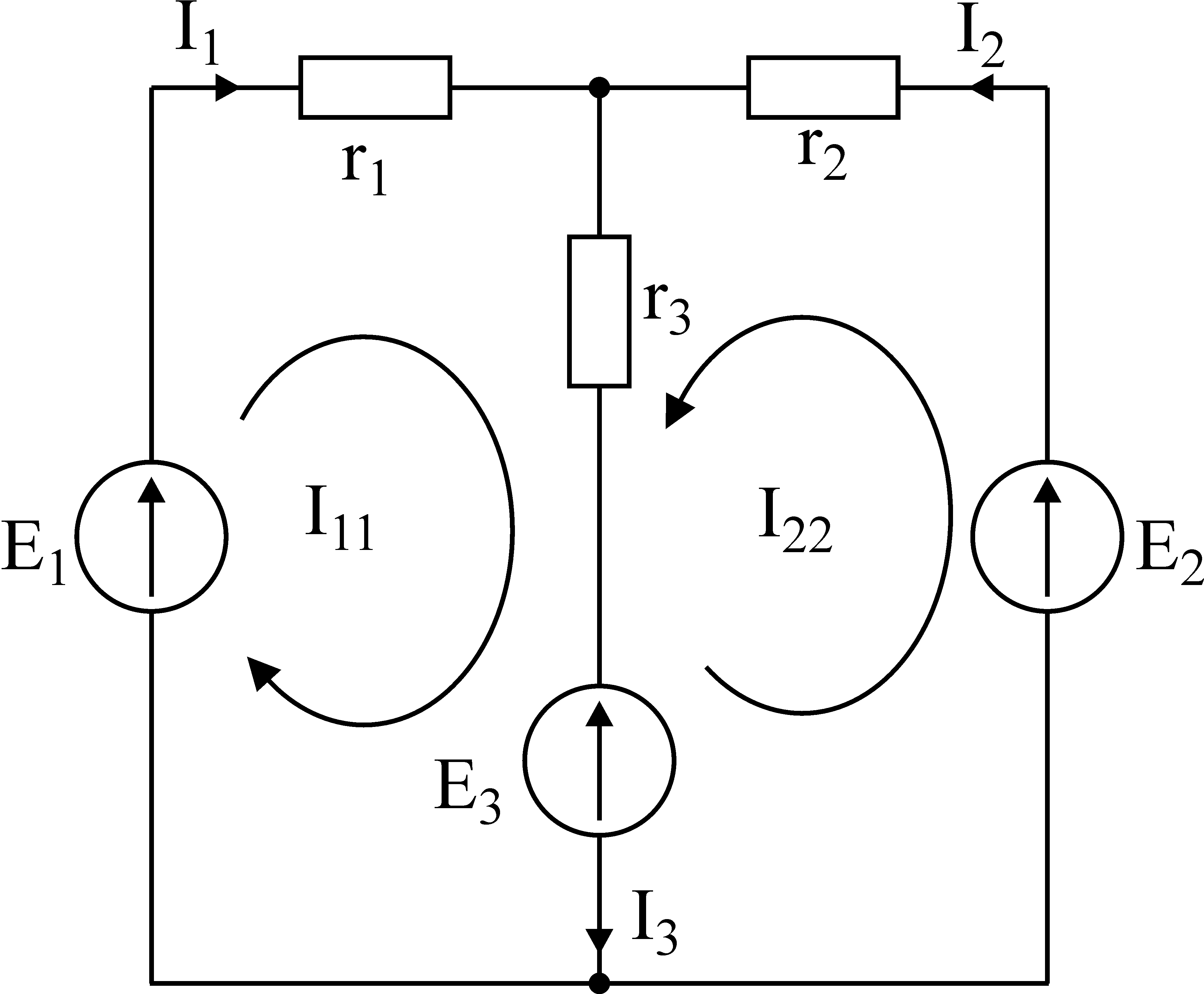
(В)
(В)
(В)
(В)
Потенциал увеличивается если обход осуществляется против направления тока, и понижается если направление обхода совпадает с направлением тока. На участке с ЭДС потенциал изменяется на величину ЭДС. Потенциал повышается в том случае, когда переход от одной точки к другой осуществляется по направлению ЭДС и понижается когда переход осуществляется против направления ЭДС.


Рис. 4. Потенциальная диаграмма. ЗАКАЗАТЬ РАБОТУ!  

Решить онлайн! (New!!!)

 

 

 

 

Задача метод контурных токов Электротехника, Схемотехника, Аналоговые…

Привет, мой друг, тебе интересно узнать все про задача метод контурных токов, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое задача метод контурных токов , настоятельно рекомендую прочитать все из категории Электротехника, Схемотехника, Аналоговые устройства

Дано:

R1 = R5 =10 Ом, R4 = R6 = 5 Ом, R3 = 25 Ом, R2 = 20 Ом, Е1 =100 В, Е2 =80 В, Е3 =50 В

Определяем количество узлов, ветвей и независимых контуров: q = 3, p = 5, контуров 3. Составляем уравнения по законам Кирхгофа: уравнений по 1-ому закону Кирхгофа равно 2, а уравнений по 2-ому закону Кирхгофа равно 3. для узлов а и b. Для контуров выбираем обходы по часовой стрелке:

Так как три контура, то будет три контурных тока I11, I22, I33 . Об этом говорит сайт https://intellect.icu . Направления этих токов выбираем по часовой стрелке рис 3. Запишем настоящие токи через контурные: 
I1 = I11 — I33, I2 = — I22, I3 = — I33, I4 = I11, I5 = I11- I22
Запишем уравнения по второму закону Кирхгофа для контурных уравнений в соответствии с правилами.
Правило: если ЭДС и ток имеют одинаковое направление с направлением обхода контура, то они берутся с «+», если нет, то с «–».

Решим систему уравнений математическим методом Гаусса или Крамера.


Решив систему, получаем значения контурных токов:

I11 = 2,48 А, I22 = — 1,84 А, I33 = — 0,72 А

Определим настоящие токи:

I1 = 3,2 А,
I2 = 1,84 А,
I3 = 0,72 А,
I4 = 2,48 А,
I5 = 4,32 А

Проверим правильность расчета токов, подставив их в уравнения по законам Кирхгофа.
Составим уравнения для расчета баланса мощностей:

Из расчета видно, что баланс мощностей сошелся. Погрешность меньше 1%

 

Как ты считаеешь, будет ли теория про задача метод контурных токов улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое задача метод контурных токов и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Электротехника, Схемотехника, Аналоговые устройства

Расчёт электрической цепи постоянного тока методом контурных токов.

Схема делится на ячейки (независимые контуры). Для каждого контура вводится свой ток Ik, который является расчётной величиной.

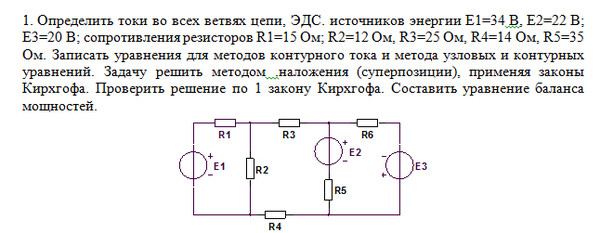
Итак, в заданной цепи (рис. 1.38) можно рассмотреть три контура-ячейки (АДСВА, ABA’А, А’СВА’) и ввести для них контурные токи Iк1 Iк2, Iк3.

Если в контуре ячейки имеется ветвь не входящая в другие контуры то она называется внешней. В таких ветвях контурные токи Ik являются действительными токами в внешних ветвях Ikn = In.

Ветви принадлежащие двум смежным контурам называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров с учётом их направления. 


Порядок расчёта:

1. Произвольно выбираем направление (против часовой или по часовой) контурных токов в контурах (ячейках).
2. Направление обхода контура принимаем таким же как направление контурного тока.
3. Составляем уравнения для каждого контура:

3.1 Смотрим, как направлена ЭДС относительно обхода контура. Если направление обхода контура совпадает, то значение ЭДС записываем со знаком «+» (в левой части уравнения), если не совпадает, то со знаком «–» (записываем также в левой части уравнения). Эдс в контуре может быть несколько — тогда выполняем выше указанное действие для каждого эдс. Если в контуре нету ни одного источника эдс то записываем ноль;

3.2 В левой части записываем:

 

3.2.1 Произведение контурного тока и сумму всех сопротивлений данного контура.

3.2.2 Произведение контурного тока который протекает по смежной ветви и сумму всех сопротивлений которые включены в смежную цепь.(знак произведения выбираем в зависимости совпадает ли направление обхода контура с направлением контурного тока протекающего по смежной цепи).

Если в контуре есть несколько смежных ветвей то повторяем пункт 3.2.2 для всех ветвей по отдельности.

После третьего пункта у вас должно получиться уравнение данного типа:
ЭДС = Контурный ток * сумма всех сопротивлений данного контура — или + контурный ток смежной цепи * сумма всех сопротивлений смежной ветви.

 

40 = 44*Iк1 + 24*Iк2 — 20*Iк3

60 = 24*Iк1 + 104*Iк2 + 40*Iк3

20 = -20*Iк1 + 40*Iк2 + 110*Iк3

 

4. Полученные уравнения записываем в систему и решаем. После решения системы получаем контурные токи равные токам действительным во внешних ветвях.

5. Находим действительные токи в смежных ветвях из алгебраической суммы контурных токов.

Решение задач Метод 📝 контурных токов Основы теории цепей

1. Сколько стоит помощь?

Цена, как известно, зависит от объёма, сложности и срочности. Особенностью «Всё сдал!» является то, что все заказчики работают со экспертами напрямую (без посредников). Поэтому цены в 2-3 раза ниже.

2. Каковы сроки?

Специалистам под силу выполнить как срочный заказ, так и сложный, требующий существенных временных затрат. Для каждой работы определяются оптимальные сроки. Например, помощь с курсовой работой – 5-7 дней. Сообщите нам ваши сроки, и мы выполним работу не позднее указанной даты. P.S.: наши эксперты всегда стараются выполнить работу раньше срока.

3. Выполняете ли вы срочные заказы?

Да, у нас большой опыт выполнения срочных заказов.

4. Если потребуется доработка или дополнительная консультация, это бесплатно?

Да, доработки и консультации в рамках заказа бесплатны, и выполняются в максимально короткие сроки.

5. Я разместил заказ. Могу ли я не платить, если меня не устроит стоимость?

Да, конечно — оценка стоимости бесплатна и ни к чему вас не обязывает.

6. Каким способом можно произвести оплату?

Работу можно оплатить множеством способом: картой Visa / MasterCard, с баланса мобильного, в терминале, в салонах Евросеть / Связной, через Сбербанк и т.д.

7. Предоставляете ли вы гарантии на услуги?

На все виды услуг мы даем гарантию. Если эксперт не справится — мы вернём 100% суммы.

8. Какой у вас режим работы?

Мы принимаем заявки 7 дней в неделю, 24 часа в сутки.

Методическая разработка урока «Метод контурных токов» (10 класс).

Профильный уровень

Методическая разработка урока физики для профильного класса

(политехнический, физико-математический)

Урок 12/114 10 класс

Тема: Метод контурных токов.

Цели урока:

1. образовательная: научить учащихся производить расчеты сложных электрических цепей;

2. развивающая: сформировать умения анализировать, развитие логики мышления, поиска способов рационального решения физических задач;

3. воспитательная: воспитание мотивации учения.

Содержание урока:

1. Организационный момент

2. Проверка знаний.

1. Фронтальный опрос.

Вопросы:

• Дайте определение узла электрической цепи. Начертите на доске электрический узел, укажите направление электрических токов в подводящих к узлу ветвях.

• Сформулируйте первое правило Кирхгофа.

• Запишите первое правило Кирхгофа для начерченного на доске (рис. 1) узла.




Рис. 1. Рис.2.

• Какое соединение элементов электрической цепи можно считать ветвью?

• Сформулируйте второе правило Кирхгофа, запишите второе правило Кирхгофа для предложенной схемы (рис. 2).

• Объясните, как записать второе правило Кирхгофа, если в ветви находятся несколько источников тока?

• Как влияет полярность включения источника тока в электрическую цепь на знак ЭДС в уравнении?

2. Индивидуальный опрос у доски с одновременным решением задачи № 1 в тетрадях учащихся.

ЗАДАЧА № 1.

В предложенной электрической цепи определите силу тока во всех резисторах, используя законы Кирхгофа.




Рис. 3

Решение задачи:

Напишем 1 закон Кирхгофа для узлов А, В, С:

А: I₁ — I₂ + I₄ = 0;

В: I₅ – I₁ + I₃ = 0;

С: I₆ – I₄ – I₅ = 0.

Выберем направление обхода контуров ADBA, BDCB и ABCA и напишем 2 закон Кирхгофа для этих контуров:

ADBA: ε₁ = I₂ ^. R₂ + I₁ ^. R₁ + I₃ ^. R₃ ;

BDCB: ε₂ = I₅ ^. R₅ — I₃ ^. R₃ + I₆ ^. R₆ ;

ABCA : 0 = I₄ ^. R₄ — I₁ ^. R₁ – I₅ ^. R₅ .

Подставим численные значения сопротивлений резисторов и источников тока в полученные уравнения и объединим их систему из шести уравнений с шестью неизвестными:

Выразим из наиболее простого уравнения системы один из неизвестных токов и, подставив это неизвестное в остальные уравнения, преобразуем уравнения системы с учетом полученного выражения, и, понижая с каждым преобразованием ранг системы уравнений, найдем численные значения неизвестных, входящих в эту систему уравнений:







Подставим полученные значения силы тока в резисторах в уравнения Кирхгофа, убедимся в правильности расчетов:




3. Изучение нового материала.

Вопросы: Расчет электрических цепей с помощью метода контурных токов.

Расчет электрической цепи методом контурных токов.

Для сравнения уровня сложности расчетов произведем расчет электрической цепи Рис. 3., предложенной в предыдущей задаче, методом контурных токов:




Основным достоинством, рассматриваемого метода расчета электрической цепи, метода контурных токов является то, что для вычисления силы токов в каждом элементе цепи количество уравнений в системе соответствует количеству контуров рассчитываемой электрической цепи. В нашем случае необходимо составить всего три уравнения, что в два раза меньше чем в системе уравнений рассчитываемой при использовании законов Кирхгофа.

Выберем в контурах ADBA, BDCB и ABCA произвольно направления контурных токов J₁, J₂ и J₃. Составим систему из трех уравнений:




Подставив в полученную систему уравнений численные значения резисторов и ЭДС, рассчитаем контурные токи:




Сила тока в отдельных резисторах определяется как векторная сумма контурных токов, протекающих через эти резисторы:

I₁ = J₁ – J₃ = 0,2 А; I₂ = J₁ = 0,6 А;

I₃ = J₂ – J₁ = 0,4 А; I₄ = J₃ = 0,4 А;

I₅ = J₂ – J₃ = 0,6 А; I₆ = J₂ = 1А.

Результаты расчета проверяются с помощью законов Кирхгофа.

4. Закрепление изученного материала.

Учащимся предлагается самостоятельно записать уравнения, необходимые для расчета следующей электрической цепи (рис. 4) методом контурных токов:

Рис. 4.

Для предложенной электрической цепи выберем 3 контура:

1 – контур: С, R₂ ,ε_1,R₁, А, R₃, С

2 – контур: С, R₃, А, R₄, В, R₆, D, R₅, С

3 – контур: D, R₆, В, R₇, ε_2, R₈, D

Составим уравнения согласно второму правилу Кирхгофа для выбранных контуров:

ε₁= J₁ ^. (R₁ + R₂ + R₃ + r₁) – J₂ ^. R₃ (1).

0 = J₂ ^. (R₃ + R₄ + R₅ + R₆) – J₁ ^. R₃ – J₃ ^. R₆ (2).

ε ₂= J₃ ^. (R₆ + R₇ + R₈ + r₂) – J₂ ^. R₆ (3).

После решения системы трех уравнений с тремя неизвестными найдем токи в элементах цепи:

I₁ = I₂ =J₁, I₃ =J₁ – J₂,

I₄ = I₅ =J₂, I₃ =J₁ – J₂,

I₆ = J₂ – J₃, I₇ = I₈ =J₃.

5. Самостоятельная работа учащихся по решению задач.

Используя метод контурных токов, вычислите численные значения силы тока в каждом элементе, найдите падение напряжения на всех резисторах, предложенной электрической цепи:

ЗАДАЧА № 2.

Рассчитайте электрическую цепь методом контурных токов:

Дано:

ε₁ = 50 В

ε₂ = 40 В

R₁ = 7 Ом

R₂ = 10 Ом

R₃ = 6 Ом

r₁ = 3 Ом

r₂ = 4 Ом.

Определить:

I₁ , I₂ , I₃,

U₁, U₂, U₃.

РЕШЕНИЕ:

В цепи два простых контура. Выберем направление контурных токов J₁ и J₂ с учетом полярности ЭДС источников тока.

Для контура C,ε_1, r_1, R₁, A, R₂,C: ε₁= J₁ ^. (R₁ + R₂ + r₁) + J₂ ^. R₂ (1).

Для контура C, R₂, A, R₃ , ε_1, r_1, ,C: ε₂= J₂ ^. (R₃ + R₂ + r₂) + J₁ ^. R₂ (2).

Подставляя в выражения (1) и (2) численные значения сопротивления резисторов и ЭДС источников тока, получаем систему из двух уравнений:




50 = J₁ ^. (7 + 10 + 3) + J₂ ^. 10, 5 = 2J₁ + J₂ , J₁ = 2 А;

40 = J₂ ^. (6 + 10 + 4) + J₁ ^. 10. 4 = 2J₂ + J₁. J₂ = 1 А.

Рассчитаем токи в отдельных резисторах: I₁ = J₁ = 2А; I₂ = J₁ + J₂ = 3А; I₃ = J₂ = 1А.

Рассчитаем падение напряжения на резисторах: U₁ = I₁ ^. R₁ = 2 ^. 7 = 14 B, U₂ = I₂ ^. R₂ = 3 ^. 10 = 30 B, U₃ = I₃ ^. R₃ = 1 ^. 6 = 6 B.

Ответ: I₁ = 2А; I₂ = 3А; I₃ = 1А. U₁ = 14 B, U₂ = 30 B, U₃ = 6 B.

6. Подведение итогов урока.

7. Задание на дом.

Рассчитайте методом контурных токов электрические цепи:

ЗАДАЧА № 1.

Дано:

ε₁ = 20 В

ε₂ = 30 В

R₁ = 16 Ом

R₂ = 10 Ом

R₃ = 20 Ом

R₄ = 7 Ом

R₅ = 10 Ом

r₁ = 3 Ом

r₂ = 4 Ом.

Определить:

I₁ , I₂ , I₃, I₄ , I₅ ,

U₁, U₂, U_3, U₄, U₅.

ЗАДАЧА № 2.

Дано:

ε₁ = 20 В

ε₂ = 30 В

R₁ = 16 Ом

R₂ = 10 Ом

R₃ = 20 Ом

R₄ = 8 Ом

R₅ = 20 Ом

r₁ = 2 Ом

r₂ = 4 Ом.

Определить:

I₁ , I₂ , I₃, I₄ , I₅ ,

U₁, U₂, U_3, U₄, U₅.

ЗАДАЧА № 3.

Дано:

ε₁ = 100 В

ε₂ = 50 В

R₁ = 20 Ом

R₂ = 30 Ом

R₃ = 20 Ом

R₄ = 20 Ом

R₅ = 75 Ом

R₆ = 78 Ом

r₁ = 5 Ом

r₂ = 2 Ом.

Определить:

I₁ , I₂ , I₃, I₄ , I₅ , I₆,

U₁, U₂, U_3, U₄, U_5, U₆.

Пример решения задачи методом контурных токов

Метод узловых напряжений

Кроме метода контурных токов, для уменьшения трудоемкости расчётов, применяют метод узловых напряжений, при этом возможно еще меньшее число уравнений, так как при этом методе их число достигает

где q – количество узлов в электрической цепи.

Принцип расчёта электрической цепи заключается в следующем:

1. Принимаем один из узлов цепи за базисный и присваиваем ему потенциал равный нулю;
2. Для оставшихся узлов составляем уравнения по первому закону Кирхгофа, заменяя токи в ветвях по закону Ома через напряжение и сопротивление;
3. После решения получившейся системы уравнений вычисляем токи в ветвях по обобщенному закону Ома.

В качестве примера возьмём предыдущую цепь и составим систему уравнений

В качестве базисного возьмём узел А и заземлим его, для остальных узлов B и D составим уравнения по первому закону Кирхгофа

Примем потенциалы узлов В = U1 и D = U2, тогда токи в ветвях выразятся через обобщённый закон Ома

В результате получившаяся система будет иметь следующий вид

Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений

В результате решения системы уравнений мы пришли к следующим результатам: потенциал в узле В – U1 = -57,14 В, а в узле D – U2 = 14,29 В. Теперь нетрудно посчитать, что токи в ветвях будут равны

Результат решения для токов I2 и I5 получился отрицательным, так как действительное направление токов противоположно направлению, изображённому на рисунке. Данные результаты совпадают с результатами, полученными для этой же схемы при расчёте по методу контурных токов.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Суть метода контурных токов

Основные принципы данного метода основываются на том факте, что протекающие в ребрах цепи токи, не все считаются независимыми. Присутствующие в системе У-1 уравнения для узлов, четко показывают зависимость от них У-1 токов. При выделении в электрической цепи независимого тока Р-У+1, вся система может быть сокращена до уравнений Р-У+1. Таким образом, метод контурных токов представляет собой очень простое и удобное выделение в цепи независимых токов Р-У+1.

Для того чтобы построить систему независимых контуров, используется простой и наглядный метод создания планарных графов. На данной схеме ветви и узлы цепи размещаются на плоскости таким образом, что взаимное пересечение ребер полностью исключается. С помощью этого метода плоскость разбивается на области, ограниченные замкнутыми цепочками ребер. Именно они и составляют систему независимых контуров. Данный метод более всего подходит для ручных расчетов схем. Однако его применение может стать затруднительным или вовсе невозможным, если рассматриваемая схема не укладывается в рамки планарного графа.

Другим способом расчетов служит метод выделения максимального дерева. Само дерево представлено в виде подмножества звеньев электрической цепи и является односвязным графом, в котором отсутствуют замкнутые контуры. Для того чтобы оно появилось, из цепи постепенно исключаются некоторые звенья. Дерево становится максимальным, когда к нему добавляется любое исключенное звено, в результате чего образуется контур.

Применение метода выделения максимального дерева представляет собой последовательное исключение из цепи заранее установленных звеньев в соответствии с определенными правилами. Каждый шаг в цепи предполагает произвольное исключение одного звена. Если такое исключение нарушает односвязность графа, разбивая его на две отдельные части, в этом случае звено может возвратиться обратно в цепь. Если граф остается односвязным, то и звено остается исключенным. В конечном итоге, количество звеньев, исключенных из цепи, оказывается равным количеству независимых контуров, расположенных в схеме. Получение каждого нового независимого контура связано с присоединением к электрической цепи конкретного исключенного звена.

Метод токовой петли | Прядильные номера

Метод тока петли — это небольшая вариация метода тока сетки. Он учитывает два особых случая, которые создают проблемы с использованием метода сетки. Мы описываем особые случаи и показываем, как с ними бороться.

Автор Вилли Макаллистер.

---

Содержание

---

Куда мы направляемся

Два особых случая — это неплоская схема (та, которую нельзя нарисовать без перекрещенных проводов) и схема с источником тока, совместно используемым между двумя сетками.

Чтобы проанализировать подобные схемы, вы включаете уравнения для некоторых контуров без сетки. Убедитесь, что каждый цикл включает в себя элемент схемы, который не является частью любого другого цикла. В остальном шаги в методе тока петли такие же, как и в методе тока сетки.

---

Метод токовой петли, как и метод токовой сетки, основан на законе напряжения Кирхгофа (KVL). Мы прибегаем к методу контурного тока в двух особых случаях.

Частный случай: неплоская схема

Метод сеточного тока работает для схем планарных .

• Схема — это планарная , если ее можно нарисовать на плоской поверхности без перекрещенных проводов. Все схемы, которые вы видели до сих пор, плоские. Схема внизу слева плоская. Для плоских схем мы используем метод Mesh Current и записываем уравнения на основе сеток . Это всегда работает для плоских схем.

• Непланарная схема показана внизу справа. Он должен быть нарисован хотя бы с одним перекрещенным проводом, его нельзя нарисовать плоско.Поскольку нет возможности перерисовать схему, чтобы избежать перекрещивания проводов, схема справа не является плоской.

Слева: плоская схема, можно рисовать без перекрещенных проводов.
Справа: неплоская схема, можно нарисовать только перекрещенным проводом.

Если цепь неплоская, мы, , должны использовать метод тока контура.

Особый случай: общий источник тока

Второй особый случай — это когда вы сталкиваетесь с текущим источником, совместно используемым двумя сетками.Это еще один раз, когда вы, , можете включить петлю без сетки в систему уравнений.

И сетка $ \ goldD {\ text I} $, и сетка $ \ goldD {\ text {II}} $ проходят через текущий источник $ \ text I_ \ text S $. Можно (но утомительно) писать и решать сеточные уравнения для этой конфигурации. (Попробуйте и посмотрите, на что это похоже. Довольно неудобно определять напряжение в узле над источником тока.)

Это время, когда вы можете захотеть использовать петлю.Вы можете отбросить одну из сеток и заменить ее петлей, охватывающей обе сетки, как показано здесь для цикла $ \ greenD {\ text {III}} $.

Затем вы решаете систему уравнений точно так же, как метод Mesh Current.

В других учебниках вы можете встретить цикл $ \ greenD {\ text {III}} $, называемый супермешом .

Выбрать петли

Мы можем внести небольшую корректировку в метод Mesh Current Method, чтобы помочь нам в двух особых случаях — в дополнение к сеткам, позволить петлям участвовать в процессе построения уравнения.

Когда вы выбираете петли,

• Убедитесь, что каждый элемент схемы участвует в петле или сетке. У каждого элемента должна быть возможность повлиять на решение.
• Убедитесь, что хотя бы один элемент в каждой петле не является частью какой-либо другой петли или сетки. Это гарантирует независимость петлевых уравнений.

Эти правила генерируют необходимое количество независимых уравнений для решения схемы.

Взгляните на предыдущую схему.Видите ли вы, как определены сетка и петля в соответствии с этими двумя принципами?

Метод токовой петли

Метод токовой петли представляет собой разновидность метода токовой петли,

• Определите сетки (открытые окна схемы) и петли (другие закрытые пути) .
• Назначьте текущую переменную каждой сетке или петле . Используйте постоянное направление (по или против часовой стрелки).
• Напишите уравнения закона напряжения Кирхгофа вокруг каждой ячейки и петли .
• Решите получившуюся систему уравнений для токов сетки и контура .
• Решите для любых токов и напряжений элементов, которые вы хотите, с помощью закона Ома.

Переключиться на метод контура полезно, если схема неплоская или есть источник тока, совместно используемый двумя сетками.

Чтобы убедиться, что у вас есть независимые уравнения, убедитесь, что каждый цикл включает в себя элемент схемы, который не является частью любого другого цикла.

(PDF) Фундаментальный метод токовой петли с использованием техники «виртуальных источников напряжения» для особых случаев

International Journal of Electrical Engineering Education 40/3

Фундаментальный метод токовой петли с использованием техники «виртуальных источников напряжения»

для

специальных дела

Джордж Э.Хатзаракис, 1 Марина Д. Торторели1 и Анастасиос Д. Циолас 2

1 Кафедры электротехники и электроники, Педагогический факультет и

Технологическое образование (ASPETE), Афины, Греция

2 Вычислительный факультет, Аристотелевский университет в Салониках 9-mail [email protected], [email protected]

Аннотация Новый метод, основанный на использовании виртуальных источников напряжения, делает любую электрическую цепь

решаемой с помощью фундаментального метода токовой петли простым и понятным способом для студентов.Таким образом, систематизируется метод

основного токового контура (особенно для неплоских цепей), и трудности

, представленные до сих пор для специальных категорий цепей, перестают существовать.

Ключевые слова основной цикл; ссылка на сайт; неконвертируемый источник тока; Особые случаи; дерево; виртуальное напряжение

источник

Систематическое решение электрической цепи требует топологических концепций, подобных

, которые упоминаются во многих учебниках по электрическим цепям.1,2,3 Наиболее важные con-

cepts — это граф, дерево и основная петля.

Каждой электрической цепи соответствует график, который представляет собой результат геометрической фигуры —

из схемы, когда каждая ветвь неактивного элемента схемы заменяется

линейной частью или изогнутой частью; источники напряжения цепи замкнуты накоротко, а источники тока

разомкнуты.

Если граф можно нарисовать на плоскости таким образом, что любые две из его ветвей имеют вид

, которые нельзя пересекать ни в какой точке, кроме узла схемы, то этот граф называется планарным графом

и схема, планарная схема (рис.1 (а, б)). В противном случае они называются

неплоским графом и неплоской схемой соответственно (рис. 1 (c)).

Граф, для которого переход от одного узла к другому осуществляется посредством следующих

непрерывных ветвей, называется связным графом (рис. 2 (а)). В противоположном случае

он называется несвязным графом (рис. 2 (б)).

Для связного графа схемы дерево (T) — это связная часть графа

, которая содержит все узлы и одновременно не содержит никаких петель.

ветвей дерева называются ветвями дерева, а остальные ветви (составляющие

в графе) называются связями (LT) или хордами.

Основное свойство, проистекающее непосредственно из определения дерева, состоит в том, что если граф

имеет n узлов, то дерево также имеет n узлов, но имеет n-1 ветвей.

На рисунке 3 показаны два дерева T1 и T2 связного графа и их связи LT1 и

LT2, соответственно.

Очевидно, возможные деревья связного графа являются результатом всех комбинаций

ветвей графа, удовлетворяющих свойствам дерева.

Для данного дерева в связном графе фундаментальный цикл (FL) — это каждый цикл, который

Примеры, решенные проблемы и их использование

В области электроники более важно анализировать даже простые схемы. Для анализа простых схем используются такие принципы, как напряжение Кирхгофа и закон Кирхгофа по току. Принимая во внимание, что в ситуации сложных схем, которые имеют несколько контролируемых источников напряжения и тока, должны быть дополнительные инструменты наряду с законами KVL и KCL.Только при использовании принципов KVL и KCL анализ оказывается неточным и ненадежным. Итак, чтобы провести точный анализ и узнать переменные в этих схемах, необходимо реализовать такие подходы, как сетка и узловая схема. С помощью этих методов можно легко узнать такие переменные, как ток и напряжение. Дайте нам четко знать об анализе сетки, анализе супер сетки в этой статье.




Что такое анализ сетки?

Сеткой считается петля, не имеющая других петель внутри схемы.Здесь токи сетки используются в качестве переменных вместо токов, чтобы выяснить весь анализ схемы. Из-за этого метод требует минимального количества уравнений для решения. Анализ сетки реализуется в схемах с использованием закона напряжения Кирхгофа, чтобы узнать неизвестные значения тока.

Это также называется методом петли тока сетки. После этого значения напряжения также можно узнать по закону Ома. Ветвь рассматривается как путь, по которому она соединяет два узла и включается в элемент схемы.Когда сетка состоит только из одной ветви, ток ветви называется током сетки. В то время как, когда сетка состоит из двух ветвей, тогда ток сетки рассматривается либо как сумма, либо как разность двух петель сетки, когда они находятся либо на аналогичных, либо на противоположных путях.




Шаги

• Зная переменные схемы, существует процедура, которой необходимо следовать для реализации анализа сетки, и шаги могут быть объяснены следующим образом:
• На первом этапе найдите сетки и отметьте отводят токи сетки либо против часовой стрелки, либо по часовой стрелке.
• Посмотрите на величину тока, протекающего через каждый элемент, в соответствии с токами сетки.
• Запишите все сеточные уравнения для наблюдаемых сеток. Уравнения сетки записываются с применением закона Кирхгофа, а затем с применением закона Ома.
• Чтобы определить токи сетки, решите наблюдаемые уравнения сетки в соответствии с шагом 3.
• Таким образом, поток значений тока и напряжения через каждый элемент в цепи можно узнать по приложению сетчатых токов.

Общая форма для установки уравнений в анализе сетки

После идентификации сеток в цепи каждая из них состоит из одного уравнения. Уравнения представляют собой сумму падения напряжения во всем контуре сетевого тока. В случае цепей, которые имеют больше, чем напряжение и ток, падение напряжения считается импедансом цепи, умноженным на конкретный ток петли петли.

Если источник напряжения существует внутри контура, то напряжение, присутствующее в источнике, может быть либо добавлено, либо вычтено в зависимости от того, является ли это потерей напряжения или увеличением напряжения для этой ячейки.Но в условии, когда текущий источник не находится между сетками, тогда ток сетки будет учитывать либо отрицательное, либо положительное значение источника в зависимости от направления источника тока сетки.

Метод тока сетки

С помощью приведенной ниже схемы можно легко узнать метод измерения тока сетки. В цепи токи контура I1 и I2 прикладываются по часовой стрелке.

В зависимости от направления тока контура на сопротивлениях R1, R2 и R3 имеет место полярность падений напряжения.Здесь токи I1 и I2 будут иметь противоположные пути протекания тока, поскольку резистор R2 разделяет оба контура.

Итак, обе полярности напряжений могут быть известны. В то время как в практических сценариях R2 можно разделить на две фазы, но токи контура особенно применимы для аналитических приложений. Не влияет на полярность источников напряжения, потому что они постоянны.

После применения закона Кирхгофа по напряжению могут быть записаны следующие два уравнения:

R2 (I1 — I2) + R1I1 = V1 — Получено из контура 1

R2 (I2 — I1) + R1I2 = -V2 — Получено из цикла 2

Сходные члены в приведенных выше уравнениях объединены, и при расположении одинаковые члены появляются в одинаковых позициях в каждом уравнении.Когда токи контура известны, можно оценить токи ответвления. Переставленные уравнения:

I1 (R1 + R2) — I2R2 = V1 — Для цикла 1

-I1R2 + (R2 — R3) I3 = -V2 — Для цикла 2

Решенные задачи анализа сетки

В этом разделе показаны решенные примеры нахождения тока в цепи с использованием метода тока сетки .

В приведенной ниже схеме найдите величину напряжения, которое проходит через источник тока 15 А, методом анализа сетки.При условии, что все они являются источниками тока.

Анализ сетки для определения напряжения

В соответствии со схемой существует вероятность изменения источника напряжения на ток с использованием параллельного сопротивления. Для этого резистор подключается последовательно к источнику напряжения, и резистор должен иметь то же значение, что и источник напряжения, и напряжение

Vs = IsRs = 4 * 4 = 16V

Найдите ответвление токи (I1 и I2) для контуров и обозначают направления тока в обоих контурах.

Назначение токов ответвления

Затем для каждой сетки (петли) примените закон KVL

Mesh — 1

Vx — (I1 — I2) — 18 = 0

Здесь I1 = 15

Итак, Vx + (6 * I2) = 90

Mesh — 2

18-6 (I2 — I1) — 4 * I2 — 16 = 0

I2 = 78/10

= 7,8 А

Согласно уравнению Mesh-1

Vx = 90 — 44,4

Vx = 45,6 V

Это решенный пример решения двух сеток с использованием анализа тока сетки

Здесь нам нужно узнать напряжение и токи ответвлений.Рассмотрим схему ниже.

Метод тока сетки через три сетки

Применяя закон KVL к первому циклу, мы получаем

V1 — R2 (I1 — I3) — R4 (I1 — I2) = 0

4 — 2 (I1) — 2 (I3) — 4 (I1) — 4 (I2) = 0

-2 (I3) — 6 (I1) = 4

При применении закона KVL ко второй сетке получаем

-Vc — R4 (I2 — I1) — R3 (I2 — I3) = 0

-Vc = -4 (I1) + 6 (I2) — 2 (I3) = 0

Поскольку I2 = -2A, мы получаем

-Vc = -4 (I1) -12-2 (I3) = 0

При применении закона KVL к третьей сетке получаем

-R1 (I3) — R3 (I3 — I2) — R2 (I3 — I1 ) = 0

Подставляя I2 = -2A

2 (I1) — 8 (I3) = 0

Bu, решая первое и третье уравнения сетки, получаем

I1 = 4.46 и I3 = -0,615

Итак, Vc = 28,61 В

И ток ветви

Iac = I1 — I3

Iac = 5,075 ампер

Это решенный пример решения трех сеток с использованием анализа токов сетки

Это примеры примеров, решенных с помощью анализа сетки. Тщательный анализ этой концепции позволяет нам решать и сложные схемы.

Анализ Super Mesh

Для анализа огромных и сложных схем, анализ Super Mesh является лучшим подходом, чем анализ Mesh, поскольку в Super Mesh будут две сетки, совместно использующие общий компонент в качестве источника тока.

Тот же метод используется для анализа цепей надузлов в качестве альтернативы для анализа узловых цепей, потому что этот метод упрощает эти сложные схемы, замыкая элемент напряжения и минимизируя количество опорных узлов для каждого источника напряжения. В анализе суперсетки текущий источник находится внутри секции суперсетки, так что можно минимизировать сетку на одну для каждого текущего источника, который присутствует.

Когда источник тока присутствует на разрешающем элементе схемы, то одиночная сетка может не рассматриваться.С другой стороны, КВЛ реализован только для тех ячеек в модифицированной электрической схеме.

Давайте рассмотрим пример анализа супер сетки для лучшего понимания.

Используя анализ супер-сетки, узнать значения V3, i1, i2 и i3 для приведенной ниже схемы?

При применении КВЛ к Меш-1 получаем

10i1 + 80 (i1 — i2) + 30 (i1 — i3) = 80

Получаем 60i1 — 20i2 — 30i3 = 80

По приложению метода супер-сетки для Mesh 2 и Mesh 3, мы получаем

30 = 40i3 + 30 (i3 — i1) + 20 (i2 — i1)

70i3 — 50i1 + 20i2 = 30

Отдельный источник тока, который находится в супер сетка соответствует ожидаемым токам сетки, которые равны

15ix = i3 — i2

I3 = 15ix + i2

Решая все три вышеупомянутых уравнения, мы получаем

i1 = 0.58 ампер, i2 = -6,16 ампер и i3 = 2,6 ампер

Чтобы найти V3, мы имеем v3 = i3 * R3, поэтому

V3 = 2,6 * 40 = 104 В

Анализ сетки использует

Основное применение анализа сетки предназначен для разрешения плоских схем, чтобы знать значения тока в любом месте как в простых, так и в сложных электрических цепях

Другое использование состоит в том, что обычные вычисления для решения уравнений являются сложными и требуется больше математических формул, тогда как при анализе сетки достаточно меньшего количества вычислений .

Другое использование анализа Mesh Current — это несбалансированный мост из пшеничных камней. Чтобы узнать это, рассмотрим приведенный ниже пример

Поскольку пропорции резисторов R1 / R4 и R2 / R5 не равны, мы можем понять, что на R3 будет протекать некоторое количество напряжения и тока. Поскольку мы знаем, что решение этих типов схем усложняется подходом общей последовательно-параллельной техники, нам нужен другой подход для решения этой проблемы.

Итак, что касается этого, мы можем применить метод тока ответвления, но для этого метода требуется шесть токов от Ia до If, что приводит к работе с любым количеством уравнений.Таким образом, эту сложность можно легко уменьшить с помощью метода Mesh current, где для этого требуется всего несколько переменных.

Что такое метод анализа течения сетки? его матричная форма

Анализ тока сетки Метод используется для анализа и решения электрической сети, имеющей различные источники, или схемы, состоящей из нескольких сеток или петель с источниками напряжения или тока. Он также известен как метод токовой петли .

В методе Mesh Current в петле предполагается отдельный ток, а полярность капель в каждом элементе петли определяется предполагаемым направлением тока петли для этого петли.

Неизвестным в анализе тока сетки является ток в различных сетках, и закон, который применим для решения схемы методом тока сетки, известен как Закон Кирхгофа (KVL) о напряжении, который гласит, что —

В любой замкнутой цепи приложенное сетевое напряжение равно сумме произведения тока и сопротивления или, другими словами, в любой замкнутой цепи сумма повышения напряжения равна сумме падений напряжения в направлении текущий поток.

Состав:

KVL уже обсуждается в теме ТАКЖЕ СМОТРИ: Текущий закон Кирхгофа и Закон Кирхгофа о напряжении

Давайте разберемся с методом Mesh Current с помощью схемы, показанной ниже

В указанной выше сети

• R ₁ , R ₂ , R ₃ , R ₄ и R ₅ — это различные сопротивления
• V ₁ и V ₂ — источник напряжения
• I ₁ — ток, протекающий в сетке ABFEA
• I ₂ — ток, протекающий в сетке BCGFB
• I ₃ — ток, протекающий в сетке CDHGC

Направление тока принято по часовой стрелке для простоты решения сети.


Шаги для решения сети методом ячеистых токов

Принимая во внимание приведенную выше принципиальную схему, ниже приведены следующие шаги для решения схемы методом Mesh Current.

Шаг 1 — Прежде всего, определите независимые цепи или петли схемы.
. Поскольку на схеме, показанной выше, есть три сетки, которые мы рассматриваем.

Шаг 2 — Назначьте циркулирующий ток каждой ячейке, как показано на принципиальной схеме, где I ₁ , I ₂ и I ₃ протекают в каждой ячейке.
Желательно назначать одинаковое направление для всех токов и по часовой стрелке, чтобы упростить расчет.

Шаг 3 — Теперь напишите уравнение KVL для каждой сетки.
Поскольку в схеме три сетки, будет три уравнения KVL, как показано ниже

Применение КВЛ в сетке ABFEA

Переставив уравнение, мы получим уравнение (1)


Наложение КВЛ в сетку BCGFB

Применение КВЛ в сетке CDHGC

Шаг 4 — Теперь решите уравнения (1) (2) и (3) одновременно, чтобы получить значение тока I ₁ , I ₂ и I ₃ .
Зная токи сетки, мы можем определить различные напряжения и токи в цепи.


Матричная форма

Вышеупомянутая схема также может быть решена методом Матрицы, как показано ниже

Вышеупомянутые уравнения (1), (2) и (3) в матричной форме могут быть выражены как

Таким образом, уравнение (4) может быть решено для получения значений различных токов.

Из уравнения (4) видно, что матрица сопротивлений [R] симметрична, т.е.

Уравнение (5) можно записать как:

Где,

[R] — сопротивление сетки

[I] — вектор-столбец токов сетки, а

[В] — вектор-столбец алгебраической суммы всех напряжений источника вокруг сетки.

Это все о методе анализа тока сетки.

Найдите токи контура I1, I2 и I3, используя Анализ петли / сетки Для данной схемы…

1. Используйте метод сеточного тока, чтобы найти токи ответвления i1, i2, и i3 в цепи …

   Используйте метод сеточного тока, чтобы найти токи ответвления i1, i2, и i3 в схеме на рисунке (рисунок 1), если v1 = 35 В и v3 = 81 V. Найдите текущий i1. Найдите текущий i2. Найдите текущий i3. 1K0 10 мА 5 Ω υ1 500 Ω ξ4 Ω 1, Ou

2. Найдите токи I1 I2 I3 I4 I5 используя петлевой (сеточный) анализ, пожалуйста, используйте указанные направления …

   Найдите токи I1 I2 I3 I4 I5 используя петлевой (сеточный) анализ, пожалуйста, используйте указанные направления для токов.Пожалуйста, покажите работу. заранее спасибо 2KC2 2 мА 12 В KC2 I, 2 1KS2 5 2K2 2KQ 4 1K (2

3. Для схемы ниже определите сеточные токи i1, i2 и i3. 2vx 1 10 Q …

   Для схемы ниже определите сеточные токи i1, i2 и i3. 2vx 1 10 Q 15 Q 6 V i3 VX 5 Q 12 В 12 +

4. Вычислите токи сетки i1, i2 и i3. Is = 2 А Рассчитайте сеточные токи 11, 12, …

   Вычислите токи сетки i1, i2 и i3. Is = 2 А Рассчитайте токи сетки 11, 12 и iz.Is = 2 А. + 01

5. Используя анализ тока сетки, выведите уравнения тока сетки для i1, i2, i3, i4, i5 и i6 ….

   Используя анализ тока сетки, выведите уравнения тока сетки для i1, i2, i3, i4, i5 и i6. Ценности зависимых источников следует заменить выражениями сеточных токов в КВЛ уравнения. 1. (20 баллов) Используя анализ тока сетки, выведите уравнения тока сетки для ii, i2, iz, 14, 15 и i6. Значения зависимых источников следует заменить выражениями сеточных токов в уравнениях КВЛ.Не нужно упрощать уравнения и не решать …

6. На рисунке показана часть схемы с направлением электрического тока. токи I1, I2, I3, I4, …

   На рисунке показана часть схемы с направлением электрического тока. токи I1, I2, I3, I4 и Ix указаны стрелками. Какой правильное выражение для Ix? Пожалуйста, объясните причину ответа 12. На рисунке показана часть схемы, направление электрических токов I1, 12, 13, 14 и IT указано стрелками.Какое правильное выражение для Ir? А. 11-12 13 С. 12-11 Г. 11 12 13 14 IX

7. Для схемы, показанной на рисунке ниже, мы хотим найти токи I1, I2 и …

   Для схемы, показанной на рисунке ниже, мы хотим найти токи I1, I2 и I3. (а) Воспользуйтесь правилами Кирхгофа, чтобы завершить уравнение для верхнего петля. (При необходимости используйте любую указанную выше переменную или символ. Все токи даны в амперах. Не вводите никакие единицы.) 30 В =? (b) Воспользуйтесь правилами Кирхгофа, чтобы завершить уравнение для нижнего петля.(При необходимости используйте любую указанную выше переменную или символ. Все токи даны в амперах. Делать…

8. В схеме, приведенной ниже, определить сеточные токи i1 (t) и i2 (t). Пусть v1 = 14 …

   В схеме, приведенной ниже, определить сеточные токи i1 (t) и i2 (t). Пусть v1 = 14 cos (4t) V и v2 = 20 cos (4t — 30 °) V. Сообщите свой ответ, чтобы величина положительная, а все углы находятся в диапазоне отрицательных От 180 градусов до положительных 180 градусов. i1 (t) = cos (4t + (˚)) А i2 (t) = cos (4t + ˚) А

9. используйте анализ тока сетки, чтобы найти значения i1 и i2 в рисунок p2.27. выберите i1 …

   используйте анализ тока сетки, чтобы найти значения i1 и i2 в рисунок p2.27. выберите i1 по часовой стрелке вокруг левой сетки, i2 по часовой стрелке вокруг правой сетки и i3 по часовой стрелке вокруг центра сетка. ν + 8 Ом w Рисунок P2.27

10. ?? Используя законы Кирхгофа, найдите токи I1, I2 и I3 в показанной цепи. Намекать:…

    ?? Используя законы Кирхгофа, найдите токи I1, I2 и I3 в показанной цепи. Подсказка: используйте как правило соединения, так и правило напряжения двух контуров.

Анализ тока в ячейке

или метод, объясненный на примерах

Анализ цепной сети и определение тока или напряжения — сложная задача. Однако анализ схемы будет легким, если мы применим правильный процесс для уменьшения сложности. Основными методами анализа цепей являются Анализ тока ячейки и анализ узлового напряжения .

Сеточный и узловой анализ

Сеточный и узловой анализ имеют определенный набор правил и ограниченные критерии для получения идеального результата.Для работы цепи требуется один или несколько источников напряжения или тока, либо оба источника. Определение техники анализа — важный шаг в решении схемы. И это зависит от количества источников напряжения или тока, доступных в конкретной цепи или сети.

Анализ сетки зависит от доступного источника напряжения, тогда как узловой анализ зависит от источника тока . Таким образом, для упрощения вычислений и уменьшения сложности более разумным выбором будет использовать анализ сетки, когда доступно большое количество источников напряжения.В то же время, если схема или сети имеют дело с большим количеством источников тока, то узловой анализ — лучший выбор.

Но что, если в цепи есть источники как напряжения, так и тока? Если в схеме имеется большее количество источников напряжения и небольшое количество источников тока, анализ сетки по-прежнему является лучшим выбором, но хитрость заключается в том, чтобы преобразовать источники тока в эквивалентный источник напряжения.

В этом руководстве мы обсудим анализ сетки и поймем, как использовать в схемной сети.

Метод или анализ тока сетки

Для анализа сети с помощью анализа сетки необходимо выполнение определенного условия. Анализ сетки применим только к схемам или сетям планировщика.

Что такое планарная схема?

Схема

Planner — это простая схема или сеть, которую можно нарисовать на плоской поверхности, где не происходит пересечения. Когда схеме нужен кроссовер, это неплоская схема.

На изображении ниже показана плоская схема . Он простой и никакого кроссовера нет.

Теперь ниже схема является неплоской схемой . Схема не может быть упрощена, так как в схеме есть кроссовер.

Анализ сетки не может быть выполнен в неплоской схеме и может быть выполнен только в плоской схеме. Чтобы применить анализ сетки, требуется несколько простых шагов, чтобы получить конечный результат.

1. Первый шаг — определить, является ли схема плоской или неплоской.
2. Если это планарная схема, то ее необходимо упростить без кроссовера.
3. Идентификация сеток.
4. Определение источника напряжения.
5. Определение текущего циркуляционного пути
6. Применение закона Кирхгофа в нужных местах.

Давайте посмотрим, как Mesh Analysis может быть полезным процессом для анализа на уровне цепей.

Определение тока в цепи с использованием метода определения тока сетки

Схема выше содержит две сетки. Это простая схема планировщика, в которой присутствуют 4 резистора. Первая сетка создается с помощью резисторов R1 и R3, а вторая сетка создается с помощью резисторов R2, R4 и R3.

Через каждую сетку протекает ток двух разных значений. Источник напряжения — V1. Циркулирующий ток в каждой ячейке можно легко определить с помощью уравнения сетки.

Для первой сетки V1, R1 и R3 соединены последовательно . Следовательно, они оба имеют один и тот же ток, который обозначается синим циркулирующим идентификатором с именем i1. Для второй сетки происходит то же самое, R2, R4 и R3 используют один и тот же ток , который также обозначен синей циркулирующей линией, обозначенной как i ₂ .

Есть особый случай для R3. R3 — это общий резистор между двумя сетками.Это означает, что через резистор R3 протекает два разных тока двух разных сеток. Каким будет ток R3? Это разница между двумя сетками или петлями тока. Итак, ток, протекающий через резистор R3, равен i ₁ — i ₂ .

Давайте рассмотрим первую сетку —

При применении закона Кирхгофа напряжение V1 равно разнице напряжений R1 и R3.

А каково напряжение на R1 и R3? В этом случае очень поможет закон Ома. Согласно закону Ома Напряжение = Ток x Сопротивление .

Итак, для R1 напряжение будет i ₁ x R ₁ , а для резистора R3 оно будет (i ₁ — i ₂ ) x R ₃

Следовательно, согласно закону напряжения Кирхгофа,

  V  1  = i  1  R  1  + R  3  (i  1  - i  2 ) ……….. [Уравнение: 1]  

Для второй ячейки нет источника напряжения, подобного V1 в первой ячейке. В таком случае, согласно закону напряжения Кирхгофа, в цепи последовательной цепи с замкнутым контуром, разности потенциалов всех резисторов равны 0.

Итак, применяя тот же закон Ома и закон Кирхгофа,

  R  3  (i  1  - i  2 )) + i  2  R  2  + i  2  R  4  = 0) ……….. [Уравнение: 2]  

Решив уравнение 1 и уравнение 2, можно определить значение i1 и i2 . Теперь мы увидим два практических примера решения схемных петель.

Решение двух сеток с использованием анализа тока сетки

Каким будет ток в ячейке следующей цепи?

Схема вышеупомянутой сети немного отличается от предыдущего примера.В предыдущем примере в схеме был один источник напряжения V1, но для этой схемы сети присутствуют два разных источника напряжения, V1 и V2 . В схеме две сетки.

Для Mesh-1 , V1, R1 и R3 соединены последовательно. Таким образом, один и тот же ток протекает через три компонента: i ₁ .

По закону Ома напряжение каждого компонента составляет —

.

  В  1  = 5 В 
  В  R1  = i  1  x 2 = 2i  1   

Для R3 через него протекают два контура тока, поскольку это общий компонент между двумя сетками.Поскольку для разных ячеек используются два разных источника напряжения, ток через резистор R3 равен i ₁ + i ₂ .

Итак, напряжение на

  В  R3  = (i  1  + i  2 ) x 5 = 5 (i  1  + i  2 )  

По закону Кирхгофа,

  В  1  = 2i  1  + 5 (i  1  + i  2 ) 
  5 = 7i  1  + 5i  2  …….(Уравнение: 1)  

Теперь в Mesh-2 , V2, R2 и R3 соединены последовательно. Таким образом, через три компонента протекает один и тот же ток: i ₂ .

По закону Ома напряжение каждого компонента составляет

  В  1  = 25 В 
  В  R2  = i  2  x 10 = 10i  2  
  В  R3  = (i  1  + i  2 ) x 5 = 5 (i  1  + i  2 )  

По закону Кирхгофа,

  В  2  = 10i  2  + 5 (i  1  + i  2 ) 
  25 = 5i  1  + 15i  2  
  5 = i  1  + 3i  2 ….. (Уравнение: 2) 
 

Итак, вот два уравнения, 5 = 7i ₁ + 5i ₂ и 5 = i ₁ + 3i ₂ .

Решая эти два уравнения, мы получаем,

  i  1  = .625A 
  i  2  = 1,875A  

Схема дополнительно смоделирована в Spice Tool для оценки результата.

Точно такая же схема воспроизводится в Orcad Pspice, и мы получаем тот же результат

Решение трех сеток с использованием анализа тока сетки

Вот еще один классический пример анализа сетки

Рассмотрим приведенную ниже схему сети.Используя анализ сетки, мы рассчитаем три тока в трех сетках.

Вышеупомянутая схемная сеть имеет три ячейки . Также доступен дополнительный источник тока .

Чтобы решить схему сети в процессе анализа сетки, Mesh-1 игнорируется, поскольку i ₁ , источник тока в десять ампер находится вне схемы сети.

В Mesh-2 , V1, R1 и R2 соединены последовательно.Таким образом, через три компонента протекает один и тот же ток: i ₂ .

По закону Ома напряжение каждого компонента составляет

  В  1  = 10 В  

Для R1 и R2 через каждый резистор протекает два контура тока. R1 является общим компонентом двух ячеек, 1 и 2. Таким образом, ток, протекающий через резистор R1, равен i ₂ — i ₂ . То же, что и R1, ток через резистор R2 равен i ₂ — i ₃ .

Следовательно, напряжение на резисторе R1

  В  R1  = (i  2  - i  1 ) x 3 = 3 (i  2  - i  1 )  

А для резистора R2

  V  R2  = 2 x (i  2  - i  3 ) = 2 (i  2  - i  3 )  

По закону Кирхгофа,

  3 (i  2  - i  1 ) + 2 (i  2  - i  3 ) + 10 = 0 или -3i  1  + 5i  2  = -10….(Уравнение: 1)  

Итак, значение i ₁ уже известно, что составляет 10А.

Предоставляя значение i ₁ , можно сформировать уравнение: 2.

  -3i  1  + 5i  2  - 2i  3  = -10 
 -30 + 5i  2  - 2i  3  = -10 
  5i  2  - 2i  3  = 20…. (Уравнение: 2)  

В Mesh-3 V1, R3 и R2 соединены последовательно.Таким образом, один и тот же ток протекает через три компонента — i3.

По закону Ома напряжение каждого компонента составляет —

.

  В  1  = 10 В 
  В  R2  = 2 (i  3  - i  2 ) 
  В  R3  = 1 x i  3  = i  3   

По закону Кирхгофа,

  i  3  + 2 (i  3  - i  2 ) = 10 
  или, -2i  2  + 3i  3  = 10….[Уравнение: 3] 
 

Следовательно, вот два уравнения, 5i ₂ — 2i ₃ = 20 и -2i ₂ + 3i ₃ = 10. Решив эти два уравнения, i ₂ = 7.27A и i ₃ = 8,18 А.

Моделирование анализа сетки в pspice показало, что точно такой же результат, как и вычисленный.

Вот как можно рассчитать ток в петлях и сетках с помощью Mesh Current Analysis .

[PDF] 3ЦЕЛИ ОБУЧЕНИЯ. Методы анализа

1 IRWI3_8232hr 9/3/4 8:54 AM Page 82 3 Узловые 3 ЦЕЛИ ИЗУЧЕНИЯ и методы анализа петель 3. Узловой анализ Анализ …

IRWI03_082-132-hr

30.09.04

8:54

Page 82

3

Методы узлового и петлевого анализа

ЦЕЛИ ОБУЧЕНИЯ 3.1 Узловой анализ Техника анализа, в которой один узел в N-узле сеть выбирается в качестве опорного узла, и текущий закон Кирхгофа применяется к оставшимся N-1 неопорным узлам.Результирующие N-1 линейно независимых одновременных уравнений записываются в терминах N-1 неизвестных узловых напряжений. Решение N-1 линейно независимых уравнений дает N-1 неизвестных узловых напряжений, которые, в свою очередь, могут использоваться с законом Ома для определения всех токов в цепи … Page 83 3.2 Анализ контура Метод анализа, в котором напряжение Кирхгофа Закон применяется к сети, содержащей N независимых петель. Каждому независимому контуру назначается ток контура, и применение KVL к каждому контуру дает набор N независимых одновременных уравнений для N неизвестных токов контура.Решение этих уравнений дает N неизвестных токов контура, которые, в свою очередь, могут использоваться с законом Ома для определения всех напряжений в цепи … Page 102

В главе 2 мы проанализировали простейшие возможные схемы, содержащие только одноузловая пара или одна петля. Мы обнаружили, что эти схемы можно полностью проанализировать с помощью одного алгебраического уравнения. В случае схемы с одноузловой парой (то есть с двумя узлами, один из которых является эталонным), как только напряжение узла известно, мы можем рассчитать все токи.В одноконтурной схеме, когда известен ток в контуре, мы можем рассчитать все напряжения. В этой главе мы систематически расширяем наши возможности, чтобы мы могли рассчитывать все токи и напряжения в цепях, содержащих несколько узлов и петель. Наш анализ основан в основном на двух законах, с которыми мы уже знакомы: текущем законе Кирхгофа (KCL) и законе напряжения Кирхгофа (KVL). В узловом анализе мы используем KCL

3.3 Пример применения … Page 118

для определения узловых напряжений, а в петлевом анализе мы используем KVL до

3.4 Пример конструкции … Page 119

Определите токи контура.

Сводка … Страница 120 Проблемы … Страница 120

Доступ к видео по решению проблем PSV и Circuit Solutions CS по адресу: http://www.justask4u.com/irwin, используя регистрационный код на внутренней стороне обложки и просмотрите сайт с ответами и не только!

●

IRWI03_082-132-hr

30.09.04

8:54

Страница 83

РАЗДЕЛ 3.1

3.1

NODALANA LY SIS

Узловой анализ

Узловой анализ переменные в цепи выбираются в качестве узловых напряжений.Напряжения в узлах определяются относительно общей точки схемы. Один узел выбирается в качестве опорного узла, а напряжения всех остальных узлов определяются по отношению к этому узлу. Нередко именно к этому узлу подключено наибольшее количество ветвей. Его обычно называют землей, потому что говорят, что он имеет нулевой потенциал, и иногда он представляет собой шасси или линию заземления в практической цепи. Мы выберем наши переменные как положительные по отношению к опорному узлу.Если одно или несколько узловых напряжений действительно отрицательны по отношению к опорному узлу, анализ покажет это. Чтобы понять ценность знания всех узловых напряжений в сети, мы еще раз рассмотрим сеть на рис. 2.32, которая перерисована на рис. 3.1. Все напряжения VS, Va, Vb и Vc измеряются относительно нижнего узла, который выбран в качестве опорного и помечен символом заземления. Следовательно, напряжение в узле 1 составляет VS = 12 В относительно опорного узла 5; напряжение в узле 2 составляет Va = 3 В относительно опорного узла 5 и так далее.Теперь внимательно обратите внимание, что как только эти напряжения узлов известны, мы можем немедленно вычислить любой ток ветви или мощность, подаваемую или потребляемую любым элементом, поскольку мы знаем напряжение на каждом элементе в сети. Например, напряжение V1 на крайнем левом резисторе 9-k представляет собой разность потенциалов между двумя концами резистора; то есть V1 = VS — Va = 12 — 3 = 9V

Это уравнение на самом деле является не чем иным, как применением KVL вокруг крайнего левого контура; то есть -VS + V1 + Va = 0

. Аналогичным образом мы находим, что V3 = Va — Vb

и V5 = Vb — Vc

. Тогда токи в резисторах равны VS — Va V1 = 9k 9k. V3 Va — Vb I3 = = 3k 3k V5 Vb — Vc I5 = = 9k 9k I1 =

Кроме того, Va — 0 6k Vb — 0 I4 = 4k I2 =

, поскольку опорный узел 5 находится под нулевым потенциалом.Va = 3 V VS 1

12 V

V + 1-

I1

2

9 k +

± — —

3 Vb = — V 2

3 Vc = — V 8

VV + 3-3 + 5I3 3 k + I5 9 k +

4

6 k

3 k

I2 5

4 k —

I4

—

Рисунок 3.1 Схема с известными напряжениями узлов.

83

IRWI03_082-132-hr

84

9/30/04

ГЛАВА 3

8:54 AM

Page 84

N O D A L A N D L O P A N A N A LY S2 Схема, используемая для иллюстрации закона Ома в многоузловой сети. Узел m

+ vm

R

Узел N

+ vN

i

—

—

Таким образом, как правило, если нам известны напряжения узлов в цепи, мы можем рассчитать ток через любой резистивный элемент по закону Ома; то есть i =

vm — vN R

3.1

, как показано на рис. 3.2. Теперь, когда мы продемонстрировали ценность знания всех узловых напряжений в сети, давайте определим способ их расчета.В узловом анализе мы используем уравнения KCL таким образом, что переменные, содержащиеся в этих уравнениях, представляют собой неизвестные узловые напряжения сети. Как мы указали, один из узлов в схеме из N узлов выбирается в качестве опорного узла, и напряжения на всех оставшихся N — 1 неопорных узлах измеряются относительно этого опорного узла. Используя топологию сети, можно показать, что для определения N-1 неизвестных узловых напряжений требуется ровно N — 1 линейно независимых уравнений KCL.Следовательно, теоретически после того, как один из узлов в схеме из N узлов был выбран в качестве опорного узла, наша задача сводится к идентификации оставшихся N — 1 неопорных узлов и написанию по одному уравнению KCL для каждого из них. В многоузловой схеме этот процесс приводит к набору N — 1 линейно независимых одновременных уравнений, в которых переменными являются N — 1 неизвестных узловых напряжений. Чтобы укрепить эту идею, рассмотрим еще раз Пример 2.5. Обратите внимание, что в этой схеме только четыре (т.е., любые четыре) из пяти уравнений KCL, одно из которых написано для каждого узла в этой пятиузловой сети, являются линейно независимыми. Кроме того, многие из токов ответвления в этом примере (те, которые не содержатся в источнике) могут быть записаны в терминах узловых напряжений, как показано на рис. 3.2 и выражено в формуле. (3.1). Таким образом, как мы продемонстрируем в следующих разделах, уравнения KCL содержат неизвестные узловые напряжения. Поучительно рассматривать узловой анализ, исследуя несколько различных типов цепей и иллюстрируя характерные особенности каждого из них.Начнем с простейшего случая. Однако в качестве прелюдии к нашему обсуждению деталей узлового анализа опыт показывает, что стоит на мгновение отвлечься, чтобы четко понять концепцию узлового напряжения. Вначале важно указать ссылку. Например, утверждение, что напряжение в узле A равно 12 В, ничего не значит, если мы не укажем точку отсчета; то есть напряжение в узле A составляет 12 В по отношению к чему? Схема на рис. 3.3 иллюстрирует часть сети, содержащую три узла, один из которых является опорным.Рисунок 3.3 Изображение узловых напряжений.

V1 = 4 В 1

V2 = –2 В R2

R1

3

2

R3

IRWI03_082-132-hr

30 сентября 2004 г.

8:54 AM Страница

85

РАЗДЕЛ 3.1

NODALANA LY SIS

85

Напряжение V1 = 4 В — это напряжение в узле 1 по отношению к опорному узлу 3. Аналогично, напряжение V2 = -2 В — это напряжение в узле 2. относительно узла 3.Кроме того, однако, напряжение в узле 1 по отношению к узлу 2 составляет ± 6 В, а напряжение в узле 2 по отношению к узлу 1 составляет –6 В. Кроме того, поскольку ток будет течь от узла с более высоким потенциалом к узел с более низким потенциалом, ток в R1 идет сверху вниз, ток в R2 — слева направо, а ток в R3 — снизу вверх. Эти концепции имеют важные разветвления в нашей повседневной жизни. Если бы человек висел в воздухе, положив одну руку на одну линию, а другую — на другую, и линейное напряжение постоянного тока каждой линии было бы одинаковым, напряжение на его сердце было бы нулевым, и он был бы в безопасности.Если, однако, он отпустит одну линию и позволит ногам коснуться земли, линейное напряжение постоянного тока будет существовать от его руки до ноги с его сердцем посередине. Он, вероятно, был бы мертв, как только его нога коснулась земли. В городе, где мы живем, молодой человек попытался забрать своего попугая, который сбежал из клетки и сидел снаружи, сидя на линии электропередачи. Он стоял на металлической лестнице и металлическим шестом тянулся к попугаям; когда металлический столб коснулся линии электропередачи, мужчина погиб мгновенно.Электроэнергия жизненно важна для нашего уровня жизни, но она также очень опасна. Материал в этой книге не дает вам права безопасно обращаться с ней. Поэтому всегда будьте предельно осторожны с электрическими цепями. Теперь, когда мы начинаем обсуждение узлового анализа, наш подход будет заключаться в том, чтобы начать с простых случаев и систематически переходить к более сложным. Многочисленные примеры будут средством демонстрации каждого аспекта этого подхода. Наконец, в конце этого раздела мы опишем стратегию атаки любой цепи с помощью узлового анализа.

ЦЕПИ, ВКЛЮЧАЮЩИЕ ТОЛЬКО НЕЗАВИСИМЫЕ ИСТОЧНИКИ ТОКА Рассмотрим сеть, показанную на рис. 3.4. Обратите внимание, что эта сеть содержит три узла, и поэтому мы знаем, что для определения N-1 = 2 неизвестных узловых напряжений потребуется ровно N-1 = 3-1 = 2 линейно независимых уравнения KCL. Сначала мы выбираем нижний узел в качестве опорного, а затем напряжение на двух оставшихся узлах, обозначенных v1 и v2, будет измеряться относительно этого узла. Предполагается, что токи ответвления протекают в направлениях, указанных на рисунках.Если один или несколько токов ответвления фактически протекают в направлении, противоположном предполагаемому, анализ просто выдаст отрицательный ток ответвления. Применение KCL в узле 1 дает -iA + i1 + i2 = 0

Используя закон Ома (i = Gv) и учитывая, что опорный узел находится под нулевым потенциалом, мы получаем -iA + G1 Av1 — 0B + G2 Av1 — v2 B = 0

или

Использование соглашения о пассивных знаках.

AG1 + G2 Bv1 — G2 v2 = iA

KCL на узле 2 дает -i2 + iB + i3 = 0

или

-G2 Av1 — v2 B + iB + G3 Av2 — 0B = 0

, что может быть выраженным как -G2 v1 + AG2 + G3 Bv2 = -iB

v1 1

iA

v2 i2

R2

2

R1 i1 3

i3 R3

iB

.4 Трехузловая схема.

IRWI03_082-132-hr

86

9/30/04

ГЛАВА 3

8:54 AM

Page 86

NODALANDLOOPANA LY две СИСТЕХНИКИ и v2 равны AG1 + G2 Bv1 — G2 v2 = iA

-G2 v1 + AG2 + G3 Bv2 = -iB

3,2

Обратите внимание, что в результате анализа были получены два одновременных уравнения с неизвестными v1 и v2.Их можно решить с помощью любой удобной техники, а современные калькуляторы и персональные компьютеры — очень эффективные инструменты для их применения. Далее мы продемонстрируем три метода решения линейно независимых одновременных уравнений: исключение Гаусса, матричный анализ и пакет математических программ MATLAB. Краткое напоминание, которое иллюстрирует использование как метода исключения Гаусса, так и матричного анализа при решении этих уравнений, содержится в справочнике по решению проблем для этого текста.Использование программного обеспечения MATLAB несложно, и мы продемонстрируем его использование, когда столкнемся с приложением. Уравнения KCL в узлах 1 и 2 дали два линейно независимых одновременных уравнения: -iA + i1 + i2 = 0 -i2 + iB + i3 = 0

Уравнение KCL для третьего узла (эталона): + iA — i1 — iB — i3 = 0

Обратите внимание, что если мы сложим первые два уравнения, мы получим третье. Кроме того, любые два уравнения можно использовать для вывода оставшегося уравнения. Следовательно, в этой схеме с N = 3 узлами только N-1 = 2 уравнений являются линейно независимыми и требуются для определения N-1 = 2 неизвестных узловых напряжений.Обратите внимание, что узловой анализ использует KCL в сочетании с законом Ома. После того, как направление токов ответвления принято, тогда закон Ома, показанный на рис. 3.2 и выраженный формулой. (3.1) используется, чтобы выразить токи ответвления через неизвестные узловые напряжения. Мы можем предположить, что токи идут в любом направлении. Однако, как только мы принимаем определенное направление, мы должны быть очень осторожны, чтобы правильно записать токи в терминах узловых напряжений, используя закон Ома.

Пример 3.1 Предположим, что сеть на рис. 3.4 имеет следующие параметры: IA = 1 мА, R1 = 12 кОм, R2 = 6 кОм, IB = 4 мА и R3 = 6 кОм. Определим все узловые напряжения и токи ответвлений. РЕШЕНИЕ

В целях иллюстрации мы решим эту проблему с помощью исключения Гаусса, матричного анализа и MATLAB. Используя значения параметра Eq. (3.2) становится V1 c

1 1 1 + d — V2 cd = 1 * 10-3 12k 6k 6k

-V1 c

1 1 1 d + V2 c + d = -4 * 10-3 6k 6k 6k

, где мы используем заглавные буквы, потому что напряжения постоянны.Уравнения можно записать как V1 V2 = 1 * 10-3 4k 6k —

V1 V2 + = -4 * 10-3 6k 3k

Используя метод исключения Гаусса, мы решаем первое уравнение для V1 в терминах V2: 2 V1 = V2 ab + 4 3

IRWI03_082-132-hr

30.09.04

8:54

Page 87

РАЗДЕЛ 3.1

Это значение затем подставляется во второе уравнение, чтобы получить V2 — 1 2 a V2 + 4 b + = -4 * 10-3 6k 3 3k

или V2 = -15 V

Это значение для V2 теперь подставляется обратно в уравнение для V1 через V2, что дает 2 V2 + 4 3

V1 =

= -6 V

Уравнения схемы также могут быть решены с помощью матричного анализа.Общая форма матричного уравнения GV = I

, где в данном случае 1 4k G = D 1 6k

1 6k V 1 * 10-3 T, V = B 1 R и I = BR 1 V2 -4. * 10-3 3k

—

Решение матричного уравнения: V = G – 1I

и, следовательно, 1 V1 4k BR = D V2 -1 6k

-1-1 6k 1 * 10-3 TBR 1 -4 * 10-3 3k

Чтобы вычислить обратное к G, нам понадобятся сопряженный элемент и определитель. Сопряженным является 1 3k Adj G = D 1 6k

1 6k T 1 4k

, а определитель G∑ = a =

1 1-1-1 ba b — a ba b 3k 4k 6k 6k

1 18k 2

Следовательно, 1 V1 3k BR = 18k 2 D V2 1 6k

1 6k 1 * 10-3 TB R 1-4 * 10-3 4k

4 1 2 3k 6k 2 = 18k 2 DT 1 1-2 6k 2 k = B

-6 R -15

NODALANA LY SIS

87

IRWI03_082-132-час

88

9/30/04

ГЛАВА 3

43

Page 88

NODALANDLOOPANA LY SISTECHNIQUES

Решение MATLAB начинается с набора уравнений, выраженных в матричной форме как G * V = I

, где символ * обозначает умножение вектора напряжения V на матрицу коэффициентов G.Затем, как только программное обеспечение MATLAB загружено в ПК, матрица коэффициентов (G) и вектор V могут быть выражены в нотации MATLAB путем ввода строк матрицы или вектора в приглашении >>. Используйте точку с запятой для разделения строк и пробелов для разделения столбцов. Скобки используются для обозначения векторов или матриц. Когда матрица G и вектор I определены, тогда решение уравнения V = inv (G) * I

, которое также вводится в командной строке >>, даст неизвестный вектор V.Матричное уравнение для нашей схемы, выраженное в десятичной системе счисления: B

0,00025 -0,00016666

-0,00016666 V 0,001 RB 1R = BR 0,0003333 V2 -0,004

Если теперь ввести матрицу коэффициентов G, затем вектор I и, наконец, уравнение V = inv (G) * I, экран компьютера, содержащий эти данные и вектор решения V, выглядит следующим образом: >> G = [0,00025 -0,000166666; -0,000166666 0,00033333] G = 1.0e-003 * 0,2500 -0,1667

-0,1667 0,3333

>> I = [0.001; -0,004] I = 0,0010 -0,0040 >> V = inv (G) * IV = -6,0001 -15,0002

Зная напряжения узлов, мы можем определить все токи по закону Ома: I1 =

V1 -6 1 = = — мА R1 12k 2

I2 =

-6 — (-15) V1 — V2 3 = = мА 6k 6k 2

I3 =

V2 -15 5 = = — mA 6k 6k 2

и

На рисунке 3.5 показаны результаты всех расчетов. Обратите внимание, что KCL выполняется на каждом узле. V1 = –6 В

Рисунок 3.5 Схема, использованная в примере 3.1.

3 мА — 2 1 мА

12 к

V2 = –15 В 6 к

5 мА — 2 4 мА

1 мА — 2

6 к

IRWI03_082-132-час

30.09.04

8:54

Страница 89

РАЗДЕЛ 3.1

R3

v1 i

2

R2

1

R1

i3

R5

R5

R5

iA

i1

Рисунок 3.6 Схема с четырьмя узлами.

v3

3

R4 i4

iB

Теперь рассмотрим схему на рис.3.6. Предполагается, что текущие направления показаны на рисунке. Отметим, что в этой сети четыре узла. Узел внизу схемы выбирается в качестве опорного узла и помечается символом заземления. Поскольку N = 4, N-1 = 3 линейно независимых уравнения KCL потребуются для определения трех неизвестных напряжений неопорных узлов, обозначенных v1, v2 и v3. В узле 1 KCL дает i1 — iA + i2 — i3 = 0

или v3 — v1 v1 v1 — v2 — iA + = 0 R1 R2 R3 v1 a

1 1 1 1 1 + + b — v2 — v3 = iA R1 R2 R3 R2 R3

На узле 2 KCL дает -i2 + i4 — i5 = 0

или —

-v1

v3 — v2 v2 v1 — v2 + = 0 R2 R4 R5

1 1 1 1 1 + v2 a + + b — v3 = 0 R2 R2 R4 R5 R5

В узле 3 уравнение i3 + i5 + iB = 0

или v3 — v1 v3 — v2 + + iB = 0 R3 R5 — v1

1 1 1 1 — v2 + v3 a + b = -iB R3 R5 R3 R5

Объединяя уравнения узлов вместе, получаем v1 a -v1

1 1 1 1 1 + + b — v2 — v3 = iA R1 R2 R3 R2 R3

1 1 1 1 1 + v2 a + + b — v3 = 0 R2 R2 R4 R5 R5 -v1

1 1 1 1 — v2 + v3 a + b = -iB R3 R5 R3 R5

3.3

NODALANA LY SIS

89

IRWI03_082-132-hr

90

9/30/04

ГЛАВА 3

8:54 AM

Page 90

НОД В результате анализа были получены три одновременных уравнения для трех неизвестных узловых напряжений v1, v2 и v3. Уравнения также могут быть записаны в матричной форме как 1 1 1 + + R1 R2 R3 1 F R2 1 R3

1 R2 1 1 1 + + R2 R4 R5 1 R5 —

1 R3 1 R5 —

1 1 + R3 R5

v1 iA VC v2 S = C 0 S v3 -iB

3.4

Здесь важно отметить симметричную форму уравнений, описывающих две предыдущие сети. Уравнения (3.2) и (3.3) имеют однотипную симметричную форму. Матрица G для каждой сети представляет собой симметричную матрицу. Эта симметрия не случайна. Узловые уравнения для сетей, содержащих только резисторы и независимые источники тока, всегда можно записать в этой симметричной форме. Мы можем воспользоваться этим фактом и научиться писать уравнения путем осмотра.Обратите внимание, что в первом уравнении (3.2) коэффициент при v1 является суммой всех проводимостей, подключенных к узлу 1, а коэффициент при v2 является отрицательным из проводимостей, подключенных между узлом 1 и узлом 2. Правая часть уравнение представляет собой сумму токов, поступающих в узел 1 через источники тока. Это уравнение представляет собой KCL в узле 1. Во втором уравнении в (3.2) коэффициент при v2 представляет собой сумму всех проводимостей, подключенных к узлу 2, коэффициент при v1 является отрицательным значением проводимости, подключенной между узлом 2 и узлом 1. , а правая часть уравнения представляет собой сумму токов, поступающих в узел 2 через источники тока.Это уравнение представляет собой KCL в узле 2. Точно так же в первом уравнении в (3.3) коэффициент при v1 представляет собой сумму проводимости, подключенной к узлу 1, коэффициент при v2 является отрицательной величиной проводимости, подключенной между узлом 1 и узлом 2. , коэффициент при v3 является отрицательным значением проводимости, подключенной между узлом 1 и узлом 3, а правая часть уравнения представляет собой сумму токов, поступающих в узел 1 через источники тока. Два других уравнения в (3.3) получаются аналогичным образом.В общем, если KCL применяется к узлу j с узловым напряжением vj, коэффициент при vj представляет собой сумму всех проводимостей, подключенных к узлу j, и коэффициентов напряжений других узлов Ae.g., vj — 1, vj + 1. B являются отрицательными значениями суммы проводимости, подключенной непосредственно между этими узлами и узлом j. Правая часть уравнения равна сумме токов, поступающих в узел через источники тока. Следовательно, левая часть уравнения представляет собой сумму токов, выходящих из узла j, а правая часть уравнения представляет собой токи, входящие в узел j.

Пример 3.2. Давайте применим то, что мы только что узнали, для написания уравнений для сети, показанной на рис. 3.7, путем проверки. Затем, учитывая следующие параметры, мы определим напряжения узлов с помощью MATLAB: R1 = R2 = 2 k, R3 = R4 = 4 k, R5 = 1 k, iA = 4 мА и iB = 2 мА. R1

Рисунок 3.7 Схема, использованная в примере 3.2.

v1

iA

v2

v3 R4

R2

R3

R5 iB

IRWI03_082-132-hr

9/30/04

3.1

РЕШЕНИЕ

Уравнения: v1 a

1 1 1 + b — v2 (0) — v3 ab = -iA R1 R2 R1

-v1 (0) + v2 a -v1 a

1 1 1 + b — v3 ab = iA — iB R3 R4 R4

1 1 1 1 1 b — v2 ab + v3 a + + b = 0 R1 R4 R1 R4 R5

, которое также может быть записано непосредственно в матричной форме как 1 1 + R1 R2 F

0 —

1 R1

0 1 1 + R3 R4 1 R4

1 R1 v1 -iA 1 VC v2 S = C iA — iB S R4 v3 0 1 1 1 + + R1 R4 R5 —

И уравнения, и матрица G демонстрируют симметрию, которая всегда будет присутствовать в схемах, содержащих только резисторы и источники тока.Если теперь используются значения компонентов, матричное уравнение принимает вид 1 1 + 2k 2k F

0 —

1 2k

1 2k v1 -0,004 1 1 1 V Cv2S = C 0,002S + 4k 4k 4k v3 0 1 1 1 1 + + 4k 2k 4k 1k 0

—

или 0,001 0 0 0,0005 C -0,0005 -0,00025

-0,0005 v1 -0,004-0,00025 SC v2 S = C 0,002 S 0,00175 v3 0

Если мы теперь будем использовать эти данные с программным обеспечением MATLAB, экран компьютера, содержащий данные и результаты анализа MATLAB, показан ниже.>> G = [0,001 0 -0,0005; 0 0,0005 -0,00025; -0,0005 -0,00025 0,00175] G = 0,0010 0 -0,0005

0 0,0005 -0,0003

>> I = [-0,004; 0,002; 0] I = -0,0040 0,0020 0 >> V = inv (G) * IV = -4,3636 3,6364 -0,7273

-0,0005 -0,0003 0,0018

NODALANA LY SIS

91

IRWI03_082-132-час 92

9/30/04

8:54

ГЛАВА 3

Page 92

NODALANDLOOPANA LY SISTECHNIQUES

РАСШИРЕНИЯ ОБУЧЕНИЯ ОТВЕТ: 1 1 VV = 4 * 10-3, 4k 1 12k 2 1 V = -2 * 10-3.12k 4k 2

E3.1 Запишите уравнения узла для схемы на рис. E3.1.

V1

Рисунок E3.1

V2 12 k 6 k

4 мА

6 k

2 мА

E3.2 Найдите все напряжения узлов в сети на рисунке E3.2, используя MATLAB. Рисунок E3.2

ОТВЕТ: V1 = 5,4286 В, V2 = 2,000 В, V3 = 3,1429 В.

1 k

V1

2 k

4 мА

V2

4 k

V3

1 k

2 мА

ЦЕПИ, СОДЕРЖАЩИЕ ЗАВИСИМЫЕ ИСТОЧНИКИ ТОКА Присутствие зависимого источника может нарушить симметричную форму узловых уравнений, определяющих схему.Рассмотрим схему, показанную на рис. 3.8, которая содержит управляемый током источник тока. Уравнения KCL для неопорных узлов: io +

v1 v1 — v2 + = 0 R1 R2

и v2 — v1 + io — iA = 0 R2

, где io = v2R3. Упрощая уравнения, получаем

AG1 + G2 Bv1 — AG2 — G3 Bv2 = 0

-G2 v1 + AG2 + G3 Bv2 = iA

или в матричной форме B

AG1 + G2 B -G2

— AG2 — G3 B v 0 RB 1R = BR AG2 + G3 B v2 iA

Обратите внимание, что наличие зависимого источника разрушило симметричный характер узловых уравнений.v1

Рисунок 3.8 Схема с зависимым источником.

v2 R2

io

R1

R3 io

iA

IRWI03_082-132-hr

9/30/04

8:54 AM

SECTION

Страница 93

SECT

Пример 3.3. Определим узловые напряжения для сети на рис. 3.8 при следующих параметрах: = 2

R 2 = 6 k R 3 = 3 k

R 1 = 12 k РЕШЕНИЕ

iA = 2 мА

Использование этих значений с уравнениями для сети дает 1 1 V + V = 0 4k 1 2k 2 1 1 V1 + V = 2 * 10-3 6k 2k 2

—

Решение этих уравнений любым удобным методом дает V1 = -245 В и V2 = 125 В.Мы можем проверить эти ответы, определив токи ответвления в сети, а затем используя эту информацию для проверки KCL в узлах. Например, ток сверху вниз через R 3 равен Io =

V2 125 4 = = A R3 3k 5k

Аналогично, ток справа налево через R 2 равен I2 =

125 — (-245) V2 — V1 6 = = A R2 6k 5k

Все результаты показаны на рис. 3.9. Обратите внимание, что KCL выполняется на каждом узле. –24 V1 = — V 5

6 I2 = — A 5k

12 V2 = — V

Рисунок 3.9 Схема, использованная в примере 3.3.

5

6 k 8 2Io = — A 5k

12 k

10 —A 5k

3 k

–2 I1 = — A 5k

4 Io = — A 5k

Пример 3.4. определить набор линейно независимых уравнений, решение которых даст значения узловых напряжений в сети, показанные на рис. 3.10. Затем, учитывая следующие значения компонентов, мы вычислим напряжения узлов с помощью MATLAB: R1 = 1 k, R2 = R3 = 2 k, R4 = 4 k, iA = 2 мА, iB = 4 мА и = 2. iA

v1

v2 R1

R3

Рисунок 3.10 Цепь, содержащая источник тока, управляемый напряжением. +

vx

— v3

R2 vx

R4

iB

93

IRWI03_082-132-час

94

9/30/04

Page 94

NODALANDLOOPANA LY SISTECHNIQUES

РЕШЕНИЕ

Применение KCL на каждом из нереференсных узлов дает уравнения G3 v1 + G1 Av1 — v2 B — iA = 0

iA + G1 Av2 — G1 B + vx + v3 B = 0

G2 Av3 — v2 B + G4 v3 — iB = 0

, где vx = v2 — v3.Упрощая эти уравнения, получаем AG1 + G3 Bv1 — G1 v2 = iA

-G1 v1 + AG1 + + G2 Bv2 — A + G2 Bv3 = -iA -G2 v2 + AG2 + G4 Bv3 = iB

Учитывая значения компонентов , уравнения принимают вид 1 1 + 1k 2k 1 F k 0

—

1 k

1 1 + 2 + k 2k 1 2k

0 v1 0,002 1 b VC v2 S = C -0,002 S 2k v3 0,004 1 1 + 2k 4k

— a2 +

или 0,0015 C -0,001 0

-0,001 2,0015 -0,0005

0 v1 0,002 -2,0005 SC v2 S = C -0.002 S 0,00075 v3 0,004

Далее показаны входные и выходные списки MATLAB. >> G = [0,0015 -0,001 0; -0,001 2,0015 -2,0005; 0 -0,0005 0,00075] G = 0,0015 -0,0010 0

-0,0010 2,0015 -0,0005

0 -2,0005 0,0008

>> I = [0,002; -0,002; 0,004] I = 0,0020 -0,0020 0,0040 >> V = inv (G) * IV = 11,9940 15,9910 15,9940

IRWI03_082-132-час

9/30/04

8:54

Страница 95

РАЗДЕЛ 3.1

NODALANA LY SIS

95

РАСШИРЕНИЕ ОБУЧЕНИЯ E3.3 Найдите узловые напряжения в цепи на рис. E3.3.

V1

Рисунок E3.3

ОТВЕТ: V1 = 16 В, V2 = -8 В.

V2 10 k 2Io

10 k

10 k

4 мА

Io

9000 Vo2 ​​ANSWER = 4 В.

E3.4 Найдите напряжение Vo в сети на рис. E3.4.

Vx

Рисунок E3.4

2 мА

3 k

Vx — 6000

+ 12 k

12 k

Vo —

ЦЕПИ, СОДЕРЖАЩИЕ НЕЗАВИСИМЫЕ ИСТОЧНИКИ НАПРЯЖЕНИЯ В нашей практике В этой теме мы перейдем от простейшего случая к более сложным.В простейшем случае к опорному узлу подключен независимый источник напряжения. Следующий пример иллюстрирует этот случай.

Пример 3.5 Рассмотрим схему, показанную на рис. 3.11а. Определим все узловые напряжения и токи ответвлений. РЕШЕНИЕ В этой сети есть три неопорных узла с помеченными узлами напряжения V1, V2 и V3. Основываясь на наших предыдущих обсуждениях, мы могли бы предположить, что для нахождения всех напряжений узла

нам потребуется написать уравнение KCL для каждого из узлов, не являющихся опорными.Полученные в результате три линейно независимых одновременных уравнения будут давать неизвестные узловые напряжения. Однако обратите внимание, что V1 и V3 являются известными величинами, потому что независимый источник напряжения подключен непосредственно между неопорным узлом и каждым из этих узлов. Следовательно, V1 = 12 В и V3 = -6 В. Кроме того, обратите внимание, что ток через резистор 9 кОм составляет [12 — (-6)] 9 кОм = 2 мА слева направо. Мы не знаем V2 или ток в остальных резисторах. Однако, поскольку напряжение только одного узла неизвестно, уравнение для одного узла даст его.Применение KCL к этому центральному узлу дает

или

V2 — V3 V2 — V1 V2 — 0 + + = 0 12k 6k 12k V2 — (-6) V2 V2 — 12 + + = 0 12k 6k 12k

, из которого мы получить V2 =

3 V 2

После того, как все напряжения узлов известны, закон Ома может быть использован для определения токов ответвления, показанных на рис. 3.11b. Диаграмма показывает, что KCL выполняется на каждом узле. Обратите внимание, что наличие источников напряжения в этом примере упростило анализ, поскольку два из трех линейных независимых уравнений равны V1 = 12 В и V3 = -6 В.Мы обнаружим, что, как правило, всякий раз, когда между узлами присутствуют источники напряжения, уравнения узловых напряжений, описывающие сеть, будут более простыми.

ПОДСКАЗКА Каждый раз, когда независимый источник напряжения подключается между эталонным узлом и неопорным узлом, напряжение неопорного узла известно.

IRWI03_082-132-hr

96

30.09.04

8:54

ГЛАВА 3

Страница 96

NODALANDLOOPANA LY SISTECHNIQUES

2

12 k

V1

12 k

V3

9 k

3 —V 2

7 —A 8k +12 V

–6 V

12 k 12 V

± —

+

6 k

6V

5 —A 8k

12 V

12 k

± —

+

6 k 23 —A 8k

1 —A 4k

6V

8k

(б)

(а) Рисунок 3.11 Схема, использованная в примере 3.5.

РАСШИРЕНИЕ ДЛЯ ОБУЧЕНИЯ E3.5 Используйте узловой анализ, чтобы найти текущий Io в сети, показанной на рис. E3.5.

ОТВЕТ: Io =

3 мА. 4

Vo

Рисунок E3.5 6 k 6V

± —

6 k 3 k

± —

3V

Io

Далее рассмотрим случай, когда независимый источник напряжения подключен между два нереференсных узла.

Пример 3.6. Предположим, мы хотим найти токи в двух резисторах в схеме на рис.3.12a. РЕШЕНИЕ

Если мы попытаемся атаковать эту проблему методом грубой силы, мы сразу же столкнемся с проблемой. До сих пор токи ветви были либо известными значениями источника, либо могли быть выражены как напряжение ветви, деленное на сопротивление ветви. Однако ток ответвления через источник 6 В, конечно, неизвестен и не может быть напрямую выражен с помощью закона Ома. Конечно, мы можем дать этому току имя и записать уравнения KCL для двух неопорных узлов в терминах этого тока.Однако этот подход не является панацеей, потому что этот метод приведет к двум линейно независимым системным уравнениям в терминах трех неизвестных, то есть двух узловых напряжений и тока в источнике напряжения. Чтобы решить эту дилемму, напомним, что N-1 линейно независимых уравнений требуется для определения N-1 напряжений неопорного узла в схеме с N-узлами. Поскольку наша сеть состоит из трех узлов, нам нужны два линейно независимых уравнения. Теперь обратите внимание, что если каким-то образом известно одно из узловых напряжений, мы немедленно узнаем другое; то есть, если известно V1, то V2 = V1 — 6.Если известно V2, то V1 = V2 + 6. Следовательно, разность потенциалов между двумя узлами ограничена источником напряжения и, следовательно, V1 — V2 = 6

Это уравнение связи является одним из двух линейно независимых уравнений. необходимо для определения узловых напряжений.

IRWI03_082-132-hr

9/30/04

8:54

Страница 97

РАЗДЕЛ 3.1

Н О Д А Л А Н А Л И С И С

97

Далее рассмотрим сеть на рис.3.12b, в котором источник 6 В полностью заключен в пунктирную поверхность. Уравнение ограничения управляет этой пунктирной частью сети. Остальное уравнение получается путем применения KCL к этой пунктирной поверхности, которую обычно называют суперузлом. Напомним, что в главе 2 мы продемонстрировали, что KCL должен выполняться для поверхности, и этот метод устраняет проблему работы с током через источник напряжения. KCL для суперузла: V1 V2 + + 4 * 10-3 = 0 6k 12k

-6 * 10-3 +

Решение этих уравнений дает V1 = 10 В и V2 = 4 В и, следовательно, I1 = 53 мА. и I2 = 13 мА.Быстрая проверка показывает, что KCL выполняется на каждом узле. Обратите внимание, что применение KCL в опорном узле дает такое же уравнение, как показано выше. Учащийся может почувствовать, что применение KCL в опорном узле избавляет от необходимости иметь дело с надузлами. Напомним, что мы не применяем KCL ни в каком узле — даже эталонном узле — который содержит независимый источник напряжения. Эту идею можно проиллюстрировать схемой в следующем примере. Рисунок 3.12 Схемы, использованные в примере 3.6. 6V

V1

± —

V2

V1 4 мА

6 мА

6 k

V2

± — 6V

12 k 6 mA

6 k

12 k

I2

(а)

4 мА

(б)

Пример 3.7 Определим ток Io в сети на рис. 3.13a. РЕШЕНИЕ

Изучая сеть, мы отмечаем, что узловые напряжения V2 и V4 известны, а узловые напряжения V1 и V3 ограничены уравнением V1 — V3 = 12

Сеть перерисована на рис. 3.13b.

V3 + 12

V1 ± —

2 к

V2

12 В

V3 1 к

6 В

2 к

V4

2 к Io

(а)

1 к

± —

12 В

2 к

V3

1 к

+

± —

2 к

Рисунок 3.13 Пример схемы с суперузлами.

6V

1 k

+

2 k Io

(b)

± —

12 V

IRWI03_082-132-hr

98

9/30/04

8:54 AM

Page 98

NODALANDLOOPANA LY SISTECHNIQUES

Поскольку мы хотим найти текущий Io, V1 (в надузле, содержащем V1 и V3) записывается как V3 + 12. Уравнение KCL в суперузле имеет вид V3 + 12 — (-6) 2k

+

V3 — (-6) V3 + 12-12 V3 — 12 V3 + + + = 0 2k 1k 1k 2k

Решение уравнения для V3 дает V3 = —

6 В 7

Io может быть вычислено немедленно как 6 7 3 Io = = — mA 2k 7 —

ОТВЕТ НА РАСШИРЕНИЕ ОБУЧЕНИЯ: Io = 3.8 мА.

E3.6 Используйте узловой анализ, чтобы найти Io в сети, показанной на рис. E3.6. Рисунок E3.6

V1

V2

12 V

— ±

V3

2 k 6V

V4 2 k

± —

1 k

2 k

±

± 4000

Io

ЦЕПИ, СОДЕРЖАЩИЕ ЗАВИСИМЫЕ ИСТОЧНИКИ НАПРЯЖЕНИЯ Как будет показано в следующих примерах, сети, содержащие зависимые (контролируемые) источники, обрабатываются таким же образом, как описано ранее.

Пример 3.8 Мы хотим найти Io в сети на рис. 3.14. РЕШЕНИЕ

Поскольку зависимый источник напряжения подключен между узлом с меткой V1 и опорным узлом, V1 = 2kIx

KCL в узле с меткой V2 равен V2 — V1 V2 4 + = 0 2k k 1k

, где Ix =

V2 1k

Решение этих уравнений дает V2 = 8 В и V1 = 16 В. Следовательно, Io =

V1 — V2 2k

= 4 мА

IRWI03_082-132-hr

9/30/04

8: 54 AM

Страница 99

РАЗДЕЛ 3.1

2 k

V1 Io 2 kIx

± —

V2

2 k

N O D A L A N A LY S I S

Рисунок 3.14 Схема, использованная в примере 3.8.

Ix

4 мА

1 k

Пример 3.9 Найдем ток Io в сети на рис. 3.15. РЕШЕНИЕ

Эта схема содержит как независимый источник напряжения, так и источник напряжения, управляемый напряжением. Обратите внимание, что V3 = 6 V, V2 = Vx, и между узлами, помеченными V1 и V2, существует суперузл.Применяя KCL к суперузлу, мы получаем V2 — V3 V1 — V3 V1 V2 + + + = 0 6k 12k 6k 12k

где уравнение ограничения для суперузла V1 — V2 = 2Vx

Окончательное уравнение V3 = 6

Решая эти уравнения, мы находим, что V1 =

9 V 2

и, следовательно, Io =

V1 3 = mA 12k 8 Рисунок 3.15 Схема, использованная в примере 3.9.

6 к

2Vx

V1

± —

12 к

V2

V3

+ 12 к

6 к

Io

Vx

000

Наконец, давайте рассмотрим две дополнительные схемы, которые в целях сравнения мы рассмотрим, используя более одного метода.

Пример 3.10 Найдем Vo в сети на рис. 3.16a. Обратите внимание, что схема содержит два источника напряжения, один из которых является управляемым, и два независимых источника тока. Схема перерисована на рис. 3.16b, чтобы маркировать узлы и идентифицировать надузел, окружающий управляемый источник. Из-за наличия независимого источника напряжения известно, что напряжение в узле 4 равно 4 В. Мы будем использовать эти знания при написании узловых уравнений для сети.

99

IRWI03_082-132-hr

100

9/30/04

8:54 AM

ГЛАВА 3

Page 100

NODALANDLOOPANA LY SISTECHNIES с четырьмя узлами линейной сети

000. независимых уравнений достаточно для определения всех узловых напряжений.В суперузле определяющим уравнением является V1 — V2 = 2Vx

, где V2 = Vx

и, следовательно, V1 = 3Vx

Кроме того, мы знаем, что одно дополнительное уравнение V4 = 4

Таким образом, с учетом этих двух уравнений только Еще два уравнения необходимы для решения неизвестных узловых напряжений. Эти дополнительные уравнения являются результатом применения KCL в суперузле и в узле V3. Уравнения: —

Vx — V3 3Vx — V3 Vx 3Vx — 4 2 + + + + = 0 k 1k 1k 1k 1k V3 — Vx V3 — 3Vx 2 + = 1k 1k k

Объединение уравнений дает два уравнения 8Vx — 2V3 = 6 -4Vx + 2V3 = 2

Решая эти уравнения, получаем Vx = 2 V и

V3 = 5 V

Vo = 3Vx — V3 = 1 V

V1 +

± —

2Vx 1 k

Vo —

2 —A k

2 мА +

Vx

± —

1 k

1 k 1 k

V2 +

2 мА

—

± —

4V

(а)

+ Vo —

2Vx

Vx

1 к

V3

1 к

V4

1 к 2 —A k

1 к

—

4V

(б)

Рисунок 3.16 Схема, использованная в примере 3.10.

Пример 3.11. Мы хотим найти Io в сети на рис. 3.17a. Обратите внимание, что эта схема содержит три источника напряжения, один из которых является управляемым источником, а другой — управляемым источником тока. Поскольку два источника напряжения подключены к опорному узлу, напряжение одного узла известно напрямую, а другое задается зависимым источником. Кроме того, разница в напряжении между двумя узлами определяется независимым источником 6 В.

IRWI03_082-132-hr

30.09.04

8:54

Страница 101

РАЗДЕЛ 3.1

101

N O D A L A N A LY S I S

Сеть перерисована на рис. 3.17b, чтобы маркировать узлы и идентифицировать надузел. Поскольку сеть состоит из шести узлов, для определения неизвестных узловых напряжений необходимо пять линейных независимых уравнений. Два уравнения для суперузла: V1 — V4 = -6 V4 — V3 V1 — V3 V4 — V5 V4 V1 — 12 + + 2Ix + + + = 0 1k 1k 1k 1k 1k

Три оставшихся уравнения: V2 = 12 V3 = 2Vx V5 V5 — V4 + = 2Ix 1k 1k

Уравнения для управляющих параметров: Vx = V1 — 12 Ix =

V4 1k

Объединение этих уравнений дает следующую систему уравнений -2V1 + 5V4 — V5 = — 36 V1 — V4 = -6 -3V4 + 2V5 = 0

Решение этих уравнений любым удобным способом дает V1 = -38 V V4 = -32 V V5 = -48 V

Тогда, поскольку V3 = 2Vx, V3 = — 100 В.Io составляет -48 мА. Читателю рекомендуется убедиться, что KCL выполняется на каждом узле.

V1 + Vx

1 к

—

+

1 к

1 к

6 В 1 к

2Ix

+ Vx V2

1 к 1 к

V

± —

1 k 1 k

2Vx

Ix

(a) Рисунок 3.17 Схема, использованная в примере 3.11.

6 В

1 к

Io

12 В

± —

± —

2Ix

V4

1 к 12 В

+

1 к

+

1 к

V5 1 k

1 k

1 k

Ix

Io

IRWI03_082-132-hr

102

9/30/04

8:54 AM

Страница 3

NODALANDLOOPANA LY SISTECHNIQUES

ПРОБЛЕМА — SO LV INGSTR AT EGY Nodal Analysis Шаг 1.Выберите один узел в схеме из N узлов в качестве опорного узла. Предположим, что напряжение узла

равно нулю, и измерьте напряжения всех узлов относительно этого узла. Шаг 2. Если в сети присутствуют только независимые источники тока, запишите уравнения KCL

в N-1 неопорных узлах. Если присутствуют зависимые источники тока, напишите уравнения KCL, как это делается для сетей только с независимыми источниками тока; затем напишите управляющие уравнения для зависимых источников.Шаг 3. Если в сети присутствуют источники напряжения, они могут быть подключены (1) между эталонным узлом и неопорным узлом или (2) между двумя неопорными узлами. В первом случае, если источником напряжения является независимый источник, то известно напряжение на одном из неопорных узлов. Если источник является зависимым, он рассматривается как независимый источник при написании уравнения KCL, но необходимо дополнительное уравнение ограничения, как описано ранее. В последнем случае, если источник является независимым, напряжение между двумя узлами ограничивается значением источника напряжения, и уравнение, описывающее это ограничение, представляет собой одно из N-1 линейно независимых уравнений, необходимых для определения N-узла. напряжения.Поверхность сети, описываемая уравнением связи (то есть источник и два соединительных узла), называется суперузлом. Одно из оставшихся N-1 линейно независимых уравнений получается путем применения KCL в этом суперузле. Если источник напряжения является зависимым, он рассматривается как независимый источник при написании уравнений KCL, но необходимо дополнительное уравнение ограничения, как описано ранее.

РАСШИРЕНИЕ ОБУЧЕНИЯ E3.7 Используйте узловой анализ, чтобы найти Io в схеме на рис.E3.7. Рисунок E3.7

V1

4 мА

+ —

2 k

Ix

3,2

2000 Ix

PSV

ANSWER: Io =

4 мА. 3

V2

2 мА

2 k

Io

Анализ петли Мы обнаружили, что при узловом анализе неизвестными параметрами являются узловые напряжения, и для их определения использовался KCL. После расчета этих узловых напряжений все токи ответвлений в сети можно легко определить с помощью закона Ома.В отличие от этого подхода, анализ контура использует KVL для определения набора токов контура в цепи. Как только эти токи контура известны, закон Ома можно использовать для расчета любых напряжений в сети. С помощью топологии сети мы можем показать, что в общем случае существует ровно B — N + 1 линейно независимых уравнений КВЛ для любой сети, где B — количество ветвей в схеме, а N — количество узлов. Например, если мы еще раз рассмотрим схему на рис. 2.5, мы обнаружим, что имеется восемь ветвей и пять узлов.Таким образом, число

IRWI03_082-132-hr

30.09.04

8:54

Page 103

РАЗДЕЛ 3.2

1

i2 (t)

i3 (t)

A0002 LY SIS

103

Рисунок 3.18 Рисунок 2.5 перерисован с контурными токами.

R2 R1 iB (t) v1 (t) i4 (t) 3 i5 (t) 4 ± —

iA (t)

i1 (t) 2

R3 R4

iC (t)

± —

i6 (t)

v2 (t) iD (t) i7 (t)

R5 i8 (t)

5

линейно независимых уравнений KVL, необходимых для определения всех токов в сети, B — N + 1 = 8-5 + 1 = 4.Схема на рис. 2.5 перерисована, как показано на рис. 3.18, с токами в 4 контурах, обозначенными, как показано. Затем токи ответвлений определяются как i1 (t) = iA (t) i2 (t) = iA (t) — iB (t) i3 (t) = iB (t) i4 (t) = iA (t) — iC (t) i5 (t) = iB (t) — iD (t) i6 (t) = -iC (t) i7 (t) = iC (t) — iD (t) i8 (t) = -iD (t )

Все схемы, которые мы рассмотрим в этом тексте, будут плоскими, что просто означает, что мы можем нарисовать схему на листе бумаги таким образом, чтобы ни один проводник не пересекал другой проводник. Если цепь плоская, петли легче идентифицировать.Например, вспомните в главе 2, что мы обнаружили, что одного уравнения достаточно для определения тока в цепи, содержащей один контур. Если схема содержит N независимых контуров, мы покажем (и для проверки можно использовать общую топологическую формулу B — N + 1), что для описания сети потребуются N независимых одновременных уравнений. Наш подход к петлевому анализу будет отражать подход, используемый в узловом анализе (т.е. мы начнем с простых случаев и систематически перейдем к более сложным).Затем в конце этого раздела мы обрисуем общую стратегию использования анализа петель.

ЦЕПИ ИСТОЧНИКИ

СОДЕРЖИТ ТОЛЬКО

НЕЗАВИСИМЫЙ

НАПРЯЖЕНИЕ

Для начала анализа рассмотрим схему, показанную на рис. 3.19. Отметим, что эта сеть имеет семь ветвей и шесть узлов, и поэтому количество линейно независимых уравнений КВЛ, необходимых для определения всех токов в цепи, равно B — N + 1 = 7 — 6 + 1 = 2. Поскольку два линейно независимых уравнения КВЛ требуются, мы идентифицируем две независимые петли, ABEFA и BCDEB.Теперь мы определяем новый набор переменных тока, называемых токами контура, которые можно использовать для определения физических токов в цепи. Предположим, что ток i1 течет в первом контуре, а ток i2 течет во втором контуре. Тогда ток ветви, протекающий от B к E через R3, равен i1 — i2. Предполагаются направления токов. Как и в случае узлового анализа, если фактические токи не в указанном направлении, вычисленные значения будут отрицательными. Применение KVL к первому циклу дает + v1 + v3 + v2 — vS1 = 0

KVL, примененное к циклу 2, дает + vS2 + v4 + v5 — v3 = 0

, где v1 = i1R1, v2 = i1R2, v3 = Ai1 — i2 B R3, v4 = i2R4 и v5 = i2R5.

СОВЕТ В уравнениях используется условное обозначение пассивных знаков.

IRWI03_082-132-hr

104

9/30/04

8:54

ГЛАВА 3

Page 104

NODALANDLOOPANA LY SISTECHNIQUES

. уравнения, необходимые для определения двух контурных токов; то есть i1 AR1 + R2 + R3 B — i2 AR3 B = vS1

-i1 AR3 B + i2 AR3 + R4 + R5 B = -vS2

или в матричной форме B

R1 + R2 + R3 -R3

-R3 iv RB 1 R = B S1 R R3 + R4 + R5 i2 -vS2

На этом этапе важно определить то, что называется сеткой.Сетка — это особый вид цикла, в котором нет никаких петель. Поэтому, когда мы проходим путь сетки, мы не обводим никакие элементы схемы. Например, сеть на рис. 3.19 содержит две ячейки, определяемые путями A-B-E-F-A и B-C-D-E-B. Путь A-B-C-D-E-F-A является петлей, но не сеткой. Поскольку большая часть нашего анализа в этом разделе будет включать в себя написание уравнений KVL для сеток, мы будем называть токи токами сетки, а анализ — анализом сетки.Рисунок 3.19 Двухконтурная схема.

A

v + 1R1

vS1 ± — —

C

± —

+

i1

R3 v3 —

R2 F

vS2

B

B

B

+

i2

R4 v4

R5

—

v5 + D

Пример 3.12 Рассмотрим сеть на рис. 3.20a. Мы хотим найти текущий Ио. РЕШЕНИЕ

Мы начнем анализ с написания уравнений сетки.Обратите внимание, что на резисторах нет знаков + и -. Однако они не нужны, поскольку мы будем применять закон Ома к каждому резистивному элементу при написании уравнений КВЛ. Уравнение для первой сетки: -12 + 6kI1 + 6kAI1 — I2 B = 0

Уравнение KVL для второй сетки: 6kAI2 — I1 B + 3kI2 + 3 = 0

, где Io = I1 — I2. Решение двух одновременных уравнений дает I1 = 54 мА и I2 = 12 мА. Следовательно, Io = 34 мА. Все напряжения и токи в сети показаны на рис.3.20b. Вспомните из узлового анализа, что после определения узловых напряжений мы могли проверить наш анализ, используя KCL на узлах. В этом случае мы знаем токи ответвления и можем использовать KVL вокруг любого замкнутого пути, чтобы проверить наши результаты. Например, применение KVL к внешнему циклу дает -12 +

15 3 + + 3 = 0 2 2 0 = 0

Поскольку мы хотим вычислить текущее Io, мы могли бы использовать анализ цикла, как показано на рис. 3.20. c. Обратите внимание, что контурный ток I1 проходит через центральную ветвь сети и, следовательно, I1 = Io.Два уравнения контура в этом случае: и

-12 + 6kAI1 + I2 B + 6kI1 = 0

-12 + 6kAI1 + I2 B + 3kI2 + 3 = 0

Решение этих уравнений дает I1 = 34 мА и I2 = 12 мА. Поскольку ток в источнике 12 В составляет I1 + I2 = 54 мА, эти результаты согласуются с анализом сетки.

IRWI03_082-132-hr

9/30/04

8:54

Page 105

РАЗДЕЛ 3.2

Наконец, для сравнения, давайте найдем Io с помощью узлового анализа.Наличие двух источников напряжения указывает на то, что это жизнеспособный подход. Применяя KCL к верхнему центральному узлу, мы получаем Vo Vo — 3 Vo — 12 + + = 0 6k 6k 3k

и, следовательно, Vo =

9 V 2

, а затем Io =

Vo 3 = mA 6k 4

Обратите внимание, что в этом случае нам пришлось решать только одно уравнение вместо двух. 15 —V + 2 —

Vo 6 k

5 — mA 4

3 k 6 k

12 В

± —

I1

± —

I2

3V

3 —V + 2 —

Io

3 k + 9 — mA 6 k 2 3 — mA 4

1 — mA 2

6 k

± —

12 В

Vo

(a)

± —

3V

(b) 6 k

12 V

± —

Vo

I1

3 k

6 k

I2

± —

3V

Рисунок 3.20 Схемы, использованные в примере 3.12.

Еще раз мы вынуждены отметить симметричную форму уравнений сетки, описывающих схему на рис. 3.19. Обратите внимание, что матрица коэффициентов для этой схемы симметрична. Поскольку эта симметрия обычно проявляется в сетях, содержащих резисторы и независимые источники напряжения, мы можем научиться писать уравнения сетки путем осмотра. В первом уравнении коэффициент при i1 является суммой сопротивлений, через которые протекает ток сетки 1, а коэффициент при i2 является отрицательным из суммы сопротивлений, общих для тока 1 сетки и тока 2 сетки.Правая часть уравнения представляет собой алгебраическую сумму источников напряжения в ячейке 1. Знак источника напряжения положительный, если он способствует предполагаемому направлению потока тока, и отрицательный, если он противодействует предполагаемому потоку. Первое уравнение — это KVL для сетки 1. Во втором уравнении коэффициент при i2 представляет собой сумму всех сопротивлений в сетке 2, коэффициент при i1 является отрицательным из суммы сопротивлений, общих для сетки 1 и сетки 2, а правая часть уравнения представляет собой алгебраическую сумму источников напряжения в сетке 2.В общем, если мы предположим, что все токи сетки имеют одинаковое направление (по часовой стрелке или против часовой стрелки), то, если KVL применяется к сетке j с током сетки ij, коэффициент ij является суммой сопротивлений в ячейке j и коэффициенты других токов сетки Ae.g., ij — 1, ij + 1 B являются отрицательными значениями сопротивлений, общих для этих сеток и сетки j. Правая часть уравнения равна алгебраической сумме источников напряжения в ячейке j. Эти источники напряжения имеют положительный знак, если они способствуют протеканию тока ij, и отрицательный знак, если они противодействуют ему.

LOOPANA LY SIS

105

IRWI03_082-132-hr

106

9/30/04

8:54 AM

ГЛАВА 3

Page 106

NODAL запишите уравнения сетки, проверив сеть на рис. 3.21. Затем мы будем использовать MATLAB для определения токов сетки. РЕШЕНИЕ

Три линейно независимых одновременных уравнения: (4k + 6k) I1 — (0) I2 — (6k) I3 = -6 — (0) I1 + (9k + 3k) I2 — (3k) I3 = 6 — ( 6k) I1 — (3k) I2 + (3k + 6k + 12k) I3 = 0

или в матричной форме 10k C 0-6k

0 12k -3k

-6k I1-6-3k SC I2 S = C 6 S 21k I3 0

Обратите внимание на симметричную форму уравнений.Общая форма матричного уравнения — RI = V

, а решение этого матричного уравнения — I = R – 1V

. Входные / выходные данные для решения MATLAB следующие: >> R = [10e3 0 -6e3 ; 0 12e3 -3e3; -6e3 -3e3 21e3] R = 10000 0-6000

0 12000-3000

-6000-3000 21000

>> V = [-6; 6; 0] V = -6 6 0 >> I = inv (R) * V I = 1.0e-003 * -0,6757 0,4685 -0,1261 4 k

Рисунок 3.21 Схема, использованная в примере 3.13.

I1

6 k

+ 6V

I2

I3

12 k

3 k

ЦЕПИ, СОДЕРЖАЩИЕ НЕЗАВИСИМЫЕ ИСТОЧНИКИ ТОКА. наличие источника тока упрощает анализ петли.Следующие примеры иллюстрируют это.

IRWI03_082-132-hr

9/30/04

8:54 AM

Page 107

РАЗДЕЛ 3.2

LOOPANA LY SIS

РАСШИРЕНИЕ ОБУЧЕНИЯ E3.8 Используйте уравнения схемы в VO, чтобы найти Рис. E3.8.

ОТВЕТ: Vo =

6V

Рисунок E3.8

+ 4 k

+ 2 k

2 k

6 k

± —

Vo

3V

-9 .14 Найдем как Vo, так и V1 в схеме на рис. 3.22. РЕШЕНИЕ

Хотя кажется, что существуют два неизвестных тока сетки, ток I1 проходит непосредственно через источник тока, и, следовательно, I1 ограничен равным 2 мА. Следовательно, неизвестен только ток I2. KVL для самой правой сетки составляет 2k (I2 — I1) — 2 + 6kI2 = 0

И, конечно, I1 = 2 * 10-3

Эти уравнения можно записать как — 2kI1 + 8kI2 = 2 I1 = 2k

Входные / выходные данные для решения MATLAB следующие: >> R = [-2000 8000; 1 0] R = -2000 1

8000 0

>> V = [2; 0.002] V = 2,0000 0,0020 >> I = inv (R) * VI = 0,0020 0,0008

33 V. 5

107

IRWI03_082-132-hr

108

9/30/04

8:54 AM

ГЛАВА 3

Страница 108

NODALANDLOOPANA LY SISTECHNIQUES

>> format long >> II = 0,00200000000000 0,00075000000000

Обратите внимание, что первое решение для I2 содержит одну цифру в последнем десятичном разряде. Естественно, возникает вопрос, было ли число округлено до этого значения.Если мы введем «длинный формат», MATLAB предоставит ответ с использованием 15 цифр. Таким образом, вместо 0,008 более точный ответ — 0,0075. Следовательно, Vo = 6kI2 =

9 V 2

Чтобы получить V1, мы применяем KVL вокруг любого замкнутого пути. Если мы используем внешний контур, уравнение KVL будет -V1 + 4kI1 — 2 + 6kI2 = 0

И, следовательно, 21 В 2

V1 =

Обратите внимание, что, поскольку ток I1 известен, резистор 4-k не входить в уравнение при поиске Vo. Однако он появляется в каждом цикле, содержащем текущий источник, и, таким образом, используется при поиске V1.Рисунок 3.22. Схема, использованная в примере 3.14.

2V

V1

+

4 k 2 mA

+

I1

I2

6 k

Vo

2 k —

Пример 3.15 Мы хотим найти Vo в сети . 3.23. РЕШЕНИЕ

Поскольку токи I1 и I2 проходят непосредственно через источник тока, два из трех требуемых уравнений следующие: I1 = 4 * 10-3 I2 = -2 * 10-3

Третье уравнение — это KVL для сетки, содержащей источник напряжения; то есть 4kAI3 — I2 B + 2kAI3 — I1 B + 6kI3 — 3 = 0

Эти уравнения дают I3 =

1 мА 4

и, следовательно, Vo = 6kI3 — 3 =

-3 В 2

IRWI03_082 -132-час

30.09.04

8:54

Страница 109

РАЗДЕЛ 3.2

L O P A N A LY S I S

109

Рис. 3.23. Схема, использованная в примере 3.15.

4 мА

+ I1

2 k

6 k

I3

Vo

4 k 2 мА

+

4 k

I2

3V

— в предыдущем примере — общий подход к работе с независимыми источниками тока при написании уравнений КВЛ; то есть использовать одну петлю для каждого источника тока.Количество «оконных стекол» в сети говорит нам, сколько уравнений нам нужно. Дополнительные уравнения KVL записываются для покрытия остальных элементов схемы в сети. Следующий пример иллюстрирует этот подход.

Пример 3.16

СОВЕТ

Найдем Io в сети на рис. 3.24a. РЕШЕНИЕ

Сначала мы выбираем два контура тока I1 и I2 так, чтобы I1 проходил напрямую через источник 2 мА, а I2 проходил напрямую через источник 4 мА, как показано на рис.3.24b. Следовательно, два из наших трех линейно независимых уравнений: I1 = 2 * 10-3 I2 = 4 * 10-3

Остающийся контурный ток I3 должен проходить через элементы схемы, не охваченные двумя предыдущими уравнениями, и, конечно, не может пройти через источники тока. Путь для этого оставшегося контура тока может быть получен путем разомкнутой цепи источников тока, как показано на рис. 3.24c. Когда все токи обозначены в исходной цепи, уравнение KVL для этой последней петли, как показано на рис.3.24d, равно -6 + 1kI3 + 2kAI2 + I3 B + 2kAI3 + I2 — I1 B + 1kAI3 — I1 B = 0

Решение уравнений дает I3 =

-2 мА 3

и, следовательно, Io = I1 — I2 — I3 =

-4 мА 3

Затем рассмотрим метод супер-сетки. В этом случае заданы три тока сетки, как показано на рис. 3.24e, и, поскольку напряжение на источнике тока 4 мА неизвестно, предполагается, что оно равно Vx. Токи сетки, ограниченные источниками тока, равны I1 = 2 * 10-3 I2 — I3 = 4 * 10-3

Уравнения КВЛ для ячеек 2 и 3 соответственно: 2kI2 + 2kAI2 — I1 B — Vx = 0

-6 + 1kI3 + Vx + 1kAI3 — I1 B = 0

В этом случае источник тока 4 мА расположен на границе между двумя сетками.Таким образом, мы продемонстрируем два метода работы с подобными ситуациями. Один из них — это особый метод цикла, а другой известен как подход суперсетки.

IRWI03_082-132-hr

110

9/30/04

8:54

ГЛАВА 3

Страница 110

NODALANDLOOPANA LY SISTECHNIQUES

000 9VI

000
000

000

1 к

+ 4 мА

1 к

2 к 2 мА

I1

2 к

I2 2 к

2 мА

Io

4 мА

1 к

(б)

6В

6В

1 к

+

1 к

+ I3

1 к

2 к

I3

1 к

000

2 2 к

2 мА

6 В 1 к

+ I3

—

2 к

I1

I2

I3 1 к 2 к

I1

2 к

Io

1 к

+

Vx + 4 мА

2 к

I2

(d)

6V

1 k

4 мА

Io

(c)

2 мА

2 k

Io

2 мА

Io (f)

Рисунок 3.24 Цепи, использованные в примере 3.16.

Сложение последних двух уравнений дает -6 + 1kI3 + 2kI2 + 2kAI2 — I1 B + 1kAI3 — I1 B = 0

Обратите внимание, что неизвестное напряжение Vx было исключено. Два уравнения связи вместе с этим последним уравнением дают желаемый результат. Цель суперячейки — избежать введения неизвестного напряжения Vx. Суперсетка создается мысленным удалением источника тока 4 мА, как показано на рис. 3.24f. Затем запишите уравнение KVL вокруг пунктирного пути, определяющего суперсетку, используя исходные токи сетки, как показано на рис.3.20e, дает -6 + 1kI3 + 2kI2 + 2kAI2 — I1 B + 1kAI3 — I1 B = 0

Обратите внимание на то, что это уравнение суперсетки такое же, как полученное ранее путем введения напряжения Vx.

IRWI03_082-132-hr

9/30/04

8:54

Page 111

РАЗДЕЛ 3.2

LOOPANA LY SIS

ОБУЧАЮЩИЕ РАСШИРЕНИЯ E3.9 Найдите Vo. E3 в сети. 9.

ОТВЕТ: Vo =

33 В. 5

ОТВЕТ: Vo =

32 В.5

+ Vo —

Рисунок E3.9 4 мА

6 k 2 k

± —

4 k

5V

E3.10 Найдите Vo в сети на рисунке E3.10. 4 мА

Рисунок E3.10

± —

2 мА

+

1 k

2 k

4V

4 k

Vo —

ЦЕПИ, СОДЕРЖАЩИЕ ЗАВИСИМОСТЬ ЦЕПЕЙ С ЗАВИСИМОСТЬЮ ЗАПРЕЩЕННЫХ ЦЕПЕЙ источники такие же, как и в прошлом. Во-первых, мы рассматриваем зависимый источник как независимый источник при написании уравнений KVL.Затем мы пишем управляющее уравнение для зависимого источника. Следующие примеры иллюстрируют это.

Пример 3.17. Найдем Vo в схеме на рис. 3.25, которая содержит источник напряжения, управляемый напряжением. РЕШЕНИЕ

Уравнение для токов контура, показанное на рисунке: — 2Vx + 2k (I1 + I2) + 4kI1 = 0 — 2Vx + 2k (I1 + I2) — 3 + 6kI2 = 0

, где Vx = 4kI1

Эти уравнения можно объединить для получения — 2kI1 + 2kI2 = 0 — 6kI1 + 8kI2 = 3

Входные / выходные данные для решения MATLAB: >> R = [-2000 2000; -6000 8000] R = -2000 -6000

2000 8000

111

IRWI03_082-132-час

112

9/30/04

8:54 AM

ГЛАВА 3

Страница 112

Страница 112 NODALANDLOOPANA LY SISTECHNIQUES

>> V = [0; 3] V = 0 3 >> I = inv (R) * V I = 0.00150000000000 0,00150000000000

и, следовательно, Vo = 6kI2 = 9 В

Для сравнения мы также решим задачу с помощью узлового анализа. Наличие источников напряжения указывает на то, что этот метод может быть проще. Рассмотрение источника 3-V и его соединительных узлов как надузла и записи уравнения KCL для этого супеузла дает Vx — 2Vx Vx Vx + 3 + + = 0 2k 4k 6k

, где Vo = Vx + 3

Эти уравнения также дают Vo = 9 В. Рисунок 3.25 Схема, использованная в примере 3.17.

Vx 2 k 2 Vx

± —

I1

3V

+ 4 k

+ 6 k

I2

Vo —

Пример 3.18 Найдем Vo в схеме на рис. 3.26, который содержит источник тока, управляемый напряжением. РЕШЕНИЕ

Токи I1 и I2 проходят через источники тока. Следовательно, два необходимых уравнения: Vx 2000 I2 = 2 * 10 — 3 I1 =

Уравнение KVL для третьей сетки — 3 + 2k (I3 — I1) + 6kI3 = 0

, где Vx = 4k (I1 — I2)

Объединение этих уравнений дает — I1 + 2I2 = 0 I2 = 2k — 2kI2 + 8kI3 = 3

IRWI03_082-132-hr

9/30/04

8:54 AM

Страница 113

РАЗДЕЛ 3.2

L O O P A N A LY S I S

Решение MATLAB для этих уравнений: >> R = [-1 2 0; 0 1 0; -2000 0 8000] R = -1 0 -2000

2 1 0

0 0 8000

>> V = [0; 0,002; 3] V = 0 0,00200000000000 3.00000000000000 >> I = inv (R) * VI = 0,00400000000000 0,00200000000000 0,00137500000000

И, следовательно, Vo = 8,25 V

+

Vx — 2000

I1 —

2 k

Vx +

I3

6 k

4 k 2 мА

I2

Рисунок 3.26 Схема, использованная в примере 3.18.

± —

Vo

3V —

Пример 3.19. Схема на рис. 3.27 содержит как источник тока, управляемый током, так и источник тока, управляемый напряжением. Давайте использовать MATLAB для определения токов контура. РЕШЕНИЕ

Уравнения для токов контура, показанные на рисунке: 4 k Vx I2 = 2k I1 =

-1kIx + 2kAI3 — I1 B + 1kAI3 — I4 B = 0

, где

1kAI4 — I3 B + 1kAI4 — I2 B + 12 = 0 Vx = 2kAI3 — I1 B Ix = I4 — I2

113

IRWI03_082-132-час

114

30.09.04

8:54 AM

ГЛАВА 3

114

NODALANDLOOPANA LY SISTECHNIQUES

Объединение этих уравнений дает 4 k I1 + I2 — I3 = 0 I1 =

1kI2 + 3kI3 — 2kI4 = 8 1kI2 + 1kI3 — 2kI4 = 1

. 1 D 0 1k 0 1k

0-1 3k 1k

4 0 I1 k 0 ITD 2T = E 0 U -2k I3 8-2k I4 12

Входные и выходные данные для решения MATLAB следующие:> > R = [1 0 0 0; 1 1 -1 0; 0 1000 1000 -2000]

0 1000 3000 -2000;

R = 1 1 0 0

0 1 1000 1000

0-1 3000 1000

0 0 -2000-2000

>> V = [0.004; 0; 8; 12] V = 0,0040 0 8,0000 12,0000 >> I = inv (R) * V I = 0,0040 -0,0060 -0,0020 -0,0100

Рисунок 3.27 Схема, использованная в примере 3.19.

2 к

I1

4 мА +

1kIx

± —

Vx

Vx

I2 —

— 2k

Ix

Ix

1 k

± —

12 V

IRWI03_082-132-hr

9/30/04

8:54 AM

Страница 115

РАЗДЕЛ 3.2

L O P A N A LY S I S

Пример 3.20 На этом этапе мы снова рассмотрим схему из примера 3.10 и проанализируем ее с помощью уравнений контура. Напомним, что поскольку сеть имеет два источника напряжения, узловой анализ был несколько упрощен. Аналогичным образом наличие источников тока должно упростить анализ контура. Ясно, что сеть имеет четыре контура, и поэтому для определения токов контура требуются четыре линейно независимых уравнения. Сеть перерисована на рис.3.28, где указаны токи контура. Обратите внимание, что мы провели по одному току через каждый из независимых источников тока. Такой выбор токов упрощает анализ, поскольку два из четырех уравнений имеют вид I1 = 2k I3 = -2k

Два оставшихся уравнения KVL для токов контура I2 и I4 равны -2Vx + 1kI2 + (I2 — I3) 1k = 0 (I4 + I3 — I1) 1k — 2Vx + 1kI4 + 4 = 0

, где Vx = 1k (I1 — I3 — I4)

Подставляя уравнения для I1 и I3 в два уравнения KVL, получаем 2kI2 + 2kI4 = 6 4kI4 = 8

Решая эти уравнения для I2 и I4, мы получаем I4 = 2 мА I2 = 1 мА

и, таким образом, Vo = 1 В Рисунок 3.28 Схема, использованная в примере 3.20.

± —

2Vx 2 —A k

I1

I2

Vx 1 k

I3

1 k

I4

1 k

+

—

0003 A k

± —

4V

Пример 3.21. Еще раз рассмотрим Пример 3.11. В этом случае мы исследуем сеть с помощью анализа петель. Хотя существует четыре источника, два из которых являются зависимыми, только один из них является текущим.Таким образом, с самого начала мы ожидаем, что петлевой анализ будет сложнее узлового анализа. Ясно, что в схеме шесть контуров. Таким образом, для решения всех неизвестных токов необходимо шесть линейно независимых уравнений. Сеть перерисована на рис. 3.29, где указаны петли. Шесть уравнений KVL, описывающих сеть: 1kI1 + 1kAI1 — I2 B + 1kAI1 — I4 B = 0 1kAI2 — I1 B — 6 + 1kAI2 — I5 B = 0 I3 = 2Ix

115

IRWI03_082-132-hr

116

9/30/04

8:54

ГЛАВА 3

Страница 116

NODALANDLOOPANA LY SISTECHNIQUES

-12 + 1kAI4 — I1 B + 2Vx = 0

— I0002k + Ix 1kAI5 — Io B = 0

1kAIo — I5 B + 1kAIo — I3 B + 1kIo = 0

Рисунок 3.29 Схема, использованная в примере 3.21.

+

1 к

Vx

1 к

6 В

+

I1

I2

1 к

1 к

2Ix

000 9000 9000 9000

I3 —

I4

2Vx

1 k 1 k

± —

I5

1 k

I6 Ix

Io

И управляющие переменные для двух зависимых источников Vx = -1kI1 Ix = — Io

Подстановка параметров управления в шесть уравнений KVL дает 3I1 -I1 0 -3I1 2I1 0

-I2 0 + 2I2 0 0 I3 0 0 -I2 0 0 0

-I4 0 0 0 -I5 0 0 -2I5 + 2Io + I4 0 0 0 + 2I5 -Io 0 -3I5 + 5Io

= = = = = =

0 6k 0 12k 0 0

, что может быть записано в матричной форме как 3-1 0-1 -1 2 0 0 0 0 1 0 F -3 0 0 1 2-1 0 0 0 0 0 0

0-1-2 0 2-3

0 I1 0 I2 0 6k 2 I 0 VF 3V = FV 0 I4 12k -1 I5 0 5 Io 0

Хотя эти шесть линейных Независимые системы уравнений могут быть решены любым удобным способом, мы будем использовать решение MATLAB.Как показывают результаты, перечисленные ниже, ток Io составляет -48 мА. >> R = [3 -1 0 -1 0 0; -1 2 0 0 -1 0; 0 0 1 0 -2 2; -3 0 0 1 0 0; 2-1 0 0 2 -1; 0 0 0 0-3 5] R = 3-1 0-3 2 0

-1 2 0 0-1 0

0 0 1 0 0 0

-1 0 0 1 0 0

0-1 -2 0 2 -3

>> V = [0; 0,006; 0; 0,012; 0; 0]

0 0 2 0 -1 5

IRWI03_082-132-hr

9/30/04

8:54 AM

Страница 117

РАЗДЕЛ 3.2

V = 0 0.0060 0 0,0120 0 0 >> I = inv (R) * V I = 0,0500 -0,0120 -0,0640 0,1620 -0,0800 -0,0480 >>

Наконец, очень важно внимательно изучить схему перед выбором подхода к анализу. Один метод может быть намного проще другого, и немного времени, потраченное заранее, может сэкономить много времени в долгосрочной перспективе.

P R O B L E M — S O LV I N G S T R AT E G Y Анализ контура Шаг 1. Один ток контура назначается каждому независимому контуру в цепи, которая содержит

N независимых контуров.Шаг 2. Если в сети присутствуют только независимые источники напряжения, напишите линейно независимые уравнения KVL N

, по одному для каждого контура. Если присутствуют зависимые источники напряжения, запишите уравнение KVL, как это делается для цепей только с независимыми источниками напряжения; затем напишите управляющие уравнения для зависимых источников. Шаг 3. Если в сети присутствуют источники тока, можно использовать любой из двух методов

. В первом случае выбирается один контурный ток, который проходит через один из источников тока.Это делается для каждого источника тока в сети. Остальные токи контура (N — количество источников тока) определяются путем размыкания цепи источников тока в сети и использования этой модифицированной сети для их выбора. Как только все эти токи определены в исходной сети, можно записать N петлевых уравнений. Второй подход аналогичен первому, за исключением того, что если два тока сетки проходят через конкретный источник тока, вокруг этого источника образуется суперячейка.Два требуемых уравнения для сеток, содержащих этот источник, — это уравнения связи для двух сеточных токов, которые проходят через источник, и уравнение суперсетки. Как указывалось ранее, при наличии зависимых источников тока также необходимы управляющие уравнения для этих источников.

L O P A N A LY S I S

117

IRWI03_082–132-час

118

9/30/04

8:54 AM

ГЛАВА 3

ГЛАВА 3

ПЛАН И Е Н И Е

Page 11811 Используйте анализ сетки, чтобы найти Vo в цепи на рис. E3.11. Рисунок E3.11

12 В

2 k

+ 2000Ix

± —

ОТВЕТ: Vo = 12 В.

PSV

Ix

4 k

+

Vo

9000

—

E3.12 Используйте анализ петель для решения сети в примере 3.5 и сравните время и усилия, затраченные на эти два метода решения. E3.13 Используйте узловой анализ для решения схемы из примера 3.15 и сравните время и усилия, затраченные на две стратегии решения.

3.3

Пример приложения Пример приложения 3.22 Концептуальная схема для ручной установки скорости электродвигателя постоянного тока показана на рисунке 3.30a. Резисторы R1 и R2 находятся внутри компонента, называемого потенциометром или потенциометром, который представляет собой не что иное, как регулируемый резистор, например, регулятор громкости. Вращение ручки изменяет соотношение a = R2 (R1 + R2), но общее сопротивление Rpot = R1 + R2 не изменяется. Таким образом, потенциометр образует делитель напряжения, который устанавливает напряжение Vspeed.Выходной сигнал усилителя мощности VM в четыре раза больше Vspeed. Усилители мощности могут выдавать высокие токи, необходимые для привода двигателя. Наконец, скорость двигателя постоянного тока пропорциональна VM, то есть скорость в оборотах в минуту равна некоторой постоянной k умноженной на V. Не зная подробностей усилителя мощности, можем ли мы проанализировать эту систему? В частности, можем ли мы установить взаимосвязь между оборотами в минуту и ​​крутящим моментом?

5V

Rpot

µ

R1 R2

= 1 = 0

+ Vspeed —

Power amp

+

VM / Vspeed = 4

VM —

двигатель ) Модель усилителя мощности

5V

Rpot

µ

R1 R2

= 1 = 0

+ Vspeed —

+ 4Vspeed —

± —

+

VM —

VM — 3.30 (а) простой драйвер двигателя постоянного тока и (б) модель схемы, используемая для его анализа.

IRWI03_082-132-hr

9/30/04

8:54 AM

Page 119

РАЗДЕЛ 3.4

РЕШЕНИЕ

Поскольку выходное напряжение усилителя мощности пропорционально его входу, мы можем смоделировать усилитель как простой зависимый источник. Полученная принципиальная схема показана на рис. 3.30b. Теперь мы можем легко установить взаимосвязь между скоростью двигателя и положением кастрюли: a. Уравнения, которые управляют работой двигателя, усилителя мощности и делителя напряжения: скорость (об / мин) = KM VM VM = 4Vspeed Vspeed = 5

R2 R2 = 5c d = 5a R1 + R2 Rpot R1 = (1 — a ) Rpot

R2 = aRpot

Объединение этих соотношений для исключения Vspeed дает соотношение между скоростью двигателя и a, то есть об / мин = 20a.Если, например, постоянная KM двигателя составляет 50 об / минV, то об / мин = 1000a

Это соотношение указывает, что скорость двигателя пропорциональна положению ручки потенциометра. Поскольку максимальное значение a равно 1, частота вращения двигателя находится в диапазоне от 0 до 1000 об / мин. Обратите внимание, что в нашей модели усилитель мощности, смоделированный зависимым источником, может выдавать любой ток, необходимый двигателю. Конечно, это невозможно, но это демонстрирует некоторые компромиссы, с которыми мы сталкиваемся при моделировании. Выбрав простую модель, мы смогли быстро наладить необходимые отношения.Однако другие характеристики реального усилителя мощности в этой модели не учитываются.

3.4

Пример проектирования

Пример проектирования 3.23 Источник 8 В должен использоваться вместе с двумя стандартными резисторами для разработки делителя напряжения, который будет выдавать 5 В при подключении к нагрузке 100 А. Сохраняя потребляемую мощность на минимально возможном уровне, мы хотим минимизировать ошибку между фактическим выходом и требуемыми 5 вольтами. РЕШЕНИЕ Разделитель можно смоделировать, как показано на рис.3.31. Применяя KCL к выходному узлу

, получаем уравнение VS — Vo Vo = + Io R1 R2

Используя указанные параметры для входного напряжения, желаемого выходного напряжения и источника тока, получаем R1 =

3R2 5 + ( 100) R2

Методом проб и ошибок мы обнаружили, что отличные значения для двух стандартных резисторов равны R1 = 10 кОм и R2 = 27 кОм. Для минимизации энергопотребления используются резисторы большого номинала. При таком выборе резисторов выходное напряжение составляет 5,11 В, что составляет всего 2 процента погрешности.15%. Рис. 3.31. Простая схема делителя напряжения с нагрузкой 100 мкА.

R1 VS ± —

+

8V

R2

Io

Vo 100 A —

ПРИМЕР КОНСТРУКЦИИ

119

IRWI03_082-132-час

000

120 9/0003

000

120 9/000 8:54

ГЛАВА 3

Страница 120

NODALANDLOOPANA LY SISTECHNIQUES

РЕЗЮМЕ Узловой анализ для N-узловой цепи

Анализ петли для N-петлевой схемы

●

— Выберите один схема узла в качестве опорного узла.Предположим, что напряжение узла равно нулю, и измерьте напряжения всех узлов относительно этого узла.

●

Один контурный ток назначается каждому независимому контуру в цепи, содержащей N независимых контуров.

●

●

Если в сети присутствуют только независимые источники тока, запишите уравнения KCL в N — 1 неопорных узлах. Если присутствуют зависимые источники тока, напишите уравнения KCL, как это делается для сетей только с независимыми источниками тока; затем напишите управляющие уравнения для зависимых источников.

Если в сети присутствуют только независимые источники напряжения, напишите N линейно независимых уравнений KVL, по одному для каждого контура. Если присутствуют зависимые источники напряжения, запишите уравнения KVL, как это делается для цепей только с независимыми источниками напряжения; затем напишите управляющие уравнения для зависимых источников.

●

●

Если в сети присутствуют источники напряжения, они могут быть подключены (1) между эталонным узлом и неопорным узлом или (2) между двумя неопорными узлами.В первом случае, если источником напряжения является независимый источник, то известно напряжение на одном из неопорных узлов. Если источник является зависимым, он рассматривается как независимый источник при написании уравнений KCL, но необходимо дополнительное уравнение ограничения. В последнем случае, если источник является независимым, напряжение между двумя узлами ограничивается значением источника напряжения, и уравнение, описывающее это ограничение, представляет собой одно из N — 1 линейно независимых уравнений, необходимых для определения напряжений в N узлах. .Поверхность сети, описываемая уравнением связи (то есть источник и два соединительных узла), называется суперузлом. Одно из оставшихся N — 1 линейно независимых уравнений получается путем применения KCL в этом суперузле. Если источник напряжения является зависимым, он рассматривается как независимый источник при написании уравнений KCL, но необходимо дополнительное уравнение ограничения.

Если в сети присутствуют источники тока, можно использовать любой из двух методов. В первом случае выбирается один контурный ток, который проходит через один из источников тока.Это делается для каждого источника тока в сети. Остальные токи контура (N — количество источников тока) определяются путем размыкания цепи источников тока в сети и использования этой модифицированной сети для их выбора. Как только все эти токи определены в исходной сети, можно записать N-петлевые уравнения. Второй подход аналогичен первому, за исключением того, что если два тока сетки проходят через конкретный источник тока, вокруг этого источника образуется суперячейка.Два требуемых уравнения для сеток, содержащих этот источник, — это уравнения связи для двух сеточных токов, которые проходят через источник, и уравнение суперсетки. При наличии зависимых источников тока также необходимы управляющие уравнения для этих источников.

ПРОБЛЕМЫ PSV

CS

оба доступны в Интернете по адресу: http://www.justask4u.com/irwin

РАЗДЕЛ 3.1 3.1 Найдите Io в схеме на рис. P3.1 с помощью узлового анализа.

КС

3.2 Используйте узловой анализ, чтобы найти V1 в цепи на рис. P3.2. 2 k

10 k + 12 k

6 мА

6 k

Io

3 k 3 k

6 мА

V1

2 k 4 мА

Рисунок P3.1 Рисунок P3.2

2 k

IRWI03_082-132-hr

9/30/04

8:54

Page 121

ПРОБЛЕМЫ

3.3 Используйте узловой анализ, чтобы найти как V1, так и Vo в схеме на рис. P3. 3. П С В

121

3.7 Найдите Vo в сети на рис. P3.7, используя узловой анализ. CS

Vo

+

—

2 мА

V1

V2 2 к

6 к

6 к

3 к

12 мА

+

6 к 1 к

12 В

12 к

± —

± —

6 к

6 В

Рисунок P3.3

Рисунок P3.7

3.8 Найдите Vo в цепи на рисунке P3.8 с использованием узлового анализа.

3.4 Найдите V1 и V2 в схеме на рис. P3.4, используя узловой анализ. Затем решите проблему с помощью MATLAB и сравните свои ответы.

PSV

6 к 2 к

6 мА

+

V1

4 мА

+

4 к +

V2

6 к

—

3 кОм

6 к

8 мА +

Vo

4 к

—

—

Рисунок P3.4

Рисунок P3.8

3.5 Найдите Io в схеме на рисунке P3.5, используя узловой анализ.

CS

3.9 Используйте узловой анализ, чтобы найти Vo в цепи на рис. P3.9. 4 k

9V

Io

2 k

3 k

± —

6 k

2 k

2 k

Рисунок P3.5

2 k 6V

± + 9000

Vo

4 k

8 k 8 k

2 мА

Рисунок P3.9

3.6 Найдите Io в сети на рис. P3.6, используя узловой анализ.

3.10 Найдите Io в схеме на рис. P3.10, используя узловой анализ.

Io

Io 6 k 6V

—

+

Рисунок P3.6

4 k

4 k 6 k

± —

24 V

6V

± — 9000 .10

4 k 4 k

4 k

2 mA

IRWI03_082-132 часа

122

9/30/04

8:54 AM

ГЛАВА 3

Страница 122 9000A LY SISTECHNIQUES

3.11 Используйте узловой анализ, чтобы найти Vo в сети, показанной на рис. P3.11. Затем решите проблему с помощью MATLAB и сравните свои ответы.

3.14 Найдите Io в сети на рис. P3.14.

± — 6V

4 k 6V

4 k

± —

12 k

+ 12 k

2 мА

CS

3 мА

3 мА

6 k

3 k

6 k

Vo —

Рисунок P3.11

Io Рисунок P3.14

3.15 Найдите I1 в сети на рис. P3.15.

CS

3V

3.12 Используйте узловой анализ, чтобы найти Vo в цепи на рис. P3.12. 2 k

6 k

± — 2 мА

+

3 k

I1

3 k

5V

6 k

± —

Рисунок P3.15

Vo 3.160003 Найти Io в сети на рис. P3.16. 6 мА

6 В

+

Io —

4 k

Рисунок P3.12

6 k

3.13 Используйте узловой анализ, чтобы найти Vo в цепи на рис. P3.13. 6 к

3 к

+

2 мА

± —

12 В

6 В

2 к

Рисунок P3.16

3.17 Используйте узловой анализ, чтобы найти Vx и Vy в цепи на рисунке P3.17.

4 к 8 к

5A

1A 12 В

+

+

+ —

24 В +

Vx

R = 132

Vo

4 к

Vy

+

10 44

± —

88

—

110 В

12

Рисунок P3.13

Рисунок P3.17

3.18 Для сети на рисунке P3.17 объясните, почему резистор R не играет роли в определении Vx и Vy. 3.19. Используйте узловой анализ, чтобы найти Vo в сети, показанной на рис. P3.19. + 2 k

± —

14 V

3 k

Vo

10 k

—

1 k 1 k

7 k

2 k

± —

Рисунок P3.19

2Vx

9 k +

Vx —

9 k

18 k 1 mA

IRWI03_082-132-hr

9/30/04

8:54 AM

Страница 123

PRO 3.24 Используйте узловой анализ, чтобы найти Io в цепи на рис. P3.24.

3.20 Используйте узловой анализ, чтобы найти VA и VB в сети, показанной на рис. P3.20. Упростите анализ, сделав правильный выбор для опорного узла. +

VA

—

+

3

6

Io 8 k

VB

—

4 мА

2 1A

6

2 1A

6

V

± —

5

± —

12 В

2 k

4 k

Рисунок P3.20 Рисунок P3.24

3.21 Найдите Io в цепи на рис. P3.21. 3.25. Найдите Io в сети на рис. P3.25, используя узловой анализ. 4 к

4 к 2 к 2 к

± —

24 В

2 мА

Io ± —

2 к

3 к

— ±

6 В

6 В

6 к

Io Рисунок P3.25

Рисунок P3.21

3.26 Используйте узловой анализ, чтобы найти Io в сети, показанной на рисунке P3.26.

3.22 Используйте узловой анализ, чтобы найти Io и IS в схеме на рис.P3.22.

± —

Io 3 k

3 k

1 k

6V

2 k 2 k

± —

1 k

4 k

6V

0002 2 mA

4 k

2 k 4 мА

2 k

Io

IS Рисунок P3.26 Рисунок P3.22

3.27 Используйте узловой анализ, чтобы найти Vo в сети на рисунке P3.27. Затем решите эту проблему с помощью MATLAB и сравните свои ответы. C S

3.23 Используйте узловой анализ, чтобы найти Vo в сети на рис.P3.23. 3 мА

1 к

4 к 2 к

2 к

± —

6 В

6 к

+ 1 к

12 В

Vo

— ±

+ 1 к0003

1 k

Рисунок P3.23

Vo

1 k 2 mA

Рисунок P3.27

—

IRWI03_082-132-час

124

9/30/04

8:54 AM

ГЛАВА 3

Страница 124

NODALANDLOOPANA LY SISTECHNIQUES

3.28 Найдите Vo в цепи на рис. P3.28 с помощью узлового анализа.

3.32 Найдите Vo в сети на рис. P3.32, используя узловой анализ.

PSV

CS

— ±

6V

4 k 6V

1 k

4 k

± —

2 k

2 мА

+ 2 k

мА k

+

1 k

12 V

± —

Vo

2 k

—

Рисунок P3.32

3.33 Используйте узловой анализ, чтобы найти Vo в сети, показанной на рис. P3.33.

Рисунок P3.28

3.29 Используйте узловой анализ, чтобы найти Vo в цепи на рисунке P3.29.

1 к

2 к

1 к

CS

2 к

1 к +

9 мА

6 В

± —

± —

12 В

Vo +

Vo + k

2 мА

Vo

1 k

—

—

6 k

4 k

6 мА

Рисунок P3.33

3.34 Найдите Vo в цепи на рис. P3.34, используя узловой анализ. Рисунок P3.29 +

3.30 Используйте узловой анализ, чтобы найти Vo в цепи на рис. P3.30.

12 В

1 к

1 к 2 к 8 В

± —

2 к

Vo —

2 к

4 к +

± —

Vo

— 60003

2 k

+

2 мА

1 k

4 k 2 мА

Рисунок P3.34

Рисунок P3.30

3.35 Используйте узловой анализ, чтобы найти Vo в сети, показанной на рис. P3.35.

3.31 Используйте узловой анализ, чтобы найти Vo в цепи на рис. P3.31.

6 мА

6 мА + 12 к 12 В

+

12 к

Vo

1 к 1 к

—

2 к

12 В

+ +

6 к 2 мА

6V

± —

1 k

2 k

Vo —

Рисунок P3.31

Vo

Рисунок P3.35

IRWI03_082-132-hr

9/30/04

8:54 AM

Page 125

ПРОБЛЕМЫ

3.36 Используйте MATLAB, чтобы найти узловые напряжения в сети на рис. P3.36. C S

V1

125

3.39 Найдите Vo в сети на рис. P3.39.

± —

2 к

± —

6 В

12 В

1 к

2 к 1 к

2 мА

1 к

+ +

2 В

В 12 В

2 к

V4

+

2 к

1 к

4 В

1 к

Vo

4 мА

± —

2 к

—

—

—

—

P3.39

3.40 Используйте узловой анализ, чтобы найти Vo в цепи на рис. P3.40. Рисунок P3.36

3.37 Определите Vo в сети, показанной на рисунке P3.37, с помощью узлового анализа.

± —

2 к

6 В

1 к

2 мА

+ 2 к

4 мА

1 к

1 к

2 к

+

12 В мА 1 к

1 к

Vo

6 В

± —

—

+ +

12 В 1 к

2 к

Рисунок P3.40

Vo

1 k

3.41 Определите Vo в сети на рис. P3.41.

Рисунок P3.37

2 k

1 k

3.38 Найдите Vo в цепи на рис. P3.38.

+

2 В

1 к

12 В

2 к

+ + 4 мА 2 к

1 к

2 к

+

6 мА

2 мА

2 мА

2 к

6 В

—

4 мА

+ 6 В 1 к

1 к

± —

12 В

1 к

+

Рисунок P3.41

Vo

3.42 Найдите Vo в схеме на рис. P3.42.

Рисунок P3.38

12 В

+ —

2 k 2 k

4 мА

1 k

2 k +

4V

+

2 k

1 k

k

Vo —

Рисунок P3.42

IRWI03_082-132-hr

126

9/30/04

8:54

ГЛАВА 3

Страница 126

NODALANDLES .43 Найдите Io в схеме на рис. P3.43, используя узловой анализ.

3.47 Найдите Io в сети на рис. P3.47.

± — 4000Ix

2 к 4 мА

1 к

2 к

12 В

1 к

1 к

1 к

4 к

1 к

12 к I 9000

+

PSV

12 мА

Io

Рисунок P3.47 1 k

2 мА

1 k

1 k

Io

3.48 Найдите Io в схеме на рис. P3.48, используя узловой анализ.

Рисунок P3.43

12 k 12 k

3.44 Используйте узловой анализ, чтобы найти Vo на рисунке P3.44.

Ix

2Ix 3 мА

10 k

4Ix

12 мА

Vo

Ix

Io

Рисунок P3.48

+ 10 k

9000

12 k сеть на рис. P3.49 с использованием узлового анализа. CS

—

Ix

Рисунок P3.44

10 k

3.45 Найдите Vo в схеме на рис. P3.45, используя узловой анализ.

4000Ix

+

+

Vo

10 к

4 мА

10 к

± 1 к

Vo — 2

+

12 В

± —

± — 9000

Рисунок P3.49

Vo

2 k

—

3,50 Найдите Vo в цепи на рисунке P3.50.

PSV

Рисунок P3.45 1 k

+

3.46 Найдите Vo в цепи на рис. P3.46 с помощью узлового анализа. Затем решите проблему с помощью MATLAB и сравните свои ответы. CS

Vx

1 k

2 k 2 mA

+ 2Vx — 1000

1 k

—

Vo —

Рисунок P3.50

+ 2Ix

1 k

000 1 k

12 В

1 k

Ix

1 k

Vo

3.51 Используйте узловой анализ, чтобы найти Vo в цепи на рис.P3.51. Кроме того, найдите все токи ответвления и проверьте свои ответы с помощью KCL на каждом узле.

—

+ 2000Ix

Рисунок P3.46 12 k 6V

+

4 k

Ix Рисунок P3.51

2 k 2 mA

+ 4 k

Vo —

3

IRWI -hr

30.09.04

8:55

Page 127

127

ПРОБЛЕМЫ

3.52 Найдите мощность, подаваемую источником тока 2 А в сети на рис.P3.52 с использованием узлового анализа.

3.56 Используя узловой анализ, найдите Vo в сети на рис. P3.56.

Ix 4 мА

1 к

4

1 к

12 В 10 В

+ —

4

5

2Ix

2A

+ —

+ —

+ —

Рисунок P3.52

± —

Vo

2 k

1 k

—

3.53 Используйте узловые уравнения для схемы на рис.P3.53 для определения Vo.

Рисунок P3.56

3.57 Используйте узловой анализ, чтобы найти Vo в цепи на рисунке P3.57.

± — –12 В 4

Ix

4

2 1 к

+

Vo

6

2

4A

2Ix

± —

000 1 0003

1 кОм 2Vx

12 В

+ —

+

+

+ 2 к

—

2 к

4 мА

2 к

Vx

1 к

1 к —

Рисунок P3.53

3.54 Определите Vo в сети на рис. P3.54, используя узловой анализ.

2Ix

Ix

1 k

1 k

+

Ix

—

2Vx

1 k

1 k

1 k

9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000

1 k

+

1 k

+

1 k 12 В

3.58 Используйте узловой анализ для определения Io в цепи на рис. P3.58.

2 мА

1 к

1 к

Рисунок P3.57

± —

2Ix

2 мА

12 В

1 k

+

Vx —

Рисунок P3.54

3.55 Рассчитайте Vo в схеме на рис. P3.55 с помощью узлового анализа .

Рисунок P3.58

3.59 Найдите Io в сети на рисунке P3.59, используя узловой анализ.

+ 2 к

1 к

1 к

Vx

± —

1 к

—

12 В

Io

2 к + 12 В

+
+

Vo

2Vx

— ±

Рисунок P3.55

Рисунок P3.59

1 k + 2Ix

1 k

Ix

—

6 мА

1 k

1 k

2 мА

+ —

1 k k

Vx —

IRWI03_082-132-hr

128

9/30/04

8:55 AM

ГЛАВА 3

Страница 128

NODALANDLOOPANA LOOPANA LYS

в сети. P3.60, мы хотим определить мощность, рассеиваемую на резисторе R3.

3.61 В схеме на рис. P3.61 используйте метод исключения Гаусса для определения Vo. (a) Будет ли сеточный или узловой анализ наиболее эффективным

(a) Является ли сеточный или узловой анализ наиболее эффективным подходом

? Почему?

подход? Почему? (b) Для узлового анализа прокомментируйте преимущества

(b) Если используется анализ сетки, требуются ли какие-либо суперсетки

? Напишите уравнения сетки. Если используется узловой анализ, требуются ли какие-либо надузлы? Если да, то сколько? Как лучше всего разместить опорный узел и почему? Напишите уравнения узла.

выбор узла 1 в качестве опорного узла. Повторите эти действия для узлов 2, 3 и 4. (c) Основываясь на ваших результатах в (b), напишите уравнения узлов. 1

R1

R2

R1

V — S1 +

R3

4

+

R2

VS1

2

VS1

R5

R4

R4

R3

-V + S2

+

R4

3

R5

Vo —

Рисунок P3.60 Рисунок P3.61

РАЗДЕЛ 3.2 3.62 Используйте уравнения сетки, чтобы найти Vo в цепи на рис. P3.62. 2 k

3.64 Используйте анализ сетки, чтобы найти Vo в цепи на рис. P3.64. 4 к

4 к

4 к +

+ 6V

± —

2 к

6 к

Vo

2 к

—

2 к

2 к

Рисунок P3.62

Vo

12 В —

3.63 Найдите Vo в сети на рис.P3.63 с использованием уравнений сетки. P S V 4V

Рисунок P3.64

3.65 Используйте анализ сетки, чтобы найти Vo в цепи на рисунке P3.65.

12 В

± —

+

4 к

+ 4 к

4 к

4 к

10 к +

Vo

6 к

8 к

2 к Vo

Рисунок P3.63

+

6V —

Рисунок P3.65

IRWI03_082-132-hr

9/30/04

8:55 AM

Страница 129

PROBLEMS

PROBLEMS .66 Используйте анализ сетки, чтобы найти Vo в сети на рис. P3.66. C S

3 k

± —

12 В

3.70 Используйте как узловой анализ, так и анализ сетки, чтобы найти Io в схеме на рис. P3.70. 6 мА

+

2 k 6 k

2 мА

129

Vo 12 В

4 k

Рисунок P3.66

— ±

3.67 Используйте анализ контура, чтобы найти Vo в цепи в Рис. P3.67.

2 мА

2 к

4 к

Io 4 к 6 В

+

2 к

± —

2 мА

4 к

Рисунок P3.70

Vo

3.71 Найдите Io в сети на рис. P3.71, используя анализ петель. Затем решите проблему с помощью MATLAB и сравните свои ответы. C S

Рисунок P3.67

6 k

3.68 Используйте анализ петель, чтобы найти Vo в сети, показанной на рисунке P3.68. PSV

6 к

— ± 2 к 1 к

2 к

12 В

2 мА

1 к

6 к

+ 6 В

Vo

+

5 мА

k

Io

Рисунок P3.71

Рисунок P3.68

3.69 Найдите Io в сети на рисунке P3.69, используя анализ сетки.

3.72 Найдите Vo в сети на рис. P3.72, используя как сеточный, так и узловой анализ. PSV

CS

+

Io 2 мА

4 к

2 к 2 к

2 к 2 мА

6 к

± —

12 В

4 к

4 мА 12 В

+ —

Vo

2 k —

Рисунок P3.69 Рисунок P3.72

IRWI03_082-132-hr

130

9/30/04

8:55 AM

ГЛАВА

Page 130

NODALANDLOOPANA LY SISTECHNIQUES

3.73 Используйте анализ петель, чтобы найти Io в сети, показанной на рис. P3.73. CS

3.82 Напишите сеточные уравнения для схемы на рис. P3.82, используя заданные токи.

1 к

12 В

2A

+ —

1 к

2 мА

I3 4

1 к

1 к

5

Io 12 В 1 к

— Vx +

4 мА

1 k

0,5Vx

+ —

I1

2

I2

+ —

I4

20 V

Рисунок P3.82 Рисунок P3.73

3.74 Найдите Io в цепи на рисунке P3.74.

3.83 Используйте анализ сетки, чтобы найти Vo в цепи на рис. P3.83.

CS

PSV

Io 6V

+ —

4 k

2 k 2 mA

+

4 k 6V

2 k

VA-

± —

+

4 ВА 6 к

Vo

12 к

6 к

1 мА

2 к

Рисунок P3.83

3.84 Найдите Vo в цепи на рис. P3.84 с помощью анализа сетки. Рисунок P3.74

CS

3.75 Решите задачу 3.33, используя анализ петель.

2 k

3.76 Решите задачу 3.34, используя анализ петель. 2000 Ix

3.78 Решите задачу 3.37, используя анализ петель.

± —

4 k

3.80 Решите задачу 3.43, используя анализ петель.

Ix

4 k

6V

+ —

Рисунок P3.81

I5

2 k

2 k

1 k

I3

I4

Vo

—

Vo

1 k Рисунок P3.85

1 k

+ 12 V

+ 12 V —

2 Ix 2 k

—

3.85 Используйте анализ петель, чтобы найти Vo в сети на рис. P3.85.

2 k

I2

Vo

Рисунок P3.84

3.81 Используйте MATLAB, чтобы найти токи ячейки в сети, показанной на рисунке P3.81. C S

I1

2 k

Ix

3.79 Решите задачу 3.40, используя анализ петель.

2 мА

+

6 В

3.77 Решите задачу 3.35, используя анализ петель.

1 k

+ —

IRWI03_082-132-hr

9/30/04

8:55 AM

Page 131

ПРОБЛЕМЫ

3.86 Используйте анализ контура, чтобы найти Vo в цепи на рис. P3.86. 2 k

3.90 Решите задачу 3.54, используя анализ петель. 3.91. Решите задачу 3.55, используя анализ петель.

2 k +

± —

12 В

3.92 Решите задачу 3.56, используя анализ контура. 3.93 Решите задачу 3.57 с использованием анализа петель.

2 Vo — 1000

1 k

Vo

3.94 Решите задачу 3.58, используя анализ петель.

—

3.95 Решите задачу 3.59, используя анализ петель. 3.96. Используйте анализ сетки, чтобы определить мощность, выдаваемую независимым источником 3 В в сети, показанной на рис. P3.96.

Рисунок P3.86

3.87 Используйте как узловой анализ, так и анализ сетки, чтобы найти Vo в цепи на рис. P3.87. 6 Вx

100200

40 мА

6 Вx

± —

± —

300 6 мА

3 В

8 к +

100

+

—

3.97 Используйте анализ сетки, чтобы найти мощность, выдаваемую источником напряжения с регулируемым током в цепи, показанной на рис. P3.97.

—

+ 6

2 k

4 k

Vx

Vx — 8

4 k

—

Рисунок P3.97

Рисунок P3.88

3.89 Найти Vo в сети на рис. P3.89.

Vx

—

PSV

+ +

1 к 12 мА

1 к

1 к

Vo —

1 к

1 к 1 к

4 мА

6

15 Ix

+ —

Vo

+

Рисунок P3.89

Vx +

4 k

+

Vx

Рисунок P3.96

—

3.88 Используя анализ сетки, найдите Vo в цепи на рисунке P3.88.

6 мА

600

—

Рисунок P3.87

Vx — 4000

± —

Vo

12 k

4 k

Vx — 1000

131

1

IRWI03_082-132-hr

132

9/30/04

8:55 AM

ГЛАВА 3

Page 132

NODALANDLOOPANA LY SISTECHNIQUES

PRO НАЙТИ НАЙТИ НАЙТИ
PRO

FE Vo в схеме на рис.