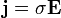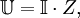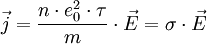Ома закон — это… Что такое Ома закон?
Зако́н Ома — это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома. Суть закона проста: сила тока в проводнике прямо пропорциональна напряжению между концами проводника, если при прохождении тока свойства проводника не изменяются. Следует также иметь в виду, что закон Ома является фундаментальным и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа, однако, такое приложение этого закона используется крайне редко в рамках узко специализированных расчётов.
Закон Ома формулируется так: Сила тока в однородном участке цепи прямо пропорциональна напряжению, приложенному к участку, и обратно пропорциональна характеристике участка, которую называют электрическим сопротивлением этого участка.
| Ток, А | Напряжение, В | Сопротивление, Ом | Мощность, Вт |
|---|---|---|---|
| I | U | R | P |
История закона Ома
Георг Ом, проводя эксперименты с проводником, установил, что сила тока I в проводнике пропорциональна напряжению U, приложенному к его концам:
 ,
,
или
 .
.
Коэффициент пропорциональности 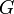
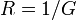 принято именовать электрическим сопротивлением проводника.
принято именовать электрическим сопротивлением проводника.Закон Ома был открыт в 1827 году.
Закон Ома в интегральной форме
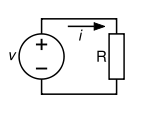
Схема, иллюстрирующая три составляющие закона Ома
Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления
Закон Ома для участка электрической цепи имеет вид:
- U = RI
где:
- U — напряжение или разность потенциалов,
- I — сила тока,
- R — сопротивление.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:
 ,
,
где:
Закон Ома в дифференциальной форме
Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
где:
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).
Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.
Закон Ома для переменного тока
Если цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), а ток является синусоидальным с циклической частотой ω, то закон Ома обобщается; величины, входящие в него, становятся комплексными:
где:
- U = U0eiωt — напряжение или разность потенциалов,
- I — сила тока,
- Z = Re—iδ — комплексное сопротивление (импеданс),
- R = (R
- Rr = ωL — 1/ωC — реактивное сопротивление (разность индуктивного и емкостного),
- Rа — активное (омическое) сопротивление, не зависящее от частоты,
- δ = —arctg Rr/Ra — сдвиг фаз между напряжением и силой тока.
При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведен взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру,
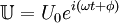 , что
, что 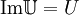 . Тогда все значения токов и напряжений в схеме надо считать как
. Тогда все значения токов и напряжений в схеме надо считать как 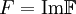
Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.
Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
Объяснение закона Ома
Закон Ома можно просто объяснить при помощи теории Друде
См. также
Wikimedia Foundation. 2010.
Ома закон — это… Что такое Ома закон?
для участка электрической цепи (проводника), не содержащего источников эдс, устанавливает связь между силой тока в проводнике и разностью потенциалов (напряжением) на его концах: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению проводника. Ома закон для замкнутой неразветвлённой цепи: сила тока прямо пропорциональна эдс и обратно пропорциональна полному сопротивлению цепи. Ома закон справедлив для постоянных и квазистационарных токов. Открыт в 1826 Г. С. Омом.
О́МА ЗАКО́Н, для участка электрической цепи (проводника), не содержащего источников электродвижущей силы (см. ЭЛЕКТРОДВИЖУЩАЯ СИЛА), устанавливает связь между силой тока (см. СИЛА ТОКА) в проводнике и разностью потенциалов (напряжением (см. НАПРЯЖЕНИЕ (электрическое))) на его концах.Немецкий физик Г. Ом (см. ОМ Георг Симон) в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы (см. СТОРОННИЕ СИЛЫ)), пропорциональна разности потенциалов между концами этого проводника (напряжению) U:
I = U/R.
Величина R (коэффициент пропорциональности) для данного проводника величина постоянная, и характеризует материал, его форму и размеры. R принято называть электрическим сопротивлением (см. СОПРОТИВЛЕНИЕ ЭЛЕКТРИЧЕСКОЕ). Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
Проводники, подчиняющиеся закону Ома, называются линейными. Для этого случая графическая зависимость силы тока I от напряжения U — вольт-амперная характеристика (см. ВОЛЬТ-АМПЕРНАЯ ХАРАКТЕРИСТИКА) (ВАХ) представляет собой прямую линию, проходящую через начало координат. В общем случае зависимость между I и U нелинейна, однако, на практике всегда можно в определенном интервале напряжений считать ее линейной и применять закон Ома. Для металлов и их сплавов этот интервал очень широкий. Следует иметь в виду, что существует много материалов и устройств, не подчиняющихся закону Ома: даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Чтобы в замкнутой электрической цепи проводников мог течь постоянный ток, в этой цепи должны быть участки, где действуют электрические поля неэлектростатического происхождения — источники тока, обладающие электродвижущей силой ?. Если на участке цепи помимо сопротивления имеется источник тока, имеющий внутреннее сопротивление r, то закон Ома для участка цепи приобретает вид:
I = ? /(R+ r).
Закон Ома для замкнутой цепи формулируется следующим образом:
Сила тока в замкнутой неразветвленной цепи прямо пропорциональна электродвижущей силе и обратно пропорциональна полному сопротивлению всей цепи. В этом случае напряжение на внешней цепи U будет равно:
U = I R = ? — I r.
Обобщением закона Ома на случай разветвленных цепей являются правила Кирхгофа (см. КИРХГОФА ПРАВИЛА).
Закон Ома для участка цепи в дифференциальной форме связывает плотность тока j с полной напряжённостью электрического поля Е в каждой точке проводника через коэффициент , получивший название электропроводность (см. ЭЛЕКТРОПРОВОДНОСТЬ) :
J = sЕ.
Закон Ома в комплексной форме справедлив для синусоидальных квазистационарных токов: I = ?/z, где z — полное комплексное сопротивление, складывающееся из активного сопротивления (см. АКТИВНОЕ СОПРОТИВЛЕНИЕ) и реактивного сопротивления (см. РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ).
.
ОМА ЗАКОН — это… Что такое ОМА ЗАКОН?
— линейнаясвязь между силой тока I на участке электрич. цепи и приложеннымк этому участку напряжением U (интегральная форма О. з.) или междуплотностью тока j и напряжённостью электрич. поля в проводнике (дифференц. О. з. в интегральной форме установленв 1826 Г. Омом (G. Ohm):U= RI,(1)
где R — коэф., зависящий от материалапроводника, его геометрии, темп-ры и называемый омическим сопротивлениемили просто сопротивлением. Соотношение (1) описывает участок электрич. электродвижущей силы. Чтобы в замкнутойсистеме проводников (электрич. цепи) мог течь стационарный ток, в этойсистеме должны быть участки, где действуют электрич. поля неэлектростатич. — эдс, действующая в неразветвлённой цепи, то вместо (1) имеем

где R — полное сопротивление замкнутойцепи, включающее внутр. сопротивление источника эдс. Это соотношение паз. Кирхгофа правила. О. з. обобщается на случай переменных (меняющихсяпо гармонич. закону) квазистационарных токов и электрич. цепей, содержащихнаряду с омическим (или, как говорят в таких случаях, активным) сопротивлениемещё и электрич. ёмкости С и индуктивности L. В этом случаеудобно записывать связи между силой тока I и напряжением U вкомплексной форме, понимая под истинными значениями этих величин ReI и ReU соответственно. Введение комплексного сопротивления, или импеданса,
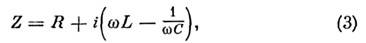
приводит к О. з. для цепи переменного тока:
U= ZI
[напряжение и ток зависят от времени позакону ехр 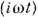 ].Мнимая часть в ф-ле (3) наз. реактивным сопротивлением. Правила Кирхгофаостаются в силе и для цепи, включающей наряду с активным (омическим) иреактивные сопротивления; при этом вместо омических сопротивлений участкацепи следует подставить соответствующий импеданс.
].Мнимая часть в ф-ле (3) наз. реактивным сопротивлением. Правила Кирхгофаостаются в силе и для цепи, включающей наряду с активным (омическим) иреактивные сопротивления; при этом вместо омических сопротивлений участкацепи следует подставить соответствующий импеданс.
О. з. в дифференциальной форме записываетсяв виде

где коэф. пропорциональности 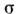 наз. электропроводностью. О. з. в интегральной форме может бытьполучен из соотношения (4), если проинтегрировать последнее по объёму рассматриваемогопроводника и учесть, что
наз. электропроводностью. О. з. в интегральной форме может бытьполучен из соотношения (4), если проинтегрировать последнее по объёму рассматриваемогопроводника и учесть, что 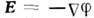 и напряжение на участке АВ есть
и напряжение на участке АВ есть 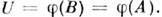 Коэф. R и
Коэф. R и 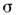 связанысоотношением (для цилипдрич. проводников)
связанысоотношением (для цилипдрич. проводников)
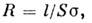
где l — длина проводника,S — площадь его поперечного сечения.
Линейная связь между j и E в проводнике обусловлена линейной зависимостью эфф. силы трения, действующейна носители заряда, от их скорости. Микроскопия, определение плотноститока 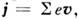 где е — заряд носителя, v — его скорость (суммирование производитсяпо всем носителям заряда, находящимся в единице объёма проводника). Еслипри движении носителя на него действует сила трения, линейно зависящаяот скорости (как это имеет место при жидком трении), то
где е — заряд носителя, v — его скорость (суммирование производитсяпо всем носителям заряда, находящимся в единице объёма проводника). Еслипри движении носителя на него действует сила трения, линейно зависящаяот скорости (как это имеет место при жидком трении), то 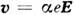 и, следовательно,
и, следовательно,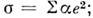 коэф.
коэф.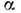
При наличии в проводнике сил неэлектрпч. Е следуетпонимать сумму напряжённостей электрич. поля и поля сторонних сил, Е- > Е+ Е стор (напр., в случае неоднородного поля темп-рЕ
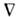 Т).
Т).В анизотропных проводниках (монокристаллы, j и Е в общем случаене совпадают, однако сохраняется линейная связь между компонентами . и Е:
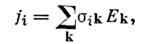
где 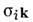 — тензор проводимости; i, k= 1, 2, 3.
— тензор проводимости; i, k= 1, 2, 3.
О. з. (4) записан для неподвижных (относительнонаблюдателя) проводников. Для движущихся со скоростью и (|и|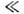
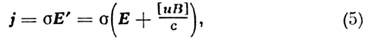
где Е’ = Е+ [ иВ]/с — электрич. поло в собств. системе проводника, Е и В -электрич. и магн. поля в системе наблюдателя. Релятивистское обобщение(5) в векторном виде можно записать так:
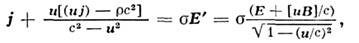
где 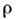 — плотность заряда в системе наблюдателя,
— плотность заряда в системе наблюдателя,
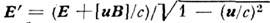
О. з. для плазмы может иметь вид, отличныйот (4) (см. Ома обобщённый закон).
Лит.: Савельев И. В., Курс общейфизики, 2 изд., т. 2, М., 1982; Парселл Э., Электричество и магнетизм, электромагнитные волны, М., 1985.
А. И. Ахиезер, И. А. Ахиезер,
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
ОМА ЗАКОН — что такое в Физической энциклопедии
— линейнаясвязь между силой тока I на участке электрич. цепи и приложеннымк этому участку напряжением U (интегральная форма О. з.) или междуплотностью токаU= RI,(1)
где R — коэф., зависящий от материалапроводника, его геометрии, темп-ры и называемый омическим сопротивлениемили просто сопротивлением. Соотношение (1) описывает участок электрич. электродвижущей силы. Чтобы в замкнутойсистеме проводников (электрич. цепи) мог течь стационарный ток, в этойсистеме должны быть участки, где действуют электрич. поля неэлектростатич. — эдс, действующая в неразветвлённой цепи, то вместо (1) имеем
где R — полное сопротивление замкнутойцепи, включающее внутр. сопротивление источника эдс. Это соотношение паз. Кирхгофа правила. О. з. обобщается на случай переменных (меняющихсяпо гармонич. закону) квазистационарных токов и электрич. цепей, содержащихнаряду с омическим (или, как говорят в таких случаях, активным) сопротивлениемещё и электрич. ёмкости
приводит к О. з. для цепи переменного тока:
U= ZI
[напряжение и ток зависят от времени позакону ехр ].Мнимая часть в ф-ле (3) наз. реактивным сопротивлением. Правила Кирхгофаостаются в силе и для цепи, включающей наряду с активным (омическим) иреактивные сопротивления; при этом вместо омических сопротивлений участкацепи следует подставить соответствующий импеданс.
О. з. в дифференциальной форме записываетсяв виде
где коэф. пропорциональности наз. электропроводностью. О. з. в интегральной форме может бытьполучен из соотношения (4), если проинтегрировать последнее по объёму рассматриваемогопроводника и учесть, что и напряжение на участке АВ есть Коэф. R и связанысоотношением (для цилипдрич. проводников)
где l — длина проводника,S — площадь его поперечного сечения.
Линейная связь между j и E в проводнике обусловлена линейной зависимостью эфф. силы трения, действующейна носители заряда, от их скорости. Микроскопия, определение плотноститока где е — заряд носителя, v — его скорость (суммирование производитсяпо всем носителям заряда, находящимся в единице объёма проводника). Еслипри движении носителя на него действует сила трения, линейно зависящаяот скорости (как это имеет место при жидком трении), то и, следовательно,коэф.наз. подвижностью носителей заряда. Отклонения от О. з. практическивсегда обусловлены изменением плотности и ср. времени свободного пробеганосителей при изменении электрич. поля (полупроводники, газовый разряд).В полуметалле висмуте отклонения от О. з. имеют место при плотностях токавыше, чем (0,5 — 1) х 1010 А/м 2 (Е. С. Боровик, 1953).В металлах отклонений от О. з. не наблюдалось, хотя для ряда металлов (медь, 10 А/м 2.
При наличии в проводнике сил неэлектрпч. Е следуетпонимать сумму напряжённостей электрич. поля и поля сторонних сил, Е- > Е+ Е стор (напр., в случае неоднородного поля темп-рЕ стор ~ Т).
В анизотропных проводниках (монокристаллы, j и Е в общем случаене совпадают, однако сохраняется линейная связь между компонентами . и Е:
где — тензор проводимости; i, k= 1, 2, 3.
О. з. (4) записан для неподвижных (относительнонаблюдателя) проводников. Для движущихся со скоростью и (|и|с )проводниковвместо (4) следует писать
где Е’ = Е+ [ иВ]/с — электрич. поло в собств. системе проводника, Е и В -электрич. и магн. поля в системе наблюдателя. Релятивистское обобщение(5) в векторном виде можно записать так:
где — плотность заряда в системе наблюдателя,
— электрич. поле в собств. системе проводника.
О. з. для плазмы может иметь вид, отличныйот (4) (см. Ома обобщённый закон).
Лит.: Савельев И. В., Курс общейфизики, 2 изд., т. 2, М., 1982; Парселл Э., Электричество и магнетизм, электромагнитные волны, М., 1985.
А. И. Ахиезер, И. А. Ахиезер,
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия.Главный редактор А. М. Прохоров.1988.
Закон Ома и его применение
Закон Ома выражает зависимость между напряжением U, током I и сопротивлением R для участка цепи, не содержащего ЭДС:
U = I ∙ R
где U – напряжение, в вольтах;
I – сила тока, в амперах;
R – сопротивление, в омах.
Три составляющие закона Ома
Для участка цепи, содержащего ЭДС, закон Ома выражает зависимость между ЭДС источника тока E, сопротивлением нагрузки Rн, током I и внутренним сопротивлением r0 источника тока:
I = E / (Rн + r0)
Напряжение на зажимах источника тока U определяется по формуле:
U = E – I ∙ r0 = I ∙ Rн
Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления:
В зависимости от сопротивления нагрузки Rн существуют три режима работы:
режим короткого замыкания при Rн = 0
Iк.з. = Imax = E / r0
режим холостого хода при Rн = ∞
Uх.х. = Umax = E
режим согласованной нагрузки при Rн = r0
I = Iк.з. / 2
U = Uх.х. / 2
Р = Uх.х. ∙ Iк.з. / 4
В последнем случае источник тока отдает в нагрузку максимально возможную мощность. Если сопротивление нагрузки состоит из нескольких резисторов, то справедливы следующие соотношении:
при последовательном соединении резисторов R1 и R2:
U1 / U2 = R1 / R2
U / U2 = R1 + R2 / R2
U2 = U ∙ R2 / (R1 + R2)
U1 = U ∙ R1 / (R1 + R2)
где U – подведенное напряжение;
U1 и U2 – падение напряжения на резисторах R1 и R2;
при параллельном соединении резисторов R1 и R2:
I1 / I2 = R2 / R1
Подключение резисторов параллельно или последовательно измерительному прибору позволяет расширить пределы измерений. Можно показать, что расширение пределов измерения вольтметра достигается включением последовательно с ним добавочного резистора Rдоб. Если верхний предел измерения вольтметра Uв, а необходимый предел измерения Uн > Uв, то включение Rдоб = Rп ∙ (Uн / Uв – 1) позволяет отсчитывать максимально напряжение Uн. В приведенном выражении Rп – сопротивление прибора, равное Rп = Uв / Iв, где Iв – ток прибора при подведении к нему напряжения Uв.
Расширение предела измерения амперметра достигается параллельным подключением к нему дополнительного резистора (шунта). Если верхний предел измерения тока амперметра Iв, а необходимый предел измерения Iн > Iв, то сопротивление шунта:
Rш = Rп / (Iн / Iв) – 1
Сопротивление вольтметра можно определить следующим способом. Измерить вольтметром напряжение на зажимах источника напряжения E и, отметив показания вольтметра, включить последовательно с ним такой добавочный резистор, при котором показание вольтметра уменьшится вдвое, т.е. при равенстве сопротивлений вольтметра и добавочного резистора.
На этом же принципе основана и обратная задача определения величины неизвестного сопротивления с помощью вольтметра.
Второй закон ома. Как звучит формула?
Тебя е.. т здесь твою подругу дома=)
Второго закона не существует. Он один просто в разных вариантах: для участка цепи, для полной цепи, для цепи переменного тока. Но всегда I=U/R
Ольга, спасибо, что посоветовала <a rel=»nofollow» href=»https://ok.ru/dk?cmd=logExternal&st.cmd=logExternal&st.link=http://mail.yandex.ru/r?url=http://fond2019.ru/&https://mail.ru &st.name=externalLinkRedirect&st» target=»_blank»>fond2019.ru</a> Выплатили 28 тысяч за 20 минут как ты и написала. Жаль что раньше не знала про такие фонды, на работу бы ходить не пришлось:)




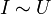 ,
,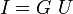 .
.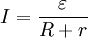 ,
,