1.6. Холостой ход и короткое замыкание тока.

Рис. 1.8. Режим холостого хода
В режиме холостого хода внешняя цепь разомкнута (рис. 1.8.) При этом ее сопротивление равно бесконечности, а величина тока в цепи равна нулю. Следовательно, напряжение на зажимах генератора: Uxx= E.
Короткое замыкание возникает обычно в результате повреждения изоляции соединительных проводов. При этом зажимы генератора оказываются замкнуты проводником с ничтожно малым сопротивлением (рис. 1.9).
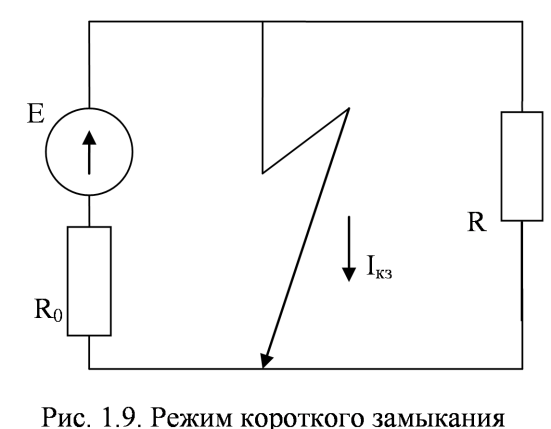
Рис. 1.9 Режим короткого замыкания.
Практически
напряжение на зажимах генератора в
режиме короткого замыкания равно нулю,
и сопротивление цепи равно внутреннему
сопротивлению генератора R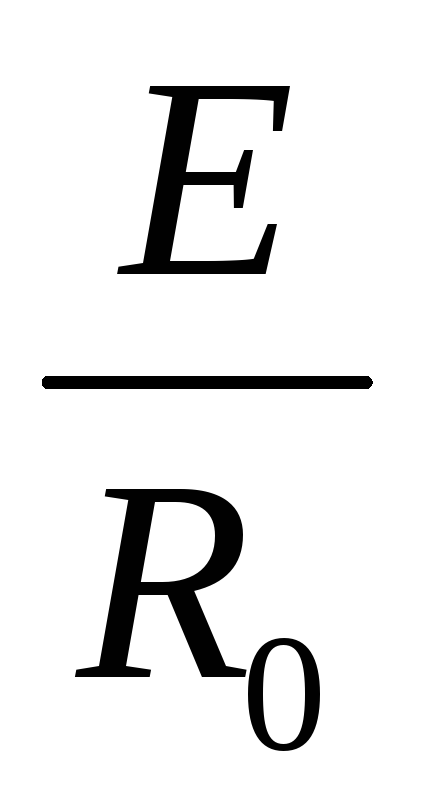 оказывается очень большой.
оказывается очень большой.
Короткое замыкание является аварийным режимом работы и представляет собой большую опасность для электрических установок, т.к. может повлечь за собой их разрушение, вследствие перегрева, вызванного большими токами.
1.7. Расчет сложных электрических цепей постоянного тока.
Приведем основные понятия сложной цепи. Несколько последовательно соединенных элементов цепи, по которым проходит один и тот же ток, образуют ветвь. В общем случае ветвь может содержать как сопротивления, так и ЭДС.
Точка соединения трех и более ветвей называют узловой точкой или узлом.
Несколько ветвей, образующих замкнутую электрическую цепь называют контуром.
1.7.1. Метод непосредственного применения законов Кирхгофа
Универсальным методом расчета токов в сложных цепях постоянного тока с несколькими источниками электрической энергии, является метод непосредственного применения I и II законов Кирхгофа.
К узловым точкам схемы применяется I закон Кирхгофа, согласно которому сумма токов, притекающих к узлу равна сумме токов уходящих от него, т.е. алгебраическая сумма токов в узле равна нулю. ∑I =0
К контурам применяется II закон Кирхгофа, согласно которому алгебраическая сумма ЭДС, действующих в контуре, равна сумме падений напряжений на всех сопротивлениях контура.
∑E = ∑IR
По первому и второму законам Кирхгофа составляют столько уравнений, сколько неизвестных токов в цепи. По первому закону Кирхгофа составляют n-1 уравнений, где n – число узлов в цепи. Недостающие уравнения составляют по второму закону Кирхгофа.
Рассмотрим применение метода на примере сложной электрической цепи, схема которой представлена на рис. 1.10

Рис. 1.10. Сложная электрическая цепь постоянного тока.
Расчет токов, протекающих в ветвях сложной цепи, проводят по следующим правилам:
По возможности упрощают схему, заменяя параллельно соединенные сопротивления одним эквивалентным. Для рассматриваемой схемы имеем
R567 = 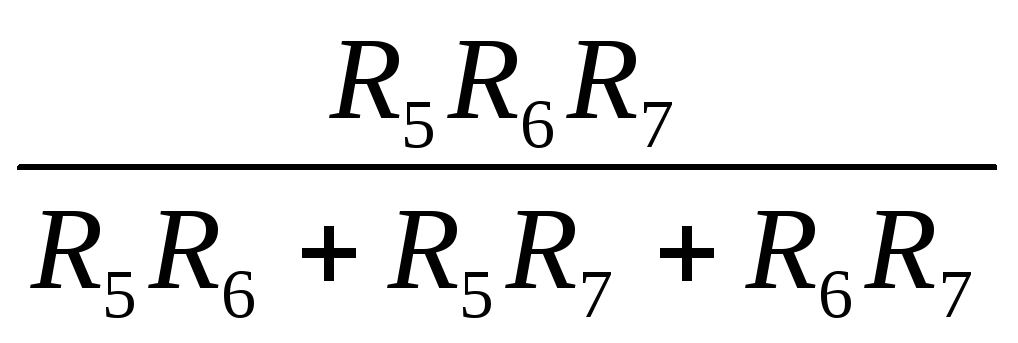
Определяют количество искомых токов в цепи и произвольно задают их направления. Количество искомых токов равно количеству ветвей в цепи. В рассматриваемой цепи после упрощения остается три ветви abcd, ad, afed, следовательно, требуется найти значения трех токов I
Определяют количество узлов в цепи и для всех узловых точек, кроме одной составляют уравнения по первому закону Кирхгофа. В рассматриваемой цепи две узловые точки a и d. Поэтому, по первому закону Кирхгофа составляется одно уравнение для узловой точки a, в соответствии с заданными направлениями токов
I
Выбирают произвольное направление обхода контуров по или против часовой стрелки и по второму закону Кирхгофа составляют недостающие уравнения. Для рассматриваемой цепи необходимо составить еще два уравнения. Они составляются по второму закону Кирхгофа, для контуров adef и abcd в соответствии с выбранными направлениями их обхода. При этом ЭДС и токи, совпадающие с направлением обхода контура, принимают со знаком плюс, а ЭДС и токи, противоположные этому направлению, со знаком минус. В результате получаем
E
E2 = I2 (R567+R4) + I3R8 (1.13)
5. Определяют неизвестные токи в ветвях, решая полученную систему уравнений (1.11), (1.12), (1.13). Если какие-то значения при расчете получаются со знаком минус, то это означает, что направления реальных токов противоположны заданным в начале расчета.
Проверку решения
задачи осуществляют путем расчета
уравнения баланса мощностей: алгебраическая
сумма мощностей развиваемых всеми
источниками ЭДС равна сумме мощностей,
потребляемых всеми сопротивлениями
нагрузки. В общем виде уравнение баланса
мощностей записывается как ∑EI=∑I
Применительно к рассматриваемой цепи, уравнение баланса мощностей принимает вид:
E1I1+E2I2 = I (R1+R2+R3)
+ I
(R1+R2+R3)
+ I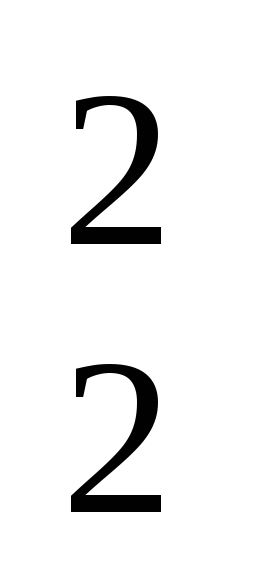
 R8 (1.14)
R8 (1.14)Если направление ЭДС совпадает с направлением тока в ветви, то их произведение включается в левую часть уравнения со знаком плюс, а если не
с



Метод х/х и к/з | ВолАмпер
Этот метод определения тока в какой нибудь ветви сложной разветвленной цепи заключается в том, что точки, к которым приключена в заданной системе исследуемая ветвь, рассматриваются как полюсы некоторого источника тока со сложным внутренним сопротивлением. Для обыкновенной цепи мы можем написать, что ток во внешней цепи равен напряжению между его полюсами U0, когда внешняя цепь разомкнута, деленному на сумму внутреннего (rk) и внешнего (r) сопротивлений: I=U0/rk+r





поэтому искомый ток в ветви будет

или

В случае, если мостик уравновешен, т. е. в r ток равен нулю (I=0), то r2r3 = r1r4 и мы имеем пропорциональность четырех сопротивлений: r1/r2=r3/r4 позволяющую определить одно сопротивление, например, r1, когда известны три остальных. Для случая равновесия моста (I=0) это соотношение может быть выведено более простым способом, так как в этом случае I1=I2 и I3=I4 и падения напряжений в r1 и r3, так же как и в r3 и r4, должны быть равны: I1r1 = I3r3 и I1r2=I3r4, откуда получается то же соотношение:
r1/r2=r3/r4

Метод короткого замыкания и холостого хода
 |
Более точные результаты можно получить при расположении образца на расстоянии, равном от закороченного конца. В этом случае образец находится в пучности электрического поля и, следовательно, более эффективно с ним взаимодействует. Четверть волновой отрезок со стороны образца имеет бесконечное сопротивление, в связи с этим метод носит название метода холостого хода.
Для такого положения уравнение (7) переписываем в виде:
 (11)
(11)
Сочетание метода короткого замыкания и холостого хода дает еще одну возможность избежать решения трансцендентного уравнения. Перемножая (7) и (11), можно исключить гиперболическую функцию:
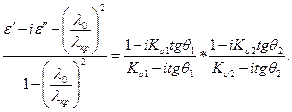 (12)
(12)
Практически это можно осуществить путем использования подвижного поршня, который в первом положении устанавливается вплотную к образцу, а во втором отодвинут от него на расстоянии .
Метод «бесконечного» слоя
В методе используется слой диэлектрика, условно названный «бесконечным». Толщина «бесконечного» слоя выбирается из условия полного затухания прошедшей волны. Соотношения, связывающие электрические характеристики диэлектрика с измеряемыми величинами, выражаются через элементарные функции при самом общем рассмотрении данной задачи.
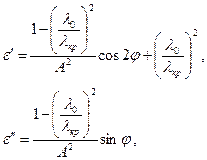 (13)
(13)
где  определяются из условия:
определяются из условия:
(14)
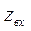 — входное сопротивление бесконечного образца, определяемое по измеренным значениям с помощью круговой диаграммы.
— входное сопротивление бесконечного образца, определяемое по измеренным значениям с помощью круговой диаграммы.
Метод волноводных мостов
 |
Этот метод основан на измерении фазового сдвига и затухания волны, проходящей через заполненный исследуемым материалом участок волновода.
В данной схеме энергия генератора делится на две равные части, одна из которых идет в верхнее плечо моста, содержащего образец толщиной d. В другом плече находится калибровочный аттенюатор и фазовращатель, служащие для установления нулевого баланса индикаторного прибора.
Процесс измерения состоит в установлении нулевого баланса сначала без образца, а затем с образцом. Измеряемые величины, которые являются разностью соответствующих показаний фазовращателя и аттенюатора, позволяют вычислить действительную и мнимую части диэлектрической проницаемости материала образца.
Экспериментальная часть
Описание установки
Генератор СВЧ возбуждает электромагнитные волны в волноводе, в качестве которого используется волновод измерительной линии.
 |
Чтобы измерительная линия, представляющая в режиме стоячей волны реактивную нагрузку, не влияла на работу генератора, она подключается через аттенюатор (отрезок волновода, в который погружается пластина, поглощающая СВЧ мощность). Измерение рекомендуется проводить в положении аттенюатора 10 дБ. Обычно генератор имеет собственный аттенюатор.
Исследуемый диэлектрик помещен в отрезок волновода. Положение максимума поля относительно диэлектрика регулируется короткозамыкателем.
Определение
Определение производится сочетанием методов холостого хода и короткого замыкания. При этом используется соотношение (12)
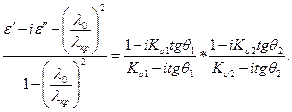
Для этого сначала берется пустой отрезок волновода, закорачивается пластиной. Затем измеряется длина волны в волноводе  и координата любого максимума поля стоячей волны. После этого на месте пустого отрезка волновода ставится отрезок с диэлектриком известной толщины. Измеряется смещение максимума
и координата любого максимума поля стоячей волны. После этого на месте пустого отрезка волновода ставится отрезок с диэлектриком известной толщины. Измеряется смещение максимума  и коэффициент бегущей волны:
и коэффициент бегущей волны:
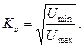
Смещение максимума и длины волны в волноводе позволяет определить:
Затем короткозамыкатель устанавливается на расстояние 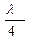 от образца, и измеряются те же параметры, что и в первом случае.
от образца, и измеряются те же параметры, что и в первом случае.
Таким образом, зная 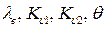 можно решить уравнение (12), что дает возможность определить
можно решить уравнение (12), что дает возможность определить 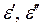 .
.
Контрольные вопросы
1. Запишите уравнения Максвелла для диэлектрика.
2. Что такое комплексная диэлектрическая проницаемость? Каков ее физический смысл.
3. Что такое ?
4. Каков критерий разделения сред на проводники и диэлектрики?
5. Охарактеризуйте методы измерения диэлектрической проницаемости?
6. В чем отличие метода полного заполнения сечения волновода от методов короткого замыкания и холостого хода?
7. Охарактеризуйте достоинства метода волноводных мостов.
8. В каких случаях удобен метод «бесконечного слоя».
9. Опишите установку и используемую методику определения диэлектрической проницаемости.
Литература:
1. Григорьев А.Д. Электродинамика и техника СВЧ. – М.В.Ш.,1990.
2. Брандт А.А. Исследование диэлектриков на сверхвысоких частотах. М. Физматгиз, 1963.
3. Описание измерительной линии.
4.4. Параметры холостого хода и короткого замыкания четырехполюсника
Входное
сопротивление четырехполюсника. Если
к одной паре зажимов четырехполюсника,
например 2
— 2′, подключить
произвольное сопротивление ZH (рис.
12.14, а), то
со стороны другой пары зажимов, т. е. 1
— 1′, четырехполюсник
можно рассматривать как двухполюсник
с входным сопротивлением ZBX1,
которое называют входным сопротивлением
четырехполюсника. Следовательно,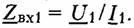
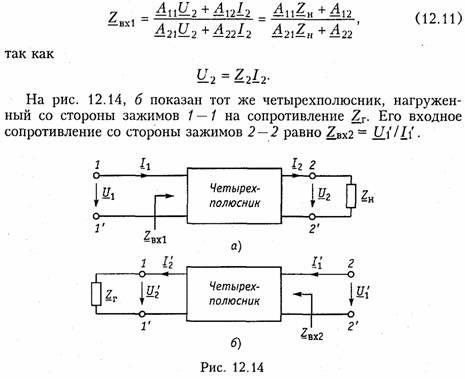
Входное сопротивление можно выразить через параметры четырехполюсника. Проще всего это сделать, воспользовавшись выражениями для U1, и I1 из уравнений передачи в А-параметрах (12.4). В этом случае
В связи с тем, что изменилось направление передачи энергии, следует воспользоваться уравнениями передачи (12.6). Тогда
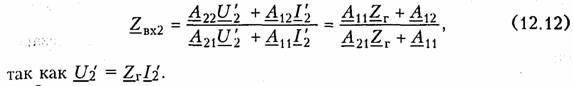
Заметим, что при изменении направления передачи энергии через четырехполюсник в выражениях (12.11) и (12.12) параметры A11, и A22 поменялись местами (см. свойство 4, § 12.2).
Входное сопротивление четырехполюсника не является его внутренним параметром, так как оно зависит не только от свойств четырехполюсника, но и от свойств внешней цепи (нагрузки), на которую замкнута пара зажимов четырехполюсника.
Параметры холостого хода и короткого замыкания. Формулы (12.11) и (12.12) описывают входные сопротивления четырехполюсника при произвольных сопротивлениях нагрузки ZHи Zr. Из них легко получить значения ZBX1 и ZBX2 при разомкнутых и замкнутых накоротко зажимах четырехполюсника.
В режиме холостого хода на зажимах 2—2′ (выходные зажимы разомкнуты) входное сопротивление четырехполюсника со стороны зажимов 1 — 1′ обозначается Zxx1 и определяется из формулы (12.11) при ZH = ∞:

Величины 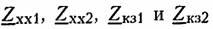 называются параметрами
холостого хода и короткого
замыкания. Значения
этих параметров для любой данной частоты
могут быть измерены с помощью специального
прибора для измерения комплексных
сопротивлений — моста переменного
тока. Это особенно удобно, когда
четырехполюсник представляется в
виде «черного ящика» и нет возможности
узнать его содержимое или рассчитать
какие-либо другие системы параметров,
либо когда влияние паразитных элементов
четырехполюсника трудно учесть
аналитически. Измерение же других систем
параметров часто представляет значительную
сложность.
называются параметрами
холостого хода и короткого
замыкания. Значения
этих параметров для любой данной частоты
могут быть измерены с помощью специального
прибора для измерения комплексных
сопротивлений — моста переменного
тока. Это особенно удобно, когда
четырехполюсник представляется в
виде «черного ящика» и нет возможности
узнать его содержимое или рассчитать
какие-либо другие системы параметров,
либо когда влияние паразитных элементов
четырехполюсника трудно учесть
аналитически. Измерение же других систем
параметров часто представляет значительную
сложность.
Из
приведенных выше соотношений для
параметров XX и
КЗ легко получить, что  т.е.
только три параметра из четырех являются
независимыми. Этих параметров достаточно
для составления уравнений передачи
пассивного четырехполюсника, причем
из параметров XX и
КЗ может быть получена любая система
параметров-коэффициентов.
т.е.
только три параметра из четырех являются
независимыми. Этих параметров достаточно
для составления уравнений передачи
пассивного четырехполюсника, причем
из параметров XX и
КЗ может быть получена любая система
параметров-коэффициентов.
У активного четырехполюсника все четыре параметра независимы, поэтому их нельзя найти по параметрам XX и КЗ.
В
случае симметричного пассивного
четырехполюсника параметры  симметричный
четырехполюсник характеризуется только
двумя параметрами XX и
КЗ.
симметричный
четырехполюсник характеризуется только
двумя параметрами XX и
КЗ.
4.5. Характеристические параметры четырехполюсника
Согласованное
включение четырехполюсника. При
передаче сигналов на расстояние может
участвовать большое число каскадно
соединенных четырехполюсников. На
практике используется такое включение
четырехполюсников, которое получило
название согласованного. Если
рассматривать четырехполюсник,
включенный по схеме рис. 12.1, то это
означает, что должны выполняться два
условия: 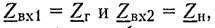 т.
е. входное сопротивление четырехполюсника
должно быть согласовано с сопротивлением
генератора, а выходное — с сопротивлением
нагрузки.
т.
е. входное сопротивление четырехполюсника
должно быть согласовано с сопротивлением
генератора, а выходное — с сопротивлением
нагрузки.
В случае каскадного включения нескольких четырехполюсников обеспечивают согласованное включение каждого из них.
Режим согласованного включения является наиболее благоприятным при передаче сигналов, поскольку при этом отсутствуют отражения электрической энергии (а значит, ее рассеяние) на стыках «генератор —четырехполюсник» и «четырехполюсник —нагрузка» и искажение сигнала.
Характеристические сопротивления четырехполюсника. Остается не ясным, всегда ли можно включить четырехполюсник согласованно, т. е. всегда ли можно подобрать такие сопротивления Zr и ZH, при которых
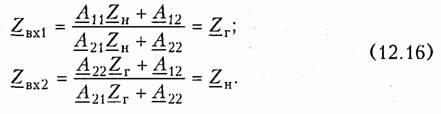
Оказывается, для любого четырехполюсника всегда существует такая пара сопротивлений, для которой выполняется условие (12.16). Эти сопротивления называютсяхарактеристическими (собственными) сопротивлениями четырехполюсника и обозначаются Zc1 и Zс2. Индекс «1» указывает на то, что характеристическое сопротивление определяется со стороны зажимов 1 — 1′, а индекс «2» — со стороны зажимов 2—2′.

Таким
образом, если в качестве внутреннего
сопротивления генератора
выбрать 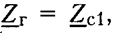 качестве
сопротивления нагрузки
качестве
сопротивления нагрузки 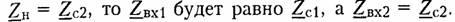 Рисунок
12.15 иллюстрирует это свойство
характеристических сопротивлений.
Рисунок
12.15 иллюстрирует это свойство
характеристических сопротивлений.
Можно теперь уточнить определение режима согласованного включения. Режимом согласованного включения четырехполюсника называется такой режим его работы, когда внутреннее сопротивление генератора выбрано равным характеристическому сопротивлению четырехполюсника Zc1, а сопротивление нагрузки равным характеристическому сопротивлению ZC2.

Совместное решение этих уравнений относительно величин Zс1, и Zс2 дает выражение характеристических сопротивлений через А-параметры:
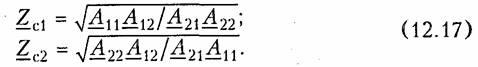
Характеристическое сопротивление можно выразить через параметры XX и КЗ. Проще всего это получить из (12.17), если воспользоваться формулами (12.13) — (12.15), где параметры XXи КЗ выражены через А-параметры:

Последние формулы удобны для экспериментального определения характеристических сопротивлений методами XX и КЗ.
Пример. Дан резистивный Г- образный четырехполюсник (см. рис. 12.2, б) с элементами Z1 = 1600 Ом, Z2 =900 Ом. Включим его согласованно с генератором и нагрузкой. Для согласования четырехполюсника с генератором нужно выбрать его внутреннее сопротивление равным характеристическому сопротивлению
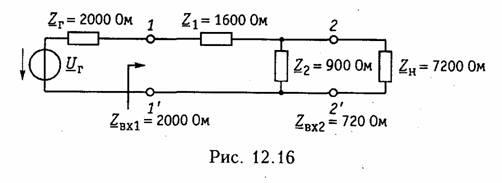
четырехполюсника со стороны зажимов 1 —1′, т. е. Zr = Zc1. Чтобы согласовать четырехполюсник с нагрузкой, следует подключить к его зажимам 2—2′ сопротивление нагрузки ZH = ZC2.
Матрица А четырехполюсника имеет вид

Характеристическая постоянная передачи четырехполюсника.
При согласованном включении на стыках «генератор —четырехполюсник» и «четырехполюсник —нагрузка» рассеяние электрической энергии будет происходить только в четырехполюснике (например, она будет превращаться в тепловую энергию на резистивных элементах схемы).
Чтобы учесть эти потери, вводят меру передачи энергии — характеристическую (собственную) постоянную передачи четырехполюсника, определяемую через отношение произведения напряжения и тока на входе четырехполюсника к произведению напряжения и тока на его выходе, взятое-в логарифмическом масштабе


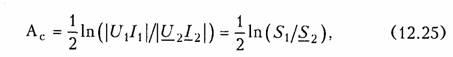
где S1 и S2 — полные мощности на входе и выходе четырехполюсника при согласованном его включении, называется характеристическим (собственным) ослаблением четырехполюсника. Она показывает в логарифмическом масштабе, на сколько уменьшилась мощность на выходе четырехполюсника по сравнению с мощностью на его входе при передаче энергии через четырехполюсник в режиме согласованного включения.
Для симметричного четырехполюсника из (12.21) получаем
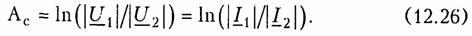

Бел достаточно крупная единица измерения. Вместо нее обычно применяют в 10 раз меньшую единицу — децибел (сокращенно дБ). Поскольку 1 Б = 10 дБ, то
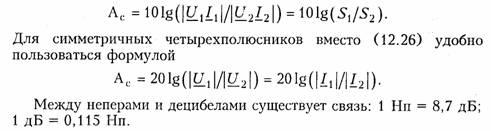
Пример. Несимметричный и симметричный четырехполюсники включены согласованно. Мощность на выходе первого из них уменьшается по сравнению с мощностью на входе в 1000 раз, на выходе второго по сравнению с его входом — в 10 000 раз. Определим характеристические (собственные) ослабления четырехполюсников.
Характеристическое ослабление по мощности для несимметричного четырехполюсника согласно формуле (12.25) составляет Ас = 10 lg 1000 = 30 дБ, а для симметричного — Ас = 10 lg 10 000 = 40 дБ. Кроме того, для симметричного четырехполюсника можно указать характеристическое ослабление по напряжению и току. В соответствии с (12.25) оно равно 20 lg 10 000 = 80 дБ.
Второе слагаемое в формуле (12.24)
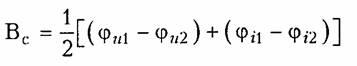
учитывает изменение начальных фаз напряжений и токов при передаче энергии через согласованно включенный четырехполюсник и носит название характеристической (собственной) фазыили фазовой постоянной четырехполюсника.
Преобразование (12.21) для симметричного четырехполюсника приводит к характеристической (собственной) фазовой постоянной, равной разности фаз входного и выходного напряжений или токов:
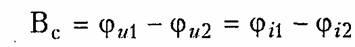
Измеряется фазовая постоянная в радианах (сокращенно рад) или градусах (сокращенно град).
Величины Zc1, Zc2 и Гс образуют систему характеристических {собственных) параметров четырехполюсника. Она полностью описывает пассивный четырехполюсник.
Связь с другими системами параметров. Вычисление характеристических параметров по А-параметрам осуществляется с помощью формул (12.17), (12.22), а по параметрам XX и КЗ — с помощью формул (12.18) и (12.23). Установим обратные соотношения, т. е. выразим А-параметры и параметры XX и КЗ через характеристическое.
Из (12.22) следует:


Заметим, что из этих формул легко выводится формула (12.23), приведенная ранее без вывода.
Расчет каскадного согласованного соединения четырехполюсников. При расчете каскадного соединения четырехполюсников ранее был использован матричный метод, в котором матрица А результирующего четырехполюсника определялась произведением матриц А составляющих четырехполюсников. Если четырехполюсники соединены согласованно, то удобнее пользоваться характеристическими параметрами.
На рис. 12.17 показано каскадное согласованное включение трех четырехполюсников с характеристическими постоянными передачи Гс1, ГС2 и ГсЗ.
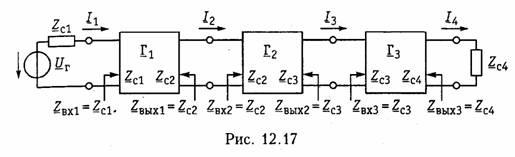
Согласование четырехполюсников состоит в том, что характеристические сопротивления со стороны их соединения выбраны равными друг другу, а внутреннее сопротивление генератора и сопротивление нагрузки — равными характеристическим сопротивлениям крайних четырехполюсников. Действительно, крайний справа четырехполюсник нагружен на сопротивление, равное его характеристическому Zс4, значит, входное сопротивление этого крайнего четырехполюсника будет равно характеристическому сопротивлению Zc3 предшествующего четырехполюсника. В свою очередь, входное сопротивление среднего четырехполюсника оказывается равным характеристическому сопротивлению Zc2 крайнего левого четырехполюсника. Следовательно, входное сопротивление крайнего слева четырехполюсника равно Zc1и согласовано с внутренним сопротивлением генератора.
Аналогичным образом можно провести рассуждения, начиная с левого четырехполюсника.
На рис. 12.17 во избежание путаницы входные сопротивления четырехполюсников со стороны зажимов 2—2′ названы выходными сопротивлениями четырехполюсников. Определим характеристическую постоянную передачи результирующего четырехполюсника. Согласно (12.20)
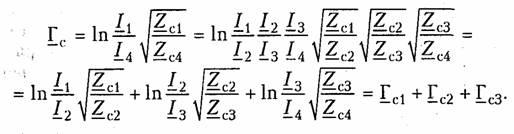
Таким образом, результирующий четырехполюсник, составленный из каскадно и согласованно соединенных отдельных четырехполюсников, имеет характеристические сопротивления, равные характеристическим сопротивлениям крайних четырехполюсников, и оказывается включенным согласованно с генератором и нагрузкой. Его характеристическая постоянная передачи равна сумме характеристических постоянных передачи соединяемых четырехполюсников. Учитывая, что Гс = Ас + jВс, можно записать:
Определение а–параметров с помощью режимов короткого замыкания и холостого хода
Режимам холостого хода (ХХ) и короткого замыкания (КЗ) при прямом и обратном питании четырехполюсника соответствуют схемы рис. 3.4 (а, б – режимы ХХ и КЗ при прямом питании; в, г – при обратном питании).
Прямое питание
Режим холостого хода.Принимая во внимание, что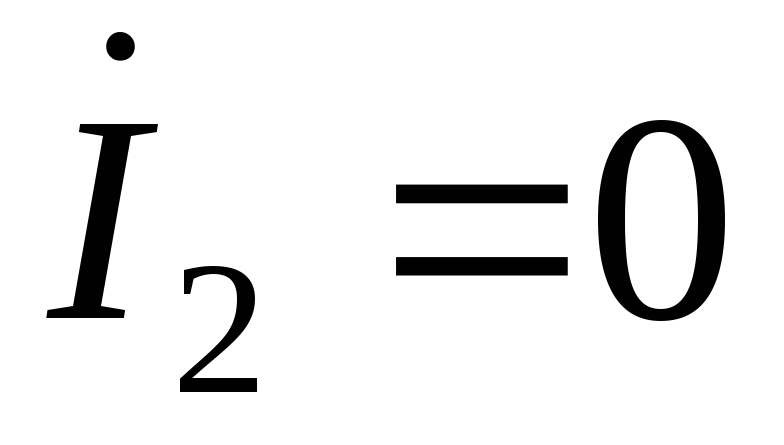 ,
,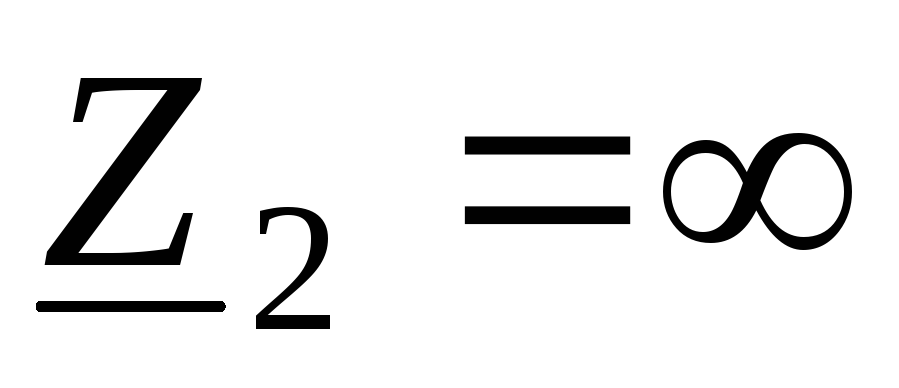 ,
формула (3.9) принимает вид
,
формула (3.9) принимает вид

Со стороны выводов 1–1в режиме холостого хода входное сопротивление четырехполюсника
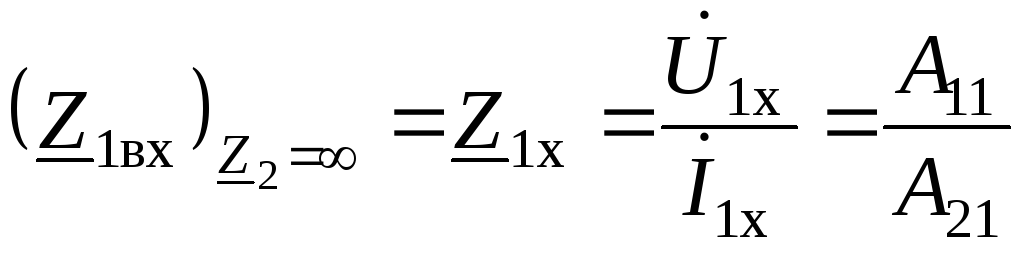 . (3.12)
. (3.12)
Режим короткого замыкания.
Учитывая, что в этом случае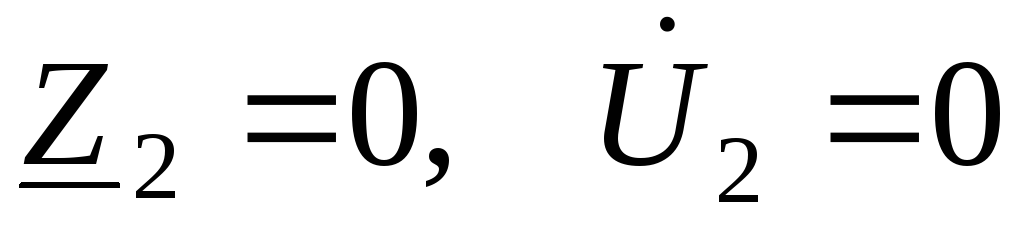 (рис. 3.4, б), соотношение (3.9) будет иметь
вид
(рис. 3.4, б), соотношение (3.9) будет иметь
вид
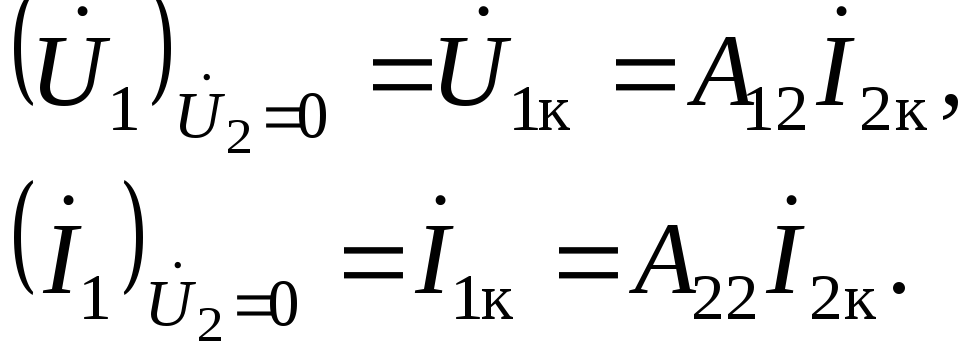
В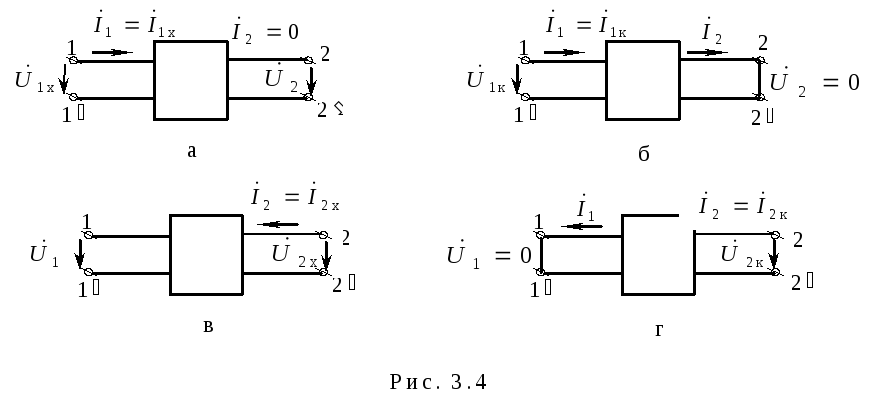 ходное
сопротивление четырехполюсника со
стороны выводов 1–1
ходное
сопротивление четырехполюсника со
стороны выводов 1–1
 . (3.13)
. (3.13)
Обратное питание
Учитывая, что при обратном питании А11иА22меняются местами, можно получить еще два уравнения (рис. 3.4, в, г).
Входное сопротивление со стороны выводов 2–2в режиме холостого хода
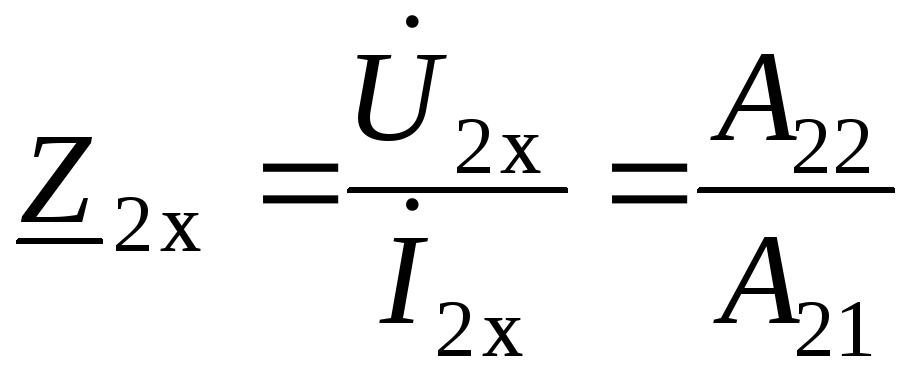 . (3.14)
. (3.14)
Входное сопротивление четырехполюсника со стороны выводов 2–2в режиме короткого замыкания
 . (3.15)
. (3.15)
Сопротивления  ,
,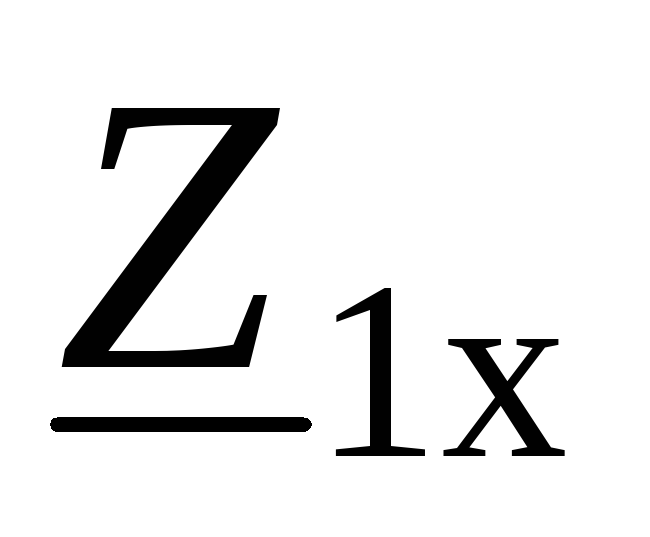 ,
,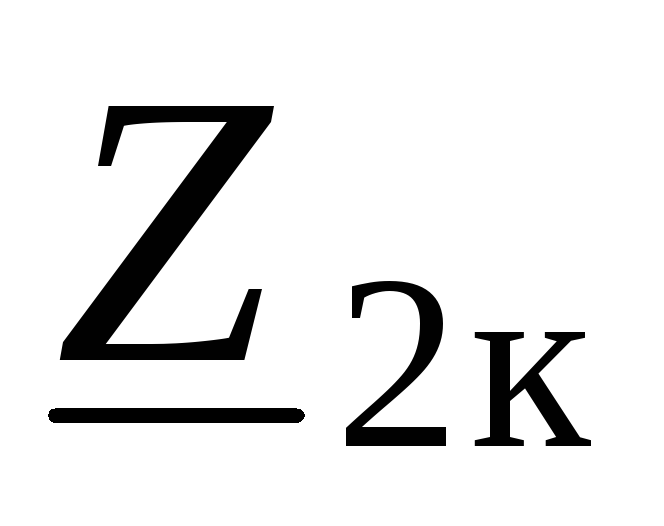 ,
, называютпараметрами короткого
замыкания и холостого хода. ВыразимА–параметры через эти сопротивления.
С этой целью из (3.14) вычтем (3.13)
называютпараметрами короткого
замыкания и холостого хода. ВыразимА–параметры через эти сопротивления.
С этой целью из (3.14) вычтем (3.13)
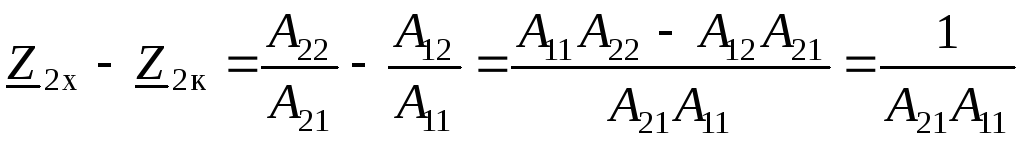 .
.
После деления
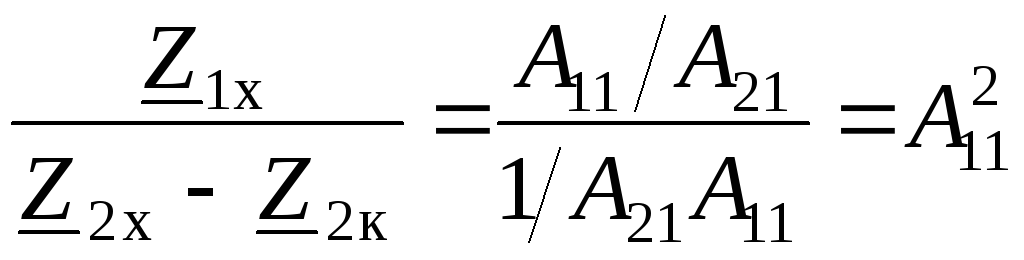 ,
,
получим
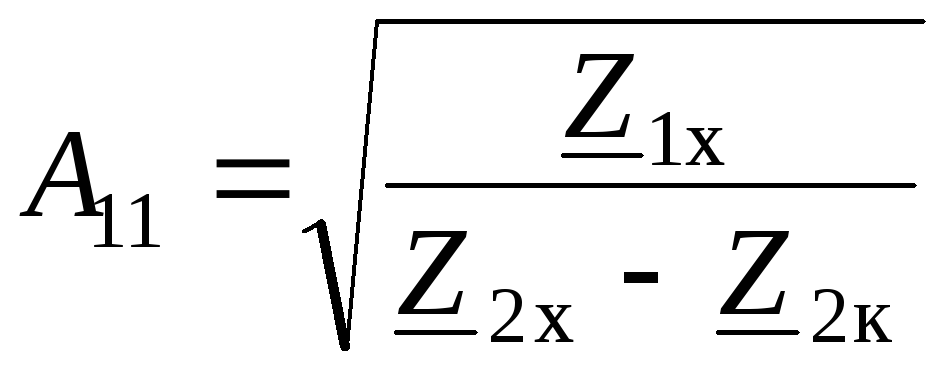 . (3.16)
. (3.16)
Учитывая (3.14), (3.12), (3.13), получим
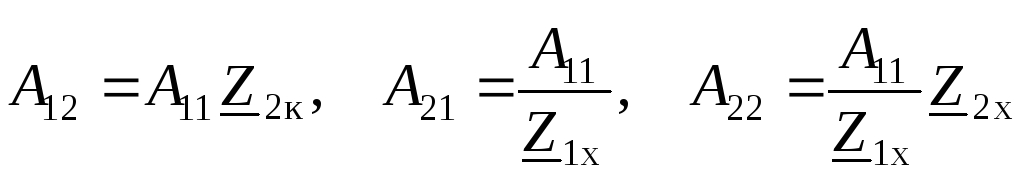 . (3.17)
. (3.17)
Уравнение 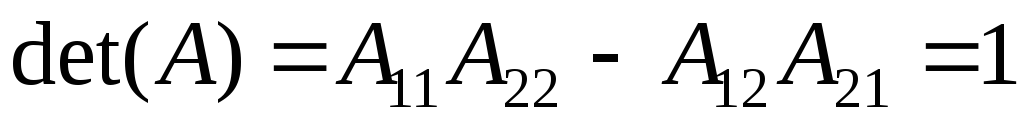 – проверочное.
– проверочное.
Нагрузочный режим четырехполюсника как результат наложения режимов холостого хода и короткого замыкания
Пусть к выводам 2–2четырехполюсника подключено сопротивление
нагрузки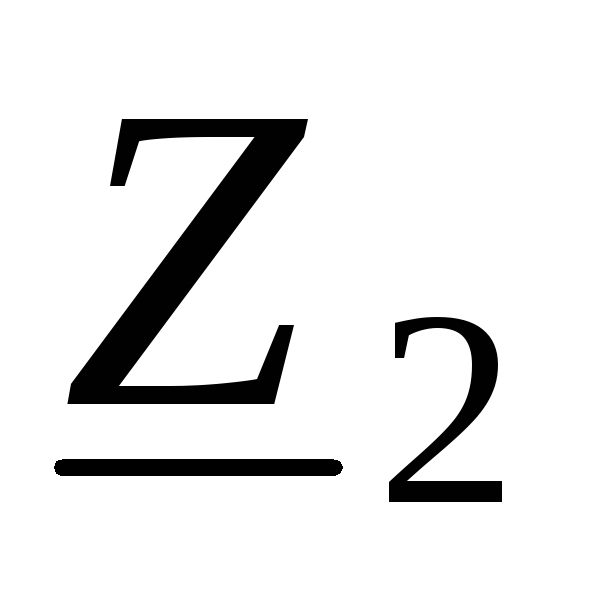 .
При этом
.
При этом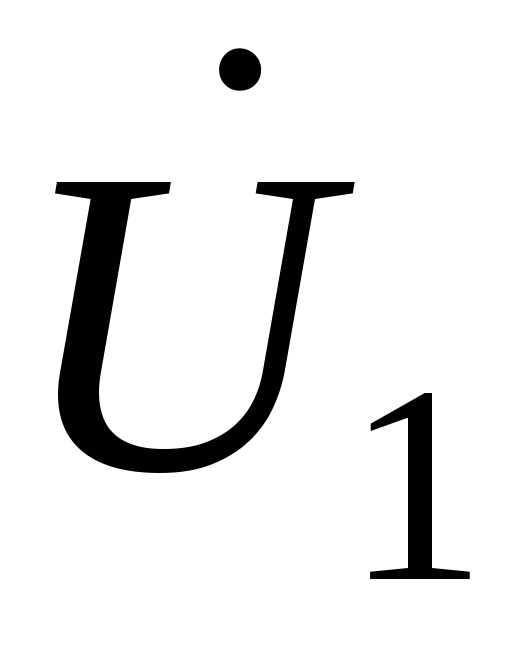 ,
, и
и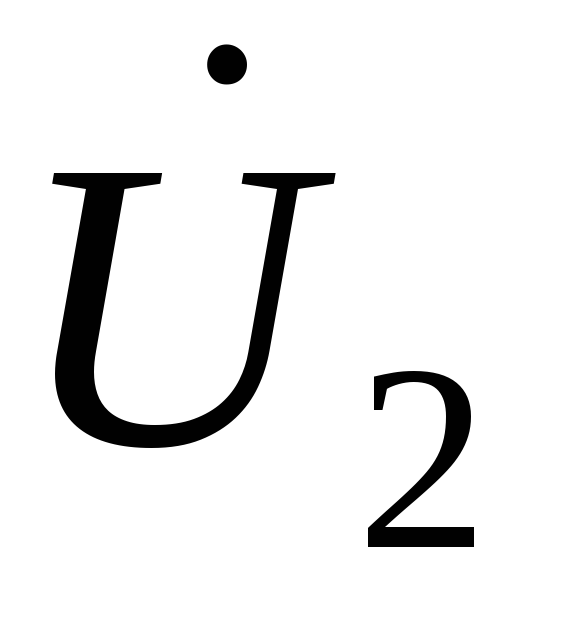 ,
, связаны соотношениями (3.9). Отсоединим
сопротивление
связаны соотношениями (3.9). Отсоединим
сопротивление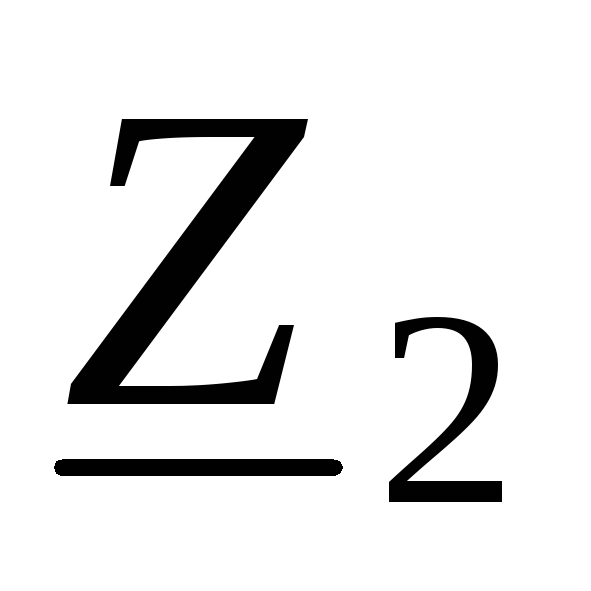 (режим холостого хода). Отрегулируем
входное напряжение
(режим холостого хода). Отрегулируем
входное напряжение так, чтобы напряжение на выходных
разомкнутых зажимах
так, чтобы напряжение на выходных
разомкнутых зажимах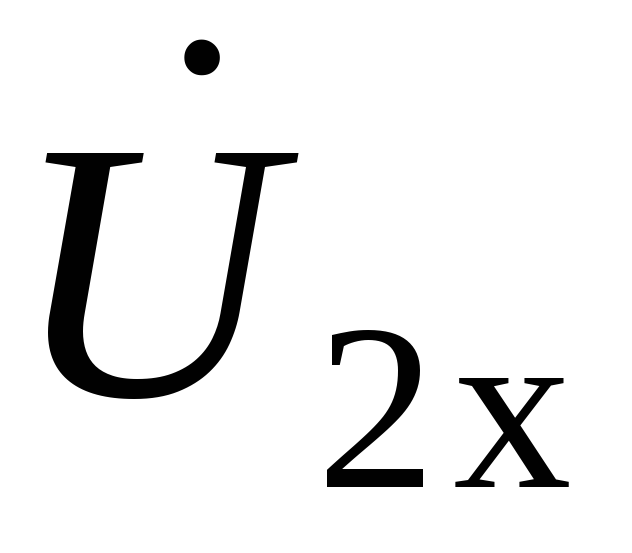 стало равным напряжению
стало равным напряжению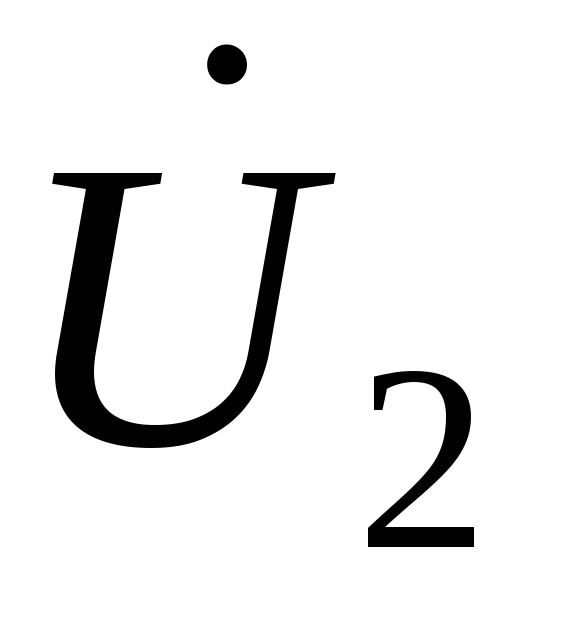 в нагрузочном режиме:
в нагрузочном режиме:
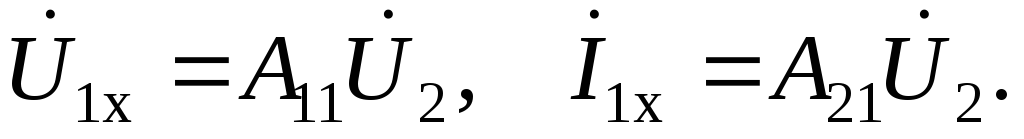
Замкнем выводы 2–2(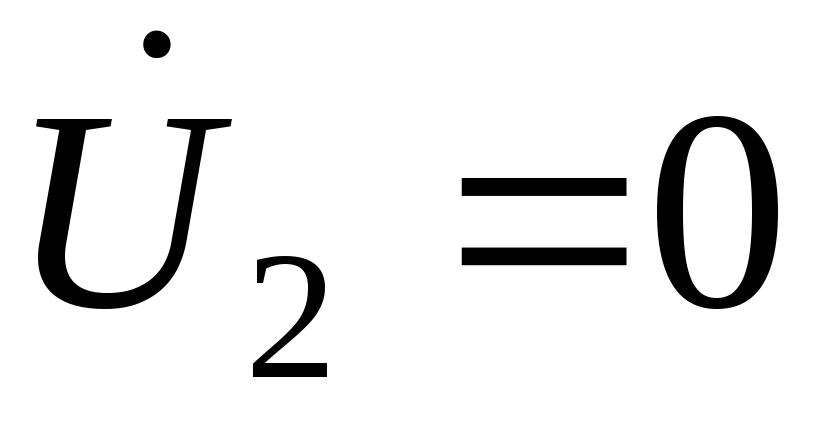 ,
режим короткого замыкания). Отрегулируем
входное напряжение
,
режим короткого замыкания). Отрегулируем
входное напряжение так, чтобы ток на выходных зажимах
так, чтобы ток на выходных зажимах стал равным току
стал равным току в нагрузочном режиме. Тогда
в нагрузочном режиме. Тогда

При сложении получим
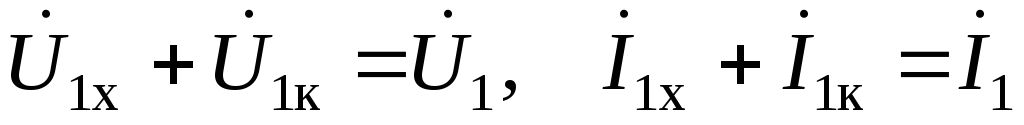 .
.
Полученные соотношения
показывают, что рабочий режим
четырехполюсника (нагрузка 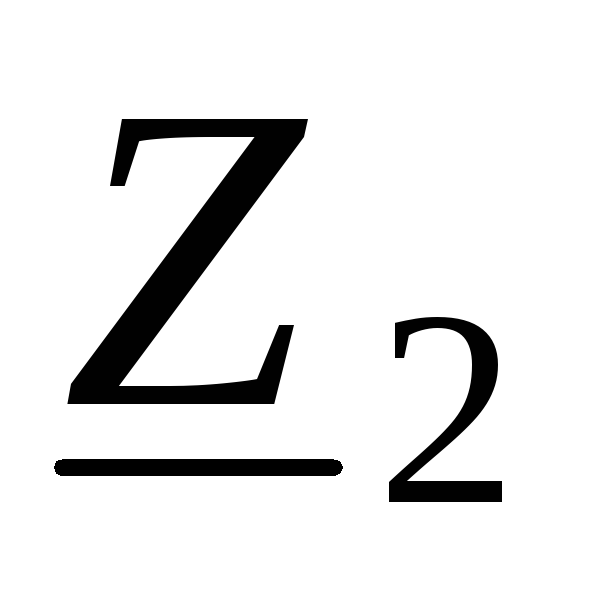 подключена к выводам 2–2)
можно воспроизвести путем наложения
режимов холостого хода и короткого
замыкания, т.е. можно смоделировать
нагрузочный режим, в некоторых случаях
требующий источников большой мощности,
наложением крайних нагрузочных режимов
(холостого хода и короткого замыкания),
когда такие источники не нужны (нагрузка
не потребляет мощности!).
подключена к выводам 2–2)
можно воспроизвести путем наложения
режимов холостого хода и короткого
замыкания, т.е. можно смоделировать
нагрузочный режим, в некоторых случаях
требующий источников большой мощности,
наложением крайних нагрузочных режимов
(холостого хода и короткого замыкания),
когда такие источники не нужны (нагрузка
не потребляет мощности!).
Эквивалентные схемы замещения четырехполюсника
Л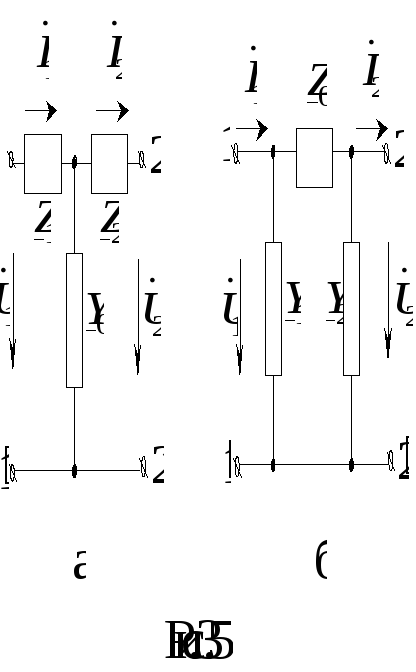 юбой
четырехполюсник можно свести к
сопротивлениям или проводимостям,
соединенным по Т– или П–образной схеме
(рис. 3.5). Эквивалентной схемой замещения
реального четырехполюсника называется
простейший трехэлементный четырехполюсник
(Т– или П–образный), имеющий такие же
юбой
четырехполюсник можно свести к
сопротивлениям или проводимостям,
соединенным по Т– или П–образной схеме
(рис. 3.5). Эквивалентной схемой замещения
реального четырехполюсника называется
простейший трехэлементный четырехполюсник
(Т– или П–образный), имеющий такие же илиA–параметры, как
и заданный четырехполюсник.
илиA–параметры, как
и заданный четырехполюсник.
Три сопротивления Т– или П–схем должны быть рассчитаны с учетом того, что схема замещения должна обладать такими же А-параметрами, какими обладает заменяемый ей четырехполюсник.
Выразим 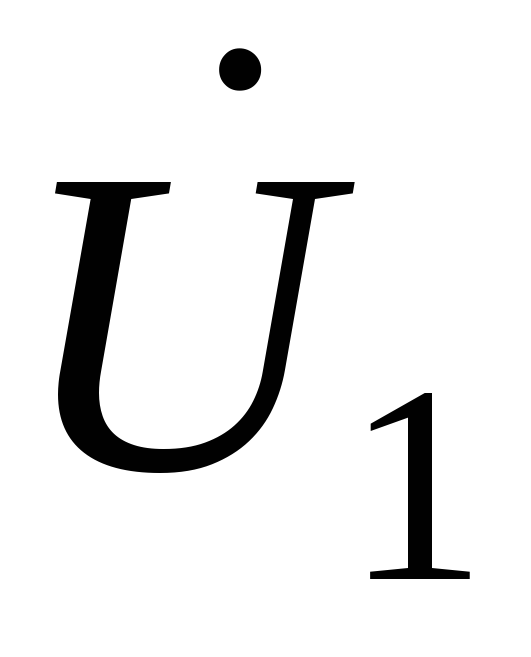 и
и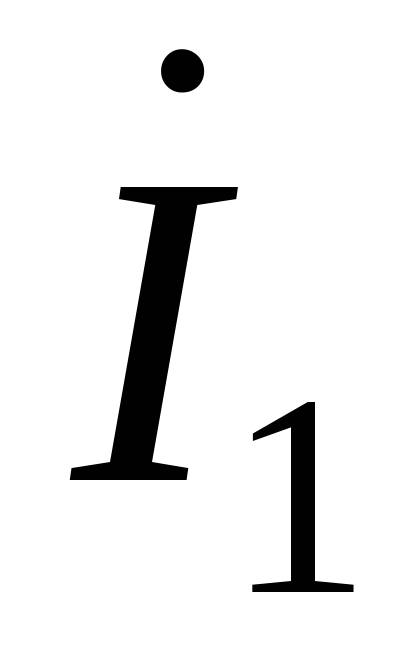 Т–образной схемы через
Т–образной схемы через ,
,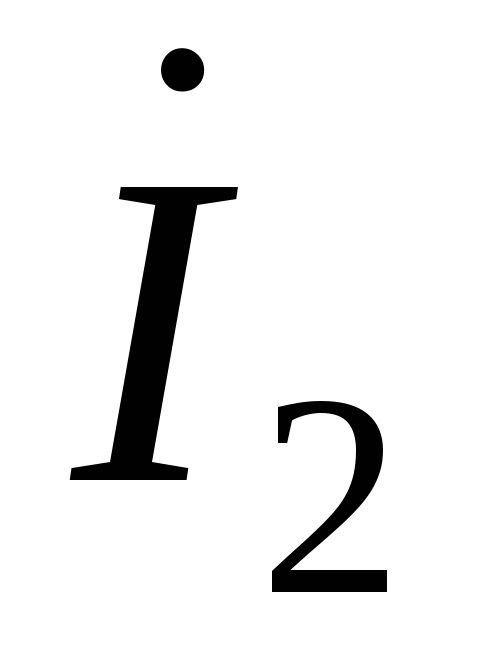 ,
используя уравнения, составленные по
законам Кирхгофа:
,
используя уравнения, составленные по
законам Кирхгофа:
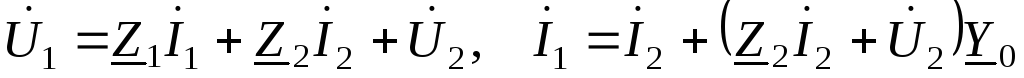 (3.18)
(3.18)
Подставляя 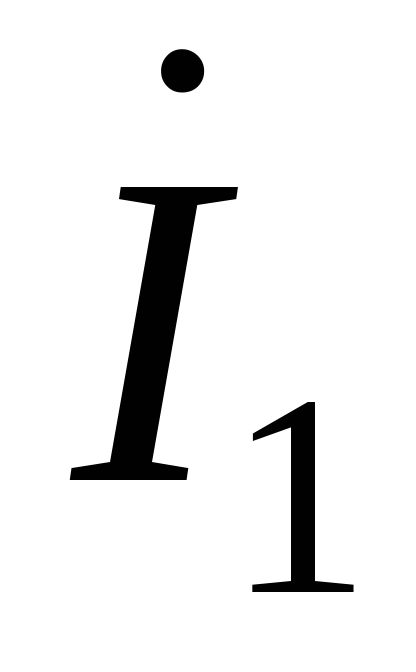 в выражение для определения
в выражение для определения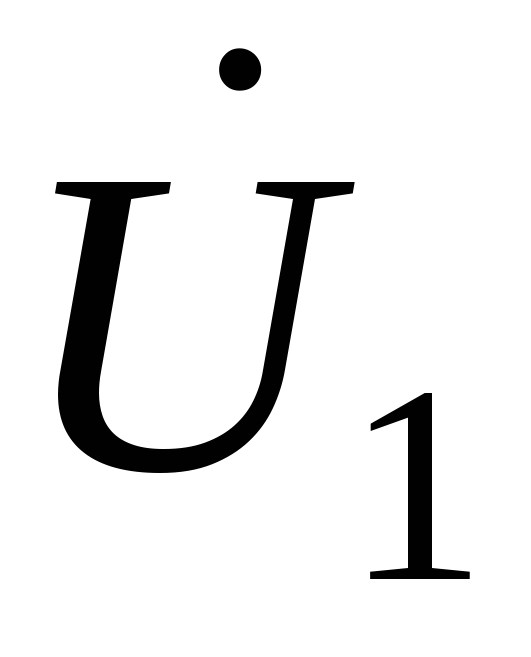 и группируя однородные члены, получим
и группируя однородные члены, получим

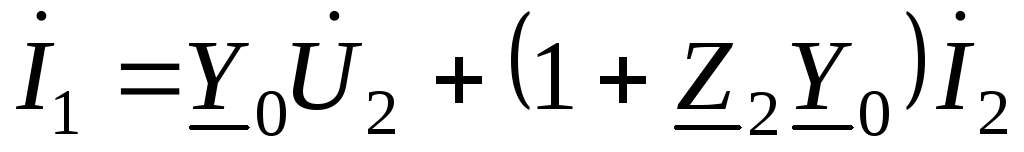 .
.
С другой стороны для данной схемы справедлива общая запись уравнений четырехполюсника в А–параметрах:

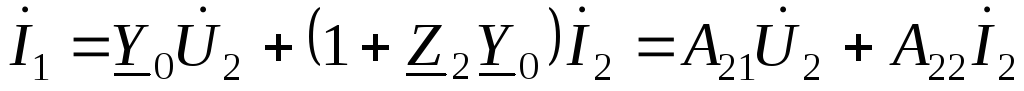 .
.
Приравняв
коэффициенты при  и
и ,
получимА–параметры как функции
параметров Т-образной схемы замещения:
,
получимА–параметры как функции
параметров Т-образной схемы замещения:
 (3.19)
(3.19)
Проведя аналогичные действия, можно получить подобные соотношения для П–образной схемы четырехполюсника:
 (3.20)
(3.20)
Два четырехполюсника эквивалентны, если у них равны А–параметры. Это следует из уравнений (3.9). Следовательно, если известныА–параметры какого-то четырехполюсника, то его можно заменить на эквивалентную ему Т– или П–образную схемы замещения, если определить параметры этих схем замещения в выражениях (3.19) и (3.20). При этом для Т–образной схемы замещения
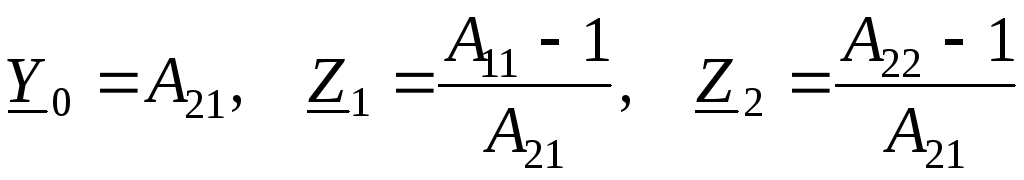 . (3.21)
. (3.21)
Параметры элементов П–образной схемы замещения
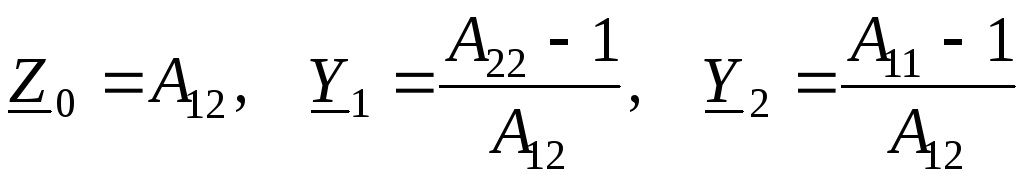 .
.
Опыт холостого хода и короткого замыкания
В СССР стандартными группами являются следующие:
В стандартных схемах обмотки высшего напряжения соединены звездой, так как при такой схеме фазное напряжение в раз меньше линейного, благодаря чему упрощается изоляция обмоток. Обмотки низшего напряжения чаще соединяются треугольником, гак как при таком соединении трансформатор менее чувствителен к несимметрии нагрузки фаз.
Обмотки низшего напряжения соединяются также по схеме звезда с нулем, так как при такой схеме можно в четырехпроводной сети получить два различных напряжения — линейное и фазное (например, 327 и 220 в, 220 и 380 в и т. д.).
§ 84. ОПЫТ ХОЛОСТОГО ХОДА И КОРОТКОГО ЗАМЫКАНИЯ
Для испытания трансформатора служит опыт холостого хода и опыт короткого замыкания.
При опыте холостого хода трансформатора (рис. 103) его вторичная обмотка разомкнута и тока в этой обмотке нет (/2—0).
Если первичную обмотку трансформатора включить в сеть источника электрической энергии переменного тока, то в этой обмотке будет протекать ток холостого хода I0, который представляет собой малую величину по сравнению с номинальным током трансформатора. В трансформаторах больших мощностей ток холостого хода может достигать значений порядка 5— 10% номинального тока. В трансформаторах малых мощностей этот ток достигает значения 25—30% номинального тока. Ток холостого хода I0 создает магнитный поток в магнитопроводе трансформатора. Для возбуждения магнитного потока трансформатор потребляет реактивную мощность из сети. Что же касается активной мощности, потребляемой трансформатором при холостом ходе, то она расходуется на покрытие потерь мощности в магнитопроводе, обусловленных гистерезисом и вихревыми токами.
Так как реактивная мощность при холостом ходе трансформатора значительно больше активной мощности, то коэффициент мощности cos φ его весьма мал и обычно равен 0,2-0,3.
По данным опыта холостого хода трансформатора определяется сила тока холостого хода I0, потери в стали сердечника Рст и коэффициент трансформации К.
Силу тока холостого хода I0 измеряет амперметр, включенный в цепь первичной обмотки трансформатора.
При испытании трехфазного трансформатора определяется фазный ток холостого хода.
О потерях в стали сердечника Pст судят по показаниям ваттметра, включенного в цепь первичной обмотки трансформатора.
Коэффициент трансформации трансформатора равен отношению показаний вольтметров, включенных в цепь первичной и вторичной обмоток.
При коротком замыкании вторичной обмотки сопротивление трансформатора очень мало и ток короткого замыкания во много раз больше номинального. Такой большой ток вызывает сильный нагрев обмоток трансформатора и приводит к выходу его из строя. Поэтому трансформаторы снабжаются защитой, отключающей его при коротких замыканиях.
При опыте короткого замыкания (рис. 104) вторичная обмотка трансформатора замкнута накоротко, т. е. напряжение на зажимах вторичной обмотки равно нулю. Первичная обмотка включается в сеть с таким пониженным напряжением, при котором токи в обмотках равны номинальным. Такое пониженное напряжение называется напряжением короткого замыкания и обычно равно 5,5% от номинального значения.
По данным опыта короткого замыкания определяется напряжение короткого замыкания uк %, его активная uа % и реактивная ux % составляющие, потери на нагревание обмоток трансформатора Pобм при номинальной нагрузке и активное, реактивное и полное сопротивления трансформатора при коротком замыкании rk, xk и zk.
Потери в обмотках указываются ваттметром. Активное, реактивное и полное сопротивления короткого замыкания трансформатора определяются следующими выражениями:
где Uk, I и Pk — напряжение, сила тока, мощность, указываемые измерительными приборами, включенными в цепь первичной обмотки трансформатора.
При испытании трехфазного трансформатора следует в приведенных выше выражениях подставить фазные значения напряжения, тока и мощности.
Напряжение короткого замыкания и его активная и реактивная составляющие равны:
где Uн и Iн — номинальные напряжения и сила тока вторичной (первичной) обмотки трансформатора.
§ 85. ОПРЕДЕЛЕНИЕ РАБОЧИХ СВОЙСТВ ТРАНСФОРМАТОРОВ ПО ДАННЫМ ОПЫТОВ ХОЛОСТОГО ХОДА И КОРОТКОГО ЗАМЫКАНИЯ
Свойства трансформатора при работе его под нагрузкой могут быть определены непосредственным его испытанием. Если включить трансформатор на какую-либо нагрузку и изменить ее, то по показаниям приборов можно определить, каким образом будет изменяться напряжение на зажимах вторичной обмотки и к. п. д. трансформатора. Однако при испытании трансформатора под нагрузкой происходит очень большой расход электроэнергии (тем больший, чем больше мощность трансформатора), и для создания активной, индуктивной и емкостной нагрузок необходимо очень громоздкое оборудование (реостаты, индуктивные катушки и конденсаторы). Кроме этого, непосредственное испытание трансформатора дает очень неточные результаты.
Все рабочие свойства трансформатора могут быть определены по данным опытов холостого хода и короткого замыкания. При этом требуется сравнительно малая затрата энергии и отпадает надобность в громоздком нагрузочном оборудовании, кроме того, такое определение рабочих свойств дает высокую точность.
При опыте холостого хода измеряют напряжение первичной и вторичной обмотки 171 и U2, ток холостого хода /0 и потребляемую при холостом ходе мощность Р0, которая расходуется на покрытие потерь в стали магнитопровода, т. е. Рст=Ро.
При опыте короткого замыкания измеряют напряжение короткого замыкания UK, силу тока первичной обмотки, равную номинальной Iн, и мощность Рк, потребляемую трансформатором при опыте короткого замыкания и расходуемую на покрытие потерь в обмотках при номинальной нагрузке, т. е. Робм=РК.
По данным опыта короткого замыкания определяются сопротивление (полное, активное и реактивное) трансформатора при коротком замыкании zK, rK и хК, а также напряжение короткого замыкания uк и активная uа и реактивная uх составляющие напряжения короткого замыкания.
При испытании трехфазного трансформатора все величины определяются для одной фазы.
По данным опытов холостого хода и короткого замыкания можно найти напряжение на зажимах вторичной обмотки и к. трансформатора при любой нагрузке.
Процентное понижение вторичного напряжения при любой грузке равно:
где
где U20 — напряжение при холостом ходе.
Таким образом, напряжение вторичной обмотки зависит не только от величины, но и от характера нагрузки.
При индуктивном характере нагрузки напряжение понижается с ростом нагрузки в большей степени, чем при чисто активной. При емкостном характере нагрузки происходит повышение напряжения с ростом нагрузки.
Пример. Напряжение вторичной обмотки трансформатора при холостом ходе U20=400 в. Определить вторичное напряжение при номинальной нагрузке Iн и cos φ2=1 (чисто активная нагрузка), cos φ 2=0,8 (для активно-индуктивной и активно-емкостной нагрузки), если напряжение короткого замыкания и его активная составляющая равны:
Р е ш е н и е. Реактивная составляющая напряжения короткого замыкания трансформатора
1.2 Метод двух коротких замыканий

| 1 |
| ln |
| 1+ thgl |
| 1,15 | lg | 1 + thgl | , | ||||||||||||
a |
|
|
|
|
| = |
|
|
|
|
|
|
|
| = | |||||||
|
|
|
|
|
|
| l | |||||||||||||||
|
| 2l | 1- thgl |
|
|
|
|
|
| 1- thgl | (1.8) | |||||||||||
| 1 |
|
|
|
|
| 1 рад | . |
|
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
b |
| = | j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
| T 57,3 км |
|
|
|
|
|
|
| ||||||||||||||
| 2l |
|
|
|
|
|
|
|
|
|
|
| ||||||||||
где jТ – аргумент выражения |
| 1+ thgl | = |
| Т |
| e jjТ . |
|
| |||||||||||||
|
|
|
|
| ||||||||||||||||||
|
|
|
| |||||||||||||||||||
|
|
|
|
|
| 1- thgl |
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
Коэффициент 57,3 необходим для перевода полученного аргумента в ра-
дианы. |
|
Далее можно определить коэффициент распространения: |
|
g =a + jb. | (1.9) |
Первичные параметры определяются из очевидных соотношений:
zр | = zв g; | ||
| (1.10) | ||
zб | = | zв | . |
| |||
|
| g | |
При увеличении затухания рельсовой линии(увеличение длины или сни-
жение сопротивления изоляции) входное сопротивление в режиме холостого хода падает, а в режиме короткого замыкания увеличивается, поэтому исполь-
зование метода холостого хода и короткого замыкания приводит к значитель-
ным погрешностям. При затухании a×l =15 Дб [1] модули входных сопротив-
лений равны и расчет указанным методом приводит к значительным погрешно-
стям. Поэтому, если условие
zx.x |
| ³1, 2 | (1.11) | |
zк.з | ||||
|
| |||
не выполняется, то пользуются при измерениях методом двух коротких замы-
каний. При этом методе определяется входное сопротивление при коротком за-
мыкании рельсовой линии на релейном конце на расстоянии2l от питающего конца и в середине, т. е. на расстоянии l , т. е.

zк.з2l | = zв th 2gl; | (1.12) |
zк.зl | = zв thgl. | (1.13) |
Как известно, |
|
|
th3gl = |
|
|
| 2thgl | . |
|
|
|
| ||||
|
|
|
|
|
|
| |||||||
|
|
| 1+ th3gl |
| |||||||||
Подставляя это выражение в формулу (1.12), получим: |
| ||||||||||||
z | = z |
|
|
| 2thgl | . |
|
|
| ||||
|
|
|
|
|
|
| |||||||
к.з2l |
|
| в 1+ th3gl |
| |||||||||
Заменив в полученном выражении произведение zв thgl | на zк.зl , соглас- | ||||||||||||
но (1.13) получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
zк.з2l = |
|
|
| 2zк.зl |
| ||||||||
|
|
| . |
|
|
| |||||||
1+ th3gl |
| ||||||||||||
Из полученного выражения находим |
| ||||||||||||
|
|
|
|
|
|
|
| ||||||
thgl = |
| 2zк.зl — zк.з2l | . | (1.14) | |||||||||
|
|
|
| ||||||||||
|
|
|
|
|
| zк.з2l |
| ||||||
Далее определяем |
|
|
|
|
|
|
|
|
|
|
|
|
|
| zв = | zк.зl | . | (1.15) | |||||||||
|
| ||||||||||||
|
|
|
|
| thgl |
| |||||||
Определение gl выполняется по формуле(1.14). Расчет остальных пара-
метров рельсовой цепи осуществляется по формулам (1.8), (1.9) и (1.10).
Приведенные выше способы могут быть использованы в рельсовых цепях как постоянного, так и переменного тока. При измерениях в рельсовых цепях переменного тока обязательным является определение угла сдвига фаз между напряжением и током в начале рельсовой цепи.
1.3 Определение параметров рельсовой линии для постоянного тока методом измерения напряжений и токов в начале и конце
Метод холостого хода и короткого замыкания, как и метод двух коротких
замыканий, имеет тот недостаток, что требует выключения рельсовой цепи.



