Вывод закона ома: 18.2. Вывод закона Ома в дифференциальной форме в классической электронной теории

Содержание

Закон Ома для полной цепи | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Рис. 5.19. Внутренняя и внешняя части электрической цепи

Рассмотрим замкнутую электрическую цепь, состоящую из двух частей: собственно источника с электродвижущей силой Ɛ и внутренним сопротивлением r и внешней части цепи — проводника с сопротивлением R (рис. 5.19).

Закон Ома для полной цепи устанавливает зависимость силы тока в замкнутой цепи I от электродвижущей силы источника Ɛ и полного сопротивления цепи R + r. Эту зависимость можно установить на основании закона сохранения энергии и закона Джоуля-Ленца. Если через поперечное сечение проводника за время Δt заряженными частицами переносится заряд Δq, то работа сторонних сил

A_ст.

= ƐΔq = ƐIΔt.

Если в цепи электрическая энергия превращается лишь в тепловую, то по закону сохранения энергии А_ст. = Q и общее количество теплоты, выделяющееся в замкнутой цепи, равно сумме количеств теплоты, выделяющихся во внешней и внутренней частях цепи

Q = I²RΔt + I²rΔt.

Если

A_ст. = Q = (Ɛ / R + r) • IΔt,

то

ƐIΔt = I²RΔt + I²rΔt.

Итак,

Ɛ = IR + Ir

I = Ɛ / (R + r),

что и выражает закон Ома для полной цепи.

Закон Ома для полной цепи. Сила тока в замкнутой цепи измеряется отношением электродвижущей силы источника тока, имеющегося в этой цепи, к полному ее сопротивлению.

Из сказанного выше можно сделать вывод, что

закон Ома для полной цепи является одним из выражений закона сохранения энергии.

Во многих случаях для характеристики источников тока недостаточно использовать лишь

ЭДС. Пусть, например, необходимо установить, ток какой максимальной силы может дать определенный источник тока. Если исходить из закона Ома для полной цепи

I = Ɛ / (R + r), Материал с сайта http://worldofschool.ru

то очевидно, что максимальной сила тока в цепи будет тогда, когда внешнее сопротивление цепи R стремится к нулю — это короткое замыкание в цепи. При этом ток короткого замыкания имеет силу I_max = Ɛ / r, поскольку Ɛ и r изменить для данного источника мы не можем, они являются характеристиками источника.

Если представить, что сопротивление внешней части цепи стремится к бесконечности (цепь становится разомкнутой), то напряжение на полюсах источника тока IR стремится к электродвижущей силе, то есть:

электродвижущая сила источника тока равна напряжению на полюсах разомкнутого источника.

На этой странице материал по темам:

Запишите формулу закона ома для полной цепи.
Шпаргалка закон ома, что такое ток
Реферат на тему -закон ома на полной цепи википедия
Закон ома при параллельном соединении источников
Реферат на тему закон ома на полной цепи

Вопросы по этому материалу:

Как определяется работа сторонних сил?
Сформулируйте закон Ома для полной цепи.
Запишите формулу закона Ома для полной цепи.
Что такое ток короткого замыкания?

Как можно определить ток короткого замыкания?
Как связаны между собой максимально возможное напряжение на полюсах источника и электродвижущая сила источника?

Закон Ома для полной цепи | Полезные статьи

Вывод закона Ома для полного участка цепи.

Возьмем источник постоянного тока, состоящий из сосуда с серной кислотой и помещёнными в него цинковым и угольным электродами. Цинк отдаёт в кислоту двухвалентные ионы, становясь согласно закону сохранения заряда отрицательно заряженным. Для рассмотрения закона Ома для полной цепи на участке между электродами помещается резистор, замыкающий цепь, что приводит к появлению постоянного электрического тока – избыток электронов цинка начнёт движение в угольный электрод. В ходе химической реакции совершается работа А по переносу заряда q. Её целесообразно выразить через ЭДС:

ε = A/q

Кроме того, по закону сохранения энергии работа расходуется на выделение тепла Q в нагрузке и в самом источнике:

A = Q

Количество теплоты согласно закону Джоуля-Ленца для источника и нагрузки:

Q = I²• r • t, где r – сопротивление источника
и
Q = I²• R • t, где R – сопротивление нагрузки.

Выразим количество электричества (заряд) через силу тока:

q = I • t

Для вывода закона Ома продолжаем преобразования и получаем ЭДС для полной цепи:

ε • I • t = I²• r • t + I²• R • t
⇓
ε = I•r + I•R – из этого выражения выводится формула закона Ома для полной цепи:

I = ε/(r+R)

Классическая формулировка закона Ома для полной цепи: сила тока полной цепи прямопропорциональна ЭДС источника и обратноспропорциональна полному сопротивлению цепи.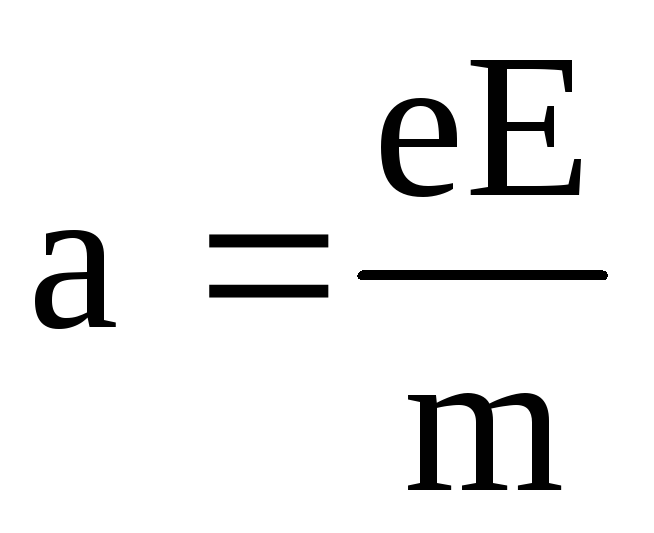

Обычно сопротивление источника значительно ниже сопротивления нагрузки: R ≫ r. В таких случаях ε ≈ U, а формула принимает вид уравнения закона Ома для участка цепи:

I = U/R.

Примечательно, что изначально принятые Георгом Омом символы отличаются от используемых сегодня.

Закон Ома для переменного тока.

Рис. 2. Модель идеализированной цепи переменного тока

В случае токов, подчиняющихся гармоническому закону, нагрузка проявляет ряд особенностей. В реальной цепи наравне с активной (резистивной) нагрузкой в той или иной степени обязательно присутствуют ёмкость и индуктивность, создавая колебательный контур. Эти элементы представляют собой реактивную составляющую нагрузки, расчёт которой несколько сложнее.

Возьмем последовательную цепь из резистора, конденсатора и катушки в установившемся режиме, питающуюся от источника ЭДС с пренебрежимым сопротивлением (при этом e ≈ U), соединённую идеальными проводниками:

За основу векторной диаграммы возьмем ток, так как он одинаковый на всех элементах схемы.

Напряжение на резисторе совпадает по направлению с током. В катушке появляется ЭДС индукции, противодействующая изменению напряжения, а в конденсаторе напряжение препятствует току, соответственно, фазы колебаний в них отличаются: в катушке напряжение опережает ток, в конденсаторе зависимость обратная:

где ω – радиальная частота, равняющаяся 2πf, т. е. 100π при 50 Гц.

Результирующее напряжение согласно параллелограмму сил:

Емкостное сопротивление обозначается X_С, а индуктивное X_L. Полное сопротивление обозначается Z и называется импедансом. Для простоты его называют сопротивлением, учитывающим частоту.

Выразим отсюда полное сопротивление, т. е. сопротивление, определяющее активно-реактивный характер нагрузки:

Имея все параметры рассматриваемой модели в установившемся режиме можно записать закон Ома для полной цепи переменного тока в установившемся режиме:

Основы классической теории электропроводности металлов

1.

Лекция 6 Основы классической теории
электропроводности
металлов
2.10. Природа носителей тока в металлах.
2.11.
Основные
положения
классической
электронной теории проводимости металлов
Друде – Лоренца.
2.12. Вывод законов Ома, Джоуля-Ленца и
Видемана-Франца на основе теории Друде Лоренца.
2.13.
Затруднения
классической
теории
электропроводности
металлов.
Сверхпроводимость
металлов.
Открытие
высокотемпературной сверхпроводимости.

3. 2.10. Природа носителей тока в металлах.

Для выяснения природы носителей тока в металлах был поставлен ряд опытов.
Опыт Рикке (Riecke C., 1845-1915). В 1901г. Рикке осуществил опыт, в котором
он пропускал ток через стопку цилиндров с тщательно отполированными
торцами Cu-Al-Cu. Перед началом опыта образцы были взвешены с высокой
степенью точности (Δm = ±0,03 мг). Ток пропускался в течение года. За это
время через цилиндры прошел заряд q = 3,5∙106 Кл.

По окончании опыта цилиндры были вновь взвешены. Взвешивание показало, что

пропускание тока не оказало никакого влияния на вес цилиндров. При
исследовании торцевых поверхностей под микроскопом также не было
обнаружено проникновения одного металла в другой. Результаты опыта Рикке
свидетельствовали о том, что носителями тока в металлах являются не
атомы, а какие-то частицы, которые входят в состав всех металлов.
Такими частицами могли быть электроны, открытые в 1897 г. Томсоном (Thomson
J., 1856-1940) в опытах с катодными лучами. Чтобы отождествить носители
тока в металлах с электронами, необходимо было определить знак и величину
удельного
заряда носителей. Это
_
Cu
было осуществлено в
+
опыте Толмена и
Al
Стюарта (Tolman R.,
Cu
1881-1948, Stewart B.,
1828-1887).
Рис.6.1. Опыт Рикке.
Опыт Толмена и Стюарта. Суть опыта, проведенного в 1916 г.,
состояла в определении удельного заряда носителей тока при резком
торможении проводника.

В опыте для этой цели использовалась
катушка из медного провода длиной 500 м, которая приводилась в
быстрое вращение (линейная скорость витков составляла 300 м/с), а
затем резко останавливалась. Заряд, протекавший по цепи за время
торможения, измерялся с помощью баллистического гальванометра.
Найденный из опыта удельный заряд носителя тока q / m 1,71 1011 Кл / кг ,
оказался очень близким к величине удельного заряда электрона
(e / m 1,76 1011 Кл / кг ) , откуда был сделан вывод о том, что ток в металлах
переносится электронами.
_
V
V
a 0 U 0
a
К опыту Толмена-Стюарта с инерцией электронов.
U
ma
d
q

5. 2.11. Основные положения классической электронной теории проводимости металлов Друде – Лоренца.

Исходя из представлений о свободных электронах как основных носителях тока в металлах,
Друде (Drude P., 1863-1906) разработал классическую теорию электропроводности металлов,
которая затем была усовершенствована Лоренцем (Lorentz H.

, 1853-1928).
Основные положения этой теории сводятся к следующим:
1). Носителями тока в металлах являются электроны, движение которых подчиняется
законом классической механики.
2). Поведение электронов подобно поведению молекул идеального газа (электронный
газ).
3). При движении электронов в кристаллической решетке можно не учитывать
столкновения электронов друг с другом.
4). При упругом столкновении электронов с ионами электроны полностью передают
им накопленную в электрическом поле энергию.
Средняя тепловая скорость хаотического движения электронов при Т ≈ 300К составляет
8kT
8 1,38 10 23 300
10 5 м / с 100км / c
.
31
m
3,14 9,1 10
При включении электрического поля на хаотическое движение электронов накладывается
упорядоченное движение (называемое иногда «дрейфовым»), происходящее с некоторой
средней скоростью u ; возникает направленное
движение
электронов – электрический ток.

Плотность тока определяется по формуле
.
j ne u
Оценки показывают, что при максимально допустимой
плотности тока в металлах j = 107 А/м2
и концентрации носителей 1028 – 1029м-3 ,
. Таким
образом, даже при очень
u 10 3 м / с 1мм
/c
больших плотностях тока средняя скорость упорядоченного движения электронов
u .
Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов
Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в
кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным
электрическим полем. Масштабы дрейфа
сильно преувеличены

7. 2.12. Вывод законов Ома, Джоуля-Ленца и Видемана-Франца на основе теории Друде-Лоренца.

Закон Ома.
Ускорение, приобретаемое электроном в электрическом поле
e
На пути свободного пробега
величины
eE
a
.
m
Е
λ максимальная
скорость электрона достигнет
u max
eE
m
,
где τ — время свободного пробега: / .

Среднее значение скорости упорядоченного
движения есть:
u
eE
u
.
2
2m
Подставив это значение в формулу для плотности тока, будем иметь:
ne
j u ne
E ,
2m v
max
2
Полученная формула представляет собой закон Ома в дифференциальной форме:
ne 2
j E ,
2m
где σ – удельная электропроводность металла:
ne 2
ne 2
2m
2m
.
Закон Джоуля — Ленца
Кинетическая энергия электрона, которую он имеет к моменту
соударения с ионом:
2
m 2
mumax
E кин
.
2
2
При столкновении с ионом энергия, полученная электроном в
2
электрическом поле E mumax , полностью передается иону. Число
кин
1
2
соударений одного электрона в единицу времени равно
, где λ
– длина свободного пробега электрона. Общее число столкновений
за единицу времени в единице объема равно N n
. Тогда
количество тепла, выделяющегося в единице объема проводника за
единицу времени будет:
2
2
Q уд N
mumax
ne 2
E
2
2m
.

Последнюю формулу можно представить в виде закона Джоуля-Ленца в
дифференциальной форме:
1
Q уд Е 2 E 2
,
где ρ =1/σ – удельное сопротивление металла.
Закон Видемана-Франца.
Из
опыта
известно,
что
металлы,
наряду
с
высокой
электропроводностью, обладают также высокой теплопроводностью.
Видеман (Wiedemann G., 1826-1899) и Франц (Franz R.,) установили в
1853 г. эмпирический закон, согласно которому отношение
коэффициента
теплопроводности
κ
к
коэффициенту
электропроводности σ для всех металлов приблизительно одинаково и
изменяется пропорционально абсолютной температуре:
.
8
2
,
3
10
Т
Рассматривая электроны как одноатомный
газ, можем на основании
кинетической
теории
газов
написать
для
коэффициента
теплопроводности электронного газа:
1
1
,
nm cv nk
3
2 при постоянном
3 k — удельная теплоемкость одноатомного
где
газа
cv
объеме.

2m
Разделив κ на σ, приходим к закону Видемана-Франца:
.
k
3 T
e и е = 1,6·10-19 Кл, найдем, что
Подставив сюда k = 1,38·10-23 Дж/К
2
,
что очень хорошо согласуется с
2,23 10 8 Т
экспериментальными
данными.

10. 2.13. Затруднения классической теории электропроводности металлов. Сверхпроводимость металлов. Открытие высокотемпературной сверхпроводи

2.13. Затруднения классической теории
электропроводности металлов. Сверхпроводимость
металлов. Открытие высокотемпературной
сверхпроводимости.
Несмотря на достигнутые успехи, классическая электронная теория
проводимости металлов Друде-Лоренца не получила дальнейшего
развития.
Связано это с двумя основными причинами:
1) трудностями, с которыми столкнулась эта теория при объяснении
некоторых свойств металлов;
2) созданием более совершенной квантовой теории проводимости
твердых тел, устранившей затруднения классической теории и
предсказавшей ряд новых свойств металлов.

Выделим основные затруднения теории Друде-Лоренца:
1. Согласно классической теории, зависимость удельного сопротивления
металлов от температуры ~ T в то время, как на опыте в широком
интервале температур вблизи Т≈300К для большинства металлов
наблюдается зависимость ρ ~ Т.
2. Хорошее количественное совпадение с законом Видемана-Франца
оказалось в известной степени случайным. В первоначальном
варианте теории Друде не учитывал распределение электронов по
скоростям. Позже, когда Лоренц учел это распределение, оказалось,
2
что отношение будет
k
2 T
,
e
что значительно хуже согласуется с экспериментом. Согласно же
2
квантовой теории,
2 k
8
T 2,45 10 Т
.
3 e
3. Теория дает неправильное значение теплоемкости металлов. С
учетом теплоемкости электронного газа С=9/2R, а на практике С=3R,
что примерно соответствует теплоемкости диэлектриков.
4. Наконец, теория оказалась полностью неспособной объяснить
открытое в 1911г.

Камерлинг-Оннесом (Kamerligh-Onnes H., 18531926)
явления
сверхпроводимости
(полного
исчезновения
сопротивления) металлов при низких температурах, а также
существования остаточного сопротивления, в сильной степени
зависящего от чистоты металла.
1
2
Тк
1-металл с
примесями
2-чистый металл
Т
Зависимость сопротивления металлов от температуры.
(Тк – температура перехода в сверхпроводящее состояние)
Интересно отметить, что в отношении
низкотемпературных сверхпроводников
(металлов) действует правило: металлы с
более высоким удельным сопротивлением
ρ имеют и более высокую критическую
температуру сверхпроводящего перехода
Ткр (см. таблицу).
.
Таблица. Свойства низкотемпературных
сверхпроводников
Металл
ρ
Тк , К
Титан
1,7
0,4
Алюминий
2,5
1,2
Ртуть
9,4
4,1
Свинец
22
7,2
Феноменологическая теория низкотемпературной сверхпроводимости
была создана в 1935г.

Ф.и Г. Лондонами (London F., 1900-1954, London
H., 1907-1970), но лишь спустя почти полвека (в 1957г.) явление
сверхпроводимости получило окончательное объяснение в рамках
микроскопической (квантовой) теории, созданной Дж.Бардиным, Л.
Купером и Дж. Шриффером (Bardeen J., Cooper L., Schrieffer J.).
В 1986г. Дж. Беднорцем (Bednorz J.) и К. Мюллером (Müller K.) было
открыто явление высокотемпературной сверхпроводимости в
керамических металлоксидах (лантана, бария и др. элементов),
являющихся диэлектриками при комнатной температуре. Критическая
температура перехода в сверхпроводящее состояние для этих
материалов около 100К.
Теория высокотемпературной сверхпроводимости в настоящее время
находится в стадии разработки и пока далека от своего завершения.
Неясен даже механизм возникновения высокотемпературной
сверхпроводимости.

Откуда берется закон Ома | Великий Шизик

Чем больше работаем, тем больше результат. Это не всегда случается в человеческой жизни, но в случае электрических цепей чаще всего это так. Работа электрического поля по перемещению единицы заряда — это напряжение. В результате этой работы по цепи течет электрический ток. Чем больше напряжение, тем больше сила тока.

Зависимость вида «чем больше, тем больше» может выглядеть следующим образом:

Рис. 1. Характер возможной зависимости силы тока от напряжения: а) Суперлинейная б)Линейная в) Сублинейная

Возможно три варианта:

суперлинейная, когда сила тока увеличивается быстрее, чем напряжение.
линейная, когда сила тока пропорциональна напряжению
сублинейная, когда сила тока увеличивается медленнее, чем напряжение.

Эти варианты реализуются в разных системах:

а) Суперлинейная зависимость имеет место в вакууме или в случае пробоя диэлектрика, а также в полупроводниковых диодах, включенных в прямом направлении.
б) Линейная зависимость характерна для проводников при не слишком больших напряжениях, без учета нагрева. Здесь имеет место тот самый закон Ома, который будет выведен далее.
в) Сублинейная реализуется в проводниках, которые нагреваются под действием протекающего в них тока, а также в полупроводниковых диодах, включенных в обратном направлении.

В этой статье мы остановимся на проводниках, в которых реализуется линейная зависимость, и получим закон Ома для участка цепи. Надо сказать, что несмотря на всю простоту этого закона, получается он довольно непросто, и требуется много модельных предположений. В школе его не выводят, в вузе выводят в дифференциальном виде, а я дам нечто среднее — выведу из готовых школьных формул с дополнительной информацией.

Силы, действующие на электрон

Рассмотрим электрон, находящийся внутри кристаллической решетки проводника. В школе их называют «свободные электроны» в противоположность «связанным», но надо понимать, «связанные» связаны с одним атомом, а «свободные» могут перемещаться внутри металла, но не могут его покинуть, так как связаны со всем кристаллом. В университетском курсе вместо «связанных» и «свободных» используют термины «валентные электроны» и «электроны проводимости»

Со стороны электрического поля на электрон действует сила Кулона, пропорциональная заряду электрона и напряженности поля (F_е на рисунке). Сила Кулона не зависит от скорости электрона, она разгоняет его в направлении, противоположном вектору напряженности поля, так как электрон имеет отрицательный заряд. Со стороны кристаллической решетки действует сила сопротивления (F_c), пропорциональная скорости и направленная противоположно движению электрона.

Рис. 2. Силы, действующие на электрон проводимости. e — заряд электрона, Е — напряженность электрического поля, V* — равновесная скорость дрейфа электронов.

Почему сила сопротивления зависит от скорости? Чем быстрее движется электрон, тем чаще он сталкивается с дефектами. Вопреки распространенному мнению, электронам при движении мешают вовсе не атомы кристаллической решетки, а различные дефекты и неоднородности. При сравнительно небольших скоростях, при которых не создается значительный нагрев, эта зависимость будет иметь линейный характер. На графике эта зависимость изображена прямой линией, и наклон этой прямой определяется свойствами вещества.

Электрон разгоняется под действием электрического поля, и при некоторой скорости V* сила сопротивления становится равна силе электрического поля. Начиная с этого момента разгон прекращается, и электрон движется равномерно со скоростью V* — это равновесная скорость дрейфа. Далее мы будем обозначать ее просто V.

Подвижность электронов

Для разных величин электрического поля равновесная скорость дрейфа электронов будет различной (см. рисунок 3а). Рисунок 3 получен из рисунка 2 просто делением на заряд электрона — чем выше напряженность поля, тем дальше она пересекает прямую, характеризующую силу сопротивления. Так как зависимость силы сопротивления от скорости является линейной, то и зависимость скорости дрейфа от напряженности электрического поля тоже будет линейной (см. формулу на рисунке 3)

Рис. 3. Связь равновесной скорости и напряженности электрического поля.

Эта линейная связь выражается простой формулой, выделенной желтеньким на рисунке. Коэффициент пропорциональности, обозначенный греческой буквою «мю», называется подвижностью электронов. Подвижность определяется углом наклона прямой зависимости силы сопротивления от скорости, причем чем круче идет прямая (больше сила сопротивления), тем меньше подвижность. На рисунке 3 б) изображена такая ситуация, вторая прямая идет ниже первой, равновесная скорость больше, и подвижность больше.

Вывод закона Ома

От рассмотрения движения электронов в рамках выбранной модели можно приступить к выводу закона Ома. Мы воспользуемся школьной формулой для силы тока, в которую входит заряд электрона, концентрация электронов, скорость их движения и площадь (формула 1 на рисунке). Также нам понадобится приведенная выше формула с подвижностью (формула 2). И еще одна школьная формула связи напряжения и напряженности поля (формула 3).

Вывод закона Ома. Комбинируем три формулы и объединяем в группу всё, что касается параметров материала. R — сопротивление, ро — удельное сопротивление, n — концентрация электронов, l — длина проводника, S — площадь поперечного сечения.

Из этих трех формул, группируя всё и вводя новые обозначения, мы получаем и закон Ома, и выражение для сопротивления через длину и площадь проводника.

Получается, что линейность закона Ома вытекает из линейности формулы подвижности. Важным фактором также является то, что концентрация электронов в проводниках не зависит от напряжения. В полупроводниках, например, это не так, и там закон Ома не выполняется.

Итак, вывод закона Ома довольно нетривиален, не зря в школе его не выводят. Экспериментально доказать этот закон тоже было нелегко. Сам Георг Симон Ом столкнулся с рядом трудностей, например, необходимо было исключить влияние нагрева, и современники не сразу оценили полученную им зависимость — казалось, это слишком просто.

Удивительно то, что этот закон, выведенный из большого количества нетривиальных фактов, так прост и так часто реализуется на практике. Воистину повезло школьникам и электрикам! Насколько сложнее было бы рассчитывать цепи и решать задачи, если бы что-то пошло не так.

На этом заканчиваю статью, если возникли вопросы, пишите в комментариях.

Понравилась статья? Что-то стало понятно? Ставьте лайк!

Буду рада новым подписчикам!

Изучение закона ома для полной цепи вывод. Лабораторная работа

Цель работы:

Углубление знаний о законе Ома для участков цепи и о законе Ома для полной цепи. Применения правил Кирхгофа для расчета цепей постоянного тока.

Оборудование : учебно-лабораторный стенд «Законы постоянного тока», мультиметр, три-четыре резистора с известными сопротивлениями, два гальванических элемента разных типов, соединительные провода.

Введение

Постановка задачи о расчете цепи постоянного тока: «Зная величины действующих в цепи э.д.с., внутренние сопротивления источников тока и сопротивления всех элементов цепи, рассчитать силы токов на каждом участке цепи и падение напряжения на каждом элементе».

При решении этой задачи используются:

закон Ома для участка цепи

I – сила тока, U – напряжение на участке цепи, R – сопротивление участка;

закон Ома для полной цепи

I – сила тока, e — э.д.с. источника тока, R – сопротивление внешней цепи, r – внутреннее сопротивление источника тока.

Непосредственный расчет разветвленных цепей, содержащих несколько замкнутых контуров и несколько источников тока, производится с помощью двух правил Кихгофа.

Любая точка в разветвленной цепи, в которой сходится не менее трех проводников с током, называется узлом . При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла, — отрицательным.

Первое правило Кирхгофа : алгебраическая сила токов, сходящихся в узле, равна нулю:

Второе правило Кирхгофа : в любом замкнутом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме э.д.с., встречающихся в контуре:

(4)

Описание стенда «Законы постоянного тока»

В работе используется стенд, состоящий из двух источников тока (гальванических элементов), набора из четырёх резисторов с известными сопротивлениями, мультиметра и набора соединительных проводов.

1. При сборке электрических цепей необходимо обеспечить хороший контакт в каждом соединении.

2. Соединительные провода закручиваются под клеммы по часовой стрелке .

3. При измерении сил токов и напряжений щупы мультиметра должны быть плотно прижаты к клеммам.

4. Измерения производятся при кратковременном замыкании цепи кнопкой.

5. Не следует длительное время оставлять цепь в собранном состоянии.

Прежде всего, изучите правила измерений с помощью универсального электроизмерительного прибора – мультиметра.

Измерение, обработка и представление результатов измерений

Задание 1.

Э.д.с. источника тока можно с достаточно большой степенью точности измерить непосредственно с помощью вольтметра. Но при этом следует иметь в виду, что при этом измеряемое напряжение меньше истинного значения э.д.с. на величину падения напряжения на самом источнике тока.

, (5)

где U – показания вольтметра.

Разница между истинным значением э.д.с. и измеренным напряжением при этом равна:

. (6)

При этом относительная погрешность измерения э.д.с. равна:

(7)

Обычно сопротивление источника тока (гальванического элемента) равно несколько Ом (например, 1Ом ). Если даже сопротивление вольтметра мало (например, 100 Ом ), то и в этом случае погрешность прямого измерения э.д.с. составляет всего » 1%. Хороший вольтметр, в том числе используемый в мультиметре, имеет сопротивление порядка 10 6 Ом . Ясно, что при использовании такого вольтметра можно считать, что показание вольтметра практически равно измеряемой э.д.с источника тока.

1. Подготовьте мультиметр к измерению постоянного напряжения до 2 В .

2. Не вынимая гальванические элементы из креплений, измерьте и запишите их э.д.с. с точностью до сотых долей вольта.

3. Э.д.с. величина всегда положительная. Соблюдайте полярность при подключении мультиметра к источникам тока. Красный щуп мультиметра присоединяется к «+» источника тока.

Задание 2.

Внутреннее сопротивление источника тока можно вычислить с помощью закона Ома:

1. Подготовьте мультиметр для измерения силы постоянного тока до 10(20) А .

2. Составьте электрическую цепь из последовательно соединенного источника тока, резистора (одного из набора) и амперметра.

3. Измерьте силу тока в цепи.

4. Рассчитайте и запишите величину внутреннего сопротивления источника.

5. Аналогичные измерения проделайте для другого элемента.

Задание 3. Расчёт электрической цепи постоянного тока

1. Соберите электрическую цепь по схеме, предложенной преподавателем (схемы 1-7).

2. Зачертите схему в отчет по работе и укажите номиналы выбранных резисторов.

3. С помощью правил Кирхгофа рассчитайте силы токов во всех ветвях цепи. Вычислите падения напряжений на каждом резисторе.

4. С помощью мультимета измерьте силу тока в доступном для измерения месте. Измерьте падение напряжения на каждом резисторе.

5. В выводе сравните измеренные и расчетные значения и укажите причины возможных расхождений.

Задание 4. Соединение источников тока в батареи

1. Источники тока могут соединятся в батареи двумя основными способами: параллельно и последовательно. Если источники соединяются последовательно, то их э.д.с. и внутренние сопротивления складываются:

При параллельном соединении одинаковых источников тока общая э.д.с. батареи равна э.д.с. одного источника, а внутреннее сопротивление батареи в n раз меньше внутреннего сопротивления одного источника тока:

(10)

Соберите цепи по схемам 8, 9, в которых реализуются обе схемы соединения. Рассчитайте и измерьте силу тока в цепи при этих соединениях. В выводе сравните расчетные и измеренные значения.

Отчет по лабораторной работе № 3

Изучение применения закона Ома для расчета цепей постоянного тока

выполненной учащимся школы «Поиск»

…………………………………………………………………………………

«…….»………….. 200….

Задание 1. Определение э.д.с. источников тока

Первый источник тока e 1 = ……… В

Второй источник тока e 2 = ……… В

Задание 2. Измерение внутреннего сопротивления источников тока

Первый источник тока

R = ……… Ом, I = ……… А, r 1 = ……… Ом

Второй источник тока

R = ……… Ом, I = ……… А, r 2 = ……… Ом

Таблица 1

Вывод: ………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

При проектировании и ремонте схем различного назначения обязательно учитывается закон Ома для полной цепи. Поэтому тем, кто собирается этим заниматься, для лучшего понимания процессов этот закон надо знать. Законы Ома разделяют на две категории:

для отдельного участка электрической цепи;
для полной замкнутой цепи.

В обоих случаях учитывается внутреннее сопротивление в структуре источника питания. В вычислительных расчетах используют закон Ома для замкнутой цепи и другие определения.

Простейшая схема с источником ЭДС

Чтобы понять закон Ома для полной цепи, для наглядности изучения рассматривается самая простая схема с минимальным количеством элементов, ЭДС и активной резистивной нагрузки. Можно прибавить в комплект соединительные провода. Для питания идеально подходит автомобильный аккумулятор 12В, он рассматривается как источник ЭДС со своим сопротивлением в элементах конструкции.

Роль нагрузки играет обычная лампа накаливания с вольфрамовой спиралью, которая имеет сопротивление в несколько десятков Ом. Данная нагрузка преобразует электрическую энергию в тепловую. Всего несколько процентов расходуются на излучение потока света. При расчете таких схем применяют закон Ома для замкнутой цепи.

Принцип пропорциональности

Экспериментальными исследованиями в процессе измерений величин при разных значениях параметров полной цепи:

Силы тока – I А;
Суммы сопротивлений батареи и нагрузки – R+r измеряют в омах;
ЭДС – источник тока, обозначают как Е. измеряется в вольтах

было замечено, что сила тока имеет прямо пропорциональную зависимость относительно ЭДС и обратную пропорциональную зависимость относительно суммы сопротивлений, которые замыкаются последовательно в контуре цепи. Алгебраически это сформулируем следующим образом:

Рассматриваемый пример схемы с замкнутым контуром цепи – с одним источником питания и одним внешним элементом сопротивления нагрузки в виде лампы со спиралью накаливания. При расчете сложных схем с несколькими контурами и множеством элементов нагрузки применяют закон Ома для всей цепи и другие правила. В частности надо знать законы Киргофа, понимать, что такое двухполюсники, четырехполюсники, отводящие узлы и отдельные ветви. Это требует детального рассмотрения в отдельной статье, раньше этот курс ТЭРЦ (теория электро- радиотехнических цепей) в институтах учили не менее двух лет. Поэтому ограничиваемся простым определением только для полной электрической цепи.

Особенности сопротивлений в источниках питания

Важно! Если сопротивление спирали на лампе мы видим на схеме и в реальной конструкции, то внутреннего сопротивления в конструкции гальванической батарейки, или аккумулятора, не видно. В реальной жизни, даже если разобрать аккумулятор, найти сопротивление невозможно, оно не существует как отдельная деталь, иногда его отображают на схемах.

Внутреннее сопротивление создается на молекулярном уровне. Токопроводящие материалы аккумулятора или другого источника питания генератора с выпрямителем тока не обладают 100% проводимостью. Всегда присутствуют элементы с частицами диэлектрика или металлов другой проводимости, это создает потери тока и напряжения в батарее. На аккумуляторах и батарейках нагляднее всего отображается влияние сопротивления элементов конструкции на величину напряжения и тока на выходе. Способность источника выдавать максимальный ток определяет чистота состава токопроводящих элементов и электролита. Чем чище материалы, тем меньше значение r, источник ЭДС выдает больший ток. И, наоборот, при наличии примесей ток меньше, r увеличивается.

В нашем примере аккумулятор имеет ЭДС 12В, к нему подключается лампочка, способная потреблять мощность 21 Вт, в этом режиме спираль лампы раскаляется до максимально допустимого накала. Формулировка проходящего через нее тока записывается как:

I = P\U = 21 Вт / 12В = 1,75 А.

При этом спираль лампы горит в половину накала, выясним причину этого явления. Для расчетов сопротивления общей нагрузки (R + r ) применяют законы Ома для отдельных участков цепей и принципы пропорциональности:

(R + r) = 12\ 1,75 = 6,85 Ом.

Возникает вопрос, как выделить из суммы сопротивлений величину r. Допускается вариант – измерить мультиметром сопротивление спирали лампы, отнять его от общего и получить значение r – ЭДС. Этот способ будет не точен – при нагревании спирали сопротивление значительно изменяет свою величину. Очевидно, что лампа не потребляет заявленной в ее характеристиках мощности. Ясно, что напряжение и ток для накаливания спирали малы. Для выяснения причины измерим падение напряжения на аккумуляторе при подключенной нагрузке, к примеру, оно будет 8 Вольт. Предположим, что сопротивление спирали рассчитывается с использованием принципов пропорциональности:

U/ I = 12В/1,75А = 6,85 Ом.

При падении напряжения сопротивление лампы остается постоянным, в этом случае:

I = U/R = 8В/6,85 Ом = 1,16 А при требуемом 1.75А;
Потери по току = (1,75 -1.16) = 0,59А;
По напряжению = 12В – 8В = 4В.

Потребляемая мощность будет Р = UxI = 8В х 1.16А = 9,28 Вт вместо положенных 21 Вт. Выясняем, куда уходит энергия. За пределы замкнутого контура не может, остаются только провода и конструкция источника ЭДС.

Сопротивление ЭДС – r можно вычислить, используя потерянные величины напряжения и тока:

r = 4В/0.59А = 6,7 Ом.

Получается внутреннее сопротивление источника питания «сжирает» половину выделяемой энергии на себя, и это, конечно, не нормально.

Такое бывает в старых отработавших свой срок или бракованных аккумуляторах. Сейчас производители стараются следить за качеством и чистотой применяемых токоведущих материалов, чтобы снизить потери. Для того чтобы в нагрузку отдавалась максимальная мощность, технологии изготовления источников ЭДС контролируют, чтобы величина не превышала 0,25 Ом.

Зная закон Ома для замкнутой цепи, используя постулаты пропорциональности, можно легко вычислить необходимые параметры для электрических цепей для определения неисправных элементов или проектирования новых схем различного назначения.

Видео

Закон Ома для полной цепи – эмпирический (полученный из эксперимента) закон, который устанавливает связь между силой тока, электродвижущей силой (ЭДС) и внешним и внутренним сопротивлением в цепи.

При проведении реальных исследований электрических характеристик цепей с постоянным током необходимо учитывать сопротивление самого источника тока. Таким образом в физике осуществляется переход от идеального источника тока к реальному источнику тока, у которого есть свое сопротивление (см. рис. 1).

Рис. 1. Изображение идеального и реального источников тока

Рассмотрение источника тока с собственным сопротивлением обязывает использовать закон Ома для полной цепи.

Сформулируем закона Ома для полной цепи так (см. рис. 2): сила тока в полной цепи прямо пропорциональна ЭДС и обратно пропорциональна полному сопротивлению цепи, где под полным сопротивлением понимается сумма внешних и внутренних сопротивлений.

Рис. 2. Схема закона Ома для полной цепи.

R – внешнее сопротивление [Ом];
r – сопротивление источника ЭДС (внутреннее) [Ом];
I – сила тока [А];
ε– ЭДС источника тока [В].

Рассмотрим некоторые задачи на данную тему. Задачи на закон Ома для полной цепи, как правило, дают ученикам 10 класса, чтобы они могли лучше усвоить указанную тему.

I. Определите силу тока в цепи с лампочкой, сопротивлением 2,4 Ом и источником тока, ЭДС которого равно 10 В, а внутреннее сопротивление 0,1 Ом.

По определению закона Ома для полной цепи, сила тока равна:

II. Определить внутреннее сопротивление источника тока с ЭДС 52 В. Если известно, что при подключении этого источника тока к цепи с сопротивлением 10 Ом амперметр показывает значение 5 А.

Запишем закон Ома для полной цепи и выразим из него внутреннее сопротивление:

III. Однажды школьник спросил у учителя по физике: «Почему батарейка садится?» Как грамотно ответить на данный вопрос?

Мы уже знаем, что реальный источник обладает собственным сопротивлением, которое обусловлено либо сопротивлением растворов электролитов для гальванических элементов и аккумуляторов, либо сопротивлением проводников для генераторов. Согласно закону Ома для полной цепи:

следовательно, ток в цепи может уменьшаться либо из-за уменьшения ЭДС, либо из-за повышения внутреннего сопротивления. Значение ЭДС у аккумулятора почти постоянный. Следовательно, ток в цепи понижается за счет повышения внутреннего сопротивления. Итак, «батарейка» садится, так как её внутреннее сопротивление увеличивается.

Тема: «Изучение закона Ома для участка цепи»

Цель работы : установить на опыте зависимость силы тока от напряжения и сопротивления.

Оборудование : амперметр лабораторный, вольтметр лабораторный, источник питания, набор из трёх резисторов сопротивлениями 1 Ом, 2 Ом, 4 Ом, реостат, ключ замыкания тока, соединительные провода.

Ход работы.

Краткие теоритические сведения

Электрический ток — упорядоченное движение заряженных частиц

Количественной мерой электрического тока служит сила тока I

Сила тока — – скалярная физическая величина, равная отношению заряда q, переносимого через поперечное сечение проводника за интервал времени t, к этому интервалу времени:

В Международной системе единиц СИ сила тока измеряется в амперах [А] .

Прибор для измерения силы тока Амперметр. Включается в цепь последовательно

Напряжение – это физическая величина, характеризующая действие электрического поля на заряженные частицы, численно равно работе электрического поля по перемещению заряда из точки с потенциалом φ 1 в точку с потенциалом φ 2

U 12 = φ 1 – φ 2

U – напряжение

A – работа тока

q – электрический заряд

Единица напряжения – Вольт [В]

Прибор для измерения напряжения – Вольтметр. Подключается в цепь параллельно тому участку цепи, на котором измеряется разность потенциалов.

На схемах электрических цепей амперметр обозначается .

Величина, характеризующая противодействие электрическому току в проводнике, которое обусловлено внутренним строением проводника и хаотическим движением его частиц, называется электрическим сопротивлением проводника.

Электрическое сопротивление проводника зависит от размеров и формы проводника и от материала , из которого изготовлен проводник .

S – площадь поперечного сечения проводника

l – длина проводника

ρ – удельное сопротивление проводника

В СИ единицей электрического сопротивления проводников служит ом [Ом].

Графическая зависимость силы тока I от напряжения U — вольт-амперная характеристика

Закон Ома для однородного участка цепи : сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

Назван в честь его первооткрывателя Георга Ома .

Практическая часть

1. Для выполнения работы соберите электрическую цепь из источника тока, амперметра, реостата, проволочного резистора сопротивлением 2 Ом и ключа. Параллельно проволочному резистору присоедините вольтметр (см. схему).

2. Опыт 1.

Таблица 1 . Сопротивление участка 2 Ом

4. Опыт 2 .

Таблица 2.

6. Ответьте на контрольные вопросы.

Контрольные вопросы

1. Что такое электрический ток?

2. Дайте определение силы тока. Как обозначается? По какой формуле находится?

3. Какова единица измерения силы тока?

4. Каким прибором измеряется сила тока? Как он включается в электрическую цепь?

5. Дайте определение напряжения. Как обозначается? По какой формуле находится?

6. Какова единица измерения напряжения?

7. Каким прибором измеряется напряжение? Как он включается в электрическую цепь?

8. Дайте определение сопротивления. Как обозначается? По какой формуле находится?

9. Какова единица измерения сопротивления?

10. Сформулируйте закон Ома для участка цепи.

Вариант выполнения измерений.

Опыт 1. Исследование зависимости силы тока от напряжения на данном участке цепи . Включите ток. При помощи реостата доведите напряжение на зажимах проволочного резистора до 1 В, затем до 2 В и до 3 В. Каждый раз при этом измеряйте силу тока и результаты записывайте в табл. 1.

Таблица 1 . Сопротивление участка 2 Ом

По данным опытов постройте график зависимости силы тока от напряжения. Сделайте вывод.

Опыт 2. Исследование зависимости силы тока от сопротивления участка цепи при постоянном напряжении на его концах . Включите в цепь по той же схеме проволочный резистор сначала сопротивлением 1 Ом, затем 2 Ом и 4 Ом. При помощи реостата устанавливайте на концах участка каждый раз одно и то же напряжение, например, 2 В. Измеряйте при этом силу тока, результаты записывайте в табл 2.

Таблица 2. Постоянное напряжение на участке 2 В

По данным опытов постройте график зависимости силы тока от сопротивления. Сделайте вывод.

Презентация: «Лабораторная работа: «Изучение закона Ома для участка цепи» .

{edocs}fizpr/lr7f.pptx,800,600{/edocs}

Лабораторная работа №10. «Изучение закона Ома для полной цепи – 3 способ». Цель работы: изучить закон Ома для полной цепи. Задачи работы:  определение ЭДС и внутреннего сопротивления источника постоянного тока по его вольтамперной характеристике;  исследование графической зависимости мощности, выделяющейся во внешней цепи от величины силы электрического тока P  f I  . Оборудование: источник постоянного тока, амперметр, вольтметр, соединительные провода, ключ, реостат. Теория и метод выполнения работы: Закон I  Rr Ома для полной цепи I  Rr . Преобразуем    I  R  r   I  R  I  r  U  I  r    U  I  r  U    I  r . выражение Следовательно, зависимость напряжения на выходе источника постоянного тока от величины силы тока (вольтамперная характеристика) имеет вид (см. рис. 1): рис. 1 Анализ вольт-амперной характеристики источника постоянного тока: 1) для т.C: I=0, тогда U    0  r   2) для т.D: U=0, тогда 0    I  r    I  r  I  3) tg  U   r I I к.з   I к.з r Выражение для мощности, выделяющейся во внешней электрической цепи имеет вид P  I  U  I    I  r   I    I 2  r . Поэтому графическая зависимость P  f I  представляет собой параболу, ветви которой направлены вниз (см. рис. 2). рис. 2 Анализ графической зависимости P  f I  (см. рис. 3): рис. 3 1) для т.B: P=0, тогда 0  I   I 2  r  0    I  r  I   r  I к. з. , т.е. абсцисса т.B соответствует току короткого замыкания; 2) т.к. парабола является симметричной, то абсцисса т.А составляет половину тока короткого замыкания I  3) т.к. в т.А I  I к. з.   , а ордината – соответствует максимальному значению мощности; 2 2r  Rr и I  2r , то после преобразований получаем R=r – условие, при котором мощность выделяющаяся во внешней цепи с источником постоянного тока принимает максимальное значение; 2     r  4) максимальное значение мощности P  I 2  R   .  4r 2r 2 Ход работы: 1. Подключить вольтметр к клеммам источника постоянного тока (см. рис. 4). Напряжение, показанное вольтметром принять за величину ЭДС источника постоянного тока и считать как эталонное для данной лабораторной работы. Результат записать в виде: (U±U) В. Абсолютную погрешность принять равной цене деления вольтметра. рис. 4 2. Собрать экспериментальную установку по схеме, приведённой на рисунке 5: рис. 5 3. Провести серию из 5-10 экспериментов, при плавном перемещении ползунка реостата, результаты измерений заносить в таблицу: Сила тока Напряжение I U А В 4. По полученным экспериментальным данным построить вольт-амперную характеристику источника постоянного тока. 5. Определить возможное значение ЭДС источника постоянного тока и тока короткого замыкания. 6. Применить методику графической обработки экспериментальных данных и вычислений для расчёта внутреннего сопротивления источника постоянного тока. 7. Результаты вычислений представить в виде:  ЭДС источника постоянного тока: (ср±ср) В;  внутреннее сопротивление источника постоянного тока: r=(rср±rср) Ом. 8. Построить графическую зависимость U  f I  в Microsoft Excel, используя мастер диаграмм с добавлением линии тренда и указанием уравнения прямой. По основным параметрам уравнения определить возможное значение ЭДС источника постоянного тока, тока короткого замыкания и внутреннее сопротивление. 9. На числовых осях указать интервал значений ЭДС, внутреннего сопротивления источника постоянного тока и тока короткого замыкания, полученных различными методами определения. 10. Исследовать мощность, выделяющуюся во внешней цепи от величины силы электрического тока. Для этого заполнить таблицу и построить графическую зависимость P  f I  : Сила тока Мощность I P А Вт 11. По построенному графику определить максимальное значение мощности, ток короткого замыкания, внутреннее сопротивление источника тока и ЭДС. 12. Возможен вариант построения графической зависимости P  f I  в Microsoft Excel, используя мастер диаграмм с добавлением полиномиальной линии тренда со степенью 2, пересечением кривой с осью OY (P) в начале координат и указанием уравнения на диаграмме. По основным параметрам уравнения определить максимальное значение мощности, ток короткого замыкания, внутреннее сопротивление источника тока и ЭДС. 13. Сформулировать общий вывод по работе.

Урок 30. Лабораторная работа № 07. Изучение закона Ома для участка цепи.

Тема: «Изучение закона Ома для участка цепи»

Цель работы: установить на опыте зависимость силы тока от напряжения и сопротивления.

Оборудование: амперметр лабораторный, вольтметр лабораторный, источник питания, набор из трёх резисторов сопротивлениями 1 Ом, 2 Ом, 4 Ом, реостат, ключ замыкания тока, соединительные провода.

Ход работы.

Краткие теоритические сведения

Электрический ток — упорядоченное движение заряженных частиц

Количественной мерой электрического тока служит сила тока I

В Международной системе единиц СИ сила тока измеряется в амперах [А].

[1A=1Кл/1с]

Прибор для измерения силы тока Амперметр. Включается в цепь последовательно

На схемах электрических цепей амперметр обозначается .

U₁₂ = φ₁ – φ₂

U – напряжение

A – работа тока

q – электрический заряд

Единица напряжения – Вольт [В]

[1B=1Дж/1Кл]

На схемах электрических цепей амперметр обозначается .

Электрическое сопротивление проводника зависит от размеров и формы проводника и от материала, из которого изготовлен проводник.

S – площадь поперечного сечения проводника

l – длина проводника

ρ – удельное сопротивление проводника

В СИ единицей электрического сопротивления проводников служит ом [Ом].

Графическая зависимость силы тока I от напряжения U — вольт-амперная характеристика

Закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

Назван в честь его первооткрывателя Георга Ома.

Практическая часть

2. Опыт 1. Исследование зависимости силы тока от напряжения на данном участке цепи. Включите ток. При помощи реостата доведите напряжение на зажимах проволочного резистора до 1 В, затем до 2 В и до 3 В. Каждый раз при этом измеряйте силу тока и результаты записывайте в табл. 1.

Таблица 1. Сопротивление участка 2 Ом

Напряжение, В
Сила тока, А

3. По данным опытов постройте график зависимости силы тока от напряжения. Сделайте вывод.

4. Опыт 2. Исследование зависимости силы тока от сопротивления участка цепи при постоянном напряжении на его концах. Включите в цепь по той же схеме проволочный резистор сначала сопротивлением 1 Ом, затем 2 Ом и 4 Ом. При помощи реостата устанавливайте на концах участка каждый раз одно и то же напряжение, например, 2 В. Измеряйте при этом силу тока, результаты записывайте в табл 2.

Таблица 2. Постоянное напряжение на участке 2 В

Сопротивление участка, Ом
Сила тока, А

5. По данным опытов постройте график зависимости силы тока от сопротивления. Сделайте вывод.

6. Ответьте на контрольные вопросы.

Контрольные вопросы

1. Что такое электрический ток?

2. Дайте определение силы тока. Как обозначается? По какой формуле находится?

3. Какова единица измерения силы тока?

4. Каким прибором измеряется сила тока? Как он включается в электрическую цепь?

5. Дайте определение напряжения. Как обозначается? По какой формуле находится?

6. Какова единица измерения напряжения?

7. Каким прибором измеряется напряжение? Как он включается в электрическую цепь?

8. Дайте определение сопротивления. Как обозначается? По какой формуле находится?

9. Какова единица измерения сопротивления?

10. Сформулируйте закон Ома для участка цепи.

Вариант выполнения измерений.

Опыт 1. Исследование зависимости силы тока от напряжения на данном участке цепи. Включите ток. При помощи реостата доведите напряжение на зажимах проволочного резистора до 1 В, затем до 2 В и до 3 В. Каждый раз при этом измеряйте силу тока и результаты записывайте в табл. 1.

Таблица 1. Сопротивление участка 2 Ом

Напряжение, В	1	2	3
Сила тока, А	0,5	1,0	1,5

По данным опытов постройте график зависимости силы тока от напряжения. Сделайте вывод.

Опыт 2. Исследование зависимости силы тока от сопротивления участка цепи при постоянном напряжении на его концах. Включите в цепь по той же схеме проволочный резистор сначала сопротивлением 1 Ом, затем 2 Ом и 4 Ом. При помощи реостата устанавливайте на концах участка каждый раз одно и то же напряжение, например, 2 В. Измеряйте при этом силу тока, результаты записывайте в табл 2.

Таблица 2. Постоянное напряжение на участке 2 В

Сопротивление участка, Ом	1	2	4
Сила тока, А	2,0	1,0	0,5

По данным опытов постройте график зависимости силы тока от сопротивления. Сделайте вывод.

Презентация: «Лабораторная работа: «Изучение закона Ома для участка цепи» .

{edocs}fizpr/lr7f.pptx,800,600{/edocs}

Лабораторная работа. Изучение закона Ома для участка цепи.

Школа-гимназия № 31

Методическая разработка

открытого урока по физике.

Лабораторная работа. Изучение закона Ома для участка цепи.

10 класс

Учитель физики Иванченко Галина Николаевна.

Пос. Жалагаш, Кызылординская область, Казахстан

22.02.2017 год

Лабораторная работа № 8. Изучение закона Ома для участка цепи.

Цель работы: установить зависимость между силой тока, напряжением и сопротивлением участка цепи.

Оборудование: амперметр, вольтметр, источник питания напряжением 4 В, набор из трёх резисторов сопротивлениями 100 Ом, 200 Ом, 300 Ом, реостат, ключ замыкания тока, соединительные, виртуальная физическая лаборатория программа «Eleсtron.exe»?

Ход урока

Орг. момент.

2.Откройте тетради и запишите тему урока: « Лабораторная работа № 8. Изучение закона Ома для участка цепи.

На предыдущем уроке вы познакомились с физическими величинами: сила тока, плотность тока, электродвижущая сила, источники тока. Повторим домашнее задание.

Выберите правильный ответ

Ученики выполняют задание, отвечают на вопросы тестов:

Задание № 1

1. Электрическим током называют:

А. Движение электронов по проводнику

Б. Упорядочное движение электронов по проводнику

В. Упорядочное движение электрических зарядов по проводнику

2. Какие превращения происходят в гальванических элементах, элементах Вольта, аккумуляторах?

А. Внутренняя энергия превращается в электрическую

Б. Химическая энергия превращается в электрическую

В. Электрическая энергия превращается в механическую

3. Для получения электрического тока в проводнике необходимо:

А. Создать в нем электрические заряды

Б. Разделить в нем электрические заряды

В. Создать в нем электрическое поле

4. За направление электрического тока в цепи принято направление:

А.От отрицательного полюса источника к положительному

Б.От положительного полюса источника к отрицательному

В.По которому перемещаются электроны в проводнике

5.Что представляет собой электрический ток в металлах и какое действие тока на проводник используется в электрических лампах?

А.Упорядочное движение электрических зарядов, химическое

Б. Упорядочное движение положительно и отрицательно заряженных ионов, магнитное

В. Упорядочное движение электронов, тепловое

6. Прибор для измерения силы тока называется:

А.Барометр

Б. Гальванометр

В. Амперметр

7. Формула для определения силы тока:

А. I = q / t

Б. I = q t

В. I = t /q

8. Выразите 0,025 А в миллиамперметрах

А.250 мА

Б. 25 мА

В. 2,5мА

Проверьте ответы:

Задание № 1
Выполните тренировочные вопросы и задания, продолжив предложения:

Сила тока — это :

Единицы силы тока:

Электродвижущая сила- это:

Источники тока:

4.Скажите какие физические величины, определяют электрический ток в цепи?

Сила тока, напряжение, сопротивление.

На сегодняшнем уроке нам необходимо решить следующую задачу:

выяснить, как зависит сила тока на участке цепи от приложенного напряжения и величины сопротивления одновременно. Это является главной целью нашего урока.

Работу на сегодняшнем уроке будем проводить по этапам.

Сначала установим зависимость силы тока от напряжения, запишем математически эту зависимость и проверим на опыте.

Второй этап будет состоять в установлении зависимости между силой тока и сопротивлением, при постоянном напряжении; запишем результаты в таблицу, сделаем вывод о характере этой зависимости.

На третьем этапе мы совместно сделаем общий вывод о том, как зависит сила тока одновременно от напряжения и сопротивления, т.е. решим основную задачу урока.

Ребята, зависимость силы тока от напряжения и сопротивления была впервые установлена немецким ученым Георгом Омом в 1827 году, и поэтому носит название закона Ома для участка цепи.

Давайте с вами посмотрим, как же все-таки устанавливается эта зависимость между I, U и R.

5.Итак, сила тока прямо пропорциональна напряжению. А так ли это?

Убедимся в этом на опыте.

Задание 1.

Установите связь между силой тока , напряжением и сопротивлением участка цепи.

На демонстрационной доске виртуальной лаборатории соберите электрическую цепь:

начертите схему по рис.13.7 учебника, стр 390 в тетради.

сказать из чего состоит цепь: источник тока, резистор, ключ, амперметр, вольтметр

Измерить напряжение на концах проводника. Какую силу тока показывает амперметр?

Увеличить напряжение. Изменились ли показания амперметра?

Да, сила тока в цепи изменилась.

Запишем полученные результаты в таблице.

Вывод: U/R.

Задание 2.

Определите сопротивления участка цепи, пользуясь законом Ома.

Теперь перейдем ко второму этапу наших рассуждений. начертите схему по рис.13.8 учебника, стр 390 в тетради. Вычислите сопротивление.

Начертим таблицу в тетрадь и будем ее заполнять по ходу опыта.

Какой ток в цепи?
10 А
Увеличим сопротивление в 2 раза, не меняя напряжение, какой ток в цепи сейчас?
5 А
Итак, глядя на таблицу, что можно сказать о зависимости между силой тока и сопротивлением?
Эта зависимость обратно пропорциональная.
Вывод: I ~ 1/R
Итак, вот мы и подошли к третьему этапу.
Задание 3. Определите напряжение на участке цепи, пользуясь законом Ома. Начертите схему по рис.13.9 учебника, стр 390 в тетради.
Пользуясь этим законом, мы можем рассчитать силу тока, зная напряжение и сопротивление, то есть, зная две величины мы всегда можем найти третью.
Задание 4. Начертите схему по рис.13.9 учебника, стр 391 в тетради.
Итак, ребята, между какими величинами устанавливает зависимость закон Ома?
между силой тока, напряжением и сопротивлением.
Как зависит сила тока от напряжения?
Прямо пропорционально.
Как зависит сила тока от сопротивления?
6. Закрепление материала
Динамическая пауза «Отгадать слова»
РЕМАП (единица физической величины) АМПЕР
ЛУНОК (единица физической величины) КУЛОН
РОЗОЛТИЯ (тело, которое сделано из диэлектрика) ИЗОЛЯТОР
НОРТКЕЛЭ (частица, обладающая самым маленьким зарядом в природе) ЭЛЕКТРОН
Рефлексия.
Ребята, что сегодня вы узнали на уроке?
Оцените свою деятельность на уроке
15-20 баллов — «4»
20-25 баллов – «5»

Закон
Ома и его вывод
ПОДВИЖНОСТЬ ЭЛЕКТРОНА И ТОК
Подвижность электрона (u _e) определяется как дрейфовая скорость электрона на единицу приложенного электрического поля.
u _e = скорость дрейфа / электрическое поле = V _d / E
Таким образом, V _d = u _e E
Единица измерения мобильности в системе СИ: м ² с ^-1 В ^-1 или мс ^-1 N ^-1 C
По соотношению скорости течения и скорости дрейфа (уже обсуждалось)
I = Анев _д (1)
Положив значение v _d в уравнение выше, мы получим
I = Aneu _e E
ЗАКОН ОМА
Заявление: — Закон Ома гласит, что ток (I), протекающий через проводник, прямо пропорционален разности потенциалов (V) на концах проводника, при условии, что физические условия проводников, такие как температура, механическое напряжение и т. Д.Поддерживаются постоянными, т.е. IαV
Или VαI или V = RI
или V / I = R = постоянная
Где R — сопротивление проводника. Это зависит от длины, формы и характера материала проводника. Разница между разностью потенциалов (V) и током (I) через проводник представляет собой прямую линию.
Вычисление по закону Ома:
Как скорость дрейфа равна определяется по V _d = eEt / m
Но электрическое поле на проводнике длиной l равно
.
E = об / л
Таким образом, V _d = e V / мл
Также I = Anev _d
Подставив значение v _d в уравнение I (уравнение 1 связи тока и скорости дрейфа), мы получим
I = Ane (эВ / мл) = (Ane ² / мл) V
Или V / I = ml / Ane ² = R
Где R — постоянная для данного проводника.Он известен как сопротивление проводника.
Таким образом, V = RI
Это закон Ома. 2 \ frac {\ tau} {m_e} σ = ne e2me τ
с nen_ene объемная плотность электронов проводимости, eee заряд электрона, mem_eme масса электрона и τ \ tauτ среднее свободное время электронов, представляющее, сколько в среднем электрон проводимости проходит до взаимодействия с проводником. .Также часто используют величину ρ = 1σ \ rho = \ frac {1} {\ sigma} ρ = σ1, удельное сопротивление .
Используя эту формулу, плотность тока электронов можно переписать в терминах средней скорости электронов, часто называемой дрейфовой скоростью :
J⃗ = −enev⃗ˉ. \ Vec {J} = -en_e \ bar {\ vec {v}}. J = −ene vˉ.
Для движения электронов в стержне микроскопический закон Ома может быть связан с макроскопическим законом Ома V = IRV = IRV = IR. Обратите внимание, что плотность тока — это ток на единицу площади J = IAJ = \ frac {I} {A} J = AI.Точно так же электрическое поле — это напряжение на единицу длины: E = VLE = \ frac {V} {L} E = LV. Комбинируя два, получаем
V = (LAσ) I.V = \ left (\ frac {L} {A \ sigma} \ right) I.V = (AσL) I.
В проводящем стержне с площадью поперечного сечения AAA и длиной LLL с проводимостью σ \ sigmaσ сопротивление, следовательно, определяется как
R = LAσ = ρLA.R = \ frac {L} {A \ sigma} = \ frac {\ rho L} {A} .R = AσL = AρL.
В сложных материалах, где проводимость изменяется по длине проводника, сопротивление определяется путем обработки всего вышеперечисленного как бесконечно малой величины и интегрирования.L \ frac {1} {xA} dx = \ frac {\ log (L)} {A}. \ _ \ SquareR = ∫1L xA1 dx = Alog (L). □
Медный провод с некоторым сопротивлением RRR. Затем проволоку сплющивают и растягивают, так что длина удваивается, а площадь поперечного сечения уменьшается в 14 раз без изменения удельного сопротивления. На какой коэффициент изменяется сопротивление провода?
Проволока из чистого германия с удельным сопротивлением ρ = 1.{-3} \: \ Omega \ cdot \ text {m} ρ = 1,2 × 10−3Ω⋅m и длиной 10 см10 \ text {cm} 10 см подключается к любому выводу 9 V9 \ text {V} 9 Аккумулятор V. Предположим, что общая масса проволоки составляет 20 г20 \ text {g} 20 г и что на один атом германия проводит только один электрон. Найдите скорость дрейфа электронов в проводе.
Величина плотности тока, указанная выше, составляет
.
J = enev, J = en_e v, J = ene v,
где vvv — скорость дрейфа. Необходимо вычислить две вещи: плотность nen_ene проводящих электронов и плотность тока JJJ.
Плотность тока определяется из
.
J = σE = VρL, J = \ sigma E = \ frac {V} {\ rho L}, J = σE = ρLV,
где LLL — указанная общая длина провода.
Число проводящих электронов можно вычислить из общего числа атомов германия, поскольку каждый атом обеспечивает только один проводящий электрон. Число атомов германия можно вычислить из общей массы: поскольку германий весит 72,3 г 72,3 \ text {g} 72,3 г на моль, их
20 г × 1 моль 72.{-5} \ text {m} / \ text {s}. \ end {выровнен} v = ene J = ρLene V = (1,2 · 10−3Ω⋅m) (10 см) (1,6 · 10−19 C) (4,59 · 1022 см − 3) 9 V = 1,02 · 10− 5 м / с.
Это очень низкая скорость! Большая часть скорости электрических сигналов происходит от распространения «дырок» в заряде через материалы, а не от реальных физических зарядов. □ _ \ квадрат □
0.{-3} 3 × 1029 м-3, найдите скорость дрейфа электронов проводимости в миллиметрах в секунду.
1 Закон Ома и его выводы 2 Скорость дрейфа по физике класса 12 CBSE
Совет Закон Ома объясняет взаимосвязь между разностью потенциалов и током. Мы должны найти выражение для этого отношения. Свободные электроны обладают дрейфовой скоростью, и мы также должны вывести связь между дрейфовой скоростью электронов и током.
Полный пошаговый ответ:
Джордж Саймон Ом установил связь между разностью потенциалов в проводнике и током, протекающим через проводник. Этот закон называется законом Ома.
Согласно закону Ома, при постоянной температуре ток, протекающий через проводник, будет прямо пропорционален разности потенциалов между концами проводника.
Примем разность потенциалов равной $ V $
Пусть ток через проводник будет, $ I $
Согласно закону Ома, $ V $ и $ I $ прямо пропорциональны
I.е.
$ V \ propto I $
Знак пропорциональности можно заменить на знак равенства, умножив его на коэффициент пропорциональности.
Следовательно, мы можем написать,
$ V = IR $
Где константа пропорциональности $ R $ известна как сопротивление проводника. Единица сопротивления — Ом $ \ left (\ Omega \ right) $
Скорость дрейфа электронов.
Средняя скорость, с которой свободные электроны дрейфуют под действием электрического поля, называется дрейфовой скоростью.
Скорость дрейфа может быть обозначена как $ {v_d} $.
Связь между током и скоростью дрейфа может быть получена следующим образом:
Рассмотрим проводник длиной $ l $ и площадью поперечного сечения $ A $. Пусть количество свободных электронов в единице объема равно $ n $. $ {V_d} $ — скорость дрейфа.
Ток, протекающий по проводнику за секунду, можно записать как,
$ I = \ dfrac {q} {t} $
Пусть $ N $ будет полным числом электронов, а $ e $ — зарядом электрона. .
Тогда мы можем записать общий заряд $ q $ как $ q = Ne $
Тогда $ I = \ dfrac {{Ne}} {t} $
Объем проводника можно записать как,
$ V = Al $
Где $ A $ — площадь проводника, а $ l $ — длина проводника.
Количество электронов в единице объема будет,
$ n = \ dfrac {N} {{Al}} $
Отсюда мы можем написать,
$ N = nAl $
Подставив это значение в уравнение тока, получаем
$ I = \ dfrac {{nAle}} {t} $
Пусть количество зарядов, пересекающих любое поперечное сечение за одну секунду, будет электронами, содержащимися на длине, равной дрейфовой скорости проводника.
, т.е.
$ l = {v_d} t $
Подставляя это значение в приведенное выше уравнение для тока, мы получаем
$ I = \ dfrac {{nA {v_d} te}} {t} = nAe {v_d} $
Примечание
Закон Ома остается в силе только тогда, когда ток, протекающий по проводнику, является постоянным.По закону Ома график, соединяющий напряжение и ток, будет прямой линией. Подвижность можно определить как скорость дрейфа на единицу электрического поля. Это положительная величина.
Основы закона Ома — Inst Tools
В 1827 году немецкий физик Джордж Ом опубликовал брошюру под названием «Гальваническая цепь, исследованная математически». Он содержал одну из первых попыток измерить токи и напряжения, а также описать и связать их математически.Одним из результатов было утверждение фундаментальной взаимосвязи, которую мы теперь называем законом Ома.
Рассмотрим однородный цилиндр из проводящего материала, к которому подключено напряжение. Напряжение вызовет протекание заряда, т. Е. Ток:
Ом обнаружил, что во многих проводящих материалах, например в металле, ток всегда пропорционален напряжению. Поскольку напряжение и ток прямо пропорциональны, существует константа пропорциональности R , называемая сопротивлением , такая, что:
Это закон Ома.Единица сопротивления (вольт на ампер) обозначается как Ом, и обозначается заглавной греческой буквой омега, Ом.
Мы называем конструкцию, в которой соблюдается закон Ома, резистором .
Идеальное соотношение резисторов — прямая линия , проходящая через начало координат :
Несмотря на то, что сопротивление определяется как R = v / i , следует отметить, что R является чисто геометрическим свойством и зависит только от формы проводника и материала, используемого в конструкции.Например, для равномерного резистора можно показать, что сопротивление определяется как:
, где l — длина резистора, а A — площадь поперечного сечения. Удельное сопротивление , , r, является постоянной величиной проводящего материала, используемого для изготовления резистора.
Обозначение схемы резистора показано ниже, вместе с направлением тока и полярностью напряжения, которые делают закон Ома алгебраически правильным:
Пример
Рассмотрим схему, показанную ниже.
Напряжение на резисторе 1 кОм по определению идеального источника напряжения равно
v ( t ) = 10 В. Таким образом, по закону Ома получаем:
i1 = v / R = 10/1000 = 0,01 A = 10 мА
i2 = — v / R = -10/1000 = -0,01 A = -10 мА
Обратите внимание, что i 2 = — i 1, как и ожидалось
Закон Ома и классическая физика
Закон Ома и классическая физика
Для этого базового модуля мы просто возьмите подходящий модуль из гиперперсонал « Introduction to Materials Science II » с это самая новая и обновленная версия.
Модуль в том виде, в котором он существовал в сентябре 2001 г. воспроизведено ниже.
Закон Ома и классический Физика
В этом подразделе мы рассмотрим классический трактовка движения электронов в электрическом поле. Это прямой продолжение подраздел 1.1.3 в backbone II (гиперкрипта «Введение в материалы»). Наука II ») и снова более точно соответствует самой лекции.
В этом предыдущем подразделе мы получили самые основные материальная формулировка закона Ома.
s = q · n · m
Для однородных и изотропных материалов (например, поликристаллических металлов или монокристалла кубических полупроводников), концентрация носителей n и их подвижность м не зависят по координатам — они имеют одинаковое значение везде в материале и удельная проводимость с является скаляром.
В целом у нас может быть более одного типа перевозчиков. (это обычная ситуация в полупроводниках), и n и m все еще могут быть более или менее сложными функциями температура T , местная напряженность поля E _loc в результате приложенного внешнего напряжения детальная структура материала (например, дефекты решетки) и т. д. на.
Мы увидим, что эти сложности являются сутью современные электронные материалы, особенно полупроводники, но для того, чтобы облегчить жизнь, теперь ограничимся особым классом омических материалы. У нас есть видимый до этого требуется, чтобы n и m не зависели от местной напряженности поля. Мы еще может иметь температурную зависимость с ; в конце концов, даже коммерческие омические резисторы демонстрируют более или менее выраженный температурная зависимость, которая примерно линейно возрастает с ростом T.
Короче говоря, мы обрабатываем металлы, для которых характерны постоянная плотность одного вида носителей (= электронов) порядка 1 … 3 электронов на атом в металле.
Основные уравнения и природа «Сила трения»
Мы считаем электроны в металле «свободные», т.е. могут беспрепятственно двигаться в любом направлении.
Электрическое поле E затем создает силу F = -e · E на любом данном электроне и, таким образом, ускоряет электроны в направлении поля (точнее, противоположном полю направление, потому что вектор поля указывает от + до -, тогда как электрон перемещается с — на +).
В летающий рой аналогии, электрическое поле будет соответствовать постоянному воздушному потоку — некоторые ветер — который перемещает рой с постоянной скоростью дрейфа.
Основная механика дает для отдельной частицы с импульсом p
F = d p / d t = m · dv / d t с p = импульс электрона.
Обратите внимание, что p не обязательно должно быть нулевым при переключении поля. на.
Если бы это было все, то скорость данного электрон приобретал бы все возрастающую компоненту в направлении поля и со временем приблизиться к бесконечности. Очевидно, это невозможно, поэтому мы должны ввести механизм, который разрушает неограниченное увеличение v
В классической механике это делается путем введения сила трения F _fr = k _fr · v где k _fr — некоторая постоянная трения.Но это пока математически достаточен, лишен какого-либо физического смысла в отношении движущиеся электроны. Поэтому нам нужно искать другой подход.
Лучший способ понять это — предположить, что электрон, летящий с возрастающей скоростью, в своем время от времени, что изменит его импульс (и, следовательно, величину и направление v ), а также его кинетическая энергия 1/2 · м · об. ² .
Другими словами, мы рассматриваем столкновения с другими частицы, в которых сохраняется полная энергия и импульс частиц, но отдельные частицы теряют «память» о своей скорости перед столкновением и начинает с нового импульса после каждого столкновения.
Какие «партнеры» при коллизиях электрона, или выражаясь стандартным языком, каковы механизмы рассеяния ? Есть несколько возможностей:
Другие электроны .Пока такое случается, в большинстве случаев это не самый важный процесс.
Дефекты , например иностранный атомы, точечные дефекты или дислокации. Это более важное рассеяние механизм и, более того, механизм, с помощью которого электрон может передавать свои излишки энергия (полученная за счет ускорения в электрическом поле) решетки это означает, что материал нагревается
Фононы , т.е.е. «локализованный» колебания решетки, распространяющиеся через кристалл. В квантовой механике При рассмотрении колебаний решетки можно показать, что эти колебания, которые содержат тепловую энергию кристалла, проявляют типичные свойства (квантовые) частицы: у них есть импульс и энергия, равная h · n ( h = постоянная Планка, n = частота вибрации), и взаимодействие электрона с колебанием решетки как столкновение с phonon дает правильные результаты. Это самый важный механизм рассеяния .
Было бы далеко от истины предполагать, что только разлетаются ускоренные электроны; рассеяние происходит постоянно. Если электроны ускоряются в электрическом поле и, таким образом, набирают энергию, рассеяние — это способ передать эту избыточную энергию решетке, которая затем нагреется. Как правило, рассеяние — это механизм достижения теплового равновесия и равнораспределение энергии кристалла.
Давайте посмотрим на некоторые рисунки, иллюстрирующие процессы рассеяния.
Здесь показана величина скорости электрона в x и -x направление без внешнего поля. В электрон движется с постоянной скоростью, пока не рассеется, а затем продолжает движение. с новой скоростью.
Процессы рассеяния, хотя и непредсказуемые, как одиночные событий, должно привести к средней характеристике для материал и его условия.
Тогда как < v > = 0 , < v > имеет конечное значение и x > = — -x > . Это немного сложно, поскольку мы пишем формулы здесь мы не можем легко различить между векторами и скалярами: здесь, чтобы подчеркнуть точку, v — это вектор , а v — скаляр (его величина).
От классический Из термодинамики известно, что электронный газ находится в тепловом равновесии с окружающая среда обладает энергией E _кин = (1/2) k T на частицу и степень свободы с k = постоянная Больцмана и T = абсолютная температура.
Мы пишем энергии E пурпурным цветом , чтобы избежать путаницы с электрическими полями E .
Три степени свободы — это скорости в x -, y — и z -направление, поэтому мы должны иметь
E _{кин, x} = 1 / 2m x > ² = 1/2 k T или
x > = (k T / m) ^1/2 .
Аналогично для полной энергии
E _кин = 1 / 2m x > ² + 1 / 2м y > ² + 1 / 2m z > ² = 1 / 2m ² = 1 / 2mv ₀ ² ,
имеем
E _кин = 1 / 2m ² = 1 / 2mv ₀ ² = 3/2 к т
с v ₀ = .
Теперь давайте вращаемся в электрическом поле Е . Он будет ускорять электроны между столкновениями; их скорость увеличивается линейно.
На нашей диаграмме сверху это выглядит так:
Здесь у нас есть электрическое поле в направлении x .Между столкновениями электрон набирает скорость в направлении + x . с постоянной скоростью.
Средняя скорость в + x направлениях, + x > , теперь больше, чем в -x направление, -x > . Однако для реальных электронов разница очень небольшая; рисунок очень преувеличен.
Скорость дрейфа содержится в разности + x > — -x > ; это полностью описывается увеличением скорости между столкновениями.Таким образом, мы можем символически пренебречь скоростью сразу после столкновения, потому что она в среднем равна нулю в любом случае, и просто нанесите на график прирост скорости в упрощенная картинка; всегда начиная с нуля после столкновения.
Теперь картина выглядит довольно простой; но помните, что это содержит некоторые не так простое усреднение.
Здесь стоит отметить, что мы можем определить новое среднее значение : Среднее время между столкновения, или более условно, среднее время t для достижения скорости дрейфа v _D на упрощенной схеме.
Это легче всего увидеть, еще раз упростив диаграмму рассеяния : Мы просто используйте всего за один раз — в среднем — за время, которое проходит между событиями рассеяния и получением.
Это стандарт диаграмма , иллюстрирующая рассеяние электронов в кристалле обычно встречается в учебниках; в определение времени рассеяния т включено
Хотя эта диаграмма не ошибочна, это очень абстрактный рендеринг основных процессов после нескольких усреднений процедуры.Только из этой диаграммы нельзя сделать никаких выводов относительно средние скорости электронов без электрического поля!
Используя концепцию рассеяния, теперь мы можем ввести два новых (связанных) параметра материала:
Среднее значение (рассеяние) время t между двумя столкновениями как определенное ранее и непосредственно связанное количество:
означает бесплатный путь L между столкновениями; я.е. расстояние, пройденное электрон (в среднем), прежде чем он столкнется с чем-то еще и изменит свое импульс. Имеем
L = 2t · (v ₀ + v _D) .
Обратите внимание, что в уравнение входит v ₀ !
Использование т в качестве нового параметра, мы можем переписать уравнения механики:
dv / d t можно записать как Dv / D t = v _D / t
потому что изменение скорости за время т это всего лишь v _D .Отсюда получаем
v _D / t = — E · e / m , или
v _D = — ( E · e · t) / m .
Вставка этого уравнения для v _D в старом определении нынешнего плотность, j = — n · e · v _D дает
j = — E · ( n · e ² т) / м: = s · E ,
и таким образом
s = ( n · e ² t) / м
Это классическая формула проводимости классического «электронного газа» материал; я.е. металлы. Мы еще не знаем t _class , но мы можем изменить уравнение вокруг и с его помощью вычислить порядок величины т _класс , так как у нас знать порядок величины электропроводности металлов. В результат:
т _класс = _ок. (10 ^-13 …. 10 ^-15) сек
«Очевидно» (как утверждается во многих учебники), это тоже значение small и, следовательно, классический подход должен быть неправильным.Но разве это действительно слишком маленький? Как можно сказать, не зная больше об электронах в металлах? Ну ты не можешь . Итак, начнем вместо этого посмотрите на длину свободного пробега L .
Имеем
t = L / (2 (v ₀ + v _D)) или L = 2t (v ₀ + v _D) и
v ₀ ² = (3kT / m) ^1/2
.
Это дает нам значение v ₀ = _ок. 10 ⁵ м / с при комнатной температуре! Теперь нам понадобится v _D , и это мы можем оценить из уравнения v _D / t = — E · e / m с учетом выше:
v _D = — E · т · э / м = _ок. 1 мм / сек
если мы воспользуемся значением т , продиктованным измеренные электропроводности.Это намного меньше, чем v ₀ !
Средняя длина свободного пробега между столкновениями, таким образом, равно
L = 2t (v ₀ + v _D) = _ок. 2tv ₀ = _ок. (10 ¹ ..10 ^-1) нм
и это уж точно слишком мало! .
Почему длина свободного пробега в порядке размера? атома слишком мало? Что ж, подумайте о механизмах рассеивания.Расстояние между дефектами, конечно, намного больше, а сам фонон «побольше» тоже. Кроме того, подумайте, что происходит при температурах ниже комнатные температуры: л стало бы еще меньше — как-то это без разницы.
Тратить больше не окупается время на это. Как ни крути, какие хитрые устройства вы ввести, чтобы сделать приближения лучше (и физики очень постарались трудно!), вы не сможете решить проблему: средняя длина свободного пробега равна никогда даже не приближаясь к тому, кем они должны быть, и к выводу — может быть неохотно, но неизбежно — должно быть:
Нет способа описать
электропроводность (в металлах)
с классической физикой.
С рамой
2.2.1 Внутренние свойства в равновесии
2.2.2 Легирование и плотность носителей
2.2.3 Срок службы и длина диффузии
2.3.2 Квазиэнергии Ферми
2.3.5 Пересмотр перекрестка
5.3.2 Изотипические переходы, модуляционное допирование и квантовые эффекты
8.1.2 Основные трудоемкие процессы
© Х.Föll (Semiconductors — Script)
4.2: Сопротивление и закон Ома
Когда на электродах в электролитической ячейке поддерживается разность потенциалов, через электролит протекает ток. Этот ток переносится положительными ионами, движущимися от положительного электрода к отрицательному, а также одновременно отрицательными ионами, движущимися от отрицательного электрода к положительному. Обычное направление потока электричества — это направление, в котором движутся положительные заряды.То есть электричество течет от положительного электрода к отрицательному. Таким образом, положительные ионы движутся в том же направлении, что и обычное направление потока электричества, а отрицательные ионы движутся в противоположном направлении.
Когда ток течет по металлу , ток переносится исключительно посредством отрицательно заряженных электронов, и поэтому ток переносится исключительно посредством частиц, которые движутся в направлении, противоположном обычному потоку электричества.Таким образом, «электричество» течет из точки с высоким потенциалом в точку с низким потенциалом; электроны перемещаются из точки с низким потенциалом в точку с более высоким потенциалом.
Когда на резистор подается разность потенциалов \ (V \), отношение разности потенциалов на резисторе к току \ (I \), протекающему через него, называется сопротивлением , \ (R \), резистора. Таким образом,
\ [V = IR. \ Label {4.2.1} \]
Это уравнение, которое определяет сопротивление, на первый взгляд кажется, что ток через резистор пропорционален разности потенциалов на нем , и это закон Ома. Уравнение \ ref {4.2.1}, однако, подразумевает простую пропорциональность между \ (V \) и \ (I \), только если \ (R \) постоянна и не зависит от \ (I \) или \ (V \). На практике, когда через резистор протекает ток, резистор нагревается, и его сопротивление увеличивается — и тогда \ (V \) и \ (I \) больше не пропорциональны друг другу. Таким образом, можно было бы сформулировать закон Ома в форме, что ток через резистор пропорционален разности потенциалов на нем, при условии, что температура поддерживается постоянной .Тем не менее, существуют вещества (и различные электронные устройства), в которых сопротивление не зависит от приложенной разности потенциалов даже при постоянной температуре. Таким образом, лучше рассматривать уравнение \ ref {4.2.1} как определение сопротивления, а не как фундаментальный закон, при этом признавая, что оно является хорошим описанием поведения большинства реальных веществ в самых разных условиях, если только поскольку температура поддерживается постоянной.
Определение: сопротивление и проводимость
Если через резистор протекает ток в один ампер при разности потенциалов в один вольт, сопротивление будет равно одному Ом (\ (\ Omega \)).{-2}. \]
Сопротивление равно , проводимость , \ (G \) . Таким образом, \ (I = GV \). Обычной неформальной практикой является выражение проводимости в «mhos», где «mho» — это ом ^-1. Однако официальной единицей проводимости в системе СИ является сименс (S), то же самое, что и «mho», а именно A V ^-1.
Сопротивление резистора пропорционально его длине \ (l \) и обратно пропорционально его площади поперечного сечения A :
\ [R = \ dfrac {\ rho l} {A} \ label {4.2.2} \]
Константа пропорциональности \ (\ rho \) называется сопротивлением материала, из которого изготовлен резистор. Его размеры: ML ³ T ^-1 Q ^-2, а его единица измерения в системе СИ — омметр или \ (\ Omega \) м.
Сопротивление обратно пропорционально проводимости , \ (\ sigma \). Его размеры: M ^-1 L ^-3 TQ ², а его единица СИ — сименс на метр, См ^-1.
Для тех, кто любит собирать малоизвестные единицы, есть забавная единица, с которой я когда-то столкнулся, а именно единица удельного сопротивления поверхности.Один касается сопротивления тонкого листа проводящего материала, такого как, например, тонкая металлическая пленка, нанесенная на стекло. Сопротивление некоторой прямоугольной области этого прямоугольника пропорционально длине l прямоугольника и обратно пропорционально его ширине w :
.
\ [R = \ dfrac {\ rho l} {w} \ nonumber \]
Таким образом, сопротивление зависит от отношения \ (l / w \), то есть от формы прямоугольника, а не от его размера. Таким образом, сопротивление прямоугольника 2 мм \ (\ times \) 3 мм такое же, как у прямоугольника 2 м \ (\ times \) 3 м, но сильно отличается от сопротивления 3 мм \ (\ times \) Прямоугольник 2 мм.Поверхностное сопротивление определяется как сопротивление прямоугольника единичной длины и ширины (т. Е. Квадрата) — и не имеет значения, каков размер квадрата. Таким образом, единицы удельного поверхностного сопротивления — Ом на квадрат. (Конец предложения!)
Что касается их удельного сопротивления, обнаружено, что вещества можно разделить на металлов , непроводников (изоляторы) и полупроводников . Металлы имеют довольно низкие удельные сопротивления, порядка 10 ^-8 \ (\ Omega \) м.Например:
Серебро: 1,6 \ (\ times \) 10 ^-8 \ (\ Omega \) м
Медь: 1,7 \ (\ раз \) 10 ^-8
Алюминий: 2,8 \ (\ раз \) 10 ^-8
Вольфрам: 5,5 \ (\ раз \) 10 ^-8
Утюг: 10 \ (\ times \) 10 ^-8
Непроводники обычно имеют удельное сопротивление порядка от 10 ¹⁴ до 10 ¹⁶ \ (\ Omega \) м или более. То есть для большинства практических целей и условий они вообще не проводят легко измеримое электричество.
Полупроводники имеют промежуточное удельное сопротивление, например
Углерод: 1500 \ (\ times \) 10 ^-8 \ (\ Omega \) м
Германий: 4,5 \ (\ times \) 10 ^-1
Кремний 6,4 \ (\ раз \) 10 ⁺²
Существует еще один способ, помимо уравнения 4.2.1, который обычно используется для выражения закона Ома. См. Рисунок IV.1.

\ (\ text {РИСУНОК IV.1} \)
У нас есть металлический стержень длиной \ (l \), площадью поперечного сечения A, , электропроводностью \ (\ sigma \), поэтому его сопротивление составляет l / (\ (\ sigma \) A ).Мы зажимаем его между двумя точками, между которыми существует разность потенциалов В , и, следовательно, величина электрического поля в металле равна \ (E = V / l \). Таким образом, уравнение 4.2.1 (закон Ома) принимает вид \ (El = Il / (\ sigma A) \). Теперь введите \ (J = I / A \) как плотность тока (ампер на квадратный метр). Их закон Ома принимает вид \ (J = \ sigma E \). Обычно это записывается в векторной форме, поскольку ток и поле являются векторами, так что закон Ома записывается как
\ [\ textbf {J} = \ sigma \ textbf {E} \ label {4.2.3} \]
состояние и вывод класса закона Ома 10 Архив
Загрузите лучшее приложение для подготовки к экзаменам в Индии
Класс 9-10, JEE и NEET
Скачать приложение eSaral Эй, вы хотите узнать о том, как сформулировать и объяснить закон Ома? Если да. Тогда продолжайте читать.
Закон Ома:
Если физическое состояние, то есть температура, природа материала и размеры проводника, остаются неизменными, то отношение разности потенциалов, приложенной к его концам, к току, протекающему по нему, остается постоянным.{2} 9 15 10 $
Вещества, подчиняющиеся закону Ома, называются омическими или линейными проводниками. Сопротивление таких проводников не зависит от величины и полярности приложенных разностей потенциалов. Здесь график между I и V представляет собой прямую линию, проходящую через начало координат. Обратная величина наклона прямой дает сопротивление $ R = \ frac {V} {I} = \ frac {1} {\ tan \ theta} $ = constant например серебро, медь, ртуть, углерод, слюда и др.

Вещества, не подчиняющиеся закону Ома, называются неомными или нелинейными проводниками.Кривая ВАХ не является прямой линией. p n диод, транзисторы, термоэмиссионные клапаны, выпрямители и т. д.

V = IR определяет сопротивление и, следовательно, применимо ко всем омическим и неомическим проводникам. Если R константа или $ V \ propto I $, то оно представляет закон Ома.

Отношение $ R = \ frac {V} {I} $ — это макроскопическая форма , а $ \ rho = \ frac {E} {J} $ — микроскопическая форма закона Ома.

Сопротивление проводника зависит от температуры, типа материала, длины и площади поперечного сечения.{\ circ} \ mathrm {C} $ so $ \ mathrm {R} = \ mathrm {R} _ {0} \ left (1+ \ frac {\ Delta \ theta} {273} \ right) $$ = \ mathrm {R} _ {0} \ left (\ frac {273+ \ Delta \ theta} {273} \ right) $
$ = \ mathrm {R} _ {0} \ frac {\ mathrm {T}} {273} $
так $ R \ propto T $
т.е. сопротивление чистого металлического проводника пропорционально его абсолютной температуре.
$ R \ propto L $ и $ \ mathrm {R} \ propto \ frac {1} {\ mathrm {~ A}} $, поэтому $ R \ propto \ frac {L} {A} $ или
$ R = \ rho \ frac {L} {A} $
, где $ \ rho $ называется удельным сопротивлением или удельным сопротивлением.
Относительное изменение сопротивления без изменения объема или массы:
(a) При небольшом изменении длины $ (\ leq 5 \%) $ дробное изменение в $ \ mathrm {R} $ равно $ \ frac {\ Delta R} {R} = \ frac {2 \ Delta L} {L} $
(b) Когда изменение радиуса небольшое $ (\ leq 5 \%) $, относительное изменение R равно
$ \ frac {\ Delta R} {R} = \ frac {-4 \ Delta r} {r} $
(c) Когда изменение площади небольшое $ (\ leq 5 \%) $, относительное изменение R равно
$ \ frac {\ Delta \ mathrm {R}} {\ mathrm {R}} = \ frac {-2 \ Delta \ mathrm {A}} {\ mathrm {A}} $
Важные сведения об удельном сопротивлении:
В микроскопических величинах $ E = \ rho J $, поэтому удельное сопротивление численно равно отношению величины электрического поля к плотности тока.{2} \ tau} {m} = $ ne $ \ mu $

Удельное сопротивление не зависит от формы и размера тела и зависит от природы материала тела. Удельное сопротивление — это свойство материала, а сопротивление — свойство объекта.

Температурная зависимость удельного сопротивления определяется соотношением $ \ rho = \ rho_ {0} (1+ \ propto \ Delta \ theta) $, где $ \ propto $ — температурный коэффициент удельного сопротивления, а $ \ Delta \ theta $ — изменение температуры. Для металлов $ \ alpha $ положительно, поэтому удельное сопротивление увеличивается с температурой, а для неметаллов $ \ alpha $ отрицательно, поэтому удельное сопротивление уменьшается с температурой.{\ circ} \ mathrm {C} $.

Плавкая проволока изготовлена из сплава олово-свинец , так как он имеет низкую температуру плавления и низкое удельное сопротивление. Предохранитель используется последовательно и плавится, чтобы вызвать разрыв цепи, когда ток превышает безопасный предел.

Сопротивления ящиков сопротивления изготовлены из манганина или константана , потому что они имеют умеренное удельное сопротивление и очень малый температурный коэффициент сопротивления. Удельное сопротивление почти не зависит от температуры.

Нить накала колбы состоит из вольфрама , потому что он имеет низкое удельное сопротивление, высокую температуру плавления 3300 K и излучает свет при 2400 K. Колба заполнена инертным газом, поскольку при высокой температуре он реагирует с воздухом, образующим оксид.

Соединительные провода изготовлены из меди , поскольку она имеет низкое сопротивление и удельное сопротивление.

Итак, это все из этой статьи. Надеюсь, вы получили представление о том, как сформулировать и объяснить закон Ома.Если вы нашли эту статью информативной, поделитесь ею с друзьями.

Закон Ома для полной цепи | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Запишите формулу закона ома для полной цепи.

Шпаргалка закон ома, что такое ток

Реферат на тему -закон ома на полной цепи википедия

Закон ома при параллельном соединении источников

Реферат на тему закон ома на полной цепи

Как определяется работа сторонних сил?

Сформулируйте закон Ома для полной цепи.

Запишите формулу закона Ома для полной цепи.

Что такое ток короткого замыкания?

Как можно опре­делить ток короткого замыкания?

Как связаны между собой максимально возможное напряжение на полюсах источника и электродвижущая сила источника?

Закон Ома для полной цепи | Полезные статьи

Вывод закона Ома для полного участка цепи.

Закон Ома для переменного тока.

Основы классической теории электропроводности металлов

1.

3. 2.10. Природа носителей тока в металлах.

5. 2.11. Основные положения классической электронной теории проводимости металлов Друде – Лоренца.

7. 2.12. Вывод законов Ома, Джоуля-Ленца и Видемана-Франца на основе теории Друде-Лоренца.

10. 2.13. Затруднения классической теории электропроводности металлов. Сверхпроводимость металлов. Открытие высокотемпературной сверхпроводи

Откуда берется закон Ома | Великий Шизик

Силы, действующие на электрон

Подвижность электронов

Вывод закона Ома

Изучение закона ома для полной цепи вывод. Лабораторная работа

Описание стенда «Законы постоянного тока»

Простейшая схема с источником ЭДС

Принцип пропорциональности

Особенности сопротивлений в источниках питания

Видео

Урок 30. Лабораторная работа № 07. Изучение закона Ома для участка цепи.

Лабораторная работа. Изучение закона Ома для участка цепи.

Ома и его вывод

1 Закон Ома и его выводы 2 Скорость дрейфа по физике класса 12 CBSE

Основы закона Ома — Inst Tools

Закон Ома и классическая физика

4.2: Сопротивление и закон Ома

состояние и вывод класса закона Ома 10 Архив

Закон Ома:

Важные сведения об удельном сопротивлении:

Добавить комментарий Отменить ответ

Как можно определить ток короткого замыкания?