24.Вывод закона Ома по электронной теории.
Пусть в металлическом проводнике существует электрическое поле напряженностью Е=const. Co стороны поля заряд е испытывает действие силы F=eE и приобретает ускорение а=F/m=еЕ/т. Таким образом, во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость
vmax= еE<t>.
где <t>—среднее время между двумя последовательными соударениями электрона с ионами решетки.
Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в поле энергию, поэтому скорость его упорядоченного движения становится равной нулю. Следовательно, средняя скорость направленного движения электрона
<v>=(vmax+0)/2=eE<t>/(2m). (103.1)
Классическая теория металлов не учитывает распределения электронов по скоростям, поэтому среднее время <t> свободного пробега определяется средней длиной свободного пробега <l> и средней скоростью движения электронов относительно кристаллической решетки проводника, равной <u>+(v) (<u>—средняя скорость теплового движения электронов). В §102 было показано, что (v)<< <u>, поэтому
<t>=<l>/<u>.
Подставив значение <t> в формулу (103.1), получим
<v>=eE<l>/(2m<u>).
Плотность тока в металлическом проводнике, по (96.1),

откуда видно, что плотность тока пропорциональна напряженности поля,
т. е. получили закон Ома в дифференциальной форме (ср. с (98.4)). Коэффициент пропорциональности между j и Е есть не что иное, как удельная проводимость материала

которая тем больше, чем больше концентрация свободных электронов и средняя длина их свободного пробега.
25. Вывод закона Джоуля – Ленца по электронной теории.
К концу свободного пробега электрон под действием поля приобретает дополнительную кинетическую энергию

При соударении электрона с ионом эта энергия полностью передается решетке и идет на увеличение внутренней энергии металла, т. е. на его нагревание.
За единицу времени электрон испытывает с узлами решетки в среднем <z> столкновений:
<z>=<
Если n — концентрация электронов, то в единицу времени происходит n<z> столкновений и решетке передается энергия
w=n<z><Eк>, (103.5)
которая идет на нагревание проводника. Подставив (103.3) и (103.4) в (103.5), получим таким образом энергию, передаваемую решетке в единице объема проводника за единицу времени,

Величина w называется удельной тепловой мощностью тока (см. §99). Коэффициент пропорциональности между
26.Закон Видемана-Франца. Связь между электро и теплопроводностью металлов и ее объяснение электронной теорией.
Закон Видемана — Франца. Металлы обладают как большой электропроводностью, так и высокой теплопроводностью. Это объясняется тем, что носителями тока и теплоты в металлах являются одни и те же частицы — свободные электроны, которые, перемещаясь в металле, переносят не только электрический заряд, но и присущую им энергию хаотического теплового движения, т. е. осуществляют перенос теплоты.
Видеманом и Францем в 1853 г. экспериментально установлен закон, согласно которому отношение теплопроводности
/=T,
где — постоянная, не зависящая от рода металла.
Элементарная классическая теория электропроводности металлов позволила найти значение : =3(k/e)2, где k — постоянная Больцмана. Это значение хорошо согласуется с опытными данными. Однако, как оказалось впоследствии, это согласие теоретического значения с опытным случайно. Лоренц, применив к электронному газу статистику Максвелла — Больцмана, учтя тем самым распределение электронов по скоростям, получил
Таким образом, классическая теория электропроводности металлов объяснила законы Ома и Джоуля — Ленца, а также дала качественное объяснение закона Видемана — Франца. Однако она помимо рассмотренных противоречий в законе Видемана — Франца столкнулась еще с рядом трудностей при объяснении различных опытных данных. Температурная зависимость сопротивления. Из формулы удельной проводимости (103.2) следует, что сопротивление металлов, т. е. величина, обратно пропорциональная , должна возрастать пропорционально T (в (103.2)
Оценка средней длины свободного пробега электронов в металлах. Чтобы по формуле (103.2) получить , совпадающие с опытными значениями, надо принимать <l> значительно больше истинных, иными словами, предполагать, что электрон проходит без соударений с ионами решетки сотни междоузельных расстояний, что не согласуется с теорией Друде — Лоренца.
Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость диэлектриков, у которых нет свободных электронов. Согласно закону Дюлонга и Пти (см. §73), теплоемкость одноатомного кристалла равна 3R. Учтем, что теплоемкость одноатомного электронного газа равна 3/2R. Тогда атомная теплоемкость металлов должна быть близка к 4,5R. Однако опыт доказывает, что она равна 3R, т. е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классической электронной теорией.
Указанные расхождения теории с опытом можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла — Больцмана, а квантовой статистикой. Поэтому объяснить затруднения элементарной классической теории электропроводности металлов можно лишь квантовой теорией, которая будет рассмотрена в дальнейшем. Надо, однако, отметить, что классическая электронная теория не утратила своего значения и до настоящего времени, так как во многих случаях (например, при малой концентрации электронов проводимости и высокой температуре) она дает правильные качественные результаты и является по сравнению с квантовой теорией простой и наглядной.
18.2. Вывод закона Ома в дифференциальной форме в классической электронной теории
Друде считал, что сразу после очередного соударения электрона с ионом кристаллической решетки скорость упорядоченного движения электрона равна нулю. Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение равное

и к концу пробега скорость упорядоченного движения достигнет значения
| (18.2) |
где t
— среднее время между двумя последовательными
соударениями электрона с ионами решетки.
Друде не учитывал распределение
электронов по скоростям и приписывал
всем электронам одинаковое значение
средней скорости 
 ,
где
,
где 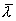 —
среднее значение длины свободного
пробега,
—
среднее значение длины свободного
пробега,  —
скорость теплового движения электронов.
Подставим это значение t в формулу (18.2)
—
скорость теплового движения электронов.
Подставим это значение t в формулу (18.2) 
Скорость изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального

Подставив это выражение в

получим

Плотность
тока оказалась пропорциональной
напряженности поля. Следовательно, мы
получили закон Ома. Согласно  коэффициент
пропорциональности между j и Е представляет
собой проводимость
коэффициент
пропорциональности между j и Е представляет
собой проводимость
| (18.3) |
Если бы электроны не сталкивались с ионами решетки, длина свободного пробега, а, следовательно, и проводимость были бы бесконечно велики. Таким образом, электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами.
18.3. Вывод закона Джоуля-Ленца в дифференциальной форме в классической теории электропроводности
К концу
свободного пробега электрон приобретает
скорость  ,
и, следовательно, дополнительную
кинетическую энергию, средняя величина
которой
,
и, следовательно, дополнительную
кинетическую энергию, средняя величина
которой

Столкнувшись
с ионом, электрон по предположению
полностью теряет приобретенную им за
время пробега скорость, и передает
энергию кристаллической решетке. Эта
энергия идет на увеличение внутренней
энергии металла, проявляющееся в его
нагревании. Каждый электрон претерпевает
за секунду в среднем 1/t соударений,
сообщая всякий раз решетке энергию  .
Следовательно, в единице объема за
единицу времени должно выделяться тепло
.
Следовательно, в единице объема за
единицу времени должно выделяться тепло

где n
— число электронов проводимости в единице
объема. Величина  есть
не что иное, как удельная мощность тока.
Множитель при
есть
не что иное, как удельная мощность тока.
Множитель при  совпадает
со значением
совпадает
со значением  (18.3)
для закона Ома. Таким образом. Мы пришли
к выражению закона Джоуля-Ленца в
дифференциальной форме.
(18.3)
для закона Ома. Таким образом. Мы пришли
к выражению закона Джоуля-Ленца в
дифференциальной форме.

18.4. Связь между теплопроводностью и электропроводностью металлов (закон Видемана-Франца)
Из опыта известно, что наряду с высокой электропроводностью металлы отличаются также большой теплопроводностью. Видеман и Франц установили в 1853 г. эмпирический закон, согласно которому отношение коэффициента теплопроводности к коэффициенту электропроводности для всех металлов приблизительно одинаково и изменяется пропорционально абсолютной температуре. Способностью проводить тепло обладают и неметаллические кристаллы. Однако теплопроводность металлов значительно превосходит теплопроводность диэлектриков. Из этого можно заключить, что теплопередача в металлах осуществляется в основном не кристаллической решеткой, а электронами. Рассматривая электроны как одноатомный газ, для коэффициента теплопроводности можно заимствовать выражение кинетической теории газа

где  —
плотность газа;
—
плотность газа; 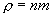 .
.
Тогда
| (18.4) |
Удельная теплоемкость одноатомного газа равна

Подставляя эти значения в выражение (18.4), получим
| (18.5) |
Разделив (18.5) на (18.3), имеем

Произведя
замену  приходим
к соотношению
приходим
к соотношению
| (18.6) |
которое
выражает закон Видемана-Франца, При
T=300°К для отношения получается значение  ,
очень хорошо согласующееся с
экспериментальными данными.
,
очень хорошо согласующееся с
экспериментальными данными.
5.11. Вывод закона Ома
16
Постоянный ток Н. Ф. Шемяков
___________________________________________________________________________________________________________________
Лекция 8
5.10. Классическая теория электропроводности металлов
На основании ряда экспериментальных данных, полученных учеными Рикке, Мандельштамом и Папалекси, Толменом и Стюартом в начале XX в. было установлено, что носителями тока в металлах являются электроны.
Некоторые свойства электрона были описаны Томсоном в 1895-97 гг.
Большая концентрация электронов в металлах (no 1028 — 1029 м3) обуславливает в них высокую тепло- и электопроводимость. Позднее была создана классическая теория электропроводности металлов Друде—Лоренца.
В основу теории были положены выводы классической молекулярно-кинетической теории, в которой электроны проводимости рассматриваются как электронный газ и его свойства подобны свойствам одноатомного, идеального газа. Число свободных электронов равно примерно числу атомов.
Согласно классической электронной теории проводимости металлов в отсутствии электрического поля в них электроны проводимости (электронный газ) находятся в состоянии теплового хаотического движения в кристаллической решетке, образованной положительно заряженными ионами.
Ионы совершают
тепловые колебания около положений
равновесия —
узлов кристаллической решетки. При
своем движении электроны испытывают
столкновения с ионами. Длина свободного
пробега электронов  ,
т. е. по порядку равна периоду кристаллической
решетки. В соответствии с выводами
молекулярно-кинетической
теории средняя кинетическая энергия
теплового движения электронов
,
т. е. по порядку равна периоду кристаллической
решетки. В соответствии с выводами
молекулярно-кинетической
теории средняя кинетическая энергия
теплового движения электронов  ,
,
где m — масса электрона; vкв — средняя квадратичная скорость теплового движения. Например, при температуре Т = 273 К, vкв 105 м/c.
При создании электрического поля в металлических проводниках возникает электрический ток, плотность которого
 ,
(5.38)
,
(5.38)
где n0 — концентрация электронов; qe — заряд электрона; v — средняя скорость упорядоченного движения. Электроны имеют скорость v = <u> + v.
Следовательно, под действием напряженности электрического поля электроны в проводнике приходят в упорядоченное движение в направлении противоположном вектору напряженности электрического поля.
При максимально допустимой плотности тока в металлах cредняя скорость упорядоченного движения v 103 м/c, т. е. v u, что объясняется малым значением средней длины свободного пробега электрона между двумя последовательными столкновениями его с ионами.
По классической теории проводимости металлов при соударении электрона с ионом он полностью теряет свою скорость.
Уравнение движения электрона в электрическом поле в процессе свободного пробега является равноускоренным.
Поэтому на основании второго закона Ньютона
F
= ma
= m ,
,
где F = qeE; Е — напряженность электрического поля.
Средняя скорость упорядоченного движения
v
= .
.
Если средняя продолжительность времени свободного пробега t, то после интегрирования
F
= ma
= m
получим, что
vмах
=
или
v
= .
(5.39)
.
(5.39)
Если u всех электронов одинаковы, но v u, найдем среднее время пробега электрона
 .
.
С учетом этого формулу (5.39) перепишем в виде:
 .
(5.40)
.
(5.40)
Следовательно, плотность тока
 ,
(5.41)
,
(5.41)
где  (5.42)
(5.42)
— удельная электропроводимость проводника.
Таким образом, на основании классической теории проводимости металлов был теоретически получен закон Ома в дифференциальной форме
j = E.
5.12. Вывод закона Джоуля — Ленца
После соударения электрона с ионами кристаллической решетки его энергия упорядоченного движения переходит во внутреннюю энергию, что приводит к нагреванию проводника.
Под действием электрического поля за время свободного пробега электрон увеличивает свою кинетическую энергию на величину
 .
(5.43)
.
(5.43)
Из-за теплового хаотического движения электронов, их средняя кинетическая энергия
 .
(5.44)
.
(5.44)
В единице объема проводника содержится n0 электронов, причем ежесекундно каждый из них испытывает в среднем число столкновений с ионами
 .
(5.45)
.
(5.45)
Энергия электрического тока, которая преобразуется во внутреннюю энергию за 1 с в единице объема, называется объемной плотностью тепловой мощности
 ,
(5.46)
,
(5.46)
где
vмах = 2v.
Используя формулу (5.39) и

окончательно получим
 (5.47)
(5.47)
или
w = E2.
Последняя формула выражает закон Джоуля-Ленца в дифференциальной форме, т. е.
 .
(5.48)
.
(5.48)
Закон Ома в дифференциальной и интегральной форме
Закон Ома для участка цепи утверждает: сила тока I прямо пропорциональна напряжению U на участке цепи и обратно пропорциональна сопротивлению R
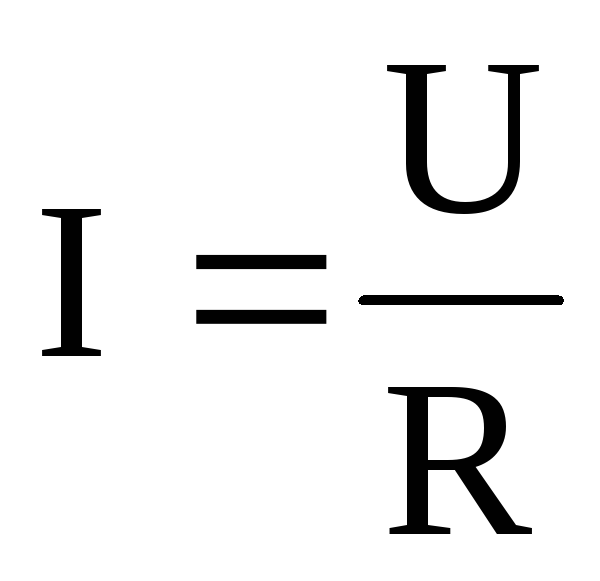 .
.
Закон Ома можно
представить в дифференциальной форме.
Через поперечное сечение проводника
течет ток силой dI
равной dI
= jdS.
Напря- жение, приложенное на концах
проводника, будет равно Е·dl (т.к.  и dφ
= -Edl).
Для проводника постоянного сечения
длиной l будем иметь
и dφ
= -Edl).
Для проводника постоянного сечения
длиной l будем иметь
 .
.
Отсюда  ,
где
,
где — удельная проводимость проводника.
Таким образом, выражениезакона
Ома в дифференциальной форме в векторном виде будет
— удельная проводимость проводника.
Таким образом, выражениезакона
Ома в дифференциальной форме в векторном виде будет
j = γ E.
Плотность тока в проводнике прямо пропорциональна напряженности электрического поля в нем.
Рассмотрим замкнутую электрическую цепь, содержащую ЭДС. Источник тока в такой цепи обладает внутренним сопротивлением r. Сопротивление внешней части цепи R называют внешним или сопротивлением нагрузки. Падение напряжения на внутреннем участке цепи равно U1 = Ir, а на внешнем — U =IR. При замкнутой внешней цепи ЭДС источника тока ؏ равна сумме падений напряжения на внутреннем сопротивлении источника тока и во внешней цепи, ؏ = Ir + IR, откуда
I = ؏ / (r + R).
Это есть выражение закона Ома в интегральной форме.
Закон Джоуля-Ленца в дифференциальной и интегральной форме
Опытом установлено, что если в проводнике течет ток, то работа сторонних сил расходуется на его нагревание. Предположим, что на концах участка проводника имеется разность потенциалов U = φ1 – φ2.
Тогда работа по переносу заряда q на этом участке равна
A = q(φ1 – φ2) = qU.
Если
ток постоянный, то  иA
= I
U
t.
иA
= I
U
t.
Эта работа равна количеству теплоты Q и формула Q = I U t выражает закон Джоуля-Ленца в интегральной форме.
Используя
выражение закона Ома  получим
получим
 .
.
Преобразуем закон Джоуля–Ленца. Введем плотность тепловой мощности w – величину, равную энергии, выделяемой за время t прохождения тока в единице объема проводника:

 ,
,
где
S
— сечение, l — длина проводника. Подставляя Q
= I2 R
t
и  ,
получим
,
получим  .
.
Здесь  — плотность тока,
— плотность тока, ,
и учитывая, чтоj
= γE,
получим
,
и учитывая, чтоj
= γE,
получим
 .
.
Это есть выражение закона Джоуля-Ленца в дифференциальной форме. Плотность тепловой мощности в проводнике, по которому течет ток, прямо пропорциональна квадрату напряженности поля в проводнике. Коэффициентом пропорциональности является удельная проводимость проводника.
Вывод законов Ома и Джоуля-Ленца из классических электронных представлений
Какова природа носителей тока в металлах? В 1901 г. Рикке проделал опыты: через 3 цилиндра, установленных друг на друга в течение 3-х лет пропускал постоянный ток. Был пропущен заряд, равный 3,5·106 Кл. Взвешивание показало неизменный вес цилиндров. Исследование торцов цилиндров не показало следов переноса вещества. Из этого был сделан вывод, что носители заряда не ионы, а открытые Томпсоном в 1897 г. электроны.
Чтобы отождествить носители заряда с электронами, нужно было определить знак и величину удельного заряда носителей.
Если в металле имеются легко перемещающиеся заряженные частицы, то при торможении металлического проводника эти частицы должны некоторое время продолжать двигаться по инерции, в результате чего в проводнике возникнет импульс тока и будет перенесен некоторый заряд.
Мандельштам и Папалекси в 1913 г. проделали такой опыт – они приводили в быстрое крутильное колебание катушку с проводом вокруг ее оси. К концам катушки подключили телефон, в котором был слышен звук, обусловленный импульсами тока. Был получен качественный результат – зарегистрирован импульс тока.
Толмен и Стюарт в 1916 г. получили количественный результат. Катушка с проводом длиной 500 м приводилась во вращение со скоростью v=300 м/с. Катушка резко тормозилась и с помощью баллистического гальванометра измеряли заряд, протекавший в цепи во время торможения. Вычисленное значение отношения заряда к массе e/m получалось очень близким для электронов. Таким образом было доказано, что носителем тока являются электроны. Исходя из представлений о свободных электронах была создана классическая теория электропроводности металлов в предположении, что:
— электроны в металле ведут себя подобно молекулам идеального газа;
— движение электронов подчиняется законам классической механики;
— взаимодействие электронов сводится к соударениям с ионами кристалли-ческой решетки;
— силами взаимодействия между электронами можно пренебречь и они между собой не сталкиваются;
— электроны в отсутствие электрического поля движутся хаотически.
Вычислим плотность тока j в проводнике, возникающего под действием поля напряженностью Е.
По определению плотность тока j = n e <v> — это заряд, переносимый через единицу площади S = 1м2 за единицу времени t=1 с; n – концентрация электронов, е – заряд электрона, <v> — средняя скорость упорядоченного движения электронов.
На
каждый электрон действует сила F
= eE
= ma,
поэтому электрон приобретает ускорение 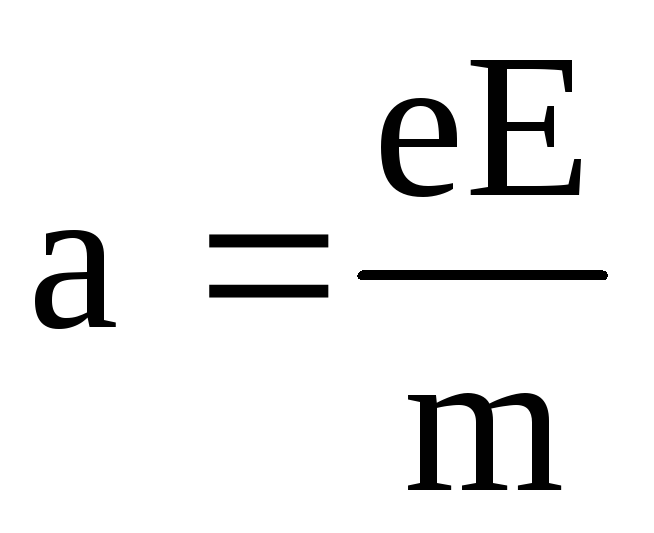 и к концу свободного пробега он
достигнет скорости
и к концу свободного пробега он
достигнет скорости ,
а средняя скорость <v>=vmax/2.
,
а средняя скорость <v>=vmax/2.
Если
<vT>
— средняя скорость теплового хаотичного
движения электронов, а средняя длина
свободного пробега электронов <λ>,
то среднее время между соударениями
<t>
= 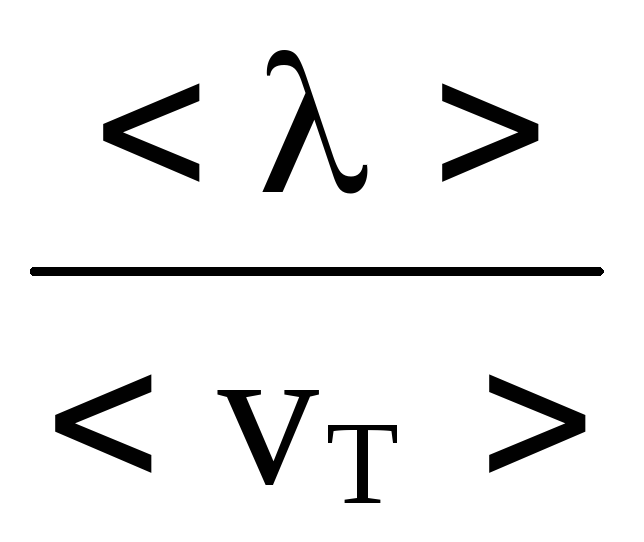 .
Подставляя <t>
в формулу для <v>
получим:
.
Подставляя <t>
в формулу для <v>
получим:
 .
.
Подставляя <v> в формулу для j, получим
 ,
,
т.е. плотность тока прямо пропорциональна Е, а это и есть выражение закона Ома в дифференциальной форме. Если положить, что
 то j = γ E.
то j = γ E.
Удельная проводимость
γ ~
n
и < λ>, <vт>
~
T,
поэтому проводимость снижается с
ростом температуры, а удельное
сопротивление  повышается с ростом температуры. К
концу свободного пробега электрон
приобретает кинетическую энергию
повышается с ростом температуры. К
концу свободного пробега электрон
приобретает кинетическую энергию

Предполагается, что вся энергия при соударении передается узлу кристаллической решетки и переходит в тепло. За 1 с электрон испытывает <vT>/ < λ > cоударений, а значит выделяет во столько же раз больше тепла. Если в единице объема n электронов, то в единице объема за единицу времени выделится количество тепла
 .
.
Таким
образом, 
 —
выражение закона Джоуля-Ленца в
дифференциальной форме.
—
выражение закона Джоуля-Ленца в
дифференциальной форме.
§ 103. Вывод основных законов электрического тока в классической теории электропроводности металлов
1. Закон Ома. Пусть в металлическом проводнике существует электрическое поле напряженностью Е=const. Co стороны поля заряд е испытывает действие силы F=eE и приобретает ускорение а=F/m=еЕ/т. Таким образом, во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость
vmax= еE<t>.
где <t>—среднее время между двумя последовательными соударениями электрона с ионами решетки.
Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в поле энергию, поэтому скорость его упорядоченного движения становится равной нулю. Следовательно, средняя скорость направленного движения электрона
<v>=(vmax+0)/2=eE<t>/(2m). (103.1)
Классическая теория металлов не учитывает распределения электронов по скоростям, поэтому среднее время <t> свободного пробега определяется средней длиной свободного пробега <l> и средней скоростью движения электронов относительно кристаллической решетки проводника, равной <u>+(v) (<u>—средняя скорость теплового движения электронов). В §102 было показано, что (v)<< <u>, поэтому
<t>=<l>/<u>.
Подставив значение <t> в формулу (103.1), получим
<v>=eE<l>/(2m<u>).
Плотность тока в металлическом проводнике, по (96.1),

откуда видно, что плотность тока пропорциональна напряженности поля,
165
т. е. получили закон Ома в дифференциальной форме (ср. с (98.4)). Коэффициент пропорциональности между j и Е есть не что иное, как удельная проводимость материала

которая тем больше, чем больше концентрация свободных электронов и средняя длина их свободного пробега.
2. Закон Джоуля — Ленца. К концу свободного пробега электрон под действием поля приобретает дополнительную кинетическую энергию

При соударении электрона с ионом эта энергия полностью передается решетке и идет на увеличение внутренней энергии металла, т. е. на его нагревание.
За единицу времени электрон испытывает с узлами решетки в среднем <z> столкновений:
<z>=<u>/<l>. (103.4)
Если n — концентрация электронов, то в единицу времени происходит n<z> столкновений и решетке передается энергия
w=n<z><Eк>, (103.5)
которая идет на нагревание проводника. Подставив (103.3) и (103.4) в (103.5), получим таким образом энергию, передаваемую решетке в единице объема проводника за единицу времени,

Величина w называется удельной тепловой мощностью тока (см. §99). Коэффициент пропорциональности между w и Е2 по (103.2) есть удельная проводимость ; следовательно, выражение (103.6) —закон Джоуля — Ленца в дифференциальной форме (ср. с (99.7)).
3. Закон Видемана — Франца. Металлы обладают как большой электропроводностью, так и высокой теплопроводностью. Это объясняется тем, что носителями тока и теплоты в металлах являются одни и те же частицы — свободные электроны, которые, перемещаясь в металле, переносят не только электрический заряд, но и присущую им энергию хаотического теплового движения, т. е. осуществляют перенос теплоты.
Видеманом и Францем в 1853 г. экспериментально установлен закон, согласно которому отношение теплопроводности () к удельной проводимости () для всех металлов при одной и той же температуре одинаково и увеличивается пропорционально термодинамической температуре:
/=T,
где — постоянная, не зависящая от рода металла.
Элементарная классическая теория электропроводности металлов позволила найти значение : =3(k/e)2, где k — постоянная Больцмана. Это значение хорошо согласуется с опытными данными. Однако, как оказалось впоследствии, это согласие теоретического значения с опытным случайно. Лоренц, применив к электронному газу статистику Максвелла — Больцмана, учтя тем самым распределение электронов по скоростям, получил =2(k/e)2, что привело к резкому расхождению теории с опытом.
Таким образом, классическая теория электропроводности металлов объяснила законы Ома и Джоуля — Ленца, а также дала качественное объяснение закона Видемана — Франца. Однако она помимо рассмотренных противоречий в законе Видемана — Франца столкнулась еще с рядом трудностей при объяснении различных опытных данных. Рассмотрим некоторые из них.
Температурная зависимость сопротивления. Из формулы удельной проводимости (103.2) следует, что сопротивление металлов, т. е. величина, обратно пропорциональная , должна возрастать пропорционально T (в (103.2) n и <l> от температуры не зависят, а <u>~Т). Этот вывод электронной теории противоречит опытным данным, согласно которым R~T (см. §98).
166
Оценка средней длины свободного пробега электронов в металлах. Чтобы по формуле (103.2) получить , совпадающие с опытными значениями, надо принимать <l> значительно больше истинных, иными словами, предполагать, что электрон проходит без соударений с ионами решетки сотни междоузельных расстояний, что не согласуется с теорией Друде — Лоренца.
Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость диэлектриков, у которых нет свободных электронов. Согласно закону Дюлонга и Пти (см. §73), теплоемкость одноатомного кристалла равна 3R. Учтем, что теплоемкость одноатомного электронного газа равна 3/2R. Тогда атомная теплоемкость металлов должна быть близка к 4,5R. Однако опыт доказывает, что она равна 3R, т. е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классической электронной теорией.
Указанные расхождения теории с опытом можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла — Больцмана, а квантовой статистикой. Поэтому объяснить затруднения элементарной классической теории электропроводности металлов можно лишь квантовой теорией, которая будет рассмотрена в дальнейшем. Надо, однако, отметить, что классическая электронная теория не утратила своего значения и до настоящего времени, так как во многих случаях (например, при малой концентрации электронов проводимости и высокой температуре) она дает правильные качественные результаты и является по сравнению с квантовой теорией простой и наглядной.
Вывод закона Ома на основе КЭТ — Мегаобучалка
Исследование температурной зависимости электрического сопротивления металлов и полупроводников
Цель работы: ознакомление с классическим методом измерения сопротивления при помощи резистивного моста; вычисление удельного сопротивления, температурного коэффициента сопротивления металла; определение энергии активации примесей в полупроводнике.
Оборудование: мост постоянного тока, нагреватель, измеритель температуры, медный провод, полупроводник.
Краткие теоретические сведения
Закон Ома
В 1826 г. немецкий физик Георг Симон Ом экспериментально установил закон, согласно которому сила тока I, протекающего по однородному проводнику, пропорциональна напряжению U на его концах:
, (5.1)
где R — электрическое сопротивление проводника.
Это соотношение не является универсальным законом, так как электрическое сопротивление R не является константой материала. Оно зависит от формы и размеров электрического проводника. Однако можно выделить в сопротивлении R константу материала — удельное сопротивление r.
Наиболее просто это сделать для проводников правильной формы. Так, для однородного проводника цилиндрической формы сопротивление R выражается через удельное сопротивление ρ следующим образом:
(5.2)
где — длина проводника; S — площадь его поперечного сечения.
Чтобы понять, какие физические величины определяют удельное сопротивление, его необходимо выразить через другие константы материала, как это делается в классической электронной теории (КЭТ).
Вывод закона Ома на основе КЭТ
КЭТ металлов основана на следующих представлениях. Атом можно представлять как совокупность двух систем электронов. Одна из систем сильно связана с ядром и образует так называемый остов. Другая система, система валентных электронов, у некоторых атомов, например, у атомов щелочных элементов, слабо связана с ядром. При объединении таких атомов в твердое тело, каждый остов занимает вполне определенное место — узел, а совокупность узлов образует кристаллическую решетку. Валентные электроны уже не принадлежат тому или иному остову, а образуют «электронный газ», газ свободных электронов, принадлежащий всему твердому телу в целом. Электронному газу приписываются свойства идеального одноатомного газа. Свободные электроны непрерывно хаотически движутся, причем средняя кинетическая энергия их движения
, (5.3)
где m — масса электрона; — средняя скорость теплового движения; k- постоянная Больцмана; T — термодинамическая температура.
Под действием внешнего электрического поля свободные электроны приобретают дополнительную скорость, направленную противоположно направлению поля. Это медленное (по сравнению с тепловым движением) направленное движение электронов называется дрейфом, а дополнительная скорость – скоростью дрейфа , или дрейфовой скоростью. Максимальная величина дрейфовой скорости определяется частотой соударений электронов с тем или иным остовом. Каждый остов совершает колебательные движения, амплитуда колебаний определяется температурой твердого тела. При повышении температуры возрастает амплитуда колебаний ионов и, следовательно, увеличивается вероятность столкновения электронов с ионами. В результате скорость дрейфа электронов уменьшается, соответственно уменьшается и ток I. При неизменной разности потенциалов на концах проводника уменьшение тока означает по закону Ома (5.1) рост сопротивления проводника R. С уменьшением же температуры остовы колеблются все менее интенсивно, все реже соударения электронов с ионами. Поэтому сопротивление проводника убывает с уменьшением температуры.
На основе этих представлений КЭТ найдем связь удельного сопротивления с другими константами материала.
В промежутке между двумя следующими друг за другом соударениями электроны под действием кулоновской силы F = eE двигаются с ускорением
, (5.4)
где e — заряд; m -масса электрона; E — напряженность электрического поля.
Скорость дрейфа и время между двумя последующими соударениями являются случайными величинами. Можно предполагать, что эти величины распределены в интервале от нуля до некоторых максимальных значений. Если — среднее время между двумя последующими соударениями, или среднее время свободного пробега электронов, то максимальная дрейфовая скорость, которую электрон приобретает перед соударением, равна
(5.5)
Средняя скорость дрейфа электронов равна, очевидно, половине максимальной, так как сразу же после соударения скорость дрейфа равна нулю, а затем растет со временем линейно. Используя это соображение и заменяя в (5.5) ускорение его значением из (5.4), получим:
(5.6)
Здесь величина
(5.7)
называется подвижностью электронов, имеет размерность м2/В с и численно равна средней дрейфовой скорости в единичном поле.
Для однородного проводника цилиндрической формы с площадью поперечного сечения S силу тока I можно выразить через скорость дрейфа . За время t электроны проходят вдоль проводника расстояние . Пусть в единице объема имеется n электронов проводимости. Число электронов, пересекающих сечение S проводника за время t, составляет nSL. Заряд Q, проходящий через это сечение, равен . Так как сила тока I равна Q/t, тогда
, (5.8)
где n — концентрация электронов.
Подставляя в (5.8) значение дрейфовой скорости из (5.6) и учитывая, что , где — длина проводника, получим
(5.9)
Из сравнения полученного выражения с законом Ома (5.1) получим, что
(5.10)
Сопоставляя выражения (5.10) и (5.2), можно легко получить искомую связь материальной константы r с фундаментальными константами (заряд и масса электрона) и другими материальными константами (концентрация и среднее время свободного пробега электронов):
(5.11)
2. Формула Друде – Лоренца
Преобразуя (5.11) с учетом (5.7), удельное сопротивление можно выразить через подвижность электронов:
(5.12)
Величина, обратная удельному сопротивлению (, называется удельной проводимостью (. Используя понятие удельной проводимости, выражение (5.12) можно записать в виде
EMBED Equation.DSMT4 (5.13)
Как видно из (5.13), удельная проводимость пропорциональна концентрации электронов проводимости n и их подвижности (.
Соотношение (5.13) носит универсальный характер, является справедливым как для твердых тел (металлов, полупроводников, диэлектриков), так и для жидкостей и газов и известно под названием формула Друде-Лоренца.
2)Вывод закона Ома
Закон Ома.
Математически
закон Ома выражается формулой(дифф.форма):  где
где  -постоянная
для данного материала величина, называемая
его удельной
электрической проводимостью.
Она зависит от температуры, давления и
пр. Закон Ома справедлив лишь для
физически однородных тел.
-постоянная
для данного материала величина, называемая
его удельной
электрической проводимостью.
Она зависит от температуры, давления и
пр. Закон Ома справедлив лишь для
физически однородных тел.  . Вывод
Закона Ома
. Вывод
Закона Ома
Обозначим за
 -скорость
беспорядочного движения электронов в
металле.
-скорость
беспорядочного движения электронов в
металле.  -дрейфовая
скорость (направленное
движение носителей
заряда под
действием электрического поля).
-дрейфовая
скорость (направленное
движение носителей
заряда под
действием электрического поля).Тогда полная скорость электрона

Движение электрона описывается уравнением(из механики):



Предположим, что
 и что в начальный момент времени
и что в начальный момент времени  электроны совершают дрейфовое движение
со скоростью
электроны совершают дрейфовое движение
со скоростью  ,
тогда из уравнения (3) получаем:,
,
тогда из уравнения (3) получаем:,

Воспользовавшись соотношение о плотности электрического тока
 и введя обозначения
и введя обозначения  ,
преобразуем уравнение (3) к виду
,
преобразуем уравнение (3) к виду
 (6),
(6),

Если
ток стационарный, то объемная плотность
электричества в однородном проводнике
равна нулю.  или
или  . Так
как среда по предположению однородна,
то
. Так
как среда по предположению однородна,
то  ,
,  и рассматриваемое уравнение сводится
к виду
и рассматриваемое уравнение сводится
к виду  .
Отсюда с учетом теоремы Гаусса находим
.
Отсюда с учетом теоремы Гаусса находим  .
.




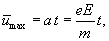




 -скорость
беспорядочного движения электронов в
металле.
-скорость
беспорядочного движения электронов в
металле.  -дрейфовая
скорость (направленное
движение носителей
заряда под
действием электрического поля).
-дрейфовая
скорость (направленное
движение носителей
заряда под
действием электрического поля).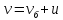
 и что в начальный момент времени
и что в начальный момент времени  электроны совершают дрейфовое движение
со скоростью
электроны совершают дрейфовое движение
со скоростью  ,
тогда из уравнения (3) получаем:,
,
тогда из уравнения (3) получаем:, и введя обозначения
и введя обозначения  ,
преобразуем уравнение (3) к виду
,
преобразуем уравнение (3) к виду