Магнитное поле прямого тока | Все формулы
Магнитное поле прямого тока — создается током, текущего по тонкому прямому бесконечному проводу
Вывод формулы для магнитного поля прямого тока :
За постоянную интегрирования возьмем угол α (угол между векторами dl и r) и выразим через него все остальные величины
Магнитная индукция, которая создавается одним элементом проводника, равна
Поскольку угол α для всех элементов прямого тока изменяется в пределах от 0 до π, то
Посчитаем интеграл, и получим формулу Магнитной индукции поля прямого тока
Так же есть :
Магнитное поле кругового тока:
В Формуле мы использовали :
— Магнитная индукция прямого тока
— Магнитная проницаемость среды
— Магнитная постоянная
— Сила тока
— Расстояние от провода до точки, где мы вычисляем магнитную индукцию
— Угол между вектором dl и r
Магнитное поле прямого тока
Применим закон Био–Савара–Лапласа для расчета магнитных полей простейших токов.
Рассмотрим магнитное поле прямого тока (рис. 1.6).
Рис. 1.6
Все векторы от произвольных элементарных участков имеют одинаковое направление. Поэтому сложение векторов можно заменить сложением модулей.
Пусть точка, в которой определяется магнитное поле, находится на расстоянии b от провода. Из рисунка 1.6 видно, что:
Подставив найденные значения r и dl в закон Био–Савара–Лапласа, получим:
Для конечного проводника угол α изменяется от
| , | (1.5.1) |
Для бесконечно длинного проводника а , тогда
или, что удобнее для расчетов,
| , | (1.5.2) |
Линии магнитной индукции прямого тока представляют собой систему концентрических окружностей, охватывающих ток (рис. 1.3).
Другие аудио-видео демонстрации по теме или смежным темам:1. Силовые линии магнитов. 2. Линии магнитной индукции.
Закон Био — Савара — Лапласа. Магнитное поле прямого, кругового и соленоидального токов.

Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Значение магнитной индукции для любого проводника определяется законом Био — Савара — Лапласа.
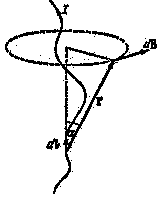
Рис. 15.8.
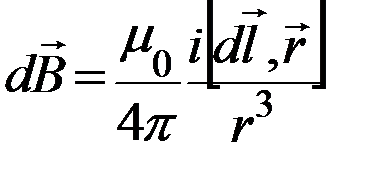 -в векторной форме, (15.6)
-в векторной форме, (15.6)
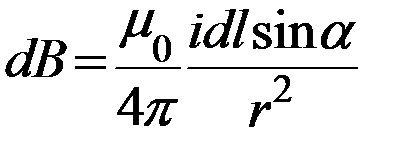 — в скалярной форме. (15.7)
— в скалярной форме. (15.7)
Вектор  всегда перпендикулярен плоскости, построенной на векторах
всегда перпендикулярен плоскости, построенной на векторах 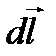 и
и 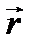
Вывод формулы напряжённости магнитного поля прямого тока (рис. 15.9; рис. 15.10) .
Применим формулу 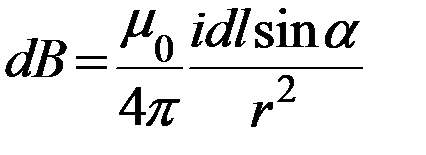 для вычисления полей простейших токов. Рассмотрим поле, создаваемое током, текущим по бесконечному прямому проводу (Рис. 15.9) .Все dBв данной точке имеют одинаковое направление. Поэтому сложение векторов dBможно заменить сложением их модулей. Точка, для которой мы вычисляем магнитную индукцию, находится на расстоянии b от провода. Из рисунка 15.9 видно, что:
для вычисления полей простейших токов. Рассмотрим поле, создаваемое током, текущим по бесконечному прямому проводу (Рис. 15.9) .Все dBв данной точке имеют одинаковое направление. Поэтому сложение векторов dBможно заменить сложением их модулей. Точка, для которой мы вычисляем магнитную индукцию, находится на расстоянии b от провода. Из рисунка 15.9 видно, что:
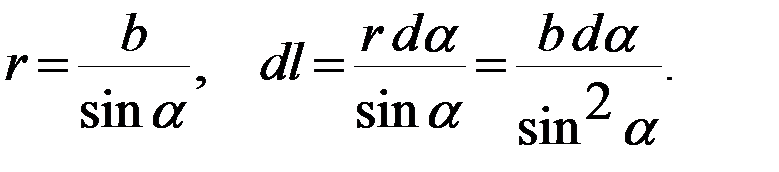
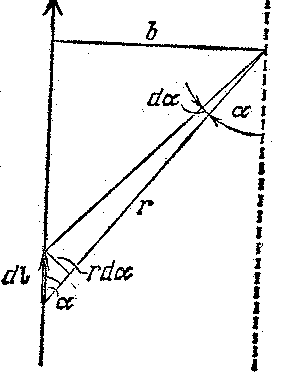
Рис. 15.9.
Подставим эти значения в формулу магнитной индукции:

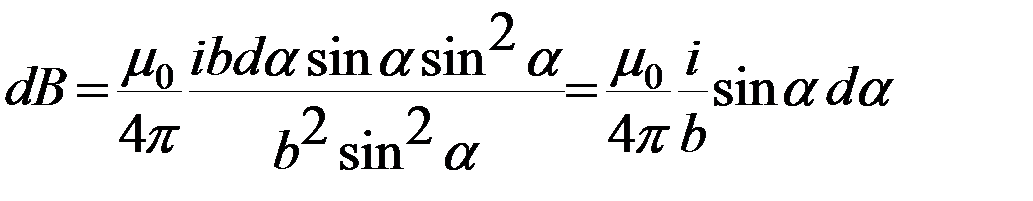 .
.
Угол 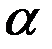 для всех элементов бесконечно прямого тока изменяется в пределах от 0 до
для всех элементов бесконечно прямого тока изменяется в пределах от 0 до 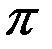
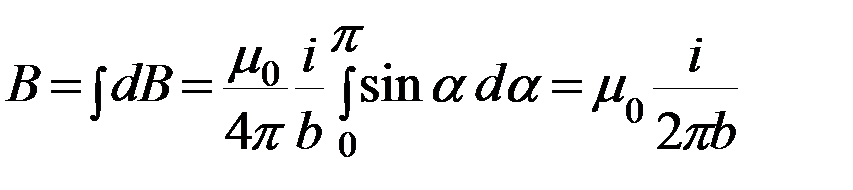 .
.
Таким образом, магнитная индукция поля прямого тока определяется формулой: 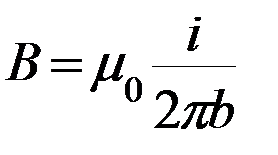 . (15.8 )
. (15.8 )
Для того, чтобы получить напряженность магнитного поля, необходимо разделить правую часть формулы (15.8) на 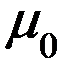
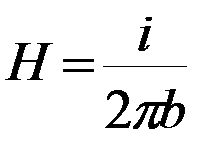
 . (15.9)
. (15.9)
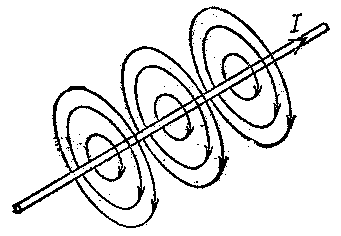
Рис. 15.10
Вывод формулы напряжённости магнитного поля кругового тока (рис. 15.11).
Рассмотрим поле, создаваемое током, текущим по тонкому проводу, имеющему форму окружности (круговой ток). Определим магнитную индукцию кругового тока
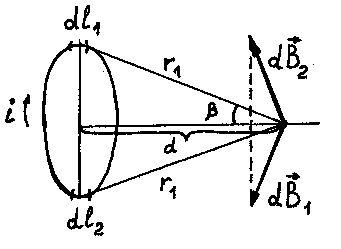
Рис. 15.11
Рассмотрим индукции 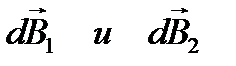 , создаваемых двумя элементами контура dl1 и dl2. Т. к. угол между r и dl равен 90°, то sin 90°=1.
, создаваемых двумя элементами контура dl1 и dl2. Т. к. угол между r и dl равен 90°, то sin 90°=1.
Закон Био — Савара — Лапласа для двух элементов:
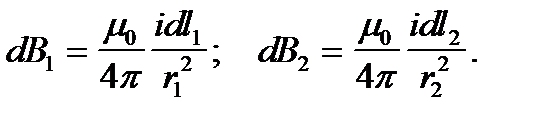
Выбрав dl1=dl2 и принимая, что r1=r2, получим:
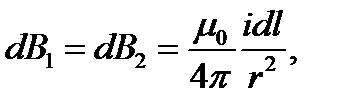
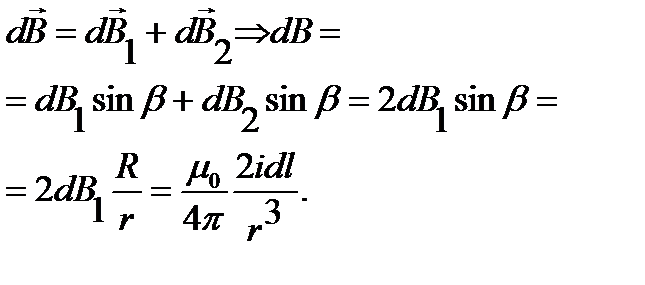
Проинтегрируем это выражение по всему контуру и заменим r на 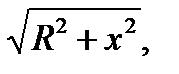 получим:
получим:
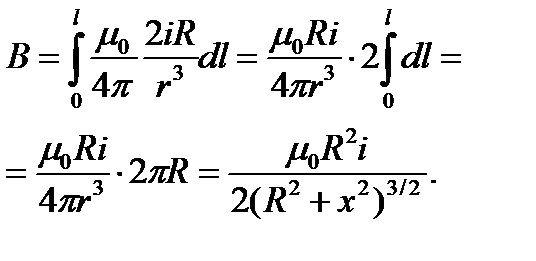 (15.10)
(15.10)
В частности, при x=0 имеем:
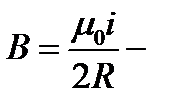 (15.11)
(15.11)
магнитная индукция в центре кругового тока
Напряженность магнитного поля в центре кругового тока равна:
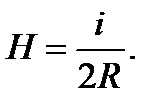 (15.12)
(15.12)
Формула для расчета напряженности магнитного поля кругового тока на его оси принимает вид:
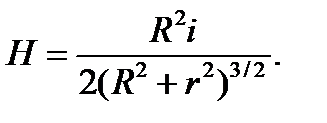 (15.13)
(15.13)
Вывод формулы напряжённости магнитного поля соленоидального тока.
Соленоид представляет собой тонкий провод, навитый плотно, виток к витку, на цилиндрический каркас. В отношении создаваемого им поля соленоид эквивалентен системе одинаковых круговых токов с общей прямой осью. Бесконечно длинный соленоид симметричен относительно любой перпендикулярной к его оси плоскости. Взятые попарно симметричные относительно такой плоскости витки создают поле, магнитная индукция которого перпендикулярна к плоскости. Следовательно, в любой точке внутри и вне соленоида вектор 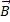 может иметь лишь направление, параллельное оси.
может иметь лишь направление, параллельное оси.
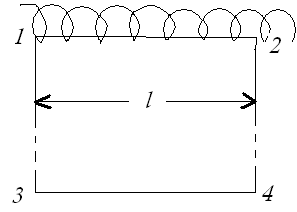
Рис. 15.12.
Возьмем прямоугольный контур 1-2-3-4. Циркуляцию вектора 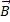 по этому контуру можно представить следующим образом:
по этому контуру можно представить следующим образом:
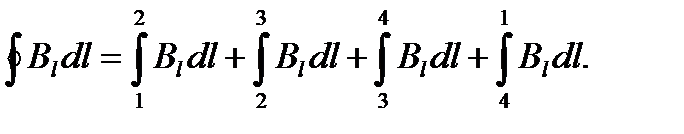
Из четырех интегралов, стоящих в правой части, второй и четвертый равны нулю, так как вектор 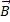 перпендикулярен к участкам контура, по которым они берутся.
перпендикулярен к участкам контура, по которым они берутся.
Взяв участок 3-4 на большом расстоянии от соленоида(где поле заведомо должно быть очень слабым), третьим слагаемым можно пренебречь. Следовательно, можно утверждать, что :
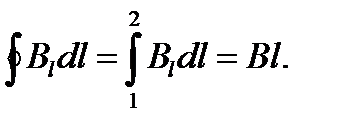
Здесь В — магнитная индукция поля в тех точках, где располагается отрезок 1-2, 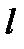 -длина этого отрезка.
-длина этого отрезка.
Если отрезок 1-2 проходит внутри соленоида на любом расстоянии от его оси, контур охватывает суммарный ток  , где
, где 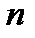 — число витков соленоида, приходящееся на единицу его длинны,
— число витков соленоида, приходящееся на единицу его длинны, 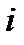 — сила тока в соленоиде. Поэтому согласно :
— сила тока в соленоиде. Поэтому согласно :
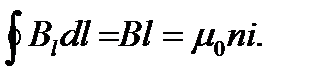
Откуда: 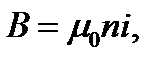 (15.14)
(15.14)
а напряженность магнитного поля соленоидального тока равна:
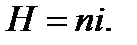 (15.15)
(15.15)
Отметим, что полученный нами результат не зависит от того, на каком расстоянии от оси (но внутри соленоида) располагается отрезок 1-2. Если этот отрезок располагается вне соленоида, то охватываемый контуром ток равен нулю, вследствие чего:
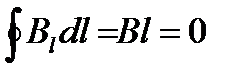 .
.
Откуда В=0. Таким образом, вне бесконечного длинного соленоида магнитная индукция равна нулю, внутри — всюду одинакова и имеет величину, определяемую формулой (15.14). По этой причине в учении о магнетизме бесконечно длинный соленоид играет такую же роль, как плоский конденсатор в учении об электричестве. В обоих случаях поле однородно и полностью заключено внутри конденсатора (электрическое) и внутри соленоида(магнитное).
Произведение 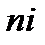 называется числом ампер — витков на метр.
называется числом ампер — витков на метр.
Тесты к лекции №15
Тест 15.1.Магнитная индукция поля, создаваемого отрезком бесконечно тонкого прямолинейного проводника, вычисляется по формуле…
£ 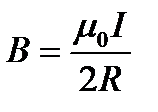
£ 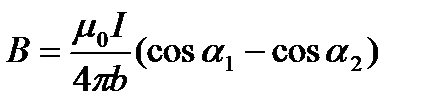
£ 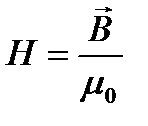
£ 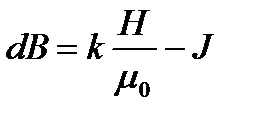
Тест 15.2.Магнитная индукция в центре кругового тока определяется по формуле…
£ 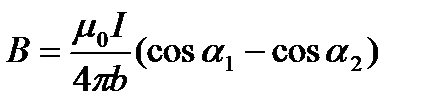
£ 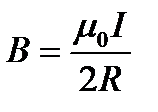
£ 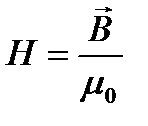
£ 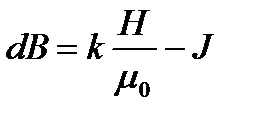
Тест 15.3.Форма существования материи, обладающая свойством передавать магнитное взаимодействие.
£ магнитное поле
£ магнитная индукция
£ пробный контур
£ магнитный момент
Тест 15.4.Дайте определение пробного контура.
£ контур, вносящий помехи в исходное поле.
£ контур, усиливающий исходное поле.
£ контур, ослабляющий исходное поле.
£ контур, который не создает заметных искажений исходного поля.
Тест 15.5.Формула 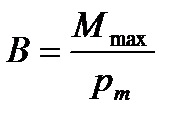 выражает:
выражает:
£ вектор магнитной индукции
£ напряженность магнитного поля
£ магнитную индукцию
£ магнитный момент
Вихревой характер магнитного поля. Циркуляция вектора индукции магнитного поля. Магнитный поток. Сила Ампера. Работа по перемещению проводника с током в магнитном поле. Сила Лоренца. Определение удельного заряда электрона[11]
16.1. Вихревой характер магнитного поля. Циркуляция вектора индукции магнитного поля. Магнитный поток
16.2. Сила Ампера
16.3. Работа по перемещению проводника с током в магнитном поле
16.4. Сила Лоренца
16.5. Определение удельного заряда электрона
9.2. Закон Био-Савара- Лапласа и его применение к расчету полей прямого и кругового токов.

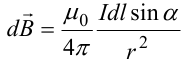
Направление вектора dB определяется правилом правого винта, которое заключается в
следующем: буравчик с правым винтом (штопор) нужно вращать от вектора dl к вектору r по
кратчайшему пути, тогда на правление движения острия бу равчика rпокажет ориентацию вектора dB .
Магнитное поле прямого тока
 Рассчитаем,
используя закон Био-Савара-Лапласа,
магнит ное поле, создаваемое бесконечным
прямым проводником с то ком, в точке М,
отстоящей на расстоянии а от проводника.
Рассчитаем,
используя закон Био-Савара-Лапласа,
магнит ное поле, создаваемое бесконечным
прямым проводником с то ком, в точке М,
отстоящей на расстоянии а от проводника.
Выделим элемент проводника dl. Пусть элемент dl виден из точки М под малым углом dα. Положение точки М относительно элемента dl определяется вектором r. Из
рис. видно, что выполняются следующие соотношения
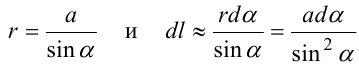
Используя закон Био-Савара-Лапласа, запишем индукцию магнитного поля, создаваемого элементом тока dl в точке М
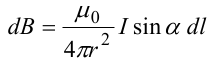
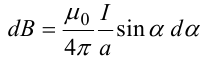
Для того, чтобы найти индукцию магнитного поля, создаваемого всем проводом, нужно, используя принцип суперпозиции, найти сумму векторов dBi от всех элементов dli.
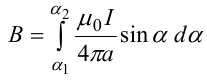
В случае бесконечного прямого тока α1=0 и α2=π, тогда

В общем случае индукция магнитного поля, создаваемого прямым проводником с ток конечной длины равна
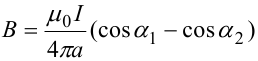
odmin
Магнитное поле на оси кругового витка с током.
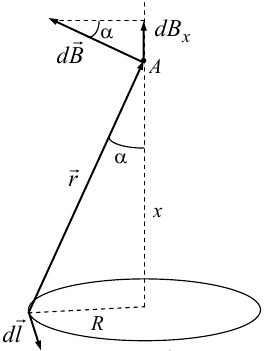 Возьмем
на оси кругового витка точку А, отстоящую
от плоскости витка на расстоянии х.
Выберем ось х вдоль оси витка. Выделим
на витке с током элемент тока dl. Оче
видно, что при суммировании векторов
dB от всех элементов витка горизонтальные
составляющие векторов dB взаимно
компенсируются, а вертикальные
составляющие (dBx) складываются скалярно.
Тогда индукция магнитного поля в точке
А будет
Возьмем
на оси кругового витка точку А, отстоящую
от плоскости витка на расстоянии х.
Выберем ось х вдоль оси витка. Выделим
на витке с током элемент тока dl. Оче
видно, что при суммировании векторов
dB от всех элементов витка горизонтальные
составляющие векторов dB взаимно
компенсируются, а вертикальные
составляющие (dBx) складываются скалярно.
Тогда индукция магнитного поля в точке
А будет
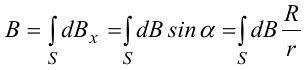
здесь S − длина витка, R − его радиус.
Согласно закону Био-Савара-Лапласа
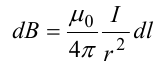
(угол между векторами r и dl равен π/2).
Окончательно

10.1. Закон полного тока (теорема о циркуляции вектора магнитной индукции).
В случае нескольких токов вrсилу принципа суперпозиции
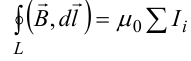
применение к расчету полей соленоида
10.2. Применение к расчету поля соленоида.
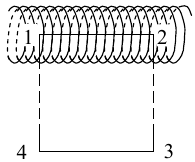 Рассмотрим
бесконечно длинный соленоид по которому
течет ток I и который имеет n витков на
единицу длины. Выберем прямоугольный
контур интегрирования 1-2-3-4. Сторона 1-2
совпадает с осью соленоида, а 3-4 удалена
на очень большое расстояние от оси. В
силу симметрии вектор B внутри соленоида
дол жен быть параллелен его оси, т.е.
Внутри соленоида магнитное поле должно
быть однородно.
Рассмотрим
бесконечно длинный соленоид по которому
течет ток I и который имеет n витков на
единицу длины. Выберем прямоугольный
контур интегрирования 1-2-3-4. Сторона 1-2
совпадает с осью соленоида, а 3-4 удалена
на очень большое расстояние от оси. В
силу симметрии вектор B внутри соленоида
дол жен быть параллелен его оси, т.е.
Внутри соленоида магнитное поле должно
быть однородно.
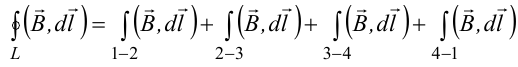
Последний интеграл в правой части равен нулю, т.к. На большом расстоянии от соленоида В=0. Второй и третий интегралы в правой части также равны нулю, т.к. для каждого элемента dl выполняется условие B ⊥ dl , а на участке 1-2, очевидно, B параллелен dl r. Тогда

, где l − длина участка 1-2.
С другой стороны, полученное выражение должно быть пропорционально сумме токов, охватываемых контуром 1-2-3-4. Рассматриваемый контур охватывает nl витков, в
каждом из которых течет ток I, тогда
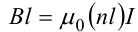
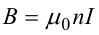
Откуда
10.3. Поле тороида.
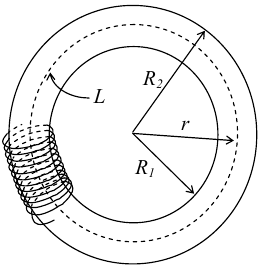 Пусть
мы имеем тороид (”бублик”) с плотно
намотанными на него N витками тонкого
провода с током I. Пусть R1 и R2 − внешний
и внутренний радиусы то роида. Найдем
индукцию магнитного поля на средней
линии тороида, т.е. на окружности радиуса
r=(R1+R2)/2.
Пусть
мы имеем тороид (”бублик”) с плотно
намотанными на него N витками тонкого
провода с током I. Пусть R1 и R2 − внешний
и внутренний радиусы то роида. Найдем
индукцию магнитного поля на средней
линии тороида, т.е. на окружности радиуса
r=(R1+R2)/2.
В качестве контура интегрирования L выберем саму среднюю линию. В силу симметрии вектор индукции магнитного поля B в каждой точке контура L должен быть направлен по касательной к этому контуру и быть постоянным по модулю. Выбранный нами контур охватывает все N витков.
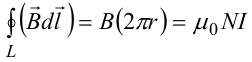
Откуда
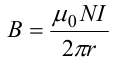
Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током, –
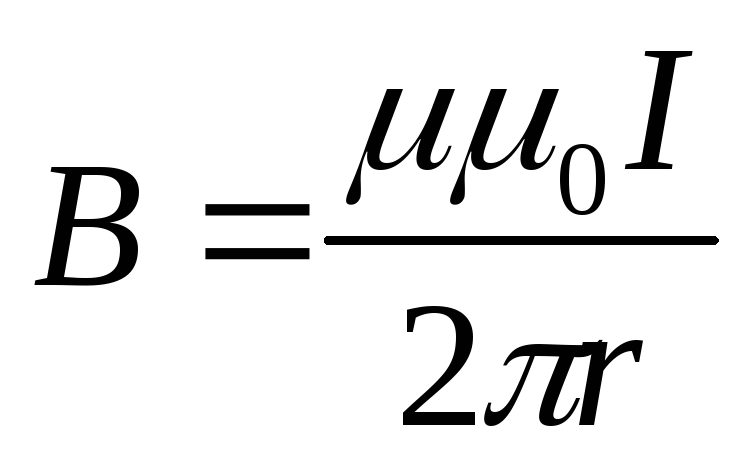 ,
,
где r – расстояние от оси проводника до точки.
Согласно
предположению Ампера в любом теле
существуют микроскопические токи
(микротоки), обусловленные движением
электронов в атомах. Они создают свое
магнитное поле и ориентируются в
магнитных полях макротоков. Макроток
— это ток в проводнике под действием ЭДС
или разности потенциалов.
Вектор магнитной индукции 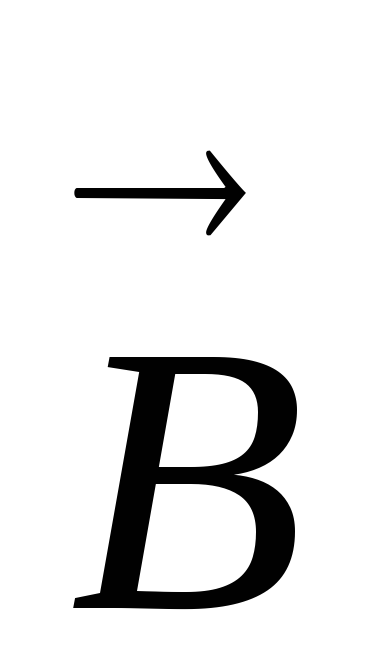 характеризует результирующее магнитное
поле, создаваемое всеми макро- и
микротоками. Магнитное поле макротоков
описывается также и вектором напряженности
характеризует результирующее магнитное
поле, создаваемое всеми макро- и
микротоками. Магнитное поле макротоков
описывается также и вектором напряженности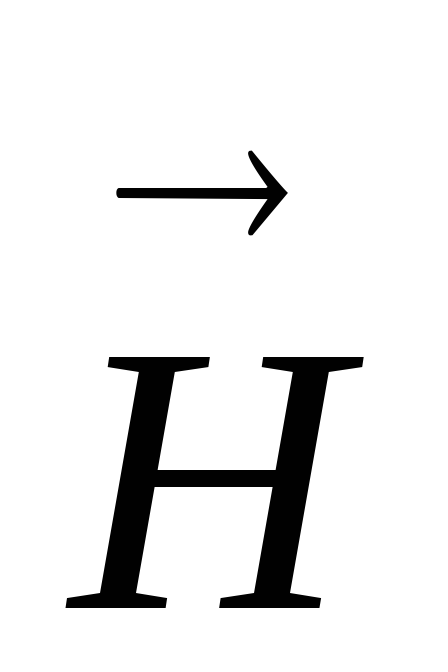 .
В случае однородной изотропной среды
вектор магнитной индукции связан с
вектором напряженности соотношением
.
В случае однородной изотропной среды
вектор магнитной индукции связан с
вектором напряженности соотношением
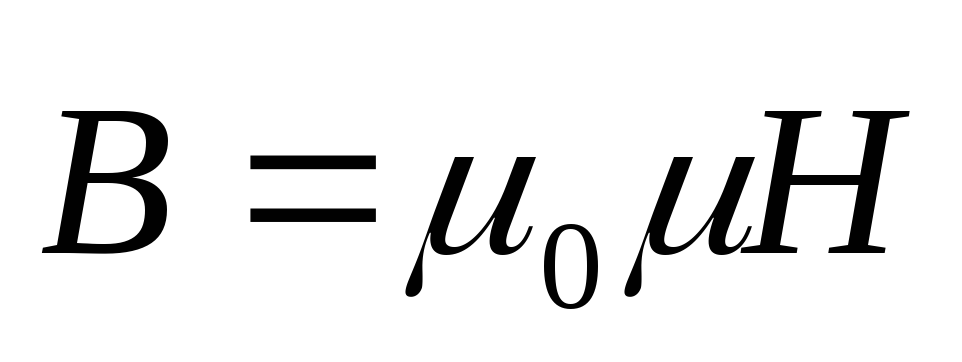 (5)
(5)
где μ0 — магнитная постоянная; μ- магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков усиливается или ослабляется за счет микротоков среды. Иначе говоря, μ показывает, во сколько раз вектор индукции магнитного поля в среде больше или меньше, чем в вакууме.
Единица
напряженности магнитного поля — А/м.
1А/м — напряженность такого поля,
магнитная индукция которого в вакууме
равна  Тл.
Земля представляет
собой огромный шарообразный магнит.
Действие магнитного поля Земли
обнаруживается на ее поверхности и в
окружающем пространстве.
Тл.
Земля представляет
собой огромный шарообразный магнит.
Действие магнитного поля Земли
обнаруживается на ее поверхности и в
окружающем пространстве.
Магнитным
полюсом Земли называют ту точку на ее
поверхности, в которой свободно
подвешенная магнитная стрелка
располагается вертикально. Положения
магнитных полюсов подвержены постоянным
изменениям, что обусловлено
внутренним строением нашей планеты.
Поэтому магнитные полюса не
совпадают с географическими. Южный
полюс магнитного поля Земли расположен
у северных берегов Америки, а Северный
полюс — в Антарктиде. Схема
силовых линий магнитного поля Земли
показана на рис. 5 (пунктиром обозначена
ось вращения Земли):  — горизонтальная
составляющая индукции магнитного
поля; Nr,
Sr — географические полюсы Земли; N,
S
— магнитные полюсы
Земли.
— горизонтальная
составляющая индукции магнитного
поля; Nr,
Sr — географические полюсы Земли; N,
S
— магнитные полюсы
Земли.
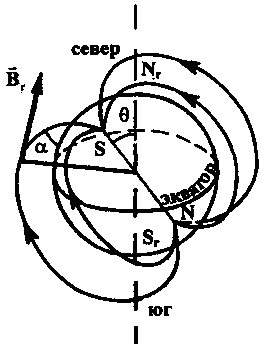
Рис. 5
Направление
силовых линий магнитного поля Земли
определяется с помощью
магнитной стрелки. Если свободно
подвесить магнитную стрелку, то она
установится по направлению касательной
к силовой линии. Так как магнитные
полюсы находятся внутри Земли, магнитная
стрелка устанавливается не горизонтально,
а под некоторым углом α к плоскости
горизонта. Этот угол α
называют
магнитным наклонением. С приближением
к магнитному полюсу угол
α увеличивается. Вертикальная плоскость,
в которой расположена стрелка, называется
плоскостью магнитного меридиана, а угол  между магнитным игеографическим
меридианами — магнитным склонением.
Силовой характеристикой
магнитного поля, как уже отмечалось,
является магнитная индукция В. Ее
значение невелико и изменяется от
0,42∙10-4 Тл на экваторе до 0,7∙10-4 Тл у
магнитных полюсов.
между магнитным игеографическим
меридианами — магнитным склонением.
Силовой характеристикой
магнитного поля, как уже отмечалось,
является магнитная индукция В. Ее
значение невелико и изменяется от
0,42∙10-4 Тл на экваторе до 0,7∙10-4 Тл у
магнитных полюсов.
Вектор
индукции магнитного поля Земли можно
разделить на две составляющие:
горизонтальную 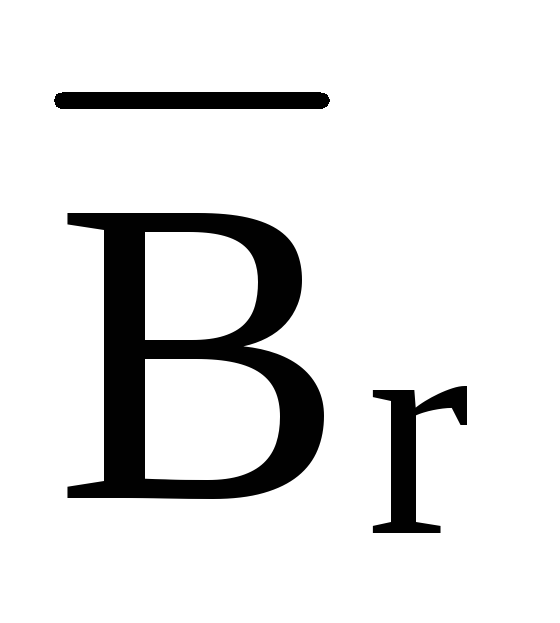 и
вертикальную
и
вертикальную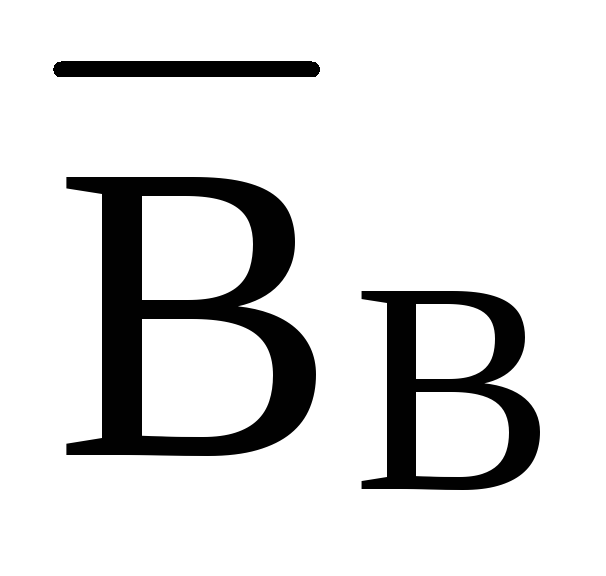 (рис. 5). Укрепленная навертикальной
оси магнитная стрелка устанавливается
в направлении горизонтальной
составляющей Земли
(рис. 5). Укрепленная навертикальной
оси магнитная стрелка устанавливается
в направлении горизонтальной
составляющей Земли 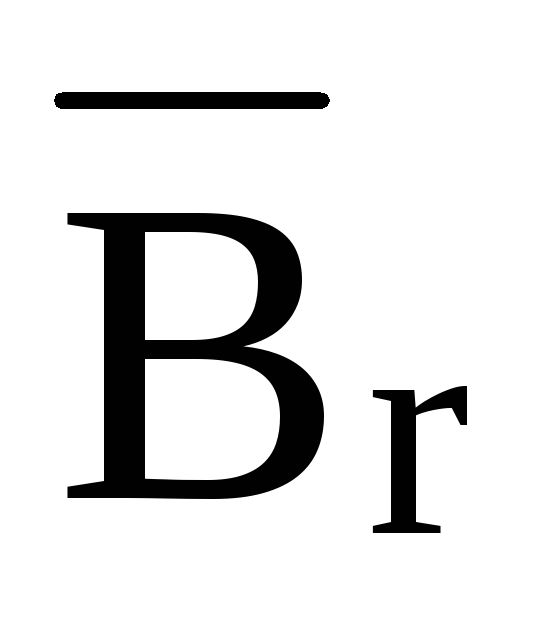 .
Магнитное склонение
.
Магнитное склонение ,
наклонение α и горизонтальная
составляющая магнитного поля
,
наклонение α и горизонтальная
составляющая магнитного поля  являются основными параметрами
магнитного поля Земли.
являются основными параметрами
магнитного поля Земли.
Значение 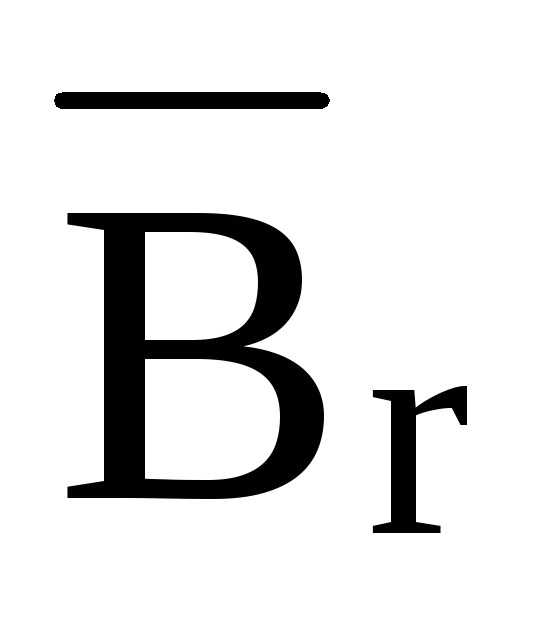 определяют магнитометрическим методом,
который основан на взаимодействии
магнитного поля катушки с магнитной
стрелкой. Прибор, называемый
тангенс-буссолью, представляет собой
небольшую буссоль (компас с лимбом,
разделенным на градусы), укрепленную
внутри катушки 1 из нескольких
витков изолированной проволоки.
определяют магнитометрическим методом,
который основан на взаимодействии
магнитного поля катушки с магнитной
стрелкой. Прибор, называемый
тангенс-буссолью, представляет собой
небольшую буссоль (компас с лимбом,
разделенным на градусы), укрепленную
внутри катушки 1 из нескольких
витков изолированной проволоки.
Катушка
расположена в вертикальной плоскости.
Она создает добавочное магнитное
поле  к (диаметр катушки и число витков указываются
на приборе).
к (диаметр катушки и число витков указываются
на приборе).
В
центре катушки помещается магнитная
стрелка 2. Она должна быть небольшой,
чтобы можно было принимать индукцию,
действующую на ее полюсы,
равной индукции в центре кругового
тока. Плоскость контура катушки
устанавливается
так, чтобы она совпадала с направлением
стрелки и была перпендикулярна
горизонтальной составляющей земного
поля 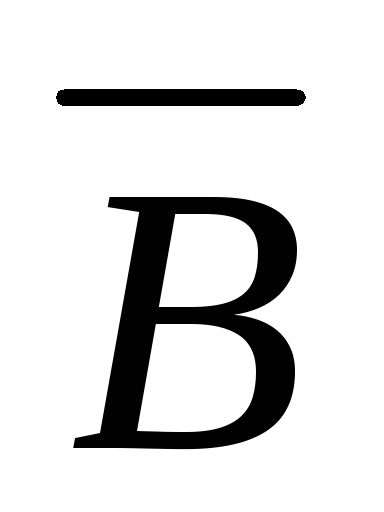 r.
Под действием
r.
Под действием 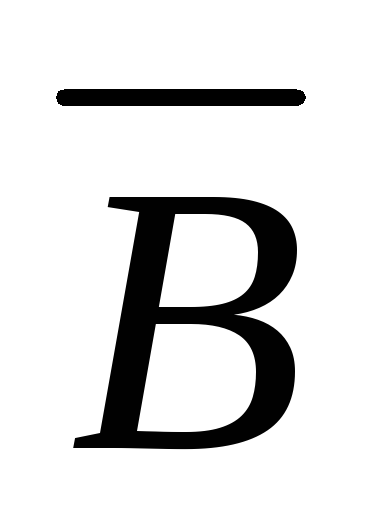 r индукции
поля Земли и индукции поля катушки
стрелка устанавливается по направлению
равнодействующей индукции р(рис.
6 а, б).
r индукции
поля Земли и индукции поля катушки
стрелка устанавливается по направлению
равнодействующей индукции р(рис.
6 а, б).

Рис. 6
Из рис. 6 видно, что
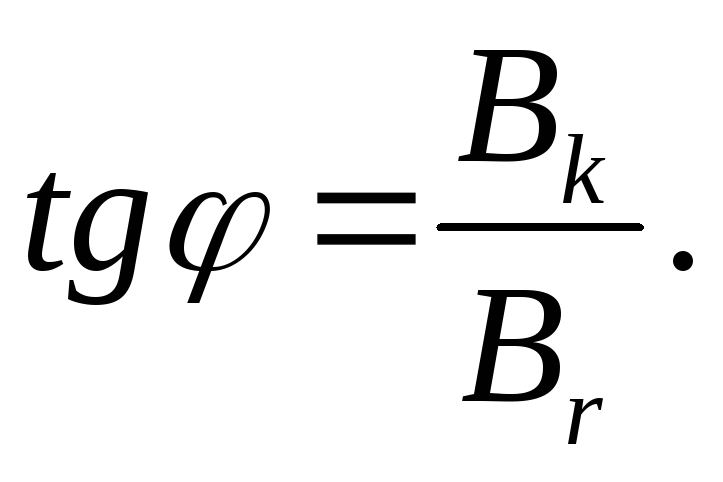 (6)
(6)
Индукция магнитного поля катушки в центре –
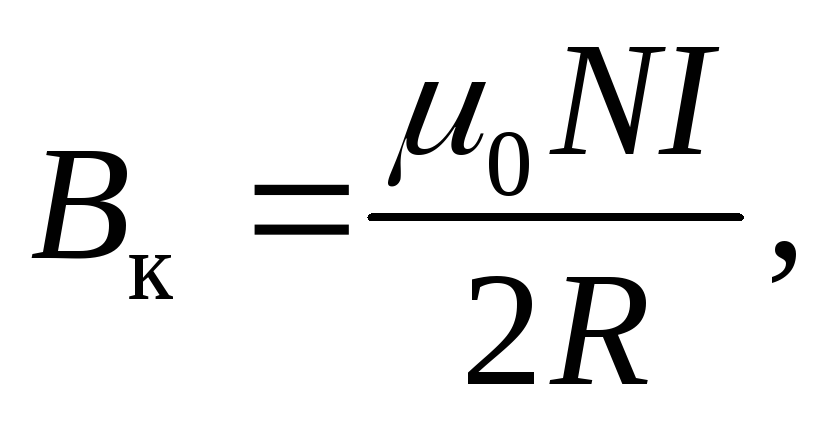 7)
7)
где N — число витков катушки; I — ток, идущий по ней; R — радиус катушки. Из (6) и (7) следует, что

Или
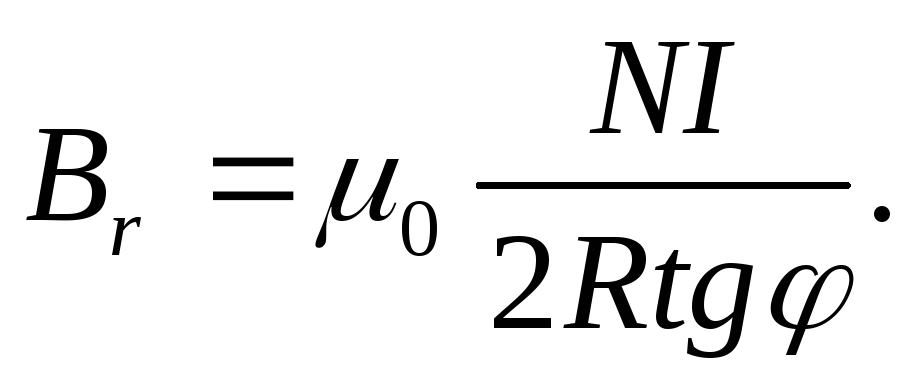 (8)
(8)
Важно понять, что формула (8) является приближенной, т.е. она верна только в том случае, когда размер магнитной стрелки намного меньше радиуса контура R. Минимальная ошибка при измерении фиксируется при угле отклонения стрелки ≈45°. Соответственно этому и подбирается сила тока в катушке тангенс-буссоли.
Порядок выполнения работы
Установить катушку тангенс-буссоли так, чтобы ее плоскость совпала с на правлением магнитной стрелки.
Собрать цепь по схеме (рис. 7).
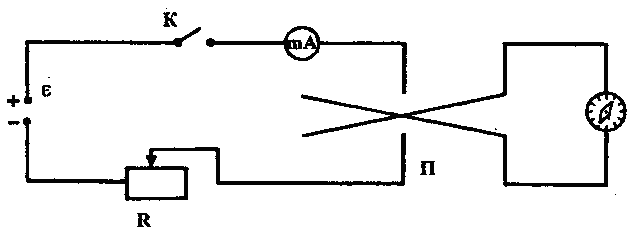
Рис. 7
3.
Включить ток и измерить углы отклонения
у концов стрелки  и
и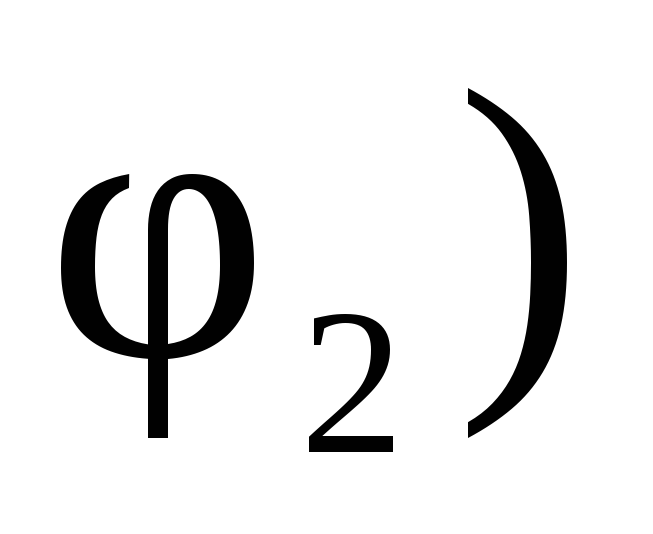 .
Данные занести в таблицу. Затем с помощью
переключателя П изменить направление
тока на противоположное, не
меняя величины силы тока, и измерить
углы отклонения у обоих концов стрелки
.
Данные занести в таблицу. Затем с помощью
переключателя П изменить направление
тока на противоположное, не
меняя величины силы тока, и измерить
углы отклонения у обоих концов стрелки  и
и 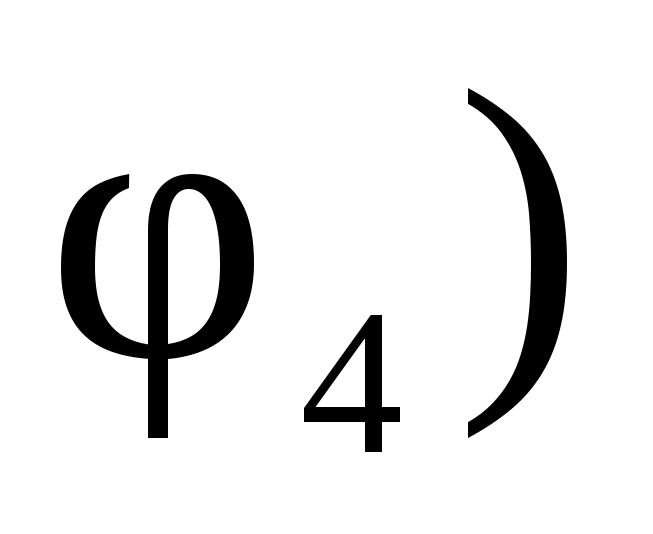 вновь. Данные занести в таблицу. Таким
образом, устраняется ошибка определения
угла, связанная с несовпадением плоскости
катушки тангенс-буссоли с плоскостью
магнитного
меридиана. Вычислить
вновь. Данные занести в таблицу. Таким
образом, устраняется ошибка определения
угла, связанная с несовпадением плоскости
катушки тангенс-буссоли с плоскостью
магнитного
меридиана. Вычислить
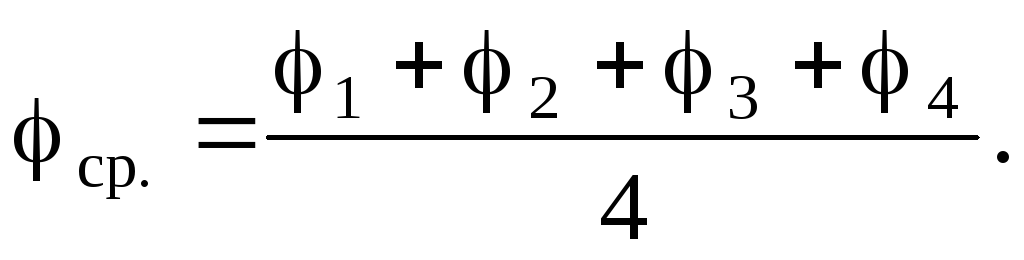
Результаты
измерений I
и  занести
в таблицу 1.
занести
в таблицу 1.
Таблица 1
Опыт повторить для 5-ти различных значений тока, но при условии, чтобы углы
 были не меньше 25° и не больше 45°. Ток в
цепи изменять резисторомR.
были не меньше 25° и не больше 45°. Ток в
цепи изменять резисторомR.По формуле (8) вычислить Вr — значение горизонтальной составляющей земного поля в системе СИ (для каждого значения силы тока).
Вычислить Вср. по формуле
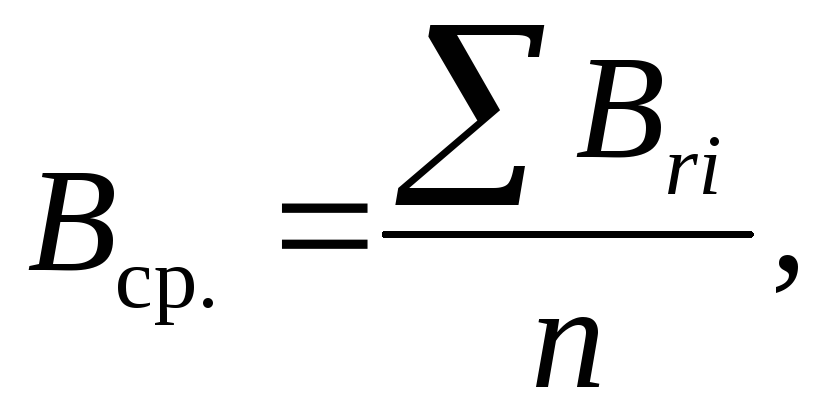
где n — число измерений.
Найти доверительную границу общей погрешности по формуле
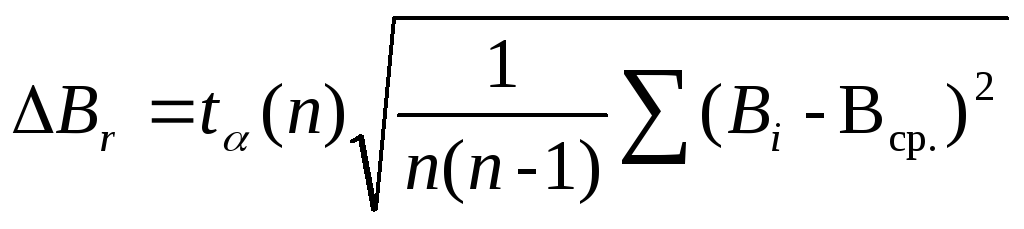 ,
,
Где  — коэффициент Стьюдента (при
— коэффициент Стьюдента (при =0,95
иn=5
=0,95
иn=5 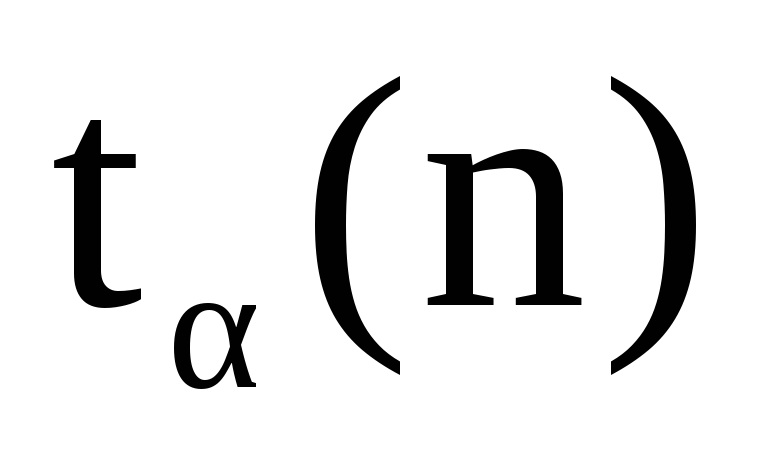 =2,8).
=2,8).
Результаты записать в виде выражения
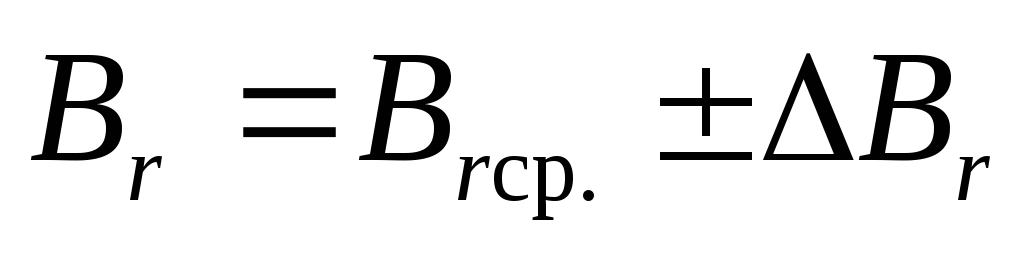 .
.
Контрольные вопросы
Что называется индукцией магнитного поля? Какова единица ее измерения? Как определяется направление вектора магнитной индукции?
Что называется напряженностью магнитного поля? Какова ее связь с магнитной индукцией?
Сформулировать закон Био-Савара-Лапласа, вычислить на его основе индукцию магнитного поля в центре кругового тока, индукцию поля прямого тока и соленоида.
Как определяется направление индукции магнитного поля прямого и кругового токов?
В чем заключается принцип суперпозиции магнитных полей?
Какое поле называют вихревым?
Сформулируйте закон Ампера.
Расскажите об основных параметрах магнитного поля Земли.
Каким образом можно определить направление силовых линий магнитного поля Земли?
Почему измерение горизонтальной составляющей индукции магнитного по ля выгоднее проводить при угле отклонения стрелки в 45°?
ЛАБОРАТОРНАЯ РАБОТА №7
Закон Био-Савара-Лапласа. Вывод формулы для напряженности и индукции магнитного поля на оси кругового витка с током.
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
Нижегородский Государственный Технический Университет им. Р.Е.Алексеева
Выксунский филиал
Кафедра общеобразовательных и общепрофессиональных дисциплин
Методическое пособие
к выполнению лабораторной работы №2-6
«Магнитное поле соленоида. Датчик Холла»
Для студентов всех специальностей и всех форм обучения ВФ НГТУ
г. Выкса
2009г.
Составители: В.П. Маслов, О.Д. Честнова, С.А.Ковыляев
Определение индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.: методическое пособие к выполнению лаб. работы №2-6 по дисциплине «Физика» для студентов всех специальностей и всех форм обучения ВФ НГТУ; сост.: В.П.Маслов и др. г.Н.Новгород, 2009. -9с.
Дана методика определения индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.. При написании использованы описания лабораторных работ НГТУ, МАИ, МИФИ, СФТИ и др. вузов.
Научный редактор А.А. Радионов
Редактор Э.Б. Абросимова
Подписано в печать Формат 60х48 1/16. Бумага газетная.
Печать офсетная. Усл. п. л. 0,75. Уч.-изд. л. 0,75. Тираж 200 экз. Заказ 14.
Нижегородский Государственный Технический Университет им. Р.Е.Алексеева
Типография НГТУ. 603950, ГСП-41, г. Нижний Новгород, ул. Минина, 24.
© Нижегородский государственный технический
университет им. Р.Е.Алексеева, 2009
Цель работы: ознакомиться с определением индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
В
пространстве, окружающем проводники с
током, движущиеся заряды, магниты,
возникает магнитное поле, которое можно
обнаружить по воздействию его на другой
проводник с током или магнитную стрелку.
Магнитное поле в каждой точке пространства
количественно может быть описано с
помощью вектора напряженности магнитного
поля 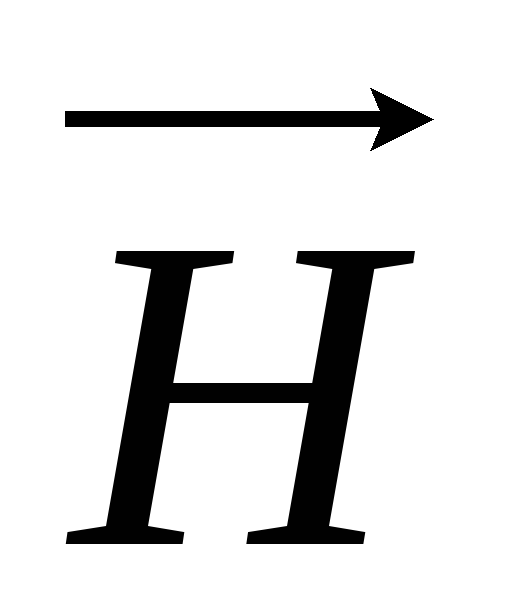 или с помощью вектора индукции магнитного
поля
или с помощью вектора индукции магнитного
поля 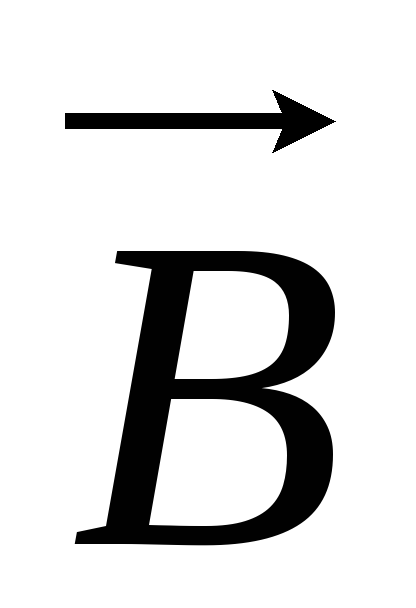 .
В вакууме векторы
.
В вакууме векторы 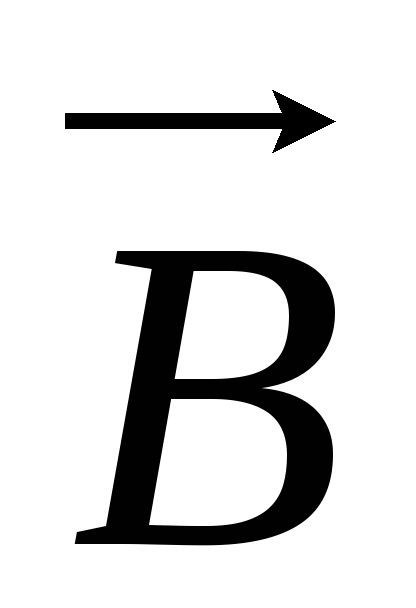 и
и 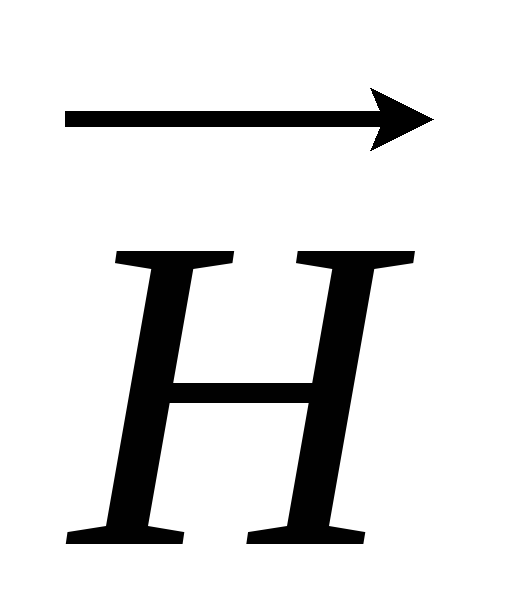 связаны соотношением:
связаны соотношением:
 ,
(1)
,
(1)
где μ0 = 4π·10 -7 Гн/м — магнитная постоянная.
Единицы
измерения 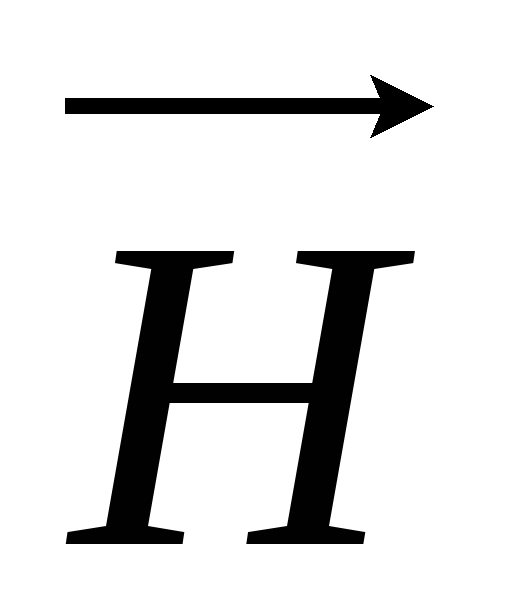 и
и 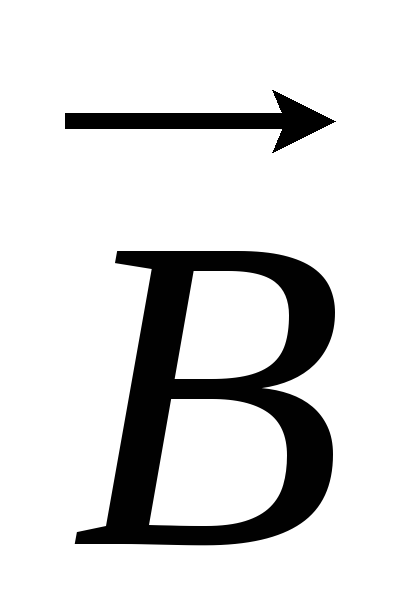 А/м и
Тл соответственно. В среде с магнитной
проницаемостью μ
А/м и
Тл соответственно. В среде с магнитной
проницаемостью μ
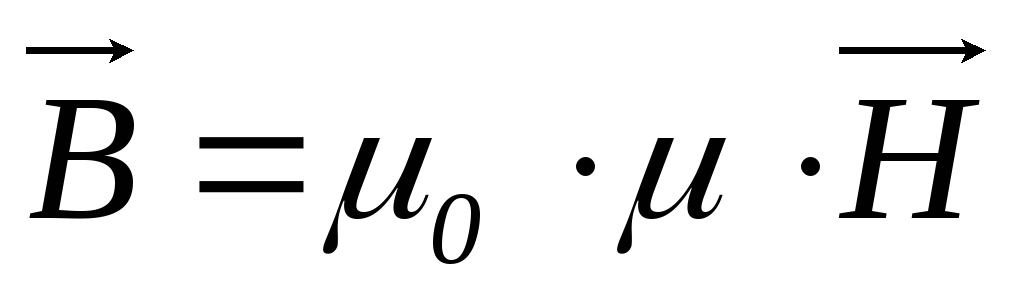
Для
вычисления напряженности и индукции
магнитного поля, используют закон
Био-Савара-Лапласа, согласно которому
элементарная напряженность магнитного
поля 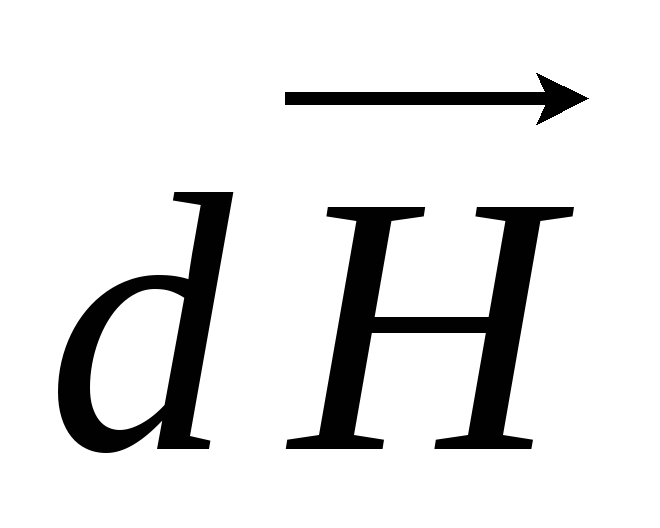 ,
создаваемая элементом проводника с
током
,
создаваемая элементом проводника с
током 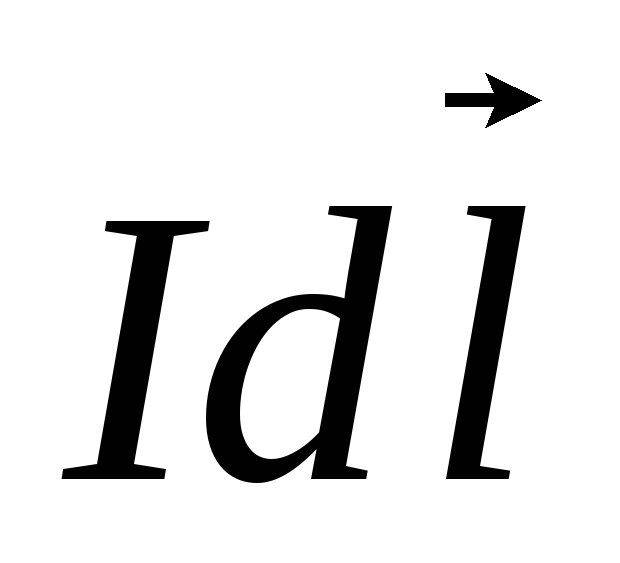 в некоторой точке пространства на
расстоянии
в некоторой точке пространства на
расстоянии 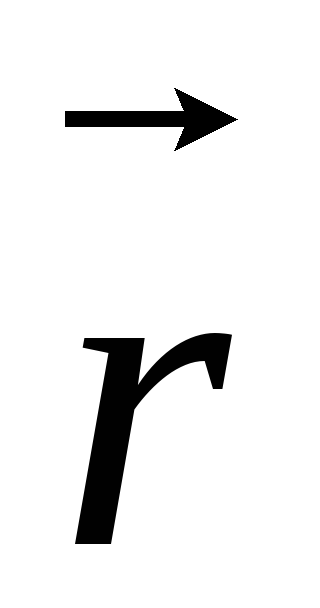 ,
определяется выражением:
,
определяется выражением:
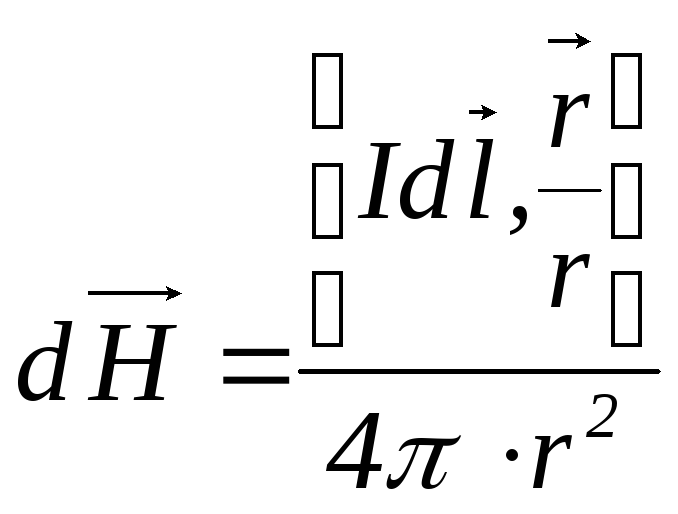 ,
(2)
,
(2)
где 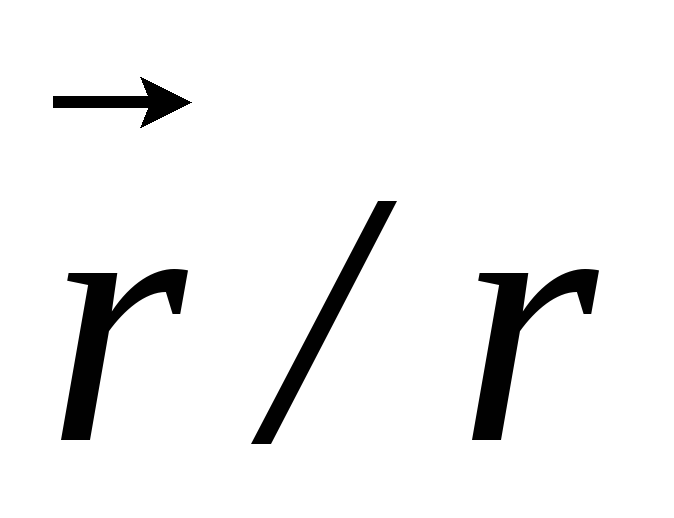 – единичный вектор, направленный вдоль
– единичный вектор, направленный вдоль 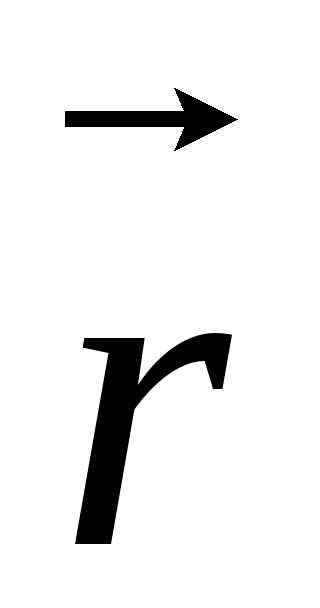 .
.
Модуль вектора:
 ,
,
где  – угол между векторами
– угол между векторами 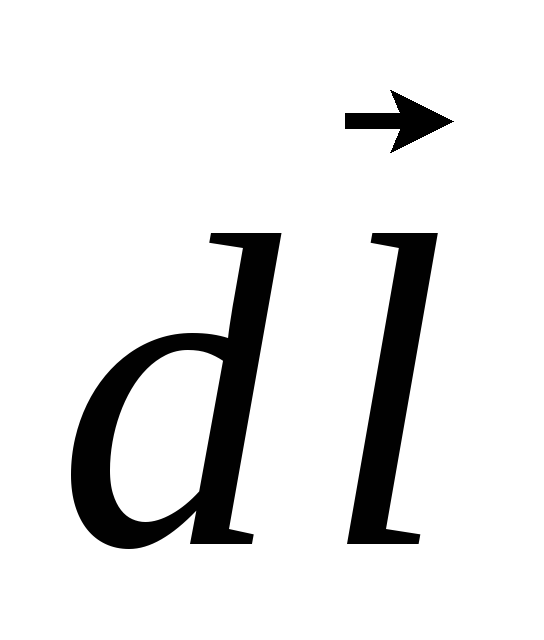 и
и 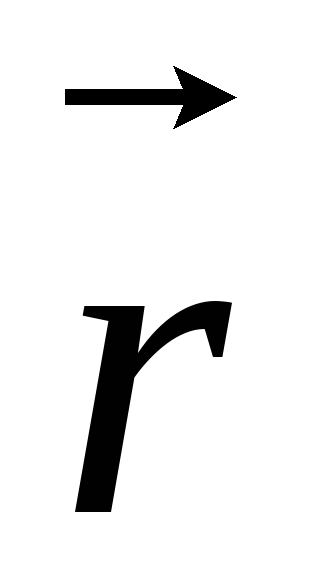 .
.
Для
нахождения результирующей напряженности,
создаваемой проводником конечных
размеров, надо воспользоваться принципом
суперпозиции магнитных полей и найти
векторную сумму элементарных напряженностей 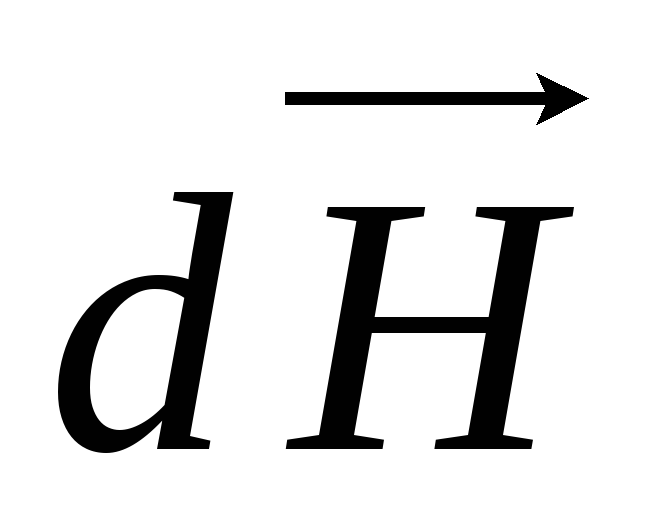 от
всех элементов
от
всех элементов 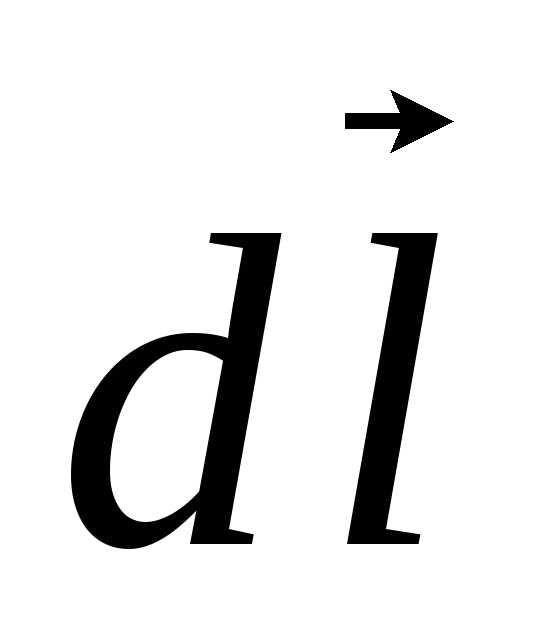 проводника. Применим формулу (2) для
вычисления напряженности магнитного
поля на оси кругового витка с током
(рис.1).
проводника. Применим формулу (2) для
вычисления напряженности магнитного
поля на оси кругового витка с током
(рис.1).
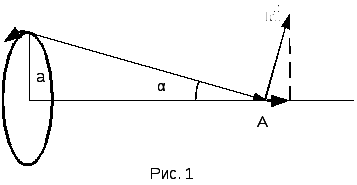
На
рис.1 компонента 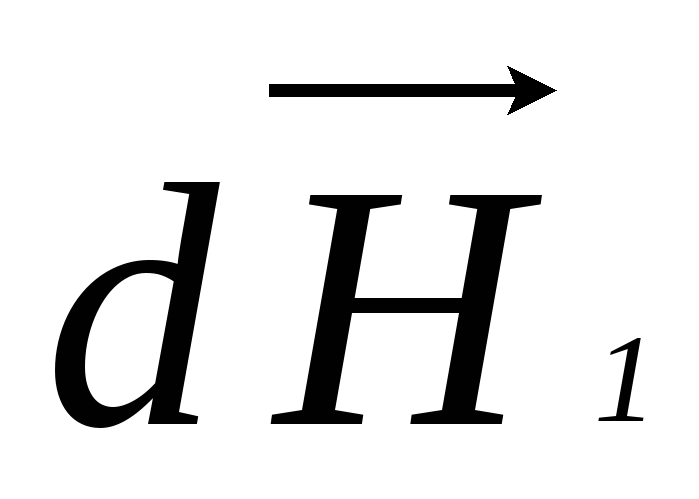 ,
созданная элементом тока
,
созданная элементом тока 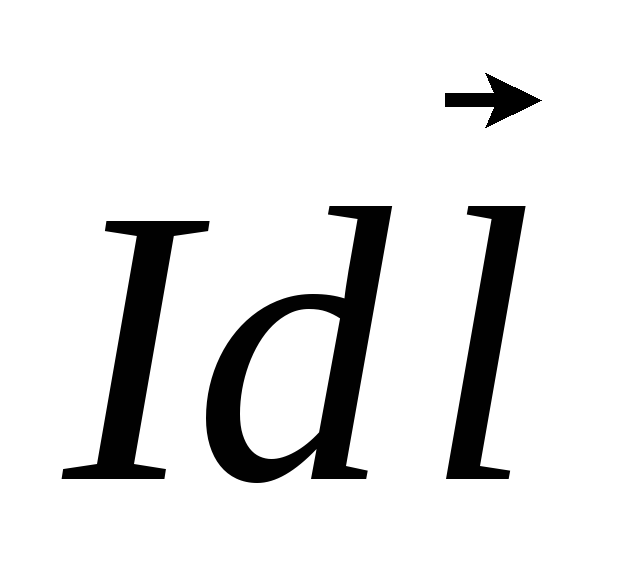 ,
согласно (2) определяется как
,
согласно (2) определяется как
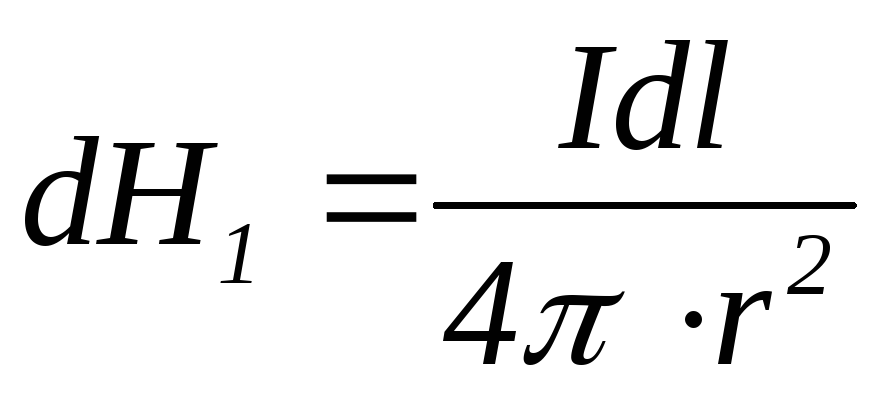 ,
,
где
учтено, что угол между 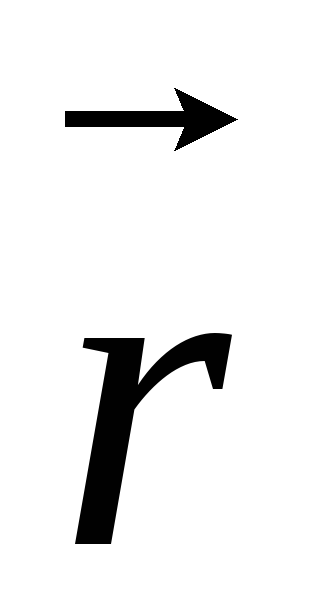 и
и 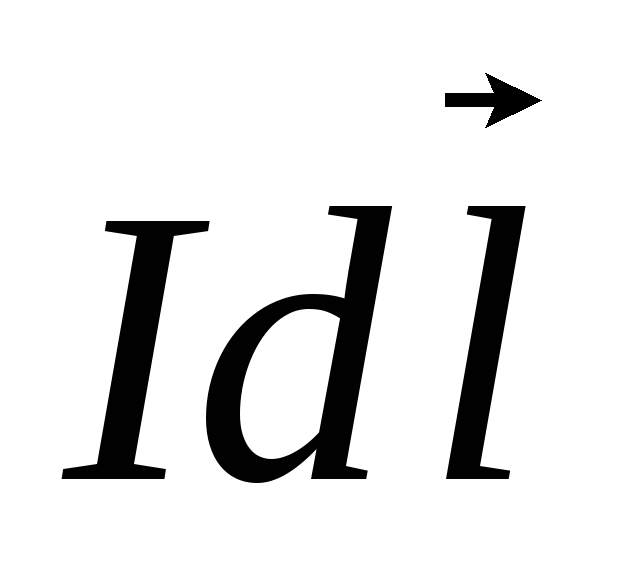 прямой. Из симметрии элементов
прямой. Из симметрии элементов 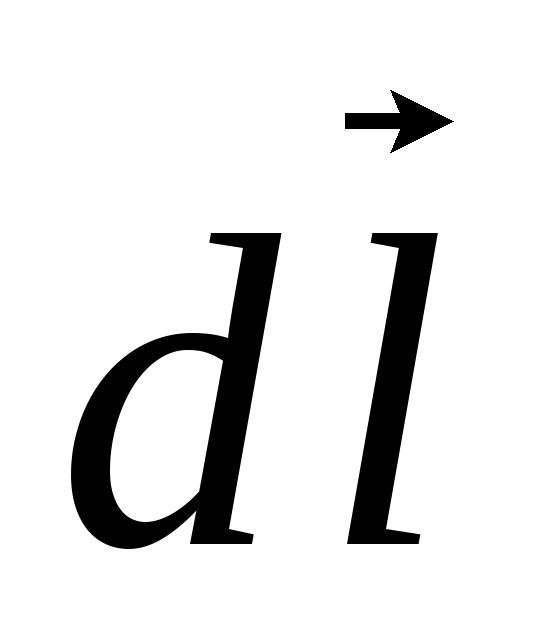 витка по отношению к точке А видно, что
результирующая напряженность магнитного
поля направлена вдоль оси так, что
витка по отношению к точке А видно, что
результирующая напряженность магнитного
поля направлена вдоль оси так, что 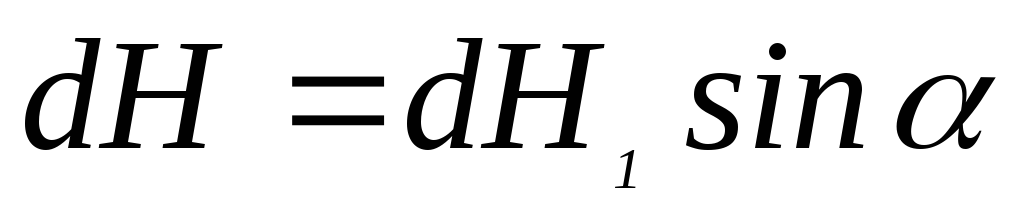 ,
то есть
,
то есть
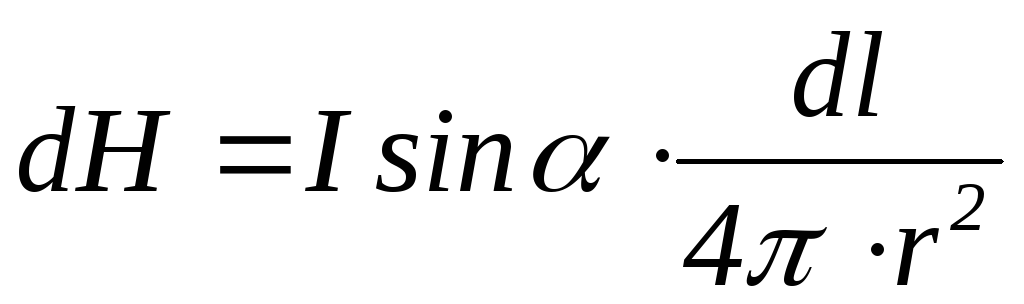 .
.
В
правой части последней формулы
все-величины, кроме  ,
постоянны (для данной точки А), поэтому
интегрирование no
,
постоянны (для данной точки А), поэтому
интегрирование no  дает
дает
 ,
,
или согласно рис.1
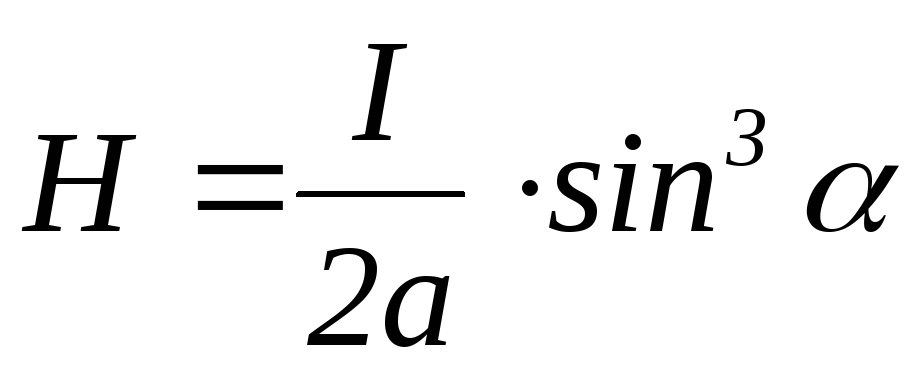 (3)
(3)
Величину  можно найти по формуле (1).
можно найти по формуле (1).
Вывод формулы для напряженности и индукции магнитного поля на оси соленоида (на расстоянии z от средней точки на оси)
Пусть
на единицу длины соленоида приходится n витков (рис.2), тогда участок 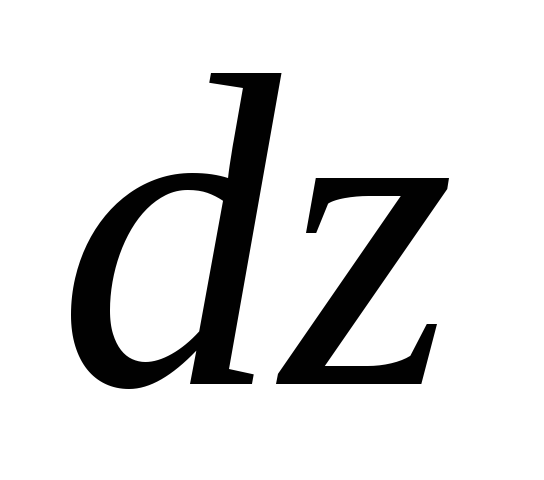 содержит
содержит 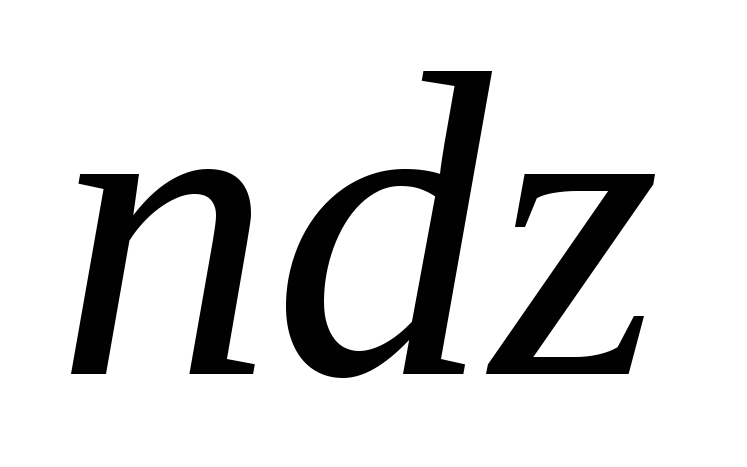 витков,
которые,
согласно (3), в точке А на оси создадут
напряженность
витков,
которые,
согласно (3), в точке А на оси создадут
напряженность
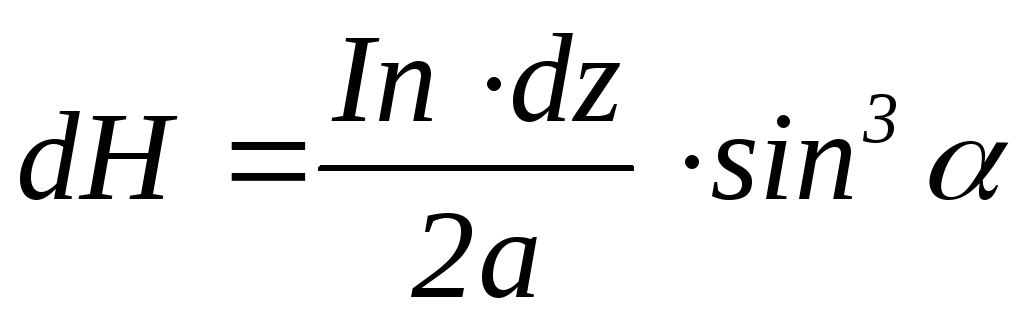 .
(4)
.
(4)
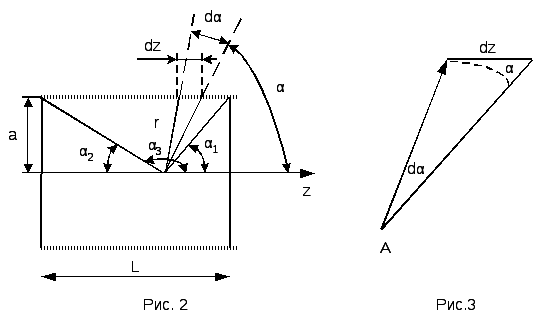
На
рис.2 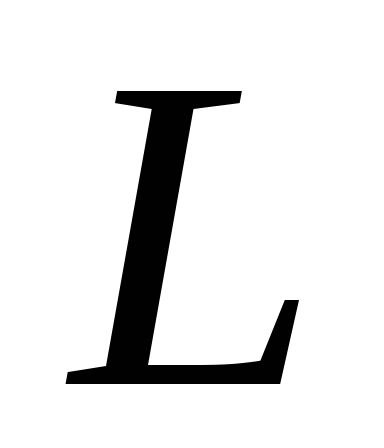 – длина соленоида, а — радиус витков
обмотки, 0 -центральная точка на оси
соленоида. ОА=z – координата точки А.
– длина соленоида, а — радиус витков
обмотки, 0 -центральная точка на оси
соленоида. ОА=z – координата точки А.
На
рис. 3 отдельно изображены элементы dz,
радиус-вектор 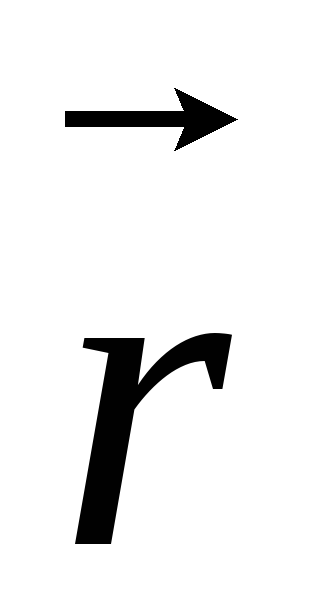 и углы
и углы  и
и 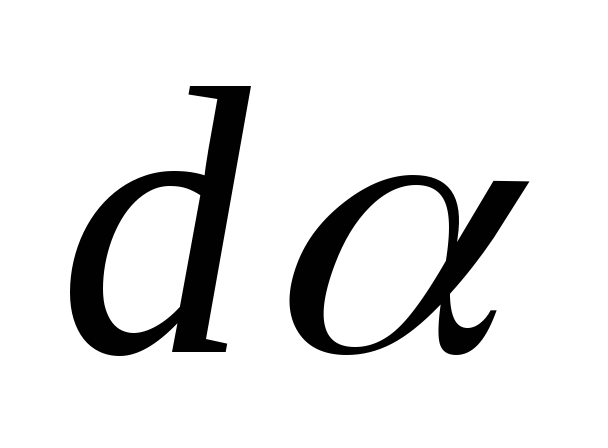 .
Из геометрических построений рис.2 и 3
следует:
.
Из геометрических построений рис.2 и 3
следует:
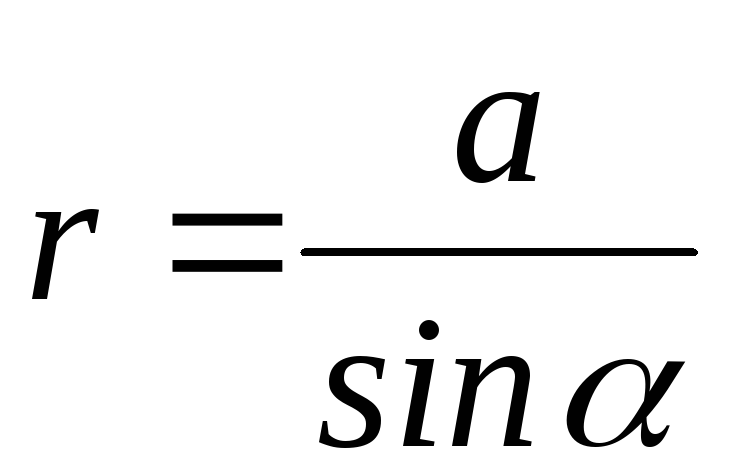 ;
; 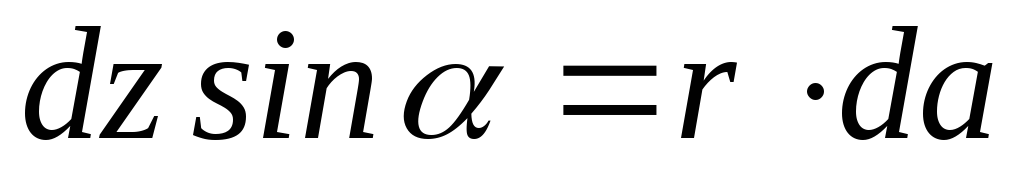 ;
; 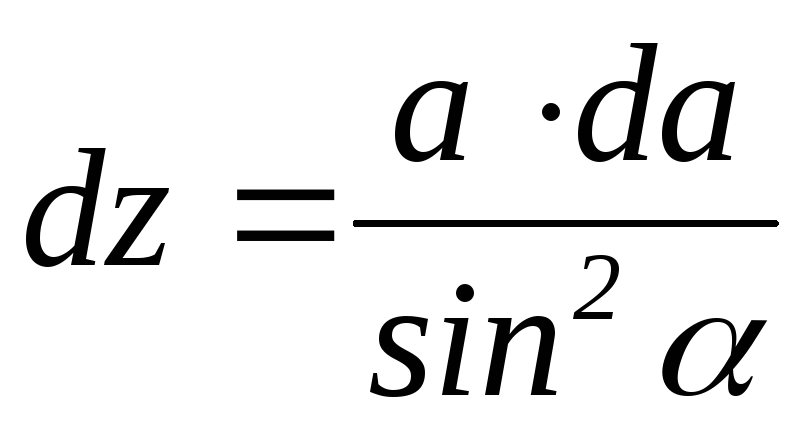 .
.
Подставим
эти соотношения в (4) и проинтегрируем
по  в пределах от
в пределах от  до
до 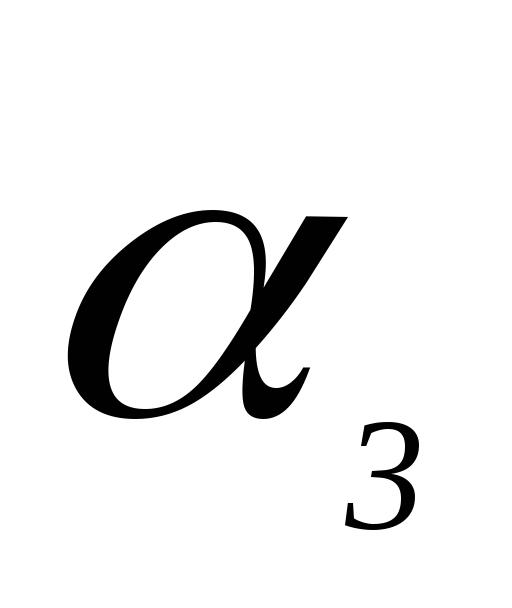 :
:
 .
.
Учитывая,
что 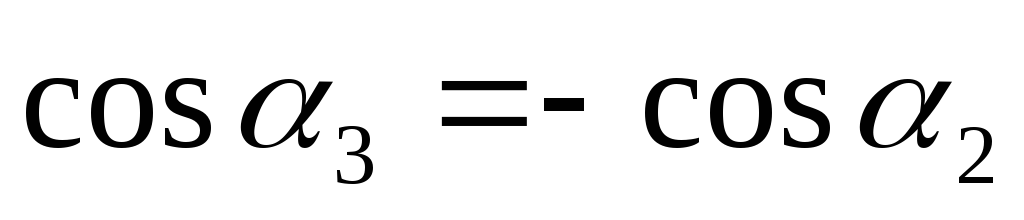 ,
получим
,
получим
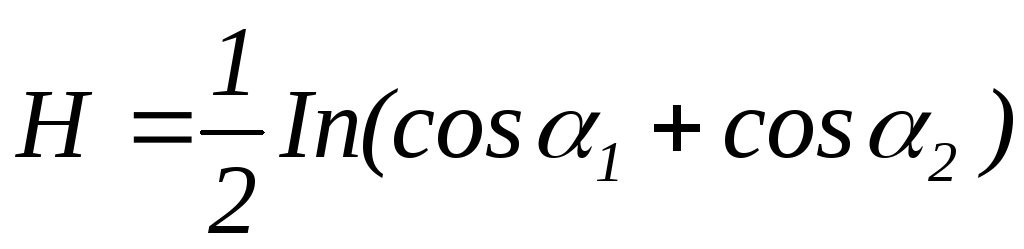 (5)
(5)
В
случае бесконечно длинного соленоида
(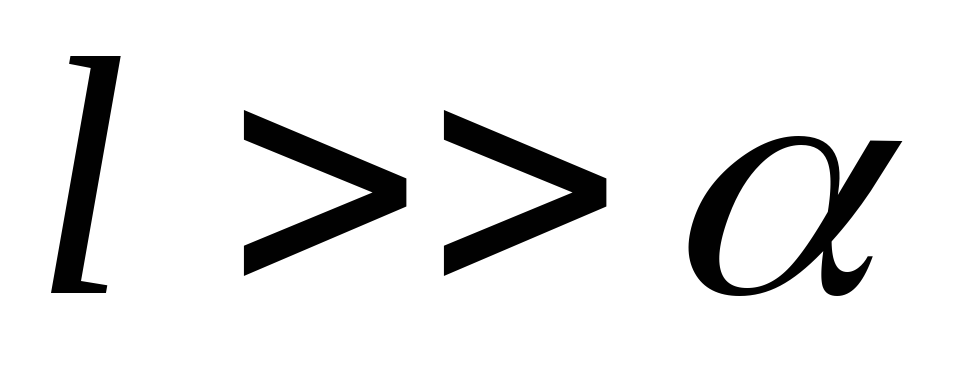 )
в центральной точке 0
)
в центральной точке 0 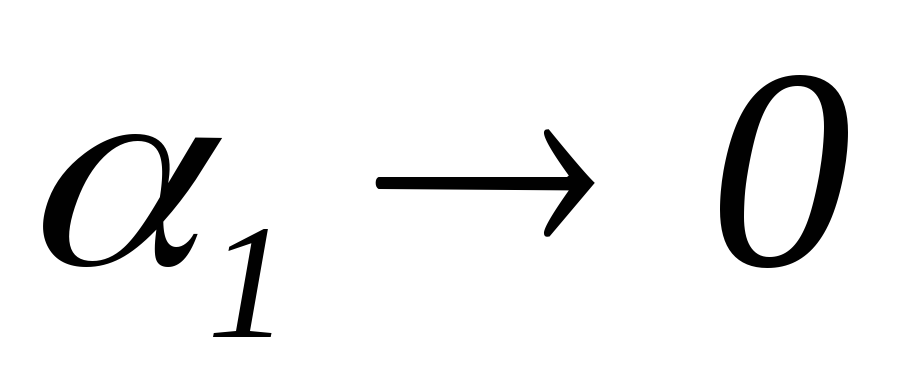 ,
, 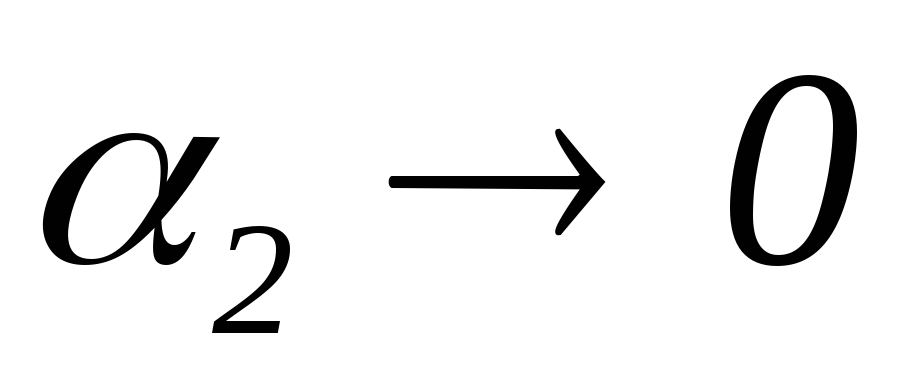
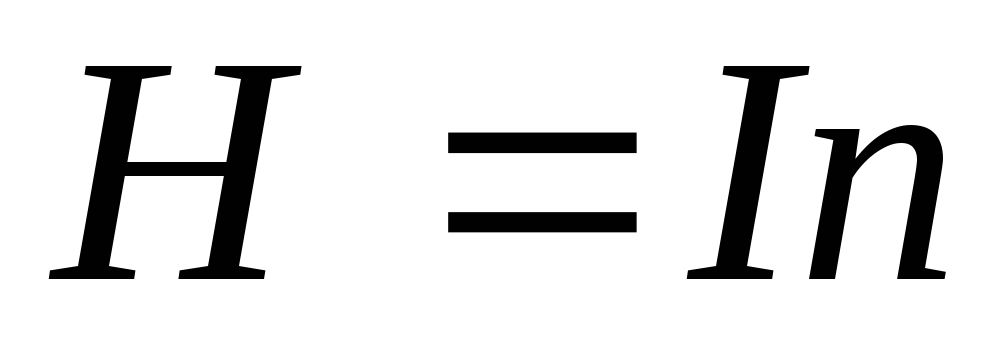 .
(6)
.
(6)
Из (5) также следует, что при переходе от центра к краю полубесконечного соленоида (на краю z=0,5L, α1=π/2, α2→0) напряженность уменьшается вдвое:
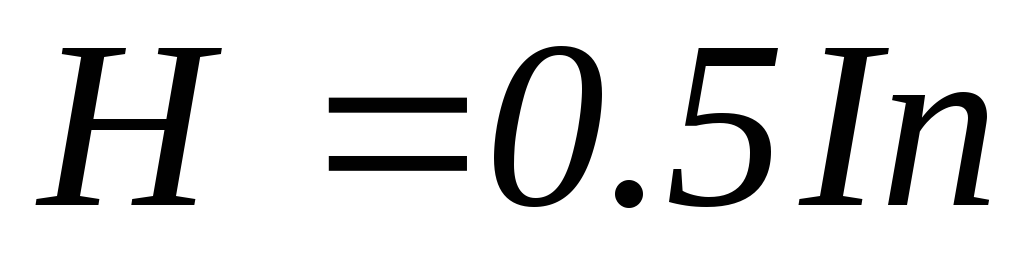 . (7)
. (7)
Индукцию, магнитного поля получим, добавив к выражениям (5), (б), (7) формулу (1). Отметим, что вывод формулы (6) для бесконечно длинного соленоида получается существенно проще на основе закона полного тока.
20. Магнитное поле тока. Закон Био-Савара-Лапласа и его применение к расчету индукции магнитного поля прямолинейного тока.
Магнитное поле тока:
Магнитное поле создается вокруг электрических зарядов при их движении. Так как движение электрических зарядов представляет собой электрический ток, то вокруг всякого проводника с током всегда существует магнитное поле тока.
Чтобы убедиться в существовании магнитного поля тока, поднесем сверху к проводнику, по которому протекает электрический ток, обыкновенный компас. Стрелка компаса тотчас же отклонится в сторону. Поднесем компас к проводнику с током снизу — стрелка компаса отклонится в другую сторону (рисунок 1).

Применим закон Био–Савара–Лапласа для расчета магнитных полей простейших токов. Рассмотрим магнитное поле прямого тока.
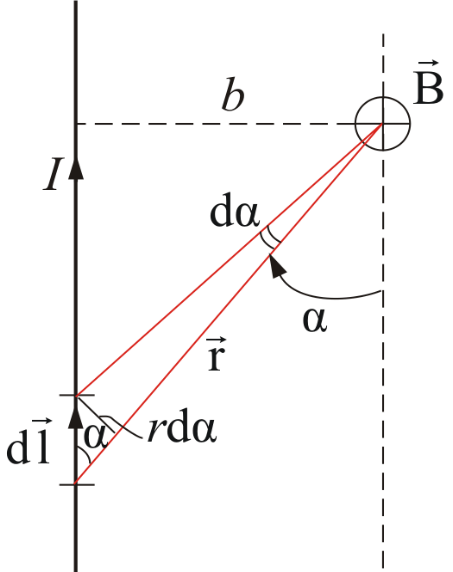
Все векторы dB от произвольных элементарных участков dl имеют одинаковое направление. Поэтому сложение векторов можно заменить сложением модулей.
Пусть точка, в которой определяется магнитное поле, находится на расстоянии b от провода. Из рисунка видно, что:
 ;
; 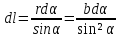
Подставив найденные значения r и dl в закон Био–Савара–Лапласа, получим:

Для конечного
проводника угол
α изменяется от  ,
до
,
до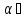 .
Тогда
.
Тогда
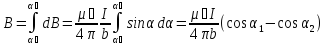
Для бесконечно
длинного проводника  ,
а
,
а 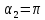 ,
тогда
,
тогда
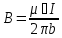 или,
что удобнее для расчетов,
или,
что удобнее для расчетов,  .
.
Линии магнитной индукции прямого тока представляют собой систему концентрических окружностей, охватывающих ток.
21. Закон Био-Савара-Лапласа и его применение к расчету индукции магнитного поля кругового тока.
Магнитное поле кругового проводника с током.
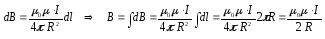
22. Магнитный момент витка с током. Вихревой характер магнитного поля.
Магнитный момент витка с током это физическая величина, как и любой другой магнитный момент, характеризует магнитные свойства данной системы. В нашем случае систему представляет круговой виток с током. Этот ток создает магнитное поле, которое взаимодействует с внешним магнитным полем. Это может быть как поле земли, так и поле постоянного или электромагнита.

Рисунок — 1 круговой виток с током
Круговой виток с током можно представить в виде короткого магнита. Причем этот магнит будет направлен перпендикулярно плоскости витка. Расположение полюсов такого магнита определяется с помощью правила буравчика. Согласно которому северный плюс будет находиться за плоскостью витка, если ток в нем будет двигаться по часовой стрелке.
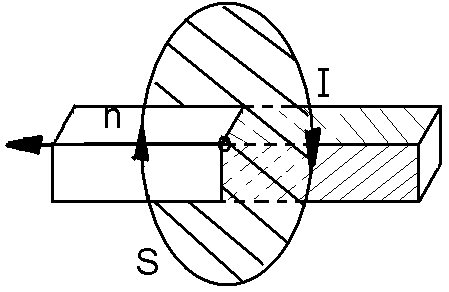
Рисунок— 2 Воображаемый полосовой магнит на оси витка
На этот магнит, то есть на наш круговой виток с током, как и на любой другой магнит, будет воздействовать внешнее магнитное поле. Если это поле будет однородным, то возникнет вращающий момент, который будет стремиться развернуть виток. Поле буде поворачивать виток так чтобы его ось расположилась вдоль поля. При этом силовые линии самого витка, как маленького магнита, должны совпасть по направлению с внешним полем.
Если же внешнее поле будет не однородным, то к вращающему моменту добавится и поступательное движение. Это движение возникнет вследствие того что участки поля с большей индукцией будут притягивать наш магнит в виде витка больше чем участки с меньшей индукцией. И виток начнет двигаться в сторону поля с большей индукцией.
Величину магнитного момента кругового витка с током можно определить по формуле.

Где, I ток протекающий по витку
S площадь витка с током
n нормаль к плоскости в которой находится виток
Таким образом, из формулы видно, что магнитный момент витка это векторная величина. То есть кроме величины силы, то есть ее модуля он обладает еще и направлением. Данное свойство магнитный момент получил из-за того что в его состав входит вектор нормали к плоскости витка.




 были не меньше 25° и не больше 45°. Ток в
цепи изменять резисторомR.
были не меньше 25° и не больше 45°. Ток в
цепи изменять резисторомR.