Электрическое сопротивление | Все формулы
Электрическое сопротивление — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему
Высокая электропроводность металлов связана с тем, что в них имеется большое количество носителей тока — электронов проводимости, образующихся из валентных электронов атомов металла, которые не принадлежат определённому атому. Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение электронов. Движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решётки (на примесях, дефектах решётки, а также нарушениях периодической структуры, связанной с тепловыми колебаниями ионов). При этом электроны теряют импульс, а энергия их движения преобразуются во внутреннюю энергию кристаллической решётки, что и приводит к нагреванию проводника при прохождении по нему электрического тока.
В формуле мы использовали :
— Электрическое сопротивление
— Длина проводника
— Площадь поперечного сечения проводника
— Удельное сопротивление проводника
— Напряжение, поданное на проводник
— Сила тока в проводнике
Сопромат для чайников ℹ️ основы сопротивления материалов, характеристика, основные задачи, обозначения и формулы, условия расчетов, методы и примеры решений
Многочисленные учебники «Cопромат для чайников» создают для развенчания мифа о непостижимой сложности дисциплины. Этой наукой пугают на первых курсах вузов. Для начала расшифруем грозный термин «сопротивление материалов».
На деле – проста и решение почти не выходит за рамки школьной задачи о растяжении и сжатии пружины. Другое дело – найти слабое звено конструкции и свести расчет к несложной постановке. Так что не стоит зевать на лекциях по основам механики. При подготовке к урокам можно пользоваться решениями онлайн, но на экзаменах помогут только свои знания.
Что такое сопромат
Это методика расчета деталей, конструкций на способность выдерживать нагрузки в требуемой степени. Или хотя бы для предсказания последствий. Не более, хотя почему-то относят руководство к наукам.
Этой «наукой» прекрасно владели древнегреческие и древнеримские инженеры, сооружавшие сложнейшие механизмы. Понятия не имея о структуре, уравнении состояния вещества и прочих теориях, египтяне строили исполинские плотины и пирамиды.
Основные задачи по сопротивлению материалов
Задача следует напрямую из определения. А вот каковы критерии упомянутого слова «выдерживать»? Неясно, что скрывается под «материалом» и как реальные вещи схематизировать.
Требования
Перечислены далеко не все, но для статики и базовой программы хватит:
-
Прочность – способность образца воспринимать внешние силы без разрушения. Слегка мнущаяся под весом оборудования подставка никого не интересует. Основную-то функцию она выполняет.
-
Жесткость – свойство воспринимать нагрузку без существенного нарушения геометрии. Гнущийся под силой резания инструмент даст дополнительную погрешность обработки. К ошибке приведет деформация станины агрегата.
-
Устойчивость – способность конструкции сохранять стабильность равновесия. Поясним на примере: стержень находится под грузом, будучи прямым – выдерживает, а чуть изогнется – характер напряжения изменится, груз рухнет.
Материал и силы
Как всякая методика, сопромат принимает массу упрощений и прямо неверных допущений:
-
материал однороден, среда сплошная. Внутренние особенности в расчет не берутся;
-
свойства не зависят от направления;
-
образец восстанавливает начальные параметры при снятии нагрузки;
-
поперечные сечения не меняются при деформации;
-
в удаленных от места нагрузки местах усилие распределяется равно по сечению;
-
результат воздействия нагрузок равен сумме последствий от каждой;
-
деформации не влияют на точки приложения сил;
-
отсутствуют изначальные внутренние напряжения.
Схемы
Служат для создания возможности расчета реальных конструкций:
-
тело – объект с практически одинаковыми «длина х ширина х высота»;
-
брус (балка, стержень, вал) – характеризуется значительной длиной.
На рисунке показаны опоры с воспринимаемыми реакциями (обозначены красным цветом):
Рис. 1. Опоры с воспринимаемыми реакциями:
а) шарнирно-подвижная;
б) шарнирно-неподвижная;
в) жесткая заделка (защемление).
Силы в сопромате
Приложенные извне, уравновешиваются возникающими изнутри. Напомним, рассматривается статическая ситуация. Материал «сопротивляется».
Разделим нагруженное тело виртуальным сечением P (см. рис. 2).
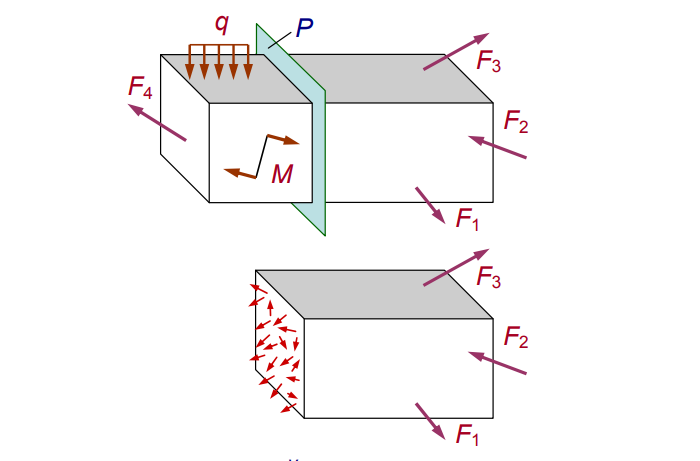
Рис. 2
Заменим хаос равнодействующей R и моментом M (см. рис. 3):
Рис. 3
Распределив по осям, получим картину нагрузки сечения (см. рис. 4):
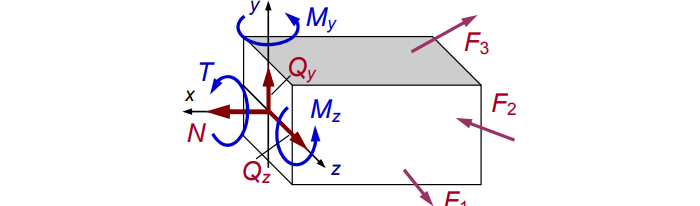
Рис. 4
Нагрузки и деформации, изучаемые в сопромате
Изучим несколько принятых терминов.
Напряжения
В теле приложенные силы распределяются по сечению. Нагружен каждый элементарный «кусочек». Разложим силы:
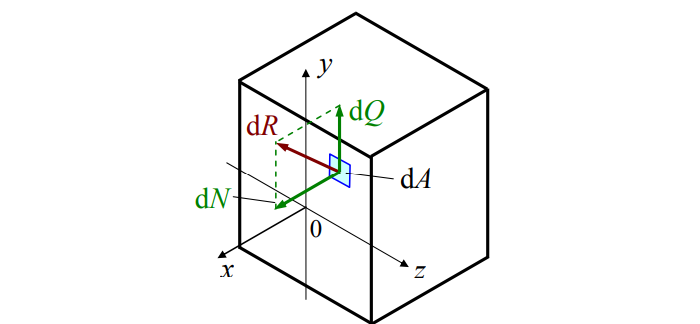
Элементарные усилия таковы:
-
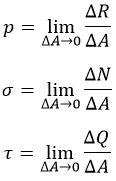
σ – «сигма», нормальное напряжение. Перпендикулярно сечению. Характерно для сжатия / растяжения;
-
τ – «тау», касательное напряжение. Параллельно сечению. Появляется при кручении;
-
p – полное напряжение.
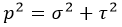
Просуммировав элементы, получим:
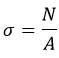
Здесь:
В принятой в России системе СИ сила измеряется в ньютонах (Н). Напряжения – в паскалях (Па). Длины в метрах (м).
Деформации
Различают деформацию упругую (с индексом «e») и пластическую (с индексом «p»). Первая исчезает по снятии растягивающей / сжимающей силы, вторая – нет.
Полная деформация будет равна:
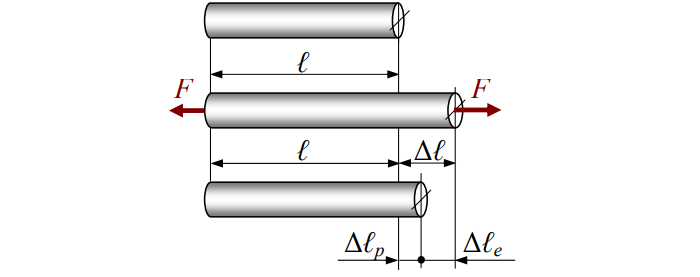
Деформация относительная обозначается «ε» и рассчитывается так:
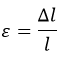
Под «сдвигом» понимается смещение параллельных слоев. Рассмотрим рисунок:
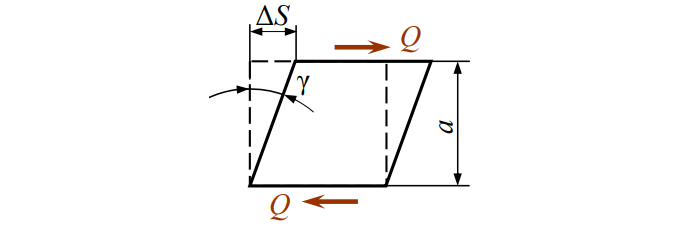
Здесь γ – относительный сдвиг.
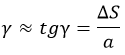
Виды нагрузки
Перечислены основные.
-
Растяжение и сжатие – нагрузка нормальной силой (по оси стержня).
-
Кручение – действует момент. Обычно рассчитываются передающие усилия валы.
-
Изгиб – воздействие направлено на искривление.
Основные формулы
Базовый принцип сопромата единственный. В упомянутой задаче о пружине применим закон Гука:
E – модуль упругости (Юнга). Величина зависит от используемого материала. Для стали полагают равным 200 х 106 Па.
Сопротивление материала прямо пропорционально деформации:
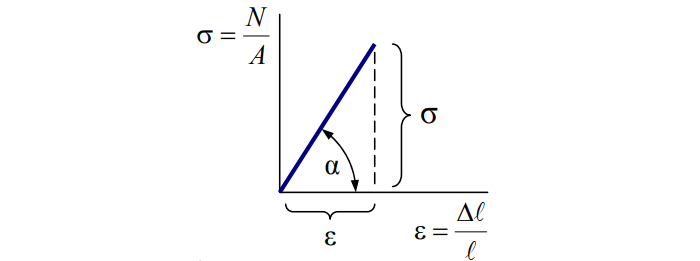
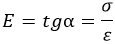
Закон верен не всегда и не для всех материалов. Как уже упоминалось, принимается как одно из допущений.
Реальная диаграмма
Растяжение стержня из низкоуглеродистой стали выглядит следующим образом:
Принимаемые схемы:
График (б) относится к большей части конструкционных материалов: подкаленные стали, сплавы цветных металлов, пластики.
Расчеты обычно ведут по σт (а) и σ0.2 (б). С незначительными пластическими деформациями конструкции или без таковых.
Пример решения задачи
Какой груз допустимо подвесить на пруток из стали 45 Ø10 мм?
Решение.
σ0,2 для стали 45 равна 245 МПа (из ГОСТ).
Площадь сечения прутка:
Допустимая сила тяжести:
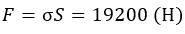
Для получения веса следует разделить на ускорение свободного падения g:
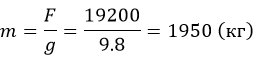
Ответ: необходимо подвесить груз массой 1950 кг.
Как найти опасное сечение
Наиболее простой способ – построение эпюры. На закрепленную балку действуют точечные и распределенные силы. Считаем на характерных участках, начиная с незакрепленного конца.
Усилие положительно, если направлено на растяжение.
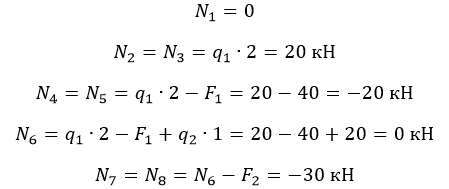
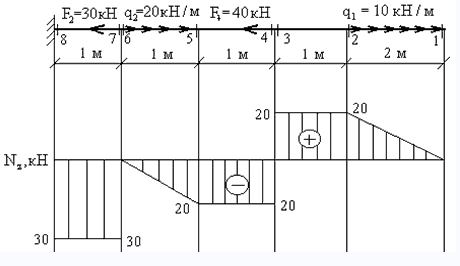
На схеме показано, что:
Зачем и кому нужен сопромат
Даже не имеющий отношения к прочностным расчетам инженер-универсал должен иметь понятие о приблизительных (на 10-20%) значениях. Знать конструкционные материалы, представлять свойства. Чувствовать заранее слабые места агрегатов.
Совершенно необходим разработчикам различных конструкций, машиностроительных изделий. Будущим архитекторам в вузах преподается в виде предмета «Строительная механика».
Методика помогает на стадии проектирования обеспечивать необходимый запас прочности изделий. Стойкость к постоянным и динамичным нагрузкам. Это сберегает массу времени и затрат в дальнейших изготовлении, испытании и эксплуатации изделия. Обеспечивает надежность и долговечность.
Формула сопротивления тока. Как найти, вычислить электрическое сопротивление.
Тема: по какой форуле можно рассчитать электрическое сопротивление.
В сфере электрики и электроники такая вещь (и понятие) как сопротивление встречается повсеместно. Хоть может и показаться, что электрическое сопротивление это плохо, так как она препятствует свободному течению электрических зарядов по проводникам, но это не совсем так. Возможно вы уже сталкивались с тем, что во всем нужна своя мера. Любой вид энергии (в нашем случае электрической, электромагнитной) в той или иной системе нуждается в своем определенном количестве. Если энергии становится больше или меньше нужной меры, то как правило возникают различные нарушения правильной ее работы. Так что сопротивление в определенных случаях это даже очень хорошо.
Ну, а какая есть формула сопротивления тока? Основополагающей формулой, по которой можно найти электрическое сопротивление является та, которая исходит из обычного закона Ома.
Сама формула электрического сопротивления выражается так — сопротивление это отношение напряжения к силе тока. То есть, чтобы найти электрическое сопротивление нужно напряжение (разность потенциалов) разделить на силу тока. Все очень просто. Единицей измерения электрического сопротивления является «Ом» (названная в честь своего ученого открывателя). Напряжение измеряется в вольтах, а сила тока в амперах. В итоге мы имеем, 1 Ом равен 1 вольт деленный на 1 ампер. Используется и другие более крупные единицы измерения сопротивления — это килоомы (1 кОм = 1000 Ом), мегаомы (1 мОм = 1000 кОм = 1000 000 Ом).
Но всеже есть одно НО! Формулу нахождения сопротивления по закону Ома можно применять для постоянного и переменного тока лишь при наличии именно активного сопротивления (обычные резисторы, нагреватели, лампы накаливания и т.д.). Для случая реактивного сопротивления используется немного другая формула сопротивления тока. Она учитывает кроме напряжения и силы тока еще частоту, индуктивность, ёмкость.
Помимо этих формул еще можно привести такую, которая показывает зависимость сопротивления от вида и размеров проводника. Формула сопротивления тока уже будет содержать такие понятия как сечение проводника, его длина, удельное сопротивления (зависящее от конкретного материала).
А что собственно представляет собой это самое электрическое сопротивление? Думаю не лишним будет пояснить это. Итак, из физики нам известно, что любой проводник имеет так называемую кристаллическую решетку, состоящую из атомов и молекул, соединенных достаточно жесткими связями, что формирует устойчивую, фиксированную структуру. Атомы имеют ядро (состоящее из протонов и нейтронов), у которого положительный заряд. Вокруг ядра вращаются более мелкие частицы, называемые электронами, имеющими отрицательный электрический заряд.
Так вот, те электроны, что удалены от ядра дальше всего могут достаточно легко отрываться от своего атома и переходить к соседнему. При определенных условиях, а именно при подключении внешнего источника питания (а конкретнее внешнего электромагнитного поля) эти свободные электроны могут уже перемещаться упорядоченно в одном направлении. что порождает электрический ток. Но при своем движении электроны постоянно сталкиваются с другими атомами, что находятся на их пути. Вот именно это и является фактором электрического сопротивления. Следовательно предположить, что чем длиннее и тоньше будет проводник, тем больше препятствий будет на пути движения электронов, тем больше будет электрическое сопротивление. Ну, а еще одни проводники, в силу особенностей своей кристаллической решетки, будут иметь большее сопротивление, а другие — меньшее.
Напряжение можно еще сравнить с давлением (по аналогии с водой в трубах, к примеру), электрический ток это упорядоченное движение заряженных частиц, то есть в прямом смысле «поток зарядов (их количество, которое движется в одном направлении)». Вот и получается, что чем больше мы имеем (видим) напряжение на определенном участке электрической цепи (давление воды в водопроводе), при определенном потоке электронов, тем значит больше будет электрическое сопротивление, которое оказывается на движение этого самого потока электрических зарядов, внутри проводника. Все логично.
P.S. Если хорошо уметь представлять те физические процессы, что происходят внутри электрических схем, цепей, будет намного проще понять их изначальную суть. После этого любая формула становится более понятной, с точки зрения зависимости определенных физических величин. Это уже не просто набор каких-то знаков, это конкретная зависимость единиц измерения, что строго отображают в теории то, что работает на практике (в схемах, электрических устройствах и т.д.).
Коэффициент сопротивления, формула и примеры
Коэффициент сопротивления дает возможность учитывать потери энергии при движении тела. Чаще всего рассматривают два типа движения: движение по поверхности и движение в веществе (жидкости или газе). Если рассматривают движение по опоре, то обычно говорят о коэффициенте трения. В том случае, если рассматривают движение тела в жидкости или газе, то имеют в виду коэффициент сопротивления формы.
Определение коэффициента сопротивления (трения) скольжения
Речь идет о коэффициенте трения скольжения, который зависит от совокупных свойств трущихся поверхностей и является безразмерной величиной. Коэффициент трения зависит от: качества обработки поверхностей, трущихся тел, присутствия на них грязи, скорости движения тел друг относительно друга и т.д. Коэффициент трения определяют эмпирически (опытным путем).
Определение коэффициент сопротивления (трения) качения
Данный коэффициент, имеет размерность длины. Основной его единицей в системе СИ будет метр.
Определение коэффициента сопротивления формы
Иногда, если рассматривают движение вытянутого тела, то считают:
где V — объем тела.
Рассматриваемый коэффициент сопротивления является безразмерной величиной. Он не учитывает эффектов на поверхности тел, поэтому формула (3) может стать не пригодна, если рассматривается вещество, которое имеет большую вязкость. Коэффициент сопротивления (C) является постоянной величиной пока число Рейнольдса (Re) является неизменным. В общем случае .
Если тело имеет острые ребра, то эмпирически получено, что для таких тел коэффициент сопротивления остается постоянным в широкой области чисел Рейнольдса. Так опытным путем получено, что для круглых пластинок поставленных поперек воздушного потока, при значения коэффициента сопротивления находятся в пределах от 1,1 до 1,12. При уменьшении числа Рейнольдса () закон сопротивления переходит в закон Стокса, который для круглых пластинок имеет вид:
Сопротивление шаров было исследовано для широкой области чисел Рейнольдса до Для получили:
При , .
В справочниках представлены коэффициенты сопротивления для круглых цилиндров, шаров и круглых пластинок в зависимости от числа Рейнольдса.
В авиационной технике задача о нахождении формы тела с минимальным сопротивлением имеет особое значение.