Вихревой характер магнитного поля

Определение 1

Вихревой характер магнитного поля заключается в непрерывности линий индукции любого магнитного поля при отсутствии начала и конца, так как они либо замкнуты, либо уходят в бесконечность. На порождение полей не влияет характер контуров с током. Векторные поля, обладающие непрерывными силовыми линиями, называются вихревыми полями. Магнитное поле также можно считать вихревым.

Электростатические поля имеют силовые линии, начинающиеся и заканчивающиеся на электрических зарядах, причем, всегда находятся в разомкнутом состоянии. Линии магнитного поля замкнуты. Это говорит об отсутствии магнитных зарядов в природе.

Электрический ток образуется благодаря движению электрических зарядов. Так как магнитных зарядов нет, это объясняет отсутствие магнитного тока. Данное утверждение можно выразить при помощи уравнения:

Определение вихревого поля также выполнимо другим способом.

Вихревое магнитное поле

Определение 2

Векторные поля, вектор которых не равен нулю – это

вихревые магнитные поля.

Следуя из теоремы о циркуляции локального вида, которая влияет на вихревой характер магнитного поля:

rot B→=μ0j→ (2), где j→ считается объемной плотностью тока, и второй формы определения вихревого поля можно заключить, что магнитное поле будет вихревым там, где проходят токи, а безвихревым там, где их нет.

При отсутствии токов вектор магнитной индукции B→ представляется в виде градиента скалярного магнитного потенциала φm:

B→=-gradφm (3).

Если имеются токи, то данное представление невозможно.

Различие между потенциальными и вихревыми полями

Основными уравнениями магнитного поля постоянных токов считаются выражения вида:

rot B→=μ0j→div B→=0 (4).

Произведем сравнение с основными уравнениями электростатики:

rot E→=0div E→=1ε0ρ (5).

Рассматривая систему (5), видно, что электрическое поле всегда потенциально, а его источниками являются электростатические (неподвижные) заряды.

Вихревой характер магнитного поля

Линии магнитной индукции непрерывны: они не имеют ни начала, ни конца. Это имеет место для любого магнитного поля, вызванного какими угодно контурами с током. Векторные поля, обладающие непрерывными линиями, получили название вихревых полей. Мы видим, что магнитное поле есть вихревое поле. В этом заключается существенное отличие магнитного поля от электростатического.

23. Циркуляция вектора напряженности магнитного поля в вакууме и его применение к расчету магнитного поля длинного соленоида и тороида.

Закон полного тока (теорема о циркуляции вектора ): циркуляция векторапо произвольному замкнутому контуру равна произведению магнитной постояннойна алгебраическую сумму токов, охватываемых этим контуром

,                                    (6)

где – вектор элементарной длины контура, направленный вдоль обхода контура;– индукция магнитного поля;– проекция вектора на направление касательной к контуру;– угол между векторамии

.

·     Магнитная индукция поля внутри соленоида

,                                       (7)

где – магнитная постоянная;– длина соленоида;– число витков соленоида;

– число витков соленоида на единице его длины.

·     Магнитная индукция поля внутри тороида

,                                           (8)

где – радиус оси тороида.

24. Действие магнитного поля на движущийся заряд. Сила Лоренца.

• Из опыта известно, что магнитное поле оказывает действие не только на проводники с током, но и на отдельные заряды, которые движутся в магнитном поле. Сила, которая действует на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца

Магнитное поле не оказывает действия на покоящийся электрический заряд. Этим магнитное поле существенно отличается от электрического. Магнитное поле действует только на движущиеся в нем заряды.

Сила действующая на эл. заряд Q движущийся в магн. поле со скоростью v называется силой Лоренца. F=Q[vB]. Направление силы Лоренца определяется по правилу левой руки. Магнитное поле не действует на покоящийся заряд. Если на движущийся заряд помимо магн. поля действует эл. поле то результирующая сила равна векторной сумме сил. F=QE+Q[vB].

Соленоидальное векторное поле — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2016; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июня 2016; проверки требуют 2 правки.

Векторное поле называется соленоидальным или вихревым^{[источник не указан 499 дней]}, если через любую замкнутую поверхность S его поток равен нулю:

∫Sa→⋅ds→=0{\displaystyle \int \limits _{S}{\vec {a}}\cdot {\vec {ds}}=0}.

Другое определение соленоидального поля: Векторное поле a→{\displaystyle {\vec {a}}}называют соленоидальным, если оно является вихрем некоторого поля b→{\displaystyle {\vec {b}}},a→=rotb→{\displaystyle {\vec {a}}=rot{\vec {b}}}. При этом векторное поле b→{\displaystyle {\vec {b}}} называют

векторным потенциалом поля a→{\displaystyle {\vec {a}}}.^[1]

Если это условие выполняется для любых замкнутых S в некоторой области (по умолчанию — всюду), то это условие равносильно тому, что равна нулю дивергенция векторного поля a→{\displaystyle {\vec {a}}}:

diva→≡∇⋅a→=0{\displaystyle \mathrm {div} \,{\vec {a}}\equiv \nabla \cdot {\vec {a}}=0}

всюду на этой области (подразумевается, что дивергенция всюду на этой области существует). Поэтому соленоидальные поля называют также

бездивергентными.

Для широкого класса областей это условие выполняется тогда и только тогда, когда a→{\displaystyle {\vec {a}}} имеет векторный потенциал, то есть существует некое такое векторное поле A→{\displaystyle {\vec {A}}} (векторный потенциал), что a→{\displaystyle {\vec {a}}} может быть выражено как его ротор:

a→=∇×A→≡rotA→.{\displaystyle {\vec {a}}=\nabla \times {\vec {A}}\equiv \mathrm {rot} \,{\vec {A}}.}

Иначе говоря, поле является вихревым, если оно не имеет источников. Силовые линии такого поля не имеют ни начала, ни конца, и являются замкнутыми. Вихревое поле порождается не покоящимися зарядами (источниками), а изменением связанного с ним поля (например, для электрического поля порождается изменением магнитного). Поскольку в природе не существует магнитных зарядов, то магнитное поле

всегда является вихревым, и его силовые линии всегда замкнуты. Силовые линии постоянного магнита, несмотря на то, что выходят из его полюсов (словно имеют источники внутри), на самом деле замыкаются внутри магнита. Поэтому, разрезав магнит надвое, не удастся получить два отдельных магнитных полюса.

Слово соленоидальное происходит от греческого соленоид (σωληνοειδές, sōlēnoeidēs), означающее «трубообразно» или «как в трубе», содержащего слово σωλην (Solen) — труба. В данном контексте это означает фиксацию объема для модели текущей жидкости, отсутствие источников и стоков (как при течении в трубе, где новая жидкость не появляется и не пропадает).

[источник не указан 499 дней]

1. ↑ А.Н. Канатников. Курс лекций (неопр.). МГТУ им. Н.Э.Баумана. Дата обращения 8 января 2019.

Вихревое электрическое поле

Вихревое электрическое поле — это электрическое поле, которое порождается переменным магнитным полем и линии напряженности которго замкнуты.

Переменное магнитное поле порождает инду­цированное электрическое поле. Если магнитное поле постоянно, то индуциро­ванного электрического поля не возникнет. Следовательно, индуцированное электрическое поле не связано с зарядами, как это имеет место в случае элект­ростатического поля; его силовые линии не начинаются и не заканчиваются на зарядах, а замкнуты сами на себя, подобно силовым линиям магнитного поля. Это означает, что 

индуцированное электрическое поле, подобно магнитному, является вихревым.

   Если неподвижный проводник поместить в переменное магнитное поле, то в нем индуцируется э. д. с. Электроны приводятся в направленное движение электрическим полем, индуцированным переменным магнитном полем; возни­кает индуцированный электрический ток. В этом случае проводник является лишь индикатором индуцированного электрического поля. Поле приводит в движение свободные электроны в проводнике и тем самым обнаруживает себя. Теперь можно утверждать, что и без проводника это поле существует, обладая запасом энергии.

   Сущность явления электромагнитной индукции заключается не столько в появлении индуцированного тока, сколько в возникновении вихревого электрического поля.

   Это фундаментальное положение электродинамики установлено Максвел­лом как обобщение закона электромагнитной индукции Фарадея.

   В отличие от электростатического поля индуцированное электрическое поле является непотенциальным, так как работа, совершаемая в индуцированном электрическом поле, при перемещении единичного положительного заряда по замкнутому контуру равна э. д. с. индукции, а не нулю.

   Направление вектора напряженности вихревого электрического поля уста­навливается в соответствии с законом электромагнитной индукции Фарадея и правилом Ленца. Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока.

   Так как вихревое электрическое поле существует и в отсутствие проводника, то его можно применять для ускорения заряженных частиц до скоростей, со­измеримых со скоростью света. Именно на использовании этого принципа основано действие ускорителей электронов — бетатронов.

   Индукционное электрическое поле имеет совершенно другие свойства в отличии от электростатического поля.

Отличие вихревого электрического поля от электростатического

1) Оно не связано с электрическими зарядами; 
2) Силовые линии этого поля всегда замкнуты; 
3) Работа сил вихревого поля по перемещению зарядов на замкнутой траектории не равна нулю.

электростатическое поле	индукционное электрическое поле ( вихревое электр. поле )
1. создается неподвижными электр. зарядами	1. вызывается изменениями магнитного поля
2. силовые линии поля разомкнуты — потенциальное поле	2. силовые линии замкнуты — вихревое поле
3. источниками поля являются электр. заряды	3. источники поля указать нельзя
4. работа сил поля по перемещению пробного заряда по замкнутому пути = 0.	4. работа сил поля по перемещению пробного заряда по замкнутому пути = ЭДС индукции

Вихревой характер магнитного поля

Задание: Использовать понятие скалярного магнитного потенциала (${\varphi }_m$) можно только в области пространства, где $\overrightarrow{j}=0.$ Однако и в этой части пространства ${\varphi }_m$ функция не однозначная. Покажите это.

Решение:

Рассмотрим магнитное поле возле контура с током (рис.1). В соответствии с теоремой о циркуляции для любого контура выполняется равенство:

\[\oint\limits_L{\overrightarrow{B}\overrightarrow{dl}=}0\ \left(2.1\right).\]

Рис. 1

Так как при отсутствии токов магнитное поле становистя потенциальным, интеграл, который берется между точками A и B не зависит от пути интегрирования, то можно записать:

\[\int\limits_{AaB}{\overrightarrow{B}\overrightarrow{dl}}=\int\limits_{AbB}{\overrightarrow{B}\overrightarrow{dl}}\ \left(2.2\right).\]

Следовательно:

\[\int\limits_{AbB}{\overrightarrow{B}\overrightarrow{dl}}=\int\limits^B_A{\overrightarrow{B}\overrightarrow{dl}}={\varphi }_{mA}-{\varphi }_{mB}\left(2.3\right).\]

Выражение (2.3) можно рассматривать как разность скалярных магнитных потенциалов в точках A и B. Если поступить, как делалось для потенциала в электростатике, то есть принять, что в какой то точке, например токе B потенциал равне нулю, то запишем:

\[\int\limits^B_A{\overrightarrow{B}\overrightarrow{dl}}={\varphi }_{mA}\left(2.4\right).\]

Однако, если выбрать контур, который будет охватывать какой-либо ток, например контур AcbB (рис.1) в таком случае линейный интеграл по замкнутому контуру от циркуляции вектора индукции по нему будет отличен от нуля:

\[\oint\limits_{AcbB}{\overrightarrow{B}\overrightarrow{dl}\ne }0\ \left(2.5\right).\]

или

\[\oint\limits_{AcBbА}{\overrightarrow{B}\overrightarrow{dl}=\int\limits_{AсB}{\overrightarrow{B}\overrightarrow{dl}}}-\int\limits_{AbB}{\overrightarrow{B}\overrightarrow{dl}}=I\ne 0\left(2.6\right).\]

В таком случае:

\[\int\limits_{AсB}{\overrightarrow{B}\overrightarrow{dl}}=\int\limits_{AbB}{\overrightarrow{B}\overrightarrow{dl}}+I=ц_{mA}-ц_{mB}+I\ \left(2.7\right).\]

Так, если мы выберем какой — то путь AnB, который охватывает ток n- раз, то получим:

\[\int\limits_{AnB}{\overrightarrow{B}\overrightarrow{dl}}={\varphi }_{mA}-{\varphi }_{mB}+nI(2.8)\]

Зададим нулевой потенциал в точке B, тогда имеем, что:

\[\int\limits_{AnB}{\overrightarrow{B}\overrightarrow{dl}}={\varphi }_{mA}+nI\left(2.9\right).\]

Уравнение (2.9) показывает, что скалярный магнитный потенциал — не однозначная величина.

Вихревое электрическое поле. Видеоурок. Физика 11 Класс

Как же возникает электродвижущая сила в проводнике, который находится в переменном магнитном поле? Что такое вихревое электрическое поле, его природа и причины возникновения? Какие основные свойства этого поля? На все эти и многие другие вопросы ответит сегодняшний урок.

Тема: Электромагнитная индукция

Урок: Вихревое электрическое поле

Вспомним о том, что правило Ленца позволяет определять направление индукционного тока в контуре, находящемся во внешнем магнитном поле с переменным потоком. Отталкиваясь от этого правила, удалось сформулировать закон электромагнитной индукции.

Закон электромагнитной индукции

При изменении магнитного потока, пронизывающего площадь контура, в этом контуре возникает электродвижущая сила, численно равная скорости изменения магнитного потока, взятой со знаком минус.

 

Как же возникает эта электродвижущая сила? Оказывается, ЭДС в проводнике, который находится в переменном магнитном поле, связано с возникновением нового объекта – вихревого электрического поля.

Рассмотрим опыт. Есть катушка из медной проволоки, в которую вставлен железный сердечник для того, чтобы усилить магнитное поле катушки. Катушка через проводники подключена к источнику переменного тока. Также есть виток из проволоки, помещенной на деревянную основу. К этому витку подключена электрическая лампочка. Материал проволоки покрыт изоляцией. Основание катушки сделано из дерева, т. е. из материала, не проводящего электрический ток. Каркас витка также изготовлен из дерева. Таким образом, исключается всякая возможность контакта лампочки с цепью, подключённой к источнику тока. При замыкании источника лампочка загорается, следовательно, в витке протекает электрический ток – значит, сторонние силы в этом витке совершают работу. Необходимо выяснить, откуда берутся сторонние силы.

Магнитное поле, пронизывающее плоскость витка, не может вызвать появление электрического поля, поскольку магнитное поле действует только на движущиеся заряды. Согласно электронной теории проводимости металлов, внутри них существуют электроны, которые могут свободно двигаться внутри кристаллической решётки. Однако, это движение в отсутствие внешнего электрического поля носит беспорядочный характер. Такая беспорядочность приводит к тому, что суммарное действие магнитного поля на проводник с током равно нулю. Этим электромагнитное поле отличается от электростатического, которое действует и на неподвижные заряды. Так, электрическое поле действует на движущиеся и на неподвижные заряды. Однако, та разновидность электрического поля, которая, изучалась ранее, создаётся только электрическими зарядами. Индукционный ток, в свою очередь, создаётся переменным магнитным полем.

Предположим, что электроны в проводнике приходят в упорядоченное движение под действием некой новой разновидности электрического поля. И это электрическое поле порождается не электрическими зарядами, а переменным магнитным полем. К подобной идее пришли Фарадей и Максвелл. Главное в этой идее то, что переменное во времени магнитное поле порождает электрическое. Проводник с имеющимися в нём свободными электронами позволяет обнаружить это поле. Это электрическое поле приводит в движение электроны, находящиеся в проводнике. Явление электромагнитной индукции состоит не столько в появлении индукционного тока, сколько в появлении новой разновидности электрического поля, которое приводит в движение электрические заряды в проводнике (рис. 1).

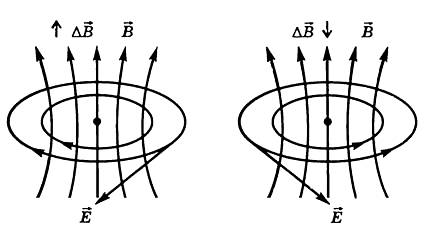
Рис. 1. Вихревое поле (Источник)

 

Вихревое поле отличается от статического. Оно не порождается неподвижными зарядами, следовательно, линии напряженности этого поля не могут начинаться и заканчиваться на заряде. Согласно исследованиям, линии напряжённости вихревого поля представляют собой замкнутые линии подобно линиям индукции магнитного поля. Следовательно, это электрическое поле является вихревым – таким же, как и магнитное поле.

Второе свойство касается работы сил этого нового поля. Изучая электростатическое поле, выяснили, что работа сил электростатического поля по замкнутому контуру равна нулю. Так как при движении заряда в одном направлении перемещение и действующая сила сонаправлены и работа положительна, то при движении заряда в обратном направлении перемещение и действующая сила противоположно направлены и работа отрицательна, суммарная работа будет равна нулю. В случае вихревого поля работа по замкнутому контуру будет отлична от нуля. Так при движении заряда вдоль замкнутой линии электрического поля, имеющего вихревой характер, работа на разных участках будет сохранять постоянный знак, поскольку сила и перемещение на разных участках траектории будут сохранять одинаковое направление друг относительно друга. Работа сил вихревого электрического поля по перемещению заряда вдоль замкнутого контура отлична от нуля, следовательно, вихревое электрическое поле может порождать электрический ток в замкнутом контуре, что совпадает с результатами эксперимента. Тогда можно утверждать то, что сила, действующая на заряды со стороны вихревого поля, равна произведению переносимого заряда на напряжённость этого поля.

                                                                   (9.2.)

Эта сила и есть сторонняя сила, совершающая работу. Работа этой силы, отнесённая к величине перенесённого заряда, – ЭДС индукции. Направление вектора напряженности вихревого электрического поля в каждой точке линий напряжённости определяется по правилу Ленца и совпадает с направлением индукционного тока.

В неподвижном контуре, находящемся в переменном магнитном поле, возникает индукционный электрический ток. Само магнитное поле не может быть источником сторонних сил, поскольку оно может действовать только на упорядоченно движущиеся электрические заряды. Электростатического поля быть не может, поскольку оно порождается неподвижными зарядами. После предположения о том, что переменное во времени магнитное поле порождает электрическое поле, узнали, что это переменное поле носит вихревой характер, т. е. его линии замкнуты. Работа вихревого электрического поля по замкнутому контуру отлична от нуля. Сила, действующая на переносимый заряд со стороны вихревого электрического поля, равна величине этого переносимого заряда, умноженной на напряжённость вихревого электрического поля. Эта сила и является той сторонней силой, которая приводит к возникновению ЭДС в контуре. Электродвижущая сила индукции, т. е. отношение работы сторонних сил к величине переносимого заряда, равна взятой со знаком минус скорости изменения магнитного потока. Направление вектора напряженности вихревого электрического поля в каждой точке линий напряжённости определяется по правилу Ленца.             

 

Список рекомендованной литературы

1. Касьянов В.А., Физика 11 кл.: Учебн. для общеобразоват. учреждений. – 4-е изд., стереотип. – М.: Дрофа, 2004. – 416 с.: ил., 8 л. цв. вкл.
2. Генденштейн Л.Э., Дик Ю.И., Физика 11. – М.: Мнемозина.
3. Тихомирова С.А., Яровский Б.М., Физика 11. – М.: Мнемозина.
   

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Электронный учебник физики (Источник).
2. Классная физика (Источник).
3. Xvatit.com (Источник).

 

Рекомендованное домашнее задание

1. Касьянов В.А., Физика 11 кл.: Учебн. для общеобразоват. учреждений. – 4-е изд., стереотип. – М.: Дрофа, 2004. – 416 с.: ил., 8 л. цв. вкл., ст. 119, в. 1, з. 5.
2. Внутри стеклянного кольца с разрезом расположен постоянный магнит (рис. 2). Что будет наблюдаться на концах разреза АВ в процессе удаления магнита из кольца влево?
   

Рис. 2. Постоянный магнит (Источник).

3. Как объяснить тот факт, что удар молнии может расплавить предохранители, вывести из строя чувствительные электроприборы и полупроводниковые устройства?
4. ^* При размыкании кольца в катушке возникла ЭДС самоиндукции 300 В. Какова напряжённость вихревого электрического поля в витках катушки, если их количество равно 800, а радиус витков – 4 см?

Вихревое электрическое поле

Из закона электромагнитной индукции следует, что любое изменение сцепленного с контуром магнитного потока Ф приводит к возникновению ЭДС индукции ε_iи появлению индукционного тока i

Возникновение ЭДС индукции возможно и в неподвижном контуре при условии, что существует переменное магнитное поле. Из­вестно, что ЭДС в цепи возникает тогда, когда в ней на носители тока действуют сторонние силы. При электромагнитной индукции эти силы не связаны ни с тепловыми, химическими и другими про­цессами в контуре. Они не являются силами Лоренца, т.к. на не­подвижные заряды сила Лоренца не действует, Для объяснения ЭДС индукции в неподвижных проводниках Максвелл высказал ги­потезу, что всякое переменное поле (магнитное), возбуждает в ок­ружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. При этом контур, в котором возникает ЭДС, играет второстепенную роль инструмента для обнаружения возникающего электрического поля. Циркуляция вектора Е_В напряженности этого поля по любому замкнутому контуру L представляет собой ЭДС индукции

ε_i = = —.

Учитывая, что dФ = ВdS, можно записать = и тогда

= — .

Поля, для которых циркуляция вектора по замкнутому контуру не равна нулю, называются вихревыми. Таким образом, электрическое поле напряженностью Е_В, возбуж­даемое переменным магнитным полем, является вихревым, как и само магнитное поле. Напомним, что циркуляция вектора Е_q элек­тростатического поля равна нулю, т.к. электростатическое поле яв­ляется не вихревым, а потенциальным.

Ток смещения

По гипотезе Максвелла всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле. Основная же идея Максвелла заключается в том, что между электрическим и магнитным полями существует и обратное соот­ношение, т.е. изменяющееся во времени электрическое поле должно приводить к появлению переменного магнитного поля. Для установления количественных соотношений между изменяющимся электрическим и возникающим магнитным полями Максвелл ввел в рассмотрение так называемыйток смещения, плотность которого обозначим j_см. Рассмотрим участок цепи переменного тока, содержащего конденсатор.

Движение свободных носителей заряда имеет место во всей цепи, кроме зазора между обкладками конденсатора. При зарядке конденсатора (рис. 131а) ток течет в направлении к положительно заряженной обкладке, поверхностная плотность заряда на которой +σ. Между обкладками будет существовать электрическое поле с напряженно­стью Е и индукцией D.

D = ε ε₀E; D = σ.

При зарядке индукция D в зазоре возрастает, т.е. и по направлению совпадает с направлением j_пр плотности тока проводимости в обкладке конденсатора. Величина j_пр тока проводимости в обкладке площадью S можно выразить так

.

По Максвеллу переменное электрическое поле в конденсаторе создает такое магнитное поле, как если бы между обкладками конденсатора существовал ток проводимости плотностью такой же, как в обкладке конденсатора, т.е.

j_пр = j_см.

Из этого следует, что

При разрядке конденсатора (рис. 131б) изменяется во времени по­верхностная плотность заряда σ на обкладках, а значит, изменяется и индукция D в зазоре. Индукция D убывает, Это значит, чтоj_см =совпадает по направлению и по величине сj_пр как и при зарядке конденсатора. Из сказанного можно заключить, что ток проводимости и ток смещения равны по величине и одина­ковы по направлению.

Ток смещения следует понимать в том смысле, что перемен­ное электрическое поле в конденсаторе в любой момент времени создает такое же магнитное поле, как если бы между обкладками существовал ток проводимости, имеющий силу, равную силе тока в подводящих проводниках. Из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно – способность создавать в окружающем пространства магнитное поле, т.е. ток смещения эквивалентен току проводимости только по способности создавать магнитное поле.

Если в проводнике течет переменный ток, то внутри про­водника существует переменное электрическое поле, а значит, име­ются ток проводимости и ток смещения. Магнитное поле в нем оп­ределяется суммой токов, т.е. полным током. При расчетах магнит­ных полей в формулы нужно подставлять полную плотность тока j_полн = j_пр + j_см = j_пр + В зависимости от электропроводности среды и быстроты изменения поля (частоты тока) оба слагаемых играют разную роль. В хорошо проводящих веществах плотность тока смещения мала и им можно пренебречь. В плохо проводящих средах и при высоких частотах ток смещения играет основную роль.

Уравнения Максвелла.

Теория электромагнитного поля Максвелла основана на двух основных положениях:

• всякое изменение магнитного поля вызывает появление вихревого магнитного поля;

• всякое изменение электрического поля вызывает появ­ление вихревого электрического поля.

Эта теория в строгой форме выражена в виде уравнений Максвелла. В учении об электричестве и магнетизме эти уравнения играют такую же роль, как законы Ньютона в механике или основ­ные законы в термодинамике.

Полная система уравнений Максвелла в интегральной форме:

1. 3.

2. 4. .

1. Электрическое поле может быть потенциальным ( Е_Q) и вих­ревым ( Е_В ), поэтому напряженность суммарного поля Е равна Е = Е_Q + Е_В. Циркуляция вектора Е_Q равна нулю, а циркуляция век­тора Е_В отражает закон электромагнитной индукции

.

Из этого уравнения следует, что электриче­ские поля создаются электрическими зарядами и изменяющимися во времени магнитными полями.

2. Это уравнение — закон полного тока в обобщенном виде и показывает, что магнитные поля создаются движущимися зарядами (токами) либо (и) переменными электрическими полями.

3. Это уравнение – есть выражение теоремы Остроградского-Га­усса для электростатического поля в диэлектрике, где ρ – объ­емная плотность заряда в рассматриваемом объеме V.

4. Теорема Остроградского-Гаусса для потока магнитной индукции означает, что линии магнитной индукции замкнуты.

Для решения этих уравнений необходимо знать связь между вхоя­щими в них величинами

D = εε₀E ; B = μμ₀H ; j = γE.

Для стационарных полей ( E = const, B = const ) Уравнения Мак­свелла примут вид:

.

В этом случае электрические и магнитные поля независимы друг от друга и могут изучаться отдельно друг от друга.

Уравнения Максвелла в дифференциальной форме имеют вид:

.

Контрольные вопросы.

1. Магнитное поле. Индукция магнитного поля. Сила Лоренца. Движе­ние заряженной частицы в магнитном поле.

2. Сила Ампера. Работа, совершаемая при перемещении проводника с током в магнитном поле.

3. Контур с током в магнитном поле. Момент сил, действующих на кон­тур. Магнитный момент. Энергия контура с током в магнитном поле.

4. Закон Био-Савара-Лапласа и его применение к расчёту магнитного поля.

5. Теорема Гаусса и теорема о циркуляции (закон полного тока) для магнитного поля. Применение закона полного тока к расчёту магнит­ного поля.

6. Магнитное поле длинного соленоида. Потокосцепление. Индуктив­ность, Индуктивность длинного соленоида.

7. Индукция токов в движущихся проводниках. Электродвижущая сила индукции. Вращение рамки в магнитном поле. Генераторы переменного тока.

8. Явление электромагнитной индукции. Закон электромагнитной ин­дукции. Правило Ленца. Вихревое электрическое поле.

9. Явление самоиндукции. Электродвижущая сила самоиндукции. Магнит­ная энергия тока. Объёмная плотность энергии магнитного поля.

10. Магнитные моменты атомов. Диа- и парамагнетизм. Намагниченность. Закон полного тока для магнитного поля в веществе. Напряжённость магнитного поля. Магнитная восприимчивость и магнитная проницаемость.

11. Ферромагнетики. Кривая намагничивания. Магнитный гистерезис, Остаточное намагничивание. Коэрцитивная сила. Магнитная проницаемость ферромагнетика.

12. Ток смещения. Система уравнений Максвелла в интегральной форме. Физический смысл уравнений Максвелла. Дифференциальные уравнения.